Передаточная функция замкнутой системы по ошибке
Для замкнутой
системы существенной характеристикой
является ее ошибка
![]() .
.
Величину
ошибки можно найти, зная входное
воздействие и передаточную функцию
разомкнутой системы:
![]() ,
,
откуда
![]() .
.
С учетом
ошибки системы (характеризует точность
управления в системе) вводится
характеристика замкнутой системы,
называемая передаточной функцией
замкнутой системы по ошибке:
![]() .
.
Передаточная
функция замкнутой системы по ошибке
позволяет определить ошибку управления
в замкнутой системе в том случае, когда
необходимо обеспечить заданное значение
управляемой величины
![]() с заданной точностью. Эта характеристика
с заданной точностью. Эта характеристика
замкнутой системы позволяет оценивать
точность обеспечения заданного значения
управляемой величины (точность
управления).
Построение частотных характеристик системы
Структура
обыкновенной линейной системы
автоматического управления всегда
будет состоять из типовых звеньев,
рассмотренных выше. Эти звенья будут
входить в структуру в составе различных
соединений: последовательного,
параллельного, соединения с обратной
связью.
Передаточная
функция системы, состоящей из различных
соединений типовых звеньев, выразится
зависимостью вида
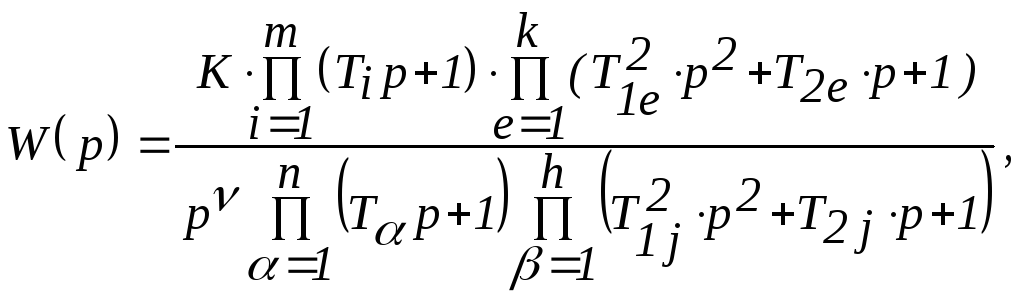 гдеK – коэффициент
гдеK – коэффициент
усиления системы.
Сомножители
вида
![]() ,
,
стоящие в знаменателе выражения,
соответствуют инерционным звеньям,
входящим в последовательные соединения.
Сомножители![]() в знаменателе соответствуют колебательным
в знаменателе соответствуют колебательным
звеньям, соединённым последовательно.
Предполагается, что в системеn
инерционных звеньев иhколебательных звеньев.
Параметр pв знаменателе передаточной функции
появляется при наличии в структуре
системы интегрирующих звеньев. Таких
звеньев может быть в системеν,
поскольку при наличии в системе
интегрирующего звена система становится
астатической, то число интегрирующих
звеньевνназываютстепенью
астатизма системы.
Структура
системы может содержать параллельные
соединения звеньев. Пусть, например, в
системе присутствует параллельное
соединение усилительного и интегрирующего
звена, тогда передаточная функция этого
соединения
 .
.
Из-за присутствия
в системе параллельного соединения
типовых звеньев в числителе передаточной
функции появляются сомножители вида
![]() .
.
Для обозначения таких сомножителей их
условно приписываютфорсирующим
звеньям первого порядка. Форсирующее
звено первого порядка имеет динамические
свойства, обратные свойствам инерционного
звена. Аналогично, сомножители вида![]() приписывают форсирующим звеньям
приписывают форсирующим звеньям
второго порядка, свойства которых
противоположны свойствам колебательного
звена.
Таким образом,
передаточная функция обыкновенной
линейной системы будет состоять из
произведений типовых сомножителей.
Поскольку каждый сомножитель соответствует
структурному звену с типовыми динамическими
свойствами, то и динамические свойства
системы в целом будут комбинацией
типовых свойств. Это обстоятельство, в
частности, позволяет упростить построение
частотных характеристик линейной
системы.
Сделав
подстановку
![]() в приведенное выше выражение для
в приведенное выше выражение для
передаточной функции системы, можно
перейти к частотной передаточной функции

модуль которой
![]()
Используя
последнее выражение для амплитудной
логарифмической частотной характеристики
системы, можно записать

В соответствии
с последним выражением для нахождения
суммарной амплитудной логарифмической
характеристики системы необходимо
построить ЛАХ для входящих в систему
звеньев, а затем геометрически их
суммировать.
Исходя из
общего выражения для частотной
передаточной функции, можно записать
выражение для фазового угла системы

Сомножители
числителя частотной передаточной
функции обеспечивают положительные
фазовые сдвиги, а сомножители знаменателя
– отрицательные. Фазовая частотная
характеристика системы получается
суммированием фазовых частотных
характеристик составляющих систему
типовых звеньев.
Асимптотическая
ЛАХ строится ещё проще, и ее построение
рассмотрим на примере. Пусть передаточная
функция системы имеет вид
![]()
тогда частотная передаточная функция
запишется в виде
![]()
а модуль частотной передаточной функции
![]()
Логарифмическая
амплитудная характеристика
![]()
при этом слагаемое
![]() будет влиять на ход характеристики при
будет влиять на ход характеристики при![]() ,
,
слагаемое![]() при
при![]() и т.д.
и т.д.
Частоты
![]() называются частотами сопряжения. Учет
называются частотами сопряжения. Учет
влияния каждого следующего звена при
построении асимптотической характеристики
ведется для частот, более высоких, чем
соответствующая частота сопряжения,
путем изменения наклона характеристики
на![]() ,
,
в зависимости от знака, стоящего перед
слагаемым (на -20 дБ/дек для инерционного
звена и +20 дБ/дек для форсирующего звена
первого порядка).
В результате суммарная асимптотическая
логарифмическая амплитудная характеристика
для рассматриваемого примера примет
вид, изображенной на рис. 72, где для
определенности принято
![]() .
.
Е сли
сли
одно из звеньев системы колебательное,
то на соответствующей ему частоте
сопряжения![]() наклон характеристики изменяется на
наклон характеристики изменяется на![]() (-40 дБ/дек для колебательного звена и
(-40 дБ/дек для колебательного звена и
+40 дБ/дек для форсирующего звена второго
порядка).
Общие правила построения асимптотической
ЛАХ линейной системы следующие:
-
асимптотическая ЛАХ состоит из
прямолинейных отрезков, имеющих разный
наклон к оси частот, кратный 20 дБ/дек; -
низкочастотный участок ЛАХ проходит
через точку
 и имеет наклон0 дБ/дек для статической
и имеет наклон0 дБ/дек для статической
системы и дБ/дек для астатической системы с
дБ/дек для астатической системы с
астатизмомνпорядка; -
влияние каждого звена на ЛАХ системы
учитывается начиная с частоты сопряжения,
определяемой постоянной времени звена; -
учет влияния звена сводится к изменению
наклона очередного отрезка ЛАХ на
частоте сопряжения следующим образом:
-
наклон увеличивается на –20 дБ/декдля инерционного звена,
-
наклон
уменьшается на +20 дБ/декдля
форсирующего звена первого порядка, -
наклон
увеличивается на –40 дБ/декдля
колебательного звена, -
наклон
уменьшается на +40 дБ/декдля
форсирующего звена второго порядка.
Суммарная
логарифмическая фазовая характеристика
получается суммированием фазовых
характеристик звеньев системы. Для
рассмотренного примера фазовая частотная
логарифмическая характеристика показана
на рис. 73: 1 – ЛФХ интегрирующего звена,
2 – ЛФХ форсирующего звена первого
порядка, 3 и 4 – ЛФХ инерционных звеньев,
5 – суммарная фазовая частотная
характеристика.
 Суммарная
Суммарная
фазовая характеристика 5 получена
суммированием ординат (с учетом знака)
фазовых характеристик звеньев. На рис.
73 положительная полуось фазовых углов
направлена вниз.
При построении
частотных характеристик системы замена
действительной ЛАХ асимптотической
ЛАХ для колебательного звена даёт
значительную погрешность при малой
степени успокоения звена. Если для
колебательного звена степень успокоения
выходит за пределы
![]() ,
,
то асимптотическая ЛАХ нуждается в
уточнении. Для этого строится точная
характеристика путем расчета точек по
формулам для колебательного звена (в
пределах![]() дек
дек
от частоты сопряжения). Учесть особенности
характеристики можно также, используя
график поправок для ЛАХ колебательного
звена, который приводится в литературе
по теории управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Время на прочтение
7 мин
Количество просмотров 15K
Продолжаем публикацию лекций по курсу «Управление в Технических Системах» автор — Олег Степанович Козлов на кафедре Э7 МГТУ им. Н.Э. Баумана.
Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:
1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности. 4 Структурные преобразования систем автоматического регулирования.
Будет как всегда позновательной увлекательно и жестко
5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)
Используя структурные преобразования (см. раздел 4), структурную схему практически любой линейной или линеаризованной САР (САУ) можно привести к виду:
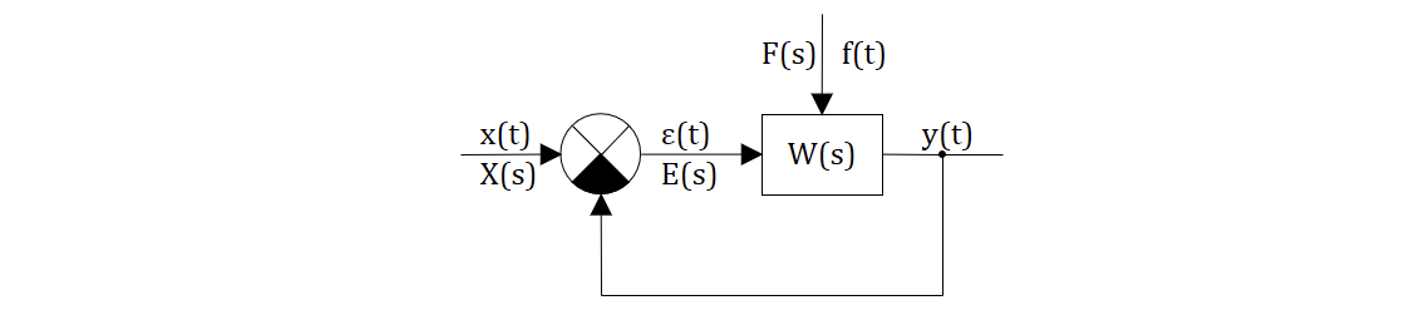
Где функции по времени:
— управляющее воздействие;
– регулируемая величина (выходное воздействие);
– возмущающее воздействие;
Или в изображениях:
Определение: Если единичная обратная связь охватывает все элементы (звенья) САР – она называется главной.
Определение: Если главная обратная связь отсутствует — САР считается разомкнутой.
Передаточная функция может быть любой сложности (т.е. содержать местные обратные связи, параллельные и последовательные цепи и т.д.).
Возмущающих воздействий может быть несколько и приложены они могут быть в любом месте структурной схемы.
Передаточную функцию которую в Теории Управления называют передаточной функцией разомкнутой САР, будем представлять в следующем виде (для единообразия):
где – общий коэффициент усиления;
– полиномы по степеням переменной
, причем свободные члены в них равны 1 (единице).
Учитывая, что САР линейна или линеаризована, разделим на структурной схеме каналы прохождения управляющего и возмущающего воздействий. Выделим в отдельное звено (может быть и очень сложное) ту часть системы, через которую проходит возмущающее воздействие обозначим ее через
Структурная схема САР принимает вид:

где:
В Теории Управления используют 3 основных передаточных функций замкнутой САР:
-
главная передаточная функция
;
-
передаточная функция по возмущающему воздействию
;
-
передаточная функция для ошибки (рассогласования)
Рассмотрим более подробно вышеупомянутые передаточные функции.
Главная передаточная функция
Главная передаточная функция -передаточная функция по управляющему воздействию математическое определение этой передаточной функции:
выведем формулу при условии если возмущеющие воздействие равно . «Обойдем» структурную схемв по контуру:
Примечание. Формула (5.3) совпадает с формулой для передаточной функции цепи с местной единичной обратной связью (см. раздел 4 – «Структурные преобразования»).
Подставляя вместо ее выражение через полиномы
и
где:
Анализ выражения (5.4) показывает, что свойства главной передаточной функции замкнутой САР однозначно определяются свойствами разомкнутой САР, т.е. через полиномы и
.
Передаточная функция замкнутой САР по внешнему возмущающему воздействию
Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействи , а возмущеющие воздействие отличное от нуля
. В этом случае (см. рисунок 5.1.2) получается:
Перрейдем к изображением и «обойдем» схему (см. рис. 5.1.2) по контуру
Подставляя вместо ее выражение через полиномы
и
получаем:
где: — вид данного полинома зависит от места приложения возмущающего воздействия;
Формулы 5.4 и 5.6 имеют общий занаменатель
Передаточная функция замкнутой САР для ошибки (рассогласования)
Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействиt отлично от 0 , а возмущеющие воздействие равно 0
. В этом случае для передаточной функции получается (см. рис. 5.1.2):
Сделаем вывод соответствующих формул, выполнив «обход» по контуру схемы (см. рис. 5.1.2)
Учитывая формулу для главной передаточной функции можно записать выражения для передаточной функции рассоглаосвания:
Подставляя вместо ее выражение через полиномы
и
получаем:
где:
Опять замечаем, что знаменатель передаточной функции равен полиному
следовательно, характерным признаком передаточных функций замкнутой САР является общность знаменателей ! ! !
В Теории Управления выражение имеет «собственное» название: характеристический полином замкнутой САР.
5.2 Уравнения динамики замкнутой САР
Как указывалось в подразделе 5.1, любую замкнутую САР можно привести к виду представленному на рисунке 5.2.1:
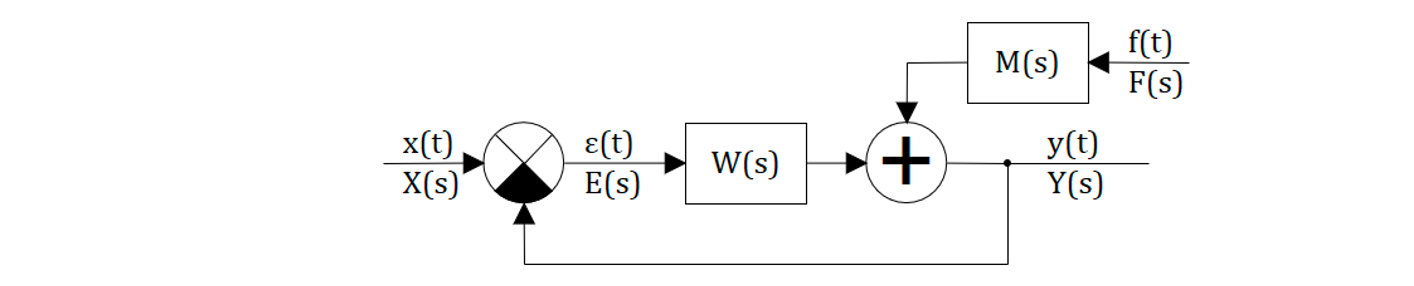
Выведены соотношения для 3-х основных передаточных функций замкнутой САР позволяют записать выражения для регулируемой величины в изображениях:
Подставляя значения и
через полиномы
и
разомкнутой САР получаем:
подставим значения для характеристического полинома получим выражение для динамического уравнения замкнутой САР в изображениях:
Переходя к оригиналам получаем символическую форму записи обыкновенного дифференциального уравнения замкнутой САР:
Решение диференциального уравнения состоит из двух частей:
где: — собственная часть, решение однородного дифференциального уравнения
;
— вынужденная часть решения (частное решение), определяемая правой частью уравнения ( 5.2.3 ).
Решения однородного уравнения замкнутой САР:
записываем соответствующее характеристическое уравнение:
находим корни степенного уравнения если все корни уравнения разные:
Если есть совпадающие корни характеристического уравнения, то формула для изменится (см. Математическое описание систем автоматического управления).
Обычно находят по виду правой части уравнения (5.2.3) или, используя другие методы (например, метод вариаций постоянных).
Необходимо отметить, что порядок дифференциального уравнения (5.2.3) равен «n», т.е. такой же, как и у разомкнутой САР
если нет возмущающего воздействия, т.к. порядок дифференциального оператора L(p) обычно значительно выше, чем N(p).
По аналогии с выводом уравнения (5.2.3) можно получить уравнение динамики для рассогласования :
подставляя значения и
(см. 5.6 и 5.9) получаем:
Уравнение (5.2.5)- уравнение динамики замкнутой САР в ихображениях для рассогласования (ошибки) при наличии управляющего и возмущающего воздействий.
Особенностью данного уравнения (5.2.5) является то, что левая часть его практически совпадает с левой частью (5.2.2), в то время, как порядок правой части заметно выше , т.к. порядок многочленов D (s) и L (s) — одинаков, а порядок N(s) меньше L(s).
Это означает, что внешние воздействия и
влияют на
более сильным образом.
Дифференциальное уравнение замкнутой САР для ошибки:
Способы решения уравнения ( 5.2.6 ) такие же, как и для уравнения ( 5.2.3 ) .
5.3. Частотные характеристики замкнутой САР.
Наибольший интерес при анализе замкнутых САР имеет АФЧХ замкнутой САР по управляющему воздействию:
где передаточная функция:
Учитывая, что — комплексное число, по аналогии имеем:
Где — вещественная часть функции,
— мнимая часть функиции.
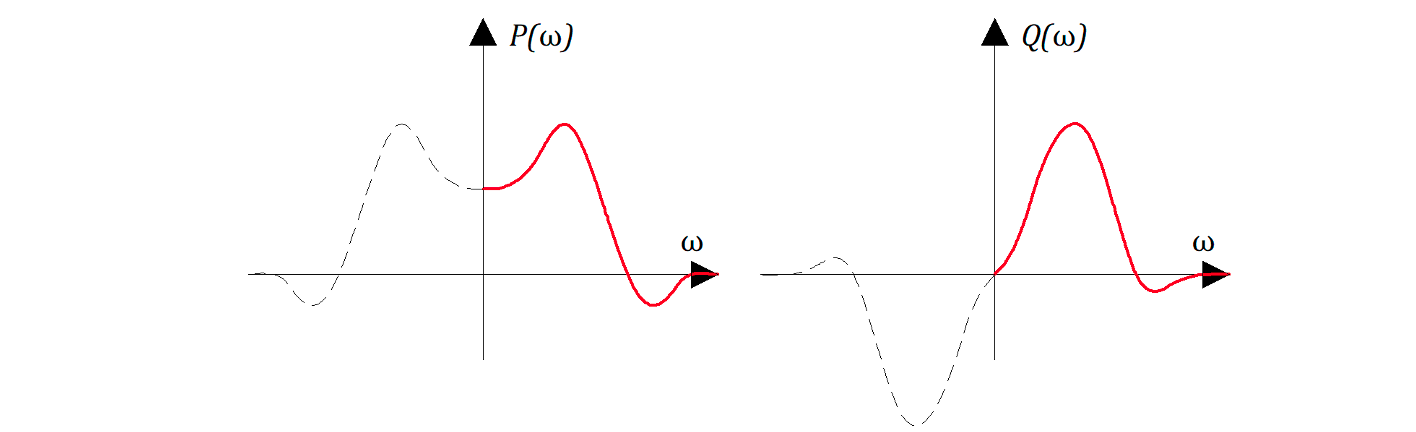
На этих рисунках представлен «примерный» вид зависимостей P (w)и Q(w) для «какой-то» замкнутой САР причем P(w) — четная функция, т.е. P(w) = P(-w); Q(w) — нечетная функция, т.е. Q(w) = — Q(-w).
Если известны частотные свойства разомкнутой САР, то можно определить частотные свойства замкнутой САР. Воспользуемся показательной формой для АФЧХ
Где — амплитуда (модуль),
— сдвиг фазы (фаза). Подставляя это в (5.3.1), имеем получаем:
Учитывая, что
Приравнивая чисто вещественные и чисто мнимые части, имеем
Для нахождения амплитуды и сдвига фазы
замкнутой передаточной функции как функции от амплитуды
и сдвига фазы
разомкнутой системы. Разделив (2) на (1) получим:
Сдвиг фазы замкнутой системы через характеристики разомкнутой системы:
Для получения амплитуды замкнутоей системы возведем оба уравнения системы (5.3.5) в квадрат:
складываем эти два уравнения:
Аналогичным образом можно выразить, например, P(w) и Q(w) — характеристики замкнутой САР через u(w) и u(w) — характеристики разомкнутой САР.
Пример
В качестве примера на рисунке 5.4.1 приведена модель помещения, в котором с помощью интегрирующего звена обеспечивается подвод тепла для поддержания температуры. Температура задается в виде ступенчатой функции. В качестве внешнего воздействия используется внешняя температура.
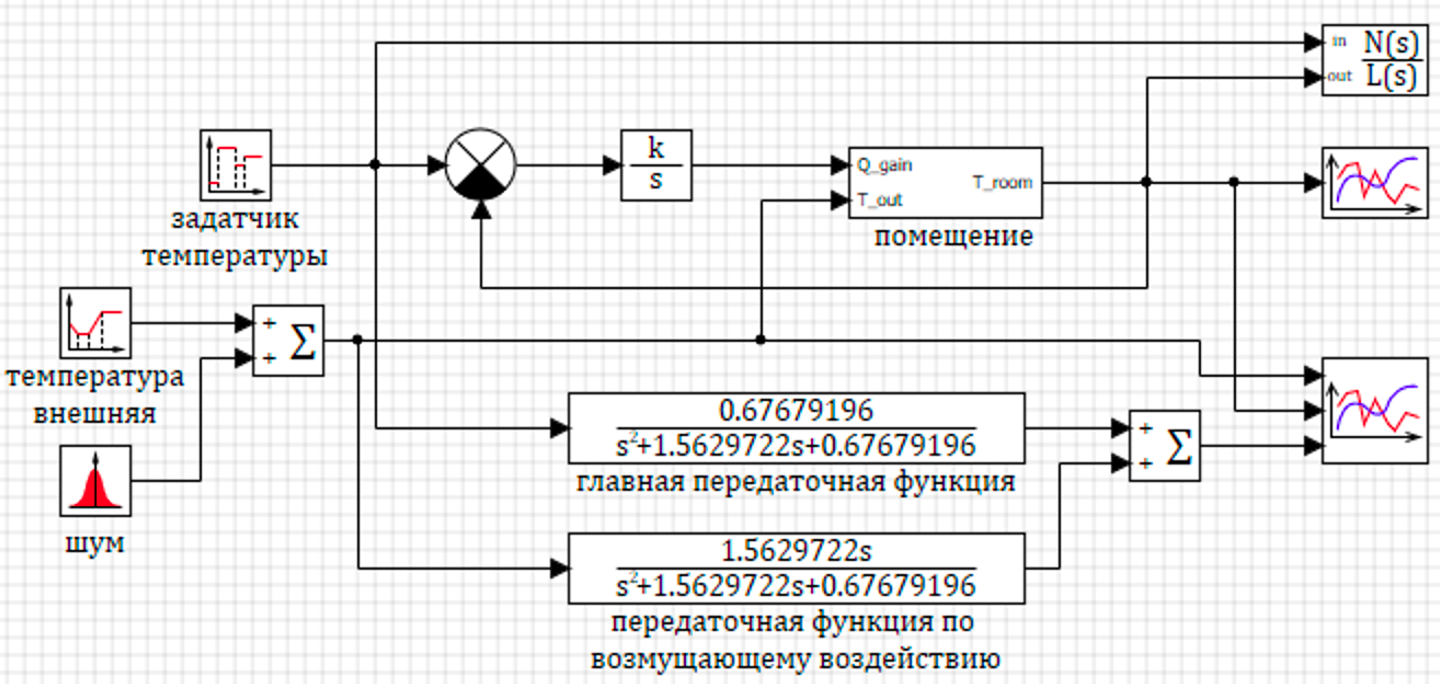
Передаточные функции построены средтвами автоматического анализа. Видно, что знаменатель главной передаточной функции и знаменатель передаточной функции по возмущающиму воздействию одинаковы.
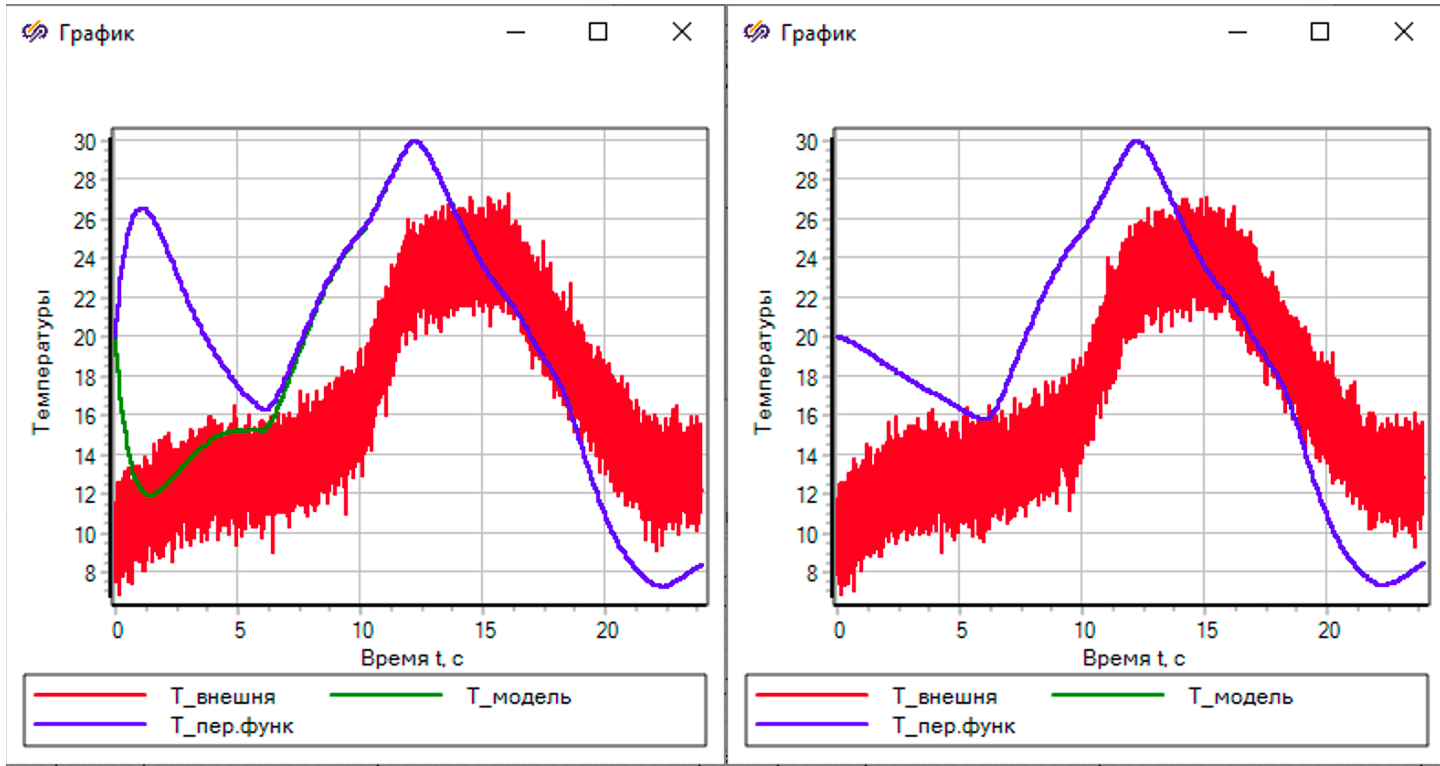
График справа показывает расхождение результаты модели (зеленая линия) и передаточных функций (синит линя) в начале расчета, но потом функции сходятся. Расхождение объясняются разными начальными условиями по производным. Слева тот же самый график, но в это случае начальное состояние определено с помощю загрузки стационарного состояния, полученного предварительным моделированием. В этом случае совпадение модели и передаточных функций полное.
Ссылку на модель примера можено взять здесь…
ЗАДАНИЕ
НА РАБОТУ
1. По имеющейся в
исходных данных передаточной функции разомкнутой системы записать передаточную
функцию замкнутой системы.
2. Записать
передаточную функцию для ошибки от регулирующего воздействия.
3. Изобразить
структурную схему исследуемой системы, считая систему следящей.
4. Записать
характеристические полиномы разомкнутой и замкнутой системы.
5. Исследовать систему
на устойчивость по критерию Гурвица.
6. Исследовать систему
на устойчивость по критерию Михайлова методом чередующихся корней.
7. Построить годограф
Михайлова с указанием масштабов по обеим осям.
8. Исследовать систему
на устойчивость по критерию Найквиста.
9. Построить годограф
Найквиста с указанием масштабов по обеим осям.
10. Определить запас
устойчивости по модулю и по фазе.
11. Вычислить
коэффициенты ошибки и найти ошибку регулирования системы в установившемся
режиме ξ(t) при заданной входной функции.
12. Построить график ξ(t)
в масштабе по обеим осям.
ИСХОДНЫЕ
ДАННЫЕ
Структура системы: 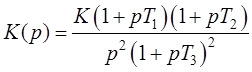
Входное воздействие: ![]()
Численные
значения коэффициентов
|
|
|
|
|
|
|
|
|
|
|
6 |
0.05 |
2 |
0.02 |
0.1 |
-5 |
1.5 |
2 |
1 |
1.
Передаточная функция замкнутой системы.
Для следящих систем (т.е. систем, для которых
передаточная функция канала обратной передачи равна 1) передаточная функция
замкнутой системы определяется как:
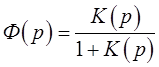 (1.1)
(1.1)
Подставим в выражение (1.1) заданную передаточную
функцию разомкнутой системы:
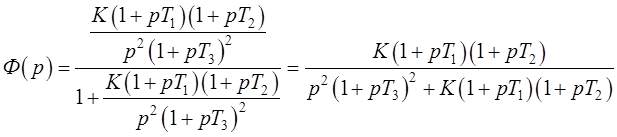 (1.2)
(1.2)
2.
Передаточная функция ошибки от регулирующего воздействия.
Передаточная функция
ошибки от регулирующего воздействия ![]() может быть записана по
может быть записана по
формуле:
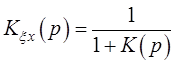
(2.1)
Интересной особенностью
функции является тот факт, что она представляет собой отношение двух
характеристических полиномов: разомкнутой системы ![]() и
и
замкнутой системы ![]() . В самом деле, если обозначим
. В самом деле, если обозначим
передаточную функцию разомкнутой системы в виде
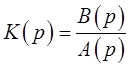
(2.2)
то знаменатель этой
передаточной функции будет называться характеристическим полиномом разомкнутой
системы.
С другой стороны, передаточная функция замкнутой
системы тоже имеет свой знаменатель:
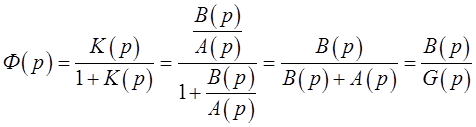 (2.3)
(2.3)
Полином ![]() называется характеристическим
называется характеристическим
полиномом замкнутой системы. Теперь, переходя к формуле (2.3),
можно записать:
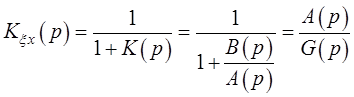 (2.4)
(2.4)
что и является отношением двух характеристических
полиномов.
Подставим в выражение (2.1) заданную передаточную
функцию разомкнутой системы:
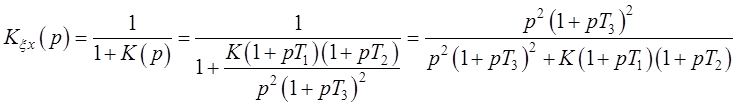 (2.5)
(2.5)
3.
Структурная схема исследуемой системы.
 Исследуемая система состоит из двух форсирующих,
Исследуемая система состоит из двух форсирующих,
двух инерционных и двух интегрирующих звеньев. Считая систему следящей,
необходимо все звенья расположить в канале прямой передачи. С учетом этого
структурная схема имеет следующий вид:
Рис.
3.1.
Структурная схема исследуемой системы.
4.
Характеристические полиномы разомкнутой и замкнутой системы.
Характеристическим полиномом разомкнутой системы ![]() называется знаменатель передаточной
называется знаменатель передаточной
функции разомкнутой системы (см. формулу (2.2)):
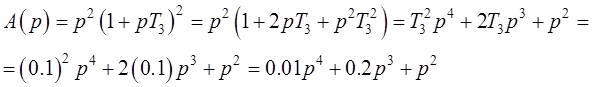 (4.1)
(4.1)
Характеристическим полиномом замкнутой системы ![]() называется знаменатель передаточной
называется знаменатель передаточной
функции замкнутой системы. Этот полином есть не что иное, как сумма полиномов
числителя и знаменателя передаточной функции разомкнутой системы (см. формулу
(2.3)):
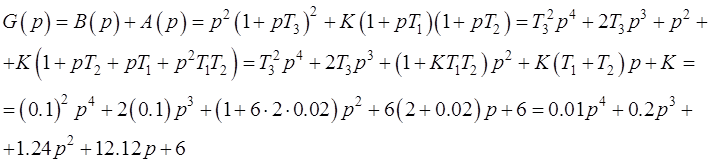 (4.2)
(4.2)
5.
Исследование устойчивости системы по критерию Гурвица.
Согласно критерию Гурвица, для того, чтобы система
была устойчива, необходимо наложить определенные условия на коэффициенты
характеристического уравнения системы (5.1).
![]() (5.1)
(5.1)
Эти условия можно разделить на необходимые и
достаточные. Необходимым условием устойчивости является положительность всех
коэффициентов уравнения (5.1):
![]()
(5.2)
Если это условие не выполняется, дальнейший анализ
можно не проводить – система неустойчива. Если же условие (5.2) выполняется, то
проверяется достаточное условие – положительность всех диагональных
определителей матрицы Гурвица.
Запишем характеристическое уравнение для заданной
системы (уравнение![]() ):
):
![]() (5.3)
(5.3)
Поскольку все коэффициенты характеристического
уравнения положительны, то необходимое условие устойчивости Гурвица
выполняется.
Для проверки достаточного условия необходимо
сформировать матрицу Гурвица. Для системы с дифференциальным уравнением 4-го
порядка характеристическое уравнение будет иметь вид:
![]()
(5.4)
а матрица Гурвица выглядит следующим образом:
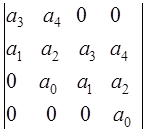
(5.5)
Достаточные условия устойчивости – положительные
значения всех диагональных определителей:
![]()
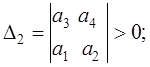
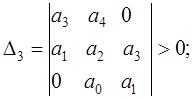
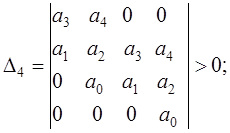 (5.6)
(5.6)
В результате для уравнения 4-степени условия Гурвица
сводятся к неравенству:
![]()
(5.7)
Для заданной системы характеристический полином
имеет вид (4.2):
![]()
Обозначим коэффициенты характеристического полинома:
![]()
![]()
![]()
![]()
![]() (5.8)
(5.8)
Подставим коэффициенты в неравенство (5.7):
![]() (5.9)
(5.9)
Это есть условие устойчивости. Если неравенство
превратить в равенство, возникает так называемое критическое состояние системы,
когда она находится на грани между устойчивым и неустойчивым состояниями.
Коэффициент усиления при этом называют критическим ![]() .
.
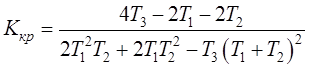 (5.10)
(5.10)
Подставим в (5.10)
численные значения постоянных времени звеньев:
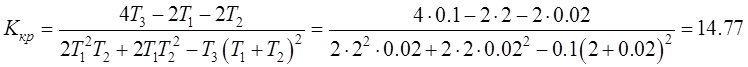
Следовательно, данная
система устойчива, т.к. ее коэффициент усиления более чем в два раза меньше
критического.
6.
Исследование устойчивости системы по критерию Михайлова методом чередующихся
корней.
Запишем характеристический полином заданной системы
согласно (4.2):
![]()
Перейдем в частотную область:
![]() (6.1)
(6.1)
Обозначим и вычислим коэффициенты:
![]()
![]()
![]()
![]()
![]()
Найдем частоты пересечения мнимой оси, для чего
приравняем к нулю вещественную часть и найдем корни полученного уравнения.
![]() (6.2)
(6.2)
Заменим переменную:
![]()
(6.3)
