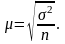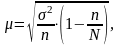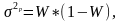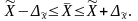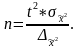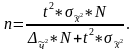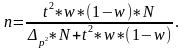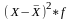Цель
работы:
1. Научиться распространять
результаты выборочного наблюдения на
генеральную совокупность.
2. Научиться определять
необходимую численность выборки для
получения результата по генеральной
совокупности.
Рекомендации
по выполнению задания:
1.Последовательность
выполнения практической работы:
-
Ознакомиться
с рекомендациями по выполнению задания
и с содержанием рекомендуемых задач. -
Уяснить,
какие показатели необходимо определить. -
Выполнить
необходимые расчеты и оформить их с
подробным объяснением. -
По
результатам расчетов сделать выводы.
2.
Выборочное наблюдение – это такое
несплошное наблюдение, при котором
отбор подлежащих обследованию единиц
осуществляется в случайном порядке,
отобранная часть изучается, а результаты
распространяются на всю исходную
совокупность. Наблюдение организуется
таким образом, что эта часть отобранных
единиц в уменьшенном масштабе
репрезентирует (представляет) всю
совокупность.
Формулы
необходимые для расчета:
Для
характеристики надежности выборочных
показателей различают среднюю и
предельную ошибки выборки.
а)
повторный отбор:
|
|
б)
бесповторный отбор:
|
|
где
n
– численность выборочной совокупности;
N
– численность генеральной совокупности;
2
– дисперсия средней или доли;

процент
выборки
Дисперсия
средней
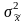
находится с использованием формул,
указанных в п. 5.
Дисперсия
выборочной доли:
|
|
где
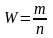
— доля единиц, обладающих данным признаком
в выборочной совокупности;
m
– единицы выборочной совокупности,
обладающие данным признаком.
Предельная
ошибка выборки (
):
|
|
где
t
– коэффициент кратности (доверия).
Доверительные
интервалы:
|
а) |
|
|
|
б) |
|
Объем
выборки при повторном отборе:
|
а) |
|
|
|
б) |
|
Объем
выборки при бесповторном отборе:
|
а) |
|
|
|
б) |
|
Вариант №1
Задание
1.
В
целях изучения затрат времени на
изготовление детали рабочими завода
проведена 10% случайная бесповторная
выборка в результате которой получено
данное распределение деталей по затратам
времени, представлено в следующей
таблице:
|
Затраты времени на |
Число деталей, шт. |
Расчетные |
||
|
Середина |
|
|
||
|
до 10 |
10 |
9 |
90 |
136,9 |
|
до 12 |
20 |
11 |
220 |
57,8 |
|
12 – 14 |
50 |
13 |
650 |
4,5 |
|
14 – 16 |
15 |
15 |
225 |
79,35 |
|
16 |
5 |
17 |
85 |
92,45 |
|
Итого |
100 |
— |
1270 |
371 |
На
основе этих данных вычислить:
1.
С вероятностью 0.954 предельную ошибку
выборочной средней и возможные границы,
в которых ожидаются средние затраты
времени на изготовление одной детали
на заводе;
2.
С вероятностью 0.954 предельную ошибку
выборочной доли и границы удельного
веса числа деталей с затратами времени
на их изготовление от 10 до 14 мин.
Задание
2.
Для
определения среднего возраста 1200
студентов факультета необходимо провести
выборочное обследование методом
случайного бесповторного отбора.
Предварительно установлено, что среднее
квадратическое отклонение возраста
студентов равно 3 года.
Определить
количество студентов, которое нужно
обследовать, чтобы с вероятностью 0,954
средняя ошибка выборки не превышала 3
года.
Задание
№3
Для
изучения возрастной структуры рабочих
завода по состоянию на 1 июля было
проведено 3% выборочное обследование
по методу случайного бесповторного
отбора. Результаты обследования
распределения рабочих по возрасту
представлены в следующей таблице:
|
Группы лет. |
Число чел. |
|
до |
10 |
|
20 – 30 |
18 |
|
30 – 40 |
40 |
|
40 –50 |
24 |
|
50 |
8 |
|
Итого |
100 |
На
основании данных выборочного обследования
вычислите:
1.
По «способу моментов»:
а)
средний возраст рабочего;
б)
дисперсию.
2.
Среднее квадратическое отклонение.
3.
Коэффициент вариации.
4.
С вероятностью 0.997 возможные границы
среднего возраста рабочих завода.
5.
С вероятностью 0.954 возможные границы
доли рабочих завода, возраст которых
составляет менее 20 лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ Юридический колледж)
ПЛАН-КОНСПЕКТ учебного занятия
по ОП.11 Статистика
учебной дисциплине/междисциплинарному курсу
для обучающихся 2 курса
специальность 40.02.01 Право и организация социального обеспечения
(набор 2016 г.)
(углубленная подготовка)
дата проведения занятия по расписанию
Тема 3.1. Выборочное наблюдение
Занятие 15. ПЗ №8 Определение ошибки репрезентативности.
Определение объема выборочной совокупности
Цель занятия: отработать практические навыки по определению доверительных пределов и исчислению ошибок выборки
Задачи занятия:
Обучающая: Обеспечить усвоение обучающимися материала о понятиях: ошибки репрезентативности, выборка, выборочная совокупность;
Воспитательная: воспитывать навыки самостоятельной работы, чувство ответственности за порученный участок работы, дисциплину умственного труда, уверенность в своих силах, стремление к достижению результата;
Развивающая: создавать условия для развития самостоятельности мышления, способности высказывания собственной точки зрения, систематизировать необходимую информацию, анализировать, сравнивать и обобщать информацию, развивать монологическую речь.
Основная литература:
Глава 11. Выборочное наблюдение. (211-220) Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Дополнительная литература:
Савюк Л.К. Правовая статистика: Учебник. — М.: Юрист, 2016
Интернет-ресурсы:
- Информационно-издательский центр «Статистика России» http://www.statbook.ru
- Электронный фонд правовой и технической документации http://docs.cntd.ru
- Информационно правовой портал http://www.garant.ru/
Междисциплинарные связи: Право социальное обеспечение
Внутридисциплинарные связи: Тема 2.1. Сводка и группировка статистических данных
1. Актуализация знаний по ранее пройденному материалу учебного курса
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 1.
|
Вопрос (тестовое задание) |
Ответ |
|
|
|
|
|
|
|
|
|
2. Изучаемые вопросы занятия
|
1. Определение ошибки репрезентативности. |
|
2. Определение объема выборочной совокупности. |
Вопрос 1. Определение ошибки репрезентативности
В статистике выделяют два основных метода исследования – сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны Ошибки смещения, т. е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки – Случайная ошибка репрезентативности (M) – Является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. ошибки репрезентативности
2. доверительных границ средних (или относительных) величин в генеральной совокупности
3. достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):

 , где σ – среднее квадратическое отклонение; n – численность выборки (>30).
, где σ – среднее квадратическое отклонение; n – численность выборки (>30).
Расчет ошибки репрезентативности (mР) относительной величины (Р):
 , где Р – соответствующая относительная величина (рассчитанная, например, в %);
, где Р – соответствующая относительная величина (рассчитанная, например, в %);
Q =100 – Ρ% – величина, обратная Р; n – численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.
 ;
;  .
.
Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ – дельта), которая определяется по формуле:
Δ=t * m, где t – доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% – 3,0; при вероятности безошибочного прогноза 99,7% – 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.
Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной).
Для определения доверительных границ используются следующие формулы:
- для средних величин:
 ,где Мген – доверительные границы средней величины в генеральной совокупности;
,где Мген – доверительные границы средней величины в генеральной совокупности;
Мвыб – средняя величина, Полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM – ошибка репрезентативности средней величины.
2) для относительных величин:
 , где Рген – доверительные границы относительной величины в генеральной совокупности; Рвыб – относительная величина, полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент; mP – ошибка репрезентативности относительной величины.
, где Рген – доверительные границы относительной величины в генеральной совокупности; Рвыб – относительная величина, полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент; mP – ошибка репрезентативности относительной величины.
Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, Указывающей на имеющееся число степеней свободы (n), Которое равно n-1.
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной совокупности (Мген).
Решение.
- Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m): m = σ / √n = 6 / √36 = ±1 удар в минуту
- Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо:
- а) задать степень вероятности безошибочного прогноза (Р = 95 %);
- б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2×1 = 80 ± 2 удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген).
Решение.
- Вычисление ошибки репрезентативности относительного показателя: m = √P x q / n = √18 x (100 — 18) / 164 = ± 3%
- Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом:
- необходимо задать степень вероятности безошибочного прогноза (Р=95%);
- при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 ч после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч работы.
Решение.

Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.

Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено влиянием возраста детей.
|
Источники информации по 1 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 1
- Записать в тетрадь конспект (1-2 стр.)
Вопрос 2. Определение объема выборочной совокупности
Социологические исследования редко бывают сплошными, как, например, перепись населения. Обычно сплошное исследование проводится при небольшой генеральной совокупности.
Чаще всего исследования носят выборочный характер, при котором наиболее важным основанием является возможность распространения полученных результатов и выводов на всю генеральную совокупность. В таком случае сплошное исследование нецелесообразно. Обеспечение этой нецелесообразности — вопрос о репрезентативности выборки, т.е. достаточной количественной и качественной представительности генеральной совокупности в выборке.
Условиями соблюдения репрезентативности выборки являются:
1) равная возможность каждого члена генеральной совокупности попасть в выборку;
2) отбор необходимо проводить независимо от изучаемого признака (иначе в выборку могут попасть, например, только спортсмены);
3) отбор по возможности должен производиться из однородных совокупностей;
4) величина выборки должна быть достаточно большой.
Далее возникает вопрос: как определить достаточный объем выборки? Для этого необходимо иметь характеристики генеральной совокупности по важнейшим (с точки зрения исследования) признакам. К ним, например, можно отнести сведения о количестве желающих заниматься физической культурой и спортом, о числе занимающихся и т.д. Но, как правило, такие характеристики (или многие из них) не известны. Пилотажные исследования как раз и направлены на их выявление.
Приведем пример определения объема выборочной совокупности. В ходе подготовки к проведению конкретно-социологического исследования на основании теоретических посылок были выделены характеристики и признаки, подлежащие изучению. Например, желание заниматься физической культурой, спортом, величина потребности, участие в видах деятельности и др.
На основании результатов изучения этих признаков в пробном исследовании (30 и более респондентов) определяется объем выборки.
Предположим, что в пробном исследовании опрошено 147 студентов 4-х курсов в четырех вузах Республики Беларусь.
Для желания заниматься физической культурой получены следующие распределения:
1.«Нет, не хочу» — 5 человек;
2.«Скорее не хочу, чем хочу» — 3 человека;
3.«Безразлично» — 11 человек;
4.«Скорее хочу, чем не хочу» — 34 человека;
5.«Да, хочу» — 72 человека.
Для расчета объема выборки используются формулы:

t — 1,96 — распределение Стьюдента для вероятности 0,95 или 95% (т.е., если требуемая вероятность соответствия характеристик выборки и характеристик генеральной совокупности 95%, всегда = 1,96. Их соответствие на 95% — общепринятое требование в социологических исследованиях.
Для нашего распределения:

При условии, что выборка в пробном исследовании представляла бы собой модель генеральной совокупности, величина выборочной совокупности для изучения желания заниматься физической культурой должна быть не меньше 147 человек. Тогда с вероятностью 95% можно утверждать, что генеральное среднее лежит в пределах 4,39+0,155.
Поскольку модель выборки в пробном исследовании во вузам не представляет собой модели генеральной совокупности (опрос был в четырех вузах из 30), то увеличиваем полученное n (30/4) в 7,5 раза. Тогда необходимый объем выборки — 1102 респондента.
Качественная представительность полученной выборки оценивается сравнением существенных характеристик (либо связанных с существенными) генеральной совокупности и выборки. Для студенчества, например, такими характеристиками являются: соотношение по полу, охват учебными занятиями по физическому воспитанию, соотношение форм занятий и др.
Когда информация о признаках элементов генеральной совокупности отсутствует, исключается возможность определения объема выборочной совокупности при помощи формул. В этом случае можно опереться на многолетний опыт социологов — практиков, свидетельствующий о том, что для пробных опросов достаточна выборка объемом 100-250 человек. При массовых опросах, если величина генеральной совокупности 5000 человек, достаточный объем выборочной совокупности — не менее 500 человек, если же величина генеральной совокупности 5000 человек и более, то — 10% ее состава (но не более 2000-2500 человек). Это характеризует достаточно достоверные результаты исследования.
ПРИМЕР 1
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200
 =30г
=30г
 =4г — СКО
=4г — СКО
p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:

 =0,84 г
=0,84 г
 г
г
Определяем величину средней ошибки.

Ответ: пределы в которых находится средний вес изделий: г
г
ПРИМЕР 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает: n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:

Найдем среднее число детей в выборочной совокупности:
 ребенка
ребенка
Определим дисперсию

 ребенка – средняя величина ошибки
ребенка – средняя величина ошибки
Т.к p = 0,954, то t = 2
 ребенка
ребенка
 ребенка
ребенка
Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
|
Источники информации по 2 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 3-е издание, стер. – М.: КНОРУС, 2019. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 2
- Записать в тетрадь конспект (1-2 стр.)
3. Подведение итогов учебного занятия
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 2.
|
Наименование изученного вопроса учебного занятия |
Контрольное задание по изученному вопросу |
Ответ |
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 1 Условие задачи: при медицинском осмотре 126 детей 6 летнего возраста, проживающих в одном из районов городе А., в 12% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген). |
|
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 2. Условие задачи: при медицинском осмотре детей 6 летнего возраста в 15% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 7-летнего возраста составила 24% (m = ± 2,64%). Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп. |
|
|
Определение объема выборочной совокупности |
ЗАДАНИЕ 3. В городе проживает 300 тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей: P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Сформулируйте понятие генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Перечислите способы отбора единиц для выборочного наблюдения |
- Домашнее задание на следующее занятие
- Выучить основные понятия. Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО (стр. 211-220)
- Выполнить задание 11.1. в тетради (стр. 224) учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Преподаватель Ю.В. Древаль
|
СОГЛАСОВАНО Протокол заседания ЦК дисциплин профессионального цикла специальности «Право и организация социального обеспечения» ГБПОУ Юридический колледж от ____________ 2017 г. № ___ |
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.
Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.
Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.
Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.
Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.
Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.
В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:

где µx– стандартная ошибка.
Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µx зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).
Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:

В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.
Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:

Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.
Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности x и величину предельной ошибки этой средней ?x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна

Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
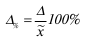
Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.
Данный текст является ознакомительным фрагментом.
Читайте также
Наблюдения за объемом
Наблюдения за объемом
Имеет значение не сам объем, а его соотношения в различные периоды рыночного движения. Соотношения объемов – очень важный, но и наименее объективный из технических инструментов, так как здесь нет никаких непреложных правил. Вместо этого есть набор
Закономерности и наблюдения
Закономерности и наблюдения
Я верю в существование закономерностей на рынке и считаю, что отношусь к числу людей, которые способны их улавливать. Но я также хорошо помню и о том, что все закономерности нечеткие. Нечеткие они потому, что в них присутствует фактор
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
8. Способы статистического наблюдения
8. Способы статистического наблюдения
Способами получения статистической информа–ции являются документальный способ наблюдения; способ непосредственного наблюдения: опрос.Документальное наблюдение основано на исполь–зовании в качестве источника информации данных
9. Формы статистического наблюдения
9. Формы статистического наблюдения
В теории статистики рассматриваются и формы статистического наблюдения: отчетность; специально организованное статистическое наблюдение; реги–стры.Статистическая отчетность – основная форма статистического наблюдения, которая
2. Ошибки выборочного наблюдения
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но
19. Наблюдения
19. Наблюдения
Наблюдение представляет собой сбор первичной информации об объекте наблюдения для построения гипотез, проверки исходных данных и т. д.К способам проведения наблюдения относят:1) прямой, который предполагает непосредственное наблюдение за объектом
6. Организация статистического наблюдения
6. Организация статистического наблюдения
Начальным этапом статистического исследования является статистическое наблюдение.В процессе статистического наблюдения формируется оснавная информация, которая является основной для статистического
11. Ошибки статистического наблюдения и контроль материалов наблюдения
11. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Любое статистическое наблюдение предполагает получение данных, которые будут
34. Определение выборочного наблюдения
34. Определение выборочного наблюдения
Так как сплошное наблюдение дорого и трудоемко, то его заменили выборочным.Выборочное наблюдение – это способ несплошного наблюдения, при котором лишь часть совокупности, отобранная по определенным правилам выборки и
Часть 5 Наблюдения
Часть 5
Наблюдения
За свою тридцатипятилетнюю карьеру в бизнесе я смотрел на мир с разных точек зрения. Я был свидетелем взлетов и падений в экономике и отрасли, появления на рынке новых продуктов и их исчезновения. Я представлял новые товары, возрождал старые, закрывал
Введение процедуры наблюдения
Введение процедуры наблюдения
Наблюдение вводится с целью сохранения активов должника, проведения оценки его финансового состояния, изучения объективной возможности восстановления платежеспособности и продолжения функционирования организации.С момента введения
1. Организация статистического наблюдения
1. Организация статистического наблюдения
Статистическое наблюдение – это организованная работа по сбору первичных сведений об изучаемых массовых явлениях и процессах общественной жизни. Статистическое наблюдение проводится организованно и по заранее разработанным
5. Ошибки статистического наблюдения и контроль материалов наблюдения
5. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Точность – это уровень соответствия значения какого–либо признака или
1. Определение выборочного наблюдения
1. Определение выборочного наблюдения
Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности
Общие наблюдения и впечатления
Общие наблюдения и впечатления
Члены команды систематически выполняли требования восьми этапов цикла кайдзен и обнаружили, что с их помощью смогли построить процесс решения проблем в правильной последовательности. Использование таких инструментов, как «рыбий скелет»
Подборка по базе: Зуев К.А. Практическое задание..docx, Практическое занятие 3.rtf, Зуев К.А. Практическое задание. (2).docx, Общий Психологический Практикум Практическое задание.docx, Зуев К.А. Практическое задание..docx, Зуев К.А. Практическое задание..docx, Зуев К.А. Практическое задание..docx, Зуев К.А. Практическое задание. (1).docx, Пожидаева К.М. Практическое задание 3.doc, 3 Практическое задание № 3 английский2.docx
Практическое занятие №3. Ошибки выборки
3.1 Ошибки регистрации и ошибки репрезентативности
В результате статистической обработки данных могут возникнуть ошибки наблюдения, получаемые вследствие расхождения между величиной какого-либо показателя, найденного при статистическом наблюдении данных и действительными его размерами. Их еще называют выбросами. Это данные среди исходных результатов измерений (или данные, занесенные в таблицу и полученные из результатов измерений), которые настолько отклоняются от сопоставимых данных, внесенных в ту же самую таблицу, что признаются несовместимыми.
В зависимости от причин возникновения различаю ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации возникают в результате неправильного установления фактов или ошибочной записи в процессе наблюдения. Они бывают случайными и систематическими. Случайные ошибки регистрации могут быть допущены как в опрашиваемыми в их ответах, так и регистраторами. Систематические ошибки могут быть и преднамеренными, и непреднамеренными. Преднамеренные ошибки – сознательные, тенденциозные искажения действительного положения дел. Непреднамеренные ошибки могут быть вызваны различными случайными причинами (небрежность, невнимательность).
Ошибки репрезентативности (представительности) возникают в результате неполного обследования и в случае, если обследуемая совокупность недостаточно полно воспроизводит генеральную совокупность. Они могут быть случайными и систематическими.
Ошибки репрезентативности присущи выборочному наблюдению и возникают в связи с тем, что выборочная совокупность не полностью воспроизводит генеральную.
Выборка является репрезентативной (или представительной), если она достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки является, согласно закону больших чисел, соблюдение случайности отбора, т.е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку.
Анализ репрезентативности выборки особенно важен на начальном этапе исследований, когда численность генеральной совокупности неизвестна, но известны некоторые параметры опыта, позволяющие оценить репрезентативность.
Ошибки выборки – разность между характеристиками выборочной и генеральной совокупностей. Для среднего значения определяют предельную ошибку выборки по формуле
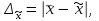 (3.1)
(3.1)
где
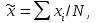 (3.2)
(3.2)
N– объем выборки.
Грубые ошибки и промахи обнаруживают и исключают из расчетов следующим образом:
- находят среднее арифметическое
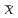 результата n—кратного измерения величины хi;
результата n—кратного измерения величины хi; - определяют среднее квадратическое отклонение S; Если базовый элемент ijсодержит лишь два результата измерений, то внутриэлементное расхождение (аналог стандартного отклонения) равно
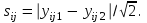 (3.3)
(3.3)
Таким образом, если во всех базовых элементах содержится по два результата измерений, для простоты вместо стандартных отклонений могут быть использованы абсолютные расхождения;
- вычисляют вспомогательную величину t(S) (табл. 3.1).
Таблица 3.1 – Значения вспомогательной величины t(S) в зависимости от числа nповторных измерений (степень достоверности 0,95)
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| t(S) | 15,56 | 4,97 | 3,56 | 3,04 | 2,78 | 2,62 | 2,51 | 2,43 | 2,37 |
При |хi —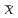 |>t(S) результат измерения хiявляется грубой ошибкой, поэтому его исключают из расчетов и среднее значение
|>t(S) результат измерения хiявляется грубой ошибкой, поэтому его исключают из расчетов и среднее значение 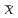 вычисляют заново для оставшихся достоверных результатов измерения.
вычисляют заново для оставшихся достоверных результатов измерения.
Ошибки (промахи) могут быть исключены из генеральной совокупности с помощью следующего правила:
Если k больше допустимого значения, то делается вывод о том, что xi не принадлежит к генеральной совокупности.
Значения допустимых k дано в таблице 3.2.
Таблица 3.2 – Значения допустимых kв зависимости от числа измерений
| Число измерений | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 25 |
| Значение k | 1,49 | 1,94 | 2,22 | 2,41 | 2,55 | 2,66 | 2,75 | 2,82 | 2,88 | 3,01 |
В литературе известны также критерии 3s, Граббса (Смирнова) [ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений], Шарлье, Шовенэ, Диксона и др., которые позволяют исключить грубые промахи.
3.2 Критерий Романовского
Используя критерий Романовского можно определить грубую погрешность в зависимости от числа измерений и уровня значимости α. Для этого необходимо вычислить расчетное значение Vрасч сомнительного результата по формулам:
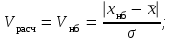
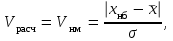 (3.4)
(3.4)
где Vнб, Vнм – соответственно расчетные значения соответствующие наибольшему (хнб) и наименьшему (хнм) значениям сомнительного результата.
Для принятых значений числа измерений n и уровня значимости α определяется максимально допустимое значение Vдоп по таблице 3.3, которое сравнивается с расчетным. Если Vдоп<Vрасч, то сомнительные значения (хнб, хнм) являются грубыми погрешностями и должны быть исключены из дальнейших рассмотрений.
Если Vдоп>Vрасч, то хнб и хнм необходимо оставить в данном ряду измерений и учитывать при обработке результатов измерений.
Таблица 3.3 – Значение критерия Романовского Vдоп в зависимости от числа измерений и уровня значимости
| Число измерений n | Уровень значимости | |||
| 0,1 | 0,05 | 0,025 | 0,01 | |
| 3 | 1,41 | 1,41 | 1,41 | 1,41 |
| 4 | 1,65 | 1,69 | 1,71 | 1,72 |
| 5 | 1,79 | 1,87 | 1,92 | 1,96 |
| 6 | 1,89 | 2,00 | 2,07 | 2,13 |
| 7 | 1,97 | 2,09 | 2,18 | 2,27 |
| 8 | 2,04 | 2,17 | 2,27 | 2,37 |
| 9 | 2,10 | 2,24 | 2,35 | 2,46 |
| 10 | 2,15 | 2,29 | 2,41 | 2,54 |
| 11 | 2,19 | 2,34 | 2,47 | 2,61 |
| 12 | 2,23 | 2,39 | 2,52 | 2,66 |
| 13 | 2,26 | 2,43 | 2,56 | 2,71 |
| 14 | 2,30 | 2,46 | 2,60 | 2,76 |
| 15 | 2,33 | 2,49 | 2,64 | 2,8 |
| 16 | 2,35 | 2,52 | 2,67 | 2,84 |
| 17 | 2,38 | 2,55 | 2,70 | 2,87 |
| 18 | 2,40 | 2,58 | 2,73 | 2,90 |
| 19 | 2,43 | 2,60 | 2,75 | 2,93 |
| 20 | 2,45 | 2,62 | 2,78 | 2,96 |
| 21 | 2,47 | 2,64 | 2,8.’ | 2,98 |
| 22 | 2,49 | 2,66 | 2,82 | 3,01 |
| 23 | 2,50 | 2,68 | 2,84 | 3,03 |
| 24 | 2,52 | 2,7 | 2,86 | 3,05 |
| 25 | 2,54 | 2,72 | 2,88 | 3,07 |
Пример 3.1. Проверить результат хнб = 17,15 на соответствие грубой погрешности при =0,05. Выполнено измерений п = 12; разброс значений составил = 0,03, 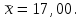
Решение. Рассчитаем критерий Романовского по формуле (3.4):
Vрасч = (17,15 – 17,00)/0,03 = 5.
Для заданных = 0,05 и п = 12 найти по таблице 3 допустимое значение критерия Романовского Vдоп = 2,39. Сравнивая табличное значение с расчетным, получаем 2,39<5, т.е. Vдоп<Vрасч, следовательно, хнб является грубой погрешностью и должно быть исключено из дальнейших рассмотрений.
3.3 Статистическая обработка экспериментальных данных. Собственно-случайная выборка (простая случайная)
Выборочное наблюдение относится к разновидности несплошного наблюдения, цель которого – по отобранной части единиц дать характеристику всей совокупности единиц. Необходимо, чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц).
Используя теорему Чебышева П.Л. можно вычислить величину 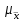 , выражающую среднее квадратическое отклонение выборочной средней от математического ожидания:
, выражающую среднее квадратическое отклонение выборочной средней от математического ожидания:
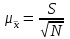 , (3.5)
, (3.5)
которую называют средней ошибкой выборки.
С учетом выбранного уровня вероятности и соответствующего ему значения t (выбирается по табл. 2.5) предельная ошибка выборки составит:
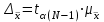 , (3.6)
, (3.6)
где tα(N-1) – квантиль распределения Стьюдента для вероятности α и числа степеней свободы f = (N-1).
С учётом (3.5) и (3.6) можно утверждать, что при заданной вероятности генеральная средняя 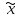 будет находиться в следующих границах:
будет находиться в следующих границах:
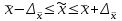 (3.7)
(3.7)
Пример 3.2. Предположим, в результате выборочного обследования жилищных условий жителей города, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 3.4).
Таблица 3.4 – Результаты выборочного обследования жилищных условий жителей города
| Общая площадь жилищ, приходящаяся на 1 чел., кв. м. | До 5,0 | 5,0…10,0 | 10,0…15,0 | 15,0…20,0 | 20,0…25,0 | 25,0…30,0 | 30,0 и более |
| Число жителей | 8 | 95 | 204 | 207 | 210 | 130 | 83 |
Рассмотрим определение границ генеральной средней, в данном случае – средней площади жилищ в расчёте на 1 чел. в целом по городу, опираясь только на результаты выборочного обследования. Для определения средней ошибки выборки нам необходимо, прежде всего, рассчитать выборочную среднюю величину и дисперсию изучаемого признака (табл. 3.5).
В случае, когда данные сгруппированы по интервалам, т. е. представлены в виде интервальных рядов распределения, при расчёте средней арифметической в качестве значения признака принимают середину интервала, исходя из предположения о равномерном распределении единиц совокупности на данном интервале.
Таблица 3.5 – Расчёт средней (полезной) площади жилищ, приходящейся на 1 чел., и дисперсии
| Общая (полезная) площадь жилищ,
приходящаяся на 1 чел., м2 |
Число
жителей mi |
Середина
интервала xi |
xi·mi | 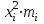 |
| До 5,0
5,0 … 10,0 10,0 … 15,0 15,0 … 20,0 20,0 … 25,0 25,0 … 30,0 30,0 и более |
8
95 204 270 210 130 83 |
2,5
7,5 12,5 17,5 22,5 27,5 32,5 |
20,0
712,5 2550,0 4725,0 4725,0 3575,0 2697,5 |
50,0
5343,75 31875,0 82687,5 106312,5 98312,5 87668,75 |
| Итого: | 1000 | – | 19005,0 | 412250,0 |
Расчёт ведется по формулам:
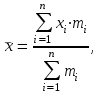 (3.8)
(3.8)
где xi – середина интервала.
В нашем примере:
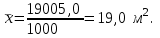
Дисперсию определим по формуле:
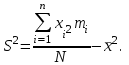 (3.9)
(3.9)
Тогда получаем:
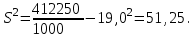
Откуда получаем значение выборочного среднего квадратичного отклонения:
S = 7,16м2.
Средняя ошибка выборки составит:
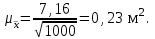
Определим предельную ошибку выборки с вероятностью 0,954 (t=2):
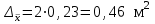 .
.
Установим границы генеральной средней:
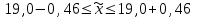 или
или 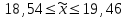 .
.
Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний размер общей площади, приходящейся на 1 чел., в целом по городу лежит в пределах от 18,5 до 19,5 м2.
При расчёте средней ошибки собственно-случайной бесповторной выборки необходимо учитывать поправку на бесповторность отбора:
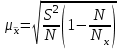 , (3.10)
, (3.10)
где Nx – генеральная совокупность. Если предположить, что представленные в таблице 6 данные являются результатом 5%-го бесповторного отбора (следовательно, генеральная совокупность включает 20 000 ед.), т.е. средняя ошибка выборки согласно (3.10) будет несколько меньше:
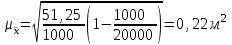 .
.
Соответственно уменьшится и предельная ошибка выборки, что вызовет сужение границ генеральной средней. Особенно ощутимо влияние поправки на бесповторность отбора при относительно большом проценте выборки.
Варианты заданий к практическому занятию №3
| Вариант | в | хср | хнб | сигма | n |
| 1 | 0,1 | 24 | 24,48 | 0,12 | 3 |
| 2 | 0,05 | 24 | 26,16 | 0,12 | 4 |
| 3 | 0,025 | 18 | 19,26 | 0,09 | 5 |
| 4 | 0,01 | 5 | 5,3 | 0,09 | 6 |
| 5 | 0,1 | 25 | 26,75 | 0,11 | 7 |
| 6 | 0,05 | 10 | 10,8 | 0,1 | 8 |
| 7 | 0,025 | 18 | 19,62 | 0,11 | 9 |
| 8 | 0,01 | 8 | 8,48 | 0,09 | 10 |
| 9 | 0,1 | 18 | 18,18 | 0,13 | 11 |
| 10 | 0,05 | 18 | 18,36 | 0,1 | 20 |
| 11 | 0,025 | 18 | 19,08 | 0,1 | 21 |
| 12 | 0,01 | 14 | 15,4 | 0,09 | 22 |
| 13 | 0,1 | 16 | 17,6 | 0,09 | 23 |
| 14 | 0,05 | 9 | 9,18 | 0,11 | 24 |
| 15 | 0,025 | 7 | 7,63 | 0,12 | 25 |
| 16 | 0,01 | 23 | 23,23 | 0,09 | 3 |
| 17 | 0,1 | 17 | 18,36 | 0,11 | 4 |
| 18 | 0,05 | 21 | 21,63 | 0,1 | 5 |
| 19 | 0,025 | 6 | 6,18 | 0,11 | 6 |
| 20 | 0,01 | 10 | 10,5 | 0,12 | 7 |
| 21 | 0,1 | 6 | 6,66 | 0,11 | 8 |
| 22 | 0,05 | 12 | 12,6 | 0,09 | 9 |
| 23 | 0,025 | 15 | 15,6 | 0,09 | 10 |
| 24 | 0,01 | 12 | 12,36 | 0,12 | 11 |
| 25 | 0,1 | 22 | 23,54 | 0,11 | 20 |
| 26 | 0,05 | 15 | 16,35 | 0,13 | 21 |
| 27 | 0,025 | 5 | 5,35 | 0,08 | 22 |
| 28 | 0,01 | 18 | 19,62 | 0,11 | 23 |
| 29 | 0,1 | 10 | 10,9 | 0,11 | 24 |
| 30 | 0,05 | 15 | 16,5 | 0,1 | 25 |
| Вариант | Общая площадь на 1 чел, кв. м. | до 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | больше 30 | P |
| 1 | Число жителей | 100 | 98 | 121 | 61 | 12 | 180 | 72 | 0,953 |
| 2 | 71 | 61 | 90 | 184 | 87 | 60 | 102 | 0,939 | |
| 3 | 67 | 105 | 63 | 165 | 123 | 105 | 51 | 0,931 | |
| 4 | 57 | 41 | 188 | 124 | 127 | 85 | 30 | 0,937 | |
| 5 | 199 | 146 | 146 | 72 | 101 | 7 | 156 | 0,971 | |
| 6 | 178 | 55 | 85 | 102 | 182 | 60 | 85 | 0,974 | |
| 7 | 45 | 136 | 136 | 37 | 62 | 31 | 33 | 0,926 | |
| 8 | 152 | 13 | 80 | 67 | 144 | 73 | 23 | 0,953 | |
| 9 | 199 | 111 | 75 | 61 | 197 | 198 | 78 | 0,962 | |
| 10 | 66 | 6 | 12 | 61 | 171 | 123 | 178 | 0,955 | |
| 11 | 169 | 36 | 177 | 35 | 132 | 147 | 101 | 0,975 | |
| 12 | 40 | 120 | 17 | 42 | 53 | 116 | 140 | 0,967 | |
| 13 | 38 | 158 | 107 | 194 | 26 | 204 | 166 | 0,923 | |
| 14 | 83 | 201 | 110 | 23 | 161 | 93 | 46 | 0,942 | |
| 15 | 64 | 151 | 84 | 162 | 188 | 96 | 49 | 0,958 | |
| 16 | 115 | 20 | 183 | 198 | 84 | 190 | 109 | 0,922 | |
| 17 | 189 | 106 | 89 | 138 | 148 | 132 | 38 | 0,977 | |
| 18 | 144 | 9 | 156 | 81 | 204 | 148 | 11 | 0,979 | |
| 19 | 31 | 150 | 202 | 125 | 182 | 62 | 119 | 0,947 | |
| 20 | 16 | 78 | 148 | 35 | 30 | 147 | 132 | 0,971 | |
| 21 | 6 | 136 | 123 | 132 | 163 | 29 | 64 | 0,97 | |
| 22 | 99 | 160 | 159 | 165 | 29 | 64 | 196 | 0,969 | |
| 23 | 89 | 198 | 56 | 71 | 152 | 15 | 198 | 0,967 | |
| 24 | 153 | 54 | 150 | 36 | 134 | 40 | 189 | 0,95 | |
| 25 | 112 | 161 | 66 | 65 | 182 | 28 | 146 | 0,923 | |
| 26 | 37 | 90 | 88 | 136 | 25 | 20 | 149 | 0,943 | |
| 27 | 187 | 59 | 13 | 7 | 148 | 156 | 194 | 0,922 | |
| 28 | 84 | 118 | 159 | 200 | 62 | 127 | 7 | 0,961 | |
| 29 | 66 | 86 | 11 | 24 | 54 | 155 | 202 | 0,956 | |
| 30 | 50 | 144 | 179 | 104 | 86 | 10 | 49 | 0,968 |
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ Юридический колледж)
ПЛАН-КОНСПЕКТ учебного занятия
по ОП.11 Статистика
учебной дисциплине/междисциплинарному курсу
для обучающихся 2 курса
специальность 40.02.01 Право и организация социального обеспечения
(набор 2017 г.)
(углубленная подготовка)
Тема 3.1. Выборочное наблюдение
ПЗ Расчет ошибок выборочной средней и выборочной доли для разных способов отбора
Цель занятия: отработать практические навыки по определению ошибок выборочной средней и выборочной доли для разных способов отбора
Задачи занятия:
Обучающая: Обеспечить усвоение обучающимися материала о понятиях: выборочной средней, выборка, выборочная совокупность;
Воспитательная: воспитывать навыки самостоятельной работы, чувство ответственности за порученный участок работы, дисциплину умственного труда, уверенность в своих силах, стремление к достижению результата;
Развивающая: создавать условия для развития самостоятельности мышления, способности высказывания собственной точки зрения, систематизировать необходимую информацию, анализировать, сравнивать и обобщать информацию, развивать монологическую речь.
Основная литература:
Глава 11. Выборочное наблюдение. (211-220) Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Дополнительная литература:
Савюк Л.К. Правовая статистика: Учебник. — М.: Юрист, 2016
Интернет-ресурсы:
- Информационно-издательский центр «Статистика России» http://www.statbook.ru
- Электронный фонд правовой и технической документации http://docs.cntd.ru
- Информационно правовой портал http://www.garant.ru/
Междисциплинарные связи: Право социальное обеспечение
Внутридисциплинарные связи: Тема 2.1. Сводка и группировка статистических данных
1. Актуализация знаний по ранее пройденному материалу учебного курса
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 1.
|
Вопрос (тестовое задание) |
Ответ |
|
|
|
|
|
|
|
|
|
2. Изучаемые вопросы занятия
1. ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора
Вопрос 1. ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора
При бесповторном оборе с каждой отобранной единицей или серией вероятность отбора оставшихся единиц или серий повышается, при этом средняя ошибка выборочной средней уменьшается по сравнению с повторным отбором и имеет следующий вид:
1) для механического или собственно случайного бесповторного отбора:

При достаточно большом объеме совокупности N можно воспользоваться формулой:

2) для серийного бесповторного отбора равновеликих серий:

При достаточно большом числе серий в генеральной совокупности R можно воспользоваться формулой:
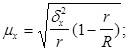
3) для типического отбора с бесповторным случайном отборе внутри групп, пропорциональном объему групп:



Межсерийная дисперсия выборочных средних и средняя из выборочных дисперсий типических групп вычисляются следующим образом:


где — среднее значение показателя в j — й серии;
— дисперсия признака x в j — й типической группе;
nj — число единиц в j -й типической группе Предельная ошибка выражается следующим образом:

и зависит от вариации изучаемого признака в генеральной совокупности, объема и доли выборки, способа отбора единиц из генеральной совокупности и от величины вероятности, с которой гарантируются результаты выборочного наблюдения.
Средняя величина количественного признака в генеральной совокупности определяется с у четом предельной ошибки выборочной средней
Из всего вышесказанного можно сделать следующие выводы:
1. Определение объема выборки зависит от метода отбора, который может быть механический бесповторный и механический повторный отбор, серийный при повторном и серийный при бесповторном отборе, типический при повторном случайном и типический при бесповторном случайном отборе. В зависимости от принадлежности к тому или иному методу, объем выборки рассчитывается по определенным формулам.
2. Планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который входит в план всего статистического анализа выборочного наблюдения и включает вопросы методологии, организации, техники сбора информации, контроля ее достоверности и оформления итоговых результатов.
3. Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. Во 2 и 3 разделе были представлены формулы расчета ошибок выборочного наблюдения в статистическом анализе в зависимости от способов отбора выборочной совокупности.
ПРИМЕР
При обследовании 500 образцов изделий, отобранных из партии готовой продукции предприятия в случайном порядке, 40 оказались нестандартными.
С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции, выпускаемой заводом.
Решение:
Рассчитаем долю нестандартной продукции в выборочной совокупности:

Средняя ошибка выборочной доли при повторном отборе рассчитывается по формуле:

где n – численность выборки.
С вероятностью 0,954 рассчитаем предельную ошибку выборочной доли по формуле:
Δ = μ × t
где
t – коэффициент доверия.
Значение коэффициента доверия t определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного наблюдения и берётся из готовых таблиц.
При Р = 0,954, t = 2.
Δ = t * μ = 2 * 0,012 = 0,024
С вероятностью 0,954 можно утверждать, что доля нестандартной продукции в партии товара колеблется:
ω – Δ ˂ р ˂ ω + Δ
0,08 – 0,02 ˂ р ˂ 0,08+0,02
0,06 ˂ р ˂ 0,10
или
6% ˂ р ˂ 10%
ПРИМЕР
Для определения скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 20 дням со средним квадратическим отклонением 7 дней.
Необходимо с вероятностью P=0,954 определить предельную ошибку выборочной средней и доверительные пределы в которых будет находится средняя продолжительность расчетов предприятий данной корпорации с кредиторами.
Решение:
Средняя продолжительность расчетов предприятий корпорации с кредиторами находится в пределах
Так как выборка случайная повторная, то предельная ошибка выборки определяется по формуле (1):
 дня.
дня.
И, значит, пределы средней продолжительности расчетов равны


С вероятностью 0,954 можно утверждать, что средняя продолжительность расчетов предприятий корпорации с кредиторами в коммерческом банке может изменяться от 18,6 дня до 21,4 дня.
|
Источники информации по 1 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 1
- Записать в тетрадь конспект (1-2 стр.)
Вопрос 2. Определение объема выборочной совокупности
3. Подведение итогов учебного занятия
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 2.
|
Наименование изученного вопроса учебного занятия |
Контрольное задание по изученному вопросу |
Ответ |
|
ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора |
ЗАДАНИЕ 1 При обследовании 1000 образцов изделий, отобранных из партии готовой продукции предприятия в случайном порядке, 70 оказались нестандартными. С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции, выпускаемой заводом. |
|
|
ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора |
ЗАДАНИЕ 2. Для определения скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 10 дням со средним квадратическим отклонением 8 дней. Необходимо с вероятностью P=0,954 определить предельную ошибку выборочной средней и доверительные пределы в которых будет находится средняя продолжительность расчетов предприятий данной корпорации с кредиторами. |
|
|
ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора |
ЗАДАНИЕ 3. По математическим формулам можно осуществить расчет:
|
|
|
ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора |
|
|
|
ПЗ №9 Расчет ошибок выборочной средней и выборочной доли для разных способов отбора |
|
- Домашнее задание на следующее занятие
- Повторить основные понятия. Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО (стр. 211-220)
- Выполнить задание 11.2. в тетради (стр. 224) учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Преподаватель Ю.В. Древаль
|
СОГЛАСОВАНО Протокол заседания ЦК дисциплин профессионального цикла специальности «Право и организация социального обеспечения» ГБПОУ Юридический колледж от ____________ 2018 г. № ___ |
Цель
работы:
1. Научиться распространять
результаты выборочного наблюдения на
генеральную совокупность.
2. Научиться определять
необходимую численность выборки для
получения результата по генеральной
совокупности.
Рекомендации
по выполнению задания:
1.Последовательность
выполнения практической работы:
-
Ознакомиться
с рекомендациями по выполнению задания
и с содержанием рекомендуемых задач. -
Уяснить,
какие показатели необходимо определить. -
Выполнить
необходимые расчеты и оформить их с
подробным объяснением. -
По
результатам расчетов сделать выводы.
2.
Выборочное наблюдение – это такое
несплошное наблюдение, при котором
отбор подлежащих обследованию единиц
осуществляется в случайном порядке,
отобранная часть изучается, а результаты
распространяются на всю исходную
совокупность. Наблюдение организуется
таким образом, что эта часть отобранных
единиц в уменьшенном масштабе
репрезентирует (представляет) всю
совокупность.
Формулы
необходимые для расчета:
Для
характеристики надежности выборочных
показателей различают среднюю и
предельную ошибки выборки.
а)
повторный отбор:
|
|
б)
бесповторный отбор:
|
|
где
n
– численность выборочной совокупности;
N
– численность генеральной совокупности;
2
– дисперсия средней или доли;

процент
выборки
Дисперсия
средней
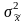
находится с использованием формул,
указанных в п. 5.
Дисперсия
выборочной доли:
|
|
где
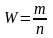
— доля единиц, обладающих данным признаком
в выборочной совокупности;
m
– единицы выборочной совокупности,
обладающие данным признаком.
Предельная
ошибка выборки (
):
|
|
где
t
– коэффициент кратности (доверия).
Доверительные
интервалы:
|
а) |
|
|
|
б) |
|
Объем
выборки при повторном отборе:
|
а) |
|
|
|
б) |
|
Объем
выборки при бесповторном отборе:
|
а) |
|
|
|
б) |
|
Вариант №1
Задание
1.
В
целях изучения затрат времени на
изготовление детали рабочими завода
проведена 10% случайная бесповторная
выборка в результате которой получено
данное распределение деталей по затратам
времени, представлено в следующей
таблице:
|
Затраты времени на |
Число деталей, шт. |
Расчетные |
||
|
Середина |
|
|
||
|
до 10 |
10 |
9 |
90 |
136,9 |
|
до 12 |
20 |
11 |
220 |
57,8 |
|
12 – 14 |
50 |
13 |
650 |
4,5 |
|
14 – 16 |
15 |
15 |
225 |
79,35 |
|
16 |
5 |
17 |
85 |
92,45 |
|
Итого |
100 |
— |
1270 |
371 |
На
основе этих данных вычислить:
1.
С вероятностью 0.954 предельную ошибку
выборочной средней и возможные границы,
в которых ожидаются средние затраты
времени на изготовление одной детали
на заводе;
2.
С вероятностью 0.954 предельную ошибку
выборочной доли и границы удельного
веса числа деталей с затратами времени
на их изготовление от 10 до 14 мин.
Задание
2.
Для
определения среднего возраста 1200
студентов факультета необходимо провести
выборочное обследование методом
случайного бесповторного отбора.
Предварительно установлено, что среднее
квадратическое отклонение возраста
студентов равно 3 года.
Определить
количество студентов, которое нужно
обследовать, чтобы с вероятностью 0,954
средняя ошибка выборки не превышала 3
года.
Задание
№3
Для
изучения возрастной структуры рабочих
завода по состоянию на 1 июля было
проведено 3% выборочное обследование
по методу случайного бесповторного
отбора. Результаты обследования
распределения рабочих по возрасту
представлены в следующей таблице:
|
Группы лет. |
Число чел. |
|
до |
10 |
|
20 – 30 |
18 |
|
30 – 40 |
40 |
|
40 –50 |
24 |
|
50 |
8 |
|
Итого |
100 |
На
основании данных выборочного обследования
вычислите:
1.
По «способу моментов»:
а)
средний возраст рабочего;
б)
дисперсию.
2.
Среднее квадратическое отклонение.
3.
Коэффициент вариации.
4.
С вероятностью 0.997 возможные границы
среднего возраста рабочих завода.
5.
С вероятностью 0.954 возможные границы
доли рабочих завода, возраст которых
составляет менее 20 лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лабораторная работа: Проведение выборочного наблюдения
Федеральное агентство по
образованию
Государственное
образовательное учреждение высшего профессионального образования
«Санкт-Петербургский
государственный политехнический университет»
Факультет экономики и
менеджмента
Кафедра «Предпринимательство
и коммерция»
ЛАБОРАТОРНАЯ РАБОТА №2
По дисциплине
«Статистика»
На тему
«Проведение выборочного
наблюдения»
Санкт-Петербург 2008
Введение
Целью лабораторной работы является освоение
методики организации и проведения выборочного наблюдения; статистических
методов и методов компьютерной обработки полученной информации; методов оценки
параметров генеральной совокупности на основе выборочных данных.
Выборочное наблюдение – важнейший вид не
сплошного наблюдения. Теория выборочного наблюдения, т.н. выборочный метод, –
совокупность принципов и способов отбора единиц совокупности, а также способов
и методов оценки параметров генеральной совокупности на основе выборочных
единиц. Выборочный метод в настоящее время получил широкое практическое
применение, поскольку обладает целым рядом преимуществ по сравнению со сплошным
наблюдением и иными видами несплошного наблюдения.
Преимущества выборочного наблюдения по сравнению со
сплошным:
1.
Экономия
времени, финансовых, трудовых, материальных ресурсов.
2.
Возможность
расширить программу наблюдения.
С другими видами не сплошного наблюдения:
3.
Благодаря
хорошо разработанной теории выборки и используемых при выборочных наблюдениях
способах формирования выборки появляется возможность дать вероятностную оценку
параметров генеральной совокупности.
Генеральная совокупность – совокупность, которая
собственно интересует исследователя и из которой отбираются единицы в
выборочную совокупность. Выборочная совокупность – совокупность отобранных
единиц, по которым будут фиксироваться значения тех или иных признаков.
Основной принцип формирования выборочной
совокупности – случайность отбора, т.е. всем единицам генеральной совокупности
должна быть обеспечена равная вероятность попадания в выборку. Этот принцип
обеспечивает объективность выборочного наблюдения, поскольку позволяет сформировать
репрезентативную выборку. Репрезентативность способствует получению несмещённой
выборки, т.е. структура или закономерность распределения в выборочной
совокупности соответствует распределению единиц в генеральной совокупности.
Способы отбора единиц в выборочную совокупность:
1.
Случайный
отбор. Реализуют методом жеребьёвки или с использованием таблиц случайных
чисел.
2.
Механический
отбор – частный случай случайного отбора. Рассчитывается шаг отбора, который
равен отношению объёма совокупности к объёму выборки: ![]() .
.
Отбор может проводиться по принципу бесповторного
отбора, когда, извлекаемая из генеральной совокупности, единица назад не
возвращается, и повторного отбора [1].
Виды выборки:
1.
Собственно
случайная.
2.
Типологическая
(стратифицированная).
3.
Гнездовая
(серийная).
4.
Многоступенчатая.
5.
Многофазная.
Лабораторная работа выполнена на основе исходных
данных первой лабораторной: данные сборника Росстата Регионы России [2], а
именно статистическая информация о числе собственных легковых автомобилей на
1000 человек населения в различных регионах России в 1990 году. Объём исходной
совокупности – 88 единиц.
1.
Расчёт необходимого объёма выборочной совокупности
Ошибка выборки – это различие в значениях
какого-либо параметра генеральной совокупности и его оценки, полученной на
основе выборки. Ошибка выборки присутствует всегда, т.к. её возникновение
связано с самой сутью выборочного наблюдения: по части судят о целом.
Распределение единиц выборочной совокупности не может в полной мере соответствовать
распределению единиц генеральной совокупности. Понятию ошибки выборки и
методике её определения посвящены многие работы теории выборки (учёные –
Я. Бернулли, П.Л. Чебышев, А.М. Ляпунов, А.А. Марков,
А.А. Чупров и др.).
Теорема Чебышева. При неограниченном
увеличении числа наблюдений в генеральной совокупности с ограниченной
дисперсией с вероятностью, близкой к единице, можно утверждать, что величина
ошибки выборки не превысит сколь угодно малой положительной величины ξ.
![]()
![]() ,
,
где ![]() – выборочное
– выборочное
среднее, ![]() – генеральное среднее,
– генеральное среднее, ![]() – вероятность события, заключённого
– вероятность события, заключённого
в скобки.
Теорема Чебышева доказывает принципиальную
возможность оценки параметров генеральной совокупности на основе выборочных
данных, утверждая, что в условиях большой выборки вероятность получить
незначительную величину ошибки близка к 1. Однако, практически не ясно, чему
равна эта вероятность, и какова величина ошибки выборки.
Теорема Ляпунова. При неограниченном увеличении
числа наблюдений в генеральной совокупности с ограниченной дисперсией
вероятность того, что ошибка выборки не превысит величины tμ, равна
нормированной функции Лапласа:
![]() ,
,
где μ – средняя ошибка выборки,  ,
, ![]() – среднее выборочное по i‑й
– среднее выборочное по i‑й
выборке, n – число выборок.
Математической статистикой доказано, что величина
μ2 прямо пропорциональна дисперсии генеральной совокупности (s2) и обратно
пропорциональна объёму выборки (n): ![]() .
.
Известно, что ![]() (S2 – дисперсия выборки).
(S2 – дисперсия выборки).
Если выборка большого объёма, то ![]() ,
,
следовательно, на практике сомножитель ![]() опускают
опускают
и ![]() .
.
Предельная ошибка выборки ![]() . Плотность нормального
. Плотность нормального
распределения: ![]() , где
, где
нормированное отклонение выборочной средней от генеральной средней ![]() .
.
Данное исследование проводится с вероятностью
0,95. Этому значению в таблице Лапласа соответствует t=1,96, которое на
практике округляют до 2. В этом случае ![]() .
.
Тогда ![]() .
.
Важным вопросом подготовки выборочного наблюдения
является определение объема выборочной совокупности, необходимой и достаточной
для оценки тех или иных свойств генеральной совокупности. В практике
экономико-статистических исследований, как правило, используется процедура
бесповторного отбора единиц в выборочную совокупность. Первым этапом подготовки
выборочного наблюдения является расчет объема выборки. Расчет, как правило,
проводится по следующей формуле: ![]() [3].
[3].
Расчёт объёма выборки проводится многократно с
учётом разной величины ошибки и с разным уровнем вероятности. По полученным
результатам выбирают оптимальный вариант. В лабораторной работе будет
сформировано три выборки, объёмом 70, 25 и 15 единиц каждая.
2.
Формирование выборочных совокупностей и обработка выборочных
данных
Методом случайного бесповторного отбора
формируются большая (70 единиц) и две малых выборки (25 и 15 единиц). Затем,
при помощи ППП Statistica рассчитываются основные статистические характеристики,
данные занесены в таблицу ниже.
Таблица 2.1 . Основные
статистические характеристики выборок

В таблице 2.1 «NewVar1» обозначает выборку
размером 70 единиц, «NewVar2» – 25 единиц, «NewVar3» – 15 единиц. В графе «Mean» указаны значения
средних по каждой выборке, «Std. Dv.» – стандартное отклонение, «N» – объём выборки, «Std. Err.» – средняя ошибка
выборки, «Confidence -95,000%» и «Confidence +95,000%» – соответственно нижняя и верхняя
границы доверительного интервала при вероятности 95%, «Reference» – гипотетическое
значение генеральной средней величины (известно из первой лабораторной работы),
«t-value» – расчетное значение t‑критерия для
проверки гипотезы о значении генеральной средней, «df» – число степеней
свободы, «p»
– расчетный уровень значимости t‑критерия.
Среднее значение выборки, состоящей из 70 единиц,
равно 53,64286, оно отличается от генеральной средней на 2,06309, величина
среднеквадратического отклонения равна 16,66183. Средняя ошибка этой выборки –
1,991470, а интервал оптимальности ![]() , т.е.
, т.е.
с вероятностью 95% можно утверждать, что в среднем по России число собственных
легковых автомобилей на 1000 человек населения в 1990 году находилось в
указанных пределах. Расчётное значение t-критерия составляет -1,03596, меньше
2, следовательно, различия между генеральной и выборочной средней случайны, и
выборочное среднее является достоверной оценкой генеральной средней. Расчётный
уровень значимости t-критерия также подтверждает это (![]() ).
).
3.
Распространение результатов выборочного наблюдения на генеральную
совокупность
Теперь необходимо провести оценку существенности
разности двух выборочных средних. Если разность между средними величинами
статистически значима, это означает, что различие вызвано неслучайными
факторами, или выборки не принадлежат одной генеральной совокупности. Иначе эта
задача формулируется как проверка статистической гипотезы о равенстве двух
средних: ![]() .
.
В лабораторной работе содержательно гипотеза
формулируется следующим образом: взяты выборки из одной или из разных
генеральных совокупностей? В контексте решаемой задачи ответ очевиден – выборки
взяты из одной и той же совокупности. Но следует обратить особое внимание на
проявление эффекта случайной ошибки репрезентативности. Реализация процедуры
проверки гипотезы может дать, в редких случаях, парадоксальный результат, а
именно, показать на основе t‑критерия, что выборки как бы взяты из разных
генеральных совокупностей с разными значениями средних величин. С дидактической
точки зрения такой результат весьма полезен для понимания существа
статистических выводов и степени их условности. Для демонстрации этого эффекта
рекомендуется взять такие две выборки, из ранее полученных, для которых
разность между средними выборочными значениями максимальна [3].
В данной работе для сравнения взяты выборки,
объёмом 70 и 25 единиц. Результаты анализа занесены в таблицу ниже.
Таблица 3.1 . Результаты
расчёта t-критерия для выборок, объёмом 70 и 25 единиц
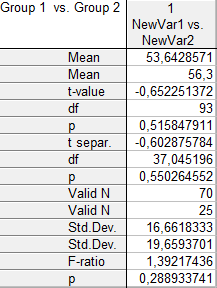
В полученной таблице рассчитаны следующие
показатели:
—
Mean – среднее значение по двум выборкам.
—
t-value – t‑критерий, необходимый для оценки
существенности разности двух средних: 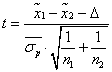 , т. к.
, т. к. ![]() , то
, то 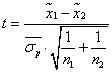 .
.
—
df – число степеней свободы.
—
p
– расчётный уровень значимости t‑критерия.
—
t-separ – расчетное значение t‑критерия с учетом
различных дисперсий. Очевидно, что в этом примере оно не изменяется, однако
программа выдаёт другой результат.
—
df – число степеней свободы t‑критерия при
условии неравных дисперсий. 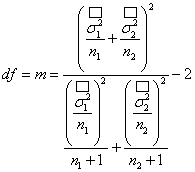 .
.
Расчетное значение m округляется до целого значения в силу того, что число степеней
свободы есть целое число по определению.
—
p –
расчетный уровень значимости t‑критерия при условии неизвестных и неравных дисперсий.
—
Valid N – объём каждой выборки.
—
Std. Dev. – среднее квадратическое отклонение: 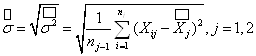
—
F-ratio – F‑критерий (дисперсионное
отношение), используемый для оценки существенности различия значений двух
дисперсий: 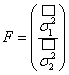 .
.
—
p – расчетный уровень
значимости P‑критерия.
Гипотеза принимается, если ![]() . Здесь
. Здесь ![]() . Табличное значение t‑критерия равно
. Табличное значение t‑критерия равно ![]() . Таким образом
. Таким образом ![]() , следовательно, испытуемая
, следовательно, испытуемая
гипотеза принимается. Аналогичный вывод можно получить на основе сравнения
расчетного и принятого уровней значимости: ![]() .
.
4.
Проверка статистических гипотез о значении генеральной средней и о
равенстве двух выборочных средних
Для наглядного и компактного представления
результатов проведенного выборочного наблюдения необходимо воспользоваться
графическими возможностями ППП STATISTICA. Весьма существенным, с дидактической точки
зрения, является то, что последовательное выполнение рассматриваемых
лабораторных работ, дает возможность наглядного сравнения результатов
выборочного и сплошного наблюдений. Вполне очевидно, что, по определению, такое
сравнение исключено в реальных практических условиях [3].
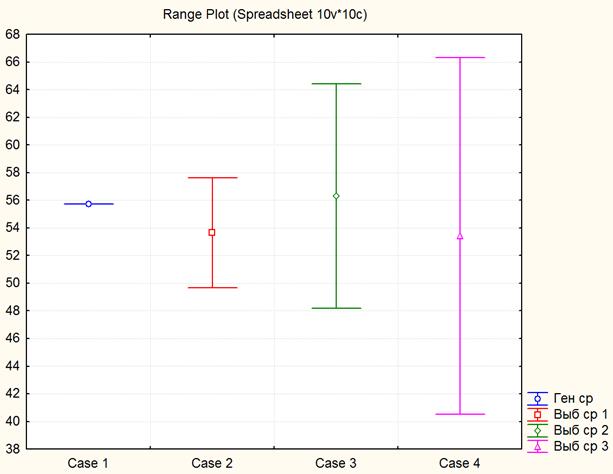
Рисунок 4.1. Графическое сравнение результатов сплошного и выборочного
наблюдения
График наглядно показывает, что доверительные
интервалы, построенные по всем выборкам, накрывают генеральную среднюю, что
естественно. Если бы, какой либо доверительный интервал, рассчитанный по
результатам выборки, не включал в себя значение генеральной средней, то в
реальных условиях, это означало бы получение ошибочного вывода на основе
выборки.
Диаграмма наглядно демонстрирует возможный
результат выборочного зондирования исследуемой генеральной совокупности и
убедительно иллюстрирует объективную неоднозначность выводов, формулируемых на
основе выборочных данных.
Заключение
Среднее значение выборки, состоящей из 70 единиц,
равно 53,64286, оно отличается от генеральной средней на 2,06309, величина
среднеквадратического отклонения равна 16,66183. Средняя ошибка этой выборки –
1,991470, а интервал оптимальности ![]() , т.е.
, т.е.
с вероятностью 95% можно утверждать, что в среднем по России число собственных
легковых автомобилей на 1000 человек населения в 1990 году находилось в
указанных пределах. Расчётное значение t-критерия составляет -1,03596, меньше
2, следовательно, различия между генеральной и выборочной средней случайны, и
выборочное среднее является достоверной оценкой генеральной средней. Расчётный
уровень значимости t-критерия также подтверждает это (![]() ).
).
По результатам проверки гипотезы о равенстве двух
выборочных средних получены следующие выводы: расчётное значение t-критерия
меньше табличного, следовательно, с вероятностью 95% можно утверждать, что две
выборочных средних равны и получены не случайным образом (это подтверждает и
расчётный уровень значимости, больший 0,05).
График наглядно показывает, что доверительные
интервалы, построенные по всем выборкам, накрывают генеральную среднюю, что
естественно. Если бы, какой либо доверительный интервал, рассчитанный по результатам
выборки, не включал в себя значение генеральной средней, то в реальных
условиях, это означало бы получение ошибочного вывода на основе выборки.
Список использованных источников
1.
Лекции
по дисциплине статистика. Лектор – доц. О.А. Пономарёва, 2008.
2.
Сборник
Росстата Регионы России. Социально-экономические показатели. 2006.
3.
Учебное
пособие. Статистика. Методы анализа распределений. Выборочное наблюдение. Н.В. Куприенко,
О.А. Пономарёва, Д.В. Тихонов. 132 с. – 2008.
| Теория экономического прогнозирования | |
|
Министерство образования Российской Федерации Тюменский государственный нефтегазовый университет В.Г.НАНИВСКАЯ, И.В.АНДРОНОВА ТЕОРИЯ ЭКОНОМИЧЕСКОГО … В качестве исходных данных могут быть взяты выборочные наблюдения и динамические ряды. Подбор модели в каждом конкретном случае осуществляется по целому статистически ряду критериев (дисперсии, корреляционному отношению и др.) |
Раздел: Рефераты по экономико-математическому моделированию Тип: реферат |
| Обработка лесоводственной информации | |
|
Содержание Введение 1 Обработка лесоводственной информации 1.1 Исходные данные и их характеристика 1.2 Группировка результатов наблюдения 1.3 … Поэтому между статистическими показателями выборочной совокупности и действительными значениями этих показателей генеральной совокупности всегда будут некоторые расхождения … Так, с вероятностью, равной 0,68, можно утверждать, что расхождение между действительным значением данного показателя в генеральной совокупности и вычисленным его значением для … |
Раздел: Рефераты по экономике Тип: отчет по практике |
| Маркетинговое исследование рынка | |
|
1 билет Вопрос 1: Цели, задачи и предмет изучения учебной дисциплины. Значение МИ для отраслей н/х. МИ — сбор, обработка и анализ данных по разным … 4. выборки — так как полное исследования генеральной совокупности является слишком дорогим, а иногда невозможным, необходимо ограничиваться выборкой. 7) механический способ (определяется по формуле n= (t^2 б^2 N) / (t^2 б^2 + предельно_заданная_ошибка_выборки^2 N), где |
Раздел: Рефераты по маркетингу Тип: шпаргалка |
| Эконометрика | |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Тихоокеанский государственный … ü Методы коррекции статистических выводов при неоднородности дисперсий ошибок. Выборочное распределение — это ряд всех возможных значений выборочной статистики, который может быть получен из генеральной совокупности для выборки данного объёма. |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Учебное пособие по курсу всего маркетинга | |
|
Оглавление Введение 4 1. Основной текст 6 1.1. Сущность и цели маркетинга. Организация маркетинга 6 Окружающая среда маркетинга и сегментирование … … небольших партий товаров, изучение реакции потребителей на изменение факторов (условий продажи); лабораторный — построение по данным полевых наблюдений имитационной модели типа: 8. Панель потребителей — это: а) часть мостовой; б) деревянная обивка стены; в) выборочная совокупность семей потребителей, представляющих фирме информацию о доходах, расходах … |
Раздел: Рефераты по маркетингу Тип: реферат |