Предельная ошибка не должна геодезия

Человеку свойственно ошибаться. Это касается не только общих вопросов и знаний жизни. Но и распространяется на любые сферы его деятельности, в том числе в области геодезии. В ней все проводимые измерения выполняются с ошибками. Значительная часть работ в геодезическом производстве основывается на измерениях. А измерения — своего рода сравнение с какой-то эталонной или истинной величиной. Если понимать, что истинного значения в идеале не существует, то все сравнения в измерениях сводятся к сравнению с конкретно полученным значением и принятому, как верное. Одним из наиболее приближенных к истинному значению, считается среднее арифметическое.

Понятие погрешности, её абсолютная и относительная величины

Если переходить на понятие погрешности, то отклонение отдельного замера от среднего арифметического из выполненных измерений и считается абсолютной его ошибкой. Числовая форма погрешности не дает представления о качестве произведенного измерения. Для этого существует понятие относительной погрешности. Под ним понимают отношение значения собственно ошибки к замеренной величине. Применяется этот параметр в определении точности работ при линейных замерах в полигонометрических и теодолитных ходах.

В нивелирных ходах для его оценки точности существует так называемая приведенная погрешность. Это тоже своего рода относительный показатель. Только он подразумевает под собой отношение абсолютного значения ошибки к конкретному принятому значению определяемой величины (для нивелировок на 1 км хода).

Погрешности по источникам возникновения

При производстве геодезических работ после окончания каждой выполненной операции в полевых условиях можно говорить об ошибках. Присутствуют они и при проведении камеральных работ. Так при установке приборов в рабочее положение возникают отклонения в центрировании инструмента над центром знака. Также возникают неточности при выставлении прибора в отвесное состояние, когда выводим его цилиндрический уровень в верхнее горизонтальное положение и круглый уровень на середину. Следующими причинами возникновения погрешностей считаются визирование и снятие отсчетов в момент исполнения наблюдений.  Влияние внешних условий окружающей среды: рефракция воздуха, дымка, туман, осадки, формирует еще одну группу ошибок. Помимо человеческого фактора и влияния внешней среды существуют конструктивные особенности приборов, с заложенными в них вероятностными составляющими точности измерений. Еще одной из причин возникновения погрешностей считается несовершенство методик их определений. Резюмируя выше сказанное, можно выделить следующий перечень ошибок по источникам их возникновения:

• инструментальные;
• индивидуальные;
• из-за условий окружающей среды;
• методические.

Погрешности по характеру действий

По данному признаку все ошибки можно разделить на следующие отклонения:

• грубые, то есть значительно превышающие ожидаемые ошибки, возникающие в результате просчетов, неверных действий и обнаруженные при дополнительном контроле;
• систематические отклонения, отличающиеся постоянством возникновения и закономерностями изменений при повторных операциях; к ним можно отнести периодические и функциональные погрешности;
• случайные, значения величин, которых не значительны, большая часть их мала, чем велика, встречаются как с положительными, так и с отрицательными значениями, в каждом конкретном случае они возникают отдельно случайным образом и в своей массе подчинены определенным вероятностным закономерностям;

Именно изучение случайных погрешностей в геодезии дает возможность производить оценки точности и получать наиболее надежные результаты.

Предельные и допустимые отклонения

При определенных факторах случайные ошибки по абсолютному значению своей величины не могут превышать определенного предела. Этот предел в геодезической и маркшейдерской практике имеет название предельной погрешности.

В строительном производстве нормативными документами введен термин предельного отклонения, который может иметь как положительное, так и отрицательное значения. Алгебраическая сумма этих параметров (предельных отклонений) имеет название допуска.

В геодезии крайние предельные значения отклонений, допускаемые нормативной документацией, называются допустимыми.

Средние, вероятные и средне квадратические погрешности

При различных оценках точности выполненных замеров применяются некоторые критерии случайных ошибок. К таким мерилам оценки относятся понятия:

• средне арифметического отклонения от всех случайных ошибок, имеющее название среднего уклонения;
• срединного отклонения, то есть находящегося в середине измеренного ряда по абсолютным значениям с учетом убывания и возрастания, именуемое вероятной ошибкой;
• средне квадратическое отклонение (СКО) – это параметр функции дисперсии (рассеивания) случайных величин результатов измерений. Он равен математическому ожиданию (среднему арифметическому значению) квадратов отклонений в измерениях от математического ожидания (среднего арифметического значения) результатов замеров.

Случайные погрешности подчиняются нормальному закону распределения и находятся в интервале от нуля до трех СКО. Большинство из них в пределах шестидесяти восьми процентов находятся в интервале до одного СКО. Девяносто пять процентов случайных величин попадает в интервал от нуля до двух СКО. Девяносто девять процентов случайных ошибок находится в интервале от нуля до трех СКО.

На основании этого в теоретических расчетах при предварительных оценках точности выполнения работ за предельные принимаются три средне квадратические ошибки. При геодезических и маркшейдерских работах на практике к расчетам принимаются двойные величины средне квадратических отклонений. 

Нормы точности геодезических работ при возведении зданий и сооружений приводятся в нормативных документах: строительных нормах и правилах (СНиП), государственных стандартах (ГОСТ), в сводах правил (СП), ведомственных инструкциях и в других нормативных документах.

Нормы точности в этих документах могут быть указаны в явном виде, непосредственно относящиеся к построению линий, осей или высотных отметок. Точность может быть прописана к выполнению тех или иных геодезических измерений, например, угловых, линейных или высотных, как это сделано в СНиП 3.01.03-84 «Геодезические работы в строительстве».

Погрешности при разбивочных работах неизбежны, они зависят от целого ряда факторов, а именно:

• подготовленности площадки для производства измерений;
• квалификации исполнителей работ;
• применяемых технических средств;
• способов и приемов выполняемых работ;
• влияния внешней среды.

Точность геометрических параметров определяется характеристиками действительной и нормативной точности, которые установлены ГОСТ 21778-81

В практике измерений различают действительный размер Xi и номинальный Xпот. Отклонение действительного размера от номинального размера, называют погрешностью.

В практике геодезических измерений следует различать такие понятия, «погрешность» и «ошибка». Под погрешностью обычно понимают инструментальные погрешности, а с ошибками связывают неточности измерений или вычислений, обусловленных человеческим фактором.

Действительный размер — это размер, полученный в результате измерений или построений с допустимой погрешностью. Номинальный размер это основной проектный размер, определенный исходя из его функционального назначения и служащий отправным пунктом отсчета отклонений. Учитывая погрешности изготовления, разбивки и монтажа конструкции, в стандартах и других нормативных документах, а также на чертежах помимо номинального (проектного) размера Xпот указывают два предельно допустимых размера, наибольший Xmax и наименьший Xmin. Разность между наибольшим и наименьшим предельными размерами, или интервал значений размера, называют допуском Δ, или полем допуска, т.е.:

Δ = Xmax — Xmin

Половина допуска δ=0,5 Δ является предельным отклонением параметра X от середины поля допуска.

Точность, которая устанавливается нормативными документами, называется нормативной, а фактическая (действительная) точность характеризуется величиной отклонения, определяемой как разность между действительными и номинальными значениями.

Vi = Xi — Xпот

Для нормального распределения результатов измерений согласно теории ошибок, истинному значению измеряемой величины (Xпот) соответствует среднее арифметическое результатов измерений при количестве измерений, стремящихся к бесконечности. Характеристикой результата измерения одной величины является средняя квадратическая ошибка м, определяемая по формуле Бесселя. Ее доверительная вероятность составляет 68%. Предельной погрешности δ может соответствовать удвоенное значение средней квадратической ошибки (δ = 2м) с доверительной вероятностью 95%. Для особо ответственных работ предельную погрешность принимают δ = 3м доверительная вероятность при этом соответствует 99,7%.

Точность разбивочных работ регламентируется технологическими допусками но ГОСТ 21779-82, такими как:

• допуск разбивки точек и осей в плане;
• допуск передачи точек и осей но вертикали;
• допуски разбивки и передачи высотных отметок.

Все допуски разбивочных работ сгруппированы в шесть классов точности. Класс точности определяет величину допуска для конкретных условий. От величины допуска зависит выбор метода и геодезических приборов для производства работ.

Допуски разбивки точек и осей в плане охватывают размеры осей от 2500 до 160000 мм. Допуски передачи точек и осей по вертикали и створности точек и осей разбиты на девять линейных интервалов. Данные разбивки точек по высоте представлены в нижней таблице. Допуски одного класса точности имеют одинаковую относительную точность.

Примечание: Классы точности не связаны с видами сооружений. Класс точности выбирается в зависимости от средств геодезического обеспечения разбивочных работ и контроля качества.

Точность измерения линий, углов, превышений и вынос проекта в натуру на застроенной территории указывается на пунктах внутренней геодезической основы, на не застроенной — в ППГР.

Предельная погрешность взаимного положения габаритных осей зданий и сооружений не должна превышать в плане 5 мм, а по высоте — 10 мм.

Разбивочные работы в процессе строительства должны обеспечивать вынос в натуру осей и отметок реперов с заданной точностью. Параметры точности разбивочных работ приводятся в Своде правил СП 126.13330.2012 Актуализированная редакция СНиП 3.01.03-84 «Геодезические работы в строительстве».

В таблице приведены средние квадратические ошибки, которые допускаются при выносе проекта в натуру. В том случае, если в проектной документации указаны допуски на изготовление и возведение конструкций зданий, не предусмотренные стандартами, нормами и правилами, необходимую точность разбивочных работ определяют специальным расчетом по условиям, заложенным в проектной документации. Для приведения в соответствие расчетов, выполненных по ГОСТ 21779-82 и СП 126.13330.2012, следует иметь в виду, что при наличии расхождений, приоритетность необходимо отдавать расчетам, выполненных по ГОСТ. Геодезический контроль точности геометрических параметров здания является составной частью производственного контроля, осуществляемого в процессе возведения здания или сооружения.

Плановое и высотное положение элементов здания отображается в документации по исполнительной съемке.

Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.

По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.

Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.

Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)

Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:

1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.

Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)

где: ;
n – количество измерений одной величины.

Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.

Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.

Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:

F = f( X, Y, Z … ),                        (1.28)

здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.

В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
(1.29)

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.

Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:

Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)

Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)

Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим

В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)

Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,

F = x * y * z,

то для нее можно записать выражение относительной ошибки функции:
(1.33)

которое в некоторых случаях оказывается более удобным, чем формула (1.32).

Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)

Величина   (1.36)

называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде

по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде

и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

или

Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:

M2 = m2/n

или
(1.37)

то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.

Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.

Пусть имеется ряд равноточных измерений величины X:

l1, l2 , …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем разности:
(1.38)

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:

[V] = 0.                   (1.39)

Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)

Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:
(1.41)

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.

Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.

Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)

Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,

,
откуда ;

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).

Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)

Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.

Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:

p = C/m2                  (1.45)

где C – в общем случае произвольное положительное число.

При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или              X0 = [l*p] / [p] .

Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем

откуда  (1.47)

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)

Согласно (1.46) и (1.32) напишем:

Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:

Подставим это выражение в формулу (1.48) и получим,

P = [p],                 (1.49)

то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.

В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:

P = n.                  (1.50)

При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)

где pi – вес i-того элемента.

---

Подборка по базе: Физ. Тема «Челночный бег с переноской 2-3 предметов с передачей , Тема 3.4. Договор как основание возникновения обязательства. Общ, ТЕСТОВЫЕ ВОПРОСЫ К ЭКЗАМЕНУ ПО ПРЕДМЕТУ ДОУ.docx, сводная ведомость по моим предметам.docx, 1. Протокол входного контроля отчетности — Статистика (прочие)_ , Сенсорные способности являются базой для успешного овладения раз, Тест с ответами по предмету электрические измерения.doc, Лекция 4. Общие проблемы малой группы. Динамические процессы в м, Форма анализа воспитательной работы для руководителей предметных, Цель, задачи, предмет и объект антикоррупционной экспертизы. Суб

---

Тема: Элементы теории ошибок измерений.

1. Классификация ошибок измерений.

Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые, систематические и случайные.

К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.

Систематические ошибки происходят от неизвестного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.

Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений.

В основу теории ошибок положены следующие свойства случайных ошибок:
1. Малые ошибки встречаются чаще, а большие реже.

2. Ошибки не превышают известного предела.

3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине,

одинаково часто встречаются.

4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе

измерений.
По источнику происхождения различают ошибки приборов, внешние и личные.

Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.

Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира

солнечными лучами.

Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.

,

2. Арифметическая средина.

Если одна величина измерена n раз и получены результаты: l₁, l_2, l_3, l_4, l_5, l_6,….., l_n,

то

Величина x называется арифметической срединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:
l₁ – x = v₁

l₂ – x = v₂

l₃ – x = v₃

. . . . . . . .

l_n – x = v_n

Или в общем виде получим:
[ l ] – nx = [v]

Тогда [v] = 0.
2. Средняя квадратическая ошибка.
Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

[v²]

m = √ n — 1
где [v²] – сумма квадратов вероятнейших ошибок; n – число измерений.

Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

m

[v²]

M = ———— = √ —————

√n n ( n – 1 )
Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е.
ε = 3m.

Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной ве-

личины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной

l = 110 м, при m = 2 см равна m/l = 1/5500.
Пример. Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата.

Вычисления приведены в таблице:

№ п/п	Длина линии в м	v, см	v2	Вычисления
1	225,26	+6	36	m = 5,6 см; М = 5,6/ √6 = 2,3 см
2	225,23	+3	9
3	225,22	+2	4
4	226,14	-6	36
5	225,23	+3	9
6	225,12	-8	64
xср.= 225, 20	[v] = 0	[v2] = 158

По формулам вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна
2,3 1

———- = ————

22520 9 800

1. Оценка точности измерений

Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:

1. Находят вероятнейшее (наиболее точное для данных условий) значение

измеренной величины по формуле арифметической средины х = [1]/n.

1. Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: [v] = 0;
2. По формуле вычисляют среднюю квадратическую ошибку одного измерения.
3. По формуле вычисляют среднюю квадратическую ошибку арифметической средины.
4. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.
5. При необходимости подсчитывают предельную ошибку одного измерения,

которая может служить допустимым значением погрешностей аналогичных

измерений.

ЛЕКЦИЯ 7

Тема: Геодезические сети.
Для составления карт и планов, решения геодезических задач в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат. Эти точки маркируют на поверхности Земли или в зданиях и сооружениях центрами (знаками).

Геодезическая сеть – это система закрепленных точек земной поверхности, положение которых определено в общей для них системе геодезических координат.

Геодезические сети подразделяют на плановые и высотные: первые служат для определения координат X и Y геодезических центров, вторые — для определения их высот.

Принцип построения плановых геодезических сетей заключается в следующем. На местности выбирают точки, взаимное положение которых представляется в виде геометрических фигур: треугольников, четырехугольников, ломаных линий и т.д. Причем

точки выбирают с таким расчетом, чтобы некоторые элементы фигур (стороны, углы) можно было бы непосредственно измерить, а все другие элементы вычислить по данным измерений. Например, в треугольнике достаточно измерить одну сторону и три угла (один для контроля правильности измерений) или две стороны и два угла (один для контроля правильности измерений), а остальные стороны и углы вычислить. Для вычисления плановых координат вершин выбранных точек необходимо кроме элементов геометрических фигур знать еще дирекционный угол стороны одной из фигур и координаты одной из вершин.

Сети строят по принципу перехода от общего к частному, т. е. от сетей с большими расстояниями между пунктами и высокоточными измерениями к сетям с меньшими расстояниями и менее точным.

Геодезические сети подразделяют на четыре вида: государственные, сгущения, съемочные и специальные. Государственные геодезические сети служат исходными для построения всех других видов сетей. Началом единого отсчета плановых координат в Российской Федерации служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.

1. Методы создания геодезических сетей.

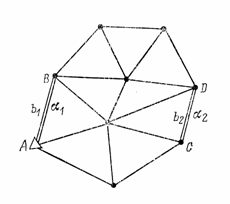
Плановые геодезические сети создаются методами триангуляции, полигонометрии и трилатерации. При построении геодезической сети методом триангуляции на местности закрепляется ряд точек, которые в своей совокупности образуют систему треугольников. В треугольниках измеряются все углы и некоторые стороны, которые называются базисными. По длине базисной стороны и измеренным углам, вычисляют длины всех сторон, а затем координаты всех пунктов сети.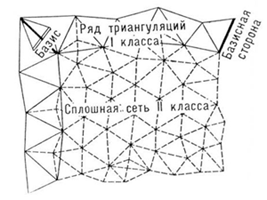

Метод полигонометрии заключается в построении на местности системы ломанных линий, называемых полигонометрическими ходами. Эти ходы прокладывают обычно между пунктами триангуляции. В полигонометрических ходах измеряются все углы поворота и длины всех сторон.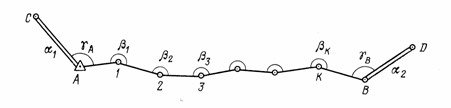

При построении сети методом трилатерации на местности также строится сеть треугольников, в которых при помощи высокоточных дальномеров измеряются все стороны.

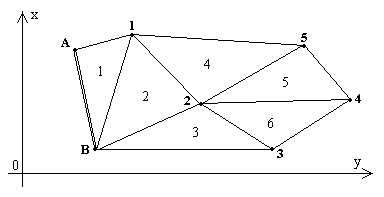
Сети сгущения строят для дальнейшего увеличения плотности (числа пунктов, приходящихся на единицу площади) государственных сетей. Плановые сети сгущения подразделяют на 1-й.и 2-й разряды.

Съемочные сети — это тоже сети сгущения, но с еще большей плотностью. С точек съемочных сетей производят непосредственно съемку предметов местности и рельефа для составления карт и планов различных масштабов.

Специальные геодезические сети создают для геодезического обеспечения строительства сооружений. Плотность пунктов, схема построения и точность этих сетей зависят от специфических особенностей строительства.

Государственные высотные геодезические сети создают для

распространения по всей территории страны единой системы

высот. За начало высот в Российской Федерации и некоторых других странах принят средний уровень Балтийского моря, определение которого проводилось в период с 1825 до 1840 г. Этот уровень отмечен горизонтальной чертой на медной металличе-

ской пластине, укрепленной в устое моста через обводной канал в Кронштадте.

Между пунктами государственных высотных геодезических сетей высокой точности (1-го класса) размещают пункты высотных сетей низших классов (2-го, 3-го и т.д.). Несколь-

ко пересекающихся ходов называют сетями. Как правило, сети создают из ходов, прокладываемых между тремя или более точек. В целом точки (реперы) высотных сетей, называемых нивелирными, достаточно равномерно распределены на территории страны.

На незастроенной территории расстояния между реперами составляют 5…7 км, в го-

родах сеть реперов в 10 раз плотнее.

Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса.

Как правило, сети образуют полигоны с узловыми точками (общими точками пересечения двух или более ходов одного и того же класса). Каждый нивелирный ход опирается обоими концами на реперы ходов более высокого класса или узловые точки.

1. Закрепление на местности пунктов геодезических сетей.

Точки геодезических сетей закрепляют на местности знаками. По местоположению знаки бывают: грунтовые и стенные, заложенные в стены зданий и сооружений; металлические, железобетонные, деревянные, в виде откраски и т.д.; по назначению —

постоянные, к которым относятся все знаки государственных геодезических сетей, и временные, устанавливаемые на период изысканий, строительства, реконструкции, наблюдений и т.д.

Постоянные знаки. Их закрепляют подземными знаками — центрами. Конструкции центров обеспечивают их сохранность и неизменность положения в течение длительного периода времени. Как правило, подземный центр представляет собой бетонный

монолит , закладываемый ниже глубины промерзания грунта и не в насыпной массив. У поверхности земли в монолите устанавливают чугунную марку, на которой наносят центр в виде креста или точки. Положению этого центра соответствуют коор-

динаты Хи Y и во многих случаях отметки.

Для того чтобы с одного знака был виден другой (смежный),

над подземными центрами устанавливают наружные знаки в виде

металлических или деревянных трех- или четырехгранных пира-

мид или сигналов.

Пирамиды или сигналы имеют высоту 3…30 м и более. Геодезический сигнал с под-

земным центром и столиком предназначен для установки измерительных приборов и на-

стила при работе на нем наблюдателя. Верх сигнала или пирамиды заканчивается визир-

ной целью , на которую при измерении углов направляют зрительную трубу теодолита. На

столик устанавливают также отражатель, если измеряют расстояния между пунктами светодалъномером. Для спутниковых измерений сигналы и пирамиды строить не надо.

Как правило, пункты плановых разбивочных сетей и сетей сгущения закрепляют подземными центрами, такими же как и пункты государственных сетей. Так как расстояния между этими пунктами сравнительно небольшие, оформления их наружными знаками не требуется. Знаки могут закладывать в зданиях и сооружениях, в этом случае их называют стенными.

Координаты всех пунктов плановой геодезической сети, а также отметки пунктов высотной геодезической сети заносятся в специальные каталоги, в которых кроме названия пунктов дается описание их местоположения.

Иногда для различных целей могут создаваться местные геодезические сети.

Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей).

Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.

ЛЕКЦИЯ 8

Тема: Угловые измерения на местности.

Основными элементами любых геодезических работ на местности являются угловые и линейные измерения. Для производства угловых измерений служат специальные приборы, называемые теодолитами.

1. Теодолит. Устройство теодолита

Теодолит – это геодезический прибор, предназначенный для измерения горизонтальных углов, углов наклона и расстояний.

В соответствии с действующим ГОСТом в настоящее время

промышленностью выпускаются теодолиты следующих типов:

Основными частями любого теодолита являются лимб, алидада, зрительная труба.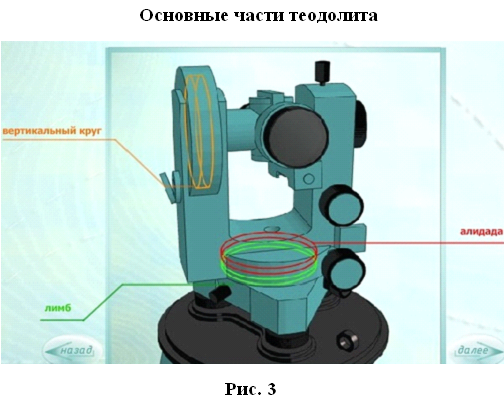

Угломерный круг, по краю которого нанесена шкала с градусными делениями, называется лимбом.
В плоскости угломерного круга с лимбом вращается второй круг – алидада.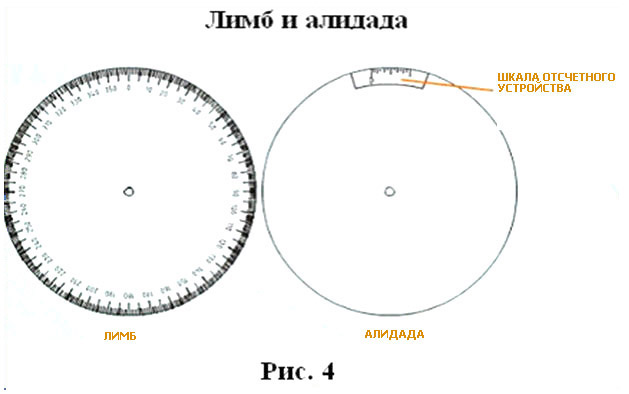

На алидаде имеется устройство для отсчета по лимбу. В современных теодолитах угломерные круги стеклянные, такие теодолиты называются оптическими.
Алидада жестко связана со зрительной трубой с помощью колонок. Лимб, алидада и зрительная труба имеют закрепительные и наводящие винты.


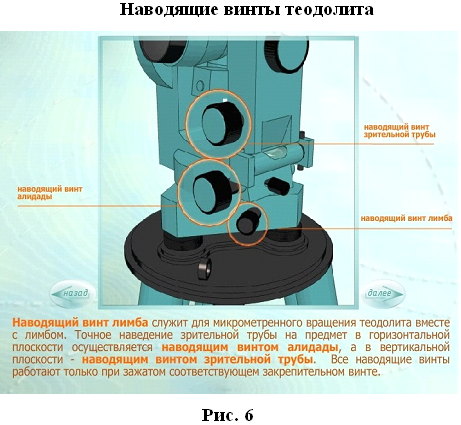
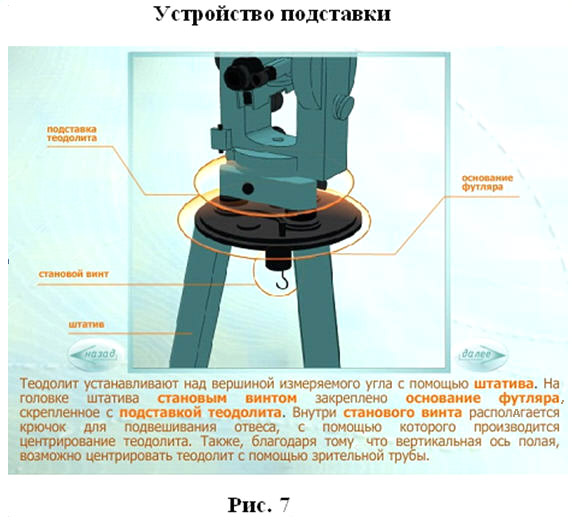
Плоскость лимба приводится в горизонтальное положение с помощью трех подъемных винтов и цилиндрического уровня. Центр лимба устанавливается над вершиной измеряемого угла. Для грубой наводки трубы на предмет служит оптический визир.
Для измерения вертикальных углов наклона имеется вертикальный круг.
Для производства отсчетов по лимбу рядом с окуляром зрительной трубы располагается микроскоп, свет в который направляется с помощью специального зеркальца. Для прикрепления теодолита к штативу служит становой винт.

2. Отсчетные устройства
При измерении углов производится отсчет по лимбу.
Угловая величина дуги, соответствующая одному делению шкалы лимба, называется ценой деления лимба.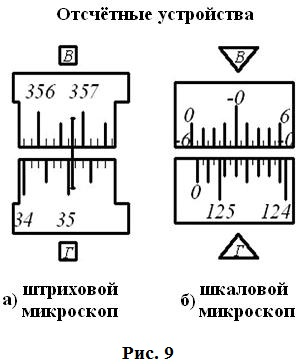

Отсчет по лимбу производится относительно индекса, нанесенного на алидаду.

Для оценки долей деления лимба служат отсчетные устройства. В оптических теодолитах в качестве отсчетных устройств служат штриховые (Т30) и шкаловые

(2Т30 и Т15) микроскопы.

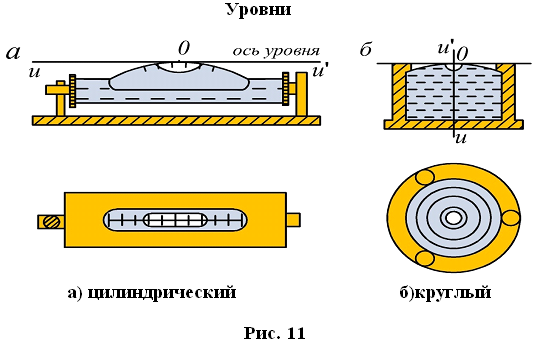
3. Уровни
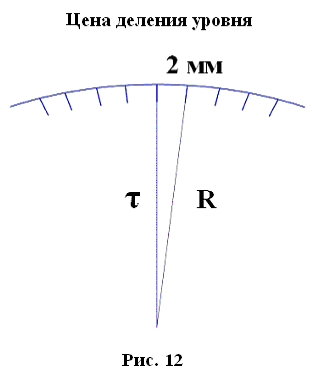
Уровни бывают круглыми и цилиндрическими. Цилиндрический уровень состоит из стеклянной трубки, верхняя часть которой представляет дугу большого радиуса. На верхней части ампулы имеется шкала делений через 2 мм. Центральный штрих шкалы называется нуль – пунктом.
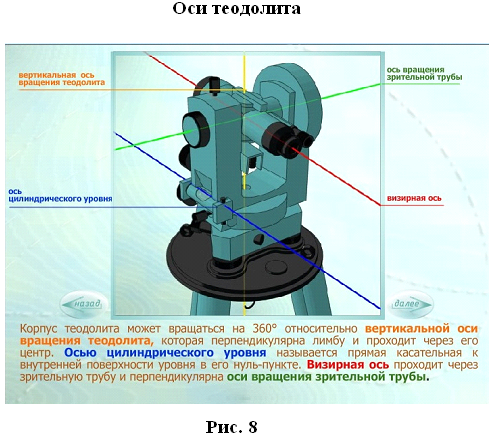
Прямая, касательная к внутренней поверхности уровня в его нуль–пункте, называется осью цилиндрического уровня.
Чем больше радиус, тем меньше цена деления и тем уровень точнее.

4. Зрительные трубы
Зрительная труба геодезических приборов состоит из объектива и окуляра. Трубы большинства геодезических приборов дают обратное (перевернутое) изображение предмета. Вблизи переднего фокуса окуляра помещается металлическое кольцо, называемое диафрагмой со стеклянной пластинкой, на которой награвированы тонкие нити, составляющие сетку нитей. Сетка нитей снабжена четырьмя исправительными винтами, позволяющими перемещать сетку нитей в своей плоскости.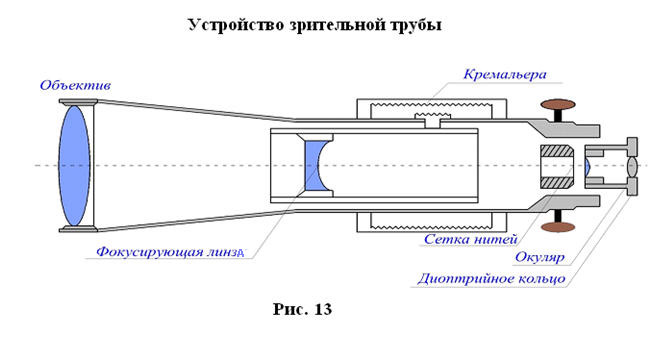

Прямая, соединяющая перекрестки сетки нитей с оптическим центром объектива, называется визирной осью трубы.
Установка трубы для наблюдений складывается из установки ее «по глазу» и «по предмету». При недостаточно тщательной фокусировке трубы будет наблюдаться перемещение предмета относительно сетки при изменении положения глаза наблюдателя перед окуляром. Перемещение предмета относительно сетки при изменении положения глаза наблюдателя перед окуляром называется параллаксом сетки нитей. Устраняется дополнительным вращением кремальеры.

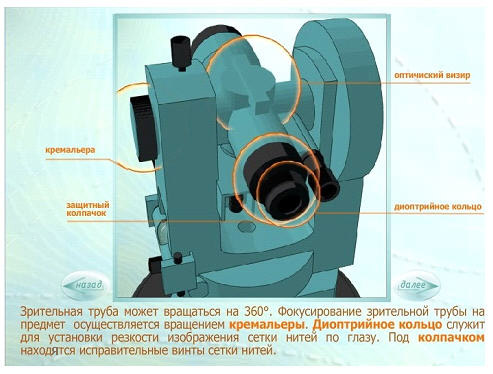
Установка трубы «по глазу» заключается в получении резкого изображения сетки нитей. Выполняется перемещением диоптрийного кольца.

Установка трубы «по предмету» выполняется с помощью кремальеры, при этом внутри трубы перемещается фокусирующая линза (труба с внутренней фокусировкой).

ЛЕКЦИЯ 9

Человеку свойственно ошибаться. Это касается не только общих вопросов и знаний жизни. Но и распространяется на любые сферы его деятельности, в том числе в области геодезии. В ней все проводимые измерения выполняются с ошибками. Значительная часть работ в геодезическом производстве основывается на измерениях. А измерения — своего рода сравнение с какой-то эталонной или истинной величиной. Если понимать, что истинного значения в идеале не существует, то все сравнения в измерениях сводятся к сравнению с конкретно полученным значением и принятому, как верное. Одним из наиболее приближенных к истинному значению, считается среднее арифметическое.

Понятие погрешности, её абсолютная и относительная величины

Если переходить на понятие погрешности, то отклонение отдельного замера от среднего арифметического из выполненных измерений и считается абсолютной его ошибкой. Числовая форма погрешности не дает представления о качестве произведенного измерения. Для этого существует понятие относительной погрешности. Под ним понимают отношение значения собственно ошибки к замеренной величине. Применяется этот параметр в определении точности работ при линейных замерах в полигонометрических и теодолитных ходах.

В нивелирных ходах для его оценки точности существует так называемая приведенная погрешность. Это тоже своего рода относительный показатель. Только он подразумевает под собой отношение абсолютного значения ошибки к конкретному принятому значению определяемой величины (для нивелировок на 1 км хода).

Погрешности по источникам возникновения

При производстве геодезических работ после окончания каждой выполненной операции в полевых условиях можно говорить об ошибках. Присутствуют они и при проведении камеральных работ. Так при установке приборов в рабочее положение возникают отклонения в центрировании инструмента над центром знака. Также возникают неточности при выставлении прибора в отвесное состояние, когда выводим его цилиндрический уровень в верхнее горизонтальное положение и круглый уровень на середину. Следующими причинами возникновения погрешностей считаются визирование и снятие отсчетов в момент исполнения наблюдений.  Влияние внешних условий окружающей среды: рефракция воздуха, дымка, туман, осадки, формирует еще одну группу ошибок. Помимо человеческого фактора и влияния внешней среды существуют конструктивные особенности приборов, с заложенными в них вероятностными составляющими точности измерений. Еще одной из причин возникновения погрешностей считается несовершенство методик их определений. Резюмируя выше сказанное, можно выделить следующий перечень ошибок по источникам их возникновения:

• инструментальные;
• индивидуальные;
• из-за условий окружающей среды;
• методические.

Погрешности по характеру действий

По данному признаку все ошибки можно разделить на следующие отклонения:

• грубые, то есть значительно превышающие ожидаемые ошибки, возникающие в результате просчетов, неверных действий и обнаруженные при дополнительном контроле;
• систематические отклонения, отличающиеся постоянством возникновения и закономерностями изменений при повторных операциях; к ним можно отнести периодические и функциональные погрешности;
• случайные, значения величин, которых не значительны, большая часть их мала, чем велика, встречаются как с положительными, так и с отрицательными значениями, в каждом конкретном случае они возникают отдельно случайным образом и в своей массе подчинены определенным вероятностным закономерностям;

Именно изучение случайных погрешностей в геодезии дает возможность производить оценки точности и получать наиболее надежные результаты.

Предельные и допустимые отклонения

При определенных факторах случайные ошибки по абсолютному значению своей величины не могут превышать определенного предела. Этот предел в геодезической и маркшейдерской практике имеет название предельной погрешности.

В строительном производстве нормативными документами введен термин предельного отклонения, который может иметь как положительное, так и отрицательное значения. Алгебраическая сумма этих параметров (предельных отклонений) имеет название допуска.

В геодезии крайние предельные значения отклонений, допускаемые нормативной документацией, называются допустимыми.

Средние, вероятные и средне квадратические погрешности

При различных оценках точности выполненных замеров применяются некоторые критерии случайных ошибок. К таким мерилам оценки относятся понятия:

• средне арифметического отклонения от всех случайных ошибок, имеющее название среднего уклонения;
• срединного отклонения, то есть находящегося в середине измеренного ряда по абсолютным значениям с учетом убывания и возрастания, именуемое вероятной ошибкой;
• средне квадратическое отклонение (СКО) – это параметр функции дисперсии (рассеивания) случайных величин результатов измерений. Он равен математическому ожиданию (среднему арифметическому значению) квадратов отклонений в измерениях от математического ожидания (среднего арифметического значения) результатов замеров.

Случайные погрешности подчиняются нормальному закону распределения и находятся в интервале от нуля до трех СКО. Большинство из них в пределах шестидесяти восьми процентов находятся в интервале до одного СКО. Девяносто пять процентов случайных величин попадает в интервал от нуля до двух СКО. Девяносто девять процентов случайных ошибок находится в интервале от нуля до трех СКО.

На основании этого в теоретических расчетах при предварительных оценках точности выполнения работ за предельные принимаются три средне квадратические ошибки. При геодезических и маркшейдерских работах на практике к расчетам принимаются двойные величины средне квадратических отклонений.