11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ( ).
).
В теории выборочного наблюдения выведены формулы для определения  , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то  определяется как:
определяется как:
 — при оценивании среднего значения признака;
— при оценивании среднего значения признака;
 — если признак альтернативный, и оценивается доля.
— если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):
 — для среднего значения признака;
— для среднего значения признака;
 — для доли.
— для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки ( ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
 .
.
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ( )
)
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака

- Определяем среднюю ошибку повторной случайной выборки

- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна

- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
 ;
;
- средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

- установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки ( ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп

Здесь  — средняя из групповых дисперсий типических групп.
— средняя из групповых дисперсий типических групп.
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:

аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:

- Средняя из внутригрупповых дисперсий

- Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

- Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно

- Значение среднего квадратического отклонения составляет

- Средняя ошибка выборки:

- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:

- Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Средняя квадратическая, предельная и относительная ошибки
Для суждения о степени точности ряда измерений нужно иметь среднее значение ошибки. Среднее арифметическое из измерений нельзя брать, так как из-за разных знаков ряд с отдельными крупными ошибками может оказаться точнее ряда с меньшими ошибками:
25,04; 24,97; 25,04 – mср.=0,02 м
Если взять ошибки по абсолютной величине, то два ряда измерений с одинаковыми по абсолютной величине средними ошибками могут быть
ошибочно приняты равноточными и наличие крупных ошибок не будет отражено:
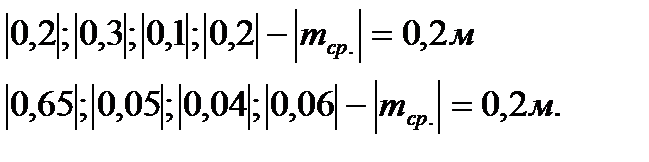
Поэтому в качестве критерия для оценки точности ряда измерений используют не зависящую от знаков отдельных ошибок и рельефно показывающую наличие крупных ошибок среднюю квадратическую ошибку. Квадрат этой ошибки принимают равным среднему арифметическому из квадратов отдельных случайных ошибок, то есть:
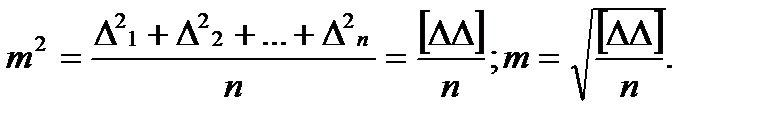 – формула Гаусса, где Δ – истинная ошибка измерения.
– формула Гаусса, где Δ – истинная ошибка измерения.
По теории вероятностей подсчитано, что при большом количестве измерений случайная ошибка одного измерения превосходит m.
∆>1m – в 32 случаях из 100 измерений.
∆>2m – в 5 случаях из 100 измерений.
∆>3m – в 3 случаях из 1000 измерений.
Поэтому утроенную среднюю квадратическую ошибку считают предельной
Часто точность произведенных измерений лучше оценивается относительной ошибкой, то есть отношением абсолютной ошибки к измеряемой величине, выражаемой правильной дробью с числителем, равным 1. Эта ошибка характеризует в основном линейные измерения и измерения площади участков. Например, в замкнутом полигоне теодолитного хода линейные измерения оцениваются относительной ошибкой  ; где
; где 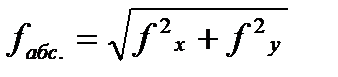 – абсолютная ошибка, Р – периметр полигона.
– абсолютная ошибка, Р – периметр полигона.
Дата добавления: 2015-08-11 ; просмотров: 767 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Тема: Элементы теории ошибок измерений.
1. Классификация ошибок измерений
_______ Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.
_______ К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.
_______ Систематические ошибки происходят от известного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.
_______ Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений _______
_______ В основу теории ошибок положены следующие свойства случайных ошибок :
_______ 1. Малые ошибки встречаются чаще, а большие реже.
_______ 2. Ошибки не превышают известного предела.
_______ 3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются.
_______ 4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений.
_______ По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.
_______ Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами.
_______ Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.
2. Арифметическая середина

_______ Величина x называется арифметической серединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:

_______ Или в общем виде получим:
3. Средняя квадратическая ошибка
_______ Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

где [v 2 ] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

_______ Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.
_______ Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. ___
_______ Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной:
_______ l = 110 м, при m = 2 см, равна m/ l = 1/5500.
_______ Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:

Таб. 1
_______ По формулам вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна

4. Оценка точности измерений
_______ Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:
_______ 1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической середины х = [ l ]/n.
_______ 2. Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: [v] = 0;
_______ 3. По формуле вычисляют среднюю квадратическую ошибку одного измерения.
_______ 4. По формуле вычисляют среднюю квадратическую ошибку арифметической средины.
_______ 5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.
_______ 6. При необходимости подсчитывают предельную ошибку одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.
5. Понятие о неравноточных измерениях
_______ Неравноточными измерениями называются такие, которые выполнены различным числом приемов, приборами различной точности и т.д. Если измерения неодинаковой точности, то для определения общей арифметической середины пользуются формулой:

________ Весом называется число, которое выражает степень доверия к результату измерения. В тех случаях, когда неизвестны веса измеренных величин, а известны их средние квадратические ошибки, то веса можно вычислить по формуле:

т.е. вес результата измерений обратно пропорционален квадрату средней квадратической ошибки.
_______ При неравноточных измерениях средняя квадратическая ошибка измерения, вес которого равен единице, определяется по формуле:

где δ – разность между отдельными результатами измерений и общей арифметической серединой.
Источник
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Начальные сведения из теории ошибок
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измере ний. При многократных измерениях одной и той же величины резуль таты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.
Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:  (1.25)
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:  (1.26)
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:  (1.27)
(1.27)
где:  ;
;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.
Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:  (1.29)
(1.29)
где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки: 
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:  (1.30)
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:  (1.31)
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим 

В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,  (1.32)
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций: 
Если функция имеет вид произведения нескольких аргументов,
то для нее можно записать выражение относительной ошибки функции:  (1.33)
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,  (1.34)
(1.34)
Сложим эти равенства, суммарное уравнение разделим на n и получим:  (1.35)
(1.35)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде 
по третьему свойству ошибок (1.26) можно написать: 
что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде 
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем: 
или 
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
Вычислим арифметическую середину X0 = [1]/n и образуем разности:  (1.38)
(1.38)
Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:  (1.40)
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:  (1.41)
(1.41)
Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):  (1.42)
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:  .
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,  .
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:  (1.43)
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой  ; такая замена практически не изменит правой части формулы (1.43). Итак,
; такая замена практически не изменит правой части формулы (1.43). Итак,
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:  (1.44)
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
где C – в общем случае произвольное положительное число.
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем 
откуда  (1.47)
(1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:  (1.48)
(1.48)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:  (1.51)
(1.51)
Источник
Средняя квадратическая, предельная и относительная погрешности



Для правильного использования результатов измерений необходимо знать, с какой точностью, т.е. с какой степенью близости к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории погрешностей служит предложенная Гауссом средняя квадратическая погрешность m, вычисляемая по формуле
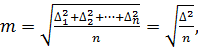
где n – число измерений данной величины.
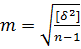
где 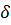 — отклонения отдельных значений измеренной величины от арифметической средины, называемые вероятнейшими погрешностями, причем [
— отклонения отдельных значений измеренной величины от арифметической средины, называемые вероятнейшими погрешностями, причем [ 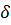 ] = 0.
] = 0.
Точность арифметической средины, естественно, будет выше точности отдельного измерения. Ее средняя квадратическая погрешность M определяется по формуле
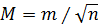
где m – средняя квадратическая погрешность одного измерения, вычисляемая по формуле 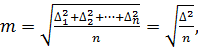 или
или 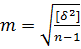 .
.
Часто в практике для контроля и повышения точности определяемую величину измеряют дважды – в прямом и обратном направлениях, например, длину линий, превышения между точками. Из двух полученных значений за окончательное применяется среднее из них. В этом случае средняя квадратическая погрешность одного измерения подсчитывается по формуле
а среднего результата из двух измерений – по формуле
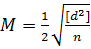 ,
,
где d – разность двукратно измеренных величин, n – число разностей (двойных измерений).
В соответствии с первым свойством случайных погрешностей для абсолютной величины случайной погрешности при данных условиях измерений существует допустимый предел, называемый предельной погрешностью. В строительных нормах предельная погрешность называется допускаемым отклонением.
Теорией погрешностей измерений доказывается, что абсолютное большинство случайных погрешностей (68,3%) данного ряда измерений находится в интервале от 0 до ±m; в интервал от 0 до ±2m попадает 95,4%, а от 0 до ±3m – 99,7% погрешностей. Таким образом, из 100 погрешностей данного ряда измерений лишь пять могут оказаться больше или равны 2m, а из 1000 погрешностей только три будут больше или равны 3m. На основании этого в качестве предельной погрешности ∆пред для данного ряда измерений принимается утроенная средняя квадратическая погрешность, т.е. ∆пред = 3m. На практике во многих работах для повышения требований точности измерений принимают ∆пред = 2m. Погрешность измерений, величины которых превосходят ∆пред, считают грубыми.
Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной погрешности.
Источник

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:
 (в данной формуле не используется показатель объема генеральной совокупности N)
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ( ).
).
В теории выборочного наблюдения выведены формулы для определения  , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то  определяется как:
определяется как:
 — при оценивании среднего значения признака;
— при оценивании среднего значения признака;
 — если признак альтернативный, и оценивается доля.
— если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):
 — для среднего значения признака;
— для среднего значения признака;
 — для доли.
— для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки ( ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
 .
.
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ( )
)
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака

- Определяем среднюю ошибку повторной случайной выборки

- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна

- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
 ;
;
- средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

- установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки ( ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп

Здесь  — средняя из групповых дисперсий типических групп.
— средняя из групповых дисперсий типических групп.
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:

аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:

- Средняя из внутригрупповых дисперсий

- Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

- Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно

- Значение среднего квадратического отклонения составляет

- Средняя ошибка выборки:

- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:

- Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
В
конкретной выборке действительная
ошибка может быть больше средней, меньше
средней или равна средней. Каждое из
этих расхождений имеет определенную
вероятность.
![]()
![]()
Предельная
ошибка выборки
– это максимальное различие между
выборочной и генеральной характеристикой,
гарантируемое с определенной вероятностью.
где
t – нормированное
отклонение, зависящее от вероятности,
определяемое как аргумент интегральной
функции Лапласа
Ф(t).
Определение предельной ошибки выборки
основано на теореме Чебышева –Ляпунова.
Теорема
Чебышева-Ляпунова:
С![]()
вероятностью сколь угодно близкой к
единице можно утверждать, что при
достаточно большом объеме выборки и
ограниченной дисперсии выборочная
характеристика будет очень мало
отличаться от генеральной характеристики.
З![]()
начение
этой функций находиться в таблице,
поэтому, зная вероятность P
=Ф(t),
можно определить аргумент
t.
Наиболее часто используемые значения
приведем в таблице:
|
Р(t) |
0,683 |
0,95 |
0,954 |
0,99 |
0,997 |
|
t |
1 |
1,96 |
2 |
2,58 |
3 |
Чем
больше вероятность, с которой гарантируются
результаты, тем больше будет предельная
ошибка и менее надежные результаты
выборки. Поэтому
в экономических исследованиях используется
Р=0,95 и Р=0,954.
6. Распределение результатов выборки на генеральную совокупность
Конечным
итогом выборочного обследования
является оценка неизвестных генеральных
характеристик на основе данных выборки.
По
этой оценке строится доверительный
интервал для генеральной средней
![]()
![]()
и
генеральной доли.
Ошибка
выборки зависит не только от вероятности,
но и от того, как было организовано
выборочное обследование.
Выделим
основные
этапы
выборочного обследования:
-
определение
объекта исследования; -
постановка
цели и задач; -
определение
процедуры отбора, проведение отбора
единиц в выборку; -
подготовка
кадров и инструментария; -
сбор
данных; -
определение
выборочных характеристик, ошибок
выборки; -
оценка
доверительных интервалов; -
о
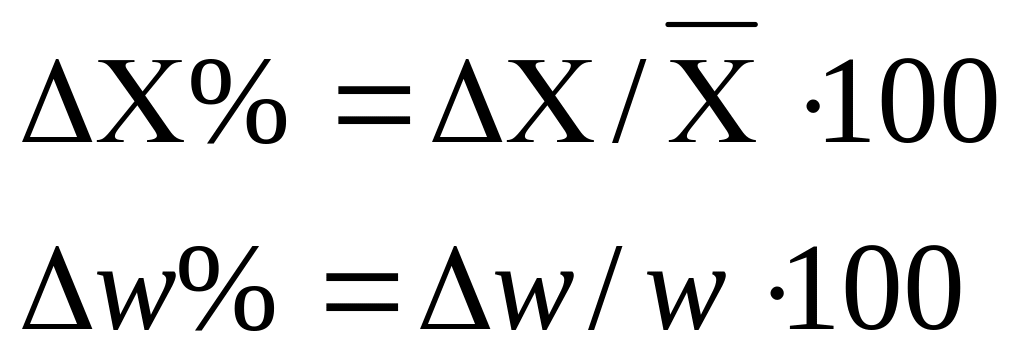
ценка
возможностей распространения результатов
на генеральную совокупность. Для этого
определяют относительные ошибки
выборки:
Если
эти ошибки не превышают заранее заданной
величины, то результаты можно распространить
на генеральную совокупность, если
превышает, то изменить процедуру отбора
или методы ремонта выборки.
9.
Распространение результатов. Для этого
применяются следующие способы:
1.
Прямой пересчет, т.е.
границы доверительного интервала
умножаются на объем генеральной
совокупности.
2.
Способ поправочных коэффициентов –
используется в тех случаях, когда
корректируются данные сплошного
обследования. По выборке рассчитывается
поправочный коэффициент, и данные
сплошного обследования исправляются
на этот коэффициент.
7. Определение необходимой численности выборки.
При
проведении выборочного обследования
возникает вопрос, сколько нужно отобрать
единиц в выборку, чтобы результаты
обследования удовлетворяли заранее
заданным величинам, т.е. предельная
ошибка не превышала определенного
значения. Для определения необходимой
численности выборки применяются формулы,
которые выводятся из предельной ошибки.
Возьмем
собственно-случайный повторный отбор:
______
∆x
= t∙μx
= t∙√Sx2
/ n
=> n
=
t2·
Sx2
∆x2
Для
бесповторного отбора:
___________
∆x
= t·√Sx
/ n·(1-n/N) =>
t2·N·Sx2
n
=
____________
∆x2·N
+ t2·
Sx2
Для
других способов отбора формулы необходимой
численности выборки аналогичны,
изменяется только дисперсия.
Значения
дисперсии при определении необходимой
численности выборки достаточно часто
бывает неизвестно. В этом случае ее
определяют:
-
из
предыдущего обследования на данную
тему; -
рассчитывают
приближенно Sx2≈(R/6)2
по пробному обследованию малого
количества единиц; -
неизвестную
дисперсию для доли берут равной 0,25.
Области
применения выборочного метода
обследования.
В
настоящее время выборочный метод сбора
данных является одним из наиболее часто
используемых. Выборочное наблюдение
используется для:
-
статистического
оценивания и проверки различных гипотез; -
при
контроле технологических процессов и
показателей качества продукции; -
при
различных отраслевых обследованиях; -
при
решении задач в сфере предпринимательства. -

Пример:
Имеются данные выборочного
собственно-случайного бесповторного
обследования 30% работников коммерческого
банка об их стаже работы.
Результаты
обследования представлены в таблице.
|
Стаж |
До |
3-5 |
5-7 |
7-9 |
Свыше |
Итого |
|
Число |
10 |
48 |
28 |
10 |
4 |
100 |
С
вероятностью 0,997 определить возможные
пределы среднего стажа работы по всем
работникам банка, а также возможные
пределы для доли работников банка,
имеющих стаж работы менее 5 лет.
Решение:
1
Для
расчетов построим расчетную таблицу
|
Стаж, |
Число fi |
Середина xi |
xi*fi |
_ (xi |
_ (xi |
_ (xi |
|
До |
10 |
2 |
20 |
— |
9 |
90 |
|
3-5 |
48 |
4 |
192 |
— |
1 |
48 |
|
5-7 |
28 |
6 |
168 |
1 |
1 |
28 |
|
7-9 |
10 |
8 |
80 |
3 |
9 |
90 |
|
Свыше |
4 |
10 |
40 |
5 |
25 |
100 |
|
Итого |
100 |
— |
500 |
— |
— |
356 |
С![]()
редний
стаж работников равен
Д![]()
исперсия
равна
Среднеквадратическое
отклонение равно
= 2
=
3,56
= 1,887 лет.
Определим
ошибки выборки. Так как вероятность Р=
0,997, то коэффициент доверия t
= 3.
Рассчитаем выборочную долю для признака
– стаж работы менее 5 лет. Так как данный
стаж работы имеют 1 и 2 группы работников
в выборке, то w
= m/n = (10+48)/100 = 0.58.
Дисперсия выборочной доли 2w
= w*(1 – w) = 0,58*0,42 =0,2434.
Определим
предельную ошибку выборки для среднего
О![]()
пределим
предельную ошибку выборки для доли
![]()
Построим
доверительный интервал для среднего.
П![]()
остроим
доверительный интервал для выборочной
доли
В![]()
ывод
2. С
вероятностью 0,997 можно утверждать, что
средний стаж работы всех работников
банка находится в пределах от 4,526 до
5,474 лет, а доля всех работников банка,
имеющих стаж работы менее 5 лет, находится
в пределах от 45,6% до 70,4%.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10.02.201516.87 Mб211321388933_cifrovaya_obrabotka_izobrageniy.djvu
Если
одна величина измерена n
раз и получены результаты: l1,
l2,
l3,
l4,
l5,
l6,…..,
ln,
то

Величина
x
называется
арифметической
срединой или
вероятнейшим значением измеренной
величины. Разности между каждым измерением
и арифметической срединой называют
вероятнейшими ошибками измерений:
l 1
1
– x
= v1
l2
– x = v2
l3
– x = v3
.
. . . . . . .
ln
– x
= vn
Или
в общем виде получим:
[ l
]
– nx = [v]
Тогда
[v]
= 0.
2. Средняя квадратическая ошибка.
Точность
результатов измерений оценивается
средней
квадратической ошибкой.
Средняя квадратическая ошибка одного
измерения вычисляется по формуле:

[v2]
m=
√
n
— 1
где
[v2]
– сумма квадратов вероятнейших ошибок;
n – число измерений.
Средняя
квадратическая ошибка арифметической
середины вычисляется по формуле:

m
[v2]
M
= ———— = √
—————
 √n n
√n n
(
n – 1 )
Предельная
ошибка не должна превышать утроенной
средней квадратической ошибки, т.е.
ε
= 3m.
Иногда
о точности измерений судят не по
абсолютной величине средней квадратической
или предельной погрешности, а по величине
относительной ошибки. Относительной
ошибкой
называется отношение абсолютной ошибки
к значению самой измеренной ве-
личины.
Относительную ошибку выражают в виде
простой дроби, числитель которой —
единица, а знаменатель — число, округленное
до двух-трех значащих цифр с нулями.
Например, относительная средняя
квадратическая погрешность измерения
линии длиной
l
= 110 м, при m
= 2 см равна m/l
= 1/5500.
Пример.
Линия измерена шесть раз. Определить
ее вероятнейшую длину и оценить точность
этого результата.
Вычисления
приведены в таблице:
|
№ п/п |
Длина |
v, |
v2 |
Вычисления |
|
1 |
225,26 |
+6 |
36 |
m М |
|
2 |
225,23 |
+3 |
9 |
|
|
3 |
225,22 |
+2 |
4 |
|
|
4 |
226,14 |
-6 |
36 |
|
|
5 |
225,23 |
+3 |
9 |
|
|
6 |
225,12 |
-8 |
64 |
|
|
xср.= |
[v] |
[v2] |
По
формулам вычислены абсолютные средние
квадратические ошибки, а оценивать
точность измерения длины линии необходимо
по относительной ошибке. Поэтому нужно
абсолютную ошибку разделить на длину
линии. Для нашего примера относительная
ошибка вероятнейшего значения измеренной
линии равна
2,3
1
———-
= ————
22520 9
800
-
Оценка
точности измерений
Точность
результатов многократных измерений
одной и той же величины оценивают в
такой последовательности:
-
Находят
вероятнейшее (наиболее точное для
данных условий) значение
измеренной
величины по формуле арифметической
средины х = [1]/n.
-
Вычисляют
отклонения для каждого значения
измеренной величины от значения
арифметической средины. Контроль
вычислений: [v]
= 0; -
По
формуле вычисляют среднюю квадратическую
ошибку одного измерения. -
По
формуле вычисляют среднюю квадратическую
ошибку арифметической средины. -
Если
измеряют линейную величину, то
подсчитывают относительную среднюю
квадратическую ошибку каждого измерения
и арифметической средины. -
При
необходимости подсчитывают предельную
ошибку одного измерения,
которая
может служить допустимым значением
погрешностей аналогичных
измерений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Физ. Тема «Челночный бег с переноской 2-3 предметов с передачей , Тема 3.4. Договор как основание возникновения обязательства. Общ, ТЕСТОВЫЕ ВОПРОСЫ К ЭКЗАМЕНУ ПО ПРЕДМЕТУ ДОУ.docx, сводная ведомость по моим предметам.docx, 1. Протокол входного контроля отчетности — Статистика (прочие)_ , Сенсорные способности являются базой для успешного овладения раз, Тест с ответами по предмету электрические измерения.doc, Лекция 4. Общие проблемы малой группы. Динамические процессы в м, Форма анализа воспитательной работы для руководителей предметных, Цель, задачи, предмет и объект антикоррупционной экспертизы. Суб
Тема: Элементы теории ошибок измерений.
- Классификация ошибок измерений.
Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.
При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые, систематические и случайные.
К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.
Систематические ошибки происходят от неизвестного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.
Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений.
В основу теории ошибок положены следующие свойства случайных ошибок:
1. Малые ошибки встречаются чаще, а большие реже.
2. Ошибки не превышают известного предела.
3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине,
одинаково часто встречаются.
4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе
измерений.
По источнику происхождения различают ошибки приборов, внешние и личные.
Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.
Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира
солнечными лучами.
Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.
,
2. Арифметическая средина.
Если одна величина измерена n раз и получены результаты: l1, l2, l3, l4, l5, l6,….., ln,
то
Величина x называется арифметической срединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:
l 1 – x = v1
1 – x = v1
l2 – x = v2
l3 – x = v3
. . . . . . . .
ln – x = vn
Или в общем виде получим:
[ l ] – nx = [v]
Тогда [v] = 0.
2. Средняя квадратическая ошибка.
Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

[v2]
m = √ n — 1
= √ n — 1
где [v2] – сумма квадратов вероятнейших ошибок; n – число измерений.
Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

m
[v2]
M = ———— = √ —————
 √n n ( n – 1 )
√n n ( n – 1 )
Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е.
ε = 3m.
Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной ве-
личины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной
l = 110 м, при m = 2 см равна m/l = 1/5500.
Пример. Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата.
Вычисления приведены в таблице:
| № п/п | Длина линии в м | v, см | v2 | Вычисления |
| 1 | 225,26 | +6 | 36 |
m = 5,6 см; М |
| 2 | 225,23 | +3 | 9 | |
| 3 | 225,22 | +2 | 4 | |
| 4 | 226,14 | -6 | 36 | |
| 5 | 225,23 | +3 | 9 | |
| 6 | 225,12 | -8 | 64 | |
|
xср.= 225, 20 |
[v] = 0 |
[v2] = 158 |
По формулам вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна
2,3 1
———- = ————
22520 9 800
- Оценка точности измерений
Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:
- Находят вероятнейшее (наиболее точное для данных условий) значение
измеренной величины по формуле арифметической средины х = [1]/n.
- Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: [v] = 0;
- По формуле вычисляют среднюю квадратическую ошибку одного измерения.
- По формуле вычисляют среднюю квадратическую ошибку арифметической средины.
- Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.
- При необходимости подсчитывают предельную ошибку одного измерения,
которая может служить допустимым значением погрешностей аналогичных
измерений.
ЛЕКЦИЯ 7
Тема: Геодезические сети.
Для составления карт и планов, решения геодезических задач в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат. Эти точки маркируют на поверхности Земли или в зданиях и сооружениях центрами (знаками).
Геодезическая сеть – это система закрепленных точек земной поверхности, положение которых определено в общей для них системе геодезических координат.
Геодезические сети подразделяют на плановые и высотные: первые служат для определения координат X и Y геодезических центров, вторые — для определения их высот.
Принцип построения плановых геодезических сетей заключается в следующем. На местности выбирают точки, взаимное положение которых представляется в виде геометрических фигур: треугольников, четырехугольников, ломаных линий и т.д. Причем
точки выбирают с таким расчетом, чтобы некоторые элементы фигур (стороны, углы) можно было бы непосредственно измерить, а все другие элементы вычислить по данным измерений. Например, в треугольнике достаточно измерить одну сторону и три угла (один для контроля правильности измерений) или две стороны и два угла (один для контроля правильности измерений), а остальные стороны и углы вычислить. Для вычисления плановых координат вершин выбранных точек необходимо кроме элементов геометрических фигур знать еще дирекционный угол стороны одной из фигур и координаты одной из вершин.
Сети строят по принципу перехода от общего к частному, т. е. от сетей с большими расстояниями между пунктами и высокоточными измерениями к сетям с меньшими расстояниями и менее точным.
Геодезические сети подразделяют на четыре вида: государственные, сгущения, съемочные и специальные. Государственные геодезические сети служат исходными для построения всех других видов сетей. Началом единого отсчета плановых координат в Российской Федерации служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.
- Методы создания геодезических сетей.
Плановые геодезические сети создаются методами триангуляции, полигонометрии и трилатерации. При построении геодезической сети методом триангуляции на местности закрепляется ряд точек, которые в своей совокупности образуют систему треугольников. В треугольниках измеряются все углы и некоторые стороны, которые называются базисными. По длине базисной стороны и измеренным углам, вычисляют длины всех сторон, а затем координаты всех пунктов сети.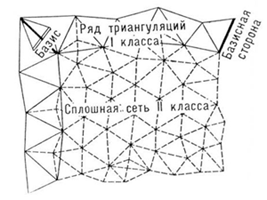
Метод полигонометрии заключается в построении на местности системы ломанных линий, называемых полигонометрическими ходами. Эти ходы прокладывают обычно между пунктами триангуляции. В полигонометрических ходах измеряются все углы поворота и длины всех сторон.
При построении сети методом трилатерации на местности также строится сеть треугольников, в которых при помощи высокоточных дальномеров измеряются все стороны.
Сети сгущения строят для дальнейшего увеличения плотности (числа пунктов, приходящихся на единицу площади) государственных сетей. Плановые сети сгущения подразделяют на 1-й.и 2-й разряды.
Съемочные сети — это тоже сети сгущения, но с еще большей плотностью. С точек съемочных сетей производят непосредственно съемку предметов местности и рельефа для составления карт и планов различных масштабов.
Специальные геодезические сети создают для геодезического обеспечения строительства сооружений. Плотность пунктов, схема построения и точность этих сетей зависят от специфических особенностей строительства.
Государственные высотные геодезические сети создают для
распространения по всей территории страны единой системы
высот. За начало высот в Российской Федерации и некоторых других странах принят средний уровень Балтийского моря, определение которого проводилось в период с 1825 до 1840 г. Этот уровень отмечен горизонтальной чертой на медной металличе-
ской пластине, укрепленной в устое моста через обводной канал в Кронштадте.
Между пунктами государственных высотных геодезических сетей высокой точности (1-го класса) размещают пункты высотных сетей низших классов (2-го, 3-го и т.д.). Несколь-
ко пересекающихся ходов называют сетями. Как правило, сети создают из ходов, прокладываемых между тремя или более точек. В целом точки (реперы) высотных сетей, называемых нивелирными, достаточно равномерно распределены на территории страны.
На незастроенной территории расстояния между реперами составляют 5…7 км, в го-
родах сеть реперов в 10 раз плотнее.
Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса.
Как правило, сети образуют полигоны с узловыми точками (общими точками пересечения двух или более ходов одного и того же класса). Каждый нивелирный ход опирается обоими концами на реперы ходов более высокого класса или узловые точки.
- Закрепление на местности пунктов геодезических сетей.
Точки геодезических сетей закрепляют на местности знаками. По местоположению знаки бывают: грунтовые и стенные, заложенные в стены зданий и сооружений; металлические, железобетонные, деревянные, в виде откраски и т.д.; по назначению —
постоянные, к которым относятся все знаки государственных геодезических сетей, и временные, устанавливаемые на период изысканий, строительства, реконструкции, наблюдений и т.д.
Постоянные знаки. Их закрепляют подземными знаками — центрами. Конструкции центров обеспечивают их сохранность и неизменность положения в течение длительного периода времени. Как правило, подземный центр представляет собой бетонный
монолит , закладываемый ниже глубины промерзания грунта и не в насыпной массив. У поверхности земли в монолите устанавливают чугунную марку, на которой наносят центр в виде креста или точки. Положению этого центра соответствуют коор-
динаты Хи Y и во многих случаях отметки.

Для того чтобы с одного знака был виден другой (смежный),
над подземными центрами устанавливают наружные знаки в виде
металлических или деревянных трех- или четырехгранных пира-
мид или сигналов.
Пирамиды или сигналы имеют высоту 3…30 м и более. Геодезический сигнал с под-
земным центром и столиком предназначен для установки измерительных приборов и на-
стила при работе на нем наблюдателя. Верх сигнала или пирамиды заканчивается визир-
ной целью , на которую при измерении углов направляют зрительную трубу теодолита. На
столик устанавливают также отражатель, если измеряют расстояния между пунктами светодалъномером. Для спутниковых измерений сигналы и пирамиды строить не надо.
Как правило, пункты плановых разбивочных сетей и сетей сгущения закрепляют подземными центрами, такими же как и пункты государственных сетей. Так как расстояния между этими пунктами сравнительно небольшие, оформления их наружными знаками не требуется. Знаки могут закладывать в зданиях и сооружениях, в этом случае их называют стенными.
Координаты всех пунктов плановой геодезической сети, а также отметки пунктов высотной геодезической сети заносятся в специальные каталоги, в которых кроме названия пунктов дается описание их местоположения.
Иногда для различных целей могут создаваться местные геодезические сети.
Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей).
Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.
ЛЕКЦИЯ 8
Тема: Угловые измерения на местности.
Основными элементами любых геодезических работ на местности являются угловые и линейные измерения. Для производства угловых измерений служат специальные приборы, называемые теодолитами.
1. Теодолит. Устройство теодолита
Теодолит – это геодезический прибор, предназначенный для измерения горизонтальных углов, углов наклона и расстояний.
В соответствии с действующим ГОСТом в настоящее время
промышленностью выпускаются теодолиты следующих типов:
Основными частями любого теодолита являются лимб, алидада, зрительная труба.
Угломерный круг, по краю которого нанесена шкала с градусными делениями, называется лимбом.
В плоскости угломерного круга с лимбом вращается второй круг – алидада.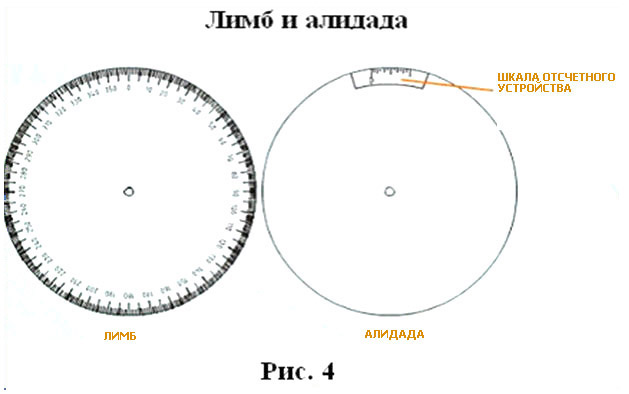
На алидаде имеется устройство для отсчета по лимбу. В современных теодолитах угломерные круги стеклянные, такие теодолиты называются оптическими.
Алидада жестко связана со зрительной трубой с помощью колонок. Лимб, алидада и зрительная труба имеют закрепительные и наводящие винты.
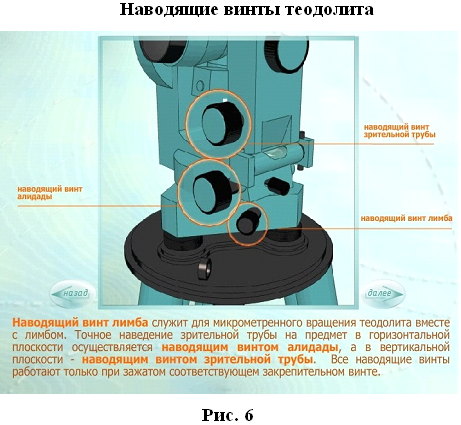
Плоскость лимба приводится в горизонтальное положение с помощью трех подъемных винтов и цилиндрического уровня. Центр лимба устанавливается над вершиной измеряемого угла. Для грубой наводки трубы на предмет служит оптический визир.
Для измерения вертикальных углов наклона имеется вертикальный круг.
Для производства отсчетов по лимбу рядом с окуляром зрительной трубы располагается микроскоп, свет в который направляется с помощью специального зеркальца. Для прикрепления теодолита к штативу служит становой винт.
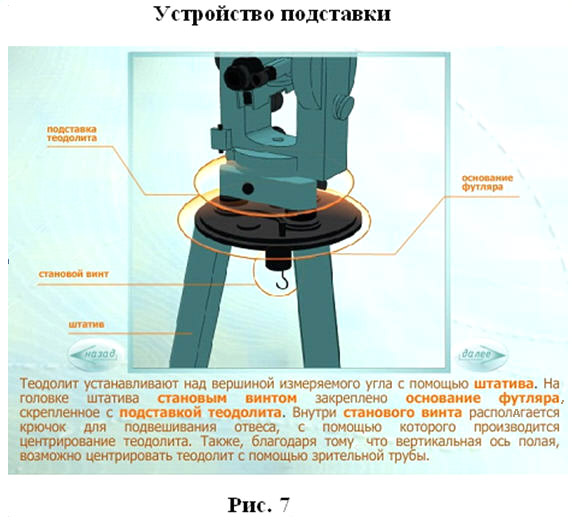
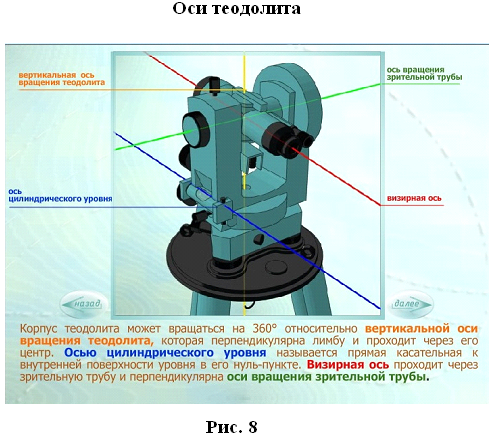
2. Отсчетные устройства
При измерении углов производится отсчет по лимбу.
Угловая величина дуги, соответствующая одному делению шкалы лимба, называется ценой деления лимба.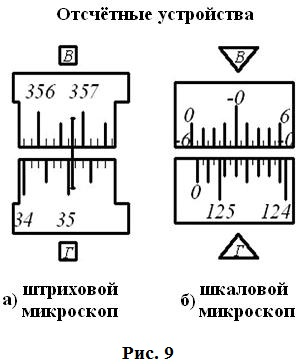
Отсчет по лимбу производится относительно индекса, нанесенного на алидаду.
Для оценки долей деления лимба служат отсчетные устройства. В оптических теодолитах в качестве отсчетных устройств служат штриховые (Т30) и шкаловые
(2Т30 и Т15) микроскопы.
3. Уровни
Уровни бывают круглыми и цилиндрическими. Цилиндрический уровень состоит из стеклянной трубки, верхняя часть которой представляет дугу большого радиуса. На верхней части ампулы имеется шкала делений через 2 мм. Центральный штрих шкалы называется нуль – пунктом.
Прямая, касательная к внутренней поверхности уровня в его нуль–пункте, называется осью цилиндрического уровня.
Чем больше радиус, тем меньше цена деления и тем уровень точнее.
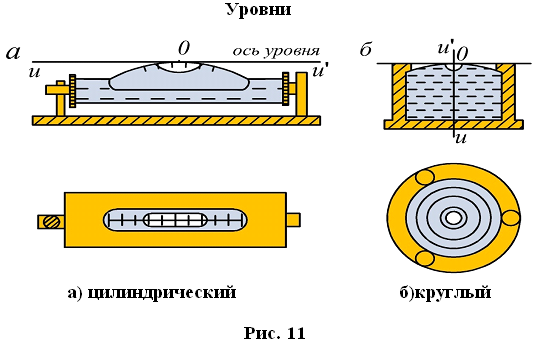
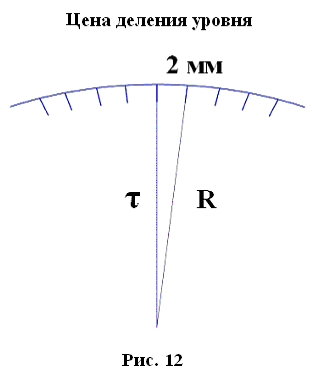
4. Зрительные трубы
Зрительная труба геодезических приборов состоит из объектива и окуляра. Трубы большинства геодезических приборов дают обратное (перевернутое) изображение предмета. Вблизи переднего фокуса окуляра помещается металлическое кольцо, называемое диафрагмой со стеклянной пластинкой, на которой награвированы тонкие нити, составляющие сетку нитей. Сетка нитей снабжена четырьмя исправительными винтами, позволяющими перемещать сетку нитей в своей плоскости. 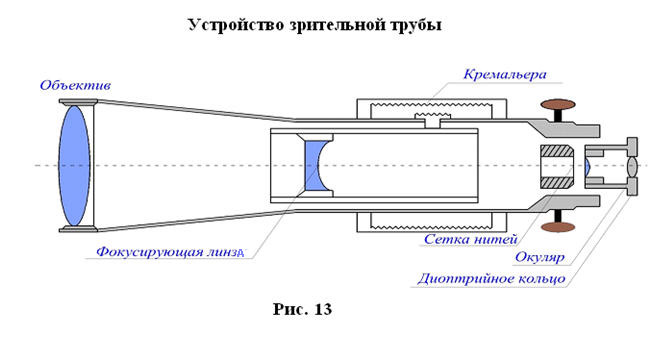
Прямая, соединяющая перекрестки сетки нитей с оптическим центром объектива, называется визирной осью трубы.
Установка трубы для наблюдений складывается из установки ее «по глазу» и «по предмету». При недостаточно тщательной фокусировке трубы будет наблюдаться перемещение предмета относительно сетки при изменении положения глаза наблюдателя перед окуляром. Перемещение предмета относительно сетки при изменении положения глаза наблюдателя перед окуляром называется параллаксом сетки нитей. Устраняется дополнительным вращением кремальеры.
Установка трубы «по глазу» заключается в получении резкого изображения сетки нитей. Выполняется перемещением диоптрийного кольца.
Установка трубы «по предмету» выполняется с помощью кремальеры, при этом внутри трубы перемещается фокусирующая линза (труба с внутренней фокусировкой).
ЛЕКЦИЯ 9




 = 5,6/
= 5,6/