Предельная ошибка прогноза это

Посчитать ошибку прогноза

4. Решение типовых задач

По районам региона приводятся данные за 200Х г. (табл. 1.1).

Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х

Среднедневная заработная плата, руб., У

1. Построить линейное уравнение парной регрессии у от х.

2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х, составляющем 107% от среднего уровня.

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу (табл. 1.2).

;

YI—

.

Получено уравнение регрессии: .

С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

2. Тесноту линейной связи оценит коэффициент корреляции:

; .

Это означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации:

.

Качество построенной модели оценивается как хорошее, так как средняя относительная ошибка аппроксимации не превышает 8-10%.

3. Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.

Выдвигаем гипотезу Н0 о статистически незначимом отличии показателя от нуля: .

Определим случайные ошибки Ma, mb, :

;

;

.

; ;

.

Фактические значения t-статистики превосходят табличные значения:

; ; ,

Поэтому гипотеза Н0 отклоняется, т. е. A, B и Rxy не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительный интервал для A и B. Для этого определим предельную ошибку для каждого показателя:

; .

;

;

;

;

;

.

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры A и B, находясь в указанных границах, не принимают нулевые значения, т. е. не являются статистики незначимыми и существенно отличаются от нуля.

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение промежуточного минимума составит: тыс. руб., тогда прогнозное значение прожиточного минимума составит: тыс. руб.

5. Ошибка прогноза составит:

тыс. руб.

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

.

Доверительный интервал прогноза:

;

руб.;

руб.

Выполненный прогноз среднемесячной заработной платы оказался надежным, но неточным, т. к. диапазон верхней и нижней границ доверительного интервала составляет 1,95 раза (121/62,2).

Зависимость потребления продукта А от среднедушевого дохода по данным 20 семей характеризуется следующим образом:

— уравнение регрессии ;

— индекс корреляции ;

— остаточная дисперсия .

Требуется провести дисперсионный анализ полученных результатов.

Результаты дисперсионного анализа приведены в табл. 1.3.

Почему мы не считаем MAPE, RMSE и другие математические ошибки при прогнозировании спроса

Когда перед компанией встают задачи прогнозирования спроса для управления товарными запасами, обычно появляется вопрос, связанный с выбором метода прогнозирования. Но как определить, какой метод лучше? Однозначного ответа на этот вопрос нет. Однако, исходя из нашей практики, самым распространенным методам оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE). Также используются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка прогнозирования (RMSE).

Ошибка прогноза в данном случае – это разница между фактическим значением спроса и его прогнозным значением. Т.е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Изначально MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки прогноза спроса. На практике ошибку могут рассчитывать по каждой позиции товара, а также среднюю оценку по всем товарным группам.

Несмотря на то, что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они не достаточно корректны и не подходят для применения в реальном бизнесе. Для простоты изложения, выделим три ключевых момента, которые приводят к некорректным выводам при использовании вышеописанных методов оценки. Назовем их ошибка №1, №2 и №3. Сначала мы подробно опишем эти ошибки, а потом расскажем, как наши методы сравнения помогаю их ликвидировать.

О некорректности использования MAPE, RMSE и других распространенных ошибок

Ошибка № 1 заключается в том, что используемые методы больше относятся к математике, нежели к бизнесу, по той причине, что это обезличенные цифры (или проценты), которые ничего не говорят про деньги. Бизнесу же нужно принимать решения на основе выгоды, которую он получит в деньгах. Например, ошибка в 80% на первый взгляд звучит устрашающие. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 0,5 рублей – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Ко всему прочему также больше значение имеет объем продукции, что тоже никак не учитывается данными ошибками прогнозирования.

Второй важный момент (ошибка №2), который не учитывают данные оценки прогнозирования – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и как следствие стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути мы имеет одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.

Третий ключевой момент (ошибка №3) – описанные ошибки распространяются только на точечный прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный не был прогноз с точки зрения описанных выше методов, мы все равно не оцениваем точность страхового запаса, а значит реальные данные могут быть значительно искажены.

Критерии, привязанные к прибыльности бизнеса

Учитывая описанные выше недостатки ошибок прогнозирования, такой подход не является корректным и надежным для сравнения алгоритмов. Ко всему прочему он зачастую оторван от реального бизнеса. Используемый же нами подход позволяет оценить точность алгоритмов в деньгах, рассчитать стоимость ошибки прогнозирования на понятном для бизнеса языке финансов. Таким образом это позволяет нам ликвидировать ошибку №1.

В случае с ошибкой № 2, мы рассчитываем два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается, как количество недопроданных товаров, умноженное на разность цен закупки и реализации. Например, вы закупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. Экономический урон будет равен:

(1200-1000)*(4000-3000)=200 000 рублей.

В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. Экономический урон будет равен сумме затрат на нереализованную продукцию, помноженную на ставку альтернативных вложений за этот период. Предположим, что реальный спрос в предыдущем примере оказался 800 дисков и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда экономический урон будет равен

(1000-800)*3000*0,2/12=10 000 рублей.

Соответственно, в каждом конкретном случае, мы будет учитывать одно из этих значений.

Для того, чтобы ликвидировать ошибку № 3, мы сравниваем алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее — уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течении периода их пополнения. Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыть от реализации, в случае если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.

Подробнее о уровне сервиса, его видах и примерах расчета читайте в статье «Что такое уровень сервиса и почему он важен.»

Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т.д.). Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.

В качестве основного критерия (критерий №1) качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше (исправление ошибки №2). Таким образом мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери — тем точнее работает алгоритм.

Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую, либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом мы можем проверить, насколько хорошо в целом работает модель.

Для компаний, которые, считают оптимальный уровень сервиса мы используем дополнительный критерий (критерий №2) для оценки. В общем виде он выглядит как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту). Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным.

Что проиллюстрировать применение данного критерия, вернемся к нашему примеру с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:

(3300-3000)*(4000-3000)=300 000 рублей.

Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку равную 20% годовых). Итоговое значение критерия будет равно:

(3000-2850)*3000*0,2/12 = 7500 рублей

Конечно, в идеальном случае, мы должны рассчитывать ошибку только при оптимальном уровне сервиса, между прогнозным и реальным значениями. Но так как не все компании еще перешли на оптимальный уровень сервиса, мы вынуждены использовать два критерия.

Используемые нами критерии в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволят бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.

Пример сравнения точности прогнозирования системы Forecast NOW c методом ARIMA (на базе номенклатуры бытовой химии):

Методы оценки качества прогноза

Часто при составлении любого прогноза — забывают про способы оценки его результатов. Потому как часто бывает, прогноз есть, а сравнение его с фактом отсутствует. Еще больше ошибок случается, когда существуют две (или больше) модели и не всегда очевидно — какая из них лучше, точнее. Как правило одной цифрой (R 2 ) сложно обойтись. Как если бы вам сказали — этот парень ходит в синей футболке. И вам сразу все стало про него ясно )

В статьях о методах прогнозирования при оценке полученной модели я постоянно использовал такие аббревиатуры или обозначения.

• R 2
• MSE
• MAPE
• MAD
• Bias

Попробую объяснить, что я имел в виду.

Остатки

Суровые MSE и R 2

Когда нам требуется подогнать кривую под наши данные, то точность этой подгонки будет оцениваться программой по среднеквадратической ошибке (mean squared error, MSE). Рассчитывается по незамысловатой формуле

где n-количество наблюдений.

Соотвественно, программа, рассчитывая кривую подгонки, стремится минимизировать этот коэффициент. Квадраты остатков в числителе взяты именно по той причине, чтобы плюсы и минусы не взаимоуничтожились. Физического смысла MSE не имеет, но чем ближе к нулю, тем модель лучше.

Вторая абстрактная величина это R 2 — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. В отличии от MSE не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле:

где Var(Y) — дисперсия исходных данных.

Безусловно коэффициент детерминации — важный критерий выбора модели. И если модель плохо коррелирует с исходными данными, она вряд ли будет иметь высокую предсказательную силу.

MAPE и MAD для сравнения моделей

Статистические методы оценки моделей вроде MSE и R 2 , к сожалению, трудно интерпретировать, поэтому светлые головы придумали облегченные, но удобные для сравнения коэффициенты.

Среднее абсолютное отклонение (mean absolute deviation, MAD) определяется как частное от суммы остатков по модулю к числу наблюдений. То есть, средний остаток по модулю. Удобно? Вроде да, а вроде и не очень. В моем примере MAD=43. Выраженный в абсолютных единицах MAD показывает насколько единиц в среднем будет ошибаться прогноз.

MAPE призван придать модели еще более наглядный смысл. Расшифровывается выражение как средняя абсолютная ошибка в процентах (mean percentage absolute error, MAPE).

где Y — значение исходного ряда.

Выражается MAPE в процентах, и в моем случае означает, что в модель может ошибаться в среднем на 16%. Что, согласитесь, вполне допустимо.

Наконец, последняя абсолютно синтетическая величина — это Bias, или просто смещение. Дело в том, что в реальном мире отклонения в одну сторону зачастую гораздо болезненнее, чем в другую. К примеру, при условно неограниченных складских помещениях, важнее учитывать скачки реального спроса вверх от спрогнозированных значений. Поэтому случаи, где остатки положительные относятся к общему числу наблюдений. В моем случае 44% спрогнозированных значений оказались ниже исходных. И можно пожертвовать другими критериями оценки, чтобы минимизировать этот Bias.

Можете попробовать это сами в Excel и Numbers

Интересно узнать — какие методы оценки качества прогнозирования вы используете в своей работе?

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

1. Для каждой позиции рассчитывается ошибка прогноза (факт вычитается из прогноза) — Error
2. Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
3. Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (факт вычитается из прогноза по модулю) — Absolute Error
2. Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
3. Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (факт вычитается из прогноза, по модулю) — Absolute Error
2. Находится сумма всех фактов по всем позициям (общий фактический объем)
3. Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

1. Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
2. Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
3. Извлекаем корень из полученного результат — RMSE
4. Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
   1. Разделить на разницу между максимальным и минимальным значением показателей
   2. Разделить на разницу между третьим и первым квартилем значений показателей
   3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Эконометрика — это быстро развивающаяся отрасль науки, характеризующаяся математическим описанием рядов экономических данных и представлением таких данных в геометрической или графической форме.

Термин «эконометрика» был впервые использован в 1910 году. Эконометрика означает измерение экономики. Предпосылкой для возникновения эконометрики послужила давняя необходимость получить достаточное представление о количественных взаимосвязях в современной экономической жизни, которое не могли дать статистика, экономическая теория и математика по отдельности. Это подчеркивает междисциплинарный характер предмета. Кроме того, предпосылками возникновения эконометрики являются развитие количественных методов в экономических исследованиях, накопление бухгалтерских и статистических данных, а также создание современной микро- и макроэкономики. Современная экономика определяет эконометрику как «науку о моделировании экономических явлений для объяснения и прогнозирования их развития, а также для выявления и измерения их детерминант». Таким образом, эконометрика — это наука об измерении и анализе экономических явлений и экономических отношений с помощью математических и статистических методов.

Если у вас нет времени на выполнение заданий по эконометрике, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.

Ответы на вопросы по заказу заданий по эконометрике:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете «Эконометрика«, если у вас есть желание и много свободного времени!

Содержание:

1. Ответы на вопросы по заказу заданий по эконометрике:
2. Парная регрессия и корреляция
3. Задача 1
4. Решение:
5. Задача 2
6. Решение:
7. Задача 3
8. Решение:
9. Множественная регрессия и корреляция
10. Задача 4
11. Решение:
12. Задача 5
13. Решение:
14. Задача 6
15. Реализация типовых задач на компьютере
16. Система эконометрических уравнений
17. Задача 7
18. Решение:
19. Задача 8
20. Решение:
21. Задача 8
22. Решение:
23. Задача 9
24. Решение:

Парная регрессия и корреляция

Задача 1

По территориям региона приводятся данные за 199Х г. (табл. 1.6). Таблица 1.6

Требуется:

1. Построить линейное уравнение парной регрессии

2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума составляющем 107% от среднего уровня.

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Решение:

I. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу (табл. 1.7). Таблица !.7

Получено уравнение регрессии:

С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

2. Тесноту линейной связи оценит коэффициент корреляции:

Это означает, что 52% вариации заработной платы объясняется вариацией фактора — среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации:

Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.

3. Оценку статистической значимости параметров регрессии проведем с помощью статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.

Выдвигаем гипотезу о статистически незначимом отличии показателей от нуля:

для числа степеней свободы составит 2,23.

Определим случайные ошибки

Тогда

Фактические значения статистики превосходят табличные значения:

поэтому гипотеза отклоняется, т.е. не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительный интервал для Для этого определим предельную ошибку для каждого показателя:

Доверительные интервалы:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: тыс. руб., тогда

прогнозное значение прожиточного минимума составит:

5. Ошибка прогноза составит:

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

Доверительный интервал прогноза:

Выполненный прогноз среднемесячной заработной платы оказался надежным но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 1,95 раза:

Возможно, вас также заинтересует эта ссылка:

Задача 2

По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов, приведенных в табл. 1.8. Таблица 1.8

Требуется:

1. Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат.

2. Ранжировать факторы по силе влияния.

Решение:

1. Для уравнения равносторонней гиперболы

Для уравнения прямой

Для уравнения степенной зависимости

Для уравнения показательной зависимости

2. Сравнивая значения ранжируем по силе их влияния на себестоимость единицы продукции:

Для формирования уровня себестоимости продукции группы предприятий первоочередное значение имеют цены на энергоносители; в гораздо меньшей степени влияют трудоемкость продукции и отчисляемая часть прибыли. Фактором снижения себестоимости выступает размер производства: с ростом его на 1% себестоимость единицы продукции снижается на -0,97%.

Возможно, вас также заинтересует эта ссылка:

Задача 3

Зависимость потребления продукта от среднедушевого дохода по данным 20 семей характеризуется следующим образом:

уравнение регрессии

индекс корреляции

остаточная дисперсия

Требуется:

Провести дисперсионный анализ полученных результатов.

Решение:

Результаты дисперсионного анализа приведены в табл. 1.9. Таблица 1.9

В силу того что гипотеза о случайности различий факторной и остаточной дисперсий отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость потребления продукта от среднедушевого дохода.

Реализация типовых задач на компьютере

Решение с помощью ППП Excel

1. Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной репрессии Порядок вычисления следующий:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 — для получения только оценок коэффициентов регрессии;

3) активизируйте Мастер функций любым из способов:

а) в главном меню выберите Вставка/Функция;

б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;

4) в окне Категория (рис. 1.1) выберите Статистические, в окне Функция — ЛИНЕЙН. Щелкните по кнопке ОК;

5) заполните аргументы функции (рис. 1.2):

Известные значения — диапазон, содержащий данные результативного признака;

Известные значения — диапазон, содержащий данные факторов независимого признака;

Константа — логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа — 0, то свободный член равен 0; Статистика — логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация

выводится, если Статистика 23 0, то выводятся только оценки параметров уравнения. Щелкните по кнопке ОК;

6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем — на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Для вычисления параметров экспоненциальной кривой

в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.

Для данных из примера 2 результат вычисления функции ЛИНЕИН представлен на рис. 1.3, функции ЛГРФПРИБЛ — на рис. 1.4.

2. С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис /Надстройки. Установите флажок Пакет анализа (рис. 1.5);

2) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

3) заполните диалоговое окно ввода данных и параметров вывода (рис. 1.6):

Входной интервал — диапазон, содержащий данные результативного признака;

Входной интервал — диапазон, содержащий данные факторов независимого признака;

Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист — можно задать произвольное имя нового листа.

Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Результаты регрессионного анализа для данных из примера 2 представлены на рис. 1.7.

Возможно, вас также заинтересует эта ссылка:

Множественная регрессия и корреляция

Задача 4

По 20 территориям России изучаются следующие данные (табл. 2.2): зависимость среднегодового душевого дохода (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности заняты (%) и от доли экономически активного населения в численности всего населения (%) Таблица 2.2

Требуется:

1. Составить таблицу дисперсионного анализа для проверки при уровне значимости статистической значимости уравнения множественной регрессии и его показателя тесноты связи.

2. С помощью частных критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактора после фактора и насколько целесообразно включение после

3. Оценить с помощью критерия Стыодента статистическую значимость коэффициентов при переменных множественного уравнения регрессии.

Решение:

1. Задача дисперсионного анализа состоит в проверке нулевой гипотезы о статистической незначимости уравнения регрессии в целом и показателя тесноты связи.

Анализ выполняется при сравнении фактического и табличного (критического) значений кригерия Фишера факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: где — число единиц совокупности;

— число факторов в уравнении линейной регрессии;

— фактическое значение результативного признака;

— расчетное значение результативного признака.

Результаты дисперсионного анализа представлены в табл. 2.3. Таблица 2.3

Сравнивая приходим к выводу о необходимости отклонить гипотезу и сделать вывод о статистической значимости

уравнения регрессии в целом и значения так как они статистически надежны и сформировались под систематическим действием неслучайных причин. Вероятность того, что допускаются ошибки при отклонении нулевой гипотезы, не превышает 5%, и это является достаточно малой величиной.

2. Частный критерий Фишера оценивает статистическую целесообразность включения фактора в модель после того, как в нее включен фактор Частный критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторами Результаты дисперсионного анализа представлены в табл. 2.4.

Таблица 2.4

Включение фактора после фактора оказалось статистически значимым и оправданным: прирост фак торной дисперсии (в расчете на одну степень свободы) оказался существенным, т.е. следствием дополнительного включения в модель систематически действующего фактора так как

Аналогично проверим целесообразность включения в модель дополнительного фактора после включенного ранее фактора Расчет выполним с использованием показателей тесноты связи

В силу того что приходим к выводу, что включение после оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы был несуществен, статистически незначим, т.е. влияние не является устойчивым, систематическим. Вполне возможно было ограничиться построением линейного уравнения парной регрессии

3. Оценка с помощью критерия Стьюдента значимости коэффициентов связана с сопоставлением их значений с величиной их случайных ошибок: Расчет значений случайных ошибок достаточно сложен и трудоемок. Поэтому предлагается более простой способ: расчет значения критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного критерия Фишера:

Табличные (критические) значения критерия Стьюдента зависят от принятого уровня значимости (обычно это 0,1; 0,05 или 0,01) и от числа степеней свободы где число единиц совокупности, число факторов в уравнении.

В нашем примере при Сравнивая приходим к выводу, что так как

коэффициент регрессии является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе. Так как приходим к заключению, что величина является статистически незначимой, ненадежной в силу того, что она формируется преимущественно под воздействием случайных факторов. Еще раз подтверждается статистическая значимость влияния (доли занятых тяжелым физическим трудом) на (среднедушевой доход) и ненадежность, незначимость влияния (доли экономически активного населения в численности всего населения).

Возможно, вас также заинтересует эта ссылка:

Задача 5

Зависимость спроса на свинину от цены на нее и от цены на говядину представлена уравнением

Требуется:

1. Представить данное уравнение в естественной форме (не в логарифмах).

2. Оценить значимость параметров данного уравнения, если известно, что критерий для параметра при составил 0,827, а для параметра при — 1,015.

Решение:

1. Представленное степенное уравнение множественной регрессии приводим к естественной форме путём потенцирования обеих частей уравнения:

Значения коэффициентов регрессии в степенной функции равны коэффициентам эластичности результата

Спрос на свинину сильнее связан с ценой на говядину — он увеличивается в среднем на 2,83% при росте цен на 1%. С ценой на свинину спрос на нее связан обратной зависимостью: с ростом цен на 1% потребление снижается в среднем на 0,21%.

2. Табличное значение критерия для обычно лежит в интервале 2 — 3 — в зависимости от степеней свободы. В данном примере Это весьма небольшие значения критерия,

которые свидетельствуют о случайной природе взаимосвязи, о статистической ненадежности всего уравнения, поэтому применять полученное уравнение для прогноза не рекомендуется.

Возможно, вас также заинтересует эта ссылка:

Задача 6

По 20 предприятиям региона (табл. 2.5) изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%). Таблица 2.5

Требуется:

1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.

2. Проанализировать линейные коэффициенты парной и частной корреляции.

3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.

4. С помощью критерия Фишера оценить статистическую надежность уравнения регрессии и Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.

5. С помощью частных критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после

6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

Реализация типовых задач на компьютере

1. Решение примера проведем с использованием ППП MS Excel и Statgraphics.

Решение с помощью ППП Excel

Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) в главном меню выберите последовательно пункты Сервис / Анализ данных / Описательная статистика, после чего щелкните по кнопке ОК;

3) заполните диалоговое окно ввода данных и параметров вывода (рис. 2.1);

Входной интервал — диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов); Группирование — по столбцам или по строкам — необходимо указать дополнительно;

Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист — можно задать произвольное имя нового листа.

Если необходимо получить дополнительную информацию Итоговой статистики, Уровня надежности, наибольшего и наименьшего значений. установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 2.2.

Решение с помощью ППП Statgraphics

Для проведения многофакторного анализа в ППП Statgraphics используется пункт меню Multiple Variable Analysis. Для получения показателей описательной статистики необходимо проделать следующие операции:

1) ввести исходные данные или открыть существующий файл, содержащий анализируемые данные;

2) в главном меню выбрать Describe/Numeric Data/Multiple Variable Analysis;

3) заполнить диалоговое окно ввода данных (рис. 2.3). Ввести названия всех столбцов, значения которых вы хотите включить в анализ; щелкнуть по кнопке ОК;

4) в окне табличных настроек поставить флажок напротив Summary Statistics (рис. 2.4). Итоговая статистика — показатели вариации -появится в отдельном окне.

Для данных примера 4 результат применения функции Multiple Variable Analysis представлен на рис. 2.5.

Сравнивая значения средних квадратических отклонений и средних величин и определяя коэффициенты вариации:

приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%.

Совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

Решение с помощью ППП Excel

К сожалению, в ППП MS Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:

1) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;

2) заполните диалоговое окно ввода данных и параметров вывода (см. рис. 2.1);

3) результаты вычислений — матрица коэффициентов парной корреляции — представлены на рис. 2.6.

Решение с помощью ППП Statgraphics

При проведении многофакторного анализа — Multiple Variable Analysis — вычисляются линейные коэффициенты парной корреляции и линейные коэффициенты частной корреляции. Последовательность операций описана в п.1 этого примера. Для отображения результатов вычисления на экране необходимо установить флажки напротив Correlations и Partial Correlations в окне табличных настроек (рис. 2.7).

В результате получим матрицы коэффициентов парной и частной корреляции (рис. 2.8).

Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки как с коэффициентом обновления основных фондов — так и с долей рабочих высокой квалификации —

Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очишают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно связаны связь и гораздо слабее: а межфакторная зависимость и выше, чем парная Все это приводит к выводу о необходимости исключить фактор — доля высококвалифицированных рабочих — из правой части уравнения множественной регрессии.

Если сравнить коэффициенты парной и часгной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи:

Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

3. Вычисление параметров линейного уравнения множественной регрессии.

Система эконометрических уравнений

Задача 7

Изучается модель вида

где — валовой национальный доход;

— валовой национальный доход предшествующего года;

— личное потребление;

— конечный спрос (помимо личного потребления);

— случайные составляющие.

Информация за девять лет о приростах всех показателей дана в табл. 3.1

Таблица 3.1

Для данной модели была получена система приведенных уравнений:

Требуется:

1. Провести идентификацию модели.

2. Рассчитать параметры первого уравнения структурной модели.

Решение:

1. В данной модели две эндогенные переменные и две экзогенные переменные Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.

Первое уравнение сверхидентифицировано, так как в нем на параметры при наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная Переменная в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверх-идентифицирована.

2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.

Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной Для этого в приведенное уравнение

подставим значения имеющиеся в условии задачи. Получим:

Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения на теоретические и рассчитываем новую переменную (табл. 3.2). Таблица 3.2

Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную через Решаем уравнение

Система нормальных уравнений составит:

Итак, первое уравнение структурной модели будет таким:

Задача 8

Имеются данные за 1990-1994 гг. (табл. 3.3). 4 Таблица 3.3

Требуется: Построить модель вида

рассчитав соответствующие структурные коэффициенты.

Решение:

Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид

В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2=1 + 1. Это означает, что каждое уравнение и система в целом идентифицированы.

Для определения параметров такой системы применяется косвенный метод наименьших квадратов.

С этой целью структурная форма модели преобразуется в приведенную форму:

в которой коэффициенты при определяются методом наименьших квадратов.

Для нахождения значений запишем систему нормальных уравнений:

При ее решении предполагается, что выражены через отклонения от средних уровней, т. е. матрица исходных данных составит:

Применительно к ней необходимые суммы оказываются следующими:

Система нормальных уравнений составит:

Решая ее, получим:

Итак, имеем

Аналогично строим систему нормальных уравнений для определения коэффициентов

Следовательно,

тогда второе уравнение примет вид

Приведенная форма модели имеет вид

Из приведенной формы модели определяем коэффициенты структурной модели:

Итак, структурная форма модели имеет вид

Возможно, вас также заинтересует эта ссылка:

• Решение задач

Задача 8

Имеются следующие данные о величине дохода на одного члена семьи и расхода на товар (табл. 4.3).

Таблица 4.3

Требуется:

1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда.

2. Перечислить основные пути устранения тенденции для построения модели спроса на товар в зависимости от дохода.

3. Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов.

4. Пояснить экономический смысл коэффициента регрессии.

5. Построить линейную модель спроса на товар включив в нее фактор времени. Интерпретировать полученные параметры.

Решение:

1. Обозначим расходы на товар через а доходы одного члена семьи — через Ежегодные абсолютные приросты определяются по формулам

Расчеты можно оформить в виде таблицы (табл. 4.4). Таблица 4.4

2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. если ряды динамики характеризуются линейной тенденцией.

Другой возможный путь учета тенденции при построении моделей — найти по каждому ряду уравнение тренда:

и отклонения от него:

Далее модель строится по отклонениям от тренда:

При построении эконометрических моделей чаще используется другой путь учета тенденции — включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т.е.

3. Модель имеет вид

Для определения параметров применяется МНК. Система нормальных уравнений следующая:

Применительно к нашим данным имеем

Решая эту систему, получим:

откуда модель имеет вид

4. Коэффициент регрессии руб. Он означает, что с ростом прироста душевого дохода на 1%-ный пункт расходы на товар увеличиваются со средним ускорением, равным 0,565 руб.

5. Модель имеет вид

Применяя МНК, получим систему нормальных уравнений:

Расчеты оформим в виде табл. 4.5. Таблица 4.5

Система уравнений примет вид

Решая ее, получим

Уравнение регрессии имеет вид

Параметр фиксирует силу связи Его величина означает, что с ростом дохода на одного члена семьи на 1%-ный пункт при условии неизменной тенденции расходы на товар возрастают в среднем на 0,322 руб. Параметр характеризует среднегодовой абсолютный прирост расходов на товар под воздействием прочих факторов при условии неизменного дохода.

Задача 9

По данным за 30 месяцев некоторого временного ряда были получены значения коэффициентов автокорреляции уровней:

— коэффициенты автокорреляции порядка

Требуется:

1. Охарактеризовать структуру этого ряда, используя графическое изображение.

2. Для прогнозирования значений в будущие периоды предполагается построить уравнение авторегрессии. Выбрать наилучшее уравнение, обосновать выбор. Указать общий вид этого уравнения.

Решение:

1. Так как значения всех коэффициентов автокорреляции достаточно высокие, ряд содержит тенденцию. Поскольку наибольшее абсолютное значение имеет коэффициент автокорреляции 4-го порядка ряд содержит периодические колебания, цикл этих колебаний равен 4.

График этого ряда можно представить на рис. 4.1.

2. Наиболее целесообразно построение уравнения авторегрессии:

так как значение свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 4 месяца.

Кроме того, возможно построение и множественного уравнения авторегрессии так как

Сравнить полученные уравнения и выбрать наилучшее решение можно с помощью скорректированного коэффициента детерминации.

Реализация типовых задач на компьютере

Решение с использованием ППП MS Excel

1. Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда -ЛГРФПРИБЛ. Порядок вычисления был рассмотрен в 1-м разделе практикума. В качестве зависимой переменной в данном примере

выступает время Приведем результаты вычисления

функций ЛИНЕЙН и ЛГРФПРИБЛ (рис. 4.2 и 4.3).

Запишем уравнения линейного и экспоненциального тренда, используя данные рис. 4.2 и 4.3:

2. Построение графиков осуществляется с помощью Мастера диаграмм.

Порядок построения следующий:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) активизируйте Мастер диаграмм любым из следующих способов:

а) в главном меню выберите Вставка/Диаграмма;

б) на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;

3) в окне Тип выберите График (рис. 4.4); вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее;

4) заполните диапазон данных, как показано на рис. 4.5. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее;

5) заполните параметры диаграммы на разных закладках (рис. 4.6): названия диаграммы и осей, значения осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкните по кнопке Далее;

6) Укажите место размещения диаграммы на отдельном или имеющимся листе(рис. 4.7) Щелкните по кнопке далее. Готовая диаграмма, отражающая динамику уровней изучаемого ряда, представлена на рис 4.8

В ППП MS Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:

1) выделите область построения диаграммы; в главном меню выберите Диаграмма/Добавить линию тренда;

2) в появившемся диалоговом окне (рис. 4.9) выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома, для скользящего среднего — количество точек усреднения.

В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение среднеквадратического отклонения, установив соответствующие флажки на закладке Параметры (рис. 4.10). Щелкните по кнопке ОК.

На рис 4.11-4.15 представлены различные виды трендов, описывающие исходные данные задачи

3. Сравним значения по разным уравнениям трендов:

Исходные данные лучше всего описывает полином 6-й степени. Следовательно, в рассматриваемом примере для расчета прогнозных значений следует использовать полиномиальное уравнение.

Возможно, вас также заинтересует эта ссылка:

1. Модели временных рядов

1. Основные понятия
   и показатели

Временные ряды
(ряды динамики, хронологические ряды,
Time Series) — это ряды чисел, показывающие
изменение изучаемого явления во времени.

Временные ряды
бывают интервальными и моментными.

В интервальных
рядах приводятся уровни явления за
последовательные интервалы времени.

Пример интервального
ряда дается ниже.

Таблица 4.1. Добыча
угля в Ростовской области, млн. т

Год	Добыча угля, млн. т
1995	19,4
1996	16,7
1997	14,1
1998	10,9
1999	10,1

В моментных рядах
данные приводятся на последовательные
моменты времени.

Пример моментного
ряда:

Таблица 4.2.
Численность наличного населения
Ростовской области на начало года, тыс.
чел.

Год	1996	1997	1998	1999	2000
Наличное население, тыс. чел.		4420,0	4403,9	4384,2	4357,9

К числу показателей,
характеризующих временные ряды, относятся
следующие:

— средний уровень
ряда,

— абсолютные
приросты (цепные и базисные),

— темпы (коэффициенты)
роста (цепные и базисные),

— темпы (коэффициенты)
прироста (цепные и базисные),

— абсолютное
содержание одного процента прироста,

— средний абсолютный
прирост,

— средний темп
роста,

— средний темп
прироста²и др.

1. Анализ и
   прогнозирование временных рядов

Уровни временного
ряда формируются под влиянием действия
множества факторов, часть из которых
определяет основную тенденцию развития
явления (тренд), а остальные – обусловливают
колебания уровней ряда вокруг линии
тренда. При этом колеблемость вокруг
линии тренда также можно разложить на
части: некую систематическую составляющую
(например, сезонные колебания) и случайную
колеблемость.

Таким образом,
динамика уровней ряда включает три
составляющих:

— основную тенденцию
развития (тренд);

— систематическую
колеблемость вокруг линии тренда;

— случайную
(несистематическую) колеблемость вокруг
линии тренда.

4.2.1. Анализ и прогнозирование временных рядов с трендом

К числу приемов
выявления основной тенденции временных
рядов можно отнести укрупнение интервалов,
сглаживание и аналитическое выравнивание.

Укрупнение
интервалов представляет собой замену
данных, имеющих отношение к мелким
временным периодам, данными по более
крупным периодам. Например, можно
заменить суточные данные недельными
или декадными, декадные – месячными,
месячные – квартальными и т.д.

Например, объем
продажи валюты на биржах меняется изо
дня в день под влиянием самых разнообразных
факторов, включая и чисто случайные.
Относительно меньшую колеблемость
обнаруживают недельные объемы продажи
валюты, еще меньшую — месячные и далее
— квартальные. Объединив мелкие интервалы
в крупные, мы погасим известную часть
случайной колеблемости и получим
возможность более отчетливо показать
основную тенденцию развития событий
на валютных биржах.

Недостатком этого
приема является то, что с переходом к
более крупным интервалам длина ряда
сильно укорачивается. Поэтому, имея
очень короткий ряд, выявить с его помощью
какую-либо тенденцию развития невозможно.
Таким образом, применение этого приема
приходится ограничить лишь теми случаями,
когда исходный временной ряд достаточно
длинен.

Сглаживание
временных рядов осуществляется с
помощью скользящей средней. Эта средняя
исчисляется для нескольких уровней,
входящих в интервал сглаживания, и затем
(при центрировании) относится к середине
этого интервала.

Расчет скользящей
средней по данным примера о динамике
добычи угля в Ростовской области (таблица
4.1.) имеет следующий вид:

Таблица 4.3.
Сглаживание ряда добычи угля в Ростовской
области с помощью скользящей средней

Год	Добыча угля
Фактические данные	Данные, сглаженные с помощью скользящей средней
1995	19,4	—
1996	16,7	(19,4+16,7+14,1):3 = 16,73
1997	14,1	(16,7+14,1+10,9):3 = 13,9
1998	10,9	(14,1+10,9+10,1):3 = 11,97
1999	10,1	—

В общем виде расчет
скользящей средней для i-того периода
можно записать так:

(4.1)

Эта формула верна
для сглаживания по трем точкам.

Для для сглаживания
по пяти точкам она примет следующий
вид:

Сглаживание
методом скользящей средней можно
проводить по любому числу членов т,
но удобнее, если т
— нечетное
число, так как в этом случае скользящая
средняя сразу относится к конкретной
временной точке — середине (центру)
интервала. Если же т
— четное,
то скользящая средняя относится к
промежутку между временными точками:
например, при сглаживании по четырем
членам средняя из первых четырех уровней
будет находиться между второй и третьей
датой, следующая средняя — между третьей
и четвертой и т.д. Тогда, чтобы сглаженные
уровни относились непосредственно к
конкретным временным точкам (датам), из
каждой пары смежных промежуточных
значений скользящих средних находят
среднюю арифметическую, которую и
относят к определенной дате (периоду).
Такой прием называется центрированием.

Недостатком
метода скользящей средней является то,
что сглаженный ряд «укорачивается» по
сравнению с фактическим с двух концов:
при нечетном т
на (m
— 1)/2 с каждого конца, а при четном — на
т/2
с каждого конца.

Применяя этот
метод, надо помнить, что он сглаживает
(устраняет) лишь случайные колебания.

Если же, например,
ряд содержит сезонную волну, она
сохранится и после сглаживания методом
скользящей средней.

Кроме того, этот
метод сглаживания, как и укрупнение
интервалов, является механическим,
эмпирическим и не позволяет выразить
общую тенденцию изменения уровней в
виде математической модели.

Аналитическое
выравнивание. Более
совершенный метод обработки временных
рядов в целях устранения случайных
колебаний и выявления тренда —
выравнивание уровней ряда по аналитическим
формулам (аналитическое выравнивание).
Суть аналитического выравнивания
заключается в замене эмпирических
(фактических) уровней y
теоретическими
,
которые
рассчитаны по определенному уравнению,
принятому за математическую модель
тренда, где теоретические уровни
рассматриваются как функция времени:

.

При
этом каждый фактический уровень y
рассматривается как сумма двух
составляющих:
,
где
—
систематическая составляющая, отражающая
тренд и выраженная определенным
уравнением, а
—
случайная величина, вызывающая колебания
уровней вокруг тренда.

Задача аналитического
выравнивания сводится к следующему:

• определение
  на основе фактических данных вида
  (формы) гипотетической функции
  ,
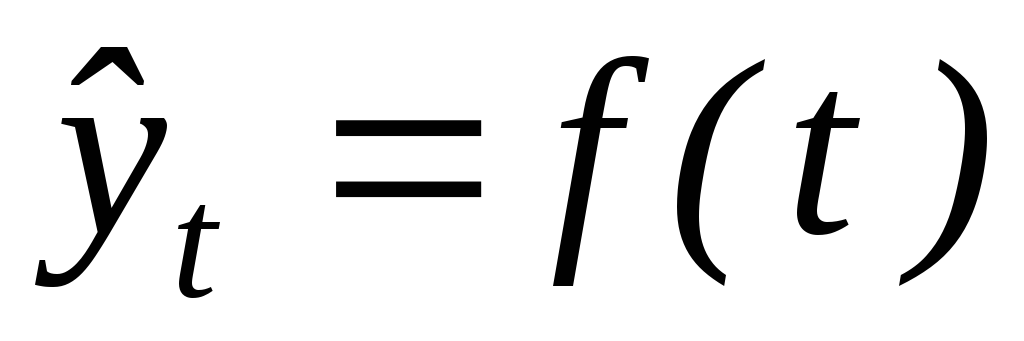  способной наиболее адекватно отразить
  тенденцию развития исследуемого
  показателя;

• нахождение по
  эмпирическим данным параметров указанной
  функции (уравнения);

• расчет по найденному
  уравнению теоретических (выравненных)
  уровней.

Наиболее простые
модели аналитического выравнивания:

—
линейная:
;

—
показательная:
;

—
экспоненциальная: ;

—
гиперболическая:
;

—
парабола 2-го порядка:

и
др.

Несложно
заметить, что в качестве объясняющей
переменной в трендовых уравнениях
регрессии выступает фактор времени t.

Выбор аналитической
функции для выравнивания временного
ряда осуществляется, как правило, на
основании графического изображения
эмпирических данных, дополняемого
содержательным анализом особенностей
развития исследуемого показателя
(явления). Вспомогательную роль при
выборе аналитической функции играют
механические приемы сглаживания
(укрупнение интервалов и метод скользящей
средней). Частично устраняя случайные
колебания, они помогают более точно
определить тренд и выбрать адекватную
модель для аналитического выравнивания.

Существует ряд
рекомендаций для выбора аналитической
функции:

1.
Выравнивание по прямой (линейной) функции
эффективно для рядов, уровни которых
изменяются примерно в арифметической
прогрессии, т.е. когда первые разности
уровней (абсолютные приросты)
примерно постоянны.

2.
Если примерно постоянны вторые разности
уровней (ускорения), то такое развитие
хорошо описывается параболой 2-го порядка
.
Если постоянны п-е
разности уровней, можно использовать
параболу п-го
порядка ,
позволяющую
«улавливать» перегибы, смену направлений
изменения уровней. Парабола 2-го порядка
отражает развитие с ускоренным или
замедленным изменением уровней ряда.

3.
Если при последовательном расположении
t
(меняющемся в арифметической прогрессии)
значения уровней меняются в геометрической
прогрессии, т.е. цепные коэффициенты
роста примерно постоянны, то такое
развитие можно отразить показательной
или экспоненциальной функцией.

4. Если обнаружено
замедленное снижение уровней ряда,
которые по логике не могут снизиться
до нуля, для описания характера тренда
выбирают гиперболу и т.д.

Рассмотрим выбор
формы уравнения тренда на следующем
примере:

Таблица 4.4. Динамика
среднегодовой численности
промышленно-производственного персонала
в промышленности в Ростовской области
(тыс.чел.)

Годы	Среднегодовая численность промышленно-производственного персонала в промышленности
1993	569,7
1994	516,4
1995	472,0
1996	431,0
1997	395,8
1998	365,1

Расчитаем первые
и вторые разности, а также коэффициенты
роста.

	yt
1993	569,7
1994	516,4	-53,3		0,906
1995	472,0	-44,4	8,9	0,914
1996	431,0	-41,0	3,4	0,913
1997	395,8	-35,2	5,8	0,918
1998	365,1	-30,7	4,5	0,922

Наибольшей
стабильностью отличаются коэффициенты
роста, поэтому, видимо, для описания
тренда следует выбрать либо показательную,
либо экспоненциальную функцию.

К аналогичным
выводам можно прийти, анализируя график
динамики среднегодовой численности
ППП в Ростовской области (рис. 12).

Судя по графику
динамики среднегодовой численности
ППП в Ростовской области, для прогноза
лучше всего использовать показательную,
экпоненциальную либо линейную функцию.

Рис.12. Динамика
среднегодовой численности ППП в
Ростовской области

Несмотря на эти
выводы, рассмотрим механизм расчета
параметров всех вышеперечисленных
моделей.

Параметры искомых
уравнений при аналитическом выравнивании
могут быть определены различными
способами. Чаще всего для этого
используется метод наименьших квадратов.

В частности для
нахождения параметров уравнения
прямойможет быть использован следующий
алгоритм:

(4.2)

Если периоды или
моменты времени пронумеровать так,
чтобы получилось
,
то вышеприведенные алгоритмы существенно
упростятся и примут следующий вид:

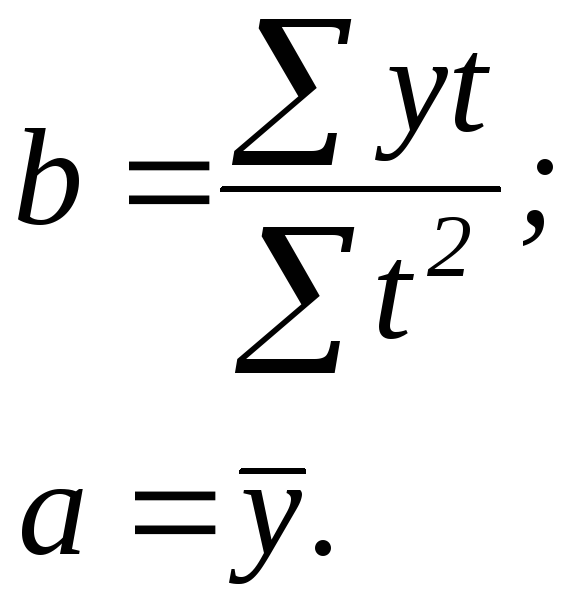(4.3)

В нашем примере –
6 уровней ряда. Для того, чтобы сумма
порядковых номеров уровней ряда была
равна нулю, нулевым моментом следует
принять промежуток между 1995 и 1996 гг.
Тогда порядковый номер 1993 года будет
равен -2,5, 1994 — -1,5 и т.д. Их сумма равна
нулю, что в дальнейшем упростит расчеты.
Для их осуществления составим рабочую
таблицу 4.5:

Таблица 4.5.

Годы	T	y	Yt	t2
1993	-2,5	569,7	-1424,25	6,25
1994	-1,5	516,4	-774,6	2,25
1995	-0,5	472,0	-236	0,25
1996	0,5	431,0	215,5	0,25
1997	1,5	395,8	593,7	2,25
1998	2,5	365,1	912,75	6,25
Суммы	0	2750	-712,9	17,5

Отсюда:

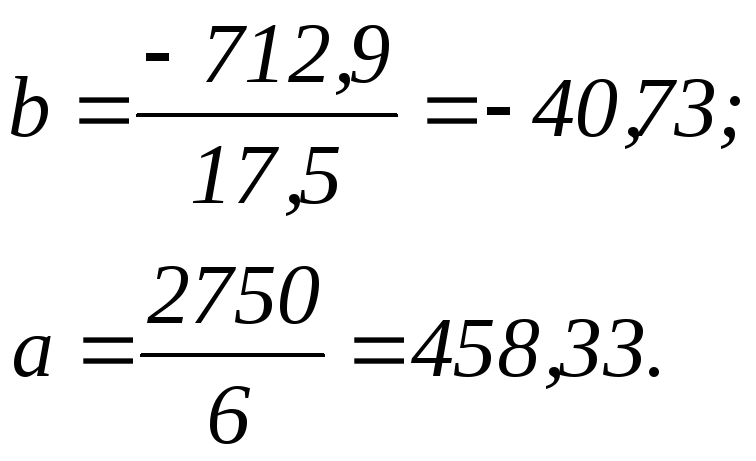
При таких параметрах
уравнение получит следующий вид:

Дадим интерпретацию
параметров тренда.

Коэффициент
регрессии (b)
в линейном тренде показывает средний
за период цепной абсолютный прирост
уровней ряда. В нашем примере b = -40,73,
следовательно среднегодовая численность
ППП в среднем за год снижается на 40,73
тыс.чел. Свободный член (а)
в линейном тренде выражает начальный
уровень ряда в момент (период времени)
t
= 0. В нашей нумерации t
= 0 приходится на период времени между
1996 и 1997 гг., что несколько затрудняет
его интерпретацию. В нашем случае а
= 458,33 тыс.чел. – это средняя численность
ППП за вторую половину 1996 и первую
половину 1997 гг.

С помощью этого
уравнения найдем выравненные уровни и
рассчитаем стандартную ошибку уравнения
регрессии S_yx.

.

Расчеты проведем
в рабочей таблице 4.6:

Таблица 4.6.

	T
1994	-2,5	569,7	560,1762	9,5238	90,7029
1995	-1,5	516,4	519,4390	-3,0390	9,2358
1996	-0,5	472,0	478,7019	-6,7019	44,9155
1997	0,5	431,0	437,9648	-6,9648	48,5079
1998	1,5	395,8	397,2276	-1,4276	2,0381
1999	2,5	365,1	356,4905	8,6095	74,1239
Суммы	0	2750	2750	0	269,5242

Чем меньше
стандартная ошибка, тем лучше подобрана
модель тренда. Сравнение S_yx
, рассчитанных для различных
моделей дает возможность выбрать лучшую
из них.

Рассмотрим
использование для аналитического
выравнивания других (нелинейных) моделей.

Для определения
параметров нелинейных уравнений
регрессии необходимо привести их к
линейному виду. Рассмотрим алгоритмы
линеаризации некоторыхиз них.

Уравнение
гиперболы:
.

Чтобы привести к
линейному виду уравнение гиперболы,
необходимо ввести переменную
.
Тогда уравнение примет линейный вид:
и
его параметры можно рассчитывать обычным
МНК.

Расчет по данным
нашего примера даст следующие результаты
(при условии, что
):

b= -26,5222;a= 458,3333;S_yx= 75,5534.

При таких параметрах
уравнение получит следующий вид:

.

Учитывая, что S_yx– намного больше, чем в уравнении прямой,
можно сделать вывод, модель гиперболы
хуже описывает динамику численности
ППП в Ростовской области.

Уравнение
параболы:
.

Аналогичный прием
используется и при определении параметров
уравнения параболы. Приняв
,
получим:
—
линейное уравнение множественной
регрессии.

Расчет по данным
нашего примера даст следующие результаты
(при условии, что
):

b₁= -40,7371;b₂= 2,6750;a= 450,5313;S_yx= 0,8909.

При таких параметрах
уравнение получит следующий вид:

.

Как мы видим, в
данном случае S_yx– меньше, чем в уравнении прямой, т.е.
парабола 2-го порядка лучше других
моделей описывает динамику численности
ППП в Ростовской области.

Показательная
функция:
.

Линеаризация
показательной функции достигается
путем ее логарифмирования:

.

Это – линейное
уравнение. Правда, при определении его
параметров мы получим десятичные
логарифмы aиb.

Расчет по данным
нашего примера даст следующие результаты
(при условии, что
):

lgb= -0,0386;lga= 2,6562;S_yx= 2,7977.

При таких параметрах
уравнение получит следующий вид:

.

Найдем aиb.

b
= 10^-0,0386 = 0,915.

Данная величина
является среднегодовым коэффициентом
роста. В нашем примере его величина
указывает на то, что среднегодовая
численность ППП в Ростовской области
снижалась на 8,5 % в среднем за год.

a
= 10^2,6562 = 453,1062.

Таким образом,
искомое уравнение будет иметь такой
вид:

.

Судя по величине
стандартной ошибки S_yx= 2,7977, показательная функция лучше, чем
линейная, но хуже, чем параболическая
описывает динамику ППП в Ростовской
области.

Экспоненциальная
функция:
.

В данным случае
для линеаризации лучше использовать
натуральные логарифмы:

.

Снова имеем линейное
уравнение.

Расчет по данным
нашего примера даст следующие результаты
(при условии, что
):

b= -0,089;lna= 6,116;S_yx= 2,7573.

При таких параметрах
уравнение получит следующий вид:

.

Найдем
a:

a =
e^6,116 =
453,0489.

b
= -0,089. Данная величина является
среднегодовым коэффициентом прироста.
В нашем примере его величина указывает
на то, что среднегодовая численность
ППП в Ростовской области снижалась на
8,9 % в среднем за год.

Таким образом,
искомое уравнение будет иметь такой
вид:

.

Судя по величине
стандартной ошибки S_yx= 2,7573, экспоненциальная функция лучше,
чем линейная, но хуже, чем параболическая
описывает динамику ППП в Ростовской
области.

Разумеется, решение
относительно функциональной формы
уравнения тренда принимаются, не только
исходя из величины стандартной ощибки
уравнения тренда. Необходимо, принимать
во внимание цели аналитического
выравнивания, оценивать значимость
уравнения регрессии в целом, а также
его параметров.

Так, в нашем примере
наименьшую стандартную ошибку имеет
уравнени параболы. Однако его лучше
всего использовать для интерполяции
(расчета промежуточных значений).
Очевидно, что прогноз (экстраполяцию)
с помощью уравнения параболы делать
нельзя.

Так как наименьшую
и примерно одинаковую стандартную
ошибку имеют показательная и
экспоненциальная функции, для
прогнозирования, видимо, лучше использовать
одну из них.

Таким образом, мы
пришли к тем же выводам, что и в начале
анализа данного временного ряда.

Несмотря на все
вышеприведенные соображения, необходимо
проверять значимость трендового
уравнения регрессии. Алгоритм проверки
ничем не отличается от проверки значимости
любого другого уравненния регрессии.

В качестве критерия
проверки статистической гипотезы о
значимости уравнения регрессии
используется критерий F– Фишера-Снедекора.

Несложно убедиться
в том, что в нашем примере на уровне
значимости α = 0,05 можно доверять всем
уравнениям за исключением уравнения
гиперболы.

Прогнозирование
временных рядов с трендом.

Если не учитывать
систематическую колеблемость вокруг
линии тренда (например, сезонную
колеблемость), то прогнозирование
сводится к подстановке в уравнения
регрессии значений t,
относящихся к соответствующему периоду
упреждения.

Прогноз бывает
точечным и интервальным.

Точечный
прогноз по уравнению тренда — это
расчетное значение переменной y,
полученное путем подстановки в уравнение
тренда соответствующих значений t.

По сравнению с
точечным значительно большую практическую
ценность имеет интервальный прогноз,
позволяющий с заданной надежностью
(доверительной вероятностью) γопределить границы интервала, в которых
будет находиться уровень изучаемого
призака в прогнозируемый период времени.
Надежность точечного прогноза равна
нулю.

Интервальный
прогноз определяется двойным неравенством:

,
(4.6)

где
-прогноз
значения переменнойy
на момент (период) времени t;

—
точечная оценка значения переменной y
на момент (период) времени t;

—
предельная ошибка прогноза.

Предельная ошибка
прогноза рассчитывается по формуле:

,
(4.7)

где
— табличное значение t — критерия Стьюдента
для уровня значимости α = 1 — γ и числа
степеней свободы (k
= n — 2);

—
стандартная ошибка точечного прогноза,
которая, в свою очередь, рассчитывается
по формуле:

,
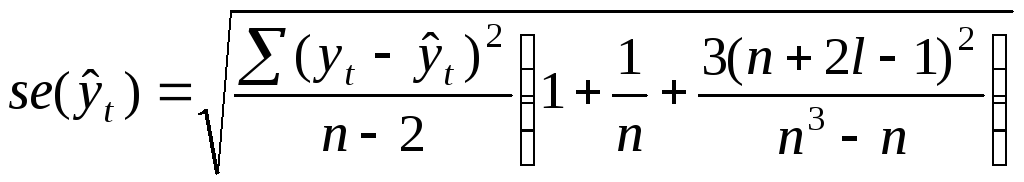(4.8)

где
— длина периода упреждения (срок прогноза).

Рассмотрим
использование для прогнозирования
линейного уравнения регрессии в примере
о динамике среднегодовой численности
ППП в Ростовской области.

Дадим точечный и
интервальный прогноз численности ППП
на 1999 год.

В
нашей нумерации 1999 год соответствует
моменту времени t
= 3,5. Линейное уравнение динамики
среднегодовой численности ППП в
Ростовской области имеет вид:

Отсюда,

Следовательно,
точечный прогноз среднегодовой
численности ППП в Ростовской области
на 1999 год составляет 315,75 тыс.чел.

Определим границы
доверительного интервала, в котором с
заданной надежностью γ будет находится
среднегодовая численности ППП в
Ростовской области в 1999 году.

Общепринятый в
экономике уровень надежности γ = 1 — α =
1 — 0,05 = 0,95.

Найдем стандартную
ошибку прогноза:

.

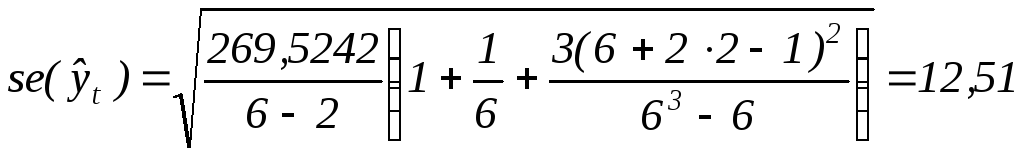Табличное
значение t — критерия Стьюдента для
уровня значимости α = 0,05 и числа степеней
свободы k = 6 – 2 = 4 составляет 2,78, т.е.
=2,78.

Отсюда,

Таким образом,

;

.

С вероятностью
0,95 можно ожидать, что в 1999 году среднегодовая
численность ППП в Ростовской области
будут находиться в пределах от 280,96 до
350,54 тыс. чел.

Обратите внимание
на то, что приведенные формулы верны
только для уравнения парной регрессии,
линейной по параметрам.

Эконометрика

Вариант 1

Задание 1. Модель парной линейной регрессии.

Имеются данные о размере среднемесячных доходов в разных группах семей

Номер группы	Среднедушевой денежный доход в месяц, руб., X	Доля оплаты труда в структуре доходов семьи, %, Y
1	79,8	64,2
2	152,1	66,1
3	199,3	69,0
4	240,8	70,6
5	282,4	72,4
6	301,8	74,3
7	385,3	76,0
8	457,8	77,1
9	577,4	78,4

Задания:

1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы

2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.

3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.

4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.

Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.

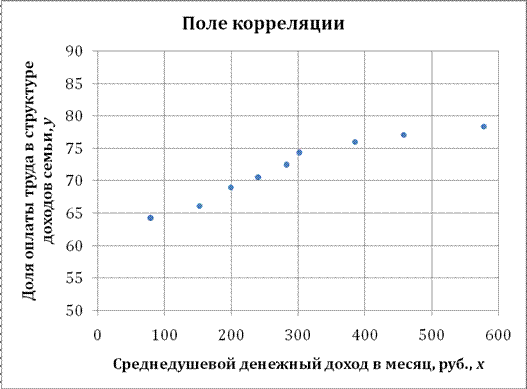
Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .

Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.

№ п/п	X	Y	X×Y	X2	Y2
1	79,8	64,2	5123,16	6368,04	4121,64
2	152,1	66,1	10053,81	23134,41	4369,21
3	199,3	69,0	13751,70	39720,49	4761,00
4	240,8	70,6	17000,48	57984,64	4984,36
5	282,4	72,4	20445,76	79749,76	5241,76
6	301,8	74,3	22423,74	91083,24	5520,49
7	385,3	76,0	29282,80	148456,09	5776,00
8	457,8	77,1	35296,38	209580,84	5944,41
9	577,4	78,4	45268,16	333390,76	6146,56
S	2676,7	648,1	198645,99	989468,27	46865,43
Среднее	297,41	72,01	22071,78	109940,92	5207,27

Вычислим коэффициент корреляции. Используем следующую формулу:

= 0,9568.

Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.

Среднюю ошибку коэффициента корреляции определим по формуле:

= 0,032.

Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.

TТабл(0,05; 7) = 2,36.

Запишем доверительный интервал для коэффициента корреляции.

Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.

Вычислим параметры уравнения регрессии.

= 0,03.

= 72,01 – 0,03×297,41 = 63,09.

Получим следующее уравнение: .

Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

= 23,04.

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.

Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.

Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:

Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.

№ п/п	X	Y
1	79,8	64,2	65,48	1,6384	47354,1
2	152,1	66,1	67,65	2,4025	21115,0
3	199,3	69,0	69,07	0,0049	9625,6
4	240,8	70,6	70,31	0,0841	3204,7
5	282,4	72,4	71,56	0,7056	225,3
6	301,8	74,3	72,14	4,6656	19,3
7	385,3	76,0	74,65	1,8225	7724,7
8	457,8	77,1	76,82	0,0784	25725,0
9	577,4	78,4	80,41	4,0401	78394,4
S	2676,7	648,1	648,09	15,4421	193388,1

Вычислим стандартные ошибки коэффициентов уравнения.

= 1,2.

= 0,003.

Вычислим T-статистики.

Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и , т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.

Сделаем рисунок.

Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.

Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

= 75,81.

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.

Fтабл(0,05; 1; 7) = 5,59.

Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.

Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.

XP = 297,41 × 1,11 = 330,1.

Вычислим прогнозное значение Yp с помощью уравнения регрессии.

» 73%.

Доверительный интервал прогноза имеет вид

(УP – Tкр×My, УP + Tкр×My),

Где , M = 2 – число параметров уравнения.

= 1,695 » 1,7.

Запишем доверительный интервал прогноза:

Þ

Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.

Задание 2. Модель парной нелинейной регрессии.

По территориям Центрального района известны данные за 1995 г.

Район	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y
Брянская обл.	178	240
Владимирская обл.	202	226
Ивановская обл.	197	221
Калужская обл.	201	226
Костромская обл.	189	220
Орловская обл.	166	232
Рязанская обл.	199	215
Смоленская обл.	180	220
Тверская обл.	181	222
Тульская обл.	186	231
Ярославская обл.	250	229

Задания:

1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной () парной регрессии. Сделать рисунки.

2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.

3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии

4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.

Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.

Получим следующий рисунок.

По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.

Построение полулогарифмической модели регрессии.

Уравнение логарифмической кривой: .

Обозначим:

Получим линейное уравнение регрессии:

Y = A + B×X.

Произведем линеаризацию модели путем замены . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Xy	X2	Y2				Ai
1	178	240	5,1818	1243,63	26,85	57600	226,40	206,314	184,904	6,006
2	202	226	5,3083	1199,67	28,18	51076	225,17	0,132	0,694	0,370
3	197	221	5,2832	1167,59	27,91	48841	225,41	21,496	19,464	1,957
4	201	226	5,3033	1198,55	28,13	51076	225,22	0,132	0,615	0,348
5	189	220	5,2417	1153,18	27,48	48400	225,82	31,769	33,833	2,576
6	166	232	5,1120	1185,98	26,13	53824	227,08	40,496	24,172	2,165
7	199	215	5,2933	1138,06	28,02	46225	225,31	113,132	106,362	4,577
8	180	220	5,1930	1142,45	26,97	48400	226,29	31,769	39,601	2,781
9	181	222	5,1985	1154,07	27,02	49284	226,24	13,223	17,968	1,874
10	186	231	5,2257	1207,15	27,31	53361	225,97	28,769	25,273	2,225
11	250	229	5,5215	1264,41	30,49	52441	223,09	11,314	34,980	2,651
Итого	2129	2482	57,862	13054,74	304,48	560528	2482,00	498,545	487,867	27,530
Среднее	193,5	225,6	5,260	1186,79	27,68	50957,091	225,636	45,322	44,352	2,503

= -9,76.

= 225,6 – (-9,76)×5,26 = 276,99.

Уравнение модели имеет вид:

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Рассчитаем средний коэффициент эластичности по формуле:

= -0,04%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид: .

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

.

Произведем линеаризацию модели путем замены и . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Y = ln(Y)	XY	X2	Y2					Ai
1	178	240	5,1818	5,4806	28,3995	26,851	30,037	226,3	206,3	188,391	241,661	6,07
2	202	226	5,3083	5,4205	28,7737	28,178	29,382	225,1	0,132	0,835	71,479	0,406
3	197	221	5,2832	5,3982	28,5196	27,912	29,140	225,3	21,496	18,671	11,934	1,918
4	201	226	5,3033	5,4205	28,7467	28,125	29,382	225,1	0,132	0,753	55,570	0,385
5	189	220	5,2417	5,3936	28,2720	27,476	29,091	225,7	31,769	32,607	20,661	2,530
6	166	232	5,1120	5,4467	27,8437	26,132	29,667	226,9	40,496	25,675	758,752	2,233
7	199	215	5,2933	5,3706	28,4284	28,019	28,844	225,2	113,132	104,576	29,752	4,540
8	180	220	5,1930	5,3936	28,0089	26,967	29,091	226,2	31,769	38,059	183,479	2,728
9	181	222	5,1985	5,4027	28,0858	27,024	29,189	226,1	13,223	16,950	157,388	1,821
10	186	231	5,2257	5,4424	28,4407	27,308	29,620	225,9	28,769	26,413	56,934	2,275
11	250	229	5,5215	5,4337	30,0021	30,487	29,525	223,1	11,314	34,846	3187,116	2,646
Итого	2129	2482	57,862	59,603	313,521	304,479	322,969	2480,927	498,545	487,777	4774,727	27,548
Среднее	193,5	225,6	5,260	5,418	28,502	27,680	29,361	225,539	45,322	44,343	434,066	2,504

С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.

= -0,042.

= 5,418 – 0,959×5,26 = 5,637.

Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.

A = eA = e5,637 = 280,76

Получим уравнение степенной модели регрессии: .

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Для степенной модели средний коэффициент эластичности равен коэффициенту B.

= -0,042%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Сводная таблица вычислений

Параметры	Модель
Полулогарифмическая	Степенная
Уравнение связи
Индекс корреляции	0,1464	0,147
Коэффициент детерминации	0,021	0,021
Средняя ошибка аппроксимации, %	2,5	2,5

Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.

Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.

Прогнозное значение составит:

= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:

= 224,6 тыс. р.

Определим доверительный интервал прогноза для уровня значимости a = 0,05.

Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

, где

Получаем: = 7,55.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.

= 14,8.

Запишем доверительный интервал прогноза.

= 224,6 – 14,8 = 209,8 тыс. р.

= 224,6 + 14,8 = 239,4 тыс. р.

Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.

Задание 3. Моделирование временных рядов

Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.

Номер квартала	Товарооборот % к предыдущему периоду	Номер квартала	Товарооборот % к предыдущему периоду
1	100	11	98,8
2	93,9	12	101,9
3	96,5	13	113,1
4	101,8	14	98,4
5	107,8	15	97,3
6	96,3	16	112,1
7	95,7	17	97,6
8	98,2	18	93,7
9	104	19	114,3
10	99	20	108,4

Задания:

1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.

2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.

3. Рассчитать трендовую компоненту временного ряда и построить его график

4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.

Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.

Построим мультипликативную модель временного ряда.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.

Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1)  Выравнивание исходного ряда методом скользящей средней.

2)  Расчет значений сезонной компоненты S.

3)  Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.

4)  Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.

5)  Расчет полученных по модели значений T×E.

6)  Расчет абсолютных и/или относительных ошибок.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).

Таблица 2.1

№ месяца, T	Товарооборот, Yi	Итого за четыре месяца	Скользящая средняя за четыре месяца	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	100,0	–	–	–	–
2	93,9	392	98	–	–
3	96,5	400	100	99	0,975
4	101,8	402	100,5	100,25	1,015
5	107,8	402	100,5	100,5	1,073
6	96,3	398	99,5	100	0,963
7	95,7	394	98,5	99	0,967
8	98,2	397	99,25	98,875	0,993
9	104,0	400	100	99,625	1,044
10	99,0	404	101	100,5	0,985
11	98,8	413	103,25	102,125	0,967
12	101,9	412	103	103,125	0,988
13	113,1	411	102,75	102,875	1,099
14	98,4	309	77,25	90	1,093
15	97,3	196	49	63,125	1,541
16	112,1	303	75,75	62,375	1,797
17	97,6	418	104,5	90,125	1,083
18	93,7	414	103,5	104	0,901
19	114,3	–	–	–	–
20	108,4	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Таблица 2.2

Показатели	Год	№ квартала, I
I	II	III	IV
	1	–	–	0,975	1,015
	2	1,073	0,963	0,967	0,993
	3	1,044	0,985	0,967	0,988
	4	1,099	1,093	1,541	1,797
	5	1,083	0,901	–	–
Всего за I-й квартал		4,299	3,942	4,45	4,793
Средняя оценка сезонной компоненты для I-го квартала,		0,860	0,788	0,890	0,959
Скорректированная сезонная компонента,		0,984	0,901	1,018	1,097

Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.

Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.

Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент K.

Проверяем условие: равенство 4 суммы значений сезонной компоненты:

0,984 + 0,901 + 1,018 + 1,097 = 4.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.

Таблица 2.3

T	Yt	St		T	T×S
1	2	3	4	5	6	7
1	100,0	0,984	101,6	100,02	98,42	1,016
2	93,9	0,901	104,2	100,19	90,27	1,040
3	96,5	1,018	94,8	100,36	102,17	0,945
4	101,8	1,097	92,8	100,53	110,28	0,923
5	107,8	0,984	109,6	100,7	99,09	1,088
6	96,3	0,901	106,9	100,87	90,88	1,060
7	95,7	1,018	94,0	101,04	102,86	0,930
8	98,2	1,097	89,5	101,21	111,03	0,884
9	104,0	0,984	105,7	101,38	99,76	1,043
10	99,0	0,901	109,9	101,55	91,50	1,082
11	98,8	1,018	97,1	101,72	103,55	0,954
12	101,9	1,097	92,9	101,89	111,77	0,912
13	113,1	0,984	114,9	102,06	100,43	1,126
14	98,4	0,901	109,2	102,23	92,11	1,068
15	97,3	1,018	95,6	102,4	104,24	0,933
16	112,1	1,097	102,2	102,57	112,52	0,996
17	97,6	0,984	99,2	102,74	101,10	0,965
18	93,7	0,901	104,0	102,91	92,72	1,011
19	114,3	1,018	112,3	103,08	104,94	1,089
20	108,4	1,097	98,8	103,25	113,27	0,957
Среднее	101,4					1,0011

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.

Таблица 2.4

	T		T2
	1	2	3	4	5	6	7
	1	101,6	1	101,6	2,5	1,58	2,0
	2	104,2	4	208,4	13,2	3,87	56,3
	3	94,8	9	284,4	32,1	5,88	24,0
	4	92,8	16	371,2	71,9	8,33	0,2
	5	109,6	25	548	75,9	8,08	41,0
	6	106,9	36	641,4	29,4	5,63	26,0
	7	94,0	49	658	51,3	7,48	32,5
	8	89,5	64	716	164,6	13,07	10,2
	9	105,7	81	951,3	18,0	4,08	6,8
	10	109,9	100	1099	56,3	7,58	5,8
	11	97,1	121	1068,1	22,6	4,81	6,8
	12	92,9	144	1114,8	97,4	9,69	0,3
	13	114,9	169	1493,7	160,5	11,20	136,9
	14	109,2	196	1528,8	39,6	6,39	9,0
	15	95,6	225	1434	48,2	7,13	16,8
	20	102,2	400	2044	0,2	0,37	114,5
	21	99,2	441	2083,2	12,3	3,59	14,4
	22	104,0	484	2288	1,0	1,05	59,3
	23	112,3	529	2582,9	87,6	8,19	166,4
	24	98,8	576	2371,2	23,7	4,49	49,0
Сумма	230	2035,2	3670	23588	1008,3	122,49	778,2
Среднее	11,5	101,8	183,5	1179,4	50,4	6,12	38,91

Вычислим параметры уравнения тренда.

= 0,17.

= 99,85.

В результате получим уравнение тренда:

T = 99,85 + 0,17×T.

Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.

Расчет ошибки в мультипликативной модели произведем по формуле:

Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).

Рассчитаем сумму квадратов абсолютных ошибок .

Используя 5-й столбец таблицы 2.4, получим:

= 7,099.

Рассчитаем среднюю относительную ошибку: .

Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.

< Предыдущая		Следующая >

« Назад

По территориям региона приводятся данные:

Таблица 1

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, ден.ед., x	Среднедневная заработная плата, ден.ед., y
1	85	139
2	86	148
3	87	142
4	79	154
5	106	164
6	113	195
7	67	139
8	98	164
9	79	152
10	87	162
11	86	152
12	117	173

Требуется:

1. Построить линейное уравнение парной регрессии y по x.

Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 2.

Таблица 2

№	x	y	y*x	x2	y2				ki
1	2	3	4	5	6	7	8	9	10
1	85	139	11815	7225	19321	151,80	-12,80	163,93	9,21
2	86	148	12728	7396	21904	152,69	-4,69	22,04	3,17
3	87	142	12354	7569	20164	153,59	-11,59	134,21	8,16
4	79	154	12166	6241	23716	146,46	7,54	56,88	4,90
5	106	164	17384	11236	26896	170,51	-6,51	42,40	3,97
6	113	195	22035	12769	38025	176,75	18,25	333,16	9,36
7	67	139	9313	4489	19321	135,77	3,23	10,45	2,33
8	98	164	16072	9604	26896	163,38	0,62	0,38	0,38
9	79	152	12008	6241	23104	146,46	5,54	30,71	3,65
10	87	162	14094	7569	26244	153,59	8,41	70,81	5,19
11	86	152	13072	7396	23104	152,69	-0,69	0,48	0,46
12	117	173	20241	13689	29929	180,31	-7,31	53,45	4,23
Итого	1090	1884	173282	101424	298624	1884	0,00	918,89	54,99
Среднее значение	90,83	157	14440,17	8452	24885,33	157	–	76,57	4,58
	14,19	15,37	–	–	–	–	–		–
	201,31	236,33	–	–	–	–	–		–

По формулам находим параметры регрессии

Получено уравнение регрессии:

.

Параметр регрессии позволяет сделать вывод, что с увеличением среднедушевого прожиточного минимума на 1 ден.ед. среднедневная заработная плата возрастает в среднем на 0,89 ден.ед.

После нахождения уравнения регрессии заполняем столбцы 7 – 10 таблицы 2.

2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.

Тесноту линейной связи оценит коэффициент корреляции:

Т.к. значение коэффициента корреляции больше 0,7, то это говорит о наличии весьма тесной линейной связи между признаками.

Коэффициент детерминации:

Это означает, что 67,6% вариации заработной платы (y) объясняется вариацией фактора x – среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации:

Качество построенной модели оценивается как хорошее, так как  не превышает 10%.

3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью -критерия Фишера и t-критерия Стьюдента.

Оценку статистической значимости уравнения регрессии в целом проведем с помощью F-критерия Фишера. Фактическое значение F-критерия по формуле составит

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k₁=1 и k₂=12-2=10 составляет F_табл=4,96. Так как , то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии и корреляции проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из параметров.

Табличное значение t-критерия для числа степеней свободы df=n-2=12-2=10 и уровня значимости 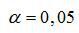 составит t_табл=2,23.

Определим стандартные ошибки   (остаточная дисперсия на одну степень свободы

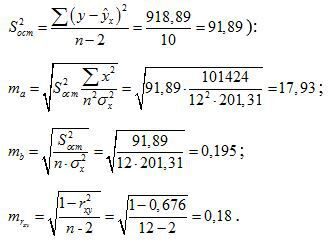
Тогда

Фактические значения t-статистики превосходят табличное значение:

Поэтому параметры a, b и r_xy не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регрессии a и b. Для этого определим предельную ошибку для каждого показателя:

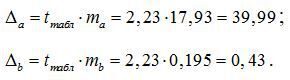
Доверительные интервалы

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью  параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.

4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от  среднего уровня.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:  ден.ед., тогда индивидуальное прогнозное значение заработной платы составит:  ден.ед.

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Ошибка прогноза составит:

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

Доверительный интервал прогноза:

Выполненный прогноз среднемесячной заработной платы является надежным () и находится в пределах от 140,16 ден.ед. до 185,0 ден.ед.

6. На одном графике отложить исходные данные и теоретическую прямую.

7. Проверить вычисления в MS Excel.

Выбираем Сервис®Анализ данных®Регрессия. Заполняем диалоговое окно ввода данных и параметров вывода. Получаем следующие результаты:

Откуда выписываем.

Уравнение регрессии:

Коэффициент корреляции:

Коэффициент детерминации:

Фактическое значение F-критерия Фишера:

Остаточная дисперсия на одну степень свободы:

Корень квадратный из остаточной дисперсии (стандартная ошибка):

Стандартные ошибки для параметров регрессии:

Фактические значения t-критерия Стьюдента:

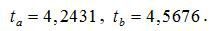
Доверительные интервалы:

Как видим, найдены все рассмотренные выше параметры и характеристики уравнения регрессии, за исключением средней ошибки аппроксимации (значение t-критерия Стьюдента для коэффициента корреляции совпадает с t_b). Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).

     
Далее определяется предельная ошибка прогноза по тренду:

. Предельная ошибка определяется с заданной вероятно-

стью оценки прогноза (Р(t)) и с учётом степеней
свободы изучаемой системы (n-m) по таблице значений t-критерия
Стьюдента, здесь n – число уровней ряда, а m – число параметров
тренда. Границы доверительного интервала прогноза по тренду определяются,
исходя из предельной ошибки прогноза:

     
Доверительный интервал прогноза говорит о том, что прогнозное значение
показателя, полученное по тренду, не выйдет за пределы границ доверительного
интервала с заданной вероятностью. Так как колеблемость существенно ухудшает
оценку прогноза, выполняют расчёт доверительного интервала прогноза с учётом
случайных колебаний уровней ряда. Средняя возможная ошибка прогноза с учётом
случайных колебаний рассчитывается по формуле:  Затем определяется предельная ошибка прогноза с учётом
случайных колебаний уровней ряда:  Далее
определяются границы доверительного интервала прогноза с учётом случайных
колебаний уровней ряда:

4.6. Изучение
сезонности в статистике внешней торговли.

Индексы сезонности. Учет сезонных колебаний при

прогнозировании

      Как известно, сезонностью называют процесс
изменения общей тенденции развития явлений и процессов под влиянием смены
времён года.Что касается внешней торговли, то сезонность наблюдается в товаропотоках
тех товаров, производство которых носит сезонный характер. Это, прежде всего,
некоторые виды продовольственных товаров и сельскохозяйственная продукция. Сезонность
наблюдается как в объёмах внешней торговли указанными товарами, так и в ценах
на них. Для изучения сезонности явления или процесса необходимо иметь временной
ряд изучаемого показателя внешней торговли либо по квартальным, либо по
ежемесячным данным за ряд лет. Прежде всего, выявляется тенденция динамики
рассматриваемого показателя в форме линейного или нелинейного уравнения тренда.
Далее определяются теоретические  (выровненные) уровни по полученному тренду  . В
фактических уровнях временного ряда содержатся
как случайные, так и сезонные колебания. В теоретических уровнях ряда какие либо
колебания отсутствуют. Отношения фактических и теоретических уровней отражают
суммарную величину колебаний уровней ряда и называются индексами колеблемости: