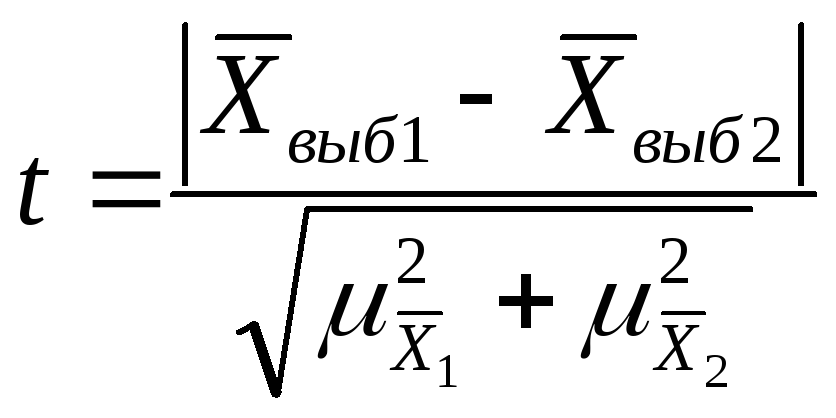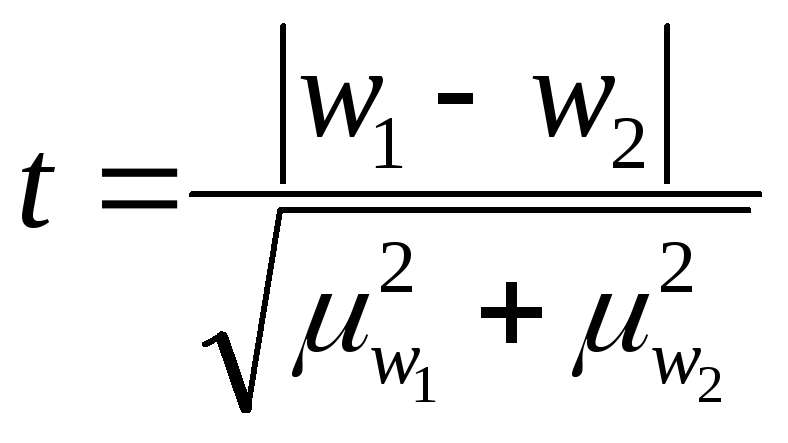Предельная ошибка выборки представляет собой - Ремонт и установка крупной бытовой техники

Определение ошибок выборки

Разность между показателями выборочной
и генеральной совокупностей называется
ошибкой выборки:

—
генеральное среднее;

—
выборочное среднее;

—
генеральная дисперсия;

—
выборочная дисперсия;

Ошибки выборки подразделяют на ошибки
регистрации и ошибки репрезентативности.

Ошибки регистрации возникают из-за
неправильных или неточных сведений.
Источником таких ошибок могут быть
непонимание вопроса, невнимательность
регистратора, пропуск или повторный
счет некоторых единиц совокупности.

Среди ошибок регистрации выделяют
систематические, т.е. обусловленные
причинами, действующими в каком-то одном
направлении и искажающие результаты
работы (округление цифр, тяготение к
полным десяткам и сотням и т.д.), и
случайные, проявляющиеся в различных
направлениях, уравновешивающих друг
друга и лишь изредка дающих заметный
суммарный итог.

Ошибки репрезентативности также могут
быть систематическими и случайными.

Изучение и измерение случайных ошибок
репрезентативности является основной
задачей выборочного метода.

При случайном и механическом отборах
средняя ошибка выборки для средней
величины определяется по формуле:

—
при повторном отборе;

—
при бесповторном отборе,

—
объем выборки,

—
объем генеральной совокупности.

На практике значение генеральных
параметров, как правило, не известно.
Поэтому их заменяют исправленными
выборочными характеристиками:

При

Формулы для расчета средней ошибки
выборочной доли имеют следующий вид:

—
при повтор. отборе;

—
при бесповторном отборе;

—
дисперсия доли;

Это так называемые средние или стандартные
ошибки.

Предельная ошибка выборки

представляет
собой t-кратную среднюю
ошибку.

Здесь t – коэффициент
доверия, который определяется по таблице
значений интегральной функции Лапласа
при заданной доверительной вероятности.

	0,683	0,954	0,997
t	1	2	3

Зная предельную ошибку можно определить
доверительные интервалы, в которых
находятся значения генеральных
параметров.

Пример:

Для определения среднего срока пользования
краткосрочным кредитом в банке была
произведена 5% механическая выборка, в
которую попали 200 счетов. По результатам
выборки установлено, что средний срок
пользования кредитом составляет 60 дней
при среднеквадратичном отклонении 20
дней.

В 8 счетах срок пользования кредитом
превышал 6 месяцев. Необходимо с
вероятностью 0,99 определить пределы, в
которых находится срок пользования
краткосрочным кредитом банка и доля
краткосрочных кредитов со сроком
пользования более полугода.

Решение:

Среднюю ошибку выборки определяют по
формуле для бесповторного отбора.

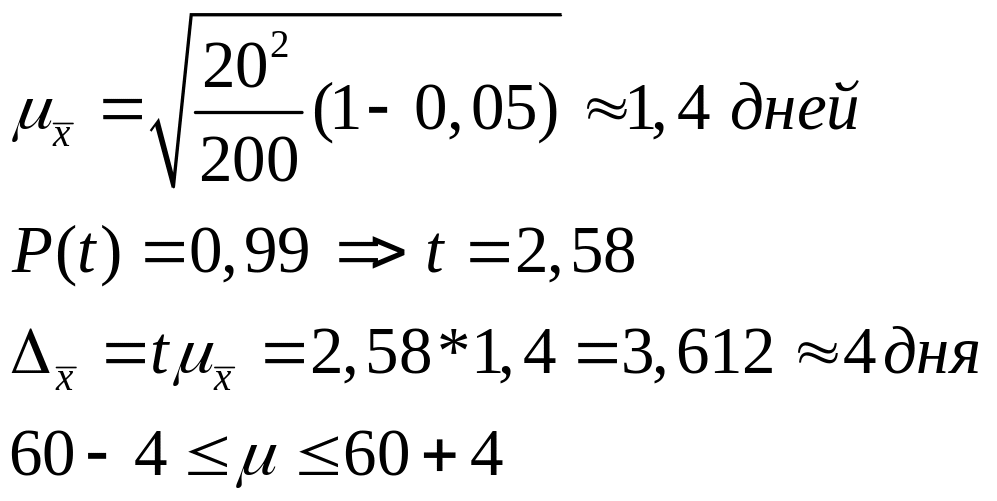
Т.е. с вероятностью 0,99 можно утверждать,
что средний срок пользования краткосрочным
кредитом составляет от 56 до 64 дней.

По итогам выборки определим долю кредитов
со сроком пользования более полугода.

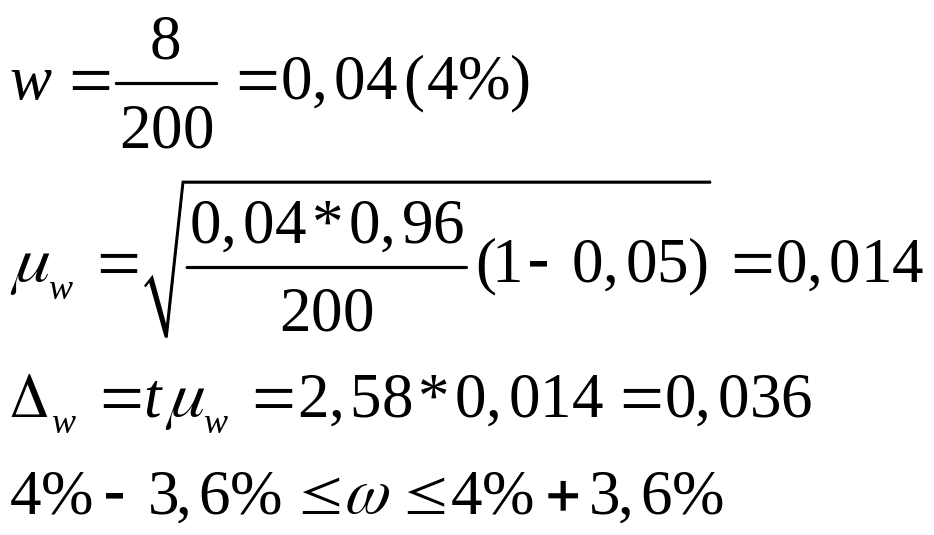
С вероятностью 0,99 можно гарантировать,
что доля кредитов банка со сроком
использования более полугода оставляет

общего числа кредитов.

Определение
оптимальной численности выборки

На
практике обычно расчет объема выборки
производят по формуле для повторного
отбора:

Если
полученный объем выборки превышает 5%
численности генеральной совокупности,
то расчеты корректируют на бесповторность:

В
данных формулах присутствуют значения
генеральной дисперсии, которые как
правило неизвестны. Для ее оценки можно
использовать:

1.
Выборочную дисперсию по данным прошлых
или пробных обследований.

2.
Дисперсию найденную из соотношения для
среднего квадратичного отклонения:

(если
все х >0 и х_min
0)

3.
Дисперсию, вычисленную из соотношения
для нормального распределения

4.
Дисперсию, определенную из соотношения
для асимметричного распределения

В
качестве оценки генеральной дисперсии
доли используют максимально возможную
дисперсию альтернативного признака:

Пример:
Определить численность выборки по
следующим данным. Для определения
средней цены говядины на 5000 рынках
города предполагается провести выборочную
регистрацию цен. Известно, что цены на
говядину колеблются от 40 до 70 руб/кг.
Сколько торговых точек необходимо
обследовать, чтобы с вероятностью 0,954
ошибка выборки при определении средней
цены не превышала 2 руб. за 1 кг.

Решение:
Предположим, что распределение цен
соответствует нормальному закону. Тогда

P(t)
= 0,954. Следовательно t
= 2.

Поскольку
доля отбора не превышает 5%, то к формуле
бемповторного отбора можно не переходить.
Т.е. для того, чтобы с вероятностью 0, 954
гарантировать, что ошибка при определении
функцией цены говядины не превысит 2
руб/кг необходимо исследовать 25 торговых
точек на рынках города.

Определение:
Относительная ошибка выборки– это
отношение предельной ошибки выборки к
среднему значению признака, выраженного
в %.

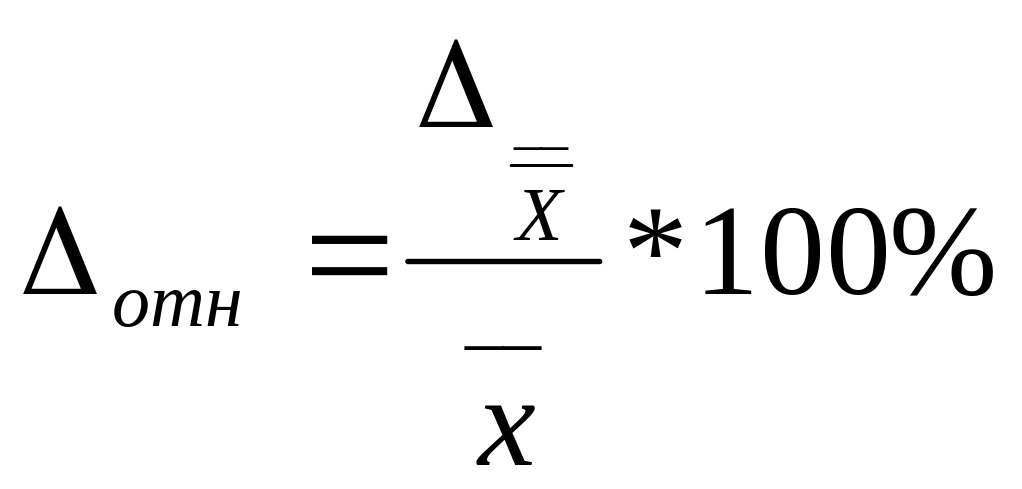
Расчёт
объема выборки при заданном уровне
относительной ошибки выборки осуществляется
по формулам:

—
коэффициент вариации

Пример:
В городе зарегистрировано 30000 безработных.
Для определения средней продолжительности
безработицы организуется выборочное
обследование. По данным прошлых лет
известно, что коэффициент вариации
объема продолжительности безработицы
составляет 40%. Какое число безработных
необходимо охватить выборочным
наблюдением, чтобы с вероятностью 0,997
утверждать, что полученным предельная
ошибка выборки не превышает 5% средней
продолжительности безработицы.

Решение:
P(t)
= 0,997. Следовательно t
= 3.

Объем выборки всегда округляют в большую
сторону.

Ответ: 566.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Средняя и предельная ошибки выборки

Средняя ошибка выборкивсегда
присутствует в выборочных исследованиях
и появляется вследствие того, что
обследуются не все единицы статистической
совокупности, а лишь ее часть.

Средняя ошибка выборки превращается в
предельную ошибкуΔ
при умножении ее на коэффициент
доверияt, который задается
предварительно, исходя из требуемой
точности наблюдения. Предельная ошибка
позволяет судить об «истинном» размере
параметра в генеральной совокупности
с определенной степенью вероятности

-предельная
ошибка ,-средняя
ошибка, t – коэффициент доверия

При типическом и серийном
отборе, при расчете ошибки выборки
вместо общей дисперсии (σ²)
следует использовать
среднюю из внутригрупповых дисперсий
и межгрупповую дисперсию,
где—
частная дисперсия i группы,объем i группы

Формулы предельной ошибки случайной
выборки при определении средней

Для повторного отбора

где
средняя
ошибка выборки

Для бесповторного отбора

Формулы предельной ошибки случайной
выборки при определении доли

Для повторного отбора

где
средняя ошибка выборочной доли

Для бесповторного отбора

где
средняя ошибка выборочной доли

Формулы численности случайной
выборки при определении средней величины

Для повторного отбора	Для бесповторного отбора

Формулы численности случайной выборки при определении доли изучаемого признака

Для повторного отбора	Для бесповторного отбора

Предельная разница между генеральной
и выборочной средней соответствует
величине предельной ошибки

для средней	для доли:

Значения вероятности и соответственно
tнаходятся по таблицам
распределения:

Лапласа
Стьюдента (в случае малой выборки)

Формулы случайной выборки подходят и
для механической выборки.

При необходимости округления, при
случайной выборке – округление в большую
сторону, при механической – в меньшую.

Малая выборка

Если численность выборочной совокупности
не более 30 единиц, то средняя ошибка
малой выборки при определении средней
величины рассчитывается по формуле:

	при определении доли по формуле:

Для расчета ошибки малой выборки
применяется уточненная формула дисперсии

где n-1 —
представляет собой «число степеней
свободы», т.е. количество вариантов,
могущих принимать произвольные
значения, не меняющие величины средней.

Типы задач выборочного наблюдения

определение ошибки выборки,
определение численности выборочной
совокупности n
,
определение вероятности того, что
выборочная средняя (или доля) отклонится
от генеральной не более, чем на заданную
величину t=Δ/μ,
оценка случайности расхождений
показателей выборочных наблюдений,
перенос выборочных характеристик на
генеральную совокупность.

Проверка гипотез о средней и доле

Оценка случайности расхождений
показателей выборочных наблюдений

Если при n>30 коэффициент t<3, то делается
вывод о случайности расхождений.
Если n≤ 30 , то полученное
значение t сравнивают с табличным,
определяемым по таблице распределения
Стьюдента
Если,
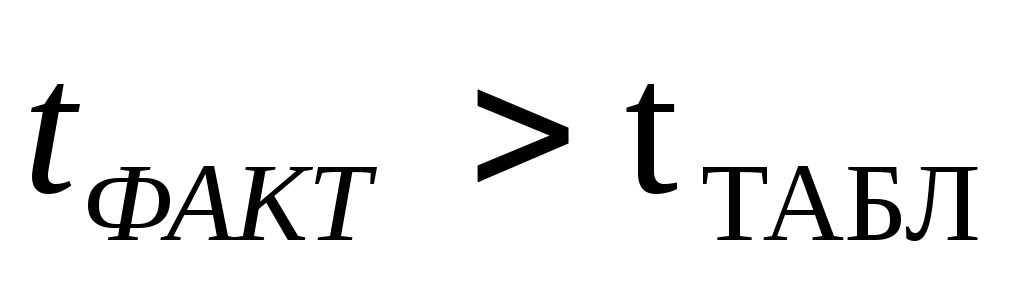расхождение считается существенным.
Если
,
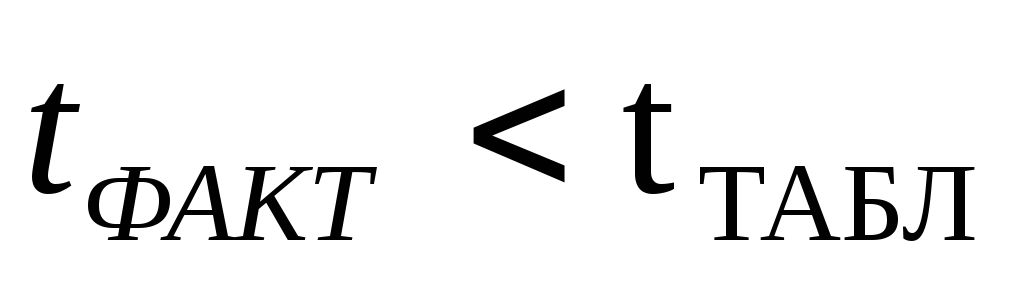расхождение считается случайным.

Методы переноса выборочных данных на
генеральную совокупность

метод взвешивания;
метод перевзвешивания;
метод заполнения случайным подбором
в классах замещения.

11.2. Оценка результатов выборочного наблюдения

11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли

Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ().

В теории выборочного наблюдения выведены формулы для определения , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.

Например, если применяется повторная собственно случайная выборка, то определяется как:

— при оценивании среднего значения признака;

— если признак альтернативный, и оценивается доля.

При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):

— для среднего значения признака;

— для доли.

Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.

Предельная ошибка выборки ( Delta ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):

Delta =t mu .

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.

Уровень предельной ошибки выборки зависит от следующих факторов:

степени вариации единиц генеральной совокупности;
объема выборки;
выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
уровня доверительной вероятности.

Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.

Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.

Таблица
11.2.

Значение доверительной вероятности P	0,683	0,954	0,997
Значение коэффициента доверия t	1,0	2,0	3,0

Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:

Ошибки выборки при различных видах отбора

Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.

Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ()

где $sigma^{2}$ — дисперсия признака в выборочной совокупности.

Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.

Таблица
11.4.

Уровень фондоотдачи, руб.	До 1,4	1,4-1,6	1,6-1,8	1,8-2,0	2,0-2,2	2,2 и выше	Итого
Количество предприятий	13	15	17	15	16	14	90

В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:

По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:

Таблица
11.5.

Результаты наблюдения	Расчетные значения
уровень фондоотдачи, руб., x_i	количество предприятий, f_i	середина интервала, x_i^xb4	x_i^xb4f_i	x_i^xb4²f_i
До 1,4	13	1,3	16,9	21,97
1,4-1,6	15	1,5	22,5	33,75
1,6-1,8	17	1,7	28,9	49,13
1,8-2,0	15	1,9	28,5	54,15
2,0-2,2	16	2,1	33,6	70,56
2,2 и выше	14	2,3	32,2	74,06
Итого	90	—	162,6	303,62

Выборочная средняя

Выборочная дисперсия изучаемого признака

Определяем среднюю ошибку повторной случайной выборки
Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.

Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.

Предельная ошибка выборки с вероятностью 0,954 равна
$delta_{x}= tmu_{x}= 2*0.035 = 0.07$
Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.

Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

$delta_{x}= tmu_{x}= 2*0.027 = 0.054$

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.

По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:

рассчитаем выборочную долю.

Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда

m = 60, n = 90, w = m/n = 60 : 90 = 0,667;

рассчитаем дисперсию доли в выборочной совокупности

$sigma_{w}^{2}= w(1 - w) = 0,667(1 - 0,667) = 0,222$ ;

средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

зададим доверительную вероятность и определим предельную ошибку выборки.

При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

$delta_{x}= tmu_{x}= 3*0.04 = 0.12$

установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.

Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда

N₁ + N₂ + … + N_i + … + N_k = N.

Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки

n₁ + n₂ + … + n_i + … + n_k = n.

Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.

Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:

n = n_i · N_i/N

где n_i — количество извлекаемых единиц для выборки из i-й типической группы;

n — общий объем выборки;

N_i — количество единиц генеральной совокупности, составивших i-ю типическую группу;

N — общее количество единиц генеральной совокупности.

Отбор единиц внутри групп происходит в виде случайной или механической выборки.

Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

Таблица
11.6.
Формулы для расчета средней ошибки выборки () при использовании типического отбора, пропорционального объему типических групп

Здесь $sigma^{2}$ — средняя из групповых дисперсий типических групп.

Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:

Таблица
11.7.

Номер курса	Всего студентов, чел., N_i	Обследовано в результате выборочного наблюдения, чел., n_i	Среднее число посещений библиотеки одним студентом за семестр, x_i	Внутригрупповая выборочная дисперсия, $sigma_{i}^{2}$
1	650	33	11	6
2	610	31	8	15
3	580	29	5	18
4	360	18	6	24
5	350	17	10	12
Итого	2 550	128	8	—

Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:

общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
количество единиц, отобранных из каждой типической группы:

аналогично для других групп:

n₂ = 31 (чел.);

n₃ = 29 (чел.);

n₄ = 18 (чел.);

n₅ = 17 (чел.).

Проведем необходимые расчеты.

Выборочная средняя, исходя из значений средних типических групп, составит:
Средняя из внутригрупповых дисперсий
Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

$delta_{x} = tmu_{x} = 2*0.334 = 0.667$
Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.

Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.

Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

$delta_{MB}= tmu_{MB}$

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.

Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.

Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.

Среднее значение признака в выборке равно
Значение среднего квадратического отклонения составляет
Средняя ошибка выборки:
Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
Предельная ошибка выборки:
$delta_{MB}= tmu_{MB}=2,365*0,344 = 0,81356 ~ 0,81 (ч)$
Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.

11.2.2. Определение численности выборочной совокупности

Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):

вид предполагаемой выборки;
способ отбора (повторный или бесповторный);
выбор оцениваемого параметра (среднего значения признака или доли).

Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.

Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.

Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.

При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.

Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.

Источник

11.2. Оценка результатов выборочного наблюдения

11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли

Например, если применяется повторная собственно случайная выборка, то определяется как:

— при оценивании среднего значения признака;

— если признак альтернативный, и оценивается доля.

При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):

— для среднего значения признака;

— для доли.

Delta =t mu .

Уровень предельной ошибки выборки зависит от следующих факторов:

степени вариации единиц генеральной совокупности;
объема выборки;
выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
уровня доверительной вероятности.

Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.

Таблица
11.2.

Значение доверительной вероятности P	0,683	0,954	0,997
Значение коэффициента доверия t	1,0	2,0	3,0

Итак, определение границ генеральной средней и доли состоит из следующих этапов:

Ошибки выборки при различных видах отбора

Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.

Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ()

где $sigma^{2}$ — дисперсия признака в выборочной совокупности.

Таблица
11.4.

Уровень фондоотдачи, руб.	До 1,4	1,4-1,6	1,6-1,8	1,8-2,0	2,0-2,2	2,2 и выше	Итого
Количество предприятий	13	15	17	15	16	14	90

По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:

Таблица
11.5.

Результаты наблюдения	Расчетные значения
уровень фондоотдачи, руб., x_i	количество предприятий, f_i	середина интервала, x_i^xb4	x_i^xb4f_i	x_i^xb4²f_i
До 1,4	13	1,3	16,9	21,97
1,4-1,6	15	1,5	22,5	33,75
1,6-1,8	17	1,7	28,9	49,13
1,8-2,0	15	1,9	28,5	54,15
2,0-2,2	16	2,1	33,6	70,56
2,2 и выше	14	2,3	32,2	74,06
Итого	90	—	162,6	303,62

Выборочная средняя

Выборочная дисперсия изучаемого признака

Определяем среднюю ошибку повторной случайной выборки
Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.

Предельная ошибка выборки с вероятностью 0,954 равна
$delta_{x}= tmu_{x}= 2*0.035 = 0.07$
Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

$delta_{x}= tmu_{x}= 2*0.027 = 0.054$

рассчитаем выборочную долю.

m = 60, n = 90, w = m/n = 60 : 90 = 0,667;

рассчитаем дисперсию доли в выборочной совокупности

$sigma_{w}^{2}= w(1 - w) = 0,667(1 - 0,667) = 0,222$ ;

средняя ошибка выборки при использовании повторной схемы отбора составит

зададим доверительную вероятность и определим предельную ошибку выборки.

$delta_{x}= tmu_{x}= 3*0.04 = 0.12$

установим границы для генеральной доли с вероятностью 0,997:

Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда

N₁ + N₂ + … + N_i + … + N_k = N.

n₁ + n₂ + … + n_i + … + n_k = n.

n = n_i · N_i/N

где n_i — количество извлекаемых единиц для выборки из i-й типической группы;

n — общий объем выборки;

N_i — количество единиц генеральной совокупности, составивших i-ю типическую группу;

N — общее количество единиц генеральной совокупности.

Отбор единиц внутри групп происходит в виде случайной или механической выборки.

Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

Здесь $sigma^{2}$ — средняя из групповых дисперсий типических групп.

Таблица
11.7.

Номер курса	Всего студентов, чел., N_i	Обследовано в результате выборочного наблюдения, чел., n_i	Среднее число посещений библиотеки одним студентом за семестр, x_i	Внутригрупповая выборочная дисперсия, $sigma_{i}^{2}$
1	650	33	11	6
2	610	31	8	15
3	580	29	5	18
4	360	18	6	24
5	350	17	10	12
Итого	2 550	128	8	—

Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:

общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
количество единиц, отобранных из каждой типической группы:

аналогично для других групп:

n₂ = 31 (чел.);

n₃ = 29 (чел.);

n₄ = 18 (чел.);

n₅ = 17 (чел.).

Проведем необходимые расчеты.

Выборочная средняя, исходя из значений средних типических групп, составит:
Средняя из внутригрупповых дисперсий
Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

$delta_{x} = tmu_{x} = 2*0.334 = 0.667$
Доверительные границы для среднего значения признака в генеральной совокупности:

Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.

Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

$delta_{MB}= tmu_{MB}$

Среднее значение признака в выборке равно
Значение среднего квадратического отклонения составляет
Средняя ошибка выборки:
Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
Предельная ошибка выборки:
$delta_{MB}= tmu_{MB}=2,365*0,344 = 0,81356 ~ 0,81 (ч)$
Доверительный интервал для среднего значения признака в генеральной совокупности:

11.2.2. Определение численности выборочной совокупности

вид предполагаемой выборки;
способ отбора (повторный или бесповторный);
выбор оцениваемого параметра (среднего значения признака или доли).

Таблица
11.8.
Формулы для определения численности выборочной совокупности

При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.

Источник

Предельная ошибка выборки

Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.

1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:

Предельная ошибка выборки для средней при повторном отборе

где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;

мю х — средняя ошибка выборки.

2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:

Предельная ошибка выборки для доли при повторном отборе

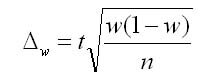
3. Предельная ошибка выборки для средней при бесповторном отборе:

Предельная ошибка выборки при бесповторном отборе

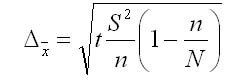
4. Предельная ошибка выборки для доли при бесповторном отборе:

Предельная ошибка выборки для доли при бесповторном отборе

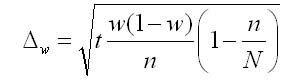
Предельная относительная ошибка выборки

Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:

Предельная относительная ошибка выборки

Малая выборка

Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.

Межсерийная дисперсия

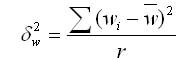
Средняя и предельная ошибки для малой выборки

В малой выборке средняя ошибка рассчитывается по формуле:

средняя ошибка малой выборки

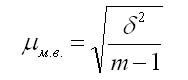
Предельная ошибка малой выборки рассчитывается по формуле:

Предельная ошибка малой выборки

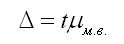
где t — отношение Стьюдента

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

Материалы сайта

Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.

Источник