2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка
выборки
показывает, насколько отклоняется в
среднем параметр выборочной
совокупности
от соответствующего параметра генеральной.
Если рассчитать среднюю из ошибок всех
возможных выборок определенного вида
заданного объема (n),
извлеченных из одной и той же генеральной
совокупности,
то получим их обобщающую характеристику
среднюю
ошибку выборки
().
В
теории выборочного наблюдения
выведены формулы для определения ,
которые индивидуальны для разных
способов отбора (повторного и
бесповторного), типов используемых
выборок и видов оцениваемых статистических
показателей.
Например, если
применяется повторная собственно
случайная выборка, то
определяется как:
![]()
при
оценивании среднего значения признака;
![]()
если
признак альтернативный, и оценивается
доля.
При бесповторном
собственно случайном отборе в формулы
вносится поправка
![]()
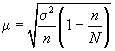
для
среднего значения признака;
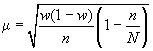
для
доли.
Вероятность
получения именно такой величины ошибки
всегда равна 0,683. На практике же
предпочитают получать данные с большей
вероятностью, но это приводит к возрастанию
величины ошибки выборки.
Предельная
ошибка выборки ()
равна t-кратному
числу средних ошибок выборки (в теории
выборки принято коэффициент t
называть
коэффициентом доверия):
t
.
Если ошибку выборки
увеличить в два раза (t
2), то получим гораздо большую вероятность
того, что она не превысит определенного
предела (в нашем случае
двойной средней ошибки)
0,954. Если взять t
3, то доверительная вероятность составит
0,997
практически достоверность.
Уровень предельной
ошибки выборки зависит от следующих
факторов:
степени вариации
единиц генеральной совокупности;
объема выборки;
выбранных схем
отбора (бесповторный отбор дает меньшую
величину ошибки);
уровня
доверительной вероятности.
Если объем выборки
больше 30, то значение t
определяется по таблице нормального
распределения, если меньше
по таблице распределения Стьюдента
(Приложение
1).
Приведем некоторые
значения коэффициента доверия из таблицы
нормального распределения.
![]()
Доверительный
интервал для среднего значения признака
и для доли в генеральной
совокупности
устанавливается следующим образом:
![]()
Итак, определение
границ генеральной средней и доли
состоит из следующих этапов:
нахождение в
выборке среднего значения признака
(или доли);
определение
в соответствии с выбранной схемой отбора
и вида выборки;
задание
доверительной вероятности Р
и определение коэффициента доверия t
по
соответствующей таблице;
вычисление
предельной ошибки выборки ;
построение
доверительного интервала для средней
(или доли).
Ошибки выборки
при различных видах отбора
1. Собственно
случайная и механическая выборка.
Средняя
ошибка собственно случайной и механической
выборки находятся по формулам,
представленным в табл. 11.1.
Таблица 1
Формулы для
расчета средней ошибки
собственно
случайной и механической выборки ()

где
2
дисперсия
признака в выборочной совокупности.
Пример 2. Для
изучения уровня фондоотдачи было
проведено выборочное обследование 90
предприятий из 225 методом случайной
повторной выборки, в результате которого
получены данные, представленные в
таблице.

В рассматриваемом
примере имеем 40%-ную выборку (90 : 225
0,4, или 40%). Определим ее предельную ошибку
и границы для среднего значения признака
в генеральной совокупности по шагам
алгоритма:
1. По результатам
выборочного обследования рассчитаем
среднее значение и дисперсию в выборочной
совокупности:
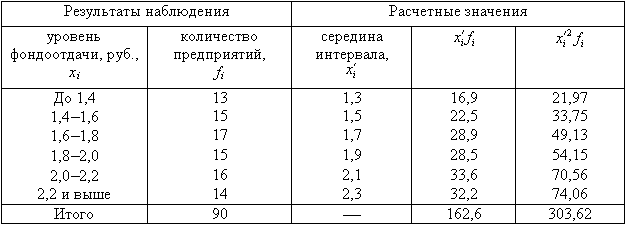
Выборочная средняя
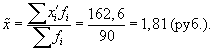
Выборочная
дисперсия изучаемого признака
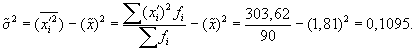
2. Определяем
среднюю ошибку повторной случайной
выборки
![]()
3. Зададим
вероятность, на уровне которой будем
говорить о величине предельной ошибки
выборки. Чаще всего она принимается
равной 0,999; 0,997; 0,954.
Для наших данных
определим предельную ошибку выборки,
например, с вероятностью 0,954. По таблице
значений вероятности функции нормального
распределения (см. выдержку из нее,
приведенную в Приложении 1) находим
величину коэффициента доверия t,
соответствующего вероятности 0,954. При
вероятности 0,954 коэффициент t
равен 2.
4. Предельная
ошибка выборки с вероятностью 0,954 равна
![]()
5. Найдем доверительные
границы для среднего значения уровня
фондоотдачи в генеральной совокупности
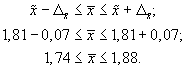
Таким образом, в
954 случаях из 1000 среднее значение
фондоотдачи будет не выше 1,88 руб. и не
ниже 1,74 руб.
Выше была
использована повторная схема случайного
отбора. Посмотрим, изменятся ли результаты
обследования, если предположить, что
отбор осуществлялся по схеме бесповторного
отбора. В этом случае расчет средней
ошибки проводится по формуле
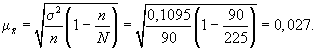
Тогда при вероятности
равной 0,954 величина предельной ошибки
выборки составит:
![]()
Доверительные
границы для среднего значения признака
при бесповторном случайном отборе будут
иметь следующие значения:
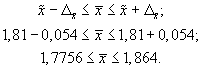
Сравнив результаты
двух схем отбора, можно сделать вывод
о том, что применение бесповторной
случайной выборки дает более точные
результаты по сравнению с применением
повторного отбора при одной и той же
доверительной вероятности. При этом,
чем больше объем выборки, тем существеннее
сужаются границы значений средней при
переходе от одной схемы отбора к другой.
По данным примера
определим, в каких границах находится
доля предприятий с уровнем фондоотдачи,
не превышающим значения 2,0 руб., в
генеральной совокупности:
1) рассчитаем
выборочную долю.
Количество
предприятий в выборке с уровнем
фондоотдачи, не превышающим значения
2,0 руб., составляет 60 единиц. Тогда
m
60, n
90, w
m/n
60 : 90
0,667;
2) рассчитаем
дисперсию доли в выборочной совокупности
w2
w(1
w)
0,667(1
0,667)
0,222;
3) средняя ошибка
выборки при использовании повторной
схемы отбора составит
![]()
Если предположить,
что была использована бесповторная
схема отбора, то средняя ошибка выборки
с учетом поправки на конечность
совокупности составит
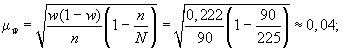
4) зададим
доверительную вероятность и определим
предельную ошибку выборки.
При значении
вероятности Р
0,997 по таблице нормального распределения
получаем значение для коэффициента
доверия t
3 (см. выдержку из нее, приведенную в
Приложении 1):
![]()
5) установим границы
для генеральной доли с вероятностью
0,997:

Таким образом, с
вероятностью 0,997 можно утверждать, что
в генеральной совокупности доля
предприятий с уровнем фондоотдачи, не
превышающим значения 2,0 руб., не меньше,
чем 54,7%, и не больше 78,7%.
2. Типическая
выборка. При
типической выборке генеральная
совокупность объектов разбита на k
групп, тогда
N1
N2
…
Ni
…
Nk
N.
Объем извлекаемых
из каждой типической группы единиц
зависит от принятого способа отбора;
их общее количество образует необходимый
объем выборки
n1
n2
…
ni
…
nk
n.
Существуют
следующие два способа организации
отбора внутри типической группы:
пропорциональной объему типических
групп и пропорциональной степени
колеблемости значений признака у единиц
наблюдения в группах. Рассмотрим первый
из них, как наиболее часто используемый.
Отбор, пропорциональный
объему типических групп, предполагает,
что в каждой из них будет отобрано
следующее число единиц совокупности:
![]()
где ni
количество извлекаемых единиц для
выборки из i-й
типической группы;
n
общий объем выборки;
Ni
количество единиц генеральной
совокупности, составивших i-ю
типическую группу;
N
общее количество единиц генеральной
совокупности.
Отбор единиц
внутри групп происходит в виде случайной
или механической выборки.
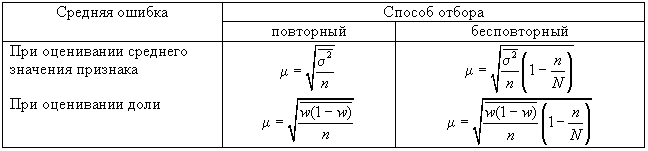
Формулы для
оценивания средней ошибки выборки для
среднего и доли представлены в табл.
11.2.
Таблица 2
Формулы для
расчета средней ошибки выборки ()
при использовании типического отбора,
пропорционального объему типических
групп
Здесь
![]()
средняя из групповых дисперсий типических
групп.
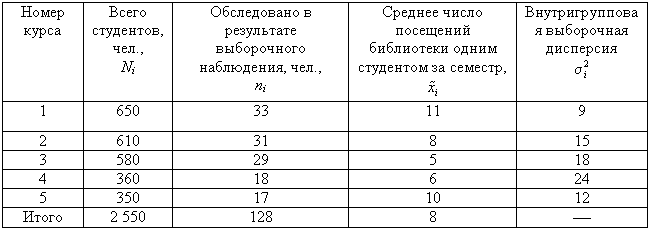
Пример 3. В
одном из московских вузов проведено
выборочное обследование студентов с
целью определения показателя средней
посещаемости вузовской библиотеки
одним студентом за семестр. Для этого
была использована 5%-ная бесповторная
типическая выборка, типические группы
которой соответствуют номеру курса.
При отборе, пропорциональном объему
типических групп, получены следующие
данные:
Число студентов,
которое необходимо обследовать на
каждом курсе, рассчитаем следующим
образом:
общий объем
выборочной совокупности:
![]()
количество
единиц, отобранных из каждой типической
группы:
![]()
аналогично для
других групп:
п2
31 (чел.);
п3
29 (чел.);
п4
18 (чел.);
п5
17 (чел.).
Проведем необходимые
расчеты.
1. Выборочная
средняя, исходя из значений средних
типических групп, составит:
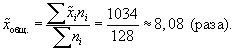
2. Средняя из
внутригрупповых дисперсий
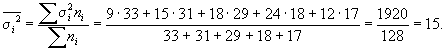
3. Средняя ошибка
выборки:
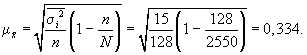
С вероятностью
0,954 находим предельную ошибку выборки:
![]()
4. Доверительные
границы для среднего значения признака
в генеральной совокупности:
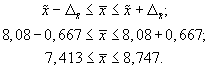
Таким образом, с
вероятностью 0,954 можно утверждать, что
один студент за семестр посещает
вузовскую библиотеку в среднем от семи
до девяти раз.
3.
Малая выборка. В
связи с небольшим объемом выборочной
совокупности
те формулы для определения ошибок
выборки,
которые использовались нами ранее при
«больших» выборках, становятся
неподходящими и требуют корректировки.
Среднюю ошибку
малой выборки
определяют по формуле
![]()
Предельная
ошибка малой выборки:
![]()
Распределение
значений выборочных средних всегда
имеет нормальный закон распределения
(или приближается к нему) при п
100, независимо от характера распределения
генеральной
совокупности.
Однако в случае малых выборок действует
иной закон распределения
распределение Стьюдента.
В этом случае коэффициент доверия
находится по таблице t-распределения
Стьюдента в зависимости от величины
доверительной вероятности Р
и объема выборки п.
В Приложении
1
приводится фрагмент таблицы t-распределения
Стьюдента, представленной в виде
зависимости доверительной вероятности
от объема выборки и коэффициента доверия
t.
Пример 4.
Предположим,
что выборочное обследование восьми
студентов академии показало, что на
подготовку к контрольной работе по
статистике они затратили следующее
количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4;
6,6.
Оценим выборочные
средние затраты времени и построим
доверительный интервал для среднего
значения признака в генеральной
совокупности, приняв доверительную
вероятность равной 0,95.
1. Среднее значение
признака в выборке равно
![]()
2. Значение среднего
квадратического отклонения составляет
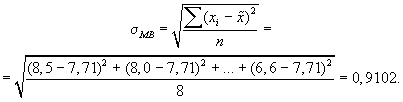
3. Средняя ошибка
выборки:
![]()
4. Значение
коэффициента доверия t
2,365 для п
8 и Р
0,95 (Приложение 1).
5. Предельная
ошибка выборки:
![]()
6. Доверительный
интервал для среднего значения признака
в генеральной совокупности:
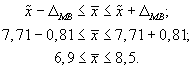
То есть с вероятностью
0,95 можно утверждать, что затраты времени
студента на подготовку к контрольной
работе находятся в пределах от 6,9 до 8,5
ч.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предельная ошибка выборки
Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.
1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:

где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;
мю х — средняя ошибка выборки.
2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:
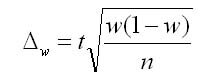
3. Предельная ошибка выборки для средней при бесповторном отборе:
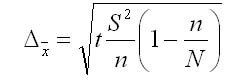
4. Предельная ошибка выборки для доли при бесповторном отборе:
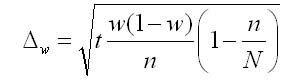
Предельная относительная ошибка выборки
Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:

Малая выборка
Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.
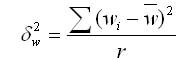
Средняя и предельная ошибки для малой выборки
В малой выборке средняя ошибка рассчитывается по формуле:
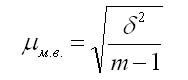
Предельная ошибка малой выборки рассчитывается по формуле:
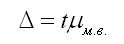
где t — отношение Стьюдента
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
2. Виды отбора.
3. Ошибки выборки, определение объема выборочной совокупности.
4. Способы распространения выборочных характеристик.
1. Понятие выборочного наблюдения, репрезентативность выборочного наблюдения.
1. Выборочное наблюдение несложное наблюдение, при котором обследуется не вся совокупность, а лишь часть, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При проведении выборочного наблюдения нельзя получить абсолютно точные данные, как при сплошном, т. к. обследованию подвергается не вся совокупность, а ее часть. Поэтому при проведении выборочного наблюдения неизбежна некоторая свойственная ему погрешность, ошибка.
Ошибки, свойственные выборочному наблюдению, называются ошибками репрезентативности, т. е. представительства. Они характеризуют размер расхождения между данными выборочного наблюдения и всей совокупности.
Ошибки репрезентативности делятся на случайные и систематические.
Случайные ошибки возникают вследствие того, что выборочная совокупность недостаточно точно воспроизводит совокупность, вследствие несплошного характера наблюдения. Случайные ошибки м. б. доведены до незначительных размеров, а главное размеры и пределы их можно определить с достаточной точностью на основании закона больших чисел и теории вероятности.
Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения.
Вся совокупность единиц, из которой производится отбор, называется генеральной совокупностью и обозначается буквой N. Часть генеральной совокупности, попавшая в выборку, называется выборочной совокупностью и обозначается n.
Обобщающие показатели генеральной совокупности средняя, дисперсия, доля называются генеральными и соответственно обозначаются ![]() доля отнесения М единиц, обладающих определенным признаком, ко всей численности генеральной совокупности, т. е. М/N.
доля отнесения М единиц, обладающих определенным признаком, ко всей численности генеральной совокупности, т. е. М/N.
Обобщающие характеристики в выборочной совокупности называются выборочными и обозначаются соответственно x*, ![]() частость отношение числа единиц, обладающих данным признаком, в выборочной совокупности n, т. е.
частость отношение числа единиц, обладающих данным признаком, в выборочной совокупности n, т. е. ![]()
![]()
Теория выборочного метода дает возможность определить случайные ошибки обобщающих характеристик в выборочной совокупности.
Ошибка репрезентативности разность между выборочной средней и генеральной средней при достаточно большом числе наблюдений будет сколько угодно малой, т. е.
![]()
где ![]() абсолютная величина расхождения между генеральной средней и выборочной средней, составляющая ошибку репрезентативности.
абсолютная величина расхождения между генеральной средней и выборочной средней, составляющая ошибку репрезентативности.
![]() — среднее квадратическое отклонение вариантов выборочной средней от генеральной средней (средняя ошибка выборки). Она зависит от колеблемости признака в генеральной совокупности
— среднее квадратическое отклонение вариантов выборочной средней от генеральной средней (средняя ошибка выборки). Она зависит от колеблемости признака в генеральной совокупности ![]() и числа отобранных единиц n:
и числа отобранных единиц n: ![]() . Величина m зависит также от способа образования выборочной совокупности, т. к. между
. Величина m зависит также от способа образования выборочной совокупности, т. к. между ![]() средней ошибкой выборки и n числом отбираемых единиц существует обратно пропорциональная связь. Отсюда вытекает следующее правило: если надо уменьшить ошибку выборки, например, в 3 раза, необходимо увеличить объем выборки в девять раз.
средней ошибкой выборки и n числом отбираемых единиц существует обратно пропорциональная связь. Отсюда вытекает следующее правило: если надо уменьшить ошибку выборки, например, в 3 раза, необходимо увеличить объем выборки в девять раз.
Увеличение колеблемости признака в генеральной совокупности влечет за собой увеличение среднего квадратического отклонения, и следовательно и ошибки выборки.
Доказано, что соотношение между дисперсиями генеральной и выборочной совокупностей выражаются формулой:
![]() , т. к.
, т. к. ![]() при больших n приближается к 1, то
при больших n приближается к 1, то ![]()
Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью, на величину которой указывает коэффициент доверия t.
Величина ![]() обозначается
обозначается ![]() называется предельной ошибкой выборки. Следовательно предельная ошибка выборки определяется формулой
называется предельной ошибкой выборки. Следовательно предельная ошибка выборки определяется формулой ![]() =
= ![]() . С увеличением t увеличивается вероятность нашего утверждения, но вместе с тем увеличивается и величина ошибки.
. С увеличением t увеличивается вероятность нашего утверждения, но вместе с тем увеличивается и величина ошибки.
2. Виды и схемы отбора.
Формирование выборочной совокупности из генеральной может осуществляться по-разному: в зависимости от вида и схемы отбора, и т. д. От их особенностей зависит размер ошибки и методы определения. Различаются 4 вида отбора:
1. собственно-случайный
2. механический
3. типический
4. серийный (гнездовой)
Собственно-случайный отбор включение единиц совокупности осуществляется наудачу. Наиболее распространенным способом отбора в случайной выборке является жеребьевка, при которой на каждую единицу заготавливают билет с порядковым номером. Затем в случайном порядке отбирают необходимое количество единиц совокупности. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку.
Механический отбор вся совокупность разбивается на равные по объему группы по случайному признаку. Затем из каждой группы случайно отбирается одна единица.
Типичный отбор совокупность расчленяется по существенному, типическому признаку на качественно однородные, однотипные группы. Затем из каждой группы случайным или механическим способом отбирается количество единиц, пропорциональное удельному весу группы во всей совокупности.
Типический отбор дает более точные результаты чем случайный или механический, потому что при нем в выборку в такой же пропорции как и в генеральной совокупности, попадают представители всех типических групп.
Серийный отбор (гнездовой) отбору подлежат не отдельные единицы совокупности, а целые группы, серии, гнезда, отобранные случайным или механическим способом. В каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.
Точность выборки зависит и от схемы отбора. Выборка м. б. проведена по схеме повторного или бесповторного отбора.
Повторный отбор каждая отобранная единица или серия возвращается во всю совокупность и может вновь попасть в выборку.
Бесповторный отбор каждая обследованная единица не возвращается в совокупность и не м. б. подвергнута повторному обследованию. Бесповторный отбор дает более точные результаты, т. к. при одном и том же объеме выборки наблюдение охватывает большее количество единиц изучаемой совокупности.
Обе схемы отбора могут применяться в сочетании с разными видами отбора, за исключением механического, который всегда бывает бесповторным.
3. Ошибки выборки, определение объема выборочной совокупности
Для суждения о праве распространения данных выборочного наблюдения на генеральную совокупность определяют величину ошибок между сводимыми показателями выборочной и генеральной совокупностей.
Обычно сопоставляют такие показатели:
1. Среднюю выборочной совокупности со средней генеральной совокупности, в результате чего получаем ошибку средней.
![]()
2. Частость выборочной совокупности с долей генеральной совокупности, что дает возможность определить ошибку частостей:
![]()
Разность между показателями выборочной и генеральной совокупностей называется ошибкой репрезентативности. Если эти показатели достаточно близки, то выборка считается репрезентативной.
Выборочная средняя и частость являются переменными величинами, т. е. могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются переменными величинами и также могут принимать различные значения в зависимости от единиц совокупности, попавшие в выборку. Вот почему определяется средняя из возможных ошибок, которая обозначается буквой ![]() . Величина
. Величина ![]() зависит от степени колеблемости значений признака в генеральной совокупности и от численности выборки n. Степень колеблемости в генеральной совокупности определяется средним квадратом отклонений или дисперсией
зависит от степени колеблемости значений признака в генеральной совокупности и от численности выборки n. Степень колеблемости в генеральной совокупности определяется средним квадратом отклонений или дисперсией ![]() . Из математических теорем и закона больших чисел следует, что при случайном отборе, проведенном по системе повторной выборки, между
. Из математических теорем и закона больших чисел следует, что при случайном отборе, проведенном по системе повторной выборки, между ![]() и п существует следующая зависимость:
и п существует следующая зависимость:
![]()
Ошибка выборочного наблюдения это разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения
![]()
Чебышев доказал, что при достаточно большом числе независимых наблюдений можно с вероятностью, близкой к единице утверждать, что отклонение выборочной средней от генеральной будет сколь угодно малым.
![]() , величину
, величину ![]() называют средней ошибкой выборки.
называют средней ошибкой выборки.
Соотношение между дисперсиями генеральной и выборочной совокупности выражается формулой
![]()
Если выборочное наблюдение применяется для определения доли признака, то средняя ошибка доли исчисляется по формуле
![]() , т. к. дисперсия альтернативного признака
, т. к. дисперсия альтернативного признака ![]() , где p доля единиц совокупности, обладающих данным признаком, а q не обладающим данным признаком.
, где p доля единиц совокупности, обладающих данным признаком, а q не обладающим данным признаком.
В этих формулах ![]() и pq характеристики генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности, что вполне правомерно, т. к. основано на законе больших чисел, по которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
и pq характеристики генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности, что вполне правомерно, т. к. основано на законе больших чисел, по которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
При бесповторном отборе средняя ошибка выборки равна
![]() , а ошибка доли
, а ошибка доли ![]() , где N численность единиц генеральной совокупности.
, где N численность единиц генеральной совокупности.
Множитель ![]() всегда меньше единицы, т. к. n < N. Поэтому величина средней ошибки выборки при бесповторном отборе меньше чем при повторном.
всегда меньше единицы, т. к. n < N. Поэтому величина средней ошибки выборки при бесповторном отборе меньше чем при повторном.
Для решения практических задач выборочного обследования средней ошибки выборки недостаточно, потому что при исчислении ошибки конкретной выборки фактическая ошибка м. б. больше или меньше средней ошибки выборки ![]() . Поэтому пользуются не средней, а предельной ошибкой выборки, т. е. пределами, за которые не выйдет фактическая ошибка выборки.
. Поэтому пользуются не средней, а предельной ошибкой выборки, т. е. пределами, за которые не выйдет фактическая ошибка выборки.
Предельная ошибка выборки зависит от того, с какой вероятностью должна гарантироваться ошибка выборки. Уровень вероятности определяется на основе теорем Чебышева и Ляпунова при помощи специального коэффициента t.
Если предельную ошибку выборки обозначить буквой ![]() , то
, то  , где t коэффициент, зависящий от вероятности, с которой гарантируется ошибка выборки. Он называется еще коэффициентом доверия. Чтобы определить величину вероятности для различных значений t на практике пользуются готовой таблицей.
, где t коэффициент, зависящий от вероятности, с которой гарантируется ошибка выборки. Он называется еще коэффициентом доверия. Чтобы определить величину вероятности для различных значений t на практике пользуются готовой таблицей.
Систематизируем формулы для определения предельной ошибки средней и доли
|
Схема отбора |
Предельная ошибка выборки |
|
|
Для средней |
Для доли |
|
|
Повторный отбор Бесповторный отбор |
|
|
Из формул видно, что предельная ошибка выборки прямо пропорциональна коэффициенту t, дисперсии ![]() и обратно пропорциональна корню квадратному из численности выборки.
и обратно пропорциональна корню квадратному из численности выборки.
Дисперсия ![]() величина конкретная, свойственная данной совокупности. Обычно она неизвестна, а известна
величина конкретная, свойственная данной совокупности. Обычно она неизвестна, а известна ![]() *, которой и заменяют величину
*, которой и заменяют величину ![]() , потому что в силу действия закона больших чисел при достаточно большом объеме выборки n распределение признака x в выборочной совокупности близко воспроизводит распределение этого признака в генеральной совокупности.
, потому что в силу действия закона больших чисел при достаточно большом объеме выборки n распределение признака x в выборочной совокупности близко воспроизводит распределение этого признака в генеральной совокупности.
Ошибка выборки зависит и от ее объема n. Чем больше объем выборки, тем меньше предельная ошибка (при данных ![]() и t)
и t)
Рассмотренные формулы средней и предельной ошибки и доли применяются при случайном и механическом видах отбора.
При типическом отборе предельная ошибка выборки и доли определяется по формулам:
|
Схема отбора |
Предельная ошибка выборки |
|
|
Для средней |
Для доли |
|
|
Повторный отбор Бесповторный отбор |
|
|
т. е. при типичном отборе надо брать средние из внутригрупповых дисперсий и доли, полученные по каждой типической группе.
Из этих формул видно, что при типическом отборе в отличие от случайного исключается влияние межгрупповой вариации на точность выборки, т. к. в выборку обязательно попадают представители всех групп в тех же пропорциях, что и в генеральной совокупности. Ошибка выборки при типичном отборе зависит только от средней из внутригрупповых дисперсий, а не от общей дисперсии, как при случайном отборе т. к.
![]() , откуда
, откуда 
Следовательно ошибка выборки при типическом отборе всегда меньше ошибки выборки, проведенной случайным отбором.
При серийном отборе каждая серия рассматривается как единица совокупности, и мерой колеблемости будет межсерийная выборочная дисперсия, т. е. средний квадрат отклонений серийных средних от общей выборочной средней:
![]() , где
, где ![]() средняя по каждой серии, x* общая выборочная средняя, s число отобранных серий.
средняя по каждой серии, x* общая выборочная средняя, s число отобранных серий.
Предельная ошибка выборки и доли при серийном отборе с равновеликими сериями определяется по формулам, где S общее число серий в генеральной совокупности.
|
Схема отбора |
Предельная ошибка выборки |
|
|
Для средней |
Для доли |
|
|
Повторный отбор Бесповторный отбор |
|
|
Выборочное наблюдение, объем которого превышает 20 единиц, называется малой выборкой. Для определения средней и предельной ошибок при малой выборке пользуются теми же формулами, что и при большой, но только с некоторыми особенностями, так ![]() , а
, а  .
.
Кроме того, в случае малой выборки действует особый закон распределения величин t, и при определении вероятности учитывается не только коэффициент t, но и объем выборки n.
Необходимая численность выборки (n) определяется на основе формул предельной ошибки выборки.
Если выборка повторная, то при случайном и механическом отборах определяется по формуле
![]() , при бесповторном отборе
, при бесповторном отборе ![]()
4. Способы распространения выборочных характеристик.
Есть два способа распространения выборочных характеристик на всю совокупность прямой пересчет и способ коэффициентов
Способ прямого пересчета заключается в том, что средние или частости выборочной совокупности умножаются на числа единиц генеральной совокупности.
Когда выборочное обследование проводится в целях уточнения данных сплошного наблюдения, применяется способ коэффициентов. В этом случае данные сплошного наблюдения сопоставляют с данными выборочного наблюдения и устанавливают процент расхождения между ними, т. е. процент надоучета или переучета. Коэффициенты, полученные в результате такого сопоставления, используются для внесения поправок в данные сплошного учета.
Пример.
1) способ прямого пересчета
Для определения качества продукции проверено 500 изделий из 10000. В результате чего установлено, что средний % изделий 3-го сорта всей партии будет находиться в пределах 6,1-13,9%. Способом прямого пересчета определяем, что обще кол-во изделий 3-го сорта всей партии составит от 610 до 1390
10000*0,061= 610
10000*0,139 = 1390
2) способ коэффициентов
Пример
Необходимо определить численность выборки, которая позволила бы оценить долю брака в партии продукции с точностью до 2%, с вероятностью Р =0,954. Партия состоит из 10000 изделий
![]() ,
, ![]()
![]()
 , P =0,954, t =2
, P =0,954, t =2
![]() pq=0,25 (p=0,5; q=0,5)
pq=0,25 (p=0,5; q=0,5)

