11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ( ).
).
В теории выборочного наблюдения выведены формулы для определения  , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то  определяется как:
определяется как:
 — при оценивании среднего значения признака;
— при оценивании среднего значения признака;
 — если признак альтернативный, и оценивается доля.
— если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):
 — для среднего значения признака;
— для среднего значения признака;
 — для доли.
— для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки ( ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
 .
.
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака

- Определяем среднюю ошибку повторной случайной выборки

- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна

- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
 ;
;
- средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

- установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь  — средняя из групповых дисперсий типических групп.
— средняя из групповых дисперсий типических групп.
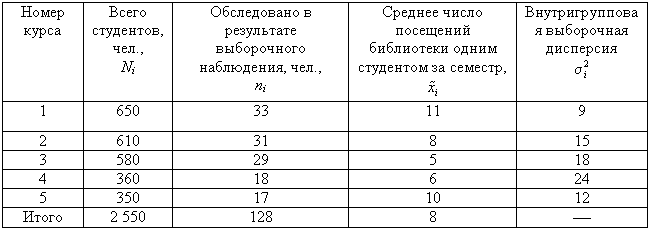
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:

аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:

- Средняя из внутригрупповых дисперсий

- Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

- Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно

- Значение среднего квадратического отклонения составляет

- Средняя ошибка выборки:

- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:

- Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка
выборки
показывает, насколько отклоняется в
среднем параметр выборочной
совокупности
от соответствующего параметра генеральной.
Если рассчитать среднюю из ошибок всех
возможных выборок определенного вида
заданного объема (n),
извлеченных из одной и той же генеральной
совокупности,
то получим их обобщающую характеристику
среднюю
ошибку выборки
().
В
теории выборочного наблюдения
выведены формулы для определения ,
которые индивидуальны для разных
способов отбора (повторного и
бесповторного), типов используемых
выборок и видов оцениваемых статистических
показателей.
Например, если
применяется повторная собственно
случайная выборка, то
определяется как:
![]()
при
оценивании среднего значения признака;
![]()
если
признак альтернативный, и оценивается
доля.
При бесповторном
собственно случайном отборе в формулы
вносится поправка
![]()
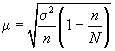
для
среднего значения признака;
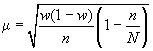
для
доли.
Вероятность
получения именно такой величины ошибки
всегда равна 0,683. На практике же
предпочитают получать данные с большей
вероятностью, но это приводит к возрастанию
величины ошибки выборки.
Предельная
ошибка выборки ()
равна t-кратному
числу средних ошибок выборки (в теории
выборки принято коэффициент t
называть
коэффициентом доверия):
t
.
Если ошибку выборки
увеличить в два раза (t
2), то получим гораздо большую вероятность
того, что она не превысит определенного
предела (в нашем случае
двойной средней ошибки)
0,954. Если взять t
3, то доверительная вероятность составит
0,997
практически достоверность.
Уровень предельной
ошибки выборки зависит от следующих
факторов:
степени вариации
единиц генеральной совокупности;
объема выборки;
выбранных схем
отбора (бесповторный отбор дает меньшую
величину ошибки);
уровня
доверительной вероятности.
Если объем выборки
больше 30, то значение t
определяется по таблице нормального
распределения, если меньше
по таблице распределения Стьюдента
(Приложение
1).
Приведем некоторые
значения коэффициента доверия из таблицы
нормального распределения.
![]()
Доверительный
интервал для среднего значения признака
и для доли в генеральной
совокупности
устанавливается следующим образом:
![]()
Итак, определение
границ генеральной средней и доли
состоит из следующих этапов:
нахождение в
выборке среднего значения признака
(или доли);
определение
в соответствии с выбранной схемой отбора
и вида выборки;
задание
доверительной вероятности Р
и определение коэффициента доверия t
по
соответствующей таблице;
вычисление
предельной ошибки выборки ;
построение
доверительного интервала для средней
(или доли).
Ошибки выборки
при различных видах отбора
1. Собственно
случайная и механическая выборка.
Средняя
ошибка собственно случайной и механической
выборки находятся по формулам,
представленным в табл. 11.1.
Таблица 1
Формулы для
расчета средней ошибки
собственно
случайной и механической выборки ()

где
2
дисперсия
признака в выборочной совокупности.
Пример 2. Для
изучения уровня фондоотдачи было
проведено выборочное обследование 90
предприятий из 225 методом случайной
повторной выборки, в результате которого
получены данные, представленные в
таблице.

В рассматриваемом
примере имеем 40%-ную выборку (90 : 225
0,4, или 40%). Определим ее предельную ошибку
и границы для среднего значения признака
в генеральной совокупности по шагам
алгоритма:
1. По результатам
выборочного обследования рассчитаем
среднее значение и дисперсию в выборочной
совокупности:
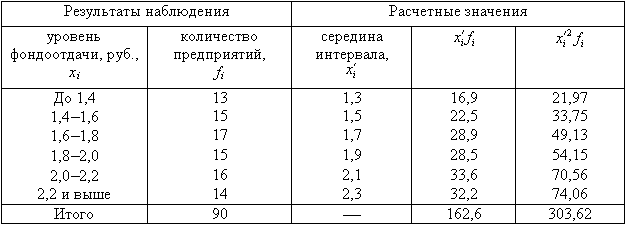
Выборочная средняя
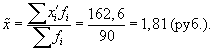
Выборочная
дисперсия изучаемого признака
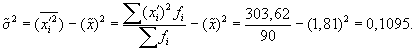
2. Определяем
среднюю ошибку повторной случайной
выборки
![]()
3. Зададим
вероятность, на уровне которой будем
говорить о величине предельной ошибки
выборки. Чаще всего она принимается
равной 0,999; 0,997; 0,954.
Для наших данных
определим предельную ошибку выборки,
например, с вероятностью 0,954. По таблице
значений вероятности функции нормального
распределения (см. выдержку из нее,
приведенную в Приложении 1) находим
величину коэффициента доверия t,
соответствующего вероятности 0,954. При
вероятности 0,954 коэффициент t
равен 2.
4. Предельная
ошибка выборки с вероятностью 0,954 равна
![]()
5. Найдем доверительные
границы для среднего значения уровня
фондоотдачи в генеральной совокупности
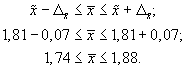
Таким образом, в
954 случаях из 1000 среднее значение
фондоотдачи будет не выше 1,88 руб. и не
ниже 1,74 руб.
Выше была
использована повторная схема случайного
отбора. Посмотрим, изменятся ли результаты
обследования, если предположить, что
отбор осуществлялся по схеме бесповторного
отбора. В этом случае расчет средней
ошибки проводится по формуле
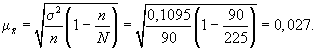
Тогда при вероятности
равной 0,954 величина предельной ошибки
выборки составит:
![]()
Доверительные
границы для среднего значения признака
при бесповторном случайном отборе будут
иметь следующие значения:
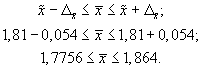
Сравнив результаты
двух схем отбора, можно сделать вывод
о том, что применение бесповторной
случайной выборки дает более точные
результаты по сравнению с применением
повторного отбора при одной и той же
доверительной вероятности. При этом,
чем больше объем выборки, тем существеннее
сужаются границы значений средней при
переходе от одной схемы отбора к другой.
По данным примера
определим, в каких границах находится
доля предприятий с уровнем фондоотдачи,
не превышающим значения 2,0 руб., в
генеральной совокупности:
1) рассчитаем
выборочную долю.
Количество
предприятий в выборке с уровнем
фондоотдачи, не превышающим значения
2,0 руб., составляет 60 единиц. Тогда
m
60, n
90, w
m/n
60 : 90
0,667;
2) рассчитаем
дисперсию доли в выборочной совокупности
w2
w(1
w)
0,667(1
0,667)
0,222;
3) средняя ошибка
выборки при использовании повторной
схемы отбора составит
![]()
Если предположить,
что была использована бесповторная
схема отбора, то средняя ошибка выборки
с учетом поправки на конечность
совокупности составит
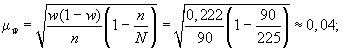
4) зададим
доверительную вероятность и определим
предельную ошибку выборки.
При значении
вероятности Р
0,997 по таблице нормального распределения
получаем значение для коэффициента
доверия t
3 (см. выдержку из нее, приведенную в
Приложении 1):
![]()
5) установим границы
для генеральной доли с вероятностью
0,997:

Таким образом, с
вероятностью 0,997 можно утверждать, что
в генеральной совокупности доля
предприятий с уровнем фондоотдачи, не
превышающим значения 2,0 руб., не меньше,
чем 54,7%, и не больше 78,7%.
2. Типическая
выборка. При
типической выборке генеральная
совокупность объектов разбита на k
групп, тогда
N1
N2
…
Ni
…
Nk
N.
Объем извлекаемых
из каждой типической группы единиц
зависит от принятого способа отбора;
их общее количество образует необходимый
объем выборки
n1
n2
…
ni
…
nk
n.
Существуют
следующие два способа организации
отбора внутри типической группы:
пропорциональной объему типических
групп и пропорциональной степени
колеблемости значений признака у единиц
наблюдения в группах. Рассмотрим первый
из них, как наиболее часто используемый.
Отбор, пропорциональный
объему типических групп, предполагает,
что в каждой из них будет отобрано
следующее число единиц совокупности:
![]()
где ni
количество извлекаемых единиц для
выборки из i-й
типической группы;
n
общий объем выборки;
Ni
количество единиц генеральной
совокупности, составивших i-ю
типическую группу;
N
общее количество единиц генеральной
совокупности.
Отбор единиц
внутри групп происходит в виде случайной
или механической выборки.
Формулы для
оценивания средней ошибки выборки для
среднего и доли представлены в табл.
11.2.
Таблица 2
Формулы для
расчета средней ошибки выборки ()
при использовании типического отбора,
пропорционального объему типических
групп
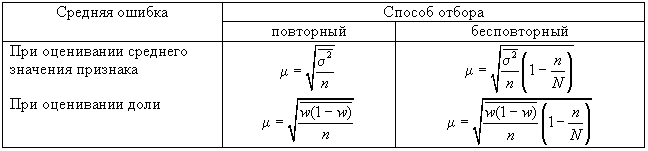
Здесь
![]()
средняя из групповых дисперсий типических
групп.
Пример 3. В
одном из московских вузов проведено
выборочное обследование студентов с
целью определения показателя средней
посещаемости вузовской библиотеки
одним студентом за семестр. Для этого
была использована 5%-ная бесповторная
типическая выборка, типические группы
которой соответствуют номеру курса.
При отборе, пропорциональном объему
типических групп, получены следующие
данные:
Число студентов,
которое необходимо обследовать на
каждом курсе, рассчитаем следующим
образом:
общий объем
выборочной совокупности:
![]()
количество
единиц, отобранных из каждой типической
группы:
![]()
аналогично для
других групп:
п2
31 (чел.);
п3
29 (чел.);
п4
18 (чел.);
п5
17 (чел.).
Проведем необходимые
расчеты.
1. Выборочная
средняя, исходя из значений средних
типических групп, составит:
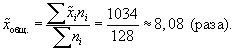
2. Средняя из
внутригрупповых дисперсий
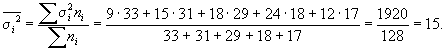
3. Средняя ошибка
выборки:
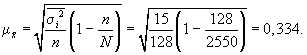
С вероятностью
0,954 находим предельную ошибку выборки:
![]()
4. Доверительные
границы для среднего значения признака
в генеральной совокупности:
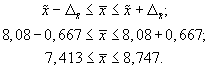
Таким образом, с
вероятностью 0,954 можно утверждать, что
один студент за семестр посещает
вузовскую библиотеку в среднем от семи
до девяти раз.
3.
Малая выборка. В
связи с небольшим объемом выборочной
совокупности
те формулы для определения ошибок
выборки,
которые использовались нами ранее при
«больших» выборках, становятся
неподходящими и требуют корректировки.
Среднюю ошибку
малой выборки
определяют по формуле
![]()
Предельная
ошибка малой выборки:
![]()
Распределение
значений выборочных средних всегда
имеет нормальный закон распределения
(или приближается к нему) при п
100, независимо от характера распределения
генеральной
совокупности.
Однако в случае малых выборок действует
иной закон распределения
распределение Стьюдента.
В этом случае коэффициент доверия
находится по таблице t-распределения
Стьюдента в зависимости от величины
доверительной вероятности Р
и объема выборки п.
В Приложении
1
приводится фрагмент таблицы t-распределения
Стьюдента, представленной в виде
зависимости доверительной вероятности
от объема выборки и коэффициента доверия
t.
Пример 4.
Предположим,
что выборочное обследование восьми
студентов академии показало, что на
подготовку к контрольной работе по
статистике они затратили следующее
количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4;
6,6.
Оценим выборочные
средние затраты времени и построим
доверительный интервал для среднего
значения признака в генеральной
совокупности, приняв доверительную
вероятность равной 0,95.
1. Среднее значение
признака в выборке равно
![]()
2. Значение среднего
квадратического отклонения составляет
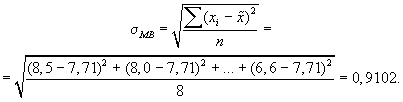
3. Средняя ошибка
выборки:
![]()
4. Значение
коэффициента доверия t
2,365 для п
8 и Р
0,95 (Приложение 1).
5. Предельная
ошибка выборки:
![]()
6. Доверительный
интервал для среднего значения признака
в генеральной совокупности:
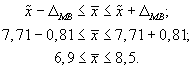
То есть с вероятностью
0,95 можно утверждать, что затраты времени
студента на подготовку к контрольной
работе находятся в пределах от 6,9 до 8,5
ч.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание курса лекций “Статистика”
Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.
Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.
При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.
Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:
N ‑ объем (число единиц) генеральной совокупности;
n ‑ объем (число единиц) выборочной совокупности;
![]()
‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);
![]()
‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);
р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как
m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,
определяется как ;
![]()
‑ средняя ошибка выборки;
![]()
‑ предельная ошибка выборки;
![]()
‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.
Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.
Таким образом среднюю ошибку выборки можно представить как

(10.1)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

(10.2)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.
Учитывая, что при достаточно большом объеме выборки отношение  близко к 1, формула средней ошибки повторной выборки принимает следующий вид:
близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

(10.3)
Где ‑ ![]() дисперсия изучаемого признака по выборочной совокупности.
дисперсия изучаемого признака по выборочной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.
При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Таблица 10.1 ‑ !!!Некоторые значения t
| Вероятность, рi. | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.
Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:
- Определение цели обследования.
- Установление границ генеральной совокупности.
- Составление программы наблюдения и программы разработки данных
- Определение вида выборки, процента отбора и метода отбора
- Отбор и регистрация наблюдаемых признаков у отобранных единиц.
- Насчет выборочных характеристик и их ошибок.
- Распространение полученных результатов на генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.
К наиболее распространенным на практике видам относятся:
- собственно-случайная (простая случайная) выборка;
- механическая (систематическая) выборка;
- типическая (стратифицированная, расслоенная) выборка;
- серийная (гнездовая) выборка.
Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.
Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.
Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:

(10.4)
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:

(10.5)
а при расчете средней ошибки собственно-случайной бесповторной выборки:

(10.6)
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

(10.7)
где ![]() и
и ![]() ‑ генеральная и выборочная средняя соответственно;
‑ генеральная и выборочная средняя соответственно;
![]() ‑ предельная ошибка выборочной средней.
‑ предельная ошибка выборочной средней.
Пример.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:
Определим пределы генеральной средней:
 или
или

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2.
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 10.2 ‑ Распределение семей по числу детей в городе N
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество
семей |
1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей
|
Число детей в семье, х; |
Количество семей, f | ||||
|
0 1 2 3 4 5 |
1000 2000 1200 400 200 200 |
0
2000 2400 1200 800 1000 |
-1,5
-0,5 0,5 1,5 2,5 3,5 |
2,25
0,25 0,25 2,25 6,25 12,25 |
2250 500 300 900 1250 2450 |
|
Итого |
5000 | 7400 | – | – | 7650 |


Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).

Следовательно, пределы генеральной средней:

Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.
В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

(10.8)
где ![]() ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

(10.9)
Соответственно, при бесповторном отборе:

(10.10)
Пределы доли признака в генеральной совокупности p выглядят следующим образом:

(10.11)
Рассмотрим пример.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности:
n= 480 х 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:

Пределы доли признака в генеральной совокупности:

Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:

(10.12)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.
С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:

Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

(10.13)
Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.
Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит

Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.
Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.
Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.
Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.
Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.
При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).

С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.
Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.
Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:

(10.14)
Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.
Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:

Средняя ошибка типической выборки определяется по формулам:

(10.15)
 (10.16)
(10.16)
где ![]() – средняя из внутригрупповых дисперсий.
– средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

(10.17)
Где ![]() ‑ среднее отклонение признака в i-ой группе.
‑ среднее отклонение признака в i-ой группе.
Cредняя ошибка такого отбора определяется следующим образом:

(10.18)

(10.19)
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Таблица 10.4 ‑ Результаты обследования рабочих предприятия
| Цех | Всего рабочих, человек | Обследовано, человек | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| I
II III |
1000
1400 800 |
100
140 80 |
18
12 15 |
49
25 16 |
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)
Рассчитаем среднюю из внутригрупповых дисперсий:

Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):

Рассчитаем выборочную среднюю:

С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:

Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:


С учетом полученных значений рассчитаем среднюю ошибку выборки:

В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

(10.20)

(10.21)
Где r ‑ число отобранных серий; R ‑ общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
 (10.22)
(10.22)
где ![]() ‑ средняя i-й серии;
‑ средняя i-й серии;
![]() ‑ общая средняя по всей выборочной совокупности.
‑ общая средняя по всей выборочной совокупности.
Пример.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.
Решение. Рассчитаем общую среднюю:

Межгрупповая (межсерийная) дисперсия равна:

Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):

Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:

Определение необходимого объема выборки
При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:
– собственно-случайная и механическая выборка:

(10.23)

(10.24)
– типическая выборка:

(10.25)

(10.26)
– серийная выборка:

(10.27)

(10.28)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.
Решение. Рассчитаем необходимый объем выборки:

Пример.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки:

Вычислим теперь объем отдельных типических групп:

Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.
Пример.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:

Содержание курса лекций “Статистика”
Контрольные задания
Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.
Для изучения мнения студентов о проведении определенных мероприятий из совокупности, состоящей из 10 тыс. человек, методом случайного бесповторного отбора опрошено 600 студентов. Из них 240 одобрили план мероприятий. С вероятностью 0,954 определите предел, в котором находится доля студентов, одобривших мероприятия, во всей совокупности.
Решение:
При собственно-случайном бесповторном отборе среднюю ошибку выборочной доли рассчитывают по формуле:
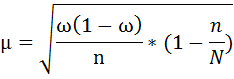
где
ω — доля единиц выборочной совокупности, обладающих изучаемым признаком,
n – численность выборочной совокупности,
N – численность генеральной совокупности.
Доля студентов одобривших мероприятия из числа опрошенных студентов составила:
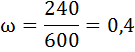
Рассчитаем среднюю ошибку выборочной доли:
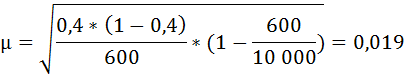
Предельная ошибка выборочной доли с вероятностью 0,954 составит:
Δ = μ * t = 0,019 * 2 = 0,039 (или 3,9%).
t — коэффициент доверия.
Значение t табличное (смотри Задачу №32).
При Р = 0,954, t = 2,0.
Определим пределы, доли признака в генеральной совокупности следующим образом:
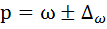
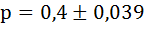
Пределы генеральной доли признака в генеральной совокупности:
0,4 – 0,039 ˂ р ˂ 0,4 + 0,039
или
0,361 ˂ р ˂ 0,439
С вероятностью 0,954 можно утверждать, что доля студентов, одобривших мероприятия, во всей совокупности находится в пределах от 36,1% до 43,9%.
2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка
выборки
показывает, насколько отклоняется в
среднем параметр выборочной
совокупности
от соответствующего параметра генеральной.
Если рассчитать среднюю из ошибок всех
возможных выборок определенного вида
заданного объема (n),
извлеченных из одной и той же генеральной
совокупности,
то получим их обобщающую характеристику
среднюю
ошибку выборки
().
В
теории выборочного наблюдения
выведены формулы для определения ,
которые индивидуальны для разных
способов отбора (повторного и
бесповторного), типов используемых
выборок и видов оцениваемых статистических
показателей.
Например, если
применяется повторная собственно
случайная выборка, то
определяется как:
![]()
при
оценивании среднего значения признака;
![]()
если
признак альтернативный, и оценивается
доля.
При бесповторном
собственно случайном отборе в формулы
вносится поправка
![]()
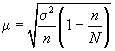
для
среднего значения признака;
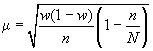
для
доли.
Вероятность
получения именно такой величины ошибки
всегда равна 0,683. На практике же
предпочитают получать данные с большей
вероятностью, но это приводит к возрастанию
величины ошибки выборки.
Предельная
ошибка выборки ()
равна t-кратному
числу средних ошибок выборки (в теории
выборки принято коэффициент t
называть
коэффициентом доверия):
t
.
Если ошибку выборки
увеличить в два раза (t
2), то получим гораздо большую вероятность
того, что она не превысит определенного
предела (в нашем случае
двойной средней ошибки)
0,954. Если взять t
3, то доверительная вероятность составит
0,997
практически достоверность.
Уровень предельной
ошибки выборки зависит от следующих
факторов:
степени вариации
единиц генеральной совокупности;
объема выборки;
выбранных схем
отбора (бесповторный отбор дает меньшую
величину ошибки);
уровня
доверительной вероятности.
Если объем выборки
больше 30, то значение t
определяется по таблице нормального
распределения, если меньше
по таблице распределения Стьюдента
(Приложение
1).
Приведем некоторые
значения коэффициента доверия из таблицы
нормального распределения.
![]()
Доверительный
интервал для среднего значения признака
и для доли в генеральной
совокупности
устанавливается следующим образом:
![]()
Итак, определение
границ генеральной средней и доли
состоит из следующих этапов:
нахождение в
выборке среднего значения признака
(или доли);
определение
в соответствии с выбранной схемой отбора
и вида выборки;
задание
доверительной вероятности Р
и определение коэффициента доверия t
по
соответствующей таблице;
вычисление
предельной ошибки выборки ;
построение
доверительного интервала для средней
(или доли).
Ошибки выборки
при различных видах отбора
1. Собственно
случайная и механическая выборка.
Средняя
ошибка собственно случайной и механической
выборки находятся по формулам,
представленным в табл. 11.1.
Таблица 1
Формулы для
расчета средней ошибки
собственно
случайной и механической выборки ()

где
2
дисперсия
признака в выборочной совокупности.
Пример 2. Для
изучения уровня фондоотдачи было
проведено выборочное обследование 90
предприятий из 225 методом случайной
повторной выборки, в результате которого
получены данные, представленные в
таблице.

В рассматриваемом
примере имеем 40%-ную выборку (90 : 225
0,4, или 40%). Определим ее предельную ошибку
и границы для среднего значения признака
в генеральной совокупности по шагам
алгоритма:
1. По результатам
выборочного обследования рассчитаем
среднее значение и дисперсию в выборочной
совокупности:

Выборочная средняя
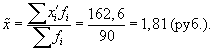
Выборочная
дисперсия изучаемого признака
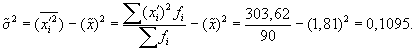
2. Определяем
среднюю ошибку повторной случайной
выборки
![]()
3. Зададим
вероятность, на уровне которой будем
говорить о величине предельной ошибки
выборки. Чаще всего она принимается
равной 0,999; 0,997; 0,954.
Для наших данных
определим предельную ошибку выборки,
например, с вероятностью 0,954. По таблице
значений вероятности функции нормального
распределения (см. выдержку из нее,
приведенную в Приложении 1) находим
величину коэффициента доверия t,
соответствующего вероятности 0,954. При
вероятности 0,954 коэффициент t
равен 2.
4. Предельная
ошибка выборки с вероятностью 0,954 равна
![]()
5. Найдем доверительные
границы для среднего значения уровня
фондоотдачи в генеральной совокупности
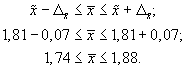
Таким образом, в
954 случаях из 1000 среднее значение
фондоотдачи будет не выше 1,88 руб. и не
ниже 1,74 руб.
Выше была
использована повторная схема случайного
отбора. Посмотрим, изменятся ли результаты
обследования, если предположить, что
отбор осуществлялся по схеме бесповторного
отбора. В этом случае расчет средней
ошибки проводится по формуле
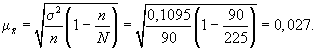
Тогда при вероятности
равной 0,954 величина предельной ошибки
выборки составит:
![]()
Доверительные
границы для среднего значения признака
при бесповторном случайном отборе будут
иметь следующие значения:
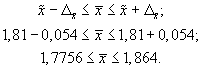
Сравнив результаты
двух схем отбора, можно сделать вывод
о том, что применение бесповторной
случайной выборки дает более точные
результаты по сравнению с применением
повторного отбора при одной и той же
доверительной вероятности. При этом,
чем больше объем выборки, тем существеннее
сужаются границы значений средней при
переходе от одной схемы отбора к другой.
По данным примера
определим, в каких границах находится
доля предприятий с уровнем фондоотдачи,
не превышающим значения 2,0 руб., в
генеральной совокупности:
1) рассчитаем
выборочную долю.
Количество
предприятий в выборке с уровнем
фондоотдачи, не превышающим значения
2,0 руб., составляет 60 единиц. Тогда
m
60, n
90, w
m/n
60 : 90
0,667;
2) рассчитаем
дисперсию доли в выборочной совокупности
w2
w(1
w)
0,667(1
0,667)
0,222;
3) средняя ошибка
выборки при использовании повторной
схемы отбора составит
![]()
Если предположить,
что была использована бесповторная
схема отбора, то средняя ошибка выборки
с учетом поправки на конечность
совокупности составит
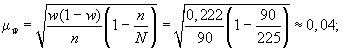
4) зададим
доверительную вероятность и определим
предельную ошибку выборки.
При значении
вероятности Р
0,997 по таблице нормального распределения
получаем значение для коэффициента
доверия t
3 (см. выдержку из нее, приведенную в
Приложении 1):
![]()
5) установим границы
для генеральной доли с вероятностью
0,997:

Таким образом, с
вероятностью 0,997 можно утверждать, что
в генеральной совокупности доля
предприятий с уровнем фондоотдачи, не
превышающим значения 2,0 руб., не меньше,
чем 54,7%, и не больше 78,7%.
2. Типическая
выборка. При
типической выборке генеральная
совокупность объектов разбита на k
групп, тогда
N1
N2
…
Ni
…
Nk
N.
Объем извлекаемых
из каждой типической группы единиц
зависит от принятого способа отбора;
их общее количество образует необходимый
объем выборки
n1
n2
…
ni
…
nk
n.
Существуют
следующие два способа организации
отбора внутри типической группы:
пропорциональной объему типических
групп и пропорциональной степени
колеблемости значений признака у единиц
наблюдения в группах. Рассмотрим первый
из них, как наиболее часто используемый.
Отбор, пропорциональный
объему типических групп, предполагает,
что в каждой из них будет отобрано
следующее число единиц совокупности:
![]()
где ni
количество извлекаемых единиц для
выборки из i-й
типической группы;
n
общий объем выборки;
Ni
количество единиц генеральной
совокупности, составивших i-ю
типическую группу;
N
общее количество единиц генеральной
совокупности.
Отбор единиц
внутри групп происходит в виде случайной
или механической выборки.
Формулы для
оценивания средней ошибки выборки для
среднего и доли представлены в табл.
11.2.
Таблица 2
Формулы для
расчета средней ошибки выборки ()
при использовании типического отбора,
пропорционального объему типических
групп

Здесь
![]()
средняя из групповых дисперсий типических
групп.
Пример 3. В
одном из московских вузов проведено
выборочное обследование студентов с
целью определения показателя средней
посещаемости вузовской библиотеки
одним студентом за семестр. Для этого
была использована 5%-ная бесповторная
типическая выборка, типические группы
которой соответствуют номеру курса.
При отборе, пропорциональном объему
типических групп, получены следующие
данные:

Число студентов,
которое необходимо обследовать на
каждом курсе, рассчитаем следующим
образом:
общий объем
выборочной совокупности:
![]()
количество
единиц, отобранных из каждой типической
группы:
![]()
аналогично для
других групп:
п2
31 (чел.);
п3
29 (чел.);
п4
18 (чел.);
п5
17 (чел.).
Проведем необходимые
расчеты.
1. Выборочная
средняя, исходя из значений средних
типических групп, составит:
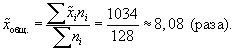
2. Средняя из
внутригрупповых дисперсий
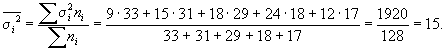
3. Средняя ошибка
выборки:
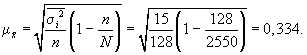
С вероятностью
0,954 находим предельную ошибку выборки:
![]()
4. Доверительные
границы для среднего значения признака
в генеральной совокупности:
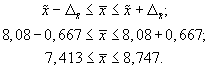
Таким образом, с
вероятностью 0,954 можно утверждать, что
один студент за семестр посещает
вузовскую библиотеку в среднем от семи
до девяти раз.
3.
Малая выборка. В
связи с небольшим объемом выборочной
совокупности
те формулы для определения ошибок
выборки,
которые использовались нами ранее при
«больших» выборках, становятся
неподходящими и требуют корректировки.
Среднюю ошибку
малой выборки
определяют по формуле
![]()
Предельная
ошибка малой выборки:
![]()
Распределение
значений выборочных средних всегда
имеет нормальный закон распределения
(или приближается к нему) при п
100, независимо от характера распределения
генеральной
совокупности.
Однако в случае малых выборок действует
иной закон распределения
распределение Стьюдента.
В этом случае коэффициент доверия
находится по таблице t-распределения
Стьюдента в зависимости от величины
доверительной вероятности Р
и объема выборки п.
В Приложении
1
приводится фрагмент таблицы t-распределения
Стьюдента, представленной в виде
зависимости доверительной вероятности
от объема выборки и коэффициента доверия
t.
Пример 4.
Предположим,
что выборочное обследование восьми
студентов академии показало, что на
подготовку к контрольной работе по
статистике они затратили следующее
количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4;
6,6.
Оценим выборочные
средние затраты времени и построим
доверительный интервал для среднего
значения признака в генеральной
совокупности, приняв доверительную
вероятность равной 0,95.
1. Среднее значение
признака в выборке равно
![]()
2. Значение среднего
квадратического отклонения составляет
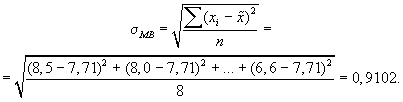
3. Средняя ошибка
выборки:
![]()
4. Значение
коэффициента доверия t
2,365 для п
8 и Р
0,95 (Приложение 1).
5. Предельная
ошибка выборки:
![]()
6. Доверительный
интервал для среднего значения признака
в генеральной совокупности:
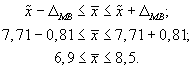
То есть с вероятностью
0,95 можно утверждать, что затраты времени
студента на подготовку к контрольной
работе находятся в пределах от 6,9 до 8,5
ч.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание курса лекций “Статистика”
Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.
Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.
При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.
Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:
N ‑ объем (число единиц) генеральной совокупности;
n ‑ объем (число единиц) выборочной совокупности;
![]()
‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);
![]()
‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);
р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как
m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,
определяется как ;
![]()
‑ средняя ошибка выборки;
![]()
‑ предельная ошибка выборки;
![]()
‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.
Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.
Таким образом среднюю ошибку выборки можно представить как

(10.1)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

(10.2)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.
Учитывая, что при достаточно большом объеме выборки отношение  близко к 1, формула средней ошибки повторной выборки принимает следующий вид:
близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

(10.3)
Где ‑ ![]() дисперсия изучаемого признака по выборочной совокупности.
дисперсия изучаемого признака по выборочной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.
При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Таблица 10.1 ‑ !!!Некоторые значения t
| Вероятность, рi. | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.
Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:
- Определение цели обследования.
- Установление границ генеральной совокупности.
- Составление программы наблюдения и программы разработки данных
- Определение вида выборки, процента отбора и метода отбора
- Отбор и регистрация наблюдаемых признаков у отобранных единиц.
- Насчет выборочных характеристик и их ошибок.
- Распространение полученных результатов на генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.
К наиболее распространенным на практике видам относятся:
- собственно-случайная (простая случайная) выборка;
- механическая (систематическая) выборка;
- типическая (стратифицированная, расслоенная) выборка;
- серийная (гнездовая) выборка.
Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.
Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.
Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:

(10.4)
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:

(10.5)
а при расчете средней ошибки собственно-случайной бесповторной выборки:

(10.6)
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

(10.7)
где ![]() и
и ![]() ‑ генеральная и выборочная средняя соответственно;
‑ генеральная и выборочная средняя соответственно;
![]() ‑ предельная ошибка выборочной средней.
‑ предельная ошибка выборочной средней.
Пример.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:
Определим пределы генеральной средней:
 или
или

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2.
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 10.2 ‑ Распределение семей по числу детей в городе N
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество
семей |
1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей
|
Число детей в семье, х; |
Количество семей, f | ||||
|
0 1 2 3 4 5 |
1000 2000 1200 400 200 200 |
0
2000 2400 1200 800 1000 |
-1,5
-0,5 0,5 1,5 2,5 3,5 |
2,25
0,25 0,25 2,25 6,25 12,25 |
2250 500 300 900 1250 2450 |
|
Итого |
5000 | 7400 | – | – | 7650 |


Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).

Следовательно, пределы генеральной средней:

Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.
В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

(10.8)
где ![]() ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

(10.9)
Соответственно, при бесповторном отборе:

(10.10)
Пределы доли признака в генеральной совокупности p выглядят следующим образом:

(10.11)
Рассмотрим пример.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности:
n= 480 х 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:

Пределы доли признака в генеральной совокупности:

Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:

(10.12)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.
С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:

Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

(10.13)
Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.
Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит

Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.
Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.
Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.
Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.
Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.
При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).

С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.
Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.
Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:

(10.14)
Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.
Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:

Средняя ошибка типической выборки определяется по формулам:

(10.15)
 (10.16)
(10.16)
где ![]() – средняя из внутригрупповых дисперсий.
– средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

(10.17)
Где ![]() ‑ среднее отклонение признака в i-ой группе.
‑ среднее отклонение признака в i-ой группе.
Cредняя ошибка такого отбора определяется следующим образом:

(10.18)

(10.19)
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Таблица 10.4 ‑ Результаты обследования рабочих предприятия
| Цех | Всего рабочих, человек | Обследовано, человек | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| I
II III |
1000
1400 800 |
100
140 80 |
18
12 15 |
49
25 16 |
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)
Рассчитаем среднюю из внутригрупповых дисперсий:

Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):

Рассчитаем выборочную среднюю:

С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:

Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:


С учетом полученных значений рассчитаем среднюю ошибку выборки:

В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

(10.20)

(10.21)
Где r ‑ число отобранных серий; R ‑ общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
 (10.22)
(10.22)
где ![]() ‑ средняя i-й серии;
‑ средняя i-й серии;
![]() ‑ общая средняя по всей выборочной совокупности.
‑ общая средняя по всей выборочной совокупности.
Пример.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.
Решение. Рассчитаем общую среднюю:

Межгрупповая (межсерийная) дисперсия равна:

Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):

Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:

Определение необходимого объема выборки
При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:
– собственно-случайная и механическая выборка:

(10.23)

(10.24)
– типическая выборка:

(10.25)

(10.26)
– серийная выборка:

(10.27)

(10.28)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.
Решение. Рассчитаем необходимый объем выборки:

Пример.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки:

Вычислим теперь объем отдельных типических групп:

Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.
Пример.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:

Содержание курса лекций “Статистика”
Контрольные задания
Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.

 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп