При проверке нулевой основной гипотезы возможны следующие ошибки ошибка парной гипотезы - Ремонт и установка крупной бытовой техники

2.1.1. Основные понятия о статистической гипотезе

Полученные
в экспериментах выборочные данные
всегда ограничены и носят в значительной
степени случайный характер. Именно
поэтому для анализа таких данных и
используется математическая статистика,
позволяющая обобщать закономерности,
полученные на выборке, и распространять
их на всю генеральную совокупность.

Однако,
в связи с действием случайных причин,
оценка параметров генеральной
совокупности, сделанная на основании
экспериментальных (выборочных) данных,
всегда будет сопровождаться погрешностью,
и поэтому подобного рода оценка должна
рассматриваться как предположительное,
а не как окончательное утверждение.
Подобные предположения о свойствах и
параметрах генеральной совокупности
носят название статистических гипотез.

Сущность
проверки статистической гипотезы
заключается в том, чтобы установить,
согласуются ли экспериментальные
данные и выдвинутая гипотеза, допустимо
ли отнести расхождение между гипотезой
и результатом статистического анализа
экспериментальных данных за счет
случайных причин?

Рассмотрим
простой пример. Подбросим монету 10 раз.
Если монета не имеет дефектов формы,
то количество выпадений герба и цифры
должно быть примерно одинаковым. Таким
образом, возможны гипотезы:

—
монета правильная и частота выпадений
герба и цифры примерно одинакова,

—
монета деформирована и чаще выпадает
герб,

—
монета деформирована и чаще выпадает
цифра.

Но
нам надо выразить понятия «правильная»
или «деформированная» монета в
математических параметрах. В качестве
параметра выбираем вероятность Р
выпадения герба. Тогда приведенные выше
гипотезы можно записать (в порядке
упоминания) так:

—
Р = ½,

—
Р > ½,

—
Р < ½.

При
проведении эксперимента надо ответить
на вопрос, какая же из приведенных
гипотез верна?

При
проверке статистических гипотез
используется два понятия: нулевая
гипотеза (ее обозначают Н0) и альтернативная
гипотеза (обозначение Н1). Как правило,
принято считать, что нулевая гипотеза
Н0 – это гипотеза о сходстве, а
альтернативная Н1 – гипотеза о различии.
Таким образом, принятие нулевой гипотезы
свидетельствует об отсутствии различий,
а альтернативной – о наличии различий.

Для
нашего примера в качестве нулевой
(будем называть ее основной) гипотезы
Н0 принимаем – монета правильная, а
качестве альтернативной гипотезы Н1 –
монета деформированная. Альтернативных
гипотез может быть несколько. В нашем
случае их две (больше и меньше ½).

2.1.2. Ошибки при проверке статистических гипотез

Обозначим
через N множество всевозможных
результатов наблюдений (выборок) m.
Выделим в N область n , исходя из следующих
соображений: если гипотеза Н0 верна,
то наступление события m ∈
n маловероятно. Это записывается так:

Р
{ m ∈
n/Но} = α ,

где
α – малое число, близкое к нулю.

Иными
словами, вероятность Р события m ∈
n при условии, что верна гипотеза Н0,
равна α. Если это событие все же произошло,
то гипотеза Н0 отвергается. При этом
сохраняется небольшая вероятность
(учитывая, что α мало, но не равно нулю),
что гипотеза Н0 отвергается, хотя она
верна. Такая ошибка называется ошибкой
первого рода. Ее вероятность равна α.

Возможна
и ошибка второго рода β, которая состоит
в том, что гипотеза Н0 принимается, хотя
она неверна, а верна альтернативная
гипотеза Н1.

Р
{m ∈
n/Н1} = β.

Разберем
порядок проверки статистических гипотез
на примере. Допустим, что проводится
приемочный контроль партии продукции.
Известно, что в партии могут содержаться
дефектные изделия. Поставщик полагает,
что доля дефектных изделий составляет
не более 3%, а заказчик считает, что
качество изготовления изделий низкое
и доля дефектных изделий значительна
и составляет 20%. Между поставщиком и
заказчиком достигнута следующая
договоренность: партия продукции
принимается, если в выборке из 10 изделий
будет обнаружено не более одного
дефектного изделия.

Требуется
в процессе решения примера сформулировать:

—
нулевую (основную) и альтернативную
гипотезы,

—
определить критическую область и
область принятия нулевой гипотезы,

—
определить, в чем состоят ошибки первого
и второго рода, и найти их вероятность.

Если
смотреть на ситуацию с точки зрения
заказчика (потребителя), учитывая, что
заказчик всегда прав, то нулевой гипотезой
Н0 следует принять гипотезу, что
продукция содержит 20% брака. Альтернативная
гипотеза Н1 соответствует версии
поставщика – 3% брака.

Поскольку
отбирается 10 изделий, то множество
возможных результатов (наличие дефектного
изделия) составит N = (0,1,2,3…10), так как в
выборке может оказаться и 0, и 10 дефектных
изделий. По условиям поставок, принятым
и заказчиком, и поставщиком, гипотеза
заказчика Н0 считается:

− отвергнутой,
если число дефектов находится в области
n = {0,1};

− принятой,
если число дефектов находится в области
n = {2,3,4…10}.

Область
результатов выборки, при попадании в
которую принятая гипотеза отвергается,
называется критической. В нашем
случае это – область n = {0,1}.

Напомним,
что ошибка первого рода возникает тогда,
когда гипотеза Н0 отвергается, хотя
она верна. Для нашего примера это
означает, что партия изделий принимается
(закупается), хотя в ней 20% дефектных
изделий. Ошибка второго рода для
нашего примера возникает тогда, когда
нулевая гипотеза принимается (т.е.
партия бракуется), в то время как верна
альтернативная гипотеза (дефектных
изделий всего 3%). Найдем вероятность
этих ошибок.

Сначала
заметим, что число дефектных изделий m
является биномиальной, случайной
величиной. Если допустить, что гипотеза
Н0 верна то в выборке N=10 этому
соответствует 2 случая: m =0 и m = 1. Тогда
биномиальная величина имеет вид Bi
(10;2). Найдем вероятность каждого из двух
событий:

Р(m
= 0) = (0,8)¹⁰=
0,107,

Р(m
= 1) = 10·(0,8)⁹·0,2
= 0,268.

Тогда
ошибка первого рода α будет равна сумме
этих вероятностей:

α
= Р (m ≤ 1) = Р (m=0/Н0) + Р (m =1/Н0) = 0,375.

Если
верна гипотеза Н1, то вероятность
выбрать дефектное изделие составляет
по условию примера 0,03 (3%). Ошибка
второго рода произойдет, если из 10
изделий в выборке окажутся дефектных
2 и более. В этом случае биномиальная
величина имеет вид Bi (10;0,03). Тогда для
событий m ≤ 1 вероятность составит:

Р(m=0)
= (0,97)¹⁰=
0,737,

Р(m=1)
= 10·(0,97)^9·0,03
= 0,228.

Таким
образом, вероятность альтернативных
событий (m > 1) составит величину ошибки
второго рода β:

β
= Р(m>1/Н1) = 1 – Р(m ≤ 1/Н1) = 1 – Р(m =0/Н1) –
Р(m=1/Н1) = =1 – 0,737 – 0,228 = 0,035.

Из
сравнения ошибок α и β можно заключить,
что оговоренная процедура по приему
партии выгодна скорее поставщику, чем
потребителю (заказчику).

Соседние файлы в папке УК работы

#
#
#
11.08.201936.84 Кб25ЛР 6 УК1.xlsx
#
11.08.201919.67 Кб23ЛР 6 УК2.xlsx
#
11.08.201941.03 Кб24лр7.xlsx
#
11.08.201977.53 Кб25лр8.xlsx

План:

1. Статистические гипотезы. Основные понятия.

2. Гипотезы о законе распределения.

3. Гипотезы о числовом значении генерального
среднего и дисперсии.

1.
Статистические гипотезы. Основные понятия.

Статистическая гипотеза— это утверждение о виде неизвестного
распределения или параметрах известного распределения. Статистические гипотезы
проверяются по результатам выборки статистическими методами в ходе эксперимента
(эмпирическим путем) с помощью статистических критериев.

В тех случаях, когда
известен закон, но неизвестны значения его параметров (дисперсия или
математическое ожидание) в конкретной ситуации, статистическую гипотезу
называют параметрической.

Например, предположение
об ожидаемом среднем доходе по акциям или разбросе дохода являются
параметрическими гипотезами.

Когда закон
распределения генеральной совокупности не известен, но есть основания
предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его
распределения называются непараметрическими.

Например, можно
выдвинуть гипотезу, что число дневных продаж в магазине или доход населения
подчинены нормальному закону распределения.

По содержанию статистические гипотезы можно классифицировать:

1.
Гипотезы о типе вероятностного закона
распределения случайной величины, характеризующего явление или процесс.

2.
Гипотезы об однородности двух или более
обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных
совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые
выборочные характеристики различаются между собой статистически значимо или
нет.

3.
Гипотезы о свойствах числовых значений
параметров исследуемой генеральной совокупности. Больше ли значения параметров
некоторого заданного номинала или меньше и т.д.

4.
Гипотезы о вероятностной зависимости двух
или более признаков, характеризующих различные свойства рассматриваемого
явления или процесса. При этом определяется характер этой зависимости.

Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).

Выдвинутую гипотезу называют основной или нулевой и обозначают H₀
. Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают
H₁.

Под статистическим
критерием понимают однозначно определенное правило, устанавливающее
условие, при котором проверяемая гипотеза отвергается либо не отвергается.

Пример:

Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных условиях используются статистические
данные, на основании которых делается вывод о том, является ли данное массовое
заболевание эпидемией. Предполагается, что существует некоторый критерий-
уровень доли заболевших, критический для этого заболевания, который
устанавливается по ранее имевшимся случаям.

Различают три вида критериев:

1.
Параметрические критерии—
критерии значимости, которые служат для проверки гипотез о параметрах
распределения генеральной совокупности при известном виде распределения.

2.
Критерии согласия—
позволяют проверить гипотезы о соответствии распределений генеральной
совокупности известной теоретической модели.

3.
Непараметрические критерии—
используются в гипотезах, когда не требуется знаний о конкретном виде
распределения.

Проверка
параметрических гипотез проводится на основе критериев значимости., а
непараметрических- критериев согласия.

Задача проверки
статистических гипотез сводится к исследованию генеральной совокупности по
выборке. Множество возможных значений элементов выборки может быть разделено на
два непересекающихся подмножества- критическую область и область принятия
гипотезы.

Областью принятия гипотезы или областью допустимых значений I_доп

называют совокупность значений критерия,
при которых эту гипотезу принимают.

Критической областью
I_кр называют множество значений критерия, при
котором гипотезу отвергают.

Наблюдаемые значения критерия (статистика)
K_набл
называют такое значение критерия, которое
находится по данным выборки.

Границы критической области, отделяющие ее от
области принятия гипотезы, называют критическими точками и обозначают
K_кр.

Для определения
критической области задается уровень значимости
—
некая малая вероятность попадания критерия в критическую область.

Уровень значимости— вероятность принятия
конкурирующей гипотезы, тогда как справедлива основная.

С помощью уровня
значимости определяются границы критической области.

Основной принцип проверки статистических гипотез
состоит в следующем: если наблюдаемое значение статистики критерия попадает (не
попадает) в критическую область, то гипотеза H₀

отвергается (принимается), а гипотеза H₁

принимается (отвергается) в качестве одного из
возможных решений с формулировкой «гипотеза
H₀ противоречит (не противоречит) выборочным
данным на уровне значимости
».

В зависимости от
содержания альтернативной гипотезы осуществляется выбор критической области:
левосторонней, правосторонней, двусторонней. Если смысл исследования заключается
в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения
или увеличения), то говорят об односторонней критической области. Если смысл
исследования- выявить различия в изучаемых параметрах, но характер их
отклонения от контрольных (или теоретических) не известен, то говорят о
двусторонней критической области.

Однако, принятие той
или иной гипотезы не дает оснований утверждать, что она верна. Результат
проверки статистической гипотезы лишь устанавливают на определенном уровне
значимости ее соответствие (несоответствие) результатам эксперимента.

При проверке
статистических гипотез возможны следующие ошибки:

1.
Отвергнута правильная
H₀, а принята неправильная гипотеза
H₁ — ошибка
первого рода.

2. Отвергнута правильная альтернативная
гипотеза
H₁ и
принята неправильная нулевая гипотеза H₀
—
ошибка второго рода.

Заметим, что уровень значимости —
есть вероятность ошибки первого рода. Ошибка первого рода называется
-риском. Обычно они задаются
некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго
рода называются -риском, а вероятность ее
допустить обозначается
(вероятность того, что принята гипотеза
H₀
, когда на самом деле справедлива
альтернативная гипотеза H₁
.

Можно доказать, что с
уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода
и наоборот. Поэтому, на практике пытаются подбирать значения параметров
и
опытным путем в целях минимизации суммарного
эффекта от возможных ошибок. При принятии управленческих решений для
одновременного уменьшения ошибок первого и второго рода самым действенным
средством является увеличение объема выборки, что согласуется с законом больших
чисел.

На бытовом уровне
ошибки второго рода могут иметь более трагические последствия, чем ошибки
первого рода.

2. Гипотеза о законе распределения. Критерий согласия Пирсона (
X²
-критерий).

Критериями согласия называют критерии, в
которых гипотеза определяет закон распределения либо полностью, либо с
точностью до небольшого числа параметров.

Причины расхождения
результатов эксперимента и теоретических характеристик могут быть вызваны малым
объемом выборки, неудачным способом группировки наблюдений, ошибками в
выборе гипотезы о виде распределения
генеральной совокупности и др.

Рассмотрим
универсальный критерий согласия Пирсона. Проверка гипотезы о том, что
эмпирическая частота мало отличается от соответствующей теоретической частоты,
осуществляется с помощью величины X²
—
меры расхождения между ними.

Для произвольной
выборки, когда распределение непрерывно или число различных вариант велико, все
пространство наблюдаемых вариант делят на конечное число непересекающихся
областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую
вероятность.

Для применения критерия
согласия Пирсона необходимо:

1. Вычислить значение статистики по формуле:
, где
p_i –вероятность
принятия значения
x_i, n_i.
— эмпирическая частота для
соответствующего
x_i. n— объем выборки. s— число вариант выборки.

2.
По
соответствующей таблице распределения Пирсона найти критическое значение , где k = s –
r
– 1 – число степеней свободы, s—
число различных вариант или интервалов группировки, r— число неизвестных параметров
предполагаемого теоретического распределения,
— выбранный уровень значимости. Это
значит, что строится правосторонний интервал.

3.
Если
,
то основная гипотеза отвергается, в противном случае- принимается, т.е. чем
больше отклонение, тем меньше согласованы теоретическое и эмпирическое
распределение. Поэтому принято использовать только правостороннюю критическую
область.

Расчетная таблица имеет вид:

Интервалы

Середины
i-го
интервала x_i

Эмпирические
частоты n_i

Вероятности p_i

Теоретические
частоты np_i

Пример:

По таблице
эмпирического распределения изменения в процентах темпа роста акций проверьте
гипотезу о нормальном распределении выборки.

Интервалы	(-2; -1)	(-1; 0)	(0; 1)	(1; 2)	Итого
n_i	7	14	18	11	50
p_i	0,157	0,341	0,341	0,157	1

Решение:

Гипотезу о нормальном
распределении проверим по критерию Пирсона.

Интервалы	Эмпирические частоты n_i	Вероятности p_i	Теоретические частоты np_i
(-2; -1)	7	0,157	7,85	0,7225	0,092
(-1; 0)	14	0,341	17,05	9,3025	0,546
(0; 1)	18	0,341	17,05	0,9025	0,053
(1; 2)	11	0,157	7,85	9,925	1,264
Итого					=1,955

По таблице найдем
при =0,05
и k = s – r – 1 = 4 – 2 – 1 = 1. s = 4 – число
интервалов. r
= 2- число параметров теоретического (нормального) распределения.

Имеем . Т.к. 1,955 < 3,841, то
, т.е. гипотеза о нормальном
распределении подтверждается.

3. Гипотезы о числовом значении генерального
среднего и дисперсии.

Установление двусторонней критической
области на уровне значимости
для
проверки гипотезы соответствует отысканию соответствующего доверительного
интервала с надежностью
.

Рассмотрим условия применения некоторых
статистических гипотез.

Тип гипотезы H₀	Границы критической области на уровне значимости	Статистика наблюдений
О числовом значении генерального среднего нормального распределения M(X) = m = , с известным среднеквадратическим отклонением.
О числовом значении генерального среднего нормального распределения M(X) = m = m₀, с неизвестной среднеквадратическим отклонением	Распределение Стьюдента
О числовом значении дисперсии нормального распределения , или	Распределение Пирсона

Пример:

Результаты исследований в течение 35 лет
показали, что среднее изменение доходности векселей равно 5,5 %. Полагая, что
изменение доходности подчиняется нормальному закону распределения с
среднеквадратическим отклонением равным 2 %, на уровне значимости
, решите: можно ли принять 6 % в качестве нормативного процента
(математического ожидания) изменения доходности.

Решение:

По условию задачи
нулевая гипотеза
. Так как
, то в качестве альтернативной гипотезы
возьмем гипотезу:
, которой соответствует левосторонняя
критическая область с интервалом.

Найдем границы
критической области:

По таблице значений
функции Ф(х) найдем
, т.е. левосторонняя критическая область
лежит в интервале.

Найдем статистику
наблюдений:
.

Имеем:, нет основания отвергать нулевую
гипотезу. Значит, в качестве нормативного процента можно принять 6 %.

Пример:

Точность работы
программы проверяют по дисперсии контролируемого количества символов в коде,
которая не должна превышать 0,1. По выборке из 15 сообщений вычислена
исправленная оценка дисперсии 0,22. При
уровне значимости 0,05 проверьте, обеспечивает ли программа необходимую
точность.

Решение:

Имеем: n = 15, s² = 0,22
, ,
.

Сформулируем гипотезу о
числовом значении дисперсии:

H₀ — программа обеспечивает необходимую точность
;

H₁ —
программа не обеспечивает необходимую точность
.

Определим статистику: .

Найдем границы
критической области:
.

Поскольку 30,8 >
23,7;
, принимаем гипотезу H₁, т.к.
H₀ противоречит опытным данным. Вывод: программа
не обеспечивает необходимую точность.

Все, что вам нужно знать о проверке гипотез — часть I

Перевод

Ссылка на автора

Статистика — это все о данных, но одни данные не интересны. Это интерпретация данных, которые нас интересуют …

Область Data Science развивается как никогда раньше. Многие компании в настоящее время ищут профессионалов, которые могут просеять свои данные о добыче золота и помочь им эффективно принимать быстрые бизнес-решения. Это также дает возможность многим работающим профессионалам переключить свою карьеру на область Data Science.

Имея этот ИИ, Data Science окружает многих студентов колледжей и хочет продолжить свою карьеру в области Data Science. И эта шумиха вокруг Data Science правильно провозглашена Томасом Х. Давенпортом и Д.Дж. Патил в одной из статей Harvard Business Review,

«Data Scientist: самая сексуальная работа XXI века»

В современном мире аналитики модели машинного обучения в строительстве стали сравнительно простыми (благодаря более надежным и гибким инструментам и алгоритмам), но фундаментальные концепции по-прежнему сбивают с толку. Одним из таких понятий является проверка гипотез.

В этом посте я пытаюсь прояснить основные понятия проверки гипотез с помощью иллюстраций.

Что такое проверка гипотез? Чего мы пытаемся достичь? Зачем нам нужно проверять гипотезы? Мы должны знать ответы на все эти вопросы, прежде чем мы продолжим.

Статистика это все о данных. Данные сами по себе не интересны. Это интерпретация данных, которые нас интересуют. ИспользованиеПроверка гипотезымы пытаемся интерпретировать или делать выводы о населении, используя выборочные данные.Проверка гипотезоценивает два взаимоисключающих утверждения о совокупности, чтобы определить, какое утверждение лучше всего подтверждается данными выборки. Всякий раз, когда мы хотим заявить о распределении данных или о том, отличается ли один набор результатов от другого набора результатов в прикладном машинном обучении, мы должны полагаться на статистические проверки гипотез.

Есть два возможных результата: если результат подтверждает гипотезу, то вы произвели измерение. Если результат противоречит гипотезе, то вы сделали открытие — Энрико Ферми

Давайте посмотрим на терминологию, которую мы должны знать вПроверка гипотезы

1. Параметр и статистика:

параметрявляется кратким описанием фиксированной характеристики или показателя целевой группы населения. Параметр обозначает истинное значение, которое будет получено при проведении переписи, а не выборки.

Пример:Среднее (μ), дисперсия (σ²), стандартное отклонение (σ), пропорция (π)

Население: Население — это совокупность объектов, которые мы хотим изучить / протестировать. Коллекция объектов может быть города, студенты, фабрики и т. Д. Это зависит от изучения под рукой.

В реальном мире сложно получить полную информацию о населении. Следовательно, мы выбираем выборку из этой совокупности и получаем те же статистические показатели, упомянутые выше. И эти меры называются выборочной статистикой. Другими словами,

статистикаявляется кратким описанием характеристики или меры выборки. Выборочная статистика используется в качестве оценки параметра совокупности.

Пример:Среднее значение выборки (x̄), дисперсия выборки (S²), стандартное отклонение выборки (S), пропорция выборки (п)

Фото от CliffsNotes

2. Распределение выборки:

Распределение выборки — это распределение вероятностей статистики, полученной с помощью большого числа выборок, взятых из определенной совокупности.

Пример:Предположим, что простая выборка из пяти больниц должна быть взята из населения 20 больниц. Возможны следующие варианты: (20, 19, 18, 17, 16) или (1,2,4,7,8) или любая из 15 504 (с использованием комбинаций 20C)) различных образцов размера 5.

В целом среднее значение распределения выборки будет приблизительно эквивалентно среднему значению для населения, т.е. E (x̄) = μ

Чтобы узнать больше о распределении выборки, пожалуйста, проверьте это ниже видео:

Видео из ханской академии

3. Стандартная ошибка (SE):

Стандартная ошибка (SE) очень похожа на стандартное отклонение. Оба являются мерами распространения. Чем выше число, тем больше разбросаны ваши данные. Проще говоря, два термина по сути равны, но есть одно важное отличие. Пока стандартная ошибка используетстатистика(пример данных) использование стандартного отклоненияпараметры(данные о населении)

Стандартная ошибка говорит вам, насколько далеко ваша выборочная статистика (например, среднее значение выборки) отклоняется от фактического среднего значения населения. Чем больше размер вашей выборки, тем меньше SE. Другими словами, чем больше размер выборки, тем ближе среднее значение выборки к среднему значению популяции.

Чтобы узнать больше о стандартной ошибке (SE), пожалуйста, смотрите видео ниже

Теперь давайте рассмотрим следующий пример, чтобы лучше понять остальные концепции.

4. (а) Нулевая гипотеза (H₀):

Заявление, в котором не ожидается никакой разницы или эффекта. Если нулевая гипотеза не отклонена, никакие изменения не будут внесены.

Слово «ноль» в данном контексте означает, что общепринятый факт, что исследователи аннулируют. Это не означает, что само утверждение является нулевым! (Возможно, этот термин следует называть «недействительной гипотезой», поскольку это может вызвать меньше путаницы)

4. (б). Альтернативная гипотеза (H₁):

Утверждение, что ожидается некоторое различие или эффект. Принятие альтернативной гипотезы приведет к изменению мнений или действий. Это противоположность нулевой гипотезы.

Чтобы узнать больше о нулевых и альтернативных гипотезах, пожалуйста, посмотрите это видео ниже

5. (а). Односторонний тест:

Односторонний тест — это тест статистической гипотезы, в котором критическая область распределения является односторонней, так что она либо превышает определенное значение, либо меньше, но не одновременно. Если тестируемый образец попадает в одностороннюю критическую область, альтернативная гипотеза будет принята вместо нулевой гипотезы.

Односторонний тест также известен как направленная гипотеза или направленный тест.

Критический регион:Критическая область — это область значений, которая соответствует отклонению нулевой гипотезы на некотором выбранном уровне вероятности.

5. (б). Двусторонний тест:

Двухсторонний тест — это метод, в котором критическая область распределения является двусторонней, и он проверяет, является ли выборка больше или меньше определенного диапазона значений. Если тестируемый образец попадает в одну из критических областей, альтернативная гипотеза принимается вместо нулевой гипотезы.

По соглашению, двусторонние тесты используются для определения значимости на уровне 5%, то есть каждая сторона распределения сокращается на 2,5%.

6. Тестовая статистика:

тестовая статистикаизмеряет, насколько близко образец пришел к нулевой гипотезе. Его наблюдаемое значение изменяется случайным образом от одной случайной выборки к другой выборке. Тестовая статистика содержит информацию о данных, которые имеют значение для принятия решения о том, следует ли отклонить нулевую гипотезу или нет.

Различные тесты гипотез используют разные статистические тесты, основанные на вероятностной модели, принятой в нулевой гипотезе. Общие тесты и их тестовая статистика включают в себя:

Изображение из https://support.minitab.com

В общем, выборочные данные должны предоставить достаточные доказательства, чтобы отвергнуть нулевую гипотезу и сделать вывод, что эффект существует в популяции. В идеале, проверка гипотезы не позволяет отклонить нулевую гипотезу, когда эффект отсутствует в популяции, и отвергает нулевую гипотезу, когда эффект существует.

К настоящему времени мы понимаем, что вся проверка гипотез работает на основе имеющегося образца. Мы можем прийти к другому выводу, если образец будет изменен. Есть два типа ошибок, которые относятся к неверным выводам о нулевой гипотезе.

7. (а). Ошибка типа I:

Тип-IОшибка возникает, когда результаты выборки приводят к отклонению нулевой гипотезы, когда она на самом деле верна.Тип-Iошибки эквивалентны ложным срабатываниям.

Тип-Iошибки можно контролировать. Значение альфа, которое связано суровень значимостичто мы выбрали, имеет прямое отношение кТип-Iошибки.

7. (б). Ошибка типа II:

Тип-IIошибка возникает, когда на основании результатов выборки нулевая гипотеза не отклоняется, если она фактически ложна.Тип-IIошибки эквивалентны ложным негативам.

Уровень значимости (α):

Вероятность сделатьТип-Iошибка, и это обозначаетсяальфа (α), Альфа это максимальная вероятность того, что у нас естьТип-Iошибка. Для уровня достоверности 95% значение альфа составляет 0,05. Это означает, что существует 5% вероятность того, что мы отвергнем истинную нулевую гипотезу.

P-значение:

р-значениеиспользуется во всей статистике, от t-тестов до простого регрессионного анализа до моделей на основе дерева, почти во всех моделях машинного обучения. Мы все используемP-значениеопределить статистическую значимость в тесте гипотезы. Несмотря на то чтоР-значениескользкая концепция, которую люди часто неправильно интерпретируют.

P-значениеоцените, насколько хорошо выборочные данные подтверждают аргумент защитника дьявола о том, что нулевая гипотеза верна. Он измеряет, насколько совместимы ваши данные с нулевой гипотезой. Насколько вероятен эффект, наблюдаемый в ваших данных выборки, если нулевая гипотеза верна?

Другими словами, если нулевая гипотеза верна,Р-значениевероятность получения результата как экстремального или более экстремального, чем результат выборки, только по случайной случайности

Высокие значения P:Ваши данные, скорее всего, с истинным нулем

Низкие значения P:Ваши данные вряд ли с истинным нулем

Пример: Предположим, что вы проверяете следующую гипотезу на уровне значимости (α) 5%, и вы получаете значение p как 3%, и ваша выборочная статистикаИксзнак равно25

H₀: μ = 20

H₁: μ> 20

Интерпретация р-значения выглядит следующим образом:

Мы видели выше, чтоαтакже известен как совершениеТип-Iошибка. Когда мы говорим, αзнак равно5%, мы можем отклонить нашу нулевую гипотезу 5 из 100 раз, даже если это правда. Теперь, когда нашиР-значение3%, что меньшеα(мы определенно ниже порога совершенияТип-Iошибка),означает получение выборочной статистики как можно более экстремальной (x̄>знак равно25) учитывая, что H₀ истинно, очень меньше. Другими словами, мы не можем получить нашу выборочную статистику, если предположим, что H₀ истинно. Следовательно, мы отвергаем H₀ и принимаем H₁. Предположим, вы получаетеР-значениекак 6%, т. е. вероятность получения выборочной статистики как можно более экстремальной, тем выше, учитывая, что нулевая гипотеза верна. Таким образом, мы не можем отказаться от H₀, по сравнению сαмы не можем рисковатьТип-Iошибка больше, чем согласованный уровень значимости. Следовательно, мы не можем отвергнуть нулевую гипотезу и отвергнуть альтернативную гипотезу.

Теперь, когда мы поняли основную терминологию вПроверка гипотезы,Теперь давайте рассмотрим этапы проверки гипотез и приведем пример с примером.

Например, крупный универмаг рассматривает возможность введения услуги интернет-магазина. Новая услуга будет введена, если более 40 процентов интернет-пользователей совершают покупки через Интернет.

Шаг 1: сформулируйте гипотезы:

Подходящий способ сформулировать гипотезы:

H₀: π ≤ 0,40

H₁: π> 0,40

Если нулевая гипотеза H₀ отклонена, то будет принята альтернативная гипотеза H₁ и введена новая услуга интернет-покупок. С другой стороны, если мы не сможем отклонить H₀, то новая услуга не должна быть введена, пока не будут получены дополнительные доказательства. Этот тест нулевой гипотезы являетсяодин хвостТест, потому что альтернативная гипотеза выражается направленно: доля интернет-пользователей, которые используют Интернет для покупок, превышает 0,40.

Шаг 2: Выберите подходящий тест:

Чтобы проверить нулевую гипотезу, необходимо выбрать соответствующий статистический метод. Для этого примераZстатистика, которая соответствует стандартному нормальному распределению, будет уместной.

z = (p-π) / σₚ, где σₚ = sqrt (π (1-π) / n)

Шаг 3: Выберите уровень значимости, α:

Мы поняли чтоУровень значимостиотносится кТип-Iошибка. В нашем примере ошибка Типа I произошла бы, если бы мы пришли к выводу, основываясь на выборочных данных, что доля клиентов, предпочитающих новый тарифный план, была больше 0,40, тогда как на самом деле она была меньше или равна 0,40.

Ошибка типа II возникла бы, если бы мы пришли к выводу, основываясь на выборочных данных, что доля клиентов, предпочитающих новый тарифный план, была меньше или равна 0,40, тогда как фактически она была больше 0,40.

Необходимо сбалансировать два типа ошибок. В качестве компромисса α часто устанавливается на 0,05; иногда это 0,01; другие значения α редки. Мы рассмотрим 0,05 для нашего примера.

Шаг 4: Соберите данные и рассчитайте статистику теста:

Размер выборки определяется после учета требуемого значения α и других качественных соображений, таких как бюджетные ограничения для сбора данных выборки. Для нашего примера, скажем, 30 пользователей были опрошены, а 17 указали, что они использовали Интернет для покупок.

Таким образом, значение пропорции выборки составляетр = 17/30 = 0,567.

Значениеσₚ = SQRT ((0,40) (0,60) / 30) = 0,089.

Тестовая статистикаZможно рассчитать как

г = (р-π) / σₚ = (0.567-0.40) /0.089=1.88

Шаг 5: Определите вероятность (или критическое значение):

Используя стандартные нормальные таблицы из приведенного выше, вероятность полученияZзначение 1,88 составляет 0,96995, т.е.Р (z≤1.88) = 0,96995,Но мы хотели вычислить вероятность справа отz (потому что мы заинтересованы в получении значения вероятности, которое попадает в область отклонения или критическую область),то есть1-0.96995знак равно0,03005, Эта вероятность прямо сопоставима с(поскольку α совершает ошибку Типа I, а рассчитанное нами значение вероятности также попадает в критическую область)

Если вы хотите понять, как искать значения вероятностей для данных z-оценок, посмотрите видео ниже:

В качестве альтернативы, критическое значениег,который даст область справа от критического значения 0,05, находится между 1,64(при 1,64 вероятность составляет 0,94950)и 1,65(при 1,65 вероятность равна 0 95053)и равен 1,645(вероятность равна 0,95, то есть слева от нормального распределения, что означает, что справа она равна 0,05),

Обратите внимание, что при определении критического значения статистики теста, область в хвосте за критическим значением либоα или α / 2.этоαдля одностороннего теста иα / 2для двустороннего теста. Наш пример — односторонний тест.

Если вы хотите понять, как искать критическое значениеα,Пожалуйста, посмотрите видео ниже:

Шаг 6 и 7: сравните вероятность (или критическое значение) и примите решение:

Вероятность, связанная с вычисленным или наблюдаемым значением статистики теста, составляет 0,03005. Это вероятность полученияР-значение0,567 (доля образца =п)когда π = 0,40. Это меньше уровня значимости 0,05. Следовательно, нулевая гипотеза отвергается.

В качестве альтернативы рассчитывается значение тестовой статистикиг = 1,88лежит в области отклонения, за пределами значения 1,645. Снова, тот же самый вывод отклонить нулевую гипотезу сделан.

Обратите внимание, что два способа проверки нулевой гипотезы эквивалентны, но математически противоположны в направлении сравнения. Если вероятность, связанная с вычисленным или наблюдаемым значением тестовой статистики (TSCAL), равнаменьше, чемНа уровне значимости (α) нулевая гипотеза отвергается. Однако, если абсолютное значение рассчитанного значения статистики тестабольше чемабсолютное значение критического значения тестовой статистики (TSCR), нулевая гипотеза отклоняется. Причина этого смещения знака состоит в том, что чем больше абсолютное значение TSCAL, тем меньше вероятность получения более экстремального значения тестовой статистики при нулевой гипотезе.

если вероятность TSCAL <уровень значимости (α), то отклонить H₀.

Но, если | TSCAL | > | TSCR |, затем отклонить H₀

Шаг 8: Вывод:

В нашем примере мы заключаем, что есть свидетельства того, что доля интернет-пользователей, совершающих покупки через Интернет, значительно превышает 0,40. Следовательно, рекомендация для универмага будет заключаться в том, чтобы ввести новый сервис интернет-магазинов.

Этот пример относится к одному образцу теста пропорций. Тем не менее, существует несколько типов тестов, которые зависят от знаний о населении и рассматриваемой проблемы.

Например, у нас есть t-тест, Z-тест. Тест хи-квадрат, тест Манна-Уитни, тест Вилкоксона и т. Д.

На этом я хотел бы завершить часть I «Все, что вам нужно знать о проверке гипотез». Я буду обсуждать параметрические и непараметрические тесты и какой тест использовать в каком сценарии в части II. До тех порСчастливого обучения…

Спасибо за чтение!

Пожалуйста, поделитесь своим мнением в разделе комментариев ниже.

Ссылки:

Маркетинговые исследования — прикладная ориентация Naresh K Malhotra и Satyabhushan Dash
https://www.cliffsnotes.com/study-guides/statistics/sampling/populations-samples-parameters-and-statistics
https://www.statisticshowto.datasciencecentral.com
https://www.khanacademy.org
https://blog.minitab.com

Ошибки I и II рода при проверке гипотез, мощность

Общий обзор

Принятие неправильного решения

Мощность и связанные факторы

Проверка множественных гипотез

Общий обзор

Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.

Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.

Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.

Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:

отвергнуть нулевую гипотезу и принять альтернативную гипотезу
остаться в рамках нулевой гипотезы

Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).

Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.

Принятие неправильного решения

Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.

	Верная гипотеза
H₀	H₁
Результат применения критерия	H₀	H₀ верно принята	H₀ неверно принята (Ошибка второго рода)
H₁	H₀ неверно отвергнута (Ошибка первого рода)	H₀ верно отвергнута

Верная гипотеза

H₀

H₁

Результат

применения

критерия

H₀

H₀ верно принята

H₀ неверно принята

(Ошибка второго рода)

H₁

H₀ неверно отвергнута

(Ошибка первого рода)

H₀ верно отвергнута

Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.

Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.

Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.

Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.

Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.

В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.

К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.

Мощность и связанные факторы

Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).

Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.

Ряд факторов имеют прямое отношение к мощности критерия.

Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.

Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.

Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.

Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.

Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).

Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.

Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.

Проверка множественных гипотез

Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.

Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.

Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.

Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.

Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии

В начало

Содержание портала

Источник

2.1.1. Основные понятия о статистической гипотезе

—
монета правильная и частота выпадений
герба и цифры примерно одинакова,

—
монета деформирована и чаще выпадает
герб,

—
монета деформирована и чаще выпадает
цифра.

—
Р = ½,

—
Р > ½,

—
Р < ½.

При
проведении эксперимента надо ответить
на вопрос, какая же из приведенных
гипотез верна?

2.1.2. Ошибки при проверке статистических гипотез

Р
{ m ∈
n/Но} = α ,

где
α – малое число, близкое к нулю.

Р
{m ∈
n/Н1} = β.

Требуется
в процессе решения примера сформулировать:

—
нулевую (основную) и альтернативную
гипотезы,

—
определить критическую область и
область принятия нулевой гипотезы,

—
определить, в чем состоят ошибки первого
и второго рода, и найти их вероятность.

− отвергнутой,
если число дефектов находится в области
n = {0,1};

− принятой,
если число дефектов находится в области
n = {2,3,4…10}.

Р(m
= 0) = (0,8)¹⁰=
0,107,

Р(m
= 1) = 10·(0,8)⁹·0,2
= 0,268.

Тогда
ошибка первого рода α будет равна сумме
этих вероятностей:

α
= Р (m ≤ 1) = Р (m=0/Н0) + Р (m =1/Н0) = 0,375.

Р(m=0)
= (0,97)¹⁰=
0,737,

Р(m=1)
= 10·(0,97)^9·0,03
= 0,228.

Таким
образом, вероятность альтернативных
событий (m > 1) составит величину ошибки
второго рода β:

β
= Р(m>1/Н1) = 1 – Р(m ≤ 1/Н1) = 1 – Р(m =0/Н1) –
Р(m=1/Н1) = =1 – 0,737 – 0,228 = 0,035.

Соседние файлы в папке УК работы

#
#
#
11.08.201936.84 Кб34ЛР 6 УК1.xlsx
#
11.08.201919.67 Кб31ЛР 6 УК2.xlsx
#
11.08.201941.03 Кб37лр7.xlsx
#
11.08.201977.53 Кб33лр8.xlsx

Источник

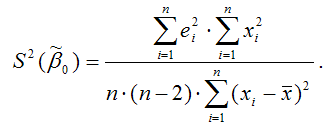
Оценка дисперсии МНК-оценки коэффициента β1линейной модели парной регрессии будет определяться по формуле:

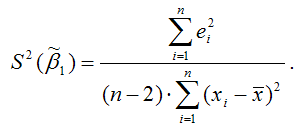
Для модели множественной регрессии общую формулу расчёта матрицы ковариаций МНК-оценок коэффициентов на основе оценки дисперсии случайной ошибки модели регрессии можно записать следующим образом:

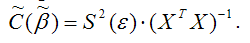
18. Характеристика качества модели регрессии

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.
   Для оценки качества модели регрессии используются специальные показатели.
   Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
   1) парной линейный коэффициент корреляции, который рассчитывается по формуле:

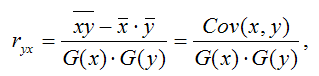
   где G(x) – среднеквадратическое отклонение независимой переменной;
   G(y) – среднеквадратическое отклонение зависимой переменной.
   Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии

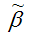
по формуле:

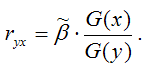
   Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.
   2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.
   Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.
   Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:
   G2(y)=σ2(y)+δ2(y),
   где G2(y) – это общая дисперсия зависимой переменной;
   σ2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:

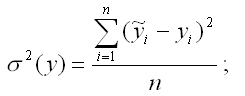
δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:

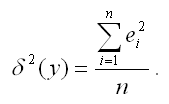
С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:
1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:

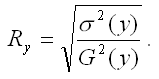
Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.
2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:

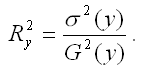
Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;
3) показатель

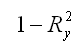
характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;
4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):

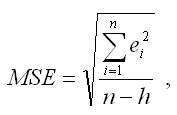
   где h– это количество параметров, входящих в модель регрессии.
   Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.
   Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:

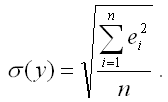
5) показатель средней ошибки аппроксимации рассчитывается по формуле:

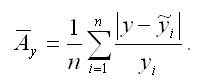
Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.

19. Понятие статистической гипотезы. Общая постановка задачи проверки статистической гипотезы

   Проверка статистических гипотез – это один из основных методов математической статистики, который используется в эконометрике.
   С помощью методов математической статистики можно проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например, математического ожидания или дисперсии), о наличии корреляционной зависимости между случайными величинами, определенными на множестве объектов одной и той же генеральной совокупности.
   Предположим, что на основании имеющихся данных у исследователя есть основания выдвинуть предположения о законе распределения или о параметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов которой определена эта случайная величина). Задача проверки статистической гипотезы заключается в подтверждении или опровержении этого предположения на основании выборочных (экспериментальных) данных.
   Статистической гипотезой называется любое предположение о виде неизвестного закона распределения или о параметрах известных распределений.
   Параметрической гипотезой называется гипотеза о значениях параметров распределения или о сравнительной величине параметров двух распределений.
   Примером параметрической статистической гипотезы является гипотеза о равенстве математических ожиданий двух нормальных совокупностей.
   Непараметрическими гипотезами называются гипотезы о виде распределения случайной величины.
   Проверка статистической гипотезы означает проверку соответствия выборочных данных выдвинутой гипотезе.
   Параллельно с выдвигаемой основной гипотезой рассматривают и противоречащую ей гипотезу, которая называется конкурирующей или альтернативной. Противоречащая гипотеза считается справедливой, если основная выдвинутая гипотеза отвергается.
   Нулевой, основной или проверяемой гипотезой называется первоначально выдвинутая гипотеза, которая обозначается Н0.
   Конкурирующей или альтернативной гипотезой называется гипотеза, которая противоречит основной гипотезе Н0 и обозначается Н1.
   Например, основная гипотеза Н0 состоит в том, что математическое ожидание μ равно значению μ0. В этом случае конкурирующая гипотеза Н1 может состоять в предположении, что математическое ожидание μ не равно (больше или меньше) значения μ0:
   Н0: μ=μ0;
   Н1: μ≠μ0,
   или
   Н1: μ>μ0,
   или
   Н1: μ<μ0.
   Простой гипотезой называется гипотеза, которая содержит только одно предположение. Например, гипотеза о том, что параметр распределения Пуассона λ равен значению λ0, является простой. Основная гипотеза о том, что математическое ожидание нормального распределения равно 5 (при известной дисперсии), т.е.
   Н0: а=5,
   также является простой.
   Сложной гипотезой называется гипотеза, которая состоит из нескольких простых гипотез. Например, сложная гипотеза вида:
   Н0: λ>4,
   состоит из множества простых гипотез вида:
   Н0: λ>m,
   где m – это люблое число, большее четырёх.

20. Ошибки первого и второго рода. Понятие о статистических критериях. Критическая область, критические точки

   Проверка статистической гипотезы означает проверку согласования исходных выборочных данных с выдвинутой основной гипотезой. При этом возможно возникновение двух ситуаций – основная гипотеза может подтвердиться, а может и опровергнуться. Следовательно, при проверке статистических гипотез существует вероятность допустить ошибку, приняв или опровергнув верную гипотезу.
   При проверке статистических гипотез можно допустить ошибки первого или второго рода
   Ошибкой первого рода называется ошибка, состоящая в опровержении верной гипотезы.
   Ошибкой второго рода называется ошибка, состоящая в принятии ложной гипотезы.
   Уровнем значимостиа называется вероятность совершения ошибки первого рода.
   Значение уровеня значимости а обычно задаётся близким к нулю (например, 0,05; 0,01;0,02 и т. д.), потому что чем меньше значение уровеня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Н0.
   Вероятность совершения ошибки второго рода, т. е. принятия ложной гипотезы, обозначается β.
   При проверке нулевой гипотезы Н0возможно возникновение следующих ситуаций:

   Проверка справедливости сттатистическвх гипотез осуществляется с помощью различных статистических критериев.
   Статистическим критерием называется случайная величина, которая используется с целью проверки нулевой гипотезы.
   Статистические критерии называются соответственно тому закону распределения, которому они подчиняются, т. е. F-критерий подчиняется распределению Фишера-Снедекора, χ2-критерий подчиняется χ2-распределению, Т-критерий подчиняется распределению Стьюдента, U-критерий подчиняется нормальному распределению.
   Наблюдаемым значением статистического критерия называется значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения.
   Множество всех возможных значений выбранного статистического критерия делится на два непересекающихся подмножества. Первое подмножество включает в себя те значения критерия, при которых основная гипотеза отвергается, а второе подмножество – те значения критерия, при которых основная гипотеза принимается.
   Критической областью называется множество возможных значений статистического критерия, при которых основная гипотеза отвергается.
   Областью принятия гипотезы или областью допустимых значений называется множество возможных значений статистического критерия, при которых основная гипотеза принимается.
   Если наблюдаемое значение статистического критерия, рассчитанное по данным выборочной совокупности, принадлежит критической области, то основная гипотеза отвергается. Если наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то основная гипотеза принимается.
   Критическими точками или квантилями называются точки, разграничивающие критическую область и область принятия гипотезы.
   Критические области могут быть как односторонними, так и двусторонними.

21. Правосторонняя критическая область. Левосторонняя и двусторонняя критические области. Мощность критерия

   При проверке статистических гипотез используют правосторонние, левосторонние и двусторонние критические области.
   Правосторонняя критическая область характеризуется неравенством вида:
   L>lкр,
   где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
   lкр, – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия.
   Следовательно, для определения правосторонней критической области необходимо рассчитать положительное значение статистического критерия lкр.
   Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет больше значения lкр, равна заданному уровню значимости, т.е. P(L>lкр)=a.
   Для каждого статистического критерия рассчитаны специальные таблицы, с помощью которых определяют критическую точку, удовлетворяющую заданному уровню значимости.
   Левосторонняя критическая область характеризуется неравенством вида:
   L<lкр,
   где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
   lкр, — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия.
   Следовательно, для определения левосторонней критической области необходимо найти рассчитать отрицательное значение статистического критерия lкр.
   Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет меньше значения lкр, равна заданному уровню значимости, т.е. P(L<lкр)=a.
   Двусторонняя критическая область характеризуется двумя неравенствами вида:
   L>lкр1 и L<lкр2,
   где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
   lкр1 – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия;
   lкр2 — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия;
   lкр1> lкр2.
   Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, сумма вероятностей того, что значение статистического критерия L будет больше значения lкр1 или меньше значения lкр2, равна заданному уровню значимости, т.е. P(L>lкр1)+(L<lкр2)=a.
   Выбор критической области осуществляется исходя из вида конкурирующей гипотезы Н1. При этом применяются следующие правила:
   1) правосторонняя критическая область выбирается в том случае, если Н1:>;
   2) левосторонняя критическая область выбирается в том случае, если Н1:‹;
   3) двусторонняя критическая область выбирается в том случае, если Н1:≠.
   Предположим, что заданы следующие параметры:
   1) статистический критерий L;
   2) критическая область W, где H0 отклоняется;
   3) область принятия гипотезы

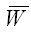
   где H0 не отклоняется;
   4) вероятность совершить ошибку первого рода a;
   5) вероятность совершить ошибку второго рода β.
   Тогда справедливо утверждение о том, что выражение

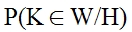
   является вероятностью того, что статистический критерий L попадёт в критическую область, если верна гипотеза H.
   При построении критической области учитываются два требования:
   1) вероятность того, что статистический критерий L попадёт в критическую область, если верна Н0, равна а:

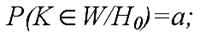
данное равенство задаёт вероятность совершения ошибки первого рода;
2) вероятность того, что статистический критерий L попадёт в критическую область (область отклонения гипотезы Н0 в пользу гипотезы Н1), если верна гипотеза Н1:

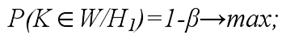
   данное равенство задаёт вероятность принятия правильной гипотезы.
   Мощностью статистического критерия называется вероятность попадания данного критерия в критическую область, при условии, что справедлива конкурирующая гипотеза Н1, т. е.выражение 1-β является мощностью критерия.
   Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования обеспечивает минимальную ошибку второго рода, состоящую в том, что будет принята неправильная гипотеза.

22. Проверка гипотезы о значимости коэффициентов модели парной регрессии

Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.
   Необходимость проверки гипотез о значимости параметров модели вызвана тем, что в дальнейшем построенную модель будут использовать для дальнейших экономических расчётов.
   Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости оценок неизвестных коэффициентов модели, полученных методом наименьших квадратов.
   Основная гипотеза состоит в предположении о незначимости коэффициентов регрессии, т. е.
   Н0:β0=0, или Н0:β1=0.
   Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов регрессии, т.е.
   Н1:β0≠0, или Н1:β1≠0.
   Данные гипотезы проверяются с помощью t-критерия Стьюдента.
   Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают со значением t-критерия, которое определяется по таблице распределения Стьюдента и называется критическим.
   Критическое значение t-критерия зависит от уровня значимости и числа степеней свободы.
   Уровнем значимостиа называется величина, которая рассчитывается по формуле:
   а=1-γ,
   где γ – это доверительная вероятность попадания оцениваемого параметра в доверительный интервал. Значение доверительной вероятности должно быть близким к единице, например, 0.95, 0.99. Следовательно, уровень значимости а можно определить как вероятность того, что оцениваемый параметр не попадёт в доверительный интервал.
   Числом степеней свободы называется показатель, который рассчитывается как разность между объёмом выборочной совокупности n и числом оцениваемых параметров по данной выборке h. Для линейной модели парной регрессии число степеней свободы рассчитывается как (n-2), потому что по данным выборочной совокупности оцениваются только два параметра – β0 и β1.
   Таким образом, критическое значение t-критерия Стьюдента определяется как tкрит(а;n-h).
   При проверке основной гипотезы вида Н0:β1=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

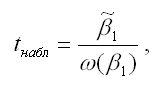
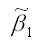
   где – оценка параметра модели регрессии β1;
   ω(β1) – величина стандартной ошибки параметра модели регрессии β1.
   Показатель стандартной ошибки параметра модели регрессии β1 для линейной модели парной регрессии рассчитывается по формуле:

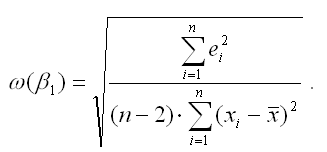
Числитель стандартной ошибки может быть рассчитан через парный коэффициент детерминации следующим образом:

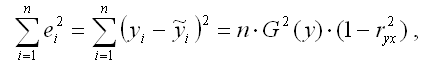
   где G2(y) – общая дисперсия зависимой переменной;
   r2yx – парный коэффициент детерминации между зависимой и независимой переменными.
   При проверке основной гипотезы β0=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

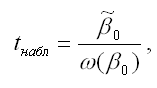
где

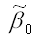
   – оценка параметра модели регрессии β0;
   ω(β0) – величина стандартной ошибки параметра модели регрессии β0.
   Показатель стандартной ошибки параметра β0 модели регрессии для линейной модели парной регрессии рассчитывается по формуле:

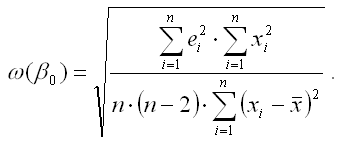
   При проверке основных гипотез возможны следующие ситуации:
   Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|›tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости параметров модели регрессии отвергается.
   Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости параметров модели регрессии принимается.

23. Проверка гипотезы о значимости парного коэффициента корреляции

   Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной переменной у и факторной переменной х.
   Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.
   Н0:rxy=0.
   Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.
   Н1:rxy≠0.
   Данные гипотезы проверяются с помощью t-критерия Стьюдента.
   Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
   При проверке значимости парного коэффициента корреляции критическое значение t-критерия определяется как tкрит(a;n-h), где а – уровень значимости, (n-h) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
   При проверке основной гипотезы вида Н0:rxy=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

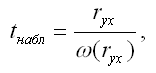
где ryx – выборочный парный коэффициент корреляции между результативной переменной у и факторной переменной х, который рассчитывается по формуле:

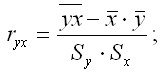
ω(ryx) – величина стандартной ошибки парного выборочного коэффициента корреляции.
Показатель стандартной ошибки парного выборочного коэффициента корреляции для линейной модели парной регрессии рассчитывается по формуле:

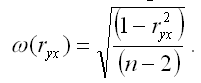
Если данное выражение подставить в формулу для расчёта наблюдаемого значения t-критерия для проверки гипотезы вида Н0:rxy=0, то получим:

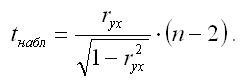
   При проверке основной гипотезы возможны следующие ситуации:
   Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.
   tнабл|>tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости парного коэффициента корреляции отвергается.
   Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости парного коэффициента корреляции принимается. В этом случае корреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.
   Применение t-статистики Стьюдента для проверки гипотезы вида Н0:rxy=0 основано на выполнении двух условий:
   1) если объём выборочной совокупности достаточно велик (n≥30);
   2) коэффициент корреляции по модулю значительно меньше единицы:
   0,45≤|ryx|≤0.75.
   В том случае, если модуль парного выборочного коэффициента корреляции близок к единице, то гипотеза вида Н0:rxy=0 также может быть проверена с помощью z-статистики. Данный метод оценки значимости парного коэффициента корреляции был предложен Р. Фишером.

Источник