В специальной
литературе можно встретить различные
рекомендации для обнаружения грубых
погрешностей измерений и отсева промахов.
Если имеется
выборка небольшого объёма n,
то можно воспользоваться методом
сравнения максимального относительного
отклонения |![]()
—
|![]()
/S
с
критическим (при выбранном уровне
значимости и числе степеней свободы
f
= n
– 2),
значение которого
определяют по таблице.
Здесь мы впервые
сталкиваемся с понятием о статистической
гипотезе.
Статистической
называют гипотезу
о виде неизвестного распределения
случайных величин или о параметрах
известных распределений. Решение на
основе выборочных наблюдений о том,
таков ли параметр генеральной совокупности
или нет, называется проверкой гипотезы.
Если выдвинутая гипотеза неверна, мы
её отбрасываем.
Наряду с выдвинутой
гипотезой, которую обычно называют
нулевой или основной и обозначают Н0,
рассматривают и альтернативную гипотезу
Н1,
противоречащую нулевой.
Вероятность
того, что будет отброшена верная гипотеза
Н0,
называют уровнем значимости и обычно
обозначают α.
Величина α
выбирается равной 0,05
или 0,01
и связана
с величиной надёжности статистической
оценки
следующим
соотношением:
α
= 1
–
.
(5.74)
Так, α
= 0,05, т.е.
5%-ный уровень значимости соответствует
доверительной вероятности (надёжности)
вывода
=
0,95.
Ошибка, при
которой гипотеза неверно отбрасывается,
называемую ошибкой
первого рода.
Принимая гипотезу, которая на самом
деле неверна, мы совершаем ошибку,
которая называется ошибкой
второго рода,
её вероятность обычно обозначается β.
Возвратимся к
названному выше методу обнаружения
промахов. Вычисляют абсолютную величину
максимального относительного отклонения
![]()
(5.75)
и выдвигают
гипотезу о том, что оно меньше критической
величины τ,
определяемой по таблицам при выбранном
уровне значимости α
и числе степеней свободы f
= n
– 2:
τ
≤ τтабл.α;f.
(5.76)
Если это соотношение
соблюдается, то проверяемый результат
измерения признаётся доброкачественным.
В противном случае гипотеза о
доброкачественности проверяемого
результата измерения отбрасывается.
Этот результат должен быть исключён из
выборки.
Сначала проверяют
наибольший и/или наименьший по абсолютной
величине элементы выборки, по которой
рассчитывались
и S,
затем процедуру проверки можно повторить
и для следующих по величине результатов
измерений и их отклонений.
Допускается
исключение одного или двух промахов из
выборки. При этом целесообразно, по
возможности, выполнить дополнительные
измерения для восстановления
первоначального объёма выборки. Если
же обнаруживается более двух промахов,
то вся выборка признаётся недоброкачественной.
После исключения
того или иного наблюдения характеристики
эмпирического распределения должны
быть пересчитаны по доброкачественным
данным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Грубая
погрешность, промах —
погрешность результата отдельного измерения, входящего в ряд измерений, которая
для данных условий резко отличается от остальных результатов этого
ряда.
Вопрос
о том, содержит ли результат наблюдений промах, решается общими методами
проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что
результат
наблюдения X, не содержит грубой
погрешности,
т.е. является одним из значений измеряемой величины. Пользуясь определенными
статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это
удается, то результат наблюдений рассматривают как содержащий грубую погрешность
и его исключают.
Одним
из критериев для проверки на грубые промахи является Q – тест.
Для
проверки на наличие грубых промахов проводят упорядочивание по величине вариант
с последующей проверкой крайних членов выборки. Формулы для вычислений:
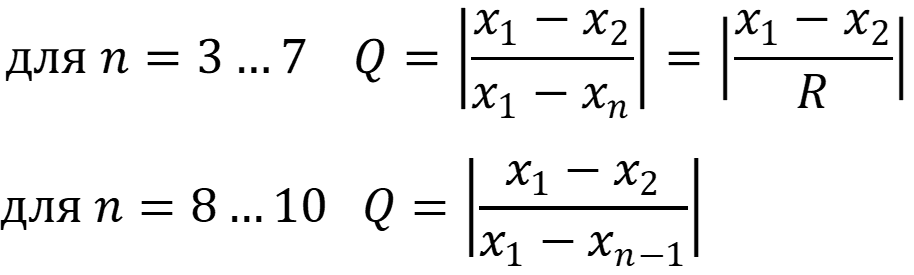
Найденное
значение Q для данной варианты X сравнивается с табличным значением Qтабл. для заданной
степени вероятности. При отсутствии данных Р = 0,95.
Если
Q > Qтабл., то X можно считать грубым промахом. Если Q ≤
Qтабл., то результат не отбрасывают.
Задача
№1:
При
определении фосфора в листьях спектрофотометрическим методом были получены
следующие результаты (мкг/кг): 3,4; 3,7; 3,5; 3,6; 4,2; 3,5. Проверить данные на
наличие грубых промахов.
Решение:
Расположим
варианты выборки в порядке убывания величины: 4,2; 3,7; 3,6; 3,5; 3,5; 3,4.
Сомнительной по величине вариантой является 4,2. Проверим по Q –
тесту:
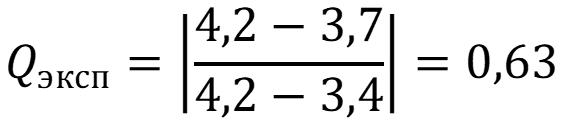
Qтабл. при Р = 0,95 равно 0,56
Ответ:
Qэксп
> Qтабл. – варианта 4,2 является грубым промахом.
Вариантом
для более объёмных выборок является критерий Романовского (10 < n <
20)
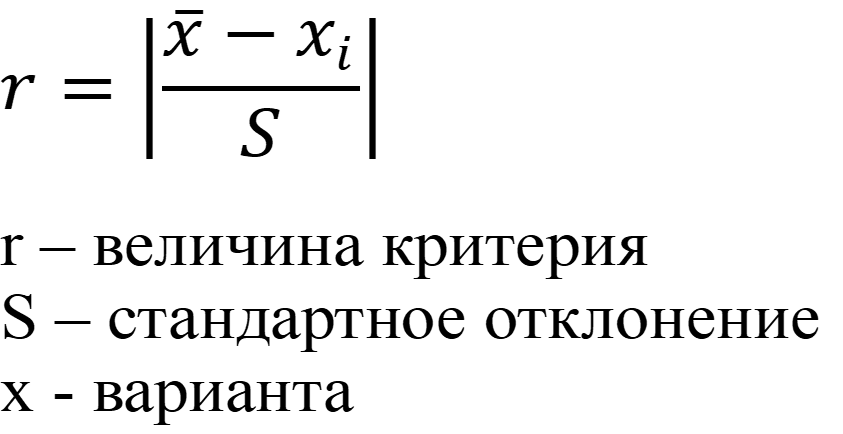
Найденное
значение r для данной варианты X сравнивается с табличным значением rтабл. для заданной
степени вероятности.
При
отсутствии данных Р = 0,95.
Если
r > rтабл., то можно считать грубым промахом. Если r ≤
rтабл., то результат не отбрасывают.
Задача
№2:
При
определении меди в почвах методом ААС были получены следующие результаты
(мг/кг): 17; 18; 20; 17; 23; 25; 27; 19; 15; 17; 18; 22. Проверить данные на
наличие грубых промахов.
Решение:
Расположим
варианты выборки в порядке убывания величины: 27; 24; 23; 22; 20; 19; 18; 18;
17; 17; 17; 15.
Сомнительными
по величине вариантами являются 27 и 15.
Рассчитаем
среднее арифметическое для вариант без учёта подозрительных:
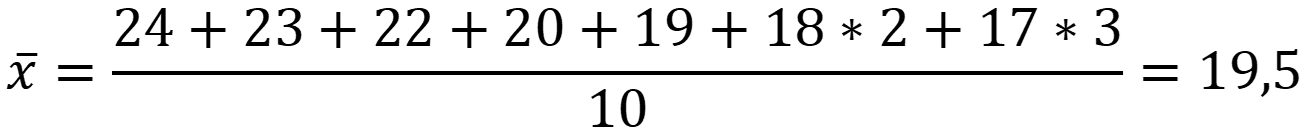
Рассчитаем
стандартное отклонение для выборки:
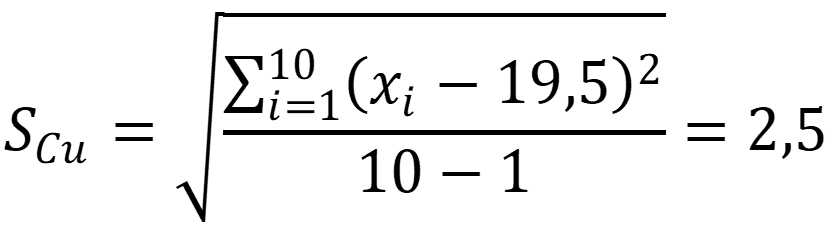
Рассчитаем
экспериментальное значение r для каждой сомнительной варианты:
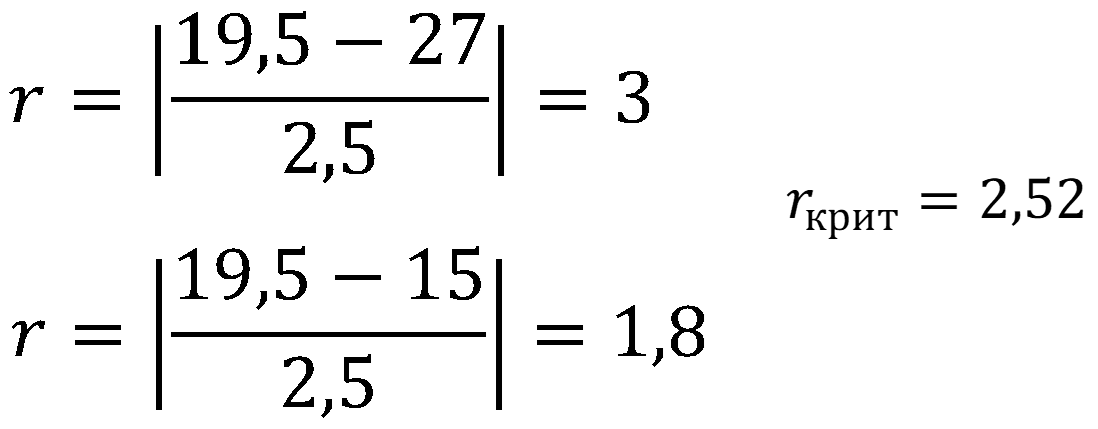
Ответ:
варианта 27 является грубой погрешностью так как экспериментальное значение
критерия больше критического.
Видео
можно посмотреть тут.
1. Практическое занятие
2.
1. Проверка выборки на наличие грубых ошибок
Проверка статистической выборки на наличие грубых ошибок осуществляется
по теореме Фишера:
N 0 1
(1)
xNi x S t α r
1
N 0
2
где α — уровень значимости
x Ni — значение составляющей выборки, вызывающее сомнение;
х
— среднеарифметическое
значение выборки, определяемое:
1 N 0
x
xi
N(0) 1
S — среднеквадратическое отклонение случайной величины, определяемое:
S
t
1
α
2
r
N
1
2
xi x
N 0 1 1
— квантиль t- распределения Стьюдента, выбираемый из таблицы в зависимости
от числа степеней свободы r и уровня значимости вероятности α.
r N(0) 1 , где N 0 Nв nот
r — число степеней свободы, равное
здесь Nв — число выборки; nот — число отклонений, проверяемых на ошибку выборки.
3. Пример выполнения задания
Пример. Время срабатывания пружинного клапана при отсекании давления
в канале нагнетания составило 9;10;11;7;8;14;17;12;7;10;5;13;9;10;12;8;9 мс.
Проверить однородность статистической выборки на наличие грубых ошибок при
уровне значимости α = 0,05.
Решение:
1. Выстраивается вариационный ряд и подсчитывается число наблюдений Nв,
попавших в выборку:
5;7;7;8;8;9;9;9;10;10;10;11;12;12;13;14;17.
Nв = 17
2. Определяется объем выборки без двух сомнительных ее крайних членов
N(0) = Nв – nот = 17 – 2 = 15
3. Вычисляется среднее арифметическое значение выборки без учета
сомнительных наблюдений:
1 N 0 15
7 7 8 8 9 9 9 10 10 10 11 12 12 13 14
x
x
9,9 мс;
i
N 0 i 1
15
4. Продолжение
4. Вычисляется среднеквадратическое отклонение случайной величины
так же без учета сомнительных значений:
1 N 0 15
1
2
S
62,95 2,12
xi x
N(0) 1 i 1
15 1
N 0 15
где
i 1
xi x 2
=(7-9,9)2 + (7-9,9)2 + (8-9,9)2 + (8-9,9)2 + (9-9,9)2 + (9-9,9)2 +
(9-9,9)2 + (10-9,9)2 + (10-9,9)2 + (10-9,9)2 + (11-9,9)2 + (12-9,9)2 +
(12-9,9)2 + (13-9,9)2 + (14-9,9)2= 62,95;
5. Определяется значение t — распределения Стьюдента для уровня значимости
α = 0,05 и числа степеней свободы r = N(0) – 1 = 15 – 1 = 14
t
1
α
2
r t1 0,05 14 2,145
2
6. Вычисляется правый член неравенства (1)
S t
α
1
2
r
N 0 1
15 1
2,12 2,145
4,7
N 0
15
5. Продолжение
7. Полученное значение сопоставляется с левым членом неравенства (1)
x 5 x 5 9,9 4,9 4,7,
x 17 x 17 9,9 7,1 4,7.
Как видно, неравенство (1) не выполняется в обоих случаях.
Следовательно, значения выборки xi= 5 и хi= 17 относятся к грубым ошибкам
и из статистического анализа исключаются.
Методы робастного оценивания — это статистические методы, которые позволяют получать достаточно надежные оценки статистической совокупности(См.[6]).
Единицы статистической совокупности, у которых значения анализируемого признака существенно отклоняются от основного массива, называются аномальными явлениями, «грубыми ошибками» или выбросами.
При решении задач статистического анализа проблема наличия в выборке аномальных измерений имеет чрезвычайно важное значение. Присутствие единственного аномального наблюдения может приводить к оценкам, которые совершенно не согласуются с выборочными данными.
Для данных индексов построим точечный график (Рисунок 7). В ходе визуального анализа выявляем наличие в выборке аномальных значений (выбросов).

Рисунок 7. Точечный график
Самым простым методом обнаружения грубых ошибок считается метод, на основании Т — Критерия Граббса:

, где (1.4)
— среднее значение, x — аномальное значение, s — выборочное среднеквадратическое отклонение СВ.
Данный критерий можно использовать для выделения аномальных результатов измерений только в случае нормального закона.
Так как выборка распределена нормально, мы можем найти Тк, и проверить наличие грубых ошибок в выборке.
Результаты расчетов по выборке представлены на Рисунке 8:

Рисунок 8.Результаты вычисления
Полученные значения сравнивают с табличными значениями процентных точек критерия Смирнова Граббса (Таблица 1). В том случае, если >, мы может утверждать, что проверяемое значение является грубой ошибкой и относится к классу выбросов.
Таблица 1. Значения процентных точек критерия Смирнова Граббса
|
0.99 |
0.95 |
|
|
30 |
0.4257 |
0.4791 |
|
31 |
0.4376 |
0.4885 |
|
32 |
0.4477 |
0.4995 |
|
33 |
0.4558 |
0.5099 |
|
34 |
0.4688 |
0.5189 |
|
35 |
0.4779 |
0.5285 |
|
36 |
0.4874 |
0.5374 |
|
37 |
0.4970 |
0.5459 |
|
38 |
0.5048 |
0.5540 |
|
39 |
0.5145 |
0.5617 |
|
40 |
0.5211 |
0.5692 |
|
41 |
0.5307 |
0.5767 |
|
42 |
0.5385 |
0.5835 |
|
43 |
0.5450 |
0.5902 |
|
44 |
0.5522 |
0.5970 |
|
45 |
0.5599 |
0.6033 |
|
46 |
0.5675 |
0.6090 |
|
47 |
0.5742 |
0.6154 |
|
48 |
0.5789 |
0.6211 |
|
49 |
0.5861 |
0.6270 |
|
50 |
0.5910 |
0.6324 |
Сравним полученные значения с табличным (при = 0,01) при числе наблюдений равном 48, а Ткр = 0,5789.
Так как Тк(1) =1,9> = 0,5789, то проверяемое значение является грубой ошибкой и относится к классу выбросов.
Аналогично Тк(2) =3,33> = 0,5789, что подтверждает, что рассматриваемое значение является аномальным значением.
Критерий Граббса имеет некоторые недостатки. Он не точен, и не чувствителен к засорениям, когда ошибки группируются на расстоянии от общей совокупности.
Далее подтвердим наличие грубых ошибок на основании L- критерия Титьена-Мура (См.[9]).
Решающее правило для исключения k наибольших членов вариационного ряда основано на статистике:

, где (1.5)
 Воспользовавшись формулами, было найдено значение L-критерия Титьена-Мура для рассматриваемой выборки (Рисунок 9)
Воспользовавшись формулами, было найдено значение L-критерия Титьена-Мура для рассматриваемой выборки (Рисунок 9)
Рисунок 9. Значение L-критерия Титьена-Мура
Сравниваем полученное значение с критическим пределом (Таблица 2). При наличии выбросов статистика Lk должна быть меньше критического предела. В данном случае Lk = 0,67887 <Cкр = 0,696, что подтверждает наличие аномальных значений в выборке (См.[9]).
Таблица 2. Критические значения оценки для L — критерия Титьена и Мура (a=0,05)

Для избавления от выбросов изменим данные доходностей, исключим значение 0,076594461 и -0,125593848, что приведет к нормальному распределению.
Гистограмма при этом теперь имеет вид (Рисунок 10):

Рисунок 10.Гистограмма
Оценка функции распределения и построение ее графика. Интерпретация полученных результатов и предварительный закон распределения
Каждая случайная величина полностью определяется своей функцией распределения.
Если X — случайная величина, то функция F(x) = FX (x) = P (X <x) называется функцией распределения случайной величины X. Здесь P (X <x) — вероятность того, что случайная величина X принимает значение, меньшее x.
Важно понимать, что функция распределения содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
1. F(x) определена на всей числовой прямой R;
2. F(x) не убывает, т.е. если x1x2, то F(x1) F(x2);

3. F(-)=0, F(+)=1, т.е. и ;

4. F(x) непрерывна справа, т.е.

Для построения функции распределения необходимо взять накопленные частоты. Они определяются путем последовательного суммирования частот предшествующих интервалов (Рисунок 11).

Рисунок 11. Накопленные частоты
Таким образом график оценки функции имеет вид (Рисунок 12):

Рисунок 12. График оценки функции
Полученная функция распределения соответствует нормальному закону распределения, поэтому логично предположить, что финансовые индексы валютной пары евро/рубль распределены нормально.
В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.
Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.
Ключевые слова:
грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.
Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.
Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.
На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.
Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят
,
однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.
Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:
- Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
- Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
- Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).
В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.
В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].
Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.
Задаются вероятностью
Р
или уровнем значимости
α
(
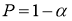
) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».
Проверяемая гипотеза состоит в утверждении, что результат наблюдения
x
i
не содержит грубой погрешности, т. е. является одним из значений случайной величины
x
с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
max
или наименьший xmin из результатов наблюдений.
Предложим для практического использования наиболее простые методы отсева грубых погрешностей.
Если в распоряжении экспериментатора имеется выборка небольшого объема
n
≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:
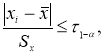
(1)
где
x
i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения
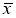
и среднеквадратичного отклонения
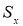
;
τ
1-
p
— табличное значение статистики
τ
, вычисленной при доверительной вероятности
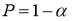
.
Таким образом, для выделения аномального значения вычисляют значение статистики,
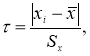
(2)
которое затем сравнивают с табличным значением
τ
1-α
:
τ
≤
τ
1-α
. Если неравенство
τ
≤
τ
1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.
Квантили распределения статистики
τ
при уровнях значимости
α
= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности
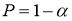
=
0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости
α
= 0,05 (результат получается с 95 %-й доверительной вероятностью).
Функции распределения статистики
τ
определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности
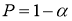
или уровне значимости
α
можно для чисел измерения п = 3–25 найти те наибольшие значения
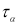
которые случайная величина
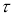
может еще принять по чисто случайным причинам.
Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения
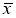
и среднеквадратичного отклонения
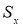
для выборки нового объема
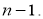
Таблица 1
Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]
|
|
Уровень значимости |
|
Уровень значимости |
||||||
|
0,10 |
0,05 |
0,025 |
0,01 |
0,10 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2,98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
|||||
В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.
-
Критерий «трех сигм» применяется для случая, когда измеряемая величина
x
распределена по нормальному закону. По этому критерию считается, что с вероятностью
Р
= 0,9973 и значимостью
α
= 0,0027 появление даже одной случайной погрешности, большей, чем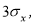
маловероятное событие и ее можно считать промахом, если
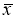
−
x
i
> 3
S
x
, где
S
x
—
оценка среднеквадратического отклонения (СКО) измерений. Величины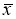
и
S
x
вычисляют без учета экстремальных значений
x
i
. Данный критерий надежен при числе измерений
n
≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при
6 <
n
≤100 она равна 4
S
x
; при 100 <
n
≤1000 − 4,5
S
x
; при 1000 <
n
≤10000–5
Sx
. Данное правило также используется только при нормальном распределении.
Практические вычисления проводят следующим образом [5, с. 65]:
- Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
-
Вычисляют среднее арифметическое значение выборки
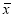
без учета сомнительного значения
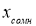
измеряемой величины.
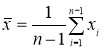
(3)
-
Вычисляют оценку СКО выборки
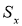
без учета сомнительного значения
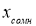
измеряемой величины.
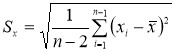
(4)
- Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.
Если
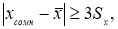
то сомнительное значение отбрасывают, как промах.
Если
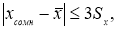
то сомнительное значение оставляют как равноправное в ряду наблюдений.
Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.
-
Критерий В. И. Романовского применяется, если число измерений невелико,
n
≤ 20. При этом вычисляется соотношение
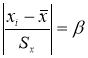
(5)
где
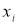
— результат, вызывающий сомнение,
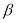
— коэффициент, предельное значение которого
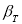
определяют по таблице 2. Если
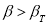
, сомнительное значение
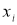
исключают («отбрасывают») как промах. Если
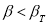
,
сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].
Таблица 2
Значение критерия Романовского
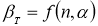
|
Уровень значимости, |
Число измерений, |
||||||
|
|
|
|
|
|
|
|
|
|
0,01 |
1,73 |
2,16 |
2,43 |
2,62 |
2,75 |
2,90 |
3,08 |
|
0,02 |
1,72 |
2,13 |
2,37 |
2,54 |
2,66 |
2,80 |
2,96 |
|
0,05 |
1,71 |
2,10 |
2,27 |
2,41 |
2,52 |
2,64 |
2,78 |
|
0,10 |
1,69 |
2,00 |
2,17 |
2,29 |
2,39 |
2,49 |
2,62 |
Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.
- Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.
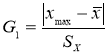
и
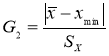
(6)
Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев
t
-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.
Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.
Если G1
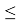
GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2
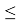
GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.
Отсев грубых погрешностей можно производить и для больших выборок (
n
= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].
Известно, что критическое значение
τ
p
(
p
— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента
t
α, n-2
[6, с. 26]:
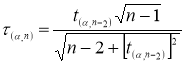
(7)
Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (
n
= 100):
1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;
2)
по формуле
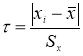
вычисляют значение статистики
τ
;
3)
по таблице (или в программе Excel) находят процентные точки
t
-распределения Стьюдента
t
(
α,
n
-2
)
:
t
(95
%, 98)
= 1,6602, и
t
(
99
%, 98)
= 3,1737;
По предыдущей формуле в программе Excel вычисляют соответствующие точки
t
(95
%, 100)
= 1,66023и
t
(99
%, 100)
=3,17374.
Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.
Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)
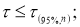
2)
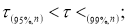
3)
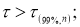
.
Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.
Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.
Пример 1.
Имеется выборка из 100 шт. резисторов с номинальным сопротивлением
R
н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.
- Заносим данные измерений в таблицу Excel в ячейки В2:В101
- Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)
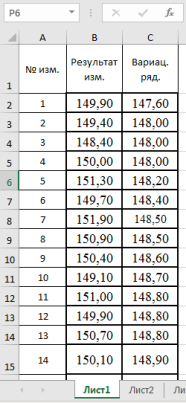
Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).
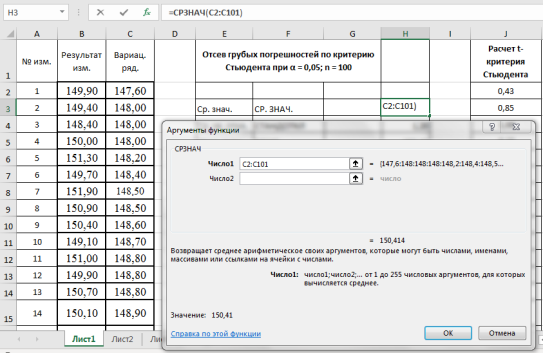
Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки
-
Находим среднеквадратическое отклонение —
S
x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).
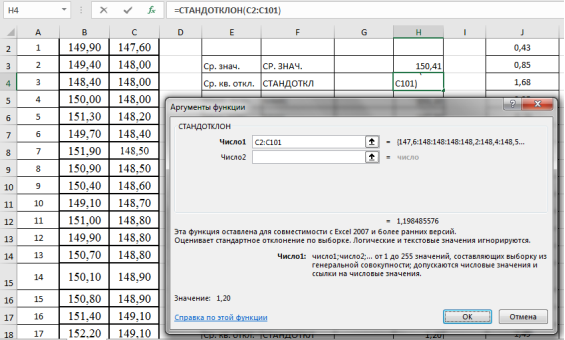
Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения
-
Находим максимальное значение в выборке —
x
макс
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).
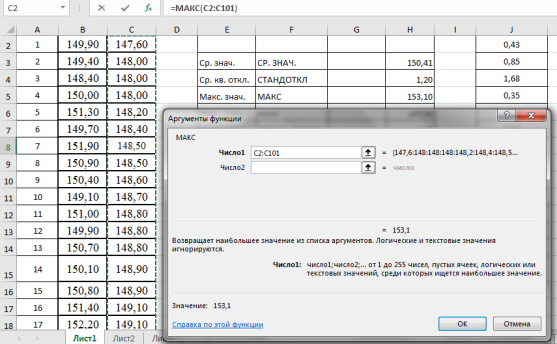
Рис. 4. Фрагмент диалогового окна при нахождении максимального значения
-
Находим минимальное значение в выборке —
x
мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).
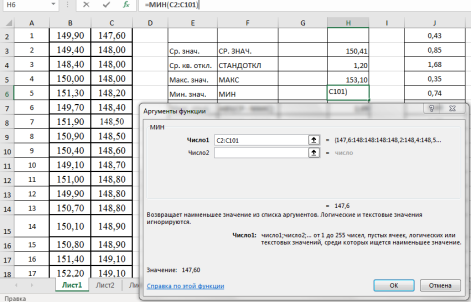
Рис. 5. Фрагмент диалогового окна при нахождении минимального значения
-
Находим максимальное и минимальное отклонения — Δ
макс
и Δ
мин
. Вводим в ячейки Н7 и Н8 формулы:
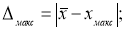
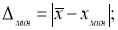
-
Находим теоретическое значение —
t
теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу
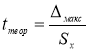
. и
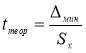
-
Находим табличное значение
t
табл.
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (
n
-2) — 98, результат в ячейке Н10–1,66 (рис. 6).
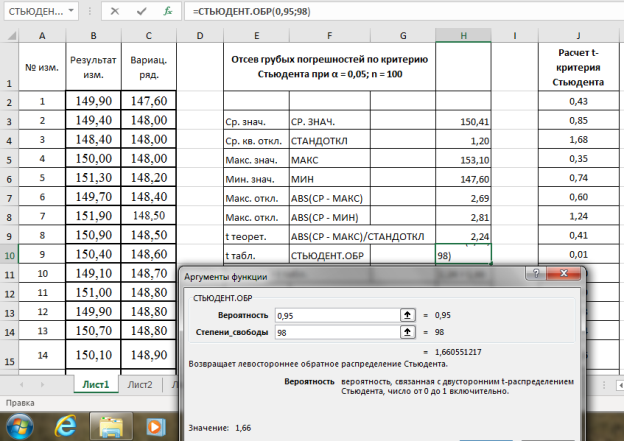
Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента
-
Сравниваем теоретическое значение
t
теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:
t
табл
.= 1,6605. - Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).
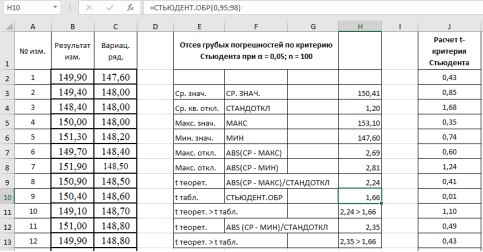
Рис. 7. Фрагмент диалогового окна при окончательном анализе данных
- Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.
Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений
n
= 20, β
табл
= 2,78 (из таблицы 2).

Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского
Выводы
- Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
- Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.
Литература:
1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.
2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.
3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.
4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.
5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.
6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.
Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.
