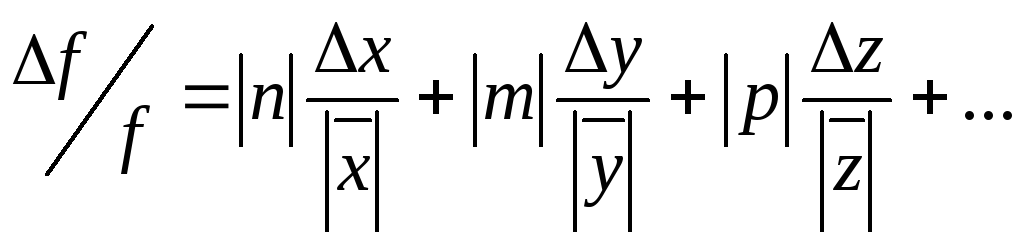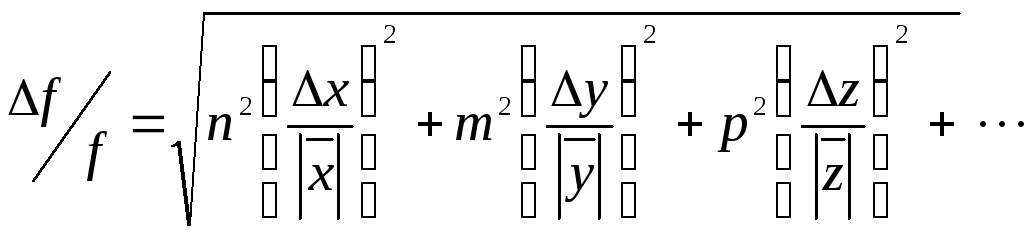Расчет ошибок результатов полученных косвенным путем

26

В
результате прямого измерения получается
не истинное значение х
измеряемой величины, а серия
изn
значений
.
Пусть теперь

Суммируя последнее
равенство, получим

или

Но

(7)

где
средне арифметическое измеренных
значений.
Таким образом,

(8)

Из
этого простого результата вытекают
весьма важные следствия. Действительно,
при
и.

значит,
при бесконечно большом числе измерений
и, следовательно, при конечныхn
результат тем ближе к среднему
арифметическому, чем больше число
измерений. Отсюда также следует, что
при оценке ∆Х
в качестве

целесообразно
взять
.

На
практике n
конечно и
.
В задачу математической теории случайной
погрешности входит оценка интервала

(9)

в
котором заключено истинное значение
измеряемой величины. Интервал (9)
называется доверительным
интервалом,
а величина
–абсолютной
погрешностью результата серии измерений.
Теория оценки ∆х
достаточно сложна, поэтому здесь будут
рассмотрены лишь её основные результаты.
Прежде всего нужно отметить, что,
поскольку х
– случайная величина, ошибка ∆х
может быть определенна лишь с той или
иной степенью надежности
α,
которую также называют доверительной
вероятностью.
Доверительная вероятность – это
вероятность того, что истинное значение
измеряемой величины х
попадает в доверительный интервал (9).
Если положить α=1
(100%), то это будет соответствовать
достоверному событию, т.е. вероятности
того, что х
принимает
какое-то значение в интервале ().
При этом.
Очевидно, такой выбор надёжностиα
нецелесообразен.
При малых α
доверительный интервал ∆х
определяется с малой достоверностью.
В дальнейшем мы будем полагать α=0.90
или 0.95. Доверительный интервал и
надёжность взаимосвязаны. Для оценки
границ доверительного интервала
английский математик В. Госсет
(публиковавший свои работы под псевдонимом
Стьюдент) ввёл в 1908 г. коэффициент:

(10)

равный
отношению погрешности ∆х
к средней
квадратичной ошибке*

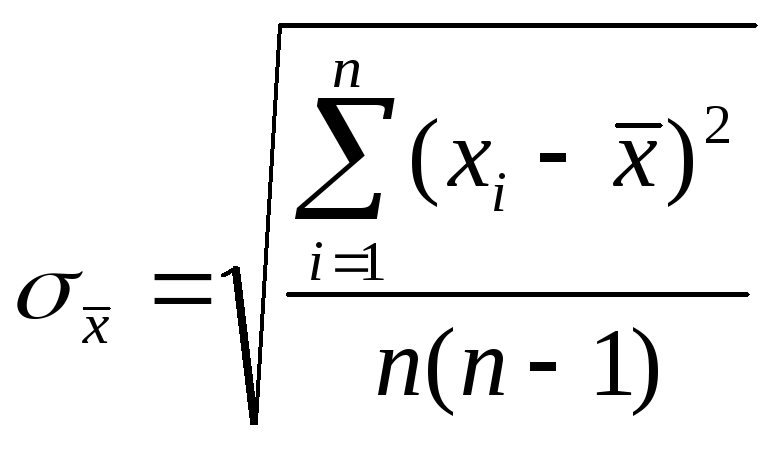(11)

Коэффициент
зависит от надёжностиα,
а также от числа измерений n
и называется коэффициентом
Стьюдента.
Этот коэффициент табулирован (см.
приложение 1), поэтому рассчитав
и задав доверительную вероятностьα,
нетрудно найти случайную ошибку:

(12)

Расчёт погрешности косвенных измерений.

При
косвенных измерениях измеряемая величина
f
находится
из функциональной зависимости:

где
x,
y,
z
– результаты прямых измерений. Формулу
для ∆f
можно
получить, заменив в (2) дифференциалы
погрешностями и взяв все слагаемые по
модулю

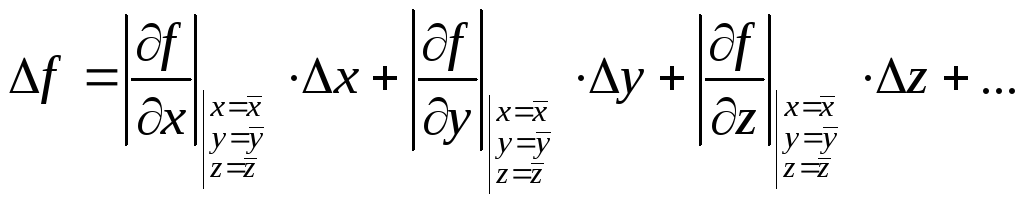(13)

Соотношение
(13) рекомендуется для оценки погрешности
∆f
, обусловленной
приборными погрешностями величины x,
y, z,… Для
оценки погрешности, связанной со
случайными ошибками прямых измерений,
рекомендуется соотношение:

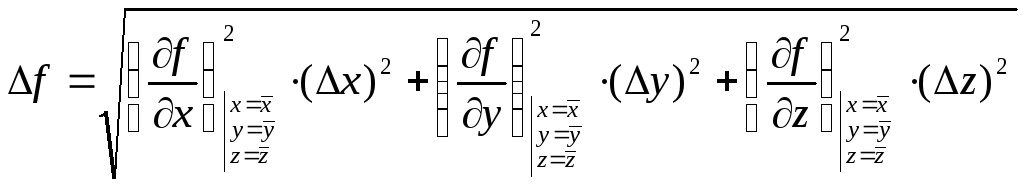(14)

Следует
правда отметить, что формулы (13) и (14)
приводят практически к одинаковым
результатам. Производные в (13) и (14)
берутся при средних, т.е. при измеренных
значениях аргументов.

Очень
часто функция f
представлена
степенной зависимостью от аргументов

(15)

где
c, n, m и p – постоянные. Частным случаями
формулы (15) являются соотнощения
,и
др.

Задание.
Покажите, что для функции вида (15) формулы
(13) и (14) принимают вид:

(13)

(14)

Из
соотношений (13) и (14) следует, что для
степенных функций расчёт погрещностей
существенно упрощается, причём
целесообразно сначала найти относительную
погрешность, которая выражается через
относительную погрешность прямых
измерений, а затем найти абсолютную
погрешность

(16)

Под
понимается
функция от средних (измеренных) значений
аргументов

.

Алгоритм расчета погрешностей

—
Для прямых измерений

1.
Вычислить среднее арифметическое
результатов

серии из n
измерений:

Замечание:
при расчете
удобнее исходить из формулы:

где
— любое удобное значение, близкое к.

2. Найти отклонения
отдельных измерений от среднего значения

3. Исключить промахи.

4. Рассчитать
среднюю квадратичную погрешность
результата серии измерений

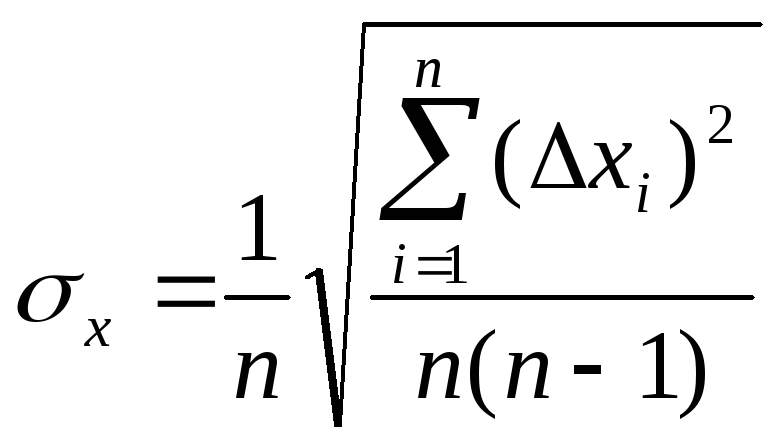
Замечание.
При

можно положить

и рассчитывать
по формуле

5.
Если
,
то случайную ошибку можно не рас­считывать.

6.
В противном случае задать доверительную
вероятность
и найти по таблице коэффициент Стьюдента
.

7. Рассчитать
границы доверительного интервала

Замечание
1. Если
приборная погрешность
имеет тот же порядок величины что и, то абсолютная погрешность результата
серии измерений находится по формуле:

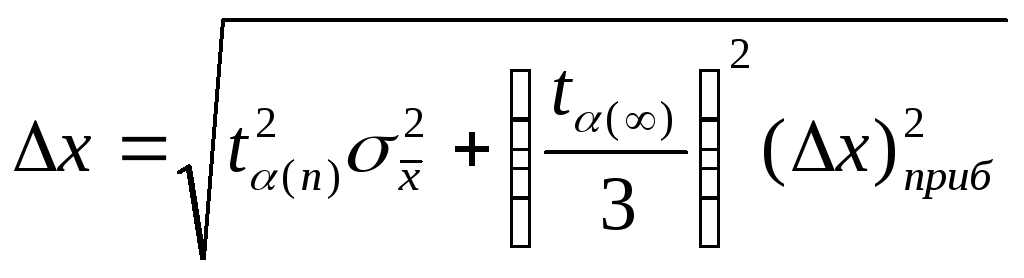
где
Практически в качествеможно
взять табличное значениеотвечающее самому большо­му из
приведенных в ней значенийп
(например, п=500
).

Замечание
2. При большом
числе измерений
можно по­ложить

где

.

8. Результат
измерения представить в виде:

— Для косвенных
измерений

Погрешность

косвенного
измерения можно рассчитать по одной из
формул (13), (14), (13*), (14*). Две последние
формулы выпол­няются для степенных
зависимостей, а соотношения (13) и (14)
име­ют общий характер.

Сводка
соотношений для расчета погрешности
косвенного измере­ния
для
некоторых простых функциональных
за­висимостей представлена в таблице.

Таблица

Функция	Формулы для расчета погрешностей
	;
	;

Пример.
Пусть джоулево тепло Q рассчитывается
по формуле

Поскольку это
степенная зависимость, целесообразно
воспользоваться формулой (13*)

Правила
представления результатов измерений
и их погрешностей

Погрешности
могут лишь оцениваться, поэтому обычно
достаточно указать погрешность с одной
значащей цифрой. Например, Δm=0,2 г.
г.
Запись т
= 3,0 г
означает, что измерение произведено
с точностью до десятых долей грамма.
Однако при про­межуточных вычислениях
целесообразно оставлять больше значащих
цифр.

Правила округления
чисел (результатов измерений)
иллюстрируют­ся в таблице (обратите
внимание на особенности округления
цифры 5).

Таблица Округление
до десятых значащих цифр

До округления	После округления	Пояснения
734,7 736 735,0 745,0 745,1	730 740 740 740 750	4<5 6>5 3 – нечетное 4 — четное после 5 стоит не 0

Результат измерения
принято округлять так, чтобы числовое
зна­чение оканчивалось цифрой того
же разряда, что и значение погреш­ности.
Например, запись

см.

непреемлема,
т.к. само значение погрешности Δl = 0,1 см
указыва­ет
на то, что
цифры 018 результата не могут гарантироваться.
Нуж­но
записать
так:
см.

Соседние файлы в предмете Физика

• #
• #
• #

---

Подборка по базе: Реферат Общественный и государственный строй Древнего Рима в рес, Московский финансово-промышленный университет «Синергия.pdf, Эпидемиология госпитальных инфекций мочевыводящих путей.docx, 1. Университет Синергия с 06.05.22.docx, Устные сообщения АТПз 2 курс.docx, 5847 — Государственный строй Рима в период республики — курсовая, Федеральный государственный образовательный стандарт среднего об, Сообщение по истории Средневековые университеты.Схоластика.docx, АО «КАЗАХСКИЙ НАЦИОНАЛЬНЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМЕНИ С.Д., Использование приемов убеждающей коммуникации в сообщениях СМИ.p

---

ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ
В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого измеряются другие величины (аргументы) и т.д., а затем искомая величина вычисляется на основе заданной функциональной зависимости

(11)

Если для каждого аргумента в выражении (11) экспериментально найдены средние значения и вычислены погрешности , то за наилучшее приближение для величины принимается значение

получающееся при подстановке в выражение (11) вместо истинных значений аргументов их средних экспериментальных значений.

Доверительная погрешность косвенных измерений величины определяется погрешностями прямых измерений (однократных или многократных) всех аргументов , входящих в формулу (11).

Полное приращение функции , обусловленное изменением ее аргументов на малые величины , может быть, как известно из курса высшей математики, c достаточной точностью вычислено по формуле

, (12)

где , , –

частные производные функции по ее соответствующим аргументам. При вычислении частной производной все аргументы функции кроме того, по которому производится дифференцирование, считаются постоянными.

Рассматривая в выражении (12) величины как погрешности прямых (однократных или многократных) измерений аргументов , можем считать каждый из слагаемых правой части этой формулы вкладом в общую погрешность измерений функции . Полагая эти вклады независимыми, по принятому в математической статистике закону сложения погрешностей получаем общую формулу для вычисления погрешности при косвенных измерениях

. (13)

Таким образом, для того чтобы определить абсолютную погрешность результата косвенного измерения, следует найти частные производные функции по всем аргументам, подставить в них найденные на предыдущем этапе измерений средние значения аргументов и провести расчет по формуле (13).

При расчете погрешностей по формуле (13) допустимо пренебрегать теми слагаемыми подкоренного выражения, которые по крайней мере в 2 – 3 раза меньше максимального. (коэффициент 3 применяется в тех случаях, когда слагаемых много и малые погрешности могут внести заметный вклад в общую погрешность). Это соображение существенно упрощает расчет погрешности, а также позволяет четко выявить тот аргумент, погрешность которого имеет определяющее значение. Данный подход удобен при обсуждении результатов и важен для поиска путей повышения точности результатов.

Если искомая функция удобна для логарифмирования (представляет собой произведение простых функций измеряемых аргументов), учитывают, что полное приращение функции может быть с достаточной точностью рассчитано по формуле

, (14)

и вместо выражения (13) получают следующее соотношение

. (15)

Заметим, что правая часть выражения (15) дает значение относительной погрешности результата данного косвенного измерения.

Окончательно рекомендуется следующий алгоритм обработки результатов косвенных измерений.

1. Выполнить (однократные или многократные) прямые измерения аргументов измеряемой функции

; ;.

(Подразумевается, что величина является результатом однократного прямого измерения.)

2. Найти среднеарифметические значение аргументов

; ; .

3. Вычислить абсолютные погрешности отдельных результатов наблюдений для каждого аргумента (при многократных его измерениях), а также их квадраты и соответствующие суммы

;

4. Для данных значений и найти по таблице коэффициент Стьюдента и вычислить погрешности аргументов (случайные или приборные)

...

5. Если функция удобна для логарифмирования, прологарифмировать ее и по формуле (15) вычислить относительную погрешность

.

В противном случае опредлить доверительную погрешность результата измерений по общей формуле (13)

.

6. Вычислить предварительный результат измерений

.

7. Округлив результат измерений и погрешность, записать окончательный результат в виде

НЕВОСПРОИЗВОДИМЫЕ КОСВЕННЫЕ ИЗМЕРЕНИЯ
Иногда при выполнении косвенных измерений невозможно повторить наблюдения в тождественных условиях относительно одного или нескольких аргументов измеряемой функции. Например, при измерении коэффициента вязкости жидкости в нее бросают металлические шарики (дробинки). Каждый из брошенных в жидкость шариков сразу же достать нельзя. Условия опытов, повторенных с разными шариками, не будут одинаковыми из-за различия размеров и формы шариков, различного состояния их поверхностей и т.д. В этом случае говорят, что косвенные измерения

невоспроизводимы. Тем не менее коэффициент вязкости характеризует одну и ту же исследуемую жидкость, и расчет должен давать близкие значения этого коэффициента для всех шариков.

Для невоспроизводимых косвенных измерений рекомендуется следующий порядок обработки их результатов.

1) Определить значение искомой функции для каждого ого невоспроизводимого наблюдения, исходя из найденных экспериментальных значений аргументов ,

2) Каждое из определенных таким образом значений рассматривается затем как случайная величина с нормальным законом распределения погрешностей . Иначе говоря, значения рассматриваются как результаты прямых многократных измерений физической величины . В соответствии с этим в качестве наиболее вероятного значения берется среднее арифметическое

,

а погрешность вычисляется по формуле (как случайная погрешность)

,

т.е. по правилам обработки результатов прямых многократных измерений.
ПРИМЕРЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ
Пример 1. В работе № 103 коэффициент поверхностного натяжения жидкости определяется по расчетной формуле

(16)

где – сила поверхностного натяжения, и – внутренний и внешний диаметры кольца соответственно.

Для получения расчетной формулы погрешности учтем, что выражение (16) относительно удобно для логарифмирования (содержит три множителя:) и, следовательно, целесообразно искать погрешность по формуле (15) с учетом замены соответствующих значений функции и аргументов:

Прологарифмировав выражение (16), получим

Находим частные производные

Выражение для расчета относительной погрешности будет

Отсутствие в данной формуле значения относительной погрешности числа обусловлено тем, что в настоящее время значение этого числа известно с высокой точностью.
Пример 2. В работе № 108 требуется определить отношение теплоемкостей (коэффициент Пуассона) воздуха . Расчетная формула имеет вид

(17)

где и – разности уровней жидкости (воды) в манометре для некоторых двух состояний воздуха в сосуде.

Косвенные измерения в данном эксперименте являются невоспроизводимыми, поскольку, повторяя опыт, накачать и выпустить каждый раз одинаковое количество воздуха невозможно. Значения вычисляются в каждом наблюдении по результатам прямых измерений величин и , а затем обрабатываются как результаты прямых многократных измерений. Следовательно, доверительная погрешность определяется как случайная по формуле

.
Пример 3. В лабораторной работе № 117 коэффициент жесткости пружины определяется по формуле

, (18)

где – коэффициент жесткости, – масса груза, – среднее удлинение пружины при увеличении массы груза на 50 г, – ускорение свободного падения (на широте Санкт–Петербурга).

Воспользовавшись алгоритмом обработки результатов косвенных измерений в случае удобной для логарифмирования расчетной формулы, получим (см. пример 1) выражение

в котором погрешностью ускорения свободного падения можно пренебречь в силу ее малости.

В этой работе требуется также найти экспериментальное и расчетное значения периодов колебания груза и (масса груза задается преподавателем). Соответствующие формулы погрешностей имеют следующий вид:

а) для расчетного значения периода колебания груза

б) для периода колебаний, измеренного с помощью секундомера,

.
Пример 4. В работе № 131 термический коэффициент линейного расширения твердых тел определяется соотношением

(19)

где – приращение длины образца при изменении температуры на , – длина исследуемого образца при комнатной температуре.

Выражение (19) удобно для логарифмирования, поэтому относительную погрешность измеряемой величины находим как в примере 1, выполняя математические операции логарифмирования и дифференцирования. В результате получаем формулу

где – доверительные погрешности соответствующих аргументов.

В данной работе может быть использован и алгоритм обработки результатов косвенных невоспроизводимых измерений, если полученные на разных участках исследуемого температурного диапазона значения термического коэффициента линейного расширения не будут соответствовать четко выраженной монотонной зависимости.
ОСНОВНЫЕ ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ
Важным методом обработки результатов опыта является представление их в виде графика. При минимальной обработке графики представляют результаты измерений в наиболее компактной форме с легкой обозримостью всего объема информации. Они позволяют проверить соответствие теории и результата эксперимента, выявить области изменения переменных, требующие более детального исследования.

Графический метод обработки результатов эффективен только при его грамотном применении, что предполагает овладение элементарными навыками работы с графическим материалом.

Выбор бумаги. Графики выполняют на миллиметровой бумаге. Размер листа для графика равен примерно мм. При этом график еще достаточно масштабен, им удобно пользоваться (например, вклеивать или подшивать в лабораторный отчет). Очень удобны в этом отношении листы из ’’Блокнота для диаграмм’’.Построение координатных осей. Графики принято строить в декартовой (прямугольной) системе координат, где по оси абсцисс откладывается переменная, выбранная за независимую (аргумент), а по оси ординат – функция. При нанесении осей следует оставить место для заголовка, поясняющих записей и полей для вклейки или подшивки в лабораторный отчет.Выбор интервала изменения переменных и оцифровка шкал. Интервалы изменения переменных по обеим осям выбираются независимо друг от друга, так чтобы на графике была представлена лишь экспериментально исследованная область изменения переменных величин. Сам график при этом занимает все поле чертежа. Не следует стремиться к тому, чтобы начало координат (точка 0,0) обязательно поместилось на графике. Делать это разумно в тех случаях, когда при этом существенно не увеличиваются размеры графика или когда эта точка является наиболее надежным результатом измерений. Например, при измерении силы тока в зависимости от напряжения точка (0,0) – очевидный и самый надежный результат этой зависимости.

Ценность графика во многом определяется удачным выбором масштаба. Рекомендуется выбирать удобные для восприятия и расчетов единицы масштаба шкал. Допустимы значения единиц масштаба, равные только

одной, двум или пяти единицам измеряемой величины, умноженным на порядковый множитель , где – положительное или отрицательное целое число (порядок величины).

Число оцифрованных делений на каждой оси должно быть минимально необходимым для ясного понимания шкалы и составляет обычно от 4 до 10. По оси цифры пишутся под масштабными рисками, обозначение откладываемой величины и ее единица измерения указываются справа под осью. По оси цифры пишутся слева от рисок, а обозначение соответствующей величины и единица измерения указываются вверху слева от оси. Стрелки на осях не ставятся. Порядковый множитель следует включать в буквенное обозначение или использовать десятичные приставки к названиям единиц. Например, ’’’’, ’’’’, ’’’’.

Ни в коем случае не следует отмечать и оцифровывать на осях экспериментальные значения аргумента и функции, а тем более проводить штриховые линии для помещения экспериментальных точек на поле графика. Изобилие линий резко ухудшает восприятие графической информации. Следует помнить, что на графике прежде всего должны выделяться экспериментальные точки – именно они являются главным результатом работы экспериментатора.

Выбрав масштаб и проведя оцифровку осей, проверьте себя. Найдите координаты 2–3 произвольно взятых точек. Если на определение двух координат каждой точки затрачивается более 10 с или возникают ошибки – масштаб и оцифровка осей выбраны неудачно.

Нанесение экспериментальных точек и их погрешностей. Экспериментальные точки нужно наносить на график точно и аккуратно, отмечая их кружками (квадратами, треугольниками, крестиками). Полезно применять разные знаки для разных кривых, если они изображаются на одном графике. Погрешности на графиках, когда это позволяет масштаб, можно указывать для одной или обеих измеряемых величин в виде отрезков, полудлина которых равна доверительной погрешности. Исключение составляют случаи, когда по одной из осей откладываются величины, известные точно (например, принимающие только целочисленные значения).

Обычно указание погрешностей либо загромождает график, либо их нельзя указать в данном масштабе (при точных измерениях). Поэтому допустимо иногда вообще не указывать погрешности или делать это для одной–двух точек. О точности измерений тогда можно весьма приближенно судить по разбросу точек относительно проведенной кривой.

Проведение кривой по экспериментальным точкам. Экспериментальные точки соединяются карандашом плавной кривой так, чтобы они располагались примерно поровну и в среднем на равном удалении по обе стороны от кривой. Ни в коем случае не следует соединять экспериментальные точки на графике ломаной линией (от точки к точке). Обычно зависимости физических величин соответствуют гладким, плавно изменяющимся функциям без резких изломов и перегибов. Если же все точки последовательно соединить, то получится ломаная линия, которая не имеет ничего общего с истинной физической зависимостью. Это следует хотя бы из того факта, что форма полученной ломаной линии не будет воспроизводиться при повторных сериях измерений.

Проводимая на графике кривая не должна заслонять экспериментальные точки. Следует помнить, что именно точки являются результатом измерений, а кривая – лишь наше (не обязательно верное) толкование результата.

Оформление графиков. Графики должны быть снабжены заголовками и пояснениями, кратко и точно отражающими содержание графика. Обязательно указываются откладываемые по осям величины и их размерности. Если на одном графике располагается несколько кривых, то каждая из них должна быть четко обозначена цифрой или буквой, поясняемой в подписи к графику. Заголовок и пояснения располагают либо под графиком, либо на незанятой части координатной сетки.Лабораторная работа №100
Измерение электронным секундомером интервалов времени, задаваемых по механическому секундомеру с секундной стрелкой
Цель работы – освоение алгоритма обработки результатов прямых многократных прямых измерений, построение гистограммы экспериментальных значений определяемой величины и оценка параметров распределения Гаусса из кривой закона распределения.
Теоретическая часть
1. Измерение физических величин и графическое представление результатов измерений.
При измерении физических величин в лабораторном практикуме из систематических погрешностей во внимание принимаются, как правило, только приборные как легко учитываемые. В таком случае в погрешность определяемой величины входят две составляющие: случайная (статистическая) и систематическая (приборная) (предполагаем, что промахи отсутствуют):

Если приборная погрешность значительно больше случайной, то при многократных измерениях практически получается один и тот же результат. Этот недостаток присущ, в основном, стрелочным приборам, подвижная часть которых, связанная со стрелкой, бывает настолько инерционной, что либо не реагирует на малые случайные отклонения, либо эти отклонения настолько малы, что их практически невозможно регистрировать. Такой прибор принято называть

грубым. Точный прибор характеризуется меньшей систематической (приборной) погрешностью по сравнению со случайной, и поэтому на распределение полученных с его помощью результатов измерений сказывается случайный разброс. Точными приборами являются цифровые вольтметры, электронные секундомеры и весы, измерители сопротивлений, емкостей и индуктивностей и т.д. Полученные с их помощью значений одной и той же измеряемой физической величины при неизменных контролируемых условиях следует обрабатывать как результаты прямых многократных измерений.

Если измерения проводят с помощью грубого и точного приборов, то необходимо исключить просчеты (промахи), связанные с отсутствием навыков измерения. Особое значение это имеет для уменьшения различия в показаниях механического и электронного секундомеров, обусловленного реакцией исследователя и проявляющегося в недновременности как включения, так и выключения счетного устройства. После нескольких измерений отрезков времени (длительностью, например, 60 секунд) с помощью электронного секундомера удается их фиксировать с погрешностью в несколько сотых секунды. Просчетов на механическом секундомере в силу его большей приборной погрешности избежать значительно легче.

Перед проведением статистического анализа целесообразно проверить, не изменяются ли измеренные значения регулярным образом со временем. Такое изменение называется

дрейфом. Для выяснения этого вопроса необходимо построить график зависимости результатов измерения от времени (рис. 2).

а) б)
Рис.2. Зависимость значений результатов измерения от порядкового номера отсчета (от времени): а – дрейф отсутствует, б – дрейф наблюдается. Точки – экспериментальные значения, прямые – аппроксимация точек (проведена от руки).
На горизонтальной оси обычно откладывают порядковый номер результата отдельного измерения, на вертикальной оси – сам результат. На рис.2а дрейф отсутствует, на рис.2б результаты систематически увеличиваются с течением времени (с увеличением порядкового номера наблюдения ).

При наличии дрейфа следует установить, связан ли он с неисправностью прибора (устранить ее или заменить прибор) или с закономерным изменением определяемой величины (здесь необходимо специальное исследование). При отсутствии дрейфа нужно построить экспериментальную

гистограмму, показывающую, как часто получаются те или иные значения . Если – число измерений, попадающих в любой из одинаковых интервалов (ячейка гистограммы), на которые разбивается весь диапазон значений определяемой величины, то величина

является оценкой вероятности того, что величина находится в пределах ячейки. Кривая, наилучшим образом описывающая экспериментальное распределение вероятности, называется

законом распределения. В случае нормального распределения в качестве оценки берут среднее квадратическое отклонение отдельного измерения (5). Относительная погрешность такой оценки зависит от числа измерений и при небольшом она велика. При 50 измерениях относительная погрешность составляет приблизительно 22%, поэтому достаточно сделать 40–50 измерений. Оценить величину можно, не прибегая к формуле (5), а используя кривую закона распределения: величина параметра равна полуширине кривой на уровне долей ее максимального значения.
2. Пример построения гистограммы экспериментальных значений определяемой величины и оценки параметров и из кривой закона распределения.
Пусть проведено 50 отсчетов величины напряжения, из которых , а . Эти значения укладываются в диапазоне напряжений . Если принять, что в одну ячейку гистограммы попадает не менее 4 значений, то при общем числе наблюдений 50 весь диапазон величины можно разбить не более, чем на одинаковых интервалов или ячеек гистограммы. Учтем неравномерность распределения результатов наблюдений по всему диапазону. Это уменьшает число ячеек примерно в 1,5 – 2 раза. Возьмем 6 ячеек. Длина ячеек будет равна примерно . Так как измеренные значения содержат сотые доли, то длину ячейки нужно брать равной 0,09 или 0,10 В. Выбрав значение 0,09 В, мы уменьшим общую длину всех ячеек и потеряем часть измерений при построении гистограммы ( место ). Поэтому следует несколько расширить диапазон значений так, чтобы он включал в себя разность . В данном конкретном случае в качестве минимального целесообразно взять значение , а в качестве максимального – , размер ячейки – . Обозначение ячеек, полученных при таком разбиении, приведены во второй колонке таблицы 4.

Распределим полученные значения величины по ячейкам и числа результатов, отнесенных к соответствующим интервалам, запишем в третью колонку таблицы 4. Поделив эти числа на общее число наблюдений , получим значения , которые занесем в четвертую колонку.

Гистограмму и график закона распределения следует нанести на миллиметровую бумагу, как это показано на рис.3. По оси абсцисс принято откладывать измеряемую величину , по оси ординат – числа измерений и величину . Масштаб удобно выбрать таким, чтобы единице измеряемой величины (или 10; 100 единицам; 0,1 единицы и т.д.) соответствовал 1 см на миллиметровой бумаге. Удобным является также масштаб, при котором 1 см соответствует 2 или 5 единицам.

Напомним, что пересечение координатных осей не должно обязательно совпадать с нулевыми значениями аргумента и функции (необходимо полностью использовать все поле чертежа).

При построении кривой закона распределения через точки на ступеньках гистограммы (эти точки соответствуют середине интервалов ) следует наилучшим образом провести колоколообразную кривую. Так как значения функции в указанных точках имеют погрешности, то необязательно все экспериментальные точки должны лежать на кривой.
Таблица 4

№ п/п	Ячейки гистограммы , В	Число наблюдений в ячейке,
1.	19,75 – 19,85	2	0,04
2.	19,85 – 19,95	6	0,12
3.	19,95 – 20,05	17	0,34
4.	20,05 – 20,15	18	0,36
5.	20,15 – 20,25	6	0,12
6.	20,25 – 20,35	1	0,02

Из рисунка 3 видно, что на уровне 0,6 от максимального значения ширина кривой закона распределения , откуда следует, что , а , соответствующее максимальному значению ординаты, приближенно равно .

Рис.3. Гистограмма экспериментальных значений (1) и закона распределения (кривая 2).
Описание установки
В данной работе требуется провести многократные измерения интервала времени с помощью механического (грубый прибор) и электронного секундомеров (более точный прибор).
Порядок выполнения работы
1. Прежде чем приступить к выполнению работы необходимо ознакомиться с правилами пользования электронным секундомером. Соответствующая инструкция выдается лаборантом.

2. Получить у лаборанта механический секундомер. Интервал времени задается преподавателем.

3. С разрешения преподавателя включить тумблер электронного секундомера ’’Сеть’’ и дать прибору прогреться в течение 3 – 5 минут.

4. Измерить промежуток времени несколько раз механическим и электронным секундомерами, чтобы освоить технику измерений и исключить промахи, связанные с отсутствием опыта измерений (тренировочные измерения).

5. Провести многократные измерения интервалов времени электронным секундомером при условии одновременного запуска и остановки электронного и механического секундомеров (50 – 100 раз по заданию преподавателя). Результаты опыта занести в таблицу 5.

Таблица 5

№ п/п	Результаты отдельных измерений	Случайные отклонения от выборочного среднего
1. 2. 3.

Обработка результатов измерений
Задание 1. Исследование дрейфа.

Проанализировать изменение со временем значений измеряемой величины, для чего по данным таблицы 5 построить график зависимости результатов наблюдений от времени (рис.2).

Задание 2. Статистический анализ выборки.

2.1. Определить выборочное среднее по формуле

.

2.2. Определить отклонения отдельных результатов наблюдений от среднего

и убедиться в выполнении равенства

2.3. Вычислить значения и сумму .

2.4. Рассчитать с

реднеквадратичную погрешность отдельного результата измерения

.

2.5. Определить с

реднеквадратичную погрешность среднего арифметического результата измерения по формуле

,

2.6. Для заданных значений числа измерений и доверительной вероятности найти по таблице коэффициент Стьюдента и вычислить случайную погрешность

.

2.7. Оценить приборную погрешность электронного секундомера по формуле (9). Проверить, что она меньше случайной более чем в два раза. В согласии с формулой (10) доверительную погрешность результата измерений приравнять случайной:

.

2.8. Округлив погрешность и предварительный результат, записать окончательный результат измерений в виде

.

Задание 3. Оценка параметров закона распределения вероятностей с помощью гистограммы.
3.1. По результатам наблюдений составить таблицу, необходимую для построения гистограммы и кривой, описывающей закон распределения (табл.4).

3.2. Построить гистограмму, кривую закона распределения и оценить по этой кривой значение величины среднего квадратического отклонения .

3.3. Сравнить величину со значением , полученным по гистограмме и кривой закона распределения.

Контрольные вопросы:
1. Какие измерения называются прямыми? косвенными?

2. Как рассчитывается доверительная погрешность при прямых многократных измерениях?

3. Почему при записи окончательного результата необходимо указывать доверительную вероятность?

4. Доверительная вероятность результата . Что это означает?

5. Какие погрешности называются систематическими? случайными? приборными?

6. Какая кривая называется гистограммой? законом распределения?

СОДЕРЖАНИЕ

Стр.

Введение 3

Абсолютная и относительная погрешности измерений 4

Доверительная вероятность и доверительная погрешность 4

Виды погрешностей 5

Прямые и косвенные измерения 6

Погрешности многократных прямых измерений 6

Округление результатов и погрешностей результатов измерений. Запись окончательного результата 11

Погрешности прямых однократных измерений 13

Вычисление погрешностей при косвенных измерениях 16

Невоспроизводимые косвенные измерения 19

Примеры обработки результатов косвенных измерений 19

Основные правила построения графиков 22

Лабораторная работа № 100 24

Контрольные вопросы 31