Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
![]()
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
![]() измеряемой
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
![]()
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
![]()
(14)
Отношения
![]()
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
![]()
к среднему арифметическому значению
![]()
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
![]()
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
![]()
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
![]()
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
![]()
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
![]()
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
![]() :
:
![]() ,
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
![]() ,
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
![]()
(15)

(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
![]()
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
![]()
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
![]() —
—
среднее квадратичное отклонение;
![]() —
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
![]()
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
![]()
теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
![]()
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
![]() —
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n

-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
![]()
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
![]() (или
(или
высотой
![]()
– плотностью относительной частоты
![]() ).
).
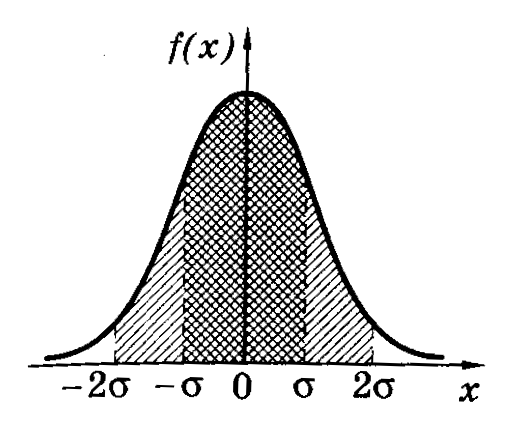
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
![]()
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
![]()
(25)
Где
![]()
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:

(26)
Как рассчитать экспериментальную ошибку в химии
На чтение 1 мин Просмотров 394 Опубликовано 05.06.2021
Ошибка – это мера точности значений в вашем эксперименте. Важно уметь вычислить экспериментальную ошибку, но есть несколько способов ее вычислить и выразить. Вот наиболее распространенные способы вычисления экспериментальной ошибки:
Содержание
- Формула ошибки
- Формула относительной ошибки
- Формула процента ошибки
- Пример расчета ошибки
Формула ошибки
В общем, ошибка – это разница между принятым или теоретическое значение и экспериментальное значение.
Ошибка = экспериментальное значение – известное значение
Формула относительной ошибки
Относительная ошибка = ошибка/известное значение
Формула процента ошибки
% Error = относительная ошибка x 100%
Пример расчета ошибки
Допустим, исследователь измеряет массу образца, который должен быть 5,51 грамм. Известно, что фактическая масса образца составляет 5,80 грамма. Рассчитайте погрешность измерения.
Экспериментальное значение = 5,51 грамма
Известное значение = 5,80 грамма
Ошибка = экспериментальное значение – известное значение
Ошибка = 5,51 г – 5,80 грамма
Ошибка = – 0,29 грамма
Относительная ошибка = ошибка/известное значение
Относительная ошибка = – 0,29 г/5,80 г
Относительная ошибка = – 0,050
% Error = относительная ошибка x 100%
% Error = – 0,050 x 100%
% Error = – 5,0%
Например,
в основе колориметрического метода
определения концентрации какого-либо
соединения лежит следующая зависимость:
G
= K
D,
(3.14)
где
G
– концентрация растворенного вещества;
K
– коэффициент пропорциональности; D
– оптическая плотность раствора.
При
этом, согласно закону распространения
ошибок, по данным Доерфеля,
относительная ошибка при определении
составляет
![]()
![]()
![]() ,
,
(3.15)
где
![]() –
–
сумма квадратов относительных
погрешностей, связанных с приготовлением
пробы исследуемого образца.
Коэффициент
пропорциональности можно найти
экспериментально калибровкой, но он
также содержит ошибку, которая, согласно
закону распространения ошибок,
составляет
![]() ,
,
(3.16)
где
![]()
– относительная погрешность при взятии
навески вещества;
![]()
– сумма квадратов прочих относительных
погрешностей, связанных с приготовлением
раствора, для построения калибровочной
кривой.
Таким образом:
![]() .
.
(3.17)
Максимально
допустимая погрешность измерения
оптической плотности на ФЭК-Н-57 составляет
0,01. При расчете были использованы
максимально допустимые абсолютные
ошибки для мерной посуды, приведенные
Доерфелем:
![]()
![]() ,
,
т.
е. относительная погрешность метода
при количественном определении вещества
составляет 1,4 %.
4. Методы математического планирования эксперимента
Современное
развитие биотехнологии невозможно без
широкого применения методов математического
планирования экспериментов. Начало
математическому планированию экспериментов
положили в 30-х годах работы Р. Фишера.
В частности, им были разработаны планы
полного факторного эксперимента. В
последнее время фундаментальные работы
Бокса позволили применять высокоэффективные
схемы планирования, такие, как метод
крутого восхождения и планы высших
порядков. Эти методы, в первую очередь,
нашли широкое применение при решении
задач оптимизации химико-технологиче-ских
процессов и только в последнее время
начали использоваться в биологии.
Основным
преимуществом математического
планирования, по сравнению с классическими
методами исследования, является
возможность одновременного влияния на
эффективность процесса боль-шого числа
факторов. Кроме того, этот метод позволяет,
наряду с количественным учетом каждого
отдельного фактора, установить наличие
в системе межфакторных взаимодействий
и оценить эффект последних, а также
определить значения параметров при
оптимальной эффективности процессов.
4.1. Анализ результатов экспериментов
В
результате анализа информационного
массива необходимо установить
непрерывность или дискретность
(прерывистость) исследуемого параметра
(исследуемых параметров) в зависимости
от входных данных.
В
непрерывных объектах все входные сигналы
представляют собой
непрерывные функции выходных параметров
от входных. В
дискретных объектах все входные сигналы
колеблются с определенной амплитудой
вокруг теоретического значения.
Практические
задачи требуют иногда простого
математического аппарата для описания
эмпирической зависимости выходного
параметра от входного (входных параметров)
только в определенном диапазоне. В более
сложных случаях требуется определить
твердо установленные закономерности
и структурные параметры. Закономерности
определяют, как правило, на основе
создания и решения математических
моделей процесса.
В
результате поискового эксперимента и
анализа априорного информационного
массива устанавливают схемы взаимодействия
рассматриваемого объекта с внешней
средой по соотношению входных и выходных
параметров. В принципе возможно
установление четырех схем взаимодействия:
– одномерно-одномерной
(рис. 4.1, а) – на объект воздействует
только один фактор (один входной сигнал),
а его поведение рассматривается по
одному показателю (один выходной сигнал);
– одномерно-многомерной
(см. рис. 4.1, б) – на объект
воздействует один фактор, а его поведение
оценивается по нескольким показателям;
– многомерно-одномерной
(см. рис. 4.1, в)
– на объект воздействуют несколько
факторов, а их поведение оценивается
по одному показателю;
– многомерно-многомерной
(рис. 4.1, г)
– на объект воздействует большое
количество факторов, а их поведение
оценивается по большому количеству
показателей.
а
б



y1
х



у
х
y2

y3
в
г
х



 1
1
х1
у1
х
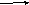

 2
2
у
х2
у2
х

 3
3
х3
у3
Рис.
4.1. Схемы взаимодействия объекта с
внешней средой:
а
– одномерно-одномерная; б –
одномерно-многомерная;
в –
многомерно-одномерная; г –
многомерно-многомерная
При
проведении исследования часто приходится
находить оптимальные параметры, при
которых показатели процессов принимают
экстремальные (максимальные или
минимальные) значения.
Относительная ошибка — опыт
Cтраница 1
Относительная ошибка опыта не превышает 4 — МО % для частиц размером 21ч — 31 мк и возрастает до 24 % при увеличении размеров частиц до 90 мк.
[2]
Относительная ошибка опытов составляла 5 % при определении коэффициентов тепло — и температуропроводности и 7 % при определении удельной теплоемкости и энтальпии.
[3]
Определить относительную ошибку опыта, если известно, что при нейтрализации 1 граммэквивалента сильной кислоты таким же количеством сильной щелочи выделяется 13 7 ккал тепла.
[4]
Определить относительную ошибку опыта, если известно, что при нейтрализации 1 граммэквивалента сильной кислоты таким же количеством сильной щелочи выделяется 13 7 ккал тепла.
[5]
Определить относительную ошибку опыта, если известно, что при нейтрализации 1 грамм-эквивалента сильной кислоты таким же количеством сильной щелочи выделяется 13 7 ккал тепла.
[6]
Определить относительную ошибку опыта, если известно, что три ( нейтрализация 1 грамм-эквивалента сильной кислоты таким ( же количеством сильной щелочи выделяется 13 7 ккал тепла.
[7]
Определить относительную ошибку опыта в процентах, зная, что при нейтрализации 1 г-экв сильной кислоты щелочью выделяется 13 64 ккал тепла.
[8]
Количественной оценкой точности результатов измерений является относительная ошибка опыта.
[9]
Количественной оценкой точности результатов опыта является относительная ошибка опыта.
[10]
Количественной оценкой точности результатов опыта является относительная ошибка опыта.
[11]
Таким образом, при уменьшении навески возрастает относительная ошибка опыта.
[13]
Сравнив полученную величину с теоретической, вычисляют относительную ошибку опыта в процентах.
[14]
По экспериментальным данным и истинному значению эквивалентной массы металла определяют относительную ошибку опыта.
[15]
Страницы:
1
2
Не пойму, что я делаю не правильно:
p.s. по лабораторной работе «определение теплоты нейтрализации»
Чтобы найти относительную погрешность опыта надо: е = (Qтеорит-Qэксп)/Qтеорит * 100%
Qтеорит = 56,9 кдж/моль, а Qэксп я нашла , получилось 1161,4 Дж и перевела в килоджоули 1,1614 кДж.
Но когда я их подставляю в формулу, у меня получается значение 98!
Такое может быть? Или где-то ошибка?
