Материал из Викиконспекты
Перейти к: навигация, поиск
<wikitex>
Дискретная математика, алгоритмы и структуры данных, 1 семестр
- Пусть $R$ и $S$ — рефлексивные отношения на $A$. Будет ли рефлексивным их а) объединение? б) пересечение? В этом и следующих заданиях, если ответ отрицательный, при демонстрации контрпримера удобно использовать представление отношения в виде ориентированного графа.
- Пусть $R$ и $S$ — симметричные отношения на $A$. Будет ли симметричным их а) объединение? б) пересечение?
- Пусть $R$ и $S$ — транзитивные отношения на $A$. Будет ли транзитивным их а) объединение? б) пересечение?
- Пусть $R$ и $S$ — антисимметричные отношения на $A$. Будет ли антисимметричным их а) объединение? б) пересечение?
- Определим $R^{-1}$ следующим образом: если $xRy$, то $yR^{-1}x$. Выполнено ли соотношение $RR^{-1} = I$, где $I$ — отношение равенства? Выполнен ли закон сложения степенией $R^iR^j=R^{i+j}$, если $i$ и $j$ разного знака?
- Пусть $R$ обладает свойством $X$. Будет ли обладать свойством $X$ отношение $R^{-1}$? Следует проанализировать $X$ — рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность
- Пусть $R$ и $S$ — транзитивные отношения на $A$. Будет ли транзитивным их композиция?
- Пусть $R$ и $S$ — антисимметричные отношения на A. Будет ли антисимметричным их композиция?
- Постройте пример рефлексивного, симметричного, но не транзитивного отношения
- Постройте пример рефлексивного, антисимметричного, но не транзитивного отношения
- Пусть $R$ — отношение на $A$. Рассмотрим $Tr(R)$ — пересечение всех транзитивных отношений на $A$, содержащих $R$. Докажите, что $Tr(R) = R^{+}$.
- Пусть $R$ — транзитивное антисимметричное отношение. Предложите способ за полиномиальное время построить минимальное отношение $S$, такое что $S^+ = R$.
- Является ли отношение $R$, такое что $(a, b) R (c, d)$, если $ad = bc$ на ${mathbb Z}^+ times {mathbb N}$ отношением эквивалентности?
- В каком случае транзитивное замыкание отношения будет отношением эквивалентности?
- В каком случае транзитивное замыкание отношения будет отношением частичного порядка?
- Выразите в явном виде «и», «или» и «не» через стрелку Пирса
- Выразите в явном виде «и», «или» и «не» через штрих Шеффера
- Является ли пара ${xto y, neg x}$ базисом?
- Является ли набор ${x to y, langle xyzrangle, neg x}$ базисом?
- Является ли набор ${{mathbf 0}, langle xyz rangle, neg x}$ базисом?
- Можно ли выразить «и» через «или»?
- Выразите медиану 5 через медиану 3
- Выразите медиану $2n+1$ через медиану 3
- Докажите, что любую монотонную самодвойственую функцию можно выразить через медиану
- Докажите, что любую функцию, кроме тождественной единицы, можно записать в СКНФ
- Докажите, что любую функцию от $n$ переменных можно представить с использованием стрелки Пирса формулой, длиной не больше чем $2^ncdot poly(n)$, где $poly(n)$ — полином, общий для всех функций
- Булева функция называется пороговой, если $f(x_1, x_2, ldots, x_n) = 1$ тогда и только тогда, когда $a_1x_1+a_2x_2+ldots+a_nx_n ge b$, где $a_i$ и $b$ — вещественные числа. Докажите, что «и» и «или» — пороговые функции.
- Приведите пример непороговой функции
- Рассмотрим булеву функцию $f$. Обозначим как $N(f)$ число наборов аргументов, на которых $f$ равна 1. Например, $N(vee) = 3$. Обозначим как $Sigma(f)$ сумму всех наборов аргументов, на которых $f$ равна 1 как векторов. Например, $Sigma(vee) = (2, 2)$. Докажите, что если для пороговой функции $f$ и функции $g$ выполнено $N(f) = N(g)$ и $Sigma(f) = Sigma(g)$, то $f = g$
- Сколько существует самодвойственных функций от $n$ переменных?
- Приведите пример функции, которая лежит во всех пяти классах Поста.
- Приведите пример функции, которая лежит во всех пяти классах Поста и существенно зависит хотя бы от трех переменных.
- Говорят, что формула имеет вид 2-КНФ, если она имеет вид $(t_{11}vee t_{12})wedge(t_{21}vee t_{22})wedgeldots$, где $t_{ij}$ представляет собой либо переменную, либо ее отрицание (в каждом дизъюнкте ровно два терма). Предложите полиномиальный алгоритм проверки, что формула, заданная в 2-КНФ имеет набор значений переменных, на которых она имеет значение 1.
- КНФ называется КНФ Хорна, если в каждом дизъюнкте не более одной переменной находится без отрицания. Пример: $xwedge(x vee neg y vee neg z) wedge (neg x vee neg t)$. Предложите полиномиальный алгоритм проверки, что формула, заданная в форме КНФ Хорна имеет набор аргументов, на котором она равна 1.
- Докажите, что если булеву функцию $f$ можно задать в форме Крома (в виде 2-КНФ), то выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = f(z_1, …, z_n) = 1$ $Rightarrow f(langle x_1, y_1, z_1rangle, …, langle x_n, y_n, z_n rangle) = 1$
- Докажите, что если выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = f(z_1, …, z_n) = 1$ $Rightarrow f(langle x_1, y_1, z_1rangle, …, langle x_n, y_n, z_n rangle) = 1$, то булеву функцию $f$ можно задать в форме Крома.
- Докажите, что если булеву функцию $f$ можно задать в форме Хорна, то выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = 1 Rightarrow f(x_1wedge y_1, …, x_n wedge y_n) = 1$
- Докажите, что если выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = 1 Rightarrow f(x_1wedge y_1, …, x_n wedge y_n) = 1$, то булеву функцию $f$ можно задать в форме Хорна
- Постройте схему из функциональных элементов для операции медиана трех над базисом ${ vee, wedge, neg}$. Постарайтесь использовать минимальное число элементов.
- Постройте схему из функциональных элементов для операции $x oplus y oplus z$ над базисом ${ vee, wedge, neg}$. Постарайтесь использовать минимальное число элементов.
- Предложите способ построить схему для функции $x_1 oplus … oplus x_n$ над базисом ${ vee, wedge, neg}$ с линейным числом элементов.
- Докажите, что не существует схем константной глубины для функций $x_1 vee … vee x_n$, $x_1 wedge … wedge x_n$.
- Докажите, что не существует схем константной глубины для функций $x_1 oplus … oplus x_n$.
- Докажите, что не существует схемы константной глубины для сложения.
- Постройте схему из функциональных элементов с тремя входами: $x, y, z$ и одним выходом. Значение на выходе равно $x$, если $z=0$ и $y$, если $z=1$. Используйте базис из всех не более чем бинарных функций.
- Мультиплексор — функциональная схема с $n = 2^k + k$ и одним выходом. Обозначим первые $2^k$ входов как $x_0, x_1, ldots, x_{2^k-1}$, а оставшиеся $k$ как $y_0, y_1, ldots, y_{k-1}$. Выход мультиплексора равен $x_i$, где $i$ — число, двоичное представление которого подано на входы $y_0, y_1, ldots, y_{k-1}$. Постройте схему линейного от $n$ размера для мультиплексора.
- Дешифратор — функциональная схема с $k + 1$ входом и $n = 2^k$ выходами. Обозначим первые $k$ входов как $y_0, y_1, ldots, y_{k-1}$, а последний как $z$. Обозначим выходы дешифратора как $x_0, x_1, ldots, x_{2^k-1}$. Значение на выходах дешифратора 0 на всех выходах, кроме $x_i$, где $i$ — число, двоичное представление которого подано на входы $y_0, y_1, ldots, y_{k-1}$, а на выходе $x_i$ равно значению $z$. Постройте схему линейного размера для дешифратора.
- Докажите, что для функции «большинство из $2n+1$» существует схема из функциональных элементов глубины $O(log n)$
- На одном китайском заводе в матричном умножителе случайно использовали элементы «или» вместо «и». Можно ли из получившихся значений получить произведение исходных чисел (доступа к входам нет, есть только доступ к $ntimes 2n$ выходам матричного псевдоумножителя).
- Докажите, что любую булеву функцию от $n$ аргументов можно представить схемой из функциональных элементов, содержащей $O(2^n)$ элементов.
- Докажите, что любую булеву функцию от $n$ аргументов можно представить схемой из функциональных элементов, содержащей $O(2^n/n)$ элементов.
- Контактной схемой называется ориентированный ациклический граф, на каждом ребре которого написана переменная или ее отрицание (ребра в контактных схемах называют контактами, а вершины — полюсами). Зафиксируем некоторые значения переменным. Тогда замкнутыми называются ребра, на которых записана 1, ребра, на которых записан 0, называются разомкнутыми. Зафиксируем две вершины $u$ и $v$. Тогда контактная схема вычисляет некоторую функцию $f$ между вершинами $u$ и $v$, равную 1 на тех наборах переменных, на которых между $u$ и $v$ есть путь по замкнутым ребрам. Постройте контактные схемы для функций «и», «или» и «не».
- Постройте контактную схему для функции «xor».
- Постройте контактную схему для функции медиана трех.
- Докажите, что любую булеву функцию можно представить контактной схемой.
- Постройте контактную схему «xor от $n$ переменных», содержащую $O(n)$ ребер.
- Постройте контактную схему «большинство из $2n+1$ переменных», содержащую $O(n)$ ребер.
- Постройте контактную схему, в которой для каждого из $2^n$ наборов конъюнкций переменных и их отрицаний есть пара вершин, между которыми реализуется эта конъюнкция, используя $O(2^n)$ ребер.
- Докажите, что любую булеву функцию можно представить контактной схемой, содержащей $O(2^n)$ ребер.
- Как выглядит дерево Хаффмана для частот символов $1, 2, …, 2^{n-1}$ (степени двойки) ?
- Как выглядит дерево Хаффмана для частот символов $1, 1, 2, 3, …, F_{n-1}$ (числа Фибоначчи)?
- Докажите, что если размер алфавита — степень двойки и частоты никаких двух символов не отличаются в 2 или более раз, то код Хаффмана не лучше кода постоянной длины
- Модифицируйте алгоритм Хаффмана, чтобы строить $k$-ичные префиксные коды
- Укажите, как построить дерево Хаффмана за линейное время, если символы уже отсортированы по частоте
- Предложите алгоритм построения оптимального кода среди префиксных кодов с длиной кодового слова не более L бит
- Предложите алгоритм построения оптимального кода среди префиксных кодов, для которых коды символов упорядочены лексикографически
- Предложите способ хранения информации об оптимальном префиксном коде для n-символьного алфавита, использующий не более $2n — 1 + n lceillog_2(n)rceil$ бит ($lceil xrceil$ — округление $x$ вверх)
- Можно ли разработать алгоритм, который сжимает любой файл не короче заданной величины $N$ хотя бы на 1 бит?
- Приведите пример однозначно декодируемого кода оптимальной длины, который не является ни префиксным, ни развернутым префиксным
- Для каких префиксных кодов существует строка, для которой он является кодом Хаффмана? Предложите алгоритм построения такой строки.
- Пусть заданы пары $(u_i, v_i)$. Предложите алгоритм проверки, что существует код Хаффмана для некоторой строки, в котором $i$-е кодовое слово содержит $u_i$ нулей и $v_i$ единиц.
- Докажите, что если в коде Хаффмана для некоторой строки $i$-е кодовое слово содержит $u_i$ нулей и $v_i$ единиц, то для многочлена от двух переменных $f(x, y) = sum_{i=1}^n x^{u_i}y^{v_i}$ выполнено $f(x, y) — 1 = (x + y — 1) g(x, y)$ для некоторого многочлена $g(x, y)$.
- Разработайте алгоритм кодирования Move To Front строки длиной $n$ за $O(n log n)$
- Докажите, что при оптимальном кодирование с помощью LZ77 не выгодно делать повтор блока, который можно увеличить вправо
- Верно ли утверждение из предыдущего задания при кодировании с помощью L78?
- Разработайте алгоритм оптимального кодирования текста с помощью LZ77, если на символ уходит $c$ бит, а на блок повтора $d$ бит
- Предложите семейство строк $S_1, S_2, ldots, S_n, ldots$, где $S_i$ имеет длину $i$, таких, что при их кодировании с помощью LZW длина строки увеличивается. Начальный алфавит ${0, 1}$.
- Разработайте алгоритм обратного преобразования Барроуза-Уиллера
- Разработайте алгоритм обратного преобразования Барроуза-Уиллера за $O(n)$
- Докажите, что для любого $c > 1$ существует распределение частот $p_1, p_2, .., p_n$, что арифметическое кодирование в $c$ раз лучше Хаффмана
- При арифметическом кодировании можно учитывать, что с учетом уже потраченных символов соотношения символов становятся другими и отрезок надо делить в другой пропорции. Всегда ли кодирование с таким уточнением лучше классического арифметического кодирования?
- При арифметическом кодировании трудным моментом является деление отрезка в пропорциях, не являющихся степенями двойки. Рассмотрим модификацию арифметического кодирования, когда соотношения между символами приближаются дробями со знаменателями — степенями двойки. Что можно сказать про получившийся алгоритм?
- Разработайте оптимальный код исправляющий одну ошибку при пересылке 2 битов
- Разработайте оптимальный код исправляющий одну ошибку при пересылке 3 битов
- Разработайте код, исправляющий две ошибки, использующий асимптотически не более $2n$ бит для кодирования $2^n$ символьного алфавита (для $n > n_0$)
- Перечисление всех $2^n$ двоичных векторов длины $n$ называется кодом Грея, если в нем не повторяются никакие два вектора и любые два соседних вектора отличаются ровно в одном разряде. Докажите по индукции, что для любого $n$ существует код Грея.
- Докажите, что последовательность $g_i = i oplus lfloor i / 2rfloor$ образует код Грея.
- Построим последовательность $g_i$ следующим образом: пусть $g_0 = 0$ и при переходе от $g_i$ к $g_{i+1}$ будем менять тот же бит, который меняется с 0 на 1 при переходе от $i$ к $i+1$. Докажите, что получившаяся последовательность является кодом Грея.
- Разработайте код Грея для k-ичных векторов
- При каких $a_1, a_2, …, a_n$ существует обход гиперпараллелепипеда $a_1 times a_2 times … times a_n$, который переходит каждый раз в соседнюю ячейку и бывает в каждой ячейке ровно один раз?
- При каких $a_1, a_2, …, a_n$ существует обход гиперпараллелепипеда $a_1 times a_2 times … times a_n$, который переходит каждый раз в соседнюю ячейку и бывает в каждой ячейке ровно один раз, а в конце возвращается в исходную ячейку?
- Код «антигрея» — постройте двоичный код, в котором соседние слова отличаются хотя бы в половине бит
- Троичный код «антигрея» — постройте троичный код, в котором соседние слова отличаются во всех позициях
- При каких $n$ и $k$ существует двоичный $n$-битный код, в котором соседние кодовые слова отличаются ровно в $k$ позициях?
- Докажите, что для достаточно больших $n$ существует код Грея, который отличается от любого, полученного из зеркального перестановкой столбцов, отражением и циклическим сдвигом строк
- Код Грея назвается монотонным, если нет таких слов $g_i$ и $g_j$, что $i < j$, а $g_i$ содержит на 2 или больше единиц больше, чем $g_j$. Докажите, что существует монотонный код Грея
- Докажите, что $sum_{k=0}^n C_n^k = 2^n$
- Докажите, что $sum_{k=0}^n (-1)^kC_n^k = 0$
- Коды Грея для перестановок. Предложите способ перечисления перестановок, в котором соседние перестановки отличаются обменом двух соседних элементов (элементарной транспозицией).
- Коды Грея для сочетаний. Предложите способ перечисления сочетаний, в котором соседние сочетания отличаются заменой одного элемента.
- Рассмотрим коды Грея для перестановок и коды Грея для их таблиц инверсий. Есть ли между ними связь?
- Сочетание с повторениями — это способ выбрать из $n$ элементов $k$, причем один элемент можно выбирать несколько раз. Порядок не важен. Чему равно число сочетаний с повторениями из $n$ по $k$?
- Предложите альтернативное доказательство формулы включения-исключения: посчитайте для каждого элемента, сколько раз он будет посчитан в правой части формулы и используйте формулу $sum_{k=0}^n (-1)^kC_n^k = 0$.
- Предложите алгоритм получения по перестановке ее таблицы инверсий за $O(n log n)$.
- Предложите алгоритм получения перестановки по ее таблице инверсий за $O(n log n)$.
- Максимумом в перестановке называется элемент, который больше своих соседей (одного, если он первый или последний, обоих иначе). Выведите рекуррентную формулу для числа перестановок $n$ элементами с $k$ максимумами
- Подъемом в перестановке называется пара соседних элементов, таких что $a_{i-1} < a_i$. Выведите рекуррентную формулу для числа перестановок $n$ элементов с $k$ подъемами
- Неподвижной точкой в перестановке называется элемент $a_i = i$. Выведите рекуррентную формулу для числа перестановок $n$ элементов с $k$ неподвижными точками
- Докажите, что числа Стирлинга 1 рода образуют матрицу переходов в линейном пространстве полиномов базиса возрастающих факториальных степеней к базису обычных степеней
- Докажите, что числа Стирлинга 2 рода образуют матрицу переходов в линейном пространстве полиномов от базиса обычных степеней к базису убывающих факториальных степеней
- Укажите способ подсчитать число разбиений заданного $n$-элементного множества на $k$ упорядоченных непустых подмножеств
- Докажите, что $n$-е число Каталана равно ${2n choose n}/(n+1)$
- Двоичное дерево — это подвешенное дерево, где каждая вершина может иметь двух детей: левого и правого. Каждый из них также является двоичным деревом (либо отсутствует). Докажите, что число двоичных деревьев с $n$ вершинами равно $n$-му числу Каталана.
- Подвешенное дерево с порядком на детях — это подвешенное дерево, где каждая вершина может иметь произвольное число детей, причем дети упорядочены. Каждый ребенок в свою очередь является подвешенным деревом. Докажите, что число подвешенных деревьев порядком на детях с $n$ вершинами равно $n-1$-му числу Каталана.
- Докажите, что число триангуляций правильного $n$-угольника равно $n-2$-му числу Каталана.
- Установите явное взаимно-однозначное соответствие между объектами из предыдущих трех заданий и правильными скобочными последовательностями.
- Укажите способ подсчитать число разбиений числа на слагаемые за $O(n sqrt{n})$
- Решите с помощью ДП задачу о наибольшей общей подстроке за $O(n^2)$
- Решите с помощью ДП задачу о наибольшей общей возрастающей подпоследовательности за $O(n^3)$
- Решите с помощью ДП задачу о наибольшей общей возрастающей подпоследовательности за $O(n^2)$
- Докажите, что минимальное число невозрастающих подпоследовательностей, на которые можно разбить заданную последовательность, равно длине ее наибольшей возрастающей подпоследовательности
- Решите задачу о наибольшей возрастающей подпоследовательности за $O(n log n)$ без дерева отрезков
- Решите с помощью ДП задачу о наибольшей пилообразной подпоследовательности (последовательность называется пилообразной, если никакие ее три подряд идущих элемента не образуют ни возрастающую, ни убывающую последовательность)
- Докажите, что произведение длины наибольшей возрастающей подпоследовательности и наибольшей убывающей подпоследовательности перестановки не меньше $n$
- Будем говорить, что строки a и b образуют пару подстрок строки c, если c можно представить как xaybz, где x, y и z — произвольные строки. Решите с помощью ДП задачу о наибольшей общей паре подстрок.
- Задача о редакционном расстоянии: найдите последовательность действий для превращения строки $s$ в строку $t$ с помощью операций вставки, удаления и замены символа. Длины строк $m$ и $n$, соответственно. Требуется решить задачу за $O(mn)$ с памятью $O(m + n)$.
- Решите задачу о редакционном расстоянии, если помимо операций вставки, удаления и замены символа можно использовать операцию обмена местами двух соседних символов. Стоимость всех операций одинаковая.
- Решите битоническую задачу о комивояжере: найдите во взвешенном графе гамильтонов цикл минимального веса, который удовлетворяет дополнительно следующему свойству: сначала номера посещенных вершин возрастают, а затем убывают. Время $O(n^2)$.
- Задача о рюкзаке: дано $n$ предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$. Решите задачу за время $O(nc)$ с памятью $O(c)$.
- Задача о рюкзаке без ограничения на число одинаковых предметов: дано $n$ типов предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$. Каждого предмета можно брать несколько (любое количество) экземпляров. Решите задачу за время $O(nc)$ с памятью $O(c)$.
- Непрерывная задача о рюкзаке: дано $n$ жидкостей, у каждой жидкости есть доступное количество $w_i$ и стоимость единицы жидкости $v_i$, размер рюкзака $c$, требуется выбрать для каждой жидкости число $0 le x_i le w_i$, чтобы суммарной стоимости выбранных жидкостей $sum x_iv_i$ была максимальна и суммарное объем взятых жидкостей $sum x_i$ был не более $c$.
- Задача о рюкзаке, большой рюкзак: дано $n$ типов предметов, у предмета $i$-го типа есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, предметов каждого типа можно взять любое количество, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$. Докажите, что если максимальный вес предмета $z$, то следует взять предметов с максимальным отношением $c_i/w_i$ с суммарным весом хотя бы $c — z^2$.
- Решите задачу о рюкзаке: дано $n$ предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$, время $O(2^{n/2} cdot poly(n))$, память $O(2^{n/2})$
- Решите с помощью ДП задачу о наибольшей подпоследовательности-палиндроме
- Рассмотрим задачу: расставить знаки +, * и скобки в выражении таким образом, чтобы его значение было минимальным по модулю. Приведите контрпример к решению на базе ДП, в котором для каждого подотрезка хранится минимальное и максимальное положительное и отрицательное значение, достижимое на этом отрезке?
- Решите с помощью ДП задачу о наибольшей общей подпоследовательности-палиндроме
- Решите задачу о рюкзаке: дано $n$ предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$, время $O(2^{n/2} cdot poly(n))$, память $O(2^{n/2})$
- Решите задачу: найти в дереве минимальное множество вершин, чтобы расстояние от любой вершины до одной из выбранных было не более $d$
- Выведите рекуррентную формулу для числа разбиений числа $n$ на нечетные слагаемые
- Выведите рекуррентную формулу для числа разбиений числа $n$ на нечетное число слагаемых
- Выведите рекуррентную формулу для числа разбиений числа $n$ на различные слагаемые
- Решите задачу о гамильтоновом пути в графе за $O(2^nn)$ (считайте, что $n$ не превышает размер слова в архитектуре компьютера).
- Чему равна вероятность, что две случайно вытянутые кости домино можно приложить друг к другу по правилам домино?
- Чему равна вероятность, что на двух брошенных честных игральных костях выпадут числа, одно из которых делит другое?
- Чему равна вероятность, что если вытянуть из колоды две случайные карты, одной из них можно побить другую (одна из мастей назначена козырем, картой можно побить другую, если они одинаковой масти или если одна из них козырь)?
- Чему равна вероятность, что на двадцати брошенных честных монетах выпадет поровну нулей и единиц?
- Приведите пример событий, независимых попарно, но зависимых в совокупности
- Приведите пример трех событий, для которых $P(A cap B cap C) = P(A)P(B)P(C)$, но которые не являются независимыми, причем вероятности всех трех событий больше 0
- Доказать или опровергнуть, что для независимых событий $A$ и $B$ и события $C$, где $P(C) > 0$ выполнено $P(A cap B|C) = P(A|C)P(B|C)$
- Доказать или опровергнуть, что для независимых событий $A$ и $B$ и события $C$, где $P(A) > 0$, $P(B) > 0$ выполнено $P(C|A cap B) = P(C|A)P(C|B)$
- Рассмотрим множество костей домино (неупорядоченные пары $(i, j)$, где $i$ и $j$ от 0 до 6, всего костей 28). Можно ли вероятностное пространство костей домино естественным образом представить как прямое произведение вероятностных пространств?
- Доказать или опровергнуть: если $P(A|B) = P(B|A)$, то $P(A) = P(B)$
- Доказать или опровергнуть: если $P(A|B) = P(B|A)$, то $A$ и $B$ независимы
- Доказать или опровергнуть: если $P(A|C) = P(B|C)$, то $P(C|A) = P(C|B)$
- Доказать или опровергнуть: если $A$ и $B$ независимы, то $Omega setminus A$ и $Omega setminus B$ независимы
- Можно ли ввести равномерное распределение на натуральных числах?
- Приведите пример бесконечного вероятностного простанства
- Можно ли конструкцию с произведением вероятностных пространств распространить на бесконечное множество пространств?
- Докажите, что если $f$ и $g$ независимы, то для любых $a$ и $b$ события $[f = a]$ и $[g = b]$ независимы
- Докажите, что для независимых случайных величин $Exieta =Exi Eeta$.
- Докажите, что математическое ожидание равно $Exi = sumlimits_{ainmathbb{R}}aP(xi=a)$. Здесь сумма берется по не более чем счетному числу возможных значений случайной величины.
- Дисперсией случайной величины называется $Dxi=E(xi-Exi)^2$. Докажите, что дисперсия равна $Dxi=Exi^2-(Exi)^2$
- Докажите, что дисперсия суммы независимых случайных величин равна сумме их дисперсий.
- Найдите математическое ожидание и дисперсию значения на нечестной монете
- Найдите математическое ожидание и дисперсию значения на честной игральной кости
- Найдите распределение, математическое ожидание и дисперсию следующей случайной величины: число бросков честной монеты до первого выпадения 1.
- Ковариацией случайных величин $xi$ и $eta$ называют величину $Cov(xi, eta)=E((xi-Exi)(eta-Eeta))$. Чему равна ковариация независимых случайных величин?
- Корреляцией случайных величин $xi$ и $eta$ называют величину $corr(xi, eta) = Cov(xi, eta) / sqrt{Dxi Deta}$. Докажите, что корреляция случайных величин лежит в диапазоне от -1 до 1
- Докажите или опровергните, что корреляция случайных величин равна 0 тогда и только тогда, когда они независимы
- Докажите, что корреляция случайных величин равна 1 тогда и только тогда, когда они линейно зависимы $(f = cg)$ и $c > 0$ (если $c < 0$, то корелляция равно -1)
- Случайные величины f, g и h называются независимыми в совокупности, если для любых a, b и c события [f <= a], [g <= b] и [h <= c] независимы. Приведите пример независимых попарно, но не независимых в совокупности случайных величин
- Найдите математическое ожидание числа инверсий в перестановке чисел от 1 до $n$
- Найдите математическое ожидание числа подъемов в перестановке чисел от 1 до $n$
- Предложите метод генерации случайной перестановки порядка $n$ с равновероятным распределением всех перестановок, если мы умеем генерировать равномерно распределенное целое число от 1 до $k$ для любых небольших $k$ ($k = O(n)$).
- Дает ли следующий метод равномерную генерацию всех перестановок? «p = [1, 2, …, n]; for i from 1 to n: swap(p[i], p[random(1..n)] )»
- Дает ли следующий метод равномерную генерацию всех перестановок? «p = [1, 2, …, n]; for i from 1 to n: swap(p[random(1..n)], p[random(1..n)] )»
- Предложите метод генерации случайного сочетания из $n$ по $k$ с равновероятным распределением всех сочетаний, если мы умеем генерировать равномерно распределенное целое число от 1 до $t$ для любых небольших $t$ ($t = O(n)$)
- Докажите, что для монеты энтропия максимальна в случае честной монеты
- Докажите, что для n исходов энтропия максимальна если они все равновероятны
- Зафиксируйте ваш любимый язык программирования. Колмогоровской сложностью $K(x)$ для слова $x$ называется длина минимальной программы, которая выводит слово $x$. Докажите, что колмогоровская сложность не превышает $n H(x) + O(log n)$, где $n$ — длина строки $x$, $H(x)$ — энтропия случайного источника с распределением соответствующим частотам встречания символов в $x$, константа в $O$, не зависит от слова $x$ (но может зависеть от выбранного языка программирования)
- Докажите, что для любого $c > 0$ найдется слово, для которого $K(x) < c H(x)$
- Пусть заданы полные системы событий $A = {a_1, …, a_n}$ и $B = {b_1, …, b_m}$. Определим условную энтропию $H(A | B)$ как $-sumlimits_{i = 1}^m P(b_i) sumlimits_{j = 1}^n P(a_j | b_i) log P(a_j | b_i))$. Докажите, что $H(A | B) + H(B) = H(B | A) + H(A)$
- Что можно сказать про $H(A | B)$ если $a_i$ и $b_j$ независимы для любых $i$ и $j$?
- Что можно сказать про $H(A | A)$?
- Постройте схему получения вероятности 1/3 с помощью честной монеты, имеющую минимальное математическое ожидание числа бросков. Докажите оптимальность вашей схемы.
- Докажите, что математическое ожидание числа экспериментов при симуляции одного распределения другим асимптотически равно отношению энтропий распределений (считайте, что энтропия симулируемого распределения больше).
- Пусть $f$ и $g$ — непрерывные возрастающие функции, причем $limlimits_{xto-infty}f(x)=0$, $limlimits_{xto-infty}g(x)=0$, $limlimits_{xto+infty}f(x)=1$, $limlimits_{xto+infty}g(x)=1$, кроме того считайте, что вы можете вычислять $f(x)$, $g(x)$, $f^{-1}(x)$ и $g^{-1}(x)$. У вас есть случайная величина с функцией распределения $f(x)$. Как вам получить случайную величину с функцией распределения $g(x)$?
</wikitex>
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
дискретная-математика — Дискретная математика
|
Задача А |
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
В
качестве примера (n,k)-кода,
при задании которого используется
матричное представление, рассмотрим
код Хэмминга – код с кодовым расстоянием
d=3,
позволяющий исправлять все одиночные
ошибки. Для кода Хэмминга число разрешённых
кодовых комбинаций равно верхней границе
– 2n/(n+ 1).
Первые k разрядов
кодовых комбинация используются в
качестве информационных, их число равно:
|
|
Данное уравнение имеет
целочисленные решения k=0,1,4,11,26,…,
которые и определяют соответствующие
коды Хэмминга: (3, 1), (7, 4), (15,11) и т.д.
Рассмотрим построение (7, 4)-кода. Для
этого воспользуемся каноническим
представлением порождающей матрицы.
Одним из свойств порождающей матрицы
является то, что для различных кодовых
комбинаций, составленных из информационных
разрядов, должны быть различными и
проверочные разряды. Так как все
вектор-строки единичной подматрицы
матрицы Gn,k
различны, то и подматрица проверочных
разрядов должна состоять из различных
ненулевых строк (общее число ненулевых
строк должно быть равно 2r–1).
Вычтем
из возможного числа ненулевых строк r
строк, образующих единичную матрицу ![]() ,
,
которую следует добавить к транспонированной
подматрице проверочных разрядов при
определении проверочной матрицы. Тогда
останется 2r–1–r
r-разрядных строк с
числом единиц не меньше двух. Для кода
Хэмминга это число как раз равно числу
информационных разрядов. Для (n,
k)-кода число различных
r-разрядных строк с
числом единиц не меньше двух равно числу
строк в порождающей матрице. Это свойство
позволяет составить непосредственно
один из вариантов порождающей матрицы
(7, 4)-кода, например, такой:
|
|
Учитывая связь элементов порождающей
и проверочной матриц, представленных
в канонической форме, имеем:
|
|
Проверим способность
разработанного (7, 4) кода исправлять
одиночные ошибки. Пусть передаваемая
кодовая комбинация v
(7,4)-кода образована
путём сложения первой, второй и четвёртой
строк матрицы G7,4,
тогда v=1101001.
Предположим,
что при передаче по каналу произошла
ошибка в третьем разряде кодовой
комбинации v. В этом
случае на приёмной стороне канала будет
получена кодовая комбинация v‘=1111001.
Умножим принятую кодовую комбинацию
на транспонированную проверочную
матрицу H7,4:
|
|
Отличие от нуля синдрома
говорит о том, что произошла ошибка.
Чтобы определить, в каком разряде кодовой
комбинации произошла ошибка, проверим,
с какой строкой матрицы транспонированной
матрицы H7,4
совпадает синдром. Как видно, он совпадает
с третьей строкой. Следовательно, ошибка
произошла в третьем разряде кодовой
комбинации. В декодирующих устройствах
систем передачи информации результат
перемножения принятой кодовой комбинации
на проверочную матрицу (синдром ошибки)
используется для автоматического
исправления соответствующего разряда.
13.5 Циклические коды
Циклическим
кодом называется линейный код, который
представляет собой конечное множество,
замкнутое относительно операции
циклического сдвига кодовых векторов,
образующих его. Пусть дан n-мерный
вектор v=a0a1…an-1
с координатами из конечного поля F.
Его циклическим сдвигом называется
вектор v‘=an-1a0a1…an-2.
Рассмотрим
n-мерное арифметическое
пространство над полем Галуа GF(2).
Каждому вектору a0a1…an-1
из GF(2) можно сопоставить
взаимно однозначно многочлен
a0+a1x+…+an-1xn-1
с коэффициентами из GF(2).
Сумме двух векторов a0a1…an-1
и b0b1…bn-1
ставится в соответствие сумма
соответствующих им многочленов,
произведению элементов поля на вектор
— произведение многочлена, соответствующего
этому вектору, на элемент.
Рассмотрим
некоторый многочлен g(x)
из описанного линейного пространства.
Множество всех многочленов из этого
подпространства, которые делятся без
остатка на g(x),
образует линейное подпространство.
Линейное подпространство определяет
некоторый линейный код.
Линейный
код, образованный классом многочленов
C(g(x)),
кратных некоторому полиному g(x),
называемому порождающим многочленом,
называется полиномиальным.
Покажем,
как связаны полиномиальные коды C(g(x))
и циклические коды. Пусть a=a0…an-1
– некоторое кодовое слово, а соответствующий
кодовый многочлен a(x)=a0+…+an-1xn-1.
Циклическому сдвигу a‘
соответствует кодовый многочлен
a‘(x)=an-1+a0x+…+an-2xn-1,
который можно выразить через первоначальный:
|
|
Поскольку полиномиальный
код должен делиться на g(x),
то для того, чтобы он был циклическим,
многочлен a‘(x)
должен делиться на g(x).
Из этого соображения можно сформулировать
следующую теорему. Полиномиальный код
является циклическим тогда и только
тогда, когда многочлен g(x)
является делителем многочлена xn–1.
В этом случае многочлен g(x)
называется порождающим многочленом
циклического кода.
В
теории кодирования доказывается
следующая теорема: если многочлен g(x)
имеет степень n–k
и является делителем xn–1,
то C(g(x))
является линейным циклическим
(n,k)-кодом.
Многочлен
xn–1 разложим
на множители xn–1 = (x–1)(xn-1+xn-1+…+1).
Следовательно, циклические коды
существуют при любом n.
Число циклических n-разрядных
кодов равно числу делителей многочлена
xn–1. Для
построения циклических кодов разработаны
таблицы разложения многочленов xn–1
на неприводимые многочлены, то есть на
такие, которые делятся только на единицу
и на самого себя.
Рассмотрим,
например, какие коды можно построить
на основе многочлена x7–1
над полем GF(2). Разложение
многочлена на неприводимые множители
имеет вид
|
|
Поскольку можно образовать
шесть делителей многочлена x7–1,
комбинируя неприводимые делители,
существует шесть двоичных циклических
кодов. (n,k)-код
определяется, во-первых, значением n,
а во-вторых, значением k=n–s,
s – степень
многочлена-делителя xn–1,
определяющего код. Ниже приведены
делители полинома и соответствующие
им значения k:
x– 1,s=1,k=6;
x3+x2+1,s=3,k=4;
x3+x+1,s=3,k=4;
(x–1)(x3+x2+1)=x4+x2+x+1,s=4,k=3;
(x–1)(x3+x+1)=x4+x3+x2+1,s=4,k=3;
(x3+x2+1)( x3+x+1)=x6+
x5+ x4+ x3+ x2+
x,s=6,k=1.
(7, 6)-код имеет лишь один проверочный
символ, а (7, 1)-код – лишь один
информационный. Они являются соответственно
кодом с проверкой на чётность и кодом
с повторением.
Как
и обычный линейный код, циклический код
может быть задан порождающей матрицей.
Следовательно, задача состоит в том,
чтобы найти такую матрицу, то есть найти
k линейно независимых
кодовых комбинаций, образующих её.
Воспользуемся для этого свойством
замкнутости циклического кода относительно
операции циклического сдвига. Заметим,
что циклический сдвиг вправо на один
разряд эквивалентен умножению многочлена
g(x)
на x. Тогда порождающую
матрицу можно построить, взяв в качестве
строк порождающий многочлен и k
его циклических сдвигов:
|
|
Например, рассмотрим один из
делителей многочлена x7–1,
а именно полином g(x)=1+x+x3.
Ему соответствует кодовая комбинация
1101000 (выписаны коэффициенты при степенях
0, 1, …, 6 порождающего многочлена, так
как кодовая комбинация содержит 7
символов). Тогда порождающая матрица
(7,4) имеет вид
|
|
Рассмотрим теперь, как с
помощью порождающего многочлена
g(x)=1+x+x3
осуществляется кодирование (7, 4)-кодом.
Возьмём, например, 4-разрядное слово
(0101), которому соответствует многочлен
f(x)=x+x3.
Перемножив эти два многочлена:
f(x)g(x) = (x+x3)(1+x+x3) =x+x2+x3+x6,
получим кодовую комбинацию 0111001.
Аналогично можно получить кодовые слова
для всех 4-разрядных двоичных слов.
Однако получившийся код, как видно, не
является разделимым, что неудобно для
практических нужд.
Чтобы
закодировать сообщение h(x)
циклическим кодом C(g(x)),
который является разделимым, нужно
разделить многочлен xn—kh(x)
на g(x)
и прибавит остаток от деления к многочлену
xn—kh(x).
Для
примера рассмотрим кодовую комбинацию
1101. Этому вектору соответствует полином
h(x)=1+x+x3.
Тогда xn—k h(x)=x3+x4+x6.
Разделим получившийся многочлен на
g(x)=1+x+x3,
получим остаток, равный 0. Тогда кодовый
вектор равен 0001101.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
Помехоустойчивое кодирование. Часть 1: код Хэмминга +33
Программирование
Рекомендация: подборка платных и бесплатных курсов дизайна интерьера — https://katalog-kursov.ru/

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
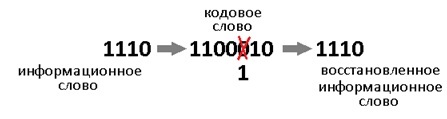
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):

Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:

В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
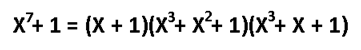
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
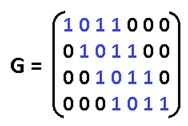
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Подведем итог рассмотренному. Мы рассмотрели двоичный симметричный канал и код, состоящий из 2 кодовых слов длины  , скорость передачи информации которого равна
, скорость передачи информации которого равна  Чтобы получить высокую скорость передачи информации, нам хотелось бы иметь как можно больше кодовых слов. В то же время мы хотели бы исправлять как можно больше ошибок. Однако эти два желания противоречат друг другу, потому что чем больше у нас кодовых слов, тем ближе они будут друг к другу и, согласно лемме 4.1.5, тем меньше будет способность кода исправлять ошибки. Например, если
Чтобы получить высокую скорость передачи информации, нам хотелось бы иметь как можно больше кодовых слов. В то же время мы хотели бы исправлять как можно больше ошибок. Однако эти два желания противоречат друг другу, потому что чем больше у нас кодовых слов, тем ближе они будут друг к другу и, согласно лемме 4.1.5, тем меньше будет способность кода исправлять ошибки. Например, если  и мы хотим исправлять не более одной ошибки, то мы можем найти код с четырьмя кодовыми словами, а именно
и мы хотим исправлять не более одной ошибки, то мы можем найти код с четырьмя кодовыми словами, а именно  . Однако если
. Однако если  и мы хотим исправлять две ошибки, то мы не можем найти больше двух слов, (0,0,0,0,0), (1,1,1,1,1). Теорема 4.1.10 показывает, что требование увеличения способности исправлять ошибки для кода фиксированной длины
и мы хотим исправлять две ошибки, то мы не можем найти больше двух слов, (0,0,0,0,0), (1,1,1,1,1). Теорема 4.1.10 показывает, что требование увеличения способности исправлять ошибки для кода фиксированной длины  приводит к уменьшению максимального возможного числа кодовых слов.
приводит к уменьшению максимального возможного числа кодовых слов.
До сего времени мы полностью игнорировали одну проблему — насколько легко может быть осуществлено декодирование. Декодер в ближайшее кодовое слово, рассматриваемый нами ранее, декодирует полученный вектор v в кодовое слово и, расстояние  до которого минимально. Однако, чтобы сделать это, декодер должен содержать таблицу всех кодовых слов, и когда вектор v поступает на вход, он определяет, к какому кодовому слову и вектор v ближе всего. Однако такой декодер требует огромной памяти, и большое время декодирования сделает декодирование в реальном времени в большинстве случаев неприемлемым.
до которого минимально. Однако, чтобы сделать это, декодер должен содержать таблицу всех кодовых слов, и когда вектор v поступает на вход, он определяет, к какому кодовому слову и вектор v ближе всего. Однако такой декодер требует огромной памяти, и большое время декодирования сделает декодирование в реальном времени в большинстве случаев неприемлемым.
Далее мы развиваем теорию линейных (термин будет определен ниже) двоичных кодов, которые имеют много желательных характеристик в отношении сложности кодирования и декодирования.
Один из простейших примеров линейного двоичного кода  с повторением, т.е.
с повторением, т.е.  . Другими словами, этот код является
. Другими словами, этот код является  -мерным подпространством всех двоичных
-мерным подпространством всех двоичных  -кортежей, которое содержит два кодовых слова:
-кортежей, которое содержит два кодовых слова:  вектор из
вектор из  нулей, и
нулей, и  вектор из
вектор из  единиц. Получив вектор длины
единиц. Получив вектор длины  , пользователь может решить, какое кодовое слово было передано, использовав различные правила; например, если число полученных нулей/единиц больше, чем число полученных единиц/нулей, то пользователь может считать, что передавалось кодовое слово, состоящее из всех нулей/единиц. Эта схема обладает большой способностью обнаружения и исправления ошибок, но скорость передачи информации у нее очень низкая.
, пользователь может решить, какое кодовое слово было передано, использовав различные правила; например, если число полученных нулей/единиц больше, чем число полученных единиц/нулей, то пользователь может считать, что передавалось кодовое слово, состоящее из всех нулей/единиц. Эта схема обладает большой способностью обнаружения и исправления ошибок, но скорость передачи информации у нее очень низкая.
Другая крайность —  —
—  -коды с одной проверкой на четность, которые содержат только один контрольный бит,
-коды с одной проверкой на четность, которые содержат только один контрольный бит,  . То есть эти коды имеют очень высокую скорость передачи информации, но нулевую корректирующую способность; они могут только обнаруживать нечетное число ошибок. (Фактически любое нечетное число ошибок неотличимо от единичной ошибки.) Контрольный бит, который называется также битом четности, определяется как сумма
. То есть эти коды имеют очень высокую скорость передачи информации, но нулевую корректирующую способность; они могут только обнаруживать нечетное число ошибок. (Фактически любое нечетное число ошибок неотличимо от единичной ошибки.) Контрольный бит, который называется также битом четности, определяется как сумма  информационных цифр по модулю 2. В проверке на четность/нечетность последняя цифра выбирается так, чтобы общее число единиц было четно/нечетно. Например, в коде с проверкой на четность кодовое слово для 1101 равно 11011. Отметим, что любое четное число ошибок канала не может быть обнаружено. (Такие коды используются для хранения данных на магнитных лентах.)
информационных цифр по модулю 2. В проверке на четность/нечетность последняя цифра выбирается так, чтобы общее число единиц было четно/нечетно. Например, в коде с проверкой на четность кодовое слово для 1101 равно 11011. Отметим, что любое четное число ошибок канала не может быть обнаружено. (Такие коды используются для хранения данных на магнитных лентах.)
Нас интересуют коды со средней скоростью передачи информации и средними способностями исправления ошибок.
Рассмотрим описанный выше код с одной проверкой на четность. Заметим, что  информационных битов можно выбрать произвольно, в то время как
информационных битов можно выбрать произвольно, в то время как  бит, проверочный разряд, — это линейная комбинация первых
бит, проверочный разряд, — это линейная комбинация первых  битов и добавляется, чтобы помочь нам обнаруживать возможные ошибки передачи. Если обозначить информационные биты через
битов и добавляется, чтобы помочь нам обнаруживать возможные ошибки передачи. Если обозначить информационные биты через  , а проверочные — через
, а проверочные — через  то в коде с единственной проверкой на четность
то в коде с единственной проверкой на четность

Обобщим эту идею следующим образом. Пусть  суть к информационных битов, и предположим, что мы добавили
суть к информационных битов, и предположим, что мы добавили  проверочных битов, чтобы сформировать кодовое слово длины
проверочных битов, чтобы сформировать кодовое слово длины
 . (Это процедура кодирования.) В то время как каждый из к информационных битов формируется независимо от предыдущих,
. (Это процедура кодирования.) В то время как каждый из к информационных битов формируется независимо от предыдущих,  проверочных битов являются линейными комбинациями информационных, т.е.
проверочных битов являются линейными комбинациями информационных, т.е.

или, поскольку сложение в GF(2) совпадает с вычитанием,

Выписанная система уравнений может быть также записала в виде

или

где  — кодовое слово, определенное предыдущей системой уравнений,
— кодовое слово, определенное предыдущей системой уравнений,  — транспонированный вектор. Более точно, вектор v является кодовым словом кода, определенного матрицей Н, тогда и только тогда, когда v удовлетворяет системе
— транспонированный вектор. Более точно, вектор v является кодовым словом кода, определенного матрицей Н, тогда и только тогда, когда v удовлетворяет системе  Выписанные уравнения называются проверочными уравнениями,
Выписанные уравнения называются проверочными уравнениями,  -матрица Н называется проверочной матрицей.
-матрица Н называется проверочной матрицей.
Если  — два кодовых слова, то
— два кодовых слова, то

из чего мы делаем вывод, что  также кодовое слово. Поэтому кодовые слова образуют подпространство векторного пространства
также кодовое слово. Поэтому кодовые слова образуют подпространство векторного пространства  Мы говорим, что код линейный тогда и только тогда, когда кодовые слова образуют подпространство пространства
Мы говорим, что код линейный тогда и только тогда, когда кодовые слова образуют подпространство пространства 
Поскольку кодовые слова образуют подпространство, они могут быть выражены в виде линейных комбинаций к линейно независимых векторов, составляющих базис этого подпространства. Эти к линейно независимых векторов можно рассматривать как строки  матрицы G размера к
матрицы G размера к  , называемой порождающей матрицей рассматриваемого кода. Каждая строка
, называемой порождающей матрицей рассматриваемого кода. Каждая строка  — сама является кодовым словом, а значит,
— сама является кодовым словом, а значит,

откуда мы делаем вывод, что

Пример. Предположим, что для кода  мы имеем следующие проверочные уравнения:
мы имеем следующие проверочные уравнения:

Тогда проверочная матрица Н имеет вид

Порождающая матрица Н этого кода (см. теорему 4.1.11 ниже) — это

Кодовые слова — это  линейных комбинаций строк матрицы
линейных комбинаций строк матрицы 
Очевидно, что векторное пространство, получающееся из строк матрицы, не изменится, если мы выполним любую из следующих элементарных операций со строками:
1. Поменять любые две строки местами.
2. Умножить любую строку на ненулевой элемент.
3. Заменить строку ее суммой с любой другой строкой.
(В двоичном случае вторая операция бессмысленна, потому что единственный ненулевой элемент — это 1.)
Поскольку мы исследуем те свойства линейных кодов, которые связаны со способностью исправлять ошибки, заметим, что два кода, отличающиеся только порядком расположения цифр, имеют одну и ту же вероятность ошибки, и такие коды называются эквивалентными. Более точно, если V — векторное пространство строк матрицы G, то код V эквивалентен V тогда и только тогда, когда V — векторное пространство строк матрицы G, полученной переупорядочением столбцов матрицы G. Таким образом переупорядочение столбцов порождающей матрицы приводит к порождающей матрице эквивалентного кода. Более того, любая из перечисленных выше трех элементарных операций, выполненная над строками матрицы G, приводит к матрице G» с тем же самым векторным пространством, и поэтому G и G» — порождающие одного и того же кода. Объединяя эти два случая, видим, что если матрица G получена из матрицы G последовательностью элементарных операций над строками и переупорядочением столбцов, то  — порождающие матрицы эквивалентных кодов.
— порождающие матрицы эквивалентных кодов.
Обычно мы хотим, чтобы порождающая матрица была представлена в следующем виде:

т.е.  где I — единичная к
где I — единичная к  -матрица,
-матрица,  произвольная к
произвольная к  —
—  -матрица. Пользуясь элементарными операциями над строками, мы всегда можем привести порождающую матрицу к такому виду, и это лучше всего иллюстрируется приводимым ниже примером.
-матрица. Пользуясь элементарными операциями над строками, мы всегда можем привести порождающую матрицу к такому виду, и это лучше всего иллюстрируется приводимым ниже примером.
Пример. Предположим, что мы имеем порождающую матрицу

На каждом шаге мы выполняем операции, необходимые для того, чтобы привести один из столбцов к требуемому виду. Мы начинаем слева направо.
Для первого столбца мы прибавим первую строку ко второй и заменим вторую строку суммой:

Для второго столбца переставим вторую строку с третьей:

и заменим первую строку суммой первой и второй строк:

Для третьего столбца заменим первую и вторую строки их суммами с третьей строкой:

Таким образом мы убеждаемся, что последовательным применением элементарных операций мы всегда можем привести порождающую матрицу G к виду 
Пусть теперь  — вектор размерности
— вектор размерности  , и рассмотрим произведение а на порождающую матрицу
, и рассмотрим произведение а на порождающую матрицу 

где

Заметим, что если мы рассматриваем вектор а как вектор с информационными битами, то в кодовом слове b кода, полученного из G, первые к битов информационные, а остальные  — к компонент — линейные комбинации первых к. Таким образом кодирование чрезвычайно просто: достаточно умножить информационный вектор на порождающую матрицу. Упорядоченный код — это код, состоящий из кодовых слов, в каждом из которых первые к битов — информационные, а остальные — проверочные. Из сказанного выше следует, что любой линейный код эквивалентен упорядоченному. Мы говорим, что линейный код с кодовыми словами длины
— к компонент — линейные комбинации первых к. Таким образом кодирование чрезвычайно просто: достаточно умножить информационный вектор на порождающую матрицу. Упорядоченный код — это код, состоящий из кодовых слов, в каждом из которых первые к битов — информационные, а остальные — проверочные. Из сказанного выше следует, что любой линейный код эквивалентен упорядоченному. Мы говорим, что линейный код с кодовыми словами длины  имеет размерность к тогда и только тогда, когда он имеет к информационных битов, и, как мы уже видели, мы называем такие коды
имеет размерность к тогда и только тогда, когда он имеет к информационных битов, и, как мы уже видели, мы называем такие коды  -кодами.
-кодами.
Подводя итоги сказанному, мы видим, что двоичный линейный код длины  и размерности к — это
и размерности к — это  -мерное подпространство
-мерное подпространство  -мерного векторного пространства над
-мерного векторного пространства над  Таким образом, код полностью определяется порождающей матрицей G, строки которой суть базисные векторы этого подпространства. В качестве альтернативы, линейный код С может быть полностью определен проверочной матрицей Н, которая удовлетворяет уравнению
Таким образом, код полностью определяется порождающей матрицей G, строки которой суть базисные векторы этого подпространства. В качестве альтернативы, линейный код С может быть полностью определен проверочной матрицей Н, которая удовлетворяет уравнению  или
или  для любого кодового слова v. Мы говорим, что векторное пространство, определяющее код, ортогонально векторному пространству, определенному строками матрицы Н. Векторное пространство, определенное строками матрицы Н, можно также рассматривать как определяющее линейный код С: Н теперь — порождающая матрица,
для любого кодового слова v. Мы говорим, что векторное пространство, определяющее код, ортогонально векторному пространству, определенному строками матрицы Н. Векторное пространство, определенное строками матрицы Н, можно также рассматривать как определяющее линейный код С: Н теперь — порождающая матрица,  проверочная. Коды С и С называются дуальными кодами, и если С есть
проверочная. Коды С и С называются дуальными кодами, и если С есть  -код, то С является
-код, то С является 
 -кодом.
-кодом.
Теорема 4.1.11. Если V — код с порождающей матрицей  , где
, где  — единичная к
— единичная к  -матрица,
-матрица,  произвольная к
произвольная к 
 -матрица, то проверочная матрица этого кода равна
-матрица, то проверочная матрица этого кода равна 
Доказательство. Если  — кодовое слово, то
— кодовое слово, то

что в точности совпадает с  (Связь между G и Н станет понятней, если заметить, что в обоих случаях
(Связь между G и Н станет понятней, если заметить, что в обоих случаях  это коэффициент при
это коэффициент при  информационном бите в сумме, определяющей
информационном бите в сумме, определяющей  проверочный бит
проверочный бит 
Пример. Для порождающей матрицы

 находим проверочную матрицу
находим проверочную матрицу

Кодовые слова — это

Теорема 4.1.12. Код с проверочной матрицей Н имеет минимальный вес (а следовательно, кодовое расстояние) w тогда и только тогда, когда любое множество из  или меньшего числа столбцов матрицы Н линейно независимо.
или меньшего числа столбцов матрицы Н линейно независимо.
Локазательство. Мы докажем теорему в одном направлении, а остальную часть оставим читателю. Вектор  является кодовым словом тогда и только тогда, когда
является кодовым словом тогда и только тогда, когда  или, что эквивалентно, тогда и только тогда, когда
или, что эквивалентно, тогда и только тогда, когда

где  есть
есть  столбец матрицы Н. Таким образом, если w — минимальный вес кода, то не существует равной 0 линейной комбинации
столбец матрицы Н. Таким образом, если w — минимальный вес кода, то не существует равной 0 линейной комбинации  или меньшего числа столбцов матрицы Н.
или меньшего числа столбцов матрицы Н. 
Из теоремы 4.1.12 мы видим, что код может иметь кодовое расстояние 3 тогда и только тогда, когда любые  столбца проверочной матрицы Н линейно независимы. Однако два ненулевых вектора в
столбца проверочной матрицы Н линейно независимы. Однако два ненулевых вектора в  над GF(2) линейно независимы, если они просто различны. Поэтому мы можем построить код с кодовым расстоянием 3 (т.е. код может исправлять одну ошибку), если будем рассматривать в качестве проверочной матрицы Н матрицу, столбцы которой составляют все отличные от нуля элементы пространства
над GF(2) линейно независимы, если они просто различны. Поэтому мы можем построить код с кодовым расстоянием 3 (т.е. код может исправлять одну ошибку), если будем рассматривать в качестве проверочной матрицы Н матрицу, столбцы которой составляют все отличные от нуля элементы пространства  Значит, мы можем построить так называемые
Значит, мы можем построить так называемые  -коды Хэмминга, т.е.
-коды Хэмминга, т.е.  .
.
Определение 4.1.13. Пусть Н — проверочная матрица линейного  Если v — полученный вектор, то вектор
Если v — полученный вектор, то вектор  длины
длины  называется синдромом вектора
называется синдромом вектора 
Из этого определения видно, что вектор является кодовым словом тогда и только тогда, когда его синдром равен О. Если учитывать это, то процесс декодирования для кодов Хэмминга очень прост. Если v — полученный, а и — переданный вектор, где  мы действуем следующим образом: сначала вычисляем синдром вектора v, который равен
мы действуем следующим образом: сначала вычисляем синдром вектора v, который равен

Если произошла одна ошибка, то  — вектор с весом 1, т.е.
— вектор с весом 1, т.е.  компонент равны 0 и мы имеем «1» в
компонент равны 0 и мы имеем «1» в  позиции, где встретилась ошибка. Таким образом, произведение
позиции, где встретилась ошибка. Таким образом, произведение  будет
будет  столбцом матрицы Н, и мы получим переданный вектор, если прибавим к v вектор
столбцом матрицы Н, и мы получим переданный вектор, если прибавим к v вектор  , который состоит из нулей, за исключением
, который состоит из нулей, за исключением  позиции, которая равна 1.
позиции, которая равна 1.
Пример. Рассмотрим  -код Хэмминга с проверочной матрицей
-код Хэмминга с проверочной матрицей

и предположим, что получен вектор  что синдром вектора v равен
что синдром вектора v равен

что совпадает с четвертым столбцом матрицы Н; следовательно, вектор ошибок равен  и, добавляя его к v, мы получаем переданный вектор
и, добавляя его к v, мы получаем переданный вектор 
Рассмотрим теперь другую процедуру декодирования линейных кодов, т.е. мы получим другой взгляд на декодирование по максимуму правдоподобия, рассматривая смежные классы кода С в 
Пусть С — линейный ( -код над
-код над  ), где этот код рассматривается как подпространство пространства
), где этот код рассматривается как подпространство пространства  векторного пространства всех двоичных
векторного пространства всех двоичных  -кортежей. Факторпространство
-кортежей. Факторпространство  состоит из всех смежных классов
состоит из всех смежных классов 
для произвольного  , где каждый смежный класс содержит
, где каждый смежный класс содержит  векторов. Имеется разбиение множества
векторов. Имеется разбиение множества  вида
вида

Если получен вектор у, то у должен быть элементом одного из этих смежных классов, скажем  Если передано кодовое слово
Если передано кодовое слово  то вектор ошибок
то вектор ошибок  равене
равене  Следовательно, мы имеем следующее правило декодирования: если получен вектор у, то возможные векторы ошибки
Следовательно, мы имеем следующее правило декодирования: если получен вектор у, то возможные векторы ошибки  — это векторы из смежного класса, содержащего у. Наиболее вероятная ошибка — вектор
— это векторы из смежного класса, содержащего у. Наиболее вероятная ошибка — вектор  с минимальным весом в классе смежности вектора у. Поэтому у декодируется как
с минимальным весом в классе смежности вектора у. Поэтому у декодируется как  . (Вектор наименьшего веса в смежном классе называется лидером смежного класса. Если имеется несколько таких векторов, то произвольный из них выбирается в качестве лидера смежного класса.)
. (Вектор наименьшего веса в смежном классе называется лидером смежного класса. Если имеется несколько таких векторов, то произвольный из них выбирается в качестве лидера смежного класса.)
Чтобы использовать указанную схему декодирования, нам нужны таблицы смежных классов, и ниже мы покажем, как создавать таблицу декодирования Слепиана.
Пусть С — упомянутый выше  -линейиый код, и пусть
-линейиый код, и пусть  — кодовые слова, где
— кодовые слова, где  — нулевой вектор кода. Кодовые слова располагают в первой строке с нулевым вектором слева. Затем выбирают один из оставшихся векторов пространства
— нулевой вектор кода. Кодовые слова располагают в первой строке с нулевым вектором слева. Затем выбирают один из оставшихся векторов пространства  например
например  и помещают его под нулевым вектором. (Обычно
и помещают его под нулевым вектором. (Обычно  выбирается так, что он имеет наибольшую вероятность поступить на приемник, если передан нулевой вектор.) После этого заполняют вторую строку, помещая под каждым кодовым словом
выбирается так, что он имеет наибольшую вероятность поступить на приемник, если передан нулевой вектор.) После этого заполняют вторую строку, помещая под каждым кодовым словом  — вектор
— вектор  . Аналогично, второй вектор
. Аналогично, второй вектор  из
из  который еще не появился в таблице, помещают в первом столбце третьей строки, и строка заполняется тем же способом. Этот процесс продолжается до тех пор, пока все векторы из
который еще не появился в таблице, помещают в первом столбце третьей строки, и строка заполняется тем же способом. Этот процесс продолжается до тех пор, пока все векторы из  не появятся в таблице. Множество элементов строки образует смежный класс, и, если на каждом шаге вектор g выбирался как вектор наименьшего веса, не представленный в первых i столбцах, то элементы первого столбца гарантированно будут лидерами смежных классов (проверьте это на следующем ниже примере).
не появятся в таблице. Множество элементов строки образует смежный класс, и, если на каждом шаге вектор g выбирался как вектор наименьшего веса, не представленный в первых i столбцах, то элементы первого столбца гарантированно будут лидерами смежных классов (проверьте это на следующем ниже примере).
Два элемента  которые принадлежат одному и тому же смежному классу к, обладают следующим свойством:
которые принадлежат одному и тому же смежному классу к, обладают следующим свойством:  т.е. их сумма равна кодовому слову. Кроме того, каждый вектор из пространства
т.е. их сумма равна кодовому слову. Кроме того, каждый вектор из пространства  появляется в таблице ровно один раз. (В этом легко убедиться,
появляется в таблице ровно один раз. (В этом легко убедиться,
если предположить, что два вектора  совпадают, где
совпадают, где  смежных классов. Равенство
смежных классов. Равенство  имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда  где
где  кодовое слово; но тогда
кодовое слово; но тогда  принадлежит смежному классу, который имеет
принадлежит смежному классу, который имеет  в качестве лидера, а это противоречит методу построения таблицы, согласно которому первый элемент в каждой строке — это не появлявшийся ранее вектор.)
в качестве лидера, а это противоречит методу построения таблицы, согласно которому первый элемент в каждой строке — это не появлявшийся ранее вектор.)
Пример. Рассмотрим ( -линейный код, проверочные биты которого определяются уравнениями
-линейный код, проверочные биты которого определяются уравнениями

Тогда таблица Слепиана этого кода имеет вид

Отметим, что имеется  смежных класса, каждый из которых содержит
смежных класса, каждый из которых содержит  элементов. Следующие две теоремы показывают, как описанная выше таблица Слепиана мажет использоваться для декодирования линейных кодов.
элементов. Следующие две теоремы показывают, как описанная выше таблица Слепиана мажет использоваться для декодирования линейных кодов.
Теорема 4.1.14. Если мы пользуемся таблицей Слепиана для декодирования полученного вектора в кодовое слово, расположенное над ним, то полученный вектор v правильно декодируется в переданный вектор и тогда и только тогда, когда вектор ошибки  лидер смежного класса.
лидер смежного класса.
Доказательство. Если  лидер
лидер  смежного класса, то
смежного класса, то  — появляется в
— появляется в  смежном классе таблицы Слепиана под кодовым словом и и будет правильно декодирован. Однако если
смежном классе таблицы Слепиана под кодовым словом и и будет правильно декодирован. Однако если  не является лидером смежного класса, то полученный вектор v появится в некотором смежном классе, скажем
не является лидером смежного класса, то полученный вектор v появится в некотором смежном классе, скажем  с лидером
с лидером  Тогда v принадлежит
Тогда v принадлежит  строке таблицы, но не находится под и, потому что
строке таблицы, но не находится под и, потому что 
Теорема 4.1.15. Два вектора  принадлежат одному и тому же смежному классу тогда и только тогда, когда их синдромы равны.
принадлежат одному и тому же смежному классу тогда и только тогда, когда их синдромы равны.
Локазательство. Если и  принадлежат
принадлежат  смежному классу, то
смежному классу, то  . Значит,
. Значит,  откуда следует, что
откуда следует, что  .
.
Обратно, если  , то
, то  , откуда следует, что
, откуда следует, что  и если
и если  , то
, то  , откуда следует, что
, откуда следует, что  принадлежат одному и тому же смежному классу.
принадлежат одному и тому же смежному классу. 
Теперь мы в состоянии представить упрощенную процедуру декодирования, которая работает следующим образом. Сформируем таблицу декодирования, которая состоит из двух столбцов, первый составлен из  синдромов, а второй — из соответствующих лидеров смежных классов. Когда получен вектор v, то мы сначала вычисляем его синдром, а затем находим из таблицы соответствующий лидер смежного класса. Мы полагаем, что лидер смежного класса — это вектор ошибки, и, прибавляя его к вектору v, получаем переданный вектор и.
синдромов, а второй — из соответствующих лидеров смежных классов. Когда получен вектор v, то мы сначала вычисляем его синдром, а затем находим из таблицы соответствующий лидер смежного класса. Мы полагаем, что лидер смежного класса — это вектор ошибки, и, прибавляя его к вектору v, получаем переданный вектор и.
Пример. Для линейного  -кода, описанного в предыдущем примере, мы имеем следующую таблицу декодирования:
-кода, описанного в предыдущем примере, мы имеем следующую таблицу декодирования:

Мы видим, что декодирующей таблице для 
 -кода требуется список синдромов и лидеров смежных классов, соответствующих
-кода требуется список синдромов и лидеров смежных классов, соответствующих  смежным классам. Это может оказаться как дороже, так и дешевле, чем сравнивать полученный вектор со всеми возможными
смежным классам. Это может оказаться как дороже, так и дешевле, чем сравнивать полученный вектор со всеми возможными  кодовыми словами и выбирать ближайший. В
кодовыми словами и выбирать ближайший. В  -коде, например, имеется только
-коде, например, имеется только  смежных классов в противовес 280 кодовым словам, хотя
смежных классов в противовес 280 кодовым словам, хотя  — очень большое число.
— очень большое число.
Теорема 4.1.16. Пусть С есть  -линейный код, кодовые слова которого имеют одинаковую вероятность передачи. Тогда использование построенной выше таблицы Слепиана (т.е. лидеров смежных классов, имеющих наименьший вес в смежном классе) максимизирует вероятность правильного декодирования.
-линейный код, кодовые слова которого имеют одинаковую вероятность передачи. Тогда использование построенной выше таблицы Слепиана (т.е. лидеров смежных классов, имеющих наименьший вес в смежном классе) максимизирует вероятность правильного декодирования.
Доказательство Пусть  вектор в
вектор в  строке и
строке и  столбца таблицы Слепиана. Кодовые слова
столбца таблицы Слепиана. Кодовые слова  находятся в 0-й строк и наверху каждого столбца. Пусть
находятся в 0-й строк и наверху каждого столбца. Пусть  расстояние Хэмминга между полученным вектором
расстояние Хэмминга между полученным вектором  и кодовым словом
и кодовым словом  в которое декодируется
в которое декодируется  Мы уже видели, что вероятность правильного декодирования максимизируется, когда полученный вектор декодируется в ближайшее кодовое слово.
Мы уже видели, что вероятность правильного декодирования максимизируется, когда полученный вектор декодируется в ближайшее кодовое слово.
Предположим теперь, что вектор v появляется в таблице Слепиана под кодовым словом и, где  и пусть g — лидер смежного класса, содержащего v; более того, предположим, что
и пусть g — лидер смежного класса, содержащего v; более того, предположим, что  — ближайшее к v кодовое слово, причем
— ближайшее к v кодовое слово, причем  Тогда вес вектора
Тогда вес вектора  — и равен
— и равен  в то время как элемент
в то время как элемент  имеет вес
имеет вес  и находятся в том же самом смежном классе. Поскольку по определению g имеет наименьший вес в смежном классе,
и находятся в том же самом смежном классе. Поскольку по определению g имеет наименьший вес в смежном классе,  и, таким образом, v по крайней мере так же близок к и, как И к
и, таким образом, v по крайней мере так же близок к и, как И к 
Материал из Викиконспекты
Перейти к: навигация, поиск
<wikitex>
Дискретная математика, алгоритмы и структуры данных, 1 семестр
- Пусть $R$ и $S$ — рефлексивные отношения на $A$. Будет ли рефлексивным их а) объединение? б) пересечение? В этом и следующих заданиях, если ответ отрицательный, при демонстрации контрпримера удобно использовать представление отношения в виде ориентированного графа.
- Пусть $R$ и $S$ — симметричные отношения на $A$. Будет ли симметричным их а) объединение? б) пересечение?
- Пусть $R$ и $S$ — транзитивные отношения на $A$. Будет ли транзитивным их а) объединение? б) пересечение?
- Пусть $R$ и $S$ — антисимметричные отношения на $A$. Будет ли антисимметричным их а) объединение? б) пересечение?
- Определим $R^{-1}$ следующим образом: если $xRy$, то $yR^{-1}x$. Выполнено ли соотношение $RR^{-1} = I$, где $I$ — отношение равенства? Выполнен ли закон сложения степенией $R^iR^j=R^{i+j}$, если $i$ и $j$ разного знака?
- Пусть $R$ обладает свойством $X$. Будет ли обладать свойством $X$ отношение $R^{-1}$? Следует проанализировать $X$ — рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность
- Пусть $R$ и $S$ — транзитивные отношения на $A$. Будет ли транзитивным их композиция?
- Пусть $R$ и $S$ — антисимметричные отношения на A. Будет ли антисимметричным их композиция?
- Постройте пример рефлексивного, симметричного, но не транзитивного отношения
- Постройте пример рефлексивного, антисимметричного, но не транзитивного отношения
- Пусть $R$ — отношение на $A$. Рассмотрим $Tr(R)$ — пересечение всех транзитивных отношений на $A$, содержащих $R$. Докажите, что $Tr(R) = R^{+}$.
- Пусть $R$ — транзитивное антисимметричное отношение. Предложите способ за полиномиальное время построить минимальное отношение $S$, такое что $S^+ = R$.
- Является ли отношение $R$, такое что $(a, b) R (c, d)$, если $ad = bc$ на ${mathbb Z}^+ times {mathbb N}$ отношением эквивалентности?
- В каком случае транзитивное замыкание отношения будет отношением эквивалентности?
- В каком случае транзитивное замыкание отношения будет отношением частичного порядка?
- Выразите в явном виде «и», «или» и «не» через стрелку Пирса
- Выразите в явном виде «и», «или» и «не» через штрих Шеффера
- Является ли пара ${xto y, neg x}$ базисом?
- Является ли набор ${x to y, langle xyzrangle, neg x}$ базисом?
- Является ли набор ${{mathbf 0}, langle xyz rangle, neg x}$ базисом?
- Можно ли выразить «и» через «или»?
- Выразите медиану 5 через медиану 3
- Выразите медиану $2n+1$ через медиану 3
- Докажите, что любую монотонную самодвойственую функцию можно выразить через медиану
- Докажите, что любую функцию, кроме тождественной единицы, можно записать в СКНФ
- Докажите, что любую функцию от $n$ переменных можно представить с использованием стрелки Пирса формулой, длиной не больше чем $2^ncdot poly(n)$, где $poly(n)$ — полином, общий для всех функций
- Булева функция называется пороговой, если $f(x_1, x_2, ldots, x_n) = 1$ тогда и только тогда, когда $a_1x_1+a_2x_2+ldots+a_nx_n ge b$, где $a_i$ и $b$ — вещественные числа. Докажите, что «и» и «или» — пороговые функции.
- Приведите пример непороговой функции
- Рассмотрим булеву функцию $f$. Обозначим как $N(f)$ число наборов аргументов, на которых $f$ равна 1. Например, $N(vee) = 3$. Обозначим как $Sigma(f)$ сумму всех наборов аргументов, на которых $f$ равна 1 как векторов. Например, $Sigma(vee) = (2, 2)$. Докажите, что если для пороговой функции $f$ и функции $g$ выполнено $N(f) = N(g)$ и $Sigma(f) = Sigma(g)$, то $f = g$
- Сколько существует самодвойственных функций от $n$ переменных?
- Приведите пример функции, которая лежит во всех пяти классах Поста.
- Приведите пример функции, которая лежит во всех пяти классах Поста и существенно зависит хотя бы от трех переменных.
- Говорят, что формула имеет вид 2-КНФ, если она имеет вид $(t_{11}vee t_{12})wedge(t_{21}vee t_{22})wedgeldots$, где $t_{ij}$ представляет собой либо переменную, либо ее отрицание (в каждом дизъюнкте ровно два терма). Предложите полиномиальный алгоритм проверки, что формула, заданная в 2-КНФ имеет набор значений переменных, на которых она имеет значение 1.
- КНФ называется КНФ Хорна, если в каждом дизъюнкте не более одной переменной находится без отрицания. Пример: $xwedge(x vee neg y vee neg z) wedge (neg x vee neg t)$. Предложите полиномиальный алгоритм проверки, что формула, заданная в форме КНФ Хорна имеет набор аргументов, на котором она равна 1.
- Докажите, что если булеву функцию $f$ можно задать в форме Крома (в виде 2-КНФ), то выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = f(z_1, …, z_n) = 1$ $Rightarrow f(langle x_1, y_1, z_1rangle, …, langle x_n, y_n, z_n rangle) = 1$
- Докажите, что если выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = f(z_1, …, z_n) = 1$ $Rightarrow f(langle x_1, y_1, z_1rangle, …, langle x_n, y_n, z_n rangle) = 1$, то булеву функцию $f$ можно задать в форме Крома.
- Докажите, что если булеву функцию $f$ можно задать в форме Хорна, то выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = 1 Rightarrow f(x_1wedge y_1, …, x_n wedge y_n) = 1$
- Докажите, что если выполнено следствие: $f(x_1, …, x_n) = f(y_1, …, y_n) = 1 Rightarrow f(x_1wedge y_1, …, x_n wedge y_n) = 1$, то булеву функцию $f$ можно задать в форме Хорна
- Постройте схему из функциональных элементов для операции медиана трех над базисом ${ vee, wedge, neg}$. Постарайтесь использовать минимальное число элементов.
- Постройте схему из функциональных элементов для операции $x oplus y oplus z$ над базисом ${ vee, wedge, neg}$. Постарайтесь использовать минимальное число элементов.
- Предложите способ построить схему для функции $x_1 oplus … oplus x_n$ над базисом ${ vee, wedge, neg}$ с линейным числом элементов.
- Докажите, что не существует схем константной глубины для функций $x_1 vee … vee x_n$, $x_1 wedge … wedge x_n$.
- Докажите, что не существует схем константной глубины для функций $x_1 oplus … oplus x_n$.
- Докажите, что не существует схемы константной глубины для сложения.
- Постройте схему из функциональных элементов с тремя входами: $x, y, z$ и одним выходом. Значение на выходе равно $x$, если $z=0$ и $y$, если $z=1$. Используйте базис из всех не более чем бинарных функций.
- Мультиплексор — функциональная схема с $n = 2^k + k$ и одним выходом. Обозначим первые $2^k$ входов как $x_0, x_1, ldots, x_{2^k-1}$, а оставшиеся $k$ как $y_0, y_1, ldots, y_{k-1}$. Выход мультиплексора равен $x_i$, где $i$ — число, двоичное представление которого подано на входы $y_0, y_1, ldots, y_{k-1}$. Постройте схему линейного от $n$ размера для мультиплексора.
- Дешифратор — функциональная схема с $k + 1$ входом и $n = 2^k$ выходами. Обозначим первые $k$ входов как $y_0, y_1, ldots, y_{k-1}$, а последний как $z$. Обозначим выходы дешифратора как $x_0, x_1, ldots, x_{2^k-1}$. Значение на выходах дешифратора 0 на всех выходах, кроме $x_i$, где $i$ — число, двоичное представление которого подано на входы $y_0, y_1, ldots, y_{k-1}$, а на выходе $x_i$ равно значению $z$. Постройте схему линейного размера для дешифратора.
- Докажите, что для функции «большинство из $2n+1$» существует схема из функциональных элементов глубины $O(log n)$
- На одном китайском заводе в матричном умножителе случайно использовали элементы «или» вместо «и». Можно ли из получившихся значений получить произведение исходных чисел (доступа к входам нет, есть только доступ к $ntimes 2n$ выходам матричного псевдоумножителя).
- Докажите, что любую булеву функцию от $n$ аргументов можно представить схемой из функциональных элементов, содержащей $O(2^n)$ элементов.
- Докажите, что любую булеву функцию от $n$ аргументов можно представить схемой из функциональных элементов, содержащей $O(2^n/n)$ элементов.
- Контактной схемой называется ориентированный ациклический граф, на каждом ребре которого написана переменная или ее отрицание (ребра в контактных схемах называют контактами, а вершины — полюсами). Зафиксируем некоторые значения переменным. Тогда замкнутыми называются ребра, на которых записана 1, ребра, на которых записан 0, называются разомкнутыми. Зафиксируем две вершины $u$ и $v$. Тогда контактная схема вычисляет некоторую функцию $f$ между вершинами $u$ и $v$, равную 1 на тех наборах переменных, на которых между $u$ и $v$ есть путь по замкнутым ребрам. Постройте контактные схемы для функций «и», «или» и «не».
- Постройте контактную схему для функции «xor».
- Постройте контактную схему для функции медиана трех.
- Докажите, что любую булеву функцию можно представить контактной схемой.
- Постройте контактную схему «xor от $n$ переменных», содержащую $O(n)$ ребер.
- Постройте контактную схему «большинство из $2n+1$ переменных», содержащую $O(n)$ ребер.
- Постройте контактную схему, в которой для каждого из $2^n$ наборов конъюнкций переменных и их отрицаний есть пара вершин, между которыми реализуется эта конъюнкция, используя $O(2^n)$ ребер.
- Докажите, что любую булеву функцию можно представить контактной схемой, содержащей $O(2^n)$ ребер.
- Как выглядит дерево Хаффмана для частот символов $1, 2, …, 2^{n-1}$ (степени двойки) ?
- Как выглядит дерево Хаффмана для частот символов $1, 1, 2, 3, …, F_{n-1}$ (числа Фибоначчи)?
- Докажите, что если размер алфавита — степень двойки и частоты никаких двух символов не отличаются в 2 или более раз, то код Хаффмана не лучше кода постоянной длины
- Модифицируйте алгоритм Хаффмана, чтобы строить $k$-ичные префиксные коды
- Укажите, как построить дерево Хаффмана за линейное время, если символы уже отсортированы по частоте
- Предложите алгоритм построения оптимального кода среди префиксных кодов с длиной кодового слова не более L бит
- Предложите алгоритм построения оптимального кода среди префиксных кодов, для которых коды символов упорядочены лексикографически
- Предложите способ хранения информации об оптимальном префиксном коде для n-символьного алфавита, использующий не более $2n — 1 + n lceillog_2(n)rceil$ бит ($lceil xrceil$ — округление $x$ вверх)
- Можно ли разработать алгоритм, который сжимает любой файл не короче заданной величины $N$ хотя бы на 1 бит?
- Приведите пример однозначно декодируемого кода оптимальной длины, который не является ни префиксным, ни развернутым префиксным
- Для каких префиксных кодов существует строка, для которой он является кодом Хаффмана? Предложите алгоритм построения такой строки.
- Пусть заданы пары $(u_i, v_i)$. Предложите алгоритм проверки, что существует код Хаффмана для некоторой строки, в котором $i$-е кодовое слово содержит $u_i$ нулей и $v_i$ единиц.
- Докажите, что если в коде Хаффмана для некоторой строки $i$-е кодовое слово содержит $u_i$ нулей и $v_i$ единиц, то для многочлена от двух переменных $f(x, y) = sum_{i=1}^n x^{u_i}y^{v_i}$ выполнено $f(x, y) — 1 = (x + y — 1) g(x, y)$ для некоторого многочлена $g(x, y)$.
- Разработайте алгоритм кодирования Move To Front строки длиной $n$ за $O(n log n)$
- Докажите, что при оптимальном кодирование с помощью LZ77 не выгодно делать повтор блока, который можно увеличить вправо
- Верно ли утверждение из предыдущего задания при кодировании с помощью L78?
- Разработайте алгоритм оптимального кодирования текста с помощью LZ77, если на символ уходит $c$ бит, а на блок повтора $d$ бит
- Предложите семейство строк $S_1, S_2, ldots, S_n, ldots$, где $S_i$ имеет длину $i$, таких, что при их кодировании с помощью LZW длина строки увеличивается. Начальный алфавит ${0, 1}$.
- Разработайте алгоритм обратного преобразования Барроуза-Уиллера
- Разработайте алгоритм обратного преобразования Барроуза-Уиллера за $O(n)$
- Докажите, что для любого $c > 1$ существует распределение частот $p_1, p_2, .., p_n$, что арифметическое кодирование в $c$ раз лучше Хаффмана
- При арифметическом кодировании можно учитывать, что с учетом уже потраченных символов соотношения символов становятся другими и отрезок надо делить в другой пропорции. Всегда ли кодирование с таким уточнением лучше классического арифметического кодирования?
- При арифметическом кодировании трудным моментом является деление отрезка в пропорциях, не являющихся степенями двойки. Рассмотрим модификацию арифметического кодирования, когда соотношения между символами приближаются дробями со знаменателями — степенями двойки. Что можно сказать про получившийся алгоритм?
- Разработайте оптимальный код исправляющий одну ошибку при пересылке 2 битов
- Разработайте оптимальный код исправляющий одну ошибку при пересылке 3 битов
- Разработайте код, исправляющий две ошибки, использующий асимптотически не более $2n$ бит для кодирования $2^n$ символьного алфавита (для $n > n_0$)
- Перечисление всех $2^n$ двоичных векторов длины $n$ называется кодом Грея, если в нем не повторяются никакие два вектора и любые два соседних вектора отличаются ровно в одном разряде. Докажите по индукции, что для любого $n$ существует код Грея.
- Докажите, что последовательность $g_i = i oplus lfloor i / 2rfloor$ образует код Грея.
- Построим последовательность $g_i$ следующим образом: пусть $g_0 = 0$ и при переходе от $g_i$ к $g_{i+1}$ будем менять тот же бит, который меняется с 0 на 1 при переходе от $i$ к $i+1$. Докажите, что получившаяся последовательность является кодом Грея.
- Разработайте код Грея для k-ичных векторов
- При каких $a_1, a_2, …, a_n$ существует обход гиперпараллелепипеда $a_1 times a_2 times … times a_n$, который переходит каждый раз в соседнюю ячейку и бывает в каждой ячейке ровно один раз?
- При каких $a_1, a_2, …, a_n$ существует обход гиперпараллелепипеда $a_1 times a_2 times … times a_n$, который переходит каждый раз в соседнюю ячейку и бывает в каждой ячейке ровно один раз, а в конце возвращается в исходную ячейку?
- Код «антигрея» — постройте двоичный код, в котором соседние слова отличаются хотя бы в половине бит
- Троичный код «антигрея» — постройте троичный код, в котором соседние слова отличаются во всех позициях
- При каких $n$ и $k$ существует двоичный $n$-битный код, в котором соседние кодовые слова отличаются ровно в $k$ позициях?
- Докажите, что для достаточно больших $n$ существует код Грея, который отличается от любого, полученного из зеркального перестановкой столбцов, отражением и циклическим сдвигом строк
- Код Грея назвается монотонным, если нет таких слов $g_i$ и $g_j$, что $i < j$, а $g_i$ содержит на 2 или больше единиц больше, чем $g_j$. Докажите, что существует монотонный код Грея
- Докажите, что $sum_{k=0}^n C_n^k = 2^n$
- Докажите, что $sum_{k=0}^n (-1)^kC_n^k = 0$
- Коды Грея для перестановок. Предложите способ перечисления перестановок, в котором соседние перестановки отличаются обменом двух соседних элементов (элементарной транспозицией).
- Коды Грея для сочетаний. Предложите способ перечисления сочетаний, в котором соседние сочетания отличаются заменой одного элемента.
- Рассмотрим коды Грея для перестановок и коды Грея для их таблиц инверсий. Есть ли между ними связь?
- Сочетание с повторениями — это способ выбрать из $n$ элементов $k$, причем один элемент можно выбирать несколько раз. Порядок не важен. Чему равно число сочетаний с повторениями из $n$ по $k$?
- Предложите альтернативное доказательство формулы включения-исключения: посчитайте для каждого элемента, сколько раз он будет посчитан в правой части формулы и используйте формулу $sum_{k=0}^n (-1)^kC_n^k = 0$.
- Предложите алгоритм получения по перестановке ее таблицы инверсий за $O(n log n)$.
- Предложите алгоритм получения перестановки по ее таблице инверсий за $O(n log n)$.
- Максимумом в перестановке называется элемент, который больше своих соседей (одного, если он первый или последний, обоих иначе). Выведите рекуррентную формулу для числа перестановок $n$ элементами с $k$ максимумами
- Подъемом в перестановке называется пара соседних элементов, таких что $a_{i-1} < a_i$. Выведите рекуррентную формулу для числа перестановок $n$ элементов с $k$ подъемами
- Неподвижной точкой в перестановке называется элемент $a_i = i$. Выведите рекуррентную формулу для числа перестановок $n$ элементов с $k$ неподвижными точками
- Докажите, что числа Стирлинга 1 рода образуют матрицу переходов в линейном пространстве полиномов базиса возрастающих факториальных степеней к базису обычных степеней
- Докажите, что числа Стирлинга 2 рода образуют матрицу переходов в линейном пространстве полиномов от базиса обычных степеней к базису убывающих факториальных степеней
- Укажите способ подсчитать число разбиений заданного $n$-элементного множества на $k$ упорядоченных непустых подмножеств
- Докажите, что $n$-е число Каталана равно ${2n choose n}/(n+1)$
- Двоичное дерево — это подвешенное дерево, где каждая вершина может иметь двух детей: левого и правого. Каждый из них также является двоичным деревом (либо отсутствует). Докажите, что число двоичных деревьев с $n$ вершинами равно $n$-му числу Каталана.
- Подвешенное дерево с порядком на детях — это подвешенное дерево, где каждая вершина может иметь произвольное число детей, причем дети упорядочены. Каждый ребенок в свою очередь является подвешенным деревом. Докажите, что число подвешенных деревьев порядком на детях с $n$ вершинами равно $n-1$-му числу Каталана.
- Докажите, что число триангуляций правильного $n$-угольника равно $n-2$-му числу Каталана.
- Установите явное взаимно-однозначное соответствие между объектами из предыдущих трех заданий и правильными скобочными последовательностями.
- Укажите способ подсчитать число разбиений числа на слагаемые за $O(n sqrt{n})$
- Решите с помощью ДП задачу о наибольшей общей подстроке за $O(n^2)$
- Решите с помощью ДП задачу о наибольшей общей возрастающей подпоследовательности за $O(n^3)$
- Решите с помощью ДП задачу о наибольшей общей возрастающей подпоследовательности за $O(n^2)$
- Докажите, что минимальное число невозрастающих подпоследовательностей, на которые можно разбить заданную последовательность, равно длине ее наибольшей возрастающей подпоследовательности
- Решите задачу о наибольшей возрастающей подпоследовательности за $O(n log n)$ без дерева отрезков
- Решите с помощью ДП задачу о наибольшей пилообразной подпоследовательности (последовательность называется пилообразной, если никакие ее три подряд идущих элемента не образуют ни возрастающую, ни убывающую последовательность)
- Докажите, что произведение длины наибольшей возрастающей подпоследовательности и наибольшей убывающей подпоследовательности перестановки не меньше $n$
- Будем говорить, что строки a и b образуют пару подстрок строки c, если c можно представить как xaybz, где x, y и z — произвольные строки. Решите с помощью ДП задачу о наибольшей общей паре подстрок.
- Задача о редакционном расстоянии: найдите последовательность действий для превращения строки $s$ в строку $t$ с помощью операций вставки, удаления и замены символа. Длины строк $m$ и $n$, соответственно. Требуется решить задачу за $O(mn)$ с памятью $O(m + n)$.
- Решите задачу о редакционном расстоянии, если помимо операций вставки, удаления и замены символа можно использовать операцию обмена местами двух соседних символов. Стоимость всех операций одинаковая.
- Решите битоническую задачу о комивояжере: найдите во взвешенном графе гамильтонов цикл минимального веса, который удовлетворяет дополнительно следующему свойству: сначала номера посещенных вершин возрастают, а затем убывают. Время $O(n^2)$.
- Задача о рюкзаке: дано $n$ предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$. Решите задачу за время $O(nc)$ с памятью $O(c)$.
- Задача о рюкзаке без ограничения на число одинаковых предметов: дано $n$ типов предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$. Каждого предмета можно брать несколько (любое количество) экземпляров. Решите задачу за время $O(nc)$ с памятью $O(c)$.
- Непрерывная задача о рюкзаке: дано $n$ жидкостей, у каждой жидкости есть доступное количество $w_i$ и стоимость единицы жидкости $v_i$, размер рюкзака $c$, требуется выбрать для каждой жидкости число $0 le x_i le w_i$, чтобы суммарной стоимости выбранных жидкостей $sum x_iv_i$ была максимальна и суммарное объем взятых жидкостей $sum x_i$ был не более $c$.
- Задача о рюкзаке, большой рюкзак: дано $n$ типов предметов, у предмета $i$-го типа есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, предметов каждого типа можно взять любое количество, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$. Докажите, что если максимальный вес предмета $z$, то следует взять предметов с максимальным отношением $c_i/w_i$ с суммарным весом хотя бы $c — z^2$.
- Решите задачу о рюкзаке: дано $n$ предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$, время $O(2^{n/2} cdot poly(n))$, память $O(2^{n/2})$
- Решите с помощью ДП задачу о наибольшей подпоследовательности-палиндроме
- Рассмотрим задачу: расставить знаки +, * и скобки в выражении таким образом, чтобы его значение было минимальным по модулю. Приведите контрпример к решению на базе ДП, в котором для каждого подотрезка хранится минимальное и максимальное положительное и отрицательное значение, достижимое на этом отрезке?
- Решите с помощью ДП задачу о наибольшей общей подпоследовательности-палиндроме
- Решите задачу о рюкзаке: дано $n$ предметов, у каждого предмета есть вес $w_i$ и стоимость $v_i$, размер рюкзака $c$, требуется выбрать предметы максимальной суммарной стоимости с весом не более $c$, время $O(2^{n/2} cdot poly(n))$, память $O(2^{n/2})$
- Решите задачу: найти в дереве минимальное множество вершин, чтобы расстояние от любой вершины до одной из выбранных было не более $d$
- Выведите рекуррентную формулу для числа разбиений числа $n$ на нечетные слагаемые
- Выведите рекуррентную формулу для числа разбиений числа $n$ на нечетное число слагаемых
- Выведите рекуррентную формулу для числа разбиений числа $n$ на различные слагаемые
- Решите задачу о гамильтоновом пути в графе за $O(2^nn)$ (считайте, что $n$ не превышает размер слова в архитектуре компьютера).
- Чему равна вероятность, что две случайно вытянутые кости домино можно приложить друг к другу по правилам домино?
- Чему равна вероятность, что на двух брошенных честных игральных костях выпадут числа, одно из которых делит другое?
- Чему равна вероятность, что если вытянуть из колоды две случайные карты, одной из них можно побить другую (одна из мастей назначена козырем, картой можно побить другую, если они одинаковой масти или если одна из них козырь)?
- Чему равна вероятность, что на двадцати брошенных честных монетах выпадет поровну нулей и единиц?
- Приведите пример событий, независимых попарно, но зависимых в совокупности
- Приведите пример трех событий, для которых $P(A cap B cap C) = P(A)P(B)P(C)$, но которые не являются независимыми, причем вероятности всех трех событий больше 0
- Доказать или опровергнуть, что для независимых событий $A$ и $B$ и события $C$, где $P(C) > 0$ выполнено $P(A cap B|C) = P(A|C)P(B|C)$
- Доказать или опровергнуть, что для независимых событий $A$ и $B$ и события $C$, где $P(A) > 0$, $P(B) > 0$ выполнено $P(C|A cap B) = P(C|A)P(C|B)$
- Рассмотрим множество костей домино (неупорядоченные пары $(i, j)$, где $i$ и $j$ от 0 до 6, всего костей 28). Можно ли вероятностное пространство костей домино естественным образом представить как прямое произведение вероятностных пространств?
- Доказать или опровергнуть: если $P(A|B) = P(B|A)$, то $P(A) = P(B)$
- Доказать или опровергнуть: если $P(A|B) = P(B|A)$, то $A$ и $B$ независимы
- Доказать или опровергнуть: если $P(A|C) = P(B|C)$, то $P(C|A) = P(C|B)$
- Доказать или опровергнуть: если $A$ и $B$ независимы, то $Omega setminus A$ и $Omega setminus B$ независимы
- Можно ли ввести равномерное распределение на натуральных числах?
- Приведите пример бесконечного вероятностного простанства
- Можно ли конструкцию с произведением вероятностных пространств распространить на бесконечное множество пространств?
- Докажите, что если $f$ и $g$ независимы, то для любых $a$ и $b$ события $[f = a]$ и $[g = b]$ независимы
- Докажите, что для независимых случайных величин $Exieta =Exi Eeta$.
- Докажите, что математическое ожидание равно $Exi = sumlimits_{ainmathbb{R}}aP(xi=a)$. Здесь сумма берется по не более чем счетному числу возможных значений случайной величины.
- Дисперсией случайной величины называется $Dxi=E(xi-Exi)^2$. Докажите, что дисперсия равна $Dxi=Exi^2-(Exi)^2$
- Докажите, что дисперсия суммы независимых случайных величин равна сумме их дисперсий.
- Найдите математическое ожидание и дисперсию значения на нечестной монете
- Найдите математическое ожидание и дисперсию значения на честной игральной кости
- Найдите распределение, математическое ожидание и дисперсию следующей случайной величины: число бросков честной монеты до первого выпадения 1.
- Ковариацией случайных величин $xi$ и $eta$ называют величину $Cov(xi, eta)=E((xi-Exi)(eta-Eeta))$. Чему равна ковариация независимых случайных величин?
- Корреляцией случайных величин $xi$ и $eta$ называют величину $corr(xi, eta) = Cov(xi, eta) / sqrt{Dxi Deta}$. Докажите, что корреляция случайных величин лежит в диапазоне от -1 до 1
- Докажите или опровергните, что корреляция случайных величин равна 0 тогда и только тогда, когда они независимы
- Докажите, что корреляция случайных величин равна 1 тогда и только тогда, когда они линейно зависимы $(f = cg)$ и $c > 0$ (если $c < 0$, то корелляция равно -1)
- Случайные величины f, g и h называются независимыми в совокупности, если для любых a, b и c события [f <= a], [g <= b] и [h <= c] независимы. Приведите пример независимых попарно, но не независимых в совокупности случайных величин
- Найдите математическое ожидание числа инверсий в перестановке чисел от 1 до $n$
- Найдите математическое ожидание числа подъемов в перестановке чисел от 1 до $n$
- Предложите метод генерации случайной перестановки порядка $n$ с равновероятным распределением всех перестановок, если мы умеем генерировать равномерно распределенное целое число от 1 до $k$ для любых небольших $k$ ($k = O(n)$).
- Дает ли следующий метод равномерную генерацию всех перестановок? «p = [1, 2, …, n]; for i from 1 to n: swap(p[i], p[random(1..n)] )»
- Дает ли следующий метод равномерную генерацию всех перестановок? «p = [1, 2, …, n]; for i from 1 to n: swap(p[random(1..n)], p[random(1..n)] )»
- Предложите метод генерации случайного сочетания из $n$ по $k$ с равновероятным распределением всех сочетаний, если мы умеем генерировать равномерно распределенное целое число от 1 до $t$ для любых небольших $t$ ($t = O(n)$)
- Докажите, что для монеты энтропия максимальна в случае честной монеты
- Докажите, что для n исходов энтропия максимальна если они все равновероятны
- Зафиксируйте ваш любимый язык программирования. Колмогоровской сложностью $K(x)$ для слова $x$ называется длина минимальной программы, которая выводит слово $x$. Докажите, что колмогоровская сложность не превышает $n H(x) + O(log n)$, где $n$ — длина строки $x$, $H(x)$ — энтропия случайного источника с распределением соответствующим частотам встречания символов в $x$, константа в $O$, не зависит от слова $x$ (но может зависеть от выбранного языка программирования)
- Докажите, что для любого $c > 0$ найдется слово, для которого $K(x) < c H(x)$
- Пусть заданы полные системы событий $A = {a_1, …, a_n}$ и $B = {b_1, …, b_m}$. Определим условную энтропию $H(A | B)$ как $-sumlimits_{i = 1}^m P(b_i) sumlimits_{j = 1}^n P(a_j | b_i) log P(a_j | b_i))$. Докажите, что $H(A | B) + H(B) = H(B | A) + H(A)$
- Что можно сказать про $H(A | B)$ если $a_i$ и $b_j$ независимы для любых $i$ и $j$?
- Что можно сказать про $H(A | A)$?
- Постройте схему получения вероятности 1/3 с помощью честной монеты, имеющую минимальное математическое ожидание числа бросков. Докажите оптимальность вашей схемы.
- Докажите, что математическое ожидание числа экспериментов при симуляции одного распределения другим асимптотически равно отношению энтропий распределений (считайте, что энтропия симулируемого распределения больше).
- Пусть $f$ и $g$ — непрерывные возрастающие функции, причем $limlimits_{xto-infty}f(x)=0$, $limlimits_{xto-infty}g(x)=0$, $limlimits_{xto+infty}f(x)=1$, $limlimits_{xto+infty}g(x)=1$, кроме того считайте, что вы можете вычислять $f(x)$, $g(x)$, $f^{-1}(x)$ и $g^{-1}(x)$. У вас есть случайная величина с функцией распределения $f(x)$. Как вам получить случайную величину с функцией распределения $g(x)$?
</wikitex>
дискретная-математика — Дискретная математика
|
Задача А |
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Код Хэмминга. Пример работы алгоритма
Время на прочтение
4 мин
Количество просмотров 519K
Вступление.
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.

На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:
 и
и 
После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:
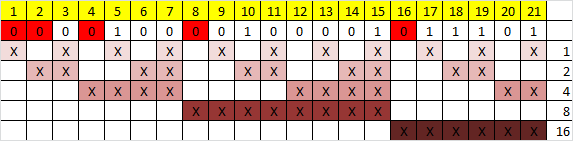
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Источники.
1. Википедия
2. Calculating the Hamming Code
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.









