Регрессия
– способ предсказания значения одних
переменных по значениям других.
Регрессионная
модель –
это уравнение, в котором объясняемая
переменная представляется в виде функций
от объясняющих переменных факторов.
Задача:
на основе эмпирических данных определить
объясняемую часть и получить оценку
распределения случайной части. Суть:
построить регрессию и определить
параметры модели.
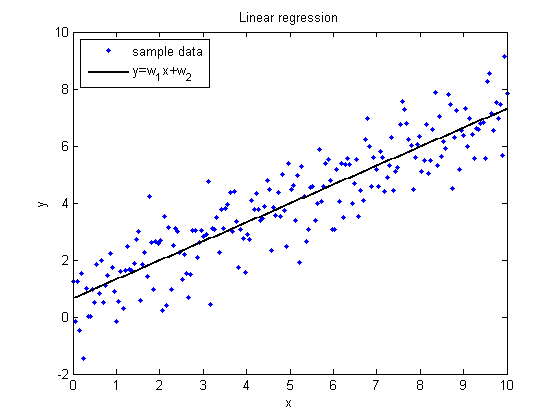
Парная
линейная регрессия —
модель статистической линейной связи
между двумя количественными переменными
х и у, представленная уравнением y = a +
bx, где х — переменная независимая , y —
переменная зависимая – либо в другой
записи Y=B0+B1Xt+Et; Xt-детерминированная
величина, Yt-объясняемая переменная, Et
– случайная величина.
Детерминированной
называется переменная, которая в
результате любого числа испытаний
принимается одно и тоже конкретное
значение из своего множества возможных
значений, например, число этажей в
конкретном доме
Парная регрессия.
(xi,yi);
i=1,…,n
Предполагаем,
что yi представляем в виде
Yi=α+βxi+
εi
Смысл
εi – однозначно для каждого х мы
прогнозировать у не можем
Возникает
вопрос о причинах
обязательного присутствия в регрессионных
моделях случайного фактора (отклонения).
Среди таких причин можно выделить
наиболее
существенные:
не включение в модель всех объясняющих
переменных, неправильный выбор
функциональной формы модели, агрегирование
переменных, ошибки измерений,
ограниченность
статистических данных, непредсказуемость
человеческого фактора.
М(у/Х=хi)=
α+βxi (мат ожидание у при условии, что
Х=хi…)
α
и β – истинные значения коэф регрессии
По
заданным х и у надо найти α и β
Пусть
есть набор значений двух переменных X
и Y:
![]()
,…,![]()
.
Между
ними есть объективная связь Y=f(X). Нужно
по имеющимся данным наблюдений подобрать
функцию
![]()
,
которая наилучшим образом показывает
истинную зависимость.
![]()
,
![]()
-неизвестные.
Е
сли
каждую пару представить точкой, то
картинка будет – диаграмма рассеяния
(корреляционное поле). Требуется найти
значения коэффициентов в этой зависимости.
Зависимость линейная ŷ= a + bx a^=y
– b^x
b^=( xy — xy)
/ (x2
– (x)2)
– в числителе: среднее произведение
минус произведение средних. В знаменателе:
средний квадрат фактора минус квадрат
среднего.
Наблюдаемые
и расчетные значения объясняющей
переменной

e
– остаток
(отклонение, ошибка) – разность между
наблюдаемым и расчетным значением.
Остаток всегда имеет знак. Остатки
наблюдаемы. Надо провести линию регрессии
так, чтобы остатки были меньше. Т.о.
задача линейной регрессии – провести
прямую линию, наилучшим образом
приближающую наблюдаемые точки. Провести
прямую – найти а и b.
Метод наименьших квадратов
Это
метод для оценки неизвестных величин
по результатам измерений, содержащим
случайные ошибки. МНК применяется также
для приближённого представления заданной
функции другими (более простыми)
функциями.
В методе
наименьших квадратов (МНК) по заданным
экспериментальным точкам строится
теоретическая функциональная зависимость.
Для функции одной переменной по n точкам
(xi,yi) ищется «наилучшая» теоретическая
кривая y=f(x).
Суть
– найти такие коэффициенты a и b, кот.
минимизируют сумму квадратов отклонений
расчетных значений объясняемой переменной
от наблюдаемых значений.
Ŷi=a+bxi
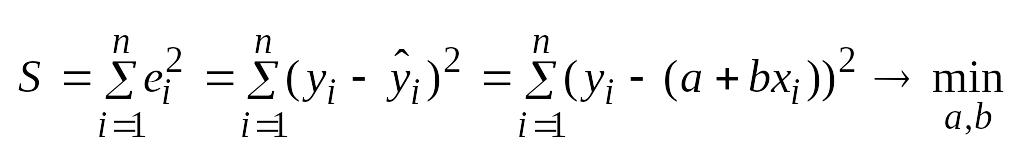
в
точке
![]()
.
ei=y-ŷ
→ ei2
=
(y-ŷ)2
ŷ
= a+bx
Надо
построить необходимое
условие экстремума (частные производные
каждого bj приравниваем к нулю) и решить
полученную нормальную систему уравнений
линейной регрессии.
Необходимое
условие экстремума:
если есть функция нескольких переменных
S(a,b) то, чтобы найти её экстремум нужно
приравнять нулю все её частные производные
и решить полученную систему уравнений:
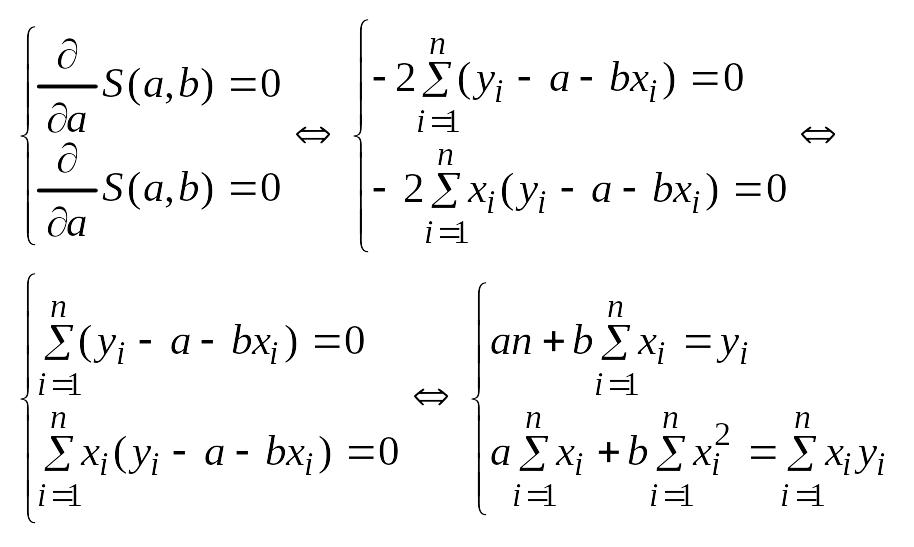
[(yi-(α+βxi)2]’α=
-2(yi-(α+βxi))
[(yi-(α+βxi)2]’β
= -2(yi-(α+βxi))xi
Реш-е
системы это оценка а и b
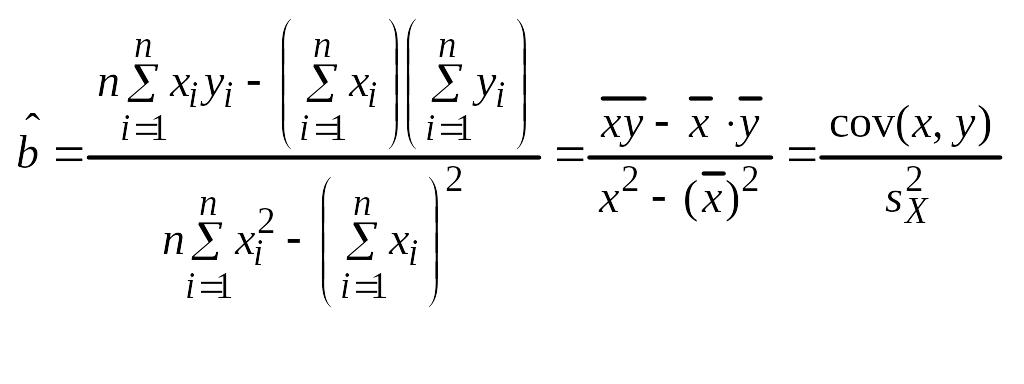
В
X(c чер)
= 1/n Σn
i=1 xi
Y(c чер)
= 1/n Σn
i=1 yi
числителе – выборочная оценка
ковариации; в знаменателе – выборочная
оценка дисперсии фактора.
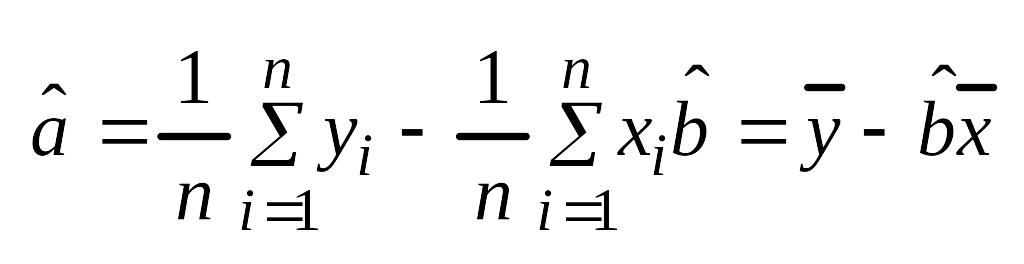
Интерпретация
— С ростом Х на 1, Y изменится на значение
b.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the ‘outcome’ or ‘response’ variable, or a ‘label’ in machine learning parlance) and one or more independent variables (often called ‘predictors’, ‘covariates’, ‘explanatory variables’ or ‘features’). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters (e.g., quantile regression or Necessary Condition Analysis[1]) or estimate the conditional expectation across a broader collection of non-linear models (e.g., nonparametric regression).
Regression analysis is primarily used for two conceptually distinct purposes.
First, regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of machine learning.
Second, in some situations regression analysis can be used to infer causal relationships between the independent and dependent variables. Importantly, regressions by themselves only reveal relationships between a dependent variable and a collection of independent variables in a fixed dataset. To use regressions for prediction or to infer causal relationships, respectively, a researcher must carefully justify why existing relationships have predictive power for a new context or why a relationship between two variables has a causal interpretation. The latter is especially important when researchers hope to estimate causal relationships using observational data.[2][3]
History[edit]
The earliest form of regression was the method of least squares, which was published by Legendre in 1805,[4] and by Gauss in 1809.[5] Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the Sun (mostly comets, but also later the then newly discovered minor planets). Gauss published a further development of the theory of least squares in 1821,[6] including a version of the Gauss–Markov theorem.
The term «regression» was coined by Francis Galton in the 19th century to describe a biological phenomenon. The phenomenon was that the heights of descendants of tall ancestors tend to regress down towards a normal average (a phenomenon also known as regression toward the mean).[7][8]
For Galton, regression had only this biological meaning,[9][10] but his work was later extended by Udny Yule and Karl Pearson to a more general statistical context.[11][12] In the work of Yule and Pearson, the joint distribution of the response and explanatory variables is assumed to be Gaussian. This assumption was weakened by R.A. Fisher in his works of 1922 and 1925.[13][14][15] Fisher assumed that the conditional distribution of the response variable is Gaussian, but the joint distribution need not be. In this respect, Fisher’s assumption is closer to Gauss’s formulation of 1821.
In the 1950s and 1960s, economists used electromechanical desk «calculators» to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the result from one regression.[16]
Regression methods continue to be an area of active research. In recent decades, new methods have been developed for robust regression, regression involving correlated responses such as time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other complex data objects, regression methods accommodating various types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with error, regression with more predictor variables than observations, and causal inference with regression.
Regression model[edit]
In practice, researchers first select a model they would like to estimate and then use their chosen method (e.g., ordinary least squares) to estimate the parameters of that model. Regression models involve the following components:
In various fields of application, different terminologies are used in place of dependent and independent variables.
Most regression models propose that 




The researchers’ goal is to estimate the function 






Once researchers determine their preferred statistical model, different forms of regression analysis provide tools to estimate the parameters 










It is important to note that there must be sufficient data to estimate a regression model. For example, suppose that a researcher has access to 








More generally, to estimate a least squares model with 






Underlying assumptions[edit]
By itself, a regression is simply a calculation using the data. In order to interpret the output of regression as a meaningful statistical quantity that measures real-world relationships, researchers often rely on a number of classical assumptions. These assumptions often include:
A handful of conditions are sufficient for the least-squares estimator to possess desirable properties: in particular, the Gauss–Markov assumptions imply that the parameter estimates will be unbiased, consistent, and efficient in the class of linear unbiased estimators. Practitioners have developed a variety of methods to maintain some or all of these desirable properties in real-world settings, because these classical assumptions are unlikely to hold exactly. For example, modeling errors-in-variables can lead to reasonable estimates independent variables are measured with errors. Heteroscedasticity-consistent standard errors allow the variance of 


Linear regression[edit]
In linear regression, the model specification is that the dependent variable, 




- straight line:
In multiple linear regression, there are several independent variables or functions of independent variables.
Adding a term in 
- parabola:
This is still linear regression; although the expression on the right hand side is quadratic in the independent variable 



In both cases, 

Returning our attention to the straight line case: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:
The residual, 


Minimization of this function results in a set of normal equations, a set of simultaneous linear equations in the parameters, which are solved to yield the parameter estimators, 

Illustration of linear regression on a data set
In the case of simple regression, the formulas for the least squares estimates are
where 



Under the assumption that the population error term has a constant variance, the estimate of that variance is given by:
This is called the mean square error (MSE) of the regression. The denominator is the sample size reduced by the number of model parameters estimated from the same data, 




The standard errors of the parameter estimates are given by
Under the further assumption that the population error term is normally distributed, the researcher can use these estimated standard errors to create confidence intervals and conduct hypothesis tests about the population parameters.
General linear model[edit]
In the more general multiple regression model, there are 
where 


If the first independent variable takes the value 1 for all 


The least squares parameter estimates are obtained from 
The normal equations are
In matrix notation, the normal equations are written as
where the 














Diagnostics[edit]
Once a regression model has been constructed, it may be important to confirm the goodness of fit of the model and the statistical significance of the estimated parameters. Commonly used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-test of the overall fit, followed by t-tests of individual parameters.
Interpretations of these diagnostic tests rest heavily on the model’s assumptions. Although examination of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model’s assumptions are violated. For example, if the error term does not have a normal distribution, in small samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can be invoked such that hypothesis testing may proceed using asymptotic approximations.
Limited dependent variables[edit]
Limited dependent variables, which are response variables that are categorical variables or are variables constrained to fall only in a certain range, often arise in econometrics.
The response variable may be non-continuous («limited» to lie on some subset of the real line). For binary (zero or one) variables, if analysis proceeds with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than two values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest. An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an event, then count models like the Poisson regression or the negative binomial model may be used.
Nonlinear regression[edit]
When the model function is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences between linear and non-linear least squares.
Interpolation and extrapolation[edit]

In the middle, the interpolated straight line represents the best balance between the points above and below this line. The dotted lines represent the two extreme lines. The first curves represent the estimated values. The outer curves represent a prediction for a new measurement.[20]
Regression models predict a value of the Y variable given known values of the X variables. Prediction within the range of values in the dataset used for model-fitting is known informally as interpolation. Prediction outside this range of the data is known as extrapolation. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.
It is generally advised[citation needed] that when performing extrapolation, one should accompany the estimated value of the dependent variable with a prediction interval that represents the uncertainty. Such intervals tend to expand rapidly as the values of the independent variable(s) moved outside the range covered by the observed data.
For such reasons and others, some tend to say that it might be unwise to undertake extrapolation.[21]
However, this does not cover the full set of modeling errors that may be made: in particular, the assumption of a particular form for the relation between Y and X. A properly conducted regression analysis will include an assessment of how well the assumed form is matched by the observed data, but it can only do so within the range of values of the independent variables actually available. This means that any extrapolation is particularly reliant on the assumptions being made about the structural form of the regression relationship. Best-practice advice here[citation needed] is that a linear-in-variables and linear-in-parameters relationship should not be chosen simply for computational convenience, but that all available knowledge should be deployed in constructing a regression model. If this knowledge includes the fact that the dependent variable cannot go outside a certain range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly near such bounds. The implications of this step of choosing an appropriate functional form for the regression can be great when extrapolation is considered. At a minimum, it can ensure that any extrapolation arising from a fitted model is «realistic» (or in accord with what is known).
Power and sample size calculations[edit]
There are no generally agreed methods for relating the number of observations versus the number of independent variables in the model. One method conjectured by Good and Hardin is 





Other methods[edit]
Although the parameters of a regression model are usually estimated using the method of least squares, other methods which have been used include:
- Bayesian methods, e.g. Bayesian linear regression
- Percentage regression, for situations where reducing percentage errors is deemed more appropriate.[23]
- Least absolute deviations, which is more robust in the presence of outliers, leading to quantile regression
- Nonparametric regression, requires a large number of observations and is computationally intensive
- Scenario optimization, leading to interval predictor models
- Distance metric learning, which is learned by the search of a meaningful distance metric in a given input space.[24]
Software[edit]
All major statistical software packages perform least squares regression analysis and inference. Simple linear regression and multiple regression using least squares can be done in some spreadsheet applications and on some calculators. While many statistical software packages can perform various types of nonparametric and robust regression, these methods are less standardized. Different software packages implement different methods, and a method with a given name may be implemented differently in different packages. Specialized regression software has been developed for use in fields such as survey analysis and neuroimaging.
See also[edit]
- Anscombe’s quartet
- Curve fitting
- Estimation theory
- Forecasting
- Fraction of variance unexplained
- Function approximation
- Generalized linear model
- Kriging (a linear least squares estimation algorithm)
- Local regression
- Modifiable areal unit problem
- Multivariate adaptive regression splines
- Multivariate normal distribution
- Pearson correlation coefficient
- Quasi-variance
- Prediction interval
- Regression validation
- Robust regression
- Segmented regression
- Signal processing
- Stepwise regression
- Taxicab geometry
- Trend estimation
References[edit]
- ^ Necessary Condition Analysis
- ^ David A. Freedman (27 April 2009). Statistical Models: Theory and Practice. Cambridge University Press. ISBN 978-1-139-47731-4.
- ^ R. Dennis Cook; Sanford Weisberg Criticism and Influence Analysis in Regression, Sociological Methodology, Vol. 13. (1982), pp. 313–361
- ^ A.M. Legendre. Nouvelles méthodes pour la détermination des orbites des comètes, Firmin Didot, Paris, 1805. “Sur la Méthode des moindres quarrés” appears as an appendix.
- ^ a b Chapter 1 of: Angrist, J. D., & Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press.
- ^ C.F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. (1821/1823)
- ^
Mogull, Robert G. (2004). Second-Semester Applied Statistics. Kendall/Hunt Publishing Company. p. 59. ISBN 978-0-7575-1181-3. - ^ Galton, Francis (1989). «Kinship and Correlation (reprinted 1989)». Statistical Science. 4 (2): 80–86. doi:10.1214/ss/1177012581. JSTOR 2245330.
- ^ Francis Galton. «Typical laws of heredity», Nature 15 (1877), 492–495, 512–514, 532–533. (Galton uses the term «reversion» in this paper, which discusses the size of peas.)
- ^ Francis Galton. Presidential address, Section H, Anthropology. (1885) (Galton uses the term «regression» in this paper, which discusses the height of humans.)
- ^ Yule, G. Udny (1897). «On the Theory of Correlation». Journal of the Royal Statistical Society. 60 (4): 812–54. doi:10.2307/2979746. JSTOR 2979746.
- ^ Pearson, Karl; Yule, G.U.; Blanchard, Norman; Lee, Alice (1903). «The Law of Ancestral Heredity». Biometrika. 2 (2): 211–236. doi:10.1093/biomet/2.2.211. JSTOR 2331683.
- ^ Fisher, R.A. (1922). «The goodness of fit of regression formulae, and the distribution of regression coefficients». Journal of the Royal Statistical Society. 85 (4): 597–612. doi:10.2307/2341124. JSTOR 2341124. PMC 1084801.
- ^ Ronald A. Fisher (1954). Statistical Methods for Research Workers (Twelfth ed.). Edinburgh: Oliver and Boyd. ISBN 978-0-05-002170-5.
- ^ Aldrich, John (2005). «Fisher and Regression». Statistical Science. 20 (4): 401–417. doi:10.1214/088342305000000331. JSTOR 20061201.
- ^ Rodney Ramcharan. Regressions: Why Are Economists Obessessed with Them? March 2006. Accessed 2011-12-03.
- ^ Fotheringham, A. Stewart; Brunsdon, Chris; Charlton, Martin (2002). Geographically weighted regression: the analysis of spatially varying relationships (Reprint ed.). Chichester, England: John Wiley. ISBN 978-0-471-49616-8.
- ^ Fotheringham, AS; Wong, DWS (1 January 1991). «The modifiable areal unit problem in multivariate statistical analysis». Environment and Planning A. 23 (7): 1025–1044. doi:10.1068/a231025. S2CID 153979055.
- ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Rouaud, Mathieu (2013). Probability, Statistics and Estimation (PDF). p. 60.
- ^ Chiang, C.L, (2003) Statistical methods of analysis, World Scientific. ISBN 981-238-310-7 — page 274 section 9.7.4 «interpolation vs extrapolation»
- ^ Good, P. I.; Hardin, J. W. (2009). Common Errors in Statistics (And How to Avoid Them) (3rd ed.). Hoboken, New Jersey: Wiley. p. 211. ISBN 978-0-470-45798-6.
- ^ Tofallis, C. (2009). «Least Squares Percentage Regression». Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. SSRN 1406472.
- ^ YangJing Long (2009). «Human age estimation by metric learning for regression problems» (PDF). Proc. International Conference on Computer Analysis of Images and Patterns: 74–82. Archived from the original (PDF) on 2010-01-08.
Further reading[edit]
- William H. Kruskal and Judith M. Tanur, ed. (1978), «Linear Hypotheses,» International Encyclopedia of Statistics. Free Press, v. 1,
- Evan J. Williams, «I. Regression,» pp. 523–41.
- Julian C. Stanley, «II. Analysis of Variance,» pp. 541–554.
- Lindley, D.V. (1987). «Regression and correlation analysis,» New Palgrave: A Dictionary of Economics, v. 4, pp. 120–23.
- Birkes, David and Dodge, Y., Alternative Methods of Regression. ISBN 0-471-56881-3
- Chatfield, C. (1993) «Calculating Interval Forecasts,» Journal of Business and Economic Statistics, 11. pp. 121–135.
- Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 978-0-471-17082-2.
- Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage
- Hardle, W., Applied Nonparametric Regression (1990), ISBN 0-521-42950-1
- Meade, Nigel; Islam, Towhidul (1995). «Prediction intervals for growth curve forecasts». Journal of Forecasting. 14 (5): 413–430. doi:10.1002/for.3980140502.
- A. Sen, M. Srivastava, Regression Analysis — Theory, Methods, and Applications, Springer-Verlag, Berlin, 2011 (4th printing).
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner, ISBN 978-3-8348-1022-9.
- Stulp, Freek, and Olivier Sigaud. Many Regression Algorithms, One Unified Model: A Review. Neural Networks, vol. 69, Sept. 2015, pp. 60–79. https://doi.org/10.1016/j.neunet.2015.05.005.
- Malakooti, B. (2013). Operations and Production Systems with Multiple Objectives. John Wiley & Sons.
- Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). «The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation». PeerJ Computer Science. 7 (e623): e623. doi:10.7717/peerj-cs.623. PMC 8279135. PMID 34307865.
External links[edit]
- «Regression analysis», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Earliest Uses: Regression – basic history and references
- What is multiple regression used for? – Multiple regression
- Regression of Weakly Correlated Data – how linear regression mistakes can appear when Y-range is much smaller than X-range

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the ‘outcome’ or ‘response’ variable, or a ‘label’ in machine learning parlance) and one or more independent variables (often called ‘predictors’, ‘covariates’, ‘explanatory variables’ or ‘features’). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters (e.g., quantile regression or Necessary Condition Analysis[1]) or estimate the conditional expectation across a broader collection of non-linear models (e.g., nonparametric regression).
Regression analysis is primarily used for two conceptually distinct purposes.
First, regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of machine learning.
Second, in some situations regression analysis can be used to infer causal relationships between the independent and dependent variables. Importantly, regressions by themselves only reveal relationships between a dependent variable and a collection of independent variables in a fixed dataset. To use regressions for prediction or to infer causal relationships, respectively, a researcher must carefully justify why existing relationships have predictive power for a new context or why a relationship between two variables has a causal interpretation. The latter is especially important when researchers hope to estimate causal relationships using observational data.[2][3]
History[edit]
The earliest form of regression was the method of least squares, which was published by Legendre in 1805,[4] and by Gauss in 1809.[5] Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the Sun (mostly comets, but also later the then newly discovered minor planets). Gauss published a further development of the theory of least squares in 1821,[6] including a version of the Gauss–Markov theorem.
The term «regression» was coined by Francis Galton in the 19th century to describe a biological phenomenon. The phenomenon was that the heights of descendants of tall ancestors tend to regress down towards a normal average (a phenomenon also known as regression toward the mean).[7][8]
For Galton, regression had only this biological meaning,[9][10] but his work was later extended by Udny Yule and Karl Pearson to a more general statistical context.[11][12] In the work of Yule and Pearson, the joint distribution of the response and explanatory variables is assumed to be Gaussian. This assumption was weakened by R.A. Fisher in his works of 1922 and 1925.[13][14][15] Fisher assumed that the conditional distribution of the response variable is Gaussian, but the joint distribution need not be. In this respect, Fisher’s assumption is closer to Gauss’s formulation of 1821.
In the 1950s and 1960s, economists used electromechanical desk «calculators» to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the result from one regression.[16]
Regression methods continue to be an area of active research. In recent decades, new methods have been developed for robust regression, regression involving correlated responses such as time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other complex data objects, regression methods accommodating various types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with error, regression with more predictor variables than observations, and causal inference with regression.
Regression model[edit]
In practice, researchers first select a model they would like to estimate and then use their chosen method (e.g., ordinary least squares) to estimate the parameters of that model. Regression models involve the following components:
In various fields of application, different terminologies are used in place of dependent and independent variables.
Most regression models propose that 




The researchers’ goal is to estimate the function 






Once researchers determine their preferred statistical model, different forms of regression analysis provide tools to estimate the parameters 










It is important to note that there must be sufficient data to estimate a regression model. For example, suppose that a researcher has access to 








More generally, to estimate a least squares model with 






Underlying assumptions[edit]
By itself, a regression is simply a calculation using the data. In order to interpret the output of regression as a meaningful statistical quantity that measures real-world relationships, researchers often rely on a number of classical assumptions. These assumptions often include:
A handful of conditions are sufficient for the least-squares estimator to possess desirable properties: in particular, the Gauss–Markov assumptions imply that the parameter estimates will be unbiased, consistent, and efficient in the class of linear unbiased estimators. Practitioners have developed a variety of methods to maintain some or all of these desirable properties in real-world settings, because these classical assumptions are unlikely to hold exactly. For example, modeling errors-in-variables can lead to reasonable estimates independent variables are measured with errors. Heteroscedasticity-consistent standard errors allow the variance of 


Linear regression[edit]
In linear regression, the model specification is that the dependent variable, 




- straight line:
In multiple linear regression, there are several independent variables or functions of independent variables.
Adding a term in 
- parabola:
This is still linear regression; although the expression on the right hand side is quadratic in the independent variable 



In both cases, 

Returning our attention to the straight line case: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:
The residual, 


Minimization of this function results in a set of normal equations, a set of simultaneous linear equations in the parameters, which are solved to yield the parameter estimators, 

Illustration of linear regression on a data set
In the case of simple regression, the formulas for the least squares estimates are
where 



Under the assumption that the population error term has a constant variance, the estimate of that variance is given by:
This is called the mean square error (MSE) of the regression. The denominator is the sample size reduced by the number of model parameters estimated from the same data, 




The standard errors of the parameter estimates are given by
Under the further assumption that the population error term is normally distributed, the researcher can use these estimated standard errors to create confidence intervals and conduct hypothesis tests about the population parameters.
General linear model[edit]
In the more general multiple regression model, there are 
where 


If the first independent variable takes the value 1 for all 


The least squares parameter estimates are obtained from 
The normal equations are
In matrix notation, the normal equations are written as
where the 














Diagnostics[edit]
Once a regression model has been constructed, it may be important to confirm the goodness of fit of the model and the statistical significance of the estimated parameters. Commonly used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-test of the overall fit, followed by t-tests of individual parameters.
Interpretations of these diagnostic tests rest heavily on the model’s assumptions. Although examination of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model’s assumptions are violated. For example, if the error term does not have a normal distribution, in small samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can be invoked such that hypothesis testing may proceed using asymptotic approximations.
Limited dependent variables[edit]
Limited dependent variables, which are response variables that are categorical variables or are variables constrained to fall only in a certain range, often arise in econometrics.
The response variable may be non-continuous («limited» to lie on some subset of the real line). For binary (zero or one) variables, if analysis proceeds with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than two values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest. An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an event, then count models like the Poisson regression or the negative binomial model may be used.
Nonlinear regression[edit]
When the model function is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences between linear and non-linear least squares.
Interpolation and extrapolation[edit]

In the middle, the interpolated straight line represents the best balance between the points above and below this line. The dotted lines represent the two extreme lines. The first curves represent the estimated values. The outer curves represent a prediction for a new measurement.[20]
Regression models predict a value of the Y variable given known values of the X variables. Prediction within the range of values in the dataset used for model-fitting is known informally as interpolation. Prediction outside this range of the data is known as extrapolation. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.
It is generally advised[citation needed] that when performing extrapolation, one should accompany the estimated value of the dependent variable with a prediction interval that represents the uncertainty. Such intervals tend to expand rapidly as the values of the independent variable(s) moved outside the range covered by the observed data.
For such reasons and others, some tend to say that it might be unwise to undertake extrapolation.[21]
However, this does not cover the full set of modeling errors that may be made: in particular, the assumption of a particular form for the relation between Y and X. A properly conducted regression analysis will include an assessment of how well the assumed form is matched by the observed data, but it can only do so within the range of values of the independent variables actually available. This means that any extrapolation is particularly reliant on the assumptions being made about the structural form of the regression relationship. Best-practice advice here[citation needed] is that a linear-in-variables and linear-in-parameters relationship should not be chosen simply for computational convenience, but that all available knowledge should be deployed in constructing a regression model. If this knowledge includes the fact that the dependent variable cannot go outside a certain range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly near such bounds. The implications of this step of choosing an appropriate functional form for the regression can be great when extrapolation is considered. At a minimum, it can ensure that any extrapolation arising from a fitted model is «realistic» (or in accord with what is known).
Power and sample size calculations[edit]
There are no generally agreed methods for relating the number of observations versus the number of independent variables in the model. One method conjectured by Good and Hardin is 





Other methods[edit]
Although the parameters of a regression model are usually estimated using the method of least squares, other methods which have been used include:
- Bayesian methods, e.g. Bayesian linear regression
- Percentage regression, for situations where reducing percentage errors is deemed more appropriate.[23]
- Least absolute deviations, which is more robust in the presence of outliers, leading to quantile regression
- Nonparametric regression, requires a large number of observations and is computationally intensive
- Scenario optimization, leading to interval predictor models
- Distance metric learning, which is learned by the search of a meaningful distance metric in a given input space.[24]
Software[edit]
All major statistical software packages perform least squares regression analysis and inference. Simple linear regression and multiple regression using least squares can be done in some spreadsheet applications and on some calculators. While many statistical software packages can perform various types of nonparametric and robust regression, these methods are less standardized. Different software packages implement different methods, and a method with a given name may be implemented differently in different packages. Specialized regression software has been developed for use in fields such as survey analysis and neuroimaging.
See also[edit]
- Anscombe’s quartet
- Curve fitting
- Estimation theory
- Forecasting
- Fraction of variance unexplained
- Function approximation
- Generalized linear model
- Kriging (a linear least squares estimation algorithm)
- Local regression
- Modifiable areal unit problem
- Multivariate adaptive regression splines
- Multivariate normal distribution
- Pearson correlation coefficient
- Quasi-variance
- Prediction interval
- Regression validation
- Robust regression
- Segmented regression
- Signal processing
- Stepwise regression
- Taxicab geometry
- Trend estimation
References[edit]
- ^ Necessary Condition Analysis
- ^ David A. Freedman (27 April 2009). Statistical Models: Theory and Practice. Cambridge University Press. ISBN 978-1-139-47731-4.
- ^ R. Dennis Cook; Sanford Weisberg Criticism and Influence Analysis in Regression, Sociological Methodology, Vol. 13. (1982), pp. 313–361
- ^ A.M. Legendre. Nouvelles méthodes pour la détermination des orbites des comètes, Firmin Didot, Paris, 1805. “Sur la Méthode des moindres quarrés” appears as an appendix.
- ^ a b Chapter 1 of: Angrist, J. D., & Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press.
- ^ C.F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. (1821/1823)
- ^
Mogull, Robert G. (2004). Second-Semester Applied Statistics. Kendall/Hunt Publishing Company. p. 59. ISBN 978-0-7575-1181-3. - ^ Galton, Francis (1989). «Kinship and Correlation (reprinted 1989)». Statistical Science. 4 (2): 80–86. doi:10.1214/ss/1177012581. JSTOR 2245330.
- ^ Francis Galton. «Typical laws of heredity», Nature 15 (1877), 492–495, 512–514, 532–533. (Galton uses the term «reversion» in this paper, which discusses the size of peas.)
- ^ Francis Galton. Presidential address, Section H, Anthropology. (1885) (Galton uses the term «regression» in this paper, which discusses the height of humans.)
- ^ Yule, G. Udny (1897). «On the Theory of Correlation». Journal of the Royal Statistical Society. 60 (4): 812–54. doi:10.2307/2979746. JSTOR 2979746.
- ^ Pearson, Karl; Yule, G.U.; Blanchard, Norman; Lee, Alice (1903). «The Law of Ancestral Heredity». Biometrika. 2 (2): 211–236. doi:10.1093/biomet/2.2.211. JSTOR 2331683.
- ^ Fisher, R.A. (1922). «The goodness of fit of regression formulae, and the distribution of regression coefficients». Journal of the Royal Statistical Society. 85 (4): 597–612. doi:10.2307/2341124. JSTOR 2341124. PMC 1084801.
- ^ Ronald A. Fisher (1954). Statistical Methods for Research Workers (Twelfth ed.). Edinburgh: Oliver and Boyd. ISBN 978-0-05-002170-5.
- ^ Aldrich, John (2005). «Fisher and Regression». Statistical Science. 20 (4): 401–417. doi:10.1214/088342305000000331. JSTOR 20061201.
- ^ Rodney Ramcharan. Regressions: Why Are Economists Obessessed with Them? March 2006. Accessed 2011-12-03.
- ^ Fotheringham, A. Stewart; Brunsdon, Chris; Charlton, Martin (2002). Geographically weighted regression: the analysis of spatially varying relationships (Reprint ed.). Chichester, England: John Wiley. ISBN 978-0-471-49616-8.
- ^ Fotheringham, AS; Wong, DWS (1 January 1991). «The modifiable areal unit problem in multivariate statistical analysis». Environment and Planning A. 23 (7): 1025–1044. doi:10.1068/a231025. S2CID 153979055.
- ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Rouaud, Mathieu (2013). Probability, Statistics and Estimation (PDF). p. 60.
- ^ Chiang, C.L, (2003) Statistical methods of analysis, World Scientific. ISBN 981-238-310-7 — page 274 section 9.7.4 «interpolation vs extrapolation»
- ^ Good, P. I.; Hardin, J. W. (2009). Common Errors in Statistics (And How to Avoid Them) (3rd ed.). Hoboken, New Jersey: Wiley. p. 211. ISBN 978-0-470-45798-6.
- ^ Tofallis, C. (2009). «Least Squares Percentage Regression». Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. SSRN 1406472.
- ^ YangJing Long (2009). «Human age estimation by metric learning for regression problems» (PDF). Proc. International Conference on Computer Analysis of Images and Patterns: 74–82. Archived from the original (PDF) on 2010-01-08.
Further reading[edit]
- William H. Kruskal and Judith M. Tanur, ed. (1978), «Linear Hypotheses,» International Encyclopedia of Statistics. Free Press, v. 1,
- Evan J. Williams, «I. Regression,» pp. 523–41.
- Julian C. Stanley, «II. Analysis of Variance,» pp. 541–554.
- Lindley, D.V. (1987). «Regression and correlation analysis,» New Palgrave: A Dictionary of Economics, v. 4, pp. 120–23.
- Birkes, David and Dodge, Y., Alternative Methods of Regression. ISBN 0-471-56881-3
- Chatfield, C. (1993) «Calculating Interval Forecasts,» Journal of Business and Economic Statistics, 11. pp. 121–135.
- Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 978-0-471-17082-2.
- Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage
- Hardle, W., Applied Nonparametric Regression (1990), ISBN 0-521-42950-1
- Meade, Nigel; Islam, Towhidul (1995). «Prediction intervals for growth curve forecasts». Journal of Forecasting. 14 (5): 413–430. doi:10.1002/for.3980140502.
- A. Sen, M. Srivastava, Regression Analysis — Theory, Methods, and Applications, Springer-Verlag, Berlin, 2011 (4th printing).
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner, ISBN 978-3-8348-1022-9.
- Stulp, Freek, and Olivier Sigaud. Many Regression Algorithms, One Unified Model: A Review. Neural Networks, vol. 69, Sept. 2015, pp. 60–79. https://doi.org/10.1016/j.neunet.2015.05.005.
- Malakooti, B. (2013). Operations and Production Systems with Multiple Objectives. John Wiley & Sons.
- Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). «The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation». PeerJ Computer Science. 7 (e623): e623. doi:10.7717/peerj-cs.623. PMC 8279135. PMID 34307865.
External links[edit]
- «Regression analysis», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Earliest Uses: Regression – basic history and references
- What is multiple regression used for? – Multiple regression
- Regression of Weakly Correlated Data – how linear regression mistakes can appear when Y-range is much smaller than X-range
Материал из MachineLearning.
Перейти к: навигация, поиск
Термину регрессионная модель, используемому в регрессионном анализе, можно сопоставить синонимы: «теория», «гипотеза».
Эти термины пришли из статистики, в частности из раздела «проверка статистических гипотез».
Регрессионная модель есть прежде всего гипотеза, которая должна быть подвергнута статистической проверке, после чего она принимается или отвергается.
Регрессионная модель — это параметрическое семейство функций, задающее отображение
где — пространтсво параметров,
— пространство свободных переменных,
— пространство зависимых переменных.
Так как регрессионный анализ предполагает поиск зависимости матожидания случайной величины от свободных переменных
, то в её состав входит аддитивная случайная величина
:
Предположение о характере распределения случайной величины называются гипотезой порождения данных.
Эта гипотеза играет центральную роль в выборе критерия оценки качества модели и, как следствие, в способе настройки параметров модели.
Модель является настроенной (обученной) когда зафиксированы её параметры, то есть модель задаёт отображение
для фиксированного значения .
Различают математическую модель и регрессионную модель.
Математическая модель предполагает участие аналитика в конструировании функции, которая описывает некоторую известную закономерность.
Математическая модель является интерпретируемой — объясняемой в рамках исследуемой закономерности.
При построении математической модели сначала создаётся параметрическое семейство функций, затем с помощью измеряемых данных выполняется идентификация модели — нахождение её параметров.
Известная функциональная зависимость объясняющей переменной и переменной отклика — основное отличие математического моделирования от регрессионного анализа.
Недостаток математического моделирования состоит в том, что измеряемые данные используются для верификации, но не для построения модели, вследствие чего можно получить неадекватную модель.
Также затруднительно получить модель сложного явления, в котором взаимосвязано большое число различных факторов.
Регрессионная модель объединяет широкий класс универсальных функций, которые описывают некоторую закономерность.
При этом для построения модели в основном используются измеряемые данные, а не знание свойств исследуемой закономерности.
Такая модель часто неинтерпретируема, но более точна.
Это объясняется либо большим числом моделей-претендентов, которые используются для построения оптимальной модели, либо большой сложностью модели.
Нахождение параметров регрессионной модели называется обучением модели.
Недостатки регрессионного анализа: модели, имеющие слишком малую сложность, могут оказаться неточными, а модели, имеющие избыточную сложность, могут оказаться переобученными.
Примеры регрессионных моделей: линейные функции, алгебраические полиномы, ряды Чебышёва, нейронные сети без обратной связи, например, однослойный персептрон Розенблатта, радиальные базисные функции и прочее.
И регрессионная, и математическая модель, как правило, задают непрерывное отображение.
Требование непрерывности обусловлено классом решаемых задач: чаще всего это описание физических, химических и других явлений,
где требование непрерывности выставляется естественным образом.
Иногда на отображение накладываться ограничения монотонности, гладкости, измеримости, и некоторые другие.
Теоретически, никто не запрещает работать с функциями произвольного вида, и допускать в моделях существование не только точек разрыва, но и задавать конечное, неупорядоченное множество значений свободной переменной, то есть, превращать задачи регрессии в задачи классификации.
При решении задач регрессионного анализа встают следующие вопросы.
- Как выбрать тип и структуру модели, какому именно семейству она должна принадлежать?
- Какова гипотеза порождения данных, каково распределение случайной переменной?
- Какой целевой функцией оценить качество аппроксимации?
- Каким способом отыскать параметры модели, каков должен быть алгоритм оптимизации параметров?
Смотри также
- Модель зависимости
- Регрессионный анализ
- Анализ регрессионных остатков
- Символьная регрессия
- Линейная регрессия (пример)
- Алгоритмы выбора линейных регрессионных моделей (практика)
- Регрессионный анализ (рекомендуемые обозначения)
Литература
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Издательский дом «Вильямс». 2007.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
- Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: ВЦ РАН, 2010. 60 с. Брошюра, PDF.
Литература
- Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.
- MacKay, D. Information, inference, learning algorithms. Cambridge University Press. 2003.
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Издательский дом «Вильямс». 2007.
- Nabney, Yan T., Netlab: Algorithms for pattern recognition. Springer. 2004.
- Lehmann, E. L., Romano, J. P. Testing Statistical Hypotheses. Springer. 2005.
- Burnham, K., Anderson, D. R. Model Selection and Multimodel Inference. Springer. 2002.
- Grunwald, P D., Myung, I. J. (eds.) Advances In Minimum Description Length: Theory And Applications. Springer. 2005.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Регрессия как задача машинного обучения
38 мин на чтение
(55.116 символов)
Постановка задачи регрессии
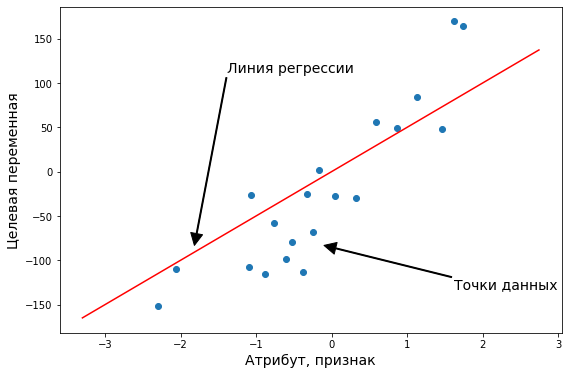
Источник: Analytics Vidhya.
Задача регрессии — это одна из основных задач машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, наборы данных для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (dependent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Так же надо сказать, что иногда регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия почти не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Линейная регрессия с одной переменной
Функция гипотезы
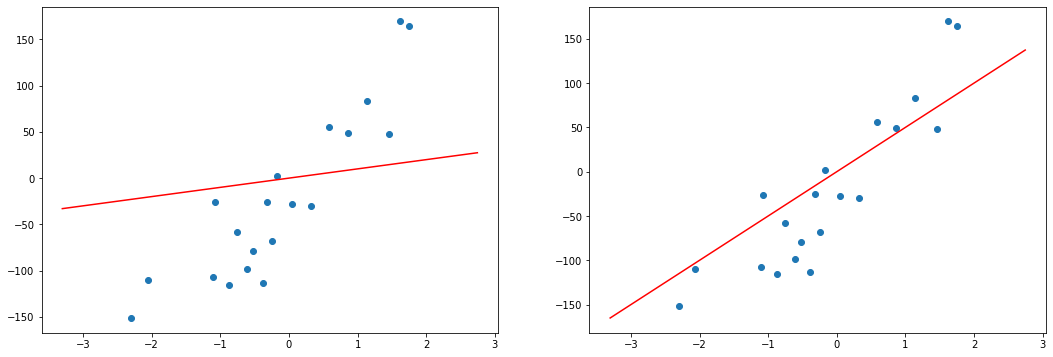
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y.
Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$б которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно, или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
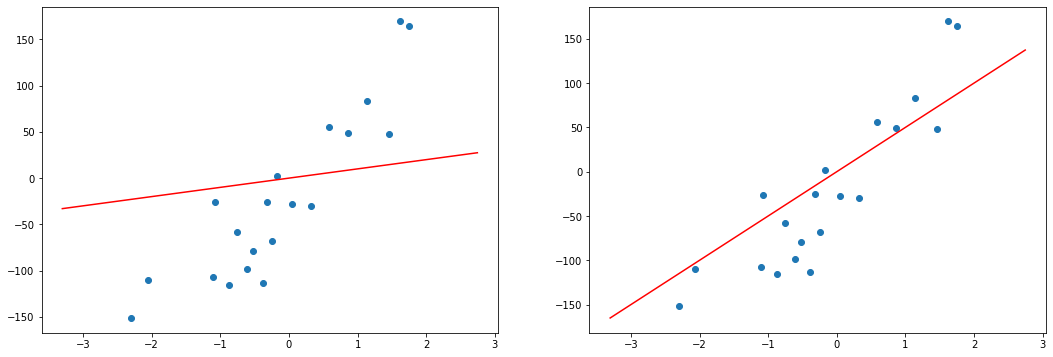
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
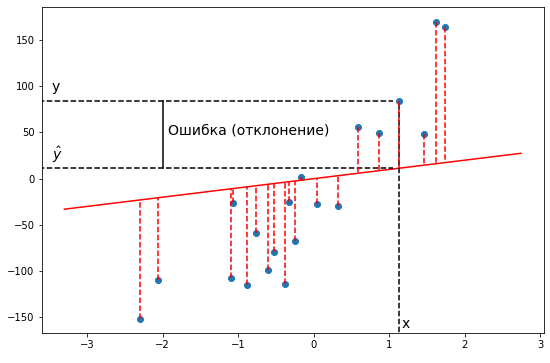
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Возведение в квадрат в этой формуле нужно для того, чтобы положительные отклонения не компенсировали отрицательные. Можно было бы для этого брать, например, абсолютное значение, но эта функция не везде дифференцируема, а это станет нам важно позднее.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
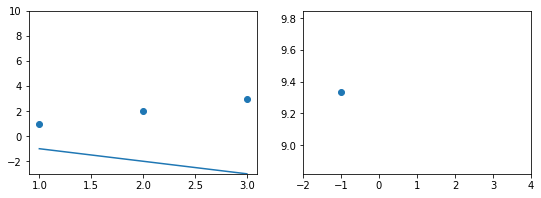
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
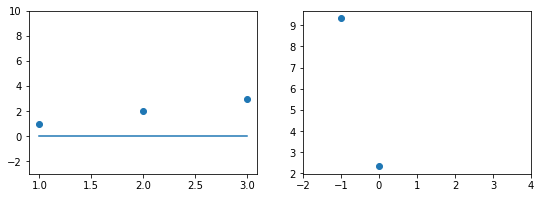
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
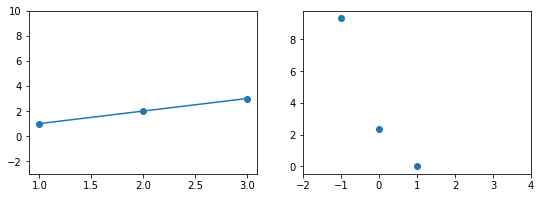
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
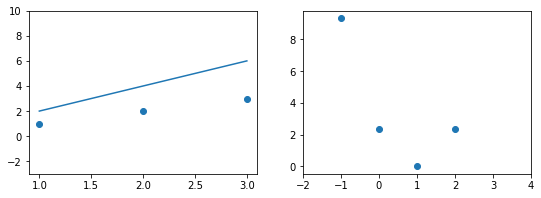
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
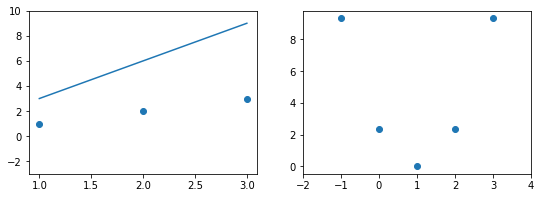
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
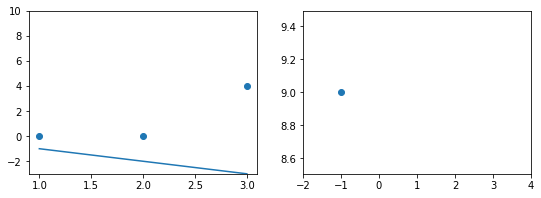
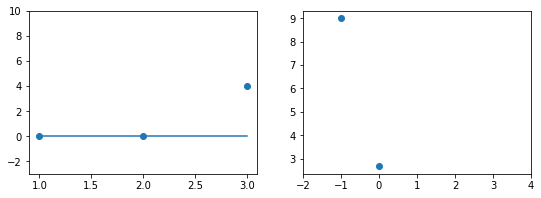
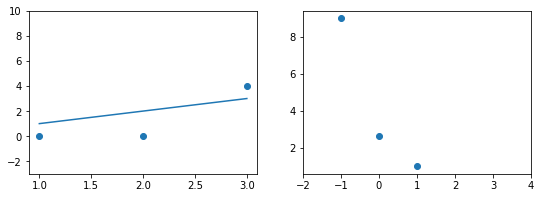
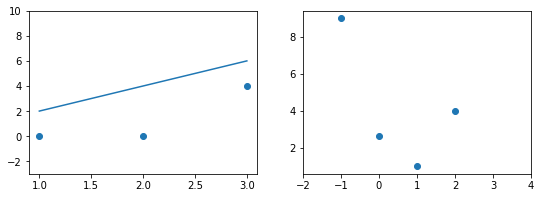
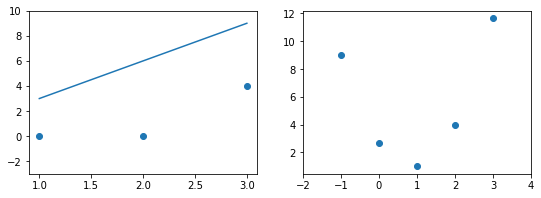
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
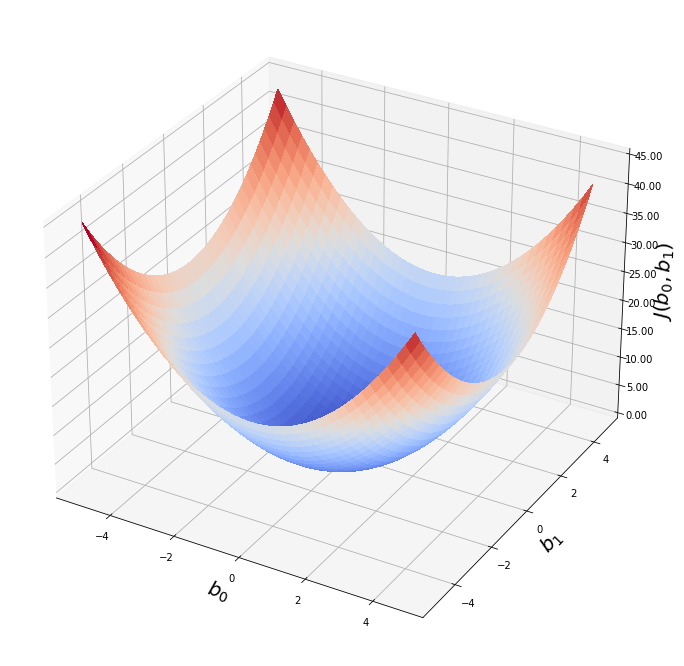
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
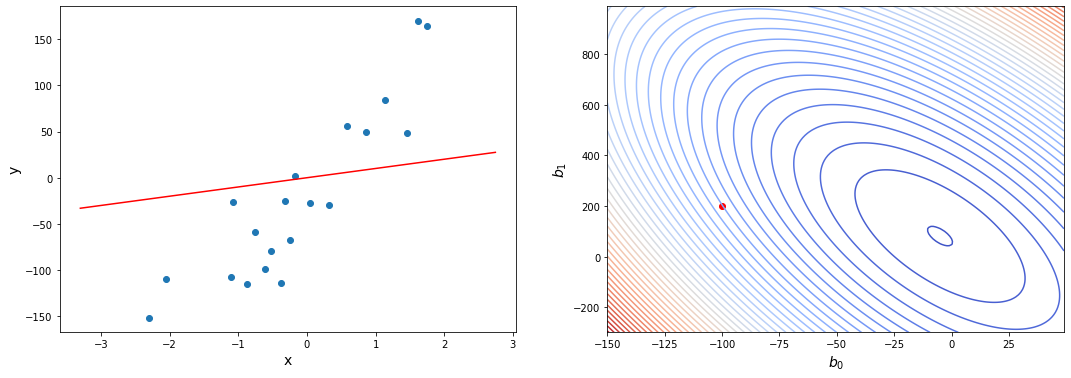
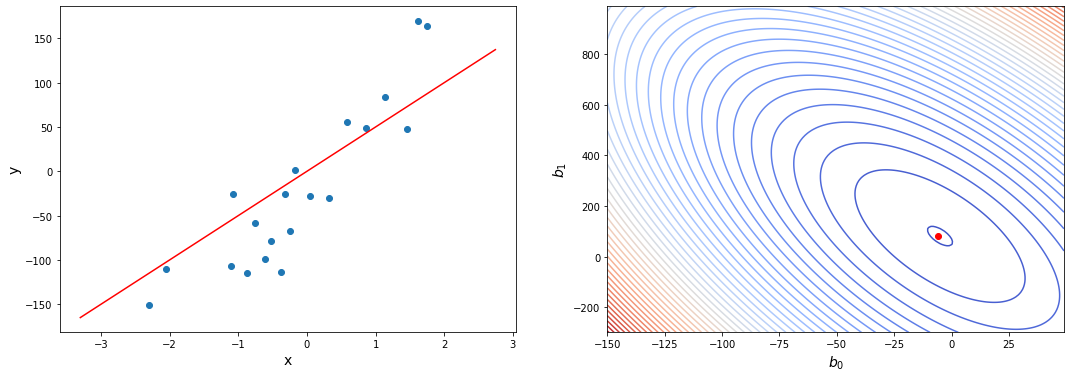
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска.
Это происходит при помощи производной функции ошибки. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит, от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
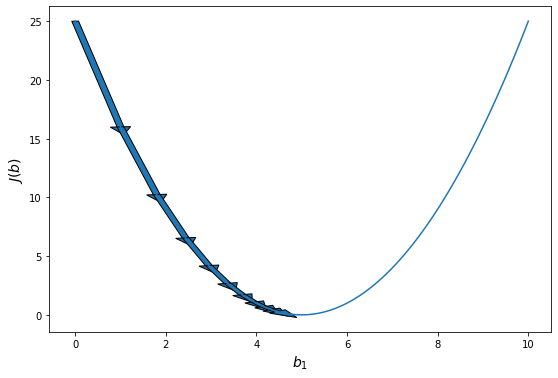
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.

Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки:
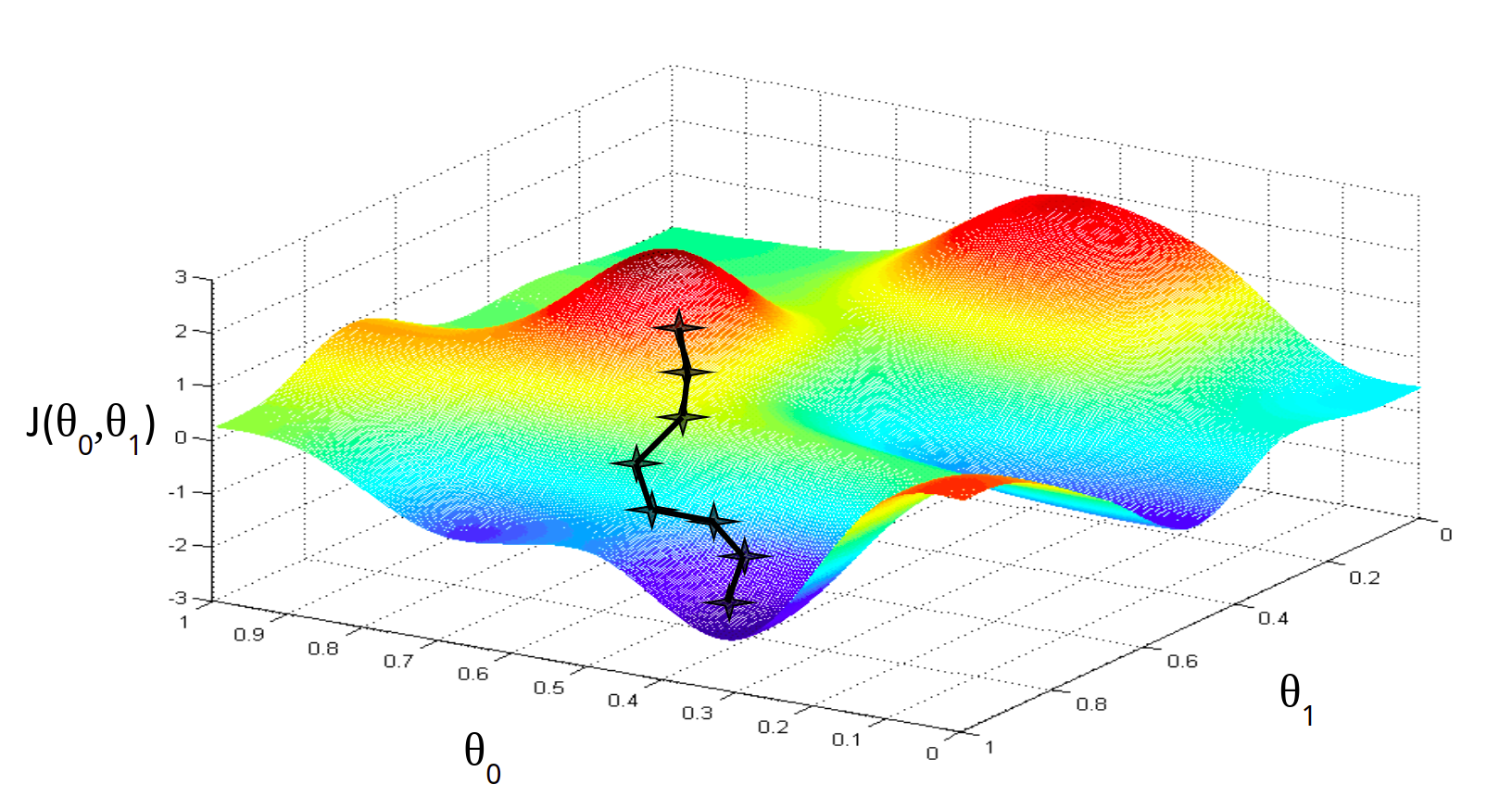
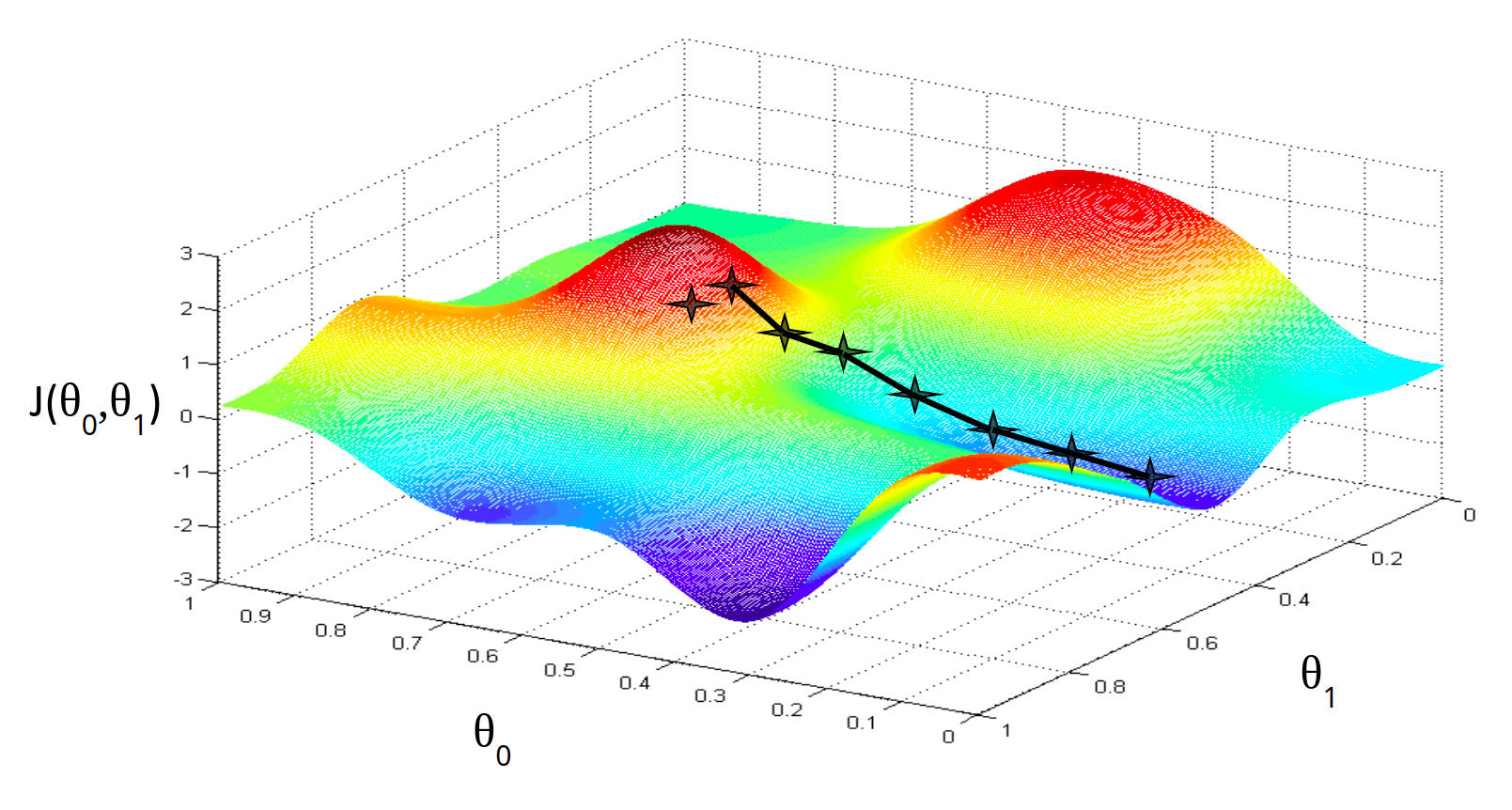
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
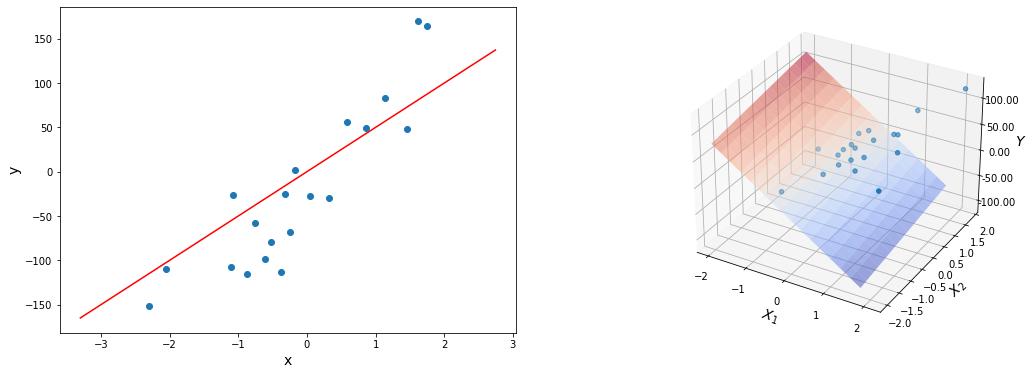
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Целевая переменная не нормируется.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
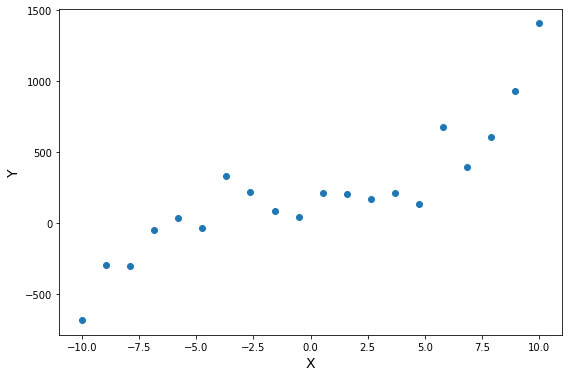
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.

Источник: Wikimedia.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данном разделе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данного раздела предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
Это код генерирует вот такой вот график:
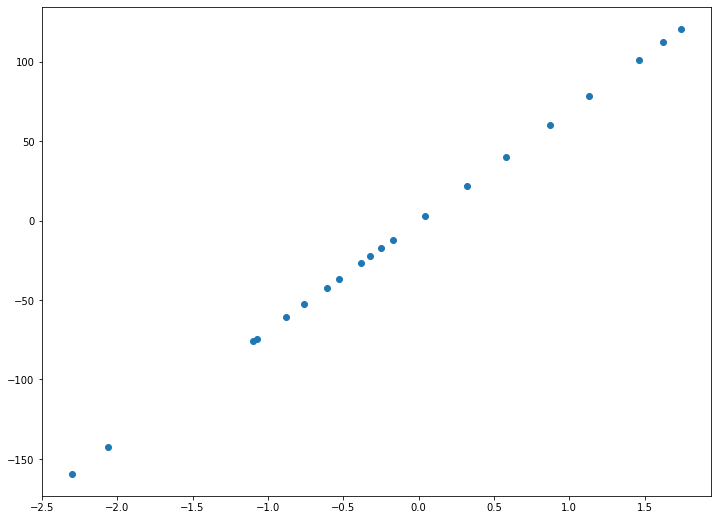
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
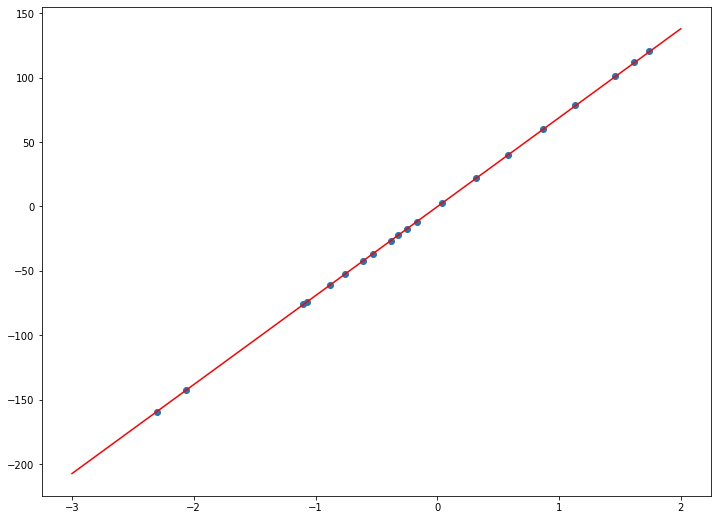
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()

На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
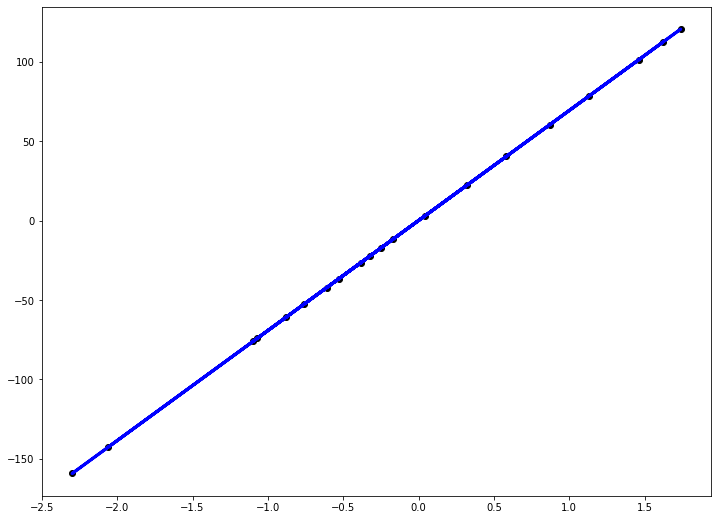
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение 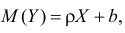
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии  неизвестны, неизвестна и величина коэффициента корреляции
неизвестны, неизвестна и величина коэффициента корреляции 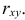 Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений:
Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений: 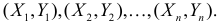 Эти результаты могут служить источником информации о неизвестных значениях
Эти результаты могут служить источником информации о неизвестных значениях 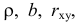 надо только уметь эту информацию извлечь оттуда.
надо только уметь эту информацию извлечь оттуда.
Неизвестная нам линия регрессии 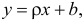 как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для
как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для  можно принять те их значения, при которых имеет минимум функция
можно принять те их значения, при которых имеет минимум функция 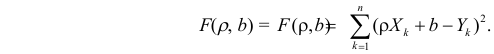
Такие значения  , согласно необходимым условиям экстремума, находятся из системы уравнений:
, согласно необходимым условиям экстремума, находятся из системы уравнений:
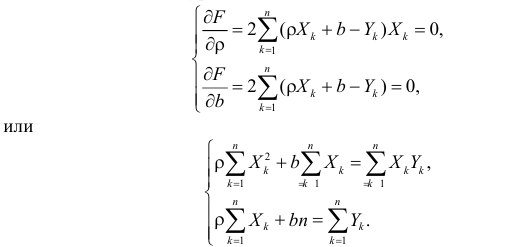
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.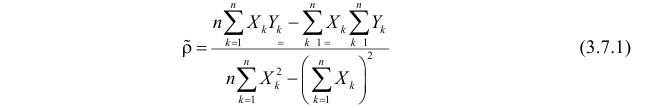
и
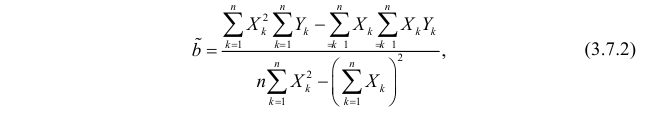
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 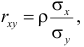 где
где 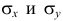 средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через
средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через 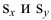 оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку
оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку 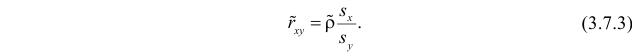
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 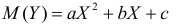 оценки параметров
оценки параметров 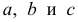 находятся из условия минимума функции
находятся из условия минимума функции
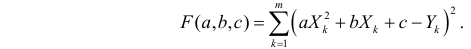
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X 
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
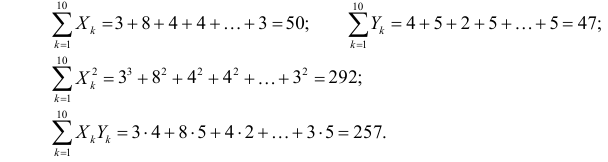
По формулам (3.7.1) и (3.7.2) получим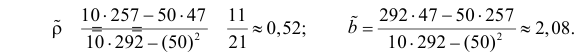
Итак, оценка линии регрессии имеет вид 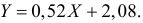 Так как
Так как 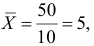 то по формуле (3.1.3)
то по формуле (3.1.3)
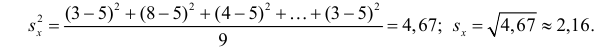
Аналогично, 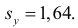 Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину
Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину 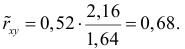
Ответ. 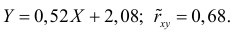
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 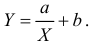 Найти оценки параметров
Найти оценки параметров 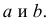
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 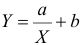 играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)
играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)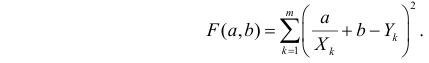
Необходимые условия экстремума приводят к системе из двух уравнений: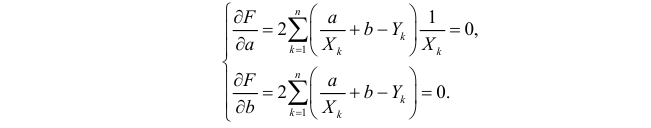
Откуда
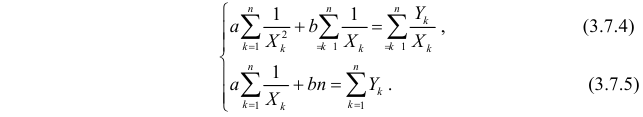
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров 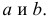
На основе опытных данных вычисляем: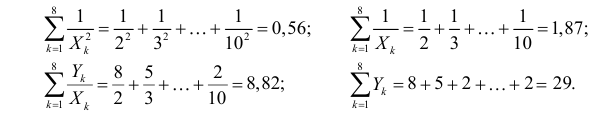
В итоге получаем систему уравнений (?????) и (?????) в виде 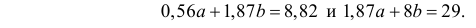
Эта система имеет решения 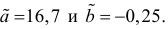
Ответ. 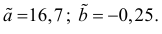
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 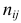 равно числу наблюдений, для которых X находится в интервале
равно числу наблюдений, для которых X находится в интервале 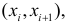 а Y – в интервале
а Y – в интервале 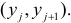 Через
Через 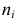 обозначено число наблюдений, при которых
обозначено число наблюдений, при которых 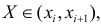 а Y произвольно. Число наблюдений, при которых
а Y произвольно. Число наблюдений, при которых 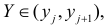 а X произвольно, обозначено через
а X произвольно, обозначено через 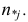
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 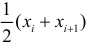 и
и 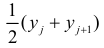 наблюдались
наблюдались 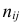 раз.
раз.
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.

Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 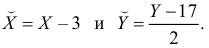 Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 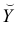 при фиксированных значениях
при фиксированных значениях 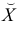 :
:
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).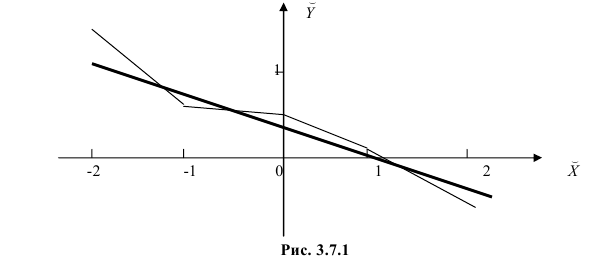
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33): 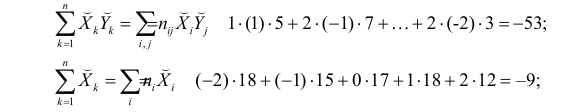
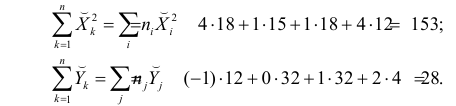
Тогда
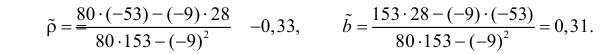
В новом масштабе оценка линии регрессии имеет вид 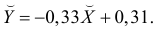 График этой прямой линии изображен на рис. 3.7.1.
График этой прямой линии изображен на рис. 3.7.1.
Для оценки 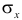 по корреляционной таблице можно воспользоваться формулой (3.1.3):
по корреляционной таблице можно воспользоваться формулой (3.1.3):
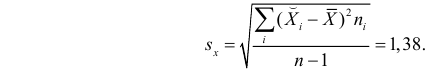
Подобным же образом можно оценить 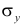 величиной
величиной 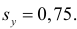 Тогда оценкой коэффициента корреляции может служить величина
Тогда оценкой коэффициента корреляции может служить величина 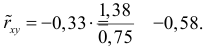
Вернемся к старому масштабу:
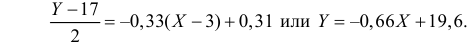
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ. 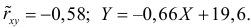
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 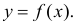 Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то
Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то 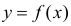 играет роль линии регрессии и все свойства линии регрессии приложимы к
играет роль линии регрессии и все свойства линии регрессии приложимы к 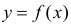 . В частности,
. В частности, 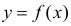 обычно находят по методу наименьших квадратов.
обычно находят по методу наименьших квадратов.
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
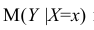 можно представить в виде
можно представить в виде 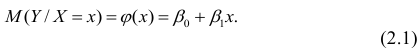
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 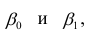 называемые коэффициентами регрессии, а также
называемые коэффициентами регрессии, а также 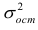 — остаточная дисперсия.
— остаточная дисперсия.
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей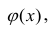 которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости
которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости 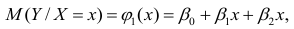
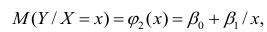
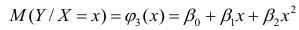 линейны относительно параметров
линейны относительно параметров 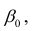
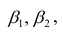 хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости
хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости 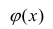 выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
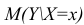 можно представить в виде (2.1).
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 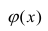 линейна и по оцениваемым параметрам, и
линейна и по оцениваемым параметрам, и
по переменным. Оценки параметров модели (2.1) 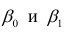 обозначил
обозначил 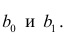 Оценку остаточной дисперсии
Оценку остаточной дисперсии 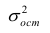 обозначим
обозначим 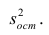 Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии
Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии 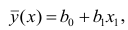 коэффициенты которого
коэффициенты которого 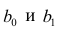 находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака
находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака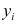 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 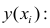
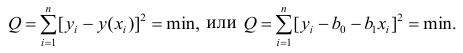
Составим систему нормальных уравнений: первое уравнение
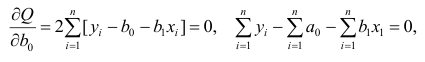
откуда 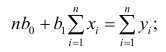
второе уравнение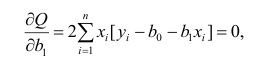
откуда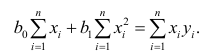
Итак,
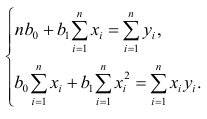
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно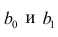 найдём оценки параметров
найдём оценки параметров 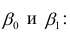
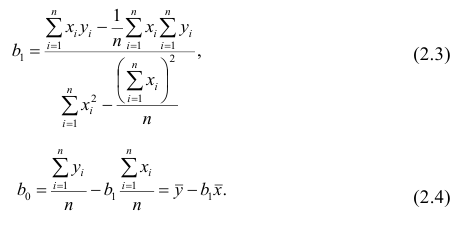
Остаётся получить оценку параметра 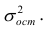 . Имеем
. Имеем
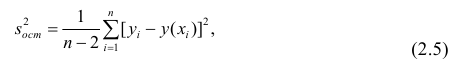
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы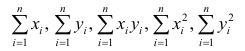 заменяют на
заменяют на
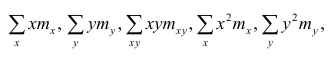
где 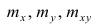 — частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
— частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
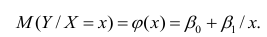
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
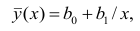
где 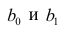 —оценки коэффициентов регрессии
—оценки коэффициентов регрессии 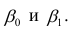
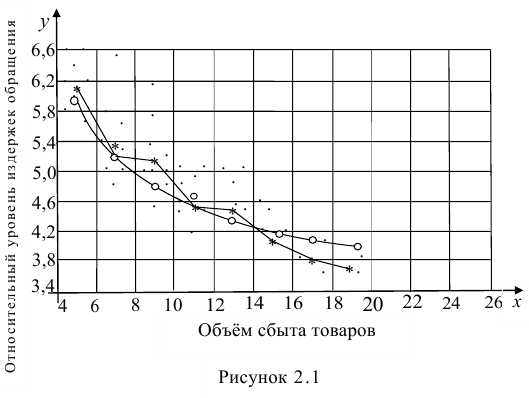
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
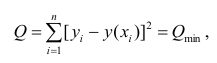
или
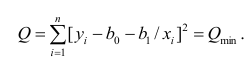
Дифференцируя последнее равенство по 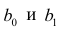 и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
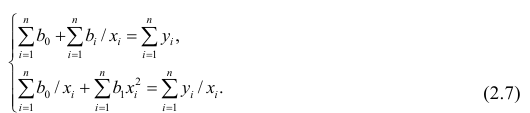
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
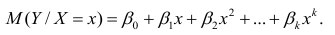
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
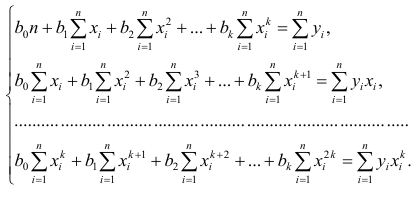
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 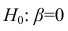 статистика
статистика

имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 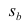 — оценка среднеквадратического отклонения
— оценка среднеквадратического отклонения
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение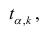 удовлетворяющее условию
удовлетворяющее условию 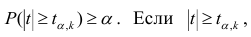 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При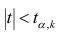 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
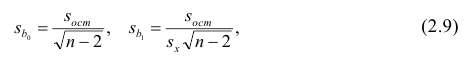
где 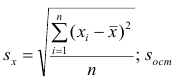 — оценка остаточной дисперсии, вычисляемая по
— оценка остаточной дисперсии, вычисляемая по
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
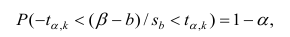
где а — уровень значимости, находим

Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 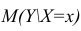 является условное среднее
является условное среднее 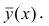 Кроме точечной оценки для
Кроме точечной оценки для 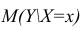 можно
можно
построить доверительный интервал в точке 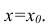
Известно, что 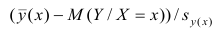 имеет распределение
имеет распределение
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания 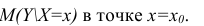
Оценку дисперсии условного среднего вычисляют по формуле
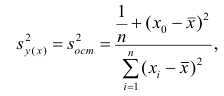
или для интервального ряда
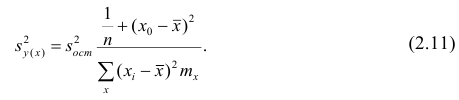
Доверительный интервал находят из условия
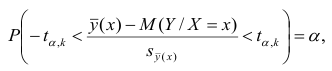
где а — уровень значимости. Отсюда
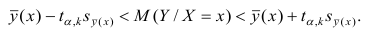
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
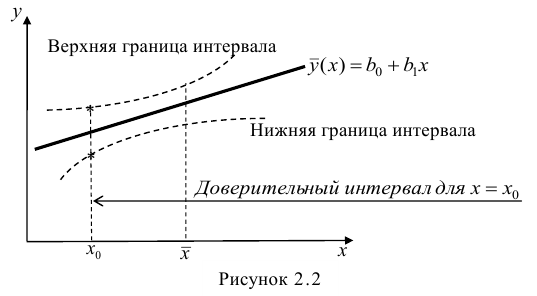
Из рис. 2.2 видно, что в точке 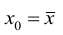 границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 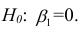 Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением
Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением 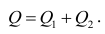 — Общая сумма квадратов отклонений результативного признака
— Общая сумма квадратов отклонений результативного признака
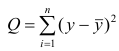 разлагается на
разлагается на 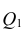 (сумму, характеризующую влияние признака
(сумму, характеризующую влияние признака
X) и 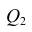 (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
(остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
Для проверки нулевой гипотезы вычисляют статистику 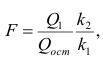 которая имеет распределение Фишера-Снедекора с А
которая имеет распределение Фишера-Снедекора с А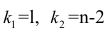 степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы
степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы 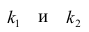 находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение
находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение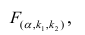 удовлетворяющее условию
удовлетворяющее условию 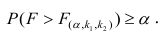 . Если
. Если 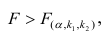 нулевую гипотезу отвергают, уравнение считают значимым. Если
нулевую гипотезу отвергают, уравнение считают значимым. Если 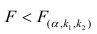 то нет оснований отвергать нулевую гипотезу.
то нет оснований отвергать нулевую гипотезу.
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 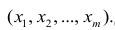 Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним
Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним 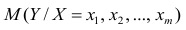 и постоянной дисперсией
и постоянной дисперсией 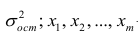 — линейно независимые векторы
— линейно независимые векторы 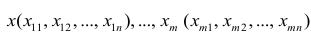 . Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
. Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
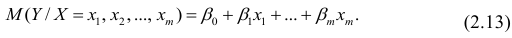
Оценке подлежат параметры 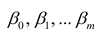 и остаточная дисперсия.
и остаточная дисперсия.
Заменив параметры их оценками, запишем уравнение регрессии
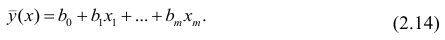
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 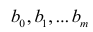 является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:
является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:

Как и в двумерном случае, составляют систему нормальных уравнений
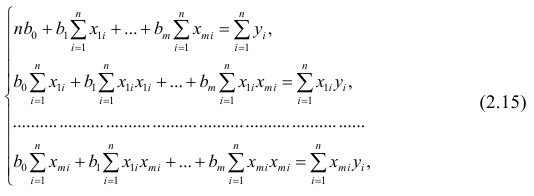
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 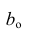 через остальные параметры:
через остальные параметры:
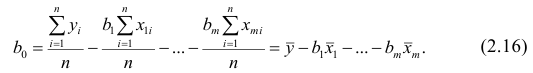
Подставим в остальные уравнения системы вместо 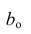 полученное выражение:
полученное выражение:
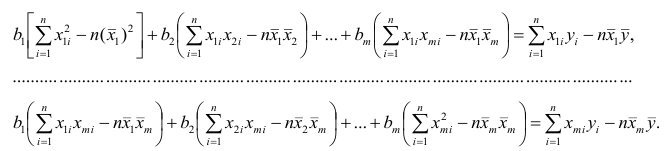
Пусть С — матрица коэффициентов при неизвестных параметрах 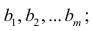
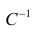 — матрица, обратная матрице С;
— матрица, обратная матрице С; 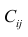 — элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы
— элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы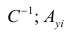 — выражение
— выражение
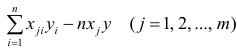 . Тогда, используя формулы линейной алгебры,
. Тогда, используя формулы линейной алгебры,
запишем окончательные выражения для параметров:
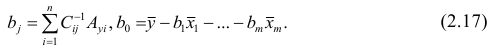
Оценкой остаточной дисперсии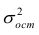 является
является
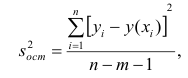
где 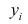 — измеренное значение результативного признака;
— измеренное значение результативного признака;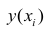 значение результативного признака, вычисленное по уравнению регрессий.
значение результативного признака, вычисленное по уравнению регрессий.
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику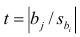 вычисляют для каждого j-го коэффициента регрессии
вычисляют для каждого j-го коэффициента регрессии
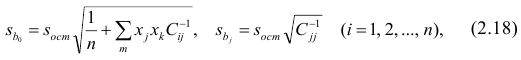
где 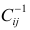 —элемент обратной матрицы, стоящий на пересечении i-й строки и j-
—элемент обратной матрицы, стоящий на пересечении i-й строки и j-
го столбца;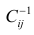 —диагональный элемент обратной матрицы.
—диагональный элемент обратной матрицы.
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 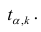 Если
Если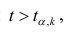 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если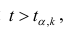 то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: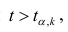
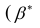 — вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики
— вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики 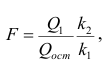 , где
, где 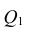 — сумма квадратов, характеризующая влияние признаков X;
— сумма квадратов, характеризующая влияние признаков X; 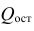 — остаточная сумма квадратов, характеризующая влияние неучтённых факторов;
— остаточная сумма квадратов, характеризующая влияние неучтённых факторов; 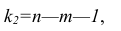
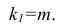 Для уровня значимости а и числа степеней свободы
Для уровня значимости а и числа степеней свободы 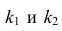 по табл. 3 приложений находят критическое значение
по табл. 3 приложений находят критическое значение 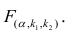 Если
Если 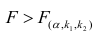 то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При
то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При 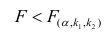 нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 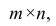 аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений
аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений 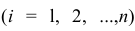 столбцы — признакам
столбцы — признакам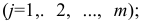 таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных
таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных 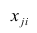 переходят к переменным
переходят к переменным 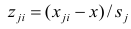 В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
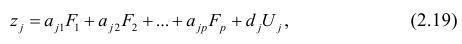
где 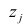 -j-й признак (величина случайная);
-j-й признак (величина случайная); 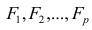 — общие факторы (величины случайные, имеющие нормальный закон распределения);
— общие факторы (величины случайные, имеющие нормальный закон распределения); 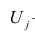 — характерный фактор;
— характерный фактор; 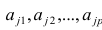 — факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);
— факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);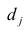 — нагрузка характерного фактора.
— нагрузка характерного фактора.
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 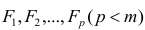 и характерного фактора
и характерного фактора 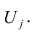
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков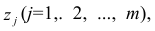 , т.е.
, т.е.
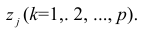
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы 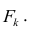
Факторные нагрузки 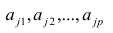 . характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
. характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
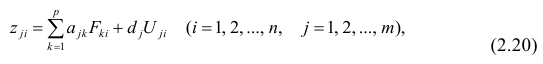
где 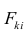 значение k-го фактора для i-го объекта.
значение k-го фактора для i-го объекта.
Дисперсию признака 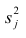 можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность
можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность 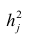 и часть, обусловленную действием j-го характера фактора, характерность
и часть, обусловленную действием j-го характера фактора, характерность 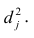 Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака
Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака 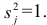 Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
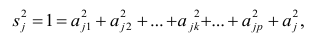
где 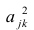 —доля дисперсии признака
—доля дисперсии признака 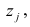 приходящаяся на k-й фактор.
приходящаяся на k-й фактор.
Полный вклад k-го фактора в суммарную дисперсию признаков
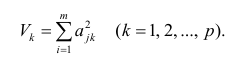
Вклад общих факторов в суммарную дисперсию 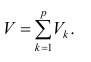
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
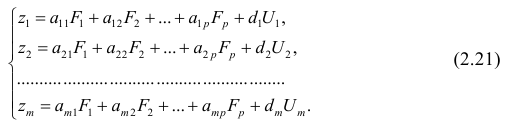
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
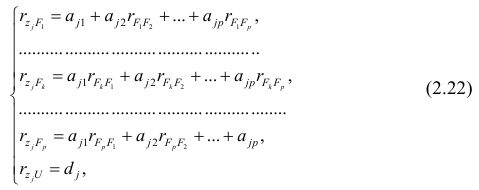
где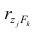 — выборочный коэффициент корреляции между j-м параметром и к-
— выборочный коэффициент корреляции между j-м параметром и к-
м фактором;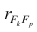 — коэффициент корреляции между к-м и р-м факторами.
— коэффициент корреляции между к-м и р-м факторами.
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
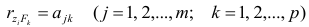 , т.е. коэффициенты отображения равны
, т.е. коэффициенты отображения равны
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам: 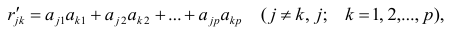
где 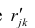 —вычисленный по отображению коэффициент корреляции между j-м
—вычисленный по отображению коэффициент корреляции между j-м
и к-м признаком. Остаточный коэффициент корреляции
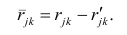
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
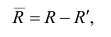
где 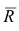 — матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
— матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
Результаты факторного анализа удобно представить в виде табл. 2.10.

Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
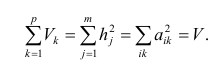
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции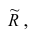 у которой на главной диагонали стоят значения общностей
у которой на главной диагонали стоят значения общностей 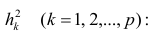 :
: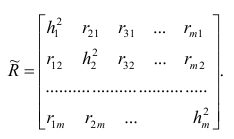
Редуцированная и полная матрицы связаны соотношением

где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 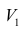 должен быть найден при условии
должен быть найден при условии
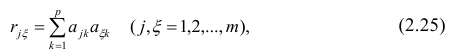
где 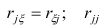 —общность
—общность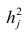 параметра
параметра
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора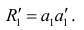 Имея эту матрицу, получают первую матрицу остатков:
Имея эту матрицу, получают первую матрицу остатков: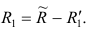
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 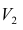 находят из условия
находят из условия
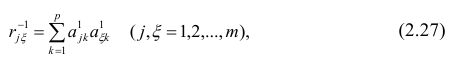
где 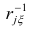 — коэффициент корреляции из первой матрицы остатков;
— коэффициент корреляции из первой матрицы остатков; 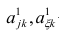 — факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков:
— факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков: 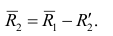
Факторный анализ учитывает суммарную общность. Исходная суммарная общность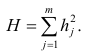 Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на
Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на 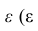 — наперёд заданное малое число).
— наперёд заданное малое число).
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных 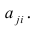
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
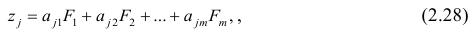
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 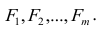 По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
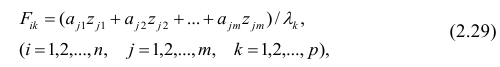
где 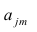 — элементы факторного решения:
— элементы факторного решения: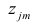 — исходные переменные;
— исходные переменные; 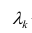 .— k-е собственное значение; р — количество оставленных главных
.— k-е собственное значение; р — количество оставленных главных
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента 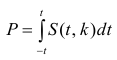
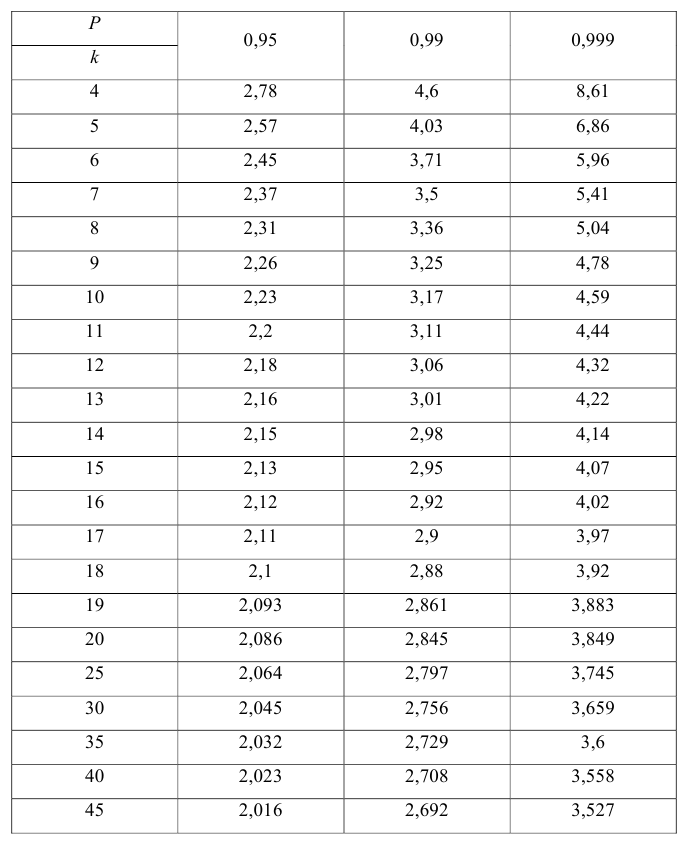
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 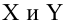 связаны линейной корреляционной зависимостью
связаны линейной корреляционной зависимостью 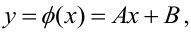 для отыскания которой проведено
для отыскания которой проведено 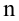 независимых измерений
независимых измерений 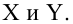
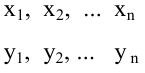
Диаграмма рассеяния (разброса, рассеивания)
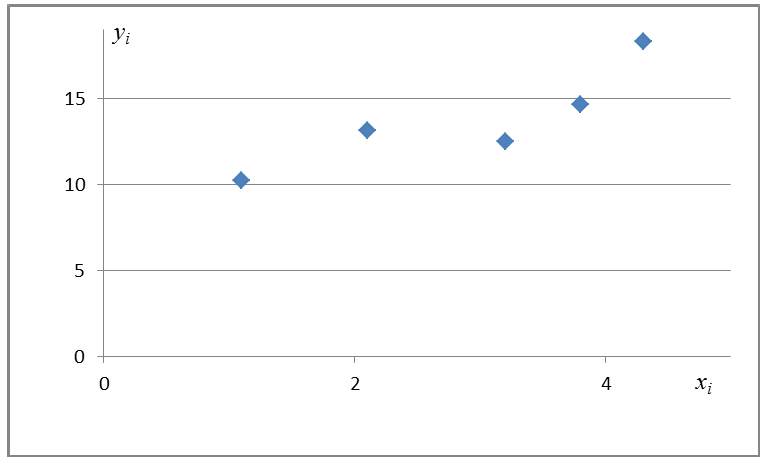
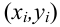 — координаты экспериментальных точек.
— координаты экспериментальных точек.
Выборочное уравнение прямой линии регрессии 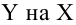 имеет вид
имеет вид
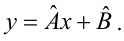
Задача: подобрать 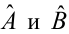 таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой
таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой 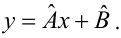
Для того, что бы провести прямую 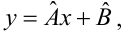 воспользуемся МНК. Потребуем,
воспользуемся МНК. Потребуем,
чтобы 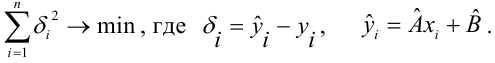
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
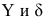 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.- Дисперсия
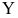 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения. - Результаты наблюдений
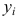 в разных точках независимы.
в разных точках независимы. - Входные переменные
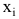 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 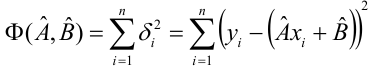 и найдём её минимальное значение
и найдём её минимальное значение
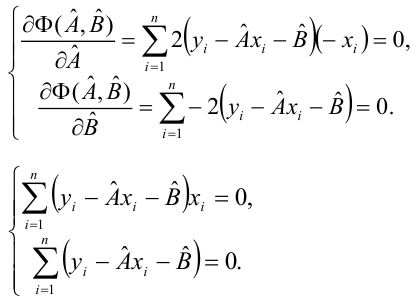
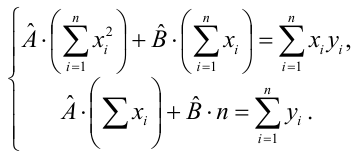
Решив систему, получим искомые значения 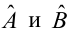
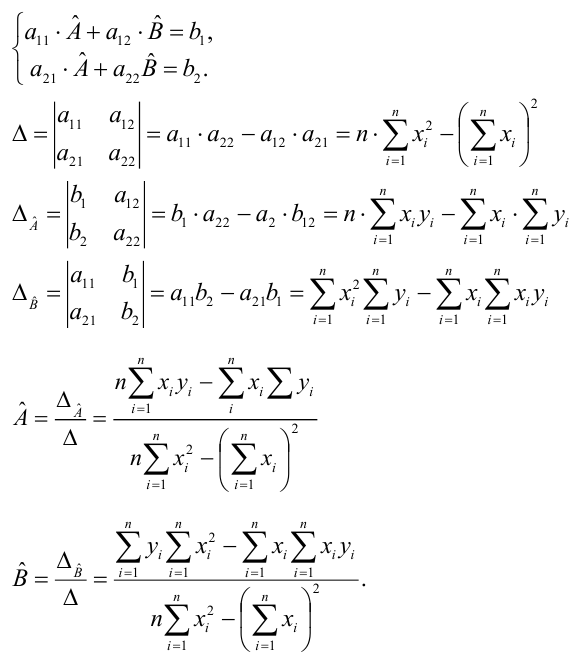
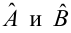 является несмещенными оценками истинных значений коэффициентов
является несмещенными оценками истинных значений коэффициентов 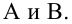
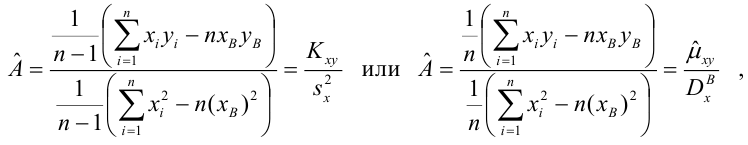 где
где
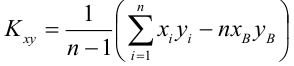 несмещенная оценка корреляционного момента (ковариации),
несмещенная оценка корреляционного момента (ковариации),
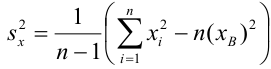 несмещенная оценка дисперсии
несмещенная оценка дисперсии 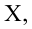
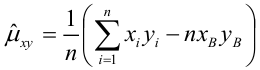 выборочная ковариация,
выборочная ковариация,
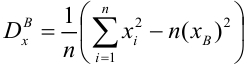 выборочная дисперсия
выборочная дисперсия 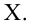
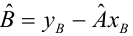
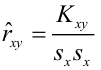 — выборочный коэффициент корреляции
— выборочный коэффициент корреляции
Коэффициент детерминации
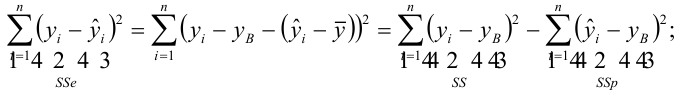
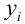 — наблюдаемое экспериментальное значение
— наблюдаемое экспериментальное значение 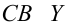 при
при 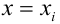
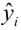 — предсказанное значение
— предсказанное значение 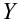 удовлетворяющее уравнению регрессии
удовлетворяющее уравнению регрессии
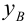 — средневыборочное значение
— средневыборочное значение 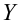
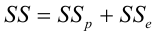
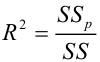 — коэффициент детерминации, доля изменчивости
— коэффициент детерминации, доля изменчивости 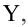 объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии
объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии 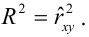
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
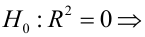 регрессия незначима
регрессия незначима
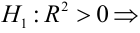 регрессия значима
регрессия значима
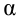 — уровень значимости
— уровень значимости
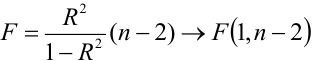 — статистический критерий
— статистический критерий
Критическая область — правосторонняя; 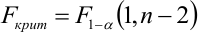
Если 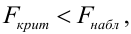 то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
Мощность статистического критерия. Функция мощности
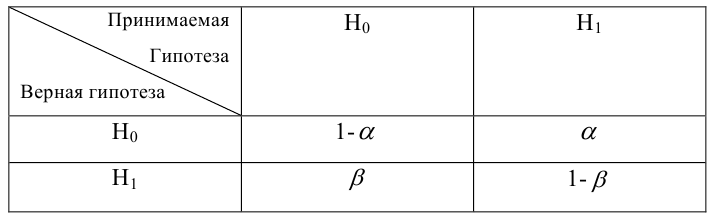
Определение. Мощностью критерия 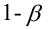 называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода 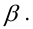
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 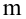 и дисперсией
и дисперсией 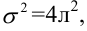 проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
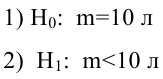
3) Уровень значимости 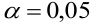
4) Статистический критерий
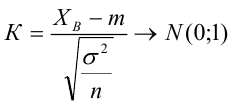
5) Критическая область — левосторонняя
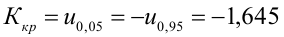
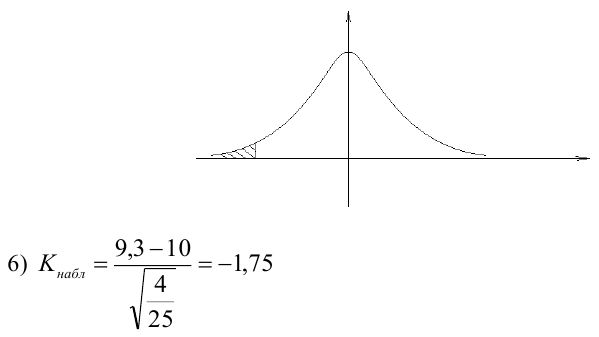
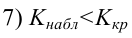 следовательно
следовательно 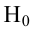 отвергается на уровне значимости
отвергается на уровне значимости 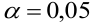
Пример:
В условиях примера 1 предположим, что наряду с 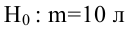 рассматривается конкурирующая гипотеза
рассматривается конкурирующая гипотеза 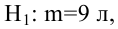 а критическая область задана неравенством
а критическая область задана неравенством 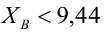 Найти вероятность ошибок I рода и II рода.
Найти вероятность ошибок I рода и II рода.
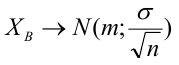
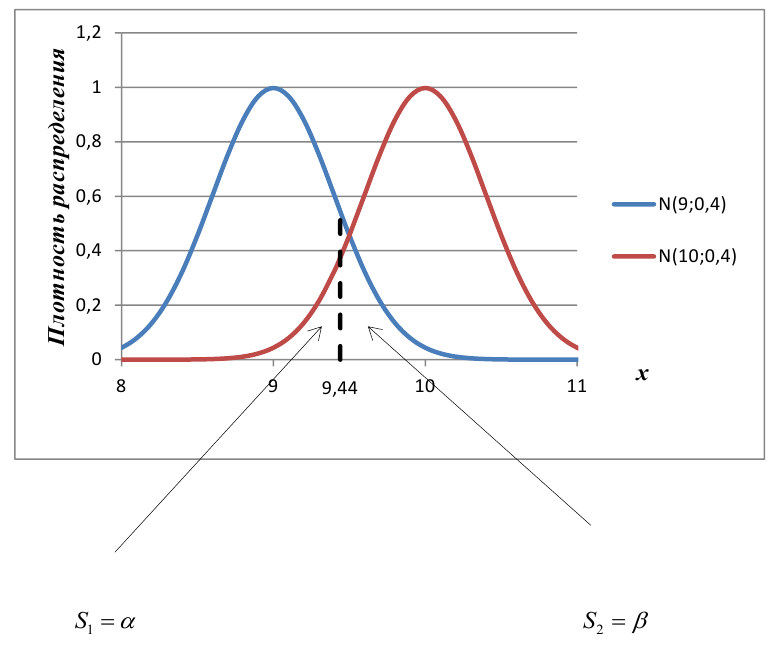
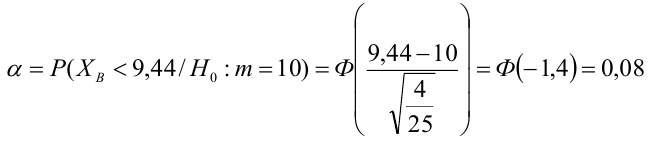
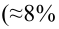 автомобилей имеют меньший расход топлива)
автомобилей имеют меньший расход топлива)
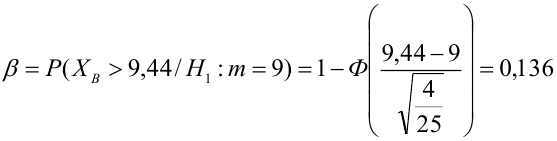
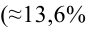 автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
Определение. Пусть проверяется 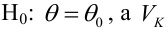 — критическая область критерия с заданным уровнем значимости
— критическая область критерия с заданным уровнем значимости 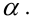 Функцией мощности критерия
Функцией мощности критерия 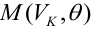 называется вероятность отклонения
называется вероятность отклонения  как функция параметра
как функция параметра 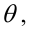 т.е.
т.е.
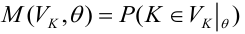
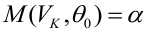 — ошибка 1-ого рода
— ошибка 1-ого рода
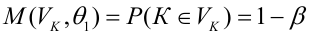 — мощность критерия
— мощность критерия
Пример:
Построить график функции мощности из примера 2 для 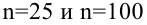
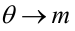
 попадает в критическую область.
попадает в критическую область.
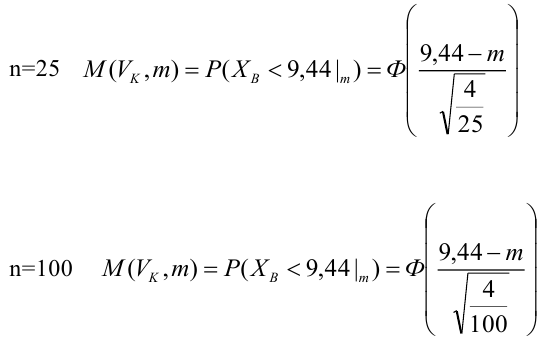
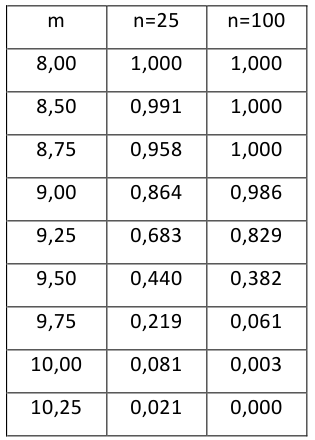
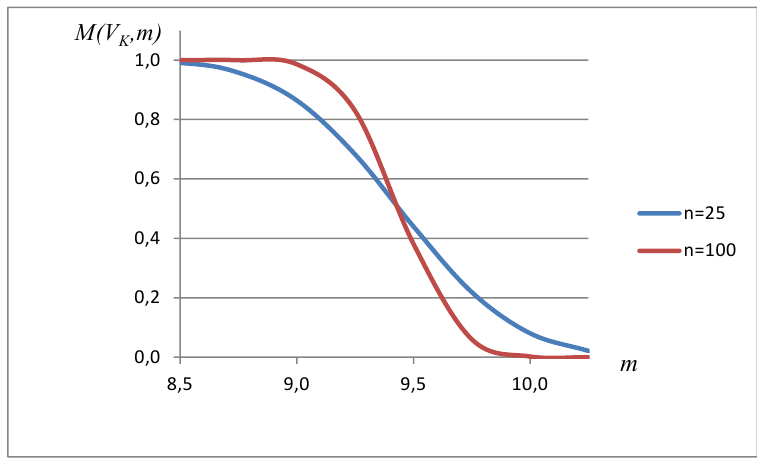
Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить 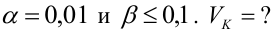
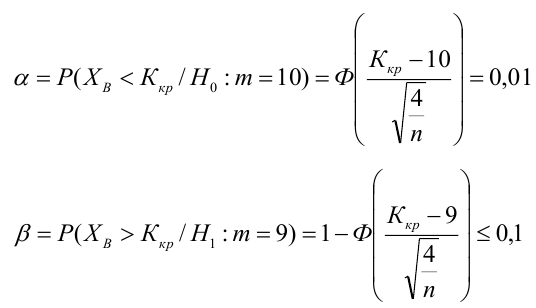
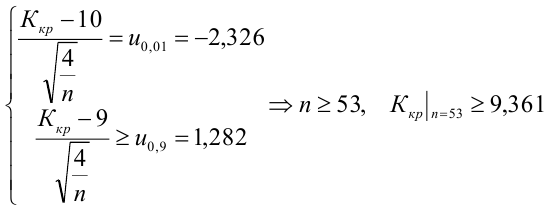
Лемма Неймана-Пирсона.
При проверке простой гипотезы 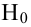 против простой альтернативной гипотезы
против простой альтернативной гипотезы 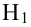 наилучшая критическая область (НКО) критерия заданного уровня значимости
наилучшая критическая область (НКО) критерия заданного уровня значимости 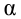 состоит из точек выборочного пространства (выборок объема
состоит из точек выборочного пространства (выборок объема 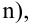 для которых справедливо неравенство:
для которых справедливо неравенство:
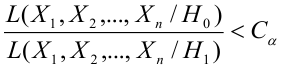
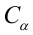 — константа, зависящая от
— константа, зависящая от 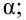
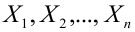 — элементы выборки;
— элементы выборки;
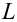 — функция правдоподобия при условии, что соответствующая гипотеза верна.
— функция правдоподобия при условии, что соответствующая гипотеза верна.
Пример:
Случайная величина 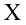 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 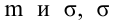 известно. Найти НКО для проверки
известно. Найти НКО для проверки 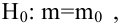 против
против 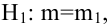 причем
причем 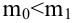
Решение:
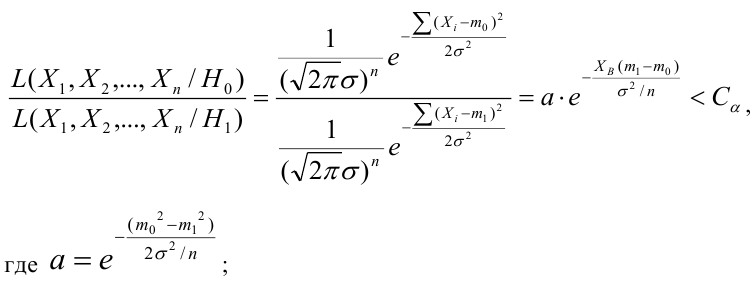
Ошибка первого рода: 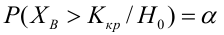
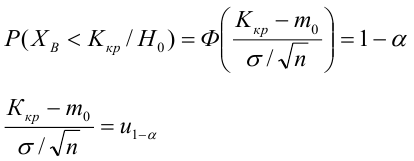
НКО: 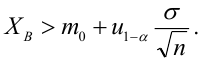
Пример:
Для зависимости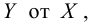 заданной корреляционной табл. 13, найти оценки параметров
заданной корреляционной табл. 13, найти оценки параметров 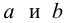 уравнения линейной регрессии
уравнения линейной регрессии 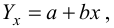 остаточную дисперсию; выяснить значимость уравнения регрессии при
остаточную дисперсию; выяснить значимость уравнения регрессии при 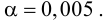
Решение. Воспользуемся предыдущими результатами
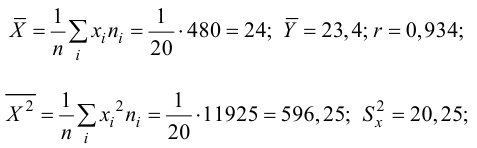
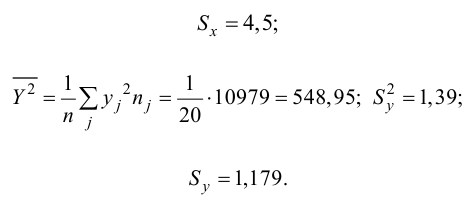
Согласно формуле (24), уравнение регрессии будет иметь вид 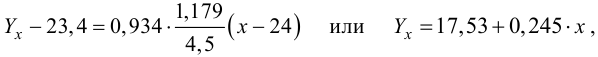 тогда
тогда 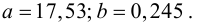
Для выяснения значимости уравнения регрессии вычислим суммы 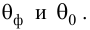 Составим расчетную таблицу:
Составим расчетную таблицу:
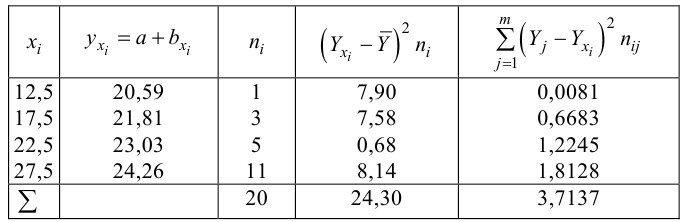
Из (27) и (28) по данным таблицы получим 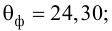
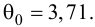
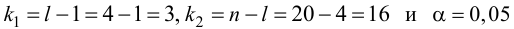 по табл. П7 находим
по табл. П7 находим 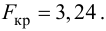
Вычислим статистику
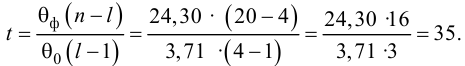
Так как 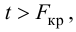 то уравнение регрессии значимо. Остаточная дисперсия равна
то уравнение регрессии значимо. Остаточная дисперсия равна 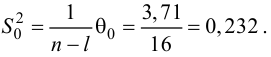
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
Корреляция и регрессия
Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
Уравнение регрессии:
y = 68.16 x — 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (yi— y ) 2 | (y-y(x)) 2 | (xi— x ) 2 | |y — yx|:y |
| 0.371 | 15.6 | 0.1376 | 243.36 | 5.79 | 14.11 | 780.89 | 2.21 | 0.1864 | 0.0953 |
| 0.399 | 19.9 | 0.1592 | 396.01 | 7.94 | 16.02 | 559.06 | 15.04 | 0.163 | 0.1949 |
| 0.502 | 22.7 | 0.252 | 515.29 | 11.4 | 23.04 | 434.49 | 0.1176 | 0.0905 | 0.0151 |
| 0.572 | 34.2 | 0.3272 | 1169.64 | 19.56 | 27.81 | 87.32 | 40.78 | 0.0533 | 0.1867 |
| 0.607 | 44.5 | .3684 | 1980.25 | 27.01 | 30.2 | 0.9131 | 204.49 | 0.0383 | 0.3214 |
| 0.655 | 26.8 | 0.429 | 718.24 | 17.55 | 33.47 | 280.38 | 44.51 | 0.0218 | 0.2489 |
| 0.763 | 35.7 | 0.5822 | 1274.49 | 27.24 | 40.83 | 61.54 | 26.35 | 0.0016 | 0.1438 |
| 0.873 | 30.6 | 0.7621 | 936.36 | 26.71 | 48.33 | 167.56 | 314.39 | 0.0049 | 0.5794 |
| 2.48 | 161.9 | 6.17 | 26211.61 | 402 | 158.07 | 14008.04 | 14.66 | 2.82 | 0.0236 |
| 7.23 | 391.9 | 9.18 | 33445.25 | 545.2 | 391.9 | 16380.18 | 662.54 | 3.38 | 1.81 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим tкрит:
tкрит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx i ± ε)
где
| xi | y = -11.17 + 68.16xi | εi | ymin | ymax |
| 0.371 | 14.11 | 19.91 | -5.8 | 34.02 |
| 0.399 | 16.02 | 19.85 | -3.83 | 35.87 |
| 0.502 | 23.04 | 19.67 | 3.38 | 42.71 |
| 0.572 | 27.81 | 19.57 | 8.24 | 47.38 |
| 0.607 | 30.2 | 19.53 | 10.67 | 49.73 |
| 0.655 | 33.47 | 19.49 | 13.98 | 52.96 |
| 0.763 | 40.83 | 19.44 | 21.4 | 60.27 |
| 0.873 | 48.33 | 19.45 | 28.88 | 67.78 |
| 2.48 | 158.07 | 25.72 | 132.36 | 183.79 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — ta)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
Случайная ошибка модели регрессии в уравнении регрессии
Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования зависимостей между социально-экономическими переменными. Эту задачу мы рассмотрим в рамках самой распространенной в статистических пакетах классической модели линейной регрессии.
Специфика социологических исследований состоит в том, что очень часто необходимо изучать и предсказывать социальные события. Вторая часть данной главы будет посвящена логистической регрессии, целью которой является построение моделей, предсказывающих вероятности событий.
Линейная модель связывает значения зависимой переменной Y со значениями независимых показателей X k (факторов) формулой:
Y=B 0 +B 1 X 1 +:+B p X p + e
где e — случайная ошибка. Здесь X k означает не «икс в степени k «, а переменная X с индексом k .
Традиционные названия «зависимая» для Y и «независимые» для X k отражают не столько статистический смысл зависимости, сколько их содержательную интерпретацию.
Величина e называется ошибкой регрессии. Первые математические результаты, связанные с регрессионным анализом, сделаны в предположении, что регрессионная ошибка распределена нормально с параметрами N(0,? 2 ) , ошибка для различных объектов считаются независимыми. Кроме того, в данной модели мы рассматриваем переменные X как неслучайные значения, Такое, на практике, получается, когда идет активный эксперимент, в котором задают значения X (например, назначили зарплату работнику), а затем измеряют Y (оценили, какой стала производительность труда). За это иногда зависимую переменную называют откликом. Теория регрессионных уравнений со случайными независимыми переменными сложнее, но известно, что, при большом числе наблюдений, использование метода разработанного для неслучайных X корректно.
Благодаря полученным оценкам коэффициентов уравнения регрессии могут быть оценены прогнозные значения зависимой переменной , причем они могут быть вычислены и там, где значения y определены, и там где они не определены. Прогнозные значения являются оценками средних, ожидаемых по модели значений Y , зависящих от X .
Поскольку коэффициенты регрессии — случайные величины, линия регрессии также случайна. Поэтому прогнозные значения случайны и имеют некоторое стандартное отклонение , зависящее от X . Благодаря этому можно получить и доверительные границы для прогнозных значений регрессии (средних значений y ).
Кроме того, с учетом дисперсии остатка могут быть вычислены доверительные границы значений Y (не средних, а индивидуальных!).
Для каждого объекта может быть вычислен остаток e i =  . Остаток полезен для изучения адеквантности модели данным. Это означает, что должны быть выполнены требования о независимости остатков для отдельных наблюдений, дисперсия не должна зависеть от X .
. Остаток полезен для изучения адеквантности модели данным. Это означает, что должны быть выполнены требования о независимости остатков для отдельных наблюдений, дисперсия не должна зависеть от X .
Для изучения отклонений от модели удобно использовать стандартизованный остаток — деленный на стандартную ошибку регрессии.
Случайность оценки прогнозных значений Y вносит дополнительную дисперсию в регрессионный остаток, из-за этого дисперсия остатка зависит от значений независимых переменных (  ). Стьюдентеризованный остаток — это остаток деленный на оценку дисперсии остатка:
). Стьюдентеризованный остаток — это остаток деленный на оценку дисперсии остатка:  .
.
Таким образом, мы можем получить: оценку (прогнозную) значений зависимой переменной Unstandardized predicted value), ее стандартное отклонение (S.E. of mean predictions), доверительные интервалы для среднего Y(X) и для Y(X) (Prediction intervals — Mean, Individual).
Это далеко не полный перечень переменных, порождаемых SPSS.
Пусть прогнозируется вес ребенка в зависимости от его возраста. Ясно, что дисперсия веса для четырехлетнего младенца будет значительно меньше, чем дисперсия веса 14-летнего юноши. Таким образом, дисперсия остатка e i зависит от значений X , а значит условия для оценки регрессионной зависимости не выполнены. Проблема неоднородности дисперсии в регрессионном анализе называется проблемой гетероскедастичности.
В SPSS имеется возможность корректно сделать соответствующие оценки за счет приписывания весов слагаемым минимизируемой суммы квадратов. Эта весовая функция должна быть равна 1/? 2 (x) , где ? 2 (x) — дисперсия y как функция от x . Естественно, чем меньше дисперсия остатка на объекте, тем больший вес он будет иметь. В качестве такой функции можно использовать ее оценку, полученную при фиксированных значениях X .
Например, в приведенном примере на достаточно больших данных можно оценить дисперсию для каждой возрастной группы и вычислить необходимую весовую переменную. Увеличение влияния возрастных групп с меньшим возрастом в данном случае вполне оправдано.
В диалоговом окне назначение весовой переменной производится с помощью кнопки WLS (Weighed Least Squares — метод взвешенных наименьших квадратов).
В меню — это команда Linear Regression. В диалоговом окне команды:
— Назначаются независимые и зависимая переменные,
— Назначается метод отбора переменных. STEPWISE — пошаговое включение/удаление переменных. FORWARD — пошаговое включение переменных. BACKWARD — пошаговое исключение переменных. При пошаговом алгоритме назначаются значимости включения и исключения переменных (OPTIONS). ENTER — принудительное включение.
— Имеется возможность отбора данных, на которых будет оценена модель (Selection). Для остальных данных могут быть оценены прогнозные значения функции регрессии, его стандартные отклонения и др.
— Назначения вывода статистик (Statistics) — доверительные коэффициенты коэффициентов регресии, их ковариационная матрица, статистики Дарбина-Уотсона и пр.
— Задаются графики рассеяния остатков, их гистограммы (Plots)
— Назначаются сохранение переменных(Save), порождаемых регрессией.
— Если используется пошаговая регрессия, назначаются пороговые значимости для включения (PIN) и исключения (POUT) переменных (Options).
— Если обнаружена гетероскедастичность, назначается и весовая переменная.
Обычно демонстрацию модели начинают с простейшего примера, и такие примеры Вы можете найти в Руководстве по применению SPSS. Мы пойдем немного дальше и покажем, как получить полиномиальную регрессию.
Курильский опрос касался населения трудоспособного возраста. Как показали расчеты, в среднем меньшие доходы имеют молодые люди и люди старшего возраста. Поэтому, прогнозировать доход лучше квадратичной кривой, а не простой линейной зависимостью. В рамках линейной модели это можно сделать, введя переменную — квадрат возраста. Приведенное ниже задание SPSS предназначено для прогноза логарифма промедианного дохода (ранее сформированного).
REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2
/SAVE PRED MCIN ICIN.
*регрессия с сохранением предсказанных значений и доверительных интервалов средних и индивидуальных прогнозных значений.
Таблица 5.1 показывает, что уравнение объясняет всего 4.5% дисперсии зависимой переменной (коэффициент детерминации R 2 =.045), скорректированная величина коэффициента равна 0.042, а коэффициент множественной корреляции равен 0.211. Много это или мало, трудно сказать, поскольку у нас нет подобных результатов на других данных, но то, что здесь есть взаимосвязь, можно понять, рассматривая таблицу 6.2.
Таблица 6.1. Общие характеристики уравнения
Adjusted R Square
Std. Error of the Estimate
a Predictors: (Constant), V9_2, V9 Возраст
b Dependent Variable: LNV14M логарифм промедианного дохода
Результаты дисперсионного анализа уравнения регрессии показывает, что гипотеза равенства всех коэффициентов регрессии нулю должна быть отклонена.
Таблица 6.2. Дисперсионный анализ уравнения
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
источники:
http://masters.donntu.org/2005/fvti/scherbak/library/doc_1.htm
http://statistica.ru/theory/osnovy-lineynoy-regressii/
Регрессия
– способ предсказания значения одних
переменных по значениям других.
Регрессионная
модель –
это уравнение, в котором объясняемая
переменная представляется в виде функций
от объясняющих переменных факторов.
Задача:
на основе эмпирических данных определить
объясняемую часть и получить оценку
распределения случайной части. Суть:
построить регрессию и определить
параметры модели.
Парная
линейная регрессия —
модель статистической линейной связи
между двумя количественными переменными
х и у, представленная уравнением y = a +
bx, где х — переменная независимая , y —
переменная зависимая – либо в другой
записи Y=B0+B1Xt+Et; Xt-детерминированная
величина, Yt-объясняемая переменная, Et
– случайная величина.
Детерминированной
называется переменная, которая в
результате любого числа испытаний
принимается одно и тоже конкретное
значение из своего множества возможных
значений, например, число этажей в
конкретном доме
Парная регрессия.
(xi,yi);
i=1,…,n
Предполагаем,
что yi представляем в виде
Yi=α+βxi+
εi
Смысл
εi – однозначно для каждого х мы
прогнозировать у не можем
Возникает
вопрос о причинах
обязательного присутствия в регрессионных
моделях случайного фактора (отклонения).
Среди таких причин можно выделить
наиболее
существенные:
не включение в модель всех объясняющих
переменных, неправильный выбор
функциональной формы модели, агрегирование
переменных, ошибки измерений,
ограниченность
статистических данных, непредсказуемость
человеческого фактора.
М(у/Х=хi)=
α+βxi (мат ожидание у при условии, что
Х=хi…)
α
и β – истинные значения коэф регрессии
По
заданным х и у надо найти α и β
Пусть
есть набор значений двух переменных X
и Y:
![]()
,…,![]()
.
Между
ними есть объективная связь Y=f(X). Нужно
по имеющимся данным наблюдений подобрать
функцию
![]()
,
которая наилучшим образом показывает
истинную зависимость.
![]()
,
![]()
-неизвестные.
Е
сли
каждую пару представить точкой, то
картинка будет – диаграмма рассеяния
(корреляционное поле). Требуется найти
значения коэффициентов в этой зависимости.
Зависимость линейная ŷ= a + bx a^=y
– b^x
b^=( xy — xy)
/ (x2
– (x)2)
– в числителе: среднее произведение
минус произведение средних. В знаменателе:
средний квадрат фактора минус квадрат
среднего.
Наблюдаемые
и расчетные значения объясняющей
переменной

e
– остаток
(отклонение, ошибка) – разность между
наблюдаемым и расчетным значением.
Остаток всегда имеет знак. Остатки
наблюдаемы. Надо провести линию регрессии
так, чтобы остатки были меньше. Т.о.
задача линейной регрессии – провести
прямую линию, наилучшим образом
приближающую наблюдаемые точки. Провести
прямую – найти а и b.
Метод наименьших квадратов
Это
метод для оценки неизвестных величин
по результатам измерений, содержащим
случайные ошибки. МНК применяется также
для приближённого представления заданной
функции другими (более простыми)
функциями.
В методе
наименьших квадратов (МНК) по заданным
экспериментальным точкам строится
теоретическая функциональная зависимость.
Для функции одной переменной по n точкам
(xi,yi) ищется «наилучшая» теоретическая
кривая y=f(x).
Суть
– найти такие коэффициенты a и b, кот.
минимизируют сумму квадратов отклонений
расчетных значений объясняемой переменной
от наблюдаемых значений.
Ŷi=a+bxi
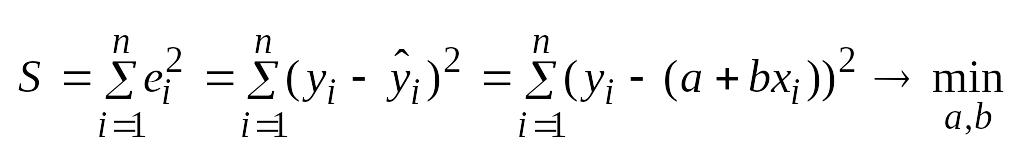
в
точке
![]()
.
ei=y-ŷ
→ ei2
=
(y-ŷ)2
ŷ
= a+bx
Надо
построить необходимое
условие экстремума (частные производные
каждого bj приравниваем к нулю) и решить
полученную нормальную систему уравнений
линейной регрессии.
Необходимое
условие экстремума:
если есть функция нескольких переменных
S(a,b) то, чтобы найти её экстремум нужно
приравнять нулю все её частные производные
и решить полученную систему уравнений:
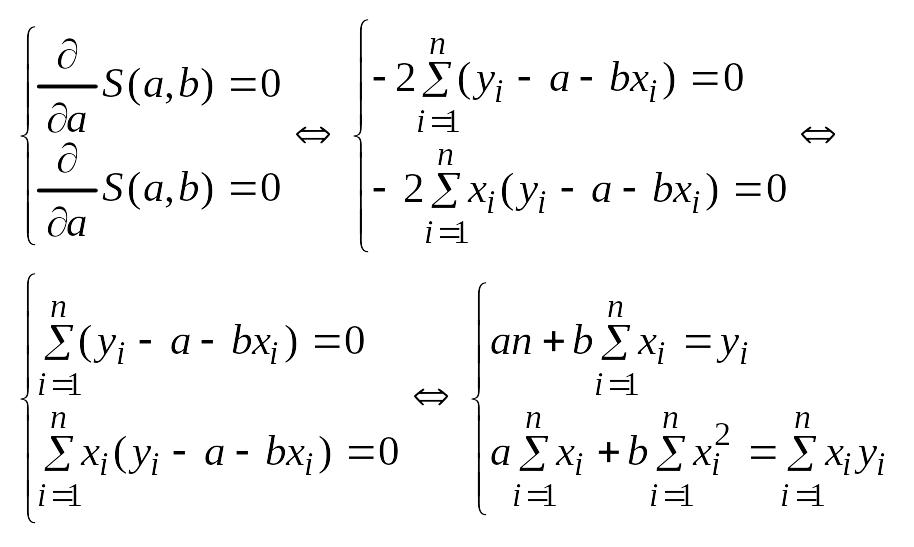
[(yi-(α+βxi)2]’α=
-2(yi-(α+βxi))
[(yi-(α+βxi)2]’β
= -2(yi-(α+βxi))xi
Реш-е
системы это оценка а и b
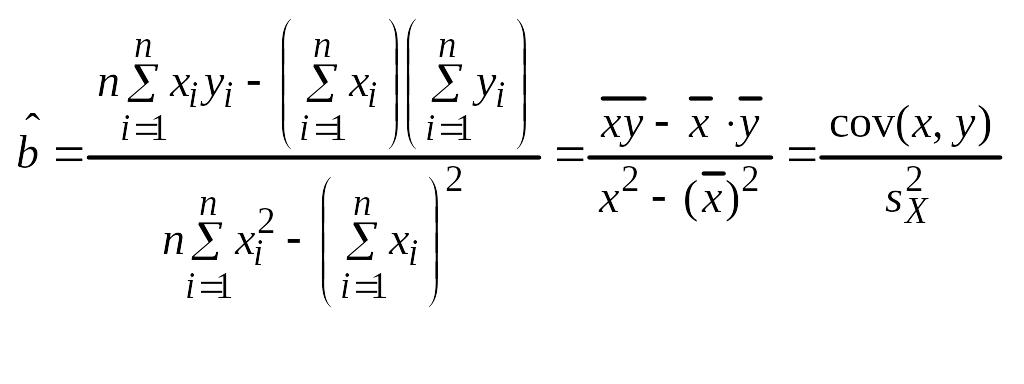
В
X(c чер)
= 1/n Σn
i=1 xi
Y(c чер)
= 1/n Σn
i=1 yi
числителе – выборочная оценка
ковариации; в знаменателе – выборочная
оценка дисперсии фактора.
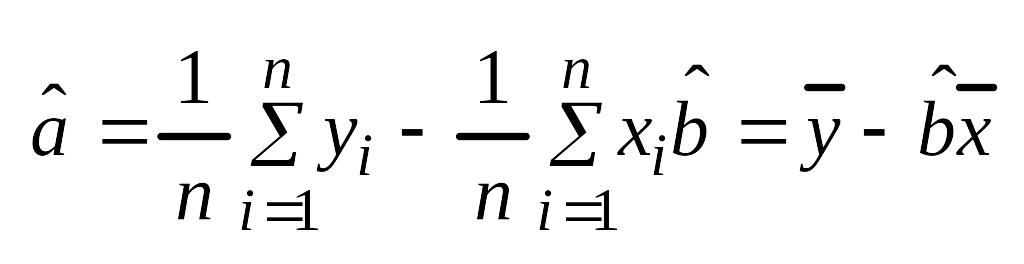
Интерпретация
— С ростом Х на 1, Y изменится на значение
b.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the ‘outcome’ or ‘response’ variable, or a ‘label’ in machine learning parlance) and one or more independent variables (often called ‘predictors’, ‘covariates’, ‘explanatory variables’ or ‘features’). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters (e.g., quantile regression or Necessary Condition Analysis[1]) or estimate the conditional expectation across a broader collection of non-linear models (e.g., nonparametric regression).
Regression analysis is primarily used for two conceptually distinct purposes. First, regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of machine learning. Second, in some situations regression analysis can be used to infer causal relationships between the independent and dependent variables. Importantly, regressions by themselves only reveal relationships between a dependent variable and a collection of independent variables in a fixed dataset. To use regressions for prediction or to infer causal relationships, respectively, a researcher must carefully justify why existing relationships have predictive power for a new context or why a relationship between two variables has a causal interpretation. The latter is especially important when researchers hope to estimate causal relationships using observational data.[2][3]
History[edit]
The earliest form of regression was the method of least squares, which was published by Legendre in 1805,[4] and by Gauss in 1809.[5] Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the Sun (mostly comets, but also later the then newly discovered minor planets). Gauss published a further development of the theory of least squares in 1821,[6] including a version of the Gauss–Markov theorem.
The term «regression» was coined by Francis Galton in the 19th century to describe a biological phenomenon. The phenomenon was that the heights of descendants of tall ancestors tend to regress down towards a normal average (a phenomenon also known as regression toward the mean).[7][8]
For Galton, regression had only this biological meaning,[9][10] but his work was later extended by Udny Yule and Karl Pearson to a more general statistical context.[11][12] In the work of Yule and Pearson, the joint distribution of the response and explanatory variables is assumed to be Gaussian. This assumption was weakened by R.A. Fisher in his works of 1922 and 1925.[13][14][15] Fisher assumed that the conditional distribution of the response variable is Gaussian, but the joint distribution need not be. In this respect, Fisher’s assumption is closer to Gauss’s formulation of 1821.
In the 1950s and 1960s, economists used electromechanical desk calculators to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the result from one regression.[16]
Regression methods continue to be an area of active research. In recent decades, new methods have been developed for robust regression, regression involving correlated responses such as time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other complex data objects, regression methods accommodating various types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with error, regression with more predictor variables than observations, and causal inference with regression.
Regression model[edit]
In practice, researchers first select a model they would like to estimate and then use their chosen method (e.g., ordinary least squares) to estimate the parameters of that model. Regression models involve the following components:
In various fields of application, different terminologies are used in place of dependent and independent variables.
Most regression models propose that 




The researchers’ goal is to estimate the function 






Once researchers determine their preferred statistical model, different forms of regression analysis provide tools to estimate the parameters 










It is important to note that there must be sufficient data to estimate a regression model. For example, suppose that a researcher has access to 








More generally, to estimate a least squares model with 






Underlying assumptions[edit]
By itself, a regression is simply a calculation using the data. In order to interpret the output of regression as a meaningful statistical quantity that measures real-world relationships, researchers often rely on a number of classical assumptions. These assumptions often include:
A handful of conditions are sufficient for the least-squares estimator to possess desirable properties: in particular, the Gauss–Markov assumptions imply that the parameter estimates will be unbiased, consistent, and efficient in the class of linear unbiased estimators. Practitioners have developed a variety of methods to maintain some or all of these desirable properties in real-world settings, because these classical assumptions are unlikely to hold exactly. For example, modeling errors-in-variables can lead to reasonable estimates independent variables are measured with errors. Heteroscedasticity-consistent standard errors allow the variance of 


Linear regression[edit]
In linear regression, the model specification is that the dependent variable, 




- straight line:
In multiple linear regression, there are several independent variables or functions of independent variables.
Adding a term in 
- parabola:
This is still linear regression; although the expression on the right hand side is quadratic in the independent variable 



In both cases, 

Returning our attention to the straight line case: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:
The residual, 


Minimization of this function results in a set of normal equations, a set of simultaneous linear equations in the parameters, which are solved to yield the parameter estimators, 

Illustration of linear regression on a data set
In the case of simple regression, the formulas for the least squares estimates are
where 



Under the assumption that the population error term has a constant variance, the estimate of that variance is given by:
This is called the mean square error (MSE) of the regression. The denominator is the sample size reduced by the number of model parameters estimated from the same data, 




The standard errors of the parameter estimates are given by
Under the further assumption that the population error term is normally distributed, the researcher can use these estimated standard errors to create confidence intervals and conduct hypothesis tests about the population parameters.
General linear model[edit]
In the more general multiple regression model, there are 
where 


If the first independent variable takes the value 1 for all 


The least squares parameter estimates are obtained from 
The normal equations are
In matrix notation, the normal equations are written as
where the 














Diagnostics[edit]
Once a regression model has been constructed, it may be important to confirm the goodness of fit of the model and the statistical significance of the estimated parameters. Commonly used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-test of the overall fit, followed by t-tests of individual parameters.
Interpretations of these diagnostic tests rest heavily on the model’s assumptions. Although examination of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model’s assumptions are violated. For example, if the error term does not have a normal distribution, in small samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can be invoked such that hypothesis testing may proceed using asymptotic approximations.
Limited dependent variables[edit]
Limited dependent variables, which are response variables that are categorical variables or are variables constrained to fall only in a certain range, often arise in econometrics.
The response variable may be non-continuous («limited» to lie on some subset of the real line). For binary (zero or one) variables, if analysis proceeds with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than two values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest. An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an event, then count models like the Poisson regression or the negative binomial model may be used.
Nonlinear regression[edit]
When the model function is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences between linear and non-linear least squares.
Prediction (interpolation and extrapolation) [edit]

In the middle, the interpolated straight line represents the best balance between the points above and below this line. The dotted lines represent the two extreme lines. The first curves represent the estimated values. The outer curves represent a prediction for a new measurement.[20]
Regression models predict a value of the Y variable given known values of the X variables. Prediction within the range of values in the dataset used for model-fitting is known informally as interpolation. Prediction outside this range of the data is known as extrapolation. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.
It is generally advised[citation needed] that when performing extrapolation, one should accompany the estimated value of the dependent variable with a prediction interval that represents the uncertainty. Such intervals tend to expand rapidly as the values of the independent variable(s) moved outside the range covered by the observed data.
For such reasons and others, some tend to say that it might be unwise to undertake extrapolation.[21]
However, this does not cover the full set of modeling errors that may be made: in particular, the assumption of a particular form for the relation between Y and X. A properly conducted regression analysis will include an assessment of how well the assumed form is matched by the observed data, but it can only do so within the range of values of the independent variables actually available. This means that any extrapolation is particularly reliant on the assumptions being made about the structural form of the regression relationship. Best-practice advice here[citation needed] is that a linear-in-variables and linear-in-parameters relationship should not be chosen simply for computational convenience, but that all available knowledge should be deployed in constructing a regression model. If this knowledge includes the fact that the dependent variable cannot go outside a certain range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly near such bounds. The implications of this step of choosing an appropriate functional form for the regression can be great when extrapolation is considered. At a minimum, it can ensure that any extrapolation arising from a fitted model is «realistic» (or in accord with what is known).
Power and sample size calculations[edit]
There are no generally agreed methods for relating the number of observations versus the number of independent variables in the model. One method conjectured by Good and Hardin is 





Other methods[edit]
Although the parameters of a regression model are usually estimated using the method of least squares, other methods which have been used include:
- Bayesian methods, e.g. Bayesian linear regression
- Percentage regression, for situations where reducing percentage errors is deemed more appropriate.[23]
- Least absolute deviations, which is more robust in the presence of outliers, leading to quantile regression
- Nonparametric regression, requires a large number of observations and is computationally intensive
- Scenario optimization, leading to interval predictor models
- Distance metric learning, which is learned by the search of a meaningful distance metric in a given input space.[24]
Software[edit]
All major statistical software packages perform least squares regression analysis and inference. Simple linear regression and multiple regression using least squares can be done in some spreadsheet applications and on some calculators. While many statistical software packages can perform various types of nonparametric and robust regression, these methods are less standardized. Different software packages implement different methods, and a method with a given name may be implemented differently in different packages. Specialized regression software has been developed for use in fields such as survey analysis and neuroimaging.
See also[edit]
- Anscombe’s quartet
- Curve fitting
- Estimation theory
- Forecasting
- Fraction of variance unexplained
- Function approximation
- Generalized linear model
- Kriging (a linear least squares estimation algorithm)
- Local regression
- Modifiable areal unit problem
- Multivariate adaptive regression spline
- Multivariate normal distribution
- Pearson correlation coefficient
- Quasi-variance
- Prediction interval
- Regression validation
- Robust regression
- Segmented regression
- Signal processing
- Stepwise regression
- Taxicab geometry
- Linear trend estimation
References[edit]
- ^ Necessary Condition Analysis
- ^ David A. Freedman (27 April 2009). Statistical Models: Theory and Practice. Cambridge University Press. ISBN 978-1-139-47731-4.
- ^ R. Dennis Cook; Sanford Weisberg Criticism and Influence Analysis in Regression, Sociological Methodology, Vol. 13. (1982), pp. 313–361
- ^ A.M. Legendre. Nouvelles méthodes pour la détermination des orbites des comètes, Firmin Didot, Paris, 1805. “Sur la Méthode des moindres quarrés” appears as an appendix.
- ^ a b Chapter 1 of: Angrist, J. D., & Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press.
- ^ C.F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. (1821/1823)
- ^
Mogull, Robert G. (2004). Second-Semester Applied Statistics. Kendall/Hunt Publishing Company. p. 59. ISBN 978-0-7575-1181-3. - ^ Galton, Francis (1989). «Kinship and Correlation (reprinted 1989)». Statistical Science. 4 (2): 80–86. doi:10.1214/ss/1177012581. JSTOR 2245330.
- ^ Francis Galton. «Typical laws of heredity», Nature 15 (1877), 492–495, 512–514, 532–533. (Galton uses the term «reversion» in this paper, which discusses the size of peas.)
- ^ Francis Galton. Presidential address, Section H, Anthropology. (1885) (Galton uses the term «regression» in this paper, which discusses the height of humans.)
- ^ Yule, G. Udny (1897). «On the Theory of Correlation». Journal of the Royal Statistical Society. 60 (4): 812–54. doi:10.2307/2979746. JSTOR 2979746.
- ^ Pearson, Karl; Yule, G.U.; Blanchard, Norman; Lee, Alice (1903). «The Law of Ancestral Heredity». Biometrika. 2 (2): 211–236. doi:10.1093/biomet/2.2.211. JSTOR 2331683.
- ^ Fisher, R.A. (1922). «The goodness of fit of regression formulae, and the distribution of regression coefficients». Journal of the Royal Statistical Society. 85 (4): 597–612. doi:10.2307/2341124. JSTOR 2341124. PMC 1084801.
- ^ Ronald A. Fisher (1954). Statistical Methods for Research Workers (Twelfth ed.). Edinburgh: Oliver and Boyd. ISBN 978-0-05-002170-5.
- ^ Aldrich, John (2005). «Fisher and Regression». Statistical Science. 20 (4): 401–417. doi:10.1214/088342305000000331. JSTOR 20061201.
- ^ Rodney Ramcharan. Regressions: Why Are Economists Obessessed with Them? March 2006. Accessed 2011-12-03.
- ^ Fotheringham, A. Stewart; Brunsdon, Chris; Charlton, Martin (2002). Geographically weighted regression: the analysis of spatially varying relationships (Reprint ed.). Chichester, England: John Wiley. ISBN 978-0-471-49616-8.
- ^ Fotheringham, AS; Wong, DWS (1 January 1991). «The modifiable areal unit problem in multivariate statistical analysis». Environment and Planning A. 23 (7): 1025–1044. doi:10.1068/a231025. S2CID 153979055.
- ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Rouaud, Mathieu (2013). Probability, Statistics and Estimation (PDF). p. 60.
- ^ Chiang, C.L, (2003) Statistical methods of analysis, World Scientific. ISBN 981-238-310-7 — page 274 section 9.7.4 «interpolation vs extrapolation»
- ^ Good, P. I.; Hardin, J. W. (2009). Common Errors in Statistics (And How to Avoid Them) (3rd ed.). Hoboken, New Jersey: Wiley. p. 211. ISBN 978-0-470-45798-6.
- ^ Tofallis, C. (2009). «Least Squares Percentage Regression». Journal of Modern Applied Statistical Methods. 7: 526–534. doi:10.2139/ssrn.1406472. SSRN 1406472.
- ^ YangJing Long (2009). «Human age estimation by metric learning for regression problems» (PDF). Proc. International Conference on Computer Analysis of Images and Patterns: 74–82. Archived from the original (PDF) on 2010-01-08.
Further reading[edit]
- William H. Kruskal and Judith M. Tanur, ed. (1978), «Linear Hypotheses,» International Encyclopedia of Statistics. Free Press, v. 1,
- Evan J. Williams, «I. Regression,» pp. 523–41.
- Julian C. Stanley, «II. Analysis of Variance,» pp. 541–554.
- Lindley, D.V. (1987). «Regression and correlation analysis,» New Palgrave: A Dictionary of Economics, v. 4, pp. 120–23.
- Birkes, David and Dodge, Y., Alternative Methods of Regression. ISBN 0-471-56881-3
- Chatfield, C. (1993) «Calculating Interval Forecasts,» Journal of Business and Economic Statistics, 11. pp. 121–135.
- Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 978-0-471-17082-2.
- Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage
- Hardle, W., Applied Nonparametric Regression (1990), ISBN 0-521-42950-1
- Meade, Nigel; Islam, Towhidul (1995). «Prediction intervals for growth curve forecasts». Journal of Forecasting. 14 (5): 413–430. doi:10.1002/for.3980140502.
- A. Sen, M. Srivastava, Regression Analysis — Theory, Methods, and Applications, Springer-Verlag, Berlin, 2011 (4th printing).
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner, ISBN 978-3-8348-1022-9.
- Stulp, Freek, and Olivier Sigaud. Many Regression Algorithms, One Unified Model: A Review. Neural Networks, vol. 69, Sept. 2015, pp. 60–79. https://doi.org/10.1016/j.neunet.2015.05.005.
- Malakooti, B. (2013). Operations and Production Systems with Multiple Objectives. John Wiley & Sons.
- Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). «The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation». PeerJ Computer Science. 7 (e623): e623. doi:10.7717/peerj-cs.623. PMC 8279135. PMID 34307865.
External links[edit]
- «Regression analysis», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Earliest Uses: Regression – basic history and references
- What is multiple regression used for? – Multiple regression
- Regression of Weakly Correlated Data – how linear regression mistakes can appear when Y-range is much smaller than X-range
Корреляция и регрессия
Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
Уравнение регрессии:
y = 68.16 x — 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (yi— y ) 2 | (y-y(x)) 2 | (xi— x ) 2 | |y — yx|:y |
| 0.371 | 15.6 | 0.1376 | 243.36 | 5.79 | 14.11 | 780.89 | 2.21 | 0.1864 | 0.0953 |
| 0.399 | 19.9 | 0.1592 | 396.01 | 7.94 | 16.02 | 559.06 | 15.04 | 0.163 | 0.1949 |
| 0.502 | 22.7 | 0.252 | 515.29 | 11.4 | 23.04 | 434.49 | 0.1176 | 0.0905 | 0.0151 |
| 0.572 | 34.2 | 0.3272 | 1169.64 | 19.56 | 27.81 | 87.32 | 40.78 | 0.0533 | 0.1867 |
| 0.607 | 44.5 | .3684 | 1980.25 | 27.01 | 30.2 | 0.9131 | 204.49 | 0.0383 | 0.3214 |
| 0.655 | 26.8 | 0.429 | 718.24 | 17.55 | 33.47 | 280.38 | 44.51 | 0.0218 | 0.2489 |
| 0.763 | 35.7 | 0.5822 | 1274.49 | 27.24 | 40.83 | 61.54 | 26.35 | 0.0016 | 0.1438 |
| 0.873 | 30.6 | 0.7621 | 936.36 | 26.71 | 48.33 | 167.56 | 314.39 | 0.0049 | 0.5794 |
| 2.48 | 161.9 | 6.17 | 26211.61 | 402 | 158.07 | 14008.04 | 14.66 | 2.82 | 0.0236 |
| 7.23 | 391.9 | 9.18 | 33445.25 | 545.2 | 391.9 | 16380.18 | 662.54 | 3.38 | 1.81 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим tкрит:
tкрит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx i ± ε)
где
| xi | y = -11.17 + 68.16xi | εi | ymin | ymax |
| 0.371 | 14.11 | 19.91 | -5.8 | 34.02 |
| 0.399 | 16.02 | 19.85 | -3.83 | 35.87 |
| 0.502 | 23.04 | 19.67 | 3.38 | 42.71 |
| 0.572 | 27.81 | 19.57 | 8.24 | 47.38 |
| 0.607 | 30.2 | 19.53 | 10.67 | 49.73 |
| 0.655 | 33.47 | 19.49 | 13.98 | 52.96 |
| 0.763 | 40.83 | 19.44 | 21.4 | 60.27 |
| 0.873 | 48.33 | 19.45 | 28.88 | 67.78 |
| 2.48 | 158.07 | 25.72 | 132.36 | 183.79 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — ta)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
Случайная ошибка модели регрессии в уравнении регрессии
Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования зависимостей между социально-экономическими переменными. Эту задачу мы рассмотрим в рамках самой распространенной в статистических пакетах классической модели линейной регрессии.
Специфика социологических исследований состоит в том, что очень часто необходимо изучать и предсказывать социальные события. Вторая часть данной главы будет посвящена логистической регрессии, целью которой является построение моделей, предсказывающих вероятности событий.
Линейная модель связывает значения зависимой переменной Y со значениями независимых показателей X k (факторов) формулой:
Y=B 0 +B 1 X 1 +:+B p X p + e
где e — случайная ошибка. Здесь X k означает не «икс в степени k «, а переменная X с индексом k .
Традиционные названия «зависимая» для Y и «независимые» для X k отражают не столько статистический смысл зависимости, сколько их содержательную интерпретацию.
Величина e называется ошибкой регрессии. Первые математические результаты, связанные с регрессионным анализом, сделаны в предположении, что регрессионная ошибка распределена нормально с параметрами N(0,? 2 ) , ошибка для различных объектов считаются независимыми. Кроме того, в данной модели мы рассматриваем переменные X как неслучайные значения, Такое, на практике, получается, когда идет активный эксперимент, в котором задают значения X (например, назначили зарплату работнику), а затем измеряют Y (оценили, какой стала производительность труда). За это иногда зависимую переменную называют откликом. Теория регрессионных уравнений со случайными независимыми переменными сложнее, но известно, что, при большом числе наблюдений, использование метода разработанного для неслучайных X корректно.
Благодаря полученным оценкам коэффициентов уравнения регрессии могут быть оценены прогнозные значения зависимой переменной , причем они могут быть вычислены и там, где значения y определены, и там где они не определены. Прогнозные значения являются оценками средних, ожидаемых по модели значений Y , зависящих от X .
Поскольку коэффициенты регрессии — случайные величины, линия регрессии также случайна. Поэтому прогнозные значения случайны и имеют некоторое стандартное отклонение , зависящее от X . Благодаря этому можно получить и доверительные границы для прогнозных значений регрессии (средних значений y ).
Кроме того, с учетом дисперсии остатка могут быть вычислены доверительные границы значений Y (не средних, а индивидуальных!).
Для каждого объекта может быть вычислен остаток e i = . Остаток полезен для изучения адеквантности модели данным. Это означает, что должны быть выполнены требования о независимости остатков для отдельных наблюдений, дисперсия не должна зависеть от X .
Для изучения отклонений от модели удобно использовать стандартизованный остаток — деленный на стандартную ошибку регрессии.
Случайность оценки прогнозных значений Y вносит дополнительную дисперсию в регрессионный остаток, из-за этого дисперсия остатка зависит от значений независимых переменных ( ). Стьюдентеризованный остаток — это остаток деленный на оценку дисперсии остатка: .
Таким образом, мы можем получить: оценку (прогнозную) значений зависимой переменной Unstandardized predicted value), ее стандартное отклонение (S.E. of mean predictions), доверительные интервалы для среднего Y(X) и для Y(X) (Prediction intervals — Mean, Individual).
Это далеко не полный перечень переменных, порождаемых SPSS.
Пусть прогнозируется вес ребенка в зависимости от его возраста. Ясно, что дисперсия веса для четырехлетнего младенца будет значительно меньше, чем дисперсия веса 14-летнего юноши. Таким образом, дисперсия остатка e i зависит от значений X , а значит условия для оценки регрессионной зависимости не выполнены. Проблема неоднородности дисперсии в регрессионном анализе называется проблемой гетероскедастичности.
В SPSS имеется возможность корректно сделать соответствующие оценки за счет приписывания весов слагаемым минимизируемой суммы квадратов. Эта весовая функция должна быть равна 1/? 2 (x) , где ? 2 (x) — дисперсия y как функция от x . Естественно, чем меньше дисперсия остатка на объекте, тем больший вес он будет иметь. В качестве такой функции можно использовать ее оценку, полученную при фиксированных значениях X .
Например, в приведенном примере на достаточно больших данных можно оценить дисперсию для каждой возрастной группы и вычислить необходимую весовую переменную. Увеличение влияния возрастных групп с меньшим возрастом в данном случае вполне оправдано.
В диалоговом окне назначение весовой переменной производится с помощью кнопки WLS (Weighed Least Squares — метод взвешенных наименьших квадратов).
В меню — это команда Linear Regression. В диалоговом окне команды:
— Назначаются независимые и зависимая переменные,
— Назначается метод отбора переменных. STEPWISE — пошаговое включение/удаление переменных. FORWARD — пошаговое включение переменных. BACKWARD — пошаговое исключение переменных. При пошаговом алгоритме назначаются значимости включения и исключения переменных (OPTIONS). ENTER — принудительное включение.
— Имеется возможность отбора данных, на которых будет оценена модель (Selection). Для остальных данных могут быть оценены прогнозные значения функции регрессии, его стандартные отклонения и др.
— Назначения вывода статистик (Statistics) — доверительные коэффициенты коэффициентов регресии, их ковариационная матрица, статистики Дарбина-Уотсона и пр.
— Задаются графики рассеяния остатков, их гистограммы (Plots)
— Назначаются сохранение переменных(Save), порождаемых регрессией.
— Если используется пошаговая регрессия, назначаются пороговые значимости для включения (PIN) и исключения (POUT) переменных (Options).
— Если обнаружена гетероскедастичность, назначается и весовая переменная.
Обычно демонстрацию модели начинают с простейшего примера, и такие примеры Вы можете найти в Руководстве по применению SPSS. Мы пойдем немного дальше и покажем, как получить полиномиальную регрессию.
Курильский опрос касался населения трудоспособного возраста. Как показали расчеты, в среднем меньшие доходы имеют молодые люди и люди старшего возраста. Поэтому, прогнозировать доход лучше квадратичной кривой, а не простой линейной зависимостью. В рамках линейной модели это можно сделать, введя переменную — квадрат возраста. Приведенное ниже задание SPSS предназначено для прогноза логарифма промедианного дохода (ранее сформированного).
REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2
/SAVE PRED MCIN ICIN.
*регрессия с сохранением предсказанных значений и доверительных интервалов средних и индивидуальных прогнозных значений.
Таблица 5.1 показывает, что уравнение объясняет всего 4.5% дисперсии зависимой переменной (коэффициент детерминации R 2 =.045), скорректированная величина коэффициента равна 0.042, а коэффициент множественной корреляции равен 0.211. Много это или мало, трудно сказать, поскольку у нас нет подобных результатов на других данных, но то, что здесь есть взаимосвязь, можно понять, рассматривая таблицу 6.2.
Таблица 6.1. Общие характеристики уравнения
Adjusted R Square
Std. Error of the Estimate
a Predictors: (Constant), V9_2, V9 Возраст
b Dependent Variable: LNV14M логарифм промедианного дохода
Результаты дисперсионного анализа уравнения регрессии показывает, что гипотеза равенства всех коэффициентов регрессии нулю должна быть отклонена.
Таблица 6.2. Дисперсионный анализ уравнения
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.
- Остатки нормально распределены с нулевым средним значением;
- Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.
Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
http://masters.donntu.org/2005/fvti/scherbak/library/doc_1.htm
http://statistica.ru/theory/osnovy-lineynoy-regressii/
Материал из MachineLearning.
(Перенаправлено с Регрессия)
Перейти к: навигация, поиск
Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств.
Данные состоят из пар значений зависимой переменной (переменной отклика)
и независимой переменной (объясняющей переменной).
Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.
Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные.
Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка: сумма квадратов разности значений
модели и зависимой переменной для всех значений независимой переменной в качестве аргумента.
Регрессионный анализ — раздел математической статистики и машинного обучения.
Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины.
Относительно характера распределения этой величины делаются предположения, называемые гипотезой порождения данных.
Для подтверждения или опровержения этой гипотезы выполняются статистические тесты,
называемые анализом остатков.
При этом предполагается, что независимая переменная не содержит ошибок.
Регрессионный анализ используется для прогноза, анализа временных рядов,
тестирования гипотез и выявления скрытых взаимосвязей в данных.
Содержание
- 1 Определение регрессионного анализа
- 2 Линейная регрессия
- 3 Нелинейная регрессия
- 4 О терминах
- 5 Смотри также
- 6 Литература
- 7 Внешние ссылки
Определение регрессионного анализа
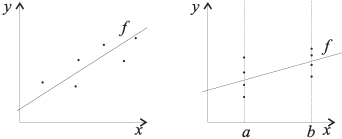
Выборка может быть не функцией, а отношением. Например, данные для построения регрессии могут быть такими: . В такой выборке одному значению переменной
соответствует несколько значений переменной
.
Регрессия — зависимость математического ожидания (например, среднего значения)
случайной величины от одной или нескольких других случайных величин (свободных переменных),
то есть .
Регрессионным анализом называется поиск такой функции , которая описывает эту зависимость.
Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих.
где — функция регрессионной зависимости, а
— аддитивная случайная величина с нулевым матожиданием.
Предположение о характере распределения этой величины называется гипотезой порождения данных.
Обычно предполагается, что величина имеет гауссово распределение с нулевым средним и дисперсией
.
Задача нахождения регрессионной модели нескольких свободных переменных ставится следующим образом.
Задана выборка — множество значений свободных
переменных и множество соответствующих им значений зависимой переменной.
Эти множества обозначаются как , множество исходных данных
.
Задана регрессионная модель — параметрическое семейство функций зависящая от параметров
и свободных переменных
.
Требуется найти наиболее вероятные параметры :
Функция вероятности зависит от гипотезы порождения данных и задается Байесовским выводом или методом наибольшего правдоподобия.
Линейная регрессия
Линейная регрессия предполагает, что функция зависит от параметров
линейно.
При этом линейная зависимость от свободной переменной необязательна,
В случае, когда функция линейная регрессия имеет вид
здесь — компоненты вектора
.
Значения параметров в случае линейной регрессии находят с помощью метода наименьших квадратов.
Использование этого метода обосновано предположением о гауссовском распределении случайной переменной.
Разности между фактическими значениями зависимой переменной и восстановленными называются регрессионными остатками (residuals). В литературе используются также синонимы: невязки и ошибки.
Одной из важных оценок критерия качества полученной зависимости является сумма квадратов остатков:
Здесь — Sum of Squared Errors.
Дисперсия остатков вычисляется по формуле
Здесь — Mean Square Error, среднеквадратичная ошибка.
|
|
|
На графиках представлены выборки, обозначенные синими точками, и регрессионные зависимости, обозначенные сплошными линиями.
По оси абсцисс отложена свободная переменная, а по оси ординат — зависимая.
Все три зависимости линейны относительно параметров.
Нелинейная регрессия
Нелинейные регрессионные модели — модели вида
которые не могут быть представлены в виде скалярного произведения
где — параметры регрессионной модели,
— свободная переменная из пространства
,
— зависимая переменная,
— случайная величина и
— функция из некоторого
заданного множества.
Значения параметров в случае нелинейной регрессии находят с помощью одного из методов градиентного спуска, например алгоритма Левенберга-Марквардта.
О терминах
Термин «регрессия» был введён Фрэнсисом Гальтоном в конце 19-го века.
Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот
феномен «регрессия к посредственности».
Сначала этот термин использовался исключительно в биологическом смысле.
После работ Карла Пирсона этот термин стали использовать и в статистике.
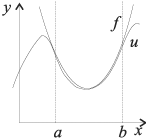
Аппроксимация функций: непрерывная функция приближает непрерывную или дискретную функцию
В статистической литературе различают регрессию с участием одной свободной переменной и с несколькими свободными переменными —
одномерную и многомерную регрессию.
Предполагается, что мы используем несколько свободных переменных,
то есть, свободная переменная — вектор .
В частных случаях, когда свободная переменная является скаляром,
она будет обозначаться .
Различают линейную и нелинейную регрессию.
Если регрессионную модель не является линейной комбинацией функций
от параметров, то говорят о нелинейной регрессии.
При этом модель может быть произвольной суперпозицией функций из некоторого набора.
Нелинейными моделями являются, экспоненциальные,
тригонометрические и другие (например, радиальные базисные функции или персептрон Розенблатта),
полагающие зависимость между параметрами и зависимой переменной нелинейной.
Различают параметрическую и непараметрическую регрессию.
Строгую границу между этими двумя типами регрессий провести сложно.
Сейчас не существует общепринятого критерия отличия одного типа моделей от другого.
Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной —непараметрическими.
Пример параметрической регресионной модели: линейный предиктор, многослойный персептрон.
Примеры смешанной регрессионной модели: функции радиального базиса.
Непараметрическая модель — скользящее усреднение в окне некоторой ширины.
В целом, непараметрическая регрессия отличается от параметрической тем,
что зависимая переменная зависит не от одного значения свободной переменной,
а от некоторой заданной окрестности этого значения.
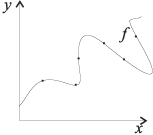
Интерполяция: функция задана значениями узловых точек
Есть различие между терминами: «приближение функций», «аппроксимация», «интерполяция», и «регрессия».
Оно заключается в следующем.
Приближение функций. Дана функция дискретного или непрерывного аргумента.
Требуется найти функцию из некоторого параметрическую семейства, например, среди алгебраических
полиномов заданной степени. Параметры функции должны
доставлять минимум некоторому функционалу, например,
Термин аппроксимация — синоним термина «приближение функций».
Чаще используется тогда, когда речь идет о заданной функции, как о функции дискретного аргумента.
Здесь также требуется отыскать такую функцию , которая проходит наиболее близко ко всем точкам заданной функции.
При этом вводится понятие невязки — расстояния между точками непрерывной функции и соответствующими точками функции
дискретного аргумента.
Интерполяция функций — частный случай задачи приближения,
когда требуется, чтобы в определенных точках, называемых
узлами интерполяции совпадали значения функции и
приближающей ее функции . В более общем случае накладываются
ограничения на значения некоторых производных производных.
То есть, дана функция дискретного аргумента.
Требуется отыскать такую функцию , которая проходит через все точки
.
При этом метрика обычно не используется, однако часто вводится понятие «гладкости» искомой функции.
Регрессия и классификация тесно связаны друг с другом.
Термин алгоритм в классификации мог бы стать синонимом термина модель в регрессии,
если бы алгоритм не оперировал с дискретным множеством ответов-классов, а модель — с непрерывно-определенной свободной переменной.
Смотри также
- Регрессионная модель
- Линейная регрессия (пример)
- Метод наименьших квадратов
- Нелинейная регрессия
- Алгоритм Левенберга-Марквардта
- Связанный Байесовский вывод
- Метод группового учета аргументов
- Анализ регрессионных остатков
- Применение методов регрессионного анализа на практике
- Регрессионный анализ (рекомендуемые обозначения)
Литература
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Издательский дом «Вильямс». 2007.
- Айвазян С.А. Прикладная статистика и основы эконометрики. М.: Юнити. 2001.
- Брандт З. Анализ данных. М.: Мир. 2003.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
- Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: ВЦ РАН, 2010. 60 с. Брошюра, PDF.
Внешние ссылки
- Wikipedia.org, Категория «Regression analysis»
- Non linear regression and curve fitting, NLREG software
- Netlab neural network software by Yan Nabney
- Curvefit.com, A complete guide to nonlinear regression