3.1. Постановка задачи. Ряд Тейлора
В теории функциональных
рядов центральное место занимает раздел,
посвященный разложению функции в ряд.
Таким образом,
ставится задача: по заданной функции
![]()
требуется
найти такой степенной ряд
![]() ,
,
который на некотором
интервале сходился и его сумма была
равна
![]() ,
,
т.е.
![]() =
= ![]() ..
..
Эта задача называется
задачей
разложения функции в степенной ряд.
Необходимым
условием разложимости функции в степенной
ряд является
её дифференцируемость бесконечное
число раз – это следует из свойств
сходящихся степенных рядов. Такое
условие выполняется, как правило, для
элементарных функций в их области
определения.
Итак, предположим,
что функция
![]() имеет производные любого порядка. Можно
имеет производные любого порядка. Можно
ли её разложить в степенной ряд, если
можно, то как найти этот ряд? Проще
решается вторая часть задачи, с неё и
начнем.
Допустим, что
функцию![]() можно представить в виде суммы степенного
можно представить в виде суммы степенного
ряда, сходящегося в интервале, содержащем
точкух0:
![]() =
= ![]() ..
..
(*)
где а0,а1,а2,,…,ап,…
– неопределенные
(пока) коэффициенты.
Положим в равенстве
(*) значение х
= х0,
тогда получим
![]() .
.
Продифференцируем
степенной ряд (*) почленно
![]() =
= ![]() ..
..
и полагая здесь
х = х0,
получим
![]() .
.
При следующем
дифференцировании получим ряд
![]() =
= ![]() ..
..
полагая х
= х0,
получим![]() ,
,
откуда
![]() .
.
После п
-кратного
дифференцирования получим
![]()
Полагая в последнем
равенстве х
= х0,
получим
![]() ,
,
откуда
![]()
Итак, коэффициенты
найдены
![]() ,
,
![]() ,
,
![]() ,
,
…,
![]() ,….,
,….,
подставляя которые
в ряд (*), получим
![]()
Полученный
ряд называется рядом
Тейлора
для функции
![]() .
.
Таким образом, мы
установили, что если
функцию можно разложить в степенной
ряд по степеням (х — х0),
то это разложение единственно и полученный
ряд обязательно является рядом Тейлора.
Заметим,
что ряд Тейлора можно получить для любой
функции, имеющей производные любого
порядка в точке х
= х0.
Но это еще
не означает, что между функцией и
полученным рядом можно поставить знак
равенства, т.е. что сумма ряда равна
исходной функции. Во-первых, такое
равенство может иметь смысл только в
области сходимости, а полученный для
функции ряд Тейлора может и расходиться,
во-вторых, если ряд Тейлора будет
сходиться, то его сумма может не совпадать
с исходной функцией.
3.2. Достаточные условия разложимости функции в ряд Тейлора
Сформулируем
утверждение, с помощью которого будет
решена поставленная задача.
Если функция
![]() в некоторой
в некоторой
окрестности точки х0
имеет производные до (n+1)-го
порядка включительно, то в этой окрестности
имеет место формула
Тейлора
![]()
где Rn(х)-остаточный
член формулы Тейлора – имеет вид (форма
Лагранжа)
![]()
где
точка ξ
лежит между
х и х0.
Отметим, что между
рядом Тейлора и формулой Тейлора имеется
различие: формула Тейлора представляет
собой конечную сумму, т.е. п
— фиксированное
число.
Напомним, что сумма
ряда S(x)
может быть
определена как предел функциональной
последовательности частичных сумм
Sп(x)
на некотором
промежутке Х:
![]() .
.
Согласно этому,
разложить функцию в ряд Тейлора означает
найти такой ряд, что для любого х
X
![]()
Запишем формулу
Тейлора в виде![]() ,
,
где
![]() .
.
Заметим, что ![]() определяет ту
определяет ту
ошибку, которую мы получаем, заменяй
функцию f(x)
многочленом
Sn(x).
Если
![]() ,
,
то![]() ,т.е. функция
,т.е. функция
разлагается в ряд
Тейлора. И
наоборот,
если
![]() ,
,
то![]() .
.
Тем самым
мы доказали
критерий
разложимости функции в ряд Тейлора.
Для того, чтобы
в некотором промежутке функция f(х)
разлагалась в ряд Тейлора, необходимо
и достаточно, чтобы на этом промежутке
![]() ,
,
где Rn(x)
— остаточный член ряда Тейлора.
С помощью
сформулированного критерия можно
получить достаточные
условия
разложимости функции в ряд Тейлора.
Если в некоторой
окрестности точки х0
абсолютные величины всех производных
функции ограничены одним и тем же числом
М ≥ 0,
т.е.
![]() ,
,
то в этой
окрестности функция разлагается в ряд
Тейлора.
Из вышеизложенного
следует алгоритм
разложения
функции f(x)
в ряд Тейлора в
окрестности точки х0:
1.
Находим
производные функции f(x):
f(x),
f’(x), f”(x), f’”(x), f(n)
(x),…
2. Вычисляем значение
функции и значения её производных в
точке х0
f(x0),
f’(x0),
f”(x0),
f’”(x0),
f(n)
(x0),…
3. Формально
записываем ряд Тейлора и находим область
сходимости полученного степенного
ряда.
4. Проверяем
выполнение достаточных условий, т.е.
устанавливаем, для каких х
из области
сходимости, остаточный член Rn(x)
стремится
к нулю при
![]() или
или
![]() .
.
Разложение функций
в ряд Тейлора по данному алгоритму
называют разложением
функции в ряд Тейлора по определению
или
непосредственным
разложением.
Соседние файлы в папке Ряды
- #
- #
- #
- #
- #
Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots — постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,limn→∞Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{»}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{»}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{»}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1xf(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=11+tf(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
1x=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=∑k=0∞(−1)k(x−1)k,∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=∑k=0nf(k)(x0)k!(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=f(n+1)(ξ)(n+1)!xn+1,x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+o(xn),∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+o(x2n),∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+o(x2n+1),∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+o(x2n+2),∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=x1!−x22!+x33!−…+(−1)n+1xnn!+o(xn),x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(t21!−(t2)22!+(t2)33!+o((t2)3))=t3−t52+t76+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−(x+1)52+(x+1)76+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−(2t)22!−(2t)44!+o(t5))=(t2−4)(1−2t2+2t43+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+8t43+o(t5))=−4+9t2−143t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−143(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(1xn)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=1xt=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−x2−1f(x)=2x-sqrt{x^2-1}
с точностью до o(1×3)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=2t−1t2−1=2−(1−t2)1/2tg(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=2−(1−t22−t48)+o(t4)t=1t+t2−t38+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+12x−18×3+o(1×3),x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (00)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
limx→1ex−ecos(x−1)sin(x−1)limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
limx→1ex−ecos(x−1)sin(x−1)=limx→1(e+e(x−1)+e(x−1)22!+e(x−1)33!+…)−e(1−(x−1)22!+…)(x−1)−(x−1)33!+…=elimx→1(x−1)+(x−1)2+(x−1)36+…(x−1)−(x−1)36+…=elimx→11+(x−1)+(x−1)26+…1−(x−1)26+…=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e
Тест по теме «Формула и ряд Тейлора»
Выражение функции в виде бесконечной суммы
 По мере увеличения степени полинома Тейлора она приближается к правильной функции. На этом изображении показан грех x и его приближения Тейлора, полиномы степени 1, 3, 5, 7, 9, 11и 13.
По мере увеличения степени полинома Тейлора она приближается к правильной функции. На этом изображении показан грех x и его приближения Тейлора, полиномы степени 1, 3, 5, 7, 9, 11и 13.
В математике ряд Тейлора функции является бесконечная сумма члены, которые выражены в терминах производных функций в одной точке. Для наиболее распространенных функций функция и сумма ее ряда Тейлора вблизи этой точки равны. Ряды Тейлора названы в честь Брука Тейлора, который представил их в 1715 году.
Если ноль — это точка, в которой рассматриваются производные, ряд Тейлора также называется серией Маклорена, после Колина Маклорена, который широко использовал этот частный случай из серии Тейлора в 18 веке.
частичная сумма, образованная первыми членами ряда Тейлора, полиномом степени n, который называется n-м полиномом Тейлора функции. Полиномы Тейлора — это приближения, которые обычно становятся лучше при увеличении. Теорема Тейлора дает количественные оценки погрешностей, обеспечивает использование таких приближений. Если ряд Тейлора функции является сходящейся, его сумма составляет предел бесконечной последовательности полиномов Тейлора. Функция может быть не равна сумме своего ряда Тейлора, даже если ее ряд Тейлора сходится. Функция является аналитической в точке x, если она равна сумме своего ряда Тейлора в некотором открытом интервале (или открытом диске в комплексная плоскость ), содержащая x. Это означает, что функция аналитична в каждой точке интервала (или круга).
Содержание
- 1
- 2 Примеры
- 3 История
- 4 Аналитические функции
- 5 Ошибка аппроксимации и сходимость
- 5.1 Обобщение
- 6 Список рядов Маклорена некоторых общих функций
- 6.1 Экспоненциальная функция
- 6.2 Натуральный логарифм
- 6.3 Геометрический ряд
- 6.4 Биномиальный ряд
- 6.5 Тригонометрические функции
- 6.6 Гиперболические функции
- 7 Вычисление ряда Тейлора
- 7.1 Первый пример
- 7.2 Второй пример
- 7.3 Третий пример
- 8 Ряд Тейлора как определения
- 9 Ряд Тейлора с переменными
- 9.1 Пример
- 10 Сравнение с рядом Фурье
- 11 См. Также
- 12 Примечания
- 13 Ссылки
- 14 Внешние ссылки
Определение
Ряд Тейлора вещественной или комплекснозначной функции f (x), который бесконечно дифференцируем при действительном или комплексном числе a, является степенным рядом
- f (a) + f ′ (a) 1! (х — а) + е ″ (а) 2! (Икс — а) 2 + е ‴ (а) 3! (Икс — а) 3 + ⋯, { displaystyle f (a) + { frac {f ‘(a)} {1!}} (Xa) + { frac {f’ ‘(a)} {2! }} (xa) ^ {2} + { frac {f » ‘(a)} {3!}} (xa) ^ {3} + cdots,}
где n! обозначает факториал число n. В более компактной сигма-нотации это можно записать как
- ∑ n = 0 ∞ f (n) (a) n! (Икс — а) п, { Displaystyle сумма _ {п = 0} ^ { infty} { гидроразрыва {е ^ {(п)} (а)} {п!}} (Ха) ^ {п},}
где f (a) обозначает n-ю производную функции f, вычисленную в точке a. (Производная нулевого порядка функции f определяет как сама f, а (x — a) и 0! оба как 1.)
Когда a = 0, ряд также называется рядом Маклорена.
Примеры
Ряд Тейлора для любого многочлена является самим многочленом.
Ряд Маклорена для 1/1 — x — это геометрический ряд
- 1 + x + x 2 + x 3 + ⋯, { displaystyle 1 + x + x ^ {2} + x ^ {3} + cdots,}
поэтому ряд Тейлора для 1 / x при a = 1 равенстве
- 1 — (x — 1) + (x — 1) 2 — (x — 1) 3 + ⋯. { displaystyle 1- (x-1) + (x-1) ^ {2} — (x-1) ^ {3} + cdots.}
Интегрируя вышеуказанный ряд Маклорена, мы находим ряд Маклорена для ln ( 1 — x), где ln обозначает натуральный логарифм :
- — x — 1 2 x 2 — 1 3 x 3 — 1 4 x 4 — ⋯. { displaystyle -x — { tfrac {1} {2}} x ^ {2} — { tfrac {1} {3}} x ^ {3} — { tfrac {1} {4}} x ^ {4} — cdots.}
Соответствующий ряд Тейлора для ln x при a = 1 равенстве
- (x — 1) — 1 2 (x — 1) 2 + 1 3 (x — 1) 3 — 1 4 (х — 1) 4 + ⋯, { displaystyle (x-1) — { tfrac {1} {2}} (x-1) ^ {2} + { tfrac {1} {3}} ( x-1) ^ {3} — { tfrac {1} {4}} (x-1) ^ {4} + cdots,}
и, в более общем смысле, соответствующий ряд Тейлора для ln x в произвольная ненулевая точка a равна:
- ln a + 1 a (x — a) — 1 a 2 (x — a) 2 2 + ⋯. { displaystyle ln a + { frac {1} {a}} (xa) — { frac {1} {a ^ {2}}} { frac { left (xa right) ^ {2} } {2}} + cdots.}
Ряд Тейлора для экспоненциальной функции e при a = 0 равен
- ∑ n = 0 ∞ xnn! = х 0 0! + х 1 1! + х 2 2! + х 3 3! + х 4 4! + х 5 5! + ⋯ знак равно 1 + x + x 2 2 + x 3 6 + x 4 24 + x 5120 + ⋯. { displaystyle { begin {align} sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = { frac {x ^ {0}} { 0!}} + { Frac {x ^ {1}} {1!}} + { Frac {x ^ {2}} {2!}} + { Frac {x ^ {3}} {3! }} + { frac {x ^ {4}} {4!}} + { frac {x ^ {5}} {5!}} + cdots = 1 + x + { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {6}} + { frac {x ^ {4}} {24}} + { frac {x ^ {5}} {120}} + cdots. End {align}}}
Вышеупомянутое расширение верно, потому что производная e по x также равна e, а e равно 1. Это оставляет (x — 0) в числитель и п! в знаменателе для каждого члена в бесконечной сумме.
История
Греческий философ Зенон рассматривал проблему суммирования бесконечного ряда для достижения конечного результата, но отвергал ее как невозможную; Результатом стал парадокс Зенона. Позже Аристотель показал философское разрешение парадокса, но математическое содержание, по-видимому, оставалось неразрешенным, пока его не подхватил Архимед, как это было до Аристотеля досократическим атомистом Демокрит. Именно с помощью архимедова метода исчерпания можно было выполнить бесконечное количество последовательных последовений для конечного результата. Лю Хуэй независимо использовал аналогичный метод несколько столетий спустя.
В 14 самые ранние примеры использования рядов Тейлора и близких к ним методов были даны Мадхавой из Сангамаграмы. Хотя записи о его работе не сохранились, работы более поздних индийских математиков предполагают, что он обнаружил ряд частных случаев ряда Тейлора, в числе для тригонометрических функций от синуса., косинус, тангенс и арктангенс. Керальская школа астрономии и математики дополнительно расширила его работы с помощью различных расширений рядов и рациональных приближений до 16 века.
В 17 веке Джеймс Грегори также работал в этой области и опубликовал несколько серий Маклорена. Однако только в 1715 году общий метод построения этих рядов для всех функций, которые они существуют, был наконец предоставлен Бруком Тейлором, в честь которого теперь назван ряд.
Серия Maclaurin была названа в честь Колина Маклорена, который опубликовал частный случай результата Тейлора в 18 веке.
Аналитические функции
 Функция не является аналитической при x = 0: ряд Тейлора идентично 0, хотя функция не является.
Функция не является аналитической при x = 0: ряд Тейлора идентично 0, хотя функция не является.
Если f (x) равно заданный сходящимся степенным прямым прямым прямым расстоянием в точке b на комплексной плоскости, он называется аналитическим в круге. Таким образом, для x в этом круге f задается сходящимся степенным рядом
- f (x) = ∑ n = 0 ∞ a n (x — b) n. { displaystyle f (x) = sum _ {n = 0} ^ { infty} a_ {n} (xb) ^ {n}.}
Дифференцируя приведенную выше формулу по xn раз, затем установить x = b дает:
- f (n) (b) n! = a n { displaystyle { frac {f ^ {(n)} (b)} {n!}} = a_ {n}}
, и поэтому разложение в степенной ряд согласуется с рядом Тейлора. Таким образом, функция является аналитической в открытом положении с центром в точке b тогда и только тогда, когда ее ряд Тейлора сходится к значению функции в каждой точке диска.
Если f (x) равен своему ряду Тейлора для всех x в комплексной плоскости, он называется целым. Полиномы, экспоненциальная функция e и тригонометрические функции синус и косинус, являются примерами целых функций. Примеры неполных функций включают квадратный корень , логарифм , тангенс тригонометрической функции , и обратный ему арктангенс. Для этих функций ряды Тейлора не сходятся, если x далеко от b. То есть Тейлора расходится на в точке x, если расстояние между x и b больше, чем радиус сходимости. Ряд Тейлора можно использовать для вычислений значения функций в каждой точке, если значение функции и всех ее производных известно в одной точке.
Использование ряда Тейлора для аналитических функций включает:
- Частные суммы (полиномы Тейлора ) ряд как приближения функции. Эти аппроксимации хороши.
- Дифференцирование и интегрирование степенных рядов может работать построчно, и поэтому это особенно легко.
- Аналитическая функция однозначно продолжается до голоморфной функции на открытом диске в комплексной плоскости. Это делает доступным механизмом комплексного анализа.
- (Усеченный) ряд программных вычислений для выполнения определенных вычислений функций (часто путем преобразования полинома в форму Чебышева и вычисляя его с помощью алгоритма Кленшоу ).
- Алгебраические операции могут быть легко выполнены с представлением степенного ряда; например, формула Эйлера следует из разложений в ряд Тейлора для тригонометрических и экспоненциальных функций. Этот результат имеет фундаментальное значение в таких областях, как гармонический анализ.
- Аппроксимации с использованием первых нескольких функций.
Ошибка аппроксимации и сходимость
 Синусоидальная функция (синий) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного периода с большой степенью 7 (розовый) для полного периода сходимости
Синусоидальная функция (синий) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного периода с большой степенью 7 (розовый) для полного периода сходимости
 Многочлены Тейлора для ln (1 + x) обеспечивают только точные приближения В диапазоне −1 < x ≤ 1. For x>1, м Нагчлены Тейлора более высокой степени худшие приближения.
Многочлены Тейлора для ln (1 + x) обеспечивают только точные приближения В диапазоне −1 < x ≤ 1. For x>1, м Нагчлены Тейлора более высокой степени худшие приближения.  Приближения Тейлора для ln (1 + x) (черный). Для x>1 приближения расходятся.
Приближения Тейлора для ln (1 + x) (черный). Для x>1 приближения расходятся.
На рисунке справа показано точное приближение sin x вокруг точки x = 0. Розовая кривая представляет собой полином седьмой степени:
- sin (x) ≈ x — х 3 3! + х 5 5! — х 7 7!. { displaystyle sin left (x right) приблизительно x — { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} {5!}} — { гидроразрыв {x ^ {7}} {7!}}. !}
Ошибка в этом приближении не более | х | / 9!. В частности, для -1 < x < 1, the error is less than 0.000003.
Напротив, также показано изображение функций натурального логарифма ln (1 + x) и некоторых из ее многочленов Тейлора около a = 0. Эти приближения сходятся с функциями только в области — 1 < x ≤ 1; outside of this region the higher-degree Taylor polynomials are worse approximations for the function.
Ошибка, возникающая при аппроксимации функции ее полиномом Тейлора n-й степени, называется остатком или остатком и обозначается функцией R n (x). Теорема Тейлора может Номинация для оценки размера остатка.
В общем, ряды Тейлора не обязательно должны быть сходящимися. И фактически набор функций со сходящимся рядом Тейлора представляет собой скудное множество в дизай Фреше гладких функций. И даже если ряд Тейлора функции f действительно сходится, его предел не обязательно должен быть равен значению функции f (x). Например функция,
- f (x) = {e — 1 x 2, if x ≠ 0 0, if x = 0 { displaystyle f (x) = { begin {cases} e ^ {- { frac { 1} {x ^ {2}}}} { text {if}} x neq 0 0 { text {if}} x = 0 end {cases}}}
равно бесконечно дифференцируема в точке x = 0 и имеет там все производные нулю. Следовательно, Тейлора функции f (x) относительно x = 0 тождественно равен нулю. Однако вокруг f (x) не является нулевой функцией, поэтому не равна ее ряду Тейлора начала координат. Таким образом, f (x) является примером неаналитической гладкой функции.
В анализа этот пример показывает, что существуют бесконечно дифференцируемые функции f (x), ряд Тейлора не равен f (x), даже если они сходятся. Напротив, голоморфные функции, изучаемые в комплексном анализе, всегда обладают сходящимся рядом Тейлора, и даже ряд Тейлора мероморфных функций, которые могут иметь особенности, никогда не сходятся к значению, отличному от самой функции. Однако комплексная функция не приближается к 0, когда z приближается к 0 вдоль мнимой оси, поэтому она не непрерывна в комплексной плоскости, и ее ряд Тейлора не определен в 0.
В более общем В смысле, каждая последовательность действительных или комплексных чисел может появиться как коэффициенты в ряду Тейлора бесконечно дифференцируемой функции, определенной на вещественной прямой, как следствие леммы Бореля. В результате радиус сходимости ряда Тейлора может быть равенством нулю. Существуют даже бесконечно дифференцируемые функции, функции на вещественной прямой, чьи ряды Тейлора везде имеют радиус сходимости 0.
Функцию нельзя записать в виде ряда Тейлора с центром в сингулярности ; в этих случаях все же можно разложить в ряд, если допустить также отрицательные переменные x; см. серию Лоран. Например, f (x) = e можно записать в виде ряда Лорана.
Обобщение
Однако существует обобщение ряда Тейлора, которое сходится к значению самой функции для любой ограниченной непрерывной функции на (0, ∞), используя исчисление конечных разностей. В частности, имеется следующая теорема, благодаря Эйнару Хилле, что для любого t>0
- lim h → 0 + ∑ n = 0 ∞ t n n! Δ h n f (a) h n = f (a + t). { displaystyle lim _ {h to 0 ^ {+}} sum _ {n = 0} ^ { infty} { frac {t ^ {n}} {n!}} { frac { Delta _ {h} ^ {n} f (a)} {h ^ {n}}} = f (a + t).}
Здесь Δ. h- n-й оператор конечных разностей с шагом h. Этот ряд в точности совпадает с рядом Тейлора, за исключением того, что вместо дифференцирования появляются отдельные различия: ряд формально аналогичен ряду серии Ньютона. Эта функция является аналитической в составе ряда сходятся к ряду Тейлора и в этом смысле обобщают ряд Тейлора.
В общем, для любой бесконечной следовать a i выполняется следующее тождество степенного ряда:
- ∑ n = 0 ∞ u n n! Δ N а я знак равно е — и ∑ J знак равно 0 ∞ U J J! а я + j. { displaystyle sum _ {n = 0} ^ { infty} { frac {u ^ {n}} {n!}} Delta ^ {n} a_ {i} = e ^ {- u} sum _ {j = 0} ^ { infty} { frac {u ^ {j}} {j!}} a_ {i + j}.}
Так, в частности,
- f (a + t) = lim h → 0 + е — й ∑ j знак равно 0 ∞ f (a + jh) (th) jj!. { displaystyle f (a + t) = lim _ {h to 0 ^ {+}} e ^ {- { frac {t} {h}}} sum _ {j = 0} ^ { infty } f (a + jh) { frac { left ({ frac {t} {h}} right) ^ {j}} {j!}}.}
Ряд справа — это математическое ожидание для f (a + X), где X — распределенная по Пуассону случайная величина, которая принимает значение jh с вероятностью e · (t / h) / j!. Следовательно,
- f (a + t) = lim h → 0 + ∫ — ∞ ∞ f (a + x) d P t h, h (x). { displaystyle f (a + t) = lim _ {h to 0 ^ {+}} int _ {- infty} ^ { infty} f (a + x) dP _ {{ frac {t } {h}}, h} (x).}
закон больших чисел подразумевает, что тождество выполнено.
Список серий Маклорена некоторых общих функций
Далее следуют несколько важных расширений серии Маклорена. Все эти разложения действительны для сложных аргументов x.
Экспоненциальная функция
 Экспоненциальная функция e (синим цветом) и сумма первых n + 1 элементов Тейлора в 0 (красным).
Экспоненциальная функция e (синим цветом) и сумма первых n + 1 элементов Тейлора в 0 (красным).
экспоненциальная функция ex { displaystyle e ^ {x}}
- ex = ∑ п = 0 ∞ xnn! Знак равно 1 + х + х 2 2! + х 3 3! + ⋯ { displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2}} {2!}} + { Frac {x ^ {3}} {3!}} + Cdots}
.
Он сходится для всех x.
Натуральный логарифм
натуральный логарифм (с основанием e ) имеет ряд Маклорена
- ln (1 — x) = — ∑ n Знак равно 1 ∞ xnn = — x — x 2 2 — x 3 3 — ⋯, ln (1 + x) = ∑ n = 1 ∞ (- 1) n + 1 xnn = x — x 2 2 + x 3 3 — ⋯. { displaystyle { begin {align} ln (1-x) = — sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n}} = — x- { frac {x ^ {2}} {2}} — { frac {x ^ {3}} {3}} — cdots, ln (1 + x) = sum _ {n = 1} ^ { infty} (- 1) ^ {n + 1} { frac {x ^ {n}} {n}} = x — { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {3}} — cdots. end {align}}}
Они сходятся для | х | < 1 {displaystyle |x|<1}
Геометрический ряд
Геометрический ряд и его производные имеют ряд Маклорена
- 1 1 — x = ∑ n = 0 ∞ xn 1 (1 — x) 2 = ∑ n = 1 ∞ nxn — 1 1 (1 — Икс) 3 знак равно ∑ N знак равно 2 ∞ (N — 1) N 2 Иксn — 2. { displaystyle { begin {align} { frac {1} {1-x}} = sum _ {n = 0} ^ { infty} x ^ {n} { frac {1} {(1-x) ^ {2}}} = sum _ {n = 1} ^ { infty} nx ^ {n- 1} { frac {1} {(1-x) ^ {3}}} = sum _ {n = 2} ^ { infty} { frac {(n-1) n} {2 }} х ^ {п-2}. end {align}}}
Все сходятся для | х | < 1 {displaystyle |x|<1}
Биномиальный ряд
биномиальный ряд — это степенной ряд
- (1 + x) α = ∑ n = 0 ∞ (α n) xn { displaystyle ( 1 + x) ^ { alpha} = sum _ {n = 0} ^ { infty} { binom { alpha} {n}} x ^ {n}}
, коэффициенты которого являются обобщенными биномиальные коэффициенты
- (α n) = ∏ k = 1 n α — k + 1 k = α (α — 1) ⋯ (α — n + 1) n!. { displaystyle { binom { alpha} {n}} = prod _ {k = 1} ^ {n} { frac { alpha -k + 1} {k}} = { frac { alpha ( alpha -1) cdots ( alpha -n + 1)} {n!}}.}
(Если n = 0, этот продукт является пустым продуктом и имеет значение 1.) сходится для | х | < 1 {displaystyle |x|<1}
Когда α = −1, это, по сути, бесконечный геометрический ряд, упомянутый в предыдущем разделе. Частные случаи α = 1/2 и α = −1/2 дают функцию квадратного корня и ее обратную функцию :
- (1 + x) 1 2 = 1 + 1 2 x — 1 8 x 2 + 1 16 x 3 — 5 128 x 4 + 7 256 x 5 -…, (1 + x) — 1 2 = 1 — 1 2 x + 3 8 x 2 — 5 16 x 3 + 35 128 x 4 — 63 256 х 5 +…. { displaystyle { begin {align} (1 + x) ^ { frac {1} {2}} = 1 + { tfrac {1} {2}} x — { tfrac {1} {8} } x ^ {2} + { tfrac {1} {16}} x ^ {3} — { tfrac {5} {128}} x ^ {4} + { tfrac {7} {256}} x ^ {5} — ldots, (1 + x) ^ {- { frac {1} {2}}} = 1 — { tfrac {1} {2}} x + { tfrac {3 } {8}} x ^ {2} — { tfrac {5} {16}} x ^ {3} + { tfrac {35} {128}} x ^ {4} — { tfrac {63} { 256}} x ^ {5} + ldots. end {align}}}
Когда сохраняется только линейный член, это упрощается до биномиального приближения.
Тригонометрические функции
Обычные тригонометрические функции и обратные к ним имеют следующий ряд Маклорена:
- sin x = ∑ n = 0 ∞ (- 1) n (2 n + 1)! Икс 2 N + 1 знак равно Икс — Икс 3 3! + х 5 5! — для всех x cos x знак равно ∑ n знак равно 0 ∞ (- 1) n (2 n)! Икс 2 N знак равно 1 — Икс 2 2! + х 4 4! — ⋯ для всех x загар x знак равно ∑ n = 1 ∞ B 2 n (- 4) n (1 — 4 n) (2 n)! x 2 n — 1 = x + x 3 3 + 2 x 5 15 + ⋯ для | х | < π 2 sec x = ∑ n = 0 ∞ ( − 1) n E 2 n ( 2 n) ! x 2 n = 1 + x 2 2 + 5 x 4 24 + ⋯ for | x | < π 2 arcsin x = ∑ n = 0 ∞ ( 2 n) ! 4 n ( n !) 2 ( 2 n + 1) x 2 n + 1 = x + x 3 6 + 3 x 5 40 + ⋯ for | x | ≤ 1 arccos x = π 2 − arcsin x = π 2 − ∑ n = 0 ∞ ( 2 n) ! 4 n ( n !) 2 ( 2 n + 1) x 2 n + 1 = π 2 − x − x 3 6 − 3 x 5 40 − ⋯ for | x | ≤ 1 arctan x = ∑ n = 0 ∞ ( − 1) n 2 n + 1 x 2 n + 1 = x − x 3 3 + x 5 5 − ⋯ for | x | ≤ 1, x ≠ ± i {displaystyle {begin{aligned}sin x=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-cdots {text{for all }}x[6pt]cos x=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-cdots {text{for all }}x[6pt]tan x=sum _{n=1}^{infty }{frac {B_{2n}(-4)^{n}left(1-4^{n}right)}{(2n)!}}x^{2n-1}=x+{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}+cdots {text{for }}|x|<{frac {pi }{2}}[6pt]sec x=sum _{n=0}^{infty }{frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}=1+{frac {x^{2}}{2}}+{frac {5x^{4}}{24}}+cdots {text{for }}|x|<{frac {pi }{2}}[6pt]arcsin x=sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}=x+{frac {x^{3}}{6}}+{frac {3x^{5}}{40}}+cdots {text{for }}|x|leq 1[6pt]arccos x={frac {pi }{2}}-arcsin x={frac {pi }{2}}-sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}={frac {pi }{2}}-x-{frac {x^{3}}{6}}-{frac {3x^{5}}{40}}-cdots {text{for }}|x|leq 1[6pt]arctan x=sum _{n=0}^{infty }{frac {(-1)^{n}}{2n+1}}x^{2n+1}=x-{frac {x^{3}}{3}}+{frac {x^{5}}{5}}-cdots {text{for }}|x|leq 1, xneq pm iend{aligned}}}
Все углы выражены в радианах. Числа B k, появляющиеся в разложениях tan x, являются числами Бернулли. E k в разложении sec x — это числа Эйлера.
гиперболические функции
гиперболические функции имеют ряды Маклорена, тесно связанные с рядами для соответствующие тригонометрические функции:
- sinh x = ∑ n = 0 ∞ x 2 n + 1 (2 n + 1)! знак равно х + х 3 3! + х 5 5! + ⋯ для всех x cosh x = ∑ n = 0 ∞ x 2 n (2 n)! Знак равно 1 + х 2 2! + х 4 4! + ⋯ для всех x tanh x = ∑ n = 1 ∞ B 2 n 4 n (4 n — 1) (2 n)! x 2 n — 1 = x — x 3 3 + 2 x 5 15 — 17 x 7 315 + ⋯ для | х | < π 2 arsinh x = ∑ n = 0 ∞ ( − 1) n ( 2 n) ! 4 n ( n !) 2 ( 2 n + 1) x 2 n + 1 for | x | ≤ 1 artanh x = ∑ n = 0 ∞ x 2 n + 1 2 n + 1 for | x | ≤ 1, x ≠ ± 1 {displaystyle {begin{aligned}sinh x=sum _{n=0}^{infty }{frac {x^{2n+1}}{(2n+1)!}}=x+{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}+cdots {text{for all }}x[6pt]cosh x=sum _{n=0}^{infty }{frac {x^{2n}}{(2n)!}}=1+{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}+cdots {text{for all }}x[6pt]tanh x=sum _{n=1}^{infty }{frac {B_{2n}4^{n}left(4^{n}-1right)}{(2n)!}}x^{2n-1}=x-{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}-{frac {17x^{7}}{315}}+cdots {text{for }}|x|<{frac {pi }{2}}[6pt]operatorname {arsinh} x=sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}{text{for }}|x|leq 1[6pt]operatorname {artanh} x=sum _{n=0}^{infty }{frac {x^{2n+1}}{2n+1}}{text{for }}|x|leq 1, xneq pm 1end{aligned}}}
Числа B k, появляющиеся в ряду для tanh x, являются числами Бернулли.
Расчет ряда Тейлора
Существует несколько методов вычисления ряда Тейлора для большое количество функций. Можно попытаться использовать определение ряда Тейлора, хотя это часто требует обобщения формы коэффициентов в соответствии с очевидной закономерностью. В качестве альтернативы можно использовать такие манипуляции, как подстановка, умножение или деление, сложение или вычитание стандартных рядов Тейлора, чтобы построить ряд Тейлора функции, поскольку ряд Тейлора является степенным рядом. В некоторых случаях можно также получить ряд Тейлора, многократно применяя интегрирование по частям. Особенно удобно использовать системы компьютерной алгебры для вычисления рядов Тейлора.
Первый пример
Для вычисления полинома Маклорена 7-й степени для функции
- f (x) = ln (cos x), x ∈ (- π 2, π 2) { displaystyle f (x) = ln ( cos x), quad x in left (- { frac { pi} {2}}, { frac { pi} {2}} right)}
,
сначала можно переписать функцию как
- f (x) = ln (1 + (cos x — 1)) { displaystyle f (x) = ln { bigl (} 1 + ( cos x-1) { bigr)} !}
.
Ряд Тейлора для натурального логарифма (с использованием нотации большого O )
- ln (1 + x) = x — Икс 2 2 + Икс 3 3 + О (Икс 4) { Displaystyle ln (1 + х) = х — { frac {x ^ {2}} {2}} + { frac {x ^ {3} } {3}} + {O} left (x ^ {4} right) !}
и для функции косинуса
- cos x — 1 = — x 2 2 + x 4 24 — x 6 720 + О (x
{ displaystyle cos x-1 = — { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) !}
.
В последнем разложении ряда есть нулевой постоянный член, который позволяет заменить вторую серию на первую и легко опустить члены более высокого порядка r, чем 7-я степень, используя большую нотацию O:
- f (x) = ln (1 + (cos x — 1)) = (cos x — 1) — 1 2 (cos x — 1) 2 + 1 3 (cos x — 1) 3 + O ((cos x — 1) 4) = (- x 2 2 + x 4 24 — x 6 720 + O (x 8)) — 1 2 ( — x 2 2 + x 4 24 + O (x 6)) 2 + 1 3 (- x 2 2 + O (x 4)) 3 + O (x
= — x 2 2 + x 4 24 — x 6 720 — x 4 8 + x 6 48 — x 6 24 + O (x
= — x 2 2 — x 4 12 — x 6 45 + O (x 8). { Displaystyle { begin {align} е (х) = ln { bigl (} 1 + ( соз х-1) { bigr)} = ( соз х-1) — { tfrac {1} {2}} ( cos x-1) ^ {2} + { tfrac {1} {3}} ( cos x-1) ^ {3} + {O} left (( cos x-1) ^ {4} right) = left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) right) — { frac {1} {2}} left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} + {O} left (x ^ {6} right) right) ^ {2} + { frac {1} {3}} left (- { frac {x ^ {2}} {2}} + O left (x ^ {4} right) right) ^ {3} + {O } left (x ^ {8} right) = — { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} — { frac {x ^ {4}} {8}} + { frac {x ^ {6}} {48}} — { frac {x ^ {6 }} {24}} + O left (x ^ {8} right) = — { frac {x ^ {2}} {2}} — { frac {x ^ {4}} { 12}} — { frac {x ^ {6}} {45}} + O left (x ^ {8} right). End {align}} !}
Поскольку косинус равен четная функция, коэффициенты для всех нечетных степеней x, x, x, x,… должны быть равны нулю.
Второй пример
Предположим, нам нужен ряд Тейлора в 0 функции
- g (x) = e x cos x. { displaystyle g (x) = { frac {e ^ {x}} { cos x}}. !}
У нас есть экспоненциальная функция
- e x = ∑ n = 0 ∞ x n n! Знак равно 1 + х + х 2 2! + х 3 3! + х 4 4! + ⋯ { displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ { 2}} {2!}} + { Frac {x ^ {3}} {3!}} + { Frac {x ^ {4}} {4!}} + Cdots !}
и, как и в первом примере,
- cos x = 1 — x 2 2! + х 4 4! — ⋯ { displaystyle cos x = 1 — { frac {x ^ {2}} {2!}} + { Frac {x ^ {4}} {4!}} — cdots !}
Предположим, что степенной ряд равен
- ex cos x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + ⋯ { displaystyle { frac {e ^ {x}} { cos x} } = c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + cdots !}
Затем умножение на знаменатель и замена Ряд косинуса дает
- ex = (c 0 + c 1 x + c 2 x 2 + c 3 x 3 + ⋯) cos x = (c 0 + c 1 x + c 2 x 2 + c 3 x 3 + с 4 Икс 4 + ⋯) (1 — Икс 2 2! + Икс 4 4! -) знак равно с 0 — с 0 2 Икс 2 + с 0 4! Икс 4 + С 1 Икс — С 1 2 Икс 3 + С 1 4! х 5 + с 2 х 2 — с 2 2 х 4 + с 2 4! х 6 + с 3 х 3 — с 3 2 х 5 + с 3 4! x 7 + c 4 x 4 + ⋯ { displaystyle { begin {align} e ^ {x} = left (c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + cdots right) cos x = left (c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + c_ {4} x ^ {4} + cdots right) left (1 — { frac {x ^ {2}} {2!}} + { Frac {x ^ {4}) } {4!}} — cdots right) = c_ {0} — { frac {c_ {0}} {2}} x ^ {2} + { frac {c_ {0}} { 4!}} X ^ {4} + c_ {1} x — { frac {c_ {1}} {2}} x ^ {3} + { frac {c_ {1}} {4!}} X ^ {5} + c_ {2} x ^ {2} — { frac {c_ {2}} {2}} x ^ {4} + { frac {c_ {2}} {4!}} X ^ {6} + c_ {3} x ^ {3} — { frac {c_ {3}} {2}} x ^ {5} + { frac {c_ {3}} {4!}} X ^ { 7} + c_ {4} x ^ {4} + cdots end {align}} !}
Сбор членов до четвертого порядка дает
- ex = c 0 + c 1 x + (c 2 — c 0 2) x 2 + (c 3 — c 1 2) x 3 + (c 4 — c 2 2 + c 0 4!) X 4 + ⋯ { displaystyle e ^ {x} = c_ {0} + c_ {1} x + left (c_ {2} — { frac {c_ {0}} {2}} right) x ^ {2} + left (c_ {3} — { frac {c_ {1 }} {2}} right) x ^ { 3} + left (c_ {4} — { frac {c_ {2}} {2}} + { frac {c_ {0}} {4!}) } right) x ^ {4} + cdots !}
Значения ci { displaystyle c_ {i}}

- e x cos x = 1 + x + x 2 + 2 x 3 3 + x 4 2 + ⋯. { displaystyle { frac {e ^ {x}} { cos x}} = 1 + x + x ^ {2} + { frac {2x ^ {3}} {3}} + { frac {x ^ {4}} {2}} + cdots. !}
Третий пример
Здесь мы используем метод, называемый «косвенное расширение», чтобы раскрыть данную функцию. В этом методе используется известное разложение Тейлора экспоненциальной функции. Чтобы разложить (1 + x) e как ряд Тейлора по x, мы используем известный ряд Тейлора функции e:
- e x = ∑ n = 0 ∞ x n n! Знак равно 1 + х + х 2 2! + х 3 3! + х 4 4! + ⋯. { displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2} } {2!}} + { Frac {x ^ {3}} {3!}} + { Frac {x ^ {4}} {4!}} + Cdots.}
Таким образом,
- (1 + x) ex = ex + xex = ∑ n = 0 ∞ xnn! + ∑ N знак равно 0 ∞ Икс N + 1 N! Знак равно 1 + ∑ N знак равно 1 ∞ Икс N N! + ∑ N знак равно 0 ∞ Икс N + 1 N! Знак равно 1 + ∑ N знак равно 1 ∞ Икс N N! + ∑ N знак равно 1 ∞ Икс N (N — 1)! Знак равно 1 + ∑ N знак равно 1 ∞ (1 N! + 1 (N — 1)!) Икс N знак равно 1 + ∑ N знак равно 1 ∞ N + 1 N! Икс N знак равно ∑ N знак равно 0 ∞ N + 1 N! х п. { displaystyle { begin {align} (1 + x) e ^ {x} = e ^ {x} + xe ^ {x} = sum _ {n = 0} ^ { infty} { frac { x ^ {n}} {n!}} + sum _ {n = 0} ^ { infty} { frac {x ^ {n + 1}} {n!}} = 1+ sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n!}} + Sum _ {n = 0} ^ { infty} { frac {x ^ {n + 1}} { n!}} = 1+ sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n!}} + sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {(n-1)!}} = 1+ sum _ {n = 1} ^ { infty} left ({ frac {1} {n!} } + { frac {1} {(n-1)!}} right) x ^ {n} = 1+ sum _ {n = 1} ^ { infty} { frac {n + 1} {n!}} X ^ {n} = sum _ {n = 0} ^ { infty} { frac {n + 1} {n!}} X ^ {n}. End {выровнены}}}
Определения ряда Тейлора
Классически алгебраические функции определяются алгебраическим уравнением, а трансцендентные функции (включая те, которые обсуждались выше) определяются некоторым свойством, которое выполняется для них, например, дифференциальным уравнением . Например, экспоненциальная функция — это функция, которая везде равна своей производной и принимает значение 1 в начале координат. Однако с равным успехом можно определить аналитическую функцию с помощью ее ряда Тейлора.
Ряды Тейлора используются для определения функций и «операторов » в различных областях математики. В частности, это верно в тех областях, где классические определения функций не работают. Например, используя ряд Тейлора, можно расширить аналитические функции до наборов матриц и операторов, таких как экспоненциальная матрица или матричный логарифм.
. В других областях, таких как формальный анализ, это удобнее работать непосредственно с самими сериями power series. Таким образом, можно определить решение дифференциального уравнения как степенной ряд, который, как мы надеемся доказать, является рядом Тейлора искомого решения.
Ряд Тейлора от нескольких переменных
Ряд Тейлора также может быть обобщен на функции более чем одной переменной с
- T (x 1,…, xd) = ∑ n 1 = 0 ∞ ⋯ ∑ nd знак равно 0 ∞ (x 1 — a 1) N 1 ⋯ (xd — ad) ndn 1! ⋯ н д! (∂ n 1 + ⋯ + ndf ∂ x 1 n 1 ⋯ ∂ xdnd) (a 1,…, ad) = f (a 1,…, ad) + ∑ j = 1 d ∂ f (a 1,…, ad) ∂ xj (xj — aj) + 1 2! ∑ j знак равно 1 d ∑ k знак равно 1 d ∂ 2 е (a 1,…, a d) ∂ x j ∂ x k (x j — a j) (x k — a k) + 1 3! ∑ j = 1 d ∑ k = 1 d ∑ l = 1 d ∂ 3 f (a 1,…, ad) ∂ xj ∂ xk ∂ xl (xj — aj) (xk — ak) (xl — al) + ⋯ { Displaystyle { begin {align} T (x_ {1}, ldots, x_ {d}) = sum _ {n_ {1} = 0} ^ { infty} cdots sum _ {n_ {d } = 0} ^ { infty} { frac {(x_ {1} -a_ {1}) ^ {n_ {1}} cdots (x_ {d} -a_ {d}) ^ {n_ {d} }} {n_ {1}! cdots n_ {d}!}} , left ({ frac { partial ^ {n_ {1} + cdots + n_ {d}} f} { partial x_ { 1} ^ {n_ {1}} cdots partial x_ {d} ^ {n_ {d}}}} right) (a_ {1}, ldots, a_ {d}) = f (a_ {1}, ldots, a_ {d}) + sum _ {j = 1} ^ {d} { frac { partial f (a_ {1}, ldots, a_ {d})} { partial x_ {j}}} (x_ {j} -a_ {j}) + { frac {1} {2!}} sum _ {j = 1} ^ {d} sum _ {k = 1} ^ {d} { frac { partial ^ {2} f (a_ {1}, ldots, a_ {d})} { partial x_ {j} partial x_ {k}}} (x_ {j} — a_ {j}) (x_ {k} -a_ {k}) qquad qquad + { frac {1} {3!}} sum _ {j = 1} ^ {d} sum _ {k = 1} ^ {d} sum _ {l = 1} ^ {d} { frac { partial ^ {3} f (a_ {1}, ldots, a_ {d})} { partial x_ {j} partial x_ {k} partial x_ {l}}} (x_ {j} -a_ {j}) (x_ {k} -a_ {k}) (x_ {l} -a_ {l})) + cdots end {align}}}
Например, для функции f (x, y) { displaystyle f (x, y)}
- f (a, b) + (x — a) fx ( а, б) + (у — б) fy (а, б) + 1 2! ((Икс — a) 2 fxx (a, b) + 2 (x — a) (y — b) fxy (a, b) + (y — b) 2 fyy (a, b)) { displaystyle f ( a, b) + (xa) f_ {x} (a, b) + (yb) f_ {y} (a, b) + { frac {1} {2!}} { Big (} (xa) ^ {2} f_ {xx} (a, b) +2 (xa) (yb) f_ {xy} (a, b) + (yb) ^ {2} f_ {yy} (a, b) { Big)}}
где нижние индексы обозначают соответствующие частные производные.
Разложение в ряд Тейлора второго порядка скалярной функции более чем одной переменной можно компактно записать как
- T (x) знак равно е (а) + (х — а) TD е (а) + 1 2! (Икс — а) T {D 2 е (а)} (Икс — а) + ⋯, { Displaystyle Т ( mathbf {x}) = F ( mathbf {a}) + ( mathbf {x} — mathbf {a}) ^ { mathsf {T}} Df ( mathbf {a}) + { frac {1} {2!}} ( mathbf {x} — mathbf {a}) ^ { mathsf {T}} left {D ^ {2} f ( mathbf {a}) right } ( mathbf {x} — mathbf {a}) + cdots,}
где D f (a) is the gradient of f evaluated at x= aand D f (a) is the Hessian matrix. Applying the multi-index notation the Taylor series for several variables becomes
- T ( x) = ∑ | α | ≥ 0 ( x − a) α α ! ( ∂ α f) ( a), {displaystyle T(mathbf {x})=sum _{|alpha |geq 0}{frac {(mathbf {x} -mathbf {a})^{alpha }}{alpha !}}left({mathrm {partial } ^{alpha }}fright)(mathbf {a}),}
which is to be understood as a still more abbreviated multi-index version of the first equation of this paragraph, with a full analogy to the single variable case.
Example
 Second-order Taylor series approximation (in orange) of a function f (x,y) = e ln(1 + y) around the origin.
Second-order Taylor series approximation (in orange) of a function f (x,y) = e ln(1 + y) around the origin.
In order to compute a second-order Taylor series expansion around point (a, b) = (0, 0) of the function
- f ( x, y) = e x ln ( 1 + y), {displaystyle f(x,y)=e^{x}ln(1+y),}
one first computes all the necessary partial derivatives:
- f x = e x ln ( 1 + y) f y = e x 1 + y f x x = e x ln ( 1 + y) f y y = − e x ( 1 + y) 2 f x y = f y x = e x 1 + y. {displaystyle {begin{aligned}f_{x}=e^{x}ln(1+y)[6pt]f_{y}={frac {e^{x}}{1+y}}[6pt]f_{xx}=e^{x}ln(1+y)[6pt]f_{yy}=-{frac {e^{x}}{(1+y)^{2}}}[6pt]f_{xy}=f_{yx}={frac {e^{x}}{1+y}}.end{aligned}}}
Evaluating these derivatives at the origin gives the Taylor coefficients
- f x ( 0, 0) = 0 f y ( 0, 0) = 1 f x x ( 0, 0) = 0 f y y ( 0, 0) = − 1 f x y ( 0, 0) = f y x ( 0, 0) = 1. {displaystyle {begin{aligned}f_{x}(0,0)=0f_{y}(0,0)=1f_{xx}(0,0)=0f_{yy}(0,0)=-1f_{xy}(0,0)=f_{yx}(0,0)=1.end{aligned}}}
Substituting these values in to the general formula
- T ( x, y) = f ( a, b) + ( x − a) f x ( a, b) + ( y − b) f y ( a, b) + 1 2 ! ( ( x − a) 2 f x x ( a, b) + 2 ( x − a) ( y − b) f x y ( a, b) + ( y − b) 2 f y y ( a, b)) + ⋯ {displaystyle T(x,y)=f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)+{frac {1}{2!}}{Big (}(x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b){Big)}+cdots }
produces
- T ( x, y) = 0 + 0 ( x − 0) + 1 ( y − 0) + 1 2 ( 0 ( x − 0) 2 + 2 ( x − 0) ( y − 0) + ( − 1) ( y − 0) 2) + ⋯ = y + x y − y 2 2 + ⋯ {displaystyle {begin{aligned}T(x,y)=0+0(x-0)+1(y-0)+{frac {1}{2}}{Big (}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{Big)}+cdots =y+xy-{frac {y^{2}}{2}}+cdots end{aligned}}}
Since ln(1 + y) is analytic in |y| < 1, we have
- e x ln ( 1 + y) = y + x y − y 2 2 + ⋯, | y | < 1. {displaystyle e^{x}ln(1+y)=y+xy-{frac {y^{2}}{2}}+cdots,qquad |y|<1.}
Comparison with Fourier series
The trigonometric Fourier series enables one to express a periodic function (or a function определенная на отрезке [a, b]) как бесконечная сумма тригонометрических функций (синусов и косинусов ). В этом смысле ряд Фурье аналогичен ряду Тейлора, поскольку последний позволяет выразить функцию в виде бесконечной суммы степеней. Тем не менее, эти две серии отличаются друг от друга в нескольких важных вопросах:
- Конечные усечения ряда Тейлора функции f (x) относительно точки x = a все в точности равны f в точке a. Напротив, ряд Фурье вычисляется путем интегрирования по всему интервалу, поэтому обычно нет такой точки, где бы все конечные усечения ряда были точными.
- Вычисление ряда Тейлора требует знания функции на произвольной малой окрестности точки, тогда как вычисление ряда Фурье требует знания функции во всей области интервала. В определенном смысле можно сказать, что ряд Тейлора является «локальным», а ряд Фурье — «глобальным».
- Ряд Тейлора определен для функции, которая имеет бесконечно много производных в одной точке, тогда как Ряд Фурье определяется для любой интегрируемой функции. В частности, функция не могла быть дифференцируемой. (Например, f (x) может быть функцией Вейерштрасса.)
- Сходимость обоих рядов имеет очень разные свойства. Даже если ряд Тейлора имеет положительный радиус сходимости, результирующий ряд может не совпадать с функцией; но если функция аналитическая, то ряд сходится поточечно к функции и равномерно на каждом компактном подмножестве интервала сходимости. Что касается ряда Фурье, если функция квадратная -интегрируемый, то ряд сходится в среднем квадратичном, но необходимы дополнительные требования для обеспечения точечной или равномерной сходимости (например, если периодическая функция класса C, то сходимость будет равномерной).
- Наконец, на практике аппроксимировать функцию конечным устройством, скажем, многочленом Тейлора или частичной суммой тригонометрической серии, соответственно, в случае ряда Тейлора ошибка очень мала в окрестности точки. к она может быть очень большой в удаленной точке. В случае ряда Фурье ошибка распределяется по области определения функции.
См. Также
- Асимптотическое разложение
- Производящая функция
- Ряд Мадхавы
- Интерполяция разделенных разностей Ньютона
- Аппроксимация Паде
- Серия Пюизо
- Оператор сдвига
Примечания
Ссылки
- Абрамовиц, Милтон ; Стегун, Ирен А. (1970), Справочник по математическим функциям с формулами, графики и математическими таблицами, Нью-Йорк: Dover Publications, девятое издание
- Томас, Джордж Б., младший ; Финни, Росс Л. (1996), Исчисление и аналитическая геометрия (9-е изд.), Эддисон Уэсли, ISBN 0-201-53174-7
- Гринберг, Майкл (1998), Высшая инженерная математика (2-е изд.), Прентис Холл, ISBN 0-13-321431-1
Внешние ссылки
- , Энциклопедия математики, EMS Press, 2001 [1994]
- Вайсштейн, Эрик У. «Серия Тейлора». MathWorld.
- многочлен Тейлора — практическое введение
- Мадхава из Сангамаграммы
- «обсуждение метода Паркера-Сохацки «
- Другая визуализация Тейлора — где вы можете выбрать точку приближения и количество производных
- пересмотр Тейлора для численных методов в Численные методы для студентов STEM
- Золушка 2: расширение Тейлора
- Ряд Тейлора
- Обратные тригонометрические функции Ряд Тейлора
- «Суть исчисления: серия Тейлора» — через YouTube.
-
Понятие ряда Тейлора.
Начать изучение
-
Остаточный член формулы Тейлора.
Начать изучение
-
Разложение элементарных функций в ряд Тейлора.
Начать изучение
-
Разложение показательной и гиперболической функций в ряд Тейлора.
Начать изучение
-
Разложение тригонометрических функций в ряд Тейлора.
Начать изучение
-
Разложение логарифмической функции в ряд Тейлора.
Начать изучение
-
Разложение степенной функции в ряд Тейлора.
Начать изучение
-
Элементарные функции комплексного переменного.
Начать изучение
Понятие ряда Тейлора.
Определение.
Если функция (f(x)) определена в некоторой окрестности точки (x_{0}) и имеет в точке (x_{0}) производные всех порядков, то степенной ряд
$$
f(x_{0}) + sum_{n=1}^{infty}frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}label{ref1}
$$
называется рядом Тейлора функции (f) в точке (x_{0}).
Пусть функция (f) регулярна в точке (x_{0}), то есть представляется в некоторой окрестности точки (x_{0}) сходящимся к этой функции степенным рядом
$$
f(x) = sum_{n = 0}^{infty}a_{n}(x-x_{0})^{n},quad |x-x_{0}| < rho, rho > 0.label{ref2}
$$
Тогда по теореме, доказанной здесь, функция (f) бесконечно дифференцируема в окрестности точки (x_{0}), причем коэффициенты ряда eqref{ref2} выражаются формулами
$$
a_{0} = f(x_{0}),quad a_{n} = frac{f^{(n)}(x_{0})}{n!},quad n in mathbb{N}.label{ref3}
$$
Таким образом, степенной ряд для функции (f(x)), регулярной в данной точке (a), совпадает с рядом Тейлора функции (f) в точке (a).
Если известно, что функция (f(x)) бесконечно дифференцируема в точке (a) (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный для этой функции ряд Тейлора eqref{ref1} сходится при (x neq x_{0}) к функции (f(x)).
Рассмотрим функцию (f(x) = e^{-1/x^{2}}), (x neq 0), (f(0) = 0). Эта функция определена на (R),
$$
f'(x) = frac{2}{x^{3}}e^{-1/x^{2}}, f″(x) = left(frac{4}{x^{6}}-frac{6}{x^{4}}right)e^{-1/x^{2}}quadmbox{при} x neq 0,nonumber
$$
откуда с помощью индукции легко показать, что
$$
f^{(n)}(x) = e^{-1/x^{2}} Q_{3n} left(frac{1}{x}right) mbox{при} x neq 0,nonumber
$$
где (Q_{3n}(t)) — многочлен степени (3n) от (t). Воспользуемся тем, что (displaystylelim_{x rightarrow 0}frac{1}{|x|^{k}}e^{-1/x^{2}}=0) для любого (k in mathbb{N}) (решение можно посмотреть здесь), и докажем, что
$$
f^{(k)}(0) = 0 mbox{для любого} k in mathbb{N}.label{ref4}
$$
Утверждение eqref{ref4} верно при (k = 1), так как (f'(0) = displaystylelim_{x rightarrow 0}frac{e^{-1/x^{2}}}{x} = 0), откуда, предположив, что формула eqref{ref4} справедлива при (k = n), находим
$$
f^{(n + 1)}(0) = lim_{x rightarrow 0}frac{f^{(n)}(x)-f^{(n)}(0)}{x} = lim_{x rightarrow 0} frac{1}{x} Q_{3n} left(frac{1}{x}right) e^{-1/x^{2}} = 0.nonumber
$$
Таким образом, по индукции доказано равенство eqref{ref4}, и поэтому все коэффициенты ряда Тейлора eqref{ref1} в точке (x_{0} = 0) для рассматриваемой функции равны нулю.
Так как (e^{-1/x^{2}} neq 0) при (x neq 0), то сумма ряда Тейлора для функции (f) не совпадает с (f(x)) при (x neq 0). Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки (x_{0} = 0).
Причина этого явления становится понятной, если функцию (f) рассматривать в комплексной плоскости. В самом деле, функция (f(z) = e^{-1/z^{2}}) не является непрерывной в точке (z = 0), так как (f(x) = e^{-1/x^{2}} rightarrow 0) при (x rightarrow 0), a (f(iy) = e^{1/y^{2}} rightarrow +infty) при (y rightarrow 0).
Остаточный член формулы Тейлора.
Пусть функция (f(x)) бесконечно дифференцируема в точке (x_{0}). Тогда ей можно поставить в соответствие ряд eqref{ref1}. Обозначим
$$
S_{n}(x) = sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k},label{ref5}
$$
$$
r_{n}(x) = f(x)-S_{n}(x)label{ref6}
$$
и назовем (r_{n}(x)) остаточным членом формулы Тейлора для функции (f) в точке (x_{0}). Если существует
$$
lim_{x rightarrow 0} r_{n}(x) = 0,label{ref7}
$$
то согласно определению сходимости ряда ряд eqref{ref1} сходится к функции (f(x)) в точке (x), то есть
$$
f(x) = sum_{n = 0}^{infty}frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}.label{ref8}
$$
Теорема 1.
Если функции (f(x)), (f'(x)), …, (f^{(n + 1)}(x)) непрерывны на интервале (Delta = (x_{0}-delta, x_{0} + delta)), где (delta > 0), то для любого (x in Delta) остаточный член формулы Тейлора для функции (f) в точке (x_{0}) можно представить:
- в интегральной форме
$$
r_{n}(x) = frac{1}{n!} intlimits_{x_{0}}^{x} (x-t)^{n}f^{(n + 1)}(t) dt;label{ref9}
$$ - в форме Лагранжа
$$
r_{n}(x) = frac{f^{(n + 1)}(xi)}{(n + 1)!}(x-x_{0})^{n + 1},label{ref10}
$$
где (xi) принадлежит интервалу с концами (x_{0}) и (x).
Доказательство.
(circ) Формула eqref{ref10} доказана в здесь. Докажем формулу eqref{ref9} методом индукции. В силу равенств eqref{ref5} и eqref{ref6} нужно показать, что
$$
f(x)-f(x_{0}) = sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k} + frac{1}{n!} intlimits_{x_{0}}^{x} (x-t)^{n}f^{(n + 1)}(t) dt.label{ref11}
$$
Воспользуемся равенством (displaystyleintlimits_{x_{0}}^{x} f'(t) dt = f(x)-f(x_{0})) и преобразуем его левую часть с помощью формулы интегрирования по частям:
$$
intlimits_{x_{0}}^{x} f'(t) dt =-left.intlimits_{x_{0}}^{x} f'(t)d(x-t) = [-f'(x)(x-t)]right|_{t = x_{0}}^{t = x} + intlimits_{x_{0}}^{x} (x-t)f″(t) dt == f'(x_{0})(x-x_{0}) + intlimits_{x_{0}}^{x} (x-t)f″(t) dt.nonumber
$$
Таким образом,
$$
f(x)-f(x_{0}) = f'(x_{0})(x-x_{0}) + intlimits_{x_{0}}^{x} (x-t)f″(t) dt,nonumber
$$
то есть формула eqref{ref11} верна при (n = 1). Предположим, что формула eqref{ref11} является верной для номера (n-1), то есть
$$
f(x)-f(x_{0}) = sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k} + frac{1}{(n-1)!} intlimits_{x_{0}}^{x} (x-t)^{n-1}f^{(n)}(t) dt.label{ref12}
$$
Преобразуем интеграл в правой части формулы eqref{ref12}, применив формулу интегрирования по частям:
$$
frac{1}{(n-1)!} intlimits_{x_{0}}^{x} (x-t)^{n-1}f^{(n)}(t) dt = -frac{1}{n!} intlimits_{x_{0}}^{x} f^{n}(t)dt((x-t)^{n}) == left.left(-frac{1}{n!}f^{n}(t)(x-t)^{n}right)right|_{t = x_{0}}^{t = x} + frac{1}{n!} intlimits_{x_{0}}^{x}(x-t)^{n}f^{(n + 1)}(t) dt == frac{1}{n!}f^{(n)}(x_{0})(x-x_{0})^{n} + frac{1}{n!} intlimits_{x_{0}}^{x}(x-t)^{n}f^{(n + 1)}(t) dt.nonumber
$$
Отсюда следует, что равенство eqref{ref12} можно записать в виде eqref{ref11}. Формула eqref{ref9} доказана. (bullet)
Теорема 2.
Если функция (f) и все ее производные ограничены в совокупности на интервале (Delta = (x_{0}-delta, x_{0} + delta)), то есть
$$
exists M > 0: forall x in Delta rightarrow |f^{(n)}(x)| leq M, n = 0,1,2,ldots,label{ref13}
$$
то функция (f) представляется сходящимся к ней в каждой точке интервала (Delta) рядом Тейлора eqref{ref8}.
Доказательство.
(circ) Пусть (x in (x_{0}-delta, x_{0} + delta)). Тогда, используя формулу eqref{ref10} и условие eqref{ref13}, получаем
$$
|r_{n}(x)| leq M frac{|x-x_{0}|^{n + 1}}{(n + 1)!}.label{ref14}
$$
Так как (displaystylelim_{x rightarrow 0} frac{a^{n}}{n!} = 0) для любого (a > 0) (пример разобран здесь), то из eqref{ref14} следует, что выполняется условие eqref{ref7}, то есть в точке (x) справедливо равенство eqref{ref8}. (bullet)
Замечание 1.
Теорема 2 остается в силе, если условие eqref{ref13} заменить следующим условием:
$$
exists M > 0 exists C > 0: forall x in Delta rightarrow |f^{(n)}(x)| leq MC^{n}, n = 0, 1, 2, ldotsnonumber
$$
Разложение элементарных функций в ряд Тейлора.
Найдем разложение основных элементарных функций в ряд Тейлора в окрестности точки (x_{0} = 0), то есть в ряд вида
$$
f(x) = sum_{n = 0}^{infty}frac{f^{(n)}(0)}{n!}x^{n},label{ref15}
$$
который называют рядом Маклорена. Заметим, что коэффициенты (displaystylefrac{f^{(n)}(0)}{n!}) разложения eqref{ref15} для основных элементарных функций (показательной, гиперболических, тригонометрических и других) были найдены в разделе про формулу Тейлора.
Разложение показательной и гиперболической функций в ряд Тейлора.
Пусть (f(x) = e^{x}). Тогда для любого (x in (-rho, rho)), где (rho > 0), выполняются неравенства
$$
0 < f(x) < e^{rho},quad 0 < f^{(n)}(x) < e^{rho}, n in mathbb{N}.nonumber
$$
По теореме 2 ряд eqref{ref15} для функции (f(x) = e^{x}) сходится к этой функции на интервале ((-rho, rho)) при любом (rho > 0), то есть радиус сходимости этого ряда (R = +infty). Так как для функции (f(x) = e^{x}) выполняются равенства (f(0) = 1), (f^{(n)}(0) = 1) для любого (n), то по формуле eqref{ref15} получаем разложение в ряд Маклорена показательной функции
$$
e^{x} = sum_{n = 0}^{infty}frac{x^{n}}{n!},label{ref16}
$$
Используя разложение eqref{ref16} и формулы
$$
operatorname{ch} x = frac{e^{x} + e^{-x}}{2},quad operatorname{sh} x = frac{e^{x}-e^{-x}}{2},nonumber
$$
находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса:
$$
operatorname{ch} x = sum_{n = 0}^{infty}frac{x^{2n}}{2n!},label{ref17}
$$
$$
operatorname{sh} x = sum_{n = 0}^{infty}frac{x^{2n + 1}}{(2n + 1)!},label{ref18}
$$
Радиус сходимости каждого из рядов eqref{ref17}, eqref{ref18} (R = +infty).
Разложение тригонометрических функций в ряд Тейлора.
Пусть (f(x) = sin x). Тогда (|f(x)| leq 1) и (|f^{(n)}(x)| leq 1) для всех (n in mathbb{N}) и для всех (x in R). По теореме 2 ряд eqref{ref15}для функции (f(x) = sin x) сходится для любого (x in (-infty, +infty)), то есть радиус сходимости этого ряда (R = +infty).
Если (f(x) = sin x), то (f(0) = 0), (f^{(2n)}(0) = 0), (f'(0) = 1), (f^{(2n + 1)}(0) = (-1)^{n}) для любого (n), и по формулеeqref{ref15}получаем разложение синуса в ряд Маклорена:
$$
sin x = sum_{substack{n = 0}}^{infty} frac{(-1)^{n}}{(2n + 1)!}x^{2n + 1}.label{ref19}
$$
Пусть (f(x) = cos x). Тогда (|f(x)| leq 1), (|f^{(n)}(x)| leq 1) для всех (n) и для всех (x in R), (f(0) = 1), (f'(0) = 0), (f^{(2n)}(0) = (-1)^{n}) и, (f^{(2n + 1)}(0) = 0) для всех (n). По формуле eqref{ref15} получаем
$$
cos x = sum_{n = 0}^{infty} frac{(-1)^{n}}{2n!}x^{2n}.label{ref20}
$$
Радиус сходимости каждого из рядов eqref{ref19} и eqref{ref20} (R = +infty).
Разложение логарифмической функции в ряд Тейлора.
Пусть (f(x) = ln(1 + x)). Тогда
$$
f^{(n)}(x) = frac{(-1)^{n-1}(n-1)!}{(1 + x)^{n}},label{ref21}
$$
откуда находим
$$
frac{f^{(n)}(0)}{n!} = frac{(-1)^{n-1}}{n}.label{ref22}
$$
(circ) Оценим остаточный член (r_{n}(x)), пользуясь формулой eqref{ref9} при (x_{0} = 0). Преобразуем эту формулу, полагая (t = tau x). Тогда (dt = x dtau), (1-x =x(1-tau)) и формула eqref{ref9} примет вид
$$
r_{n}(x) = frac{x^{n + 1}}{n!} intlimits_0^1 (1-tau) f^{(n + 1)}(tau x) dtau.label{ref23}
$$
Если (f(x) = ln(x + 1)), то по формуле eqref{ref23}, используя равенство eqref{ref21}, получаем
$$
r_{n}(x) = (-1)^{n}x^{n + 1} intlimits_0^1 frac{(1-tau)^{n}}{(1 + tau x)^{n + 1}} d tau.label{ref24}
$$
Пусть (|x| < 1). Тогда справедливы неравенства
$$
|1 + tau x| geq 1-tau|x| geq 1-tau,label{ref25}
$$
$$
|1 + tau x| geq 1-|x|,label{ref26}
$$
так как (0 leq tau leq 1). Отсюда следует, что при любом (n in mathbb{N}) выполняется неравенство
$$
|1 + tau x|^{n + 1} geq (1-tau)^{n}(1-|x|).label{ref27}
$$
Используя неравенство eqref{ref27}, из формулы eqref{ref24} получаем следующую оценку остаточного члена:
$$
|r_{n}(x)| leq |x|^{n + 1} intlimits_0^1 frac{dtau}{1-|x|} = frac{|x|^{n + 1}}{1-|x|},nonumber
$$
откуда следует, что (r_{n}(x) rightarrow 0) при (n rightarrow infty), если (|x| < 1).
Пусть (x = 1). Тогда (1 + tau x = 1 + tau), ((1 + tau)^{n + 1} geq 1), (1-tau geq 0), так как (0 leq tau leq 1). Поэтому из формулы eqref{ref24} следует, что (|r_{n}(1)| leq displaystyleintlimits_0^1 (1-tau)^{n}dtau = frac{1}{n + 1}), откуда получаем: (r_{n}(1) rightarrow 0) при (n rightarrow infty).
Итак, если (x in (-1, 1]), то остаточный член (r_{n}(x)) для функции (f(x) = ln (1 + x)) стремится к нулю при (n rightarrow infty), то есть ряд Маклорена сходится к (f(x)). (bullet)
Из формулeqref{ref15}и eqref{ref22} получаем разложение функции (ln (1 + x)) в ряд Маклорена
$$
ln (1 + x) = sum_{n=1}^{infty} frac{(-1)^{n-1}}{n} x^{n},label{ref28}
$$
радиус сходимости которого (R = 1).
Формула eqref{ref28} справедлива при (x = 1), и поэтому
$$
ln 2 = sum_{n=1}^{infty} frac{(-1)^{n-1}}{n} = 1-frac{1}{2} + frac{1}{3}-frac{1}{4} + ldots + frac{(-1)^{n-1}}{n} + ldotsnonumber
$$
Заменяя в формуле eqref{ref28} (x) на (-x), получаем
$$
ln (1-x) =-sum_{n=1}^{infty} frac{x^{n}}{n}.label{ref29}
$$
Разложение степенной функции в ряд Тейлора.
Пусть (f(x) = (1 + x)^{alpha}). Если (alpha = 0), то (f(x) = 1), а если (alpha = n), где (n in mathbb{N}), то (f(x)) — многочлен степени (n), который можно записать по формуле бинома Ньютона в виде конечной суммы:
$$
f(x) = sum_{k=0}^{n} C_{n}^{k}x^{k}.nonumber
$$
Покажем, что если (alpha notin mathbb{N}) и (a neq 0), то функция (f(x) = (1 + x)^{alpha}) представляется при каждом (x in (-1, 1)) сходящимся к ней рядом Маклорена
$$
(1 + x)^{alpha} = sum_{n = 0}^{infty} C_{alpha}^{n}x^{n},label{ref30}
$$
где
$$
C_{alpha}^{0} = 1,quad C_{alpha}^{n} = frac{alpha(alpha-1)ldots(alpha-(n-1))}{n!}.label{ref31}
$$
(circ) Так как
$$
f^{(n + 1)}(x) = alpha(alpha-1)ldots(alpha-n)(1 + x)^{alpha-(n-1)},label{ref32}
$$
то по формуле eqref{ref23} получаем
$$
r_{n}(x) = A_{n}x^{n + 1} intlimits_0^1 left(frac{1-tau}{1 + tau x}right)^{n} (1 + tau x)^{alpha-1} dtau,label{ref33}
$$
где
$$
A_{n} = frac{alpha(alpha-1)ldots(alpha-n)}{n!}.
$$
Выберем число (m in mathbb{N}) таким, чтобы выполнялось условие (|a| leq m). Тогда при всех (n geq m) справедливы неравенства
$$
|A_{n}| leq frac{m(m + 1)ldots(m + n)}{n!} leq frac{(m + n)!}{n!} = (n + 1)ldots(n + m) leq (2n)^{m}.label{ref34}
$$
Используя неравенства eqref{ref25} и eqref{ref26}, а также неравенство (|1 + tau x| leq 1 + |x|), получаем
$$
0 leq frac{1-tau}{1 + xtau} leq 1,label{ref35}
$$
$$
|1 + tau x|^{alpha-1}leq beta(x)=left{begin{array}{lc}(1 + |x|)^{alpha-1},&mbox{если} alpha geq 1, (1-|x|)^{alpha-1},&mbox{если} alpha < 1,end{array} right.label{ref36}
$$
Из формулы eqref{ref33} и оценок eqref{ref34}-eqref{ref36} следует неравенство
$$
|r_{n}(x)| leq beta(x) 2^{m}n^{m}|x|^{n + 1},label{ref37}
$$
которое справедливо при всех (n geq m) и для каждого (x in (-1, 1)).
Так как (displaystylelim_{t rightarrow +infty} frac{t^{m}}{a^{t}}) при (a > 1), то (displaystylelim_{n rightarrow infty} frac{n^{m}}{(1/|x|)^{n + 1}} = 0). Поэтому из соотношения eqref{ref37} следует, что (r_{n}(x) rightarrow 0) при (n rightarrow infty) для каждого (x in (-1, 1)), то есть справедливо равенство eqref{ref30}, причем радиус сходимости ряда eqref{ref30} в случае, когда (alpha neq 0) и (alpha notin mathbb{N}), равен 1. (bullet)
Отметим важные частные случаи формулы eqref{ref30}:
$$
frac{1}{1 + x} = sum_{n = 0}^{infty} (-1)^{n}x^{n},label{ref38}
$$
$$
frac{1}{1-x} = sum_{n = 0}^{infty} x^{n}.label{ref39}
$$
В заключение заметим, что при разложении функций в ряд Тейлора обычно используют формулы eqref{ref16}—eqref{ref20}, eqref{ref28}-eqref{ref30} и применяют такие приемы, как: представление данной функции в виде линейной комбинации функций, ряды Тейлора для которых известны; замена переменного; почленное дифференцирование и интегрирование ряда.
Пример 1.
Разложить в ряд Маклорена функцию (f(x)) и найти радиус сходимости (R) ряда, если:
- (displaystyle f(x) = frac{1}{1 + x^{2}});
- (displaystyle f(x) = frac{1}{sqrt{1 + x^{2}}});
- (displaystyle f(x) = frac{2x-1}{x^{2}-x-6}).
Решение.
- (triangle) Используя формулу eqref{ref38}, получаем ряд
$$
frac{1}{1 + x^{2}} = sum_{n = 0}^{infty} (-1)^{n}x^{2n},label{ref40}
$$
радиус сходимости которого (R = 1). - Из равенства eqref{ref30} следует, что (displaystylefrac{1}{sqrt{1 + x^{2}}} = sum_{n = 0}^{infty} C_{-1/2}^{n}x^{2n}), где
$$
C_{-1/2}^{n} = frac{displaystyleleft(-frac{1}{2}right)left(-frac{1}{2}-1right)ldotsleft(-frac{1}{2}-(n-1)right)}{n!} = frac{(-1)^{n}1cdot3ldots(2n-1)}{2^{n}n!} = frac{(-1)^{n}(2n-1)!!}{2^{n}n!}.nonumber
$$
Следовательно,
$$
frac{1}{sqrt{1 + x^{2}}} = 1 + sum_{n=1}^{infty} frac{(-1)^{n}(2n-1)!!}{2^{n}n!}x^{2n}, R = 1.label{ref41}
$$ - Так как (f(x) = displaystylefrac{1}{x + 2} + frac{1}{x-3} = frac{1}{displaystyle2left(1 + frac{x}{2}right)}-frac{1}{displaystyle3left(1-frac{x}{3}right)}), то, применяя формулы eqref{ref38} и eqref{ref39}, получаем ряд
$$
frac{2x-1}{x^{2}-x-6} = sum_{n = 0}^{infty} left(frac{(-1)^{n}}{2^{n + 1}}-frac{1}{3^{n + 1}}right)x^{n}, R = 2. blacktrianglenonumber
$$
Пример 2.
Разложить в ряд Маклорена функции
$$
operatorname{arctg} x,nonumber
$$
$$
operatorname{arcsin} x,nonumber
$$
$$
ln(x + sqrt{1 + x^{2}}),nonumber
$$
и найти радиусы сходимости (R) рядов.
Решение.
- (triangle) Почленно интегрируя ряд eqref{ref40}, получаем
$$
operatorname{arctg} x = intlimits_0^x frac{dt}{1 + t^{2}} = sum_{n = 0}^{infty} (-1)^{n} frac{x^{2n + 1}}{2n + 1},quad R = 1.nonumber
$$ - Заменяя в формуле eqref{ref41} (x^{2}) на (-x^{2}), получаем
$$
frac{1}{sqrt{1-x^{2}}} = 1 + sum_{n=1}^{infty} frac{(2n-1)!!}{2^{n}n!}x^{2n},quad R = 1.nonumber
$$
откуда следует, что
$$
operatorname{arcsin} x = intlimits_0^x frac{dt}{1-t^{2}} = x + sum_{n=1}^{infty} frac{(2n-1)!!}{2^{n}n!(2n + 1)}x^{2n + 1}, R = 1.nonumber
$$ - Почленно интегрируя ряд eqref{ref41}, получаем
$$
ln(x + sqrt{1 + x^{2}}) = intlimits_0^x frac{dt}{1 + t^{2}} = x + sum_{n=1}^{infty} frac{(-1)^{n}(2n-1)!!}{2^{n}n!(2n + 1)}x^{2n + 1}, R = 1. blacktrianglenonumber
$$
Пример 3.
Разложить в ряд Тейлора в точке (x_{0} = 2) функцию (f(x) = ln(4 + 3x-x^{2})).
Решение.
(triangle) Так как (4 + 3x-x^{2} = -(x-4)(x + 1)), то, полагая (t = x-2), получаем
$$
f(x) = ln(4-x)(x + 1) = g(t) = ln(2-t)(3 + t) = ln 6 + lnleft(1-frac{t}{2}right) + lnleft(1 + frac{t}{3}right).nonumber
$$
Используя формулы eqref{ref28} и eqref{ref29}, отсюда находим
$$
g(t) = ln 6-sum_{n=1}^{infty} frac{t^{n}}{n2^{n}} + sum_{n=1}^{infty} frac{(-1)^{n-1}t^{n}}{n3^{n}},quad |t| < 2.nonumber
$$
Следовательно,
$$
ln(4 + 3x-x^{2}) = ln 6 + sum_{n=1}^{infty} left(frac{(-1)^{n-1}}{3n}-frac{1}{2^{n}}right)frac{(x-2)^{n}}{n}, R = 2. blacktrianglenonumber
$$
Элементарные функции комплексного переменного.
Показательная, гиперболические и тригонометрические функции комплексного переменного (z) определятся соответственно формулами
$$
e^{z} = sum_{n = 0}^{infty} frac{z^{n}}{n!},label{ref42}
$$
$$
operatorname{ch} z = sum_{n = 0}^{infty} frac{z^{2n}}{(2n)!},label{ref43}
$$
$$
operatorname{sh} z = sum_{n = 0}^{infty} frac{z^{2n + 1}}{(2n + 1)!},label{ref44}
$$
$$
cos z = sum_{n = 0}^{infty} frac{(-1)^{n}z^{2n}}{(2n)!},label{ref45}
$$
$$
sin z = sum_{n = 0}^{infty} frac{(-1)^{n}z^{2n + 1}}{(2n + 1)!}.label{ref46}
$$
Радиус сходимости (R) каждого из рядов eqref{ref42}-eqref{ref46} равен (+infty). Заменяя в равенстве eqref{ref42} (z) на (iz) и (-iz), получаем
$$
e^{iz} = sum_{n = 0}^{infty} frac{i^{n}z^{n}}{n!},qquad e^{-iz} = sum_{n = 0}^{infty} frac{(-1)^{n}i^{n}z^{n}}{n!}.label{ref47}
$$
Используя равенства eqref{ref47} и формулы eqref{ref45}, eqref{ref46}, находим
$$
frac{e^{iz} + e^{-iz}}{2} = cos z, frac{e^{iz}-e^{-iz}}{2i} = sin z,label{ref48}
$$
откуда следует, что
$$
e^{iz} = cos z + i sin z.label{ref49}
$$
Полагая в формуле eqref{ref42} (z = z_{1}) и (z = z_{2}). и перемножая соответствующие ряды, можно показать, что
$$
e^{z_{1}}e^{z_{2}} = e^{z_{1} + z_{2}}.label{ref50}
$$
Пусть (z = x + iy), где (x in R), (y in R). Тогда из равенства eqref{ref50} и формулы eqref{ref49} находим
$$
e^{z} = e^{x + iy} = e^{x}(cos y + i sin y).label{ref51}
$$
Из формулы eqref{ref51} следует, что
$$
e^{z + 2pi i} = e^{z},nonumber
$$
то есть (e^{z}) — периодическая функция с периодом (2pi i). Поэтому для каждого комплексного (z neq 0) уравнение
$$
e^{w} = zlabel{ref52}
$$
имеет бесконечное множество решений вида (w + i2pi n), где (w) — одно из решений уравнения eqref{ref52}, (n in Z).
Если (w = u + iv), то (z = e^{w} = e^{u}(cos v + i sin v)), откуда получаем
$$
|z| = e^{u},quad u = ln |z|,quad v = arg z.nonumber
$$
Пусть (varphi) — какое-нибудь значение аргумента числа (z). Тогда
$$
v = varphi + 2pi n, n in Z.nonumber
$$
Таким образом, все решения уравнения eqref{ref52}, если их обозначить символом (operatorname{Ln} z), задаются формулой
$$
operatorname{Ln} z = ln |z| + i(varphi + 2pi n),label{ref53}
$$
где (varphi) — одно из значений аргумента числа (z) ((z neq 0)), (n in Z).
По заданному значению (z) значение (w) из уравнения eqref{ref52} определяется, согласно формуле eqref{ref53}, неоднозначно (говорят, что логарифмическая функция (operatorname{Ln} z) является многозначной).
Пример 4.
Разложить в степенной ряд в окрестности точки (z = 0) функцию (f(z) = e^{z}sin z).
Решение.
(triangle) Используя формулы eqref{ref48} и eqref{ref50}, получаем
$$
f(z) = e^{z}left(frac{e^{iz}-e^{-iz}}{2i}right) = frac{1}{2i}(e^{z(1 + i)}-e^{z(1-i)}).nonumber
$$
Так как (1 + i = sqrt{2}e^{ipi/4}), (1-i = sqrt{2}e^{-ipi/4}), то по формуле eqref{ref42} находим
$$
f(z) = sum_{n = 0}^{infty} frac{2^{n/2}}{n!} left(frac{e^{ipi n/4}-e^{-ipi n/4}}{2i}right)z^{n},nonumber
$$
откуда в силу второго из равенств eqref{ref48} следует, что
$$
e^{z}sin z = sum_{n = 0}^{infty} frac{2^{n/2}}{n!} sin frac{pi n}{4}z^{n}.nonumber
$$
Радиус сходимости ряда (R = +infty). (blacktriangle)
Разложение функций в степенные ряды. Ряд Тейлора
Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции , определенной в области и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида который бы сходился в области и его сумма в этой области совпадала с .
Постановка задачи разложения функции в степенной ряд
Для функции , аналитической в области , найти ряд , сходящийся к в круге , принадлежащем области , то есть
Равенство (3.15) означает, что является суммой ряда в круге .
Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции ; найти круг сходимости ряда и установить сходимость ряда именно к . Последнее, напомним, означает, что для точек круга выполняется неравенство для любого и .
Все поставленные вопросы решаются с помощью следующей теоремы.
Теорема Тейлора о разложении функции в степенной ряд
Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки этой области представляется в виде степенного ряда (3.15), радиус сходимости которого не меньше, чем расстояние от точки до границы области . Коэффициенты ряда вычисляются по формуле
где — произвольный контур, принадлежащий области и охватывающий точку , в частности, — окружность или по формуле
На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.
Алгоритм разложения аналитической функции в степенной ряд
1. Найти производные от данной функции: .
2. Вычислить значения производных в точке ; записать коэффициенты по формуле (3.17). Составить ряд по степеням с этими коэффициентами, который соответствует данной функции
3. Найти область сходимости полученного ряда и записать разложение (3.15).
Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, .
Утверждение 3.3
1. Функция, аналитическая в точке , раскладывается в окрестности этой точки в степенной ряд.
2. На границе круга сходимости ряда есть хотя бы одна особая точка функции, т.е. радиус сходимости круга равен расстоянию от центра разложения до ближайшей особой точки функции.
3. Степенной ряд в круге сходимости является рядом Тейлора для своей суммы, т.е. коэффициенты ряда вычисляются по формулам (3.16), (3.17).
Примеры разложения функций по степеням z
Пример 3.13. Записать разложения по степеням функций .
Решение
Задачу решаем по вышеприведенному алгоритму.
1. Найдем производные:
В поставленной задаче . По формуле (3.17) имеем
3. Нетрудно убедиться, что все составленные ряды сходятся во всей комплексной плоскости, . В результате получаем формулы, которые ранее были приняты за определения соответствующих функций:
В результате получены так называемые основные разложения.
Пример 3.14. Записать разложения по степеням функций: а) ; б) .
Решение
Задачу можно решать, пользуясь алгоритмом, а можно использовать формулы (3.13) для суммы членов геометрической профессии. Заданные функции являются аналитическими во всей комплексной плоскости за исключением одной точки . Для каждого случая получаем:
заметим, что здесь для .
Пример 3.15. Записать разложения по степеням функций: а) ; б) .
Решение
Разложения записываются для однозначных ветвей многозначного выражения. Выбор ветви определяется заданием функции в точке .
a) Функция определена во всей комплексной плоскости за исключением , т.е. в двусвязной области . Чтобы получить односвязную область из , проведем разрез, соединяющий точки и . Из условия следует, что точка должна быть внутренней точкой области. Поэтому выбираем разрез, не проходящий через . например по лучу . В полученной односвязной области, где , функция является однозначной аналитической функцией. Далее решаем задачу по алгоритму.
1. Находим производные (формулу устанавливаем по индукции):
2. По формуле (3.17):
3. Находим радиус сходимости ряда: , где . В результате получаем
б) Функция определена всюду в за исключением , т.е. в двусвязной области. В односвязной области, полученной из путем разреза по лучу , функция является однозначной , аналитической. Задачу можно решать, как и выше, т.е. по алгоритму, а можно использовать полученный выше результат, введя обозначение . Для , удовлетворяющих неравенству имеем разложение . Заменяя на , получаем результат
Разложения основных функция в степенной ряд
Разложения, полученные в результате решения примеров 3.13-3.15, носят название основных (табличных) разложений. Выпишем их:
Основные разложения позволяют при решении примеров на разложение функции в ряд Тейлора не пользоваться сформулированным выше алгоритмом, сложность которого связана с техникой дифференцирования и составления формулы общего члена.
Утверждение 3.4. При разложении функции в ряд Тейлора используются основные (табличные) разложения и действия над рядами. Радиус сходимости ряда может быть получен по виду раскладываемой функции без использования формулы общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полученного при разложении данной функции в окрестности точки , равен расстоянию от центра разложения — точки до ближайшей особой точки функции. Если функция является аналитической всюду, то .
Пример 3.16. Разложить по степеням функции комплексного переменного:
Решение
а) Обозначим через и, используя табличное разложение для функции , получим ответ:
, то есть .
б) Запишем функцию в виде произведения и, используя разложение для , получим ответ:
, то есть .
в) Чтобы воспользоваться одним из основных разложений, применим тригонометрическую формулу — формулу «понижения». Получим:
Заметим, что свободный член разложения в этой записи встречается дважды, поэтому нужно привести подобные члены. Для этого в записи рада отделим слагаемое при — свободный член:
В результате имеем .
Из этого разложения можно найти значение производной любого порядка функции в точке , так как эти значения связаны формулой (3.17) с коэффициентами разложения: . Поэтому, учитывая, что в разложении присутствуют только четные степени, заключаем, что все производные нечетных порядков от в точке равны нулю, а производная, например, десятого порядка не равна нулю. Найдем ее, используя равенство , где — коэффициент в разложении при , т.е. в записанном выше разложении нужно взять . Получим
г) Функция определена всюду, кроме . В односвязной области, например в плоскости с разрезом по лучу , где , возможно выделение однозначных ветвей многозначного выражения (рис. 3.1). Выбираем ту ветвь, для которой , то есть из получаем . Разложим аналитическую функцию по степеням в круге ; радиус круга — расстояние от центра разложения до граничной точки .
Чтобы воспользоваться основным разложением, преобразуем функцию следующим образом:
Тогда, обозначая через и используя основное разложение для , получаем при условии , т.е. в круге .
Пример 3.17. Разложить в окрестности точки ветвь функции , для которой .
Решение
Функция определена всюду в , кроме точек , т.е. в трехсвязной области — плоскости с выколотыми точками и . Чтобы получить односвязную область, проведем разрезы по лучам, выходящим из этих точек. Например, луч из точки выберем параллельным мнимой оси, , а луч из точки — по действительной оси: . В полученной односвязной области (рис. 3.2) каждая ветвь является аналитической функцией и раскладывается в ряд в круге ( — расстояние от до границы). Здесь ветвь задается условием:
, то есть из при .
Далее, чтобы использовать основное разложение, преобразуем функцию:
Для числа в силу выбора ветви берем , а функции и раскладываем в ряды, как в предыдущем примере:
В области , принадлежащей выбранной односвязной области, сходятся оба ряда. Используя свойство сложения рядов, получаем окончательный результат:
При разложении функции в ряд в окрестности точки , т.е. по степеням , удобно использовать замену и полученную после замены функцию раскладывать по степеням .
Пример 3.18. Разложить по степеням функции: a) ; б) в) .
Решение
а) Обозначим через , и, используя тригонометрическую формулу для функции , получим: . Здесь и — постоянные величины, а для функций и используем основные разложения. В результате получим
то есть ряд вида , где коэффициент определяется следующим образом: для и для .
б) Можно, как и выше, использовать вспомогательную переменную, а можно сделать то же самое, применив простое преобразование: . Здесь — постоянная величина, функция раскладывается в ряд как функция по степеням . Получаем ответ:
, или .
в) Обозначая через , получаем функцию . Разложение этой функции по степеням найдено в примере 3.16:
Возвращаясь к исходной переменной, получаем разложение исходной функции в круге (рис. 3.3):
Пример 3.19. Разложить по степеням функции: .
Решение
Данные функции являются простейшими рациональными (элементарными) дробями. Для их разложения используется формула суммы членов бесконечно убывающей геометрической прогрессии . В первом случае формула используется непосредственно, при , во втором — после преобразования получаем . Разложение заданных функций имеет вид
Соотношения (3.18),(3.19) обобщают формулу , которая получается из них при .
При разложении дроби замечаем, что она является производной от , то есть , поэтому ее разложение можно получить, используя дифференцирование ряда:
Ответ удобнее записать в виде .
Очевидно, повторяя процедуру дифференцирования, можно получить разложение элементарных дробей вида при любом натуральном .
Алгоритм разложения рациональных дробей в ряд Тейлора
Рассмотрим примеры на разложение в ряд Тейлора рациональных дробей
где и — многочлены. Первые этапы решения задачи аналогичны этапам интегрирования этих дробей. Приведем полный алгоритм.
1. Если дробь неправильная , следует выделить целую часть дроби многочлен.
2. Правильную рациональную дробь разложить на элементарные дроби:
а) записать дробь в виде суммы элементарных дробей вида с неопределенными коэффициентами , где — корень знаменателя, — его кратность;
б) найти неопределенные коэффициенты.
3. Разложить элементарные дроби в степенные ряды. Основными приемами при этом являются применение формул (3.13),(3.18),(3.19) и правила дифференцирования ряда (см. пример 3.19)).
При разложении по степеням можно предварительно ввести вспомогательную переменную .
Пример 3.20. Разложить по степеням функции: а) ; б) .
Решение
а) Воспользуемся алгоритмом.
1. Дробь неправильная, поэтому выделяем целую часть: .
2. Полученная правильная дробь является элементарной дробью.
3. Записываем разложение элементарной дроби и получаем:
Для разложения дроби можно было использовать формулу (3.19) при .
Для нахождения окончательного ответа нужно сделать преобразование приведения подобных членов, так как в полученном выражении свободный член встречается дважды. Имеем
, то есть .
б) Воспользуемся алгоритмом.
1. Дробь неправильная, выделяем целую часть. Можно, как и выше, применить преобразование дроби:
Можно для выделения целой части применить метод деления «углом», или, обозначая i + 2 = t, произвести почленное деление на одночлен
2,3. Записываем разложение заданной функции, используя формулу (3.19) для правильной дроби:
Окончательный ответ: .
Получен ряд вида , где . Нетрудно проверить равенство: .
Пример 3.21. Функцию разложить в ряд Тейлора в окрестности точки , если а) ; б) .
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем ее на элементарные дроби. Для этого представим дробь в виде
где и — неопределенные коэффициенты, которые находим из тождества
Полагая последовательно и , получаем .
Записываем дробь в виде суммы дробей: .
3. Раскладываем по степеням г каждую элементарную дробь:
В общей области сходимости — круге — записываем сумму рядов разложение исходной дроби:
б) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Разложение дроби на элементарные получено в предыдущем пункте:
3. Раскладываем по степеням каждую элементарную дробь:
Записываем разложение исходной дроби в круге
При разложении по степеням, можно было сделать замену в исходной дроби.
Радиусы сходимости в обоих случаях можно определить заранее, до записи» разложения — по виду функции. Ее особыми точками являются точки и . В первом случае ближайшей к точке является точка , расстояние между точками равно единице и, следовательно, ; во втором — обе особые точки удалены от на расстояние, равное двум, и .
Пример 3.22. Разложить по степеням функции (рациональные дроби): а) ; б) .
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем правильную дробь на элементарные дроби, предварительно разложив знаменатель на множители:
, где и .
Представим дробь в виде . Находим коэффициенты и из тождества , т.е. из системы
Дробь представлена в виде суммы: .
3. Раскладываем элементарные дроби по степеням
Записываем ответ:
б) Воспользуемся алгоритмом.
1,2. Раскладываем дробь на элементарные:
, где — неопределенные коэффициенты.
Находим коэффициенты из тождества .
Приравнивая коэффициенты при одинаковых степенях , имеем
3. Раскладываем элементарные дроби по степеням
Для исходной дроби получаем разложение:
или, складывая ряды: .
Окончательный ответ: .
Пример 3.23. Разложить по степеням функции: а) ; б) .
Решение
Обе дроби правильные; раскладывать на более простые нет необходимости. Используя основные разложения, получаем ответы:
а) ;
б) или .
Пример 3.24. Используя разложение функции по степеням , найти значение производной седьмого порядка в точке .
Решение
Пример 3.25. Записать разложение функций a) и б) по степеням до члена, содержащего .
Решение
а) Применим метод подстановки ряда в ряд, используя основные разложения для функций и . Имеем
, или, подставляя:
где . Записывать большее число слагаемых нет необходимости, так как уже у следующего (первого отброшенного) младшая степень равна .
Возведение в степень рядов, как и перемножение рядов, производится по правилам действий с многочленами, в частности применяется формула бинома Ньютона:
Так как младшая степень выражения равна трем, следовательно, — шести, то для записи результата следует взять из первых двух скобок по два слагаемых, а из остальных по одному, т.е.
Приводя подобные члены, получим окончательный ответ:
или .
Разложение, очевидно, можно получить, вычисляя коэффициенты разложения по формуле (3.17), что более громоздко.
б) Разложение можно получить, используя формулу (3.17) для коэффициентов либо произведя деление ряда на ряд методом деления «утлом» или методом неопределенных коэффициентов.
Применим последний прием. Разложение по степеням ищем в виде
По определению деления имеем тождество
Перемножаем ряды справа и приравниваем коэффициенты полученного ряда известным коэффициентам при соответствующих степенях ряда, записанного слева. Получаем систему уравнений
из которой находим коэффициенты .
Ответ получаем в виде . Это разложение справедливо в круге , так как — ближайшая к особая точка функции тангенса .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Разложение в ряд Тейлора
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
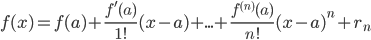 ,
,
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
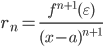 , где число x заключено между х и а.
, где число x заключено между х и а.
- Решение онлайн
- Видеоинструкция
Если для некоторого значения х rn→0 при n→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
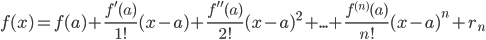
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
- она имеет производные всех порядков;
- построенный ряд сходится в этой точке.
При а=0 получаем ряд, называемый рядом Маклорена:
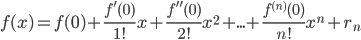
Разложение простейших (элементарных) функций в ряд Маклорена:
Пример №1. Разложить в степенной ряд функцию f(x)=2x.
Решение
. Найдем значения функции и ее производных при х=0
f(x) = 2x, f(0) = 20=1;
f'(x) = 2xln2, f'(0) = 20 ln2= ln2;
f»(x) = 2x ln22, f»(0) = 20 ln22= ln22;
…
f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.
Пример №2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex.
Решение
. Находим производные функции ex и их значения в точке х=-4.
f(x) = еx, f(-4) = е-4;
f'(x) = еx, f'(-4) = е-4;
f»(x) = еx, f»(-4) = е-4;
…
f(n)(x) = еx, f(n)( -4) = е-4.
Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -∞<x<+∞.
Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение
. Находим производные данной функции.
f(x)=lnx,  ,
,  ,
,  ,
, 

f(1)=ln1=0, f'(1)=1, f»(1)=-1, f»'(1)=1*2,…, f(n)=(-1)n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно,

Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Пример №4. Разложить в степенной ряд функцию  .
.
Решение
. В разложении (1) заменяем х на -х2, получаем:
 , -∞<x<∞
, -∞<x<∞
Пример №5. Разложить в ряд Маклорена функцию  .
.
Решение
. Имеем 
Пользуясь формулой (4), можем записать:

подставляя вместо х в формулу –х, получим:

Отсюда находим: ln(1+x)-ln(1-x) =  —
— 
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
 . Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример №5а. Разложить в ряд Маклорена функцию  , указать область сходимости.
, указать область сходимости.
Решение. Сначала найдем 1-x-6x2=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.
 на элементарные:
на элементарные: 
Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

с областью сходимости |x| < 1/3.
Пример №6. Разложить функцию  в ряд Тейлора в окрестности точки х=3.
в ряд Тейлора в окрестности точки х=3.
Решение
. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):
 =
= 
Полученный ряд сходится при  или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).
Решение
.


Ряд сходится при  , или -2 < x < 5.
, или -2 < x < 5.
Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение
. Сделаем замену t=х-2:

Воспользовавшись разложением (3), в котором на место х подставим π/4t, получим:

Полученный ряд сходится к заданной функции при -∞<π/4t<+∞, т.е. при (-∞<x<+∞).
Таким образом,
 , (-∞<x<+∞)
, (-∞<x<+∞)
Приближенные вычисления с помощью степенных рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд:

Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:

Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток rn(x). Для этого применяют следующие приемы:
- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).
Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение
. Воспользуемся разложением  , где x=1/2 (см. пример 5 в предыдущей теме):
, где x=1/2 (см. пример 5 в предыдущей теме):

Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:

Таким образом, мы можем отбросить этот остаток и получаем 
Пример №2. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
Решение
. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
 , поэтому его и следующие за ним члены можно отбросить.
, поэтому его и следующие за ним члены можно отбросить.
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10-5.
Решение
. Соответствующий неопределенный интеграл  не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:


Так как полученный ряд удовлетворяет условиям Лейбница и  достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим

Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.
Решение
.

![]()
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
 ≈0.0001<0.001
≈0.0001<0.001
Следовательно,  .
.

As the degree of the Taylor polynomial rises, it approaches the correct function. This image shows sin x and its Taylor approximations by polynomials of degree 1, 3, 5, 7, 9, 11, and 13 at x = 0.
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function’s derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century.
The partial sum formed by the first n + 1 terms of a Taylor series is a polynomial of degree n that is called the nth Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as n increases. Taylor’s theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of the infinite sequence of the Taylor polynomials. A function may differ from the sum of its Taylor series, even if its Taylor series is convergent. A function is analytic at a point x if it is equal to the sum of its Taylor series in some open interval (or open disk in the complex plane) containing x. This implies that the function is analytic at every point of the interval (or disk).
Definition[edit]
The Taylor series of a real or complex-valued function f (x) that is infinitely differentiable at a real or complex number a is the power series
where n! denotes the factorial of n. In the more compact sigma notation, this can be written as
where f(n)(a) denotes the nth derivative of f evaluated at the point a. (The derivative of order zero of f is defined to be f itself and (x − a)0 and 0! are both defined to be 1.)
With a = 0, the Maclaurin series takes the form:[1]
or in the compact sigma notation:
Examples[edit]
The Taylor series of any polynomial is the polynomial itself.
The Maclaurin series of 1/1 − x is the geometric series
So, by substituting x for 1 − x, the Taylor series of 1/x at a = 1 is
By integrating the above Maclaurin series, we find the Maclaurin series of ln(1 − x), where ln denotes the natural logarithm:
The corresponding Taylor series of ln x at a = 1 is
and more generally, the corresponding Taylor series of ln x at an arbitrary nonzero point a is:
The Maclaurin series of the exponential function ex is
The above expansion holds because the derivative of ex with respect to x is also ex, and e0 equals 1. This leaves the terms (x − 0)n in the numerator and n! in the denominator of each term in the infinite sum.
History[edit]
The ancient Greek philosopher Zeno of Elea considered the problem of summing an infinite series to achieve a finite result, but rejected it as an impossibility;[2] the result was Zeno’s paradox. Later, Aristotle proposed a philosophical resolution of the paradox, but the mathematical content was apparently unresolved until taken up by Archimedes, as it had been prior to Aristotle by the Presocratic Atomist Democritus. It was through Archimedes’s method of exhaustion that an infinite number of progressive subdivisions could be performed to achieve a finite result.[3] Liu Hui independently employed a similar method a few centuries later.[4]
In the 14th century, the earliest examples of specific Taylor series (but not the general method) were given by Madhava of Sangamagrama.[5][6] Though no record of his work survives, writings of his followers in the Kerala school of astronomy and mathematics suggest that he found the Taylor series for the trigonometric functions of sine, cosine, and arctangent (see Madhava series). During the following two centuries his followers developed further series expansions and rational approximations.
In late 1670, James Gregory was shown in a letter from John Collins several Maclaurin series (











In 1691–1692, Isaac Newton wrote down an explicit statement of the Taylor and Maclaurin series in an unpublished version of his work De Quadratura Curvarum. However, this work was never completed and the relevant sections were omitted from the portions published in 1704 under the title Tractatus de Quadratura Curvarum.
It was not until 1715 that a general method for constructing these series for all functions for which they exist was finally published by Brook Taylor,[8] after whom the series are now named.
The Maclaurin series was named after Colin Maclaurin, a professor in Edinburgh, who published the special case of the Taylor result in the mid-18th century.
Analytic functions[edit]

The function e(−1/x2) is not analytic at x = 0: the Taylor series is identically 0, although the function is not.
If f (x) is given by a convergent power series in an open disk centred at b in the complex plane (or an interval in the real line), it is said to be analytic in this region. Thus for x in this region, f is given by a convergent power series
Differentiating by x the above formula n times, then setting x = b gives:
and so the power series expansion agrees with the Taylor series. Thus a function is analytic in an open disk centered at b if and only if its Taylor series converges to the value of the function at each point of the disk.
If f (x) is equal to the sum of its Taylor series for all x in the complex plane, it is called entire. The polynomials, exponential function ex, and the trigonometric functions sine and cosine, are examples of entire functions. Examples of functions that are not entire include the square root, the logarithm, the trigonometric function tangent, and its inverse, arctan. For these functions the Taylor series do not converge if x is far from b. That is, the Taylor series diverges at x if the distance between x and b is larger than the radius of convergence. The Taylor series can be used to calculate the value of an entire function at every point, if the value of the function, and of all of its derivatives, are known at a single point.
Uses of the Taylor series for analytic functions include:
- The partial sums (the Taylor polynomials) of the series can be used as approximations of the function. These approximations are good if sufficiently many terms are included.
- Differentiation and integration of power series can be performed term by term and is hence particularly easy.
- An analytic function is uniquely extended to a holomorphic function on an open disk in the complex plane. This makes the machinery of complex analysis available.
- The (truncated) series can be used to compute function values numerically, (often by recasting the polynomial into the Chebyshev form and evaluating it with the Clenshaw algorithm).
- Algebraic operations can be done readily on the power series representation; for instance, Euler’s formula follows from Taylor series expansions for trigonometric and exponential functions. This result is of fundamental importance in such fields as harmonic analysis.
- Approximations using the first few terms of a Taylor series can make otherwise unsolvable problems possible for a restricted domain; this approach is often used in physics.
Approximation error and convergence[edit]

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full period centered at the origin.

The Taylor polynomials for ln(1 + x) only provide accurate approximations in the range −1 < x ≤ 1. For x > 1, Taylor polynomials of higher degree provide worse approximations.

The Taylor approximations for ln(1 + x) (black). For x > 1, the approximations diverge.
Pictured is an accurate approximation of sin x around the point x = 0. The pink curve is a polynomial of degree seven:
The error in this approximation is no more than |x|9 / 9!. For a full cycle centered at the origin (−π < x < π) the error is less than 0.08215. In particular, for −1 < x < 1, the error is less than 0.000003.
In contrast, also shown is a picture of the natural logarithm function ln(1 + x) and some of its Taylor polynomials around a = 0. These approximations converge to the function only in the region −1 < x ≤ 1; outside of this region the higher-degree Taylor polynomials are worse approximations for the function.
The error incurred in approximating a function by its nth-degree Taylor polynomial is called the remainder or residual and is denoted by the function Rn(x). Taylor’s theorem can be used to obtain a bound on the size of the remainder.
In general, Taylor series need not be convergent at all. And in fact the set of functions with a convergent Taylor series is a meager set in the Fréchet space of smooth functions. And even if the Taylor series of a function f does converge, its limit need not in general be equal to the value of the function f (x). For example, the function
is infinitely differentiable at x = 0, and has all derivatives zero there. Consequently, the Taylor series of f (x) about x = 0 is identically zero. However, f (x) is not the zero function, so does not equal its Taylor series around the origin. Thus, f (x) is an example of a non-analytic smooth function.
In real analysis, this example shows that there are infinitely differentiable functions f (x) whose Taylor series are not equal to f (x) even if they converge. By contrast, the holomorphic functions studied in complex analysis always possess a convergent Taylor series, and even the Taylor series of meromorphic functions, which might have singularities, never converge to a value different from the function itself. The complex function e−1/z2, however, does not approach 0 when z approaches 0 along the imaginary axis, so it is not continuous in the complex plane and its Taylor series is undefined at 0.
More generally, every sequence of real or complex numbers can appear as coefficients in the Taylor series of an infinitely differentiable function defined on the real line, a consequence of Borel’s lemma. As a result, the radius of convergence of a Taylor series can be zero. There are even infinitely differentiable functions defined on the real line whose Taylor series have a radius of convergence 0 everywhere.[9]
A function cannot be written as a Taylor series centred at a singularity; in these cases, one can often still achieve a series expansion if one allows also negative powers of the variable x; see Laurent series. For example, f (x) = e−1/x2 can be written as a Laurent series.
Generalization[edit]
There is, however, a generalization[10][11] of the Taylor series that does converge to the value of the function itself for any bounded continuous function on (0,∞), using the calculus of finite differences. Specifically, one has the following theorem, due to Einar Hille, that for any t > 0,
Here Δn
h is the nth finite difference operator with step size h. The series is precisely the Taylor series, except that divided differences appear in place of differentiation: the series is formally similar to the Newton series. When the function f is analytic at a, the terms in the series converge to the terms of the Taylor series, and in this sense generalizes the usual Taylor series.
In general, for any infinite sequence ai, the following power series identity holds:
So in particular,
The series on the right is the expectation value of f (a + X), where X is a Poisson-distributed random variable that takes the value jh with probability e−t/h·(t/h)j/j!. Hence,
The law of large numbers implies that the identity holds.[12]
List of Maclaurin series of some common functions[edit]
Several important Maclaurin series expansions follow.[13] All these expansions are valid for complex arguments x.
Exponential function[edit]

The exponential function ex (in blue), and the sum of the first n + 1 terms of its Taylor series at 0 (in red).
The exponential function 
.
It converges for all x.
The exponential generating function of the Bell numbers is the exponential function of the predecessor of the exponential function:
Natural logarithm[edit]
The natural logarithm (with base e) has Maclaurin series
They converge for 
Geometric series[edit]
The geometric series and its derivatives have Maclaurin series
All are convergent for 
Binomial series[edit]
The binomial series is the power series
whose coefficients are the generalized binomial coefficients
(If n = 0, this product is an empty product and has value 1.) It converges for 
When α = −1, this is essentially the infinite geometric series mentioned in the previous section. The special cases α = 1/2 and α = −1/2 give the square root function and its inverse:
When only the linear term is retained, this simplifies to the binomial approximation.
Trigonometric functions[edit]
The usual trigonometric functions and their inverses have the following Maclaurin series:
All angles are expressed in radians. The numbers Bk appearing in the expansions of tan x are the Bernoulli numbers. The Ek in the expansion of sec x are Euler numbers.
Hyperbolic functions[edit]
The hyperbolic functions have Maclaurin series closely related to the series for the corresponding trigonometric functions:
The numbers Bk appearing in the series for tanh x are the Bernoulli numbers.
Polylogarithmic functions[edit]
The polylogarithms have these defining identities:
The Legendre chi functions are defined as follows:
And the formulas presented below are called inverse tangent integrals:
In statistical thermodynamics these formulas are of great importance.
Elliptic functions[edit]
The complete elliptic integrals of first kind K and of second kind E can be defined as follows:
The Jacobi theta functions describe the world of the elliptic modular functions and they have these Taylor series:
The regular partition number sequence P(n) has this generating function:
The strict partition number sequence Q(n) has that generating function:
Calculation of Taylor series[edit]
Several methods exist for the calculation of Taylor series of a large number of functions. One can attempt to use the definition of the Taylor series, though this often requires generalizing the form of the coefficients according to a readily apparent pattern. Alternatively, one can use manipulations such as substitution, multiplication or division, addition or subtraction of standard Taylor series to construct the Taylor series of a function, by virtue of Taylor series being power series. In some cases, one can also derive the Taylor series by repeatedly applying integration by parts. Particularly convenient is the use of computer algebra systems to calculate Taylor series.
First example[edit]
In order to compute the 7th degree Maclaurin polynomial for the function
,
one may first rewrite the function as
.
The Taylor series for the natural logarithm is (using the big O notation)
and for the cosine function
.
The latter series expansion has a zero constant term, which enables us to substitute the second series into the first one and to easily omit terms of higher order than the 7th degree by using the big O notation:
Since the cosine is an even function, the coefficients for all the odd powers x, x3, x5, x7, … have to be zero.
Second example[edit]
Suppose we want the Taylor series at 0 of the function
We have for the exponential function
and, as in the first example,
Assume the power series is
Then multiplication with the denominator and substitution of the series of the cosine yields
Collecting the terms up to fourth order yields
The values of 

Third example[edit]
Here we employ a method called «indirect expansion» to expand the given function. This method uses the known Taylor expansion of the exponential function. In order to expand (1 + x)ex as a Taylor series in x, we use the known Taylor series of function ex:
Thus,
Taylor series as definitions[edit]
Classically, algebraic functions are defined by an algebraic equation, and transcendental functions (including those discussed above) are defined by some property that holds for them, such as a differential equation. For example, the exponential function is the function which is equal to its own derivative everywhere, and assumes the value 1 at the origin. However, one may equally well define an analytic function by its Taylor series.
Taylor series are used to define functions and «operators» in diverse areas of mathematics. In particular, this is true in areas where the classical definitions of functions break down. For example, using Taylor series, one may extend analytic functions to sets of matrices and operators, such as the matrix exponential or matrix logarithm.
In other areas, such as formal analysis, it is more convenient to work directly with the power series themselves. Thus one may define a solution of a differential equation as a power series which, one hopes to prove, is the Taylor series of the desired solution.
Taylor series in several variables[edit]
The Taylor series may also be generalized to functions of more than one variable with[14][15]
For example, for a function 
where the subscripts denote the respective partial derivatives.
Second-order Taylor series in several variables[edit]
A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written compactly as
where D f (a) is the gradient of f evaluated at x = a and D2 f (a) is the Hessian matrix. Applying the multi-index notation the Taylor series for several variables becomes
which is to be understood as a still more abbreviated multi-index version of the first equation of this paragraph, with a full analogy to the single variable case.
Example[edit]

Second-order Taylor series approximation (in orange) of a function f (x,y) = ex ln(1 + y) around the origin.
In order to compute a second-order Taylor series expansion around point (a, b) = (0, 0) of the function
one first computes all the necessary partial derivatives:
Evaluating these derivatives at the origin gives the Taylor coefficients
Substituting these values in to the general formula
produces
Since ln(1 + y) is analytic in |y| < 1, we have
Comparison with Fourier series[edit]
The trigonometric Fourier series enables one to express a periodic function (or a function defined on a closed interval [a,b]) as an infinite sum of trigonometric functions (sines and cosines). In this sense, the Fourier series is analogous to Taylor series, since the latter allows one to express a function as an infinite sum of powers. Nevertheless, the two series differ from each other in several relevant issues:
- The finite truncations of the Taylor series of f (x) about the point x = a are all exactly equal to f at a. In contrast, the Fourier series is computed by integrating over an entire interval, so there is generally no such point where all the finite truncations of the series are exact.
- The computation of Taylor series requires the knowledge of the function on an arbitrary small neighbourhood of a point, whereas the computation of the Fourier series requires knowing the function on its whole domain interval. In a certain sense one could say that the Taylor series is «local» and the Fourier series is «global».
- The Taylor series is defined for a function which has infinitely many derivatives at a single point, whereas the Fourier series is defined for any integrable function. In particular, the function could be nowhere differentiable. (For example, f (x) could be a Weierstrass function.)
- The convergence of both series has very different properties. Even if the Taylor series has positive convergence radius, the resulting series may not coincide with the function; but if the function is analytic then the series converges pointwise to the function, and uniformly on every compact subset of the convergence interval. Concerning the Fourier series, if the function is square-integrable then the series converges in quadratic mean, but additional requirements are needed to ensure the pointwise or uniform convergence (for instance, if the function is periodic and of class C1 then the convergence is uniform).
- Finally, in practice one wants to approximate the function with a finite number of terms, say with a Taylor polynomial or a partial sum of the trigonometric series, respectively. In the case of the Taylor series the error is very small in a neighbourhood of the point where it is computed, while it may be very large at a distant point. In the case of the Fourier series the error is distributed along the domain of the function.
See also[edit]
- Asymptotic expansion
- Generating function
- Laurent series
- Madhava series
- Newton’s divided difference interpolation
- Padé approximant
- Puiseux series
- Shift operator
Notes[edit]
- ^ Thomas & Finney 1996, §8.9
- ^ Lindberg, David (2007). The Beginnings of Western Science (2nd ed.). University of Chicago Press. p. 33. ISBN 978-0-226-48205-7.
- ^ Kline, M. (1990). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 35–37. ISBN 0-19-506135-7.
- ^ Boyer, C.; Merzbach, U. (1991). A History of Mathematics (Second revised ed.). John Wiley and Sons. pp. 202–203. ISBN 0-471-09763-2.
- ^ «Neither Newton nor Leibniz – The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala» (PDF). MAT 314. Canisius College. Archived (PDF) from the original on 2015-02-23. Retrieved 2006-07-09.
- ^ S. G. Dani (2012). «Ancient Indian Mathematics – A Conspectus». Resonance. 17 (3): 236–246. doi:10.1007/s12045-012-0022-y. S2CID 120553186.
- ^ Turnbull, Herbert Westren, ed. (1939). James Gregory; Tercentenary Memorial Volume. G. Bell & Sons. pp. 168–174.Roy, Ranjan (1990). «The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha» (PDF). Mathematics Magazine. 63 (5): 291–306. doi:10.1080/0025570X.1990.11977541.Malet, Antoni (1993). «James Gregorie on Tangents and the «Taylor» Rule for Series Expansions». Archive for History of Exact Sciences. 46 (2): 97–137. doi:10.1007/BF00375656. JSTOR 41133959.
- ^ Taylor, Brook (1715). Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (in Latin). London. p. 21–23 (Prop. VII, Thm. 3, Cor. 2). Translated into English in Struik, D. J. (1969). A Source Book in Mathematics 1200–1800. Harvard University Press. pp. 329–332. ISBN 978-0-674-82355-6. Re-translated into English by Ian Bruce (2007) as Methodus Incrementorum Directa & Inversa, 17centurymaths.com.Feigenbaum, L. (1985). «Brook Taylor and the method of increments». Archive for History of Exact Sciences. 34 (1–2): 1–140. doi:10.1007/bf00329903.
- ^ Rudin, Walter (1980), Real and Complex Analysis, New Delhi: McGraw-Hill, p. 418, Exercise 13, ISBN 0-07-099557-5
- ^ Feller, William (2003) [1971]. An introduction to probability theory and its applications. Vol. 2 (3rd ed.). Wiley. pp. 230–2. ISBN 9789971512989. OCLC 818811840.
- ^ Hille, Einar; Phillips, Ralph S. (1957), Functional analysis and semi-groups, AMS Colloquium Publications, vol. 31, American Mathematical Society, pp. 300–327.
- ^ Feller 2003, p. 231
- ^ Most of these can be found in (Abramowitz & Stegun 1970).
- ^ Hörmander, Lars (2002) [1990]. «1. Test Functions §1.1. A review of Differential Calculus». The analysis of partial differential operators. Vol. 1 (2nd ed.). Springer. Eqq. 1.1.7 and 1.1.7′. doi:10.1007/978-3-642-61497-2_2. ISBN 978-3-642-61497-2.
- ^ Kolk, Johan A.C.; Duistermaat, J.J. (2010). «Taylor Expansion in Several Variables». Distributions: Theory and applications. Birkhauser. pp. 59–63. doi:10.1007/978-0-8176-4675-2_6. ISBN 978-0-8176-4672-1.
References[edit]
- Abramowitz, Milton; Stegun, Irene A. (1970), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, Ninth printing
- Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.), Addison Wesley, ISBN 0-201-53174-7
- Greenberg, Michael (1998), Advanced Engineering Mathematics (2nd ed.), Prentice Hall, ISBN 0-13-321431-1
- Roy, Ranjan (2021) [1st ed. 2011]. Series and Products in the Development of Mathematics. Vol. 1 (2nd ed.). Cambridge University Press.
External links[edit]
- «Taylor series», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. «Taylor Series». MathWorld.
Выражение функции в виде бесконечной суммы
 По мере увеличения степени полинома Тейлора она приближается к правильной функции. На этом изображении показан грех x и его приближения Тейлора, полиномы степени 1, 3, 5, 7, 9, 11и 13.
По мере увеличения степени полинома Тейлора она приближается к правильной функции. На этом изображении показан грех x и его приближения Тейлора, полиномы степени 1, 3, 5, 7, 9, 11и 13.
В математике ряд Тейлора функции является бесконечная сумма члены, которые выражены в терминах производных функций в одной точке. Для наиболее распространенных функций функция и сумма ее ряда Тейлора вблизи этой точки равны. Ряды Тейлора названы в честь Брука Тейлора, который представил их в 1715 году.
Если ноль — это точка, в которой рассматриваются производные, ряд Тейлора также называется серией Маклорена, после Колина Маклорена, который широко использовал этот частный случай из серии Тейлора в 18 веке.
частичная сумма, образованная первыми членами ряда Тейлора, полиномом степени n, который называется n-м полиномом Тейлора функции. Полиномы Тейлора — это приближения, которые обычно становятся лучше при увеличении. Теорема Тейлора дает количественные оценки погрешностей, обеспечивает использование таких приближений. Если ряд Тейлора функции является сходящейся, его сумма составляет предел бесконечной последовательности полиномов Тейлора. Функция может быть не равна сумме своего ряда Тейлора, даже если ее ряд Тейлора сходится. Функция является аналитической в точке x, если она равна сумме своего ряда Тейлора в некотором открытом интервале (или открытом диске в комплексная плоскость ), содержащая x. Это означает, что функция аналитична в каждой точке интервала (или круга).
Содержание
- 1
- 2 Примеры
- 3 История
- 4 Аналитические функции
- 5 Ошибка аппроксимации и сходимость
- 5.1 Обобщение
- 6 Список рядов Маклорена некоторых общих функций
- 6.1 Экспоненциальная функция
- 6.2 Натуральный логарифм
- 6.3 Геометрический ряд
- 6.4 Биномиальный ряд
- 6.5 Тригонометрические функции
- 6.6 Гиперболические функции
- 7 Вычисление ряда Тейлора
- 7.1 Первый пример
- 7.2 Второй пример
- 7.3 Третий пример
- 8 Ряд Тейлора как определения
- 9 Ряд Тейлора с переменными
- 9.1 Пример
- 10 Сравнение с рядом Фурье
- 11 См. Также
- 12 Примечания
- 13 Ссылки
- 14 Внешние ссылки
Определение
Ряд Тейлора вещественной или комплекснозначной функции f (x), который бесконечно дифференцируем при действительном или комплексном числе a, является степенным рядом
- f (a) + f ′ (a) 1! (х — а) + е ″ (а) 2! (Икс — а) 2 + е ‴ (а) 3! (Икс — а) 3 + ⋯, { displaystyle f (a) + { frac {f ‘(a)} {1!}} (Xa) + { frac {f’ ‘(a)} {2! }} (xa) ^ {2} + { frac {f » ‘(a)} {3!}} (xa) ^ {3} + cdots,}
где n! обозначает факториал число n. В более компактной сигма-нотации это можно записать как
- ∑ n = 0 ∞ f (n) (a) n! (Икс — а) п, { Displaystyle сумма _ {п = 0} ^ { infty} { гидроразрыва {е ^ {(п)} (а)} {п!}} (Ха) ^ {п},}
где f (a) обозначает n-ю производную функции f, вычисленную в точке a. (Производная нулевого порядка функции f определяет как сама f, а (x — a) и 0! оба как 1.)
Когда a = 0, ряд также называется рядом Маклорена.
Примеры
Ряд Тейлора для любого многочлена является самим многочленом.
Ряд Маклорена для 1/1 — x — это геометрический ряд
- 1 + x + x 2 + x 3 + ⋯, { displaystyle 1 + x + x ^ {2} + x ^ {3} + cdots,}
поэтому ряд Тейлора для 1 / x при a = 1 равенстве
- 1 — (x — 1) + (x — 1) 2 — (x — 1) 3 + ⋯. { displaystyle 1- (x-1) + (x-1) ^ {2} — (x-1) ^ {3} + cdots.}
Интегрируя вышеуказанный ряд Маклорена, мы находим ряд Маклорена для ln ( 1 — x), где ln обозначает натуральный логарифм :
- — x — 1 2 x 2 — 1 3 x 3 — 1 4 x 4 — ⋯. { displaystyle -x — { tfrac {1} {2}} x ^ {2} — { tfrac {1} {3}} x ^ {3} — { tfrac {1} {4}} x ^ {4} — cdots.}
Соответствующий ряд Тейлора для ln x при a = 1 равенстве
- (x — 1) — 1 2 (x — 1) 2 + 1 3 (x — 1) 3 — 1 4 (х — 1) 4 + ⋯, { displaystyle (x-1) — { tfrac {1} {2}} (x-1) ^ {2} + { tfrac {1} {3}} ( x-1) ^ {3} — { tfrac {1} {4}} (x-1) ^ {4} + cdots,}
и, в более общем смысле, соответствующий ряд Тейлора для ln x в произвольная ненулевая точка a равна:
- ln a + 1 a (x — a) — 1 a 2 (x — a) 2 2 + ⋯. { displaystyle ln a + { frac {1} {a}} (xa) — { frac {1} {a ^ {2}}} { frac { left (xa right) ^ {2} } {2}} + cdots.}
Ряд Тейлора для экспоненциальной функции e при a = 0 равен
- ∑ n = 0 ∞ xnn! = х 0 0! + х 1 1! + х 2 2! + х 3 3! + х 4 4! + х 5 5! + ⋯ знак равно 1 + x + x 2 2 + x 3 6 + x 4 24 + x 5120 + ⋯. { displaystyle { begin {align} sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = { frac {x ^ {0}} { 0!}} + { Frac {x ^ {1}} {1!}} + { Frac {x ^ {2}} {2!}} + { Frac {x ^ {3}} {3! }} + { frac {x ^ {4}} {4!}} + { frac {x ^ {5}} {5!}} + cdots \ = 1 + x + { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {6}} + { frac {x ^ {4}} {24}} + { frac {x ^ {5}} {120}} + cdots. End {align}}}
Вышеупомянутое расширение верно, потому что производная e по x также равна e, а e равно 1. Это оставляет (x — 0) в числитель и п! в знаменателе для каждого члена в бесконечной сумме.
История
Греческий философ Зенон рассматривал проблему суммирования бесконечного ряда для достижения конечного результата, но отвергал ее как невозможную; Результатом стал парадокс Зенона. Позже Аристотель показал философское разрешение парадокса, но математическое содержание, по-видимому, оставалось неразрешенным, пока его не подхватил Архимед, как это было до Аристотеля досократическим атомистом Демокрит. Именно с помощью архимедова метода исчерпания можно было выполнить бесконечное количество последовательных последовений для конечного результата. Лю Хуэй независимо использовал аналогичный метод несколько столетий спустя.
В 14 самые ранние примеры использования рядов Тейлора и близких к ним методов были даны Мадхавой из Сангамаграмы. Хотя записи о его работе не сохранились, работы более поздних индийских математиков предполагают, что он обнаружил ряд частных случаев ряда Тейлора, в числе для тригонометрических функций от синуса., косинус, тангенс и арктангенс. Керальская школа астрономии и математики дополнительно расширила его работы с помощью различных расширений рядов и рациональных приближений до 16 века.
В 17 веке Джеймс Грегори также работал в этой области и опубликовал несколько серий Маклорена. Однако только в 1715 году общий метод построения этих рядов для всех функций, которые они существуют, был наконец предоставлен Бруком Тейлором, в честь которого теперь назван ряд.
Серия Maclaurin была названа в честь Колина Маклорена, который опубликовал частный случай результата Тейлора в 18 веке.
Аналитические функции
 Функция не является аналитической при x = 0: ряд Тейлора идентично 0, хотя функция не является.
Функция не является аналитической при x = 0: ряд Тейлора идентично 0, хотя функция не является.
Если f (x) равно заданный сходящимся степенным прямым прямым прямым расстоянием в точке b на комплексной плоскости, он называется аналитическим в круге. Таким образом, для x в этом круге f задается сходящимся степенным рядом
- f (x) = ∑ n = 0 ∞ a n (x — b) n. { displaystyle f (x) = sum _ {n = 0} ^ { infty} a_ {n} (xb) ^ {n}.}
Дифференцируя приведенную выше формулу по xn раз, затем установить x = b дает:
- f (n) (b) n! = a n { displaystyle { frac {f ^ {(n)} (b)} {n!}} = a_ {n}}
, и поэтому разложение в степенной ряд согласуется с рядом Тейлора. Таким образом, функция является аналитической в открытом положении с центром в точке b тогда и только тогда, когда ее ряд Тейлора сходится к значению функции в каждой точке диска.
Если f (x) равен своему ряду Тейлора для всех x в комплексной плоскости, он называется целым. Полиномы, экспоненциальная функция e и тригонометрические функции синус и косинус, являются примерами целых функций. Примеры неполных функций включают квадратный корень , логарифм , тангенс тригонометрической функции , и обратный ему арктангенс. Для этих функций ряды Тейлора не сходятся, если x далеко от b. То есть Тейлора расходится на в точке x, если расстояние между x и b больше, чем радиус сходимости. Ряд Тейлора можно использовать для вычислений значения функций в каждой точке, если значение функции и всех ее производных известно в одной точке.
Использование ряда Тейлора для аналитических функций включает:
- Частные суммы (полиномы Тейлора ) ряд как приближения функции. Эти аппроксимации хороши.
- Дифференцирование и интегрирование степенных рядов может работать построчно, и поэтому это особенно легко.
- Аналитическая функция однозначно продолжается до голоморфной функции на открытом диске в комплексной плоскости. Это делает доступным механизмом комплексного анализа.
- (Усеченный) ряд программных вычислений для выполнения определенных вычислений функций (часто путем преобразования полинома в форму Чебышева и вычисляя его с помощью алгоритма Кленшоу ).
- Алгебраические операции могут быть легко выполнены с представлением степенного ряда; например, формула Эйлера следует из разложений в ряд Тейлора для тригонометрических и экспоненциальных функций. Этот результат имеет фундаментальное значение в таких областях, как гармонический анализ.
- Аппроксимации с использованием первых нескольких функций.
Ошибка аппроксимации и сходимость
 Синусоидальная функция (синий) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного периода с большой степенью 7 (розовый) для полного периода сходимости
Синусоидальная функция (синий) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного периода с большой степенью 7 (розовый) для полного периода сходимости
 Многочлены Тейлора для ln (1 + x) обеспечивают только точные приближения В диапазоне −1 < x ≤ 1. For x>1, м Нагчлены Тейлора более высокой степени худшие приближения.
Многочлены Тейлора для ln (1 + x) обеспечивают только точные приближения В диапазоне −1 < x ≤ 1. For x>1, м Нагчлены Тейлора более высокой степени худшие приближения.  Приближения Тейлора для ln (1 + x) (черный). Для x>1 приближения расходятся.
Приближения Тейлора для ln (1 + x) (черный). Для x>1 приближения расходятся.
На рисунке справа показано точное приближение sin x вокруг точки x = 0. Розовая кривая представляет собой полином седьмой степени:
- sin (x) ≈ x — х 3 3! + х 5 5! — х 7 7!. { displaystyle sin left (x right) приблизительно x — { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} {5!}} — { гидроразрыв {x ^ {7}} {7!}}. !}
Ошибка в этом приближении не более | х | / 9!. В частности, для -1 < x < 1, the error is less than 0.000003.
Напротив, также показано изображение функций натурального логарифма ln (1 + x) и некоторых из ее многочленов Тейлора около a = 0. Эти приближения сходятся с функциями только в области — 1 < x ≤ 1; outside of this region the higher-degree Taylor polynomials are worse approximations for the function.
Ошибка, возникающая при аппроксимации функции ее полиномом Тейлора n-й степени, называется остатком или остатком и обозначается функцией R n (x). Теорема Тейлора может Номинация для оценки размера остатка.
В общем, ряды Тейлора не обязательно должны быть сходящимися. И фактически набор функций со сходящимся рядом Тейлора представляет собой скудное множество в дизай Фреше гладких функций. И даже если ряд Тейлора функции f действительно сходится, его предел не обязательно должен быть равен значению функции f (x). Например функция,
- f (x) = {e — 1 x 2, if x ≠ 0 0, if x = 0 { displaystyle f (x) = { begin {cases} e ^ {- { frac { 1} {x ^ {2}}}} { text {if}} x neq 0 \ 0 { text {if}} x = 0 end {cases}}}
равно бесконечно дифференцируема в точке x = 0 и имеет там все производные нулю. Следовательно, Тейлора функции f (x) относительно x = 0 тождественно равен нулю. Однако вокруг f (x) не является нулевой функцией, поэтому не равна ее ряду Тейлора начала координат. Таким образом, f (x) является примером неаналитической гладкой функции.
В анализа этот пример показывает, что существуют бесконечно дифференцируемые функции f (x), ряд Тейлора не равен f (x), даже если они сходятся. Напротив, голоморфные функции, изучаемые в комплексном анализе, всегда обладают сходящимся рядом Тейлора, и даже ряд Тейлора мероморфных функций, которые могут иметь особенности, никогда не сходятся к значению, отличному от самой функции. Однако комплексная функция не приближается к 0, когда z приближается к 0 вдоль мнимой оси, поэтому она не непрерывна в комплексной плоскости, и ее ряд Тейлора не определен в 0.
В более общем В смысле, каждая последовательность действительных или комплексных чисел может появиться как коэффициенты в ряду Тейлора бесконечно дифференцируемой функции, определенной на вещественной прямой, как следствие леммы Бореля. В результате радиус сходимости ряда Тейлора может быть равенством нулю. Существуют даже бесконечно дифференцируемые функции, функции на вещественной прямой, чьи ряды Тейлора везде имеют радиус сходимости 0.
Функцию нельзя записать в виде ряда Тейлора с центром в сингулярности ; в этих случаях все же можно разложить в ряд, если допустить также отрицательные переменные x; см. серию Лоран. Например, f (x) = e можно записать в виде ряда Лорана.
Обобщение
Однако существует обобщение ряда Тейлора, которое сходится к значению самой функции для любой ограниченной непрерывной функции на (0, ∞), используя исчисление конечных разностей. В частности, имеется следующая теорема, благодаря Эйнару Хилле, что для любого t>0
- lim h → 0 + ∑ n = 0 ∞ t n n! Δ h n f (a) h n = f (a + t). { displaystyle lim _ {h to 0 ^ {+}} sum _ {n = 0} ^ { infty} { frac {t ^ {n}} {n!}} { frac { Delta _ {h} ^ {n} f (a)} {h ^ {n}}} = f (a + t).}
Здесь Δ. h- n-й оператор конечных разностей с шагом h. Этот ряд в точности совпадает с рядом Тейлора, за исключением того, что вместо дифференцирования появляются отдельные различия: ряд формально аналогичен ряду серии Ньютона. Эта функция является аналитической в составе ряда сходятся к ряду Тейлора и в этом смысле обобщают ряд Тейлора.
В общем, для любой бесконечной следовать a i выполняется следующее тождество степенного ряда:
- ∑ n = 0 ∞ u n n! Δ N а я знак равно е — и ∑ J знак равно 0 ∞ U J J! а я + j. { displaystyle sum _ {n = 0} ^ { infty} { frac {u ^ {n}} {n!}} Delta ^ {n} a_ {i} = e ^ {- u} sum _ {j = 0} ^ { infty} { frac {u ^ {j}} {j!}} a_ {i + j}.}
Так, в частности,
- f (a + t) = lim h → 0 + е — й ∑ j знак равно 0 ∞ f (a + jh) (th) jj!. { displaystyle f (a + t) = lim _ {h to 0 ^ {+}} e ^ {- { frac {t} {h}}} sum _ {j = 0} ^ { infty } f (a + jh) { frac { left ({ frac {t} {h}} right) ^ {j}} {j!}}.}
Ряд справа — это математическое ожидание для f (a + X), где X — распределенная по Пуассону случайная величина, которая принимает значение jh с вероятностью e · (t / h) / j!. Следовательно,
- f (a + t) = lim h → 0 + ∫ — ∞ ∞ f (a + x) d P t h, h (x). { displaystyle f (a + t) = lim _ {h to 0 ^ {+}} int _ {- infty} ^ { infty} f (a + x) dP _ {{ frac {t } {h}}, h} (x).}
закон больших чисел подразумевает, что тождество выполнено.
Список серий Маклорена некоторых общих функций
Далее следуют несколько важных расширений серии Маклорена. Все эти разложения действительны для сложных аргументов x.
Экспоненциальная функция
 Экспоненциальная функция e (синим цветом) и сумма первых n + 1 элементов Тейлора в 0 (красным).
Экспоненциальная функция e (синим цветом) и сумма первых n + 1 элементов Тейлора в 0 (красным).
экспоненциальная функция ex { displaystyle e ^ {x}}
- ex = ∑ п = 0 ∞ xnn! Знак равно 1 + х + х 2 2! + х 3 3! + ⋯ { displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2}} {2!}} + { Frac {x ^ {3}} {3!}} + Cdots}
.
Он сходится для всех x.
Натуральный логарифм
натуральный логарифм (с основанием e ) имеет ряд Маклорена
- ln (1 — x) = — ∑ n Знак равно 1 ∞ xnn = — x — x 2 2 — x 3 3 — ⋯, ln (1 + x) = ∑ n = 1 ∞ (- 1) n + 1 xnn = x — x 2 2 + x 3 3 — ⋯. { displaystyle { begin {align} ln (1-x) = — sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n}} = — x- { frac {x ^ {2}} {2}} — { frac {x ^ {3}} {3}} — cdots, \ ln (1 + x) = sum _ {n = 1} ^ { infty} (- 1) ^ {n + 1} { frac {x ^ {n}} {n}} = x — { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {3}} — cdots. end {align}}}
Они сходятся для | х | < 1 {displaystyle |x|<1}
Геометрический ряд
Геометрический ряд и его производные имеют ряд Маклорена
- 1 1 — x = ∑ n = 0 ∞ xn 1 (1 — x) 2 = ∑ n = 1 ∞ nxn — 1 1 (1 — Икс) 3 знак равно ∑ N знак равно 2 ∞ (N — 1) N 2 Иксn — 2. { displaystyle { begin {align} { frac {1} {1-x}} = sum _ {n = 0} ^ { infty} x ^ {n} \ { frac {1} {(1-x) ^ {2}}} = sum _ {n = 1} ^ { infty} nx ^ {n- 1} \ { frac {1} {(1-x) ^ {3}}} = sum _ {n = 2} ^ { infty} { frac {(n-1) n} {2 }} х ^ {п-2}. end {align}}}
Все сходятся для | х | < 1 {displaystyle |x|<1}
Биномиальный ряд
биномиальный ряд — это степенной ряд
- (1 + x) α = ∑ n = 0 ∞ (α n) xn { displaystyle ( 1 + x) ^ { alpha} = sum _ {n = 0} ^ { infty} { binom { alpha} {n}} x ^ {n}}
, коэффициенты которого являются обобщенными биномиальные коэффициенты
- (α n) = ∏ k = 1 n α — k + 1 k = α (α — 1) ⋯ (α — n + 1) n!. { displaystyle { binom { alpha} {n}} = prod _ {k = 1} ^ {n} { frac { alpha -k + 1} {k}} = { frac { alpha ( alpha -1) cdots ( alpha -n + 1)} {n!}}.}
(Если n = 0, этот продукт является пустым продуктом и имеет значение 1.) сходится для | х | < 1 {displaystyle |x|<1}
Когда α = −1, это, по сути, бесконечный геометрический ряд, упомянутый в предыдущем разделе. Частные случаи α = 1/2 и α = −1/2 дают функцию квадратного корня и ее обратную функцию :
- (1 + x) 1 2 = 1 + 1 2 x — 1 8 x 2 + 1 16 x 3 — 5 128 x 4 + 7 256 x 5 -…, (1 + x) — 1 2 = 1 — 1 2 x + 3 8 x 2 — 5 16 x 3 + 35 128 x 4 — 63 256 х 5 +…. { displaystyle { begin {align} (1 + x) ^ { frac {1} {2}} = 1 + { tfrac {1} {2}} x — { tfrac {1} {8} } x ^ {2} + { tfrac {1} {16}} x ^ {3} — { tfrac {5} {128}} x ^ {4} + { tfrac {7} {256}} x ^ {5} — ldots, \ (1 + x) ^ {- { frac {1} {2}}} = 1 — { tfrac {1} {2}} x + { tfrac {3 } {8}} x ^ {2} — { tfrac {5} {16}} x ^ {3} + { tfrac {35} {128}} x ^ {4} — { tfrac {63} { 256}} x ^ {5} + ldots. end {align}}}
Когда сохраняется только линейный член, это упрощается до биномиального приближения.
Тригонометрические функции
Обычные тригонометрические функции и обратные к ним имеют следующий ряд Маклорена:
- sin x = ∑ n = 0 ∞ (- 1) n (2 n + 1)! Икс 2 N + 1 знак равно Икс — Икс 3 3! + х 5 5! — для всех x cos x знак равно ∑ n знак равно 0 ∞ (- 1) n (2 n)! Икс 2 N знак равно 1 — Икс 2 2! + х 4 4! — ⋯ для всех x загар x знак равно ∑ n = 1 ∞ B 2 n (- 4) n (1 — 4 n) (2 n)! x 2 n — 1 = x + x 3 3 + 2 x 5 15 + ⋯ для | х | < π 2 sec x = ∑ n = 0 ∞ ( − 1) n E 2 n ( 2 n) ! x 2 n = 1 + x 2 2 + 5 x 4 24 + ⋯ for | x | < π 2 arcsin x = ∑ n = 0 ∞ ( 2 n) ! 4 n ( n !) 2 ( 2 n + 1) x 2 n + 1 = x + x 3 6 + 3 x 5 40 + ⋯ for | x | ≤ 1 arccos x = π 2 − arcsin x = π 2 − ∑ n = 0 ∞ ( 2 n) ! 4 n ( n !) 2 ( 2 n + 1) x 2 n + 1 = π 2 − x − x 3 6 − 3 x 5 40 − ⋯ for | x | ≤ 1 arctan x = ∑ n = 0 ∞ ( − 1) n 2 n + 1 x 2 n + 1 = x − x 3 3 + x 5 5 − ⋯ for | x | ≤ 1, x ≠ ± i {displaystyle {begin{aligned}sin x=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-cdots {text{for all }}x\[6pt]cos x=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-cdots {text{for all }}x\[6pt]tan x=sum _{n=1}^{infty }{frac {B_{2n}(-4)^{n}left(1-4^{n}right)}{(2n)!}}x^{2n-1}=x+{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}+cdots {text{for }}|x|<{frac {pi }{2}}\[6pt]sec x=sum _{n=0}^{infty }{frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}=1+{frac {x^{2}}{2}}+{frac {5x^{4}}{24}}+cdots {text{for }}|x|<{frac {pi }{2}}\[6pt]arcsin x=sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}=x+{frac {x^{3}}{6}}+{frac {3x^{5}}{40}}+cdots {text{for }}|x|leq 1\[6pt]arccos x={frac {pi }{2}}-arcsin x\={frac {pi }{2}}-sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}={frac {pi }{2}}-x-{frac {x^{3}}{6}}-{frac {3x^{5}}{40}}-cdots {text{for }}|x|leq 1\[6pt]arctan x=sum _{n=0}^{infty }{frac {(-1)^{n}}{2n+1}}x^{2n+1}=x-{frac {x^{3}}{3}}+{frac {x^{5}}{5}}-cdots {text{for }}|x|leq 1, xneq pm iend{aligned}}}
Все углы выражены в радианах. Числа B k, появляющиеся в разложениях tan x, являются числами Бернулли. E k в разложении sec x — это числа Эйлера.
гиперболические функции
гиперболические функции имеют ряды Маклорена, тесно связанные с рядами для соответствующие тригонометрические функции:
- sinh x = ∑ n = 0 ∞ x 2 n + 1 (2 n + 1)! знак равно х + х 3 3! + х 5 5! + ⋯ для всех x cosh x = ∑ n = 0 ∞ x 2 n (2 n)! Знак равно 1 + х 2 2! + х 4 4! + ⋯ для всех x tanh x = ∑ n = 1 ∞ B 2 n 4 n (4 n — 1) (2 n)! x 2 n — 1 = x — x 3 3 + 2 x 5 15 — 17 x 7 315 + ⋯ для | х | < π 2 arsinh x = ∑ n = 0 ∞ ( − 1) n ( 2 n) ! 4 n ( n !) 2 ( 2 n + 1) x 2 n + 1 for | x | ≤ 1 artanh x = ∑ n = 0 ∞ x 2 n + 1 2 n + 1 for | x | ≤ 1, x ≠ ± 1 {displaystyle {begin{aligned}sinh x=sum _{n=0}^{infty }{frac {x^{2n+1}}{(2n+1)!}}=x+{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}+cdots {text{for all }}x\[6pt]cosh x=sum _{n=0}^{infty }{frac {x^{2n}}{(2n)!}}=1+{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}+cdots {text{for all }}x\[6pt]tanh x=sum _{n=1}^{infty }{frac {B_{2n}4^{n}left(4^{n}-1right)}{(2n)!}}x^{2n-1}=x-{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}-{frac {17x^{7}}{315}}+cdots {text{for }}|x|<{frac {pi }{2}}\[6pt]operatorname {arsinh} x=sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}{text{for }}|x|leq 1\[6pt]operatorname {artanh} x=sum _{n=0}^{infty }{frac {x^{2n+1}}{2n+1}}{text{for }}|x|leq 1, xneq pm 1end{aligned}}}
Числа B k, появляющиеся в ряду для tanh x, являются числами Бернулли.
Расчет ряда Тейлора
Существует несколько методов вычисления ряда Тейлора для большое количество функций. Можно попытаться использовать определение ряда Тейлора, хотя это часто требует обобщения формы коэффициентов в соответствии с очевидной закономерностью. В качестве альтернативы можно использовать такие манипуляции, как подстановка, умножение или деление, сложение или вычитание стандартных рядов Тейлора, чтобы построить ряд Тейлора функции, поскольку ряд Тейлора является степенным рядом. В некоторых случаях можно также получить ряд Тейлора, многократно применяя интегрирование по частям. Особенно удобно использовать системы компьютерной алгебры для вычисления рядов Тейлора.
Первый пример
Для вычисления полинома Маклорена 7-й степени для функции
- f (x) = ln (cos x), x ∈ (- π 2, π 2) { displaystyle f (x) = ln ( cos x), quad x in left (- { frac { pi} {2}}, { frac { pi} {2}} right)}
,
сначала можно переписать функцию как
- f (x) = ln (1 + (cos x — 1)) { displaystyle f (x) = ln { bigl (} 1 + ( cos x-1) { bigr)} !}
.
Ряд Тейлора для натурального логарифма (с использованием нотации большого O )
- ln (1 + x) = x — Икс 2 2 + Икс 3 3 + О (Икс 4) { Displaystyle ln (1 + х) = х — { frac {x ^ {2}} {2}} + { frac {x ^ {3} } {3}} + {O} left (x ^ {4} right) !}
и для функции косинуса
- cos x — 1 = — x 2 2 + x 4 24 — x 6 720 + О (x
 { displaystyle cos x-1 = — { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) !}
{ displaystyle cos x-1 = — { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) !}.
В последнем разложении ряда есть нулевой постоянный член, который позволяет заменить вторую серию на первую и легко опустить члены более высокого порядка r, чем 7-я степень, используя большую нотацию O:
- f (x) = ln (1 + (cos x — 1)) = (cos x — 1) — 1 2 (cos x — 1) 2 + 1 3 (cos x — 1) 3 + O ((cos x — 1) 4) = (- x 2 2 + x 4 24 — x 6 720 + O (x 8)) — 1 2 ( — x 2 2 + x 4 24 + O (x 6)) 2 + 1 3 (- x 2 2 + O (x 4)) 3 + O (x
 = — x 2 2 + x 4 24 — x 6 720 — x 4 8 + x 6 48 — x 6 24 + O (x
= — x 2 2 + x 4 24 — x 6 720 — x 4 8 + x 6 48 — x 6 24 + O (x  = — x 2 2 — x 4 12 — x 6 45 + O (x 8). { Displaystyle { begin {align} е (х) = ln { bigl (} 1 + ( соз х-1) { bigr)} \ = ( соз х-1) — { tfrac {1} {2}} ( cos x-1) ^ {2} + { tfrac {1} {3}} ( cos x-1) ^ {3} + {O} left (( cos x-1) ^ {4} right) \ = left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) right) — { frac {1} {2}} left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} + {O} left (x ^ {6} right) right) ^ {2} + { frac {1} {3}} left (- { frac {x ^ {2}} {2}} + O left (x ^ {4} right) right) ^ {3} + {O } left (x ^ {8} right) \ = — { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} — { frac {x ^ {4}} {8}} + { frac {x ^ {6}} {48}} — { frac {x ^ {6 }} {24}} + O left (x ^ {8} right) \ = — { frac {x ^ {2}} {2}} — { frac {x ^ {4}} { 12}} — { frac {x ^ {6}} {45}} + O left (x ^ {8} right). End {align}} !}
= — x 2 2 — x 4 12 — x 6 45 + O (x 8). { Displaystyle { begin {align} е (х) = ln { bigl (} 1 + ( соз х-1) { bigr)} \ = ( соз х-1) — { tfrac {1} {2}} ( cos x-1) ^ {2} + { tfrac {1} {3}} ( cos x-1) ^ {3} + {O} left (( cos x-1) ^ {4} right) \ = left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) right) — { frac {1} {2}} left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} + {O} left (x ^ {6} right) right) ^ {2} + { frac {1} {3}} left (- { frac {x ^ {2}} {2}} + O left (x ^ {4} right) right) ^ {3} + {O } left (x ^ {8} right) \ = — { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} — { frac {x ^ {6}} {720}} — { frac {x ^ {4}} {8}} + { frac {x ^ {6}} {48}} — { frac {x ^ {6 }} {24}} + O left (x ^ {8} right) \ = — { frac {x ^ {2}} {2}} — { frac {x ^ {4}} { 12}} — { frac {x ^ {6}} {45}} + O left (x ^ {8} right). End {align}} !}
Поскольку косинус равен четная функция, коэффициенты для всех нечетных степеней x, x, x, x,… должны быть равны нулю.
Второй пример
Предположим, нам нужен ряд Тейлора в 0 функции
- g (x) = e x cos x. { displaystyle g (x) = { frac {e ^ {x}} { cos x}}. !}
У нас есть экспоненциальная функция
- e x = ∑ n = 0 ∞ x n n! Знак равно 1 + х + х 2 2! + х 3 3! + х 4 4! + ⋯ { displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ { 2}} {2!}} + { Frac {x ^ {3}} {3!}} + { Frac {x ^ {4}} {4!}} + Cdots !}
и, как и в первом примере,
- cos x = 1 — x 2 2! + х 4 4! — ⋯ { displaystyle cos x = 1 — { frac {x ^ {2}} {2!}} + { Frac {x ^ {4}} {4!}} — cdots !}
Предположим, что степенной ряд равен
- ex cos x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + ⋯ { displaystyle { frac {e ^ {x}} { cos x} } = c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + cdots !}
Затем умножение на знаменатель и замена Ряд косинуса дает
- ex = (c 0 + c 1 x + c 2 x 2 + c 3 x 3 + ⋯) cos x = (c 0 + c 1 x + c 2 x 2 + c 3 x 3 + с 4 Икс 4 + ⋯) (1 — Икс 2 2! + Икс 4 4! -) знак равно с 0 — с 0 2 Икс 2 + с 0 4! Икс 4 + С 1 Икс — С 1 2 Икс 3 + С 1 4! х 5 + с 2 х 2 — с 2 2 х 4 + с 2 4! х 6 + с 3 х 3 — с 3 2 х 5 + с 3 4! x 7 + c 4 x 4 + ⋯ { displaystyle { begin {align} e ^ {x} = left (c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + cdots right) cos x \ = left (c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + c_ {4} x ^ {4} + cdots right) left (1 — { frac {x ^ {2}} {2!}} + { Frac {x ^ {4}) } {4!}} — cdots right) \ = c_ {0} — { frac {c_ {0}} {2}} x ^ {2} + { frac {c_ {0}} { 4!}} X ^ {4} + c_ {1} x — { frac {c_ {1}} {2}} x ^ {3} + { frac {c_ {1}} {4!}} X ^ {5} + c_ {2} x ^ {2} — { frac {c_ {2}} {2}} x ^ {4} + { frac {c_ {2}} {4!}} X ^ {6} + c_ {3} x ^ {3} — { frac {c_ {3}} {2}} x ^ {5} + { frac {c_ {3}} {4!}} X ^ { 7} + c_ {4} x ^ {4} + cdots end {align}} !}
Сбор членов до четвертого порядка дает
- ex = c 0 + c 1 x + (c 2 — c 0 2) x 2 + (c 3 — c 1 2) x 3 + (c 4 — c 2 2 + c 0 4!) X 4 + ⋯ { displaystyle e ^ {x} = c_ {0} + c_ {1} x + left (c_ {2} — { frac {c_ {0}} {2}} right) x ^ {2} + left (c_ {3} — { frac {c_ {1 }} {2}} right) x ^ { 3} + left (c_ {4} — { frac {c_ {2}} {2}} + { frac {c_ {0}} {4!}) } right) x ^ {4} + cdots !}
Значения ci { displaystyle c_ {i}}

- e x cos x = 1 + x + x 2 + 2 x 3 3 + x 4 2 + ⋯. { displaystyle { frac {e ^ {x}} { cos x}} = 1 + x + x ^ {2} + { frac {2x ^ {3}} {3}} + { frac {x ^ {4}} {2}} + cdots. !}
Третий пример
Здесь мы используем метод, называемый «косвенное расширение», чтобы раскрыть данную функцию. В этом методе используется известное разложение Тейлора экспоненциальной функции. Чтобы разложить (1 + x) e как ряд Тейлора по x, мы используем известный ряд Тейлора функции e:
- e x = ∑ n = 0 ∞ x n n! Знак равно 1 + х + х 2 2! + х 3 3! + х 4 4! + ⋯. { displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2} } {2!}} + { Frac {x ^ {3}} {3!}} + { Frac {x ^ {4}} {4!}} + Cdots.}
Таким образом,
- (1 + x) ex = ex + xex = ∑ n = 0 ∞ xnn! + ∑ N знак равно 0 ∞ Икс N + 1 N! Знак равно 1 + ∑ N знак равно 1 ∞ Икс N N! + ∑ N знак равно 0 ∞ Икс N + 1 N! Знак равно 1 + ∑ N знак равно 1 ∞ Икс N N! + ∑ N знак равно 1 ∞ Икс N (N — 1)! Знак равно 1 + ∑ N знак равно 1 ∞ (1 N! + 1 (N — 1)!) Икс N знак равно 1 + ∑ N знак равно 1 ∞ N + 1 N! Икс N знак равно ∑ N знак равно 0 ∞ N + 1 N! х п. { displaystyle { begin {align} (1 + x) e ^ {x} = e ^ {x} + xe ^ {x} = sum _ {n = 0} ^ { infty} { frac { x ^ {n}} {n!}} + sum _ {n = 0} ^ { infty} { frac {x ^ {n + 1}} {n!}} = 1+ sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n!}} + Sum _ {n = 0} ^ { infty} { frac {x ^ {n + 1}} { n!}} \ = 1+ sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n!}} + sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {(n-1)!}} = 1+ sum _ {n = 1} ^ { infty} left ({ frac {1} {n!} } + { frac {1} {(n-1)!}} right) x ^ {n} \ = 1+ sum _ {n = 1} ^ { infty} { frac {n + 1} {n!}} X ^ {n} \ = sum _ {n = 0} ^ { infty} { frac {n + 1} {n!}} X ^ {n}. End {выровнены}}}
Определения ряда Тейлора
Классически алгебраические функции определяются алгебраическим уравнением, а трансцендентные функции (включая те, которые обсуждались выше) определяются некоторым свойством, которое выполняется для них, например, дифференциальным уравнением . Например, экспоненциальная функция — это функция, которая везде равна своей производной и принимает значение 1 в начале координат. Однако с равным успехом можно определить аналитическую функцию с помощью ее ряда Тейлора.
Ряды Тейлора используются для определения функций и «операторов » в различных областях математики. В частности, это верно в тех областях, где классические определения функций не работают. Например, используя ряд Тейлора, можно расширить аналитические функции до наборов матриц и операторов, таких как экспоненциальная матрица или матричный логарифм.
. В других областях, таких как формальный анализ, это удобнее работать непосредственно с самими сериями power series. Таким образом, можно определить решение дифференциального уравнения как степенной ряд, который, как мы надеемся доказать, является рядом Тейлора искомого решения.
Ряд Тейлора от нескольких переменных
Ряд Тейлора также может быть обобщен на функции более чем одной переменной с
- T (x 1,…, xd) = ∑ n 1 = 0 ∞ ⋯ ∑ nd знак равно 0 ∞ (x 1 — a 1) N 1 ⋯ (xd — ad) ndn 1! ⋯ н д! (∂ n 1 + ⋯ + ndf ∂ x 1 n 1 ⋯ ∂ xdnd) (a 1,…, ad) = f (a 1,…, ad) + ∑ j = 1 d ∂ f (a 1,…, ad) ∂ xj (xj — aj) + 1 2! ∑ j знак равно 1 d ∑ k знак равно 1 d ∂ 2 е (a 1,…, a d) ∂ x j ∂ x k (x j — a j) (x k — a k) + 1 3! ∑ j = 1 d ∑ k = 1 d ∑ l = 1 d ∂ 3 f (a 1,…, ad) ∂ xj ∂ xk ∂ xl (xj — aj) (xk — ak) (xl — al) + ⋯ { Displaystyle { begin {align} T (x_ {1}, ldots, x_ {d}) = sum _ {n_ {1} = 0} ^ { infty} cdots sum _ {n_ {d } = 0} ^ { infty} { frac {(x_ {1} -a_ {1}) ^ {n_ {1}} cdots (x_ {d} -a_ {d}) ^ {n_ {d} }} {n_ {1}! cdots n_ {d}!}} , left ({ frac { partial ^ {n_ {1} + cdots + n_ {d}} f} { partial x_ { 1} ^ {n_ {1}} cdots partial x_ {d} ^ {n_ {d}}}} right) (a_ {1}, ldots, a_ {d}) \ = f (a_ {1}, ldots, a_ {d}) + sum _ {j = 1} ^ {d} { frac { partial f (a_ {1}, ldots, a_ {d})} { partial x_ {j}}} (x_ {j} -a_ {j}) + { frac {1} {2!}} sum _ {j = 1} ^ {d} sum _ {k = 1} ^ {d} { frac { partial ^ {2} f (a_ {1}, ldots, a_ {d})} { partial x_ {j} partial x_ {k}}} (x_ {j} — a_ {j}) (x_ {k} -a_ {k}) \ qquad qquad + { frac {1} {3!}} sum _ {j = 1} ^ {d} sum _ {k = 1} ^ {d} sum _ {l = 1} ^ {d} { frac { partial ^ {3} f (a_ {1}, ldots, a_ {d})} { partial x_ {j} partial x_ {k} partial x_ {l}}} (x_ {j} -a_ {j}) (x_ {k} -a_ {k}) (x_ {l} -a_ {l})) + cdots end {align}}}
Например, для функции f (x, y) { displaystyle f (x, y)}
- f (a, b) + (x — a) fx ( а, б) + (у — б) fy (а, б) + 1 2! ((Икс — a) 2 fxx (a, b) + 2 (x — a) (y — b) fxy (a, b) + (y — b) 2 fyy (a, b)) { displaystyle f ( a, b) + (xa) f_ {x} (a, b) + (yb) f_ {y} (a, b) + { frac {1} {2!}} { Big (} (xa) ^ {2} f_ {xx} (a, b) +2 (xa) (yb) f_ {xy} (a, b) + (yb) ^ {2} f_ {yy} (a, b) { Big)}}
где нижние индексы обозначают соответствующие частные производные.
Разложение в ряд Тейлора второго порядка скалярной функции более чем одной переменной можно компактно записать как
- T (x) знак равно е (а) + (х — а) TD е (а) + 1 2! (Икс — а) T {D 2 е (а)} (Икс — а) + ⋯, { Displaystyle Т ( mathbf {x}) = F ( mathbf {a}) + ( mathbf {x} — mathbf {a}) ^ { mathsf {T}} Df ( mathbf {a}) + { frac {1} {2!}} ( mathbf {x} — mathbf {a}) ^ { mathsf {T}} left {D ^ {2} f ( mathbf {a}) right } ( mathbf {x} — mathbf {a}) + cdots,}
где D f (a) is the gradient of f evaluated at x= aand D f (a) is the Hessian matrix. Applying the multi-index notation the Taylor series for several variables becomes
- T ( x) = ∑ | α | ≥ 0 ( x − a) α α ! ( ∂ α f) ( a), {displaystyle T(mathbf {x})=sum _{|alpha |geq 0}{frac {(mathbf {x} -mathbf {a})^{alpha }}{alpha !}}left({mathrm {partial } ^{alpha }}fright)(mathbf {a}),}
which is to be understood as a still more abbreviated multi-index version of the first equation of this paragraph, with a full analogy to the single variable case.
Example
 Second-order Taylor series approximation (in orange) of a function f (x,y) = e ln(1 + y) around the origin.
Second-order Taylor series approximation (in orange) of a function f (x,y) = e ln(1 + y) around the origin.
In order to compute a second-order Taylor series expansion around point (a, b) = (0, 0) of the function
- f ( x, y) = e x ln ( 1 + y), {displaystyle f(x,y)=e^{x}ln(1+y),}
one first computes all the necessary partial derivatives:
- f x = e x ln ( 1 + y) f y = e x 1 + y f x x = e x ln ( 1 + y) f y y = − e x ( 1 + y) 2 f x y = f y x = e x 1 + y. {displaystyle {begin{aligned}f_{x}=e^{x}ln(1+y)\[6pt]f_{y}={frac {e^{x}}{1+y}}\[6pt]f_{xx}=e^{x}ln(1+y)\[6pt]f_{yy}=-{frac {e^{x}}{(1+y)^{2}}}\[6pt]f_{xy}=f_{yx}={frac {e^{x}}{1+y}}.end{aligned}}}
Evaluating these derivatives at the origin gives the Taylor coefficients
- f x ( 0, 0) = 0 f y ( 0, 0) = 1 f x x ( 0, 0) = 0 f y y ( 0, 0) = − 1 f x y ( 0, 0) = f y x ( 0, 0) = 1. {displaystyle {begin{aligned}f_{x}(0,0)=0\f_{y}(0,0)=1\f_{xx}(0,0)=0\f_{yy}(0,0)=-1\f_{xy}(0,0)=f_{yx}(0,0)=1.end{aligned}}}
Substituting these values in to the general formula
- T ( x, y) = f ( a, b) + ( x − a) f x ( a, b) + ( y − b) f y ( a, b) + 1 2 ! ( ( x − a) 2 f x x ( a, b) + 2 ( x − a) ( y − b) f x y ( a, b) + ( y − b) 2 f y y ( a, b)) + ⋯ {displaystyle T(x,y)=f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)+{frac {1}{2!}}{Big (}(x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b){Big)}+cdots }
produces
- T ( x, y) = 0 + 0 ( x − 0) + 1 ( y − 0) + 1 2 ( 0 ( x − 0) 2 + 2 ( x − 0) ( y − 0) + ( − 1) ( y − 0) 2) + ⋯ = y + x y − y 2 2 + ⋯ {displaystyle {begin{aligned}T(x,y)=0+0(x-0)+1(y-0)+{frac {1}{2}}{Big (}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{Big)}+cdots \=y+xy-{frac {y^{2}}{2}}+cdots end{aligned}}}
Since ln(1 + y) is analytic in |y| < 1, we have
- e x ln ( 1 + y) = y + x y − y 2 2 + ⋯, | y | < 1. {displaystyle e^{x}ln(1+y)=y+xy-{frac {y^{2}}{2}}+cdots,qquad |y|<1.}
Comparison with Fourier series
The trigonometric Fourier series enables one to express a periodic function (or a function определенная на отрезке [a, b]) как бесконечная сумма тригонометрических функций (синусов и косинусов ). В этом смысле ряд Фурье аналогичен ряду Тейлора, поскольку последний позволяет выразить функцию в виде бесконечной суммы степеней. Тем не менее, эти две серии отличаются друг от друга в нескольких важных вопросах:
- Конечные усечения ряда Тейлора функции f (x) относительно точки x = a все в точности равны f в точке a. Напротив, ряд Фурье вычисляется путем интегрирования по всему интервалу, поэтому обычно нет такой точки, где бы все конечные усечения ряда были точными.
- Вычисление ряда Тейлора требует знания функции на произвольной малой окрестности точки, тогда как вычисление ряда Фурье требует знания функции во всей области интервала. В определенном смысле можно сказать, что ряд Тейлора является «локальным», а ряд Фурье — «глобальным».
- Ряд Тейлора определен для функции, которая имеет бесконечно много производных в одной точке, тогда как Ряд Фурье определяется для любой интегрируемой функции. В частности, функция не могла быть дифференцируемой. (Например, f (x) может быть функцией Вейерштрасса.)
- Сходимость обоих рядов имеет очень разные свойства. Даже если ряд Тейлора имеет положительный радиус сходимости, результирующий ряд может не совпадать с функцией; но если функция аналитическая, то ряд сходится поточечно к функции и равномерно на каждом компактном подмножестве интервала сходимости. Что касается ряда Фурье, если функция квадратная -интегрируемый, то ряд сходится в среднем квадратичном, но необходимы дополнительные требования для обеспечения точечной или равномерной сходимости (например, если периодическая функция класса C, то сходимость будет равномерной).
- Наконец, на практике аппроксимировать функцию конечным устройством, скажем, многочленом Тейлора или частичной суммой тригонометрической серии, соответственно, в случае ряда Тейлора ошибка очень мала в окрестности точки. к она может быть очень большой в удаленной точке. В случае ряда Фурье ошибка распределяется по области определения функции.
См. Также
- Асимптотическое разложение
- Производящая функция
- Ряд Мадхавы
- Интерполяция разделенных разностей Ньютона
- Аппроксимация Паде
- Серия Пюизо
- Оператор сдвига
Примечания
Ссылки
- Абрамовиц, Милтон ; Стегун, Ирен А. (1970), Справочник по математическим функциям с формулами, графики и математическими таблицами, Нью-Йорк: Dover Publications, девятое издание
- Томас, Джордж Б., младший ; Финни, Росс Л. (1996), Исчисление и аналитическая геометрия (9-е изд.), Эддисон Уэсли, ISBN 0-201-53174-7
- Гринберг, Майкл (1998), Высшая инженерная математика (2-е изд.), Прентис Холл, ISBN 0-13-321431-1
Внешние ссылки
- , Энциклопедия математики, EMS Press, 2001 [1994]
- Вайсштейн, Эрик У. «Серия Тейлора». MathWorld.
- многочлен Тейлора — практическое введение
- Мадхава из Сангамаграммы
- «обсуждение метода Паркера-Сохацки «
- Другая визуализация Тейлора — где вы можете выбрать точку приближения и количество производных
- пересмотр Тейлора для численных методов в Численные методы для студентов STEM
- Золушка 2: расширение Тейлора
- Ряд Тейлора
- Обратные тригонометрические функции Ряд Тейлора
- «Суть исчисления: серия Тейлора» — через YouTube.
Наиболее простым
и достаточно эффективным способом
приближения функций является использование
формулы Тейлора для их разложения в
степенной ряд. Пусть задана непрерывная
функция
,
имеющая непрерывные производные до
порядка
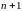
включительно. Такую функцию можно
разложить в некоторой окрестности точки

по степеням

по формуле Тейлора:

,
(3.1)
где
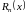
– остаточный член (ошибка, погрешность),
связанный с заменой при вычислении
бесконечного степенного ряда первыми
его
членами.
Ошибку ограничения
можно оценить по формуле,
где
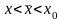
:
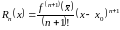
.
Формула Тейлора
не только дает возможность организовать
численный метод вычисления значений
функции
,
но и позволяет оценить величину ошибки
приближения, возникающей в результате
ограничения количества рассматриваемых
членов ряда. При ее использовании
требуется определить точку

,
в окрестностях которой будет производиться
разложение функции, при этом следует
руководствоваться соображениями
точности представления коэффициентов
ряда (3.1) и величиной используемого
интервала области определения, внутри
которого будут производиться вычисления.
Рассмотрим
разложение в ряд Тейлора функции
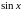
.
Найдем соответствующие производные и
в результате получим последовательность
функций:
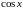
,
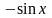
,

,
,
,
,
,
,
… . Если положить

,
то последовательность функций
преобразуется в ряд чисел 1, 0, –1, 0, 1, 0,
–1, 0, …, тогда по формуле (3.1) мы имеем:

.
Оценим величину
ошибки приближения при рассмотрении
первых четырех членов ряда

и

,

,
поскольку
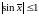
для любых
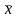
.
Из полученной
оценки погрешности видно, что ошибка
приближения зависит от
и если не изменить число членов ряда в
представлении функции
,
то для достаточно больших
значение погрешности может превысить
1.
3.1.2. Полиномы Чебышева
Формула Тейлора
при разложении функции в степенной ряд
дает сходимость, зависящую от значения
.
Возникает идея поиска такого многочлена

,
чтобы максимальная ошибка приближения
функции
была бы наименьшей. Данная задача была
решена великим русским математиком
П.Л.Чебышевым и получила название задачи
о наилучшем приближении.
Пусть задана
некоторая функция
,
которую на отрезке
требуется приблизить многочленом

таким образом, чтобы

,
т.е. подобрать
такие коэффициенты

,
чтобы максимальная величина модуля
разности между
и
была наименьшей для любых
.
Определение.
Полиномом Чебышева называется многочлен
вида
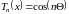
,
где

.
Заметим, что
полиномы Чебышева не являются
тригонометрическими функциями, однако
доказательство данного утверждения
приводить не будем. Используя известные
формулы тригонометрии, найдем первые
три многочлена:

,

,

.
Для вычисления
многочленов Чебышева практичнее
использовать следующее рекуррентное
соотношение:

.
(3.2)
Свойства
многочленов Чебышева:
-
Учитывая формулу
(3.2), можно установить, что
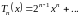
,
,
то есть коэффициент
при старшей степенимногочлена Чебышева равен
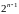
. -
Полиномы Чебышева

образуют ортогональный базис (с весом

)
на множестве функций, непрерывных на
отрезке
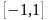
,
и удовлетворяют следующим равенствам:

(3.3)
3. Многочлены
Чебышева доставляют минимум максимальной
ошибки приближения, то есть являются
многочленами наилучшего приближения
для класса функции, непрерывных на
отрезке
.
Докажем данный факт.
Чебышев показал,
что точная верхняя грань (supremum,
супремум) многочлена
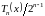
среди всех многочленов

с коэффициентом 1 при старшей степени
на отрезке
наименьшая. Действительно,

,
откуда
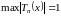
,
тогда

,
причем экстремумы принимают попеременно
положительные и отрицательные значения
на отрезке [–1,1], так как

– гармоническая функция. Количество
экстремумов равно

.
Рассмотрим разность:
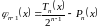
,
которая является многочленом степени
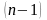
(поскольку члены

уничтожаются). Если экстремальное
значение
меньше, чем у
,
то в
экстремальных точках полинома
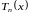
функция
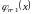
принимает по очереди положительные и
отрицательные значения. Следовательно,
имеет
действительных
корней, чего не тожет быть, так как
степень многочлена равна
.
Тогда выполняется тождество
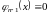
или

.
Последнее свойство
полиномов Чебышева представляет большой
интерес для численного анализа. Если
какая-либо ошибка приближения может
быть выражена многочленом Чебышева
степени
,
то любое другое выражение для ошибки в
виде многочлена степени
,
имеющего тот же самый коэффициент при
старшей степени
,
будет иметь на отрезке [–1,1] большую
максимальную ошибку, чем чебышевское.
Практика
использования полиномов Чебышева для
решения задачи приближения функции
заключается в следующем. Поскольку
система функций
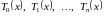
образует базис, то на отрезке [–1,1] любую
функцию можно представить как линейную
комбинацию

,
:

.
(3.4)
Коэффициенты
разложения можно определить, используя
свойство ортогональности (3.3) полиномов
Чебышева. Для определения
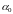
почленно умножим левую и правую часть
выражения (3.4) на
и проинтегрируем:

.
Учитывая
ортогональность, имеем:
или

.
Аналогично можно
вычислить остальные коэффициенты
разложения (3.4):
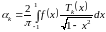
,
.
(3.5)
Единственной
проблемой разложения функции
по полиномам Чебышева является вычисление
достаточно сложных интегралов вида
(3.5).
Соседние файлы в папке 3-й семестр
- #
- #
Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=<msubsup>∑k=0∞</msubsup>ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots — постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,<mspace width=»1em»/><munder>limn→∞</munder>Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′(x0)1!</mfrac></mstyle>(x−x0)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′′(x0)2!</mfrac></mstyle>(x−x0)2+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(n)(x0)n!</mfrac></mstyle>(x−x0)n+…=<msubsup>∑k=0∞</msubsup><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(k)(x0)k!</mfrac></mstyle>(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{»}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′(0)1!</mfrac></mstyle>x+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′′(0)2!</mfrac></mstyle>(x−x0)2+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(n)(x0)n!</mfrac></mstyle>(x−x0)n+…=<msubsup>∑k=0∞</msubsup><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(k)(x0)k!</mfrac></mstyle>(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{»}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,<mspace width=»1em»/>f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′(x0)1!</mfrac></mstyle>t+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′′(x0)2!</mfrac></mstyle>t2+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(n)(x0)n!</mfrac></mstyle>tn+…=<msubsup>∑k=0∞</msubsup><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(k)(x0)k!</mfrac></mstyle>tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{»}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>g′(0)1!</mfrac></mstyle>t+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>g(n)(0)n!</mfrac></mstyle>tn+…=<msubsup>∑k=0∞</msubsup><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>g(k)(0)k!</mfrac></mstyle>tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1x</mfrac></mstyle>f(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>11+t</mfrac></mstyle>f(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>11+t</mfrac></mstyle>=1−t+t2−t3+…+(−1)ntn+…=<msubsup>∑k=0∞</msubsup>(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1x</mfrac></mstyle>=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=<msubsup>∑k=0∞</msubsup>(−1)k(x−1)k,<mspace width=»1em»/>∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f′(x0)1!</mfrac></mstyle>(x−x0)+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(n)(x0)n!</mfrac></mstyle>(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=<msubsup>∑k=0n</msubsup><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(k)(x0)k!</mfrac></mstyle>(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>f(n+1)(ξ)(n+1)!</mfrac></mstyle>xn+1,<mspace width=»1em»/>x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x1!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x22!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x33!</mfrac></mstyle>+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>xnn!</mfrac></mstyle>+o(xn),<mspace width=»1em»/>∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x1!</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x33!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x55!</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x77!</mfrac></mstyle>+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(−1)n+1x2n−1(2n−1)!</mfrac></mstyle>+o(x2n),<mspace width=»1em»/>∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x22!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x44!</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x66!</mfrac></mstyle>+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(−1)n+1x2n(2n)!</mfrac></mstyle>+o(x2n+1),<mspace width=»1em»/>∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x33</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x55</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x77</mfrac></mstyle>+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(−1)nx2n+12n+1</mfrac></mstyle>+o(x2n+2),<mspace width=»1em»/>∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x1!</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x22!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>x33!</mfrac></mstyle>−…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(−1)n+1xnn!</mfrac></mstyle>+o(xn),<mspace width=»1em»/>x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>α1!</mfrac></mstyle>x+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>α(α−1)2!</mfrac></mstyle>x2+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>α(α−1)(α−2)3!</mfrac></mstyle>x3+…+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>α(α−1)…(α−n+1)n!</mfrac></mstyle>xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t21!</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(t2)22!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(t2)33!</mfrac></mstyle>+o((t2)3))=t3−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t52</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t76</mfrac></mstyle>+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x+1)52</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x+1)76</mfrac></mstyle>+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,<mspace width=»1em»/>x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(2t)22!</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(2t)44!</mfrac></mstyle>+o(t5))=(t2−4)(1−2t2+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>2t43</mfrac></mstyle>+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>8t43</mfrac></mstyle>+o(t5))=−4+9t2−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>143</mfrac></mstyle>t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>143</mfrac></mstyle>(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1xn</mfrac></mstyle>)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1x</mfrac></mstyle>t=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−<msqrt>x2−1</msqrt>f(x)=2x-sqrt{x^2-1}
с точностью до o(<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1×3</mfrac></mstyle>)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1x</mfrac></mstyle>,<mspace width=»1em»/>x=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1t</mfrac></mstyle>t=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>2t</mfrac></mstyle>−<msqrt><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1t2</mfrac></mstyle>−1</msqrt>=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>2−(1−t2)1/2t</mfrac></mstyle>g(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>2−(1−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t22</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t48</mfrac></mstyle>)+o(t4)t</mfrac></mstyle>=<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1t</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t2</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>t38</mfrac></mstyle>+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>12x</mfrac></mstyle>−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>18×3</mfrac></mstyle>+o(<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1×3</mfrac></mstyle>),<mspace width=»1em»/>x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>00</mfrac></mstyle>)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
<munder>limx→1</munder><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>ex−ecos(x−1)sin(x−1)</mfrac></mstyle>limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
<munder>limx→1</munder><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>ex−ecos(x−1)sin(x−1)</mfrac></mstyle>=<munder>limx→1</munder><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(e+e(x−1)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>e(x−1)22!</mfrac></mstyle>+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>e(x−1)33!</mfrac></mstyle>+…)−e(1−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)22!</mfrac></mstyle>+…)(x−1)−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)33!</mfrac></mstyle>+…</mfrac></mstyle>=e<munder>limx→1</munder><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)+(x−1)2+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)36</mfrac></mstyle>+…(x−1)−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)36</mfrac></mstyle>+…</mfrac></mstyle>=e<munder>limx→1</munder><mstyle displaystyle=»true» scriptlevel=»0″><mfrac>1+(x−1)+<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)26</mfrac></mstyle>+…1−<mstyle displaystyle=»true» scriptlevel=»0″><mfrac>(x−1)26</mfrac></mstyle>+…</mfrac></mstyle>=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e






















![{ displaystyle { begin {align} sin x = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n +1)!}} X ^ {2n + 1} = x - { frac {x ^ {3}} {3!}} + { Frac {x ^ {5} } {5!}} - cdots { text {для всех}} x [6pt] cos x = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n)!}} x ^ {2n} = 1 - { frac {x ^ {2}} {2!}} + { frac {x ^ {4}} {4! }} - cdots { text {для всех}} x [6pt] tan x = sum _ {n = 1} ^ { infty} { frac {B_ {2n} (- 4) ^ {n} left (1-4 ^ {n} right)} {(2n)!}} X ^ {2n-1} = x + { frac {x ^ {3}} {3}} + { frac {2x ^ {5}} {15}} + cdots { text {for}} | х | <{ frac { pi} {2}} [6pt] sec x = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} E_ {2n }} {(2n)!}} X ^ {2n} = 1 + { frac {x ^ {2}} {2}} + { frac {5x ^ {4}} {24}} + cdots { text {for}} | х | <{ frac { pi} {2}} [6pt] arcsin x = sum _ {n = 0} ^ { infty} { frac {(2n)!} {4 ^ {n} (n!) ^ {2} (2n + 1)}} x ^ {2n + 1} = x + { frac {x ^ {3}} {6}} + { frac {3x ^ {5} } {40}} + cdots { text {for}} | х | leq 1 [6pt] arccos x = { frac { pi} {2}} - arcsin x = { frac { pi} {2}} - sum _ {n = 0} ^ { infty} { frac {(2n)!} {4 ^ {n} (n!) ^ {2} (2n + 1)}} x ^ {2n + 1} = { frac { pi} {2}} - x - { frac {x ^ {3}} {6}} - { frac {3x ^ {5}} {40}} - cdots { text {for}} | х | leq 1 [6pt] arctan x = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {2n + 1}} x ^ {2n + 1} = x - { frac {x ^ {3}} {3}} + { frac {x ^ {5}} {5}} - cdots { text {for}} | х | Leq 1, x neq pm i end {выровнять ed}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/158a0ae14d1c9e0d1dc21c268f7e2169b9066dc7)
![{ displaystyle { begin {align} sinh x = sum _ {n = 0} ^ { infty} { frac {x ^ {2n + 1}} {(2n +1)!}} = x + { frac {x ^ {3}} {3!}} + { Frac {x ^ { 5}} {5!}} + Cdots { text {для всех}} x [6pt] cosh x = sum _ {n = 0} ^ { infty} { frac {x ^ {2n}} {(2n)!}} = 1 + { frac {x ^ {2}} {2!}} + { Frac {x ^ {4}} {4!}} + Cdots { text {для всех}} x [6pt] tanh x = sum _ {n = 1} ^ { infty} { frac {B_ {2n} 4 ^ {n} left (4 ^ {n} -1 right)} {(2n)!}} x ^ {2n -1} = x - { frac {x ^ {3}} {3}} + { frac {2x ^ {5}} {15}} - { frac {17x ^ {7}} {315}} + cdots { текст {for}} | х | <{ frac { pi} {2}} [6pt] operatorname {arsinh} x = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} (2n)!} {4 ^ {n} (n!) ^ {2} (2n + 1)}} x ^ {2n + 1} { текст {for}} | х | leq 1 [6pt] operatorname {artanh} x = sum _ {n = 0} ^ { infty} { frac {x ^ {2n + 1}} {2n + 1}} { текст {for}} | х | Leq 1, x neq pm 1 end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec241364ffd161564c83602d06608a450cdea5fd)
















![{ Displaystyle { begin {align} f_ {x} = e ^ {x} ln (1 + y) [6pt] f_ { y} = { frac {e ^ {x}} {1+ y}} [6pt] f_ {xx} = e ^ {x} ln (1 + y) [6pt] f_ { yy} = - { frac {e ^ {x}} {(1 + y) ^ {2}}} [6pt] f_ {xy} = f_ {yx} = { frac {e ^ { x}} {1 + y}}. End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80a9f65e179df2db5256dc15097892be2ded7c6d)








![{displaystyle f(x)={begin{cases}e^{-1/x^{2}}&{text{if }}xneq 0\[3mu]0&{text{if }}x=0end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae050e61cde6a0fdeda1f237f75846465579462d)




![{displaystyle {begin{aligned}sinh x&=sum _{n=0}^{infty }{frac {x^{2n+1}}{(2n+1)!}}&&=x+{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}+cdots &&{text{for all }}x\[6pt]cosh x&=sum _{n=0}^{infty }{frac {x^{2n}}{(2n)!}}&&=1+{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}+cdots &&{text{for all }}x\[6pt]tanh x&=sum _{n=1}^{infty }{frac {B_{2n}4^{n}left(4^{n}-1right)}{(2n)!}}x^{2n-1}&&=x-{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}-{frac {17x^{7}}{315}}+cdots &&{text{for }}|x|<{frac {pi }{2}}\[6pt]operatorname {arsinh} x&=sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{frac {x^{3}}{6}}+{frac {3x^{5}}{40}}-cdots &&{text{for }}|x|leq 1\[6pt]operatorname {artanh} x&=sum _{n=0}^{infty }{frac {x^{2n+1}}{2n+1}}&&=x+{frac {x^{3}}{3}}+{frac {x^{5}}{5}}+cdots &&{text{for }}|x|leq 1, xneq pm 1end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cda808c97562eca785bd172eb7739711b338730a)






![{displaystyle {frac {2}{pi }}K(x)=sum _{n=0}^{infty }{frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc8e464983f3fdf2071ed149ed55bba842544a2d)
![{displaystyle {frac {2}{pi }}E(x)=sum _{n=0}^{infty }{frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85daf53e01f72f0f0c820811910a77974657052e)


![{displaystyle vartheta _{00}(x)^{-1/6}vartheta _{01}(x)^{-2/3}{biggl [}{frac {vartheta _{00}(x)^{4}-vartheta _{01}(x)^{4}}{16,x}}{biggr ]}^{-1/24}=sum _{n=0}^{infty }P(n)x^{n}=prod _{k=1}^{infty }{frac {1}{1-x^{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c898219336ceb853f972d83f60a14049d671523)
![{displaystyle vartheta _{00}(x)^{1/6}vartheta _{01}(x)^{-1/3}{biggl [}{frac {vartheta _{00}(x)^{4}-vartheta _{01}(x)^{4}}{16,x}}{biggr ]}^{1/24}=sum _{n=0}^{infty }Q(n)x^{n}=prod _{k=1}^{infty }{frac {1}{1-x^{2k-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5dd403c225903926ad0c45788a5f1a0a5fb67c)


