Формула для определения случайной ошибки - Ремонт и установка крупной бытовой техники

Вычисление случайных погрешностей при измерениях

Пусть при измерениях
систематические погрешности пренебрежимо
малы. Рассмотрим случай, когда измерение
проведено большое число раз (n→∞).

Как показывает
опыт, отклонение результатов измерений
от их среднего значения в большую или
меньшую сторону одинаковы. Результаты
измерений с малым отклонением от среднего
значения наблюдается значительно чаще,
чем с большими отклонениями.

Расположим все
численные значения результатов измерений
в ряд в порядке их возрастания и разделим
этот ряд на равные интервалы.
Пусть–
число измерений с результатом, попавшим
в интервал [].
Величинаесть вероятность ΔP_i(х)
получения результата со значением в
интервале [].

Графически
представим
,
соответствующее каждому интервалу []
(рис.1). Изображенная на рис.1 ступенчатая
кривая называется гистограммой. Допустим,
что измерительный прибор обладает
чрезвычайно высокой чувствительностью.
Тогда ширину интервала можно сделать
бесконечно малой величинойdx.
Ступенчатая кривая в этом случае
заменяется кривой, представляемой
функцией φ(х) (рис.2). Функцию φ(х) принято
называть функцией плотности распределения.
Её смысл состоит в том, что произведение
φ(х)dx
есть вероятность dP(x)
получения результатов со значением в
интервале от х до х+dх.
Графически значение вероятности
представляется в виде площади
заштрихованного прямоугольника.
Аналитически функция плотности
распределения записывается следующим
образом:

.
(5)

Представленную в
виде (5) функцию φ(х) называют функцией
Гаусса, а соответствующее распределение
результатов измерений Гауссовым или
нормальным.

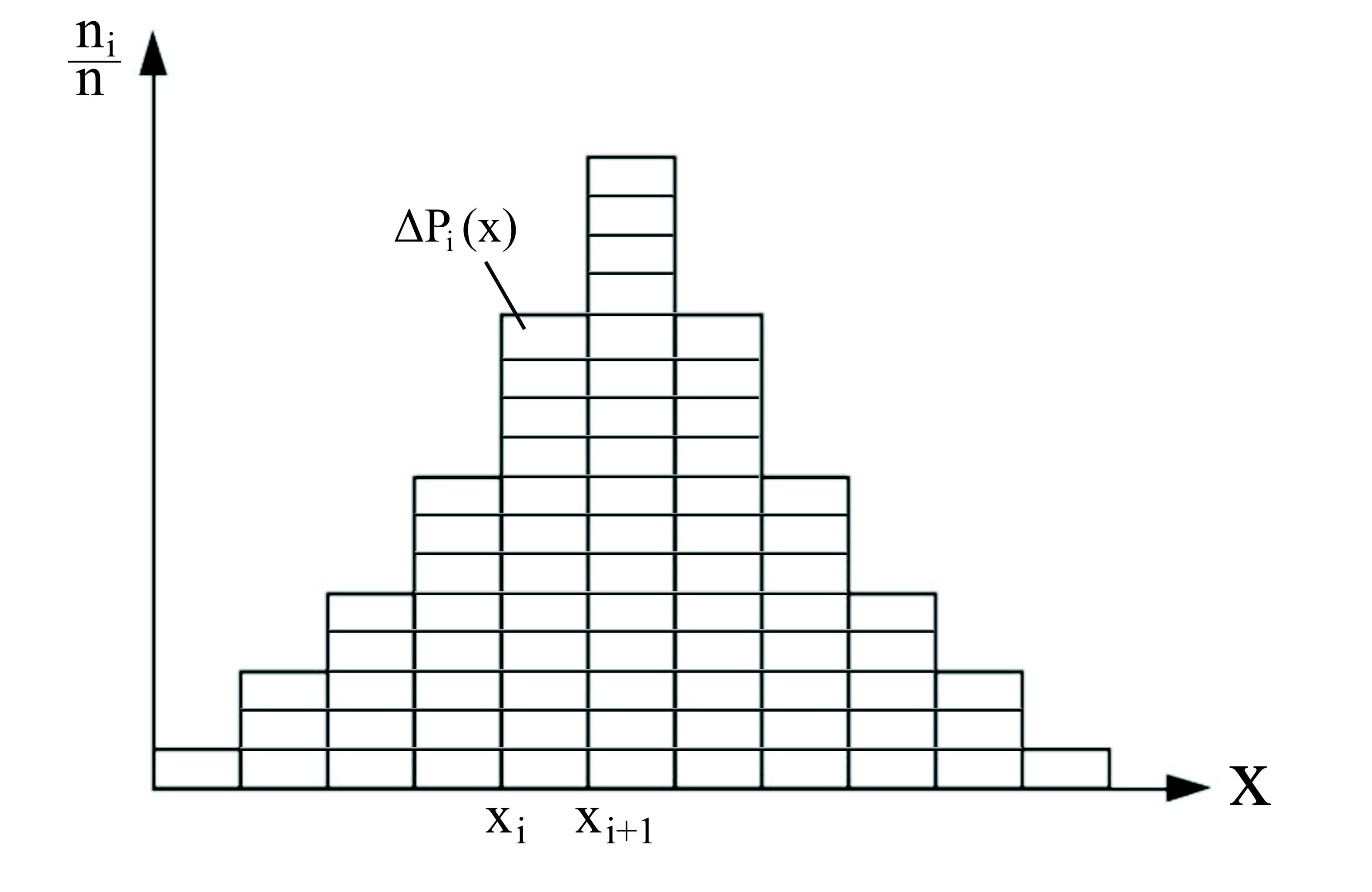
рис.1

Параметры
иσ
имеют следующий смысл (рис.2).

–среднее значение
результатов измерений. При
=функция Гаусса достигает максимального
значения. Если число измерений бесконечно
велико, торавно истинному значению измеряемой
величины.

σ
– характеризует степень разброса
результатов измерения от их среднего
значения. Параметр σ
вычисляется по формуле:

.
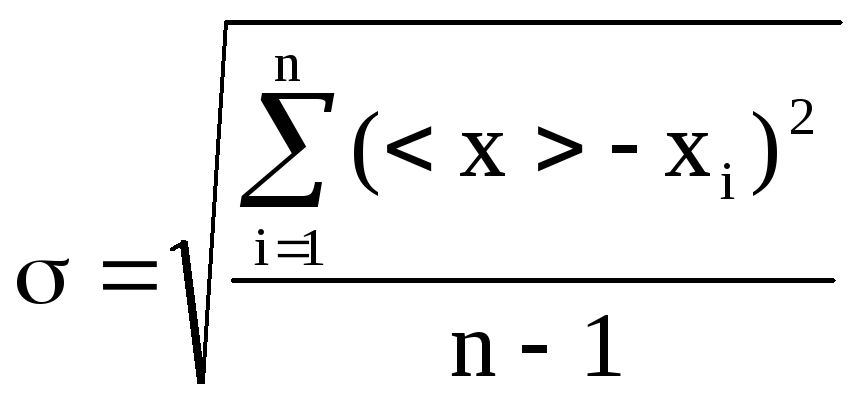(6)

Этот параметр
представляет собой среднеквадратичную
погрешность. Величину σ²в теории
вероятностей называют дисперсией
функции φ(х).

Чем выше точность
измерений, тем ближе располагаются
результаты измерений к истинному
значению измеряемой величины, и,
следовательно, меньше σ.

Вид функции φ(х),
очевидно, не зависит от числа измерений.

В теории вероятностей
показано, что 68% всех измерений дадут
результат, который располагается в
интервале
,
95% – в интервале []
и 99,7% в интервале [].

рис.2

Таким образом, с
вероятностью (надёжностью) 68% величина
отклонения результата измерения от
среднего значения лежит в интервале
[],
с вероятностью (надёжностью) 95% – в
интервале []
и с вероятностью (надежностью) 99,7% – в
интервале [].

Интервал,
соответствующий той или иной вероятности
отклонения от среднего значения,
называется доверительным.

В реальных
экспериментах число измерений, очевидно,
не может быть бесконечно большим, поэтому
маловероятно, чтобы
совпало с истинным значением измеряемой
величины.
В связи с этим важно оценить на основе
теории вероятностей величину возможного
отклоненияот.

Расчеты показывают,
что при числе измерений более 20 с
вероятностью 68%
попадает в доверительный интервал [],
с вероятностью 95% – в интервале[],
с вероятностью 99,7% – в интервале [].

Величина
,
определяющая границы доверительного
интервала, называется стандартным
отклонением или просто – стандартом.

Стандарт
вычисляется по формуле:

.
(7)

С
учетом формулы (6), выражение (7) приобретает
следующий вид:

.
(8)

Чем больше число
измерений n,
тем ближе Х располагается к
.
Если число измерений не велико меньше
15, то вместо распределения Гаусса
используют распределение Стьюдента,
которое приводит к увеличению ширины
доверительного интервала возможного
отклонения Х отвt_n_,_p
раз.

Сомножитель t_n_,_p
называется коэффициентом Стьюдента.
Индексы Р и n
указывают, с какой надежностью и какому
числу измерений соответствует коэффициент
Стьюдента. Величина коэффициента
Стьюдента для данного числа измерений
и заданной надежности определяется по
таблице 1.

Таблица
1

Коэффициент
Стьюдента.

Число измерений

Надежность Р,%

0,5

0,6

0,7

0,8

0,9

0,95

0,98

0,999

120

∞

1,00

0,82

0,77

0,74

0,73

0,72

0,71

0,70

0,69

0,68

0,67

1,38

1,06

0,98

0,94

0,92

0,90

0,88

0,87

0,86

0,85

0,84

2,0

1,3

1,2

1,1

1,0

3,1

1,9

1,6

1,5

1,4

1,3

6,3

2,9

2,1

2,0

1,9

1,8

1,7

1,6

12,7

4,3

3,2

2,8

2,6

2,4

2,3

2,1

2,0

31,8

7,0

4,5

3,7

3,4

3,1

3,0

2,9

2,8

2,6

2,5

2,4

2,3

36,6

31,6

12,9

8,6

6,9

6,0

5,4

5,0

4,8

4,1

3,9

3,6

3,5

3,4

3,3

Например, при
заданной надежности 95% и числе измерений
n=20
коэффициент Стьюдента t_20,95=2,1
(доверительный интервал
)
при числе измеренийn=4,
t_4,95=3,2
(доверительный интервал
).
То есть, при увеличении числа измерений
с 4 до 20 возможное отклонениеотX
уменьшается в 1,524 раза.

Таким образом,
чтобы рассчитать абсолютную случайную
погрешность необходимо:

Провести несколько
измерений.
Найти средний
арифметический результат измерений.
Вычислить по
формуле (8) стандартное отклонение.
По таблице найти
для заданной надежности коэффициент
Стьюдента. Величина t_n_,_p
S_m
есть абсолютная погрешность
в определении Х.
Результат записать
в виде Х=(с надежностью Р).

Ниже приводится
пример расчета абсолютной случайной
погрешности

№

Х_i

Х_i
– <X>

(Х_i
– <X>)²

20,2

19,6

19,9

20,4

20,2

20,3

-0.1

+0.5

+0.2

-0.3

-0.1

-0.2

0.01

0.25

0.04

0.09

0.01

0.04

∑

120,6

0,44

По формуле (2)
находим среднее значение измеряемой
величины
(без указания размерности физической
величины)

По
формуле (8) вычисляем величину стандартного
отклонения

Коэффициент
Стьюдента, определенный для n=6,
и Р=95%, t_6,95=2,6
окончательный результат:

Х=20,1±2,6·0,121=20,1±0,315
(с Р=95%).

Вычисляем
относительную погрешность:

При записи
окончательного результата измерений
нужно иметь в виду, что погрешность
должна содержать только одну значащую
цифру (отличную от нуля). Две значащие
цифры в погрешности записываются лишь
в том случае, если предпоследняя цифра
1. Большее число значащих цифр записывать
бесполезно, поскольку они будут не
достоверны. В записи среднего значения
измеряемой величины последняя цифра
должна принадлежать тому же разряду,
что и последняя цифра в записи погрешности.

Примеры:

Х=531±2;

Х=(243±5)·10²;

Х=232,567±0,003.

При проведении
нескольких измерений может получится
один и тот же результат. Это возможно в
том случае, если чувствительность
измерительного прибора низкая. Когда
измерение производится прибором с
низкой чувствительностью достаточно
и однократного измерения. Не имеет
смысла, например, многократно измерять
длину стола рулеткой с сантиметровыми
делениями. Результат измерения в этом
случае будет один и тот же. Погрешность
при проведении однократного измерения
определяется ценой наименьшего деления
прибора. Она называется приборной
погрешностью. Её значение
вычисляется по следующей формуле:

,
(10)

где γ – цена деления
прибора;

t_∞,_p
– коэффициент Стьюдента, соответствующий
бесконечно большому числу измерений.

С учетом приборной
погрешности, абсолютная погрешность с
заданной надежностью определяется по
формуле:

,
(11)

где
.

С учетом формул
(8) и (10), (11) записывается так:

.
(12)

В литературе для
сокращения записи величину погрешности
иногда не указывают. Предполагается,
что величина погрешности составляет
половину единицы последней значащей
цифры. Так, например, величина радиуса
Земли записана в виде
м.
Это означает, что в качестве погрешности
следует взять величину, равную ±м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.

2.1 Случайная величина

Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.

Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].

Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δ⁢x] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δ⁢x: x∈[x0,x0+δ⁢x].
Устремим интервал
δ⁢x к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w⁢(x0)=P[x0,x0+δ⁢x]δ⁢x будет оставаться конечным.
Функцию w⁢(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.

Замечание. В математической литературе распределением часто называют не функцию
w⁢(x), а её интеграл W⁢(x)=∫w⁢(x)⁢𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.

Гистограммы.

Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[k⁢h,(k+1)⁢h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.

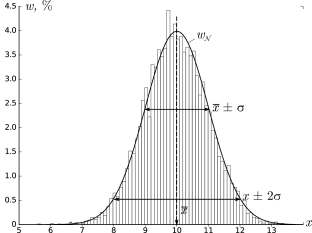
Рис. 2.1: Пример гистограммы для нормального распределения (x¯=10,
σ=1,0, h=0,1, n=104)

Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w⁢(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w⁢(x).

Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w⁢(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.

Свойства распределений.

Из определения функции w⁢(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:

Px∈[a,b]=∫abw⁢(x)⁢𝑑x.

(2.1)

Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w⁢(x) по всей области
значений x (то есть суммарная площадь под графиком w⁢(x)) равен единице:

Это соотношение называют условием нормировки.

Среднее и дисперсия.

Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как

Переходя к пределу, получим следующее определение среднего значения
случайной величины:

где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину

σ2=(x-x¯)2¯=∫(x-x¯)2⁢w⁢𝑑x

(2.3)

называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.

Доверительный интервал.

Обозначим как P|Δ⁢x|<δ вероятность
того, что отклонение от среднего Δ⁢x=x-x¯ составит величину,
не превосходящую по модулю значение δ:

P|Δ⁢x|<δ=∫x¯-δx¯+δw⁢(x)⁢𝑑x.

(2.4)

Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.

2.2 Нормальное распределение

Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).

Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.

Плотность нормального распределения выражается следующей формулой:

w𝒩⁢(x)=12⁢π⁢σ⁢e-(x-x¯)22⁢σ2.

(2.5)

Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.

Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩⁢(x)).

При значительном отклонении x от среднего величина
w𝒩⁢(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.

Замечание. Точки x=x¯±σ являются точками
перегиба графика w⁢(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w⁢(x¯±σ)/w⁢(x¯)=e-1/2≈0,61
от высоты вершины.

Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.

x-x0σ2=2w⁢(x)σ1=1

Рис. 2.2: Плотность нормального распределения

Доверительные вероятности.

Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.

Замечание. Значение интеграла вида ∫e-x2/2⁢𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.

Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна

P|Δ⁢x|<σ=∫x¯-σx¯+σw𝒩⁢𝑑x≈0,68.

Вероятность отклонения в пределах x¯±2⁢σ:

а в пределах x¯±3⁢σ:

Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2⁢σ;x¯+2⁢σ],
и лишь 0,27% окажутся за пределами
[x¯-3⁢σ;x¯+3⁢σ].

Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.

Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись

означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δ⁢x;x¯+δ⁢x] с
вероятностью 68%. Таким образом погрешность ±δ⁢x считается
равной одному среднеквадратичному отклонению: δ⁢x=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δ⁢x=2⁢σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.

Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.

Сравнение результатов измерений.

Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.

Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2⁢σ.

Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если

Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.

Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.

Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.

2.3 Независимые величины

Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:

Обозначим отклонения величин от их средних как Δ⁢x=x-x¯ и
Δ⁢y=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δ⁢x¯=x¯-x¯=0,
Δ⁢y¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δ⁢x⋅Δ⁢y¯
равно произведению средних Δ⁢x¯⋅Δ⁢y¯
и, следовательно, равно нулю:

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=0.

(2.6)

Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.

Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2⁢x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2⁢x=2⁢σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2⁢x=2⁢σx.

Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.

Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.

Пример. Пусть σy=σx/3,
тогда σz=σx⁢1+19≈1,05⁢σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.

2.4 Погрешность среднего

Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.

Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых

Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать

σZ=σx12+σx22+…+σxn2=n⁢σx,

поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем

Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.

Подчеркнём отличия между σx и σ⟨x⟩:

величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;

величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.

2.5 Результирующая погрешность опыта

Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?

Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:

Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δ⁢xслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δ⁢xсист=x¯-xист=const:

Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:

σполн2=⟨δ⁢xсист2⟩+⟨δ⁢xслуч2⟩≤Δсист2+σслуч2.

(2.9)

Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.

Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:

Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.

Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.

Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:

Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2⁢σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)

d=386±6⁢мкм,εd=1,5%.

Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.

Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=162,0⁢м/с,
среднеквадратичное отклонение σv=13,8⁢м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6⁢м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δ⁢v, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6⁢м/с
(ε≈4%), так и значение σv≈14⁢м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.

Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=163,3⁢м/с,
σv=12,1⁢м/c, σ⟨v⟩=5⁢м/с,
σполн≈11,2⁢м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11⁢м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.

2.6 Обработка косвенных измерений

Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.

2.6.1 Случай одной переменной

Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f⁢(x).

В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:

Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δ⁢x=x-x⋆, и пользуясь определением производной,
при условии, что функция y⁢(x) — гладкая
вблизи x≈x⋆, запишем

где f′≡d⁢yd⁢x — производная фукнции f⁢(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δ⁢y2⟩,
σx2=⟨Δ⁢x2⟩), и затем снова извлечём
корень. В результате получим

Пример. Для степенной функции
y=A⁢xn имеем σy=n⁢A⁢xn-1⁢σx, откуда

σyy=n⁢σxx,или εy=n⁢εx,

то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.

Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.

Упражнение. Найдите погрешность логарифма y=ln⁡x, если известны x
и σx.

Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.

2.6.2 Случай многих переменных

Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f⁢(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:

Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:

где символом fx′≡∂⁡f∂⁡x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f⁢(x,y,…):

σu2=fx′⁣2⁢σx2+fy′⁣2⁢σy2+…

(2.11)

Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.

Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …

Остановимся на некоторых важных частных случаях формулы
(2.11).

Пример. Для суммы (или разности) u=∑i=1nai⁢xi имеем

σu2=∑i=1nai2⁢σxi2.

(2.12)

Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что

σu2u2=α2⁢σx2x2+β2⁢σy2y2+…

или через относительные погрешности

εu2=α2⁢εx2+β2⁢εy2+…

(2.13)

Пример. Вычислим погрешность произведения и частного: u=x⁢y или u=x/y.
Тогда в обоих случаях имеем

εu2=εx2+εy2,

(2.14)

то есть при умножении или делении относительные погрешности складываются
квадратично.

Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу

u=arctgyx.

В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′⁢zx′=-yx2+y2,
uy′=uz′⁢zy′=xx2+y2, и наконец

σu2=y2⁢σx2+x2⁢σy2(x2+y2)2.

Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.

По итогам данного раздела можно дать следующие практические рекомендации.

•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью.
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной.
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.

Источник

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Формула абсолютной погрешности

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Формула относительной погрешности

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Формула приведенной погрешности

Классификация оценочной погрешности

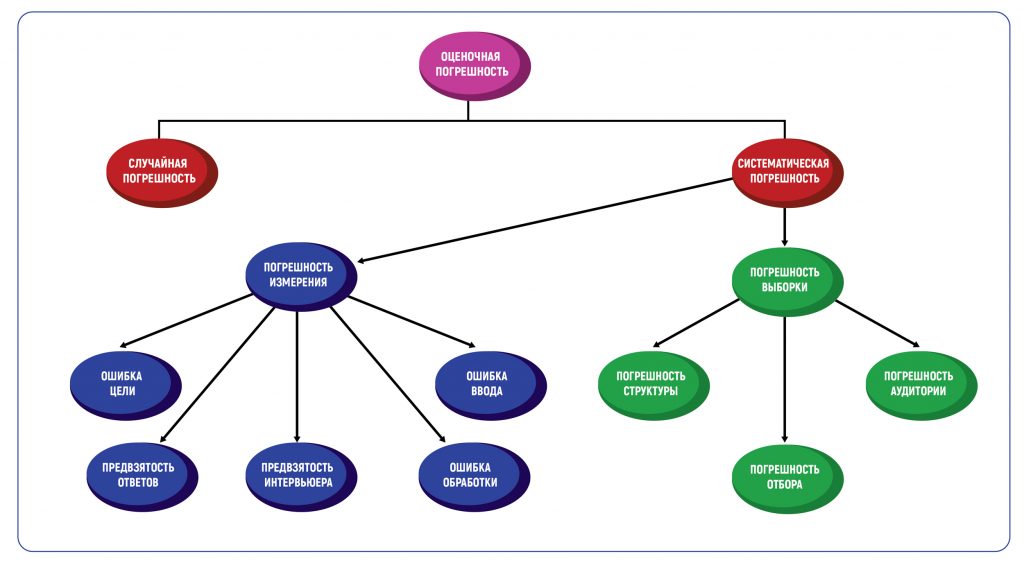
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

Классификация оценочной погрешности

Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.

Источник

Случайная погрешность — это ошибка в измерениях, которая носит неконтролируемый характер и очень труднопредсказуема. Так происходит из-за того, что существует огромное количество параметров, находящихся вне контроля экспериментатора, которые влияют на итоговые показатели. Случайные погрешности с абсолютной точностью вычислить невозможно. Они вызваны не сразу очевидными источниками и требуют много времени на выяснение причины их возникновения.

случайная погрешность это

Как определить наличие случайной погрешности

Непредсказуемые ошибки присутствует не во всех измерениях. Но для того чтобы полностью исключить ее возможное влияние на результаты измерений, необходимо повторить эту процедуру несколько раз. Если итог не меняется от эксперимента к эксперименту либо изменяется, но на определенное относительное число — величина этой случайной погрешности равна нулю, и о ней можно не думать. И, наоборот, если полученный результат измерений каждый раз другой (близкий к какому-то среднему значению, но отличный), и отличия носят неопределенный характер, следовательно, на него влияет непредсказуемая ошибка.

Пример возникновения

Случайная составляющая погрешности возникает вследствие действия различных факторов. Например, при измерении сопротивления проводника, необходимо собрать электрическую цепь, состоящую из вольтметра, амперметра и источника тока, которым служит выпрямитель, подключенный в осветительную сеть. Первым делом нужно измерить напряжение, записав показания с вольтметра. Затем перенести взгляд на амперметр, чтобы зафиксировать его данные о силе тока. После использовать формулу, где R = U / I.

случайная погрешность формула

Но может случиться так, что в момент снятия показаний с вольтметра в соседней комнате включили кондиционер. Это довольно мощный прибор. В результате этого напряжение сети немного уменьшилось. Если бы не пришлось отводить взгляд на амперметр, можно было заметить, что показания вольтметра изменились. Поэтому данные первого прибора уже не соответствуют записанным ранее значениям. Из-за непредсказуемого включения кондиционера в соседней комнате получается результат уже со случайной погрешностью. Сквозняки, трения в осях измерительных приборов — потенциальные источники ошибок в измерениях.

Как проявляется

Допустим, необходимо рассчитать сопротивление круглого проводника. Для этого нужно знать его длину и диаметр. Помимо этого, учитывается удельное сопротивление материала, из которого он изготовлен. При измерении длины проводника случайная погрешность себя проявлять не будет. Ведь этот параметр всегда один и тот же. Но вот при измерении диаметра штангенциркулем или микрометром окажется, что данные разняться. Так происходит потому, что идеально круглый проводник невозможно изготовить в принципе. Поэтому, если измерить диаметр в нескольких местах изделия, то он может оказаться разным вследствие действия непредсказуемых факторов в момент его изготовления. Это случайная погрешность.

Иногда она также называется статистической погрешностью, поскольку эту величину можно уменьшить, увеличив количество экспериментов при одинаковых условиях их проведения.

величина случайной погрешности

Природа возникновения

В отличие от систематической ошибки, простое усреднение нескольких итоговых показателей одной и той же величины компенсирует случайные погрешности результатов измерений. Природа их возникновения определяется очень редко, и поэтому никогда не фиксируется, как постоянная величина. Случайная погрешность — это отсутствие каких-либо природных закономерностей. Например, она не пропорциональна измеряемой величине или никогда не остается постоянной при проведении нескольких измерений.

Может существовать ряд возможных источников случайных ошибок в экспериментах, и он полностью зависит от типа эксперимента и используемых приборов.

Например, биолог, изучающий размножение конкретного штамма бактерии, может столкнуться с непредсказуемой ошибкой из-за небольшого изменения температуры или освещения в помещении. Однако когда эксперимент будет повторяться в течение определенного периода времени, он избавится от этих различий в результатах путем их усреднения.

случайные погрешности результатов измерений

Формула случайной погрешности

Допустим, нужно определить какую-то физическую величину x. Чтобы исключить случайную погрешность необходимо провести несколько измерений, итогом которых будет серия результатов N количества измерений — x_1,x_2,…,x_n.

Чтобы обработать эти данные следует:

За результат измерений х₀принять среднее арифметическое х̅. Иными словами, х₀= (x₁ +x₂ +… +x_n)/ N_.
Найти стандартное отклонение. Обозначается оно греческой буквой σ и вычисляется следующим образом: σ = √((х₁— х̅ )²+ (х₂-х̅ )²+ … + (х_n— х̅ )²/ N — 1). Физический смысл σ состоит в том, что если провести еще одно измерение (N+1), то оно с вероятностью 997 шансов из 1000 ляжет в интервал х̅ -3σ < х_n+1< с + 3σ.
Найти границу абсолютной погрешности среднего арифметического х̅. Находится она по следующей формуле: Δх = 3σ / √N.
Ответ: х = х̅ + (-Δх).

Относительная погрешность будет равна ε = Δх /х̅.

случайная составляющая погрешности

Пример вычисления

Формулы расчета случайной погрешности достаточно громоздкие, поэтому, чтобы не запутаться в вычислениях, лучше использовать табличный способ.

Пример:

При измерении длины l, были получены следующие значения: 250 см, 245 см, 262 см, 248 см, 260 см. Количество измерений N = 5.

N п/п	l, см	I _{ср. арифм.,}см	\|l-l _{ср. арифм.}\|	(l-l _{ср. арифм.})²	σ, см	Δ l, см
1	250	253,0	3	9	7,55	10,13
2	245	8	64
3	262	9	81
4	248	5	25
5	260	7	49
	Σ = 1265			Σ = 228

Относительная погрешность равна ε = 10,13 см / 253,0 см = 0,0400 см.

Ответ: l = (253 + (-10)) см, ε = 4 %.

Практическая польза высокой точности измерений

Следует учитывать, что достоверность результатов тем выше, чем большее количество измерений проводится. Чтобы повысить точность в 10 раз, необходимо провести в 100 раз больше измерений. Это достаточно трудоемкое занятие. Однако оно может привести к очень важным результатам. Иногда приходится иметь дело со слабыми сигналами.

абсолютная случайная погрешность

Например, в астрономических наблюдениях. Допустим, необходимо изучить звезду, блеск которой изменяется периодически. Но это небесное тело настолько далеко, что шум электронной аппаратуры или датчиков, принимающих излучения, может быть во много раз больше, чем сигнал, который необходимо обработать. Что же делать? Оказывается, если проводить миллионы измерений, то возможно среди этого шума выделить необходимый сигнал с очень большой достоверностью. Однако для этого потребуется совершать огромное количество измерений. Такая методика используется, чтобы различать слабые сигналы, которые едва заметны на фоне различных шумов.

Причина, по которой случайные погрешности могут быть решены путем усреднения, заключается в том, что они имеют нулевое ожидаемое значение. Они действительно непредсказуемы и разбросаны по среднему значению. Исходя из этого, среднее арифметическое ошибок ожидается равным нулю.

Случайная погрешность присутствуют в большинстве экспериментов. Поэтому исследователь должен быть подготовлен к ним. В отличие от систематических, случайные погрешности не предсказуемы. Это затрудняет их обнаружение, но от них легче избавиться, поскольку они являются статистическими и удаляются математическим методом, таким как усреднение.

Источник