Формула для вычисления абсолютной ошибки силы тока

Федеральное
Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И
РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра физики

ОТЧЕТ

Лабораторная
работа по курсу «Общая физика»

ИЗУЧЕНИЕ МАГНИТНОГО
ПОЛЯ КРУГОВОГО ТОКА

Преподаватель Студент
группы

___________ /____________.
/ __________ / /

___________201_
г. __________ 2011 г.

2011

Целью
настоящей работы является определение
величины удельного заряда электрона
методом магнетрона.

2. ОПИСАНИЕ УСТАНОВКИ
И МЕТОДИКИ ЭКСПЕРИМЕНТА

В качестве магнетрона
используется электронная лампа 3Ц22С,
которая имеет цилиндрические анод и
катод. Диаметр катода равен 1 мм.
Несоосность между осями катода и анода
порядка 1 мм. Поэтому для данной лампы
расстояние от катода до анода можно
принять R
= (8 ± 1) мм.

На лампу надевается
соленоид с большим числом витков на
единицу длины. Густота намотки соленоида
для разных блоков (вариантов) приведена
в Журнале измерений.

Погрешность густоты
намотки соленоида составляет 5 вит./см.

Для определения
зависимости анодного тока от тока
соленоида используется следующая схема
измерения (рис. 2.1).

Рисунок 2.1 – Схема
экспериментальной установки

Значение анодного
тока измеряется микроамперметром (μA),
который вмонтирован в основную панель
лабораторного макета. Значение тока
соленоида измеряется миллиамперметром
(mA),
который также вмонтирован в основную
панель. Регулировка тока соленоида
осуществляется с помощью ручки
потенциометра RP1,
выведенную на основную панель. Ручка
потенциометра RP2
для регулирования анодного напряжения
выведена на малую панель (блок питания
лабораторного макета). В эту же панель
вмонтирован вольтметр (V),
измеряющий анодное напряжение.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ
ФОРМУЛЫ

Для расчёта
удельного заряда электрона будем
использовать формулу:

, (3.1)

где e
– заряд электрона, m
– масса электрона

μ
– относительная магнитная проницаемость
среды (для вакуума μ
= 1);

μ₀
– магнитная
постоянная (в СИ
μ₀
= 4·π·10^-7
Гн/м);

n –
число витков, приходящихся на единицу
длины соленоида;

I_кр
– значение
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения.

R
– расстояние от катода до анода

U_a
—
анодное напряжение лампы

Расчет погрешности:

Абсолютная
погрешность расчёта удельного заряда
электрона равна:

, (3.2)

где

— коэффициент Стьюдента,

(3.3)

Или

Относительная
погрешность расчёта удельного заряда
электрона

, (3.4)

где

— относительная погрешность измерения
анодного напряжения лампы ()

— относительная
погрешность расстояние от катода до
анода (

Относительная
погрешность квадрата расстояния от
катода до анода
(3.5)

— относительная
погрешность расчёта значения квадрата
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения ()

Относительная
погрешность расчёта значения силы тока
в соленоиде, при котором индукция
магнитного поля достигает критического
значения рассчитывается как:

, (3.6)

где

— абсолютная погрешность расчёта значения
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения, она вычисляется
по формуле

(3.7)

4. РЕЗУЛЬТАТЫ РАБОТЫ
И ИХ АНАЛИЗ.

Измеренные значения
и результаты их обработки приведены в
таблице.

Таблица 4.1

Зависимость
анодного тока I_а
от тока
соленоида I_с
при
различных значениях анодного напряжения
U_а

Номер опыта	Uа = 6,18 В	Uа = 8,4 В	Uа = 11,84 В	Uа = 15,47 В
Iс, mA	Iа, μA	Iс, MA	Iа, μA	Iс, mA	Iа, μA	Iс, mA	Iа, μA
1	50,286	500	49,615	500	50,016	500	50,061	500
2	54,486	500	73,173	500	87,873	500	98,231	500
3	64,4	486	75,172	475	89,233	475	101,89	486
4	64,629	438	75,882	327	89,848	373	103,19	299
5	64,559	450	76,42	228	91,117	167	103,44	260
6	65,322	276	76,633	192	91,479	111	104,0	185
7	66,011	131	77,199	82	91,652	82	104,54	116
8	71,368	34	77,944	55	99,23	9	105,43	55
9	75,093	10	86,133	17	102,77	11	113,01	32
10	78,522	10	89,103	10	106,09	10	120,82	10
	Iкр,= 64,5 (mA)	Iкр,= 75 (mA)	Iкр,= 89 (mA)	Iкр,= 102 (mA)

Рассчитаем удельный
заряд электрона по формуле (3.1),
густота намотки соленоида n
= 26000вит/м, расстояние от катода до анода
R
= 8 мм подробности
расчёта в таблице 2

Найдём значение
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения из графиков:

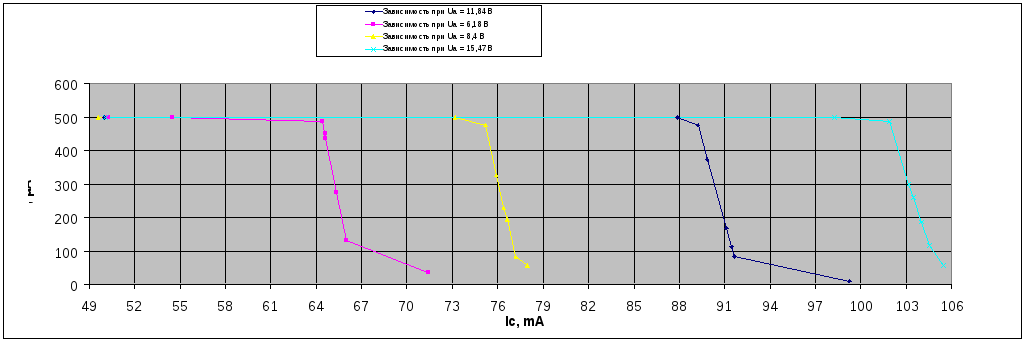
Рис 4.1 Зависимость
анодного тока от тока от тока в соленоиде
при Uа = 6.18В , Uа = 8.4В, Uа = 11,84В, Uа = 15,47В

Занесём данные
значение силы
тока в соленоиде, при котором индукция
магнитного поля достигает критического
значения от
анодного напряжение лампы в таблицу
4.2

Таблица 4.2

Зависимость силы
тока в соленоиде, при котором индукция
магнитного поля достигает критического
значения от
анодного напряжение лампы

Uа ,(В)	Iкр ,(mA)
6,18	64,5
8,4	75
11,84	89
15,7	102

Найдём абсолютную
погрешность значения силы тока в
соленоиде, при котором индукция магнитного
поля достигает критического значения
по формуле (3.7).

Т.к. в нашем
эксперименте приборы цифровые, то их
приборная погрешность будет равняться
младшему разряду, значит

= 0.01 мА
=
0.001 мкА

Тогда

=1×10^-5
А

Относительная
погрешность расчёта значения силы тока
в соленоиде, при котором индукция
магнитного поля достигает критического
значения рассчитывается по формуле
(3.3) подробности в таблице 2

Относительная
погрешность расчёта значения силы тока
в соленоиде, при котором индукция
магнитного поля достигает критического
значения рассчитывается по формуле
(3.6).

Относительная
погрешность расчёта значения квадрата
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения представлена в
таблице 2.

Абсолютная
погрешность расстояние
от катода до анода равна
1
мм, а само расстояние 8 мм, значит:

=0.125

Относительная
погрешность квадрата расстояние
от катода до анода рассчитывается по
формуле (3.5).

Т.к. измеритель
напряжения — цифровой прибор, то абсолютную
приборную погрешность можно принять
равной наименьшему разряду, значит
0.01
(В), тогда относительная погрешность
равна
,
расчет приведён в таблице 4.3.

Относительная
погрешность расчёта удельного заряда
электрона рассчитаем по формуле (3.4)

Таблица 4.3.
Погрешности расчёта удельного заряда
электрона

	,В	,А
1	6,18	0,0645	0,0016	0.25	3E-05	0,25	4,346E+10
2	8,4	0,075	0,0012	0.25	3E-05	0,25	4,369E+10
3	11,84	0,089	0,0008	0.25	2E-05	0,25	4,373E+10
4	15,7	0,102	0,0006	0.25	2E-05	0,25	4,415E+10

По формуле (3.3)
находим стандартную ошибку
=
1×10⁸
(Кл/кг), далее по формуле (3.2) находим
общую абсолютную ошибку (доверительную
вероятность возьмем равной ά=0.95, значение
Стьюдента равно t=
3.2)

5×10⁸
(Кл/кг)

Итак, удельного
заряда электрона с учётом погрешности
равен:

=(
1,751+0.005)×10¹¹
Кл/кг

Сравнивая с
табличным значением
=
1.7588×10¹¹
Кл/кг, рассчитанное значение в данной
лабораторной работе в пределах погрешности
равно табличному значению.

5. ВЫВОДЫ

В данной лабораторной
работе была определена фундаментальная
константа удельный
заряд электрона
=(1,751+0.004)×10¹¹
Кл/кг. Различия с табличными данными
можно объяснить тем, что недостаточно
точно определялся Iкр.

6. ОТВЕТЫ НА
КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1 Как устроена
магнетронная система?

Между анодом и
катодом приложено постоянное напряжение,
создающее радиальное электрическое
поле. На лампу надевают соленоид, по
которому протекает постоянный ток,
создающий постоянное магнитное поле,
направленное вдоль оси анода. Электроны,
испускаемые накалённым катодом, в
отсутствии магнитного поля движутся к
аноду так, что проекция их траектории
на плоскость YOX представляет собой
отрезки прямых.

При включении тока
в соленоиде, его магнитное поле будет
действовать на движущейся электрон с
силой Лоренца:
F_Л
= e[v,B],
где e
– заряд электрона;v
– скорость электрона;B
– индукция магнитного поля.

6.2 От чего зависит
радиус кривизны траектории электрона
в магнетроне?

Радиус кривизны
траектории электрона в магнетроне от
заряда частицы, индукции магнитного
поля, массы и скорости частицы.

6.3 Какая сила
называется силой Лоренца и как определяется
её направление?

Сила, действующая
на движущуюся заряженную частицу в
магнитном поле, называется силой Лоренца.
Сила Лоренца определяется по правилу
векторного произведения с учётом знака
заряда. Вектор силы всегда перпендикулярен
вектору скорости электрона

6.4 Почему сила
Лоренца не изменяет кинетической энергии
заряженной частицы?

Потому что, она
направлена перпендикулярно движению
и изменяет только траекторию движения.

6.5 По какому правилу
и как определяется направление вектора
магнитной индукции в соленоиде при
заданном направлении тока в нём?

Направление вектора
индукции магнитного поля В
определяется
по правилу буравчика

6.6 Что означают
величины, входящие в формулу для
определения магнитной индукции?

,
где e
– заряд электрона, m
– масса электрона, v
– скорость электрона, R
– радиус окружности, по которой движется
электрон.

6.7 Что происходит
с электронами, вылетевшими из катода,
если величина магнитной индукции В
≥ В_кр?

Увеличивая магнитную
индукцию В
до В_кр
электроны перестанут достигать анода.

6.8 Какие из
характеристик, измеренных и рассчитанных
в данной работе, зависят от величины
напряжения?

От величины
напряжения
зависит сила тока в соленоиде, при
котором индукция магнитного поля
достигает критического значения

6.9 В какой цепи
токи больше: в анодной цепи или в цепи
соленоида?

Ответ: С цепи
соленоида токи больше.

6.10 Каким способом
в данной работе определяется величина
критического тока I_кр?

Ответ: в данной
работе величина критического тока I_кр
определяется
из графиков.

6.11 Ток эмиссии
катода постоянен при постоянном токе
накала. Почему при увеличении тока в
соленоиде (I
>
I_кр)
наблюдается снижение анодного тока?

Потому что часть
электронов возвращается на катод.

6.12 Почему в
экспериментальной зависимости I_а=
f(I_с)
не наблюдается
резкого спада
анодного тока при величине магнитной
индукции B ≥
B_кр?

Ответ: Это
связано с тем, что в экспериментальной
установке катод установлен не точно по
оси анода. Кроме этого, радиус катода
отличен от нуля, т.е. катод не представляет
собой бесконечно тонкую нить. Он является
цилиндром малого диаметра. Так же
начальные скорости электронов, вылетевших
с поверхности катода, не равны нулю, а
имеют различные значения (согласно
распределению Максвелла).

6.13 Два электрона
с кинетическими энергиями Е₁
и Е₂
движутся в
магнитном поле, перпендикулярно
направлению поля. Найти отношение их
периодов обращения и радиусов траекторий.

Ответ: период
обращения электрона равен

Из формулы

найдем
отношение
=

— таким образом,
период обращения электрона не зависит
от кинетической скорости, и отношение
периодов равно 1.

6.14 Определить
частоту вращения (циклотронную частоту)
частицы массы m
и зарядом
q в магнитном
поле индукции
B.

Ответ: Период
обращения частицы равен
,
с одной стороны, и с другой

Из формулы

найдем
отношение
=

Тогда

6.15 Выполняется ли
принцип независимости движения для
заряженных частиц, движущихся одновременно
в электрическом и магнитном полях?

Нет, т.к. движущийся
заряд создает магнитное поле, а изменение
магнитного поля может создавать ток
(т.е. заряд в единицу времени).

6.16 Электрон,
обладающий скоростью v,
попадает в однородное магнитное поле,
индукция которого перпендикулярна
скорости v.
Окружность, какого радиуса описывает
электрон?

Ответ: Из формулы

вытекает, что
=

6.17 Заряженная
частица, пролетая некоторую область
пространства, не отклоняется от
первоначального направления движения.
Можно ли на основании этого факта
утверждать, что магнитное поле в этой
области отсутствует?

Нет, т.к. линии
магнитной индукции могут быть направлены
вдоль вектора скорости, тогда сила
Лоренса равна 0.

6.18 Пучок протонов,
попадая в некоторую область пространства,
отклоняется на некоторый угол. Можно
ли на основании этого факта определить,
каким полем вызвано отклонение,
электрическим или магнитным?

Нет, пучок протонов
мог отклониться как из-за сил Кулона,
так и из-за силы Лоренса, если априорно
нет данных, то нельзя сказать чем вызвано
отклонение пучка протонов.

6.19 Протон и электрон,
имеющие одинаковую скорость, попадают
в однородное магнитное поле, индукция
В
которого перпендикулярна скорости
частиц. Как будут различаться их
траектории?

В

— раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона и они будут вращаться в разные
стороны, т.к. у них разные знаки заряда

6.20 Протон и электрон,
ускоренные одинаковой разностью
потенциалов, влетают в однородное
магнитное поле. Во сколько раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона?

Ответ: Из формулы

определим радиуса
кривизны траектории электрона:

Для протона

Тогда

В

— раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона

6.21 Протон и электрон
влетают в однородное магнитное поле с
одинаковой скоростью. Во сколько раз
радиус кривизны траектории протона
будет больше радиуса кривизны траектории
электрона?

Ответ: Из формулы

определим радиуса
кривизны траектории электрона:

Для протона

Тогда

В

— раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона

6.22 Показать, что
какой бы скоростью
v ни обладал
электрон, влетающий в однородное
магнитное поле с индукцией В,
и каким бы ни был угол между векторами
v
и В,
время Т,
за которое он опишет виток винтовой
линии, будет одним и тем же.

Запишем силу
Лоренца

,
где e
– заряд электрона; v
– скорость электрона; B
– индукция магнитного поля.

Сила Лоренца
является центростремительной силой,
значит

Тогда

или

6.23 Показать, что
радиус кривизны траектории заряженной
частицы, движущейся в однородном
магнитном поле, перпендикулярном её
скорости, пропорционален импульсу
частицы.

Сила Лоренца
является центростремительной силой,
значит, скорость всегда будет направлена
по касательной и перпендикулярна радиусу
кривизны траектории заряженной частицы

7. ПРИЛОЖЕНИЕ

К работе прилагается
регистрационный файл (*.REG).

Была ли эта статья полезной?

Оценка погрешностей электрических измерений

Абсолютная
погрешность измерений, производимых
электроизмерительными приборами,
оценивается, исходя из класса точности
приборов. Обозначение класса точности
0,2; 0,5; 1,0 и т.д. не только характеризует
прибор в зависимости от системы,
конструкции, качества материалов,
точности градуировки и других факторов,
но и указывает, что погрешность показаний
прибора соответствующего класса в любом
месте шкалы не должна превышать 0,2%;
0,5%; 1%.

Если
обозначим через
максимально возможное показание прибора,
а через—
номер класса прибора, то получим
абсолютную погрешность прибора

.

Например,
вольтметр 0,2 класса (n
= 0,002),
шкала которого рассчитана на 50 В, имеет
абсолютную погрешность

,

а
амперметр класса 1,5, рассчитанный
на максимальное показание 5 А, имеет
абсолютную погрешность

.

Так
как абсолютная погрешность считается
одинаковой по всей шкале данного
электроизмерительного прибора, то
относительная погрешность
будет тем больше, чем меньше измеряемая
величина. Если, например, при помощи
указанного амперметра измерить ток
около 4А, то относительная погрешность
будет составлять 1,9%, а при измерении
силы тока около 1А – 7,5%.

При точных
измерениях следует пользоваться такими
приборами, чтобы предполагаемое значение
измеряемой величины составило 70-80% от
максимального (номинального) значения.
Поэтому применяют приборы, имеющие
несколько пределов измерений; при работе
с таким прибором его включают в цепь на
тот предел измерений, который достаточно
близок к предполагаемому значению
измеряемой величины.

Рассмотрим
вычисление погрешностей на следующем
примере.

Определить
погрешность измерения внутреннего
сопротивления элемента, электродвижущая
сила которого Е, напряжение на полюсах
U
и величина тока I.
Для измерения применены вольтметр
класса 0,5 ()
и
амперметр класса 1,0 ().Результаты
измерений следующие: Е = 2В, U
= 1,3 В,
I
= 1,2 А.

Абсолютные
погрешности измерений:

;

.

Вычисление
внутреннего сопротивления производим
по формуле

. (1)

Максимальная
относительная погрешность может быть
определена общеизвестным методом.
Логарифмируя выражение (1)

lnr
= ln(E-U)
– lnI,

находим относительную
погрешность

;

.

Эта
погрешность,
выраженная в процентах, составляет:

.

С
помощью формулы (1) находим внутренне
сопротивление r
и абсолютную погрешность
r:

Ом;

=
0,029 Ом =0,03 Ом.

Следовательно,
внутреннее сопротивление

0,03)
Ом.

ЛАБОРАТОРНАЯ
РАБОТА № 2.1

Изучение электростатических полей методом электролитического моделирования

Цель
работы:

1. Ознакомиться
   с одним из наиболее распространенных
   способов изучения характеристик
   электростатического поля с помощью
   электролитической ванны.

2. Практически
   исследовать некоторые электростатические
   поля.

Приборы и
принадлежности: электростатическая
ванна, набор электродов; индикатор нуля,
пантограф.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лабораторная работа № 1.

Расчет погрешностей емкости с помощью коэффициента Стьюдента.

Расчет погрешности измерения мощности и сопротивления

Цели занятия:

1. Общеобразовательная – Умение решать задачи по теме погрешности.

2. Развивающая — Углубление знаний .

3. Воспитательная – Проверить сформированность качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А (1)

Действительная относительная погрешность представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:

(2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,

т .е. к показанию прибора

(3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора

(4)

Для приборов с двухсторонней шкалой А_макс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального значения, то А_макс равно разности между конечным и начальным значениями шкалы.

Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как

,

где а₁, а₂, …, а_n – результаты отдельных измерений;

n – число измерений.

Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:

где Р₁ = а₁ – А_ср; Р₂ = а₂ – А_ср; Р_n = а_n – А_ср.

Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента t_n, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:

А = Аср t_n

Контрольное задание

Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):

• Действительное значение измеряемой емкости;

• Среднюю квадратическую и максимальную погрешности однократного измерения;

• Доверительный интервал для результата измерения при доверительной вероятности Р_д (табл.3).

• Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения С_ср (таб.1, таб.2).

Таблица 1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица 2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание. Количество и номера наблюдений значений емкости для каждого варианта определяются данными таблицы 1 и 2, например для варианта 1 следует взять результаты измерений 1-3 табл.2.

Указания к решению

1. Для удобства выполнения и проверки расчетов по заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица 3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

1. Далее определить среднеквадратическую погрешность :

1. По таблице (4) определить коэффициент Стьюдента.

2. В конце решения следует записать окончательный (с учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание 2._. Используя формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей измерения мощности и сопротивления. Расчет выполняется в соответствии с вариантами указанными в задании.

Задача 1. Для определения сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены напряжение и ток. Зная основные параметры измерительных приборов (амперметра и вольтметра), определить ошибку косвенных измерений мощности и сопротивления.

Пример. Определить абсолютную и относительную погрешности измерения мощности, выделяемой на резисторе, если известны показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А = 1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем мощность Р = U * I ( Вт)

2. Абсолютная ошибка измерения напряжения, В

1. Абсолютная ошибка измерения тока, _М А

1. В соответствии с таблицей абсолютная ошибка измерения мощности, Вт

Относительная ошибка

1. Формула для сопротивления R = U / I

2. 

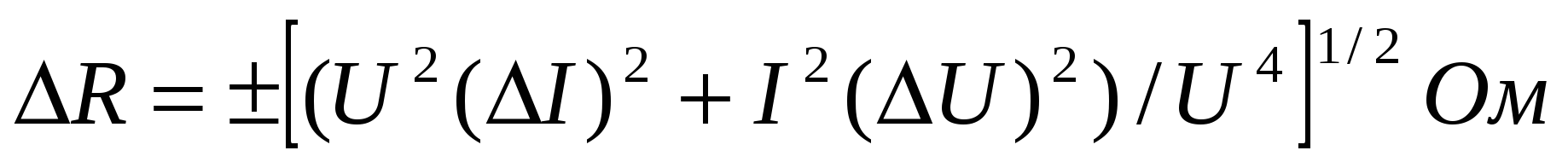
3. Относительная погрешность

Примечание:

1. Для вычисления погрешностей измерения мощности используются формулы 1,2,3,4,

2. Для вычисления погрешностей измерения сопротивления используются формулы 2,3,5,6,7.

Формулы для выполнения контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

3 Номинальная относительная погрешность

4.Приведенная относительная погрешность

1. Сопротивление шунта

R_Ш = R_А / Р-1 (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1) (Ом)

1. Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

1. Напряжение сети:

U_C = K_U* U (В)

1. Активная мощность сети:

P_C = K_i * K_U *P (Вт)

1. Реактивная мощность сети :

Q = U*I* sinφ (Вар)

1. Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление сети :

Z_C = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C / S_C

1. Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

1. Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

1. Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%

Задача 1

Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности N_B
с пределом измерений U_m, ток I амперметром класса точности N_a
с пределом измерений I_m. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.

Дано:

Найти:

Решение:

1)  Найдем
мощность, потребляемую приемником

2)  Класс
точности определяет приведенную погрешность

3)  Найдем
абсолютную погрешность измерения тока и напряжения

,

.

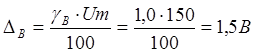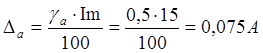4)  Найдем
абсолютную погрешность измерения мощности при косвенном измерении

5)  Найдем
относительную погрешность измерения мощности

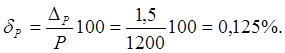
6)  Доверительный
интервал результата измерения с вероятностью .

Задача 2

Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.

Дано:

Найти:

Решение:

1)  Определим
среднее арифметическое результатов измерения

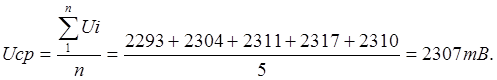
2)  Определяем
среднее квадратичное результатов измерения

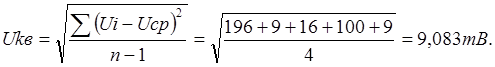
3)  Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется     , где

— коэффициент Стьюдента,

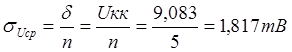 — среднее квадратичное отклонение
результата измерения.

4)  Находим
доверительный интервал

5)  Результат
измерения

Задача 3

Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление R_O  и рассчитана на предельный длительный ток I_O, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений I_m
и вольтметр с пределом измерений U_m?

Дано:

Найти: ,

Решение:

1)  Расчет
измерительной цепи амперметра

1.1 
Определяем коэффициент расширения пределов измерения по току

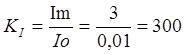
1.2     Определяем сопротивление
шунта

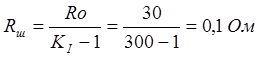
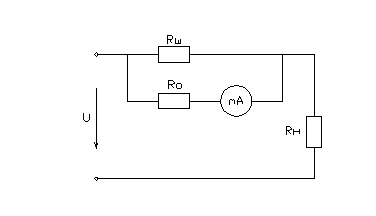
1.3 
 Схема измерительной цепи

2)  Расчет
цепи вольтметра

2.1 Определяем коэффициент
расширения пределов измерения по напряжению

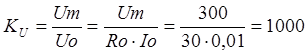
2.2  Определяем добавочное
сопротивление

2.3 
Схема включения

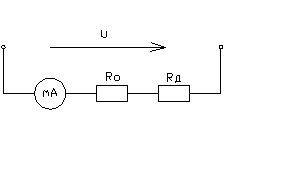
Задача 4

Определить
цену деления измерительных приборов:

1) амперметра, имеющего на шкале n_a делений и предел измерения I_m;

2)вольтметра, имеющего n_в делений шкалы и предел измерения U_m;

3) ваттметра, имеющего n_ВТ делений шкалы и пределы измерений по току I_{m ВТ} и напряжению U_m
ВТ.

Дано:

Найти:

Решение:

1) Цена деления
амперметра

2) Цена деления
вольтметра

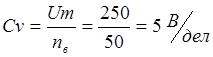
3) Цена
деления ваттметра

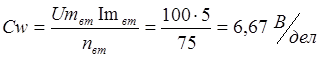
Задача 5

У вольтметра и
амперметра с пределами измерений U_m и I_m, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U₂ и I₂.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов N_a и N_в и
измерительных трансформаторов N_тн и N_тт. Привести схему измерения.

Дано:

Найти:

Решение:

1) Определим
коэффициенты трансформации трансформатора напряжения и тока

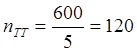
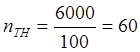
2) Определим
ток и напряжение в сети

3) Определим
абсолютные погрешности амперметра и вольтметра

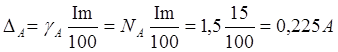
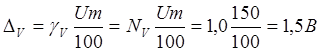
4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения

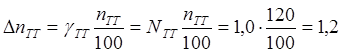
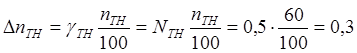
5) Результирующие
абсолютные погрешности измерения тока и напряжения равны

6)
Относительные погрешности измерения тока и напряжения

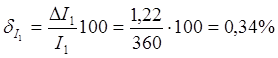
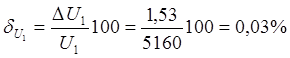
Задача 6

Определить
относительные погрешности измерения сопротивления R_x
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – R_a,
вольтметра – R_в. Сделать вывод о
целесообразности использования той или иной схемы.

Дано:

Найти: .

Решение:

Принципиальные
схемы

 

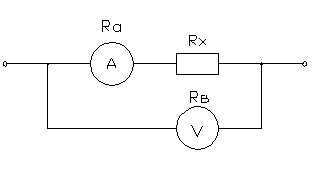
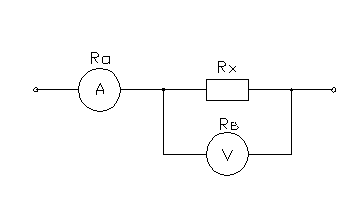
Схема
1                                              Схема 2

1)  Для
схемы включения 1.

1.1. 
Измеренное сопротивление.

1.2. 
Определяем абсолютную погрешность.

1.3. 
Определяем относительную погрешность.