3
Занятие 3
Анализ формы
эмпирического распределения.
Коэффициент
асимметрии приближенно можно оценить
по следующей формуле:
![]()
(1)
или
![]()
(более точная формула)
где
М – среднее арифметическое, s
— среднее квадратическое отклонение, n
– объем выборки.
Ошибка показателя
асимметрии:
mAs
=
![]()
![]() (2)
(2)
или
![]()
(более точная формула)
Для
нахождения коэффициента асимметрии и
его ошибки (воспользуемся приближенными
формулами 1 и 2) по материалам нашей
задачи составим таблицу
Расчет коэффициента
асимметрии:
|
Объем |
|
|
Среднее |
|
|
Стандартное |
|
|
Сумма(xi-M)3 |
|
|
Асимметрия |
|
|
Ошибка |
ЭКСЦЕСС.
Показатель
эксцесса «Е»
приближенно рассчитывается по выражению::
Е
=
(Xi—M)4/ns4
— 3
(3)
где
М – среднее арифметическое, s
— среднее квадратическое отклонение, n
– объем выборки, цифра 3 является,
поправкой связанной с нормальным
распределением.
Более точная
формула;
![]()
Ошибка
показателя эксцесса: mE
= 2![]()
(4)
Или более точная
формула:
![]()
Для
нахождения коэффициента эксцесса и его
ошибки (формулы 3 и 4 для приближенных
расчетов по материалам нашей задачи
составим таблицу
|
Расчет |
|
|
Объем |
|
|
Среднее |
|
|
Стандартное |
|
|
Сумма(xi-M)4 |
|
|
Эксцесс |
|
|
Ошибка |
Коэффициенты
асимметрии и эксцесса можно рассчитать
в приложении Exel
с помощью вставки соответствующей
функции: выделяем ячейку, где будет
находиться нужный нам показатель.
Выбираем раздел меню
«Вставка»-«Функция»-«Статистические»-
«СКОС» (если
мы хотим оценить, коэффициент асимметрии)
или «ЭКСЦЕСС» (если
мы хотим оценить коэффициент эксцесса
(Рис. 1)).
Указываем диапазон значений, по которым
будет оценена средняя. Затем «ОК».

Рис.
1
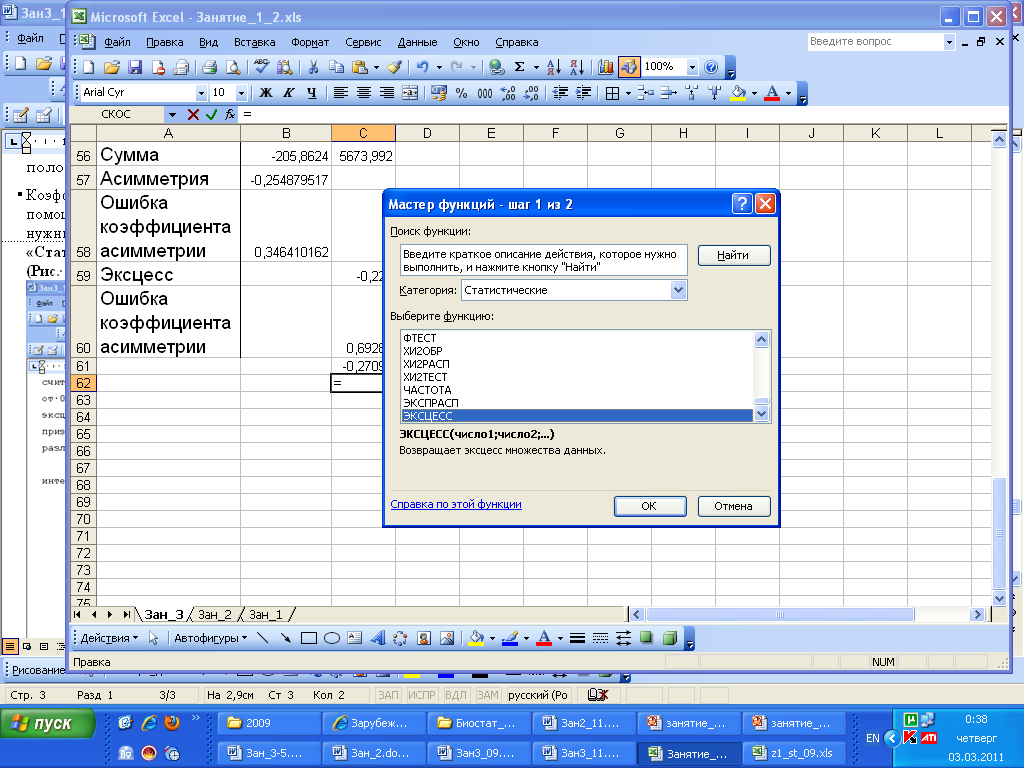

Оценка коэффициентов
асимметрии и эксцесса с помощью
приложения «Статистика».
Вставляем
исходные данные в специальную таблицу
Spreadsheet.
Выбираем последовательно разделы
Statistics—Basic
Statistics/Tables—Descriptive
statistics
(как показано на Рисунке
2).

Рис.
2



В
открывшемся окне выбираем раздел
Advanced
(Рис.
5),
где мы указываем, в каком столбце
находятся данные (Variables),
какие показатели хотим рассчитать:
коэффициент асимметрии и его ошибка –
«Skewness» и «Std. err.
Skewness» соответственно; и коэффициент
эксцесса и его ошибка – «Kurtosis»
и «Std. err.
Kurtosis»
соответственно (расставляем отметки,
как показано на Рисунке
3
и нажимаем «Summary».

Рис.
3


Соседние файлы в папке Задание 3
- #
- #
16.04.201536.35 Кб41Схема_отчета_3.xls
Коэффициент асимметрии. Эксцесс распределения
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:
Число 3 вычитается из отношения
потому, что для наиболее часто встречающегося
нормального распределения отношение
.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную
таблицу
Средняя:
Найдем моду — варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент
3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент
4-го порядка:
Получаем:
Задача 2
Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем
3-ю варианту
0
Условные варианты вычислим по
формуле:
где
4
(разность между соседними вариантами)
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии можно найти
по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
3
Занятие 3
Анализ формы
эмпирического распределения.
Коэффициент
асимметрии приближенно можно оценить
по следующей формуле:
![]()
(1)
или
![]()
(более точная формула)
где
М – среднее арифметическое, s
— среднее квадратическое отклонение, n
– объем выборки.
Ошибка показателя
асимметрии:
mAs
=
![]()
![]() (2)
(2)
или
![]()
(более точная формула)
Для
нахождения коэффициента асимметрии и
его ошибки (воспользуемся приближенными
формулами 1 и 2) по материалам нашей
задачи составим таблицу
Расчет коэффициента
асимметрии:
|
Объем |
|
|
Среднее |
|
|
Стандартное |
|
|
Сумма(xi-M)3 |
|
|
Асимметрия |
|
|
Ошибка |
ЭКСЦЕСС.
Показатель
эксцесса «Е»
приближенно рассчитывается по выражению::
Е
=
(Xi—M)4/ns4
— 3
(3)
где
М – среднее арифметическое, s
— среднее квадратическое отклонение, n
– объем выборки, цифра 3 является,
поправкой связанной с нормальным
распределением.
Более точная
формула;
![]()
Ошибка
показателя эксцесса: mE
= 2![]()
(4)
Или более точная
формула:
![]()
Для
нахождения коэффициента эксцесса и его
ошибки (формулы 3 и 4 для приближенных
расчетов по материалам нашей задачи
составим таблицу
|
Расчет |
|
|
Объем |
|
|
Среднее |
|
|
Стандартное |
|
|
Сумма(xi-M)4 |
|
|
Эксцесс |
|
|
Ошибка |
Коэффициенты
асимметрии и эксцесса можно рассчитать
в приложении Exel
с помощью вставки соответствующей
функции: выделяем ячейку, где будет
находиться нужный нам показатель.
Выбираем раздел меню
«Вставка»-«Функция»-«Статистические»-
«СКОС» (если
мы хотим оценить, коэффициент асимметрии)
или «ЭКСЦЕСС» (если
мы хотим оценить коэффициент эксцесса
(Рис. 1)).
Указываем диапазон значений, по которым
будет оценена средняя. Затем «ОК».

Рис.
1


Оценка коэффициентов
асимметрии и эксцесса с помощью
приложения «Статистика».
Вставляем
исходные данные в специальную таблицу
Spreadsheet.
Выбираем последовательно разделы
Statistics—Basic
Statistics/Tables—Descriptive
statistics
(как показано на Рисунке
2).

Рис.
2



В
открывшемся окне выбираем раздел
Advanced
(Рис.
5),
где мы указываем, в каком столбце
находятся данные (Variables),
какие показатели хотим рассчитать:
коэффициент асимметрии и его ошибка –
«Skewness» и «Std. err.
Skewness» соответственно; и коэффициент
эксцесса и его ошибка – «Kurtosis»
и «Std. err.
Kurtosis»
соответственно (расставляем отметки,
как показано на Рисунке
3
и нажимаем «Summary».

Рис.
3


Соседние файлы в папке Задание 3
- #
- #
16.04.201536.35 Кб37Схема_отчета_3.xls
Коэффициент асимметрии. Эксцесс распределения
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:
Число 3 вычитается из отношения
потому, что для наиболее часто встречающегося
нормального распределения отношение
.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Составим расчетную
таблицу
Средняя:
Найдем моду — варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент
3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент
4-го порядка:
Получаем:
Задача 2
Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем
3-ю варианту
0
Условные варианты вычислим по
формуле:
где
4
(разность между соседними вариантами)
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии можно найти
по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
Функция СКОС в Excel предназначена для определения коэффициента асимметрии для последовательности числовых данных и возвращает соответствующее числовое значение.
Расчет коэффициента асимметрии распределения чисел в Excel
Коэффициент асимметрии показывает степень несимметричности распределения числовых данных относительно среднего значения. Может принимать следующие значения:
- Из диапазона отрицательных чисел – отклонение в сторону отрицательных значений (отрицательные величины преобладают).
- Из диапазона положительных чисел – отклонение в сторону положительных значений (преобладание положительных величин).
- 0 – асимметрия отсутствует (например, для последовательности 1, 2, 3, -1, -2, -3 асимметрический коэффициент равен нулю – 0).
Для определения коэффициента асимметрии используется уравнение:
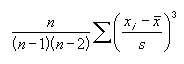
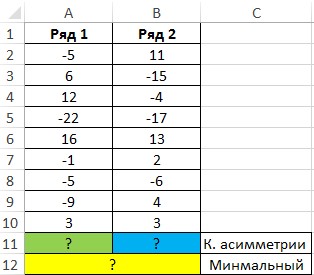
Пример 1. В таблице Excel содержатся два ряда числовых данных. Определить, какой из числовых рядов характеризуется наименьшим коэффициентом асимметрии.
Вид таблицы данных:
Для решения используем следующую формулу:
С помощью функции ЕСЛИ выполняем проверку коэффициента симметрии («имеет ли второй ряд большее значение скоса?») и возвращаем соответствующее значение с пояснением.
Результат вычислений:
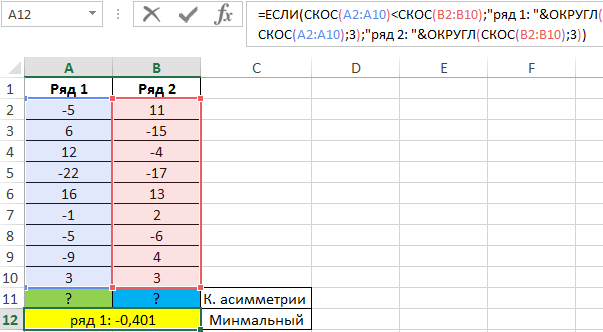
Проверим значения для каждого ряда по отдельности с помощью функций:
=ОКРУГЛ(СКОС(A2:A10);3)
=ОКРУГЛ(СКОС(B2:B10);3)
Полученные результаты:
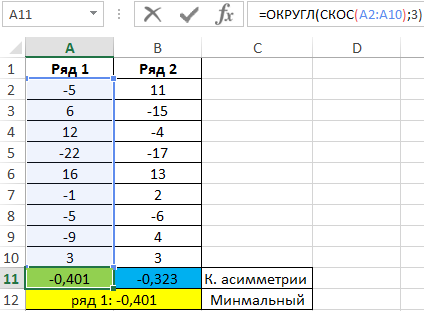
Обе последовательности имеют отклонения в отрицательную сторону, но у ряда 1 это выражено в большей степени.
Коэффициент асимметрии и аппроксимация нормальным распределением в Excel
Пример 2. Имеем последовательность чисел. Необходимо проанализировать данную последовательность и сделать вывод о возможности аппроксимации нормальным распределением.
Вид таблицы данных:
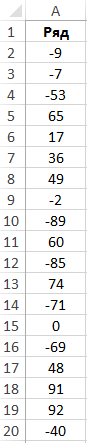
Для проверки нормального распределения величины применяют довольно сложные статистические критерии. Однако, в простейшем случае можно определить две величины (коэффициент асимметрии и эксцесс), чтобы сделать определенные выводы. Если они близки к нулю, аппроксимация нормальным распределением допустима.
Определим значения асимметрии и эксцесса следующими функциями:
=СКОС(A2:A20)
=ЭКСЦЕСС(A2:A20)
Результаты:
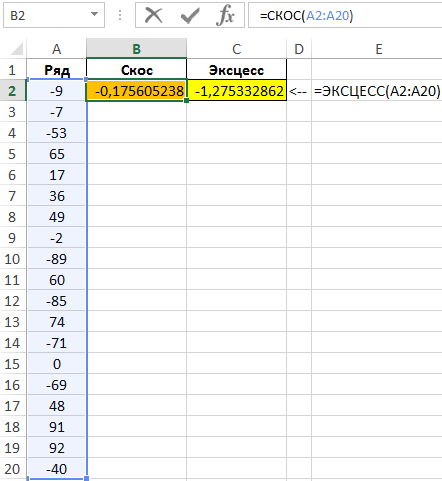
Отклонения от 0 значительны, поэтому аппроксимация невозможна. Чтобы автоматизировать подобные расчеты введем некоторые условия:
В данном случае принято допущение о том, что максимальное допустимое отклонение модулей асимметрии и эксцесса составляет 0,1
Результат:
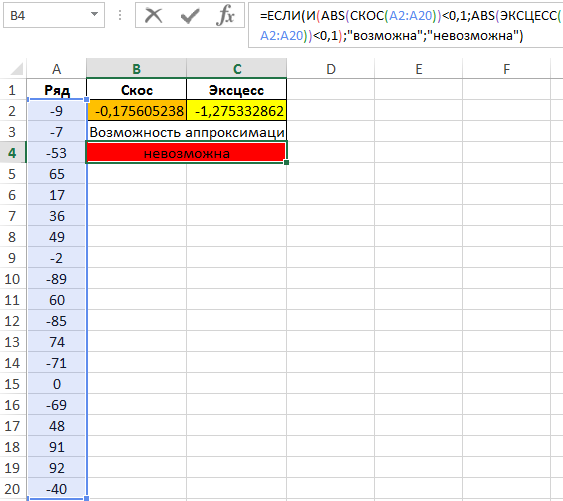
Правила использования функции СКОС в Excel
Функция имеет следующую синтаксическую запись:
=СКОС(число1;[число2];…)
Описание аргументов:
- число1 – обязательный, принимает первое значение числовой последовательности или ссылку на диапазон ячеек с числовыми данными.
- [число2];… — второй и последующие необязательные аргументы, принимающие числовые значения второго и последующих чисел исследуемого ряда.
Примечания:
- Функция принимает в качестве аргументов числа или данные, которые могут быть преобразованы к числовым данным, а также ссылки на ячейки с числами или преобразуемыми к числам данными. Иначе СКОС будет возвращать код ошибки #ЗНАЧ!
- Не преобразуемые к числам значения, содержащиеся в ячейках, в расчете не учитываются. Логические ИСТИНА и ЛОЖЬ также игнорируются рассматриваемой функцией.
- Если исследуемый ряд значений содержит менее трех числовых значений, функция СКОС вернет код ошибки # ЧИСЛО!
