
Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
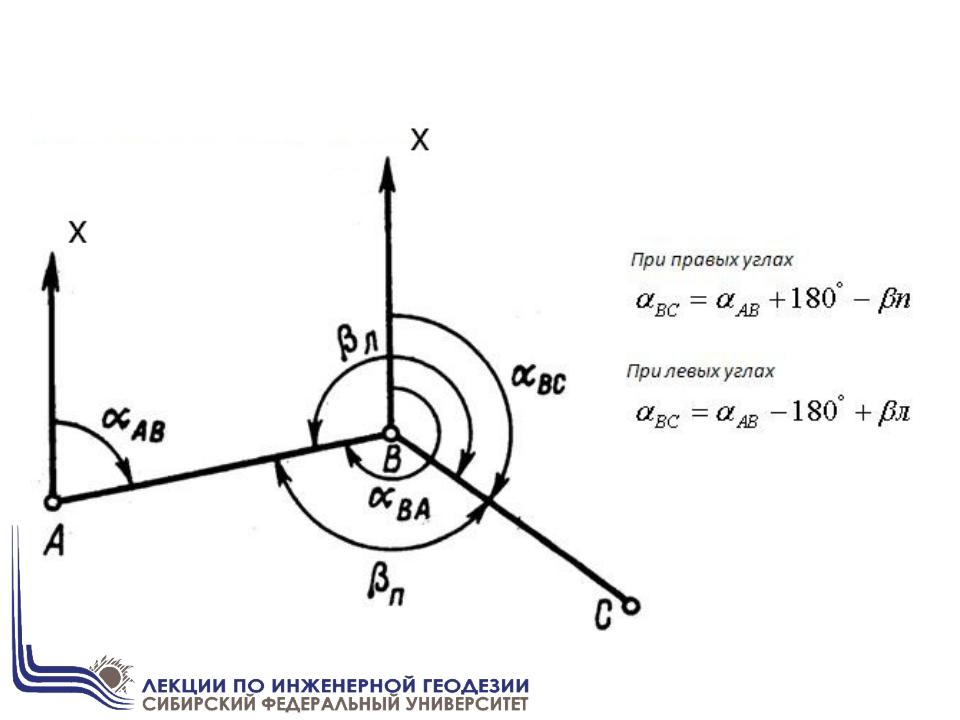
Контроль вычисления приращений координат: d АВ 
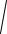 2 2
2 2
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |
ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
Результатом теодолитной съёмки является плановое положение контуров и местных предметов. Теодолитная съёмка обычно производится сравнительно на небольших участках местности, изображаемых в последующем на топографических планах крупных масштабов.
Геодезической основой для теодолитной съёмки являются теодолитные ходы, сгущаемые от пунктов Государственной геодезической сети 1-4 классов, а также пунктов сетей 1 и 2 разрядов. Формы ходов зависят от характера снимаемой местности. Так, при съёмке площадных объектов целесообразно использовать замкнутые ходы в сочетании с диагональными и висячими ходами, при съёмках линейных сооружений – разомкнутые в сочетании, в основном, с висячими ходами.
Теодолитная (горизонтальная, плановая) съёмка выполняется при помощи теодолита и мер длины (лента, рулетка) или дальномеров. Предельная погрешность (mS) положения пунктов плановой съёмочной сети относительно пунктов ГГС или ГСС не должна превышать 0,2 мм в масштабе плана.
Теодолитные ходы прокладываются с предельными относительными погрешностями 1:3000, 1:2000, 1:1000 в зависимости от условий съёмки (см.таблицу)
Допустимые относительные погрешности в теодолитных ходах
| Масштаб плана | mS | ||
|---|---|---|---|
| 1:3000 | 1:2000 | 1:1000 | |
| Допустимые длины ходов между исходными пунктами, км | |||
| 1 : 5000 | 6,0 | 4,0 | 2,0 |
| 1 : 2000 | 3,0 | 2,0 | 1,0 |
| 1 : 1000 | 1,8 | 1,2 | 0,6 |
| 1 : 500 | 0,9 | 0,6 | 0,3 |
Теодолитная съёмка ситуации выполняется способами угловой и линейной засечек, полярных координат, перпендикуляров, обхода, створов и комбинированными способами. Часть указанных способов была рассмотрена ранее в гл. 7 при пояснениях вопросов привязки точек съёмочного обоснования.
Способ угловой засечки используют для съёмки точек, недоступных для непосредственных линейных измерений. На план снятые пикеты наносят графически либо по координатам, предварительно вычисленным по формулам Юнга. В частности, указанный способ использован для получения положения острова (точки а – ж) – рис. 8.2. Вокруг озера проложен для выполнения съёмки способом обхода замкнутый теодолитный ход, привязанный к исходной геодезической основе АВ.
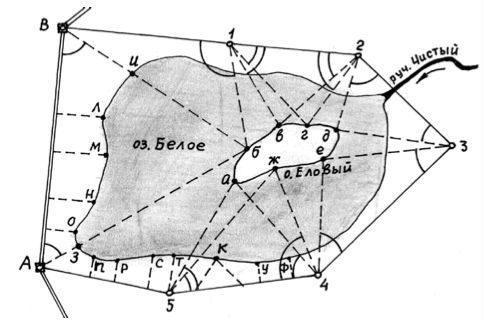
Способы теодолитной съёмки рис.1
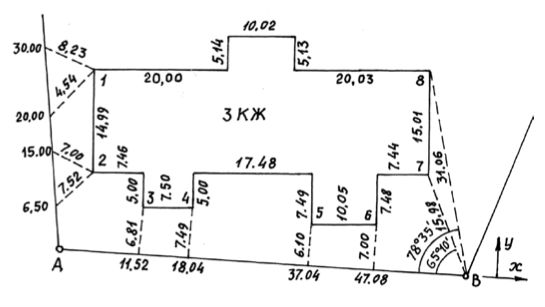
Способы теодолитной съёмки рис.2
На рис. 1 способом линейной засечки получено положение точки к, находящейся на берегу озера. На рис. 2 таким же способом получено положение точек 1 и 2 здания. Обычно точки местности, полученные способом линейной засечки, наносят на план графически по соответствующим расстояниям.
Способ полярных координат применяют для съёмки точек, находящихся в прямой видимости сравнительно недалеко от точек и линий теодолитного хода. При этом целесообразно, чтобы измеряемые расстояния не превышали длины мерного прибора (ленты или рулетки). При больших углах наклона в измеренное расстояние вводят поправку за наклон для получения горизонтального проложения. На рис. 1 таким способом получены точки и и з одновременно с выполнением угловой засечки. На рис. 2 указанный способ использован для съёмки точек 7 и 8 сооружения. Точки на план наносят графически по значению горизонтального угла и горизонтального проложения либо по координатам, предварительно вычисленным из решения прямой геодезической задачи с точек съёмочного обоснования.
Если съёмочные пикеты находятся вблизи от линии съемочного обоснования, то удобно использовать для их съёмки способ перпендикуляров (прямоугольных координат). На рис. 1 таким способом получено положение точек л – ф береговой линии озера, а на рис. 2 – точки 3, 4, 5 и 6 здания. Часто линию съёмочного обоснования принимают за ось х, а перпендикулярную к ней линию – за ось y условной системы координат. При этом значения координат х и y съемочных пикетов могут быть положительными и отрицательными. Результаты измерений оформляют в виде таблицы и соответствующего абриса, похожего на приведённые рисунки, с полным указанием на нем результатов измерений и привязок к точкам и линиям съёмочного обоснования. Абрис составляют обычно на одну из линий съёмочного обоснования либо на две-три таких смежных линии. Пикеты, полученные способом перпендикуляров, наносят на план графически. В отдельных случаях вычисляют и прямоугольные координаты этих пикетов. При этом необходимо преобразовать принятую для съёмки условную систему координат в используемую систему координат съёмочного обоснования. Решение такой задачи сложности не представляет: для этого достаточно только определить дирекционный угол направления условной оси х и координаты начала условной системы координат, если выбранная ось х (линия створа) не совпадает с линией съёмочного обоснования. Если же ось х совпадает с линией съёмочного обоснования, то задача определения координат съёмочных пикетов сразу сводится к решению прямой геодезической задачи.
О способе обхода уже было сказано выше (см. рис. 1). Этот способ чаще используется для съёмки контуров, имеющих значительную площадь. Вокруг контура прокладывают дополнительный замкнутый теодолитный ход и с точек и линий этого хода любыми известными способами получают положение искомых пикетов.
Ответственные точки местности часто снимают повторно с других станций либо на той же станции, но другим способом (комбинированный способ съёмки). Комбинированный способ съёмки может быть реализован, например, одновременным получением координат точки способом угловой и линейной засечек при использовании электронных тахеометров.
Если линия съёмочного обоснования пересекает контур объекта местности, линейный контур сооружения, то положение точки пересечения фиксируют промерами в створе линии съёмочного обоснования. Такой способ называют способом створов. Часто створ задают отдельно от линии съёмочного обоснования направлением, а положение точек местности от него получают способом перпендикуляров. В этом случае как раз и необходимо для получения координат съёмочных пикетов определить дирекционный угол линии створа и координаты одной из его точек, например, начала координат условной системы.
При съёмках зданий обязательно производят полные их обмеры. Это позволяет пополнить недостающие элементы контура здания, а также является надежным контролем результатов съёмки. Контрольные промеры выполняют и между точками твердых контуров, полученных с разных станций либо с одной станции, но независимо от другой точки.
Такие промеры могут быть выполнены между углами двух соседних зданий, между углами одного и того же здания сложной конфигурации, между точкой-ориентиром и углом здания и т.п.
Горизонтальные углы при теодолитной съёмке измеряют теодолитом полным приёмом, во многих случаях и расстояния измеряют дважды – в прямом и обратном направлениях, если они значительно превышают длину мерного прибора. Центрирование теодолита в точке съёмочного обоснования должно обеспечить необходимую точность измерения горизонтальных углов.
Теодолитный ход является наиболее востребованной частью геодезических работ, переплетаясь со многими видами инженерной деятельности. В чем же его назначение и какие особенности выполнения разберем по порядку в нашей статье.
Содержание
- 1 Назначение и основные разновидности
- 2 Порядок проведения
- 3 Основные технические требования к линейным измерениям
- 4 Съемка ситуации и ее виды
- 5 Обработка полученных результатов измерений
- 5.1 Создавайте будущее вместе с нами
- 6 Составление плана
Назначение и основные разновидности
Проводится с целью точного отображения местности и расположенных на ней объектов на крупномасштабной карте, плане или специальных схемах.
Данная процедура подразумевает создание системы точек, закрепленных в натуре, и определение их горизонтальных углов при помощи теодолита или тахеометра. Расстояние между пунктами определяется при помощи светодальномеров, рулеток и других приборов, позволяющих обеспечить необходимую точность. По форме обычно принято различать следующие виды ходов:
– разомкнутый;
– замкнутый;
– висячий.
В разомкнутом первая и последняя точка базируется на разные пункты и направления геодезической сети, чьи координаты и дирекционные углы уже определены, а замкнутый образует геометрическую фигуру, поэтому может опираться только на один. Особенность же висячего хода состоит в том, что один его конец примыкает к пункту геодезического обоснования, а второй остается свободным.
Его форма во многом зависит от того, на какой территории проводятся измерения. Например, для автодорог и трубопроводов хорошо подойдет разомкнутый ход, а на строительных площадках и земельных участках обязательно должен быть построен замкнутый полигон.
Достаточно распространённой процедурой является прокладывание внутри больших полигонов дополнительных сетей, чтобы полностью отобразить ситуацию на плане.
Порядок проведения
Выполнение теодолитного хода начинают с рекогносцировки, подразумевающей изучение ее особенностей и определение наиболее подходящих мест для установки точек.
Расстояние между ними должно варьироваться в пределах от 20 до 350 метров, но оно зависит также и от масштаба съемки. Наилучшей точности можно добиться, если расстояние будет одинаковым, но особенности территории далеко не всегда позволяют это сделать.
Съемку осуществляют на открытом пространстве с хорошей взаимной видимостью между пунктами, закрепленными специальными кольями из дерева, металла и других материалов. Для их долговременной сохранности нередко используются бетонные монолитные столпы. Также рекомендуется привязать каждый знак к твердым объектам поблизости, чтобы можно было восстановить его в случае потери.

Когда все подготовительные процедуры завершены и определено местоположение пунктов начинаются полевые работы. Прибор устанавливают на точке и измеряют угол за один прием, визируясь на соседние, после чего определяют расстояния между ними.
Если строится замкнутый полигон, за начальный берут магнитный азимут одной из сторон. Привязка к пункту геодезической сети необходима для определения дирекционного угла и координат, что позволит обеспечить должный контроль полученных результатов.
Все данные записываются в специальный журнал или автоматически заносятся в память электронного измерительного устройства. В дальнейшем они используются для камеральной обработки, которая подразумевает проведение расчетов с целью вычисления координат пунктов и жестких контуров.
Параллельно со съемкой составляется схематический чертеж, отображающий местоположение объектов на местности, который называется абрисом. Он представляет собой полноценный документ, является неотъемлемой частью технической документации и служит источником информации при построении плана или карты.
Во время составления абриса необходимо отобразить на нем как можно больше информации. Особенно важно обозначить все метрические данные и сделать его понятным для прочтения.
Во время снегопада, дождей и других неблагоприятных погодных условий, а также при плохой освещенности, проводить измерения запрещается.
Основные технические требования к линейным измерениям
Любые геодезические работы должны быть выполнены с четким соблюдением всех правил, дабы обеспечить получение самых точных результатов измерений. Основные требования к данной процедуре изложены в инструкции по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500, а также ряда других нормативных документов.
В зависимости от предельной относительной погрешности длина теодолитного хода должна соотносится со следующими показателями, приведенными в табл.1.
Таблица 1.
| Буровая установка | № скважины | Литологический тип | Коэф. крепости | Размер отдельности, м | Скорость фактическая, м/c |
|---|---|---|---|---|---|
| DM LP | 6,0 | 4,0 | 2,0 | 6,0 | 3,0 |
| СБШ | 3,0 | 2,0 | 1,0 | 3,6 | 1,5 |
| 1:1000 | 1,8 | 1,2 | 0,6 | 1,5 | 1,5 |
| 1:500 | 0,9 | 0,6 | 0,3 | — | — |
(m_{s}) – среднеквадратическая ошибка измеренных расстояний.
Показатели предельно допустимых длин между узловой точкой и исходной уменьшается на 30%, а также должны быть:
– больше 20 м, но меньше 350 м на застроенных участках;
– свыше 40 м и не более 350 м.
Аналогичные требования (табл. 2) есть и к висячим теодолитным ходам:
Таблица 2.
| Масштаб | Местность | |
| Застроенная | Не застроенная | |
| 1:5000 | 350 | 500 |
| 1:2000 | 200 | 300 |
| 1:1000 | 150 | 200 |
| 1:500 | 100 | 150 |
Измерение длин необходимо проводить в обе стороны и высчитать их среднее значение, а точность приборов должна быть не менее 30”. Допустимое отклонение при центрировании – не более 3 мм.
Съемка ситуации и ее виды
Прокладывание теодолитного хода, как правило, проводят для последующего отображения особенностей территории работ. Конечная цель – получения данных о местоположении снимаемых объектов в пространстве и составление контурной карты или плана местности без отображения рельефа. Фиксируются наиболее значимые элементы окружения:
– деревья и крупная растительность;
– инженерные конструкции;
– государственные геодезические пункты;
– контуры зданий, сооружений и других жестких объектов.

Процесс их измерения называется съемкой ситуации, которая выполняется следующими способами:
- Способ перпендикуляров. Применяют для съемки объектов вытянутой формы, которые расположены преимущественно на открытом пространстве и близко к пунктам. Основной принцип выполнения этого способа строится на определении основания перпендикуляра, а также измерении его длины до станции.
- Полярных координат. Проводится, если снимаемая цель находится на большом расстоянии от пункта. Одна сторона принимается за полярную ось, а ее вершина – за полюс. Измеряются горизонтальные углы направления на заданную точку и определяют линейное расстояния до нее.
- Угловая засечка. Хорошо подходит для съемки труднодоступных точек. Их местоположение определяют совмещением сторон углов, измеренных от вершины теодолитного хода до заданного пункта с двух направлений.
- Метод створа (линейных промеров) используется, когда контуры местности пересекают уже построенный ход или его продолжение, а также для определения дополнительных точек посредством линейных измерений. Данный способ активно применяется на сильно застроенных участках.
- Способ обхода используют, как правило, на закрытой местности, если необходимо снять особо важный объект, но от вершин сторон это сделать невозможно по причине наличия препятствий или дальности. Прокладывают дополнительные пикеты, которые и привязывают к основным пунктам, а границы контура снимают методом перпендикуляра.
Геодезические работы основаны на принципе «от общего к частному». Поэтому, в теории, лучше всего сперва построить теодолитный ход, а потом уже провести съемку подробностей.
Обработка полученных результатов измерений
Выполнение контурной съемки проводится с целью получения данных, необходимых для дальнейшего расчета координат:
– горизонтальных углов;
– длин сторон теодолитного хода;
– дирекционных углов;
– румбов.
Подсчет теоретической суммы угловых измерений () хода осуществляют по формуле (табл. 3).
Таблица 3.
| замкнутый | разомкнутый |
| (beta _{T}= 180left ( n-2 right )) | (beta _{T}=left ( alpha _{р}+alpha _{к} right )pm 180^{o}cdot left ( n+1 right )) |
n – количество точек;
(alpha _{н})– значение начального дирекционного угла, –конечного;
Далее производят расчет угловой невязки:
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
(f_{beta }=sum beta _{изм}- sum beta _{т})
(beta _{изм})– сумма измеренных углов.
Следующим шагом будет сравнение (f_{beta })с допуском (f_{beta доп}). Если результат не соответствует приведенному ниже выражению, необходимо перепроверь данные:
(f_{beta}< f_{beta доп})
(f_{beta доп}={1,5·t}sqrt{n}), где t – приборная точность измерения углов; n – количество измеряемых углов.
В дальнейшем (f_{beta}) равномерно распределяется между измеренными величинами с противоположным знаком и проводится расчет поправки измеренных углов ((delta _{beta })):
(delta _{beta} = – frac{f_{beta }}{n})
При правильном выполнении расчетов сумма поправок будет иметь отрицательное значение:
(sum delta _{beta }=-f_{beta })
Далее следует вычисление дирекционного угла (α), который начинают отчитывать от северного направления осевого меридиана по часовой стрелке.
(alpha _{n}=alpha _{n-1}+180^{o}-beta _{пр.исп})
(alpha _{n}=alpha _{n-1}-180^{o}+beta _{л.исп})
В данном выражении (alpha _{n-1})– дирекционный угол предыдущей точки, (alpha _{n})– последующей.
(beta _{пр.исп})– исправленное значение правого по ходу угла, (beta _{л.исп})– исправленное значение левого по ходу угла.
Начальный α должен равняться конечному. Если же полученный α больше 360°, то перед тем, как занести показатели в журнал из них вычитают 360°.
Теперь вычисляется румб (r), который отсчитывают от самого близкого окончания осевого меридиана до ориентированной линии. Рассчитывается в зависимости от своего местоположения относительно четверти координат (табл. 4).
Таблица 4. Формула румба для каждой четверти.
| Четверть и ее название | Пределы α | Формула | Знаки приращения координат | |
| ΔХ | ΔУ | |||
| 1 С.В. | 0° – 90° | r = α | + | + |
| 2 Ю.В. | 90°-180° | r = 180° – α | – | + |
| 3 Ю.З. | 180°-270° | r = α – 180° | – | – |
| 4 С.З. | 270°-360° | r = 360° – α | + | – |
Приращение геодезических координат определяют:
(X = d · cos(r))
(Y = d · sin(r))
где: d – горизонтальное проложение;
r – румб стороны.
Уравнивание проводят при помощи приведенных ниже формул:
(f_{Delta X}=sum Delta X_{B}-sum Delta X_{T})
(f_{Delta Y}=sum Delta Y_{B}-sum Delta Y_{T})
( sum Delta X_{B}) и (sum Delta Y_{B})– сумма приращений координат, которые были определены с учетом знаков;
(sum Delta X_{T}) и (sum Delta Y_{T}) – теоретическая сумма приращения значений координат.
Стоит отметить, что в замкнутом полигоне последние значение равняются нулю, поэтому невязки должны быть равны сумме приращений или приближенными к нему.
Проверка условия допустимости:
1. Абсолютного значения:
(f_{абс}=sqrt{fDelta X^{2}+fDelta Y^{2}})
2. Относительного:
(f_{отн}=frac{f_{абс}}{P})
где Р – периметр хода (сумма его горизонтальных проложений).
Условие допустимости:
(left | f_{отн} right |leq left | f_{абс} right |)
Невязки раскидывают с обратным знаком, предварительно выполнив поправки на приращение каждой стороны при помощи таких формул:
(delta X_{imath }=frac{f_{x}cdot d_{imath }}{P})
(delta Y_{imath }=frac{f_{Delta y}cdot d_{imath }}{P})
(imath) – номер точки;
Все координаты вершин рассчитываются таким образом:
(X_{n}=X_{n-1}+Delta X_{n-1(исп)})
(Y_{n}=Y_{n-1}+Delta Y_{n-1(исп)})
Составление плана
Полученные в процессе съемки и дальнейшей обработки данные используются для построения картографического материала, как с помощью специальных программ, так и вручную.

Выполняется в крупном масштабе и содержит подробную информацию о местности. Последовательность построения следующая:
- Создание координатной сетки. Берутся либо уже заранее подготовленные листы или чертятся с помощью линейки Дробышева. Также можно построить ее посредством проведения через плотный лист бумаги двух диагональных линий и последующего откладывания отрезков от их пересечения. Очень важно начертить сетку таким образом, чтобы схема хода и прилегающие территории находились в середине.
Правильность нанесения пунктов на план можно проверить по расстоянию между ними, которое не должно быть больше 0,2 мм. Кроме того, отображают ситуацию на нем при помощи методов, используемых во время полевых работ.
- Нанесение вершин и отображение ситуации. Точки пикетов отображаются на плане или карте, а потом переносят элементы окружающей местности, которые были предварительно зарисованы на абрисе. Отображаются они в виде символических графических обозначений, передающие информации об объекте, существующем в реальности – условных знаков.
- Зарамочное оформление. Обязательно указывают в каком масштабе выполнен план и какая местность и ситуация на нем изображена.
На сегодняшний день обработку и создание графических материалов выполняют при помощи специально созданного для этих целей программного обеспечения (ГЕОМИКС). Благодаря ему процессы камеральной обработки стали значительно проще и занимают гораздо меньше времени. Но только на на этом возможности геодезических программ не заканчиваются. Осуществив все необходимые вычисления и уравнивания, можно построить план в электронном виде и распечатать, а в случае необходимости провести коррективы.
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
-

- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
какую информацию можно извлечь из относительной ошибки? например линейная погрешность или что то в этом роде. пожалуйста привидите пример.
#1
-

Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.141
- Симпатии:
- 630
- Адрес:
-
Химки
1/2000 = 1 м на 2 км
То есть, линейная погрешность в 1 м на 2 км хода дает 1/2000.#2
-

- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
это я знаю, а еще что нибудь из нее нельзя извлечь?
#3
-

Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.141
- Симпатии:
- 630
- Адрес:
-
Химки
Попробуйте, может, получится;)
#4
-

Форумчанин
а вы что хотите извлечь то, вы расскажите причину столь странного интереса…
#5
-

- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
нам преподаватель говорит, что относительная ошибка дает много информации, но не рассказывает, мол мы сами все знаем. а я кроме линейной погрешности ничего незнаю

#6
-

Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
ну, скажем, на первый взгляд: в теодолитном ходе если угловая невязка в допуске а относительная ошибка слишком большая, то это логично говорит о том что у вас есть ошибка в длинах линий, если же вы проверили все длины линий и поняли что они все верны, а относительная ошибка хода по-прежнему вас не устраивает, то у вас ошибка как минимум в двух углах поворота, причем эти ошибки взаимно исключают друг друга.. (а преподаватели, к слову, пользуются относительной ошибкой часто для того что бы определить подгонялись ли углы в ходе или нет.. )
Случай с ошибкой в исходных данных тоже может быть выявлен таким образом..
#7
-

Форумчанин
Самую полезную для студента информацию несет не относительная ошибка, а абсолютные ошибки приращений координат. В случае, если в небольшом ходе Вы где-то пролетели с измерением длин линий лентой (на метр, двадцать метров, остаток до другого края ленты), ним легко узнать дир. угол линии, в которой сидит промах. Как — не скажу, сами догадайтесь.
 И тогда в поисках ошибки не придется перемерять весь полигон.
И тогда в поисках ошибки не придется перемерять весь полигон.#8
-

Форумчанин
Для теодолитного хода относительная ошибка вычисляется по формуле =√ΣΔX²+ ΣΔY²/P<1/2000, где ΣΔX, ΣΔY — суммы приращений координат, Р — периметр полигона, т.е. относительная ошибка позволяет определить еще и ошибку в вычислениях превышений.
Относительная ошибка как правило характеризует точность линейных измерений. Например, относительная ошибка нитяного дальномера составляет 1/300, ошибка измерения рулеткой 1/2000, значит линия в 50 м в первом случае будет определена с точностью ±17 см, а во втором ±2,5см#9
-

Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
не понял.. а это то откуда?
#10
-

Форумчанин
- Регистрация:
- 30 ноя 2007
- Сообщения:
- 2.709
- Симпатии:
- 2.444
- Адрес:
-
Сибирь
А если промахнулись в двух линиях?
#11
-

Форумчанин
Извините приращений координат
#12
-

- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
спасибо за участие в этом вопросе.
#13
-

Форумчанин
Тогда уже не узнать

Если трасса, и углы близки к 180 градусам, то тоже.
Но в теодолито-рулеточную эпоху этим методом пользовались частенько. Помогало.
#14
Поделиться этой страницей

|
Ведомость координат разомкнутого теодолитного хода |
Таблица 7.7 |
||||||
|
№ |
ГоризонДирекционГоризон- |
Приращения |
|||||
|
№ |
тальные |
ные углы |
тальные |
координат, м |
Координаты, м |
||
|
то- |
углы β |
α |
проложе- |
(поправки) |
|||
|
чек |
(поправки) |
ния, м |
Х |
Y |
X |
Y |
|
|
А |
d |
5635,22 |
6081,33 |
||||
|
115о36,3′ |
189,04 |
(+0,04) |
(+0,03) |
||||
|
1 |
|||||||
|
(-0,2′) |
-81,70 |
+170,48 |
5553,56 |
6251,84 |
|||
|
2 |
150о31,0′ |
86о07,1′ |
113,86 |
(+0,02) |
(+0,02) |
||
|
(-0,2′) |
+7,71 |
+113,60 |
5561,29 |
6365,46 |
|||
|
3 |
163о07,5′ |
69о14,4′ |
121,57 |
(+0,02) |
(+0,02) |
||
|
(-0,3′) |
+43,09 |
+113,68 |
5604,40 |
6479,16 |
|||
|
4 |
167о29,0′ |
56о43,1′ |
93,39 |
(+0,02) |
(+0,01) |
||
|
(-0,2′) |
+51,25 |
+78,07 |
5655,67 |
6557,24 |
|||
|
D |
241о21,5′ |
118о04,4′ |
163,61 |
(+0,03) |
(+0,02) |
||
|
å d |
-77,00 |
+144,36 |
5578,70 |
6701,62 |
|||
|
å β ИЗМ |
fX |
fY |
(5578,703) |
(6701,622) |
|||
|
681,47 м |
-0,13 м |
-0,10 м |
|||||
|
722о29,0′ |
fАБС= |
fОТН = |
|||||
|
å β ТЕОР |
0,17 м |
1 |
|||||
|
2о28,1′ |
fОТН ДОП |
4000 |
|||||
|
fβ |
+0,9′ |
1 |
|||||
|
2000 |
|||||||
|
fβ доп |
± 2,0′ |
Приращения координат (прямая геодезическая задача) вычисляют по формулам (7.3):
|
Х = d cos α ; |
Y = d sin α . |
|||||
|
Запишем схему передачи координат с начальной точки хода на |
||||||
|
конечную в виде системы уравнений и составим суммы этих уравнений: |
||||||
|
Х1 = Х Н + Х1 |
Y1 = YН + Y1 |
|||||
|
Х 2 = Х1 + Х 2 |
Y2 = Y1 + Y2 |
|||||
|
………. ………. …… |
………. |
………. …… |
(7.77) |
|||
|
Х К = Х n−1 + Х К |
YК = Yn−1 + YК |
|||||
|
− − − − − − − − − − − |
− − − − − − − − − − − |
|||||
|
Х К = Х Н + å |
Х |
YК |
= YН + å |
Y |
||
|
Поскольку значения ХН , ХК, YH , YK |
являются исходными (известными), то |
по результатам вычислений можно получить невязки в приращениях координат:
|
f X = å X − ( X K − X H ) ; fY = å Y − (YK − YH ). |
(7.78) |
Физический смысл невязок в приращениях координат пояснен на рис. 7.24. При построении теодолитного хода реальное его положение определяется точками А, 1, 2, …, В, жестко закрепленными на местности и имеющими абсолютно точные, но неизвестные нам координаты. В результате неизбеж-
207

ных погрешностей в измерениях (углов и расстояний) и возможных погрешностей при вычислениях получается реальный ход А—1′—2′— … — В’, т.е. ход, не замыкающийся в конечной исходной точке В. Величина незамыкания хода (невязка) по оси Х – fX , по оси Y – fY.
Эти невязки могут быть получены и как разности координат:
|
f X = X B′ − X B ; fY = YB′ − YB . |
(7.79) |
Общая линейная (абсолютная) невязка хода составляет
(7.80)
Очевидно, что сама абсолютная (линейная) невязка не всегда может являться непосредственным критерием качества измерений, поскольку длины ходов могут быть различными при одном и том же значении абсолютной невязки. В связи с этим для оценки точности теодолитных ходов пользуются относительной невязкой, определяемой по формуле
|
1 |
|||||
|
fОТН = |
|||||
|
çæ å d |
ö , |
(7.81) |
|||
|
ç |
|||||
|
è |
f АБС ø |
||||
|
где |
å d — |
длина |
теодо- |
||
|
литного хода (периметр – |
|||||
|
Рис. 7.24. Физический смысл невязок в |
для замкнутого хода; сум- |
||||
|
приращениях координат |
ма горизонтальных проло- |
||||
|
жений). |
|||||
|
Критерием качества работ является выполнение условия |
(7.82) |
||||
|
fОТН ≤ fОТН .. ДОП . |
|||||
|
Величина допустимой относительной невязки |
fОТН .. ДОП |
определяется |
со-ответствующими инструкциями, а также техническим заданием, устанавли-вающими необходимую точность построения съемочного обоснования. Так, для технических теодолитных ходов, в зависимости от условий измерений, особенно длин линий, величина относительной допустимой невязки (погреш-ности) может находиться в пределах от 1:1000 до 1:3000.
Пример 7.14. Оценка качества теодолитного хода. Исходные данные см. в табл. 7.7 (ведомость координат).
208

В ведомости координат выполнены вычисления приращений координат и получены их суммы по всему ходу: å Х = − 56 ,65 м; å Y = + 620 ,19 м. Теоретические разности
координат: ( Х К − Х Н ) = ( Х D − X A ) = − 56,516 м;(YK − YH ) = (YD − YA ) = + 620,295 м. Невя зки:
f X = − 56,65 − (− 56,516 ) = − 0,134 м; fY = + 620 ,19 − (+ 620 ,295 ) = − 0,105 м ;
fАБС = 0,1702 м ;
fОТН = 1 (681,47
(681,47 0,1702 ) = 1
0,1702 ) = 1 4000 . (Значение знаменателя относительной невязки можно
4000 . (Значение знаменателя относительной невязки можно
округлять до пятидесяти). Если заданная допустимая относительная невязка равна, например, 1:2000, то необходимое качество построения съемочного обоснования обеспечено.
75.4. Рекомендации к поиску вероятных погрешностей в измерениях и вычислениях при обработке ведомости координат
Конечная оценка точности теодолитного хода производится на основе всех (линейных и угловых) измерений, выполненных при создании съемочного обоснования. Кроме того, оценке точности теодолитного хода предшествует и большой объем вычислений, что, даже несмотря на ряд контрольных вычислений, повышает вероятность появления погрешностей, в результате чего условие (7.62) может не выполниться.
Чаще всего отступление от неравенства (7.62) сравнительно небольшое, что как раз и затрудняет поиск погрешностей. Грубые погрешности (просчеты) находятся сравнительно быстро и легко. В некоторых случаях, если небольшие погрешности допущены при измерениях в двух или нескольких линиях (в углах или расстояниях), то отыскание их только в камеральных условиях чаще всего не представляется возможным. Необходимы повторные измерения, которые обычно начинают с самых сложных участков.
Если же погрешности были допущены только в одной линии (в ее длине или ее направлении), то поиск их может быть сравнительно легко осуществлен по величинам и знакам невязок fХ и fY в приращениях координат. Для этого предварительно определяют дирекционный угол линейной невязки fАБС, по той же схеме, как это производится при решении обратной геодезической задачи при определении дирекционных углов исходных направлений
|
rf |
æ |
f |
ö |
f . |
(7.83) |
|
|
= arctgç |
Y |
Þ α |
||||
|
è |
fX ø |
Затем следует образовать группы дирекционных углов: А) — совпадающих с направлением невязки (αf ± 180o);
Б) — перпендикулярных к направлению невязки [( af + 90o) ± 180o]. Если погрешность допущена в длине линии, то наиболее вероятно, что
она присутствует в тех линиях, для которых их направление (дирекционный угол) совпадает с направлением невязки (сравнение производится по группе А). Так, например, наиболее вероятна погрешность в длине линии С-5 для разомкнутого теодолитного хода (рис. 7.24 а), либо для линий 4-1 и 2-3 для замкнутого теодолитного хода (рис. 7.24 б).
209

Если погрешность допущена в направлении линии, то наибольшая вероятность этого для тех линий, дирекционные углы которых отличаются от направления невязки на 90о. (Сравнение производится по группе В). Таким образом, для разомкнутого теодолитного хода, изображенного на рис. 7.24 а, наиболее вероятна погрешность в направлении линии 6-В. Для замкнутого теодолитного хода более вероятна погрешность в направлении линий 1-2 и 3-4 .
В том случае, если указанный алгоритм поиска погрешностей не даст результатов, то следует ожидать, что погрешности присутствуют в двух или более линиях. Это требует повторения полевых измерений, перед которыми необходимо еще раз внимательно выверить полевые журналы предшествующих работ, а также повторно проверить все вычисления. Повторные полевые измерения целесообразно начинать с проверки длин линий и их горизонтальных проложений (при этом в первую очередь проверяют наиболее сложные для измерений участки). Проверку горизонтальных углов также начинают с вершин, наблюдения с которых по каким-либо причинам выполнялись с большими помехами: видимость соседних пунктов была недостаточной, производилась перестановка вех и т.п. Особое внимание здесь следует уделять центрированию теодолита и устнановке вехи в наблюдаемых точках.
Пример 7.15. Поиск вероятных погрешностей в теодолитных ходах. Исходные данные см. в табл. 7.7 (ведомость координат).
Рассмотрим результаты обработки данных, приведенные в табл. 7.7. (На самом деле невязки в ходах допустимы, в связи с чем нет необходимости в поиске погрешностей).
Данный пример приводится исключительно в учебных целях только для пояснения схемы поиска погрешностей измерений в теодолитных ходах.
|
rf = arctg |
(— 0,105 |
— 0,134 ) |
» 38 0 Þ |
(III ..четверть ) Þ α f |
» 218 0. |
||
|
Для погрешностей в длине линий |
Для погрешностей в направлениях линий |
||||||
|
αf = 38o и |
αf = 218o |
αf = 128o |
и αf = 308o |
В соответствии со значениями дирекционных углов линий теодолитного хода наибо-
лее близким является α4D ≈ 118о и α34 ≈ 57о. Таким образом, можно предположить, что существует погрешность в определении направления линии 4-D (эта погрешность может быть и грубой. Неправильно, например, выписано значение дирекционного угла в ведомость координат, а также возможна погрешность в измерении длины линии 3-4.
При определенном навыке оценки величин дирекционных углов выполняются устно, без вычислений, по значениям невязок и их знакам.
75.5. Уравнивание приращений координат и вычисление координат точек хода
В приращения координат, при обеспечении условия (7.82), вводят весовые поправки ν Хi и ν Yi , зависящие от величины горизонтального проложения, по которому было вычислено данное приращение. Знаки поправок должны быть обратными знаку невязки:
210
Теодолитный ход является наиболее востребованной частью геодезических работ, переплетаясь со многими видами инженерной деятельности. В чем же его назначение и какие особенности выполнения разберем по порядку в нашей статье.
Содержание
- 1 Назначение и основные разновидности
- 2 Порядок проведения
- 3 Основные технические требования к линейным измерениям
- 4 Съемка ситуации и ее виды
- 5 Обработка полученных результатов измерений
- 5.1 Создавайте будущее вместе с нами
- 6 Составление плана
Назначение и основные разновидности
Проводится с целью точного отображения местности и расположенных на ней объектов на крупномасштабной карте, плане или специальных схемах.
Данная процедура подразумевает создание системы точек, закрепленных в натуре, и определение их горизонтальных углов при помощи теодолита или тахеометра. Расстояние между пунктами определяется при помощи светодальномеров, рулеток и других приборов, позволяющих обеспечить необходимую точность. По форме обычно принято различать следующие виды ходов:
– разомкнутый;
– замкнутый;
– висячий.
В разомкнутом первая и последняя точка базируется на разные пункты и направления геодезической сети, чьи координаты и дирекционные углы уже определены, а замкнутый образует геометрическую фигуру, поэтому может опираться только на один. Особенность же висячего хода состоит в том, что один его конец примыкает к пункту геодезического обоснования, а второй остается свободным.
Его форма во многом зависит от того, на какой территории проводятся измерения. Например, для автодорог и трубопроводов хорошо подойдет разомкнутый ход, а на строительных площадках и земельных участках обязательно должен быть построен замкнутый полигон.
Достаточно распространённой процедурой является прокладывание внутри больших полигонов дополнительных сетей, чтобы полностью отобразить ситуацию на плане.
Порядок проведения
Выполнение теодолитного хода начинают с рекогносцировки, подразумевающей изучение ее особенностей и определение наиболее подходящих мест для установки точек.
Расстояние между ними должно варьироваться в пределах от 20 до 350 метров, но оно зависит также и от масштаба съемки. Наилучшей точности можно добиться, если расстояние будет одинаковым, но особенности территории далеко не всегда позволяют это сделать.
Съемку осуществляют на открытом пространстве с хорошей взаимной видимостью между пунктами, закрепленными специальными кольями из дерева, металла и других материалов. Для их долговременной сохранности нередко используются бетонные монолитные столпы. Также рекомендуется привязать каждый знак к твердым объектам поблизости, чтобы можно было восстановить его в случае потери.

Когда все подготовительные процедуры завершены и определено местоположение пунктов начинаются полевые работы. Прибор устанавливают на точке и измеряют угол за один прием, визируясь на соседние, после чего определяют расстояния между ними.
Если строится замкнутый полигон, за начальный берут магнитный азимут одной из сторон. Привязка к пункту геодезической сети необходима для определения дирекционного угла и координат, что позволит обеспечить должный контроль полученных результатов.
Все данные записываются в специальный журнал или автоматически заносятся в память электронного измерительного устройства. В дальнейшем они используются для камеральной обработки, которая подразумевает проведение расчетов с целью вычисления координат пунктов и жестких контуров.
Параллельно со съемкой составляется схематический чертеж, отображающий местоположение объектов на местности, который называется абрисом. Он представляет собой полноценный документ, является неотъемлемой частью технической документации и служит источником информации при построении плана или карты.
Во время составления абриса необходимо отобразить на нем как можно больше информации. Особенно важно обозначить все метрические данные и сделать его понятным для прочтения.
Во время снегопада, дождей и других неблагоприятных погодных условий, а также при плохой освещенности, проводить измерения запрещается.
Основные технические требования к линейным измерениям
Любые геодезические работы должны быть выполнены с четким соблюдением всех правил, дабы обеспечить получение самых точных результатов измерений. Основные требования к данной процедуре изложены в инструкции по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500, а также ряда других нормативных документов.
В зависимости от предельной относительной погрешности длина теодолитного хода должна соотносится со следующими показателями, приведенными в табл.1.
Таблица 1.
| Буровая установка | № скважины | Литологический тип | Коэф. крепости | Размер отдельности, м | Скорость фактическая, м/c |
|---|---|---|---|---|---|
| DM LP | 6,0 | 4,0 | 2,0 | 6,0 | 3,0 |
| СБШ | 3,0 | 2,0 | 1,0 | 3,6 | 1,5 |
| 1:1000 | 1,8 | 1,2 | 0,6 | 1,5 | 1,5 |
| 1:500 | 0,9 | 0,6 | 0,3 | — | — |
(m_{s}) – среднеквадратическая ошибка измеренных расстояний.
Показатели предельно допустимых длин между узловой точкой и исходной уменьшается на 30%, а также должны быть:
– больше 20 м, но меньше 350 м на застроенных участках;
– свыше 40 м и не более 350 м.
Аналогичные требования (табл. 2) есть и к висячим теодолитным ходам:
Таблица 2.
| Масштаб | Местность | |
| Застроенная | Не застроенная | |
| 1:5000 | 350 | 500 |
| 1:2000 | 200 | 300 |
| 1:1000 | 150 | 200 |
| 1:500 | 100 | 150 |
Измерение длин необходимо проводить в обе стороны и высчитать их среднее значение, а точность приборов должна быть не менее 30”. Допустимое отклонение при центрировании – не более 3 мм.
Съемка ситуации и ее виды
Прокладывание теодолитного хода, как правило, проводят для последующего отображения особенностей территории работ. Конечная цель – получения данных о местоположении снимаемых объектов в пространстве и составление контурной карты или плана местности без отображения рельефа. Фиксируются наиболее значимые элементы окружения:
– деревья и крупная растительность;
– инженерные конструкции;
– государственные геодезические пункты;
– контуры зданий, сооружений и других жестких объектов.

Процесс их измерения называется съемкой ситуации, которая выполняется следующими способами:
- Способ перпендикуляров. Применяют для съемки объектов вытянутой формы, которые расположены преимущественно на открытом пространстве и близко к пунктам. Основной принцип выполнения этого способа строится на определении основания перпендикуляра, а также измерении его длины до станции.
- Полярных координат. Проводится, если снимаемая цель находится на большом расстоянии от пункта. Одна сторона принимается за полярную ось, а ее вершина – за полюс. Измеряются горизонтальные углы направления на заданную точку и определяют линейное расстояния до нее.
- Угловая засечка. Хорошо подходит для съемки труднодоступных точек. Их местоположение определяют совмещением сторон углов, измеренных от вершины теодолитного хода до заданного пункта с двух направлений.
- Метод створа (линейных промеров) используется, когда контуры местности пересекают уже построенный ход или его продолжение, а также для определения дополнительных точек посредством линейных измерений. Данный способ активно применяется на сильно застроенных участках.
- Способ обхода используют, как правило, на закрытой местности, если необходимо снять особо важный объект, но от вершин сторон это сделать невозможно по причине наличия препятствий или дальности. Прокладывают дополнительные пикеты, которые и привязывают к основным пунктам, а границы контура снимают методом перпендикуляра.
Геодезические работы основаны на принципе «от общего к частному». Поэтому, в теории, лучше всего сперва построить теодолитный ход, а потом уже провести съемку подробностей.
Обработка полученных результатов измерений
Выполнение контурной съемки проводится с целью получения данных, необходимых для дальнейшего расчета координат:
– горизонтальных углов;
– длин сторон теодолитного хода;
– дирекционных углов;
– румбов.
Подсчет теоретической суммы угловых измерений () хода осуществляют по формуле (табл. 3).
Таблица 3.
| замкнутый | разомкнутый |
| (beta _{T}= 180left ( n-2 right )) | (beta _{T}=left ( alpha _{р}+alpha _{к} right )pm 180^{o}cdot left ( n+1 right )) |
n – количество точек;
(alpha _{н})– значение начального дирекционного угла, –конечного;
Далее производят расчет угловой невязки:
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
(f_{beta }=sum beta _{изм}- sum beta _{т})
(beta _{изм})– сумма измеренных углов.
Следующим шагом будет сравнение (f_{beta })с допуском (f_{beta доп}). Если результат не соответствует приведенному ниже выражению, необходимо перепроверь данные:
(f_{beta}< f_{beta доп})
(f_{beta доп}={1,5·t}sqrt{n}), где t – приборная точность измерения углов; n – количество измеряемых углов.
В дальнейшем (f_{beta}) равномерно распределяется между измеренными величинами с противоположным знаком и проводится расчет поправки измеренных углов ((delta _{beta })):
(delta _{beta} = – frac{f_{beta }}{n})
При правильном выполнении расчетов сумма поправок будет иметь отрицательное значение:
(sum delta _{beta }=-f_{beta })
Далее следует вычисление дирекционного угла (α), который начинают отчитывать от северного направления осевого меридиана по часовой стрелке.
(alpha _{n}=alpha _{n-1}+180^{o}-beta _{пр.исп})
(alpha _{n}=alpha _{n-1}-180^{o}+beta _{л.исп})
В данном выражении (alpha _{n-1})– дирекционный угол предыдущей точки, (alpha _{n})– последующей.
(beta _{пр.исп})– исправленное значение правого по ходу угла, (beta _{л.исп})– исправленное значение левого по ходу угла.
Начальный α должен равняться конечному. Если же полученный α больше 360°, то перед тем, как занести показатели в журнал из них вычитают 360°.
Теперь вычисляется румб (r), который отсчитывают от самого близкого окончания осевого меридиана до ориентированной линии. Рассчитывается в зависимости от своего местоположения относительно четверти координат (табл. 4).
Таблица 4. Формула румба для каждой четверти.
| Четверть и ее название | Пределы α | Формула | Знаки приращения координат | |
| ΔХ | ΔУ | |||
| 1 С.В. | 0° – 90° | r = α | + | + |
| 2 Ю.В. | 90°-180° | r = 180° – α | – | + |
| 3 Ю.З. | 180°-270° | r = α – 180° | – | – |
| 4 С.З. | 270°-360° | r = 360° – α | + | – |
Приращение геодезических координат определяют:
(X = d · cos(r))
(Y = d · sin(r))
где: d – горизонтальное проложение;
r – румб стороны.
Уравнивание проводят при помощи приведенных ниже формул:
(f_{Delta X}=sum Delta X_{B}-sum Delta X_{T})
(f_{Delta Y}=sum Delta Y_{B}-sum Delta Y_{T})
( sum Delta X_{B}) и (sum Delta Y_{B})– сумма приращений координат, которые были определены с учетом знаков;
(sum Delta X_{T}) и (sum Delta Y_{T}) – теоретическая сумма приращения значений координат.
Стоит отметить, что в замкнутом полигоне последние значение равняются нулю, поэтому невязки должны быть равны сумме приращений или приближенными к нему.
Проверка условия допустимости:
1. Абсолютного значения:
(f_{абс}=sqrt{fDelta X^{2}+fDelta Y^{2}})
2. Относительного:
(f_{отн}=frac{f_{абс}}{P})
где Р – периметр хода (сумма его горизонтальных проложений).
Условие допустимости:
(left | f_{отн} right |leq left | f_{абс} right |)
Невязки раскидывают с обратным знаком, предварительно выполнив поправки на приращение каждой стороны при помощи таких формул:
(delta X_{imath }=frac{f_{x}cdot d_{imath }}{P})
(delta Y_{imath }=frac{f_{Delta y}cdot d_{imath }}{P})
(imath) – номер точки;
Все координаты вершин рассчитываются таким образом:
(X_{n}=X_{n-1}+Delta X_{n-1(исп)})
(Y_{n}=Y_{n-1}+Delta Y_{n-1(исп)})
Составление плана
Полученные в процессе съемки и дальнейшей обработки данные используются для построения картографического материала, как с помощью специальных программ, так и вручную.

Выполняется в крупном масштабе и содержит подробную информацию о местности. Последовательность построения следующая:
- Создание координатной сетки. Берутся либо уже заранее подготовленные листы или чертятся с помощью линейки Дробышева. Также можно построить ее посредством проведения через плотный лист бумаги двух диагональных линий и последующего откладывания отрезков от их пересечения. Очень важно начертить сетку таким образом, чтобы схема хода и прилегающие территории находились в середине.
Правильность нанесения пунктов на план можно проверить по расстоянию между ними, которое не должно быть больше 0,2 мм. Кроме того, отображают ситуацию на нем при помощи методов, используемых во время полевых работ.
- Нанесение вершин и отображение ситуации. Точки пикетов отображаются на плане или карте, а потом переносят элементы окружающей местности, которые были предварительно зарисованы на абрисе. Отображаются они в виде символических графических обозначений, передающие информации об объекте, существующем в реальности – условных знаков.
- Зарамочное оформление. Обязательно указывают в каком масштабе выполнен план и какая местность и ситуация на нем изображена.
На сегодняшний день обработку и создание графических материалов выполняют при помощи специально созданного для этих целей программного обеспечения (ГЕОМИКС). Благодаря ему процессы камеральной обработки стали значительно проще и занимают гораздо меньше времени. Но только на на этом возможности геодезических программ не заканчиваются. Осуществив все необходимые вычисления и уравнивания, можно построить план в электронном виде и распечатать, а в случае необходимости провести коррективы.
