Повторный и бесповторный отбор.
Ошибка выборки
Краткая теория
На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.
При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.
Выборка может осуществляться по схеме повторного и бесповторного
отбора.
В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.
Выборка может осуществляться отдельными единицами или сериями
(гнездами).
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.
На основании приемов классической выборки решаются следующие
задачи:
а) определяются границы среднего значения показателя по генеральной
совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
;
при
;
при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной
совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным
значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:
где
– доля признака по генеральной совокупности.
Типическая (районированная) выборка
Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.
Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:
где
– средняя из внутригрупповых дисперсий
по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:
где
– численности единиц совокупности групп по выборке.
Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю
из частных выборочных средних
.
Для случая пропорционального отбора это определяется по формуле:
При непропорциональном отборе средняя из внутригрупповых дисперсий вычисляется по
формуле:
где
– численность единиц групп по генеральной
совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:
Средняя дисперсия доли
признака из групповых дисперсий доли
при
типической пропорциональной выборке вычисляется по формуле:
Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:
Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:
а средняя доля признака:
Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель
.
Серийная выборка
Серийная ошибка выборки
может применяться в двух вариантах:
а) объем серий различный
б) все серии имеют
одинаковое число единиц (равновеликие серии).
Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии
и
производится отбор не единиц совокупности, а серий
. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки
при
серийном отборе исчисляются по формулам:
а) при повторном отборе
б) при бесповторном отборе
где
– число
серий в генеральной совокупности;
– число
отобранных серий;
– межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:
где
–
среднее значение признака в каждой из отобранных серий;
– межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:
Определение численности выборочной совокупности
При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.
Примеры решения задач
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Задача 2
В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.
Решение
Численность
выборки можно найти по формуле:
В нашем случае:
Вывод к задаче
Таким образом численность
выборки должна составить 2661 чел.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала |
Средняя месячная заработная плата, руб. |
Среднее квадратическое отклонение, руб. |
Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.
Чтобы
получить суждение о точности результатов
выборочного наблюдения, математическая
статистика дает аппарат характеристики
состава генеральной совокупности и
формулу
средней ошибки,
т.е. средней величины из всех возможных
ошибок при бесчисленном множестве
случайных выборок.
Средняя
ошибка выборки для средней величины
признака
определяется по формуле:
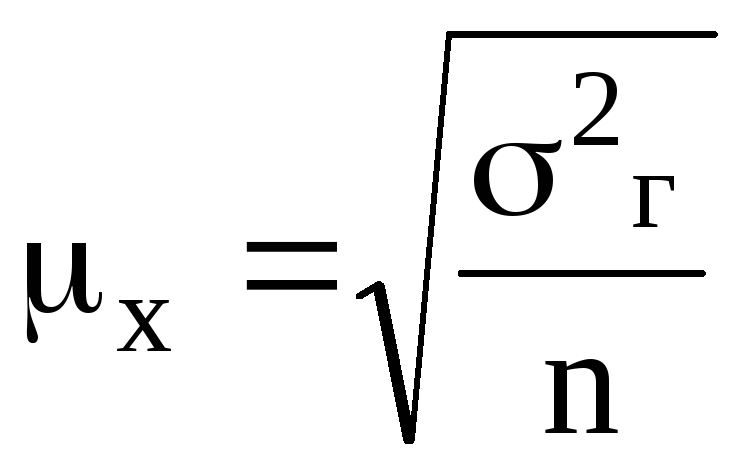 ,
,
где
2г
– дисперсия количественного признака
в генеральной совокупности.
Если
при выборочном наблюдении изучению
подлежит альтернативный признак (доля
признака), то средняя
ошибка выборки для доли единиц,
обладающих данным признаком, определяется
по теореме Я. Бернулли:
![]() ,
,
где
p – доля единиц, обладающих данным
качеством, в генеральной совокупности;
p(1-p) – дисперсия альтернативного признака
в генеральной совокупности.
Средняя
ошибка выборки
по значениям выборочной дисперсии 2
для средней и w(1–w) для доли признака
при повторном
способе
выборки определяется по формуле:
![]() ,
,
![]() ,
,
где w – доля признака в выборочной
совокупности.
На
практике повторная выборка, при которой
численность генеральной совокупности
остается неизменной и для каждой единицы
вероятность попасть в выборку одинакова,
встречается редко (например, при изучении
населения в качестве пользователей,
пациентов, избирателей).
При
бесповторной
выборке
численность генеральной совокупности
в процессе отбора сокращается на 1–n/N,
где n/N – доля отобранных единиц. В связи
с этим формулы средней
ошибки выборки
приобретают следующий вид:
![]() ;
;
![]() .
.
Так
как доля единиц генеральной совокупности,
не попавших в выборку (1–n/N), всегда
меньше единицы, то ошибка
выборки при бесповторном отборе при
прочих равных условиях меньше, чем при
повторном отборе.
Как
и сама выборочная характеристика, ошибка
выборки является случайной величиной,
она может быть в каждом конкретном
случае меньше, равна или больше .
Академик А.М. Ляпунов доказал, что
вероятность
появления случайной ошибки выборки
при достаточно большом ее объеме
подчиняется закону нормального
распределения:
![]() ,
,
где
∆ — предельная
ошибка
выборки, t – коэффициент доверия,
зависящий от вероятности (Р), с которой
предельная ошибка определяется,
— средняя ошибка выборки.
Значения функции
Ф(t) табулированы при разных значениях,
например:
при
t=1 P()
= Ф(1) = 0,683;
при
t=2 P(2)
= Ф(2) = 0,9545;
при
t=3 P(3)
= Ф(3) = 0,9973 и т.д.
В
общем виде
= t*
характеризует предельную
ошибку
выборки, показывающую максимально
возможное расхождение выборочной и
генеральной характеристик при заданной
вероятности этого утверждения. Так, при
t=2 возможная ошибка
не превысит 2,
что гарантируется с вероятностью 0,9545.
Это значит, что в 9545 выборках из 10000
подобных максимальная ошибка не выйдет
за пределы 2.
При
проведении выборочного учета массовых
социально-экономических явлений
считается
достаточным максимальный размах 3.
Возможная
ошибка выборки указывается с определенной
вероятностью Р, с которой гарантируются
границы рассчитанной случайной ошибки
репрезентативности. На практике наиболее
часто пользуются значениями вероятности
Р=0,95 (t=1,96), Р=0,99 (t=2,58) и Р=0,999 (t=3,28),
гарантирующими репрезентативность
выборки соответственно с ошибкой 5; 1;
0,1%.
Возможная
ошибка выборки позволяет определять
предельные значения характеристик
генеральной совокупности при заданной
вероятности, т.е. их доверительные
интервалы. Поэтому вероятность
Р называется доверительной,
она представляет собой вероятность
того, что ошибка выборки не превысит
некоторую заданную величину .
Доверительные интервалы для:
генеральной
средней —
![]() (от
(от![]() до
до![]() ),
),
генеральной
доли –
![]() (от w–
(от w–
до w+).
Наряду
с абсолютной величиной предельной
ошибки выборки рассчитывается и
относительная
ошибка
выборки, которая определяется отношением
предельной ошибки средней или доли к
соответствующей характеристике
выборочной совокупности:
![]() %;
%;
![]() %.
%.
При
проведении выборочного наблюдения в
экономических исследованиях преимущественно
стремятся к тому, чтобы относительная
ошибка репрезентативности выборки не
превышала 5 … 10%.
5.3
Определение необходимого объёма выборки
для обеспечения репрезентативности
выборочных наблюдений при повторном и
бесповторном способе отбора. Виды
отбора (случайный, механический,
типический, стратифицированный,
комбинированный).
Необходимый
объем выборки (![]() )определяется
)определяется
из формул предельных ошибок выборки ,
соответствующих различным способам
отбора.
Так,
для случайного
повторного отбора
имеем:
x
=
![]() , откуда
, откуда![]() .
.
Уменьшение
(увеличение) предельной ошибки в несколько
раз ведет к увеличению (уменьшению)
выборочной совокупности в квадрат раз.
Для уменьшения предельной ошибки,
например, в 2 раза численность выборки
должна быть увеличена в 4 раза. Из трех
параметров два (t и )
задаются исследователем.
При
бесповторном
отборе
необходимая численность выборки
рассчитывается по формуле:
![]() .
.
При прочих равных
условиях при бесповторном отборе
требуется меньший объем выборочной
совокупности, чем при повторном.
При
изучении альтернативного признака
(доли р) необходимый объем выборки
определяется по формулам при отборе:
повторном:
![]() ,
,
бесповторном:![]() .
.
Репрезентативность
выборки зависит не только от количества
отобранных единиц совокупности и степени
их колеблемости по изучаемым признакам,
но и от способа отбора.
В
зависимости от способа выборки единиц
из генеральной совокупности различают
следующие виды
отбора (выборки):
собственно
случайный; механический;
типический
(районированный, стратифицированный);
серийный
(гнездовой); комбинированный, многофазный
и др.
При
собственно
случайном
отборе
единицы отбираются из генеральной
совокупности в строгом соответствии с
научными принципами и правилами
случайного отбора.
Формировать
выборку в строгом соответствии с
правилами случайного отбора практически
очень сложно. Используются таблицы
случайных чисел, нумеруются все единицы
генеральной совокупности, при жеребьевке
на каждую единицу заготавливаются
соответствующие карточки или фишки.
При большой генеральной совокупности
проводить такую предварительную работу
практически невозможно и нецелесообразно.
Для
удобства проведения выборочного
наблюдения на практике применяют другие
формы отбора, организуемые таким образом,
чтобы была обеспечена случайность
выборки.
При
механическом
отборе
генеральная совокупность делится на n
равных частей
в соответствии с естественным расположением
ее границ (географическим, пространственным,
алфавитным и др.) и из каждой части
обследуется одна единица. Например,
если нужно отобрать 10% рабочих, то
обследуют каждого десятого рабочего
по списку, упорядоченного по алфавиту.
Ошибки репрезентативности при механическом
отборе возникают не в результате
случайности отбора, а в результате
случайности размещения единиц изучаемой
совокупности.
Если
единицы в генеральной совокупности
размещены случайно в отношении изучаемого
признака (в алфавитном порядке, в порядке
времени поступления писем, телеграмм,
телефонных соединений), то ошибка
механической выборки становится
случайной и ее можно определять по
формуле ошибки случайной выборки.
Механический отбор удобно проводить,
когда уже имеются списки единиц
совокупности и когда имеют дело с
генеральной совокупностью, численность
которой известна лишь приблизительно
и единицы которой появляются постепенно,
например, при контроле качества услуг
и средств связи.
Типический
(районированный, стратифицированный)
отбор
осуществляется на основе предварительного
разделения единиц генеральной совокупности
на типические группы (районы, страты)
по изучаемым признакам. В качестве
групп, страт в зависимости от характера
изучаемого признака могут использоваться
округа, регионы, отрасли, предприятия.
Отбор из каждой группы может осуществляться
в случайном (повторном или бесповторном)
или механическом порядке.
Объем
выборки в каждой типической группе
обычно устанавливается пропорционально
ее удельному весу в генеральной
совокупности или дифференцированному
признаку. Это повышает точность
выборочного наблюдения, поскольку более
точно, чем при собственно случайной
выборке, отражается структура генеральной
совокупности.
При
типической выборке устраняется влияние
межгрупповой вариации изучаемого
признака на точность ее результатов,
так как имеется представительство в
выборочной совокупности каждой из
типических групп. Средняя ошибка выборки
здесь зависит не от общей дисперсии 2,
а от средней из групповых дисперсий
![]() .
.
Так как средняя из групповых дисперсий
всегда меньше общей дисперсии, при
прочих равных условияхошибка
типической выборки меньше ошибки
собственно случайного отбора.
При
определении ошибки типической выборки
в случае пропорционального
отбора для
расчета предельной
ошибки
выборки применяется формула случайной
выборки, в которой применяется средняя
из групповых дисперсий
![]() .
.
∆ = t*µ или для
выборки:
повторной
—
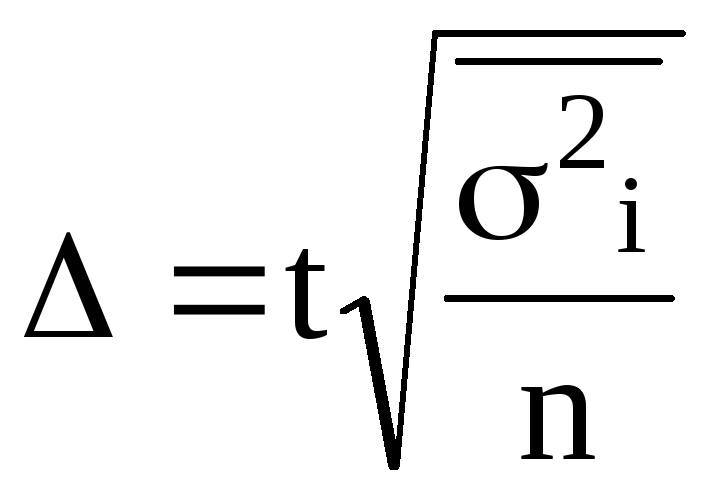
; бесповторной —
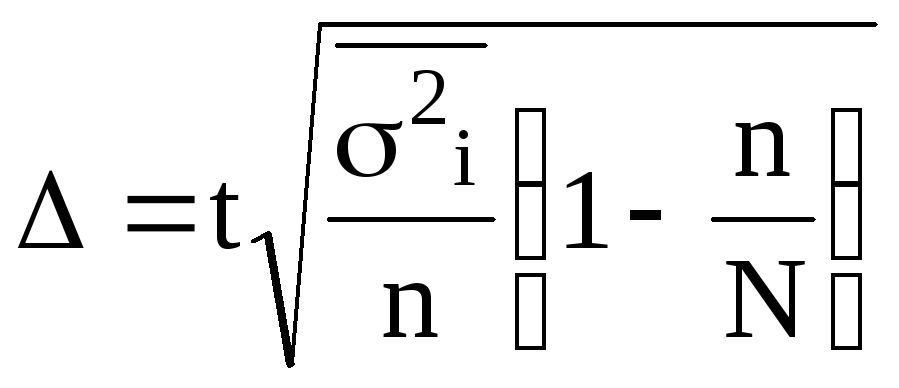 .
.
Отбор
единиц в типическую выборку производится
пропорционально объему типических
групп:
![]() ,
,
где
![]() =2ini/ni;
=2ini/ni;
ni
– численность единиц выборочной
совокупности i-й группы; 2i
– выборочная дисперсия i-й группы; N
– объем всей совокупности;
![]() —
—
объем типических групп.
При
определении ошибки типической выборки
в случае отбора
по
дифференциальному признаку
для расчета предельной
ошибки
выборки применяется формула случайной
выборки, в которой применяется
внутригрупповые дисперсии 2i.
∆ = t*µ или для
выборки:
повторной
—
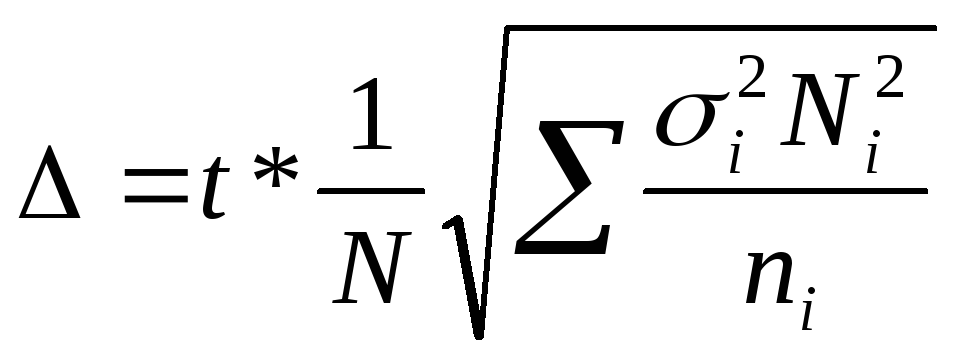
; бесповторной —
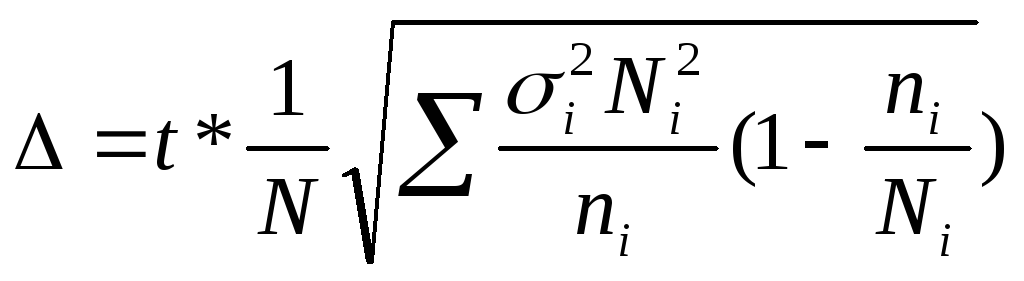 .
.
Отбор
единиц в типическую выборку производится
пропорционально дифференциальному
признаку — среднему квадратическому
отклонению
![]() :
:
![]() .
.
Выделение
типических групп в генеральной
совокупности значительно повышает
репрезентативность выборки.
Примером
типической выборки является уровень
потребления услуг связи с разделением
потребителей на население и организации
с разбивкой последних на две группы –
бюджетные и хозрасчетные.
При
серийном
(гнездовом) отборе
в случайном порядке отбираются не
единицы, а группы единиц (серии, гнезда).
Серии, или группы, единиц отбираются по
принципу случайного отбора или
механическим способом, внутри отобранных
серий (гнезд) обследованию подвергаются
все единицы. Если общее число серий в
генеральной совокупности обозначить
через R, а число отобранных серий – r, то
средняя ошибка выборки может быть
определена по формулам:
x
=
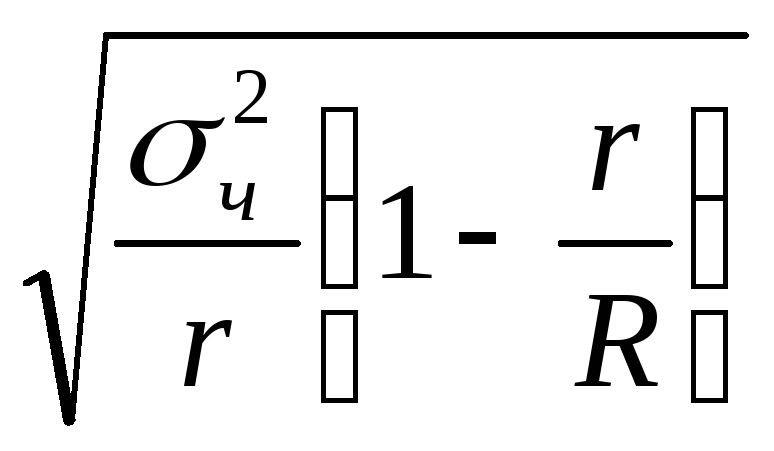
для бесповторной выборки, x
=
![]() ,
,
повторной выборки,
где
![]() –
–
межсерийная (межгрупповая) дисперсия.
Объём
серийной выборки определяется по
формуле:
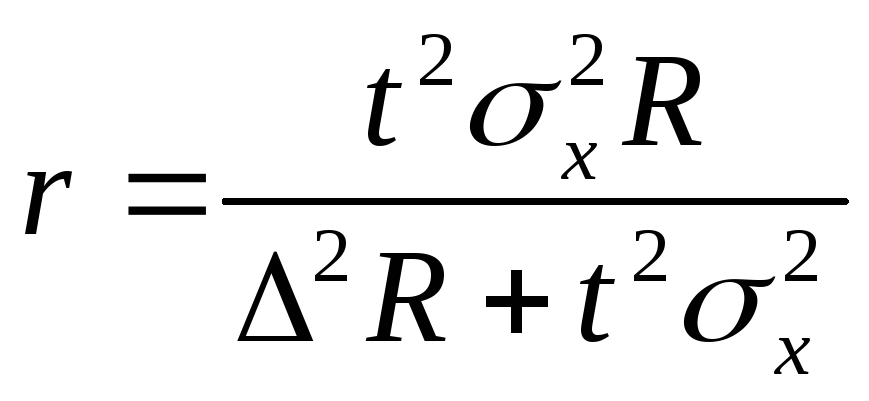
Чем
меньше серийные средние отличаются
одна от другой, т.е. чем ближе друг к
другу серии по уровню изучаемого
признака, тем точнее серийная выборка.
При
значительной вариации серийных средних
увеличивается ошибка репрезентативности
выборки.
Серийная
выборка применяется в организациях
связи для определения скорости пересылки
письменной корреспонденции и телеграмм,
доли неисправных таксофонов, массы
писем, объема передаваемой информации
электронных сообщений и т.д. В качестве
серии здесь выступает совокупность
писем, телеграмм, разговоров за сутки,
количество суток (дней) обследования
равно количеству серий, попавших в
выборочную совокупность.
На
практике в зависимости от цели и задач
выборочного обследования часто выборки
производят на основе сочетания двух и
более способов, образующих ступени
отбора:
механический и серийный, типический и
механический, серийный и собственно
случайный. Такие выборки
получили название комбинированных
(ступенчатых).
При комбинированном отборе общая ошибка
выборки состоит из ошибок на каждой ее
ступени. Например, единовременно скорость
прохождения письменной корреспонденции
учитывается с помощью трех способов,
образующих три ступени отбора: на основе
случайного отбора определяются регионы
страны, механического отбора – города
и сельские населенные пункты регионов,
серийного отбора – группы писем,
представляющие определенные направления
пересылки и подлежащие сплошному учету.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ( ).
).
В теории выборочного наблюдения выведены формулы для определения  , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то  определяется как:
определяется как:
 — при оценивании среднего значения признака;
— при оценивании среднего значения признака;
 — если признак альтернативный, и оценивается доля.
— если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):
 — для среднего значения признака;
— для среднего значения признака;
 — для доли.
— для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки ( ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
 .
.
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака

- Определяем среднюю ошибку повторной случайной выборки

- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна

- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
 ;
;
- средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

- установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь  — средняя из групповых дисперсий типических групп.
— средняя из групповых дисперсий типических групп.
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:

аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:

- Средняя из внутригрупповых дисперсий

- Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

- Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно

- Значение среднего квадратического отклонения составляет

- Средняя ошибка выборки:

- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:

- Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Средние ошибки повторной и бесповторной выборки
Средняя ошибка выборки
Средняя ошибка выборки представляет из себя такое расхождение между средними выборочной и генеральной совокупностями, которое не превышает ±б (дельта).
На основании теоремы Чебышева П. Л. величина средней ошибки при случайном повторном отборе в контрольных работах по статистике рассчитывается по формуле (для среднего количественного признака):
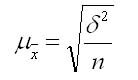
где числитель — дисперсия признака х в выборочной совокупности;
n — численность выборочной совокупности.
Для альтернативного признака формула средней ошибки выборки для доли по теореме Я. Бернулли рассчитывается по формуле:
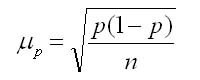
где р(1- р) — дисперсия доли признака в генеральной совокупности;
n — объем выборки.
Вследствие, того что дисперсия признака в генеральной совокупности точно не известна, на практике используют значение дисперсии, которое рассчитано для выборочной совокупности на основании закона больших чисел. Согласно данному закону выборочная совокупность при большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Поэтому расчетные формулы средней ошибки при случайном повторном отборе будут выглядеть таким образом:
1. Для среднего количественного признака:
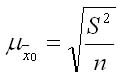
где S^2 — дисперсия признака х в выборочной совокупности;
n — объем выборки.
2. Для доли (альтернативного признака):
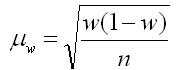
где w (1 — w) — дисперсия доли изучаемого признака в выборочной совокупности.
В теории вероятностей было показано, что генеральная дисперсия выражается через выборочную согласно формуле:
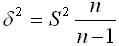
В случаях малой выборки, когда её объем меньше 30, необходимо учитывать коэффициент n/(n-1). Тогда среднюю ошибку малой выборки рассчитывают по формуле:
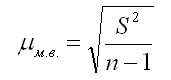
Так как в процессе бесповторной выборки сокращается численность единиц генеральной совокупности, то в представленных выше формулах расчета средних ошибок выборки нужно подкоренное выражение умножить на 1- (n/N).
Расчетные формулы для такого вида выборки будут выглядеть так:
1. Для средней количественного признака:
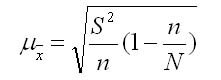
где N — объем генеральной совокупности; n — объем выборки.
2. Для доли (альтернативного признака):
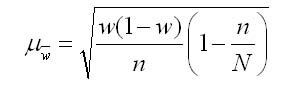
где 1- (n/N) — доля единиц генеральной совокупности, не попавших в выборку.
Поскольку n всегда меньше N, то дополнительный множитель 1 — (n/N) всегда будет меньше единицы. Это означает, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. Когда доля единиц генеральной совокупности, которые не попали в выборку, существенная, то величина 1 — (n/N) близка к единице и тогда расчет средней ошибки производится по общей формуле.
Средняя ошибка зависит от следующих факторов:
1. При выполнении принципа случайного отбора средняя ошибка выборки определяется во-первых объемом выборки: чем больше численность, тем меньше величины средней ошибки выборки. Генеральная совокупность характеризуется точнее тогда, когда больше единиц данной совокупности охватывает выборочное наблюдение
2. Средняя ошибка также зависит от степени варьирования признака. Степень варьирования характеризуется дисперсией. Чем меньше вариация признака (дисперсия), тем меньше средняя ошибка выборки. При нулевой дисперсии (признак не варьируется) средняя ошибка выборки равна нулю, таким образом, любая единица генеральной совокупности будет характеризовать всю совокупность по этому признаку.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
1.1. Ошибки
выборочного наблюдения
Средняя
ошибка выборки показывает, как генеральная средняя отклоняется в среднем от выборочной средней в ту или другую сторону. Формула
расчета средней ошибки выборки определяется видом исследуемого признака единиц
совокупности (количественный или альтернативный) и
способом отбора (бесповторный или повторный).
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
![]() , где
, где ![]() — дисперсия признака в выборочной совокупности
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный
 , где N—
, где N—
число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный
 , где w-выборочная
, где w-выборочная
доля
·
Если отбор бесповторный, а признак
альтернативный

Предельная ошибка выборки— показывающая с определенной степенью вероятности
отклонения средней от выборочной средней.
Предельная ошибка выборки
![]() , где параметр t зависит
, где параметр t зависит
от вероятности
Некоторые значения параметра t приведены
в таблице:
|
Вероятность, p |
0.95 |
0.954 |
0.9876 |
0.9907 |
0.9973 |
0.9999 |
|
Параметр t |
1.96 |
2.0 |
2.5 |
2.6 |
3.0 |
4.0 |
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
![]() , где
, где ![]() — дисперсия признака в выборочной совокупности
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный
 , где N—
, где N—
число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный
 , где w-выборочная
, где w-выборочная
доля
·
Если отбор бесповторный, а признак
альтернативный

Доверительный интервал для генеральной средней
![]()
Доверительный интервал для
генеральной доли
![]()
Пример расчета доверительного
интервала:
При выборочном обследовании 5% продукции по методу случайного
бесповторного отбора получены данные о содержании сахара в образцах:
|
Сахарность, % |
Число |
|
16-17 17-18 18-19 19-20 20-21 |
10 158 154 50 28 |
|
На основании этих данных вычислите:
1. Средний процент сахаристости.
2. Дисперсию и среднее квадратическое
отклонение.
3. С вероятностью 0.954 возможные пределы среднего значения
сахаристости продукции для всей партии.
4. С вероятностью 0.997 возможный процент продукции высшего
сорта по всей партии, если известно, что из 400 проб, попавших в выборку , 80
ед. отнесены к продукции высшего сорта.
Решение.
1.
Средний процент сахаристости найдем по формуле средней взвешенной
![]() , где xi–
, где xi–
середина i-го интервала
![]() =18,32 %
=18,32 %
2.
Дисперсия
![]()
![]()
![]() =336,49
=336,49
D(X)=336.49–
18.322=0.8676
Среднее квадратическое отклонение
![]() =0,93%
=0,93%
5. Предельная ошибка для
среднего процента сахаристости
![]()
для вероятности 0,954 параметр t=2.0
![]()
Доверительный интервал для среднего значения процента
сахаристости
![]()
![]()
![]()
С вероятностью 0,954 можно утверждать, что в генеральной
совокупности средний процент сахаристости лежит в пределах от 18,23% до 18,41%.
5. Доля продукции высшего сорта в выборочной совокупности
![]()
Предельная ошибка для
доли продукции высшего сорта
![]()
для вероятности 0,997 параметр t=3.0
![]()
Доверительный интервал для доли продукции высшего сорта
![]()
![]()
![]()
С вероятностью 0,997 можно утверждать, что в генеральной
совокупности доля продукции высшего сорта лежит в пределах от 14,0% до 26,0%.

 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп