|
0 / 0 / 0 Регистрация: 07.06.2010 Сообщений: 10 |
|
|
1 |
|
Определить вероятность допустимой погрешности измерений03.06.2011, 06:20. Показов 10914. Ответов 1
Добрый день! Помогите решить задачку по метрологии , если можно с объяснениями! : В результате поверки амперметра установлено, что 80 % погрешностей результатов измерений, произведенных с его помощью, не превосходит ± 20 мА. Считая, что погрешности распределены по нормальному закону с нулевым математическим ожиданием, найдите вероятность того, что погрешность результата измерения превзойдет ± 40 мА.
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
01.12.2012, 18:02 |
2 |
|
Помогите решить задачку по метрологии , если можно с объяснениями! 1. Вероятность попадания в интервал Удачи
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
01.12.2012, 18:02 |
|
Помогаю со студенческими работами здесь Дифракция Фраунгофера, расчёт погрешности косвенных измерений Нахождение коэффициента вязкости и расчет погрешности его измерений Методы уменьшения/устранения систематической составляющей погрешности средств измерений Для чего предназначены структурные схемы средств измерений с автоматической коррекцией погрешности Какова вероятность, что ошибочных измерений у них поровну? Оценить вероятность того, что случайная погрешность измерений не превысит указанного значения Найти вероятность того,что в одном из измерений ошибка превысит заданную точность. Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 2 |
Задание 3:
|
Вариант |
Задание |
|
1 |
Определите методическую погрешность |
|
2 |
Электронные весы c СКП |
|
3 |
Произведено 5 наблюдений измеряемой |
|
4 |
Определите методическую погрешность |
|
5 |
Вольтметр с пределом 10 В и классом |
|
6 |
Определите результат косвенных |
|
7 |
Чему равна э.д.с. генератора, если два |
|
8 |
Оцените методическую погрешность |
|
9 |
Погрешность вольтметра характеризуется |
|
10 |
Оцените погрешность измерителя |
|
11 |
Последовательно соединены 10 резисторов |
|
12 |
Цифровой вольтметр класса точности |
|
13 |
Последовательно соединены 10 резисторов |
|
14 |
Измерительный усилитель содержит |
|
15 |
Оцените методическую погрешность |
|
16 |
Вольтметр с пределом 10 В и классом |
|
17 |
Оцените инструментальную ошибку |
|
18 |
Чему равна э.д.с. генератора, если два |
|
19 |
Оцените погрешность измерителя |
|
20 |
К вольтметру класса точности 1.5 с |
|
21 |
Определите число наблюдений, необходимых |
|
22 |
Погрешность вольтметра характеризуется |
|
23 |
Электронный уровень (измеритель малых |
|
24 |
Погрешность вольтметра характеризуется |
|
25 |
Погрешность вольтметра характеризуется |
|
26 |
Произведено 5 наблюдений измеряемой |
|
27 |
Структурная схема цифрового мультиметра |
|
28 |
Оцените погрешность измерителя |
|
29 |
Определите какой результат измерения |
|
30 |
В каком диапазоне измеряемых напряжений |
|
31 |
Чему равна э.д.с. генератора, если два |
|
32 |
Произведено 5 наблюдений измеряемой |
|
33 |
Оцените необходимое время прогрева |
|
34 |
Определите погрешность какого |
|
35 |
Произведено 7 наблюдений измеряемой |
|
36 |
Оцените погрешность аналогового |
|
37 |
Оцените мощность, рассеиваемую на |
|
38 |
Последовательно соединены 10 резисторов |
|
39 |
Чему равна э.д.с. генератора, если два |
|
40 |
Погрешность вольтметра характеризуется |
|
41 |
Определите методическую погрешность |
|
42 |
Оцените инструментальную ошибку |
|
43 |
Вольтметр с пределом 10 В и классом |
|
44 |
Определите число наблюдений, необходимых |
|
45 |
Измерительный усилитель содержит |
|
46 |
Выведите формулу определения входного |
|
47 |
Оцените методическую погрешность |
|
48 |
По результатам прямых измерений |
|
49 |
Последовательно соединены 10 резисторов |
|
50 |
Определите какой результат измерения |
|
51 |
Определите число наблюдений, необходимых |
|
52 |
Погрешность вольтметра характеризуется |
|
53 |
Входное сопротивление вольтметра |
|
54 |
Определите класс точности амперметра |
|
55 |
Оцените методическую погрешность |
|
56 |
Определите число наблюдений, необходимых |
|
57 |
Чему Чему равна э.д.с. генератора, если |
|
58 |
Электронные весы c СКП |
|
59 |
Определите какой результат измерения |
|
60 |
Определите методическую погрешность |
|
61 |
Определите результат косвенного |
|
62 |
Осциллограф показал размах сигнала |
|
63 |
Определите методическую погрешность |
|
64 |
Оцените методическую погрешность |
|
65 |
Определите вероятность превышения |
|
66 |
Оцените погрешность измерения амплитуды |
|
67 |
Образцовый динамометр с СКП 0.01%, |
|
68 |
Параллельно соединены 8 резисторов |
|
69 |
Оцените инструментальную ошибку |
|
70 |
В каком диапазоне измеряемых напряжений |
|
71 |
Определите методическую погрешность |
|
72 |
Измерительный усилитель содержит |
|
73 |
Определите какой результат измерения |
|
74 |
Чему равна э.д.с. генератора, если два |
|
75 |
. Определите методическую погрешность |
|
76 |
Оцените величину искажений передачи |
|
77 |
Структурная схема цифрового мультиметра |
|
78 |
Определите границы доверительного |
|
79 |
Мостовым измерителем измерено |
|
80 |
Определите величину тепловой постоянной |
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Слайд 2
Задача 1. Определить максимальную абсолютную, относительную, приведѐнную
погрешности и сделать запись результата измерения напряжения
аналоговым вольтметром с классом точности 1,5 с пределом 1 В для показания 0,87 В.

Слайд 3
Решение: Для аналогового вольтметра с классом точности
р = 1,5 максимальная абсолютная погрешность равна
:
±∆ = p ∙XN/100 =1,5∙1/100 =0,015 B ,
где р – класс точности; XN – нормирующее значение измеряемой величины

Слайд 4
±γ =p% =1,5%
Приведѐнная погрешность: р% = 1,5%
±δ
= p∙XN/X = 1,5 ∙ 1/0.87 =1,72
Относительная погрешность: 1,72%
В соответствии с правилами округления результат измерения имеет вид 0,870 ± 0,015 В

Слайд 5
Задача 2. Определить абсолютную погрешность и сделать
запись результата измерения напряжения цифровым вольтметром с
классом точности 0,1/0,05 с пределом 10 В для показания 7,93 В.

Слайд 6
Решение Для цифрового вольтметра относительная погрешность равна
:
±δ=(с + d(XK/ X -1))=0,1 +
0,05 (10/7,93 -1 )=0,113%
Здесь XК = 10 В предел измерений; c/d = 0,1/0,05 – класс точности; Х =7,93 В – показание цифрового вольтметра.
По относительной погрешности определяется абсолютная:
±∆=δ ∙X/100 =0,113 ∙ 7,93/100=0,009 B
В соответствии с правилами округления результат измерения имеет вид 7,930± 0,009 В

Слайд 7
Задача 3.
Определить доверительный интервал и записать результат
измерения напряжения 37,86 В при погрешности однократного
измерения 0,14 В, если число измерений равно 5, доверительная вероятность 0,93.

Слайд 8
Решение: Доверительный интервал результата измерения при доверительной
вероятности равен ∆ = ± tα∙σ
tα — коэффициент распределения Стьюдента, зависящий от α и числа измерений N.
При α =0,93 и N= 5 в соответствии с табл.1 имеем значение t = 2,456.
Средняя квадратическая погрешность результата измерений х равна
σx= ± σ/N =0,14/√5 =0,0625 B

Слайд 9
Доверительный интервал результата измерения получается равным
∆
= ±2,456 ∙0,0623 = 0,153 В
Результат:
37,86 ±9,15B, α=0,93

Слайд 10
Задача 4. Дан результат измерения физической величины,
выраженный в делениях шкалы и равный α.
Дано: α = 49 дел., α макс = 150 дел., Iн = 7,5 А, Кл = 0,5.

Слайд 11
Измерение произведено прибором с указанными параметрами (класс
точности, верхний предел измерения, число делений шкалы).
Вычислить значение измеренной величины и наибольшую ожидаемую абсолютную и относительную погрешности. Записать результат измерения с учетом погрешности.

Слайд 12
Решение: 1) цена деления CI амперметра (вольтметра
– CB, ваттметра – СP)
равна
CI =Iн /αmax =7,5/150 =0,05 А/дел;
2) измеренное значение тока
I = α ∙ CI =49∙0,05 =2,45 A;
3) допускаемая наибольшая погрешность прибора
∆I =± K∙Iн /100 =±0,5∙7,5 /100 =±0,0375 A=0,04 A;

Слайд 13
4) наибольшая ожидаемая относительная погрешность измерения;
δI =
± ∆I∙100 / I = ± 0,04∙100
/2,45 = ±1,6 %
5) наибольшая ожидаемая абсолютная погрешность измерения равна наибольшей допускаемой погрешности прибора, т. е.
∆I =±0,04 A;
Результат измерения: I = 2,45 ±0,04 A= 2,45(1±0,016) A.

Слайд 14
Задача 5. Приведены данные ряда многократных замеров
частоты. Считая, что систематическая составляющая погрешности измерения
пренебрежимо мала, а случайные погрешности распределены по нормальному закону, вычислить среднее арифметическое значение результата частоты f ,оценку среднего квадратического значения случайной погрешности отдельного замера s,

Слайд 15
оценку среднего квадратического значения случайной погрешности в
определении среднего арифметического S. Проверить, нет ли
среди погрешностей отдельных измерений грубых погрешностей ( по правилу « 3-х сигм»). Задавшись доверительной вероятностью, вычислить границы доверительного интервала. Записать результат измерений.

Слайд 16
50,06; 49,82; 48,98: 50,30; 50,15; 50,08; 49,93;
49,76; 49,92; всего – 9 значений.
Решение:
1) определяем среднее арифметическое значение частоты:
x = ∑xi /n = (50,06 + 49,82+ 48,98 + 50,30+ 50,15+ 50,08+ 49,93+ 49,76+ 49,92) / 9 =50,003=50,00 Гц;
2) определяем оценку среднеквадратического отклонения отдельного замера S.
Для этого находим погрешности отдельных замеров: ∆i

Слайд 17
Получаем следующий ряд значений : +0,06;
–0,18; –0,02; +0,30; +0,15; +0,08; –0,07; 0,24;
–0,08.
Вычисляем S по формуле: S = √∑ ∆i2/ n-1 , S = ± 0,1674 Гц = ±0,17 Гц;

Слайд 18
3) проверим, имеются ли грубые ошибки (промахи)
по правилу: ∆i >3σ, 3S =0,51 Гц;
. Среди имеющихся девяти остаточных погрешностей наибольшая – в четвертом замере, равная 0,30 и не превосходит 3S = 0,51, поэтому повторного расчета S не требуется. В противном случае необходимо исключить грубые ошибки и вновь выполнить расчеты по пунктам 1 и 2;
4) находим оценку среднеквадратического отклонения (ошибки) среднего арифметического значения: Sx= ±S/√n =±0,1674/3 = ±0,0558 = ±0,06 Гц;

Слайд 19
5) определим границы доверительного интервала, приняв
доверительную вероятность равной Р = 0,95;
по
табл. 1. находим коэффициент Стьюдента tα для заданной доверительной вероятности
Р = 0,95 и n = 9: tα = 2,3;
доверительный интервал равен ∆ = ± tα ∙Sx =±2,3∙0,6 = ±0,138 =0,14 Гц;
6) результат измерения частоты x = 50,00 ±0,14 Гц, при Р = 0,95.

Слайд 20
Задача 6. Дано: α1 = 30 дел.,
α2 = 45 дел.
Амперметр: Кл=1,5, верхний
предел измерения тока Iн = 1,5 A,
αмакс = 75 дел.
Вольтметр: верхний предел измерения напряжения Uн = 300 В, αмакс = 150, Кл =1,0.

Слайд 21
Решение:
1) цена деления амперметра:
CI =Iн
/αmax =1,5/75 =0,02 А/дел;
2) наибольшая
допускаемая погрешность амперметра:
∆I =± K∙Iн /100 =±1,5∙1,5 /100 =±0,0225 A=0,02 A;
3) измеренный ток равен I = α ∙ CI =30∙0,02 =0,60 A;

Слайд 22
4) относительная погрешность измерения тока:
δI =
± ∆I / I = ± 0,0225
/0,6 = ±0,0375А=0,04А
5) цена деления вольтметра:
CU =Uн /αmax =300 / 150 = 2 B/дел;
6) наибольшая допускаемая погрешность вольтметра:
∆U =± K∙Uн /100 =±1,0∙ 300 /100 =± 3B;

Слайд 23
7) измеренное напряжение равно U= α2 ∙
CU =45∙ 2 =90 В;
 относительная
относительная
погрешность измерения напряжения составляет
δU = ± ∆U / U = ±3, / 90 = ±0,033B=0,03B
9) мощность и сопротивление резистора:
P = U ∙ I = 90 ∙ 0,6 =54 Bt, R = U / I = 90 / 0,6 = 150 Oм;

Слайд 24
10) относительная погрешность измерения мощности (наибольшая ожидаемая,
то же и для измерения сопротивления) равна
δP
= δR = δU + δI = ± ( 0,03 + 0,04) = ±0,07
т. к. и при умножении, и при делении двух измеренных значений относительная погрешность результата измерения равна сумме относительных погрешностей измерения каждого значения

Слайд 25
11) абсолютная погрешность и результат измерения мощности
составят
∆?= δ? ∙ ? = ±(0,07
∙ 54) = 3,78 ≈ 4 Вт, ? = (54 ± 4) Вт;
12) абсолютная погрешность и результат определении сопротивления:
∆?= δ? ∙ ? = ±(0,07 ∙ 150) = 10,5 ≈ 11 Ом, ? = (150 ± 11) Ом.

23.Учебник издан тиражом 50000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0002. Найти вероятность того, что тираж содержит: а) четыре бракованные книги; б) менее двух бракованных книг.
24.Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется: а) 5 бракованных; б) хотя бы одна бракованная.
25.Автоматическая телефонная станция получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно два вызова?
26.Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10?
27.Аппаратура содержит 2000 одинаково надежных элементов, вероятность отказа для каждого из которых равна p = 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов?
28.Сообщение содержит 1000 символов. Вероятность искажения одного символа равна 0,004. Найти среднее число искаженных символов; вероятность того, что будет искажено не более 3–х символов.
29.Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов равно 5000.
30.Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность, что в течение часа позвонят 5 абонентов?
31.Имеется общество из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна 1/365.
ЗАДАНИЕ 17
1.Поезда метро идут равномерно с интервалом 3 минуты. Какова вероятность, что подошедший пассажир будет ожидать ближайший поезд менее полминуты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
2.Случайная величина равномерно распределена на интервале (1;5). Найти еѐ плотность и функцию распределения. Построить их графики.
3.Автобусы некоторого маршрута следуют строго по расписанию с интервалом 5 минут. Найти вероятность, что подошедший к остановке пассажир
будет ожидать не менее 1 минуты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
4. Для случайной величины Х , равномерно распределенной на интервале (2;6), найти Р( 2< Х <3) , плотность и функцию распределения.
93
5.Интервал движения трамваев равен 4 мин. Какова вероятность, что подошедший к остановке пассажир будет ожидать вагон не более 2 минут Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
6.Радиус окружности измерен приближенно на интервале (а;b). Полагая, что радиус является случайной величиной Х, равномерно распределенной на этом интервале, найти математическое ожидание и дисперсию длины окружности.
7.Паром для перевозки машин через реку подходит к причалу через каждые
40минут. X – время прибытия машины к причалу. Найти вероятность, что подъехавшая случайным образом автомашина будет ожидать прибытия парома не более 10 мин. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
8.Для случайной величины Х, равномерно распределенной на промежутке (–1;5), математическое ожидание и Р(0 < X < 3).
9.Кабинки фуникулѐра подъезжают к подножию горы через каждые полчаса. Какова вероятность, что подошедшим лыжникам ждать придется менее 5 минут. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
10.Математическое ожидание равномерно распределенной случайной величины Х на интервале (1; b) равно 2. Найти параметр b и D(X).
11.Время ожидания троллейбуса на остановке имеет равномерное распределение на промежутке (0;10) минут. Какова вероятность, что ожидать ближайший троллейбус придется более 8 мин. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
12.Станок – автомат выдает обработанную деталь через каждые 7 минут. Найти вероятность, что подошедший контролѐр будет ожидать готовую деталь менее 30 секунд. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
13.Х – равномерно распределенная случайная величина на интервале (а;5). Дисперсия еѐ равна 1/3 . Найти параметр а и математическое ожидание.
14.Паром для перевозки пассажиров и машин через залив приплывает к причалу через каждые 3 часа. Какова вероятность, что подъехавшая машина попадет на паром менее, чем через полчаса? Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
15.Ребро куба приближенно измерено в интервале (а;b). Найти математическое ожидание и среднее квадратическое отклонение площади повер х- ности куба, если его ребро рассматривать как случайную величину, равномерно распределѐнную на этом интервале.
16.Время ожидания автобуса на остановке имеет равномерное распределение в промежутке (0;20) мин. Найти вероятность ожидания автобуса бо-
94
лее 15 минут. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
17.Вычислить математическое ожидание и дисперсию для площади равностороннего треугольника, сторона которого приближенно измерена в интервале (а;b) и равномерно распределена на данном интервале.
18.Цена деления шкалы амперметра 0,1А. Показания округляются до ближайшего целого деления. Найти вероятность, что при измерении будет допущена ошибка, не превышающая 0,03А.
19.Вычислить среднее время ожидания троллейбуса и среднее квадратическое отклонение при условии строгого соблюдения графика движения с интервалом 6 минут.
20.Случайная величина Х равномерно распределена на интервале (3;7). Найти Р(4<X<6 ), плотность и функцию распределения.
21.Цена деления шкалы измерительного прибора равна 0,5. Показания прибора округляются до ближайшего целого деления. Найти вероятность, что при измерении будет допущена ошибка, не превышающая 0,02.
22.Минутная стрелка электронных часов перемещается скачком в конце каждой минуты. Найти вероятность, что в данный момент часы покажут время, которое отличается от истинного не более чем на 10 секунд.
23.Диагональ квадрата приближенно измерена на промежутке (а;b). Найти математическое ожидание и среднее квадратическое отклонение площади квадрата, если считать диагональ случайной величиной, равномерно распределенной на данном промежутке.
24.Найти математическое ожидание и дисперсию случайной величины Х, равномерно распределенной на интервале (8;11).
25.Цена деления штангенциркуля равна 0,1 мм. Показания при измерении округляются до ближайшего целого деления. Найти вероятность, что при измерении детали будет допущена ошибка, превышающая 0,03 мм.
26.Случайная величина Х равномерно распределена на интервале (1;b). Вероятность попадания в интервал (2;5) равна 0,3. Найти параметр b, математическое ожидание и дисперсию.
27.Экспресс курсирует между аэропортом и ж/д вокзалом с интервалом полтора часа. Найти вероятность, что пассажиры, не знающие его расписание, будут ждать ближайший рейс менее 20 минут.
28.Для случайной величины Х, имеющей равномерное распределение на интервале (0,6), найти Р (1 < X < 4), математическое ожидание, дисперсию и среднее квадратическое отклонение.
29.Плотность распределения равномерной случайной величины Х на промежутке (а;11) равна 0,1. Найти параметр а, математическое ожидание и дисперсию.
95

30. Время бегуна на дистанции фиксировалось секундомером с ценой деления 0,1 секунд и оказалось выше мирового рекорда на 0,02 секунды. Какова вероятность, что спортсмен, по крайней мере, повторил рекорд?
ЗАДАНИЕ 18
1. Средний срок службы коробки передач до капитального ремонта у автомобиля определенной марки составляет 56 месяцев со стандартным отклонением σ = 16 месяцев. Привлекая покупателей, производитель хочет дать гарантию на этот узел, обещая сделать ремонт коробки передач нового автомобиля в случае ее поломки до определенного срока. Пусть срок службы коробки передач подчиняется нормальному закону. На сколько месяцев в таком случае производитель должен дать гарантию для этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей?
2. X – нормальная случайная величина с математическим ожиданием a = 4. Вероятность попадания X в интервал (3,5; 4,5) равна 0,7. Найти вероятность того, что из трех значений случайной величины X две попадут в интервал (2,5; 3,5).
3. Случайная величина X имеет плотность распределения вероятностей
|
2 |
x 1 2 |
|||||
|
f (x) |
e |
4.,5 . Найдите M(X) – математическое ожидание X, D(X) – |
||||
|
18 |
||||||
дисперсию X, вероятность того, что абсолютная величина отклонения X от математического ожидания не превысит 3.
4. Задана случайная величина X=N(3,1; 0.5) и точки х1 1 и х2 2 , разделяющие числовую ось на три интервала. Найти вероятность того, что случайная величина X принимает значения в этих интервалах
5. Плотность вероятности распределения случайной величины имеет вид
|
1 |
x |
2 2 |
|||||
|
f (x) |
e |
2 |
. Найти вероятность того, что из 4 независимых случайных |
||||
|
2 |
|||||||
величин, распределенных по данному закону, две окажутся на интервале ( ∞; 3).
6.Автоматически изготовленные детали по длине распределены нормально и расположены в интервале от 29,7 до 30,3 см. Какой длины проектировалась деталь, и с каким допуском?
7.Длина изготовляемой детали является нормально распределенной случайной величиной со средним значением a=100 мм и средним квадратическим отклонением =2 мм. Каких деталей окажется в большой партии больше – тех, у кого длина превосходит 103 мм или тех, у кого она заключается в пределах от 101 мм до 102 мм?
8.Коробки с деталями упаковываются автоматически. Их средняя масса равна 900 г. Известно, что 1% коробок имеют массу, большую 1 кг.
96
Каков % коробок, масса которых не превышает 850 г., если вес коробок – случайная величина, распределенная по нормальному закону?
9.Длина заготовок распределена по нормальному закону с математическим ожиданием 1минута и средним квадратическим отклонением 9 мм. Найти вероятность того, что в партии из 10 деталей не будет ни одной детали длиной более 105 см?
10.Диаметр болтов подчиняется нормальному распределению с параметрами M(x)=20, σ=0.1. Найти плотность распределения и количество болтов размером меньше 19,9, если всего болтов 12 штук.
11.Деталь, изготовленная автоматом, считается годной, если отклонение ее фактического размера от проектного не превосходит по абсолютной величине 8 мм. Случайные отклонения фактического размера от проектного подчинены нормальному закону со средним квадратическим отклонением σ=5 мм и математическим ожиданием a=0. Сколько процентов годных деталей изготавливает автомат?
12.Размер детали задан полем допуска 10мм – 12 мм. Оказалось, что средний размер детали равен 11,4 мм, а среднее квадратическое отклонение – 0,7 мм. Считая, что размер детали подчиняется нормальному закону распределения, определить вероятность брака по заниженному и завышенному размеру.
13.Менеджер торгово-посреднической фирмы получает жалобы от некоторых клиентов на то, что служащие фирмы затрачивают слишком много времени на выполнение их заказов. Собрав и проанализировав соответствующую информацию, он выяснил, что среднее время выполнения заказа составляет 6,6 дней, однако, для выполнения 20% заказов потребовалось 15 дней и более. Учитывая, что время выполнения заказа есть случайная величина, распределенная по нормальному закону, определите фактическое стандартное отклонение времени обслуживания клиентов.
14.Ошибка измерения некоторого параметра технической системы является случайной величиной, распределенной по нормальному закону. Если номинальное значение измеряемого параметра равно a, а стандартное отклонение от него равно 2, то какую точность измерения параметра технической системы можно гарантировать с вероятностью 0,8?
15.Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 120 мм. Фактическая длина изготовленных деталей не менее 116,5 мм и не более 123,5 мм. Найти вероятность того, что длина наудачу взятой детали меньше 117,2 мм.
16.По данным центрального банка России случайная величина Х – недельная потребность в купюрах достоинством 100 рублей подчиняется закону нормального распределения со средним значением а = 1160 и сред-
97
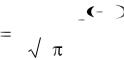
ним квадратичным отклонением σ = 240. Требуется записать функцию плотности вероятности и построить ее график.
17. Размер диаметров втулок, изготовленных цехом, можно считать нормально распределенной случайной величиной со средним 2,5 см и дисперсией 0,0001 см2. Какое следует установить поле допуска относительно номинального диаметра, чтобы брак составлял 1%?
18. Параметр X детали распределѐн нормально с m = 2, равным номиналу. Каким должно быть σ, чтобы с вероятностью 0,9 отклонение X по модулю не превышало 1% номинала?
19. Плотность вероятности нормально распределенной случайной величи-
|
1 |
x 14 2 |
||||||
|
ны Х имеет вид |
f (x) |
e |
32 |
. В каком промежутке она с большей |
|||
|
4 |
2 |
вероятностью принимает значения (6; или (18; 20)?
20.В результате поверки амперметра установлено, что 70% погрешностей результатов измерений, произведенных с его помощью, не превосходит ± 20 %. Считая, что погрешности распределены по нормальному закону с нулевым математическим ожиданием, определить среднеквадратическую погрешность.
21.Браковка шаров для подшипников производится следующим образом:
если шарик не проходит через отверстия d1 =5,9 мм, но проходит через отверстие d 2 =6,1 мм, то его размер считается приемлемым. Если какое–нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика есть нормально распределенная случайная величина X и M(X)=6 мм, D(X)=0.0025 мм2. Какова вероятность, что шарик забракован?
22.Изделия, выпускаемые цехом, по своим линейным размерам распределяются по нормальному закону с математическим ожиданием, равным 6 см. Известна вероятность, равная 0,9758, что наудачу взятое изделие будет иметь размеры в границах от 5,95см до 6,05 см. Найти дисперсию этой случайной величины.
23.Валик, изготовленный автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметров валиков подчиняются нормальному закону со средним квадратичным отклонением 1,6 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в процентах) изготавливает автомат?
24.Еженедельный выпуск продукции на заводе распределен по нормальному закону. Известно, что вероятность того, что еженедельный выпуск продукции превысит 150000 ед. равна 0,221, а вероятность того, что он окажется ниже 100000 ед. равна 0,0038. Определите, сколько в среднем единиц продукции в неделю выпускает завод.
98

25.Диаметр электродвигателя есть нормально распределенная случайная величина с параметрами а = 100 мм и σ = 1.6 мм. Найти вероятность того, что диаметр случайно взятого электродвигателя находится в интервале (98, 101).
26.Случайные ошибки измерения детали подчинены нормальному закону с параметром = 20 мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
27.Пусть X – случайная величина, подчиненная нормальному закону с математическим ожиданием а = 16 и средним квадратическим отклонением
 1. Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?
1. Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?
28.Пусть диаметр изготовляемой в цехе детали является случайной величиной,
распределенной по нормальному закону с параметрами а = 4,5 см, = 0, 05см. Найти вероятность того, что размер диаметра взятой наудачу детали отличается от математического ожидания не более чем на 1 мм.
29.Цех изготовляет детали, длины которых представляют собой случайную величину X, распределенную по нормальному закону. Математическое ожидание и среднее квадратическое отклонение величины X соответственно равны
15см и 0,1 см. Найти вероятность того, что отклонение длины детали в ту или другую сторону от математического ожидания не превзойдет 0,25 см.
30.Автомат изготавливает шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине
меньше 0,7 мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением = 0,4мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.
ЗАДАНИЕ 19
1. Найти при каких значениях А функция является функцией плотности
|
распределения. Найти M 0 , M x , Dx , As , Ex (указать их при b |
2, 1) . |
|
x Ax 2b 3e x 0, b 1 . |
|
|
2. Для геометрического распределения P m 1 p m p, m |
0,1, 2…Найти |
M x , Dx , As , Ex (указать их при p 0,5) .
3. Найти при каких значениях А функция является функцией плотности
|
распределения. Найти M 0 , M x , Dx , As , Ex (указать их при |
1) . |
|
x2 |
x Axe 2 2 .
Axe 2 2 .
4. Найти при каких значениях А функция является функцией плотности
|
распределения |
случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
|
(указать их при |
0,5) . |
99
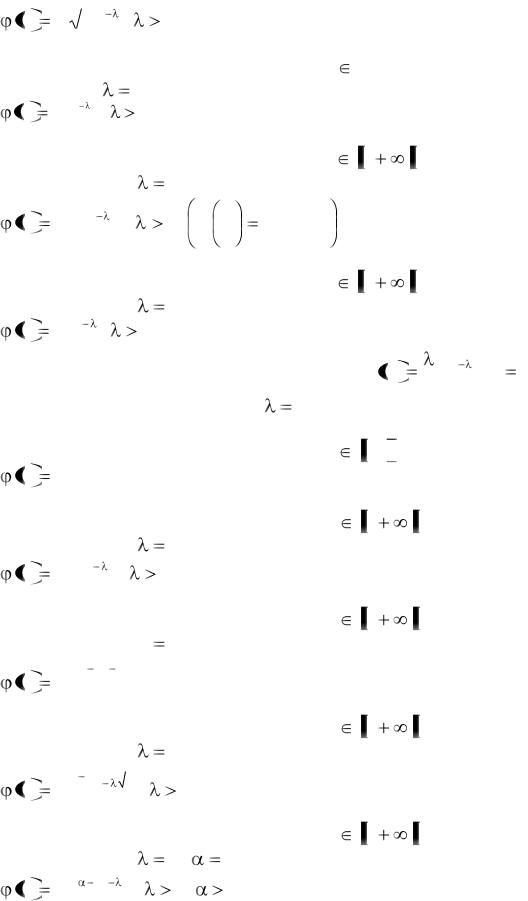
|
x |
A |
x e x , |
0. |
||||||||||||
|
5. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения |
случайной величины x |
R . Найти M 0 , M x , Dx , As , Ex (ука- |
|||||||||||||
|
зать их при |
1). |
||||||||||||||
|
x |
A e |
x |
, |
0 |
|||||||||||
|
6. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения |
случайной величины x |
0, |
. Найти M 0 , M x , Dx , As , Ex |
||||||||||||
|
(указать их при |
|
||||||||||||||
|
x |
Ax 2e x2 , |
0, Г |
1 |
2,68014 . |
|||||||||||
|
3 |
|||||||||||||||
|
7. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения |
случайной величины x |
0, |
. Найти M 0 , M x , Dx , As , Ex |
||||||||||||
|
(указать их при |
1). |
||||||||||||||
|
x |
A e |
х , |
0. |
||||||||||||
|
m |
|||||||||||||||
|
8. |
Для |
распределения |
Пуассона |
P m |
e , m 0,1, 2,… Найти |
||||||||||
|
m! |
|||||||||||||||
|
M x , Dx , As , Ex (указать их при |
2 ). |
||||||||||||||
|
9. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения случайной величины x |
1; 3 . Найти M 0 , M x , Dx , As , Ex |
xc.
10.Найти при каких значениях А функция является функцией плотности
|
распределения |
случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
||
|
(указать их при |
1). |
|||
|
3 |
x 2 |
, |
0. |
|
|
x Ax e |
11. Найти при каких значениях А функция является функцией плотности
|
распределения случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
|||
|
(указать их при n 4). |
||||
|
n |
1 |
x |
||
|
x Ax 2 |
e 2 . |
12. Найти при каких значениях А функция является функцией плотности
|
распределения случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
||||
|
(указать их при |
4). |
||||
|
1 |
|||||
|
e 3 x2 , |
|||||
|
x Ax |
3 |
0. |
13. Найти при каких значениях А функция является функцией плотности
|
распределения |
случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
||
|
(указать их при |
2, |
0,5). |
||
|
1 x2 |
, |
0, |
0. |
|
|
x Ax e |
100

14. Найти при каких значениях А функция является функцией плотности
|
распределения случайной величины x |
0, |
. Найти M 0 , M x , Dx , As , Ex |
|||||||||
|
(указать их при |
2 ). |
||||||||||
|
x2 |
|||||||||||
|
x Ax2e 2 |
2 . |
||||||||||
|
15. Для биномиального закона распределения P m |
C m pmqn m , m 0,1, 2,…, n |
||||||||||
|
n |
n |
||||||||||
|
Найти M |
, D |
, A , E |
(Указать их при p |
1 |
, n |
100 ). |
|||||
|
x |
x |
||||||||||
|
x |
s |
2 |
|||||||||
ЗАДАНИЕ 20
Варианты 1 – 10
Оценить вероятность того, что частота некоторого события А отклонится от его вероятности р в каждом испытании из серии n независимых испытаний по абсолютной величине не более чем на 0,01.
|
1. |
p = |
1 |
; n = 7500. |
2. |
p |
1 |
; n 9000. |
||
|
3 |
|||||||||
|
3 |
|||||||||
|
3. |
p = |
1 |
; n = 9500. |
4. |
p = |
1 |
; n = 10000. |
||
|
3 |
3 |
||||||||
|
5. |
p = |
1 |
; n = 6000. |
6. |
p = |
1 |
; n = 8000. |
||
|
3 |
4 |
||||||||
|
7. |
p = |
1 |
; n = 2000. |
8. |
p = |
1 |
; n = 1500. |
||
|
4 |
4 |
||||||||
|
p = |
1 |
; n = 1500. |
1 |
||||||
|
9. |
10. p = |
; n = 2500. |
|||||||
|
6 |
5 |
Варианты 11 – 20
Вероятность некоторого события А в каждом испытании из серии n независимых испытаний равна р. Найти наименьшее число испытаний так, чтобы с вероятностью не меньшей 0,99 частота события А отклонялась по абсолютной величине от его вероятности р не более, чем на .
|
11. |
p = |
1 |
; |
= 0,01. |
12. |
p = |
1 |
; |
= 0,02. |
|
3 |
4 |
||||||||
|
13. |
p = |
1 |
; |
= 0,03. |
14. |
p = |
1 |
; |
= 0,04. |
|
5 |
6 |
||||||||
|
15. |
p = |
2 |
; |
= 0,01. |
16. |
p = |
2 |
; |
= 0,02. |
|
3 |
5 |
||||||||
|
17. |
p = |
1 |
; |
= 0,03. |
18. |
p = |
4 |
; |
= 0,04. |
|
2 |
7 |
101

|
19. p = |
3 |
; = 0,01. |
20. p = |
4 |
; = 0,02. |
|
8 |
9 |
Варианты 21 – 30
Вероятность некоторого события А в каждом испытании из серии n независимых испытаний равна р. Найти границу абсолютной величины отклонения частоты события А от его вероятности р, которую можно ожидать с вероятностью 0,99, произведя n испытаний.
|
21. |
p = |
1 |
; n = 12100. |
22. |
p = |
1 |
; n = 13200. |
|
3 |
3 |
||||||
|
23. |
p = |
1 |
; n = 14300. |
24. |
p = |
1 |
; n = 15100. |
|
3 |
3 |
||||||
|
25. |
p = |
1 |
; n = 16200. |
26. |
p = |
1 |
; n = 17200. |
|
3 |
3 |
||||||
|
27. |
p = |
1 |
; n = 18100. |
28. |
p = |
1 |
; n = 19200. |
|
3 |
3 |
||||||
|
29. |
p = |
1 |
; n = 20100. |
30. |
p = |
1 |
; n = 21200. |
|
3 |
3 |
ЗАДАНИЕ 21
Варианты 1 ÷ 15
За значение некоторой величины принимают среднее арифметическое достаточно большого числа еѐ измерений. Предполагая, что среднее квадратическое отклонение σ возможных результатов каждого измерения не превосходит α см, оценить вероятность того, что при n измерениях неизвестной, величина отклонений принятого значения от истинного по абсо-
|
лютной величине не превзойдет ε см. |
|||
|
1. |
α = 1 , n = 2000 , ε = 0,001. |
2. |
α = 1,2, n = 2500, ε = 0,01. |
|
3. |
α = 1,4, n = 3000, ε = 0,001. |
4. |
α = 1,6, n = 3500, ε = 0,01. |
|
5. |
α = 1,8, n = 4000, ε = 0,001. |
6. |
α = 1, n = 4500, ε = 0,01. |
|
7. |
α = 1,1, n = 5000, ε = 0,001. |
8. |
α = 1,3, n = 5500, ε = 0,01. |
|
9. |
α = 1,5, n = 6000, ε = 0,001. |
10. |
α = 1,7, n = 6500, ε = 0,01. |
|
11. |
α = 1,9, n = 7000, ε = 0,001. |
12. |
α = 1,2, n = 7500, ε = 0,01. |
|
13. |
α = 1,4, n = 8000, ε = 0,001. |
14. |
α = 1,5 , n = 8500, ε = 0,01. |
15.α = 1,6, n = 9000, ε = 0,001.
Варианты 16 ÷ 30
Дана последовательность независимых случайных величин Х1, Х2, Хn, для каждой из которых задан закон распределения, Применим ли к этой последовательности закон больших чисел?
102
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибка измерения некоторого параметра технической системы является случайной величиной.doc
Зарегистрируйся в два клика и получи неограниченный доступ к материалам, а также
промокод

на новый заказ в Автор24. Это бесплатно.
Условие
Ошибка измерения некоторого параметра технической системы является случайной величиной, распределенной по нормальному закону со стандартным отклонением σ=1. Какую точность измерения параметра технической системы можно гарантировать с вероятностью 0,9?
Решение
Случайная величина X – ошибка измерения некоторого параметра технической системы.
a – математическое ожидание; σ=1 – стандартное отклонение.
Для нормально распределенной случайной величины X, вероятность
PX-a<δ=2Фδσ
Фx – функция Лапласа (находим по таблице).
Тогда
PX-a<δ=2Фδ1=2Фδ=0,9
2Фδ=0,9
Фδ=0,45
δ=1,65
С вероятностью 0,9 можно гарантировать ошибку измерения в пределах ±1,65.
Ответ: 1,65.
50% решения задач недоступно для прочтения
Закажи написание решения задач по выбранной теме всего за пару кликов. Персональная работа в кратчайшее
время!
А.А. Данилов.
ОБУ «Пензенский ЦСМ»,
Россия, г.Пенза, pcsm@sura.ru
Е.Ю. Лукашов.
Федеральное государственное унитарное предприятие «Всероссийский чно-исследовательский институт метрологической службы» (ФГУП ИИМС»),
Москва, Россия, e-mail: sva@vniims.ru
В статье рассматриваются вопросы измеримости погрешности средств измерений. Приводится обоснование того, что погрешность — есть величина случайная и не может быть представлена конкретным значением, можно определить лишь характеристики погрешности.
Ключевые слова: погрешность средств измерений, случайные величины, характеристики погрешности.
This article describes the questions of a measurability of the inaccuracy of a measuring instrument. It gives an explanation that the inaccuracy is a random quantity and it cannot be a constant value. It is only possible to determine the characteristics of the inaccuracy.
Key words: inaccuracy of a measuring instruments, random variables, inaccuracy characteristics.
Наши взгляды — как наши часы: все они показывают разное время, но каждый верит только своим.
Александр Поуп
Мое дело сказать правду, а не заставлять верить в нее.
Жан Жак Руссо
Погрешность СИ — разность между показанием СИ и действительным значением измеряемой величины
РМГ 29-99 ГСП. Метрология. Термины и определения
Поводом для написания настоящей статьи послужило распространенное в последнее время заблуждение (приверженцами которого являются не только начинающие метрологи, но и некоторые метрологи со стажем), основанное на неправильном толковании определения погрешности средства измерений (СИ), приведённом в РМГ 29-99 [1]:
«Погрешность средства измерений — разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины…
Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением», т.е.
ε = Х-Хд (1)
где ε -погрешность СИ, Х — показание СИ, Хд — действительное значение измеряемой величины.
Анализируя эту формулу, наши оппоненты делают неправильный вывод, а именно: погрешность СИ — есть значение, равное правой части формулы (1). Некоторые из оппонентов идут дальше, отстаивая второй, тоже неправильный вывод: если СИ — объект, а погрешность СИ — одно из свойств объекта, то, поскольку свойства объекта подлежат измерению, следовательно, можно говорить и об измерении погрешности СИ. Более того, некоторые СИ, например, В1-8 и др., имеют отсчетное устройство с наименованием «Погрешность поверяемого прибора», предназначенное «для снятия отсчета погрешности поверяемого вольтметра» [2], что придает оппонентам излишней уверенности в своей правоте.
Попробуем разобраться.
Для применения формулы (1) воспользуемся определением действительного значения [1]: «Действительное значение — значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него».
Используя указанное определение, оппоненты считают, что при проведении поверки СИ, эталон выбран правильно, следовательно, его погрешностью, в сравнении с погрешностью поверяемого СИ, можно пренебречь. Это дает возможность получить погрешность СИ, вычислив разность «между показанием СИ и действительным значением измеряемой физической величины».
Где здесь противоречие?
Во-первых, в правой части формулы (1) обе величины являются случайными. Поэтому и погрешность тоже является случайной величиной. А, следовательно, можно говорить об отдельной реализации случайной величины. Если же говорить о погрешности вообще, то её оценку необходимо рассматривать, как оценку одной или нескольких характеристик случайной величины.
Во-вторых, в частном случае Х-Хд из (1) можно сделать неправильный вывод: погрешность ε =0, следовательно, погрешность СИ в проверяемой точке диапазона измерений меньше погрешности эталона. Правильный же вывод из этого результата при поверке СИ — погрешность СИ не превышает установленных для неё пределов. И только.
В-третьих, используя один экземпляр эталона и выполнив необходимые измерения, можно получить одно значение ε1, погрешности СИ в проверяемой точке диапазона его измерений. Используя же другой экземпляр эталона, также выполнив необходимые измерения, можно получить второе значение ε2 погрешности СИ. Для n-го экземпляра эталона будет получено n-е значение εn погрешности СИ. Какое из них принять за погрешность СИ?
Почему такое возможно? Потому, что каждый из экземпляров эталонов хранит, воспроизводит и передает свое значение единицы величины, которое отличается от номинального значения и находится в некоторых допускаемых пределах отклонения от него.
Те же рассуждения можно повторить в отношении повторных экспериментов с тем же эталоном и в той же точке диапазона измерений и в отношении других точек диапазона измерений СИ.
И, наконец, в-четвертых, если бы кому-нибудь удалось получить истинную погрешность СИ, тогда этот уникальный человек смог бы определить истинное значение измеряемой величины. Возможно ли такое?
Нет! И вот почему.
Во-первых, при повторении эксперимента в силу случайных причин, устранить которые (либо свести к нулю их влияние) не представляется возможным, будут зафиксированы показания СИ, в общем случае отличающиеся между собой. На этом основании Шишкин И.Ф. в предложенной им аксиоматике формулирует третью аксиому метрологии, согласно которой «результат измерения без округления является случайным» [3]. Из этой аксиомы следует, что результат измерения имеет вполне конкретное значение, которое следует рассматривать, как реализацию случайной величины.
Во-вторых, действительное значение измеряемой величины, приписанное эталону, при его воспроизведении в силу случайных причин в действительности также не постоянно. Кроме того, это действительное значение также неизвестно абсолютно точно, в том числе и для первичного эталона. Именно поэтому для эталонов регламентируют неисключенную систематическую погрешность, случайную погрешность и нестабильность [4].
Из этих утверждений следует, что погрешность может быть представлена и представляется на практике совершенно конкретными значениями. Но, надо иметь в виду, что любая оценка погрешности — есть оценка случайной величины. Именно поэтому может быть указан лишь интервал значений, в котором находится погрешность СИ с заданной вероятностью, либо числовые характеристики этого интервала [5].
Таким образом, с помощью формулы (1) для конкретного момента времени может быть получено лишь одно из возможных значений погрешности СИ, принадлежащих указанному интервалу с некоторой вероятностью. Именно поэтому наличие упомянутого выше отсчетного устройства -с наименованием «Погрешность поверяемого прибора» у установки для поверки вольтметров В1-8 предназначено лишь «для снятия отсчета погрешности поверяемого вольтметра» [2] и реализации формулы (1) в этой установке, который может быть использован для определения характеристик погрешности.
Рассмотрим теперь следующий тезис оппонентов, утверждающих, что погрешность можно измерить.
В соответствии с РМГ 29-99 [1]:
«Измерение — совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значеш, этой величины».
Из этого определения следует, что
— во-первых, измерению подлежит величина,
— во-вторых, техническое средство предназначенное для измерения должно хранить единицу величины.
— в-третьих, в результате рений получают оценку значения величины.
Так можно ли говорить об изме рении погрешности?
Нет! Погрешность измерить невозможно! Можно лишь говорить об определении характеристик погрешности [5].
Погрешность измерить невозможно. Можно определить лишь характеристики погрешности
Несмотря на то, что погрешность может быть выражена в единицах измеряемой величины, гносеологически измерение погрешности невозможно, ибо: — во-первых, погрешность — не есть физическая величина, а потому не подлежит измерению, во-вторых, для погрешности может быть указан лишь интервал значений, в котором находится погрешность СИ с заданной вероятностью, либо числовые характеристики этого интервала.
ВЫВОДЫ
1. Погрешность — есть величина случайная и не может быть оценена на основе единичной реализации.
2. Погрешность измерить невозможно. Можно определить лишь характеристики погрешности.
ЛИТЕРАТУРА
1. РМГ 29-99. ГСИ. Метрология. Основные термины и определения.
2. Установка для поверки вольтметров В1-8. Техническое описание и инструкция по эксплуатации,- С. 31.
3. Шишкин И. Ф. Теоретическая метрология. Часть 1. Общая теория измерений. Учебник для вузов.-СПб.: Питер,- 2010.- С. 52.
4. ГОСТ8.381-2009. ГСИ. Эталоны. Способы выражения точности.
5. МИ 1317-2004. ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров.
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.
поделиться знаниями или
запомнить страничку
- Все категории
- экономические
43,606 - гуманитарные
33,643 - юридические
17,916 - школьный раздел
611,332 - разное
16,894
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Макеты страниц
Ошибки измерений и способ наименьших квадратов
9.1.21. Ошибки измерений и нормальный закон распределения.
Измерения всегда сопровождаются ошибками. Различают ошибки двух основных видов: систематические и случайные. Систематические ошибки имеют определенные причины, которые искажают измерение всегда в одном направлении и часто на постоянную величину. Они возникают за счет неисправности или плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого выполнения технологии и т. д. Во многих случаях можно найти причины таких ошибок и устранить их.
Случайные ошибки неопределенны, и причина их неизвестна. Свое незнание причины ошибок мы обычно маскируем, говоря, что их порождает случай. А это просто означает, что их можно приписать большому количеству причин, действующих в любом направлении и создающих каждая свою погрешность. Такие случайные ошибки можно учитывать статистическими методами.
Существует еще одна категория ошибок, о которой будет кратко сказано в п. 9.1.27; это категория отдельных промахов, происходящих по однократной вине экспериментатора, например, если он по рассеянности один раз неправильно считает показания со шкалы измерительного прибора. В этом случае мы имеем дело с анормальным результатом измерения. Существует простое правилу, позволяющее исключить из таблицы результатов измерений ошибки этой категории.
Мы займемся в основном категорией случайных ошибок. Допустим, что имеется несколько в одинаковой степени надежных измерений физической величины, истинное значение которой равно  Ошибки, соответствующие измерениям
Ошибки, соответствующие измерениям  будут равны
будут равны

Это чисто случайные ошибки.
Мы не знаем точного значения величины X и не можем определить ее на опыте, так как всякое измерение, сделанное для ее определения, искажается ошибкой. Обозначим через X наиболее вероятное значение величины 
Рассмотрим величины

Величины  называются отклонениями. Так как речь здесь идет только о случайных ошибках, то величины х и у могут быть а положительными, и отрицательными, а малые значения будут встречаться чаще, чем большие. Примем допущение, что эти величины, следуют нормальному закону распределения
называются отклонениями. Так как речь здесь идет только о случайных ошибках, то величины х и у могут быть а положительными, и отрицательными, а малые значения будут встречаться чаще, чем большие. Примем допущение, что эти величины, следуют нормальному закону распределения

Положим

 как известно, называется мерой точности. При этом
как известно, называется мерой точности. При этом  примет вид
примет вид

где  относительное число ошибок, равных х.
относительное число ошибок, равных х.
Вычертим кривые Гаусса при двух различных значениях мерь; точности  Легко заметить, что чем больше
Легко заметить, что чем больше  тем кривые острее, тем круче их склоны. Это означает, что чем больше параметр
тем кривые острее, тем круче их склоны. Это означает, что чем больше параметр  тем реже встречаются большие ошибки. Поэтому величину
тем реже встречаются большие ошибки. Поэтому величину  и называют мерой точности.
и называют мерой точности.
Вероятность того, что ошибка будет заключаться между  равна
равна



