
Важной задачей кодологии при обработке информационных потоков кодированных сообщений в каналах систем связи и компьютерных является разделение потоков и селектирование их по заданным признакам. Выделенный поток расчленяется на отдельные сообщения и для каждого из них выполняется углубленный анализ с целью установления кода и его характеристик с последующим декодированием и доступом к семантике сообщения.
Так, например, для определенного Рида-Соломона кода (РС-кода) необходимо установить:
- длину n кодового слова (блока);
- количество k информационных и N-k проверочных символов;
- неприводимый многочлен р(х), задающий конечное поле GF(2r);
- примитивный элемент α конечного поля;
- порождающий многочлен g(x);
- параметр j кода;
- используемое перемежение;
- последовательность передачи кодовых слов или символов в канал и еще некоторые другие.
Здесь в работе рассматривается несколько другая частная задача — моделирование собственно РС-кода, являющаяся центральной основной частью названной выше задачи анализа кода.
Описание РС-кода и его характеристик
Для удобства и лучшего уяснения сущности устройства РС-кода и процесса кодирования вначале приведем основные понятия и термины (элементы) кода.
Рида – Соломона коды (РС-код) можно интерпретировать как недвоичные коды БЧХ (Боуза – Чоудхури – Хоквингема), значения кодовых символов которых взяты из поля GF(2r), т. е. r информационных символов отображаются отдельным элементом поля. Коды Рида – Соломона – это линейные недвоичные систематические циклические коды, символы которых представляют собой r-битовые последовательности, где r – целое положительное число, большее 1.
Коды Рида – Соломона (n, k) определены на r-битовых символах при всех n и k, для которых:
0 < k < n < 2r + 2, где
k – число информационных символов, подлежащих кодированию,
n – число кодовых символов в кодируемом блоке.
Для большинства (n, k)-кодов Рида – Соломона; (n, k) = (2r–1, 2r–1–2∙t), где
t – количество ошибочных символов, которые может исправить код, а
n–k = 2t – число контрольных символов.
Код Рида – Соломона обладает наибольшим минимальным расстоянием (числом символов, которыми отличаются последовательности), возможным для линейного кода. Для кодов Рида – Соломона минимальное расстояние определяется следующим образом: dmin = n–k +1.
Определение. РС-кодом над полем GF(q=рm), с длиной блока n = qm-1, исправляющим t ошибок, является множество всех кодовых слов u(n) над GF(q), для которых 2t последовательных компонентов спектра с номерами равны 0.
Тот факт, что 2t последовательных степеней α — корни порождающего многочлена g(x) или что спектр содержит 2t последовательных нулевых компонентов, является важным свойством кода, позволяющим исправлять t ошибок.
Информационный многочлен Q. Задает текст сообщения, которое делится на блоки (слова) постоянной длины и оцифровывается. Это то, что подлежит передаче в системе связи.
Порождающий многочлен g(x) РС-кода — многочлен, который преобразует информационные многочлены (сообщения) в кодовые слова путем перемножения Q·g(x)= С =u(n) над GF(q).
Проверочный многочлен h(x) позволяет устанавливать наличие искаженных символов в слове.
Синдромный многочлен S(z). Многочлен, содержащий компоненты соответствующие ошибочным позициям. Вычисляется для каждого принятого декодером слова.
Многочлен ошибок E. Многочлен с длиной равной кодовому слову, с нулевыми значениями во всех позициях, кроме тех, что содержат искажения символов кодового слова.
Многочлен локаторов ошибок Λ(z) обеспечивает нахождение корней, указывающих позиции ошибок в словах, принятых приемной стороной канала связи (декодером). Корни его могут быть найдены методом проб и ошибок, т.е. путем подстановки по очереди всех элементов поля, пока Λ(z) не станет равным нулю.
Многочлен значений ошибок Ω(z)≡Λ(z)·S(z) (modz2t) сравним по модулю z2t с произведением многочлена локаторов ошибок на синдромный многочлен.
Неприводимый многочлен поля р(x). Конечные поля существуют не при любом числе элементов, а только в случае, если число элементов является простым числом р или степенью q=рm простого числа. В первом случае поле называется простым (его элементы-вычеты чисел по модулю простого числа р), во втором-расширением соответствующего простого поля (его q элементов-многочленов степени m-1 и менее — это вычеты многочленов по модулю неприводимого над простым полем многочлена р(x) степени m)
Примитивный многочлен. Если корнем неприводимого многочлена поля является примитивный элемент α, то р(x) называют неприводимым примитивным многочленом.
В ходе изложения действий с РС-кодом нам потребуется неоднократно обращение к полю Галуа, поэтому сразу здесь поместим рабочую таблицу с элементами этого поля при разных представлениях элементов (десятичным числом, двоичным вектором, многочленом, степенью примитивного элемента).
Таблица П — Характеристики элементов конечного поля расширения GF(24), неприводимый многочлен p(x) = x4+x+1, примитивный элемент α =0010= 210
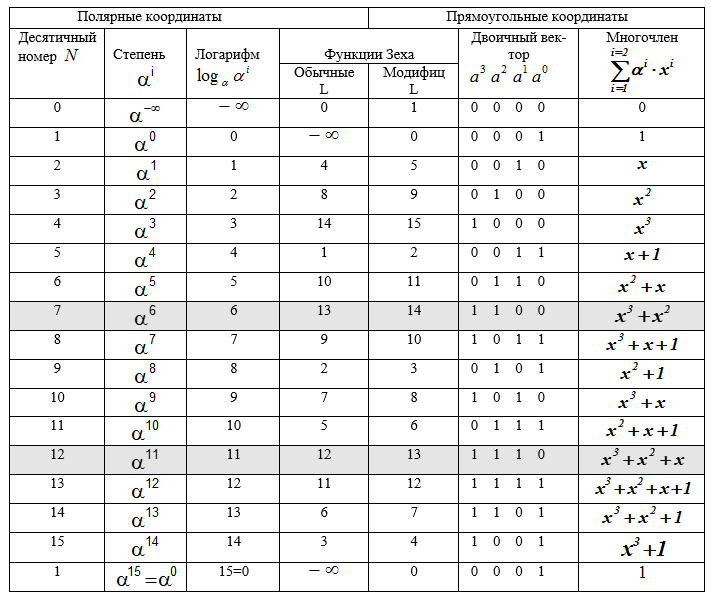
Пример 1. Над конечным полем GF(24), задан неприводимый многочлен поля p(x) = x4 + x + 1, примитивный элемент α =2, и задан (n, k)- код Рида-Соломона (РС-код). Кодовое расстояние этого кода равно d = n — k + 1 = 7. Такой код может исправлять до трёх ошибок в блоке (кодовом слове) сообщения.
Порождающий многочлен g(z) кода имеет степень m =n-k = 15-9 = 6 (его корнями являются 6 элементов поля GF(24) в десятичном представлении, а именно элементы 2, 3, 4, 5, 6, 7) и определяется соотношением, т.е. многочленом от z с коэффициентами (элементами) из GF(24) в десятичном представлении при i = 1(1)6. В рассматриваемом РС-коде 29 = 512 кодовых слов.
Кодирование сообщений РС-кодом
В таблице П эти корни имеют и степенное представление .

Здесь z- абстрактная переменная, а α -примитивный элемент поля, через его степени выражены все (16) элементы поля. Многочленное представление элементов поля использует переменную х.
Вычисление порождающего многочлена g(x)=А·В РС-кода выполним частями (по три скобки):

Векторное представление (через коэффициенты g(z) элементами поля в десятичном представлении) порождающего многочлена имеет вид
g(z) = G<7>= (1, 11, 15, 5, 7, 10, 7).
После формирования порождающего многочлена РС-кода, ориентированного на обнаружение и исправление ошибок, задается сообщение. Сообщение представляется в цифровом виде (например, ASCII- кодом), от которого переходят к многочленному или векторному представлению.
Информационный вектор (слово сообщения) имеет k — компонентов из (n, k). В примере k = 9, вектор получается 9-компонентный, все компоненты – это элементы поля GF(24) в десятичном представлении Q<9> = (11, 13, 9, 6, 7, 15, 14, 12, 10).
Из этого вектора формируется кодовое слово u<15> — вектор с 15 компонентами. Кодовые слова, как и сами коды, бывают систематическими и несистематическими. Несистематическое кодовое слово получают умножением информационного вектора Q на вектор, соответствующий порождающему многочлену
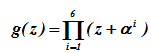
После преобразований получаем несистематическое кодовое слово (вектор) в виде
Q·g = <11, 15, 3, 9, 6, 14, 7, 5, 12, 15, 14, 3, 3, 7, 1>.
При систематическом кодировании сообщение (информационный вектор) представляют многочленом Q(z) в форме Q(z)=q(z)·g(z) + R(z), где степень degR(z)<m = 6. После этого к вектору Q справа приписывается остаток R (всё в десятичном виде). Это делается так.
Многочлен Q сдвигают в сторону старших разрядов на величину m = n — k, что достигается путём умножения Q(z) на Zn — k (в примере Zn — k = Z 6) и выполняют после сдвига деление Q(z)·Zn — k на g(z). В результате находят остаток от деления R(z). Все операции выполняют над полем GF(24)
(11, 13, 9, 6, 7, 15, 14, 12, 10, 0, 0, 0, 0, 0, 0) =
=(1, 11, 15, 5, 7, 10, 7)·(11, 15, 9, 10,12,10,10,10, 3) + (1, 2, 3, 7, 13, 9) = G·S + R.
Остаток при делении многочленов вычисляется обычным способом (уголком см.здесь Пример 6). Деление выполняется по образцу: Пусть Q = 26, g(z) = 7 тогда 26 = 7·3 +R(z), R(z)=26 -7·3 =26-21 = 5. Вычисление остатка R(z) от деления многочленов. Приписываем к вектору Q справа остаток R.
Получаем u<15> — кодовое слово в систематическом виде. Этот вид явно содержит информационное сообщение в k старших разрядах кодового слова
u<15> = (11,13,9,6,7,15,14,12,10; 1, 2, 3, 7, 13, 9)
Разряды вектора нумеруются справа налево от 0(1)14. Шесть младших разрядов справа являются проверочными.
Декодирование кодов Рида-Соломона
После получения блока декодер обрабатывает каждый блок (кодовое слово) и исправляет ошибки, которые возникли во время передачи или хранения. Декодер делит полученный многочлен на порождающий многочлен кода РС. Если остаток равен нулю, то ошибок не обнаружено, в противном случае — имеют место ошибки.
Типичный РС-декодер выполняет пять этапов в цикле декодирования, а именно:
- Вычисление синдромного многочлена (его коэффициентов ), обнаруживаются ошибки.
- Решается ключевое уравнение Падэ — вычисление значений ошибок и их позиций соответствующих местоположений.
- Реализуется процедура Ченя — нахождение корней многочлена локатора ошибок.
- Используется алгоритм Форни для вычисления значения ошибки.
- Вносятся корректирующие поправки в искаженные кодовые слова;
Завершается цикл извлечением сообщения из кодовых слов (снятие кода).
Вычисление синдрома.
Генерация синдрома из принятого кодового слова является первым этапом процесса
декодирования. Здесь вычисляются синдромы и определяется, есть ли ошибки в полученном кодовом слове или нет
Декодирование кодовых слов РС – кода может быть организовано разными способами. К классическим способам относится декодирование с привлечением алгоритмов, работающих во временной или в частотной области, которые используют вычисление синдрома, либо не используют. Не углубляясь в теорию этого вопроса, остановим свой выбор на декодировании с вычислением синдромов кодовых слов во временной области.
Обнаружение искажений
Синдромный , где
вектор последовательно определяется для каждого из полученных декодером на его входе кодовых слов. При нулевых значениях компонентов вектора синдрома
, декодер считает, что в принятом слове ошибки нет. Если же хотя бы для одного
, то декодер делает вывод о наличии ошибок в кодовом векторе и приступает к их выявлению, что является 1-м шагом работы декодера.
Вычисление синдромного многочлена
Умножение на приемной стороне кодового слова С на проверочную матрицу Н может давать в результате два исхода:
- синдромный вектор S=0, что соответствует отсутствию ошибок в векторе C;
- синдромный вектор S≠0, что означает наличие ошибок (одной или более) в компонентах вектора C.
Интерес представляет второй случай.
Кодовый вектор с ошибками представлен в виде C(E) =C + E, E– вектор ошибок. Тогда
Компоненты Sj синдрома определяются либо соотношением суммирования
для n = q-1 и j = 1(1)m = n-k, либо схемой Горнера:
Пример 2. Пусть вектор ошибок имеет вид Е =<0 0 0 0 12 0 0 0 0 0 0 8 0 0 0>. Он искажает в кодовом векторе символы на 3-й и 10-й позициях. Значения ошибок соответственно 8 и 12 — эти значения также являются элементами поля GF(24) и заданы в десятичном (табл. П) представлении. В векторе Е нумерация позиций от младших справа налево, начиная с 0(1)14.
Сформируем теперь кодовый вектор с двумя ошибками в 3-ем разряде и в 10-ом со значениями 8 и 12 соответственно. Это осуществляется суммированием в поле GF(24) по правилам арифметики этого поля. Суммирование элементов поля с нулем не изменяет их значения. Ненулевые значения (элементы поля) суммируются после преобразования их к многочленному представлению, как обычно суммируются многочлены, но коэффициенты при неизвестной приводятся по mod 2.
После получения результата суммирования они вновь преобразуются к десятичному представлению, пройдя предварительно через степенное представление

Ниже показано вычисление искажённых ошибками значений в 10 и 3 позициях кодового слова:
Декодер вычисления выполняет по общей формуле для компонентов Sj, j=1(1)m. Здесь (в модели) используем соотношение , так как E задаём (моделируем) в программе сами, то ненулевые слагаемые получаются только при i = 3 и i = 10.

Специально ниже покажем вычисления по этой формуле в развернутом виде.
Проверочная матрица РС – кода
Как только сформулирован порождающий многочлен кода, появляется возможность построения проверочной матрицы для кодовых слов, а также определение количества исправляемых ошибок (см.здесь, декодер ). Построим вспомогательную матрицу [7×15], из которой могут быть получены две разные проверочные матрицы: первые шесть строк – одна и последние шесть строк – другая.
Сама матрица формируется специальным образом. Первые две строки очевидны, третья строка и все последующие получены вычитанием из предыдущей (второй) строки отрезка чисел натурального ряда 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 по mod 15. При возникновении нулевого значения оно заменяется числом 15, отрицательные вычеты преобразуются в положительные.
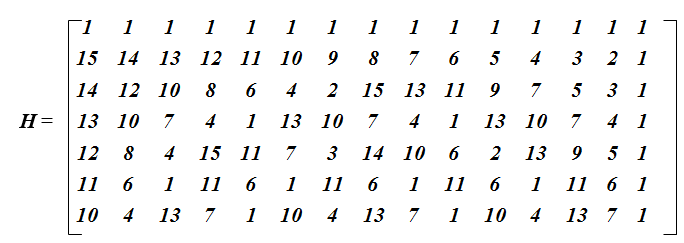
Каждая матрица соответствует своему порождающему многочлену для систематического и несистематического кодирования.
Определение коэффициентов синдромного многочлена
Далее будем определять коэффициенты синдромного многочлена при j=1(1)6.
Относительно кодового слова с длиной , поступающего на вход декодера мы допускаем, что оно искажено ошибками.
Относительно вектора ошибок для его выявления необходимо знать следующее:
Как вычисляется и используется далее синдромный вектор (многочлен) S? Его роль при декодировании кодовых слов очень значительна. Покажем это с иллюстрацией на числовом примере.
Пример 3. (Вычисление компонентов синдромного вектора )
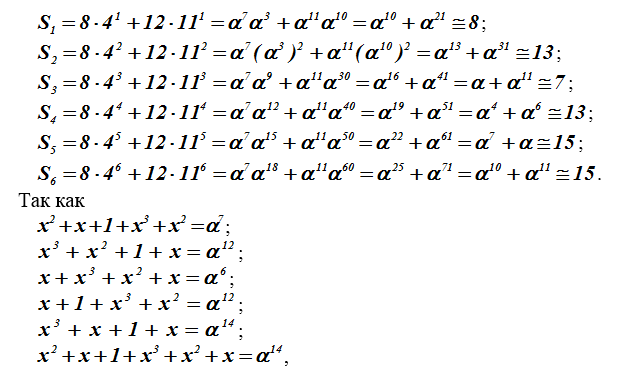
то в итоге имеем =<8,13,7,13,15,15>
Для дальнейшего рассмотрения введем новые понятия. Величину будем называть локатором ошибок, здесь искаженный символ кодового слова на позиции
, α – примитивный элемент поля GF(24).
Множество локаторов ошибок конкретного кодового слова рассматривается далее как коэффициенты многочлена локаторов ошибок σ(z), корнями которого являются значения
, обратные локаторам.
При этом выражения обращаются в нуль.
всегда свободный член уравнения всегда свободный член уравнения .
Степень многочлена локаторов ошибок равна v – количеству ошибок и не превышает величины .
Все искаженные символы находятся на разных позициях слова, следовательно, среди локаторов , не может быть повторяющихся элементов поля, а многочлен σ(z)=0 не имеет кратных корней.
Величины ошибок для удобства записи переобозначим символом . Для коэффициентов синдромного многочлена ранее рассматривались нелинейные уравнения. В нашем случае v=1 начало отсчета компонентов синдрома.
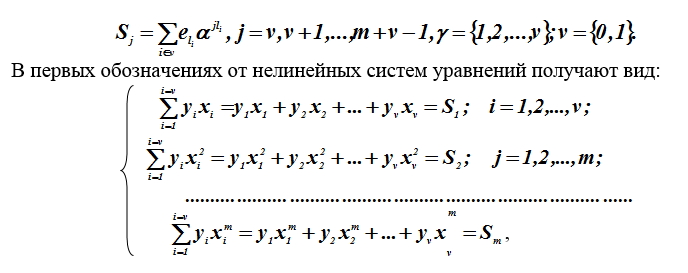
где — неизвестные величины, а
— известные, вычисляемые на первом этапе декодирования, параметры (компоненты синдромного вектора).
Методы решения подобных систем нелинейных уравнений неизвестны, но решения отыскивают, используя ухищрения (обходные пути). Выполняется переход к Ганкелевой (теплицевой) системе линейных уравнений относительно коэффициентов многочлена локаторов.
Преобразование к системе линейных уравнений
В уравнение многочлена локаторов ошибок подставляется значение его корней
. При этом многочлен обращается в нуль. Образуется тождество, обе части которого умножаем на
, получаем:
.
Таких равенств получаем
Суммируем эти равенства по всем , при которых эти равенства выполняются. Так как многочлен σ(z) имеет v корней
, раскроем скобки и перенесем коэффициенты
за знак суммы:

В этом равенстве согласно системе нелинейных уравнений, приведенной
ранее, каждая сумма равна одному из компонентов вектора синдрома. Отсюда заключает, что относительно коэффициентов можно выписать систему уже линейных уравнений.
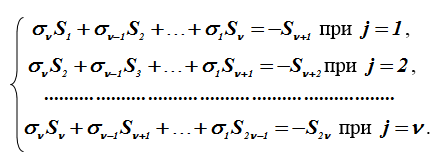
Знаки «–» при вычислениях над двоичным полем опускаются, так как со-ответствуют «+». Полученная система линейных уравнений является ганкелевой и ей соответствует матрица с размерами бит.

Эта матрица не вырождена, если число ошибок в кодовом слове C(E) строго равно , т.е. способность помехоустойчивости данного кода не нарушилась.
Решение системы линейных уравнений
Полученная система линейных уравнений в качестве неизвестных содержит коэффициенты многочлена локаторов ошибок для кодового слова C(E). Известными считаются вычисленные ранее компоненты синдромного вектора
. Здесь t – количество ошибок в слове, m – количество проверочных позиций в слове.
Существуют разные методы решения сформированной системы.
Отметим, что матрица (ганкелева) не вырождена для размерностей, ограниченных количеством допустимым в отдельном слове (меньшем 0.5m) ошибок. При этом система уравнений однозначно разрешается, а задача может быть сведена просто к обращению ганкелевой матрицы. Желательно было бы снять ограничение на размерность матриц, т.е. над бесконечным полем.
Над бесконечными полями известны методы решения ганкелевой системы линейных уравнений:
- итеративный метод Тренча – Берлекэмпа — Месси (ТБМ-метод); (1)
- прямой детерминированный Питерсона — Горенштейна — Цирлера; (ПГЦ — метод); (2)
- метод Сугиямы, использующий алгоритм Евклида для нахождения НОД (С-метод).(3)
Не рассматривая других методов, остановим свой выбор на ТБМ-методе. Мотивировка выбора следующая.
Метод (ПГЦ) прост и хорош, но для малого количества исправляемых ошибок, С-метод сложен для реализации на ЭВМ и ограниченно опубликован (освещен) в источниках, хотя С-метод как и ТБМ-метод по известному многочлену синдромов S(z) обеспечивает решение уравнения Падэ над полем Галуа. Это уравнение сформировано для многочлена локаторов ошибок σ(z) и многочлена ω(z), в теории кодирования называется ключевым уравнением Падэ:
.
Решением ключевого уравнения является совокупность корней многочлена σ(z), и соответственно локаторов
, т.е. позиции ошибок. Значения (величины) ошибок
определяются из формулы Форни в виде
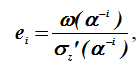
где и
— значения многочленов σ(z) и ω(z) в точке
, обратной корню многочлена σ(z);
i — позиция ошибки; — формальная производная многочлена σ(z) по z;
Формальная производная многочлена в конечном поле
Имеются различия и сходство для производной по переменной в поле вещественных чисел и формальной производной в конечном поле. Рассмотрим многочлен

– это элементы поля, i = 1(1)n
Элементы поля. Задан код над вещественным полем GF(24). Производная по z имеет вид:

В бесконечном вещественном поле операции умножить на n и суммировать n раз совпадают. Для конечных полей производная определяется иначе.
Производная по аналогии определяется соотношением:

где ((i)) = 1+1+…+1, (i) раз, суммируемых по правилам конечного поля: знак + обозначает операцию «суммировать столько-то раз», т.е. элемент повторить 2 раза, элемент
повторить 3 раза, элемент
повторить n раз.
Ясно, что эта операция не совпадает с операции умножения в конечном поле. В частности, в полях GF(2r) сумма четного числа одинаковых слагаемых берется по mod2 и обнуляется, а нечетного – равна самому слагаемому без изменений. Следовательно, в поле GF(2r) производная получает вид

вторая и старшие четные производные в этом поле равны нулю.
Из алгебры известно, если многочлен имеет кратные корни (кратность р ), то производная многочлена будет иметь этот же корень, но с кратностью р-1. Если р = 1, то f(z) и f ‘(z) не имеет общего корня. Следовательно, если многочлен и его производная имеют общий делитель, то существует кратный корень. Все корни производной f ‘(z) эти корни кратные в f(z).
Метод решения ключевого уравнения
ТМБ (Тренча-Берлекэмпа-Месси) — метод решения ключевого уравнения. Итеративный алгоритм обеспечивает определение многочленов σ(z) и ω(z), и решение уравнения Падэ (ключевого).
Исходные данные: коэффициенты многочлена степени n-1.
Цель. Определение в явном (аналитическом) виде многочленов σ(z) и ω(z).
В алгоритме используются обозначения: j — номер шага, — степень многочлена,
— разложение многочлена по степеням
и
— промежуточные переменные и функции на j-м шаге алгоритма;
Начальные условия необходимо задавать, так как здесь используется рекурсия.
Начальные условия:

Пример 4. Выполнение итеративного алгоритма для вектора
S=(8,13,7,13,15,15). Определяются многочлены и
.
Таблица 2 – Расчет многочленов локаторов ошибок
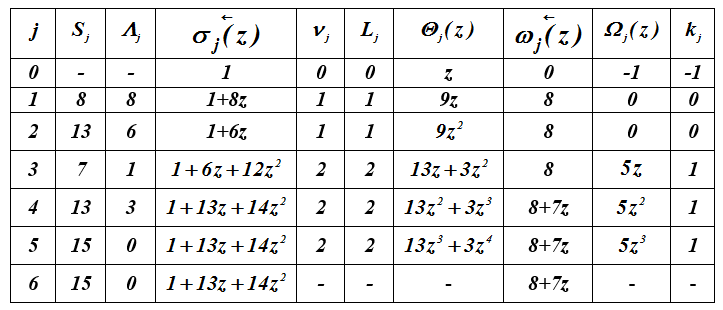
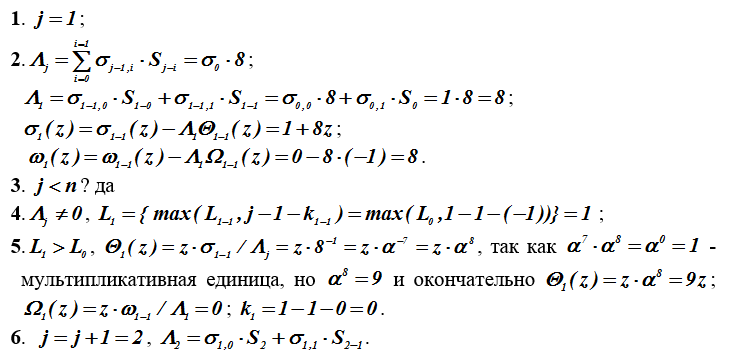
Итак ,
=7z+8.
Многочлен локаторов ошибок σ(z) над полем GF(24) с неприводимым многочленом p(x) = x4 + x + 1 имеет корни
и
, в этом легко убедиться непосредственной проверкой, т.е.
и
. Подстановка корней в
=
=;
=
=.
Взяв формальную производную от σ(z), получаем σ_2(z) =2·14+13 =13, так как 14z берется в сумме 2 раза и по mod 2 обращается в нуль.
С использованием формулы Форни найдем выражения для расчета величин ошибок .
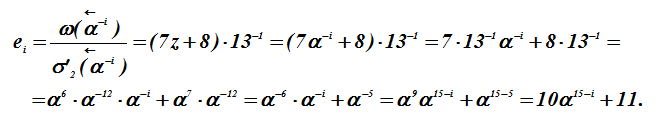
Подстановкой значений i = 3 и i = 10 позиций в последнее выражение
находим
= =
;
= =
.
Архитектура построения программного комплекса
Для построения программного комплекса предлагается использовать следующее архитектурное решение. Программный комплекс реализуется в виде приложения с графическим интерфейсом пользователя.
Исходными данными для программного комплекса является цифровой поток информации, выгруженной с помощью дампа из файла. Для удобства анализа и наглядности работы комплекса предполагается использование .txt файлов.
Загруженный цифровой поток представляется в виде массивов данных, в ходе работы комплекса над которыми применяются различные вычислительные действия.
На каждом этапе работы комплекса предоставляется возможность наглядного представления промежуточных результатов работы.
Результаты работы программного комплекса представляются в виде числовых данных, отображающихся в таблицах.
Сохранение промежуточных и окончательных результатов анализа производится в файлы.
Схема функционирования программного комплекса
Работа с комплекса начинается с загрузки цифрового потока с помощью дампа из файла. После загрузки пользователю предоставляется возможность визуального представления двоичного содержимого файла и его текстового содержимого.
В рамках данного интерфейса должны реализовываться следующие функциональные задачи:
- Загрузка исходного сообщения;
- Преобразование сообщения в дамп;
- Кодирование сообщения;
- Моделирование перехваченного сообщения
- Построение спектров полученных кодовых слов с целью анализа их визуального представления;
- Вывод на экран параметров кода.
Описание работы программного комплекса
При запуске исполняемого файла программы на экране появляется окно представленное на рисунке 2, в котором отображён основной интерфейс программы.
На вход программы подается файл, который нужно передать по каналу связи. Для его передачи по реальным каналам связи требуется кодирование – добавление к нему проверочных символов, необходимых для однозначного декодирования слова на источнике-получателе. Для начала работы комплекса необходимо с помощью кнопки “Загрузить файл” выбрать нужный текстовый файл. Его содержимое будет отображено в нижнем поле главного окна программы.
Двоичное представление сообщения будет представлено в соответствующем поле, двоичное представление информационных слов – в поле “Двоичное представление информационных слов”.
Число бит исходного сообщения и общее число слов в нем отображаются в полях “Количество бит в передаваемом сообщении” и “Количество слов в передаваемом сообщении”.
Сформированные информационные и кодовые слова отображаются в таблицах в правой части основного окна программы.
Окно программы с промежуточными результатами представлено на рисунке 3.

Рисунок 3 – Промежуточное представление результатов работы программного комплекса

Рисунок 4. Результаты загрузки файла сообщения
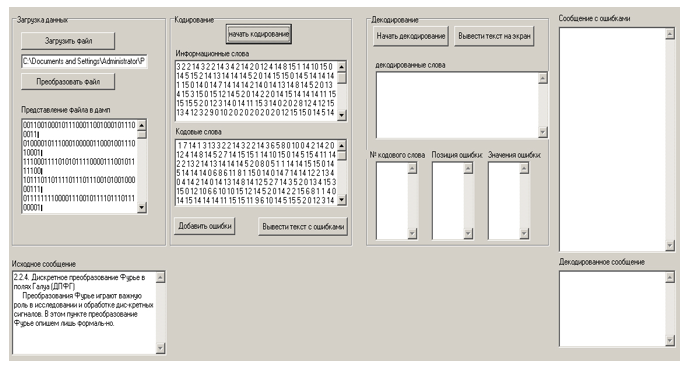
Рисунок 5. Результаты кодирования файла

Рисунок 6. Вывод сообщения с внесенными в него ошибками.

Рисунок 7. Вывод результатов декодирования и сообщения с внесенными в него ошибками
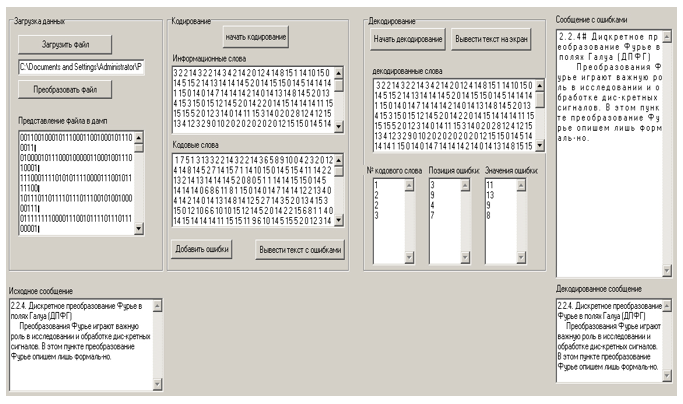
Рисунок 8. Вывод декодированного сообщения.
Заключение
АНБ США является главным оператором глобальной системы перехвата «Эшелон». «Эшелон» располагает разветвлённой инфраструктурой, включающей в себя станции наземного слежения, расположенные по всему миру. Отслеживаются практически все мировые информационные потоки.
Исследование возможностей получения доступа к семантике кодированных информационных сообщений в настоящее время активной информационной борьбы как в области технологий, так и в политике — стало очередным вызовом и одной из актуальных и востребованных задач современности.
В подавляющем большинстве кодов кодирование и декодирование сообщений (информации) реализуется на строгой математической основе конечных расширенных полей Галуа. Работа с элементами таких полей отличается от общепринятых в арифметике и требует при использовании вычислительных средств написания специальных процедур манипулирования с элементами полей.
Предлагаемая вниманию читателей работа слегка приоткрывает завесу тайны над подобной деятельностью на уровне фирм, компаний и государств в целом.
Список используемой литературы
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. – М.: Мир, 1986. – 576 с.
- Мак-Вильямс Ф. Дж, Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. – М.: Связь, 1979. – 744 с.
- Берлекэмп Э. Алгебраическая теория кодирования. – М.: Мир, 1971. – 478 с.
- Габидулин Э.М., Афанасьев В.Б. Кодирование в радиоэлектронике. – М.: Радио и связь, 1986. – 176 с., ил.
- Вернер М. Основы кодирования. Учебник для ВУЗов. – М.: Техносфера, 2004. – 288 с.
- Трифонов П.В. Адаптивное кодирование в многочастотных системах. Диссертация на соискание ученой степени кандидата технических наук. – СПб: Санкт-Петербургский государственный политехнический университет, 2005. – 147 с.
- Фомичев С. М., Абилов А.В. Обзор математических моделей каналов связи и их применение в телекоммуникационных системах. – Ижевск: Ижевский государственный технический университет, 2001. – 60 с.
- Касами Т., Токура Н., Ивадари Е., Инагаки Я. Теория кодирования. – М.: Мир, 1978. – 576 с.
- Муттер В. М. Основы помехоустойчивой телепередачи информации. – Л.: Энергоатомиздат. Ленинградское отделение, 1990. – 288 с.
- Ваулин А. Е., Смирнов С.И. «Моделирование помехозащищенного канала передачи сообщения в системе связи»/Сборник алгоритмов и программ типовых задач. Вып.26. под редакцией ктн доц. И.А. Кудряшова –. СПб.: ВКА им А.Ф. Можайского, 2007. – стр. 121-130.
- Карпушев С.И Конспект лекций по алгебре (часть 2. Абстрактная алгебра). – ВИКУ им. А. Ф. Можайского, 2002. – 97 с.
- Зайцев И. Е. Методика определения параметров помехоустойчивого каскадного кодирования. – Л.: ВИКИ, 1987 – 120 с.
| Reed–Solomon codes | |
|---|---|
| Named after | Irving S. Reed and Gustave Solomon |
| Classification | |
| Hierarchy | Linear block code Polynomial code Reed–Solomon code |
| Block length | n |
| Message length | k |
| Distance | n − k + 1 |
| Alphabet size | q = pm ≥ n (p prime) Often n = q − 1. |
| Notation | [n, k, n − k + 1]q-code |
| Algorithms | |
| Berlekamp–Massey Euclidean et al. |
|
| Properties | |
| Maximum-distance separable code | |
|
Reed–Solomon codes are a group of error-correcting codes that were introduced by Irving S. Reed and Gustave Solomon in 1960.[1]
They have many applications, the most prominent of which include consumer technologies such as MiniDiscs, CDs, DVDs, Blu-ray discs, QR codes, data transmission technologies such as DSL and WiMAX, broadcast systems such as satellite communications, DVB and ATSC, and storage systems such as RAID 6.
Reed–Solomon codes operate on a block of data treated as a set of finite-field elements called symbols. Reed–Solomon codes are able to detect and correct multiple symbol errors. By adding t = n − k check symbols to the data, a Reed–Solomon code can detect (but not correct) any combination of up to t erroneous symbols, or locate and correct up to ⌊t/2⌋ erroneous symbols at unknown locations. As an erasure code, it can correct up to t erasures at locations that are known and provided to the algorithm, or it can detect and correct combinations of errors and erasures. Reed–Solomon codes are also suitable as multiple-burst bit-error correcting codes, since a sequence of b + 1 consecutive bit errors can affect at most two symbols of size b. The choice of t is up to the designer of the code and may be selected within wide limits.
There are two basic types of Reed–Solomon codes – original view and BCH view – with BCH view being the most common, as BCH view decoders are faster and require less working storage than original view decoders.
History[edit]
Reed–Solomon codes were developed in 1960 by Irving S. Reed and Gustave Solomon, who were then staff members of MIT Lincoln Laboratory. Their seminal article was titled «Polynomial Codes over Certain Finite Fields». (Reed & Solomon 1960). The original encoding scheme described in the Reed & Solomon article used a variable polynomial based on the message to be encoded where only a fixed set of values (evaluation points) to be encoded are known to encoder and decoder. The original theoretical decoder generated potential polynomials based on subsets of k (unencoded message length) out of n (encoded message length) values of a received message, choosing the most popular polynomial as the correct one, which was impractical for all but the simplest of cases. This was initially resolved by changing the original scheme to a BCH code like scheme based on a fixed polynomial known to both encoder and decoder, but later, practical decoders based on the original scheme were developed, although slower than the BCH schemes. The result of this is that there are two main types of Reed Solomon codes, ones that use the original encoding scheme, and ones that use the BCH encoding scheme.
Also in 1960, a practical fixed polynomial decoder for BCH codes developed by Daniel Gorenstein and Neal Zierler was described in an MIT Lincoln Laboratory report by Zierler in January 1960 and later in a paper in June 1961.[2] The Gorenstein–Zierler decoder and the related work on BCH codes are described in a book Error Correcting Codes by W. Wesley Peterson (1961).[3] By 1963 (or possibly earlier), J. J. Stone (and others) recognized that Reed Solomon codes could use the BCH scheme of using a fixed generator polynomial, making such codes a special class of BCH codes,[4] but Reed Solomon codes based on the original encoding scheme, are not a class of BCH codes, and depending on the set of evaluation points, they are not even cyclic codes.
In 1969, an improved BCH scheme decoder was developed by Elwyn Berlekamp and James Massey, and has since been known as the Berlekamp–Massey decoding algorithm.
In 1975, another improved BCH scheme decoder was developed by Yasuo Sugiyama, based on the extended Euclidean algorithm.[5]

In 1977, Reed–Solomon codes were implemented in the Voyager program in the form of concatenated error correction codes. The first commercial application in mass-produced consumer products appeared in 1982 with the compact disc, where two interleaved Reed–Solomon codes are used. Today, Reed–Solomon codes are widely implemented in digital storage devices and digital communication standards, though they are being slowly replaced by Bose–Chaudhuri–Hocquenghem (BCH) codes. For example, Reed–Solomon codes are used in the Digital Video Broadcasting (DVB) standard DVB-S, in conjunction with a convolutional inner code, but BCH codes are used with LDPC in its successor, DVB-S2.
In 1986, an original scheme decoder known as the Berlekamp–Welch algorithm was developed.
In 1996, variations of original scheme decoders called list decoders or soft decoders were developed by Madhu Sudan and others, and work continues on these types of decoders – see Guruswami–Sudan list decoding algorithm.
In 2002, another original scheme decoder was developed by Shuhong Gao, based on the extended Euclidean algorithm.[6]
Applications[edit]
Data storage[edit]
Reed–Solomon coding is very widely used in mass storage systems to correct
the burst errors associated with media defects.
Reed–Solomon coding is a key component of the compact disc. It was the first use of strong error correction coding in a mass-produced consumer product, and DAT and DVD use similar schemes. In the CD, two layers of Reed–Solomon coding separated by a 28-way convolutional interleaver yields a scheme called Cross-Interleaved Reed–Solomon Coding (CIRC). The first element of a CIRC decoder is a relatively weak inner (32,28) Reed–Solomon code, shortened from a (255,251) code with 8-bit symbols. This code can correct up to 2 byte errors per 32-byte block. More importantly, it flags as erasures any uncorrectable blocks, i.e., blocks with more than 2 byte errors. The decoded 28-byte blocks, with erasure indications, are then spread by the deinterleaver to different blocks of the (28,24) outer code. Thanks to the deinterleaving, an erased 28-byte block from the inner code becomes a single erased byte in each of 28 outer code blocks. The outer code easily corrects this, since it can handle up to 4 such erasures per block.
The result is a CIRC that can completely correct error bursts up to 4000 bits, or about 2.5 mm on the disc surface. This code is so strong that most CD playback errors are almost certainly caused by tracking errors that cause the laser to jump track, not by uncorrectable error bursts.[7]
DVDs use a similar scheme, but with much larger blocks, a (208,192) inner code, and a (182,172) outer code.
Reed–Solomon error correction is also used in parchive files which are commonly posted accompanying multimedia files on USENET. The distributed online storage service Wuala (discontinued in 2015) also used Reed–Solomon when breaking up files.
Bar code[edit]
Almost all two-dimensional bar codes such as PDF-417, MaxiCode, Datamatrix, QR Code, and Aztec Code use Reed–Solomon error correction to allow correct reading even if a portion of the bar code is damaged. When the bar code scanner cannot recognize a bar code symbol, it will treat it as an erasure.
Reed–Solomon coding is less common in one-dimensional bar codes, but is used by the PostBar symbology.
Data transmission[edit]
Specialized forms of Reed–Solomon codes, specifically Cauchy-RS and Vandermonde-RS, can be used to overcome the unreliable nature of data transmission over erasure channels. The encoding process assumes a code of RS(N, K) which results in N codewords of length N symbols each storing K symbols of data, being generated, that are then sent over an erasure channel.
Any combination of K codewords received at the other end is enough to reconstruct all of the N codewords. The code rate is generally set to 1/2 unless the channel’s erasure likelihood can be adequately modelled and is seen to be less. In conclusion, N is usually 2K, meaning that at least half of all the codewords sent must be received in order to reconstruct all of the codewords sent.
Reed–Solomon codes are also used in xDSL systems and CCSDS’s Space Communications Protocol Specifications as a form of forward error correction.
Space transmission[edit]

Deep-space concatenated coding system.[8] Notation: RS(255, 223) + CC («constraint length» = 7, code rate = 1/2).
One significant application of Reed–Solomon coding was to encode the digital pictures sent back by the Voyager program.
Voyager introduced Reed–Solomon coding concatenated with convolutional codes, a practice that has since become very widespread in deep space and satellite (e.g., direct digital broadcasting) communications.
Viterbi decoders tend to produce errors in short bursts. Correcting these burst errors is a job best done by short or simplified Reed–Solomon codes.
Modern versions of concatenated Reed–Solomon/Viterbi-decoded convolutional coding were and are used on the Mars Pathfinder, Galileo, Mars Exploration Rover and Cassini missions, where they perform within about 1–1.5 dB of the ultimate limit, the Shannon capacity.
These concatenated codes are now being replaced by more powerful turbo codes:
| Years | Code | Mission(s) |
|---|---|---|
| 1958–present | Uncoded | Explorer, Mariner, many others |
| 1968–1978 | convolutional codes (CC) (25, 1/2) | Pioneer, Venus |
| 1969–1975 | Reed-Muller code (32, 6) | Mariner, Viking |
| 1977–present | Binary Golay code | Voyager |
| 1977–present | RS(255, 223) + CC(7, 1/2) | Voyager, Galileo, many others |
| 1989–2003 | RS(255, 223) + CC(7, 1/3) | Voyager |
| 1989–2003 | RS(255, 223) + CC(14, 1/4) | Galileo |
| 1996–present | RS + CC (15, 1/6) | Cassini, Mars Pathfinder, others |
| 2004–present | Turbo codes[nb 1] | Messenger, Stereo, MRO, others |
| est. 2009 | LDPC codes | Constellation, MSL |
Constructions (encoding)[edit]
The Reed–Solomon code is actually a family of codes, where every code is characterised by three parameters: an alphabet size q, a block length n, and a message length k, with k < n ≤ q. The set of alphabet symbols is interpreted as the finite field of order q, and thus, q must be a prime power. In the most useful parameterizations of the Reed–Solomon code, the block length is usually some constant multiple of the message length, that is, the rate R = k/n is some constant, and furthermore, the block length is equal to or one less than the alphabet size, that is, n = q or n = q − 1.[citation needed]
Reed & Solomon’s original view: The codeword as a sequence of values[edit]
There are different encoding procedures for the Reed–Solomon code, and thus, there are different ways to describe the set of all codewords.
In the original view of Reed & Solomon (1960), every codeword of the Reed–Solomon code is a sequence of function values of a polynomial of degree less than k. In order to obtain a codeword of the Reed–Solomon code, the message symbols (each within the q-sized alphabet) are treated as the coefficients of a polynomial p of degree less than k, over the finite field F with q elements.
In turn, the polynomial p is evaluated at n ≤ q distinct points 
Formally, the set 
Since any two distinct polynomials of degree less than 







Being a code that achieves this optimal trade-off, the Reed–Solomon code belongs to the class of maximum distance separable codes.
While the number of different polynomials of degree less than k and the number of different messages are both equal to 

Simple encoding procedure: The message as a sequence of coefficients[edit]
In the original construction of Reed & Solomon (1960), the message 

The codeword of 





This function 




This matrix is the transpose of a Vandermonde matrix over 

Systematic encoding procedure: The message as an initial sequence of values[edit]
There is an alternative encoding procedure that also produces the Reed–Solomon code, but that does so in a systematic way. Here, the mapping from the message 



To compute this polynomial 

Once it has been found, it is evaluated at the other points 
The alternative encoding function 
Since the first 


Since Lagrange interpolation is a linear transformation, 

Discrete Fourier transform and its inverse[edit]
A discrete Fourier transform is essentially the same as the encoding procedure; it uses the generator polynomial p(x) to map a set of evaluation points into the message values as shown above:
The inverse Fourier transform could be used to convert an error free set of n < q message values back into the encoding polynomial of k coefficients, with the constraint that in order for this to work, the set of evaluation points used to encode the message must be a set of increasing powers of α:
However, Lagrange interpolation performs the same conversion without the constraint on the set of evaluation points or the requirement of an error free set of message values and is used for systematic encoding, and in one of the steps of the Gao decoder.
The BCH view: The codeword as a sequence of coefficients[edit]
In this view, the message is interpreted as the coefficients of a polynomial 











For a «narrow sense code», 
Systematic encoding procedure[edit]
The encoding procedure for the BCH view of Reed–Solomon codes can be modified to yield a systematic encoding procedure, in which each codeword contains the message as a prefix, and simply appends error correcting symbols as a suffix. Here, instead of sending 









Formally, the construction is done by multiplying 





The remainder has degree at most 





As a result, the codewords 


Properties[edit]
The Reed–Solomon code is a [n, k, n − k + 1] code; in other words, it is a linear block code of length n (over F) with dimension k and minimum Hamming distance 
The error-correcting ability of a Reed–Solomon code is determined by its minimum distance, or equivalently, by 




Theoretical BER performance of the Reed-Solomon code (N=255, K=233, QPSK, AWGN). Step-like characteristic.
The theoretical error bound can be described via the following formula for the AWGN channel for FSK:[11]
and for other modulation schemes:
where 




For practical uses of Reed–Solomon codes, it is common to use a finite field 


The sender sends the data points as encoded blocks, and the number of symbols in the encoded block is 






The Reed–Solomon code properties discussed above make them especially well-suited to applications where errors occur in bursts. This is because it does not matter to the code how many bits in a symbol are in error — if multiple bits in a symbol are corrupted it only counts as a single error. Conversely, if a data stream is not characterized by error bursts or drop-outs but by random single bit errors, a Reed–Solomon code is usually a poor choice compared to a binary code.
The Reed–Solomon code, like the convolutional code, is a transparent code. This means that if the channel symbols have been inverted somewhere along the line, the decoders will still operate. The result will be the inversion of the original data. However, the Reed–Solomon code loses its transparency when the code is shortened. The «missing» bits in a shortened code need to be filled by either zeros or ones, depending on whether the data is complemented or not. (To put it another way, if the symbols are inverted, then the zero-fill needs to be inverted to a one-fill.) For this reason it is mandatory that the sense of the data (i.e., true or complemented) be resolved before Reed–Solomon decoding.
Whether the Reed–Solomon code is cyclic or not depends on subtle details of the construction. In the original view of Reed and Solomon, where the codewords are the values of a polynomial, one can choose the sequence of evaluation points in such a way as to make the code cyclic. In particular, if 












[edit]
Designers are not required to use the «natural» sizes of Reed–Solomon code blocks. A technique known as «shortening» can produce a smaller code of any desired size from a larger code. For example, the widely used (255,223) code can be converted to a (160,128) code by padding the unused portion of the source block with 95 binary zeroes and not transmitting them. At the decoder, the same portion of the block is loaded locally with binary zeroes. The Delsarte–Goethals–Seidel[12] theorem illustrates an example of an application of shortened Reed–Solomon codes. In parallel to shortening, a technique known as puncturing allows omitting some of the encoded parity symbols.
BCH view decoders[edit]
The decoders described in this section use the BCH view of a codeword as a sequence of coefficients. They use a fixed generator polynomial known to both encoder and decoder.
Peterson–Gorenstein–Zierler decoder[edit]
Daniel Gorenstein and Neal Zierler developed a decoder that was described in a MIT Lincoln Laboratory report by Zierler in January 1960 and later in a paper in June 1961.[13] The Gorenstein–Zierler decoder and the related work on BCH codes are described in a book Error Correcting Codes by W. Wesley Peterson (1961).[14]
Formulation[edit]
The transmitted message, 
As a result of the Reed-Solomon encoding procedure, s(x) is divisible by the generator polynomial g(x):
where α is a primitive element.
Since s(x) is a multiple of the generator g(x), it follows that it «inherits» all its roots.
Therefore,
The transmitted polynomial is corrupted in transit by an error polynomial e(x) to produce the received polynomial r(x).
Coefficient ei will be zero if there is no error at that power of x and nonzero if there is an error. If there are ν errors at distinct powers ik of x, then
The goal of the decoder is to find the number of errors (ν), the positions of the errors (ik), and the error values at those positions (eik). From those, e(x) can be calculated and subtracted from r(x) to get the originally sent message s(x).
Syndrome decoding[edit]
The decoder starts by evaluating the polynomial as received at points 
Note that 


The advantage of looking at the syndromes is that the message polynomial drops out. In other words, the syndromes only relate to the error, and are unaffected by the actual contents of the message being transmitted. If the syndromes are all zero, the algorithm stops here and reports that the message was not corrupted in transit.
Error locators and error values[edit]
For convenience, define the error locators Xk and error values Yk as:
Then the syndromes can be written in terms of these error locators and error values as
This definition of the syndrome values is equivalent to the previous since 
The syndromes give a system of n − k ≥ 2ν equations in 2ν unknowns, but that system of equations is nonlinear in the Xk and does not have an obvious solution. However, if the Xk were known (see below), then the syndrome equations provide a linear system of equations that can easily be solved for the Yk error values.
Consequently, the problem is finding the Xk, because then the leftmost matrix would be known, and both sides of the equation could be multiplied by its inverse, yielding Yk
In the variant of this algorithm where the locations of the errors are already known (when it is being used as an erasure code), this is the end. The error locations (Xk) are already known by some other method (for example, in an FM transmission, the sections where the bitstream was unclear or overcome with interference are probabilistically determinable from frequency analysis). In this scenario, up to 
The rest of the algorithm serves to locate the errors, and will require syndrome values up to 

Error locator polynomial[edit]
There is a linear recurrence relation that gives rise to a system of linear equations. Solving those equations identifies those error locations Xk.
Define the error locator polynomial Λ(x) as
The zeros of Λ(x) are the reciprocals 


Let 


Sum for k = 1 to ν and it will still be zero.
Collect each term into its own sum.
Extract the constant values of 
These summations are now equivalent to the syndrome values, which we know and can substitute in! This therefore reduces to
Subtracting 
Recall that j was chosen to be any integer between 1 and v inclusive, and this equivalence is true for any and all such values. Therefore, we have v linear equations, not just one. This system of linear equations can therefore be solved for the coefficients Λi of the error location polynomial:
The above assumes the decoder knows the number of errors ν, but that number has not been determined yet. The PGZ decoder does not determine ν directly but rather searches for it by trying successive values. The decoder first assumes the largest value for a trial ν and sets up the linear system for that value. If the equations can be solved (i.e., the matrix determinant is nonzero), then that trial value is the number of errors. If the linear system cannot be solved, then the trial ν is reduced by one and the next smaller system is examined. (Gill n.d., p. 35)
Find the roots of the error locator polynomial[edit]
Use the coefficients Λi found in the last step to build the error location polynomial. The roots of the error location polynomial can be found by exhaustive search. The error locators Xk are the reciprocals of those roots. The order of coefficients of the error location polynomial can be reversed, in which case the roots of that reversed polynomial are the error locators 

Calculate the error values[edit]
Once the error locators Xk are known, the error values can be determined. This can be done by direct solution for Yk in the error equations matrix given above, or using the Forney algorithm.
Calculate the error locations[edit]
Calculate ik by taking the log base 
Fix the errors[edit]
Finally, e(x) is generated from ik and eik and then is subtracted from r(x) to get the originally sent message s(x), with errors corrected.
Example[edit]
Consider the Reed–Solomon code defined in GF(929) with α = 3 and t = 4 (this is used in PDF417 barcodes) for a RS(7,3) code. The generator polynomial is
If the message polynomial is p(x) = 3 x2 + 2 x + 1, then a systematic codeword is encoded as follows.
Errors in transmission might cause this to be received instead.
The syndromes are calculated by evaluating r at powers of α.
Using Gaussian elimination:
Λ(x) = 329 x2 + 821 x + 001, with roots x1 = 757 = 3−3 and x2 = 562 = 3−4
The coefficients can be reversed to produce roots with positive exponents, but typically this isn’t used:
R(x) = 001 x2 + 821 x + 329, with roots 27 = 33 and 81 = 34
with the log of the roots corresponding to the error locations (right to left, location 0 is the last term in the codeword).
To calculate the error values, apply the Forney algorithm.
Ω(x) = S(x) Λ(x) mod x4 = 546 x + 732
Λ'(x) = 658 x + 821
e1 = −Ω(x1)/Λ'(x1) = 074
e2 = −Ω(x2)/Λ'(x2) = 122
Subtracting 
Berlekamp–Massey decoder[edit]
The Berlekamp–Massey algorithm is an alternate iterative procedure for finding the error locator polynomial. During each iteration, it calculates a discrepancy based on a current instance of Λ(x) with an assumed number of errors e:
and then adjusts Λ(x) and e so that a recalculated Δ would be zero. The article Berlekamp–Massey algorithm has a detailed description of the procedure. In the following example, C(x) is used to represent Λ(x).
Example[edit]
Using the same data as the Peterson Gorenstein Zierler example above:
| n | Sn+1 | d | C | B | b | m |
|---|---|---|---|---|---|---|
| 0 | 732 | 732 | 197 x + 1 | 1 | 732 | 1 |
| 1 | 637 | 846 | 173 x + 1 | 1 | 732 | 2 |
| 2 | 762 | 412 | 634 x2 + 173 x + 1 | 173 x + 1 | 412 | 1 |
| 3 | 925 | 576 | 329 x2 + 821 x + 1 | 173 x + 1 | 412 | 2 |
The final value of C is the error locator polynomial, Λ(x).
Euclidean decoder[edit]
Another iterative method for calculating both the error locator polynomial and the error value polynomial is based on Sugiyama’s adaptation of the extended Euclidean algorithm .
Define S(x), Λ(x), and Ω(x) for t syndromes and e errors:
The key equation is:
For t = 6 and e = 3:
The middle terms are zero due to the relationship between Λ and syndromes.
The extended Euclidean algorithm can find a series of polynomials of the form
Ai(x) S(x) + Bi(x) xt = Ri(x)
where the degree of R decreases as i increases. Once the degree of Ri(x) < t/2, then
Ai(x) = Λ(x)
Bi(x) = −Q(x)
Ri(x) = Ω(x).
B(x) and Q(x) don’t need to be saved, so the algorithm becomes:
R−1 := xt R0 := S(x) A−1 := 0 A0 := 1 i := 0 while degree of Ri ≥ t/2 i := i + 1 Q := Ri-2 / Ri-1 Ri := Ri-2 - Q Ri-1 Ai := Ai-2 - Q Ai-1
to set low order term of Λ(x) to 1, divide Λ(x) and Ω(x) by Ai(0):
Λ(x) = Ai / Ai(0)
Ω(x) = Ri / Ai(0)
Ai(0) is the constant (low order) term of Ai.
Example[edit]
Using the same data as the Peterson–Gorenstein–Zierler example above:
| i | Ri | Ai |
|---|---|---|
| −1 | 001 x4 + 000 x3 + 000 x2 + 000 x + 000 | 000 |
| 0 | 925 x3 + 762 x2 + 637 x + 732 | 001 |
| 1 | 683 x2 + 676 x + 024 | 697 x + 396 |
| 2 | 673 x + 596 | 608 x2 + 704 x + 544 |
Λ(x) = A2 / 544 = 329 x2 + 821 x + 001
Ω(x) = R2 / 544 = 546 x + 732
Decoder using discrete Fourier transform[edit]
A discrete Fourier transform can be used for decoding.[15] To avoid conflict with syndrome names, let c(x) = s(x) the encoded codeword. r(x) and e(x) are the same as above. Define C(x), E(x), and R(x) as the discrete Fourier transforms of c(x), e(x), and r(x). Since r(x) = c(x) + e(x), and since a discrete Fourier transform is a linear operator, R(x) = C(x) + E(x).
Transform r(x) to R(x) using discrete Fourier transform. Since the calculation for a discrete Fourier transform is the same as the calculation for syndromes, t coefficients of R(x) and E(x) are the same as the syndromes:
Use 

Let v = number of errors. Generate E(x) using the known coefficients 

Then calculate C(x) = R(x) − E(x) and take the inverse transform (polynomial interpolation) of C(x) to produce c(x).
Decoding beyond the error-correction bound[edit]
The Singleton bound states that the minimum distance d of a linear block code of size (n,k) is upper-bounded by n − k + 1. The distance d was usually understood to limit the error-correction capability to ⌊(d−1) / 2⌋. The Reed–Solomon code achieves this bound with equality, and can thus correct up to ⌊(n−k) / 2⌋ errors. However, this error-correction bound is not exact.
In 1999, Madhu Sudan and Venkatesan Guruswami at MIT published «Improved Decoding of Reed–Solomon and Algebraic-Geometry Codes» introducing an algorithm that allowed for the correction of errors beyond half the minimum distance of the code.[16] It applies to Reed–Solomon codes and more generally to algebraic geometric codes. This algorithm produces a list of codewords (it is a list-decoding algorithm) and is based on interpolation and factorization of polynomials over 
Soft-decoding[edit]
The algebraic decoding methods described above are hard-decision methods, which means that for every symbol a hard decision is made about its value. For example, a decoder could associate with each symbol an additional value corresponding to the channel demodulator’s confidence in the correctness of the symbol. The advent of LDPC and turbo codes, which employ iterated soft-decision belief propagation decoding methods to achieve error-correction performance close to the theoretical limit, has spurred interest in applying soft-decision decoding to conventional algebraic codes. In 2003, Ralf Koetter and Alexander Vardy presented a polynomial-time soft-decision algebraic list-decoding algorithm for Reed–Solomon codes, which was based upon the work by Sudan and Guruswami.[17]
In 2016, Steven J. Franke and Joseph H. Taylor published a novel soft-decision decoder.[18]
MATLAB example[edit]
Encoder[edit]
Here we present a simple MATLAB implementation for an encoder.
function encoded = rsEncoder(msg, m, prim_poly, n, k) % RSENCODER Encode message with the Reed-Solomon algorithm % m is the number of bits per symbol % prim_poly: Primitive polynomial p(x). Ie for DM is 301 % k is the size of the message % n is the total size (k+redundant) % Example: msg = uint8('Test') % enc_msg = rsEncoder(msg, 8, 301, 12, numel(msg)); % Get the alpha alpha = gf(2, m, prim_poly); % Get the Reed-Solomon generating polynomial g(x) g_x = genpoly(k, n, alpha); % Multiply the information by X^(n-k), or just pad with zeros at the end to % get space to add the redundant information msg_padded = gf([msg zeros(1, n - k)], m, prim_poly); % Get the remainder of the division of the extended message by the % Reed-Solomon generating polynomial g(x) [~, remainder] = deconv(msg_padded, g_x); % Now return the message with the redundant information encoded = msg_padded - remainder; end % Find the Reed-Solomon generating polynomial g(x), by the way this is the % same as the rsgenpoly function on matlab function g = genpoly(k, n, alpha) g = 1; % A multiplication on the galois field is just a convolution for k = mod(1 : n - k, n) g = conv(g, [1 alpha .^ (k)]); end end
Decoder[edit]
Now the decoding part:
function [decoded, error_pos, error_mag, g, S] = rsDecoder(encoded, m, prim_poly, n, k) % RSDECODER Decode a Reed-Solomon encoded message % Example: % [dec, ~, ~, ~, ~] = rsDecoder(enc_msg, 8, 301, 12, numel(msg)) max_errors = floor((n - k) / 2); orig_vals = encoded.x; % Initialize the error vector errors = zeros(1, n); g = []; S = []; % Get the alpha alpha = gf(2, m, prim_poly); % Find the syndromes (Check if dividing the message by the generator % polynomial the result is zero) Synd = polyval(encoded, alpha .^ (1:n - k)); Syndromes = trim(Synd); % If all syndromes are zeros (perfectly divisible) there are no errors if isempty(Syndromes.x) decoded = orig_vals(1:k); error_pos = []; error_mag = []; g = []; S = Synd; return; end % Prepare for the euclidean algorithm (Used to find the error locating % polynomials) r0 = [1, zeros(1, 2 * max_errors)]; r0 = gf(r0, m, prim_poly); r0 = trim(r0); size_r0 = length(r0); r1 = Syndromes; f0 = gf([zeros(1, size_r0 - 1) 1], m, prim_poly); f1 = gf(zeros(1, size_r0), m, prim_poly); g0 = f1; g1 = f0; % Do the euclidean algorithm on the polynomials r0(x) and Syndromes(x) in % order to find the error locating polynomial while true % Do a long division [quotient, remainder] = deconv(r0, r1); % Add some zeros quotient = pad(quotient, length(g1)); % Find quotient*g1 and pad c = conv(quotient, g1); c = trim(c); c = pad(c, length(g0)); % Update g as g0-quotient*g1 g = g0 - c; % Check if the degree of remainder(x) is less than max_errors if all(remainder(1:end - max_errors) == 0) break; end % Update r0, r1, g0, g1 and remove leading zeros r0 = trim(r1); r1 = trim(remainder); g0 = g1; g1 = g; end % Remove leading zeros g = trim(g); % Find the zeros of the error polynomial on this galois field evalPoly = polyval(g, alpha .^ (n - 1 : - 1 : 0)); error_pos = gf(find(evalPoly == 0), m); % If no error position is found we return the received work, because % basically is nothing that we could do and we return the received message if isempty(error_pos) decoded = orig_vals(1:k); error_mag = []; return; end % Prepare a linear system to solve the error polynomial and find the error % magnitudes size_error = length(error_pos); Syndrome_Vals = Syndromes.x; b(:, 1) = Syndrome_Vals(1:size_error); for idx = 1 : size_error e = alpha .^ (idx * (n - error_pos.x)); err = e.x; er(idx, :) = err; end % Solve the linear system error_mag = (gf(er, m, prim_poly) gf(b, m, prim_poly))'; % Put the error magnitude on the error vector errors(error_pos.x) = error_mag.x; % Bring this vector to the galois field errors_gf = gf(errors, m, prim_poly); % Now to fix the errors just add with the encoded code decoded_gf = encoded(1:k) + errors_gf(1:k); decoded = decoded_gf.x; end % Remove leading zeros from Galois array function gt = trim(g) gx = g.x; gt = gf(gx(find(gx, 1) : end), g.m, g.prim_poly); end % Add leading zeros function xpad = pad(x, k) len = length(x); if len < k xpad = [zeros(1, k - len) x]; end end
Reed Solomon original view decoders[edit]
The decoders described in this section use the Reed Solomon original view of a codeword as a sequence of polynomial values where the polynomial is based on the message to be encoded. The same set of fixed values are used by the encoder and decoder, and the decoder recovers the encoding polynomial (and optionally an error locating polynomial) from the received message.
Theoretical decoder[edit]
Reed & Solomon (1960) described a theoretical decoder that corrected errors by finding the most popular message polynomial. The decoder only knows the set of values 



Berlekamp Welch decoder[edit]
In 1986, a decoder known as the Berlekamp–Welch algorithm was developed as a decoder that is able to recover the original message polynomial as well as an error «locator» polynomial that produces zeroes for the input values that correspond to errors, with time complexity 

Example[edit]
Using RS(7,3), GF(929), and the set of evaluation points ai = i − 1
a = {0, 1, 2, 3, 4, 5, 6}
If the message polynomial is
p(x) = 003 x2 + 002 x + 001
The codeword is
c = {001, 006, 017, 034, 057, 086, 121}
Errors in transmission might cause this to be received instead.
b = c + e = {001, 006, 123, 456, 057, 086, 121}
The key equations are:
Assume maximum number of errors: e = 2. The key equations become:
Using Gaussian elimination:
Q(x) = 003 x4 + 916 x3 + 009 x2 + 007 x + 006
E(x) = 001 x2 + 924 x + 006
Q(x) / E(x) = P(x) = 003 x2 + 002 x + 001
Recalculate P(x) where E(x) = 0 : {2, 3} to correct b resulting in the corrected codeword:
c = {001, 006, 017, 034, 057, 086, 121}
Gao decoder[edit]
In 2002, an improved decoder was developed by Shuhong Gao, based on the extended Euclid algorithm.[6]
Example[edit]
Using the same data as the Berlekamp Welch example above:
| i | Ri | Ai |
|---|---|---|
| −1 | 001 x7 + 908 x6 + 175 x5 + 194 x4 + 695 x3 + 094 x2 + 720 x + 000 | 000 |
| 0 | 055 x6 + 440 x5 + 497 x4 + 904 x3 + 424 x2 + 472 x + 001 | 001 |
| 1 | 702 x5 + 845 x4 + 691 x3 + 461 x2 + 327 x + 237 | 152 x + 237 |
| 2 | 266 x4 + 086 x3 + 798 x2 + 311 x + 532 | 708 x2 + 176 x + 532 |
Q(x) = R2 = 266 x4 + 086 x3 + 798 x2 + 311 x + 532
E(x) = A2 = 708 x2 + 176 x + 532
divide Q(x) and E(x) by most significant coefficient of E(x) = 708. (Optional)
Q(x) = 003 x4 + 916 x3 + 009 x2 + 007 x + 006
E(x) = 001 x2 + 924 x + 006
Q(x) / E(x) = P(x) = 003 x2 + 002 x + 001
Recalculate P(x) where E(x) = 0 : {2, 3} to correct b resulting in the corrected codeword:
c = {001, 006, 017, 034, 057, 086, 121}
See also[edit]
- BCH code
- Cyclic code
- Chien search
- Berlekamp–Massey algorithm
- Forward error correction
- Berlekamp–Welch algorithm
- Folded Reed–Solomon code
Notes[edit]
- ^ Authors in Andrews et al. (2007), provide simulation results which show that for the same code rate (1/6) turbo codes outperform Reed-Solomon concatenated codes up to 2 dB (bit error rate).[9]
References[edit]
- ^ Reed & Solomon (1960)
- ^ D. Gorenstein and N. Zierler, «A class of cyclic linear error-correcting codes in p^m symbols», J. SIAM, vol. 9, pp. 207–214, June 1961
- ^ Error Correcting Codes by W_Wesley_Peterson, 1961
- ^ Error Correcting Codes by W_Wesley_Peterson, second edition, 1972
- ^ Yasuo Sugiyama, Masao Kasahara, Shigeichi Hirasawa, and Toshihiko Namekawa. A method for solving key equation for decoding Goppa codes. Information and Control, 27:87–99, 1975.
- ^ a b Gao, Shuhong (January 2002), New Algorithm For Decoding Reed-Solomon Codes (PDF), Clemson
- ^ Immink, K. A. S. (1994), «Reed–Solomon Codes and the Compact Disc», in Wicker, Stephen B.; Bhargava, Vijay K. (eds.), Reed–Solomon Codes and Their Applications, IEEE Press, ISBN 978-0-7803-1025-4
- ^ J. Hagenauer, E. Offer, and L. Papke, Reed Solomon Codes and Their Applications. New York IEEE Press, 1994 — p. 433
- ^ a b Andrews, Kenneth S., et al. «The development of turbo and LDPC codes for deep-space applications.» Proceedings of the IEEE 95.11 (2007): 2142-2156.
- ^ See Lin & Costello (1983, p. 171), for example.
- ^ «Analytical Expressions Used in bercoding and BERTool». Archived from the original on 2019-02-01. Retrieved 2019-02-01.
- ^ Pfender, Florian; Ziegler, Günter M. (September 2004), «Kissing Numbers, Sphere Packings, and Some Unexpected Proofs» (PDF), Notices of the American Mathematical Society, 51 (8): 873–883, archived (PDF) from the original on 2008-05-09, retrieved 2009-09-28. Explains the Delsarte-Goethals-Seidel theorem as used in the context of the error correcting code for compact disc.
- ^ D. Gorenstein and N. Zierler, «A class of cyclic linear error-correcting codes in p^m symbols,» J. SIAM, vol. 9, pp. 207–214, June 1961
- ^ Error Correcting Codes by W Wesley Peterson, 1961
- ^ Shu Lin and Daniel J. Costello Jr, «Error Control Coding» second edition, pp. 255–262, 1982, 2004
- ^ Guruswami, V.; Sudan, M. (September 1999), «Improved decoding of Reed–Solomon codes and algebraic geometry codes», IEEE Transactions on Information Theory, 45 (6): 1757–1767, CiteSeerX 10.1.1.115.292, doi:10.1109/18.782097
- ^ Koetter, Ralf; Vardy, Alexander (2003). «Algebraic soft-decision decoding of Reed–Solomon codes». IEEE Transactions on Information Theory. 49 (11): 2809–2825. CiteSeerX 10.1.1.13.2021. doi:10.1109/TIT.2003.819332.
- ^ Franke, Steven J.; Taylor, Joseph H. (2016). «Open Source Soft-Decision Decoder for the JT65 (63,12) Reed–Solomon Code» (PDF). QEX (May/June): 8–17. Archived (PDF) from the original on 2017-03-09. Retrieved 2017-06-07.
Further reading[edit]
- Gill, John (n.d.), EE387 Notes #7, Handout #28 (PDF), Stanford University, archived from the original (PDF) on June 30, 2014, retrieved April 21, 2010
- Hong, Jonathan; Vetterli, Martin (August 1995), «Simple Algorithms for BCH Decoding» (PDF), IEEE Transactions on Communications, 43 (8): 2324–2333, doi:10.1109/26.403765
- Lin, Shu; Costello, Jr., Daniel J. (1983), Error Control Coding: Fundamentals and Applications, New Jersey, NJ: Prentice-Hall, ISBN 978-0-13-283796-5
- Massey, J. L. (1969), «Shift-register synthesis and BCH decoding» (PDF), IEEE Transactions on Information Theory, IT-15 (1): 122–127, doi:10.1109/tit.1969.1054260
- Peterson, Wesley W. (1960), «Encoding and Error Correction Procedures for the Bose-Chaudhuri Codes», IRE Transactions on Information Theory, IT-6 (4): 459–470, doi:10.1109/TIT.1960.1057586
- Reed, Irving S.; Solomon, Gustave (1960), «Polynomial Codes over Certain Finite Fields», Journal of the Society for Industrial and Applied Mathematics, 8 (2): 300–304, doi:10.1137/0108018
- Welch, L. R. (1997), The Original View of Reed–Solomon Codes (PDF), Lecture Notes
- Berlekamp, Elwyn R. (1967), Nonbinary BCH decoding, International Symposium on Information Theory, San Remo, Italy
- Berlekamp, Elwyn R. (1984) [1968], Algebraic Coding Theory (Revised ed.), Laguna Hills, CA: Aegean Park Press, ISBN 978-0-89412-063-3
- Cipra, Barry Arthur (1993), «The Ubiquitous Reed–Solomon Codes», SIAM News, 26 (1)
- Forney, Jr., G. (October 1965), «On Decoding BCH Codes», IEEE Transactions on Information Theory, 11 (4): 549–557, doi:10.1109/TIT.1965.1053825
- Koetter, Ralf (2005), Reed–Solomon Codes, MIT Lecture Notes 6.451 (Video), archived from the original on 2013-03-13
- MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York, NY: North-Holland Publishing Company
- Reed, Irving S.; Chen, Xuemin (1999), Error-Control Coding for Data Networks, Boston, MA: Kluwer Academic Publishers
External links[edit]
Information and tutorials[edit]
- Introduction to Reed–Solomon codes: principles, architecture and implementation (CMU)
- A Tutorial on Reed–Solomon Coding for Fault-Tolerance in RAID-like Systems
- Algebraic soft-decoding of Reed–Solomon codes
- Wikiversity:Reed–Solomon codes for coders
- BBC R&D White Paper WHP031
- Geisel, William A. (August 1990), Tutorial on Reed–Solomon Error Correction Coding, Technical Memorandum, NASA, TM-102162
- Concatenated codes by Dr. Dave Forney (scholarpedia.org).
- Reid, Jeff A. (April 1995), CRC and Reed Solomon ECC (PDF)
Implementations[edit]
- FEC library in C by Phil Karn (aka KA9Q) includes Reed–Solomon codec, both arbitrary and optimized (223,255) version
- Schifra Open Source C++ Reed–Solomon Codec
- Henry Minsky’s RSCode library, Reed–Solomon encoder/decoder
- Open Source C++ Reed–Solomon Soft Decoding library
- Matlab implementation of errors and-erasures Reed–Solomon decoding
- Octave implementation in communications package
- Pure-Python implementation of a Reed–Solomon codec
4.2. Введение в коды Рида-Соломона: принципы, архитектура и реализация
Коды Рида-Соломона были предложены в 1960 году Ирвином Ридом (Irving S. Reed) и Густавом Соломоном (Gustave Solomon), являвшимися сотрудниками Линкольнской лаборатории МТИ. Ключом к использованию этой технологии стало изобретение эффективного алгоритма декодирования Элвином Беликамфом (Elwyn Berlekamp; http://en.wikipedia.org/wiki/Berlekamp-Massey_algorithm), профессором Калифорнийского университета (Беркли). Коды Рида-Соломона (см. также http://www.4i2i.com/reed_solomon_codes.htm) базируются на блочном принципе коррекции ошибок и используются в огромном числе приложений в сфере цифровых телекоммуникаций и при построении запоминающих устройств. Коды Рида-Соломона применяются для исправления ошибок во многих системах:
- устройствах памяти (включая магнитные ленты, CD, DVD, штриховые коды, и т.д.);
- беспроводных или мобильных коммуникациях (включая сотовые телефоны, микроволновые каналы и т.д.);
- спутниковых коммуникациях;
- цифровом телевидении / DVB (digital video broadcast);
- скоростных модемах, таких как ADSL, xDSL и т.д.
На
рис.
4.3 показаны практические приложения (дальние космические проекты) коррекции ошибок с использованием различных алгоритмов (Хэмминга, кодов свертки, Рида-Соломона и пр.). Данные и сам рисунок взяты из http://en.wikipedia.org/wiki/Reed-Solomon_error_correction.
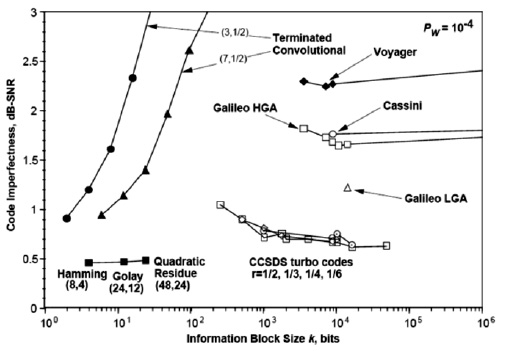
Рис.
4.3.
Несовершенство кода, как функция размера информационного блока для разных задач и алгоритмов
Типовая система представлена ниже (см. http://www.4i2i.com/reed_solomon_codes.htm)

Рис.
4.4.
Схема коррекции ошибок Рида-Соломона
Кодировщик Рида-Соломона берет блок цифровых данных и добавляет дополнительные «избыточные» биты. Ошибки происходят при передаче по каналам связи или по разным причинам при запоминании (например, из-за шума или наводок, царапин на CD и т.д.). Декодер Рида-Соломона обрабатывает каждый блок, пытается исправить ошибки и восстановить исходные данные. Число и типы ошибок, которые могут быть исправлены, зависят от характеристик кода Рида-Соломона.
Свойства кодов Рида-Соломона
Коды Рида-Соломона являются субнабором кодов BCH и представляют собой линейные блочные коды. Код Рида-Соломона специфицируются как RS(n,k) s -битных символов.
Это означает, что кодировщик воспринимает k информационных символов по s битов каждый и добавляет символы четности для формирования n символьного кодового слова. Имеется nk символов четности по s битов каждый. Декодер Рида-Соломона может корректировать до t символов, которые содержат ошибки в кодовом слове, где 2t = n–k.
Диаграмма, представленная ниже, показывает типовое кодовое слово Рида-Соломона:
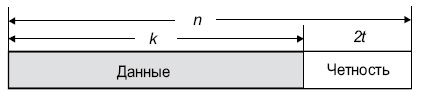
Рис.
4.5.
Структура кодового слова R-S
Пример. Популярным кодом Рида-Соломона является RS(255, 223) с 8-битными символами. Каждое кодовое слово содержит 255 байт, из которых 223 являются информационными и 32 байтами четности. Для этого кода
n = 255, k = 223, s = 8
2t = 32, t = 16
Декодер может исправить любые 16 символов с ошибками в кодовом слове: то есть ошибки могут быть исправлены, если число искаженных байт не превышает 16.
При размере символа s, максимальная длина кодового слова ( n ) для кода Рида-Соломона равна n = 2s – 1.
Например, максимальная длина кода с 8-битными символами ( s = 8 ) равна 255 байтам.
Коды Рида-Соломона могут быть в принципе укорочены путем обнуления некоторого числа информационных символов на входе кодировщика (передавать их в этом случае не нужно). При передаче данных декодеру эти нули снова вводятся в массив.
Пример. Код (255, 223), описанный выше, может быть укорочен до (200, 168). Кодировщик будет работать с блоком данных 168 байт, добавит 55 нулевых байт, сформирует кодовое слово (255, 223) и передаст только 168 информационных байт и 32 байта четности.
Объем вычислительной мощности, необходимой для кодирования и декодирования кодов Рида-Соломона, зависит от числа символов четности. Большое значение t означает, что большее число ошибок может быть исправлено, но это потребует большей вычислительной мощности по сравнению с вариантом при меньшем t.
Ошибки в символах
Одна ошибка в символе происходит, когда 1 бит символа оказывается неверным или когда все биты неверны.
Пример. Код RS(255,223) может исправить до 16 ошибок в символах. В худшем случае, могут иметь место 16 битовых ошибок в разных символах (байтах). В лучшем случае, корректируются 16 полностью неверных байт, при этом исправляется 16 x 8 = 128 битовых ошибок.
Коды Рида-Соломона особенно хорошо подходят для корректировки кластеров ошибок (когда неверными оказываются большие группы бит кодового слова, следующие подряд).
Декодирование
Алгебраические процедуры декодирования Рида-Соломона могут исправлять ошибки и потери. Потерей считается случай, когда положение неверного символа известно. Декодер может исправить до t ошибок или до 2t потерь. Данные о потере (стирании) могут быть получены от демодулятора цифровой коммуникационной системы, т.е. демодулятор помечает полученные символы, которые вероятно содержат ошибки.
Когда кодовое слово декодируется, возможны три варианта.
- Если 2s + r < 2t ( s ошибок, r потерь), тогда исходное переданное кодовое слово всегда будет восстановлено. В противном случае
- Декодер детектирует ситуацию, когда он не может восстановить исходное кодовое слово. или
- Декодер некорректно декодирует и неверно восстановит кодовое слово без какого-либо указания на этот факт.
Вероятность каждого из этих вариантов зависит от типа используемого кода Рида-Соломона, а также от числа и распределения ошибок.
4.2. Введение в коды Рида-Соломона: принципы, архитектура и реализация
Коды Рида-Соломона были предложены в 1960 году Ирвином Ридом (Irving S. Reed) и Густавом Соломоном (Gustave Solomon), являвшимися сотрудниками Линкольнской лаборатории МТИ. Ключом к использованию этой технологии стало изобретение эффективного алгоритма декодирования Элвином Беликамфом (Elwyn Berlekamp; http://en.wikipedia.org/wiki/Berlekamp-Massey_algorithm), профессором Калифорнийского университета (Беркли). Коды Рида-Соломона (см. также http://www.4i2i.com/reed_solomon_codes.htm) базируются на блочном принципе коррекции ошибок и используются в огромном числе приложений в сфере цифровых телекоммуникаций и при построении запоминающих устройств. Коды Рида-Соломона применяются для исправления ошибок во многих системах:
- устройствах памяти (включая магнитные ленты, CD, DVD, штриховые коды, и т.д.);
- беспроводных или мобильных коммуникациях (включая сотовые телефоны, микроволновые каналы и т.д.);
- спутниковых коммуникациях;
- цифровом телевидении / DVB (digital video broadcast);
- скоростных модемах, таких как ADSL, xDSL и т.д.
На
рис.
4.3 показаны практические приложения (дальние космические проекты) коррекции ошибок с использованием различных алгоритмов (Хэмминга, кодов свертки, Рида-Соломона и пр.). Данные и сам рисунок взяты из http://en.wikipedia.org/wiki/Reed-Solomon_error_correction.

Рис.
4.3.
Несовершенство кода, как функция размера информационного блока для разных задач и алгоритмов
Типовая система представлена ниже (см. http://www.4i2i.com/reed_solomon_codes.htm)

Рис.
4.4.
Схема коррекции ошибок Рида-Соломона
Кодировщик Рида-Соломона берет блок цифровых данных и добавляет дополнительные «избыточные» биты. Ошибки происходят при передаче по каналам связи или по разным причинам при запоминании (например, из-за шума или наводок, царапин на CD и т.д.). Декодер Рида-Соломона обрабатывает каждый блок, пытается исправить ошибки и восстановить исходные данные. Число и типы ошибок, которые могут быть исправлены, зависят от характеристик кода Рида-Соломона.
Свойства кодов Рида-Соломона
Коды Рида-Соломона являются субнабором кодов BCH и представляют собой линейные блочные коды. Код Рида-Соломона специфицируются как RS(n,k) s -битных символов.
Это означает, что кодировщик воспринимает k информационных символов по s битов каждый и добавляет символы четности для формирования n символьного кодового слова. Имеется nk символов четности по s битов каждый. Декодер Рида-Соломона может корректировать до t символов, которые содержат ошибки в кодовом слове, где 2t = n–k.
Диаграмма, представленная ниже, показывает типовое кодовое слово Рида-Соломона:

Рис.
4.5.
Структура кодового слова R-S
Пример. Популярным кодом Рида-Соломона является RS(255, 223) с 8-битными символами. Каждое кодовое слово содержит 255 байт, из которых 223 являются информационными и 32 байтами четности. Для этого кода
n = 255, k = 223, s = 8
2t = 32, t = 16
Декодер может исправить любые 16 символов с ошибками в кодовом слове: то есть ошибки могут быть исправлены, если число искаженных байт не превышает 16.
При размере символа s, максимальная длина кодового слова ( n ) для кода Рида-Соломона равна n = 2s – 1.
Например, максимальная длина кода с 8-битными символами ( s = 8 ) равна 255 байтам.
Коды Рида-Соломона могут быть в принципе укорочены путем обнуления некоторого числа информационных символов на входе кодировщика (передавать их в этом случае не нужно). При передаче данных декодеру эти нули снова вводятся в массив.
Пример. Код (255, 223), описанный выше, может быть укорочен до (200, 168). Кодировщик будет работать с блоком данных 168 байт, добавит 55 нулевых байт, сформирует кодовое слово (255, 223) и передаст только 168 информационных байт и 32 байта четности.
Объем вычислительной мощности, необходимой для кодирования и декодирования кодов Рида-Соломона, зависит от числа символов четности. Большое значение t означает, что большее число ошибок может быть исправлено, но это потребует большей вычислительной мощности по сравнению с вариантом при меньшем t.
Ошибки в символах
Одна ошибка в символе происходит, когда 1 бит символа оказывается неверным или когда все биты неверны.
Пример. Код RS(255,223) может исправить до 16 ошибок в символах. В худшем случае, могут иметь место 16 битовых ошибок в разных символах (байтах). В лучшем случае, корректируются 16 полностью неверных байт, при этом исправляется 16 x 8 = 128 битовых ошибок.
Коды Рида-Соломона особенно хорошо подходят для корректировки кластеров ошибок (когда неверными оказываются большие группы бит кодового слова, следующие подряд).
Декодирование
Алгебраические процедуры декодирования Рида-Соломона могут исправлять ошибки и потери. Потерей считается случай, когда положение неверного символа известно. Декодер может исправить до t ошибок или до 2t потерь. Данные о потере (стирании) могут быть получены от демодулятора цифровой коммуникационной системы, т.е. демодулятор помечает полученные символы, которые вероятно содержат ошибки.
Когда кодовое слово декодируется, возможны три варианта.
- Если 2s + r < 2t ( s ошибок, r потерь), тогда исходное переданное кодовое слово всегда будет восстановлено. В противном случае
- Декодер детектирует ситуацию, когда он не может восстановить исходное кодовое слово. или
- Декодер некорректно декодирует и неверно восстановит кодовое слово без какого-либо указания на этот факт.
Вероятность каждого из этих вариантов зависит от типа используемого кода Рида-Соломона, а также от числа и распределения ошибок.
Есть способ передавать данные, теряя часть по пути, но так, чтобы потерянное можно было вернуть по прибытии. Это третья, завершающая часть моего простого изложения алгоритма избыточного кодирования по Риду-Соломону. Реализовать это в коде не прочитав первую, или хотя бы вторую часть на эту тему будет проблематично, но чтобы понять для себя что можно сделать с использованием кодировки Рида-Соломона, можно ограничиться прочтением этой статьи.
Что может этот код?
И так, что из себя представляет избыточный код Рида-Соломона с практической точки зрения? Допустим, есть у нас сообщение – «DON’T PANIC». Если добавить к нему несколько избыточных байт, допустим 6 штук: «rrrrrrDON’T PANIC» (каждый r – это рассчитанный по алгоритму байт), а затем передать через какую-нибудь среду с помехами, или сохранить там, где данные могут понемногу портиться, то по окончании передачи или хранения у нас может остаться такое, например: «rrrrrrDON’AAAAAAA» (6 байт оказались с ошибкой). Если мы знаем номера байтов, где вместо букв, которые были при создании кода, вдруг оказались какие-нибудь «A», то мы можем полностью восстановить сообщение в исходное «rrrrrrDON’T PANIC». После этого можно для красоты убрать избыточные символы. Теперь текст можно печатать на обложку.
Вообще, избыточных символов к сообщению мы можем добавить сколько угодно. Количество избыточных символов равно количеству исправляемых ошибок (это верно лишь в том случае, когда нам известны номера позиций ошибок). Как правило, ошибки, положение которых известно, называют erasures. Благозвучного перевода найти не могу («стирание» мне не кажется благозвучным), так что в дальнейшем я буду применять термин «опечатки» и ставить его в кавычки (прекрасно понимаю, что этот термин обычно несёт похожий, но другой смысл). Исправление «опечаток» полезно, например, при восстановлении блоков QR кода, которые по какой-либо причине не удалось прочитать.
Также код Рида-Соломона позволяет исправлять ошибки, положение которых неизвестно, но тогда на каждую одну исправляемую ошибку должно приходиться 2 избыточных символа. «rrrrrrDON’T PANIC», принятые как «rrrrrrDO___ PANIC» легко будут исправлены без дополнительной информации. Неправильно принятый байт, положение которого неизвестно, в дальнейшем я буду называть «ошибкой» и тоже брать в кавычки.
Можно комбинировать исправление «ошибок» и «опечаток». Если, например, есть 3 избыточных символа, то можно исправить одну «ошибку» и одну «опечатку». Ещё раз обращу внимание на то, что чтобы исправить «опечатку», нужно каким-то образом (не связанным с алгоритмом Рида-Соломона) узнать номер байта «опечатки». Что важно, и «ошибки» и «опечатки» могут быть исправлены алгоритмом и в избыточных байтах тоже.
Стоит отметить, что если количество переданных и принятых байт отличается, то здесь код Рида-Соломона практически бессилен. То есть, если на расшифровку попадёт такое: «rrrrrrDO’AIC», то ничего сделать не получится, если, конечно, неизвестно какие позиции у пропавших букв.
Как закодировать сообщение?
Здесь уже не обойтись без понимания арифметики с полиномами в полях Галуа. Ранее мы научились представлять сообщения в виде полиномов и проводить операции сложения, умножения и деления над ними. Уже этого почти достаточно, чтобы создать код Рида-Соломона из сообщения. Единственно, для того, чтобы это сделать понадобится ещё полином-генератор. Это результат такого произведения:
Где – это примитивный член поля (как правило, выбирают 2), а
– это количество избыточных символов. То есть, прежде чем создавать код Рида-Соломона из сообщения, нужно определиться с количеством избыточных символов, которое мы считаем достаточным, затем перемножить биномы вида
в количестве
штук по правилам перемножения полиномов. Для любого сообщения можно использовать один и тот же полином-генератор, и любое сообщение в таком случае будет закодировано с одним и тем же количеством избыточных символов.
Пример: Мы решили использовать 4 избыточных символа, тогда нужно составить такое выражение:
Так как мы работаем с полем Галуа, то вместо минуса можно смело писать плюс, не боясь никаких последствий. Жаль, что это не работает с количеством денег после похода в магазин. И так, возводим в степень, и перемножаем (по правилам поля Галуа GF[256], порождающий полином 285):
Необязательное дополнение
Легко заметить (правда легко – надо лишь взглянуть на произведение биномов), что корнями получившегося полинома будут как раз степени примитивного члена: 2, 4, 8, 16. Что самое интересное, если взять какой-нибудь другой полином, умножить его на (4 – в данном случае это количество избыточных символов), получится тот же самый полином, только с нулями в коэффициентах перед первыми 4 младшими степенями, а затем разделить его на полином-генератор, и прибавить остаток от деления к нашему полиному с 4 нулями, то его корнями также будут эти 4 числа (2, 4, 8, 16).
Выражение выше есть полином-генератор, который необходим для того, чтобы закодировать сообщение любой длины, добавив к нему 4 избыточных символа, которые позволят скорректировать 2 «ошибки» или 4 «опечатки».
Прежде чем приводить пример кодирования, нужно договориться об обозначениях. Полиномы, записанные «по-математически» с иксами и степенями выглядят довольно-таки громоздко. На самом деле, при написании программы достаточно знать коэффициенты полинома, а степени можно узнать из положения этих коэффициентов. Таким образом полученный в примере выше полином-генератор можно записать так: {116, 167, 224, 30, 1}. Также, для ещё большей компактности, можно опустить скобки и запятые и записать всё в шестнадцатеричном представлении: 74 E7 D8 1E 01. Выходит в 2 раза короче. Надо отметить, что если в «математической» записи мы не пишем члены, коэффициенты которых равны нулю, то при принятой здесь шестнадцатеричной записи они обязательны, и, например,
нужно записывать так:
или 00 00 00 00 0A. Там, где «математическая» запись позволит более понятно объяснить суть, я буду прибегать к ней.
И так, чтобы представить сообщение «DON’T PANIC» в полиномиальной форме, с учётом соглашения выше достаточно просто записать его байты:
44 4F 4E 27 54 20 50 41 4E 49 43.
Чтобы создать код Рида-Соломона с 4 избыточными символами, сдвигаем полином вправо на 4 позиции (что эквивалентно умножению его на ):
00 00 00 00 44 4F 4E 27 54 20 50 41 4E 49 43
Теперь делим полученный полином на полином-генератор (74 E7 D8 1E 01), берём остаток от деления (DB 22 58 5C) и записываем вместо нулей к полиному, который мы делили. (это эквивалентно операции сложения):
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43
Вот эта строка как раз и будет кодом Рида-Соломона для сообщения «DON’T PANIC» с 4 избыточными символами.
Некоторые пояснения
Порядок записи степеней при представлении сообщения в виде полинома имеет значение, ведь полином не эквивалентен полиному
, поэтому следует определиться с этим порядком один раз и его придерживаться. Ещё раз: когда мы преобразуем:
сообщение -> полином, порядок имеет значение.
Так как избыточные символы подставляются именно в младшие степени при кодировании, то от выбора порядка степеней при представлении сообщения зависит положение избыточных символов – в начале или в конце закодированного сообщения.
Изменение порядка записи никоим образом не влияет на арифметику с полиномами, ведь как полином не запиши другим он не становится. . Это очевидно, но при составлении алгоритма легко запутаться.
В некоторых статьях полином-генератор начинается не с первой степени, как здесь: , а с нулевой:
. Это не эквивалентные записи одного и того же, последующие вычисления будут отличаться в зависимости от этого выбора.
Также при создании кода можно не делить на полином-генератор, получая остаток, а умножать на него. Это слегка другая разновидность кода Рида-Соломона, в которой в закодированном сообщении не содержится в явном виде исходное.
Как раскодировать сообщение?
Здесь всё посложнее будет. Ненамного, но всё же. Вопрос про раскодировать, собственно «не вопрос!» – убираем избыточные символы и остаётся исходное сообщение. Вопрос в том, как узнать, были ли ошибки при передаче, и если были, то как их исправить.
В первую очередь нужно отметить, что при проверке на наличие ошибок нужно знать количество избыточных символов. А во-вторую – надо научиться считать значение полинома при определённом . Про количество избыточных символов нам должен заранее сообщить тот, кто кодировал сообщение, а вот чтобы вычислить значение полинома нужно написать ещё одну функцию для работы с полиномами. Это элементарщина – просто вместо
подставляется нужное значение. Но пример, всё же, никогда не помешает.
Пример: Нужно вычислить полиномпри
. Подставляем, возводим в степень:
, перемножаем,
, складываем и получаем число
. Сложение, умножение и возведение в степень здесь по правилам поля Галуа GF[256] (порождающий полином 285)
Код приводить не буду, оставлю ссылку на гитхаб: https://github.com/AV-86/Reed-Solomon-Demo/releases Там всё что я описывал в этой и предыдущих статьях реализовано на C#, в виде демо-приложения (собирается под win в VS2019, бинарник тоже выложен). Можно посмотреть как работает арифметика в поле Галуа, а также посмотреть, как работает кодирование Рида-Соломона.
И так, прежде чем исправлять «ошибки» или «опечатки» нужно узнать есть ли они. Элементарно. Нужно вычислить полином принятого сообщения с избыточными символами при равном степеням примитивного члена. Это те же числа, которые мы использовали при составлении полинома-генератора:
,
– количество избыточных символов,
– примитивный член. Если ошибок нет, то все вычисленные значения будут равны нулю. Закодированное ранее сообщение «DON’T PANIC» с 4 избыточными символами, в виде полинома в шестнадцатеричном представлении:
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43,
если вычислить этот полином при равном 2, 4, 8, 16, то получатся значения: 0, 0, 0, 0, ведь здесь сообщение точно в таком же виде, в котором оно и было закодировано. Если изменить хотя бы один байт, например, последний символ сделаем более правильным: 42 вместо 43:
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 42,
то результат такого же вычисления станет равным 13, 18, B5, 5D. Эти значения называются синдромами. Их тоже можно принять за полином. Тогда это будет полином синдромов.
И так, чтобы узнать есть ли ошибки в принятом сообщении, нужно посчитать полином синдромов. Если он состоит из одних нулей (также можно говорить, что он равен нулю), то ошибок нет.
Важное, но совсем занудное дополнение
Может случиться так, что сообщение с ошибками будет иметь синдром равным нулю. Это случится в том случае, когда полином амплитуд ошибок (о нём будет ниже) кратен полиному-генератору. Так что проверку ошибок по полиному синдромов кода Рида-Соломона нельзя считать 100% гарантией отсутствия ошибок. Можно даже посчитать вероятность такого случая.
Допустим мы кодируем сообщение из 4 символов четырьмя же избыточными символами, то есть передаём 8 байт. Также возьмём для примера вероятность ошибки при передаче одного символа в 10%. То есть, в среднем на каждые 10 символов приходится один, который передался как случайное число от 00 до FF. Это, конечно же совсем синтетическая ситуация, которая вряд ли будет в реальности, но здесь можно точно вычислить вероятности.
Для рассчёта я рассуждаю так: Полиномы, кратные полиному-генератору получаются умножением генератора на другие полиномы. Пятизначный кратный полином — получается умножением на константу от 1 до 255. Шестизначный — умножением на бином первой степени а их, без нулей ровно Те же рассуждения для 7 и 8 -значных полиномов, кратных генератору. Затем надо найти вероятности выпадения 5, 6, 7 и 8 ошибок подряд, и для каждой из них вычислить вероятность, что такая случайная последовательность ошибок окажется кратной полиному-генератору. Сложить их, и тогда мы получим вероятность того, что при передаче 4 байт с 4 избыточными символами, при вероятности ошибки при передаче одного символа 10% получится не обнаруживаемая кодом Рида-Соломона ошибочная передача. Рассчёт в маткаде:

Итого, на каждые ~500 Тб при такой передаче окажется один блок из 4 ошибочных символов, которые алгоритм посчитает корректными. Цифры большие, но вероятность не 0. При вероятности ошибки в 1% речь идёт об эксабайтах. Рассчёт, конечно не эталон, может быть даже с ошибками, но даёт понять об порядках чисел.
Что же делать, если синдром не равен нулю? Конечно же исправлять ошибки! Для начала рассмотрим случай с «опечатками», когда мы точно знаем номера позиций некорректно принятых байт. Ошибёмся намеренно в нашем закодированном сообщении 4 раза, столько же, сколько у нас избыточных символов:
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
41 – это буква A, поэтому их 5 подряд получилось. Позиции ошибок считаются слева направо, начиная с 0. Для удобства используем шестнадцатеричную систему при нумерации:
00 01 02 03 04 05 06 07 08 09 0A 0B 0C 0D 0E
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
Позиции ошибок: 0A 0C 0D 0E.
И так, если мы находимся на стороне приёмника, то у нас есть следующая информация:
-
Сообщение с 4 избыточными символами;
-
само сообщение: DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41;
-
В сообщении есть ошибки в позициях 0A 0C 0D 0E.
Этого достаточно, чтобы восстановить сообщение в исходное состояние. Но обо всём по порядку.
Для продолжения необходимо разучить ещё одну операцию с полиномами в полях Галуа — взятие формальной производной от полинома. Формальная производная полинома в поле Галуа похожа на обычную производную. Формальной она называется потому, что в полях вроде GF[256] нет дробных чисел, и соответственно нельзя определить производную, как отношение бесконечно малых величин. Вычисляется похоже на обычную производную, но с особенностями. Если при обычном дифференцировании , то для формальной производной в поле Галуа с основанием 2, формула для дифференцирования члена такая:
. Это значит, что достаточно просто переписать полином, начиная с первой степени (нулевая выкидывается) и у оставшегося убрать (обнулить, извиняюсь) члены с нечётными степенями. Пример:
Необходимо найти производную
(Это рандомный полином, не связан с примером). Производная суммы равна сумме производных, соответственно применяем формулу для производной члена и получаем:
Или, если записывать в шестнадцатеричном виде, то это же самое выглядит так:
(01 2D A5 C6 8C DF )’ = 2D 00 C6 00 DF .
Думаю, что из примера в шестнадцатеричном виде проще всего составить алгоритм нахождения формальной производной.
Теперь можно уже исправить «опечатки»? Как бы не так! Нужно ещё два полинома. Полином-локатор и полином ошибок.
Полином-локатор – это полином, корнями которого являются числа обратные примитивному члену в степени позиции ошибки. Сложно? Можно проще. Полином-локатор это произведение вида
где – это примитивный член,
и так далее – это позиции ошибок.
Пример: у нас есть позиции ошибок 10, 12, 13, 14; примитивный член тогда полином локатор будет таким:
Перемножаем и получаем полином-локатор для позиций ошибок 10, 12, 13, 14:
Или в шестнадцатеричной записи: 01 2D A5 C6 8C.
Про полином-локатор нужно понять следующее: из него можно получить позиции ошибок, и наоборот – из позиций ошибок можно получить полином-локатор. По сути, это две разные записи одного и того же – позиций ошибок.
Полином ошибок – его по-разному называют в разных статьях, он не так уж и сложен. Представляет из себя произведение полинома синдромов и полином-локатора, с отброшенными старшими степенями. Продолжая пример, найдём полином ошибок для искажённого сообщения:
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
Полином синдромов: 72 BD 22 5B
Произведение полинома синдромов и полинома-локатора не буду расписывать в «математическом» виде, напишу так:
(72 BD 22 5B)(01 2D A5 C6 8C) = 72 4B 10 22 D9 C0 57 15
У результата оставляем количество младших членов, равное количеству избыточных символов, в нашем случае их 4, старшие степени просто выбрасываем, они не нужны. Остаётся
72 4B 10 22
Это и есть полином ошибок.
Осталось посчитать амплитуды ошибок. Звучит угрожающе, но на деле это просто значения, которые нужно прибавить к искажённым символам сообщения чтобы получились неискажённые символы. Для этого воспользуемся алгоритмом Форни. Здесь придётся привести фрагмент кода, словами расписать так, чтобы было понятно, очень сложно.
Функция принимает на входе
-
полином синдромов (Syndromes),
-
полином, в котором члены – позиции ошибок (ErrPos),
-
количество избыточных символов (NumOfErCorrSymbs).
Класс GF_Byte — это просто байт, для которого переопределены арифметические операции так, чтобы они выполнялись по правилам поля Галуа GF[256], класс GF_Poly – Это полином в поле Галуа. По сути, массив GF_Byte. Для него также переопределны арифметические операции так, чтобы они выполнялись по правилам арифметики с полиномами в полях Галуа.
public static GF_Poly FindMagnitudesFromErrPos(
GF_Poly Syndromes,
GF_Poly ErrPos,
uint NumOfErCorrSymbs)
{
//Вычисление локатора из позиций ошибок
GF_Poly Locator = CalcLocatorPoly(ErrPos);
//Произведение для вычисления полинома ошибок
GF_Poly Product = Syndromes * Locator;
//Полином ошибок. DiscardHiDeg оставляет указаное количество младших степеней
GF_Poly ErrPoly = Product.DiscardHiDeg(NumOfErCorrSymbs);
//Производная локатора
GF_Poly LocatorDer = Locator.FormalDerivative();
//Здесь будут амплитуды ошибок. Количество членов - это самая большая позиция ошибки
GF_Poly Magnitudes = new GF_Poly(ErrPos.GetMaxCoef());
//Перебор каждой заданной позиции ошибки
for (uint i = 0; i < ErrPos.Len; i++) {
//число обратное примитивному члену в степени позиции ошибки
GF_Byte Xi = 1 / GF_Byte.Pow_a(ErrPos[i]);
//значение полинома ошибок при x = Xi
GF_Byte W = ErrPoly.Eval(Xi);
//значение производной локатора при x = Xi
GF_Byte L = LocatorDer.Eval(Xi);
//Это как раз и будет найденное значение ошибки,
//которое надо вычесть из ошибочного символа, чтобы он стал не ошибочным
GF_Byte Magnitude = W / L;
//запоминаем найденную амплитуду в текущей позиции ошибки
Magnitudes[ErrPos[i]] = Magnitude;
}
return Magnitudes;
}Если скормить функции следующие параметры:
-
полином синдромов 72 BD 22 5B
-
полином, в котором члены — позиции ошибок 0A 0C 0D 0E
-
количество символов коррекции ошибок 4,
то на выходе она даст полином амплитуд ошибок:
00 00 00 00 00 00 00 00 00 00 11 00 0F 08 02.
Теперь можно прибавить полученное к искажённому сообщению
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41
(по правилам сложения полиномов, конечно же), и на выходе получится исходное сообщение:
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43.
Первые 4 байта — это избыточные символы. Если бы в них оказались «опечатки», то разницы никакой для алгоритма нет, разве что они нам не нужны после исправления. Можно их просто отбросить:
44 4F 4E 27 54 20 50 41 4E 49 43 Это исходное сообщение «DON’T PANIC».
Здесь должно быть понятно, как исправлять ошибки, положение которых известно. Само по себе уже это может нести практическую пользу. В QR кодах на обшарпанных стенах могут стереться некоторые квадратики, и программа, которая их расшифровывает сможет определить в каких именно местах находятся байты, которые не удалось прочитать, которые «стёрлись» – erasures, или как мы договорились писать по-русски «опечатки». Но нам этого, конечно же недостаточно. Мы хотим уметь выявлять испорченные байты без дополнительной информации, чтобы передавать их по радио, или по лазерному лучу, или записывать на диски (кого я обманываю? CD давно мертвы), может быть, захотим реализовать передачу через ультразвук под водой, чтобы управлять моделью подводной лодки, а какие-нибудь неблагодарные дельфины будут портить случайные данные своими песнями. Для всего этого нам понадобится уметь выявлять, в каких именно байтах при передаче попортились биты.
Как найти позиции ошибок?
Вспомним про полином-локатор. Его можно составить из заранее известных позиций ошибок, а ещё его можно вычислить из полинома-синдромов и количества избыточных символов. Есть не один алгоритм, который позволяет это сделать. Здесь будет алгоритм алгоритм Берлекэмпа-Мэсси. Если хочется много математики, то гугл с википедией на неё не скупятся. Я, если честно, не вник до конца в циклические полиномы и прочее-прочее-прочее. Стыдно, немножко, конечно, но я взял реализацию этого алгоритма с сайта Wikiversity переписал его на C#, и постарался сделать его более доходчивым и читаемым:
public static GF_Poly CalcLocatorPoly(GF_Poly Syndromes, uint NumOfErCorrSymbs) {
//Алгоритм Берлекэмпа-Мэсси
GF_Poly Locator;
GF_Poly Locator_old;
//Присваиваем локатору инициализирующее значение (1*X^0)
Locator = new GF_Poly(new byte[] { 1 });
Locator_old = new GF_Poly(Locator);
uint Synd_Shift = 0;
for (uint i = 0; i < NumOfErCorrSymbs; i++) {
uint K = i + Synd_Shift;
GF_Byte Delta = Syndromes[K];
for (uint j = 1; j < Locator.Len; j++) {
Delta += Locator[j] * Syndromes[K - j];
}
//Умножение полинома на икс (эквивалентно сдвигу вправо на 1 байт)
Locator_old = Locator_old.MultiplyByXPower(1);
if (Delta.val != 0) {
if (Locator_old.Len > Locator.Len) {
GF_Poly Locator_new = Locator_old.Scale(Delta);
Locator_old = Locator.Scale(Delta.Inverse());
Locator = Locator_new;
}
//Scale – умножение на константу. Можно было бы
//вместо использования Scale
//умножить на полином нулевой степени. Разницы нет, но так короче:
Locator += Locator_old.Scale(Delta);
}
}
return Locator;
}Пояснения по коду
Приведённый алгоритм считает локатор. Если количество «ошибок» больше, чем количество избыточных символов, поделённое на 2, то алгоритм не сработает правильно.
Если в сообщении, которое мы используем для примера –
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43,
ошибиться в нулевом и последнем символе (2 «ошибки», мы притворяемся, что не знаем в каких позициях ошиблись), получится такой полином:
02 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 01,
Полином синдромов для него 4B A7 E8 BD. Если выполнить функцию, приведённую выше с параметрами 4B A7 E8 BD, и 4 (количество избыточных символов), то она вернёт нам такой полином: 01 12 13. Это не похоже на позиции ошибок, которые мы ожидаем, но полином-локатор содержит в себе информацию о позициях ошибок, ведь это «полином, корнями которого являются числа обратные примитивному члену в степени позиции ошибки». Из этого, если немного поскрипеть мозгами или ручкой по бумаге следует, что позиция ошибки – это логарифм числа по основанию примитивного члена, обратного корню полинома.
E – позиция ошибки, a – примитивный член (2, как правило), R – корень полинома.
Что-ж, будем искать корни в поле. Поиск корней полинома в поле Галуа занятие лёгкое и непыльное. В GF[256] может быть 256 числел всего, так что иксу негде разгуляться. Просто считаем полином 256 раз, подставляя вместо x число, и если полином посчитался как нуль, то записываем к массиву с корнями текущее значение x. Дальше считаем по формуле и получаем позиции ошибок 00 и 0E, именно там где они и были допущены. Теперь эти значения вместе с синдромами и цифрой 4 можно скармливать алгоритму Форни, чтобы он исправил «ошибки» также, как он исправлял «опечатки».
Ещё пара пояснений
-
Существуют более эффективные алгоритмы поиска корней полинома в поле Галуа. Перебор просто самый наглядный.
-
В позиции 00 в текущем примере находится избыточный символ. Алгоритмам Берлекэмпа-Месси и Форни это абсолютно неважно.
Если у нас есть 4 избыточных символа, при этом мы знаем что есть 2 «опечатки» в известных позициях, то алгоритм Берлекэмпа-Мэсси сможет найти ещё одну «ошибку». Но для этого его нужно будет совсем немного модифицировать. Всего то надо там где мы писали
//Присваиваем локатору инициализирующее значение (1*X^0)
Locator = new GF_Poly(new byte[] { 1 });нужно локатор инициализировать не единичным полиномом, а полиномом-локатором, рассчитанным из известных позиций ошибок. И ещё изменить пару строчек. Весь код, напомню, есть на гитхабе: https://github.com/AV-86/Reed-Solomon-Demo/releases
Надеюсь материал в этой статье поможет тем, кто захочет в каком-нибудь своём проекте реализовать избыточное кодирование без сторонних библиотек. Просьба: Если что-то не понятно, не стесняйтесь комментировать. Постараюсь ответить на вопросы, или внести правки в статью.
8.1.1. Вероятность появления ошибок для кодов Рида-Соломона
8.1.2. Почему коды Рида-Соломона эффективны при борьбе c импульсными помехами
8.1.3. Рабочие характеристики кода Рида-Соломона как функция размера, избыточности и степени кодирования
8.1.4. Конечные поля
8.1.4.1.Операция сложения в поле расширения GF(2m)
8.1.4.2. Описание конечного поля с помощью примитивного полинома
8.1.4.3. Поле расширения GF(23)
8.1.4.4. Простой тест для проверки полинома на примитивность
8.1.5. Кодирование Рида-Соломона
8.1.5.1. Кодирование в систематической форме
8.1.5.2. Систематическое кодирование с помощью (n-k)-разрядного регистра сдвига
8.1.6. Декодирование Рида-Соломона
8.1.6.1. Вычисление синдрома
8.1.6.2. Локализация ошибки
8.1.6.3. Значения ошибок
8.1.6.4. Исправление принятого полинома с помощью найденного полинома ошибок
Коды Рида-Соломона (Reed-Solomon code, R-S code) — это недвоичные циклические коды, символы которых представляют собой m-битовые последовательности, где т—положительное целое число, большее 2. Код (n, K) определен на m-битовых символах при всех п и k, для которых
![]() (8.1)
(8.1)
где k — число информационных битов, подлежащих кодированию, а n — число кодовых символов в кодируемом блоке. Для большинства сверточных кодов Рида-Соломона (n,k)
![]() (8.2)
(8.2)
где t — количество ошибочных битов в символе, которые может исправить код, а и ![]() — число контрольных символов. Расширенный код Рида-Соломона можно получить при
— число контрольных символов. Расширенный код Рида-Соломона можно получить при ![]() , но не более того.
, но не более того.
Код Рида-Соломона обладает наибольшим минимальным расстоянием, возможным для линейного кода с одинаковой длиной входных и выходных блоков кодера. Для недвоичных кодов расстояние между двумя кодовыми словами определяется (по аналогии с расстоянием Хэмминга) как число символов, которыми отличаются последовательности. Для кодов Рида-Соломона минимальное расстояние определяется следующим образом [1].
![]() (8.3)
(8.3)
Код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, где t приведено в уравнении (6.44), можно выразить следующим образом.
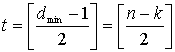 (8.4)
(8.4)
Здесь [x] означает наибольшее целое, не превышающее х. Из уравнения (8.4) видно, что коды Рида-Соломона, исправляющие t символьных ошибок, требуют не более 2t контрольных символов. Из уравнения (8.4) следует, что декодер имеет п-k «используемых» избыточных символов, количество которых вдвое превышает количество исправляемых ошибок. Для каждой ошибки один избыточный символ используется для обнаружения ошибки и один — для определения правильного значения. Способность кода к коррекции стираний выражается следующим образом.
![]() (8.5)
(8.5)
Возможность одновременной коррекции ошибок и стираний можно выразить как требование.
![]() (8.6)
(8.6)
Здесь ![]() — число символьных ошибочных комбинаций, которые можно исправить, а
— число символьных ошибочных комбинаций, которые можно исправить, а ![]() — количество комбинаций символьных стираний, которые могут быть исправлены. Преимущества недвоичных кодов, подобных кодам Рида-Соломона, можно увидеть в следующем сравнении. Рассмотрим двоичный код (п, k) = (7, 3). Полное пространство n-кортежей содержит
— количество комбинаций символьных стираний, которые могут быть исправлены. Преимущества недвоичных кодов, подобных кодам Рида-Соломона, можно увидеть в следующем сравнении. Рассмотрим двоичный код (п, k) = (7, 3). Полное пространство n-кортежей содержит ![]() n-кортежей, из которых
n-кортежей, из которых ![]() (или 1/16 часть всех n-кортежей) являются кодовыми словами. Затем рассмотрим недвоичный код (n, k)=(7, 3), где каждый символ состоит из т = 3 бит. Пространство n-кортежей содержит
(или 1/16 часть всех n-кортежей) являются кодовыми словами. Затем рассмотрим недвоичный код (n, k)=(7, 3), где каждый символ состоит из т = 3 бит. Пространство n-кортежей содержит ![]() 2 097 152 n-кортежа, из которых
2 097 152 n-кортежа, из которых ![]() (или 1/4096 часть всех n-кортежей) являются кодовыми словами. Если операции производятся над недвоичными символами, каждый из которых образован т битами, то только незначительная часть (т.е.
(или 1/4096 часть всех n-кортежей) являются кодовыми словами. Если операции производятся над недвоичными символами, каждый из которых образован т битами, то только незначительная часть (т.е. ![]() из большого числа
из большого числа ![]() ) возможных n-кортежей является кодовыми словами. Эта часть уменьшается с ростом т. Здесь важным является то, что если в качестве кодовых слов используется незначительная часть пространства n-кортежей, то можно достичь большего
) возможных n-кортежей является кодовыми словами. Эта часть уменьшается с ростом т. Здесь важным является то, что если в качестве кодовых слов используется незначительная часть пространства n-кортежей, то можно достичь большего ![]() .
.
Любой линейный код дает возможность исправить n—k комбинаций символьных стираний, если все n—k стертых символов приходятся на контрольные символы. Однако коды Рида-Соломона имеют замечательное свойство, выражающееся в том, что они могут исправить любой набор п-k символов стираний в блоке. Можно сконструировать коды с любой избыточностью. Впрочем, с увеличением избыточности растет сложность ее высокоскоростной реализации. Поэтому наиболее привлекательные коды Рида-Соломона обладают высокой степенью кодирования (низкой избыточностью).
8.1.1. Вероятность появления ошибок для кодов Рида-Соломона
Коды Рида-Соломона чрезвычайно эффективны для исправления пакетов ошибок, т.е. они оказываются эффективными в каналах с памятью. Также они хорошо зарекомендовали себя в каналах с большим набором входных символов. Особенностью кода Рида-Соломона является, то, что к коду длины n можно добавить два информационных символа, не уменьшая при этом минимального расстояния. Такой расширенный код имеет длину п + 2 и то же количество символов контроля четности, что и исходный код. Из уравнения (6.46) вероятность появления ошибки в декодированном символе, РЕ, можно записать через вероятность появления ошибки в канальном символе, ![]() .
.
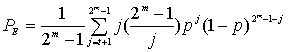 (8.7)
(8.7)
Здесь t — количество ошибочных битов в символе, которые может исправить код, а символы содержат т битов каждый.
Для некоторых типов модуляции вероятность битовой ошибки можно ограничить сверху вероятностью символьной ошибки. Для модуляции MFSK с М=![]() связь РВи РЕвыражается формулой (4.112).
связь РВи РЕвыражается формулой (4.112).
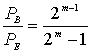 (8.8)
(8.8)
На рис. 8.1 показана зависимость ![]() от вероятности появления ошибки в канальном символе p, полученная из уравнений (8,7) и (8.8) для различных ортогональных 32-ричных кодов Рида-Соломона с возможностью коррекции t ошибочных бит в символе и n = 31 (тридцать один 5-битовый символ в кодовом блоке). На рис.8.2 показана зависимость
от вероятности появления ошибки в канальном символе p, полученная из уравнений (8,7) и (8.8) для различных ортогональных 32-ричных кодов Рида-Соломона с возможностью коррекции t ошибочных бит в символе и n = 31 (тридцать один 5-битовый символ в кодовом блоке). На рис.8.2 показана зависимость ![]() от
от ![]() /N0 для таких систем кодирования при использовании модуляции MFSK и некогерентной демодуляции в канале AWGN [2]. Для кодов Рида-Соломона вероятность появления ошибок является убывающей степенной функцией длины блока, n, а сложность декодирования пропорциональна небольшой степени длины блока [1]. Иногда коды Рида-Соломона применяются в каскадных схемах. В таких системах внутренний сверточный декодер сначала осуществляет некоторую защиту от ошибок за счет мягкой схемы решений на выходе демодулятора; затем сверточный декодер передает данные, оформленные согласно жесткой схеме, на внешний декодер Рида-Соломона, что снижает вероятность появления ошибок. В разделах 8.2.3 и 8.3 мы рассмотрим каскадное декодирование и декодирование Рида-Соломона на примере системы цифровой записи данных на аудиокомпакт-дисках (compact disc — CD).
/N0 для таких систем кодирования при использовании модуляции MFSK и некогерентной демодуляции в канале AWGN [2]. Для кодов Рида-Соломона вероятность появления ошибок является убывающей степенной функцией длины блока, n, а сложность декодирования пропорциональна небольшой степени длины блока [1]. Иногда коды Рида-Соломона применяются в каскадных схемах. В таких системах внутренний сверточный декодер сначала осуществляет некоторую защиту от ошибок за счет мягкой схемы решений на выходе демодулятора; затем сверточный декодер передает данные, оформленные согласно жесткой схеме, на внешний декодер Рида-Соломона, что снижает вероятность появления ошибок. В разделах 8.2.3 и 8.3 мы рассмотрим каскадное декодирование и декодирование Рида-Соломона на примере системы цифровой записи данных на аудиокомпакт-дисках (compact disc — CD).
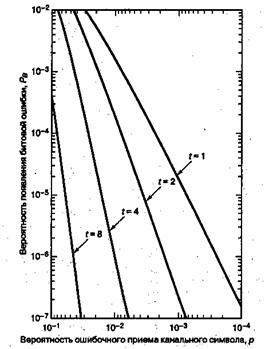
Рис. 8.1. Зависимость Рв от р для различных ортогональных 32-ринных кодов Рида-Соломона с возможностью коррекции t бит в символе и п = 31.(Перепечатано с разрешения автора из Data Communications, Network, and Systems, ed. Thomas C, Bartee, Howard W. Sams Company,Indianapolis,Ind., 1985, p. 311. Ранее публиковалось в J. P. Odenwalder, Error Control Coding Handbook, M/A-COM LINKABIT, Inc., San Diego, Calif., . ./ — . July,15, 1976,p.
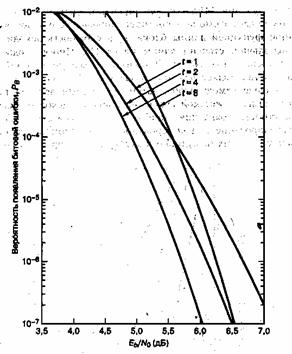
Рис. 8.2. Зависимость рв от Et/NQ для различных ортогональных кодов Рида-Соломона с возможностью коррекции t бит в символе и п = 31, при 32-ринной модуляции MFSK в канале AWGN. (Перепечатано с разрешения автора из Data Communications, Network, and Systems, ed. Thomas C. Bartee, Howard W. Sams Company, Indianapolis, Ind.f 1985, p. 312. Ранее публиковалось в J. P. Odenwalder, Error Control Coding Handbook, M/A-COM LINKABIT, Inc., San Diego, Calif., July, 15, 1976, p. 92.)
8.1.2. Почему коды Рида-Соломона эффективны при борьбе с импульсными помехами
Давайте рассмотрим код (n, k) = (255, 247), в котором каждый символ состоит из т = 8 бит (такие символы принято называть байтами). Поскольку п-k=8, из уравнения (8.4) можно видеть, что этот код может исправлять любые 4-символьные ошибки в блоке длиной до 255. Пусть блок длительностью 25 бит в ходе передачи поражается помехами, как показано на рис. 8.3. В этом примере пакет шума, который попадает на 25 последовательных битов, исказит точно 4 символа. Декодер для кода (255, 247) исправит любые 4-символьные ошибки без учета характера повреждений, причиненных символу. Другими словами, если декодер исправляет байт (заменяет неправильный правильным), то ошибка может быть вызвана искажением одного или всех восьми битов. Поэтому, если символ неправильный, он может быть искажен на всех двоичных позициях. Это дает коду Рида-Соломона огромное преимущество при наличии импульсных помех по сравнению с двоичными кодами (даже при использовании в двоичном коде чередования). В этом примере, если наблюдается 25-битовая случайная помеха, ясно, что искаженными могут оказаться более чем 4 символа (искаженными могут оказаться до 25 символов). Конечно, исправление такого числа ошибок окажется вне возможностей кода (255, 247).
8.1.3. Рабочие характеристики кода Рида-Соломона как функция размера, избыточности и степени кодирования
Для того чтобы код успешно противостоял шумовым эффектам, длительность помех должна составлять относительно небольшой процент от количества кодовых слов. Чтобы быть уверенным, что так будет большую часть времени, принятый шум необходимо усреднить за большой промежуток времени, что снизит эффект от неожиданной или необычной полосы плохого приема. Следовательно, можно предвидеть, что код с коррекцией ошибок будет более эффективен (повысится надежность передачи) при увеличении размера передаваемого блока, что делает код Рида-Соломона более привлекательным, если желательна большая длина блока [3]. Это можно оценить по семейству кривых, показанному на рис. 8.4, где степей кодирования взята равной 7/8, при этом длина блока возрастает с n = 32 символов (при w = 5 бит на символ) до n=256 символов (при n=8 бит на символ). Таким образом, размер блока возрастает с 160 бит до 2048 бит.
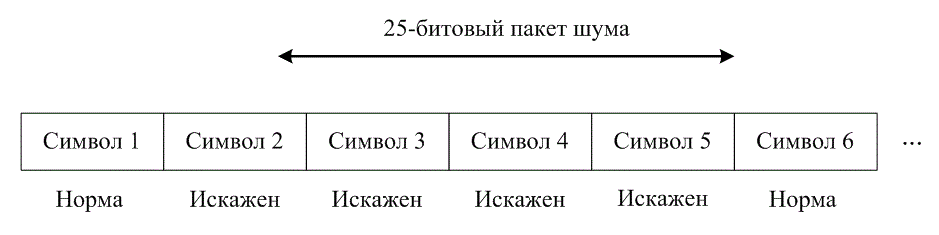
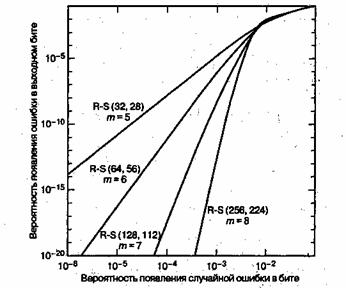
Рис. 8.4. Характеристики декодера Рида-Соломона как функция размера символов (степень кодирования = 7/8)
По мере увеличения избыточности кода (и снижения его степени кодирования), сложность реализации этого кода повышается (особенно для высокоскоростных устройств). При этом для систем связи реального времени должна увеличиться ширина полосы пропускания. Увеличение избыточности, например увеличение размера символа, приводит к уменьшению вероятности появления битовых ошибок, как можно видеть на рис. 8.5, еще кодовая длина п равна постоянному значению 64 при снижении числа символов данных с k = 60 до k = 4 (избыточность возрастает с 4 до 60символов).
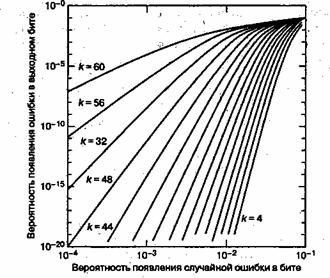
Рис. 8.5. Характеристики декодера Рида-Соломона (64, k) как функция избыточности
На рис. 8.5 показана передаточная функция (выходная вероятность появлений битовой ошибки, зависящая от входной вероятности появления символьной ошибки) гипотетических декодеров. Поскольку здесь не имеется в виду определенная система или канал (лишь вход-выход декодера), можно заключить, что надежность передачи является монотонной функцией избыточности и будет неуклонно возрастать с приближением степени кодирования к нулю. Однако это не так для кодов, используемых в системах связи реального времени. По мере изменения степени кодирования кода от максимального значения до минимального (от 0 до 1), интересно было бы понаблюдать за эффектами, показанными на рис. 8.6. Здесь кривые рабочих характеристик показаны при модуляции BPSK и кодах (31, к) для разных типов каналов. На рис. 8.6 показаны системы связи реального времени, в которых за кодирование с коррекцией ошибок приходится платить расширением полосы пропускания, пропорциональным величине, равной обратной степени кодирования. Приведенные кривые показывают четкий оптимум степени кодирования, минимизирующий требуемое значение ![]() [4]. Для гауссова канала оптимальное значение степени кодирования находится где-то между 0,6 и 0,7, для канала с райсовским замиранием — около 0,5 (с отношением мощности прямого сигнала к мощности отраженного К = 7 дБ) и 0,3 — для канала с релеевским замиранием. (Каналы с замиранием будут рассматриваться в главе 15.) Почему здесь как при очень высоких степенях кодирования (малой избыточности), так и при очень низких (значительной избыточности) наблюдается ухудшение
[4]. Для гауссова канала оптимальное значение степени кодирования находится где-то между 0,6 и 0,7, для канала с райсовским замиранием — около 0,5 (с отношением мощности прямого сигнала к мощности отраженного К = 7 дБ) и 0,3 — для канала с релеевским замиранием. (Каналы с замиранием будут рассматриваться в главе 15.) Почему здесь как при очень высоких степенях кодирования (малой избыточности), так и при очень низких (значительной избыточности) наблюдается ухудшение ![]() ? Для высоких степеней кодирования это легко объяснить, сравнивая высокие степени кодирования с оптимальной степенью кодирования. Любой код в целом обеспечивает все преимущества кодирования; следовательно, как только степень кодирования приближается к единице (нет кодирования), система проигрывает в надежности передачи. Ухудшение характеристик при низких степенях кодирования является более тонким вопросом, поскольку в системах связи реального времени используется и модуляция, и кодирование, т.е. работает два механизма. Один механизм направлен на снижение вероятности появления ошибок, другой повышает ее. Механизм, снижающий вероятность появления ошибки, — это кодирование; чем больше избыточность, тем больше возможности кода в коррекции ошибок. Механизм, повышающий эту вероятность, — это снижение энергии, приходящейся на канальный символ (по сравнению с информационным символом), что следует из увеличения избыточности (и более быстрой передачи сигналов в системах связи реального времени). Уменьшенная энергия символа вынуждает демодулятор совершать больше ошибок. В конечном счете второй механизм подавляет первый, поэтому очень низкие степени кодирования вызывают ухудшение характеристик кода.
? Для высоких степеней кодирования это легко объяснить, сравнивая высокие степени кодирования с оптимальной степенью кодирования. Любой код в целом обеспечивает все преимущества кодирования; следовательно, как только степень кодирования приближается к единице (нет кодирования), система проигрывает в надежности передачи. Ухудшение характеристик при низких степенях кодирования является более тонким вопросом, поскольку в системах связи реального времени используется и модуляция, и кодирование, т.е. работает два механизма. Один механизм направлен на снижение вероятности появления ошибок, другой повышает ее. Механизм, снижающий вероятность появления ошибки, — это кодирование; чем больше избыточность, тем больше возможности кода в коррекции ошибок. Механизм, повышающий эту вероятность, — это снижение энергии, приходящейся на канальный символ (по сравнению с информационным символом), что следует из увеличения избыточности (и более быстрой передачи сигналов в системах связи реального времени). Уменьшенная энергия символа вынуждает демодулятор совершать больше ошибок. В конечном счете второй механизм подавляет первый, поэтому очень низкие степени кодирования вызывают ухудшение характеристик кода.
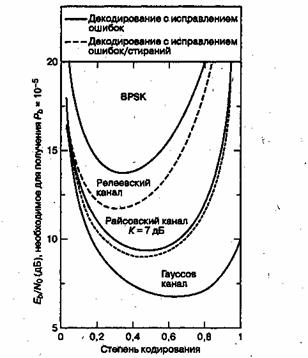
Рис. 8.6. Характеристики декодера Рида-Соломона (31, k) как функция степени кодирования (модуляция BPSK)
Давайте попробуем подтвердить зависимость вероятности появления ошибок от степени кодирования, показанную на рис. 8.6, с помощью кривых, изображенных на рис. 8.2. Непосредственно сравнить рисунки не удастся, поскольку на рис. 8.6 применяется модуляция BPSK, а на рис. 8.2 — 32-ричная модуляция MFSK. Однако, пожалуй, нам удастся показать, что зависимость характеристик кода Рида-Соломона от его степени кодирования выглядит одинаково как при BPSK, так и при MFSK. На рис. 8.2 вероятность появления ошибки в канале AWGN снижается при увеличении способности кода t к коррекции символьных ошибок с t = 1 до t = 4; случаи t = 1 и t = 4 относятся к кодам (31, 29) и (31,23) со степенями кодирования 0,94 и 0,74. Хотя при t = 8, что отвечает коду (31,15) со степенью кодирования 0,48, достоверность передачи ![]() достигается при примерно на 0,5 дБ большем отношении
достигается при примерно на 0,5 дБ большем отношении ![]() , по сравнению со случаем t = 4. Из рис. 8.2 можно сделать вывод, что если нарисовать график зависимости достоверности передачи от степени кодирования кода, то кривая будет иметь вид, подобный приведенному на рис. 8.6. Заметим, что это утверждение нельзя получить из рис. 8.1, поскольку там представлена передаточная функция декодера, которая несет в себе сведения о канале и демодуляции. Поэтому из двух механизмов, работающих в канале, передаточная функция (рис. 8.1) представляет только выгоды, которые проявляются на входе/выходе декодера, и ничего не говорит о потерях энергии как функции низкой степени кодирования.
, по сравнению со случаем t = 4. Из рис. 8.2 можно сделать вывод, что если нарисовать график зависимости достоверности передачи от степени кодирования кода, то кривая будет иметь вид, подобный приведенному на рис. 8.6. Заметим, что это утверждение нельзя получить из рис. 8.1, поскольку там представлена передаточная функция декодера, которая несет в себе сведения о канале и демодуляции. Поэтому из двух механизмов, работающих в канале, передаточная функция (рис. 8.1) представляет только выгоды, которые проявляются на входе/выходе декодера, и ничего не говорит о потерях энергии как функции низкой степени кодирования.
8.1.4. Конечные поля
Для понимания принципов кодирования и декодирования недвоичных кодов, таких как коды Рида-Соломона, нужно сделать экскурс в понятие конечных полей, известных как поля Галуа (Galois fields — GF). Для любого простого числа p существует конечное поле, которое обозначается GF(p) и содержит p элементов. Понятие GF(p) можно обобщить на поле из ![]() элементов, именуемое полем расширения GF(p); это поле обозначается GF(
элементов, именуемое полем расширения GF(p); это поле обозначается GF(![]() ), где т — положительное целое число. Заметим, что GF(
), где т — положительное целое число. Заметим, что GF(![]() ) содержит в качестве подмножества все элементы GF(p). Символы из поля расширения GF(
) содержит в качестве подмножества все элементы GF(p). Символы из поля расширения GF(
) используются при построении кодов Рида-Соломона.
Двоичное поле GF(2) является подполем поля расширения GF(![]() ), точно так же как поле вещественных чисел является подполем поля комплексных чисел. Кроме чисел 0 и 1, в поле расширения существуют дополнительные однозначные элементы, которые будут представлены новым символом а. Каждый ненулевой элемент в GF(
), точно так же как поле вещественных чисел является подполем поля комплексных чисел. Кроме чисел 0 и 1, в поле расширения существуют дополнительные однозначные элементы, которые будут представлены новым символом а. Каждый ненулевой элемент в GF(![]() ) можно представить как степень
) можно представить как степень ![]() . Бесконечное множество элементов, F, образуется из стартового множества
. Бесконечное множество элементов, F, образуется из стартового множества ![]() и генерируется дополнительными элементами путем последовательного умножения последней записи на
и генерируется дополнительными элементами путем последовательного умножения последней записи на ![]() .
.
![]() (8.9)
(8.9)
Для вычисления из F конечного множества элементов GF(![]() ) на F нужно наложить условия: оно может содержать только
) на F нужно наложить условия: оно может содержать только ![]() элемента и быть замкнутым относительно операции умножения. Условие замыкания множества элементов поля по отношению к операции умножения имеет вид неприводимого полинома.
элемента и быть замкнутым относительно операции умножения. Условие замыкания множества элементов поля по отношению к операции умножения имеет вид неприводимого полинома.
![]() (8.9)
(8.9)
или, что тоже самое,
![]() (8.10)
(8.10)
С помощью полиномиального ограничения любой элемент со степенью, большей или равной ![]() , можно следующим образом понизить до элемента со степенью, меньшей
, можно следующим образом понизить до элемента со степенью, меньшей ![]() .
.
![]() (8.11)
(8.11)
Таким образом, как показано ниже, уравнение (8.10) можно использовать для формирования конечной последовательности F* из бесконечной последовательности F.
![]() (8.12)
(8.12)
Следовательно, из уравнения (8.12) можно видеть, что элементы конечного поля GF(![]() ) даются следующим выражением.
) даются следующим выражением.
![]() (8.13)
(8.13)
8.1.4.1. Операция сложения в поле расширения GF(2m)
Каждый из ![]() элементов конечного поля GF(
элементов конечного поля GF(![]() ) можно представить как отдельный полином степени от m-1 или меньше. Степенью полинома называется степень члена максимального порядка. Обозначим каждый ненулевой элемент GF(
) можно представить как отдельный полином степени от m-1 или меньше. Степенью полинома называется степень члена максимального порядка. Обозначим каждый ненулевой элемент GF(![]() ) полиномом
) полиномом ![]() , в котором последние т коэффициентов
, в котором последние т коэффициентов ![]() нулевые. Для
нулевые. Для ![]() ,
,
![]() (8.14)
(8.14)
Рассмотрим случай m = 3, в котором конечное поле обозначается GF(23). На рис. 8.7 показано отображение семи элементов {![]() } и нулевого элемента в слагаемые базисных элементов
} и нулевого элемента в слагаемые базисных элементов ![]() , описываемых уравнением (8.14). Поскольку из уравнения (8.10)
, описываемых уравнением (8.14). Поскольку из уравнения (8.10) ![]() , в этом поле имеется семь ненулевых элементов или всего восемь элементов. Каждая строка на рис. 8.7 содержит последовательность двоичных величин, представляющих коэффициенты
, в этом поле имеется семь ненулевых элементов или всего восемь элементов. Каждая строка на рис. 8.7 содержит последовательность двоичных величин, представляющих коэффициенты ![]() ,
, ![]() и
и ![]() из уравнения (8.14). Одним из преимуществ использования элементов
из уравнения (8.14). Одним из преимуществ использования элементов ![]() поля расширения, вместо двоичных элементов, является компактность записи, что оказывается удобным при математическом описании процессов недвоичного кодирования и декодирования. Сложение двух элементов конечного поля, следовательно, определяется как суммирование по модулю 2 всех коэффициентов при элементах одинаковых степеней.
поля расширения, вместо двоичных элементов, является компактность записи, что оказывается удобным при математическом описании процессов недвоичного кодирования и декодирования. Сложение двух элементов конечного поля, следовательно, определяется как суммирование по модулю 2 всех коэффициентов при элементах одинаковых степеней.
![]() (8.15)
(8.15)
8.1.4.2. Описание конечного поля с помощью примитивного полинома
Класс полиномов, называемых примитивными полиномами, интересует нас, поскольку такие объекты определяют конечные поля GF(![]() ), которые, в свою очередь, нужны для описания кодов Рида-Соломона. Следующее утверждение является необходимым и достаточным условием примитивности полинома. Неприводимый полином f(X) порядка т будет примитивным, если наименьшим положительным целым числом п, для которого
), которые, в свою очередь, нужны для описания кодов Рида-Соломона. Следующее утверждение является необходимым и достаточным условием примитивности полинома. Неприводимый полином f(X) порядка т будет примитивным, если наименьшим положительным целым числом п, для которого ![]() делится на f(X), будет
делится на f(X), будет ![]() . Заметим, что неприводимый полином — это такой полином, который нельзя представить в виде произведения полиномов меньшего порядка; делимость А на В означает, что А делится на В с нулевым остатком и ненулевым частным. Обычно полином записывают в порядке возрастания степеней. Иногда более удобным является обратный формат записи (например, при выполнении полиномиального деления).
. Заметим, что неприводимый полином — это такой полином, который нельзя представить в виде произведения полиномов меньшего порядка; делимость А на В означает, что А делится на В с нулевым остатком и ненулевым частным. Обычно полином записывают в порядке возрастания степеней. Иногда более удобным является обратный формат записи (например, при выполнении полиномиального деления).
|
Образующие элементы |
||||
|
Элементы поля |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
|
|
|
1 |
1 |
0 |
|
|
|
0 |
1 |
1 |
|
|
|
1 |
1 |
1 |
|
|
|
1 |
0 |
1 |
|
|
|
1 |
0 |
0 |
Рис. 8.7. Отображение элементов поля в базисные элементы GF(8) с помощью ![]()
Пример 8.1. Проверка полинома на примитивность
Основываясь на предыдущем определении примитивного полинома, укажите, какие из следующих неприводимых полиномов будут примитивными.
а) ![]()
б) ![]()
Решение
а) Мы можем проверить этот полином порядка т = 4, определив, будет ли он делителем ![]() для значений п из диапазона 1 < n < 15. Нетрудно убедиться, что
для значений п из диапазона 1 < n < 15. Нетрудно убедиться, что ![]() + 1 делится на
+ 1 делится на ![]() (см. раздел 6.8.1), и после повторения вычислений можно проверить, что при любых значениях п из диапазона 1<n<15 полином
(см. раздел 6.8.1), и после повторения вычислений можно проверить, что при любых значениях п из диапазона 1<n<15 полином ![]() +1 не делится на
+1 не делится на ![]() . Следовательно,
. Следовательно, ![]() является примитивным полиномом.
является примитивным полиномом.
б) Легко проверить, что полином является делителем ![]() . Проверив, делится ли
. Проверив, делится ли ![]() на
на ![]() , для значений n, меньших 15, можно также видеть, что указанный полином является делителем Xs+1. Следовательно, несмотря на то что полином
, для значений n, меньших 15, можно также видеть, что указанный полином является делителем Xs+1. Следовательно, несмотря на то что полином ![]() является неприводимым, он не будет примитивным.
является неприводимым, он не будет примитивным.
8.1.4.3. Поле расширения GF(23)
Рассмотрим пример, в котором будут задействованы примитивный полином и конечное поле, которое он определяет. В табл. 8.1 содержатся примеры некоторых примитивных полиномов. Мы выберем первый из указанных там полиномов, ![]() , который определяет конечное поле GF(
, который определяет конечное поле GF(![]() ), где степень полинома т=3. Таким образом, в поле, определяемом полиномом f(Х), имеется 2m = 23 = 8 элементов. Поиск корней полинома f(Х) — это поиск таких значений X, при которых
), где степень полинома т=3. Таким образом, в поле, определяемом полиномом f(Х), имеется 2m = 23 = 8 элементов. Поиск корней полинома f(Х) — это поиск таких значений X, при которых ![]() . Привычные нам двоичные элементы 0 и 1 не подходят полиному
. Привычные нам двоичные элементы 0 и 1 не подходят полиному ![]() (они не являются корнями), поскольку
(они не являются корнями), поскольку ![]() (в рамках операции по модулю 2). Кроме того, основная теорема алгебры утверждает, что полином порядка m должен иметь в точности m корней. Следовательно, в этом примере выражение
(в рамках операции по модулю 2). Кроме того, основная теорема алгебры утверждает, что полином порядка m должен иметь в точности m корней. Следовательно, в этом примере выражение ![]() должно иметь 3 корня. Возникает определенная проблема, поскольку 3 корня не лежат в одном конечном поле, что и коэффициенты f(X). А если они находятся где-то еще, то, наверняка, в поле расширения
должно иметь 3 корня. Возникает определенная проблема, поскольку 3 корня не лежат в одном конечном поле, что и коэффициенты f(X). А если они находятся где-то еще, то, наверняка, в поле расширения ![]() . Пусть,
. Пусть, ![]() , элемент поля расширения, определяется как корень полинома f(X). Следовательно, можно записать следующее.
, элемент поля расширения, определяется как корень полинома f(X). Следовательно, можно записать следующее.
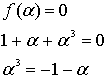 (8.16)
(8.16)
Поскольку при операциях над двоичным полем +1=-1, то ![]() можно представить следующим образом.
можно представить следующим образом.
![]() (8.17)
(8.17)
Таблица 8.1. Некоторые примитивные полиномы
|
m |
m |
||
|
3 |
|
14 |
|
|
4 |
|
15 |
|
|
5 |
|
16 |
|
|
6 |
|
17 |
|
|
7 |
|
18 |
|
|
8 |
|
19 |
|
|
9 |
|
20 |
|
|
10 |
|
21 |
|
|
11 |
|
22 |
|
|
12 |
|
23 |
|
|
13 |
|
24 |
|
Таким образом, ![]() представляется в виде взвешенной суммы всех
представляется в виде взвешенной суммы всех ![]() — членов более низкого порядка. Фактически так можно представить все степени
— членов более низкого порядка. Фактически так можно представить все степени ![]() . Например, рассмотрим следующее.
. Например, рассмотрим следующее.
![]() (8.18,а)
(8.18,а)
А теперь взглянем на следующий случай.
![]() (8.18,б)
(8.18,б)
Из уравнений (8.17) и (8.18), получаем следующее.
Из уравнений (8.17) и (8.18), получаем следующее.
![]() (8.18,в)
(8.18,в)
Из уравнений (8.17) и (8.18), получаем следующее.
![]() (8.18,г)
(8.18,г)
А теперь из уравнения (8.18,г) вычисляем
![]() (8.18,д)
(8.18,д)
Заметим, что ![]() и, следовательно, восьмью элементами конечного поля GF(
и, следовательно, восьмью элементами конечного поля GF(![]() ) ,будут
) ,будут
![]() (8.19)
(8.19)
Отображение элементов поля в базисные элементы, короче описывается уравнением (8.14), можно проиллюстрировать с помощью схемы линейного регистра сдвига с обратной связью (linear feedback shift register – LFSR) (рис 8.8). Схема генерирует (при m = 3) ![]() ненулевых элементов поля и, таким образом, обобщает процедуры, описанные в уравнениях (8.17) – (8.19). Следует отметить, что показанная на рис. 8.8. обратная связь соответствует коэффициентам полинома
ненулевых элементов поля и, таким образом, обобщает процедуры, описанные в уравнениях (8.17) – (8.19). Следует отметить, что показанная на рис. 8.8. обратная связь соответствует коэффициентам полинома ![]() , как и в случае двоичных циклических кодов (см. раздел 6.7.5.). Пусть вначале схема находится в некотором состоянии, например 1 0 0; при выполнении правого сдвига на один такт можно убедиться, что каждый из элементов поля (за исключением нулевого), показанных на рис.8.7, циклически будет появляться в разрядах регистра сдвига. На данном конечном поле GF(
, как и в случае двоичных циклических кодов (см. раздел 6.7.5.). Пусть вначале схема находится в некотором состоянии, например 1 0 0; при выполнении правого сдвига на один такт можно убедиться, что каждый из элементов поля (за исключением нулевого), показанных на рис.8.7, циклически будет появляться в разрядах регистра сдвига. На данном конечном поле GF(![]() ) можно определить две арифметические операции – сложение и умножение. В таб. 8.2. показана операция сложения, а в таб. 8.3. – операция умножения, но только для ненулевых элементов. Правила суммирования следуют из уравнений (8.17) и (8.18,д); и их можно рассчитать путем сложения (по модулю 2) соответствующих коэффициентов из базисных элементов. Правила умножения, указанные в табл. 8.3, следуют из обычной процедуры, в которой произведение элементов поля вычисляются путем сложения по модулю
) можно определить две арифметические операции – сложение и умножение. В таб. 8.2. показана операция сложения, а в таб. 8.3. – операция умножения, но только для ненулевых элементов. Правила суммирования следуют из уравнений (8.17) и (8.18,д); и их можно рассчитать путем сложения (по модулю 2) соответствующих коэффициентов из базисных элементов. Правила умножения, указанные в табл. 8.3, следуют из обычной процедуры, в которой произведение элементов поля вычисляются путем сложения по модулю ![]() их показателей степеней или, для данного случая, по модулю 7.
их показателей степеней или, для данного случая, по модулю 7.
Таблица 8.2. Таблица сложения для GF(8) при ![]()
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
Таблица 8.3. Таблица умножения для GF(8) при ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.1.4.4. Простой тест для проверки полинома на примитивность
Существует еще один, чрезвычайно простой способ проверки, является ли полином примитивным. У неприводимого полинома, который является примитивным, по крайней мере, хотя бы один из корней должен быть примитивным элементом. Примитивным элементом называется такой элемент поля, который, будучи возведенным в более высокие степени, даст ненулевые элементы поля. Поскольку данное поле является конечным, количество таких элементов также конечно.
Пример 8.2. Примитивный полином должен иметь, по крайней мере, хотя бы один примитивный элемент.
Найдите m = 3 корня полинома ![]() и определите, примитивен ли полином. Для этого проверьте, имеется ли среди корней полинома хотя бы один примитивный элемент. Каковы корни полинома? Какие из них примитивны?
и определите, примитивен ли полином. Для этого проверьте, имеется ли среди корней полинома хотя бы один примитивный элемент. Каковы корни полинома? Какие из них примитивны?
Решение
Корни будут найдены прямым перебором. Итак, ![]() не будет корнем, поскольку
не будет корнем, поскольку ![]() .Теперь, чтобы проверить, является ли корнем
.Теперь, чтобы проверить, является ли корнем ![]() , воспользуемся табл. 8.2. Поскольку
, воспользуемся табл. 8.2. Поскольку ![]() , значит,
, значит, ![]() будет корнем полинома. Далее проверим, будет ли корнем
будет корнем полинома. Далее проверим, будет ли корнем ![]() .
.![]() Значит, и
Значит, и ![]() также будет корнем полинома. Теперь проверим
также будет корнем полинома. Теперь проверим ![]() .
. ![]() Следовательно,
Следовательно, ![]() корнем полинома не является. Будет ли корнем
корнем полинома не является. Будет ли корнем ![]() ?
? ![]() Да,
Да, ![]() будет корнем полинома. Значит, корнями полинома
будет корнем полинома. Значит, корнями полинома ![]() будут
будут ![]() . Нетрудно убедиться, что, последовательно возводя в степень любой из этих корней, можно получить все 7 ненулевых элементов поля. Таким образом, все корни будут примитивными элементами. Поскольку в определении требуется, чтобы по крайней мере один из корней был примитивным, полином является примитивным.
. Нетрудно убедиться, что, последовательно возводя в степень любой из этих корней, можно получить все 7 ненулевых элементов поля. Таким образом, все корни будут примитивными элементами. Поскольку в определении требуется, чтобы по крайней мере один из корней был примитивным, полином является примитивным.
В этом примере описан относительно простой метод проверки полинома на примитивность. Для проверяемого полинома нужно составить регистр LFSR с контуром обратной связи, соответствующий коэффициентам полинома, как показана на рис. 8.8. Затем в схему регистра следует загрузить любое ненулевое состояние и выполнить за каждый такт правый сдвиг. Если за один период схема сгенерирует все ненулевые элементы поля, то данный полином с полем GF(![]() ) будет примитивным.
) будет примитивным.
8.1.5. Кодирование Рида-Соломона
В уравнении (8.2) представлена наиболее распространенная форма кодов Рида-Соломона через параметры n, k, t и некоторое положительное число m > 2. Приведем это уравнение повторно.
![]() (8.20)
(8.20)
Здесь ![]() — число контрольных символов, а t – количество ошибочных битов в символе, которые может исправить код. Генерирующий полином для кода Рида-Соломона имеет следующий вид.
— число контрольных символов, а t – количество ошибочных битов в символе, которые может исправить код. Генерирующий полином для кода Рида-Соломона имеет следующий вид.
![]() (8.21)
(8.21)
Степень полиномиального генератора равна числу контролируемых символов. Коды Рида-Соломона являются подмножеством кодов БЧХ, которые обсуждались в разделе 6.8.3. и показаны в табл. 6.4. Поэтому связь между степенью полиномиального генератора и числом контрольных символов, как и в кодах БЧХ, не должна оказаться неожиданностью. В этом можно убедиться, подвергнув проверке любой генератор из табл. 6.4. Поскольку полиномиальный генератор имеет порядок 2t, мы должны иметь в точности 2t последовательные степени ![]() , которые являются корнями полинома. Обозначим корни
, которые являются корнями полинома. Обозначим корни ![]() как:
как: ![]() . Нет необходимости начинать именно с корня
. Нет необходимости начинать именно с корня ![]() , это можно сделать с помощью любой степени
, это можно сделать с помощью любой степени ![]() . Возьмем, к примеру, код (7,3) с возможностью коррекции двухсимвольных ошибок. Мы выразим полиномиальный генератор через
. Возьмем, к примеру, код (7,3) с возможностью коррекции двухсимвольных ошибок. Мы выразим полиномиальный генератор через ![]() корня следующим образом.
корня следующим образом.
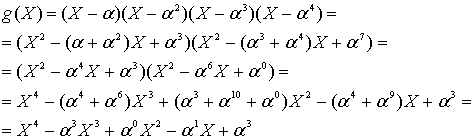
8.1.5.1. Кодирование в систематической форме
Так как код Рида-Соломона является циклическим, кодирование в систематической форме аналогично процедуре двоичного кодирования, разработанной в разделе 6.7.3. Мы можем осуществить сдвиг полинома сообщения m(X) в крайние правые k разряды регистра кодового слова и провести последующее прибавление полинома четности p(X) в крайние левые n – k разряды. Поэтому мы умножаем m(X) на ![]() , проделав алгебраическую операцию таким образом, что m(X) оказывается сдвинутым вправо на n – k позиций. В главе 6 это показано в уравнении (6.61) на примере двоичного кодирования. Далее мы делим
, проделав алгебраическую операцию таким образом, что m(X) оказывается сдвинутым вправо на n – k позиций. В главе 6 это показано в уравнении (6.61) на примере двоичного кодирования. Далее мы делим ![]() на полиномиальный генератор g(X), что можно записать следующим образом.
на полиномиальный генератор g(X), что можно записать следующим образом.
![]()
![]()
Здесь q(X) и p(X) – это частное и остаток от полиномиального деления. Как и в случае двоичного кодирования, остаток будет четным. Уравнение (8.23) можно представить следующим образом.
![]() (8.24)
(8.24)
Результирующий полином кодового слова U(X), показанный в уравнении (6.64), можно переписать следующим образом.
![]() (8.25)
(8.25)
Продемонстрируем шаги, подразумеваемые уравнениями (8.24) и (8.25), закодировав сообщение из трех символов
![]()
с помощью кода (7,3), генератор которого определяется уравнением (8.22). Сначала мы умножаем (сдвиг вверх) полином сообщения ![]() , что дает
, что дает ![]() Далее мы делим такой сдвинутый вверх полином сообщения на полиномиальный генератор из уравнения (8.22),
Далее мы делим такой сдвинутый вверх полином сообщения на полиномиальный генератор из уравнения (8.22), ![]() Полиномиальное деление недвоичных коэффициентов – это еще более утомительная процедура, чем ее двоичный аналог (см. пример 6.9), поскольку операции сложения (вычитания) и умножения (деления) выполняются согласно табл. 8.2 и 8.3. Мы оставим числителю в качестве вспомогательного упражнения проверку того, что полиномиальное деление даст в результате следующей полиномиальный остаток (полином четности).
Полиномиальное деление недвоичных коэффициентов – это еще более утомительная процедура, чем ее двоичный аналог (см. пример 6.9), поскольку операции сложения (вычитания) и умножения (деления) выполняются согласно табл. 8.2 и 8.3. Мы оставим числителю в качестве вспомогательного упражнения проверку того, что полиномиальное деление даст в результате следующей полиномиальный остаток (полином четности).
![]()
Заметим, из уравнения (8.25), полином кодового слова можно записать следующим образом.
![]()
8.1.5.2. Систематическое кодирование с помощью (n-k)-разрядного регистра сдвига
Как показано на рис. 8.9, кодирование последовательности из 3 символов в систематической форме на основе кода (7,3), определяемого генератором g(X) из уравнения (8.22), требует реализации регистра LFSR. Нетрудно убедиться, что элементы умножителя на рис. 8.9, взятые справа налево, соответствуют коэффициентам полинома в уравнении (8.22). Этот процесс кодирования является недвоичным аналогом циклического кодирования, которое описывалась в разделе 6.7.5. Здесь, в соответствии с уравнением (8.20), ненулевые кодовые слова образованы ![]() символами, и каждый символ состоит из m = 3 бит.
символами, и каждый символ состоит из m = 3 бит.
Следует отметить сходство между рис. 8.9, 6.18 и 6.19. Во всех трех случаях количество разрядов в регистре равно n – k. Рисунки в главе 6 отображают пример двоичного кодирования, где каждый разряд содержит 1 бит. В данной главе приведен пример двоичного кодирования, так что каждый разряд регистра сдвига, изображенного на рис. 8.9, содержит 3-битовый символ. На рис. 6.18 коэффициенты, обозначенные ![]() являются двоичными. Поэтому они принимают одно из значений 0 или 1, просто указывая на наличие или отсутствие связи в LFSR. На рис. 8.9 каждый коэффициент является 3-битовым, так что они могут принимать одно из 8 значений.
являются двоичными. Поэтому они принимают одно из значений 0 или 1, просто указывая на наличие или отсутствие связи в LFSR. На рис. 8.9 каждый коэффициент является 3-битовым, так что они могут принимать одно из 8 значений.
Недвоичные операции, осуществляемые кодером, показанным на рис. 8.9, создают кодовые слова в систематической форме, так же как и в двоичном случае. Эти операции определяются следующими шагами.
1. Переключатель 1 в течение первых k тактовых импульсов закрыт, для того чтобы подавать символы сообщения в (n — k)-разрядный регистр сдвига.
2. В течение первых k тактовых импульсов переключатель 2 находится в нижнем положении, что обеспечивает одновременную процедуру всех символов сообщения непосредственно на регистр выхода (на рис. 8.9 не показан).
3. После передачи k-го символа на регистр выхода, переключатель 1 открывается, а переключатель 2 переходит в верхнее положение.
4. Остальные (n—k) тактовых импульсов очищают контрольные символы, содержащиеся в регистре, подавая из на регистр выхода.
5. Общее число тактовых импульсов равно n, и содержимое регистра выхода является полиномом кодового слова ![]() , где p(X) представляет собой кодовые символы, а m(X) – символы сообщения в полиномиальной форме.
, где p(X) представляет собой кодовые символы, а m(X) – символы сообщения в полиномиальной форме.
Для проверки возьмем те же последовательность символов, что и в разделе 8.1.5.1.
![]()
Здесь крайний правый символ является самым первым и крайний правый бит также является самым первым. Последовательность действий в течение первых k = 3 сдвигов в цепи кодирования на рис. 8.9 будет иметь следующий вид.
Очередь ввода Такт Содержимое регистра обратная связь
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
||
|
— |
3 |
|
|
|
|
— |
Как можно видеть, после третьего такта регистр содержит 4 контрольных символа, ![]() . Затем переключатель 1 переходит в верхнее положение, и контрольные символы, содержащиеся в регистре, подаются на выход. Поэтому выходное слово, записанное в полиномиальной форме, можно представить в следующим виде.
. Затем переключатель 1 переходит в верхнее положение, и контрольные символы, содержащиеся в регистре, подаются на выход. Поэтому выходное слово, записанное в полиномиальной форме, можно представить в следующим виде.
![]()
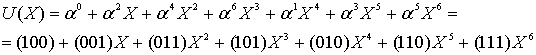 (8.26)
(8.26)
Процесс проверки содержимого регистра во время разных тактов несколько сложнее, чем в случае бинарного кодирования. Здесь сложение и умножение элементов поля должны выполняться согласно табл. 8.2 и 8.3.
Корни полиномиального генератора g(X) должны быть и корнями кодового слова, генерируемого g(X), поскольку правильное кодовое слово имеет следующий вид.
![]() (8.27)
(8.27)
Следовательно, произвольное кодовое слово, выражаемое через корень генератора g(X), должно давать нуль. Представляется интересным, действительно ли полином кодового слова в уравнении (8.26) дает нуль, когда он выражается через какой-либо из четырех корней g(X). Иными словами, это означает проверку следующего.
![]()
Независимо выполнив вычисления для разных корней, получим следующее.
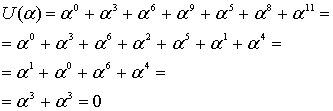
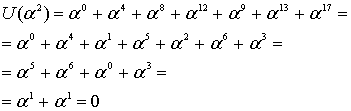
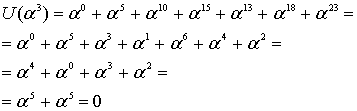
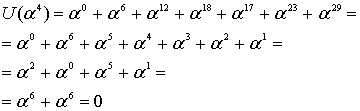
Эти вычисления показывают, что, как и ожидалось, кодовое слово, выражаемое через любой корень генератора g(X), должно давать нуль.
8.1.6. Декодирование Рида-Соломона
В разделе 8.1.5 тестовое сообщение кодируется в систематической форме с помощью кода (7,3), что дает в результате полином кодового слова, описываемый уравнением (8.26). Допустим, что в ходе передачи это кодовое слово подверглось искажению: 2 символа были приняты с ошибкой. (Такое количество ошибок соответствует максимальной способности кода к коррекции ошибок.) При использовании 7-символьного кодового слова ошибочную комбинацию можно представить в полиномиальной форме следующим образом.
![]() (8.28)
(8.28)
Пусть двухсимвольная ошибка будет такой, что
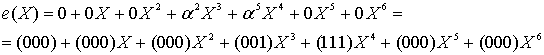 (8.29)
(8.29)
Другими словами, контрольный символ искажен 1-битовой ошибкой (представленной как ![]() ), а символ сообщения — 3-битовой ошибкой (представленной как
), а символ сообщения — 3-битовой ошибкой (представленной как ![]() ). В данном случае принятый полином поврежденного кодового слова r(Х) представляется в виде суммы полинома переданного кодового слова и полинома ошибочной комбинации, как показано ниже.
). В данном случае принятый полином поврежденного кодового слова r(Х) представляется в виде суммы полинома переданного кодового слова и полинома ошибочной комбинации, как показано ниже.
![]()
![]() (8.30)
(8.30)
Следуя уравнению (8.30), мы суммируем U(X) из уравнения (8.26) и e(Х) из уравнения (8.29) и имеем следующее.
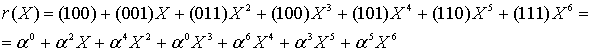 (8.31)
(8.31)
В данном примере исправления 2-символьной ошибки имеется четыре неизвестных — два относятся к расположению ошибки, а два касаются ошибочных значений. Отметим важное различие между недвоичным декодированием r(Х), которое мы показали в уравнении (8.31), и двоичным, которое описывалось в главе 6. При двоичном декодировании декодеру нужно знать лишь расположение ошибки. Если известно, где находится ошибка, бит нужно поменять с 1 на 0 или наоборот. Но здесь недвоичные символы требуют, чтобы мы не только узнали расположение ошибки, но и определили правильное значение символа, расположенного на этой позиции. Поскольку в данном примере у нас имеется четыре неизвестных, нам нужно четыре уравнения, чтобы найти их.
8.1.6.1. Вычисление синдрома
Вернемся к разделу 6.4.7 и напомним, что синдром — это результат проверки четности, выполняемой над r, чтобы определить, принадлежит ли r набору кодовых слов. Если r является членом набора, то синдром S имеет значение, равное 0. Любое ненулевое значение S означает наличие ошибок. Точно так же, как и в двоичном случае, синдром S состоит из n—k символов, ![]()
![]() . Таким образом, для нашего кода (7, 3) имеется по четыре символа в каждом векторе синдрома; их значения можно рассчитать из принятого полинома r(Х). Заметим, кдк облегчаются вычисления благодаря самой структуре кода, определяемой уравнением (8.27).
. Таким образом, для нашего кода (7, 3) имеется по четыре символа в каждом векторе синдрома; их значения можно рассчитать из принятого полинома r(Х). Заметим, кдк облегчаются вычисления благодаря самой структуре кода, определяемой уравнением (8.27).
![]()
Из этой структуры можно видеть, что каждый правильный полином кодового слова U(X) является кратным полиномиальному генератору g(X). Следовательно, корни g(X) также должны быть корнями U(X). Поскольку ![]() , то r(Х), вычисляемый с каждым корнем g(X), должен давать нуль, только если r(Х) будет правильным кодовым словом. Любые ошибки приведут в итоге к ненулевому результату в одном (или более) случае. Вычисления символов синдрома можно записать следующим образом.
, то r(Х), вычисляемый с каждым корнем g(X), должен давать нуль, только если r(Х) будет правильным кодовым словом. Любые ошибки приведут в итоге к ненулевому результату в одном (или более) случае. Вычисления символов синдрома можно записать следующим образом.
![]() (8.32)
(8.32)
Здесь, как было показано в уравнении (8.29), r(Х) содержит 2-символьные ошибки. Если r(Х) окажется правильным кодовым словом, то это приведет к тому, что все символы синдрома ![]() будут равны нулю. В данном примере четыре символа синдрома находятся следующим образом.
будут равны нулю. В данном примере четыре символа синдрома находятся следующим образом.
![]()
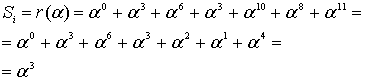 (8.33)
(8.33)
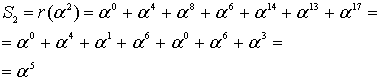 (8.34)
(8.34)
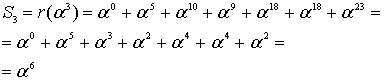 (8.35)
(8.35)
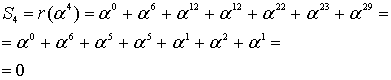 (8.36)
(8.36)
Результат подтверждает, что принятое кодовое слово содержит ошибку (введенную нами), поскольку ![]() .
.
Пример 8.3. Повторная проверка значений синдрома
Для рассматриваемого кода (7, 3) ошибочная комбинация известна, поскольку мы выбрали ее заранее. Вспомним свойство кодов, обсуждаемое в разделе 6.4.8.1, когда была введена нормальная матрица. Все элементы класса смежности (строка) нормальной матрицы имеют один и тот же синдром. Нужно показать, что это свойство справедливо и для кода Рида-Соломона, путем вычисления полинома ошибок e(Х) со значениями корней g(X). Это должно дать те же значения синдрома, что и вычисление r(Х) со значениями корней g(X). Другими словами, это должно дать те же значения, которые были получены в уравнениях (8.33)-(8.36).
Решение
![]()
![]()
![]()
Из уравнения (8.29) следует, что ![]() , поэтому
, поэтому
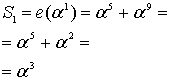
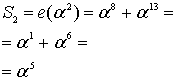
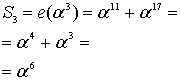
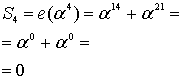
Из этих результатов можно заключить, что значения синдрома одинаковы — как полученные путем вычисления e(Х) со значениями корней g(X), так и полученные путем вычисления r(Х) с теми же значениями корней g(X).
8.1.6.2. Локализация ошибки
Допустим, в кодовом слове имеется ![]() ошибок, расположенных на позициях
ошибок, расположенных на позициях ![]() . Тогда полином ошибок, определяемый уравнениями (8.28) и (8.29), можно записать следующим образом.
. Тогда полином ошибок, определяемый уравнениями (8.28) и (8.29), можно записать следующим образом.
![]() (8.37)
(8.37)
Индексы 1, 2, …, ![]() обозначают 1-ю, 2-ю, …,
обозначают 1-ю, 2-ю, …, ![]() -ю ошибки, а индекс
-ю ошибки, а индекс ![]() — расположение ошибки. Для коррекции искаженного кодового слова нужно определить каждое значение ошибки
— расположение ошибки. Для коррекции искаженного кодового слова нужно определить каждое значение ошибки ![]() и ее расположение
и ее расположение ![]() , где
, где ![]() . Обозначим номер локатора ошибки как
. Обозначим номер локатора ошибки как ![]() . Далее вычисляем
. Далее вычисляем ![]() символа синдрома, подставляя
символа синдрома, подставляя ![]() в принятый полином при
в принятый полином при ![]() .
.
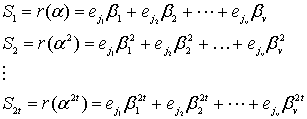 (8.38)
(8.38)
У нас имеется 2t неизвестных (t значений ошибок и t расположений) и система 2t уравнений. Впрочем, эту систему 2t уравнений нельзя решить обычным путем, поскольку уравнения в ней нелинейны (некоторые неизвестные входят в уравнение в степени). Методика, позволяющая решить эту систему уравнений, называется алгоритмом декодирования Рида-Соломона.
Если вычислен ненулевой вектор синдрома (один или более его символов не равны нулю), это означает, что была принята ошибка. Далее нужно узнать расположение ошибки (или ошибок). Полином локатора ошибок можно определить следующим образом.
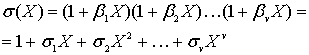 (8.39)
(8.39)
Корнями ![]() будут
будут ![]() . Величины, обратные корням
. Величины, обратные корням ![]() , будут представлять номера расположений ошибочной комбинации e(Х). Тогда, воспользовавшись авторегрессионной техникой моделирования [5], мы составим из синдромов матрицу, в которой первые t синдромов будут использоваться для предсказания следующего синдрома.
, будут представлять номера расположений ошибочной комбинации e(Х). Тогда, воспользовавшись авторегрессионной техникой моделирования [5], мы составим из синдромов матрицу, в которой первые t синдромов будут использоваться для предсказания следующего синдрома.
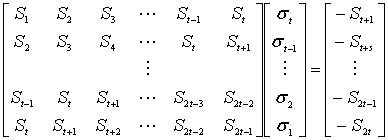 (8.40)
(8.40)
Мы воспользовались авторегрессионной моделью уравнения (8.40), взяв матрицу наибольшей размерности с ненулевым определителем. Для кода (7, 3) с коррекцией двухсимвольных ошибок матрица будет иметь размерность ![]() , и модель запишется следующим образом.
, и модель запишется следующим образом.
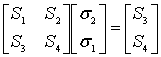 (8.41)
(8.41)
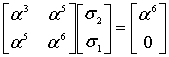 (8.42)
(8.42)
Чтобы найти коэффициенты ![]() и
и ![]() полинома локатора ошибок
полинома локатора ошибок ![]() ,. сначала необходимо вычислить обратную матрицу для уравнения (8.42). Обратная матрица для матрицы [А] определяется следующим образом.
,. сначала необходимо вычислить обратную матрицу для уравнения (8.42). Обратная матрица для матрицы [А] определяется следующим образом.
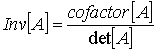
Следовательно,
det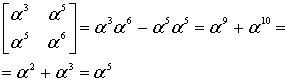 (8.43)
(8.43)
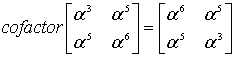 (8.44)
(8.44)
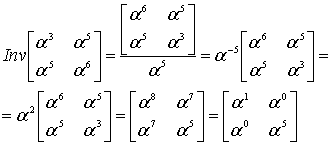 (8.45)
(8.45)
Проверка надежности
Если обратная матрица вычислена правильно, то произведение исходной и обратной матрицы должно дать единичную матрицу.
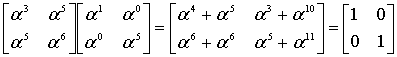 (8.46)
(8.46)
С помощью уравнения (8.42) начнем поиск положений ошибок с вычисления коэффициентов полинома локатора ошибок ![]() , как показано далее.
, как показано далее.
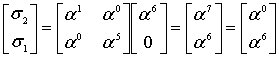 (8.47)
(8.47)
Из уравнений (8.39) и (8.47)
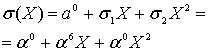 (8.48)
(8.48)
Корни ![]() являются обратными числами к положениям ошибок. После того как эти корни найдены, мы знаем расположение ошибок. Вообще, корни
являются обратными числами к положениям ошибок. После того как эти корни найдены, мы знаем расположение ошибок. Вообще, корни ![]() могут быть одним или несколькими элементами поля. Определим эти корни путем полной проверки полинома
могут быть одним или несколькими элементами поля. Определим эти корни путем полной проверки полинома ![]() со всеми элементами поля, как будет показано ниже. Любой элемент X, который дает
со всеми элементами поля, как будет показано ниже. Любой элемент X, который дает ![]() , является корнем, что позволяет нам определить расположение ошибки.
, является корнем, что позволяет нам определить расположение ошибки.
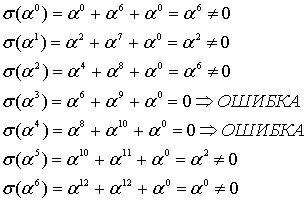
Как видно из уравнения (8.39), расположение ошибок является обратной величиной к корням полинома. А значит, ![]() означает, что один корень получается при
означает, что один корень получается при ![]() . Отсюда
. Отсюда ![]() . Аналогично
. Аналогично ![]() означает, что другой корень появляется при
означает, что другой корень появляется при ![]() , где (в данном примере)
, где (в данном примере) ![]() и
и ![]() обозначают 1-ю и 2-ю ошибки. Поскольку мы имеем дело с 2-символьными ошибками, полином ошибок можно записать следующим образом.
обозначают 1-ю и 2-ю ошибки. Поскольку мы имеем дело с 2-символьными ошибками, полином ошибок можно записать следующим образом.
![]() (8.49)
(8.49)
Здесь были найдены две ошибки на позициях ![]() и
и ![]() . Заметим, что индексация номеров расположения ошибок является сугубо произвольной. Итак, в этом примере мы обозначили величины
. Заметим, что индексация номеров расположения ошибок является сугубо произвольной. Итак, в этом примере мы обозначили величины ![]() как
как ![]()
![]() и
и ![]() .
.
8.1.6.3. Значения ошибок
Мы обозначили ошибки ![]() , где индекс j обозначает расположение ошибки, а индекс l — l-ю ошибку. Поскольку каждое значение ошибки связано с конкретным меcторасположением, систему обозначений можно упростить, обозначив
, где индекс j обозначает расположение ошибки, а индекс l — l-ю ошибку. Поскольку каждое значение ошибки связано с конкретным меcторасположением, систему обозначений можно упростить, обозначив ![]() просто как
просто как ![]() . Теперь, приготовившись к нахождению значений ошибок
. Теперь, приготовившись к нахождению значений ошибок ![]() и
и ![]() , связанных с позициями
, связанных с позициями ![]() и
и ![]() можно использовать любое из четырех синдромных уравнений. Выразим из уравнения (8.38)
можно использовать любое из четырех синдромных уравнений. Выразим из уравнения (8.38) ![]() , и
, и ![]() .
.
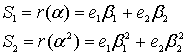 (8.50)
(8.50)
Эти уравнения можно переписать в матричной форме следующим образом.
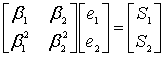 (8.51)
(8.51)
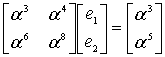 (8.52)
(8.52)
Чтобы найти значения ошибок ![]() и
и ![]() , нужно, как обычно, выполнить поиск обратной матрицы для уравнения (8.52).
, нужно, как обычно, выполнить поиск обратной матрицы для уравнения (8.52).
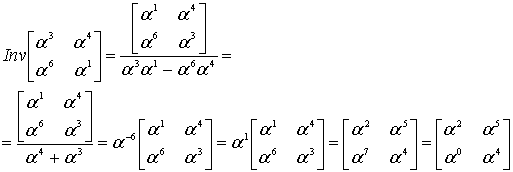 (853)
(853)
Теперь мы можем найти из уравнения (8.52) значения ошибок.
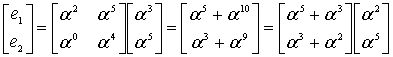 (8.54)
(8.54)
8.1.6.4. Исправление принятого полинома с помощью найденного полинома ошибок
Из уравнений (8.49) и (8.54) мы находим полином ошибок.
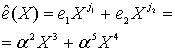 (8.55)
(8.55)
Показанный алгоритм восстанавливает принятый полином, выдавая в итоге предполагаемое переданное кодовое слово и, в конечном счете, декодированное сообщение.
![]() (8.56)
(8.56)
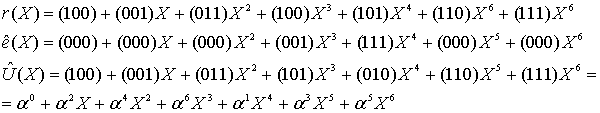 (8.57)
(8.57)
Поскольку символы сообщения содержатся в крайних правых k = 3 символах, декодированным будет следующее сообщение.
![]()
![]()
![]()
Это сообщение в точности соответствует тому, которое было выбрано для этого примера в разделе 8.1.5. (Для более детального знакомства с кодированием Рида-Соломона обратитесь к работе [6].)
| Коды Рида – Соломона | |
|---|---|
| Названный в честь | Ирвинг С. Рид и Гюстав Соломон |
| Классификация | |
| Иерархия | Линейный блочный код Полиномиальный код Код Рида – Соломона |
| Длина блока | п |
| Длина сообщения | k |
| Расстояние | п − k + 1 |
| Размер алфавита | q = пм ≥ п (п премьер) Часто п = q − 1. |
| Обозначение | [п, k, п − k + 1]q-код |
| Алгоритмы | |
| Берлекамп – Мэсси Евклидово и другие. |
|
| Свойства | |
| Разделимый код максимального расстояния | |
Коды Рида – Соломона группа коды с исправлением ошибок которые были представлены Ирвинг С. Рид и Гюстав Соломон в 1960 г.[1]У них много приложений, наиболее известными из которых являются потребительские технологии, такие как Компакт-диски, DVD, Блю рей диски, QR коды, передача информации такие технологии как DSL и WiMAX, трансляция такие системы, как спутниковая связь, DVB и ATSC, и системы хранения, такие как RAID 6.
Коды Рида – Соломона работают с блоком данных, рассматриваемым как набор конечное поле элементы, называемые символами. Коды Рида – Соломона способны обнаруживать и исправлять множественные символьные ошибки. Добавлением т = п − k проверять символы в данных, код Рида – Соломона может обнаруживать (но не исправлять) любую комбинацию до включительно т ошибочные символы, или найти и исправить до включительно ⌊т/2⌋ ошибочные символы в неизвестных местах. Как код стирания, он может исправить до т стирание в местах, которые известны и предоставлены алгоритму, или он может обнаруживать и исправлять комбинации ошибок и стираний. Коды Рида – Соломона также подходят в качестве многократныхвзрыв коды с исправлением битовых ошибок, поскольку последовательность б + 1 последовательные битовые ошибки могут повлиять не более чем на два символа размера б. Выбор т зависит от разработчика кода и может быть выбран в широких пределах.
Существует два основных типа кодов Рида – Соломона — исходный вид и BCH view — наиболее распространенным является представление BCH, поскольку декодеры представления BCH работают быстрее и требуют меньше памяти, чем исходные декодеры представления.
История
Коды Рида – Соломона были разработаны в 1960 г. Ирвинг С. Рид и Гюстав Соломон, которые тогда были сотрудниками Лаборатория Линкольна Массачусетского технологического института. Их основополагающая статья называлась «Полиномиальные коды над некоторыми конечными полями». (Рид и Соломон 1960 ). Исходная схема кодирования, описанная в статье Рида и Соломона, использовала переменный многочлен на основе сообщения, которое нужно кодировать, где кодировщику и декодеру известен только фиксированный набор значений (точек оценки), которые должны быть закодированы. Первоначальный теоретический декодер генерировал потенциальные многочлены на основе подмножеств k (длина незашифрованного сообщения) из п (длина закодированного сообщения) значения полученного сообщения, выбирая наиболее популярный полином в качестве правильного, что было непрактично во всех случаях, кроме простейшего. Первоначально это было решено путем изменения исходной схемы на Код BCH подобная схема основана на фиксированном полиноме, известном как кодеру, так и декодеру, но позже были разработаны практические декодеры на основе исходной схемы, хотя и более медленные, чем схемы BCH. Результатом этого является то, что существует два основных типа кодов Рида-Соломона: те, которые используют исходную схему кодирования, и те, которые используют схему кодирования BCH.
Также в 1960 году практический фиксированный полиномиальный декодер для Коды BCH разработан Даниэль Горенштейн и Нил Зирлер был описан в отчете лаборатории Линкольна Массачусетского технологического института Зирлера в январе 1960 года, а затем в статье в июне 1961 года.[2] Декодер Горенштейна – Цирлера и связанная с ним работа над кодами BCH описаны в книге «Коды с исправлением ошибок» автора. В. Уэсли Петерсон (1961).[3] К 1963 году (или, возможно, раньше) Дж. Дж. Стоун (и другие) признали, что коды Рида-Соломона могут использовать схему БЧХ с использованием фиксированного порождающего полинома, что делает такие коды особым классом кодов БЧХ,[4] но коды Рида-Соломона, основанные на исходной схеме кодирования, не являются классом кодов BCH, и в зависимости от набора точек оценки они даже не циклические коды.
В 1969 году усовершенствованный декодер схемы BCH был разработан Элвин Берлекамп и Джеймс Мэсси, и с тех пор известен как Алгоритм декодирования Берлекампа-Месси.
В 1975 году Ясуо Сугияма разработал еще один улучшенный декодер схемы BCH, основанный на расширенный алгоритм Евклида.[5]

В 1977 году коды Рида – Соломона были реализованы в Программа «Вояджер» в виде составные коды исправления ошибок. Первое коммерческое применение в массовых потребительских товарах появилось в 1982 году с компакт-диск, где два чередующийся Используются коды Рида – Соломона. Сегодня коды Рида – Соломона широко применяются в цифровое хранилище устройства и цифровая связь стандартов, хотя они постепенно заменяются более современными коды с низкой плотностью проверки четности (LDPC) или турбокоды. Например, коды Рида – Соломона используются в Цифровое видеовещание (DVB) стандарт DVB-S, но коды LDPC используются в его преемнике, DVB-S2.
В 1986 году оригинальная схема декодера, известная как Алгоритм Берлекампа – Велча был развит.
В 1996 году Мадху Судан и другие разработали варианты декодеров исходных схем, называемые декодерами списков или программными декодерами, и работа над этими типами декодеров продолжается — см. Алгоритм декодирования списка Гурусвами – Судан.
В 2002 году Шухонг Гао разработал еще одну оригинальную схему декодера, основанную на расширенный алгоритм Евклида Gao_RS.pdf .
Приложения
Хранилище данных
Кодирование Рида – Соломона очень широко используется в системах хранения данных для исправления пакетных ошибок, связанных с дефектами носителя.
Кодирование Рида – Соломона — ключевой компонент компакт-диск. Это было первое использование сильного кодирования с исправлением ошибок в массовом потребительском продукте, и DAT и DVD использовать аналогичные схемы. На компакт-диске два уровня кодирования Рида – Соломона, разделенные 28-полосным сверточный перемежитель дает схему, называемую кодированием Рида – Соломона с перекрестным чередованием (CIRC ). Первым элементом декодера CIRC является относительно слабый внутренний (32,28) код Рида – Соломона, сокращенный от кода (255,251) с 8-битовыми символами. Этот код может исправить до 2-х байтовых ошибок на 32-байтовый блок. Что еще более важно, он помечает как стирающие любые неисправимые блоки, то есть блоки с ошибками более 2 байтов. Декодированные 28-байтовые блоки с индикацией стирания затем распространяются обращенным перемежителем на разные блоки внешнего кода (28,24). Благодаря обратному чередованию стертый 28-байтовый блок внутреннего кода становится одним стертым байтом в каждом из 28 внешних кодовых блоков. Внешний код легко исправляет это, так как он может обрабатывать до 4 таких стираний на блок.
Результатом является CIRC, который может полностью исправить пакеты ошибок размером до 4000 бит или около 2,5 мм на поверхности диска. Этот код настолько силен, что большинство ошибок при воспроизведении компакт-дисков почти наверняка вызваны ошибками отслеживания, которые приводят к смене трека лазером, а не пакетами неисправимых ошибок.[6]
DVD используют аналогичную схему, но с гораздо большими блоками, внутренним кодом (208,192) и внешним кодом (182,172).
Исправление ошибок Рида – Соломона также используется в архивировать файлы, которые обычно размещаются вместе с мультимедийными файлами на USENET. Служба распределенного онлайн-хранилища Wuala (выпуск прекращен в 2015 г.) также использовался для использования кода Рида – Соломона при разделении файлов.
Штрих-код
Почти все двумерные штрих-коды, такие как PDF-417, MaxiCode, Datamatrix, QR код, и Кодекс ацтеков используйте исправление ошибок Рида – Соломона, чтобы обеспечить правильное считывание, даже если часть штрих-кода повреждена. Когда сканер штрих-кода не может распознать символ штрих-кода, он будет рассматривать его как стирание.
Кодирование Рида – Соломона менее распространено в одномерных штрих-кодах, но используется PostBar символика.
Передача информации
Специализированные формы кодов Рида – Соломона, в частности Коши -RS и Vandermonde -RS, может использоваться для преодоления ненадежного характера передачи данных по каналы стирания. Процесс кодирования предполагает код RS (N, K), что приводит к N кодовые слова длины N символы, каждый хранящий K символы генерируемых данных, которые затем отправляются по каналу стирания.
Любая комбинация K кодовых слов, полученных на другом конце, достаточно, чтобы восстановить все N кодовые слова. Кодовая скорость обычно устанавливается равной 1/2, если вероятность стирания канала не может быть адекватно смоделирована и не считается меньшей. В заключении, N обычно 2K, что означает, что по крайней мере половина всех отправленных кодовых слов должна быть получена, чтобы восстановить все отправленные кодовые слова.
Коды Рида – Соломона также используются в xDSL системы и CCSDS с Спецификации протокола космической связи как форма упреждающее исправление ошибок.
Космическая передача

Система конкатенированного кодирования глубокого космоса.[7] Замечание: RS (255, 223) + CC («длина ограничения» = 7, кодовая скорость = 1/2).
Одним из важных применений кодирования Рида-Соломона было кодирование цифровых изображений, отправленных обратно Вояджер Космический зонд.
Вояджер представил кодирование Рида-Соломона соединенный с участием сверточные коды, практика, которая с тех пор стала очень распространенной в дальнем космосе и спутниковой связи (например, прямое цифровое вещание).
Декодеры Витерби имеют тенденцию производить ошибки короткими пакетами. Исправление этих пакетных ошибок лучше всего выполнять с помощью коротких или упрощенных кодов Рида – Соломона.
Современные версии конкатенированного сверточного кодирования с декодированием Рида – Соломона / Витерби использовались и используются на Марс-следопыт, Галилео, Марсоход для исследования Марса и Кассини миссии, где они выполняются в пределах 1–1,5 дБ конечного предела, будучи Емкость Шеннона.
Эти объединенные коды теперь заменяются более мощными турбокоды:
Схемы кодирования каналов, используемые миссиями НАСА[8]
| Лет | Код | Миссия (и) |
|---|---|---|
| 1958-настоящее время | Некодированный | Explorer, Mariner, многие другие |
| 1968-1978 | сверточные коды (CC) (25, 1/2) | Пионер, Венера |
| 1969-1975 (32, 6) | Код Рида-Мюллера | Моряк, Викинг |
| 1977-настоящее время | Двоичный код Голея | Вояджер |
| 1977-настоящее время | RS (255, 223) + CC (7, 1/2) | «Вояджер», «Галилей» и многие другие. |
| 1989-2003 | RS (255, 223) + CC (7, 1/3) | Вояджер |
| 1958-настоящее время | RS (255, 223) + CC (14, 1/4) | Галилео |
| 1996-настоящее время | RS + CC (15, 1/6) | Кассини, Марс-следопыт, другие |
| 2004-настоящее время | Турбо коды[nb 1] | Посланник, стерео, ТОиР, другие |
| оценка 2009 г. | Коды LDPC | Созвездие, MSL |
Конструкции
Код Рида – Соломона на самом деле представляет собой семейство кодов, в котором каждый код характеризуется тремя параметрами: алфавит размер q, а длина блока п, а длина сообщения k, с участием к <п ≤ q. Набор символов алфавита интерпретируется как конечное поле порядка q, и поэтому, q должен быть основная сила. В наиболее полезных параметризациях кода Рида – Соломона длина блока обычно является некоторым постоянным кратным длине сообщения, то есть показатель р = k/п — некоторая константа, и, кроме того, длина блока равна или на единицу меньше размера алфавита, то есть п = q или п = q − 1.[нужна цитата ]
Исходный взгляд Рида и Соломона: кодовое слово как последовательность значений
Для кода Рида – Соломона существуют разные процедуры кодирования, и, следовательно, есть разные способы описания набора всех кодовых слов. Рид и Соломон (1960), каждое кодовое слово кода Рида – Соломона представляет собой последовательность значений функции полинома степени меньше k. Чтобы получить кодовое слово кода Рида – Соломона, сообщение интерпретируется как описание полинома п степени меньше чем k над конечным полем F с участием q элементов, а многочлен п оценивается в п ≤ q отдельные точки 
Формально набор 
Поскольку любые два отчетливый многочлены степени меньше чем 







В то время как количество различных многочленов степени меньше k и количество разных сообщений равно 

Простая процедура кодирования: сообщение как последовательность коэффициентов
В оригинальной конструкции Рид и Соломон (1960), сообщение 

Кодовое слово 





Эта функция 




Эта матрица является транспонированной Матрица Вандермонда над 

Систематическая процедура кодирования: сообщение как начальная последовательность значений.
Существует альтернативная процедура кодирования, которая также производит код Рида – Соломона, но делает это в систематический путь. Здесь отображение из сообщения 



относится ко всем
.
Чтобы вычислить этот полином 



С первого 




Дискретное преобразование Фурье и его обратное
А дискретное преобразование Фурье по сути такая же, как и процедура кодирования; он использует полином генератора п(x), чтобы сопоставить набор точек оценки со значениями сообщения, как показано выше:
Обратное преобразование Фурье можно использовать для преобразования безошибочного набора п < q значения сообщения обратно в полином кодирования k коэффициентов, с ограничением, что для того, чтобы это работало, набор точек оценки, используемых для кодирования сообщения, должен быть набором возрастающих степеней α:
Однако интерполяция Лагранжа выполняет то же преобразование без ограничения на набор точек оценки или требования безошибочного набора значений сообщения и используется для систематического кодирования, и на одном из этапов Декодер гао.
Представление BCH: кодовое слово как последовательность коэффициентов
В этом представлении отправитель снова отображает сообщение 
















Передатчик отправляет 



Систематическая процедура кодирования
Процедура кодирования для представления кодов Рида – Соломона BCH может быть изменена для получения систематическая процедура кодирования, в котором каждое кодовое слово содержит сообщение в качестве префикса и просто добавляет символы исправления ошибок в качестве суффикса. Здесь вместо отправки 









Формально построение осуществляется путем умножения 





Остальные имеют степень не выше 





В результате кодовые слова 


Свойства
Код Рида – Соломона — это [п, k, п − k + 1] код; другими словами, это линейный блочный код длины п (над F) с участием измерение k и минимум Расстояние Хэмминга 
Исправляющая способность кода Рида – Соломона определяется его минимальным расстоянием или, что эквивалентно, 




Теоретическая производительность BER кода Рида-Соломона (N = 255, K = 233, QPSK, AWGN). Ступенчатая характеристика.
Теоретическая граница ошибки может быть описана следующей формулой для AWGN канал для ФСК:[11]
и для других схем модуляции:
где 




Для практического использования кодов Рида – Соломона обычно используется конечное поле 









Свойства кода Рида – Соломона, обсужденные выше, делают его особенно подходящим для приложений, в которых возникают ошибки в всплески. Это связано с тем, что для кода не имеет значения, сколько битов в символе ошибочно — если несколько битов в символе повреждены, это считается только одной ошибкой. И наоборот, если поток данных характеризуется не пакетами ошибок или выпадениями, а случайными одиночными ошибками, код Рида – Соломона обычно является плохим выбором по сравнению с двоичным кодом.
Код Рида – Соломона, как и сверточный код, это прозрачный код. Это означает, что если символы канала были перевернутый где-то по ходу дела декодеры все равно будут работать. Результатом будет инверсия исходных данных. Однако код Рида – Соломона теряет прозрачность при сокращении кода. «Недостающие» биты в сокращенном коде необходимо заполнить нулями или единицами, в зависимости от того, дополняются ли данные или нет. (Другими словами, если символы инвертированы, то заполнение нулями должно быть инвертировано в заполнение одним.) По этой причине обязательно, чтобы смысл данных (то есть истинный или дополняемый) был разрешен до декодирования Рида – Соломона.
Является ли код Рида – Соломона циклический или нет, зависит от тонких деталей конструкции. В исходной точке зрения Рида и Соломона, где кодовые слова являются значениями полинома, можно выбрать последовательность точек оценки таким образом, чтобы сделать код циклическим. В частности, если 












От разработчиков не требуется использовать «естественные» размеры блоков кода Рида – Соломона. Метод, известный как «сокращение», может производить меньший код любого желаемого размера из большего кода. Например, широко используемый код (255,223) можно преобразовать в код (160,128), добавив в неиспользуемую часть исходного блока 95 двоичных нулей и не передав их. В декодере эта же часть блока загружается локально двоичными нулями. Дельсарт-Гёталь-Зайдель[12] Теорема иллюстрирует пример применения сокращенных кодов Рида – Соломона. Параллельно с сокращением используется метод, известный как прокалывание позволяет опустить некоторые закодированные символы четности.
Декодеры просмотра BCH
Декодеры, описанные в этом разделе, используют представление BCH кодового слова как последовательности коэффициентов. В них используется фиксированный полином генератора, известный как кодировщику, так и декодеру.
Декодер Петерсона – Горенштейна – Цирлера
Дэниел Горенштейн и Нил Цирлер разработали декодер, который был описан Цирлером в отчете лаборатории Линкольна Массачусетского технологического института в январе 1960 года, а затем в статье в июне 1961 года.[13] Декодер Горенштейна – Цирлера и связанные с ним работы по кодам BCH описаны в книге. Коды исправления ошибок от В. Уэсли Петерсон (1961).[14]
Формулировка
Переданное сообщение, 
В результате процедуры кодирования Рида-Соломона, s(Икс) делится на порождающий полином г(Икс):
где α первобытный корень.
поскольку s(Икс) кратна образующей г(Икс), то он «наследует» все свои корни:
Переданный полином искажается при передаче полиномом ошибки е(Икс) для получения полученного многочлена р(Икс).
где ея — коэффициент при я-я степень Икс. Коэффициент ея будет равен нулю, если нет ошибки при этой степени Икс и ненулевое значение, если есть ошибка. Если есть ν ошибки при разных мощностях яk из Икс, тогда
Задача декодера — найти количество ошибок (ν), положения ошибок (яk), а значения ошибок в этих положениях (еяk). От тех, е(Икс) можно вычислить и вычесть из р(Икс), чтобы получить изначально отправленное сообщение s(Икс).
Расшифровка синдрома
Декодер начинает с оценки полинома, полученного в определенных точках. Мы называем результаты этой оценки «синдромами», Sj. Они определяются как:
Преимущество рассмотрения синдромов состоит в том, что полином сообщения выпадает. Другими словами, синдромы связаны только с ошибкой и не зависят от фактического содержания передаваемого сообщения. Если все синдромы равны нулю, алгоритм останавливается на этом и сообщает, что сообщение не было повреждено при передаче.
Локаторы ошибок и значения ошибок
Для удобства определим локаторы ошибок Иксk и значения ошибок Yk так как:
Тогда синдромы могут быть записаны в терминах этих локаторов ошибок и значений ошибок как
Это определение значений синдрома эквивалентно предыдущему, поскольку 
Синдромы дают систему п − k ≥ 2ν уравнения в 2ν неизвестных, но эта система уравнений нелинейна в Иксk и не имеет очевидного решения. Однако если Иксk были известны (см. ниже), то синдромные уравнения представляют собой линейную систему уравнений, которую легко решить для Yk значения ошибок.
Следовательно, проблема заключается в поиске Иксk, потому что тогда была бы известна самая левая матрица, и обе части уравнения можно было бы умножить на ее обратную, давая Yk
В варианте этого алгоритма, где места ошибок уже известны (когда он используется как код стирания ), это конец. Расположение ошибок (Иксk) уже известны каким-либо другим методом (например, в FM-передаче участки, где битовый поток был нечетким или преодолен помехами, можно определить с помощью частотного анализа с вероятностью). В этом сценарии до 
Остальная часть алгоритма служит для поиска ошибок и потребует значений синдрома до 

Полином локатора ошибок
Существует линейное рекуррентное соотношение, порождающее систему линейных уравнений. Решение этих уравнений позволяет определить места ошибок. Иксk.
Определить многочлен локатора ошибок Λ (Икс) так как
Нули Λ (Икс) являются обратными 


Позволять 


Сумма за k = От 1 до ν и все равно будет ноль.
Соберите каждый член в отдельную сумму.
Извлеките постоянные значения 
Эти суммы теперь эквивалентны значениям синдромов, которые мы знаем и можем подставить! Следовательно, это сводится к
Вычитание 
Напомним, что j было выбрано любое целое число от 1 до v включительно, и эта эквивалентность верна для любых без исключения таких значений. Следовательно, мы имеем v линейные уравнения, а не одно. Таким образом, эта система линейных уравнений может быть решена относительно коэффициентов Λя полинома определения места ошибки:
Вышесказанное предполагает, что декодер знает количество ошибок. ν, но это количество еще не определено. Декодер PGZ не определяет ν напрямую, а скорее ищет его, пробуя последовательные значения. Декодер сначала принимает наибольшее значение для пробной версии. ν и устанавливает линейную систему для этого значения. Если уравнения могут быть решены (т. Е. Определитель матрицы отличен от нуля), то пробным значением является количество ошибок. Если линейная система не может быть решена, то испытание ν сокращается на единицу и исследуется следующая меньшая система. (Гилл н.д., п. 35)
Найдите корни полинома локатора ошибок
Используйте коэффициенты Λя найденный на последнем шаге для построения полинома местоположения ошибки. Корни полинома определения местоположения ошибки могут быть найдены путем исчерпывающего поиска. Локаторы ошибок Иксk являются обратными этим корням. Порядок коэффициентов полинома определения ошибки может быть изменен на обратный, и в этом случае корни этого обратного полинома являются локаторами ошибок. 

Рассчитайте значения ошибок
Как только локаторы ошибок Иксk известны, значения ошибок могут быть определены. Это можно сделать прямым решением для Yk в уравнения ошибок матрицу, приведенную выше, или используя Алгоритм Форни.
Рассчитайте места ошибок
Рассчитать яk взяв базу журнала 
Исправьте ошибки
Наконец, e (x) генерируется из яk и еяk а затем вычитается из r (x), чтобы получить первоначально отправленное сообщение s (x) с исправленными ошибками.
пример
Рассмотрим код Рида – Соломона, определенный в GF(929) с участием α = 3 и т = 4 (это используется в PDF417 штрих-коды) для кода RS (7,3). Генераторный полином равен
Если полином сообщения п(Икс) = 3 Икс2 + 2 Икс + 1, то систематическое кодовое слово кодируется следующим образом.
Ошибки при передаче могут привести к получению этого сообщения.
Синдромы рассчитываются путем оценки р во власти α.
С помощью Гауссово исключение:
- Λ (х) = 329 х2 + 821 x + 001, с корнями x1 = 757 = 3−3 и х2 = 562 = 3−4
Коэффициенты можно поменять местами, чтобы получить корни с положительными показателями, но обычно это не используется:
- R (х) = 001 х2 + 821 x + 329, с корнями 27 = 33 и 81 = 34
с журналом корней, соответствующим местоположениям ошибок (справа налево, ячейка 0 — это последний член в кодовом слове).
Чтобы вычислить значения ошибок, примените Алгоритм Форни.
- Ω (x) = S (x) Λ (x) mod x4 = 546 х + 732
- Λ ‘(х) = 658 х + 821
- е1 = −Ω (x1) / Λ ‘(x1) = 074
- е2 = −Ω (x2) / Λ ‘(x2) = 122
Вычитание е1 Икс3 и е2 Икс4 от полученного многочлена р воспроизводит исходное кодовое слово s.
Декодер Берлекампа – Месси
В Алгоритм Берлекампа-Месси является альтернативной итерационной процедурой поиска полинома локатора ошибок.Во время каждой итерации он вычисляет несоответствие на основе текущего экземпляра Λ (x) с предполагаемым количеством ошибок. е:
а затем регулирует Λ (Икс) и е так что пересчитанное Δ будет равно нулю. Статья Алгоритм Берлекампа-Месси есть подробное описание процедуры. В следующем примере C(Икс) используется для представления Λ (Икс).
пример
Используя те же данные, что и в приведенном выше примере Peterson Gorenstein Zierler:
| п | Sп+1 | d | C | B | б | м |
|---|---|---|---|---|---|---|
| 0 | 732 | 732 | 197 Икс + 1 | 1 | 732 | 1 |
| 1 | 637 | 846 | 173 Икс + 1 | 1 | 732 | 2 |
| 2 | 762 | 412 | 634 Икс2 + 173 Икс + 1 | 173 Икс + 1 | 412 | 1 |
| 3 | 925 | 576 | 329 Икс2 + 821 Икс + 1 | 173 Икс + 1 | 412 | 2 |
Окончательное значение C — многочлен локатора ошибок, Λ (Икс).
Евклидов декодер
Другой итерационный метод вычисления как полинома локатора ошибок, так и полинома значения ошибки основан на адаптации Сугиямы расширенный алгоритм Евклида .
Определим S (x), Λ (x) и Ω (x) для т синдромы и е ошибки:
Ключевое уравнение:
Для т = 6 и е = 3:
Средние члены равны нулю из-за связи между Λ и синдромами.
Расширенный алгоритм Евклида может найти серию многочленов вида
- Ая(Икс) S(Икс) + Bя(Икс) Икст = ря(Икс)
где степень р уменьшается как я увеличивается. Однажды степень ря(Икс) < т/ 2, то
Ая(х) = Λ (х)
Bя(х) = −Q (х)
ря(х) = Ω (х).
B (x) и Q (x) не нужно сохранять, поэтому алгоритм становится:
- р−1 = хт
- р0 = S (х)
- А−1 = 0
- А0 = 1
- я = 0
- а степень Rя ≥ т / 2
- я = я + 1
- Q = Ri-2 / Ря-1
- ря = Ri-2 — Q Rя-1
- Ая = Аi-2 — Q Aя-1
чтобы установить младший член Λ (x) равным 1, разделите Λ (x) и Ω (x) на Aя(0):
- Λ (х) = Ая / Ая(0)
- Ω (x) = Rя / Ая(0)
Ая(0) — постоянный член (младшего порядка) Aя.
пример
Используя те же данные, что и в приведенном выше примере Петерсона – Горенштейна – Цирлера:
| я | ря | Ая |
|---|---|---|
| −1 | 001 х4 + 000 х3 + 000 х2 + 000 х + 000 | 000 |
| 0 | 925 х3 + 762 х2 + 637 х + 732 | 001 |
| 1 | 683 х2 + 676 х + 024 | 697 х + 396 |
| 2 | 673 х + 596 | 608 х2 + 704 х + 544 |
- Λ (х) = А2 / 544 = 329 х2 + 821 х + 001
- Ω (x) = R2 / 544 = 546 х + 732
Декодер с использованием дискретного преобразования Фурье
Для декодирования можно использовать дискретное преобразование Фурье.[15] Чтобы избежать конфликта с названиями синдромов, позвольте c(Икс) = s(Икс) закодированное кодовое слово. р(Икс) и е(Икс) такие же, как указано выше. Определить C(Икс), E(Икс), и р(Икс) как дискретные преобразования Фурье c(Икс), е(Икс), и р(Икс). поскольку р(Икс) = c(Икс) + е(Икс), и поскольку дискретное преобразование Фурье является линейным оператором, р(Икс) = C(Икс) + E(Икс).
Преобразовать р(Икс) к р(Икс) с помощью дискретного преобразования Фурье. Поскольку расчет для дискретного преобразования Фурье такой же, как расчет для синдромов, т коэффициенты р(Икс) и E(Икс) такие же, как синдромы:
Использовать 

Пусть v = количество ошибок. Сгенерируйте E (x), используя известные коэффициенты 

Затем вычислите C(Икс) = р(Икс) − E(Икс) и обратное преобразование (полиномиальная интерполяция) C(Икс) производить c(Икс).
Декодирование за пределами исправления ошибок
В Граница синглтона заявляет, что минимальное расстояние d линейного блочного кода размером (п,k) ограничена сверху п − k + 1. Расстояние d обычно понималось, что возможность исправления ошибок ограничивается ⌊d/ 2⌋. Код Рида – Соломона достигает этой границы с равенством и, таким образом, может исправлять до (п − k + 1) / 2⌋ ошибок. Однако этот предел исправления ошибок не точен.
В 1999 году, Мадху Судан и Венкатесан Гурусвами в Массачусетском технологическом институте опубликовал «Улучшенное декодирование кодов Рида – Соломона и алгебраической геометрии», в котором представлен алгоритм, позволяющий исправлять ошибки, превышающие половину минимального расстояния кода.[16] Это относится к кодам Рида – Соломона и в более общем смысле к алгебро-геометрические коды. Этот алгоритм создает список кодовых слов (это список-декодирование алгоритм) и основан на интерполяции и факторизации многочленов по 
Мягкое декодирование
Алгебраические методы декодирования, описанные выше, являются методами жесткого решения, что означает, что для каждого символа принимается жесткое решение о его значении. Например, декодер может связать с каждым символом дополнительное значение, соответствующее каналу. демодулятор уверенность в правильности обозначения. Появление LDPC и турбокоды, которые используют повторяющиеся мягкое решение методы декодирования распространения убеждений для достижения производительности исправления ошибок, близкой к теоретический предел, вызвало интерес к применению декодирования с мягким решением к обычным алгебраическим кодам. В 2003 году Ральф Кёттер и Александр Варди представил алгоритм полиномиального алгебраического декодирования списков с мягким решением для кодов Рида – Соломона, который был основан на работе Судана и Гурусвами.[17]В 2016 году Стивен Дж. Франке и Джозеф Х. Тейлор опубликовали новый декодер с мягким решением.[18]
Пример Matlab
Кодировщик
Здесь мы представляем простую реализацию Matlab для кодировщика.
функция[закодировано] =rsEncoder(msg, m, prim_poly, n, k)% RSENCODER Кодировать сообщение с помощью алгоритма Рида-Соломона % m - количество бит на символ % prim_poly: Примитивный многочлен p (x). Т.е. для DM - 301 % k - размер сообщения % n - общий размер (k + избыточный) % Пример: msg = uint8 ('Тест') % enc_msg = rsEncoder (сообщение, 8, 301, 12, число (сообщение)); % Получить альфа альфа = gf(2, м, prim_poly); % Получите порождающий многочлен Рида-Соломона g (x) g_x = генполия(k, п, альфа); % Умножьте информацию на X ^ (n-k) или просто добавьте нули в конце, чтобы % получить место для добавления избыточной информации msg_padded = gf([сообщение нули(1, п - k)], м, prim_poly); % Получить остаток от деления расширенного сообщения на % Порождающий многочлен Рида-Соломона g (x) [~, остаток] = деконв(msg_padded, g_x); % Теперь верните сообщение с избыточной информацией закодированный = msg_padded - остаток;конец% Найдите порождающий многочлен Рида-Соломона g (x), между прочим, это% то же, что и функция rsgenpoly в Matlabфункцияг =генполия(k, n, альфа)г = 1; % Умножение на поле Галуа - это просто свертка для k = mod (1: n - k, n) г = Конв(г, [1 альфа .^ (k)]); конецконец
Декодер
Теперь расшифровка:
функция[декодировано, error_pos, error_mag, g, S] =rsDecoder(закодировано, m, prim_poly, n, k)% RSDECODER Расшифровать сообщение, закодированное Ридом-Соломоном % Пример: % [dec, ~, ~, ~, ~] = rsDecoder (enc_msg, 8, 301, 12, numel (сообщение)) max_errors = этаж((п - k) / 2); orig_val = закодированный.Икс; % Инициализировать вектор ошибки ошибки = нули(1, п); г = []; S = []; % Получить альфа альфа = gf(2, м, prim_poly); % Найдите синдромы (проверьте, не разбивает ли сообщение генератор % полином результат равен нулю) Synd = поливал(закодированный, альфа .^ (1:п - k)); Синдромы = отделка(Synd); % Если все синдромы нулевые (полностью делимые), ошибок нет если пусто (Syndromes.x) расшифрованный = orig_val(1:k); error_pos = []; error_mag = []; г = []; S = Synd; вернуть; конец% Подготовьтесь к эвклидовому алгоритму (используется для поиска ошибки % полиномов) r0 = [1, нули(1, 2 * max_errors)]; r0 = gf(r0, м, prim_poly); r0 = отделка(r0); size_r0 = длина(r0); r1 = Синдромы; f0 = gf([нули(1, size_r0 - 1) 1], м, prim_poly); f1 = gf(нули(1, size_r0), м, prim_poly); g0 = f1; g1 = f0; % Выполните алгоритм Евклида на многочленах r0 (x) и Syndromes (x) в %, чтобы найти многочлен обнаружения ошибки в то время как правда % Сделайте длинное деление [частное, остаток] = деконв(r0, r1); % Добавьте нули частное = подушечка(частное, длина(g1)); % Найти частное * g1 и дополнить c = Конв(частное, g1); c = отделка(c); c = подушечка(c, длина(g0)); % Обновить g как коэффициент g0 * g1 г = g0 - c; % Проверить, меньше ли степень остатка (x) max_errors если все (остаток (1: конец - max_errors) == 0) перерыв; конец% Обновить r0, r1, g0, g1 и удалить ведущие нули r0 = отделка(r1); r1 = отделка(остаток); g0 = g1; g1 = г; конец% Удалить ведущие нули г = отделка(г); % Найдите нули полинома ошибок на этом поле Галуа evalPoly = поливал(г, альфа .^ (п - 1 : - 1 : 0)); error_pos = gf(найти(evalPoly == 0), м); % Если ошибочной позиции не обнаружено, мы возвращаем полученную работу, потому что % по сути это ничего, что мы могли бы сделать и возвращаем полученное сообщение если isempty (error_pos) расшифрованный = orig_val(1:k); error_mag = []; вернуть; конец% Подготовьте линейную систему для решения полинома ошибок и нахождения ошибки % величины size_error = длина(error_pos); Синдром_Вальс = Синдромы.Икс; б(:, 1) = Синдром_Вальс(1:size_error); для idx = 1: size_error е = альфа .^ (idx * (п - error_pos.Икс)); ошибаться = е.Икс; э(idx, :) = ошибаться; конец% Решите линейную систему error_mag = (gf(э, м, prim_poly) gf(б, м, prim_poly))'; % Поместите величину ошибки в вектор ошибки ошибки(error_pos.Икс) = error_mag.Икс; % Принесите этот вектор в поле галуа errors_gf = gf(ошибки, м, prim_poly); % Теперь, чтобы исправить ошибки, просто добавьте закодированный код decoded_gf = закодированный(1:k) + errors_gf(1:k); расшифрованный = decoded_gf.Икс;конец% Удалить ведущие нули из массива Галуафункцияgt =отделка(г)gx = г.Икс; gt = gf(gx(найти(gx, 1) : конец), г.м, г.prim_poly);конец% Добавить ведущие нулифункцияxpad =подушечка(х, к)len = длина(Икс); если (len < k) xpad = [нули(1, k - len) Икс]; конецконец
Оригинальные декодеры вида Рида Соломона
Декодеры, описанные в этом разделе, используют исходное представление кодового слова Рида-Соломона как последовательность полиномиальных значений, где полином основан на кодируемом сообщении. Один и тот же набор фиксированных значений используется кодером и декодером, и декодер восстанавливает полином кодирования (и, возможно, полином обнаружения ошибки) из полученного сообщения.
Теоретический декодер
Рид и Соломон (1960) описал теоретический декодер, который исправляет ошибки, находя самый популярный полином сообщений. Декодер знает только набор значений 



Декодер Berlekamp Welch
В 1986 году декодер, известный как Алгоритм Берлекампа – Велча был разработан как декодер, который может восстанавливать исходный полином сообщения, а также полином «локатора» ошибок, который производит нули для входных значений, соответствующих ошибкам, с временной сложностью O (n ^ 3), где n — число значений в сообщении. Восстановленный многочлен затем используется для восстановления (при необходимости пересчета) исходного сообщения.
пример
Используя RS (7,3), GF (929) и набор точек оценки ая = я − 1
- а = {0, 1, 2, 3, 4, 5, 6}
Если полином сообщения
- п(Икс) = 003 Икс2 + 002 Икс + 001
Кодовое слово
- c = {001, 006, 017, 034, 057, 086, 121}
Ошибки при передаче могут привести к получению этого сообщения.
- б = c + е = {001, 006, 123, 456, 057, 086, 121}
Ключевые уравнения:
Предположим максимальное количество ошибок: е = 2. Ключевые уравнения становятся:
С помощью Гауссово исключение:
- Q(Икс) = 003 Икс4 + 916 Икс3 + 009 Икс2 + 007 Икс + 006
- E(Икс) = 001 Икс2 + 924 Икс + 006
- Q(Икс) / E(Икс) = п(Икс) = 003 Икс2 + 002 Икс + 001
Пересчитать Р (х) где E (x) = 0: {2, 3} исправлять б в результате получено исправленное кодовое слово:
- c = {001, 006, 017, 034, 057, 086, 121}
Декодер гао
В 2002 году Шухонг Гао разработал улучшенный декодер на основе расширенного алгоритма Евклида. Gao_RS.pdf .
пример
Используя те же данные, что и в приведенном выше примере Берлекампа Велча:
Интерполяция Лагранжа
для я = От 1 до п
| я | ря | Ая |
|---|---|---|
| −1 | 001 х7 + 908 х6 + 175 х5 + 194 х4 + 695 х3 + 094 х2 + 720 х + 000 | 000 |
| 0 | 055 х6 + 440 х5 + 497 х4 + 904 х3 + 424 х2 + 472 х + 001 | 001 |
| 1 | 702 х5 + 845 х4 + 691 х3 + 461 х2 + 327 х + 237 | 152 х + 237 |
| 2 | 266 х4 + 086 х3 + 798 х2 + 311 х + 532 | 708 х2 + 176 х + 532 |
- Q(Икс) = р2 = 266 Икс4 + 086 Икс3 + 798 Икс2 + 311 Икс + 532
- E(Икс) = А2 = 708 Икс2 + 176 Икс + 532
делить Q(x) и E(x) по старшему коэффициенту при E(x) = 708. (Необязательно)
- Q(Икс) = 003 Икс4 + 916 Икс3 + 009 Икс2 + 007 Икс + 006
- E(Икс) = 001 Икс2 + 924 Икс + 006
- Q(Икс) / E(Икс) = п(Икс) = 003 Икс2 + 002 Икс + 001
Пересчитать п(Икс) где E(Икс) = 0 : {2, 3} исправлять б в результате получено исправленное кодовое слово:
- c = {001, 006, 017, 034, 057, 086, 121}
Смотрите также
- Код BCH
- Циклический код
- Чиен поиск
- Алгоритм Берлекампа-Месси
- Прямое исправление ошибок
- Алгоритм Берлекампа – Велча
- Сложенный код Рида – Соломона
Заметки
- ^ Авторы в[8] предоставить результаты моделирования, которые показывают, что для той же кодовой скорости (1/6) турбокоды превосходят сцепленные коды Рида-Соломона до 2 дБ (частота ошибок по битам ).
использованная литература
- Джилл, Джон (нет данных), EE387 Заметки № 7, Раздаточный материал № 28 (PDF), Стэнфордский университет, архив из оригинал (PDF) 30 июня 2014 г., получено 21 апреля, 2010
- Хонг, Джонатан; Веттерли, Мартин (август 1995), «Простые алгоритмы декодирования BCH» (PDF), Транзакции IEEE по коммуникациям, 43 (8): 2324–2333, Дои:10.1109/26.403765
- Линь, Шу; Костелло-младший, Дэниел Дж. (1983), Кодирование с контролем ошибок: основы и приложения, Нью-Джерси, Нью-Джерси: Прентис-Холл, ISBN 978-0-13-283796-5
- Мэсси, Дж. Л. (1969), «Синтез регистров сдвига и декодирование BCH» (PDF), IEEE Transactions по теории информации, ИТ-15 (1): 122–127, Дои:10.1109 / tit.1969.1054260
- Петерсон, Уэсли В. (1960), «Процедуры кодирования и исправления ошибок для кодов Бозе-Чаудхури», Сделки IRE по теории информации, IT-6 (4): 459–470, Дои:10.1109 / TIT.1960.1057586
- Рид, Ирвинг С.; Соломон, Гюстав (1960), «Полиномиальные коды над некоторыми конечными полями», Журнал Общества промышленной и прикладной математики, 8 (2): 300–304, Дои:10.1137/0108018
- Уэлч, Л. Р. (1997), Первоначальный взгляд на коды Рида – Соломона (PDF), Конспект лекций
дальнейшее чтение
- Берлекамп, Элвин Р. (1967), Недвоичное декодирование BCH, Международный симпозиум по теории информации, Сан-Ремо, Италия
- Берлекамп, Элвин Р. (1984) [1968], Алгебраическая теория кодирования (Пересмотренное издание), Laguna Hills, CA: Aegean Park Press, ISBN 978-0-89412-063-3
- Сипра, Барри Артур (1993), «Вездесущие коды Рида – Соломона», Новости SIAM, 26 (1)
- Форни младший, Г. (Октябрь 1965 г.), «О декодировании кодов BCH», IEEE Transactions по теории информации, 11 (4): 549–557, Дои:10.1109 / TIT.1965.1053825
- Кёттер, Ральф (2005), Коды Рида – Соломона, MIT Lecture Notes 6.451 (видео), архивировано с оригинал на 2013-03-13
- MacWilliams, F.J .; Слоан, Н. Дж. А. (1977), Теория кодов, исправляющих ошибки, Нью-Йорк, Нью-Йорк: Издательская компания Северной Голландии.
- Рид, Ирвинг С.; Чен, Сюэминь (1999), Кодирование с контролем ошибок для сетей передачи данных, Бостон, Массачусетс: Kluwer Academic Publishers
внешние ссылки
Информация и учебные пособия
- Введение в коды Рида – Соломона: принципы, архитектура и реализация (CMU)
- Учебное пособие по кодированию Рида – Соломона для обеспечения отказоустойчивости в RAID-подобных системах
- Алгебраическое мягкое декодирование кодов Рида – Соломона
- Викиверситет: коды Рида – Соломона для программистов
- Белая книга BBC R&D WHP031
- Гейзель, Уильям А. (август 1990 г.), Учебное пособие по кодированию с исправлением ошибок Рида – Соломона (PDF), Технический меморандум, НАСА, TM-102162
- Гао, Шухун (январь 2002 г.), Новый алгоритм декодирования кодов Рида-Соломона (PDF), Клемсон
- Составные коды автор Dr. Дэйв Форни (scholarpedia.org).
Реализации
- Кодек Рида – Соломона Schifra с открытым исходным кодом C ++
- Библиотека RSCode Генри Мински, кодировщик / декодер Рида – Соломона
- Библиотека программного декодирования Рида – Соломона с открытым исходным кодом C ++
- Реализация в Matlab ошибок и стираний декодирования Рида – Соломона
- Реализация Octave в коммуникационном пакете
- Реализация кодека Рида – Соломона на чистом Python
- ^ Рид и Соломон (1960)
- ^ Д. Горенштейн и Н. Цирлер, «Класс циклических линейных кодов с исправлением ошибок в символах p ^ m», J. SIAM, vol. 9, стр. 207-214, июнь 1961 г.
- ^ Коды исправления ошибок, автор W_Wesley_Peterson, 1961 г.
- ^ Коды исправления ошибок, автор W_Wesley_Peterson, второе издание, 1972 г.
- ^ Ясуо Сугияма, Масао Касахара, Сигейчи Хирасава и Тошихико Намекава. Метод решения ключевого уравнения для декодирования кодов Гоппа. Информация и контроль, 27: 87–99, 1975.
- ^ Имминк, К.А.С. (1994), «Коды Рида – Соломона и компакт-диск», в Wicker, Stephen B .; Бхаргава, Виджай К. (ред.), Коды Рида – Соломона и их приложения, IEEE Press, ISBN 978-0-7803-1025-4
- ^ Дж. Хагенауэр, Э. Оффер и Л. Папке, Коды Рида-Соломона и их приложения. Нью-Йорк IEEE Press, 1994 — стр. 433
- ^ а б Эндрюс, Кеннет С. и др. «Разработка кодов турбо и LDPC для приложений дальнего космоса». Протоколы IEEE 95.11 (2007): 2142-2156.
- ^ Лидл, Рудольф; Пильц, Гюнтер (1999). Прикладная абстрактная алгебра (2-е изд.). Вайли. п. 226.
- ^ Увидеть Лин и Костелло (1983), п. 171), например.
- ^ «Аналитические выражения, используемые в кодировании и BERTool». В архиве с оригинала на 2019-02-01. Получено 2019-02-01.
- ^ Пфендер, Флориан; Циглер, Гюнтер М. (сентябрь 2004 г.), «Целующиеся числа, упаковки сфер и некоторые неожиданные доказательства» (PDF), Уведомления Американского математического общества, 51 (8): 873–883, в архиве (PDF) из оригинала 2008-05-09, получено 2009-09-28. Объясняет теорему Дельсарта-Гётальса-Зейделя в контексте кода исправления ошибок для компакт-диск.
- ^ Д. Горенштейн и Н. Цирлер, «Класс циклических линейных кодов с исправлением ошибок в символах p ^ m», J. SIAM, vol. 9. С. 207–214, июнь 1961 г.
- ^ Коды исправления ошибок Уэсли Петерсон, 1961 г.
- ^ Шу Линь и Дэниел Дж. Костелло-младший, «Кодирование с контролем ошибок», второе издание, стр. 255–262, 1982, 2004
- ^ Гурусвами, V .; Судан, М. (сентябрь 1999 г.), «Улучшенное декодирование кодов Рида – Соломона и кодов алгебраической геометрии», IEEE Transactions по теории информации, 45 (6): 1757–1767, CiteSeerX 10.1.1.115.292, Дои:10.1109/18.782097
- ^ Кёттер, Ральф; Варди, Александр (2003). «Алгебраическое декодирование с мягким решением кодов Рида – Соломона». IEEE Transactions по теории информации. 49 (11): 2809–2825. CiteSeerX 10.1.1.13.2021. Дои:10.1109 / TIT.2003.819332.
- ^ Franke, Стивен Дж .; Тейлор, Джозеф Х. (2016). «Декодер Soft-Decision с открытым исходным кодом для кода Рида-Соломона JT65 (63,12)» (PDF). QEX (Май / июнь): 8–17. В архиве (PDF) из оригинала на 2017-03-09. Получено 2017-06-07.
В современных
системах цифрового телевидения для
обеспечения помехоустойчивой передачи
цифровых телевизионных сигналов по
радиоканалу используются наиболее
совершенные коды Рида-Соломона(Reed-Solomon),требующие добавления двух проверочных
символов в расчете на одну исправляемую
ошибку. Коды Рида-Соломона обладают
высокими корректирующими свойствами,
для них разработаны относительно
простые и конструктивные методы
кодирования. Коды Рида-Соломона не
являются двоичными. Это надо понимать
в том смысле, что символами кодовых
слов являются не двоичные знаки, а
элементы множества чисел, состоящего
более чем из двух знаков (хотя, конечно,
при передаче каждый символ заменяется
соответствующей двоичной комбинацией).
Коды Рида-Соломона,
относящиеся к классу циклических
кодов, образуют подгруппублоковых
кодов. Они получаются из любой
разрешенной комбинации путем циклического
сдвига ее разрядов. Кодирование и
декодирование, обнаруживающее и
исправляющее ошибки, – это вычислительные
процедуры, которые для циклических
кодов удобно выполнять как действия с
многочленами и реализацию в виде
цифровых устройств на базе регистров
сдвига с обратными связями.
Чтобы получить
более детальное представление о кодах
Рида-Соломона посмотрим, какое место
они занимают в классификации корректирующих
кодов (рис. 4.4).
Корректирующие
коды разделяются на блочные и сверточные
(непрерывные). Блочные кодыоснованы на перекодировании исходной
кодовой комбинации (блока), содержащейkинформационных
символов, в передаваемую кодовую
комбинацию, содержащуюn>kсимволов.
Дополнительныер = n – kсимволов зависят только отkсимволов исходной кодовой комбинации.
Следовательно, кодирование и
декодирование осуществляются всегда
в пределах одной кодовой комбинации
(блока). В противоположность этому всверточных кодахкодирование и
декодирование осуществляются непрерывно
над последовательностью двоичных
символов.
Блочные коды
бывают разделимые и неразделимые. В
разделимых кодахможно в каждой
кодовой комбинации указать, какие
символы являются информационными,
а какие проверочными. Внеразделимых
кодахтакая возможность отсутствует.
Следующая ступень
классификации – систематические
коды. Они отличаются тем, что в них
проверочные символы формируются из
информационных символов по определенным
правилам, выражаемым математическими
соотношениями. Например, каждый
проверочный символхpjполучается как линейная комбинация
информационных символов

Рис. 4.4.Место
кодов Рида-Соломона в классификации
корректирующих кодов
![]() ,
,
где
![]() – коэффициенты, принимающие значения
– коэффициенты, принимающие значения
0 или 1;![]() .
.
Соотношение для формирования
контрольного бита проверки на четность
является частным случаем .
Перейдем к более
подробному знакомству с циклическими
кодами.
В первую очередь
введем запись кодовой комбинации или,
как часто называют ее в литературе,
кодового вектора в виде полинома. Пусть
имеется кодовая комбинация
a0a1a2…an–1,
гдеа0– младший разряд кода,an–1– старший разряд кода. Соответствующий
ей полином имеет вид
![]() ,
,
где х–
формальная переменная, вводимая только
для получения записи кодовой
комбинации в виде полинома.
Над полиномами,
представляющими кодовые комбинации,
определена математическая операция
умножения. Особенность этой операции
по сравнению с общепринятой заключается
в том, что коэффициенты при хвсех
степеней суммируются по модулю 2, а
показатели степенихпри перемножении
суммируются по модулюn,
поэтомухn= 1.
Далее
введем понятие производящего
полинома.
Производящим
полиномом порядка (n – k)
может быть
полином со старшей степенью х,
равной (n – k),
на который без
остатка делится двучлен (1 + хn).
Разрешенные кодовые комбинации
получаются перемножением полиномов
порядка k – 1,
выражающих исходные кодовые комбинации,
на производящий полином.
Циклические коды
имеют следующее основное свойство.
Если кодовая комбинация a0a1a2…an–1является разрешенной, то получаемая
из нее путем циклического сдвига
кодовая комбинацияan–1a0a1…an–2также является разрешенной в данном
коде. При записи в виде полиномов
операция циклического сдвига кодового
слова сводится к умножению соответствующего
полинома нахс учетом приведенных
ранее правил выполнения операции
умножения.
Циклический код
с производящим полиномом
![]() строится следующим образом.
строится следующим образом.
1. Берутся
полиномы
![]() ,
,![]() ,
,![]() ,
,
…,![]() .
.
2. Кодовые
комбинации, соответствующие этим
полиномам, записывают в виде строк
матрицы G, называемойпроизводящей матрицей.
3. Формируется
набор разрешенных кодовых комбинаций
кода. В него входит нулевая кодовая
комбинация, k
кодовых комбинаций, указанных в п. 1,
а также суммы их всевозможных сочетаний.
Суммирование осуществляется поразрядно,
причем каждый
разряд суммируется по модулю 2.
Общее число полученных таким образом
разрешенных кодовых комбинаций равно
2k,
что соответствует числу информационных
разрядов кода.
Для построения
декодера в первую очередь получают
производящий полином
![]() порядкаkдля построенияисправляющей матрицыН:
порядкаkдля построенияисправляющей матрицыН:
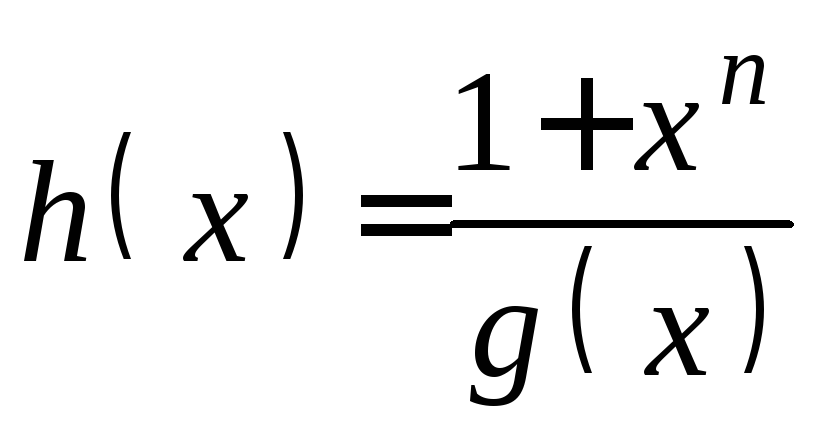 .
.
Строками исправляющей
матрицы Нбудут кодовые комбинации,
определяемые полиномами![]() ,
,![]() ,
,
…,![]() ,
,
где![]() – это записанный в обратном порядке
– это записанный в обратном порядке
полином![]() .
.
Исправляющая матрица имеетnстолбцов иn – kстрок.
При декодировании
принятая кодовая комбинация a0a1a2…an–1скалярно умножается на каждую строку
исправляющей матрицы. Эта операция
может быть записана в виде соотношения:
![]() ,
,
где hji– элементыj-той
строки матрицыН. Полученныеn – kчиселcjобразуютисправляющий векторилисиндром. Если ошибок нет, то всеcj= 0. Если же при передаче данной кодовой
комбинации возникла ошибка, то некоторые
из чиселcjне равны 0. По тому, какие именно элементы
исправляющего вектора отличны от нуля,
можно сделать вывод о том, в каких
разрядах принятой кодовой комбинации
есть ошибка и, следовательно, исправить
эти ошибки.
Рассмотрим пример,
часто встречающийся в литературе.
Построим циклический код с n= 7;k= 4. Для этого
представим двучлен 1 +х7в
виде произведения [4]:
![]() .
.
В
обычной алгебре это равенство, конечно,
не выполняется, но если использовать
для приведения подобных вместо обычного
сложения операцию суммирования по
модулю 2, а при сложении показателей
степеней –
операцию суммирования по модулю 7, то
равенство окажется справедливым.
В качестве
производящего многочлена возьмем 1 + х+х3. Умножаем его нах,х2их3и получаем многочленых+х2+х4;х2+х3+х5;х3+х4+х6. Затем
записываем производящую матрицуG,
причем в каждой строке матрицы младший
разряд кодовой комбинации расположен
первым слева.
 .
.
Далее формируем
набор из 15 допустимых кодовых комбинаций:
00000000, 1101000, 0110100, 0011010, 0001101, 1011100, 0101110,
0010111, 1000110, 0100011, 1111111, 1010001, 1000110, 0100011,
1001011. В этих записях младшие биты
слева, а старшие – справа.
Перемножив первые
два сомножителя в , получаем производящий
многочлен для исправляющей матрицы:
1 + х+х+х4. Затем
умножаем его нахих2и
получаем еще две строки этой матрицы,
которая в результате имеет такой вид
(в отличие от матрицыGздесь младшие разряды соответствующих
полиномов расположены справа):
 .
.
Пусть принята
кодовая комбинация 0001101, входящая в
набор допустимых. Найдем скалярные
произведения этой кодовой комбинации
со всеми строками матрицы Н:

Пусть теперь
принята кодовая комбинация 0001100, в
которой последний (старший) бит содержит
ошибку. Скалярные произведения принятой
кодовой комбинации на строки исправляющей
матрицы имеют вид:

Таким образом,
получен синдром (1, 0, 0). Если ошибка
оказывается в другом бите кодовой
комбинации, то получается другой
синдром.
Одним из важных
достоинств циклических кодов является
возможность построения кодирующих и
декодирующих устройств в виде сдвиговых
регистров с обратными связями через
сумматоры по модулю 2.
Различные виды
циклических кодов получаются с помощью
различных производящих полиномов.
Существует развитая математическая
теория этого вопроса [15]. Среди
большого количества циклических кодов
к числу наиболее эффективных и широко
используемых относятся коды
Бозе-Чоудхури-Хоквингема (ВСН-коды –
по первым буквам фамилий Bose,Chaudhuri,Hockwinhamили в русскоязычной записи БЧХ-коды),
являющиесяобобщением кодов Хеммингана случай направления нескольких
ошибок. Они образуют наилучший среди
известных класснеслучайных кодовдля каналов, в которых ошибки в
последовательных символах возникают
независимо. Например, БЧХ-код (63, 44),
используемый в системе спутникового
цифрового радиовещания, позволяет
исправить 2 или 3 ошибки, обнаружить 4
или 5 ошибок на каждый блок из 63 символов.
Относительная скорость такого кода
равнаR= 44/63 = 0,698.
Одним
из видов ВСН-кодов являются коды
Рида-Соломона. Эти коды относятся к
недвоичным
кодам,
так как символами в них могут быть
многоразрядные двоичные числа,
например, целые байты. В Европейском
стандарте цифрового телевидения
DVB
используется код Рида-Соломона,
записываемый как (204, 188, 8), где 188 –
количество информационных байт в пакете
транспортного потока MPEG-2,
204 – количество байт в пакете после
добавления проверочных символов, 8 –
минимальное кодовое расстояние между
допустимыми кодовыми комбинациями.
Таким образом, в качестве кодовых
комбинаций берутся целые пакеты
транспортного потока, содержащие 1888
= 1504 информационных бита, а добавляемые
проверочные символы содержат 168
= 128 бит. Относительная скорость такого
кода равна 0,92. Этот код Рида-Соломона
позволяет эффективно исправлять до 8
принятых с ошибками байт в каждом
транспортном пакете.
Отметим также,
что используемый в цифровом телевизионном
вещании код Рида-Соломона часто называют
укороченным. Смысл этого термина
состоит в следующем. Из теории кодов
Рида-Соломона следует, что если символом
кода является байт, то полная длина
кодового слова должна составлять 255
байт (239 информационных и 16 проверочных).
Однако, пакет транспортного потокаMPEG-2 содержит 188 байт.
Чтобы согласовать размер пакета с
параметрами кода, перед кодированием
в начало каждого транспортного пакета
добавляют 51 нулевой информационный
байт, а после кодирования эти
дополнительные нулевые байты
отбрасывают.
В приемнике для
каждого принятого транспортного пакета,
содержащего 204 байта, вычисляются
синдромы и находятся два полинома:
«локатор», корни которого показывают
положение ошибок, и «корректор»
(evaluator), дающий значение
ошибок. Ошибки корректируются, если
это возможно. Если же коррекция невозможна
(например, ошибочных байт более данные
в пакете не изменяются, а сам пакет
помечается путем установки флага
(первый бит после синхробайта), как
содержащий неустранимые ошибки. В обоих
случаях 16 избыточных байт удаляются,
и после декодирования длина транспортного
пакета становится равной 188 байт.
| Код Рида — Соломона | |
|---|---|
| Назван в честь | Ирвинг Рид[d] и Густав Соломон[d] |
| Тип |
|
| Длина блока | |
| Длина сообщения | |
| Расстояние | |
| Размер алфавита | для простого , часто |
| Обозначение | |
Коды Рида — Соломона (англ. (b) Reed–Solomon codes) — недвоичные циклические коды (b) , позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида — Соломона, работающие с байтами (октетами).
Код Рида — Соломона является частным случаем БЧХ-кода (b) .
В настоящее время широко используется в системах восстановления данных с компакт-дисков (b) , при создании архивов с информацией для восстановления в случае повреждений, в помехоустойчивом кодировании (b) .
История
Код Рида — Соломона был изобретён в 1960 году сотрудниками лаборатории Линкольна Массачусетского технологического института (b) Ирвингом Ридом (b) (англ.) и Густавом Соломоном (b) (англ.). Идея использования этого кода была представлена в статье «Polynomial Codes over Certain Finite Fields». Эффективные алгоритмы декодирования были предложены в 1969 году (b) Элвином Берлекэмпом (b) и Джэймсом Месси (b) (алгоритм Берлекэмпа — Мэсси (b) ) и в 1977 году (b) Давидом Мандельбаумом (b) (англ.) (метод, использующий Алгоритм Евклида (b) [1]). Первое применение код Рида — Соломона получил в 1982 году (b) в серийном выпуске компакт-дисков.
Формальное описание
Коды Рида — Соломона являются важным частным случаем БЧХ-кода (b) , корни (b) порождающего полинома которого лежат в том же поле (b) , над которым строится код (). Пусть — элемент поля (b) , имеющий порядок . Если — примитивный элемент, то его порядок равен , то есть . Тогда нормированный полином (b) минимальной степени над полем , корнями (b) которого являются подряд идущих степеней элемента , является порождающим полиномом кода Рида — Соломона над полем :
где — некоторое целое число (в том числе 0 и 1), с помощью которого иногда удается упростить кодер. Обычно полагается . Степень многочлена (b) равна .
Длина полученного кода , минимальное расстояние (является минимальным из всех расстояний Хемминга (b) всех пар кодовых слов, см. Линейный код (b) ). Код содержит проверочных символов, где обозначает степень полинома; число информационных символов . Таким образом и код Рида — Соломона является разделимым кодом с максимальным расстоянием (является оптимальным в смысле границы Синглтона (b) ).
Кодовый полином может быть получен из информационного полинома , , путём перемножения и :
Свойства
Код Рида — Соломона над , исправляющий ошибок, требует проверочных символов и с его помощью исправляются произвольные пакеты ошибок длиной и меньше. Согласно теореме о границе Рейгера, коды Рида — Соломона являются оптимальными с точки зрения соотношения длины пакета и возможности исправления ошибок — используя дополнительных проверочных символов, исправляется ошибок (и менее).
Теорема (граница Рейгера). Каждый линейный блоковый код, исправляющий все пакеты длиной и менее, должен содержать, по меньшей мере, проверочных символов.
Код, двойственный коду Рида — Соломона, есть также код Рида — Соломона. Двойственным кодом для циклического кода (b) называется код, порожденный его проверочным многочленом.
Матрица порождает код Рида — Соломона тогда и только тогда когда любой минор (b) матрицы отличен от нуля.
При выкалывании или укорочении кода Рида — Соломона снова получается код Рида — Соломона. Выкалывание — операция, состоящая в удалении одного проверочного символа. Длина кода уменьшается на единицу, размерность сохраняется. Расстояние кода должно уменьшиться на единицу, ибо в противном случае удаленный символ был бы бесполезен. Укорочение — фиксируем произвольный столбец кода и выбираем только те векторы, которые в данном столбце содержат 0. Это множество векторов образует подпространство (b) .
Исправление многократных ошибок
Код Рида — Соломона является одним из наиболее мощных кодов, исправляющих многократные пакеты ошибок. Применяется в каналах, где пакеты ошибок могут образовываться столь часто, что их уже нельзя исправлять с помощью кодов, исправляющих одиночные ошибки.
Код Рида — Соломона над полем с кодовым расстоянием можно рассматривать как -код над полем , который может исправлять любую комбинацию ошибок, сосредоточенную в или меньшем числе блоков из m символов. Наибольшее число блоков длины , которые может затронуть пакет длины , где , не превосходит , поэтому код, который может исправить блоков ошибок, всегда может исправить и любую комбинацию из пакетов общей длины , если .
Практическая реализация
Кодирование с помощью кода Рида — Соломона может быть реализовано двумя способами: систематическим и несистематическим (см. , описание кодировщика).
При несистематическом кодировании информационное слово умножается на некий неприводимый полином в поле Галуа. Полученное закодированное слово полностью отличается от исходного и для извлечения информационного слова нужно выполнить операцию декодирования и уже потом можно проверить данные на содержание ошибок. Такое кодирование требует большие затраты ресурсов только на извлечение информационных данных, при этом они могут быть без ошибок.
![]()
При систематическом кодировании к информационному блоку из символов приписываются проверочных символов, при вычислении каждого проверочного символа используются все символов исходного блока. В этом случае нет затрат ресурсов при извлечении исходного блока, если информационное слово не содержит ошибок, но кодировщик/декодировщик должен выполнить операций сложения и умножения для генерации проверочных символов. Кроме того, так как все операции проводятся в поле Галуа, то сами операции кодирования/декодирования требуют много ресурсов и времени. Быстрый алгоритм декодирования, основанный на быстром преобразовании Фурье, выполняется за время порядка .

Кодирование
При операции кодирования информационный полином умножается на порождающий многочлен. Умножение исходного слова длины на неприводимый полином при систематическом кодировании можно выполнить следующим образом:
- К исходному слову приписываются нулей, получается полином .
- Этот полином делится на порождающий полином , находится остаток , , где — частное.
- Этот остаток и будет корректирующим кодом Рида — Соломона, он приписывается к исходному блоку символов. Полученное кодовое слово .
Кодировщик строится из сдвиговых регистров, сумматоров и умножителей. Сдвиговый регистр состоит из ячеек памяти, в каждой из которых находится один элемент поля Галуа.
Существует и другая процедура кодирования (более практичная и простая). Положим — примитивный элемент поля , и пусть — вектор информационных символов, а значит — информационный многочлен. Тогда вектор есть вектор кода Рида — Соломона, соответствующий информационному вектору . Этот способ кодирования показывает, что для кода РС вообще не нужно знать порождающего многочлена и порождающей матрицы кода, достаточно знать разложение поля (b) по примитивному элементу и размерность кода (длина кода в этом случае определяется как ). Все дело в том, что за разностью полностью скрывается порождающий многочлен и кодовое расстояние.
Декодирование
Декодировщик, работающий по авторегрессивному спектральному методу декодирования, последовательно выполняет следующие действия:
- Вычисляет синдром ошибки
- Строит полином ошибки
- Находит корни данного полинома
- Определяет характер ошибки
- Исправляет ошибки
Вычисление синдрома ошибки
Вычисление синдрома ошибки выполняется синдромным декодером, который делит кодовое слово на порождающий многочлен. Если при делении возникает остаток, то в слове есть ошибка. Остаток от деления является синдромом ошибки.
Построение полинома ошибки
Вычисленный синдром ошибки не указывает на положение ошибок. Степень полинома синдрома равна , что много меньше степени кодового слова . Для получения соответствия между ошибкой и её положением в сообщении строится полином ошибок. Полином ошибок реализуется с помощью алгоритма Берлекэмпа — Месси (b) либо с помощью алгоритма Евклида. Алгоритм Евклида имеет простую реализацию, но требует больших затрат ресурсов. Поэтому чаще применяется более сложный, но менее затратоемкий алгоритм Берлекэмпа — Месси. Коэффициенты найденного полинома непосредственно соответствуют коэффициентам ошибочных символов в кодовом слове.
Нахождение корней
На этом этапе ищутся корни полинома ошибки, определяющие положение искаженных символов в кодовом слове. Реализуется с помощью процедуры Ченя, равносильной полному перебору. В полином ошибок последовательно подставляются все возможные значения, когда полином обращается в ноль — корни найдены.
Определение характера ошибки и её исправление
По синдрому ошибки и найденным корням полинома с помощью алгоритма Форни определяется характер ошибки и строится маска искаженных символов. Однако для кодов РС существует более простой способ отыскания характера ошибок. Как показано в[2] для кодов РС с произвольным множеством последовательных нулей :
где формальная производная по многочлена локаторов ошибок , а
Далее после того как маска найдена, она накладывается на кодовое слово с помощью операции XOR (b) и искаженные символы восстанавливаются. После этого отбрасываются проверочные символы и получается восстановленное информационное слово.
Алгоритм Судана
В данное время стали применяться принципиально новые методы декодирования, например, алгоритм, предложенный в 1997 году Мадху Суданом[3].
Удлинение кодов РС
Удлинение кодов РС — это процедура, при которой увеличивается длина и расстояние кода (при этом код ещё находится на границе Синглтона (b) и алфавит кода не изменяется), а количество информационных символов кода не изменяется[4]. Такая процедура увеличивает корректирующую способность кода (b) . Рассмотрим удлинение кода РС на один символ. Пусть — вектор кода РС, порождающий многочлен которого есть . Пусть теперь . Покажем, что добавление к вектору символа увеличит его вес до , если . Многочлен, соответствующий вектору кода, можно расписать как , но тогда с учётом выражения для получим . , так как 1 не принадлежит списку корней порождающего многочлена. Но и , так как в этом случае , что увеличило бы расстояние кода вопреки условию, это значит что и вес кода увеличился, за счёт добавления нового символа . Новые параметры кода , удлиненный вектор . Проверочная матрица не удлиненного кода имеет вид
Тогда проверочная матрица, удлиненного на один символ РС кода будет
Применение
Сразу после появления (60-е годы XX века) коды Рида — Соломона стали применяться в качестве внешних кодов в каскадных конструкциях, использующихся в спутниковой связи. В подобных конструкциях -е символы РС (их может быть несколько) кодируются внутренними сверточными кодами (b) . На приемном конце эти символы декодируются мягкималгоритмом Витерби (b) (эффективный в каналах с АБГШ (b) ) . Такой декодер будет исправлять одиночные ошибки в q-ричных символах, когда же возникнут пакетные ошибки и некоторые пакеты q-ричных символов будут декодированы неправильно, тогда внешний декодер Рида — Соломона исправит пакеты этих ошибок. Таким образом будет достигнута требуемая надежность передачи информации ([5]).
В настоящий момент коды Рида — Соломона имеют очень широкую область применения благодаря своей способности находить и исправлять многократные пакеты ошибок.
Запись и хранение информации
Код Рида — Соломона используется при записи и чтении в контроллерах оперативной памяти, при архивировании данных, записи информации на жесткие диски (ECC (b) ), записи на CD/DVD диски. Даже если поврежден значительный объем информации, испорчено несколько секторов дискового носителя, то коды Рида — Соломона позволяют восстановить большую часть потерянной информации. Также используется при записи на такие носители, как магнитные ленты и штрихкоды.
Запись на CD-ROM
Возможные ошибки при чтении с диска появляются уже на этапе производства диска, так как сделать идеальный диск при современных технологиях невозможно. Также ошибки могут быть вызваны царапинами на поверхности диска, пылью и т. д. Поэтому при изготовлении читаемого компакт-диска используется система коррекции CIRC (Cross Interleaved Reed Solomon Code). Эта коррекция реализована во всех устройствах, позволяющих считывать данные с CD-дисков, в виде чипа с прошивкой firmware. Нахождение и коррекция ошибок основана на избыточности и перемежении (b) (redundancy & interleaving). Избыточность — примерно 25 % от исходной информации.
При записи на аудиокомпакт-диски (b) используется стандарт Red Book (b) . Коррекция ошибок происходит на двух уровнях, C1 и C2. При кодировании на первом этапе происходит добавление проверочных символов к исходным данным, на втором этапе информация снова кодируется. Кроме кодирования, осуществляется также перемешивание (перемежение (b) ) байтов, чтобы при коррекции блоки ошибок распались на отдельные биты, которые легче исправляются. На первом уровне обнаруживаются и исправляются ошибочные блоки длиной один и два байта (один и два ошибочных символа, соответственно). Ошибочные блоки длиной три байта обнаруживаются и передаются на следующий уровень. На втором уровне обнаруживаются и исправляются ошибочные блоки, возникшие в C2, длиной 1 и 2 байта. Обнаружение трех ошибочных символов является фатальной ошибкой и не может быть исправлено.
Беспроводная (b) и мобильная (b) связь
Этот алгоритм кодирования используется при передаче данных по сетям WiMAX (b) , в оптических линиях связи (b) , в спутниковой (b) и радиорелейной связи (b) . Метод прямой коррекции ошибок в проходящем трафике (Forward Error Correction, FEC) основывается на кодах Рида — Соломона.
Примеры кодирования
16-ричный (15,11) код Рида — Соломона
Пусть . Тогда
Степень равна 4, и . Каждому элементу поля можно сопоставить 4 бита. Информационный многочлен является последовательностью 11 символов из , что эквивалентно 44 битам, а все кодовое слово является набором из 60 бит.
8-ричный (7,3) код Рида — Соломона
Пусть . Тогда
Пусть информационный многочлен имеет вид:
Кодовое слово несистематического кода запишется в виде:
что представляет собой последовательность семи восьмеричных символов.
Альтернативный метод кодирования 9-ричного (8,4) кода Рида — Соломона
Построим поле Галуа (b) по модулю многочлена . Пусть его корень, тогда , таблица поля имеет вид:
Пусть информационный многочлен , далее производя соответствующие вычисления над построенным полем получим:
В итоге построен вектор кода РС с параметрами . На этом кодирование законченно. Заметим, что при этом способе нам не потребовался порождающий многочлен кода[4].
Примеры декодирования
Пусть поле генерируется примитивным элементом, неприводимый многочлен которого . Тогда . Пусть . Тогда порождающий многочлен кода РС равен . Пусть теперь принят многочлен . Тогда . Тогда ключевая система уравнений получается в виде:
Теперь рассмотрим Евклидов алгоритм решения этой системы уравнений.
- Начальные условия:
Алгоритм останавливается, так как , отсюда следует, что
Далее полный перебор по алгоритму Чени выдает нам позиции ошибок, это . Потом по формуле получаем что
Таким образом декодированный вектор . Декодирование завершено, исправлены две ошибки[6].
Применение
- Код Рида — Соломона используется в некоторых прикладных программах в области хранения данных, например в RAID 6 (b) ;
См. также
- Конечное поле (b)
- Обнаружение и исправление ошибок (b)
- Циклический код (b)
- Код Боуза — Чоудхури — Хоквингема (b)
- Турбо-код (b)
- Код Хэмминга (b)
Примечания
- ↑ Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — С. 92—93. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
- ↑ Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
- ↑ Алгоритм Судана. Дата обращения: 24 декабря 2018. Архивировано 24 декабря 2018 года.
- 1 2 Сагалович, 2007, с. 212—213.
- ↑ М. Вернер. Основы кодирования. — Техносфера, 2004. — С. 268—269. — ISBN 5-94836-019-9.
- ↑ Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — С. 116—119. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
Литература
- Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
- Блейхут Р. (b) Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир (b) , 1986. — 576 с.
- Берлекэмп Э. Алгебраическая теория кодирования = Algebraic Coding Theory. — М.: Мир, 1971. — С. 478.
- Егоров С.И. Коррекция ошибок в информационных каналах периферийных устройств ЭВМ. — Курск: КурскГТУ, 2008. — С. 252.
- Сагалович Ю. Л.Введение в алгебраические коды — М.: МФТИ (b) , 2007. — 262 с. — ISBN 978-5-7417-0191-1
- Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
- М. Вернер. Основы кодирования. — Техносфера, 2004. — 288 с. — ISBN 5-94836-019-9.
Ссылки
- Могущество кодов Рида — Соломона или информация, воскресшая из пепла (статья Криса Касперски)
- Помехоустойчивое кодирование в пакетных сетях (статья В. Варгаузина)
- Error Correcting Code (ECC)
- CD-R диски, технология изнутри
- Формат CD
- Коды Рида-Соломона
- wiki.linuxformat.ru/wiki/LXF134:par2 — использование par2, утилиты восстановления файлов методом Кода Рида-Соломона (рус.)
 КРИС КАСПЕРСКИ
КРИС КАСПЕРСКИ
Коды Рида-Соломона в практических реализациях,
или Информация, воскресшая из пепла III
В прошлых статьях этого цикла мы рассмотрели базовый математический аппарат, на который опираются коды Рида-Соломона, и исследовали простейший кодер/декодер, способный исправлять одиночные ошибки и работающий с двумя символами четности. Для подавляющего большинства задач такой корректирующей способности оказывается катастрофически недостаточно, и тогда приходится задумываться о реализации более мощного кодера/декодера.
Кодер/декодер, рассматриваемый в настоящей статье, чрезвычайно конфигурабелен и может быть настроен на работу с любым количеством символов четности, а это означает, что при разумной избыточности он способен исправлять любое мыслимое количество ошибок. Подобная универсальность не проходит даром, и конструкция такого декодера усложнятся более чем в сто (!) раз. Самостоятельное проектирование декодеров Рида-Соломона требует глубоких знаний высшей математики в целом и природы корректирующих кодов в частности, поэтому не смущайтесь, если данная статья поначалу вам покажется непонятной. Это действительно сложные вещи, не допускающие простого объяснения.
С другой стороны, для практического использования корректирующих кодов можно и не вникать в их сущность, просто откомпилировав исходные тексты кодера/декодера Рида-Соломона, приведенные в данной статье. Также вы можете воспользоваться любой законченной библиотекой, поставляемой сторонними разработчиками. В качестве альтернативного примера в заключение этой статьи будет кратно описан интерфейс библиотеки ElByECC.DLL, разработанной компанией «Elaborate Bytes» и распространяемой вместе с популярным копировщиком Clone CD. Известнейший прожигатель дисков всех времен и народов Ahead Burning ROM имеет аналогичную библиотеку, размещенную в файле NEWTRF.DLL.
Легенда
Напомним читателю основные условные обозначения, используемые в этой статье. Количество символов кодируемого сообщения (называемого также информационным словом) по общепринятому соглашению обозначается буквой k; полная длина кодового слова, включающего в себя кодируемые данные и символы четности, – n. Отсюда, количество символов четности равно: n – k. За максимальным количеством исправляемых ошибок «закреплена» буква t. Поскольку для исправления одной ошибки требуется два символа четности, общее количество символов четности равно 2t. Выражение RS(n, k) описывает определенную разновидность корректирующих кодов Рида-Соломона, оперирующую с n-символьными блоками, k-символов, из которых представляют полезные данные, а все остальные задействованы под символы четности.
Полином, порожденный на основе примитивного члена a, называется порожденным или сгенерированным (generate) полиномом.
Кодировщик (encoder)
Существует по меньшей мере два типа кодеров Рида-Соломона: несистематические и систематические кодировщики.
Вычисление несистематических корректирующих кодов Рида-Соломона осуществляется умножением информационного слова на порожденный полином, в результате чего образуется кодовое слово, полностью отличающееся от исходного информационного слова, а потому для непосредственного употребления категорически непригодное. Для приведения полученных данных в исходный вид мы должны в обязательном порядке выполнить ресурсоемкую операцию декодирования, даже если данные не искажены и не требуют восстановления!
При систематическом кодировании, напротив, исходное информационное слово останется неизменным, а корректирующие коды (часто называемые символами четности) добавляются в его конец, благодаря чему к операции декодирования приходится прибегать лишь в случае действительного разрушения данных. Вычисление несистематических корректирующих кодов Рида-Соломона осуществляется делением информационного слова на порожденный полином. При этом все символы информационного слова сдвигаются на n – k байт влево, а на освободившееся место записывается 2t байт остатка (см. рис. 1).
Поскольку рассмотрение обоих типов кодировщиков заняло бы слишком много места, сосредоточим свое внимание на одних лишь систематических кодерах как на наиболее популярных.

Рисунок 1. Устройство кодового слова
Архитектурно кодировщик представляет собой совокупность сдвиговых регистров (shift registers), объединенных посредством сумматоров и умножителей, функционирующих по правилам арифметики Галуа. Сдвиговый регистр (иначе называемый регистром сдвига) представляет последовательность ячеек памяти, называемых разрядами, каждый из которых содержит один элемент поля Галуа GF(q). Содержащийся в разряде символ, покидая этот разряд, «выстреливается» на выходную линию. Одновременно с этим разряд «засасывает» символ, находящийся на его входной линии. Замещение символов происходит дискретно, в строго определенные промежутки времени, называемые тактами.
При аппаратной реализации сдвигового регистра его элементы могут быть объединены как последовательно, так и параллельно. При последовательном объединении пересылка одного m-разрядного символа потребуем m-тактов, в то время как при параллельном она осуществляется всего за один такт.
Низкая эффективность программных реализаций кодеров Рида-Соломона объясняется тем, что разработчик не может осуществлять параллельное объединение элементов сдвигового регистра и вынужден работать с той шириной разрядности, которую «навязывает» архитектура данной машины. Однако создать 4-элементный 8-битный регистр сдвига параллельного типа на процессорах семейства IA32 вполне реально.
Цепи, основанные на регистрах сдвига, обычно называют фильтрами. Блок-схема фильтра, осуществляющего деление полинома на константу, приведена на рис. 2. Пусть вас не смущает тот факт, что деление реализуется посредством умножения и сложения. Данный прием базируется на вычислении системы двух рекуррентных равенств:
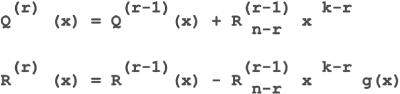
Формула 1. Деление полинома на константу посредством умножения и сложения
Здесь: Q(r)(x) и R(r)(x) – соответственно частное и остаток на r-шаге рекурсии. Поскольку сложение и вычитание, выполняемое по модулю два, тождественны друг другу, для реализации делителя нам достаточно иметь всего два устройства – устройство сложения и устройство умножения, а без устройства вычитания можно обойтись.
После n-сдвигов на выходе регистра появляется частное, а в самом регистре окажется остаток, который и представляет собой рассчитанные символы четности (они же – коды Рида-Соломона), а коэффициенты умножения с g0 по g(2t – 1) напрямую соответствуют коэффициентам умножения порожденного полинома.
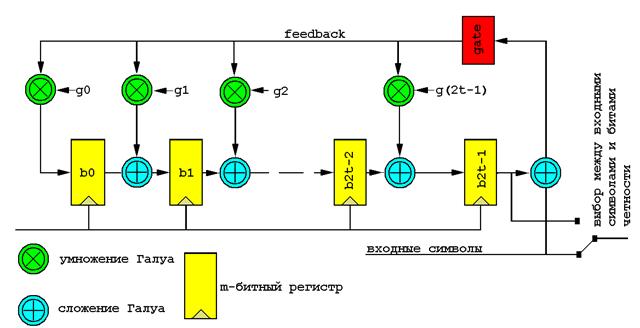
Рисунок 2. Устройство простейшего кодера Рида-Соломона
Простейший пример программной реализации такого фильтра приведен ниже. Это законченный кодер Рида-Соломона, вполне пригодный для практического использования. Конечно, при желании его можно было бы и улучшить, но тогда неизбежно пострадала бы наглядность и компактность листинга.
Листинг 1. Исходный текст простейшего кодера Рида-Соломона
/*——————————————————————————————————
*
* кодировщик Рида-Соломона
* ========================
*
* кодируемые данные передаются через массив data[i], где i=0..(k-1), а сгенерированные символы четности
* заносятся в массив b[0]..b[2*t-1]. Исходные и результирующие данные должны быть представлены
* в полиномиальной форме (т.е. в обычной форме машинного представления данных).
* Кодирование производится с использованием сдвигового feedback-регистра, заполненного соответствующими
* элементами массива g[] с порожденным полиномом внутри, процедура генерации которого уже обсуждалась
* в предыдущей статье. Сгенерированное кодовое слово описывается следующей формулой:
* с(x) = data(x)*x(n-k) + b(x)
*
* на основе исходных текстов Simon Rockliff, от 26.06.1991, распространяемых
* по лицензии GNU
–––––––––––––––––––––––––––––––––––––––––––––––––––––––––———————————————*/
encode_rs()
{
int i, j;
int feedback;
// инициализируем поле бит четности нулями
for (i = 0; i < n — k; i++) b[i] = 0;
// обрабатываем все символы исходных данных справа налево
for (i = k — 1; i >= 0; i—)
{
// готовим (data[i] + b[n – k –1]) к умножению на g[i], т.е. складываем очередной «захваченный»
// символ исходных данных с младшим символом битов четности (соответствующего «регистру» b2t-1,
// см. рис. 2) и переводим его в индексную форму, сохраняя результат в регистре feedback,
// как мы уже говорили, сумма двух индексов есть произведение полиномов
feedback = index_of[data[i] ^ b[n – k — 1]];
// есть еще символы для обработки?
if (feedback != -1)
{
// осуществляем сдвиг цепи bx-регистров
for (j=n-k-1; j>0; j—)
// если текущий коэффициент g – это действительный (т.е. ненулевой коэффициент,
// то умножаем feedback на соответствующий g-коэффициент и складываем его
// со следующим элементом цепочки
if (g[j]!=-1) ї
b[j]=b[j-1]^alpha_to[(g[j]+feedback)%n];
else
// если текущий коэффициент g – это нулевой коэффициент, выполняем один лишь
// сдвиг без умножения, перемещая символ из одного m-регистра в другой
b[j] = b[j-1];
// закольцовываем выходящий символ в крайний левый b0-регистр
b[0] = alpha_to[(g[0]+feedback)%n];
}
else
{ // деление завершено, осуществляем последний сдвиг регистра, на выходе регистра
// будет частное, которое теряется, а в самом регистре – искомый остаток
for (j = n-k-1; j>0; j—) b[j] = b[j-1] ; b[0] = 0;
}
}
}
Декодер (decoder)
Декодирование кодов Рида-Соломона представляет собой довольно сложную задачу, решение которой выливается в громоздкий, запутанный и чрезвычайно ненаглядный программный код, требующий от разработчика обширных знаний во многих областях высшей математики. Типовая схема декодирования, получившая название авторегрессионого спектрального метода декодирования, состоит из следующих шагов:
- вычисления синдрома ошибки (синдромный декодер);
- построения полинома ошибки, осуществляемое либо посредством высокоэффективного, но сложно реализуемого алгоритма Берлекэмпа-Месси, либо посредством простого, но медленного Евклидового алгоритма;
- нахождения корней данного полинома, обычно решающееся лобовым перебором (алгоритм Ченя);
- определения характера ошибки, сводящееся к построению битовой маски, вычисляемой на основе обращения алгоритма Форни или любого другого алгоритма обращения матрицы;
- наконец, исправления ошибочных символов путем наложения битовой маски на информационное слово и последовательного инвертирования всех искаженных бит через операцию XOR.

Рисунок 3. Схема авторегрессионного спектрального декодера корректирующих кодов Рида-Соломона
Синдромный декодер
Грубо говоря, синдром есть остаток деления декодируемого кодового слова c(x) на порожденный полином g(x), и, если этот остаток равен нулю, кодовое слово считается неискаженным. Ненулевой остаток свидетельствует о наличии по меньшей мере одной ошибки. Остаток от деления дает многочлен, не зависящий от исходного сообщения и определяемый исключительно характером ошибки (syndrome – греческое слово, обозначающее совокупность признаков и/или симптомов, характеризующих заболевание).
Принятое кодовое слово v с компонентами vi = ci + ei, где i = 0, … n – 1, представляет собой сумму кодового слова c и вектора ошибок e. Цель декодирования состоит в очистке кодового слова от вектора ошибки, описываемого полиномом синдрома и вычисляемого по формуле: Sj = v(aj+j0–1), где j изменяется от 1 до 2t, а a представляет собой примитивный член «альфа», который мы уже обсуждали в предыдущей статье. Да, мы снова выражаем функцию деления через умножение, поскольку деление – крайне неэффективная в смысле производительности операция.
Блок-схема устройства, осуществляющего вычисление синдрома, приведена на рис. 4. Как видно, она представляет собой типичный фильтр (сравните ее со схемой рис. 2), а потому ни в каких дополнительных пояснениях не нуждается.
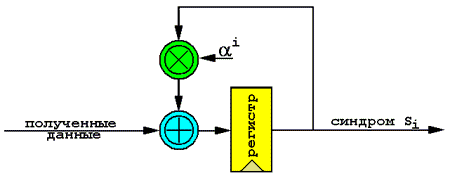
Рисунок 4. Блок-схема цепи вычисления синдрома
Вычисление синдрома ошибки происходит итеративно, так что вычисление результирующего полинома (также называемого ответом от английского «answer») завершается непосредственно в момент прохождения последнего символа четности через фильтр. Всего требуется 2t циклов «прогона» декодируемых данных через фильтр, – по одному прогону на каждый символ результирующего полинома.
Пример простой программной реализации синдромного декодера содержится в листинге 2, и он намного нагляднее его словесного описания.
Полином локатора ошибки
Полученный синдром описывает конфигурацию ошибки, но еще не говорит нам, какие именно символы полученного сообщения были искажены. Действительно, степень синдромного полинома, равная 2t, много меньше степени полинома сообщения, равной n, и между их коэффициентами нет прямого соответствия. Полином, коэффициенты которого напрямую соответствуют коэффициентам искаженных символов, называется полиномом локатора ошибки и по общепринятому соглашению обозначается греческой буквой L (лямбда).
Если количество искаженных символов не превышает t, между синдромом и локатором ошибки существует следующее однозначное соответствие, выражаемое следующей формулой НОД[xn-1, E(x)] = L(x), и вычисление локатора сводится к задаче нахождения наименьшего общего делителя, успешно решенной еще Евклидом и элементарно реализуемой как на программном, так и на аппаратном уровне. Правда, за простоту реализации нам приходится расплачиваться производительностью, точнее непроизводительностью данного алгоритма, и на практике обычно применяют более эффективный, но и более сложный для понимания алгоритм Берлекэмпа-Месси (Berlekamp-Massy), подробно описанный Кнутом во втором томе «Искусства программирования» (см. также «Теория и практика кодов, контролирующих ошибки» Блейхута) и сводящийся к задаче построения цепи регистров сдвига с линейной обратной связью и по сути своей являющегося разновидностью авторегрессионого фильтра, множители в векторах которого и задают полином L.
Декодер, построенный по такому алгоритму, требует не более 3t операций умножения в каждой из итерации, количество которых не превышает 2t. Таким образом, решение поставленной задачи укладывается всего в 6t2 операций умножения. Фактически поиск локатора сводится к решению системы из 2t уравнений – по одному уравнению на каждый символ синдрома – c t неизвестными. Неизвестные члены и есть позиции искаженных символов в кодовом слове v. Легко видеть, если количество ошибок превышает t, система уравнений становится неразрешима и восстановить разрушенную информацию в этом случае не представляется возможным.
Блок-схема алгоритма Берлекэмпа-Месси приведена на рис. 5, а его законченная программа реализация содержится в листинге 2.
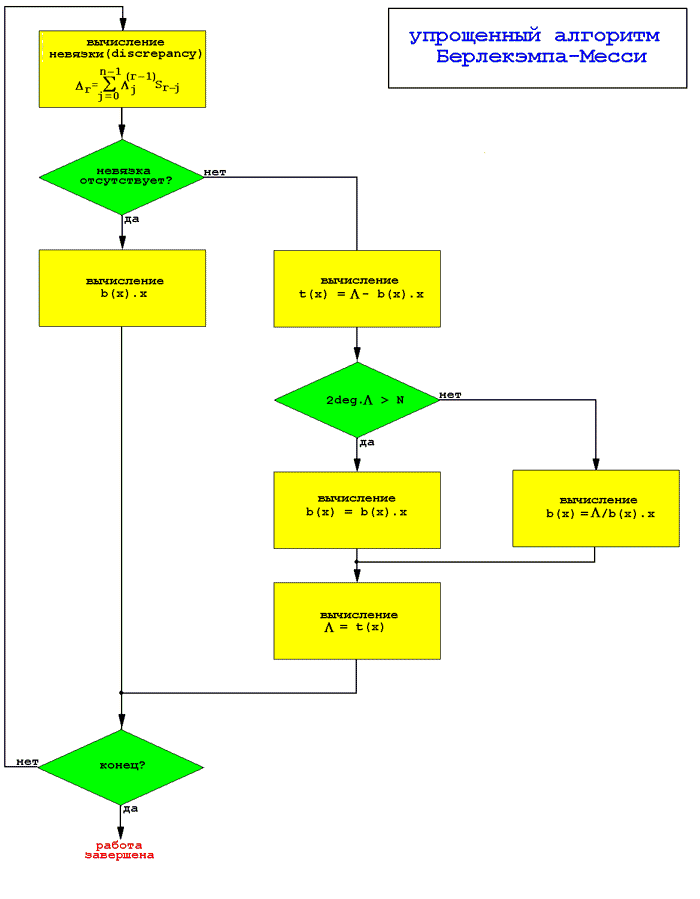
Рисунок 5. Структурная схема алгоритма Берлекэмпа-Месси
Корни полинома
Коль скоро полином локатора ошибки нам известен, его корни определяют местоположение искаженных символов в принятом кодовом слове. Остается эти корни найти. Чаще всего для этого используется процедура Ченя (Chien search), аналогичная по своей природе обратному преобразованию Фурье и фактически сводящаяся к тупому перебору (brute force, exhaustive search) всех возможных вариантов. Все 2m возможных символов один за другим подставляются в полином локатора в порядке социалистической очереди и затем выполняется расчет полинома. Если результат обращается в ноль – считается, что искомые корни найдены.
Восстановление данных
Итак, мы знаем, какие символы кодового слова искажены, но пока еще не готовы ответить на вопрос: как именно они искажены. Используя полином синдрома и корни полинома локатора, мы можем определить характер разрушений каждого из искаженных символов. Обычно для этой цели используется алгоритм Форни (Forney), состоящий из двух стадий: сначала путем свертки полинома синдрома полиномом локатора L мы получаем некоторый промежуточный полином, условно обозначаемый греческой буквой W. Затем на основе W-полинома вычисляется нулевая позиция ошибки (zero error location), которая в свою очередь делится на производную от L-полинома. В результате получается битовая маска, каждый из установленных битов которой соответствует искаженному биту и для восстановления кодового слова в исходный вид все искаженные биты должны быть инвертированы, что осуществляется посредством логической операции XOR.
На этом процедура декодирования принятого кодового слова считается законченной. Остается отсечь n – k символов четности, и полученное информационное слово готово к употреблению.
Исходный текст декодера
Ниже приводится исходный текст полноценного декодера Рида-Соломона, снабженный минимально разумным количеством комментариев. К сожалению, в рамках журнальной статьи подробное комментирование кода декодера невозможно, поскольку потребовало бы очень много места.
При возникновении трудностей в анализе этого листинга обращайтесь к блок-схемам, приведенным на рис. 3, 4 и 5 – они помогут.
Листинг 2. Исходный текст простейшего декодера Рида-Соломона
/*——————————————————————————————————
*
* декодер Рида-Соломона
* =====================
*
* Процедура декодирования кодов Рида-Соломона состоит из нескольких шагов: сначала мы вычисляем
* 2t-символьный синдром путем постановки alpha**i в recd(x), где recd – полученное кодовое слово,
* предварительно переведенное в индексную форму. По факту вычисления recd(x) мы записываем
* очередной символ синдрома в s[i], где i принимает значение от 1 до 2t, оставляя s[0] равным нулю.
* Затем, используя итеративный алгоритм Берлекэмпа, мы находим полином локатора ошибки – elp[i].
* Если степень elp превышает собой величину t, мы бессильны скорректировать все ошибки и ограничиваемся
* выводом сообщения о неустранимой ошибке, после чего совершаем аварийный выход из декодера.
* Если же степень elp не превышает t, мы подставляем alpha**i, где i = 1..n в elp для вычисления
* корней полинома. Обращение найденных корней дает нам позиции искаженных символов. Если количество
* определенных позиций искаженных символов меньше степени elp, искажению подверглось более чем t
* символов и мы не можем восстановить их. Во всех остальных случаях восстановление оригинального
* содержимого искаженных символов вполне возможно. В случае, когда количество ошибок заведомо велико,
* для их исправления декодируемые символы проходят сквозь декодер без каких-либо изменений.
*
* на основе исходных текстов Simon Rockliff, от 26.06.1991, распространяемых по лицензии GNU
–––––––––––––––––––––––––––––––––––––––––––––––––––––––––———————————————*/
decode_rs()
{
int i, j, u, q;
int s[n-k+1]; // полином синдрома ошибки
int elp[n – k + 2][n — k]; // полином локатора ошибки лямбда
int d[n-k+2];
int l[n-k+2];
int u_lu[n-k+2],
int count=0, syn_error=0, root[t], loc[t], z[t+1], err[n], reg[t+1];
// переводим полученное кодовое слово в индексную форму для упрощения вычислений
for (i = 0; i < n; i++) recd[i] = index_of[recd[i]];
// вычисляем синдром
//————————————————————————————————-
for (i = 1; i <= n — k; i++)
{
s[i] = 0; // инициализация s-регистра (на его вход по умолчанию поступает ноль)
// выполняем s[i] += recd[j]*ij т.е. берем очередной символ декодируемых данных, умножаем его
// на порядковый номер данного символа, умноженный на номер очередного оборота и складываем
// полученный результат с содержимым s-регистра по факту исчерпания всех декодируемых символов,
// мы повторяем весь цикл вычислений опять – по одному разу для каждого символа четности
for (j=0; j<n; j++) if (recd[j]!=-1) s[i]^= alpha_to[(recd[j]+i*j)%n];
if (s[i]!=0) syn_error=1; // если синдром не равен нулю, взводим флаг ошибки
// преобразуем синдром из полиномиальной формы в индексную
s[i] = index_of[s[i]];
}
// коррекция ошибок
//————————————————————————————————-
if (syn_error) // если есть ошибки, пытаемся их скорректировать
{
// вычисление полинома локатора лямбда
//————————————————————————————————
// вычисляем полином локатора ошибки через итеративный алгоритм Берлекэмпа. Следуя терминологии
// Lin and Costello (см. «Error Control Coding: Fundamentals and Applications» Prentice Hall 1983
// ISBN 013283796) d[u] представляет собой m («мю»), выражающую расхождение (discrepancy),
// где u = m + 1 и m есть номер шага из диапазона от –1 до 2t. У Блейхута та же самая величина
// обозначается D(x) («дельта») и называется невязкой. l[u] представляет собой степень elp
// для данного шага итерации, u_l[u] представляет собой разницу между номером шага и степенью elp,
// инициализируем элементы таблицы
d[0] = 0; // индексная форма
d[1] = s[1]; // индексная форма
elp[0][0] = 0; // индексная форма
elp[1][0] = 1; // полиномиальная форма
for (i = 1; i < n — k; i++)
{
elp[0][i] = -1; // индексная форма
elp[1][i] = 0; // полиномиальная форма
}
l[0] = 0; l[1] = 0; u_lu[0] = -1; u_lu[1] = 0; u = 0;
do
{
u++;
if (d[u] == -1)
{
l[u + 1] = l[u];
for (i = 0; i <= l[u]; i++)
{
elp[u+1][i] = elp[u][i];
elp[u][i] = index_of [elp[u][i]];
}
}
else
{
// поиск слов с наибольшим u_lu[q], таких что d[q]!=0
q = u — 1;
while ((d[q] == -1) && (q>0)) q—;
// найден первый ненулевой d[q]
if (q > 0)
{
j=q ;
do
{
j— ;
if ((d[j]!=-1) && (u_lu[q]<u_lu[j]))
q = j ;
} while (j>0);
};
// как только мы найдем q, такой что d[u]!=0 и u_lu[q] есть максимум
// запишем степень нового elp полинома
if (l[u] > l[q]+u-q) l[u+1] = l[u]; else l[u+1] = l[q]+u-q;
// формируем новый elp(x)
for (i = 0; i < n — k; i++) elp[u+1][i] = 0;
for (i = 0; i <= l[q]; i++)
if (elp[q][i]!=-1)
elp[u+1][i+u-q]=alpha_to [(d[u]+n-d[q]+elp[q][i])%n];
for (i=0; i<=l[u]; i++)
{
elp[u+1][i] ^= elp[u][i];
// преобразуем старый elp в индексную форму
elp[u][i] = index_of[elp[u][i]];
}
}
u_lu[u+1] = u-l[u+1];
// формируем (u + 1) невязку
//————————————————————————————————
if (u < n-k) // на последней итерации расхождение не было обнаружено
{
if (s[u + 1]!=-1) d[u+1] = alpha_to[s[u+1]]; else d[u + 1] = 0;
for (i = 1; i <= l[u + 1]; i++)
if ((s[u + 1 — i] != -1) && (elp[u + 1][i]!=0))
d[u+1] ^= alpha_to[(s[u+1-i]+index_of[elp[u+1][i]])%n];
// переводим d[u+1] в индексную форму
d[u+1] = index_of[d[u+1]];
}
} while ((u < n-k) && (l[u+1]<=t));
// расчет локатора завершен
//——————————————————
u++ ;
if (l[u] <= t)
{ // коррекция ошибок возможна
// переводим elp в индексную форму
for (i = 0; i <= l[u]; i++) elp[u][i] = index_of[elp[u][i]];
// нахождение корней полинома локатора ошибки
//———————————————-
for (i = 1; i <= l[u]; i++) reg[i] = elp[u][i]; count = 0;
for (i = 1; i <= n; i++)
{
q = 1 ;
for (j = 1; j <= l[u]; j++)
if (reg[j] != -1)
{
reg[j] = (reg[j]+j)%n;
q ^= alpha_to[reg[j]];
}
if (!q)
{ // записываем корень и индекс позиции ошибки
root[count] = i;
loc[count] = n-i;
count++;
}
}
if (count == l[u])
{ // нет корней – степень elp < t ошибок
// формируем полином z(x)
for (i = 1; i <= l[u]; i++) // Z[0] всегда равно 1
{
if ((s[i]!=-1) && (elp[u][i]!=-1))
z[i] = alpha_to[s[i]] ^ alpha_to[elp[u][i]];
else
if ((s[i]!=-1) && (elp[u][i]==-1))
z[i] = alpha_to[s[i]];
else
if ((s[i]==-1) && (elp[u][i]!=-1))
z[i] = alpha_to[elp[u][i]];
else
z[i] = 0 ;
for (j=1; j<i; j++)
if ((s[j]!=-1) && (elp[u][i-j]!=-1))
z[i] ^= alpha_to[(elp[u][i-j] + s[j])%n];
// переводим z[i] в индексную форму
z[i] = index_of[z[i]];
}
// вычисление значения ошибок в позициях loc[i]
//———————————————————————————————-
for (i = 0; i<n; i++)
{
err[i] = 0;
// переводим recd[] в полиномиальную форму
if (recd[i]!=-1) recd[i] = alpha_to[recd[i]]; else recd[i] = 0;
}
// сначала вычисляем числитель ошибки
for (i = 0; i < l[u]; i++)
{
err[loc[i]] = 1;
for (j=1; j<=l[u]; j++)
if (z[j]!=-1)
err[loc[i]] ^= alpha_to [(z[j]+j*root[i])%n];
if (err[loc[i]]!=0)
{
err[loc[i]] = index_of[err[loc[i]]];
q = 0 ; // формируем знаменателькоэффициента ошибки
for (j=0; j<l[u]; j++)
if (j!=i)
q+=index_of[1^alpha_to[(loc[j]+root[i])%n]];
q = q % n; err[loc[i]] = alpha_to [(err[loc[i]]-q+n)%n];
// recd[i] должен быть в полиномиальной форме
recd[loc[i]] ^= err[loc[i]];
}
}
}
else // нет корней, решение системы уравнений невозможно, т.к. степень elp >= t
{
// переводим recd[] в полиномиальную форму
for (i=0; i<n; i++)
if (recd[i]!=-1) recd[i] = alpha_to[recd[i]];
else
recd[i] = 0; // выводим информационное слово как есть
}
else // степень elp > t, решение невозможно
{
// переводим recd[] в полиномиальную форму
for (i=0; i<n; i++)
if (recd[i]!=-1)
recd[i] = alpha_to[recd[i]] ;
else
recd[i] = 0 ; // выводим информационное слово как есть
}
else // ошибок не обнаружено
for (i=0;i<n;i++) if(recd[i]!=-1)recd[i]=alpha_to[recd[i]]; else recd[i]=0;
}
Интерфейс с библиотекой ElByECC.DLL
Программная реализация кодера/декодера Рида-Соломона, приведенная в листингах 1, 2, достаточно наглядна, но крайне непроизводительна и нуждается в оптимизации. Как альтернативный вариант можно использовать готовые библиотеки от сторонних разработчиков, входящие в состав программных комплексов, так или иначе связанных с обработкой корректирующих кодов Рида-Соломона. Это и утилиты прожига/копирования/восстановления лазерных дисков, и драйвера ленточных накопителей (от стримера до Арвида), и различные телекоммуникационные комплексы и т. д.
Как правило, все эти библиотеки являются неотъемлемой частью самого программного комплекса и потому никак не документируется. Причем восстановление прототипов интерфейсных функций представляет весьма нетривиальную задачу, требующую от исследователя не только навыков дизассемблирования, но и знаний высшей математики, иначе смысл всех битовых манипуляций останется совершенно непонятным.
Насколько законно подобное дизассемблирование? Да, дизассемблирование сторонних программных продуктов действительно запрещено, но тем не менее оно законно. Здесь уместно провести аналогию со вскрытием пломб вашего телевизора, влекущее потерю гарантии, но отнюдь не приводящее к уголовному преследованию. Также никто не запрещает вызывать функции чужой библиотеки из своей программы. Нелегально распространять эту библиотеку в составе вашего программного обеспечения действительно нельзя, но что мешает вам попросить пользователя установить данную библиотеку самостоятельно?
Ниже приводится описание важнейших функций библиотеки ElByECC.DLL, входящей в состав известного копировщика защищенных лазерных дисков Clone CD, условно-бесплатную копию которого можно скачать c cайта: http://www.elby.ch/.
Сам Clone CD проработает всего лишь 21 день, а затем потребует регистрации, однако на продолжительность использования библиотеки ElByECC.DLL не наложено никаких ограничений.
Моими усилиями был создан h-файл, содержащий прототипы основных функций библиотеки ElByECC.DLL, специальная редакция которого была любезно предоставлена для журнала «Системный администратор».
Несмотря на то, что библиотека ElByECC.DLL ориентирована на работу с секторами лазерных дисков, она может быть приспособлена и для других целей, например, построения отказоустойчивых дисковых массивов, о которых говорилось в предыдущей статье.
Краткое описание основных функций библиотеки приводится ниже.
Подключение библиотеки ElByECC.DLL к своей программе
Существуют по меньшей мере два способа подключения динамических библиотек к вашим программам. При динамической компоновке адреса требуемых функций определяются посредством вызова GetProcAddress, причем сама библиотека ElByECC.DLL должна быть предварительно загружена через LoadLibrary. Это может выглядеть, например, так (обработка ошибок для простоты опущена):
Листинг 3. Динамическая загрузка библиотеки ElByECC.DLL
HANDLE h;
int (__cdecl *CheckECCAndEDC_Mode1) (char *userdata, char *header, char *sector);
h=LoadLibrary(«ElbyECC.dll»);
CheckECCAndEDC_Mode1 = GetProcAddress(h, «CheckECCAndEDC_Mode1»);
Статическая компоновка предполагает наличие специального lib-файла, который может быть автоматически сгенерирован утилитой implib из пакета Borland C++ любой подходящей версии, представляющую собой утилиту командной строки, вызываемую так:
implib.exe -a ElByECC.lib ElByECC.lib
GenECCAndEDC_Mode1
Функция GenECCAndEDC_Mode1 осуществляет генерацию корректирующих кодов на основе 2048-байтового блока пользовательских данных и имеет следующий прототип:
Листинг 4. Прототип функции GenECCAndEDC_Mode1
// указатель на массив из 2048 байт
GenECCAndEDC_Mode1(char *userdata_src,
// указатель на заголовок
char *header_src,
struct RAW_SECTOR_MODE1 *raw_sector_mode1_dst)
- userdata_src – указатель на 2048-байтовый блок пользовательских данных, для которых необходимо выполнить расчет корректирующих кодов. Сами пользовательские данные в процессе выполнения функции остаются неизменными и автоматически копируются в буфер целевого сектора, где к ним добавляется 104 + 172 байт четности и 4 байта контрольной суммы.
- header_src – указатель на 4-байтовый блок, содержащий заголовок сектора. Первые три байта занимает абсолютный адрес, записанный в BCD-форме, а четвертый байт отвечает за тип сектора, которому необходимо присвоить значение 1, соответствующий режиму «корректирующие коды задействованы».
- raw_sector_mode1_dst – указатель на 2352-байтовый блок, в который будет записан сгенерированный сектор, содержащий 2048-байт пользовательских данных и 104+172 байт корректирующих кодов вместе с 4 байтами контрольной суммы и представленный следующей структурой:
Листинг 5. Структура сырого сектора
struct RAW_SECTOR_MODE1
{
BYTE SYNC[12]; // синхрогруппа
BYTE ADDR[3]; // абсолютный адрес сектора
BYTE MODE; // тип сектора
BYTE USER_DATA[2048]; // пользовательские данные
BYTE EDC[4]; // контрольная сумма
BYTE ZERO[8]; // нули (не используется)
BYTE P[172]; // P-байты четности
BYTE Q[104]; // Q-байты четности
};
При успешном завершении функция возвращает ненулевое значение и ноль в противном случае.
CheckSector
Функция CheckSector осуществляет проверку целостности сектора по контрольной сумме и при необходимости выполняет его восстановление по избыточным кодам Рида-Соломона.
Листинг 6. Прототип функции CheckSector
// указатель на секторный буфер
CheckSector(struct RAW_SECTOR *sector,
int DO); // только проверка/лечение
- sector – указатель на 2352-байтовый блок данных, содержащий подопытный сектор. Лечение сектора осуществляется «вживую», т.е. непосредственно по месту возникновения ошибки. Если количество разрушенных байт превышают корректирующие способности кодов Рида-Соломона, исходные данные остаются неизменными;
- DO – флаг, нулевое значение которого указывает на запрет модификации сектора. Другими словами, соответствует режиму TEST ONLY. Ненулевое значение разрешает восстановление данных, если они действительно подверглись разрушению.
При успешном завершении функция возвращает ненулевое значение и ноль, если сектор содержит ошибку (в режиме TEST ONLY) или если данные восстановить не удалось (при вызове функции в режиме лечения). Для предотвращения возможной неоднозначности рекомендуется вызывать данную функцию в два приема. Первый раз – в режиме тестирования для проверки целостности данных, и второй раз – в режиме лечения (если это необходимо).
Финал
Ниже приведен законченный примем использования корректирующих кодов на практике, пригодный для решения реальных практических задач.
Листинг 7. Пример вызова функций ElByECC.DLL из своей программы
/*—————————————————————————————————-
*
* демонстрация ElByECC.DLL
* ========================
*
* Данная программа демонстрирует работу с библиотекой ElByECC.DLL, генерируя избыточные коды
* Рида-Соломона на основе пользовательских данных, затем умышленно искажает их и вновь восстанавливает.
* Количество разрушаемых байт передается в первом параметре командной строки (по умолчанию – 6)
——————————————————————————————————*/
#include <stdio.h>
#include «ElByECC.h» // декомпилировано автором
// рушить по умолчанию
#define _DEF_DMG 6
// сколько байт рушить?
#define N_BYTES_DAMAGE ((argc>1)?atol(argv[1]):_DEF_DMG)
main(int argc, char **argv)
{
int a;
// заголовок сектора
char stub_head[HEADER_SIZE];
// область пользовательских данных
char user_data[USER_DATA_SIZE];
// сектор для искажений
struct RAW_SECTOR_MODE1 raw_sector_for_damage;
// контрольная копия сектора
struct RAW_SECTOR_MODE1 raw_sector_for_compre;
// TITLE
//—————————————————————————————————
printf(«= ElByECC.DLL usage demo example by KKn»);
// инициализация пользовательских данных
//—————————————————————————————————
printf(«user data initialize……………»);
// user_data init
for (a = 0; a < USER_DATA_SIZE; a++) user_data[a] = a;
// src header init
memset(stub_head, 0, HEADER_SIZE); stub_head[3] = 1;
printf(«+OKn»);
// генерация кодов Рида-Соломона на основе
// пользовательских данных
//—————————————————————————————————
printf(«RS-code generate……………….»);
a = GenECCAndEDC_Mode1(user_data, stub_head, &raw_sector_for_damage);
if (a == ElBy_SECTOR_ERROR) { printf(«-ERROR!x7n»); return -1;}
memcpy(&raw_sector_for_compre, &raw_sector_for_damage, RAW_SECTOR_SIZE);
printf(«+OKn»);
// умышленное искажение пользовательских данных
//—————————————————————————————————
printf(«user-data %04d bytes damage……..», N_BYTES_DAMAGE);
for (a=0;a<N_BYTES_DAMAGE;a++) raw_sector_for_damage.USER_DATA[a]^=0xFF;
if(!memcmp(&raw_sector_for_damage, &raw_sector_for_compre,RAW_SECTOR_SIZE))
printf(«-ERR: NOT DAMAGE YETn»); else printf(«+OKn»);
// проверка целостности пользовательских данных
//—————————————————————————————————
printf(«user-data check………………..»);
a = CheckSector((struct RAW_SECTOR*) &raw_sector_for_damage, ElBy_TEST_ONLY);
if (a==ElBy_SECTOR_OK){
printf(«-ERR:data not damagex7n»);return -1;}printf(«.data damgen»);
// восстановление пользовательских данных
//—————————————————————————————————
printf(«user-data recorver……………..»);
a = CheckSector((struct RAW_SECTOR*) &raw_sector_for_damage, ElBy_REPAIR);
if (a == ElBy_SECTOR_ERROR) {
printf(«-ERR: NOT RECORVER YETx7n»); return -1; } printf(«+OKn»);
// проверка успешности восстановления
//—————————————————————————————————
printf(«user-data recorver check………..»);
if(memcmp(&raw_sector_for_damage, &raw_sector_for_compre,RAW_SECTOR_SIZE))
printf(«-ERR: NOT RECORVER YETx7n»); else printf(«+OKn»);
printf(«+OKn»);
return 1;
}
8.1.1. Вероятность появления ошибок для кодов Рида-Соломона
8.1.2. Почему коды Рида-Соломона эффективны при борьбе c импульсными помехами
8.1.3. Рабочие характеристики кода Рида-Соломона как функция размера, избыточности и степени кодирования
8.1.4. Конечные поля
8.1.4.1.Операция сложения в поле расширения GF(2m)
8.1.4.2. Описание конечного поля с помощью примитивного полинома
8.1.4.3. Поле расширения GF(23)
8.1.4.4. Простой тест для проверки полинома на примитивность
8.1.5. Кодирование Рида-Соломона
8.1.5.1. Кодирование в систематической форме
8.1.5.2. Систематическое кодирование с помощью (n-k)-разрядного регистра сдвига
8.1.6. Декодирование Рида-Соломона
8.1.6.1. Вычисление синдрома
8.1.6.2. Локализация ошибки
8.1.6.3. Значения ошибок
8.1.6.4. Исправление принятого полинома с помощью найденного полинома ошибок
Коды Рида-Соломона (Reed-Solomon code, R-S code) — это недвоичные циклические коды, символы которых представляют собой m-битовые последовательности, где т—положительное целое число, большее 2. Код (n, K) определен на m-битовых символах при всех п и k, для которых
![]() (8.1)
(8.1)
где k — число информационных битов, подлежащих кодированию, а n — число кодовых символов в кодируемом блоке. Для большинства сверточных кодов Рида-Соломона (n,k)
![]() (8.2)
(8.2)
где t — количество ошибочных битов в символе, которые может исправить код, а и ![]() — число контрольных символов. Расширенный код Рида-Соломона можно получить при
— число контрольных символов. Расширенный код Рида-Соломона можно получить при ![]() , но не более того.
, но не более того.
Код Рида-Соломона обладает наибольшим минимальным расстоянием, возможным для линейного кода с одинаковой длиной входных и выходных блоков кодера. Для недвоичных кодов расстояние между двумя кодовыми словами определяется (по аналогии с расстоянием Хэмминга) как число символов, которыми отличаются последовательности. Для кодов Рида-Соломона минимальное расстояние определяется следующим образом [1].
![]() (8.3)
(8.3)
Код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, где t приведено в уравнении (6.44), можно выразить следующим образом.
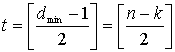 (8.4)
(8.4)
Здесь [x] означает наибольшее целое, не превышающее х. Из уравнения (8.4) видно, что коды Рида-Соломона, исправляющие t символьных ошибок, требуют не более 2t контрольных символов. Из уравнения (8.4) следует, что декодер имеет п-k «используемых» избыточных символов, количество которых вдвое превышает количество исправляемых ошибок. Для каждой ошибки один избыточный символ используется для обнаружения ошибки и один — для определения правильного значения. Способность кода к коррекции стираний выражается следующим образом.
![]() (8.5)
(8.5)
Возможность одновременной коррекции ошибок и стираний можно выразить как требование.
![]() (8.6)
(8.6)
Здесь ![]() — число символьных ошибочных комбинаций, которые можно исправить, а
— число символьных ошибочных комбинаций, которые можно исправить, а ![]() — количество комбинаций символьных стираний, которые могут быть исправлены. Преимущества недвоичных кодов, подобных кодам Рида-Соломона, можно увидеть в следующем сравнении. Рассмотрим двоичный код (п, k) = (7, 3). Полное пространство n-кортежей содержит
— количество комбинаций символьных стираний, которые могут быть исправлены. Преимущества недвоичных кодов, подобных кодам Рида-Соломона, можно увидеть в следующем сравнении. Рассмотрим двоичный код (п, k) = (7, 3). Полное пространство n-кортежей содержит ![]() n-кортежей, из которых
n-кортежей, из которых ![]() (или 1/16 часть всех n-кортежей) являются кодовыми словами. Затем рассмотрим недвоичный код (n, k)=(7, 3), где каждый символ состоит из т = 3 бит. Пространство n-кортежей содержит
(или 1/16 часть всех n-кортежей) являются кодовыми словами. Затем рассмотрим недвоичный код (n, k)=(7, 3), где каждый символ состоит из т = 3 бит. Пространство n-кортежей содержит ![]() 2 097 152 n-кортежа, из которых
2 097 152 n-кортежа, из которых ![]() (или 1/4096 часть всех n-кортежей) являются кодовыми словами. Если операции производятся над недвоичными символами, каждый из которых образован т битами, то только незначительная часть (т.е.
(или 1/4096 часть всех n-кортежей) являются кодовыми словами. Если операции производятся над недвоичными символами, каждый из которых образован т битами, то только незначительная часть (т.е. ![]() из большого числа
из большого числа ![]() ) возможных n-кортежей является кодовыми словами. Эта часть уменьшается с ростом т. Здесь важным является то, что если в качестве кодовых слов используется незначительная часть пространства n-кортежей, то можно достичь большего
) возможных n-кортежей является кодовыми словами. Эта часть уменьшается с ростом т. Здесь важным является то, что если в качестве кодовых слов используется незначительная часть пространства n-кортежей, то можно достичь большего ![]() .
.
Любой линейный код дает возможность исправить n—k комбинаций символьных стираний, если все n—k стертых символов приходятся на контрольные символы. Однако коды Рида-Соломона имеют замечательное свойство, выражающееся в том, что они могут исправить любой набор п-k символов стираний в блоке. Можно сконструировать коды с любой избыточностью. Впрочем, с увеличением избыточности растет сложность ее высокоскоростной реализации. Поэтому наиболее привлекательные коды Рида-Соломона обладают высокой степенью кодирования (низкой избыточностью).
8.1.1. Вероятность появления ошибок для кодов Рида-Соломона
Коды Рида-Соломона чрезвычайно эффективны для исправления пакетов ошибок, т.е. они оказываются эффективными в каналах с памятью. Также они хорошо зарекомендовали себя в каналах с большим набором входных символов. Особенностью кода Рида-Соломона является, то, что к коду длины n можно добавить два информационных символа, не уменьшая при этом минимального расстояния. Такой расширенный код имеет длину п + 2 и то же количество символов контроля четности, что и исходный код. Из уравнения (6.46) вероятность появления ошибки в декодированном символе, РЕ, можно записать через вероятность появления ошибки в канальном символе, ![]() .
.
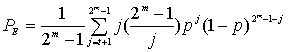 (8.7)
(8.7)
Здесь t — количество ошибочных битов в символе, которые может исправить код, а символы содержат т битов каждый.
Для некоторых типов модуляции вероятность битовой ошибки можно ограничить сверху вероятностью символьной ошибки. Для модуляции MFSK с М=![]() связь РВи РЕвыражается формулой (4.112).
связь РВи РЕвыражается формулой (4.112).
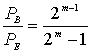 (8.8)
(8.8)
На рис. 8.1 показана зависимость ![]() от вероятности появления ошибки в канальном символе p, полученная из уравнений (8,7) и (8.8) для различных ортогональных 32-ричных кодов Рида-Соломона с возможностью коррекции t ошибочных бит в символе и n = 31 (тридцать один 5-битовый символ в кодовом блоке). На рис.8.2 показана зависимость
от вероятности появления ошибки в канальном символе p, полученная из уравнений (8,7) и (8.8) для различных ортогональных 32-ричных кодов Рида-Соломона с возможностью коррекции t ошибочных бит в символе и n = 31 (тридцать один 5-битовый символ в кодовом блоке). На рис.8.2 показана зависимость ![]() от
от ![]() /N0 для таких систем кодирования при использовании модуляции MFSK и некогерентной демодуляции в канале AWGN [2]. Для кодов Рида-Соломона вероятность появления ошибок является убывающей степенной функцией длины блока, n, а сложность декодирования пропорциональна небольшой степени длины блока [1]. Иногда коды Рида-Соломона применяются в каскадных схемах. В таких системах внутренний сверточный декодер сначала осуществляет некоторую защиту от ошибок за счет мягкой схемы решений на выходе демодулятора; затем сверточный декодер передает данные, оформленные согласно жесткой схеме, на внешний декодер Рида-Соломона, что снижает вероятность появления ошибок. В разделах 8.2.3 и 8.3 мы рассмотрим каскадное декодирование и декодирование Рида-Соломона на примере системы цифровой записи данных на аудиокомпакт-дисках (compact disc — CD).
/N0 для таких систем кодирования при использовании модуляции MFSK и некогерентной демодуляции в канале AWGN [2]. Для кодов Рида-Соломона вероятность появления ошибок является убывающей степенной функцией длины блока, n, а сложность декодирования пропорциональна небольшой степени длины блока [1]. Иногда коды Рида-Соломона применяются в каскадных схемах. В таких системах внутренний сверточный декодер сначала осуществляет некоторую защиту от ошибок за счет мягкой схемы решений на выходе демодулятора; затем сверточный декодер передает данные, оформленные согласно жесткой схеме, на внешний декодер Рида-Соломона, что снижает вероятность появления ошибок. В разделах 8.2.3 и 8.3 мы рассмотрим каскадное декодирование и декодирование Рида-Соломона на примере системы цифровой записи данных на аудиокомпакт-дисках (compact disc — CD).

Рис. 8.1. Зависимость Рв от р для различных ортогональных 32-ринных кодов Рида-Соломона с возможностью коррекции t бит в символе и п = 31.(Перепечатано с разрешения автора из Data Communications, Network, and Systems, ed. Thomas C, Bartee, Howard W. Sams Company,Indianapolis,Ind., 1985, p. 311. Ранее публиковалось в J. P. Odenwalder, Error Control Coding Handbook, M/A-COM LINKABIT, Inc., San Diego, Calif., . ./ — . July,15, 1976,p.

Рис. 8.2. Зависимость рв от Et/NQ для различных ортогональных кодов Рида-Соломона с возможностью коррекции t бит в символе и п = 31, при 32-ринной модуляции MFSK в канале AWGN. (Перепечатано с разрешения автора из Data Communications, Network, and Systems, ed. Thomas C. Bartee, Howard W. Sams Company, Indianapolis, Ind.f 1985, p. 312. Ранее публиковалось в J. P. Odenwalder, Error Control Coding Handbook, M/A-COM LINKABIT, Inc., San Diego, Calif., July, 15, 1976, p. 92.)
8.1.2. Почему коды Рида-Соломона эффективны при борьбе с импульсными помехами
Давайте рассмотрим код (n, k) = (255, 247), в котором каждый символ состоит из т = 8 бит (такие символы принято называть байтами). Поскольку п-k=8, из уравнения (8.4) можно видеть, что этот код может исправлять любые 4-символьные ошибки в блоке длиной до 255. Пусть блок длительностью 25 бит в ходе передачи поражается помехами, как показано на рис. 8.3. В этом примере пакет шума, который попадает на 25 последовательных битов, исказит точно 4 символа. Декодер для кода (255, 247) исправит любые 4-символьные ошибки без учета характера повреждений, причиненных символу. Другими словами, если декодер исправляет байт (заменяет неправильный правильным), то ошибка может быть вызвана искажением одного или всех восьми битов. Поэтому, если символ неправильный, он может быть искажен на всех двоичных позициях. Это дает коду Рида-Соломона огромное преимущество при наличии импульсных помех по сравнению с двоичными кодами (даже при использовании в двоичном коде чередования). В этом примере, если наблюдается 25-битовая случайная помеха, ясно, что искаженными могут оказаться более чем 4 символа (искаженными могут оказаться до 25 символов). Конечно, исправление такого числа ошибок окажется вне возможностей кода (255, 247).
8.1.3. Рабочие характеристики кода Рида-Соломона как функция размера, избыточности и степени кодирования
Для того чтобы код успешно противостоял шумовым эффектам, длительность помех должна составлять относительно небольшой процент от количества кодовых слов. Чтобы быть уверенным, что так будет большую часть времени, принятый шум необходимо усреднить за большой промежуток времени, что снизит эффект от неожиданной или необычной полосы плохого приема. Следовательно, можно предвидеть, что код с коррекцией ошибок будет более эффективен (повысится надежность передачи) при увеличении размера передаваемого блока, что делает код Рида-Соломона более привлекательным, если желательна большая длина блока [3]. Это можно оценить по семейству кривых, показанному на рис. 8.4, где степей кодирования взята равной 7/8, при этом длина блока возрастает с n = 32 символов (при w = 5 бит на символ) до n=256 символов (при n=8 бит на символ). Таким образом, размер блока возрастает с 160 бит до 2048 бит.


Рис. 8.4. Характеристики декодера Рида-Соломона как функция размера символов (степень кодирования = 7/8)
По мере увеличения избыточности кода (и снижения его степени кодирования), сложность реализации этого кода повышается (особенно для высокоскоростных устройств). При этом для систем связи реального времени должна увеличиться ширина полосы пропускания. Увеличение избыточности, например увеличение размера символа, приводит к уменьшению вероятности появления битовых ошибок, как можно видеть на рис. 8.5, еще кодовая длина п равна постоянному значению 64 при снижении числа символов данных с k = 60 до k = 4 (избыточность возрастает с 4 до 60символов).

Рис. 8.5. Характеристики декодера Рида-Соломона (64, k) как функция избыточности
На рис. 8.5 показана передаточная функция (выходная вероятность появлений битовой ошибки, зависящая от входной вероятности появления символьной ошибки) гипотетических декодеров. Поскольку здесь не имеется в виду определенная система или канал (лишь вход-выход декодера), можно заключить, что надежность передачи является монотонной функцией избыточности и будет неуклонно возрастать с приближением степени кодирования к нулю. Однако это не так для кодов, используемых в системах связи реального времени. По мере изменения степени кодирования кода от максимального значения до минимального (от 0 до 1), интересно было бы понаблюдать за эффектами, показанными на рис. 8.6. Здесь кривые рабочих характеристик показаны при модуляции BPSK и кодах (31, к) для разных типов каналов. На рис. 8.6 показаны системы связи реального времени, в которых за кодирование с коррекцией ошибок приходится платить расширением полосы пропускания, пропорциональным величине, равной обратной степени кодирования. Приведенные кривые показывают четкий оптимум степени кодирования, минимизирующий требуемое значение ![]() [4]. Для гауссова канала оптимальное значение степени кодирования находится где-то между 0,6 и 0,7, для канала с райсовским замиранием — около 0,5 (с отношением мощности прямого сигнала к мощности отраженного К = 7 дБ) и 0,3 — для канала с релеевским замиранием. (Каналы с замиранием будут рассматриваться в главе 15.) Почему здесь как при очень высоких степенях кодирования (малой избыточности), так и при очень низких (значительной избыточности) наблюдается ухудшение
[4]. Для гауссова канала оптимальное значение степени кодирования находится где-то между 0,6 и 0,7, для канала с райсовским замиранием — около 0,5 (с отношением мощности прямого сигнала к мощности отраженного К = 7 дБ) и 0,3 — для канала с релеевским замиранием. (Каналы с замиранием будут рассматриваться в главе 15.) Почему здесь как при очень высоких степенях кодирования (малой избыточности), так и при очень низких (значительной избыточности) наблюдается ухудшение ![]() ? Для высоких степеней кодирования это легко объяснить, сравнивая высокие степени кодирования с оптимальной степенью кодирования. Любой код в целом обеспечивает все преимущества кодирования; следовательно, как только степень кодирования приближается к единице (нет кодирования), система проигрывает в надежности передачи. Ухудшение характеристик при низких степенях кодирования является более тонким вопросом, поскольку в системах связи реального времени используется и модуляция, и кодирование, т.е. работает два механизма. Один механизм направлен на снижение вероятности появления ошибок, другой повышает ее. Механизм, снижающий вероятность появления ошибки, — это кодирование; чем больше избыточность, тем больше возможности кода в коррекции ошибок. Механизм, повышающий эту вероятность, — это снижение энергии, приходящейся на канальный символ (по сравнению с информационным символом), что следует из увеличения избыточности (и более быстрой передачи сигналов в системах связи реального времени). Уменьшенная энергия символа вынуждает демодулятор совершать больше ошибок. В конечном счете второй механизм подавляет первый, поэтому очень низкие степени кодирования вызывают ухудшение характеристик кода.
? Для высоких степеней кодирования это легко объяснить, сравнивая высокие степени кодирования с оптимальной степенью кодирования. Любой код в целом обеспечивает все преимущества кодирования; следовательно, как только степень кодирования приближается к единице (нет кодирования), система проигрывает в надежности передачи. Ухудшение характеристик при низких степенях кодирования является более тонким вопросом, поскольку в системах связи реального времени используется и модуляция, и кодирование, т.е. работает два механизма. Один механизм направлен на снижение вероятности появления ошибок, другой повышает ее. Механизм, снижающий вероятность появления ошибки, — это кодирование; чем больше избыточность, тем больше возможности кода в коррекции ошибок. Механизм, повышающий эту вероятность, — это снижение энергии, приходящейся на канальный символ (по сравнению с информационным символом), что следует из увеличения избыточности (и более быстрой передачи сигналов в системах связи реального времени). Уменьшенная энергия символа вынуждает демодулятор совершать больше ошибок. В конечном счете второй механизм подавляет первый, поэтому очень низкие степени кодирования вызывают ухудшение характеристик кода.

Рис. 8.6. Характеристики декодера Рида-Соломона (31, k) как функция степени кодирования (модуляция BPSK)
Давайте попробуем подтвердить зависимость вероятности появления ошибок от степени кодирования, показанную на рис. 8.6, с помощью кривых, изображенных на рис. 8.2. Непосредственно сравнить рисунки не удастся, поскольку на рис. 8.6 применяется модуляция BPSK, а на рис. 8.2 — 32-ричная модуляция MFSK. Однако, пожалуй, нам удастся показать, что зависимость характеристик кода Рида-Соломона от его степени кодирования выглядит одинаково как при BPSK, так и при MFSK. На рис. 8.2 вероятность появления ошибки в канале AWGN снижается при увеличении способности кода t к коррекции символьных ошибок с t = 1 до t = 4; случаи t = 1 и t = 4 относятся к кодам (31, 29) и (31,23) со степенями кодирования 0,94 и 0,74. Хотя при t = 8, что отвечает коду (31,15) со степенью кодирования 0,48, достоверность передачи ![]() достигается при примерно на 0,5 дБ большем отношении
достигается при примерно на 0,5 дБ большем отношении ![]() , по сравнению со случаем t = 4. Из рис. 8.2 можно сделать вывод, что если нарисовать график зависимости достоверности передачи от степени кодирования кода, то кривая будет иметь вид, подобный приведенному на рис. 8.6. Заметим, что это утверждение нельзя получить из рис. 8.1, поскольку там представлена передаточная функция декодера, которая несет в себе сведения о канале и демодуляции. Поэтому из двух механизмов, работающих в канале, передаточная функция (рис. 8.1) представляет только выгоды, которые проявляются на входе/выходе декодера, и ничего не говорит о потерях энергии как функции низкой степени кодирования.
, по сравнению со случаем t = 4. Из рис. 8.2 можно сделать вывод, что если нарисовать график зависимости достоверности передачи от степени кодирования кода, то кривая будет иметь вид, подобный приведенному на рис. 8.6. Заметим, что это утверждение нельзя получить из рис. 8.1, поскольку там представлена передаточная функция декодера, которая несет в себе сведения о канале и демодуляции. Поэтому из двух механизмов, работающих в канале, передаточная функция (рис. 8.1) представляет только выгоды, которые проявляются на входе/выходе декодера, и ничего не говорит о потерях энергии как функции низкой степени кодирования.
8.1.4. Конечные поля
Для понимания принципов кодирования и декодирования недвоичных кодов, таких как коды Рида-Соломона, нужно сделать экскурс в понятие конечных полей, известных как поля Галуа (Galois fields — GF). Для любого простого числа p существует конечное поле, которое обозначается GF(p) и содержит p элементов. Понятие GF(p) можно обобщить на поле из ![]() элементов, именуемое полем расширения GF(p); это поле обозначается GF(
элементов, именуемое полем расширения GF(p); это поле обозначается GF(![]() ), где т — положительное целое число. Заметим, что GF(
), где т — положительное целое число. Заметим, что GF(![]() ) содержит в качестве подмножества все элементы GF(p). Символы из поля расширения GF(
) содержит в качестве подмножества все элементы GF(p). Символы из поля расширения GF(
) используются при построении кодов Рида-Соломона.
Двоичное поле GF(2) является подполем поля расширения GF(![]() ), точно так же как поле вещественных чисел является подполем поля комплексных чисел. Кроме чисел 0 и 1, в поле расширения существуют дополнительные однозначные элементы, которые будут представлены новым символом а. Каждый ненулевой элемент в GF(
), точно так же как поле вещественных чисел является подполем поля комплексных чисел. Кроме чисел 0 и 1, в поле расширения существуют дополнительные однозначные элементы, которые будут представлены новым символом а. Каждый ненулевой элемент в GF(![]() ) можно представить как степень
) можно представить как степень ![]() . Бесконечное множество элементов, F, образуется из стартового множества
. Бесконечное множество элементов, F, образуется из стартового множества ![]() и генерируется дополнительными элементами путем последовательного умножения последней записи на
и генерируется дополнительными элементами путем последовательного умножения последней записи на ![]() .
.
![]() (8.9)
(8.9)
Для вычисления из F конечного множества элементов GF(![]() ) на F нужно наложить условия: оно может содержать только
) на F нужно наложить условия: оно может содержать только ![]() элемента и быть замкнутым относительно операции умножения. Условие замыкания множества элементов поля по отношению к операции умножения имеет вид неприводимого полинома.
элемента и быть замкнутым относительно операции умножения. Условие замыкания множества элементов поля по отношению к операции умножения имеет вид неприводимого полинома.
![]() (8.9)
(8.9)
или, что тоже самое,
![]() (8.10)
(8.10)
С помощью полиномиального ограничения любой элемент со степенью, большей или равной ![]() , можно следующим образом понизить до элемента со степенью, меньшей
, можно следующим образом понизить до элемента со степенью, меньшей ![]() .
.
![]() (8.11)
(8.11)
Таким образом, как показано ниже, уравнение (8.10) можно использовать для формирования конечной последовательности F* из бесконечной последовательности F.
![]() (8.12)
(8.12)
Следовательно, из уравнения (8.12) можно видеть, что элементы конечного поля GF(![]() ) даются следующим выражением.
) даются следующим выражением.
![]() (8.13)
(8.13)
8.1.4.1. Операция сложения в поле расширения GF(2m)
Каждый из ![]() элементов конечного поля GF(
элементов конечного поля GF(![]() ) можно представить как отдельный полином степени от m-1 или меньше. Степенью полинома называется степень члена максимального порядка. Обозначим каждый ненулевой элемент GF(
) можно представить как отдельный полином степени от m-1 или меньше. Степенью полинома называется степень члена максимального порядка. Обозначим каждый ненулевой элемент GF(![]() ) полиномом
) полиномом ![]() , в котором последние т коэффициентов
, в котором последние т коэффициентов ![]() нулевые. Для
нулевые. Для ![]() ,
,
![]() (8.14)
(8.14)
Рассмотрим случай m = 3, в котором конечное поле обозначается GF(23). На рис. 8.7 показано отображение семи элементов {![]() } и нулевого элемента в слагаемые базисных элементов
} и нулевого элемента в слагаемые базисных элементов ![]() , описываемых уравнением (8.14). Поскольку из уравнения (8.10)
, описываемых уравнением (8.14). Поскольку из уравнения (8.10) ![]() , в этом поле имеется семь ненулевых элементов или всего восемь элементов. Каждая строка на рис. 8.7 содержит последовательность двоичных величин, представляющих коэффициенты
, в этом поле имеется семь ненулевых элементов или всего восемь элементов. Каждая строка на рис. 8.7 содержит последовательность двоичных величин, представляющих коэффициенты ![]() ,
, ![]() и
и ![]() из уравнения (8.14). Одним из преимуществ использования элементов
из уравнения (8.14). Одним из преимуществ использования элементов ![]() поля расширения, вместо двоичных элементов, является компактность записи, что оказывается удобным при математическом описании процессов недвоичного кодирования и декодирования. Сложение двух элементов конечного поля, следовательно, определяется как суммирование по модулю 2 всех коэффициентов при элементах одинаковых степеней.
поля расширения, вместо двоичных элементов, является компактность записи, что оказывается удобным при математическом описании процессов недвоичного кодирования и декодирования. Сложение двух элементов конечного поля, следовательно, определяется как суммирование по модулю 2 всех коэффициентов при элементах одинаковых степеней.
![]() (8.15)
(8.15)
8.1.4.2. Описание конечного поля с помощью примитивного полинома
Класс полиномов, называемых примитивными полиномами, интересует нас, поскольку такие объекты определяют конечные поля GF(![]() ), которые, в свою очередь, нужны для описания кодов Рида-Соломона. Следующее утверждение является необходимым и достаточным условием примитивности полинома. Неприводимый полином f(X) порядка т будет примитивным, если наименьшим положительным целым числом п, для которого
), которые, в свою очередь, нужны для описания кодов Рида-Соломона. Следующее утверждение является необходимым и достаточным условием примитивности полинома. Неприводимый полином f(X) порядка т будет примитивным, если наименьшим положительным целым числом п, для которого ![]() делится на f(X), будет
делится на f(X), будет ![]() . Заметим, что неприводимый полином — это такой полином, который нельзя представить в виде произведения полиномов меньшего порядка; делимость А на В означает, что А делится на В с нулевым остатком и ненулевым частным. Обычно полином записывают в порядке возрастания степеней. Иногда более удобным является обратный формат записи (например, при выполнении полиномиального деления).
. Заметим, что неприводимый полином — это такой полином, который нельзя представить в виде произведения полиномов меньшего порядка; делимость А на В означает, что А делится на В с нулевым остатком и ненулевым частным. Обычно полином записывают в порядке возрастания степеней. Иногда более удобным является обратный формат записи (например, при выполнении полиномиального деления).
|
Образующие элементы |
||||
|
Элементы поля |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
|
|
|
1 |
1 |
0 |
|
|
|
0 |
1 |
1 |
|
|
|
1 |
1 |
1 |
|
|
|
1 |
0 |
1 |
|
|
|
1 |
0 |
0 |
Рис. 8.7. Отображение элементов поля в базисные элементы GF(8) с помощью ![]()
Пример 8.1. Проверка полинома на примитивность
Основываясь на предыдущем определении примитивного полинома, укажите, какие из следующих неприводимых полиномов будут примитивными.
а) ![]()
б) ![]()
Решение
а) Мы можем проверить этот полином порядка т = 4, определив, будет ли он делителем ![]() для значений п из диапазона 1 < n < 15. Нетрудно убедиться, что
для значений п из диапазона 1 < n < 15. Нетрудно убедиться, что ![]() + 1 делится на
+ 1 делится на ![]() (см. раздел 6.8.1), и после повторения вычислений можно проверить, что при любых значениях п из диапазона 1<n<15 полином
(см. раздел 6.8.1), и после повторения вычислений можно проверить, что при любых значениях п из диапазона 1<n<15 полином ![]() +1 не делится на
+1 не делится на ![]() . Следовательно,
. Следовательно, ![]() является примитивным полиномом.
является примитивным полиномом.
б) Легко проверить, что полином является делителем ![]() . Проверив, делится ли
. Проверив, делится ли ![]() на
на ![]() , для значений n, меньших 15, можно также видеть, что указанный полином является делителем Xs+1. Следовательно, несмотря на то что полином
, для значений n, меньших 15, можно также видеть, что указанный полином является делителем Xs+1. Следовательно, несмотря на то что полином ![]() является неприводимым, он не будет примитивным.
является неприводимым, он не будет примитивным.
8.1.4.3. Поле расширения GF(23)
Рассмотрим пример, в котором будут задействованы примитивный полином и конечное поле, которое он определяет. В табл. 8.1 содержатся примеры некоторых примитивных полиномов. Мы выберем первый из указанных там полиномов, ![]() , который определяет конечное поле GF(
, который определяет конечное поле GF(![]() ), где степень полинома т=3. Таким образом, в поле, определяемом полиномом f(Х), имеется 2m = 23 = 8 элементов. Поиск корней полинома f(Х) — это поиск таких значений X, при которых
), где степень полинома т=3. Таким образом, в поле, определяемом полиномом f(Х), имеется 2m = 23 = 8 элементов. Поиск корней полинома f(Х) — это поиск таких значений X, при которых ![]() . Привычные нам двоичные элементы 0 и 1 не подходят полиному
. Привычные нам двоичные элементы 0 и 1 не подходят полиному ![]() (они не являются корнями), поскольку
(они не являются корнями), поскольку ![]() (в рамках операции по модулю 2). Кроме того, основная теорема алгебры утверждает, что полином порядка m должен иметь в точности m корней. Следовательно, в этом примере выражение
(в рамках операции по модулю 2). Кроме того, основная теорема алгебры утверждает, что полином порядка m должен иметь в точности m корней. Следовательно, в этом примере выражение ![]() должно иметь 3 корня. Возникает определенная проблема, поскольку 3 корня не лежат в одном конечном поле, что и коэффициенты f(X). А если они находятся где-то еще, то, наверняка, в поле расширения
должно иметь 3 корня. Возникает определенная проблема, поскольку 3 корня не лежат в одном конечном поле, что и коэффициенты f(X). А если они находятся где-то еще, то, наверняка, в поле расширения ![]() . Пусть,
. Пусть, ![]() , элемент поля расширения, определяется как корень полинома f(X). Следовательно, можно записать следующее.
, элемент поля расширения, определяется как корень полинома f(X). Следовательно, можно записать следующее.
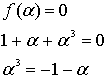 (8.16)
(8.16)
Поскольку при операциях над двоичным полем +1=-1, то ![]() можно представить следующим образом.
можно представить следующим образом.
![]() (8.17)
(8.17)
Таблица 8.1. Некоторые примитивные полиномы
|
m |
m |
||
|
3 |
|
14 |
|
|
4 |
|
15 |
|
|
5 |
|
16 |
|
|
6 |
|
17 |
|
|
7 |
|
18 |
|
|
8 |
|
19 |
|
|
9 |
|
20 |
|
|
10 |
|
21 |
|
|
11 |
|
22 |
|
|
12 |
|
23 |
|
|
13 |
|
24 |
|
Таким образом, ![]() представляется в виде взвешенной суммы всех
представляется в виде взвешенной суммы всех ![]() — членов более низкого порядка. Фактически так можно представить все степени
— членов более низкого порядка. Фактически так можно представить все степени ![]() . Например, рассмотрим следующее.
. Например, рассмотрим следующее.
![]() (8.18,а)
(8.18,а)
А теперь взглянем на следующий случай.
![]() (8.18,б)
(8.18,б)
Из уравнений (8.17) и (8.18), получаем следующее.
Из уравнений (8.17) и (8.18), получаем следующее.
![]() (8.18,в)
(8.18,в)
Из уравнений (8.17) и (8.18), получаем следующее.
![]() (8.18,г)
(8.18,г)
А теперь из уравнения (8.18,г) вычисляем
![]() (8.18,д)
(8.18,д)
Заметим, что ![]() и, следовательно, восьмью элементами конечного поля GF(
и, следовательно, восьмью элементами конечного поля GF(![]() ) ,будут
) ,будут
![]() (8.19)
(8.19)
Отображение элементов поля в базисные элементы, короче описывается уравнением (8.14), можно проиллюстрировать с помощью схемы линейного регистра сдвига с обратной связью (linear feedback shift register – LFSR) (рис 8.8). Схема генерирует (при m = 3) ![]() ненулевых элементов поля и, таким образом, обобщает процедуры, описанные в уравнениях (8.17) – (8.19). Следует отметить, что показанная на рис. 8.8. обратная связь соответствует коэффициентам полинома
ненулевых элементов поля и, таким образом, обобщает процедуры, описанные в уравнениях (8.17) – (8.19). Следует отметить, что показанная на рис. 8.8. обратная связь соответствует коэффициентам полинома ![]() , как и в случае двоичных циклических кодов (см. раздел 6.7.5.). Пусть вначале схема находится в некотором состоянии, например 1 0 0; при выполнении правого сдвига на один такт можно убедиться, что каждый из элементов поля (за исключением нулевого), показанных на рис.8.7, циклически будет появляться в разрядах регистра сдвига. На данном конечном поле GF(
, как и в случае двоичных циклических кодов (см. раздел 6.7.5.). Пусть вначале схема находится в некотором состоянии, например 1 0 0; при выполнении правого сдвига на один такт можно убедиться, что каждый из элементов поля (за исключением нулевого), показанных на рис.8.7, циклически будет появляться в разрядах регистра сдвига. На данном конечном поле GF(![]() ) можно определить две арифметические операции – сложение и умножение. В таб. 8.2. показана операция сложения, а в таб. 8.3. – операция умножения, но только для ненулевых элементов. Правила суммирования следуют из уравнений (8.17) и (8.18,д); и их можно рассчитать путем сложения (по модулю 2) соответствующих коэффициентов из базисных элементов. Правила умножения, указанные в табл. 8.3, следуют из обычной процедуры, в которой произведение элементов поля вычисляются путем сложения по модулю
) можно определить две арифметические операции – сложение и умножение. В таб. 8.2. показана операция сложения, а в таб. 8.3. – операция умножения, но только для ненулевых элементов. Правила суммирования следуют из уравнений (8.17) и (8.18,д); и их можно рассчитать путем сложения (по модулю 2) соответствующих коэффициентов из базисных элементов. Правила умножения, указанные в табл. 8.3, следуют из обычной процедуры, в которой произведение элементов поля вычисляются путем сложения по модулю ![]() их показателей степеней или, для данного случая, по модулю 7.
их показателей степеней или, для данного случая, по модулю 7.
Таблица 8.2. Таблица сложения для GF(8) при ![]()
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
Таблица 8.3. Таблица умножения для GF(8) при ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.1.4.4. Простой тест для проверки полинома на примитивность
Существует еще один, чрезвычайно простой способ проверки, является ли полином примитивным. У неприводимого полинома, который является примитивным, по крайней мере, хотя бы один из корней должен быть примитивным элементом. Примитивным элементом называется такой элемент поля, который, будучи возведенным в более высокие степени, даст ненулевые элементы поля. Поскольку данное поле является конечным, количество таких элементов также конечно.
Пример 8.2. Примитивный полином должен иметь, по крайней мере, хотя бы один примитивный элемент.
Найдите m = 3 корня полинома ![]() и определите, примитивен ли полином. Для этого проверьте, имеется ли среди корней полинома хотя бы один примитивный элемент. Каковы корни полинома? Какие из них примитивны?
и определите, примитивен ли полином. Для этого проверьте, имеется ли среди корней полинома хотя бы один примитивный элемент. Каковы корни полинома? Какие из них примитивны?
Решение
Корни будут найдены прямым перебором. Итак, ![]() не будет корнем, поскольку
не будет корнем, поскольку ![]() .Теперь, чтобы проверить, является ли корнем
.Теперь, чтобы проверить, является ли корнем ![]() , воспользуемся табл. 8.2. Поскольку
, воспользуемся табл. 8.2. Поскольку ![]() , значит,
, значит, ![]() будет корнем полинома. Далее проверим, будет ли корнем
будет корнем полинома. Далее проверим, будет ли корнем ![]() .
.![]() Значит, и
Значит, и ![]() также будет корнем полинома. Теперь проверим
также будет корнем полинома. Теперь проверим ![]() .
. ![]() Следовательно,
Следовательно, ![]() корнем полинома не является. Будет ли корнем
корнем полинома не является. Будет ли корнем ![]() ?
? ![]() Да,
Да, ![]() будет корнем полинома. Значит, корнями полинома
будет корнем полинома. Значит, корнями полинома ![]() будут
будут ![]() . Нетрудно убедиться, что, последовательно возводя в степень любой из этих корней, можно получить все 7 ненулевых элементов поля. Таким образом, все корни будут примитивными элементами. Поскольку в определении требуется, чтобы по крайней мере один из корней был примитивным, полином является примитивным.
. Нетрудно убедиться, что, последовательно возводя в степень любой из этих корней, можно получить все 7 ненулевых элементов поля. Таким образом, все корни будут примитивными элементами. Поскольку в определении требуется, чтобы по крайней мере один из корней был примитивным, полином является примитивным.
В этом примере описан относительно простой метод проверки полинома на примитивность. Для проверяемого полинома нужно составить регистр LFSR с контуром обратной связи, соответствующий коэффициентам полинома, как показана на рис. 8.8. Затем в схему регистра следует загрузить любое ненулевое состояние и выполнить за каждый такт правый сдвиг. Если за один период схема сгенерирует все ненулевые элементы поля, то данный полином с полем GF(![]() ) будет примитивным.
) будет примитивным.
8.1.5. Кодирование Рида-Соломона
В уравнении (8.2) представлена наиболее распространенная форма кодов Рида-Соломона через параметры n, k, t и некоторое положительное число m > 2. Приведем это уравнение повторно.
![]() (8.20)
(8.20)
Здесь ![]() — число контрольных символов, а t – количество ошибочных битов в символе, которые может исправить код. Генерирующий полином для кода Рида-Соломона имеет следующий вид.
— число контрольных символов, а t – количество ошибочных битов в символе, которые может исправить код. Генерирующий полином для кода Рида-Соломона имеет следующий вид.
![]() (8.21)
(8.21)
Степень полиномиального генератора равна числу контролируемых символов. Коды Рида-Соломона являются подмножеством кодов БЧХ, которые обсуждались в разделе 6.8.3. и показаны в табл. 6.4. Поэтому связь между степенью полиномиального генератора и числом контрольных символов, как и в кодах БЧХ, не должна оказаться неожиданностью. В этом можно убедиться, подвергнув проверке любой генератор из табл. 6.4. Поскольку полиномиальный генератор имеет порядок 2t, мы должны иметь в точности 2t последовательные степени ![]() , которые являются корнями полинома. Обозначим корни
, которые являются корнями полинома. Обозначим корни ![]() как:
как: ![]() . Нет необходимости начинать именно с корня
. Нет необходимости начинать именно с корня ![]() , это можно сделать с помощью любой степени
, это можно сделать с помощью любой степени ![]() . Возьмем, к примеру, код (7,3) с возможностью коррекции двухсимвольных ошибок. Мы выразим полиномиальный генератор через
. Возьмем, к примеру, код (7,3) с возможностью коррекции двухсимвольных ошибок. Мы выразим полиномиальный генератор через ![]() корня следующим образом.
корня следующим образом.
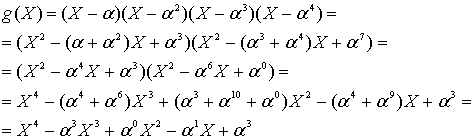
8.1.5.1. Кодирование в систематической форме
Так как код Рида-Соломона является циклическим, кодирование в систематической форме аналогично процедуре двоичного кодирования, разработанной в разделе 6.7.3. Мы можем осуществить сдвиг полинома сообщения m(X) в крайние правые k разряды регистра кодового слова и провести последующее прибавление полинома четности p(X) в крайние левые n – k разряды. Поэтому мы умножаем m(X) на ![]() , проделав алгебраическую операцию таким образом, что m(X) оказывается сдвинутым вправо на n – k позиций. В главе 6 это показано в уравнении (6.61) на примере двоичного кодирования. Далее мы делим
, проделав алгебраическую операцию таким образом, что m(X) оказывается сдвинутым вправо на n – k позиций. В главе 6 это показано в уравнении (6.61) на примере двоичного кодирования. Далее мы делим ![]() на полиномиальный генератор g(X), что можно записать следующим образом.
на полиномиальный генератор g(X), что можно записать следующим образом.
![]()
![]()
Здесь q(X) и p(X) – это частное и остаток от полиномиального деления. Как и в случае двоичного кодирования, остаток будет четным. Уравнение (8.23) можно представить следующим образом.
![]() (8.24)
(8.24)
Результирующий полином кодового слова U(X), показанный в уравнении (6.64), можно переписать следующим образом.
![]() (8.25)
(8.25)
Продемонстрируем шаги, подразумеваемые уравнениями (8.24) и (8.25), закодировав сообщение из трех символов
![]()
с помощью кода (7,3), генератор которого определяется уравнением (8.22). Сначала мы умножаем (сдвиг вверх) полином сообщения ![]() , что дает
, что дает ![]() Далее мы делим такой сдвинутый вверх полином сообщения на полиномиальный генератор из уравнения (8.22),
Далее мы делим такой сдвинутый вверх полином сообщения на полиномиальный генератор из уравнения (8.22), ![]() Полиномиальное деление недвоичных коэффициентов – это еще более утомительная процедура, чем ее двоичный аналог (см. пример 6.9), поскольку операции сложения (вычитания) и умножения (деления) выполняются согласно табл. 8.2 и 8.3. Мы оставим числителю в качестве вспомогательного упражнения проверку того, что полиномиальное деление даст в результате следующей полиномиальный остаток (полином четности).
Полиномиальное деление недвоичных коэффициентов – это еще более утомительная процедура, чем ее двоичный аналог (см. пример 6.9), поскольку операции сложения (вычитания) и умножения (деления) выполняются согласно табл. 8.2 и 8.3. Мы оставим числителю в качестве вспомогательного упражнения проверку того, что полиномиальное деление даст в результате следующей полиномиальный остаток (полином четности).
![]()
Заметим, из уравнения (8.25), полином кодового слова можно записать следующим образом.
![]()
8.1.5.2. Систематическое кодирование с помощью (n-k)-разрядного регистра сдвига
Как показано на рис. 8.9, кодирование последовательности из 3 символов в систематической форме на основе кода (7,3), определяемого генератором g(X) из уравнения (8.22), требует реализации регистра LFSR. Нетрудно убедиться, что элементы умножителя на рис. 8.9, взятые справа налево, соответствуют коэффициентам полинома в уравнении (8.22). Этот процесс кодирования является недвоичным аналогом циклического кодирования, которое описывалась в разделе 6.7.5. Здесь, в соответствии с уравнением (8.20), ненулевые кодовые слова образованы ![]() символами, и каждый символ состоит из m = 3 бит.
символами, и каждый символ состоит из m = 3 бит.
Следует отметить сходство между рис. 8.9, 6.18 и 6.19. Во всех трех случаях количество разрядов в регистре равно n – k. Рисунки в главе 6 отображают пример двоичного кодирования, где каждый разряд содержит 1 бит. В данной главе приведен пример двоичного кодирования, так что каждый разряд регистра сдвига, изображенного на рис. 8.9, содержит 3-битовый символ. На рис. 6.18 коэффициенты, обозначенные ![]() являются двоичными. Поэтому они принимают одно из значений 0 или 1, просто указывая на наличие или отсутствие связи в LFSR. На рис. 8.9 каждый коэффициент является 3-битовым, так что они могут принимать одно из 8 значений.
являются двоичными. Поэтому они принимают одно из значений 0 или 1, просто указывая на наличие или отсутствие связи в LFSR. На рис. 8.9 каждый коэффициент является 3-битовым, так что они могут принимать одно из 8 значений.
Недвоичные операции, осуществляемые кодером, показанным на рис. 8.9, создают кодовые слова в систематической форме, так же как и в двоичном случае. Эти операции определяются следующими шагами.
1. Переключатель 1 в течение первых k тактовых импульсов закрыт, для того чтобы подавать символы сообщения в (n — k)-разрядный регистр сдвига.
2. В течение первых k тактовых импульсов переключатель 2 находится в нижнем положении, что обеспечивает одновременную процедуру всех символов сообщения непосредственно на регистр выхода (на рис. 8.9 не показан).
3. После передачи k-го символа на регистр выхода, переключатель 1 открывается, а переключатель 2 переходит в верхнее положение.
4. Остальные (n—k) тактовых импульсов очищают контрольные символы, содержащиеся в регистре, подавая из на регистр выхода.
5. Общее число тактовых импульсов равно n, и содержимое регистра выхода является полиномом кодового слова ![]() , где p(X) представляет собой кодовые символы, а m(X) – символы сообщения в полиномиальной форме.
, где p(X) представляет собой кодовые символы, а m(X) – символы сообщения в полиномиальной форме.
Для проверки возьмем те же последовательность символов, что и в разделе 8.1.5.1.
![]()
Здесь крайний правый символ является самым первым и крайний правый бит также является самым первым. Последовательность действий в течение первых k = 3 сдвигов в цепи кодирования на рис. 8.9 будет иметь следующий вид.
Очередь ввода Такт Содержимое регистра обратная связь
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
||
|
— |
3 |
|
|
|
|
— |
Как можно видеть, после третьего такта регистр содержит 4 контрольных символа, ![]() . Затем переключатель 1 переходит в верхнее положение, и контрольные символы, содержащиеся в регистре, подаются на выход. Поэтому выходное слово, записанное в полиномиальной форме, можно представить в следующим виде.
. Затем переключатель 1 переходит в верхнее положение, и контрольные символы, содержащиеся в регистре, подаются на выход. Поэтому выходное слово, записанное в полиномиальной форме, можно представить в следующим виде.
![]()
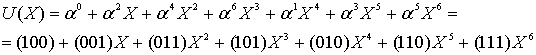 (8.26)
(8.26)
Процесс проверки содержимого регистра во время разных тактов несколько сложнее, чем в случае бинарного кодирования. Здесь сложение и умножение элементов поля должны выполняться согласно табл. 8.2 и 8.3.
Корни полиномиального генератора g(X) должны быть и корнями кодового слова, генерируемого g(X), поскольку правильное кодовое слово имеет следующий вид.
![]() (8.27)
(8.27)
Следовательно, произвольное кодовое слово, выражаемое через корень генератора g(X), должно давать нуль. Представляется интересным, действительно ли полином кодового слова в уравнении (8.26) дает нуль, когда он выражается через какой-либо из четырех корней g(X). Иными словами, это означает проверку следующего.
![]()
Независимо выполнив вычисления для разных корней, получим следующее.
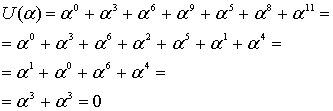
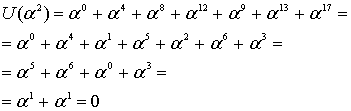
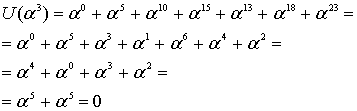
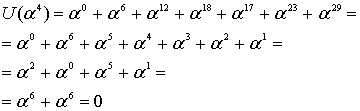
Эти вычисления показывают, что, как и ожидалось, кодовое слово, выражаемое через любой корень генератора g(X), должно давать нуль.
8.1.6. Декодирование Рида-Соломона
В разделе 8.1.5 тестовое сообщение кодируется в систематической форме с помощью кода (7,3), что дает в результате полином кодового слова, описываемый уравнением (8.26). Допустим, что в ходе передачи это кодовое слово подверглось искажению: 2 символа были приняты с ошибкой. (Такое количество ошибок соответствует максимальной способности кода к коррекции ошибок.) При использовании 7-символьного кодового слова ошибочную комбинацию можно представить в полиномиальной форме следующим образом.
![]() (8.28)
(8.28)
Пусть двухсимвольная ошибка будет такой, что
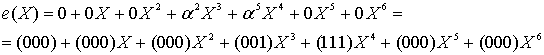 (8.29)
(8.29)
Другими словами, контрольный символ искажен 1-битовой ошибкой (представленной как ![]() ), а символ сообщения — 3-битовой ошибкой (представленной как
), а символ сообщения — 3-битовой ошибкой (представленной как ![]() ). В данном случае принятый полином поврежденного кодового слова r(Х) представляется в виде суммы полинома переданного кодового слова и полинома ошибочной комбинации, как показано ниже.
). В данном случае принятый полином поврежденного кодового слова r(Х) представляется в виде суммы полинома переданного кодового слова и полинома ошибочной комбинации, как показано ниже.
![]()
![]() (8.30)
(8.30)
Следуя уравнению (8.30), мы суммируем U(X) из уравнения (8.26) и e(Х) из уравнения (8.29) и имеем следующее.
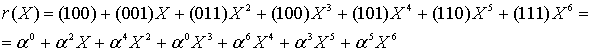 (8.31)
(8.31)
В данном примере исправления 2-символьной ошибки имеется четыре неизвестных — два относятся к расположению ошибки, а два касаются ошибочных значений. Отметим важное различие между недвоичным декодированием r(Х), которое мы показали в уравнении (8.31), и двоичным, которое описывалось в главе 6. При двоичном декодировании декодеру нужно знать лишь расположение ошибки. Если известно, где находится ошибка, бит нужно поменять с 1 на 0 или наоборот. Но здесь недвоичные символы требуют, чтобы мы не только узнали расположение ошибки, но и определили правильное значение символа, расположенного на этой позиции. Поскольку в данном примере у нас имеется четыре неизвестных, нам нужно четыре уравнения, чтобы найти их.
8.1.6.1. Вычисление синдрома
Вернемся к разделу 6.4.7 и напомним, что синдром — это результат проверки четности, выполняемой над r, чтобы определить, принадлежит ли r набору кодовых слов. Если r является членом набора, то синдром S имеет значение, равное 0. Любое ненулевое значение S означает наличие ошибок. Точно так же, как и в двоичном случае, синдром S состоит из n—k символов, ![]()
![]() . Таким образом, для нашего кода (7, 3) имеется по четыре символа в каждом векторе синдрома; их значения можно рассчитать из принятого полинома r(Х). Заметим, кдк облегчаются вычисления благодаря самой структуре кода, определяемой уравнением (8.27).
. Таким образом, для нашего кода (7, 3) имеется по четыре символа в каждом векторе синдрома; их значения можно рассчитать из принятого полинома r(Х). Заметим, кдк облегчаются вычисления благодаря самой структуре кода, определяемой уравнением (8.27).
![]()
Из этой структуры можно видеть, что каждый правильный полином кодового слова U(X) является кратным полиномиальному генератору g(X). Следовательно, корни g(X) также должны быть корнями U(X). Поскольку ![]() , то r(Х), вычисляемый с каждым корнем g(X), должен давать нуль, только если r(Х) будет правильным кодовым словом. Любые ошибки приведут в итоге к ненулевому результату в одном (или более) случае. Вычисления символов синдрома можно записать следующим образом.
, то r(Х), вычисляемый с каждым корнем g(X), должен давать нуль, только если r(Х) будет правильным кодовым словом. Любые ошибки приведут в итоге к ненулевому результату в одном (или более) случае. Вычисления символов синдрома можно записать следующим образом.
![]() (8.32)
(8.32)
Здесь, как было показано в уравнении (8.29), r(Х) содержит 2-символьные ошибки. Если r(Х) окажется правильным кодовым словом, то это приведет к тому, что все символы синдрома ![]() будут равны нулю. В данном примере четыре символа синдрома находятся следующим образом.
будут равны нулю. В данном примере четыре символа синдрома находятся следующим образом.
![]()
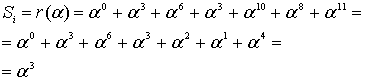 (8.33)
(8.33)
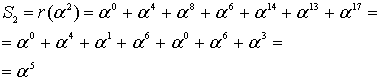 (8.34)
(8.34)
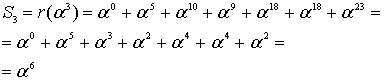 (8.35)
(8.35)
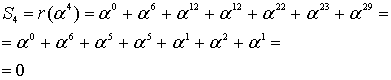 (8.36)
(8.36)
Результат подтверждает, что принятое кодовое слово содержит ошибку (введенную нами), поскольку ![]() .
.
Пример 8.3. Повторная проверка значений синдрома
Для рассматриваемого кода (7, 3) ошибочная комбинация известна, поскольку мы выбрали ее заранее. Вспомним свойство кодов, обсуждаемое в разделе 6.4.8.1, когда была введена нормальная матрица. Все элементы класса смежности (строка) нормальной матрицы имеют один и тот же синдром. Нужно показать, что это свойство справедливо и для кода Рида-Соломона, путем вычисления полинома ошибок e(Х) со значениями корней g(X). Это должно дать те же значения синдрома, что и вычисление r(Х) со значениями корней g(X). Другими словами, это должно дать те же значения, которые были получены в уравнениях (8.33)-(8.36).
Решение
![]()
![]()
![]()
Из уравнения (8.29) следует, что ![]() , поэтому
, поэтому
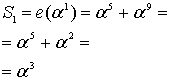
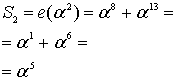
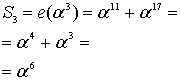
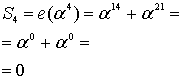
Из этих результатов можно заключить, что значения синдрома одинаковы — как полученные путем вычисления e(Х) со значениями корней g(X), так и полученные путем вычисления r(Х) с теми же значениями корней g(X).
8.1.6.2. Локализация ошибки
Допустим, в кодовом слове имеется ![]() ошибок, расположенных на позициях
ошибок, расположенных на позициях ![]() . Тогда полином ошибок, определяемый уравнениями (8.28) и (8.29), можно записать следующим образом.
. Тогда полином ошибок, определяемый уравнениями (8.28) и (8.29), можно записать следующим образом.
![]() (8.37)
(8.37)
Индексы 1, 2, …, ![]() обозначают 1-ю, 2-ю, …,
обозначают 1-ю, 2-ю, …, ![]() -ю ошибки, а индекс
-ю ошибки, а индекс ![]() — расположение ошибки. Для коррекции искаженного кодового слова нужно определить каждое значение ошибки
— расположение ошибки. Для коррекции искаженного кодового слова нужно определить каждое значение ошибки ![]() и ее расположение
и ее расположение ![]() , где
, где ![]() . Обозначим номер локатора ошибки как
. Обозначим номер локатора ошибки как ![]() . Далее вычисляем
. Далее вычисляем ![]() символа синдрома, подставляя
символа синдрома, подставляя ![]() в принятый полином при
в принятый полином при ![]() .
.
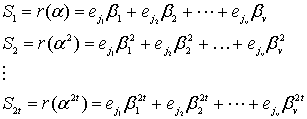 (8.38)
(8.38)
У нас имеется 2t неизвестных (t значений ошибок и t расположений) и система 2t уравнений. Впрочем, эту систему 2t уравнений нельзя решить обычным путем, поскольку уравнения в ней нелинейны (некоторые неизвестные входят в уравнение в степени). Методика, позволяющая решить эту систему уравнений, называется алгоритмом декодирования Рида-Соломона.
Если вычислен ненулевой вектор синдрома (один или более его символов не равны нулю), это означает, что была принята ошибка. Далее нужно узнать расположение ошибки (или ошибок). Полином локатора ошибок можно определить следующим образом.
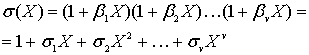 (8.39)
(8.39)
Корнями ![]() будут
будут ![]() . Величины, обратные корням
. Величины, обратные корням ![]() , будут представлять номера расположений ошибочной комбинации e(Х). Тогда, воспользовавшись авторегрессионной техникой моделирования [5], мы составим из синдромов матрицу, в которой первые t синдромов будут использоваться для предсказания следующего синдрома.
, будут представлять номера расположений ошибочной комбинации e(Х). Тогда, воспользовавшись авторегрессионной техникой моделирования [5], мы составим из синдромов матрицу, в которой первые t синдромов будут использоваться для предсказания следующего синдрома.
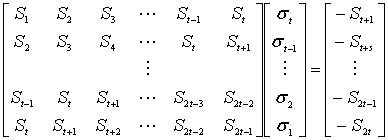 (8.40)
(8.40)
Мы воспользовались авторегрессионной моделью уравнения (8.40), взяв матрицу наибольшей размерности с ненулевым определителем. Для кода (7, 3) с коррекцией двухсимвольных ошибок матрица будет иметь размерность ![]() , и модель запишется следующим образом.
, и модель запишется следующим образом.
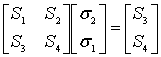 (8.41)
(8.41)
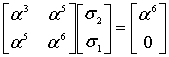 (8.42)
(8.42)
Чтобы найти коэффициенты ![]() и
и ![]() полинома локатора ошибок
полинома локатора ошибок ![]() ,. сначала необходимо вычислить обратную матрицу для уравнения (8.42). Обратная матрица для матрицы [А] определяется следующим образом.
,. сначала необходимо вычислить обратную матрицу для уравнения (8.42). Обратная матрица для матрицы [А] определяется следующим образом.
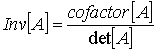
Следовательно,
det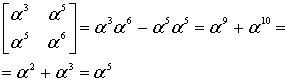 (8.43)
(8.43)
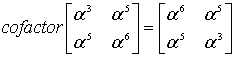 (8.44)
(8.44)
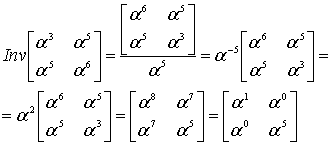 (8.45)
(8.45)
Проверка надежности
Если обратная матрица вычислена правильно, то произведение исходной и обратной матрицы должно дать единичную матрицу.
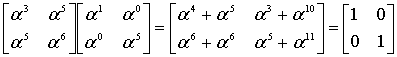 (8.46)
(8.46)
С помощью уравнения (8.42) начнем поиск положений ошибок с вычисления коэффициентов полинома локатора ошибок ![]() , как показано далее.
, как показано далее.
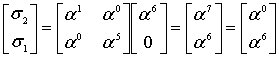 (8.47)
(8.47)
Из уравнений (8.39) и (8.47)
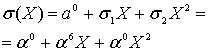 (8.48)
(8.48)
Корни ![]() являются обратными числами к положениям ошибок. После того как эти корни найдены, мы знаем расположение ошибок. Вообще, корни
являются обратными числами к положениям ошибок. После того как эти корни найдены, мы знаем расположение ошибок. Вообще, корни ![]() могут быть одним или несколькими элементами поля. Определим эти корни путем полной проверки полинома
могут быть одним или несколькими элементами поля. Определим эти корни путем полной проверки полинома ![]() со всеми элементами поля, как будет показано ниже. Любой элемент X, который дает
со всеми элементами поля, как будет показано ниже. Любой элемент X, который дает ![]() , является корнем, что позволяет нам определить расположение ошибки.
, является корнем, что позволяет нам определить расположение ошибки.
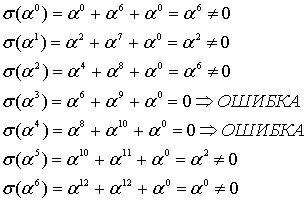
Как видно из уравнения (8.39), расположение ошибок является обратной величиной к корням полинома. А значит, ![]() означает, что один корень получается при
означает, что один корень получается при ![]() . Отсюда
. Отсюда ![]() . Аналогично
. Аналогично ![]() означает, что другой корень появляется при
означает, что другой корень появляется при ![]() , где (в данном примере)
, где (в данном примере) ![]() и
и ![]() обозначают 1-ю и 2-ю ошибки. Поскольку мы имеем дело с 2-символьными ошибками, полином ошибок можно записать следующим образом.
обозначают 1-ю и 2-ю ошибки. Поскольку мы имеем дело с 2-символьными ошибками, полином ошибок можно записать следующим образом.
![]() (8.49)
(8.49)
Здесь были найдены две ошибки на позициях ![]() и
и ![]() . Заметим, что индексация номеров расположения ошибок является сугубо произвольной. Итак, в этом примере мы обозначили величины
. Заметим, что индексация номеров расположения ошибок является сугубо произвольной. Итак, в этом примере мы обозначили величины ![]() как
как ![]()
![]() и
и ![]() .
.
8.1.6.3. Значения ошибок
Мы обозначили ошибки ![]() , где индекс j обозначает расположение ошибки, а индекс l — l-ю ошибку. Поскольку каждое значение ошибки связано с конкретным меcторасположением, систему обозначений можно упростить, обозначив
, где индекс j обозначает расположение ошибки, а индекс l — l-ю ошибку. Поскольку каждое значение ошибки связано с конкретным меcторасположением, систему обозначений можно упростить, обозначив ![]() просто как
просто как ![]() . Теперь, приготовившись к нахождению значений ошибок
. Теперь, приготовившись к нахождению значений ошибок ![]() и
и ![]() , связанных с позициями
, связанных с позициями ![]() и
и ![]() можно использовать любое из четырех синдромных уравнений. Выразим из уравнения (8.38)
можно использовать любое из четырех синдромных уравнений. Выразим из уравнения (8.38) ![]() , и
, и ![]() .
.
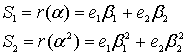 (8.50)
(8.50)
Эти уравнения можно переписать в матричной форме следующим образом.
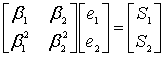 (8.51)
(8.51)
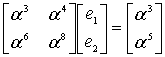 (8.52)
(8.52)
Чтобы найти значения ошибок ![]() и
и ![]() , нужно, как обычно, выполнить поиск обратной матрицы для уравнения (8.52).
, нужно, как обычно, выполнить поиск обратной матрицы для уравнения (8.52).
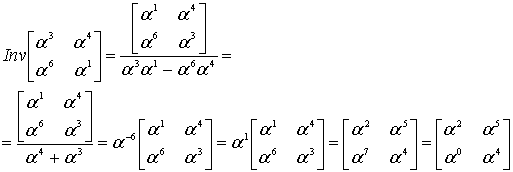 (853)
(853)
Теперь мы можем найти из уравнения (8.52) значения ошибок.
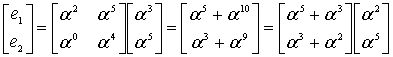 (8.54)
(8.54)
8.1.6.4. Исправление принятого полинома с помощью найденного полинома ошибок
Из уравнений (8.49) и (8.54) мы находим полином ошибок.
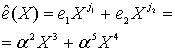 (8.55)
(8.55)
Показанный алгоритм восстанавливает принятый полином, выдавая в итоге предполагаемое переданное кодовое слово и, в конечном счете, декодированное сообщение.
![]() (8.56)
(8.56)
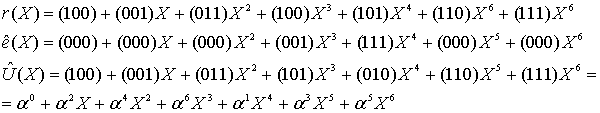 (8.57)
(8.57)
Поскольку символы сообщения содержатся в крайних правых k = 3 символах, декодированным будет следующее сообщение.
![]()
![]()
![]()
Это сообщение в точности соответствует тому, которое было выбрано для этого примера в разделе 8.1.5. (Для более детального знакомства с кодированием Рида-Соломона обратитесь к работе [6].)





























![{displaystyle {begin{aligned}&Y_{k}X_{k}^{j+nu }Lambda (X_{k}^{-1})=0.\[1ex]&Y_{k}X_{k}^{j+nu }left(1+Lambda _{1}X_{k}^{-1}+Lambda _{2}X_{k}^{-2}+cdots +Lambda _{nu }X_{k}^{-nu }right)=0.\[1ex]&Y_{k}X_{k}^{j+nu }+Lambda _{1}Y_{k}X_{k}^{j+nu }X_{k}^{-1}+Lambda _{2}Y_{k}X_{k}^{j+nu }X_{k}^{-2}+cdots +Lambda _{nu }Y_{k}X_{k}^{j+nu }X_{k}^{-nu }=0.\[1ex]&Y_{k}X_{k}^{j+nu }+Lambda _{1}Y_{k}X_{k}^{j+nu -1}+Lambda _{2}Y_{k}X_{k}^{j+nu -2}+cdots +Lambda _{nu }Y_{k}X_{k}^{j}=0.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6573fa0f429ac4349f5da794df9c4fb7831e8cbf)















![{displaystyle {begin{aligned}S(x)&=S_{t}x^{t-1}+S_{t-1}x^{t-2}+cdots +S_{2}x+S_{1}\[1ex]Lambda (x)&=Lambda _{e}x^{e}+Lambda _{e-1}x^{e-1}+cdots +Lambda _{1}x+1\[1ex]Omega (x)&=Omega _{e}x^{e}+Omega _{e-1}x^{e-1}+cdots +Omega _{1}x+Omega _{0}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a84cd05dee4a72d23c59b3f95c4efdf3c8703600)
































