Сколько ошибок может обнаружить код - Ремонт и установка крупной бытовой техники

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 63K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ( $A$ , $B$ , $C$ , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ( $rightarrow$ ), а передачу по каналу связи — волнистой стрелкой ( $rightsquigarrow$ ). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$ . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$begin{aligned} A &to 0,\ B &to 1. end{aligned}$

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$ .

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$begin{aligned} A &to 00,\ B &to 11. end{aligned}$

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$ ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$ . А может, во втором, и была передана $A$ .

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$ . Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$ . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$ .

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$ , а получили $001$ . Видно, что эта цепочка больше похожа на исходные $000$ , чем на $111$ . А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$ , равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$ . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$ , так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$ .

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
Расстояние в обе стороны одинаково.
Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$ ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$ , мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

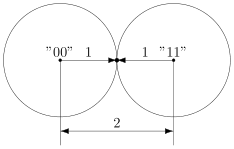
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$ . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

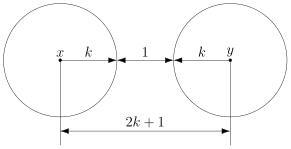
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$d_{min} geqslant 2k+1.$

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned}$

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

	A	B	C	D
A	—	3	3	4
B	3	—	4	3
C	3	4	—	3
D	4	3	3	—

Минимальное расстояние $d_{min}=3$ , а значит $3geqslant2k+1$ , откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned}$

Минимальное расстояние получилось для символа $A$ , значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned}$

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right.$

Или, если воспользоваться свойствами сложения в GF(2), получаем

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Или

$left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right.$

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}.$

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$ ) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}.$

Соответствующая система имеет вид:

$left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right.$

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$ .

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right.$

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned}$

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$a_1 x^{(1)}+a_2 x^{(2)},$

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$(a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG.$

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned}$

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0.$

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$ , а было отправлено кодовое слово $v$ . Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$begin{aligned} v &= x + e,\ x &= v + e. end{aligned}$

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$ . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100).$

Вектор ошибки равен $(00100)$ , а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Число обнаруживаемых или исправляемых ошибок.

При применении двоичных кодов учитывают
только дискретные искажения, при которых
единица переходит в нуль (1 → 0) или нуль
переходит в единицу (0 → 1). Переход 1 →
0 или 0 → 1 только в одном элементе кодовой
комбинации называют единичной ошибкой
(единичным искажением). В общем случае
под кратностью ошибки подразумевают
число позиций кодовой комбинации, на
которых под действием помехи одни
символы оказались заменёнными на другие.
Возможны двукратные (t= 2) и многократные (t> 2) искажения элементов в кодовой
комбинации в пределах 0 <t<n.

Минимальное кодовое расстояние является
основным параметром, характеризующим
корректирующие способности данного
кода. Если код используется только для
обнаружения ошибок кратностью t₀,
то необходимо и достаточно, чтобы
минимальное кодовое расстояние было
равно

d_min
> t₀
+ 1. (13.10)

В этом случае никакая комбинация из t₀ошибок не может перевести одну разрешённую
кодовую комбинацию в другую разрешённую.
Таким образом, условие обнаружения всех
ошибок кратностьюt₀можно записать в виде:

t₀≤ d_min — 1. (13.11)

Чтобы можно было исправить все ошибки
кратностью t_ии менее, необходимо иметь минимальное
расстояние, удовлетворяющее условию:

. (13.12)

В этом случае любая кодовая комбинация
с числом ошибок t_иотличается от каждой разрешённой
комбинации не менее чем вt_и+ 1 позициях. Если условие (13.12) не выполнено,
возможен случай, когда ошибки кратностиtисказят переданную
комбинацию так, что она станет ближе к
одной из разрешённых комбинаций, чем к
переданной или даже перейдёт в другую
разрешённую комбинацию. В соответствии
с этим, условие исправления всех ошибок
кратностью не болееt_иможно записать в виде:

t_и
≤(d_min
— 1) / 2 . (13.13)

Из (13.10) и (13.12) следует, что если код
исправляет все ошибки кратностью t_и,
то число ошибок, которые он может
обнаружить, равноt₀= 2∙t_и. Следует
отметить, что соотношения (13.10) и (13.12)
устанавливают лишь гарантированное
минимальное число обнаруживаемых или
исправляемых ошибок при заданномd_minи не ограничивают возможность обнаружения
ошибок большей кратности. Например,
простейший код с проверкой на чётность
сd_mi_n= 2 позволяет обнаруживать не только
одиночные ошибки, но и любое нечётное
число ошибок в пределахt₀<n.

Корректирующие возможности кодов.

Вопрос о минимально необходимой
избыточности, при которой код обладает
нужными корректирующими свойствами,
является одним из важнейших в теории
кодирования. Этот вопрос до сих пор не
получил полного решения. В настоящее
время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают
связь между максимально возможным
минимальным расстоянием корректирующего
кода и его избыточностью.

Так, граница Плоткинадаёт верхнюю
границу кодового расстоянияd_mi_nпри заданном числе разрядовnв
кодовой комбинации и числе информационных
разрядовm, и для
двоичных кодов:

(13.14)

или

при. (13.15)

Верхняя граница Хеммингаустанавливает
максимально возможное число разрешённых
кодовых комбинаций (2^m)
любого помехоустойчивого кода при
заданных значенияхnиd_min:

, (13.16)

где
—
число сочетаний изnэлементов поiэлементам.

Отсюда можно получить выражение для
оценки числа проверочных символов:

. (13.17)

Для значений (d_min/n)
≤ 0,3 разница между границей Хемминга и
границей Плоткина сравнительно невелика.

Граница Варшамова-Гильбертадля
больших значенийnопределяет нижнюю
границу для числа проверочных разрядов,
необходимого для обеспечения заданного
кодового расстояния:

. (13.18)

Отметим, что для некоторых частных
случаев Хемминг получил простые
соотношения, позволяющие определить
необходимое число проверочных символов:

дляd_min= 3,

дляd_min= 4.

Блочные коды с d_min= 3 и 4 в литературе обычно называют кодами
Хемминга.

Все приведенные выше оценки дают
представление о верхней границе числаd_minпри фиксированных значенияхnиmили оценку снизу числа проверочных
символовkпри заданныхmиd_min.

Существующие методы построения избыточных
кодов решают в основном задачу нахождения
такого алгоритма кодирования и
декодирования, который позволял бы
наиболее просто построить и реализовать
код с заданным значением d_min.
Поэтому различные корректирующие коды
при одинаковыхd_minсравниваются по сложности кодирующего
и декодирующего устройств. Этот критерий
является в ряде случаев определяющим
при выборе того или иного кода.

Соседние файлы в папке ЛБ_3

#
#
14.04.2015937 б73KodHemmig.m
#
14.04.20150 б65ЛБ_3.exe

Источник

Содержание

1 Исправление ошибок в помехоустойчивом кодировании
2 Параметры помехоустойчивого кодирования
3 Контроль чётности
4 Классификация помехоустойчивых кодов
5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

мажоритарный метод

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

где n – количество символов закодированного сообщения (результата кодирования);
m – количество проверочных символов, добавляемых при кодировании;
k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

прямоугольный код

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.

Рассчитаем скорость кода для:

1 1 0 0 0 1 0 0 | 1

Здесь R=8/9=0,88

И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.

Классификация помехоустойчивых кодов

Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.

По используемому алфавиту:

Двоичные. Оперируют битами.
Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.

Блочные коды делятся на

Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

систематический и несистематический код

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Классификация помехоустойчивых кодов

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4)

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Декодирование кода Хэмминга через синдром

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Таблица декодирования. Код Хэмминга

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

расстояние хэмминга

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.

n — количество символов на входе.
k — количество символов на выходе.
t — кратность исправляемых ошибок.
Отношение k/n — скорость кода.
G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

График помехоустойчивых кодов

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромиссы при использовании помехоустойчивых кодов

Компромисс:

Достоверность vs полоса пропускания.
Мощность vs полоса пропускания.
Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.

Пример блочного перемежения:

Пример блочного перемежения кодов

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.

Корректирующий код (также помехоустойчивый код) — код (b) , предназначенный для обнаружения и исправления ошибок (b) .

Основная техника — добавление при записи (передаче) в полезные данные специальным образом структурированной избыточной информации (например, контрольного числа (b) ), а при чтении (приёме) использование такой избыточной информации для обнаружения и исправления ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

Коды обнаружения ошибок (которые могут только установить факт ошибки) принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить бо́льшее число ошибок, чем был способен исправить). Коды, исправляющие ошибки, применяются в системах цифровой связи (b) , в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам, а также в системах хранения информации, в том числе магнитных и оптических. Коды, обнаруживающие ошибки, применяются в сетевых протоколах (b) различных уровней (b) .

По способу работы с данными коды, исправляющие ошибки, делятся на блоковые^[⇨], делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные^[⇨], работающие с данными как с непрерывным потоком.

Блоковые коды

Блоковый код, разбивающий информацию на фрагменты длиной бит и преобразующий их в кодовые слова длиной бит обычно обозначают ; при этом число называется скоростью кода. Если исходные бит код оставляет неизменными, и добавляет проверочных, такой код называется систематическим, иначе — несистематическим.

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из информационных бит сопоставляется бит кодового слова. Однако хороший код должен удовлетворять как минимум следующим критериям:

способность исправлять как можно большее число ошибок,
как можно меньшая избыточность,
простота кодирования и декодирования.

Приведённые требования в общем случае противоречат друг другу, поэтому существует большое количество кодов, каждый из которых пригоден для определённого круга задач. Практически все используемые коды являются линейными (b) , это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.

Линейные коды общего вида

Линейный блоковый код — такой код, что множество его кодовых слов образует -мерное линейное подпространство в -мерном линейном пространстве (b) , изоморфное (b) пространству -битных векторов (b) .

Это значит, что операция кодирования соответствует умножению исходного -битного вектора на невырожденную матрицу (b) , называемую порождающей матрицей.

Для ортогонального (b) по отношению к подпространства и матрицы , задающей базис (b) этого подпространства, и для любого вектора справедливо:

Минимальное расстояние и корректирующая способность

Расстоянием Хэмминга (метрикой Хэмминга) между двумя кодовыми словами и называется количество отличных бит на соответствующих позициях:

Минимальное расстояние Хэмминга является важной характеристикой линейного блокового кода. Она показывает, насколько «далеко» расположены коды друг от друга. Она определяет другую, не менее важную характеристику — корректирующую способность (b) :

Корректирующая способность (b) определяет, сколько ошибок передачи кода (типа ) можно гарантированно исправить. То есть вокруг каждого кодового слова имеем -окрестность (b) , которая состоит из всех возможных вариантов передачи кодового слова с числом ошибок () не более . Никакие две окрестности двух любых кодовых слов не пересекаются друг с другом, так как расстояние между кодовыми словами (то есть центрами этих окрестностей) всегда больше двух их радиусов.

Таким образом, получив искажённую кодовую комбинацию из , декодер принимает решение, что исходной была кодовая комбинация , исправляя тем самым не более ошибок.

Например, при наличии всего двух кодовых слов и с расстоянием Хэмминга между ними, равным 3, ошибка в одном бите слова может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову , чем к . Но если каналом были внесены ошибки в двух битах (в которых отличалось от ), то результат ошибочной передачи окажется ближе к , чем , и декодер примет решение, что передавалось слово .

Коды Хэмминга

Коды Хэмминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хэмминга может быть представлен в таком виде, что синдром:

где — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.

Общий метод декодирования линейных кодов

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова соответствует наиболее вероятное переданное слово . Однако данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора вычисляется синдром. Поскольку , где — кодовое слово, а — вектор ошибки, то . Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Линейные циклические коды

Несмотря на то, что декодирование линейных кодов значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды (b) , кроме более простого декодирования, обладают и другими важными свойствами.

Циклическим кодом является линейный код (b) , обладающий следующим свойством: если является кодовым словом, то его циклическая перестановка также является кодовым словом.

Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово представляется в виде полинома . При этом циклический сдвиг кодового слова эквивалентен умножению многочлена на по модулю (b) .

Чаще всего используются двоичные циклические коды (то есть могут принимать значения 0 или 1).

Порождающий многочлен

Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему (генераторному) многочлену . Порождающий многочлен является делителем .

С помощью порождающего многочлена осуществляется кодирование циклическим кодом. В частности:

несистематическое кодирование осуществляется путём умножения кодируемого вектора на : ;
систематическое кодирование осуществляется путём «дописывания» к кодируемому слову остатка от деления на , то есть .

Коды CRC

Коды CRC (англ. (b) cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путём деления на . Ввиду того, что исправление ошибок не требуется, проверка правильности передачи может производиться точно так же.

Таким образом, вид многочлена задаёт конкретный код CRC. Примеры наиболее популярных полиномов:

Название кода	Степень	Полином
CRC-12	12
CRC-16	16
CRC-CCITT (b)	16
CRC-32	32

Коды БЧХ

Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.

Коды коррекции ошибок Рида — Соломона

Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (b) (октетами (b) ).

Математически коды Рида — Соломона являются кодами БЧХ (b) .

Преимущества и недостатки блоковых кодов

Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ (b) ), менее высока.

Свёрточные коды

Свёрточный кодер ()

Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных. Такие коды, как правило, порождаются дискретной линейной инвариантной во времени системой (b) . Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.

Кодирование свёрточным кодом производится с помощью регистра сдвига (b) , отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.

Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби (b) , который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия (b) .

Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.

Каскадное кодирование. Итеративное декодирование

Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.

Например, популярной является следующая конструкция: данные кодируются кодом Рида — Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.

Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако декодирование требует больших ресурсов. К таким кодам относят турбо-коды (b) и LDPC-коды (b) (коды Галлагера).

Оценка эффективности кодов

Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ (b) ).

Граница Хэмминга и совершенные коды

Пусть имеется двоичный блоковый код с корректирующей способностью (b) . Тогда справедливо неравенство (называемое границей Хэмминга):

Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хэмминга (b) . Часто применяемые на практике коды с большой корректирующей способностью (b) (такие, как коды Рида — Соломона (b) ) не являются совершенными.

Литература

	Имеется викиучебник (b) по теме «Помехоустойчивое кодирование»

Блейхут Р. (b) Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир (b) , 1986. — 576 с.
Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.

7.1. Классификация корректирующих кодов

7.2. Принципы помехоустойчивого кодирования

7.3. Систематические коды

7.4. Код с четным числом единиц. Инверсионный код

7.5. Коды Хэмминга

7.6. Циклические коды

7.7. Коды с постоянным весом

7.8. Непрерывные коды

7.1. Классификация корректирующих кодов

В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим, кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны также коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.

Для того чтобы «од обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.

Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.

В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов [12]. На рис. 7.1 показана схема, поясняющая классификацию, проведенную по способам построения корректирующих кодов.

Все известные в настоящее время коды могут быть разделены

на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

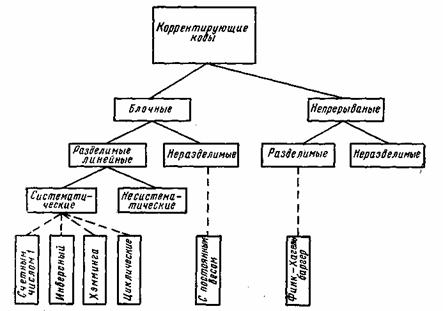
Рис. 7.1. Классификация корректирующих кодов

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат ‘исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

В свою очередь, линейные коды могут быть |разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими. Вертикальными прямоугольниками на схеме рис. 7.1 представлены некоторые конкретные коды, описанные в последующих параграфах.

7.2. Принципы помехоустойчивого кодирования

В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные моды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно M=2ⁿ, где п — значность кода. В обычном некорректирующем коде без избыточности, например в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число сообщений источника М0. Однако в.этом случае лишь М0комбинаций из общего числа используется для передачи информации. Эти комбинации называются разрешенными, а остальные М—М0комбинаций носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.

Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d между двумя комбинациями и определяется количеством единиц в сумме этих комбинаций по модулю два. Например,

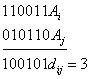
Для любого кода d. Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.

Расстояние между комбинациями и условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций и , разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация преобразовалась в другую разрешенную комбинацию , должно исказиться d символов.

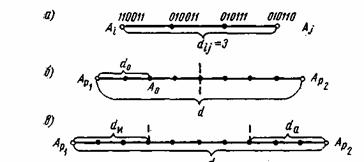
Рис. 7.2. Геометрическое представление разрешенных и запрещенных кодовых комбинаций

При искажении меньшего числа символов комбинация перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,

(7.1)

Если g>d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация ib этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d=2.

Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна:

(7.2)

где — вероятность искажения одного символа. Так как обычно <<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация (см.рис.7.2б), тогда принимается решение, что была передана комбинация . Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности

(7.3)

Минимальное значение d, при котором еще возможно исправление любых одиночных ошибок, равно 3.

Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.2в ошибки кратности исправляются, а ошибки, кратность которых лежит в пределах только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах , то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А вместо Aили наоборот.

Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания . Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов оказалось равным gc, причем

(7.4)

а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок , то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.

Если , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.

Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или .восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие «оды обычно используются для корректирования ошибок малой кратности.

Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций Мувеличение d возможно лишь за счет роста количества запрещенных комбинаций:

(7.5)

что, в свою очередь, требует избыточного числа символов r=n—k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее по аналогии с (6.12) как

(7.6)

При независимых ошибках вероятность определенного сочетания g ошибочных символов в n-значной кодовой комбинации выражается ф-лой ((7.2), а количество всевозможных сочетаний g ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний

Отсюда полная вероятность ошибки кратности g, учитывающая все сочетания ошибочных символов, равняется:

(7.7)

Используя (7.7), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема

и вероятность правильного корректирования ошибок

Здесь суммирование ‘Производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:

(7.8)

Анализ ф-лы (7.8) показывает, что при малой величине Р0и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.

Вероятность Р, избыточность и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.

Общая задача, которая ставится при создании кода, заключается, в достижении наименьших значений Р и . Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.

В соответствии с общим принципом корректирования ошибок, основанным на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться все М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках. Изучению таких кодов и посвящены последующие разделы.

7.3. Систематические коды

Изучение конкретных способов помехоустойчивого кодирования начнем с систематических кодов, которые в соответствии с классификацией (рис. 7.1) относятся к блочным разделимым кодам, т. е. к кодам, где операции кодирования осуществляются независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.

Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, а контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:, где с и е в двоичном коде принимают значения 0 или 1.

Процесс кодирования на передающем конце сводится к образованию контрольных символов, которые выражаются в виде линейной функции информационных символов:

(7.9)

Здесь — коэффициенты, равные 0 или 1, а и — знаки суммирования по модулю два. Значения выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации образуется по правилу (7.9) вторая группа контрольных символов

Затем производится сравнение обеих групп контрольных символов путем их суммирования по модулю два:

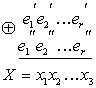(7.10)

Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы, а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае , что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.

Для исправления ошибок знание одного факта их возникновения является недостаточным. Необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить место положения ошибок и исправить их.

Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно . В этом случае должно выполняться условие

(7.11)

Формула (7.11) позволяет при заданном количестве информационных символов k определить необходимое число контрольных символов r, с помощью которых исправляются все одиночные ошибки.

7.4. Код с чётным числом единиц. Инверсионный код

Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит, помимо информационных символов, один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на

основании (7.9) в следующей форме: . Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (— суммирование по модулю):

(7.12)

Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем, случае ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются. На основании ,(7.8) вероятность необнаруженной ошибки равна:

К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую .избыточность , однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.

Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000, 11000 и 01101, 10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными. Если количество единиц в информационных символах четное, т. е. сумма этих

символов

(7.13)

равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольные символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид . При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е. , то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘=1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность: . Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.

Анализ показывает, что при наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением

Для g>4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов ро можно полагать, что полная вероятность необнаруженных ошибок

Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину =0,5.

7.5. Коды Хэмминга

К этому типу кодов обычно относят систематические коды с расстоянием d=3, которые позволяют исправить все одиночные ошибки (7.3).

Рассмотрим построение семизначного кода Хэмминга, каждая комбинация которого содержит четыре информационных и триконтрольных символа. Такой код, условно обозначаемый (7.4), удовлетворяет неравенству (7.11) и имеет избыточность

Если информационные символы с занимают в комбинация первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:

(7.14)

Декодирование осуществляется путем трех проверок на четность (7.10):

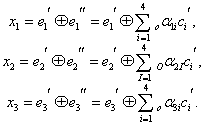(7.15)

Так как х равно 0 или 1, то всего может быть восемь контрольных чисел Х=х1х2х3: 000, 100, 010, 001, 011, 101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами я искаженными символами. Если искажен один из контрольных символов: или , то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.

Таблица 7.1

Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1. Нетрудно показать, что этому распределению контрольных чисел соответствуют коэффициенты , приведенные в табл. 7.2.

Таблица 7.2

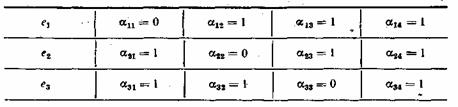
Если подставить коэффициенты в выражение (7.15), то получим:

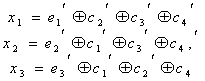(7.16)

При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов . Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются , Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:

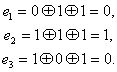
Передаваемая комбинация при этом будет . Предположим, что принята комбинация — 1001, 010 (искажен символ ). Подставляя соответствующие значения в (7.16), получим:

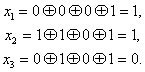
Вычисленное таким образом контрольное число 110 позволяет согласно табл. 7.1 исправить ошибку в символе.

Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблице. Вместе с тем существует более изящный метод отыскания одиночных ошибок, предложенный впервые самим Хэммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Для кода (7.4) символы в комбинации должны размещаться в следующем порядке: , а контрольное число вычисляться по формулам:

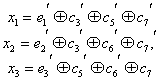(7.17)

Так, если произошла ошибка в информационном символе с’5 то контрольное число , что соответствует числу 5 в двоичной системе.

В заключение отметим, что в коде (7.4) при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.

7.6. Циклические коды

Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации дает другую комбинацию также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например, .

Комбинации циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:

Помимо цикличности, кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени , где k—значность первичного кода без избыточности, а п-значность циклического кода

Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A*(z) ,на порождающий полином G(z):

A(z)=A*(z)G(z).

Умножение производится по модулю zⁿ и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.

В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).

Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа г нулей, что эквивалентно повышению полинома A*(z) на ,г разрядов, т. е. умножению его на гг. Затем произведение z^rA*(z) делится на порождающий полином. B общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда

Вычисленный остаток К(г) я используется для образования комбинации циклического кода в виде суммы

A(z)=z^rA*(z)@R(z).

Так как сложение и вычитание по модулю два дают один и тот же результат, то нетрудно заметить, что A(z) = Q(z)G(z), т. е. полученная комбинация удовлетворяет требованию делимости на порождающий полином. Степень полинома R{z) не превышает r—1, поэтому он замещает нули в комбинации zA*(z).

Для примера рассмотрим циклический код c n = 7, k=4, r=3 и G(z)=z³-z+1=1011. Необходимо закодировать комбинацию A*(z)=z*+1 = 1001. Тогда zA*(z)=z+z= 1001000. Для определения остатка делим z³A*(z) на G(z):

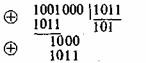
Окончательно получаем

В А(z) высшие четыре разряда занимают информационные символы, а остальные при — контрольные.

Контрольные символы в циклическом коде могут быть вычислены по общим ф-лам (7.9), однако здесь определение коэффициентов затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).

Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z). Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.

Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигнала.

В теории кодирования весом кодовых комбинаций принято называть .количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.

Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной краткости и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:

при (7.18)

В этом коде из общего числа комбинаций М = 2⁷=128 разрешенными являются лишь , поэтому в соответствии с (7.6) коэффициент избыточности

Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.

7.8. Непрерывные коды

Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка—Хагельбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:

; (7.19)

Расстояние между информационными символами l=k—i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода =0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются между информационными символами с задержкой на два шага сложения.

Рис. 7.3. Образование и размещение контрольных символов в цепном коде Финка—Хагельбаргера

При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов е», которая сравнивается с принятой последовательностью контрольных символов е’ (рис. 7.36). Если произошла ошибка в информационном символе, например, c‘k, то это вызовет искажения сразу двух символов e«k и e«km, что и обнаружится в результате их сравнения с и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление такой ошибки не требуется.

Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но я группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2l, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2l при интервале между пакетами не менее 6l+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения, а следовательно, и с усложнением кодирующих и декодирующих устройств.

Вопросы для повторения

1. Как могут быть классифицированы корректирующие коды?

2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?

3. В чем состоят основные принципы корректирования ошибок?

4. Дайте определение кодового расстояния.

5. При каких условиях код может обнаруживать или исправлять ошибки?

6. Как используется корректирующий код в системах со стиранием?

7. Какие характеристики определяют корректирующие способности кода?

8. Как осуществляется построение кодовых комбинаций в систематических кодах?

9. На чем основан принцип корректирования ошибок с использованием контрольного числа?

10. Объясните метод построения кода с четным числом единиц.

11. Как осуществляется процедура кодирования в семизначном коде Хэмминга?

12. Почему семизначный код 3/4 не обнаруживает ошибки смещения?

13. Каким образом производится непрерывное кодирование?

14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?

Источник

запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Исправление ошибок в помехоустойчивом кодировании

мажоритарный метод

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

где n – количество символов закодированного сообщения (результата кодирования);
m – количество проверочных символов, добавляемых при кодировании;
k – количество информационных символов.

Контроль чётности

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

прямоугольный код

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.

Рассчитаем скорость кода для:

1 1 0 0 0 1 0 0 | 1

Здесь R=8/9=0,88

И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Классификация помехоустойчивых кодов

Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.

По используемому алфавиту:

Двоичные. Оперируют битами.
Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.

Блочные коды делятся на

Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.

систематический и несистематический код

Классификация помехоустойчивых кодов

Код Хэмминга

Код Хэмминга (7,4)

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Декодирование кода Хэмминга через синдром

Таблица декодирования. Код Хэмминга

Расстояние Хэмминга

расстояние хэмминга

Помехоустойчивые коды

Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.

n — количество символов на входе.
k — количество символов на выходе.
t — кратность исправляемых ошибок.
Отношение k/n — скорость кода.
G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

График помехоустойчивых кодов

Компромиссы при использовании помехоустойчивых кодов

Компромисс:

Достоверность vs полоса пропускания.
Мощность vs полоса пропускания.
Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Пример блочного перемежения:

Пример блочного перемежения кодов

Источник

I’m having that question:

The code: let $m$ be some binary word when $|m|<32000$. Create a word $m’$ that is the word $m$ with a parity bit. Now encode $m’$ with CRC with the generator polynomial $x^{15}+x^{14}+1$.

Prove that this code can detect every one, two or three errors.

Ok, so the every one error is easy: The error polynomial of one bit is $x^i$ when $0<=i<32000$. If the generator polynomial contains an $x^0$ term, it will not have $x^k$ factor, so the reminder can never be zero.

Every two errors is also easy: The error polynomial of two bits is $x^j(x^{i-j}+1)$ when $0<=i<j<32000$. Since $x^{15}+x^{14}+1$ dose not divide by $x$, we need to check only $(x^{i-j}+1)$. But $x^{15}+x^{14}+1$ will not divide $x^k+1$ for any value of $k<32768$ and the code word length is less then 32000. So the the code will detect every two errors.

But I have problems with three errors. If the error polynomial will be $x^3(x^{15}+x^{14}+1) = x^{18}+x^{17}+x^3$, it will divide by $x^{15}+x^{14}+1$ and the reminder will be zero. Then the CRC will not detect the error. So we need to check the parity bit. But since the parity bit created before the CRC, it can check only the bits that are in position $i$ where $16<=i<=|m|$. But since the error polynomial is $x^{18}+x^{17}+x^3$ only the bits 17 and 18 will be checked, and because there are only two errors in this range, the parity bit will also miss the error.

So how can I prove that this code can detect every three errors with that example?

Источник