§ 19.1. Статические и скоростные ошибки автоколебательных систем
В предыдущих главах исследовались симметричные автоколебания как результат свободного движения системы (т. е. без внешнего воздействия) при симметричных нелинейностях. Однако, как будет показано, важное практическое значение имеет также рассмотрение несимметричных автоколебаний.
Несимметрия автоколебаний может вызываться различными причинами;
1) несимметричностью нелинейной характеристики как при наличии, так и при отсутствии внешних воздействий;
2) наличием постоянного или медленно меняющегося внешнего воздействия при симметричных нелинейностях;
3) наличием постоянной или медленно меняющейся скорости изменения внешнего воздействия при симметричных нелинейностях (для тех случаев, когда постоянное воздействие не вызывает смещения центра колебаний; обычно это имеет место в следящих системах и вообще в астатических системах).
В самом деле, если имеется несимметричная нелинейная характеристика (например, рис. 19.1, а, б), то даже при симметричных колебаниях переменной возникают несимметричные по амплитуде колебания переменной (рис. 19.1, б).
Рис. 19.1.
Если же нелинейность симметрична (например, рис. 19.2, а, б), то при наличии постоянного внешнего воздействия (или в астатических системах при наличии постоянной скорости изменения внешнего
воздействия) смещается центр колебаний переменной вследствие чего колебания переменной становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, б).
Рис. 19.2.
Пусть задана автоматическая система, динамика которой описывается уравнением
В данном параграфе будем считать для статических систем или же для астатических систем. Астатической системой называется такая, в которой многочлен имеет общий множитель , т. е. .
Поэтому запишем уравнение (19.1) в виде
где соответственно
При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме
причем а, являются неизвестными постоянными.
С учетом величины смещения первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде
где при обозначении
Отсюда видно, что в общем случае все три коэффициента являются функциями трех неизвестных:
В частных случаях эти зависимости могут быть более простыми.
Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает
Это уравнение разбивается на два:
При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается нелинейная взаимосвязь обоих уравнений через соотношения (19.7).
Можно предложить два метода решения задачи.
Первый метод состоит в следующем. Уравнение (19.9) совпадает с прежним уравнением (18.33); отличие состоит лишь в том, что теперь коэффициенты q и согласно (19.7) зависят не только от а и , но и от смещения Поэтому, написав как прежде, характеристическое уравнение
заменив на ивыделив вещественную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:
Эти уравнения дают возможность определить амплитуду и частоту автоколебаний как функции постоянной составляющей
Для решения этой задачи можно применять любой из способов, описанных в § 18.2, в зависимости от того, какой из них лучше подходит к условиям заданной конкретной задачи. Таким же способом можно определить зависимость а и не только от но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики и , то здесь их необходимо строить в виде серии кривых при разных постоянных значениях (рис. 19.3).
После того как из уравнений (19.11) определены зависимости (19.12), можно, воспользовавшись первым из выражений (19.7), найти функцию смещения
Подставив ее в (19.8), получим алгебраическое уравнение
с одной неизвестной которая отсюда и определяется. Чаще всего это уравнение относительно является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда и частота
Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины смещения центра колебаний, характерную именно для нелинейных систем (в линейных системах смещение центра колебаний не играет роли), надо всегда иметь в виду.
Рис. 19.3.
При одних нелинейностях она может быть весьма существенной, при других — менее существенной.
Второй метод решения той же задачи состоит, наоборот, в том, что сначала решается уравнение (19.8), где согласно (19.7) будет или часто . Решение получает вид
Это решение подставляется затем в уравнения (19.11), которые, таким образом, буду! содержать только две неизвестные: Определив последние (по любому из способов § 18.2), вычисляем потом по (19.15) и величину которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия
Величина и является искомой статической или скоростной ошибкои соответственно для статической и астатической систем.
В тех случаях, когда передаточная функция линейной части системы имеет нулевой корень в знаменателе (что часто бывает), т. е. когда вместо (19.14) получаем уравнение
откуда определяется статическое отклонение или скоростная ошибка
В случае, когда при отсутствии внешнего воздействия определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью или же для которой
вместо уравнения (19.8) получаем
Оно решается любым из тех же двух методов, описанных выше для уравнения (19.8). Одновременно согласно (19.11) определяются
Если в этом случае знаменатель передаточной функции линейной части системы имеет нулевой корень, то и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид
откуда определяется Это означает, что в указанных системах возникает такое смещение колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F (т. е. обеспечивается ), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.
Приведем пример исследования совместного влияния двух внешних воздействий, причем из дальнейшего будет видно, что, в отличие от линейных систем, здесь нельзя просто складывать статические ошибки от отдельно взятых в ействий.
Уравнения автоматической системы (рис. 19.5) заданы в виде
где — простейшая симметричная релейная характеристика, показанная на рис. 19.5:
Чтобы воспользоваться выведенными выше общими формулами, надо сначала привести заданную систему уравнений (19.20) — (19.22) к одному уравнению типа (19.1).
Рис. 19.4.
Рис. 19.5.
В результате получаем
Пусть является задающим воздействием, изменяющимся с постоянной скоростью:
которое требуется воспроизвести на выходе системы в виде Допустим также, что второе внешнее воздействие является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):
Его влияние требуется свести к минимуму. Найдем установившуюся ошибку на выходе системы. Правая часть уравнения (19.24) будет при этом постоянной, и установившееся решение для х с учетом автоколебаний следует искать
в виде
Гармоническая линеаризация нелинейности (19.23) при этом согласно (19.6) дает
В данной задаче согласно (19.24) уравнение (19.9) для периодических составляющих получит вид
а уравнение (19.8) для постоянных составляющих будет
где согласно (19 24)-(19.26)
Выше были указаны два метода решения задачи. Для иллюстрации обоих методов решим данную задачу каждым из них.
Согласно первому методу сначала решается уравнение (19.29) для определения зависимостей
Характеристическое уравнение здесь будет
и уравнения (19.11) поэтому примут вид
Исключая отсюда находим частоту автоколебаний
Частота в данной задаче оказалась не зависящей от смещения , а следовательно, и от величины внешнего воздействия. Затем, подставляя в первое из уравнений (19.33) выражение q из (19.28) и из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний от смещения
где величина
представляет собой амплитуду автоколебаний в данной системе при отсутствии смещения (при ). Отсюда
Полученное выражение мояшо записать также в виде
если обозначить
Результат (19.37) или (19.38) и представляет собой искомую зависимость
Далее, согласно первому методу решения задачи подставим полученное значение амплитуды из (19.38) в выражение (19.28) для откуда с использованием (19.39) найдем функцию смещения
где А определяется через параметры системы формулой (19.36).
Подставив величину (19.40) в уравнение (19.30) для постоянных составляющих, с учетом (19.31) и (19.36) получим
Сравнивая это с формулой (19.39), видим, что для искусственно введенной ранее величины а можно записать следующее выражение:
Эта величина характеризует совокупность приложенных к системе внешних воздействий. Учитывая это, из формулы (19.38) находим амплитуду автоколебаний
Существенно то, что амплитуда автоколебаний зависит не только от параметров системы (см. (19.36)), но еще и от величины внешних воздействий. Эта зависимость нелинейная. В данном случае при увеличении внешних воздействий амплитуда уменьшается по закону косинуса, в то время как частота не зависит от внешних воздействий.
Из формулы (19.43) видно, что автоколебания существуют до тех пор, пока величины внешних воздействий удовлетворяют условию
При этом амплитуда автоколебаний изменяется в пределах
Таков первый метод определения установившихся величин смещения амплитуды и частоты автоколебаний при наличии внешних воздействий.
Проиллюстрируем также и второй метод. Согласно второму методу сначала решается уравнение (19.30). По (19.30) и первой из формул (19.28) находим
или, с учетом (19.31),
Для отыскания входящей сюда амплитуды а воспользуемся уравнением (19.29). Характеристическое уравнение для него будет (19.32), и уравнения (19.11) поэтому примут вид:
где согласно (19.28) и (19.45)
Исключая из уравнений (19.46) величину находим частоту автоколебаний
Подставив найденные выражения q в первое из уравнений (19.46), найдем амплитуду автоколебаний
где величина
является амплитудой автоколебаний при отсутствии внешних воздействий (при
Подставив найденное выражение амплитуды (19.49) в формулу (19.45) получим окончательно величину смещения
Как видно, второй метод в данной задаче приводит к тем же самым результатам значительно более коротким путем, чем первый, что очень важно для практических расчетов (принципиально же оба метода эквивалентны друг другу). По-видимому, большая простота второго метода будет иметь место и в большинстве других задач.
В этом втором методе, в отличие от первого, функция смещения не определяется. Однако последняя может понадобиться в дальнейшем для других целей. Но ее тоже легко можно определить при использовании второго метода. Здесь величины и их отношение выражены через величины внешних воздействий. Функция же смещения не должна содержать ни величин внешних воздействий, ни амплитуды зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим
а подставив это в первую из формул (19.28), сразу получим искомую функцию смещения
где А выражается только через параметры системы согласно (19.50).
Важно отметить, что функция смещения не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи.
Итак, двумя разными методами определена величина смещения автоколебаний на входе реле. Найдем теперь установившуюся ошибку на выходе системы Поскольку на выходе должно воспроизводиться внешнее воздействие то согласно рис. 19.5 и второму уравнению (19.20) ошибка данной системы выражается величиной установившееся решение для которой, следовательно, и надо искать. Выразив переменную через х, которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем
Учитывая (19.25) и (19.27), перепишем данное уравнение в виде
В соответствии с видом правой части установившееся решение этого линейного уравнения следует искать в виде
где — постоянные, а — периодическая составляющая.
Подставив это в (19.54), получим три уравнения для отыскания указанных величин:
Второе из них дает
Тогда из (19.56) находим
где определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной
где определяется формулой (19.49) через внешнее воздействие, а — формулой (19.48).
Итак, в данной системе имеются все три составляющие ошибки (19.55), зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной из них является составляющая возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при кос согласно (19.59) будет Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи на гибкую . Тогда в уравнении (19.54) величина заменится на :
Как видим, составляющая, пропорциональная времени, в правой части уравнения исчезла, вследствие чего установившееся решение для ошибки х в отличие от (19.55), будет
При этом из (19.62) находимз
причем изменяются, конечно, и формулы для (их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний ошибки можно сделать весьма малой.
Определение динамических ошибок (по
скорости, по ускорению) для статической и астатических систем.
Точность АС
характеризуется величиной ошибки в установившемся режиме и зависит от характера
воздействия, а также структуры и параметров системы.
Реальные воздействия
в радиотехнических следящих системах описывается сложными (случайными)
функциями времени. Однако при анализе точности управления часто используют
простые детерминированные воздействия: постоянное ступенчатое, линейное,
квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить
в модели задающего воздействия наиболее существенные признаки (начальное
значение, скорость изменения, ускорение). Большинство систем радиоавтоматики
описываются передаточными функциями вида
, (11.1)
где Ki — общее усиление
разомкнутой системы, i – число интегрирующих
звеньев, определяющее порядок астатизма системы;
– полиномы, порядок которых определяется числом типовых
звеньев (n и m соответственно инерционных и форсирующих), а
коэффициенты полиномов – постоянными времени типовых звеньев.
11.1. Статические ошибки
Ошибка системы при постоянном
(ступенчатом) воздействии x(t)=x0=const при t³0
называется статическойeст.
Для установившейся
ошибки, учитывая, что изображение X(p)=x0/p,
запишем:
. (11.2)
Для статической
системы (не содержащей интегрирующих звеньев) статическая ошибка равна
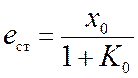 . (11.3)
. (11.3)
Таким образом, в
статических системах установившееся значение управляемой переменной не равно
заданному: меньше на величину ошибки, значение которой обратно пропорционально
усилению К0 по постоянному току (обычно К0>>1).
Для астатических
систем (i ³ 1) ошибка при постоянном воздействии
![]() ,
,
так как числитель в (11.2) равен нулю, а знаменатель равен
Кi.
Отсутствие
статической ошибки обусловило название таких систем – астатические.
11.2. Динамические ошибки
Ошибка,
характеризующая точность замкнутой системы при меняющемся воздействии,
называется динамической eд(t).
Любое детерминированное
воздействие (при условии существования его производных d(k)/dt(k),
k=1, 2, …) можно представить в виде ряда
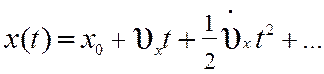 , (11.4)
, (11.4)
где x0 — начальное значение, ![]() — скорость изменения,
— скорость изменения, ![]() — ускорение и т. д.
— ускорение и т. д.
Для вычисления
динамических ошибок при типовых воздействиях (линейном и квадратическом)
представим выражение для ошибки в операторной форме:
![]() (11.5)
(11.5)
Используя разложение
передаточной функции Ke(p) в ряд Маклорена по степеням
переменной р, перепишем (11.5) в виде
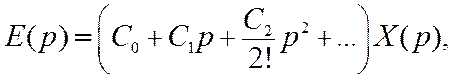 (11.6)
(11.6)
где C0, C1, C2,
… — коэффициенты ошибок, определяемые
как
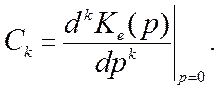 (11.7)
(11.7)
Установившееся
значение ошибки при произвольном воздействии x(t)
на основании (11.6) определяется временным рядом
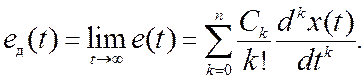 (11.8)
(11.8)
Чем меньше
коэффициенты ошибок, тем выше точность системы при произвольном
детерминированном воздействии. При вычислении коэффициентов Ck
обычно ограничиваются только первыми тремя (для систем с астатизмом не выше
второго порядка).
Коэффициент C0
в соответствии с (11.7) равен
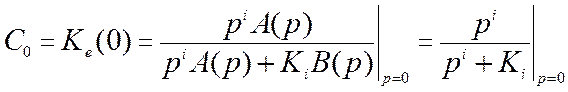 .
.
Для статических
систем (i=0) C0=1/(1+K0), а для
астатических систем C0=0.
Определим динамические
ошибки типовых систем при линейном воздействии (изменение с постоянной
скоростью) x(t)=nxt.
В соответствии с
формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как
![]() .
.
Для статической
системы она равна
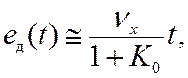
так как вклад составляющей C1nx
значительно меньше, чем C0 x(t), которая растет
линейно со временем. Таким образом, скоростная ошибка в статических системах
накапливается со временем со скоростью nx/(1+K0), что делает неприемлемым использование
таких систем при меняющемся воздействии. Для астатических систем C0=0 и скоростная ошибка
![]() .
.
Нахождение
коэффициента ошибки C1 с использованием формулы (11.7)
затруднительно. Более простой способ его вычисления основан на сравнении
точного выражения для передаточной функции Ke(p) и
аппроксимирующего ее ряда:
 (11.9)
(11.9)
Уравнение (11.9)
можно представить в виде
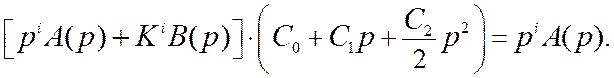 (11.10)
(11.10)
Полагая i= 1 (астатическая система первого порядка) и приравнивая
коэффициенты при переменной p в левой и правой частях уравнения, находим
![]()
или C1=1/K1, так как C0=0.
Таким образом,
скоростная ошибка системы первого порядка астатизма eд=nx/K1
определяется усилением разомкнутой системы K1 и не зависит от
времени. Параметр K1, имеющий размерность c –1,
называется добротностью системы по скорости (чем выше добротность, тем
точнее система).
Для астатической
системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C0=C1=0.
Равенство C1=0 вытекает из уравнения (11.10), так как в
правой части уравнения не содержится слагаемого, в которое входит переменная p
(есть только с p2 и выше).
Оценим динамические
ошибки типовых систем при квадратичном воздействии (изменение с постоянным
ускорением)![]() .
.
В соответствии с (11.8)
для динамической ошибки (ошибки по ускорению) запишем
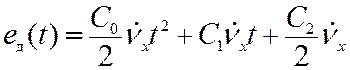 . (11.11)
. (11.11)
Для статической
системы ошибка по ускорению равна
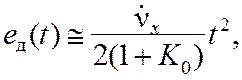 (11.12)
(11.12)
так как составляющие ошибки с коэффициентами C1 и C2
вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по
квадратичному закону исключает применение статических систем при наличии
ускорения.
Для системы первого
порядка астатизма ошибка по ускорению равна
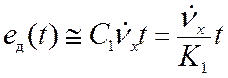 (11.13)
(11.13)
(вкладом составляющей ![]() можно
можно
пренебречь). Накопление ошибки со временем (со скоростью ![]() ) не позволяет применять такие
) не позволяет применять такие
системы при наличии ускорения. Для астатической системы второго порядка ошибка
по ускорению равна
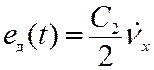 . (11.14)
. (11.14)
Определение
коэффициента ошибки C2 с использованием уравнения (11.7)
сводится к приравниванию коэффициентов при p2 в обеих частях
уравнения:
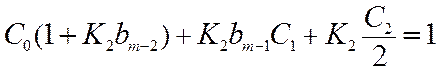 . (11.15)
. (11.15)
Откуда
C2/2=1/K2, так как C0=C1=0.
Определение
установившихся ошибок.
Одно из основных требований, которым
должна удовлетворять система управления,
заключается в обеспечении необходимой
точности воспроизведения задающего
воздействия в установившемся режиме.
Для оценки точности системы определяется
установившаяся ошибка, которая может
быть получена из выражения (4.4) с помощью
теоремы операционного исчисления о
конечном значении функции:
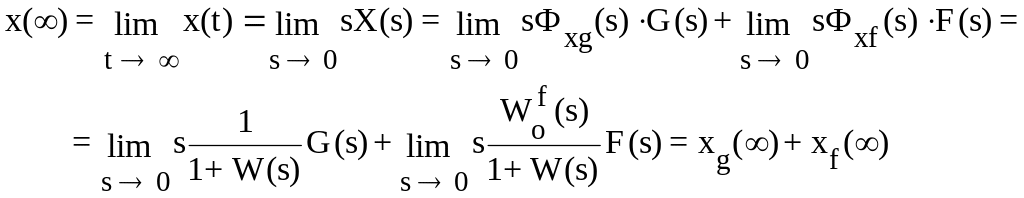
(6.4)
где
![]()
—
установившаяся ошибка от задающего
воздействия;
![]()
—
установившаяся ошибка от возмущающего
воздействия.
Если
задающее воздействие g(t) имеет произвольный
характер, то ошибка системы может быть
найдена с помощью коэффициентов
ошибок.
Изображение ошибки по задающему
воздействию имеет вид
Xg(s)=
Фxg(s)G(s),
где
Фxg(s)
— передаточная функция замкнутой системы
по ошибке относительно задающего
воздействия.
Для
получения коэффициентов ошибок
передаточная функция Фxg(s)
раскладывается в степенной ряд
Фxg(s)
= c0
+
c1s
+ c2s2
+
c3s3
+
… ,
сходящийся при
малых s, что соответствует установившемуся
режиму или достаточно большим значениям
времени t.
Коэффициенты
ci этого
ряда называются коэффициентами ошибок
и определяются из выражения

при
i = 0, 1, 2, 3, … (6.5)
Коэффициенты
c0,
c1
и c2
называются
соответственно коэффициентами позиционной
ошибки, скоростной ошибки и ошибки от
ускорения.
Выражение
для изображение ошибки по задающему
воздействию примет вид
Xg(s)
= (c0+
c1s+
c2s2+
c3s3+…)G(s).
Перейдя к оригиналу,
выразим установившуюся ошибку через
коэффициенты ошибок, задающее воздействие
и его производные:
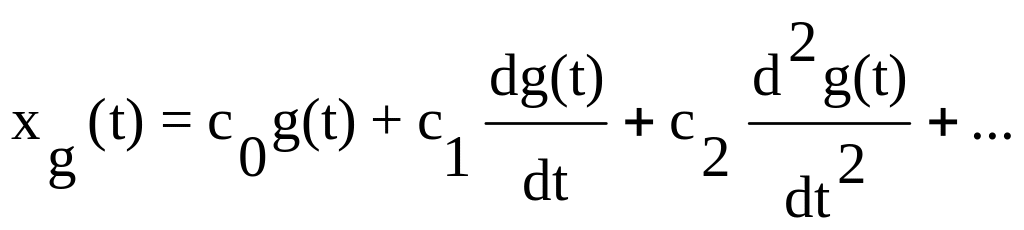
.
(6.6)
Аналогично
можно ввести понятие коэффициентов
ошибок по возмущающему воздействию.
Точность
в типовых режимах. Для
оценки
точности системы управления
используется
величина ошибки в различных типовых
режимах, близких к реальным или наиболее
трудным. В качестве типовых входных
воздействий выбираются воздействия,
изменяющиеся по закону g(t)=gntn
(где n=0,1,2), и гармоническое воздействие
g(t)=gmsint.
Рассмотрим
установившийся режим системы при
постоянных задающем g(t)=g0=const
и возмущающем f(t)=f0=const
воздействиях. В этом случае ошибка
системы называется статической и
находится с помощью выражения (6.7):
![]()
=
![]()
+
![]()
=
![]()
g0
+
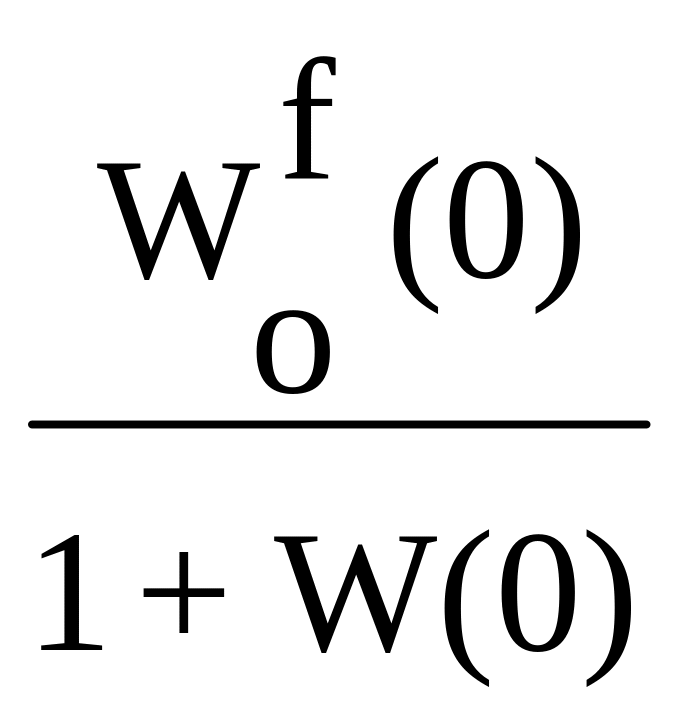
f0.
(6.7)
В
статических системах управления значение
W(0)=k, где k — общий коэффициент передачи
разомкнутой системы. При этом составляющая
статической ошибки от задающего
воздействия
=
g0/(1+k).
(6.8)
Составляющая
статической ошибки от возмущающего
воздействия
=
kf
f0/(1+k),
(6.9)
где
kf
— коэффициент передачи разомкнутой
системы по возмущающему воздействию.
Из
выражений (6.8) и (6.9) следует, что для
повышения точности управления необходимо
увеличивать общий коэффициент передачи
разомкнутой системы k. Тут выявляется
противоречие между требованием точности
(увеличение k) и устойчивости (ограничение
k).
В
астатических системах W(0),
поэтому составляющая ошибки
=
0. Вторая составляющая ошибки
при W(0)
не всегда обращается в нуль, так как
возможен случай, когда и
![]()
.
Режим
работы при постоянных задающих и
возмущающих воздействий наиболее
характерен для систем стабилизации.
Рассмотрим
теперь установившееся состояние при
изменении задающего воздействия с
постоянной скорость g(t)=g1t
(где g1=const)
и постоянном значении возмущающего
воздействия f(t)=f0=const.
По (6.4) найдем установившуюся ошибку:

(6.10)
Первый
член этого выражения в статической
системе при W(0)=k стремится к бесконечности,
поэтому система, работающая в режиме
слежения с постоянной скоростью, должна
быть астатической относительно задающего
воздействия. Второе слагаемое определяет
статическую ошибку системы от возмущающего
воздействия.
Для систем с
астатизмом первого порядка установившаяся
ошибка от задающего воздействия
=
g1/kv,
(6.11)
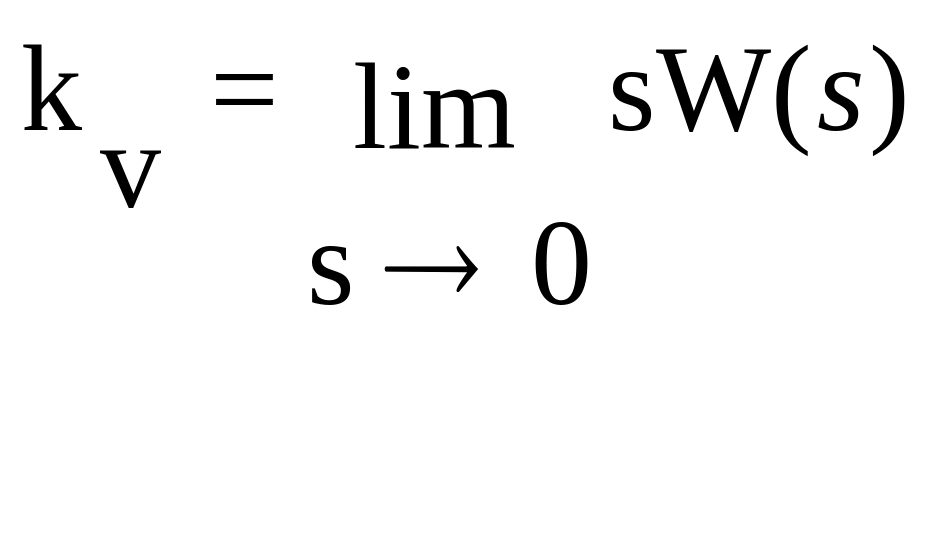
где
kv
— коэффициент передачи (добротность)
системы по скорости.
Ошибка
![]()
называется скоростной ошибкой от
задающего воздействия.
В
системах с астатизмом второго порядка
и выше скоростная ошибка равна нулю
(так как kv),
поэтому режим с задающим воздействием,
изменяющимся с постоянной скоростью,
используется только для оценки точности
следящих систем с астатизмом первого
порядка.
Рассмотрим
установившийся режим в системе при
изменении задающего воздействия с
постоянным ускорением g(t)=g2t2/2
(где g2=const)
и постоянным значением возмущающего
воздействия f(t)=f0=const.
Аналогично
определяется установившаяся ошибка по
(6.4):
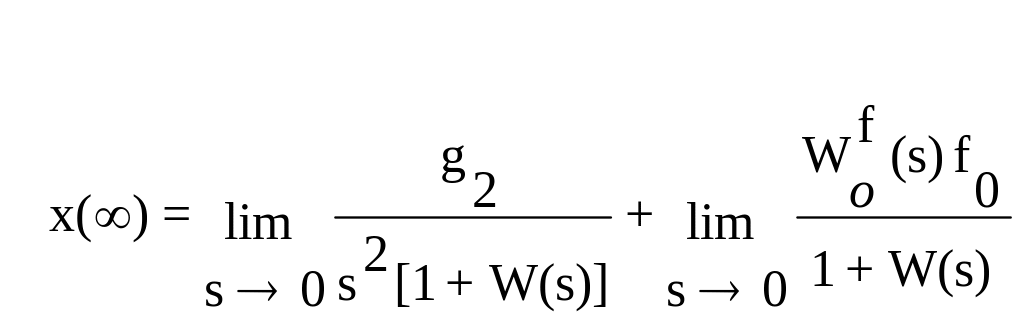
(6.12)
В
статических и астатических системах
первого порядка первая составляющая
ошибки стремится к бесконечности,
поэтому этот режим имеет смысл только
для следящих систем с астатизмом второго
порядка, для которых ошибка по задающему
воздействию
=
g2/ka,
(6.13)
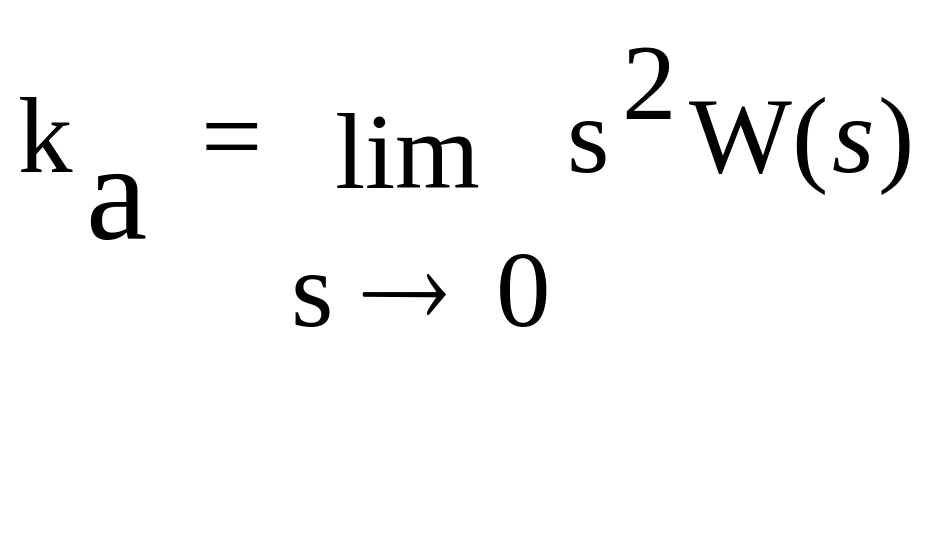
где
ka
— коэффициент передачи (добротность)
системы по ускорению.
Ошибка
называется установившейся ошибкой
системы от ускорения. Этот режим работы
обычно применяется для оценки точности
следящих систем с астатизмом второго
порядка.
Второе
слагаемое, как и в предыдущем случае,
определяет статическую ошибку системы
от возмущающего воздействия.
Рассмотрим теперь
установившийся режим системы управления
при изменении задающего воздействия
по гармоническому закону
g(t)
= gmsint.
Для упрощения
предположим, что возмущающее воздействие
равно нулю.
В линейной системе
ошибка в установившемся режиме также
изменяется по гармоническому закону с
той же частотой:
x(t)
= xmsin(t+).
Точность
системы в этом режиме оценивается по
величине амплитуды ошибки. Амплитудные
значения связаны между собой модулем
частотной передаточной функции замкнутой
системы, то есть можно записать
![]()
или
![]()
(6.14)
Систему
всегда проектируют таким образом, чтобы
величина ошибки была меньше задающего
воздействия, т.е. выполняется условие
W(j)>>1.
В связи с этим единицей в знаменателе
приведенной выше формулы можно пренебречь.
Таким образом, амплитуда ошибки
определяется как
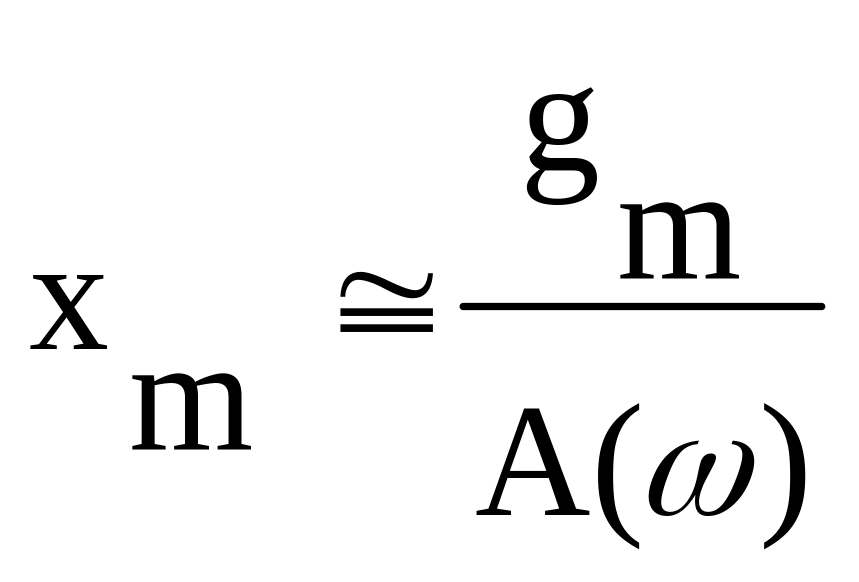
,
(6.15)
где
A()
— модуль частотной передаточной функции
разомкнутой системы.
Пример.
Определить
установившиеся ошибки в системе
управления, заданной передаточными
функциями:
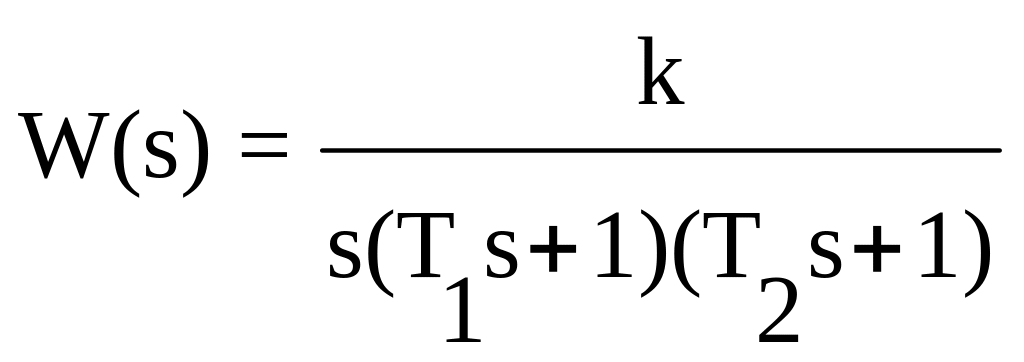
и
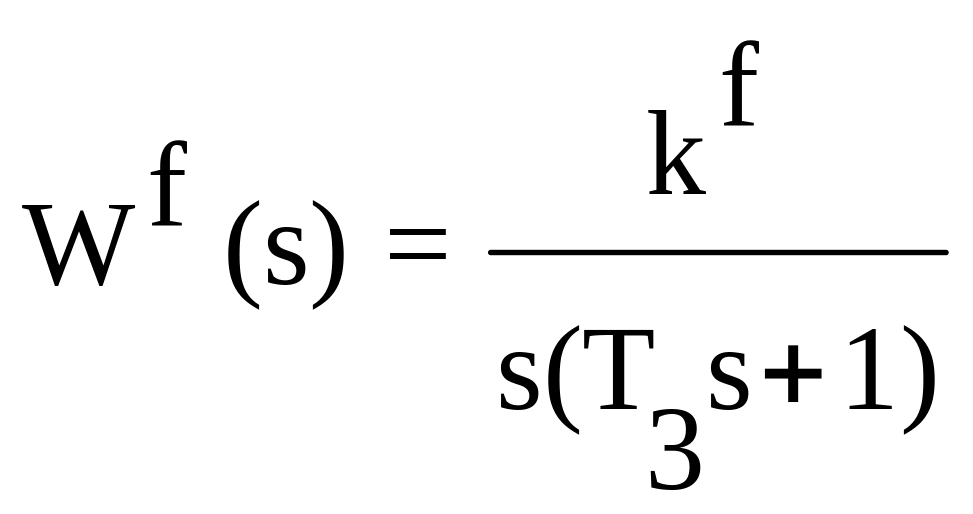
.
Решение.
Найдем установившиеся ошибки системы
при различных внешних воздействиях.
1.
g(t)=g01(t),
f(t)=f01(t).
Тогда
G(s)= g0
/s,
F(s)= f0
/s.
Установившаяся
ошибка от задающего воздействия:

Установившаяся
ошибка от возмущающего воздействия:

-
g(t)=g1t,
f(t)=f01(t).
Тогда
G(s)=g1/s2,
F(s)=f0
/s.
Установившаяся
ошибка от задающего воздействия:

-
g(t)=g2t2,
f(t)=f01(t).
Тогда
G(s)=2g2/s3,
F(s)=f0
/s.
Установившаяся
ошибка от задающего воздействия:
4.
g(t) = gmsint,
f(t)=0.
При
k=40 c-1,
T1=
0.05 c, T2=
0.01 c, =1
c-1 ,
gm=300
.
Амплитуда ошибки

5.
g(t) = g0+
g1t+
g2t2/2,
f(t)=f01(t).
Определим
коэффициенты ошибок c0,
c1,
c2.
Остальные коэффициенты ошибок находить
нет необходимости, так как степень
полинома задающего воздействия равняется
двум.
Передаточная
функция замкнутой системы по ошибке
относительно задающего воздействия
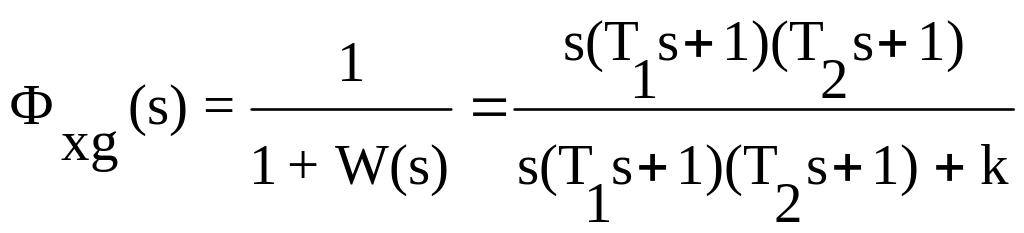
,
откуда
![]()
,
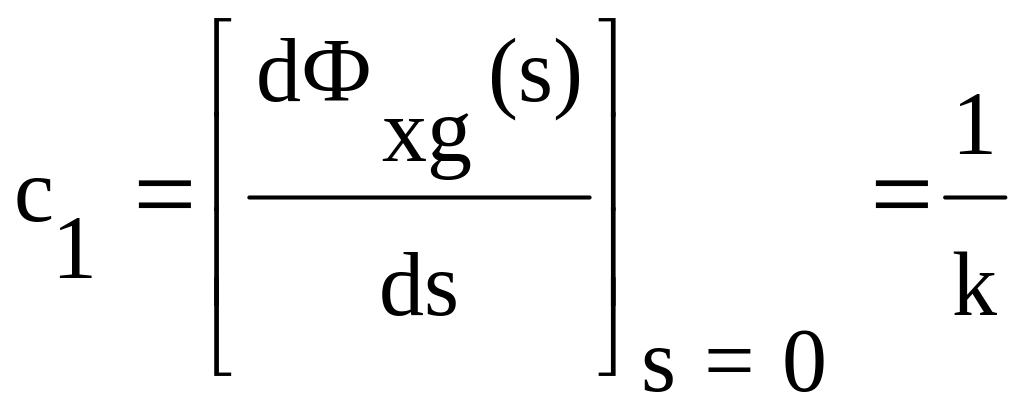
,
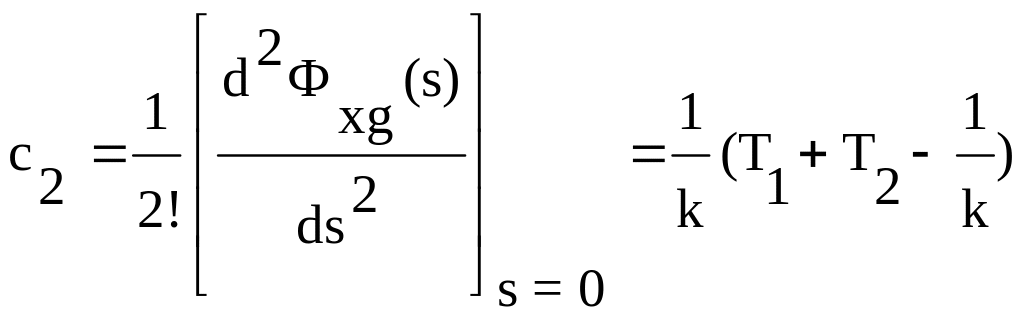
.
Установившаяся
ошибка от задающего воздействия:
![]()
,
где
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Большая Энциклопедия Нефти и Газа
Динамическая ошибка представляет собой дополнительное рассогласование между входной и выходной величинами, появляющееся при движении следящей системы. Эта ошибка определяется, с одной стороны, формой входного сигнала, с другой — инерционностью элементов, составляющих следящую систему. [2]
Динамическая ошибка в процессе регулирования определяется в основном величиной коэффициента колебательности т а / для доминирующих комплексных полюсов и степенью близости к началу плоскости р остальных полюсов и нулей замкнутой системы. При этом близкие к началу плоскости р нули увеличивают перерегулирование, а близкие, но не доминирующие полюсы — его уменьшают. [4]
Динамическая ошибка в этом случае носит колебательно-затухающий характер. [5]
Динамические ошибки в неустановившихся режимах движения могут дополнительно увеличиваться за счет переходных составляющих. Так как при уменьшении ап, ас и ат колебательность системы увеличивается, переходные составляющие ошибки могут возрастать, в то время как установившаяся динамическая ошибка ( 11 — 27) при этом уменьшается. [6]
Динамические ошибки возникают в установившемся режиме и обусловлены параметрами следящей системы и характером изменения измеряемого параметра. Флук-туационные ошибки вызваны влиянием помех и возмущений, которые воздействуют на следящую систему. [7]
Динамическая ошибка интегрирующих скоростных счетчиков, датчик которых реагирует на мгновенный расход, будет значительно больше, чем объемных счетчиков, отмеряющих определенные объемные порции потока. [9]
Динамическая ошибка не накапливается в процессе работы ШД и, как правило, остается в пределах я эл. [10]
Динамическая ошибка , ее величина, характер изменения во времени может быть различной в зависимости от параметров системы автоматического регулирования. [11]
Динамические ошибки в равной степени присущи как астатическим, так и статическим САУ. [12]
Динамические ошибки равны: стационарные — до 2 мкм, переходные — до 3 мкм. Прочие ошибки не превышают 4 мкм. Сложение этих ошибок как случайных величин с нормальным законом распределения в сумме дает ошибку в 13 мкм. [13]
Динамическая ошибка , ее величина, характер изменения во времени может быть различной в зависимости от параметров системы автоматического регулирования. [14]
Динамические ошибки в равной степени присущи как астатическим, так и статическим САУ. [15]
Как найти динамическую ошибку
Точность систем управления является важнейшим показателем их качества. Чем выше точность, тем выше качество системы. Однако предъявление повышенных требований к точности вызывает неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная точность может привести к несоответствию характеристик системы условиям функционирования и необходимости ее повторной разработки. Поэтому на этапе проектирования системы должно быть проведено тщательное обоснование требуемых показателей точности.
В этом разделе рассматриваются методы определения ошибок, возникающих при работе систем управления с детерминированными входными воздействиями. Вначале анализируются ошибки систем в переходном режиме. Затем особое внимание уделено простым способам расчета ошибок систем в установившемся режиме. Будет показано, что все системы управления можно разделить по величине установившихся ошибок на системы без памяти, так называемые статические системы, и системы, обладающие памятью, – астатические системы управления.
Типовые входные воздействия
Для оценки качества работы систем управления рассматривают их поведение при некоторых типовых воздействиях. Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = , g(p) = ;
б) линейное воздействие: g(t) = t , t > 0 ; ;
в) квадратичное воздействие: /2 , t > 0 ; g(p) = .
В некоторых случаях рассматривают обобщенное полиномиальное воздействие:
Ступенчатое воздействие является одним из простейших, но именно с его помощью определяется ряд важных свойств систем управления, связанных с видом переходного процесса. Линейное и квадратичное воздействия часто бывают связаны с задачами слежения за координатами движущегося объекта. Тогда линейное воздействие соответствует движению объекта с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых воздействиях можно построить следующим образом. Пусть задана передаточная функция замкнутой системы управления W(p). Тогда
где g(p) – изображение соответствующего воздействия.
Например, если , то и для g(t) = g0 получим .
С помощью вычетов или по таблицам находим обратное преобразование Лапласа и получаем вид переходного процесса x(t) для заданного входного воздействия:
где Res x(p) – вычет функции x(p) в точке a.
Обычно реакция системы на ступенчатое воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
Переходный процесс, как правило, характеризуют двумя параметрами – длительностью переходного процесса (временем установления) и величиной перерегулирования.
Под временем установления tу понимают временной интервал, по истечении которого отклонение |x(t) — xуст | выходного процесса от установившегося значения xуст не превышает определенную величину, например, 0,1gо. Время установления является важным параметром САУ, позволяющим оценить ее быстродействие. Величину tу можно оценить приближенно по амплитудно-частотной характеристике системы. При заданной частоте среза . Для оценки качества системы используется также величина перерегулирования, определяемая соотношением .
В зависимости от характера собственных колебаний системы переходный процесс в ней может быть колебательным, как это показано на рис. 21, б, или плавным гладким, называемым апериодическим (рис. 21,а). Если корни характеристического уравнения системы действительны, то переходный процесс в ней апериодический. В случае комплексных корней характеристического уравнения собственные колебания устойчивой системы управления являются затухающими гармоническими и переходный процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее собственные колебания затухают медленно, и перерегулирование в переходном режиме получается значительным. Как следствие, величина перерегулирования может служить мерой запаса устойчивости системы. Для многих систем запас устойчивости считается достаточным, если величина перерегулирования .
Установившийся режим
При проектировании систем управления часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной или бесконечно большой величиной.
Очень важно, что величина установившейся ошибки может быть легко найдена с помощью теоремы о предельном значении оригинала: .
При использовании этой теоремы нужно выразить величину ошибки e (p) через g(p). Для этого рассмотрим структурную схему замкнутой системы управления (рис. 22).
Очевидно, e (p) = g(p) — x(p) = g(p) — H(p)e(p). Отсюда или e (p) = He(p)g(p) , где He(p) = называется передаточной функцией системы управления от входного воздействия g(p) к ошибке слежения e(p). Таким образом, величину установившейся ошибки можно найти с помощью следующего соотношения:
где He(p) = 1/(1+H(p)); g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим систему управления, в составе которой нет интеграторов, например,
Найдем величину установившейся ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0. В этом случае
Предположим теперь, что входное воздействие изменяется линейно t или .
Тогда . Соответствующие входные воздействия и переходные процессы можно представить графиками на рис. 23,а и б.
Пример 2. Рассмотрим теперь систему, содержащую один интегратор. Типичным примером может быть система сервопривода (рис. 6) с .
Для ступенчатого воздействия g(t) = g0 или g(p) = получим
При линейном входном воздействии
Такие процессы можно проиллюстрировать соответствующими кривыми на рис.24, а и б.
Пример 3. Рассмотрим систему с двумя интеграторами. Пусть, например, . При ступенчатом воздействии .
Наконец, если входное воздействие квадратичное g(t) = at2/2 (g(p) = a/p3), то
Таким образом, в системе с двумя интеграторами может осуществляться слежение за квадратичным входным воздействием при конечной величине установившейся ошибки. Например, можно следить за координатами объекта, движущегося с постоянным ускорением.
Статические и астатические системы управления
Анализ рассмотренных примеров показывает, что системы управления, содержащие интегрирующие звенья, выгодно отличаются от систем без интеграторов. По этому признаку все системы делятся на статические системы, не содержащие интегрирующих звеньев, и астатические системы, которые содержат интеграторы. Системы с одним интегратором называются системами с астатизмом первого порядка. Системы с двумя интеграторами – системами с астатизмом второго порядка и т.д.
Для статических систем даже при неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет конечную величину g(t) = g0 . В системах с астатизмом первого порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно изменяющемся воздействии . Наконец, в системах с астатизмом второго порядка ненулевая установившаяся ошибка появляется только при квадратичных входных воздействиях g(t) = at2 /2 и составляет величину eуст = a/k.
Какие же физические причины лежат в основе таких свойств астатических систем управления?
Рассмотрим систему управления с астатизмом второго порядка (рис. 25)
Пусть входной сигнал системы управления изменяется линейно: t. Как было установлено, в такой системе установившаяся ошибка равна нулю, т.е. e (t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t) = t , то на входе второго интегратора должен быть сигнал . Действительно, при нулевом рассогласовании e (t) =0 в системе с интеграторами возможно существование ненулевого выходного сигнала первого интегратора . Первый интегратор после окончания переходного процесса «запоминает» скорость изменения входного воздействия и в дальнейшем работа системы управления осуществляется по «памяти». Таким образом, физическим объяснением такого значительного различия статических и астатических систем является наличие памяти у астатических систем управления.
Итак, существуют простые возможности определения важнейшего показателя систем управления – величины их динамических ошибок. Детальный анализ переходных процессов в системах управления обычно выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины установившихся ошибок легко находятся аналитически. При этом астатические системы управления, т.е. системы с интеграторами, имеют существенно лучшие показатели качества по сравнению со статическими системами.
© 2022 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
Радиоавтоматика: основы теории и принципы построения автоматических систем , страница 25
Определение динамических ошибок (по скорости, по ускорению) для статической и астатических систем.
Точность АС характеризуется величиной ошибки в установившемся режиме и зависит от характера воздействия, а также структуры и параметров системы.
Реальные воздействия в радиотехнических следящих системах описывается сложными (случайными) функциями времени. Однако при анализе точности управления часто используют простые детерминированные воздействия: постоянное ступенчатое, линейное, квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить в модели задающего воздействия наиболее существенные признаки (начальное значение, скорость изменения, ускорение). Большинство систем радиоавтоматики описываются передаточными функциями вида
где Ki — общее усиление разомкнутой системы, i – число интегрирующих звеньев, определяющее порядок астатизма системы;
– полиномы, порядок которых определяется числом типовых звеньев (n и m соответственно инерционных и форсирующих), а коэффициенты полиномов – постоянными времени типовых звеньев.
11.1. Статические ошибки
Ошибка системы при постоянном (ступенчатом) воздействии x(t)=x0=const при t³0 называется статическойeст.
Для установившейся ошибки, учитывая, что изображение X(p)=x0/p, запишем:
Для статической системы (не содержащей интегрирующих звеньев) статическая ошибка равна
Таким образом, в статических системах установившееся значение управляемой переменной не равно заданному: меньше на величину ошибки, значение которой обратно пропорционально усилению К0 по постоянному току (обычно К0>>1).
Для астатических систем (i ³ 1) ошибка при постоянном воздействии
так как числитель в (11.2) равен нулю, а знаменатель равен Кi.
Отсутствие статической ошибки обусловило название таких систем – астатические.
11.2. Динамические ошибки
Ошибка, характеризующая точность замкнутой системы при меняющемся воздействии, называется динамической eд(t).
Любое детерминированное воздействие (при условии существования его производных d (k) /dt (k) , k=1, 2, …) можно представить в виде ряда
где x0 — начальное значение, — скорость изменения, — ускорение и т. д.
Для вычисления динамических ошибок при типовых воздействиях (линейном и квадратическом) представим выражение для ошибки в операторной форме:
Используя разложение передаточной функции Ke(p) в ряд Маклорена по степеням переменной р, перепишем (11.5) в виде
где C0, C1, C2, … — коэффициенты ошибок, определяемые как
Установившееся значение ошибки при произвольном воздействии x(t) на основании (11.6) определяется временным рядом
Чем меньше коэффициенты ошибок, тем выше точность системы при произвольном детерминированном воздействии. При вычислении коэффициентов Ck обычно ограничиваются только первыми тремя (для систем с астатизмом не выше второго порядка).
Коэффициент C0 в соответствии с (11.7) равен
Для статических систем (i=0) C0=1/(1+K0), а для астатических систем C0=0.
Определим динамические ошибки типовых систем при линейном воздействии (изменение с постоянной скоростью) x(t)=nxt.
В соответствии с формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как
Для статической системы она равна
так как вклад составляющей C1nx значительно меньше, чем C0x(t), которая растет линейно со временем. Таким образом, скоростная ошибка в статических системах накапливается со временем со скоростью nx/(1+K0), что делает неприемлемым использование таких систем при меняющемся воздействии. Для астатических систем C0=0 и скоростная ошибка
Нахождение коэффициента ошибки C1 с использованием формулы (11.7) затруднительно. Более простой способ его вычисления основан на сравнении точного выражения для передаточной функции Ke(p) и аппроксимирующего ее ряда:
Уравнение (11.9) можно представить в виде
Полагая i= 1 (астатическая система первого порядка) и приравнивая коэффициенты при переменной p в левой и правой частях уравнения, находим
Таким образом, скоростная ошибка системы первого порядка астатизма eд=nx/K1 определяется усилением разомкнутой системы K1 и не зависит от времени. Параметр K1, имеющий размерность c –1 , называется добротностью системы по скорости (чем выше добротность, тем точнее система).
Для астатической системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C0=C1=0. Равенство C1=0 вытекает из уравнения (11.10), так как в правой части уравнения не содержится слагаемого, в которое входит переменная p (есть только с p 2 и выше).
Оценим динамические ошибки типовых систем при квадратичном воздействии (изменение с постоянным ускорением).
В соответствии с (11.8) для динамической ошибки (ошибки по ускорению) запишем
Для статической системы ошибка по ускорению равна
так как составляющие ошибки с коэффициентами C1 и C2 вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по квадратичному закону исключает применение статических систем при наличии ускорения.
Для системы первого порядка астатизма ошибка по ускорению равна
(вкладом составляющей можно пренебречь). Накопление ошибки со временем (со скоростью ) не позволяет применять такие системы при наличии ускорения. Для астатической системы второго порядка ошибка по ускорению равна
Определение коэффициента ошибки C2 с использованием уравнения (11.7) сводится к приравниванию коэффициентов при p 2 в обеих частях уравнения:

 возникают несимметричные по амплитуде колебания переменной
возникают несимметричные по амплитуде колебания переменной  (рис. 19.1, б).
(рис. 19.1, б).

 вследствие чего колебания переменной
вследствие чего колебания переменной  становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, б).
становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, б).


 для статических систем или же
для статических систем или же  для астатических систем. Астатической системой называется такая, в которой многочлен
для астатических систем. Астатической системой называется такая, в которой многочлен  имеет общий множитель
имеет общий множитель  , т. е.
, т. е.  .
.



 а,
а,  являются неизвестными постоянными.
являются неизвестными постоянными.
 первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде
первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде






 согласно (19.7) зависят не только от а и
согласно (19.7) зависят не только от а и  , но и от смещения
, но и от смещения  Поэтому, написав как прежде, характеристическое уравнение
Поэтому, написав как прежде, характеристическое уравнение

 на
на  ивыделив вещественную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:
ивыделив вещественную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:

 и частоту
и частоту  автоколебаний как функции постоянной составляющей
автоколебаний как функции постоянной составляющей 

 не только от
не только от  но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики
но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики  и
и  , то здесь их необходимо строить в виде серии кривых при разных постоянных значениях
, то здесь их необходимо строить в виде серии кривых при разных постоянных значениях  (рис. 19.3).
(рис. 19.3).


 которая отсюда и определяется. Чаще всего это уравнение относительно
которая отсюда и определяется. Чаще всего это уравнение относительно  является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда
является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда  и частота
и частота 

 или часто
или часто  . Решение получает вид
. Решение получает вид

 Определив последние (по любому из способов § 18.2), вычисляем потом по (19.15) и величину
Определив последние (по любому из способов § 18.2), вычисляем потом по (19.15) и величину  которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия
которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия 
 и является искомой статической или скоростной ошибкои соответственно для статической и астатической систем.
и является искомой статической или скоростной ошибкои соответственно для статической и астатической систем.
 имеет нулевой корень в знаменателе (что часто бывает), т. е. когда
имеет нулевой корень в знаменателе (что часто бывает), т. е. когда  вместо (19.14) получаем уравнение
вместо (19.14) получаем уравнение


 определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью
определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью  или же
или же  для которой
для которой



 передаточной функции линейной части системы имеет нулевой корень, то
передаточной функции линейной части системы имеет нулевой корень, то  и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид
и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид

 Это означает, что в указанных системах возникает такое смещение
Это означает, что в указанных системах возникает такое смещение  колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F (т. е. обеспечивается
колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F (т. е. обеспечивается  ), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.
), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.
 ействий.
ействий.

 — простейшая симметричная релейная характеристика, показанная на рис. 19.5:
— простейшая симметричная релейная характеристика, показанная на рис. 19.5:




 является задающим воздействием, изменяющимся с постоянной скоростью:
является задающим воздействием, изменяющимся с постоянной скоростью:

 Допустим также, что второе внешнее воздействие
Допустим также, что второе внешнее воздействие  является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):
является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):









 находим частоту автоколебаний
находим частоту автоколебаний

 в данной задаче оказалась не зависящей от смещения
в данной задаче оказалась не зависящей от смещения  , а следовательно, и от величины внешнего воздействия. Затем, подставляя в первое из уравнений (19.33) выражение q из (19.28) и
, а следовательно, и от величины внешнего воздействия. Затем, подставляя в первое из уравнений (19.33) выражение q из (19.28) и  из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний
из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний  от смещения
от смещения 


 ). Отсюда
). Отсюда




 из (19.38) в выражение (19.28) для
из (19.38) в выражение (19.28) для  откуда с использованием (19.39) найдем функцию смещения
откуда с использованием (19.39) найдем функцию смещения 





 амплитуды
амплитуды  и частоты
и частоты  автоколебаний при наличии внешних воздействий.
автоколебаний при наличии внешних воздействий. 



 находим частоту автоколебаний
находим частоту автоколебаний 




 не определяется. Однако последняя может понадобиться в дальнейшем для других целей. Но ее тоже легко можно определить при использовании второго метода. Здесь величины
не определяется. Однако последняя может понадобиться в дальнейшем для других целей. Но ее тоже легко можно определить при использовании второго метода. Здесь величины  и их отношение выражены через величины внешних воздействий. Функция же смещения
и их отношение выражены через величины внешних воздействий. Функция же смещения  не должна содержать ни величин внешних воздействий, ни амплитуды
не должна содержать ни величин внешних воздействий, ни амплитуды  зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим
зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим 

 не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи.
не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи.  автоколебаний на входе реле. Найдем теперь установившуюся ошибку на выходе системы
автоколебаний на входе реле. Найдем теперь установившуюся ошибку на выходе системы  Поскольку на выходе должно воспроизводиться внешнее воздействие
Поскольку на выходе должно воспроизводиться внешнее воздействие  то согласно рис. 19.5 и второму уравнению (19.20) ошибка данной системы выражается величиной
то согласно рис. 19.5 и второму уравнению (19.20) ошибка данной системы выражается величиной  установившееся решение для которой, следовательно, и надо искать. Выразив переменную
установившееся решение для которой, следовательно, и надо искать. Выразив переменную  через х, которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем
через х, которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем 


 — постоянные, а
— постоянные, а  — периодическая составляющая.
— периодическая составляющая. 


 определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной
определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной 

 определяется формулой (19.49) через внешнее воздействие, а
определяется формулой (19.49) через внешнее воздействие, а  — формулой (19.48).
— формулой (19.48).  возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать
возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать  Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при кос
Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при кос  согласно (19.59) будет
согласно (19.59) будет  Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи
Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи  на гибкую
на гибкую  . Тогда в уравнении (19.54) величина
. Тогда в уравнении (19.54) величина  заменится на
заменится на  :
: 


 (их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний ошибки
(их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний ошибки  можно сделать весьма малой.
можно сделать весьма малой. 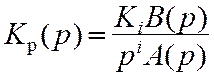 , (11.1)
, (11.1)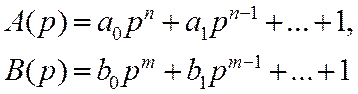
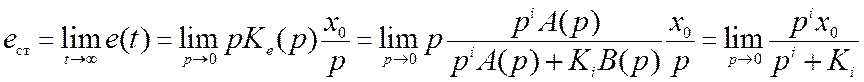 . (11.2)
. (11.2)






