Математика,
вопрос задал stanislava67,
9 месяцев назад
Добавить свой ответ
Ответы на вопрос
Ответил 68tata
7
Ответ:
1) Прямоугольником называется четырехугольник у которого противоположные стороны равны и все четыре угла равны.
2) верно
3)сложением называется действие при котором числа складываются: если все числа положительные или отрицательные, либо вычитаются: если числа и положительные и отрицательные.
4. Равносторонним треугольником называется треугольник у которого равны все стороны или углы
5. верно
Добавить свой ответ
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Қазақ тiлi,
1 месяц назад
Помогите по казахскому языку просклонять слова Домбыра…
Русский язык,
1 месяц назад
Составить по первым слогам предложение. На картинках изображены: улитка, ель, жаба, ягода( малина или ежевика), пиджак, тарелка.
Химия,
9 месяцев назад
Найдите степень окисления в формуле :CH2Cl2…
ОБЖ,
9 месяцев назад
Доведіть, що харчування, яке є оздоровчим для однієї людини, може нашкодити іншій.
История,
6 лет назад
Кто эти люди? И какой город их связывает?
Математика,
6 лет назад
сторона квадрата равна 17 см длина прямоугольника периметр которого равен периметру этого квадрата на 8 см больше его ширины Найдите стороны прямоугольника…
ФГБОУ ВПО САХАЛИНСКИЙ ГОСУДВРСТВЕННЫЙ УНИВЕРСИТЕТ
ЮЖНО-САХАЛИНСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ
ДОКЛАД
ПО МАТЕМАТИКЕ
НА ТЕМУ:ТРЕБОВАНИЯ К ОПРЕДЕЛЕНИЮ ПОНЯТИЙ.
Выполнила:
Шемякина Т.Е.
Южно-Сахалинск
Основные правила составления определений.
Одно и то же математическое понятие может быть определено различными способами. Например, такое простейшее понятие, как «треугольник», в разных учебниках по математике определяется по-разному:
-
Треугольник — это замкнутая ломаная линия, состоящая из трех звеньев»;
-
Многоугольник, имеющий три стороны, называется треугольником;
-
Если А, В и С — любые три точки, не лежащие на одной прямой, то объединение трех отрезков АВ, ВС и АС называется треугольником.
Все эти определения, как и ранее приведенное, правильные. Однако иногда, воспроизводя определения, имеющиеся в учебнике, или строя определения самостоятельно, ученики и, не только они, допускают разные ошибки. Чтобы строить и воспроизводить определения математических понятий правильно, нужно знать основные требования к логическому определению понятий.
Рассмотрим эти требования, попутно указывая наиболее часто встречающиеся ошибки в определении математических понятий.
Определения должны быть научно правильными.
Это означает, что, определяя то или иное понятие, надо это сделать так, чтобы не исказить научный смысл этого понятия. Так, например, смысл понятия «отношение» (в математике) состоит в том, что оно есть какое-то число. Между тем иногда это понятие определяют так: «Отношение есть сравнение двух чисел или величин посредством деления». Но сравнение есть некоторый процесс, а не число. В данном случае неверно выбрано родовое понятие и тем самым искажен научный смысл определяемого понятия. Другой пример. Иногда приходится слышать от ученика такое определение: «Абсолютной величиной, или модулем числа, называется это число без знака». Получается, что существуют какие-то числа без знака, но таких чисел (кроме нуля) математика не знает: в математике рассматриваются лишь положительные, отрицательные числа и нуль, других чисел нет. Если число написано без знака, то это положительное число, а не какое-то «беззначное». Поэтому приведенное определение неверное.
Определения не должны содержать «порочного круга».
Один ученик на вопрос, что такое умножение, например, ответил: «Умножением называется действие отыскания произведения». Когда же его спросили, а что такое произведение, он с уверенностью заявил, что это результат умножения. Следовательно, у этого ученика получается, что умножение определяется через понятие произведения, а произведение через понятие умножения. Получается «порочный круг» в определении. Ясно, что такой способ определения является грубо ошибочным. Еще пример ошибки «порочного круга» в определении: «Угол называется прямым, если его стороны перпендикулярны» и «Прямые называются перпендикулярными, если при пересечении они образуют прямые углы». Схему этих двух определений можно изобразить так.
Как видим, эти определения действительно образуют «порочный круг». Следовательно, строя определения математических понятий, надо следить за тем, чтобы они не образовали друг с другом «порочного круга».
Определение должно содержать указание на ближайшее родовое понятие.
Как бы ни было построено определение математического понятия, в нем должно быть указано ближайшее родовое понятие к определяемому понятию. Нарушение этого требования приводит к различным ошибкам. Так, например, иногда учащиеся, формулируя определения, вовсе не указывают родовое понятие. На вопрос, какие фигуры называется равновеликими, они отвечают: «Это если две фигуры имеют равные площади». Что означает «это», можно лишь догадываться. Или: на предложение сформулировать определение равнобедренных треугольников, иногда можно услышать такой ответ: «Это такие, у которых две стороны равны». Такая небрежность в формулировке определений недопустима. Другой тип ошибок связан с тем, что в определении указывается не ближайшее родовое понятие, а более широкое. Вот пример такого определения: «Параллелограмм есть фигура, у которой противоположные стороны параллельны». В этом определении указано не ближайшее для параллелограмма родовое понятие — «четырехугольник», а более далекое, более широкое — «фигура». И тем самым это определение становится неверным, ибо фигурой, у которой противоположные стороны параллельны, может быть не только параллелограмм, но и, например, правильный шестиугольник. Или другой пример. Давая определение диаметра круга, ученик сформулировал его так: «Диаметр круга есть прямая, проходящая через центр круга». Ученик указал в качестве родового понятия прямую, а ведь диаметр — это не вся прямая, а лишь отрезок прямой.
Определение не должно быть тавтологией, т. е. повторяющей в иной словесной форме ранее сказанное.
Сущность такой ошибки заключается в том, что понятие определяется через само себя. Вот примеры тавтологии в некоторых определениях: «Сложением называется действие, при котором числа складываются»(здесь сложение определено через понятие «складывание», что одно и то же). «Фигура А называется симметричной фигуре В, если они расположены симметрично относительно оси симметрии» (здесь «симметричные фигуры» определены через понятие «фигуры, расположенные симметрично»). Ясно, что такие определения являются грубо ошибочными.
Определение должно быть достаточным.
Это означает, что в определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия. Если же это требование нарушается, то под определение можно подвести не только объекты определяемого понятия, но и другие объекты. Так, например, иногда ученики дают такое 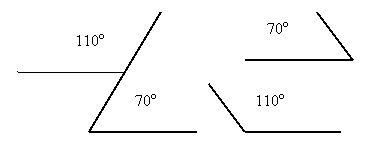 определение смежных углов: «Смежными называются углы, которые в сумме составляют 180°». Недостаточность этого определения становится очевидной, если взглянуть на рисунок. На нем изображены две пары углов, сумма которых равна 180°, но они не смежные. Ошибка здесь в том, что указано лишь одно свойство смежных углов, оно недостаточно для их определения. Можно было бы, например, так определить их: «Смежными называются два угла, имеющие общую сторону, которые расположены в разных полуплоскостях от этой общей стороны и в сумме составляют 180°».
определение смежных углов: «Смежными называются углы, которые в сумме составляют 180°». Недостаточность этого определения становится очевидной, если взглянуть на рисунок. На нем изображены две пары углов, сумма которых равна 180°, но они не смежные. Ошибка здесь в том, что указано лишь одно свойство смежных углов, оно недостаточно для их определения. Можно было бы, например, так определить их: «Смежными называются два угла, имеющие общую сторону, которые расположены в разных полуплоскостях от этой общей стороны и в сумме составляют 180°».
Например, медиану треугольника определили следующим образом: «Медианой треугольника называется отрезок, делящий его сторону пополам». Очевидно, что и в этом определении указано недостаточное число признаков медианы. Поэтому под это определение подходят не только медиана треугольника, но и средняя линия (ведь и она делит сторону треугольника пополам) и вообще любой отрезок, делящий сторону треугольника пополам. Для построения правильного определения медианы треугольника надо добавить еще и такой признак: «Медиана выходит из вершины треугольника». Тогда получаем такое правильное определение: «Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны».
Определение не должно быть избыточным.
Это означает, что в определении не должно быть указано лишних признаков, являющихся следствием других признаков определяемого понятия. Например, весьма часто встречается такое определение ромба: «Ромбом называется параллелограмм, все стороны которого равны между собой». Это определение явно избыточное, ибо достаточно равенства двух смежных сторон параллелограмма для того, чтобы были равны все его стороны. Следовательно, правильнее определять ромб следующим образом: «Ромбом называется параллелограмм, две смежные стороны которого равны». Вот другой пример: «Диаметром круга называется наибольшая хорда, проходящая через центр круга». Здесь первый признак «наибольшая» является следствием второго признака «проходящая через центр», а второй является следствием первого. Поэтому правильное определение такое: «Диаметром круга называется хорда, проходящая через центр круга» или: «Диаметром крута называется наибольшая хорда».
Мы указали лишь основные требования к определению математических понятий и привели примеры ошибок, возникающих при нарушении этих требований. Для того чтобы избежать таких ошибок, надо знать эти требования, учитывать их при формулировании тех или иных определений, учиться строить правильные определения.
Определяемое понятие — понятие существенные признаки которого отыскиваются. Определяющее понятие — понятие посредством которого определяется неизвестное понятие.
В определении понятия через ближайший род и видовые отличиня нужно следиить за тем, чтобы использовался ближайший род, но не образовывался порочный круг.
Тавтология в определении — логическая ошибка заключающаяся в том, что понятие определяется само через себя.
Слишком узкое определение понятия — логическая ошибка, состоящее в том, что нарушается принцип соразмерности, в результате чего объем определяемого понятия оказывается меньше объема определяющего понятия.
В определении понятия через ближайший род и видовые отличиня нужно следиить за тем, чтобы использовалось минимальное и в тоже время достаточное количество существенных признаков видовых отличий.
1)
Что нужно знать об объекте, чтобы иметь
представление о нем? Чтобы
иметь представление об объекте нужно
знать его существенные свойства.
2)
Какие свойства объекта различают?
Среди
свойств какого-либо объекта имеются
существенные и несущественные для его
определения.
3)
Что называют содержанием понятия?
Содержание
понятия
— это
совокупность существенных и отличительных
признаков предмета, качества или
множества однородных предметов,
отражённых в этом понятии
4)
Дать определения объема понятия.
Объем
понятия- это отображенное в нашем
сознании множество предметов, каждый
из которых имеет признаки, зафиксированные
в исследуемом понятии.
5)
Какова взаимосвязь между объемом и
содержанием понятия?
Они
взаимосвязаны: чем больше объем понятия,
тем меньше его содержание, и наоборот:
чем меньше объем, тем больше содержание
понятия.
Так,
например, объем понятия «равнобедренный
треугольник» меньше объема понятия
«треугольник», в объем первого понятия
входят не все треугольники, а лишь
равнобедренные. А содержание первого
понятия больше содержания второго, так
как равнобедренный треугольник обладает
не только всеми свойствами треугольника,
но и особыми свойствами, присущими
только равнобедренным треугольникам.
6)
Что называется определением понятия?
Определение
понятия — это логическая операция, в
процессе которой раскрывается содержание
понятия.
7)
Приведите примеры явных определений
(неявных определений).
Явные
определения раскрывают существенные
признаки предмета; к неявным относятся
определение через отношение предмета
к своей противоположности, контекстуальное,
остенсивное и некоторые другие виды
определений. Явное определение:
«Радиус-это отрезок, соединяющий центр
окружности с любой точкой окружности».,
«Уравнение- это равенство, содержащее
неизвестную величину». Неявные
определения: «Свобода
-есть познанная необходимость»;
«Возможность — потенциальная
действительность»; «Действительность
— реализованная возможность».
Какие определения называются
контекстуальными? Остенсивные?
В
контекстуальном определении содержание
понятия раскрывается в относительно
самостоятельном по смыслу отрывке
письменной или устной речи (контексте).
Определение остенсивное(от лат. ostentus —
показывание, выставление напоказ)
неявное определение, раскрывающее
содержание понятия путем непосредственного
показа, ознакомления обучаемого с
предметами, действиями и ситуациями,
обозначаемыми данным понятием. Можно,
напр., предъявить стол и сказать: «Это
— стол, и все вещи, похожие на него, тоже
столы»
9)
Как определить понятие через род и
видовое отличие? (приведите примеры).
Определение
через ближайший род и видовые отличие
— это логический прием определения
понятия, который заключается в том, что
отыскивается ближайший род и отличительные
признаки, имеющиеся только у данного
вида предметов. Например
: «четные числа- это натуральные числа
кратные 2», родовое понятие — натуральные
числа, видовые отличия — кратны числу
2. «Параллелограммом называется
четырехугольник, противоположные
стороны которого параллельны»
Четырехугольник – родовое понятие,
видовые отличия- противоположные стороны
параллельны»
10)
Какие требования предъявляются для
оценки правильности явных определений?
Определения
должны быть научно правильными.
Это означает, что, определяя то или иное
понятие, надо это сделать так, чтобы не
исказить научный смысл этого понятия.
Так, например, смысл понятия «отношение»
(в математике) состоит в том, что оно
есть какое-то число. Между тем иногда
это понятие определяют так: «Отношение
есть сравнение двух чисел или величин
посредством деления». Но сравнение есть
некоторый процесс, а не число. Определения
не должны содержать «порочного круга».
В
определении понятия через ближайший
род и видовые отличия нужно следить за
тем, чтобы использовался ближайший род,
но не образовывался порочный круг. «Угол
называется прямым, если его стороны
перпендикулярны». Определение
должно содержать указание на ближайшее
родовое понятие.
Как
бы ни было построено определение
математического понятия, в нем должно
быть указано ближайшее родовое понятие
к определяемому понятию. Нарушение
этого требования приводит к различным
ошибкам. «Параллелограмм есть фигура,
у которой противоположные стороны
параллельны». В этом определении указано
не ближайшее для параллелограмма родовое
понятие — «четырехугольник», а более
далекое, более широкое — «фигура». И
тем самым это определение становится
неверным, ибо фигурой, у которой
противоположные стороны параллельны,
может быть не только параллелограмм,
но и, например, правильный шестиугольник.
Определение не должно быть тавтологией,
т.
е. повторяющей в иной словесной форме
ранее сказанное. Сущность такой ошибки
заключается в том, что понятие определяется
через само себя. Вот примеры тавтологии
в некоторых определениях: «Сложением
называется действие, при котором числа
складываются»
Определение
должно быть достаточным.
Это
означает, что в определении должны быть
указаны все признаки, позволяющие
однозначно выделить объекты определяемого
понятия. Если же это требование нарушается,
то под определение можно подвести не
только объекты определяемого понятия,
но и другие объекты.
Например,
медиану треугольника определили
следующим образом: «Медианой треугольника
называется отрезок, делящий его сторону
пополам». Очевидно, что и в этом определении
указано недостаточное число признаков
медианы. Поэтому под это определение
подходят не только медиана треугольника,
но и средняя линия (ведь и она делит
сторону треугольника пополам) и вообще
любой отрезок, делящий сторону треугольника
пополам. Для построения правильного
определения медианы треугольника надо
добавить еще и такой признак: «Медиана
выходит из вершины треугольника». Тогда
получаем такое правильное определение:
«Медианой треугольника называется
отрезок, соединяющий вершину треугольника
с серединой противоположной стороны».
Определение
не должно быть избыточным.
Это
означает, что в определении не должно
быть указано лишних признаков, являющихся
следствием других признаков определяемого
понятия. Например, весьма часто встречается
такое определение ромба: «Ромбом
называется параллелограмм, все стороны
которого равны между собой». Это
определение явно избыточное, ибо
достаточно равенства двух смежных
сторон параллелограмма для того, чтобы
были равны все его стороны.
Темы:
№2, №3 Математические предложения.
Математические доказательства.
1)
Чем характеризуется математическое
предложение? Суждение
–
это такая форма мышления, в которой
отражается наличие или отсутствие
самого объекта, наличие или отсутствие
его свойств, связей. Математическое
суждение принято называть предложением.
2)
Что называют логическими связками?
Логические
связки представляют собой формальные
аналоги союзов нашего родного естественного
языка. Как сложные предложения строятся
из простых с помощью союзов «однако»,
«так как», «или» и т.п., так и сложные
суждения образуются из простых с помощью
логических связок. Логическая
связка — это любая логическая операция
над высказыванием. Например, употребляемые
в обычной речи слова и словосочетания
«не», «и», «или», «если… , то», «тогда и
только тогда» являются логическими
связками.
3)
Дайте определение высказывания.
Высказывание
—
термин математической логики, обозначающий
формализованную структурированную
запись мысли с помощью буквенных символов
и логических связок, рассматриваемую
с точки зрения истинностных значений.
4)
Когда высказывание «А и В» истинно?
«А
и В» истинно только тогда, когда они
одновременно истинны.
5)
Когда
истинно высказывание вида «А или В»?
Отрицание
высказывания А?
высказывание
вида «А или В»
истинное только тогда, когда хотя бы
одно из них истинно. Отрицание
высказывания А
логическое высказывание, принимающее
значение «истинно», если исходное
высказывание ложно, и наоборот.
6)
Какие слова называются кванторами?
КВАНТОР
[< лат. quantum сколько] — символ математической
логики; логическая операция, дающая
количественную характеристику области
предметов, к которым относится выражение,
получаемое в результате ее применения.
7)
Назовите кванторы общности и
существования.
—
квантор
общности (для любого, все и т. д.)
— квантор
существования (существует, для некоторых).
Как устанавливается истинность
высказываний с кванторами общности и
существования?
Для
доказательства утверждения с квантором
общности необходимо убедиться в том,
что при подстановке каждого из значений
х высказывание обращается в истинное
. Если множество Х конечно, то это можно
сделать путем перебора всех случаев;
если же множество Х бесконечно, то
необходимо провести рассуждения в общем
виде. Чтобы убедиться в истинности
высказывания с квантором существования,
достаточно привести пример и таким
образом доказать.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: праткическая работа 1.docx, Практическая работа.docx, Практическая работа 2.1.docx, Контрольная работа.docx, курсовая работа по роману.docx, Практическая работа № 1.doc, Самостоятельная работа к теме 1.2 «Техносфера современной школы», Практическая работа №3 раздел программы 3.6.1.doc, Практическая работа по Механике жидкости и газа.pdf, Самостоятельная работа к теме 2.5.2.ppt
Практическая работа по математике
Выполнила студентка гр. ПНОз-181
Юненко А.С.
Стр. 45 п.13 №1-6.
№1
Начертите три геометрические фигуры, принадлежащие объёму понятий:
А) параллелограмм
Б) трапеция
В) окружность
№2
Назовите пять существенных свойств понятия:
А) Треугольник.
1) Против большей стороны лежит больший угол, и наоборот.
2) Против равных сторон лежат равные углы, и наоборот.
3)Сумма углов треугольника равно 180° (можно сказать, что каждый угол равностороннем треугольнике равна 60°).
4)Продолжая одну из сторон треугольника, получаем внешний угол.
5) Любая сторона треугольника меньше суммы двух других сторон и больше из разности.
Б) Круг
1) Круг является выпуклой фигурой.
2) При вращении плоскости относительно центра круг переходит сам в себя.
3) Круг является фигурой, имеющей наибольшую площадь при заданном периметре. Или что тоже самое, образующей наименьшим периметром при заданной S.
4) Площадь круга радиуса R, обозначаемая S, равна S=πR², где π=3,14.
5) Периметр круга (длина граничной окружности): L=2πR.
№3
Каков объём понятия:
А) однозначное число – всегда записано одной цифрой;
Б) натуральное число – начинается с 1 и по порядку до бесконечности;
В) луч – имеет начало, но не имеет конца.
№4
Назовите несколько свойств, общих для прямоугольника и квадрата. Какое из утверждений верное:
А) Всякое свойство квадрата присуще прямоугольнику. (Неверно)
Б) Всякое свойство прямоугольника присуще квадрату. (Верно)
Свойства:
- У прямоугольника и квадрата прямые углы;
- Противоположные стороны равны;
- Диагонали равны и точкой пересечения делятся пополам.
№5
Находятся ли в отношении рода и вида следующие пары понятий:
А) многоугольник и треугольник – отношение рода и вида.
Б) угол и острый угол – отношение рода и вида
В) луч и прямая – отношение «часть и целое»
Г) ромб и квадрат — – отношение рода и вида
Д) круг и окружность — – отношение «часть и целое»
№6
Изобрази при помощи кругов Эйлера отношения между объёмами понятий a, b, c, если:
А
А)
В
С
A – «четырёхугольник»,
B – «трапеция»,
c – «прямоугольник»
В
Б)
А
A – «натуральное число, кратное 3»,
B – «натуральное число, кратное 4»,
c – «натуральное число» С
В)
С
A – «треугольник», А В
B – «равнобедренный треугольник»,
c – «равносторонний треугольник»
Стр. 51 п.14 № 1,2,3,6
№1
Переформулируйте следующие определения, используя слова «тогда и только тогда, когда»:
А) Чётным называется число тогда и только тогда, когда оно делится на 2.
Б) Множество А называется подмножеством В тогда и только тогда, когда каждый элемент множества А принадлежит множеству В.
В) Множества А и В называется равными тогда и только тогда, когда А ⸦ В и В ⸦ А.
Г) Треугольником называется фигура тогда и только тогда, когда состоит из трех точек, не лежавших на одной прямой, и трех попарно соединяющих их отрезков.
№2
В следующих определениях выделите определяемое и определяющие понятие, родовое понятие (по отношению к определяемому) и видовое отличие:
А) Параллелограммом называют четырёхугольник, у которого противоположные стороны попарно параллельны.
Определяемое понятие – параллелограммом
Определяющие понятие – четырёхугольник, у которого противоположные стороны попарно параллельны
Родовое понятие (по отношению к определяемому) – четырёхугольник
Видовое отличие — у которого противоположные стороны попарно параллельны
Б) Отрезок, соединяющий середины двух сторон треугольника, называется средней линией.
Определяемое понятие – средней линией
Определяющие понятие – отрезок, соединяющий середины двух сторон треугольника
Родовое понятие (по отношению к определяемому) – отрезок
Видовое отличие — соединяющий середины двух сторон треугольника
№3
Назовите все свойства, которые содержатся в видовом отличие из следующих определений:
А) Биссектрисой угла называется луч, входящий из вершины угла делящий угол пополам.
Ответ: это геометрическое место точек, равноудалённых от сторон этого угла.
Б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Ответ: если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
№6
Есть ли логические ошибки в следующих определениях? Если можете, исправьте их.
А) Прямоугольником называется четырёхугольник, у которого противоположные стороны равны и все четыре угла равны.
Б) Биссектрисой угла называется прямая, делящая угол пополам.
В) Сложением называется действие, при котором числа складываются: если все числа положительные или отрицательные, либо вычитаются: если все числа положительные или отрицательные.
Г) Равносторонним треугольником называется треугольник, у которого равны все стороны или углы.
Д) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.
Начнём по порядку рассматривать эти высказывания.
1) Квадрат — четырехугольник, у которого все стороны равны;
утверждение не совсем верное, так как ромб — тоже четырёхугольник, у которого все стороны равны;
2) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией, верное утверждение;
3) Сложением называется действие, при котором числа складываются, верно, но отчасти, только для положительных чисел, для отрицательных, сложение становится по сути вычитанием;
4) Луч – прямая, ограниченная с одной стороны, верное утверждение.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Конспект урока по ТОНКМ с МП по теме «Требования к определению математических понятий»
Ищем педагогов в команду «Инфоурок»
Тема: Требования к определению понятий
Цель: добиться осознанного усвоения студентами требований, предъявляемых к определению математического понятия
Познакомиться с основными требованиями, предъявляемыми к определению математических понятий, учиться находить ошибки, допущенные в формулировке определения;
Развивать математическую речь, мышление, анализ, синтез, обобщение, классификацию;
Воспитывать познавательный интерес, коммуникативную культуру
Оборудование: учебные пособия по ТОНКМ (Л.П. Стойлова, А.М. Пышкало), математике (Л.П. Стойлова); раздаточный материал.
I . Организационный момент.
III . Открытие нового знания
Чтобы оценить правильность явных определений, надо знать правила определения понятий. Так как преобладающее большинство определений в школьном курсе математики — это определения через род и видовое отличие, то речь будет идти о правилах этих определений.
Прежде всего, определяемое и определяющее понятия должны быть соразмерны . Это значит, что совокупности предметов, охватываемые ими, должны совпадать. Соразмерны, например, понятия «прямоугольник» и «четырехугольник, в котором все углы прямые». Если же объем определяющего понятия включает в себя объем понятия определяемого, то говорят об ошибке слишком широкого определения. Так, определение «Прямые а и b называются параллельными, если они не имеют общих точек или совпадают» слишком широко, поскольку ему удовлетворяют и скрещивающиеся прямые. Если же объем определяющего понятия уже объема определяемого понятия, то имеет место ошибка слишком узкого определения. Например, определение «Прямые а и b называются параллельными, если они не имеют общих точек» слишком узко, поскольку ему не удовлетворяют совпадающие прямые.
Второе правило определения запрещает порочный круг : нельзя определять понятие через само себя или определять его через другое понятие, которое, в свою очередь, определяется через него. Возьмем такие понятия начальной математики, как «умножение» и «произведение», и дадим им следующие определения:
Умножением чисел называется действие, при помощи которого находят произведение этих чисел.
Произведением чисел называется результат их умножения.
Видим, что умножение определяется через понятие произведения, а произведение — через понятие умножения. Определения образовали, как говорят в математике, порочный круг. В результате цепочка последовательных определений, выстроенных в рамках курса, прерывается.
Порочный круг содержится и в таком определении: «Решением уравнения называется число, которое является его решением». Здесь Понятие «решение уравнения» определяется, по сути дела, через решение уравнения.
Третьим важным требованием к логически правильному определению понятия является следующее: в определении должны быть указаны все свойства, позволяющие однозначно выделять объекты, принадлежащие объему определяемого понятия .
Рассмотрим, например, такое определение Понятия «смежные углы»: «Смежными называются углы, которые в сумме составляют 180°». Нетрудно увидеть, что под данное определение можно подвести не только углы, изображенные на рисунке 2 и действительно являющиеся смежными, но и углы, изображенные на рисунке 3. Почему так произошло? Дело в том, что в приведенном определении смежных углов указано лишь одно их свойство, а именно свойство составлять в сумме 180°, но его недостаточно для выделения смежных углов из всех других.
Рассмотрим определение: «Прямоугольником называется четырехугольник, у которого противоположные стороны равны и все углы прямые». Можно показать, что включенное в определение свойство «иметь равные стороны» вытекает из свойства «иметь прямые углы». Следовательно, данное определение прямоугольника избыточное и правильнее определять прямоугольник таким образом: «Прямоугольником называется четырехугольник, у которого все углы прямые».
Следует сказать, что в любом определении понятия есть элемент произвола, что проявляется во-первых в выборе термина (прямоугольник в котором все стороны равны, мог бы называться и по-другому), а во-вторых, в выборе свойств, включаемых в определение. В принципе понятие квадрата можно определить так: «Квадратом называется ромб, у которого все углы прямые» – или так: «Квадратом называется параллелограмм, у которого все стороны равны, а углы прямые». Различные определения одного и того же понятия возможны потому, что из большого числа свойств, входящих в содержание этого понятия, в определение включаются только некоторые.
Если одному и тому же понятию даются, например, два различных определения, то они должны быть равносильными. Это означает, что из свойств, включенных в одно определение, должны вытекать свойства, положенные в основу другого определения, и наоборот.
Чем же руководствуются, когда из возможных определений некоторого понятия выбирают одно? Исходят из того, какое определение проще, естественнее или целесообразнее для дальнейшего построения теории.
Если же какие-либо свойства оказываются включенными в определение, то другие свойства тех же объектов могут быть логически выведены из тех, что вошли в определение. Это важное положение используют при решении задач на распознавание. Если объект А принадлежит объему определяемого понятия, то он обладает всеми свойствами, которые указаны в определении понятия. Справедливо и обратное утверждение, т. е. если известно, что объект А обладает всеми свойствами, которые указаны в он определении понятия, называемого некоторым термином, то и объект А можно назвать этим термином.
Пример. Используя определение диаметра окружности, установим, в каком из случаев, представленных на рисунке 4, отрезок CD является диаметром.
Определим диаметр окружности следующим образом: диаметром окружности называется хорда, проходящая через ее центр. Чтобы отрезок CD оказался диаметром окружности, достаточно одновременное выполнение двух условий: отрезок С D должен быть хордой окружности и проходить через ее центр. Этим двум условиям удовлетворяет отрезок С D в случае «а». В случае «б» отрезок С D — хорда, но он не проходит через центр окружности; в случае «в» отрезок С D проходит через центр окружности, но не является хордой.
Заметим, что в математике для ответа на вопрос, существует ли объект, удовлетворяющий данному определению, как правило, доказывают специальную теорему, подтверждающую возможность существования объекта, о котором говорится в определении. В геометрии существование объекта, удовлетворяющего определению, иногда обосновывают, построив его.
III . Первичное закрепление изученного материала
Найдите логические ошибки (если они есть) в следующих определениях и исправьте их.
1) Прямоугольником называется четырехугольник, у которого противоположные стороны равны;
2) Биссектрисой угла называется прямая, делящая угол пополам;
3) Сложение – это когда числа складываются;
4) Равносторонним треугольником называется треугольник, у которого все стороны и все углы равны;
5) Параллелограмм – это многоугольник, у которого противоположные стороны попарно параллельны;
6) Квадрат – это ромб с прямым углом;
7) Квадрат – это когда все стороны равны;
Прямоугольник – это параллелограмм с прямым углом;
9) Равные треугольники – это треугольники, которые равны.
10) Прямоугольник, у которого диагонали взаимно перпендикулярны, есть квадрат.
V . Подведение итогов урока
– Назовите основные требования, предъявляемые к определению математических понятий
V . Домашнее задание (с инструктажем)
Источник
Выполнение заданий
Задание 1. Назовите по три понятий, принадлежащих объему понятий:
а) рациональное число б) четырехугольник в) математика г) мебель д)музыкальный национальный инструмент
тувинского народа е) часы
ж) специальности в колледже
e) предметы на 1 курсе
Задание 2. Укажите общие свойства следующих пар понятий:
a) трапеции и ромба; б) треугольника и параллелограмма;
в) прямоугольника и круга.
Задание 3. Определите, в каких отношениях находятся следующие понятия а, в, с и изобразите их объемы А, В, С на диаграммах Эйлера-Венна:
a) «прямая», «луч», «отрезок» б) «дерево», «растение», «кустарник»
b) «целое число», «натуральное число», «отрицательное число»
г) «треугольник», «многоугольник», «геометрическая фигура».
Задание 4. Для каждого из понятий укажите родовое понятие:
a) «кустарник», б) «квадрат», в) «стол», г) «нечетное число».
Задание 5. Для каждого из понятий укажите два видовых понятия:
a) «животное», б) «часть речи», в) «одежда», г) «параллелограмм».
Задание 6. Укажите три понятия, являющееся родовыми для понятия «прямоугольник». Какое из них ближайшее?
Задание 7. Приведите примеры разных определений из учебников математики начальных классов, разработанных по требованиям фгос ноо и выясните, к каким определениям они относятся.
Задание 8. Выясните с помощью
учебников математики начальных классов каким способом определяются в начальном курсе математики понятия:
а) «числовое выражение»; «однозначное число»;
в) «уменьшаемое»; г) «разность»; д) «площадь»; е) «квадрат».
Задание 9. Выясните, какие из определений верны (соразмерны):
a) Правильный треугольник
треугольник, у которого все стороны равны.
6) Остроугольный треугольник треугольник с острым углом.
Прямоугольник четырехугольник, у которого все углы прямые и смежные стороны равны.
Задание 10. Укажите логические ошибки, опустите лишние слова или добавьте нужные слова B следующих определениях:
a) Луч есть прямая, ограниченная с одной стороны.
6) Отрезком называется прямая, ограниченная с двух сторон.
b) Квадратом называется прямоугольник, диагонали которого равны и делят друг друга пополам.
г) Секущей называется бесконечная прямая, проходящая через какие- нибудь точки окружности.
Задание 11. Найдите ошибки в определениях, выясните тип ошибки:
б) Дуб-это дерево, которое растет в лесу.
b) Прямая, делящая сторону треугольника пополам, называется медианой.
г) Сложением называется действие, при котором числа складываются.
Задание 12. Проверьте правильность следующих классификаций понятий:
a) понятие «треугольник» делится на понятия: «остроугольный треугольник», «прямоугольный треугольник», «тупоугольный треугольник», «равносторонний треугольник», «равнобедренный треугольник»;
6) под понятие «натуральное число» делится на понятия: «четное число», «нечетное число», «число, кратное на 3»;
b) понятие «четырехугольник» делится на понятия: «параллелограмм» и «трапеция».
B случае, если классификация выполнена неправильно, укажите какое условие нарушено и
Задание 13. Выполните правильные классификации следующих понятий:
Вуз, студент, угол, музыкальный инструмент, мебель, обувь, домашнее животное, домашняя птица, посуда, часы, учитель, здание, дерево, число, буква русского алфавита, множество, житель города.
Задание 14. Докажите, что понятие «четырехугольник» родовое по отношению к понятию «квадрат». В какой зависимости находятся содержания этих понятий?
Источник
Есть ли логические ошибки в следующих определениях? Если можете исправьте их 1. Прямоугольником называется четырехугольник у которого противоположные.
Есть ли логические ошибки в следующих определениях? Если можете исправьте их 1. Прямоугольником называется четырехугольник у которого противоположные стороны равны 2. Биссектрисой угла называется прямая делящая угол пополам 3. сложением называется действие при котором числа складываются 4. Равносторонним треугольником называется треугольник у которого равны все стороны и углы 5. Параллелограммом называется многоугольник у которого противоположные стороны попарно параллельны
Ответы
1) Прямоугольником называется четырехугольник у которого противоположные стороны равны и все четыре угла равны.
3)сложением называется действие при котором числа складываются: если все числа положительные или отрицательные, либо вычитаются: если числа и положительные и отрицательные.
4. Равносторонним треугольником называется треугольник у которого равны все стороны или углы
а)периметр квадрата равен сумме четырех его сторон:
б)площадь прямоугольника равна произведению двух его сторон:
с)площадь круга равна произведению числа пи на квадрат его радиуса:
г)длина окружности равна удвоенному произведению радиуса окружности на число пи:
Источник
Задания по математике. В педагогическом университете профиль начальное образование.
1. Начертите три геометрические фигуры, принадлежащие объему понятия: а) параллелограмм; б) трапеция; в) окружность.
2. Назовите пять существенных свойств понятия: а) треугольник; б) круг.
3. Каков объем понятия: а) однозначное число; б) натуральное число; в) луч?
4. Назовите несколько свойств, общих для прямоугольника и квадрата. Какое из следующих утверждений верное: а) Всякое свойство квадрата присуще прямоугольнику. б) Всякое свойство прямоугольника присуще квадрату?
5. Находятся ли в отношении рода и вида следующие пары понятий: а) многоугольник и треугольник; б) угол и острый угол; в) луч и прямая; г) ромб и квадрат; д) круг и окружность?
6. Изобразите при помощи кругов Эйлера отношения между объемами понятий а, в и с, если: а) а – «четырехугольник», в – «трапеция», с – «прямоугольник»; б) а – «натуральное число, кратное 3», в – «натуральное число, кратное 4», с – «натуральное число»; в) а – «треугольник», в – «равнобедренный треугольник», с – «равносторонний треугольник».
7. Приведите примеры понятий, отношения между которыми изображены на рисунке.
8. Среди понятий, изучаемых в начальном курсе математики, есть такие, как «четное число», «треугольник», «многоугольник», «число», «трехзначное число», «прямой угол», «сумма», «слагаемое», «выражение». Есть ли среди них понятия, находящиеся в отношении: а) рода и вида; б) целого и части?
9. Какие свойства понятий «прямоугольник» и «сложение» изучают в начальном курсе математики?
10. Переформулируйте следующие определения, используя слова «тогда и только тогда, когда»:
а) Четным называется число, которое делится на 2.
б) Множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
в) Множества А и В называются равными, если А Ì В и В Ì А.
г) Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.
11. В следующих определениях выделите определяемое и определяющее понятие, родовое понятие (по отношению к определяемому) и видовое отличие: а) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны; б) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
12. Назовите все свойства, которые содержатся в видовом отличии каждого из следующих определений: а) Биссектрисой угла называется луч, выходящий из вершины угла и делящий угол пополам; б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
13. Соразмеримы ли следующие определения: а) Остроугольным треугольником называется треугольник, у которого есть острый угол; б) Прямоугольным треугольником называется треугольник, у которого есть прямой угол.
14. Учащийся определил прямой угол, стороны которого взаимно перпендикулярны, а взаимно перпендикулярные прямые как прямые, образующие при пересечении прямые углы. Какую ошибку допустил учащийся?
15. Есть ли логические ошибки в следующих определениях? Если есть, то исправьте их.
а) Прямоугольником называется четырехугольник, у которого противоположные стороны равны.
б) Биссектрисой угла называется прямая, делящая угол пополам.
в) Сложением называется действие, при котором числа складываются.
г) Равносторонним треугольником называется треугольник, у которого равны все стороны и все углы.
д) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.
16. Дайте определение: тупоугольного треугольника, равнобедренного треугольника, трапеции. Какие понятия вы выбрали в качестве родового в каждом случае? Какие свойства включили в видовое отличие?
Источник
Исправьте логические ошибки в предложениях.
Исправьте логические ошибки в предложениях.
1. Налицо незаконное разбазаривание государственного имущества.
2. День был жаркий, но ярко светило солнце.
3. Народные войска встречали тысячи жителей города.
4. Каждый рабочий закреплен за определенным станком, который следит за его состоянием.
5. Пророческие слова великого певца народной скорби и печали в нашей стране сбылись.
6. Книги у меня лежат справа, а свет слева.
7. Условия жизни города отличны от села.
8. Сидя на диване, Коля читал книгу, задумчиво уставившись в потолок.
9. Археологи заметили, что покойники из южного захоронения перекликаются с покойниками из северного захоронения.
1. На лицо незаконная кража государственного имущества.
2. День был пасмурный, но солнце светило ярко.
3. Тысячи жителей города встречали народные войска.
4. На каждый станок определён свой рабочий, который следит за его состоянием.
5. Пророческие слова и печали великого певца народной скорби в нашей стране сбылись.
6. Книги у меня лежат справа, а свечи слева.
7. Условия жизни города отличаются от условий в селе.
8. Коля читал книгу, сидя на диване.
9. Археологи заметили, что покойники из южного захоронения пересекаются с покойниками из северного захоронения.
1. Явное незаконное разбазаривание государственного имущества.
2.День был жаркий, т. к. ярко светило солнце.
3. Народные войска были встречены тысячами жителей города.
4. Каждый рабочий закреплен за определенным станком, при этом в обязанности рабочего входит контроль за состоянием оборудования.
5. Пророческие слова великого певца народной скорби и печали сбылись для нашей страны.
6. Книги у меня лежат справа, а свет направлен слева.
7. Условия жизни города отличаются от условий жизни села.
8. Сидя на диване, Коля читал книгу, иногда задумчиво уставившись в потолок.
9. Археологи заметили, что у покойников из южного захоронения есть сходства с покойниками из северного захоронения.
Источник







 Б) трапеция
Б) трапеция






 В) окружность
В) окружность













