Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
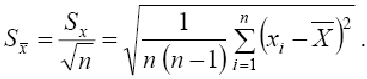
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
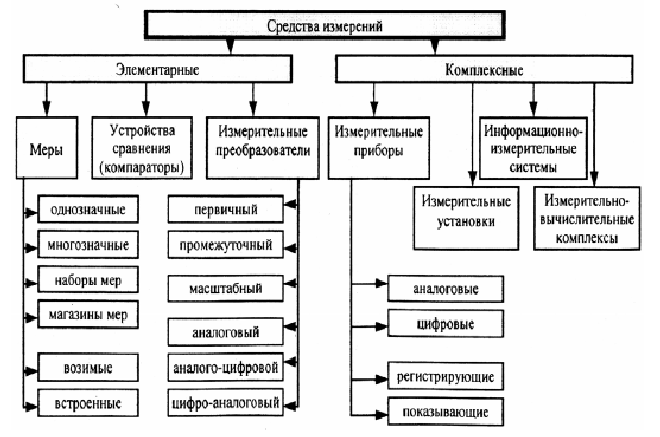
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
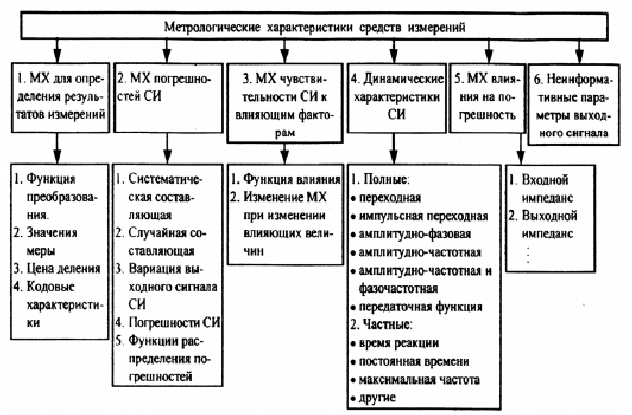
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
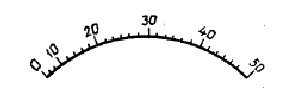
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.

Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.

Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
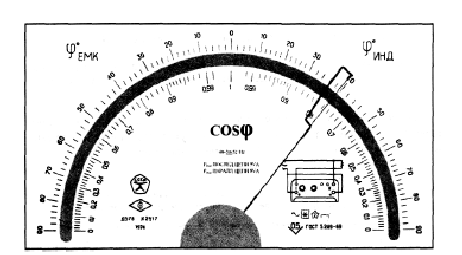
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).

Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
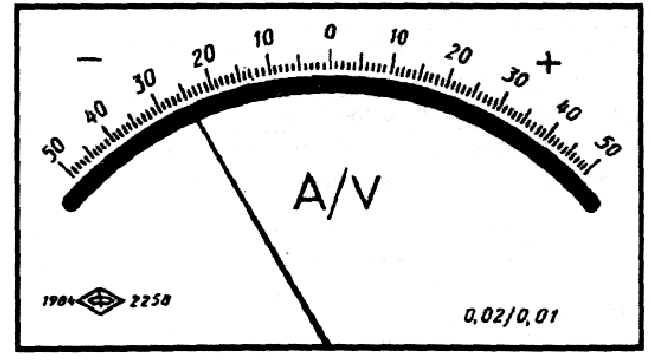
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
![]() ,
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
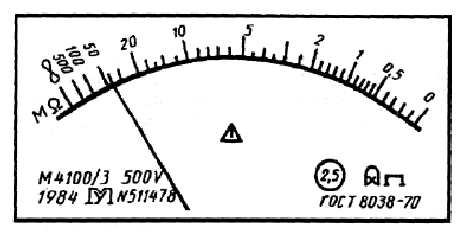
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
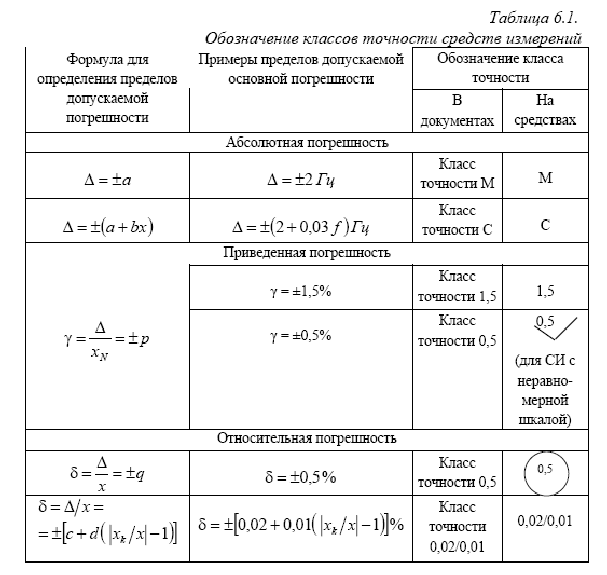
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Способы уменьшения случайных погрешностей.
1 Метод многократных измерений.
2. Метод комплексирования.
Проводят измерения одной и той же величины при следующих условиях:
А) несколькими однотипными СИ одновременно
С) различными методами( разными группами экспериментаторов)
В дальнейшем проводится объединение результатов наблюдений по алгоритму средневзвешенной оценки, более точным наблюдениям больший вес. Объединение может быть только для равноточных результатов по систематической погрешности.
3. Метод косвенных измерений.
В отдельных случаях позволяет уменьшить случайную погрешность.
Средства измерений. Характеристики СИ для определения результатов измерений.
Средство измерений – это техническое средство (или комплекс), предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящие и (или) хранящие единицу физической величины, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени [24]. Данное определение раскрывает метрологическую сущность СИ, заключающуюся в умении хранить (или воспроизводить) единицу ФВ
и в неизменности размера хранимой единицы во времени. Первое обуславливает возможность выполнения измерения, суть которого, как известно, состоит в сравнении измеряемой величины с ее единицей. Второе принципиально необходимо, поскольку при изменении размера хранимой единицы ФВ с помощью данного СИ нельзя получить результат с требуемой точностью. Под метрологическими характеристиками (MX) понимают такие характеристики СИ, которые позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью. В отличие от СИ приборы или вещества, не имеющие нормированных MX, называют индикаторами. СИ — это техническая основа метрологического обеспечения.
Классификация средств измерений по их роли в процессе измерения и
Эталон – средство измерений (или их комплекс), предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера нижестоящим по поверочной схеме СИ и утвержденное в качестве эталона в установленном порядке.
Меры — это СИ, воспроизводящие или хранящие физическую величину заданного размера. Меры могут быть однозначными, воспроизводящими одно значение физической величины (гиря, калибр на заданный размер, образцы твердости, шероховатости, катушка сопротивления, нормальный элемент, воспроизводящий значение ЭДС), и
многозначными — для воспроизведения плавно или дискретно ряда значений одной и той же физической величины (измерительный конденсатор переменной емкости, набор конечных мер, магазин емкостей, индуктивности и сопротивления, измерительные линейки).
Для ряда областей измерений, и в первую очередь для физико-химических измерений, чрезвычайно перспективным средством повышения эффективности поверочных работ является применение стандартных образцов (СО). Правила работы с СО устанавливает ГОСТ 8.315—97. Согласно этому документу,
стандартный образец состава и свойств веществ и материалов — это средство измерений в виде вещества (материала), состав или свойства которого установлены аттестацией. Можно дать и другое определение: стандартный образец — образец вещества (материала) с установленными в результате метрологической аттестации
значениями одной или более величин, характеризующими свойство или состав этого вещества (материала).
Стандартные образцы предназначены для обеспечения единства и требуемой точности измерений посредством:
• градуировки, метрологической аттестации и поверки СИ;
• метрологической аттестации методик выполнения измерений;
• контроля показателей точности измерений;
• измерения ФВ, характеризующих состав или свойства веществ материалов, методами сравнения.
По своему назначению СО исполняют роль мер, однако в отличие от «классических» мер они имеют ряд особенностей. Например, образцы состава воспроизводят значения ФВ,
характеризующих состав или свойства именно того материала (вещества), из которого они изготовлены. Стандартные образцы, как правило не являются изделиями, они реализованы обычно в виде части или порции однородного вещества (материала), причем эта часть является полноценным носителем воспроизводимой единицы ФВ, а не ее части Эта особенность образцов отражена в требованиях к их однородности по составу и свойствам. Однородность материала, из которого сделан образец, имеет принципиальное значение, в то время как для меры такая характеристик часто является второстепенной.
Измерительные преобразователи — СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не доступной для непосредственного восприятия наблюдателем. Это термопары, измерительные трансформаторы,
усилители, преобразователи давления. По месту, занимаемому в измерительной цепи, они делятся на первичные, промежуточные и т. п. Конструктивно они выполняются либо отдельными блоками, либо составной частью СИ. Не следует отождествлять измерительные преобразователи с преобразовательными элементам. Последние не имеют метрологических характеристик, как, например, трансформатор тока или напряжения.
Измерительный прибор — СИ, предназначенное для переработки сигнала измерительной информации в другие, доступные для непосредственного восприятия наблюдателем формы. Различают приборы прямого действия (амперметры, вольтметры,
манометры) и приборы сравнения (компараторы). По способу отсчета измеряемой величины СИ делятся на показывающие (аналоговые, цифровые), регистрирующие (на
бумажную или магнитную ленту) и т. п.
Измерительная установка — совокупность функционально объединенных СИ и вспомогательных устройств, расположенных в одном месте. Например, поверочные установки, установки для испытания электротехнических, магнитных и других материалов. Измерительная установка позволяет предусмотреть определенный
метод измерения и заранее оценить погрешность измерения.
Измерительная система — это комплекс СИ и вспомогательных
устройств с компонентами связи (проводные, предназначенный для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи
и/или использования в автоматических системах управления. В отличие от измерительных установок, предусматривающих изменения режима и условий функционирования, измерительная система не воздействует на режимы работы, а предназначена только для сбора и/или хранения информации. Частными случаями измерительной системы являются информационно-вычислительный комплекс (ИВК), информационно-измерительные системы (ИИС). К последним можно отнести системы автоматического контроля, системы технического диагностирования, системы распознавания образов, системы для передачи неизмерительной информации. При организации поверки рабочих СИ используют различные эталоны и образцовые СИ. СИ, как правило, работают совместно с датчиками (измерительными преобразователями), имеющими свои MX.
При использовании средств измерений принципиально важно знать степень соответствия информации об измеряемой величине, содержащейся в выходном сигнале, ее истинному значению. С этой целью для каждого СИ вводятся и нормируются определенные метрологические характеристики (МХ). Метрологическими называются характеристики свойств СИ, оказывающие влияние на результат измерения и его погрешности. Характеристики, устанавливаемые нормативными документами, называются нормируемыми, а определяемые экспериментально – действительными.
Номенклатура метрологических характеристик средств измерений
Неинформативным называется параметр входного сигнала СИ, не связанный функционально с измеряемым параметром. Например, частота переменного тока при измерении его амплитуды. Нормальные метрологические характеристики (НМХ) устанавливаются документами. MX, определенные документами, считаются действительными. На практике наиболее распространены следующие MX СИ.
Диапазон измерений — область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей — это диапазон преобразования):
Предел измерения — наибольшее или наименьшее значение диапазона измерения. Для мер — это номинальное значение воспроизводимой величины.
Рис 32 Неравномерная шкала СИ
Например, у шкалы на рис. 32 начальный участок (
20%) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10. 50 единиц.
Цена деления шкалы — разность значений величин, соответствующих двум соседним
отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.
Чувствительность — отношение изменения сигнала Δу на выде СИ к вызвавшему это изменение изменению Δх сигнала на входе
Например, для стрелочного СИ — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины
Таким образом, для неравномерных шкал величина S= var, и степень неравномерности шкалы оценивают через коэффициент
Для равномерных шкал S = Sср = const и Sср = l/хN где xN — диапазон измерений.
Поскольку х и у могут быть выражены в различных единицах то величина S имеет размерность [мм/А], [мм/В], [градус/В]и т.д. Говоря о чувствительности, указывают чувствительность тока, напряжения и т. д. Иногда для оперирования безразмерными единицами вводят понятие относительной чувствительности
где х0, у0 — номинальные (или средние) величины. Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора. Величину, обратную чувствительности, называют постоянной прибора С = 1/S.
Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления. Поэтому для СИ с неравномерной шкалой чувствительность — величина переменная.
Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:
где хв, ху — значения измерений образцовыми СИ при возрастании и убывании величины х. Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.
Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой (или статической характеристикой преобразования),которая может быть представлена аналитически, графически или в виде таблицы. Градуировочная характеристика может изменяться под воздей ствием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает «следить» за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.
Дата добавления: 2016-04-14 ; просмотров: 4124 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Методы повышения точности измерений
Анализ причин появления погрешностей измерений, выбор способов их обнаружения и уменьшения являются основными этапами процесса измерений. Погрешности измерений, принято делить на систематические и случайные. В процессе измерений систематические и случайные погрешности проявляются совместно и образуют нестационарный случайный процесс. Деление погрешностей на систематические и случайные является удобным приемом для их анализа и разработки методов уменьшения их влияния на результат измерения.
Рассмотрим способы обнаружения и исключения систематических погрешностей, поскольку они зависят от выбора метода измерений и его осуществелния.
По характеру изменения систематические погрешности делятся:
- постоянные – погрешности, связанные с неточной градуировкой шкалы прибора, отклонением размера меры от номинального значения, неточным выбором моделей объектов.
- переменные
– периодические – погрешность изменяющаяся по периодическому закону, например погрешность отсчета при определении времени по башенным часам, если смотреть на стрелку снизу, температурная погрешность от изменения температуры в течение суток и т.п.
– прогрессирующие – погрешности монотонно изменяющиеся (увеличивающиеся или уменьшающиеся) в общем случае по сложному, обычно неизвестному закону. Прогрессирующие погрешности во многих случаях обусловлены старением элементов средств измерений и могут быть скорректированы при его периодической поверке.
По причине возникновения погрешности измерений разделяются на три основные группы:
- методические – погрешности обусловленные неадекватностью принимаемых моделей реальным объектам, несовершенством методов измерений, упрощением зависимостей, положенных в основу измерений, неопределенностью объекта измерения;
- инструментальные – погрешности обусловленные прежде всего особенностями используемых в средствах измерений принципов и методов измерений, а также схемным, конструктивным и технологическим несовершенством средств измерений.
- взаимодейтствия – обусловлены взаимным влиянием средства измерений, объекта исследования и экспериментатора. Погрешности из-за взаимного влияния средства и объекта измерений обычно принято относить к методическим погрешностям, а погрешности, связанные с действиями экспериментатора, называются личными погрешностями. Однако такая классификация недостаточно полно отражает суть рассматриваемых погрешностей.
Выявление и устранение причин возникновения погрешностей – наиболее распространенный способ уменьшения всех видов систематических погрешностей. Примерами такого способа являются: термостатирование отдельных узлов или прибора в целом, а также проведение измерений в термостатированных помещениях для исключения температурной погрешности, применение экранов, фильтров и специальных цепей (например, эквипотенциальных цепей) для устранения погрешностей из-за влияния электромагнитных полей, наводок и токов утечек, применение стабилизированных источников питания.
Для уменьшения прогрессирующей погрешности из-за старения элементов средств измерений, параметры таких элементов стабилизируют путем искусственного и естественного старения. Кроме этого систематические погрешности можно уменьшить рациональным расположением средств измерений по отношению друг к другу, к источнику влияющих воздействий и к объекту исследования. Например магнитоэлектрические приборы должны быть удалены друг от друга, оси катушек индуктивности, должны быть расположены под углом 90°, выводы термопары должны располагаться по изотермическим линиям объекта.
Многие систематические погрешности, являющиеся не изменяющимися во времени функциями влияющих величин или обусловленные стабильными физическими эффектами, могут быть теоретически рассчитаны и устранены введением поправок или использованием специальных корректирующих цепей.
Другим радикальным способом устранения систематических погрешностей является поверки средств измерений в рабочих условиях с целью определения поправок к результатам измерения. Это дает возможность учесть все систематические погрешности без выяснения причин их возникновения. Степень коррекции систематических погрешностей в этом случае, естественно, зависит от метрологических характеристик используемых эталонных приборов и случайных погрешностей поверяемых приборов.
Фактически поверка средств измерений перед их использованием и введение поправок адекватна применению средств измерений более высоких классов точности при условии, что случайные погрешности средств измерений малы по сравнению с систематическими, а сами систематические погрешности медленно изменяются во времени.
Метод инвертирования широко используется для устранения ряда постоянных и медленно изменяющихся систематических погрешностей. Этот метод и ряд его разновидностей (метод исключения погрешности по знаку, коммутационного инвертирования, структурной модуляции, двукратных измерений, инвертирования функции преобразования и др.) основаны на выделении алгебраической суммы чесного числа сигналов измерительной информации, которые вследствие инвертирования отличаются направлением информативного сигнала, опорного сигнала или знаком погрешности.
Метод модуляции – метод близкий к методу инвертирования, в котором производится периодическое инвертирование входного сигнала и подавление помехи, имеющей однонаправленное действие.
Метод исключения погрешности по знаку — вариант метода инвертирования, который часто применяется для исключения известных по природе погрешностей, источники которых имеют направленное действие, например погрешностей из-за влияния постоянных магнитных полей, ТЭДС и др.
Метод замещения (метод разновременного сравнения) является наиболее универсальным методом, который дает возможность устранить большинство систематических погрешностей. Измерения осуществляются в два приема. Сначала по отсчетному устройству прибора делают отсчет измеряемой величины, затем, сохраняя все условия эксперимента неизменными, вместо измеряемой величины на вход прибора подают известную величину, значение которой с помощью регулируемой меры (калибратором) устанавливают таким образом, чтобы показание прибора было таким же, как при включении измеряемой величины.
Метод равномерного компарирования является разновидностью метода замещения, он используется при измерениях таких величин, которые нельзя с высокой точностью воспроизводить с помощью регулируемых мер или других технических средств. Обычно это величины, изменяющиеся с высокой частотой или по сложному закону. В качестве известных регулируемых величин при этом используются величины такого же рода, как измеряемые, но отличаютщиеся от них спектральным составом (обычно постоянные во времени и в пространстве) и создающие такой же, как и измеряемая величина, сигнал на выходе компарирующего преобразователя.
Метод эталонных сигналов заключается в том, что на вход средств измерений периодически вместо измеряемой величины подаются эталонные сигналы такого же рода, что и измеряемая величина. Разность между реальной градуировочной характеристикой используется для коррекции чувствительности или для автоматического введения поправки в результат измерения. При этом, как и при методе замещения, устраняются все систематические погрешности, но только в тех точках диапазона измерений, которые соответствуют эталонным сигналам. Метод широко используется в современных точных цифровых приборах и в информационно-измерительных системах. Примером использования этого метода является периодическая подстройка рабочего тока в компенсаторах и цифровых вольтметрах постоянного тока при помощи нормального элемента.
Тестовый метод – при использовании данного метода значение измеряемой величины определяется по результатам нескольких наблюдений, при которых в одном случае входным сигналом средства измерений является сама измеряемая величина Х, а в других – так называемые тесты, являющиеся функциями измеряемой величины.
Метод вспомагательных измерений используется для исключения погрешностей из-за влияющих величин и неинформативных параметров входного сигнала. Для реальзации этого метода одновременно с измеряемой величиной Х с помощью вспомогательных измерительных устройств производится измерение каждой из влияющих величин и вычисление с помощью вычислительного устройства, а также формул и алгоритмов поправок к результатам измерения.
Метод симметричных наблюдений заключается в проведении многократных наблюдений через равные промежутки времени и усреднении результатов наблюдений, симметрично расположенных относительно среднего наблюдения. Обычно этот метод применяется для исключения прогрессирующих погрешностей, изменяющихся по линейному закону. Так, при измерении сопротивления резистора путем сравнения напряжения на измеряемом и эталонном резисторах, включенных последовательно и питаемых от общего аккумулятора, может возникнуть погрешность вследствие разряда источника питания.
Для исключения этой погрешности проводят три измерения падения напряжения:
- на эталонном резисторе U01 = I·R0;
- через равные промежутки времени на измеряемом резисторе UX = (I — ΔI1)·RX;
- снова на эталонном резисторе U02 = (I — ΔI2)·R0.
- Если ток изменяется во времени по линейному закону, то ΔI2 = 2ΔI1; I — ΔI1 = (U01 + U02) / (2R0) и RX = R0·2·UX / (U01 + U02).
Метод симметричных наблюдений можно также использовать для устранения других видов погрешностей, например систематических погрешностей из-за влияющих величин, изменяющихся по периодическому закону. В этом случае симметричные наблюдения проводят через половину периода, когда погрешность имеет разные знаки, но одинаковые значения. Таким образом, например, можно исключить погрешность из-за наличия четных гармоник при измерении амплитудного значения напряжения при искаженной форме кривой.
Источник
Например, один из способов оценить количество времени, которое требуется, – это просто время, когда это один раз с секундомом часовым. Вы можете уменьшить неопределенность в этой оценке, сделав это одинаковое измерение в несколько раз и приняв среднее значение.
Как уменьшить систематические и случайные ошибки?
Систематическая ошибка может быть сведена к минимуму путем регулярной калибровки оборудования , используя элементы управления в экспериментах, разогревая инструменты до получения чтения и сравнение значений со стандартами. Хотя случайные ошибки могут быть сведены к минимуму путем увеличения размера выборки и усреднения данных, труднее компенсировать систематическую ошибку.
Как лучше всего минимизировать неопределенности для случайного процесса?
Чтобы помочь организациям достичь этой цели, я составил список из трех высокоэффективных методов для снижения неопределенности измерений.
- Проверьте и собирайте данные. «Посмотрите на комбинации, которые дают меньшую изменчивость. …
- Выберите лучшую калибровочную лабораторию. …
- Удалите смещение и охарактеризуйте.
Что является примером случайной ошибки?
Случайные ошибки в экспериментальных измерениях вызваны неизвестными и непредсказуемыми изменениями в эксперименте. … Примерами причин случайных ошибок являются: Электронный шум в схеме электрического прибора , нерегулярные изменения скорости тепла от солнечного коллектора из -за изменений ветра.
Как увеличение размера выборки уменьшает случайную ошибку?
Как этот доверительный интервал сравнивается с тем, который вы вычислили по данным, сообщенным Lye et al.? Ключ к уменьшению случайной ошибки составляет для увеличения размера выборки . … Как видите, доверительный интервал существенно сужается по мере увеличения размера выборки, отражая менее случайную ошибку и большую точность.
влияют ли случайные ошибки?
Случайная ошибка в основном влияет на точность , которая воспроизводима, одно и то же измерение при эквивалентных обстоятельствах. Напротив, систематическая ошибка влияет на точность измерения или насколько близко наблюдаемое значение к истинному значению.
Каковы причины случайных ошибок?
Случайная ошибка может быть вызвана множеством вещей, такими как несоответствия или неточность в оборудовании, используемом для измерения данных, в измерениях экспериментатора, в индивидуальных различиях между участниками, которые измеряются, или в экспериментальных процедурах.
Как вы контролируете случайные ошибки?
способы уменьшения случайных ошибок
- Пытание повторяющихся измерений для получения среднего значения.
- Построение графика для установления шаблона и получения линии или кривой наилучшего соответствия. Таким образом, расхождения или ошибки уменьшаются.
- Поддержание хорошей экспериментальной техники (например, чтение с правильной позиции)
Почему неопределенность вызывает беспокойство?
Эта способность напрямую связана с нашим уровнем уверенности в отношении будущих событий – насколько они вероятно, когда они произойдут, и на что они будут похожи. Неопределенность уменьшает то, насколько эффективно и эффективно мы можем подготовиться к будущему и, таким образом, способствует тревоге.
Что такое неопределенность при примере?
Неопределенность определяется как сомнение . Когда вы чувствуете, что не уверены, хотите ли вы устроиться на новую работу или нет, это пример неопределенности. Когда экономика становится плохо, и заставляет всех беспокоиться о том, что произойдет дальше, это пример неопределенности.
Каковы три стратегии снижения неопределенности?
Эти три варианта отражают три стратегии URT для получения информации и, следовательно, снижения неопределенности: пассивный, активный и интерактивный (Berger, 1979; Berger & Bradac, 1982).
Каковы 3 типа ошибок в науке?
Ошибки обычно классифицируются по трем категориям: Систематические ошибки, случайные ошибки и ошибки . Систематические ошибки связаны с выявленными причинами и в принципе могут быть устранены. Ошибки этого типа приводят к измеренным значениям, которые неизменно слишком высоки или неизменно слишком низки.
Как мы можем предотвратить человеческую ошибку?
Пять способов уменьшить человеческую ошибку на рабочем месте
- Не делайте цели и сроки недостижимыми. …
- Убедитесь, что персонал имеет доступ к необходимым им инструментам. …
- Работайте над вашими внутренними линиями связи. …
- Предлагайте регулярное обучение и личное развитие. …
- Рассмотрим облачное хранилище и управление документами.
Что хуже систематической или случайной ошибки?
Эти ошибки бывают в двух формах; Один гораздо хуже, чем другой: Случайная ошибка (может быть исправлена для – см. Ниже) Систематическая ошибка (чрезвычайно серьезно, если вы не знаете, что она существует)
можно исправить случайную ошибку?
Случайная ошибка может быть уменьшена на: с использованием среднего измерения из набора измерений , или. Увеличение размера выборки.
Почему случайная ошибка неизбежна?
Каждое измерение, которое вы принимаете, будет неверным на одинаковую сумму, потому что есть проблема с вашим измерительным устройством. Случайные ошибки неизбежны и являются результатом возникновения трудностей, проведенных измерениями или попытки измерить величины , которые варьируются со временем.
может ли скорректировать случайную ошибку в собранных данных?
случайная ошибка в собранных данных не может быть исправлена . Для научных данных необходима только одна точка данных для расчета его стандартного отклонения. … должно быть определено стандартное отклонение и среднее значение набора данных. Относительная ошибка является указанием точности собранных данных.
Какой тип ошибки возникает из -за плохой точности?
Плохая точность результатов систематических ошибок . Это ошибки, которые повторяются точно одинаково каждый раз, когда проводится измерение.
Какой тип ошибки нельзя контролировать?
случайная ошибка (или случайная вариация) обусловлена факторами, которые не могут или не будут контролироваться.
Можно ли устранить систематические ошибки?
Систематическая ошибка, как указано выше, может быть исключена – не совсем полностью , но обычно в достаточной степени. Этот процесс устранения называется «калибровкой». Калибровка – это просто процедура, когда результат измерения, записанного прибором, сравнивается с результатом измерения стандарта.
Как увеличивает достоверность размера выборки?
Если ваш размер эффекта невелик, вам понадобится большой размер выборки, чтобы обнаружить разницу, в противном случае эффект будет маскирован случайностью в ваших образцах. … Итак, Большие размеры выборки дают более надежные результаты с большей точностью и мощностью, но они также стоят больше времени и денег.
может ли выбора размер влиять на смещение?
Увеличение размера выборки имеет тенденцию уменьшать ошибку выборки; То есть это делает образец статистики менее переменной. Однако увеличение размера выборки не влияет на смещение обследования . Большой размер выборки не может исправить методологические проблемы (под прикрытием, смещение без ответа и т. Д.), Которые вызывают смещение обследования.
влияет ли размер выборки на систематическую ошибку?
Случайные ошибки приводят к переменным различиям от истинного значения и непредсказуемо приводят к измерениям, которые выше или меньше истинного значения. Не зная истинного значения измеренной величины, невозможно определить величину любой систематической ошибки, которая может существовать.
Связанный QNA:
Уменьшение — влияние — случайная погрешность
Cтраница 1
Уменьшение влияния случайных погрешностей на результат измерений достигается путем многократных измерений величины в одинаковых условиях.
[1]
Уменьшение влияния случайных погрешностей на результат измерений достигается путем многократных измерений величины в одинаковых условиях. Если принять, что систематические погрешности близки к нулю, то наиболее достоверное значение, которое можно приписать измеряемой величине на основании ряда измерений, есть среднее арифметическое из полученных значений.
[2]
Уменьшение влияния случайных погрешностей на результат измерений достигается путем многократных измерений величины в одинаковых условиях.
[3]
Для уменьшения влияния случайных погрешностей на результат измерения рекомендуется производить измерение данной величины в одинаковых условиях и по возможности большее число раз и из полученных значений брать среднее арифметическое, которое считается наиболее вероятным значением измеренной величины, так как случайные погрешности, одинаковые по абсолютной величине, но разные по знакам, при большом числе измерений встречаются одинаково часто.
[4]
Для уменьшения влияния случайных погрешностей измерения при каждом сочетании пикового ускорения и длительности действия проводят три-четыре измерения.
[5]
Для уменьшения влияния случайных погрешностей показаний индикатор многократно проверяют в каждой точке шкалы и затем вычисляют среднее значение.
[6]
Как уже указывалось ( § 13), для уменьшения влияния случайных погрешностей на результат анализа обычно проводят не одно, а два и более определения интересующего нас элемента в данном веществе. Как правило, ни при одном из этих определений не получается истинного значения определяемой величины, так как все они содержат ошибки. Поэтому задачей анализа является нахождение наиболее вероятного значения определяемой величины и оценка точности полученного результата.
[7]
Как уже указывалось ( § 13), для уменьшения влияния случайных погрешностей на результат анализа обычно проводят не одно, а два или несколько определений интересующего нас элемента в данном веществе. Как правило, ни при одном из этих определений не получается истинного значения определяемой величины, так как все они содержат ошибки. Поэтому задачей анализа является нахождение наиболее вероятного значения определяемой величины и оценка степени точности полученного результата.
[8]
Как уже указывалось ( § 13), для уменьшения влияния случайных погрешностей на результат анализа обычно проводят не одно, а два или несколько определений интересующего нас элемента в данном веществе. Как правило, ни при одном у из этих определений не получается истинного значения определяемой величины, так как все они содержат ошибки. Поэтому задачей анализа является нахождение наиболее вероятного значения определяемой величины и оценка степени точности полученного результата.
[10]
Рассмотрим прежде всего статистические измерения, при которых многократные измерения проводятся для уменьшения влияния случайных погрешностей. Результат каждого измерения при этом дает оценку измеряемой величины.
[11]
Повышение точности результата измерений может быть достигнуто исключением грубых и систематических погрешностей из результатов измерений и уменьшением влияния случайных погрешностей. При этом во всех случаях грубые погрешности ( промахи) следует исключать из результатов измерений. Систематические погрешности следует исключать тогда, когда это обеспечивает заметное повышение точности. Способы уменьшения влияния случайных погрешностей изложены в § 1.4. Необходимо иметь в виду, что, если принять за результат измерений среднее арифметическое из ряда — измерений, точность повышается в У — п раз.
[12]
В ряде случаев — при измерении заведомо постоянной величины — возникает задача повышения точности измерения за счет уменьшения влияния случайных погрешностей, для чего проводят ряд повторных наблюдений. Повторные наблюдения имеет смысл производить в том случае, если систематические погрешности исключены или если они значительно меньше случайных погрешностей, так как систематические погрешности нельзя исключить увеличением числа наблюдений. Кроме того, необходимо также учитывать, что погрешность результата измерения, обусловленная случайными погрешностями, не может быть снижена до значения, меньшего порога чувствительности используемых средств изменений.
[13]
В § 1.3 было показано, что проведение многократных наблюдений с последующим усреднением результатов — эффективный способ уменьшения влияния случайной погрешности на результат измерения.
[14]
Повышение точности измерительных приборов достигается за счет автоматической компенсации ( исключения) систематической погрешности, в частности автоматической установки нуля перед началом измерений, автоматического выполнения градуировочной операции ( самокалибровки), осуществления самоконтроля, уменьшения влияния случайных погрешностей путем проведения многократных измерений с последующим усреднением их результатов, выявления и исключения грубых погрешностей, выведения на дисплей информации о числовых значениях погрешностей по ходу измерений.
[15]
Страницы:
1
2
