Методы исключения грубых ошибок
При
получении результата измерения, резко
отличающегося
от всех других результатов, естественно
возникает
подозрение, что допущена грубая ошибка.
В этом случае
необходимо сразу же проверить, не
нарушены ли основные
условия измерения.
Если
же такая проверка не была сделана
вовремя, то
вопрос о целесообразности браковки
одного «выскакивающего»
значения решается путем сравнения его
с
остальными результатами измерения. При
этом применяются различные критерии,
в зависимости от того, известна или нет
средняя квадратическая ошибка, а
измерений
(предполагается, что все измерения
производятся с
одной и той же точностью и независимо
друг от друга).
Метод
исключения при известной
![]() .
.
Обозначим
«выскакивающее»
значение через х*,
а
все остальные результаты
измерения через
![]() ,
,
![]() ……….
……….
![]() .
.
Подсчитаем
среднее арифметическое значение
![]()
и
сравним абсолютную величину
разности
![]() с величиной
с величиной![]() .
.
Дляполученного
отношения
![]()
подсчитаем
вероятность 1—2Ф(t)
(Приложение табл.2.)
Это даст вероятность того, что
рассматриваемое
отношение случайно примет значение,
не
меньшее чем t,
при
условии, что значение х*
не
содержит
грубой ошибки (что ошибка результата
х* только случайна). Если подсчитанная
указанным образом вероятность
окажется очень малой, то «выскакивающее»
значение
содержит грубую ошибку и его следует
исключить из
дальнейшей обработки результатов
измерений.
Какую
именно вероятность считать очень малой,
зависит
от конкретных условий решаемой задачи:
если назначить
слишком низкий уровень малых вероятностей,
то
грубые ошибки могут остаться, если
же взять этот уровень
неоправданно большим, то можно
исключить результаты
со случайными ошибками, необходимые
для правильной
обработки результатов измерения.
Обычно применяют
один из трех уровней малых вероятностей:
5%
уровень (исключаются ошибки, вероятность
появления
которых меньше 0,05);
1
%
уровень
(исключаются ошибки, вероятность
появления
которых меньше 0,01);
0,1%
уровень
(исключаются ошибки, вероятность
появления
которых меньше 0,001).
При
выбранном уровне
![]() малых вероятностей «выскакивающее»
малых вероятностей «выскакивающее»
значение х*
считают
содержащим грубую ошибку,
если для соответствующего отношения t
вероятность
1—2Ф(t)<![]() .
.
Чтобы подчеркнуть вероятностный
характер этого заключения, говорят, что
значение
х*
содержит
грубую ошибку с надежностью вывода
Р=1—![]() .
.
Значение t
= t(Р),
для
которого 1—2Ф(t)
=![]()
и,
значит, 2Ф(t)
=Р, называется критическим
значением
отношения
t
при надежности Р. Так, если
![]()
= 0,01 (1%
уровень),
то Р = 0,99, критическое значение t
= tР)
= 2,576,
и как только отношение t
превзойдет
это критическое значение, мы можем
браковать
«выскакивающее» значение х*
с
надежностью вывода
0,99.
Пример.
Пусть
среди 41 результата независимых измерений,
произведенных
со средней квадратической ошибкой
![]() =0,133,
=0,133,
обнаружено
одно «выскакивающее» значение x*=6,866,
в то время как среднее
из остальных 40 результатов составляет
![]() =6,500.
=6,500.
Можно ли считать,
что «выскакивающее» значение содержит
грубую ошибку, и исключить
его из дальнейшей обработки?
Решение.
Разность между «выскакивающим» значением
и средним составляет
![]() = 0,366, поэтому отношениеt
= 0,366, поэтому отношениеt
равно
![]()
По
табл.2 для t=2,72
оцениваем вероятность 1— 2Ф (t)=
0,0066 < 0,007. Следовательно, с надежностью
вывода Р
> 0,993
можно
считать, что значение x*
содержит
грубую ошибку, и исключить
это значение из дальнейшей обработки
результатов измерения.
Подчеркнем,
что указанный прием применяется только
тогда,
когда величина
![]() средней квадратической ошибкиточно
средней квадратической ошибкиточно
известна заранее.
Метод
исключения при
неизвестной
![]() .
.
Если
величина
![]()
заранее
неизвестна, то она оценивается приближенно
по результатам измерений, т. е. вместо
нее применяют эмпирический стандарт:
![]()
(1)
При
этом абсолютную величину разности
![]() между
между
«выскакивающим» значением х*
и
средним значением
![]()
остальных
(приемлемых) результатов делят на
эмпирический
стандарт и полученное отношение(2)
сравнивают с критическими значениями
![]() (Приложение табл. 3).
(Приложение табл. 3).
![]() (2)
(2)
Если
при данном числе п
приемлемых
результатов отношение (2) оказывается
между двумя
критическими значениями при надежностях
![]()
и
![]() (
(
![]() >
>![]() ),
),
то с надежностью вывода, большей
![]()
можно считать,
что «выскакивающее» значение содержит
грубую ошибку, и исключить его из
дальнейшей обработки результатов.
Заметим,
что если надежность вывода окажется
недостаточной,
то это свидетельствует не об отсутствии
грубой ошибки,
а лишь об отсутствии достаточных
оснований для
исключения «выскакивающего» значения.
Пример.
Пусть для n
результатов независимых равноточных
измерений
некоторой величины среднее значение
равно
![]() = 6,500,а
= 6,500,а
эмпирический стандарт s
=
0,133, и пусть (n
+ 1)-е измерение дало результат
х* = 6,866. Можно ли исключить этот результат
из дальнейшей
обработки?
Решение.
Здесь отношение (2) равно t
= 0,366/0,133 = 2,75. Если
число приемлемых результатов n
= 40, то полученное отношение превосходит
критическое значение 2,742 при надежности
P
= 0,99 и
значение х*
можно
исключить с надежностью вывода, большей
0,99. Если
же число приемлемых результатов n
= 6, то полученное отношение
меньше критического значения 2,78 даже
при надежности P=0,95
и значение x*
исключать не следует.
Грубые ошибки
возникают вследствие нарушения основных
условий измерения или в результате
недосмотра экспериментатора. Внешним
признаком результата, содержащего
грубую ошибку, является его резкое
отличие по величине от результатов
остальных измерений.
Выбор метода
зависит от того, известна ли
среднеквадратическая ошибка измерений
σ
(съёмка данных на конкретном элементарном
объекте измерений проводится с помощью
одного и того же устройства и в одних и
тех же условиях, поэтому можно считать,
что все измерения проводятся с одной и
той же точностью и, кроме того, независимо
друг от друга).
При известной
среднеквадратической ошибке измерений
применяют следующий метод:
Для каждого
экспериментального значения X*
находят выражение
![]() ,
,
(3)
где
![]() — среднее арифметическое всех значений
— среднее арифметическое всех значений
(кроме
X*),
n
– количество этих значений;
Ф(t)
– функция, возвращаемый результат
которой определяется с помощью массива
значений или с помощью формулы
![]() ,
,
(4)
где
![]() t
t
> 0,
ф( — t
) = — ф( t),
(5)
Если α
< А, значит
с вероятностью (1-
α)*100% можно
утверждать, что X*
— грубая ошибка.
Принято выбирать
А
из 0.05, 0.01,
0.001 для
вероятностей 95,
99, 99.9%
соответственно.
Отличительной
чертой исключения грубых ошибок при
неизвестной σ
является её замена в формуле (1) эмпирическим
стандартом
 ,
,
(6)
где i
– номер любого значения, кроме номера
исследуемого значения X*
.
После удаления
грубых ошибок из набора значений, можно
найти интервал, в котором будет находиться
действительное значение.
Xд
= Xcp
± sigma,
где sigma
= σ,
если известно среднеквадратическое
отклонение, или
![]() ,
,
если σ
неизвестно.
Но полученный
интервал можно будет считать верным,
только в определённом случае.
Все
доверительные оценки, как средних
значений, так и дисперсий основаны на
гипотезе нормальности закона распределения
случайных ошибок измерения
и поэтому могут применяться лишь до тех
пор,
пока результаты эксперимента не
противоречат этой гипотезе.
Если
результаты эксперимента вызывают
сомнение в
нормальности закона распределения
случайных ошибок, то
для решения вопроса о пригодности или
непригодности
нормального закона распределения надо
произвести достаточно
большое число измерений и применить
один из
описанных ниже критериев.
Критерий
соответствия
![]() 2
2
(«хи-квадрат»).
Результаты
измерений (разумеется, свободные от
систематических
ошибок) группируют по интервалам таким
образом,
чтобы эти интервалы покрывали всю ось
(-![]() ,
,
+![]() )
)
и чтобы количество данных в каждом
интервале былодостаточно
большим (во всяком случае не менее пяти,
лучше
десяти). Для каждого интервала (![]() )
)
подсчитывают
число
![]()
результатов
измерения, попавших в
этот интервал. Затем вычисляют вероятность
![]() попадания
попадания
в этот интервал при нормальном законе
распределения
вероятностей:
![]() (7)
(7)
где
![]() — среднее арифметическое значение
— среднее арифметическое значение
результатовизмерения,
s—эмпирический
стандарт (средняя квадратическая
ошибка), Ф — интеграл вероятностей,
представленный
таблицами 1 и 2(см. приложение).
Затем, вычисляют сумму
![]() (8)
(8)
где
L — число всех интервалов число всех
результатов измерений (-![]() ,
,![]() ),
),
(![]() ),…,(
),…,(![]() ),
),
n — число всех результатов измерений
(![]() ).
).
Если
сумма (8) окажется больше критического
значения
![]() по табл. 4 принекоторой
по табл. 4 принекоторой
доверительной вероятности P
и
числе степеней
свободы k
= L-3,
то
с надежностью P
можно
считать, что распределение вероятностей
случайных ошибок в
рассматриваемой серии измерений
отличается от нормального.
В противном случае для такого вывода
нет достаточных оснований.
При
отсутствии достаточных оснований для
того, чтобы отвергнуть
гипотезу о нормальном распределении
случайных
ошибок измерения, эта гипотеза
принимается, так как в обычных ситуациях
эта гипотеза часто может быть обоснована
теоретически. Однако следует иметь в
виду, что даже малая величина суммы (8)
не может служить доказательством
нормальности закона распределения.
Отметим
еще важное свойство критерия
![]() :
:
если
распределение
отлично от нормального, то при достаточно
большом числе измерений сумма (8) превысит
соответствующее
критическое значение
![]() .
.
Поэтому,
если при произведенном числе измерений
критерий
![]()
дал малую надежность,
но сомнение в нормальности распределения
осталось,
то следует увеличить число измерений
(в несколько
раз!).
Указанное
выше число степеней свободы k
= L-3
относится только к тому случаю, когда
оба параметра нормального закона
распределения определяются по результатам
измерений, т.е. когда вместо точных
значений а
и
![]() применяются
применяются
их эмпирические значения
![]()
и
s.
Если
значение а
точно
известно (например, при измерении
эталона), то число степеней свободы
равно k
= L-2,
если известны оба параметра а
и
![]() ,
,
то число степеней свободы равно k
= L-1.
На практике такая ситуация встречается
редко, и поэтому для получения числа
степеней свободы не менее пяти надо
брать число интервалов не менее
восьми.
В
заключение заметим, что эффективность
критерия
![]() повышается,
повышается,
если в каждый из выделенных интервалов
попадает примерно одинаковое количество
данных. Это следует
учитывать при группировке первичного
материала (если
возможно).
Пример.
Приведем пример расчета вероятностей
для применения
критерия
![]() .Возьмем
.Возьмем
интервальный ряд данных, значения
параметров нормального распределения
для которого были посчитаны:
![]() =8,63,
=8,63,
s
= 0,127. Для применения критерия
![]() 2
2
объединим крайние интервалы,
чтобы число данных в каждом интервале
стало не менее пяти.
Полученные данные представлены в первых
двух столбцах табл. 1. Крайние интервалы
взяты бесконечными. В третьем столбце
подсчитаны отношения
![]()
для
правых концов интервалов, например,
![]() = (8,425-8,63)/0,127 =-1,614.
= (8,425-8,63)/0,127 =-1,614.
В четвертом столбце приведены
соответствующие значения интеграла
вероятностей Ф (![]() )(Приложение
)(Приложение
табл. 1). При
этом произведена линейная интерполяция.
По значениям
Ф (![]() )-в
)-в
пятом столбце вычислены вероятности![]() —
—
как разностисоответствующих
значений Ф (t):
![]()
например,
р2
= -0,3888 — (-0,4467) = 0,0579. При вычислении
вероятности
![]() учтено, что Ф(-
учтено, что Ф(-![]() )
)
= -0,5. Последние столбцы таблицы
не нуждаются в пояснении. Сумма чисел
последнего столбца дает
нужное значение
![]() 2
2
=2,528. Сравнение этого значения с
критическими
значениями при числе степеней свободы
k
=10-3
= 7 показывает, что нет оснований
сомневаться в нормальности распределения
(основания для подобного сомнения могли
бы возникнуть, если
бы вычисленное значение
![]() 2
2
было бы по крайней мере раз в
5—6 больше).
Таблица
1
|
Интервалы |
|
|
|
|
|
|
|
|
||||||
|
(-
(8,425;
(8,475;
(8,525;
(8,575;
(8,625;
(8,675;
(8,725;
(8,775;
(8,825; |
7 5 8 10 18 17 12 9 7 7 |
-1,614 -1,220 -0,827 -0,433 -0,039 0,354 0,748 1,142 1,536
+ |
-0,4467 -0,3888 -0,2959 -0,1676 -0,0156 0,1383 0,2728 0,3733 0,4377 0,5000 |
0,0533 0,0579 0,0929 0,1283 0,1520 0,1539 0,1345 0,1005 0,0644 0,0623 |
1,67 -0,79 -1,29 -2,83 2,80 1,61 -1,45 -1,05 0,56 0,77 |
0,523 0,108 0,179 0,624 0,516 0,168 0,157 0,110 0,048 0,095 |
|
Суммы |
100=n |
— |
— |
1,0000 |
— |
2,528= |
Для
этого определяется критерий соответствия
χ2, который должен быть достаточно мал.
В этом случае с определённой достоверностью
можно будет говорить о нормальности
распределения набора значений, а как
следствие этого – право с определённой
вероятностью утверждать, что полученный
интервал верен.
Результаты
измерений, освобождённые от грубых
ошибок, группируют по интервалам таким
образом, чтобы они покрыли всю ось и
чтобы количество данных в каждом
интервале было достаточно большим.
Для
каждого интервала подсчитывают число
результатов измерения mi , попавших в
этот интервал.
Затем
вычисляется вероятность pi попадания в
этот интервал при нормальном законе
распределения вероятностей
![]() ,
,
где
Xi – правая граница i-го интервала.
Необходимо заметить,
что для первого интервала
![]() ,
,
Для последнего
интервала
![]()
В
качестве проверки правильности расчёта
значений pi можно использовать равенство
![]() .
.
Непосредственно
χ2 находится по формуле:
![]() ,
,
где
l – количество интервалов.
Если
полученное значение χ2 окажется больше
критического значения χ2кр
, при некоторой доверительной вероятности
Р и числе степеней свободы k = l – 3, то с
надёжностью Р можно считать, что
распределение вероятностей случайных
ошибок в рассматриваемой серии измерений
отличается от нормального. В противном
случае для такого вывода нет достаточных
оснований.
При
отсутствии достаточных оснований для
того, чтобы отвергнуть гипотезу о
нормальном распределении случайных
ошибок измерения, эта гипотеза
принимается, а следовательно интервал
Xд = Xcp ± sigma можно считать верным.
Разработанная автоматизированная
система позволяет оперативно проводить
оценку грубых ошибок эксперимента и
достоверность нормального распределения
результатов. Ввод данных осуществляется
автоматически с устройства либо из
предварительно подготовленного файла
данных.

Рис.1. Пример работы
автоматизированной системы оценки
статистических данных
В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.
Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.
Ключевые слова:
грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.
Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.
Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.
На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.
Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят
,
однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.
Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:
- Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
- Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
- Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).
В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.
В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].
Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.
Задаются вероятностью
Р
или уровнем значимости
α
(
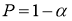
) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».
Проверяемая гипотеза состоит в утверждении, что результат наблюдения
x
i
не содержит грубой погрешности, т. е. является одним из значений случайной величины
x
с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
max
или наименьший xmin из результатов наблюдений.
Предложим для практического использования наиболее простые методы отсева грубых погрешностей.
Если в распоряжении экспериментатора имеется выборка небольшого объема
n
≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:
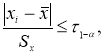
(1)
где
x
i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения
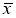
и среднеквадратичного отклонения
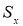
;
τ
1-
p
— табличное значение статистики
τ
, вычисленной при доверительной вероятности
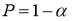
.
Таким образом, для выделения аномального значения вычисляют значение статистики,
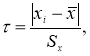
(2)
которое затем сравнивают с табличным значением
τ
1-α
:
τ
≤
τ
1-α
. Если неравенство
τ
≤
τ
1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.
Квантили распределения статистики
τ
при уровнях значимости
α
= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности
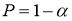
=
0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости
α
= 0,05 (результат получается с 95 %-й доверительной вероятностью).
Функции распределения статистики
τ
определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности
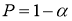
или уровне значимости
α
можно для чисел измерения п = 3–25 найти те наибольшие значения
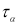
которые случайная величина
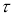
может еще принять по чисто случайным причинам.
Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения
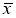
и среднеквадратичного отклонения
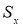
для выборки нового объема
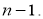
Таблица 1
Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]
|
|
Уровень значимости |
|
Уровень значимости |
||||||
|
0,10 |
0,05 |
0,025 |
0,01 |
0,10 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2,98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
|||||
В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.
- Критерий «трех сигм» применяется для случая, когда измеряемая величина
x
распределена по нормальному закону. По этому критерию считается, что с вероятностью
Р
= 0,9973 и значимостью
α
= 0,0027 появление даже одной случайной погрешности, большей, чем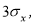
маловероятное событие и ее можно считать промахом, если
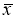
−
x
i
> 3
S
x
, где
S
x
—
оценка среднеквадратического отклонения (СКО) измерений. Величины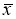
и
S
x
вычисляют без учета экстремальных значений
x
i
. Данный критерий надежен при числе измерений
n
≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при
6 <
n
≤100 она равна 4
S
x
; при 100 <
n
≤1000 − 4,5
S
x
; при 1000 <
n
≤10000–5
Sx
. Данное правило также используется только при нормальном распределении.
Практические вычисления проводят следующим образом [5, с. 65]:
- Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
- Вычисляют среднее арифметическое значение выборки
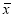
без учета сомнительного значения
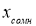
измеряемой величины.
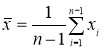
(3)
- Вычисляют оценку СКО выборки
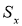
без учета сомнительного значения
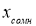
измеряемой величины.
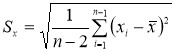
(4)
- Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.
Если
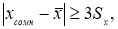
то сомнительное значение отбрасывают, как промах.
Если
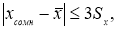
то сомнительное значение оставляют как равноправное в ряду наблюдений.
Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.
- Критерий В. И. Романовского применяется, если число измерений невелико,
n
≤ 20. При этом вычисляется соотношение
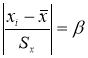
(5)
где
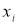
— результат, вызывающий сомнение,
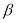
— коэффициент, предельное значение которого
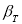
определяют по таблице 2. Если
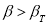
, сомнительное значение
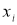
исключают («отбрасывают») как промах. Если
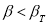
,
сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].
Таблица 2
Значение критерия Романовского
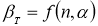
|
Уровень значимости, |
Число измерений, |
||||||
|
|
|
|
|
|
|
|
|
|
0,01 |
1,73 |
2,16 |
2,43 |
2,62 |
2,75 |
2,90 |
3,08 |
|
0,02 |
1,72 |
2,13 |
2,37 |
2,54 |
2,66 |
2,80 |
2,96 |
|
0,05 |
1,71 |
2,10 |
2,27 |
2,41 |
2,52 |
2,64 |
2,78 |
|
0,10 |
1,69 |
2,00 |
2,17 |
2,29 |
2,39 |
2,49 |
2,62 |
Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.
- Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.
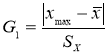
и
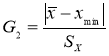
(6)
Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев
t
-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.
Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.
Если G1
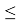
GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2
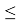
GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.
Отсев грубых погрешностей можно производить и для больших выборок (
n
= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].
Известно, что критическое значение
τ
p
(
p
— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента
t
α, n-2
[6, с. 26]:
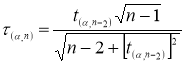
(7)
Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (
n
= 100):
1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;
2)
по формуле
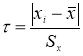
вычисляют значение статистики
τ
;
3)
по таблице (или в программе Excel) находят процентные точки
t
-распределения Стьюдента
t
(
α,
n
-2
)
:
t
(95
%, 98)
= 1,6602, и
t
(
99
%, 98)
= 3,1737;
По предыдущей формуле в программе Excel вычисляют соответствующие точки
t
(95
%, 100)
= 1,66023и
t
(99
%, 100)
=3,17374.
Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.
Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)
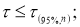
2)
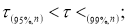
3)
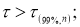
.
Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.
Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.
Пример 1.
Имеется выборка из 100 шт. резисторов с номинальным сопротивлением
R
н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.
- Заносим данные измерений в таблицу Excel в ячейки В2:В101
- Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)
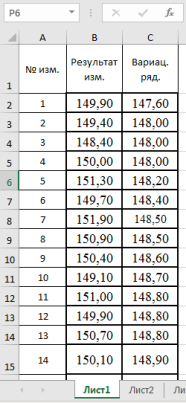
Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).
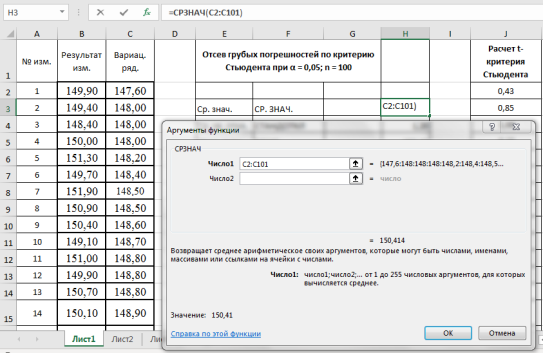
Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки
- Находим среднеквадратическое отклонение —
S
x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).
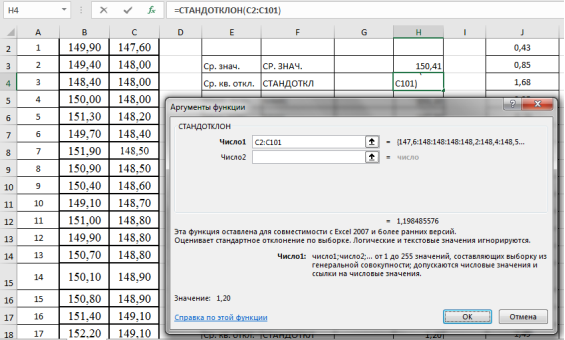
Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения
- Находим максимальное значение в выборке —
x
макс
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).
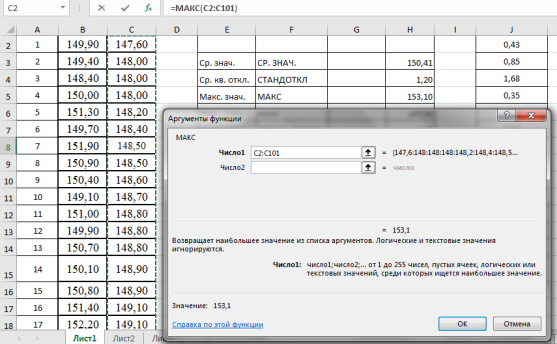
Рис. 4. Фрагмент диалогового окна при нахождении максимального значения
- Находим минимальное значение в выборке —
x
мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).
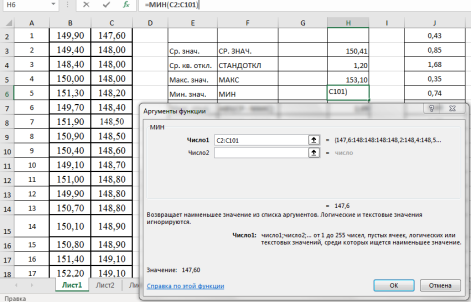
Рис. 5. Фрагмент диалогового окна при нахождении минимального значения
- Находим максимальное и минимальное отклонения — Δ
макс
и Δ
мин
. Вводим в ячейки Н7 и Н8 формулы:
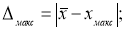
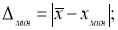
- Находим теоретическое значение —
t
теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу
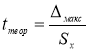
. и
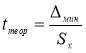
- Находим табличное значение
t
табл.
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (
n
-2) — 98, результат в ячейке Н10–1,66 (рис. 6).
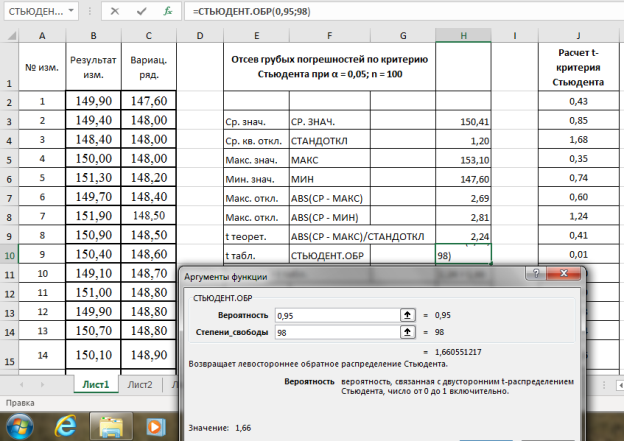
Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента
- Сравниваем теоретическое значение
t
теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:
t
табл
.= 1,6605. - Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).
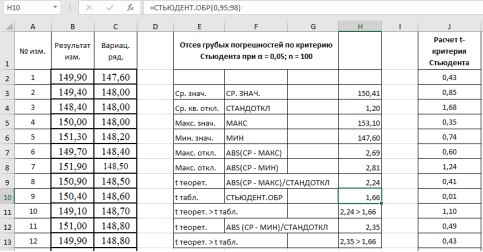
Рис. 7. Фрагмент диалогового окна при окончательном анализе данных
- Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.
Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений
n
= 20, β
табл
= 2,78 (из таблицы 2).

Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского
Выводы
- Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
- Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.
Литература:
1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.
2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.
3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.
4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.
5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.
6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.
Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.
Системы оценивания письменных работ по
математике
При проверке
усвоения материала необходимо выявлять полноту, прочность усвоения
учащимися теории и
умения применять ее на практике в знакомых и незнакомых ситуациях.
Формами контроля качества освоения содержания
учебной программы учащимися являются:
·
Письменная
проверка предполагает письменный
ответ учащегося на один или систему вопросов (заданий). К письменным ответам
относятся: домашние, проверочные, практические, контрольные, творческие работы,
письменные ответы на вопросы теста, рефераты и пр.
·
Устная проверка предполагает устный ответ учащегося на один
или систему вопросов в форме рассказа, беседы, собеседования и другое.
·
Комбинированная проверка
предполагает сочетание устных и письменных форм работы.
Рассмотрим оценивание письменной проверки.
Оценка ответа
учащегося при письменном опросе проводится по пятибалльной системе, т.
е. за ответ выставляется одна из отметок:5 (отлично), 4
(хорошо), 3 (удовлетворительно), 2 (неудовлетворительно), 1 (плохо) на
практике такую оценку практически не используют.
Учителю
важно знать, как соотнести фактические знания ученика и оценку, отражающую эти
знания.
В
зависимости от поставленных целей по-разному строится программа контроля,
подбираются различные типы вопросов и заданий. Но применение примерных норм
оценки знаний должно внести единообразие в оценку знаний и умений учащихся и
сделать ее более объективной. Примерные нормы представляют основу, исходя из
которой, учитель оценивает знания и умения учащихся.
Содержание и объем материала, подлежащего проверке и оценке, определяются программой по математике
для средней школы. В задания для проверки включаются основные, типичные и
притом различной сложности вопросы, соответствующие проверяемому разделу
программы.
При
проверке знаний и умений, учащихся учитель выявляет не только степень усвоения
учащимися теории и умения применять ее на практике, но также умение
самостоятельно мыслить.
Основными формами проверки знаний и умений учащихся по математике в средней школе являются устный
опрос и письменная контрольная работа, наряду с которыми применяются и другие
формы проверки. Письменная контрольная работа позволяет оценить умение учащихся
излагать свои мысли на бумаге; навыки грамотного и фактически грамотного
оформления выполняемых ими заданий.
При оценке письменных контрольных работ учитель в первую очередь учитывает имеющиеся у
учащегося фактические знания и умения, их полноту, прочность, умение применять
на практике в различных ситуациях. Результат оценки зависит также от наличия и
характера погрешностей, допущенных при письменной контрольной работе.
Среди
погрешностей выделяются ошибки, недочеты и мелкие погрешности.
Погрешность
считается ошибкой, если она свидетельствует о том, что ученик не овладел
основными знаниями, умениями и их применением.
К
недочетам относятся погрешности, свидетельствующие о недостаточно полном
или недостаточно прочном усвоении основных знаний и умений или об отсутствии
знаний, не считающихся в соответствии с программой основными. К недочетам относятся
погрешности, объясняющиеся рассеянностью или недосмотром, но которые не привели
к искажению смысла полученного учеником задания или способа его выполнения.
Грамматическая ошибка, допущенная в написании известного учащемуся
математического термина, небрежная запись, небрежное выполнение чертежа
считаются недочетом.
К
мелким погрешностям относятся погрешности в письменной речи, не
искажающие смысла ответа или решения, случайные описки и т. п.
Граница между ошибками и недочетами является в некоторой степени условной. В одно время
при одних обстоятельствах допущенная учащимися погрешность может
рассматриваться как ошибка, в другое время и при других обстоятельствах она
может рассматриваться как недочет.
Решение
задачи считается безупречным, если получен верный ответ при правильном ходе
решения, выбран соответствующий задаче способ решения, правильно выполнены
необходимые вычисления и преобразования, последовательно и аккуратно оформлено
решение.
Оценивание письменных контрольных работ.
Ответ оценивается отметкой «5»,
если:
·
работа выполнена
полностью;
·
в логических рассуждениях
и обосновании решения нет пробелов и ошибок;
·
в решении нет
математических ошибок (возможна одна неточность, описка, которая не является
следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
·
работа выполнена
полностью, но обоснования шагов решения недостаточны (если умение обосновывать
рассуждения не являлось специальным объектом проверки);
·
допущены одна ошибка или
есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти
виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
·
допущено более одной
ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но
учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
·
допущены существенные
ошибки, показавшие, что учащийся не обладает обязательными умениями по данной
теме в полной мере.
Отметка «1» ставится в случае:
·
полного незнания
изученного материала, отсутствия элементарных умений и навыков.
Общая классификация ошибок
При оценке знаний, умений и навыков учащихся
следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
·
незнание определения
основных понятий, законов, правил, основных положений теории, незнание формул,
общепринятых символов обозначений величин, единиц их измерения;
·
незнание наименований
единиц измерения;
·
неумение выделить в ответе
главное;
·
неумение применять знания,
алгоритмы для решения задач;
·
неумение делать выводы и
обобщения;
·
неумение читать и строить
графики;
·
неумение пользоваться
первоисточниками, учебником и справочниками;
·
потеря корня или
сохранение постороннего корня;
·
отбрасывание без
объяснений одного из них;
·
равнозначные им ошибки;
·
вычислительные ошибки,
если они не являются опиской;
·
логические ошибки
·
вычислительные ошибки в
примерах и задачах;
·
-ошибки на незнание
порядка выполнения арифметических действий;
·
-неправильное решение
задачи (пропуск действий, неправильный выбор действий, лишнее действие);
·
-недоведение до конца
решения задачи или примера;
·
-невыполненное задание
·
-неправильный выбор
порядка выполнения действий в выражении;
·
-пропуск нуля в частном
при делении натуральных чисел или десятичных дробей;
·
-неправильный выбор знака
в результате выполнения действий над положительными и отрицательными числами; а
так же при раскрытии скобок и при переносе слагаемых из одной части уравнения в
другую;
·
— неправильный выбор
действий при решении текстовых задач;
·
-неправильное измерение
или построение угла с помощью транспортира, связанное с отсутствием умения
выбирать нужную шкалу;
·
-неправильное проведение
перпендикуляра к прямой или высот в тупоугольном треугольнике;
·
-умножение показателей при
умножении степеней с одинаковыми основаниями;
·
-“сокращение” дроби на
слагаемое;
·
-замена частного
десятичных дробей частным целых чисел в том случае, когда в делителе после
запятой меньше цифр, чем в делимом;
·
-сохранение знака
неравенства при делении обеих его частей на одно и тоже отрицательное число;
·
-неверное нахождение
значения функции по значению аргумента и ее графику;
·
-потеря корней при решении
тригонометрических уравнений;
·
-непонимание смысла
решения системы двух уравнений с двумя переменными как пары чисел;
·
-незнание определенных
программой формул (формулы корней квадратного уравнения, формул производной
частного и произведения, формул приведения, основных тригонометрических
тождеств и др.);
·
-приобретение посторонних
корней при решении иррациональных, показательных и логарифмических уравнений;
·
-погрешность в нахождении
координат вектора;
·
-погрешность в разложении
вектора по трем неколлинеарным векторам, отложенным от разных точек;
·
-неумение сформулировать
предложение, обратное данной теореме;
·
-ссылка при доказательстве
или обосновании решения на обратное утверждение, вместо прямого;
·
— использование вместо
коэффициента подобия обратного ему числа.
К негрубым ошибкам следует
отнести:
·
неточность формулировок,
определений, понятий, теорий, вызванная неполнотой охвата основных признаков
определяемого понятия или заменой одного — двух из этих признаков
второстепенными;
·
неточность графика;
·
нерациональный метод
решения задачи или недостаточно продуманный план ответа (нарушение логики,
подмена отдельных основных вопросов второстепенными);
·
нерациональные методы
работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в
общем виде
·
неправильная постановка
вопроса к действию при решении задачи;
·
неверно сформулированный
ответ задачи;
·
неправильное списывание
данных чисел, знаков;
·
недоведение до конца
преобразований.
·
неправильная ссылка на
сочетательный и распределительный законы при вычислениях;
·
неправильное использование
в отдельных случаях наименований, например, обозначение единиц длины для единиц
площади и объема;
·
сохранение в окончательном
результате при вычислениях или преобразованиях выражений неправильной дроби или
сократимой дроби;
·
приведение алгебраических
дробей не к наиболее простому общему знаменателю;
·
случайные погрешности в
вычислениях при решении геометрических задач и выполнении тождественных
преобразований.
Недочетами являются:
·
нерациональные приемы
вычислений и преобразований; небрежное выполнение записей, чертежей, схем,
графиков.
Оценивание решения одной задачи, одного примера, ответа на один вопрос.
Это
необходимо, т. к. у доски, да часто и самостоятельно в классе учащиеся решают
одну задачу. К тому же умение оценивать решение одной задачи облегчает оценку
комплексного задания.
Решение
задачи обычно состоит из нескольких этапов:
а)
осмысление условия и цели задачи;
б)
возникновение плана решения;
в)
осуществление намеченного плана;
г)
проверка полученного результата.
Оценивая
выполненную работу, естественно учитывать результаты деятельности учащегося на
каждом этапе; правильность высказанной идеи, плана решения, а так же степень
осуществления этого плана при выставлении оценки нужно считать решающими. Т.о.,
при оценке решения задачи необходимо учитывать, насколько правильно учащийся
понял ее, высказал ли он плодотворную идею и как осуществил намеченный план
решения, какие навыки и умения показал, какие использовал знания.
Приведем пример.
Ученик
решает задачу, где важнейшим является составление системы уравнений. Если он
получил систему, но не довел решение до конца, то можно выставить “4”. Если же
основная задача состоит в решении полученной системы, то за ее составление
можно выставить “3”.
Оценка письменной работы по выполнению
вычислительных заданий и алгебраических преобразований
Оценка «5» ставится за безукоризненное выполнение письменной
работы, т.е.:
а) если решение всех примеров верное;
б) если все действия и преобразования
выполнены правильно, без ошибок; все записи хода решения расположены
последовательно, а также сделана проверка решения в тех случаях, когда это
требуется.
Оценка «4» ставится за работу, в которой допущена одна (негрубая)
ошибка или два-три недочета.
Оценка «3» ставится в следующих случаях:
а) если в работе имеется одна грубая ошибка и
не более одной негрубой ошибки;
б) при наличии одной грубой ошибки и
одного-двух недочетов;
в) при отсутствии грубых ошибок, но при
наличии от двух до четырех (негрубых) ошибок;
г) при наличии двух негрубых ошибок и не более
трех недочетов;
д) при отсутствии ошибок, но при наличии
четырех и более недочетов;
е) если неверно выполнено не более половины
объема всей работы.
Оценка «2» ставится, когда число ошибок превосходит норму, при
которой может быть выставлена положительная оценка, или если правильно
выполнено менее половины всей работы.
Оценка «1» ставится, если ученик совсем не выполнил работу.
Примечание. Оценка «5» может быть поставлена,
несмотря на наличие одного-двух недочетов, если ученик дал оригинальное решение
заданий, свидетельствующее о его хорошем математическом развитии.
Оценка письменной работы на решение текстовых
задач
Оценка «5» ставится в том случае, когда задача решена правильно:
ход решения задачи верен, все действия и преобразования выполнены верно и
рационально; в задаче, решаемой с вопросами или пояснениями к действиям, даны
точные и правильные формулировки; в задаче, решаемой с помощью уравнения, даны необходимые
пояснения; записи правильны, расположены последовательно, дан верный и
исчерпывающий ответ на вопросы задачи; сделана проверка решения (в тех случаях,
когда это требуется).
Оценка «4» ставится в том случае, если при правильном ходе
решения задачи допущена одна негрубая ошибка или два-три недочета.
Оценка «3» ставится в том случае, если ход решения правилен, но
допущены:
а) одна грубая ошибка и не более одной
негрубой;
б) одна грубая ошибка и не более двух
недочетов;
в) три-четыре негрубые ошибки при отсутствии
недочетов;
г) допущено не более двух негрубых ошибок и
трех недочетов;
д) более трех недочетов при отсутствии ошибок.
Оценка «2» ставится в том случае, когда число ошибок превосходит
норму, при которой может быть выставлена положительная оценка.
Оценка «1» ставится в том случае, если ученик не выполнил ни одного
задания работы.
Примечания:
1. Оценка «5» может быть поставлена
несмотря на наличие описки или недочета, если ученик дал оригинальное решение, свидетельствующее
о его хорошем математическом развитии.
2. Положительная оценка «3» может быть
выставлена ученику, выполнившему работу не полностью, если он безошибочно выполнил
более половины объема всей работы.
Оценка комбинированных письменных работ по
математике
Письменная работа по математике, подлежащая
оцениванию, может состоять из задач и примеров (комбинированная работа). В таком
случае преподаватель сначала дает предварительную оценку каждой части работы, а
затем общую, руководствуясь следующим:
а) если обе части работы оценены одинаково, то
эта оценка должна быть общей для всей работы в целом;
б) если оценки частей разнятся на один балл,
например, даны оценки «5» и «4» или «4» и «3» и т. п., то за работу в целом,
как правило, ставится балл, оценивающий основную часть работы;
в) если одна часть работы оценена баллом «5»,
а другая — баллом «3», то преподаватель может оценить такую работу в целом баллом
«4» при условии, что оценка «5» поставлена за основную часть работы;
г) если одна из частей работы оценена баллом
«5» или «4», а другая — баллом «2» или «1», то преподаватель может оценить всю
работу баллом «3» при условии, что высшая из двух данных оценок поставлена за
основную часть работы.
Примечание. Основной считается та часть работы, которая включает
больший по объему или наиболее важный по значению материал по изучаемым темам
программы.
Оценка текущих письменных работ
При оценке повседневных обучающих работ по
математике учитель руководствуется указанными нормами оценок, но учитывает
степень самостоятельности выполнения работ учащимися.
Обучающие письменные работы, выполненные
учащимися вполне самостоятельно с применением ранее изученных и хорошо закрепленных
знаний, оцениваются так же, как и контрольные работы.
Обучающие письменные работы, выполненные
вполне самостоятельно, на только что изученные и недостаточно закрепленные правила,
могут оцениваться менее строго.
Письменные работы, выполненные в классе с предварительным
разбором их под руководством учителя, оцениваются более строго.
Домашние письменные работы оцениваются так же,
как классная работа обучающего характера.
В соответствии с особенностями математики как
учебного предмета оценки за письменные работы имеют большее значение, чем
оценки за устные ответы и другие виды работ.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Методы робастного оценивания — это статистические методы, которые позволяют получать достаточно надежные оценки статистической совокупности(См.[6]).
Единицы статистической совокупности, у которых значения анализируемого признака существенно отклоняются от основного массива, называются аномальными явлениями, «грубыми ошибками» или выбросами.
При решении задач статистического анализа проблема наличия в выборке аномальных измерений имеет чрезвычайно важное значение. Присутствие единственного аномального наблюдения может приводить к оценкам, которые совершенно не согласуются с выборочными данными.
Для данных индексов построим точечный график (Рисунок 7). В ходе визуального анализа выявляем наличие в выборке аномальных значений (выбросов).

Рисунок 7. Точечный график
Самым простым методом обнаружения грубых ошибок считается метод, на основании Т — Критерия Граббса:

, где (1.4)
— среднее значение, x — аномальное значение, s — выборочное среднеквадратическое отклонение СВ.
Данный критерий можно использовать для выделения аномальных результатов измерений только в случае нормального закона.
Так как выборка распределена нормально, мы можем найти Тк, и проверить наличие грубых ошибок в выборке.
Результаты расчетов по выборке представлены на Рисунке 8:

Рисунок 8.Результаты вычисления
Полученные значения сравнивают с табличными значениями процентных точек критерия Смирнова Граббса (Таблица 1). В том случае, если >, мы может утверждать, что проверяемое значение является грубой ошибкой и относится к классу выбросов.
Таблица 1. Значения процентных точек критерия Смирнова Граббса
|
0.99 |
0.95 |
|
|
30 |
0.4257 |
0.4791 |
|
31 |
0.4376 |
0.4885 |
|
32 |
0.4477 |
0.4995 |
|
33 |
0.4558 |
0.5099 |
|
34 |
0.4688 |
0.5189 |
|
35 |
0.4779 |
0.5285 |
|
36 |
0.4874 |
0.5374 |
|
37 |
0.4970 |
0.5459 |
|
38 |
0.5048 |
0.5540 |
|
39 |
0.5145 |
0.5617 |
|
40 |
0.5211 |
0.5692 |
|
41 |
0.5307 |
0.5767 |
|
42 |
0.5385 |
0.5835 |
|
43 |
0.5450 |
0.5902 |
|
44 |
0.5522 |
0.5970 |
|
45 |
0.5599 |
0.6033 |
|
46 |
0.5675 |
0.6090 |
|
47 |
0.5742 |
0.6154 |
|
48 |
0.5789 |
0.6211 |
|
49 |
0.5861 |
0.6270 |
|
50 |
0.5910 |
0.6324 |
Сравним полученные значения с табличным (при = 0,01) при числе наблюдений равном 48, а Ткр = 0,5789.
Так как Тк(1) =1,9> = 0,5789, то проверяемое значение является грубой ошибкой и относится к классу выбросов.
Аналогично Тк(2) =3,33> = 0,5789, что подтверждает, что рассматриваемое значение является аномальным значением.
Критерий Граббса имеет некоторые недостатки. Он не точен, и не чувствителен к засорениям, когда ошибки группируются на расстоянии от общей совокупности.
Далее подтвердим наличие грубых ошибок на основании L- критерия Титьена-Мура (См.[9]).
Решающее правило для исключения k наибольших членов вариационного ряда основано на статистике:

, где (1.5)
 Воспользовавшись формулами, было найдено значение L-критерия Титьена-Мура для рассматриваемой выборки (Рисунок 9)
Воспользовавшись формулами, было найдено значение L-критерия Титьена-Мура для рассматриваемой выборки (Рисунок 9)
Рисунок 9. Значение L-критерия Титьена-Мура
Сравниваем полученное значение с критическим пределом (Таблица 2). При наличии выбросов статистика Lk должна быть меньше критического предела. В данном случае Lk = 0,67887 <Cкр = 0,696, что подтверждает наличие аномальных значений в выборке (См.[9]).
Таблица 2. Критические значения оценки для L — критерия Титьена и Мура (a=0,05)

Для избавления от выбросов изменим данные доходностей, исключим значение 0,076594461 и -0,125593848, что приведет к нормальному распределению.
Гистограмма при этом теперь имеет вид (Рисунок 10):

Рисунок 10.Гистограмма
Оценка функции распределения и построение ее графика. Интерпретация полученных результатов и предварительный закон распределения
Каждая случайная величина полностью определяется своей функцией распределения.
Если X — случайная величина, то функция F(x) = FX (x) = P (X <x) называется функцией распределения случайной величины X. Здесь P (X <x) — вероятность того, что случайная величина X принимает значение, меньшее x.
Важно понимать, что функция распределения содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
1. F(x) определена на всей числовой прямой R;
2. F(x) не убывает, т.е. если x1x2, то F(x1) F(x2);

3. F(-)=0, F(+)=1, т.е. и ;

4. F(x) непрерывна справа, т.е.

Для построения функции распределения необходимо взять накопленные частоты. Они определяются путем последовательного суммирования частот предшествующих интервалов (Рисунок 11).

Рисунок 11. Накопленные частоты
Таким образом график оценки функции имеет вид (Рисунок 12):

Рисунок 12. График оценки функции
Полученная функция распределения соответствует нормальному закону распределения, поэтому логично предположить, что финансовые индексы валютной пары евро/рубль распределены нормально.
