Минимальная
дисперсия шумовой ошибки определяет
потенциальную точность измерения
координат.
Среднеквадратичная
ошибка измерения дальности:
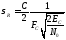, гдеFC– эффективная ширина спектра сигнала.
Среднеквадратичная
ошибка измерения радиальной скорости:
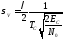где ТC– длительность
сигнала (пачки когерентных импульсов).
СКО измерения
угла:
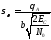где θА–ширина диаграммы
направленности антенны;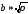
— коэффициент
Шумовые
ошибки измерения координат тем меньше,
чем больше отношение сигнал/шум.
Для уменьшения
ошибки дальности – расширить спектр
сигнала.
Для уменьшения
ошибки измерения скорости – увеличить
длительность сигнала.
Для увеличения
СКО угловой координаты – сужать Д.Н.
антенны.
29. Реализация измерителей в многоканальном и следящем виде
Многоканальный
фильтровой измеритель скорости:
Обозначения: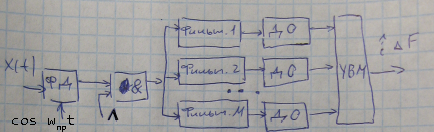
ФД – фазовый
детектор;
ДО – детектор
огибающей;
УВМ –
устройство выбора максимума.
Расчёты
для его реализации.
Требуемое
число фильтров определяется диапазоном
доплеровских частот и полосой одного
фильтра:
Полоса одного
фильтра:
Разная частота
фильтров
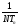или
.
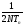Число фильтров
будет вдвое больше, что уменьшает
вероятность пропуска сигнала из-за
«провалов» на АЧХ соседних фильтров
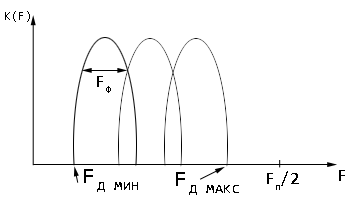
Многоканальный
измеритель при М>20 реализуется в виде
вычислителя дискретного преобразования
Фурье (ДПФ). Практически реализуется в
виде быстрого преобразования Фурье
(БПФ). При размере выборки Nчерез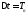
ДПФ запишется так:
, гдеan
– весовые коэффициенты.
Каждому
коэффициенту
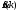соответствует
полоса эквивалентного фильтра
Следящий
измеритель скорости
Устройство
должно оценивать доплеровский сдвиг и
осуществлять слежение за изменением
Fд(t).
Схема
реализации устройства:
СМ – смеситель;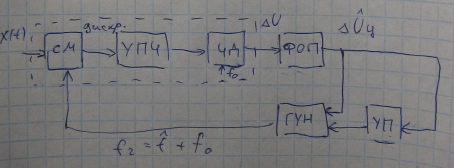
ЧД – частотный
детектор;
ФОП – фильтр
оценки доплеровского сдвига (ФНЧ);
ГУН – генератор
управляемый напряжением;
УП – устройство
поиска;
(стр. 116
Сперанский)
30. Импульсный метод измерения дальности. Цифровой и визуальный съем дальности
Дальность в
радиолокации измеряется путем прямой
или косвенной оценки задержки радиосигнала
от цели. При импульсном методе производится
прямое измерение задержки сигнала
,
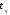отраженного от цели относительно момента
излучения зондирующего сигнала радиоволн.
С учетом скорости распространения
радиоволн дальность равна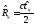
.
Визуальный
– по экрану электронно-лучевой трубки,
путем подсчета импульсов меток между
пусковым и импульсом цели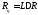
,
гдеL– оценка числа
счётных импульсов.
31. Частотный метод измерения дальности. Радиовысотомер малых высот
При этом
методе применяется непрерывный
зондирующий сигнал с линейной или
синусоидальной частотной модуляцией.
Максимальное
отклонение частоты называется девиацией
частоты. модуляция применяется
периодическая с периодом модуляции
.
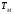Частота зондирующего сигнала в момент
времениtравна:
,
где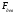
— частота девиации.
За время
распространения сигнала за счёт частотной
модуляции частота опорного сигнала
меняется: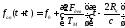
Разность
частот называется частотой биения:
.
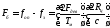Измерив
частоту биений, можно оценить дальность
до цели:
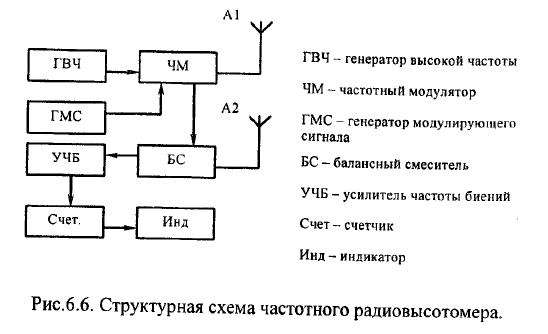
Радиовысотомер:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание раздела «Точность радиолокационных измерений»
- Точность определения дальности
- Случайная ошибка измерения
- Математические соотношения
- Систематические ошибки измерения
- Точность измерения угловых координат
- Как выполняется измерение для оценки точности радиолокатора?
- Примеры
Точность радиолокационных измерений
Точность это степень соответствия между оцениваемыми или измеряемыми значениями параметров
(координаты и/или скорость движения) лоцируемого объекта в определенный момент времени и их истинными значениями.
В радиолокации точность измерения обычно представляется как статистическая мера систематической ошибки,
которая характеризуется следующими свойствами:
- Предсказуемость: Точность позиционирования определяется при использовании географических или геодезических систем координат Земли.
- Повторяемость: Означает то, что результаты измерения одной и той же системой в сходных условиях,
будут характеризоваться близкими значениями точности в пределах некоторого интервала времени. - Относительность: Точность измерений относительно одной позиции может быть пересчитана для другой позиции (пренебрегая всевозможными ошибками).
Заявленное значение требуемой точности показывает,
что определяемое системой измерения значение того или иного параметра может отклоняться от его истинного значения,
и указывает интервал значений, в котором находится истинное значение с заданной вероятностью.
Рекомендуемое значение вероятности 95%, что соответствует интервалу,
равному удвоенному среднеквадратическому отклонению относительно среднего значения для нормального (Гауссового) распределения случайной величины.
Предположение, что все известные поправки учтены, означает, что ошибки оценивания будут иметь средние значения (смещения), близкие к нулю.
Любое остаточное смещение должно быть небольшим по сравнению с заявленной точностью.
Истинное значение — это значение, которое в рабочих условиях наилучшим образом характеризует измеряемую величину,
наблюдаемую в пределах репрезентативного (достаточного) интервала времени, площади и / или объема с учетом расположения и влияющих факторов.
ошибка измерения
импульс+шум
порог
идеальный импульс
Рисунок 1. Искажение фронта импульса под воздействием шумов
ошибка измерения
импульс+шум
порог
идеальный импульс
Рисунок 1. Искажение фронта импульса под воздействием шумов
Точность определения дальности
Теоретическая максимально достижимая точность измерения дальности методом радиолокационной импульсной дальнометрии
зависит от точности измерения времени запаздывания отраженного сигнала.
Случайные ошибки измерения
Случайные ошибки измерения в
импульсных радиолокаторах
возникают когда передний фронт отраженного сигнала искажается под воздействием шумов.
На отраженный сигнал всегда накладываются шумы, в результате чего увеличивается амплитуда принятого сигнала.
Это вызывает смещение переднего фронта импульса и, следовательно, является причиной ошибки измерения времени запаздывания отраженного сигнала.
На Рисунке 1 показано влияние шумов на обнаруживаемый передний фронт эхо-сигнала.
Сплошной линией (фиолетовой) изображен идеальный трапецеидальный импульс с довольно крутыми фронтом и спадом.
Этот импульс не может быть слишком близким к прямоугольному, поскольку это потребовало бы бесконечно широкой полосы частот.
Время задержки импульса измеряется в момент времени, когда его амплитуда достигает порогового значения, обычно на уровне 0,707 от максимальной амплитуды.
Однако на отраженный импульс накладывается шум (зеленая линия).
Измеренным может быть только напряжение, являющееся суммой мгновенных значений амплитуды импульса и шума
(желтая синяя пунктирная линия).
Это напряжение достигнет порогового значения раньше, чем напряжение идеального (в отсутствии шумов) импульса.
Разница между ними — это случайная ошибка измерения времени задержки, вызванная влиянием
шумов[1].
Если длительность импульса известна (что невозможно для первичного радиолокатора, а только для
вторичного радиолокатора),
то эта случайная ошибка может быть уменьшена математически путем одновременной оценки переднего фронта и спада (заднего фронта) импульса.
В других случаях, какой-либо учет случайной ошибки не представляется возможным.
Математический контекст
Как следует из Рисунка 1, точность измерения дальности в основном зависит от
уровня шума
или, точнее, от соотношения между амплитудой импульса и уровнем шума.
Количественно это соотношение описывается отношением «сигнал-шум».
Уровень шума, в свою очередь, зависит от ширины полосы пропускания приемного тракта.
Крутизна фронта и спада прошедшего тракт отраженного импульса также зависит от этой ширины.
Для значений отношения «сигнал-шум», значительно больших единицы, между этими величинами существует следующее
соотношение:[2]
.png)
.print.png)
где δR — ошибка измерения;
c0 — скорость света
B — ширина полосы пропускания;
SNR — отношение «сигнал-шум».
(1)
Однако ширина полосы пропускания является также существенным фактором,
влияющим на
разрешение радиолокатора по дальности
Sr = c0 / 2B.
Таким образом, максимально достижимая точность измерения дальности (характеризуемая ошибкой измерения дальности)
может быть представлена как функция разрешения радиолокатора по дальности:
.png)
.print.png)
(2)
Отсюда следует, что максимально достижимая ошибка измерения дальности должна быть значительно лучше чем разрешающая способность по дальности.
Систематические ошибки измерения
Систематические ошибки измерения, в отличие от случайных ошибок, могут быть учтены или уменьшены, в случае, если удается определить причины их возникновения.
В импульсных радиолокаторах
время задержки обычно измеряется между передним фронтом излучаемого импульса и передним фронтом отраженного от цели импульса.
Точность измерения в таком случае будет зависеть от частоты следования тактовых (измерительных) импульсов,
по количеству которых между заданными моментами времени измеряется
длительность интервала.
Очевидно, что в промежутке между тактовыми импульсами измерение не может быть произведено,
что приводит к возникновению систематической ошибки измерения дальности.
На практике точность измерения дальности зависит от размера отдельной ячейки дальности, используемой при обработке сигнала.
В соответствии с рекомендациями
ИКАО[3]
для радиолокаторов систему управления воздушным движением размер ячейки должен быть 1/128 морской мили,
то есть около 14,5 м, что соответствует интервалу времени почти 10 нс.
В
радиолокаторах непрерывного излучения
измерение сдвига фазы принятого сигнала относительно текущей фазы передатчика может содержать (хотя и неоднозначную) информацию о дальности.
Точность измерения дальности в
радиолокаторах непрерывного излучения с частотной модуляцией
также определяется параметрами передатчика, особенно наклоном и линейностью закона изменения частоты.
Точность измерения углов
стандартные требования в
зависимости от дальности
точность измерения азимута:
методом скользящего окна
моноимпульсным методом
дальность от радара (в морских милях)
Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)
стандартные требования в
зависимости от дальности
точность измерения азимута:
методом скользящего окна
моноимпульсным методом
дальность от радара (в морских милях)
Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)
Точность измерения углов зависит как от внутренних методов обработки сигнала так и от внешних условий.
Аномальные условия распространения,
которые часто возникают из-за изменений давления воздуха,
влияют на измерение угла места и могут влиять на измерение горизонтального угла (азимута), вызывая возникновение случайной ошибки измерения.
Однако более частые источники возникновения систематических ошибок определяются внутренними факторами.
Например, измерение угла
методом скользящего окна
является довольно неточным.
На практике половина ширины диаграммы направленности антенны делится на число квантований, определяемое используемым методом
(например, 8 или 16 периодов следования импульсов) и таким образом приводит к систематической ошибке порядка одного градуса. В
корреляционных методах,
где выполняется интерполяция промежуточных значений, достигается более высокая точность измерения.
Наилучшая точность измерения угловых координат на данный момент достигается при использовании метода
конического сканирования и при
моноимпульсной пеленгации.
Как выполняются измерения для оценки точности радиолокатора?
Порядок проведения таких измерений определяется их целью, а именно: координаты, измеренные радиолокатором сравниваются с действительными координатами цели.
Для радиолокаторов наблюдения за воздушным движением для этой цели выполняется испытательный полет (облет), например, компанией
FCS Flight Calibration Services GmbH.
На борту самолета Learjet 35 располагается регистратор, который записывает текущие координаты самолета,
получаемые дифференциальной системой спутниковой навигации GPS
с ошибками менее одного метра.
В то же время траектория полета самолета регистрируется на радиолокаторе.
Оба регистратора синхронизируются при помощи сигналов единого времени, получаемых ими от системы GPS,
и результаты измерений сравниваются между собой.
При обработке результатов сравнения измеренных и действительных значений координат цели применяются методы математической статистики.
Явные ошибочные измерения исключаются из анализа, поскольку необходимо определить систематическую составляющую ошибки измерения радиолокатора.
Это не означает, однако, что требуется значительное количество зондирующих импульсов (возможно, для получения хорошего значения).
В радиолокаторах, использующих моноимпульсный метод пеленгации значение ошибки измерения определяется для каждого импульса.
Если используется метод скользящего окна, то соответствующее значение определяется для конкретного требуемого числа импульсов.
Для достижения хорошей точности измерения дальности требуется, чтобы зондирующие импульсы имели стабильный и крутой фронт.
Такой фронт часто не наблюдается при использовании
внутриимпульсной модуляции.
Но тут необходимо учитывать, что измерение дальности выполняется после сжатия отраженного импульса.
В этой точке, уже после сжатия, импульс вновь имеет крутой фронт.
Единственным условием проведения подобных измерений является отсутствие помех.
Это означает, что эхо-сигнал не должен смешиваться с внешними помехами.
Однако внутренние шумы всегда будут присутствовать в тракте прохождения отраженного сигнала.
Поэтому результативные измерения возможны когда уровень отраженного от летательного аппарата сигнала будет существенно выше
уровня шума.
Наконец, калибровка полета должна выявлять возможные дополнительные систематические ошибки, а не случайные ошибки.
Примеры
В таблице 1 приведены характеристики точности для некоторых радиолокаторов.
| Название радиолокатора | Ошибка измерения углов |
Ошибка измерения дальности |
Ошибка измерения высоты |
|---|---|---|---|
| BOR–A 550 | < ±0.3° | < 20 м | |
| LANZA | < ±0.14° | < 50 м | 340 м ≈ 1150 футов (на дальности 100 морских миль) |
| GM 400 | < ±0,3° | < 50 м | 600 м ≈ 2000 футов (на дальности 100 морских миль) |
| RRP–117 | < ±0,18° | < 463 м | 1000 м ≈ 3000 футов (на дальности 100 морских миль) |
| MSSR-2000 | < ±0.049° | < 44.4 м | |
| STAR-2000 | < ±0.16° | < 60 м | |
| Variant | < ±0.25° | < 25 м |
Таблица 1. Примеры
Примітки
- Merrill I. Skolnik: »Introduction to Radar Systems» McGraw-Hill Europe, 2001, ISBN 007-118189-x, S. 317,
Topic 6.3 Theoretical Accuracy of Radar Measurements - G. Richard Curry: »Radar System Performance Modeling» 2005, ISBN 978-1-58053-816-9, S.168
- ICAO Annex 10 — Volume 4. Aeronautical Telecommunications — Surveillance and Collision Avoidance Systems, Topic 4.3.2.1.3 Range and Bearing Accuracy,
(Bundesamt für Zivilluftfahrt, Schweiz)
Под лобовым стеклом, в центре?
Между передними сидениями?
Или подвесить как-нибудь сбоку?
Часть первая
Ответ можно получить с помощью эксперимента. В конечном счете, мы так и поступим,
поэтому, если Вы торопитесь, то можете сразу переходить к концу статьи, непосредственно
к ответу. Мы же, чтобы понимать физику процесса, предварительно рассмотрим некоторые,
относящиеся к делу, теоретические вопросы.
Сначала несколько общих слов о принципе работы спутникового навигационного приемника.
Радиосигналы, передаваемые каждым навигационным спутником, принимаются, усиливаются,
переводятся на промежуточную частоту и подвергаются дальнейшей обработке. Эта обработка
заключается в извлечении информационного сообщения спутника и определении времени
распространения сигнала от спутника до приемника. Информационное сообщение спутника
содержит эфемериды его орбиты, которые используются для определения его координат
на момент передачи сигнала. Задержка принятого сигнала используется для определения
расстояния до спутника. Зная координаты нескольких спутников и расстояния до них,
навигационный приемник вычисляет координаты потребителя.
До скольких спутников требуется знать расстояния? Положение потребителя в пространстве
определяется тремя независимыми величинами (например, долготой, широтой и высотой
над уровнем моря). Кроме того, поскольку величина измеряемой задержки сигнала напрямую
связана с уходом часов приемника, величина этого ухода также подлежит определению.
Таким образом, в процессе решения навигационной задачи требуется определить четыре
независимых неизвестных величины: долгота, широта, высота над уровнем моря и уход
часов приемника.
Для определения этих неизвестных требуется минимум четыре уравнения. При этом, уравнения
должны быть независимы, т.е. ограничения, накладываемые любым из них не должны дублировать
ограничения остальных трех. Фактически, независимость уравнений определяется взаимным
расположением выбранных спутников. Проиллюстрируем сказанное двумерным случаем,
в котором для простоты рассуждений часы приемника полагаются абсолютно точными,
в силу чего для решения навигационной задачи достаточно двух спутников (положение
на плоскости определяется двумя независимыми координатами).
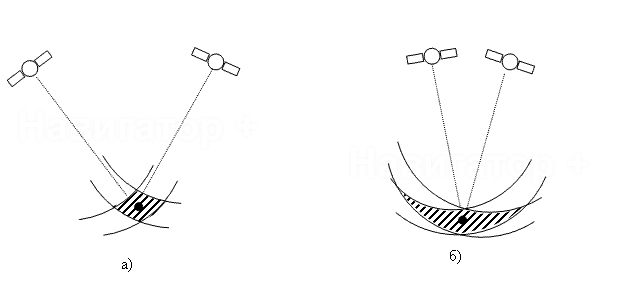
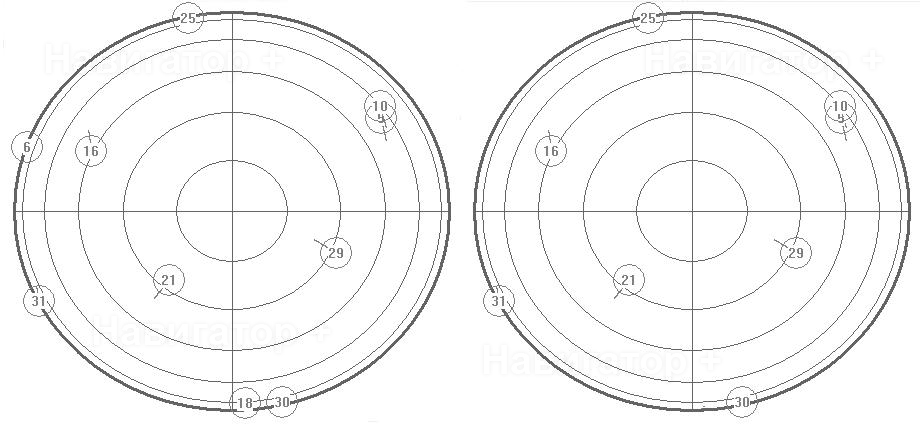
Рис 1. Влияние взаимного расположения спутников на точность определения координат
На рис. 1 конечная ширина концентрических колец обозначает конечную точность определения
расстояний до спутников. В результате измерения параметров сигнала одного спутника
GPS приемник выясняет, что размер заштрихованной области пересечения колец соответствует
точности определения координат потребителя. Точность в случае рис. 1а выше точности
в случае рис. 1б, что связано с различием угловых расстояний между направлениями
на спутники. При уменьшении этого углового расстояния ограничения, накладываемые
уравнениями, становятся более похожими друг на друга, то-есть становятся более зависимыми,
а точность определения координат падает. В пределе, при совпадении угловых положений
спутников, потребитель не может быть локализован.
В действительности, для увеличения точности, GPS приемник стремится использовать
как можно больше спутников (рис 2). Большее число колец дает меньшую площадь их
области пересечения, что соответствует увеличению точности. В трехмерном случае
все эти рассуждения остаются справедливыми, только концентрические круги на плоскости
необходимо заменить сферами с конечной толщиной поверхности.
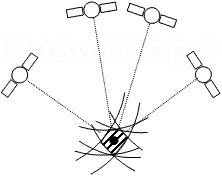
Рис 2.
Для некоторого числа спутников можно определить такое их расположение, при котором
будет обеспечена максимальная точность (оптимальное созвездие). Например, для 4
спутников это созвездие будет таким: один спутник в зените, остальные три располагаются
в плоскости горизонта, отстоя друг от друга на одинаковый азимутальный угол. Если
спутников больше 4-х, оптимальная конфигурация спутников будет похожей. Можно показать,
что для нее объем многоугольника, вершины которого совпадают с концами единичных
векторов, направленных от наблюдателя к спутникам, максимален. Отсюда интуитивно
понятно требование распределить часть спутников оптимального созвездия равномерно
по горизонту. Качество созвездия с точки зрения точности определения координат принято
характеризовать коэффициентом PDOP (Position Dilution Of Precision), который равен
отношению ошибки измерения координат к ошибке определения дальности. Чем меньше
этот коэффициент, тем точнее определяются координаты. Для созвездия на рис. 1а PDOP
меньше, чем для созвездия на рис. 1б. Для оптимального созвездия PDOP достигает
минимального значения.
В случае системы мониторинга транспорта высота объекта над уровнем моря, как правило,
менее значима, чем его положение в плане. Тут вместо PDOP можно воспользоваться
HDOP (Horizontal Dilution Of Precision) – отношение ошибки определения координат
в плане к ошибке определения дальности до спутника. Оптимальное созвездие с точки
зрения HDOP отличается от оптимального с точки зрения PDOP. В частности, для минимизации
HDOP спутник в зените ни к чему – минимум HDOP достигается при равномерном по азимуту
распределении спутников в плоскости горизонта.
Теперь пора вернуться к обсуждаемому вопросу: как расположение антенны внутри автомобиля
влияет на точность определения его координат? Во-первых, созвездие «видимых спутников»
для антенны внутри автомобиля может отличаться от созвездия фактически имеющихся:
кузов автомобиля может влиять на принципиальную возможность приема сигнала. Во-вторых,
точность измерений параметров сигнала, а следовательно, и дальностей до спутников,
внутри автомобиля может ухудшаться. Рассмотрим сначала первую часть вопроса:
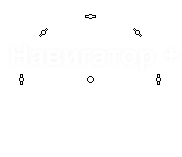
Ухудшение точности определения координат, связанное с уменьшением количества видимых спутников.
Допустим, антенна внутри автомобиля «видит» только некоторые из оптимального с точки
зрения HDOP созвездия, состоящего из 8 спутников. Как при этом изменится точность
определения координат в плане, если точность определения дальности до «видимых»
спутников остается неизменной? Чтобы ответить на этот вопрос нам придется записать
пару формул. Если Вы и их и так знаете, или Вам вообще все равно, можете просто
прочитать ответ ниже. Мы же для начала введем в рассмотрение декартову систему координат
с центром в точке расположения антенны, ось Z которой направлена вверх, ось Y –
на север, а ось X, соответственно, на восток. Поскольку в оптимальном, с точки зрения
HDOP, созвездии спутники расположены в плоскости горизонта их координаты Z в выбранной
системе будут равны 0. Для исходного оптимального созвездия можно записать следующую
систему уравнений, связывающую измеренную дальность с ошибками определения координат
и уходом часов GPS приемника:
 |
|
 |
|
 |
|
 |
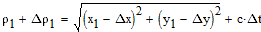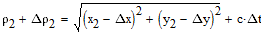(1) |
 |
|
 |
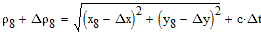В уравнениях отсутствует ошибка определения координат по оси Z. Предполагается,
что эта координата нам достоверно известна, и равна 0 в выбранной системе координат.
Правую часть каждого из уравнений (1) можно разложить в ряд по степеням
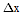
и
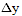. Поскольку ошибки определения координат много меньше любого
из расстояний до спутников, в разложениях можно оставить только члены, связанные
с первыми степенями. В результате получим:
 |
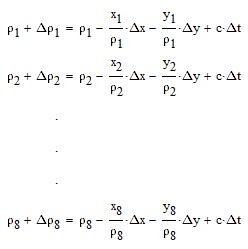(2) |
Поскольку
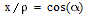, а
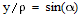, где
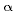
— азимутальный угол в сферической системе координат, соответствующей исходной декартовой,
в (2) можно избавиться от координат спутников, заменив их соответсвующими азимутальными
углами:
 |
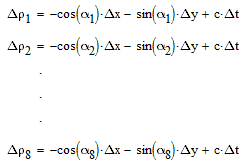(3) |
или в матричном виде:
Полученная система уравнений устанавливает связь между ошибками измерения дальностей
до спутников и определения координат в плане. Ее решение, минимизирующее сумму квадратов
невязок, выглядит так:
 |
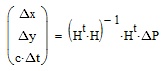(5) |
где
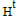— транспонированная матрица H.
Выражение (5) устанавливает связь между конкретными реализациями ошибок. Однако,
ошибки измерения дальностей до спутников суть случайные величины, поэтому, оперировать
надо не их конкретными реализациями, а статистическими характеристиками. В некотором
приближении, приемлемом в данном контексте, можно считать, что результаты измерений
подчинены нормальному закону, независимы друг от друга и имеют одинаковую дисперсию.
То-есть в целом их можно охарактеризовать диагональной ковариационной матрицей с
одинаковыми элементами на диагонали:
 |
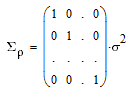(6) |
где
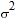— дисперсия измерения дальности
Тогда неизвестный вектор ошибок определения координат и ухода часов тоже будет случайным
и подчиненным нормальному закону. Его ковариационная матрица
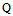
определится законом распространения ошибок:
 |
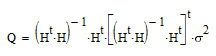(7) |
Поскольку в оптимальном по HDOP созвездии спутники равномерно распределены по азимуту,
а из интуитивных соображений ясно, что при повороте всей системы спутников на некоторый
угол вокруг оси Z ничего не изменится, матрица H однозначно определена. Это означает,
что матричный сомножитель в (6) может быть вычислен. Выполнив эти вычисления, получим:
 |
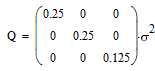(8) |
То-есть дисперсия ошибки определения координат по каждой из осей в оптимальном по
HDOP созвездии из 8-ми спутников в четыре раза меньше дисперсии ошибки измерения
дальности.
Как изменится ковариационная матрица
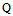, если сигнал одного из спутников будет потерян? Это несложно
выяснить, достаточно в системе уравнений (3) убрать одно уравнение и повторить только
что выполненные вычисления:
 |
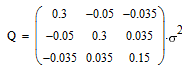(9) |
Ковариационная матрица уже не диагональная, ошибки по осям X и Y кореллированы,
поэтому, чтобы определить дисперсию ошибки диагональных элементов матрицы недостаточно,
необходимо найти собственные числа ковариационной матрицы. Выполнив это получим
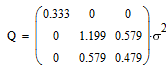
значение максимальной дисперсии ошибки
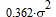
Аналогично, вычислим ковариационные матрицы для случая исчезновения сигнала 2-х,
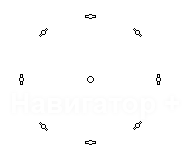
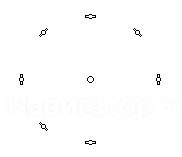
3-х и 4-х соседних спутников, и сведем все результаты в одну таблицу:
| Конфигурация спутников | Ковариационная матрица | Дисперсия |
|---|---|---|
 |
|
 |
 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
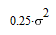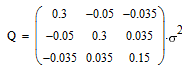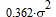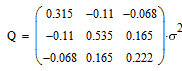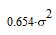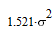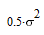Характерной является 2-я снизу строка таблицы: при исчезновении сигнала от половины
соседних спутников дисперсия ошибки увеличивается в 20 раз, то-есть среднеквадратичная
ошибка возрастает в 4.5 раза (корень из 20).
Если среднеквадратичная ошибка измерения дальности до спутника 8 метров (что недалеко
от истины), то в для оптимального созвездия среднеквадратичная ошибка измерения
координат составит 4 метра, а при исчезновении 4-х соседних спутников увеличится
до 17.9 метров.
Такое ухудшение точности хоть и не критично с точки зрения типичных задач мониторинга
транспорта, но, тем не менее, может расстроить пользователя системы «Навигатор+».
Можно ли как-нибудь определить, как будут меняться созвездия видимых спутников для
представленных в начале статьи способов расположения антенны? Простые геометрические
построения в данном случае не помогут. Дело в том, что если размеры объекта, препятствующего
приему сигнала, соизмеримы с длиной волны, то интенсивность сигнала вблизи границы
области геометрической тени будет определяться дифракцией электромагнитных волн
на объекте. Проще говоря, куском железа размером в пару длин волн сложно «загородиться»
от спутника. Более того, даже если размеры экранирующего объекта много больше длины
волны, но расстояние от границы объекта до точки наблюдения соизмеримо с длиной
волны, дифракционными эффектами также нельзя пренебречь. Длина волны, соответствующая
несущей частоте GPS сигнала, равна приблизительно 190 мм. Размер если и не близкий
к размерам характерным конструктивных эелементов кузова автомобиля, то по крайней
мере соизмеримый с ними. Поэтому, для GPS антенны, расположенной в салоне эффекты
дифракции на элементах конструкции могут быть существенны.
На практике это может означать, как то, что, например, антенна, спрятанная под крышей
автомобиля, может, тем не менее, обеспечивать прием GPS сигнала, так и то, что сигнал
от спутника, находящегося в геометрической видимости может быть не принят.
Для определения условий видимости спутников можно было бы попытаться составить электродинамическую
модель автомобиля и решить задачу дифракции, однако, это довольно сложно. Упрощенная
модель, не учитывающая подробности элементов кузова, может не обеспечить адекватной
точности, а составление строгой модели сопряжено со значительными математическими
и вычислительными трудностямии. Поэтому, мы поступили проще: провели эксперимент.
Антенну одного GPS приемника резместили на крыше неподвижного автомобиля, а антенну
другого поочередно размещали в салоне тремя указанными выше способами, и сравнивали
два видимых созвездия друг с другом.
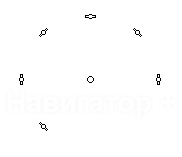
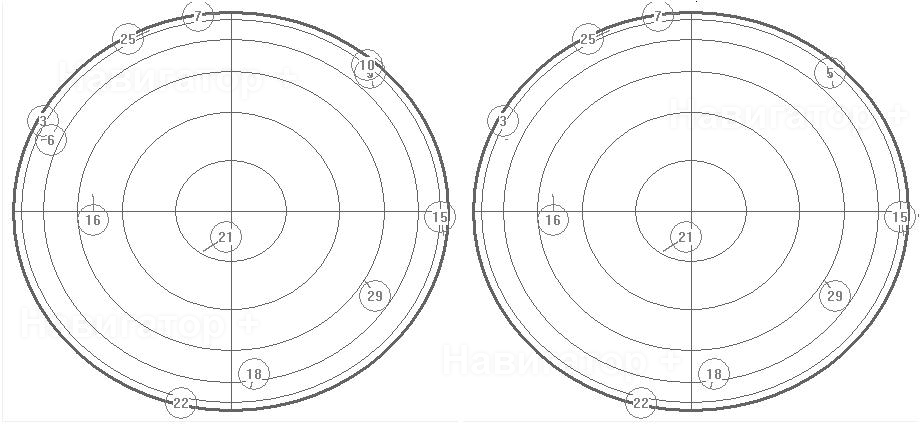
Для демонстрации видимых созвездий использовалась диаграмма, получающаяся отображением
координат спутников на плоскую область, ограниченную кругом, при котором азимут
спутника равен полярному углу соответствующей ему точки, отсчитываему по часовой
стрелке от вертикальной оси, а косинус угла возвышения пропорционален расстоянию
от точки до центра круга. Если, находясь в точке расположения антенны, повернуться
лицом на север, а потом каким-нибудь непостижимым образом моментально взлететь строго
вертикально на пару сотен тысяч километров, и посмотреть оттуда на навигационные
спутники, то они будут расположены так же, как на диаграмме. Например, спутнику,
расположенному в зените, будет соответствует точка в центре круга, а спутнику, только
появляющемуся из-за горизонта, соответствует точка вверху диаграммы. GPS спутники
принято идентифицировать числами, поэтому они обозначаются кружками с номером спутника
внутри. Окружности сетки диаграммы соответствуют углам возвышения 0, 15, 30, 45,
60 и 75 градусов.
Вот результаты эксперимента:
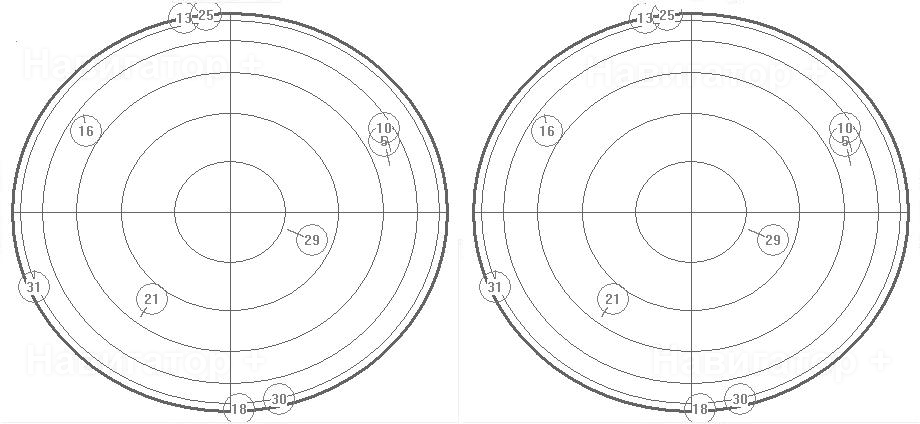
| Антенна на крыше автомобиля | Антенна под лобовым стеклом в центре (1) |
Рис. 3
| Антенна на крыше автомобиля | Антенна между передними сидениями (2) |
Рис. 4
| Антенна на крыше автомобиля | Развернутая на 90 градусов антенна (3) |
Рис. 5
В целом, как ни странно, кузов автомобиля не очень сильно влияет на количество видимых
спутников. Антенна под лобовым стеклом видит те же спутники, что и антенна на крыше,
антенна между сидениями «потеряла» всего лишь два спутника (6 и 18), и то же самое
сделала антенна, перевернутая на 90 градусов: тоже потеряла пару спутников, на этот
раз 6 и 10. Вспоминая полученные выше результаты можно заключить, что геометрический
фактор изменится не сильно.
Таким образом, мы рассмотрели первую часть поставленного вопроса о размещении антенны
внутри автомобиля, связанную с изменением количества видимых спутников. Вторую часть
вопроса рассмотрим во второй части статьи.
Минимальная
дисперсия шумовой ошибки определяет
потенциальную точность измерения
координат.
Среднеквадратичная
ошибка измерения дальности:
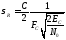, гдеFC– эффективная ширина спектра сигнала.
Среднеквадратичная
ошибка измерения радиальной скорости:
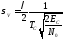где ТC– длительность
сигнала (пачки когерентных импульсов).
СКО измерения
угла:
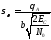где θА–ширина диаграммы
направленности антенны;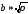— коэффициент
Шумовые
ошибки измерения координат тем меньше,
чем больше отношение сигнал/шум.
Для уменьшения
ошибки дальности – расширить спектр
сигнала.
Для уменьшения
ошибки измерения скорости – увеличить
длительность сигнала.
Для увеличения
СКО угловой координаты – сужать Д.Н.
антенны.
29. Реализация измерителей в многоканальном и следящем виде
Многоканальный
фильтровой измеритель скорости:
Обозначения:
ФД – фазовый
детектор;
ДО – детектор
огибающей;
УВМ –
устройство выбора максимума.
Расчёты
для его реализации.
Требуемое
число фильтров определяется диапазоном
доплеровских частот и полосой одного
фильтра:
Полоса одного
фильтра:
Разная частота
фильтров
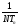или.
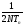Число фильтров
будет вдвое больше, что уменьшает
вероятность пропуска сигнала из-за
«провалов» на АЧХ соседних фильтров
Многоканальный
измеритель при М>20 реализуется в виде
вычислителя дискретного преобразования
Фурье (ДПФ). Практически реализуется в
виде быстрого преобразования Фурье
(БПФ). При размере выборки Nчерез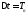ДПФ запишется так:
, гдеan
– весовые коэффициенты.
Каждому
коэффициенту
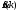соответствует
полоса эквивалентного фильтра
Следящий
измеритель скорости
Устройство
должно оценивать доплеровский сдвиг и
осуществлять слежение за изменением
Fд(t).
Схема
реализации устройства:
СМ – смеситель;
ЧД – частотный
детектор;
ФОП – фильтр
оценки доплеровского сдвига (ФНЧ);
ГУН – генератор
управляемый напряжением;
УП – устройство
поиска;
(стр. 116
Сперанский)
30. Импульсный метод измерения дальности. Цифровой и визуальный съем дальности
Дальность в
радиолокации измеряется путем прямой
или косвенной оценки задержки радиосигнала
от цели. При импульсном методе производится
прямое измерение задержки сигнала
,
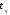отраженного от цели относительно момента
излучения зондирующего сигнала радиоволн.
С учетом скорости распространения
радиоволн дальность равна.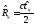
Визуальный
– по экрану электронно-лучевой трубки,
путем подсчета импульсов меток между
пусковым и импульсом цели,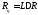
гдеL– оценка числа
счётных импульсов.
31. Частотный метод измерения дальности. Радиовысотомер малых высот
При этом
методе применяется непрерывный
зондирующий сигнал с линейной или
синусоидальной частотной модуляцией.
Максимальное
отклонение частоты называется девиацией
частоты. модуляция применяется
периодическая с периодом модуляции
.
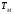Частота зондирующего сигнала в момент
времениtравна:
,
где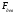— частота девиации.
За время
распространения сигнала за счёт частотной
модуляции частота опорного сигнала
меняется: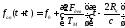
Разность
частот называется частотой биения:
.
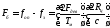Измерив
частоту биений, можно оценить дальность
до цели:
Радиовысотомер:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание раздела «Точность радиолокационных измерений»
- Точность определения дальности
- Случайная ошибка измерения
- Математические соотношения
- Систематические ошибки измерения
- Точность измерения угловых координат
- Как выполняется измерение для оценки точности радиолокатора?
- Примеры
Точность радиолокационных измерений
Точность это степень соответствия между оцениваемыми или измеряемыми значениями параметров
(координаты и/или скорость движения) лоцируемого объекта в определенный момент времени и их истинными значениями.
В радиолокации точность измерения обычно представляется как статистическая мера систематической ошибки,
которая характеризуется следующими свойствами:
- Предсказуемость: Точность позиционирования определяется при использовании географических или геодезических систем координат Земли.
- Повторяемость: Означает то, что результаты измерения одной и той же системой в сходных условиях,
будут характеризоваться близкими значениями точности в пределах некоторого интервала времени. - Относительность: Точность измерений относительно одной позиции может быть пересчитана для другой позиции (пренебрегая всевозможными ошибками).
Заявленное значение требуемой точности показывает,
что определяемое системой измерения значение того или иного параметра может отклоняться от его истинного значения,
и указывает интервал значений, в котором находится истинное значение с заданной вероятностью.
Рекомендуемое значение вероятности 95%, что соответствует интервалу,
равному удвоенному среднеквадратическому отклонению относительно среднего значения для нормального (Гауссового) распределения случайной величины.
Предположение, что все известные поправки учтены, означает, что ошибки оценивания будут иметь средние значения (смещения), близкие к нулю.
Любое остаточное смещение должно быть небольшим по сравнению с заявленной точностью.
Истинное значение — это значение, которое в рабочих условиях наилучшим образом характеризует измеряемую величину,
наблюдаемую в пределах репрезентативного (достаточного) интервала времени, площади и / или объема с учетом расположения и влияющих факторов.
ошибка измерения
импульс+шум
порог
идеальный импульс
Рисунок 1. Искажение фронта импульса под воздействием шумов
ошибка измерения
импульс+шум
порог
идеальный импульс
Рисунок 1. Искажение фронта импульса под воздействием шумов
Точность определения дальности
Теоретическая максимально достижимая точность измерения дальности методом радиолокационной импульсной дальнометрии
зависит от точности измерения времени запаздывания отраженного сигнала.
Случайные ошибки измерения
Случайные ошибки измерения в
импульсных радиолокаторах
возникают когда передний фронт отраженного сигнала искажается под воздействием шумов.
На отраженный сигнал всегда накладываются шумы, в результате чего увеличивается амплитуда принятого сигнала.
Это вызывает смещение переднего фронта импульса и, следовательно, является причиной ошибки измерения времени запаздывания отраженного сигнала.
На Рисунке 1 показано влияние шумов на обнаруживаемый передний фронт эхо-сигнала.
Сплошной линией (фиолетовой) изображен идеальный трапецеидальный импульс с довольно крутыми фронтом и спадом.
Этот импульс не может быть слишком близким к прямоугольному, поскольку это потребовало бы бесконечно широкой полосы частот.
Время задержки импульса измеряется в момент времени, когда его амплитуда достигает порогового значения, обычно на уровне 0,707 от максимальной амплитуды.
Однако на отраженный импульс накладывается шум (зеленая линия).
Измеренным может быть только напряжение, являющееся суммой мгновенных значений амплитуды импульса и шума
(желтая синяя пунктирная линия).
Это напряжение достигнет порогового значения раньше, чем напряжение идеального (в отсутствии шумов) импульса.
Разница между ними — это случайная ошибка измерения времени задержки, вызванная влиянием
шумов[1].
Если длительность импульса известна (что невозможно для первичного радиолокатора, а только для
вторичного радиолокатора),
то эта случайная ошибка может быть уменьшена математически путем одновременной оценки переднего фронта и спада (заднего фронта) импульса.
В других случаях, какой-либо учет случайной ошибки не представляется возможным.
Математический контекст
Как следует из Рисунка 1, точность измерения дальности в основном зависит от
уровня шума
или, точнее, от соотношения между амплитудой импульса и уровнем шума.
Количественно это соотношение описывается отношением «сигнал-шум».
Уровень шума, в свою очередь, зависит от ширины полосы пропускания приемного тракта.
Крутизна фронта и спада прошедшего тракт отраженного импульса также зависит от этой ширины.
Для значений отношения «сигнал-шум», значительно больших единицы, между этими величинами существует следующее
соотношение:[2]
где δR – ошибка измерения;
c0 – скорость света
B – ширина полосы пропускания;
SNR – отношение «сигнал-шум».
(1)
Однако ширина полосы пропускания является также существенным фактором,
влияющим на
разрешение радиолокатора по дальности
Sr = c0 / 2B.
Таким образом, максимально достижимая точность измерения дальности (характеризуемая ошибкой измерения дальности)
может быть представлена как функция разрешения радиолокатора по дальности:
(2)
Отсюда следует, что максимально достижимая ошибка измерения дальности должна быть значительно лучше чем разрешающая способность по дальности.
Систематические ошибки измерения
Систематические ошибки измерения, в отличие от случайных ошибок, могут быть учтены или уменьшены, в случае, если удается определить причины их возникновения.
В импульсных радиолокаторах
время задержки обычно измеряется между передним фронтом излучаемого импульса и передним фронтом отраженного от цели импульса.
Точность измерения в таком случае будет зависеть от частоты следования тактовых (измерительных) импульсов,
по количеству которых между заданными моментами времени измеряется
длительность интервала.
Очевидно, что в промежутке между тактовыми импульсами измерение не может быть произведено,
что приводит к возникновению систематической ошибки измерения дальности.
На практике точность измерения дальности зависит от размера отдельной ячейки дальности, используемой при обработке сигнала.
В соответствии с рекомендациями
ИКАО[3]
для радиолокаторов систему управления воздушным движением размер ячейки должен быть 1/128 морской мили,
то есть около 14,5 м, что соответствует интервалу времени почти 10 нс.
В
радиолокаторах непрерывного излучения
измерение сдвига фазы принятого сигнала относительно текущей фазы передатчика может содержать (хотя и неоднозначную) информацию о дальности.
Точность измерения дальности в
радиолокаторах непрерывного излучения с частотной модуляцией
также определяется параметрами передатчика, особенно наклоном и линейностью закона изменения частоты.
Точность измерения углов
стандартные требования в
зависимости от дальности
точность измерения азимута:
методом скользящего окна
моноимпульсным методом
дальность от радара (в морских милях)
Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)
стандартные требования в
зависимости от дальности
точность измерения азимута:
методом скользящего окна
моноимпульсным методом
дальность от радара (в морских милях)
Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)
Точность измерения углов зависит как от внутренних методов обработки сигнала так и от внешних условий.
Аномальные условия распространения,
которые часто возникают из-за изменений давления воздуха,
влияют на измерение угла места и могут влиять на измерение горизонтального угла (азимута), вызывая возникновение случайной ошибки измерения.
Однако более частые источники возникновения систематических ошибок определяются внутренними факторами.
Например, измерение угла
методом скользящего окна
является довольно неточным.
На практике половина ширины диаграммы направленности антенны делится на число квантований, определяемое используемым методом
(например, 8 или 16 периодов следования импульсов) и таким образом приводит к систематической ошибке порядка одного градуса. В
корреляционных методах,
где выполняется интерполяция промежуточных значений, достигается более высокая точность измерения.
Наилучшая точность измерения угловых координат на данный момент достигается при использовании метода
конического сканирования и при
моноимпульсной пеленгации.
Как выполняются измерения для оценки точности радиолокатора?
Порядок проведения таких измерений определяется их целью, а именно: координаты, измеренные радиолокатором сравниваются с действительными координатами цели.
Для радиолокаторов наблюдения за воздушным движением для этой цели выполняется испытательный полет (облет), например, компанией
FCS Flight Calibration Services GmbH.
На борту самолета Learjet 35 располагается регистратор, который записывает текущие координаты самолета,
получаемые дифференциальной системой спутниковой навигации GPS
с ошибками менее одного метра.
В то же время траектория полета самолета регистрируется на радиолокаторе.
Оба регистратора синхронизируются при помощи сигналов единого времени, получаемых ими от системы GPS,
и результаты измерений сравниваются между собой.
При обработке результатов сравнения измеренных и действительных значений координат цели применяются методы математической статистики.
Явные ошибочные измерения исключаются из анализа, поскольку необходимо определить систематическую составляющую ошибки измерения радиолокатора.
Это не означает, однако, что требуется значительное количество зондирующих импульсов (возможно, для получения хорошего значения).
В радиолокаторах, использующих моноимпульсный метод пеленгации значение ошибки измерения определяется для каждого импульса.
Если используется метод скользящего окна, то соответствующее значение определяется для конкретного требуемого числа импульсов.
Для достижения хорошей точности измерения дальности требуется, чтобы зондирующие импульсы имели стабильный и крутой фронт.
Такой фронт часто не наблюдается при использовании
внутриимпульсной модуляции.
Но тут необходимо учитывать, что измерение дальности выполняется после сжатия отраженного импульса.
В этой точке, уже после сжатия, импульс вновь имеет крутой фронт.
Единственным условием проведения подобных измерений является отсутствие помех.
Это означает, что эхо-сигнал не должен смешиваться с внешними помехами.
Однако внутренние шумы всегда будут присутствовать в тракте прохождения отраженного сигнала.
Поэтому результативные измерения возможны когда уровень отраженного от летательного аппарата сигнала будет существенно выше
уровня шума.
Наконец, калибровка полета должна выявлять возможные дополнительные систематические ошибки, а не случайные ошибки.
Примеры
В таблице 1 приведены характеристики точности для некоторых радиолокаторов.
| Название радиолокатора | Ошибка измерения углов |
Ошибка измерения дальности |
Ошибка измерения высоты |
|---|---|---|---|
| BOR–A 550 | < ±0.3° | < 20 м | |
| LANZA | < ±0.14° | < 50 м | 340 м ≈ 1150 футов (на дальности 100 морских миль) |
| GM 400 | < ±0,3° | < 50 м | 600 м ≈ 2000 футов (на дальности 100 морских миль) |
| RRP–117 | < ±0,18° | < 463 м | 1000 м ≈ 3000 футов (на дальности 100 морских миль) |
| MSSR-2000 | < ±0.049° | < 44.4 м | |
| STAR-2000 | < ±0.16° | < 60 м | |
| Variant | < ±0.25° | < 25 м |
Таблица 1. Примеры
Примітки
- Merrill I. Skolnik: »Introduction to Radar Systems» McGraw-Hill Europe, 2001, ISBN 007-118189-x, S. 317,
Topic 6.3 Theoretical Accuracy of Radar Measurements - G. Richard Curry: »Radar System Performance Modeling» 2005, ISBN 978-1-58053-816-9, S.168
- ICAO Annex 10 – Volume 4. Aeronautical Telecommunications – Surveillance and Collision Avoidance Systems, Topic 4.3.2.1.3 Range and Bearing Accuracy,
(Bundesamt für Zivilluftfahrt, Schweiz)
2. Расчет реальной разрешающей способности по дальности и азимуту.
Реальную разрешающую способность по дальности при использовании в качестве выходного устройства индикатора кругового обзора определим по формуле
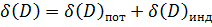(2. 1)
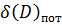— потенциальная разрешающая способность по дальности.
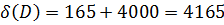
Для сигнала в виде некогерентной пачки прямоугольных импульсов
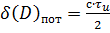(2. 2)
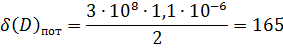
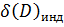— разрешающая способность индикатора по дальности вычисляется по формуле
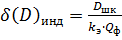(2. 3)
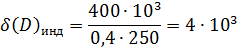
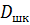— предельно значение шкалы дальности,
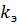— 0, 4 — коэффициент использования экрана,
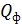— качество фокусировки трубки.
Реальную разрешающую способность по азимуту рассчитаем по формуле:
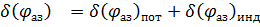(2. 4)
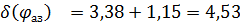
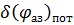— потенциальная разрешающая способность по азимуту при аппроскимации диаграммы направленности гауссовой кривой;
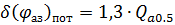(2. 5)
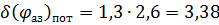
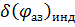— разрешающая способность индикатора по азимуту
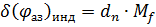(2. 6)
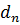— диаметр пятна электронно-лучевой трубки
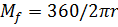— масштаб шкалы
r — удаление отметки от центра экрана
Принимая r=kэdэ / 2, (отметка на краю экрана), получим
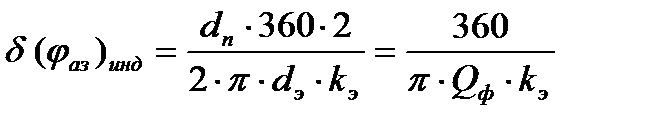(2. 7)
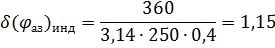
3. Расчет реальной точности измерения дальности и азимута
Точность характеризуется ошибкой измерения, результирующую среднеквадратическую ошибку измерения дальности рассчитаем по формуле:
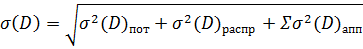(3. 1)
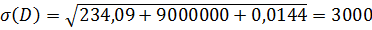
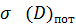—потенциальная ошибка измерения дальности.
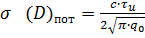(3. 2)
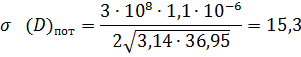
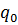— удвоенное отношение сигнал/шум
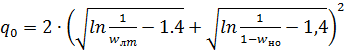(3. 3)
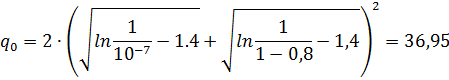
Ошибкой из-за непрямолинейности распространения 
принебрегаем. Аппаратурные ошибки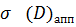 
сводятся к ошибкам отсчета по шкале индикатора 
.
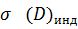Принимаем метод отсчета по электронным меткам (масштабным кольцам) на экране индикатора кругового обзора.
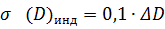(3. 4)
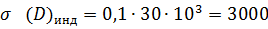
Результирующую среднеквадратическую ошибку измерения азимута определим аналогично.
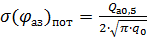(3. 5)
Слайд 1
Лазерные и телевизионные системы траекторных измерений
Лекция 9
Принципы
измерения дальности в лазерной локации
2016 г.
9 семестр, кафедра РТП
иАС, лектор:
доцент, к.т.н. Бугаев Юрий Николаевич
Слайд 2
Классический для лазерной локации принцип измерения дальности ,
с помощью заполнения счетными импульсами временного интервала между зондирующим
и отраженным сигналов используется во многих отечественных и зарубежных лазерных
дальномерах и дальномерных каналах лазерных станций траекторных измерений (Аток-В, Аток-ВК, «Виола» «Контрейс» (США, Швейцария, Япония).
Дальность до цели в лазерных импульсных дальномерах измерееся в соответствии с известной формулой радиолокации
Д = (С * T)/ 2
Где:
Д – наклонная дальность до цели;
Т – время распространения сигнала до цели и обратно;
С – скорость света в вакууме.
Дальномер должен обеспечить обнаружение объекта в режиме ручного (либо полуавтоматического) наведения с предварительным целеуказанием по азимуту и углу места
Классичечкий лазерный канал измерения дальности
Слайд 3
Среднеквадратическую инструментальную погрешность (СКП) измерений дальности станции «Аток»
-0,5 м.
Станция Аток относиться по нашей классификации к
станциям среднего радиуса действия 50 км днем и 70 км
начью.
Станция имеет два отдельных канала –дальномерный с объективом МТО-1000 (Диаметр 10 см) и угломерный с объективом «Слюссар-230» — 23 см.
Дальномерный канал станции Аток
Слайд 5
Станция делалась в ОКБ МЭИ на основе кинотеодолита
производства БЕЛОМО. Было выпущено три модификации «Аток-П» (1978г.), «Аток-В»
(1984-1987 гг.) и «Аток-ВК» (1992-1994 гг).
Станция «Аток-ВК» выпускалась специально
для Китая в стационарном варианте.
Лазерный передатчик- твердотельный с ламповой накачкой- 50 МДж, частотой 50 Гц и длительностью импульса 15 нсек.
Лазерная станция Аток
Слайд 6
На рисунке представлена типовая форма зондирующего лазерного импульса
в дальномерах типа ALTM канадской компании Optech Inc., а
на рисунке 9.3. показана принципиальная схема приемопередатчика при реализации данной
схемы измерения.
Форма зондирующего импульса
. Принципиальная схема приемопередатчика при импульсном методе
Слайд 7
Блок схема канала измерения дальности
Приемный телескоп D=1000 мм
5
Мгц
Строб
Старт
Стоп
Шум, Уровни
Слайд 8
Для старт-импульса задача фиксации решается достаточно легко, поскольку
сигнал характеризуется амплитудной и временной стабильностью. Хотя это справедливо
только для сравнительно невысоких точностей (до 0,3 – 0,5 м)
Решить
же аналогичную задачу для принимаемого от цели импульса значительно сложнее. В зависимости от дальности, состояния локационной трассы и типа цели амплитуда сигнала может меняться на 4–6 порядков. При этом существенно меняется форма сигнала из-за его ограничения в приемном тракте. Кроме того, сигнал может искажаться шумами и помехами аддитивного и мультипликативного характера.
. Погрешность временной фиксации
Слайд 9
Наиболее распространен метод временной привязки сигнала путем фиксации
его по уровню, когда момент фиксации определяется моментом пересечения
сигналом порога срабатывания формирователя (рис.9.4.). Этот момент фиксируется генерацией стандартного
стоп-импульса. видно, что его положение нестабильно и зависит от амплитуды импульса. Максимальный разброс момента фиксации равен длительности фронта импульса. Существуют способы устранения этой нестабильности, однако они довольно сложны в схемной реализации.
Слайд 10
Дисперсия и среднеквадратичная ошибка оценки дальности
D изм
= r2W(r)dr при R2/6
а СКОиви ~
1 м.
При тактовой частоте Измерителя временных интервалов (ИВИ) = 300
МГц
При тактовой частоте Измерителя временных интервалов (ИВИ) = 300 МГц а СКОиви ~ 1 м.
Слайд 11
Временная фиксация отраженного импульса по фиксированному порогу U
пор. Максимальный и минимальный сигналы; Uпор – порог срабатывания
Временная фиксация по фиксированному порогу
ФП
ВУ
ПФ
К ИВИ
Слайд 12
Если требования к точности измерения дальности и соответственно
фиксации положения импульса высоки применяют различные схемные методы коррекции:
—
метод работы по центру тяжести или по максимуму импульса;
— метод
работы методом схемы детектора половинной мощности (шестидецибельный детектор);
— метод измерения амплитуды отраженного сигнала и введение поправки на величину задержки сигнала из-за измерения амплитуды;
— вариант многопороговая схема.
Методы коррекции
Слайд 13
Структура приемного тракта с устройством временной привязки по
методу фиксации нуля производной (а) и устройство временной привязки
с двумя производными (б).
Слайд 14
Детектор половинной мощности
Принцип метода детектора половинной мощности.
Временные
диаграммы н0.
Слайд 15
Блок схема канала измерения дальности
Приемный телескоп D=1000 мм
5
Мгц
Строб
Старт
Стоп
Шум, Уровни
Слайд 16
В ДП световой сигнал проходит через блок светофильтров
и
попадает на фотоумножитель, расположенный в блоке фотоприемника,
где вместе с
сигналом СТАРТ преобразуется в электрический сигнал
ИНТЕРВАЛ.
Кроме того,
блок фотоприемника вырабатывает код амплитуды
сигнального импульса, используемый в дальнейшем для управления
режимом работы ДП Режим работы фотоприемника (задается соответствующими органами управления, расположенными на пульте и управления или автоматически Возможны два режима установки чувствительности и положения светофильтров:
ручной и автоматический. Режим канала ДП обеспечивается блоком АРУ ДП
Преобразование временного интервала в код дальности осущест-
вляется блоком ИВИ На выходе блока ИВИ имеется 17-разрядный параллельный двоичный код, поступающий в ЭВМ, а
также двоично-десятичный код, поступающий на индикацию дальности.
Индикатор конструктивно расположен на пульте наведения (ЦПН) и
включает 6 десятичных цифр.
Слайд 17
В измерителе дальности предусмотрен ввод трех
поправок:
поправка, учитывающая состояние атмосферы;
ручная поправка,
позволяющая скорректировать начальное положение; амплитудная
поправка,
зависящая от амплитуды отраженного сигнала.
Синхронизатор станции обеспечивает синхрочастоты от 5 мГц
до 1 Гц, необходимые для работы всех устройств.
Синхронизатор включает в себя задающий кварцевый генератор (КГ) на
5 мГц, формирователь, обеспечивающий согласование уровней сигнала
и последующего делителя частоты.
Слайд 18
Одновременно с излучением сигнала в направлении цели,
часть
энергии этого сигнала поступает через светопровод и нейтральный
светофильтр (поз.
4) на входе устройства Л4ПП01 на фотоумножитель и
используется для формирования
опорного сигнала СТАРТ (для тестовой
проверки приемника и всего тракта используется тестовый светодиод
В фотоумножителе ФЭУ-83 происходит преобразование оптических
импульсов сигналов опорного и отраженного в электрические сигналы
для формирования сигналов СТАРТ и СТОП.
Конструктивно фотоумножитель с делителем питания, тестовый
светодиод, узел полевой диафрагмы с интерференционным фильтром
расположены в узле ФЭУ.
Сигналы СТАРТ и СТОП с фотокатода ФЭУ 83 усиливаются в динодной
системе с анодной нагрузкой ФЭУ R 15 (см. ЯЮ5. 421.000 Э3),
и поступают на вход усилителя-формирователя сигналов СТАРТ, СТОП.
Усилитель-формирователь собран на отдельной плате и помещен в
тепловой и электрический экран.
Одновременно сигнал с ФЭУ поступает на четыре канала
дискриминатора амплитуды отраженного сигнала. Сигналы с выхода
формирователей каналов дискриминации амплитуды используются для ввода поправки в данные измерения дальности в зависимости от амплитуды отраженного сигнала.
Слайд 19
Работа канала по шумовым сигналам (Рл.тр.) В
блоке АРУ установлен счетчик последовательности сигналов, который задает два
интервала счета шумовых сигналов равных 400 мс и 1с.
Для подсчета шумовых сигналов в определенном интервале работы
вырабатывается Строб Рл.тр. в течении времени когда приход сигнала невозможен.
Далее работа канала по шумовым сигналам происходит следующим
образом. С дальномерного фотоприемника подаются шумовые сигналы на вход счетчика Рл.тр. в стробе Рл.тр.
Счетчик производит подсчет шумовых сигналов за установленный интервал времени 400 мс или 1с.
Слайд 20
— введения коррекции в
двоичный код дальности по следующему
алгоритму:
Д = Дизм. К — Дv +
Дсист (9.2.)
Дизм. — 17 разрядный двоичный код дальности, поступающий в
блок
ВК из блока ФК;
К — коэффициент поправки, задается соответствующим
набором тумблеров и учитывающий состояние атмосферы т.е. скорость света.
Дv — поправка, зависящая от амплитуды сигнала СТОП,
Запуск счетчика осуществляется импульсом СТАРТ
Дсист. — поправка систематической ошибки, задается набором
тумблеров на наборном поле в виде 6 разрядов
двоичного кода. Систематическая поправка может
набираться от 0 до 32 м с дискретом 0,5 м.
Д — 17 разрядный двоичный код дальности на выходе блока
ВК, соответствует дальности до цели в метрах. Макси-
мально возможная дальность 65535 м с дискретом
0,5 м.
Если имеются по меньшей мере 2 юстировочные вышки, с заранее известным расстоянием, то поправки можно вводить автоматически в ЭВМ.
— преобразования информации о дальности до цели, из двоичного
коде, в двоично-десятичный код для индикации дальности на пульте
управления станции.
Введения коррекции
Слайд 21
Дальномер ЛТЛС ближнего действия
Слайд 23
Особенности работы дальномерного канала ЛТЛС дальнего действия рассмотрим
на примере станции траекторных измерений типа «Юкон-М».
В качестве дальномерного
приемника – ФЭУ Хамаматца
Дальномер ЛТЛС дальнего действия
Слайд 24
В приемнике дальномерного канала В приемнике дальномерного канала
в каждый момент времени формируется в приемной матрице 16×16
изображение части общего поля зрения 1,7о×1,7о размером 3×3 угл.мин., центр
которого в данный момент облучается лазерным передатчиком и из приходящего отраженного светового сигнала формируется электрический импульс “СТОП”. На основании измерения времени запаздывания между зондирующим сигналом “СТАРТ” и отраженным сигналом “СТОП” вычисляется наклонная дальность до цели с учетом атмосферной и инструментальной погрешностей. Сам процесс измерения и вычисления дальности производится в измерителе временных
интервалов (ИВИ), который входит в состав устройства первичной обработки дальномерного канала. Работой ИВИ управляет микропроцессор дальномерного приемника. Информация о дальности в последовательном коде через интерфейс поступает через устройство последовательной передачи информации на блок вторичной обработки станции.
из приходящего отраженного светового сигнала формируется электрический импульс “СТОП”. На основании измерения времени запаздывания между зондирующим сигналом “СТАРТ” и отраженным сигналом “СТОП” вычисляется наклонная дальность до цели с учетом атмосферной и инструментальной погрешностей. Сам процесс измерения и вычисления дальности производится в измерителе временных
интервалов (ИВИ), который входит в состав устройства первичной обработки дальномерного канала. Работой ИВИ управляет микропроцессор дальномерного приемника. Информация о дальности в последовательном коде через интерфейс поступает через устройство последовательной передачи информации на блок вторичной обработки станции.