Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
![]()
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
![]()
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
![]()
(2.39)
Для
нашего примера эта величина составит:
![]()
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
![]()
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
![]()
;
S2
– остаточная сумма квадратов отклонений
![]()
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
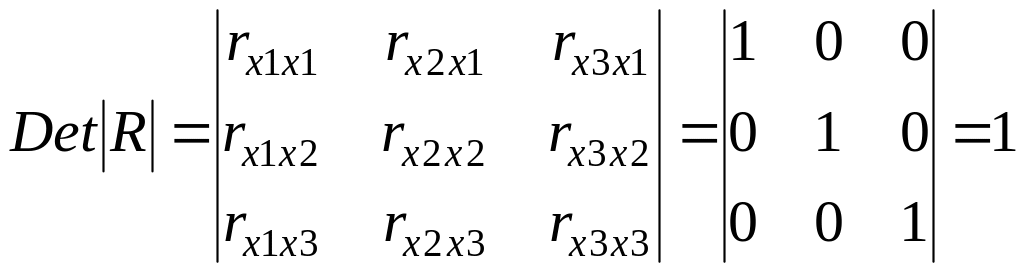
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
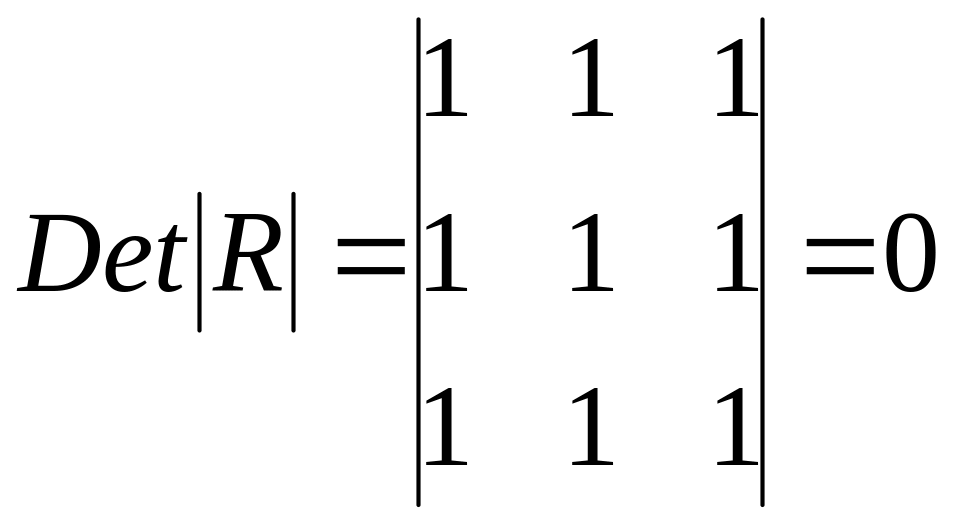
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
![]()
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
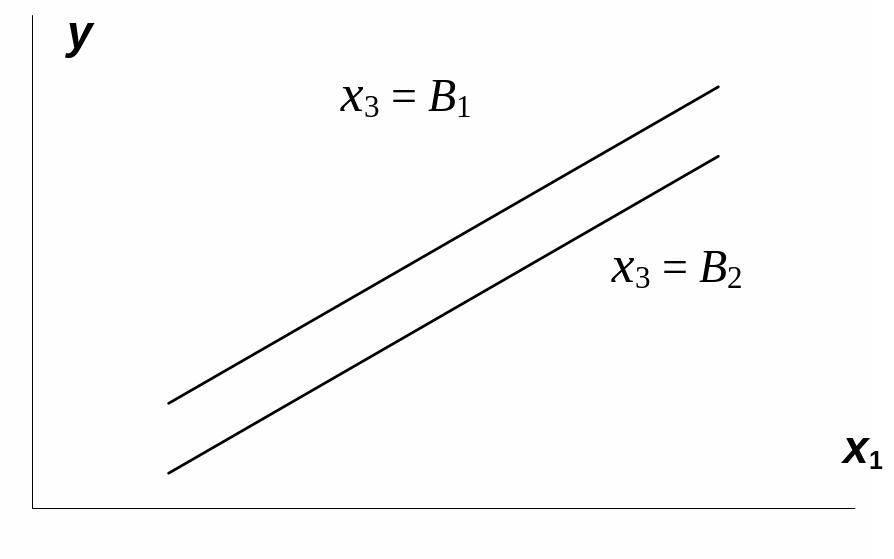
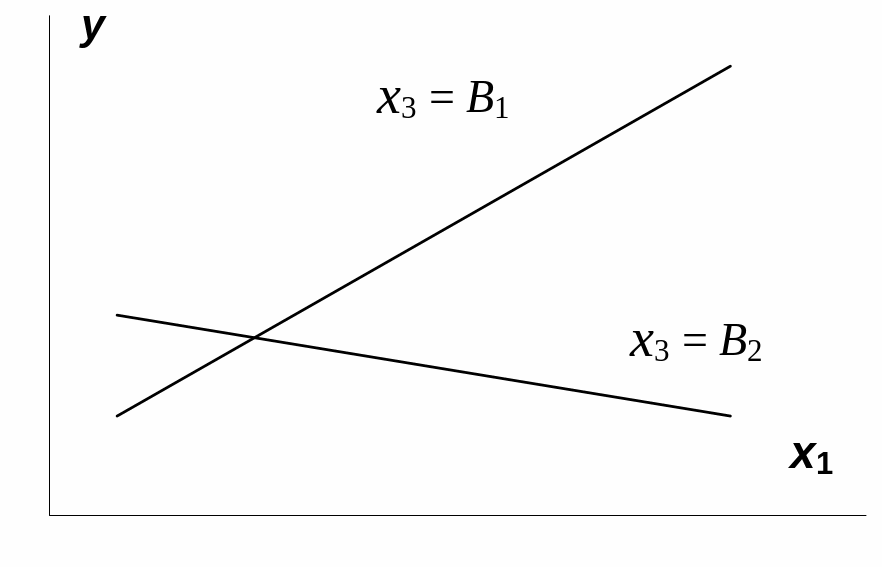
Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
![]()
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
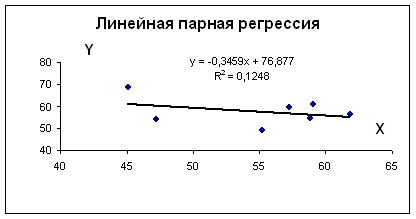
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
 .
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости  .
.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
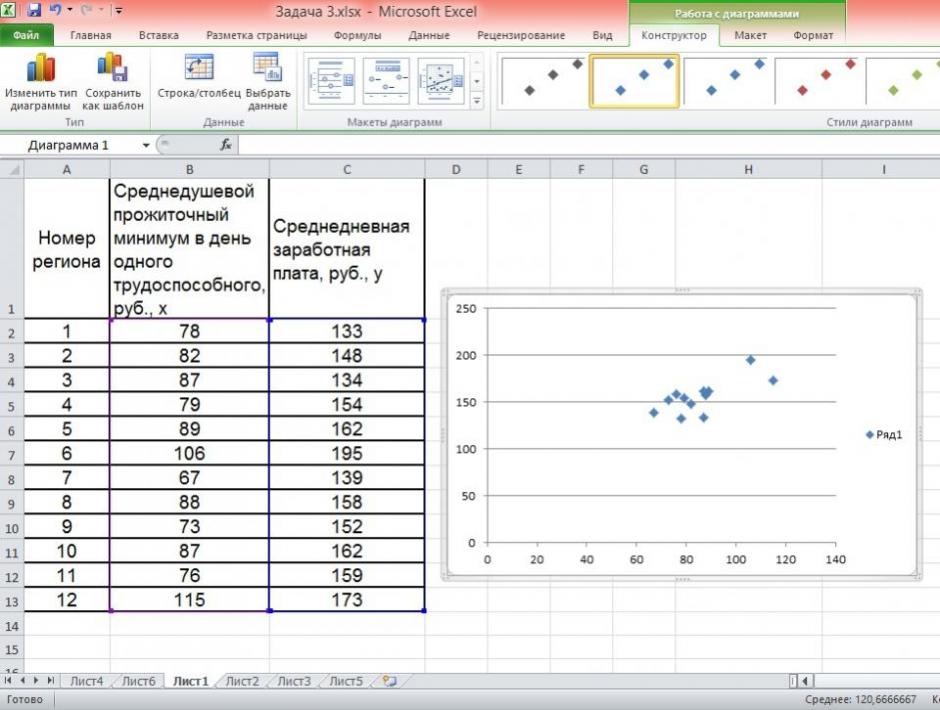
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
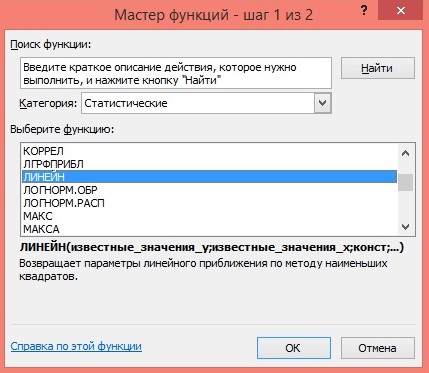
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
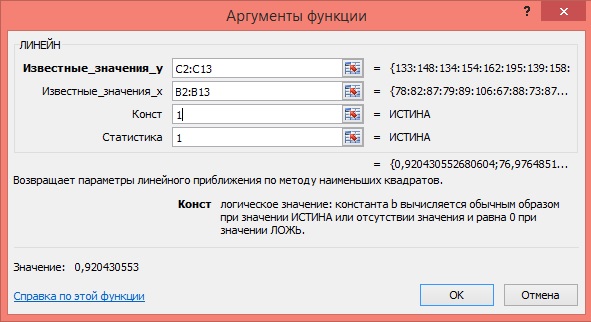
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
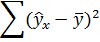
Остаточная сумма квадратов
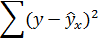
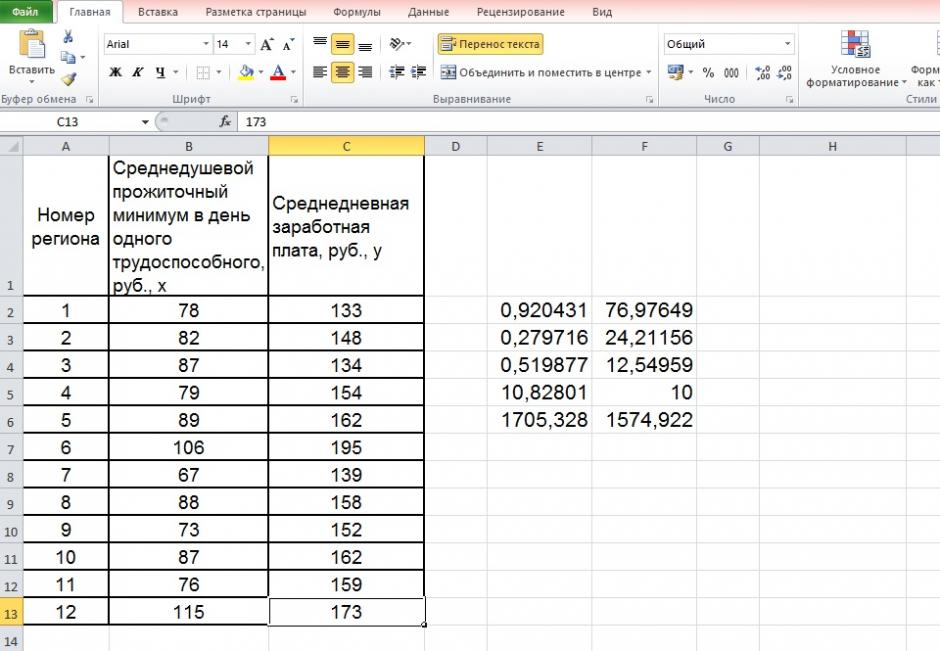
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
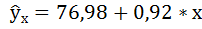
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации  означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации  можно рассчитать коэффициент корреляции:
можно рассчитать коэффициент корреляции: 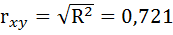 .
.
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 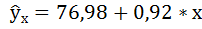 средний (общий) коэффициент эластичности определим по формуле:
средний (общий) коэффициент эластичности определим по формуле:
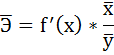
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
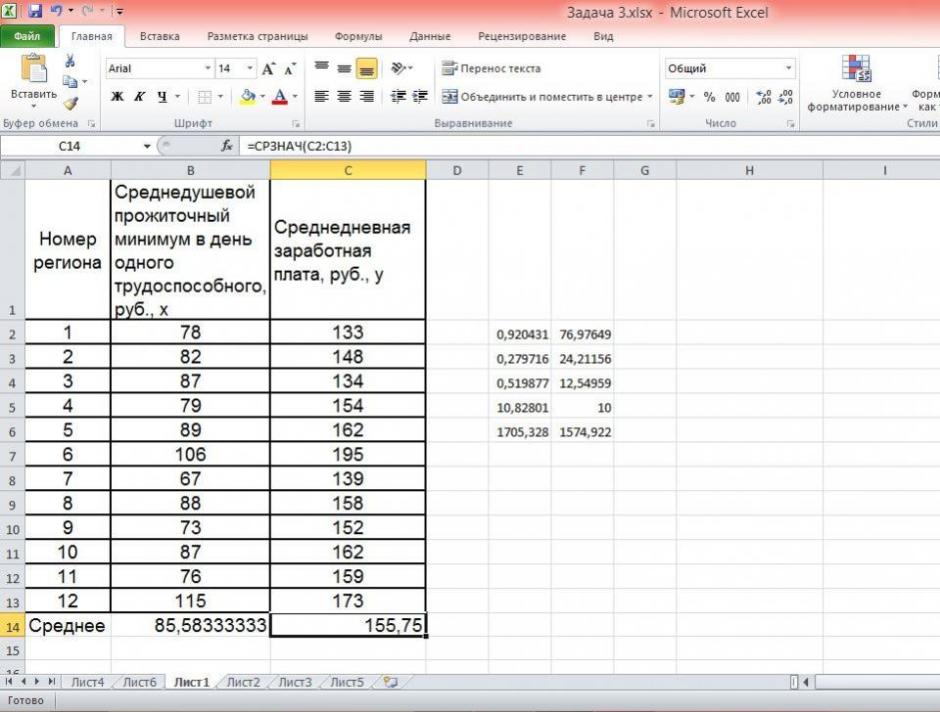
Рисунок 5 Расчёт средних значений функции и аргумент
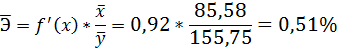
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
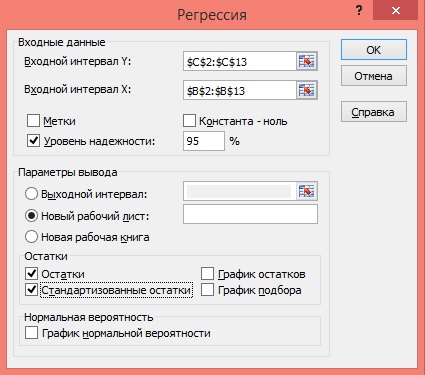
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
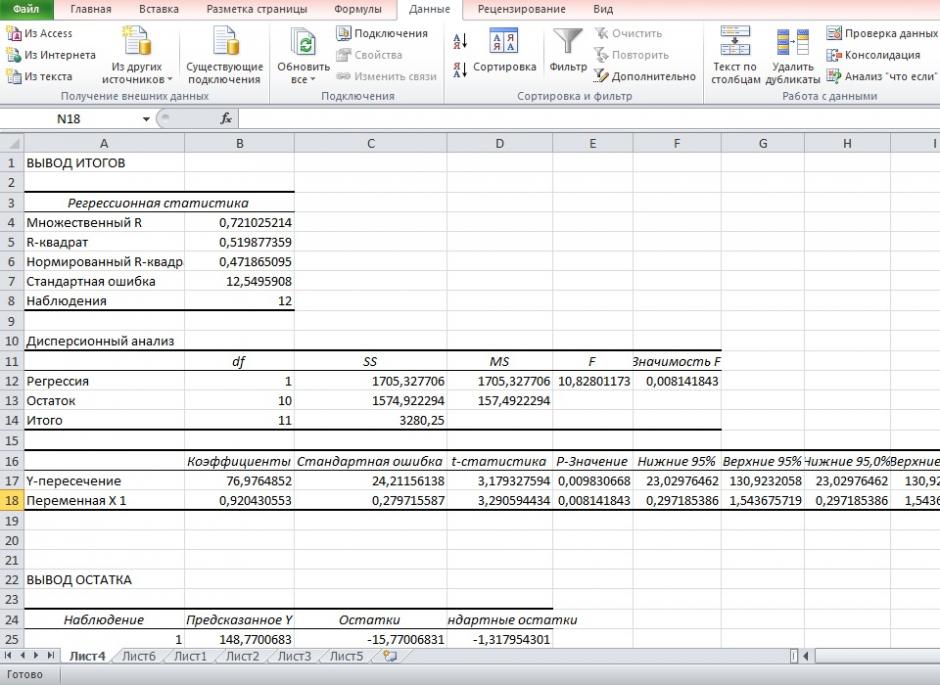
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
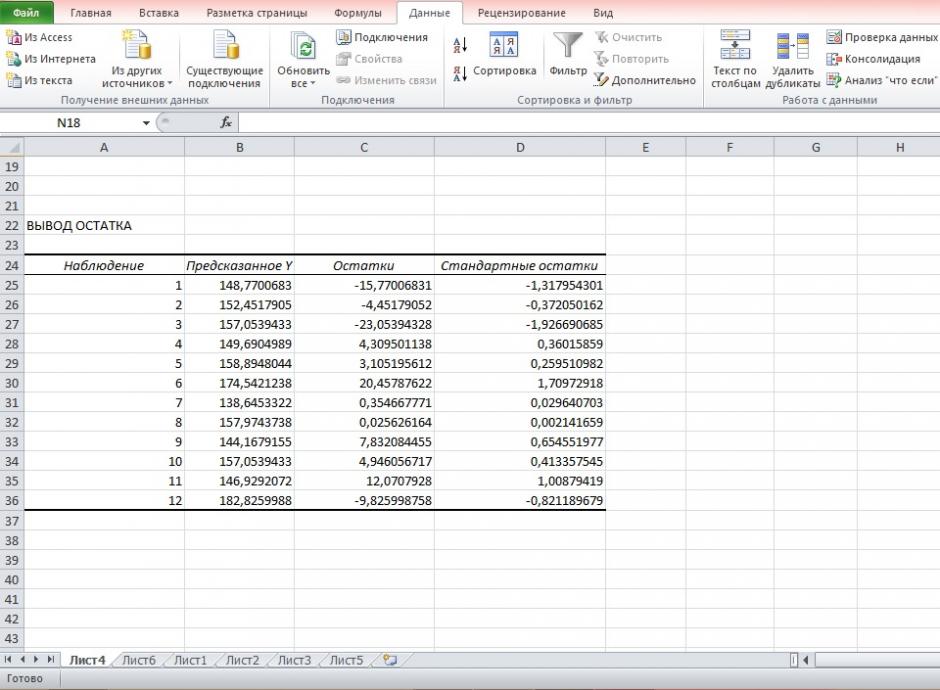
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
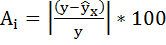
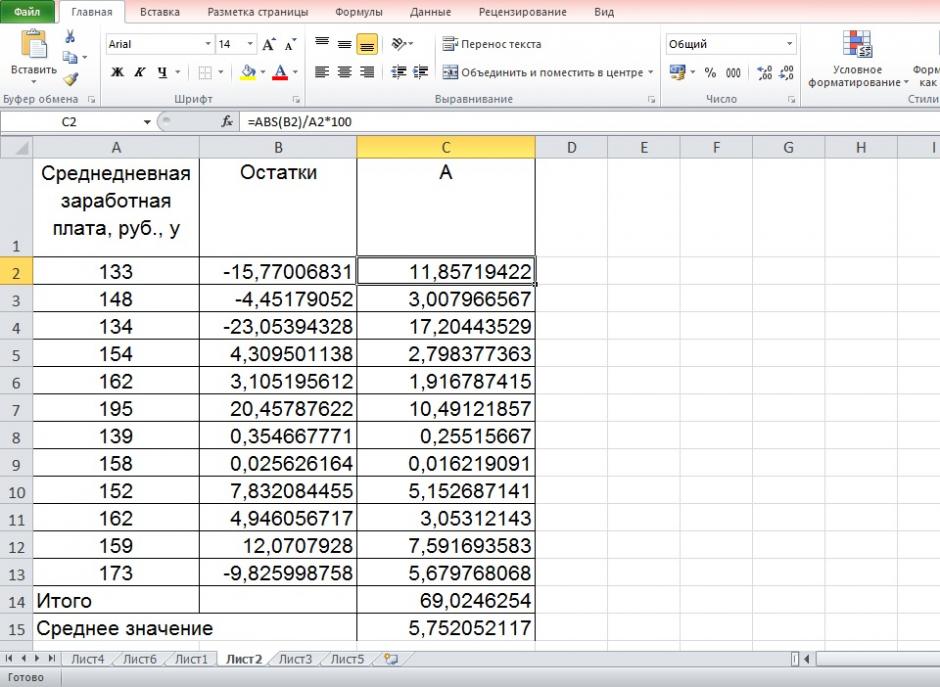
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
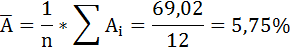
Качество построенной модели оценивается как хорошее, так как 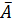 не превышает 8 – 10%.
не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера: 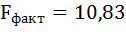
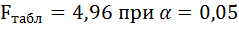
Поскольку 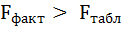 при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
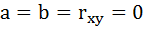 .
.
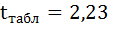 для числа степеней свободы
для числа степеней свободы 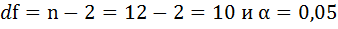
На рисунке 7 имеются фактические значения t-статистики:
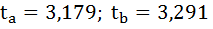
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 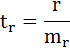
где 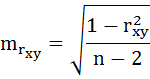 – случайная ошибка коэффициента корреляции.
– случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
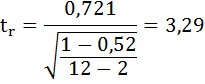
II способ: 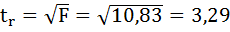
Фактические значения t-статистики превосходят табличные значения:
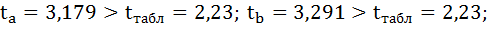
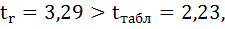
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
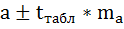
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
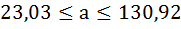
Доверительный интервал для коэффициента регрессии определяется как
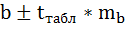
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
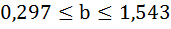
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 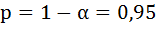 параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
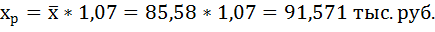
Тогда прогнозное значение прожиточного минимума составит:
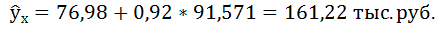
Ошибку прогноза рассчитаем по формуле:
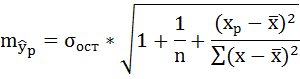
где 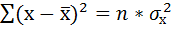
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
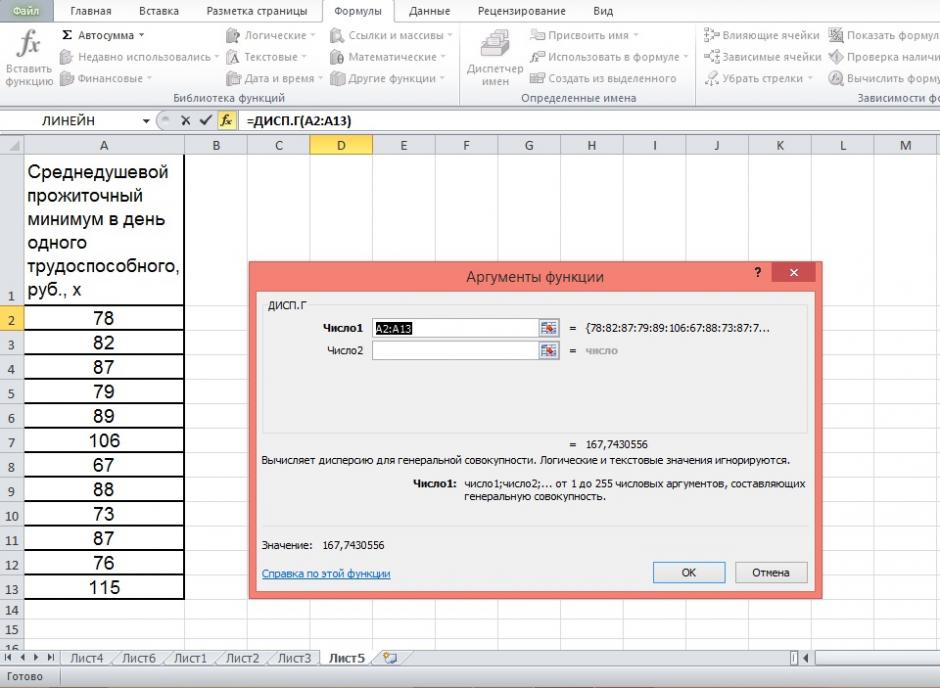
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии 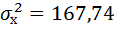
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
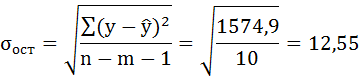
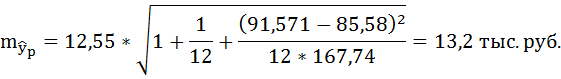
Доверительные интервалы прогноза индивидуальных значений у при 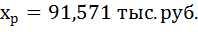 с вероятностью 0,95 определяются выражением:
с вероятностью 0,95 определяются выражением:
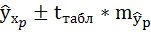
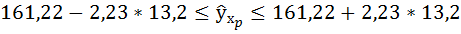
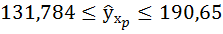
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Средней ошибки аппроксимации качество уравнений
Оценка этой формы связи по коэффициенту множественной корреляции и средней ошибке аппроксимации показывает, что адекватность данной модели не подтверждается. Действительно, хотя значение коэффициента достаточно высокое (0,92), средняя ошибка аппроксимации составляет более 10% (I = 14,5%). Поэтому данная форма должна быть исключена из перебора известных уравнений регрессии. [c.29]
Анализ полученной формы связи по той же причине, что и в первом случае, позволяет сделать вывод о непригодности и этой модели. Коэффициент множественной корреляции хотя и имеет более высокое значение, чем в линейной зависимости (0,93), но по величине средней ошибки аппроксимации (б = 12,4%) это уравнение регрессии подлежит исключению из дальнейшего перебора. [c.29]
Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации. [c.30]
Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%. [c.39]
Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /»табл = 3,01, корреляционное отношение равно 0,9959, ее»стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]
Средняя ошибка аппроксимации [c.94]
Средняя ошибка аппроксимации. [c.95]
В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. 7.4). [c.144]
Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. [c.145]
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( ), коэффициенты множественной корреляции (/ ) и детерминации (D). [c.151]
Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации [c.152]
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. [c.152]
После построения уравнения регрессии необходимо сделать проверку его значимости с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации [c.123]
Модель считается адекватной, т.е. пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 15%. [c.123]
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. [c.6]
Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических [c.6]
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ух. По ним рассчитаем показатели тесноты связи — индекс корреляции рху и среднюю ошибку аппроксимации 7, [c.13]
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. [c.16]
Это означает, что 52% вариации заработной латы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации [c.18]
Оцените с помощью средней ошибки аппроксимации качество уравнений. [c.38]
Оцените качество уравнений с помощью средней ошибки аппроксимации. [c.42]
Оцените качество уравнения через среднюю ошибку аппроксимации. [c.92]
Оцените качество каждого тренда через среднюю ошибку аппроксимации, линейный коэффициент автокорреляции отклонений. [c.166]
СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ [c.87]
Представим расчет средней ошибки аппроксимации для уравнения ух = 9,876 + 5,129 hue в табл. 2.7. А = — 7,3 = 1,2%, что [c.88]
Расчет средней ошибки аппроксимации [c.88]
В стандартных программах чаще используется первая формула для расчета Средней ошибки аппроксимации. [c.88]
В чем смысл средней ошибки аппроксимации и как она определяется [c.89]
Средняя ошибка аппроксимации [c.10]
Выбор вида модели основан на логическом анализе изучаемых показателей, сравнении статистических характеристик (средняя ошибка аппроксимации, критерий Фишера, коэффициенты множественной корреляции и детерминации), рассчитанных для различных функций по одним и тем же первичным данным. [c.31]
Проверка приведенной в формуле (154) себестоимости по фактическим данным 103 СМУ показала, что средняя ошибка аппроксимации, определяющая степень соответствия расчетных значений фактическим, составила всего 1,5%, что вполне допустимо. [c.227]
Исчисляемый коэффициент детерминации получился равным 0,869. Это говорит о том, что размер заработной платы водителей на 86,9% зависит от Р и Л ри на 13,1% — от неучтенных в модели факторов. Средняя ошибка аппроксимации составила всего лишь 0,17%. Модель была получена на основе конкретных показателей ряда автотранспортных предприятий Владимирского транспортного управления, поэтому она может -быть использована в практической работе только на этих предприятиях. Предлагаемая же методика может быть использована в любом транспортном управлении, министерстве при планировании и анализе себестоимости автомобильных перевозок и установлении нормативов по заработной плате водителей за время работы на линии. [c.36]
источники:
http://ecson.ru/economics/econometrics/zadacha-3.raschyot-parametrov-regressii-i-korrelyatsii-s-pomoschju-excel.html
http://economy-ru.info/info/119599/
Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.

Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
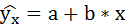
Решаем систему нормальных уравнений относительно a и b:
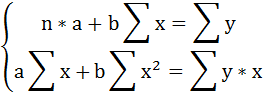
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 |  |
 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 |
8,4988 | 11,1431 | х | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
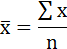
Cреднее квадратическое отклонение рассчитаем по формуле:
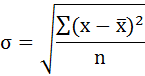
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
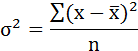
Параметры уравнения можно определить также и по формулам:
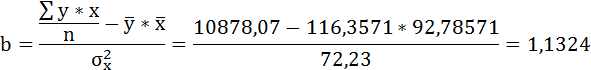
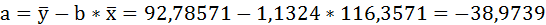
Таким образом, уравнение регрессии:
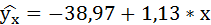
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
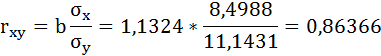
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
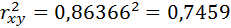
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения  .
.
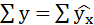 ,
,
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
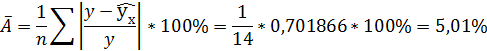
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
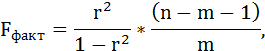
где n – число единиц совокупности;
m – число параметров при переменных х.
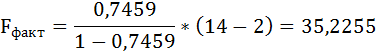
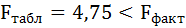
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
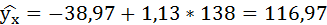
2. Степенная регрессия имеет вид:
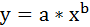
Для определения параметров производят логарифмирование степенной функции:
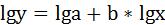
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
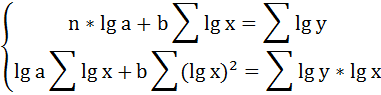
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 |
8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 |
72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
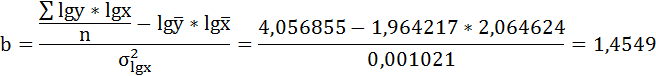
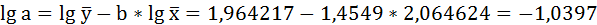
Получим линейное уравнение:
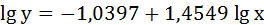
Выполнив его потенцирование, получим:
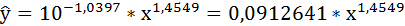
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 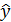 . По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
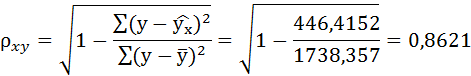
Связь достаточно тесная.
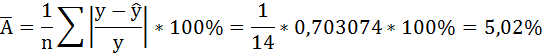
В среднем расчётные значения отклоняются от фактических на 5,02%.
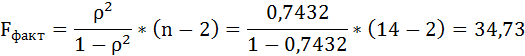
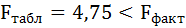
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
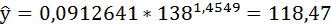
3. Уравнение равносторонней гиперболы
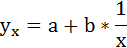
Для определения параметров этого уравнения используется система нормальных уравнений:
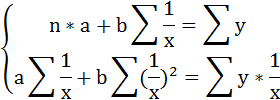
Произведем замену переменных
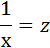
и получим следующую систему нормальных уравнений:
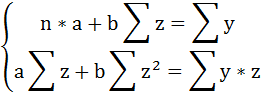
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 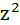 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 |
8,4988 | 11,1431 | 0,000640820 | х | х | х |
 |
72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
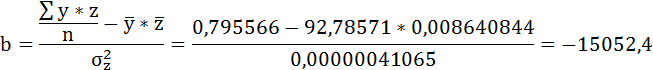
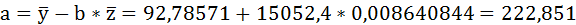
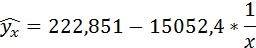
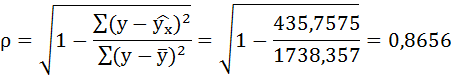
Связь достаточно тесная.
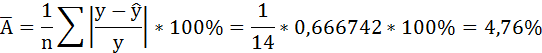
В среднем расчётные значения отклоняются от фактических на 4,76%.
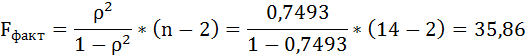
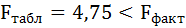
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
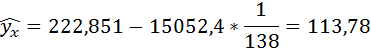
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
Оценка корреляции для нелинейной регрессии
Оценка тесноты корреляционной зависимости в случае нелинейной регрессии производится с помощью индекса корреляции (R):
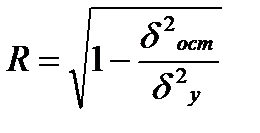 , (39.1)
, (39.1)
где 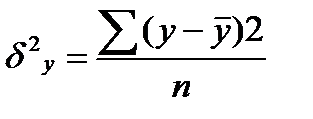 ,
, 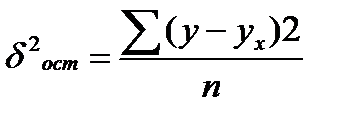 ,
, 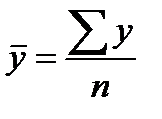 (39.2)
(39.2)
y¯x значения результативного признака, рассчитанные по уравнению регрессии.
Величина данного показателя находится в границах: 0≤ R ≤ 1 , чем она ближе к единице, тем теснее связь рассматриваемых признаков, тем надежнее найденное уравнение регрессии.
Следует помнить, что если для линейной зависимости имеет место равенство: ryx =rxy , то при криволинейной зависимости y=f(x) Ryx не равен Rxy.
Величина R 2 называется индексом детерминации.
Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:
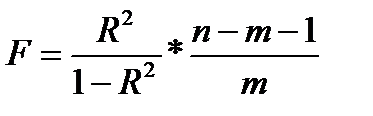 , (39.3)
, (39.3)
где R 2 — индекс детерминации;
n — число наблюдений;
m — число параметров при переменных х.
Индекс детерминации R 2 yx можно сравнивать с коэффициентом детерминации r 2 yx для обоснования возможности применения линейной функции.
Если величина (R 2 yx — r 2 yx) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия между R 2 yx и r 2 yx , вычисленных по одним и тем же исходным данным, через t — критерий Стьюдента:
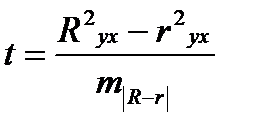 , (39.4)
, (39.4)
где 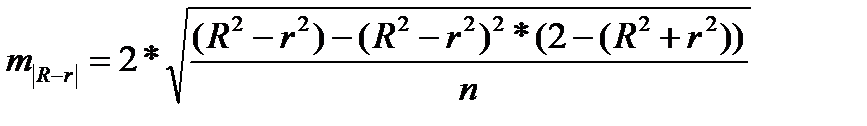 , (39.5)
, (39.5)
Если t факт> t табл, то различия между Ryx и ryx существенны и замена нелинейной регрессии линейной — невозможна. Практически, если t ≤ 2, то различия между Ryx и ryx несущественны, и, следовательно, возможно применение линейной регрессии.
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. y и yx. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:
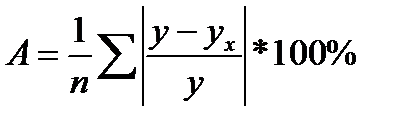 (39.6)
(39.6)
Существует и другая формула определения средней ошибки аппроксимации:
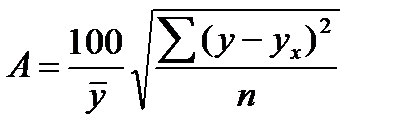 , (39.7)
, (39.7)
где 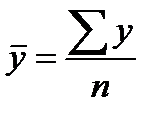 . (39.8)
. (39.8)
Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.
Возможность построения нелинейных моделей, как с помощью их приведения к линейному виду, так и путем использования нелинейной регрессии, значительно повышает универсальность регрессионного анализа, но и усложняет задачу исследователя.
Возникает вопрос: с чего начать — с линейной зависимости или с нелинейной, и если с последней, то, какого типа.
Если ограничиться парной регрессией, то можно построить график наблюдений у и х и принять решение. Однако очень часто несколько разных нелинейных функцией приблизительно соответствуют наблюдениям, если они лежать на некоторой кривой. А в случае множествен6ной регрессии невозможно даже построить график.
37. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
Хотя во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат, однако ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Так близость линейного коэффициента корреляции к нулю еще не значит, что связь между соответствующими экономическими переменными отсутствует. При слабой линейной связи может быть очень тесной, например, не линейная связь. Поэтому необходимо рассмотреть и нелинейные регрессии, построение и анализ которых имеют свою специфику.
В случае, когда между экономическими явлениями существует нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей.
38. Двухфакторная производственная функция Кобба-Дугласа
Производственная функцию Кобба –Дугласа выглядит следующим образом:
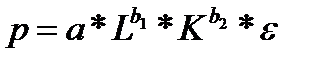 (44.1)
(44.1)
где Р –объем продукции
L— затраты труда;
К — величина капитала;
Логарифмируя ее, получим линейное в логарифмах уравнение
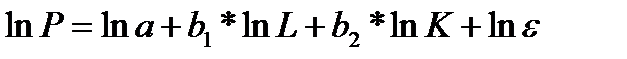 (44.2)
(44.2)
Оценив параметры этого уравнения по МНК, можно найти теоретические значения объема продукции Р^ и соответственно остаточную сумму квадратов Σ (Р — Р^) 2 которая используется в расчете индекса детерминации:
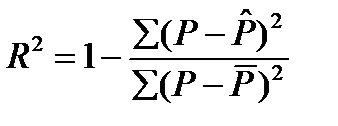 (44.3)
(44.3)
Следует помнить, что МНК применяется не к исходным данным продукции, а к их логарифмам. Поэтому в индексе корреляции с общей суммой квадратов Σ (Р — Р¯) 2 сравнивается остаточная дисперсия, которая определена по теоретическим значениям логарифмов продукции:
Σ (Р — антилогарифм (ln Р)) 2 . Т.е. Р^ находится в следствии потенцированиия ln Р.
39. Отбор факторов для экономертических моделей
Хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа, который обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе показателей корреляции определяют t-статистики для параметров регрессии. Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если 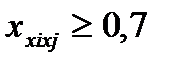 . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Включение в модель мультиколлинеарныхфакторов нежелательно в силу следующих последствий:
. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Включение в модель мультиколлинеарныхфакторов нежелательно в силу следующих последствий:
1. затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;
2. оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей. Для включающего три объясняющих переменных уравнения: y=a+b1x1+b2+b3x3+e.Матрица коэф-в корреляции м/у факторами имела бы определитель равный
Det 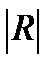 =1, т.к. rx1x1=rx2x2=1 и rx1x2=rx1x3=rx2x3=0.
=1, т.к. rx1x1=rx2x2=1 и rx1x2=rx1x3=rx2x3=0.
Если м/у факторами сущ-ет полная линейная зависимость и все коэф-ты корреляции =1, то определитель такой матрицы =0. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
40. Метод наименьших квадратов для двухфакторной производственной функции.
Метод наименьших квадратов.Некоторые более общие типы регрессионных моделей рассмотрены в разделе Основные типы нелинейных моделей. После выбора модели возникает вопрос: каким образом можно оценить эти модели? Если вы знакомы с методами линейной регрессии (описанными в разделе Множественная регрессия) или дисперсионного анализа (описанными в разделе Дисперсионный анализ), то вы знаете, что все эти методы используют оценивание по методу наименьших квадратов. Основной смысл этого метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. (Термин наименьшие квадраты впервые был использован в работе Лежандра — Legendre, 1805.)
Функция потерь.В стандартной множественной регрессии оценивание коэффициентов регрессии происходит “подбором” коэффициентов, минимизирующих дисперсию остатков (сумму квадратов остатков). Любые отклонения наблюдаемых величин от предсказанных означают некоторые потери в точности предсказаний, например, из-за случайного шума (ошибок). Поэтому можно сказать, что цель метода наименьших квадратов заключается в минимизации функции потерь. В этом случае, функция потерь определяется как сумма квадратов отклонений от предсказанных значений (термин функция потерь был впервые использован в работе Вальда — Wald, 1939). Когда эта функция достигает минимума, вы получаете те же оценки для параметров (свободного члена, коэффициентов регрессии), как, если бы мы использовали Множественную регрессию. Полученные оценки называются оценками по методу наименьших квадратов.
Продолжая в том же духе, можно рассмотреть другие функции потерь. Например, при минимизации функции потерь, почему бы вместо суммы квадратов отклонений не рассмотреть сумму модулей отклонений? В самом деле, иногда это бывает полезно для уменьшения влияния выбросов. Влияние, оказываемое крупными остатками на всю сумму, существенно увеличивается при их возведении в квадрат. Однако если вместо суммы квадратов взять сумму модулей выбросов, влияние остатков на результирующую регрессионную кривую существенно уменьшится.
Существуют несколько методов, которые могут быть использованы для минимизации различных видов функций пот
41. Двухфакторная производственная функция Солоу
Производственная функция – это зависимость между набором факторов производства и максимально возможным объемом продукта, производимым с помощью данного набора факторов.
Производственная функция всегда конкретна, т.е. предназначается для данной технологии. Новая технология – новая производительная функция.
С помощью производственной функции определяется минимальное количество затрат, необходимых для производства данного объема продукта.
Производственные функции, независимо от того, какой вид производства ими выражается, обладают следующими общими свойствами:
1) Увеличение объема производства за счет роста затрат только по одному ресурсу имеет предел (нельзя нанимать много рабочих в одно помещение – не у всех будут места).
2) Факторы производства могут быть взаимодополняемы (рабочие и инструменты) и взаимозаменяемы (автоматизация производства).
В наиболее общем виде производственная функция выглядит следующим образом:
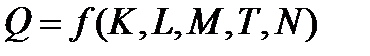 ,
,
где 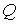 — объем выпуска;
— объем выпуска;
K- капитал (оборудование);
М- сырье, материалы;
Т – технология;
N – предпринимательские способности.
Наиболее простой является двухфакторная модель производственной функции Кобба – Дугласа, с помощью которой раскрывается взаимосвязь труда (L) и капитала (К). Эти факторы взаимозаменяемы и взаимодополняемы
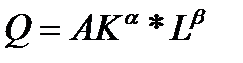 ,
,
где А – производственный коэффициент, показывающий пропорциональность всех функций и изменяется при изменении базовой технологии (через 30-40 лет);
K, L- капитал и труд;
α, β -коэффициенты эластичности объема производства по затратам капитала и труда.
Если 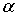 = 0,25, то рост затрат капитала на 1% увеличивает объем производства на 0,25%.
= 0,25, то рост затрат капитала на 1% увеличивает объем производства на 0,25%.
На основе анализа коэффициентов эластичности в производственной функции Кобба — Дугласа можно выделить:
1) пропорционально возрастающую производственную функцию, когда
α + β =1(Q=K 0,5 *L 0,2 ) .
2) непропорционально – возрастающую α + β > 1 (Q = K 0,9 *L 0,8 );
3) убывающую α + β 0,4 *L 0,2 ).
Рассмотрим короткий период деятельности фирмы, в котором из двух факторов переменным является труд. В такой ситуации фирма может увеличить производство за счет использования большего количества трудовых ресурсов. График производственной функции Кобба – Дугласа с одной переменной изображен на рис. 10.1 (кривая ТРн).
В краткосрочном периоде действует закон убывающей предельной производительности.
Закон убывающей предельной производительности действует в краткосрочном временном интервале, когда один производственный фактор остается неизменным. Действие закона предполагает неизменное состояние техники и технологии производства, если в производственном процессе будут применены новейшие изобретения и другие технические усовершенствования, то рост объема выпуска может быть достигнут при использовании тех же самых производственных факторов. То есть технический прогресс может изменить границы действия закона.
Если капитал является фиксированным фактором, а труд – переменным, то фирма может увеличить производство за счет использования большего количества трудовых ресурсов. Но по закону убывающей предельной производительности, последовательное увеличение переменного ресурса при неизменности других ведет к убывающей отдаче данного фактора, то есть к снижению предельного продукта или предельной производительности труда. Если же наем рабочих будет продолжаться, то в конечном итоге, они будут мешать друг другу (предельная производительность станет отрицательной) и объем выпуска сократится.
Предельная производительность труда (предельный продукт труда – MPL) – это прирост объема производства от каждой последующей единицы труда
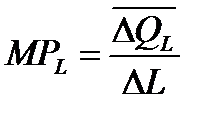 ,
,
т.е. прирост производительности к совокупному продукту (TPL)
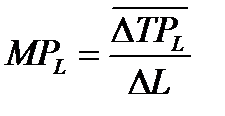 .
.
Аналогично определяется предельный продукт капитала MPK.
Основываясь на законе убывающей производительности, проанализируем взаимосвязь общего (TPL), среднего (АPL) и предельного продуктов (MPL) (рис. 10.1).
В движении кривой общего продукта (ТР) можно выделить три этапа. На этапе 1 она поднимается вверх ускоряющимися темпами, так как предельность продукта (MP) возрастает (каждый новый рабочий приносит больше продукции, чем предыдущий) и достигает максимума в точке А, то есть скорость роста функции максимальна. После точки А (этап 2) в силу действия закона убывающей отдачи, кривая MP падает, то есть каждый нанятый рабочий дает меньшее приращение общего продукта по сравнению с предшествующим, поэтому темп роста ТР после ТС замедляется. Но пока МР будет положительным, ТР будет все равно увеличиваться и достигнет максимума при МР=0.
На 3 этапе, когда количество рабочих становится избыточным по отношению к фиксированному капиталу (станки), МР приобретает отрицательное значение, поэтому ТР начинает снижаться.
Конфигурация кривой среднего продукта АР также обусловлена динамикой кривой МР. На 1 этапе обе кривые растут, пока приращение объема выпуска от вновь нанятых рабочих будет большим, чем средняя производительность (АРL) ранее нанятых рабочих. Но после точки А (max MP), когда четвертый рабочий добавляет к совокупному продукту (ТР) меньше чем третий, МР уменьшается, поэтому средняя выработка четырех рабочих также сокращается.
Производственные функции Солоу, представляют собой одно из ближайших обобщений многофакторных функций с постоянной и одинаковой эластичностью замены факторов.
42. Гомоскедастичность и гетероскедастичность остатков модели регрессии. Последствия гетероскедастичности
С определения гомоскедастичности и гетероскедастичности остатков модели регрессии строиться график зависимости остатков ei от теоретических значений результативного признака:
Если на графике получена горизонтальная полоса, то остатки ei представляют собой случайные величины и МНК оправдан, теоретические значения ух хорошо аппроксимируют фактические значения у.
Возможны варианты: если ei зависит от уx, то: 1.остатки ei не случайны.2. остатки ei, не имеют постоянной дисперсии. 3. Остатки ei носят систематический характер в данном случае отрицательные значения ei, соответствуют низким значениям ух, а положительные — высоким значениям. В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию.
Гомоскедастичность остатков означает, что дисперсия остатков ei одинакова для каждого значения х.Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. а — дисперсия остатков растет по мере увеличения х; б — дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных и максимальных значениях х; в — максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х. Графики гомо- и гетеро-ти.
Оценка отсутствия автокорреляции остатков(т.е. значения остатков ei распределены независимо друг от друга). Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между ei и ej , где ei — остатки текущих наблюдений, ej — остатки предыдущих наблюдений, может быть определен по обычной формуле линейного коэффициента корреляции 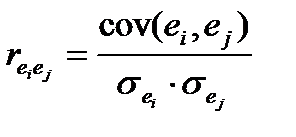 . (51.1)
. (51.1)
Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности F(e) зависит j-й точки наблюдения и от распределения значений остатков в других точках наблюдения. Для регрессионных моделей по статической информации автокорреляция остатков может быть подсчитана, если наблюдения упорядочены по фактору х. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динамики, где ввиду наличия тенденции последующие уровни динамического ряда, как правило, зависят от своих предыдущих уровней.
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным методом. Обобщенный МНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Обобщенный МНК для корректировки гетероскедастичности. В общем виде для уравнения yi=a+bxi+ei при 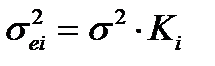 где Ki – коэффициент пропорциональности. Модель примет вид: yi=
где Ki – коэффициент пропорциональности. Модель примет вид: yi= 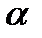 +
+ 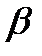 xi+
xi+ 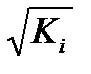 ei .
ei .
В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе i-го наблюдения на 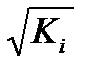 . Тогда дисперсия остатков будет величиной постоянной. От регрессии у по х перейдем к регрессии на новых переменных: y/
. Тогда дисперсия остатков будет величиной постоянной. От регрессии у по х перейдем к регрессии на новых переменных: y/ 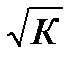 и х/
и х/ 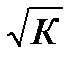 . Уравнение регрессии примет вид:
. Уравнение регрессии примет вид: 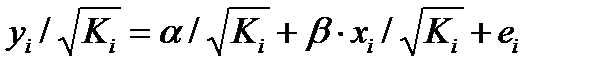 . (51.2)
. (51.2)
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные у и х взяты с весами 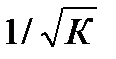 . Коэф-т регрессии b можно определить как
. Коэф-т регрессии b можно определить как 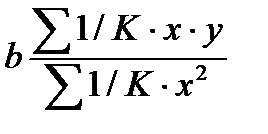 (51.3)
(51.3)
Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Модель примет вид:
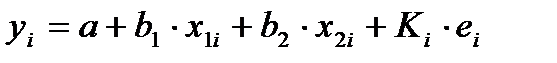 . (51.4)
. (51.4)
Модель с преобразованными переменными составит
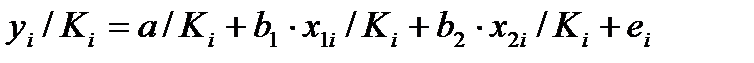 . (51.5)
. (51.5)
Это уравнение не содержит свободного члена, применяя обычный МНК получим:
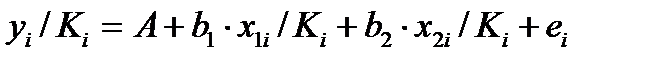 (51.5)
(51.5)
Применение в этом случае обобщенного МНК приводит к тому, что наблюдения с меньшими значениями преобразованных переменных х/К имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменными.
43. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии
Наличие гетероскедастичности в отдельных случаях может привести к смущенности оценок коэффициентов регрессии, хотя несмещенности оценок коэффициентов регрессии в основном зависит от соблюдения второй предпосылки МНК, т. е. независимости остатков и величин факторов. Гетероскедастичность будет сказываться на уменьшении эффективности оценок bi,. В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии mbi, предполагающую единую дисперсию остатков для любых значений фактора.
Тест Глейзера основывается на регрессии абсолютных значений остатков | ε | , т.е. рассматривается функция | εi| = a +bxi c + ui ,. Регрессия | εi| от xi cстроится при разных значениях параметра с, и далее отбирается та функция, для которой коэффициент регрессии b оказывается наиболее значимым, т.е. имеет место наибольшее значение (критерия Стьюдента или F-критерия Фишера и R 2 .
При обнаружении гетероскедастичности остатков регрессии ставится цель ее устранения, чему служит применение обобщенного метода наименьших квадратов
44. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии
При малом объеме выборки, для оценки гетероскедастичности используют метод Гольфреда — Квандта, разработанный в 1965 г. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально Квадрату фактора. Для того чтобы оценить нарушение гомоскедастичности они предложили параметрический тест. Данный тест заключается в следующих стадиях:
1) Упорядочение n наблюдений по мере возрастания переменной х.
2) Исключение из рассмотрения С центральных наблюдений;
при этом (n — С)/ 2 > р, где р — число оцениваемых параметров.
3) Разделение совокупности из ( n — С) наблюдений на две группы (соответственно с малыми и большими значениями факторах) и определение по каждой из групп уравнений регрессии.
4) Определение остаточной суммы квадратов для первой (S1) и второй (S2) групп и нахождение их отношения R=S1/S2, где S1> S2.
При выполнении нулевой гипотезы о гомоскедастичности от ношение R будет удовлетворять F-критерию с (n — С- 2р) : 2 степенями свободы для каждой остаточной суммы квадратов. Чем сильнее R превышает табличное значение F -критерия тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
45. Устранение гетероскедастичности остатков модели регрессии
Автокорреляция остатков может быть вызвана следующими причинами:
1) Ошибками измерения при первоначальном сборе данных по результативному признаку;
2) Неправильно выбранная формулировка исходной модель.
При формировании модели мог быть упущен из виду фактор, оказывающий существенное влияние на результат. В итоге влияние этого фактора отражается в остатках в виде автокорреляции остатков. Часто этим фактором является показатель времени. Кроме того, в качестве таких существенных факторов могут выступать лаговые значения переменных включенных в модель. Либо модель не учитывает несколько равнозначных факторов, которые оказывают совместное влияние при совпадении тенденций и циклов колебаний. От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму связи факторных и результативного признаков, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции остатков.
46. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора хj остатки i имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков от теоретических значений результативного признака уx.
Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности.
При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения i распределены независимо друг от друга.
Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений.
Отсутствие автокорреляции остатков обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t и F. Вместе с тем оценки регрессии, найденные с применением МНК, обладает хорошими свойствами даже при отсутствии нормального распределения остатков.
При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы и т.д.
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным МНК.
Обобщенный МНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии
47. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии
Существуют два наиболее распространенных метода определения автокорреляции остатков:
1) путем построения графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции; 2) использование критерия Дарбина-Уотсона и расчет величины
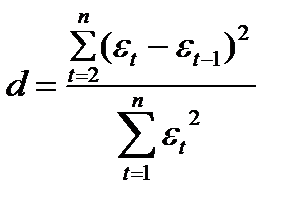 (56.1)
(56.1)
d – отношение суммы квадратов разностей последовательных занчений остатков к остаточной сумме квадратов по модели регрессии. Чащен всего критерий Дарбина –Уотсона указывается наряду с коэффициентом детерминации, значениями t- и F-критерия
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости 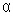 . По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1-) производится на основе данных, приведенных в таблице 5.1.
. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1-) производится на основе данных, приведенных в таблице 5.1.
Таблица 47.1 Механизм проверки гипотезы о наличии автокорреляции остатков.
| Есть положительная автокорреляция остатков. Н0 отклоняется. С вероятностью Р=(1-) принимается гипотеза Н1 | Зона неопределенности | Нет оснований отклонять Н0 (автокорреляция остатков отсутствует) | Зона неопределенности | Есть отрицательная автокорреляция остатков. Н0 отклоняется. С вероятностью Р=(1- 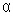 ) принимается гипотеза ) принимается гипотеза |
| 0 dL dU 2 4-dU 4-dL 4 |
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу Н0.
Есть несколько существенных ограничений на применение критерия Дарбина – Уотсона:
— он непременим к модели авторегрессии;
— данный критерий можно использовать только для выявления автокорреляции остатков 1-го порядка;
— критерий дает достоверные результаты только для больших выборок.
источники:
http://ecson.ru/economics/econometrics/zadacha-1.postroenie-regressii-raschyot-korrelyatsii-oshibki-approximatsii-otsenka-znachimosti-i-prognoz.html
http://helpiks.org/3-55677.html



Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции:  .
.
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:

Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.

Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .
Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y — диапазон, содержащий данные результативного признака;
Входной интервал X — диапазон, содержащий данные факторного признака;
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК .

Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.

Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.

Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:


Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:

Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера: 
Поскольку  при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:
 .
.
 для числа степеней свободы
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
где  — случайная ошибка коэффициента корреляции.
— случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.

Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как

Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как

Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью  параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:

где 
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .

Рисунок 10 Расчёт дисперсии
Получили значение дисперсии 
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.

Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:

Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Для общей оценки качества построенной эконометрической определяются такие характеристики как коэффициент детерминации, индекс корреляции, средняя относительная ошибка аппроксимации, а также проверяется значимость уравнения регрессии с помощью F -критерия Фишера. Перечисленные характеристики являются достаточно универсальными и могут применяться как для линейных, так и для нелинейных моделей, а также моделей с двумя и более факторными переменными. Определяющее значение при вычислении всех перечисленных характеристик качества играет ряд остатков ε i , который вычисляется путем вычитания из фактических (полученных по наблюдениям) значений исследуемого признака y i значений, рассчитанных по уравнению модели y рi .
показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.
Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.
Индекс корреляции можно легко вычислить, зная коэффициент детерминации:
Индекс корреляции R характеризует тесноту выбранного при построении модели типа связи между учтёнными в модели факторами и исследуемой переменной. В случае линейной парной регрессии его значение по абсолютной величине совпадает с коэффициентом парной корреляции r (x, y) , который мы рассмотрели ранее, и характеризует тесноту линейной связи между x и y . Значения индекса корреляции, очевидно, также лежат в интервале от 0 до 1. Чем ближе величина R к единице, тем теснее выбранный вид функции связывает между собой факторные переменные и исследуемый признак, тем лучше качество модели.
 (2.11)
(2.11)
выражается в процентах и характеризует точность модели. Приемлимая точность модели при решении практических задач может определяться, исходя из соображений экономической целесообразности с учётом конкретной ситуации. Широко применяется критерий, в соответствии с которым точность считается удовлетворительной, если средняя относительная погрешность меньше 15%. Если E отн.ср. меньше 5%, то говорят, что модель имеет высокую точность. Не рекомендуется применять для анализа и прогноза модели с неудовлетворительной точностью, то есть, когда E отн.ср. больше 15%.
F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:
 . (2.12)
. (2.12)
Критическое значение F -критерия определяется по таблицам при заданном уровне значимости α и степенях свободы (можно использовать функцию FРАСПОБР в Excel). Здесь, по-прежнему, m – число факторов, учтённых в модели, n – количество наблюдений. Если расчётное значение больше критического, то уравнение модели признаётся значимым. Чем больше расчётное значение F -критерия, тем лучше качество модели.
Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :
Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.
 .
.
Значение индекса корреляции в случае парной линейной модели как мы видим, действительно по модулю равно коэффициенту корреляции между соответствующими переменными (объём продаж и температура). Поскольку полученное значение достаточно близко к единице, то можно сделать вывод о наличии тесной линейной связи между исследуемой переменной (объём продаж) и факторной переменноё (температура).

Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.
Средняя относительная ошибка аппроксимации
Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.
В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.


Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.


Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.


В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.


Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.


Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Контрольная работа: Парная регрессия
Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1 , Х2 , … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у иx :
,
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия:.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней
•равносторонняя гипербола
Регрессии, нелинейные по оцениваемым параметрам:
• степенная ;
• показательная
• экспоненциальная
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии
и индекс корреляции — для нелинейной регрессии ():
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений – не более 8 – 10%.
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
где – общая сумма квадратов отклонений;
– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
–остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F -критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл Fфакт , то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо .
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
Если tтабл tфакт , то гипотеза Но не отклоняется и признается случайная природа формирования a , b или .
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :
где
и строится доверительный интервал прогноза:
где
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
| Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать |
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
1. Поле корреляции для:
· Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
· Степенной регрессии :
Гипотеза о форме связи : степенная функция имеет вид Y=ax b .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
· Экспоненциальная регрессия :
· Равносторонняя гипербола :
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
· Обратная гипербола :
· Полулогарифмическая регрессия :
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
где
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: .
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель к линейному виду, заменив , тогда
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы к линейному виду, заменив , тогда
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: . Получим уравнение регрессии: .
3. Оценка тесноты связи с помощью показателей корреляции и детерминации :
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy =b=7,122*, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy =(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции =, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy =0,7175. Это означает, что 71,75% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy =0,8448 и коэффициент корреляции rxy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy =0,8114 и коэффициент корреляции rxy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой:y = 5,777+7,122∙x
· Для уравнениястепенноймодели :
· Для уравненияэкспоненциальноймодели :
Для уравненияполулогарифмическоймодели :
· Для уравнения обратной гиперболической модели :
· Для уравнения равносторонней гиперболической модели :
Сравнивая значения , характеризуем оценку силы связи фактора с результатом:
·
·
·
·
·
·
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :
В среднем расчетные значения отклоняются от фактических на:
· Линейная регрессия. =*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Степенная регрессия. =*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Экспоненциальная регрессия. =*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Полулогарифмическая регрессия. =*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Гиперболическая регрессия. =*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Обратная регрессия. =*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
6. Рассчитаем F-критерий:
· Линейная регрессия. = *19= 47,579
http://welom.ru/srednyaya-oshibka-approksimacii-v-excel-ocenka-kachestva-uravneniya/
http://www.bestreferat.ru/referat-268496.html
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
![]()
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
![]()
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
![]()
(2.39)
Для
нашего примера эта величина составит:
![]()
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
![]()
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
![]()
;
S2
– остаточная сумма квадратов отклонений
![]()
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
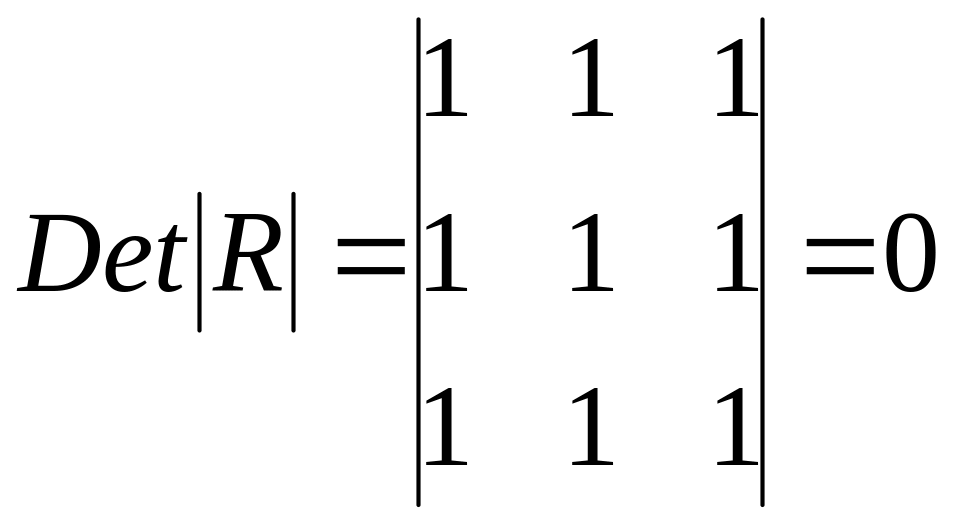
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
![]()
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
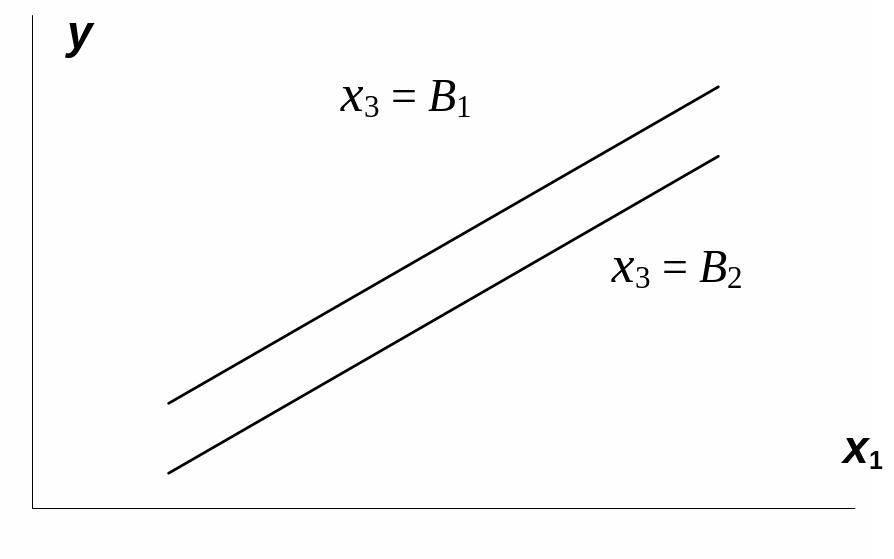

Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
![]()
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.

Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Средняя ошибка аппроксимации
Оценку качества построенной модели дает коэффициент детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений зависимой переменной от фактических:
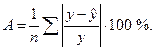
Допустимый предел значений A – не более 8-10 %.
Пример 2.5. Построим регрессионные зависимости: а) расходов на питание (y) и личным доходом (x); б) расходов на питание (y) и временем (t) по следующим данным (усл. ед.):
и оценим качество подгонки.
а) Пусть истинная модель описывается выражением y = a + b x + e.
По выборочным наблюдениям определяем оценки (a; b).
Исходные данные и расчетные показатели представим в виде следующей расчетной таблицы:
| Год | X | Y | X 2 | Xy | 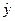 |
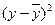 |
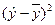 |
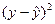 |
| -0,2 | 38,44 | 1,44 | ||||||
| 2,9 | 9,61 | 0,81 | ||||||
| 9,1 | 9,61 | 3,61 | ||||||
| 12,2 | 38,44 | 0,04 | ||||||
| Итого | 96,1 | 9,9 | ||||||
| Сред. | 84,8 | 21,2 | 19,22 | 1,98 | ||||
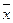 |
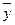 |
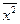 |
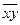 |
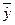 |
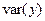 |
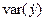 |
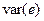 |
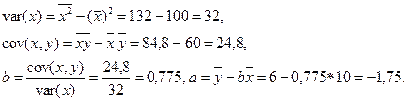
Cледовательно, 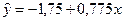 .
.
Коэффициент b = 0,775 показывает, что при увеличения дохода на 1 усл. ед расходы на питание увеличиваются в среднем на 0,775 усл. ед.
Замечание.В Excel оценки (a, b) можно также определить с помощью функций:
Условие 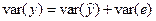 выполняется.
выполняется.
Качество подгонки оцениваем коэффициентом детерминации:
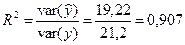 , т.е. 90,7 % вариации зависимой переменной (расходы на питание) объясняется регрессией.
, т.е. 90,7 % вариации зависимой переменной (расходы на питание) объясняется регрессией.
Значимость коэффициента R 2 проверяем по F-тесту
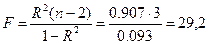 .
.
Произведем проверку значимости R 2 двумя способами.
1. При α = 0,05, n1= 1 и n2 = 3 по таблице или с помощью функции FРАСПОБР(α; n1; n2) находим Fкр = 10,13. Поскольку F = 29,2 > Fкр = 10,13, то R 2 = 0,952 значим при 5 % уровне.
2. Наблюдаемому (расчетному) значению критерия F = 29,2 соответствует значимость F =0,0124, которую можно определить в Excel с помощью функции FРАСП(F; n1; n2).
Поскольку значимостьF = 0,0124 2 значим при уровне 5 %.
б) Пусть истинная модель y = a + b t + e, (модель временного ряда). Выборочная регрессия 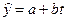 , где t – время, определяемое как t = 1 для 1990 г., t = 2 для 1991 г. и т.д.
, где t – время, определяемое как t = 1 для 1990 г., t = 2 для 1991 г. и т.д.
Представим исходные и расчетные показатели в виде расчетной таблицы:
| Год | t | Y | t 2 | ty | 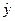 |
| –0,2 | |||||
| 2,9 | |||||
| 9,1 | |||||
| 12,2 | |||||
| Итого | |||||
| Среднее | 24,2 | ||||
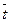 |
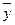 |
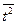 |
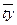 |
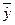 |
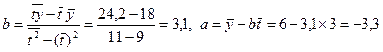 , следовательно,
, следовательно, 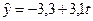 .
.
Коэффициент b = 3,1 показывает, что за год расходы на питание в среднем возрастают на 3,1 единиц.
Пример 2.6. Покажем, что в модели регрессии без свободного члена
Y = b X + e оценка МНК дляbесть:
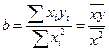 .
.
Выборочная регрессия для этой модели есть 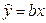 . Наблюдаемые значения зависимой переменной связаны с расчетными уравнением
. Наблюдаемые значения зависимой переменной связаны с расчетными уравнением 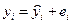 . Оценку b найдем из минимизации величины:
. Оценку b найдем из минимизации величины:
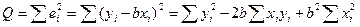 .
.
Запишем необходимые условия экстремума:
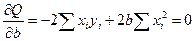 , откуда
, откуда 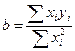 .
.
Вычисление R 2 при отсутствии свободного члена некорректно; при этом не выполняется условие 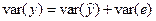 .
.
Пример 2.7. Покажем, что в модели регрессии Y = a + e оценка МНК для a есть: 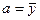 .
.
Выборочная регрессия для заданной модели есть 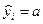 . Наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением:
. Наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением: 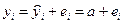 . Оценку a найдем из минимизации величины
. Оценку a найдем из минимизации величины
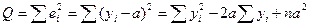 .
.
Запишем необходимые условия экстремума:
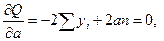 откуда
откуда 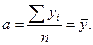
Выборочная регрессия 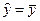 .
.
Расчет средней ошибки аппроксимации. Практическое применение
СОА показывает среднее отклонение расчетных данных результативного признака от фактических. Допустимый предел 8-10%.
Величина отклонений фактических и расчетных значений результативного признака  по каждому наблюдению представляет собой ошибку аппроксимации.
по каждому наблюдению представляет собой ошибку аппроксимации.
Поскольку  может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения  можно рассматривать как абсолютную ошибку аппроксимации, а
можно рассматривать как абсолютную ошибку аппроксимации, а  — как относительную ошибку аппроксимации
— как относительную ошибку аппроксимации
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации: 
Возможно и иное определение средней ошибки аппроксимации: 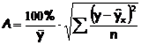
Если А =10-12%, то можно говорить о хорошем качестве модели.
Смысл средней ошибки аппроксимации в том, что это один из многих способов оценить разницу между аппроксимированнм и реальным значениями изучаемой величины. То есть это «квантификатор» потерь (в экономическом смысле) или риска.
27) Эластичность в социально-экономических моделях. Частные коэффициенты эластичности. Практическое применение.
Эластичность — мера чувствительности одной переменной (например: спроса или предложения) к изменению другой (например: цены, дохода), показывающая, на сколько процентов изменится первый показатель при изменении второго на 1 %.
Внимание отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае двухфакторной модели вычисляются по формулам:
 Частные коэффициенты эластичности показывают, на сколько процентов измениться результирующий признак, если значение одного из факторных признаков измениться на 1%, а значение другого факторного признака останется не низменным.
Частные коэффициенты эластичности показывают, на сколько процентов измениться результирующий признак, если значение одного из факторных признаков измениться на 1%, а значение другого факторного признака останется не низменным.
В экономических исследованиях широкое применение находит такой показатель, как коэффициент эластичности. Если зависимость между переменными x и y имеет вид y=f(x) , то коэффициент эластичности Э вычисляется по формуле

Коэффициент эластичности Э показывает, на сколько процентов в среднем изменится результативный признак у при изменении фактора х на 1 % от своего номинального значения. Для линейной регрессии коэффициент эластичности равен



28. t-критерий Стьюдента. Алгоритм выполнения. Практическое применение.
t – критерий Стьюдента проводится с целью проверки значимости каждого параметра в отдельности.
Если проверяется значимость каждого параметра, то выбирают t – критерий Стьюдента и гипотеза строится  … и все остальные параметры при факторе проверяются на = 0 по отдельности.
… и все остальные параметры при факторе проверяются на = 0 по отдельности.



Алгоритм t – критерия:
1) Выдвигается H0 и H1 гипотезы, рассчитываются значения статистики, лежащей в основе критерия и дающей ему название – t-статистика.
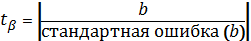
Сконфигурировав линейнуб ф-ию (вызвав «линейн») и вызвав предварительно выбранный диапазон ячеек (2×5) статистику (в поле «статистика» = 1), стандартная ошибка соответствующего коэф-та находится под ним:
2) Из таблицы t-распределения с заданным уровнем значимости, кот задает № столбца и числом степеней свободы, рассчитанному на основе числа наблюдений № — кол-во оцениваемых параметров задает № строки, выбирается t-табличное.
| Число степеней свободы Уровни значимости | 1% | 5% | 10% |
| … | |||
| t 1% | t 5% |
N=10; Число степеней свободы = 8. Уровень значимости всегда берется по двустороннему критерию.
3) Сравниваем  с каждым из табличных значений:
с каждым из табличных значений:


Следовательно, делается вывод о статистической значимости.
28. F-критерий Фишера. Алгоритм выполнения. Практическое применение.
F-критерий Фишера проводится с целью проверки значимости всей модели в целом.
Алгоритм F– критерия:
1) При выдвижении Н0 сравниваются (строятся отношения) дисперсий (Дфак – факторной и Дост – остаточной). И на основе их соотношения рассчитывается F-статистика:
F-статистика – величина, лежащая в основе критерия и дающая ему название.
Дисперсия рассчитывается в рамках дисперсионного анализа (см далее).
| B | A |
| СО (b) | СО (a) |
| R 2 | СО (y) |
| F-статистика | ЧСС |
 |
СО – стандартная ошибка
В нулевой гипотезе (Н0) делается предположение о равенстве дисперсии факторной и дисперсии остаточной.
H1 : Дф  Дост
Дост
В случае, если удастся принять альтернативную гипотезу дополнительно делается сравнение дисперсии через неравенства: Дф  Дост (делается дополнительно через дисперсионный анализ).
Дост (делается дополнительно через дисперсионный анализ).
2) Из таблиц F-распределения выбираются критические (табличные) значения F -статистики. Таблица сформирована с учетом:
1. Уровня значимости (в заголовке таблицы);
2. Числа степеней свободы – ЧСС (равно номеру строки, номер строки в таблице F-критерий, t-критерий), для парной модели ЧСС = n -2 (n – число наблюдений);
3. Кол-во независимых переменных – НП (номер столбца).
Число степеней свободы рассчитывается в общем виде по формуле:
ЧСС = n-k-1, k – кол-во независимых переменных
3) Выполняется сравнение F-статистики из п. 1 с F-критическими из п. 2 (2 при 1%, и 5%).
Для отклонения нулевой гипотезы требуется выполнение неравенства: 

В противном случае делается вывод о статистической значимости уравнения регрессии в целом.
Дисперсионный анализ
В дисперсионном анализе и в F-критерии Фишера рассматривают условно сконструированные дисперсии на основе соответствующих сумм квадратов. В основе лежит равенство (**) – разложение общей суммы квадратов отклонений СВ от среднего на факторную и остаточную сумму квадратов.

Для перехода к дисперсиям соответствующая сумма квадрата делится на ЧСС (свое для каждой суммы).

Определить ЧСС для расчета среднего значения СВ y, имеющей 5 значений.
| yi | Y1 | y2 | y3 | y4 | y5 |
 |
|||||
 |
-2 | -1 |
а — СО (а)* t табл 1%
Для линейной парной модели выполняется след связь между F и t критериями:

Таким образом, говорят о равносильности в данном частном случае этих двух критериев на практике.
В ряде прикладных программ и задач требуется оценить значимость коэффициента корреляции. Для этого строится гипотеза:
Н0: r генерал = 0
H1: r генерал не равно 0

Проверка осуществляется на основе расчета t – статистики через выборочный коэф-т корреляции, а затем на основе таблиц t – распределения выполняется сравнение рассчитанного значения с табличным.

Для линейной парной модели r 2 – это формула для расчета коэф-та детерминации: R 2 = r 2 .
Чем ближе R 2 к единице, тем лучше регрессия аппроксимирует эмпирические данные (приближает наблюдаемые данные).
Если R 2 = 1, то эмпирические точки лежат на линии регрессии, и между экзогенной и эндогенной переменными сущ-ет лин функциональная зависимость.
Если R 2 = 0, то изменение эндогенной переменной у всецело опр-ся изменением всех неучтенных в модели факторов (от изменения x не зависит).
| yi = |  |
+ |  |
 |
 R 2 = 0,3 R 2 = 0,3 |
 1 – R 2 = 0,7 1 – R 2 = 0,7 |
В прикладных задачах всегда начинают исследование с линейной функции, затем берут либо степенную, либо показательную. Затем полином второй степени и в редком случае третьей.
источники:
http://helpiks.org/7-5944.html
http://lektsii.org/6-58481.html
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Фондовые рынки во все времена своего существования привлекали большое внимание инвесторов, которые рассматривают фондовые рынки в качестве возможности эффективного вложения собственного капитала в ценные бумаги и дальнейшего приумножения капитала.
Вопрос выгодного вложения собственного капитала в ценные бумаги не теряет с годами свою актуальность, а наоборот, с развитием «информационной» экономики в информационную эпоху с использованием новейших технологий и инноваций, подобный способ заработка становится все более популярным. Преимущества его состоят прежде всего в удобстве: возможность работать в любых условиях, где есть быстрый интернет, необходимо лишь наличие мощного компьютера или ноутбука, а также источников информации для проведения быстрой оценки макроэкономической ситуации или анализа отдельных эмитентов. Важнейшими факторами для проведения успешных операций на фондовом рынке являются знания, информация и интуиция, в противном случае капитал легко потерять на фондовом рынке.
Умение прогнозировать возможное движение цены зачастую является главным фактором, позволяющим извлекать прибыль из операций не только на фондовом, но также на валютном и товарном рынках. Прогнозирование с использованием математических моделей существенно увеличивает позитивную вероятность прогноза, то есть соответствие прогноза фактическим значениям цен в будущем.
В этой связи можно выделить актуальность данной курсовой работы, где была сделана попытка построения адекватной эконометрической регрессионной модели прогноза доходности по индексу РТС. В настоящее время многие российские инвесторы ищут выгодные средства вложения собственного капитала, и фондовый рынок может служить одним из них. Поэтому исследования в области прогнозирования доходности по тому или иному инструменту актуальны в наши дни.
Цели исследования заключаются в разработке статистически значимой регрессионной модели прогноза доходности по индексу РТС, а также в построении краткосрочных прогнозов динамики доходности индекса РТС в соответствии с тремя сценариями развития международной экономической ситуации.
Для достижения целей исследования были поставлены следующие задачи :
- сбор и анализ статистической базы по динамике индексов РТС, MSCI EM и MSCI World, а также статистики по ценам на нефть марок Brent и WTI за 2005-2011 гг.;
- анализ теоретической базы по созданию эконометрической регрессионной модели;
- подведение итогов и оценка полученных результатов.
Практическая значимость работы состоит в возможности прикладного использования полученной регрессионной модели для прогнозирования доходности по индексу РТС, что увеличит вероятность принятия инвестором правильных управленческих решений, что соответственно приведет к увеличению дохода инвестора.
Работа включает введение, основную часть, заключение и список литературы. Основная часть состоит из двух глав. Глава 1 называется: «Внешние факторы, влияющие на рынок РТС». Название главы 2: «Создание и тестирование эконометрической модели динамики доходности по индексу РТС». В заключении рассматриваются результаты проведенного исследования и подводятся итоги.
Список литературы насчитывает 12 наименований.
ГЛАВА 1. ВНЕШНИЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИНДЕКС РТС
Индекс РТС является официальным индикатором Фондовой биржи РТС и общепризнанным показателем состояния российского фондового рынка. Впервые был рассчитан 1 сентября 1995 г. Индекс рассчитывается в режиме реального времени в течение всей торговой сессии биржи РТС (с 10:30 до 18:00 по московскому времени) при каждом изменении цены акции, включенной в список для его расчета[1]. Расчет индекса РТС ведется в пунктах. Значение индекса РТС составляет отношение суммарной рыночной капитализации акций, включенных в список для расчета индекса, к суммарной рыночной капитализации на начальную дату, умноженное на значение индекса на начальную дату и на корректирующий коэффициент. Таким образом, рыночная капитализация рассчитывается на основе данных о ценах акций и количестве выпущенных эмитентом акций, с учетом доли акций, находящихся в свободном обращении.
В настоящее время индекс РТС включает 50 наиболее капитализированных и ликвидных акций[2]. Список акций для расчета индекса пересматривается раз в квартал на основании показателей капитализации, ликвидности и экспертной оценки. Среди компаний, которые включены в данный индекс, можно назвать Газпром (15,00% в индексе), ЛУКОЙЛ (14,24%), Сбербанк России (12,89%), Роснефть (6,07%), Норильский никель (4,24%), Сургутнефтегаз (4,49%), НОВАТЭК (6,38%), РусГидро (1,78%), Банк ВТБ (3,01%), Уралкалий (5,88%) (по данным на май 2010 г.)[3].
Индекс РТС отражает общее состояние крупнейших российских эмитентов, перспективы их развития в будущем. Расчет индекса стремится к максимально адекватному отражению структуры российской экономики.
Значения индекса РТС подвергаются постоянному влиянию фундаментальных факторов, которые будут рассмотрены в данной работе.
Известно, что совокупный индекс капитализации компаний, которым является РТС, отражает экономическое положение страны. Российская экономика подвержена влиянию внешних факторов, являясь прежде всего экспортно-ориентированной, с основной статьей экспорта — минеральные ресурсы и энергоносители. Цены на энергоносители определяются спросом и предложением на международном рынке и зависят от развития экономик стран-импортеров энергоресурсов, которые предоставляют платежеспособный спрос. То есть если страны готовы платить за энергоресурсы и спрос на данный вид ресурсов растет, соответственно при прочих равных условиях растут цены на энергоресурсы. При завышенных ценах на энергосырье страдают все экономики, как энергоэкспортеров, так и энергоимпортеров.
Таким образом Россия, являясь крупнейшей страной-энергоэкспортером, не может оказывать сильное влияние на цены на энергоресурсы и минеральное сырье на международном рынке. Еще одной причиной этому служит существование конкуренции на рынке энергоресурсов, действуют международные организации, защищающие собственные интересы (ОПЕК и другие).
Поскольку международная ситуация сильнейшим образом сказывается на развитии российской экономики, постольку основные индексы капитализации компаний на фондовом рынке (индексы РТС и ММВБ) подвержены влиянию внешних факторов.
Если проанализировать динамику движения индекса РТС, к примеру, за период с начала 2008 г. по ноябрь 2011 г. (рис. 1), можно заметить взаимосвязь показателей индекса РТС и основных международных тенденций в экономике.
Источник: Официальный сайт биржи РТС. — http://www.rts.ru/ru/index/idxgraph.html
На графике видно, что минимальное значение индекса РТС за 2008-2011 г. было в январе 2009 г., составив 78,4% коррекции вниз, если за нулевую отметку принять значение индекса РТС в июне 2008 г. Причины столь значительного падения капитализации российских компаний-эмитентов можно связать с мировым финансовым кризисом 2008-2009 гг., стагнацией экономик развитых стран, что отразилось и на состоянии российской экономики.
Следующий минимум показателей индекса РТС пришелся на июль 2009 г., коррекция составила -64% по отношению к июню 2008 г., когда российская экономика находилась в состоянии пика роста. Здесь повлияла негативная статистика по российским экономическим показателям за первый квартал 2009 г., но прежде всего причиной данного падения стало появление макроэкономической статистики из США 10.07.2009. В этот день стало известно, что дефицит торгового баланса США в мае 2009 г. вырос по сравнению с апрелем на 11%, что является минимальным показателем с ноября 1999 г. по итогам торговой сессии 10 июля индекс РТС снизился на 5,62%.[4]
Следующее падение индекса РТС случилось в мае 2010 г., коррекция составила -45% к показателю июня 2008г. Здесь также особое влияние на рынки Emerging Markets оказало стремительное обесценение сырья (нефти и металлов)[5].
Минимум октября 2011 г. по индексу РТС обновил предыдущий минимум, коррекция составила -49%. В этот день Индекс РТС опустился ниже 1260 пунктов вслед за основными мировыми индексами на фоне опасений дефолта Греции. Европейские индексы FTSE, S&P 350 и DAX потеряли 2,7-3,4%. Нефть также подешевела, фьючерс на нефть марки WTI снизился до 76,19 долл. за баррель[6].
Подобная динамика взаимосвязи показателей индекса РТС с политическими и экономическими событиями за рубежом позволяет сделать вывод о наличии значительного влияния внешних факторов на индекс РТС.
Проанализируем факторы, которые наиболее значительным образом влияют на показатели индекса РТС. Очевидно, что одним из подобных факторов являются цены на энергоресурсы, прежде всего на европейской и американской товарных биржах. В качестве эталона можно взять цены на нефть американской марки WTI и европейской марки Brent.
На индекс РТС также оказывает влияние международная экономическая обстановка. Для отражения состояния экономики определенных групп стран рассчитываются специальные индексы. Например, в группу индексов MSCI (Morgan Stanley Capital International) входит совокупный индекс фондовых рынков развивающихся стран или индекс развивающихся стран (The MSCI Emerging Markets Index)[7]. Данный индекс оценивает рыночную капитализацию компаний развивающихся рынков. Индекс включает показатели 21 странового индекса следующих развивающихся рынков: Бразилия, Китай, Чили, Колумбия, Чехия, Египет, Венгрия, Индия, Индонезия, Корея, Малайзия, Мексика, Марокко, Перу, Филиппины, Польша, Россия, ЮАР, Тайвань, Таиланд и Турция.
Группа индексов MSCI (Morgan Stanley Capital International) включает также взвешенный индекс капитализации компаний развитых рынков (The MSCI World Index). Данный индекс рассчитывается на основе данных индексов капитализации компаний 23 развитых стран: Австралия, Австрия, Бельгия, Канада, Дания, Финляндия, Франция, Германия, Греция, Ирландия, Израиль, Италия, Япония, Голландия, Новая Зеландия, Норвегия, Португалия, Сингапур, Испания, Швейцария, Швеция, Великобритания и США, а также 1 специального административного района Китая — Гонконг.
Таким образом, можно сделать предположение, что на индекс РТС будут оказывать влияние показатели индексов MSCI EM, а также MSCI World, которые отражают состояние экономик развивающихся и развитых стран, то есть международную экономическую ситуацию в целом.
Взаимосвязь показателей по индексу РТС с индексами MSCI EM и MSCI World, а также ценами на нефть марок Brent и WTI можно наблюдать графически (диаграмма 1). Можно заметить, что графики цен нефти марок Brent и WTI практически повторяют друг друга. График индекса MSCI World менее волатилен, чем график MSCI EM, что объясняется достаточно устойчивым развитием экономик развитых стран. Экономики развивающихся стран, а также капитализация их компаний на фондовом рынке, росли более быстрыми темпами, чем экономики развитых стран, но тем стремительней и глубже оказалось снижение капитализации компаний развивающихся стран в январе 2009 г. При этом индекс РТС упал ниже, чем совокупный индекс развивающихся стран. Очевидно также, что падение цен на нефть в январе 2009 г. оказало влияние как на индекс развивающихся стран, так и на индекс развитых стран.
Таким образом, еще раз подтверждается тот факт, что показатели индекса РТС подвержены влиянию внешних факторов.
В практической части данной работы проведена попытка построения эконометрической модели, где в качестве экзогенных переменных выступают вышеописанные внешние факторы, и доходность по индексу РТС, то есть его изменение, является эндогенной переменной.
ГЛАВА 2. СОЗДАНИЕ И ТЕСТИРОВАНИЕ ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ ДИНАМИКИ ДОХОДНОСТИ ПО ИНДЕКСУ РТС
Для создания и тестирования регрессионной модели были собраны статистические данные по индексам РТС, MSCI EM и MSCI World, а также статистика по ценам нефти марок Brent за 2005-2010 гг. Так как графики цен на нефть марки Brent и WTI практически повторяют друг друга, доходность по WTI не следует включать в уравнение регрессии с целью избежания явления мультиколлинеарности.
В качестве эндогенной переменной У выступает значение доходности по индексу РТС, то есть значение последующего значения индекса к предыдущему. Подобным образом была рассчитана доходность по индексам развитых и развивающихся стран, а также изменение цен на нефть.
Экзогенная переменная Х1 представляет собой отношение последующего значения цены Brent к предыдущему; переменная Х2 — отношение последующего значения индекса MSCI EM к предыдущему; переменная Х3 — отношение последующего значения индекса MSCI World к предыдущему.
Все данные взяты в месячном выражении. Количество наблюдений — 81. Так как все переменные уравнения отражают изменение каких-либо показателей, единицами измерения являются проценты.
Были рассчитаны основные статистические показатели для выборки (таблица 1):
|
Таблица 1. Статистические показатели |
||||
|
У |
Х1 |
Х2 |
Х3 |
|
|
Среднее |
1.0159 |
1.0154125 |
1.0129 |
1.00501 |
|
Стандартная ошибка |
0.0111 |
0.009928 |
0.0086 |
0.00602 |
|
Медиана |
1.0292 |
1.0260904 |
1.0123 |
1.01055 |
|
Мода |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
|
Стандартное отклонение |
0.1001 |
0.089352 |
0.0777 |
0.05418 |
|
Дисперсия выборки |
0.01 |
0.0079838 |
0.006 |
0.00294 |
|
Эксцесс |
3.3464 |
1.4162704 |
1.4482 |
1.8354 |
|
Асимметричность |
-1.12 |
-1.012141 |
-0.701 |
-0.7918 |
|
Интервал |
0.6389 |
0.4528938 |
0.445 |
0.31687 |
|
Минимум |
0.5893 |
0.7309171 |
0.7265 |
0.80209 |
|
Максимум |
1.2282 |
1.1838108 |
1.1714 |
1.11896 |
|
Сумма |
82.289 |
82.24841 |
82.044 |
81.4058 |
|
Счет |
81 |
81 |
81 |
81 |
|
Уровень надежности(95.0%) |
0.0221 |
0.0197573 |
0.0172 |
0.01198 |
Для определения уравнения регрессии была использована двойная логарифмическая модель (log-log модель), то есть линеаризованная степенная функция. В линейном виде ее можно записать следующим образом:
log(Y)= + log(X1)+ log(X2)+ log(X3)+
Следует ожидать положительные знаки коэффициентов регрессии, так как с увеличением цен на нефть и доходности по основным мировым индексам доходность по индексу РТС также должна возрастать.
Для оценки коэффициентов линеаризованной регрессии возможно использование метода наименьших квадратов остатков, однако прежде следует проверить соблюдение некоторых требований. При выполнении условий Гаусса-Маркова оценки МНК будут наиболее эффективны:
1. Математическое ожидание случайных возмущений равно 0: E( =0;
2. Дисперсия возмущений постоянна и не зависит от номера наблюдений:
Var( = для любого номера наблюдений;
Для проверки первых двух условий достаточно произвести расчеты математического ожидания и дисперсии случайных возмущений.
3. Возмущения различных наблюдений некоррелированы, то есть отсутствует систематическая связь между значениями случайного члена в любых двух наблюдениях: Cov( =0 при i не равно j.
Для проверки третьего условия Гаусса-Маркова для начала можно воспользоваться графическим методом. На диаграмме 2 заметно, что предыдущие и последующие значения мало связаны между собой.
Чтобы математически выявить наличие или неналичие автокорреляции, воспользуемся критерием Дарбина-Уотсона. Сформулируем гипотезу Н0: ro=0 (автокорреляции нет). Гипотеза Н1: ro>0 (наличие положительной автокорреляции).
Значение статистики Дарбина-Уотсона равно 1,896.
Левая граница dL при трех факторах и 81 наблюдении составляет 1,56; правая граница dU — 1,72. Так как значение статистики Дарбина-Уотсона находится в пределах от dU до 2, следовательно можно говорить о наличии отрицательной автокорреляции остатков. Принимается гипотеза Н0, гипотеза Н1 отвергается.
Полученные результаты позволяют утверждать о соблюдении требований Гаусса-Маркова и о возможности использования метода МНК для оценки коэффициентов линеаризованной регрессии.
С использованием функции ЛИНЕЙН в Excel были получены следующие оценки:
|
Таблица 2. Оценки коэффициентов |
|||
|
0.149 |
0.582 |
0.556 |
-0.002 |
|
0.336 |
0.234 |
0.080 |
0.007 |
|
0.685 |
0.061 |
#Н/Д |
#Н/Д |
|
55.866 |
77.000 |
#Н/Д |
#Н/Д |
|
0.629 |
0.289 |
#Н/Д |
#Н/Д |
Методом МНК получены следующие коэффициенты и уравнение регрессии по выборке:
log(Y^)=-0,002+0,556log(X1)+0,582log(X2)+0,149log(X3)
где Y — доходность по индексу РТС
Х1 — месячный индекс цен на нефть марки Brent (как отношение последующего значения цены
к предыдущему, в долларах)
Х2 — доходность по индексу MSCI Emerging Markets
X3 — доходность по индексу MSCI World
1. Проведем оценку статистической значимости уравнения на основе статистических гипотез. Гипотеза Н0 означает, что полученное уравнение незначимо (между У и Х нет систематической связи, полученные оценки случайны)
Тогда гипотеза Н1 предполагает значимость уравнения.
Проверим гипотезу Н0:
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера. Фактическое значение F-критерия (статистика Фишера) найдем из таблицы, полученной по функции ЛИНЕЙН: Fстат = 55,87
Fкр (5%, 77, 3)@2,7 — табличное значение критерия Фишера на 5%-м уровне значимости, с тремя факторами и 77 степенями свободы.
Уравнение признается статистически значимым на 5% уровне значимости, между факторами и результирующей переменной существует систематическая связь, гипотеза Н0 отвергается.
Рассчитаем среднюю ошибку аппроксимации:
Аср = 4.8%
Средняя ошибка аппроксимации составила 4,8%, что указывает на относительно хорошее качество составленной модели.
2. Проверим коэффициенты регрессии на значимость.
Воспользуемся гипотезами: Гипотеза Н0 соответствует утверждению, что полученные коэффициенты регрессии получены случайным образом и являются незначимыми; тогда гипотеза Н1 означает, что коэффициенты регрессии и свободный коэффициент значимы.
Проверим гипотезу Н0 при помощи t — статистики Стьюдента и путем расчета доверительного интервала каждого из коэффициентов.
Табличное значение двустороннего t — критерия для числа степеней свободы 77 и доверительного интервала 0,05 составит: tкр @ 1,99
Рассчитаем t — статистику для каждого из коэффициентов, для этого коэффициент разделим на его стандартную ошибку:
tстат (Х1) 6.92
tстат (Х2) 2.49
tстат (Х3) 0.44
tстат (а) -0.28 Тест Стьюдента показывает, что в отношении факторов Х1 и Х2 гипотеза Н0 отвергается, так как значения t-статистики коэффициентов при Х1 и Х2 превосходят критическое значение t-статистики, подтверждается гипотеза Н1, то есть данные коэффициенты являются статистически значимыми.
Значение t — статистики для коэффициентов при регрессоре Х3 и при свободном коэффициенте по модулю меньше критического значения t — статистики, следовательно здесь подтверждается гипотеза Н0, то есть данные коэффициенты получены случайным образом и не обладают статистической значимостью.
Рассчитаем доверительные интервалы для параметров регрессионного уравнения при уровне значимости 5%: нижняя граница параметра = значение параметра — станд. ошибка параметра * tкр
верхняя граница параметра = значение параметра + станд. ошибка параметра * tкр
|
Таблица 3. Доверительные интервалы коэффициентов |
||
|
Нижняя граница |
Верхняя граница |
|
|
Свободный коэффициент |
-0.016 |
0.012 |
|
Коэффициент при Х1 |
0.396 |
0.715 |
|
Коэффициент при Х2 |
0.117 |
1.048 |
|
Коэффициент при Х3 |
-0.519 |
0.817 |
Нижние и верхние границы параметров регрессионного уравнения близки к значениям соответствующих расчетных коэффициентов.
3. Проинтерпретируем полученные коэффициенты детерминации, корреляции и эластичности.
Коэффициент детерминации R = 0,685 (из оценки по функции ЛИНЕЙН)
Коэффициент детерминации показывает, насколько факторы уравнения объясняют значение эндогенной переменной. В данном случае индекс цен на нефть марки Brent, доходность по индексам MSCI EM и MSCI World на 68,5% объясняют доходность по индексу РТС.
Проинтерпретируем коэффициенты эластичности расчетного уравнения log(Y^)=-0,002+0,556log(X1)+0,582log(X2)+0,149log(X3)
Коэффициент эластичности доходности индекса РТС по индексу цен на нефть марки Brent составляет 0,556 и показывает, что при росте цены на нефть на 1% доходность по индексу РТС вырастет на 0,556% при неизменности прочих факторов.
Коэффициент эластичности доходности индекса РТС по доходности индекса MSCI EM составляет 0,58, то есть при росте доходности по индексу MSCI EM на 1%, доходность по индексу РТС также вырастет на 0,58%.
Коэффициент эластичности доходности индекса РТС по доходности индекса MSCI World составляет 0,15, то есть при росте доходности по индексу MSCI World на 1%, доходность по индексу РТС вырастет на 0,15%.
|
Таблица 4. Коэффициенты межфакторной и парной корреляции |
||||
|
У |
Х1 |
Х2 |
Х3 |
|
|
У |
1.00 |
|||
|
Х1 |
0.67 |
1.00 |
||
|
Х2 |
0.67 |
0.37 |
1.00 |
|
|
Х3 |
0.64 |
0.37 |
0.93 |
1 |
Коэффициент корреляции между индексом цен марки Brent и доходностью по индексу РТС составляет 0,67, то есть между двумя показателями существует прямая и довольно сильная связь.
Коэффициент корреляции между показателями доходности по индексу MSCI EM и доходностью по индексу РТС составляет 0,67 и показывает, что доходность по РТС и доходность по MSCI EM также сильно взаимосвязаны.
Коэффициент корреляции между показателями доходности по индексу MSCI World и доходностью по индексу РТС составил 0,64, указывая на наличие сильной прямой связи между показателями.
Проанализируем межфакторные коэффициенты корреляции.
Межфакторная корреляция между индексом цен на нефть и доходностью по индексу MSCI EM незначительна, корреляция между индексом цен на нефть и доходностью по индексу MSCI World также мала (0,37). Что касается межфакторной корреляции между показателями доходности по индексу MSCI EM и индексу MSCI World, здесь наблюдается сильная межфакторная корреляция (0,93), присутствует явление мультиколлинеарности.
4. Рассчитаем стандартизированные коэффициенты регрессии ty=ß1tx1+ß2tx2++ß3tx3+?.
Стандартизированный коэффициент равен произведению коэффициента при регрессоре и среднеквадратического отклонения регрессора, которое затем делится на среднеквадратическое отклонение эндогенной переменной.
Рассчитаем средние квадратические отклонения:
|
Таблица 5. Средние кв. отклонения |
||
|
У |
0.10 |
|
|
Х1 |
0.09 |
|
|
Х2 |
0.08 |
|
|
Х3 |
0.05 |
|
|
Таблица 6. Стандартизованные коэффициенты |
||
|
ß1 |
0.50 |
|
|
ß2 |
0.45 |
|
|
ß3 |
0.08 |
Стандартизированное уравнение будет иметь вид:
ty^=0,5tx1+0,45tx2+0,08tx3
Коэффициенты стандартизированного уравнения показывают, что цены на нефть оказывают большее влияние на доходность по индексу РТС, влияние доходности по индексам MSCI EM и MSCI World меньше, так как коэффициет ß1>ß2 и ß1>ß3. Стандартизованный коэффициент при индексе цен на нефть также показывает, что если индекс цен на нефть изменится на свое стандартное отклонение (+- 0,09), тогда доходность по индексу РТС изменится на величину стандартное отклонение доходности по индексу РТС * коэффициент при tx1(%).
Если значение доходности по индексу MSCI EM изменится на свое стандартное отклонение (+-0,8), тогда доходность по индексу РТС изменится на величину стандартное отклонение доходности по индексу РТС * коэффициент при tx2(%).
Если значение доходности по индексу MSCI World изменится на свое стандартное отклонение (+-0,05), тогда доходность по индексу РТС изменится на величину стандартное отклонение доходности по индексу РТС * коэффициент при tx3(%).
Если сравнить тесноту связи, характеризуемую стандартизированными коэффициентами, и силу связи, объясняемую коэффициентом эластичности, между экзогенными и эндогенной переменными (Эх1=0,556, Эх2=0,58, Эх3=0,15), можно увидеть, что теснота и сила связи между доходностью по индексу РТС и доходностью по индексу MSCI World самая небольшая в сравнении с другими факторами. По тесноте и по силе связи цена на нефть марки Brent и индекс MSCI EM в равной степени влияют на динамику индекса РТС
5. Проанализируем частные коэффициенты корреляции первого и второго порядков, которые характеризуют тесноту связимежду результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Для расчетов частных коэффициентов корреляции используем парные и межфакторные коэффициенты корреляции.
|
Таблица 4. Коэффициенты межфакторной и парной корреляции |
||||
|
У |
Х1 |
Х2 |
Х3 |
|
|
У |
1.00 |
|||
|
Х1 |
0.67 |
1.00 |
||
|
Х2 |
0.67 |
0.37 |
1.00 |
|
|
Х3 |
0.64 |
0.37 |
0.93 |
1 |
при постоянном действии фактора Х2 корреляция У и Х1 оказывается более низкой.
ryx1.x2=0.62
ryx2.x1=0.61
при неизменности фактора Х1 влияние фактора Х2 на У оказывается менее сильным.
ryx3.x2=0.07
при неизменности фактора Х2 влияние фактора Х3 на У оказалось абсолютно незначительным, по сравнению с парным коэффициентом корреляции.
ryx3.x1=0.57
при фиксированном влиянии фактора Х1 корреляция фактора Х3 с У снизилась.
rx1х3.x2 0.07
при неизменности фактора Х2 межфакторная корреляция между Х1 и Х3 снижается до 7% (на 30%).
rx2х3.x1=0.91
при фиксации фактора Х1 межфакторная корреляция между факторами Х2, Х3 незначительно снизилась, по-прежнему наблюдается явление мультиколлинеарности.
Приведем частные коэффициенты корреляции второго порядка:
rуx1.х3×2 0.62
при фиксированном влиянии факторов Х2 и Х3 корреляция Х1 и У незначительно снизилась и равна корреляции Х1 и У при элиминировании лишь одного фактора Х2.
rуx2.х3×1=0.27
Корреляция фактора Х2 с У снизилась с 0,67 до 0,27 при элиминировании факторов Х1 и Х3.
rуx3.х1×2=0.04
при устранении влияния факторов Х1 и Х2 значение корреляции фактора Х3 с У снизилось до 4%.
Частные коэффициенты корреляции обычно не обладают собственным значением и используются на стадии формирования модели.
В данном случае коэффициенты парной и частной корреляции больше всего отличны при факторе Х3. Коэффициент корреляции rx2х3.×1 = 0.91 подтвердил наличие мультиколлинеарности между факторами Х2 и Х3. Коэффициенты корреляции ryx3.x2 = 0,07 и rуx3.х1×2 = 0,04 также демонстрируют сильную взаимосвязь между доходностями по индексам MSCI EM и MSCI World. При устранении влияния факторов индекса цен на нефть и доходности по MSCI EM коэффициент корреляции между доходностью по индексу РТС и доходностью по индексу MSCI World составит 4%. Высокий коэффициент парной корреляции = 0,64 между доходностью по индексу РТС и доходностью по индексу MSCI World объясняется высокой взаимосвязью показателей MSCI EM и MSCI World.
На основании показателей частных коэффициентов корреляции первого и второго порядков, стандартизированных коэффициентов регрессии, а также значений стандартных ошибок в трехфакторной модели есть смысл исключить фактор Х3 из уравнения регрессии и составить новое расчетное уравнение.
6. Для определения нового уравнения регрессии снова используем двойную логарифмическая модель (log-log модель). В линейном виде ее можно записать следующим образом:
log(Y)= + log(X1)+ log(X2)+
С помощью функции ЛИНЕЙН найдем коэффициенты двухфакторного уравнения регрессии.
|
Таблица 7. Оценка параметров регрессии |
||
|
0.677 |
0.558 |
-0.002 |
|
0.093 |
0.080 |
0.007 |
|
0.684 |
0.061 |
#Н/Д |
|
84.572 |
78.000 |
#Н/Д |
|
0.628 |
0.290 |
#Н/Д |
Тогда новое уравнение регрессии получит вид:
log(Y^)=-0,002+0,558log(X1)+0,667log(X2)
Проведем оценку статистической значимости нового уравнения на основе статистических гипотез. Пусть гипотеза Н0 означает, что полученное уравнение незначимо (между У и Х нет систематической связи, полученные оценки случайны) Тогда гипотеза Н1 предполагает значимость уравнения. Проверим гипотезу Н0: Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера.
Фактическое значение F-критерия (статистика Фишера) найдем из таблицы, полученной по функции ЛИНЕЙН: Fстат = 84,57
Fкр (5%, 78,2)@3,1 — табличное значение критерия Фишера на 5%-м уровне значимости, с двумя факторами и 78 степенями свободы Уравнение признается статистически значимым на 5% уровне значимости, между факторами и результирующей переменной существует систематическая связь, гипотеза Н0 отвергается.
Рассчитаем среднюю ошибку аппроксимации:
Аср = 4,7%
Средняя ошибка аппроксимации составила 4,7%, что указывает на относительно хорошее качество составленной модели.
7. Проверим коэффициенты регрессии на значимость.
Воспользуемся гипотезами: Пусть гипотеза Н0 соответствует утверждению, что полученные коэффициенты регрессии получены случайным образом и являются незначимыми; тогда гипотеза Н1 означает, что коэффициенты регрессии и свободный коэффициент значимы.
Проверим гипотезу Н0 при помощи t — статистики Стьюдента и путем расчета доверительного интервала каждого из коэффициентов.
Табличное значение двустороннего t — критерия для числа степеней свободы 78 и доверительного интервала 0,05 составит:
tкр @ 1,99
Рассчитаем t — статистику для каждого из коэффициентов, для этого коэффициент разделим на его стандартную ошибку:
tстат (Х1)=7.00
tстат (Х2)=7.27
tстат (а)=-0.35
Тест Стьюдента показывает, что в отношении факторов Х1 и Х2 гипотеза Н0 отвергается, так как значения t — статистики коэффициентов при Х1 и Х2 превосходят критическое значение t — статистики, подтверждается гипотеза Н1, то есть данные коэффициенты являются статистически значимыми.
Значение t — статистики для свободного коэффициента по модулю меньше критического значения t — статистики, следовательно здесь подтверждается гипотеза Н0, то есть данный коэффициент получен случайным образом и не обладает статистической значимостью.
Рассчитаем доверительные интервалы для параметров регрессионного уравнения при уровне значимости 5%:
нижняя граница параметра = значение параметра — станд. ошибка параметра * tкр
верхняя граница параметра = значение параметра + станд. ошибка параметра * tкр
|
Таблица 8. Доверительные интервалы параметров |
||
|
Нижняя граница |
Верхняя граница |
|
|
Свободный коэффициент |
-0.016 |
0.011 |
|
Коэффициент при Х1 |
0.399 |
0.716 |
|
Коэффициент при Х2 |
0.492 |
0.863 |
Нижние и верхние границы параметров регрессионного уравнения близки к значениям соответствующих расчетных коэффициентов. Заметно, что доверительный интервал для свободного коэффициента содержит 0, соответственно подтверждается гипотеза о незначимости данного коэффициента.
8. Проинтерпретируем полученные коэффициенты детерминации, корреляции и эластичности.
Коэффициент детерминации R = 0,684 (из оценки по функции ЛИНЕЙН)
Коэффициент детерминации показывает, насколько факторы уравнения объясняют значение эндогенной переменной. В данном случае индекс цен на нефть марки Brent, доходность по индексам MSCI EM на 68,4% объясняют доходность по индексу РТС.
В трехфакторной модели коэффициент детерминации равнялся 0,65, снизившись на 0,1 в двухфакторной модели.
Проинтерпретируем коэффициенты эластичности нового уравнения регрессии:
log(Y^)=-0,002+0,558log(X1)+0,667log(X2)
Коэффициент эластичности доходности индекса РТС по индексу цен на нефть марки Brent составляет 0,558 и показывает, что при росте цены на нефть на 1% доходность по индексу РТС вырастет на 0,558% при неизменности прочих факторов.
Коэффициент эластичности доходности индекса РТС по доходности индекса MSCI EM вырос по сравнению с предыдущим показателем коэффициента эластичности и в двухфакторной модели составляет 0,667, то есть при росте доходности по индексу MSCI EM на 1%, доходность по индексу РТС также вырастет на 0,667%.
Проанализируем коэффициенты межфакторной и парной корреляции в двухфакторной модели:
|
Таблица 9. Коэффициенты корреляции |
|||
|
У |
Х1 |
Х2 |
|
|
У |
1.00 |
||
|
Х1 |
0.67 |
1.00 |
|
|
Х2 |
0.67 |
0.37 |
1.00 |
Коэффициенты корреляции не изменились, однако в двухфакторной модели отсутствует явление мультиколлинеарности в связи с отсутствием фактора Х3, фактора доходности по индексу MSCI World.
9. Рассчитаем новые стандартизированные коэффициенты регрессии ty=ß1tx1+ß2tx2+?.
Стандартизированный коэффициент равен произведению коэффициента при регрессоре и среднеквадратического отклонения регрессора, которое затем делится на среднеквадратическое отклонение эндогенной переменной.
Средние квадратические отклонения:
|
Таблица 10. Среднеквадратические отклонения |
||||
|
У |
0.10 |
|||
|
Х1 |
0.09 |
Таблица 11. Стандартизованные коэффициенты |
||
|
Х2 |
0.08 |
ß1 |
0.50 |
|
|
ß2 |
0.53 |
|||
Стандартизированное уравнение будет иметь вид: ty^=0,5tx1+0,53tx2
Коэффициенты стандартизированного уравнения показывают, что в новой двухфакторной модели цены на нефть оказывают меньшее влияние на доходность по индексу РТС, и доходность по индексу MSCI EM больше влияет на индекс РТС (ß1=0,5, ß2=0,53)
Стандартизованный коэффициент при индексе цен на нефть показывает, что если индекс цен на нефть изменится на свое стандартное отклонение (+- 0,09), тогда доходность по индексу РТС изменится на величину стандартное отклонение доходности по индексу РТС * коэффициент при tx1(%).
Если значение доходности по индексу MSCI EM изменится на свое стандартное отклонение (+-0,8), тогда доходность по индексу РТС изменится на величину стандартное отклонение доходности по индексу РТС * коэффициент при tx2(%).
Если сравнить тесноту связи, характеризуемую стандартизированными коэффициентами, и силу связи, объясняемую коэффициентом эластичности, между экзогенными и эндогенной переменными (Эх1=0,558, Эх2=0,667), можно констатировать наличие более тесной и сильной связи между доходностью по индексу MSCI EM и доходностью по индексу РТС, изменение цен на нефть чуть в меньшей степени влияет на доходность по индексу РТС.
10. Частные коэффициенты корреляции, характеризующие тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение двухфакторной регрессии, уже известны. Для расчетов частных коэффициентов корреляции используем парные и межфакторные коэффициенты корреляции.
|
Таблица 9. Коэффициенты корреляции |
|||
|
У |
Х1 |
Х2 |
|
|
У |
1.00 |
||
|
Х1 |
0.67 |
1.00 |
|
|
Х2 |
0.67 |
0.37 |
1.00 |
ryx1.x2=0.62
ryx2.x1=0.61
При постоянном действии фактора доходности по индексу MSCI EM корреляция между изменением цен на нефть и доходностью по индексу РТС снижается. При фиксации цен на нефть корреляция между индексом MSCI EM и индексом РТС также уменьшается.
Коэффициенты частной корреляции показывают, что чуть более сильное влияние на индекс РТС оказывает изменение цен на нефть, чем изменение индекса MSCI EM.
Вывод: исключение фактора Х3 из трехфакторной регрессионной модели благоприятно отразилось на качестве модели. Прежде всего, исчезло явление мультиколлинеарности между факторами доходности по индексу MSCI EM и доходности по MSCI World. Одновременно увеличился коэффициент эластичности доходности РТС по доходности MSCI EM.
Коэффициент детерминации двухфакторной модели снизился на 0,001, сумма квадратов остатков увеличилась 0,001, ошибка аппроксимации снизилась на 0,1 процентных пункта, межфакторная корреляция исчезла, что делает двухфакторную модель в данном случае более предпочтительной.
В полученной модели коэффициент детерминации показывает, что вариация факторов изменения цен на нефть марки Brent и доходности по индексу MSCI EM на 68,4% объясняют вариацию доходности по индексу РТС, поэтому качество модели можно было бы улучшить путем дополнения каким-либо фактором (факторами).
На диаграмме 3 построены графики реальной и расчетной доходности по индексу РТС на основе полученной регрессионной модели. Заметно, что в некоторые периоды сумма квадратов остатков между расчетным и фактическим значением доходности особенно велика. Однако график расчетной доходности практически с точностью указывал на направление краткосрочных и долгосрочных трендов в целом, иногда различалась амплитуда колебаний. Полезно знать направление тренда, однако в будущем необходимо специфицировать модель с целью получения большего процента объясненной вариации значений доходности по индексу РТС вариацией экзогенных переменных.
СЦЕНАРИИ ИЗМЕНЕНИЯ ДОХОДНОСТИ РТС ПО ИЗМЕНИЮ ЦЕН НА НЕФТЬ
На основе полученной двухфакторной регрессионной модели построим двухмесячный прогноз доходности по индексу РТС. Рассмотрим 2 сценария развития ситуации: оптимистичный и пессимистичный, в зависимости от изменения цен на нефть марки Brent при постоянной доходности индексу MSCI EM.
Сценарий 1: Предположим, что цены на нефть будут расти на 5% каждый месяц при неизменности доходности по MSCI EM:
|
Таблица 12. Прогноз доходности в случае роста цен на нефть |
||||
|
Отношение последующего значения индекса РТС к предыдущему p/p0 |
Отношение последующего значения цены Brent к предыдущему p/p0 |
Отношение последующего значения индекса MSCI EM к предыдущему p/p0 |
Расчетное значение |
|
|
У |
Х1 |
Х2 |
Y^ |
|
|
Декабрь 2011 |
105% |
100% |
103% |
|
|
Ноябрь 2011 |
105% |
100% |
103% |
|
|
Октябрь 2011 |
93% |
99% |
113% |
108% |
|
Сентябрь 2011 |
91% |
101% |
85% |
90% |
|
Август 2011 |
86% |
95% |
91% |
91% |
|
Июль 2011 |
103% |
102% |
100% |
101% |
|
Июнь 2011 |
101% |
99% |
99% |
98% |
|
Май 2011 |
91% |
93% |
97% |
94% |
|
Апрель 2011 |
103% |
108% |
103% |
106% |
|
Март 2011 |
105% |
110% |
106% |
109% |
|
Февраль 2011 |
101% |
108% |
99% |
103% |
|
Январь 2011 |
108% |
105% |
97% |
101% |
Для нахождения расчетного значения эндогенной переменной воспользуемся уравнением регрессии:
log(Y^)=-0,002+0,558log(X1)+0,667log(X2)
При росте цен на нефть в ноябре и октябре на 5%, к примеру, доходность по индексу РТС также должна возрасти. Расчетные значения для ноября и декабря составили 103%.
Сценарий 2: Пусть цены на нефть будут падать в ноябре и декабре на 4% и на 10% соответственно.
При снижении цен на нефть в ноябре и декабре на 4% и на 10% соответственно, а также при неизменности доходности по индексу MSCI EM, в ноябре значение доходности по индексу РТС снизится на 2%, и в декабре еще на 6%.
|
Таблица 13. Прогноз доходности в случае снижения цен на нефть |
||||
|
Отношение последующего значения индекса РТС к предыдущему p/p0 |
Отношение последующего значения цены Brent к предыдущему p/p0 |
Отношение последующего значения индекса MSCI EM к предыдущему p/p0 |
Расчетное значение |
|
|
У |
Х1 |
Х2 |
Y^ |
|
|
Декабрь 2011 |
90% |
100% |
94% |
|
|
Ноябрь 2011 |
96% |
100% |
98% |
|
|
Октябрь 2011 |
93% |
99% |
113% |
108% |
|
Сентябрь 2011 |
91% |
101% |
85% |
90% |
|
Август 2011 |
86% |
95% |
91% |
91% |
|
Июль 2011 |
103% |
102% |
100% |
101% |
|
Июнь 2011 |
101% |
99% |
99% |
98% |
|
Май 2011 |
91% |
93% |
97% |
94% |
|
Апрель 2011 |
103% |
108% |
103% |
106% |
|
Март 2011 |
105% |
110% |
106% |
109% |
|
Февраль 2011 |
101% |
108% |
99% |
103% |
|
Январь 2011 |
108% |
105% |
97% |
101% |
Поскольку ноябрь-месяц уже закончился, можно сравнить прогнозное значение доходности по индексу РТС и расчетное. Среднемесячное значение цен на нефть выросло на 1%, однако доходность по индексу MSCI EM снизилась на 7%. Реальная доходность по индексу РТС увеличилась на 6%. Расчетное значение доходности по индексу РТС показало снижение на 4%, ошибка модели для данного наблюдения составила 10%.
|
Таблица 13. Показатели в ноябре |
|||||
|
Отношение последующего значения индекса РТС к предыдущему p/p0 |
Отношение последующего значения цены Brent к предыдущему p/p0 |
Отношение последующего значения индекса MSCI EM к предыдущему p/p0 |
Расчетное значение |
Остатки модели |
|
|
У |
Х1 |
Х2 |
Y^ |
E=Y-Y^ |
|
|
Ноябрь 2011 |
106% |
101% |
93% |
96% |
10% |
ЗАКЛЮЧЕНИЕ
В данном исследовании была рассмотрена статистически значимая регрессионная модель прогноза доходности по индексу РТС на основе поведения различных внешних факторов (цена на нефть, доходность по индексу MSCI EM). Было установлено, что данные факторы практически одинаково влияют на индекс РТС. Вместе они на 68% объясняют поведение индекса РТС. Цена на нефть марок Brent и WTI в своем направленном движении определяет изменение индексов как РТС, так и, возможно, MSCI EM, так как на диаграмме 1 заметно, что практически всегда изменения индексов следуют за изменением цен на нефть. Однако, для более точного результат следует ввести в модель, возможно, какие-либо внутренние факторы.
Для определения уравнения регрессии была использована двойная логарифмическая модель (log-log модель), то есть линеаризованная степенная функция, которую в линейном виде можно записать следующим образом:
log(Y)= + log(X1)+ log(X2)+
Для оценки коэффициентов линеаризованной регрессии использовался метод наименьших квадратов остатков, так как были соблюдены основные предпосылки Гаусса-Маркова:
- Математическое ожидание случайных возмущений равно 0;
- Дисперсия возмущений постоянна и не зависит от номера наблюдений;
- Возмущения различных наблюдений некоррелированы, то есть отсутствует систематическая связь между значениями случайного члена в любых двух наблюдениях.
На основе полученной регрессионной модели был построен прогноз доходности по индексу РТС на ноябрь и декабрь 2011 г. Были разработаны 2 сценария развития ситуации в зависимости от поведения цен на нефть марки Brent при неизменном значении доходности по индексу MSCI EM:
- Оптимистичный, если цена на нефть будет расти;
- Пессимистичный, если цена на нефть будет падать.
При равномерном изменении цен на нефть (на одинаковое количество процентов за период) доходность по индексу РТС будет равномерно изменяться в сторону изменения цен на нефть.
При неравномерном (скачкообразном) изменении цен на нефть (на неодинаковое количество процентов за период) доходность по индексу РТС также будет неравномерно изменяться. Данный вариант является естественным образом наиболее вероятным.
К тому же, варианты сценария были разработаны с учетом неизменного поведения других факторов, однако в динамично меняющейся обстановке постоянство факторов редко возможно наблюдать. Как видно из таблицы 13, цена на нефть выросла, доходность по индексу MSCI EM снизилась. Индекс РТС последовал за ростом цен на нефть, показывая доходность 6%.
СПИСОК ЛИТЕРАТУРЫ
- Анализ фондового рынка России за май 2010 года / Департамент по финансовому и фондовому рынку Краснодарского края. — Электронный ресурс. Режим доступа: http://www.finmarket.kubangov.ru/content/%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7-%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D0%BE%D0%B3%D0%BE-%D1%80%D1%8B%D0%BD%D0%BA%D0%B0-%D0%A0%D0%BE%D1%81%D1%81%D0%B8%D0%B8-%D0%B7%D0%B0-%D0%BC%D0%B0%D0%B9-2010-%D0%B3%D0%BE%D0%B4%D0%B0
- Балашова С.А. Динамика факторов риска российского фондового рынка / Аудит и финансовый анализ. -2010. — №5. — С. 225-231
- Елисеева И.И. Эконометрика. — Москва «Финансы и статистика»: 2003. — 346 с.
- Иванченко И., Наливайский В. Исследование степени эффективности российского фондового рынка / РЦБ Архив. — Электронный ресурс. Режим доступа: http://www.old.rcb.ru/Archive/articles.asp?id=4330
- Индекс РТС и индекс ММВБ. Справка / РИА Новости. — 07.05.2010. — Электронный ресурс. Режим доступа: http://www.rian.ru/spravka/20100507/231593218.html
- Индекс РТС обновил минимум с конца мая 2010 года / Forbes.ru. — 04.10.2011. — Электронный ресурс. Режим доступа: http://www.forbes.ru/news/74761-indeks-rts-obnovil-minimum-s-kontsa-maya-2010-goda
- Прытин Д. 13 самых неудачных дней на рынке акций в 2009 году / РБК.Рейтинг. — Электронный ресурс. Режим доступа: http://rating.rbc.ru/article.shtml?2010/01/14/32675247
- Список акций для расчета Индекса РТС (действует с 16 декабря 2011 года по 15 марта 2012 года) / РТС Биржа. — Электронный ресурс. Режим доступа: http://www.rts.ru/s288
- Трегуб А.Я., Посохов Ю.Е. Российский фондовый рынок: первое полугодие 2011 / Аналитический обзор НАУФОР. — Электронный ресурс. Режим доступа: http://naufor.ru/download/pdf/factbook/ru/RFR2011_1.pdf
- Index Definitions / MSCI. — Электронный ресурс. Режим доступа: http://www.msci.com/products/indices/tools/index.html#EM
- Crude Oil (petroleum); West Texas Intermediate Daily Price / Index Mundi. — Электронный ресурс. Режим доступа: http://www.indexmundi.com/commodities/?commodity=crude-oil-west-texas-intermediate&months=120
- Crude Oil (petroleum); Dated Brent Daily Price / Index Mundi. — Электронный ресурс. Режим доступа: http://www.indexmundi.com/commodities/?commodity=crude-oil-brent&months=120
[1] Индекс РТС и индекс ММВБ. Справка / РИА Новости. — 07.05.2010. — Электронный ресурс. Режим доступа: http://www.rian.ru/spravka/20100507/231593218.html
[2] Трегуб А.Я., Посохов Ю.Е. Российский фондовый рынок: первое полугодие 2011 / Аналитический обзор НАУФОР. — Электронный ресурс. Режим доступа: http://naufor.ru/download/pdf/factbook/ru/RFR2011_1.pdf
[3] Список акций для расчета Индекса РТС (действует с 16 декабря 2011 года по 15 марта 2012 года) / РТС Биржа. — Электронный ресурс. Режим доступа: http://www.rts.ru/s288
[4] Д. Прытин13 самых неудачных дней на рынке акций в 2009 году / РБК.Рейтинг. — Электронный ресурс. Режим доступа: http://rating.rbc.ru/article.shtml?2010/01/14/32675247
[5] Анализ фондового рынка России за май 2010 года / Департамент по финансовому и фондовому рынку Краснодарского края. — Электронный ресурс. Режим доступа: http://www.finmarket.kubangov.ru/content/%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7-%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D0%BE%D0%B3%D0%BE-%D1%80%D1%8B%D0%BD%D0%BA%D0%B0-%D0%A0%D0%BE%D1%81%D1%81%D0%B8%D0%B8-%D0%B7%D0%B0-%D0%BC%D0%B0%D0%B9-2010-%D0%B3%D0%BE%D0%B4%D0%B0
[6] Индекс РТС обновил минимум с конца мая 2010 года / Forbes.ru. — 04.10.2011. — Электронный ресурс. Режим доступа: http://www.forbes.ru/news/74761-indeks-rts-obnovil-minimum-s-kontsa-maya-2010-goda
[7] Index Definitions / MSCI. — Электронный ресурс. Режим доступа: http://www.msci.com/products/indices/tools/index.html#EM
