Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
![]()
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
![]()
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
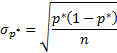
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
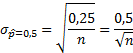
Изобразим эту зависимость на диаграмме.
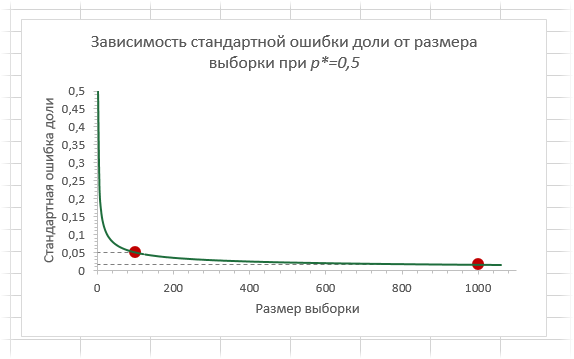
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
![]()
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
![]()
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
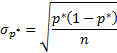
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
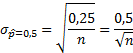
Изобразим эту зависимость на диаграмме.

График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.

Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
![]()
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.

Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:

Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы


Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
![]()
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
![]()
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
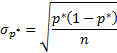
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
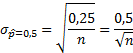
Изобразим эту зависимость на диаграмме.

График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.

Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
![]()
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.

Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:

Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы


Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.

Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
![]()
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.

Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:

Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы


Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
From Wikipedia, the free encyclopedia

For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.
The standard error (SE)[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).[1]
The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.
Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.
In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).
Standard error of the sample mean[edit]
Exact value[edit]
Suppose a statistically independent sample of 




.
Practically this tells us that when trying to estimate the value of a population mean, due to the factor 
Estimate[edit]
The standard deviation 


.
As this is only an estimator for the true «standard error», it is common to see other notations here such as:
or alternately
.
A common source of confusion occurs when failing to distinguish clearly between:
Accuracy of the estimator[edit]
When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.[4] See unbiased estimation of standard deviation for further discussion.
Derivation[edit]
The standard error on the mean may be derived from the variance of a sum of independent random variables,[5] given the definition of variance and some simple properties thereof. If 



which due to the Bienaymé formula, will have variance
where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements 
.
The variance of the mean is then
The standard error is, by definition, the standard deviation of 
.
For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.
Independent and identically distributed random variables with random sample size[edit]
There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size 

[6]
If 




(since the standard deviation is the square root of the variance)
Student approximation when σ value is unknown[edit]
In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.
Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.
Assumptions and usage[edit]
An example of how 


- Upper 95% limit
and
- Lower 95% limit
In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or SE.
Standard errors provide simple measures of uncertainty in a value and are often used because:
- in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
- when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
- when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
- as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.
Standard error of mean versus standard deviation[edit]
In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.[7]
Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.
Extensions[edit]
Finite population correction (FPC)[edit]
The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.
If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):[9]
[10]
which, for large N:
to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.
This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.
Correction for correlation in the sample[edit]

Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −½.
If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:
where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.[11] See also unbiased estimation of standard deviation for more discussion.
See also[edit]
- Illustration of the central limit theorem
- Margin of error
- Probable error
- Standard error of the weighted mean
- Sample mean and sample covariance
- Standard error of the median
- Variance
- Variance of the mean and predicted responses
References[edit]
- ^ a b c d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
- ^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. CUP. ISBN 978-0-521-81099-9.
- ^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
- ^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
- ^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
- ^ Cornell, J R, and Benjamin, C A, Probability, Statistics, and Decisions for Civil Engineers, McGraw-Hill, NY, 1970, ISBN 0486796094, pp. 178–9.
- ^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
- ^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
- ^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
- ^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
- ^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.









