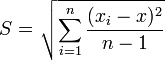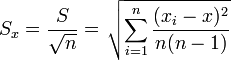Стандартная ошибка измерения: определение и пример
17 авг. 2022 г.
читать 2 мин
Стандартная ошибка измерения , часто обозначаемая как SE m , оценивает отклонение от «истинного» показателя для индивидуума при повторных измерениях.
Он рассчитывается как:
SE m = s√ 1-R
куда:
- s: стандартное отклонение измерений
- R: коэффициент надежности теста.
Обратите внимание, что коэффициент надежности находится в диапазоне от 0 до 1 и рассчитывается путем двукратного проведения теста для многих людей и расчета корреляции между их результатами теста.
Чем выше коэффициент надежности, тем чаще тест дает стабильные результаты.
Пример: расчет стандартной ошибки измерения
Предположим, человек проходит определенный тест 10 раз в течение недели, целью которого является измерение общего интеллекта по шкале от 0 до 100. Он получает следующие баллы:
Очки: 88, 90, 91, 94, 86, 88, 84, 90, 90, 94.
Среднее значение выборки равно 89,5, а стандартное отклонение выборки равно 3,17.
Если известно, что тест имеет коэффициент надежности 0,88, то мы рассчитываем стандартную ошибку измерения как:
SE м = с√1 -R = 3,17√1-0,88 = 1,098
Как использовать SE m для создания доверительных интервалов
Используя стандартную ошибку измерения, мы можем создать доверительный интервал, который, вероятно, будет содержать «истинную» оценку человека по определенному тесту с определенной степенью достоверности.
Если человек получает по тесту оценку x , мы можем использовать следующие формулы для расчета различных доверительных интервалов для этой оценки:
- 68% доверительный интервал = [ x – SE m , x + SE m ]
- 95% доверительный интервал = [ x – 2*SE m , x + 2*SE m ]
- 99% доверительный интервал = [ x – 3*SE m , x + 3*SE m ]
Например, предположим, что человек набрал 92 балла по определенному тесту, который, как известно, имеет SE m 2,5. Мы могли бы рассчитать 95% доверительный интервал как:
- 95% доверительный интервал = [92 – 2*2,5, 92 + 2*2,5] = [87, 97]
Это означает, что мы на 95% уверены в том, что «истинный» результат этого теста человека находится между 87 и 97.
Надежность и стандартная ошибка измерения
Существует простая зависимость между коэффициентом надежности теста и стандартной ошибкой измерения:
- Чем выше коэффициент надежности, тем меньше стандартная ошибка измерения.
- Чем ниже коэффициент надежности, тем выше стандартная ошибка измерения.
Чтобы проиллюстрировать это, рассмотрим человека, который проходит тест 10 раз и имеет стандартное отклонение баллов, равное 2 .
Если тест имеет коэффициент надежности 0,9 , то стандартная ошибка измерения будет рассчитываться как:
- SE m = s√1 -R = 2√1-0,9 = 0,632
Однако, если тест имеет коэффициент надежности 0,5 , то стандартная ошибка измерения будет рассчитываться как:
- SE м = с√ 1-R = 2√ 1-,5 = 1,414
Это должно иметь смысл интуитивно: если результаты теста менее надежны, то ошибка измерения «истинного» результата будет выше.
Стандартная ошибка измерения: определение и пример
17 авг. 2022 г.
читать 2 мин
Стандартная ошибка измерения , часто обозначаемая как SE m , оценивает отклонение от «истинного» показателя для индивидуума при повторных измерениях.
Он рассчитывается как:
SE m = s√ 1-R
куда:
- s: стандартное отклонение измерений
- R: коэффициент надежности теста.
Обратите внимание, что коэффициент надежности находится в диапазоне от 0 до 1 и рассчитывается путем двукратного проведения теста для многих людей и расчета корреляции между их результатами теста.
Чем выше коэффициент надежности, тем чаще тест дает стабильные результаты.
Пример: расчет стандартной ошибки измерения
Предположим, человек проходит определенный тест 10 раз в течение недели, целью которого является измерение общего интеллекта по шкале от 0 до 100. Он получает следующие баллы:
Очки: 88, 90, 91, 94, 86, 88, 84, 90, 90, 94.
Среднее значение выборки равно 89,5, а стандартное отклонение выборки равно 3,17.
Если известно, что тест имеет коэффициент надежности 0,88, то мы рассчитываем стандартную ошибку измерения как:
SE м = с√1 -R = 3,17√1-0,88 = 1,098
Как использовать SE m для создания доверительных интервалов
Используя стандартную ошибку измерения, мы можем создать доверительный интервал, который, вероятно, будет содержать «истинную» оценку человека по определенному тесту с определенной степенью достоверности.
Если человек получает по тесту оценку x , мы можем использовать следующие формулы для расчета различных доверительных интервалов для этой оценки:
- 68% доверительный интервал = [ x – SE m , x + SE m ]
- 95% доверительный интервал = [ x – 2*SE m , x + 2*SE m ]
- 99% доверительный интервал = [ x – 3*SE m , x + 3*SE m ]
Например, предположим, что человек набрал 92 балла по определенному тесту, который, как известно, имеет SE m 2,5. Мы могли бы рассчитать 95% доверительный интервал как:
- 95% доверительный интервал = [92 – 2*2,5, 92 + 2*2,5] = [87, 97]
Это означает, что мы на 95% уверены в том, что «истинный» результат этого теста человека находится между 87 и 97.
Надежность и стандартная ошибка измерения
Существует простая зависимость между коэффициентом надежности теста и стандартной ошибкой измерения:
- Чем выше коэффициент надежности, тем меньше стандартная ошибка измерения.
- Чем ниже коэффициент надежности, тем выше стандартная ошибка измерения.
Чтобы проиллюстрировать это, рассмотрим человека, который проходит тест 10 раз и имеет стандартное отклонение баллов, равное 2 .
Если тест имеет коэффициент надежности 0,9 , то стандартная ошибка измерения будет рассчитываться как:
- SE m = s√1 -R = 2√1-0,9 = 0,632
Однако, если тест имеет коэффициент надежности 0,5 , то стандартная ошибка измерения будет рассчитываться как:
- SE м = с√ 1-R = 2√ 1-,5 = 1,414
Это должно иметь смысл интуитивно: если результаты теста менее надежны, то ошибка измерения «истинного» результата будет выше.
Методы
тестирования
.
Широко распространенные диагностические
методы. Их существует множество, и они
разделяются на группы по следующим
признакам: индивидуальные и групповые
(коллективные), вербальные и невербальные,
количественные и качественные, общие
и специальные и др.
Тесты
являются
специализированными методами
диагностического обследования, применяя
которые, можно получать количественную
или качественную характеристику
изучаемого явления. В отличие от других
методов, они предполагают четкую
процедуру сбора и обработки первичных
данных, а также своеобразие их последующей
интерпретации. Существуют варианты
теста: тест-опросник и тест-задание.
Тест-опросник
—
тщательно продуманные и проверенные
вопросы, по ответам на которые можно
судить о психологических качествах
испытуемого.
Тест-задание
—
оценка психологии и поведения человека
на базе того, что он делает. Испытуемый
выполняет специальные задания, по
которым можно судить о наличии или
отсутствии степени развития у него
изучаемого качества.
Положительная
сторона тестов состоит в том, что они
могут применяться к категориям населения,
различающимся по возрасту, культуре,
профессии, жизненному опыту и т.д.
Недостаток их в том, что испытуемый по
желанию может сознательно влиять на
результаты, зная механизм теста.
В
этих случаях применяется тест-проектирование.
Создается определенный тип проекции,
согласно которому неосознаваемые
собственные качества, особенно недостатки,
человек склонен приписывать другим.
Этот тест требует повышенного
интеллектуального уровня как от
испытуемого, так и высокой профессиональной
квалификации со стороны самого диагноста.
Технология социальной работы
Зайнышев И.Г.
Социальная
педагогика и социальная работа сайт
Здоровы
ли вы душевно?
Узнайте
— все ли в порядке у вас с вашим душевным
здоровьем?
Тест
на выявление уровня самооценки
Как
высоко вы цените себя? Пройдите этот
тест чтобы выяснить это!
Зависите
ли вы от общественного мнения?
Пройдите
тест и выясните это!
стандартная
ошибка измерения
Надежность
психодиагностических методик. Стандартная
ошибка измерения. Понятие о методе
измерения ретестовой надежности
Надежность
– одно из трех главных психометрических
свойств любой измерительной
психодиагностической методики (теста).
Надежность
– это помехоустойчивость теста,
независимость его результата от действия
всевозможных случайных
факторов:
а) разнообразие
внешних материальных условий тестирования,
меняющихся от одного испытуемого к
другому;
б) динамичные
внутренние факторы, по-разному действующие
на разных испытуемых в ходе тестирования;
в) информационно-социальные
обстоятельства. Разнообразие и
изменчивость этих факторов так велики,
что они обусловливают появление у
каждого испытуемого непрогнозируемого
по размерам и направлению отклонения
измеренного тестового балла от истинного
тестового балла (который можно было бы,
в принципе, получать в идеальных
условиях). Величина этого отклонения
определяется как «стандартная
ошибка измерения» (Se).
Ошибка
измерения (Se) и надежность измерения
(R), согласно общепринятой психометрической
теории, связаны следующей формулой:
R
= 1 – Se2 / Sx2, (1)
где
Sx – дисперсия тестовых показателей Х.
Лучинин
Алексей Сергеевич
Психодиагностика конспект лекций
стандартная
ошибка измерения
— относительная доля случайного изменения
(дисперсии) измеряемого показателям по
отношению к совокупного изменению этого
показателя (общей дисперсии). Чем выше
СОИ, тем ниже точность и НАДЕЖНОСТЬ
теста.
СТАНДАРТНАЯ
ОШИБКА ИЗМЕРЕНИЯ
(standard
error of measurement)
— статистическая величина, отражающая
степень точности отдельных (педагогических)
измерений; диапазон изменения показателей,
в который попадает теоретический
показатель (например, истинный балл),
при данном выборочном показателе, с
различной степенью вероятности
Информационно просветительский портал
Ханта Мансийского округа
Стандартная Ошибка Измерения
Оценка
степени, в которой можно ожидать, что
определенный набор измерений, полученных
в данной ситуации (например, в тесте или
в одной из нескольких параллельных форм
теста), будет отклоняться от истинных
значений. Обозначается как а (М).
Психологическая энцеклопедия
Основы теории тестов
1. Основные понятия теории тестов
Измерение
или испытание, проводимое с целью
определения состояния или способностей
спортсмена, называется тестом.
Не
всякие измерения могут быть использованы
как тесты, а только те, которые отвечают
специальным требованиям. К ним относятся:
1.
стандартизованность (процедура и условия
тестирования должны быть одинаковыми
во всех случаях применения теста);
2.
надежность;
3. информативность;
4.
наличие системы оценок.
Тесты,
удовлетворяющие требованиям надежности
и информативности, называют добротными
или аутентичными
(греч. аутентико — достоверным образом).
Процесс
испытаний называется тестированием;
полученное в итоге измерения числовое
значение — результатом
тестирования
(или результатом теста). Например, бег
100 м — это тест, процедура проведения
забегов и хронометража — тестирование,
время забега — результат теста.
Тесты,
в основе которых лежат двигательные
задания, называют двигательными
или моторными
. Результатами их могут быть либо
двигательные достижения (время прохождения
дистанции, число повторений, пройденное
расстояние и т.п.), либо физиологические
и биохимические показатели.
Иногда
используется не один, а несколько тестов,
имеющих единую конечную цель (например,
оценку состояния спортсмена в
соревновательном периоде тренировки).
Такая группа тестов называется комплексом
или батареей
тестов.
Один
и тот же тест, примененный к одним и тем
же исследуемым, должен дать в одинаковых
условиях совпадающие результаты (если
только не изменились сами исследуемые).
Однако при самой строгой стандартизации
и точной аппаратуре результаты
тестирования всегда несколько варьируют.
Например, исследуемый, только что
показавший в тесте становой динамометрии
результат 215 кГ, при повторном выполнении
показывает лишь 190 кГ.
2. Надежность тестов и пути ее определения
Надежностью
теста называется степень совпадения
результатов при повторном тестировании
одних и тех же людей (или других объектов)
в одинаковых условиях.
Вариацию
результатов при повторном тестировании
называют внутри индивидуальной, или
внутри групповой, либо внутриклассовой.
Четыре
основные причины вызывают эту вариацию:
1.
Изменение состояния исследуемых
(утомление, врабатывание, научение,
изменение мотивации, концентрации
внимания и т.п.).
2. Неконтролируемые
изменения внешних условий и аппаратуры
(температура, ветер, влажность, напряжение
в электросети, присутствие посторонних
лиц и т.п.), т.е. все то, что объединяется
термином “случайная ошибка измерения”.
3.
Изменение состояния человека, проводящего
или оценивающего тест (и, конечно, замена
одного экспериментатора или судьи
другим).
4. Несовершенство теста (есть
такие тесты, которые заведомо малонадежные.
Например, если исследуемые выполняют
штрафные броски в баскетбольную корзину,
то даже баскетболист, имеющий высокий
процент попаданий, может случайно
ошибиться при первых бросках).
Основное
различие теории надежности тестов от
теории ошибок измерения состоит в том,
что в теории ошибок измеряемая величина
считается неизменной, а в теории
надежности тестов предполагается, что
она меняется от измерения к измерению.
Например, если необходимо измерить
результат выполненной попытки в прыжках
в длину с разбега, то он вполне определенный
и с течением времени значительно
измениться не может. Конечно, в силу
случайных причин (например, неодинакового
натяжения рулетки) нельзя с идеальной
точностью (скажем до 0,0001 мм) измерить
этот результат. Однако используя более
точный измерительный инструмент
(например, лазерный измеритель), можно
повысить их точность до необходимого
уровня. Вместе с тем, если стоит задача
определить подготовленность прыгуна
на отдельных этапах годичного цикла
тренировки, то самое точное измерение
показанных им результатов мало чем
поможет: ведь они от попытки к попытке
изменятся.
Чтобы
разобраться в идее методов, используемых
для суждения о надежности тестов,
рассмотрим упрощенный пример. Предположим,
что необходимо сравнить результаты
прыжков в длину с места у двух спортсменов
по двум выполненным попыткам. Допустим,
что результаты каждого из спортсменов
варьируют в пределах ± 10 см от средней
величины и равны соответственно 230 ± 10
см (т.е. 220 и 240 см) и 280± 10 см (т.е. 270 и 290
см). В таком случае вывод, конечно, будет
совершенно однозначным: второй спортсмен
превосходит первого (различия между
средними в 50см явно выше случайных
колебаний в ± 10 см). Если же при той же
самой внутригрупповой вариации ( ± 10
см) различие между средними значениями
исследуемых (межгрупповая вариация)
будут маленькими, то сделать вывод будет
гораздо труднее. Допустим, что средние
значения будут примерно равны 220 см (в
одной попытке — 210, в другой — 230 см) и
222 см (212 и 232 см). При этом первый исследуемый
в первой попытке прыгает на 230 см, а
второй — только на 212 см; и создается
впечатление, что первый существенно
сильнее второго. Из этого примера видно,
что основное значение имеет не сама по
себе внутриклассовая изменчивость, а
ее соотношение с межклассовыми различиями.
Одна и та же внутриклассовая изменчивость
дает разную надежность при равных
различиях между классами (в частном
случае между исследуемыми, рис. 14).
Например,
если зарегистрировать у исследуемых
их результаты в каком-либо тесте, повторяя
этот тест в разные дни, причем каждый
день делать по несколько попыток,
периодически меняя экспериментаторов,
то будут иметь место вариации:
а)
от испытуемого к испытуемому;
б)
ото дня ко дню;
в)
от экспериментатора к экспериментатору;
г)
от попытки к попытке.
Дисперсионный
анализ дает возможность выделить и
оценить эти вариации.
Таким
образом, чтобы оценить практически
надежность теста надо, во-первых,
выполнить дисперсионный анализ,
во-вторых, рассчитать внутриклассовый
коэффициент корреляции (коэффициент
надежности).
При
двух попытках величина внутриклассового
коэффициента корреляции практически
совпадает со значениями обычного
коэффициента корреляции между результатами
первой и второй попыток. Поэтому в таких
ситуациях для оценки надежности можно
использовать обычный коэффициент
корреляции (он при этом оценивает
надежность одной, а не двух попыток).
Говоря
о надежности тестов, необходимо различать
их стабильность (воспроизводимость),
согласованность, эквивалентность.
Под
стабильностью
теста понимают воспроизводимость
результатов при его повторении через
определенное время в одинаковых условиях.
Повторное тестирование обычно называют
ретестом.
Согласованность
теста характеризуется независимостью
результатов тестирования от личных
качеств лица, проводящего или оценивающего
тест.
При
выборе теста из определенного числа
однотипных тестов (например, спринтерский
бег на 30, 60 и 100 м) методом параллельных
форм оценивается степень совпадения
результатов. Рассчитанный между
результатами коэффициент корреляции
называют коэффициентом
эквивалентности.
Если
все тесты, входящие в какой-либо комплекс
тестов, высоко эквивалентны, он называется
гомогенным.
Весь этот комплекс измеряет одно какое-то
свойство моторики человека (например,
комплекс, состоящий из прыжков с места
в длину, вверх и тройного; оценивается
уровень развития скоростно-силовых
качеств). Если в комплексе нет эквивалентных
тестов, то есть тесты, входящие в него,
измеряют разные свойства, то он называется
гетерогенным
(например,
комплекс, состоящий из становой
динамометрии, прыжка вверх по Абалакову,
бега на 100 м).
Надежность
тестов может быть повышена до определенной
степени путем:
а)
более строгой стандартизации тестирования;
б)
увеличения числа попыток;
в)
увеличения числа оценщиков (судей,
экспериментов) и повышения согласованности
их мнений;
г)
увеличения числа эквивалентных тестов;
д)
лучшей мотивации исследуемых.
Кубанский
государственный университет физ культуры
спорта и туризма
Популярные
тестовые методики, применяемые в практике
профессионального отбора и тестирования
персонала:
Проективные
тесты
Тест
Роршаха.
Испытуемому предъявляются для
интерпретации картинки с абстрактными
изображениями — пятнами различной
конфигурации и цвета (напоминающими
чернильные кляксы). На основании того,
что увидит испытуемый, диагностируются
его скрытые установки, побуждения,
свойства характера.
Тест
Люшера
позволяет исследовать личность работника
путем анализа его субъективных
предпочтений при выборе цветовых
стимулов. В оригинале стимульный материал
представляют 73 карточки различного
цвета, в российской психодиагностике
распространена упрощенная тестовая
методика, применяющая восемь основных
цветов. При этом каждому цвету приписывается
определенное значение. Важен порядок
выбора цветов: первые выбранные цвета
выражают явные цели деятельности
личности и способы их достижения,
последние — подавленные, вытесненные
стремления.
Тематический
апперцептивный тест (ТАТ)
направлен на исследование психических
свойств личности по спонтанному описанию
тестируемым тех или иных стандартных
ситуаций, изображенных на предъявляемых
ему рисунках. Это один из наиболее
известных тестов на мотивацию достижений.
Надежность в практике тестирования
персонала не является доказанной. По
мнению специалистов, ответы на вопросы
ТАТ могут быть подвержены влиянию
сторонних факторов. Тем не менее,
успешность прохождения данного теста
коррелирует как с общими успехами
человека в учебе, так и с его экономическим
преуспеванием.
Тест
Майнера
на завершение предложений позволяет
прогнозировать управленческий и
творческий потенциал менеджеров. Этот
тест состоит из 40 незаконченных
предложений, которые тестируемый должен
дописать самостоятельно. По нему можно
судить о различных аспектах мотивации
менеджерской деятельности. В других
тестах на завершение предлагается
досочинить рассказ или дорисовать
рисунки.
По
критерию измеряемого психологического
качества можно выделить следующие
группы тестов:
Тесты
на уровень интеллекта (тесты на IQ —
интеллектуальные тесты)
Тестов,
измеряющих уровень интеллекта, очень
много, большинство из них происходят
от двух классических методик: теста
Бине-Симона
и теста
Векслера.
Оба теста прошли испытание на протяжении
70-летней практики их применения и
являются наиболее изученными и надежными.
К примеру, баллы по результатам
словесно-речевых IQ-тестов (тест Векслера)
всегда хорошо коррелируют с успехами
в учебе.
Применяя
тот или иной тест интеллекта, важно
знать, что автор или авторы теста
вкладывают в понятие «интеллект». В
настоящее время психологами выделяется
несколько видов интеллекта: словесно-речевой,
математический, визуально-пространственный,
художественный, двигательный, музыкальный
и прикладной. При этом многие психологи
говорят о так называемом «общем (едином)
интеллекте», позволяющим человеку
довольно эффективно проявлять себя в
разных областях жизнедеятельности.
Тесты
на IQ (коэффициент интеллекта) помогают
выявить наличие отдельных интеллектуальных
способностей человека, в том числе:
-
словесно-речевых;
-
способностей
оперировать с числами — математический
интеллект; -
визуально-пространственных;
-
исполнительских
(особых) — прикладной интеллект.
Недостатком
интеллектуальных тестов является то,
что они нацелены на получение некоторого
суммарного балла, отражающего
интеллектуальные способности «вообще».
Но за этим суммарным баллом остаются
неразличимыми отдельные сильные и
слабые способности человека. Выполняя
интеллектуальные тесты, человек
использует главным образом конвергентное
мышление.
Это мышление «специализируется» на
решении задач, у которых есть только
один правильный ответ. Однако на многие
вопросы нельзя дать однозначный, верный
или неверный ответ. Например, когда
нужно найти новую генеральную линию
развития фирмы, которая позволила бы
ей обогнать своих конкурентов, или
выработать новый действенный слоган —
в этих случаях у задачи множество
вариантов решения. Некоторые из них
будут лучше, другие хуже (зачастую это
может показать лишь время), но ни один
из них не является единственно верным.
Такие вопросы требуют дивергентного
мышления.
Тесты на IQ реально зондируют лишь
конвергентное мышление.
К
тому же высокий коэффициент интеллекта
сам по себе не является гарантией
успешной работы сотрудника. Многое
определяется тем, что требуется для
выполнения конкретной работы, а в этом
случае на первом месте далеко не всегда
выходят интеллектуальные качества. К
примеру, финансовому директору
недостаточно иметь хороший математический
интеллект, ему очень важно уметь верно
оценивать степень риска и принимать
правильные финансовые решения.
Тесты
на личностные качества
Отличительная
особенность данных тестов в том, что в
них оценивается не правильность ответов
тестируемого, а его личностные качества.
Хотя не все стороны характера можно
оценить с помощью тестов, поскольку
каждый человек уникален, но некоторые
личностные черты поддаются количественной
оценке.
В
практике кадровой работы часто
используются MMPI
(Миннесотский многопрофильный личностный
опросник), СМИЛ
(стандартизированный метод исследования
личности), тест
Айзенка,
16-факторный
опросник Кеттелла
(тест 16PF), тесты
Лири, Стреляу, Леонгарда,
«рисуночные тесты», тесты цветовых
предпочтений, а также такие экзотические,
как графологические
(анализ почерка)
и физиогномические (анализ черт лица).
Эти тесты могут применяться при
профотборе, если в службе персонала
есть квалифицированные психологи,
способные интерпретировать получаемые
с их помощью данные. При этом следует
учитывать, что ни один из этих тестов
не рассчитывался на специальное
применение в кадровых службах. Личностные
тесты обладают недостатком: как правило
они достаточно громоздки и сложны. В то
же время большинство служб персонала
при определении личностных качеств
кандидата стремятся использовать более
простые тесты.
Многофакторный
метод исследования личности (СМИЛ)
— это модифицированный (адаптированный
к российским условиям) вариант теста
MMPI, разработанного в 40-х годах американскими
психологами Дж. Маккинли и С. Хатэуэем
для профессионального отбора военных
летчиков. Методика построена по типу
опросника, при этом оценка результата
базируется не на прямом анализе ответов
испытуемого, а на данных статистически
подтвержденной значимости каждого
ответа в сравнении со средненормативными
показателями. Одно из важных достоинств
метода состоит в том, что автоматизированный
способ обработки данных практически
исключает зависимость получаемых
результатов от личностных особенностей
и опыта специалиста, проводящего
тестирование. В основу методики положена
статистически достоверная математическая
база.
Тест
эффективен в решении сложных вопросов
профотбора и профориентации, комплектовании
рабочих коллективов, расстановки кадров,
при изучении социального климата в
организациях и на предприятиях. Он
находит активное применение в
профконсультировании и профориентационной
работе психологов.
Тест
Кеттелла (16PF)
выводит баллы для разных качеств личности
(17 факторов первого порядка). Данные по
некоторым из этих шкал коррелируют друг
с другом, поэтому в итоге образуются 5
факторов (показателей) второго (высшего)
порядка. Полный вариант теста Кеттелла
позволяет исследовать и уровень
интеллекта, и личностные качества. Тест
Кеттелла, а также тест Айзенка наиболее
результативны в диагностике степени
нервозности личности, что профессионально
значимо для некоторых профессий.
Тест
Майерс-Бриггс,
в основе которого лежит психологическая
теория личности К.Г. Юнга, содержит более
ста утверждений и позволяет описать
личность человека по четырем составляющим:
-
Экстравертированность
— Интравертированность; -
Осознание
— Интуиция (что из них для вас более
значимо, приоритетно); -
Размышления
— Чувства; -
Суждения
— Ощущения.
Однако
этот тест больше подходит для оценки
возможности карьерного роста сотрудников
внутри организации, чем для решения
вопроса о приеме на работу.
На
входном контроле (при приеме на работу)
используют тесты самооценки, например,
тест
Лири,
личностный
дифференциал
(ЛД) или опросник
деловой направленности
(ОДН) личности, а также СМИЛ,
результаты которого коррелируют с
результатами, полученными другими
методами.
Тесты
на творческое мышление
Существуют
следующие виды:
-
Тесты
на генерирование идей; -
Тесты
на межпредметные связи (умение создавать
«творческие композиции» особенно важно
в рекламном и маркетинговом деле); -
Визуальные
тесты (на умение создавать визуальные
каламбуры или рассказы по картинкам); -
Тесты
на «боковое мышление» (которое, в отличие
от обычного, позволяет взглянуть на
задачу под нестандартным углом зрения).
Нередко
в тестах на творческое мышление
применяются сюрреалистические либо
иронические рисунки.
Управление
персоналом Словарь-справочник
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
- 1 Определение погрешности
- 2 Классификация погрешностей
- 2.1 По форме представления
- 2.2 По причине возникновения
- 2.3 По характеру проявления
- 2.4 По способу измерения
- 3 См. также
- 4 Литература
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
- Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
- Средняя квадратическая погрешность:
- Средняя квадратическая погрешность среднего арифметического:
Классификация погрешностей
По форме представления
- Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом равенство:
ΔX = | Xtrue − Xmeas | ,
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
- Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:
 .
.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
- Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
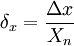 ,
,
где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность — безразмерная величина (может измеряться в процентах).
По причине возникновения
- Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
- Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
- Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.
По характеру проявления
- Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
- Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
- Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
- Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).
По способу измерения
- Погрешность прямых измерений
- Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если F = F(x1,x2…xn), где xi — непосредственно измеряемые независимые величины, имеющие погрешность Δxi, тогда:
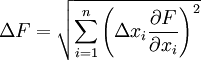
См. также
- Измерение физических величин
- Класс точности
- Метрология
- Система автоматизированного сбора данных со счетчиков по радиоканалу
- Методы электроаналитической химии
Литература
- Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
- Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.
Wikimedia Foundation.
2010.
Методы
тестирования
.
Широко распространенные диагностические
методы. Их существует множество, и они
разделяются на группы по следующим
признакам: индивидуальные и групповые
(коллективные), вербальные и невербальные,
количественные и качественные, общие
и специальные и др.
Тесты
являются
специализированными методами
диагностического обследования, применяя
которые, можно получать количественную
или качественную характеристику
изучаемого явления. В отличие от других
методов, они предполагают четкую
процедуру сбора и обработки первичных
данных, а также своеобразие их последующей
интерпретации. Существуют варианты
теста: тест-опросник и тест-задание.
Тест-опросник
—
тщательно продуманные и проверенные
вопросы, по ответам на которые можно
судить о психологических качествах
испытуемого.
Тест-задание
—
оценка психологии и поведения человека
на базе того, что он делает. Испытуемый
выполняет специальные задания, по
которым можно судить о наличии или
отсутствии степени развития у него
изучаемого качества.
Положительная
сторона тестов состоит в том, что они
могут применяться к категориям населения,
различающимся по возрасту, культуре,
профессии, жизненному опыту и т.д.
Недостаток их в том, что испытуемый по
желанию может сознательно влиять на
результаты, зная механизм теста.
В
этих случаях применяется тест-проектирование.
Создается определенный тип проекции,
согласно которому неосознаваемые
собственные качества, особенно недостатки,
человек склонен приписывать другим.
Этот тест требует повышенного
интеллектуального уровня как от
испытуемого, так и высокой профессиональной
квалификации со стороны самого диагноста.
Технология социальной работы
Зайнышев И.Г.
Социальная
педагогика и социальная работа сайт
Здоровы
ли вы душевно?
Узнайте
— все ли в порядке у вас с вашим душевным
здоровьем?
Тест
на выявление уровня самооценки
Как
высоко вы цените себя? Пройдите этот
тест чтобы выяснить это!
Зависите
ли вы от общественного мнения?
Пройдите
тест и выясните это!
стандартная
ошибка измерения
Надежность
психодиагностических методик. Стандартная
ошибка измерения. Понятие о методе
измерения ретестовой надежности
Надежность
– одно из трех главных психометрических
свойств любой измерительной
психодиагностической методики (теста).
Надежность
– это помехоустойчивость теста,
независимость его результата от действия
всевозможных случайных
факторов:
а) разнообразие
внешних материальных условий тестирования,
меняющихся от одного испытуемого к
другому;
б) динамичные
внутренние факторы, по-разному действующие
на разных испытуемых в ходе тестирования;
в) информационно-социальные
обстоятельства. Разнообразие и
изменчивость этих факторов так велики,
что они обусловливают появление у
каждого испытуемого непрогнозируемого
по размерам и направлению отклонения
измеренного тестового балла от истинного
тестового балла (который можно было бы,
в принципе, получать в идеальных
условиях). Величина этого отклонения
определяется как «стандартная
ошибка измерения» (Se).
Ошибка
измерения (Se) и надежность измерения
(R), согласно общепринятой психометрической
теории, связаны следующей формулой:
R
= 1 – Se2 / Sx2, (1)
где
Sx – дисперсия тестовых показателей Х.
Лучинин
Алексей Сергеевич
Психодиагностика конспект лекций
стандартная
ошибка измерения
— относительная доля случайного изменения
(дисперсии) измеряемого показателям по
отношению к совокупного изменению этого
показателя (общей дисперсии). Чем выше
СОИ, тем ниже точность и НАДЕЖНОСТЬ
теста.
СТАНДАРТНАЯ
ОШИБКА ИЗМЕРЕНИЯ
(standard
error of measurement)
— статистическая величина, отражающая
степень точности отдельных (педагогических)
измерений; диапазон изменения показателей,
в который попадает теоретический
показатель (например, истинный балл),
при данном выборочном показателе, с
различной степенью вероятности
Информационно просветительский портал
Ханта Мансийского округа
Стандартная Ошибка Измерения
Оценка
степени, в которой можно ожидать, что
определенный набор измерений, полученных
в данной ситуации (например, в тесте или
в одной из нескольких параллельных форм
теста), будет отклоняться от истинных
значений. Обозначается как а (М).
Психологическая энцеклопедия
Основы теории тестов
1. Основные понятия теории тестов
Измерение
или испытание, проводимое с целью
определения состояния или способностей
спортсмена, называется тестом.
Не
всякие измерения могут быть использованы
как тесты, а только те, которые отвечают
специальным требованиям. К ним относятся:
1.
стандартизованность (процедура и условия
тестирования должны быть одинаковыми
во всех случаях применения теста);
2.
надежность;
3. информативность;
4.
наличие системы оценок.
Тесты,
удовлетворяющие требованиям надежности
и информативности, называют добротными
или аутентичными
(греч. аутентико — достоверным образом).
Процесс
испытаний называется тестированием;
полученное в итоге измерения числовое
значение — результатом
тестирования
(или результатом теста). Например, бег
100 м — это тест, процедура проведения
забегов и хронометража — тестирование,
время забега — результат теста.
Тесты,
в основе которых лежат двигательные
задания, называют двигательными
или моторными
. Результатами их могут быть либо
двигательные достижения (время прохождения
дистанции, число повторений, пройденное
расстояние и т.п.), либо физиологические
и биохимические показатели.
Иногда
используется не один, а несколько тестов,
имеющих единую конечную цель (например,
оценку состояния спортсмена в
соревновательном периоде тренировки).
Такая группа тестов называется комплексом
или батареей
тестов.
Один
и тот же тест, примененный к одним и тем
же исследуемым, должен дать в одинаковых
условиях совпадающие результаты (если
только не изменились сами исследуемые).
Однако при самой строгой стандартизации
и точной аппаратуре результаты
тестирования всегда несколько варьируют.
Например, исследуемый, только что
показавший в тесте становой динамометрии
результат 215 кГ, при повторном выполнении
показывает лишь 190 кГ.
2. Надежность тестов и пути ее определения
Надежностью
теста называется степень совпадения
результатов при повторном тестировании
одних и тех же людей (или других объектов)
в одинаковых условиях.
Вариацию
результатов при повторном тестировании
называют внутри индивидуальной, или
внутри групповой, либо внутриклассовой.
Четыре
основные причины вызывают эту вариацию:
1.
Изменение состояния исследуемых
(утомление, врабатывание, научение,
изменение мотивации, концентрации
внимания и т.п.).
2. Неконтролируемые
изменения внешних условий и аппаратуры
(температура, ветер, влажность, напряжение
в электросети, присутствие посторонних
лиц и т.п.), т.е. все то, что объединяется
термином “случайная ошибка измерения”.
3.
Изменение состояния человека, проводящего
или оценивающего тест (и, конечно, замена
одного экспериментатора или судьи
другим).
4. Несовершенство теста (есть
такие тесты, которые заведомо малонадежные.
Например, если исследуемые выполняют
штрафные броски в баскетбольную корзину,
то даже баскетболист, имеющий высокий
процент попаданий, может случайно
ошибиться при первых бросках).
Основное
различие теории надежности тестов от
теории ошибок измерения состоит в том,
что в теории ошибок измеряемая величина
считается неизменной, а в теории
надежности тестов предполагается, что
она меняется от измерения к измерению.
Например, если необходимо измерить
результат выполненной попытки в прыжках
в длину с разбега, то он вполне определенный
и с течением времени значительно
измениться не может. Конечно, в силу
случайных причин (например, неодинакового
натяжения рулетки) нельзя с идеальной
точностью (скажем до 0,0001 мм) измерить
этот результат. Однако используя более
точный измерительный инструмент
(например, лазерный измеритель), можно
повысить их точность до необходимого
уровня. Вместе с тем, если стоит задача
определить подготовленность прыгуна
на отдельных этапах годичного цикла
тренировки, то самое точное измерение
показанных им результатов мало чем
поможет: ведь они от попытки к попытке
изменятся.
Чтобы
разобраться в идее методов, используемых
для суждения о надежности тестов,
рассмотрим упрощенный пример. Предположим,
что необходимо сравнить результаты
прыжков в длину с места у двух спортсменов
по двум выполненным попыткам. Допустим,
что результаты каждого из спортсменов
варьируют в пределах ± 10 см от средней
величины и равны соответственно 230 ± 10
см (т.е. 220 и 240 см) и 280± 10 см (т.е. 270 и 290
см). В таком случае вывод, конечно, будет
совершенно однозначным: второй спортсмен
превосходит первого (различия между
средними в 50см явно выше случайных
колебаний в ± 10 см). Если же при той же
самой внутригрупповой вариации ( ± 10
см) различие между средними значениями
исследуемых (межгрупповая вариация)
будут маленькими, то сделать вывод будет
гораздо труднее. Допустим, что средние
значения будут примерно равны 220 см (в
одной попытке — 210, в другой — 230 см) и
222 см (212 и 232 см). При этом первый исследуемый
в первой попытке прыгает на 230 см, а
второй — только на 212 см; и создается
впечатление, что первый существенно
сильнее второго. Из этого примера видно,
что основное значение имеет не сама по
себе внутриклассовая изменчивость, а
ее соотношение с межклассовыми различиями.
Одна и та же внутриклассовая изменчивость
дает разную надежность при равных
различиях между классами (в частном
случае между исследуемыми, рис. 14).
Например,
если зарегистрировать у исследуемых
их результаты в каком-либо тесте, повторяя
этот тест в разные дни, причем каждый
день делать по несколько попыток,
периодически меняя экспериментаторов,
то будут иметь место вариации:
а)
от испытуемого к испытуемому;
б)
ото дня ко дню;
в)
от экспериментатора к экспериментатору;
г)
от попытки к попытке.
Дисперсионный
анализ дает возможность выделить и
оценить эти вариации.
Таким
образом, чтобы оценить практически
надежность теста надо, во-первых,
выполнить дисперсионный анализ,
во-вторых, рассчитать внутриклассовый
коэффициент корреляции (коэффициент
надежности).
При
двух попытках величина внутриклассового
коэффициента корреляции практически
совпадает со значениями обычного
коэффициента корреляции между результатами
первой и второй попыток. Поэтому в таких
ситуациях для оценки надежности можно
использовать обычный коэффициент
корреляции (он при этом оценивает
надежность одной, а не двух попыток).
Говоря
о надежности тестов, необходимо различать
их стабильность (воспроизводимость),
согласованность, эквивалентность.
Под
стабильностью
теста понимают воспроизводимость
результатов при его повторении через
определенное время в одинаковых условиях.
Повторное тестирование обычно называют
ретестом.
Согласованность
теста характеризуется независимостью
результатов тестирования от личных
качеств лица, проводящего или оценивающего
тест.
При
выборе теста из определенного числа
однотипных тестов (например, спринтерский
бег на 30, 60 и 100 м) методом параллельных
форм оценивается степень совпадения
результатов. Рассчитанный между
результатами коэффициент корреляции
называют коэффициентом
эквивалентности.
Если
все тесты, входящие в какой-либо комплекс
тестов, высоко эквивалентны, он называется
гомогенным.
Весь этот комплекс измеряет одно какое-то
свойство моторики человека (например,
комплекс, состоящий из прыжков с места
в длину, вверх и тройного; оценивается
уровень развития скоростно-силовых
качеств). Если в комплексе нет эквивалентных
тестов, то есть тесты, входящие в него,
измеряют разные свойства, то он называется
гетерогенным
(например,
комплекс, состоящий из становой
динамометрии, прыжка вверх по Абалакову,
бега на 100 м).
Надежность
тестов может быть повышена до определенной
степени путем:
а)
более строгой стандартизации тестирования;
б)
увеличения числа попыток;
в)
увеличения числа оценщиков (судей,
экспериментов) и повышения согласованности
их мнений;
г)
увеличения числа эквивалентных тестов;
д)
лучшей мотивации исследуемых.
Кубанский
государственный университет физ культуры
спорта и туризма
Популярные
тестовые методики, применяемые в практике
профессионального отбора и тестирования
персонала:
Проективные
тесты
Тест
Роршаха.
Испытуемому предъявляются для
интерпретации картинки с абстрактными
изображениями — пятнами различной
конфигурации и цвета (напоминающими
чернильные кляксы). На основании того,
что увидит испытуемый, диагностируются
его скрытые установки, побуждения,
свойства характера.
Тест
Люшера
позволяет исследовать личность работника
путем анализа его субъективных
предпочтений при выборе цветовых
стимулов. В оригинале стимульный материал
представляют 73 карточки различного
цвета, в российской психодиагностике
распространена упрощенная тестовая
методика, применяющая восемь основных
цветов. При этом каждому цвету приписывается
определенное значение. Важен порядок
выбора цветов: первые выбранные цвета
выражают явные цели деятельности
личности и способы их достижения,
последние — подавленные, вытесненные
стремления.
Тематический
апперцептивный тест (ТАТ)
направлен на исследование психических
свойств личности по спонтанному описанию
тестируемым тех или иных стандартных
ситуаций, изображенных на предъявляемых
ему рисунках. Это один из наиболее
известных тестов на мотивацию достижений.
Надежность в практике тестирования
персонала не является доказанной. По
мнению специалистов, ответы на вопросы
ТАТ могут быть подвержены влиянию
сторонних факторов. Тем не менее,
успешность прохождения данного теста
коррелирует как с общими успехами
человека в учебе, так и с его экономическим
преуспеванием.
Тест
Майнера
на завершение предложений позволяет
прогнозировать управленческий и
творческий потенциал менеджеров. Этот
тест состоит из 40 незаконченных
предложений, которые тестируемый должен
дописать самостоятельно. По нему можно
судить о различных аспектах мотивации
менеджерской деятельности. В других
тестах на завершение предлагается
досочинить рассказ или дорисовать
рисунки.
По
критерию измеряемого психологического
качества можно выделить следующие
группы тестов:
Тесты
на уровень интеллекта (тесты на IQ —
интеллектуальные тесты)
Тестов,
измеряющих уровень интеллекта, очень
много, большинство из них происходят
от двух классических методик: теста
Бине-Симона
и теста
Векслера.
Оба теста прошли испытание на протяжении
70-летней практики их применения и
являются наиболее изученными и надежными.
К примеру, баллы по результатам
словесно-речевых IQ-тестов (тест Векслера)
всегда хорошо коррелируют с успехами
в учебе.
Применяя
тот или иной тест интеллекта, важно
знать, что автор или авторы теста
вкладывают в понятие «интеллект». В
настоящее время психологами выделяется
несколько видов интеллекта: словесно-речевой,
математический, визуально-пространственный,
художественный, двигательный, музыкальный
и прикладной. При этом многие психологи
говорят о так называемом «общем (едином)
интеллекте», позволяющим человеку
довольно эффективно проявлять себя в
разных областях жизнедеятельности.
Тесты
на IQ (коэффициент интеллекта) помогают
выявить наличие отдельных интеллектуальных
способностей человека, в том числе:
-
словесно-речевых;
-
способностей
оперировать с числами — математический
интеллект; -
визуально-пространственных;
-
исполнительских
(особых) — прикладной интеллект.
Недостатком
интеллектуальных тестов является то,
что они нацелены на получение некоторого
суммарного балла, отражающего
интеллектуальные способности «вообще».
Но за этим суммарным баллом остаются
неразличимыми отдельные сильные и
слабые способности человека. Выполняя
интеллектуальные тесты, человек
использует главным образом конвергентное
мышление.
Это мышление «специализируется» на
решении задач, у которых есть только
один правильный ответ. Однако на многие
вопросы нельзя дать однозначный, верный
или неверный ответ. Например, когда
нужно найти новую генеральную линию
развития фирмы, которая позволила бы
ей обогнать своих конкурентов, или
выработать новый действенный слоган —
в этих случаях у задачи множество
вариантов решения. Некоторые из них
будут лучше, другие хуже (зачастую это
может показать лишь время), но ни один
из них не является единственно верным.
Такие вопросы требуют дивергентного
мышления.
Тесты на IQ реально зондируют лишь
конвергентное мышление.
К
тому же высокий коэффициент интеллекта
сам по себе не является гарантией
успешной работы сотрудника. Многое
определяется тем, что требуется для
выполнения конкретной работы, а в этом
случае на первом месте далеко не всегда
выходят интеллектуальные качества. К
примеру, финансовому директору
недостаточно иметь хороший математический
интеллект, ему очень важно уметь верно
оценивать степень риска и принимать
правильные финансовые решения.
Тесты
на личностные качества
Отличительная
особенность данных тестов в том, что в
них оценивается не правильность ответов
тестируемого, а его личностные качества.
Хотя не все стороны характера можно
оценить с помощью тестов, поскольку
каждый человек уникален, но некоторые
личностные черты поддаются количественной
оценке.
В
практике кадровой работы часто
используются MMPI
(Миннесотский многопрофильный личностный
опросник), СМИЛ
(стандартизированный метод исследования
личности), тест
Айзенка,
16-факторный
опросник Кеттелла
(тест 16PF), тесты
Лири, Стреляу, Леонгарда,
«рисуночные тесты», тесты цветовых
предпочтений, а также такие экзотические,
как графологические
(анализ почерка)
и физиогномические (анализ черт лица).
Эти тесты могут применяться при
профотборе, если в службе персонала
есть квалифицированные психологи,
способные интерпретировать получаемые
с их помощью данные. При этом следует
учитывать, что ни один из этих тестов
не рассчитывался на специальное
применение в кадровых службах. Личностные
тесты обладают недостатком: как правило
они достаточно громоздки и сложны. В то
же время большинство служб персонала
при определении личностных качеств
кандидата стремятся использовать более
простые тесты.
Многофакторный
метод исследования личности (СМИЛ)
— это модифицированный (адаптированный
к российским условиям) вариант теста
MMPI, разработанного в 40-х годах американскими
психологами Дж. Маккинли и С. Хатэуэем
для профессионального отбора военных
летчиков. Методика построена по типу
опросника, при этом оценка результата
базируется не на прямом анализе ответов
испытуемого, а на данных статистически
подтвержденной значимости каждого
ответа в сравнении со средненормативными
показателями. Одно из важных достоинств
метода состоит в том, что автоматизированный
способ обработки данных практически
исключает зависимость получаемых
результатов от личностных особенностей
и опыта специалиста, проводящего
тестирование. В основу методики положена
статистически достоверная математическая
база.
Тест
эффективен в решении сложных вопросов
профотбора и профориентации, комплектовании
рабочих коллективов, расстановки кадров,
при изучении социального климата в
организациях и на предприятиях. Он
находит активное применение в
профконсультировании и профориентационной
работе психологов.
Тест
Кеттелла (16PF)
выводит баллы для разных качеств личности
(17 факторов первого порядка). Данные по
некоторым из этих шкал коррелируют друг
с другом, поэтому в итоге образуются 5
факторов (показателей) второго (высшего)
порядка. Полный вариант теста Кеттелла
позволяет исследовать и уровень
интеллекта, и личностные качества. Тест
Кеттелла, а также тест Айзенка наиболее
результативны в диагностике степени
нервозности личности, что профессионально
значимо для некоторых профессий.
Тест
Майерс-Бриггс,
в основе которого лежит психологическая
теория личности К.Г. Юнга, содержит более
ста утверждений и позволяет описать
личность человека по четырем составляющим:
-
Экстравертированность
— Интравертированность; -
Осознание
— Интуиция (что из них для вас более
значимо, приоритетно); -
Размышления
— Чувства; -
Суждения
— Ощущения.
Однако
этот тест больше подходит для оценки
возможности карьерного роста сотрудников
внутри организации, чем для решения
вопроса о приеме на работу.
На
входном контроле (при приеме на работу)
используют тесты самооценки, например,
тест
Лири,
личностный
дифференциал
(ЛД) или опросник
деловой направленности
(ОДН) личности, а также СМИЛ,
результаты которого коррелируют с
результатами, полученными другими
методами.
Тесты
на творческое мышление
Существуют
следующие виды:
-
Тесты
на генерирование идей; -
Тесты
на межпредметные связи (умение создавать
«творческие композиции» особенно важно
в рекламном и маркетинговом деле); -
Визуальные
тесты (на умение создавать визуальные
каламбуры или рассказы по картинкам); -
Тесты
на «боковое мышление» (которое, в отличие
от обычного, позволяет взглянуть на
задачу под нестандартным углом зрения).
Нередко
в тестах на творческое мышление
применяются сюрреалистические либо
иронические рисунки.
Управление
персоналом Словарь-справочник
Стандартная ошибка
Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.
Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.
В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.

![]()
Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.
Как найти стандартную ошибку среднего значения
Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.
Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.
S E x ¯ = s n {displaystyle SE_{bar {x}} ={frac {s}{sqrt {n}}}}
где
s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и
n — количество измерений в выборке.
Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.
Исправления для некоторых случаев
Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:
Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.
Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.
Полезность
Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!
Стандартные ошибки легко вычисляются и часто используются, потому что:
- Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
- Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
- Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
- Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).
Относительная стандартная ошибка
Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).
На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. []
Пример
Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).
Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.
Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.

![]()
.jpg)
![]()
Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-

1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-

2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-

3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-

4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-

5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-

6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-

1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-

2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-

3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-

4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-

5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-

1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 49 776 раз.