Стандартная ошибка надежности равна 3 см это значит что - Ремонт и установка крупной бытовой техники

history 23 ноября 2016 г.

Статистический вывод

Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в MS EXCEL .

СОВЕТ : Для понимания терминов Уровень значимости и Уровень надежности потребуется знание следующих понятий:

Уровень значимости статистического теста – это вероятность отклонить нулевую гипотезу , когда на самом деле она верна. Другими словами, это допустимая для данной задачи вероятность ошибки первого рода (type I error).

Уровень значимости обычно обозначают греческой буквой α ( альфа ). Чаще всего для уровня значимости используют значения 0,001; 0,01; 0,05; 0,10.

Например, при построении доверительного интервала для оценки среднего значения распределения , его ширину рассчитывают таким образом, чтобы вероятность события « выборочное среднее (Х _ср ) находится за пределами доверительного интервала » было равно уровню значимости . Реализация этого события считается маловероятным (практически невозможным) и служит основанием для отклонения нулевой гипотезы о равенстве среднего заданному значению .

Ошибка первого рода часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина ошибки первого рода задается перед проверкой гипотезы , таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи.

Чрезмерное уменьшение уровня значимости α (т.е. вероятности ошибки первого рода ) может привести к увеличению вероятности ошибки второго рода , то есть вероятности принять нулевую гипотезу , когда на самом деле она не верна. Подробнее об ошибке второго рода см. статью Ошибка второго рода и Кривая оперативной характеристики .

Уровень значимости обычно указывается в аргументах обратных функций MS EXCEL для вычисления квантилей соответствующего распределения: НОРМ.СТ.ОБР() , ХИ2.ОБР() , СТЬЮДЕНТ.ОБР() и др. Примеры использования этих функций приведены в статьях про проверку гипотез и про построение доверительных интервалов .

Уровень надежности

Уровень доверия (этот термин более распространен в отечественной литературе, чем Уровень надежности ) — означает вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра распределения.

Уровень доверия равен 1-α, где α – уровень значимости .

Термин Уровень надежности имеет синонимы: уровень доверия, коэффициент доверия, доверительный уровень и доверительная вероятность (англ. Confidence Level , Confidence Coefficient ).

В математической статистике обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.

Например, Уровень доверия 95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор уровня доверия полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.

Примечание : Стоит отметить, что математически не корректно говорить, что Уровень доверия является вероятностью, того что оцениваемый параметр распределения принадлежит доверительному интервалу , вычисленному на основе выборки . Поскольку, считается, что в математической статистике отсутствуют априорные сведения о параметре распределения. Математически правильно говорить, что доверительный интервал , с вероятностью равной Уровню доверия, накроет истинное значение оцениваемого параметра распределения.

Уровень надежности в MS EXCEL

В MS EXCEL Уровень надежности упоминается в надстройке Пакет анализа . После вызова надстройки, в диалоговом окне необходимо выбрать инструмент Описательная статистика .

После нажатия кнопки ОК будет выведено другое диалоговое окно.

В этом окне задается Уровень надежности, т.е.значениевероятности в процентах. После нажатия кнопки ОК в выходном интервале выводится значение равное половине ширины доверительного интервала . Этот доверительный интервал используется для оценки среднего значения распределения, когда дисперсия не известна (подробнее см. статью про доверительный интервал ).

Необходимо учитывать, что данный доверительный интервал рассчитывается при условии, что выборка берется из нормального распределения . Но, на практике обычно принимается, что при достаточно большой выборке (n>30), доверительный интервал будет построен приблизительно правильно и для распределения, не являющегося нормальным (если при этом это распределение не будет иметь сильной асимметрии ).

Примечание : Понять, что в диалоговом окне речь идет именно об оценке среднего значения распределения , достаточно сложно. Хотя в английской версии диалогового окна это указано прямо: Confidence Level for Mean .

Если Уровень надежности задан 95%, то надстройка Пакет анализа использует следующую формулу (выводится не сама формула, а лишь ее результат):

или эквивалентную ей

где =СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) – является стандартной ошибкой среднего (формулы приведены в файле примера ).

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))

Решение задач описательной статистики средствами пакета анализа Microsoft Excel Текст научной статьи по специальности « Компьютерные и информационные науки»

CC BY

Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Трущелёв Сергей Андреевич

Представлено определение описательной статистики , изложены методика вычисления основных ее показателей, а также пошаговая процедура статистического анализа. Сообщение содержит обучающий компонент.

Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel

Текст научной работы на тему «Решение задач описательной статистики средствами пакета анализа Microsoft Excel»

МЕТОДОЛОГИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ

Уважаемые читатели, коллеги!

В связи с возрастающими требованиями к качеству публикаций результатов научно-исследовательских работ в «Российском психиатрическом журнале» открыта новая рубрика «Методология научно-исследовательской деятельности». Планируется публикация обучающих и информационно-разъяснительных материалов по разным разделам науковедения, организации научной работы, биоинформатике, биостатистике, биоэтике и т.д. Приглашаем ученых и исследователей поделиться опытом в этой области. Надеемся, что наша инициатива будет поддержана не только в научном сообществе, но и воспринята в среде практикующих специалистов.

УДК 311:004 Трущелёв Сергей Андреевич — кандидат медицинских наук,

доцент, ведущий научный сотрудник ФГБУ «Московский научно-исследовательский институт психиатрии Минздрава России»

Адрес: 107076, г. Москва, ул. Потешная, д. 3 Телефон: (495) 963-25-31 E-mail: sat-geo@mail.ru

Решение задач описательной статистики средствами пакета анализа Microsoft Excel

Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel

The paper presents a definition of descriptive statistics, and its main indicators. The necessity of their calculation is set out step by step in the procedure of statistical analysis. The message is a training component with. Key words: science of science, biostatistics, descriptive statistics, data analysis toolpak, Excel

ФГБУ «Московский научно-исследовательский институт психиатрии Минздрава России»

Moscow Research Institute of Psychiatry

Представлено определение описательной статистики, изложены методика вычисления основных ее показателей, а также пошаговая процедура статистического анализа. Сообщение содержит обучающий компонент.

Ключевые слова: науковедение, биостатистика, описательная статистика, пакет анализа, Excel

Каждое явление (предмет исследования) определяется многими факторами. В научном исследовании полностью учесть все факторы и обеспечить их стабильность удается редко. Следовательно, явление, определяемое этими факторами, не поддается точному предсказанию — оно приобретает вероятностные черты, т.е. ведет себя случайным образом. Этому подвержены многие явления, поэтому они определяются случайной величиной, которая принимает в результате опыта или наблюдения одно из множества значений. Случайные величины могут быть дискретными (прерывными) и непрерывными. Немаловажно их распределение — правило, которое устанавливает связь между значениями случайной величины и вероятностями (частотами) их появления.

Наглядное представление о распределении случайных величин дает разброс песчинок, образующих кучу при высыпании (рассеивании) из некоторого точечного источника. Его проекция является параметром положения и соответствует математическому ожиданию распределения, если куча симметрична. Разброс песчинок (параметр рассеяния) характеризуется радиусом кучи на высоте примерно 2/3. Такой параметр рассеяния соответствует так называемому стандартному (среднеквадратичному) отклонению случайных величин в распределении. Горизонтальные расстояния песчинок от проекции источника (математического ожидания) моделируют рассеяние случайной величины. Поверхность кучи (ее высоты) соответствует частоте случайных величин на разных расстояниях от центра. Вершина кучи, расположенная под источником, отвечает максимуму частоты. На периферии высота кучи уменьшается до нуля, что соответствует уменьшению частот больших отклонений от центра рассеяния. Статистическая обработка совокупности данных состоит в некоторых осредняющих вычислительных процедурах, погашающих сугубо индивидуальные особенности — отклонения от общей закономерности и подчеркивающих типичные (популяцион-ные) свойства явления в целом. Начальный раздел математической статистики — описательная статистика — занимается характеристикой (описанием) картины случайного рассеяния по совокупности данных. В соответствии с законом распределения данных решаются вопросы выбора и вычислений надлежащих показателей. Описательная статистика включает методы организации, суммирования и описания данных. Дескриптивные (от англ. descriptive — описательный) показатели позволяют быстро обобщать данные. К описательным методам относят частотные распределения, меры централь-

ной тенденции и меры относительного положения [4, с. 95].

К основным показателям описательной статистики относятся среднее значение (среднее арифметическое, медиана, мода), усредненное значение, разброс (диапазон разброса данных), дисперсия, стандартное среднеквадратное отклонение (СКО), квартили, доверительный интервал [2, с. 28].

Статистическая обработка результатов исследований и получение показателей описательной статистики в недалеком прошлом обычно занимали много времени, однако с внедрением средств компьютерной техники многое изменилось — вычислительные процессы стали происходить очень быстро. Для проведения статистических расчетов в электронной таблице Microsoft Excel имеется пакет анализа. Надстройка «Анализ данных» располагается во вкладке «Данные», в крайне правом блоке ленты (рис. 1).

Для демонстрации вычислений будем использовать гипотетический набор данных. Далее приведем пошаговую инструкцию по созданию описательной статистики признака (показателя систолического давления), измеренного до лечения и после него, в группе наблюдения (n=60).

Для проведения вычисления обратитесь к ленте: Данные ^ Анализ данных ^ Описательная статистика ^ ОК. Затем, перейдя в окно инструмента, выберите входной интервал, группирование (по столбцам), поставьте галочку, если в первой строке выделены метки; в параметрах вывода на поле электронной страницы выберите ячейку вывода результатов, установите галочку рядом с итоговой статистикой. Потом нажмите кнопку ОК. После этого вы получите результаты описательной статистики выбранных признаков (рис. 2 и 3).

[й1 A «ï- V m И^ЭгшИ Главная Ш I» 1 Описательная статистика — Microsoft Excel □ 0 й Вставка Разметка страницы Формулы Данные Рецензирование Вид Разработчик Надстройки MetaXL Л □ S3

П внец m 1олучение jних данныхт ч [^Подключения ^Свойства Обновить все т && Изменить связи Подключения A I AIЯ I Я + Я 1А1 Я| Сортировка Со pi ч Ш ^ Очистить ^ Повторить Фильтр ™ № Дополнительно ировка и фильтр S Ii ы» вш а в Текст по Удалить ,—, столбцам дубликаты » Работа сданными Ф Фор» орма Jbi ssprfa ф ^ ^Анализданных Поиск решения Стр^И^ра Анализ

А в с D Е F G У 1 J К 1 L _

1 Номер_исс Признак_1 Признак_2 у

3 2 178 143 Анализ данным lia

Инструменты анализа У _ 1 о, 1

4 3 320 188 Двухфакторный дисперсионный^нализ без повторений Корреляция Л* 3 J d Отмена |

6 5 159 161 Экспоненциальное сглаживание Двухвыборочный Р-тест для дисперсии Анализ Фурье Гистограмма Скользящее среднее 1 Генерация случайных чисел_| Справка

Рис. 1. Пошаговый выбор инструмента анализа данных

Рис. 2. Окно инструмента описательной статистики

Среднее (арифметическое; М; х ) — одна из наиболее распространенных мер центральной тенденции, представляющая собой сумму всех значений, деленную на их количество. Если значения интересующего нас признака у большинства объектов близки к их среднему и с равной вероятностью отклоняются от него в большую или меньшую сторону, лучшими характеристиками совокупности будут само среднее значение и стандартное отклонение. Напротив, когда значения признака распределены несимметрично относительно среднего, совокупность лучше описать с помощью медианы и процен-тилей [1, с. 27].

Стандартная ошибка (т) — показатель надежности расчетного параметра; стандартное отклонение оценок, которые будут получены при многократной случайной выборке данного размера из одной и той же совокупности. Стандартная ошибка — это убывающая функция объема выборки: чем меньше стандартная ошибка, тем более достоверной является оценка параметра. Весьма часто для описания непрерывных количественных данных используют стандартную ошибку, которая (в отличие от СКО) является не характеристикой, описывающей распределение наблюдений исследуемой выборки по области значений, а только мерой точности оценки популяционного среднего и, следовательно, не характеризует дисперсию (разброс) в анализируемой выборке. Однако часто именно стандартную ошибку среднего приводят в качестве параметра описательной статистики, пытаясь продемонстрировать тем самым малую вариабельность своих данных, так как всегда (по определению) т Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

60 Среднее 161,77 Среднее 134,03

61 Стандартная ошибка 12,46 Стандартная ошибка 6.59

62 Медиана 167 Медиана 121,5

63 Мода 72 Мода 141

64 Стандартное отклонение 96.54 Стандартное отклонение 51,03

65 Дисперсия выборки 9320.59 Дисперсия выборки 2604.34

66 Эксцесс 0.89 Эксцесс 2.75

67 Асимметричность 0.96 Асимметричность 1,43

68 Интервал 420 Интервал 254

69 Минимум 50 Минимум 55

70 Максимум 470 Максимум 309

71 Сумма 9706 Сумма 8042

72 Счет 60 Счет 60

73 74 Уровень надежности(95.0%) 24.94 Уровень надежности(95.0%) 13,18

Коэффициент вариации 60% Коэффициент вариации 38%

Рис. 3. Результаты описательной статистики двух признаков

Медиану и интерквартильный размах рекомендуется применять для описания распределения, не являющегося нормальным (а это большинство распределений медико-биологических параметров) [1, с. 34]. Интерквартильный размах указывают в виде процентилей. Рекомендуется указывать уровни 25 и 75%, которые соответствуют верхней границе 1-го и нижней границе 4-го квартилей. Пример описания: Me (25%; 75%) = 60 (23; 78).

Мода (Мо) — значение, которое встречается наиболее часто во множестве. Иногда в совокупности встречается более одной моды. Тогда говорят, что совокупность мультимодальна — свидетельство того, что набор данных не подчиняется нормальному распределению. Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Например, в группе пациентов наибольшая частота тяжести болезни будет равна моде. При экспертной оценке с помощью этого показателя определяют предпочтения участников исследования. Недостаток — показатель не учитывает поведение распределения в других точках.

Стандартное отклонение (синонимы: среднеквадратичное отклонение, квадратичное отклонение; стандартный разброс; СКО; в; о) — в теории вероятностей и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно ее математического ожидания. Измеряется в единицах случайной величины. Равно корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчете стандартной ошибки среднего арифметического, построении доверительных интервалов, статистической проверке гипотез, измерении линейной взаимосвязи между случайными величинами. Большое значение СО показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения во множестве сгруппированы вокруг среднего. Если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратичного отклонения), то полученные значения или метод их получения следует перепроверить.

Дисперсия (D; о2) — мера разброса случайной величины, т.е. ее отклонения от математического ожидания. Квадратный корень из дисперсии называется стандартным отклонением. Дисперсия измеряется в квадратах единицы измерения. Однако в самостоятельном виде (как, например, средняя арифметическая) дисперсия используется редко. Это скорее вспомогательный и промежуточный показатель, который применяют в других методах статистического анализа.

Эксцесс — скалярная характеристика островершинности графика плотности вероятности унимо-

дального распределения, которую используют в качестве некоторой меры отклонения рассматриваемого распределения от нормального. Если коэффициент эксцесса равен нулю или близок к нему, то плотность вероятности распределения имеет нормальный эксцесс. Если коэффициент эксцесса сильно больше нуля, то плотность вероятности имеет положительный эксцесс. Это, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. Когда коэффициент эксцесса сильно больше нуля, говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона. Для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.

Асимметричность (коэффициент асимметрии или скоса) — величина, характеризующая асимметрию распределения данной случайной величины. Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в альтернативном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.

Интервал — размах показателей, т.е. разность между максимумом и минимумом значений вариант.

Максимум — наибольшее значение вариант.

Минимум — наименьшее значение вариант.

Сумма — сумма значений вариант.

Счет — количество вариант.

Уровень надежности — свойство объекта сохранять в установленных пределах значения всех параметров. Показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.

Коэффициент вариации случайной величины -мера относительного разброса случайной величины. Показывает, какую долю среднего значения этой величины составляет ее средний разброс. Исчисляется в процентах. Вычисляется только для количественных данных. В отличие от стандартного отклонения, он измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. В Excel нет готовой функции для расчета коэффициента вариации. Расчет можно провести простым делением стандартного отклонения на среднее значение. Эти значения имеются в таблице описательной статистики. Для вычисления этого важного показателя в ячейке ниже надписи Уровень надежности пишем Коэффициент вариации, затем в ячейке справа делаем запись: =G64/G60. То же необходимо по-

вторить для вычисления коэффициента вариации для другого измерения.

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на панели инструментов в закладке «Главная». Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что совокупность данных является однородной, если коэффициент вариации менее 33%, неоднородной — если более 33%. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений.

Анализ показателей описательной статистики

При сравнении значений среднего, медианы, моды в каждом измерении следует отметить, что эти показатели сильно отличаются друг от друга.

Коэффициенты эксцесса и асимметрии значимо отличаются от установленных границ, коэффициенты вариации больше критического (предельного) значения. Следовательно, распределение данных в обеих группах измерений отлично от нормального. В последующем необходимо применять непараметрические методы статистического анализа. Для быстрой сравнительной оценки можно использовать показатели доверительных интервалов.

Для представления результатов сравнения обычно используют формат в виде М (95% ДИ) — значение среднего и указание 95% доверительного интервала. В тексте публикации запись может выглядеть следующим образом: Средний уровень систолического давления в группе пациентов до лечения составил 161,77 мм рт. ст. (95% ДИ от 136,83 до 186,71 мм рт. ст.), после лечения -134,03 мм рт. ст. (95% ДИ от 120,85 до 147,21 мм рт. ст.). Указанные доверительные интервалы имеют зону совмещения, следовательно, существенного различия в изменении признака нет. Исходя из этого с большой долей вероятности можно утверждать, что для данной группы пациентов лекарственный препарат, примененный для снижения уровня систолического артериального давления, был не эффективен.

1. Гланц С. Медико-биологическая статистика / Пер. с англ. -М., Практика, 1998. — 459 с.

2. Ланг Т.А., Сесик М. Как описывать статистику в медицине. Аннотированное руководство для авторов, редакторов и рецензентов / Пер. с англ. под ред. В.П. Леонова. -М.: Практическая медицина, 2011. — 480 с.

3. Леонов В.П. Ошибки статистического анализа биомедицинских данных // Междунар. журн. мед. практики. — 2007. -№ 2. — С. 19-35.

4. Трущелев С.А. Медицинская диссертация: руководство: 3-е изд. / Под ред. проф. И.Н. Денисова. — М.: ГЭОТАР-Медиа, 2009. — 416 с.

Источник

Ниже приводится пример метрологически корректного описания теста «Отжимание на гимнастических брусьях».

1.Цель применения теста: определение силовой выносливости рук и пле чевого пояса.

2.Возраст спортсменов: 16—18 лет.

3.Пол: упражнение выполняют только юноши.

4.Оборудование и материалы: параллельные брусья; их высота относи тельно пола такова, чтобы испытуемый любого роста, выполняя упражнения, не касался пола ногами.

5.Порядок выполнения теста: исходное положение — упор на прямых ру ках. Сгибая руки в локтях, опуститься вниз до полного сгибания. Затем выпрямить руки, приняв исходное положение. При выполнении упражнения тело держать в вертикальном положении, раскачивание не допускается. Выполнить максимальное количество повторений («до отказа»).

6.Надежность теста: rtt*=0,90, если повторное измерение проводилось на следующий день. Если же обе попытки выполнялись подряд, то надежность низка: rtt=0,56.

7.Согласованность оценок результатов в тесте: 0,99.

8.Информативность теста: по результа

там логической экспертизы признана высокой. 9. Оценка результатов: баллы начисляют ся в зависимости от количества повторений

теста по следующей шкале (см. табл.). 10. Дополнительные указания:

а) подсчет повторений теста заканчива ется, когда испытуемый останавливается;

б) специалист, . проводящий измерения, должен следить за действиями испытуемого и вносить коррективы, если последний иска жает порядок выполнения теста;

в) можно поддерживать испытуемого ру кой, если он начинает раскачиваться.

3.4. НАДЕЖНОСТЬ ТЕСТОВ

3.4.1. Основные понятия теории надежности

Надежностью теста называется степень совпадения результатов при повторном тестировании одних и тех же людей в одина-

ковых условиях. Как уже отмечалось, полное совпадение результатов при повторных измерениях практически невозможно, и поэтому основное уравнение измерений выглядит так:

где xt — зарегистрированный в процессе измерений результат теста; xист — так называемый истинный результат. Условно он соответствует среднему значению измеряемой величины при беско-

* rtt—коэффициент надежности, о котором более подробно будет рассказано в разделе 3.4.

нечно большом числе измерений одного показателя в одних и тех же условиях. Видно, что xист — абстрактная величина и измерить ее в действительности невозможно. В идеальных условиях значе ние xист должно соответствовать реально существующей величине искомого показателя. Но такого соответствия никогда не бывает и вот почему. Рассмотрим следующий пример. Из определения теста следует, что его надежность — это, по сути дела, надеж ность оценки состояния спортсмена, его способностей. Чем ближе значения xt и xист , тем надежнее оценка. Из формулы (1) видно,

что степень близости xt и xист зависит от величин е1 ,е2 и е3. Что они представляют собой?

Величина e1—это систематические и случайные ошибки измерений, причины появления которых рассмотрены в разделе 2.3.2. Величина е2 отражает различия в процедуре тестирования при повторных измерениях. И наконец, величина е3 характеризует внутреннюю нестабильность функциональных систем организма.

Подтвердим сказанное следующим примером. При измерении времени простой реакции спортсмена на световой раздражитель были получены следующие результаты: первая попытка — 0,225 с; вторая — 0,296 с; третья — 0,203 с. Точность работы измерительных устройств (±2%) позволяет сравнительно легко вычислить значение e1 и учесть его при анализе результатов.

Предположим, что во второй попытке яркость светового раздражителя была вдвое меньшей, чем в первой и третьей. Если провести исследование о зависимости яркости светового сигнала и времени реакции, то можно определить, как изменение процедуры тестирования изменяет результат теста. Полученная в результате такого исследования величина и будет характеризовать составляющую е2.

Отметим сразу, что процедура тестирования во всех случаях должна быть стандартной, но в реальной практике это не всегда достижимо. К сожалению, меняются внешние условия тестирования, его могут проводить разные специалисты и т. д., и все это будет сказываться на результате.

Предположим теперь, что при измерении времени реакции использовали высокоточную аппаратуру, погрешности работы которой не превышают сотых долей процента. Тестирование проводилось в идеально стандартных условиях. В этом случае результаты повторных измерений также будут различаться: мера их вариативности численно будет равна составляющей е3. Причина же различий в значениях времени повторного реагирования будет теперь заключаться в нестабильности работы зрительного и нервномышечного аппаратов спортсмена. Эта нестабильность и будет определять надежность измерений.

С учетом всего сказанного можно сформулировать следующее положение: в практике необходимо использовать тесты, результаты xt которых есть сумма xист + e3 (составляющие е1 и е2 предполагаются пренебрежимо малыми). Проиллюстрируем его следующим примером. На чемпионате СССР в индивидуальной

гонке преследования на 4 км измерение результатов проводится с высокой точностью (составляющая е1 пренебрежимо мала и одинакова во всех заездах). Условия заездов одинаковы (поэтому составляющая е2 одинакова во всех измерениях).

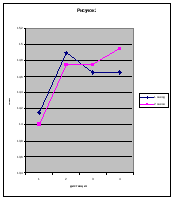
Если взять два равных по времени заезда одного и того же спортсмена, то различия в скорости на разных участках дистанции будут определяться исключительно состоянием и действиями самого спортсмена. Такие данные приведены на рис. 3. Видны высокая стабильность скорости чемпиона СССР Екимова и относи-

тельная	вариативность этого	же
показателя у второго призера —
Шкундова.
С течением времени (например,
на разных этапах годичного цикла)
вариативность	показателей	мо-
жет меняться. На рис. 4 показано,
что в соревновательном	периоде
(по сравнению с подготовительным)
время	достижения	максимальной
скорости стало более стабильным.
Если его использовать как тест,
то он в этот момент характеризуется
большей надежностью.
В спортивной практике мы од-
новременно сталкиваемся как ми-
нимум	с	тремя	разновидностями
вариативности.	1)	внутриклассовая
Вариант	А:
(внутрииндивидуальная) — вариа-
тивность	индивидуальных	резуль-
татов в серии повторных измере-
ний; 2) межклассовая (межиндиви-
дуальная) — вариативность ре-
зультатов разных спортсменов.
Вариант	Б:	1)	внутриклассовая
(как в варианте А); 2) межклассовая
— вариативность серий инди-
видуальных данных, зарегистриро-
ванных на разных этапах трениро-
вочного цикла.		1)			Рис. 3. Вариативность прохожде-
Вариант	В:		внутриклассо- ния дистанции в	индивидуальной
вая— различия между спортсменами вгонке преследования на чемпиона-
измерениях,	проведенных	в	те СССР 1986 года: а — два заезда
одинчемпиона СССР Екимова; б — два
день;	2)		межклассовая—различиязаезда второго	призера —
между сериями измерений спортсмена, Шкундова
проведенных	на	разных	этапах
тренировочного цикла *.

* Отметим, что здесь одними терминами (например, внутриклассовая) обозначены разные признаки. Для устранения путаницы необходимо в каждом случае специально оговаривать, что и каким термином обозначается.

Рис, 4. Динамика стартового разгона в пяти забегах на 100 м спортсмена К.:

а —различия по времени достижения Vmax; б—различия по уровню Vmax

От соотношения внутриклассовой и межклассовой вариативности зависит надежность тестов. Пример, подтверждающий это, представлен в следующем разделе.

Вернемся вновь к основному уравнению измерения, представив его в следующем виде:

(В этом уравнении опущены методические погрешности измерений.)

Если показатели вариативности в повторных измерениях случайны (их сумма равна нулю и в разных попытках они не зависят друг от друга), то тогда из математической статистики следует:

σt 2=σист2+ σе2 ,	(3)
2	2

где σt2 — дисперсия результатов измерений; σист2 — межклассовая

вариация (она рассматривается как свободная от ошибок); σе2 — внутриклассовая вариативность.

Коэффициент надежности (rt t )—это отношение ис-

тинной дисперсии к дисперсии, зарегистрированной в процессе измерений:

(4)

На практике можно использовать индекс надежности. Он

и рассматривается как тео-

рассчитывается по формуле

ретический кеэффициент корреляции измеренных результатов теста- с истинными.

Еще один критерий — стандартная ошибка надежно-

сти. Она рассчитывается по ризует среднее квадратическое отклонение измеренных результатов теста от линии регрессии. В свою очередь эта линия отражает меру теоретической зависимости между измеренными и истинными результатами. На рис. 5 представлен пример использования стандартной ошибки надежности, по которой можно узнать, каково среднее стандартное

отклонение	результатов	от-	Рис. 5. Определение стандартной ошиб-
дельных спортсменов	от	их
собственных	средних	величин.	ки надежности

Например, если стандартная ошибка надежности равна ±3 см, это значит, что в 68% случаев индивидуальные результаты повторных измерений отклоняются на ±3 см от того среднего результата, который каждый из них показал.

3.4.2.Определение надежности в практической работе

Взначительном большинстве случаев комплексный контроль проводится с помощью тестов, надежность которых была заранее определена специалистами в области, спортивной метрологии. Однако имеющиеся в справочниках значения надежности тестов не всегда могут быть обобщены для всех случаев тренерской работы, так как были получены в определенных условиях у конкретной группы людей. Так, например, надежность такого сравнительно простого теста, как бег на 30 м, различна у квалифицированных спринтеров, баскетболистов, гимнастов, школьников-физкультур- ников и т. д.

Кроме того, у тренера иногда возникает идея проверить подготовленность спортсменов с помощью созданного им самим теста или теста, в который внесены какие-либо изменения. Такие приме-

Самый простой способ проверки — визуальное сравнение значений первой и второй попыток в тесте для каждого спортсмена. В среднем в группе обычно тренируются не более 20 спортсменов, и после тестирования такое сравнение результатов не занимает много времени. Если результаты повторных измерений совпадают, значит, использованный тест характеризуется высокой надежностью.

Однако такие ситуации встречаются сравнительно редко; кроме того, при визуальном сравнении получаем качественную оценку: тест «надежен» или «ненадежен». Обычно в контроле используется несколько тестов, и достоверность результатов каждого из них зависит от уровня надежности. Его количественную меру и нужно определять в виде коэффициента надежности.

Для этого можно использовать два метода.

Первый — д и с п е р с и о н н ы й анализ . Он позволяет не только рассчитать значение коэффициента надежности, но и установить влияние различных факторов на изменчивость результатов в тесте.

Рассмотрим следующий пример. У группы гимнастов в конце каждого тренировочного микроцикла измеряют достижения в комплексе тестов, характеризующих их координационные и силовые способности. Полученные результаты

будут варьировать:
1)	у каждого спортсмена	(внутрииндивидуальная изменчивость);
2)	между спортсменами	(межиндивидуальная изменчивость);
3)	в разные дни тестирования.

Дисперсионный анализ позволяет выявить и оценить каждый из этих факторов изменчивости. Техника такой работы ясна из следующего примера. Группе юных баскетболистов тренер предложил выполнить три раза по десять штрафных бросков. Цель этого теста — определение точности заданий. Необходимо узнать, надежен он или нет. Сделаем это по данным табл. 3.

Видно, что надежность этого теста при трех попытках невысока, Если число попыток увеличить до 6, то надежность теста увеличится так:

Второй метод определения надежности тестов значительно проще, но может использоваться только в случае двух попыток и отсутствии тренда (т. е. постоянного, от попытки к попытке, повышения или понижения результатов теста). Здесь можно рассчитывать обычный коэффициент корреляции (при этом оценивается надежность не двух, а одной попытки).

Для примера, представленного в табл. 4, коэффициент корреляции между первой и второй попытками равен 0,43; между второй и третьей — 0,48. Оценка надежности в зависимости от величины

ее коэффициента представлена в табл. 5.

Тесты, надежность которых меньше указанных в таблице значений, использовать не рекомендуется.

3.4.3. Методы повышения надежности тестов

Контроль с помощью малонадежных тестов приводит к ошибкам в оценке состояния спортсменов. Если эти ошибочные данные используются как основа для планирования нагрузок, то и оно будет ошибочным. Поэтому необходимо стремиться повысить надежность информативных тестов для оценки каких-либо сторон подготовленности спортсменов. Для этого необходимо устранить причины, которые вызывают увеличение вариативности измерений. В некоторых случаях, помимо выполнения требований, изложенных в разделе 3.1, полезно увеличить количество попыток в тесте и использовать больше экспертов (судей, оценщиков).

Надежность оценки контролируемых показателей повышается также и при применении большего количества эквивалентных тестов.

3.4.4. Стабильность тестов

Стабильность теста — это такая разновидность надежности, которая проявляется в степени совпадения результатов тестирования, когда первое и последующие измерения разделены определенным временным интервалом. При этом повторное тестиро-

вание обычно называют ретестом.

Высокая стабильность теста свидетельствует о сохранении приобретенного в ходе тренировок технико-тактического мастерст-

ва, двигательных и психических качеств. Пример такой динамики показателей представлен на рис. 6. Из него видно, что МПК четырех сильнейших футболистов Голландии в соревновательном периоде (а именно оно в значительной степени определяет работоспособность спортсменов) поддерживается в течение двух лет на стабильном уровне.

Рис. 6. Динамика максимального потребления кислорода у сильнейших футболистов Голландии (n=4)

Стабильность теста прежде всего зависит от содержания тренировочного процесса: при исключении (или уменьшении), например, силовых упражнений результаты ретеста, как правило, уменьшаются. Кроме того, на стабильность влияют также: сложность теста и длительность временного интервала между тестом и ретестом.

Для количественной оценки стабильности используется дисперсионный анализ по той же схеме, что и в случае расчета обычной надежности.

3.4.5. Согласованность тестов

Согласованность тестов характеризуется независимостью результатов тестирования от личных качеств лица, проводящего или оценивающего тест. Если результаты спортсменов в тесте, который проводят разные специалисты (эксперты, судьи, оценщики), совпадают, то это свидетельствует о высокой степени согласованности теста. Это свойство теста зависит от совпадения методик тестирования у разных специалистов.

Когда создается новый тест, нужно обязательно проверить его на согласованность. Делается это так: разрабатывается унифицированная методика проведения теста, а потом два или более специалиста по очереди в стандартных условиях тестируют одних и тех же спортсменов.

В случае инструментальной регистрации (например, времени бега на 30 м с помощью фотоэлектронных устройств) не должно быть несовпадения результатов у разных специалистов. Но на самом деле оно бывает, и вовсе не потому, что один специалист хорошо владеет навыками измерений, а другой — плохо (такая ситуация вообще недопустима). Некоторые экспериментаторы более требовательны, умеют лучше мотивировать спортсменов, и это сказывается на результатах. Вот этот вклад «личных» качеств специалиста в результат теста и оценивается по коэффициенту согласованности. Он также рассчитывается с помощью дисперсионного анализа.

В случае качественной оценки результатов теста (особенно если тест — сложнокоординационное упражнение) отклонения их значений могут быть большими. Причина — невозможность строго стандартизировать процедуру оценки, разные возможности восприятия качественных особенностей движения у специалистов.

Специальные методы повышения согласованности оценок в таких случаях изложены в главе 5.

3.4.6. Эквивалентность тестов

Одно и то же двигательное качество (способность, сторону подготовленности) можно измерить с помощью нескольких тестов. Например, максимальную скорость — по результатам пробегания с ходу отрезков в 10, 20 или 30 м. Силовую выносливость — по числу подтягиваний на перекладине, отжиманий в упоре, количеству подъемов штанги в положении лежа на спине и т. д. Такие тесты называют э к в и в а л е н т н ы м и .

Эквивалентность тестов определяется следующим образом: спортсмены выполняют одну разновидность теста и затем, после небольшого отдыха, вторую и т. д.

Если результаты оценок совпадают (например, лучшие в подтягивании оказываются лучшими и в отжимании), то это свидетельствует об эквивалентности тестов. Коэффициент эквивалентности определяется с помощью корреляционного или дисперсионного анализа.

Применение эквивалентных тестов повышает надежность оценки контролируемых свойств моторики спортсменов. Поэтому если нужно провести углубленное обследование, то лучше применить несколько эквивалентных тестов. Такой комплекс называется гомогенным. Во всех остальных случаях лучше использовать гетерогенные комплексы: они состоят из неэквивалентных тестов.

Не существует универсальных гомогенных или гетерогенных комплексов. Так, например, для слабо подготовленных людей такой комплекс, как бег на 100 и 800 м, прыжок в длину с места, подтягивание на перекладине, будет гомогенным. Для спортсменов высокой квалификации он может оказаться гетерогенным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Подборка по базе: ОП.09. Метрология.doc, Чудинов КВ РБ-11з КР метрология.docx, КР Метрология.doc, Задачи метрология.docx, ДЗ 1 Метрология.docx, Реферат Метрология.docx, реферат метрология.docx, 4 Зертханалық жұмыс Метрология (1).docx, Лабораторная работа Метрология.docx, Папа, мама, я — спортивная семья.docx

нечно большом числе измерений одного показателя в одних и тех же условиях. Видно, что ист — абстрактная величина и измерить ее в действительности невозможно. В идеальных условиях значение ист должно соответствовать реально существующей величине искомого показателя. Но такого соответствия никогда не бывает и вот почему. Рассмотрим следующий пример. Из определения теста следует, что его надежность — это, по сути дела, надежность оценки состояния спортсмена, его способностей. Чем ближе значения и ист , тем надежнее оценка. Из формулы (1) видно, что степень близости и ист зависит от величине ,е
2
и е. Что они представляют собой Величина это систематические и случайные ошибки измерений, причины появления которых рассмотрены в разделе
2.3.2. Величина е
2
отражает различия в процедуре тестирования при повторных измерениях. И наконец, величина е характеризует внутреннюю нестабильность функциональных систем орга- низма.
Подтвердим сказанное следующим примером. При измерении времени простой реакции спортсмена на световой раздражитель были получены следующие результаты первая попытка — 0,225 с вторая — 0,296 с третья — 0,203 с. Точность работы измерительных устройств (±2%) позволяет сравнительно легко вычислить значение и учесть его при анализе результатов.
Предположим, что во второй попытке яркость светового раздражителя была вдвое меньшей, чем впервой и третьей. Если провести исследование о зависимости яркости светового сигнала и времени реакции, то можно определить, как изменение процедуры тестирования изменяет результат теста. Полученная в результате такого исследования величина и будет характеризовать составляющую е
2
.
Отметим сразу, что процедура тестирования во всех случаях должна быть стандартной, нов реальной практике это не всегда достижимо. К сожалению, меняются внешние условия тестирования, его могут проводить разные специалисты и т. д, и все это будет сказываться на результате.
Предположим теперь, что при измерении времени реакции использовали высокоточную аппаратуру, погрешности работы которой не превышают сотых долей процента. Тестирование проводилось в идеально стандартных условиях. В этом случае результаты повторных измерений также будут различаться мера их вариативности численно будет равна составляющей е. Причина же различий в значениях времени повторного реагирования будет теперь заключаться в нестабильности работы зрительного и нервно- мышечного аппаратов спортсмена. Эта нестабильность и будет определять надежность измерений.
С учетом всего сказанного можно сформулировать следующее положение в практике необходимо использовать тесты, результаты которых есть сумма ист + e
3
(составляющие е
1
и е предполагаются пренебрежимо малыми. Проиллюстрируем его следующим примером. На чемпионате СССР в индивидуальной

гонке преследования на 4 км измерение результатов проводится с высокой точностью (составляющая е
1
пренебрежимо мала и одинакова во всех заездах. Условия заездов одинаковы (поэтому составляющая е
2
одинакова во всех измерениях).
Если взять два равных повремени заезда одного итого же спортсмена, то различия вскорости на разных участках дистанции будут определяться исключительно состоянием и действиями самого спортсмена. Такие данные приведены на рис. 3. Видны высокая стабильность скорости чемпиона СССР Екимова и относительная вариативность этого же показателя у второго призера —
Шкундова.
С течением времени (например, на разных этапах годичного цикла) вариативность показателей может меняться. На рис. 4 показано, что в соревновательном периоде по сравнению с подготовительным) время достижения максимальной скорости стало более стабильным. Если его использовать как тест, то он в этот момент характеризуется большей надежностью.
В спортивной практике мы одновременно сталкиваемся как минимум стремя разновидностями вариативности.
Вариант А 1) внутриклассовая
(внутрииндивидуальная) — вариативность индивидуальных результатов в серии повторных измерений) межклассовая (межиндиви- дуальная) — вариативность результатов разных спортсменов.
Вариант Б 1) внутриклассовая как в варианте А 2) межклассовая
— вариативность серий индивидуальных данных, зарегистрированных на разных этапах тренировочного цикла.
Вариант В 1) внутриклассо- вая— различия между спортсменами в измерениях, проведенных в один день 2) межклассовая—различия между сериями измерений спортсмена, проведенных на разных этапах тренировочного цикла *.
* Отметим, что здесь одними терминами (например, внутриклассовая) обозначены разные признаки. Для устранения путаницы необходимо в каждом случае специально оговаривать, что и каким термином обозначается.
23
Рис. 3. Вариативность прохождения дистанции в индивидуальной гонке преследования на чемпионате СССР 1986 года а — два заезда чемпиона СССР Екимова; б — два заезда второго призера —
Шкундова

Рис, 4. Динамика стартового разгона в пяти забегах нам спортсмена Ка различия повремени достижения V
max
; б—различия по уровню От соотношения внутриклассовой и межклассовой вариативности зависит надежность тестов. Пример, подтверждающий это, представлен в следующем разделе.
Вернемся вновь к основному уравнению измерения, представив его в следующем виде:
x
t
=x
ист
+e В этом уравнении опущены методические погрешности измере- ний.)
Если показатели вариативности в повторных измерениях случайны (их сумма равна нулю ив разных попытках они не зависят друг от друга, то тогда из математической статистики следует:
σ
t
2
=σ
ист
2
+ е,
(3)
2 где
σ
t
2
— дисперсия результатов измерений ист — межклассовая вариация (она рассматривается как свободная от ошибок е внутриклассовая вариативность.
Коэффициент надежности (r
t это отношение истинной дисперсии к дисперсии, зарегистрированной в процессе измерений На практике можно использовать индекс надежности. Он рассчитывается по формуле ретический кеэффициент корреляции измеренных результатов теста- с истинными.
Еще один критерий — стандартная ошибка надежно- ризует среднее квадратическое отклонение измеренных результатов теста от линии регрессии. В свою очередь эта линия отражает меру теоретической зависимости между измеренными и истинными результатами. На рис. 5 представлен пример использования стандартной ошибки надежности, по которой можно узнать, каково среднее стандартное отклонение результатов отдельных спортсменов от их собственных средних величин. Например, если стандартная ошибка надежности равна ±3 см, это значит, что в 68% случаев индивидуальные результаты повторных измерений отклоняются на ±3 см оттого среднего результата, который каждый из них показал. Определение надежности в практической работе В значительном большинстве случаев комплексный контроль проводится с помощью тестов, надежность которых была заранее определена специалистами в области, спортивной метрологии. Однако имеющиеся в справочниках значения надежности тестов не всегда могут быть обобщены для всех случаев тренерской работы, так как были получены в определенных условиях у конкретной группы людей. Так, например, надежность такого сравнительно простого теста, как бег нам, различна у квалифицированных спринтеров, баскетболистов, гимнастов, школьников-физкультур- ников и т. д.
Кроме того, у тренера иногда возникает идея проверить подготовленность спортсменов с помощью созданного им самим теста или теста, в который внесены какие-либо изменения. Такие приме и рассматривается как тео- сти. Она рассчитывается по формуле и характе-
Рис. 5. Определение стандартной ошибки надежности

ры довольно часты в спортивных единоборствах и играх, где система комплексного контроля еще окончательно не сложилась. В этом случае также необходима проверка надежности тестов.
Самый простой способ проверки — визуальное сравнение значений первой и второй попыток в тесте для каждого спортсмена. В среднем в группе обычно тренируются не более 20 спортсменов, и после тестирования такое сравнение результатов не занимает много времени. Если результаты повторных измерений совпадают, значит, использованный тест характеризуется высокой надеж- ностью.
Однако такие ситуации встречаются сравнительно редко кроме того, при визуальном сравнении получаем качественную оценку тест надежен или ненадежен. Обычно в контроле используется несколько тестов, и достоверность результатов каждого из них зависит от уровня надежности. Его количественную меру и нужно определять в виде коэффициента надежности.
Для этого можно использовать два метода.
Первый — дисперсионный анализ. Он позволяет не только рассчитать значение коэффициента надежности, но и установить влияние различных факторов на изменчивость результатов в тесте.
Рассмотрим следующий пример. У группы гимнастов в конце каждого тренировочного микроцикла измеряют достижения в комплексе тестов, характеризующих их координационные и силовые способности. Полученные результаты будут варьировать) у каждого спортсмена (внутрииндивидуальная изменчивость
2) между спортсменами (межиндивидуальная изменчивость
3) в разные дни тестирования. Дисперсионный анализ позволяет выявить и оценить каждый из этих факторов изменчивости. Техника такой работы ясна из следующего примера. Группе юных баскетболистов тренер предложил выполнить три раза по десять штрафных бросков. Цель этого теста — определение точности заданий. Необходимо узнать, надежен он или нет. Сделаем это поданным табл. 3.
26

Второй метод определения надежности тестов значительно прощено может использоваться только в случае двух попыток и отсутствии тренда (те. постоянного, от попытки к попытке, повышения или понижения результатов теста. Здесь можно рассчитывать обычный коэффициент корреляции при этом оценивается надежность не двух, а одной попытки).
Для примера, представленного в табл. 4, коэффициент корреляции между первой и второй попытками равен 0,43; между второй и третьей — 0,48. Оценка надежности в зависимости от величины ее коэффициента представлена в табл. Тесты, надежность которых меньше указанных в таблице значений, использовать не рекомендуется. Методы повышения надежности тестов
Контроль с помощью малонадежных тестов приводит к ошибкам в оценке состояния спортсменов. Если эти ошибочные данные используются как основа для планирования нагрузок, то и оно будет ошибочным. Поэтому необходимо стремиться повысить надежность информативных тестов для оценки каких-либо сторон подготовленности спортсменов. Для этого необходимо устранить причины, которые вызывают увеличение вариативности измерений. В некоторых случаях, помимо выполнения требований, изложенных в разделе 3.1, полезно увеличить количество попыток в тесте и использовать больше экспертов (судей, оценщиков).
Надежность оценки контролируемых показателей повышается также и при применении большего количества эквивалентных тестов. Стабильность тестов
Стабильность теста — это такая разновидность надежности, которая проявляется в степени совпадения результатов тестирования, когда первое и последующие измерения разделены определенным временным интервалом. При этом повторное тестирование обычно называют ретестом.
Высокая стабильность теста свидетельствует о сохранении приобретенного входе тренировок технико-тактического мастерст-
28
Видно, что надежность этого теста при трех попытках невысока, Если число попыток увеличить до 6, то надежность теста увеличится так

ва, двигательных и психических качеств. Пример такой динамики показателей представлен на рис. 6. Из него видно, что МПК четырех сильнейших футболистов Голландии в соревновательном периоде (а именно оно в значительной степени определяет работоспособность спортсменов) поддерживается в течение двух лет на стабильном уровне.
Рис. 6. Динамика максимального потребления кислорода у сильнейших футболистов Голландии (Стабильность теста прежде всего зависит от содержания тренировочного процесса при исключении (или уменьшении, например, силовых упражнений результаты ретеста, как правило, уменьшаются. Кроме того, на стабильность влияют также сложность теста и длительность временного интервала между тестом и ре- тестом.
Для количественной оценки стабильности используется дисперсионный анализ по той же схеме, что ив случае расчета обычной надежности. Согласованность тестов
Согласованность тестов характеризуется независимостью результатов тестирования отличных качеств лица, проводящего или оценивающего тест. Если результаты спортсменов в тесте, который проводят разные специалисты (эксперты, судьи, оценщики, совпадают, то это свидетельствует о высокой степени согласованности теста. Это свойство теста зависит от совпадения методик тестирования у разных специалистов.
Когда создается новый тест, нужно обязательно проверить его на согласованность. Делается это так разрабатывается унифицированная методика проведения теста, а потом два или более специалиста по очереди в стандартных условиях тестируют одних и тех же спортсменов

В случае инструментальной регистрации (например, времени бега нам с помощью фотоэлектронных устройств) не должно быть несовпадения результатов у разных специалистов. Нона самом деле оно бывает, и вовсе не потому, что один специалист хорошо владеет навыками измерений, а другой — плохо (такая ситуация вообще недопустима. Некоторые экспериментаторы более требовательны, умеют лучше мотивировать спортсменов, и это сказывается на результатах. Вот этот вклад личных качеств специалиста в результат теста и оценивается по коэффициенту согласованности. Он также рассчитывается с помощью дисперсионного анализа.
В случае качественной оценки результатов теста (особенно если тест — сложнокоординационное упражнение) отклонения их значений могут быть большими. Причина — невозможность строго стандартизировать процедуру оценки, разные возможности восприятия качественных особенностей движения у специалистов.
Специальные методы повышения согласованности оценок в таких случаях изложены в главе 5.
3.4.6. Эквивалентность тестов
Одно и тоже двигательное качество (способность, сторону подготовленности) можно измерить с помощью нескольких тестов. Например, максимальную скорость — по результатам пробегания сходу отрезков вили м. Силовую выносливость — по числу подтягиваний на перекладине, отжиманий в упоре, количеству подъемов штанги в положении лежа на спине и т. д. Такие тесты называют эквивалентными Эквивалентность тестов определяется следующим образом спортсмены выполняют одну разновидность теста и затем, после небольшого отдыха, вторую и т. д.
Если результаты оценок совпадают (например, лучшие в подтягивании оказываются лучшими ив отжимании, то это свидетельствует об эквивалентности тестов. Коэффициент эквивалентности определяется с помощью корреляционного или дисперсионного анализа.
Применение эквивалентных тестов повышает надежность оценки контролируемых свойств моторики спортсменов. Поэтому если нужно провести углубленное обследование, то лучше применить несколько эквивалентных тестов. Такой комплекс называется гомогенным. Во всех остальных случаях лучше использовать гетерогенные комплексы они состоят из неэквивалентных тестов.
Не существует универсальных гомогенных или гетерогенных комплексов. Так, например, для слабо подготовленных людей такой комплекс, как бег наим, прыжок в длину с места, подтягивание на перекладине, будет гомогенным. Для спортсменов высокой квалификации он может оказаться гетерогенным

3.5. ИНФОРМАТИВНОСТЬ ТЕСТОВ
Информативным * называется тест, по результатам которого можно судить о свойстве (качестве, способности и т. п, измеряемом входе контроля. Если говорить об оценке подготовленности спортсменов, то наиболее информативным показателем является результат в соревновательном упражнении. Однако он зависит от большого количества факторов, и один и тот же результат в соревновательном упражнении могут показывать люди, заметно отличающиеся друг от друга по структуре подготовленности. Например, спортсмен с отличной техникой плавания и относительно невысокой физической работоспособностью и спортсмен со средней техникой, нос высокой работоспособностью будут соревноваться одинаково успешно (при прочих равных условиях).
Для выявления ведущих факторов, от которых зависит результат в соревновательном упражнении, и используются информативные тесты. Но как узнать меру информативности каждого из них Например, какие из перечисленных тестов информативны при оценке подготовленности теннисистов время простой реакции, время реакции выбора, прыжок вверх с места, бег нам Для ответа на этот вопрос необходимо знать методы определения информативности. Их два логический (содержательный) и эмпирический. Логический метод определения информативности тестов Суть этого метода определения информативности заключается в логическом (качественном) сопоставлении биомеханических, физиологических, психологических и других характеристик критерия и тестов.
Предположим, что мы хотим подобрать тесты для оценки подготовленности высококвалифицированных бегунов нам. Расчеты показывают, что в этом упражнении при результате 45,0 с примерно 72% энергии поставляется за счет анаэробных механизмов энергопродукции и за счет аэробных. Следовательно, наиболее информативными будут тесты, позволяющие выявить уровень и структуру анаэробных возможностей бегуна бег на отрезках 200—
ЗОО мс максимальной скоростью, прыжки с ноги на ногу в максимальном темпе на дистанции 100—200 м, повторный бег на отрезках дом сочень короткими интервалами отдыха. Как показывают клинико-биохимические исследования, по результатам этих заданий можно судить о мощности и емкости анаэробных источников энергии и, следовательно, их можно использовать в качестве информативных тестов,
Приведенный выше простой пример имеет ограниченное значение, так как в циклических видах спорта логическая информа-
* В литературе, особенно в вышедшей в свет дог, вместо термина информативность применяется адекватный ему термин валидность Анаэробные процессы — это образование энергии при мышечной работе за счет распада энергосодержащих веществ (аденозинтрифосфата и креатин- фосфата) без доступа кислорода. Аэробными называют энергетические процессы, протекающие с помощью кислорода.

Источник

Степень совпадения результатов детей при повторном тестировании

Ответ на тест по дисциплине «Спортивная метрология»:

Степень совпадения результатов при повторном тестировании одних и тех же людей в одинаковых условиях — это ____________________ теста.
• надежность

Ответы на другие тесты по дисциплине «Спортивная метрология»:

► Основные операции, проводимые с помощью шкалы порядка, — это установление …

► Изменения в организме, которые происходят в результате суммирования следов многих тренировочных занятий, называются ____________________ тренировочным эффектом.

► Метод статистического анализа, основанный на оценке различия дисперсий сравниваемых статистических совокупностей, — это метод …

► Перевод какой-либо системы в желаемое состояние — это:

Степень совпадения результатов детей при повторном тестировании

Надежностью тестов называется степень совпадения результатов при повторном тестировании одних и тех же людей в одинаковых условиях. Вполне понятно, что полное совпадение результатов при повторных измерениях практически невозможно.

Вариацию результатов при повторных измерениях называют внутрииндивидуальной или внутригрупповой, либо внутриклассовой. Основными причинами такой вариации результатов тестирования, которая искажает оценку истинного состояния подготовленности спортсмена, т.е. вносит определенную ошибку или погрешность в эту оценку, являются следующие обстоятельства:

1) случайные изменения состояния испытуемых в процессе тестирования (психологический стресс, привыкание, утомление, изменение мотивации к выполнению теста, изменение концентрации внимания, нестабильность исходной позы и других условий процедуры измерений при тестировании);

2) неконтролируемые изменения внешних условий ( температура, влажность , ветер, солнечная радиация , присутствие посторонних лиц и т.п.);

3) нестабильность метрологических характеристик технических средств измерения (ТСИ), используемых при тестировании. Нестабильность может быть вызвана несколькими причинами, обусловленными несовершенством применяемых ТСИ: погрешностью результатов измерения из-за изменений напряжения сети, нестабильностью характеристик электронных измерительных приборов и датчиков при изменениях температуры, влажности, наличием электромагнитных помех и т.п. Следует отметить, что по этой причине погрешности измерений могут составлять значительные величины;

4) изменения состояния экспериментатора (оператора, тренера, педагога, судьи), осуществляющего или оценивающего результаты тестирования

и замена одного экспериментатора другим;

5) несовершенство теста для оценки данного качества или конкретного показателя подготовленности.

Существуют специальные математические формулы для определения коэффициента надежности теста .

В таблице 2 приведена градация уровней надежности тестов.

Тесты, надежность которых меньше указанных в таблице значений, использовать не рекомендуется.

Говоря о надежности тестов, различают их стабильность (воспроизводимость), согласованность, эквивалентность.

Под стабильностью теста понимают вопроизводимостъ результатов при его повторении через определенное время в одинаковых условиях. Повторное тестирование обычно называют ретестом. Стабильность теста зависит от :

-вида теста;

— контингента испытуемых;

— временного интервала между тестом и ретестом.

Для количественной оценки стабильности используется дисперсионный анализ, по той же схеме, что и в случае расчета обычной надежности.

Согласованность теста характеризуется независимостью результатов тестирования от личных качеств лица, проводящего или оценивающего тест. Если результаты спортсменов в тесте, который проводят разные специалисты (эксперты, судьи), совпадают, то это свидетельствует о

высокой степени согласованности теста. Это свойство зависит от совпадения методик тестирования у разных специалистов.

Эквивалентность тестов.Одно и то же двигательное качество (способность, сторону подготовленности) можно измерить с помощью нескольких тестов. Например, максимальную скорость — по результатам пробегания с ходу отрезков в 10, 20 или 30 м. Силовую выносливость — по числу подтягивании на перекладине, отжиманий в упоре, количеству подъемов штанги в положении лежа на спине и т. д. Такие тесты называют эквивалентными.

Применение эквивалентных тестов повышает надежность оценки контролируемых свойств моторики спортсменов. Поэтому если нужно провести углубленное обследование, то лучше применить несколько эквивалентных тестов, Такой комплекс называется гомогенным. Во всех остальных случаях лучше использовать гетерогенные комплексы: они состоят из неэквивалентных тестов.

Не существует универсальных гомогенных или гетерогенных комплексов. Так, например, для слабо подготовленных людей такой комплекс, как бег на 100 и 800 м, прыжок и длину с места, подтягивание на перекладине, будет гомогенным. Для спортсменов высокой квалификации он может оказаться гетерогенным.

До определенной степени надежность тестов может быть повышена путем:

— более строгой стандартизации тестирования,

— увеличения числа попыток,

— увеличения числа оценщиков (судей, экспертов) и повышения согласованности их мнений,

— увеличения числа эквивалентных тестов,

— лучшей мотивации испытуемых,

— метрологически обоснованный выбор технических средств ихмерений, обеспечивающий заданную точность измерений в процессе тестирования.

Надёжность является одним из основных свойств тестов. Надежность теста — степень совпадения результатов при повторном тестировании одних и тех же людей в одинаковых условиях. По сути надёжность характеризует помехоустойчивость теста и позволяет судить о том, насколько внушают доверие полученные результаты.

В широком смысле надёжность инструмента показывает в какой степени индивидуальные различия в тестовых показателях могут быть отнесены за счёт «истинных» различий, а в какой могут быть приписаны другим факторам.

Основное различие теории надежности тестов от теории ошибок измерения состоит в том, что в теории ошибок измеряемая величина считается неизменной, а в теории надежности тестов предполагается, что она меняется от измерения к измерению.

Вариацию результатов при повторном тестировании называют внутрииндивидуальной, или внутри групповой, либо внутриклассовой.

Причины вариативности результатов при повторном тестировании:

· Изменение состояния исследуемых, нестабильность изучаемого свойства (утомление, врабатывание, научение, изменение мотивации, концентрации внимания и т.п.).

· Неконтролируемые изменения внешних условий и аппаратуры (температура, ветер, влажность, напряжение в электросети, присутствие посторонних лиц и т.п.), т.е. все то, что объединяется термином “случайная ошибка измерения”.

· Изменение состояния человека, проводящего или оценивающего тест, элементы субъективности (или замена одного экспериментатора или судьи другим).

· Несовершенство теста

Причины вариативности тестирования можно выразить следующей формулой:

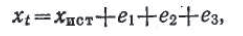
(х_t – зарегистрированный результат; х_ист – истинное значение результата (условно соответствует среднему значению результата при бесконечно большом числе изменений; е₁— систематические и случайные ошибки_, е₂– различия в процедуре тестирования при повторных измерениях, е₃ – внутренняя нестабильность функциональных систем организма).

Составляющие надежности тестов

· Стабильностьтеста — воспроизводимость результатов тестирования при его повторении (тест-ретест) через определенное время в одинаковых условиях. Стабильность зависит от вида теста, контингента испытуемых, временнóго интервала.

· Согласованность теста (объективность) — независимость результатов тестирования от личных качеств лица, проводящего тест. Особое значение согласованность имеет в квалиметрии. Согласованность теста предполагает его стандартизацию.

· Эквивалентностьсовпадение результатов при выполнении однотипных тестов, оценивающих один и тот же параметр, свойство, функцию и т.д.Применение эквивалентных тестов повышает надёжность оценки. Например, силовую выносливость можно оценить по числу подтягиваний на перекладине, отжиманий в упоре лежа, количеству подъемов штанги и т. д. Комплекс, составленный из эквивалентных тестов, является гомогенным, а из неэквивалентных – гетерогенным.

Методы определения надёжности

Согласованность между измерениями показателей можно выразить в виде коэффициента корреляции (r), выражающего степень взаимосвязи между двумя или более множествами показателей.

Существуют различные виды корреляционного анализа, которые детально описываются в учебниках по статистике. Остановимся лишь на интерпретации значений r. Коэффициент корреляции характеризует не только силу взаимосвязи между показателями, но и направление. Значения коэффициента корреляции могут варьировать от плюс 1 до минус 1. Плюс означает положительную корреляцию между измерениями, т.е., при увеличении значений одного множества возрастают значения и другого. Минус говорит об отрицательно корреляции, т.е. увеличению значений в одном множестве соответствует уменьшение в другом. При этом, чем ближе значение r приближается к единице (со знаком плюс или минус), тем сильнее корреляция. Нулевая корреляция указывает на полное отсутствие связи.

Надёжность теста можно оценить методом дисперсионного анализа и выразить в виде коэффициента надёжности и стандартной ошибки измерения (стандартной ошибки показателя). Второй показатель более удобен для интерпретации индивидуальных показателей.

Таблица 1. Интерпретация надежности тестов

Надежность	r
Отличная	0,95 и более
Хорошая	0,90 – 0,94
Средняя	0,80 – 0,89
Приемлемая	0,70 – 0,79
Низкая	0,60 – 0,69

Типы надёжности

·Ретестовая надёжность (test-retest reliability). Заключается в повторном обследовании участников (через небольшой интервал времени) с помощью того же инструмента и методики. О стабильности признака судят по величине внутриклассового коэффициента корреляции (ВКК) между результатами первого и повторного обследования.

· Внутриэкспертная надёжность (inter-rater reliability) –определяет стабильность результатов, полученных при измерении 2 или более раз одним экспериментатором в одной и той же группе с использованием одной и той же методики и теста. Оценивается по величине ВКК.

· Межэкспертная надёжность (inter-rater reliability) — определяет стабильность результатов, полученных при обследовании одной и той же группы 2-мя или более экспериментаторами. Трактуется как и результаты внутриэкспертного тестирования.

Способы повышения надежности тестов:

· стандартизация тестирования;

· увеличение числа попыток;

· увеличение числа экспертов;

· увеличение числа эквивалентных тестов;

· лучшая мотивация испытуемых;

· выбор технических средств, обеспечивающих заданную точность измерений в процессе тестирования.

При определении надежности тестов необходимо учитывать возможность такого явления, как тренд — систематическое повышение или понижение результатов тестирования от попытки к попытке. Причинами тренда являются, с одной стороны, адаптация (привыкание), а, с другой – утомление.

Теория
тестов.

1.
Степень совпадения результатов при
повторном тестировании одних и тех же
людей в одинаковых условиях называется
… .

А)
надежностью.

Б)
конгруэнтгостью.

В)
тожественностью.

Г)
согласованностью.

Степень
совпадения результатов при повторном
тестировании одних и тех же людей в
одинаковых условиях называется
надежностью.

Конгруэ́нтность —
равенство, адекватность друг другу
различных экземпляров чего-либо.

Тождественность
— отношение между объектами,
рассматриваемыми как одно и то же;
предельный случай отношения равенства.

Согласованность
– степень независимости получаемых
результатов от личных качеств человека,
проводящего тестирование.

Тестом
(от англ, test— проба, испытание) в спортивной
практике называется измерение или
испытание, проводимое с целью определения
состояния или способностей человека.

Смирнов
Ю. И., Полевщиков М. М. Спортивная
метрология: Учеб.для студ. пед. вузов. —
М.: Издательский центр «Академия», 2000.
— 232 с. (с. 40).

2.
Процедура проведения забегов и
хронометража называется … .

А)
тестированием.

Б)
результатом теста.

В)
контролем теста.

Г)
организацией теста.

Процедура
проведения забегов и хронометража
называется тестированием.

Полученное
в итоге измерения или испытания числовое
значение является результатом
тестирования.

Годик
М. А. Спортивная метрология: Уч. для ифк.
— М.: Физкультура и спорт, 1988.— 192 с. (с.
117)

3.
… — количественный показатель выраженности
измеряемого свойства у данного
испытуемого, полученный при помощи
данного теста.

А)
Балл

Б)
Единица

В)
Условная единица

Г)
Общее число

Балл
— количественный показатель выраженности
измеряемого свойства у данного
испытуемого, полученный при помощи
данного теста.

Единица
— физическая величина определенного
размера, принятая для количественного
отображения однородных с ней величин.

Условная
единица – это оценка определенной
трудоемкости труда безразмерным
коэффициентом (единицей). Смирнов Ю. И.,
Полевщиков М. М. Спортивная метрология:
Учеб.для студ. пед. вузов. — М.: Издательский
центр «Академия», 2000. — 232 с. (с. 38)

4.
… вид контроля, имеющий цель
экспресс-коррективы состояния организма.

А)
Оперативный.

Б)
Стратегический.

В)
Поэтапный.

Г)
Нормативный.

Оперативный
— вид контроля, имеющий цель
экспресс-коррективы состояния организма.

Стратегический
контроль – это вид контроля, который
заключается в наблюдении за процессом
стратегического управления и его оценке
с тем, чтобы обеспечить правильное
функционирование предприятия.

Поэтапный контроль
— вид контроля, охватывающий отдельные этапы
функционирования сети связи.

Нормативный
контроль – это контроль в
технической и иной документации норм и
требований, установленных стандартами
и другими нормативными документами.

Смирнов
Ю. И., Полевщиков М. М. Спортивная
метрология: Учеб.для студ. пед. вузов. —
М.: Издательский центр «Академия», 2000.
— 232 с. (с.38)

5.
Соотнесите определения с понятиями.

Тест, удовлетворяющий требованиям надежности и информативности, называется	аутентичным.
Тест, результаты которого зависит от двух и более факторов, называется	гетерогенным.
Тест, результаты которого зависит от одного фактора , называется	гомогенным.
Тест, в основе которого лежат двигательные задания, называется	моторным.
	Нормативно-ориентированным.
	Критериально-ориентированным.

Тест,
удовлетворяющий требованиям надежности
и информативности, называется аутентичным.

Тест,
результаты которого зависит от двух и
более факторов, называется гетерогенным.

Тест,
результаты которого зависит от одного
фактора , называется гомогенным.

Тест,
в основе которого лежат двигательные
задания, называется моторным.

Тест,
позволяющий сравнивать достижения
(уровень подготовки) отдельных испытуемых
друг с другом называется
нормативно-ориентированным.

Тест,
позволяющий оценивать, в какой степени
испытуемые овладели необходимым
заданием (двигательным качеством,
техникой движений и т.д.) называется
критериально-ориентированным.

Афанасьев
В.В., Муравьёв А.В., Осетров И.А., Михайлов
П.В. Спортивная метрология : уч. пособие
/ под ред. В.В. Афанасьева / В.В. Афанасьев,
А.В. Муравьёв, И.А. Осетров, П.В. Михайлов.
– Ярославль : Изд-во ЯГПУ, 2009. – 242 с. (с
. 126-127)

6.
К результатам теста по двигательным
параметрам относятся:

А)
пройденное расстояние;

Б)
число повторений;

В)
объем работы;

Г) скорость выполнения движения.

Двигательные
параметры характеризуют
нормирование двигательной активности.
К ним относятся: пройденное расстояние,
число повторений.

Годик
М. А. Спортивная метрология: Уч. для ифк.
— М.: Физкультура и спорт, 1988.— 192 с. (с.
117)

7.
Укажите рисунок (рисунки), на которых
изображен график с высокой стабильностью
результатов прохождения спортсменом
дистанции в два заезда.

А)
1

Б)
2

В)
Ни один из рисунков

Г)
На обоих рисунках

Стабильность
теста — это такая разновидность
надежности, которая проявляется в
степени совпадения результатов
тестирования, когда первое и последующие
измерения разделены определенным
временным интервалом.

Годик
М. А. Спортивная метрология: Уч. для ифк.
— М.: Физкультура и спорт, 1988.— 192 с. (с.
117)

8.
Валидность – это …

А)
степень точности, с какой тест измеряет
свойство, для оценки которого используется.

Б)
способность проводить тесты с целью
определения состояния или способностей
спортсмена.

В)
метод, отражающий связь между парой
тестов, проведенных в разное время.

Г)
метод, при котором происходит взаимное
влияние тестов друг на друга.

Валидность
— степень точности, с какой тест измеряет
свойство, для оценки которого используется.

Смирнов
Ю. И., Полевщиков М. М. Спортивная
метрология: Учеб.для студ. пед. вузов. —
М.: Издательский центр «Академия», 2000.
— 232 с. (с. 43)

9.
Тест имеет следующие свойства:

А)
содержательное,

Б) эмпирическое,

В)концептуальное,

г)
опознанное,

В)
конструктивное,

Г)
прогностическое.

Содержательное
свойство — характеристика теста,
выражающая показатель охвата заданиями
теста той области знания, подготовленность
в которой этот тест оценивает.

Эмпирическое
свойство теста – характеристика теста,
имеющая отношение к фактам, опыту,
экспериментам или процедурам, основанным
на опыте.

Концептуальное
свойство теста— понимается как
обоснование с позиции соответствия
авторским представлениям об особенностях
диагностируемых свойств, как мера
соответствия заданий теста авторской
концепции этих свойств.

Герасимов
Е.Н. Теория дидактических систем и
реализующая ее технология обучения. –
ЧГИФК, 2008г.-284 с.

10.
Стандартная ошибка надежности равна
±3 см, это значит, что… .

А)
результаты повторных измерений
отклоняются на ±3 см среднего результата.

Б)
результаты теста изменяются в интервале
от -3 до 3.

В)
групповой результат остался неизменным,
так как наблюдается улучшение и ухудшение
индивидуальных результатов.

Г)
результаты остались неизменны.

Стандартная
ошибка среднего — величина, характеризующая
стандартное отклонение выборочного
среднего, рассчитанное по выборке
размера из генеральной совокупности.

Годик
М. А. Спортивная метрология: Уч. для ифк.
— М.: Физкультура и спорт, 1988.— 192 с. (с.
117)

11.
Укажите таблицу (таблицы), по которым
можно определить коэффициент надежности
теста.

Таблица
1

Таблица
2

А)
По таблице 1.

Б)
По таблице 2.

В)
По обеим таблицам.

Г)
Ни по одной из таблиц.

Коэффициент
надежности —это отношение истинной
дисперсии к дисперсии, зарегистрированной
в процессе измерений.

Надежность
теста – степень совпадения результатов
при повторном тестировании одних и тех
же людей в одинаковых условиях.

12.
Укажите таблицу (таблицы), по которым
можно определить информативность теста.

Таблица
1

Таблица
2

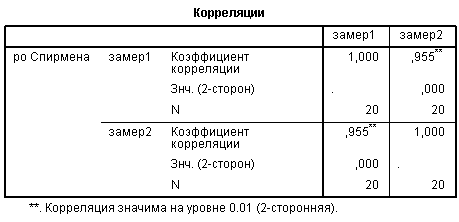
А)
По таблице 1.

Б)
По таблице 2.

В)
По обеим таблицам.

Г)
Ни по одной из таблиц.

Информативность
теста – степень точности с какой он
измеряет свойство, для оценки которого
используется.

Соседние файлы в папке 36

1. С помощью Международной системы единиц (СИ) измеряются показатели:
а) физические +
б) биологические
в) педагогические

2. Величина, характеризующая какое-либо свойство системы, называется:
а) константой
б) переменной +
в) регулятором

3. Степень совпадения результатов при повторном тестировании одних и тех же людей в одинаковых условиях – это … теста:
а) информативность
б) валидность
в) надежность +

4. Если двигательный опыт отстает от календарного возраста, то таких детей называют:
а) ретардантами +
б) юниорами
в) аутсайдерами

5. В случаях, когда одному значению одного показателя соответствует несколько значений другого, взаимосвязь называют:
а) линейной
б) параметрической
в) статистической +

6. Основные операции, проводимые с помощью шкалы отношений – это установление:
а) соотношений «больше» или «меньше»
б) равенства отношений +
в) равенства интервалов

7. Шкала оценивания, в которой число начисляемых очков приравнивается к проценту лиц, которых опередил данный участник – это шкала:
а) параметрическая
б) выбранных точек
в) перцентильная +

8. Состояние спортсмена, которое изменяется под влиянием одного или нескольких занятий, называется:
а) текущим +
б) переходным
в) оперативным

9. Метод для количественной оценки качественных показателей:
а) метрология
б) статистика
в) квалиметрия +

10. Шкала, по которой чем выше спортивный результат, тем большей прибавкой очков оценивается его улучшение:
а) пропорциональная
б) прогрессирующая +
в) сигмовидная

11. Метод сбора мнений посредством заполнения анкет:
а) анкетирование +
б) тестирование
в) интервьюирование

12. Шкала, по которой за один и тот же прирост результата начисляют по мере возрастания спортивных достижений все меньшее число очков:
а) сигмовидная
б) регрессирующая +
в) прогрессирующая

13. Шкала, предполагающая начисление одинакового числа очков за равный прирост результатов:
а) пропорциональная +
б) прогрессирующая
в) регрессирующая

14. Метод статистического анализа, основанный на оценке различия дисперсий сравниваемых статистических совокупностей:
а) репрезентативный
б) корреляционный
в) дисперсионный +

15. Шкала оценивания, построенная по двум (линейная) либо нескольким (нелинейная шкала) выбранным опорным значениям результата испытания (измерения) и соответствующим им количеством очков (баллов, рейтинга), называется шкалой:
а) выбранных точек +
б) перцентильной
в) стандартной

16. Слово «метрология» в переводе с древнегреческого означает наука о:
а) статистике
б) измерениях +
в) изменениях

17. Сбор информации и сравнение его с действительного состояния с должным:
а) обратная связь
б) управление
в) контроль +

18. Независимость результатов теста от личных качеств лица, проводящего или оценивающего тест:
а) надежность
б) согласованность +
в) информативность

19. Человек, заполняющий анкету:
а) ответчик
б) интервьюер
в) респондент +

20. Величина ∆А = А — Ао, равная разности между показаниями измерительного прибора (А) и истинным значением измеряемой величины (Ао), называется, погрешностью:
а) относительной
б) абсолютной +
в) основной

21. Нормы, основанные на сравнении показателей одного и того же спортсмена в разных состояниях, называются:
а) индивидуальными +
б) общими
в) второстепенными

22. Контроль, который осуществляется с помощью тестов, мало зависящих от повседневных колебаний состояния спортсмена:
а) общий
б) этапный +
в) пошаговый

23. Независимость результатов теста от личных качеств лица, проводящего или оценивающего тест:
а) несогласованность
б) согласие
в) согласованность +

24. Метод оценивания, при котором попарно сравнивают объекты, называют методом:
а) тройного сравнения
б) парного сравнения +
в) одинарного сравнения

25. Показатели, не имеющие определенных единиц измерения:
а) показательные
б) количественные
в) качественные +

26. Основной задачей общей метрологии является обеспечение:
а) многообразие точности измерений
б) единства и точности измерений +
в) единства и точности поведения

27. Управляемый и управляющий объекты всегда соединены:
а) связями +
б) узами
в) тренировками

28. Степень согласованности мнения нескольких экспертов, оценивается по величине коэффициента:
а) координации
б) деградации
в) конкордации +

29. Пригодность норм только для той совокупности, для которой они разработаны:
а) релевантность +
б) релевативность
в) левантность

30. Нормы, имеющие в своей основе сравнение людей, принадлежащих к одной и той же совокупности, называются:
а) сравнительными
б) сопоставительными +
в) сопоставимыми

Источник

Стандартная ошибка измерения: определение и пример

17 авг. 2022 г.
читать 2 мин

Стандартная ошибка измерения , часто обозначаемая как SE m , оценивает отклонение от «истинного» показателя для индивидуума при повторных измерениях.

Он рассчитывается как:

SE m = s√ 1-R

куда:

s: стандартное отклонение измерений
R: коэффициент надежности теста.

Обратите внимание, что коэффициент надежности находится в диапазоне от 0 до 1 и рассчитывается путем двукратного проведения теста для многих людей и расчета корреляции между их результатами теста.

Чем выше коэффициент надежности, тем чаще тест дает стабильные результаты.

Пример: расчет стандартной ошибки измерения

Предположим, человек проходит определенный тест 10 раз в течение недели, целью которого является измерение общего интеллекта по шкале от 0 до 100. Он получает следующие баллы:

Очки: 88, 90, 91, 94, 86, 88, 84, 90, 90, 94.

Среднее значение выборки равно 89,5, а стандартное отклонение выборки равно 3,17.

Если известно, что тест имеет коэффициент надежности 0,88, то мы рассчитываем стандартную ошибку измерения как:

SE м = с√1 -R = 3,17√1-0,88 = 1,098

Как использовать SE m для создания доверительных интервалов

Используя стандартную ошибку измерения, мы можем создать доверительный интервал, который, вероятно, будет содержать «истинную» оценку человека по определенному тесту с определенной степенью достоверности.

Если человек получает по тесту оценку x , мы можем использовать следующие формулы для расчета различных доверительных интервалов для этой оценки:

68% доверительный интервал = [ x – SE m , x + SE m ]
95% доверительный интервал = [ x – 2*SE m , x + 2*SE m ]
99% доверительный интервал = [ x – 3*SE m , x + 3*SE m ]

Например, предположим, что человек набрал 92 балла по определенному тесту, который, как известно, имеет SE m 2,5. Мы могли бы рассчитать 95% доверительный интервал как:

95% доверительный интервал = [92 – 2*2,5, 92 + 2*2,5] = [87, 97]

Это означает, что мы на 95% уверены в том, что «истинный» результат этого теста человека находится между 87 и 97.

Надежность и стандартная ошибка измерения

Существует простая зависимость между коэффициентом надежности теста и стандартной ошибкой измерения:

Чем выше коэффициент надежности, тем меньше стандартная ошибка измерения.
Чем ниже коэффициент надежности, тем выше стандартная ошибка измерения.

Чтобы проиллюстрировать это, рассмотрим человека, который проходит тест 10 раз и имеет стандартное отклонение баллов, равное 2 .

Если тест имеет коэффициент надежности 0,9 , то стандартная ошибка измерения будет рассчитываться как:

SE m = s√1 -R = 2√1-0,9 = 0,632

Однако, если тест имеет коэффициент надежности 0,5 , то стандартная ошибка измерения будет рассчитываться как:

SE м = с√ 1-R = 2√ 1-,5 = 1,414

Это должно иметь смысл интуитивно: если результаты теста менее надежны, то ошибка измерения «истинного» результата будет выше.

Источник

history 23 ноября 2016 г.

Уровень надежности

Уровень надежности в MS EXCEL

Решение задач описательной статистики средствами пакета анализа Microsoft Excel Текст научной статьи по специальности « Компьютерные и информационные науки»

Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Трущелёв Сергей Андреевич

Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Трущелёв Сергей Андреевич

Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel

Текст научной работы на тему «Решение задач описательной статистики средствами пакета анализа Microsoft Excel»

Ответ на тест по дисциплине «Спортивная метрология»:

Ответы на другие тесты по дисциплине «Спортивная метрология»:

Стандартная ошибка измерения: определение и пример

Пример: расчет стандартной ошибки измерения

Как использовать SE m для создания доверительных интервалов

Надежность и стандартная ошибка измерения