Суть
МНК состоит в:
—минимизации
суммы квадратов коэффициентов регрессии
—минимизации
суммы квадратов значений зависимой
переменной
+—минимизации
суммы квадратов отклонений точек
наблюдений от уравнения регрессии
—минимизации
суммы квадратов отклонений точек
эмпирического уравнения регрессии от
точек теоретического уравнения регрессии
Коэффициент
уравнения регрессии показывает
—на
сколько % изменится результат при
изменении фактора на 1%
—на
сколько % изменится фактор при изменении
результата на 1%
+—на
сколько единиц изменится результат при
изменении фактора на 1 единицу
—на
сколько единиц изменится фактор при
изменении результата на 1 единицу
—во
сколько раз изменится результат при
изменении фактора на 1 единицу
Коэффициент
эластичности показывает
—на
сколько единиц изменится фактор при
изменении результата на 1 единицу
—на
сколько единиц изменится результат при
изменении фактора на 1 единицу
—во
сколько раз изменится результат при
изменении фактора на одну единицу
+—на
сколько % изменится результат при
изменении фактора на 1 %
—на
сколько %изменится фактор при изменении
результата на 1%
Не
является предпосылкой классической
модели предположение:
—факторы
экзогенны
—длина
исходного ряда данных больше, чем
количество факторов
—матрица
факторов содержит все важные факторы,
влияющие на результат
+—факторы
являются случайными величинами
На
основании наблюдений за 100 домохозяйствами
построено эмпирическое уравнение
регрессии, у- потребление, х -доход:
У=145,65+0,825*х
Соответствуют
ли знаки и значения коэффициентов
регрессии теоретическим представлениям
+—да
—нет
—частично
соответствуют
В
производственной функции Кобба-Дугласа
параметр
соответствует коэффициенту:
—корреляции
—вариации
+—эластичности
—детерминации
Найдите
предположение, не являющееся предпосылкой
классической модели
—Случайное
отклонение имеет нулевое математическое
ожидание
—Случайное
отклонение имеет постоянную дисперсию
—Отсутствует
автокорреляция случайных отклонений
—Случайное
отклонение независимо от объясняющих
переменных
+—Случайное
отклонение не обладает нормальным
распределением
По
месячным данным за 6 лет построена
следующая регрессия:
Y=-12,23+0,91*x1-2,1*x2,
R2=0,976,
DW=1,79
t
(-3,38) (123,7) (3,2)
y-
потребление, х1 –располагаемый доход,
х2 – процентная банковская ставка по
вкладам
Оцените
качество построенной модели, не прибегая
к таблицам, совпадает ли направление
влияния объясняющих переменных с
теоретическим?
+—качество
модели высокое, направление влияния
совпадает
—качество
модели низкое, направление влияния
совпадает
—качество
модели высокое, но направление влияния
не совпадает
—качество
модели низкое, направление влияния
совпадает
Критерий
Стьюдента предназначен для:
—Определения
экономической значимости каждого
коэффициента уравнения
+—Определения
статистической значимости каждого
коэффициента уравнения
—Проверки
модели на автокорреляцию остатков
—Определения
экономической значимости модели в целом
—Проверки
на гомоскедастичность
Если
коэффициент уравнения регрессии (k)
статистически значим, то
—k
>
1
—|k
|
>
1
+—k
0
—k
>
0
—0
<
k
<
1
Табличное
значение критерия Стьюдента зависит
—Только
от уровня доверительной вероятности
—Только
от числа факторов в модели
—Только
от длины исходного ряда
—Только
от уровня доверительной вероятности и
длины исходного ряда
+—И
от доверительной вероятности, и от числа
факторов, и от длины исходного ряда
Имеется
уравнение, полученное МНК:
![]()
Зная,
что регрессионная сумма квадратов
составила 110,32, остаточная сумма квадратов
21,43, найдите коэффициент детерминации:
+—0,837
—0,999
—1,000
—0,736
Суть
коэффициента детерминации
![]()
состоит
в следующем:
+—коэффициент
определяет долю общего разброса значений
![]()
,
объясненного уравнением регрессии
—коэффициент
свидетельствует о значимости коэффициентов
регрессии
—коэффициент
определяет тесноту связи между признаками
—коэффициент
свидетельствует о наличии / отсутствии
автокорреляции
Какое
из уравнений регрессии нельзя свести
к линейному виду?
+—![]()
—![]()
—![]()
—![]()
—![]()
Какое
из уравнений регрессии является
степенным?
—
+—![]()
—![]()
—![]()
—![]()
Парная
регрессия представляет собой модель
вида:
+—y=f(x)
—y=f(x1,x2,…xm)
—y=f(y
t-1)
Уравнение
парной регрессии характеризует связь
между:
+—двумя
переменными
—несколькими
переменными
Согласно
содержанию регрессии, наблюдаемая
величина зависимой переменной складывается
из:
+—теоретического
значения зависимой переменной, найденного
из уравнения регрессии, и случайного
отклонения
—теоретического
значения зависимой переменной, найденного
из уравнения регрессии, скорректированного
на величину стандартной ошибки
—теоретического
значения зависимой переменной, найденного
из уравнения регрессии и остаточной
дисперсии
Использование
парной регрессии вместо множественной
является примером:
+—ошибки
спецификации
—ошибки
выборки
—ошибки
измерения
Включение
в совокупность единиц с “выбросами”
данных является примером:
+—ошибки
выборки
—ошибки
спецификации
—ошибки
измерения
Заниженная
балансовая прибыль в отчетности является
примером:
+—ошибки
измерения
—ошибки
спецификации
—ошибки
выборки
Аналитический
метод подбора вида уравнения регрессии
основан на:
+—изучении
природы связи признаков
—изучении
поля корреляции
—сравнении
величины остаточной дисперсии при
разных моделях
Графический
метод подбора вида уравнения регрессии
основан на:
+—изучении
поля корреляции
—изучении
природы связи признаков
—сравнении
величины остаточной дисперсии при
разных моделях
Экспериментальный
метод подбора вида уравнения регрессии
основан на:
+—сравнении
величины остаточной дисперсии при
разных моделях
—изучении
поля корреляции
—изучении
природы связи признаков
Классический
подход к оцениванию коэффициентов
регрессии основан на:
+—методе
наименьших квадратов
—графической
оценке
—методе
максимального правдоподобия
Величина
коэффициента регрессии показывает:
+—среднее
изменение результата с изменением
фактора на одну единицу
—среднее
изменение результата с изменением
фактора на один процент
—изменение
результата в процентах с изменением
фактора на один процент
Уравнение
парной регрессии дополняется коэффициентом
парной корреляции потому, что:
+—необходимо
знать тесноту связи в линейной форме
—это
требуется для получения оценок
коэффициентов регрессии
—это
необходимо для расчета величины
остаточной дисперсии
Коэффициент
детерминации характеризует:
+—долю
факторной дисперсии в общей дисперсии
результативного признака
—соотношение
факторной и остаточной дисперсий
—долю
остаточной дисперсии в общей дисперсии
результативного признака
F-критерий
характеризует:
+—соотношение
факторной и остаточной дисперсий
—долю
факторной дисперсии в общей дисперсии
результативного признака
—долю
остаточной дисперсии в общей дисперсии
результативного признака
Оценка
значимости уравнения регрессии в целом
дается с помощью:
+—F-критерия
Фишера
—коэффициента
детерминации
—стандартной
ошибки регрессии
«Объясненная»
сумма квадратов отклонений отражает
влияние на разброс y:
+—изучаемого
фактора х
—прочих
факторов
—изучаемого
фактора х и прочих факторов
Остаточная
сумма квадратов отклонений отражает
влияние на разброс у:
—изучаемого
фактора х
+—прочих
факторов
—изучаемого
фактора х и прочих факторов
Если
фактор не оказывает влияния на результат,
то линия регрессии на графике:
+—параллельна
оси ох
—параллельна
оси оу
—является
биссектрисой первой четверти декартовой
системы координат
Остаточная
сумма квадратов равна нулю в том случае,
когда:
+—у
связан с х функционально
—значения
у, рассчитанные по уравнению регрессии,
равны среднему значению у
—вся
общая дисперсия у обусловлена влиянием
прочих факторов
Общая
сумма квадратов отклонений совпадает
с остаточной, когда:
+—фактор
х не оказывает влияния на результат
—прочие
факторы не влияют на результат
—фактор
х и прочие факторы в равной степени
влияют на результат
Уравнение
регрессии статистически значимо, если
+—«объясненная»
сумма квадратов отклонений значимо
больше остаточной суммы квадратов
отклонений
—остаточная
сумма квадратов отклонений значимо
больше «объясненной» суммы квадратов
отклонений
—«объясненная»
и остаточная суммы квадратов отклонений
равны
Число
степеней свободы связано с:
+—числом
единиц совокупности n
и числом определяемых по совокупности
констант
—числом
определяемых по совокупности констант
—числом
единиц совокупности n
“Объясненная”
(факторная) сумма квадратов отклонений
в парной регрессии имеет число степеней
свободы, равное:
+—1
—n-1
—n-2
Остаточная
сумма квадратов отклонений в парной
регрессии имеет число степеней свободы,
равное:
+—n-2
—n-1
—1
Общая
сумма квадратов отклонений в парной
регрессии имеет число степеней свободы,
равное:
+—n-1
—1
—n-2
Какое
из утверждений истинно:
+—оценки
коэффициентов регрессии будут иметь
нормальное распределение, если случайные
отклонения распределены нормально
—чем
больше стандартная ошибка регрессии
(остаточная дисперсия), тем точнее оценки
коэффициентов
—90%-й
доверительный интервал для условного
математического ожидания зависимой
переменной определяет область возможных
значений для 90 % -ов наблюдений за
зависимой переменной при соответствующем
уровне объясняющей переменной
Для
оценки значимости коэффициентов
регрессии рассчитывают:
+—t-статистику
Стьюдента
—F-критерий
Фишера
—коэффициент
детерминации
Какой
нелинейной функцией можно заменить
параболу, если не наблюдается смена
направленности связи признаков:
+—степенной
функцией
—гиперболой
—логистической
функцией
В
большинстве случаев зависимости между
экономическими переменными являются:
+—стохастическими
—функциональными
—строгими
Компонента
![]()
в уравнении линейной регрессии отражает:
+—связь
в генеральной совокупности
—случайность
—связь
в генеральной совокупности и случайность
Коэффициент
а в уравнении линейной регрессии
измеряет:
+—сдвиг
по оси ординат
—наклон
прямой
—среднее
значение y
Коэффициент
b
в уравнении линейной регрессии измеряет:
+—наклон
прямой
—сдвиг
по оси ординат
—среднее
значение у
По
выборке данных можно построить так
называемое:
+—эмпирическое
уравнение регрессии
—теоретическое
уравнение регрессии
—любое
уравнение регрессии
Эмпирические
коэффициенты регрессии а и b
являются точечными оценками:
+—теоретических
коэффициентов регрессии
—условного
математического ожидания у
—теоретического
случайного отклонения
![]()
есть точечная
оценка:
+—![]()
—![]()
—![]()
Коэффициент
регрессии b
пропорционален:
+—коэффициенту
корреляции
—стандартному
отклонению х
—стандартному
отклонению у
Эмпирическая
прямая регрессии обязательно проходит
через точку:
+—![]()
—![]()
—![]()
Эмпирическое
уравнение регрессии построено таким
образом, что:
+—![]()
—![]()
—![]()
Коэффициент
b
регрессии Y
на X
имеет тот же знак, что и:
+—![]()
—![]()
—![]()
Если
по одной и той же выборке рассчитаны
регрессии У на Х и Х на У, то совпадут ли
в этом случае линии регрессии:
+—нет
—да
Если
переменная Х принимает среднее по
выборке значение х, то:
+—наблюдаемая
величина зависимой переменной У равна
среднему значению у
—регрессионная
величина Ух
в среднем
равна среднему значению у, но не
обязательно в каждом конкретном случае
—регрессионная
величина Ух
равна
среднему значению у
—регрессионный
остаток минимален среди всех других
отклонений
Выберите
истинное утверждение:
+—коэффициенты
эмпирического уравнения регрессии
являются по сути случайными величинами
—коэффициент
b
эмпирического парного линейного
уравнения регрессии показывает процентное
изменение зависимой переменной у при
однопроцентном изменении х
—коэффициент
a
эмпирического парного линейного
уравнения регрессии показывает значение
переменной y
при среднем значении переменной x
Случайное
отклонение в среднем не оказывает
влияние на зависимую переменную, если:
—![]()
+—![]()
—![]()
Случайное
отклонение приведет к увеличению
дисперсии оценок, если
+—![]()
—![]()
—
Гомоскедастичность
подразумевает:
+—![]()
—![]()
—![]()
Отсутствие
автокорреляции случайных отклонений
влечет соотношение:
+—
—
—![]()
Эмпирический
коэффициент регрессии b
является несмещенной оценкой
если:
+—![]()
—![]()
—![]()
Эмпирический
коэффициент регрессии b
является состоятельной оценкой
если:
+—
—![]()
—
Эмпирический
коэффициент регрессии b
является эффективной оценкой
если:
+—
—
—
С
увеличением числа наблюдений n
дисперсии оценок а и b:
+—уменьшаются
—увеличиваются
—не
изменяются
С
увеличением дисперсии х дисперсия
оценок a
и b:
+—уменьшается
—увеличивается
—не
изменяется
С
увеличением наклона прямой регрессии
(b)
разброс значений свободного члена а:
+—увеличивается
—уменьшается
—не
изменяется
Разброс
значений свободного члена а:
+—тем
больше, чем больше среднее значение
квадрата х
—тем
больше, чем меньше среднее значение
квадрата х
—не
зависит от величины х
Свободным
членом уравнения парной линейной
регрессии (а) можно пренебречь, когда:
+—![]()
—![]()
—![]()
Значимая
линейная связь между х и у имеет место,
когда:
+—![]()
—![]()
—![]()
С
увеличением объема выборки:
+—увеличивается
точность оценок
—увеличивается
точность прогноза по модели
—уменьшается
коэффициент детерминации
При
оценке парной линейной регрессии
получена завышенная оценка b1
теоретического коэффициента
![]()
.
Какая оценка наиболее вероятна для
коэффициента
![]()
+—заниженная
—завышенная
—несмещенная
Доверительный
интервал для среднего значения У при
Х=хр
будет:
+—уже,
чем таковой для индивидуальных значений
у
—шире,
чем таковой для индивидуальных значений
у
Дополнительные
вопросы
Для
уравнения
![]()
значение коэффициента корреляции
составило 2. Следовательно . . . .
+
значение коэффициента корреляции
рассчитано с ошибкой;
—
теснота связи в 2 раза сильнее, чем для
функциональной связи;
—
связь функциональная;
—
при увеличении фактора на единицу
значение результата увеличивается в 2
раза.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
…
—
регрессии;
+
корреляции;
—
случайных воздействий;
—
автокорреляции.
Факторная
дисперсия служит для оценки влияния:
—
как учтенных факторов, так и случайные
воздействия;
+
учтенных явно в модели факторов;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение …
—
линейного коэффициента корреляции для
исследуемой зависимости близко к 1;
—
индекса корреляции для исследуемой
зависимости близко к 0;
+
индекса детерминации, рассчитанного
для данной модели достаточно близко к
1;
—
доля остаточной дисперсии результативного
признака в его общей дисперсии стремится
к 1.
Система
нормальных уравнений метода наименьших
квадратов строится на основании:
+
таблицы исходных данных;
—
отклонений фактических значений
результативного признака от его
теоретических значений;
—
предсказанных значений результативного
признака;
—
отклонений фактических значений
объясняющей переменной от ее теоретических
значений.
Общая
дисперсия служит для оценки влияния …
—
учтенных явно в модели факторов;
+
как учтенных факторов, так и случайных
воздействий;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Экспоненциальным
не является
уравнение регрессии:
—
![]()
;
—
![]()
;
+
![]()
;
—
![]()
.
Объем
выборки определяется …
—
числовыми значениями переменных,
отбираемых в выборку;
—
объемом генеральной совокупности;
+
числом параметров при независимых
переменных;
—
числом результативных переменных.
При
расчете значения коэффициента детерминации
используется отношение:
—
математических ожиданий;
—
остаточных величин;
—
параметров уравнения регрессии;
+
дисперсий.
Предпосылкой
метода наименьших квадратов является
…
—
присутствие автокорреляции между
результатом и фактором;
—
отсутствие корреляции между результатом
и фактором;
—
присутствие автокорреляции в остатках;
+
отсутствие автокорреляции в остатках.
Смысл
расчета средней ошибки аппроксимации
состоит в определении среднего
арифметического значения . . . .
—
теоретических значений результативного
признака, выраженных в процентах от его
фактических значений;
+
отклонений
![]()
,
выраженных в процентах от фактических
значений результативного признака;
—
теоретических значений результативного
признака, выраженных в процентах от его
фактических значений признака;
—
отклонений
,
выраженных в процентах от фактических
значений независимой переменной.
Для
моделирования зависимости предложения
от цены не
может быть
использовано уравнение регрессии:
—
![]()
;
—
![]()
;
+
![]()
;
—
![]()
.
Основной
целью линеаризации уравнения регрессии
является. . . .
—
повышения существенности связи между
рассматриваемыми переменными;
—
получение новых нелинейных зависимостей;
+
возможность применения метода наименьших
квадратов для оценки параметров;
—
улучшение качества модели.
Требованием
к уравнениям регрессии, параметры
которых можно найти при помощи МНК
является:
+
линейность параметров;
—
равенство нулю средних значений
результативной переменной;
—
нелинейность параметров;
—
равенство нулю средних значений
факторного признака.
Совокупность
значений критерия, при которых принимается
нулевая гипотеза, называется областью
_____________ гипотезы:
+
принятия;
—
нулевых значений;
—
допустимых значений;
—
отрицания.
Качество
подбора уравнения оценивает коэффициент
. . . .
—
корреляции;
+
детерминации;
—
эластичности;
—
регрессии.
Увеличение точности
оценок с увеличением объема выборки
описывает свойство ___________ оценки
—
несмещенности;
—
смещенности;
+
состоятельности;
—
эффективности.
Оценки
параметров, найденных при помощи метода
наименьших квадратов, обладают свойствами
эффективности, состоятельности и
несмещенности, если предпосылки метода
наименьших квадратов . . .
+
выполняются;
—
не выполняются;
—
можно не учитывать;
—
можно исключить.
Нелинейным
не является уравнение . . . .
+![]()
;
—
;
—![]()
;
—![]()
.
Критерий
Стьюдента предназначен для определения
значимости . . .
—
построенного уравнения в целом;
—
каждого коэффициента корреляции;
—
уравнения;
+
каждого коэффициента регрессии.
Для
моделирования зависимости предложения
от цены не
может быть
использовано уравнение регрессии:
—
;
—
;
+
;
—
.
Для
уравнения
значение коэффициента корреляции
составило 2. Следовательно . . . .
+
значение коэффициента корреляции
рассчитано с ошибкой;
—
теснота связи в 2 раза сильнее, чем для
функциональной связи;
—
связь функциональная;
—
при увеличении фактора на единицу
значение результата увеличивается в 2
раза.
Назовите
показатель корреляции для нелинейных
моделей регрессии:
—
парный коэффициент линейной корреляции;
—
индекс детерминации;
—
линейный коэффициент корреляции;
+
индекс корреляции.
Если
спецификация модели
![]()
нелинейного уравнения регрессии, то
нелинейной является функция:
—
![]()
;
—
![]()
;
+
![]()
;
—
![]()
.
Значение
коэффициента корреляции не характеризует
…
+
статистическую значимость уравнения;
—
корень из значения коэффициента
детерминации;
—
тесноту связи;
—
силу связи.
Расчетное
значение критерия Фишера определяется
как отношение ….
+
дисперсий;
—
результата к фактору;
—
математических ожиданий;
—
случайных величин.
Парабола
второй степени может быть использована
для зависимостей экономических
показателей,
—
если исходные данные не обнаруживают
изменения направленности;
—
если для определенного интервала
значений фактора меняется скорость
изменений значений результата, то есть
возрастает динамика роста или спада;
—
если характер связи зависит от случайных
факторов;
+
если для определенного интервала
значений фактора меняется характер
связи рассматриваемых показателей:
прямая связь изменяется на обратную
или обратная на прямую.
Оценки
параметров уравнений регрессии при
помощи метода наименьших квадратов
находятся на основании:
—
решения уравнения регрессии;
—
решения системы нормальных неравенств;
—
решения двойственной задачи;
+
решения системы нормальных уравнений.
Для
уравнения зависимости выручки от
величины оборотных средств получено
значение коэффициента детерминации,
равное 0,7. Следовательно, _______ процентов
дисперсии обусловлено случайными
факторами.
+
30%;
—
100%;
—
70%;
—
0%.
Если
доверительный интервал для параметра
проходит через точку ноль, следовательно
…
—
значение параметра может принимать как
отрицательные, так и положительные
значения;
+
параметр является несущественным;
—
параметр является существенным;
—
параметр признается статистически
значимым.
Уравнение
регрессии
![]()
характеризует ________ зависимость.
+
обратно пропорциональную;
—
линейную;
—
функциональную;
—
прямо пропорциональную
Значения
коэффициента корреляции может находиться
в отрезке:
—
[-1;0];
—
[0;1];
+
[-1;1];
—
[-2;2].
Оценка
значимости уравнения в целом осуществляется
по критерию:
+
Фишера;
—
Дарбина-Уотсона;
—
Пирсона;
—
Стьюдента.
Метод
наименьших квадратов позволяет оценить
_______ уравнений регрессии
—
переменные и случайные величины;
+
параметры;
—
переменные;
—
параметры и переменные
Расчет
средней ошибки аппроксимации для
нелинейных уравнений регрессии связан
с расчетом разности между …
+
фактическим и теоретическим значениями
результативной переменной;
—
фактическим и теоретическим значениями
независимой переменной;
—
прогнозным и теоретическим значениями
результативной переменной;
—
прогнозным и теоретическим значениями
независимой переменной.
Предпосылкой
метода наименьших квадратов является
то, что …
—
при увеличении моделируемых значений
результативного признака значение
остатка увеличивается;
+
остаточные величины имеют случайный
характер;
—
при уменьшении моделируемых значений
результативного признака значение
остатка уменьшается;
—
остаточные величины имеют неслучайный
характер.
Проводится
исследование финансовых результатов
деятельности предприятий, среди которых
обнаруживаются как прибыльные, так и
убыточные. Среди факторов, влияющих на
прибыль, был выделен доминирующий. При
этом нельзя
использовать
спецификацию:
—
![]()
;
—
;
+
![]()
;
—
![]()
.
Значение
коэффициента детерминации рассчитывается
как отношение дисперсии результативного
признака, объясненной регрессией, к
___________ дисперсии результативного
признака.
—
средней;
—
факторной;
—
остаточной;
+
общей
Расчет
значения коэффициента детерминации не
позволяет
оценить:
—
качество подбора уравнения регрессии;
—
долю факторной дисперсии результативного
признака в общей дисперсии результативного
признака;
+
существенность коэффициента регрессии;
—
долю остаточной дисперсии результативного
признака в общей дисперсии результативного
признака.
Предпосылкой
метода наименьших квадратов является
то, что остатки …
—
не подчиняются закону больших чисел;
+
подчиняются закону нормального
распределения;
—
не подчиняются закону нормального
распределения;
—
подчиняются закону больших чисел.
Критическое
значение критерия Стьюдента определяет:
—
максимально возможную величину,
допускающую принятие гипотезы о
существенности параметра;
+
максимально возможную величину,
допускающую принятие гипотезы о
несущественности параметра;
—
минимально возможную величину, допускающую
принятие гипотезы о равенстве нулю
значения параметра;
—
минимально возможную величину, допускающую
принятие гипотезы о несущественности
параметра.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
…
—
регрессии;
+
корреляции;
—
случайных воздействий;
—
автокорреляции.
В
линейном уравнении парной регрессии
![]()
коэффициентом регрессии является
значение …
—
параметров
![]()
и
![]()
;
—
параметра
;
—
переменной
![]()
;
+
параметра
.
Линеаризация
подразумевает процедуру …
—
приведения уравнения множественной
регрессии к парной;
+
приведения нелинейного уравнения к
линейному виду;
—
приведения линейного уравнения к
нелинейному виду;
—
приведения нелинейного уравнения
относительно параметров к уравнению,
линейному относительно результата.
Система
нормальных уравнений метода наименьших
квадратов строится на основании:
—
таблицы исходных данных;
+
отклонений фактических значений
результативного признака от его
теоретических значений;
—
предсказанных значений результативного
признака;
—
отклонений фактических значений
объясняющей переменной от ее теоретических
значений.
При
помощи модели степенного уравнения
регрессии вида
![]()
не может быть
описана
зависимость …
—
выработки от уровня квалификации;
—
заработной платы от выработки;
—
объема предложения от цены;
+
выработки от трудоемкости.
Замена
![]()
не подходит
для уравнения …
—
;
—
![]()
;
—
![]()
;
+
.
При
хорошем качестве модели допустимым
значением средней ошибки аппроксимации
является …
+
5-7%;
—
50%;
—
90-95%;
—
20-25%.
Простая
линейная регрессия предполагает …
—
наличие двух и более факторов и
нелинейность уравнения регрессии;
+
наличие одного фактора и линейность
уравнения регрессии;
—
наличие одного фактора и нелинейность
уравнения регрессии;
—
наличие двух и более факторов и линейность
уравнения регрессии.
Минимальная
дисперсия остатков характерна для
оценок, обладающих свойством …
+
эффективности;
—
несостоятельности;
—
состоятельности;
—
несмещенности.
Нелинейным
является уравнение:
+
;
—
![]()
;
+
![]()
;
—
![]()
.
Построена
модель парной регрессии зависимости
предложения от цены
.
Влияние случайных факторов на величину
предложения в этой модели учтено
посредством …
—
константы
;
—
параметра
;
—
случайной величины
;
+
случайной величины
.
При
расчете значения коэффициента детерминации
используется отношение:
—
математических ожиданий;
—
остаточных величин;
—
параметров уравнения регрессии;
+
дисперсий.
Случайными
воздействиями обусловлено 12% дисперсии
результативного признака, следовательно,
значение коэффициента детерминации
составило:
—
88;
—
0,12;
+
0,88;
—
12.
Свойствами
оценок МНК являются:
—
эффективность, состоятельность и
смещенность;
—
эффективность, несостоятельность и
несмещенность;
—
эффективность, несостоятельность и
смещенность;
+
эффективность, состоятельность и
несмещенность.
Спецификация
модели нелинейная парная (простая)
регрессия подразумевает нелинейную
зависимость и …
+
независимую переменную;
—
пару существенных переменных;
—
пару независимых переменных;
—
пару зависимых переменных.
Значение
линейного коэффициента корреляции
характеризует тесноту ________ связи.
-нелинейной;
+
линейной;
-случайной;
—
множественной линейной.
Для
нелинейных уравнений метод наименьших
квадратов применяется к …
—
не преобразованным линейным уравнениям;
—
обратным уравнениям;
+
преобразованным линеаризованным
уравнениям;
—
нелинейным уравнениям.
Величина
коэффициента детерминации при включении
существенного фактора в эконометрическую
модель …
+
будет увеличиваться;
—
будет равно нулю;
—
существенно не изменится;
—
будет уменьшаться.
К
линейному виду нельзя
привести:
—
линейную модель внутренне линейную;
+
нелинейную модель внутренне нелинейную;
—
линейную модель внутренне нелинейную;
—
нелинейную модель внутренне линейную.
Математическое
ожидание остатков равно нулю, если
оценки параметров обладают свойством…
—
смещенности;
+
несмещенности;
—
состоятельности;
—
эффективности.
В
нелинейной модели парной регрессии
функция
является:
—
равной нулю;
—
несущественной;
—
линейной;
+
нелинейной.
Критические
значения критерия Фишера определяются
по:
+
уровню значимости и степеням свободы
факторной и остаточной дисперсий;
—
уровню значимости и степени свободы
общей дисперсии;
—
уровню значимости;
—
степени свободы факторной и остаточной
дисперсий.
В
качестве показателя тесноты связи для
линейного уравнения парной регрессии
используется:
—
множественный коэффициент линейной
корреляции;
+
линейный коэффициент корреляции;
—
линейный коэффициент регрессии;
—
линейный коэффициент детерминации.
Предпосылки
метода наименьших квадратов исследуют
поведение …
—
параметров уравнения регрессии;
—
неслучайных величин;
+
остаточных величин;
—
переменных уравнения регрессии.
Величина
параметра
в уравнении парной линейной регрессии
характеризует значение …
—
факторной переменной при нулевом
значении результата;
—
результирующей переменной при нулевом
значении случайной величины;
—
факторной переменной при нулевом
значении случайного фактора;
+
результирующей переменной при нулевом
значении фактора.
Если
значение индекса корреляции для
нелинейного уравнения регрессии
стремится к 1, следовательно, …
—
нелинейная связь недостаточно тесная;
—
линейная связь достаточно тесная;
+
нелинейная связь достаточно тесная;
—
нелинейная связь отсутствует.
Состоятельность
оценки характеризуется …
—
независимостью от объема выборки
значения математического ожидания
остатков;
+
увеличением ее точности с увеличением
объема выборки;
—
уменьшением ее точности с увеличением
объема выборки;
—
зависимостью от объема выборки значения
математического ожидания остатков.
Если
предпосылки метода наименьших квадратов
нарушены, то …
—
полученное уравнение статистически
незначимо;
+
оценки параметров могут не обладать
свойствами эффективности, состоятельности
и несмещенности;
—
коэффициент регрессии является
несущественным;
—
коэффициент корреляции является
несущественным.
Общая
дисперсия служит для оценки влияния …
—
учтенных явно в модели факторов;
+
как учтенных факторов, так и случайных
воздействий;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Значение
коэффициента корреляции равно -1.
Следовательно …
—
связь отсутствует;
—
связь слабая;
+
связь функциональная;
—
ситуация неопределенна.
Нелинейным
называется уравнение регрессии, если
…
—
параметры входят нелинейным образом,
а переменные линейны;
+
независимые переменные входят в уравнение
нелинейным образом;
—
параметры и зависимые переменные входят
в уравнение нелинейным образом;
—
зависимые переменные входят в уравнение
нелинейным образом.
Если
коэффициент регрессии является
несущественным, то его значения
приравниваются к …
—
табличному значению и соответствующий
фактор не включается в модель;
+
нулю и соответствующий фактор не
включается в модель;
—
единице и не влияет на результат;
—
нулю и соответствующий фактор включается
в модель.
Величина
отклонений фактических значений
результативного признака от его
теоретических значений представляет
собой …
—
ошибку корреляции;
—
значение критерия Фишера;
+
ошибку аппроксимации;
—
показатель эластичности.
Объем
выборки должен превышать число
рассчитываемых параметров при исследуемых
факторах ..
—
в 2-3 раза;
—
в 20-25 раз;
—
в 10-12 раз;
+
в 5-6 раз.
Остаточная
дисперсия служит для оценки влияния …
+
случайных воздействий;
—
величины постоянной составляющей в
уравнении;
—
учтенных явно в модели факторов;
—
как учтенных факторов, так и случайных
воздействий.
Значение
коэффициента корреляции равно 0,9.
Следовательно, значение коэффициента
детерминации составит …
—
0,3;
+
0,81;
—
0,95;
—
0,1.
По
результатам исследования было выявлено,
что рентабельность производства падает
с увеличением трудоемкости. Какую
спецификацию уравнения регрессии можно
использовать для построения модели
такой зависимости?
—
;
+
![]()
;
—
;
—
![]()
.
Случайный
характер остатков предполагает …
—
независимость предсказанных по модели
значений результативного признака от
значений факторного признака;
+
независимость остатков от величины
предсказанных по модели значений
результативного признака;
—
зависимость остатков от величины
предсказанных по модели значений
результативного признака;
—
зависимость предсказанных по модели
значений результативного признака от
значений факторного признака.
Статистические
гипотезы используются для оценки:
—
тесноты связи между результатом и
фактором;
—
тесноты связи между результатом и
случайными факторами;
—
автокорреляции в остатках;
+
значимости уравнения регрессии в целом.
Параметр
является существенным, если …
+
доверительный интервал не проходит
через ноль;
—
доверительный интервал проходит через
ноль;
—
расчетное значение критерия Стьюдента
меньше табличного значения;
—
стандартная ошибка превышает половину
значения самого параметра.
Замена
![]()
,
![]()
подходит
для уравнения:
—
![]()
;
—
![]()
;
—
![]()
;
+
.
В
исходном соотношении МНК сумма квадратов
отклонений фактических значений
результативного признака от его
теоретических значений …
—
приравнивается к нулю;
+
минимизируется;
—
максимизируется;
—
приравнивается к системе нормальных
уравнений.
При
выборе спецификации нелинейная регрессия
используется, если …
—
нелинейная зависимость для исследуемых
экономических показателей является
несущественной;
+
между экономическими показателями
обнаруживается нелинейная зависимость;
—
между экономическими показателями не
обнаруживается нелинейная зависимость;
—
между экономическими показателями
обнаруживается линейная зависимость.
Табличное
значение критерия Фишера служит для …
+
проверки статистической гипотезы о
равенстве факторной и остаточной
дисперсий;
—
проверки статистической гипотезы о
равенстве дисперсии некоторой
гипотетической величины;
—
проверки статистической гипотезы о
равенстве двух математических ожиданий;
—
проверки статистической гипотезы о
равенстве математического ожидания
некоторой гипотетической величины.
Предпосылкой
метода наименьших квадратов является
то, что остатки …
—
не подчиняются закону больших чисел;
+
подчиняются закону нормального
распределения;
—
не подчиняются закону нормального
распределения;
—
подчиняются закону больших чисел.
Расчетное
значение критерия Фишера определяется
как …
—
разность факторной дисперсии и остаточной,
рассчитанных на одну степень свободы;
—
отношение факторной дисперсии к
остаточной;
+
отношение факторной дисперсии к
остаточной, рассчитанных на одну степень
свободы;
—
суммы факторной дисперсии к остаточной,
рассчитанных на одну степень свободы.
Предпосылкой
метода наименьших квадратов не
является
условие …
—
гомоскедастичности остатков;
—
случайный характер остатков;
—
отсутствие автокорреляции в остатках;
+
неслучайный характер остатков.
Нелинейное
уравнение регрессии означает нелинейную
форму зависимости между:
—
фактором и результатом;
—
фактором и случайной величиной;
+
результатом и факторами;
—
результатом и параметрами.
Несмещенность
оценки на практике означает …
—
уменьшение точности с увеличением
объема выборки;
—
невозможность перехода от точечного
оценивания к интервальному;
—
что найденное значение коэффициента
регрессии нельзя рассматривать как
среднее значение из возможного большого
количества несмещенных оценок;
+
что при большом числе выборочных
оцениваний остатки не будут накапливаться.
Стандартная
ошибка рассчитывается для проверки
существенности …
+
параметра;
—
коэффициента детерминации;
—
случайной величины;
—
коэффициента корреляции.
Факторная
дисперсия служит для оценки влияния:
—
как учтенных факторов, так и случайные
воздействия;
+
учтенных явно в модели факторов;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Экспоненциальным
не является
уравнение регрессии:
—
;
—
;
+
;
—
.
Известно,
что с увеличением объема производства
себестоимость единицы продукции
уменьшается за счет того, что происходит
перераспределение постоянных издержек.
Пусть
— совокупная величина постоянных
издержек, а
—
величина переменных издержек в расчете
на 1 изделие. Тогда зависимость
себестоимости единицы продукции от
объема производства можно описать с
помощью модели:
—
![]()
;
—
![]()
;
+
![]()
;
—
![]()
.
В
основе метода наименьших квадратов
лежит …
—
равенство нулю суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений;
—
минимизация суммы квадратов отклонений
фактических значений результативного
признака от его средних значений;
+
минимизация суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений;
—
максимизация суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений.
Объем
выборки определяется …
—
числовыми значениями переменных,
отбираемых в выборку;
—
объемом генеральной совокупности;
+
числом параметров при независимых
переменных;
—
числом результативных переменных.
При
оценке статистической значимости
уравнения и существенности связи
осуществляется проверка …
—
существенности параметров;
—
существенности коэффициента корреляции;
+
существенности коэффициента детерминации;
—
нулевой гипотезы.
Для
модели зависимости дохода населения
(р.) от объема производства (млн р.)
получено уравнение
![]()
.
При изменении объема производства на
1 млн р. доход в среднем изменится на …
+
0,003 млн р.;
—
1200 млн р.;
—
1200 р.;
—
0,003 р.
Относительно
формы зависимости различают …
—
простую и множественную регрессию;
—
положительную и отрицательную регрессию;
—
непосредственную и косвенную регрессию;
+
линейную и нелинейную регрессию.
В
матрице парных коэффициентов корреляции
отображены значения парных коэффициентов
линейной корреляции между …
—
переменными и случайными факторами;
+
переменными;
—
параметрами;
—
параметрами и переменными.
Уравнение
регрессии
может быть реализовано при помощи
подстановки:
—
![]()
;
—
![]()
;
+
;
—
![]()
.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение …
—
линейного коэффициента корреляции для
исследуемой зависимости близко к 1;
—
индекса корреляции для исследуемой
зависимости близко к 0;
+
индекса детерминации, рассчитанного
для данной модели достаточно близко к
1;
—
доля остаточной дисперсии результативного
признака в его общей дисперсии стремится
к 1.
Если
значение коэффициента корреляции равно
единице, то связь между результатом и
фактором …
—
стохастическая;
—
вероятностная;
+
функциональная;
—
отсутствует.
Эффективность
оценки на практике характеризуется …
—
невозможностью перехода от точечного
оценивания к интервальному;
—
отсутствием накапливания значений
остатков при большом числе выборочных
оцениваний;
—
уменьшением точности с увеличением
объема выборки;
+
возможность перехода от точечного
оценивания к интервальному
.
Линеаризация
не подразумевает
процедуру …
+
включение в модель дополнительных
существенных факторов;
—
приведение нелинейного уравнения к
линейному;
—
замены переменных;
—
преобразования уравнения.
Основной
задачей эконометрики является …
—
установление связей между различными
процессами в обществе и техническим
процессом;
—
анализ технического процесса на примере
социально-экономических показателей;
—
отражение особенности социального
развития общества;
+
исследование взаимосвязей экономических
явлений и процессов.
При
применении метода наименьших остатков
уменьшить гетероскедастичность остатков
удается путем …
+
преобразования переменных;
—
преобразования параметров;
—
введения дополнительных результатов
в модель;
—
введения дополнительных факторов в
модель.
Значение
индекса детерминации, рассчитанное для
нелинейного уравнения регрессии
характеризует …
+
долю дисперсии результативного признака,
объясненную нелинейной регрессией в
общей дисперсии результативного
признака;
—
долю дисперсии результативного признака,
объясненную линейной корреляцией в
общей дисперсии результативного
признака;
Предпосылкой
метода наименьших квадратов является
…
—
присутствие автокорреляции между
результатом и фактором;
—
отсутствие корреляции между результатом
и фактором;
—
присутствие автокорреляции в остатках;
+
отсутствие автокорреляции в остатках.
Было
замечено, что при увеличении количества
вносимых удобрений урожайность также
возрастает, однако, по достижении
определенного значения фактора
моделируемый показатель начинает
убывать. Для исследования данной
зависимости можно использовать
спецификацию уравнения регрессии …
—
![]()
;
—
![]()
;
—
;
+
![]()
.
Если
оценка параметра эффективна, то это
означает …
—
максимальную дисперсию остатков;
—
уменьшение точности с увеличением
объема выборки;
—
равенство нулю математического ожидания
остатков;
+
наименьшую дисперсию остатков.
При
выборе спецификации модели парная
регрессия используется в случае, когда
…
—
среди множества факторов, влияющих на
результат, можно выделить лишь случайные
факторы;
—
среди множества факторов, влияющих на
результат, можно выделить несколько
факторов;
+
среди множества факторов, влияющих на
результат, можно выделить доминирующий
фактор;
—
среди множества факторов, влияющих на
результат, нельзя выделить доминирующий
фактор.
Нелинейную
модель зависимостей экономических
показателей нельзя привести к линейному
виду, если …
+
нелинейная модель является внутренне
нелинейной;
—
нелинейная модель является внутренне
линейной;
—
линейная модель является внутренне
нелинейной;
—
линейная модель является внутренне
линейной.
Для
существенного параметра расчетное
значение критерия Стьюдента …
—
равно нулю;
+
больше табличного значения критерия;
—
не больше табличного значения критерия;
—
меньше табличного значения критерия.
Оценить
статистическую значимость нелинейного
уравнения регрессии можно с помощью …
—
средней ошибки аппроксимации;
+
критерия Фишера;
—
линейного коэффициента корреляции;
—
показателя эластичности.
Расчетное
значение критерия Фишера определяется
как ___________факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы
—
произведение;
—
разность;
—
сумма;
+
отношение.
Критическое
значение критерия Стьюдента определяет
минимально возможную величину, допускающую
принятие гипотезы о …
—
несущественности параметра;
+
существенности параметра;
—
статистической незначимости значения
параметра;
—
равенства нулю значения параметра.
Если
между экономическими показателями
существует нелинейная связь, то …
—
нецелесообразно использовать спецификацию
нелинейного уравнения регрессии;
+
целесообразно использовать спецификацию
нелинейного уравнения регрессии;
—
целесообразно использовать линейное
уравнение парной регрессии;
—
необходимо включить в модель другие
факторы и использовать линейное уравнение
множественной регрессии.
Оценка
значимости параметров уравнения
регрессии осуществляется по критерию
…
—
Ингла-Гренджера (Энгеля-Грангера);
+
Стьюдента;
—
Фишера;
—
Дарбина-Уотсона.
Назовите
показатель тесноты связи для нелинейных
моделей регрессии:
+
индекс корреляции;
—
индекс детерминации;
—
линейный коэффициент корреляции;
—
парный коэффициент линейной корреляции.
Объем
выборки определяется числом параметров
при …
—
зависимых переменных;
+
независимых переменных;
—
случайных факторах;
—
независимых и зависимых переменных.
Значение
индекса корреляции, рассчитанное для
нелинейного уравнения регрессии
характеризует …
—
тесноту случайной связи;
—
тесноту линейной связи;
+
тесноту нелинейной связи;
—
тесноту обратной связи.
Тема
Парная регрессия (Задачи)
Зависимость
спроса на кухонные комбайны y
от цены x
по 12 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,4 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Нет,
на любом уровне (0,1; 0,05 и 0,1)
—Да,
на любом уровне (0,1; 0,05 и 0,1)
—Нет,
только на уровнях 0,05 и 0,1
—Нет,
только на уровне 0,1
Зависимость
спроса на кухонные комбайны y
от цены x
по 18 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,5 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровне значимости 0,01
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 15 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,3 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
на любом уровне (0,1, 0,05 и 0,01)
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
только на уровне значимости 0,01
Зависимость
спроса на кухонные комбайны y
от цены x
по 12 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,3 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровнях 0,01 и 0,05
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 14 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,2%. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 15 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,1 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровнях 0,01 и 0,05
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 20 торговым точкам компании имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,3 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровне значимости 0,01
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=50
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—
![]()
![]()
—![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=60
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—
![]()
![]()
![]()
—![]()
![]()
—![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=80
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—
![]()
![]()
—![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—
![]()
![]()
![]()
—![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=25
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
—![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=30
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
—
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—
![]()
![]()
—![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=45
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
—![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
—![]()
![]()
—
![]()
![]()
—![]()
![]()
![]()
+—![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=55
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
—
![]()
![]()
—
![]()
![]()
![]()
—
![]()
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 15 наблюдениям. При этом r=-0.7.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-11,11;
-0,89) с вероятностью 0,99
—(-9,67;-2,33)
с вероятностью 0,99
—(-9,01;
-2,99) с вероятностью 0,95
—(-8,53;
-2,32) с вероятностью 0,9
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 18 наблюдениям. При этом r=-0.75.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-6,92;
-3,08) с вероятностью 0,9
—(-6,92;-3,08)
с вероятностью 0,95
—(-8,22;
-1,78) с вероятностью 0,95
—(-7,34;
-2,66) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 20 наблюдениям. При этом r=-0.65.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-6,32;-1,68)
с вероятностью 0,95
—(-5,91;-2,09)
с вероятностью 0,99
—(-6,32;
-1,68) с вероятностью 0,99
—(-5,91;
-2,09) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 22 наблюдениям. При этом r=0.73.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(1,69;
4,31) с вероятностью 0,95
—(-0,49;6,49)
с вероятностью 0,95
—(-1,76;
7,76) с вероятностью 0,99
—(1,23;
4,77) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 24 наблюдениям. При этом r=0.68.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(2,46;11,54)
с вероятностью 0,99
—(2,50;
11,50) с вероятностью 0,99
—(6,36;
7,64) с вероятностью 0,90
—(3,68;
10,32) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 20 наблюдениям. При этом r=0.86.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(2,27;3,73)
с вероятностью 0,90
—(2,14;3,86)
с вероятностью 0,95
—(2,28;
3,72) с вероятностью 0,99
—(1,85;
4,15) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 15 наблюдениям. При этом r=0,53.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(0,20;9,80)
с вероятностью 0,95
—(0,05;9,95)
с вероятностью 0,99
—(1,17;
8,83) с вероятностью 0,90
—(0,35;
9,65) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 18 наблюдениям. При этом r=-0,6.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-3,42;-0,58)
с вероятностью 0,95
—(-3,7;-0,3)
с вероятностью 0,99
—(-3,21;
-0,79) с вероятностью 0,90
—(-3,56;
-0,44) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 16 наблюдениям. При этом r=![]()
.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-4,80;-1,2)
с вероятностью 0,99
—(-4,36;-1,64)
с вероятностью 0,95
—(-3,98;
-2,02) с вероятностью 0,90
—(-4,96;
-1,04) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 14 наблюдениям. При этом
![]()
.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-16,72;
0,72) с вероятностью 0,95
—(-17,32;
1,32) с вероятностью 0,99
—(-16,13;
0,13) с вероятностью 0,90
—(-15,76;
-0,24) с вероятностью 0,90
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]()
,
построенное по 18 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,360
—0,384
—0,247
—0,456
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 20 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,405
—0,428
—0,292
—0,501
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 15 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,448
—0,564
—0,356
—0,621
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 20 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,491
—0,425
—0,379
—0,531
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 18 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,327
—0,425
—0,517
—0,369
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 25 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,373
—0,321
—0,415
—0,512
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 15 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,675
—0,519
—0,631
—0,620
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 18 наблюдениям, имеет
вид:
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,461
—0,395
—0,423
—0,522
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 20 наблюдениям, имеет
вид:
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,495
—0,517
—0,444
—0,396
По
совокупности 15 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Индекс
корреляции, фактическое значение F-
критерия значимость уравнения регрессии
следующие:
+—![]()
![]()
уравнение статистически не значимо на
уровнях 0,01 и 0,05
—![]()
![]()
уравнение
статистически значимо только на уровне
0,1
—![]()
![]()
уравнение
статистически значимо только на уровнях
0,1 и 0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
По
совокупности 18 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,05 и 0,1
—
![]()
уравнение
статистически не значимо на уровне 0,01
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—
![]()
уравнение
статистически не значимо на всех уровнях
По
совокупности 25 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,1 и 0,05
—
![]()
уравнение
статистически не значимо на уровне 0,01
—
уравнение
статистически значимо на всех уровнях
—
![]()
уравнение
статистически не значимо на всех уровнях
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровне 0,1
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически не значимо на уровнях
0,05 и 0,01
По
совокупности 30 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически не значимо на уровнях
0,05 и 0,01
—![]()
![]()
уравнение
статистически значимо на уровне 0,10
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,1 и 0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически не значимо на уровне 0,01
По
совокупности 22 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровне 0,1
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически не значимо на уровне 0,1
По
совокупности 28 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,1 и 0,05
—![]()
![]()
уравнение
статистически не значимо на уровне 0,01
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровне 0,1
По
совокупности 30 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически значимо на уровне 0,1
—![]()
![]()
уравнение
статистически не значимо на уровне 0,01
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо уровне
0,1
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически не значимо на уровне 0,01
И
зучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,5
—0,7
—0,4
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,7
—0,5
—0,4
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
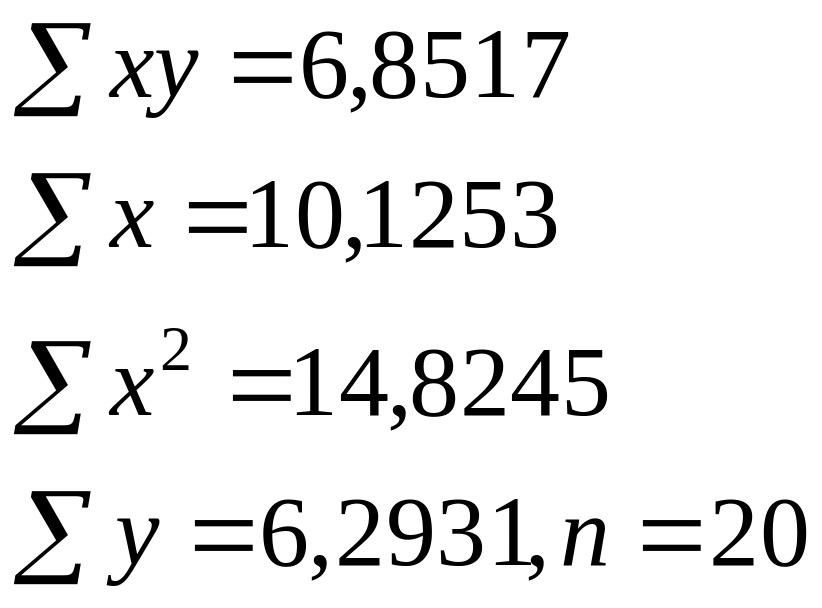
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
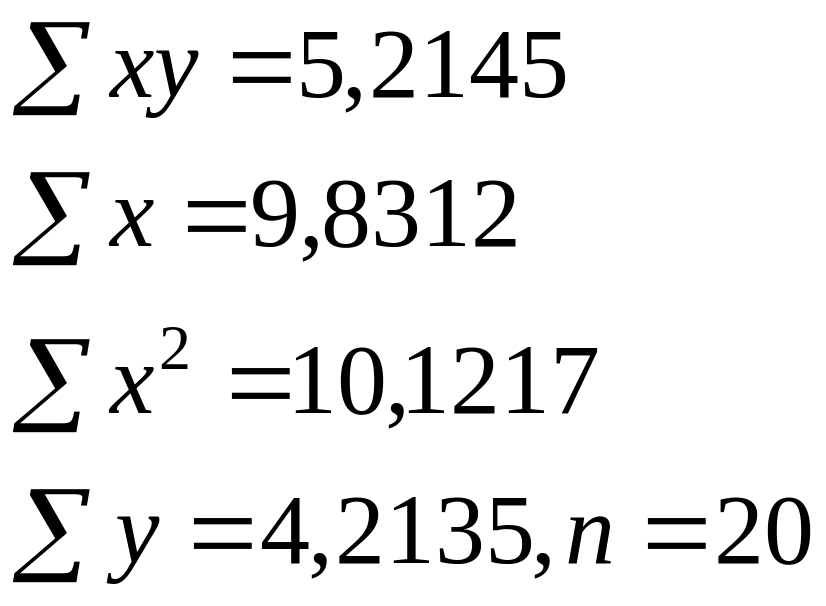
Найдите
параметр b
+—0,6
—0,4
—0,7
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,9
—0,7
—0,6
—0,8
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
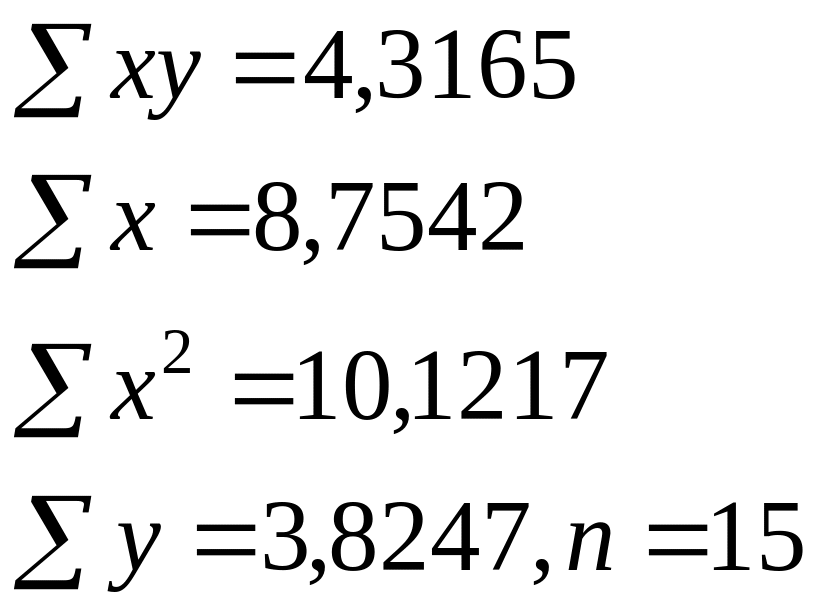
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,3
—0,4
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,5
—0,7
—0,6
—0,4
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 12 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,83;
S2регр=7,95;
F=22,04,tb=4,69
—Rxy=0,83;
S2регр=5,35;
F=12,tb=3,9
—Rxy=0,43;
S2регр=3,74;
F=5,tb=2,4
—Rxy=0,43;
S2регр=3,48;
F=7,tb=2,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 15 предприятиям
концерна следующим образом:
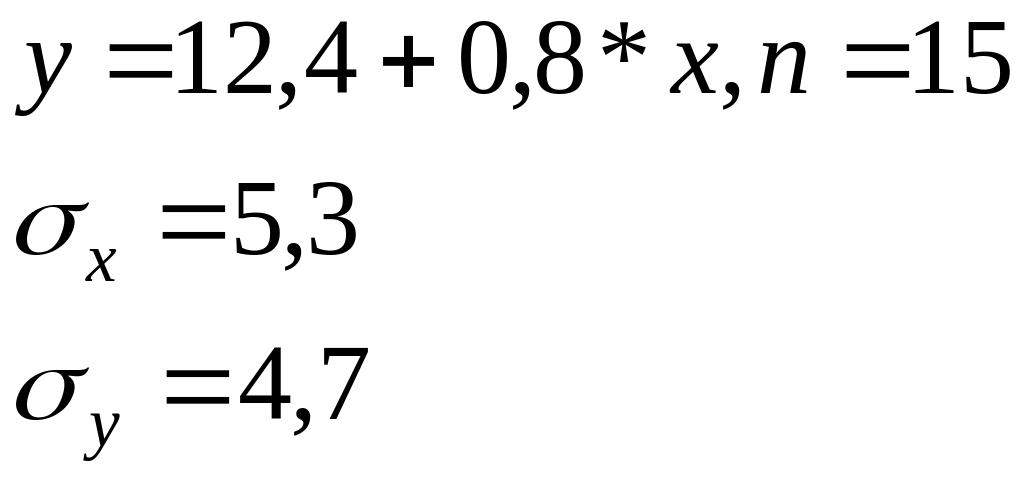
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,90;
S2регр=17,98;
F=56,83,tb=7,54
—Rxy=0,90;
S2регр=15,35;
F=32,0, tb=6,9
—Rxy=0,71;
S2регр=13,74;
F=5,0, tb=2,4
—Rxy=0,71;
S2регр=9,48;
F=7,0, tb=2,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:
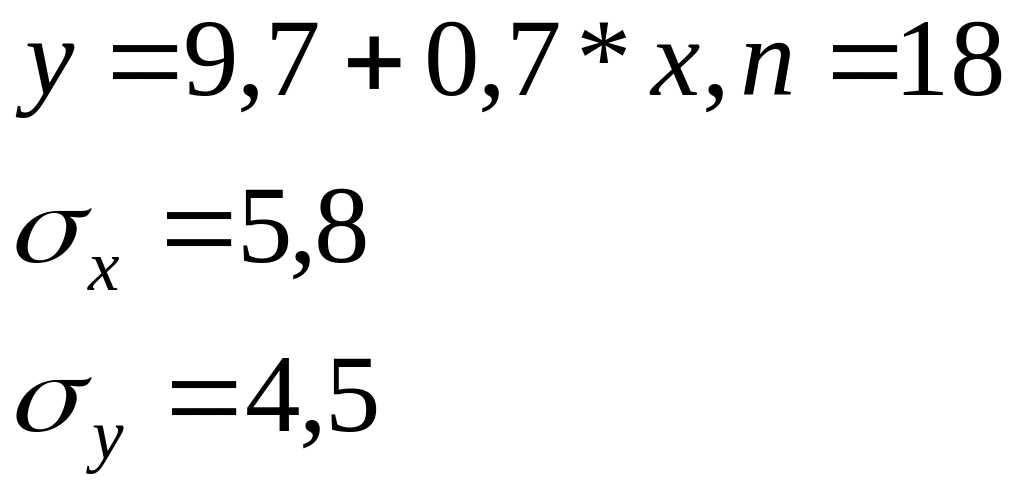
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,90;
S2регр=16,48;
F=70,02, tb=8,37
—Rxy=0,90;
S2регр=15,35;
F=50,01, tb=5,2
—Rxy=0,54;
S2регр=9,82;
F=40,2, tb=4,8
—Rxy=0,54;
S2регр=8,32;
F=38,9, tb=4,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 15 предприятиям
концерна следующим образом:
О
пределите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,91;
S2регр=14,75;
F=66,24, tb=8,14
—Rxy=0,91;
S2регр=12,32;
F=50,1, tb=7,12
—Rxy=0,39;
S2регр=5,42;
F=10,31, tb=3,49
—Rxy=0,39;
S2регр=6,17;
F=11,32, tb=4,21
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 12 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,82;
S2регр=14,75;
F=20,08, tb=4,48
—Rxy=0,82;
S2регр=12,82;
F=18,42, tb=3,37
—Rxy=0,76;
S2регр=9,28;
F=10,12, tb=4,21
—Rxy=0,76;
S2регр=8,32;
F=12,05, tb=4,75
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,88;
S2регр=39,31;
F=56,68, tb=7,53
—Rxy=0,88;
S2регр=25,12;
F=40,12, tb=6,32
—Rxy=0,37;
S2регр=13,10;
F=16,17, tb=5,21
—Rxy=0,37;
S2регр=6,12;
F=4,31, tb=1,18
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 20 предприятиям
концерна следующим образом:
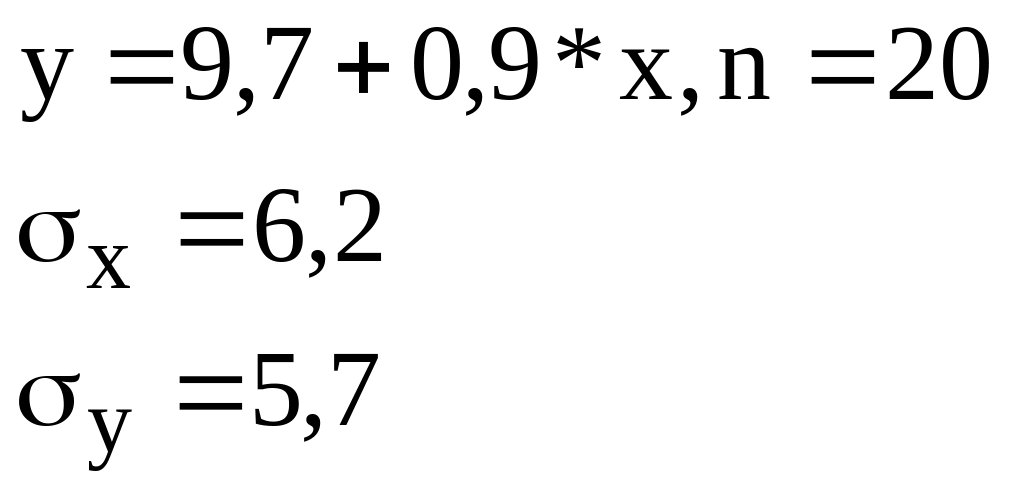
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,9789;
S2регр=31,14;
F=413,116, tb=20,33
—Rxy=0,9789;
S2регр=41,17;
F=420,08, tb=21,17
—Rxy=0,83;
S2регр=25,12;
F=57,2, tb=8,3
—Rxy=0,83;
S2регр=20,18;
F=48,1, tb=7,8
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 16 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,84;
S2регр=43,03;
F=33,83, tb=5,82
—Rxy=0,84;
S2регр=38,07;
F=25,71, tb=4,72
—Rxy=0,76;
S2регр=17,05;
F=8,3, tb=2,78
—Rxy=0,76;
S2регр=15,32;
F=6,8, tb=2,12
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,74;
S2регр=15,21;
F=18,89, tb=4,35
—Rxy=0,74;
S2регр=12,32;
F=16,05, tb=3,15
—Rxy=0,50;
S2регр=8,32;
F=12,47, tb=2,32
—Rxy=0,50;
S2регр=6,15;
F=10,16, tb=1,78
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 20 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,89;
S2регр=53,58;
F=70,62, tb=8,4
—Rxy=0,89;
S2регр=49,12;
F=51,2, tb=7,8
—Rxy=0,61;
S2регр=15,2;
F=12,3, tb=3,2
—Rxy=0,61;
S2регр=12,9;
F=5,7, tb=2,3
Уравнение регрессии
имеет вид: ln
y
= 4,5 + 0,003x
+ ln
e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,255
—0,003
—0,00066
—0,0536
—0,00063
Уравнение регрессии
имеет вид: ln
y
= 4,5 + 0,003 ln
x
+ ln
e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,003
—0,255
—0,00066
—0,0536
—0,00071
Уравнение регрессии
имеет вид: y
= 4,5 + 0,003 ln
x
+ e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,00066
—0,255
—0,003
—0,0536
—0,00063
Уравнение регрессии
имеет вид: y
= 4,5 + 0,003x
+ e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,0536
—0,255
—0,003
—0,00063
—0,0582
Уравнение регрессии
имеет вид: ln
y
= 2,3 + 0,0043x
+ ln
e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,4644
—0,0043
—0,00185
—0,168
—0,4218
Уравнение регрессии
имеет вид: ln
y
= 2,3 + 0,0043 ln
x
+ ln
e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,0043
—0,4644
—0,00185
—0,168
—0,00129
Уравнение регрессии
имеет вид: y
= 2,3 + 0,0043 ln
x
+ e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,00185
—0,0043
—0,4644
—0,168
—0,4215
Уравнение регрессии
имеет вид: y
= 2,3 + 0,0043x
+ e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,168
—0,00185
—0,0043
—0,4644
—0,00129
Уравнение регрессии
имеет вид: ln
y
= 2,2 + 0,0037x
+ ln
e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,3515
—0,0037
—0,00167
—0,137
—0,167
Уравнение регрессии
имеет вид: ln
y
= 2,2 + 0,0037 ln
x
+ ln
e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,0037
—0,3515
—0,00167
—0,137
—0,4644
Уравнение регрессии
имеет вид: y
= 2,2 + 0,0037 ln
x
+ e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,00167
—0,0037
—0,3515
—0,137
—0,00137
Уравнение регрессии
имеет вид: y
= 2,2 + 0,0037x
+ e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,137
—0,00167
—0,0037
—0,3515
—0,3218
Уравнение регрессии
имеет вид: ln
y
= 1,8 + 0,0027x
+ ln
e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,3375
—0,0015
—0,0027
—0,158
—0,3916
Уравнение регрессии
имеет вид: ln
y
= 1,8 + 0,0027 ln
x
+ ln
e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,0027
—0,3375
—0,0015
—0,158
—0,00158
Уравнение регрессии
имеет вид: y
= 1,8 + 0,0027 ln
x
+ e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,0015
—0,0027
—0,3375
—0,158
—0,00158
Уравнение регрессии
имеет вид: y
= 1,8 + 0,0027x
+ e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,158
—0,0015
—0,0027
—0,3375
—0,4218
Несмещённость, эффективность и состоятельность оценок параметров регрессии
Оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.
Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.
Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.
Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии bi имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.
Указанные критерии оценок (несмещенность, состоятельность и эффективность) обязательно учитываются при разных способах оценивания.
тест . Оценка тесноты связи
Значение линейного коэффициента корреляции не может характеризовать тесноту связи для уравнения … 

В случае стохастической зависимости множественный коэффициент корреляции R не может принимать значения …R=100 % R=1,2
Значение коэффициента детерминации, рассчитанное для линейного уравнения парной регрессии составило . Следовательно, значение линейного коэффициента парной корреляции может быть равно …- 0,9; если b. 0,9; если b > 0
В качестве показателя тесноты связи для построенного уравнения регрессии может использоваться …коэффициент множественной корреляции, если исследуется связь между зависимой переменной и несколькими независимыми переменными. коэффициент парной корреляции, если исследуется связь между зависимой переменной и одной независимой переменной
Значение коэффициента корреляции может находится в отрезке …[0; 1] [-1; 0]
Значение коэффициента корреляции может находится в отрезке …[0; 1][-1; 0]
Пусть для множественной линейной регрессии оценки параметров теоретической регрессии таковы, что гипотеза отвергается, а гипотезы принимаются. Это означает, что… добавление переменной значимо улучшает регрессионную модель по сравнению с регрессией только по переменным и. совместное добавление переменных и не приведет к значимому улучшению предсказания по сравнению с регрессией только по
Если значение коэффициента корреляции, рассчитанное для линейного уравнения регрессии равно единице, то … величина не оказывает влияния на переменную у. связь между переменными у и х функциональная
Пусть и — случайные величины, — эмпирическое корреляционное отношение. Свойствами эмпирического корреляционного отношения являются: корреляционное отношение есть неотрицательная величина, не превосходящая единицы: …. если , то между переменными корреляционная связь отсутствует
Выберите значение коэффициента корреляции, которое характеризует функциональную связь между переменными у и х. 

Тест 10.
Коэффициент детерминации …является безразмерной величиной
Пусть , где y – фактическое значение зависимой переменной, — теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), – ошибка модели. Тогда значение характеризует дисперсию …фактических значений зависимой переменной, где m– число факторных признаков. Приведена формула подсчета ______.объясненной дисперсии
Рассматривается регрессионная модель , где — линейная функция. Количество наблюдений =25. Остаточная сумма квадратов равна 440. Тогда остаточная дисперсия на одну степень свободы равна … 440/25-4-1
Значение коэффициента детерминации не является статистически значимым. Это означает, что построенное уравнение регрессии не объясняет разброс наблюдаемых значений результирующего признака относительно величины …Y
Значение коэффициента детерминации составило 0,9, следовательно …уравнением регрессии объяснено 90% дисперсии результативного признака y
Значение коэффициента детерминации составило 0,81, следовательно уравнением регрессии объяснено _____ дисперсии зависимой переменной. 81 %
Для множественной линейной регрессии с числом факторов вычисляют коэффициент детерминации с учетом величины дисперсии на одну степень свободы. В этом случае скорректированный коэффициент детерминации находят по формуле …22 н-м-1н-1
Случайными воздействиями обусловлено 12% дисперсии результативного признака, следовательно, значение коэффициента детерминации составило …0,88
Пусть исследуется линейная зависимость вида и оценена регрессия , – фактические значения, а – расчетные значения зависимой переменной, . Тогда общую дисперсию можно оценить по формуле …н-1
Тест 11.
Если расчетное значение F–критерия Фишера меньше табличного, то можно сделать вывод о …незначимости (несущественности) моделируемой зависимости…статистической незначимости построенной модели
В таблице представлены результаты дисперсионного анализа. Значение остаточной дисперсии на одну степень свободы можно определить, как …отношение чисел, определенных на пересечении строки «Остаток» и столбцов «SS» и «df»…число на пересечении строки «Остаток» и столбца «MS»
В таблице представлены результаты дисперсионного анализа. Значение остаточной суммы квадратов можно определить, как …число на пересечении строки «Остаток» и столбца «SS»…разность чисел, определенных на пересечении столбца «SS» и строк «Итого» и «Регрессия»
Статистические гипотезы используются для оценки статистической значимости …уравнения…оцениваемых параметров
В таблице представлены результаты дисперсионного анализа. Значение общей суммы квадратов можно определить, как …число на пересечении строки «Итого» и столбца «SS»…сумму чисел, определенных на пересечении столбца «SS» и строк «Регрессия» и «Остаток»
В таблице представлены результаты дисперсионного анализа. Расчетное значение F-критерия можно определить, как …отношение чисел, определенных на пересечении столбца «MS» и строк «Регрессия» и «Остаток»…число на пересечении строки «Регрессия» и столбца «F»
Какие статистические гипотезы выдвигаются при проверке статистической значимости построенной модели. нулевая о статистической незначимости….альтернативная о статистической значимости
При проверке статистической значимости построенной модели проводят сравнение …расчетного значения критерия Фишера…табличного значения критерия Фишера
В таблице представлены результаты дисперсионного анализа. Значение объясненной (факторной) дисперсии на одну степень свободы можно определить, как …отношение чисел, определенных на пересечении строки «Регрессия» и столбцов «SS» и «df»…число на пересечении строки «Регрессия» и столбца «MS»
В таблице представлены результаты дисперсионного анализа. Значение объясненной (факторной) суммы квадратов можно определить, как …разность чисел, определенных на пересечении столбца «SS» и строк «Итого» и «Остаток»…число на пересечении строки «Регрессия» и столбца «SS»
Тест 12.
Пусть t – рассчитанная для коэффициента регрессии статистика Стьюдента, а t крит — критическое значение этой статистики. Коэффициент регрессии считается статистически значимым, если выполняются следующие неравенства: t > t крит…t крит
Выберите пропущенное в таблице значение(. 4,3) – ..12
Если коэффициент регрессии является несущественным, то для него выполняются условия …доверительный интервал проходит через ноль…расчетное значение t–критерия Стьюдента по модулю меньше табличного
Какое условие не выполняется, если коэффициент регрессии является незначимым (несущественным)? его значение признается отличным от нуля
С помощью частного -критерия можно проверить значимость -го коэффициента чистой регрессии в предположении, что -й фактор в уравнение множественной регрессии …был включен последним
Если -критерий, вычисленный для оценки параметра регрессии меньше значения , вычисленного по таблицам распределения Стьюдента, то на данном уровне значимости …не отвергается гипотеза о равенстве нулю параметра для генеральной совокупности
Для парной линейной регрессии y=a+bx+e проверка гипотезы о значимости коэффициента регрессии b равносильна проверкам гипотез о значимости: коэффициента детерминации…линейной связи между x и y
Если доверительный интервал для коэффициента регрессии содержит 0, то справедливы следующие утверждения: фактическое значение статистики Стьюдента для этого коэффициента по модулю меньше критического (табличного).. коэффициент регрессии статистически незначим
Коэффициент регрессии считается статистически значимым, если справедливы следующие утверждения: доверительный интервал для этого коэффициента не содержит 0…фактическое значение статистики Стьюдента для этого коэффициента по модулю больше критического (табличного)
Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о …статистической значимости (существенности) параметра.
Гипотеза о значимости в целом уравнения нелинейной регрессии проверяется с помощью критерия…
Нелинейная связь между рассматриваемыми признаками тем теснее, чем значение индекса корреляции ближе к …
Выражение  позволяет вычислить значение …
позволяет вычислить значение …
Уравнение нелинейной регрессии  , где
, где  — общая дисперсия результативного признака
— общая дисперсия результативного признака  ;
;  — остаточная дисперсия ошибки
— остаточная дисперсия ошибки  , может оцениваться показателем тесноты связи – индексом корреляции
, может оцениваться показателем тесноты связи – индексом корреляции  , который вычисляется по формуле …
, который вычисляется по формуле …

Квадрат индекса корреляции для нелинейных форм называется …
Коэффициент детерминации для нелинейной модели часто называют…
Значение индекса корреляции находится в пределах …

Для степенной функции  формула для определения
формула для определения  –критерия
–критерия  примет вид …
примет вид …

Индекс корреляции для нелинейных форм связи находят по формуле …

Значение индекса детерминации, рассчитанное для нелинейного уравнения регрессии характеризует долю дисперсии результативного признака, _____, в общей дисперсии результативного признака.
объясненную нелинейной регрессией
Тест
1. Вопрос: Если оценка параметра эффективна, то это означает …
Выберите несколько ответов: наименьшую дисперсию остатков
возможность перехода от точечного оценивания к интервальному
2. Вопрос: Минимальная дисперсия остатков характерна для оценок, обладающих свойством …
Укажите ответ: эффективности
3. Вопрос: Несмещенная оценка параметра имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра , вычисленных по выборкам одного и того же объема . Такая оценка называется .
4. Вопрос: Если предпосылки метода наименьших квадратов не выполняются, то оценки параметров уравнения регрессии могут не обладать свойствами …
Выберите несколько ответов: эффективности несмещенности
5. Вопрос: Если оценки параметров линейного уравнения регрессии обладают свойством несмещенности, то математическое ожидание остатков …
6. Вопрос: Если оценки параметров линейного уравнения регрессии обладают свойством эффективности, то дисперсия остатков характеризуется …
7. Вопрос: Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то …
Выберите несколько ответов:
при большом числе выборочных оцениваний остатки не будут накапливаться
возможен переход от точечного оценивания к интервальному
8. Вопрос: Укажите условия, которые выполняются, если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности.
Выберите несколько ответов: наименьшая дисперсия остатков
равенство нулю математического ожидания остатков
9. Вопрос: Переход от точечного оценивания к интервальному возможен, если оценки являются …
Укажите ответ: эффективными и несмещенными
10. Вопрос: Если оценки параметров уравнения регрессии, полученных при помощи метода наименьших квадратов обладают свойствами несмещенности, эффективности и состоятельности, то …
Выберите несколько ответов: возможен переход от точечного оценивания к интервальному
математическое ожидание остатков равно нулю и они характеризуются минимальной дисперсией
Тест
1. Вопрос: Обобщенный метод наименьших квадратов не используется в случае ______ остатков.
2. Вопрос: Обобщенный метод наименьших квадратов применяется в случае…
3. Вопрос: После применения обобщенного метода наименьших квадратов удается избежать ______ остатков.
4. Вопрос: Проявление гетероскедастичности в остатках удается устранить при помощи метода обобщенного метода наименьших квадратов путем …
Выберите несколько ответов:
введения в выражение для дисперсии остатков коэффициента пропорциональности
5. Вопрос: Обобщенный метод наименьших квадратов может использоваться для корректировки _______ остатков.
Выберите несколько ответов:
6. Вопрос: Для преодоления проблемы автокорреляции служит …
обобщенный метод наименьших квадратов
7. Вопрос: Обобщенный метод наименьших квадратов применяется, когда случайные отклонения…
не имеют постоянной дисперсии и коррелированны между собой
8. Вопрос: Обобщенный метод наименьших квадратов используется для корректировки…
Укажите ответ: гетероскедастичности остатков в уравнении регрессии
9. Вопрос: Обобщенный метод наименьших квадратов применяется в случае ______ остатков.
гетероскедастичности или автокорреляции
Замена  ;
;  подходит для уравнения …
подходит для уравнения …

Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии W = b0 + b1·U + b2·V. Установите соответствие между видом нелинейной модели и соотношениями между исходными переменными Y, X, Z и новыми переменными W, U, V линеаризованной модели.
Соотношение хрен знает как делать.
Соотношение №2 хрен знает как делать.
Включение случайного отклонения мультипликативным способом позволяет линеаризовать регрессионную модель вида .

Эконометрической моделью, приводимой к линейной регрессионной модели при логарифмировании и соответствующей подстановке, является .

Эконометрическую модель, линейную по параметрам и нелинейную по переменным с аддитивным включением случайного возмущения .
всегда можно свести к классической регрессионной модели с помощью соответствующей подстановки
Соотношение №3 хрен знает как делать.
Соотношение №4 хрен знает как делать.
Эконометрическая модель  является.
является.
нелинейной по параметрам и нелинейной по переменным
Соотношение №5 хрен знает как делать.
1.Зависимость спроса  на благо от его цены
на благо от его цены  , задаваемая функцией вида
, задаваемая функцией вида  (
(  ,
,  ) является …убывающей функцией, выпуклой вниз функцией.
) является …убывающей функцией, выпуклой вниз функцией.
2. Нелинейную модель зависимостей экономических показателей нельзя привести к линейному виду, если …нелинейная модель является внутренне нелинейной
3. Зависимость  от
от  , задаваемая функцией вида
, задаваемая функцией вида  (
(  ), является возрастающей функцией …при
), является возрастающей функцией …при  , при
, при 
4. Зависимость объема производства  от использования ресурса
от использования ресурса  , задаваемая функцией вида
, задаваемая функцией вида  (
(  ,
,  ) является …выпуклой вверх функцией, возрастающей функцией
) является …выпуклой вверх функцией, возрастающей функцией
5. Функции Торнквиста относятся к классу _________ моделей…обратных
6. При выборе спецификации нелинейная регрессия используется, если …между экономическими показателями обнаруживается нелинейная зависимость
7. Зависимость спроса на товары первой необходимости от дохода (функция Торнквиста, 
 ) характеризуется обратной эконометрической моделью с начальным уровнем
) характеризуется обратной эконометрической моделью с начальным уровнем  вида …
вида … 
8. Производственная функция Кобба-Дугласа относится к классу _________ моделей…степенных
9. В модели вида  различают следующие значения параметра
различают следующие значения параметра  : 1.
: 1.  2.
2.  ; 3.
; 3.  . В зависимости от значения параметра
. В зависимости от значения параметра  возможны ситуации, изображенные на рисунках: 1в, 3а
возможны ситуации, изображенные на рисунках: 1в, 3а
10. Зависимости  от
от  , задаваемая функцией вида
, задаваемая функцией вида  (
(  ), является выпуклой вниз функцией …
), является выпуклой вниз функцией …  ,
,  .
.
1. Установите соответствие между названием модели и видом ее уравнения:
Читайте также:
- II. Оценка эффективности инвестиционного менеджмента.
- IV.Оценка эффективности деятельности структурного подразделения организации
- Анализ и оценка состояния управления инвестиционным процессом в ОАО «Дашковка»
- АНАЛИЗ ЛИКВИДНОСТИ БАЛАНСА (ОЦЕНКА ТЕКУЩЕЙ И ПЕРСПЕКТИВНОЙ ЛИКВИДНОСТИ)
- Ассортимент шерстяных и шелковых тканей. Оценка качества.
- Вживленная оценка
- Вопрос 42: оценка эффективности монетарной политики и влияние их изменений на равновесие.
- Вопрос – 130 Доказывание в ПАП. Предмет доказывания. Доказательства в производстве по делам об административных правонарушениях: понятие, виды и оценка.
- Выбор вида модели и оценка ее параметров
- Вычисление коэффициентов корреляции количественных признаков и оценка его достоверности
- ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ 1 страница
- ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ 10 страница
Пишет что не правильно( не знаю как по другому.
2. Установите соответствие между названием модели и видом ее уравнения.
3. Установите соответствие между названием модели и видом ее уравнения:
4. Установите соответствие между названием модели и видом ее уравнения:
5. Установите соответствие между характером модели и видом уравнения:
6. Установите соответствие между названием модели и видом ее уравнения:
7. Установите соответствие между характером модели и видом уравнения:
8. Установите соответствие между видом нелинейной зависимости и величинами остатков модели, к которым предъявляются предпосылки метода наименьших квадратов при оценке параметров линеаризованной модели.
9. Установите соответствие между видом уравнения и характером модели:
10. Установите соответствие между названием модели и видом ее уравнения:
При отборе факторов в модель множественной регрессии проводят анализ …
1. значений матрицы парных коэффициентов корреляции
2. остаточной дисперсии до и после включения факторов в модель
Матрица парных коэффициентов корреляции строится для …
1. отбора факторов в модель множественной регрессии
2. определения коллинеарных факторов
Матрица парных коэффициентов линейной корреляции может служить для решения следующих задач:
1. выявления мультиколлинеарных факторов
2. определения тесноты линейной связи между переменными
только 
Взаимодействие коллинеарных факторов эконометрической модели означает, что …
1. факторы дублируют влияние друг друга на результат
2. теснота связи между ними превышает по абсолютной величине 0,7
При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается…
модель с одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции
Отбор факторов в модель множественной регрессии с использованием метода включения может быть основан на сравнении ….
Из двух коллинеарных факторов из модели множественной регрессии исключается тот, для которого абсолютное значение стандартизованного коэффициента … Меньше В исходное уравнение множественной регрессии  добавляются факторы
добавляются факторы  ,
,  ,
,  . При этом
. При этом  ;
;  ;
;  и
и  . Определите, какие дополнительные факторы необходимо включить в исходное уравнение. только
. Определите, какие дополнительные факторы необходимо включить в исходное уравнение. только 
ТЕСТ 3 ФИКТИВНЫЕ ПЕРЕМЕННЫЕ
Для оценки заработной платы некоторого работника используется следующая модель  , где
, где  — заработная плата
— заработная плата  -го работника;
-го работника;  — общий стаж его работы;
— общий стаж его работы;  — переменная, принимающая значение 1, если работник с высшим образованием и 0 в противном случае;
— переменная, принимающая значение 1, если работник с высшим образованием и 0 в противном случае;  — переменная, принимающая значение 1, если у работника есть дети и 0, если нет,
— переменная, принимающая значение 1, если у работника есть дети и 0, если нет,  — переменная, принимающая значение 1, если работник мужчина и 0, если женщина. Сколько факторов необходимо представить в модели фиктивными переменными?
— переменная, принимающая значение 1, если работник мужчина и 0, если женщина. Сколько факторов необходимо представить в модели фиктивными переменными?
Фиктивная переменная может принимать значения:
Исследуется зависимость потребления кофе от ряда факторов: х1 – марки кофе, х2 – уровня крепости кофе (крепкий, средней крепости, слабой крепости), х3 – дохода потребителя, х4 – цены на кофе. Фиктивными переменными в модели не являются …
В страховой компании решили оценить влияние знака зодиака (всего 12), под которым рожден работник, на производительность его труда. Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Фиктивными переменными в уравнении множественной регрессии могут быть …
1. качественные переменные, преобразованные в количественные
2. переменные, исходные значения которых не имеют количественного значения
В модели необходимо учесть влияние возраста на производительность труда работника. На предприятии работают пенсионеры и лица, не достигшие пенсионного возраста (всего 2 категории). Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Укажите уравнения регрессии, в которых фиктивная переменная D используется только в аддитивной форме:
В модели необходимо учесть влияние уровня образования на заработную плату работника. На предприятии работают люди со средним специальным, высшим и незаконченным высшим образованием (всего 3 категории). Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Проводится эконометрическое моделирование зависимости объема продаж компании от ряда факторов: х1 – цены на товар, х2 – степени известности торговой марки фирмы, х3 – дохода потребителя, х4 – уровня интенсивности рекламной деятельности (высокий уровень – массированная реклама; средний уровень – регулярно повторяющаяся; низкий уровень – время от времени повторяющаяся). Фиктивными переменными в модели не являются …
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.034 сек.)
Учебные материалы для студентов
Методические указания, конспекты, лекции, контрольные, лабораторные работы, курсовые.
Тесты по эконометрике
1. «Белым шумом» называется ___________ процесс
чисто случайный
2. Автокорреляционной функцией временного ряда называется
последовательность значений коэффициентов автокорреляции различных порядков
3. В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений
минимизируется
4. В качестве показателя тесноты связи для линейного уравнения парной регрессии используется
линейный коэффициент корреляции
5. В качестве фиктивных переменных в модель множественной регрессии включаются факторы
не имеющие количественных значений
6. В левой части системы взаимозависимых переменных, как правило, находится
одна зависимая переменная
7. В левой части системы независимых уравнений находится
совокупность зависимых переменных
8. В линейном уравнении парной регрессии коэффициентом регрессии является значение
параметра b
9. В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между
переменными
10. В нелинейной модели парной регрессии функция является
нелинейной
11. В общем случае каждый уровень временного ряда формируется под воздействием
тенденции, сезонных колебаний и случайных факторов
12. В основе метода наименьших квадратов лежит
минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
13. В приведенной форме модели в правой части уравнений находятся
только независимые переменные
14. В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как ______________ уравнений и количества независимых факторов
сумма количества зависимых переменных предыдущих
15. В системе независимых уравнений каждое уравнение представлено
изолированным уравнением регрессии
16. В стандартизованном уравнении множественной регрессии ;. Определите, какой из факторов х1 или х2 оказывает более сильное влияние на
,так как 2,1>0,3
17. В стандартизованном уравнении множественной регрессии переменными являются
стандартизованные переменные
18. В стандартизованном уравнении свободный член
отсутствует
19. Величина коэффициента детерминации при включении существенного фактора в эконометрическую модель
будет увеличиваться
20. Величина остаточной дисперсии при включении существенного фактора в модель
будет уменьшаться
21. Величина отклонений фактических значений результативного признака от его теоретических значений представляет собой
ошибку аппроксимации
22. Величина параметра в уравнении парной линейной регрессии характеризует значение
результирующей переменной при нулевом значении фактора
23. Взаимодействие факторов эконометрической модели означает, что
влияние одного из факторов на результирующий признак не зависит от значений другого фактора
24. Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является
существенным
25. Временной ряд – это совокупность значений экономического показателя
за несколько последовательных моментов (периодов) времени
26. Временной ряд называется стационарным, если он является реализацией _____________ процесса
стационарного стохастического
27. Временной ряд характеризует
данные, описывающие один объект за ряд последовательных моментов (периодов) времени
28. Выбор формы зависимости экономических показателей и определение количества факторов в модели называется ________________ эконометрической модели
спецификацией
29. Выделяют три класса систем эконометрических уравнений
независимые, взаимозависимые и рекурсивные
30. Гетероскедастичность остатков подразумевает _____________ от значения фактора
зависимость дисперсии остатков
31. Гетероскедастичность подразумевает ________________________ от значения фактора
зависимость дисперсии остатков
32. Графическое изображение наблюдений на декартовой плоскости координат называется полем
корреляции
33. Дано уравнение регрессии . Определите спецификацию модели
линейное уравнение множественной регрессии
34. Двухшаговый метод наименьших квадратов предполагает ______ использование обычного МНК
однократное
35. Двухшаговый метод наименьших квадратов применим для решения
только сверхидентифицируемой системы одновременных уравнений
36. Двухшаговый метод наименьших квадратов применяется для оценки параметров
систем эконометрических уравнений
37. Для модели зависимости среднедушевого (в расчете на одного человека) месячного дохода населения (р.) от объема производства (млн р.) получено уравнение . При изменении объема производства на 1 млн р. доход в среднем изменится на
0,003 млн р.
38. Для моделирования зависимости предложения от цены не может быть использовано уравнение регрессии
39. Для моделирования сложных экономических систем целесообразно использовать
систему эконометрических уравнений
40. Для нелинейных уравнений метод наименьших квадратов применяется к
преобразованным линеаризованным уравнениям
41. Для оценки коэффициентов структурной формы модели не применяют _____ метод наименьших квадратов
обычный
42. Для существенного параметра расчетное значение критерия Стьюдента
больше табличного значения критерия
43. Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _% дисперсии обусловлено случайными факторами
30
44. Для уравнения у = 3,14 + 2х +e значение коэффициента корреляции составило 2. Следовательно
значение коэффициента корреляции рассчитано с ошибкой
45. Если доверительный интервал для параметра проходит через точку ноль, следовательно
параметр является несущественным
46. Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно
нелинейная связь достаточно тесная
47. Если значение коэффициента корреляции равно единице, то связь между результатом и фактором
функциональная
48. Если коэффициент регрессии является несущественным, то его значения приравниваются к
нулю и соответствующий фактор не включается в модель
49. Если между экономическими показателями существует нелинейная связь, то
целесообразно использовать спецификацию нелинейного уравнения регрессии
50. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только
тенденцию
51. Если наиболее высоким оказался коэффициент автокорреляции третьего порядка, то исследуемый ряд содержит
случайную величину, влияющую на каждый третий уровень ряда
52. Если оценка параметра эффективна, то это означает
наименьшую дисперсию остатков
53. Если предпосылки метода наименьших квадратов нарушены, то
оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности
54. Если расчетное значение критерия Фишера меньше табличного значения, то гипотеза о статистической незначимости уравнения
принимается
55. Если спецификация модели нелинейное уравнение регрессии, то нелинейной является функция
56. Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение
регрессии
57. Если факторы входят в модель как произведение, то модель называется
мультипликативной
58. Если факторы входят в модель как сумма, то модель называется
аддитивной
59. Значение индекса корреляции, рассчитанное для нелинейного уравнения регрессии характеризует тесноту ______ связи
нелинейной
60. Значение коэффициента автокорреляции второго порядка характеризует связь между
исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени
61. Значение коэффициента автокорреляции первого порядка равно 0,9 следовательно
линейная связь между последующим и предыдущим уровнями тесная
62. Значение коэффициента автокорреляции рассчитывается по аналогии с
линейным коэффициентом корреляции
63. Значение коэффициента детерминации рассчитывается как отношение дисперсии результативного признака, объясненной регрессией, к ___________ дисперсии результативного признака
общей
64. Значение коэффициента детерминации составило 0,9, следовательно
уравнение регрессии объяснено 90% дисперсии результативного признака
65. Значение коэффициента корреляции не характеризует
статистическую значимость уравнения
66. Значение коэффициента корреляции равно 0,9. Следовательно, значение коэффициента детерминации составит
0,81
67. Значение коэффициента корреляции равно 1. Следовательно
связь функциональная
68. Значение линейного коэффициента корреляции характеризует тесноту ________ связи
линейной
69. Значения коэффициента автокорреляции первого порядка равно 0,9. Следовательно
линейная связь между последующим и предыдущим уровнями тесная
70. Значения коэффициента корреляции может находиться в отрезке
[-1;1]
71. Из пары коллинеарных факторов в эконометрическую модель включается тот фактор, который при
достаточно тесной связи с результатом имеет меньшую связь с другими факторами
72. Известны значения аддитивной модели временного ряда: Yt — значение уровня ряда, Yt = 30, Т- — значение тренда, Т+15, Е- значение случайной компоненты случайных факторов Е=2. Определите значение сезонной компоненты S
13
73. Изолированное уравнение множественной регрессии может быть использовано для моделирования взаимосвязи экономических показателей, если
факторы не взаимодействуют друг с другом
74. Исследуется зависимость, которая характеризуется линейным уравнением множественной регрессии. Для уравнения рассчитано значение тесноты связи результативной переменной с набором факторов. В качестве этого показателя был использован множественный коэффициент
корреляции
75. Исходные значения фиктивных переменных предполагают значения
качественные
76. К линейному виду нельзя привести:
нелинейную модель внутренне нелинейную
77. К ошибкам спецификации относится
неправильный выбор той или иной математической функции
78. Качество подбора уравнения оценивает коэффициент
детерминации
79. Коррелограммой называется ______________________________ функции
графическое отображение автокорреляционной
80. Косвенный метод наименьших квадратов требует
преобразования структурной формы модели в приведенную
81. Критерий Стьюдента предназначен для определения значимости
каждого коэффициента регрессии
82. Критерий Фишера используется для оценки значимости
построенного уравнения
83. Критические значения критерия Фишера определяются по
уровню значимости и степеням свободы факторной и остаточной дисперсий
84. Критическое значение критерия Стьюдента определяет
максимально возможную величину, допускающую принятие гипотезы о несущественности параметра
85. Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о
существенности параметра
86. Линеаризация не подразумевает процедуру
включение в модель дополнительных существенных факторов
87. Линеаризация подразумевает процедуру приведения
нелинейного уравнения к линейному виду
88. Линейное уравнение множественной регрессии имеет вид . Определите какой из факторов или оказывает более сильное влияние на y
так как 2,5 1, то есть x возрастает и y тоже возрастает) не может быть описана зависимость
выработки от трудоемкости
167. При построении модели временного ряда проводится расчет
каждого уровня временного ряда
168. При построении систем независимых уравнений набор факторов в каждом уравнении определяется числом факторов, оказывающих ________ на моделируемый показатель
существенное влияние
169. При построении системы эконометрических уравнений необходимо учитывать
структуру связей реальной экономической системы
170. При применении метода наименьших квадратов исследуются свойства
оценок параметров уравнения регрессии
171. При применении метода наименьших квадратов исследуются свойства оценок
параметров уравнения регрессии
172. При применении метода наименьших квадратов уменьшить гетероскедастичность остатков удается путем
преобразования переменных
173. При расчете значения коэффициента детерминации используется отношение
дисперсий
174. При хорошем качестве модели допустимым значением средней ошибки аппроксимации является ___%
5-7
175. Приведенная форма модели получена из _________формы модели
структурной
176. Приведенная форма модели представляет собой систему ________ функций эндогенных переменных от экзогенных
линейных
177. Приведенная форма модели является результатом преобразования
структурной формы модели
178. Проверка является ли временной ряд «белым шумом» осуществляется с помощью
статистики Бокса-Пирса
179. Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ______ работника
уровень образования
180. Простая линейная регрессия предполагает наличие
одного фактора и линейность уравнения регрессии
181. Расчет значения коэффициента детерминации не позволяет оценить
существенность коэффициента регрессии
182. Расчет средней ошибки аппроксимации для нелинейных уравнений регрессии связан с расчетом разности между ____________________________ переменной
фактическим и теоретическим значениями результативной
183. Расчетное значение критерия Фишера определяется как
отношение факторной дисперсии к остаточной, рассчитанных на одну степень свободы
184. Расчетное значение критерия Фишера определяется как ___________ факторной дисперсии и остаточной, рассчитанных на одну степень свободы
отношение
185. Расчетное значение критерия Фишера определяется как отношение
дисперсий
186. Результатом линеаризации полиномиальных уравнений является ______________ регрессии
линейные уравнения множественной
187. Свойствами оценок МНК являются: эффективность, а также
состоятельность и несмещенность
188. Система взаимозависимых уравнений в ее классическом виде называется также системой ______ уравнений
одновременных
189. Система независимых уравнений предполагает
совокупность независимых уравнений регрессии
190. Система нормальных уравнений метода наименьших квадратов строится на основании
таблицы исходных данных
191. Система рекурсивных уравнений включает в каждое
предыдущее (должно быть последующее) уравнение в качестве факторов все зависимые переменные предшествующих уравнений с набором собственно факторов
192. Система эконометрических уравнений не используется при моделировании
взаимосвязей временных рядов данных
193. Система эконометрических уравнений предполагает наличие _________ независимых признаков
нескольких зависимых и нескольких
194. Система эконометрических уравнений представляет систему
уравнений регрессии
195. Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить
методом определителей
196. Системы эконометрических уравнений классифицируются по
способу вхождения зависимых и независимых переменных в уравнение регрессии
197. Случайный характер остатков предполагает
независимость остатков от величины предсказанных по модели значений результативного признака
198. Смысл расчета средней ошибки аппроксимации состоит в определении среднего арифметического значения
отклонений, выраженных в процентах от фактических значений результативного признака
199. Совокупность значений критерия, при которых принимается нулевая гипотеза, называется областью _____________ гипотезы
принятия
200. Состоятельность оценки характеризуется
увеличением ее точности с увеличением объема выборки
201. Спецификацию нелинейного уравнения парной регрессии целесообразно использовать, если значение
индекса детерминации, рассчитанного для данной модели достаточно близко к 1
202. Спецификация модели нелинейная парная (простая) регрессия подразумевает нелинейную зависимость и
независимую переменную
203. Стандартная ошибка рассчитывается для проверки существенности
параметра
204. Статистические гипотезы используются для оценки
значимости уравнения регрессии в целом
205. Стационарность временного ряда не подразумевает отсутствие
стационарного стохастического процесса
206. Стационарность временного ряда означает отсутствие
тренда
207. Стационарность характерна для временного ряда
типа «белый шум»
208. Стохастическим процессом называется
набор случайных переменных X(t), где t – вещественные числа
209. Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________ потребителя
доход
210. Структурной формой модели называется система _______ уравнений
взаимосвязанных
211. Структурными коэффициентами модели называются коэффициенты ___________ в структурной форме модели
при экзогенных и эндогенных переменных
212. Структуру временного ряда можно выявить с помощью коэффициента __________ уровней ряда
автокорреляции
213. Табличное значение критерия Фишера служит для проверки статистической гипотезы о равенстве
факторной и остаточной дисперсий
214. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является
линейность параметров
215. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является:
линейность параметров
216. Увеличение точности оценок с увеличением объема выборки описывает свойство _______ оценки
состоятельности
217. Уравнение может быть линеаризовано при помощи подстановки
218. Уравнение регрессии характеризует зависимость
обратно пропорциональную
219. Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированных на среднем уровне значении других переменных, называется
частным
220. Уровнем временного ряда является
значение временного ряда в конкретный момент (период) времени
221. Факторная дисперсия служит для оценки влияния
учтенных явно в модели факторов
222. Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются
фиктивными
223. Факторы эконометрической модели являются коллинеарными, если коэффициент
корреляции между ними по модулю больше 0,7
224. Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков ____________ характера
качественного
225. Фиктивные переменные включаются в уравнения ____________ регрессии
множественной
226. Циклические колебания связаны с
общей динамикой конъюнктуры рынка
227. Экзогенными переменными не являются
зависимые переменные
228. Экзогенными переменными являются
независимые переменные
229. Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются _______________________ временными рядами
нестационарными
230. Экспоненциальным не является уравнение регрессии
231. Эндогенными переменными не являются:
независимые переменные
232. Эндогенными переменными являются
зависимые переменные
233. Эффективность оценки на практике характеризуется
возможность перехода от точечного оценивания к интервальному
также в рубрике Контрольные, тесты:
источники:
http://studall.org/all4-12208.html
http://studystuff.ru/controlnaya/testyi-po-ekonometrike
Парная регрессия
и корреляция
Контрольные вопросы
- Сформулируйте задачи, решаемые эконометрикой.
Эконометрика — наука,в которой
на базе реальных статистичеких данных
строятся,анализируются и совершенствуются
модели реальных экономических явлений.
Задачи эконометрики можно
классифицировать по 3 признакам:
1. по конечным прикладным
целям
2. по уровню иерархии
3. по профилю анализируемой
экономической системы.
1. Прогноз экономических
и социальных показателей,характеризующих
состояние и развитие системы. Имитация
возможных сценариев социально-экономического
развития системы для выявления того,как
это скажется на выходных характеристиках.
2.
- макроуровень (страна в целом)
- мезоуровень (отрасль,регион,корпорация)
- микроуровень (предприятие)
3. Задачи,направленные на решение
проблем:
- рынка
- инвестиционной финансовой деятельности
- ценообразования (большая доля государственного регулирования)
- распределительных отношений
- спроса и потребления
- Дайте определение парной регрессии.
Парная регрессия –
это уравнение связи двух переменных
у и х: y=f(х),
где
— независимая переменная, объясняющая,
входная, предсказывающая,
экзогенная, фактор, регрессор, факторный
признак.
— зависимая переменная, функция
отклика, объясняемая, выходная, результирующая,
эндогенная переменная, результативный
признак
Что такое
линия регрессии?
Вычисляемая с помощью
метода наименьших квадратов прямая
линия называется линией регрессии
. Она характеризуется тем, что сумма квадратов
расстояний от точек на диаграмме до этой
линии минимальна (по сравнению со всеми
возможными линиями). Линия регрессии
дает наилучшее приближенное описание
линейной зависимости между двумя переменными.
- Поясните экономическую сущность параметров уравнения парной регрессии.
В общем случае коэффициент
регрессии показывает, как в среднем изменится
результативный признак y, если факторный
признак x увеличится
на единицу . Коэффициент a может не иметь
экономического содержания, интерпретировать
можно только знак, он показывает направления
связи. Параметр а = у, когда х = 0. Если х
не может быть равен 0, то а не имеет экономического
смысла. Интерпретировать можно только
знак при а: если а > 0. то относительное
изменение результата происходит медленнее,
чем изменение фактора, т. е. вариация результата
меньше вариации фактора: V < V. и наоборот.
- Как производится оценка параметров уравнения парной регрессии.
Построение линейной регрессии
сводится к оценке ее параметров –
a и b. Классический подход к оцениванию
параметров линейной регрессии основан
на методе наименьших квадратов (МНК).
МНК позволяет получить такие
оценки параметров a и b, при которых
сумма квадратов отклонений фактических
значений результативного признака
y от теоретических минимальна.
- Что является показателем тесноты связи в парной линейной регрессии?
Тесноту связи изучаемых
явлений оценивает линейный коэффициент
парной корреляции rxy
для линейной регрессии.
- В каких пределах находится значение коэффициента корреляции?
Коэффициент корреляции принимает
значения в интервале от -1 до +1. Теснота
линейной связи между переменными
может быть оценена на основании
шкалы Чеддока:
Положительное значение коэффициента
корреляции говорит о положительной связи
между х и у, когда с ростом одной из переменных
другая тоже растет. Отрицательное значение
коэффициента корреляции означает, с ростом
одной из переменных другая убывает, с
убыванием одной из переменной другая
растет.
- Для чего рассчитывают коэффициент детерминации и что он характеризует?
Оценку качества построенной
модели дает коэффициент (индекс) детерминации
R2.
Для оценки качества подбора
линейной функции рассчитывается квадрат
линейного коэффициента корреляции, называемый
коэффициентом детерминации. Коэффициент
детерминации показывает, сколько процентов
приходится на долю учтенных в модели
факторов:
Соответственно величина
1-R2 характеризует долю дисперсии
y, вызванную влиянием остальных, не учтенных
в модели, факторов. Коэффициентом детерминации, или долей
объясненной дисперсии называется:
.
В силу определения
.
Что такое
число степеней свободы и как
оно определяется для факторной
и остаточной суммы квадратов?
Любая сумма квадратов
отклонений связана с числом степеней
свободы, т.е. с числом свободы независимого
варьирования признака. Значит число
степеней свободы связано с числом
единиц совокупности
и с числом определяемых по ней констант.
Применительно к исследуемой проблеме
число степеней свободы должно показывать,
сколько независимых отклонений из
возможных
требуется для образования данной
суммы квадратов. Так для общей суммы квадратов
требуется
независимое отклонение, ибо по совокупности
из
единиц после расчета среднего уровня
, свободно варьируют лишь
числом отклонений. Число степеней
свободы в левой и правой частях соотношения
(*) должно совпадать, то число степеней
свободы второго слагаемого должно быть
равно (n — 2).
То есть
.
При расчете факторной
суммы квадратов — 1 степень свободы,
и при расчете остаточной суммы
квадратов — (n-2) степени свободы.
- Какова концепция F-критерия Фишера?
Разделив каждую сумму
квадратов на соответствующее ей
число степеней свободы, получим средний квадрат
отклонений, или, что тоже самое, дисперсию на
одну степень свободы D
.
Это приводит дисперсии к
сравнимому виду. Сопоставляя факторную
и остаточные дисперсии в расчете
на одну степень свободы, получим
величину F — отношения (F- критерия):
, где F- критерий для проверки нулевой
гипотезы
:
.
Если нулевая гипотеза
справедлива, то
и
не отличаются друг от друга. Для
необходимо опровержение,
то есть, чтобы факторная дисперсия превышала
остаточную в несколько раз.
— это максимальная величина
отношения дисперсий, которая
может иметь место при случайном
их расхождении для данного
уровня вероятности.
F-критерий — это оценивание качества
уравнения регрессии, которое состоит
в проверке гипотезы
о статистической незначимости
уравнения регрессии и показателя
тесноты связи. Для этого производится
сравнение фактического
и
значений F критерия Фишера-Снедекора.
определяется из соотношения значений
факторной и остаточной дисперсий, рассчитанных
на одну степень свободы
.
— это максимально возможное
значение критерия под влиянием
случайных факторов при данных
степенях свободы и уровне
значимости
. Уровень значимости
— это вероятность отвергнуть правильную
гипотезу при условии, что она верна. Обычно
.
Если
<
, то
— гипотеза о случайной природе оцениваемых
характеристик отклоняется и признается
их статистическая значимость и надежность.
Если
>
, то
— гипотеза не отклоняется и признается
статистическая незначимость, ненадежность
уравнения регрессии.
- В чем смысл средней ошибки аппроксимации и как она определяется?
Cредняя ошибка аппроксимации
дает оценку качества построенной модели.
Средняя ошибка аппроксимации — среднее
отклонение расчетных значений от фактических
в процентах:
.
Предел значений
считаем допустимым при построении
модели.
- Как оценивается значимость параметров уравнения регрессии?
Оценку статистической значимости
коэффициента корреляции проводят с помощью
t-критерия Стьюдента. Выдвигают гипотезу
Н0 о статистически незначимом отличии
коэффициента от нуля. Величина стандартной
ошибки совместно с t-распределением Стьюдента
при n-2 степенях свободы применяется для
проверки значимости коэффициента регрессии
и для расчета его доверительного интервала.
Для оценки значимости коэффициента регрессии
его величина сравнивается с его стандартной
ошибкой, т.е. определяется фактическое
значение t-критерия Стьюдента:
, причем
,причем
,т.е
.
которое затем сравнивается
с табличным значением при определенном
уровне значимости a и числе степеней свободы
n-2. Если tфакт>tтабл, то делается вывод
о значимости параметра.
От чего зависит
точность предсказания значения зависимой
переменной на основе уравнения парной
регрессии?
- Запишите все виды моделей, нелинейных относительно включаемых переменных и оцениваемых параметров.
Если между экономическими
явлениями существуют нелинейные соотношения,
то они выражаются с помощью соответствующих
нелинейных функций.
Различают два класса нелинейных
регрессий:
- Нелинейные по объясняющим параметрам:
Полиномы различных
степеней
Равносторонняя
гипербола
Полулогарифмическая
функция
- Регрессии, нелинейные по оцениваемым параметрам:
Степенная:
Показательная:
Экспоненциальная:
Логарифмическая:
Полулогарифмическая:
Обратная:
- Как осуществляется линеаризация модели?
Для нахождения параметров
регрессии необходимо провести
ее линеаризацию:Y=A+bX
Регрессии нелинейные по включенным
переменным приводятся к линейному виду
простой заменой переменных, а дальнейшая
оценка параметров производится с помощью
метода наименьших квадратов.
Несколько иначе обстоит
дело с регрессиями нелинейными по оцениваемым
параметрам, которые делятся на два типа:
нелинейные модели внутренне линейные
(приводятся к линейному виду с помощью
соответствующих преобразований, например,
логарифмированием) и нелинейные модели
внутренне нелинейные (к линейному виду
не
приводятся).
- Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков.
Уравнение нелинейной регрессии,
так же как и в линейной зависимости,
дополняется показателем корреляции,
а именно индексом корреляции (R):
где
Так как
то индекс корреляции можно
выразить как
Величина данного показателя
находится в границах
чем ближе к единице, тем теснее связь
рассматриваемых признаков, тем более
надежно найденное уравнение регрессии.
- Как определяются коэффициенты эластичности по разным видам регрессионных моделей?
Средний коэффициент эластичности
показывает, на сколько % в среднем
по совокупности изменится результат
от своей средней величины при изменении
фактора
на 1% от своего среднего значения
— характеризует соотношение
прироста результата и фактора
для соответствующей формы связи.
Т.к., коэффициент Э не
всегда const, то используем среднее значение
—
.
В таблице представлены формулы
эластичности для наиболее употребительных
функций.
|
|
||
Иногда коэффициент Э экономического
смысла не имеет. Это происходит тогда,
когда для рассматриваемых признаков
бессмысленно определение изменения значений
в процентах. Например, изменение роста
заработной платы с ростом стажа работы
на 1%.
Тест 1
1. Графическое
изображение наблюдений на декартовой
плоскости координат называется
полем …
1. регрессии;
2. корреляции;
3. случайных воздействий;
4. автокорреляции.
2. В линейном
уравнении парной регрессии у=а+bx коэффициентом
регрессии является значение
1. параметров а и b;
2. параметра a;
3. переменной x;
4. параметра b.
3. Величина параметра а в уравнении
парной линейной регрессии у=а+bx характеризует
значение …
1. факторной переменной
при нулевом значении результата;
2. результирующей переменной
при нулевом значении случайной
величины;
3. факторной переменной
при нулевом значении случайного
фактора;
4. результирующей
переменной при нулевом значении фактора.
4. Объем выборки
должен превышать число рассчитываемых
параметров при исследуемых факторах
1. в 2-3 раза;
2. в 20-25 раз;
3. в 10-12 раз;
4. в 7-8 раз.
5. Объем выборки
определяется …
1. числовыми значениями
переменных, отбираемых в выборку;
2. объёмом генеральной
совокупности;
3. числом параметров при
независимых переменных;
4. числом результативных
переменных.
6. Основной задачей
эконометрики является …
1. установление связей
между различными процессами
в обществе и техническим процессом;
2. анализ технического
процесса на примере социально-экономических
показателей;
3. отражение особенности
социального развития общества;
4. исследование
взаимосвязей экономических явлений и
процессов.
7. Наиболее наглядным
видом выбора уравнения парной
регрессии является:
1. аналитический;
2. графический;
3. экспериментальный (табличный).
8. Суть метода
наименьших квадратов состоит
в:
1. минимизации суммы остаточных
величин;
2. минимизации дисперсии
результативного признака;
3. минимизации
суммы квадратов остаточных величин.
9. Коэффициент
линейного парного уравнения
регрессии:
1. показывает среднее
изменение результата с изменением фактора
на одну единицу;
2. оценивает статистическую
значимость уравнения регрессии;
3. показывает, на сколько
процентов изменится в среднем
результат, если фактор изменится
на 1%.
10. Классический
метод к оцениванию параметров
регрессии основан на:
1. методе наименьших
квадратов;
2. методе максимального
правдоподобия;
3. шаговом регрессионном
анализе.
11. Простая линейная
регрессия предполагает …
1. наличие двух и более
факторов и нелинейность уравнения
регрессии;
2. наличие одного
фактора и линейность уравнения регрессии;
3. наличие одного фактора
и нелинейность уравнения регрессии;
4. наличие двух и более
факторов и линейность уравнения
регрессии.
12. Метод наименьших
квадратов позволяет оценить
уравнений регрессии:
1. переменные и случайные
величины;
2. параметры;
3. переменные;
4. параметры и переменные.
13. Коэффициент
регрессии в линейной регрессии
совокупного спроса на мобильные
телефоны (тыс. руб.) по цене (руб.)
оказался равным -1 Это означает:
1. увеличение цены на 1%
снижает спрос на мобильные
телефоны на 1%;
2. увеличение цена на 1
рубль снижает спрос на мобильные
телефоны на 1%;
3. увеличение цены на 1%
снижает спрос на мобильные
телефоны на 1 тысячу рублей;
4. увеличение цены на 1
рубль снижает спрос на мобильные
телефоны на 1 тысячу рублей;
5. полученное число
никак не интерпретируется.
Тест 2
1. Значение коэффициента
корреляции составило 2, следовательно
1. значение коэффициента
корреляции рассчитано с ошибкой;
2. теснота связи в 2
раза сильнее, чем для функциональной
связи;
3. связь функциональная;
4. при увеличении фактора
на единицу значение результата
увеличивается в 2 раза.
2. Значение коэффициента
корреляции не характеризует
…
1. статистическую
значимость уравнения;
2. корень из значения
коэффициента детерминации;
3. тесноту связи;
4. силу связи.
3. Для уравнения зависимости
выручки от величины оборотных
средств получено значение коэффициента
детерминации, равное 0,7.
Следовательно, _______ процентов
дисперсии обусловлено случайными
факторами.
1. 30%;
2. 100%;
3. 70%;
4. 0%.
4. Значения коэффициента
корреляции может находиться
в отрезке:
1. [-1;0];
2. [0;1];
3. [-1;1];
4. [-2;2].
5. Качество подбора
уравнения оценивает коэффициент
1. корреляции;
2. детерминации;
3. эластичности;
4. регрессии.
6. Расчётное значение
критерия Фишера определяется
как отношение
1. дисперсий;
2. результата к фактору;
3. математических ожиданий;
4. случайных величин.
7. При хорошем
качестве модели допустимым значением
средней ошибки аппроксимации
является
1. 5-7%;
2. 50%;
3. 90-95%;
4. 20-25%.
8. Случайными воздействиями
обусловлено 12% дисперсии результативного
признака, следовательно, значение
коэффициента детерминации составило:
1. 88;
2. 0,12;
3. 0,88;
4. 12.
9. Значение линейного
коэффициента корреляции характеризует
тесноту … связи.
1. нелинейной;
2. линейной;
3. случайной;
4. множественной линейной.
10. В качестве
показателя тесноты связи для
линейного уравнения парной регрессии
используется:
1. множественный коэффициент
линейной корреляции;
2. линейный коэффициент
корреляции;
03. линейный коэффициент регрессии;
4. линейный коэффициент
детерминации.
11. Значение коэффициента
корреляции равно 0,9. Следовательно,
значение коэффициента детерминации
составит …
1. 0,3;
2. 0,81;
3. 0,95;
4. 0,1.
12. Если средняя
ошибка аппроксимации равна 12%,
то говорят, что
1. качество построенной
модели плохое;
2. связь между признаком
и фактором слабая;
3. качество построенной
модели хорошее;
4. связь между признаком
и фактором сильная.
13. Если 0≤ │rxy│≤ 0,3, то о связи между
фактором и признаком можно сказать, что
она
1. умеренная;
2. сильная;
3. отсутствует;
4. слабая.
14. О сильной
связи между фактором и признаком
говорит то, что
Правильный
ответ: 2
15. «Необъяснённую»
сумму квадратов отклонений иначе
называют:
1. остаточной суммой
квадратов отклонений;
2. факторной суммой квадратов
отклонений;
3. общей суммой квадратов
отклонений;
4. средней суммой квадратов
отклонений.
16. О слабой
связи между фактором и признаком
говорит то, что
Правильный
ответ: 3
17. «Объяснённую»
сумму квадратов отклонений иначе
называют:
1. общей суммой квадратов
отклонений;
2. факторной суммой
квадратов отклонений;
3. остаточной суммой квадратов
отклонений;
4. средней суммой квадратов
отклонений.
18. Коэффициент
уравнения парной регрессии показывает:
1. тесноту связи между
зависимой и независимой переменными;
2. на сколько процентов
изменится зависимая переменная,
если независимая переменная
изменится на единицу;
3. на сколько процентов
изменится зависимая переменная,
если независимая переменная
изменится на 1%;
4. на сколько
единиц изменится зависимая переменная,
если независимая переменная изменится
на 1 ед.
19. Степень влияния
неучтённых факторов в рассматриваемой
модели можно определить на
основе:
- парного линейного коэффициента корреляции;
2. частного коэффициента
корреляции;
3. индекса корреляции;
4. коэффициента
детерминации
5. коэффициента регрессии.
20. Дисперсионный
анализ уравнения парной регрессии
проверяет:
1. значимость коэффициента
корреляции;
2. значимость уравнения
регрессии;
3. значимость коэффициента
регрессии;
4. значимость свободного
члена уравнения регрессии.
21. Коэффициент
корреляции больше нуля, это означает,
что
1. связь между
переменными тесная;
2. связь между переменными
прямая;
3. связь между переменными
обратная;
4. связь между переменными
отсутствует.
22. Оценка значимости
уравнения в целом осуществляется
по критерию:
1. Фишера;
2. Дарбина-Уотсона;
3. Пирсона;
4. Стьюдента.
23. Если расчётное
значение критерия Фишера меньше
табличного значения, то гипотеза
о статистической незначимости уравнения
1. незначима;
2. несущественна;
3. отвергается;
4. принимается.
24. Табличное значение
критерия Фишера определяется
по:
1. уровню значимости
и степеням свободы факторной и остаточной
дисперсий;
2. уровню значимости и
степени свободы общей дисперсии;
3. уровню значимости;
4. степени свободы факторной
и остаточной дисперсий.
25. Общая дисперсия
служит для оценки влияния
1. учтённых явно в модели
факторов;
2. как учтённых
факторов, так и случайных воздействий;
3. величины постоянной
составляющей в уравнении;
4. случайных воздействий.
26. Остаточная дисперсия
служит для оценки влияния
1. случайных воздействий;
2. величины постоянной
составляющей в уравнении;
3. учтённых явно в модели
факторов;
4. как учтённых факторов,
так и случайных воздействий.
27. Расчётное значение
критерия Фишера определяется
как
1. разность факторной
дисперсии и остаточной, рассчитанных
на одну степень свободы;
2. отношение факторной
дисперсии к остаточной;
3. отношение факторной
дисперсии к остаточной, рассчитанных
на одну степень свободы;
4. суммы факторной дисперсии
к остаточной, рассчитанных на одну
степень свободы.
28. Факторная дисперсия
служит для оценки влияния:
1. как учтённых факторов,
так и случайные воздействия;
2. учтённых явно
в модели факторов;
3. величины постоянной
составляющей в уравнении;
4. случайных воздействий.
29. Расчётное значение
критерия Фишера определяется
как …факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы
1. произведение;
2. разность;
3. сумма;
4. отношение.
30. Парный линейный коэффициент
корреляции характеризует наличие
слабой обратной связи, значит
он принимает следующее значение:
1. 1,2;
2. –0,82;
3. 0,23;
4. 0,92;
5. –0,24.
31. Коэффициент
корреляции равен нулю, это означает,
что
1. связь между переменными
тесная;
2. связь между переменными
прямая;
3. связь между переменными
обратная;
4. связь между
переменными отсутствует.
32. Коэффициент
корреляции меньше нуля, это означает,
что
1. связь между переменными
тесная;
2. связь между переменными
прямая;
3. связь между
переменными обратная;
4. связь между переменными
отсутствует.
33. Остаточная
сумма квадратов равна нулю:
1. когда правильно подобрана
регрессионная модель;
2. когда между признаками
существует точная функциональная
связь;
3. никогда.
34. Табличное значение F-критерия Фишера
меньше расчётного F-критерия Фишера.
Это значит:
1. уравнение регрессии
значимо;
2. уравнение регрессии
незначимо;
3. все коэффициенты уравнения
регрессии равны нулю;
4. не все коэффициенты
уравнения регрессии равны нулю.
35. Остаточная
сумма квадратов отклонений вычисляется
по формуле:1
Тест 3
1. Критерий Стьюдента
предназначен для определения
значимости
1. построенного уравнения
в целом;
2. коэффициента детерминации;
3. уравнения;
4. параметров регрессии.
2. Если доверительный
интервал для параметра проходит
через точку ноль, то
1. значение параметра
может принимать как отрицательные,
так и положительные значения;
2. параметр является
несущественным;
3. параметр является существенным;
4. параметр признается
статистически значимым.
3. Параметр является
существенным, если
1. доверительный
интервал не проходит через ноль;
2. доверительный интервал
проходит через ноль;
3. расчётное значение
критерия Стьюдента меньше табличного
значения;
4. стандартная ошибка
превышает половину значения
самого параметра.
4. Стандартная
ошибка рассчитывается для проверки
существенности
1. параметра;
2. коэффициента детерминации;
3. случайной величины;
4. коэффициента эластичности.
5. Для существенного
параметра расчётное значение
критерия Стьюдента
1. равно нулю;
2. больше табличного
значения критерия;
3. не больше табличного
значения критерия;
4. меньше табличного значения
критерия.
6. Назовите показатель
корреляции для нелинейных моделей
регрессии:
1. парный коэффициент
линейной корреляции;
2. индекс детерминации;
3. линейный коэффициент
корреляции;
4. индекс корреляции.
7. Линеаризация
подразумевает процедуру …
1. приведения уравнения
множественной регрессии к парной;
2. приведения нелинейного
уравнения к линейному виду;
3. приведения линейного
уравнения к нелинейному виду;
4. приведения нелинейного
уравнения относительно параметров к
уравнению, линейному относительно результата.
8. К линейному
виду нельзя привести:
Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода
(*ответ*) наименьших квадратов
нормальных квадратов
наибольших квадратов
средних квадратов
После применения обобщенного метода наименьших квадратов удается избежать _ остатков
(*ответ*) гетероскедастичности
случайного характера
нормального распределения
равенства нулю суммы
Предпосылкой метода наименьших квадратов является
(*ответ*) отсутствие автокорреляции в остатках
присутствие автокорреляции между результатом и фактором
отсутствие корреляции между результатом и фактором
присутствие автокорреляции в остатках
При включении фиктивных переменных в модель им присваиваются
(*ответ*) числовые метки
нулевые значения
качественные метки
одинаковые значения
При оценке статистической значимости уравнения и существенности связи осуществляется проверка
(*ответ*) существенности коэффициента детерминации
нулевой гипотезы
существенности параметров
существенности коэффициента корреляции
При применении метода наименьших квадратов уменьшить гетероскедастичность остатков удается путем
(*ответ*) преобразования переменных
введения дополнительных факторов в модель
введения дополнительных результатов в модель
преобразования параметров
Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться _ работника
(*ответ*) уровень образования
заработная плата
стаж
возраст
Расчетное значение критерия Фишера определяется как
(*ответ*) отношение факторной дисперсии к остаточной, рассчитанных на одну степень свободы
суммы факторной дисперсии к остаточной, рассчитанных на одну степень свободы
отношение факторной дисперсии к остаточной
разность факторной дисперсии и остаточной, рассчитанных на одну степень свободы
Расчетное значение критерия Фишера определяется как _ факторной дисперсии и остаточной, рассчитанных на одну степень свободы
(*ответ*) отношение
произведение
разность
сумма
Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить
(*ответ*) методом определителей
методом скользящего среднего
симплекс-методом.
методом первых разностей
Случайный характер остатков предполагает
(*ответ*) независимость остатков от величины предсказанных по модели значений результативного признака
независимость предсказанных по модели значений результативного признака от значений факторного признака
зависимость остатков от величины предсказанных по модели значений результативного признака
зависимость предсказанных по модели значений результативного признака от значений факторного признака
Стандартная ошибка рассчитывается для проверки существенности
(*ответ*) параметра
коэффициента корреляции
случайной величины
коэффициента детерминации
Линейный коэффициент детерминации. 1 страница
Предпосылки метода наименьших квадратов исследуют поведение …
— параметров уравнения регрессии;
— переменных уравнения регрессии.
Величина параметра  в уравнении парной линейной регрессии
в уравнении парной линейной регрессии  характеризует значение …
характеризует значение …
— факторной переменной при нулевом значении результата;
— результирующей переменной при нулевом значении случайной величины;
— факторной переменной при нулевом значении случайного фактора;
+ результирующей переменной при нулевом значении фактора.
Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно, …
— нелинейная связь недостаточно тесная;
— линейная связь достаточно тесная;
+ нелинейная связь достаточно тесная;
— нелинейная связь отсутствует.
Состоятельность оценки характеризуется …
— независимостью от объема выборки значения математического ожидания остатков;
+ увеличением ее точности с увеличением объема выборки;
— уменьшением ее точности с увеличением объема выборки;
— зависимостью от объема выборки значения математического ожидания остатков.
Если предпосылки метода наименьших квадратов нарушены, то …
— полученное уравнение статистически незначимо;
+ оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности;
— коэффициент регрессии является несущественным;
— коэффициент корреляции является несущественным.
Общая дисперсия служит для оценки влияния …
— учтенных явно в модели факторов;
+ как учтенных факторов, так и случайных воздействий;
— величины постоянной составляющей в уравнении;
Значение коэффициента корреляции равно -1. Следовательно …
Нелинейным называется уравнение регрессии, если …
— параметры входят нелинейным образом, а переменные линейны;
+ независимые переменные входят в уравнение нелинейным образом;
— параметры и зависимые переменные входят в уравнение нелинейным образом;
— зависимые переменные входят в уравнение нелинейным образом.
Если коэффициент регрессии является несущественным, то его значения приравниваются к …
— табличному значению и соответствующий фактор не включается в модель;
+ нулю и соответствующий фактор не включается в модель;
— единице и не влияет на результат;
— нулю и соответствующий фактор включается в модель.
Величина отклонений фактических значений результативного признака от его теоретических значений представляет собой …
— значение критерия Фишера;
Объем выборки должен превышать число рассчитываемых параметров при исследуемых факторах ..
Остаточная дисперсия служит для оценки влияния …
— величины постоянной составляющей в уравнении;
— учтенных явно в модели факторов;
— как учтенных факторов, так и случайных воздействий.
Значение коэффициента корреляции равно 0,9. Следовательно, значение коэффициента детерминации составит …
По результатам исследования было выявлено, что рентабельность производства падает с увеличением трудоемкости. Какую спецификацию уравнения регрессии можно использовать для построения модели такой зависимости?
—  ;
;
+  ;
;
—  ;
;
—  .
.
Случайный характер остатков предполагает …
— независимость предсказанных по модели значений результативного признака от значений факторного признака;
+ независимость остатков от величины предсказанных по модели значений результативного признака;
— зависимость остатков от величины предсказанных по модели значений результативного признака;
— зависимость предсказанных по модели значений результативного признака от значений факторного признака.
Статистические гипотезы используются для оценки:
— тесноты связи между результатом и фактором;
— тесноты связи между результатом и случайными факторами;
— автокорреляции в остатках;
+ значимости уравнения регрессии в целом.
Параметр является существенным, если …
+ доверительный интервал не проходит через ноль;
— доверительный интервал проходит через ноль;
— расчетное значение критерия Стьюдента меньше табличного значения;
— стандартная ошибка превышает половину значения самого параметра.
Замена  ,
,  подходит для уравнения:
подходит для уравнения:
—  ;
;
—  ;
;
—  ;
;
+  .
.
В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений …
— приравнивается к нулю;
— приравнивается к системе нормальных уравнений.
При выборе спецификации нелинейная регрессия используется, если …
— нелинейная зависимость для исследуемых экономических показателей является несущественной;
+ между экономическими показателями обнаруживается нелинейная зависимость;
— между экономическими показателями не обнаруживается нелинейная зависимость;
— между экономическими показателями обнаруживается линейная зависимость.
Табличное значение критерия Фишера служит для …
+ проверки статистической гипотезы о равенстве факторной и остаточной дисперсий;
— проверки статистической гипотезы о равенстве дисперсии некоторой гипотетической величины;
— проверки статистической гипотезы о равенстве двух математических ожиданий;
— проверки статистической гипотезы о равенстве математического ожидания некоторой гипотетической величины.
Предпосылкой метода наименьших квадратов является то, что остатки …
— не подчиняются закону больших чисел;
+ подчиняются закону нормального распределения;
— не подчиняются закону нормального распределения;
— подчиняются закону больших чисел.
Расчетное значение критерия Фишера определяется как …
— разность факторной дисперсии и остаточной, рассчитанных на одну степень свободы;
— отношение факторной дисперсии к остаточной;
+ отношение факторной дисперсии к остаточной, рассчитанных на одну степень свободы;
— суммы факторной дисперсии к остаточной, рассчитанных на одну степень свободы.
Предпосылкой метода наименьших квадратов не является условие …
— случайный характер остатков;
— отсутствие автокорреляции в остатках;
+ неслучайный характер остатков.
Нелинейное уравнение регрессии означает нелинейную форму зависимости между:
— фактором и результатом;
— фактором и случайной величиной;
+ результатом и факторами;
— результатом и параметрами.
Несмещенность оценки на практике означает …
— уменьшение точности с увеличением объема выборки;
— невозможность перехода от точечного оценивания к интервальному;
— что найденное значение коэффициента регрессии нельзя рассматривать как среднее значение из возможного большого количества несмещенных оценок;
+ что при большом числе выборочных оцениваний остатки не будут накапливаться.
Стандартная ошибка рассчитывается для проверки существенности …
Факторная дисперсия служит для оценки влияния:
— как учтенных факторов, так и случайные воздействия;
+ учтенных явно в модели факторов;
— величины постоянной составляющей в уравнении;
Экспоненциальным не является уравнение регрессии:
—  ;
;
—  ;
;
+  ;
;
—  .
.
Известно, что с увеличением объема производства себестоимость единицы продукции уменьшается за счет того, что происходит перераспределение постоянных издержек. Пусть  — совокупная величина постоянных издержек, а
— совокупная величина постоянных издержек, а  — величина переменных издержек в расчете на 1 изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели:
— величина переменных издержек в расчете на 1 изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели:
—  ;
;
—  ;
;
+  ;
;
—  .
.
В основе метода наименьших квадратов лежит …
— равенство нулю суммы квадратов отклонений фактических значений результативного признака от его теоретических значений;
— минимизация суммы квадратов отклонений фактических значений результативного признака от его средних значений;
+ минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений;
— максимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений.
Объем выборки определяется …
— числовыми значениями переменных, отбираемых в выборку;
— объемом генеральной совокупности;
+ числом параметров при независимых переменных;
— числом результативных переменных.
При оценке статистической значимости уравнения и существенности связи осуществляется проверка …
— существенности коэффициента корреляции;
+ существенности коэффициента детерминации;
Для модели зависимости дохода населения (р.) от объема производства (млн р.) получено уравнение  . При изменении объема производства на 1 млн р. доход в среднем изменится на …
. При изменении объема производства на 1 млн р. доход в среднем изменится на …
Относительно формы зависимости различают …
— простую и множественную регрессию;
— положительную и отрицательную регрессию;
— непосредственную и косвенную регрессию;
+ линейную и нелинейную регрессию.
В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между …
— переменными и случайными факторами;
— параметрами и переменными.
Уравнение регрессии 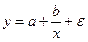 может быть реализовано при помощи подстановки:
может быть реализовано при помощи подстановки:
—  ;
;
—  ;
;
+  ;
;
—  .
.
Спецификацию нелинейного уравнения парной регрессии целесообразно использовать, если значение …
— линейного коэффициента корреляции для исследуемой зависимости близко к 1;
— индекса корреляции для исследуемой зависимости близко к 0;
+ индекса детерминации, рассчитанного для данной модели достаточно близко к 1;
— доля остаточной дисперсии результативного признака в его общей дисперсии стремится к 1.
Если значение коэффициента корреляции равно единице, то связь между результатом и фактором …
Эффективность оценки на практике характеризуется …
— невозможностью перехода от точечного оценивания к интервальному;
— отсутствием накапливания значений остатков при большом числе выборочных оцениваний;
— уменьшением точности с увеличением объема выборки;
+ возможность перехода от точечного оценивания к интервальному
Линеаризация не подразумевает процедуру …
+ включение в модель дополнительных существенных факторов;
— приведение нелинейного уравнения к линейному;
Основной задачей эконометрики является …
— установление связей между различными процессами в обществе и техническим процессом;
— анализ технического процесса на примере социально-экономических показателей;
— отражение особенности социального развития общества;
+ исследование взаимосвязей экономических явлений и процессов.
При применении метода наименьших остатков уменьшить гетероскедастичность остатков удается путем …
— введения дополнительных результатов в модель;
— введения дополнительных факторов в модель.
Значение индекса детерминации, рассчитанное для нелинейного уравнения регрессии характеризует …
+ долю дисперсии результативного признака, объясненную нелинейной регрессией в общей дисперсии результативного признака;
— долю дисперсии результативного признака, объясненную линейной корреляцией в общей дисперсии результативного признака;
Предпосылкой метода наименьших квадратов является …
— присутствие автокорреляции между результатом и фактором;
— отсутствие корреляции между результатом и фактором;
— присутствие автокорреляции в остатках;
+ отсутствие автокорреляции в остатках.
Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии …
—  ;
;
—  ;
;
—  ;
;
+  .
.
Если оценка параметра эффективна, то это означает …
— максимальную дисперсию остатков;
— уменьшение точности с увеличением объема выборки;
— равенство нулю математического ожидания остатков;
+ наименьшую дисперсию остатков.
При выборе спецификации модели парная регрессия используется в случае, когда …
— среди множества факторов, влияющих на результат, можно выделить лишь случайные факторы;
— среди множества факторов, влияющих на результат, можно выделить несколько факторов;
+ среди множества факторов, влияющих на результат, можно выделить доминирующий фактор;
— среди множества факторов, влияющих на результат, нельзя выделить доминирующий фактор.
Нелинейную модель зависимостей экономических показателей нельзя привести к линейному виду, если …
+ нелинейная модель является внутренне нелинейной;
— нелинейная модель является внутренне линейной;
— линейная модель является внутренне нелинейной;
— линейная модель является внутренне линейной.
Для существенного параметра расчетное значение критерия Стьюдента …
+ больше табличного значения критерия;
— не больше табличного значения критерия;
— меньше табличного значения критерия.
Оценить статистическую значимость нелинейного уравнения регрессии можно с помощью …
— средней ошибки аппроксимации;
— линейного коэффициента корреляции;
Расчетное значение критерия Фишера определяется как ___________факторной дисперсии и остаточной, рассчитанных на одну степень свободы
Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о …
— статистической незначимости значения параметра;
— равенства нулю значения параметра.
Если между экономическими показателями существует нелинейная связь, то …
— нецелесообразно использовать спецификацию нелинейного уравнения регрессии;
+ целесообразно использовать спецификацию нелинейного уравнения регрессии;
— целесообразно использовать линейное уравнение парной регрессии;
— необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии.
Оценка значимости параметров уравнения регрессии осуществляется по критерию …
Назовите показатель тесноты связи для нелинейных моделей регрессии:
— линейный коэффициент корреляции;
— парный коэффициент линейной корреляции.
Объем выборки определяется числом параметров при …
— независимых и зависимых переменных.
Значение индекса корреляции, рассчитанное для нелинейного уравнения регрессии характеризует …
— тесноту случайной связи;
— тесноту линейной связи;
+ тесноту нелинейной связи;
— тесноту обратной связи.
Тема Парная регрессия (Задачи)
Зависимость спроса на кухонные комбайны y от цены x по 12 торговым точкам компании имеет вид:


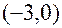
В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,4 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Нет, на любом уровне (0,1; 0,05 и 0,1)
—Да, на любом уровне (0,1; 0,05 и 0,1)
—Нет, только на уровнях 0,05 и 0,1
—Нет, только на уровне 0,1
Зависимость спроса на кухонные комбайны y от цены x по 18 торговым точкам компании имеет вид:



В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,5 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Да, только на уровне значимости 0,01
—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровнях 0,01 и 0,05
—Да, на любом уровне (0,1, 0,05 и 0,01)
Зависимость спроса на кухонные комбайны y от цены x по 15 торговым точкам компании имеет вид:
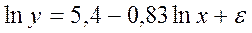


В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,3 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Да, на любом уровне (0,1, 0,05 и 0,01)
—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровнях 0,01 и 0,05
—Да, только на уровне значимости 0,01
Зависимость спроса на кухонные комбайны y от цены x по 12 торговым точкам компании имеет вид:

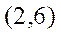

В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,3 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Да, только на уровнях 0,01 и 0,05
—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровне значимости 0,01
—Да, на любом уровне (0,1, 0,05 и 0,01)
Зависимость спроса на кухонные комбайны y от цены x по 14 торговым точкам компании имеет вид:



В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,2%. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровне значимости 0,01
—Да, только на уровнях 0,01 и 0,05
—Да, на любом уровне (0,1, 0,05 и 0,01)
Зависимость спроса на кухонные комбайны y от цены x по 15 торговым точкам компании имеет вид:

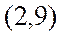

В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,1 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Да, только на уровнях 0,01 и 0,05
—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровне значимости 0,01
—Да, на любом уровне (0,1, 0,05 и 0,01)
Зависимость спроса на кухонные комбайны y от цены x по 20 торговым точкам компании имеет вид:

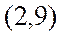

В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,3 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?
+—Да, только на уровне значимости 0,01
—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровнях 0,01 и 0,05
—Да, на любом уровне (0,1, 0,05 и 0,01)
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=50 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 


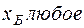
— 



— 



— 
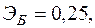


Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=60 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+— 
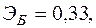


— 



— 
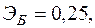


— 



Учебные материалы для студентов
Методические указания, конспекты, лекции, контрольные, лабораторные работы, курсовые.
Тесты по эконометрике
1. «Белым шумом» называется ___________ процесс
чисто случайный
2. Автокорреляционной функцией временного ряда называется
последовательность значений коэффициентов автокорреляции различных порядков
3. В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений
минимизируется
4. В качестве показателя тесноты связи для линейного уравнения парной регрессии используется
линейный коэффициент корреляции
5. В качестве фиктивных переменных в модель множественной регрессии включаются факторы
не имеющие количественных значений
6. В левой части системы взаимозависимых переменных, как правило, находится
одна зависимая переменная
7. В левой части системы независимых уравнений находится
совокупность зависимых переменных
8. В линейном уравнении парной регрессии коэффициентом регрессии является значение
параметра b
9. В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между
переменными
10. В нелинейной модели парной регрессии функция является
нелинейной
11. В общем случае каждый уровень временного ряда формируется под воздействием
тенденции, сезонных колебаний и случайных факторов
12. В основе метода наименьших квадратов лежит
минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
13. В приведенной форме модели в правой части уравнений находятся
только независимые переменные
14. В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как ______________ уравнений и количества независимых факторов
сумма количества зависимых переменных предыдущих
15. В системе независимых уравнений каждое уравнение представлено
изолированным уравнением регрессии
16. В стандартизованном уравнении множественной регрессии ;. Определите, какой из факторов х1 или х2 оказывает более сильное влияние на
,так как 2,1>0,3
17. В стандартизованном уравнении множественной регрессии переменными являются
стандартизованные переменные
18. В стандартизованном уравнении свободный член
отсутствует
19. Величина коэффициента детерминации при включении существенного фактора в эконометрическую модель
будет увеличиваться
20. Величина остаточной дисперсии при включении существенного фактора в модель
будет уменьшаться
21. Величина отклонений фактических значений результативного признака от его теоретических значений представляет собой
ошибку аппроксимации
22. Величина параметра в уравнении парной линейной регрессии характеризует значение
результирующей переменной при нулевом значении фактора
23. Взаимодействие факторов эконометрической модели означает, что
влияние одного из факторов на результирующий признак не зависит от значений другого фактора
24. Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является
существенным
25. Временной ряд – это совокупность значений экономического показателя
за несколько последовательных моментов (периодов) времени
26. Временной ряд называется стационарным, если он является реализацией _____________ процесса
стационарного стохастического
27. Временной ряд характеризует
данные, описывающие один объект за ряд последовательных моментов (периодов) времени
28. Выбор формы зависимости экономических показателей и определение количества факторов в модели называется ________________ эконометрической модели
спецификацией
29. Выделяют три класса систем эконометрических уравнений
независимые, взаимозависимые и рекурсивные
30. Гетероскедастичность остатков подразумевает _____________ от значения фактора
зависимость дисперсии остатков
31. Гетероскедастичность подразумевает ________________________ от значения фактора
зависимость дисперсии остатков
32. Графическое изображение наблюдений на декартовой плоскости координат называется полем
корреляции
33. Дано уравнение регрессии . Определите спецификацию модели
линейное уравнение множественной регрессии
34. Двухшаговый метод наименьших квадратов предполагает ______ использование обычного МНК
однократное
35. Двухшаговый метод наименьших квадратов применим для решения
только сверхидентифицируемой системы одновременных уравнений
36. Двухшаговый метод наименьших квадратов применяется для оценки параметров
систем эконометрических уравнений
37. Для модели зависимости среднедушевого (в расчете на одного человека) месячного дохода населения (р.) от объема производства (млн р.) получено уравнение . При изменении объема производства на 1 млн р. доход в среднем изменится на
0,003 млн р.
38. Для моделирования зависимости предложения от цены не может быть использовано уравнение регрессии
39. Для моделирования сложных экономических систем целесообразно использовать
систему эконометрических уравнений
40. Для нелинейных уравнений метод наименьших квадратов применяется к
преобразованным линеаризованным уравнениям
41. Для оценки коэффициентов структурной формы модели не применяют _____ метод наименьших квадратов
обычный
42. Для существенного параметра расчетное значение критерия Стьюдента
больше табличного значения критерия
43. Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _% дисперсии обусловлено случайными факторами
30
44. Для уравнения у = 3,14 + 2х +e значение коэффициента корреляции составило 2. Следовательно
значение коэффициента корреляции рассчитано с ошибкой
45. Если доверительный интервал для параметра проходит через точку ноль, следовательно
параметр является несущественным
46. Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно
нелинейная связь достаточно тесная
47. Если значение коэффициента корреляции равно единице, то связь между результатом и фактором
функциональная
48. Если коэффициент регрессии является несущественным, то его значения приравниваются к
нулю и соответствующий фактор не включается в модель
49. Если между экономическими показателями существует нелинейная связь, то
целесообразно использовать спецификацию нелинейного уравнения регрессии
50. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только
тенденцию
51. Если наиболее высоким оказался коэффициент автокорреляции третьего порядка, то исследуемый ряд содержит
случайную величину, влияющую на каждый третий уровень ряда
52. Если оценка параметра эффективна, то это означает
наименьшую дисперсию остатков
53. Если предпосылки метода наименьших квадратов нарушены, то
оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности
54. Если расчетное значение критерия Фишера меньше табличного значения, то гипотеза о статистической незначимости уравнения
принимается
55. Если спецификация модели нелинейное уравнение регрессии, то нелинейной является функция
56. Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение
регрессии
57. Если факторы входят в модель как произведение, то модель называется
мультипликативной
58. Если факторы входят в модель как сумма, то модель называется
аддитивной
59. Значение индекса корреляции, рассчитанное для нелинейного уравнения регрессии характеризует тесноту ______ связи
нелинейной
60. Значение коэффициента автокорреляции второго порядка характеризует связь между
исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени
61. Значение коэффициента автокорреляции первого порядка равно 0,9 следовательно
линейная связь между последующим и предыдущим уровнями тесная
62. Значение коэффициента автокорреляции рассчитывается по аналогии с
линейным коэффициентом корреляции
63. Значение коэффициента детерминации рассчитывается как отношение дисперсии результативного признака, объясненной регрессией, к ___________ дисперсии результативного признака
общей
64. Значение коэффициента детерминации составило 0,9, следовательно
уравнение регрессии объяснено 90% дисперсии результативного признака
65. Значение коэффициента корреляции не характеризует
статистическую значимость уравнения
66. Значение коэффициента корреляции равно 0,9. Следовательно, значение коэффициента детерминации составит
0,81
67. Значение коэффициента корреляции равно 1. Следовательно
связь функциональная
68. Значение линейного коэффициента корреляции характеризует тесноту ________ связи
линейной
69. Значения коэффициента автокорреляции первого порядка равно 0,9. Следовательно
линейная связь между последующим и предыдущим уровнями тесная
70. Значения коэффициента корреляции может находиться в отрезке
[-1;1]
71. Из пары коллинеарных факторов в эконометрическую модель включается тот фактор, который при
достаточно тесной связи с результатом имеет меньшую связь с другими факторами
72. Известны значения аддитивной модели временного ряда: Yt — значение уровня ряда, Yt = 30, Т- — значение тренда, Т+15, Е- значение случайной компоненты случайных факторов Е=2. Определите значение сезонной компоненты S
13
73. Изолированное уравнение множественной регрессии может быть использовано для моделирования взаимосвязи экономических показателей, если
факторы не взаимодействуют друг с другом
74. Исследуется зависимость, которая характеризуется линейным уравнением множественной регрессии. Для уравнения рассчитано значение тесноты связи результативной переменной с набором факторов. В качестве этого показателя был использован множественный коэффициент
корреляции
75. Исходные значения фиктивных переменных предполагают значения
качественные
76. К линейному виду нельзя привести:
нелинейную модель внутренне нелинейную
77. К ошибкам спецификации относится
неправильный выбор той или иной математической функции
78. Качество подбора уравнения оценивает коэффициент
детерминации
79. Коррелограммой называется ______________________________ функции
графическое отображение автокорреляционной
80. Косвенный метод наименьших квадратов требует
преобразования структурной формы модели в приведенную
81. Критерий Стьюдента предназначен для определения значимости
каждого коэффициента регрессии
82. Критерий Фишера используется для оценки значимости
построенного уравнения
83. Критические значения критерия Фишера определяются по
уровню значимости и степеням свободы факторной и остаточной дисперсий
84. Критическое значение критерия Стьюдента определяет
максимально возможную величину, допускающую принятие гипотезы о несущественности параметра
85. Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о
существенности параметра
86. Линеаризация не подразумевает процедуру
включение в модель дополнительных существенных факторов
87. Линеаризация подразумевает процедуру приведения
нелинейного уравнения к линейному виду
88. Линейное уравнение множественной регрессии имеет вид . Определите какой из факторов или оказывает более сильное влияние на y
так как 2,5 1, то есть x возрастает и y тоже возрастает) не может быть описана зависимость
выработки от трудоемкости
167. При построении модели временного ряда проводится расчет
каждого уровня временного ряда
168. При построении систем независимых уравнений набор факторов в каждом уравнении определяется числом факторов, оказывающих ________ на моделируемый показатель
существенное влияние
169. При построении системы эконометрических уравнений необходимо учитывать
структуру связей реальной экономической системы
170. При применении метода наименьших квадратов исследуются свойства
оценок параметров уравнения регрессии
171. При применении метода наименьших квадратов исследуются свойства оценок
параметров уравнения регрессии
172. При применении метода наименьших квадратов уменьшить гетероскедастичность остатков удается путем
преобразования переменных
173. При расчете значения коэффициента детерминации используется отношение
дисперсий
174. При хорошем качестве модели допустимым значением средней ошибки аппроксимации является ___%
5-7
175. Приведенная форма модели получена из _________формы модели
структурной
176. Приведенная форма модели представляет собой систему ________ функций эндогенных переменных от экзогенных
линейных
177. Приведенная форма модели является результатом преобразования
структурной формы модели
178. Проверка является ли временной ряд «белым шумом» осуществляется с помощью
статистики Бокса-Пирса
179. Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ______ работника
уровень образования
180. Простая линейная регрессия предполагает наличие
одного фактора и линейность уравнения регрессии
181. Расчет значения коэффициента детерминации не позволяет оценить
существенность коэффициента регрессии
182. Расчет средней ошибки аппроксимации для нелинейных уравнений регрессии связан с расчетом разности между ____________________________ переменной
фактическим и теоретическим значениями результативной
183. Расчетное значение критерия Фишера определяется как
отношение факторной дисперсии к остаточной, рассчитанных на одну степень свободы
184. Расчетное значение критерия Фишера определяется как ___________ факторной дисперсии и остаточной, рассчитанных на одну степень свободы
отношение
185. Расчетное значение критерия Фишера определяется как отношение
дисперсий
186. Результатом линеаризации полиномиальных уравнений является ______________ регрессии
линейные уравнения множественной
187. Свойствами оценок МНК являются: эффективность, а также
состоятельность и несмещенность
188. Система взаимозависимых уравнений в ее классическом виде называется также системой ______ уравнений
одновременных
189. Система независимых уравнений предполагает
совокупность независимых уравнений регрессии
190. Система нормальных уравнений метода наименьших квадратов строится на основании
таблицы исходных данных
191. Система рекурсивных уравнений включает в каждое
предыдущее (должно быть последующее) уравнение в качестве факторов все зависимые переменные предшествующих уравнений с набором собственно факторов
192. Система эконометрических уравнений не используется при моделировании
взаимосвязей временных рядов данных
193. Система эконометрических уравнений предполагает наличие _________ независимых признаков
нескольких зависимых и нескольких
194. Система эконометрических уравнений представляет систему
уравнений регрессии
195. Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить
методом определителей
196. Системы эконометрических уравнений классифицируются по
способу вхождения зависимых и независимых переменных в уравнение регрессии
197. Случайный характер остатков предполагает
независимость остатков от величины предсказанных по модели значений результативного признака
198. Смысл расчета средней ошибки аппроксимации состоит в определении среднего арифметического значения
отклонений, выраженных в процентах от фактических значений результативного признака
199. Совокупность значений критерия, при которых принимается нулевая гипотеза, называется областью _____________ гипотезы
принятия
200. Состоятельность оценки характеризуется
увеличением ее точности с увеличением объема выборки
201. Спецификацию нелинейного уравнения парной регрессии целесообразно использовать, если значение
индекса детерминации, рассчитанного для данной модели достаточно близко к 1
202. Спецификация модели нелинейная парная (простая) регрессия подразумевает нелинейную зависимость и
независимую переменную
203. Стандартная ошибка рассчитывается для проверки существенности
параметра
204. Статистические гипотезы используются для оценки
значимости уравнения регрессии в целом
205. Стационарность временного ряда не подразумевает отсутствие
стационарного стохастического процесса
206. Стационарность временного ряда означает отсутствие
тренда
207. Стационарность характерна для временного ряда
типа «белый шум»
208. Стохастическим процессом называется
набор случайных переменных X(t), где t – вещественные числа
209. Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________ потребителя
доход
210. Структурной формой модели называется система _______ уравнений
взаимосвязанных
211. Структурными коэффициентами модели называются коэффициенты ___________ в структурной форме модели
при экзогенных и эндогенных переменных
212. Структуру временного ряда можно выявить с помощью коэффициента __________ уровней ряда
автокорреляции
213. Табличное значение критерия Фишера служит для проверки статистической гипотезы о равенстве
факторной и остаточной дисперсий
214. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является
линейность параметров
215. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является:
линейность параметров
216. Увеличение точности оценок с увеличением объема выборки описывает свойство _______ оценки
состоятельности
217. Уравнение может быть линеаризовано при помощи подстановки
218. Уравнение регрессии характеризует зависимость
обратно пропорциональную
219. Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированных на среднем уровне значении других переменных, называется
частным
220. Уровнем временного ряда является
значение временного ряда в конкретный момент (период) времени
221. Факторная дисперсия служит для оценки влияния
учтенных явно в модели факторов
222. Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются
фиктивными
223. Факторы эконометрической модели являются коллинеарными, если коэффициент
корреляции между ними по модулю больше 0,7
224. Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков ____________ характера
качественного
225. Фиктивные переменные включаются в уравнения ____________ регрессии
множественной
226. Циклические колебания связаны с
общей динамикой конъюнктуры рынка
227. Экзогенными переменными не являются
зависимые переменные
228. Экзогенными переменными являются
независимые переменные
229. Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются _______________________ временными рядами
нестационарными
230. Экспоненциальным не является уравнение регрессии
231. Эндогенными переменными не являются:
независимые переменные
232. Эндогенными переменными являются
зависимые переменные
233. Эффективность оценки на практике характеризуется
возможность перехода от точечного оценивания к интервальному
также в рубрике Контрольные, тесты:
Стандартная ошибка рассчитывается для проверки существенности параметра коэффициента корреляции
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,405
- гуманитарные 33,632
- юридические 17,905
- школьный раздел 607,990
- разное 16,855
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
http://studystuff.ru/controlnaya/testyi-po-ekonometrike
http://www.soloby.ru/81297/%D1%81%D1%82%D0%B0%D0%BD%D0%B4%D0%B0%D1%80%D1%82%D0%BD%D0%B0%D1%8F-%D1%80%D0%B0%D1%81%D1%81%D1%87%D0%B8%D1%82%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%D1%81%D1%8F-%D1%81%D1%83%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D0%B8-%D0%BA%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82%D0%B0
42
Эконометрика
Тема
Основные понятия теории вероятностей
и статистики (Теоретические вопросы)
Эконометрика-
это:
+—наука,
которая дает количественное выражение
взаимосвязей в экономике
—учение
о системе показателей, дающих представление
об экономике
—различного
рода цифровые данные
Предметом
эконометрики является:
+—определение
наблюдаемых в экономике количественных
закономерностей
—сбор
цифровых данных
—изучение
экономических законов
К
одному из методов эконометрики относится:
+—анализ
временных рядов
—индексный
анализ
—счета
и двойная запись
—кластерный
анализ
Эконометрическая
модель описывает:
+—стохастические
связи между переменными
—функциональные
связи между переменными
—набор
цифровых данных
—состав
переменных
Переменные,
определяемые из уравнений модели,
называются:
+—зависимые
—независимые
—предопределенные
Переменные,
задаваемые «из вне», в определенной
степени управляемые (планируемые),
называются:
+—экзогенные
—эндогенные
—предопределенные
Переменные,
задаваемые «из вне», в определенной
степени управляемые (планируемые),
называются:
+—независимые
—зависимые
—предопределенные
Пространственные
данные фиксируются:
+—в
один и тот же момент времени по нескольким
объектам
—по
одному объекту за период времени
—по
нескольким объектам за период времени
Идентификация
модели – это:
+—статистическое
оценивание неизвестных параметров
модели
—формулировка
вида модели, состава и формы входящих
в нее связей
—сбор
необходимой статистической информации
—проверка
точности модельных данных
Верификация
модели – это:
+—проверка
точности модельных данных
—статистическое
оценивание неизвестных параметров
модели
—формулировка
вида модели, состава и формы входящих
в нее связей
—сбор
необходимой статистической информации
Статистическими
называются выводы, полученные путем:
+—обобщения
свойств выборки на генеральную
совокупность
—измерения
генеральной совокупности
—сбора
статистических данных
Выборочное
среднее является
+—оценкой
среднего в генеральной совокупности
—наиболее
часто встречающейся величиной в
генеральной совокупности
—оценкой
разброса в генеральной совокупности
Выборочное
среднее квадратическое отклонение
является:
+—оценкой
разброса в генеральной совокупности
—оценкой
среднего в генеральной совокупности
—наиболее
часто встречающейся величиной в
генеральной совокупности
Выборочный
коэффициент корреляции является:
+—оценкой
относительной меры разброса в генеральной
совокупности
—оценкой
среднего в генеральной совокупности
—наиболее
часто встречающейся величиной в
генеральной совокупности
Если
коэффициент корреляции между двумя
случайными величинами больше нуля, то
значит:
+—случайные
величины имеют прямую линейную
зависимость
—случайные
величины имеют обратную линейную
зависимость
—случайные
величины не зависимы
Если
коэффициент корреляции между двумя
случайными величинами меньше нуля, то
значит:
+—случайные
величины имеют обратную линейную
зависимость
—случайные
величины имеют прямую линейную
зависимость
—случайные
величины не зависимы
Нулевой
называется:
+—гипотеза,
подвергающаяся проверке
—гипотеза,
которая отклоняется
—гипотеза,
которая содержит одно конкретное
предположение
Альтернативной
называется:
+—гипотеза,
необходимая для проверки нулевой
гипотезы
—гипотеза,
которая отклоняется
—гипотеза,
которая содержит несколько конкретных
предположений
Уровнем
значимости называется:
+—вероятность
отвергнуть правильную нулевую гипотезу
—совокупность
значений критерия проверки, при которых
нулевую гипотезу отклоняют
—совокупность
значений критерия проверки, при которых
нулевую гипотезу не отклоняют
Случайным
называется такое событие, которое:
+—может
произойти или не произойти в условиях
данного эксперимента
—не
происходит никогда в условиях данного
эксперимента
—происходит
всегда в условиях данного эксперимента
Достоверным
называется такое событие, которое:
+—происходит
всегда в условиях данного эксперимента
—может
произойти или не произойти в условиях
данного эксперимента
—не
происходит никогда в условиях данного
эксперимента
Невозможным
называется такое событие, которое:
+—не
происходит никогда в условиях данного
эксперимента
—может
произойти или не произойти в условиях
данного эксперимента
—происходит
всегда в условиях данного эксперимента
К
несовместимым относятся события,
которые:
+—не
могут происходить одновременно
—характеризуются
тем, что одно из них происходит тогда
и только тогда, когда не происходит
другое
Вероятность
события А изменяется в пределах:
+—![]()
—![]()
—![]()
Для
вероятности достоверного события
характерно:
+—![]()
—![]()
—![]()
Для
вероятности невозможного события
характерно:
+—![]()
—![]()
—![]()
Для
вероятности несовместимых событий
характерно:
+—P(A+B)=P(A)+P(B)
—P(A+B)=0
—P(A)=1-P(B)
Для
вероятности противоположных событий
характерно:
+—P(A)=1-P(B)
—P(A+B)=P(A)+P(B)
—P(A+B)=0
Случайной
величина:
+—заранее
не известное численное значение,
зависящее от случайных обстоятельств
—количественная
мера для сравнения событий по степени
возможности их появления
—исход
или совокупность исходов вероятностного
эксперимента
Законом
распределения дискретной случайной
величины называется:
+—соответствие
между всеми возможными значениями
дискретной случайной величины и их
вероятностями
—функция,
определяющая вероятность того, что
случайная величина X примет значение,
меньшее, чем Х
—функция,
производная от функции распределения
дискретной случайной величины
Функцией
распределения случайной величины Х
называется:
+—функция,
определяющая вероятность того, что
случайная величина X примет значение,
меньшее, чем Х
—соответствие
между всеми возможными значениями
случайной величины и их вероятностями
—функция,
производная от функции распределения
непрерывной случайной величины
Плотностью
распределения вероятностей случайной
величины Х называется:
+—функция,
производная от функции распределения
случайной величины
—соответствие
между всеми возможными значениями
случайной величины и их вероятностями
—функция,
определяющая вероятность того, что
случайная величина X примет значение,
меньшее, чем Х
Плотность
распределения вероятностей можно
записать:
+—для
непрерывных случайных величин
—для
дискретных случайных величин
—для
любых случайных величин
К
числовым характеристикам положения
случайной величины относится:
+—математическое
ожидание
—дисперсия
—среднее
квадратическое отклонение
К
числовым характеристикам рассеивания
(разброса) случайной величины относится:
+—дисперсия
—математическое
ожидание
—медиана
Математическое
ожидание характеризует:
+—среднее
ожидаемое значение случайной величины
—наиболее
часто встречающееся значение случайной
величины
—серединное
значение ряда упорядоченных случайных
величин
Стандартизированное
нормальное распределение имеет
параметры:
+—![]()
—![]()
—![]()
Какими
параметрами определяется распределение
Фишера?
+—числами
степеней свободы m и n
—числом
степеней свободы n
—числом
степеней свободы n-m
Если
случайные величины X и Y независимы, то
+—![]()
—![]()
—![]()
Примером
дискретной случайной величины является:
+—списочное
число работников предприятия
—выручка
от реализации за текущий месяц
—прибыль
от реализации за текущий месяц
Примером
непрерывной случайной величины является:
+—ежедневный
курс валюты
—тарифный
разряд работников предприятия
—количество
станков в цехах
При
увеличении уровня доверительной
вероятности ширина доверительного
интервала:
—уменьшается
+—увеличивается
—остается
неизменной
В
экономике чаще всего большинство
случайных величин задается в виде:
—закрытых
случайных величин
+—непрерывных
случайных величин
—закрытых
случайных величин и непрерывных
случайных величин
К
какому закону распределения можно
отнести показатели дохода населения,
прибыли фирм в отрасли, объема потребления?
—закон
распределения Хи – квадрат
—закон
распределения Стьюдента
—закон
распределения Фишера
+—нормальный
закон распределения (распределение
Гаусса)
Законы
распределения случайной величины
необходимы для:
—определения
интервальных оценок
—проверки
статистических гипотез
+—определения
интервальных оценок и проверки
статистических гипотез
Квантиль
определяется:
—уравнением
значимости
—числом
степеней свободы
+—уровнем
значимости и числом степеней свободы
Какие
из перечисленных числовых характеристик
используются для анализа степени
взаимосвязи случайных величин?
—вероятность
—ковариация
—коэффициент
корреляции
+—ковариация
и коэффициент корреляции
—вероятность
и коэффициент корреляции
Ковариация
является:
+—абсолютной
мерой взаимосвязи
—относительной
мерой взаимосвязи
—относительной
частотой взаимосвязи
Коэффициент
корреляции является величиной:
—размерной
+—безразмерной
—имеет
ту же единицу измерения, что и случайная
величина
В
качестве оценки дисперсии при n<30
используют:
—выборочную
дисперсию
+—исправленную
дисперсию
—выборочную
и исправленную дисперсию
Способы
уменьшения вероятности ошибок при
проверке статистических гипотез состоят
в:
—минимизации
потерь от ошибок
—уменьшении
вероятностей ошибок
+—увеличении
объема выборки
Оценка
*
значения параметра модели
является несмещенной, если
—![]()
— *
обладает наименьшей дисперсией по
сравнению с другими оценками
—При
N,
вероятность отклонения *
от значения
cтремится к 0
—![]()
+—Математическое
ожидание
*
равно
Оценка
*
значения
параметра модели
является эффективной, если
—Математическое
ожидание
*
равно
+—
*
обладает
наименьшей дисперсией по сравнению с
другими оценками
—![]()
—При
N,
вероятность отклонения *
от значения
cтремится к 0
—![]()
Оценка
*
значения параметра модели
является состоятельной, если
— *
обладает
наименьшей дисперсией по сравнению с
другими оценками
—Математическое
ожидание
*
равно
—![]()
+—При
N,
вероятность отклонения
*
от значения
cтремится к 0
—![]()
Средние
расходы домохозяйств в расчете на одну
потребительскую единицу составляли,
ден. ед. в месяц:
на
питание – 62 при σ=9,3
на
одежду и обувь – 26 при σ=9,1
Степень
вариации расходов на питание и покупку
одежды и обуви:
—одинакова
—вариация
расходов на питание больше
+—вариация
расходов на питание меньше
—сравнить
вариацию невозможно
Ошибка
первого рода состоит в том, что:
+—будет
отвергнута правильная нулевая гипотеза
—будет
принята нулевая гипотеза, в то время
как в действительности верна альтернативная
гипотеза
Ошибка
второго рода состоит в том, что:
—будет
отвергнута правильная нулевая гипотеза
+—будет
принята нулевая гипотеза, в то время
как в действительности верна альтернативная
гипотеза
При
проверке статистических гипотез
вероятность совершения ошибки первого
рода обозначается через:
+—![]()
—![]()
—![]()
—![]()
Выбор
формы связи между переменными называется:
—идентифицируемостью
—верификацией
+—спецификацией
—индентификацией
К
несовместимым событиям относятся
следующие явления:
+—увеличение
налогов – рост располагаемого дохода
—увеличение
продаж – рост прибыли
—увеличение
объемов производства – снижение
издержек производства
Элементарным
называется событие, которое:
—можно
разбить на более простые события
+—нельзя
разбить на более простые события
—можно
представить в виде нескольких элементарных
событий
Вероятность
– это:
—количественная
и качественная мера, которая вводится
для сравнивания событий по степени
возможности их появления
+—количественная
мера
—качественная
мера
Дискретную
случайную величину можно задать:
—таблично
—аналитически
—графически
+—таблично,
аналитически или графически
Случайная
величина задается:
—функцией
распределения
—плотностью
вероятностей
+—функцией
распределения или плотностью вероятностей
Тема Основные
понятия теории вероятностей и статистики.
Задачи к экзамену
Пусть
X,Y
– годовые дивиденды от вложений денежных
средств в акции компаний А и В
соответственно. Риск от вложений
характеризуется дисперсиями: D(X)=25,
D(Y)=16.
Коэффициент корреляции σ =+0,8. Менее
рискованно вкладывать денежные средства:
+—в
отрасль В
—в
отрасль А
—в
обе отрасли в соотношении 30% на 70%
Пусть
X,Y
– годовые дивиденды от вложений денежных
средств в акции компаний А и В
соответственно. Риск от вложений
характеризуется дисперсиями: D(X)=4,
D(Y)=9.
Коэффициент корреляции σ =0,7. Менее
рискованно вкладывать денежные средства:
+—в
отрасль А
—в
отрасль В
—в
обе отрасли в соотношении 40% на 60%
Пусть
X,Y
– годовые дивиденды от вложений денежных
средств в акции компаний А и В
соответственно. Риск от вложений
характеризуется дисперсиями: D(X)=4,
D(Y)=9.
Коэффициент корреляции σ = -0,65. Менее
рискованно вкладывать денежные средства:
+—в
обе отрасли в соотношении 40% на 60%
—только
в отрасль А
—только
в отрасль В
Доход
Х населения имеет нормальный закон
распределения со средним значением
5000 руб. и средним квадратическим
отклонением 1000 руб. Обследуется 1000
человек. Наиболее вероятное количество
человек, имеющих доход более 6000 руб.,
будет составлять:
+—158
—159
—341
Доход
Х населения имеет нормальный закон
распределения со средним значением
4500 руб. и средним квадратическим
отклонением 700 руб. Обследуется 500
человек. Наиболее вероятное количество
человек, имеющих доход более 5500 руб.,
будет составлять:
+—38
—39
—212
Доход
Х населения имеет нормальный закон
распределения со средним значением
9000 руб. и средним квадратическим
отклонением 800 руб. Обследуется 2000
человек. Наиболее вероятное количество
человек, имеющих доход более 10400 руб.,
будет составлять:
+—80
—81
—920
Статистика
по годовым темпам инфляции в стране за
последние 10 лет составила (%): 2,6; 3,0; 5,2;
1,7; -0,5; 0,6; 2,2; 2,9; 4,2; 3,8. Несмещенные оценки
среднего темпа инфляции, дисперсии и
среднего квадратического отклонения
составляют:
+—2,57;
2,84; 1,69
—2,57;
2,56; 1,60
—2,57;
25,58; 5,06
Статистика
по годовым темпам инфляции в стране за
последние 10 лет составила (%): 2,3; 3,5; -0,8;
4,0; 2,4; 3,2; 4,1; 3,6; 2,5; 4,2. Несмещенные оценки
среднего темпа инфляции, дисперсии и
среднего квадратического отклонения
составляют:
+—2,9;
2,19; 1,481
—2,9;
2,06; 1,44
—2,9;
20,55; 4,53
Статистика
по годовым темпам инфляции в стране за
последние 10 лет составила (%): 3,8; 2,2; -0,7;
-1,0; 4,2; 5,1; 2,6; 0,8; 2,9; 1,1. Несмещенные оценки
среднего темпа инфляции, дисперсии и
среднего квадратического отклонения
составляют:
+—2,1;
4,15; 2,04
—2,1;
3,73; 1,93
—2,1;
37,34; 6,11
Предполагается,
что месячный доход граждан страны имеет
нормальное распределение с математическим
ожиданием m=500
$ и дисперсией σ2=22500.
По выборке из 500 человек определен
выборочный средний доход
![]() =450
=450
$. Доверительный интервал для среднедушевого
дохода в стране составляют при уровне
значимости 0,05:
+—436,85;
463,15
—449,87;
450,13
—438,94;
461,06
При
анализе зависимости между двумя
показателями Х и Y
по 30 наблюдениям получены следующие
данные:
![]() =
=
105;
![]() =80;
=80;
![]() =900;
=900;
![]() =252600;
=252600;
![]() =635.
=635.
Оцените наличие линейной зависимости
между Х и Y
и статистическую значимость коэффициента
корреляции ρхy:
+—rxy=0,8;
коэффициент значим на всех уровнях
значимости
—rxy=-0,8;
коэффициент значим на всех уровнях
значимости
—rxy=
0,8; коэффициент не значим на всех уровнях
значимости
—rxy=
0,8; коэффициент значим только на уровне
значимости 0,05
Предполагается,
что месячная зарплата сотрудников
фирмы составляет 500 $ при стандартном
отклонении σ
= 50 $. Выборка из 49 человек дала следующие
результаты:
![]() =450$
=450$
и S
= 60$. На основании результатов проведенных
наблюдений можно утверждать, что:
+—средняя
зарплата сотрудников меньше рекламируемой
на всех уровнях значимости, а разброс
в зарплатах больше на уровне значимости
α=0,05 и α=0,1
—средняя
зарплата сотрудников меньше рекламируемой
на всех уровнях значимости, а разброс
в зарплатах больше только на уровне
значимости α=0,01
—средняя
зарплата сотрудников меньше рекламируемой,
а разброс в зарплатах больше на всех
уровнях значимости
Предполагается,
что месячная зарплата сотрудников
фирмы составляет 600 $ при стандартном
отклонении σ
= 100 $. Выборка из 49 человек дала следующие
результаты:
![]() =500$
=500$
и S
= 120$. На основании результатов проведенных
наблюдений можно утверждать, что:
+—средняя
зарплата сотрудников меньше рекламируемой
на всех уровнях значимости, а разброс
в зарплатах больше на уровне значимости
α=0,05 и α=0,1
—средняя
зарплата сотрудников меньше рекламируемой
на всех уровнях значимости, а разброс
в зарплатах больше только на уровне
значимости α=0,01
—средняя
зарплата сотрудников меньше рекламируемой,
а разброс в зарплатах больше на всех
уровнях значимости
Предполагается,
что месячная зарплата сотрудников
фирмы составляет 800 $ при стандартном
отклонении σ
= 40 $. Выборка из 49 человек дала следующие
результаты:
![]() =780$
=780$
и S
= 50$. На основании результатов проведенных
наблюдений можно утверждать, что:
+—средняя
зарплата сотрудников меньше рекламируемой,
а разброс в зарплатах больше на всех
уровнях значимости
—средняя
зарплата сотрудников меньше рекламируемой
на всех уровнях значимости, а разброс
в зарплатах больше на уровне значимости
α=0,05 и α=0,01
—средняя
зарплата сотрудников меньше рекламируемой
на всех уровнях значимости, а разброс
в зарплатах больше только на уровне
значимости α=0,1
На
основании наблюдений за 29 кандидатами
на должность менеджера в фирме
установлено, что в среднем они тратили
10 минут на решение тестового задания
при выборочном стандартном отклонении
S=2
минуты. Предполагалось, что среднее
время решения тестового задания должно
составить 9 минут. Полученные данные
по выборочным наблюдениям:
+—не
противоречат выдвинутой гипотезе на
уровне значимости α=0,01
—противоречат
выдвинутой гипотезе на уровне значимости
α=0,01
—не
противоречат выдвинутой гипотезе на
уровне значимости α=0,1
На
основании наблюдений за 29 кандидатами
на должность менеджера в фирме
установлено, что в среднем они тратили
11 минут на решение тестового задания
при выборочном стандартном отклонении
S=2
минуты. Предполагалось, что среднее
время решения тестового задания должно
составить 10 минут. Полученные данные
по выборочным наблюдениям:
+—не
противоречат выдвинутой гипотезе на
уровне значимости α=0,01
—противоречат
выдвинутой гипотезе на уровне значимости
α=0,01
—не
противоречат выдвинутой гипотезе на
уровне значимости α=0,1
На
основании наблюдений за 29 кандидатами
на должность менеджера в фирме
установлено, что в среднем они тратили
9,2 минуты на решение тестового задания
при выборочном стандартном отклонении
S=2
минуты. Предполагалось, что среднее
время решения тестового задания должно
составить 10 минут. Полученные данные
по выборочным наблюдениям:
+—не
противоречат выдвинутой гипотезе на
уровне значимости α=0,01
—противоречат
выдвинутой гипотезе на уровне значимости
α=0,01
—не
противоречат выдвинутой гипотезе на
уровне значимости α=0,1
Расход
стирального порошка (Х) стиральной
машины марки N,
изготовляемой на предприятии, имеет
нормальный закон распределения с mx
= 200 г и σх
= 20 г. Выпустив новую модификацию
стиральной машины, предприятие
утверждает, что у нее средний расход
my
стирального порошка снижен до 100 г при
том же значении σ. Выборка из 20 стиральных
машин каждой модели дала следующие
средние расходы:
![]() =
=
190 г;
![]() =
=
120 г. По этим данным доверять рекламе
предприятия:
+—можно
на любом уровне значимости α= (0,1; 0,05;
0,01)
—можно
только на уровне значимости α = 0,01, на
уровнях значимости α = 0,05 и 0,1 доверять
нельзя
—нельзя
на любом уровне значимости
Расход
стирального порошка (Х) стиральной
машины марки N,
изготовляемой на предприятии, имеет
нормальный закон распределения с mx
= 150 г и σх
= 20 г. Выпустив новую модификацию
стиральной машины, предприятие
утверждает, что у нее средний расход
my
стирального порошка снижен до 100 г при
том же значении σ. Выборка из 25 стиральных
машин каждой модели дала следующие
средние расходы:
![]() =
=
140 г;
![]() =
=
132 г. По этим данным доверять рекламе
предприятия:
+—можно
только на уровне значимости α= 0,1
—можно
на уровне значимости α = 0,05 и 0,01
—можно
на любом уровне значимости
Расход
стирального порошка (Х) стиральной
машины марки N,
изготовляемой на предприятии, имеет
нормальный закон распределения с mx
= 150 г и σх
= 20 г. Выпустив новую модификацию
стиральной машины, предприятие
утверждает, что у нее средний расход
my
стирального порошка снижен до 100 г при
том же значении σ. Выборка из 15 стиральных
машин каждой модели дала следующие
средние расходы:
![]() =
=
145 г;
![]() =
=
130 г. По этим данным доверять рекламе
предприятия:
+—можно
на уровне значимости α=0,1 и 0,05; на уровне
значимости α=0,01 доверять нельзя
—можно
только на уровне значимости α = 0,01, на
уровнях значимости α = 0,05 и 0,1 доверять
нельзя
—нельзя
на любом уровне значимости
Средний
уровень жизни Х и Y
двух стран (США и Англии соответственно)
примерно одинаковы, но разбросы в
доходах этих стран различны. За последние
двадцать лет получены следующие
результаты:
Sx2
=280; Sy2
= 130. На основании выборочных данных
можно утверждать, что:
+—на
уровне значимости α=0,1 разброс в доходах
в США больше, чем в Англии
—на
уровне значимости α=0,05 и 0,01 разброс в
доходах США больше, чем в Англии
—на
любом уровне значимости нет оснований
утверждать, что разброс в доходах в США
больше, чем в Англии
Средний
уровень жизни Х и Y
двух стран (США и Англии соответственно)
примерно одинаковы, но разброс в доходах
этих стран различны. За последние
двадцать лет получены следующие
результаты:
Sx2
=200; Sy2
= 100. На основании выборочных данных
можно утверждать, что:
+—на
уровне значимости α=0,1 разброс в доходах
в США больше, чем в Англии
—на
уровне значимости α=0,05 и 0,01 разброс в
доходах США больше, чем в Англии
—на
любом уровне значимости нет оснований
утверждать, что разброс в доходах в США
больше, чем в Англии
Средний
уровень жизни Х и Y
двух стран (США и Англии соответственно)
примерно одинаковы, но разброс в доходах
этих стран различны. За последние
двадцать лет получены следующие
результаты:
Sx2
=300; Sy2
= 120. На основании выборочных данных
можно утверждать, что:
+—на
уровне значимости α=0,1 и 0,05 разброс в
доходах в США больше, чем в Англии
—на
уровне значимости α=0,01 разброс в доходах
США больше, чем в Англии
—на
любом уровне значимости нет оснований
утверждать, что разброс в доходах в США
больше, чем в Англии
Анализируется
зависимость между доходами горожан
(СВ Х), имеющих индивидуальные домовладения,
и рыночной стоимостью их домов (СВ Y).
По случайной выборке из 500 горожан
данной категории получены результаты:
![]() ;
;![]()
;
![]()
![]() ;
;![]()
—3,11; 3,55
—0,028; 0,094
—37,41; 44,29
+—3,05; 3,61
Имеется три вида
акций A,
B
и C
каждая стоимостью 20 у.е., дивиденды по
которым являются независимыми СВ со
средним значением 8 % и дисперсией 25.
Формируются два портфеля инвестиций.
Портфель z1
состоит из 60 акций A.
Портфель z2
включает в себя по 20 акций A,
B
и C.
Коэффициент корреляции между дивидендами
по акциям A
и C
равен -0,5, но обе величины не коррелируют
с дивидендами по акциям B.
Рассчитать риски от вложений средств
в данные портфели инвестиций:
+—z1=90000;
z2=20000
—z1=90000;
z2=29975
—z1=90000;
z2=1475
—z1=1500;
z2=1525
Имеется три вида
акций A,
B
и C,
каждая стоимостью 15 у.е., дивиденды по
которым являются независимыми СВ со
средним значением 7 % и дисперсией 16.
Формируются два портфеля инвестиций.
Портфель z1
состоит из 100 акций A
. Портфель z2
включает в себя 40 акций A,
40 акций B
и 20 акций C.
Коэффициент корреляции между дивидендами
по акциям A
и B
равен -0,6, но обе величины не коррелируют
с дивидендами по акциям C.
Рассчитать риски от вложений средств
в данные портфели инвестиций:
—z1=160000;
z2=57580,8
—z1=160000;
z2=57600
—z1=1600;
z2=1580,8
+—z1=160000;
z2=26880
Два университета
А и В готовят специалистов аналогичных
специальностей. Федеральное агентство
по образованию решило проверить качество
подготовки в обоих университетах,
организовав для этого тестовой экзамен
для студентов IV
курса. Отобранные случайным образом
студенты показали следующие суммы
баллов:
A:
55; 43; 25; 48; 37; 60; 31; 40; 44; 52; 48; 50; 53; 60
B:
53; 59; 20; 47; 39; 60; 41; 55; 48; 51; 40; 38; 36; 44; 28; 57; 39;
56; 51; 58
Можно ли утверждать
при α = 0,05, что разброс в знаниях студентов
в университете B
больше, чем в университете А:
—утверждать
нельзя, так как F=1,113
< Fкрит.=2,28
+—утверждать
нельзя, так как F=1,113
< Fкрит.=2,47
—утверждать
нельзя, так как F=0,898
< Fкрит.=2,28
—утверждать
нельзя, так как F=0,898
< Fкрит.=2,47
Два университета
A
и B
готовят специалистов аналогичных
специальностей. Федеральное агентство
по образованию решило проверить качество
подготовки в обоих университетах,
организовав для этого тестовой экзамен
для студентов IV
курса. Отобранные случайным образом
студенты показали следующие суммы
баллов:
A:
50; 54; 58; 43; 59; 30; 36; 41; 32; 45; 60; 25; 55; 47; 51; 29; 40
B:
35; 60; 28; 54; 31; 35; 49; 30; 57; 43; 55; 37; 50; 29; 42
Можно ли утверждать
при α = 0,1 что разброс в знаниях студентов
в университете А больше, чем в университете
В:
+—утверждать
нельзя, так как F=1,016
< Fкрит.=1,998
—утверждать
нельзя, так как F=1,016
< Fкрит.=1,953
—утверждать
нельзя, так как F=0,984
< Fкрит.=1,998
—утверждать
нельзя, так как F=0,984
< Fкрит.=1,953
Тема
Парная регрессия (Теоретические вопросы)
Суть
МНК состоит в:
—минимизации
суммы квадратов коэффициентов регрессии
—минимизации
суммы квадратов значений зависимой
переменной
+—минимизации
суммы квадратов отклонений точек
наблюдений от уравнения регрессии
—минимизации
суммы квадратов отклонений точек
эмпирического уравнения регрессии от
точек теоретического уравнения регрессии
Коэффициент
уравнения регрессии показывает
—на
сколько % изменится результат при
изменении фактора на 1%
—на
сколько % изменится фактор при изменении
результата на 1%
+—на
сколько единиц изменится результат
при изменении фактора на 1 единицу
—на
сколько единиц изменится фактор при
изменении результата на 1 единицу
—во
сколько раз изменится результат при
изменении фактора на 1 единицу
Коэффициент
эластичности показывает
—на
сколько единиц изменится фактор при
изменении результата на 1 единицу
—на
сколько единиц изменится результат
при изменении фактора на 1 единицу
—во
сколько раз изменится результат при
изменении фактора на одну единицу
+—на
сколько % изменится результат при
изменении фактора на 1 %
—на
сколько %изменится фактор при изменении
результата на 1%
Не
является предпосылкой классической
модели предположение:
—факторы
экзогенны
—длина
исходного ряда данных больше, чем
количество факторов
—матрица
факторов содержит все важные факторы,
влияющие на результат
+—факторы
являются случайными величинами
На
основании наблюдений за 100 домохозяйствами
построено эмпирическое уравнение
регрессии, у- потребление, х -доход:
У=145,65+0,825*х
Соответствуют
ли знаки и значения коэффициентов
регрессии теоретическим представлениям
+—да
—нет
—частично
соответствуют
В
производственной функции Кобба-Дугласа
параметр
соответствует коэффициенту:
—корреляции
—вариации
+—эластичности
—детерминации
Найдите
предположение, не являющееся предпосылкой
классической модели
—Случайное
отклонение имеет нулевое математическое
ожидание
—Случайное
отклонение имеет постоянную дисперсию
—Отсутствует
автокорреляция случайных отклонений
—Случайное
отклонение независимо от объясняющих
переменных
+—Случайное
отклонение не обладает нормальным
распределением
По
месячным данным за 6 лет построена
следующая регрессия:
Y=-12,23+0,91*x1-2,1*x2,
R2=0,976,
DW=1,79
t
(-3,38) (123,7) (3,2)
y-
потребление, х1 –располагаемый доход,
х2 – процентная банковская ставка по
вкладам
Оцените
качество построенной модели, не прибегая
к таблицам, совпадает ли направление
влияния объясняющих переменных с
теоретическим?
+—качество
модели высокое, направление влияния
совпадает
—качество
модели низкое, направление влияния
совпадает
—качество
модели высокое, но направление влияния
не совпадает
—качество
модели низкое, направление влияния
совпадает
Критерий
Стьюдента предназначен для:
—Определения
экономической значимости каждого
коэффициента уравнения
+—Определения
статистической значимости каждого
коэффициента уравнения
—Проверки
модели на автокорреляцию остатков
—Определения
экономической значимости модели в
целом
—Проверки
на гомоскедастичность
Если
коэффициент уравнения регрессии (k)
статистически значим, то
—k
>
1
—|k
|
>
1
+—k
0
—k
>
0
—0
<
k
<
1
Табличное
значение критерия Стьюдента зависит
—Только
от уровня доверительной вероятности
—Только
от числа факторов в модели
—Только
от длины исходного ряда
—Только
от уровня доверительной вероятности
и длины исходного ряда
+—И
от доверительной вероятности, и от
числа факторов, и от длины исходного
ряда
Имеется
уравнение, полученное МНК:

Зная,
что регрессионная сумма квадратов
составила 110,32, остаточная сумма квадратов
21,43, найдите коэффициент детерминации:
+—0,837
—0,999
—1,000
—0,736
Суть
коэффициента детерминации
![]() состоит
состоит
в следующем:
+—коэффициент
определяет долю общего разброса значений
![]() ,
,
объясненного уравнением регрессии
—коэффициент
свидетельствует о значимости коэффициентов
регрессии
—коэффициент
определяет тесноту связи между признаками
—коэффициент
свидетельствует о наличии / отсутствии
автокорреляции
Какое
из уравнений регрессии нельзя свести
к линейному виду?
+—![]()
—![]()
—![]()
—![]()
—![]()
Какое
из уравнений регрессии является
степенным?
—![]()
+—![]()
—![]()
—![]()
—![]()
Парная
регрессия представляет собой модель
вида:
+—y=f(x)
—y=f(x1,x2,…xm)
—y=f(y
t-1)
Уравнение
парной регрессии характеризует связь
между:
+—двумя
переменными
—несколькими
переменными
Согласно
содержанию регрессии, наблюдаемая
величина зависимой переменной
складывается из:
+—теоретического
значения зависимой переменной, найденного
из уравнения регрессии, и случайного
отклонения
—теоретического
значения зависимой переменной, найденного
из уравнения регрессии, скорректированного
на величину стандартной ошибки
—теоретического
значения зависимой переменной, найденного
из уравнения регрессии и остаточной
дисперсии
Использование
парной регрессии вместо множественной
является примером:
+—ошибки
спецификации
—ошибки
выборки
—ошибки
измерения
Включение
в совокупность единиц с “выбросами”
данных является примером:
+—ошибки
выборки
—ошибки
спецификации
—ошибки
измерения
Заниженная
балансовая прибыль в отчетности является
примером:
+—ошибки
измерения
—ошибки
спецификации
—ошибки
выборки
Аналитический
метод подбора вида уравнения регрессии
основан на:
+—изучении
природы связи признаков
—изучении
поля корреляции
—сравнении
величины остаточной дисперсии при
разных моделях
Графический
метод подбора вида уравнения регрессии
основан на:
+—изучении
поля корреляции
—изучении
природы связи признаков
—сравнении
величины остаточной дисперсии при
разных моделях
Экспериментальный
метод подбора вида уравнения регрессии
основан на:
+—сравнении
величины остаточной дисперсии при
разных моделях
—изучении
поля корреляции
—изучении
природы связи признаков
Классический
подход к оцениванию коэффициентов
регрессии основан на:
+—методе
наименьших квадратов
—графической
оценке
—методе
максимального правдоподобия
Величина
коэффициента регрессии показывает:
+—среднее
изменение результата с изменением
фактора на одну единицу
—среднее
изменение результата с изменением
фактора на один процент
—изменение
результата в процентах с изменением
фактора на один процент
Уравнение
парной регрессии дополняется коэффициентом
парной корреляции потому, что:
+—необходимо
знать тесноту связи в линейной форме
—это
требуется для получения оценок
коэффициентов регрессии
—это
необходимо для расчета величины
остаточной дисперсии
Коэффициент
детерминации характеризует:
+—долю
факторной дисперсии в общей дисперсии
результативного признака
—соотношение
факторной и остаточной дисперсий
—долю
остаточной дисперсии в общей дисперсии
результативного признака
F-критерий
характеризует:
+—соотношение
факторной и остаточной дисперсий
—долю
факторной дисперсии в общей дисперсии
результативного признака
—долю
остаточной дисперсии в общей дисперсии
результативного признака
Оценка
значимости уравнения регрессии в целом
дается с помощью:
+—F-критерия
Фишера
—коэффициента
детерминации
—стандартной
ошибки регрессии
«Объясненная»
сумма квадратов отклонений отражает
влияние на разброс y:
+—изучаемого
фактора х
—прочих
факторов
—изучаемого
фактора х и прочих факторов
Остаточная
сумма квадратов отклонений отражает
влияние на разброс у:
—изучаемого
фактора х
+—прочих
факторов
—изучаемого
фактора х и прочих факторов
Если
фактор не оказывает влияния на результат,
то линия регрессии на графике:
+—параллельна
оси ох
—параллельна
оси оу
—является
биссектрисой первой четверти декартовой
системы координат
Остаточная
сумма квадратов равна нулю в том случае,
когда:
+—у
связан с х функционально
—значения
у, рассчитанные по уравнению регрессии,
равны среднему значению у
—вся
общая дисперсия у обусловлена влиянием
прочих факторов
Общая
сумма квадратов отклонений совпадает
с остаточной, когда:
+—фактор
х не оказывает влияния на результат
—прочие
факторы не влияют на результат
—фактор
х и прочие факторы в равной степени
влияют на результат
Уравнение
регрессии статистически значимо, если
+—«объясненная»
сумма квадратов отклонений значимо
больше остаточной суммы квадратов
отклонений
—остаточная
сумма квадратов отклонений значимо
больше «объясненной» суммы квадратов
отклонений
—«объясненная»
и остаточная суммы квадратов отклонений
равны
Число
степеней свободы связано с:
+—числом
единиц совокупности n
и числом определяемых по совокупности
констант
—числом
определяемых по совокупности констант
—числом
единиц совокупности n
“Объясненная”
(факторная) сумма квадратов отклонений
в парной регрессии имеет число степеней
свободы, равное:
+—1
—n-1
—n-2
Остаточная
сумма квадратов отклонений в парной
регрессии имеет число степеней свободы,
равное:
+—n-2
—n-1
—1
Общая
сумма квадратов отклонений в парной
регрессии имеет число степеней свободы,
равное:
+—n-1
—1
—n-2
Какое
из утверждений истинно:
+—оценки
коэффициентов регрессии будут иметь
нормальное распределение, если случайные
отклонения распределены нормально
—чем
больше стандартная ошибка регрессии
(остаточная дисперсия), тем точнее
оценки коэффициентов
—90%-й
доверительный интервал для условного
математического ожидания зависимой
переменной определяет область возможных
значений для 90 % -ов наблюдений за
зависимой переменной при соответствующем
уровне объясняющей переменной
Для
оценки значимости коэффициентов
регрессии рассчитывают:
+—t-статистику
Стьюдента
—F-критерий
Фишера
—коэффициент
детерминации
Какой
нелинейной функцией можно заменить
параболу, если не наблюдается смена
направленности связи признаков:
+—степенной
функцией
—гиперболой
—логистической
функцией
В
большинстве случаев зависимости между
экономическими переменными являются:
+—стохастическими
—функциональными
—строгими
Компонента
![]()
в уравнении линейной регрессии отражает:
+—связь
в генеральной совокупности
—случайность
—связь
в генеральной совокупности и случайность
Коэффициент
а в уравнении линейной регрессии
измеряет:
+—сдвиг
по оси ординат
—наклон
прямой
—среднее
значение y
Коэффициент
b
в уравнении линейной регрессии измеряет:
+—наклон
прямой
—сдвиг
по оси ординат
—среднее
значение у
По
выборке данных можно построить так
называемое:
+—эмпирическое
уравнение регрессии
—теоретическое
уравнение регрессии
—любое
уравнение регрессии
Эмпирические
коэффициенты регрессии а и b
являются точечными оценками:
+—теоретических
коэффициентов регрессии
—условного
математического ожидания у
—теоретического
случайного отклонения
![]()
есть точечная
оценка:
+—![]()
—![]()
—![]()
Коэффициент
регрессии b
пропорционален:
+—коэффициенту
корреляции
—стандартному
отклонению х
—стандартному
отклонению у
Эмпирическая
прямая регрессии обязательно проходит
через точку:
+—![]()
—![]()
—![]()
Эмпирическое
уравнение регрессии построено таким
образом, что:
+—![]()
—![]()
—![]()
Коэффициент
b
регрессии Y
на X
имеет тот же знак, что и:
+—![]()
—![]()
—![]()
Если
по одной и той же выборке рассчитаны
регрессии У на Х и Х на У, то совпадут
ли в этом случае линии регрессии:
+—нет
—да
Если
переменная Х принимает среднее по
выборке значение х, то:
+—наблюдаемая
величина зависимой переменной У равна
среднему значению у
—регрессионная
величина Ух
в среднем
равна среднему значению у, но не
обязательно в каждом конкретном случае
—регрессионная
величина Ух
равна
среднему значению у
—регрессионный
остаток минимален среди всех других
отклонений
Выберите
истинное утверждение:
+—коэффициенты
эмпирического уравнения регрессии
являются по сути случайными величинами
—коэффициент
b
эмпирического парного линейного
уравнения регрессии показывает
процентное изменение зависимой
переменной у при однопроцентном
изменении х
—коэффициент
a
эмпирического парного линейного
уравнения регрессии показывает значение
переменной y
при среднем значении переменной x
Случайное
отклонение в среднем не оказывает
влияние на зависимую переменную, если:
—![]()
+—![]()
—![]()
Случайное
отклонение приведет к увеличению
дисперсии оценок, если
+—![]()
—![]()
—![]()
Гомоскедастичность
подразумевает:
+—![]()
—![]()
—![]()
Отсутствие
автокорреляции случайных отклонений
влечет соотношение:
+—![]()
—![]()
—![]()
Эмпирический
коэффициент регрессии b
является несмещенной оценкой
![]() если:
если:
+—![]()
—![]()
—![]()
Эмпирический
коэффициент регрессии b
является состоятельной оценкой
![]() если:
если:
+—![]()
—![]()
—![]()
Эмпирический
коэффициент регрессии b
является эффективной оценкой
![]() если:
если:
+—![]()
—![]()
—![]()
С
увеличением числа наблюдений n
дисперсии оценок а и b:
+—уменьшаются
—увеличиваются
—не
изменяются
С
увеличением дисперсии х дисперсия
оценок a
и b:
+—уменьшается
—увеличивается
—не
изменяется
С
увеличением наклона прямой регрессии
(b)
разброс значений свободного члена а:
+—увеличивается
—уменьшается
—не
изменяется
Разброс
значений свободного члена а:
+—тем
больше, чем больше среднее значение
квадрата х
—тем
больше, чем меньше среднее значение
квадрата х
—не
зависит от величины х
Свободным
членом уравнения парной линейной
регрессии (а) можно пренебречь, когда:
+—![]()
—![]()
—![]()
Значимая
линейная связь между х и у имеет место,
когда:
+—![]()
—![]()
—![]()
С
увеличением объема выборки:
+—увеличивается
точность оценок
—увеличивается
точность прогноза по модели
—уменьшается
коэффициент детерминации
При
оценке парной линейной регрессии
получена завышенная оценка b1
теоретического коэффициента
![]() .
.
Какая оценка наиболее вероятна для
коэффициента
![]()
+—заниженная
—завышенная
—несмещенная
Доверительный
интервал для среднего значения У при
Х=хр
будет:
+—уже,
чем таковой для индивидуальных значений
у
—шире,
чем таковой для индивидуальных значений
у
Дополнительные
вопросы
Для
уравнения
![]()
значение коэффициента корреляции
составило 2. Следовательно . . . .
+
значение коэффициента корреляции
рассчитано с ошибкой;
—
теснота связи в 2 раза сильнее, чем для
функциональной связи;
—
связь функциональная;
—
при увеличении фактора на единицу
значение результата увеличивается в
2 раза.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
…
—
регрессии;
+
корреляции;
—
случайных воздействий;
—
автокорреляции.
В
зависимости от количества факторов,
включенных в уравнение регрессии,
принято различать
+
простую (парную) и множественную
регрессии
Факторная
дисперсия служит для оценки влияния:
—
как учтенных факторов, так и случайные
воздействия;
+
учтенных явно в модели факторов;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение …
—
линейного коэффициента корреляции для
исследуемой зависимости близко к 1;
—
индекса корреляции для исследуемой
зависимости близко к 0;
+
индекса детерминации, рассчитанного
для данной модели достаточно близко к
1;
—
доля остаточной дисперсии результативного
признака в его общей дисперсии стремится
к 1.
Система
нормальных уравнений метода наименьших
квадратов строится на основании:
—
таблицы исходных данных;
+
отклонений фактических значений
результативного признака от его
теоретических значений;
—
предсказанных значений результативного
признака;
—
отклонений фактических значений
объясняющей переменной от ее теоретических
значений.
Общая
дисперсия служит для оценки влияния …
—
учтенных явно в модели факторов;
+
как учтенных факторов, так и случайных
воздействий;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Экспоненциальным
не является
уравнение регрессии:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Объем
выборки определяется …
—
числовыми значениями переменных,
отбираемых в выборку;
—
объемом генеральной совокупности;
+
числом параметров при независимых
переменных;
—
числом результативных переменных.
При
расчете значения коэффициента
детерминации используется отношение:
—
математических ожиданий;
—
остаточных величин;
—
параметров уравнения регрессии;
+
дисперсий.
Предпосылкой
метода наименьших квадратов является
…
—
присутствие автокорреляции между
результатом и фактором;
—
отсутствие корреляции между результатом
и фактором;
—
присутствие автокорреляции в остатках;
+
отсутствие автокорреляции в остатках.
Смысл
расчета средней ошибки аппроксимации
состоит в определении среднего
арифметического значения . . . .
—
теоретических значений результативного
признака, выраженных в процентах от
его фактических значений;
+
отклонений
![]() ,
,
выраженных в процентах от фактических
значений результативного признака;
—
теоретических значений результативного
признака, выраженных в процентах от
его фактических значений признака;
—
отклонений
![]() ,
,
выраженных в процентах от фактических
значений независимой переменной.
Для
моделирования зависимости предложения
от цены не
может быть
использовано уравнение регрессии:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Основной
целью линеаризации уравнения регрессии
является. . . .
—
повышения существенности связи между
рассматриваемыми переменными;
—
получение новых нелинейных зависимостей;
+
возможность применения метода наименьших
квадратов для оценки параметров;
—
улучшение качества модели.
Требованием
к уравнениям регрессии, параметры
которых можно найти при помощи МНК
является:
+
линейность параметров;
—
равенство нулю средних значений
результативной переменной;
—
нелинейность параметров;
—
равенство нулю средних значений
факторного признака.
Совокупность
значений критерия, при которых принимается
нулевая гипотеза, называется областью
_____________ гипотезы:
+
принятия;
—
нулевых значений;
—
допустимых значений;
—
отрицания.
Качество
подбора уравнения оценивает коэффициент
. . . .
—
корреляции;
+
детерминации;
—
эластичности;
—
регрессии.
Смысл расчета
средней ошибки аппроксимации состоит
в определении среднего арифметического
значения:
+
отклонений £ , выраженных в процентах
от фактических значений результативного
признака
—теоретических
значений результативного признака,
выраженных в процентах от его фактических
значений
—теоретических
значений результативного признака,
выраженных в процентах от его фактических
значений признака
—отклонений
£ , выраженных в процентах от фактических
значений независимой переменной
Увеличение точности
оценок с увеличением объема выборки
описывает свойство ___________ оценки
—
несмещенности;
—
смещенности;
+
состоятельности;
—
эффективности.
Оценки
параметров, найденных при помощи метода
наименьших квадратов, обладают свойствами
эффективности, состоятельности и
несмещенности, если предпосылки метода
наименьших квадратов . . .
+
выполняются;
—
не выполняются;
—
можно не учитывать;
—
можно исключить.
Нелинейным
не является уравнение . . . .
+![]() ;
;
—![]() ;
;
—![]() ;
;
—![]() .
.
Критерий
Стьюдента предназначен для определения
значимости . . .
—
построенного уравнения в целом;
—
каждого коэффициента корреляции;
—
уравнения;
+
каждого коэффициента регрессии.
Для
моделирования зависимости предложения
от цены не
может быть
использовано уравнение регрессии:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Основной целью
линеаризации уравнения регрессии
является:
+ возможность
применения метода наименьших квадратов
для оценки параметров
—повышение
существенности связи между рассматриваемыми
признаками
—получение
новых нелинейных зависимостей
—улучшение
качества модели
Для
уравнения
![]()
значение коэффициента корреляции
составило 2. Следовательно . . . .
+
значение коэффициента корреляции
рассчитано с ошибкой;
—
теснота связи в 2 раза сильнее, чем для
функциональной связи;
—
связь функциональная;
—
при увеличении фактора на единицу
значение результата увеличивается в
2 раза.
Назовите
показатель корреляции для нелинейных
моделей регрессии:
—
парный коэффициент линейной корреляции;
—
индекс детерминации;
—
линейный коэффициент корреляции;
+
индекс корреляции.
Если
спецификация модели
![]()
нелинейного уравнения регрессии, то
нелинейной является функция:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Значение
коэффициента корреляции не характеризует
…
+
статистическую значимость уравнения;
—
корень из значения коэффициента
детерминации;
—
тесноту связи;
—
силу связи.
Расчетное
значение критерия Фишера определяется
как отношение ….
+
дисперсий;
—
результата к фактору;
—
математических ожиданий;
—
случайных величин.
Парабола
второй степени может быть использована
для зависимостей экономических
показателей,
—
если исходные данные не обнаруживают
изменения направленности;
—
если для определенного интервала
значений фактора меняется скорость
изменений значений результата, то есть
возрастает динамика роста или спада;
—
если характер связи зависит от случайных
факторов;
+
если для определенного интервала
значений фактора меняется характер
связи рассматриваемых показателей:
прямая связь изменяется на обратную
или обратная на прямую.
Оценки
параметров уравнений регрессии при
помощи метода наименьших квадратов
находятся на основании:
—
решения уравнения регрессии;
+
решения системы нормальных неравенств;
—
решения двойственной задачи;
—
решения системы нормальных уравнений.
Для
уравнения зависимости выручки от
величины оборотных средств получено
значение коэффициента детерминации,
равное 0,7. Следовательно, _______ процентов
дисперсии обусловлено случайными
факторами.
+
30%;
—
100%;
—
70%;
—
0%.
Если
доверительный интервал для параметра
проходит через точку ноль, следовательно
…
—
значение параметра может принимать
как отрицательные, так и положительные
значения;
+
параметр является несущественным;
—
параметр является существенным;
—
параметр признается статистически
значимым.
Уравнение
регрессии
![]()
характеризует ________ зависимость.
+
обратно пропорциональную;
—
линейную;
—
функциональную;
—
прямо пропорциональную
Значения
коэффициента корреляции может находиться
в отрезке:
—
[-1;0];
—
[0;1];
+
[-1;1];
—
[-2;2].
Оценка
значимости уравнения в целом осуществляется
по критерию:
+
Фишера;
—
Дарбина-Уотсона;
—
Пирсона;
—
Стьюдента.
Метод
наименьших квадратов позволяет оценить
_______ уравнений регрессии
—
переменные и случайные величины;
+
параметры;
—
переменные;
—
параметры и переменные
Расчет
средней ошибки аппроксимации для
нелинейных уравнений регрессии связан
с расчетом разности между …
+
фактическим и теоретическим значениями
результативной переменной;
—
фактическим и теоретическим значениями
независимой переменной;
—
прогнозным и теоретическим значениями
результативной переменной;
—
прогнозным и теоретическим значениями
независимой переменной.
Предпосылкой
метода наименьших квадратов является
то, что …
—
при увеличении моделируемых значений
результативного признака значение
остатка увеличивается;
+
остаточные величины имеют случайный
характер;
—
при уменьшении моделируемых значений
результативного признака значение
остатка уменьшается;
—
остаточные величины имеют неслучайный
характер.
Проводится
исследование финансовых результатов
деятельности предприятий, среди которых
обнаруживаются как прибыльные, так и
убыточные. Среди факторов, влияющих на
прибыль, был выделен доминирующий. При
этом нельзя
использовать
спецификацию:
—
![]() ;
;
—
![]() ;
;
—
![]() ;
;
—
![]() .
.
Значение
коэффициента детерминации рассчитывается
как отношение дисперсии результативного
признака, объясненной регрессией, к
___________ дисперсии результативного
признака.
—
средней;
—
факторной;
—
остаточной;
+
общей
Расчет
значения коэффициента детерминации
не позволяет
оценить:
—
качество подбора уравнения регрессии;
—
долю факторной дисперсии результативного
признака в общей дисперсии результативного
признака;
+
существенность коэффициента регрессии;
—
долю остаточной дисперсии результативного
признака в общей дисперсии результативного
признака.
Предпосылкой
метода наименьших квадратов является
то, что остатки …
—
не подчиняются закону больших чисел;
+
подчиняются закону нормального
распределения;
—
не подчиняются закону нормального
распределения;
—
подчиняются закону больших чисел.
Критическое
значение критерия Стьюдента определяет:
—
максимально возможную величину,
допускающую принятие гипотезы о
существенности параметра;
+
максимально возможную величину,
допускающую принятие гипотезы о
несущественности параметра;
—
минимально возможную величину,
допускающую принятие гипотезы о
равенстве нулю значения параметра;
—
минимально возможную величину,
допускающую принятие гипотезы о
несущественности параметра.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
…
—
регрессии;
+
корреляции;
—
случайных воздействий;
—
автокорреляции.
В
линейном уравнении парной регрессии
![]()
коэффициентом регрессии является
значение …
+
параметров
![]()
и
![]() ;
;
—
параметра
![]() ;
;
—
переменной
![]() ;
;
—
параметра
![]() .
.
Линеаризация
подразумевает процедуру …
—
приведения уравнения множественной
регрессии к парной;
+
приведения нелинейного уравнения к
линейному виду;
—
приведения линейного уравнения к
нелинейному виду;
—
приведения нелинейного уравнения
относительно параметров к уравнению,
линейному относительно результата.
Система
нормальных уравнений метода наименьших
квадратов строится на основании:
—
таблицы исходных данных;
+
отклонений фактических значений
результативного признака от его
теоретических значений;
—
предсказанных значений результативного
признака;
—
отклонений фактических значений
объясняющей переменной от ее теоретических
значений.
При
помощи модели степенного уравнения
регрессии вида
![]()
не может быть
описана
зависимость …
—
выработки от уровня квалификации;
—
заработной платы от выработки;
—
объема предложения от цены;
+
выработки от трудоемкости.
Замена
![]()
не подходит
для уравнения …
—
![]() ;
;
—
![]() ;
;
—
![]() ;
;
+
![]() .
.
При
хорошем качестве модели допустимым
значением средней ошибки аппроксимации
является …
+
5-7%;
—
50%;
—
90-95%;
—
20-25%.
Простая
линейная регрессия предполагает …
—
наличие двух и более факторов и
нелинейность уравнения регрессии;
+
наличие одного фактора и линейность
уравнения регрессии;
—
наличие одного фактора и нелинейность
уравнения регрессии;
—
наличие двух и более факторов и линейность
уравнения регрессии.
Минимальная
дисперсия остатков характерна для
оценок, обладающих свойством …
+
эффективности;
—
несостоятельности;
—
состоятельности;
—
несмещенности.
Нелинейным
является уравнение:
+
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Построена
модель парной регрессии зависимости
предложения от цены
![]() .
.
Влияние случайных факторов на величину
предложения в этой модели учтено
посредством …
—
константы
![]() ;
;
—
параметра
![]() ;
;
—
случайной величины
![]() ;
;
+
случайной величины
![]() .
.
При
расчете значения коэффициента
детерминации используется отношение:
—
математических ожиданий;
—
остаточных величин;
—
параметров уравнения регрессии;
+
дисперсий.
Случайными
воздействиями обусловлено 12% дисперсии
результативного признака, следовательно,
значение коэффициента детерминации
составило:
—
88;
—
0,12;
+
0,88;
—
12.
Свойствами
оценок МНК являются:
—
эффективность, состоятельность и
смещенность;
—
эффективность, несостоятельность и
несмещенность;
—
эффективность, несостоятельность и
смещенность;
+
эффективность, состоятельность и
несмещенность.
Спецификация
модели нелинейная парная (простая)
регрессия подразумевает нелинейную
зависимость и …
+
независимую переменную;
—
пару существенных переменных;
—
пару независимых переменных;
—
пару зависимых переменных.
Значение
линейного коэффициента корреляции
характеризует тесноту ________ связи.
-нелинейной;
+
линейной;
-случайной;
—
множественной линейной.
Для
нелинейных уравнений метод наименьших
квадратов применяется к …
—
не преобразованным линейным уравнениям;
—
обратным уравнениям;
+
преобразованным линеаризованным
уравнениям;
—
нелинейным уравнениям.
Величина
коэффициента детерминации при включении
существенного фактора в эконометрическую
модель …
+
будет увеличиваться;
—
будет равно нулю;
—
существенно не изменится;
—
будет уменьшаться.
К
линейному виду нельзя
привести:
—
линейную модель внутренне линейную;
+
нелинейную модель внутренне нелинейную;
—
линейную модель внутренне нелинейную;
—
нелинейную модель внутренне линейную.
Математическое
ожидание остатков равно нулю, если
оценки параметров обладают свойством…
—
смещенности;
+
несмещенности;
—
состоятельности;
—
эффективности.
В
нелинейной модели парной регрессии
![]()
функция
![]()
является:
—
равной нулю;
—
несущественной;
—
линейной;
+
нелинейной.
Критические
значения критерия Фишера определяются
по:
+
уровню значимости и степеням свободы
факторной и остаточной дисперсий;
—
уровню значимости и степени свободы
общей дисперсии;
—
уровню значимости;
—
степени свободы факторной и остаточной
дисперсий.
В
качестве показателя тесноты связи для
линейного уравнения парной регрессии
используется:
—
множественный коэффициент линейной
корреляции;
+
линейный коэффициент корреляции;
—
линейный коэффициент регрессии;
—
линейный коэффициент детерминации.
Предпосылки
метода наименьших квадратов исследуют
поведение …
—
параметров уравнения регрессии;
—
неслучайных величин;
+
остаточных величин;
—
переменных уравнения регрессии.
Величина
параметра
![]()
в уравнении парной линейной регрессии
![]()
характеризует значение …
—
факторной переменной при нулевом
значении результата;
—
результирующей переменной при нулевом
значении случайной величины;
—
факторной переменной при нулевом
значении случайного фактора;
+
результирующей переменной при нулевом
значении фактора.
Если
значение индекса корреляции для
нелинейного уравнения регрессии
стремится к 1, следовательно, …
—
нелинейная связь недостаточно тесная;
—
линейная связь достаточно тесная;
+
нелинейная связь достаточно тесная;
—
нелинейная связь отсутствует.
Состоятельность
оценки характеризуется …
—
независимостью от объема выборки
значения математического ожидания
остатков;
+
увеличением ее точности с увеличением
объема выборки;
—
уменьшением ее точности с увеличением
объема выборки;
—
зависимостью от объема выборки значения
математического ожидания остатков.
Если
предпосылки метода наименьших квадратов
нарушены, то …
—
полученное уравнение статистически
незначимо;
+
оценки параметров могут не обладать
свойствами эффективности, состоятельности
и несмещенности;
—
коэффициент регрессии является
несущественным;
—
коэффициент корреляции является
несущественным.
Общая
дисперсия служит для оценки влияния …
—
учтенных явно в модели факторов;
+
как учтенных факторов, так и случайных
воздействий;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Значение
коэффициента корреляции равно -1.
Следовательно …
—
связь отсутствует;
—
связь слабая;
+
связь функциональная;
—
ситуация неопределенна.
Нелинейным
называется уравнение регрессии, если
…
—
параметры входят нелинейным образом,
а переменные линейны;
+
независимые переменные входят в
уравнение нелинейным образом;
—
параметры и зависимые переменные входят
в уравнение нелинейным образом;
—
зависимые переменные входят в уравнение
нелинейным образом.
Если
коэффициент регрессии является
несущественным, то его значения
приравниваются к …
—
табличному значению и соответствующий
фактор не включается в модель;
+
нулю и соответствующий фактор не
включается в модель;
—
единице и не влияет на результат;
—
нулю и соответствующий фактор включается
в модель.
Величина
отклонений фактических значений
результативного признака от его
теоретических значений представляет
собой …
—
ошибку корреляции;
—
значение критерия Фишера;
+
ошибку аппроксимации;
—
показатель эластичности.
Объем
выборки должен превышать число
рассчитываемых параметров при исследуемых
факторах ..
—
в 2-3 раза;
—
в 20-25 раз;
—
в 10-12 раз;
+
в 5-6 раз.
Остаточная
дисперсия служит для оценки влияния …
+
случайных воздействий;
—
величины постоянной составляющей в
уравнении;
—
учтенных явно в модели факторов;
—
как учтенных факторов, так и случайных
воздействий.
Значение
коэффициента корреляции равно 0,9.
Следовательно, значение коэффициента
детерминации составит …
—
0,3;
+
0,81;
—
0,95;
—
0,1.
По
результатам исследования было выявлено,
что рентабельность производства падает
с увеличением трудоемкости. Какую
спецификацию уравнения регрессии можно
использовать для построения модели
такой зависимости?
—
![]() ;
;
+
![]() ;
;
—
![]() ;
;
—
![]() .
.
Случайный
характер остатков предполагает …
—
независимость предсказанных по модели
значений результативного признака от
значений факторного признака;
+
независимость остатков от величины
предсказанных по модели значений
результативного признака;
—
зависимость остатков от величины
предсказанных по модели значений
результативного признака;
—
зависимость предсказанных по модели
значений результативного признака от
значений факторного признака.
Статистические
гипотезы используются для оценки:
—
тесноты связи между результатом и
фактором;
—
тесноты связи между результатом и
случайными факторами;
—
автокорреляции в остатках;
+
значимости уравнения регрессии в целом.
Параметр
является существенным, если …
+
доверительный интервал не проходит
через ноль;
—
доверительный интервал проходит через
ноль;
—
расчетное значение критерия Стьюдента
меньше табличного значения;
—
стандартная ошибка превышает половину
значения самого параметра.
Замена
![]() ,
,
![]() подходит
подходит
для уравнения:
—
![]() ;
;
—
![]() ;
;
—
![]() ;
;
+
![]() .
.
В
исходном соотношении МНК сумма квадратов
отклонений фактических значений
результативного признака от его
теоретических значений …
—
приравнивается к нулю;
+
минимизируется;
—
максимизируется;
—
приравнивается к системе нормальных
уравнений.
При
выборе спецификации нелинейная регрессия
используется, если …
—
нелинейная зависимость для исследуемых
экономических показателей является
несущественной;
+
между экономическими показателями
обнаруживается нелинейная зависимость;
—
между экономическими показателями не
обнаруживается нелинейная зависимость;
—
между экономическими показателями
обнаруживается линейная зависимость.
Табличное
значение критерия Фишера служит для …
+
проверки статистической гипотезы о
равенстве факторной и остаточной
дисперсий;
—
проверки статистической гипотезы о
равенстве дисперсии некоторой
гипотетической величины;
—
проверки статистической гипотезы о
равенстве двух математических ожиданий;
—
проверки статистической гипотезы о
равенстве математического ожидания
некоторой гипотетической величины.
Предпосылкой
метода наименьших квадратов является
то, что остатки …
—
не подчиняются закону больших чисел;
+
подчиняются закону нормального
распределения;
—
не подчиняются закону нормального
распределения;
—
подчиняются закону больших чисел.
Расчетное
значение критерия Фишера определяется
как …
—
разность факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы;
—
отношение факторной дисперсии к
остаточной;
+
отношение факторной дисперсии к
остаточной, рассчитанных на одну степень
свободы;
—
суммы факторной дисперсии к остаточной,
рассчитанных на одну степень свободы.
Предпосылкой
метода наименьших квадратов не
является
условие …
—
гомоскедастичности остатков;
—
случайный характер остатков;
—
отсутствие автокорреляции в остатках;
+
неслучайный характер остатков.
Нелинейное
уравнение регрессии означает нелинейную
форму зависимости между:
—
фактором и результатом;
—
фактором и случайной величиной;
+
результатом и факторами;
—
результатом и параметрами.
Несмещенность
оценки на практике означает …
—
уменьшение точности с увеличением
объема выборки;
—
невозможность перехода от точечного
оценивания к интервальному;
—
что найденное значение коэффициента
регрессии нельзя рассматривать как
среднее значение из возможного большого
количества несмещенных оценок;
+
что при большом числе выборочных
оцениваний остатки не будут накапливаться.
Стандартная
ошибка рассчитывается для проверки
существенности …
+
параметра;
—
коэффициента детерминации;
—
случайной величины;
—
коэффициента корреляции.
Факторная
дисперсия служит для оценки влияния:
—
как учтенных факторов, так и случайные
воздействия;
+
учтенных явно в модели факторов;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Экспоненциальным
не является
уравнение регрессии:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Известно,
что с увеличением объема производства
себестоимость единицы продукции
уменьшается за счет того, что происходит
перераспределение постоянных издержек.
Пусть
![]()
— совокупная величина постоянных
издержек, а
![]() —
—
величина переменных издержек в расчете
на 1 изделие. Тогда зависимость
себестоимости единицы продукции от
объема производства можно описать с
помощью модели:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
В
основе метода наименьших квадратов
лежит …
—
равенство нулю суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений;
—
минимизация суммы квадратов отклонений
фактических значений результативного
признака от его средних значений;
+
минимизация суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений;
—
максимизация суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений.
Объем
выборки определяется …
—
числовыми значениями переменных,
отбираемых в выборку;
—
объемом генеральной совокупности;
+
числом параметров при независимых
переменных;
—
числом результативных переменных.
При
оценке статистической значимости
уравнения и существенности связи
осуществляется проверка …
—
существенности параметров;
—
существенности коэффициента корреляции;
+
существенности коэффициента детерминации;
—
нулевой гипотезы.
Для
модели зависимости дохода населения
(р.) от объема производства (млн р.)
получено уравнение
![]() .
.
При изменении объема производства на
1 млн р. доход в среднем изменится на …
+
0,003 млн р.;
—
1200 млн р.;
—
1200 р.;
—
0,003 р.
Относительно
формы зависимости различают …
—
простую и множественную регрессию;
—
положительную и отрицательную регрессию;
—
непосредственную и косвенную регрессию;
+
линейную и нелинейную регрессию.
В
матрице парных коэффициентов корреляции
отображены значения парных коэффициентов
линейной корреляции между …
—
переменными и случайными факторами;
+
переменными;
—
параметрами;
—
параметрами и переменными.
Уравнение
регрессии
![]()
может быть реализовано при помощи
подстановки:
—
![]() ;
;
—
![]() ;
;
+
![]() ;
;
—
![]() .
.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение …
—
линейного коэффициента корреляции для
исследуемой зависимости близко к 1;
—
индекса корреляции для исследуемой
зависимости близко к 0;
+
индекса детерминации, рассчитанного
для данной модели достаточно близко к
1;
—
доля остаточной дисперсии результативного
признака в его общей дисперсии стремится
к 1.
Если
значение коэффициента корреляции равно
единице, то связь между результатом и
фактором …
—
стохастическая;
—
вероятностная;
+
функциональная;
—
отсутствует.
Эффективность
оценки на практике характеризуется …
—
невозможностью перехода от точечного
оценивания к интервальному;
—
отсутствием накапливания значений
остатков при большом числе выборочных
оцениваний;
—
уменьшением точности с увеличением
объема выборки;
+
возможность перехода от точечного
оценивания к интервальному
.
Линеаризация
не подразумевает
процедуру …
+
включение в модель дополнительных
существенных факторов;
—
приведение нелинейного уравнения к
линейному;
—
замены переменных;
—
преобразования уравнения.
Основной
задачей эконометрики является …
—
установление связей между различными
процессами в обществе и техническим
процессом;
—
анализ технического процесса на примере
социально-экономических показателей;
—
отражение особенности социального
развития общества;
+
исследование взаимосвязей экономических
явлений и процессов.
При
применении метода наименьших остатков
уменьшить гетероскедастичность остатков
удается путем …
+
преобразования переменных;
—
преобразования параметров;
—
введения дополнительных результатов
в модель;
—
введения дополнительных факторов в
модель.
Значение
индекса детерминации, рассчитанное
для нелинейного уравнения регрессии
характеризует …
+
долю дисперсии результативного признака,
объясненную нелинейной регрессией в
общей дисперсии результативного
признака;
—
долю дисперсии результативного признака,
объясненную линейной корреляцией в
общей дисперсии результативного
признака;
Предпосылкой
метода наименьших квадратов является
…
—
присутствие автокорреляции между
результатом и фактором;
—
отсутствие корреляции между результатом
и фактором;
—
присутствие автокорреляции в остатках;
+
отсутствие автокорреляции в остатках.
Было
замечено, что при увеличении количества
вносимых удобрений урожайность также
возрастает, однако, по достижении
определенного значения фактора
моделируемый показатель начинает
убывать. Для исследования данной
зависимости можно использовать
спецификацию уравнения регрессии …
—
![]() ;
;
—
![]() ;
;
—
![]() ;
;
+
![]() .
.
Если
оценка параметра эффективна, то это
означает …
—
максимальную дисперсию остатков;
—
уменьшение точности с увеличением
объема выборки;
—
равенство нулю математического ожидания
остатков;
+
наименьшую дисперсию остатков.
При
выборе спецификации модели парная
регрессия используется в случае, когда
…
—
среди множества факторов, влияющих на
результат, можно выделить лишь случайные
факторы;
—
среди множества факторов, влияющих на
результат, можно выделить несколько
факторов;
+
среди множества факторов, влияющих на
результат, можно выделить доминирующий
фактор;
—
среди множества факторов, влияющих на
результат, нельзя выделить доминирующий
фактор.
Нелинейную
модель зависимостей экономических
показателей нельзя привести к линейному
виду, если …
+
нелинейная модель является внутренне
нелинейной;
—
нелинейная модель является внутренне
линейной;
—
линейная модель является внутренне
нелинейной;
—
линейная модель является внутренне
линейной.
Для
существенного параметра расчетное
значение критерия Стьюдента …
—
равно нулю;
+
больше табличного значения критерия;
—
не больше табличного значения критерия;
—
меньше табличного значения критерия.
Оценить
статистическую значимость нелинейного
уравнения регрессии можно с помощью …
—
средней ошибки аппроксимации;
+
критерия Фишера;
—
линейного коэффициента корреляции;
—
показателя эластичности.
Расчетное
значение критерия Фишера определяется
как ___________факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы
—
произведение;
—
разность;
—
сумма;
+
отношение.
Критическое
значение критерия Стьюдента определяет
минимально возможную величину,
допускающую принятие гипотезы о …
—
несущественности параметра;
+
существенности параметра;
—
статистической незначимости значения
параметра;
—
равенства нулю значения параметра.
Если
между экономическими показателями
существует нелинейная связь, то …
—
нецелесообразно использовать спецификацию
нелинейного уравнения регрессии;
+
целесообразно использовать спецификацию
нелинейного уравнения регрессии;
—
целесообразно использовать линейное
уравнение парной регрессии;
—
необходимо включить в модель другие
факторы и использовать линейное
уравнение множественной регрессии.
Оценка
значимости параметров уравнения
регрессии осуществляется по критерию
…
—
Ингла-Гренджера (Энгеля-Грангера);
+
Стьюдента;
—
Фишера;
—
Дарбина-Уотсона.
Назовите
показатель тесноты связи для нелинейных
моделей регрессии:
+
индекс корреляции;
—
индекс детерминации;
—
линейный коэффициент корреляции;
—
парный коэффициент линейной корреляции.
Объем
выборки определяется числом параметров
при …
—
зависимых переменных;
+
независимых переменных;
—
случайных факторах;
—
независимых и зависимых переменных.
Значение
индекса корреляции, рассчитанное для
нелинейного уравнения регрессии
характеризует …
—
тесноту случайной связи;
—
тесноту линейной связи;
+
тесноту нелинейной связи;
—
тесноту обратной связи.
Пусть
у = утеор
+
s,
где
у —
фактическое значение зависимой
переменной,
утеор
—
теоретическое,
рассчитанное по уравнению значение
зависимой переменной (объясненное
уравнением регрессии),
е-
ошибка модели. По значению коэффициента
детерминации можно судить о доли
объясненной дисперсии результативного
признака в дисперсии…
—его
теоретических значений
—случайных
факторов
—его
фактических значений
—независимой
переменной
Подбор
аналитической формы зависимости для
уравнения парной регрессии возможен
на основе графиков разброса…
—теоретических
точек с координатами
—остатков
модели
ег,е2,…,еп
—центрированных
по факторной переменной точек с
координатами
-
(Xl
-х,у^{х2
-Х,у2),…,(хп
-Х,у„) —эмпирических
точек с координатами -
(хл),^,^
),…, (х„,у„)
Для
определения степени зависимости
результативной переменной от
факторных,
пользуются методом…
—корреляционного
анализа
—наименьших
квадратов
—кластерного
анализа
—скользящих
средних
Предпосылка
применения корреляционного анализа…
—совокупность
значений факторных и результативных
признаков распределена по нормальному
закону
—совокупность
значений факторных и результативных
признаков имеет распределение Стьюдента
—совокупность
значений факторных признаков распределена
по нормальному закону, а результативного
— по произвольному
—совокупность
значений результативного признака
распределена по нормальному закону, а
закон распределения совокупности
факторных признаков — произвольный
Уравнение нелинейной
регрессии
y
= y
+ s,
где
е2у—
общая дисперсия результативного
признака у; cro2st
-остаточная
дисперсия ошибки s
, может
оцениваться показателем тесноты связи
-индексом корреляции R,
который
вычисляется по формуле…
Тема
Парная регрессия (Задачи)
Зависимость
спроса на кухонные комбайны y
от цены x
по 12 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,4 %. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Нет,
на любом уровне (0,1; 0,05 и 0,1)
—Да,
на любом уровне (0,1; 0,05 и 0,1)
—Нет,
только на уровнях 0,05 и 0,1
—Нет,
только на уровне 0,1
Зависимость
спроса на кухонные комбайны y
от цены x
по 18 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,5 %. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Да,
только на уровне значимости 0,01
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 15 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,3 %. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Да,
на любом уровне (0,1, 0,05 и 0,01)
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
только на уровне значимости 0,01
Зависимость
спроса на кухонные комбайны y
от цены x
по 12 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,3 %. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Да,
только на уровнях 0,01 и 0,05
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 14 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,2%. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 15 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,1 %. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Да,
только на уровнях 0,01 и 0,05
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 20 торговым точкам компании имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к
уменьшению спроса на 1,3 %. Можно ли
утверждать, что приведенное уравнение
регрессии подтверждает это предположение?
+—Да,
только на уровне значимости 0,01
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=50
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=60
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=80
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=25
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=30
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=45
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
+—![]()
![]()
![]()
![]()
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
![]()
Сравнить
эластичности затрат по каждому виду
продукции при x=55
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
—![]()
![]()
![]()
![]()
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 15 наблюдениям. При этом r=-0.7.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-11,11;
-0,89) с вероятностью 0,99
—(-9,67;-2,33)
с вероятностью 0,99
—(-9,01;
-2,99) с вероятностью 0,95
—(-8,53;
-2,32) с вероятностью 0,9
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 18 наблюдениям. При этом r=-0.75.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-6,92;
-3,08) с вероятностью 0,9
—(-6,92;-3,08)
с вероятностью 0,95
—(-8,22;
-1,78) с вероятностью 0,95
—(-7,34;
-2,66) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 20 наблюдениям. При этом r=-0.65.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-6,32;-1,68)
с вероятностью 0,95
—(-5,91;-2,09)
с вероятностью 0,99
—(-6,32;
-1,68) с вероятностью 0,99
—(-5,91;
-2,09) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 22 наблюдениям. При этом r=0.73.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(1,69;
4,31) с вероятностью 0,95
—(-0,49;6,49)
с вероятностью 0,95
—(-1,76;
7,76) с вероятностью 0,99
—(1,23;
4,77) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 24 наблюдениям. При этом r=0.68.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(2,46;11,54)
с вероятностью 0,99
—(2,50;
11,50) с вероятностью 0,99
—(6,36;
7,64) с вероятностью 0,90
—(3,68;
10,32) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 20 наблюдениям. При этом r=0.86.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(2,27;3,73)
с вероятностью 0,90
—(2,14;3,86)
с вероятностью 0,95
—(2,28;
3,72) с вероятностью 0,99
—(1,85;
4,15) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 15 наблюдениям. При этом r=0,53.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(0,20;9,80)
с вероятностью 0,95
—(0,05;9,95)
с вероятностью 0,99
—(1,17;
8,83) с вероятностью 0,90
—(0,35;
9,65) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 18 наблюдениям. При этом r=-0,6.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-3,42;-0,58)
с вероятностью 0,95
—(-3,7;-0,3)
с вероятностью 0,99
—(-3,21;
-0,79) с вероятностью 0,90
—(-3,56;
-0,44) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 16 наблюдениям. При этом r=![]() .
.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-4,80;-1,2)
с вероятностью 0,99
—(-4,36;-1,64)
с вероятностью 0,95
—(-3,98;
-2,02) с вероятностью 0,90
—(-4,96;
-1,04) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
![]()
построенное
по 14 наблюдениям. При этом
![]() .
.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-16,72;
0,72) с вероятностью 0,95
—(-17,32;
1,32) с вероятностью 0,99
—(-16,13;
0,13) с вероятностью 0,90
—(-15,76;
-0,24) с вероятностью 0,90
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 18 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,360
—0,384
—0,247
—0,456
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 20 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,405
—0,428
—0,292
—0,501
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 15 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,448
—0,564
—0,356
—0,621
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 20 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,491
—0,425
—0,379
—0,531
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 18 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,327
—0,425
—0,517
—0,369
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 25 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,373
—0,321
—0,415
—0,512
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 15 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,675
—0,519
—0,631
—0,620
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 18 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,461
—0,395
—0,423
—0,522
Уравнение
регрессии потребления материалов
![]()
от объема производства
![]() ,
,
построенное по 20 наблюдениям, имеет
вид:
![]()
![]()
![]()
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,495
—0,517
—0,444
—0,396
По
совокупности 15 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
![]()
Индекс
корреляции, фактическое значение F-
критерия значимость уравнения регрессии
следующие:
+—![]()
![]()
уравнение статистически не значимо на
уровнях 0,01 и 0,05
—![]()
![]()
уравнение
статистически значимо только на уровне
0,1
—![]()
![]()
уравнение
статистически значимо только на уровнях
0,1 и 0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
По
совокупности 18 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,05 и 0,1
—![]()
![]()
уравнение
статистически не значимо на уровне
0,01
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически не значимо на всех уровнях
По
совокупности 25 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,1 и 0,05
—![]()
![]()
уравнение
статистически не значимо на уровне
0,01
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически не значимо на всех уровнях
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровне 0,1
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически не значимо на уровнях
0,05 и 0,01
По
совокупности 30 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически не значимо на уровнях
0,05 и 0,01
—![]()
![]()
уравнение
статистически значимо на уровне 0,10
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,1 и 0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически не значимо на уровне
0,01
По
совокупности 22 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровне 0,1
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически не значимо на уровне 0,1
По
совокупности 28 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
уровнях 0,1 и 0,05
—![]()
![]()
уравнение
статистически не значимо на уровне
0,01
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровне 0,1
По
совокупности 30 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо на
всех уровнях
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически значимо на уровне 0,1
—![]()
![]()
уравнение
статистически не значимо на уровне
0,01
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
![]()
на товар А и прибылью
![]()
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
![]()
![]()
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—![]()
![]()
уравнение статистически значимо уровне
0,1
—![]()
![]()
уравнение
статистически значимо на уровнях 0,1 и
0,05
—![]()
![]()
уравнение
статистически значимо на всех уровнях
—![]()
![]()
уравнение
статистически не значимо на уровне
0,01
И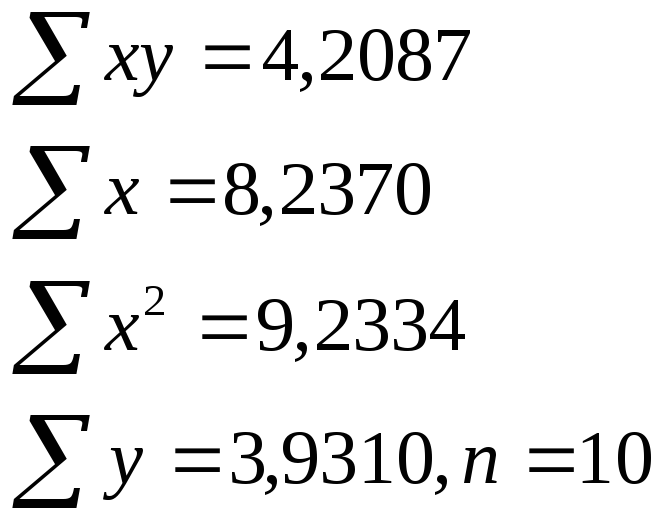
зучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,5
—0,7
—0,4
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,7
—0,5
—0,4
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,4
—0,7
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,9
—0,7
—0,6
—0,8
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
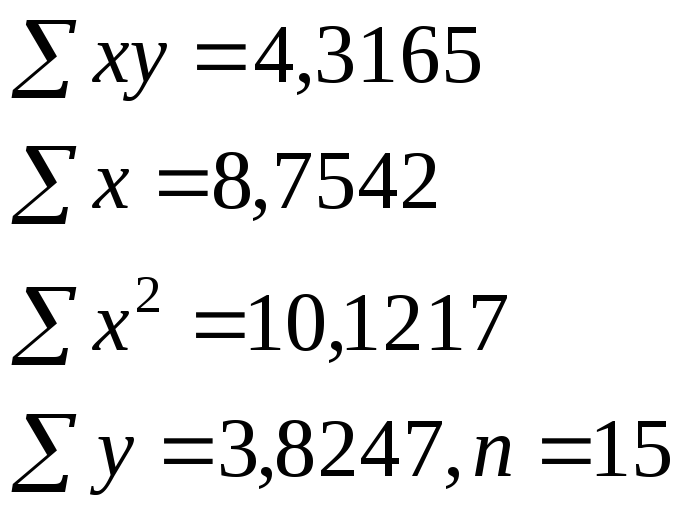
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,3
—0,4
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,5
—0,7
—0,6
—0,4
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 12 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,83;
S2регр=7,95;
F=22,04,tb=4,69
—Rxy=0,83;
S2регр=5,35;
F=12,tb=3,9
—Rxy=0,43;
S2регр=3,74;
F=5,tb=2,4
—Rxy=0,43;
S2регр=3,48;
F=7,tb=2,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 15 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,90;
S2регр=17,98;
F=56,83,tb=7,54
—Rxy=0,90;
S2регр=15,35;
F=32,0, tb=6,9
—Rxy=0,71;
S2регр=13,74;
F=5,0, tb=2,4
—Rxy=0,71;
S2регр=9,48;
F=7,0, tb=2,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,90;
S2регр=16,48;
F=70,02, tb=8,37
—Rxy=0,90;
S2регр=15,35;
F=50,01, tb=5,2
—Rxy=0,54;
S2регр=9,82;
F=40,2, tb=4,8
—Rxy=0,54;
S2регр=8,32;
F=38,9, tb=4,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 15 предприятиям
концерна следующим образом:
О
пределите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,91;
S2регр=14,75;
F=66,24, tb=8,14
—Rxy=0,91;
S2регр=12,32;
F=50,1, tb=7,12
—Rxy=0,39;
S2регр=5,42;
F=10,31, tb=3,49
—Rxy=0,39;
S2регр=6,17;
F=11,32, tb=4,21
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 12 предприятиям
концерна следующим образом:
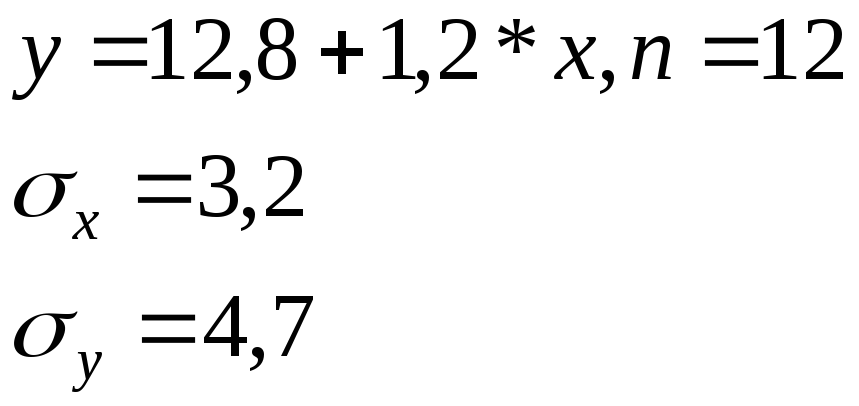
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,82;
S2регр=14,75;
F=20,08, tb=4,48
—Rxy=0,82;
S2регр=12,82;
F=18,42, tb=3,37
—Rxy=0,76;
S2регр=9,28;
F=10,12, tb=4,21
—Rxy=0,76;
S2регр=8,32;
F=12,05, tb=4,75
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,88;
S2регр=39,31;
F=56,68, tb=7,53
—Rxy=0,88;
S2регр=25,12;
F=40,12, tb=6,32
—Rxy=0,37;
S2регр=13,10;
F=16,17, tb=5,21
—Rxy=0,37;
S2регр=6,12;
F=4,31, tb=1,18
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 20 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,9789;
S2регр=31,14;
F=413,116, tb=20,33
—Rxy=0,9789;
S2регр=41,17;
F=420,08, tb=21,17
—Rxy=0,83;
S2регр=25,12;
F=57,2, tb=8,3
—Rxy=0,83;
S2регр=20,18;
F=48,1, tb=7,8
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 16 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,84;
S2регр=43,03;
F=33,83, tb=5,82
—Rxy=0,84;
S2регр=38,07;
F=25,71, tb=4,72
—Rxy=0,76;
S2регр=17,05;
F=8,3, tb=2,78
—Rxy=0,76;
S2регр=15,32;
F=6,8, tb=2,12
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:
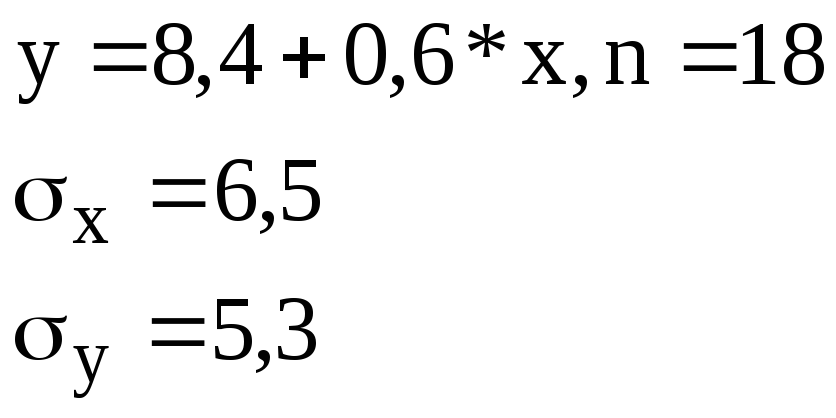
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,74;
S2регр=15,21;
F=18,89, tb=4,35
—Rxy=0,74;
S2регр=12,32;
F=16,05, tb=3,15
—Rxy=0,50;
S2регр=8,32;
F=12,47, tb=2,32
—Rxy=0,50;
S2регр=6,15;
F=10,16, tb=1,78
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 20 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,89;
S2регр=53,58;
F=70,62, tb=8,4
—Rxy=0,89;
S2регр=49,12;
F=51,2, tb=7,8
—Rxy=0,61;
S2регр=15,2;
F=12,3, tb=3,2
—Rxy=0,61;
S2регр=12,9;
F=5,7, tb=2,3
Уравнение регрессии
имеет вид: ln
y
= 4,5 + 0,003x
+ ln
e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,255
—0,003
—0,00066
—0,0536
—0,00063
Уравнение регрессии
имеет вид: ln
y
= 4,5 + 0,003 ln
x
+ ln
e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,003
—0,255
—0,00066
—0,0536
—0,00071
Уравнение регрессии
имеет вид: y
= 4,5 + 0,003 ln
x
+ e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,00066
—0,255
—0,003
—0,0536
—0,00063
Уравнение регрессии
имеет вид: y
= 4,5 + 0,003x
+ e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,0536
—0,255
—0,003
—0,00063
—0,0582
Уравнение регрессии
имеет вид: ln
y
= 2,3 + 0,0043x
+ ln
e.
При значении фактора, равном 108,
коэффициент эластичности y
по х
составит:
+—0,4644
—0,0043
—0,00185
—0,168
—0,4218
Уравнение регрессии
имеет вид: ln
y
= 2,3 + 0,0043 ln
x
+ ln
e.
При значении фактора, равном 108,
коэффициент эластичности y
по х
составит:
+—0,0043
—0,4644
—0,00185
—0,168
—0,00129
Уравнение регрессии
имеет вид: y
= 2,3 + 0,0043 ln
x
+ e.
При значении фактора, равном 108,
коэффициент эластичности y
по х
составит:
+—0,00185
—0,0043
—0,4644
—0,168
—0,4215
Уравнение регрессии
имеет вид: y
= 2,3 + 0,0043x
+ e.
При значении фактора, равном 108,
коэффициент эластичности y
по х
составит:
+—0,168
—0,00185
—0,0043
—0,4644
—0,00129
Уравнение регрессии
имеет вид: ln
y
= 2,2 + 0,0037x
+ ln
e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,3515
—0,0037
—0,00167
—0,137
—0,167
Уравнение регрессии
имеет вид: ln
y
= 2,2 + 0,0037 ln
x
+ ln
e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,0037
—0,3515
—0,00167
—0,137
—0,4644
Уравнение регрессии
имеет вид: y
= 2,2 + 0,0037 ln
x
+ e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,00167
—0,0037
—0,3515
—0,137
—0,00137
Уравнение регрессии
имеет вид: y
= 2,2 + 0,0037x
+ e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,137
—0,00167
—0,0037
—0,3515
—0,3218
Уравнение регрессии
имеет вид: ln
y
= 1,8 + 0,0027x
+ ln
e.
При значении фактора, равном 125,
коэффициент эластичности y
по х
составит:
+—0,3375
—0,0015
—0,0027
—0,158
—0,3916
Уравнение регрессии
имеет вид: ln
y
= 1,8 + 0,0027 ln
x
+ ln
e.
При значении фактора, равном 125,
коэффициент эластичности y
по х
составит:
+—0,0027
—0,3375
—0,0015
—0,158
—0,00158
Уравнение регрессии
имеет вид: y
= 1,8 + 0,0027 ln
x
+ e.
При значении фактора, равном 125,
коэффициент эластичности y
по х
составит:
+—0,0015
—0,0027
—0,3375
—0,158
—0,00158
Уравнение регрессии
имеет вид: y
= 1,8 + 0,0027x
+ e.
При значении фактора, равном 125,
коэффициент эластичности y
по х
составит:
+—0,158
—0,0015
—0,0027
—0,3375
—0,4218
Содержание
- Расчет уровня существенности
- Пример расчета
- Стандартизированный расчет уровня существенности
- Показатели для определения уровня существенности
- Три уровня существенности искажений
- Влияние уровня существенности на суждение аудитора
- Уровень существенности
- Смотреть что такое «Уровень существенности» в других словарях:
Расчет уровня существенности
Для того, чтобы при количественной оценке рассчитать уровень существенности в аудите, можно использовать абсолютные или относительные показатели. Абсолютные показатели на практике используются редко, т.к. для разных проверяемых субъектов, имеющих различный масштаб деятельности, одна и та же сумма отклонения может быть, как существенной, так и незначительной. Однако многие специалисты считают, что необходимо установить сумму, начиная с которой ошибка будет признаваться существенной для любого субъекта, независимо от размера его бизнеса.
Для того, чтобы понять, как определить уровень существенности с помощью относительных показателей, нужно сначала выбрать базу для расчета. В качестве базы может быть выбран как один показатель, так и несколько. Если применяется один критерий, то в качестве него, как правило, используется валюта баланса. Рассмотрим, как в данном случае производится расчет уровня существенности в аудите.
Пример 1
Валюта баланса предприятия на конец проверяемого периода равнялась 100 000 тыс. руб.
Аудитор принял решение использовать один показатель и коэффициент 0,02.
Уровень существенности составит:
С = 100 000 х 0,02 = 2 000 тыс. руб.
Для более точного определения уровня существенности лучше применять не один критерий, а их совокупность. Для выборки обычно используют показатели из следующего списка:
– валюта баланса
– собственный капитал
– выручка от реализации
– общие затраты предприятия
– балансовая прибыль
Рассмотрим, как при этом варианте расчета производится определение уровня существенности в аудите
Пример 2
|
Базовый показатель |
Значение базового показателя, тыс.руб. |
Доля, % |
Значение для расчета уровня существенности, тыс.руб. |
|
Валюта баланса |
100 000 |
2% |
2 000 |
|
Собственный капитал |
15 000 |
10% |
1 500 |
|
Выручка от реализации |
70 000 |
2% |
1 400 |
|
Общие затраты предприятия |
60 000 |
2% |
1 200 |
|
Балансовая прибыль |
10 000 |
5% |
Из полученного перечня обычно исключают экстремумы (в данном случае это – 500) и вычисляют среднее значение среди оставшихся показателей.
С1 = (2 000 + 1 500 + 1 400 + 1 200) / 4 = 6 100 / 4 = 1 525 тыс. руб.
Полученную величину, как правило, округляют, но так, чтобы отклонение от первоначальной суммы не превышало 20%.
В данном случае можно вычесть 25 тыс. руб., чтобы получить 1 500 тыс. руб.
Т.к. 25 / 1525 = 2% < 20%, то в итоге получим значение:
С = 1 500 тыс. руб.
Стандарты аудиторской деятельности определяют только самые общие правила проведения проверок. Поэтому аудитор сам выбирает конкретную методику, по которой определяется уровень существенности. Как рассчитать базовые показатели, какие применить коэффициенты и методику усреднения – специалист решает самостоятельно, на основании своего профессионального опыта и особенностей проверяемой компании.
Частный уровень существенности в аудите определяется путем распределения общего уровня, рассчитанного одним из указанных выше способов, по отдельным счетам бухгалтерского учета. Это распределение обычно производится пропорционально доле остатков по соответствующим счетам в валюте баланса.
Пример расчета
В таблице 1 представлен пример расчета необходимого показателя.
Таблица 1. Пример расчета
| Базовые показатели | Значение базового показателя, тыс. р. | Доля, % | Значение, применяемое для нахождения уровня существенности, тыс. р. |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| Балансовая прибыль предприятия | 63867 | 5 | 3193 |
| Выручка | 407904 | 2 | 8158 |
| Валюта баланса | 384414 | 2 | 7688 |
| Собственный капитал | 61500 | 10 | 6150 |
| Общие затраты предприятия | 304023 | 2 | 6080 |
В первом столбце таблицы 1 представлен перечень базовых показателей.
Информация о показателях, участвующих в расчете уровня существенности, принимается из бухгалтерской отчетности:
- показатели валюты баланса, собственного капитала принимаются из бухгалтерского баланса хозяйствующего субъекта;
- сведения о балансовой прибыли предприятия, выручке и общих затратах предприятия принимаются из отчета о финансовых результатах предприятия.
Во втором столбце отражены значения базового показателя, в столбце четвертом отражен показатель, который применяется для нахождения уровня. Показатель, применяемый для нахождения уровня существенности, находится умножением значения базового показателя (второй столбец) на процент (долю), отраженный в третьем столбце. Значения, которые отражены в третьем столбце (доля, %), определяются внутренними локальными актами (инструкциями) фирмы, которая проводит аудиторскую проверку. Рассчитывается значение, применяемое для нахождения данного уровня, по показателям:
- балансовой прибыли: 63867 х 5% = 3193 тыс. р.;
- выручки: 407904 х 25 = 8158 тыс. р.;
- валюты баланса: 384414 х 2% = 7688 тыс. р.;
- собственного капитала: 61500 х 10% = 6150 тыс. р.;
- общих затрат предприятия: 304023 х 2% = 6080 тыс. р.
Для расчета уровня применяется формула:
УСА = Сумма значений показателей, участвующих в расчете / количество показателей,
где УСА — уровень существенности в аудите, %.
Рассчитывается искомый уровень:
(3193 + 8158 + 7688 + 6150 + 6080) / 5 = 6253 тыс. р.
Значения, которые используются для расчета уровня, от среднего значения более чем на 20% не должны отличаться. Для проверки этого условия используется следующая формула:
Процент отклонений = (УСА – Значение показателя) / УСА х 100%, %.
Рассчитывается процент отклонений наименьшего значения от уровня: (6253 – 3193) / 6253 х 100 % = 49%.
Рассчитывается процент отклонений наибольшего значения от уровня: (8158 – 6253) / 6253 х 100% = 31%.
В результате расчетов получено, что показатель наименьшего значения (3193 тыс. р.) меньше среднего значения (6253 тыс. р.) практически в два раза.
Наименьшее значение при дальнейших расчетах отбрасывается, а наибольшее оставляется, так как наибольшее значение (8158 тыс. р.) и следующее за ним второе значение (7688 тыс.) уже не так разительно отличаются от полученного среднего показателя. В результате полученных отклонений можно сделать вывод, что наибольшее и наименьшее значения показателя отличаются от рассчитанного среднего более чем на 20%, в связи с чем возникает необходимость расчета скорректированного среднего значения показателя на основе полученных данных:
(8158 + 7688 + 6150 + 6080) / 4 = 7019 тыс. р.
Полученное значение среднего показателя округляется до 7100 тыс. р. и используется как количественный показатель уровня существенности в аудите. Округление можно производить в рамках 20% как в большую, так и в меньшую сторону.
Различие между значениями уровня до и после округления составляет:
(7100 – 7019) / 7019 x 100% = 1,16%, что находится в пределах 20%.
Полученный в ходе расчетов показатель уровня применяется при проведении аудиторской проверки для всей бухгалтерской отчетности.
>Уровень существенности
Стандартизированный расчет уровня существенности
Единый показатель уровня существенности определяется по стандартизированному методу, который применяется большинством аудиторских фирм и основан на расчете существенности в зависимости от допустимой ошибки по базовым показателям. Метод расчета на примере отчетности компании «Высокий кондитер» за 2014 год показан в таблице 1.
Таблица 1 – Стандартизированный расчет уровня существенности
|
Базовый показатель |
Значение базового показателя (руб.) |
Допустимая ошибка (%) |
Расчетное значение (руб.) |
|---|---|---|---|
|
Балансовая прибыль |
|||
|
Выручка |
|||
|
Валюта баланса |
|||
|
Собственный капитал |
|||
|
Общие затраты |
Следует отметить, что во внутренних стандартах аудиторской фирмы значения допустимой ошибки должны быть определены по всем используемым базовым показателям и применяться при проведении аудиторских проверок на постоянной основе.
Расчетное значение получается на основе произведения значения базового показателя и значения ошибки. Среднее арифметическое расчетного значения в данном случае составит 689787 руб.
Набольшее и наименьшее отклонение определяется по формулам:
(Наибольшее значение – Среднее значение) / Среднее значение * 100%
(Среднее значение – Наименьшее значение) / Среднее значение * 100%
Если отклонения наибольшего и наименьшего значения существенны, эти значения следует отбросить и пересчитать среднее значение.
(1550900 – 689787) / 689787 *100% = 125%
(689787 – 110875) / 689787 *100% = 84%
При использовании данного метода уровень существенности составит 600000 руб., если будут отброшены наибольшее и наименьшее значение.
Таким образом, при стандартизированном подходе величина в 600000 руб. будет являться планируемым уровнем существенности.
Расчет существенности может осуществляться на основе выбора базовых показателей несколькими методами.
Показатели для определения уровня существенности
При использовании метода критического компонента выбирается показатель с учетом специфики деятельности предприятия или несколько таких показателей. Для ООО «Высокий кондитер» методом критического компонента можно выбрать показатели, представленные в таблице 2. Расчет производится аналогичным образом.
Таблица 2 – Выбор показателей для определения уровня существенности методом критического компонента
|
Базовый показатель |
Значение базового показателя (руб.) |
Допустимая ошибка (%) |
Расчетное значение (руб.) |
|---|---|---|---|
|
Внеоборотные активы |
2% |
||
|
Запасы |
5% |
||
|
Дебиторская задолженность |
10% |
||
|
Денежные средства |
2% |
||
|
Итого: |
2% |
||
|
Актив баланса |
2% |
Среднее арифметическое расчетного значения составит 92649 руб.
(251708 – 92649) / 92649 *100% = 171%
(92649 – 4057) / 92649 *100% = 96%
При использовании данного метода уровень существенности составит 70000 руб., при условии того, что будут отброшены наибольшее и наименьшее значение.
При использовании метода стабильной базы отбираются показатели, которые наименее всего подвержены колебаниям за определенный период времени. Для использования данного метода в отношении отчетности ООО «Высокий кондитер» следует составить таблицу основных показателей (таблица 3).
Таблица 3 – Таблица основных показателей
|
Размещение имущества |
Изменение за период |
|||||||
|---|---|---|---|---|---|---|---|---|
|
руб. |
% к итогу |
руб. |
% к итогу |
руб. |
% к итогу |
руб. |
% |
|
|
Иммобилизованные (внеоборотные) активы (стр. 1100) |
20,50 |
17,67 |
18,52 |
54,55 |
||||
|
Оборотные активы (стр. 1200) |
79,50 |
82,33 |
81,48 |
75,33 |
||||
|
Запасы (стр. 1210) |
27,30 |
23,94 |
27,45 |
71,98 |
||||
|
Дебиторская задолженность (стр.1230) |
40,46 |
41,45 |
45,40 |
91,98 |
||||
|
Денежные средства (стр. 1240 + 1250) |
11,67 |
13,51 |
8,59 |
25,90 |
||||
|
Имущество всего (стр. 1600) |
71,07 |
|||||||
|
Собственный капитал (стр. 1300+1530) |
38,88 |
39,35 |
35,67 |
56,91 |
||||
|
Заёмный капитал (стр. 1400+1510+1520+ 1550) |
61,12 |
60,65 |
63,58 |
77,96 |
||||
|
Долгосрочные обязательства (стр. 1400) |
3,10 |
2,55 |
0,51 |
-71,72 |
||||
|
Краткосрочные обязательства (стр. 1510) |
0,06 |
4,47 |
2,41 |
6738,31 |
||||
|
Кредиторская задолженность (стр. 1520+1550) |
57,95 |
53,64 |
60,66 |
79,06 |
||||
|
Источники имущества всего (стр. 1700) |
71,07 |
Учитывая динамику абсолютных и относительных изменений, можно судить о том, что все основные показатели продемонстрировали существенные изменения. В этом случае отбор показателей по методу стабильной базы может быть осуществлен с учетом сохранения удельного веса показателя, изменение удельного веса за период не более 2-3%. С учетом этого могут быть отобраны: внеоборотные активы, оборотные активы, запасы, собственный капитал, заемный капитал.
Расчет производится аналогичным образом (таблица 4).
Таблица 4 – Выбор показателей для расчета уровня существенности методом стабильной базы
|
Базовый показатель |
Значение базового показателя (руб.) |
Допустимая ошибка (%) |
Расчетное значение (руб.) |
|---|---|---|---|
|
Внеоборотные активы |
2% |
||
|
Оборотные активы |
10% |
||
|
Запасы |
5% |
||
|
Собственный капитал |
10% |
||
|
Заемный капитал |
2% |
||
|
Валюта баланса |
2% |
Среднее арифметическое расчетного значения составит 154569 руб.
(451711 – 154569) / 154569 *100% = 192%
(154569 – 70493) / 154569 *100% = 54%
При использовании данного метода уровень существенности составит 110000 руб., при условии того, что будут отброшены наибольшее и наименьшее значение.
В рамках использования метода основного массива применительно к отчетности ООО «Высокий кондитер» следует отобрать показатели с наибольшим удельным весом в валюте баланса. Для использования данного метода в отношении отчетности ООО «Высокий кондитер» следует определить удельный вес статей баланса (таблица 5).
Таблица 5 – Удельный вес статей баланса
|
Статьи баланса |
Сумма (руб.) |
Доля в валюте баланса |
|---|---|---|
|
Основные средства |
18,22% |
|
|
Финансовые вложения |
0,25% |
|
|
Отложенные налоговые активы |
0,05% |
|
|
Запасы |
27,45% |
|
|
Дебиторская задолженность |
45,40% |
|
|
Финансовые вложения |
4,93% |
|
|
Денежные средства |
3,66% |
|
|
Прочие оборотные активы |
0,04% |
|
|
Валюта баланса |
100,00% |
|
|
Уставный капитал |
0,99% |
|
|
Нераспределенная прибыль |
34,67% |
|
|
Долгосрочные заемные средства |
0,40% |
|
|
Отложенные налоговые обязательства |
0,11% |
|
|
Краткосрочные заемные средства |
2,41% |
|
|
Кредиторская задолженность |
60,66% |
|
|
Резервы предстоящих расходов |
0,75% |
|
|
Валюта баланса |
100,00% |
Учитывая удельный вес статей баланса ООО «Высокий кондитер» можно сделать вывод, что необходимо отобрать в качестве базовых показателей запасы, дебиторскую задолженность, нераспределенную прибыль и кредиторскую задолженность. Расчет производится аналогичным образом (таблица 6).
Таблица 6 – Выбор показателей для определения уровня существенности методом основного массива
|
Базовый показатель |
Значение базового показателя (руб.) |
Допустимая ошибка (%) |
Расчетное значение (руб.) |
|---|---|---|---|
|
Запасы |
5% |
||
|
Дебиторская задолженность |
10% |
||
|
Нераспределенная прибыль |
5% |
||
|
Кредиторская задолженность |
10% |
При использовании данного метода уровень существенности составит 190000 руб., при этом отбрасывать наименьшее и наибольшее значение в данном случае нецелесообразно.
Использование метода ключевых по риску показателей и метода ключевых по последствиям показателей в данном случае представляется объективным для применения.
Представим полученные результаты в сводной таблице 7.
Таблица 7 – Сводная таблица по результатам расчета уровня существенности
|
Наименование метода |
Уровень существенности |
Характеристика применения метода |
|---|---|---|
|
Стандартный метод |
600000 руб. |
Метод применим в подавляющем большинстве случаев, но часто требует разработки специальных методик для применения аудиторскими фирмами. Эффективность метода может существенно повышаться за счет разработки внутрифирменного стандарта определения существенности. |
|
Метод критического компонента |
70000 руб. |
Метод применим в случаях, когда аудитор должен исходить из показателей, наиболее важных с учетом специфики аудируемой организации. Эффективность метода повышается за счет усреднения нескольких показателей. Использование данного метода дает наиболее точный результат с точки зрения определения уровня существенности. |
|
Метод стабильной базы |
110000 руб. |
Метод применим в случае, если возможно оценить динамику показателей и отобрать те из них, которые менее всего подвержены изменениям. |
|
Метод основного массива |
190000 руб. |
Метод применяется на основе структурного подхода и отличается простотой применения. |
|
В случае, если в ходе проведения аудиторской проверки будут выявлены ошибки, то искажения, к которым они привели, аудитор должен определить существенными и считать их таковыми, если сумма искажений каждой ошибки по отдельности или общая величина искажений превысит расчетный уровень существенности. С учетом этого, стандартный метод в ряде случаев позволяет принять к сведению достаточно значительное число ошибок, сумма которых не превышает уровень существенности. По итогам сделанных расчетов это подтвердилось. Следовательно, более объективным является использование специальных методов отбора базовых показателей для нахождения уровня существенности. |
При этом можно сделать вывод, что все ошибки и искажения, которые аудитор выявит в ходе проверки, являются существенными, если их величина превышает предельно допустимый уровень существенности.
С точки зрения содержательного значения уровня существенности, который отражает предельно возможную и допустимую величину суммы искажений, рассматриваемую аудитором как несущественную, существенность подлежит объективному определению при проведении аудиторских проверок организаций. Существенность искажений обязывает аудитора оценивать влияние таких искажений в рамках формирования профессионального суждения по итогам проведенной проверки.
Качественная оценка аудитора на основе его профессионального суждения учитывает существенность бухгалтерской информации, в контексте ее свойства оказывать прямое и косвенное влияние на решения, принимаемые на основе анализа такой информации. Таким образом, существенность оценивается аудитором с точки зрения наличия возможности искажения бухгалтерской информации, которое может повлиять на решения пользователей этой информации.
Три уровня существенности искажений
При формировании выводов аудитора в аудиторском заключении на них влияют 3 уровня существенности.
- Несущественные искажения – такие ошибки признаются аудитором неточностями или несерьезными ошибками, которые не повлияют на решения, которые могут быть приняты на основе результатов анализа проверяемой отчетности;
- Существенные искажения – такие ошибки достаточно значительны, но не влияют на оценку отчетности в целом, и хотя наличие таких искажений окажет влияние на решения, которые могут быть приняты на основе результатов анализа проверяемой отчетности, но состояние проверяемой организации отражено в отчете в целом объективно;
- Значительные искажения – наличие таких ошибок не позволяют судить об объективности и достоверности бухгалтерской отчетности в целом.
Таким образом, в случае несущественных искажений аудитор формирует стандартное заключение без оговорок. В случае существенных искажений, аудитор обязан оценить их возможное влияние на другие показатели отчетности и в случае, если оно не является существенным для отчетности в целом, то аудитор формирует условно положительное заключение, т.е. заключение с оговорками. Примером таких искажений может выступать ошибка в отражении данных в балансе по какой-либо статье в то время, как удельный вес этой статьи в валюте баланса незначителен, тогда как все остальные статьи баланса корректно отражают информацию и сформированы верно. В случае значительных искажений аудитор должен оценить их влияние как критическое, так как их наличие приведет к принятию неверных решений на основе результатов анализа проверяемой отчетности. В соответствии с этим аудитор обязан либо отказаться от выражения мнения, либо сформировать отрицательное аудиторское заключение. Такие искажения принимаются аудитором во внимание, если, например, ошибочно отражены данные в балансе по какой-либо статье баланса, которая имеет значительный удельный вес в валюте баланса.
Следует отметить, что выбор между условно-положительным и отрицательным аудиторским заключением аудитор должен основывать на результатах проверки влияния обнаруженных искажений. В этой связи, обнаруженные существенные искажения оцениваются по возможному влиянию на отчетность в целом. Аудитор распространяет выявленные ошибки на отчетность. В результате, аудитор может прийти к одному из двух выводов:
- Выявленные существенные искажения влияют только на одну статью в отчетности;
- Выявленные существенные искажения влияют на несколько статей отчетности, затрагивая несколько взаимосвязанных массивов информации.
Следовательно, если аудитор приходит к выводу второго типа, то вероятность формирования отрицательного заключения будет превалировать, так как степень распространения выявленных существенных искажений представляется более высокой и значимой.
Влияние уровня существенности на суждение аудитора
Влияние существенности на формирование профессионального суждения аудитора предполагает необходимость выражения аудитором соответствующего мнения. Аудитор выражает мнение относительно определения уровня существенности искажений в отчетности аудируемой организации. В частности, формирование профессионального суждения в области оценки риска существенных искажений требует объективизации расчета уровня существенности на этапе планирования аудиторской проверки.
Влияние величины уровня существенности на выводы аудитора в аудиторском заключении проявляется в существовании объективной зависимости от результатов аудита.
Аудитор обладает правом сделать вывод о достоверности отчетности проверяемой организации во всех существенных отношениях, если соблюдается ряд условий:
- выявлены искажения, которые намного меньше уровня существенности;
- руководство проверяемой организации согласно внести исправления аудитора согласно его рекомендациям;
- руководство проверяемой организации согласно выполнить рекомендации аудитора по недопущению выявленных искажений в будущем;
- качественные расхождения и отклонения от действующих нормативных актов и норм бухгалтерского учета, по мнению аудитора, не являются существенными.
Аудитор имеет обязательство взять на себя ответственность относительно принятия объективно взвешенного решения, модифицировать ли заключение, выражая мнение с оговоркой, либо сформировать стандартное заключение без каких-либо оговорок, в том случае, если выявленные искажения приблизительно соответствуют уровню существенности. При этом в любом случае должны соблюдаться следующие условия:
- руководство проверяемой организации согласно внести исправления аудитора согласно его рекомендациям и принять все меры для их недопущения впредь;
- качественные расхождения и отклонения от действующих нормативных актов и норм бухгалтерского учета, по мнению аудитора, не являются существенными.
Аудитор может модифицировать заключение и выразить мнение с оговоркой о достоверности отчетности проверяемой организации, если соблюдаются следующие условия:
- выявленные искажения значительно превышают уровень существенности;
- качественные расхождения и отклонения от действующих нормативных актов и норм бухгалтерского учета, по мнению аудитора, являются существенными;
- руководство проверяемой организации несогласно внести исправления аудитора согласно его рекомендациям, а дополнительные рекомендации аудитора не принимаются во внимание.
В случае невозможности однозначно выразить мнение с оговоркой о достоверности отчетности аудитор может отказаться от выражения мнения.
Следует отметить, что достаточно значимым является вопрос о регламентации порядка определения уровня существенности в договоре на проведение аудита, или формализации данного порядка в виде дополнительного приложения или соглашения к договору. С точки зрения сущностного содержания результатов определения уровня существенности, это может влиять на формируемое аудиторское заключение. Вместе с тем, ряд аудиторских фирм действуют на основе открытого характера методики определения уровня существенности, тогда как другие придерживаются точки зрения о недопустимости раскрытия фирменной методики. В пользу первого подхода следует отнести положения Стандарта №4 «Существенность в аудите», а также необходимость указания клиенту аудиторской фирмы на то, что в рамках договора на проведение аудита не содержится ответственности за не выявленные малосущественные ошибки. Некоторые аудиторы даже склонные к стоимостному выражению ответственности в договоре. В пользу второго подхода, основным аргументом является нецелесообразность посвящения клиента аудиторской фирмы в порядок определения уровня существенности в силу того, что подобное знание может позволить умышленно исказить отчетность таким образом, чтобы аудитор не выявил существующих существенных искажений и сформировал стандартное заключение без оговорок. Поэтому в рамках такого подхода аудитор склонен лишь выразить свое мнение о достоверности отчетности, а раскрывать конкретные принципы, как был сформирован такой вывод, не следует.
Следует отметить, что в данном контексте представляется наиболее объективным и целесообразным представляется разумное комбинирование данных подходов в деятельности конкретной аудиторской фирмы. В рамках комбинированного подхода аудиторская фирма придерживается определенной методики определения уровня существенности, а конкретные методы остаются внутренней информацией фирмы, не подлежащей разглашению. Данная концепция зачастую находит свое выражение в виде разработок аудиторскими организациями внутрифирменных стандартов по оценке и расчету уровня существенности. Таким образом, декларируется определенная методология определения уровня существенности, а установление уровня существенности имеет конфиденциальный характер. В соответствии с таким подходом аудиторские фирмы могут формировать специальные методики определения уровня существенности для организаций, являющихся их постоянными клиентами, для организаций, принадлежащих одной отрасли, для организаций с широким спектром хозяйственных операций, не позволяющим однозначно определить отраслевую специфику.
Таким образом, влияние существенности помимо своего непосредственного влияния на формирование профессионального суждения и выводы аудитора может проявляться и через действие внутрифирменных стандартов аудиторских фирм.
Бухгалтерская отчетность ООО «Высокий кондитер» за 2014 год



Уровень существенности
Смотреть что такое «Уровень существенности» в других словарях:
-
Уровень существенности — предельное значение искажения бухгалтерской отчетности, начиная с которой квалифицированный пользователь этой отчетности перестанет быть в состоянии делать на ее основе правильные выводы и принимать правильные экономические решения;… … Официальная терминология
-
Уровень существенности искажения бухгалтерской отчетности — под уровнем существенности понимается то предельное значение ошибки бухгалтерской отчетности, начиная с которой квалифицированный пользователь этой отчетности с большой степенью вероятности перестанет быть в состоянии делать на ее основе… … Энциклопедический словарь-справочник руководителя предприятия
-
Материальность (аудит) — Аудит Виды аудита Внутренний аудит Внешний аудит Налоговый аудит Экологический аудит Социальный аудит … Википедия
-
АУДИТОРСКАЯ ПРОВЕРКА — сбор, оценка и анализ аудиторских доказательств, касающихся финансового положения экономического субъекта, подлежащего аудиту, имеющие своим результатом выражение мнения аудитора о правильности ведения бухгалтерского учета и достоверности… … Финансово-кредитный энциклопедический словарь
-
ПЛАН АУДИТОРСКОЙ ПРОВЕРКИ — логическое описание предполагаемых направлений, объема, характера проведения аудита, особенностей экономического субъекта и его деятельности, особенностей используемых при проведении аудиторской проверки методов и технических приемов. План… … Финансово-кредитный энциклопедический словарь
-
ГОСТ Р ИСО 14064-1-2007: Газы парниковые. Часть 1. Требования и руководство по количественному определению и отчетности о выбросах и удалении парниковых газов на уровне организации — Терминология ГОСТ Р ИСО 14064 1 2007: Газы парниковые. Часть 1. Требования и руководство по количественному определению и отчетности о выбросах и удалении парниковых газов на уровне организации оригинал документа: 2.20 базовый год (base year):… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ Р ИСО 14064-3-2007: Газы парниковые. Часть 3. Требования и руководство по валидации и верификации утверждений, касающихся парниковых газов — Терминология ГОСТ Р ИСО 14064 3 2007: Газы парниковые. Часть 3. Требования и руководство по валидации и верификации утверждений, касающихся парниковых газов оригинал документа: 2.20 базовый год (base year): Исторический период, установленный для… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ Р ИСО 14065-2010: Газы парниковые. Требования к органам по валидации и верификации парниковых газов для их применения при аккредитации или других формах признания — Терминология ГОСТ Р ИСО 14065 2010: Газы парниковые. Требования к органам по валидации и верификации парниковых газов для их применения при аккредитации или других формах признания оригинал документа: 3.4.1 аккредитация (accreditation):… … Словарь-справочник терминов нормативно-технической документации
-
Стереометрическая семантика — трактовка логики как науки о получении истинных следствий из истинных посылок все более уступает место более широкой концепции,связанной либо с обобщением понятия следования, основанного на традиционной истинностной оценке и на практических… … Проективный философский словарь
-
ГОСТ Р 54134-2010: Экологический менеджмент. Руководство по применению организационных мер безопасности и оценки рисков. Выбросы парниковых газов — Терминология ГОСТ Р 54134 2010: Экологический менеджмент. Руководство по применению организационных мер безопасности и оценки рисков. Выбросы парниковых газов оригинал документа: 3.4.1 аккредитация: Аттестация третьей стороны, действие которой… … Словарь-справочник терминов нормативно-технической документации
