Задана система
точек (узлы интерполяции)
xi ,
i=1,2,…,N; a
xi
b, и значения
fi,
i = 1,2,….,N.
Требуется построить полиномы:
-
1-ой степени
P1(x)=a1+a2x, -
2-ой
степени
P2(x)=a1+a2x+a3x2, -
3-ой
степени
P3(x)=a1+a2x+a3x2+a4x3,
имеющие в узлах
интерполяции минимальное отклонение
от заданных значений fi.
Искомыми величинами являются коэффициенты
полинома (ai).
Полиномы
должны быть самым близким к заданным
точкам из всех возможных полиномов,
соответствующей степени в смысле МНК,
т.е. сумма квадратов отклонений
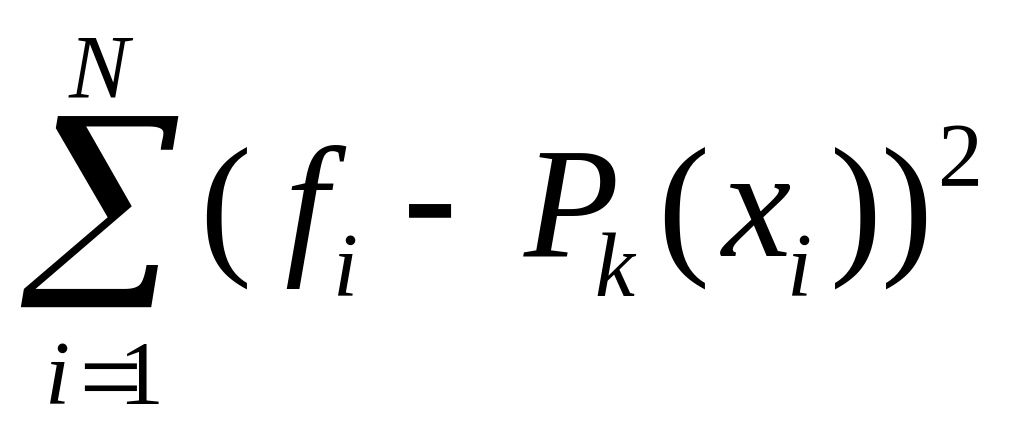
должна быть минимальной.
-
Получить систему
нормальных уравнений для каждого
полинома. -
Вычислить
коэффициенты ai
. -
Определить какой
из полиномов имеет минимальную сумму
квадратов отклонений.
|
x |
-10 |
-8,3 |
-6,7 |
-5 |
-3 |
-1,67 |
|
Вар.9 |
-100 |
-60 |
-33 |
-16 |
-7 |
-2,08 |
|
0 |
1,67 |
3,33 |
5 |
6,7 |
8,33 |
10 |
|
0 |
2,08 |
6,67 |
16 |
33 |
60,4 |
100 |
-
Полином 1-ой степени.
|
xi |
Xi^2 |
fi |
fi xi |
|
0,36 |
503,7256 |
0,07 |
3653,4903 |
|
S |
|
|
13 |
0,36 |
|
0,36 |
503,7256 |
|
S(-1) |
0,076924599 |
-5,49761E-05 |
|
-5,49761E-05 |
0,001985247 |
|
z |
|
0,07 |
|
3653,49 |
|
a |
-0,19546983 |
|
7,253077209 |
Ф(x)=-0,19547+7,25308x
Сумма квадратов
отклонений:
|
G1= |
3541,268153 |
-
Полином 2-ой степени.
|
xi |
Xi^2 |
Xi^3 |
Xi^4 |
fi |
fi xi |
fi xi^2 |
|
0,36 |
503,7256 |
16,148574 |
35060,3954 |
0,07 |
3653,4903 |
68,652523 |
|
S |
13 |
0,36 |
503,7256 |
|
0,36 |
503,7256 |
16,14857 |
|
|
503,7256 |
16,14857 |
35060,3954 |
|
S(-1) |
0,173528 |
-4,4091E-05 |
-0,00249312 |
|
-4,4E-05 |
0,001985248 |
-2,8092E-07 |
|
|
-0,00249 |
-2,8092E-07 |
6,43419E-05 |
|
z |
0,07 |
|
3653,49 |
|
|
68,65252 |
|
a |
-0,32009809 |
|
7,253062571 |
|
|
0,003216379 |
Ф(х)=-0,32009809+7,253062571*х+0,003216379*х^2
Сумма квадратов
отклонений:
|
G2 |
3541,10737 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
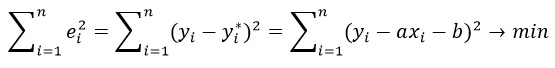
частные производные функции приравниваем к нулю
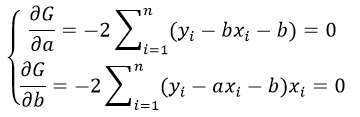
отсюда получаем систему линейных уравнений
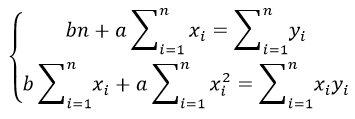
Формулы определения коэффициентов уравнения линейной регрессии:
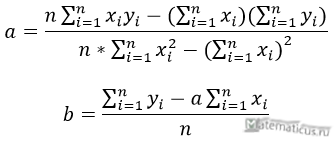
Также запишем уравнение регрессии для квадратной нелинейной функции:
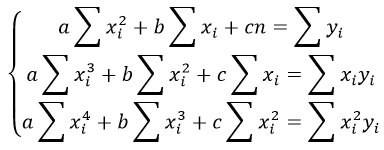
Система линейных уравнений регрессии полинома n-ого порядка:
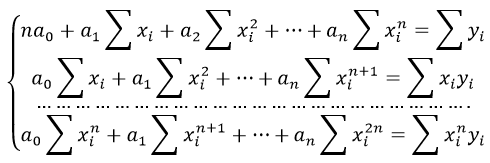
Формула коэффициента детерминации R 2 :
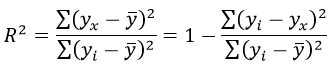
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
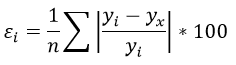
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности: 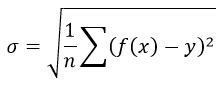
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
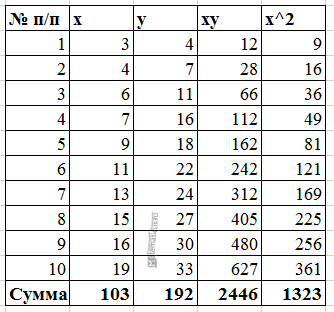
Расчет коэффициентов линейной регрессии:
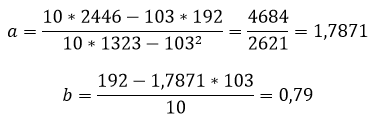
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
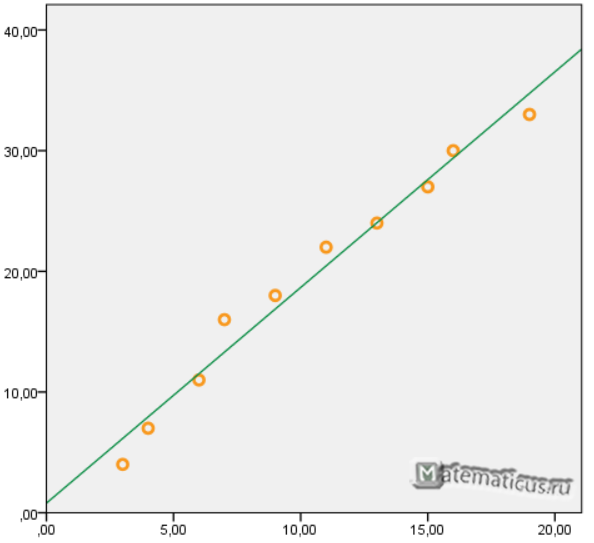
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Решения задач: метод наименьших квадратов
Метод наименьших квадратов применяется для решения различных математических задач и основан на минимизации суммы квадратов отклонений функций от исходных переменных. Мы рассмотриваем его приложение к математической статистике в простейшем случае, когда нужно найти зависимость (парную линейную регрессию) между двумя переменными, заданными выборочными данным. В этом случае речь идет об отклонениях теоретических значений от экспериментальных.
Краткая инструкция по методу наименьших квадратов для чайников: определяем вид предполагаемой зависимости (чаще всего берется линейная регрессия вида $y(x)=ax+b$), выписываем систему уравнений для нахождения параметров $a, b$. По экспериментальным данным проводим вычисления и подставляем значения в систему, решаем систему любым удобным методом (для размерности 2-3 можно и вручную). Получается искомое уравнение.
Иногда дополнительно к нахождению уравнения регрессии требуется: найти остаточную дисперсию, сделать прогноз значений, найти значение коэффициента корреляции, проверить качество аппроксимации и значимость модели. Примеры решений вы найдете ниже. Удачи в изучении!
Примеры решений МНК
Пример 1. Методом наименьших квадратов для данных, представленных в таблице, найти линейную зависимость
Пример 2. Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
1) Составьте линейную зависимость прибыли по годам деятельности фирмы.
2) Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж.
Пример 3. Экспериментальные данные о значениях переменных х и y приведены в таблице:
1 2 4 6 8
3 2 1 0,5 0
В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Пример 4. Данные наблюдений над случайной двумерной величиной (Х, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.
Пример 5. Считая, что зависимость между переменными x и y имеет вид $y=ax^2+bx+c$, найти оценки параметров a, b и c методом наименьших квадратов по выборке:
x 7 31 61 99 129 178 209
y 13 10 9 10 12 20 26
Пример 6. Проводится анализ взаимосвязи количества населения (X) и количества практикующих врачей (Y) в регионе.
Годы 81 82 83 84 85 86 87 88 89 90
X, млн. чел. 10 10,3 10,4 10,55 10,6 10,7 10,75 10,9 10,9 11
Y, тыс. чел. 12,1 12,6 13 13,8 14,9 16 18 20 21 22
Оцените по МНК коэффициенты линейного уравнения регрессии $y=b_0+b_1x$.
Существенно ли отличаются от нуля найденные коэффициенты?
Проверьте значимость полученного уравнения при $alpha = 0,01$.
Если количество населения в 1995 году составит 11,5 млн. чел., каково ожидаемое количество врачей? Рассчитайте 99%-й доверительный интервал для данного прогноза.
Рассчитайте коэффициент детерминации
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
источники:
http://www.matburo.ru/ex_ms.php?p1=msmnk
http://statistica.ru/theory/osnovy-lineynoy-regressii/
На этом занятии
мы с вами рассмотрим алгоритм, который носит название метод наименьших
квадратов. Для начала немного теории. Чтобы ее хорошо понимать нужны
базовые знания по теории вероятностей, в частности понимание ПРВ, а также
знать, что такое производная и как она вычисляется. Остальное я сейчас
расскажу.
На практике
встречаются задачи, когда производились измерения некоторой функциональной
зависимости, но из-за погрешностей приборов, или неточных сведений или еще по
какой-либо причине, измерения немного отстоят от истинных значений функции и
образуют некий разброс:
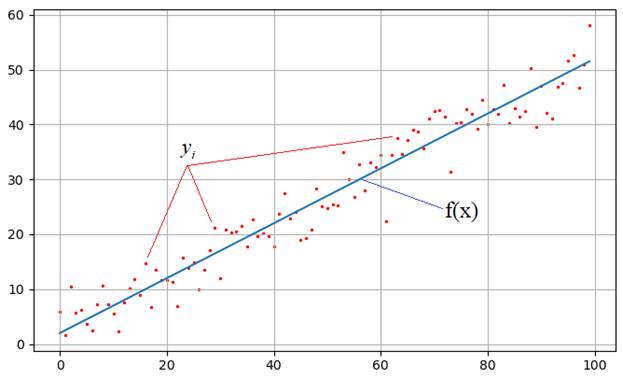
Наша задача:
зная характер функциональной зависимости, подобрать ее параметры так, чтобы она
наилучшим образом описывала экспериментальные данные ![]() Например, на
Например, на
рисунке явно прослеживается линейная зависимость. Мы это можем определить либо
чисто визуально, либо заранее знать о характере функции. Но, в любом случае
предполагается, что ее общий вид нам известен. Так вот, для линейной функции
достаточно определить два параметра k и b:
![]()
чтобы построить
аппроксимацию (приближение) линейного графика к экспериментальным зависимостям.
Конечно, вид функциональной зависимости может быть и другим, например,
квадратической (парабола), синусоидальной, или даже определяться суммой
известных функций, но для простоты понимания, мы для начала рассмотрим именно
линейный график с двумя неизвестными коэффициентами.
Итак, будем
считать, что на первый вопрос о характере функциональной зависимости
экспериментальных данных ответ дан. Следующий вопрос: как измерить качество
аппроксимации измерений ![]() функцией
функцией
![]() ? Вообще, таких
? Вообще, таких
критериев можно придумать множество, например:
— сумма квадратов
ошибок отклонений:
![]()
— сумма модулей
ошибок отклонений:
![]()
— минимум
максимальной по модулю ошибки:
![]()
и так далее. Каждый
из критериев может приводить к своему алгоритму обработки экспериментальных
значений. Так вот, в методе наименьших квадратов используется минимум суммы
квадратов ошибок. И этому есть математическое обоснование. Часто результаты
реальных измерений имеют стандартное (гауссовское) отклонение относительно
измеряемого параметра:
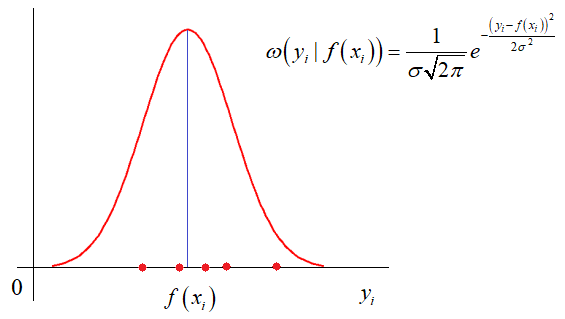
Здесь σ –
стандартное отклонение (СКО) наблюдаемых значений ![]() от функции
от функции ![]() . Отсюда хорошо
. Отсюда хорошо
видно, что чем ближе измерение к истинному значению параметра, тем больше
значение функции плотности распределения условной вероятности. И, так для всех
точек измерения. Учитывая, что они выполняются независимо друг от друга, то
можно записать следующее функциональное выражение:
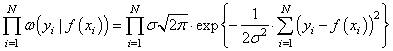
Получается, что лучшее
описание экспериментальных данных с помощью функции ![]() должно проходить по
должно проходить по
точкам, в которых достигается максимум этого выражения. Очевидно, что при
поиске максимума можно не учитывать множитель 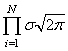 , а экспонента будет
, а экспонента будет
принимать максимальное значение при минимуме ее отрицательной степени:
![]()
Здесь также
множитель можно не учитывать, получаем критерий качества минимум суммы квадрата
ошибок:
![]()
Как мы помним,
наша цель – подобрать параметры ![]() функции
функции
![]()
которые как раз
и обеспечивают минимум этого критерия, то есть, величина E зависит от этих
подбираемых величин:
![]()
И ее можно
рассматривать как квадратическую функцию от аргументов ![]() Из школьного курса
Из школьного курса
математики мы знаем как находится точка экстремума функции – это точка, в
которой производная равна нулю:
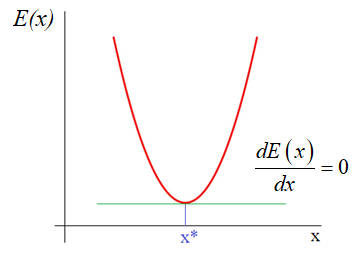
Здесь все также,
нужно взять частные производные по каждому параметру и приравнять результат
нулю, получим систему линейных уравнений:
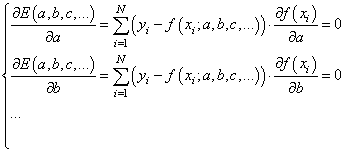
Чтобы наполнить
конкретикой эту систему, нам нужно вернуться к исходному примеру с линейной
функцией:
![]()
Эта функция
зависит от двух параметров: k и b с частными
производными:
![]()
Подставляем все
в систему, имеем:
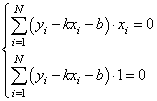
или, в виде:
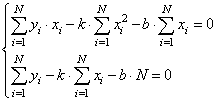
Разделим все на N:
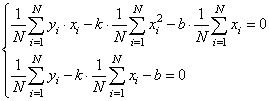
Смотрите, что в
итоге получилось. Формулы с суммами представляют собой первые и вторые
начальные моменты, а также один смешанный момент:
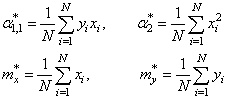
Здесь * означает
экспериментальные моменты. В этих обозначениях, получаем:
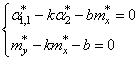
Отсюда находим,
что
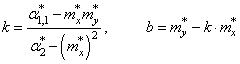
Все, мы получили
оценки параметров k и b для линейной
аппроксимации экспериментальных данных по методу наименьших квадратов. По
аналогии можно вычислять параметры для других функциональных зависимостей,
например, квадратической:
![]()
Здесь будет уже
три свободных параметра и три уравнения, решая которые будем получать лучшую
аппроксимацию по критерию минимума суммарной квадратической ошибки отклонений.
Реализация на Python
В заключение
этого занятия реализуем метод наименьших квадратов на Python. Для этого нам
понадобятся две довольно популярные библиотеки numpy и matplotlib. Если они у вас
не установлены, то делается это просто – через команды:
pip install numpy
pip install matplotlib
После этого, мы
можем их импортировать и использовать в программе:
import numpy as np import matplotlib.pyplot as plt
Первая довольно
эффективная для выполнения различных математических операций, включая векторные
и матричные. Вторая служит для построения графиков.
Итак, вначале
определим необходимые начальные величины:
N = 100 # число экспериментов sigma = 3 # стандартное отклонение наблюдаемых значений k = 0.5 # теоретическое значение параметра k b = 2 # теоретическое значение параметра b
Формируем
вспомогательный вектор
![]()
с помощью метода
array, который
возвращает объект-вектор на основе итерируемой функции range:
Затем, вычисляем
значения теоретической функции:
f = np.array([k*z+b for z in range(N)])
и добавляем к
ней случайные отклонения для моделирования результатов наблюдений:
y = f + np.random.normal(0, sigma, N)
Если сейчас
отобразить наборы точек y, то они будут выглядеть следующим
образом:
plt.scatter(x, y, s=2, c='red') plt.grid(True) plt.show()
Теперь у нас все
есть для вычисления коэффициентов k и b по экспериментальным
данным:
# вычисляем коэффициенты mx = x.sum()/N my = y.sum()/N a2 = np.dot(x.T, x)/N a11 = np.dot(x.T, y)/N kk = (a11 - mx*my)/(a2 - mx**2) bb = my - kk*mx
Здесь выражение x.T*x – это
произведение:
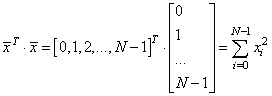
Далее, построим
точки полученной аппроксимации:
ff = np.array([kk*z+bb for z in range(N)])
и отобразим оба
линейных графика:
plt.plot(f) plt.plot(ff, c='red')
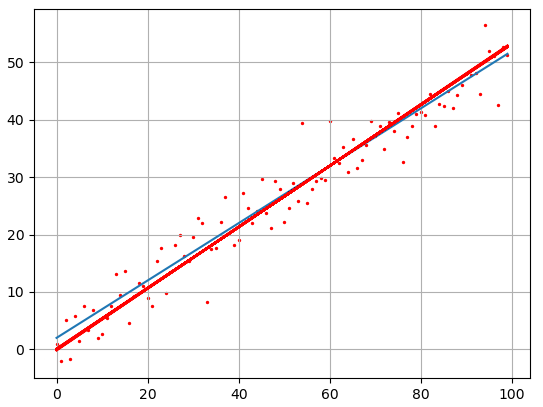
Как видите
результат аппроксимации довольно близок начальному, теоретическому графику. Вот
так работает метод наименьших квадратов.
Реализация алгоритма на Python (файл mnsq.py)
Видео по теме
Цель любого физического эксперимента — проверить, выполняется ли некоторая
теоретическая закономерность (модель), а также получить или уточнить
её параметры. Поскольку набор экспериментальных данных неизбежно ограничен,
а каждое отдельное измерение имеет погрешность, можно говорить лишь
об оценке этих параметров. В большинстве случаев измеряется не одна
величина, а некоторая функциональная зависимость величин друг от друга.
В таком случае возникает необходимость построить оценку параметров этой зависимости.
Пример. Рассмотрим процедуру измерения сопротивления некоторого резистора.
Простейшая теоретическая модель для резистора — закон Ома U=RI,
где сопротивление R — единственный параметр модели. Часто при измерениях
возможно возникновение систематической ошибки — смещение нуля напряжения или тока.
Тогда для получения более корректной оценки сопротивления стоит использовать
модель с двумя параметрами: U=RI+U0.
Для построения оценки нужны следующие компоненты
- •
данные — результаты измерений {xi,yi}
и их погрешности {σi}
(экспериментальная погрешность является неотъемлемой
частью набора данных!); - •
модель y=f(x|θ1,θ2,…) —
параметрическое описание исследуемой зависимости
(θ — набор параметров модели, например,
коэффициенты {k,b} прямой f(x)=kx+b); - •
процедура построения оценки параметров по
измеренным данным («оценщик»):
Рассмотрим самые распространенные способы построения оценки.
3.1 Метод минимума хи-квадрат
Обозначим отклонения результатов некоторой серии измерений от теоретической
модели y=f(x|θ) как
| Δyi=yi-f(xi|θ),i=1…n, |
где θ — некоторый параметр (или набор параметров),
для которого требуется построить наилучшую оценку. Нормируем Δyi
на стандартные отклонения σi и построим сумму
которую принято называть суммой хи-квадрат.
Метод минимума хи-квадрат (метод Пирсона) заключается в подборе такого
θ, при котором сумма квадратов отклонений от теоретической
модели, нормированных на ошибки измерений, достигает минимума:
Замечание. Подразумевается, что погрешность измерений σi указана только для
вертикальной оси y. Поэтому, при использовании метода следует выбирать оcи
таким образом, чтобы относительная ошибка по оси абсцисс была значительно меньше,
чем по оси ординат.
Данный метод вполне соответствует нашему интуитивному представлению
о том, как теоретическая зависимость должна проходить через экспериментальные
точки. Ясно, что чем ближе данные к модельной кривой, тем
меньше будет сумма χ2. При этом, чем больше погрешность точки, тем
в большей степени дозволено результатам измерений отклоняться от модели.
Метода минимума χ2 является частным случаем
более общего метода максимума правдоподобия (см. ниже),
реализующийся при нормальном (гауссовом) распределении ошибок.
Можно показать (см. [5]), что оценка по методу хи-квадрат является состоятельной,
несмещенной и, если данные распределены нормально,
имеет максимальную эффективность (см. приложение 5.2).
Замечание. Простые аналитические выражения для оценки методом хи-квадрат существуют
(см. п. 3.6.1, 3.6.4) только в случае линейной
зависимости f(x)=kx+b (впрочем, нелинейную зависимость часто можно
заменой переменных свести к линейной). В общем случае задача поиска
минимума χ2(θ) решается численно, а соответствующая процедура
реализована в большинстве специализированных программных пакетов
по обработке данных.
3.2 Метод максимального правдоподобия.
Рассмотрим кратко один
из наиболее общих методов оценки параметров зависимостей —
метод максимума правдоподобия.
Сделаем два ключевых предположения:
- •
зависимость между измеряемыми величинами действительно может
быть описана функцией y=f(x|θ) при некотором θ; - •
все отклонения Δyi результатов измерений от теоретической модели
являются независимыми и имеют случайный (не систематический!) характер.
Пусть P(Δyi) — вероятность обнаружить отклонение Δyi
при фиксированных {xi}, погрешностях {σi} и параметрах модели θ.
Построим функцию, равную вероятности обнаружить
весь набор отклонений {Δy1,…,Δyn}. Ввиду независимости
измерений она равна произведению вероятностей:
Функцию L называют функцией правдоподобия.
Метод максимума правдоподобия заключается в поиске такого θ,
при котором наблюдаемое отклонение от модели будет иметь
наибольшую вероятность, то есть
Замечание. Поскольку с суммой работать удобнее, чем с произведениями, чаще
используют не саму функцию L, а её логарифм:
Пусть теперь ошибки измерений имеют нормальное распределение
(напомним, что согласно центральной предельной теореме нормальное распределение
применимо, если отклонения возникают из-за большого
числа независимых факторов, что на практике реализуется довольно часто).
Согласно (2.5), вероятность обнаружить в i-м измерении
отклонение Δyi пропорциональна величине
где σi — стандартная ошибка измерения величины yi. Тогда
логарифм функции правдоподобия (3.2) будет равен (с точностью до константы)
| lnL=-∑iΔyi22σi2=-12χ2. |
Таким образом, максимум правдоподобия действительно будет соответствовать
минимуму χ2.
3.3 Метод наименьших квадратов (МНК).
Рассмотрим случай, когда все погрешности измерений одинаковы,
σi=const. Тогда множитель 1/σ2 в сумме χ2
выносится за скобки, и оценка параметра сводится к нахождению минимума суммы
квадратов отклонений:
| S(θ)=∑i=1n(yi-f(xi|θ))2→min. | (3.3) |
Оценка по методу наименьших квадратов (МНК) удобна в том случае,
когда не известны погрешности отдельных измерений. Однако тот факт, что
метод МНК игнорирует информацию о погрешностях, является и его основным
недостатком. В частности, это не позволяет определить точность оценки
(например, погрешности коэффициентов прямой σk и
σb) без привлечения дополнительных предположений
(см. п. 3.6.2 и 3.6.3).
3.4 Проверка качества аппроксимации
Значение суммы χ2 позволяет оценить, насколько хорошо данные описываются
предлагаемой моделью y=f(x|θ).
Предположим, что распределение ошибок при измерениях нормальное.
Тогда можно ожидать, что большая часть отклонений данных от модели будет
порядка одной среднеквадратичной ошибки: Δyi∼σi.
Следовательно, сумма хи-квадрат (3.1) окажется по порядку
величины равна числу входящих в неё слагаемых: χ2∼n.
Замечание. Точнее, если функция f(x|θ1,…,θp)
содержит p подгоночных параметров
(например, p=2 для линейной зависимости f(x)=kx+b),
то при заданных θ лишь n-p слагаемых в сумме хи-квадрат будут независимы.
Иными словами, когда параметры θ определены
из условия минимума хи-квадрат, сумму χ2 можно рассматривать как функцию
n-p переменных. Величину n-p называют числом степеней свободы задачи.
В теории вероятностей доказывается (см. [4] или [5]),
что ожидаемое среднее значение (математическое ожидание) суммы χ2
в точности равно числу степеней свободы:
Таким образом, при хорошем соответствии модели и данных,
величина χ2/(n-p) должна в среднем быть равна единице.
Значения существенно большие (2 и выше) свидетельствуют либо о
плохом соответствии теории и результатов измерений,
либо о заниженных погрешностях.
Значения меньше 0,5 как правило свидетельствуют о завышенных погрешностях.
Замечание. Чтобы дать строгий количественный критерий, с какой долей вероятности
гипотезу y=f(x) можно считать подтверждённой или опровергнутой,
нужно знать вероятностный закон, которому подчиняется функция χ2.
Если ошибки измерений распределены нормально, величина хи-квадрат подчинятся
одноимённому распределению (с n-p степенями свободы).
В элементарных функциях распределение хи-квадрат не выражается,
но может быть легко найдено численно: функция встроена во все основные
статистические пакеты, либо может быть вычислена по таблицам.
3.5 Оценка погрешности параметров
Важным свойством метода хи-квадрат является «встроенная» возможность
нахождения погрешности вычисленных параметров σθ.
Пусть функция L(θ) имеет максимум при θ=θ^, то есть
θ^ — решение задачи о максимуме правдоподобия. Согласно центральной предельной теореме мы ожидаем, что функция правдоподобия будем близка к нормальному распределению: L(θ)∝exp(-(θ-θ^)22σθ2),
где σθ — искомая погрешность параметра. Тогда в окрестности θ^ функция χ2(θ)=-2ln(L(θ)) имеет вид параболы:
Легко убедиться, что:
Иными словами, при отклонении параметра θ на одну ошибку σθ от значения
θ^,
минимизирующего χ2, функция χ2(θ) изменится на единицу. Таким образом для нахождения интервальной оценки для искомого параметра достаточно графическим или численным образом решить уравнение
Вероятностное содержание этого интервала будет равно 68% (его еще называют 1–σ интервалом).
Отклонение χ2 на 2 будет соответствовать уже 95% доверительному интервалу.
Замечание.
Приведенное решение просто использовать только в случае одного параметра. Впрочем, все приведенные рассуждения верны и в много-параметрическом случае. Просто решением уравнения 3.4 будет не отрезок, а некоторая многомерная фигура (эллипс в двумерном случае и гипер-эллипс при больших размерностях пространства параметров). Вероятностное содержание области, ограниченной такой фигурой будет уже не равно 68%, но может быть вычислено по соответствующим таблицам. Подробнее о многомерном случае в разделе 5.5.
3.6 Методы построения наилучшей прямой
Применим перечисленные выше методы к задаче о построении наилучшей прямой
y=kx+b по экспериментальным точкам {xi,yi}.
Линейность функции позволяет записать решение в относительно
простом аналитическом виде.
Обозначим расстояние от i-й экспериментальной точки до искомой прямой,
измеренное по вертикали, как
и найдём такие параметры {k,b}, чтобы «совокупное» отклонение
результатов от линейной зависимости было в некотором смысле минимально.
3.6.1 Метод наименьших квадратов
Пусть сумма квадратов расстояний от точек до прямой минимальна:
| S(k,b)=∑i=1n(yi-(kxi+b))2→min. | (3.5) |
Данный метод построения наилучшей прямой называют методом наименьших
квадратов (МНК).
Рассмотрим сперва более простой частный случай, когда искомая прямая
заведомо проходит через «ноль», то есть b=0 и y=kx.
Необходимое условие минимума функции S(k), как известно,
есть равенство нулю её производной. Дифференцируя сумму (3.5)
по k, считая все величины {xi,yi} константами,
найдём
| dSdk=-∑i=1n2xi(yi-kxi)=0. |
Решая относительно k, находим
Поделив числитель и знаменатель на n, этот результат можно записать
более компактно:
Напомним, что угловые скобки означают усреднение по всем экспериментальным точкам:
В общем случае при b≠0 функция S(k,b) должна иметь
минимум как по k, так и по b. Поэтому имеем систему из двух
уравнений ∂S/∂k=0, ∂S/∂b=0,
решая которую, можно получить (получите самостоятельно):
| k=⟨xy⟩-⟨x⟩⟨y⟩⟨x2⟩-⟨x⟩2,b=⟨y⟩-k⟨x⟩. | (3.7) |
Эти соотношения и есть решение задачи о построении наилучшей прямой
методом наименьших квадратов.
Замечание. Совсем кратко формулу (3.7) можно записать, если ввести обозначение
Dxy≡⟨xy⟩-⟨x⟩⟨y⟩=⟨x-⟨x⟩⟩⋅⟨y-⟨y⟩⟩.
(3.8)
В математической статистике величину Dxy называют ковариацией.
При x≡y имеем дисперсию
Dxx=⟨(x-⟨x⟩)2⟩.
Тогда
k=DxyDxx,b=⟨y⟩-k⟨x⟩.
(3.9)
3.6.2 Погрешность МНК в линейной модели
Погрешности σk и σb коэффициентов, вычисленных
по формуле (3.7) (или (3.6)), можно оценить в
следующих предположениях.
Пусть погрешность измерений величины x пренебрежимо мала: σx≈0,
а погрешности по y одинаковы для всех экспериментальных точек
σy=const, независимы и имеют случайный характер
(систематическая погрешность отсутствует).
Пользуясь в этих предположениях формулами для погрешностей косвенных
измерений (см. раздел (2.6)) можно получить следующие
соотношения:
| σk=1n-2(DyyDxx-k2), | (3.10) |
где использованы введённые выше сокращённые обозначения (3.8).
Коэффициент n-2 отражает число независимых <<степеней
свободы>>: n экспериментальных точек за вычетом двух
условий связи (3.7).
В частном случае y=kx:
| σk=1n-1(⟨y2⟩⟨x2⟩-k2). | (3.12) |
3.6.3 Недостатки и условия применимости МНК
Формулы (3.7) (или (3.6)) позволяют провести
прямую по любому набору экспериментальных данных, а полученные
выше соотношения — вычислить
соответствующую среднеквадратичную ошибку для её коэффициентов. Однако
далеко не всегда результат будет иметь физический смысл. Перечислим
ограничения применимости данного метода.
В первую очередь метод наименьших квадратов — статистический,
и поэтому он предполагает использование достаточно большого количества
экспериментальных точек (желательно n>10).
Поскольку метод предполагает наличие погрешностей только по y,
оси следует выбирать так, чтобы погрешность σx откладываемой
по оси абсцисс величины была минимальна.
Кроме того, метод предполагает, что все погрешности в опыте —
случайны. Соответственно, формулы (3.10)–(3.12)
применимы только для оценки случайной составляющей ошибки k
или b. Если в опыте предполагаются достаточно большие систематические
ошибки, они должны быть оценены отдельно. Отметим, что для
оценки систематических ошибок не существует строгих математических
методов, поэтому в таком случае проще и разумнее всего воспользоваться
графическим методом.
Одна из основных проблем, связанных с определением погрешностей методом
наименьших квадратов заключается в том, что он дает разумные погрешности даже в
том случае, когда данные вообще не соответствуют модели.
Если погрешности измерений известны, предпочтительно использовать
метод минимума χ2.
Наконец, стоит предостеречь от использования любых аналитических
методов «вслепую», без построения графиков. В частности, МНК не способен
выявить такие «аномалии», как отклонения от линейной зависимости,
немонотонность, случайные всплески и т.п. Все эти случаи требуют особого
рассмотрения и могут быть легко обнаружены визуально при построении графика.
3.6.4 Метод хи-квадрат построения прямой
Пусть справедливы те же предположения, что и для метода наименьших квадратов,
но погрешности σi экспериментальных точек различны. Метод
минимума хи-квадрат сводится к минимизации суммы квадратов отклонений,
где каждое слагаемое взято с весом wi=1/σi2:
| χ2(k,b)=∑i=1nwi(yi-(kxi+b))2→min. |
Этот метод также называют взвешенным методом наименьших квадратов.
Определим взвешенное среднее от
некоторого набора значений {xi} как
где W=∑iwi — нормировочная константа.
Повторяя процедуру, использованную при выводе (3.7), нетрудно
получить (получите) совершенно аналогичные формулы для искомых коэффициентов:
| k=⟨xy⟩′-⟨x⟩′⟨y⟩′⟨x2⟩′-⟨x⟩′2,b=⟨y⟩′-k⟨x⟩′, | (3.13) |
с тем отличием от (3.7), что под угловыми скобками
⟨…⟩′
теперь надо понимать усреднение с весами wi=1/σi2.
Записанные формулы позволяют вычислить коэффициенты прямой,
если известны погрешности σyi. Значения σyi
могут быть получены либо из некоторой теории, либо измерены непосредственно
(многократным повторением измерений при каждом xi), либо оценены из
каких-то дополнительных соображений (например, как инструментальная погрешность).
Материал из MachineLearning.
Перейти к: навигация, поиск
Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния между двумя векторами — вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.
Содержание
- 1 Постановка задачи
- 2 Пример построения линейной регрессии
- 3 Смотри также
- 4 Литература
- 5 Внешние ссылки
Постановка задачи
Задача метода наименьших квадратов состоит в выборе вектора , минимизирующего ошибку
.
Эта ошибка есть расстояние от вектора до вектора
.
Вектор лежит в простанстве столбцов матрицы
,
так как есть линейная комбинация столбцов этой матрицы с коэффициентами
.
Отыскание решения по методу наименьших квадратов эквивалентно задаче отыскания такой точки
,
которая лежит ближе всего к и находится при этом в пространстве столбцов матрицы
.
Таким образом, вектор должен быть проекцией
на пространство столбцов и вектор невязки
должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов
есть линейная комбинация столбцов с некоторыми коэффициентами , то есть это вектор
.
Для всех в пространстве
, эти векторы должны быть перпендикулярны невязке
:
Так как это равенство должно быть справедливо для произвольного вектора , то
Решение по методу наименьших квадратов несовместной системы ,
состоящей из уравнений с
неизвестными, есть уравнение
которое называется нормальным уравнением.
Если столбцы матрицы линейно независимы, то матрица
обратима
и единственное решение
Проекция вектора на пространство столбцов матрицы имеет вид
Матрица называется матрицей проектирования вектора
на пространство столбцов матрицы
.
Эта матрица имеет два основных свойства: она идемпотентна, , и симметрична,
.
Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.
Пример построения линейной регрессии
Задана выборка — таблица
Задана регрессионная модель — квадратичный полином
Назначенная модель является линейной. Для нахождения оптимального
значения вектора параметров выполняется следующая подстановка:
Тогда матрица значений подстановок свободной переменной
будет иметь вид
Задан критерий качества модели: функция ошибки
Здесь вектор . Требуется найти такие параметры
, которые бы доставляли
минимум этому функционалу,
Требуется найти такие параметры , которые доставляют минимум
— норме вектора
невязок .
Для того, чтобы найти минимум функции невязки, требуется
приравнять ее производные к нулю. Производные данной функции
по составляют
Это выражение совпадает с нормальным уравнением. Решение
этой задачи должно удовлетворять системе линейных уравнений
то есть,
После получения весов можно построить график найденной функции.
При обращении матрицы предполагается, что эта
матрица невырождена и не плохо обусловлена. О том, как работать с плохо обусловленными матрицами см. в статье Сингулярное разложение.
Смотри также
- Линейная регрессия (пример)
- Нелинейная регрессия и метод наименьших квадратов
- Регрессионный анализ
- Анализ регрессионных остатков
- Сингулярное разложение
Литература
- Стренг Г. Линейная алгебра и ее применения. М.: Мир. 1980.
- Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир. 1998.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Внешние ссылки
Wikipedia.org, Least squares

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от экспериментальных входных данных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа (b) для оценки неизвестных параметров регрессионных моделей по выборочным данным.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений (b) , в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (b) (1795) принадлежит первое применение метода, а Лежандр (b) (1805) независимо открыл и опубликовал его под современным названием (фр. (b) Méthode des moindres quarrés)[1]. Лаплас (b) связал метод с теорией вероятностей (b) , а американский математик Эдрейнru (b) en (1808) рассмотрел его теоретико-вероятностные приложения[2]. Метод распространён и усовершенствован дальнейшими изысканиями Энке (b) , Бесселя (b) , Ганзена и других.
Работы А. А. Маркова (b) в начале XX века позволили включить метод наименьших квадратов в теорию оценивания (b) математической статистики, в которой он является важной и естественной частью. Усилиями Ю. Неймана, Ф. Дэвида, А. Эйткена, С. Рао было получено множество немаловажных результатов в этой области[3].
Суть метода наименьших квадратов
Пусть , набор скалярных экспериментальных данных, , набор векторных экспериментальных данных и предполагается, что зависит от .
Вводится некоторая (в простейшем случае линейная) скалярная функция , которая определяется вектором неизвестных параметров .
Ставится задача найти вектор такой, чтобы совокупность погрешностей была в некотором смысле минимальной.
Согласно методу наименьших квадратов решением этой задачи является вектор , который минимизирует функцию
В простейшем случае , и тогда результатом МНК будет среднее арифметическое (b) входных данных.
Преимущество МНК перед минимизацией других видов ошибок состоит в том, что если дифференцируема по , то тоже дифференцируема. Приравнивание частных производных к нулю сводит задачу к решению системы уравнений, причём если зависит от линейно, то и система уравнений будет линейной.
Пример — система линейных уравнений
В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений
- ,
где прямоугольная матрица размера (то есть число строк матрицы A больше количества искомых переменных).
Такая система уравнений в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
- .
Используя оператор псевдоинверсии (b) , решение можно переписать так:
- ,
где — псевдообратная матрица для .
Эту задачу также можно «решить», используя так называемый взвешенный МНК (см. ниже), когда разные уравнения системы получают разный вес из теоретических соображений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым (b) и А. Н. Колмогоровым (b) .
МНК в регрессионном анализе (аппроксимация данных)
Пусть имеется значений некоторой переменной (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных . Задача заключается в том, чтобы взаимосвязь между и аппроксимировать некоторой функцией , известной с точностью до некоторых неизвестных параметров , то есть фактически найти наилучшие значения параметров , максимально приближающие значения к фактическим значениям . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно :
.
В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными
,
где — так называемые случайные ошибки модели.
Соответственно, отклонения наблюдаемых значений от модельных предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры , при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) будет минимальной:
- ,
где — англ. (b) Residual Sum of Squares[4] определяется как:
- .
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. (b) Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам , приравняв производные к нулю и решив полученную систему уравнений:
- .
МНК в случае линейной регрессии
Пусть регрессионная зависимость является линейной (b) :
- .
Пусть y — вектор-столбец наблюдений объясняемой переменной, а — это -матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
- .
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
- .
соответственно сумма квадратов остатков регрессии будет равна
- .
Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):
- .
В расшифрованной матричной форме эта система уравнений выглядит следующим образом:
где все суммы берутся по всем допустимым значениям .
Если в модель включена константа (как обычно), то при всех , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений , а в остальных элементах первой строки и первого столбца — просто суммы значений переменных: и первый элемент правой части системы — .
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
- .
Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
- .
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Простейшие частные случаи
В случае парной линейной регрессии , когда оценивается линейная зависимость одной переменной от другой, формулы расчёта упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:
- .
Отсюда несложно найти оценки коэффициентов:
Несмотря на то, что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид ; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели . В этом случае вместо системы уравнений имеем единственное уравнение
.
Следовательно, формула оценки единственного коэффициента имеет вид
.
Случай полиномиальной модели
Если данные аппроксимируются полиномиальной функцией регрессии одной переменной , то, воспринимая степени как независимые факторы для каждого можно оценить параметры модели исходя из общей формулы оценки параметров линейной модели. Для этого в общей формуле достаточно учесть, что при такой интерпретации и . Следовательно, матричные уравнения в данном случае примут вид:
Статистические свойства МНК-оценок
В первую очередь отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещённости (b) МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа (b) : условное по факторам математическое ожидание (b) случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
- математическое ожидание случайных ошибок равно нулю и
- факторы и случайные ошибки — независимые случайные величины (b) .
Первое условие для моделей с константой можно считать выполненным всегда, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности (b) факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (b) (то есть даже очень большой объём данных не позволяет в этом случае получить качественные оценки). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещённости (b) , оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещённых оценок), необходимо выполнение дополнительных свойств случайной ошибки:
- Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности (b) ): .
- Отсутствие корреляции (автокорреляции (b) ) случайных ошибок в разных наблюдениях между собой .
Данные предположения можно сформулировать для ковариационной матрицы (b) вектора случайных ошибок .
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными (b) , состоятельными (b) и наиболее эффективными (b) оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbiased Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова (b) ). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
.
Эффективность (b) означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация оценок коэффициентов, и в частности сами оценки коэффициентов имеют минимальную дисперсию), то есть в классе линейных несмещённых оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
.
Подставив данное значение в формулу для ковариационной матрицы, получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными (b) и состоятельными (b) . Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными (b) оценками (оставаясь несмещёнными (b) и состоятельными (b) ). Однако ещё более ухудшается оценка ковариационной матрицы: она становится смещённой (b) и несостоятельной (b) . Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения этой проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта (b) и стандартные ошибки в форме Ньюи-Уеста (b) ). Другой подход заключается в применении так называемого обобщённого МНК (b) .
Обобщённый МНК
Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определённую квадратичную форму (b) от вектора остатков , где — некоторая симметрическая положительно определённая весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно, для симметрических матриц (или операторов) существует разложение . Следовательно, указанный функционал можно представить следующим образом: , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано (теорема Айткена), что для обобщённой линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещённых оценок) являются оценки т. н. обобщённого МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
.
Ковариационная матрица этих оценок соответственно будет равна
.
Фактически сущность ОМНК заключается в определённом (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Взвешенный МНК
В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК. В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
См. также
- Обобщенный метод наименьших квадратов (b)
- Двухшаговый метод наименьших квадратов (b)
- Рекурсивный МНК (b)
- Алгоритм Гаусса — Ньютона (b)
Примечания
- ↑ Legendre, On Least Squares. Translated from the French by Professor Henry A. Ruger and Professor Helen M. Walker, Teachers College, Columbia University, New York City.Архивная копия от 7 января 2011 на Wayback Machine (b) (англ.)
- ↑ Александрова, 2008, с. 102.
- ↑ Линник, 1962, с. 21.
- ↑ Магнус, Катышев, Пересецкий, 2007, Обозначение RSS не унифицировано. RSS может быть сокращением от regression sum of squares, а ESS — error sum of squares, то есть, RSS и ESS будут иметь обратный смысл. с. 52. Издания 2004 года..
Литература
- Линник Ю. В (b) . Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
- Айвазян С. А. (b) Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6.
- Доугерти К. Введение в эконометрику: Пер. с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7.
- Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003—2004. — 311 с. — ISBN 8-86225-458-7.
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0.
- Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. — ISBN 5-279-02786-3.
- Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
- Витковский В. В. (b) Наименьшие квадраты // Энциклопедический словарь Брокгауза и Ефрона (b) : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Митин И. В., Русаков В. С. Анализ и обработка экспериментальных данных. — 5-е издание. — 24 с.
Ссылки
- Метод наименьших квадратов онлайн для зависимости y = a + bx с вычислением погрешностей коэффициентов и оцениванием автокорреляции.
На этом занятии
мы с вами рассмотрим алгоритм, который носит название метод наименьших
квадратов. Для начала немного теории. Чтобы ее хорошо понимать нужны
базовые знания по теории вероятностей, в частности понимание ПРВ, а также
знать, что такое производная и как она вычисляется. Остальное я сейчас
расскажу.
На практике
встречаются задачи, когда производились измерения некоторой функциональной
зависимости, но из-за погрешностей приборов, или неточных сведений или еще по
какой-либо причине, измерения немного отстоят от истинных значений функции и
образуют некий разброс:

Наша задача:
зная характер функциональной зависимости, подобрать ее параметры так, чтобы она
наилучшим образом описывала экспериментальные данные ![]() Например, на
Например, на
рисунке явно прослеживается линейная зависимость. Мы это можем определить либо
чисто визуально, либо заранее знать о характере функции. Но, в любом случае
предполагается, что ее общий вид нам известен. Так вот, для линейной функции
достаточно определить два параметра k и b:
![]()
чтобы построить
аппроксимацию (приближение) линейного графика к экспериментальным зависимостям.
Конечно, вид функциональной зависимости может быть и другим, например,
квадратической (парабола), синусоидальной, или даже определяться суммой
известных функций, но для простоты понимания, мы для начала рассмотрим именно
линейный график с двумя неизвестными коэффициентами.
Итак, будем
считать, что на первый вопрос о характере функциональной зависимости
экспериментальных данных ответ дан. Следующий вопрос: как измерить качество
аппроксимации измерений ![]() функцией
функцией
![]() ? Вообще, таких
? Вообще, таких
критериев можно придумать множество, например:
— сумма квадратов
ошибок отклонений:
![]()
— сумма модулей
ошибок отклонений:
![]()
— минимум
максимальной по модулю ошибки:
![]()
и так далее. Каждый
из критериев может приводить к своему алгоритму обработки экспериментальных
значений. Так вот, в методе наименьших квадратов используется минимум суммы
квадратов ошибок. И этому есть математическое обоснование. Часто результаты
реальных измерений имеют стандартное (гауссовское) отклонение относительно
измеряемого параметра:

Здесь σ –
стандартное отклонение (СКО) наблюдаемых значений ![]() от функции
от функции ![]() . Отсюда хорошо
. Отсюда хорошо
видно, что чем ближе измерение к истинному значению параметра, тем больше
значение функции плотности распределения условной вероятности. И, так для всех
точек измерения. Учитывая, что они выполняются независимо друг от друга, то
можно записать следующее функциональное выражение:
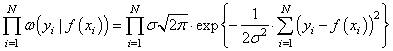
Получается, что лучшее
описание экспериментальных данных с помощью функции ![]() должно проходить по
должно проходить по
точкам, в которых достигается максимум этого выражения. Очевидно, что при
поиске максимума можно не учитывать множитель 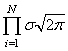 , а экспонента будет
, а экспонента будет
принимать максимальное значение при минимуме ее отрицательной степени:
![]()
Здесь также
множитель можно не учитывать, получаем критерий качества минимум суммы квадрата
ошибок:
![]()
Как мы помним,
наша цель – подобрать параметры ![]() функции
функции
![]()
которые как раз
и обеспечивают минимум этого критерия, то есть, величина E зависит от этих
подбираемых величин:
![]()
И ее можно
рассматривать как квадратическую функцию от аргументов ![]() Из школьного курса
Из школьного курса
математики мы знаем как находится точка экстремума функции – это точка, в
которой производная равна нулю:

Здесь все также,
нужно взять частные производные по каждому параметру и приравнять результат
нулю, получим систему линейных уравнений:
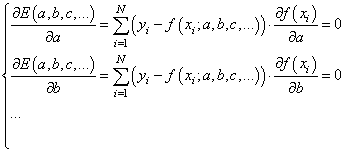
Чтобы наполнить
конкретикой эту систему, нам нужно вернуться к исходному примеру с линейной
функцией:
![]()
Эта функция
зависит от двух параметров: k и b с частными
производными:
![]()
Подставляем все
в систему, имеем:
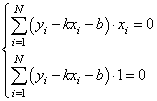
или, в виде:
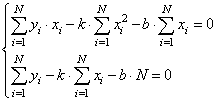
Разделим все на N:
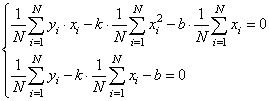
Смотрите, что в
итоге получилось. Формулы с суммами представляют собой первые и вторые
начальные моменты, а также один смешанный момент:
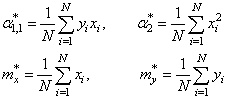
Здесь * означает
экспериментальные моменты. В этих обозначениях, получаем:
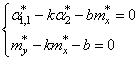
Отсюда находим,
что
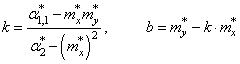
Все, мы получили
оценки параметров k и b для линейной
аппроксимации экспериментальных данных по методу наименьших квадратов. По
аналогии можно вычислять параметры для других функциональных зависимостей,
например, квадратической:
![]()
Здесь будет уже
три свободных параметра и три уравнения, решая которые будем получать лучшую
аппроксимацию по критерию минимума суммарной квадратической ошибки отклонений.
Реализация на Python
В заключение
этого занятия реализуем метод наименьших квадратов на Python. Для этого нам
понадобятся две довольно популярные библиотеки numpy и matplotlib. Если они у вас
не установлены, то делается это просто – через команды:
pip install numpy
pip install matplotlib
После этого, мы
можем их импортировать и использовать в программе:
import numpy as np import matplotlib.pyplot as plt
Первая довольно
эффективная для выполнения различных математических операций, включая векторные
и матричные. Вторая служит для построения графиков.
Итак, вначале
определим необходимые начальные величины:
N = 100 # число экспериментов sigma = 3 # стандартное отклонение наблюдаемых значений k = 0.5 # теоретическое значение параметра k b = 2 # теоретическое значение параметра b
Формируем
вспомогательный вектор
![]()
с помощью метода
array, который
возвращает объект-вектор на основе итерируемой функции range:
Затем, вычисляем
значения теоретической функции:
f = np.array([k*z+b for z in range(N)])
и добавляем к
ней случайные отклонения для моделирования результатов наблюдений:
y = f + np.random.normal(0, sigma, N)
Если сейчас
отобразить наборы точек y, то они будут выглядеть следующим
образом:
plt.scatter(x, y, s=2, c='red') plt.grid(True) plt.show()
Теперь у нас все
есть для вычисления коэффициентов k и b по экспериментальным
данным:
# вычисляем коэффициенты mx = x.sum()/N my = y.sum()/N a2 = np.dot(x.T, x)/N a11 = np.dot(x.T, y)/N kk = (a11 - mx*my)/(a2 - mx**2) bb = my - kk*mx
Здесь выражение x.T*x – это
произведение:
Далее, построим
точки полученной аппроксимации:
ff = np.array([kk*z+bb for z in range(N)])
и отобразим оба
линейных графика:
plt.plot(f) plt.plot(ff, c='red')

Как видите
результат аппроксимации довольно близок начальному, теоретическому графику. Вот
так работает метод наименьших квадратов.
Реализация алгоритма на Python (файл mnsq.py)
Видео по теме
Метод наименьших квадратов (мнк)
Данные
обычно имеют вид таблицы значений
показателей (х1 , х2 ,
у), один из которых является
результативным (у) и выражается
через оставшиеся переменные (х1 ,
х2), которые иногда называются
«факторами».
Предполагается,
что форма связи нам известна с точностью
до параметров, наилучшие значения
которых надо найти по опытным данным
(т.е. найти «МНК-оценки параметров»).
Для применения метода наименьших
квадратов крайне желательно, чтобы
параметры входили в форму связи линейным
образом, например, так:
– линейная
двухфакторная зависимость:
у = b0 + b1 x1 + b2 x2 + e;
– квадратичная
однофакторная зависимость:
у = b0 + b1 x + b2 x2 + e;
– нелинейная
двухфакторная зависимость:
lnу = b0 + b1 lnx1 + b2 lnx2 + e.
Здесь
b0 , b1 , b2 –
параметры модели, которые подлежат
определению;
е – ошибки
(остатки модели).
Далее
будем рассматривать базовую линейную
зависимость, к которой могут быть сведены
многие другие зависимости соответствующими
заменами переменных: у = ур + е,
где ур = (b0 + b1 x1 + b2 x2)
Условимся
суммирование по всем наблюдениям
обозначать квадратными скобками
(обозначения Гаусса):
![]()
;
![]()
.
По
методу наименьших квадратов (МНК)
параметры модели b0 , b1 , b2
следует определять из условия минимума
суммы квадратов ошибок по всем наблюдениям
[e2] min.
Согласно
необходимым условиям экстремума,
приравниваем нулю частные производные
суммы квадратов ошибок по каждому
параметру модели b0 , b1 , b2 .
В результате получим такую систему
«нормальных» уравнений:
[e] = 0;
[ex1] = 0;
[ex2] = 0.
При
преобразованиях были использованы
правила:
![]()
.
Название
система «нормальных» уравнений
объясняется терминологией векторного
исчисления. Значения любых переменных
![]()
представляют собой
![]()
—
мерные векторы: y = (y1 ,
y2 ,
… , yn);
x0 = (1,
1, … , 1); xj = (xj1 ,
xj2 ,
… xjn);
e = (e1 ,
e2 ,
… , en).
Два вектора перпендикулярны (ортогональны,
нормальны), если их скалярное произведение
(сумма значений одноименных компонент)
равно нулю
![]()
.
Таким образом,
система нормальных уравнений действительное
представляет собой запись условий
ортогональности (нормальности) вектора
ошибок (е)
к каждому члену модели (1, х1 ,
х2).
Помножим
равенство у = а0х0 + а1х1 + а2х2 + е
(где х0 = 1)
на каждую переменную, которые входят в
это равенство и вычислим средние
полученных выражений по всем наблюдениям.
При этом учтем требование нормальности
(ортогональности) ошибок к каждому члену
модели
![]()
Получим:
![]()
Первые
три равенства (объединенные фигурной
скобкой) представляют собой систему
нормальных уравнений в развернутой
форме, а из последних двух равенств
получаем выражение для оценки дисперсии
остатка модели
![]()
.
Аналогичную формулу имеем для расчета
суммы квадратов ошибок:
[e2] = [y2] – b0 [y] – b1 [yx1] – b2 [yx2].
Таким
образом, мы выразили сумму квадратов
ошибок через уже найденные суммы. Эта
формула понадобится в дальнейшем.
Пример расчета мнк-оценок параметров
Расчеты
по методу наименьших квадратов
продемонстрируем на оценке параметров
квадратичной модели у = b0 + b1 x + b2 x2 + e,
которая формально сводится к предыдущей
двухфакторной линейной модели заменой
переменных х1 = х,
х2 = х2 .
При этом выясняется, что аргументы х1 ,
х2
не являются «независимыми»
переменными в общепринятом понимании,
они могут быть связаны между собой, лишь
бы определитель системы нормальных
уравнений был отличен от нуля. Кроме
того, оказывается, что одной объясняющей
переменной в нелинейной модели может
соответствовать не один, а сразу несколько
членов, необходимых для описания
нелинейностей.
О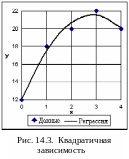
бычно
форму связи выбирают по виду расположения
эмпирических точек на графике. Например,
данные на рис. 14.3 (эмпирические точки)
явно уклоняются от прямой, видно наличие
оптимума (максимума зависимости); поэтому
сочтено, что квадратичная модель
у = b0 + b1 x + b2 x2 + e
будет более адекватно описывать эту
нелинейную зависимость.
Условия
ортогональности ошибок к каждому члену
квадратичной модели
![]()
приводят к следующей системе нормальных
уравнений:
![]()
.
Все
необходимые суммы подсчитаны в следующей
таблице:
|
Данные |
Расчет |
|||||||||
|
№ |
x |
у |
х2 |
х3 |
х4 |
ух |
ух2 |
у2 |
ур |
e |
|
1 |
0 |
12 |
0 |
0 |
0 |
0 |
0 |
144 |
12,114 |
-0,114 |
|
2 |
1 |
18 |
1 |
1 |
1 |
18 |
18 |
324 |
17,547 |
0,457 |
|
3 |
2 |
20 |
4 |
8 |
16 |
40 |
80 |
400 |
20,696 |
-0,686 |
|
4 |
3 |
22 |
9 |
27 |
81 |
66 |
198 |
484 |
21,543 |
0,457 |
|
5 |
4 |
20 |
16 |
64 |
256 |
80 |
320 |
400 |
20,114 |
-0,114 |
|
Суммы |
10 |
92 |
30 |
100 |
354 |
204 |
616 |
1752 |
0 |
Вычисленные
суммы подставляем в систему нормальных
уравнений
![]()
и
находим ее решение: b0 = 12,114;
b1 = 6,571;
b2 = –1,143.
Рачетные
значения yp = 12,114 + 6,571x – 1,143x2
приведены в той же таблице вместе с
ошибками е = у – ур .
График найденной квадратичной зависимости
изображен на рис. 14.3, при этом
наблюдается хорошее сглаживание исходных
данних.
Убеждаемся,
что сумма всех ошибок равняется нулю:
[e] = 0.
Данных
немного, поэтому подсчитаем сумму
квадратов ошибок непосредственно:
[e2] = (–0,114)2 + (0,457)2 + (–0,686)2 + (0,457)2 + (–0,114)2 = 0,914.
Для
проверки вычислим эту же сумму квадратов
по формуле:
[e2] = [y2] – b0 [y] – b1 [yx1] – b2 [yx2] =
=1752 ‑ 12,11492 ‑ 6,571204 + 1,143616 = 1,116.
Расхождение
в результатах расчета двумя способами
объясняется погрешностями в вычислении
параметров модели с 3-мя десятичными
знаками. Если вычислить эти параметры
с 4-мя десятичными знаками, то для суммы
квадратов ошибок получим значение
[e2] = 0,945,
а с 5-ю знаками – уже [e2] = 0,915.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из MachineLearning.
(Перенаправлено с МНК)
Перейти к: навигация, поиск
Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния между двумя векторами — вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.
Содержание
- 1 Постановка задачи
- 2 Пример построения линейной регрессии
- 3 Смотри также
- 4 Литература
- 5 Внешние ссылки
Постановка задачи
Задача метода наименьших квадратов состоит в выборе вектора , минимизирующего ошибку
.
Эта ошибка есть расстояние от вектора до вектора
.
Вектор лежит в простанстве столбцов матрицы
,
так как есть линейная комбинация столбцов этой матрицы с коэффициентами
.
Отыскание решения по методу наименьших квадратов эквивалентно задаче отыскания такой точки
,
которая лежит ближе всего к и находится при этом в пространстве столбцов матрицы
.
Таким образом, вектор должен быть проекцией
на пространство столбцов и вектор невязки
должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов
есть линейная комбинация столбцов с некоторыми коэффициентами , то есть это вектор
.
Для всех в пространстве
, эти векторы должны быть перпендикулярны невязке
:
Так как это равенство должно быть справедливо для произвольного вектора , то
Решение по методу наименьших квадратов несовместной системы ,
состоящей из уравнений с
неизвестными, есть уравнение
которое называется нормальным уравнением.
Если столбцы матрицы линейно независимы, то матрица
обратима
и единственное решение
Проекция вектора на пространство столбцов матрицы имеет вид
Матрица называется матрицей проектирования вектора
на пространство столбцов матрицы
.
Эта матрица имеет два основных свойства: она идемпотентна, , и симметрична,
.
Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.
Пример построения линейной регрессии
Задана выборка — таблица
Задана регрессионная модель — квадратичный полином
Назначенная модель является линейной. Для нахождения оптимального
значения вектора параметров выполняется следующая подстановка:
Тогда матрица значений подстановок свободной переменной
будет иметь вид
Задан критерий качества модели: функция ошибки
Здесь вектор . Требуется найти такие параметры
, которые бы доставляли
минимум этому функционалу,
Требуется найти такие параметры , которые доставляют минимум
— норме вектора
невязок .
Для того, чтобы найти минимум функции невязки, требуется
приравнять ее производные к нулю. Производные данной функции
по составляют
Это выражение совпадает с нормальным уравнением. Решение
этой задачи должно удовлетворять системе линейных уравнений
то есть,
После получения весов можно построить график найденной функции.
При обращении матрицы предполагается, что эта
матрица невырождена и не плохо обусловлена. О том, как работать с плохо обусловленными матрицами см. в статье Сингулярное разложение.
Смотри также
- Линейная регрессия (пример)
- Нелинейная регрессия и метод наименьших квадратов
- Регрессионный анализ
- Анализ регрессионных остатков
- Сингулярное разложение
Литература
- Стренг Г. Линейная алгебра и ее применения. М.: Мир. 1980.
- Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир. 1998.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Внешние ссылки
Wikipedia.org, Least squares
Метод наименьших квадратов (короткий MKQ или английский метод наименьших квадратов , или просто наименьших квадратов коротких: LS ; расширениям разграничить , полученные из них, как, например обобщенный метод наименьших квадратов , или двухстадийном способе наименьших квадратов , а также называется «обыкновенный» с добавлением того, что обычный метод наименьших квадратов ( английский обычный метод наименьших квадратов , сокращенно: OLS )) или метод KQ (устаревший метод суммы квадратов наименьших отклонений ) являются стандартными математическими процедурами для корректировки . В этом случае к набор данных указывает на функцию , определяет пробеги как можно ближе к точкам данных и , таким образом , наилучшим обобщающие данные. Наиболее часто используемой функцией является прямая линия , которая затем вызывается подгонкой линии . Чтобы можно было использовать метод, функция должна содержать хотя бы один параметр . Эти параметры затем определяются методом, так что, когда функция сравнивается с точками данных и расстояние между значением функции и точкой данных возводится в квадрат, сумма этих квадратов расстояний была как можно меньше. Тогда расстояния называют остатками .
Обычно этот метод используется для проверки реальных данных, таких как физические или экономические измеренные значения . Эти данные часто содержат неизбежные ошибки измерения и колебания . Предполагая, что измеренные значения близки к лежащим в основе « истинным значениям » и что между измеренными значениями существует определенная взаимосвязь, метод может использоваться для поиска функции, которая как можно лучше описывает эту взаимосвязь данных. . Этот метод также можно использовать в обратном порядке для тестирования различных функций и, таким образом, описания неизвестной взаимосвязи в данных.

Точки измерения и их расстояние от функции определяется методом наименьших квадратов. Здесь в качестве модельной кривой была выбрана логистическая функция .
В графическом примере вводятся точки данных и функция компенсации. Выбирается общая функция ( модельная функция ), которая должна соответствовать вопросу и данным, в данном случае логистическая функция . Их параметры теперь определены таким образом, чтобы минимизировать сумму квадратов отклонений наблюдений от значений функции . На графике отклонение в этой точке можно увидеть как расстояние по вертикали между наблюдением и кривой.
В стохастике метод наименьших квадратов в основном используется как метод оценки регрессионного анализа , где его также называют оценкой наименьших квадратов или обычной оценкой наименьших квадратов . Поскольку оценка методом наименьших квадратов, остаточная сумма минимизирована, это тот метод оценки, который включает максимальное определение . Метод наименьших квадратов используется как идентификация системы в связи с модельными экспериментами, например. Б. для инженеров выход из парадоксальной ситуации определения параметров модели по неизвестным законам.
история


В первый день нового 1801 года итальянский астроном Джузеппе Пиацци открыл карликовую планету Церера . Он смог идти по этому пути 40 дней, затем Церера скрылась за солнцем. В течение года многие ученые безуспешно пытались рассчитать орбиту на основе наблюдений Пиацци — предполагая круговую орбиту, потому что в то время элементы орбиты могли быть определены только математически из наблюдаемых положений неба для таких .
24-летнему Гауссу удалось вычислить орбиту с помощью нового косвенного метода определения орбиты и его расчетов компенсации, основанных на методе наименьших квадратов (хотя еще не обозначенном) таким образом, что Франц Ксавер фон Зак нашел его 7 декабря 1801 года и — подтверждено — 31 декабря 1801 года. Генрих Вильгельм Ольберс подтвердил это независимо от Зака в ходе наблюдений 1 и 2 января 1802 года.
Проблема с обнаружением Цереры как таковой заключалась в том, что в ходе наблюдений не было известно ни местоположение, ни часть орбиты, ни расстояние , а только направления наблюдения. Это приводит к поиску эллипса, а не круга, как предлагали конкуренты Гаусса. Одна из фокусных точек эллипса известна (само Солнце ), и дуги орбиты Цереры между направлениями наблюдения проходят согласно второму закону Кеплера , то есть времена ведут себя как поверхности, заметаемые направляющая балка. Кроме того, из вычислительного решения известно, что сами наблюдения предполагают коническое сечение в космосе, собственно земную орбиту.
В принципе, задача сводится к уравнению восьмой степени, тривиальным решением которого является сама орбита Земли. С помощью обширных вторичных условий и (позже) метода наименьших квадратов, разработанного Гауссом, 24-летний мужчина сумел указать вычисленное им местоположение орбиты Цереры с 25 ноября по 31 декабря 1801 года. Это позволило Заку найти Цереру в последний день прогноза. Место находилось не менее чем в 7 ° (т.е. 13,5 ширины полнолуния ) к востоку от того места, где другие астрономы подозревали Цереру, которой не только Зак, но и Ольберс должным образом воздавали должное.
Его первые вычисления все еще проводились без метода наименьших квадратов , только когда после повторного открытия Цереры стало доступно много новых данных, он использовал их для более точного определения элементов орбиты, но не раскрывая подробностей своего метода. Также была восстановлена репутация Пиацци, которая сильно пострадала из-за того, что точки его пути не соответствовали круговой траектории.
Предшественником метода наименьших квадратов является метод наименьших абсолютных отклонений , разработанный в 1760 году Руджером Йосипом Бошковичем . Гаусс разработал основы метода наименьших квадратов еще в 1795 году в возрасте 18 лет. Он был основан на идее Пьера-Симона Лапласа складывать отклонения измеренных значений от ожидаемого таким образом, чтобы сумма всех этих так называемых ошибок давала ноль. В отличие от этого метода, Гаусс использовал квадраты ошибок вместо ошибок и, таким образом, смог обойтись без требования нулевой суммы. Независимо от Гаусса француз Адриан-Мари Лежандр разработал тот же метод, опубликовал его сначала в 1805 году, в конце небольшой работы по вычислению орбит комет, и опубликовал второй трактат по нему в 1810 году. Его изложение было предельно ясным. и просто. Название Méthode des moindres carrés (метод наименьших квадратов) также происходит от Лежандра .
В 1809 году во втором томе своей работы по небесной механике Theoria motus corporum coelestium in sectionibus conicis solem ambientium (теория движения небесных тел, которые вращаются вокруг Солнца в конических сечениях) , Гаусс опубликовал метод, включающий нормальные уравнения, а также метод исключения Гаусса и метод Гаусса-Ньютона , который вышел далеко за рамки Лежандра. В нем он назвал метод наименьших квадратов своим открытием и заявил, что открыл и применил его еще в 1795 году (то есть до Лежандра), что его долгое время раздражало. Лежандр жаловался на это в длинном письме к Гауссу, которое Гаусс оставил без ответа. Гаусс лишь изредка ссылался на запись в своем математическом дневнике от 17 июня 1798 года (есть загадочная фраза на латыни: Calculus probabilitatis contra La Place defensus (исчисление вероятностей, защищенное от Лапласа) и ничего больше). Лаплас рассуждал об этом так, что Лежандр сделал первую публикацию, но Гаусс, несомненно, знал этот метод заранее, сам использовал его, а также сообщил другим астрономам в письмах. Метод наименьших квадратов быстро стал стандартным методом работы с наборами астрономических или геодезических данных после его публикации.
Гаусс интенсивно использовал этот метод в своем исследовании Королевства Ганновер с помощью триангуляции . Работа, состоящая из двух частей, была опубликована в 1821 и 1823 годах, а в 1826 году — дополнением к Theoriacommonisillanceum erroribus minimis obnoxiae (теория комбинации наблюдений, допускающих наименьшие ошибки) , в которой Гаусс обосновал успех метода наименьших квадратов с помощью заявив, что он сравнивался с другими методами, расчет поправки оптимален в широком смысле. Математическая формулировка этого утверждения известна как теорема Гаусса-Маркова , названная в честь Андрея Андреевича Маркова , который заново открыл и сделал популярной эту часть работы Гаусса, которой первоначально пренебрегали, в 20-м веке (см. Также теорему Гаусс-Маркова. # Geschichte ). Theoria Combinationis также содержит методы для эффективного решения систем линейных уравнений , таких как метод Гаусса-Зейделя и разложение LR , которые представляют собой значительный шаг вперед по математическому знанию времени.
Французский геодезист Андре-Луи Холески разработал декомпозицию Холецкого во время Первой мировой войны , которая снова продемонстрировала значительный выигрыш в эффективности по сравнению с методом решения Гаусса. В 1960-х Джин Голуб разработал идею решения возникающих систем линейных уравнений с помощью QR-разложения .
Процедура
требования
Один смотрит на зависимую переменную, на которую влияют одна или несколько переменных. Удлинение пружины зависит только от приложенной силы, но прибыльность компании зависит от нескольких факторов, таких как продажи , различные затраты или собственный капитал . Чтобы упростить обозначения, представление ограничено одной переменной в следующем . Связь между переменными и определяется функцией модели , например параболой или экспоненциальной функцией.
-
,
который зависит от и от функциональных параметров. Эта функция возникает либо от знаний пользователя, либо от более или менее трудоемкого поиска модели; возможно, придется применять различные функции модели и сравнивать результаты. Простым случаем, основанным на существующих знаниях, является, например, пружина, потому что здесь закон Гука и, следовательно, линейная функция с жесткостью пружины в качестве единственного параметра является требованием модели. Однако в более сложных случаях, например, в компании, выбору типа функции должен предшествовать сложный процесс моделирования .
Чтобы получить информацию о параметрах и, следовательно, о конкретном типе взаимосвязи, соответствующие значения наблюдений собираются для соответствующих заданных значений независимых переменных . Параметры используются для адаптации выбранного типа функции к этим наблюдаемым значениям . Теперь цель состоит в том, чтобы выбрать параметры так, чтобы функция модели как можно лучше аппроксимировала данные.

У Гаусса и Лежандра была идея сделать предположения о распределении ошибок измерения этих значений наблюдений. Они должны быть в среднем равны нулю, иметь постоянную дисперсию и быть стохастически независимыми от любой другой ошибки измерения . Это означает, что в ошибках измерения больше нет систематической информации, т.е. что они колеблются около нуля чисто случайно. Кроме того, ошибки измерения должны быть нормально распределены , что, с одной стороны, имеет вероятностные преимущества, а с другой — гарантирует, что выбросы будут настолько хороши, насколько невозможны.
Чтобы определить параметры в соответствии с этими предположениями , обычно необходимо, чтобы точек данных было значительно больше, чем параметров, поэтому это должно быть применимо.
Минимизация суммы квадратов ошибок
Критерий определения приближения следует выбирать так, чтобы большие отклонения модельной функции от данных имели больший вес, чем небольшие. Если невозможно решение без каких-либо отклонений, то наилучшим общеприменимым критерием является компромисс с наименьшим общим отклонением.
Для этого сумма квадратов ошибок, которая также называется суммой квадратов ошибок (точнее: сумма квадратов остатков ), определяется как сумма квадратов разностей между значения модельной кривой и данных .
В обозначении формул с параметрами и результатами
Затем следует выбрать те параметры, для которых сумма квадратов ошибок уравнивания минимальна:
Как именно решается эта задача минимизации, зависит от типа модельной функции.
Если сумма квадратов ошибок прогнозируется для внешнего набора данных, говорят о статистике PRESS ( англ. Предсказательная сумма квадратов остатков ).
Функция линейной модели
Функции линейной модели представляют собой линейные комбинации произвольных, как правило, нелинейных базисных функций. Для таких модельных функций проблема минимизации также может быть решена аналитически с использованием подхода экстремальных значений без итерационных шагов аппроксимации. Сначала показаны некоторые простые частные случаи и примеры.
Частный случай простой линейной прямой линии наилучшего соответствия
Вывод и процедура
Полином первого порядка
— это простая модельная функция с двумя линейными параметрами
Мы ищем коэффициенты и прямую, наиболее подходящую для заданных измеренных значений . Отклонения между искомой прямой линией и соответствующими измеренными значениями
называются ошибками подгонки или остатками . Теперь ищем коэффициенты и с наименьшей суммой квадратов ошибок
-
.
Большое преимущество подхода с этим квадратом ошибок становится очевидным, когда эта минимизация выполняется математически: функция суммы понимается как функция двух переменных и (входящие измеренные значения являются числовыми константами), затем производная (точнее: частные производные ) функции на основе этих переменных (т.е. и ) и, наконец, поиск нулевой точки из этого вывода . Результатом является линейная система уравнений
с решением
-
и ,
где представляет на сумму произведений отклонений между и , и представляет на сумму квадратов отклонений от . Это среднее арифметическое из значений, соответственно. Решение для также может быть найдено в нецентрированном виде
с помощью теоремы о смещении
можно указать. Эти результаты также могут быть получены с помощью функций действительной переменной, то есть без частных производных.
Пример с наиболее подходящей прямой линией
В этом примере вычисляется наиболее подходящая прямая линия формы, чтобы показать взаимосвязь между двумя элементами набора данных. Набор данных состоит из длины и ширины десять кораблей (см военный корабль данные ). Следует попытаться связать широту с долготой. Данные представлены в первых трех столбцах следующей таблицы. Остальные столбцы относятся к промежуточным результатам для расчета наиболее подходящей прямой. Переменная должна обозначать длину корабля и его ширину. Ищем прямую, для которой при использовании известных значений значения функции максимально приближены к известным значениям .
| Военный корабль | Длина (м) | Ширина (м) |

|

|
||||
|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
| 1 | 208 | 21,6 | 40,2 | 3,19 | 128,24 | 1616,04 | 24,88 | 3,28 |
| 2 | 152 | 15.5 | −15,8 | −2,91 | 45,98 | 249,64 | 15,86 | 0,36 |
| 3 | 113 | 10,4 | -54,8 | −8,01 | 438,95 | 3003,04 | 9,57 | -0,83 |
| 4-й | 227 | 31,0 | 59,2 | 12,59 | 745,33 | 3504,64 | 27,95 | −3,05 |
| 5 | 137 | 13,0 | −30,8 | −5,41 | 166,63 | 948,64 | 13,44 | 0,44 |
| Шестой | 238 | 32,4 | 70,2 | 13,99 | 982,10 | 4928,04 | 29,72 | −2,68 |
| 7-е | 178 | 19.0 | 10.2 | 0,59 | 6.02 | 104,04 | 20.05 | 1.05 |
| 8-е | 104 | 10,4 | −63,8 | −8,01 | 511,04 | 4070,44 | 8,12 | −2,28 |
| 9 | 191 | 19.0 | 23,2 | 0,59 | 13,69 | 538,24 | 22,14 | 3,14 |
| 10 | 130 | 11,8 | −37,8 | −6,61 | 249,86 | 1428,84 | 12,31 | 0,51 |
| Сумма Σ | 1678 | 184,1 | 3287,82 | 20391,60 |
Линия наилучшего соответствия определяется коэффициентами и , которые рассчитываются с использованием, как указано выше.
Константы и являются , соответственно, средние значения из — и метрики, так
В качестве первого промежуточного шага теперь можно рассчитать отклонение от среднего значения для каждого военного корабля: и — эти значения вводятся в четвертый и пятый столбцы приведенной выше таблицы. Это упрощает
формулу для
В качестве второго промежуточного этапа, продукты и могут быть вычислены для каждого корабля. Эти значения вводятся в шестой и седьмой столбцы таблицы, и теперь их можно легко сложить. Это можно рассчитать как
Значение уже можно интерпретировать: если предположить, что данные линейно связаны и могут быть описаны нашей рассчитанной линией наилучшего соответствия, ширина военного корабля увеличивается примерно на 0,16 метра на каждый метр, который он длиннее.
Отрезок затем
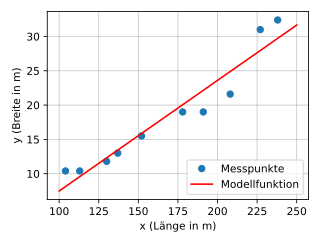
Точечная диаграмма долготы и широты десяти случайно выбранных боевых кораблей с нарисованной линейной функцией компенсации
Таким образом, уравнение наиболее подходящей линии имеет вид 
Чтобы проиллюстрировать это, данные могут быть построены как диаграмма рассеяния и вставлена наиболее подходящая линия. График показывает, что действительно существует линейная зависимость между длиной и шириной военного корабля для наших выборочных данных. Регулировка точек неплохая. Отклонение значений, предсказанных прямой линией, от измеренных значений также можно рассматривать как меру . Соответствующие значения вводятся в восьмой и девятый столбцы таблицы. Среднее отклонение составляет 2,1 м. Коэффициент детерминации как стандартизованный коэффициент также дает значение приблизительно 92,2% (100% соответствует среднему отклонению 0 м); для расчета см. пример коэффициента детерминации .
Однако отрицательный перехват означает, что в нашей линейной модели военный корабль длиной 0 метров имеет отрицательную ширину — или военные корабли начинают существовать только с определенной минимальной длины. По сравнению с реальностью это, конечно, неверно, что можно принять во внимание при оценке статистического анализа. Вероятно, что модель действительна только для области, для которой фактически доступны измеренные значения (в данном случае для военных кораблей длиной от 100 м до 240 м), и что за пределами области линейная функция больше не подходит для представления данные.
Простые полиномиальные кривые наилучшего соответствия

Диаграмма рассеяния: средний вес мужчин по возрасту с функцией параболической модели.

Набор данных с аппроксимирующими полиномами
Полиномы наилучшего соответствия являются более общими, чем линейная линия наилучшего соответствия
-
,
который теперь будет проиллюстрирован на примере (такие полиномиальные подходы с выравниванием могут — в дополнение к итерационному решению — быть решены аналитически с использованием подхода экстремальных значений).
Результаты микропереписи, проведенного Федеральным статистическим управлением, представляют собой средний вес мужчин по возрастным группам (источник: Федеральное статистическое управление, Висбаден, 2009 г.). Для анализа на смену возрастным группам пришли средние классы. Необходимо проанализировать зависимость переменного веса ( ) от переменного возраста ( ).
Диаграмма рассеяния предполагает приблизительно параболическую связь между и , которую часто можно хорошо аппроксимировать с помощью полинома. Это становится полиномиальным подходом к форме
пытается. Решением является полином 4-й степени
-
.
Точки измерения отклоняются в среднем ( стандартное отклонение ) на 0,19 кг от функции модели. Если вы уменьшите степень многочлена до 3, вы получите решение
со средним отклонением 0,22 кг и степенью полинома 2 решение
со средним отклонением 0,42 кг. Как можно видеть, если более высокие члены опущены, коэффициенты младших членов изменяются. Метод пытается извлечь максимум из любой ситуации. Соответственно, недостающие более высокие члены максимально хорошо компенсируются младшими членами до тех пор, пока не будет достигнут математический оптимум. Полином второй степени (парабола) очень хорошо описывает ход точек измерения (см. Рисунок).
Частный случай линейной настроечной функции с несколькими переменными
Если модельная функция является многомерным полиномом первого порядка, т.е. если она имеет несколько независимых переменных модели вместо одной переменной , получается линейная функция вида
-
,
те на остатках
ведет и о подходе к минимизации
можно решить.
Общий линейный случай

Далее будет показан общий случай любых линейных модельных функций любой размерности. Для заданной функции измеренного значения
с независимыми переменными — оптимально адаптированная линейная модельная функция
требуется, квадратичное отклонение которого должно быть минимальным. — координаты функции, определяемые линейные входящие параметры и любые линейно независимые функции, выбранные для адаптации к задаче.
В заданных точках измерения
получаем ошибки настройки
или в матричной записи
где вектор, который суммирует, какая матрица значений базисной функции , вектора параметров , параметров и векторных наблюдений где .

Задача минимизации с использованием евклидовой нормы по
формуле
может быть сформулирован в регулярном случае (т.е. имеет полный ранг столбца , поэтому он регулярный и, следовательно, обратимый) формулой

можно четко решить аналитически, как будет объяснено в следующем разделе. В особом случае, если он не полного ранга, система нормальных уравнений не является однозначно разрешимой, т.е. ЧАС. параметр не может быть идентифицирован (см. теорему Гаусса-Маркова # Особый случай, оцениваемые функции ).
Решение задачи минимизации
Вывод и процедура
Проблема минимизации возникает, как показано в общем линейном случае, как
Эту проблему всегда можно решить. Если матрица имеет полный ранг , решение даже единственное. Для определения экстремальной точки обнуление частных производных по ,
линейная система нормальных уравнений (также гауссовские нормальные уравнения или нормальные уравнения )
который обеспечивает решение проблемы минимизации и, как правило, должен решаться численно. Имеет полный ранг и есть , матрица положительно определена, так что найденный экстремум действительно является минимумом. Таким образом, решение задачи минимизации можно свести к решению системы уравнений. В простом случае наилучшей прямой линии ее решение, как было показано, может быть даже дано непосредственно в виде простой формулы.
В качестве альтернативы можно использовать нормальные уравнения в представлении
выпишите, при этом стандартное скалярное произведение символизирует и может также пониматься как интеграл перекрытия основных функций. Базовые функции следует читать как векторы с дискретными опорными точками в месте проведения наблюдений .
Кроме того, проблема минимизации может быть хорошо проанализирована с помощью разложения по сингулярным значениям . Это также мотивировало выражение псевдообратного , обобщения нормального обратного к матрице . Затем это дает представление о неквадратных линейных системах уравнений, которые допускают не стохастическую, а алгебраически мотивированную концепцию решения.
Численная обработка решения.
Есть два способа численного решения проблемы. С одной стороны, нормальные уравнения
которые однозначно разрешимы, если матрица имеет полный ранг. Кроме того, матрица суммы произведений имеет свойство быть положительно определенной , поэтому все ее собственные значения положительны. Вместе с симметрией из , это может быть использовано , чтобы решить эту проблему при использовании численных методов: например , с разложением Холецкого или метода CG . Поскольку оба метода сильно зависят от состояния матрицы, это иногда не рекомендуется: если условие уже плохое, то квадратичная функция плохо обусловлена. В результате ошибки округления могут быть увеличены до такой степени, что они сделают результат непригодным для использования. Однако методы регуляризации могут улучшить состояние.

Один из методов — так называемая регрессия гребня , восходящая к Hoerl и Kennard (1970). Английское слово ridge означает что-то вроде гребня, рифа, спины. Вместо плохо кондиционированной матрицы здесь используется лучше кондиционированная матрица . Вот матрица -мерной идентичности. Искусство заключается в правильном выборе . Слишком маленький усиливает состояние лишь незначительно, слишком большой ведет к искаженной адаптации.
С другой стороны, исходная задача минимизации обеспечивает более стабильную альтернативу, поскольку при малом значении минимума она имеет условие порядка величины условия , при больших значениях квадрата условие . QR-разложение используется для вычисления решения , которое генерируется с помощью преобразований домохозяйств или вращений Гивенса . Основная идея состоит в том, что ортогональные преобразования не изменяют евклидову норму вектора. Так что это
для каждой ортогональной матрицы . Чтобы решить эту проблему, можно вычислить QR-разложение , при этом правая часть также преобразуется напрямую. Это приводит к форме
с где правой верхней треугольной матрицей . Таким образом, решение задачи получается путем решения системы уравнений
Норма минимума тогда получается из оставшихся компонентов преобразованной правой части, так как связанные уравнения никогда не могут быть выполнены из-за нулевых линий в .
В статистическом регрессионном анализе с учетом нескольких переменных говорят о множественной линейной регрессии . Наиболее распространенный подход — множественная линейная модель для оценки, чем обычная оценка методом наименьших квадратов или обычный метод наименьших квадратов ( английский обычный метод наименьших квадратов , сокращенно OLS ). В отличие от метода обычный наименьших квадратов обобщенный метод наименьших квадратов , короткие VMKQ ( английский обобщен метод наименьших квадратов , вскоре GLS ) в обобщенной линейной модели регрессии используется. В этой модели члены ошибки отклоняются от предположения о распределении, например, о некоррелированности и / или гомоскедастичности . Напротив, при многомерной регрессии для каждого наблюдения существует множество значений, так что вместо вектора присутствует матрица (см. Общую линейную модель ). Модели линейной регрессии интенсивно исследуются в статистике с точки зрения теории вероятностей. В частности , в эконометрике , например, сложные рекурсивно определенные линейные структурные уравнения анализируются для моделирования экономических систем.



Проблемы с ограничениями
Часто известна дополнительная информация о параметрах, которая формулируется вторичными условиями, которые затем доступны в форме уравнений или неравенств. Уравнения появляются, например, когда необходимо интерполировать определенные точки данных. Неравенства проявляются чаще, обычно в виде интервалов по отдельным параметрам. Жесткость пружины упоминалась во вводном примере; она всегда больше нуля и всегда может быть оценена в сторону увеличения для конкретного рассматриваемого случая.
В случае уравнения их можно использовать для обоснованно поставленной задачи, чтобы преобразовать исходную задачу минимизации в задачу более низкого измерения, решение которой автоматически удовлетворяет ограничениям.
Случай неравенства сложнее. Проблема возникает здесь с линейными неравенствами
-
с ,
где неравенства подразумеваются покомпонентно. Эта проблема может быть решена однозначно как задача выпуклой и квадратичной оптимизации, и к ней можно подойти, например, с помощью методов решения таких задач .
Квадратичные неравенства возникают, например, при использовании регуляризации Тихонова для решения интегральных уравнений . Здесь не всегда дана разрешимость. Численное решение может, например, происходить с помощью специальных QR-разложений .
Нелинейные функции модели
Основная идея и процедура
С появлением мощных компьютеров нелинейная регрессия, в частности, приобретает все большее значение. Параметры включены в функцию нелинейным образом. Нелинейное моделирование, в принципе, позволяет адаптировать данные к любому уравнению формы . Поскольку эти уравнения определяют кривые , термины «нелинейная регрессия» и «подгонка кривой» в основном используются как синонимы.
Некоторые нелинейные задачи можно преобразовать в линейные с помощью подходящей замены, а затем решить, как указано выше. Мультипликативная модель вида
можно преобразовать в аддитивную систему, например, путем логарифмирования . Этот подход используется, в том числе, в теории роста .
В общем, проблема формы возникает с нелинейными модельными функциями
с нелинейной функцией . Затем частичное дифференцирование приводит к системе нормальных уравнений, которые больше не могут быть решены аналитически. Численное решение может быть выполнено итеративно с помощью метода Гаусса-Ньютона .
Современные программы часто работают с одним вариантом — алгоритмом Левенберга-Марквардта . Вот регуляризация однообразие приближенного результата гарантировано. Кроме того, метод более терпим, чем исходный метод, если имеется большее отклонение в оценочных значениях. Оба метода связаны с методом Ньютона и при подходящих условиях (начальная точка достаточно близка к локальному оптимуму) обычно сходятся прямо , то есть количество правильных десятичных знаков удваивается на каждом шаге.
Если дифференцирование занимает слишком много времени из-за сложности целевой функции, существует ряд других методов, доступных в качестве альтернативных решений, не требующих каких-либо выводов, см. Методы локальной нелинейной оптимизации .
Пример ферментативной кинетики нелинейной модельной функции
Примером полностью нелинейных регрессионных моделей является кинетика ферментов . Требование здесь состоит в том, что «только» (скорость реакции), а не (концентрация субстрата) может быть ошибкой и, таким образом, может использоваться в качестве переменной. Отношение Лайнуивера-Берка является алгебраически правильным преобразованием уравнения Михаэлиса-Ментен , но его применение дает правильные результаты только в том случае, если измеренные значения не содержат ошибок. Это происходит из-за того, что реальность возникает только при расширении отношений Михаэлиса-Ментен.

может быть описана с в качестве параметра ошибки. Это уравнение больше не может быть линеаризовано, поэтому решение здесь необходимо определять итеративно.
Неправомерное поведение при несоблюдении требований
Метод наименьших квадратов позволяет при определенных условиях вычислить наиболее вероятный из всех параметров модели. Для этого должна быть выбрана правильная модель, должно быть доступно достаточное количество измеренных значений, а отклонения измеренных значений от модельной системы должны образовывать нормальное распределение . Однако на практике этот метод также может использоваться для различных целей, если эти требования не выполняются. Однако следует отметить, что метод наименьших квадратов может дать совершенно нежелательные результаты при определенных неблагоприятных условиях. Например, в измеренных значениях не должно быть выбросов , так как они искажают результат оценки . Кроме того, мультиколлинеарность между оцениваемыми параметрами неблагоприятна, поскольку вызывает численные проблемы. Кстати, регрессоры , которые далеки от других, также могут иметь сильное влияние на результаты расчета корректировки. Здесь говорят о ценностях с большим кредитным плечом ( англ. High Leverage Value ).
Мультиколлинеарность
Явление мультиколлинеарности возникает, когда измерения двух заданных переменных и очень высокая корреляция почти линейно зависят. В линейном случае это означает, что определитель матрицы нормального уравнения очень мал и, наоборот, норма обратного очень велика; условие о , следовательно , серьезно ослаблено. Тогда нормальные уравнения трудно решить численно. Значения решения могут стать неправдоподобно большими, и даже небольшие изменения в наблюдениях вызывают большие изменения в оценках.
Убегать
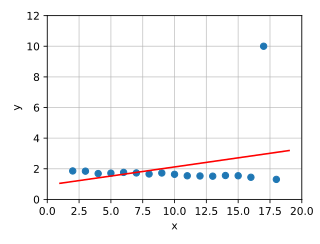
Выбросы y:
значение тянет прямую линию вверх
Значения данных, которые «не вписываются в серию измерений», определяются как выбросы . Эти значения сильно влияют на расчет параметров и искажают результат. Чтобы избежать этого, данные должны быть проверены на предмет неправильных наблюдений. Обнаруженные выбросы можно исключить, например, из серии измерений, или следует использовать альтернативные методы расчета, устойчивые к выбросам, такие как взвешенная регрессия или метод трех групп.
В первом случае после первого вычисления оценочных значений используются статистические тесты для проверки наличия выбросов в отдельных измеренных значениях. Затем эти измеренные значения отбрасываются, а оценочные значения вычисляются снова. Этот метод подходит, когда есть только несколько выбросов.
При взвешенной регрессии зависимые переменные взвешиваются в зависимости от их остатков . Выбросы, d. ЧАС. Наблюдениям с большими остатками дается низкий вес, который может быть оценен в зависимости от размера остатка. В алгоритме Мостеллера и Тьюки (1977), который называется «двойным взвешиванием», беспроблемные значения взвешиваются с 1, а выбросы с 0, что означает, что выброс подавляется. При взвешенной регрессии обычно требуется несколько итерационных шагов , пока набор выявленных выбросов больше не изменится.
Обобщенные модели наименьших квадратов
Если смягчить строгие требования в процедуре для членов ошибки, будут получены так называемые обобщенные подходы наименьших квадратов . Важные частные случаи имеют свои собственные имена, такие как взвешенный метод наименьших квадратов ( английский взвешенный метод наименьших квадратов , сокращенно WLS ), в котором ошибки действительно считаются некоррелированными, но не более той же дисперсии. Это приводит к проблеме формы
где D является диагональной матрицей . Если дисперсии сильно различаются, соответствующие нормальные уравнения имеют очень большое условие , поэтому проблема должна решаться напрямую.
Если дополнительно предположить, что ошибки в данных измерений также должны быть учтены в модельной функции, результат «общих наименьших квадратов» будет иметь вид
где ошибка в модели, а ошибка в данных.
Наконец, есть возможность не использовать нормальное распределение в качестве основы. Это соответствует, например, минимизации не по евклидовой норме, а по норме суммы . Такие модели являются предметом регрессионного анализа .
Регрессия частичных наименьших квадратов (PLS)
Частичная регрессия наименьших квадратов (англ. Partial Least Squares, PLS) или «проекция на скрытую структуру» является многомерным методом и может использоваться для уменьшения размерности, посредством чего, подобно регрессии главных компонентов , преобразование входных данных, а также целевые переменные имеют место.
литература
- Åke Björck: Численные методы для задач наименьших квадратов. SIAM, Филадельфия 1996, ISBN 0-89871-360-9 .
- Вальтер Гросманн: Основы расчета выравнивания. 3-й доб. Версия. Springer Verlag, Берлин / Гейдельберг / Нью-Йорк, 1969, ISBN 3-540-04495-7 .
- Ричард Дж. Хэнсон, Чарльз Л. Лоусон: Решение задач наименьших квадратов. SIAM, Филадельфия 1995, ISBN 0-89871-356-0 .
- Фредерик Мостеллер , Джон В. Тьюки : Анализ данных и регрессия — второй курс статистики. Аддисон-Уэсли, Ридинг, Массачусетс 1977, ISBN 0-201-04854-X .
- Герхард Жертва: Численная математика для начинающих. Введение для математиков, инженеров и компьютерных специалистов. 4-е издание. Vieweg, Брауншвейг 2002, ISBN 3-528-37265-6 .
- Петер Шенфельд: Методы эконометрики. 2 тома. Вален, Берлин / Франкфурт, 1969–1971 гг.
- Эберхард Цейдлер (ред.): Карманный справочник по математике. Оправдано v. И. Н. Бронштейн, К. А. Семендяев. Teubner, Штутгарт / Лейпциг / Висбаден 2003, ISBN 3-8171-2005-2 .
- T. Strutz: Data Fitting and Uncertainty (Практическое введение в взвешенный метод наименьших квадратов и другие аспекты). 2-е издание. Springer Vieweg, 2016 г., ISBN 978-3-658-11455-8 .
веб ссылки
Индивидуальные доказательства
- ↑ Гёттинген. In: Goettingische реклама из изученных вещей / Goettingische реклама из изученных вещей / Goettingische Learning реклама , 23 января 1802 г., стр. 1 (на сайте ANNO ).
- ^ Мориц Кантор : Gauß: Карл Фридрих Г. В: Allgemeine Deutsche Biographie (ADB). Том 8, Duncker & Humblot, Leipzig 1878, pp. 430-445., Здесь p. 436.
- ↑ Пол Карлсон: Магия чисел. Ульштайн-Верлаг, Берлин-Запад. Издание девятое, переработанное и дополненное, 1967 г., стр. 390 ф.
- ^ А. Абдулле, Герхард Ваннер : 200 лет методов наименьших квадратов . В: Элементы математики , том 57, 2002 г., стр. 45-60, DOI: 10.1007 / PL00000559 .
- ↑ См. Мориц Кантор : Гаус: Карл Фридрих Г. В: Allgemeine Deutsche Biographie (ADB). Том 8, Duncker & Humblot, Leipzig 1878, pp. 430-445., P. 436.
- ^ Лежандр: Nouvelles méthodes налить ли решимость де orbites де comètes. Париж 1805, стр. 72–80 (Приложение): Sur la Méthode des moindres Quarrés.
- ^ Карл Фридрих Гаус: Theoria Motus Corporum Coelestium в sectionibus conicis solem ambientium . Göttingen 1809; Карл Хааз (перевод): Теория движения небесных тел, которые вращаются вокруг Солнца коническими сечениями. Ганновер 1865 г.
- ^ Матрицы и определители .
- ↑ Напечатано в Gauß, Werke, Volume X / 1, p. 380.
- ↑ Абдулле, Ваннер: Элементы математики . Том 57, 2002, стр. 51. С факсимильной копией дневниковой записи.
- ^ Лаплас, цитата из Германа Голдстайна: История численного анализа . Спрингер, 1977, с. 209.
- ^ Карл Фридрих Gauß: Theoriacommonis наблюдение erroribus minimis obnoxiae. 2 части. Гёттинген 1821-1823 гг. (Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores, classis mathematicae, том 5); Supplementum Theoriacommonisationum erroribus minimis obnoxiae. Göttingen 1826/28 (Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores, classis mathematicae, Том 6.). Антон Бёрш Пауль Симон (ред.): Трактаты по методу наименьших квадратов Карла Фридриха Гаусса. На немецком языке. Берлин 1887 г., Текстархив — Интернет-архив .
- ↑ Пит Стюарт: Может быть, нам стоит называть это «Лагранжево устранение» . Дайджест НС Воскресенье, 21 июня 1991 г., 30 июня 1991 г. Том 91, выпуск 26.
- ↑ Х. Виртс: Относительная математика в регрессии и корреляции . В: Stochastik in der Schule , 1991, Issue 1, pp. 34–53.
- ↑ Ханс Р. Шварц, Норберт Кёклер: Численная математика. 7. пересмотренный Версия. Teubner, 2009, DOI: 10.1007 / 978-3-8348-9282-9 , ISBN 978-3-8348-9282-9 , стр. 141, глава 3.6 (Гауссово приближение), предложение 3.23.
- ↑ AE Hoerl и RW Kennard: Ridge regression: предвзятая оценка для неортогональных проблем , Techno Metrics 12 (1970), 55-82.
- ^ Сабина Ван Хаффель, Джоос Вандевалле: Общая проблема наименьших квадратов: вычислительные аспекты и анализ. Публикации SIAM, Филадельфия, Пенсильвания, 1991, ISBN 0-89871-275-0 .
- ↑ Мартин Плезинджер: Проблема тотальных наименьших квадратов и сокращение данных в AX ≈ B. Диссертация. ( Памятка от 24 июля 2012 г. в Интернет-архиве ; PDF; 1,6 МБ) TU Liberec и ICS Prague, 2008.
- ↑ Частичная регрессия наименьших квадратов. 3 августа 2017 г., по состоянию на 23 августа 2021 г. (немецкий).
- ↑ 1.8. Перекрестная декомпозиция — документация scikit-learn 0.24.2. Проверено 23 августа 2021 года .





















































































![v = V _ { mathrm {max}} cdot [S] / (K_ {m} + [S])](https://wikimedia.org/api/rest_v1/media/math/render/svg/27b2ab027f6b145dee50e5c62c28ad91d2f75e7c)
![nu _ {i} = { frac {V _ { max} left [S_ {i} right]} {K_ {m} + left [S_ {i} right]}} (1 + e_ {i}) { boldsymbol { nu}} _ {i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c97305e52d0907f8094ccf03835e53137f9f9b)




