1. ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ
Виды измерений и погрешностей
Измерением какой-либо физической
величины называется операция, в результате
которой мы узнаем, во сколько раз
измеряемая величина больше (или меньше)
соответствующей величины, принятой за
единицу
2.
Виды измерений классифицируются:
– по способу получения результата (прямые и
косвенные);
– по методу измерений (абсолютные,
относительные и пороговые);
– по условиям измерений (равноточные,
неравноточные);
– по степени достаточности измерений
(необходимые, избыточные)
3.
При прямых измерениях измеряется
непосредственно исследуемая величина
При косвенных измерениях исследуемая
величина измеряется как функция по
результатам измерения других величин
Например, ускорение автомобиля при
разгоне определяется по результатам
измерения расстояния и времени разгона;
вычисление плотности – по массе и объему
4.
Абсолютные измерения – это прямые
измерения в единицах измеряемой величины
Относительные измерения
представляют собой отношения измеряемой
величины к величине играющей роль единицы
или к величине, принимаемой за исходную
При пороговых измерениях фиксируется
только факт нахождения величины в
одностороннем или двухстороннем допуске
(по принципу «да/нет»)
5.
Равноточные измерения проводятся в
одинаковых условиях одними и теми же
измерительными приборами и с одинаковой
степенью тщательности.
При этом в ряду измерений нельзя отдать
предпочтение какому-либо одному или
нескольким значениям
Неравноточные измерения не отвечают
указанным выше требованиям
6.
Избыточные измерения имеют по
сравнению с необходимыми большее число
измерений либо большую точность, содержат
среди измерений зависимые, т. е. дают
избыточную информацию
Надежность результатов исследования в
значительной степени зависит от точности
измерений
Под точностью измерений понимают
степень соответствия результата
измерения действительному значению
измеряемой величины
7.
Снять показания с прибора – не значит только
измерить. Необходимо еще оценить ошибки
(погрешности) измерений
Погрешность измерения – это отклонение
результата измерения от истинного значения
измеряемой величины
8.
Под истинным значением измеряемой
величины принято считать
– среднюю арифметическую величину ряда
измерений;
– известное эталонное значение;
– величину, полученную в результате более
точных (не менее чем на порядок) измерений
9.
Основные источники ошибок
Первый источник заключен в датчике,
который неправильно реагирует на
измеряемую величину.
Например, если тензосопротивление плохо
наклеено на упругий элемент, то деформация
его решетки не будет соответствовать
деформации упругого элемента
Второй источник – измерительное
устройство, в котором возможны погрешности
из-за неправильного функционирования его
механических или электрических элементов
10.
Третий источник – сам наблюдатель,
который из-за неопытности или усталости
неправильно считывает показания прибора
Ошибки могут возникнуть из-за влияния
измерительного устройства на объект
измерения (например, при разрушающем
методе контроля), влияния окружающей среды
(температура, загазованность и т. п.),
методических погрешностей, допущенных
экспериментатором
11.
Эти источники ошибок приводят к появлению
трех типов ошибок: случайных,
систематических и грубых
Случайная погрешность – это погрешность,
которая в отдельных измерениях может
принимать случайные, заранее конкретно
неизвестные значения.
Случайные погрешности обязаны своим
происхождением ряду как объективных, так и
субъективных факторов, действие которых
неодинаково в каждом опыте и не может быть
учтено.
12.
Случайные погрешности различаются в
отдельных измерениях, сделанных в одинаковых
условиях одними и теми же измерительными
приборами. Исключить случайные погрешности
нельзя. Можно только оценить их значение
Случайные погрешности определяются по
законам теории ошибок, основанной на теории
вероятностей
13.
Систематическая погрешность – это
погрешность, вызванная факторами,
действующими одинаковым образом при
многократном повторении одних и тех же
измерений с помощью одних и тех же
измерительных приборов
В качестве примера систематической ошибки
рассмотрим случай взвешивания на чашечных
весах с помощью неточных гирь. Если взятая
нами гиря имеет ошибку, скажем 0,1 г, то вес
тела (пусть 1000 г) будет завышенным (или
заниженным) на эту величину, и чтобы
получить верное значение, необходимо учесть
эту ошибку, прибавив к полученному весу (или
вычтя из него) 0,1 г, P=(1000±0,1) г
14.
Грубая погрешность или промах
вызывается просчетом экспериментатора или
неисправностью средств измерения, или резко
изменившимися внешними условиями
Грубые погрешности приводят к явному
искажению результата, поэтому их надо
исключить из общего числа измерений
15.
По форме числового представления
погрешности делятся на абсолютные и
относительные
Абсолютная погрешность – это
разность между результатом измерения и
его истинным значением: x x a
где x – результат измерения; a – истинное
значение
Относительная погрешность – это
погрешность, приходящаяся на единицу
измеренной величины; обычно выражается в
x
процентах
a
100%.
16.
Случайные погрешности и их
распределение
Чтобы выявить случайную погрешность
измерений, необходимо повторить измерение
несколько раз
Если каждое измерение дает заметные от
других результаты, мы имеем дело с ситуацией,
когда случайная погрешность играет
существенную роль
17.
Наиболее вероятным значением измеряемой
величины из серии измерений является ее
среднее значение
Разброс измеряемой величины относительно
ее среднего значения определяется величиной
средней квадратической погрешности
отдельного измерения
18.
Пусть в эксперименте в результате
независимых и равноточных измерений
постоянной величины а получены значения х1,
х2, …, хn
Абсолютные погрешности xi xi a
рассматривают как случайные величины
Независимость измерений понимается как
взаимная независимость случайных величин xi ,
а равноточность – как подчинение величин xi
одному и тому же закону распределения (кроме
того измерения сделаны одним и тем же методом
и с одинаковой степенью тщательности)
19.
а
В качестве оценки неизвестной величины
по данным измерений обычно берут среднее
арифметическое результатов измерений
1 n
x xi .
n i 1
n
2
(
x
a
)
i
2
Дисперсия отдельных измерений i 1
обычно неизвестна, и для ее оценки
n
используется величина
2
Sn
x
( xi x )
i 1
n 1
2
.
n 1
20.
Среднюю квадратическую (стандартную)
погрешность (СКО) находятся по формуле
,
2
для ее оценки вычисляется величина
lim Sn .
Sn
2
Sn
n
Sn
100 %
Величина w
x
называется коэффициентом вариации
Обычно принимается, что погрешности
подчиняются нормальному закону распределения
случайных величин
21.
При этом предполагается:
1) погрешности измерений могут принимать
непрерывный ряд значений;
2) при большом числе наблюдений погрешности
равных значений, но разных знаков встречаются
одинаково часто;
3) частота появления погрешностей
уменьшается с увеличением величин
погрешностей
22.
Эти предположения приводят к закону
распределения погрешностей, описываемому
формулой Гаусса:
y
1
2
e
( x ) 2
2 2
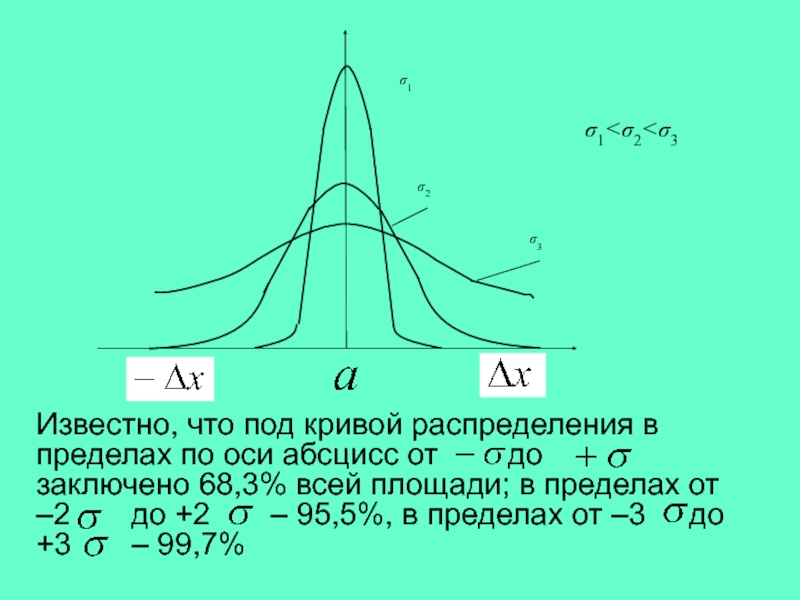
.
Форма кривых Гаусса зависит от величин
Чем больше
.
, тем больше рассеивание
случайной погрешности
23.
σ1
σ1<σ2<σ3
σ2
σ3
x
a
x
Известно, что под кривой распределения в
пределах по оси абсцисс от до
заключено 68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до
+3 – 99,7%
24.
34%
14%
34%
14%
2%
6
2%
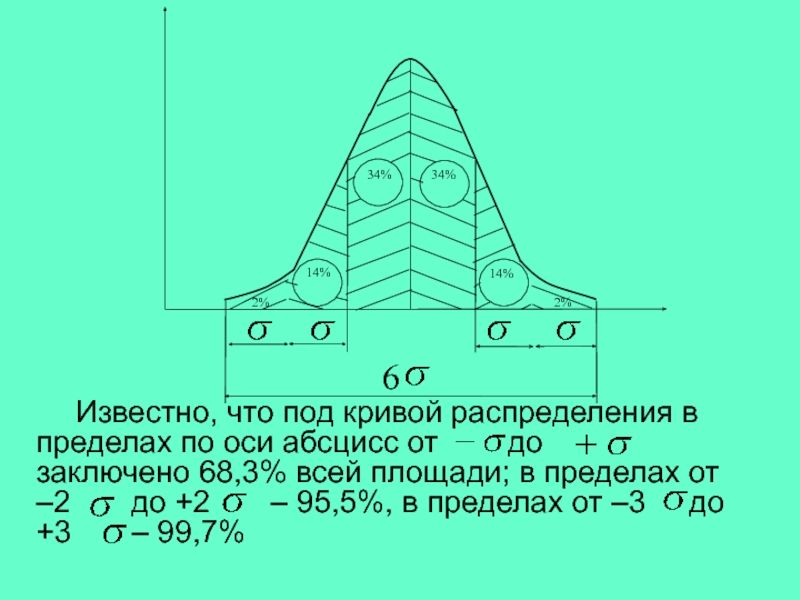
Известно, что под кривой распределения в
пределах по оси абсцисс от до
заключено 68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до
+3 – 99,7%
25.
Замечание. В ряде случаев экспериментальные
данные лучше описываются другими законами
распределения случайных величин, например,
законом Пуассона:
y
2 x 2
e
x!
.
26. Закон сложения случайных ошибок
Пусть измеряемая величина Z является суммой
(или разностью) двух величин X и Y, результаты
измерений которых независимы.
Тогда можно доказать, что S Z S X S Y
2
если S X , S Y2 , S Z2 – дисперсии величин, или
2
SZ
2
SX
2
SY
2
2
27.
Если Z является суммой не двух, а большего
числа слагаемых, то закон сложения ошибок
будет таким же, т. е. средняя квадратичная
ошибка суммы или разности двух (или
нескольких) независимых величин равна корню
квадратному из суммы дисперсий отдельных
слагаемых
Для нахождения суммарной ошибки нужно
складывать не сами ошибки, а их квадраты
28.
Средняя квадратичная ошибка суммы или
разности двух (или нескольких) независимых
величин равна корню квадратному из суммы
дисперсий отдельных слагаемых
SZ
2
SX
2
SY
29. Выводы:
1. Необходимо учитывать роль каждой из ошибок
в общей ошибке результата.
Значение отдельных ошибок очень быстро
падает по мере их уменьшения.
В первую очередь стоит уменьшать ошибку,
имеющую наибольшую величину
Относительная погрешность суммы
Sz
Z
S x2 S y2
X Y
30.
Пример: пусть X и Y – два слагаемых,
определенных со средними квадратичными
ошибками S X и S Y , причем, известно, что S Y В
два раза меньше, чем S X . Тогда ошибка суммы
будет
Z X Y
2
SZ
2
SX
2
SY
2
SX
Sx 2 5 2
( ) SX .
2
4
S Z 1,1S X .
31.
2. Средняя квадратическая погрешность
среднего арифметического равна средней
квадратической погрешности отдельного
результата, деленная на корень квадратный
Sn
из числа измерений: S x
,
n
S n – средняя квадратичная погрешность
отдельного измерения
32.
Пусть измеряемая величина Z является
разностью двух величин X и Y, результаты
измерений которых независимы.
Тогда ее относительная погрешность
Sz
Z
2
Sx
2
Sy
X Y
33.
Невозможно добиться хорошей точности
измерений какой-либо величины, строя
измерения так, что она находится как
небольшая разность результатов независимых
измерений двух величин, существенно
превышающих искомую
34.
35.
36. Доверительный интервал и доверительная вероятность
1. Необходимо учитывать роль каждой из ошибок
в общей ошибке результата.
Значение отдельных ошибок очень быстро
2
2
2
S
S
S
Тогда
можно
доказать,
что
падает по мере их уменьшения.
Z
X
Y
2
если S X , S Y2 , S Z2 – дисперсии величин, или
SZ
2
SX
2
SY
Средняя квадратичная ошибка суммы или
разности двух (или нескольких) независимых
величин равна корню квадратному из суммы
дисперсий отдельных слагаемых
37. Доверительный интервал и доверительная вероятность
1. Необходимо учитывать роль каждой из ошибок в общей
ошибке результата.
Значение отдельных ошибок очень быстро падает по мере
их уменьшения.
2
2
2
S
S
S
Тогда можно доказать, что
Z
X
Y
если S X2,
S Y2, S Z2
– дисперсии величин, или
SZ
2
SX
2
SY
Средняя квадратичная ошибка суммы или разности
двух (или нескольких) независимых величин равна корню
квадратному из суммы дисперсий отдельных слагаемых
38.
Количество опытов при ортогональном ЦКП определяется по
формуле
n
N 2 2n 1
где 2n – количество опытов, образующих полный факторный
эксперимент; 2n – число так называемых «звездных» точек в
факторном пространстве, имеющих координаты (±α, 0, 0, …, 0);
(0, ±α, 0, …, 0), …, (0, 0, …, ±α). Здесь величина α называется
«звездным» плечом; 1 – опыт в центре планирования, т. е. в
точке факторного пространства с координатами (0, 0, …, 0)
Значения «звездного» плеча α для ЦКП с различным числом
факторов n следующие:
n
α
2
1,000
3
1,215 1,414
4
5
1,547
Эти значения α выбраны из условия ортогональности
матрицы планирования
39.
40.
41. Закон сложения случайных ошибок
Если поверхность отклика не может быть описана многочленом
вида
y b0 b1 X1 b2 X 2 bn X n b12 X1 X 2 b(n 1)n X n 1 X n
для адекватного математического описания используется
многочлен более высокой степени, например, отрезок ряда
Тейлора, содержащий члены с квадратами переменных. Тогда
используют центральное композиционное планирование (ЦКП)
эксперимента.
Различают два вида ЦКП:
ортогональное и
ротатабельное
42.
Количество опытов при ортогональном ЦКП определяется по
формуле
n
N 2 2n 1
где 2n – количество опытов, образующих полный факторный
эксперимент; 2n – число так называемых «звездных» точек в
факторном пространстве, имеющих координаты (±α, 0, 0, …, 0);
(0, ±α, 0, …, 0), …, (0, 0, …, ±α). Здесь величина α называется
«звездным» плечом; 1 – опыт в центре планирования, т. е. в
точке факторного пространства с координатами (0, 0, …, 0)
Значения «звездного» плеча α для ЦКП с различным числом
факторов n следующие:
n
α
2
1,000
3
1,215 1,414
4
5
1,547
Эти значения α выбраны из условия ортогональности
матрицы планирования
43.
Уравнение регрессии при ортогональном ЦКП ищут в
следующем виде
y b0* b1 X 1 b2 X 2 … bn X n b12 X 1 X 2 … b( n 1) n X n 1 X n
b11 X 1* … bnn X n*.
Переменные величины
X ji
X 2ji
1
N
N
X 2ji
j 1
здесь j – номер опыта; i – номер фактора, введены для того,
чтобы матрица планирования была ортогональна и
коэффициенты регрессии определялись независимо друг от
друга по результатам опытов. Чтобы получить уравнение
регрессии в обычной форме
y b0 b1 X 1 b2 X 2 … bn X n b12 X 1 X 2 … b( n 1) n X n 1 X n
b11 X 12 b22 X 22 … bnn X n2 ,
b11 N 2
bnn N 2
находят величину b0 b
X ji …
X jn .
N j 1
N j 1
*
0
44. Ортогональный план
Это план 2-ого порядка nпосле преобразований (*)
2
xij
j 1
(*) x ij x ij 2
x ij 2 x i 2
n
Эти преобразования позволяют усреднить случайные
погрешности
Ортогональный план 2-ого порядка
Тогда уравнение регрессии
k
k
k
y b0 bi xi biu xi xu bii xi ;
j 1
i , u 1
i 1
В итоге уравнение регрессии преобразуется к виду
k
k
k
y b0 bi xi biu xi xu bii ( xi 2 xi 2 )
j 1
i , u 1
i 1
45.
Коэффициенты регрессии при ортогональном ЦКП считают по
следующим формулам
b0*
1
N
N
yj
j 1
N
N
X ji y j
bi
j 1
N
( X ji )
где i ≠ 0
bik
2
X ji X j k y j
j 1
N
( X ji X jk )
j 1
j 1
N
bii
j 1
N
X *ji y j
(X
j 1
*
ji
)
2
2
где i ≠ k
46.
Для расчета оценок дисперсий в определении коэфф-тов
S y2
регрессии используют следующие выражения 2
S S
2
b0
nS
2
b0*
Sb2i k N
bii
N
*
0
N
X ji
2
j 1
S
S
2
bi
где i ≠ k
2
2
y
(X
N
где i ≠ 0
N
j 1
S y2
( X ji X jk )
j 1
Sb
2
ji
)
2
S b2ii
S y2
N
(X
j 1
*
ji
)
2
Коэффициент bi, считается значимым, если bi Sb t , n .
i
Аналогично проверяется значимость остальных коэфф-тов
регрессии. Проверка адекватности уравнения регрессии
осуществляется с помощью критерия Фишера
2
S ад
Fр 2
Sвоспр
47. Метод ротатабельного центрального композиционного планирования
Метод ротатабельного планирования эксперимента позволяет
получать более точное математическое описание поверхности
отклика по сравнению с ортогональным ЦКП, что достигается
благодаря увеличению числа опытов в центре плана и
специальному выбору величины «звездного» плеча α.
Это план, у которого точки плана располагаются на
окружностях (сферах, гиперсферах)
Точность оценивания функции отклика по любому
направлению факторного пространства (для всех точек
плана) одинаковая, что позволяет наилучшим образом
извлечь максимальное количество (несмещенной)
информации из плана
48.
Ротабельный план 2-ого порядка
Для того, что бы привести план 2-ого порядка к
ротатабельному, величину плеча выбирают из условия
k
4
(**) 2 при k 5 и 2
k 1
4
при k 5
49.
При ротатабельном ЦКП для вычисления коэффициентов
регрессии и соответствующих оценок дисперсий находят
следующие константы
1
A
2 Β (n 2 )Β n
nN
Β
n 2 N N 0
C
N
N N0
где n – число факторов; N – общее число опытов
ротатабельного ЦКП; N0 – число опытов в центре плана
На основании результатов эксперимента вычисляют след.
N
N
суммы
S0 y j
Si X ji y j (где i=1,2,…,n),
j 1
j 1
N
Sik X ji X jk y j
j 1
N
(где i ≠ k),
Sii X 2ji y j
i 1
(где i=1,…, n)
50.
Формулы для расчета коэффициентов регрессии имеют
следующий вид
n
2 AΒ
b0
S0 Β n 2 C Sii
N
i 1
CSi
bi
N
C 2 Sik
bik
BN
где i ≠ k
n
AC
bii
S iiC B n 2 n C 1 B Sii 2 BS0
N
i 1
51.
Оценки дисперсий в определении коэфф-тов регрессии
вычисляют по следующим формулам
2 AB (n 2) 2
S
Sвоспр
b
N
2
C 2 Sвоспр
(где i≠k)
N
2
S
2
bi
S
0
2
воспр
(где i=1,2,…,n)
N N0
S2
bik
Sb2
ii
2
AC 2 Sвоспр
N
B n 1 n 1
Коэффициент bi, считается значимым, если bi Sb t , n .
i
Аналогично проверяется значимость остальных коэфф-тов
регрессии
52.
Оценку дисперсии адекватности рассчитывают по формуле
N
(y
2
S ад
j 1
э
j
2
y jp ) 2 Sвоспр
( N 0 1)
(n 2)( n 1)
N
( N 0 1)
2
С ней связано число степеней свободы
f ад
(n 2)(n 1)
N
( N0 1)
2
Проверку адекватности уравнения регрессии осуществляют
с помощью критерия Фишера
2
S ад
Fр 2
Sвоспр
53.
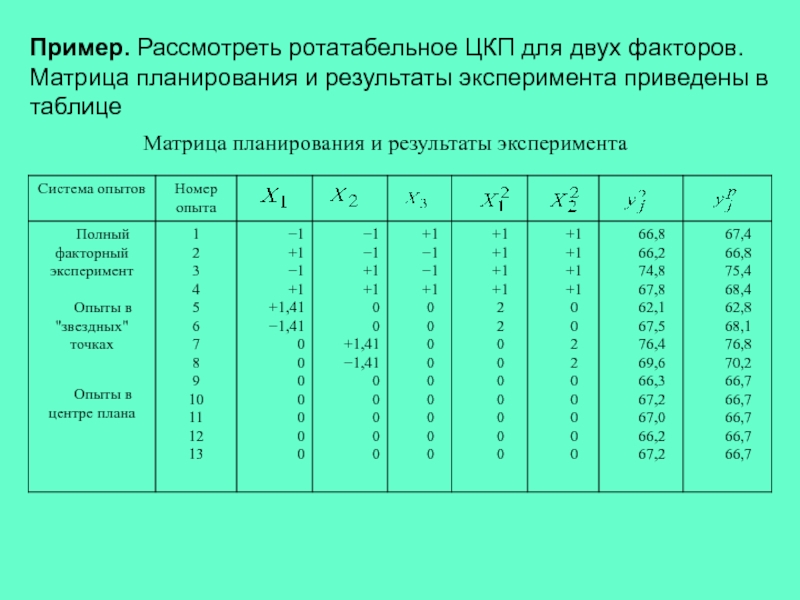
Пример. Рассмотреть ротатабельное ЦКП для двух факторов.
Матрица планирования и результаты эксперимента приведены в
таблице
Матрица планирования и результаты эксперимента
Система опытов
Номер
опыта
Полный
факторный
эксперимент
1
2
3
4
5
6
7
8
9
10
11
12
13
Опыты в
«звездных»
точках
Опыты в
центре плана
X1
1
+1
1
+1
+1,41
1,41
0
0
0
0
0
0
0
X2
1
1
+1
+1
0
0
+1,41
1,41
0
0
0
0
0
X3
+1
1
1
+1
0
0
0
0
0
0
0
0
0
X12
X 22
+1
+1
+1
+1
2
2
0
0
0
0
0
0
0
+1
+1
+1
+1
0
0
2
2
0
0
0
0
0
y эj
66,8
66,2
74,8
67,8
62,1
67,5
76,4
69,6
66,3
67,2
67,0
66,2
67,2
y jp
67,4
66,8
75,4
68,4
62,8
68,1
76,8
70,2
66,7
66,7
66,7
66,7
66,7
54.
Для нахождения коэффициентов регрессии вычислим
следующие вспомогательные коэффициенты
13
1
2 13
1,63
0,5 C
B
0,81 A
8
2 0,81 2 2 0,81 2
(2 2)(13 5)
На основании результатов опытов вычислим вспомогательные
суммы
13
S0
j 1
y эj
885,1
13
13
S 2 X j 2 y эj 19,2
S1 X j1 y эj 15,2
j 1
j 1
13
S12 X j1 X j 2 y эj 6,4
j 1
13
S11 X 2j1 y эj 535,6
j 1
13
S 22 X 2j 2 y эj 567 ,6
j 1
Коэффициенты регрессии рассчитываем по формулам
55.
2 AB
2 0,5 0,81
b0
[ S0 B(n 2) C ( S11 S22 )]
[885,1 0,81(2 2)
N
13
CS1 1,63( 15,2)
1,63(535,6 567,6)] 66,7;
b1
1,89
N
13
C 2 S12 (1,63)2 ( 6,4)
CS2 1,63 19,2
b2
2,41
b12
1,61
N
13
BN
0,81 13
AC
b11
{S11C[ B(n 2) n] C (1 B)( S11 S 22 ) 2 BS0 }
N
0,5 1,63
{535,6 1,63[0,81(2 2) 2] 1,63(1 0,81)(535,6 567 ,6)
13
2 0,81 885,1} 0,6;
AC
b22
{S 22C[ B(n 2) n] C (1 B)( S11 S 22 ) 2 BS0 }
N
0,5 1,63
{567 ,6 1,63[0,81(2 2) 2] 1,63(1 0,81)(535,6 567 ,6)
13
2 0,81 885,1} 3,4.
56.
Оценку дисперсии воспроизводимости можно найти на
основании результатов опытов, проведенных в центре плана
1
y
N0
N0
j 1
э 1
y j (66,3 67,2 67,0 66,2 67,2)
5
N
S
2
воспр
1
э
(
y
j y ) 0,3
N 0 1 j 1
67
0
Эта величина найдена при числе степеней свободы
f N0 1 5 1 4
Оценки дисперсий в определении коэфф. регрессии
2 AB (n 2) 2
2 0,5 0,81(2 2)0,3
S
Sвоспр
0,0748
N
13
2
2 2
Sy
C
S y (1,63)2 0,3
0,3
2
2
Sbi
0,0375
Sb
0,0613
N N0 13 5
ik
N
13
2
b0
Sb2ii
AC 2 S y2
N
0,5(1,63)2 0,3
[ B(n 1) (n 1)]
[0,81(2 1) (2 1)] 0,0438
13
57.
Пользуясь таблицей значений критерия Стьюдента, находим
для
f 4
и
P 0,95
t
,n
2,78
Sb t ,n 0,274 2,78 0,761
Sbi t , n 0,194 2,78 0,539
Sb t ,n 0,248 2,78 0,689
Sbii t , n 0,209 2,78 0,581
0
ik
Для проверки значимости коэффициентов регрессии рассмотрим соотнош.
b1 1,89 Sb t , n
b0 66 ,7 Sb t , n
0
i
b12 1,61 Sb t , n
b11 0,61 Sb t , n
ik
ii
b2 2,41 Sb t , n
i
b22 3,4 Sb t ,n
ii
Все коэффициенты регрессии значимы. Вычисляем оценку дисперсии
адекватности
N
(y
э
j
2
y jp ) 2 Sвоспр
( N 0 1)
3,81 0,3 4
S
0,87
(n 2)( n 1)
4 3
N
( N 0 1) 13
4
2
2
2
ад
j 1
58.
Число степеней свободы, связанных с этой оценкой дисперсии
f ад N
(n 2)(n 1)
4 3
( N 0 1) 13
4 3
2
2
Расчетное значение критерия Фишера
2
S ад
0,87
F 2
2,9
S воспр 0,3
Из таблицы значений критерия Фишера соответствующее значение
критерия FT 6,6 . Условие Fp F выполнено, следовательно,
T
уравнение регрессии
y 66,7 1,89 X 1 2,41X 2 1,61X 1 X 2 0,61X 12 3,40 X 22
адекватно представленным результатам эксперимента
Перейдем в уравнение регрессии от кодированных переменных к физическим
Пусть в нашем примере кодированные переменные X1 и X2 представляют
собой температуру и концентрацию, причем координаты центра плана
x01= 60°С и x02= 30%, а шаги варьирования Δx1= 5°С и Δх2= 1% . Тогда
x x
X1 1 01 0,2 x1 12
x1
x2 x02
X2
x2 30
x2
59.
Подставляя их в полученное
преобразуем его к виду
в этом примере уравнение регрессии,
y 2409 9,57 x1 19,7 x2 0,32 x1 x2 0,0244 x12 3,4 x22
Пользуясь таким уравнением, исследователь избавляется от необходимости
переводить всякий раз условия опыта в кодированные переменные
60. Планирование активного эксперимента
При планировании экспериментов чаще всего применяются планы
1-ого и 2-ого порядков. Планы более высоких порядков
применяются редко из-за их большой вычислительной сложности
Планы 1-ого порядка – это планы, которые позволяют провести
эксперимент для отыскания уравнения регрессии, содержащее
только первые степени факторов и их произведения
k
y b0 bi xi
i 1
k
b
i ,u 1
i i
iu
xi xu
k
b
i , j 1
i j u
iju
xi x j xu …
Планы 2-ого порядка – это планы, которые позволяют провести
эксперимент для отыскания уравнения регрессии, содержащие вторые
степени факторов
k
k
2
y b0 bi xi bii xi
i 1
i 1
k
b
i ,u 1
i u
iu
xi xu …
61. Планирование первого порядка
• В качестве факторов выбираются только
контролируемые и управляемые факторы
(переменные)
• Обеспечивается возможность независимого
изменения каждого из факторов и
поддержание его на определенном уровне
• Для каждого фактора указывается интервал
(+/-), в пределах которого ставится
исследование
62. Представления плана эксперимента (на примере эксперимента с 3-мя независимыми факторами)
b0, b1, b2, b3 – коэффициенты
регрессии
xi*xu – члены двойного
взаимодействия
Уравнением регрессии
3
y b0 bi xi
i 1
3
b
i ,u 1
i u
ui
xi xu b123 x1 x 2 x3
Табличное (матричное) представление
x1*x2*x3 – члены тройного
взаимодействия
План
Геометрическое представление
Номер
опыта
Результат
y
x0
x1
x2
x3
x1x2
x1x3
x2x3
x1x2x3
1
+1
-1
-1
-1
+1
+1
+1
-1
y1
2
+1
+1
-1
-1
-1
-1
+1
+1
y2
3
+1
-1
+1
-1
-1
+1
-1
+1
y3
4
+1
+1
+1
-1
+1
-1
-1
-1
y4
5
+1
-1
-1
+1
+1
+1
-1
+1
y5
6
+1
+1
-1
+1
-1
-1
-1
-1
y6
7
+1
-1
+1
+1
-1
+1
+1
-1
y7
8
+1
+1
+1
+1
+1
-1
+1
+1
y8
63. Свойства матрицы представления эксперимента
1. Свойство симметричности – алгебраическая сумма элементов векторстолбца каждого фактора равна нулю (за исключением столбца,
соответствующего свободному члену)
n
X
j 1
0,
ij
i = номер фактора, j – номер опыта
2. Свойство нормирования – сумма квадратов каждого столбца равна
числу опытов
n
X
j 1
2
ij
n;
3. Свойство ортогональности – скалярное произведение всех векторстолбцов (сумма почленных произведений элементов любых вектор
столбцов) равно нулю
n
X
j 1
ij
X uj 0, i u
64. Определение коэффициентов b уравнения регрессии
Методом наименьших квадратов находятся
оценки b коэффициентов
По свойствам матрицы планирования
— (ссимметри ность) b0 X 1 j 0;
y b0 b1 x1 b2 x2
(нормирования) b1 X 1 j nb1 ;
2
2
y j y j min
n
(ортогональность) b2 X 1 j X 2 j 0;
bi
j 1
n
2 y j b0 b1 X 1 j b2 X 2 j X 1 j 0;
b1
j 1
n
y
j 1
1j
n
n
j 1
j 1
n
X 1 j b0 X 1 j b1 X 1 j b2 X 1 j X 2 j 0;
2
j 1
Получаем
n
b1
y X
j 1
j
n
1j
; b2
n
y X
j 1
j
n
n
b12
y j X 1 X 2 j
j 1
n
n
2j
; b0
y X
j 1
; b123
y X
j 1
0j
n
n
j
j
1
n
X 2 X3 j
65. Планирование второго порядка
Применяется если
описание функции отклика
первым порядком
получается недостаточным
(например, процесс носит
нелинейный характер)
Каждый фактор
варьируется не менее чем
на трех уровнях – полный
эксперимент содержит 3^k
(k – количество факторов)
опытов.
Опыты проводятся
План 2-ого порядка при k=2 n=1
2
2
y b0 b1 x1 b2 x2 b11 x1 b22 x2 b12 x1 x2
1. В «крайних точках» — как в
планировании 1-ого порядка
2. В «звездных точках» — xi=(+/-)a,
xj=0, 1,…,n; 1,…,n; i!=j
3. В «центре» — xi=0, j=1,2,3,…,n
Уравнение регрессии для
эксперимента с 2-мя факторами
Слайд 1ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ
Измерением какой-либо физической величины называется операция,
в результате которой мы узнаем, во сколько раз измеряемая величина
больше (или меньше) соответствующей величины, принятой за единицу
Виды измерений и погрешностей

Слайд 2Виды измерений классифицируются:
– по способу получения результата (прямые и косвенные);
–
по методу измерений (абсолютные, относительные и пороговые);
– по условиям измерений
(равноточные, неравноточные);
– по степени достаточности измерений (необходимые, избыточные)

Слайд 3 При прямых измерениях измеряется непосредственно исследуемая величина
При косвенных
измерениях исследуемая величина измеряется как функция по результатам измерения других
величин
Например, ускорение автомобиля при разгоне определяется по результатам измерения расстояния и времени разгона; вычисление плотности – по массе и объему

Слайд 4 Абсолютные измерения – это прямые измерения в единицах измеряемой
величины
Относительные измерения представляют собой отношения измеряемой величины к величине
играющей роль единицы или к величине, принимаемой за исходную
При пороговых измерениях фиксируется только факт нахождения величины в одностороннем или двухстороннем допуске
(по принципу «да/нет»)

Слайд 5Равноточные измерения проводятся в одинаковых условиях одними и теми же
измерительными приборами и с одинаковой степенью тщательности.
При этом в
ряду измерений нельзя отдать предпочтение какому-либо одному или нескольким значениям
Неравноточные измерения не отвечают указанным выше требованиям

Слайд 6Избыточные измерения имеют по сравнению с необходимыми большее число измерений
либо большую точность, содержат среди измерений зависимые, т. е. дают
избыточную информацию
Надежность результатов исследования в значительной степени зависит от точности измерений
Под точностью измерений понимают степень соответствия результата измерения действительному значению измеряемой величины

Слайд 7Снять показания с прибора – не значит только измерить. Необходимо
еще оценить ошибки (погрешности) измерений
Погрешность измерения – это отклонение
результата измерения от истинного значения измеряемой величины

Слайд 8Под истинным значением измеряемой величины принято считать
– среднюю арифметическую
величину ряда измерений;
– известное эталонное значение;
– величину, полученную в
результате более точных (не менее чем на порядок) измерений

Слайд 9Основные источники ошибок
Первый источник заключен в датчике, который неправильно
реагирует на измеряемую величину.
Например, если тензосопротивление плохо наклеено на
упругий элемент, то деформация его решетки не будет соответствовать деформации упругого элемента
Второй источник – измерительное устройство, в котором возможны погрешности из-за неправильного функционирования его механических или электрических элементов

Слайд 10Третий источник – сам наблюдатель, который из-за неопытности или усталости
неправильно считывает показания прибора
Ошибки могут возникнуть из-за влияния измерительного
устройства на объект измерения (например, при разрушающем методе контроля), влияния окружающей среды (температура, загазованность и т. п.), методических погрешностей, допущенных экспериментатором

Слайд 11Случайная погрешность – это погрешность, которая в отдельных измерениях может
принимать случайные, заранее конкретно неизвестные значения.
Случайные погрешности обязаны своим
происхождением ряду как объективных, так и субъективных факторов, действие которых неодинаково в каждом опыте и не может быть учтено.
Эти источники ошибок приводят к появлению трех типов ошибок: случайных, систематических и грубых

Слайд 12Случайные погрешности различаются в отдельных измерениях, сделанных в одинаковых условиях
одними и теми же измерительными приборами. Исключить случайные погрешности нельзя.
Можно только оценить их значение
Случайные погрешности определяются по законам теории ошибок, основанной на теории вероятностей

Слайд 13Систематическая погрешность – это погрешность, вызванная факторами, действующими одинаковым образом
при многократном повторении одних и тех же измерений с помощью
одних и тех же измерительных приборов
В качестве примера систематической ошибки рассмотрим случай взвешивания на чашечных весах с помощью неточных гирь. Если взятая нами гиря имеет ошибку, скажем 0,1 г, то вес тела (пусть 1000 г) будет завышенным (или заниженным) на эту величину, и чтобы получить верное значение, необходимо учесть эту ошибку, прибавив к полученному весу (или вычтя из него) 0,1 г, P=(1000±0,1) г

Слайд 14Грубая погрешность или промах вызывается просчетом экспериментатора или неисправностью средств
измерения, или резко изменившимися внешними условиями
Грубые погрешности приводят к
явному искажению результата, поэтому их надо исключить из общего числа измерений

Слайд 15Абсолютная погрешность – это разность между результатом измерения и его
истинным значением:
где x – результат измерения; a – истинное значение
По форме числового представления погрешности делятся на абсолютные и относительные
Относительная погрешность – это погрешность, приходящаяся на единицу измеренной величины; обычно выражается в процентах

Слайд 16 Чтобы выявить случайную погрешность измерений, необходимо повторить измерение
несколько раз
Случайные погрешности и их распределение
Если
каждое измерение дает заметные от других результаты, мы имеем дело с ситуацией, когда случайная погрешность играет существенную роль

Слайд 17 Наиболее вероятным значением измеряемой величины из серии измерений
является ее среднее значение
Разброс измеряемой величины относительно
ее среднего значения определяется величиной средней квадратической погрешности отдельного измерения

Слайд 18Абсолютные погрешности
рассматривают как случайные величины
Пусть в эксперименте в результате независимых и равноточных измерений постоянной величины получены значения х1, х2, …, хn
Независимость измерений понимается как взаимная независимость случайных величин , а равноточность – как подчинение величин одному и тому же закону распределения (кроме того измерения сделаны одним и тем же методом и с одинаковой степенью тщательности)

Слайд 19 В качестве оценки неизвестной величины по
данным измерений обычно берут среднее арифметическое результатов измерений
Дисперсия отдельных
измерений
обычно неизвестна, и для ее оценки используется величина

Слайд 20Среднюю квадратическую (стандартную) погрешность (СКО) находятся по формуле
Величина
для
ее оценки вычисляется величина
называется коэффициентом вариации
Обычно принимается, что погрешности подчиняются нормальному закону распределения случайных величин

Слайд 21При этом предполагается:
2) при большом числе наблюдений погрешности равных
значений, но разных знаков встречаются одинаково часто;
1) погрешности измерений
могут принимать непрерывный ряд значений;
3) частота появления погрешностей уменьшается с увеличением величин погрешностей

Слайд 22Эти предположения приводят к закону распределения погрешностей, описываемому формулой Гаусса:
Форма кривых Гаусса зависит от величин .
Чем
больше , тем больше рассеивание случайной погрешности

Слайд 23Известно, что под кривой распределения в пределах по оси абсцисс
от до заключено
68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до +3 – 99,7%
Слайд 24Известно, что под кривой распределения в пределах по оси абсцисс
от до заключено
68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до +3 – 99,7%
Слайд 25Замечание. В ряде случаев экспериментальные данные лучше описываются другими законами
распределения случайных величин, например, законом Пуассона:

Слайд 26 Пусть измеряемая величина Z является суммой (или разностью)
двух величин X и Y, результаты измерений которых независимы.
Закон
сложения случайных ошибок
Тогда можно доказать, что
если , , – дисперсии величин, или

Слайд 27Если Z является суммой не двух, а большего числа слагаемых,
то закон сложения ошибок будет таким же, т. е. средняя
квадратичная ошибка суммы или разности двух (или нескольких) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых
Для нахождения суммарной ошибки нужно складывать не сами ошибки, а их квадраты

Слайд 28Средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых
величин равна корню квадратному из суммы дисперсий отдельных слагаемых

Слайд 29Необходимо учитывать роль каждой из ошибок в общей ошибке результата.
Значение отдельных ошибок очень быстро падает
по мере их уменьшения.
Выводы:
В первую очередь стоит уменьшать ошибку, имеющую наибольшую величину
Относительная погрешность суммы

Слайд 30Пример: пусть X и Y – два слагаемых, определенных со
средними квадратичными ошибками и
, причем, известно, что в два раза меньше, чем . Тогда ошибка суммы будет

Слайд 312. Средняя квадратическая погрешность среднего арифметического равна средней квадратической погрешности
отдельного результата, деленная на корень квадратный из числа измерений:
–
средняя квадратичная погрешность отдельного измерения

Слайд 32 Пусть измеряемая величина Z является разностью двух величин
X и Y, результаты измерений которых независимы.
Тогда ее относительная
погрешность

Слайд 33Невозможно добиться хорошей точности измерений какой-либо величины, строя измерения так,
что она находится как небольшая разность результатов независимых измерений двух
величин, существенно превышающих искомую

Слайд 36Необходимо учитывать роль каждой из ошибок в общей ошибке результата.
Значение отдельных ошибок очень быстро падает
по мере их уменьшения.
Доверительный интервал и доверительная вероятность
Тогда можно доказать, что
если , , – дисперсии величин, или
Средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых

Слайд 37Необходимо учитывать роль каждой из ошибок в общей ошибке результата.
Значение отдельных ошибок очень быстро падает
по мере их уменьшения.
Доверительный интервал и доверительная вероятность
Тогда можно доказать, что
если , , – дисперсии величин, или
Средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых

Слайд 38где 2n – количество опытов, образующих полный факторный эксперимент; 2n
– число так называемых «звездных» точек в факторном пространстве, имеющих
координаты (±α, 0, 0, …, 0);
(0, ±α, 0, …, 0), …, (0, 0, …, ±α). Здесь величина α называется «звездным» плечом; 1 – опыт в центре планирования, т. е. в точке факторного пространства с координатами (0, 0, …, 0)
Значения «звездного» плеча α для ЦКП с различным числом факторов n следующие:
Количество опытов при ортогональном ЦКП определяется по формуле
Эти значения α выбраны из условия ортогональности матрицы планирования

Слайд 41 Если поверхность отклика не может быть описана многочленом
вида
Закон сложения случайных ошибок
для адекватного математического описания используется многочлен более высокой степени, например, отрезок ряда Тейлора, содержащий члены с квадратами переменных. Тогда используют центральное композиционное планирование (ЦКП) эксперимента.
Различают два вида ЦКП:
ортогональное и
ротатабельное

Слайд 42где 2n – количество опытов, образующих полный факторный эксперимент; 2n
– число так называемых «звездных» точек в факторном пространстве, имеющих
координаты (±α, 0, 0, …, 0);
(0, ±α, 0, …, 0), …, (0, 0, …, ±α). Здесь величина α называется «звездным» плечом; 1 – опыт в центре планирования, т. е. в точке факторного пространства с координатами (0, 0, …, 0)
Значения «звездного» плеча α для ЦКП с различным числом факторов n следующие:
Количество опытов при ортогональном ЦКП определяется по формуле
Эти значения α выбраны из условия ортогональности матрицы планирования

Слайд 43Переменные величины
здесь j – номер опыта; i – номер
фактора, введены для того, чтобы матрица планирования была ортогональна и
коэффициенты регрессии определялись независимо друг от друга по результатам опытов. Чтобы получить уравнение регрессии в обычной форме
Уравнение регрессии при ортогональном ЦКП ищут в следующем виде
находят величину

Слайд 44Это план 2-ого порядка после преобразований (*)
Эти преобразования позволяют усреднить
случайные погрешности
Ортогональный план
Ортогональный план 2-ого порядка
Тогда уравнение регрессии
В итоге уравнение
регрессии преобразуется к виду

Слайд 45где i ≠ 0
Коэффициенты регрессии при ортогональном ЦКП считают
по следующим формулам
где i ≠ k

Слайд 46где i ≠ 0
Для расчета оценок дисперсий в определении
коэфф-тов регрессии используют следующие выражения
Коэффициент bi, считается значимым, если
. Аналогично проверяется значимость остальных коэфф-тов регрессии. Проверка адекватности уравнения регрессии осуществляется с помощью критерия Фишера
где i ≠ k

Слайд 47 Метод ротатабельного планирования эксперимента позволяет получать более точное
математическое описание поверхности отклика по сравнению с ортогональным ЦКП, что
достигается благодаря увеличению числа опытов в центре плана и специальному выбору величины «звездного» плеча α.
Метод ротатабельного центрального композиционного планирования
Это план, у которого точки плана располагаются на окружностях (сферах, гиперсферах)
Точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая, что позволяет наилучшим образом извлечь максимальное количество (несмещенной) информации из плана

Слайд 48Ротабельный план 2-ого порядка
Для того, что бы привести
план 2-ого порядка к ротатабельному, величину плеча выбирают из условия

Слайд 49 При ротатабельном ЦКП для вычисления коэффициентов регрессии и
соответствующих оценок дисперсий находят следующие константы
где n – число
факторов; N – общее число опытов ротатабельного ЦКП; N0 – число опытов в центре плана
На основании результатов эксперимента вычисляют след. суммы
(где i=1,2,…,n),
(где i ≠ k),
(где i=1,…, n)

Слайд 50Формулы для расчета коэффициентов регрессии имеют следующий вид
где i
≠ k

Слайд 51Оценки дисперсий в определении коэфф-тов регрессии вычисляют по следующим формулам
Коэффициент bi, считается значимым, если
. Аналогично проверяется значимость остальных коэфф-тов регрессии
(где i=1,2,…,n)
(где i≠k)

Слайд 52Оценку дисперсии адекватности рассчитывают по формуле
С ней связано число
степеней свободы
Проверку адекватности уравнения регрессии осуществляют с помощью критерия Фишера

Слайд 53Пример. Рассмотреть ротатабельное ЦКП для двух факторов. Матрица планирования и
результаты эксперимента приведены в таблице
Матрица планирования и результаты эксперимента
Слайд 54Для нахождения коэффициентов регрессии вычислим следующие вспомогательные коэффициенты
На основании
результатов опытов вычислим вспомогательные суммы
Коэффициенты регрессии рассчитываем по формулам

Слайд 56Оценку дисперсии воспроизводимости можно найти на основании результатов опытов, проведенных
в центре плана
Эта величина найдена при числе степеней свободы
Оценки дисперсий в определении коэфф. регрессии

Слайд 57Пользуясь таблицей значений критерия Стьюдента, находим
для
и
Для проверки значимости
коэффициентов регрессии рассмотрим соотнош.
Все коэффициенты регрессии значимы. Вычисляем оценку дисперсии адекватности

Слайд 58Число степеней свободы, связанных с этой оценкой дисперсии
Расчетное значение
критерия Фишера
Из таблицы значений критерия Фишера соответствующее значение критерия
. Условие выполнено, следовательно, уравнение регрессии
адекватно представленным результатам эксперимента
Перейдем в уравнение регрессии от кодированных переменных к физическим
Пусть в нашем примере кодированные переменные X1 и X2 представляют собой температуру и концентрацию, причем координаты центра плана
x01= 60°С и x02= 30%, а шаги варьирования Δx1= 5°С и Δх2= 1% . Тогда

Слайд 59Подставляя их в полученное в этом примере уравнение регрессии, преобразуем
его к виду
Пользуясь таким уравнением, исследователь избавляется от необходимости переводить
всякий раз условия опыта в кодированные переменные

Слайд 60Планирование активного эксперимента
При планировании экспериментов чаще всего применяются планы 1-ого
и 2-ого порядков. Планы более высоких порядков применяются редко из-за
их большой вычислительной сложности
Планы 1-ого порядка – это планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащее только первые степени факторов и их произведения
Планы 2-ого порядка – это планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащие вторые степени факторов

Слайд 61Планирование первого порядка
В качестве факторов выбираются только контролируемые и управляемые
факторы (переменные)
Обеспечивается возможность независимого изменения каждого из факторов и поддержание
его на определенном уровне
Для каждого фактора указывается интервал (+/-), в пределах которого ставится исследование

Слайд 62Представления плана эксперимента
(на примере эксперимента с 3-мя независимыми факторами)
Табличное (матричное)
представление
Геометрическое представление
Уравнением регрессии
b0, b1, b2, b3 – коэффициенты регрессии
xi*xu –
члены двойного взаимодействия
x1*x2*x3 – члены тройного взаимодействия

Слайд 63Свойства матрицы представления эксперимента
1. Свойство симметричности – алгебраическая сумма элементов
вектор-столбца каждого фактора равна нулю (за исключением столбца, соответствующего свободному
члену)
2. Свойство нормирования – сумма квадратов каждого столбца равна числу опытов
3. Свойство ортогональности – скалярное произведение всех вектор-столбцов (сумма почленных произведений элементов любых вектор столбцов) равно нулю
i = номер фактора, j – номер опыта

Слайд 64Определение коэффициентов b уравнения регрессии
По свойствам матрицы планирования
Методом наименьших квадратов
находятся оценки b коэффициентов
Получаем

Слайд 65Планирование второго порядка
Применяется если описание функции отклика первым порядком получается
недостаточным (например, процесс носит нелинейный характер)
Каждый фактор варьируется не менее
чем на трех уровнях – полный эксперимент содержит 3^k (k – количество факторов) опытов.
План 2-ого порядка при k=2 n=1
Опыты проводятся
В «крайних точках» — как в планировании 1-ого порядка
В «звездных точках» — xi=(+/-)a, xj=0, 1,…,n; 1,…,n; i!=j
В «центре» — xi=0, j=1,2,3,…,n
Уравнение регрессии для эксперимента с 2-мя факторами

Содержание ▲
- ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК… - СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В.…
- Задачи теории ошибок измерений.
Задачи теории… - 1. Задачи теории ошибок измерений.…
- Теория ошибок измерений решает
Теория ошибок… - 2. Сущность и виды измерений.
Измерения…
- Непосредственными или прямыми называ-ются…
- Под равноточными понимают измерения, полученные…
- Необходимыми считаются измерения, которые…
- Зависимыми называют измерения, имеющие некоторые…
- 3. Ошибки измерений, их классификация и…
- Причинами возникновения ошибок являются…
- В теории ошибок более важное значение имеет…
- Систематические ошибки подразделяются на…
- Случайными называются ошибки, которые не связаны…
- Случайные ошибки основного типа обладают…
- 4. Понятие о законах распределения ошибок.
4.… - Распределение случайных ошибок измерений наиболее…
- График функции (3) называется кривой нормального…
- Есть ошибки, которые подчиняются закону…
- Основными характеристиками распределения…
- Для непрерывной случайной величины с плотностью…
- Дисперсией случайной величины Х называ-ется…
- Положительное значение квадратного корня из…
- Для случайных ошибок измерений, как уже…
- 5.Числовые характеристики точности измерений.…
- При большом значении n
При большом значении… - Оценку точности измерений характеризуют также…
- Обычно для τ принимают значения 3, 2.5, или 2.…
- При нормальном распределении средняя ошибка v…
-
СПАСИБО ЗА ВНИМАНИЕ.
… - Скачать
- Похожие презентации
Вы можете ознакомиться и скачать презентацию на
тему ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ.
Доклад-сообщение содержит 31 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайды и текст этой презентации
Слайд 1

Описание слайда:
ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»
Слайд 2

Описание слайда:
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч. пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: – М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .
Слайд 3

Описание слайда:
Задачи теории ошибок измерений.
Задачи теории ошибок измерений.
Сущность и виды измерений.
Ошибки измерений, их классификация и свойства.
Понятие о законах распределения ошибок.
Числовые характеристики точности измерений.
Слайд 4

Описание слайда:
1. Задачи теории ошибок измерений.
Геодезические работы связаны с различными методами измерений длин линий, углов, превышений, площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.
Слайд 5

Описание слайда:
Теория ошибок измерений решает
Теория ошибок измерений решает
четыре основные задачи:
1. Изучение законов возникновения и распределения ошибок измерений и вычислений.
2. Оценка точности результатов измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.
Слайд 6

Описание слайда:
2. Сущность и виды измерений.
Измерения различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные (избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется результатом измерения.
Слайд 7

Описание слайда:
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например, измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.
Слайд 8

Описание слайда:
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.
Слайд 9

Описание слайда:
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Если одна величина измерена n-раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.
Слайд 10
Описание слайда:
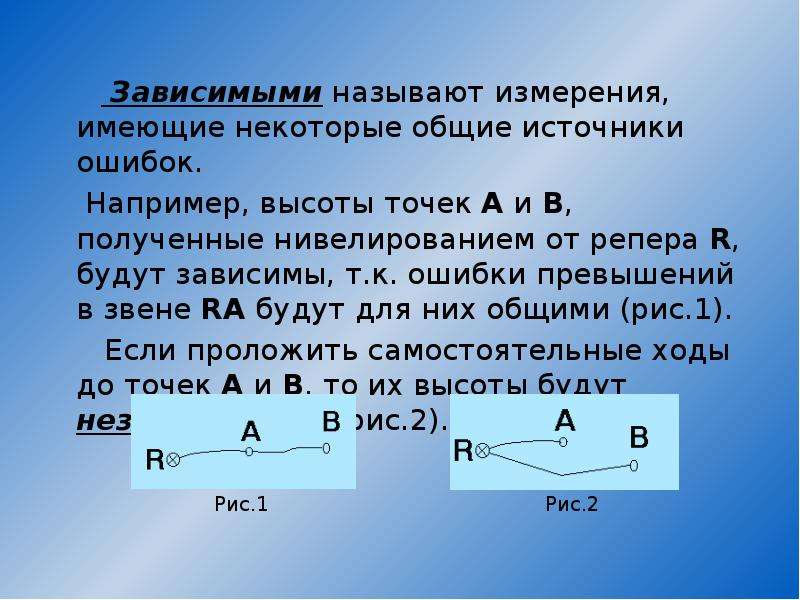
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Например, высоты точек А и В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут независимыми (рис.2).
Слайд 11

Описание слайда:
3. Ошибки измерений, их классификация и свойства.
Ошибкой результата измерения называется разность между результатом измерения и точным (истинным) значением измеряемой величины, т.е.
∆= l–x, (1)
где ∆ – ошибка измерения (иcтинная ошибка);
l – результат измерения;
x – точное значение величины.
Слайд 12

Описание слайда:
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
В соответствии с источниками возникновения различают ошибки:
1) приборов;
2) внешние;
3) личные;
4) объекта;
5) метода измерений.
Приведенная классификация ошибок по источникам возникновения имеет большое значение при изучении приборов и методов измерений.
Слайд 13

Описание слайда:
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
Грубые ошибки (промахи) вызываются невнима-тельностью наблюдателя или неисправностью прибора. Они превосходят по абсолютной величине некоторый предел, установленный для данных условий измерений.
Измерения, содержащие грубые ошибки, бракуются и заменяются новыми. Для выявления грубых ошибок производятся избыточные измерения (линии измеряют дважды, в треугольнике измеряют все три угла и т. п.).
Слайд 14

Описание слайда:
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Постоянные систематические ошибки при измерении одной и той же величины несколько раз, всякий раз появляются с одним знаком и одинаковые по величине. Например, ошибки за счет неточного центрирования теодолита при измерении углов несколькими приемами будут одинаковыми в каждом приеме.
Переменные систематические ошибки меняются от приема к приему, следуя определённому закону. Например, ошибки в направлениях, обусловленные эксцентриситетом алидады, или ошибками нанесения штрихов лимба теодолита.
Односторонне действующие систематические ошибки изменяются случайным образом, но сохраняют знак. Например, ошибка в длине линии из-за отклонения мерной ленты от створа.
Слайд 15

Описание слайда:
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Слайд 16

Описание слайда:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
1. По абсолютной величине ошибки не превосходят некоторого предела.
2. Положительные и отрицательные ошибки, равные по абсолютной величине, имеют равные вероятности, т.е. встречаются одинаково часто.
З. Чем больше ошибка по абсолютной величине, тем меньше ее вероятность появления.
4. Среднее арифметическое из значений случайных ошибок при неограниченном возрастании числа измерений одной и той же величины имеет пределом нуль, т. е. математическое ожидание ошибки равно нулю
.
Слайд 17

Описание слайда:
4. Понятие о законах распределения ошибок.
4. Понятие о законах распределения ошибок.
Свойства случайных ошибок являются проявлением закона их распределения.
В общем случае закон распределения ошибок отражает связь между размером ошибки и вероятностью ее появления.
PΔ= f(Δ)dΔ, (2)
где Р∆ – вероятность появления ошибки в интервале (∆, ∆+d∆);
∆ – случайная ошибка;
f(∆) – плотность распределения ошибок.
Слайд 18

Описание слайда:
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Плотность нормального распределения выражается формулой
(3)
где σ – среднее квадратическое отклонение случайной ошибки.
Слайд 19
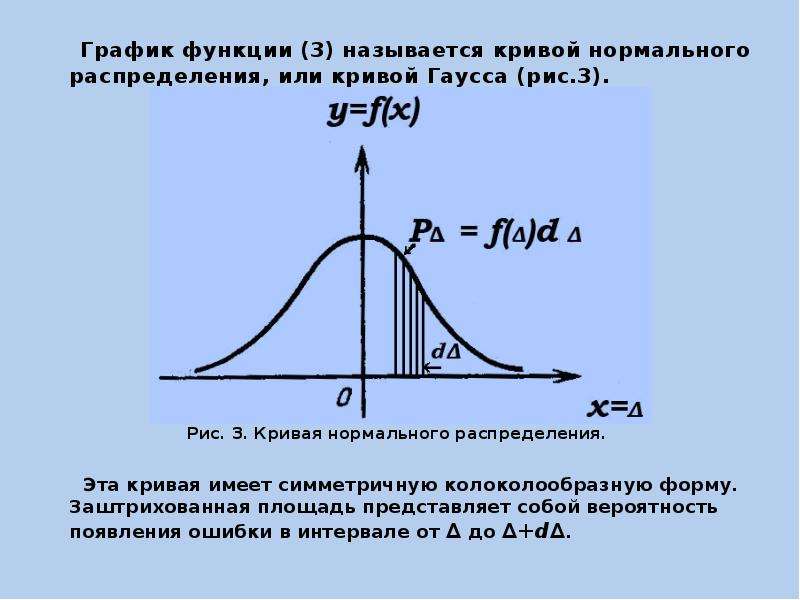
Описание слайда:
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
Рис. 3. Кривая нормального распределения.
Эта кривая имеет симметричную колоколообразную форму. Заштрихованная площадь представляет собой вероятность появления ошибки в интервале от ∆ до ∆+d∆.
Слайд 20

Описание слайда:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
(4)
где α – наибольшее значение ошибки.
Слайд 21

Описание слайда:
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Математическим ожиданием дискретной случайной величины х называют сумму произведений всех возможных значений случайной величины на соответствующие им вероятности р
. (5)
Слайд 22

Описание слайда:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
. (6)
Слайд 23

Описание слайда:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
. (7)
Слайд 24

Описание слайда:
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
. (8)
Слайд 25

Описание слайда:
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
, (9)
или
(10)
при n стремящемуся к бесконечности.
Слайд 26

Описание слайда:
5.Числовые характеристики точности измерений.
В качестве теоретической характеристики точности измерений обычно пользуются средним квадратическим отклонением σ.
Поскольку величина σ не известна, практически пользуются ее приближенным значением – средней квадратической ошибкой (СКО), определяемой по формуле:
, (11)
где ∆1, ∆2, …, ∆n – истинные ошибки измерений.
Слайд 27

Описание слайда:
При большом значении n
При большом значении n
m ≈ σ. (12)
При ограниченном числе измерений величина m будет характеризовать величину σ с некоторой ошибкой. Для оценки точности определения самой средней квадратической ошибки существует формула:
(13)
Слайд 28

Описание слайда:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
∆пр= τm, (14)
где τ – коэффициент, значение которого прини-мают таким, чтобы была мала вероятность появления ошибки больше вероятной.
Слайд 29

Описание слайда:
Обычно для τ принимают значения 3, 2.5, или 2.
Обычно для τ принимают значения 3, 2.5, или 2.
В дальнейшем при решении задач по оценке точности измерений будем пользоваться формулой
∆пр= 3m.
Для оценки точности иногда пользуются средней ошибкой v и вероятной ошибкой r. Средняя ошибка вычисляется по формуле
(15)
Слайд 30

Описание слайда:
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
(16)
Если все ошибки расположить в ряд по возрастанию абсолютных значений, то ошибка оказавшаяся в середине ряда будет вероятной. Со средней квадратической ошибкой она связана соотношением
(17)
Ошибка, выраженная в единицах измерения, называется абсолютной. Отношение ее к измеренной величине называется относительной ошибкой.
Слайд 31

Описание слайда:
СПАСИБО ЗА ВНИМАНИЕ.
Оцените презентацию от 1 до 5 баллов!
-
Тип файла:
ppt / pptx (powerpoint)
-
Всего слайдов:
31 слайд
-
Для класса:
1,2,3,4,5,6,7,8,9,10,11
-
Размер файла:
235.84 kB
-
Просмотров:
48
-
Скачиваний:
0
-
Автор:
неизвестен
Слайды и текст к этой презентации:
№1 слайд

Содержание слайда: ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»
№2 слайд

Содержание слайда: СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч. пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: – М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .
№3 слайд

Содержание слайда: Задачи теории ошибок измерений.
Задачи теории ошибок измерений.
Сущность и виды измерений.
Ошибки измерений, их классификация и свойства.
Понятие о законах распределения ошибок.
Числовые характеристики точности измерений.
№4 слайд

Содержание слайда: 1. Задачи теории ошибок измерений.
Геодезические работы связаны с различными методами измерений длин линий, углов, превышений, площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.
№5 слайд

Содержание слайда: Теория ошибок измерений решает
Теория ошибок измерений решает
четыре основные задачи:
1. Изучение законов возникновения и распределения ошибок измерений и вычислений.
2. Оценка точности результатов измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.
№6 слайд

Содержание слайда: 2. Сущность и виды измерений.
Измерения различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные (избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется результатом измерения.
№7 слайд

Содержание слайда: Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например, измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.
№8 слайд

Содержание слайда: Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.
№9 слайд

Содержание слайда: Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Если одна величина измерена n-раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.
№10 слайд

Содержание слайда: Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Например, высоты точек А и В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут независимыми (рис.2).
№11 слайд

Содержание слайда: 3. Ошибки измерений, их классификация и свойства.
Ошибкой результата измерения называется разность между результатом измерения и точным (истинным) значением измеряемой величины, т.е.
∆= l–x, (1)
где ∆ – ошибка измерения (иcтинная ошибка);
l – результат измерения;
x – точное значение величины.
№12 слайд

Содержание слайда: Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
В соответствии с источниками возникновения различают ошибки:
1) приборов;
2) внешние;
3) личные;
4) объекта;
5) метода измерений.
Приведенная классификация ошибок по источникам возникновения имеет большое значение при изучении приборов и методов измерений.
№13 слайд

Содержание слайда: В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
Грубые ошибки (промахи) вызываются невнима-тельностью наблюдателя или неисправностью прибора. Они превосходят по абсолютной величине некоторый предел, установленный для данных условий измерений.
Измерения, содержащие грубые ошибки, бракуются и заменяются новыми. Для выявления грубых ошибок производятся избыточные измерения (линии измеряют дважды, в треугольнике измеряют все три угла и т. п.).
№14 слайд

Содержание слайда: Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Постоянные систематические ошибки при измерении одной и той же величины несколько раз, всякий раз появляются с одним знаком и одинаковые по величине. Например, ошибки за счет неточного центрирования теодолита при измерении углов несколькими приемами будут одинаковыми в каждом приеме.
Переменные систематические ошибки меняются от приема к приему, следуя определённому закону. Например, ошибки в направлениях, обусловленные эксцентриситетом алидады, или ошибками нанесения штрихов лимба теодолита.
Односторонне действующие систематические ошибки изменяются случайным образом, но сохраняют знак. Например, ошибка в длине линии из-за отклонения мерной ленты от створа.
№15 слайд

Содержание слайда: Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
№16 слайд

Содержание слайда: Случайные ошибки основного типа обладают следующими вероятными свойствами:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
1. По абсолютной величине ошибки не превосходят некоторого предела.
2. Положительные и отрицательные ошибки, равные по абсолютной величине, имеют равные вероятности, т.е. встречаются одинаково часто.
З. Чем больше ошибка по абсолютной величине, тем меньше ее вероятность появления.
4. Среднее арифметическое из значений случайных ошибок при неограниченном возрастании числа измерений одной и той же величины имеет пределом нуль, т. е. математическое ожидание ошибки равно нулю
.
№17 слайд

Содержание слайда: 4. Понятие о законах распределения ошибок.
4. Понятие о законах распределения ошибок.
Свойства случайных ошибок являются проявлением закона их распределения.
В общем случае закон распределения ошибок отражает связь между размером ошибки и вероятностью ее появления.
PΔ= f(Δ)dΔ, (2)
где Р∆ – вероятность появления ошибки в интервале (∆, ∆+d∆);
∆ – случайная ошибка;
f(∆) – плотность распределения ошибок.
№18 слайд

Содержание слайда: Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Плотность нормального распределения выражается формулой
(3)
где σ – среднее квадратическое отклонение случайной ошибки.
№19 слайд

Содержание слайда: График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
Рис. 3. Кривая нормального распределения.
Эта кривая имеет симметричную колоколообразную форму. Заштрихованная площадь представляет собой вероятность появления ошибки в интервале от ∆ до ∆+d∆.
№20 слайд

Содержание слайда: Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
(4)
где α – наибольшее значение ошибки.
№21 слайд

Содержание слайда: Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Математическим ожиданием дискретной случайной величины х называют сумму произведений всех возможных значений случайной величины на соответствующие им вероятности р
. (5)
№22 слайд

Содержание слайда: Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
. (6)
№23 слайд

Содержание слайда: Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
. (7)
№24 слайд

Содержание слайда: Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
. (8)
№25 слайд

Содержание слайда: Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
, (9)
или
(10)
при n стремящемуся к бесконечности.
№26 слайд

Содержание слайда: 5.Числовые характеристики точности измерений.
В качестве теоретической характеристики точности измерений обычно пользуются средним квадратическим отклонением σ.
Поскольку величина σ не известна, практически пользуются ее приближенным значением – средней квадратической ошибкой (СКО), определяемой по формуле:
, (11)
где ∆1, ∆2, …, ∆n – истинные ошибки измерений.
№27 слайд

Содержание слайда: При большом значении n
При большом значении n
m ≈ σ. (12)
При ограниченном числе измерений величина m будет характеризовать величину σ с некоторой ошибкой. Для оценки точности определения самой средней квадратической ошибки существует формула:
(13)
№28 слайд

Содержание слайда: Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
∆пр= τm, (14)
где τ – коэффициент, значение которого прини-мают таким, чтобы была мала вероятность появления ошибки больше вероятной.
№29 слайд

Содержание слайда: Обычно для τ принимают значения 3, 2.5, или 2.
Обычно для τ принимают значения 3, 2.5, или 2.
В дальнейшем при решении задач по оценке точности измерений будем пользоваться формулой
∆пр= 3m.
Для оценки точности иногда пользуются средней ошибкой v и вероятной ошибкой r. Средняя ошибка вычисляется по формуле
(15)
№30 слайд

Содержание слайда: При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
(16)
Если все ошибки расположить в ряд по возрастанию абсолютных значений, то ошибка оказавшаяся в середине ряда будет вероятной. Со средней квадратической ошибкой она связана соотношением
(17)
Ошибка, выраженная в единицах измерения, называется абсолютной. Отношение ее к измеренной величине называется относительной ошибкой.
№31 слайд

Содержание слайда: СПАСИБО ЗА ВНИМАНИЕ.
Первый слайд презентации: Теория ошибок
это наука, изучающая те погрешности, которые возникают при измерениях. Она изучает их величины, законы их накопления и характер их проявления.

Изображение слайда
Слайд 2: Факторы измерения
1) объект измерения
2) субъект измерения
3) мерный прибор
4) метод измерения
5) внешняя среда
Измерения
Равноточными
Неравноточными
5 факторов= const.
5 факторов≠ const.

Изображение слайда
Слайд 3: Виды ошибок (погрешностей)
Грубые погрешности возникают из-за небрежности исполнителей, из-за неопытности и неправильной организации работ, которые не являются малыми величинами. Для устранения этих ошибок необходимо организовать надежный контроль.
Систематические погрешности происходящие от определенного источника и имеющие определенное направление и величину. Они появляются из-за несовершенства применяемых для измерений инструментов. Им свойственно накапливаться в рядах измерений. Они могут действовать с одним знаком, увеличивая или уменьшая результаты измерения. Задача наблюдателя состоит в том, чтобы исключить основную часть систематических ошибок из результатов измерений, а остальное влияние свести к минимуму, путем введения соответствующих поправок.
Случайные погрешности Они зависят от наблюдателя, от приборов и неучтенных колебаний внешних условий. В рядах, содержащих только случайные ошибки измерения, проявляется статистическая закономерность, которая проявляется тем сильнее, чем больше измерений содержаться в данном ряду.

Изображение слайда
Слайд 4
Δ = l -Х
где Δ – случайная ошибка;
l – измеренное значение величины;
Х – истинное значение величины.

Изображение слайда
Слайд 5: Свойства случайных погрешностей
при определенных условиях измерений случайные ошибки не могут превосходить по абсолютной величине определенного предела
чем меньше абсолютная величина случайной ошибки, тем чаще такая ошибка встречается при измерениях
положительные и отрицательные случайные ошибки одинаковых модулей равновозможны
среднее арифметическое из случайных ошибок равноточных измерений одной и той же величины стремятся к нулю при неограниченном возрастании числа измерений

Изображение слайда
Слайд 6: Критерии оценки точности измерений
1. Средняя погрешность — среднее арифметическое значение из абсолютных значений случайных ошибок
,
2. Средняя квадратическая погрешность — определяется по формуле Гаусса
m =
[Δ 2 ] = Δ 2 1 + Δ 2 2 + Δ 2 3 +…+ Δ 2 n
где гауссова сумма

Изображение слайда
Слайд 7
3. Предельная случайная погрешность-
в трех случаях из 100 превышает значения утроенной средней квадратической ошибки
Δ ПРЕД = 3 · m
4. Вероятная погрешность — это значение случайной погрешности больше или меньше которого по абсолютной величине погрешности равновозможны
r = 0,6745· m или r = 2/3 m
Абсолютные погрешности

Изображение слайда
Слайд 8: Относительные погрешности- отношение абсолютной ошибки к среднему значению измеренной величины: выраженной дробью с числителем равным единице
1. Относительная средняя погрешность —
f ОТН,СР. КВ. погреш. =
2. Относительная средняя квадратическая погрешность
f ОТН,СР.погреш. =
3. Относительная предельная случайная погрешность-
f ПРЕД.ОТН.погреш. =

Изображение слайда
Слайд 9: Линейные измерения
Непосредственные
Косвенные
мерный прибор
(рулетка, лента и т. д.) непосредственно укладывают в створ измеряемого отрезка
измеряют вспомогательные параметры (углы, базисы, физические величины и т. д.), а длину отрезка вычисляют по формуле, отображающей зависимость между определяемой и определенными величинами
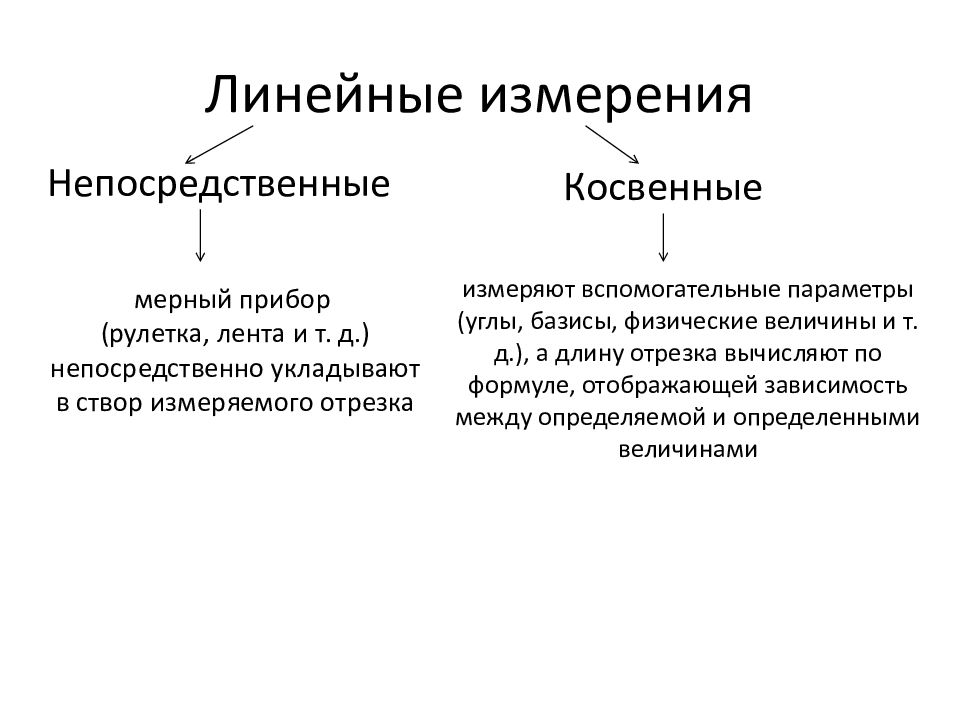
Изображение слайда
Слайд 10: Непосредственные линейные измерения
Метрами;
Рулетками;
Землемерными лентами (штриховые и шкаловые)
Инварными проволоками

Изображение слайда
Слайд 11
Рис. 6.1. Стальные рулетки: а, б — виды делений, в — карманная, автоматически сматывающаяся, г — на вилке,
д — в футляре; 1 — футляр, 2 — полотно, 3 — Г-образные окончания для фиксации,
4, 5 — ручки, 6 — кольцо, 7 — желобковый вид сечения
Рулетки
Изображение слайда
Слайд 12
а — при измерении; б — на станке;
1 — штрих, 2 — вырез, 3 — заклепка, 4 — пластина, 5 — отверстие, 6 — линия, до которой выполнено измерение,
7 — ручка
Штриховые ленты (землемерные-ЛЗ)
Изображение слайда
Слайд 13
Шкаловые ленты (землемерные- ЗЛШ)
Набор шпилек
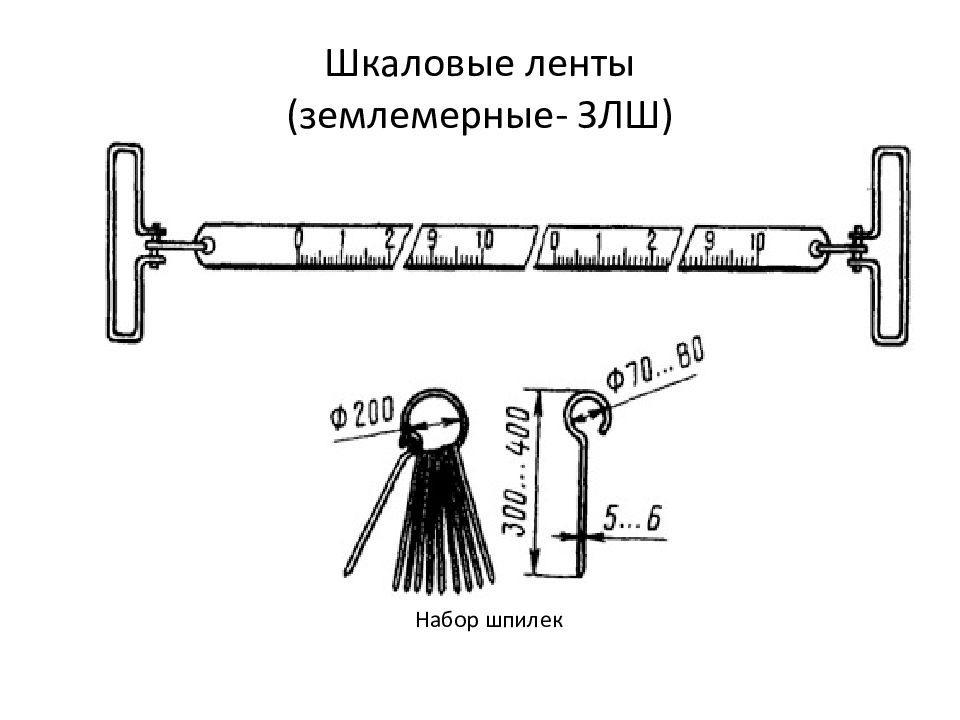
Изображение слайда
Слайд 14: Компарирование мерного прибора
До начала работы мерные приборы сравнивают с эталоном – компарируют
Компараторы
Лабораторные
Полевые
Длина l — мерного прибора (ленты, рулетки)
l = l 0 + Δ l k + Δ l t
где l 0 — номинальная длина ленты при нормальной температуре;
Δ l k – поправка за компарирование ;
Δ l t – поправка за температуру

Изображение слайда
Слайд 15
Компарирование

Изображение слайда
Слайд 16: Этапы измерения длины линии
1. Рекогносцировки (предварительный осмотр местности)
2. Вешение линий (при Д > 150 м)
3. Закрепление линии на местности
4. Непосредственное измерение

Изображение слайда
Слайд 17: Вешение линии- для обеспечения видимости на конечных точках измеряемой линии устанавливают вешки, раскрашенные полосами красного или белого цветов
вешение « на себя»
вешение через овраг
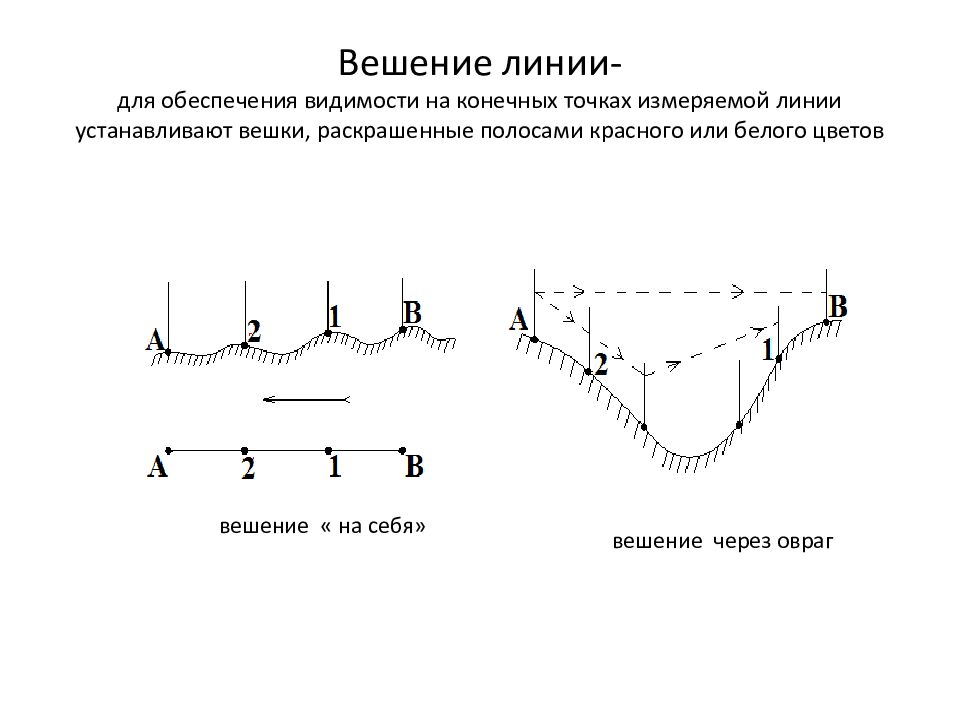
Изображение слайда
Слайд 18: Непосредственное измерение
Вешение линии: а — профиль и план, б — измерение линии;
1, 4, 7 — вехи, 2, 5 — шпильки, 3, 6 — замеры
D =200 N +20( n -1) +l
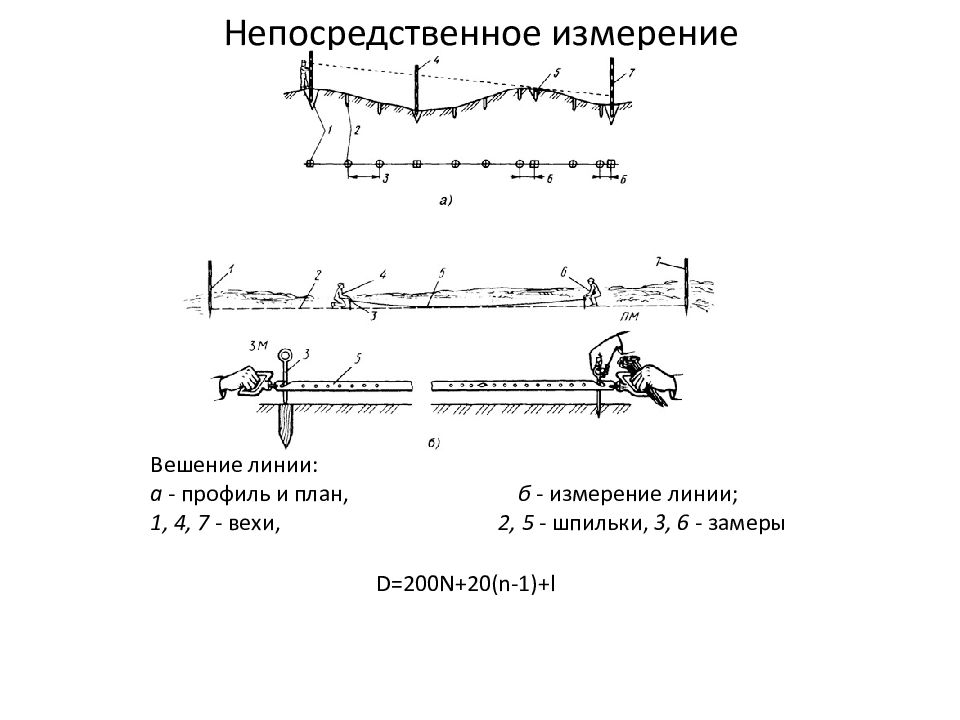
Изображение слайда
Слайд 19: Косвенные измерения
Косвенные измерения — Нитяной дальномер
D=K·n K- коэффициент дальномера=100; n — количество штрихов рейки между дальномерными штрихами
Рис. Оптический дальномер ( а ), поле зрения трубы ( б ) и схема измерения ( в )
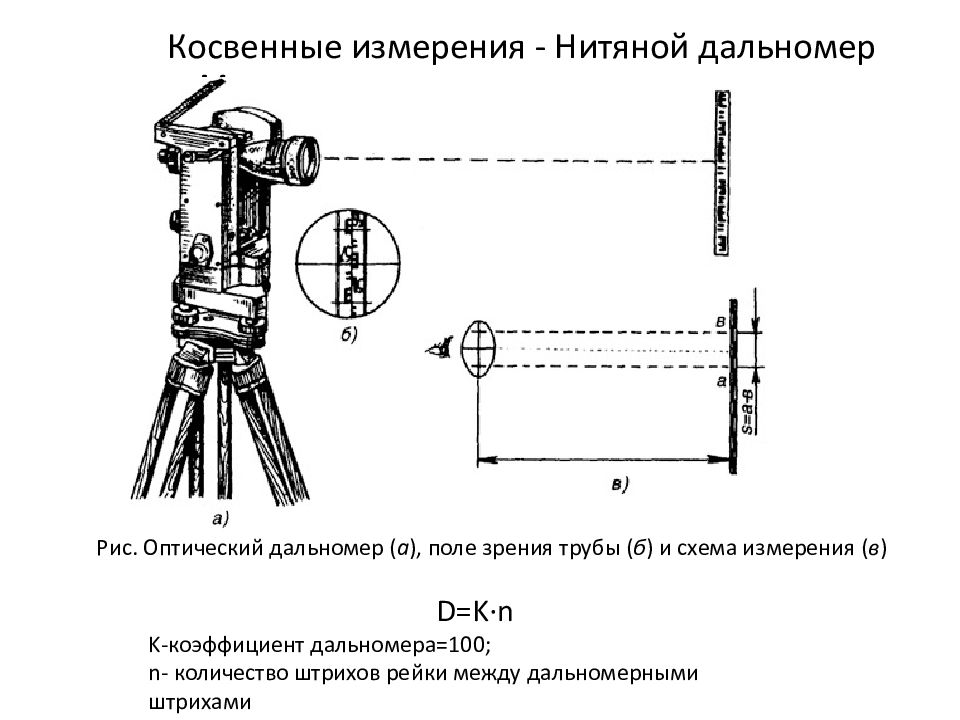
Изображение слайда
Слайд 20
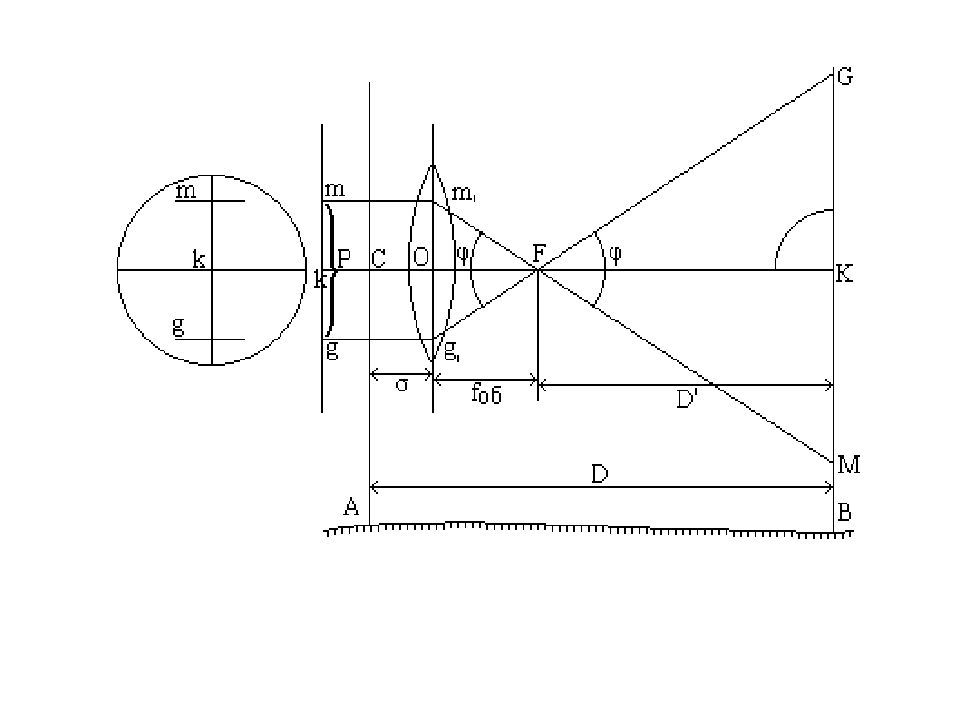
Изображение слайда
Слайд 21
Электронный дальномеры

Изображение слайда
Слайд 22
Рис. Светодальномер ( а ) и ход лучей ( б )
Светодальномеры
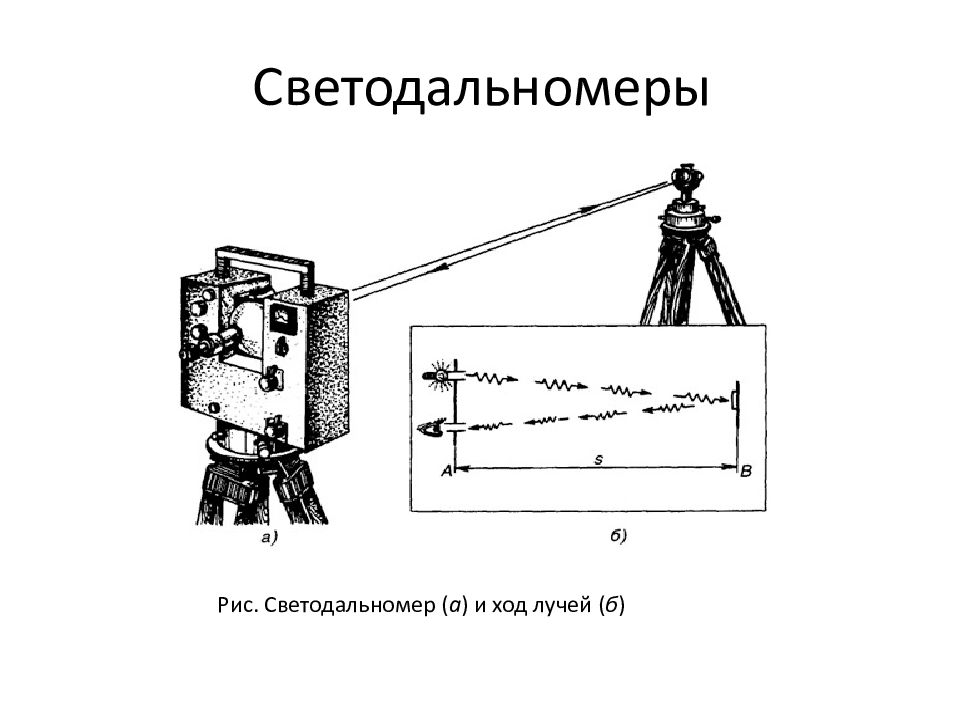
Изображение слайда
Слайд 23
Лазерные рулетки
Лазерный дальномер-рулетка disto d3a leica технические характеристики:
Диапазон измерений 0.05 — 80м (100м с отражательной пластиной)
Точность ±1.0мм
Режим измерения горизонтальных поверхностей Smart Horizontal Mode
Датчик наклона (диапазон ±45°)
Габариты 125х45х24мм
Рабочий диапазон температур 10°С..+50°С
Питание 2 батареи типа ААА
Вес 110г

Изображение слайда
Слайд 24: Угловые измерения

Изображение слайда
Слайд 25: Принцип измерения горизонтальных и вертикальных углов
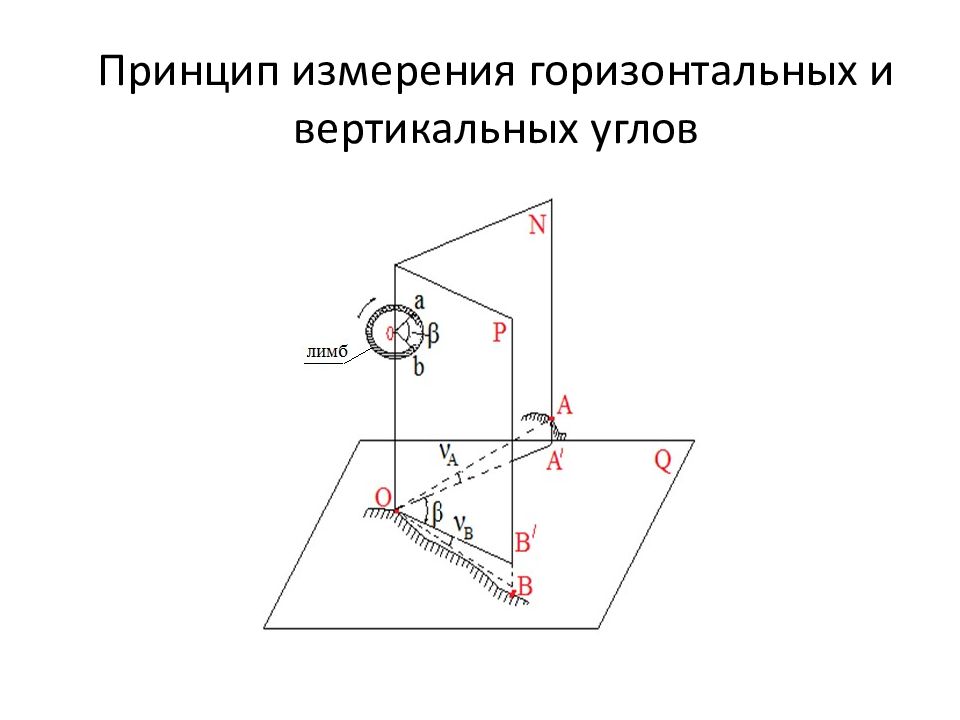
Изображение слайда
Слайд 26: Углы
Горизонтальный
Вертикальный
угол между стороной и ее проекцией на горизонтальную плоскость. Отсчитываются от проекции к стороне. Если сторона выше проекции, то угол считают положительным, если ниже – отрицательным
[-90°;+90°]
ν А > 0; ν в < 0
β = b – а
линейный угол двугранного угла, образованного плоскостями Р и N. Он определяется углом между проекциями сторон ОА и ОВ на горизонтальную плоскость Q, то есть углом АОВ [0°;360°]
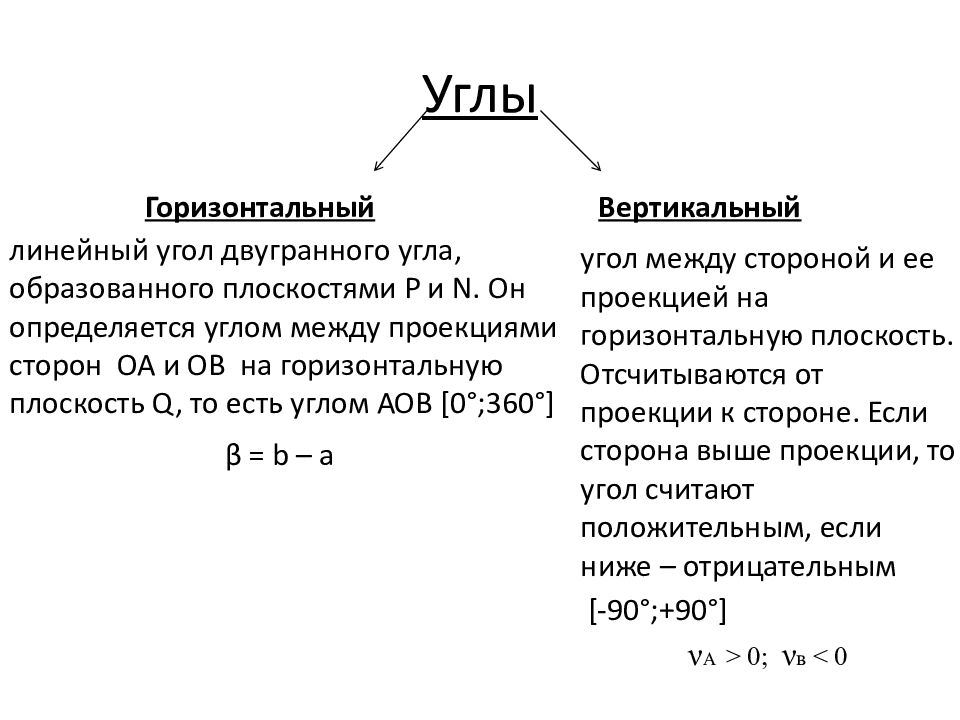
Изображение слайда
Слайд 27: Теодолит — угломерный прибор, с помощью которого измеряются горизонтальные и вертикальные углы
Виды теодолитов
По конструкции:
Механические (с металлическим лимбом);
Оптические;
Электронные;
Лазерные.
По точности:
(оптические)
1. Высокоточные: Т1
2. Точные: Т2, Т5
3. Технические: 2Т30

Изображение слайда
Слайд 28: Теодолит 2Т30
1 — наводящий винт лимба
горизонтального круга;
2 — окуляр микроскопа;
3 — зеркало;
4 — боковая крышка;
5 — паз для буссоли;
6 — оптический визир
(коллиматор, центрир);
7 — закрепительный винт трубы;
8 — наводящий винт трубы;
9 — цилиндрический уровень
горизонтального круга;
10 — наводящий винт алидады;
11 — заглушка винта;
12 — подставка теодолита;
13 — подъемные винты;
14 -основание теодолита (поддон
футляра),
15 — закрепительный винт лимба
горизонтального круга,
16 — закрепительный винт алидады
горизонтального круга,
17 — цилиндрический уровень при
зрительной трубе,
18 — кремальера, 19 — диоптрийное кольцо
2- модификация;
Т-теодолит;
30»- точность прибора ;
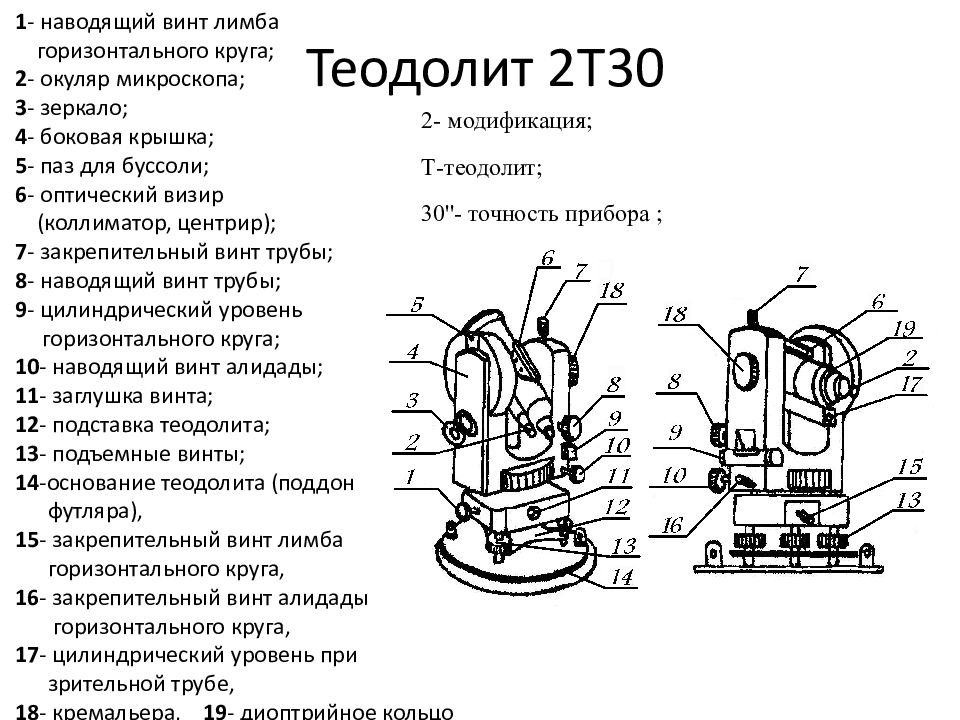
Изображение слайда
Слайд 29
Оптический теодолит 4Т30

Изображение слайда
Слайд 30: Поверки и юстировка теодолита
Поверки теодолита заключаются в установлении правильности выполнения ряда геометрических условий, предъявляемых к прибору, к его геометрическим элементам.
Если какая либо поверка не выполняется, то производят исправление или юстировку теодолита.
Основными геометрическими элементами теодолита являются:

Изображение слайда
Слайд 31
Основными осями (геометрическими элементами) теодолита являются:
1. Вертикальная (основная) ось вращения прибора VV 1 ;
2. Горизонтальная ось вращения зрительной трубы ZZ 1 ;
3. Визирная ось зрительной трубы WW 1 ;
4. Ось цилиндрического уровня при алидаде
горизонтального круга UU 1 ;
5. Сетка нитей зрительной трубы (горизонтальная, вертикальная).
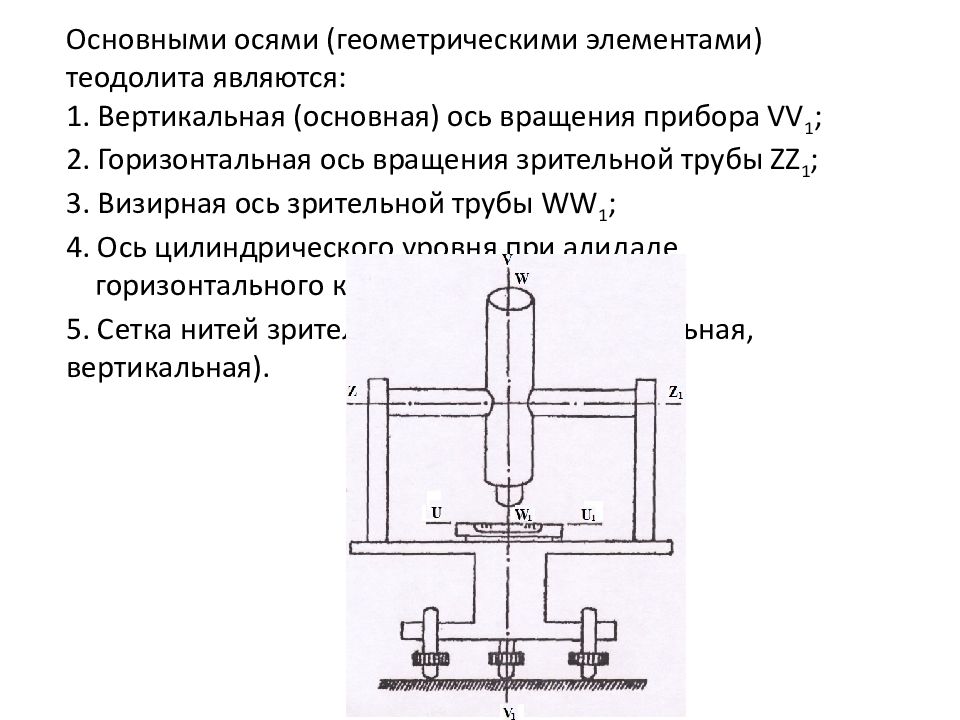
Изображение слайда
Слайд 32: Поверки теодолита
1 Ось цилиндрического уровня UU 1 при алидаде горизонтального круга должна быть перпендикулярна к оси вращения теодолита VV (поверка уровня горизонтального круга).
2 Горизонтальная нить сетки нитей зрительной трубы должна быть перпендикулярна к оси вращения теодолита VV 1.
3 Визирная ось зрительной трубы WW 1 должна быть перпендикулярна оси вращея трубы ZZ 1 (поверка коллимационной погрешности-С).
4 Ось вращения зрительной трубы ZZ 1 должна быть перпендикулярна оси вращения теодолита VV 1 (гарантируется заводом-изготовителем).
5 Ось оптического визира ( центрира ) должна быть параллельна оси вращения теодолита.

Изображение слайда
Последний слайд презентации: Теория ошибок
Электронные теодолиты

Изображение слайда
