Тесты Ферма и Миллера-Рабина на простоту
Время на прочтение
3 мин
Количество просмотров 19K
Салют хабровчане! Сегодня мы продолжаем делиться полезным материалом, перевод которого подготовлен специально для студентов курса «Алгоритмы для разработчиков».

Дано некоторое число n, как понять, что это число простое? Предположим, что n изначально нечетное, поскольку в противном случае задача совсем простая.
Самой очевидной идеей было бы искать все делители числа n, однако до сих пор основная проблема заключается в том, чтобы найти эффективный алгоритм.
Тест Ферма
По Теореме Ферма, если n – простое число, тогда для любого a справедливо следующее равенство an−1=1 (mod n). Отсюда мы можем вывести правило теста Ферма на проверку простоты числа: возьмем случайное a ∈ {1, ..., n−1} и проверим будет ли соблюдаться равенство an−1=1 (mod n). Если равенство не соблюдается, значит скорее всего n – составное.
Тем не менее, условие равенства может быть соблюдено, даже если n – не простое. Например, возьмем n = 561 = 3 × 11 × 17
Z561 = Z3 × Z11 × Z17
, где каждое a ∈ Z∗561 отвечает следующему:
(x,y,z) ∈ Z∗3×Z∗1111×Z∗17.
По теореме Ферма, x2=1, y10=1, и z16=1. Поскольку 2, 10 и 16 все являются делителями 560, это значит, что (x,y,z)560 = (1, 1, 1), другими словами a560 = 1 для любого a ∈ Z∗561.
Не имеет значения какое a мы выберем, 561 всегда будет проходить тест Ферма несмотря на то, что оно составное, до тех пор, пока a является взаимно простым с n. Такие числа называются числами Кармайкла и оказывается, что их существует бесконечное множество.
Если a не взаимно простое с n, то оно тест Ферма не проходит, но в этом случае мы можем отказаться от тестов и продолжить искать делители n, вычисляя НОД(a,n).
Тест Миллера-Рабина
Мы можем усовершенствовать тест, сказав, что n — простое тогда и только тогда, когда решениями x2 = 1 (mod n) являются x = ±1.
Таким образом, если n проходит тест Ферма, то есть an−1 = 1, тогда мы проверяем еще чтобы a(n−1)/2 = ±1, поскольку a(n−1)/2 это квадратный корень 1.
К сожалению, такие числа, как, например 1729 — третье число Кармайкла до сих пор могут обмануть этот улучшенный тест. Что если мы будем проводить итерации? То есть пока это будет возможно, мы будем уменьшать экспоненту вдвое, до тех пор, пока не дойдем до какого-либо числа, помимо 1. Если мы получим в итоге что-то, кроме -1, тогда n будет составным.
Если говорить более формально, то пускай 2S будет самой большой степенью 2, делящейся на n-1, то есть n−1=2Sq для какого-то нечетного числа q. Каждое число из последовательности
an−1 = a(2^S)q, a(2^S-1)q,…, aq.
Это квадратный корень предшествующего члена последовательности.
Тогда если n – простое число, то последовательность должна начинаться с 1 и каждое последующее число тоже должно быть 1, или же первый член последовательность может быть не равен 1, но тогда он равен -1.
Тест Миллера-Рабина берет случайное a∈ Zn. Если вышеуказанная последовательность не начинается с 1, либо же первый член последовательности не равен 1 или -1, тогда n – не простое.
Оказывается, что для любого составного n, включая числа Кармайкла, вероятность пройти тест Миллера-Рабина равна примерно 1/4. (В среднем значительно меньше.) Таким образом, вероятность того, что n пройдет несколько прогонов теста, уменьшается экспоненциально.
Если n не проходит тест Миллера-Рабина с последовательностью начинающейся с 1, тогда у нас появляется нетривиальный квадратный корень из 1 по модулю n, и мы можем эффективно находить делители n. Поэтому числа Кармайкла всегда удобно раскладывать на множители.
Когда тест применяется к числам вида pq, где p и q – большие простые числа, они не проходят тест Миллера-Рабина практически во всех случаях, поскольку последовательность не начинается с 1. Итого, так мы RSA сломать не сможем.
На практике тест Миллера-Рабина реализуется следующим образом:
- Дано
n, нужно найтиs, такое чтоn – 1 = 2Sqдля некоторого нечетногоq. - Возьмем случайное
a ∈ {1,...,n−1} - Если aq = 1, то
nпроходит тест и мы прекращаем выполнение. - Для
i= 0, ... , s−1проверить равенствоa(2^i)q = −1. Если равенство выполняется, тоnпроходит тест (прекращаем выполнение). - Если ни одно из вышеприведенных условий не выполнено, то
n– составное.
Перед выполнением теста Миллера-Рабина стоит провести еще несколько тривиальных делений на маленькие простые числа.
Строго говоря эти тесты являются тестами на то считается ли число составным, поскольку они не доказывают по сути, что проверяемое число простое, но точно доказывают, что оно может оказаться составным.
Существуют еще детерминированные алгоритма работающие за полиномиальное время для определения простоты (Agrawal, Kayal и Saxena), однако на сегодняшний день они считаются непрактичными.
Тесты Ферма и Миллера-Рабина на простоту
Салют хабровчане! Сегодня мы продолжаем делиться полезным материалом, перевод которого подготовлен специально для студентов курса «Алгоритмы для разработчиков».

Дано некоторое число n, как понять, что это число простое? Предположим, что n изначально нечетное, поскольку в противном случае задача совсем простая.
Самой очевидной идеей было бы искать все делители числа n, однако до сих пор основная проблема заключается в том, чтобы найти эффективный алгоритм.
Тест Ферма
По Теореме Ферма, если n – простое число, тогда для любого a справедливо следующее равенство an−1=1 (mod n). Отсюда мы можем вывести правило теста Ферма на проверку простоты числа: возьмем случайное a ∈ {1, ..., n−1} и проверим будет ли соблюдаться равенство an−1=1 (mod n). Если равенство не соблюдается, значит скорее всего n – составное.
Тем не менее, условие равенства может быть соблюдено, даже если n – не простое. Например, возьмем n = 561 = 3 × 11 × 17
Z561 = Z3 × Z11 × Z17
, где каждое a ∈ Z∗561 отвечает следующему:
(x,y,z) ∈ Z∗3×Z∗1111×Z∗17.
По теореме Ферма, x2=1, y10=1, и z16=1. Поскольку 2, 10 и 16 все являются делителями 560, это значит, что (x,y,z)560 = (1, 1, 1), другими словами a560 = 1 для любого a ∈ Z∗561.
Не имеет значения какое a мы выберем, 561 всегда будет проходить тест Ферма несмотря на то, что оно составное, до тех пор, пока a является взаимно простым с n. Такие числа называются числами Кармайкла и оказывается, что их существует бесконечное множество.
Если a не взаимно простое с n, то оно тест Ферма не проходит, но в этом случае мы можем отказаться от тестов и продолжить искать делители n, вычисляя НОД(a,n).
Тест Миллера-Рабина
Мы можем усовершенствовать тест, сказав, что n — простое тогда и только тогда, когда решениями x2 = 1 (mod n) являются x = ±1.
Таким образом, если n проходит тест Ферма, то есть an−1 = 1, тогда мы проверяем еще чтобы a(n−1)/2 = ±1, поскольку a(n−1)/2 это квадратный корень 1.
К сожалению, такие числа, как, например 1729 — третье число Кармайкла до сих пор могут обмануть этот улучшенный тест. Что если мы будем проводить итерации? То есть пока это будет возможно, мы будем уменьшать экспоненту вдвое, до тех пор, пока не дойдем до какого-либо числа, помимо 1. Если мы получим в итоге что-то, кроме -1, тогда n будет составным.
Если говорить более формально, то пускай 2S будет самой большой степенью 2, делящейся на n-1, то есть n−1=2Sq для какого-то нечетного числа q. Каждое число из последовательности
an−1 = a(2^S)q, a(2^S-1)q,…, aq.
Это квадратный корень предшествующего члена последовательности.
Тогда если n – простое число, то последовательность должна начинаться с 1 и каждое последующее число тоже должно быть 1, или же первый член последовательность может быть не равен 1, но тогда он равен -1.
Тест Миллера-Рабина берет случайное a∈ Zn. Если вышеуказанная последовательность не начинается с 1, либо же первый член последовательности не равен 1 или -1, тогда n – не простое.
Оказывается, что для любого составного n, включая числа Кармайкла, вероятность пройти тест Миллера-Рабина равна примерно 1/4. (В среднем значительно меньше.) Таким образом, вероятность того, что n пройдет несколько прогонов теста, уменьшается экспоненциально.
Если n не проходит тест Миллера-Рабина с последовательностью начинающейся с 1, тогда у нас появляется нетривиальный квадратный корень из 1 по модулю n, и мы можем эффективно находить делители n. Поэтому числа Кармайкла всегда удобно раскладывать на множители.
Когда тест применяется к числам вида pq, где p и q – большие простые числа, они не проходят тест Миллера-Рабина практически во всех случаях, поскольку последовательность не начинается с 1. Итого, так мы RSA сломать не сможем.
На практике тест Миллера-Рабина реализуется следующим образом:
- Дано
n, нужно найтиs, такое чтоn – 1 = 2Sqдля некоторого нечетногоq. - Возьмем случайное
a ∈ {1,...,n−1} - Если aq = 1, то
nпроходит тест и мы прекращаем выполнение. - Для
i= 0, ... , s−1проверить равенствоa(2^i)q = −1. Если равенство выполняется, тоnпроходит тест (прекращаем выполнение). - Если ни одно из вышеприведенных условий не выполнено, то
n– составное.
Перед выполнением теста Миллера-Рабина стоит провести еще несколько тривиальных делений на маленькие простые числа.
Строго говоря эти тесты являются тестами на то считается ли число составным, поскольку они не доказывают по сути, что проверяемое число простое, но точно доказывают, что оно может оказаться составным.
Существуют еще детерминированные алгоритма работающие за полиномиальное время для определения простоты (Agrawal, Kayal и Saxena), однако на сегодняшний день они считаются непрактичными.
Аннотация: Для построения многих систем защиты информации требуются простые числа большой разрядности. В связи с этим актуальной является задача тестирования на простоту натуральных чисел. В лекции 2 рассматриваются тесты техника компьютерных вычислений с многоразрядными числами.
Определение 2.1 Время работы алгоритма 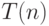 имеет верхнюю оценку
имеет верхнюю оценку  (пишут
(пишут  , читают «О большое от
, читают «О большое от 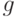 от
от  «), если существует натуральное число
«), если существует натуральное число 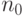 и положительная постоянная
и положительная постоянная  такие, что
такие, что  выполняется неравенство:
выполняется неравенство: 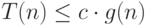 .
.
Пример 2.1 Докажем, что функция  имеет верхнюю оценку
имеет верхнюю оценку  .
.
Действительно, положим  ,
,  . Тогда
. Тогда  выполняется неравенство
выполняется неравенство  . Следовательно,
. Следовательно,  .
.
Оценка сложности алгоритма — важнейший вопрос для криптографии, поскольку от оценки сложности решающим образом зависит стойкость соответствующей криптосистемы.
Далее мы будем рассматривать алгоритмы (в основном теоретико-числовые) и в большинстве случаев будем приводить оценку сложности представленного алгоритма.
2.1 Тестирование на простоту
Существует два типа критериев простоты: детерминированные и вероятностные. Детерминированные тесты позволяют доказать, что тестируемое число — простое. Практически применимые детерминированные тесты способны дать положительный ответ не для каждого простого числа, поскольку используют лишь достаточные условия простоты.
Детерминированные тесты более полезны, когда необходимо построить большое простое число, а не проверить простоту, скажем, некоторого единственного числа.
В отличие от детерминированных, вероятностные тесты можно эффективно использовать для тестирования отдельных чисел, однако их результаты, с некоторой вероятностью, могут быть неверными. К счастью, ценой количества повторений теста с модифицированными исходными данными вероятность ошибки можно сделать как угодно малой.
На сегодня известно достаточно много алгоритмов проверки чисел на простоту. Несмотря на то, что большинство из таких алгоритмов имеет субэкспоненциальную оценку сложности, на практике они показывают вполне приемлемую скорость работы.
На практике рассмотренные алгоритмы чаще всего по отдельности не применяются. Для проверки числа на простоту используют либо их комбинации, либо детерминированные тесты на простоту.
Детерминированный алгоритм всегда действует по одной и той же схеме и гарантированно решает поставленную задачу. Вероятностный алгоритм использует генератор случайных чисел и дает не гарантированно точный ответ. Вероятностные алгоритмы в общем случае не менее эффективны, чем детерминированные (если используемый генератор случайных чисел всегда дает набор одних и тех же чисел, возможно, зависящих от входных данных, то вероятностный алгоритм становится детерминированным).
2.1.1 Вероятностные тесты простоты
Для того чтобы проверить вероятностным алгоритмом, является ли целое число  простым, выбирают случайное число
простым, выбирают случайное число  ,
,  , и проверяют условие алгоритма. Если число
, и проверяют условие алгоритма. Если число  не проходит тест по основанию
не проходит тест по основанию  , то алгоритм выдает результат «Число
, то алгоритм выдает результат «Число  составное», и число
составное», и число  действительно является составным.
действительно является составным.
Если же  проходит тест по основанию
проходит тест по основанию  , нельзя сказать о том, действительно ли число
, нельзя сказать о том, действительно ли число  является простым. Последовательно проведя ряд проверок таким тестом для разных
является простым. Последовательно проведя ряд проверок таким тестом для разных  и получив для каждого из них ответ «Число
и получив для каждого из них ответ «Число  , вероятно, простое», можно утверждать, что число
, вероятно, простое», можно утверждать, что число  является простым с вероятностью, близкой к 1. Если вероятность того, что составное число пройдёт тест, равна
является простым с вероятностью, близкой к 1. Если вероятность того, что составное число пройдёт тест, равна  , то для обеспечения вероятности
, то для обеспечения вероятности  того, что проверенное число является простым, необходимо сделать
того, что проверенное число является простым, необходимо сделать  итераций (см.
итераций (см.
рис.
1.1}).
2.1.2 Тест Ферма
Согласно малой теореме Ферма для простого числа  и произвольного целого числа
и произвольного целого числа  ,
,  , выполняется сравнение:
, выполняется сравнение:

Следовательно, если для нечетного  существует такое целое
существует такое целое  , что
, что  ,
,  и
и 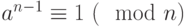 , то число
, то число  вероятно простое. Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
вероятно простое. Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
Вход: нечетное целое число  .
.
Выход: «Число  , вероятно, простое» или «Число
, вероятно, простое» или «Число  составное».
составное».
- Выбрать случайное целое число
 ,
,  .
. - Вычислить
 .
. - При
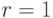 результат: «Число
результат: «Число  , вероятно, простое». В противном случае результат: «Число
, вероятно, простое». В противном случае результат: «Число  составное».
составное».
На шаге 1 алгоритма мы не рассматриваем числа  и
и  , поскольку
, поскольку  для любого целого
для любого целого  и
и  для любого нечетного
для любого нечетного  .
.
Сложность теста Ферма равна:  .
.
Тест имеет существенный недостаток в виде наличия чисел Кармайкла. Это нечетные составные числа, для которых сравнение из формулы выполняется при любом  ,
,  , взаимно простом с
, взаимно простом с  . Для всех
. Для всех  ,
,  , тест будет выдавать ошибочный результат.
, тест будет выдавать ошибочный результат.
Числа Кармайкла являются достаточно редкими. В пределах до 100000 существует лишь 16 чисел Кармайкла: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973, 75361.
2.1.3 Тест Леманна
Если для какого-либо целого числа  , меньшего
, меньшего  , не выполняется условие:
, не выполняется условие:

то число  — составное. Если это условие выполняется, то число
— составное. Если это условие выполняется, то число  — возможно простое, причем вероятность ошибки не превышает 50%.
— возможно простое, причем вероятность ошибки не превышает 50%.
Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
Вход: нечетное целое число  .
.
Выход: «Число  , вероятно, простое» или «Число
, вероятно, простое» или «Число  составное».
составное».
- Выбрать случайное целое число
 ,
,  .
. - Вычислить
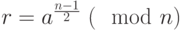 .
. - При
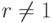 и
и  результат: «Число
результат: «Число  составное». В противном случае результат: «Число
составное». В противном случае результат: «Число  , вероятно, простое».
, вероятно, простое».
Сложность теста Леманна равна  .
.
2.1.4 Тест Соловея-Штрассена
В основе этого теста лежит следующая теорема:
Теорема 1.28 (критерий Эйлера) Нечетное число  является простым тогда и только тогда, когда для любого целого числа
является простым тогда и только тогда, когда для любого целого числа  ,
,  , взаимно простого с
, взаимно простого с  , выполняется сравнение:
, выполняется сравнение:
 |
( 2.1) |
где  — символ Якоби от параметров
— символ Якоби от параметров  и
и  .
.
Критерий Эйлера лежит в основе следующего вероятностного теста числа на простоту:
Вход: нечетное целое число  .
.
Выход: «Число  , вероятно, простое» или «Число
, вероятно, простое» или «Число  составное».
составное».
- Выбрать случайное целое число
 ,
, 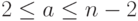 .
. - Вычислить
 .
. - При
 и
и  результат: «Число
результат: «Число  составное».
составное». - Вычислить символ Якоби
 .
. - При
 результат: «Число
результат: «Число  составное». В противном случае результат: «Число
составное». В противном случае результат: «Число  , вероятно, простое».
, вероятно, простое».
На шаге 1 мы снова не рассматриваем числа  и
и  , поскольку в силу свойств символа Якоби сравнение в формуле (2.1) для этих чисел выполняется при любом нечетном
, поскольку в силу свойств символа Якоби сравнение в формуле (2.1) для этих чисел выполняется при любом нечетном  . Если
. Если  , то
, то 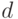 делит и число
делит и число 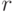 , вычисляемое на шаге 2. Таким образом, при проверке неравенства
, вычисляемое на шаге 2. Таким образом, при проверке неравенства  на шаге 3 автоматически проверяется условие
на шаге 3 автоматически проверяется условие 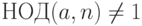 .
.
Сложность теста Соловэя-Штрассена определяется сложностью вычисления символа Якоби и равна  .
.
Для теста Соловея-Штрассена не существует чисел, подобных числам Кармайкла, то есть составных чисел, которые были бы эйлеровыми псевдопростыми по всем основаниям  .
.
2.1.5 Тест Миллера-Рабина
На сегодняшний день для проверки чисел на простоту чаще всего используется тест Миллера-Рабина, основанный на следующем наблюдении. Если  — простое, и
— простое, и  , то
, то 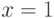 или
или  .
.
Пусть число  нечетное и
нечетное и  , где
, где 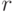 — нечетное. По малой теореме Ферма, если
— нечетное. По малой теореме Ферма, если  — простое, то
— простое, то  для любого натурального числа
для любого натурального числа  . Из нашего наблюдения следует, что, в ряду элементов
. Из нашего наблюдения следует, что, в ряду элементов 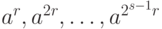 при каком-либо
при каком-либо  мы будем иметь
мы будем иметь  и
и  при
при  .
.
Это свойства лежит в основе следующего теста:
Вход: нечетное целое число  .
.
Выход: «Число  , вероятно, простое» или «Число
, вероятно, простое» или «Число  составное».
составное».
- Представить
 в виде
в виде  , где число
, где число 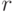 — нечетное.
— нечетное. - Выбрать случайное целое число
 ,
, 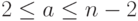 , взаимно простое с
, взаимно простое с  .
. - Вычислить
 .
. - При
 и
и  выполнить следующие действия.
выполнить следующие действия. - Результат: «Число
 , вероятно, простое».
, вероятно, простое».
В результате выполнения теста для простого числа  в последовательности
в последовательности 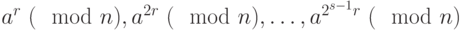 обязательно перед 1 должна появиться
обязательно перед 1 должна появиться  (или, что то же самое,
(или, что то же самое,  ). Это означает, что для простого числа
). Это означает, что для простого числа  единственными решениями сравнения
единственными решениями сравнения  являются
являются  . Если число
. Если число  составное и имеет
составное и имеет  различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует
различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует 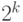 решений сравнения
решений сравнения  . Действительно, для любого простого делителя
. Действительно, для любого простого делителя 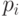 числа
числа  существует два решения указанного сравнения:
существует два решения указанного сравнения:  .
.
Поэтому  таких сравнений дают
таких сравнений дают 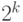 наборов решений по модулям
наборов решений по модулям 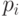 , содержащих элементы
, содержащих элементы  .
.
Сложность теста Миллера-Рабина равна  . Вероятность ошибки, то есть того, что тест объявит составное число простым, не более
. Вероятность ошибки, то есть того, что тест объявит составное число простым, не более 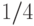 .
.
2.1.6 N — 1-алгоритмы генерации простых чисел
Перечислим некоторые теоремы, которые могут быть использованы для генерации доказуемо простых чисел [1].
Теорема 2.1 (Прот, 1878) Пусть  , где
, где  ,
,  , и
, и 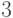 не делит
не делит  . Тогда
. Тогда  — простое тогда и только тогда, когда
— простое тогда и только тогда, когда
 |
( 2.2) |
Для генерации простого числа нужно перебирать числа  и
и  и для каждого варианта проверять условие (2.2). Когда условие будет выполнено, полученное число
и для каждого варианта проверять условие (2.2). Когда условие будет выполнено, полученное число  будет простым.
будет простым.
Недостатком этого подхода является плохое распределение генерируемых простых чисел: все они будут иметь вид  для большого
для большого  и не очень большого
и не очень большого  . В примере 1.42 мы также видели, что чем меньше простые делители числа
. В примере 1.42 мы также видели, что чем меньше простые делители числа  , тем легче осуществить дискретное логарифмирование по модулю
, тем легче осуществить дискретное логарифмирование по модулю  . Это делает генерируемые на основе теоремы Прота простые числа мало пригодными, например, для криптосистемы и электронной подписи Эль-Гамаля.
. Это делает генерируемые на основе теоремы Прота простые числа мало пригодными, например, для криптосистемы и электронной подписи Эль-Гамаля.
Теорема 2.2 (Диемитко, 1988) Пусть  , где
, где  — нечетное простое число,
— нечетное простое число,  — четное, и
— четное, и  . Если существует целое число
. Если существует целое число  такое, что
такое, что

то  простое число.
простое число.
С помощью этой теоремы генерировать простые числа можно итерационно. На вход каждой итерации подаётся какое-либо простое число  . Во время итерации перебираются числа
. Во время итерации перебираются числа  и
и  и проверяются условия теоремы Диемитко. Как только все условия выполнены, мы получили новое простое число
и проверяются условия теоремы Диемитко. Как только все условия выполнены, мы получили новое простое число  , порядок которого примерно вдвое больше, чем у исходного простого числа
, порядок которого примерно вдвое больше, чем у исходного простого числа  . Итерации можно начинать с какого-либо известного простого числа, а заканчивать, когда полученное простое число достигнет требуемого размера.
. Итерации можно начинать с какого-либо известного простого числа, а заканчивать, когда полученное простое число достигнет требуемого размера.
На заключительной итерации желательно выбирать как можно меньшее число  . Тогда у полученного простого числа
. Тогда у полученного простого числа  будет большой простой делитель
будет большой простой делитель  . Если подобрать достаточно малое
. Если подобрать достаточно малое  не получится, может потребоваться выполнить заново предыдущую итерацию для получения нового числа
не получится, может потребоваться выполнить заново предыдущую итерацию для получения нового числа  .
.
Эта теорема лежала в основе алгоритма генерации простых чисел для алгоритма цифровой подписи ГОСТ 34.10-94, пока этот алгоритм не был заменён на новый, основанный на группе точек эллиптической кривой.
В этом пункте
будут доказаны важнейшие теоремы теории
чисел и показаны их приложения к задачам
криптографии.
Теорема Эйлера.
При m
> 1, (a,
m)
= 1
![]()
aφ(m)
≡ 1 (mod
m).
Доказательство:
Если x
пробегает приведенную систему вычетов
x
= r1,
r2,…,rc
(c
= φ(m)),
составленную из наименьших неотрицательных
вычетов, то в силу того, что (a,m)=1,
наименьшие неотрицательные вычеты
чисел ax
= ρ1,
ρ2,…,
ρc
будут
пробегать ту же систему, но, возможно,
в другом порядке (это следует из
утверждения 2 пункт 3). Тогда, очевидно,
r1·…·rc
= ρ1·…
·ρc
*
Кроме того,
справедливы сравнения
ar1
≡ ρ1(mod
m),
ar2
≡ ρ2(mod
m),
… , arc
≡ ρc(mod
m).
Перемножая данные
сравнения почленно, получим
ac
·r1
·r2
·…·rc
≡ ρ
1·…· ρ
c(mod
m)
Откуда в силу (*)
получаем
ac
≡ 1 (mod
m)
А поскольку
количество чисел в приведенной системе
вычетов по модулю m
есть φ(m),
то есть c
= φ(m),
то
aφ(m)
≡ 1 (mod
m).
□
Теорема Ферма
(малая)
р
– простое, p
не делит
a
![]()
ap–1
≡ 1 (mod
m)
Доказательство:
по теореме Эйлера при m=p.
Важное следствие:
ap
≡ a
(mod
p)
![]() a,
a,
в том числе и для случая pa.
Теорема Эйлера
применяется для понижения степени в
модулярных вычислениях.
Пример:
10100
mod
11 = 109∙11+1
= 109+1
mod
11 = (–1)10
mod
11 = 1.
Следствие:
Если
![]() a:
a:
0 < a
< p,
для которого ap–1
![]() 1
1
(mod
p)
![]()
p
– составное.
Отсюда –
Тест Ферма на простоту
Вход: число n
– для проверки на простоту, t
– параметр надежности.
-
Повторяем t
раз:
а) Случайно выбираем
a
![]()
[2, n-2]
б) Если an–1
![]() 1
1
(mod
n)
![]()
«n
– составное». Выход.
-
«n
– простое с вероятностью 1–
εt
»
Этот тест может
принять составное число за простое, но
не наоборот.
Вероятность ошибки
есть εt,
где ε
![]()
В случае составного
числа n,
имеющего только большие делители, ε![]() ,
,
то есть существуют числа, для которых
вероятность ошибки при проверке их на
простоту тестом Ферма близка к 1.
Для теста Ферма
существуют так называемые числа
Кармайкла
– такие составные числа, что
![]() a:
a:
(a,n)
= 1
![]()
an–1
≡ 1(mod
n).
То есть числа Кармайкла – это такие
составные числа, которые всегда
принимаются тестом Ферма за простые,
несмотря на то, как велико число t
– параметр надежности теста.
Теорема
Кармайкла
n
– число Кармайкла
![]() 1)n
1)n
свободно от квадратов (т.е. n
= p1∙p2∙…∙pk);
2) (pi
– 1)(n
– 1), i
= 1,…,k
;
3) k
![]() .
.
Наименьшее
известное число Кармайкла
n=561
= 3∙11·17
3.7. Применение теоремы Эйлера в rsa:
Если известно
разложение числа на простые сомножители
a
= p1![]() p2
p2![]() …
…
pn![]() ,
,
то легко вычислить функцию Эйлера φ(a).
Отсюда вывод:
сложность вычисления функции Эйлера
не выше сложности задачи факторизации
.
Покажем, что в
случае n=pq
(p,q
– простые числа, p![]() q)
q)
задачи нахождения функции Эйлера и
факторизации эквивалентны. (то есть в
случае, когда n
– модуль RSA).
Учтем, что φ(n)
= (p
– 1)(q
– 1). Тогда имеем систему
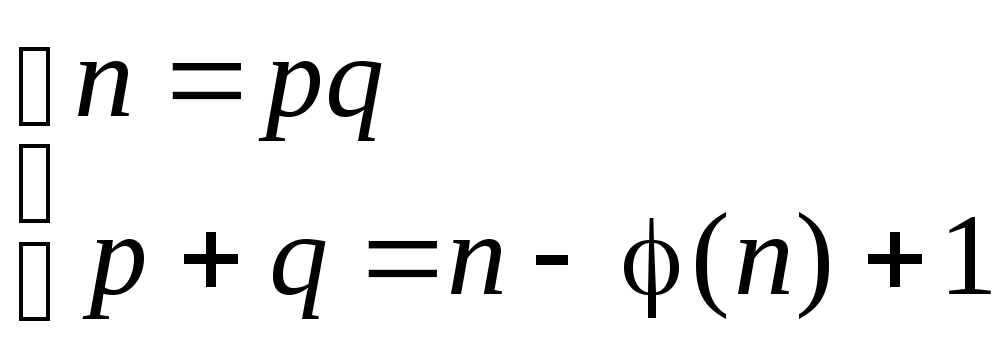 .
.
Зная n
и φ(n),
находим p
и q
из системы, приведенной выше, следующим
образом:
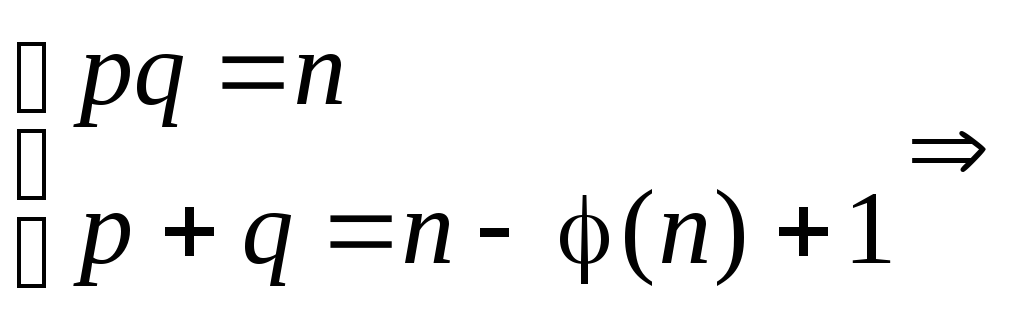
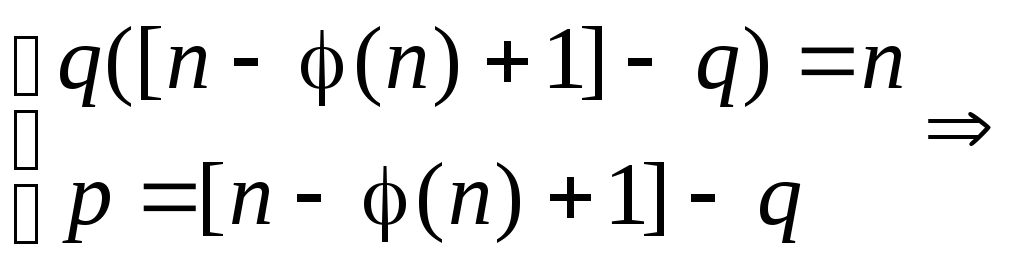

Первое уравнение
системы является квадратным уравнением
относительно q,
q
=
![]()
, где Dq
= [n–
φ(n)+1]2
– 4n.
Подставляя
полученное q
во второе уравнение системы, находим
p.
Видим, что при
нахождении чисел p,
q
по известным n,
φ(n)
применяются только «дешевые» в смысле
времени операции – сложение, деление
на 2. Только при вычислении дискриминанта
приходится применять возведение в
степень, а при вычислении q
– извлечение квадратного корня. Однако
эти операции производятся однократно,
поэтому временные затраты не столь
существенны.
Итак, для модуля
RSA
задачи нахождения функции Эйлера и
факторизации равносложны.
Формулировка
теоремы Эйлера для RSA:
n
= pq;
p≠q;
p,
q
– простые числа
![]()
![]() a
a
выполняется akφ(n)+1≡
a
(mod
n).
(на самом деле n
может быть просто свободно от квадратов,
то есть произведением произвольного
количества различных простых чисел)
Доказательство:
Возможны два
случая:
-
(a,
n)
= 1

по теореме Эйлера aφ(n)
≡ 1 (mod
n)
akφ(n)+1
= 1k
∙a
≡ a
(mod n).
-
(a,
n)
≠ 1, n
не делит a
в силу основного свойства простых
чисел, либо p
a,
либо q
a.
Не нарушая общности,
предположим, что pa,
q
не делит a.
Тогда по теореме
Ферма, akφ(n)+1≡a(mod
p),
qq–1≡1
(mod q)
![]() akφ(n)+1≡1k(p–1)·a
akφ(n)+1≡1k(p–1)·a
≡ a
(mod q).
Итак,
akφ(n)+1
≡ a
(mod p),
akφ(n)+1≡
a
(mod q).
Отсюда по
св-ву сравнений №12, akφ(n)+1≡
a(mod
НОК(p,q)).
В силу простоты p
и q,
НОК(p,q)=pq=n,
значит
akφ(n)+1≡
a
(mod n).
-
na
 a≡0(mod
a≡0(mod
n)

akφ(n)+1≡0≡a(mod
n).
□
Примечание:
Если вместо φ(n)
в теореме Эйлера для RSA
взять НОК(p–1,
q–1),
теорема все равно будет верна.
Применение
теоремы Эйлера в RSA:
Напомним, что
криптосистема RSA
является системой с открытым ключом.
В качестве параметров системы выбираются
различные большие простые числа p
и
q,
вычисляется n=pq,
φ(n)=(p–1)(q–1),
выбирается число e:
2<e<n,
(e,
φ(n))=1
и вычисляется d=e-1(mod
φ(n)).
В качестве открытого ключа берется
пара (n,
e),
в качестве закрытого, хранимого в
секрете, четверка (p,
q,
φ(n),
d).
Для того, чтобы
зашифровать открытый текст x,
абонент, пользуясь открытым ключом,
вычисляет зашифрованный текст y
по следующей формуле:
y
= xe
mod
n.
Для того, чтобы
осуществить расшифрование, владелец
секретного ключа вычисляет
x
= yd
mod
n.
В результате
такого расшифрования действительно
получится открытый текст, поскольку
yd
mod
n=xed
mod
n=xed
mod
φ(n)mod
n
=x1
mod
n=x.
Без знания простых
сомножителей p
и q
сложно вычислить значение функции
Эйлера φ(n),
а значит, и степень d,
в которую следует возводить зашифрованный
текст, чтобы получить открытый.
Более того, знание
простых сомножителей p
и q
может
значительно облегчить
процедуру возведения шифрованного
текста y
в степень d.
Действительно, пользуясь теоремой
Эйлера для RSA,
можем понизить степень d.
Разделим d
на φ(n)
с остатком:
d=kφ(n)+r
x=yd
mod
n=
ykφ(n)+r
mod
n=
yr
mod n.
Еще более можно
понизить степень, используя НОК(p–1,q–1)=![]()
вместо φ(n).
Пример:
n=19∙23=,
φ(n)=18∙22=396,
d=439.
НОК(18,22)=18∙22/2=198.
d
mod
φ(n)=43.
d
mod
НОК(p–1,q–1)=43.
Число d=439
в двоичном представлении есть 110110111.
Поэтому возведение в степень d
c
применением дихтономического алгоритма
(см. гл.2) требует 8 возведений в квадрат
и 6 умножений чисел.
Число 43 в двоичном
представлении есть 101011. Возведение в
степень 43 требует 5 возведений в квадрат
и 3 умножения чисел. Кроме того, для
вычисления φ(n)
требуется 1 операция умножения.
Таким образом,
для данного примера экономия времени
составляет 2 сложные операции.
В случае больших
простых делителей числа n
экономия оказывается более существенной.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Тест простоты — алгоритм, который по заданному натуральному числу определяет, простое ли это число. Различают детерминированные и вероятностные тесты.
Определение простоты заданного числа в общем случае не такая уж тривиальная задача. Только в 2002 году было доказано, что она полиномиально разрешима. Тем не менее, тестирование простоты значительно легче факторизации заданного числа.
*-Нравится статья? Кликни по рекламе!
Мы уже разобрали методы выбора всех простых чисел, до определенного, в статье Простые числа. Пришло время рассмотреть ряд алгоритмов, под общим названием — «Тесты простоты»:
1.) Перебор делителей:
Перебор делителей — алгоритм факторизации или тестирования простоты числа путем полного перебора всех возможных потенциальных делителей.
Описание алгоритма:
Обычно перебор делителей заключается в переборе всех целых (как вариант: простых) чисел от 2 до квадратного корня из факторизуемого числа n и в вычислении остатка от деления n на каждое из этих чисел. Если остаток от деления на некоторое число m равен нулю, то m является делителем n. В этом случае либо n объявляется составным, и алгоритм заканчивает работу (если тестируется простота n), либо n сокращается на m и процедура повторяется (если осуществляется факторизация n). По достижении квадратного корня из n и невозможности сократить n ни на одно из меньших чисел, n объявляется простым.
Примечание: если у n есть некоторый делитель p, то n/p так же будет делителем, причем одно из этих чисел не превосходит .
Реализация на Python:
def divider(n):
i = 2
j = 0 # флаг
while i**2 <= n and j != 1:
if n%i == 0:
j = 1
i += 1
if j == 1:
print ("Это составное число")
else:
print ("Это простое число")
2.) Теорема Вильсона
Теорема теории чисел, которая утверждает, что
p — простое число тогда и только тогда, когда (p − 1)! + 1 делится на p
Практическое использование теоремы Вильсона для определения простоты числа нецелесообразно из-за сложности вычисления факториала. Таким образом, время выполнения данного алгоритма = поиску факториала. Алгоритм поиска факториала мы уже рассматривали.
Реализация:
def prime(n):
if (math.factorial(n-1)+1) % n!=0:
print ("Это составное число")
else:
print ("Это простое число")
3.) Тест простоты Ферма
Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.
Если n — простое число, то an-1 1 mod n.
Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:
Простое число удовлетворяет тесту Ферма. Составной объект может пройти тест Ферма с вероятностью . Сложность разрядной операции испытания Ферма равна сложности алгоритма, который вычисляет возведение в степень.Поскольку вычисление
(mod N) довольно быстрая операция, у нас возникает быстрый тест, проверяющий, является ли данное число составным. Его называют тестом Ферма по основанию а. Заметим, что тест Ферма может лишь убедить нас в том, что число N имеет делители, но не в состоянии доказать его простоту. Действительно, рассмотрим составное число N = 11 · 13 = 341, а основание в тесте Ферма выберем равным 2. Тогда
= 1 mod 341, в то время как число 341 не простое. В этом случае говорят, что N — псевдопростое число (в смысле Ферма) по основанию 2. Существует бесконечно много псевдопростых чисел по фиксированному основанию, хотя они встречаются реже, чем простые. Можно показать, что для составного N вероятность неравенства
≠ 1 (mod N).
больше 1/2. Подводя итог сказанному, выпишем алгоритм теста Ферма.
def primFerma(a,n):
if a**(n-1)%n==1:
print "правдоподобно простое"
else:
print "составное"
Если на выходе этого алгоритма напечатано «составное, а», то мы с определенностью можем заявить, что число n не является простым, и что а свидетельствует об этом факте, т. е. чтобы убедиться в истинности высказывания, нам достаточно провести тест Ферма по основанию а. Такое а называют свидетелем того, что n составное.
Если же в результате работы теста мы получим сообщение: «правдоподобно простое», то можно заключить: n — составное с вероятностью ≤ существуют составные числа, относительно которых тест Ферма выдаст ответ правдоподобно простое, для всех взаимно простых с n оснований а. Такие числа называются числами Кармайкла. К сожалению, их бесконечно много. Первые из них — это 561, 1105 и 1729. Числа Кармайкла обладают следующими свойствами:
- они нечетны,
- имеют по крайней мере три простых делителя,
- свободны от квадратов1,
- если р делит число Кармайкла N, то р — 1 делит N — 1.
Чтобы получить представление об их распределении, посмотрим на числа, не превосходящие. Среди них окажется примерно 2, 7 •
простых чисел, но только 246 683 ≈ 2,4 •
чисел Кармайкла. Следовательно, они встречаются не очень часто, но и не настолько редко, чтобы их можно было игнорировать.
4.)Тест Миллера — Рабина
Вероятностный полиномиальный тест простоты. Тест Миллера — Рабина позволяет эффективно определять, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа. Тем не менее тест Миллера — Рабина часто используется в криптографии для получения больших случайных простых чисел.
Алгоритм был разработан Гари Миллером в 1976 году и модифицирован Майклом Рабином в 1980 году.
Пусть — нечётное число большее 1. Число
однозначно представляется в виде
, где
нечётно. Целое число
,
, называется свидетелем простоты числа
, если выполняется одно из условий:
или
Теорема Рабина утверждает, что составное нечётное число m имеет не более различных свидетелей простоты, где
— функция Эйлера.
Алгоритм Миллера — Рабина параметризуется количеством раундов r. Рекомендуется брать r порядка величины log2(m), где m — проверяемое число.
Для данного m находятся такие целое число s и целое нечётное число t, что m − 1 = 2st. Выбирается случайное число a, 1 < a < m. Если a не является свидетелем простоты числа m, то выдается ответ «m составное», и алгоритм завершается. Иначе, выбирается новое случайное число a и процедура проверки повторяется. После нахождения r свидетелей простоты, выдается ответ «m, вероятно, простое», и алгоритм завершается. Как и для теста Ферма, все числа n > 1, которые не проходят этот тест – составные, а числа, которые проходят, могут быть простыми. И, что важно, для этого теста нет аналогов чисел Кармайкла.
В 1980 году было доказано, что вероятность ошибки теста Рабина-Миллера не превышает 1/4. Таким образом, применяя тест Рабина-Миллера t раз для разных оснований, мы получаем вероятность ошибки 2-2t.
def toBinary(n):
r = []
while (n > 0):
r.append(n % 2)
n = n / 2
return r
def MillerRabin(n, s = 50):
for j in xrange(1, s + 1):
a = random.randint(1, n - 1)
b = toBinary(n - 1)
d = 1
for i in xrange(len(b) - 1, -1, -1):
x = d
d = (d * d) % n
if d == 1 and x != 1 and x != n - 1:
return True # Составное
if b[i] == 1:
d = (d * a) % n
if d != 1:
return True # Составное
return False # Простое
Ещё реализации:
- http://en.literateprograms.org/Miller-Rabin_primality_test_%28Python%29
- http://code.activestate.com/recipes/410681-rabin-miller-probabilistic-prime-test/
- http://code.activestate.com/recipes/511459-miller-rabin-primality-test/
UPD:На сладкое, нашел на Хабре статейку, где предлагали следующее регулярное выражение для определения простоты числа:
/^1?$|^(11+?)1+$/
Применять его следует не к самому целому числу. Вместо этого, нужно создать строку из единиц, где количество единиц соответствует самому числу и уже к этой строке применить регулярное выражение. Если совпадения нет — число простое. Так как же оно работает? Подвыражение (11+?) совпадает со строками вроде 11, 111, и т.д… Часть «1+» будет искать далее по строке совпадения с результатами поиска первого подвыражения. В первый раз совпадение произойдет по строке «11» и потом поиск строки «11» будет произведен снова, а затем снова до конца строки. Если поиск завершится успешно, число не является простым. Почему? Потому, что будет доказано, что длина строки делится на 2 и, соответственно, само число тоже делится на два. Если совпадения не произойдет, движок регулярных выражений начнет искать строку «111» и ее повторения. Если первое подвыражение становится достаточно длинным (n/2) и совпадений по-прежнему не будет обнаружено, число будет являться простым.
Реализовывать я его не стал, не люблю регулярки(если кто напишет, жду в комменты, добавлю).
Используемая литература:
- http://younglinux.info/algorithm/divider
- Тест простоты
- http://masteroid.ru/content/view/1292/49/
- http://www.intuit.ru/department/security/mathcryptet/
- http://www.re.mipt.ru/infsec/2005/essay/2005_Primality_tests_survey__Kuchin.htm
- http://algolist.manual.ru/maths/teornum/rabmil.php
Проверка простых чисел
Общее
В данной статье вы увидите обзор известных алгоритмов проверки чисел на простоту. На сегодня не существует единого алгоритма для определения всех простых чисел. Все методы проверки делят на две группы: вероятностные проверки и детерминированные. Детерминированные методы определяют точно, является ли число простым. Вероятностные проверки определяют число на простоту с некой вероятностью ошибки. Многократное повторение для одного числа, но с разными переменными, разрешает сделать вероятность ошибки сколь угодно малой величины.
Быстрые тесты для малых чисел и вероятно простые числа
Малые простые числа
Пока не было нужды в генерации больших простых чисел, можно было реализовывать методы проверки без применения вычислительной техники. Первым из таких методов является полный перебор всех возможных делителей. Есть модификация, которая не хуже всего перебора, называется — пробное деление. Он заключается в делении на предыдущие простые числа либо равные корню из этого числа. Для такого метода можно использовать решето Эратосфена.
Малая теорема Ферма
Французский математик Пьер Ферма в 17 веке выдал закономерность, которая лежит в основе почти всех методов проверки на простоту.
Малая теорема Ферма — Если P простое и A — любое целое, то AP = A (mod P). Если P не делит А, то АP-1 = 1 (mod P). На основе такой теоремы, можно создать мощный алгоритм на простоту:
- Тест Ферма: Для n > 1 выбираем a > и вычисляем An-1 mod n, если результат не 1, то n составное число, если 1, то n — слабо возможно простое по основанию a (a-PRP)
Часть чисел проходящие Тест Ферма являются составными, и их называют псевдопростыми.
Тест Рабина-Миллера
Можно улучшить тест Ферма, заметив, что если n — простое нечетное, то для 1 есть только два квадратных корня по модулю n: 1 и -1. По этому квадратный корень из An-1, A(n-1)/2 равен минус или плюс еденице. Если (n-1)/2 опять нечетно, то можно снова извлечь корень и тд. Первый вариант алгоритма определяет только одно деление:
- Тест Леманна: Если для любого целого числа А меньшего n не выполняется условие A(n-1)/2 = ± 1 (mod n), то число n — составное. Если это условие выполнено, то число n — возможно простое с вероятностью ошибки не больше 50%.
- Тест Рабина-Миллера: Запишем (n-1) в виде 2sd, где d нечетно, а s — неотрицательно: n называют сильно возможно простым по основанию A (A-SPRP), если реализуется одно из двух условий:
- Ad = 1 (mod n)
- (Ad)2r = -1 (mod n), для любого неотрицательного r < s
В 1980 году была доказана вероятность ошибки теста Рабина-Миллера не превышающая 1/4. Реализуя этот тест T раз для разных оснований, мы получим вероятность ошибки 2-2t
Объединение тестов
Классические тесты
Проверки чисел вида n + 1
Тест заключается в том, что мы должны знать частичное или полное разложение на множители числа n — 1. Разложение на множители n — 1 просто найти, если n имеет определенный вид.
- Тест Лукаса: N ≥ 3. Если для каждого простого q, делящего n — 1 есть целое А такое что:
- An-1 = 1 (mod n) и
- A(n-1)/q ≠ 1 (mod n), то n — простое
Для такой проверки нужно знать полное разложение n — 1 на простые множители. Более мощная версия определяет знание не полного, а частичного разложения n — 1 на простые множители. Такой вариант алгоритма был выдан Поклингтоном в 1914 году.
- Тест Поклингтона: N ≥ 3 и n = FR + 1 (F делит n-1), причем F > R, НОД (F,R) = 1 и известно разложение F на простые множители. Тогда, если для любого простого q, делящего F есть такое целое A > 1, что:
- An-1 = 1 (mod n) и
- НОД (A(n-1)/q — 1, n) = 1
- Теорема Пепина: пусть Fn это n-е число Ферма и n > 1, тогда Fn — простое тогда и только тогда, когда 3(Fn — 1)/2 = 1 (mod Fn
- Теорема Прота: Пусть n = h × 2k + 1, причем 2k > h. Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое
На основе теоремы Прота было найдено пятое по величине из известных простых чисел — 28433 × 27830457
Проверки чисел вида n — 1
Здесь рассмотрим числа только определенного вида. 7 из первых 10 позиций по самым большим известным простым числам были найдены с помощью чисел Мерсенна. Числа Мерсенна называют числа вида 2s -1.
Лукасом и Лемером в 1930 году было создано следующее утверждение: пусть s — простое, тогда число Мерсенна n = 2s — 1 является простым тогда, когда S (n — 2) = 0, где S(0) = 4 и S(k+1) = S(k)2 — 2 (mod n). На основе такого факта можно создать проверку на простоту, которая точно скажет нам, является ли для заданного s число Мерсенна простым.
- Тест Лукаса-Лемера:
- С помощью пробного деления проверяем, является ли данное s простым, если нет, то получившееся число Мерсенна — составное
- Задаем S(0) = 4
- Для k от 1 до s — 2 вычисляем S(k) = S(k-1)2 — 2 (mod n)
- Если в результате получился 0, то число Мерсенна простое
Неоклассические алгоритмы ARP и ARP-CL
Можно рассматривать числа в виде n2 + n + 1 или n2 — n + 1. А можно рассмотреть число вида nm — 1 для больших m. Тогда любое просто число q такое, что q — 1 делит m, по малой теореме Ферма будет делить nm — 1.
Было представлено, что всегда существует целое число m:
- m < (log n)log log log n
Эллиптические кривые: ECPP
Современные вариант проверок на простоту основан на теореме Поклингтона, но для эллиптических кривых. Смысл алгоритма заключается в переходе от групп порядка n — 1 и n + 1 к достаточно большему диапазону размеров групп.
AKS
В 2002 году летом индийские математики Аграавал, Саксен и Кайал нашли полиномиальный детерминированный алгоритм проверки числа на простоту. Их метод основан на версии малой теоремы Ферма:
- Теорема: Пусть A и P взаимно простые целые числа и P > 1. Число P является простым, когда (x — a)p = (xp — a) (mod p)
- Доказательство: Если p — простое, то p делит биномиальные коэффициенты pCr для r = 1,2 ..p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма)
if (n is has the form ab with b > 1) then output COMPOSITE
r := 2
while (r < n) {
if (gcd(n,r) is not 1) then output COMPOSITE
if (r is prime greater than 2) then {
let q be the largest factor of r-1
if (q > 4sqrt(r)log n) and (n(r-1)/q is not 1 (mod r)) then
break
}
r := r+1
}
for a = 1 to 2sqrt(r)log n {
if ( (x-a)n is not (xn-a) (mod xr-1,n) ) then output COMPOSITE
}
output PRIME;
Итоги
| Тест | Тип теста | Где используется |
|---|---|---|
| Пробное деление | детерминированный | Из-за большой вычислительной сложности в чистом виде не используется. Пробное деление на маленькие простые числа реализуется во многих тестах как один из шагов |
| Ферма | вероятностный | В чистом виде не реализуется. Может быть одним из первых шагов на проверку простоты для очень больших чисел |
| Леманна | верляьнлсьный | Не используется |
| Рабина-Миллера | вероятностный | В чистом виде может реализовываться в криптосистемах с открытым ключом для реализации простых ключей длиной 512, 1024 и 2048 бит. |
| Миллера | детерминированный | На практике не используется, так как пока не доказана расширенная гипотеза Римана |
| Лукаса | детерминированный | Для получения больших простых чисел определенного вида |
| Поклингтона | детерминированный | Для получения больших чисел с частично известной факторизацией n — 1 |
| Петина | детерминированный | Для получения больших простых чисел Ферма |
| Прота | детерминированный | Для получения больших простых чисел определенного вида |
| Лукаса-Лемера | детерминированный | Для получения больших простых чисел Мерсенна |
| APR | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| ECPP | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| AKS | детерминированный | В качестве детерминированной полиномиальной проверки на простоту |
Из таблицы видно, что разные методы проверки на простоту служат для двух целей:
- для получения очень больших целый чисел
- для генерации простых чисел определенного размера для реализации в криптографии
Аналитическую работу провел студент (ГУ МФТИ) кафедры радиотехники Кучин Борис.
В этом пункте
будут доказаны важнейшие теоремы теории
чисел и показаны их приложения к задачам
криптографии.
Теорема Эйлера.
При m
> 1, (a,
m)
= 1
![]()
aφ(m)
≡ 1 (mod
m).
Доказательство:
Если x
пробегает приведенную систему вычетов
x
= r1,
r2,…,rc
(c
= φ(m)),
составленную из наименьших неотрицательных
вычетов, то в силу того, что (a,m)=1,
наименьшие неотрицательные вычеты
чисел ax
= ρ1,
ρ2,…,
ρc
будут
пробегать ту же систему, но, возможно,
в другом порядке (это следует из
утверждения 2 пункт 3). Тогда, очевидно,
r1·…·rc
= ρ1·…
·ρc
*
Кроме того,
справедливы сравнения
ar1
≡ ρ1(mod
m),
ar2
≡ ρ2(mod
m),
… , arc
≡ ρc(mod
m).
Перемножая данные
сравнения почленно, получим
ac
·r1
·r2
·…·rc
≡ ρ
1·…· ρ
c(mod
m)
Откуда в силу (*)
получаем
ac
≡ 1 (mod
m)
А поскольку
количество чисел в приведенной системе
вычетов по модулю m
есть φ(m),
то есть c
= φ(m),
то
aφ(m)
≡ 1 (mod
m).
□
Теорема Ферма
(малая)
р
– простое, p
не делит
a
![]()
ap–1
≡ 1 (mod
m)
Доказательство:
по теореме Эйлера при m=p.
Важное следствие:
ap
≡ a
(mod
p)
![]() a,
a,
в том числе и для случая pa.
Теорема Эйлера
применяется для понижения степени в
модулярных вычислениях.
Пример:
10100
mod
11 = 109∙11+1
= 109+1
mod
11 = (–1)10
mod
11 = 1.
Следствие:
Если
![]() a:
a:
0 < a
< p,
для которого ap–1
![]() 1
1
(mod
p)
![]()
p
– составное.
Отсюда –
Тест Ферма на простоту
Вход: число n
– для проверки на простоту, t
– параметр надежности.
-
Повторяем t
раз:
а) Случайно выбираем
a
![]()
[2, n-2]
б) Если an–1
![]() 1
1
(mod
n)
![]()
«n
– составное». Выход.
-
«n
– простое с вероятностью 1–
εt
»
Этот тест может
принять составное число за простое, но
не наоборот.
Вероятность ошибки
есть εt,
где ε
![]()
В случае составного
числа n,
имеющего только большие делители, ε![]() ,
,
то есть существуют числа, для которых
вероятность ошибки при проверке их на
простоту тестом Ферма близка к 1.
Для теста Ферма
существуют так называемые числа
Кармайкла
– такие составные числа, что
![]() a:
a:
(a,n)
= 1
![]()
an–1
≡ 1(mod
n).
То есть числа Кармайкла – это такие
составные числа, которые всегда
принимаются тестом Ферма за простые,
несмотря на то, как велико число t
– параметр надежности теста.
Теорема
Кармайкла
n
– число Кармайкла
![]() 1)n
1)n
свободно от квадратов (т.е. n
= p1∙p2∙…∙pk);
2) (pi
– 1)(n
– 1), i
= 1,…,k
;
3) k
![]() .
.
Наименьшее
известное число Кармайкла
n=561
= 3∙11·17
3.7. Применение теоремы Эйлера в rsa:
Если известно
разложение числа на простые сомножители
a
= p1![]() p2
p2![]() …
…
pn![]() ,
,
то легко вычислить функцию Эйлера φ(a).
Отсюда вывод:
сложность вычисления функции Эйлера
не выше сложности задачи факторизации
.
Покажем, что в
случае n=pq
(p,q
– простые числа, p![]() q)
q)
задачи нахождения функции Эйлера и
факторизации эквивалентны. (то есть в
случае, когда n
– модуль RSA).
Учтем, что φ(n)
= (p
– 1)(q
– 1). Тогда имеем систему
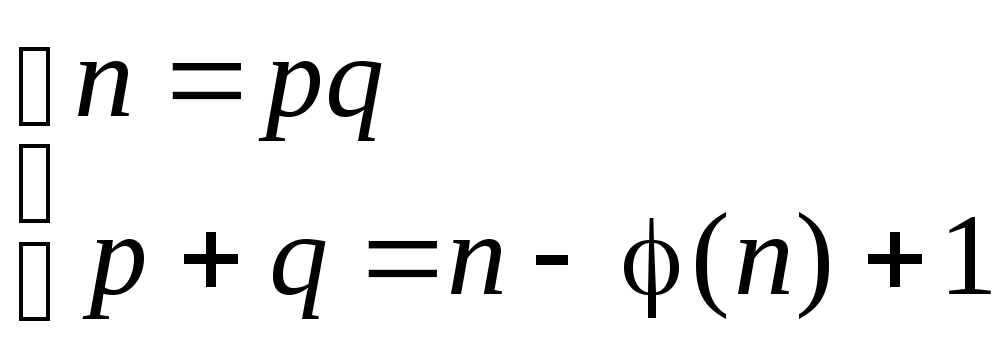 .
.
Зная n
и φ(n),
находим p
и q
из системы, приведенной выше, следующим
образом:
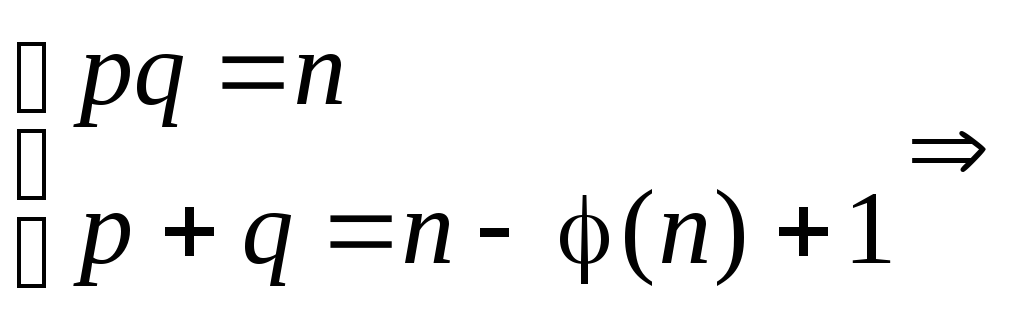
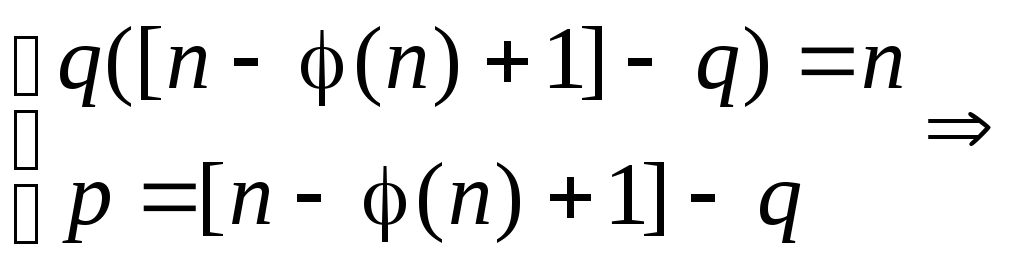

Первое уравнение
системы является квадратным уравнением
относительно q,
q
=
![]()
, где Dq
= [n–
φ(n)+1]2
– 4n.
Подставляя
полученное q
во второе уравнение системы, находим
p.
Видим, что при
нахождении чисел p,
q
по известным n,
φ(n)
применяются только «дешевые» в смысле
времени операции – сложение, деление
на 2. Только при вычислении дискриминанта
приходится применять возведение в
степень, а при вычислении q
– извлечение квадратного корня. Однако
эти операции производятся однократно,
поэтому временные затраты не столь
существенны.
Итак, для модуля
RSA
задачи нахождения функции Эйлера и
факторизации равносложны.
Формулировка
теоремы Эйлера для RSA:
n
= pq;
p≠q;
p,
q
– простые числа
![]()
![]() a
a
выполняется akφ(n)+1≡
a
(mod
n).
(на самом деле n
может быть просто свободно от квадратов,
то есть произведением произвольного
количества различных простых чисел)
Доказательство:
Возможны два
случая:
-
(a,
n)
= 1

по теореме Эйлера aφ(n)
≡ 1 (mod
n)
akφ(n)+1
= 1k
∙a
≡ a
(mod n).
-
(a,
n)
≠ 1, n
не делит a
в силу основного свойства простых
чисел, либо p
a,
либо q
a.
Не нарушая общности,
предположим, что pa,
q
не делит a.
Тогда по теореме
Ферма, akφ(n)+1≡a(mod
p),
qq–1≡1
(mod q)
![]() akφ(n)+1≡1k(p–1)·a
akφ(n)+1≡1k(p–1)·a
≡ a
(mod q).
Итак,
akφ(n)+1
≡ a
(mod p),
akφ(n)+1≡
a
(mod q).
Отсюда по
св-ву сравнений №12, akφ(n)+1≡
a(mod
НОК(p,q)).
В силу простоты p
и q,
НОК(p,q)=pq=n,
значит
akφ(n)+1≡
a
(mod n).
-
na
 a≡0(mod
a≡0(mod
n)

akφ(n)+1≡0≡a(mod
n).
□
Примечание:
Если вместо φ(n)
в теореме Эйлера для RSA
взять НОК(p–1,
q–1),
теорема все равно будет верна.
Применение
теоремы Эйлера в RSA:
Напомним, что
криптосистема RSA
является системой с открытым ключом.
В качестве параметров системы выбираются
различные большие простые числа p
и
q,
вычисляется n=pq,
φ(n)=(p–1)(q–1),
выбирается число e:
2<e<n,
(e,
φ(n))=1
и вычисляется d=e-1(mod
φ(n)).
В качестве открытого ключа берется
пара (n,
e),
в качестве закрытого, хранимого в
секрете, четверка (p,
q,
φ(n),
d).
Для того, чтобы
зашифровать открытый текст x,
абонент, пользуясь открытым ключом,
вычисляет зашифрованный текст y
по следующей формуле:
y
= xe
mod
n.
Для того, чтобы
осуществить расшифрование, владелец
секретного ключа вычисляет
x
= yd
mod
n.
В результате
такого расшифрования действительно
получится открытый текст, поскольку
yd
mod
n=xed
mod
n=xed
mod
φ(n)mod
n
=x1
mod
n=x.
Без знания простых
сомножителей p
и q
сложно вычислить значение функции
Эйлера φ(n),
а значит, и степень d,
в которую следует возводить зашифрованный
текст, чтобы получить открытый.
Более того, знание
простых сомножителей p
и q
может
значительно облегчить
процедуру возведения шифрованного
текста y
в степень d.
Действительно, пользуясь теоремой
Эйлера для RSA,
можем понизить степень d.
Разделим d
на φ(n)
с остатком:
d=kφ(n)+r
x=yd
mod
n=
ykφ(n)+r
mod
n=
yr
mod n.
Еще более можно
понизить степень, используя НОК(p–1,q–1)=![]()
вместо φ(n).
Пример:
n=19∙23=,
φ(n)=18∙22=396,
d=439.
НОК(18,22)=18∙22/2=198.
d
mod
φ(n)=43.
d
mod
НОК(p–1,q–1)=43.
Число d=439
в двоичном представлении есть 110110111.
Поэтому возведение в степень d
c
применением дихтономического алгоритма
(см. гл.2) требует 8 возведений в квадрат
и 6 умножений чисел.
Число 43 в двоичном
представлении есть 101011. Возведение в
степень 43 требует 5 возведений в квадрат
и 3 умножения чисел. Кроме того, для
вычисления φ(n)
требуется 1 операция умножения.
Таким образом,
для данного примера экономия времени
составляет 2 сложные операции.
В случае больших
простых делителей числа n
экономия оказывается более существенной.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.2. Испытание простоты чисел
Если формулы получения простых чисел, подобно формулам Ферма или Мерсенна, не гарантируют, что полученные числа — простые, то как мы можем генерировать большие простые числа для криптографии? Мы можем только выбрать случайно большое число и провести испытание, чтобы убедиться, что оно — простое.
Нахождение алгоритма, который правильно и эффективно проверяет очень большое целое число и устанавливает: данное число – простое это число или же составной объект, — всегда было проблемой в теории чисел и, следовательно, в криптографии. Однако, недавние исследования (одно из которых мы обсуждаем в этом разделе) выглядят очень перспективными.
Алгоритмы, которые решают эту проблему, могут быть разделены на две обширные категории — детерминированные алгоритмы и вероятностные алгоритмы. Ниже рассматриваются некоторые представители обеих категорий. Детерминированный алгоритм всегда дает правильный ответ. Вероятностный алгоритм дает правильный ответ в большинстве, но не во всех случаях. Хотя детерминированный алгоритм идеален, он обычно менее эффективен, чем соответствующий вероятностный.
Детерминированные алгоритмы
Детерминированный алгоритм, проверяющий простоту чисел, принимает целое число и выдает на выходе признак: это число — простое число или составной объект. До недавнего времени все детерминированные алгоритмы были неэффективны для нахождения больших простых чисел. Как мы коротко покажем, новые взгляды делают эти алгоритмы более перспективными.
Алгоритм теории делимости
Самое элементарное детерминированное испытание на простоту чисел — испытание на делимость. Мы используем в качестве делителей все числа, меньшие, чем 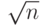 . Если любое из этих чисел делит n, тогда n — составное. Алгоритм 12.1 показывает проверку на делимость в ее примитивной и очень неэффективной форме.
. Если любое из этих чисел делит n, тогда n — составное. Алгоритм 12.1 показывает проверку на делимость в ее примитивной и очень неэффективной форме.
Алгоритм может быть улучшен, если проверять только нечетные номера. Он может быть улучшен далее, если использовать таблицу простых чисел между 2 и 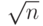 . Число арифметических операций в алгоритме 12.1 —
. Число арифметических операций в алгоритме 12.1 — 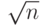 . Если мы принимаем, что каждая арифметическая операция использует только операцию на один бит (чисто условное соглашение), тогда сложность разрядной операции алгоритма 12.1 —
. Если мы принимаем, что каждая арифметическая операция использует только операцию на один бит (чисто условное соглашение), тогда сложность разрядной операции алгоритма 12.1 —  , где nb – число битов в n. В больших системах, обозначаемых О, сложность может быть оценена O(2n): экспоненциально (см. приложение L). Другими словами, алгоритм делимости неэффективен, если nb большое.
, где nb – число битов в n. В больших системах, обозначаемых О, сложность может быть оценена O(2n): экспоненциально (см. приложение L). Другими словами, алгоритм делимости неэффективен, если nb большое.
Сложность побитного испытания делимостью показательна.
Пример 12.18
Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм делимости?
Решение
Сложность побитовых операций этого алгоритма —  . Это означает, что алгоритму необходимо провести 2100 битовых операций. Если алгоритм имеет скорость 230 операций в секунду, то необходимо 270 секунд для проведения испытаний.
. Это означает, что алгоритму необходимо провести 2100 битовых операций. Если алгоритм имеет скорость 230 операций в секунду, то необходимо 270 секунд для проведения испытаний.
12.1.
AKS-алгоритм
В 2002 г. индийские ученые Агравал, Каял и Сахсена (Agrawal, Kayal и Saxena) объявили, что они нашли алгоритм для испытания простоты чисел с полиномиальной сложностью времени разрядных операций 0 ((log2nb)). Алгоритм использует тот факт, что 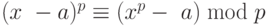 . Интересно наблюдать, что некоторые будущие разработки делают этот алгоритм стандартным тестом для определения простоты чисел в математике и информатике.
. Интересно наблюдать, что некоторые будущие разработки делают этот алгоритм стандартным тестом для определения простоты чисел в математике и информатике.
Пример 12.19
Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм AKS?
Решение
Сложность разрядной операции этого алгоритма — O((log 2 n b) 12). Это означает, что алгоритму надо только (log2 200) 12 = 39 547 615 483 битовых операций. На компьютере, способном выполнить 1 миллиард битов в секунду, алгоритму требуется только 40 секунд.
Вероятностные алгоритмы
До AKS-алгоритма все эффективные методы для испытания простоты чисел были вероятностные. Эти методы могут использоваться еще некоторое время, пока AKS формально не принят как стандарт.
Вероятностный алгоритм не гарантирует правильность результата. Однако мы можем получить вероятность ошибки настолько маленькую, что это почти гарантирует, что алгоритм вырабатывает правильный ответ. Сложность разрядной операции алгоритма может стать полиномиальной, при этом мы допускаем небольшой шанс для ошибок. Вероятностный алгоритм в этой категории возвращает результат либо простое число, либо составной объект, основываясь на следующих правилах:
a. Если целое число, которое будет проверено, — фактически простое число, алгоритм явно возвратит простое число.
b. Если целое число, которое будет проверено, — фактически составной объект, алгоритм возвращает составной объект с вероятностью  , но может возвратить простое число с
, но может возвратить простое число с 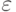 вероятности. Вероятность ошибки может быть улучшена, если мы выполняем алгоритм несколько раз с различными параметрами или с использованием различных методов. Если мы выполняем алгоритм m раз, вероятность ошибки может уменьшиться до m.
вероятности. Вероятность ошибки может быть улучшена, если мы выполняем алгоритм несколько раз с различными параметрами или с использованием различных методов. Если мы выполняем алгоритм m раз, вероятность ошибки может уменьшиться до m.
Тест Ферма
Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.
Если n — простое число, то 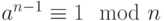 .
.
Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:
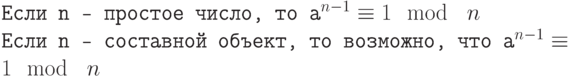
Простое число удовлетворяет тесту Ферма. Составной объект может пройти тест Ферма с вероятностью 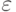 . Сложность разрядной операции испытания Ферма равна сложности алгоритма, который вычисляет возведение в степень. Позже в этой лекции мы приводим алгоритм для быстрого возведения в степень со сложностью разрядной операции O(nb ), где О — номер битов в n. Вероятность может быть улучшена, если проверка делается с несколькими числами (a1, a2 и так далее). Каждое испытание увеличивает вероятность, что испытуемое число – это простое число.
. Сложность разрядной операции испытания Ферма равна сложности алгоритма, который вычисляет возведение в степень. Позже в этой лекции мы приводим алгоритм для быстрого возведения в степень со сложностью разрядной операции O(nb ), где О — номер битов в n. Вероятность может быть улучшена, если проверка делается с несколькими числами (a1, a2 и так далее). Каждое испытание увеличивает вероятность, что испытуемое число – это простое число.
Пример 12.20
Проведите испытание Ферма для числа 561.
Решение
Используем в качестве основания число 2.
2561-1 = 1 mod 561
Число прошло тест Ферма, но это — не простое число, потому что
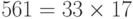 .
.
Испытание квадратным корнем
В модульной арифметике, если n — простое число, то квадратный корень равен только 1 (либо +1, либо –1). Если n — составной объект, то квадратный корень — +1 или (-1), но могут быть и другие корни. Это называют испытанием простоты чисел квадратным корнем. Обратите внимание, что в модульной арифметике –1 означает n–1.
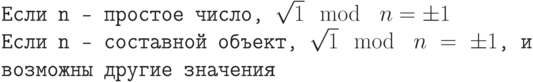
Пример 12.21
Каковы квадратные корни 1 mod n, если n равно 7 (простое число)?
Решение
Единственные квадратные корни 1 mod n – это числа 1 и –1. Мы можем видеть, что
12 = 1 mod 7 (–1)2 = 1 mod 7 22 = 4 mod 7 (–2)2 = 4 mod 7 32 = 2 mod 7 (–3)2 = 2 mod 7
Заметим, что тест не дает результатов для 4, 5 и 6, потому что 4 = –3 mod 7,
5 = –2 mod 7 и 6 = –1 mod 7.
Пример 12.22
Каков квадратный корень из 1 mod n, если n равно 8 (составное)?
Решение
Имеется три решения: 1, 3, 5 и 7 (которые дают –1). Мы можем также видеть, что
12 = 1 mod 8 (–1)2 = 1 mod 8 32 = 1 mod 8 (–5)2 = 1 mod 8
Пример 12.23
Каков квадратный корень из 1 mod n, если n равно 17 (простое)?
Решение
Имеются только два решения, соответствующие поставленной задаче: это 1 и (–1).
12 = 1 mod 17 (-1)2 = 1 mod 17 22 = 4 mod 17 (-2)2 = 4 mod 17 32 = 9 mod 17 (-3)2 = 9 mod 17 42 = 16 mod 17 (-4)2 = 16 mod 17 52 = 8 mod 17 (-5)2 = 8 mod 17 62 = 2 mod 17 (-6)2 = 2 mod 17 72 = 15 mod 17 (-7)2 = 15 mod 17 82 = 13 mod 17 (-8)2 = 13 mod 17
Заметим, что не надо проверять целые числа, большие 8, потому что 9 = –8 mod 17
Пример 12.24
Каков квадратный корень из 1 mod n, если n равно 22 (составное)?
Решение
Сюрприз в том, что имеется только два решения: +1 и –1, хотя 22 — составное число.
12 = 1 mod 22 (-1)2 = 1 mod 22
Хотя во многих случаях имеется испытание, которое показывает нам однозначно, что число составное, но это испытание провести трудно. Когда дано число n, то все числа, меньшие, чем n (кроме чисел 1 и n–1), должны быть возведены в квадрат, чтобы гарантировать, что ни одно из них не равно 1. Это испытание может использоваться для чисел (не +1 или –1), которые в квадрате по модулю n дают значение 1. Этот факт помогает в испытании Миллера–Рабина, которое рассматривается в следующем разделе.
Степан Кузнецов
«Квант» №10, 2020
Как быстро проверить, является ли данное натуральное число n простым? Такая задача часто возникает на практике. Один из примеров — шифр RSA1. Это асимметричный шифр: шифрование производится закрытым ключом (известен только отправителю), а расшифровка — открытым (известен всем). Чтобы сгенерировать такую пару ключей для шифра RSA, нужно выбрать два больших числа p и q, причем оба числа должны быть простыми — иначе шифр невозможно будет расшифровать.
Проще всего действовать по определению, перебирая все числа от 1 до n и проверяя, не является ли какое-то из них делителем. Этот способ можно немного усовершенствовать: если n = ab, то меньший из двух делителей a и b окажется меньше или равен (sqrt{n}). Значит, достаточно перебирать числа не до n, а всего лишь до (sqrt{n}).
Время работы такого алгоритма, однако, будет огромным. Например, если в двоичной записи числа n тысяча разрядов (это минимальная длина криптографического ключа RSA, гарантирующая безопасность), то число проверок равно (sqrt{n}) ≈ 2500 ≈ 3 ⋅ 2150. Если даже одна проверка делается за 1/109 секунды (частота 1 гигагерц), то для выяснения простоты числа n понадобится 3 ⋅ 10141 c ≈ 10134 лет! Можно попытаться «подобраться» к числу n с помощью решета Эратосфена, однако серьезного уменьшения времени работы это не даст. Нужны более глубокие идеи.
Начнем с малой теоремы Ферма (МТФ): если n — простое число, то для любого a от 1 до n − 1 число an − 1 при делении на n дает остаток 1 (т. е. a n − 1 ≡ 1(mod n)). Значит, если мы вдруг нашли такое a, что остаток оказался другим, то n заведомо не простое! Разумеется, перебирать все a в попытке найти нужное — затея не лучше, чем перебирать возможные делители. Но мы попробуем угадать a, выбирая его случайным образом.
Эта идея не такая безнадежная, как может показаться на первый взгляд. Действительно, пусть оказалось, что a0n − 1 (not≡) 1(mod n), а a1n − 1
≡ 1(mod n) (т. е. если мы выбрали a0 , то мы угадали, а если выбрали a1, то нет). Тогда
(a0 ⋅ a1)n − 1 ≡ a0n − 1 ⋅ a1n − 1 ≡ a0n − 1 (not≡) 1(mod n)
. Таким образом, если мы угадали с выбором a0, то также удачным будет выбор a0 ⋅ a1. Более того, если a0 взаимно просто с n, то для разных значений a1 числа a1 ⋅ a2 будут различны по модулю n. Таким образом, среди всех чисел от 1 до n − 1, взаимно простых с n, окажется не менее половины «удачных»: действительно, каждому «неудачному» числу a1 соответствует как минимум одно уникальное «удачное», равное остатку от деления a0 ⋅ a1 на n (где a0 — одно фиксированное «удачное» число).
Итак, алгоритм — его называют тестом Ферма — действует так. Выбираем случайное a в диапазоне от 2 до n − 1 (число 1 выбирать бессмысленно). Если a не взаимно просто с n — это можно быстро проверить с помощью алгоритма Евклида2 , то n заведомо составное. Иначе вычисляем остаток от деления a n − 1 на n, и если он не равен 1, то n — составное. Если же равен, то вероятность того, что мы выбрали «неудачное» a, а для другого a получился бы неединичный остаток, не превосходит 1/2. Возвести a в большую степень можно методом последовательного деления показателя пополам («быстрое возведение в степень»); при этом после каждого шага лучше брать остаток по модулю n, чтобы избежать слишком больших чисел. Повторяя алгоритм k раз, каждый раз выбирая случайное a независимо, мы уменьшим эту вероятность до 1/2k , что очень быстро стремится к нулю с ростом k.
Подведем итог. Если тест Ферма отвечает, что n составное, то он совершенно точно прав; если говорит, что простое — то может ошибиться, но с очень малой вероятностью. Эту вероятность мы контролируем за счет изменения параметра k — например, можем сделать ее меньше, чем вероятность сбоя техники. Тогда на практике алгоритм будет неотличим от точного — а работает он намного быстрее, чем перебор делителей!
К сожалению, у теста Ферма есть фатальный недостаток. Существуют так называемые числа Кармайкла: эти вредные числа не являются простыми, но удовлетворяют МТФ для любого a, взаимно простого с n. В таком случае мы не сможем найти ни одного «удачного» a0, и приведенное выше рассуждение недействительно. (Вероятность же случайно наткнуться на число a, не взаимно простое с n, мала.) Самые маленькие числа Кармайкла: 561, 1105, 1729. Числа Кармайкла относительно редки, однако, к сожалению, их бесконечно много3. (Иначе можно было бы «починить» тест Ферма, добавив в начале сверку с конечным списком чисел Кармайкла.)
Тем не менее, основную идею теста Ферма можно «спасти». Один из способов это сделать дает тест Соловея — Штрассена. Поскольку нас интересует случай нечетного n (иначе оно заведомо составное, если не равно 2), то n − 1 нацело делится на 2. Если n простое, то в силу МТФ имеем (left ( a^{frac{n-1}{2}}-1 right ) left ( a^{frac{n-1}{2}}+1 right )=a^{n-1}-1equiv0pmod{n}), откуда (a^{frac{n-1}{2}}equivpm1pmod{n}). Более того, знак (+ или –) можно вычислить, зная a и n — это символ Якоби (left (frac{a}{n} right )). Таким образом, мы получили новое сравнение, нарушение которого означает непростоту n, а именно: (a^{frac{n-1}{2}}equivleft ( frac{a}{n} right )pmod{n}). Теперь, однако, никакого аналога чисел Кармайкла нет: оказывается, что для составного n всегда найдется a0, для которого (a_0^{frac{n-1}{2}}notequivleft ( frac{a}{n} right )pmod{n}). Далее, как и для теста Ферма, можно доказать, что таких «удачных» a не менее половины среди всех чисел от 1 до n − 1, взаимно простых с n. Доказательства сформулированных выше фактов элементарные, но довольно технические. Их можно найти, например, в книге О. Н. Василенко «Теоретико-числовые алгоритмы в криптографии» (М.: МЦНМО, 2003).
Итак, получается алгоритм: выбираем случайное a от 2 до n − 1, взаимно простое с n (если нашлось не взаимно простое — немедленно отвечаем, что n составное); вычисляем остаток от деления (a^{frac{n-1}{2}}) на n и сравниваем его по модулю n с (left ( frac{a}{n} right )) . Если ответ «не равно», то a составное, иначе — предположительно простое. Во втором случае вероятность ошибки равна 1/2, теперь уже для любого n. Повторяя алгоритм k раз, снижаем вероятность ошибки до 1/2k .
Существуют и другие вероятностные тесты на простоту. А можно ли построить алгоритм проверки на простоту, который работает быстро и при этом выдает ответ точно, а не с некоторой (пусть и сколь угодно близкой к 1) вероятностью? Такие тесты называются детерминированными. Таков тест Миллера (1976). Этот тест быстрый и детерминированный, однако доказательство того, что он работает правильно, опирается на недоказанное утверждение — расширенную гипотезу Римана. Быстрый детерминированный тест, корректность которого доказана полностью, был предложен сравнительно недавно — это тест Агравала — Каяла — Саксены или AKS-тест (2002). Однако вероятностные тесты все еще работают быстрее, чем AKS-тест.
1 Подробнее о шифре RSA читайте в статье В.А. Успенского «Как теория чисел помогает в шифровальном деле» (Соросовский образовательный журнал, 1996, №6).
2 Вагутен В. Алгоритм Евклида и основная теорема арифметики («Квант», 1972, №6); Абрамов С. Самый знаменитый алгоритм («Квант», 1985, №11).
3 Alford W.R., Granville A., Pomerance C. There are infinitely many Carmichael numbers. Annals of Mathematics, 1994, vol. 139, p. 703–722.

