- Авторы
- Файлы
- Литература
Далингер В.А.
1
1 Омский государственный педагогический университет
1. Васин А.П., Лебедев А.К. Решение показательных и логарифмических уравнений и неравенств (методы решения конкурсных задач). – М.: Изд-во Центра заочного обучения «Пифагор», 1994.
2. Далингер В.А. Типичные ошибки по математике на вступительных экзаменах и как их не допускать. – Омск: Изд-во Омского ИУУ, 1991.
3. Далингер В.А. Все для обеспечения успеха на выпускных и вступительных экзаменах по математике. Выпуск 5. Показательные, логарифмические уравнения, неравенства и их системы: Учебное пособие. – Омск: Изд-во ОмГПУ, 1996.
4. Далингер В.А. Начала математического анализа: Типичные ошибки, их причины и пути предупреждения: Учебное пособие. – Омск: «Издатель-Полиграфист», 2002.
5. Далингер В.А., Зубков А.Н. Пособие для сдачи экзамена по математике: Анализ ошибок абитуриентов по математике и пути их предупреждения. – Омск: Изд-во ОмГПУ, 1991.
6. Кутасов А.Д. Показательные и логарифмические уравнения, неравенства, системы: Учебно-методическое пособие N7. – Изд-во Российского открытого университета, 1992.
Ошибки, допускаемые обучающимися при решении логарифмических уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера. об этих и других ошибках пойдет речь в этой статье.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних коней.
Рассмотрим на конкретных примерах ошибки подобного рода, но прежде обращаем внимание читателя на следующую мысль: не бойтесь приобрести посторонние корни, их можно отбросить путем проверки, бойтесь потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
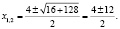
x1 = –4; x2 = 8.
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение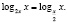 
Область определения исходного уравнения задается системой
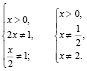
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
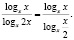
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению. Остановимся в связи с этим на примере.
Решить уравнение
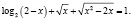
Найдем область определения этого уравнения, для чего решим систему неравенств:
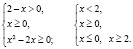
Откуда имеем x = 0. Проверим непосредственной подстановкой, является ли число x = 0 корнем исходного уравнения
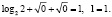
Ответ: x = 0.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Подтвердим сказанное следующим примером.
Решить уравнение
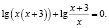
Приведем ошибочное решение этого уравнения:
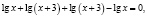
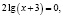
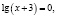
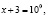
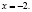
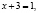х = –2.
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Проанализируем, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению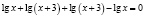 
эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
Чтобы избежать потери корня, можно поступить следующим образом: перейдем в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Покажем это на примере.
Решить неравенство
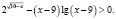
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
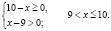
Для всех x из промежутка (9;10] выражение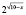 
имеет положительные значения (значения показательной функции всегда положительны).
Для всех x из промежутка (9;10] выражение x – 9 имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение (– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x∈ (9;10]. Заметим, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Решить уравнение
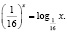
Наш опыт показывает, что учащиеся, решая это уравнение графически (заметим, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
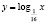и 
−
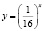это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень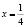 
и третий корень 
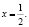Убедиться в справедливости сказанного можно непосредственной подстановкой чисел 
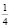и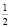 
в заданное уравнение.
Заметим, что уравнения вида logax = ax при 0 < a < e-e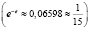 
всегда имеют три действительных корня.
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции разномонотонны (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Покажем типичные ошибки такого рода.
а) Решить уравнение xx = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
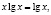
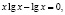
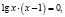
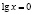или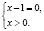 
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее мы потеряли два корня уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
б) Решить уравнение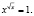 
Как и в предыдущем случае, мы имеем показательно-степенную функцию, а значит x > 0, x ≠ 1.
Для решения исходного уравнения прологарифмируем его обе части по любому основанию, например, по основанию 10: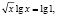 
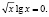
Учитывая, что произведение двух множителей равно нулю тогда, когда хотя бы один из них равен нулю, а другой при этом имеет смысл, мы имеем совокупность двух систем:
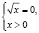или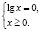 
Первая система не имеет решения; из второй системы мы получаем x = 1. Учитывая наложенные ранее ограничения, число x = 1 не должно являться корнем исходного уравнения, хотя непосредственной подстановкой мы убеждаемся в том, что это не так.
7. Рассмотрим некоторые ошибки, связанные с понятием сложной функции вида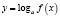 
. Ошибку покажем на таком примере.
Определить вид монотонности функции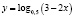 
.
Наша практика показывает, что абсолютное большинство учащихся определяют монотонность в данном случае лишь по основанию логарифма, а так как 0 < 0,5 < 1, то отсюда следует ошибочный вывод – функция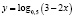 
убывает.
Нет! Эта функция возрастающая.
Условно для функции вида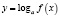 
можно записать:
– Возрастающая (Убывающая) = Убывающая;
– Возрастающая (Возрастающая) = Возрастающая;
– Убывающая (Убывающая) = Возрастающая;
– Убывающая (Возрастающая) = Убывающая;
8. Решите уравнение
.
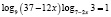Это задание взято из третьей части ЕГЭ, которое оценивается баллами (максимальный балл – 4).
Приведем решение, которое содержит ошибки, а значит за него не будет выставлен максимальный балл.
Сводим логарифмы к основанию 3. Уравнение примет вид
.
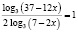Отсюда
,
.
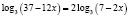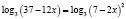Потенцируя, получаем
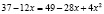или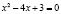 
,
х1 = 1, х2 = 3.
Выполним проверку, чтобы выявить посторонние корни
x = 1:
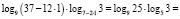
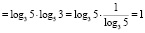, 1 = 1,
значит х = 1 – корень исходного уравнения.
х = 3:
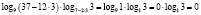, 0 ≠ 1,
значит х = 3 корнем исходного уравнения не является.
Поясним, почему это решение содержит ошибки. Суть ошибки в том, что запись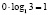 
, содержит две грубые ошибки. Первая ошибка: запись 
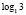вообще не имеет смысла. Вторая ошибка: не верно, что произведение двух сомножителей, один из которых 0, обязательно будет нулем. Ноль будет в том и только в том случае, если один множитель – 0, а второй множитель имеет смысл. Здесь же, как раз, второй множитель смысла не имеет.
9. Вернемся к уже прокомментированной выше ошибке, но при этом приведем и новые рассуждения.
При решении логарифмических уравнений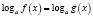 
переходят к уравнению 
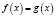. Каждый корень первого уравнения является корнем и второго уравнения. Обратное, вообще говоря, неверно, поэтому, переходя от уравнения 
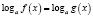к уравнению 
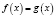, необходимо в конце проверить корни последнего подстановкой в исходное уравнение. Вместо проверки корней целесообразно заменять уравнение 
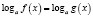равносильной системой
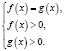
Если при решении логарифмического уравнения выражения
, 
, 
,
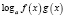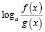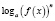где n – четное число, преобразовываются соответственно по формулам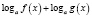 
, 
, 
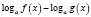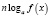, то, так как во многих случаях при этом сужается область определения уравнения, возможна потеря некоторых его корней. Поэтому указанные формулы целесообразно применять в следующем виде:
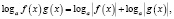
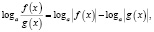
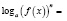
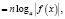
n – четное число.
Обратно, если при решении логарифмического уравнения выражения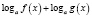 
, 
, 
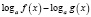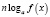, где n – четное число, преобразовываются соответственно в выражения
, 
, 
,
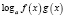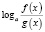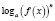то область определения уравнения может расшириться, в силу чего возможно приобретение посторонних корней. Помня об этом, в подобных ситуациях необходимо следить за равносильностью преобразований и, если область определения уравнения расширяется, делать проверку получаемых корней.
10. При решении логарифмических неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше, на стадии нахождения корней рациональной функции, получившейся в левой части неравенства. Этого делать не следует.
11. Приведем пример еще одной ошибки, связанной с решением неравенств.
Решите неравенство
.
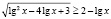Приведем ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
,
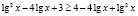откуда получаем неверное числовое неравенство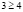 
, что позволяет сделать вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при х = 1000 имеем
, 
, 
.
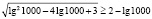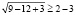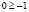Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Приведем правильное решение. Найдем область определения исходного неравенства. Она задается системой
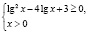или 
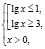
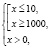откуда 
.
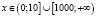Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а)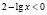 
, откуда х > 100. С учетом области определения исходного неравенства имеем промежуток 
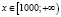. Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что 
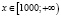– решение заданного неравенства.
б)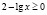 
, откуда 
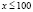. С учетом области определения исходного неравенства имеем промежуток 
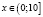. Для всех х из промежутка 
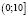имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: 
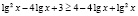, откуда 
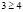. Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка 
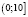решениями исходного неравенства не являются.
Ответ: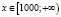 
.
12. Типичная ошибка при решении логарифмических уравнений, неравенств и их систем состоит в том, что неверно преобразовываются логарифмические выражения, входящие в них.
13. Часто допускаются ошибки при решении систем уравнений, в том числе и систем логарифмических уравнений, методом деления одного уравнения системы на другое.
Приведем пример такой ошибки, для чего указанным методом решим систему
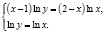
Разделив первое уравнение системы на второе, будем иметь
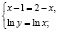
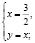
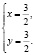
Но легко видеть, что и пара (1;1), которая удовлетворяет области определения системы уравнений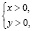 
также является решением системы. Действительно, подставляя х = 1 и у = 1 в исходную систему, имеем
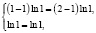откуда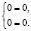 
Поясним, почему произошла потеря решения системы.
Если задана система двух уравнений с двумя неизвестными
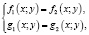
из которой мы получаем
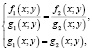
то вторая система уравнений будет следствием первой системы уравнений (значит содержит все решения первой системы) в том и только в том случае, когда нет ни одной пары (х; у), при которой бы функци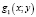и 
и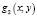 
одновременно обращались бы в ноль.
Как мы видим, такая пара (1; 1) в данном случае нашлась, потому-то и произошла потеря решения.
Более глубокий анализ этих и других ошибок читатель найдет в наших работах [2, 3, 4, 5].
Библиографическая ссылка
Далингер В.А. ТИПИЧНЫЕ ОШИБКИ УЧАЩИХСЯ ПРИ РЕШЕНИИ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ, НЕРАВЕНСТВ И ИХ СИСТЕМ И ПУТИ ИХ ПРЕДУПРЕЖДЕНИЯ // Международный журнал экспериментального образования. – 2015. – № 4-2.
– С. 445-450;
URL: https://expeducation.ru/ru/article/view?id=7437 (дата обращения: 28.06.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
План-конспект урока на тему «О типичных ошибках при решении логарифмических уравнений и неравенств».
Автор: Семёнов Илья Владимирович,
учитель ГАОУ РМЭ «Лицей Бауманский».
Цель урока: показать стандартные ошибки при решении логарифмических уравнений и неравенств с целью их предотвращения.
Задачи урок:
— образовательная: научить учащихся решать сложные логарифмические уравнения и неравенства рациональным способом, при этом правильно применять свойства логарифма;
— развивающая: развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом, развить навык рационального способа решения задач, развивать творческое мышление;
— воспитательная: воспитать культуру оформления сложных логарифмических уравнений и неравенств, культуру графической иллюстрации, самостоятельность, внимательность, умение работать в коллективе, умение вести диспут.
Тип урока: комбинированный урок.
Метод преподавания: словесный, объяснительно-иллюстративный.
Требования к учащимся:
- учащиеся должны знать: определение логарифма, его свойства; формулу перехода к новому основанию; особенности решения логарифмических неравенств по разному основанию; метод рационализации;
- учащиеся должны уметь: решать дробно-рациональные неравенства, использовать метод интервалов.
Оборудование: мел, доска.
Формы работы: фронтальная, индивидуальна, групповая.
Структура урока:
- Организационная часть урока.
Проверка учащихся и класса к уроку: наличие учебников и тетрадей, тишина в классе, чистота доски и влажность губки. Приветствие учащихся.
- Основная часть. Первичное закрепление.
Данный урок проводится после проведения входного контрольной работы. На основе проанализированных результатов (ошибок учащихся), а так же научных статей мы постарались выявить основные ошибки при решении логарифмических уравнений и неравенств.
Опишем основные из них:
А) Игнорирование модуля при вынесении четной степени из подлогарифмического выражения;
Б) Вынесение степени из подлогарифмического выражения, когда логарифм в какой-либо степени (;
В) Переменное основание (учащиеся решают логарифмические уравнения и неравенства по алгоритму, шаблонно, при этом имея скудный багаж решенных задач. По этой причине допускаются ошибки при решении логарифмического неравенства по основанию );
Г) Забывают сделать отбор корней через О.Д.З.;
Д) Хоть и не относится к логарифмическим уравнениям и неравенствам, но является частым следствием их решения решение дробно-рациональных неравенств, т.е. полное игнорирование знаменателя дроби при их решении;
Е) Нет четкой картины при использование метода интервалов;
Ж) Нет знаний элементарных функций, а в следствии и не могут верно накладывать ограничения при решении логарифмических уравнений и неравенств;
З) Неверное разложение логарифмических выражений:
—
—
И) Решая логарифмические неравенства методом замены не могут верно вернуться к введенной замене;
Й) Не видят разницы между системой и совокупностью, а в следствии не могут верно использовать равносильный переход и переход к введенной замене.
Постараемся учесть все замечания, изложенные выше и акцентировать на них внимание при решении данных проблем.
Учащимся предлагается решить логарифмические неравенства:
Начнем с первого неравенства:
О.Д.З.:
Разложив первое неравенство системы на линейные множители получаем: . Данные неравенство равносильны друг другу. Решением данной системы является промежуток
Переходим к решению логарифмического неравенства6
Разложив подлогарифмическое выражение на линейные множители получаем: .
С данного шага надо дать возможность учащимся самим выбрать путь решения:
1 способ.
С данного шага стоит уточнить порядок действий
А) можно использовать определение логарифма и перейти к выражению . В итоге мы получили сложное выражение, с которым сложно справиться.
Б) можно вынести четную степени из подлогарифмического выражения и получится выражение: . Главное в данном шаге это то, что при вынесении четной степени из подлогарифмичесокго выражения влечет то, что появляется модуль. На этом надо сделать акцент при объяснении материала.
Продолжаем решение: .
Используя определение логарифма получаем: .
По определению модуля получаем двойное неравенство:
Осталось найти пересечение множеств решения логарифмического неравенства с О.Д.З.: Решением данной системы является промежуток:
Ответ:
2 способ. Через разложение логарифма.
Приведем лишь рекомендации к решению. Используя формулы:
—
—
получаем следующее выражение:
.
Далее, решение логарифмического неравенства аналогично первому способу.
3 способ. Метод рационализации.
Объяснение по усмотрению учителя и в зависимости от профиля обучения. Так же в зависимости от доступного времени.
Переходим к решению второго неравенства.
Учащимся предлагается решать данное неравенство самостоятельно, а учитель указывает только ответ. Ответ: . На решение выделяется около 5-7 минут.
Вероятнее всего учащиеся не придут к верному ответу. Учащиеся зададутся, верен ли ответ, данный учителем. И вывод заключается в следующем – учащиеся, что то не учли. Может быть, кто-то дойдет до проблемы, если нет, то учитель объяснит сам.
Решение.
О.Д.З.: Решение системы:
Решим неравенство:
Проблема заключается в следующем – не учитывается то, что логарифм находится в квадрате (и не забываем что выносим четную степень), т.е.
Так как неравенство определено на множестве положительных чисел (по О.Д.З.), то модуль можно раскрывать с положительным значением.
Данное логарифмическое неравенство не сложно решить методом замены. Введем замену: .
Стоит спросить учащихся, а стоит ли накладывать ограничения на
Часто учащиеся не могут верно ответить на данный вопрос, потому что не имеют четкого представления о элементарных функция.
Как стоит поступить в данном случае? Стоит спросить учащихся, чем является ? А
это то, в какую степень возводят основание логарифма и получают подлогарифмическое выражение, а степень определена на множестве действительных чисел.
Продолжаем решать:
Разложив данное квадратное выражение на линейные множители получаем:
Главная проблема заключается в следующем: учащиеся находят корни квадратного выражения и бездумно возвращаются к подстановке не дорешав неравенство с введенной заменой. Стоит акцентировать внимание, что надо дорешать наше неравенство относительно .
Следующая проблема — учащиеся не могут перейти к введенной замене.
Стоит сделать следующее – спросить учащихся как представить промежуток через двойное неравенство. Ответ:
Далее задать вопрос – как данное двойное неравенство представить через систему или совокупность: И только с данного шага можно вернуться к подстановке:
Стоит спросить учащихся, какие условия есть для решения логарифмического неравенства по определению. Речь идет о том, что если , то знак неравенства сохраняется без изменений, если же
то необходимо поменять знак на противоположный.
Продолжаем решение:
Решением данной системы является промежуток: .
Осталось объединить решение логарифмического неравенства с О.Д.З.:. Решением данной системы является промежуток:
.
Ответ: .
Так же данное неравенство можно решить методом рационализации.
- Информация о домашнем задании.
На усмотрение учителя.
- Подведение итогов урока.
На данном уроке мы постарались уделить внимание основным ошибкам при решении логарифмических уравнений и неравенств.
Учитель спрашивает, полезна ли была данная информация для учащихся, весь ли материл был доступен и понятен. Есть ли у учащихся вопросы?
Учитель прощается. Урок окончен.
Конспект урока по теме «О типичных ошибках при решении логарифмических уравнений и неравенств»
план-конспект урока по алгебре (11 класс)
Даннная разработка может быть интересна для учителей, которые хотят обратить внимание учащихся на типичные ошибки при решении логарифмических уравненияхи неравенств.
Скачать:
| Вложение | Размер |
|---|---|
| plan-konspekt_uroka_3.docx | 27.89 КБ |
Предварительный просмотр:
План-конспект урока на тему «О типичных ошибках при решении логарифмических уравнений и неравенств».
Автор: Семёнов Илья Владимирович,
учитель ГАОУ РМЭ «Лицей Бауманский».
Цель урока: показать стандартные ошибки при решении логарифмических уравнений и неравенств с целью их предотвращения.
— образовательная: научить учащихся решать сложные логарифмические уравнения и неравенства рациональным способом, при этом правильно применять свойства логарифма;
— развивающая: развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом, развить навык рационального способа решения задач, развивать творческое мышление;
— воспитательная: воспитать культуру оформления сложных логарифмических уравнений и неравенств, культуру графической иллюстрации, самостоятельность, внимательность, умение работать в коллективе, умение вести диспут.
Тип урока: комбинированный урок.
Метод преподавания: словесный, объяснительно-иллюстративный.
Требования к учащимся:
- учащиеся должны знать: определение логарифма, его свойства; формулу перехода к новому основанию; особенности решения логарифмических неравенств по разному основанию; метод рационализации;
- учащиеся должны уметь: решать дробно-рациональные неравенства, использовать метод интервалов.
Оборудование: мел, доска.
Формы работы: фронтальная, индивидуальна, групповая.
- Организационная часть урока.
Проверка учащихся и класса к уроку: наличие учебников и тетрадей, тишина в классе, чистота доски и влажность губки. Приветствие учащихся.
- Основная часть. Первичное закрепление.
Данный урок проводится после проведения входного контрольной работы. На основе проанализированных результатов (ошибок учащихся), а так же научных статей мы постарались выявить основные ошибки при решении логарифмических уравнений и неравенств.
Опишем основные из них:
А) Игнорирование модуля при вынесении четной степени из подлогарифмического выражения;
Б) Вынесение степени из подлогарифмического выражения, когда логарифм в какой-либо степени ( ;
В) Переменное основание (учащиеся решают логарифмические уравнения и неравенства по алгоритму, шаблонно, при этом имея скудный багаж решенных задач. По этой причине допускаются ошибки при решении логарифмического неравенства по основанию );
Г) Забывают сделать отбор корней через О.Д.З.;
Д) Хоть и не относится к логарифмическим уравнениям и неравенствам, но является частым следствием их решения решение дробно-рациональных неравенств, т.е. полное игнорирование знаменателя дроби при их решении;
Е) Нет четкой картины при использование метода интервалов;
Ж) Нет знаний элементарных функций, а в следствии и не могут верно накладывать ограничения при решении логарифмических уравнений и неравенств;
З) Неверное разложение логарифмических выражений:
И) Решая логарифмические неравенства методом замены не могут верно вернуться к введенной замене;
Й) Не видят разницы между системой и совокупностью, а в следствии не могут верно использовать равносильный переход и переход к введенной замене.
Постараемся учесть все замечания, изложенные выше и акцентировать на них внимание при решении данных проблем.
Учащимся предлагается решить логарифмические неравенства:
Начнем с первого неравенства:
Разложив первое неравенство системы на линейные множители получаем: . Данные неравенство равносильны друг другу. Решением данной системы является промежуток
Переходим к решению логарифмического неравенства6
Разложив подлогарифмическое выражение на линейные множители получаем: .
С данного шага надо дать возможность учащимся самим выбрать путь решения:
С данного шага стоит уточнить порядок действий
А) можно использовать определение логарифма и перейти к выражению . В итоге мы получили сложное выражение, с которым сложно справиться.
Б) можно вынести четную степени из подлогарифмического выражения и получится выражение: . Главное в данном шаге это то, что при вынесении четной степени из подлогарифмичесокго выражения влечет то, что появляется модуль. На этом надо сделать акцент при объяснении материала.
Используя определение логарифма получаем: .
По определению модуля получаем двойное неравенство:
Осталось найти пересечение множеств решения логарифмического неравенства с О.Д.З.: Решением данной системы является промежуток:
2 способ. Через разложение логарифма.
Приведем лишь рекомендации к решению. Используя формулы:
—
получаем следующее выражение:
Далее, решение логарифмического неравенства аналогично первому способу.
3 способ. Метод рационализации.
Объяснение по усмотрению учителя и в зависимости от профиля обучения. Так же в зависимости от доступного времени.
Переходим к решению второго неравенства.
Учащимся предлагается решать данное неравенство самостоятельно, а учитель указывает только ответ. Ответ: . На решение выделяется около 5-7 минут.
Вероятнее всего учащиеся не придут к верному ответу. Учащиеся зададутся, верен ли ответ, данный учителем. И вывод заключается в следующем – учащиеся, что то не учли. Может быть, кто-то дойдет до проблемы, если нет, то учитель объяснит сам.
О.Д.З.: Решение системы:
Проблема заключается в следующем – не учитывается то, что логарифм находится в квадрате (и не забываем что выносим четную степень), т.е.
Так как неравенство определено на множестве положительных чисел (по О.Д.З.), то модуль можно раскрывать с положительным значением.
Данное логарифмическое неравенство не сложно решить методом замены. Введем замену: .
Стоит спросить учащихся, а стоит ли накладывать ограничения на
Часто учащиеся не могут верно ответить на данный вопрос, потому что не имеют четкого представления о элементарных функция.
Как стоит поступить в данном случае? Стоит спросить учащихся, чем является ? А это то, в какую степень возводят основание логарифма и получают подлогарифмическое выражение, а степень определена на множестве действительных чисел.
Разложив данное квадратное выражение на линейные множители получаем:
Главная проблема заключается в следующем: учащиеся находят корни квадратного выражения и бездумно возвращаются к подстановке не дорешав неравенство с введенной заменой. Стоит акцентировать внимание, что надо дорешать наше неравенство относительно .
Следующая проблема — учащиеся не могут перейти к введенной замене.
Стоит сделать следующее – спросить учащихся как представить промежуток через двойное неравенство. Ответ:
Далее задать вопрос – как данное двойное неравенство представить через систему или совокупность: И только с данного шага можно вернуться к подстановке:
Стоит спросить учащихся, какие условия есть для решения логарифмического неравенства по определению. Речь идет о том, что если , то знак неравенства сохраняется без изменений, если же то необходимо поменять знак на противоположный.
Решением данной системы является промежуток: .
Осталось объединить решение логарифмического неравенства с О.Д.З.: . Решением данной системы является промежуток: .
Так же данное неравенство можно решить методом рационализации.
- Информация о домашнем задании.
На усмотрение учителя.
На данном уроке мы постарались уделить внимание основным ошибкам при решении логарифмических уравнений и неравенств.
Учитель спрашивает, полезна ли была данная информация для учащихся, весь ли материл был доступен и понятен. Есть ли у учащихся вопросы?
math4school.ru
Ошибки в уравнениях
При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней , либо появление посторонних корней .
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного , а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10) 2 + lg x 2 = 2lg 24 .
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Комментарий . Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
Ответ: –2; 4; 6 и 12.
При делении обеих частей уравнения на выражение, содержащее неизвестное , могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3 х ( х 2 – 2 х – 3) = 9 ( х 2 – 2 х – 3) .
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
K Упражнение 2. Решить уравнение lg 2 x – lg x = 0 .
L Неправильное решение.
Разделим обе части уравнения на lg x и получим:
J Правильное решение.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину .
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0 . |
| x – 1 | x 2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х 2 – 1 и получим:
Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .
J Правильный ответ: х = 0.
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .
K Упражнение. Решить уравнение
L Неправильное решение.
Заметим, что х 2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9 . Имеем:
Комментарий . Был приобретен посторонний корень х = 9 .
J Правильный ответ: решений нет.
Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.
K Упражнение. Решить уравнение
| 2 | + х 2 – | 2 | – 4х = 0 . |
| 3х 2 | 3х 2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
Комментарий . Был приобретен посторонний корень х = 0 .
J Правильный ответ: 4 .
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .
L Неправильное решение.
И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.
Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
которое уже имеет один корень –2 , к уравнению
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3 .
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:
| tg ( x + y ) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2 x = | 2 tg x |
| 1 + tg 2 x |
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .
L Неправильное решение.
так как х ≥ 3 , то |х – 1| = х – 1 и
Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений <1>∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
Проверкой убеждаемся, что оба корня действительные.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .
K Упражнение. Решить уравнение (5 left(x-3 right)^<1/4>-6=left(x-3 right)^<1/2>.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^<1/2>=t), считают, что ( left(x-3 right)^<1/4>=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^<1/4>=t), тогда ( left(x-3 right)^<1/2>=t^2) с продолжением:
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .
K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .
L Неправильное решение.
Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .
J Правильное решение.
При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .
K Упражнение. Решить уравнение (x^2-4x-sqrt<2x^2-8x+12>=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
и исходное уравнение принимает вид:
А дальше все просто:
Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt=9.)
L Неправильное решение.
J Правильное решение.
K Упражнение 2. Решить уравнение (sqrt<(x+3)^2>=x+3.)
L Неправильное решение.
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .
J Правильное решение.
Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
На каждом из этих промежутков исходное уравнение принимает свой вид.
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
так как 4 ∈ [4; +∞) , то 4 – корень уравнения.
Так как [3; 4)∪ <4>= [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
введем новую переменную x 2 + 3х + 1 = t , тогда
1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.
K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .
L Неправильное решение.
Методом подбора находим корень уравнения х = 1 .
Комментарий . Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x) 1 /3 = 1 .
L Неправильное решение.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .
L Неправильное решение.
Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.
L Неправильное решение.
Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
K Упражнение 2. Решить уравнение lg x 2 = 4 .
L Неправильное решение.
J Правильное решение 1.
2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.
J Правильное решение 2.
lg x 2 = lg 10000; x 2 = 10000; x = ±100.
Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .
K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _<5>>^2 ;x=0.)
L Неправильное решение.
(left(1 +2 log _<5>xright)log _<5>x=0;)
Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.
K Упражнение 2. Решить уравнение (20log_<4x>sqrt+ 7log_<16x>x^3-3log _x^2=0.)
L Неправильное решение.
Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. ТИПИЧНЫЕ ОШИБКИ ПРИ РЕШЕНИИ. Рекомендацииучителю Пояснительная записка Начать работу Авторы: Мохова В.Ю. учитель математики. — презентация
Презентация была опубликована 9 лет назад пользователемtriangle.ucoz.ru
Похожие презентации
Презентация по предмету «Математика» на тему: «ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. ТИПИЧНЫЕ ОШИБКИ ПРИ РЕШЕНИИ. Рекомендацииучителю Пояснительная записка Начать работу Авторы: Мохова В.Ю. учитель математики.». Скачать бесплатно и без регистрации. — Транскрипт:
2 ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. ТИПИЧНЫЕ ОШИБКИ ПРИ РЕШЕНИИ. Рекомендацииучителю Пояснительная записка Начать работу Авторы: Мохова В.Ю. учитель математики школы 381, Хмелинина Л.А. учитель математики школы 478.
3 Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ
4 Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ X=16
5 Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ X=4 или X=-4 Посмотреть решение
6 Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ X=100
7 Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ x=10 2/3
8 log 2 x 2 =4 x 2 =2 4 x 2 =16 х = 4 или х = -4 Ответ:4;-4. Другое решение
9 log 2 x 2 =4 2·log 2 |x|=4 log 2 |x|=2 |x|=4 x = 4 или x = -4 Ответ:4;-4.
10 log 2 (4-x)+log 2 (1-2x)=2log 2 3lgx 2 +lgx 6 =8 2lgx+6lgx=8 8lgx=8 lgx=1 x=10 Ответ: 10. Найди ошибку и запиши правильное решение ПодсказкаПодсказка 2 Ответ ПодсказкаОтветПодсказка1
11 log 2 (4-x)+log 2 (1-2x)=2log 2 3 (1) log 2 ((4-x)(1-2x))=log (2) Уравнение (1) не равносильно уравнению (2), поэтому нужно сделать проверку или указать О.Д.З., тогда увидишь посторонний корень.
12 log 2 (4-x)+log 2 (1-2x)=2log 2 3lgx 2 +lgx 6 =8 2lgx+6lgx=8 8lgx=8 lgx=1 x=10 Ответ: 10. Найди ошибку и запиши правильное решение Ответ ПодсказкаПодсказка2 Ответ — Подсказка1
13 lgx 2 +lgx 6 =8 2lgx+6lgx=8 Неправильно вынесен показатель степени. Нужно сделать так: 2lg|x|+6lg|x|=8
14 log 2 (4-x)+log 2 (1-2x)=2log 2 3lgx 2 +lgx 6 =8 2lgx+6lgx=8 8lgx=8 lgx=1 x=10 Ответ: 10. Найди ошибку и запиши правильное решение Подсказка Ответ ПодсказкаОтвет 10; -10.
15 Это уравнение lgx 2 +lgx 6 =8 можно решить иначе lg(x 2 x 6 )=8 x 8 =10 8 x=10 или x=-10 Ответ: 10; -10.
16 Найди правильное решение уравнения lgxlg(2+x)=lgx /:lgx lg(2+x)=1 2+x=10 x=8 Ответ:8. проверить lgxlg(2+x)=lgx lgxlg(2+x)-lgx=0 lgx·(lg(2+x)-1)=0 lgx=0 или lg(2+x)-1=0 x=1 2+x=10 x=8 Ответ:1;8. lgxlg(2+x)=lgx Решение первоеРешение второе
17 Правильное решение — второе. В первом случае потерян корень. Посмотреть еще раз Дальше
18 В рассмотренных примерах мы отработали две ошибки: -потеря корня; -лишний корень.
19 Реши сам Если ты уверен в своих знаниях и хочешь заработать оценку «5», то выбирай задания здесь Если ты не очень уверен в своих знаниях, то выбирай задания здесь.
20 На оценку 5 реши уравнения: 1. log 3 2 (9x 2 )=log 3 81 Проверить ответПроверить ответ 2. lg(lgx)+lg(lgx 3 -2)=0 Проверить ответПроверить ответ
21 Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответПроверить ответ 2. log 3 (x-2) log 3 x=log 3 (x-2) Проверить ответ Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ Проверить ответ
22 Если решил правильно, то молодец и можешь закончить занятие.
23 На оценку 5 реши уравнения: 1. log 3 2 (9x 2 )=log 3 81 Проверить ответ 2. lg(lgx)+lg(lgx 3 -2)=0 Проверить ответПроверить ответ -1; 1; 1/9; -1/9.
24 На оценку 5 реши уравнения: 1. log 3 2 (9x 2 )=log 3 81 Проверить ответПроверить ответ 2. lg(lgx)+lg(lgx 3 -2)=0 Проверить ответ 10
25 Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответ 2. log 3 (x-2) log 3 x=log 3 (x-2) Проверить ответ Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ Проверить ответ 2
26 Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответПроверить ответ 2. log 3 (x-2) ·log 3 x=log 3 (x-2) Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ Проверить ответ 3
27 Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответПроверить ответ 2. log 3 (x-2) ·log 3 x=log 3 (x-2) Проверить ответ Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ -1/10; 1/10.
28 Если решил правильно, то молодец и можешь закончить занятие.
29 Если решил правильно, то молодец и можешь закончить занятие Или попробуй решить на «5»
30 Если у Вас осталось время, то можете заглянуть на историческую страничку или посмотреть логарифмическую комедию. Страничка истории Логарифмическая комедия
31 Действие — возведение в степень -имеет два обратных. Если a b =c, то отыскание a есть одно обратное действие – извлечение корня; нахождение же b – другое, логарифмирование. Для чего были придуманы логарифмы? Конечно, для ускорения и упрощения вычислений. Логарифмы дают возможность производить такие операции, выполнение которых без их помощи очень затруднительно (извлечение корня любой степени). Об этом можно прочитать в книге «Занимательная алгебра» Я.И.Перельмана. Немного истории Закончить работу Далее
3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)» title=»Логарифмическая комедия Докажем, что 2>3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)» > 32 Логарифмическая комедия Докажем, что 2>3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)>3lg(1/2). После сокращения на lg(1/2) Имеем: 2>3. В чем ошибка этого доказательства? Решение 3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)»> 3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)>3lg(1/2). После сокращения на lg(1/2) Имеем: 2>3. В чем ошибка этого доказательства? Решение»> 3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)» title=»Логарифмическая комедия Докажем, что 2>3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)»>
на на 33 Ошибка в том, что при сокращении на lg(1/2) не был изменен знак неравенства ( > на на на на на
источники:
http://math4school.ru/oshibki_v_uravnenijah.html
http://www.myshared.ru/slide/224744/
- Журнал
- О журнале
АНАЛИЗ И РАЗБОР ТИПИЧНЫХ ОШИБОК ЗАДАНИЙ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО ТЕМЕ: «ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ»
УДК 512:371.279.6
А. В. Таллерова
A. V. Tallerova
Таллерова Анастасия Валерьевна, студентка 2 курса магистратуры ФФМиТО УлГПУ, г. Ульяновск.
Tallerova Anastasiya Valerievna, 2-year student of a master’s degree of the faculty of physics, mathematics and technology education of ULSPU, Ulyanovsk.
АНАЛИЗ И РАЗБОР ТИПИЧНЫХ ОШИБОК ЗАДАНИЙ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО ТЕМЕ: «ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ»
ANALYSIS AND PARSING OF TYPICAL ERRORS OF THE JOBS OF THE SINGLE STATE EXAM ON THE TOPIC: «LOGARIFMIC EQUATIONS»
Аннотация. Статья посвящена анализу и разбору типичных ошибок заданий единого государственного экзамена по математике профильного уровня на примере разбора логарифмических уравнений. Приводятся примеры заданий за выбранные периоды, и рассматриваются типичные ошибки учащихся, допускаемых при решении логарифмических уравнений.
Annotation. The article is devoted to the analysis of typical errors of tasks of the unified state exam in mathematics of the profile level on the example of the analysis of logarithmic equations. Examples of assignments for the selected periods are given, and typical student mistakes made when solving logarithmic equations.
Ключевые слова: логарифмы, свойства логарифмов, уравнения, типичные ошибки.
Keywords: logarithms, properties of logarithms, equation, typical error.
Одной из важных тем в курсе алгебры в средней школе является тема «Логарифмы». Тема очень непросто дается учащимся из-за подачи многообразия материала. Однако овладеть методикой решения логарифмических уравнений очень важно, так как повышаются умственные и творческие способности обучающихся, приобретаются навыки исследовательской работы, развиваются способности к логическому мышлению, происходит более глубокое усвоение учебного материала. Но более важным фактором является присутствие логарифмов в заданиях ЕГЭ.
В настоящее время учителю необходимо непрерывно повышать свой профессиональный уровень. Если раньше, до появления ЕГЭ, учитель считал, что подготовка выпускников к поступлению в вуз не является его главной задачей и он не несет ответственности за поступление учащихся в вуз, то сейчас каждый учитель должен быть заинтересован в получении высоких результатов ЕГЭ, так как по ним судят о его профессиональном уровне.
Чтобы обучающиеся смогли успешно сдать ЕГЭ, необходимо постоянно уделять внимание решению логарифмических уравнений на уроках. Главной задачей при изучении данной темы на уроках заинтересовать их темой. Но порою незнание определений, свойств, видов и способов решения, невнимательность, ведущая к допуску типичных ошибок, затрудняют деятельность учащихся. И для того, чтобы это предотвратить, необходимо проводить анализ заданий, разбор типичных ошибок.
Логарифмические уравнения в заданиях ЕГЭ профильного уровня встречаются в 5 и 13 заданиях. Заданием 5 являются уравнения, не требующие развёрнутого решения, по сравнению с заданием 13. Заданием № 13 являются уравнения, как правило, требующее замены переменной [1], позволяющей свести уравнение к квадратному, отбора корней на заданном отрезке, обусловленного ограниченностью новой переменной, наличием выражений с переменной под знаками логарифмов.
Проведя небольшой анализ 13 задания из ЕГЭ за период с 2011 по 2018 год можно сделать вывод. Во-первых, для решения логарифмических уравнений помимо определения логарифма и его свойств, ещё необходимо знать и уметь правильно и без ошибок решать другие виды уравнений, получаемые путём преобразований: квадратные, показательные, тригонометрические. Помимо этого, также немаловажную роль играет умение работать над алгебраическими выражениями, над их преобразованиями: группировка, вынесение общего множителя за скобки, применение формул сокращенного умножения и т.д.
Например, в одном из вариантов за 2017 год было представлено уравнение вида: 
. При решении данного логарифмического уравнения по определению логарифма, в результате задача свелась к решению тригонометрического уравнения 
.
Во-вторых, задание № 13 варианта ЕГЭ часто представляет собой уравнение, которое нужно не просто решить, но и выбрать корни уравнения, удовлетворяющие условию.
Так, один из вариантов 2017 года включал следующее задание:
- Решите уравнение
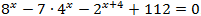. - Укажите корни этого уравнения, принадлежащие отрезку
.
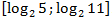Также может попасться уравнение, которое сначала не будет подавать никаких признаков пребывания здесь логарифмов. Например, уравнение попавшееся учащимся в одном из вариантов за 2014 год, имело вид 
При решении, путём алгебраических преобразований и вводом новой переменной, в итоге мы получаем два показательных уравнения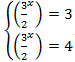 
, решая которые получаются корни 
.
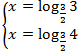Поэтому для того, чтобы довести данное уравнение до конца, необходимо знать неразрывную связь между показательной и логарифмической функциями.
В-третьих, изучение методов решения логарифмических уравнений является хорошей подготовкой к решению задачи под номером 15, так как в основных методах решения и уравнений, и неравенств фактически используются одни и те же математические идеи.
Просматривая и анализируя задания из ЕГЭ за данные периоды, можно сделать вывод, что логарифмические уравнения не сдают своих позиций и остаются одной из важных и значимых тем, хоть и уступают тригонометрическим уравнениям.
Основные методы решения логарифмических уравнений несложно запомнить, их всего пять: сведение к простейшему уравнению, использование равносильных переходов, введение новых неизвестных, логарифмирование и разложение на множители. Как правило, в задаче № 13 встречаются уравнения, требующие применения перечисленных выше пяти основных методов.
Несмотря на то, что 13 задание достаточно традиционно, процент его выполнения всего 23 %, из которых один балл получают лишь 6 % школьников. Экзаменаторы отмечают, что ученики не понимают условие задания, допускают простейшие арифметические ошибки и не умеют себя проверить – все это, естественно, очень негативно влияет на результат [3].
Какие типичные ошибки совершают экзаменуемые? По-прежнему учащиеся теряют балл в 13 задании в пункте б) по причине отсутствия обоснованного отбора корней из промежутка.
Также при решении логарифмических уравнений следует обратить внимание учащихся на то, что применение следующих формул: 
может привести как к приобретению, так и к потере корней. При решении уравнений, заменяя выражение 
на выражение 
, можно получить посторонние корни. А вот потеря корней происходит при делении обеих частей уравнения на одно и то же выражение, содержащее неизвестное. Поэтому рекомендуется следить за равносильностью уравнений [1], получаемых в результате преобразований.
Еще одна ошибка – применение свойств логарифмов без учета области допустимых значений. Например, хорошо знакомое многим свойство «логарифм произведения равен сумме логарифмов», оказывается, имеет уточнение: 
Действительно, для того, чтобы было определено выражение в левой части этого равенства, достаточно, чтобы произведение функций f и g было положительным, но сами функции при этом могут быть как одновременно больше, так и одновременно меньше нуля, поэтому при применении данного свойства необходимо использовать понятие модуля [2].
И таких примеров можно привести немало. Поэтому для эффективного освоения решения логарифмических уравнений необходимо не только прорешивать подобные задания самостоятельно, но и также обращаться за помощью к опытным преподавателям, которые расскажут обо всех «подводных камнях».
Список литературы
- Шестаков, С. А. ЕГЭ 2011. Математика. Задача С1. Уравнения и системы уравнений [Текст] / С. А. Шестаков, П. И. Захаров : под ред. А. Л. Семенова и И. В. Ященко. – М. : МЦНМО, 2011. – 120 с.
- Тишин, В. И. Логарифмические уравнения. Методическое пособие для средней школы [Текст]. / В. И. Тишин. – Брянск, 2002. – 45 с.
- Далингер, В. А. Причины типичных ошибок, допускаемых учащимися в процессе изучения математики и самоконтроль как средство организации рефлексии по предупреждению ошибок / В. А. Далингер, О. А. Тарасова : под ред. О. И. Кирикова. – Кн. 2. – Воронеж : ВГПУ, 2004. – С. 216-143.
Теги: логарифмы, свойства логарифмов, уравнения, типичные ошибки, logarithms, properties of logarithms, equation, typical error
Оставить комментарий
| Авторизация |
|---|
|
Пароль Регистрация |
1
2
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. ТИПИЧНЫЕ ОШИБКИ ПРИ РЕШЕНИИ. Рекомендацииучителю Пояснительная записка Начать работу Авторы: Мохова В.Ю. учитель математики школы 381, Хмелинина Л.А. учитель математики школы 478.
3
Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ
4
Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ X=16
5
Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ X=4 или X=-4 Посмотреть решение
6
Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ X=100
7
Устно реши уравнения Проверь ответ Проверь ответ Проверь ответ log 2 x=4log 2 x 2 =4lgx=2lgx 3 =2 Проверь ответ x=10 2/3
8
log 2 x 2 =4 x 2 =2 4 x 2 =16 х = 4 или х = -4 Ответ:4;-4. Другое решение
9
log 2 x 2 =4 2·log 2 |x|=4 log 2 |x|=2 |x|=4 x = 4 или x = -4 Ответ:4;-4.
10
log 2 (4-x)+log 2 (1-2x)=2log 2 3lgx 2 +lgx 6 =8 2lgx+6lgx=8 8lgx=8 lgx=1 x=10 Ответ: 10. Найди ошибку и запиши правильное решение ПодсказкаПодсказка 2 Ответ ПодсказкаОтветПодсказка1
11
log 2 (4-x)+log 2 (1-2x)=2log 2 3 (1) log 2 ((4-x)(1-2x))=log (2) Уравнение (1) не равносильно уравнению (2), поэтому нужно сделать проверку или указать О.Д.З., тогда увидишь посторонний корень.
12
log 2 (4-x)+log 2 (1-2x)=2log 2 3lgx 2 +lgx 6 =8 2lgx+6lgx=8 8lgx=8 lgx=1 x=10 Ответ: 10. Найди ошибку и запиши правильное решение Ответ ПодсказкаПодсказка2 Ответ — Подсказка1
13
lgx 2 +lgx 6 =8 2lgx+6lgx=8 Неправильно вынесен показатель степени. Нужно сделать так: 2lg|x|+6lg|x|=8
14
log 2 (4-x)+log 2 (1-2x)=2log 2 3lgx 2 +lgx 6 =8 2lgx+6lgx=8 8lgx=8 lgx=1 x=10 Ответ: 10. Найди ошибку и запиши правильное решение Подсказка Ответ ПодсказкаОтвет 10; -10.
15
Это уравнение lgx 2 +lgx 6 =8 можно решить иначе lg(x 2 x 6 )=8 x 8 =10 8 x=10 или x=-10 Ответ: 10; -10.
16
Найди правильное решение уравнения lgxlg(2+x)=lgx /:lgx lg(2+x)=1 2+x=10 x=8 Ответ:8. проверить lgxlg(2+x)=lgx lgxlg(2+x)-lgx=0 lgx·(lg(2+x)-1)=0 lgx=0 или lg(2+x)-1=0 x=1 2+x=10 x=8 Ответ:1;8. lgxlg(2+x)=lgx Решение первоеРешение второе
17
Правильное решение — второе. В первом случае потерян корень. Посмотреть еще раз Дальше
18
В рассмотренных примерах мы отработали две ошибки: -потеря корня; -лишний корень.
19
Реши сам Если ты уверен в своих знаниях и хочешь заработать оценку «5», то выбирай задания здесь Если ты не очень уверен в своих знаниях, то выбирай задания здесь.
20
На оценку 5 реши уравнения: 1. log 3 2 (9x 2 )=log 3 81 Проверить ответПроверить ответ 2. lg(lgx)+lg(lgx 3 -2)=0 Проверить ответПроверить ответ
21
Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответПроверить ответ 2. log 3 (x-2) log 3 x=log 3 (x-2) Проверить ответ Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ Проверить ответ
22
Если решил правильно, то молодец и можешь закончить занятие.
23
На оценку 5 реши уравнения: 1. log 3 2 (9x 2 )=log 3 81 Проверить ответ 2. lg(lgx)+lg(lgx 3 -2)=0 Проверить ответПроверить ответ -1; 1; 1/9; -1/9.
24
На оценку 5 реши уравнения: 1. log 3 2 (9x 2 )=log 3 81 Проверить ответПроверить ответ 2. lg(lgx)+lg(lgx 3 -2)=0 Проверить ответ 10
25
Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответ 2. log 3 (x-2) log 3 x=log 3 (x-2) Проверить ответ Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ Проверить ответ 2
26
Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответПроверить ответ 2. log 3 (x-2) ·log 3 x=log 3 (x-2) Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ Проверить ответ 3
27
Реши сам следующие уравнения 1. log 3 (x+4)+log 3 (x-1)=1+log 3 2 Проверить ответПроверить ответ 2. log 3 (x-2) ·log 3 x=log 3 (x-2) Проверить ответ Проверить ответ 3. lgx 2 +lgx 4 +6=0 Проверить ответ -1/10; 1/10.
28
Если решил правильно, то молодец и можешь закончить занятие.
29
Если решил правильно, то молодец и можешь закончить занятие Или попробуй решить на «5»
30
Если у Вас осталось время, то можете заглянуть на историческую страничку или посмотреть логарифмическую комедию. Страничка истории Логарифмическая комедия
31
Действие — возведение в степень -имеет два обратных. Если a b =c, то отыскание a есть одно обратное действие – извлечение корня; нахождение же b – другое, логарифмирование. Для чего были придуманы логарифмы? Конечно, для ускорения и упрощения вычислений. Логарифмы дают возможность производить такие операции, выполнение которых без их помощи очень затруднительно (извлечение корня любой степени). Об этом можно прочитать в книге «Занимательная алгебра» Я.И.Перельмана. Немного истории Закончить работу Далее
32
Логарифмическая комедия Докажем, что 2>3; «Комедия» начинается с неравенства 1/4>1/8 — бесспорно правильного. Затем следует преобразование: (1/2) 2 >(1/2) 3, также не внушающее сомнения. Большему числу соответствует больший логарифм, значит, 2lg(1/2)>3lg(1/2). После сокращения на lg(1/2) Имеем: 2>3. В чем ошибка этого доказательства? Решение
33
Ошибка в том, что при сокращении на lg(1/2) не был изменен знак неравенства ( > на < ); между тем необходимо это сделать, так как lg(1/2) есть число отрицательное.