Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
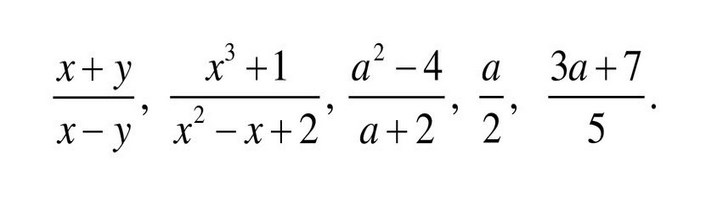
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
![]()
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Сокращение дробей с буквами и степенями проходит в три этапа:
-
Определите общий множитель.
-
Сократите коэффициенты.
-
Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
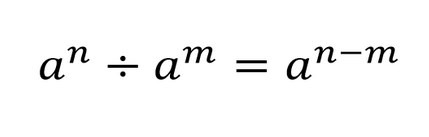
Пример сокращения дроби со степенями и буквами:
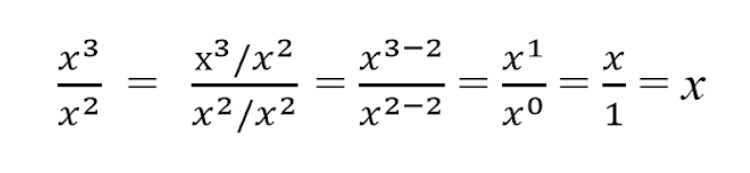
-
Следуя формуле сокращения степеней в дробях, сокращаем x3 и x2
-
Всегда делим на наименьшее значение в степени
-
Вычитаем: 3 — 1
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
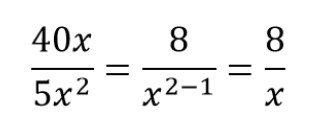
Как решаем:
-
Общий множитель для числителя и знаменателя — 8.
-
Х и x2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
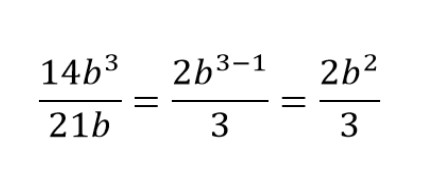
Как решаем:
-
Общий множитель для числителя и знаменателя — 7.
-
b3 и b делим на b.
-
Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
-
сокращайте многочлен в скобках только с таким же многочленом в скобках;
-
сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
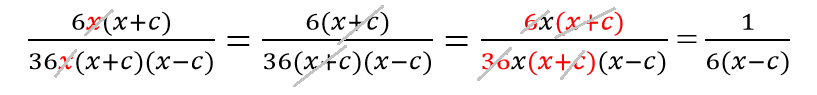
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
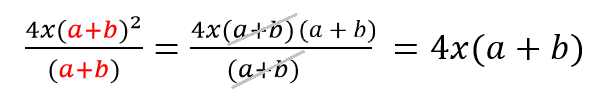
Сокращаем многочлены a+b (в дроби их 3).
Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
-
Найдите число, на которое делятся числа каждого одночлена.
-
Найдите повторяющиеся буквенные множители в каждом одночлене.
-
Вынесите найденные буквенные множители за скобку.
-
Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен.
Пример 1.
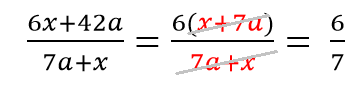
Как решаем:
-
Выносим общий множитель 6
-
Делим 42/6
-
Сокращаем получившиеся одинаковые многочлены.
Пример 2.
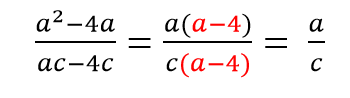
Как решаем: в числителе выносим общий множитель a за скобки, в знаменателе выносим общий множитель c за скобки и сокращаем оставшиеся в скобках многочлены.
Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b)2 = a2 + 2ab + b2 |
| Квадрат разности | (a-b)2 = a2 — 2ab — b2 |
| Разность квадратов | a2 – b2 = (a – b)(a+b) |
| Куб суммы | (a+b)3 = a3 + 3a2b + 3ab2 + b3 |
| Куб разности | (a-b)3 = a3 — 3a2b + 3ab2 — b3 |
| Сумма кубов | a3 + b3 = (a + b)(a2— ab+b2) |
| Разность кубов | a3 — b3 = (a — b)(a2+ ab+b2) |
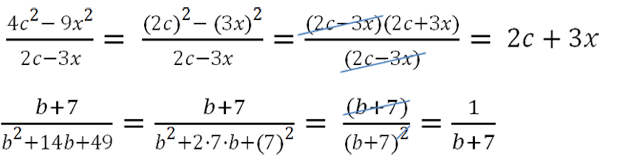
Примеры сокращения дробей с помощью формул сокращенного умножения:
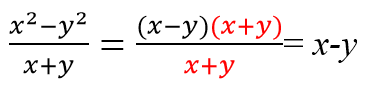
Применяем формулу разности квадратов a2 − b2 = (a − b) (a + b) и сокращаем одинаковые многочлены.
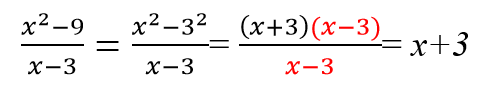
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Сократите дроби:
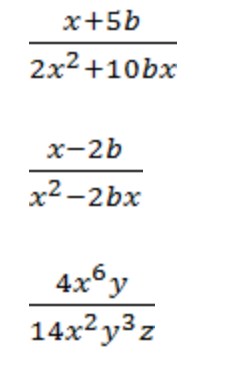
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
-
Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
-
Поделите числитель и знаменатель на общий множитель.
-
Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
-
Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
-
Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
-
Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
-
Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
Так сокращать дроби нельзя!
1 марта 2012
Работая с дробями, многие ученики допускают одни и те же ошибки. А все потому, что они забывают элементарные правила арифметики. Сегодня мы повторим эти правила на конкретных задачах, которые я даю на своих занятиях.
Вот задача, которую я предлагаю каждому, кто готовится к ЕГЭ по математике:
Задача. Морская свинья ест 150 грамм корма в день. Но она выросла и стала есть на 20% больше. Сколько грамм корма теперь ест свинья?
Неправильное решение. Это задача на проценты, которая сводится к уравнению:
![]()
Многие (очень многие) сокращают число 100 в числителе и знаменателе дроби:
![]()
Вот такую ошибку допустила моя ученица прямо в день написания этой статьи. Красным отмечены числа, которые были сокращены.
Излишне говорить, что ответ получился неправильный. Судите сами: свинья ела 150 грамм, а стала есть 3150 грамм. Увеличение не на 20%, а в 21 раз, т.е. на 2000%.
Чтобы не допускать подобных недоразумений, помните основное правило:
Сокращать можно только множители. Слагаемые сокращать нельзя!
Таким образом, правильное решение предыдущей задачи выглядит так:
![]()
Красным отмечены цифры, которые сокращаются в числителе и знаменателе. Как видите, в числителе стоит произведение, знаменателе — обыкновенное число. Поэтому сокращение вполне законно.
Работа с пропорциями
Еще одно проблемное место — пропорции. Особенно когда переменная стоит с обеих сторон. Например:
Задача. Решите уравнение:
Неправильное решение — у некоторых буквально руки чешутся сократить все на m:
![]()
Сокращаемые переменные показаны красным. Получается выражение 1/4 = 1/5 — полный бред, эти числа никогда не равны.
А теперь — правильное решение. По существу, это обыкновенное линейное уравнение. Решается либо переносом всех элементов в одну сторону, либо по основному свойству пропорции:
![]()
Многие читатели возразят: «Где ошибка в первом решении?» Что ж, давайте разбираться. Вспомним правило работы с уравнениями:
Любое уравнение можно делить и умножать на любое число, отличное от нуля.
Просекли фишку? Можно делить только на числа, отличные от нуля. В частности, можно делить на переменную m, только если m != 0. А что делать, если все-таки m = 0? Подставим и проверим:
![]()
Получили верное числовое равенство, т.е. m = 0 — корень уравнения. Для остальных m != 0 получаем выражение вида 1/4 = 1/5, что, естественно, неверно. Таким образом, не существует корней, отличных от нуля.
Выводы: собираем все вместе
Итак, для решения дробно-рациональных уравнений помните три правила:
- Сокращать можно только множители. Слагаемые — нельзя. Поэтому учитесь раскладывать числитель и знаменатель на множители;
- Основное свойство пропорции: произведение крайних элементов равно произведению средних;
- Уравнения можно умножать и делить только на числа k, отличные от нуля. Случай k = 0 надо проверять отдельно.
Помните эти правила и не допускайте ошибок.
Смотрите также:
- Как решать квадратные уравнения

- Теорема Виета

- Знаки тригонометрических функций

- Задача B1 — время, числа и проценты

- Как представить обычную дробь в виде десятичной

- Задача B2 на проценты: железнодорожные билеты



Прежде чем перейти к изучению алгебраических дробей рекомендуем вспомнить, как работать с
обыкновенными дробями.
Запомните!
![]()
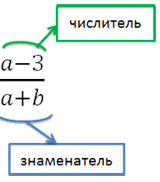
Любая дробь, в которой есть буквенный множитель, называется алгебраической дробью.
Примеры алгебраических дробей.
Как и у обыкновенной дроби, в алгебраической дроби есть числитель (наверху) и знаменатель (внизу).
Сокращение алгебраической дроби
Алгебраическую дробь можно сокращать. При сокращении
пользуются правилами
сокращения обыкновенных дробей.
Напоминаем, что при сокращении обыкновенной дроби мы делили и числитель, и знаменатель на одно и тоже число.
Алгебраическую дробь сокращают таким же образом, но только числитель и знаменатель делят
на один и тот же многочлен.
Рассмотрим пример сокращения алгебраической дроби.
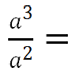
Определим наименьшую степень, в которой стоит одночлен «a» .
Наименьшая степень для одночлена «a» находится в знаменателе — это вторая степень.
Разделим, и числитель, и знаменатель на «a2».
При делении одночленов используем
свойство степени частного.
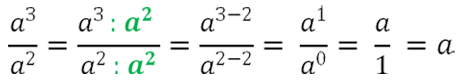
Напоминаем, что любая буква или число в нулевой степени — это единица.
Нет необходимости каждый раз подробно записывать, на что сокращали алгебраическую дробь. Достаточно держать в уме
степень, на которую сокращали, и записывать только результат.
Краткая запись сокращения алгебраической дроби выглядит следующим образом.
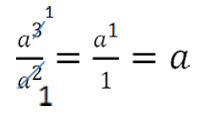
Важно!

Сокращать можно только одинаковые буквенные множители.
Нельзя сокращать
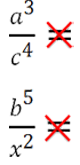
Можно сокращать
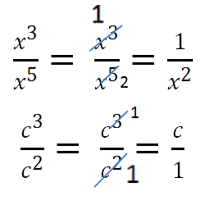
Другие примеры сокращения алгебраических дробей.
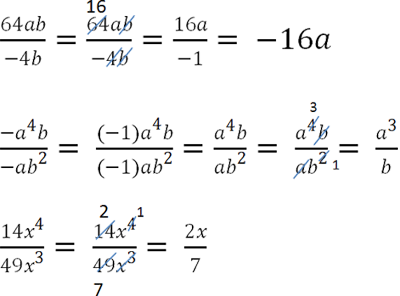
Как сократить дробь с многочленами
Рассмотрим другой пример алгебраической дроби. Требуется сократить алгебраическую дробь, у которой в числителе стоит многочлен.
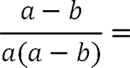
Важно!

Сокращать многочлен в скобках можно только с
точно таким же многочленом в скобках!
Ни в коем случае нельзя сокращать часть многочлена внутри скобок!
Неправильно

Правильно
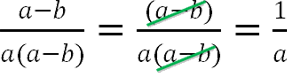
Определить, где заканчивается многочлен, очень просто. Между многочленами может быть только знак умножения.
Весь многочлен находится внутри скобок.
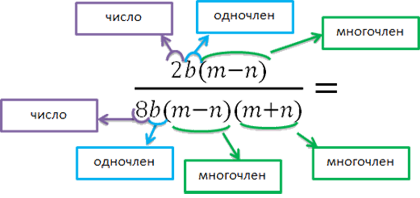
После того, как мы определили многочлены алгебраической дроби, сократим многочлен
«(m − n)» в числителе с многочленом «(m − n)»
в знаменателе.
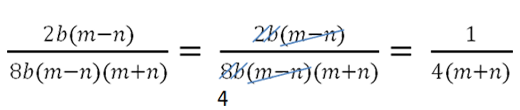
Примеры сокращения алгебраических дробей с многочленами.
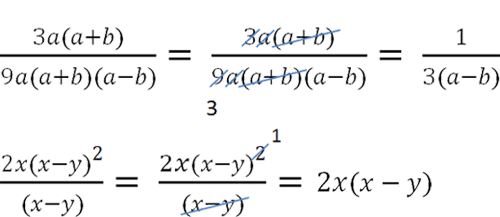
Вынесение общего множителя при сокращении дробей
Чтобы в алгебраических дробях появились одинаковые многочлены иногда нужно
вынести общий множитель за скобки.
Рассмотрим пример.
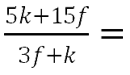
В таком виде сократить алгебраическую дробь нельзя, так как многочлен
«(3f + k)» можно сократить только со многочленом «(3f + k)».
Поэтому, чтобы в числителе получить «(3f + k)»,
вынесем общий множитель «5».
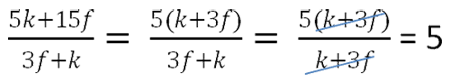
Сокращение дробей с помощью формул сокращенного умножения
В других примерах для сокращения алгебраических дробей требуется
применение формул сокращенного умножения.
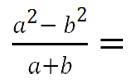
В первоначальном виде сократить алгебраическую дробь нельзя, так как нет одинаковых многочленов.
Но если применить формулу разности квадратов
для многочлена «(a2 − b2)», то одинаковые многочлены появятся.
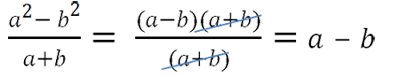
Другие примеры сокращения алгебраических дробей с помощью формул сокращенного умножения.
Отработка типичных
ошибок, связанных со свойствами степеней, при формировании вычислительных
навыков
Вычислительный навык – это высокая степень овладения
вычислительными приемами.
Навык
характеризуется такими качествами, как правильность, осознанность,
рациональность, обобщенность, автоматизм и прочность.
Я остановлюсь на
типичных ошибках, связанными со свойствами стемней и методами их ликвидации при
формировании вычислительных навыков.
И так, первая
ошибка-незнание словесных формулировок свойств. Вторая-незнание таблицы
умножения и определения степени с натуральным показателем.
Третья типичная
ошибка- неспособность выполнить переход от степени с отрицательным показателем
к степени с натуральным показателем и наоборот. Вот они, эти ошибки.
Слайд

Хочу показать, как я на разных этапах урока
отрабатываю эти ошибки.

При организации повторения уже 1сентября
(задания с №8-№ 14 как раз связаны со свойствами степеней) , их оставляю для
работы дома, а на уроке напоминаю учащимся , что еще в 4 классе они узнали, что
представляют собой квадрат и куб числа, проговариваем по цепочке -квадрат
числа, это произведение двух одинаковых множителей и пример, следующий говорит
то такое куб числа и приводит пример. Все учащиеся 1 ряда проговорили, все
остальные запомнили.
Предлагаю учащимся восстановить в тетрадях
памятку со свойствами степеней.
Слайд

1)
Сформулируйте свойства степеней, записанные на языке алгебры в памятке.
2)
используя определение степени, объяснить смысл выражений:
а)
103 б) 74 в) (-8)4 г) 3,22;
д) ![]()
е) 103; ж) 74; з) (-8)4; и)
3,22;
к) ![]()
Какие
еще можно вспомнить правила, связанные со степенями?
Отрицательное число в четной степени, есть число
положительное.
3)
Представить числа в виде квадрата или куба числа:
8,
27, 16, 81, 100, 144, 125, 64, 121, 49, 36, 216
В каждый устный счет можно включать подобные задания.
Слайд
Выполните действия:
а) а4 · а · а3а
б) (7х)2 в) р · р2 · р0
г) с · с3 · с
д) т · т4 · (т2)2 · т0
е) (23)7: (25)3
ж) –х3 · (–х)4
з) (р2)4: р5
и) (34)2 ·
(32)3 : 311
За 10-15 мин повторяется вся тема. Т.о.
организуется устный счет. Подобные вопросы включаю в математические диктанты
при изучении абсолютно любой темы. Это способствует развитию вычислительных
навыков и доведению их до автоматизма.
При изучении темы: «Алгебраические дроби», в
разделах сокращение дробей, нахождение значения алгебраической дроби при
предварительном упрощении, мы вновь возвращаемся к свойствам степеней
Слайд

Здесь использую задания — «найди ошибку в
решении или докажи, что ее нет». 5-6 человек решают у доски, сидящие на месте-
в своих тетрадях и готовятся анализировать работы товарищей. Процесс отыскания
и исправления ошибок самими учащимися под руководством учителя можно сделать
поучительным для учащихся. Такие задания так же способствуют и решению другой
проблемы-накоплению оценок. Ее получает и тот, кто решал и тот, кто проверял.
Кроме того, систематические проверки чужих
записей формируют у ученика привычку критически относиться к своему решению.
Есть возможность вернуться к этой теме и
уроках геометрии при изучении темы: «Площади», а именно, площади квадрата и при
решении задач на нахождение площади равностороннего треугольника, где
предварительно делается вывод формулы площади, отличной от классической. Во
время закрепления используем решение задач по готовым чертежам, содержащие
вопросы- — найти плошать квадрата и найти сторону квадрата, если известна его
площадь.
Слайд.
1. Сторона
квадрата равна 10; 12; 1,5; 2,5; 6; 9; 11. Найдите его площадь.
2. Периметр
квадрата равен 40; 100; Найдите площадь квадрата.
3. Найти сторону
квадрата, если его площадь 64; 144; 100; 225; 120; 36.

Слайд


1) Найти площадь равностороннего треугольника, если а= 2; 6; 8; 10; 12.
2) Найти площадь равностороннего треугольника, если его периметр равен 30;
15; 24.
К свойствам степеней мы возвращаемся и при
изучении понятия квадратного корня. Прежде чем вводить понятие корня опять
повторяем определение квадрата числа и правила работы с таблицей квадратов на
фарзаце учебника, решая два вопроса- как найти квадрат двузначного числа и как
найти число, квадрат которого известен. Это делается на этапе изучения новой
темы, т.к. найденное число квадрат которого известен, это и есть квадратный
корень.
Слайд

Затем в алгебре изучаются графики – у=√х; график квадратичной функции и опять следует
вернуться к определению степени, только здесь уже непосредственно при изучении
новой темы.
Приходится заполнять таблицы значений х и у, а
это надо делать быстро и правильно.
Слайд


![]()
Построить графики функций:
![]()
![]()
![]()
![]()
![]()
![]()
К отработке типичных ошибок в степени с
отрицательным показателем вернемся при организации итогового повторения в
разделе- «Преобразование рациональных выражений»
На этом этапе очень хорошо можно реализовать
индивидуализацию обучения.
Как реализую индивидуализацию- для начала
сообщаю, где и какой необходимо повторить теоретический материал и какие
разобрать примеры. Затем уже провожу групповую консультацию, где задают вопросы
сами ребята, иногда на эти вопросы уже могут ответить присутствующие. И
последний этап-оценочная деятельность-здесь конкретно каждый ученик выполняет
по 2-3 задания по отрабатываемой теме и получает оценку. Если
удовлетворительной оценки нет, то попытка повторяется.
Начинают с простейших и заканчивают такими
примерами, где уже требуется умение логически мыслить, обобщать, делать выводы.
В качестве образца можно взять следующие
примеры.
Слайд
1.Замените дробь степенью с целым
отрицательным показателем:
а) ![]() ;
;
б) ![]() ; в)
; в)![]() ; г)
; г) ![]() ;
;
д) ![]()
2.Замените дробью степень с целым
отрицательным показателем:
а) 5-7; б) 7-1; в) а-11;
г) х-1; д) (2у)-5
3.Вычислите:
а) 2-3; б) (-5)-1;
в) ![]() ; г) (0,2)-3;
; г) (0,2)-3;
д) ![]() ; е) 6-1+2-2;
; е) 6-1+2-2;
ж) 2780 – 0,1-2.
4. Представьте в виде дроби и сократите: (а3 +3а4 –
а6) : (3 – а2 + а—1)
5. Известно, что 3у=а. Найдите: 32у;
33у+1; 3-у; 92у
И в заключении, хочу сказать, что своим ученикам
я постоянно напоминаю- не страшно ошибиться, а страшно ошибку не искоренить…
Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.
Смысл сокращения алгебраической дроби
В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
Сокращение алгебраической дроби представляет собой аналогичное действие.
Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.
К примеру, алгебраическая дробь 3·x2+6·x·y6·x3·y+12·x2·y2 может быть сокращена на число 3, в итоге получим: x2+2·x·y6·x3·y+12·x2·y2 . Эту же дробь мы можем сократить на переменную х, и это даст нам выражение 3·x+6·y6·x2·y+12·x·y2. Также заданную дробь возможно сократить на одночлен 3·x или любой из многочленов x+2·y, 3·x+6·y, x2+2·x·y или 3·x2+6·x·y.
Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.
Все ли алгебраические дроби подлежат сокращению?
Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1.
С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.
В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3·x23·y совершенно понятно, что общим множителем является число 3.
В дроби -x·y5·x·y·z3 также мы сразу понимаем, что сократить ее возможно на х, или y, или на х·y. И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.
Например, дробь x3-1×2-1 мы можем сократить на х-1, при этом указанный общий множитель в записи отсутствует. А вот дробь x3-x2+x-1×3+x2+4·x+4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.
Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.
Правило сокращения алгебраических дробей
Правило сокращения алгебраических дробей состоит из двух последовательных действий:
- нахождение общих множителей числителя и знаменателя;
- в случае нахождения таковых осуществление непосредственно действия сокращения дроби.
Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.
Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a,b,c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a·cb·c , в котором мы сразу замечаем общий множитель c. Вторым шагом – выполняем сокращение, т.е. переход к дроби вида ab .
Характерные примеры
Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:
55=1;-23-23=1;xx=1;-3,2·x3-3,2·x3=1;12·x-x2·y12·x-x2·y;
и т.п.
Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).
К примеру, 241260=2·2·2·32·2·3·3·5·7=23·5·7=2105
Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:
241260=23·322·32·5·7=23-232-1·5·7=2105
(числитель и знаменатель разделены на общий множитель 22·3). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
241260=23·322·32·5·7=2322·332·15·7=21·13·135=2105
По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.
Задана алгебраическая дробь -27·a5·b2·c·z6·a2·b2·c7·z . Необходимо произвести ее сокращение.
Решение
Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:
-27·a5·b2·c·z6·a2·b2·c7·z=-3·3·3·a·a·a·a·a·b·b·c·z2·3·a·a·b·b·c·c·c·c·c·c·c·z==-3·3·a·a·a2·c·c·c·c·c·c=-9·a32·c6
Однако, более рациональным способом будет запись решения в виде выражения со степенями:
-27·a5·b2·c·z6·a2·b2·c7·z=-33·a5·b2·c·z2·3·a2·b2·c7·z=-332·3·a5a2·b2b2·cc7·zz==-33-12·a5-21·1·1c7-1·1=·-32·a32·c6=·-9·a32·c6 .
Ответ: -27·a5·b2·c·z6·a2·b2·c7·z=-9·a32·c6
Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).
Задана дробь 25·x0,3·x3. Необходимо выполнить ее сокращение.
Решение
Возможно сократить дробь таким образом:
25·x0,3·x3=25310·xx3=43·1×2=43·x2
Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК (5, 10) = 10. Тогда получим:
25·x0,3·x3=10·25·x10·0,3·x3=4·x3·x3=43·x2 .
Ответ: 25·x0,3·x3=43·x2
Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.
Задана рациональная дробь 2·a2·b2+28·a·b2+98·b2a2·b3-49·b3 . Необходимо ее сократить.
Решение
Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:
2·a2·b2+28·a·b2+98·b2a2·b3-49·b3=2·b2·(a2+14·a+49)b3·(a2-49)
Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:
2·b2·(a2+14·a+49)b3·(a2-49)=2·b2·(a+7)2b3·(a-7)·(a+7)
Хорошо заметно, что возможно сократить дробь на общий множитель b2·(a+7). Произведем сокращение:
2·b2·(a+7)2b3·(a-7)·(a+7)=2·(a+7)b·(a-7)=2·a+14a·b-7·b
Краткое решение без пояснений запишем как цепочку равенств:
2·a2·b2+28·a·b2+98·b2a2·b3-49·b3=2·b2·(a2+14a+49)b3·(a2-49)==2·b2·(a+7)2b3·(a-7)·(a+7)=2·(a+7)b·(a-7)=2·a+14a·b-7·b
Ответ: 2·a2·b2+28·a·b2+98·b2a2·b3-49·b3=2·a+14a·b-7·b.
Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.
Дана алгебраическая дробь 15·x-27·x3·y5·x2·y-312 . Необходимо осуществить ее сокращение, если это возможно.
Решение
На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:
15·x-27·x3·y5·x2·y-312=x·15-27·x2·y5·x2·y-312
Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x2·y. Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:
x·15-27·x2·y5·x2·y-312=x·-27·-72·15+x2·y5·x2·y-15·312==-27·x·-710+x2·y5·x2·y-710
Теперь становится виден общий множитель, осуществляем сокращение:
-27·x·-710+x2·y5·x2·y-710=-27·x5=-235·x
Ответ: 15·x-27·x3·y5·x2·y-312=-235·x .
Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.
Самые старые упоминания о таких математических явлениях, как дробь, учёные обнаружили в древнем Египте. Особенностью их было то, что у них были обозначения только вида 12, 23,13, при этом больше двойки числа, делимого они не использовали, а использовали метод сложения, к примеру, вместо дроби 56, писали 12 +13.
Но применять такие дроби было сложно, поэтому учёные разных областей пытались вывести общую универсальную формулу для удобства. Так появилась шестидесятеричная, но проводить вычисления с ней тоже было очень трудно, однако её довольно долго применяли в Вавилоне и Греции. Существовала также система называемая Асс, её суть в делении на 12, использовали её римляне. Результат такого деления, точнее одну долю, называли унцией. Самой близкой по своей системе исчисления была дробь, которую предложили в Индии, разница от современных была в формате записи, без чёрточки, и такая дробь была перевернута, в верхней части находился делитель, а в нижней делимое. Та запись, которую и по сей день используют в математике была придумана арабами.
Что такое дробь, основные понятия и виды
Определение
Дробь — число, состоящее из нескольких равных долей.
По сути дробь — это деление одного числа на другое. Выделяют два вида: обыкновенные и десятичные.
Обыкновенная дробь — означает, состоящая из целых чисел. Обыкновенные, имею два типа записи к примеру:
- 15- разделена наклонной линией, читается как одна пятая;
- [frac{1}{5}] — горизонтальной линией.
Определения:
- Числитель — число, находящееся в верхней границе дроби;
- Знаменатель — число которое мы видим в нижней границе дроби.
Например: 15, где 1- числитель, 5- знаменатель. Для того чтобы проще объяснить, что такое дробь приведём простой пример. Торт разрезан на 5 кусков, если мы взяли два и них то это 25 (две пятые части торта).
Обыкновенные дроби имеют два типа правильные и неправильные.
Правильной дробью называется дробь с значениями, в которых числитель меньше знаменателя. Такое название данный тип дроби получил не зря, ведь так логичнее и правильнее, когда часть меньше целого.
Неправильная в свою очередь имеет обратные значения, когда числитель больше знаменателя.
Примечание. Дроби, у которых знаменатель и числитель одинаковы, тоже неправильные.
Смешанная дробь. Существует также такое определение как смешанная дробь, такой вид, представляет собой дробь, состоящую из двух частей целой и дробной. Пример — [4 frac{3}{5}], где четыре это целая часть, а 35 дробная. Такой тип дроби можно получить, только при делении неправильного вида дробей.
Десятичные дроби. К десятичным, относят дроби которые в знаменателе имеют 10 в натуральной степени. К примеру [frac{5}{10},
frac{6}{100}] и тд. Такие, так же могут иметь вид строчной записи, 0,5 и 0,06. При этом в такой записи целая часть отделяется от дробной знаком запятой.
Существуют также понятия сократимой и несократимой дроби. Сократимая дробь, это та, в которой можно произвести деление числителя и знаменателя на одно и то же число.
Несократимая дробь, если такие действия выполнить нельзя.
Составная дробь, многоуровневая или выражение, имеющее несколько черт дроби. Пример [frac{frac{3}{7}}{-31}]
Равные и неравные дроби. Для того чтобы сказать, являются дроби равными или нет, нужно их сравнить.
Равные обыкновенные [frac{a}{d} frac{c}{b}] — можно вывести при помощи такого верного равенства а*b=d*c , если такое равенство не верно то данные дроби будут называться неравными.
Положительные и отрицательные дроби.
Положительные называют обыкновенные дроби, с положительными числами, при необходимость перед такими дробями ставится знак +, пример [+frac{6}{9}].
Отрицательными, считаются дроби со знаком минус, пример [-frac{6}{9}].
Стоит отметить что две дроби вида [-frac{6}{9} text { и }+frac{6}{9}] являются противоположными.
Алгебраическая дробь.
Отличается она тем, что на месте числителя и знаменателя находятся алгебраические значения, числа заменены буквами. Примеры —
[
frac{x+y}{x-y}, frac{x^{3}+1}{x^{2}-x+2}, frac{a^{2}-4}{a+2}, frac{a}{2}, frac{3 a+7}{5}
]
Если в такой дроби буквы заменить числами, то она сразу станет обыкновенной.
Одночлен — это выражение, содержащее числа, степени положительные и их произведение. Пример: ![]() в.
в.
Многочлен — это сумма одночленов. Пример: 7а+6в
Дроби на координате прямых.

Если рассматривать координату прямых, то положительные дроби на ней будут расположены справа от нулевого значения, а отрицательные слева.
Действия, которые можно выполнить с дробями
В общем то, действия с дробями это все те же действия, которые можно выполнить с числами:
- Сравнение;
- Сложение;
- Вычитание;
- Умножение;
- Деление.
Свойства дроби
Чтобы сложить или вычесть дроби, дробь обязана иметь равные знаменатели, необходимо просто выполнить это действие с их числителями
Примеры:
[
frac{4}{9}+frac{5}{9}=frac{4+5}{9} ; text { и } frac{4}{9}-frac{5}{9}=frac{5-4}{9}.
]
Что же касается дробей с разной частью делителя (Знаменателя), то тут чтобы выполнить действия сложения и вычитания с ними необходимо привести знаменатели к общему числу.
Примеры: [frac{4}{9}+frac{5}{8}=frac{4+5}{9 cdot 8}], точно так же и для вычитания.
Чтобы выполнить такое действие, как умножение обыкновенных дробей, нужно произвести умножение сначала с их числителями, а после и знаменателями.
Пример: [frac{4}{9} cdot frac{5}{8}=frac{4 cdot 5}{9 cdot 8}].
При умножении дроби на число, в такой вычислении просто умножается числитель на заданное число, а знаменатель остаётся тем же.
Пример: [frac{4}{9} cdot 6=frac{4 cdot 6}{9}];
Что же касается деления, то при делении одной дроби на другую, нужно произвести умножение, при котором первая дробь остаётся в неизменном виде, а вторая переворачивается. То есть получается мы умножаем числитель первой дроби данного примера, на знаменатель второй, и полученное число находится в верхней части дроби, а в нижней умножение знаменателя первой дроби на числитель второй.
Пример: [frac{4}{9} backslash frac{5}{8}=frac{4 cdot 8}{9 cdot 5}].
Сравнение дробей
Чтобы провести сравнение с разными делителями (знаменателями), необходимо сделать так, чтобы знаменатель стал общим только тогда можно будет сравнить числители. Соответственно, где числитель больше там и дробь больше.
Основное свойство дробей
Основным свойством дроби является выражение — «числитель и знаменатель можно делить и умножать на одно и то же число при этом значение всей дроби не поменяется.»
Еще одно определение которое пригодится нам для сокращения дроби это НОД.
НОД — наибольший общий делитель.
Общий делитель — это число, которое может быть делителем каждого из указанных чисел.
Пример: если взять число 3, то оно станет общим делителем для чисел 6 и 9. так как 9=3*3 а 6=3*2.
Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)
Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.
Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если rk+1=0, при этом rk=НОД(a, b)
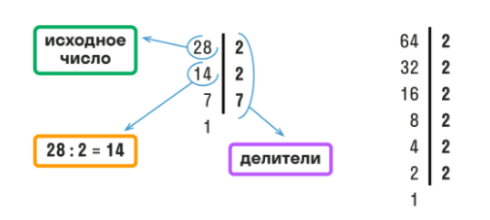
Пример. Рассчитаем НОД для 28 и 64.
Как находим:
Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (28) = 2 * 2 * 7
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Сокращение дроби
Выражение сократить дробь, фактически означает что необходимо провести деление её числителя и знаменателя на одно и то же число, не равное единице.
Результатом таких действий станет появление новой дроби, значение которой, равно первичной.
Например: возьмём обыкновенную дробь [frac{12}{44}] и произведем сокращение. Для этого разделим и числитель и знаменатель на 2, получится такая дробь [frac{12}{44} backslash 2=frac{12 backslash 2}{44 backslash 2}=frac{6}{22}].
Нет времени решать самому?
Наши эксперты помогут!
Несократимый вид дроби, приведение к такому виду
Обычно целью таких манипуляций с дробями является получение из исходного вида дроби несократимый. К примеру дробь, которая получилась у нас выше, [frac{6}{22}] при сокращении на два, как мы видим все ещё можно сократить.
Для того чтобы привести дробь к виду несократимой, нужно выполнить манипуляции по делению, числителя и знаменателя на наибольший НОД. В таком случае по свойству НОД в числителе и знаменателе окажутся простые числа, а дробь будет несократимой.
[
frac{a}{d}=frac{a backslash text { НОД }(a, d)}{d backslash text { НОД }(a, d)}
]
Из вышесказанного следует, что приведение дроби к несократимому виду значит, нужно произвести деление числителя и знаменателя на их НОД.
Пример: вернёмся к нашему примеру дроби [frac{12}{44}], для приведения ее к несократимому виду нужной сначала найти наибольший общий делитель чисел 12 и 44. таким числом НОД для них является цифра 4.
Получается: [frac{12}{44}=frac{12 backslash 4}{44 backslash 4}=frac{3}{11}].
Для чего нужно сокращение? Такие манипуляции с дробями необходимо применять, в случаях работы с большими числами.
Стоит вспомнить негласное правило математики, суть его в том, что если что-то можно сделать проще нужно упростить. Поэтому, говоря о сокращении дроби, имеется в виду именно приведение к несократимому виду, а не просто уменьшение числителя и знаменателя.
Правило сокращения
Для того чтобы сократить, необходимо:
- Найти делитель наибольшего значения, который будет общим для знаменателя и числителя;
- Разделить числитель и знаменатель на него.
Примеры:
Дана такая дробь: [frac{182}{195}]. сократим её.
Найдём такой делитель, при помощи применения алгоритма Евклида.
195 = 182 *1+13
182=13*14
Из чего следует, что НОД(182,195)=13
Поэтому для сокращения дроби [frac{182}{195}], разделим числитель 182 и знаменатель 195 на 13 и получим равенство: [frac{182}{195}=frac{182 backslash 13}{195 backslash 13}=frac{14}{25}]
Таким образом мы и получили несократимую дробь равную исходной.
Второй способ.
Второй способ основан на разложении числителя и знаменателя исходной дроби на простые множители, из которых позже все общие множители убираются.
Пример сокращения: [frac{123}{154}] для сокращения представим числитель и знаменатель дроби в виде простых множителей
[
frac{182}{195}=frac{2 cdot 7 cdot 13}{3 cdot 5 cdot 13}
]
Затем уберём все общие множители, как в числителе так и в знаменателе, [frac{182}{195}=frac{2 cdot 7 cdot 13}{3 cdot 5 cdot 13}=frac{2 cdot 7}{3 cdot 5}=frac{14}{15}]
Третий способ сокращения дроби.
Третий способ — способ последовательного сокращения. Применяя такой способ, сокращение происходит поэтапно, сокращая каждый раз на какой-либо очевидный общий множитель.
Пример: [frac{18000}{22000}]
При сокращении такой дроби сразу можно увидеть, что и числитель и знаменатель деяться на 1000 в результате такого деления получается:
[
frac{18000}{22000}=frac{18000 backslash 1000}{22000 backslash 1000}=frac{18}{22}
]
Следующим этапом мы видим, что оба значения и числителя, и знаменателя делятся на 2, получим несократимую дробь.
[
frac{18}{22}=frac{18000 backslash 2}{22000 backslash 2}=frac{9}{11}
]
Как мы видим сокращение дроби не такой сложный процесс, главное подобрать удобный способ.
Сокращение алгебраической дроби
Так же, как и в примерах выше, сокращение алгебраической дроби, это деление числителя и знаменателя на общий делитель. Отличие в том, что в алгебраической, таким общим множителем является многочлен и одночлен.
Для того чтобы сократить такие дроби нужно пройти три этапа:
- Определение множителя, который будет общим для числителя и знаменателя;
- Сокращение коэффициента;
- Деление числителя и знаменателя на множитель.
Сокращая дробь со степенями, применяется правило деления степеней с равными основаниями.
Формула:
[
a^{n} div a^{m}=a^{n-m}
]
Рассмотрим пример сокращения со степенями:
[
frac{x^{3}}{x^{2}}=frac{x^{3} / x^{2}}{x^{2} / x^{2}}=frac{x^{3-2}}{x^{2-2}}=frac{x^{1}}{x^{0}}=frac{x}{1}=x
]
Исходя из вышеописанной схемы:
- Сокращаем x3 и x2;
- Производим деление выбирая меньшее значение степени;
- Вычитаем.
В результате получаем сокращенную дробь.
Не забываем, что сократить можно только одинаковые буквенные множители.
Сокращение дробей с одночленами.
Пример: [frac{40 x}{5 x^{2}}=frac{8}{x^{2-1}}=frac{8}{x}]
Решение:
- 8 — тот самый множитель, который является общим
- Х и x2 делим на x и получаем ответ.
Дроби с многочленами: сокращение.
Для сокращения таких видов, существует два правила:
- Сократить многочлен в взятый в скобки, можно только с точно таким же многочленом в скобках;
- Сократится должен весь многочлен, взятый в скобки, нельзя сократить только часть.
Пример: [frac{x-c}{x(x-c)}=frac{1}{x}]
Вынесение общего множителя при сокращении.
Бывают случаи, когда при сокращении алгебраической дроби с многочленами, их нет одинаковых, в таком случае нужно убрать общий множитель за скобки.
Для такого вынесения тоже существуют правила их 4:
- необходимо найти число, на которое можно разделить числа каждого одночлена;
- необходимо также найти буквенный множитель, который повторяется, в каждом одночлене, их может быть несколько;
- выносим буквенный множитель, который был найден, за скобки;
- производим работу с оставшимися многочленами в скобках.
Для того чтобы умножить многочлен на одночлен, необходимо по очереди умножить каждый член многочлена на одночлен.
Приведём пример:
[frac{6 x+42 a}{7 a+x}=frac{6(x+7 a)}{7 a+x}=frac{6}{7}]
Калькулятор сокращения дробей
Подведём итоги. Для того чтобы не возникло трудностей с сокращением, стоит запомнить:
- Сокращая дробь вам необходимо найти общий множитель для числителя и знаменателя, если речь идет об алгебраических дробях, но и НОД обыкновенных;
- Разделить числитель и знаменатель на общий множительделитель;
- Если дробь алгебраическая, при делении многочлена на множитель необходимо вынести общий множитель за скобки;
- Стоит хорошо выучить все формулы и определения, связанные с дробями.
- Всегда проверять результат сокращения.
Слайд 1
Алгебраические дроби, сокращение дробей.
Слайд 2
Теория: Алгебраической дробью называют отношение двух многочленов Р и Q, т.е. , где Р — числитель, Q — знаменатель алгебраической дроби. Например , , , ,
Слайд 3
Сократить дробь – это значит, разделить одновременно числитель и знаменатель дроби на их общий множитель, одно и то же отличное от нуля число. Обрати внимание! Сначала надо разложить на множители числитель и знаменатель дроби. = =
Слайд 4
Найдите ошибку. Найдите значение выражения: 5 1 1 2
Слайд 5
№1 . 3 2 2 3 № 2 . 1 4 подсказка — 1
Слайд 6
a – b = – ( b – a) a – b b – a a – b –( а – b ) = = – 1 Замечание: для выполнении этого номера и аналогичных заданий необходимо помнить следующие равенства!
Слайд 7
№3. Сократите дробь: m 2 – n 2 m 2 + mn (m – n)(m + n) m(m + n) = = m – n m а) 4с 2 – 12с +9 4с 2 — 9 = = б) (2с – 3) 2 (2с – 3)(2с +3 ) 2с – 3 2с + 3 a 2 – 2 ab + b 2 b 2 — a 2 = в) ( a – b ) 2 ( b – a )( b + a ) подсказка (b – a) 2 (b – a)(b + a ) = b – a b + a = =
Слайд 8
( a – b) 2 =( b – a) 2 (a – b) (b – a) 2 = 1 Замечание: для выполнении этого номера и аналогичных заданий необходимо помнить следующие равенства!
Слайд 9
Сократите дроби ( письменно ) :
Слайд 10
Сократите дроби (письменно) а ) б ) в ) г)
Слайд 11
Работа с учебником, закрепление: Выполнить задание под буквами а, б № 41.6, 41.8, 41.12, 41.14, 41.16, 41.17, 41.18, 41.20, 41.21, 41.23, 41.25, 41.27, 41.28, 41.29, 41.31, 41.33, 41.37, 41.38, 41.40.
Слайд 12
Самостоятельная работа
В алгебраические дроби являются дробно-алгебраическими выражениями, у которых есть по крайней мере одно неизвестное в знаменателе. Часто есть множители, которые появляются как в числителе, так и в знаменателе этих дробей, что оставляет возможность их упрощения. Многие игнорируют то, что есть некоторые правила, которые изучаются с самого начала начальной школы, которые направляют этот процесс упрощения. Следовательно, любой упрощение у того, кто нарушает эти правила, есть большой шанс ошибиться. Поэтому ниже мы перечисляем три наиболее частые ошибки при упрощении алгебраических дробей и правильный способ выполнения этих процедур.
Прежде чем продолжить, рекомендуем прочитать статью Упрощение алгебраической дроби для тех, кто еще сомневается в этом вопросе.
1 — Вырезать элементы равно в числителе и знаменателе
Это самая частая ошибка. В начале обучения ученики хотят «вырезать» все одинаковые элементы в числителе и знаменателе алгебраическая дробь. Однако это не равнозначные элементы, которые нужно «вырезать», но, да, факторы равно.
Правило таково: Если там есть равные факторы в числителе и знаменателе эти множители можно сократить. Помните: разделение между ними будет 1, что не влияет на деление или умножение. Поскольку эти факторы просто исчезают, этот процесс получил название «резка». Также помните, что числа при умножении называются множителями.
Добавляемые или вычитаемые элементы ты не можешь быть вырезанным, потому что его деление не приводит к 1. Таким образом, взяв пример ниже, который включает в себя сумму, мы увидим правильный и неправильный способ выполнения упрощение.
Пример: Упростить следующую алгебраическую дробь.
4x + 4 года
х + у
Неверно:
4Икс + 4у = 4 + 4 = 8
Икс + у
Обратите внимание, что отсеченные неизвестные числа (выделенные красным) не являются факторами умножения, а скорее частями сложения. Следовательно, сделанный выше разрез неправильный.
Верно:
4x + 4 года
х + у
делая процесс полиномиальная факторизация по общему фактору у нас будет:
4(х + у) = 4
х + у
В числителе алгебраической дроби находим умножение, где множители равны 4 и x + y. В знаменателе находим только x + y. Обратите внимание, что x + y является фактором, поскольку он не добавляется и не вычитается никаким другим числом или неизвестными. Для лучшего обзора просто заключите круглые скобки:
4(х + у) = 4
(х + у)
Если бы вместо x + y в знаменателе стояла только цифра 4, можно было бы также упростить, сократив только цифру 4.
А теперь посмотрим на случай, когда не могло быть упрощение:
4(х + у)
х + у + k
* k — любое число, неизвестное или одночленное.
2 — Факторизация полного квадратного трехчлена с использованием процесса общего множителя в доказательстве
Почти всякий раз, когда многочлен в алгебраическая дробь, это должно быть учтено. После этого факторы, присутствующие в числителе и знаменателе, необходимо сравнить в поисках тех, которые могут быть упрощенный (другое слово для «вырезать»).
Что происходит, так это то, что студенты сталкиваются с полный квадрат трехчлена и забудьте, что это результат замечательный продукт, просто вернувшись к этому продукту, чтобы выполнить факторизация. Таким образом, делается попытка выявить общие факторы.
Не останавливайся сейчас… После рекламы есть еще кое-что;)
Люди, которые предпринимают такие попытки, часто совершают указанную выше ошибку.
Обратите внимание на следующий пример, который также показывает правильную форму и наиболее частую неправильную форму разрешения.
Пример: Упростить следующую алгебраическую дробь.
4x2 + 8xy + 4y2
х + у
Неверно:
4x2 + 8xy + 4y2
х + у
4 (х2 + 2xy + y2)
х + у
или же
4 (х + 2у) + 4у2
х + у
Обратите внимание, что это невозможно даже упростить именно потому, что процесс факторинга не был проведен должным образом.
Верно:
4x2 + 8xy + 4y2
х + у
(2x + 2г)2
х + у
(2x + 2y) (2x + 2г)
х + у
На этом этапе обратите внимание, что число 2 является общим для всех элементов двух множителей числителя. В этой ситуации необходимо учитывать фактор, общий для двух факторов. В результате мы получим:
2 · (х + у) · 2 · (х + у)
х + у
2 · 2 · (х + у) (х + у)
х + у
4 · (х + у) (х + у)
х + у
Теперь да, мы можем сократить множитель, который повторяется как в числителе, так и в знаменателе.
4 · (х + у)(Икс + у)= 4 · (х + у)
х + у
3 — Путать замечательные продукты
Обратите внимание на список примечательных продуктов ниже, который включает квадраты или произведение суммы на разницу.
(х + у)2 = х2 + 2xy + y2
(х — у)2 = х2 –2xy + y2
(х + у) (х — у) = х2 — у2
Каждый раз, когда многочлен принимает форму трехчлена полного квадрата или разности двух квадратов — находится в правая часть приведенных выше равенств -, их можно заменить замечательным продуктом, который их породил (левая часть соответствующий).
В упрощение алгебраических дробей, забвение того, что замечательное произведение соответствует идеальному квадрату трехчлена, является очень повторяющейся ошибкой, особенно когда дело доходит до разница в два квадрата. Когда он появляется, обычно думают, что он уже учтен или что показатель степени 2 может быть использован «в качестве доказательства» (и, конечно, это невозможно сделать).
Обратите внимание на следующий пример с разницей в два квадрата:
Пример: упростите следующую алгебраическую дробь.
4x2 — 4 года2
х + у
Верный:
Помните, что числитель представляет собой разность в два квадрата и может быть заменен на:
(2x — 2 года) (2x + 2y)
х + у
Упрощение будет сделано путем помещения 2 в доказательство еще раз в два фактора.
2 · (х — у) · 2 · (х + у)
х + у
2 · 2 · (х — у) · (Х + у)
х + у
4 · (х — у)·(х + у) = 4 · (х — у)
х + у
Обратите внимание, что в разности двух квадратов в одном из множителей происходит сложение, а в другом — вычитание.
Неправильно:
Используйте один из двух других замечательных кейсов продукта:
4x2 — 4 года2
х + у
(2x + 2г) (2x + 2y)
х + у
Или «приведите показатель 2 в доказательство»:
4x2 — 4 года2
х + у
4 (х — у)2
х + у
Чтобы избежать этих двух последних ошибок, предлагаем прочитать текст сумма квадрата, Общий фактор в доказательствах а также Потенцирование.
Хорошая учеба!
Луис Пауло Морейра
Окончил математику
Так сокращать дроби нельзя!
1 марта 2012
Работая с дробями, многие ученики допускают одни и те же ошибки. А все потому, что они забывают элементарные правила арифметики. Сегодня мы повторим эти правила на конкретных задачах, которые я даю на своих занятиях.
Вот задача, которую я предлагаю каждому, кто готовится к ЕГЭ по математике:
Задача. Морская свинья ест 150 грамм корма в день. Но она выросла и стала есть на 20% больше. Сколько грамм корма теперь ест свинья?
Неправильное решение. Это задача на проценты, которая сводится к уравнению:
![]()
Многие (очень многие) сокращают число 100 в числителе и знаменателе дроби:
![]()
Вот такую ошибку допустила моя ученица прямо в день написания этой статьи. Красным отмечены числа, которые были сокращены.
Излишне говорить, что ответ получился неправильный. Судите сами: свинья ела 150 грамм, а стала есть 3150 грамм. Увеличение не на 20%, а в 21 раз, т.е. на 2000%.
Чтобы не допускать подобных недоразумений, помните основное правило:
Сокращать можно только множители. Слагаемые сокращать нельзя!
Таким образом, правильное решение предыдущей задачи выглядит так:
![]()
Красным отмечены цифры, которые сокращаются в числителе и знаменателе. Как видите, в числителе стоит произведение, знаменателе — обыкновенное число. Поэтому сокращение вполне законно.
Работа с пропорциями
Еще одно проблемное место — пропорции. Особенно когда переменная стоит с обеих сторон. Например:
Задача. Решите уравнение:
Неправильное решение — у некоторых буквально руки чешутся сократить все на m:
![]()
Сокращаемые переменные показаны красным. Получается выражение 1/4 = 1/5 — полный бред, эти числа никогда не равны.
А теперь — правильное решение. По существу, это обыкновенное линейное уравнение. Решается либо переносом всех элементов в одну сторону, либо по основному свойству пропорции:
![]()
Многие читатели возразят: «Где ошибка в первом решении?» Что ж, давайте разбираться. Вспомним правило работы с уравнениями:
Любое уравнение можно делить и умножать на любое число, отличное от нуля.
Просекли фишку? Можно делить только на числа, отличные от нуля. В частности, можно делить на переменную m, только если m != 0. А что делать, если все-таки m = 0? Подставим и проверим:
![]()
Получили верное числовое равенство, т.е. m = 0 — корень уравнения. Для остальных m != 0 получаем выражение вида 1/4 = 1/5, что, естественно, неверно. Таким образом, не существует корней, отличных от нуля.
Выводы: собираем все вместе
Итак, для решения дробно-рациональных уравнений помните три правила:
- Сокращать можно только множители. Слагаемые — нельзя. Поэтому учитесь раскладывать числитель и знаменатель на множители;
- Основное свойство пропорции: произведение крайних элементов равно произведению средних;
- Уравнения можно умножать и делить только на числа k, отличные от нуля. Случай k = 0 надо проверять отдельно.
Помните эти правила и не допускайте ошибок.
Смотрите также:
- Как решать квадратные уравнения

- Теорема Виета

- Знаки тригонометрических функций

- Задача B1 — время, числа и проценты

- Как представить обычную дробь в виде десятичной

- Задача B2 на проценты: железнодорожные билеты

Основное свойство дроби: Если числитель и знаменатель алгебраической дроби поделить на одно и то же ненулевое выражение, то получится алгебраическая дробь, равная прежней: дробь не изменится.
$frac{Acdot X}{Xcdot B}=frac{Acdot X:X}{Xcdot B:X}=frac{Acdot1}{1cdot B}=frac{A}{B}$ $Xne0$ $Bne0$
Сократить дробь — значит разделить числитель и знаменатель этой дроби на один и тот же множитель.
Алгоритм сокращения алгебраических дробей
- Разложить числитель и знаменатель дроби на множители.
- Найти общие множители.
- Разделить числитель и знаменатель на общие множители.
Пример 2: Сократить дроби $frac{7a}{ax}$ $frac{6m}{-9m}$ $frac{10ab^6c}{15a^3b^2x}$ $frac{8left(a-bright)}{a-b}$
$frac{7a}{ax}=frac{7cdot a}{acdot x}=frac{7cdot [a]}{[a]cdot x}=frac{7cdot [1]}{[1]cdot x}=frac{7}{x}$ общий множитель $a$
$frac{6m}{-9m}=frac{6cdot [m]}{-9cdot [m]}=frac{2cdot3cdot [1]}{-3cdot3cdot [1]}=-frac{2}{3}$ общий множитель $3m$
$frac{10ab^6c}{15a^3b^2x}=frac{10ab^6c:[5ab^2]}{15a^3b^2x:[5ab^2]}=frac{2b^4c}{3a^2x}$ общий множитель $5ab^2$
$frac{8left(a-bright)}{a-b}=frac{8left(a-bright):[a-b]}{(a-b):[a-b]}=8$ общий множитель $a-b$
Пример 3: Сократить алгебраические дроби


Пример 4: Сократить дробь $frac{x^2+5x}{25-x^2}$
- Разложим числитель и знаменатель на множители: в числителе — вынос за скобки, в знаменателе — формула:
- $frac{x^2+5x}{25-x^2}=frac{xleft(x+5right)}{left(5-xright)left(5+xright)}$
- Появился общий множитель $x+5$. Сократим и числитель и знаменатель на общий множитель. Т.е. Поделим:
- $frac{x^2+5x}{25-x^2}=frac{xleft(x+5right)}{left(5-xright)left(5+xright)}=frac{x}{5-x}$
Пример 5: Сократить дробь $frac{a^2+4a+4}{a^2-4}$
- В числителе формула полного квадрата, в знаменателе- формула разности квадратов. Разложим их:
- $frac{a^2+4a+4}{a^2-4}=frac{(a+2)^2}{(a-2)(a+2)}$
- Вдруг, откуда — то (?) Появился общий множитель $a+2$. Сократим и числитель и знаменатель на нее:
- $frac{a^2+4a+4}{a^2-4}=frac{(a+2)^2}{(a-2)(a+2)}=frac{a+2}{a-2}$
Пример 6: Сократить дробь $frac{x^2-6x-7}{x+1}$
- В числителе выделим полный квадрат, Разложим по формуле разности квадратов:
- $frac{x^2-6x-7}{x+1}=frac{x^2-6x+9-9-7}{x+1}=frac{left(x-3right)^2-16}{x+1}=frac{left(x-3-4right)left(x-3+4right)}{x+1}=frac{left(x-7right)left(x+1right)}{x+1}=x-7$
- Вдруг, откуда — то (?) появился общий множитель $x+1$. Сократим и числитель и знаменатель на нее:

Примеры для закрепления:
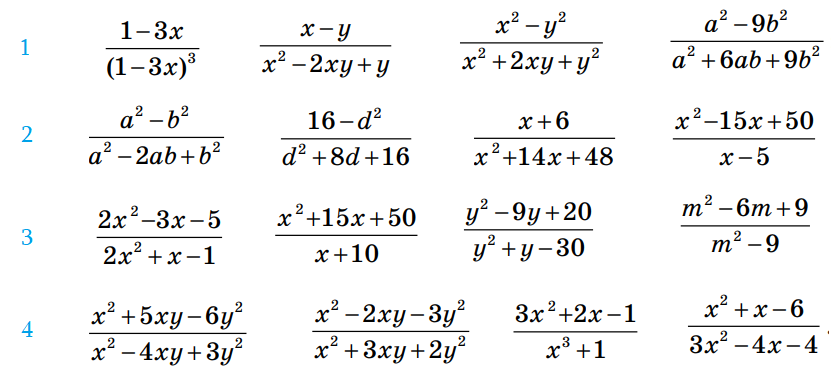
Упражнения
Подборка по базе: Технологическая карта урока 5 класс.docx, Практическая работа — разработка технологической карты урока Инф, Конспект урока по математике _Урок — сказка_ (1 класс).docx, ПРАКТИКУМ №2 _Практическая работа по разработке технологической , Подбор заданий для урока решения задач _Равновесие рычага_ (7 кл, Конспект урока по теме _Словосочетание_ (5 класс).docx, Список текстов, вопросов, конспектов.pdf, 2. Конспект лекций З. Фрейда.pdf, конспект урока Есенжарова Г. 5022Д.docx, Технологическая карта урока физики по теме _Электрические явлени
Тема урока: Сокращение алгебраических дробей
Тип урока: изучение нового материала
Задачи: Создать условия для развития умений сокращать алгебраические дроби
Планируемые результаты
Предметные: Научиться сокращать алгебраические дроби
Метапредметные:
Познавательные: ориентироваться на разнообразные способы решения задач
Регулятивные: учитывать правила в планировании и контроле способа решения
Коммуникативные: контролировать действия партнера
Личностные: формировать интерес к изучению математики и желанию применить приобретённые знания умения и навыки
Цели:
- систематизировать знания учащихся,
- ввести понятие алгебраической дроби, научить раскладывать на множители числитель и знаменатель дроби
- развивать творческую самостоятельность учащихся, коммуникативные навыки, формировать интерес к предмету.
План урока:
- Организационный момент. (2 мин)
- Актуализация опорных знаний
- Мотивационный этап
- Формулировка темы и целей урока.
- Изучение нового материала
- Закрепление изученного материала
- Итог урока.
- Рефлексия
- Домашнее задание.
Оснащение урока:
- Раздаточный материал.
- Мультимедийное приложение.
Ход урока
1 . Организационный момент.
Учитель отмечает отсутствующих, проверяет готовность к уроку.
2. Мотивационный этап
Учитель: Новое понятие в математике не появляется из неоткуда. Оно появляются тогда, когда в нём ощущается объективная необходимость. Именно так появились в математике отрицательные числа, обыкновенные и десятичные дроби.
Сегодня мы с вами ввёдем новое понятие. Предпосылки для этого у нас имеются. Вернёмся к § 23, где мы обсуждали «Деление одночлена на одночлен». Тогда мы рассмотрели ряд примеров. Выделим несколько из них:
1. Разделить одночлен  на
на 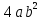 .
.
Решили мы его так: вместо записи 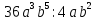 использовали черту дроби
использовали черту дроби 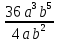
Это позволило вместо записей 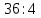 ,
,  ,
, 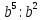 , использовать черту дроби, сделать решение примера более наглядно
, использовать черту дроби, сделать решение примера более наглядно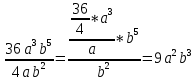
2. Разделить одночлен 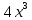 на
на  .
.
Действуя по тому же образцу, мы получили: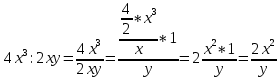
В этом случае мы заметили, что одночлен 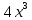 не удалось разделить на одночлен
не удалось разделить на одночлен  так, чтобы получился одночлен
так, чтобы получился одночлен
Но ведь математические модели могут содержать деление любых одночленов. Поэтому требуется ввести новое понятие, понятие алгебраической дроби.
 — алгебраическая дробь.
— алгебраическая дробь.
3. Формулировка целей и темы урока
Учитель: Сформулируйте тему урока.
Учащиеся: Тема урока: «Сокращение алгебраических дробей»
Учитель: А теперь нам нужно сформулировать цели и задачи.
Учащиеся: Цель нашего урока будет: научиться сокращать алгебраические дроби.
А задачи:
1. Повторить способы разложения на множители и формулы сокращенного умножения
2. Нам нужно сформулировать определение алгебраической дроби;
3.Нам нужно выяснить, как работать с алгебраическими дробями и сокращать их, составить алгоритм;
4 Практиковаться сокращать алгебраические дроби.
Учитель: Молодцы! Так как единственный путь, ведущий к знанию – это деятельность, теперь приступим к выполнению поставленных задач
4. Актуализация опорных знаний
Учитель: Какие способы разложения на множители вы знаете?
Учащиеся: способ вынесения общего множителя за скобки, способ группировки, разложение на множители с помощью формул сокращенного умножения.
Учитель: — Записать на доске, как разложить на множители квадрат разности двух выражений
— Записать, как разложить разность кубов двух выражений
(один из учащихся выполняет задания на доске)
Одним из основных умений, которые нам сегодня понадобятся – разложение многочлена на множители. Проверим, готовы ли мы.
Задание: Необходимо найти для многочлена, который записан в левом столбце, его разложение в правом столбце. (Выполняют задание по парам)
1. 49 + 14у + у2; А) (7 – у)(7 + у)
2. 2у2 – 20у + 50; Б) (у – 5)(у2 + 5у + 25)
3. х3 – х2у; В) 2(у – 5)2
4. 49 – у2; Г) (7 + у)2
5. у3 – 125; Д) (у – 3)3
6. у3 – 9у2 + 27у – 27; Е) х2(х – у)
Учащиеся: Ответ: Г, В, Е, А, Б, Д.
Учитель: Предлагаю учащимся оценить себя: “Отлично знаю формулы” — нет ошибок; “Хорошо знаю формулы” — 1 ошибка; “Удовлетворительно знаю формулы” — 2 ошибки
Учащиеся: Оценивают свою работу.
Учитель: Отлично! Теперь можно приступать к выполнению следующих задач.
5. Изучение нового материала
Учитель: Ребята, давайте попробуем сами сформулировать, что называется алгебраической дробью.
Учащиеся: Высказывают свои предположения
Учитель: (После ответов учеников) Алгебраическая дробь – это деление одного многочлена P на другой многочлен Q: 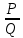 , P – числитель дроби, Q – знаменатель дроби
, P – числитель дроби, Q – знаменатель дроби
Рассмотрим примеры алгебраических дробей: ,
, 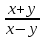 ,
, 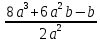
Иногда алгебраическую дробь можно заменить многочленом: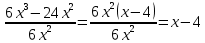
Т.е. многочлен 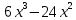 удалось разделить на
удалось разделить на 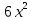 . В частном получилось
. В частном получилось 
Похожая ситуация уже встречалась нам: дробь 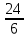 можно заменить целым числом 4, а дробь
можно заменить целым числом 4, а дробь 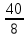 числом 5. Однако дробь
числом 5. Однако дробь 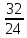 целым числом заменить не удастся, но эту дробь можно упростить. Чтобы упростить данное выражение, нужно разложить числитель и знаменатель на простые множители:
целым числом заменить не удастся, но эту дробь можно упростить. Чтобы упростить данное выражение, нужно разложить числитель и знаменатель на простые множители: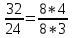
Теперь можно сократить на общий множитель 8, тогда получим 
По аналогии действия с алгебраическими дробями заключаются в следующем: нужно и числитель, и знаменатель разложить на множители, а после этого, если есть возможность общие множители сократить.
Рассмотрим примеры:
Пример 1: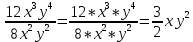
В результате деления одночленов получен новый одночлен;
Пример 2: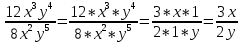
В результате деления одночленов получена алгебраическая дробь.
Пример 3:

Применим в числителе формулу для квадрата суммы, а в знаменателе формулу для разности квадратов двух выражений
Пример 4:
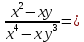
Раскладываем числитель и знаменатель на множители методом вынесения общего множителя: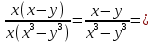
Применим в знаменателе формулу разности кубов:
Пример 5:
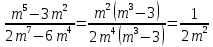
Алгоритм сокращения алгебраических дробей
1 Разложить числитель и знаменатель алгебраической дроби на множители
2 Сократить общие множители
3 Записать ответ (получившееся выражение)
6 Закрепление пройденного материала.
Сократите дробь
![]() ;
;![]() ;
;![]() ;
;
Выполните задание из учебника
35,5(б), 35.10(б, г),35.16(а, г), 35.19 (б),35.22(а),
8. Включение в систему знаний, повторение.
Учащимся предлагается из листов, на которых записаны этапы алгоритма, составить полный алгоритм. Листы нужно закрепить на доске с помощью магнитов.
Найди ошибку.
Учитель:
Каждому человеку свойственно ошибаться. Не ошибается только тот, кто ничего не делает.
Проверьте равенства:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
9 Домашнее задание. Рефлексия настроения.
Итог урока
1 Достигли ли мы поставленных целей?
2 Что мы сегодня делали на уроке?
3 Сформулируйте алгоритм сокращения алгебраических дробей
— Разложить числитель и знаменатель алгебраической дроби на множители
— Сократить общие множители
— Записать ответ (получившееся выражение)
4 Заполните таблицу.
Рефлексия
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |
Эта таблица поможет выявить ваши слабые стороны. Проработайте их, устраните пробел. На следующий урок возьмите их собой.
8. Домашнее задание
35,23 (а,б) 35,30(б) 35,33(а)
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |
| № | Вопрос | Да | Нет | Затрудняюсь |
| 1 | Знаю ли я формулы сокращённого умножения? | |||
| 2 | Умею ли я применять их при сокращении алгебраических дробей? | |||
| 3 | Смогу ли я сокращать дроби самостоятельно? |

