Типичные ошибки вычислительные ошибки - Ремонт и установка крупной бытовой техники

Типичные вычислительные ошибки учащихся при решении пробных
заданий ОГЭ и методы их предотвращения

При выполнении пробных заданий ОГЭ учащимися
допускается ряд типичных ошибок, в связи с чем, была предпринята попытка их
систематизировать и предложить методы их предотвращения.

Многие ошибки вызваны тем, что задания ОГЭ
охватывают материал фактически с 1 по 9 класс и учащиеся к 9 классу порой
забывают материал и утрачивают навыки, полученные в начальной школе и 5-6
классах, когда закладываются умения производить вычисления без использования
калькулятора.

Наиболее распространённая ошибка – «потеря
знака». В процессе вычислений учащиеся забывают о том, будет результат
положительным или отрицательным. Предлагается акцентировать внимание учащихся на
необходимости предварительно определить знак результата до осуществления
вычислений и записать его после знака «=» и лишь после этого производить
вычисления. Например: необходимо перемножить «-36» и «48», определяем, что
произведение этих чисел будет со знаком «-» и записываем его после знака «=» и
лишь после этого приступаем к умножению этих чисел столбиком.

Также часто ошибочный знак у числа или
переменной получается при действиях с дробями. Необходимо обратить внимание учащихся,
что при любых действиях с дробями желательно числитель записывать в скобках,
тогда при перемножении дробей содержащих в числителе выражение

снижается вероятность ошибки в определении
знака второго слагаемого в числителе после умножения по распределительному
закону.

Вообще необходимо акцентировать внимание, что
знак «-» относится к числу перед которым он стоит и выражение «-3+5-6+4» — это
сложение четырёх чисел, имеющих разные знаки. И при выполнении выражения
«-3*(х-1)» нужно «-3» умножить на «х», а затем «-3» умножить на «-1».

Данные проблемы могут показаться примитивом,
не заслуживающим внимания, но на практике многие учащиеся девятых классов
делают такие ошибки очень часто.

Следующий распространённый тип ошибок –
неправильный порядок вычислений, приводящий к громоздким числам и
вычислительным ошибкам. Дети начинают выполнять вычисления по порядку «в лоб»,
забывая, что, во-первых, в дробях можно сократить множители в числителе и
знаменателе в выражениях типа после сокращения которых
действие выполняется устно, при попытке же последовательно перемножить
числители и знаменатели дробей и потом разделить их «уголком» вероятность
допущения ошибки растёт с каждый разрядом числа. Во-вторых, при сложении чисел
не нужно торопиться и определить порядок сложения, например в выражении
«14+17+6+3» гораздо проще вспомнить, что можно выполнять сложение в любом
порядке и сложить «14 и 6, 17 и 3».

И в целом, часто ошибки – следствие утраты
навыка производить вычисления без калькулятора. Необходимо ещё раз напомнить
учащимся материал второго — пятого класса. Даже вполне успевающие ученики порой
делают глупые ошибки при необходимости из «9» вычесть «0,36» ибо правило
«записать запятую под запятой» часто забыто. А при делении «83» на «4» или
«2030» на «5» и других чисел, где необходимо дважды «сносить» число при делении
уголком, предварительно записав в частное «0», ошибку делают почти все
учащиеся.

Библиографическое описание:

Смородинова, Л. В. Причины вычислительных ошибок младших школьников / Л. В. Смородинова. — Текст : непосредственный // Молодой ученый. — 2016. — № 5.6 (109.6). — С. 93-94. — URL: https://moluch.ru/archive/109/27017/ (дата обращения: 31.01.2023).

В статье рассматриваются различные аспекты возникновения вычислительных ошибок младших школьников. Перечислены типы вычислительных ошибок, приведены возможные пути устранения вычислительных ошибок.

Ключевые слова: вычислительные ошибки, содержание ошибок, причины ошибок.

При формировании способов вычислений у младших школьников часто возникают типичные ошибки, поскольку процесс формирования является сложным и длительным. Под типичной вычислительной ошибкой в литературе понимают полученный несколькими учениками результат вычислений, неадекватный объективному (А.К. Артемов, П.Я. Шеварев). Успех обучения зависит от своевременного предупреждения таких ошибок [2]. Это возможно лишь в случае выявления их причин возникновения.

Различные аспекты причин ошибок, допускаемых школьниками, были исследованы в диссертациях Г. А. Асанова, Д.И. Икрамова, И.М. Кирилецкого [4], А.Г. Муханова, В.Г. Прочухаева, Д.А. Скрыпника, А.Ф. Сычикова и др. В этих работах перечислены типы допускаемых ошибок [1]. Приведено большое количество примеров ошибочных рассуждений и связанных с ними неверных решений [2].

Достаточно подробно исследованы отклонения действий учащихся от верных.

В то же время, можно констатировать, что в приведенных источниках предлагается анализ ошибок, проведенный с позиций их содержания. Однако он не гарантирует исчезновения типичных ошибок при дальнейшей работе [3].

Многие исследователи единодушны в том, что чаще всего причина появления ошибки имеет методический характер. Для анализа причин появления типичных ошибок в процессе вычислений воспользуемся методикой, разработанной А.К. Артемовым.

Будем различать содержание ошибки и причину ее возникновения. Содержание ошибки составляет то, что объективно неверно, неадекватно выполнено в действиях учащихся. Причиной ошибки называется некоторое обстоятельство (или их совокупность), повлекшие выполнение неадекватного действия. Например, если учащийся выполняет сложение чисел следующим образом: 54 + 3 = 84, то содержание ошибки составляет нарушение алгоритма сложения двузначного и однозначного чисел (вместо прибавления второго слагаемого к единицам первого слагаемого ученик прибавляет второе слагаемое к десяткам первого слагаемого). Причина ошибки остается пока неясной.

Методика выявления причин ошибок, предложенная названными авторами, предусматривает сопоставление двух ситуаций: той, в которой ученик допустил ошибку, и той, в которой он выполнил верное действие. В качестве последней может быть взят процесс объективно выполненного действия. Эти ситуации должны быть сходны (или различаться) по одному существенному компоненту. При сопоставлении ситуаций сначала устанавливается, какие условия необходимы и достаточны для верно выполненного действия. Затем путем анализа условий обучения выявляются обстоятельства, благоприятствующие зарождению ошибки. Для приведенного примера процесс объективно верного выполнения сложения будет таким: 54+3=(50+4)+3=50+(4+3)=50+7=57. При сопоставлении ошибочно и верно выполненных действий возникают следующие предположения:

− Ученик не заменил двузначное число суммой разрядных слагаемых (причиной этого может служить неполная ориентировочная основа действия сложения двузначного и однозначного чисел).

− Ученик не включил в обобщенную ориентировочную основу действия существенный для сложения признак «можно складывать только величины, измеренные в одних мерках».

Оба предположения указывают на то, что у ученика, совершившего ошибку, сформирована неполная частная ориентировочная основа действия сложения двузначного и однозначного чисел. В этом заключается ближайшая причина возникновения ошибки.

Сформированная неполная частная ориентировочная основа действия может быть причиной слишком узких и слишком широких обобщений. Поясним это утверждение.

Ориентировочная основа действия – это набор ориентиров, необходимый и достаточный для верного выполнения действия или распознавания понятия. Если хотя бы один из ориентиров отсутствует в ООД, действие становится другим и ведет к неверному результату. Если ученик не достраивает самостоятельно сформированную ООД, то будем говорить, что в этом случае ученик владеет слишком широкой ООД.

Сформированная неполная ориентировочная основа действия, в свою очередь, является следствием неверного методического подхода к обучению, рассогласованности методики обучения с закономерностями процесса усвоения знаний и умений. В частности, возможно, что неполнота ориентировочная основа действия, сформированной у детей, обусловлена игнорированием закономерности получения обобщений (Н.Ф.Талызина): «Обобщение идет только по тем признакам, которые включены в ориентировочную основу действия, направленного на анализ изучаемого объекта». Это означает, что методические ошибки являются отдаленными причинами возникновения массовых ошибок [4] .

Таким образом, для предупреждения появления ошибок необходимо не только выявить их содержание, но и определить ближайшие и отдаленные причины возникновения. Результатом этого анализа может быт разработка специальных упражнений с учетом психологических закономерностей процесса усвоения знаний и умений. [6]

Литература:

Брадис В.М. Ошибки в математических рассуждениях: Пособие для учителей. М.: Просвещение, 1967. 191 с.
Далингер В.А. Начала математического анализа. Типичные ошибки, их причины и пути их предупреждения. Омск: ООО «Издатель-полиграфист», 2002. 158 с.
Зубова С.П., Лысогорова Л.В. Математические олимпиады в современных условиях. Самарский научный вестник. 2013. № 3 (4). С. 61-63.
Зубова С.П., Лысогорова Л.В. Причины вычислительных ошибок младших школьников и пути их предупреждения. Педагогика городского пространства: теория, методология, практика. Сборник трудов по материалам Всероссийской научно-практической конференции. Самара, 2015. С. 284-288
Кочетова Н.Г., Севенюк С.А., Лысогорова Л.В. Юбилею факультета начального образования Поволжской государственной социально-гуманитарной академии посвящается//Поволжский педагогический вестник. 2014. № 4 (5). С. 5-7.
Лысогорова Л.В. Педагогические условия развития математических способностей младших школьников. Сибирский педагогический журнал. 2007. № 9. С. 228-233

Основные термины (генерируются автоматически): ошибка, однозначное число, ориентировочная основа действия, содержание ошибки, ученик, выполненное действие, действие, действие сложения, отдаленная причина возникновения, причина ошибки.

Ключевые слова

вычислительные ошибки,

содержание ошибок,

причины ошибок

вычислительные ошибки, содержание ошибок, причины ошибок

Содержание

1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
2 Виды мер точности
3 Предельные погрешности
4 Погрешности округлений при представлении чисел в компьютере
5 Погрешности арифметических операций
6 Погрешности вычисления функций
7 Числовые примеры
8 Список литературы
9 См. также

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10⁻⁶, если коэффициенты исходных уравнений задаются с точностью 10⁻².

Виды мер точности

Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой

$Delta(tilde a)=|tilde a-a|,$

где $tilde a$ – приближение к точному значению $a$ .
Относительная погрешность определяется формулой

$delta(tilde a)=frac{|tilde a-a|}{a}.$

Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, $tilde a=9348$ , абсолютная погрешность $Delta(tilde a)=15$ . Записывая число в виде

$9348=9cdot10^3+3cdot10^2+4cdot10^1+8cdot10^0,$

имеем $0,5cdot10^1<Delta(tilde a)<0,5cdot10^2$ , следовательно, число имеет две верных значащих цифр (9 и 3).

В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:

$Delta(tilde a)<0,5cdot10^{m-n+1} ,$

где $m$ — порядок (вес) старшей цифры, $n$ — количество верных значащих цифр.
В рассматриваемом примере $Delta(tilde a)le0,5cdot10^{3-2+1}le0,5cdot10^2=50$ .

Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:

$delta(tilde a)lefrac{Delta(tilde a)}{alpha_m}10^mlefrac{10^{m-n+1}}{alpha_m10^m}lefrac{1}{alpha_m10^{n-1}},$

где $alpha_m$ — старшая значащая цифра числа.

Для двоичного представления чисел имеем $delta(tilde a)le2^{-n}$ .

Тот факт, что число $tilde a$ является приближенным значением числа $a$ с абсолютной погрешностью $Delta(tilde a)$ , записывают в виде

$a=tilde apmDelta(tilde a),$

причем числа $tilde a$ и $Delta(tilde a)$ записываются с одинаковым количеством знаков после запятой, например, $a=2,347pm0,002$ или $a=2,347pm2cdot10^{-3}$ .

Запись вида

$a=tilde a(1pmdelta(tilde a))$

означает, что число $tilde a$ является приближенным значение числа $a$ с относительной погрешностью $delta(tilde a)$ .

Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.

Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений

$AX=F$

характеризуется невязкой

$R=F-Atilde X,$

где $tilde X$ — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения $Delta(X)=tilde X-X$ , причём если невязка мала, то погрешность может быть значительной.

Предельные погрешности

Пусть искомая величина $a$ является функцией параметров $t_1, ldots , t_n in Omega, qquad a*$ — приближенное значение $a$ . Тогда предельной абсолютной погрешностью называется величина

$D(a^*) = suplimits_{(t_1, ldots ,t_n) in Omega } left|{a(t_1, ldots ,t_n) - a^*}right| ,$

Предельной относительной погрешностью называется величина $D(a*)/| a*|$ .

Пусть $left|{t_j - t_j^*}right| le Delta (t_j^* ), qquad j = 1 div n$ — приближенное значение $a^* = a(t_1^*, ldots ,t_n^* )$ . Предполагаем, что $a$ — непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

$a(t_1, ldots ,t_n) - a^* = sumlimits_{j = 1}^n gamma_j (alpha )(t_j - t_j^*),$

где $gamma_j (alpha ) = a^{prime}_{t_j}(t_1^* + alpha (t_1 - t_1^*), ldots ,t_n^* + alpha (t_n - t_n^*)), qquad 0 le alpha le 1$ .

Отсюда

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_1 (a^*) = sumlimits_{j = 1}^n b_j Delta (t_j^*),$

где $b_j = suplimits_Omega left|{a^{prime}_{t_j}(t_1, ldots ,t_n)}right|$ .

Можно показать, что при малых $rho = sqrt{{(Delta (t_1^* ))}^2 + ldots + {(Delta (t_n^* ))}^2 }$ эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_2 (a^*),$

где $D_2 (a^*) = sumlimits_{j = 1} left|{gamma_j (0)}right| Delta (t^*)$ .

Несложно показать, что:

$Delta ( pm t_1^* pm , ldots , pm t_n^*) = Delta (t_1^* ) + ldots + Delta (t_n^* )$ — предельная погрешность суммы или разности равна сумме предельных погрешностей.
$delta (t_1^* cdots t_m^* cdot d_1^{* - 1} cdots d_m^{* - 1} ) = delta (t_1^* ) + ldots + delta (t_m^*) + delta (d_1^*) + ldots + delta (d_n^*)$ — предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.

Погрешности округлений при представлении чисел в компьютере

Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число $a$ , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом $tilde a$ , представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь

$a=underbrace{pm2^p}_{order}underbrace{left(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}+frac{a_{t+1}}{2^{t+1}}+dotsright)}_{mantissa},$

где $a_j={01$ , $qquad (j=1,2,...)$ — цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число

$tilde a=pm2^pleft(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}right).$

Абсолютная погрешность округления в этом случае равна

$a-tilde a=pm2^pleft(frac{a_{t+1}}{2^{t+1}}+frac{a_{t+2}}{2^{t+2}}+dotsright).$

Наибольшая погрешность будет в случае $a_{t+1}=1, qquad a_{t+2}=1,$ , тогда

$|a-tilde a|lepm2^pfrac{1}{2^{t+1}}underbrace{left(1+frac{1}{2}+frac{1}{2^2}+dotsright)}_{=2}=2^{p-t}.$

Т.к. $|M|ge0,5$ , где $M$ — мантисса числа $a$ , то всегда $a_1=1$ . Тогда $|a|ge2^pcdot2^{-1}=2^{p-1}$ и относительная погрешность равна $frac{|a-tilde a|}{|a|}le2^{-t+1}$ . Практически применяют более точные методы округления и погрешность представления чисел равна

( 1 )

$frac{|a-tilde a|}{|a|}le2^{-t},$

т.е. точность представления чисел определяется разрядностью мантиссы $t$ .
Тогда приближенно представленное в компьютере число можно записать в виде $tilde a=a(1pmepsilon)$ , где $|epsilon|le2^{-t}$ – «машинный эпсилон» – относительная погрешность представления чисел.

Погрешности арифметических операций

При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.

Округленное в системе с плавающей точкой число, соответствующее точному числу $x$ , обозначается через $fl(x)$ (от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:

$fl(abox b)=abox b(1pmepsilon),$

где $box$ — любая из арифметических операций, $|epsilon|le2^{-t}$ .

Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).

Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Если сумма точных чисел равна

$S=a_1+a_2+dots+a_n,$

сумма приближенных чисел равна

$tilde S=a_1+Delta(a_1)+a_2+Delta(a_2)+dots+a_n+Delta(a_n),$

где $Delta(a_i), qquad i=1,2,...,n$ — абсолютные погрешности представления чисел.

Тогда абсолютная погрешность суммы равна

$Delta(S)=Delta(a_1)+Delta(a_2)+dots+Delta(a_n).$

Относительная погрешность суммы нескольких чисел равна

( 2 )

$delta(S)=frac{Delta(S)}{S}=frac{a_1}{S}left(frac{Delta(a_1)}{a_1}right)+frac{a_2}{S}left(frac{Delta(a_2)}{a_2}right)+dots=frac{a_1delta(a_1)+a_2delta(a_2)+dots}{S},$

где $delta(a_i), qquad i=1,2,...,n$ — относительные погрешности представления чисел.

Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

$min quad delta(a_k)ledelta(S)le max quad delta(a_k), qquad k=1,2,...,n, quad a_k>0.$

При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых $Delta(a_i)$ величина $S$ может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.

Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.

$S=x_1+x_2+x_3,$

$tilde S_1=(x_1+x_2)(1+delta_1),$

( 3 )

$tilde S=(tilde S_1+x_3)(1+delta_2)=(x_1+x_2)(1+delta_1)(1+delta_2)+x_3(1+delta_2).$

При другой последовательности действий погрешность будет другой:

$tilde S_1=(x_3+x_2)(1+delta_1),$

$tilde S=(x_3+x_2)(1+delta_1)(1+delta_2)+x_1(1+delta_2).$

Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:

$tilde S=tilde x_1+tilde x_2+tilde x_3,$

где $tilde x_1=x_1(1+delta_1)(1+delta_2), quad tilde x_2=x_2(1+delta_1)(1+delta_2), quad tilde x_3=x_3(1+delta_2).$

При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.

$S=a_1cdot a_2,$

$tilde S=a_1cdot a_2(1+delta(a_1))(1+delta(a_2))$ ≅ $a_1cdot a_2(1+delta(a_1)+delta(a_2)),$

с точностью величин второго порядка малости относительно $delta$ .

Тогда $delta(S)=delta(a_1)+delta(a_2)$ .

Если $S=frac{a_1}{a_2}$ , то $Delta(S)=frac{a_1(1+delta_1)}{a_2(1+delta_2)}-frac{a_1}{a_2}=frac{a_1(delta_1-delta_2)}{a_2(1+delta_2)}approx frac{a_1}{a_2}(delta_1-delta_2), qquad delta(S)$ ≅ $delta_1-delta_2.$

При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:

$delta_Sigma approx delta_{fl} quad sqrt{n},$

где $delta_Sigma$ – суммарная погрешность, $|delta_{fl}|leepsilon$ – погрешность выполнения операций с плавающей точкой, $epsilon$ – погрешность представления чисел с плавающей точкой.

Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций.

Абсолютная трансформированная погрешность дифференцируемой функции $y=f(x)$ , вызываемая достаточно малой погрешностью аргумента $Delta(x)$ , оценивается величиной $Delta(y)=|f'(x)|Delta(x)$ .

Если $f(x)>0$ , то $delta(y)=frac{|f'(x)|}{f(x)}Delta(x)=left|(ln(f(x)))'right|cdotDelta(x)$ .

Абсолютная погрешность дифференцируемой функции многих аргументов $y=f(x_1, x_2, ..., x_n)$ , вызываемая достаточно малыми погрешностями $Delta(x_1), Delta(x_2), ..., Delta(x_n)$ аргументов $x_1, x_2, ...,x_n$ оценивается величиной:

$Delta(y)=sumlimits_{i=1}^nleft|frac{partial f}{partial x_i}right|Delta(x_i)$ .

Если $f(x_1,x_2,...,x_n)>0$ , то $delta(y)=sumlimits_{i=1}^nfrac{1}{f}cdotleft|frac{partial f}{partial x_i}right|cdotDelta(x_i)=sumlimits_{i=1}^{n}left|frac{partial l_n(f)}{partial x_i}right|Delta(x_i)$ .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной $y=f(x)$ , если $f(x)$ дифференцируема и $f'(x)not=0$ :

$Delta(x)=frac{1}{|f'(x)|}Delta(y)$ .

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция $y=f(x_1,x_2,...,x_n)$ наиболее критична к погрешности $Delta(x_i)$ , то:

$Delta(x_i)=frac{Delta(y)}{left|frac{partial f}{partial x_i}right|}qquad$ (погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

$Delta(x_i)=frac{Delta(y)}{nleft|frac{partial f}{partial x_i}right|},qquad i=overline{1,n}.$

Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

$x^4 - 4x^3 + 8x^2 - 16x + 15.underbrace{99999999}_8 = {(x - 2)}^4 - 10^{- 8} = 0.$

Точное решение задачи легко найти:

$(x - 2)^2 = pm 10^{- 4},$

$x_1= 2,01; x_2= 1,99; x_{3,4}= 2 pm 0,01i.$

Если компьютер работает при $delta _M > 10^{ - 8}$ , то свободный член в исходном уравнении будет округлен до $16,0$ и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение $(x-2)^4= 0$ , т.е. $x_{1,2,3,4} = 2$ , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена $approx10^{-8}$ привели, независимо от метода решения, к погрешности в решении $approx10^{-2}$ .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

$u''(t) = u(t), qquad u(0) = 1, qquad u'(0) = - 1.$

Общее решение имеет вид:

$u(t) = 0,5[u(0) + u'(0)]e^t + 0,5[u(0) - u'(0)]e^{- t}.$

При заданных начальных данных точное решение задачи: $u(x) = e^{-t}$ , однако малая погрешность $delta$ в их задании приведет к появлению члена $delta e^t$ , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

$stackrel{cdot}{u} = 10u,qquad u = u(t), u(t_0) = u_0,qquad t in [0,1].$

Его решение: $u(t) = u_0e^{10(t - t_0 )}$ , однако значение $u(t_0)$ известно лишь приближенно: $u(t_0) approx u_0^*$ , и на самом деле $u^*(t) = u_0^*e^{10(t - t_0)}$ .

Соответственно, разность $u* - u$ будет:

$u^* - u = (u_0^* - u_0)e^{10(t - t_0)}.$

Предположим, что необходимо гарантировать некоторую заданную точность вычислений $epsilon > 0$ всюду на отрезке $t in [0,1]$ . Тогда должно выполняться условие:

$|{u^*(t) - u(t)}| le varepsilon.$

Очевидно, что:

$maxlimits_{t in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| = |{u_0^* - u_0}|e^{10(1 - t_0)}.$

Отсюда можно получить требования к точности задания начальных данных $delta: qquad|u_0^* - u_0| < delta, qquad delta le varepsilon e^{ - 10}$ при $t_0= 0$ .

Таким образом, требование к заданию точности начальных данных оказываются в $e^{10}$ раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.

Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

$left{ begin{array}{l} u + 10v = 11, 100u + 1001v = 1101; end{array} right.$

является пара чисел ${1, quad 1}$ .

Изменив правую часть системы на $0,01$ , получим возмущенную систему:

$left{ begin{array}{l} u + 10v = 11.01, 100u + 1001v = 1101; end{array} right.$

с решением ${11.01, quad 0.00}$ , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность $delta_M = 0,0005$ . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки $u = 1,001,quad v = 1,002$ , разность которых составляет $Delta = |v_M - u_M| = 0,001$ .

В памяти машины эти же числа представляются в виде:

$u_M = u(1 + delta_M^u), quad v_M = v(1 + delta_M^v)$ , причем $mid delta_M^umid le delta_M$ и $mid delta_M^vmid le delta_M.$

Тогда:

$u_M - u approx udelta_M^u, quad v_M - v approx vdelta_M^v.$

Относительная ошибка при вычислении разности $u_M - v_M$ будет равна:

$delta = frac{(u_M - v_M) - (u - v)}{(u - v)} = frac{(u_M - u) - (v_M - v)}{(u - v)} = frac{delta_M^u - delta_M^v}{(u - v)}.$

Очевидно, что $delta = left|{frac{delta_M^u - delta_M^v}{Delta }} right| le frac{2delta_M}{0,001} approx 2000delta_M = 1$ , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение $u_{i+1} = qu_i, quad i ge 0, quad u_0 = a,quad q > 0, quad u_i > 0.$

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на $i$ -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением $u_i^M = u_i + delta_i$ , тогда вместо $u_{i+1}$ получим $u_{i + 1}^M = q(u_i + delta_i) = u_{i + 1} + qdelta_i$ , т.е. $delta_{i + 1} = qdelta_i,quad i = 0,1,ldots$ .

Следовательно, если $|q| > 1$ , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае $mid qmid le 1$ погрешность не возрастает и численный алгоритм устойчив.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
http://www.intuit.ru/department/calculate/calcmathbase/1/4.html

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Авторы
Файлы
Ключевые слова
Литература

Беляева Е.Р.

1 МБОУ ШР «СОШ №2»

подготовка к огэ по математике

анализ ошибок

уравнения

1. Марков С.Н., Осипенко Л.А., Лапшина Е.С. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2017 году. Методические рекомендации. – И: ГАУ ДПО ИРО, 2017. – 23с.

2. Лапшина Е. С., Марков С. Н., Осипенко Л. А. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2018 году. Методические рекомендации.– И: ГАУ ДПО ИРО, 2018. – 42 с.

3. Гаер М. А., Лапшина Е. С., Марков С. Н. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2019 году. Методические рекомендации. – И: ГАУ ДПО ИРО, 2019. – 38 с.

Введение

Структура Контрольно-измерительных материалов ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и одновременного создания условий, способствующих получению частью обучающихся подготовки повышенного уровня, достаточной для активного использования математики во время дальнейшего обучения, прежде всего при изучении её в средней школе на профильном уровне.

Чтобы быть зачисленным в профильный 10 класс на базе нашего учебного учреждения, необходимо сдать успешно экзамены по итогу 9-го класса. Успешно для меня – это значит на «отлично». Критерии оценивания экзамена по математике таковы: чтобы получить отметку «отлично», необходимо набрать минимум 22 балла. Это становится возможным лишь тогда, когда выпускник приступает к решению заданий с развёрнутым ответом с №20 — №25.

Со слов сверстников, я знаю, что не все педагоги, работающие в общеобразовательных школах, рассматривают с обучающимися задания повышенного уровня сложности, анализ типичных ошибок, которые допускают выпускники прошлых лет.

Мой вклад в решение данного проблемного вопроса заключается в том, что я предлагаю своим ровесникам, на основании моей работы, рассмотреть типичные ошибки выпускников, и самостоятельно закрепить материал, подготовиться к экзамену с помощью предложенных заданий. Мной были проанализированы КИМы с 2016-2019 годы.

Обзор литературы

Вопрос типичных ошибок, которые допускают выпускники, в тех или иных заданиях, особенно 2 части, рассматривается педагогами на совещаниях по итогам ГИА. Я не нашла ни одной исследовательской работы по данному направлению, которая была бы предложена учащимися. В основном данный проблемный вопрос представлен в виде педагогических статей.

По рекомендации своего руководителя основным источником исследования стали «Методические рекомендации результатов государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области», которые издаются Государственным автономным учреждением дополнительного профессионального образования Иркутской области «Институт развития образования Иркутской области».

Цель

Анализ типичных ошибок выпускников в решении задания №20 (2 часть) по теме «Уравнения».

Методы исследования

1.Поисковый.

2. Анализ, синтез (отбор необходимой информации, обобщение)

3.Практический

Результаты исследования

Спецификация контрольно измерительных материалов ОГЭ по математике.

Я рассмотрела спецификацию контрольных измерительных материалов для проведения ОГЭ. И сделала вывод, что задание №20 проверяет умение учащегося выполнять преобразования алгебраических выражений, решать уравнения. Задание №20 относится к повышенному уровню сложности и оценивается на 2 балла. Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.

Задание №20 подразделяется на:

-алгебраические выражения;

-уравнения;

-неравенства;

-системы неравенств;

-системы уравнений.

На данном этапе мной рассмотрены и представлены в работе:

Уравнения:

· Иррациональные.

· Дробно-рациональные.

· Уравнения, приводимые к квадратным.

· Применение свойств при решении уравнений.

Таблица 1

Основная статистика по выполнению задания №20 учащимися 9-х классов Иркутской области.

№ задания	Содержание задания	Процент участников, набравших максимальный балл по заданию
2016	2017	2018	2019
21 *	Решить уравнение или систему уравнений	6,4	21,1	10,6	14,8

*До 2020 года задание №20 значилось под №21. Изменения произошли в контрольно-измерительных материалах в 2020-2021 учебном году.

Приведённая статистика говорит о том, что в среднем лишь 13% выпускников справляются с заданием №20. [3:19]

Содержание задания №20 по годам. Типичные ошибки выпускников.

2016 год

Решите уравнение:

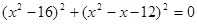
Поскольку приём использования в решении уравнений свойств отрабатывается в школе редко, с заданием справились лишь 6,4% учащихся Иркутской области.

2017 год

Решите уравнение:

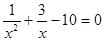
Типичные ошибки выпускников:

1.Вычислительные ошибки

2.Ошибки в формуле нахождения корней квадратного уравнения

3.Распостранённая ошибка в представлении ответа. Множество из двух корней уравнения описывалось как упорядоченная пара 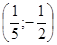, что является ошибкой в математической символике

4.Обучающиеся записывали корни в виде десятичных дробей и отбрасывали из ответа те из них, которые имели ненулевой период.

О критериях оценивания:

Решение, в котором была допущена вычислительная ошибка, но с ее учетом доведенное до конца, оценивалось в 1 балл.

Подчеркну, что ошибка в формуле нахождения корней квадратного уравнения не является вычислительной, и за ее допущение ставится 0 баллов.

Правильное решение с ошибкой в форме представления ответа – 1 балл.

Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов.[1:15]

2018 год

Решите уравнение:

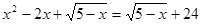
Типичные ошибки выпускников:

1) Основные ошибки в решении задачи 21 связаны с областью допустимых значений переменной, входящей в уравнение. Ошибка, как правило, заключалась либо в неэквивалентном преобразовании уравнения, произведенном без учета ограничения на область допустимых значений переменной, либо в неправильном определении (возможно, описании) области допустимых значений. Ошибки такого рода не относятся к вычислительным. Решение в таком случае оценивается в 0 баллов.

2) Вычислительные ошибки.

О критериях оценивания:

Решение, в котором была допущена вычислительная ошибка, но с ее

учетом доведенное до конца, оценивалось в 1 балл.

Подчеркну, что ошибка в определении области допустимых значений переменной не является вычислительной и за ее допущение ставится 0 баллов.

Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов. [2:15]

Рисунок 1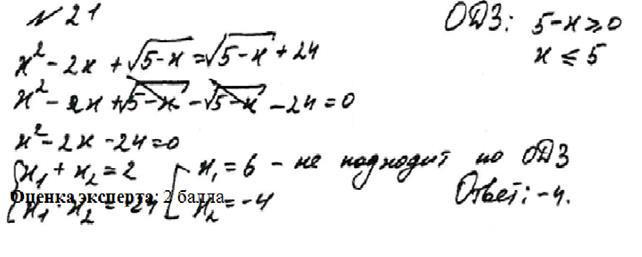

Вывод: данное уравнение решено верно. Обучающийся получил максимальное количество баллов.

Рисунок 2

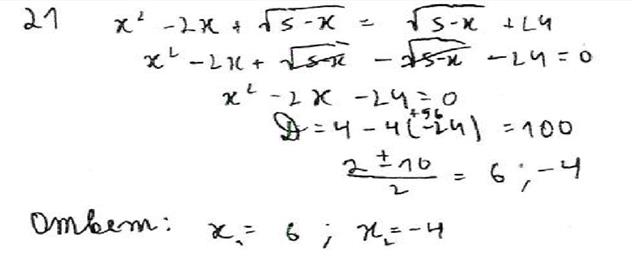
Вывод: в данном примере решения уравнения учащийся не определил ОДЗ и не учёл его при ответе. Оценка эксперта 0 баллов.

Рисунок 3

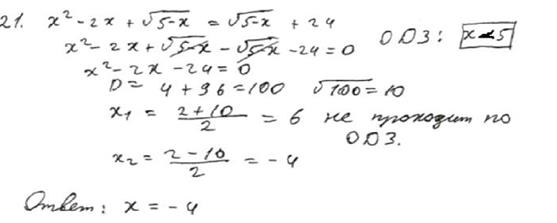
Вывод: здесь учащимся определена область допустимых значений, но неправильно: упущен случай равенства 5. Оценка эксперта 0 баллов.

2019 год

Решите уравнение:

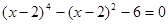
Типичные ошибки выпускников:

1.Вычислительные ошибки

2.Второй класс ошибок касается применения метода введения вспомогательной неизвестной при решении уравнения. [3:20]

Рисунок 4

Вывод: уравнение выпускником решено верно. Оценка эксперта 2 балла.

Банк заданий №20

Тщательно разобравшись в решении новых для меня уравнений, сделав анализ типичных ошибок выпускников, предлагаю небольшой банк заданий, который поможет моим сверстникам отработать задание №20.

Иррациональные уравнения (2019 год)

Решите уравнение: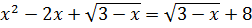

Решение:

Поскольку подкоренное выражение не может быть меньше нуля, по свойству арифметического корня, область допустимых значений ограничивается выражением 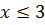значит,

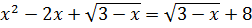ОДЗ: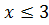

при уничтожении корней получаем:

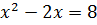
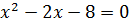решаем квадратное уравнение и получаем корни:

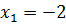
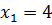Решением искомого уравнения является только 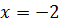, так как 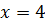не входит в область допустимых значений.

Ответ: .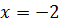

Решите уравнения самостоятельно:

a) 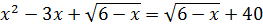(Ответ: );

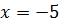b)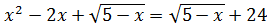 (Ответ: );

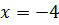c) 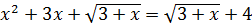(Ответ:);

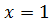d) 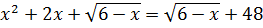(Ответ: ).

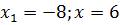Применение свойств при решении уравнений (2016 год)

Решите уравнение: .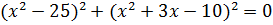

Решение:

Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:

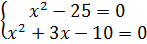
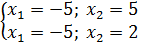
Так как системе удовлетворяет только 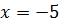, он и будет являться ответом.

Ответ: .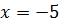

Решите уравнения самостоятельно:

a) 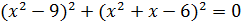(Ответ: ;

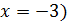b) 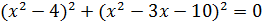(Ответ: ;

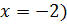c) 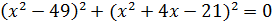(Ответ: ;

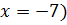d) 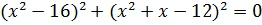(Ответ: .

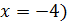Дробно-рациональные уравнения (2017 год)

Решите уравнение: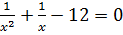

Решение:

Так как на ноль делить нельзя, обозначаем область допустимых значений 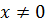и решаем:

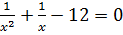ОДЗ: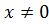

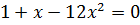
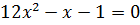
Решением через дискриминант получаем:

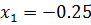
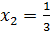Сверим корни с ОДЗ, не входят. Соответственно в ответе записываем оба корня.

Ответ: ; .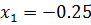

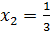Второй способ: замена переменной

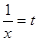
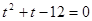, отсюда имеем, 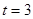и 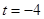, а значит ответ: ; .

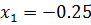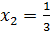Второй способ решения был предложен составителями экзаменационных материалов. Его применяет подавляющее большинство обучающихся.

Решите уравнения самостоятельно:

a) 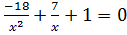(Ответ: );

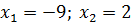b) 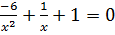(Ответ: );

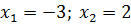c) 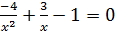(Ответ: ;

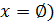d) 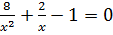(Ответ: ).

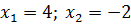Библиографическая ссылка

Беляева Е.Р. АНАЛИЗ ТИПИЧНЫХ ОШИБОК В РЕШЕНИИ УРАВНЕНИЙ, ПРЕДЛАГАЕМЫХ В КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛАХ ОГЭ. ЗАДАНИЕ №20. МАТЕМАТИКА // Международный школьный научный вестник. – 2021. – № 2.
;

URL: https://school-herald.ru/ru/article/view?id=1423 (дата обращения: 31.01.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.

Здесь мы приведем анализ типичных ошибок 2023 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

Ошибки в задачах на проценты

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.

Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.

Невнимательное прочтение условия задания

Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.

Например:

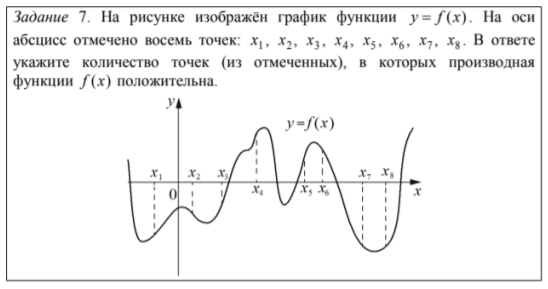
Невнимательное прочтение условия задания

В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.

Вот пример задачи:

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях.

Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.

Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.

Ошибки теоретического характера

Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.

Например:

Ошибки теоретического характера

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.

Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях.

Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Например:

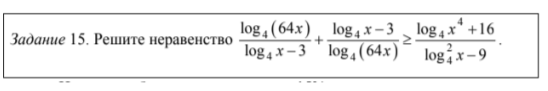
Ошибки в алгоритмах и методах решения

Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями.

Например:

Ошибки в чтении и построении чертежа

Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник.

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления.

Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.

Есть проблемы и в оформлении доказательств. Например:

Неумение обосновывать и доказывать

Основная трудность в отсутствии понимания логики построения доказательства.

Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.

Ошибки в заданиях по тригонометрии

Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.

Например:

Ошибки в заданиях по тригонометрии

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.

Ошибки математического моделирования

В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей.

В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.

Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи.

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
Задание 8 – ошибаются в наглядном решении.
Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:

прочтите условие;
выпишите данные величины, сделайте рисунок в геометрическом задании;
установите и запишите отношения и взаимосвязи между известными данными;
выпишите что найти, ответ на какой вопрос нужно дать;
определите тип задания;
сформулируйте содержание и последовательность действий.

Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок.

Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.

И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:

сориентироваться в условии,
обдумать и спланировать ее решение,
понять уровень ее сложности и решить, откладывать ли ее решение напоследок.

Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.

Математику базового уровня часто недооценивают, пренебрегая подготовкой к ней. Однако от нее зависит судьба аттестата: без «отлично» за математику отличник не получит красный аттестат, а без порогового балла выпускники в принципе рискуют уйти из школы со справкой! Типичные ошибки на ЕГЭ по математике помогут избежать этой участи.

Ошибки ЕГЭ: что повторить к математике

Типичные ошибки ЕГЭ по математике в задачах на проценты

Проблемы возникают из-за неумения рассчитывать процент от суммы. Так, стоит обратить внимание, что процент повышения или понижения стоимости вычисляется от старой, а не новой цены, поэтому принимать новую цену за 100% и исходить из нее станет причиной ошибки на ЕГЭ по математике. Новая цена — это 100% ± процент повышения (+) или понижения (-).

Частые ошибки в вычислениях

Вычислительные ошибки на ЕГЭ по математике не редкость, но от этого они не перестают быть опасными и обидными. Стоит следить за наличием минуса (и его сокращением), а также помнить правила преобразования выражений, действий с дробями. Не стоит полагаться исключительно на умение считать в уме: лучше выполнять свои вычисления на бумаге и обязательно производить проверку (подставляя значение на место неизвестной в уравнениях и производя смежные действия (сложение-вычитание, деление-умножение) в простых примерах).

Основные ошибки теоретического характера

Ошибки на ЕГЭ по математике часто возникают из-за неумение работать с чертежами и терминологией. Большинство выпускников пытается найти заданную в номере величину с помощью инструментов или на глаз, часть из них не знает терминологии и находит не ту величину. Чтобы не допустить этого, стоит научиться работать с объемными фигурами: находить площадь их поверхности (всей или боковой), объемы и их части.

Также стоит обратить внимание на важные аспекты теории: основные теоремы, аксиомы, свойства.

Распространенные ошибки в алгоритмах и методах решения

Последовательность выполнения действий проходится еще во втором классе, однако даже такие ошибки на ЕГЭ по математике встречаются. Стоит помнить как простейшие алгоритмы решения примеров: сначала действия в скобках, а потом остальные; первыми идут умножение и деление, потом сложение и вычитание, — так и более сложные. Так, в дробях ни в коем случае нельзя забывать про знаменатель, а сокращаться из числителя и знаменателя могут только множители (простые числа и выражения в скобках).

Ошибки на ЕГЭ в базе по математике

Ошибки при чтении и построении чертежа

Ошибки на ЕГЭ по математике, касающиеся чертежа, возникают при работе как с объемными фигурами, так и с расположенными в одной плоскости. Они связаны с отсутствием пространственного представления и невнимательностью, вызванной неправильным прочтением буквенной записи (угол АВС — это не то же самое, что углы АСВ и САВ). Также сложности могут возникнуть при неумении ориентироваться в основных обозначениях на чертеже (равные стороны, равные углы, прямые углы).

Типовые ошибки в заданиях по тригонометрии

Раздел тригонометрии построен на знании тригонометрических тождеств и свойств тригонометрических функций, поэтому ошибки на ЕГЭ по математике могут быть допущены из-за недостаточного владения теорией. В КИМ-е базовой математике даны основные формулы, которые могут быть полезны выпускникам, однако стоит также научиться выводить из них остальные.

Ошибки математического моделирования

Трудности, связанные с математическими моделями, вызваны неумением решать практические текстовые задачи. Для их решения необходимо понимать принцип работы действия (чаще всего, один из видов движения). Сложности возникают с подстановкой в формулу неверных данных, из-за чего искажается ответ.

Таким образом, базовая математика не так проста, как может показаться на первый взгляд. Она не займет так много времени, как профильная, но все равно требует подготовки.

Нажмите, чтобы узнать подробности

Типичные ошибки: вычислительные (умножение и деление натуральных чисел);

нахождение в уравнении неизвестного вычитаемого, уменьшаемого,

неизвестного множителя;

Анализ причин появления ошибок:

Систематизировать материал по пройденным темам.

Недостаточно развит навык применения теоретических знаний на практике.

Недостаточно сконцентрировано внимание при чтении заданий теста и при выполнении их.

Необходимо организовать уроки повторения по данным вопросам.

Необходимо обратить внимание на типичные ошибки (вычислительные ошибки сложения и вычитания, перевод единиц измерения) и включать повторение данных вопросов в устный счет на уроках.

Причины ошибок:

ЗАДЕРЖКА ПСИХИЧЕСКОГО РАЗВИТИЯ— особый тип дефицитарной аномалии психического развития ребенка. З. п. р. имеет различное происхождение: в одних случаях она связана с особенностями, а точнее — дефектами конституции ребенка, вследствие чего по своему физическому и психическому развитию он начинает соответствовать более раннему возрасту в других случаях З. п. р. возникает в результате различных соматических заболеваний (физически ослабленные дети) или органического поражения ц. н. с. (дети с минимальной мозговой дисфункцией).

У детей с З. п. р. отмечается значительное снижение работоспособности вследствие возникающих у них явлений цереброастении, психомоторной расторможенности, аффективной возбудимости. У них затруднено усвоение навыков чтения, письма, счета; страдают непосредственная память и внимание; имеются легкие нарушения речевых функций.

Пути решения:

Коррекция переключаемости и распределения внимания.
Коррекция логического мышления, зрительной и вербальной памяти.
Коррекция слухового и зрительного восприятия.
Коррекция произвольного внимания.
Коррекция мышц мелкой моторики.

Источник

Типичные вычислительные ошибки учащихся при решении пробных заданий ОГЭ и методы их предотвращения

При выполнении пробных заданий ОГЭ учащимися допускается ряд типичных ошибок, в связи с чем, была предпринята попытка их систематизировать и предложить методы их предотвращения.

Многие ошибки вызваны тем, что задания ОГЭ охватывают материал фактически с 1 по 9 класс и учащиеся к 9 классу порой забывают материал и утрачивают навыки, полученные в начальной школе и 5-6 классах, когда закладываются умения производить вычисления без использования калькулятора.

Наиболее распространённая ошибка – «потеря знака». В процессе вычислений учащиеся забывают о том, будет результат положительным или отрицательным. Предлагается акцентировать внимание учащихся на необходимости предварительно определить знак результата до осуществления вычислений и записать его после знака «=» и лишь после этого производить вычисления. Например: необходимо перемножить «-36» и «48», определяем, что произведение этих чисел будет со знаком «-» и записываем его после знака «=» и лишь после этого приступаем к умножению этих чисел столбиком.

Также часто ошибочный знак у числа или переменной получается при действиях с дробями. Необходимо обратить внимание учащихся, что при любых действиях с дробями желательно числитель записывать в скобках, тогда при перемножении дробей содержащих в числителе выражение

снижается вероятность ошибки в определении знака второго слагаемого в числителе после умножения по распределительному закону.

Вообще необходимо акцентировать внимание, что знак «-» относится к числу перед которым он стоит и выражение «-3+5-6+4» — это сложение четырёх чисел, имеющих разные знаки. И при выполнении выражения
«-3*(х-1)» нужно «-3» умножить на «х», а затем «-3» умножить на «-1».

Данные проблемы могут показаться примитивом, не заслуживающим внимания, но на практике многие учащиеся девятых классов делают такие ошибки очень часто.

Следующий распространённый тип ошибок – неправильный порядок вычислений, приводящий к громоздким числам и вычислительным ошибкам. Дети начинают выполнять вычисления по порядку «в лоб», забывая, что, во-первых, в дробях можно сократить множители в числителе и знаменателе в выражениях типа после сокращения которых действие выполняется устно, при попытке же последовательно перемножить числители и знаменатели дробей и потом разделить их «уголком» вероятность допущения ошибки растёт с каждый разрядом числа. Во-вторых, при сложении чисел не нужно торопиться и определить порядок сложения, например в выражении «14+17+6+3» гораздо проще вспомнить, что можно выполнять сложение в любом порядке и сложить «14 и 6, 17 и 3».

И в целом, часто ошибки – следствие утраты навыка производить вычисления без калькулятора. Необходимо ещё раз напомнить учащимся материал второго — пятого класса. Даже вполне успевающие ученики порой делают глупые ошибки при необходимости из «9» вычесть «0,36» ибо правило «записать запятую под запятой» часто забыто. А при делении «83» на «4» или «2030» на «5» и других чисел, где необходимо дважды «сносить» число при делении уголком, предварительно записав в частное «0», ошибку делают почти все учащиеся.

Источник

В концентре «Сотня» возможны следующие ошибки:

50 – 36=2656 – 30 = 14

50 – 30 = 20 50 – 30 = 20

20 + 6 = 26 20 – 6 = 14

80 – 27 = 87 – 20=

/ /

20+7 80+7

80 – 20 = 60 80 – 20 = 60

60 – 7 = 53 60 + 7 = 67

Список использованной литературы:

Бантова М.А. Ошибки учащихся в вычислениях и их предупреждение // Начальная школа. – 1989. – № 2.
Бельтюкова Г.В. Методические ошибки при формировании у школьников вычислительных навыков // Начальная школа. – 1980. – №8.
Белошистая А.В. Прием формирования устных вычислительных умений в пределах 100 // Начальная школа. – 2001. – №7.
Фаддейчева Т.И. Обучение устным вычислениям // Начальная школа. – 2003. –№10.
Федеральный государственный образовательный стандарт начального общего образования /Министерство образования и науки Российской Федерации. – М.: Просвещение, 2010. – 41 с.

Источник

Задание «Проблемы,
типичные ошибки учащихся»

Вспоминается расхожая истина – умные люди
учатся на чужих ошибках. В математике приходится учиться, в основном, на
собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь
необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее
использовать.

Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти
ошибки.

Решая
уравнения и неравенства учащиеся допускают типичные ошибки:

·
Незнание
правил, определений, формул.

·
Непонимание
правил, определений, формул.

·
Неумение
применять правила, определения, формулы.

·
Неверное
применение формул.

·
Невнимательное
чтение условия и вопроса задания.

·
Вычислительные
ошибки.

·
Логические
ошибки

·
Раскрытие
скобок и применение формул сокращенного умножения.

Какие же проблемы, трудности общего
характера возникают у учащихся при изучении математики ( их несомненно можно
отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения
и неравенства»):

·
Пропуски
занятий приводят к незнанию материала, пробелам в знаниях.

·
Поверхностное,
невдумчивое восприятие нового материала приводят к непониманию его.

·
Недостаточная
мозговая деятельность приводит к неумению применять правила, определения и
формулы .

·
Неряшливый,
неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не
всегда сами понимают, что именно они написали.

·
Усталость. Чрезмерная
нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и,
как следствие, к многочисленным ошибкам.

·
Кратковременное
или полное переключение внимания с одной деятельности на другую (учебную или
внеучебную) приводит к утрате только что воспринятого материала, приходится все
начинать сначала.

·
Скорость
работы. Низкая
скорость выполнения мыслительных операций часто мешает ученику контролировать
себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь
одной частью задания удаляет из «оперативной памяти» информацию о другой, в
которой допускается не вынужденная ошибка. Скорость работы определяется
физиологией конкретного школьника и навыками выполнения тех или иных операций.

·
Мотивация.
Следствие низкой мотивации – потеря внимания и ошибка.

Ошибки, допускаемые обучающимися при решении уравнений
и неравенств, самые разнообразные: от неверного оформления решения до
ошибок логического характера.

1. Самая типичная ошибка состоит в том, что учащиеся
при решении уравнений и неравенств без дополнительных пояснений используют
преобразования, нарушающие равносильность, что приводит к потере корней
и появлению посторонних корней.

Предлагаю на конкретных примерах рассмотреть ошибки
подобного рода и определить способы их предупреждения и исправления, но прежде
всего хочу обратить внимание на следующую мысль: не надо бояться
приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться
потерять корни.

а) Решить уравнение:

log3(5 – x) = 3 – log3(–1 – x).

Это уравнение учащиеся очень часто решают следующим
образом.

log3(5 – x) = 3 –
log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)(
–1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x –
32 = 0,

х₁ = –4; x₂ = 8.

Учащиеся часто, не проводя дополнительных рассуждений,
записывают оба числа в ответ. Но как показывает проверка, число
x = 8 не является корнем исходного уравнения, так как при
x = 8 левая и правая части уравнения теряют смысл. Проверка
показывает, что число x = –4 является корнем заданного
уравнения.

б) Решить уравнение

Область определения исходного уравнения задается системой

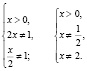
dalin3.wmf

Для решения заданного уравнения перейдем к логарифму
по основанию x, получим

Мы видим, что левая и правая части этого последнего
уравнения при x = 1 не определены, но это число является корнем
исходного уравнения (убедиться в этом можно путем непосредственной
подстановки). Таким образом, формальный переход к новому основанию привел
к потере корня. Чтобы избежать потери корня x = 1, следует
указать, что новое основание должно быть положительным числом, отличным от
единицы, и рассмотреть отдельно случай x = 1.

2. Целая группа ошибок, вернее сказать недочетов, состоит
в том, что учащиеся не уделяют должного внимания нахождению области
определения уравнений, хотя именно она в ряде случаев есть ключ
к решению.

3. Типичной ошибкой учащихся является то, что они не
владеют на нужном уровне определениями понятий, формулами, формулировками
теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.

Решить уравнение

Ученик предлагает следующее ошибочное решение этого
уравнения:

х = –2.

Поверка показывает, что х = –2 не является
корнем исходного уравнения.

Напрашивается вывод, что заданное уравнение корней не
имеет.

Однако это не так. Выполнив подстановку х =
–4 в заданное уравнение, мы можем убедиться, что это корень.

Предлагаю проанализировать, почему произошла потеря
корня.

В исходном уравнении выражения х и х +
3 могут быть одновременно оба отрицательными или оба положительными, но
при переходе к уравнению эти же выражения
могут быть только положительными. Следовательно, произошло сужение области
определения, что и привело к потере корней.

Чтобы избежать потери корня, можно поступить следующим
образом: перейти в исходном уравнении от логарифма суммы к логарифму
произведения. Возможно в этом случае появление посторонних корней, но от
них, путем подстановки, можно освободиться.

4. Многие ошибки, допускаемые при решении уравнений
и неравенств, являются следствием того, что учащиеся очень часто пытаются
решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть
это на следующем примере.

Решить неравенство

Попытка решать это неравенство привычными
алгоритмическими способами не приведет к ответу. Решение здесь должно
состоять в оценке значений каждого слагаемого левой части неравенства
на области определения неравенства.

Найдем область определения неравенства:

Для всех x из
промежутка (9;10] выражение имеет
положительные значения (значения показательной функции всегда положительны).

Для всех x из
промежутка (9;10] выражение ( x – 9) имеет положительные значения,
а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда
выражение

– (x – 9)
lg(x – 9) положительно или равно нулю.

Окончательно имеем x∈
(9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое,
стоящее в левой части неравенства, положительно (второе слагаемое может
быть равно нулю), а значит их сумма всегда больше нуля. Следовательно,
решением исходного неравенства является промежуток (9;10].

5. Одна из ошибок связана с графическим решением
уравнений.

Решить уравнение

Некоторые учащиеся, решая это уравнение графически (хочу
отметить, что его другими элементарными способами решить нельзя), получают лишь
один корень (он является абсциссой точки, лежащей на прямой y = x),
ибо графики функций

и −

это графики взаимно обратных функций.

На самом деле исходное уравнение имеет три корня: один из
них является абсциссой точки, лежащей на биссектрисе первого координатного
угла y = x, другой корень и третий корень Убедиться
в справедливости сказанного можно непосредственной подстановкой чисел и в заданное уравнение.

Этот пример удачно иллюстрирует следующий вывод:
графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны»
(одна из них возрастает, а другая – убывает), и недостаточно
математически корректно в случае одномонотонных функций (обе либо
одновременно убывают, либо одновременно возрастают).

6. Ряд типичных ошибок связан с тем, что учащиеся не
совсем корректно решают уравнения и неравенства на основе функционального
подхода. Остановлюсь на типичных ошибки такого рода.

а) Решить уравнение x^х = x.

Функция, стоящая в левой части уравнения, –
показательно-степенная и раз так, то на основание степени следует
наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе
части заданного уравнения:

или

Откуда имеем x = 1.

Логарифмирование не привело к сужению области
определения исходного уравнения. Но тем не менее произошла потеря двух корней
уравнения; непосредственным усмотрением мы находим, что x =
1 и x = –1 являются корнями исходного уравнения.

7. При решении неравенств с помощью подстановки мы
всегда сначала решаем новое неравенство относительно новой переменной,
и лишь в его решении делаем переход к старой переменной.

Школьники очень часто ошибочно делают обратный переход
раньше.Этого делать не следует.

8.Хочу привести пример еще одной ошибки, связанной
с решением неравенств.

Решите неравенство

Привожу ошибочное решение, которое очень часто
предлагают учащиеся.

Возведем обе части исходного неравенства в квадрат.
Будем иметь:

откуда получаем неверное числовое неравенство , что позволяет сделать
вывод: заданное неравенство не имеет решений.

Однако полученный вывод неверен, например, при
х = 1000 имеем

, , .

Полученное числовое неравенство верно, а значит
х = 1000 является решением.

Значит, заданное неравенство имеет решение, и, следовательно,
приведенное выше решение ошибочно.

Привожу правильное решение. Найдем область определения
исходного неравенства. Она задается системой

или

откуда .

Ясно, что на интервале (10;1000) нет решений, ибо
левая часть заданного неравенства при любом х из этого интервала не имеет
смысла.

Рассмотрим два случая.

а) , откуда х > 100. С учетом области определения
исходного неравенства имеем промежуток . Для всех х из этого промежутка левая часть
исходного неравенства неотрицательна (как значение арифметического квадратного
корня), а правая часть – отрицательна. Делаем вывод о том, что – решение заданного
неравенства.

б) , откуда . С учетом области определения исходного неравенства имеем
промежуток .
Для всех х из промежутка имеют смысл обе
части неравенства и они имеют неотрицательные значения, значит обе части
заданного неравенства мы можем возвести в квадрат. Будем иметь: , откуда . Это неверное числовое
неравенство позволяет сделать вывод: значения х из промежутка решениями исходного неравенства не
являются.

Ответ: .

9. Типичная ошибка при решении уравнений, неравенств
и их систем состоит в том, что неверно преобразовываются выражения.

Большинство
ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение
некоторых вычислительных операций до автоматизма несколько снижает вероятность
их появления.

Необходимо
осуществлять процесс обучения правилам с помощью специальной модели с
использованием приема, активизирующего рефлексивную деятельность учащихся по
предупреждению и исправлению ошибок, которые возникают в результате формального
усвоения правил.

Самостоятельная
работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ
собственных действий по решению конкретной задачи, что оказывает благоприятное
влияние на качество получаемых знаний и стимулирует развитие логического
мышления.

Пример
неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет
его корни по хорошо известной формуле, не обращая внимания на недопустимые
значения sin x.

Для
исправления и предупреждения многих ошибок важно сформировать у школьников навыки
самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой
оценки ожидаемого результата.

Каждый
учитель знает, что планомерное и систематическое повторение и есть основной
помощник в ликвидации пробелов, а, следовательно, и ошибок.

Систематические проверки чужих записей
формируют у ученика привычку критически относиться к своему решению. Для этого
подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления
ошибок самими учащимися под руководством учителя можно сделать поучительным для
учащихся.

Самоконтроль

Для исправления и предупреждения многих
ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят
из двух частей:

а) умения обнаружить ошибку;

б) умения её объяснить и исправить.

В процессе обучения применяются несколько
приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и
своевременно их исправить. К ним относятся:

·
проверка
вычисления и тождественного преобразования путём выполнения обратного действия
или преобразования;

·
проверка
правильности решения задач путём составления и решения задач, обратных к
данной;

·
оценка
результата решения задачи с точки зрения здравого смысла;

·
проверка
аналитического решения графическим способом.

Способы
исправления и предупреждения ошибок

Свести
ошибки к минимуму способствуют следующие профилактические меры:

Тексты письменных заданий должны быть
удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
Активная устная отработка основных
ЗУН, регулярный разбор типичных ошибок.
При объяснении нового материала
предугадать ошибку и подобрать систему заданий на отработку правильного усвоения
понятия. Акцентировать внимание на каждом элементе формулы, выполнение
разнотипных заданий позволит свести ошибочность к минимуму.
Подбирать задания, вызывающие
интерес, формирующие устойчивое внимание.
Прочному
усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для
запоминания, четкие алгоритмы, следуя которым заведомо придешь к
намеченной цели.

Каждый
учитель знает, что планомерное и систематическое повторение и есть основной
помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как
ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и
понимание последующего невозможно без знания предыдущего, отсюда неизбежность
повторения на каждом уроке. При объяснении нового материала следует использовать
ряд определений и теорем, которые были изучены ранее.

Источник

Ошибки учащихся в вычислениях и их предупреждение.

Одной
из главных задач обучения младших
школьников математике является
формированием у них вычислительных
навыков. Процесс овладения вычислительными
навыками довольно сложен: сначала
ученики должны усвоить тот или иной
вычислительный прием, а
затем
в результате тренировки научиться
достаточно быстро выполнять вычисления,
а
в
отношении табличных случаев —
запомнить результаты наизусть. К
тому же в каждом концентре научается
довольно большее количество приемом,
поэтому естественно, что не все ученики
сразу усваивают их часть, допускает
ошибки.

К
предлагаемой статье рассматриваются
типичные ошибки учеников при выполнении
ими арифметических действий в каждом
концентре, а
также
методические приемы предупреждения
и устранения таких ошибок.

Десяток

1.
Смешение действий сложения и
вычитания
(7+2 = 5, 6—4=10). Такие ошибки возникают
по двум причинам. Первая причина: ученики
еще не усвоили самих действий сложения
и вычитания или
же
знаков этих действий. Чаще это происходит
потому, что учитель рано стал требовать
выполнения арифметических действий
без использования счетного материала
(палочек, геометрических фигур из набора
и т. п.).

Чтобы
предупредить появление названных
ошибок, не следует запрещать ученикам
пользоваться при вычислениях счетным
материалом, если они иначе не могут
найти результат сложения или вычитания.
Для устранения уже, появившихся ошибок
надо вернуть учеников к работе со счетным
материалом. При этом важно, чтобы они
сопровождали вычислении словесным
рассуждением и соответствующей записью.
Например, выполняя сложение 5+2, ученик
берет 5 кружков и еще 2, затем, придвигая
к 5 кружкам 1 кружок, говорит: «К 5 прибавить
1, получится 6». Далее, придвигая к 6
кружкам еще кружок, он говорит: «К 6
прибавить 1 получится 7. Записываю:
5+2=7».

Вторая
причина ошибок в замене одного
арифметического действия другим — это
недостаточный анализ решаемого примера:
при вычислениях ученики больше обращают
внимание на числа, чем на знак действия.

Поэтому
важно с первых уроков обучения вычислениям
приучать учеников к тому, чтобы они
называли,
сначала
вслух, а позднее про
себя,
какое арифметическое действие надо
выполнить и над какими числами, и
только после этого вычисляли результат.
Так пусть, решая пример 6—4, они говорят:
«Это
пример
на вычитание (или: «Здесь надо вычитать
»), из 6 вычесть 4, получится 2». Воспитывая
привычку выполнять такой
анализ,
можно, полностью устранить ошибки в
замене одного, арифметического действия
другим.

Получение
результата на
единицу
больше или меньше верного (7+2=8, 9-3=7).
Подобные ошибки возникают при
присчитывании и отсчитывании чисел 2,
3, 4
по
единице
с опорой на
натуральный
ряд. Например, прибавляя к 7 число 2,
ученики должны назвать два числа,
следующие в ряду за
числом 7,
однако бывает, что
они
первым называют данное число, а
не
следующее за
ним
(7,
и думают, что они
прибавили
2 и что 7+2=8. Для предупреждения таких
ошибок полезно, чтобы при присчитывании
и отсчитывании по единице назывались
промежуточные результаты (7+1=8, 8+1=
9, значит,
7+2=9).

Неверный
результат получается иногда вследствие
использования нерациональных приемов.
Например, выполняя сложение в случаях
вида 3+6, часть учеников вместо приема
перестановки слагаемых использует
прием присчитывания по единице (по
2, по 3), а это трудно, и
ученики
часто забывают, сколько единиц они уже
прибавила и сколько осталось прибавить,
вследствие чего получают неправильный
результат (3+6=8, 3+6=10 и т. п.). Так же
объясняются, ошибки вида 9—7=4.

Предупреждению
таких ошибок помогает сравнение
рациональных и нерациональных приемов
вычислений. Так, обнаружив, что некоторые
ученики допускают ошибки при решении
примеров вида 3+6, учитель спрашивает,
как они решали пример (3+1=4, 4+1 = 5 ит.
д.), затем другие ученики объясняют, как
можно решить тот пример быстрее, легче
(надо переставить слагаемые 6+3=9, результат
помним наизусть). Здесь же ученики
указывают, в каких случаях следует
переставлять слагаемые (когда к меньшему
числу прибавляем большее).

4.
Запись или называние, вместо результата
одного из компонентов (3+5=5, 6-4=6). Такие
ошибки возникают преимущественно по
невнимательности. Как правило, ученики
сами находят ошибку и
дают
верный ответ. Для предупреждения
подобных ошибок важно научить детей
выполнять проверку решения путем,
прикидки результата: при сложении
результат должен быть больше каждого
из слагаемых (если ни одно из них не
равно нулю); при вычитании результат
доджей быть; меньше — уменьшаемого
(если вычитаемое не равно нулю); если
эти отношения не выполняются, значит,
в вычислениях допущена ошибка. Чтобы
научить детей такой проверке надо
попутно с вычислениями чаще проводить
наблюдения,
сравнивай результат с компонентами
действий сложения и вычитания. Устранению
названных ошибок помогает анализ и
обсуждение неверно решенных примеров.
Так, учитель спрашивает, верно, ли решен
пример 5+3=5
и
может ли эта сумма равняться 5.
Ученики
сравнивают сумму со слагаемыми и говорят,
что сумма должна быть больше, чем 5,
так
как к пяти еще прибавили 3.

5.
Получение
неверного результата следствие смешения
цифр. Например, ученик пишет: 4+2=9,
хотя
устно называет правильный результат.

Для
устранения подобных ошибок необходима
индивидуальная работа по запоминанию
цифр: пусть ученик нарисует названное
учителем число каких-либо — предметов
рядом напишет цифрой соответствующее
число, пусть

найдет в своем наборе
названные цифры и т.
п.

Сотня

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Типичные вычислительные ошибки учащихся при решении пробных заданий ОГЭ и методы их предотвращения

Библиографическое описание:

Ключевые слова

Похожие статьи

Как не допускать типичных вычислительных ошибок, используя…

Теория ошибки в свете различных подходов | Статья в журнале…

Теоретическое значение определения понятия «счётная ошибка»…

Обучение решению арифметических задач | Статья в журнале…

Типичные ошибки в бухгалтерском учёте и их исправление

Нормы оценки знаний обучающихся по математике

Педагогические условия устранения характерных текстовых…

Самостоятельная работа учащегося над ошибками как…

Формирование действия самоконтроля младших школьников

Похожие статьи

Как не допускать типичных вычислительных ошибок, используя…

Теория ошибки в свете различных подходов | Статья в журнале…

Теоретическое значение определения понятия «счётная ошибка»…

Обучение решению арифметических задач | Статья в журнале…

Типичные ошибки в бухгалтерском учёте и их исправление

Нормы оценки знаний обучающихся по математике

Педагогические условия устранения характерных текстовых…

Самостоятельная работа учащегося над ошибками как…

Формирование действия самоконтроля младших школьников

Материал из MachineLearning.

Содержание

Введение

Постановка вопроса. Виды погрешностей

Виды мер точности

Предельные погрешности

Погрешности округлений при представлении чисел в компьютере

Погрешности арифметических операций

Погрешности вычисления функций

Числовые примеры

Список литературы

См. также

Библиографическая ссылка

Базовый уровень математики

Ошибки в задачах на проценты

Невнимательное прочтение условия задания

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Ошибки в вычислениях

Ошибки теоретического характера

Ошибки в алгоритмах и методах решения

Ошибки в чтении и построении чертежа

Неумение обосновывать и доказывать

Ошибки в заданиях по тригонометрии

Ошибки математического моделирования

Профильный уровень

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Типичные ошибки ЕГЭ по математике в задачах на проценты

Частые ошибки в вычислениях

Основные ошибки теоретического характера

Распространенные ошибки в алгоритмах и методах решения

Ошибки при чтении и построении чертежа

Типовые ошибки в заданиях по тригонометрии

Ошибки математического моделирования

Типичные вычислительные ошибки учащихся при решении пробных заданий ОГЭ и методы их предотвращения

Ошибки учащихся в вычислениях и их предупреждение.

Десяток

Типичные вычислительные ошибки учащихся при решении пробных
заданий ОГЭ и методы их предотвращения