Если известны ошибки, допускаемые при измерении отдельных аргументов Ал ,-, и вид функции чему равна ошибка в определении величины у — Ау Эта задача называется первой илн прямой задачей теории ошибок. Отметим сразу, что сама постановка задачи исключает возможность оценки знака ошибки функции у и предполагает лишь возможность оценить некую предельную ошибку результата анализа.. [c.117]
При обработке результатов небольшого числа измерений очень важно не только найти интервальные значения измеряемой величины, но решить ц другую задачу теории ошибок найти и оценить приближенное значение стандартного отклонения а (для генеральной совокупности). Считают, что и интервальное значение о находят в виде з = 5 + о или 5— < з< 5 где 3 —точность стандартного отклонения, определенная с надежностью а при К=п—1 Оа=Я х.к (5—средняя квадратичная ошибка отдельного измерения, стандартное отклонение) —множитель, который находят по табл. 2. Для значений ( >1 левая доверительная граница интервального значения а приравнивается нулю. [c.28]
То, что нормальный закон встречается столь часто, связано с тремя обстоятельствами. Во-первых, в тех задачах, где ошибка получается как сумма большого числа слабых неконтролируемых влияний, распределение ошибки должно быть нормальным (по центральной предельной теореме теории вероятностей). Во-вторых, нормальный закон в некотором смысле —самый простой и к тому же лучше всего изученный работать с ним наиболее удобно. В-третьих, есть очень много задач, в которых хотя закон и отличается от нормального, но ошибка от принятия нормальности распределения оказывается небольшой и ею удается пренебречь. Поэтому почти во всех случаях, когда закон распределения неизвестен и нет возможности его проверить, принимают нормальность распределения ошибки. [c.51]
При обработке результатов небольшого числа измерений очень важно не только найти интервальные значения измеряемой величины, но решить и другую задачу теории ошибок найти и оценить приближенное значение стандартного отклонения а (для генеральной совокупности). Считают, что и интервальное значение а находят в виде + или 5—5а< а< 5 + 5 , где —точность стандартного отклонения, определенная с надежностью а при К=п—1 (5—средняя квадратичная ошибка отдельного [c.28]
В физико-химических исследованиях проводят как прямые, так и косвенные измерения, когда конечная величина находится по формуле, в которую входят значения одного или нескольких параметров, найденных прямым измерением по показаниям приборов. В последнем случае возникает задача расчета ошибки конеч й величины по величинам ошибок отдельных параметров, входящих в формулу. Эта задача решается с помощью математического аппарата теории приближенных вычислений. [c.14]
Первый способ состоит в приведении дифференциальных кинетических уравнений к системе нелинейных алгебраических уравнений с последующей минимизацией среднеквадратичного критерия одним из методов нелинейного программирования, что в терминах теории динамических систем означает сведение динамической задачи идентификации к статической задаче наблюдения. При этом оперирование со скоростями химических реакций как с параметрами в статической задаче наблюдения осложняется значительными ошибками, неизбежно возникающими нри экспериментальном определении скоростей химических реакций. [c.461]
Рассмотрение движения ядер в потенциальном поле можно провести в рамках уравнений классической механики. Ответ на вопрос, какую ошибку вносит классическое приближение, получается из сравнения решения квантовой и классической задач движения. Подробный анализ перехода к классическому пределу в теории молекулярных столкновений выполнен в работах Миллера [124,125]. [c.51]
Случайные ошибки отличаются от систематических тем, что увеличением числа измерений можно уменьшить их величину. Эта особенность обусловлена тем, что значения случайных ошибок с одинаковой степенью вероятности могут быть положительными и отрицательными. Казалось бы, это позволяет осуществить количественную оценку случайных ошибок. Однако это не так число повторных измерений, как правило, невелико, поэтому методы теории вероятности неприменимы. Как же следует обрабатывать результаты отдельных измерений (каждое из которых содержит случайную ошибку) для того, чтобы получить величину, более всего приближающуюся к точному значению Приступая к решению этой задачи, предполагаем, что систематические ошибки исключены. Прежде всего следует определить абсолютную и относительную погрешности измерения данной величины. [c.465]
Вторая или обратная задача общей теории ошибок формулируется.так каковы предельно допустимые ошибки Ах, Ах2,. … .., А.Хп при измерении каждого из аргументов Хи если заданная величина Аг/— предельно допустимая ошибка результата анализа [c.117]
Третья задача общей теории ошибок ставит вопрос об оптимальных условиях проведения химического анализа каким образом следует согласовать между собой условия измерения аргументов Х1, чтобы относительная ошибка функции была минимальной [c.117]
Обратная задача общей теории ошибок ставит вопрос о нахождении предельно допустимых ошибок отдельных этапов химического анализа по заданной предельной ошибке конечного результата. К сожалению, эта задача строго разрешима лишь для случая функции одного аргумента, который не представляет интереса в химическом анализе. Для функции нескольких аргументов задача не имеет единственного решения, т. е. ее решение оказывается неопределенным. Действительно, общее выражение для [c.131]
В статистической теории оптимальных систем решается задача синтеза систем, обеспечивающих выполнение статистического критерия оптимальности. При этом динамические характеристики системы определяются так, чтобы достигалась наибольшая точность преобразования случайных сигналов, характеризуемая случайной ошибкой [c.236]
Конечно, было бы большой ошибкой преувеличивать наличие субъективизма при решении конкретных задач в естественных н ках, в частности, в физике, химии и биологии Нельзя скатываться на позицию, выражаемую словами Что хотим, то и получим Подавляющее большинство фундаментальных положений и выводов этих н к является следствиями либо многократно разными способами поставленных экспериментов, либо применением хорошо обоснованных теорий Например, структурные формулы многих молекул устанавливаются, как правило, вполне однозначно с помощью серии соответствующим образом подобранных химических экспериментов или спектральными методами в диапазоне от ультрафиолета до радиоволн В объективности представлений [c.97]
В теории управления требуется следить за некоторым заданным сигналом s t) с возможно меньшей ошибкой Можно показать [6], что эта задача сводится к частному случаю задачи фильтрации, описанной выше [c.28]
Широкое применение ковариационной функции или спектральной плотности в технических задачах основано на том, что знание любой из этих функций достаточно для синтеза линейных фильтров или линейных систем регулирования с минимальной среднеквадратичной ошибкой для случаев, когда рассматриваемые сигналы искажаются шумом Теория синтеза систем с минимальной среднеквадратичной ошибкой была впервые разработана Винером [4] Она сыграла важную роль в развитии современной теории управления и теории связи [c.189]
С (Л) = Ср теор- В ЭТОМ случае для данно постановки задачи целевая функция ошибки Ди ) будет иметь вид [c.95]
Ранее в курс «Процессов и аппаратов» (и не только химической технологии) достаточно обширным разделом входила «Теория размерностей» с отдельным понятийным аппаратом, теоремами и методами исследования. Эта теория нередко использовалась для перехода к обобщенным переменным искомую величину выражали как функцию (предпочтительно — степенную) набора других величин, выбираемых исходя из имеющегося научно-производственного опыта и здравого смысла (т.е. феноменологически) сопоставление размерностей позволяло сформировать безразмерные критерии (см. разд. 1.8), контролирующие технологический процесс. С течением времени и развитием аналитических методов область применения этих подходов сушественно сузилась, уступив место иным приемам. Дело в том, что надежда на «здравый смысл» не всегда оправдывалась — были вскрыты ошибочные решения задач, обусловленные недостаточностью феноменологических представлений, возможной субъективностью в выборе переменных и т. д. (в истории науки известна «ошибка Рэлея», упустившего влияние одного из факторов и получившего деформированные [c.42]
Как бы тщательно не планировалась операционная и инвестиционная деятельность компании, всегда существует вероятность получения меньшей прибыли, чем ожидаемая. Это, в частности, проявляется в постоянных колебаниях рентабельности собственного капитала за предшествующие годы. Если бы рентабельность активов в будущем была бы гарантирована, а платежи клиентов совершенно регулярными, то компания могла бы быть уверенной в том, что ее финансовое положение не ухудшится с увеличением доли заемного капитала в пассивах. В действительности это не так и необходимо тщательно анализировать финансовые последствия долгосрочных займов, чтобы установить безопасную их долю в структуре капитала. В связи с тяжестью последствий возможной ошибки данная задача должна решаться на надежной теоретической основе. Она формировалась длительное время и поэтому для усвоения методически верных приемов расчета необходимо хорошо представлять эволюцию теории структуры капитала. [c.543]
В теории надежности такая задача, однако, часто сводится к вычислению доверительной вероятности, с которой допущенная ошибка не превзойдет некоторую наперед заданную величину. [c.133]
Не будет ошибкой оказать, что главной практической задачей такого теоретического изучения является выработка научных методов подбора катализаторов. Само собой разумеется, что для выработки таких методов нужно хорошо знать химизм и механизм каталитических реакций и иметь точные сведения о физической и химической природе катализаторов. Этими последними вопросами обыкновенно и занимается большинство исследователей, работающих в области каталитической химии, что вполне оправдано необходимостью накопления экспериментального материала при помощи современных методов исследования. Работ по теории катализа, притом не в общей форме, а в форме, применимой к конкретным реакциям, появляется значительно меньше, и особенно это относится к разработке теории подбора катализаторов, которой занимается еще меньшее число исследователей, хотя этот вопрос и очень важен. [c.3]
Перейдем к рассмотрению экспериментов. Нам уже известны свойства плазмы с точностью до порядка величины. При определении термодинамических свойств возможная точность расчета не выходит за пределы 2%. При расчетах коэффициентов переноса точность много хуже. Кроме того, чтобы избавиться от практически непреодолимых математических трудностей, мы ввели при расчетах довольно грубые допущения, обычно принимаемые и в других работах. Мы усредняли многие непостоянные величины, причем это делалось так, что оценить ошибки в конечных результатах невозможно. Возможна ошибка в 2 раза, хотя многие считают используемую нами теорию не такой уж плохой. В какой степени положение может быть исправлено экспериментом Если бы мы имели материал, способный работать при 20 000 К, то все эксперименты были бы чрезвычайно просты. Измерив градиент давления при изотермическом ламинарном течении плазмы в трубе, можно определить вязкость. Эксперименты по теплообмену позволили бы определить теплопроводность и электропроводность, измеряя другие параметры. Из-за отсутствия необходимых для этого высокотемпературных материалов мы воспользуемся другим методом, который, возможно, позволит нам использовать наш теоретический аппарат для предсказания результатов эксперимента. В этом методе в сущности нет ничего нового. Еще до постановки экспериментов по определению вязкости обычных жидкостей (например воды) была принята гипотеза о прямой пропорциональности величины касательных напряжений градиенту скорости. Затем на основании этой гипотезы была получена теоретическая формула, описывающая ламинарное течение в трубе. Совпадение полученных теоретических результатов с экспериментом позволило считать вязкость физической константой, имеющей вполне определенный смысл. Этим же путем следовало бы идти и в случае плазмы, но отсутствие подходящих конструкционных материалов не позволяет осуществить изотермические условия. Тем не менее мы попытаемся воспользоваться этим же методом, ставя простые эксперименты, результаты которых можно предсказать теоретически, а затем попытаемся скорректировать теорию. Оказывается, что лучше всего использовать обычную струю плазмы, получаемую в определенных условиях. В струе плазмы, вытекающей из сопла плазматрона, температура очень сильно изменяется и по длине и по сечению струи. Если же взять трубу и разместить электроды на ее торцах, то осевого градиента температуры быть не должно. Следовательно, задача из двумерной превращается в одномерную. Для получения стационарной дуги необходимо охлаждать стенки трубы водой, поддерживая их температуру постоянной. Для плазмы при атмосферном давлении трудно придумать эксперимент проще. Теперь надо решить, какое вещество использовать в качестве рабочего тела. Конечно, для наших целей не годятся воздух, вода и даже водород, так как в водородной плазме содержится слишком много компонент На, Н, Н+ и е . Если не удастся достигнуть локального равновесия, то необходимо рассматривать по крайней мере четыре независимые группы уравнений с соответствующим числом соотношений для скорости реакций. Лучше с этой точки зрения применить гелий при 6 83 [c.83]
К сожалению, мало надежд на то, что настоящее совещание приведет к решению указанных задач. Причиной этого является некоторое привходящее обстоятельство. Дело в том, что организация настоящего совещания и постановочный доклад находятся в руках бывших прямых отечественных сторонников лженаучных теорий Ингольда и Паулинга. Это первый случай в истории недавних научно-методологических дискуссий, когда с постановочным докладом выступает не критикующая ошибки, [c.79]
В заключение еще одно замечание. Хромосомная теория наследственности ведет свою родословную от исследований Менделя. В научной литературе имеется много самых разнообразных оценок названных исследований. Среди них оценка К- А. Тимирязева, на наш взгляд, наиболее объективна и наиболее близка к истине. В тимирязевской оценке содержится, с одной стороны, объективное определение научных заслуг Менделя в разработке проблем наследственности (см. К. А. Тимирязев, Соч., т. VII, стр. 232—236) с другой стороны, в этой оценке вскрывается несостоятельность попыток последователей Менделя, которые в первые десятилетия нашего века старались представить его достижения как а) новое эволюционное учение, призванное упразднить дарвинизм, или б) по меньшей мере универсальное учение о наследственности. Тимирязев показал, что у самого Менделя не было подобных притязаний, так как он был умный и сведущий в своем деле человек (см. К. А. Тимирязев, Соч., т. VI, стр. 264). Притязания менделистов порождались причинами не научного, а общественно-политического порядка. Тимирязев научными методами безупречно доказал, что 1) менделизм покрывает лишь какую-нибудь тысячную долю того обширного поля фактов, которые обобщаются и объясняются дарвинизмом 2) менделизм объясняет лишь небольшую часть явлений наследственности из большого их числа, на каждом шагу встречающихся в действительности (см. там же, стр. 164—195 и стр. 255—266). Последователи Менделя ограничивались единственным типом половых скрещиваний и стали использовать его как критерий для объяснения всего многообразия явлений наследственности. Иными словами, это была попытка небольшой частью подменить гигантское целое. Тимирязев, вскрыв эту ошибку, давным-давно предсказал, что менделизм, ограничивая свою собственную свободу научного исследования, сам по себе окажется не в состоянии разрешить задачи, за которые он взялся, и в конце концов будет вынужден обратиться за помощью к физиологии, к экспериментальной морфологии, к химии, к физике. А одновременно не менее необходимым окажется и научный исторический, метод мышления. [c.10]
Вторая или обратная задача общей теории ошибок формулируется так каковы предельно допустимые ошибки Ахь Лх2,. .Ах при измерении каждого из аргументов Х , если заданная величина Ау — максимально допустимая ошибка результата анализа. [c.93]
Обратная задача общей теории ошибок ставит вопрос о-нахождении предельно допустимых ошибок отдельных этапов химического анализа по заданной предельной ошибке конечного результата. [c.102]
Основным в воззрениях Менделеева на науку, на взаимоотношения между теорией и практикой было требование, чтобы теория всегда проверялась практикой, а практика щедро делилась своим опытом с теорией. Истинная теория есть вывод опыта, есть соображение, построенное на опыте. Практики часто думают, замечал Менделеев, что им нет дела до теории, но это — большая ошибка. Доказывая несостоятельность мнения подобных практиков, он приводил факты из истории технологии. Только тогда, указывал ученый, была решена, например, задача добычи дешевой соли, когда в руках практиков появился теоретический фонарь . Когда стала ясной теория образования каменной соли и соленых ключей, люди поняли, где необходимо рыть, чтобы легче всего добыть крепкие растворы и самую каменную соль. Союз промышленности и науки, говорил великий химик, двигает вперед техническую мысль. [c.80]
Случайной величиной является та, точное значение которой в предстоящем измерении невозможно предсказать. Практически случайные величины появляются двумя путями. В ряде задач величина случайна, так сказать, по сути. Так, случайно количество радиоактивных распадов в секунду для образца, обладающего низкой активностью. В других задачах мы обычно трактуем величину как в основном неслучайную (детерминированную), но становящуюся случайной вследствие того, что при измерении на нее накладывается случайная ошибка. Однако провести четкую границу между теми и другими случайными величинами вряд ли возможно. В теории вероятностей различия между ними не делают. [c.49]
Обычно независимо оценивают ошибку измерения (этим занимается теория оценок), а затем переходят к проверке годности модели и уточнению значений ее параметров (теория решений). Источниками теоретико-расчетных ошибок являются следующие причины — сама теоретическая модель, исходные данные, приближенность метода вычисления и округления при расчетах. Ошибки модели вызываются ее неадекватностью и обусловлены наличием в модели элементарных процессов, не имеющих место в действительности, или, напротив, неучетом тех или иных реальных процессов. Ошибки исходных данных имеют экспериментальную природу, связаны с неточностью измерений и, присутствуя в задаче во все время ее решения, сохраняются до конечного результата. Они иногда называются неустранимыми ошибками. Погрешность метода вычисления вызывается тем, что точный оператор заменяется приближенным (интегра.т1 — суммой, производная — разностью, функция — многочленом, замкнутая ана.чити-ческая зависимость — итерационным процессом, обры- [c.134]
Знания о механизмах и кинетике физико-хцмических нроцессов основаны на различных идеализациях и приближениях, поэтому и математическое описание, использующее теорию физико-хими-ческих нроцессов, является приближенным. Однако достигаемое приближение обычно оказывается вполне достаточным для решения технических задач в этом случае ошибка расчета не должна быть больше ошибки измерения./ [c.78]
Дополнительно заметим, что поскольку при использовании алгоритма Д-П вместо точного значения оптимума КЭгр применяется его оценка то полученный вариант декомпозиции ИЗС может привести к неоптимальному решению всей задачи синтеза ХТС. Как правило, такая ошибка приводит к несовпадению действительного значения оптимума критерия эффективности синтезированной ХТС с использованной ранее оценкой. Однако эта ситуация может и не произойти, если оценка совпадет с оптимумом КЭ некоторой ХТС с фиксированной неоптимальной технологической топологией, к синтезу которой может привести применение алгоритма, и данная ХТС будет принята за оптимальную. Таким образом, совпадение принятой оценки оптимального значения критерия эффективности с ее истинным значением для синтезированной ХТСч] в общем случае не гарантирует, что полученное с использованием теории элементарной декомпозиции (алгоритма Д-П) решение ИЗС является оптимальным в глобальном смысле. [c.151]
Если при решении задач гидродинамики вполне приемлемо допущение о существовании невозмущенного ламинарного подслоя, в котором коэффициент турбулентного обмена е = О, то при решении задач тепло-массообмена при высоких числах Прандтля (Рг > 10) двухслойная или трехслойная модели [см. уравнение (11.19)1 приводят к значительным ошибкам. Согласно теории Ландау и Левича [51, 53], подтвержденной Дайслером [103], турбулентность в пограничном слое при и] 6 подчиняется закономерности [c.28]
Очевидно, теория растворов неэлектролитов должна быть непосредственно связана с теорией чистых жидкостей и должна Г1редставлять, по существу, обобщение ее на случай жидких систем, образованных частицами разных сортов. Поскольку в растворах требуется учитывать межмолекулярные взаимодействия нескольких типов, задача расчета термодинамических функций на основании молекулярных данных оказывается, вообще говоря, еще более трудной, чем для жидкостей. Однако при исследовании растворов обычно ставится ограниченная задача — определить концентрационные н температурные зависимости термодинамических функций (допустим, найти изменение энтальпии при образовании раствора из чистых компонентов и оценить, как эта величина изменяется при изменении состава и температуры). Рассматриваются, следовательно, разности термодинамических величин для раствора и чистых компонентов при этом по крайней мере один из компонентов — жидкость. Такая постановка задачи, диктуемая опытом, вносит специфику в теоретические методы исследования растворов и во многих отношениях облегчает рассмотрение. Это относится как к строгим методам, так и к модельным. Заметим, что для растворов применение моделей, в частности решеточных, оказывается более оправданным, чем для чистых жидкостей при расчете разностей ошибки в описании раствора и чистых жидкостей в какой-то степени погашаются. [c.396]
Если система описывается линейными дифференциальными уравнениями и удовлетворяет условиям управляемости и наблюдаемости, то выбор структуры и параметров регулятора, обеспечивающих оптимальное управление системой в соответствии с заранее принятым критерием, составляет задачу об оптимальном линейном регуляторе. В реальных системах обычно не удается выполнить измерение всех необходимых переменных состояния, кроме того, измерения текущих значений переменных состояния всегда дают информацию с какой-го ошибкой, к которой добавляются ошибки вследствие неточн(Зсти действия элементов регулятора. По этим причинам решения задачи об оптимальном линейном регуляторе требуют дополнительного анализа и проверки при создании реальных систем. Несмотря на указанное ограничение, теория построения линейных оптимальных регуляторов может служить основой для более общих случаев, когда состояние систем точно неизвестно. [c.231]
Попытка приближенного теоретического решения задачи фильт рации аэрозолей была впервые предпринята Кауфманом , исхо дившим из более ранних работ Селла и Альбрехта по инер ционному осаждению аэрозолей на цилиндрах, эту попытку нельзя признать удачной, так как автор рассматривал воздух как идеаль ную а не вязкую жидкость Ту же ошибку допустили Стерменд и Ранц и Уонг , учитывавшие только инерционное осаждение ча стиц Более строгая теория Ленгмюра , основывающаяся на гидродинамике вязкой жидкости, применима лишь к тем случаям, когда инерционные эффекты пренебрежимо малы Теория, предло женная Дейвисом учитывает инерцию во всем диапазоне разме ров аэрозольных частиц и скоростей течения Все эти и ряд других [c.206]
Рассмотрение задачи о движении массы сьшучего материала на основе гидродинамической теории проведено только в работе [5], причем лишь для оптимального режима работы, т. е. для чисто осевого движения материала. Расчет основан на той же математической модели движения, ято и вычисления [3] для односпирального пгаека, но учитывает наличие двух движущихся цилиндров. Использование гидродинамической теории, по-видимому, оправдано, так как ошибка не превышает в этом случае 10—12% [5]. Можно ожидать, ято полученное на основании гидродинамической теории уравнение окажется оце более точным для случая перемещения вязких материалов. К сожалению, до настоящего времени транспортирз щая способность двухспирального шнека для вязких жидкостей не исследована. [c.218]
Некоторые дружественные критики первого, К счастью неопубликованного, (английского текста указывали, что книга недостаточно критична. Автор обязан был оценить, в какой мере это указание оказалось справедливым. Дело же читателя судить о тщательности и точности отбора материала. Многие области исследования силикатов развиты слабо в таких областях существуют заросли, в которых топор того или иного исследователя наметил лишь первую лросеку. Возможно, что кое-кто из этих иионеров в своих усилиях получить истинный ответ совершал ошибки и промахи. К счастью, однако, мы можем надеяться, что придет день, когда даже в самых густых джунглях различных теорий и гииотез забрезжит свет и станет ясным, какое направление оказалось верным. При написании настоящей книги моя скромная задача заключалась лишь в том, чтобы ввести читателя в эти чарующие джунгли, но не беру на себя смелость шролагать через них путь. [c.8]
Ошибки теории резонанса связаны с интерпретацией одного из приближенных квантово-механических методов расчета молекул (метода валентных структур). В этом можно усмотреть физический идеализм, объективизирование математических понятий. Это сказывается в работах авторов теории резонанса, а также наших, в том, что членам суммы, представляющей волновую функцию (1) (которая передает состояние молекулы в нулевом приближении), приписывается смысл определенной химической структуры. В действительности же речь идет о нулевом приближении квантовой механики (теории возмущения), т. е. об упрощенном математическом методе решения многоэлектронной задачи. [c.114]
Вместо того чтобы поправить автора и указать на его ошибки, редакция журнала Успехи химии выступила в защиту резонанса со следующим примечанием В связи с вопросом о сопоставлении теории резонаиса и теории электронных смещений редакция считает необходимым заметить следующее. Нет сомнений в законности для химика использования некоторых наглядных представлений последней теории. Эта законность оправдывается не только огромной сложностью аппарата теории резонанса, но и многими принципиальными затруднениями, встречаемыми ею при попытке решения конкретных задач химии. Однако при сопоставлении этих теорий не может иметь места их принципиальная равноправность. Напротив, одна из них покоится на наиболее общих достижениях современного естествознания, в то время как другая является все же набором продуманных моделей и механизмов. Таким образом, при попытках привести во взаимное соответствие язык и представления обеих теорий должен иметь место такой подход те положения теории электронных смещений, которые удается привестм в соответствие с языком теории резонанса, имеют право остаться в арсенале методов химика-, те же положения, для которых удается показать их противоречивость с языкам теории резонанса, должны быть исключе ш из этого арсенала (стр. 110). [c.409]
Полуэмпирические методы значительно проще, менее громоздки, более гибкие, что позволяет приспособить их для решения всевозможных разнообразных задач — от определения конфигурации системы [99, 102, 121] до расчета электронного строения и энергии переходного комплекса как функции координаты реакции [111]. По-луэмнирические методы позволяют рассчитать отдельные фрагменты соединений [108, 109], что существенно расширяет размеры системы, которые могут быть исследованы этими методами. Очень важно также то обстоятельство, что введенные в уравнения эмпирические параметры, непосредственно отражая реальную ситуацию в системе, как правило, уменьшают ошибки метода и, следовательно, улучшают теорию. Недостатком полуэмпирических методов является некоторый произвол в выборе ряда констант. [c.90]
В наиболее общей форме основные задачи общей теории ошибок можно сформулировать следующим образом. Пусть у — результат (косвенного химино-аналитического определения, X], Х2,. .Хп —аргументы, величины которых измеряются в ходе химического анализа, а f — конкретная функциональная зависимость, которая их связывает у = (х1, х2,. .., х ). Тогда, поскольку измерение величин х всегда сопряжено с ошибками ЛХг, то и определение величины у также отягощено ошибкой Ау. Но так как между у и х существует функциональная зависимость, закономерна постановка следующих задач. [c.93]
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
![]() (1.25)
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
![]() (1.26)
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
![]() (1.27)
(1.27)
где: ![]() ;
;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
 (1.29)
(1.29)
где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
![]()
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
![]() (1.30)
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
![]() (1.31)
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
![]()
![]()
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
![]() (1.32)
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
![]() (1.33)
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
 (1.34)
(1.34)
Сложим эти равенства, суммарное уравнение разделим на n и получим:
![]() (1.35)
(1.35)
Величина ![]() (1.36)
(1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
![]()
по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
![]()
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
![]()
или
![]()
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
![]() (1.37)
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:
 (1.38)
(1.38)
Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
![]() (1.40)
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:
 (1.41)
(1.41)
Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):
 (1.42)
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:
![]() .
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
![]() .
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
![]() (1.43)
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ![]() ; такая замена практически не изменит правой части формулы (1.43). Итак,
; такая замена практически не изменит правой части формулы (1.43). Итак,
![]() ,
,
откуда ![]() ;
;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
![]() (1.44)
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
![]() (1.46)
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
![]()
откуда ![]() (1.47)
(1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
![]() (1.48)
(1.48)
Согласно (1.46) и (1.32) напишем:
![]()
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
![]()
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
![]() (1.51)
(1.51)
где pi – вес i-того элемента.

ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч. пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: – М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .

1.Задачи теории ошибок измерений.
2.Сущность и виды измерений.
3.Ошибки измерений, их классификация и свойства.
4.Понятие о законах распределения ошибок.
5.Числовые характеристики точности измерений.

1. Задачи теории ошибок измерений.
Геодезические работы связаны с различными методами измерений длин линий, углов, превышений, площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.

Теория ошибок измерений решает четыре основные задачи:
1.Изучение законов возникновения и распределения ошибок измерений и вычислений.
2.Оценка точности результатов измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.

2. Сущность и виды измерений.
Измерения различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные (избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется
результатом измерения.

Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например, измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.

Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны- ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.

Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Если одна величина измерена n—раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.
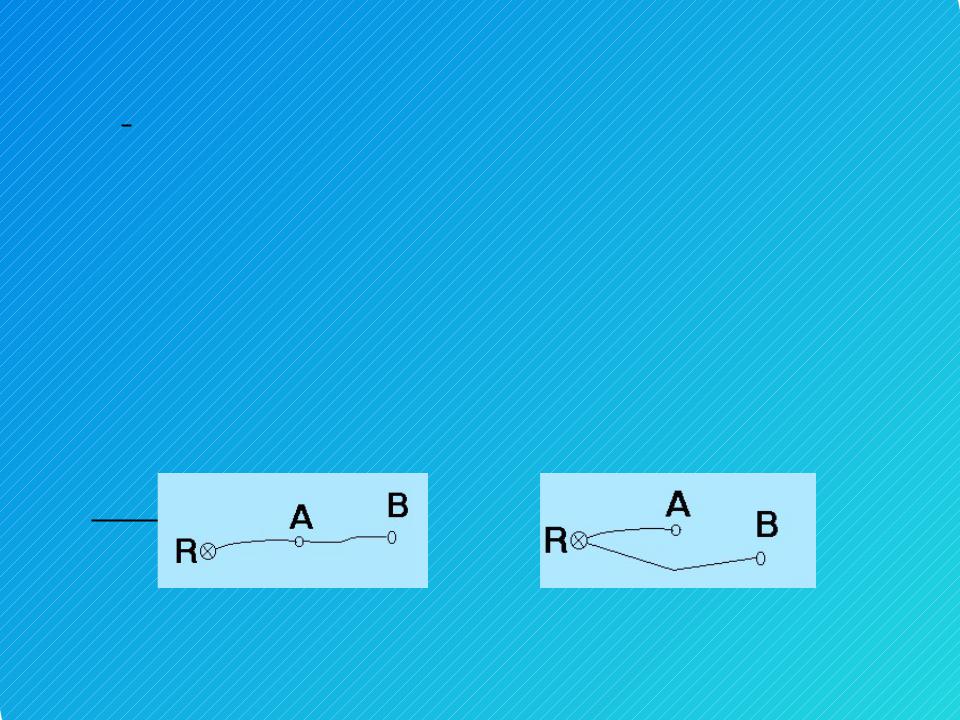
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Например, высоты точек А и В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут
(рис.2).
Соседние файлы в папке лекции по геодезии 2 курс
- #
- #
- #
29.02.20162.28 Mб32ЛЕКЦИЯ 13.pptx
- #
- #
- #
На чтение 9 мин Просмотров 1.7к. Опубликовано 03.10.2021
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
![]() (1.25)
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
![]() (1.26)
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
![]() (1.27)
(1.27)
где: ![]() ;
;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
 (1.29)
(1.29)
где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
![]()
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
![]() (1.30)
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
![]() (1.31)
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
![]()
![]()
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
![]() (1.32)
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
![]() (1.33)
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
 (1.34)
(1.34)
Сложим эти равенства, суммарное уравнение разделим на n и получим:
![]() (1.35)
(1.35)
Величина ![]() (1.36)
(1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
![]()
по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
![]()
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
![]()
или
![]()
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
![]() (1.37)
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:
 (1.38)
(1.38)
Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
![]() (1.40)
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:
 (1.41)
(1.41)
Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):
 (1.42)
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:
![]() .
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
![]() .
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
![]() (1.43)
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ![]() ; такая замена практически не изменит правой части формулы (1.43). Итак,
; такая замена практически не изменит правой части формулы (1.43). Итак,
![]() ,
,
откуда ![]() ;
;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
![]() (1.44)
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
![]() (1.46)
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
![]()
откуда ![]() (1.47)
(1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
![]() (1.48)
(1.48)
Согласно (1.46) и (1.32) напишем:
![]()
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
![]()
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
![]() (1.51)
(1.51)
где pi – вес i-того элемента.
Теория ошибок (ошибок теория)
Теория ошибок
–
раздел математической статистики, посвященный построению уточненных выводов о численных значениях приближенно измеренных величин, а также об ошибках (погрешностях) измерений.
Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, так как каждое измерение содержит некоторую ошибку. Различают 3 основных вида ошибок: систематические, грубые и случайные.
Систематические ошибки всё время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики. Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов.
Теория ошибок занимается изучением лишь грубых и случайных ошибок . Основными задачами теории ошибок являются: разыскание законов распределения случайных ошибок, разыскание оценок неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и устранение грубых ошибок .
Алфавитный указатель
