ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Ученик допустил ошибку при построении графика функции.
На каком рисунке?
На этой странице вы найдете ответ на вопрос Ученик допустил ошибку при построении графика функции?. Вопрос
соответствует категории Алгебра и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Авторы:
Год:2023
Тип:дидактические материалы
С-16. Взаимное расположение графиков на координатной плоскости > Вариант 1
Условие:
1. Постройте в одной системе координат графики функций y=-1/3*x+1; y=1/3*x-2; y=-1/3*x. Ответьте на вопросы:
1) чему равен угловой коэффициент каждой прямой;
2) каково взаимное расположение графиков функций;
3) каковы координаты точек пересечения каждого графика с осями координат?
2. Постройте в одной системе координат графики функций y=x-2; y=-2x-2; y=-2. Ответьте на вопросы:
1) в какой точке каждый график пересекает ось у, ось х;
2) каково взаимное расположение графиков?
3. В одной системе координат постройте графики функций, вычислив координаты точек пересечения графиков с осями координат: y=3x-6; y=-3x-6; y=3x+6; y=-3x+6.
Укажите пары параллельных прямых.
4. Пересекаются ли графики функций:
y=2x-4 и y=-4x+2;
y=2x-3 и y=-2x+3.
В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением.
5. Задайте формулой линейную функцию, если известны угловой коэффициент k соответствующей прямой и координаты точки A, через которую она проходит:
а) k=2/3; A(-6;-3);
б) k=-4; A(2; 7).
6. Постройте прямую, если ее угловой коэффициент равен -0,5 и она проходит через точку (-6; 4). Задайте формулой линейную функцию, график которой параллелен указанной прямой и пересекает ось x в точке (0; 5).
7. Ученик допустил ошибки при построении графиков функций:
y=1/4*x (рис. 8); y=-3x (рис. 9) и y=2x+4 (рис. 10).
Докажите, что графики построены неверно (попробуйте решить задачу не прибегая к вычислениям и построению прямых).
Описание презентации по отдельным слайдам:
-
1 слайд
«Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью».(Л.Н.Толстой)
Учитель математики:
Ветрова Л. Н. -
2 слайд
НАЙДИТЕ СООТВЕТСТВИЕ КОЭФФИЦИЕНТОВ К И В ФУНКЦИЙ
1) У=2Х-3
2) У=-3Х+6
3) У= Х 𝟐 +5
4) У=Х+1,5
5) У=-Х-7
6) У= 𝟏𝟎Х−𝟓 𝟓
7)У=5
У=2Ха) к= 1 2 ; в=5
б) к=2; в=-3
в) к=-3; в=6
г) к=-1; в=-7
д) к=2; в=-1
е) к=0; в=5
ж) к=2; в=0
з) к=1; в=1,5 -
3 слайд
Используя график, заполни таблицу
0
1
1
х
у
2.Найдите координаты точек пересечения графика с осями координат.
3.Найдите х, при которых точки графика расположены ниже оси х.
А(-5;0)
В(0;5)
А
В -
4 слайд
План исследовательской работы.
-
5 слайд
Вывод:
1)Если к>0,то угол наклона, образованный графиком линейной функции с положительным направлением оси Ох, острый.
2) Если к<0, то угол наклона , образованный графиком линейной функции с положительным направлением оси Ох, тупой.
3)Если к=0, то график линейной функции расположен параллельно оси Ох.у
х
0
y=kх+b, k>0
y=kx+b, k<0
y=b, k=0 -
6 слайд
У
Х
у=2х+4
у=2х
у=2х-2
у=2х-4
У
Х
у=-2х+4
у=-2х
у=-2х-2
у=-2х-4
Вывод: прямые параллельны, если их угловые
коэффициенты равны. -
7 слайд
Вывод: Если угловые коэффициенты линейных функций не равны, то их графики пересекаются.
х
у
0
y=2x+1
y=-3x+1 -
-
-
-
-
-
-
14 слайд
Функции заданы формулами : 1) у = -1,5х+6;
2) у = 0,5х+4;
3) у = 3+0,5х;
4) у = 0,5х+6;
5) у = 1 2 х-4
Выберите те функции, графики которых
а) параллельны
б) пересекаются
в)пересекаются в точке (0;6) -
15 слайд
х
х
х
у
у
у
0
0
0
1
1
1
1
1
1
y= 1 4 x
y=-3x
y=2x+4
Ученик допустил ошибки при построении графиков функций.
Докажите, что графики построены неверно. -
16 слайд
Задание №1
Функции заданы формулами : 1) у = -1,5х+6;
2) у = 1,5х+4;
3) у = 3+1,5х;
4) у = 0,5х+6;
5) у = 3 2 х-4
Выберите те функции, графики которых
а) параллельны
б) пересекаются -
17 слайд
Задание №2:
Задайте формулой функцию, график которой параллелен
y = -5x+8. -
18 слайд
Задание №3:
Из предложенных формул, задающих линейную функцию, выберите ту, у которой угловой коэффициент к = — 3, а точка пересечения с осью ОУ А(0; 7):
у = 3х +7; у = — 3х + 7; у = — 3х — 7 -
19 слайд
домашнее задание:
п.16 прочитать
№ 369, 372(а;в) -
20 слайд
Спасибо за урок!
Надеюсь , что вам понравилось и вы хорошо усвоили полученные результаты и выводы.
Линейная функция,
её график, свойства.
7 класс
Учитель математики Синдикова А.Ю.
Укажите линейные уравнения :
1) 5y = x
2) 3y = 0
3) y 2 + 16x 2 = 0
4) + y = 4
5) x + y =4
6) y = -x + 11
7) + 0.5x – 2 = 0
25d – 2m + 1 = 0
9) y = 3 – 2x
5
- Функция вида у = kx + b называется линейной .
- Графиком функции вида у = kx +b является прямая .
- Для построения прямой необходимы только две точки , так как через две точки проходит единственная прямая.
Найти уравнения линейных функций
y=-x+0,2; y=12,4x-5,7 ; y=-9x-18; y=5,04x;
y=-5,04x; y=126,35+8,75x;
y=x-0,2; y=x:8;
y=0,005x; y=133,133133x; y=3-10, 01x; y=2:x;
y=-0,0049; y=х:62.
y = kx + b – линейная функция
х – аргумент (независимая переменная)
у – функция (зависимая переменная)
k, b – числа (коэффициенты)
к ≠ 0
х
Х 1
у
Х 2
У 1
Х 3
У 2
У 3
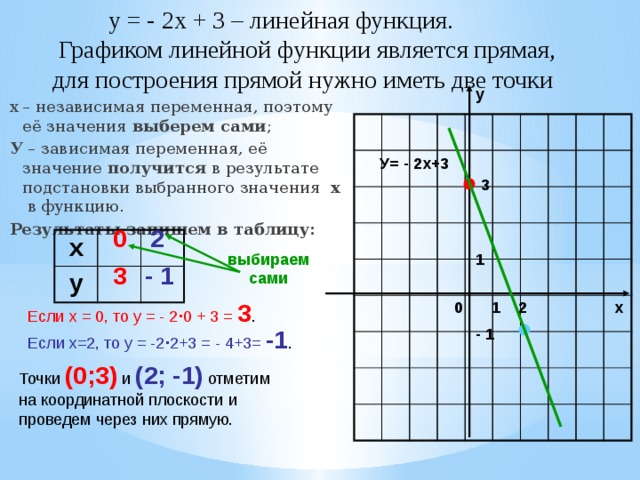
у = — 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки
у
х – независимая переменная, поэтому её значения выберем сами ;
У – зависимая переменная, её значение получится в результате подстановки выбранного значения х в функцию.
Результаты запишем в таблицу:
У= — 2х+3
3
2
0
х
у
выбираем
1
сами
— 1
3
2
0
1
Если х = 0, то у = — 2 · 0 + 3 = 3 .
х
— 1
Если х=2, то у = -2 · 2+3 = — 4+3= -1 .
Точки (0;3) и (2; -1) отметим
на координатной плоскости и
проведем через них прямую.
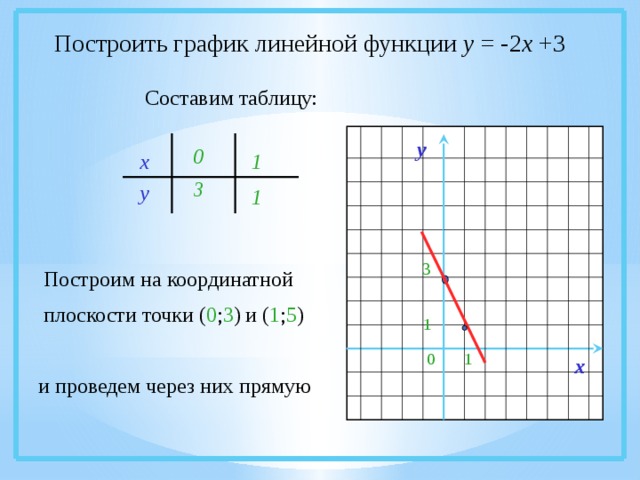
Построить график линейной функции у = -2 х +3
Составим таблицу:
у
03
х
1
у
1
3
Построим на координатной плоскости точки ( 0 ; 3 ) и ( 1 ; 5 )
1
1
0
х
и проведем через них прямую
Построить график линейной функции
I вариант II вариант
y=x-4 y=-x+4
Определить взаимосвязь коэффициентов
k и b и расположения прямых
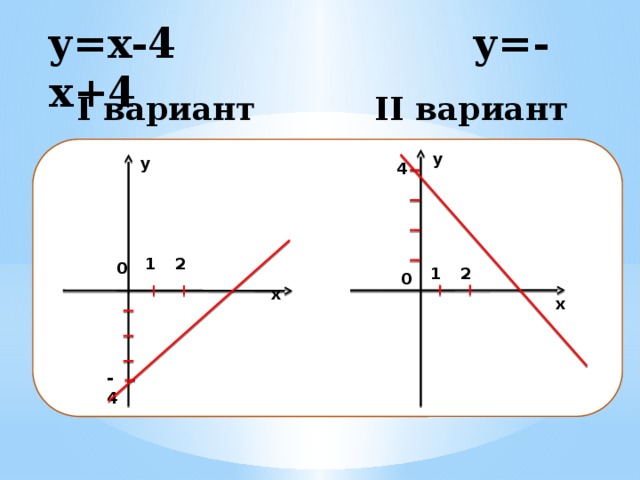
y=x-4 y=-x+4
II вариант
I вариант
y
y
4
2
1
0
1
2
0
x
x
-4
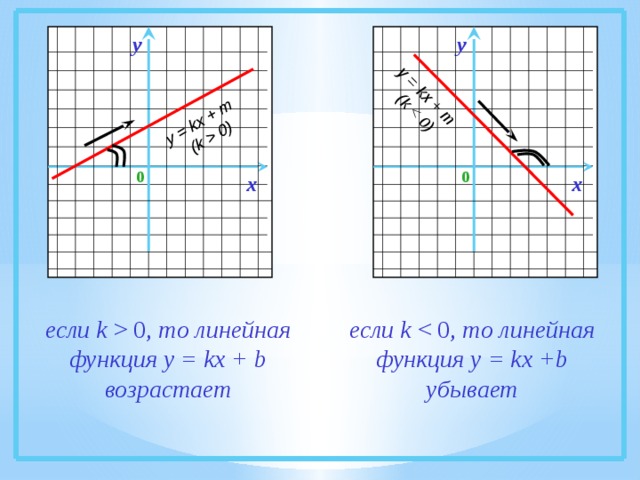0) у у 0 0 х х если k 0, то линейная функция у = kx + b возрастает если k то линейная функция у = kx +b убывает » width=»640″
y = kx + m
(k
y = kx + m
(k 0)
у
у
0
0
х
х
если k 0, то линейная функция у = kx + b возрастает
если k то линейная функция у = kx +b убывает
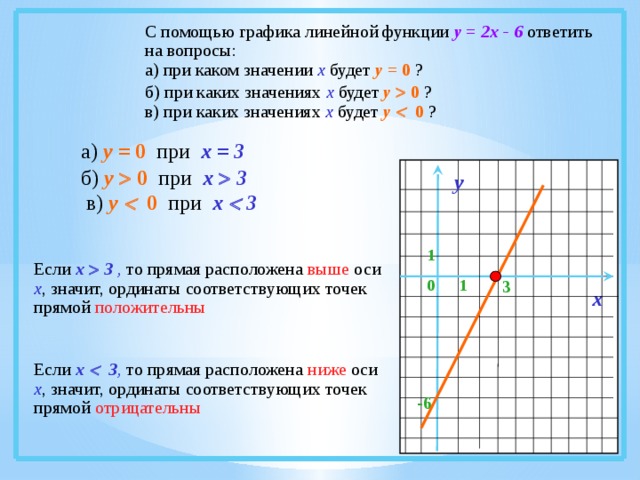
С помощью графика линейной функции у = 2х — 6 ответить на вопросы:
а) при каком значении х будет у = 0 ?
б) при каких значениях х будет у 0 ?
в) при каких значениях х будет у 0 ?
а) у = 0 при х = 3
б) у 0 при х 3
у
в) у 0 при х 3
1
Если х 3 , то прямая расположена выше оси х , значит, ординаты соответствующих точек прямой положительны
3
0
1
х
Если х 3 , то прямая расположена ниже оси х , значит, ординаты соответствующих точек прямой отрицательны
-6
Задания для самостоятельного решения: построить графики функций (выполнять в тетради)
1. у = 2х – 2
3. у = 4 – х
4. у = 1 – 3х
2. у = х + 2
Обратите внимание:
точки, выбранные вами для построения прямой, могут быть другими,
но расположение графиков обязательно должно совпадать
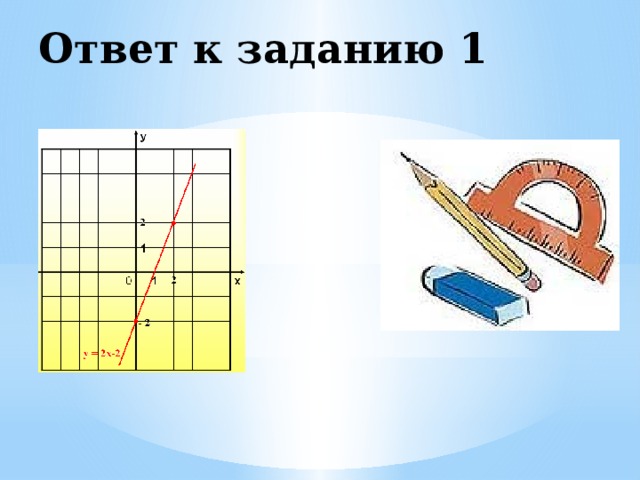
Ответ к заданию 1
12
Ответ к заданию 2
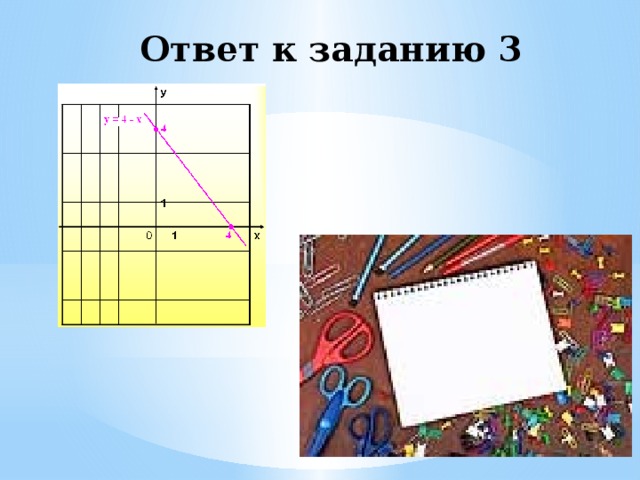
Ответ к заданию 3
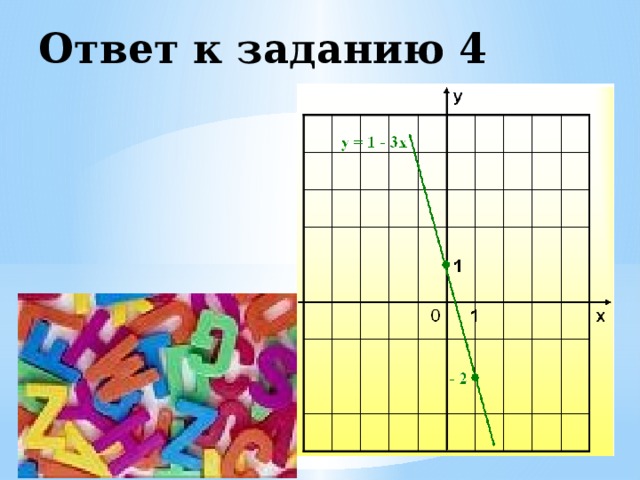
Ответ к заданию 4
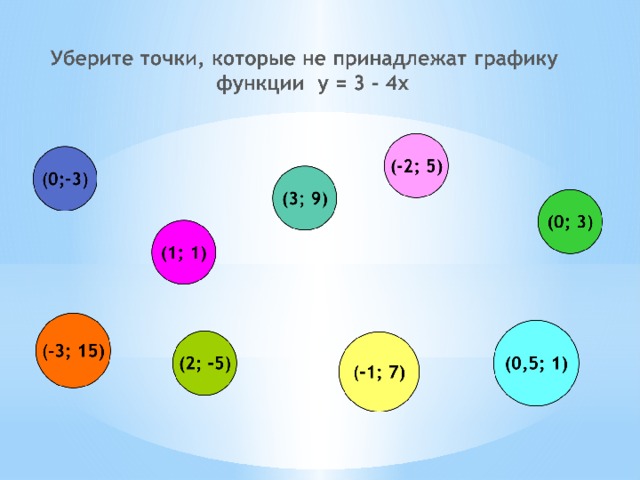
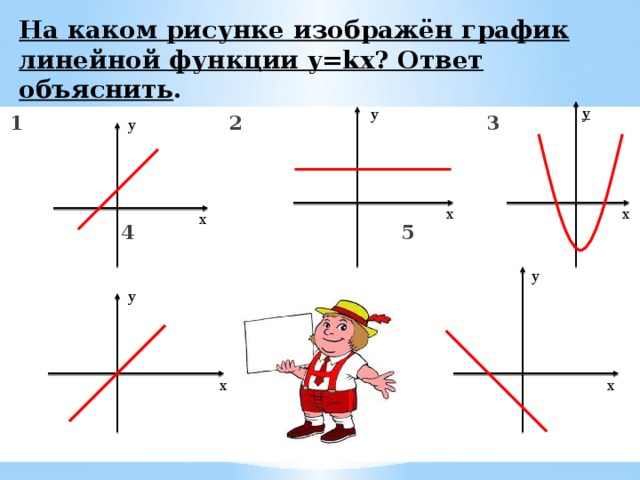
На каком рисунке изображён график линейной функции y=kx? Ответ объяснить .
y
y
1 2 3
4 5
y
x
x
x
y
y
x
x
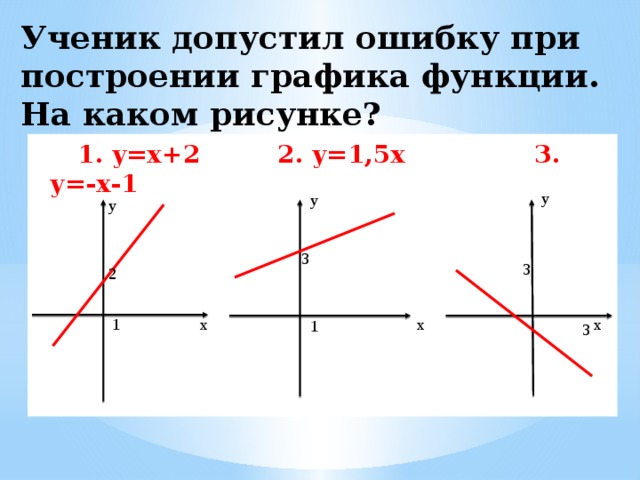
Ученик допустил ошибку при построении графика функции. На каком рисунке?
1. y=х+2 2. y=1,5х 3. y=-х-1
y
y
y
3
3
2
1
x
x
x
1
3
На каком рисунке коэффициент k отрицателен?
1 2 3
4 5
y
y
y
x
x
x
y
y
x
x
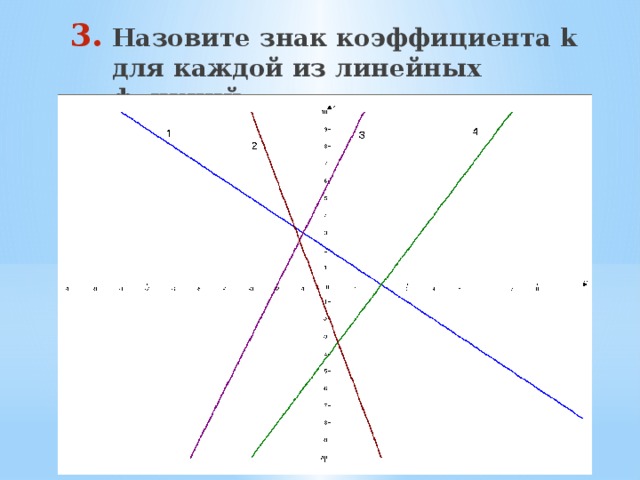
- Назовите знак коэффициента k для каждой из линейных функций:
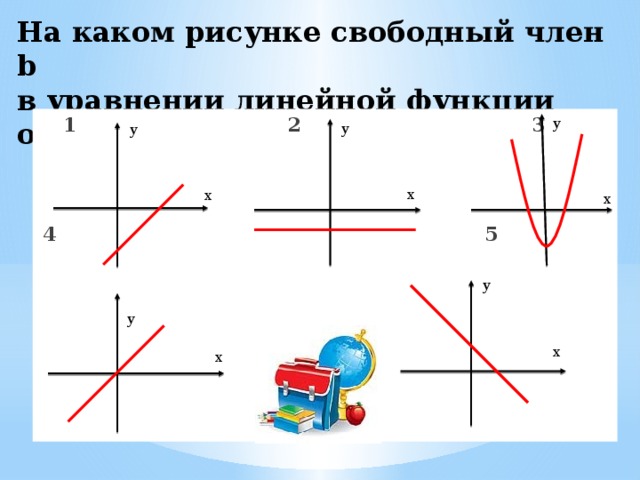
На каком рисунке свободный член b в уравнении линейной функции отрицателен?
y
1 2 3
4 5
y
y
x
х
x
y
y
x
x
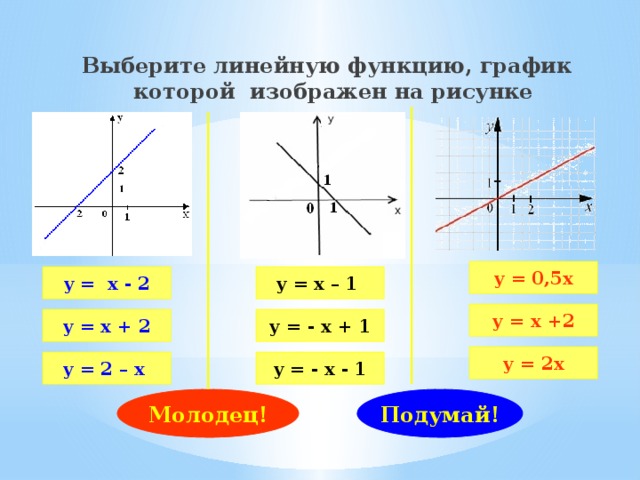
Выберите линейную функцию, график которой изображен на рисунке
у = 0,5х
у = х — 2
у = х – 1
у = х +2
у = х + 2
у = — х + 1
у = 2х
у = 2 – х
у = — х — 1
Молодец!
Подумай!
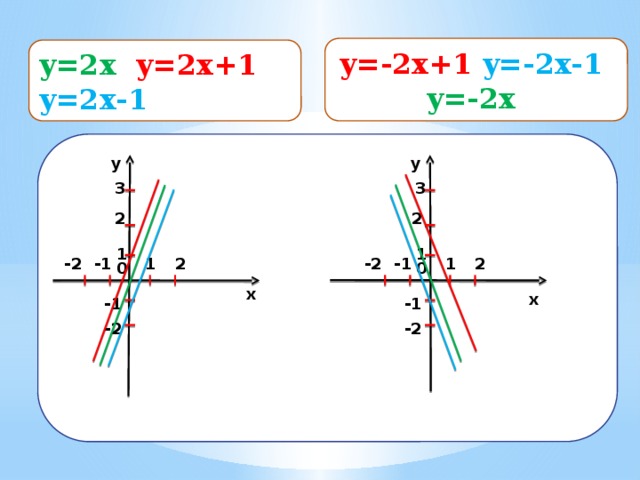
y=-2x+1 y=-2x-1
y=-2x
y=2x y=2x+1 y=2x-1
y
y
3
3
2
2
1
1
2
1
-1
2
1
-2
-1
-2
0
0
x
x
-1
-1
-2
-2
12
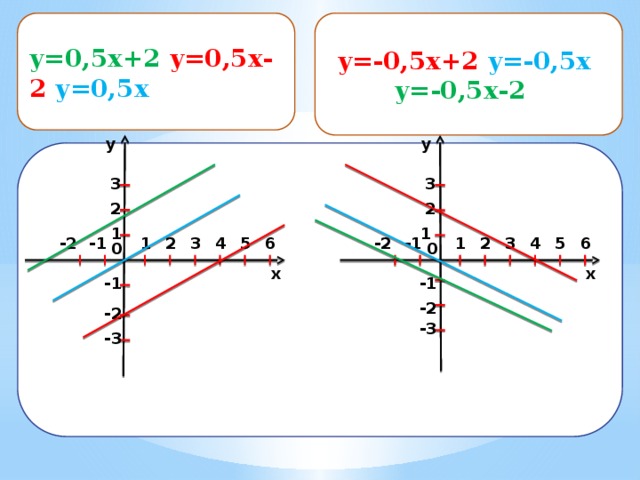
y=0,5x+2 y=0,5x-2 y=0,5x
y=-0,5x+2 y=-0,5x
y=-0,5x-2
y=-0,5x+2, y=-0,5x, y=-0,5x-2
y
y
3
3
2
2
1
1
4
6
1
2
5
3
-2
-1
1
3
6
5
4
2
-2
-1
0
0
x
x
-1
-1
-2
-2
-3
-3
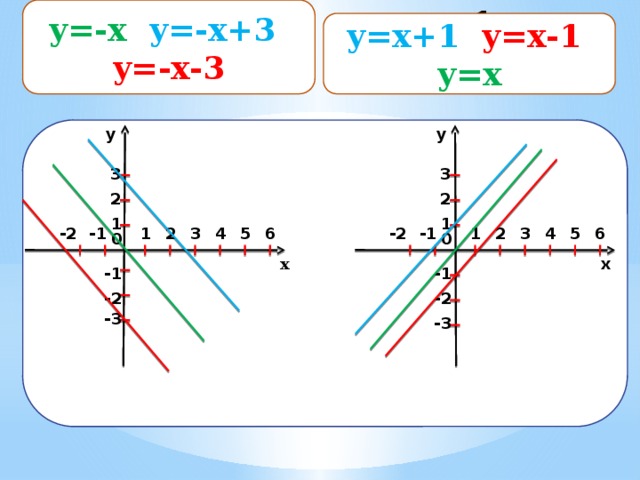
y=-x y=-x+3
y=-x-3
y=x+1 y=x-1 y=x
y=x+1 y=x-1 ,y=x
y
y
3
3
2
2
1
1
-1
1
2
6
5
4
3
1
-2
-1
4
2
-2
5
6
3
0
0
x
x
-1
-1
-2
-2
-3
-3
Составить уравнение
линейной функции по следующим условиям:
подведем
итог
Мы узнали: *Функция вида у = kx + b называется линейной. *Графиком функции вида у = kx + b является прямая. *Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая. *Коэффициент k показывает возрастает или убывает прямая. *Коэффициент b показывает, в какой точке прямая пересекает ось OY. *Условие параллельности двух прямых.
Выводы записать в тетрадь
Желаю успехов!
Алгебра – это слово произошло от названия сочинения Мухаммеда Аль-Хорезми «Аль-джебр и Аль-мукабала», в котором алгебра излагалась как самостоятельный предмет
Роберт Рекорд – это английский математик, который в 1556г. ввёл знак равенства и объяснил свой выбор тем, что ничто не может быть более равным, чем два параллельных отрезка.
- Готфрид Лейбниц – немецкий математик (1646 – 1716г.г.), который первым ввёл термин «абсцисса» — в 1695г., «ордината» — в 1684г., «координаты» — в 1692г.
12
- Рене Декарт – французский философ и математик (1596 – 1650г.г.), который первым ввёл понятие «функция»
Использованная литература
1.МордковичА.Г. и др. Алгебра: учебник для 7 класса общеобразовательных учреждений – М.:Просвещение,2010.
2.Звавич Л.И. и др. Дидактические материалы по алгебре для 7 класса — М.:Просвещение,2010.
3.Алгебра 7 класс, под редакцией Макарычев Ю.Н. и др., Просвещение, 2010 г.
4.Интернетресурсы: www.symbolsbook.ru/Article.aspx%…id%3D222
12