
-
на данном рисунке изображено сечение куба плоскостью В чём ошибка данного рисунка Дайте объяснение
-
Предмет:
Геометрия
-
Автор:
ceceliaraymond683
-
Создано:
3 года назад
Знаешь ответ? Добавь его сюда!
-
-
Русский язык
4 минуты назад
Как правильно будет? «Это два разных заведения или заведениЙ?»
-
Русский язык
9 минут назад
Вопросы по русскому языку.
-
Литература
14 минут назад
Можно ли назвать дружбой отношения Печорина и Грушницкого, Печорина и доктора Вернера?
-
СРОЧНО ПОЖАЛУЙСТА ПОМОГИТЕ
-
Обществознание
19 минут назад
Реферат по обществу на тему «религии»
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Вы не можете общаться в чате, вы забанены.
Чтобы общаться в чате подтвердите вашу почту
Отправить письмо повторно
Вопросы без ответа
-
Помогите пожалуйста
-
Помогите плиз с самостоятельной
В задании 6 нужна скобка перед 9
Топ пользователей
-

Fedoseewa27
23163
-

Sofka
7419
-

zlatikaziatik
5900
-

vov4ik329
5111
-

DobriyChelovek
4625
-

olpopovich
3461
-
TheDenty
3258
-

dobriykaban
2540
-
Udachnick
1867
-

ViktoriaBell0
1740
Войти через Google
или
Запомнить меня
Забыли пароль?
У меня нет аккаунта, я хочу Зарегистрироваться
Выберите язык и регион
Русский
Россия
English
United States

How much to ban the user?
1 hour
1 day
Слайд 1Тема: « Задачи на построение сечений».
Автор работы: Янаева
Ольга Николаевна,
учитель математики МБУ гимназии №35 г.о. Тольятти

Слайд 2Цели урока
Знать алгоритм решения задач методом «следов» и методом параллельного проецирования;
Уметь
решать задачи на построение сечений;
Уметь применять алгоритм при решении задач на построение сечений;

Слайд 3
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
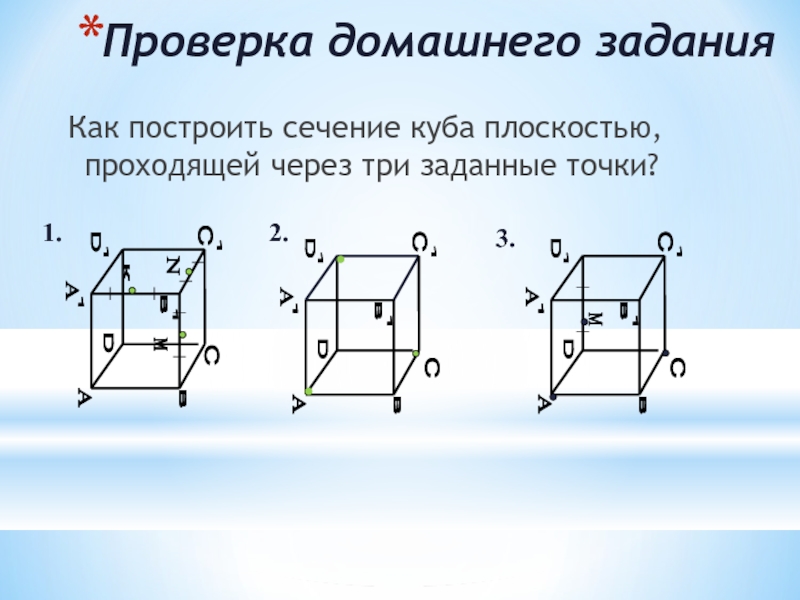
Проверка домашнего задания
Как построить сечение куба плоскостью, проходящей через три заданные точки?
1.
2.
3.
к
N
M
M
Слайд 4
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
к
N
M
M
1.
2.
3.
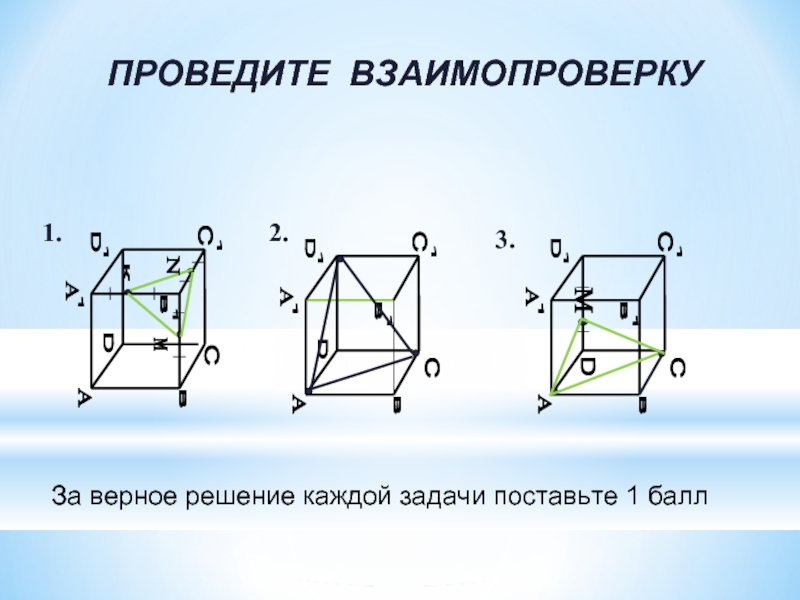
ПРОВЕДИТЕ ВЗАИМОПРОВЕРКУ
За верное решение каждой задачи поставьте 1 балл
Слайд 5
А
А
1
в
в
1
D
D
1
С
С
1
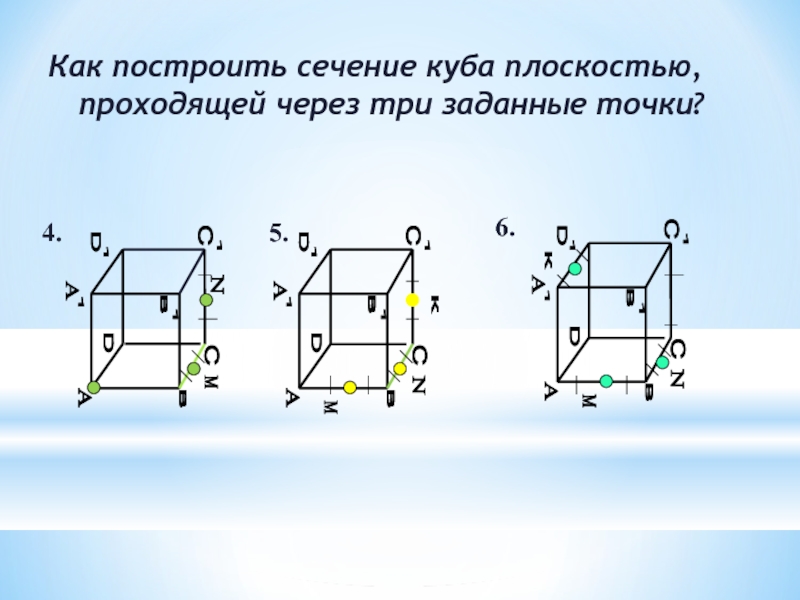
4.
N
M
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
5.
6.
Как построить сечение куба плоскостью, проходящей через три заданные точки?
Слайд 6
А
А
1
в
в
1
D
D
1
С
С
1
4.
N
M
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
5.
E
Q
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
P
Q
E
F
6.
s
s
s
T
ПРОВЕДИТЕ ВЗАИМОПРОВЕРКУ
За верное решение задач №4 и №5 по 2 балла;
За верное решение задачи №6 – 3 балла.

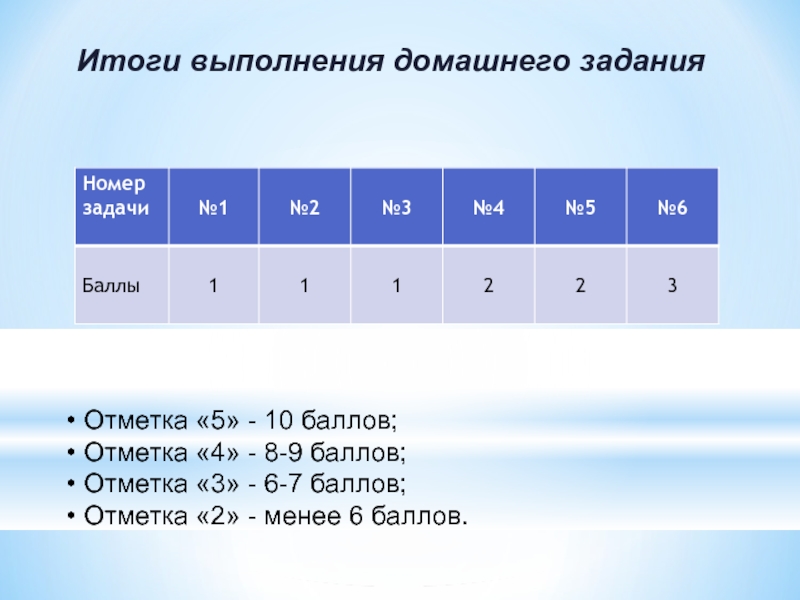
Слайд 7 Отметка «5» — 10 баллов;
Отметка «4» — 8-9 баллов;
Отметка «3» — 6-7 баллов;
Отметка «2» — менее 6 баллов.
Итоги выполнения домашнего задания
Слайд 8
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой
есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости.
Основные понятия
Рис.1
Рис.2

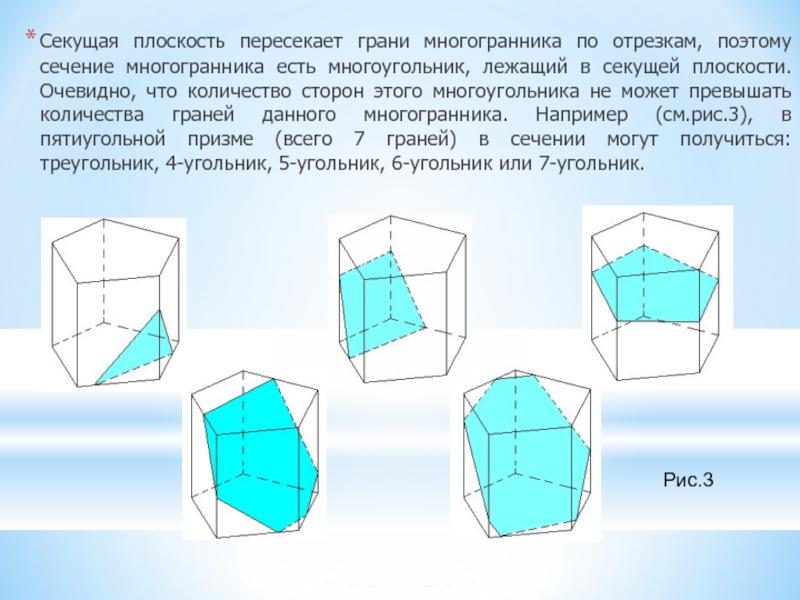
Слайд 9Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть
многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника. Например (см.рис.3), в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник.
Рис.3
Слайд 10 Две плоскости пересекаются по прямой (эта аксиома и дала названию
метода – под «следом» понимается прямая пересечения какой-либо грани многогранника и секущей плоскости).
Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?).
Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости.
ПРИМЕЧАНИЕ. Не забудьте, что прямая и плоскость являются бесконечными в пространстве фигурами!
Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K.
Метод «следов»

Слайд 11
A
B
C
D
B1
C1
D1
M
N
K
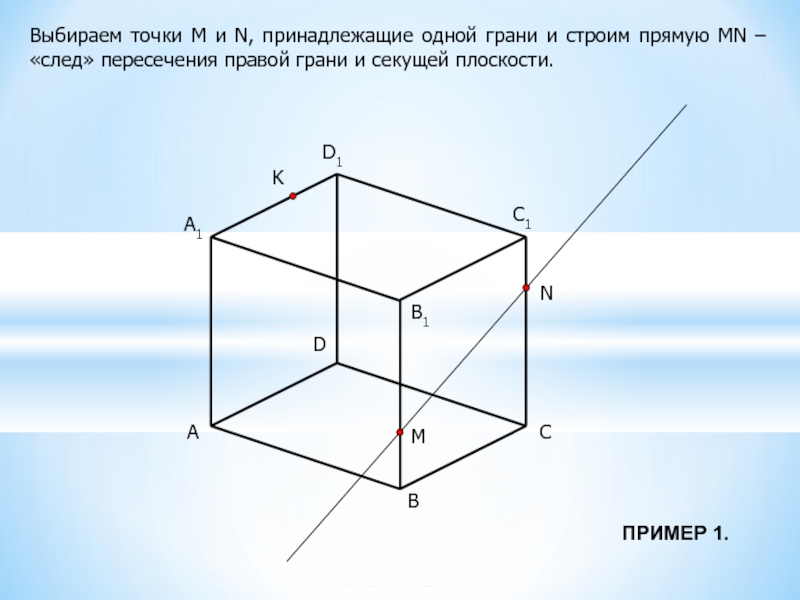
Выбираем точки М и N, принадлежащие одной грани и строим прямую
MN – «след» пересечения правой грани и секущей плоскости.
A1
ПРИМЕР 1.
Слайд 12
A
B
C
D
B1
C1
D1
M
N
K
A1
E
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной грани
с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.
ПРИМЕР 1.

Слайд 13
A
B
C
D
B1
C1
D1
M
N
K
A1
E
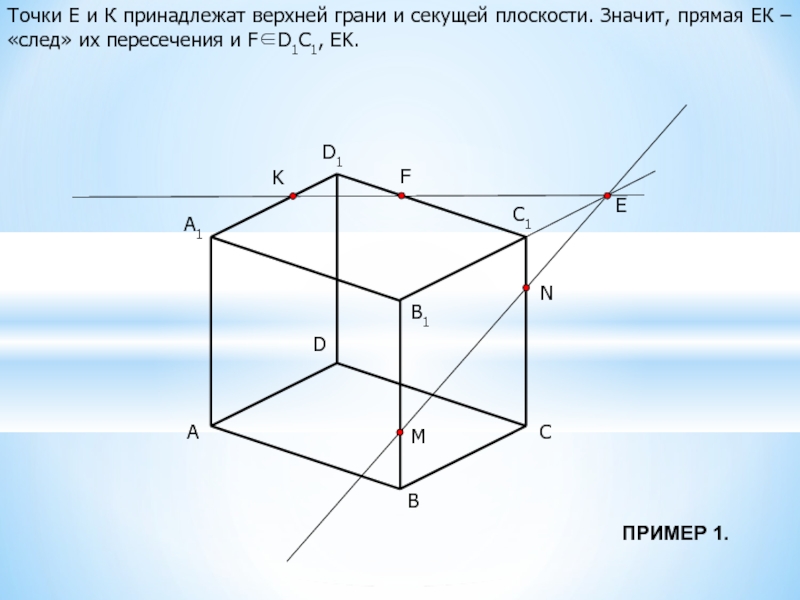
Точки Е и К принадлежат верхней грани и секущей плоскости. Значит,
прямая ЕК – «след» их пересечения и F∈D1C1, EK.
F
ПРИМЕР 1.
Слайд 14
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
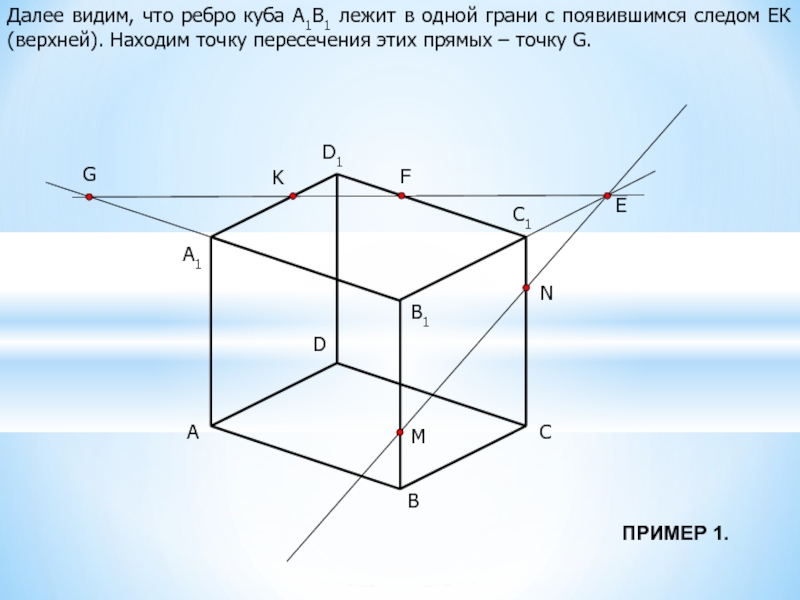
Далее видим, что ребро куба А1В1 лежит в одной грани с
появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G.
G
ПРИМЕР 1.
Слайд 15
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
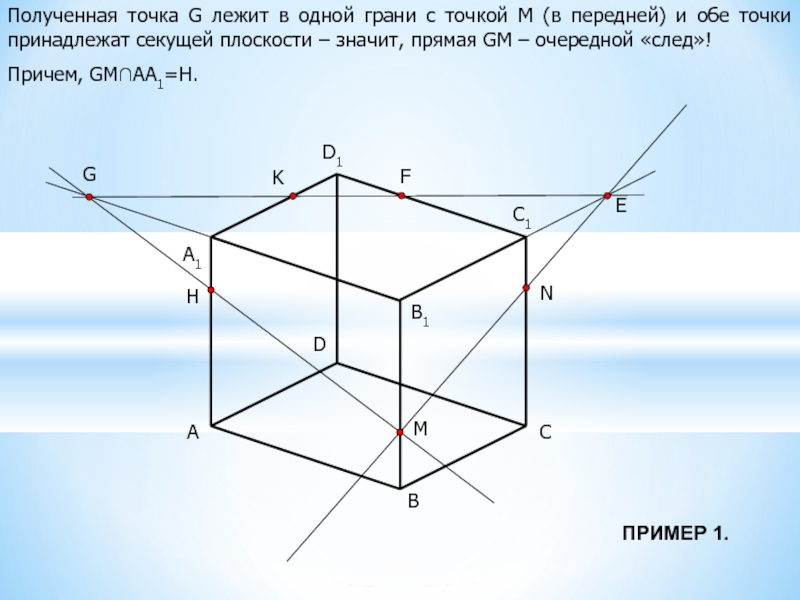
Полученная точка G лежит в одной грани с точкой М (в
передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след»!
Причем, GM∩АА1=Н.
H
ПРИМЕР 1.
Слайд 16
A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
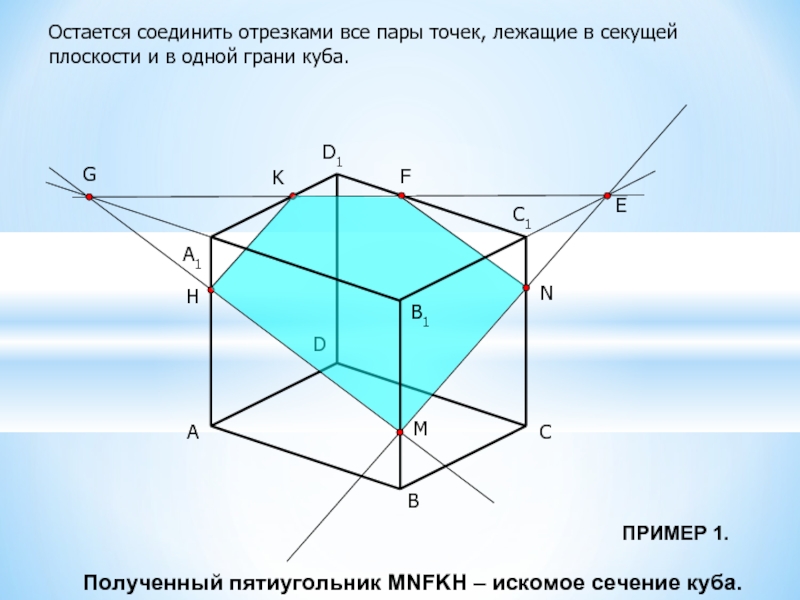
Остается соединить отрезками все пары точек, лежащие в секущей плоскости и
в одной грани куба.
Полученный пятиугольник MNFKH – искомое сечение куба.
B1
ПРИМЕР 1.
Слайд 17Плоскость сечения может задаваться:
1) тремя точками, не лежащими на одной
прямой;
2) прямой и точкой, не лежащей на ней;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.

Слайд 18Данный метод построения сечений многогранников можно применять, если найдется хотя бы
одна пара точек, лежащих в секущей плоскости и одной грани многогранника. После чего задача циклично алгоритмизируется в получение очередной точки и очередного «следа».
ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций.

Слайд 19Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то
эти отрезки параллельны.

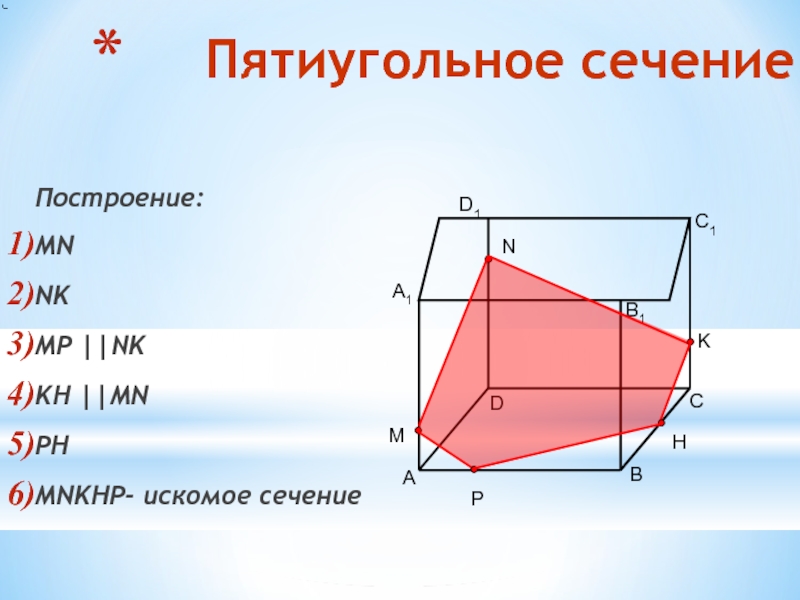
Слайд 20 Пятиугольное сечение
Построение:
MN
NK
MP ||NK
KH ||MN
PH
MNKHP- искомое сечение
A
B
D
C
A1
B1
C1
D1
N
K
M
P
H
Слайд 21Шестиугольное сечение
Построение:
MN, NK
MN∩AD=X
XY ||NK
XY∩AB=P
XY∩BC=Q
MP,PQ
QH ||MN
KH
MNKHQP- искомое сечение
A
B
D
C
A1
B1
C1
D1
N
K
M
P
H
X
Y
Q

Слайд 22Какие из данных сечений верны, а какие нет и почему?
Ответ обоснуйте.
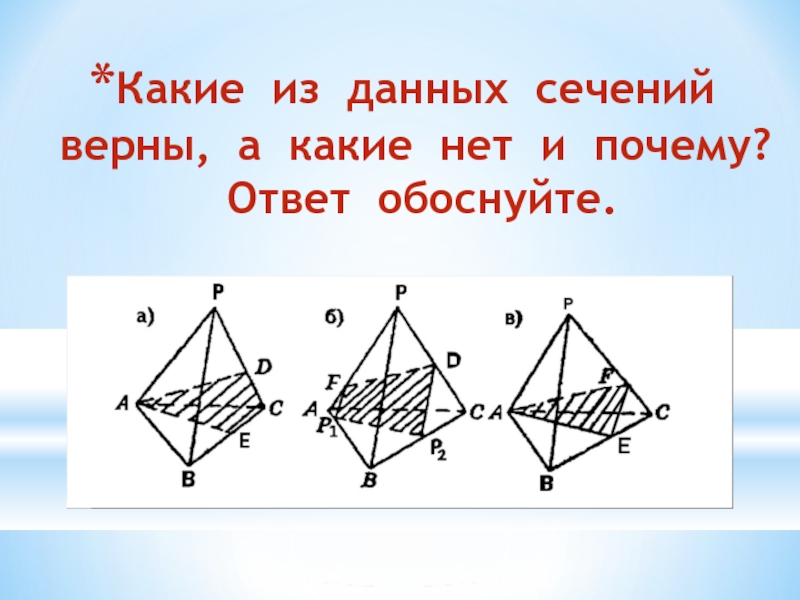
Слайд 23Какие из данных сечений верны, а какие нет и почему?
Ответ обоснуйте.

Слайд 24
A
B
D
C
A1
C1
D1
A
B
C
D
A1
D1
C1
B1
B1
Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках?


Задачи на построение сечений
Курылева С.С., учитель математики
МОУ «Лицей №1» г. Воркуты

« Я слышу – я забываю,
я вижу – я запоминаю,
я делаю – я усваиваю»
(китайская мудрость)

Попробуем решить
В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ребро CD=2 , ребро BC=√5, ребро AA 1 =2 . Точка K – середина ребра DD 1 .
Найдите площадь сечения, проходящего через точки C, B и K.

Тема урока:
Задачи на
построение
сечений

Цели на урок:
- формирование умения строить сечения тетраэдра и параллелепипеда;
- формирование умения применять полученные знания при решения задач.

Секущая плоскость многогранника – любая плоскость, по обе стороны от которой находятся точки данного многогранника

Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки называется сечением многогранника .

Сечения тетраэдра и параллелепипеда
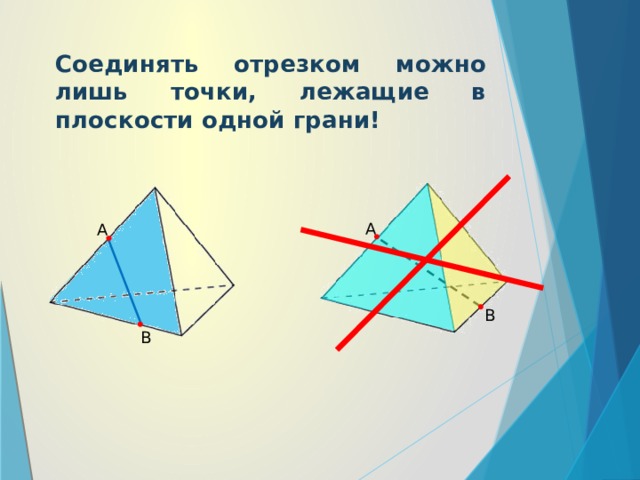
Соединять отрезком можно лишь точки, лежащие в плоскости одной грани!
А
А
В
В

Если секущая плоскость многогранника пересекает его параллельные грани по каким-либо отрезкам, то эти отрезки параллельны.
M
AB||CD
D
B
BM||CN
DM||AN
A
C
N
 m||n m α∩(ABS)=m α B А n C» width=»640″
m||n m α∩(ABS)=m α B А n C» width=»640″
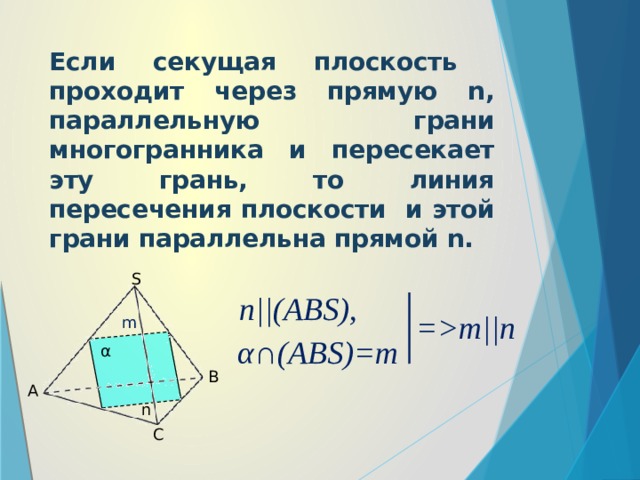
Если секущая плоскость проходит через прямую n, параллельную грани многогранника и пересекает эту грань, то линия пересечения плоскости и этой грани параллельна прямой n.
S
n||(ABS),
=m||n
m
α∩(ABS)=m
α
B
А
n
C
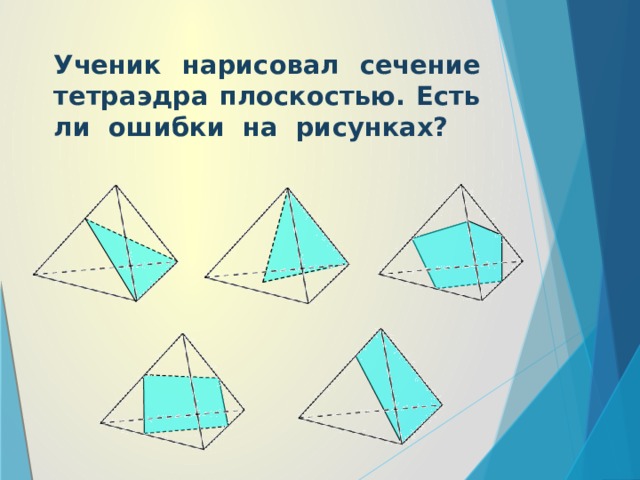
Ученик нарисовал сечение тетраэдра плоскостью. Есть ли ошибки на рисунках?
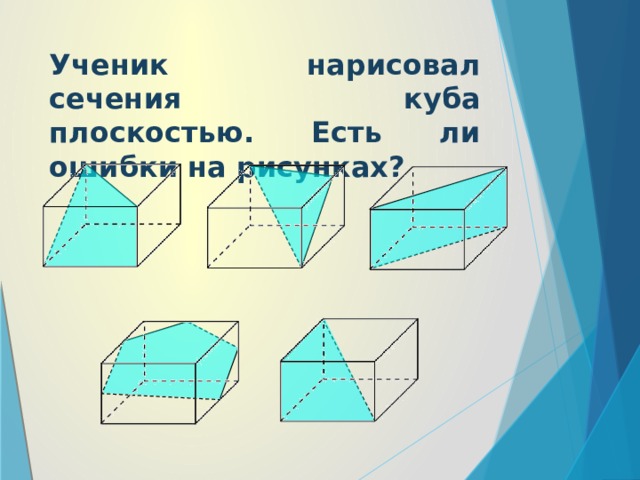
Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках?
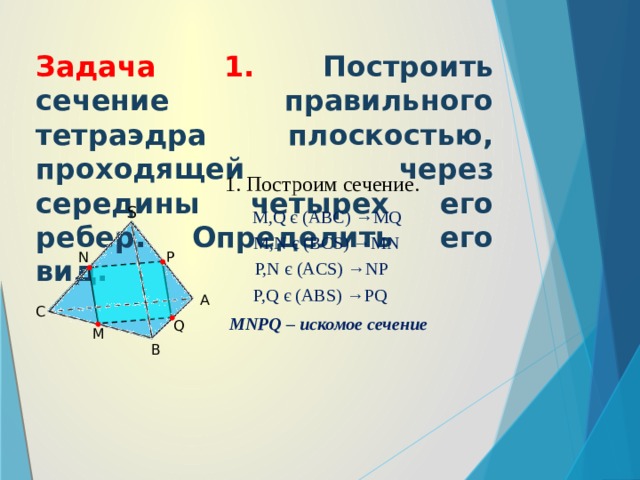
Задача 1. Построить сечение правильного тетраэдра плоскостью, проходящей через середины четырех его ребер. Определить его вид.
1. Построим сечение.
S
M,Q є (ABC) →MQ
M,N є (BCS) →MN
P
N
P,N є (ACS) →NP
P,Q є (ABS) →PQ
A
C
MNPQ – искомое сечение
Q
M
B
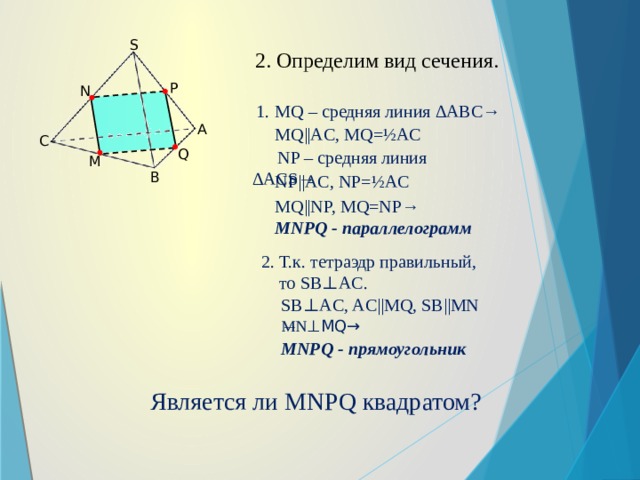
S
2. Определим вид сечения.
P
N
1. MQ – средняя линия ∆ABC→
A
MQ||AC, MQ=½AC
C
Q
NP – средняя линия ∆ACS→
M
B
NP||AC, NP=½AC
MQ||NP, MQ=NP→
MNPQ — параллелограмм
2. Т.к. тетраэдр правильный,
то SB⊥AC.
SB⊥AC, AC||MQ, SB||MN →
MN ⊥MQ→
MNPQ — прямоугольник
Является ли MNPQ квадратом?
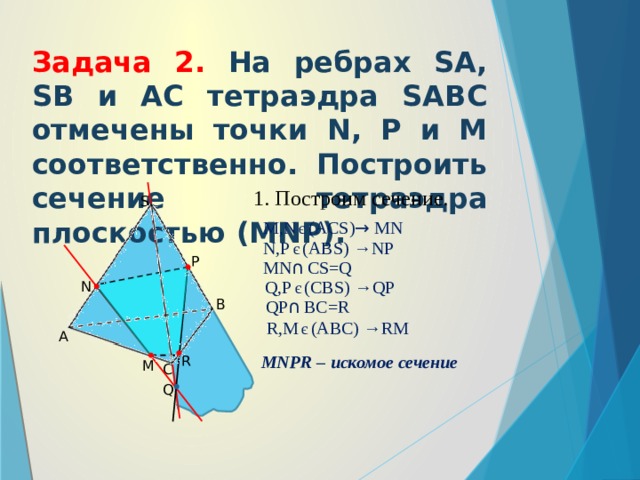
Задача 2. На ребрах SA, SB и AC тетраэдра SABC отмечены точки N, P и M соответственно. Построить сечение тетраэдра плоскостью (МNP).
1. Построим сечение.
S
M,N є (ACS) → MN
N,P є (ABS) →NP
P
MN ∩ CS=Q
Q,P є (CBS) →QP
N
QP ∩ BC=R
B
R,M є (ABC) →RM
A
MNPR – искомое сечение
R
M
C
Q
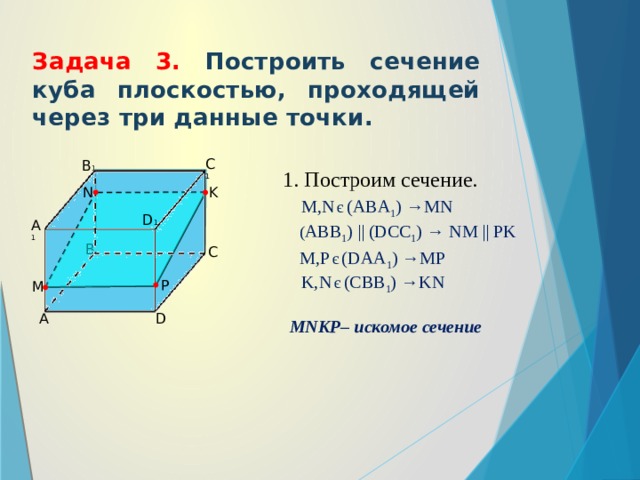
Задача 3. Построить сечение куба плоскостью, проходящей через три данные точки.
C 1
B 1
1. Построим сечение.
N
K
M,N є (ABA 1 ) →MN
D 1
A 1
( ABB 1 ) || (DCC 1 ) → NM || PK
B
C
M,P є (DAA 1 ) →MP
K,N є (CBB 1 ) →KN
P
M
A
D
MNKP– искомое сечение
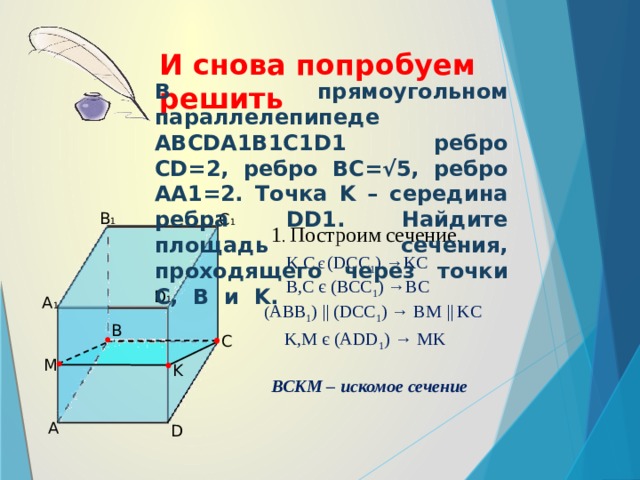
И снова попробуем решить
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро CD=2, ребро BC=√5, ребро AA1=2. Точка K – середина ребра DD1. Найдите площадь сечения, проходящего через точки C, B и K.
B 1
C 1
1 . Построим сечение .
K,C є (DCC 1 ) →KC
B,C є (BCC 1 ) →BC
D 1
A 1
( ABB 1 ) || (DCC 1 ) → BM || KC
B
K,M є (ADD 1 ) → MK
C
M
K
BCKM – искомое сечение
A
D
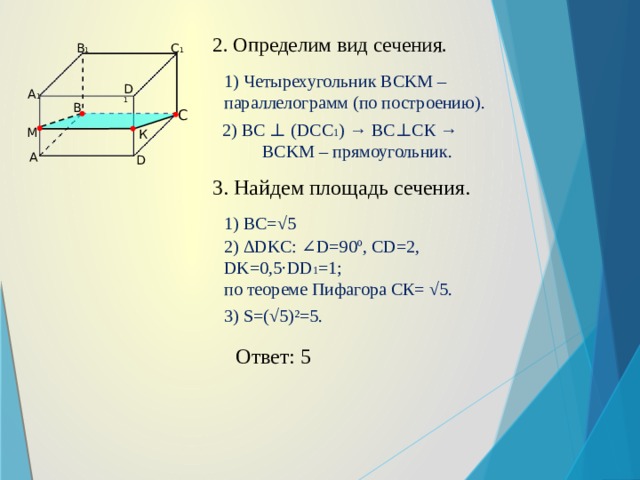
2. Определим вид сечения.
C 1
B 1
1) Четырехугольник BCKM – параллелограмм (по построению).
D 1
A 1
B
C
2) ВС ⊥ (DCC 1 ) → ВС⊥СК → BCKM – прямоугольник.
М
К
А
D
3. Найдем площадь сечения.
1) ВС=√5
2) ∆DKC: ∠D=90º, CD=2, DK=0,5·DD 1 =1;
по теореме Пифагора СК= √5.
3) S=(√5)²=5.
Ответ: 5
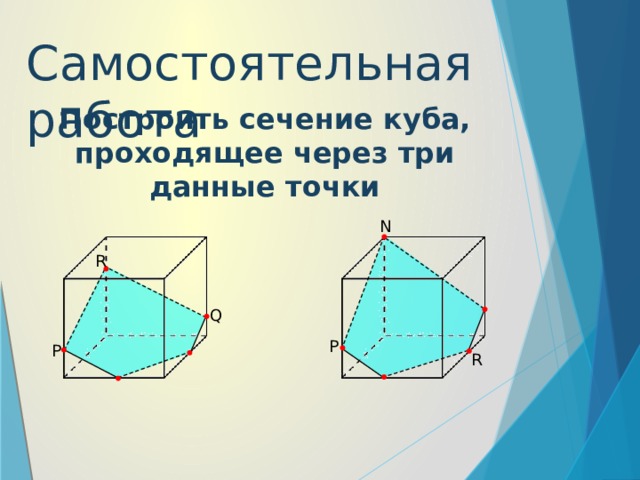
Самостоятельная работа
Построить сечение куба, проходящее через три данные точки
N
R
Q
P
P
R

Спасибо за урок!
Инфоурок
›
Геометрия
›Презентации›Презентация по геометрии на тему «Построение сечения параллелепипеда»
Презентация по геометрии на тему «Построение сечения параллелепипеда»
Скачать материал

Скачать материал




- Сейчас обучается 46 человек из 26 регионов


- Сейчас обучается 906 человек из 82 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Построение сечений
параллелепипеда
Карпова Елена Николаевна учитель высшей категории -

2 слайд
Цели урока
Определить виды сечений параллелепипеда
Установить взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда
Научиться строить сечения -

3 слайд
Треугольные сечения
A
B
D
C
A1
C1
D1
M
N
K
A
B
C
D
A1
D1
C1
B1
M
B1 -

4 слайд
Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны.
-

5 слайд
Четырехугольное сечение
Построение:
MN
MK
NK1|| MK
KK1
MNK1K -искомое
сечениеA
B
D
C
A1
B1
C1
D1
N
K
M
K1 -

6 слайд
Пятиугольное сечение
Построение:
MN
NK
MP ||NK
KH ||MN
PH
MNKHP- искомое сечениеA
B
D
C
A1
B1
C1
D1
N
K
M
P
H -

7 слайд
Шестиугольное сечение
Построение:
MN, NK
MN∩AD=X
XY ||NK
XY∩AB=P
XY∩BC=Q
MP,PQ
QH ||MN
KH
MNKHQP- искомое сечениеA
B
D
C
A1
B1
C1
D1
N
K
M
P
H
X
Y
Q -

8 слайд
Задача.
Построить сечение куба плоскостью, проходящей через точки M,N,K.
A
B
D
C
(N1 )
B1
C1
D1
M
N
K
N
X
P
M1
Q
T -

9 слайд
Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках?
A
B
D
C
A1
C1
D1
A
B
C
D
A1
D1
C1
B1
B1 -

10 слайд
1 вариант 2 вариант
A
B
D
C
A1
C1
D1
M
N
K
A
B
C
D
A1
D1
C1
B1
M
N
Р
H
H
H -

11 слайд
1 вариант 2 вариант
A
B
D
C
A1
C1
D1
M
N
K
A
B
C
D
A1
D1
C1
B1
M
N
K
B1 -

12 слайд
Домашнее задание
№110,112
Краткое описание документа:
Данная презентация учит учащихся определять виды сечений параллелепипеда,
устанавливать взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда, учит строить сечения, делать выводы:
Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 097 398 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
- Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
Тема
45. Параллелепипед
Больше материалов по этой теме
Другие материалы

Контрольная работа по теме «Многогранники»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 5. Многогранники
Рейтинг:
4 из 5
- 05.11.2017
- 18359
- 70

Тест «Аксиомы стереометрии и следствия из них»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 1. Аксиомы стереометрии и их простейшие следствия
Рейтинг:
5 из 5
- 05.11.2017
- 7928
- 30


Тест «Многогранники и тела вращения»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 6. Тела вращения
- 05.11.2017
- 12315
- 183

Презентация по математике на тему «Геометрия»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 8. Объемы и поверхности тел вращения
- 04.11.2017
- 441
- 1



Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
-
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
-
Настоящий материал опубликован пользователем Карпова Елена Николаевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 7 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 47956
- Всего материалов:
17
OBRAZOVALKA.COM
OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .
На вопросы могут отвечать также любые пользователи, в том числе и педагоги.
Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.
![]()
5
На данном рисунке изображено сечение куба плоскостью В чём ошибка данного рисунка Дайте объяснение
На данном рисунке изображено сечение куба плоскостью В чём ошибка данного рисунка Дайте объяснение
2 ответа:
![]()
0
0
Диагональ верхней грани куба и ребро нижней грани, через которое проходит сечение — скрещивающиеся прямые, значит не могут лежать в одной плоскости.
Или иначе:
Параллельные плоскости пересекаются третьей плоскостью по параллельным прямым.
Противоположные грани куба параллельны, а линии пересечения их секущей плоскостью не параллельны (прямая А₁С₁ не параллельна AD)
![]()
0
0
Ошибка в рисунки, из левого верхнего угла должна линия пройти до правого нижнего . должен получится равносторонний треугольник
Читайте также
![]()
Угол Z и внешний при нём — смежные, т.е. их сумма равна 180 градусов
Таким образом, угол Z=60 градусов
Сумма острых углов в прямоугольном тр. равна 90 градусов, т.е. угол У=30 градусов
Сторона в прямоугольном тр., лежащая напротив угла в 30 градусов равна половине гипотенузы
А гипотенуза УZ=7
Значит, XZ=7:2=3,5
Ответ: 3,5
![]()
AB = 20, AH = 12
По Пифагору, из треугольника ABH
BH = √(20²-12²) = √(400-144) = √256 = 16
MM₁ — средняя линия треугольника ABC
MN — средняя линия треугольника HBC
MN = BH/2 = 8
По Пифагору, из треугольника AMN
AN = √(AM²-MN²) = √(18² — 8²) = √(324-64) = √260 = 2√65
HN = AN-AH = 2√65 — 12
AC = AH+2*HN = 12+2*(2√65 — 12) = 4√65-12
S(ABC) = 1/2*BH*AC = 1/2*16*(4√65-12) = 32√65-96
![]()
B)#@#@#¢»_++$-#+$(-‘7#+$-+$(2(
![]()
Здесь есть одна хитрость, позволяющая не проводить длинные, хотя и несложные вычисления. Для еще большей «прозрачности» решения я увеличу размеры сторон в 2 раза (площадь всего треугольника и треугольника вдл увеличатся при этом в 4 раза).
![]()
Инфоурок
›
Геометрия
›Презентации›Презентация по геометрии на тему «Построение сечения параллелепипеда»
Презентация по геометрии на тему «Построение сечения параллелепипеда»
Скачать материал

Скачать материал


- Сейчас обучается 386 человек из 70 регионов


- Сейчас обучается 1029 человек из 80 регионов


- Сейчас обучается 31 человек из 17 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Построение сечений
параллелепипеда
Карпова Елена Николаевна учитель высшей категории -

2 слайд
Цели урока
Определить виды сечений параллелепипеда
Установить взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда
Научиться строить сечения -

3 слайд
Треугольные сечения
A
B
D
C
A1
C1
D1
M
N
K
A
B
C
D
A1
D1
C1
B1
M
B1 -

4 слайд
Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны.
-

5 слайд
Четырехугольное сечение
Построение:
MN
MK
NK1|| MK
KK1
MNK1K -искомое
сечениеA
B
D
C
A1
B1
C1
D1
N
K
M
K1 -

6 слайд
Пятиугольное сечение
Построение:
MN
NK
MP ||NK
KH ||MN
PH
MNKHP- искомое сечениеA
B
D
C
A1
B1
C1
D1
N
K
M
P
H -

7 слайд
Шестиугольное сечение
Построение:
MN, NK
MN∩AD=X
XY ||NK
XY∩AB=P
XY∩BC=Q
MP,PQ
QH ||MN
KH
MNKHQP- искомое сечениеA
B
D
C
A1
B1
C1
D1
N
K
M
P
H
X
Y
Q -

8 слайд
Задача.
Построить сечение куба плоскостью, проходящей через точки M,N,K.
A
B
D
C
(N1 )
B1
C1
D1
M
N
K
N
X
P
M1
Q
T -

9 слайд
Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках?
A
B
D
C
A1
C1
D1
A
B
C
D
A1
D1
C1
B1
B1 -

10 слайд
1 вариант 2 вариант
A
B
D
C
A1
C1
D1
M
N
K
A
B
C
D
A1
D1
C1
B1
M
N
Р
H
H
H -

11 слайд
1 вариант 2 вариант
A
B
D
C
A1
C1
D1
M
N
K
A
B
C
D
A1
D1
C1
B1
M
N
K
B1 -

12 слайд
Домашнее задание
№110,112
Краткое описание документа:
Данная презентация учит учащихся определять виды сечений параллелепипеда,
устанавливать взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда, учит строить сечения, делать выводы:
Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 303 766 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
Тема
45. Параллелепипед
Больше материалов по этой теме
Другие материалы

Контрольная работа по теме «Многогранники»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 5. Многогранники
Рейтинг:
4 из 5
- 05.11.2017
- 19922
- 75

Тест «Аксиомы стереометрии и следствия из них»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 1. Аксиомы стереометрии и их простейшие следствия
Рейтинг:
5 из 5
- 05.11.2017
- 7991
- 30


Тест «Многогранники и тела вращения»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 6. Тела вращения
- 05.11.2017
- 14411
- 211

Презентация по математике на тему «Геометрия»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Погорелов А.В.
- Тема: § 8. Объемы и поверхности тел вращения
- 04.11.2017
- 467
- 1



Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
-
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
-
Настоящий материал опубликован пользователем Карпова Елена Николаевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 7 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 56178
-
Всего материалов:
17
Слайд 1Тема: « Задачи на построение сечений».
Автор работы:
Янаева Ольга Николаевна,
учитель математики МБУ гимназии №35 г.о. Тольятти

Слайд 2Цели урока
Знать алгоритм решения задач методом «следов» и методом параллельного
проецирования;
Уметь решать задачи на построение сечений;
Уметь применять алгоритм при решении
задач на построение сечений;

Слайд 3
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
Проверка домашнего задания
Как построить сечение куба плоскостью, проходящей через три заданные точки?
1.
2.
3.
к
N
M
M

Слайд 4
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
А
А
1
в
в
1
D
D
1
С
С
1
к
N
M
M
1.
2.
3.
ПРОВЕДИТЕ ВЗАИМОПРОВЕРКУ
За верное решение каждой задачи поставьте 1 балл

Слайд 5
А
А
1
в
в
1
D
D
1
С
С
1
4.
N
M
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
5.
6.
Как построить сечение куба плоскостью, проходящей через три заданные точки?

Слайд 6
А
А
1
в
в
1
D
D
1
С
С
1
4.
N
M
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
5.
E
Q
А
А
1
в
в
1
D
D
1
С
С
1
N
M
к
P
Q
E
F
6.
s
s
s
T
ПРОВЕДИТЕ ВЗАИМОПРОВЕРКУ
За верное решение задач №4 и №5 по 2 балла;
За верное решение задачи №6 – 3 балла.

Слайд 7 Отметка «5» — 10 баллов;
Отметка «4» — 8-9
баллов;
Отметка «3» — 6-7 баллов;
Отметка «2» — менее
6 баллов.
Итоги выполнения домашнего задания

Слайд 8
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от
которой есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из
всех точек, которые являются общими для многогранника и секущей плоскости.
Основные понятия
Рис.1
Рис.2

Слайд 9Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника
есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон
этого многоугольника не может превышать количества граней данного многогранника. Например (см.рис.3), в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник.
Рис.3

Слайд 10 Две плоскости пересекаются по прямой (эта аксиома и дала
названию метода – под «следом» понимается прямая пересечения какой-либо грани
многогранника и секущей плоскости).
Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?).
Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости.
ПРИМЕЧАНИЕ. Не забудьте, что прямая и плоскость являются бесконечными в пространстве фигурами!
Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K.
Метод «следов»

Слайд 11
A
B
C
D
B1
C1
D1
M
N
K
Выбираем точки М и N, принадлежащие одной грани и строим
прямую MN – «след» пересечения правой грани и секущей плоскости.
A1
ПРИМЕР
1.

Слайд 12
A
B
C
D
B1
C1
D1
M
N
K
A1
E
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной
грани с третьей точкой сечения К (верхней) и в одной
грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.
ПРИМЕР 1.

Слайд 13
A
B
C
D
B1
C1
D1
M
N
K
A1
E
Точки Е и К принадлежат верхней грани и секущей плоскости.
Значит, прямая ЕК – «след» их пересечения и F∈D1C1, EK.
F
ПРИМЕР
1.

Слайд 14
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
Далее видим, что ребро куба А1В1 лежит в одной грани
с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых
– точку G.
G
ПРИМЕР 1.

Слайд 15
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
Полученная точка G лежит в одной грани с точкой М
(в передней) и обе точки принадлежат секущей плоскости – значит,
прямая GM – очередной «след»!
Причем, GM∩АА1=Н.
H
ПРИМЕР 1.

Слайд 16
A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
Остается соединить отрезками все пары точек, лежащие в секущей плоскости
и в одной грани куба.
Полученный пятиугольник MNFKH – искомое
сечение куба.
B1
ПРИМЕР 1.

Слайд 17Плоскость сечения может задаваться:
1) тремя точками, не лежащими на
одной прямой;
2) прямой и точкой, не лежащей на ней;
3)
двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.

Слайд 18Данный метод построения сечений многогранников можно применять, если найдется хотя
бы одна пара точек, лежащих в секущей плоскости и одной
грани многогранника. После чего задача циклично алгоритмизируется в получение очередной точки и очередного «следа».
ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций.

Слайд 19Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам,
то эти отрезки параллельны.

Слайд 20 Пятиугольное сечение
Построение:
MN
NK
MP ||NK
KH ||MN
PH
MNKHP- искомое сечение
A
B
D
C
A1
B1
C1
D1
N
K
M
P
H

Слайд 21Шестиугольное сечение
Построение:
MN, NK
MN∩AD=X
XY ||NK
XY∩AB=P
XY∩BC=Q
MP,PQ
QH ||MN
KH
MNKHQP- искомое сечение
A
B
D
C
A1
B1
C1
D1
N
K
M
P
H
X
Y
Q

Слайд 22Какие из данных сечений верны, а какие нет и почему?
Ответ обоснуйте.

Слайд 23Какие из данных сечений верны, а какие нет и почему?
Ответ обоснуйте.

Слайд 24
A
B
D
C
A1
C1
D1
A
B
C
D
A1
D1
C1
B1
B1
Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках?

