Укажите какого порядка будет максимальная ошибка метода симпсона

Упражнение 1:

Номер 1

Какие системы называют динамическими?

Ответ:

(1) системы, в которых выходные переменные являются функциями от времени или каких–либо других параметров 

(2) системы, в которых входные переменные являются функциями от времени или каких–либо других параметров 

(3) системы, в которых входные переменные являются константными значениями 

(4) системы, в которых выходные переменные являются константными значениями 

Номер 2

Какими уравнениями описываются динамические системы?

Ответ:

(1) дифференциальными 

(2) интегральными 

(3) в виде многочлена степени n 

(4) нет правильного ответа 

Номер 3

Как выглядит формула Ньютона-Лейбница?

Ответ:

(1)  

(2)  

(3)  

(4)  

Упражнение 2:

Номер 1

В каких случаях применяются численные методы интегрирования?

Ответ:

(1) подынтегральная функция f(x) задана таблично на участке [a,b] 

(2) подынтегральная функция f(x) задана аналитически, но ее первообразная выражается через элементарные функции 

(3) подынтегральная функция f(x) задана аналитически, имеет первообразную, но ее определение слишком сложно 

Номер 2

К каким методам относятся численные методы по характеру результата?

Ответ:

(1) точным 

(2) приближенным 

(3) нет правильного ответа 

Номер 3

Какой шаг при вычислении интеграла численными методами необходимо выполнить вторым?

Ответ:

(1) в каждой части деления подынтегральную функцию f(x) аппроксимируют интерполяционным многочленом. Степень многочлена n = 0,1,2… 

(2) весь участок [a,b] делят на n равных частей с шагом h=(b-a)/n 

(3) для каждой части деления определяют площадь частичной криволинейной трапеции 

(4) суммируют площади частичных криволинейных трапеций 

Упражнение 3:

Номер 1

Как называется нахождение приближенного значения интеграла?

Ответ:

(1) сплайн 

(2) кубический сплайн 

(3) квадратура 

Номер 2

По какой формуле вычисляется остаточный член?

Ответ:

(1)  

(2)  

(3)  

Номер 3

Что называется остаточным членом?

Ответ:

(1) разность между точным и приближенным значением интеграла 

(2) разность между приближенным и точным значением интеграла 

(3) сумма приближенного и точного значений интеграла 

(4) погрешностью квадратурной формулы 

Упражнение 4:

Номер 1

В каком случае квадратурная формула называется формулой прямоугольников, а  метод – методом прямоугольников?

Ответ:

(1) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. прямой, параллельной оси OX 

(2) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки 

(3) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени 

Номер 2

В каком случае квадратурная формула называется формулой трапеций, а метод – методом трапеций?

Ответ:

(1) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. прямой, параллельной оси OX 

(2) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки 

(3) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени 

Номер 3

В каком случае квадратурная формула называется формулой Симпсона, а метод – методом Симпсона?

Ответ:

(1) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки 

(2) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени 

(3) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. прямой, параллельной оси OX 

Упражнение 5:

Номер 1

Какой вид имеет квадратурная формула, если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага?

Ответ:

(1)  

(2)  

(3) нет правильного ответа 

Номер 2

Какой порядок имеет точность метода трапеций?

Ответ:

(1) h 

(2) h2 

(3) h3 

(4) h4 

Номер 3

Чем аппроксимируется подынтегральная функция в каждой части деления в методе Симпсона?

Ответ:

(1) квадратичной параболой 

(2) кубическим сплайном 

(3) многочленом степени n 

(4) нет правильного ответа 

Упражнение 6:

Номер 1

Что отражает параметр N2 в формуле по методу Симпсона ?

Ответ:

(1) заданную точность 

(2) число шагов 

(3) количество частей деления 

(4) нет правильного ответа 

Номер 2

Формула Ньютона-Лейбница используется

Ответ:

(1) для решения систем нелинейных уравнений 

(2) для численного интегрирования 

(3) для численного дифференцирования 

(4) для решения систем линейных уравнений 

Номер 3

В каком случае невозможно применить численный метод интегрирования?

Ответ:

(1) подынтегральная функция f(x) задана аналитически, имеет первообразную, но ее определение слишком сложно 

(2) подынтегральная функция f(x) задана таблично на участке [a,b] 

(3) подынтегральная функция f(x) задана на участке [a,b] таблично, но интеграл ищется на другом участке 

(4) подынтегральная функция f(x) задана аналитически, но ее первообразная не выражается через элементарные функции 

Упражнение 7:

Номер 1

Численные методы интегрирования являются

Ответ:

(1) точными 

(2) приближенными 

(3) эвристическими 

(4) аналитическими 

Номер 2

Квадратурой называется

Ответ:

(1) приближенное значение интеграла 

(2) усредненный квадрат интеграла 

(3) квадрат интеграла 

(4) среднее значение между интегралом и функцией в данной точке 

Номер 3

Какую необходимо брать высоту прямоугольника в методе прямоугольников на интервале [a,b] в общем случае? 

Ответ:

(1) значение функции в точке a 

(2) значение функции в точке b 

(3) значение функции в точке (b-a)/2 

(4) значение функции либо в точке a, либо в точке b 

(5) все варианты равнозначны 

Упражнение 8:

Номер 1

Какое количество шагов надо выполнить, чтобы проинтегрировать методом прямоугольников функцию на отрезке [a,b] с шагом h?

Ответ:

(1) (a+b)/h 

(2) (b-a)/h 

(3) h 

(4) b-a 

Номер 2

Какая максимальная степень степенного подынтегральной многочлена должна быть, чтобы гарантировать безошибочное вычисление интеграла методом трапеций?

Ответ:

(1) 1 

(2) 2 

(3) 3 

(4) любая 

(5) ошибка аппроксимации будет всегда 

Номер 3

Укажите какого порядка будет максимальная ошибка метода Симпсона

Ответ:

(1) 1 

(2) 2 

(3) 3 

(4) 4 

Упражнение 9:

Номер 1

Какой из параметров не влияет на ошибку методов Симпсона, трапеций и прямоугольников?

Ответ:

(1) производная подынтегральной функции на данном интервале 

(2) максимальное значение подынтегральной функции 

(3) размер выбранного шага 

Номер 2

Какой из методов имеет большее количество шагов?

Ответ:

(1) прямоугольников 

(2) трапеций 

(3) Симпсона 

(4) трапеций и Симпсона 

(5) все имеют одинаковое 

Номер 3

Как выглядит общий вид дифференциального уравнения?

Ответ:

(1) F(x,y,y') = 0 

(2) F(x,y,y') = 1 

(3) F(x,y,y') = -1 

(4) F(x,y,y') = N 

Упражнение 10:

Номер 1

Как выглядит нормальная форма дифференциального уравнения?

Ответ:

(1) y = f'(x,y) 

(2) y' = f(x,y) 

(3) y' = f'(x,y) 

(4) нет правильного ответа 

Номер 2

Чему равна правая часть (f(x,y)) дифференциального уравнения, представленного в нормальной форме?

Ответ:

(1) функции y(x) 

(2) первой производной функции y(x) 

(3) первообразной функции y(x) 

(4) второй производной функции y(x) 

Номер 3

Как называется дифференциальное уравнения, если функция у зависит от нескольких аргументов?

Ответ:

(1) частное дифференциальное уравнение 

(2) нормальная форма дифференциального уравнения 

(3) дифференциальное уравнение в частных производных 

Упражнение 11:

Номер 1

Что является общим решением обыкновенного дифференциального уравнения y' = f(x,y)?

Ответ:

(1) семейство функций у=у(х,с) 

(2) функция у=у(х) 

(3) функция у=с 

(4) нет правильного ответа 

Номер 2

Что называется задачей Коши?

Ответ:

(1) нахождение частного решения дифференциального уравнения y' = f(x,y) 

(2) нахождение частного решения дифференциального уравнения y' = f(x,y), удовлетворяющего начальному условию  

(3) нахождение частного решения дифференциального уравнения y = f(x,y) 

(4) нахождение частного решения дифференциального уравнения y = f(x,y), удовлетворяющего начальному условию  

Номер 3

Что такое h в постановке задачи Коши в численных методах?

Ответ:

(1) начало участка интегрирования уравнения 

(2) конец участка интегрирования уравнения 

(3) число шагов интегрирования уравнения 

(4) шаг интегрирования дифференциального уравнения 

Упражнение 12:

Номер 1

На чем основаны методы Рунге–Кутта?

Ответ:

(1) на аппроксимации искомой функции у(х) в пределах каждого шага многочленом, который получен при помощи разложения функции у(х) в окрестности шага h каждой i-ой точки в ряд Тейлора:  

(2) на аппроксимации искомой функции у(х) в пределах каждого шага многочленом, который получен при помощи разложения функции у(х) в окрестности шага h каждой i-ой точки в ряд Тейлора:  

(3) на аппроксимации искомой функции у(х) в пределах каждого шага многочленом, который получен при помощи разложения функции у(х) в ряд Тейлора:  

Номер 2

Как еще называется метод Эйлера?

Ответ:

(1) метод Рунге–Кутта первого порядка 

(2) метод Рунге–Кутта второго порядка 

(3) метод Рунге–Кутта четвертого порядка 

Номер 3

Как выглядит формула Эйлера?

Ответ:

(1)  

(2)  

(3)  

(4) нет правильного ответа 

Упражнение 13:

Номер 1

Чему равна точность метода Эйлера на каждом шаге?

Ответ:

(1)  

(2)  

(3)  

(4)  

Номер 2

Чему равен в графическом представлении метода Эйлера наклон касательной в пределах каждого шага?

Ответ:

(1) значению производной y'(x) в начальной точке шага xi 

(2) шагу интегрирования дифференциального уравнения 

(3) точности метода Эйлера 

(4) количеству шагов интегрирования дифференциального уравнения 

Номер 3

Как выглядит модифицированная или уточненная формула Эйлера?

Ответ:

(1)  

(2)  

(3)  

(4)  

Упражнение 14:

Номер 1

В какое количество этапов группируются все вычисления на каждом шаге по модифицированной или уточненной формуле Эйлера для определения предварительного значения  ?

Ответ:

(1) 2 

(2) 3 

(3) 4 

(4) 5 

Номер 2

Чему равна точность модифицированного метода Эйлера на каждом шаге?

Ответ:

(1)  

(2)  

(3)  

(4)  

Номер 3

Каким количеством прямых аппроксимируется функция у(х) на каждом шаге в модифицированном методе Эйлера?

Ответ:

(1) 1 

(2) 2 

(3) 3 

(4) 4 

Упражнение 15:

Номер 1

Какой из всех численных методов решения дифференциальных уравнений с помощью ЭВМ получил самое большое распространение?

Ответ:

(1) метод Рунге-Кутта 1-го порядка 

(2) метод Эйлера 

(3) модифицированный метод Эйлера 

(4) метод Рунге-Кутта 4-го порядка 

Номер 2

Чему равна ошибка на каждом шаге интегрирования дифференциальных уравнений в методе Рунге-Кутта 4-го порядка?

Ответ:

(1) h2 

(2) h3 

(3) h4 

(4) h5 

Номер 3

Чем аппроксимируется искомая функция y(x) на каждом шаге интегрирования дифференциальных уравнений в методе Рунге-Кутта 4-го порядка?

Ответ:

(1) рядом Тейлора, содержащим члены ряда с h2 

(2) рядом Тейлора, содержащим члены ряда с h3 

(3) рядом Тейлора, содержащим члены ряда с h4 

Упражнение 16:

Номер 1

Производные функции y(x) каких порядков необходимо определить для сохранения членов ряда, содержащих h2 , h3,h4?

Ответ:

(1) y'',y''',y(4) 

(2) y', y'',y''' 

(3) y'',y''' 

(4) y', y'' 

Номер 2

Решение дифференциального уравнения 1-го порядка представляется как

Ответ:

(1) аналитическая функция 

(2) табличная функция 

(3) графическая функция 

Номер 3

Метод Эйлера это:

Ответ:

(1) метод Рунге-Кутта 2-го порядка 

(2) метод Рунге-Кутта 1-го порядка 

(3) метод Рунге-Кутта 4-го порядка 

Упражнение 17:

Номер 1

Модифицированный метод Эйлера это:

Ответ:

(1) метод Рунге-Кутта 2-го порядка 

(2) метод Рунге-Кутта 1-го порядка 

(3) метод Рунге-Кутта 4-го порядка 

Номер 2

Методы Рунге-Кутта получены при помощи разложения функции в ряд

Ответ:

(1) Маклорена 

(2) Тейлора 

(3) Эйлера 

Номер 3

Точность h метода эйлера имеет порядок

Ответ:

(1) 4 

(2) 3 

(3) 2 

Упражнение 18:

Номер 1

Точность h метода Рунге-Кутта 4-го порядка

Ответ:

(1) 4 

(2) 3 

(3) 2 

Номер 2

Точность h модифицированного метода Эйлера

Ответ:

(1) 4 

(2) 3 

(3) 2 

Номер 3

Какой метод считается более точным

Ответ:

(1) Эйлера 

(2) Рунге-Кутта 4-го порядка 

(3) модифицированный метод Эйлера 

Упражнение 19:

Номер 1

Как добиться того чтобы результаты по методу Эйлера, модифицированному методу Эйлера и методу Рунге-Кутта 4-го порядка были почти одинаковыми

Ответ:

(1) увеличивая шаг интегрирования 

(2) уменьшая шаг интегрирования 

(3) удваивая шаг интегрирования 

Номер 2

Для решения дифференциальных уравнений 1-го порядка необходимо

Ответ:

(1) начальное значение x, начальное значение y, шаг интегрирования h, конец интервала b 

(2) начальное значение x, конечное значение y, шаг интегрирования h 

(3) начальное значение x, начальное значение y, конец интервала b 

Номер 3

К какой системе можно свести любое дифференциальное уравнение m–го порядка при помощи замен?

Ответ:

(1) к системе, состоящей из m-1 уравнения первого порядка 

(2) к системе, состоящей из m уравнений первого порядка 

(3) к системе, состоящей из m+1 уравнения первого порядка 

Упражнение 20:

Номер 1

Что является решением дифференциального уравнения m-го порядка?

Ответ:

(1) решение системы, состоящей из m дифференциальных уравнений первого порядка 

(2) решение системы, состоящей из m-1 дифференциального уравнения первого порядка 

(3) m табличных функций y, y1=y', y2=y''1, … , ym=y(m-1) 

(4) m-1 табличная функция y, y1=y', y2=y''1, … , ym-1=y(m-2) 

Номер 2

Как выглядят дифференциальные уравнения второго порядка в общем виде?

Ответ:

(1) f(x) = 0 

(2) F(x,y)= 0 

(3) F(x,y,y')= 0 

(4) F(x,y,y',y'')= 0 

Номер 3

Как выглядит нормальная форма дифференциальных уравнений второго порядка?

Ответ:

(1) y'=f(x,y) 

(2) y”=f(x,y') 

(3) y”=f(x,y,y') 

(4) y”'=f(x,y,y'') 

Упражнение 21:

Номер 1

Как звучит постановка в численных методах задача Коши для системы y(x) с учетом двух начальных условия: y(x0)=y0, y1(x0)=(y1)0?

Ответ:

(1) найти табличные функции y(x) и (y1)(x),  

(2) найти табличные функции y(x) и (y1)(x),  

(3) нет правильного ответа 

Номер 2

Что является решением задачи Коши для системы, состоящей из двух дифференциальных уравнений первого порядка, на графике?

Ответ:

(1) узловая точка 

(2) совокупность узловых точек 

(3) не существует решения задачи Коши на графике 

Номер 3

Какое условие необходимо соблюдать на каждом шаге интегрирования при применении для решения системы дифференциальных уравнений тех же методов, что и для решения одного дифференциального уравнения первого порядка?

Ответ:

(1) все уравнения системы необходимо решать последовательно 

(2) все уравнения системы необходимо решать параллельно 

(3) нет правильного ответа 

Упражнение 22:

Номер 1

Матрица какого размера получится при решении дифференциального уравнения m-го порядка (при этом каждая из табличных функций определяется на промежутке [a, b] с шагом h и включает n узловых точек)?

Ответ:

(1) n-1 m-1 

(2) n m 

(3) n+1 m+2 

Номер 2

Что представляет собой каждая i–ая строка матрицы, полученной при решении дифференциального уравнения m-го порядка?

Ответ:

(1) массив решений m табличных функций на одном i–ом шаге интегрирования 

(2) массив решений m-1 табличной функций на одном i–ом шаге интегрирования 

(3) массив решений одной j-й табличной функции по всем n шагам интегрирования 

(4) массив решений одной j-й табличной функции по всем n-1 шагам интегрирования 

Номер 3

Что является решением дифференциального уравнения m-го порядка на графике?

Ответ:

(1) одна узловая точка 

(2) 2 узловые точки 

(3) n m узловых точек 

(4) не существует решения задачи на графике 

Упражнение 23:

Номер 1

Дифференциальное уравнение высоких порядков можно

Ответ:

(1) решить методами Гаусса 

(2) решить методами Рунге-Кутта 

(3) решить методами Ньютона 

Номер 2

Чтобы решить дифференциальное уравнение высоких порядков мы их приводим к системе

Ответ:

(1) дифференциальных уравнений m-го порядка 

(2) нелинейных уравнений 

(3) дифференциальных уравнений 1-го порядка 

Номер 3

При использовании методов Рунге-Кутта для решения дифференциальных уравнений высоких порядков на каждом шаге интегрирования все уравнения системы решаются

Ответ:

(1) перпендикулярно 

(2) параллельно 

(3) независимо 

Упражнение 24:

Номер 1

Для решения дифференциальных уравнений n-го порядка задача Коши это

Ответ:

(1) начальное значение x, начальное значение y, шаг интегрирования h, конец интервала b 

(2) начальное значение x, начальное значение y, y', …, y , шаг интегрирования h, конец интервала b 

(3) начальное значение x, начальное значение y, y', …, y , конец интервала b 

Номер 2

Решение дифференциальных уравнений n-го порядка представляются как

Ответ:

(1) аналитическая функция 

(2) табличная функция 

(3) графическая функция 

Номер 3

Если целевая функция и функция ограничений известны, то это методы

Ответ:

(1) интерполяции 

(2) оптимизации 

(3) аппроксимации 

Упражнение 25:

Номер 1

В прямых методах оптимизации при поиске экстремума используются

Ответ:

(1) значения первых производных функции 

(2) наряду с первыми и значения вторых производных функции 

(3) только значения целевой функции 

Номер 2

В градиентных методах используются

Ответ:

(1) значения первых производных функции 

(2) наряду с первыми и значения вторых производных функции 

(3) только значения целевой функции 

Номер 3

В градиентных методах 2-го порядка используются

Ответ:

(1) значения первых производных функции 

(2) наряду с первыми и значения вторых производных функции 

(3) только значения целевой функции 

Упражнение 26:

Номер 1

 Метод дихотомии является методом

Ответ:

(1) прямого поиска 

(2) градиентным методом первого порядка 

(3) градиентным методом второго порядка 

Номер 2

Метод "золотого сечения" является методом

Ответ:

(1) прямого поиска 

(2) градиентным методом 

(3) градиентным методом второго порядка 

Номер 3

В методе дихотомии, если F(x-E)<F(x+E), то для определения min выбирается отрезок

Ответ:

(1) [(a+b)/2, b] 

(2) [a, (a+b)/2] 

(3) [(a+b)/2-E, (a+b)/2+E] 

Упражнение 27:

Номер 1

Метод дихотомии это

Ответ:

(1) однопараметрический метод 

(2) метод условной оптимизации 

(3) метод многомерной оптимизации 

Номер 2

В методе дихотомии если F(x-E)>F(x+E), то для определения min выбирается отрезок

Ответ:

(1) [(a+b)/2, b] 

(2) [a, (a+b)/2] 

(3) [(a+b)/2-E, (a+b)/2+E] 

Номер 3

В методе дихотомии если F(x-E)<F(x+E), то для определения max выбирается отрезок

Ответ:

(1) [(a+b)/2, b] 

(2) [a, (a+b)/2] 

(3) [(a+b)/2-E, (a+b)/2+E] 

В
основе метода Симпсона лежит следующая
лемма.

Лемма.
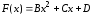Если
или,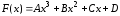
то

.
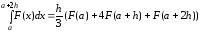(4.5)

Выполним
доказательство лишь для квадратичной
параболы. Подставим функцию
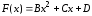под интеграл в (4.5) и вычислим его. Получим

.
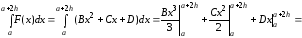
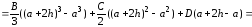
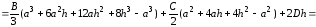
(4.6)

С
другой стороны,

,

,

.

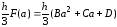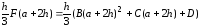Сложив
три последних выражения, мы получим
выражение (4.6), что и доказывает лемму.

Перейдем
к изложению метода Симпсона. Разделим
точки
,
разбивающие отрезок интегрированияна частичные отрезки с равномерным
шагом,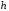
на тройки точек,,…,.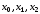
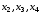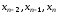Для такого разбиения число отрезковнеобходимо выбрать четным. На отрезке,
определяемом-й
тройкой точек,,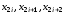
заменим подынтегральную функцию
параболой второго порядка,
проходящей через точки,,,
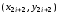и заменим точное значение интеграла на
этом отрезке интеграломот полученной параболы. На основании
леммы можно записать, что

.

Приближенное
значение интеграла на всем отрезке
интегрирования
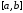получим как сумму этих частичных
интегралов:

.
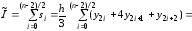
(4.7)

Мы
видим, что в методе Симпсона крайние
значения функции
суммируются с весом 1, значенияс нечетным номером– с весом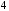и значенияс четным номером– с весом.
Суммы значений функции с различными
весами удобно вычислить отдельно, а
затем их сложить, умножить на шаг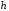и разделить на 3.

4.7 Погрешность метода Симпсона

Абсолютная
погрешность формулы Симпсона (4.7)
определяется выражением

.

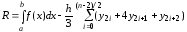Она
складывается из частичных погрешностей
,
полученных на каждой тройке точек,
используемых для аппроксимации:

.

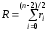Частичная
погрешность здесь определяется выражением

.

Оценка
общей погрешности имеет вид

.
(4.8)

Получим
оценки сначала для частичной, а затем
и для полной погрешностей. Для этого
рассмотрим вспомогательную функцию

,
.

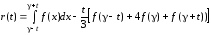При
иэта функция совпадает с.
Кроме того,.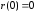
Найдем производные функции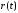до 3-го порядка включительно. Поскольку

,

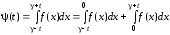то,
используя правила дифференцирования
интеграла по нижнему и верхнему пределам,
получим

,

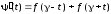а
также

,

.

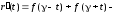
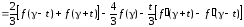Выполняя
последовательное дифференцирование,
будем иметь

,

,

,

.

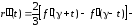
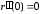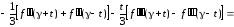
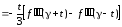Применяя
к
теорему Лагранжа, т.е. используя равенство

,
,

получим

.

Обозначая
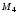максимальное по модулю значение четвертой
производной подынтегральной функции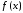на отрезке интегрирования,

,

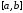получим
оценку для 3-й производной функции
:

.

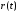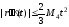Поскольку

,

то

.

Аналогично
получаем

,

,

,

.

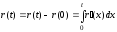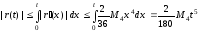Поскольку
,
то для частичной погрешности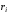получаем оценку

.

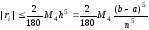Выражение
(4.8) имеет
слагаемых, следовательно, абсолютная
погрешность формулы Симпсона будет
оцениваться выражением

.

Из
последней формулы видно, что абсолютная
погрешность метода Симпсона имеет тот
же порядок, что и
.
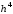Формула Симпсона точна для полиномов
третьей степени, поскольку для полинома
3-й степени.
Это является следствием того, что лемма
(4.5) справедлива также для полинома 3-й
степени.

4.8 Интерполяционные квадратурные формулы

Рассмотрим
вычисление следующего интеграла:

,
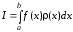(4.9)

где
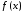– некоторая достаточно гладкая функция,
которую назовем подынтегральной,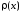– некоторая неотрицательная интегрируемая
функция, которая называется весовой.

Этот
интеграл является более общим по
сравнению с рассматриваемым ранее
интегралом (4.1). Интеграл вида (4.1) получим
из (4.9) при весовой функции
.

Для
вычисления интеграла (4.9) применим
следующий подход: выберем на отрезке
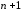точек.
В отличие от предыдущих методов, не
будем вычислять интегралы на частичных
отрезках, а заменим подынтегральную
функцию на всем отрезкеинтерполяционным полиномом (3.7),
построенным
по узлам
.
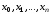В результате получим следующую
квадратурную формулу:

,
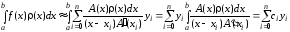(4.10)

где

,
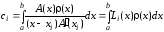(4.11)

,

и
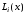– полином влияния-го
узла (3.6).

Формула
(4.10), в которой коэффициенты определяются
по выражению (4.11),
называется интерполяционной
квадратурной формулой.

Рассмотрим
вопрос погрешности интерполяционной
квадратурной формулы. Заменяя
подынтегральную функцию
полиномом Лагранжа,
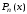получаем абсолютную грешность(3.27). Представим функциювиде

и
найдем интеграл (4.9)

.

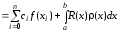Ясно,
что второе слагаемое правой части этого
выражения есть абсолютная погрешность
интерполяционной квадратурной формулы:

.

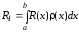Подставляя
сюда выражение (3.27) для погрешности
,
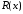получим следующую формулу абсолютной
погрешности интерполяционной квадратурной
формулы (4.10):

.

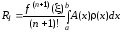
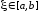Если
обозначить

,

то
для оценки абсолютной погрешности
интерполяционной квадратурной формулы
(4.10) получим выражение

.

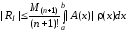Из
полученных выражений для погрешности
видно, что интерполяционная квадратурная
формула (4.10) точна для полиномов
-й
степени, поскольку в этом случае.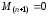
О такой квадратурной формуле говорят,
что ее степень точности равна.

Таким
образом, квадратурная формула
интерполяционного типа (4.10), построенная
по
узлам,
является точной для полиномов-й
степени. Справедливо также и обратное
утверждение, которое сформулируем в
виде теоремы.

Теорема.
Если квадратурная формула

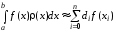(4.12)

точна
для полинома степени
,
то она является интерполяционной.

Для
доказательства достаточно показать,
что если
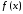– полином степени,
то коэффициенты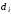определяются формулой (4.11), т.е..
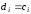Выберем в качестве такого полинома
полином влияния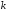-го
узла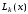(3.6). Тогда по условию теоремы квадратурная
формула (4.12) для него будет точной, т.е.

,
.

Полином
влияния обладает свойством

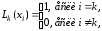
в
связи с чем предыдущий интеграл будет
равен

.

Левая
часть последнего равенства есть
,
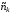т.е.,,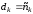
и теорема доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Аноним

Я завалил сессию, почему я не увидел данный сайт с ответами интуит до этого

14 окт 2015

К какому уравнению неприменимо отделение корней?

Точность h модифицированного метода Эйлера

Методы какой группы позволяют получить решение системы за конечное число итераций?

На чем основаны методы Рунге–Кутта?

Какая задача возникает при реализации на ЭВМ статистического моделирования?

Какое максимальное количество моделей одного объекта можно составить?

К какому классу моделей можно отнести спичечный коробок, если представить его моделью системного блока ПК при планировании своего рабочего места?

Что требуется для нахождения объективных и устойчивых характеристик процесса при статистическом моделировании?

В зависимости от характера исследуемых реальных процессов и систем, на какие группы могут быть разделены математические модели?

Какие последовательности случайных чисел называются псевдослучайными или квазислучайными?

Из какого количества этапов состоит метод Ньютона?

В чем заключается центральная предельная теорема?

это интерполяционный многочлен

Трансцендентное уравнение sin(mx-10)+sin((m-1)-10)+…+sin(10)=0 имеет

Какие задачи называются задачами интерполирования или экстраполирования?

Какой вид моделирования основывается на построении математических моделей для описания изучаемых процессов и на использовании новейших вычислительных машин, обладающих высоким быстродействием и способных вести диалог с человеком?

Как описывается функционирование элементарных явлений, подсистем и модулей при использовании имитационного моделирования?

Сколько матриц Якоби необходимо сформировать в методе Ньютона?

В каком случае квадратурная формула называется формулой трапеций, а метод – методом трапеций?

Интерполяционная функция

Если добавить экспериментальные точки, то в методе Ньютона нужно

Какой шаг при вычислении интеграла численными методами необходимо выполнить вторым?

Какой вид имеет система нелинейных уравнений?

Отец мальчика, возвращаясь домой, заметил большое количество магазинов с колбасой и решил купить для сына килограмм, он заходил в каждый магазин и записывал цены в таблицу, однако возвращаться в магазин, где он уже был он не хочет, поэтому он решил определить вероятность того, дороже или дешевле будет колбаса в следующем магазине. Какую математическую модель взять отцу за основу?

Как называется модель, если между ней и реальным объектом, процессом или системой существует полное поэлементное соответствие?

Что требуется для генерации последовательности нормально распределенной случайной величины классическими методами?

Какая модель наиболее подходит для описания движения турбулентного потока жидкости

Какой характер носят выводы, полученные в результате исследования гипотетической модели?

Какие методы применяются для решения системы нелинейных уравнений?

В методе дихотомии если F(x-E)>F(x+E), то для определения min выбирается отрезок

Математическое моделирование это средство для

Какая математическая модель не относится к стохастическим?

Какая модель не является плодом человеческой мысли в общем случае?

Материальная точка это не только математическая, но и

Во время поиска лучшего результата были построены две различные математические модели: эксперимент на ЭВМ, моделирующий систему атомов и дифференциальная система уравнений, решенная численно, от двух полученных результатов взяли среднеквадратичный. Можно ли считать такой метод моделью?

Верно ли описание: детерминированная, непрерывная, аналитическая, модель?

Сколько классов моделей существует?

Какие модели входят в состав идеальных математических моделей?

Что такое математическая модель?

Как называются модели, в которых предполагается отсутствие всяких случайных воздействий и их элементы (элементы модели) достаточно точно установлены?

От какого количества факторов зависит математическое описание исследуемых процессов и систем?

Если игровой автомат наряду со случайными комбинациями управляется устройством, которое всегда стремится, чтобы человек проиграл, можно ли к такому автомату построить какую либо из предложенных математических моделей?

Чтобы описать количество улова за день, рыбак использовал СДА модель, где получил зависимость улова от времени суток, но ему хотелось бы получить зависимость улова от времени на часах, какую модель стоит ему посоветовать?

Посредством каких конструкций, математические модели описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи?

Что не входит в предмет математического моделирования?

Какие изучаются зависимости между величинами, описывающими процессы, при их моделировании?

При исследовании гипотетической модели какого характера получатся выводы?

После исследования распространения радиоволн в прямоугольном волноводе вывели систему дифференциальных уравнений, которую решили численно на ЭВМ, какими будут полученные результаты?

В простейшем случае при расчете определенного интеграла функции его представляют в виде:

Какой из методов применяется чаще на практике?

В чем состоит суть компьютерного моделирования?

Какое преимущество имеет вычислительный эксперимент по сравнению с натурным экспериментом?

Что происходит с результатами исследований на ЭВМ при проверке адекватности математической модели и реального объекта, процесса или системы?

Для чего могут применяться результаты проверки адекватности математической модели и реального объекта, процесса или системы?

На какие группы можно разделить все методы решения математических задач?

Метод половинного деления применим для случая

Каким количеством нелинейных уравнений описывается модель, если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы?

Как называется интервал, в котором лежит уточняемый корень уравнения?

Какое количество этапов содержит процесс определения корней алгебраических и трансцендентных уравнений?

Какая из операций не входит в последовательность операций, необходимых для уточнения корня методом половинного деления?

При каком условии прекращается процесс поиска корня по методу простых итераций?

В методе простых итераций условие сходимости имеет вид

Какой рекуррентной формулой реализуется итерационный процесс схождения к корню?

Как еще называют модифицированный метод Ньютона?

Какая рекуррентная формула применяется в модифицированном методе Ньютона?

В каком из описанных случаев не рекомендуется имитационное моделирование?

Укажите численный метод, моделирующий последовательности псевдослучайных чисел с заданными вероятностными характеристиками:

Что из перечисленного не является минусом имитационного моделирования?

Возможно ли совместное использование имитационного и аналитического моделирования в рамках одной задачи?

С помощью каких типов математических моделей можно исследовать реальные процессы и системы?

Что не относится к достоинствам имитационного моделирования?

Рекомендуется ли применять имитационное моделирование в случаях, когда кроме оценки влияния параметров (переменных) процесса или системы необходимо осуществить наблюдение за поведением компонент (элементов) процесса или системы в течение определенного периода?

Чем оперируют в вероятностном имитационном моделировании?

Что такое статистическая модель случайного процесса?

Какая возникает задача при реализации на ЭВМ статистического имитационного моделирования?

Какая величина называется непрерывной?

Что называется законом распределения дискретной случайной величины?

Какое свойство не является свойством интегральной функции распределения?

В каком случае распределение вероятностей называют равномерным?

Какая функция равномерного распределения существует?

По какой формуле определяется вероятность того, что нормальная случайная величина X примет значение, принадлежащее интервалу (c, d)?

Зависимость между возможными значениями дискретной случайной величины и вероятностью ее появления называют

Вероятность того, что случайная величина X примет значение, заключенной в интервале (a,b), равна

Что не является числовой характеристикой случайной величины?

Дисперсия постоянной величины C равна

Какой метод получил название «Метод Монте-Карло»?

Какое распределение называется равномерным?

Какие требования являются общими для всех известных методов имитации равномерного распределения?

Что не является недостатком «метода середины квадрата»?

Пусть рекуррентная формула содержит в качестве переменных три предыдущих значения (например, X[N]=X[N-1]/3+(X[N-2]-X[N-3])/6) За первые три числа взяты единицы. Генерация непрерывных псевдослучайных чисел начинается с 4. Будет ли при повторном запуске генератора числа отличные от первого запуска?

Какие из методов содержат рекуррентную формулу?

Мультипликативный конгруэнтный метод характеризуется

Укажите число, которое не требуется для генерации чисел по линейно конгруэнтному методу:

Какое количество этапов в решении задачи моделирования случайных величин с нормальным законом распределения?

К какому способу формирования последовательности нормально распределенных случайных величин относится метод, основанный на центральной предельной теореме?

Среднеквадратичное отклонение двух случайных величин, сгенерированных по методу полярных координат будет

Какой метод не несет в себе цель сгенерировать нормально распределенную случайную величину?

В эксперименте было решено использовать значение текущего времени в миллисекундах, выдаваемое компьютером, чтобы сгенерировать первоначальное псевдослучайное число. В каком методе это можно применить?

Каким методом можно сгенерировать на ЭВМ нормально распределенные случайные величины в бесконечном интервале значений (в пределах доступных переменных)?

Как называется параметр bi в системе линейных уравнений?

Как выглядит матрица коэффициентов системы порядка (n n)?

В основе какого метода лежит идея последовательного исключения неизвестных?

Из какого количества этапов состоит метод Гаусса?

Какое количество шагов необходимо для того, чтобы выполнить поиск ненулевого ведущего элемента?

Укажите, какие методы не являются численными для решения систем линейных уравнений:

Формула какого рода используется на обратном шаге метода Гаусса при нахождении корней?

Для применения метода простых итераций необходима

Какой из методов обладает большей точностью при решении системы линейных уравнений в общем случае?

Что означает решить систему нелинейных уравнений?

Как называется область, в которой начальное приближение 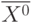сходится к искомому решению?

Для решения каких систем линейных уравнений применяется метод простых итераций?

Какой ряд более удобен для разложения в методе Ньютона?

В сколько этапов реализуется метод Ньютона?

Что означает фраза дана табличная функция?

В чем состоит задача экстраполирования функции (или задача экстраполяции)?

Каким способом решаются задачи интерполяции и экстраполяции?

Как называется интерполирование, выполняемое с помощью алгебраических многочленов?

По какой формуле интерполяционный многочлен имеет вид: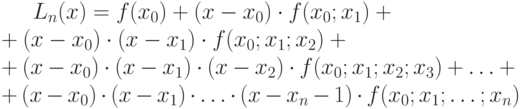

Чему равен параметр P формулы 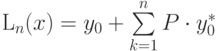, полученной в результате свертки формулы Ньютона?

Что требуют первые 2n условия сплайн-интерполяции?

В чем заключается сглаживание опытных данных методом наименьших квадратов?

Метод Лагранжа используется для

Если добавить экспериментальные точки, то в методе Лагранжа

Какие системы называют динамическими?

К каким методам относятся численные методы по характеру результата?

Что называется остаточным членом?

В каком случае квадратурная формула называется формулой прямоугольников, а метод – методом прямоугольников?

Какой порядок имеет точность метода трапеций?

Формула Ньютона-Лейбница используется

Численные методы интегрирования являются

Какое количество шагов надо выполнить, чтобы проинтегрировать методом прямоугольников функцию на отрезке [a,b] с шагом h?

Какой из параметров не влияет на ошибку методов Симпсона, трапеций и прямоугольников?

Как выглядит нормальная форма дифференциального уравнения?

Что является общим решением обыкновенного дифференциального уравнения y’ = f(x,y)?

Чему равна точность метода Эйлера на каждом шаге?

Каким количеством прямых аппроксимируется функция у(х) на каждом шаге в модифицированном методе Эйлера?

Чему равна ошибка на каждом шаге интегрирования дифференциальных уравнений в методе Рунге-Кутта 4-го порядка?

Решение дифференциального уравнения 1-го порядка представляется как

Точность h метода эйлера имеет порядок

К какой системе можно свести любое дифференциальное уравнение m–го порядка при помощи замен?

Как выглядит нормальная форма дифференциальных уравнений второго порядка?

Как звучит постановка в численных методах задача Коши для системы y(x) с учетом двух начальных условия: y(x₀)=y₀, y₁(x₀)=(y₁)₀?

Что представляет собой каждая i–ая строка матрицы, полученной при решении дифференциального уравнения m-го порядка?

При использовании методов Рунге-Кутта для решения дифференциальных уравнений высоких порядков на каждом шаге интегрирования все уравнения системы решаются

Для решения дифференциальных уравнений n-го порядка задача Коши это

В градиентных методах используются

В методе дихотомии, если F(x-E)<F(x+E), то для определения min выбирается отрезок

Метод дихотомии это

Какой способ необходим для описания непрерывной случайной величины ?

Какой метод называется градиентным?

В чем состоит суть «линейного конгруэнтного метода»?

К какой группе методов относится правило Крамера?

Как повысить точность статистического моделирования?

Методы Рунге-Кутта получены при помощи разложения функции в ряд

Как расшифровывается сокращение РПС?

Что необходимо сделать для того, чтобы проверить выводы, полученные в результате исследования гипотетической модели?

Посредством чего в вероятностных аналитических моделях учитывается влияние случайных факторов?

Равномерное распределение характеризуется тем, что

В каком случае будет формально непригоден простейший вариант метода Гаусса, называемый схемой единственного деления?

Мальчик, гуляя по проспекту, пытается установить как колеблется цена на хлеб в большом ряду хлебных магазинов. Результатом он хочет получить функцию стоимости одного и того же хлеба по пути приближения к центру города по проспекту. Какую математическую модель стоит выбрать мальчику?

В чем состоит суть «метода середины квадрата»?

В каком случае невозможно применить численный метод интегрирования?

Какой способ задания зависимости между различными параметрами исследуемых объектов, процессов и систем является наиболее удобным?

Алгебраический многочлен степени m, как правило, имеет

Сколько этапов можно выделить для решения задачи генерирования случайных чисел на ЭВМ с заданным законом распределения?

Как еще называют метод секущих?

Какие этапы входят в состав методики статистического моделирования?

Использование различных начальных значений какого параметра в обращении GAUSS (IX,S,AM,X) позволяет формировать различные последовательности нормально распределенных псевдослучайных чисел?

Может ли идеальный электрический контур быть моделью математического маятника?

По поведению математических моделей во времени их разделяют на

Чем является функционал «Х» в представлении математической модели в виде системы функционалов Ф_i (X,Y,Z,t)=0?

Какие группы математических моделей не являются результатом распределения моделей по их поведению во времени?

На какие группы можно разделить математические модели по виду входной информации?

В каком моделировании функционирование объектов, процессов или систем описывается набором алгоритмов?

Какой из шагов построения математической модели сформулирован не верно?

Что входит в предмет математического моделирования?

Укажите метод, неприменяемый для компьютерного моделирования:

Какая задача не поддается точному решению на ЭВМ в виде формул?

Из двух численных методов расчета дифференциала более точен тот, который

Какой из экспериментов наиболее выгодно применять для исследования большого числа вариантов проектируемого объекта или процесса для различных режимов его эксплуатации?

Какое направление является наиболее перспективным для проведения вычислительного эксперимента?

Укажите существующие группы решения математических задач

Для применения способа уточнения корней необходимо

Если при половинном делении оба интервала меняют знак, то это говорит о

Какое максимальное количество корней имеет нелинейное уравнение f(x)=0, если функция f(x) имеет вид многочлена степени m?

В каком случае уравнение f(x)=0 называется трансцендентным уравнением?

Какая процедура основана на следующем свойстве непрерывности функции «если функция f(x) непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) < 0, то между точками a и b имеется хотя бы один корень уравнения»?

При каком условии прекращается процесс поиска корня по методу хорд?

Какое из понятий не относится к вероятностным характеристикам системы?

Какой вид моделирования характеризуется следующим описанием «на основе математической модели с помощью ЭВМ проводится серия вычислительных экспериментов, т.е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, уточняется модель»?

В виде каких зависимостей задается поведение РПС в аналитических моделях?

Что понимается под алгоритмизацией функционирования РПС?

Какая величина называется случайной?

К какой форме представления (задания) закона распределения относится биномиальное распределение, определяемое законом Бернулли P_n(k)=C_n^kp^kq^n-k (где k = 0, 1, 2, …, n – количество возможных появлений событий, а q = 1-p – вероятность не появления событий)?

Какая функция называется интегральной функцией распределения?

В чем состоит Геометрический смысл ДФР?

Что происходит с нормальной кривой (кривой Гаусса) при изменении величины параметра (математического ожидания случайной величины)?

Если заранее не обговорен закон распределения, то имеет ввиду

Математическое ожидание есть

Аддитивные методы используются для

Можно ли методом серединного квадрата генерировать натуральные числа?

Какой из перечисленных способов не относится к основным способам формирования последовательности нормально распределенных случайных величин?

К какому способу формирования последовательности нормально распределенных случайных величин относится метод полярных координат?

Центральная теорема теории вероятности говорит о

Была поставлена задача измерить вероятностным методом число пи. Пусть в единичный квадрат случайно ставятся точки, при этом в квадрат вписана единичная окружность, как должны быть распределены случайные координаты точек (x,y), чтобы можно было измерить площадь окружности, проведя большое количество опытов и проверяя попала ли каждая точка в окружность или нет?

Будет ли обладать цикличностью метод полярных координат, если сгенерированные равновероятно распределенные числа обладают цикличностью?

К чему преобразуется исходная система n-го порядка в результате выполнения первого шага прямого хода метода Гаусса?

Какую систему линейных уравнений невозможно решать методом Гаусса?

Если в случае, когда система нелинейных уравнений имеет несколько возможных решений и по методу простых итераций найдено одно из них, то для поиска других требуется

От чего зависит эффективность всех итерационных методов?

К какому виду необходимо преобразовать исходную систему нелинейных уравнений для применения метода простых итераций?

Какая идея лежит в основе метода Ньютона?

Какое условие должно выполниться для прекращения итерационного процесса в рамках метода Ньютона?

Основная идея метода Ньютона –

Каким способом можно определить каждый элемент матрицы Якоби в методе Ньютона?

Чему будет равна степень n многочлена P_n(x), если количество узловых точек N?

Что необходимо сделать для построения интерполяционного многочлена в явном виде?

Какой из способов аппроксимации данных нашел большее применение на практике?

Степень интерполяционного многочлена Лагранжа:

Как выглядит формула Ньютона-Лейбница?

Что отражает параметр N2 в формуле по методу Симпсона ?

Какая максимальная степень степенного подынтегральной многочлена должна быть, чтобы гарантировать безошибочное вычисление интеграла методом трапеций?

Чему равна правая часть (f(x,y)) дифференциального уравнения, представленного в нормальной форме?

Что называется задачей Коши?

Как еще называется метод Эйлера?

Чему равен в графическом представлении метода Эйлера наклон касательной в пределах каждого шага?

Метод Эйлера это:

Как выглядят дифференциальные уравнения второго порядка в общем виде?

Что является решением задачи Коши для системы, состоящей из двух дифференциальных уравнений первого порядка, на графике?

Матрица какого размера получится при решении дифференциального уравнения m-го порядка (при этом каждая из табличных функций определяется на промежутке [a, b] с шагом h и включает n узловых точек)?

Решение дифференциальных уравнений n-го порядка представляются как

Метод «золотого сечения» является методом

В методе дихотомии если F(x-E)<F(x+E), то для определения max выбирается отрезок

Укажите систему, которую не следует исследовать статистическими имитационными моделями:

По какой формуле вычисляется остаточный член?

Как еще называют метод Ньютона?

Какие характеристики объекта, процесса или системы устанавливаются на этапе выбора математической модели?

Квадратурой называется

Какое количество этапов содержит методика статистического моделирования?

Что необходимо сделать, чтобы найти вероятность того, что отклонение случайной величины Х по абсолютной величине меньше заданного положительного числа ?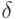

Какой из методов не относится к методам уточнения приближенных значений действительных корней?

В чем состоит задача интерполирования функции (или задача интерполяции)?

Какая характеристика не относится к числовым характеристикам случайной величины?

В каких случаях применяются численные методы интегрирования?

По какой формуле проводится проверка решения задачи, найденного посредством метода Гаусса?

К каким случайным величинам применим способ описания распределения случайной величины в виде таблицы, в виде формулы или графически?

Чему равен параметр B_j формулы 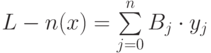, полученной в результате свертки формулы Лагранжа?

Чем аппроксимируется подынтегральная функция в каждой части деления в методе Симпсона?

Какие модели относятся к классу вещественных моделей?

Как можно охарактеризовать метод Монте-Карло?

Как называется отношение ?

Как выглядит модифицированная или уточненная формула Эйлера?

Какая из задач не имеет аналитической модели?

Какой модели быть не может?

При анализе движения электронов в диодном промежутке было построено две математические модели: сперва написана программа, моделирующая взаимодействие частиц, затем выведено уравнение движения электронов из теоретических соображений. Какие математические модели были применены в данных случаях?

Какие модели нельзя отнести к классу мысленных моделей?

На какой язык должна быть «переведена» прикладная задача для ее решения с использованием ЭВМ?

Численный метод предполагает решение в бесконечном цикле итераций. Когда следует прервать процесс вычисления?

Что лежит в основе компьютерного моделирования как нового метода научных исследований?

Что позволяют делать с математическими моделями компьютерное моделирование и вычислительный эксперимент?

Какой тип математических моделей чаще всего используется в задачах проектирования или исследования поведения реальных объектов, процессов или систем?

Интервалом изоляции называется

На заданном отрезке [a,b] имеется только один корень, если

Что такое уточнение корней?

Как еще можно назвать метод простых итераций?

Как выглядит условие сходимости, применяемое в методе простых итераций?

Укажите более точное определение имитационных моделей:

Каким методом представляется имитационное моделирование?

Какие математические модели применяются при имитационном моделировании?

Что является недостатком имитационного моделирования?

Для изучения каких систем используется аналитическое моделирование?

Для какого из методов больше подойдет характеристика: численный метод, моделирующий на ЭВМ псевдослучайные числовые последовательности с заданными вероятностными характеристиками

В чем заключается геометрический смысл интегральной функции распределения F(x)?

Как звучит центральная предельная теорема теории вероятностей?

Какой способ неприменим для описания дискретной случайной величины?

Пусть найдено, что дисперсия составляет 0.01 для некоторой непрерывной величины, чему равно среднеквадратичное отклонение?

Как называется последовательность, полученная из соотношения ?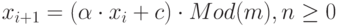

Какой из методов не содержит рекуррентной формулы?

При каком значении m реализуется последовательность Фибоначчи (1,1,2,3,5,8,13…) для метода X[N+1]=X[N]+X[N-1] mod m.

Какие формулы применяются в методе полярных координат для вычисления независимых нормально распределенные случайных величин x1 и x2?

Что означает параметр S в обращении (GAUSS (IX,S,AM,X)) к датчику, представленному в виде подпрограммы GAUSS?

Метод аппроксимации нормально распределенной случайной величины основан на сложении

Можно ли методом, основанным на центральной предельной теореме теории вероятности или полярных координат сгенерировать псевдослучайную величину с синусоидальным распределением вероятности?

Какой вид имеет система линейных уравнений?

На какое количество групп можно разделить численные методы решения систем линейных уравнений?

Как называется матрица А, применяемая в методе Ньютона, которая составленая из частных производных ?

В чем заключается аппроксимация опытных данных?

Интерполяция — это

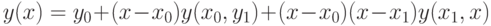это интерполяционный многочлен

Разделенные разности используются интерполяционным многочленом в формах

Какими уравнениями описываются динамические системы?

Как называется нахождение приближенного значения интеграла?

Какой вид имеет квадратурная формула, если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага?

Какую необходимо брать высоту прямоугольника в методе прямоугольников на интервале [a,b] в общем случае?

Какой из методов имеет большее количество шагов?

Как называется дифференциальное уравнения, если функция у зависит от нескольких аргументов?

Что такое h в постановке задачи Коши в численных методах?

Чем аппроксимируется искомая функция y(x) на каждом шаге интегрирования дифференциальных уравнений в методе Рунге-Кутта 4-го порядка?

Производные функции y(x) каких порядков необходимо определить для сохранения членов ряда, содержащих h² , h³,h⁴?

Модифицированный метод Эйлера это:

Какой метод считается более точным

Как добиться того чтобы результаты по методу Эйлера, модифицированному методу Эйлера и методу Рунге-Кутта 4-го порядка были почти одинаковыми

Что является решением дифференциального уравнения m-го порядка?

Чтобы решить дифференциальное уравнение высоких порядков мы их приводим к системе

В прямых методах оптимизации при поиске экстремума используются

Какой метод решения системы нелинейных уравнений обеспечивает более быструю сходимость?

Что является решением дифференциального уравнения m-го порядка на графике?

На какое количество групп можно разделить все методы решения математических задач?

Дифференциальная функция распределения это

Пересечение касательной к функции и осью абсцисс дает точку, используемую в методе

К какому виду должно быть приведено исходное уравнение f(x)=0 для того, чтобы можно было применить метод простых итераций?

Дифференциальное уравнение высоких порядков можно

К системе какого вида приводится исходная система в результате выполнения всех шагов прямого хода?

Что означает сокращенное обозначение модели СДА?

Как называется замещаемый моделью объект?

Какие процессы должны отражать математические модели в задачах проектирования или исследования поведения реальных объектов, процессов или систем?

В какое количество этапов группируются все вычисления на каждом шаге по модифицированной или уточненной формуле Эйлера для определения предварительного значения ?

Какой из шагов не входит в состав исследования объекта, процесса или системы и составления их математического описания при математическом моделировании, но является частью математического моделирования?

Каким методом является классический метод Гаусса?

Во время изучения зависимости температуры сжатого реального газа от давления построили три различных модели: имитационную детерминированную, аналитическую детерминированную и имитационную стохастическую. Какая из моделей опишет газ наиболее точно?

Инженеру во сне приснился новый шпиндель для двигателя, и он хочет его испытать, какую модель ему лучше предоставить токарям, чтобы ускорить процесс его изготовления?

На какие группы можно разделить математические модели по степени их соответствия реальным объектам, процессам или системам?

Для описания движения турбулентного потока жидкости наиболее подходит

Какой из методов решения нелинейных уравнений не является методом прямого поиска?

Какое условие должно выполняться, чтобы метод Ньютона обеспечивал быструю сходимость?

Какой рекуррентной формулой реализуется итерационный процесс схождения к корню в методе хорд

Что такое дифференциальная функция распределения (ДФР) (или плотность вероятности)?

Какой закон называют нормальным законом распределения вероятностей непрерывной случайной величины?

Что означают термины «случайные числа» и «последовательность случайных чисел»?

В чем состоит суть алгоритмических методов получения равномерно распределенных псевдослучайных чисел?

Какой метод получения случайных чисел был предложен Грином?

Может ли множитель предыдущего значения быть меньше приращения предыдущего значения для смешанного конгруэнтного метода?

Накапливается ли ошибка (связанная с округлением чисел с бесконечным периодом) от шага к шагу в методе Гаусса?

Произойдет ли зацикливание алгоритма простых итераций, если корней нет в области сходимости?

По какой формуле интерполяционный многочлен имеет вид:

Как называется группа кубических многочленов, в местах сопряжения которых первая и вторая производные непрерывны?

Проведя натурный эксперимент на электроискровом станке : по различным частотам генерации импульсов подбирали амплитуду импульсов, чтобы толщина реза была постоянна. Полученные результаты можно считать

Какой из всех численных методов решения дифференциальных уравнений с помощью ЭВМ получил самое большое распространение?

В задаче о камне, брошенном под углом к горизонту, решенной в явном виде, как зависимость координаты от времени, была применена модель

Какие виды математических моделей получаются при разделении их по принципам построения?

Как выглядит общий вид дифференциального уравнения?

Какой фактор определяет использование статистической имитационной модели?

Посмотрев на набор различных математических моделей, математик сформировал четыре общих утверждения для всех математических моделей. Какое из утверждений для произвольной математической модели верно?

Для того чтобы модель была гомоморфная необходимо и достаточно в рамках поставленной задачи

В чем заключается построение математической модели?

Какую математическую модель следует построить, чтобы определить вероятность выпадения «орла» на монете, у которой центр тяжести смещен к «решке», и поэтому она не поддается обычной теории вероятности?

С чего обычно начинается построение математической модели?

В каких процессах вычислительный эксперимент является единственно возможным?

Какой вид имеет система линейных уравнений в матричной форме?

Методы какой группы реализуют на ЭВМ нахождение корней с заданной точностью и являются итерационными методами?

В каком случае квадратурная формула называется формулой Симпсона, а метод – методом Симпсона?

Точность h метода Рунге-Кутта 4-го порядка

Если целевая функция и функция ограничений известны, то это методы

Какое название имеет первый этап метода Гаусса?

Метод дихотомии является методом

Уравнение называется трансцендентным, если

Что происходит с областью сходимости метода Ньютона при увеличении числа неизвестных?

Математическая модель в общем случае представляется через

Какими знаниями необходимо обладать для построения математической модели в прикладных задачах?

Можно ли вероятностным моделированием исследовать систему на устойчивость?

Что такое имитационное моделирование?

Можно ли сгенерировать на ЭВМ нормально распределенные случайные величины в бесконечном интервале значений методом полярных координат?

Какое условие должно быть выполнено, чтобы можно было найти функцию F(x) из класса алгебраических многочленов P_n(x)=a₀xⁿ+ a₁x^n-1+ a₂x^n-2+…+ a_n-1x¹+ a_nx⁰?

Какой многочлен называется интерполяционным многочленом?

Чему равна точность модифицированного метода Эйлера на каждом шаге?

В градиентных методах 2-го порядка используются

Бывает ли математическая модель полностью тождественна рассматриваемому объекту, процессу или системе?

Какими методами следует решать системы, состоящие из смешанных (линейных и нелинейных) уравнений?

При выполнении какого условия прекращается итерационный процесс поиска в рамках метода простых итераций?

Как называются точки с координатами (x_i, y_i)?

Какое условие необходимо соблюдать на каждом шаге интегрирования при применении для решения системы дифференциальных уравнений тех же методов, что и для решения одного дифференциального уравнения первого порядка?

Как выглядит формула Эйлера?

Какой из указанных методов не имеют периода в общем случае?

Какие методы решения применяются для поиска корней уравнения f(x)=0 с заданной степенью точности ?

Что происходит с нормальной кривой (кривой Гаусса) при изменении величины параметра 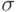(среднего квадратичного отклонения)?

Какое количество основных способов формирования последовательности нормально распределенных случайных величин различают?

Какой из методов имеет приближенный характер?

Что называется отделением корня уравнения f(x)=0?

Укажите какого порядка будет максимальная ошибка метода Симпсона

Для решения дифференциальных уравнений 1-го порядка необходимо

In numerical integration, Simpson’s rules are several approximations for definite integrals, named after Thomas Simpson (1710–1761).

The most basic of these rules, called Simpson’s 1/3 rule, or just Simpson’s rule, reads

In German and some other languages, it is named after Johannes Kepler, who derived it in 1615 after seeing it used for wine barrels (barrel rule, Keplersche Fassregel). The approximate equality in the rule becomes exact if f is a polynomial up to and including 3rd degree.

If the 1/3 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson’s 1/3 rule. Points inside the integration range are given alternating weights 4/3 and 2/3.

Simpson’s 3/8 rule, also called Simpson’s second rule, requires one more function evaluation inside the integration range and gives lower error bounds, but does not improve on order of the error.

If the 3/8 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson’s 3/8 rule.

Simpson’s 1/3 and 3/8 rules are two special cases of closed Newton–Cotes formulas.

In naval architecture and ship stability estimation, there also exists Simpson’s third rule, which has no special importance in general numerical analysis, see Simpson’s rules (ship stability).

Simpson’s 1/3 rule[edit]

Simpson’s 1/3 rule, also simply called Simpson’s rule, is a method for numerical integration proposed by Thomas Simpson. It is based upon a quadratic interpolation. Simpson’s 1/3 rule is as follows:

where is the step size.

The error in approximating an integral by Simpson’s rule for is

where (the Greek letter xi) is some number between and .^[1][2]

The error is asymptotically proportional to . However, the above derivations suggest an error proportional to . Simpson’s rule gains an extra order because the points at which the integrand is evaluated are distributed symmetrically in the interval .

Since the error term is proportional to the fourth derivative of at , this shows that Simpson’s rule provides exact results for any polynomial of degree three or less, since the fourth derivative of such a polynomial is zero at all points. Another way to see this result is to note that any interpolating cubic polynomial can be expressed as the sum of the unique interpolating quadratic polynomial plus an arbitrarily scaled cubic polynomial that vanishes at all three points in the interval, and the integral of this second term vanishes because it is odd within the interval.

If the second derivative exists and is convex in the interval , then

Derivations[edit]

Quadratic interpolation[edit]

One derivation replaces the integrand by the quadratic polynomial (i.e. parabola) that takes the same values as at the end points and and the midpoint . One can use Lagrange polynomial interpolation to find an expression for this polynomial,

Using integration by substitution, one can show that^[3][2]

Introducing the step size , this is also commonly written as

Because of the factor, Simpson’s rule is also referred to as «Simpson’s 1/3 rule» (see below for generalization).

Averaging the midpoint and the trapezoidal rules[edit]

Another derivation constructs Simpson’s rule from two simpler approximations: the midpoint rule

and the trapezoidal rule

The errors in these approximations are

and

respectively, where denotes a term asymptotically proportional to . The two terms are not equal; see Big O notation for more details. It follows from the above formulas for the errors of the midpoint and trapezoidal rule that the leading error term vanishes if we take the weighted average

This weighted average is exactly Simpson’s rule.

Using another approximation (for example, the trapezoidal rule with twice as many points), it is possible to take a suitable weighted average and eliminate another error term. This is Romberg’s method.

Undetermined coefficients[edit]

The third derivation starts from the ansatz

The coefficients α, β and γ can be fixed by requiring that this approximation be exact for all quadratic polynomials. This yields Simpson’s rule. (This derivation is essentially a less rigorous version of the quadratic interpolation derivation, where one saves significant calculation effort by guessing the correct functional form.)

Composite Simpson’s 1/3 rule[edit]

If the interval of integration is in some sense «small», then Simpson’s rule with subintervals will provide an adequate approximation to the exact integral. By «small» we mean that the function being integrated is relatively smooth over the interval . For such a function, a smooth quadratic interpolant like the one used in Simpson’s rule will give good results.

However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory or lacks derivatives at certain points. In these cases, Simpson’s rule may give very poor results. One common way of handling this problem is by breaking up the interval into small subintervals. Simpson’s rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson’s 1/3 rule, or just composite Simpson’s rule.

Suppose that the interval is split up into subintervals, with an even number. Then, the composite Simpson’s rule is given by

Dividing the interval into subintervals of length and introducing the points for (in particular, and ), we have

This composite rule with corresponds with the regular Simpson’s rule of the preceding section.

The error committed by the composite Simpson’s rule is

where is some number between and , and is the «step length».^[4][5] The error is bounded (in absolute value) by

This formulation splits the interval in subintervals of equal length. In practice, it is often advantageous to use subintervals of different lengths and concentrate the efforts on the places where the integrand is less well-behaved. This leads to the adaptive Simpson’s method.

Simpson’s 3/8 rule[edit]

Simpson’s 3/8 rule, also called Simpson’s second rule, is another method for numerical integration proposed by Thomas Simpson. It is based upon a cubic interpolation rather than a quadratic interpolation. Simpson’s 3/8 rule is as follows:

where is the step size.

The error of this method is

where is some number between and . Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value. A composite 3/8 rule also exists, similarly as above.^[6]

A further generalization of this concept for interpolation with arbitrary-degree polynomials are the Newton–Cotes formulas.

Composite Simpson’s 3/8 rule[edit]

Dividing the interval into subintervals of length and introducing the points for (in particular, and ), we have

While the remainder for the rule is shown as^[6]

we can only use this if is a multiple of three. The 1/3 rule can be used for the remaining subintervals without changing the order of the error term (conversely, the 3/8 rule can be used with a composite 1/3 rule for odd-numbered subintervals).

Alternative extended Simpson’s rule[edit]

This is another formulation of a composite Simpson’s rule: instead of applying Simpson’s rule to disjoint segments of the integral to be approximated, Simpson’s rule is applied to overlapping segments, yielding^[7]

The formula above is obtained by combining the composite Simpson’s 1/3 rule with the one consisting of using Simpson’s 3/8 rule in the extreme subintervals and Simpson’s 1/3 rule in the remaining subintervals. The result is then obtained by taking the mean of the two formulas.

Simpson’s rules in the case of narrow peaks[edit]

In the task of estimation of full area of narrow peak-like functions, Simpson’s rules are much less efficient than trapezoidal rule. Namely, composite Simpson’s 1/3 rule requires 1.8 times more points to achieve the same accuracy as trapezoidal rule.^[8] Composite Simpson’s 3/8 rule is even less accurate. Integration by Simpson’s 1/3 rule can be represented as a weighted average with 2/3 of the value coming from integration by the trapezoidal rule with step h and 1/3 of the value coming from integration by the rectangle rule with step 2h. The accuracy is governed by the second (2h step) term. Averaging of Simpson’s 1/3 rule composite sums with properly shifted frames produces the following rules:

where two points outside of the integrated region are exploited, and

where only points within integration region are used. Application of the second rule to the region of 3 points generates 1/3 Simpon’s rule, 4 points — 3/8 rule.

These rules are very much similar to the alternative extended Simpson’s rule. The coefficients within the major part of the region being integrated are one with non-unit coefficients only at the edges. These two rules can be associated with Euler–MacLaurin formula with the first derivative term and named First order Euler–MacLaurin integration rules.^[8] The two rules presented above differ only in the way how the first derivative at the region end is calculated. The first derivative term in the Euler–MacLaurin integration rules accounts for integral of the second derivative, which equals the difference of the first derivatives at the edges of the integration region. It is possible to generate higher order Euler–Maclaurin rules by adding a difference of 3rd, 5th, and so on derivatives with coefficients, as defined by Euler–MacLaurin formula.

Composite Simpson’s rule for irregularly spaced data[edit]

For some applications, the integration interval needs to be divided into uneven intervals – perhaps due to uneven sampling of data, or missing or corrupted data points. Suppose we divide the interval into even number of subintervals of widths . Then the composite Simpson’s rule is given by^[9]

where

are the function values at the th sampling point on the interval .

In case of odd number of subintervals, the above formula are used up to the second to last interval,
and the last interval is handled separately by adding the following to the result:^[10]

where

from collections.abc import Sequence

def simpson_nonuniform(x: Sequence[float], f: Sequence[float]) -> float:
    """
    Simpson rule for irregularly spaced data.

    :param x: Sampling points for the function values
    :param f: Function values at the sampling points

    :return: approximation for the integral

    See ``scipy.integrate.simpson`` and the underlying ``_basic_simpson``
    for a more performant implementation utilizing numpy's broadcast.
    """
    N = len(x) - 1
    h = [x[i + 1] - x[i] for i in range(0, N)]
    assert N > 0

    result = 0.0
    for i in range(1, N, 2):
        h0, h1 = h[i - 1], h[i]
        hph, hdh, hmh = h1 + h0, h1 / h0, h1 * h0
        result += (hph / 6) * (
            (2 - hdh) * f[i - 1] + (hph**2 / hmh) * f[i] + (2 - 1 / hdh) * f[i + 1]
        )

    if N % 2 == 1:
        h0, h1 = h[N - 2], h[N - 1]
        result += f[N]     * (2 * h1 ** 2 + 3 * h0 * h1) / (6 * (h0 + h1))
        result += f[N - 1] * (h1 ** 2 + 3 * h1 * h0)     / (6 * h0)
        result -= f[N - 2] * h1 ** 3                     / (6 * h0 * (h0 + h1))
    return result

SimpsonInt <- function(fx, dx) {
  n <- length(dx)
  h <- diff(dx)
  stopifnot(exprs = {
    length(fx) == n
    all(h >= 0)
  })
  res <- 0
  for (i in seq(1L, n - 2L, 2L)) {
    hph <- h[i] + h[i + 1L]
    hdh <- h[i + 1L] / h[i]
    res <- res + hph / 6 *
      ((2 - hdh) * fx[i] +
         hph ^ 2 / (h[i] * h[i + 1L]) * fx[i + 1L] +
         (2 - 1 / hdh) * fx[i + 2L])
  }

  if (n %% 2 == 0) {
    hph <- h[n - 1L] + h[n - 2L]
    threehth <- 3 * h[n - 1L] * h[n - 2L]
    sixh2 <- 6 * h[n - 2L]
    h1sq <- h[n - 1L] ^ 2
    res <- res +
      (2 * h1sq + threehth) / (6 * hph) * fx[n] +
      (h1sq + threehth) / sixh2 * fx[n - 1L] -
      (h1sq * h[n - 1L]) / (sixh2 * hph) * fx[n - 2L]
  }
  res
}

See also[edit]

• Newton–Cotes formulas
• Gaussian quadrature

Notes[edit]

References[edit]

• Atkinson, Kendall E. (1989). An Introduction to Numerical Analysis (2nd ed.). John Wiley & Sons. ISBN 0-471-50023-2.
• Burden, Richard L.; Faires, J. Douglas (2000). Numerical Analysis (7th ed.). Brooks/Cole. ISBN 0-534-38216-9.
• Cartwright, Kenneth V. (September 2017). «Simpson’s Rule Cumulative Integration with MS Excel and Irregularly-spaced Data» (PDF). Journal of Mathematical Sciences and Mathematics Education. 12 (2): 1–9. Retrieved 18 December 2022.
• Kalambet, Yuri; Kozmin, Yuri; Samokhin, Andrey (2018). «Comparison of integration rules in the case of very narrow chromatographic peaks». Chemometrics and Intelligent Laboratory Systems. 179: 22–30. doi:10.1016/j.chemolab.2018.06.001. ISSN 0169-7439.
• Matthews, John H. (2004). «Simpson’s 3/8 Rule for Numerical Integration». Numerical Analysis — Numerical Methods Project. California State University, Fullerton. Archived from the original on 4 December 2008. Retrieved 11 November 2008.
• Shklov, N. (December 1960). «Simpson’s Rule for Unequally Spaced Ordinates». The American Mathematical Monthly. 67 (10): 1022–1023. doi:10.2307/2309244. JSTOR 2309244.
• Süli, Endre; Mayers, David (2003). An Introduction to Numerical Analysis. Cambridge University Press. ISBN 0-521-00794-1.
• Weisstein, Eric W. «Newton-Cotes Formulas». MathWorld. Retrieved 14 December 2022.

External links[edit]

• «Simpson formula», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. «Simpson’s Rule». MathWorld.
• Simpson’s 1/3rd rule of integration — Notes, PPT, Mathcad, Matlab, Mathematica, Maple at Numerical Methods for STEM undergraduate
• A detailed description of a computer implementation is described by Dorai Sitaram in Teach Yourself Scheme in Fixnum Days, Appendix C

This article incorporates material from Code for Simpson’s rule on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

In numerical integration, Simpson’s rules are several approximations for definite integrals, named after Thomas Simpson (1710–1761).

The most basic of these rules, called Simpson’s 1/3 rule, or just Simpson’s rule, reads

In German and some other languages, it is named after Johannes Kepler, who derived it in 1615 after seeing it used for wine barrels (barrel rule, Keplersche Fassregel). The approximate equality in the rule becomes exact if f is a polynomial up to and including 3rd degree.

If the 1/3 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson’s 1/3 rule. Points inside the integration range are given alternating weights 4/3 and 2/3.

Simpson’s 3/8 rule, also called Simpson’s second rule, requires one more function evaluation inside the integration range and gives lower error bounds, but does not improve on order of the error.

If the 3/8 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson’s 3/8 rule.

Simpson’s 1/3 and 3/8 rules are two special cases of closed Newton–Cotes formulas.

In naval architecture and ship stability estimation, there also exists Simpson’s third rule, which has no special importance in general numerical analysis, see Simpson’s rules (ship stability).

Simpson’s 1/3 rule[edit]

Simpson’s 1/3 rule, also simply called Simpson’s rule, is a method for numerical integration proposed by Thomas Simpson. It is based upon a quadratic interpolation. Simpson’s 1/3 rule is as follows:

where is the step size.

The error in approximating an integral by Simpson’s rule for is

where (the Greek letter xi) is some number between and .^[1][2]

The error is asymptotically proportional to . However, the above derivations suggest an error proportional to . Simpson’s rule gains an extra order because the points at which the integrand is evaluated are distributed symmetrically in the interval .

Since the error term is proportional to the fourth derivative of at , this shows that Simpson’s rule provides exact results for any polynomial of degree three or less, since the fourth derivative of such a polynomial is zero at all points. Another way to see this result is to note that any interpolating cubic polynomial can be expressed as the sum of the unique interpolating quadratic polynomial plus an arbitrarily scaled cubic polynomial that vanishes at all three points in the interval, and the integral of this second term vanishes because it is odd within the interval.

If the second derivative exists and is convex in the interval , then

Derivations[edit]

Quadratic interpolation[edit]

One derivation replaces the integrand by the quadratic polynomial (i.e. parabola) that takes the same values as at the end points and and the midpoint . One can use Lagrange polynomial interpolation to find an expression for this polynomial,

Using integration by substitution, one can show that^[3][2]

Introducing the step size , this is also commonly written as

Because of the factor, Simpson’s rule is also referred to as «Simpson’s 1/3 rule» (see below for generalization).

Averaging the midpoint and the trapezoidal rules[edit]

Another derivation constructs Simpson’s rule from two simpler approximations: the midpoint rule

and the trapezoidal rule

The errors in these approximations are

and

respectively, where denotes a term asymptotically proportional to . The two terms are not equal; see Big O notation for more details. It follows from the above formulas for the errors of the midpoint and trapezoidal rule that the leading error term vanishes if we take the weighted average

This weighted average is exactly Simpson’s rule.

Using another approximation (for example, the trapezoidal rule with twice as many points), it is possible to take a suitable weighted average and eliminate another error term. This is Romberg’s method.

Undetermined coefficients[edit]

The third derivation starts from the ansatz

The coefficients α, β and γ can be fixed by requiring that this approximation be exact for all quadratic polynomials. This yields Simpson’s rule. (This derivation is essentially a less rigorous version of the quadratic interpolation derivation, where one saves significant calculation effort by guessing the correct functional form.)

Composite Simpson’s 1/3 rule[edit]

If the interval of integration is in some sense «small», then Simpson’s rule with subintervals will provide an adequate approximation to the exact integral. By «small» we mean that the function being integrated is relatively smooth over the interval . For such a function, a smooth quadratic interpolant like the one used in Simpson’s rule will give good results.

However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory or lacks derivatives at certain points. In these cases, Simpson’s rule may give very poor results. One common way of handling this problem is by breaking up the interval into small subintervals. Simpson’s rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson’s 1/3 rule, or just composite Simpson’s rule.

Suppose that the interval is split up into subintervals, with an even number. Then, the composite Simpson’s rule is given by

Dividing the interval into subintervals of length and introducing the points for (in particular, and ), we have

This composite rule with corresponds with the regular Simpson’s rule of the preceding section.

The error committed by the composite Simpson’s rule is

where is some number between and , and is the «step length».^[4][5] The error is bounded (in absolute value) by

This formulation splits the interval in subintervals of equal length. In practice, it is often advantageous to use subintervals of different lengths and concentrate the efforts on the places where the integrand is less well-behaved. This leads to the adaptive Simpson’s method.

Simpson’s 3/8 rule[edit]

Simpson’s 3/8 rule, also called Simpson’s second rule, is another method for numerical integration proposed by Thomas Simpson. It is based upon a cubic interpolation rather than a quadratic interpolation. Simpson’s 3/8 rule is as follows:

where is the step size.

The error of this method is

where is some number between and . Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value. A composite 3/8 rule also exists, similarly as above.^[6]

A further generalization of this concept for interpolation with arbitrary-degree polynomials are the Newton–Cotes formulas.

Composite Simpson’s 3/8 rule[edit]

Dividing the interval into subintervals of length and introducing the points for (in particular, and ), we have

While the remainder for the rule is shown as^[6]

we can only use this if is a multiple of three. The 1/3 rule can be used for the remaining subintervals without changing the order of the error term (conversely, the 3/8 rule can be used with a composite 1/3 rule for odd-numbered subintervals).

Alternative extended Simpson’s rule[edit]

This is another formulation of a composite Simpson’s rule: instead of applying Simpson’s rule to disjoint segments of the integral to be approximated, Simpson’s rule is applied to overlapping segments, yielding^[7]

The formula above is obtained by combining the composite Simpson’s 1/3 rule with the one consisting of using Simpson’s 3/8 rule in the extreme subintervals and Simpson’s 1/3 rule in the remaining subintervals. The result is then obtained by taking the mean of the two formulas.

Simpson’s rules in the case of narrow peaks[edit]

In the task of estimation of full area of narrow peak-like functions, Simpson’s rules are much less efficient than trapezoidal rule. Namely, composite Simpson’s 1/3 rule requires 1.8 times more points to achieve the same accuracy as trapezoidal rule.^[8] Composite Simpson’s 3/8 rule is even less accurate. Integration by Simpson’s 1/3 rule can be represented as a weighted average with 2/3 of the value coming from integration by the trapezoidal rule with step h and 1/3 of the value coming from integration by the rectangle rule with step 2h. The accuracy is governed by the second (2h step) term. Averaging of Simpson’s 1/3 rule composite sums with properly shifted frames produces the following rules:

where two points outside of the integrated region are exploited, and

where only points within integration region are used. Application of the second rule to the region of 3 points generates 1/3 Simpon’s rule, 4 points — 3/8 rule.

These rules are very much similar to the alternative extended Simpson’s rule. The coefficients within the major part of the region being integrated are one with non-unit coefficients only at the edges. These two rules can be associated with Euler–MacLaurin formula with the first derivative term and named First order Euler–MacLaurin integration rules.^[8] The two rules presented above differ only in the way how the first derivative at the region end is calculated. The first derivative term in the Euler–MacLaurin integration rules accounts for integral of the second derivative, which equals the difference of the first derivatives at the edges of the integration region. It is possible to generate higher order Euler–Maclaurin rules by adding a difference of 3rd, 5th, and so on derivatives with coefficients, as defined by Euler–MacLaurin formula.

Composite Simpson’s rule for irregularly spaced data[edit]

For some applications, the integration interval needs to be divided into uneven intervals – perhaps due to uneven sampling of data, or missing or corrupted data points. Suppose we divide the interval into even number of subintervals of widths . Then the composite Simpson’s rule is given by^[9]

where

are the function values at the th sampling point on the interval .

In case of odd number of subintervals, the above formula are used up to the second to last interval,
and the last interval is handled separately by adding the following to the result:^[10]

where

from collections.abc import Sequence

def simpson_nonuniform(x: Sequence[float], f: Sequence[float]) -> float:
    """
    Simpson rule for irregularly spaced data.

    :param x: Sampling points for the function values
    :param f: Function values at the sampling points

    :return: approximation for the integral

    See ``scipy.integrate.simpson`` and the underlying ``_basic_simpson``
    for a more performant implementation utilizing numpy's broadcast.
    """
    N = len(x) - 1
    h = [x[i + 1] - x[i] for i in range(0, N)]
    assert N > 0

    result = 0.0
    for i in range(1, N, 2):
        h0, h1 = h[i - 1], h[i]
        hph, hdh, hmh = h1 + h0, h1 / h0, h1 * h0
        result += (hph / 6) * (
            (2 - hdh) * f[i - 1] + (hph**2 / hmh) * f[i] + (2 - 1 / hdh) * f[i + 1]
        )

    if N % 2 == 1:
        h0, h1 = h[N - 2], h[N - 1]
        result += f[N]     * (2 * h1 ** 2 + 3 * h0 * h1) / (6 * (h0 + h1))
        result += f[N - 1] * (h1 ** 2 + 3 * h1 * h0)     / (6 * h0)
        result -= f[N - 2] * h1 ** 3                     / (6 * h0 * (h0 + h1))
    return result

SimpsonInt <- function(fx, dx) {
  n <- length(dx)
  h <- diff(dx)
  stopifnot(exprs = {
    length(fx) == n
    all(h >= 0)
  })
  res <- 0
  for (i in seq(1L, n - 2L, 2L)) {
    hph <- h[i] + h[i + 1L]
    hdh <- h[i + 1L] / h[i]
    res <- res + hph / 6 *
      ((2 - hdh) * fx[i] +
         hph ^ 2 / (h[i] * h[i + 1L]) * fx[i + 1L] +
         (2 - 1 / hdh) * fx[i + 2L])
  }

  if (n %% 2 == 0) {
    hph <- h[n - 1L] + h[n - 2L]
    threehth <- 3 * h[n - 1L] * h[n - 2L]
    sixh2 <- 6 * h[n - 2L]
    h1sq <- h[n - 1L] ^ 2
    res <- res +
      (2 * h1sq + threehth) / (6 * hph) * fx[n] +
      (h1sq + threehth) / sixh2 * fx[n - 1L] -
      (h1sq * h[n - 1L]) / (sixh2 * hph) * fx[n - 2L]
  }
  res
}