Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
![]() ;
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
![]() .
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
![]() ,
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
![]() принимают отношение исправленных
принимают отношение исправленных
выборочных дисперсий: .
.
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
![]() называют значение критерия, вычисленное
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсии![]() и
и![]() ,
,
то наблюдаемое значение критерия .
.
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
![]() — одномерная случайная величина, все её
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
![]() называют точки, отделяющие критическую
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
![]() >
>![]() ,
,
где![]() — положительное число.
— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
![]() <
<![]() ,
,
где![]() — отрицательное число.
— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
![]() где
где![]() .
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
![]() >0):
>0):
![]() ,
,
или равносильным неравенством
![]() .
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
![]() >
>![]() ,
,
где![]() >0.
>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
![]() .
.
Затем ищут критическую точку![]() ,
,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерий![]() примет значение, большее
примет значение, большее![]() ,
,
была равна принятому уровню значимости:
Р(![]() >
>![]() )=
)=![]() .
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
![]() >
>![]() ,
,
то нулевую гипотезу отвергают; если же![]() <
<![]() ,
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(![]() >
>![]() )=
)=![]() ?
?
(*)
Поскольку вероятность
события
![]() >
>![]() мала (
мала (![]() — малая вероятность), такое событие при
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше![]() ,
,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
![]() не потому, что нулевая гипотеза ложна,
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости![]() .
.
Итак, пользуясь требованием (*), мы с
вероятностью![]() рискуем совершить ошибку первого рода.
рискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
![]() <
<![]() (
(![]() <0).
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее![]() ,
,
была равна принятому уровню значимости:
Р(![]() <
<![]() )=
)=![]() .
.
Двусторонняя
критическая область определяется
неравенствами
![]() Критические
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшее![]() или большее
или большее![]() ,
,
была равна принятому уровню значимости:
![]() .
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
![]() )и
)и![]() (
(![]() >0),
>0),
то
![]() Учитывая (*), получим
Учитывая (*), получим
![]() .
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
![]() при условии, что нулевая гипотеза
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
![]() ,
,
то мощность равна 1-![]() .
.
Действительно, если![]() — вероятность ошибки второго рода, т.е.
— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —![]() .
.
Пусть мощность 1
—
![]() возрастает; следовательно, уменьшается
возрастает; следовательно, уменьшается
вероятность![]() совершить ошибку второго рода. Таким
совершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
![]() ,
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —![]() ,
,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
![]() и
и![]() невозможно; если уменьшить
невозможно; если уменьшить![]() ,
,
то![]() будет возрастать. Например, если принять
будет возрастать. Например, если принять![]() =0,
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятность![]() ошибки второго рода.
ошибки второго рода.
Как же выбрать
![]() наиболее целесообразно? Ответ на этот
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее![]() .
.
Если
![]() уже выбрано, то, пользуясь теоремой Ю.
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которой![]() будет минимальным и, следовательно,
будет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ![]() ).
).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например: 
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид: 
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение: $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение: $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Внимание!Критерий согласия (X^2) чувствителен к низкочастотным (редким) событиям и может ошибаться на таких выборках. Поэтому низкочастотные события нужно либо отбрасывать, либо объединять с другими событиями. Эта процедура называется коррекцией Йетса.
В Учи.ру мы стараемся даже небольшие улучшения выкатывать A/B-тестом, только за этот учебный год их было больше 250. A/B-тест — мощнейший инструмент тестирования изменений, без которого сложно представить нормальное развитие интернет-продукта. В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьёзные ошибки как на этапе дизайна эксперимента, так и при подведении итогов. В этой статье я расскажу о некоторых технических моментах проведения теста: как мы определяем срок тестирования, подводим итоги и как избегаем ошибочных результатов при досрочном завершении тестов и при тестировании сразу нескольких гипотез.

Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:
- Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
- Определяем срок, на который запускается тест.
- Случайно разбиваем пользователей на две группы.
- Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
- В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
- По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
- Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.
Всё выглядит логично и просто, дьявол, как всегда, в деталях.
Статистическая значимость, критерии и ошибки
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:
- Ошибка первого рода происходит, если мы фиксируем разницу между группами, хотя на самом деле её нет. В тексте также будет встречаться эквивалентный термин — ложноположительный результат. Статья посвящена именно таким ошибкам.
- Ошибка второго рода происходит, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.
При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:
- Есть A/B-тест с контрольной группой A и экспериментальной — B. Цель — проверить, что группа B отличается от группы A по какой-то метрике.
- Формулируем нулевую статистическую гипотезу: группы A и B не отличаются, а наблюдаемые различия объясняются шумом. По умолчанию всегда считаем, что разницы нет, пока не доказано обратное.
- Проверяем гипотезу строгим математическим правилом — статистическим критерием, например, критерием Стьюдента.
- В результате получаем величину p-value. Она лежит в диапазоне от 0 до 1 и означает вероятность увидеть текущую или более экстремальную разницу между группами при условии верности нулевой гипотезы, то есть при отсутствии разницы между группами.
- Значение p-value сравнивается с уровнем значимости 0.05. Если оно больше, принимаем нулевую гипотезу о том, что различий нет, иначе считаем, что между группами есть статистически значимая разница.
Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.
Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.
Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.
Проблема множественного тестирования гипотез
Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп и уровне значимости
вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:
Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.
Метод Холма — Бонферрони
Искушенный читатель знает и о методе Холма — Бонферрони, который всегда обладает большей мощностью, чем поправка Бонферрони, то есть реже совершает ошибки второго рода. В этом методе мы сортируем гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага
по формуле:
P-value первой гипотезы сравнивается с уровнем статистический значимости . Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости
, и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.
Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.
Проблема подглядывания
Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.
Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.
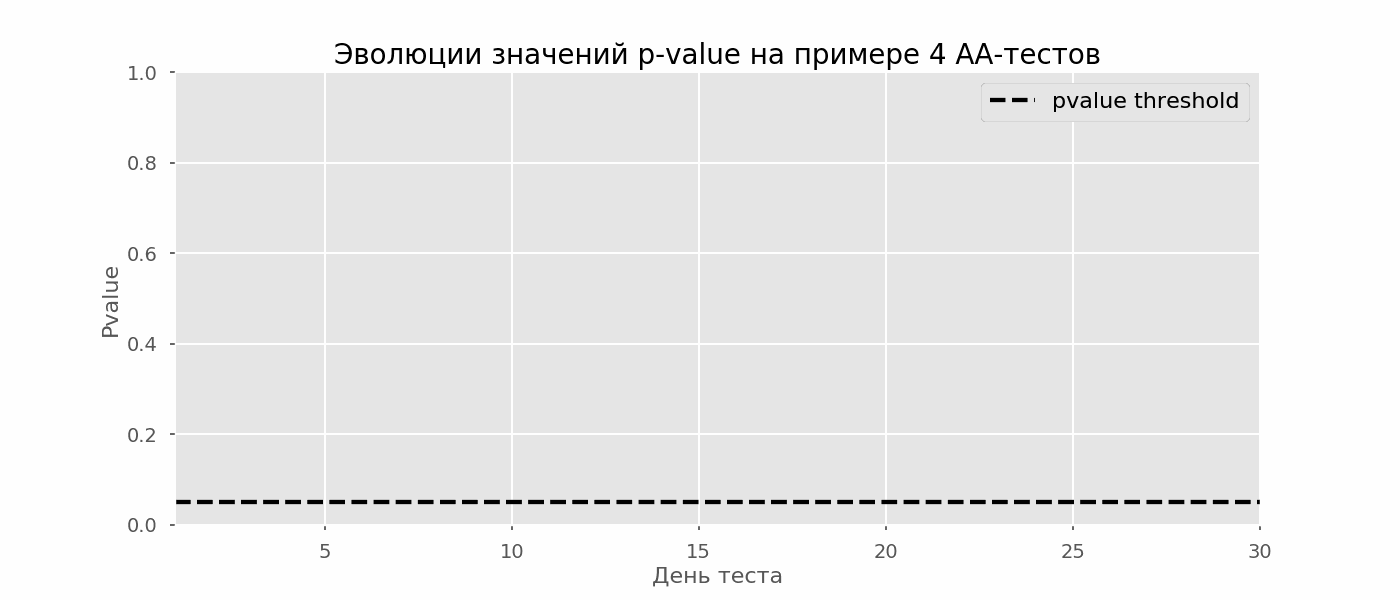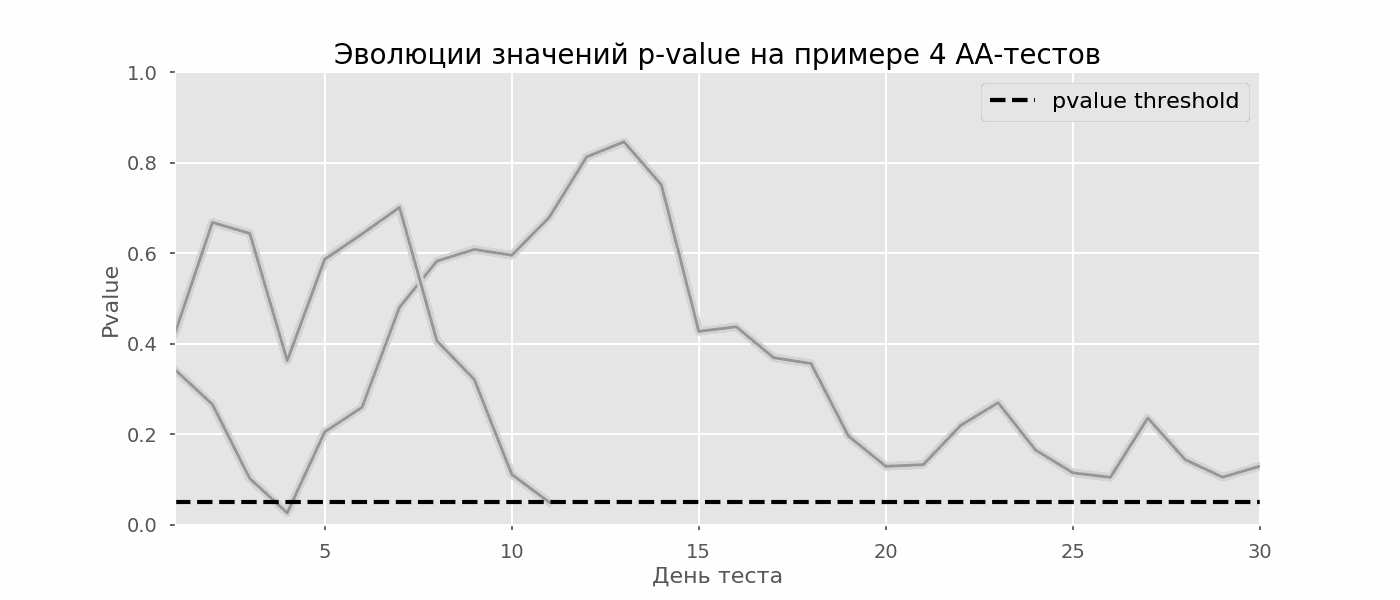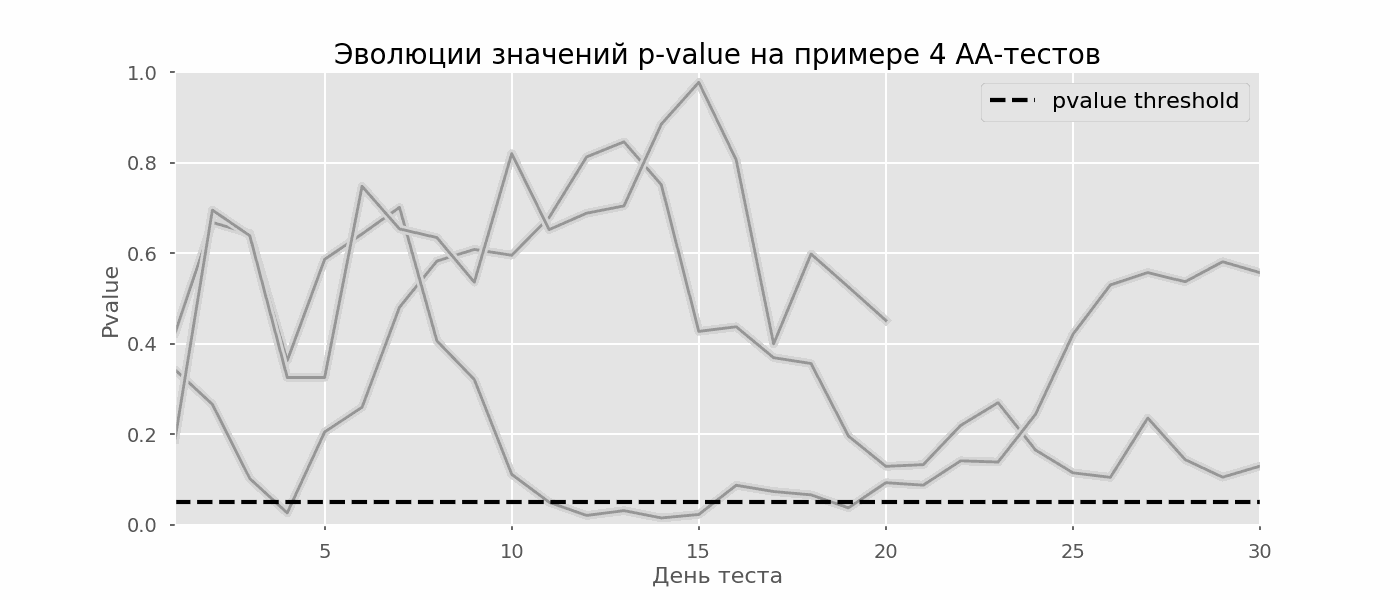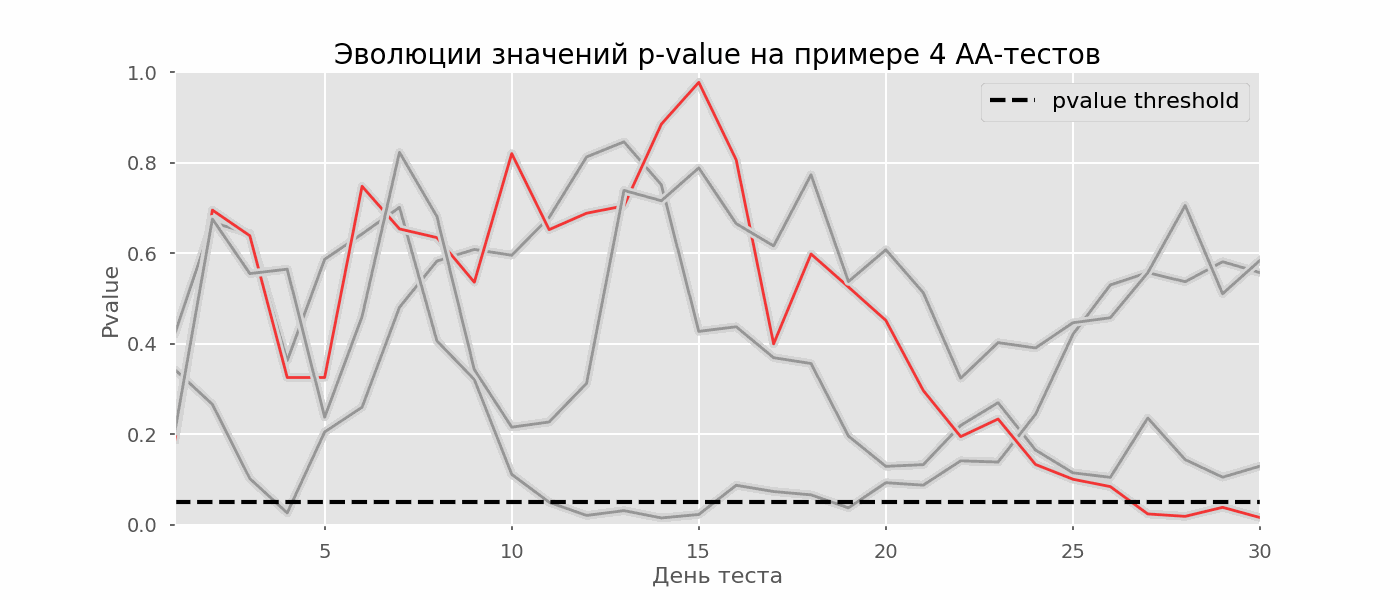
Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.
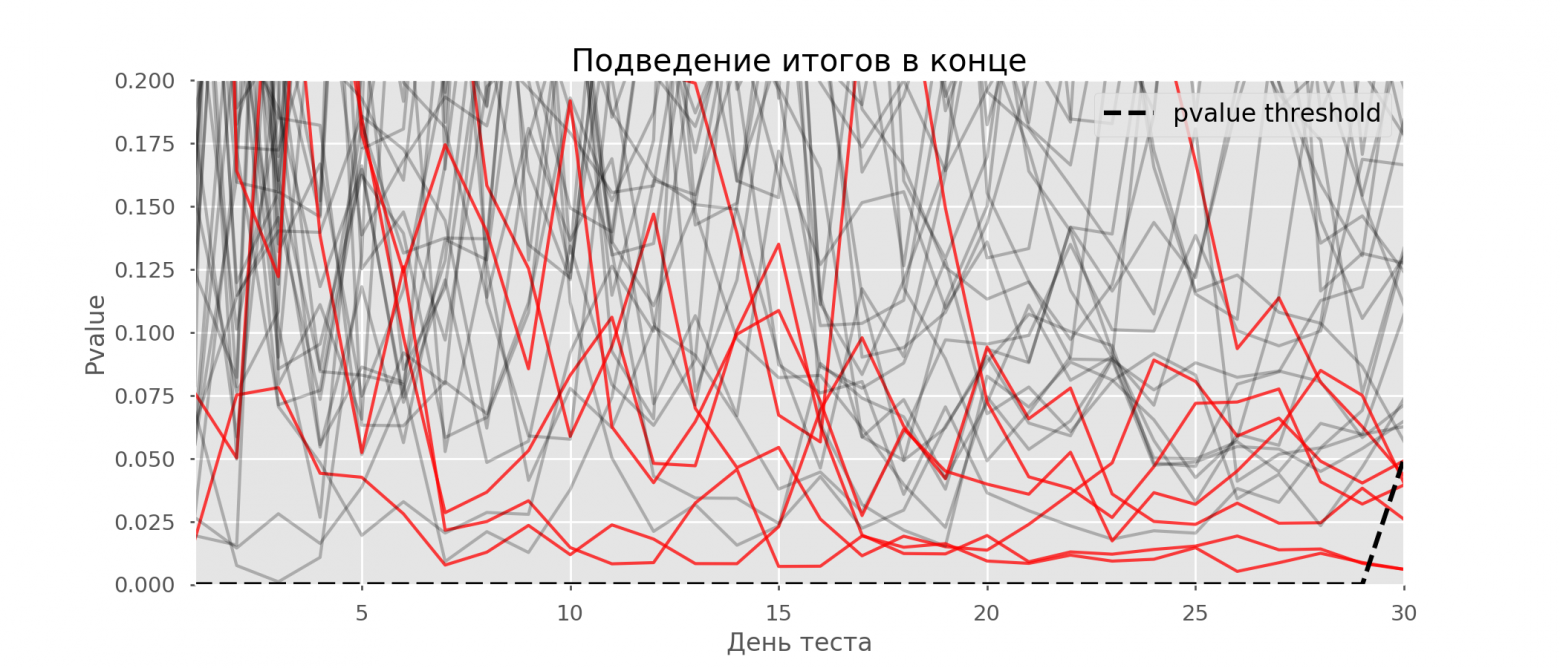
На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:
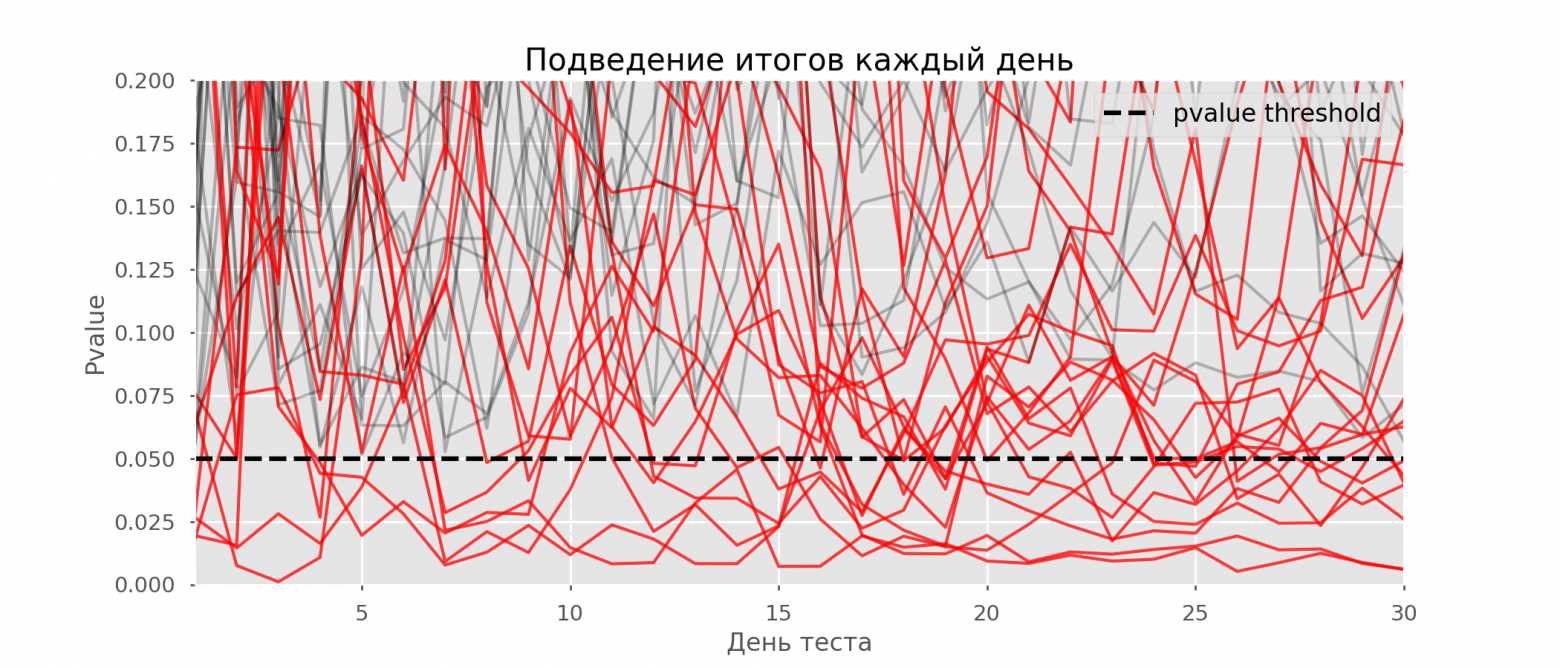
Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:

Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).
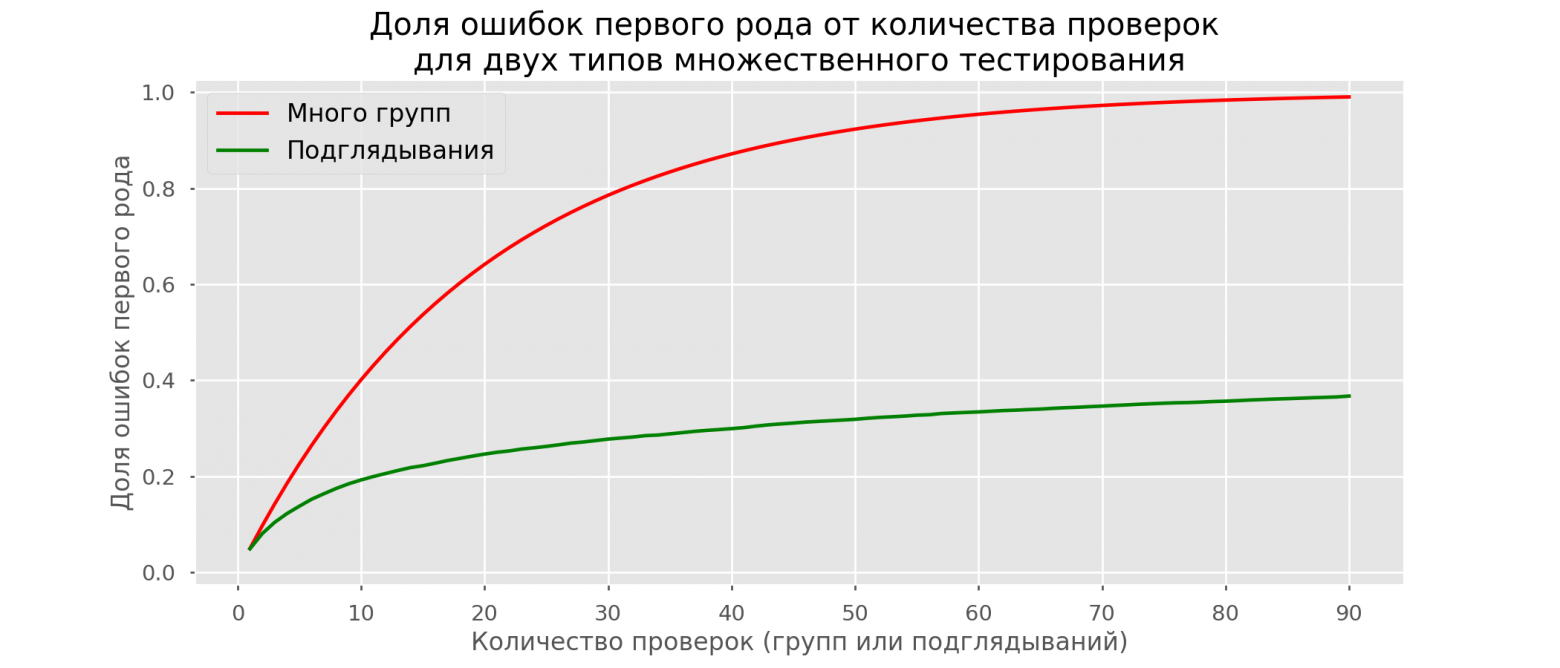
Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.
Байесовский подход и проблема подглядывания
Можно встретить мнение, что Байесовский подход к анализу A/B-тестов избавляет от проблемы подглядывания. Это не так, хотя и его можно настроить соответствующим образом. Отличную статью с дополнительными материалами можно почитать здесь.
Методы досрочного завершения теста
Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O’Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).
Pocock
Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.
O’Brien-Fleming
В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента (в том числе значение на последнем шаге
), соответствующие нужному уровню значимости, зависят от номера проверки
(принимает значения от 1 до общего количества проверок
включительно) и рассчитываются по эмпирически полученной формуле:
Код для воспроизведения коэффициентов
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt
# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081,
2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
[1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_) # [ 0.33729346, -0.63307934]
print(lr.intercept_) # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z)) # 0.999894
total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()
Соответствующие уровни значимости вычисляются через перцентиль стандартного распределения, соответствующий значению статистики Стьюдента
:
perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2
На тех же симуляциях это выглядит так:

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.
Метод Optimizely
Метод Optimizely хорош тем, что позволяет вообще не фиксировать дату окончания теста, а требуемый уровень значимости рассчитывается на каждый момент времени как функция от количества наблюдений в тесте. Интуитивно лично мне их метод нравится меньше, так как в нём жёсткость критерия увеличивается по ходу теста. То есть она минимальна в первые дни, когда случайный шум оказывает наибольшее влияние на метрики. В методе O’Brien-Fleming’a ситуация противоположная.
Калькулятор A/B-тестов
Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:
- какие классы попадают в тест;
- тест раздаётся на учителей или учеников;
- время учебного года;
- тест на всех пользователей или только на новых.
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.

Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте , среднее значение метрики
и её дисперсию
. Зафиксировав доли контрольной группы
, экспериментальной группы
и ожидаемый прирост от теста
в процентах, можно рассчитать ожидаемые значения статистики Стьюдента
и соответствующее p-value на каждый день теста:
Далее легко получить значения p-value на каждый день:
pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2
Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.
Заключение
В качестве заключения хочу напомнить основные посылы статьи:
- Если вы сравниваете средние значения метрики в группах, скорее всего, вам подойдёт критерий Стьюдента. Исключение — экстремально малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я таких не встречал).
- Если в тесте несколько групп, пользуйтесь поправками на множественное тестирование гипотез. Подойдёт простейшая поправка Бонферрони.
- Сравнения по дополнительным метрикам или срезам групп тоже подвержены проблеме множественного тестирования.
- Выбирайте дату завершения теста заранее. Вместо даты также можно зафиксировать количество наблюдений в группе.
- Не подводите итоги теста раньше этой даты. Это можно делать, только если вы заранее решили пользоваться методами, подразумевающими досрочное завершение, например, методом O’Brien-Fleming.
- Когда вносите изменения в схему A/B-тестирования, всегда проверяйте её жизнеспособность A/A-тестами.
Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.
5.3. Ошибки первого и второго рода
Ошибка первого рода состоит в том, что гипотеза ![]() будет отвергнута, хотя на самом деле она правильная. Вероятность
будет отвергнута, хотя на самом деле она правильная. Вероятность
допустить такую ошибку называют уровнем значимости и обозначают буквой ![]() («альфа»).
(«альфа»).
Ошибка второго рода состоит в том, что гипотеза ![]() будет принята, но на самом деле она неправильная. Вероятность
будет принята, но на самом деле она неправильная. Вероятность
совершить эту ошибку обозначают буквой ![]() («бета»). Значение
(«бета»). Значение ![]() называют мощностью критерия – это вероятность отвержения неправильной
называют мощностью критерия – это вероятность отвержения неправильной
гипотезы.
В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения ![]() .
.
И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении
вероятности ![]() —
—
отвергнуть правильную гипотезу растёт вероятность ![]() — принять неверную гипотезу (при прочих равных условиях).
— принять неверную гипотезу (при прочих равных условиях).
Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей ![]() и
и ![]() , при этом учитывается тяжесть последствий, которые
, при этом учитывается тяжесть последствий, которые
повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару
нестатистических примеров.
Петя зарегистрировался в почтовике. По умолчанию, ![]() – он считается добропорядочным пользователем. Так считает антиспам
– он считается добропорядочным пользователем. Так считает антиспам
фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до
адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может
совершить ошибку двух типов:
1) с вероятностью ![]() ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
за спам и Петю за спаммера) или
2) с вероятностью ![]() ошибочно принять нулевую гипотезу (хотя Петя редиска).
ошибочно принять нулевую гипотезу (хотя Петя редиска).
Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра
целесообразно уменьшить уровень значимости ![]() , «пожертвовав» вероятностью
, «пожертвовав» вероятностью ![]() (увеличив её). В результате в основной ящик будут попадать все
(увеличив её). В результате в основной ящик будут попадать все
«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность ![]() следует увеличить (в пользу уменьшения
следует увеличить (в пользу уменьшения
вероятности ![]() ). Не хотел я
). Не хотел я
приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой
дилеммой. Видимо, таки, надо рассказать:
У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение
достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному
увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.
Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные
решения (упаси вас).
Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается
на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,
достаточно, возвращаемся к теме:
 5.4. Процесс проверки статистической гипотезы
5.4. Процесс проверки статистической гипотезы
 5.2. Нулевая и альтернативная гипотезы
5.2. Нулевая и альтернативная гипотезы
| Оглавление |
-
Простые и сложные гипотезы. Статистический критерий различения гипотез. Уровень значимости и мощность критерия. Ошибки первого и второго рода.
Статистической
гипотезой называют гипотезу о виде
неизвестного распределения генеральной
совокупности или о параметрах известных
распределений. Нулевой (основной) называют
выдвинутую гипотезу Н0. Конкурирую-щей
(альтернативной) называют
гипотезу Н1, которая противоречит
нулевой. Простой называют гипотезу,
содержащую только одно предположение,сложной –
гипотезу, состоящую из конечного или
бесконечного числа простых гипотез.
В
результате проверки правильности
выдвинутой нулевой гипотезы ( такая
проверка называется статистической,
так как производится с применением
методов математичес-кой статистики)
возможны ошибки двух видов: ошибка
первого рода,
состоящая в том, что будет отвергнута
правильная нулевая гипотеза, и ошибка
второго рода,
заключаю-щаяся в том, что будет принята
неверная гипотеза.
Замечание. Какая
из ошибок является на практике более
опасной, зависит от конкретной задачи.
Например, если проверяется правильность
выбора метода лечения больного, то
ошибка первого рода означает отказ от
правильной методики, что может замедлить
лече-ние, а ошибка второго рода (применение
неправильной методики) чревата ухудшением
состояния больного и является более
опасной.
Вероятность
ошибки первого рода называется уровнем
значимости α.
Основной
прием проверки статистических гипотез
заключается в том, что по имеющейся
выборке вычисляется значение некоторой
случайной величины, имеющей известный
закон распределения.
Статистическим
критерием называется
случайная величина К с
известным законом распределения,
служащая для проверки нулевой гипотезы.
Мощностью
критерия называют
вероятность попадания критерия в
критическую область при условии, что
верна конкурирующая гипотеза.
Если
обозначить вероятность ошибки второго
рода (принятия неправильной нулевой
гипотезы) β, то мощность критерия равна
1 – β. Следовательно, чем больше мощность
критерия, тем меньше вероятность
совершить ошибку второго рода. Поэтому
после выбора уровня значимости следует
строить критическую область так, чтобы
мощность критерия была максимальной.
-
Числовые характеристики случайных процессов (определение, свойства). Корреляционная теория случайных процессов.
Каждая
случайная величина полностью определяется
своей функцией распределения.
В
то же время при решении практических
задач достаточно знать несколько
числовых параметров, которые позволяют
представить основные особенности
случайной величины в сжатой форме. К
таким величинам относятся в первую
очередь математическое ожидание и
дисперсия.
-
Характеристики
положения
-
Математическое
ожидание случайной величины
Математическое
ожидание — число,
вокруг которого сосредоточены значения
случайной величины. Математическое
ожидание случайной величины обозначается M .
Математическое
ожидание дискретной случайной
величины ,
имеющей распределение
|
x1 |
x2 |
… |
xn |
|
p1 |
p2 |
… |
pn |
называется
величина ![]()
,
если число значений случайной величины
конечно.
Если
число значений случайной величины
счетно, то ![]()
.
При этом, если ряд в правой части
равенства расходится, то говорят, что
случайная величина не имеет
математического ожидания.
Математическое
ожидание непрерывной случайной
величины с
плотностью вероятностей p(x)
вычисляется по формуле ![]()
.
При этом, если интеграл в правой части
равенства расходится, то говорят, что
случайная величина не имеет
математического ожидания.
Если
случайная величина является
функцией случайной величины , =
f(x),
то
![]()
.
Аналогичные
формулы справедливы для функций
дискретной случайной величины:
![]()
, ![]()
.
Основные
свойства математического ожидания:
-математическое
ожидание константы равно этой
константе, Mc=c ;
-математическое
ожидание — линейный функционал на
пространстве случайных величин, т.е.
для любых двух случайных величин , и
произвольных постоянных a и bсправедливо: M(a + b )
= a M( )+ b M( );
-математическое
ожидание произведения двух независимых случайных
величин равно произведению их
математических ожиданий, т.е. M( )
= M( )M( ).
Если
математическое ожидание случайной
величины не существует, то в качестве
характеристики положения случайной
величины применяют моду или медиану.
-
Мода
Модой
случайной величины X
называется такое значение x, при котором
плотность распределения вероятностей
случайной величины f(x)
принимает максимальное значение.
Из определения следует, что мода
определяется только для непрерывных
случайных величин. Аналогом моды для
дискретной случайной величины является
её наивероятнейшее значение. Мода
обозначается через Modx.
-
Медиана
Медианой
случайной величины X
называется такое значение x, которое
разбивает всю область возможных значений
случайной величины на две равновероятные
части, т. е. P|X < x} = P|X > x} = 0,5. Из
определения следует, что медиана, как
и мода, точно может быть определена
только для непрерывных случайных
величин. Медиана обычно обозначается
через Mеdx.
-
Характеристики
разброса
-
Дисперсия
случайной величины
Дисперсия
случайной величины характеризует меру
разброса случайной величины около ее
математического ожидания.
Если
случайная величина имеет
математическое ожидание M ,
то дисперсией случайной
величины называется
величина D = M( — M )2.
Легко
показать, что D = M( — M )2= M 2 — M( )2.
Эта
универсальная формула одинаково хорошо
применима как для дискретных случайных
величин, так и для непрерывных.
Величина M 2 >для
дискретных и непрерывных случайных
величин соответственно вычисляется
по формулам
![]()
, ![]()
.
-
Для
определения меры разброса значений
случайной величины часто используется
среднеквадратичное
отклонение
, связанное
с дисперсией соотношением
.
Основные
свойства дисперсии:
-дисперсия
любой случайной величины
неотрицательна, D ![]()
0;
-дисперсия
константы равна нулю, Dc=0;
-для
произвольной константы D(c )
= c2D( );
-дисперсия
суммы двух независимых случайных
величин равна
сумме их дисперсий: D( )
= D( )
+ D ( ).
-
Моменты
распределения
В
теории вероятностей и математической
статистике, помимо математического
ожидания и дисперсии, используются и
другие числовые характеристики случайных
величин. В первую очередь
это начальные и центральные моменты.
Начальным
моментом k-го порядка случайной
величины называется математическое
ожидание k-й
степени случайной величины ,
т.е. k = M k.
Центральным
моментом k-го порядка случайной
величины называется величина k,
определяемая формулой k = M( — M )k.
Заметим,
что математическое ожидание случайной
величины — начальный момент первого
порядка, 1 = M ,
а дисперсия — центральный момент второго
порядка,
2 = M 2 = M( — M )2 = D .
Существуют
формулы, позволяющие выразить центральные
моменты случайной величины через ее
начальные моменты, например:
2= 2- 12, 3 = 3 — 3 2 1 + 2 13.
Если
плотность распределения вероятностей
непрерывной случайной величины
симметрична относительно прямой x
= M ,
то все ее центральные моменты нечетного
порядка равны нулю.
-
Асимметрия
В
теории вероятностей и в математической
статистике в качестве меры асимметрии
распределения является коэффициент
асимметрии, который определяется
формулой ![]()
,
где 3 —
центральный момент третьего порядка, ![]()
—
среднеквадратичное отклонение.
-
Эксцесс
Нормальное
распределение наиболее часто используется
в теории вероятностей и в математической
статистике, поэтому график плотности
вероятностей нормального распределения
стал своего рода эталоном, с которым
сравнивают другие распределения. Одним
из параметров, определяющих отличие
распределения случайной величины ,
от нормального распределения, является
эксцесс.
Эксцесс случайной
величины определяется
равенством ![]()
.
У
нормального распределения,
естественно, = 0.
Если ( ) > 0, то это означает,
что график плотности вероятностей p (x)
сильнее “заострен”, чем у нормального
распределения, если же ( ) <
0, то “заостренность” графика p (x)
меньше, чем у нормального распределения.
КОРРЕЛЯЦИОННАЯ
ТЕОРИЯ
Корреляционная
теория случайных функций — описание
случайных ф-ций ![]()
при
помощи статистич. моментов 1-го и 2-го
порядка: ![]()
.
Аргумент случайной ф-ции x может
иметь любую размерность. Если ![]()
—
гауссова случайная ф-ция, полностью
определяемая первым и вторым моментами,
то К. т. даёт её полное описание. Обычно
К. т. применяют для таких физ. задач,
к-рые описываются линейными ур-ниями
вида ![]()
= F(x), где ![]()
—
нек-рый линейный оператор, F
(х) — случайная
ф-ция. В этом случае можно получить
ур-ния и для статистич. моментов ![]()
,
![]()
.
Для нелинейных
задач
К. т. обычно имеет приближённый характер.
К. т. наиб. приспособлена для описания
однородных (стационарных) случайных
ф-ций, для к-рых справедлива Винера-Хинчина
теорема. К.
т. используют в большинстве физ.
приложений случайных ф-ций, напр. в
теории флуктуации и
теории когерентности.
Дисциплина:
ТВ и МС Билет № 6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
27.05.201527.69 Mб12Э. Стиллмен, Дж. Грин — Изучаем C#.pdf
5.3. Ошибки первого и второго рода
Ошибка первого рода состоит в том, что гипотеза ![]() будет отвергнута, хотя на самом деле она правильная. Вероятность
будет отвергнута, хотя на самом деле она правильная. Вероятность
допустить такую ошибку называют уровнем значимости и обозначают буквой ![]() («альфа»).
(«альфа»).
Ошибка второго рода состоит в том, что гипотеза ![]() будет принята, но на самом деле она неправильная. Вероятность
будет принята, но на самом деле она неправильная. Вероятность
совершить эту ошибку обозначают буквой ![]() («бета»). Значение
(«бета»). Значение ![]() называют мощностью критерия – это вероятность отвержения неправильной
называют мощностью критерия – это вероятность отвержения неправильной
гипотезы.
В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения ![]() .
.
И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении
вероятности ![]() —
—
отвергнуть правильную гипотезу растёт вероятность ![]() — принять неверную гипотезу (при прочих равных условиях).
— принять неверную гипотезу (при прочих равных условиях).
Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей ![]() и
и ![]() , при этом учитывается тяжесть последствий, которые
, при этом учитывается тяжесть последствий, которые
повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару
нестатистических примеров.
Петя зарегистрировался в почтовике. По умолчанию, ![]() – он считается добропорядочным пользователем. Так считает антиспам
– он считается добропорядочным пользователем. Так считает антиспам
фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до
адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может
совершить ошибку двух типов:
1) с вероятностью ![]() ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
за спам и Петю за спаммера) или
2) с вероятностью ![]() ошибочно принять нулевую гипотезу (хотя Петя редиска).
ошибочно принять нулевую гипотезу (хотя Петя редиска).
Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра
целесообразно уменьшить уровень значимости ![]() , «пожертвовав» вероятностью
, «пожертвовав» вероятностью ![]() (увеличив её). В результате в основной ящик будут попадать все
(увеличив её). В результате в основной ящик будут попадать все
«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью 
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность ![]() следует увеличить (в пользу уменьшения
следует увеличить (в пользу уменьшения
вероятности ![]() ). Не хотел я
). Не хотел я
приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой
дилеммой. Видимо, таки, надо рассказать:
У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение
достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному
увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.
Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные
решения (упаси вас).
Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается
на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,
достаточно, возвращаемся к теме:
 5.4. Процесс проверки статистической гипотезы
5.4. Процесс проверки статистической гипотезы
 5.2. Нулевая и альтернативная гипотезы
5.2. Нулевая и альтернативная гипотезы
| Оглавление |
Сущность задачи проверки статистических гипотез
Статистическая гипотеза
—
представляет собой некоторое предположение о законе
распределения случайной величины или о параметрах этого закона,
формулируемое на основе выборки.
Примерами статистических гипотез являются предположения: генеральная
совокупность распределена по экспоненциальному закону; математические
ожидания двух экспоненциально распределенных выборок равны друг другу. В
первой из них высказано предположение о виде закона распределения, а во
второй – о параметрах двух распределений. Гипотезы, в основе которых
нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.
Гипотезу, утверждающую, что различие между
сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения
объясняются лишь случайными колебаниями в выборках, на основании которых
производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.
Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины.
Например, если l
является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l
=10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l
> 10 состоит из бесконечного множества простых гипотез Н0 о равенстве l
=bi , где bi – любое число, большее 10. Гипотеза Н0
о том, что математическое ожидание нормального распределения равно двум
при неизвестной дисперсии, тоже является сложной. Сложной гипотезой
будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.
Проверка гипотезы основывается на вычислении
некоторой случайной величины – критерия, точное или приближенное
распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn).
Процедура проверки гипотезы предписывает каждому значению критерия одно
из двух решений – принять или отвергнуть гипотезу. Тем самым все
выборочное пространство и соответственно множество значений критерия
делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью.
Выбор одной области однозначно определяет и другую область.
Принятие или отклонение гипотезы Н0 по
случайной выборке соответствует истине с некоторой вероятностью и, соответственно,
возможны два рода ошибок.
Ошибка первого рода
—
возникает с вероятностью a тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1.
Ошибка второго рода
—
возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1.
Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0.
Вероятность отвергнуть ложную гипотезу Н0 называется мощностью критерия.
Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл. 3.1.
Таблица 3.1.
| Гипотеза Н0 | Решение | Вероятность | Примечание |
| Верна | Принимается | 1–a | Доверительная вероятность |
| Отвергается | a | Вероятность ошибки первого рода | |
| Неверна | Принимается | b | Вероятность ошибки второго рода |
| Отвергается | 1–b | Мощность критерия |
Например, рассмотрим случай, когда некоторая несмещенная оценка параметра q
вычислена по выборке объема n, и эта оценка имеет плотность распределения f(q
), рис. 3.1.
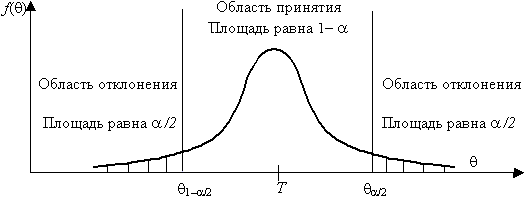
Рис. 3.1. Области и отклонения гипотезы
Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н0 о равенстве q
=Т, то насколько велико должно быть различие между q
и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос
можно в статистическом смысле, рассматривая вероятность достижения
некоторой заданной разности между q
и Т на основе выборочного распределения параметра q
.
Целесообразно полагать одинаковыми значения вероятности выхода параметра q
за нижний и верхний пределы интервала. Такое допущение во многих
случаях позволяет минимизировать доверительный интервал, т.е. повысить
мощность критерия проверки. Суммарная вероятность того, что параметр q
выйдет за пределы интервала с границами q
1–a
/2 и q
a
/2, составляет величину a
. Эту величину следует выбрать настолько
малой, чтобы выход за пределы интервала был маловероятен. Если оценка
параметра попала в заданный интервал, то в таком случае нет оснований
подвергать сомнению проверяемую гипотезу, следовательно, гипотезу
равенства q
=Т можно принять. Но если после получения
выборки окажется, что оценка выходит за установленные пределы, то в этом
случае есть серьезные основания отвергнуть гипотезу Н0. Отсюда следует, что вероятность допустить ошибку первого рода равна a
(равна уровню значимости критерия).
Если предположить, например, что истинное значение параметра в действительности равно Т+d, то согласно гипотезе Н0 о равенстве q
=Т – вероятность того, что оценка параметра q
попадет в область принятия гипотезы, составит b
, рис. 3.2.
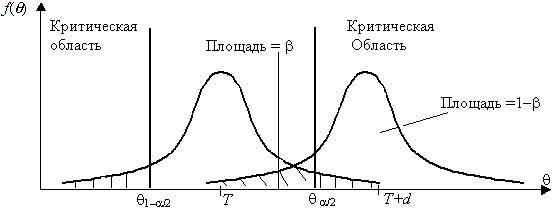
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a
. Однако при этом увеличивается вероятность ошибки второго рода b
(снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т – d.
Единственный способ уменьшить обе вероятности состоит
в увеличении объема выборки (плотность распределения оценки параметра
при этом становится более «узкой»). При выборе критической области
руководствуются правилом Неймана – Пирсона: следует так выбирать
критическую область, чтобы вероятность a
была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения a
относительно произволен. Употребительные значения лежат в пределах от
0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы
интервалов с границами q
1–a
/2 и q
a
/2 для типовых значений a
и различных способов построения критерия.
При выборе уровня значимости необходимо учитывать
мощность критерия при альтернативной гипотезе. Иногда большая мощность
критерия оказывается существеннее малого уровня значимости, и его
значение выбирают относительно большим, например 0,2. Такой выбор
оправдан, если последствия ошибок второго рода более существенны, чем
ошибок первого рода. Например, если отвергнуто правильное решение
«продолжить работу пользователей с текущими паролями», то ошибка первого
рода приведет к некоторой задержке в нормальном функционировании
системы, связанной со сменой паролей. Если же принято решения не менять
пароли, несмотря на опасность несанкционированного доступа посторонних
лиц к информации, то эта ошибка повлечет более серьезные последствия.
В зависимости от сущности проверяемой гипотезы и
используемых мер расхождения оценки характеристики от ее теоретического
значения применяют различные критерии. К числу наиболее часто
применяемых критериев для проверки гипотез о законах распределения
относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о
значениях параметров – критерии Фишера, Стьюдента.
3.2. Типовые распределения
При проверке гипотез широкое применение находит ряд
теоретических законов распределения. Наиболее важным из них является
нормальное распределение. С ним связаны распределения хи-квадрат,
Стьюдента, Фишера, а также интеграл вероятностей. Для указанных законов
функции распределения аналитически не представимы. Значения функций
определяются по таблицам или с использованием стандартных процедур
пакетов прикладных программ. Указанные таблицы обычно построены в целях
удобства проверки статистических гипотез в ущерб теории распределений –
они содержат не значения функций распределения, а критические значения
аргумента z(a
).
Для односторонней критической области z(a
) = z1–a
, т.е. критическое значение аргумента z(a
) соответствует квантили z1–a
уровня 1– a
, так как 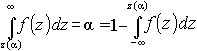 , рис. 3.3.
, рис. 3.3.
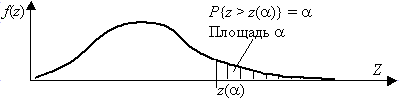
Для двусторонней критической области, с уровнем значимости a , размер левой области a 2, правой a 1 (a 1+a 2=a ), рис. 3.4. Значения z(a 2) и z(a 1) связаны с квантилями распределения соотношениями z(a 1)=z1–a 1, z(a 2)=za 2, так как 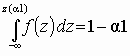 ,
, 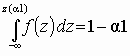 . Для симметричной функции плотности распределения f(z) критическую область выбирают из условия a 1=a 2=a /2 (обеспечивается наибольшая мощность критерия). В таком случае левая и правая границы будут равны |z(a /2)|.
. Для симметричной функции плотности распределения f(z) критическую область выбирают из условия a 1=a 2=a /2 (обеспечивается наибольшая мощность критерия). В таком случае левая и правая границы будут равны |z(a /2)|.
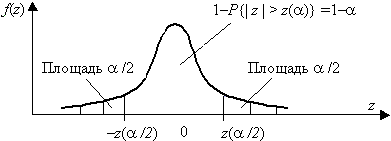
Рис. 3.4. Двусторонняя критическая область
Нормальное распределение
Этот вид распределения является наиболее важным в
связи с центральной предельной теоремой теории вероятностей:
распределение суммы независимых случайных величин стремится к
нормальному с увеличением их количества при произвольном законе
распределения отдельных слагаемых, если слагаемые обладают конечной
дисперсией. Так как реальные физические явления часто представляют собой
результат суммарного воздействия многих факторов, то в таких случаях
нормальное распределение является хорошим приближением наблюдаемых
значений. Функция плотности нормального распределения
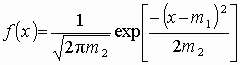
(3.1)
– унимодальная, симметричная, аргумент х может принимать любые действительные значения, рис. 3.5.
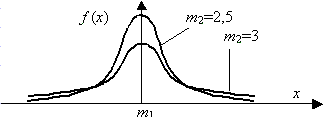
Рис. 3.5. Плотность нормального распределения
Функция плотности нормального распределения стандартизованной величины u имеет вид:
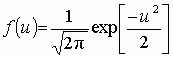
Вычисление значений функции распределения Ф(u) для стандартизованного неотрицательного аргумента u (u ³
0) можно произвести с помощью полинома наилучшего приближения [9, стр. 694]
Ф(u)= 1– 0,5(1 + 0,196854u + 0,115194u2 +
+ 0,000344u3 + 0,019527u4)– 4.(3.2)
Такая аппроксимация обеспечивает абсолютную ошибку не более 0,00025. Для вычисления Ф(u) в области отрицательных значений стандартизованного аргумента u (u<0) следует воспользоваться свойством симметрии нормального распределения Ф(u) = 1 –Ф(–u).
Иногда в справочниках вместо значений функции Ф(u) приводят значения интеграла вероятностей
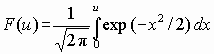
, u > 0.(3.3)
Интеграл вероятностей связан с функцией нормального распределения соотношением Ф(u) = 0,5 + F(u).
Распределение хи-квадрат
Распределению хи-квадрат (c
2-распределению) с k степенями свободы соответствует распределение суммы 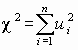 квадратов n стандартизованных случайных величин ui, каждая из которых распределена по нормальному закону, причем k из них независимы, n ³
квадратов n стандартизованных случайных величин ui, каждая из которых распределена по нормальному закону, причем k из них независимы, n ³
k. Функция плотности распределения хи-квадрат с k степенями свободы
![]()
, xі0,(3.4)
где х = c
2, Г(k/2) – гамма-функция.
Число степеней свободы k определяет количество независимых слагаемых в выражении для c
2. Функция плотности при k, равном одному или двум, – монотонная, а при k >2 – унимодальная, несимметричная, рис. 3.6.
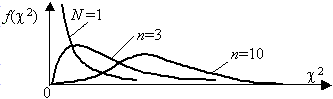
Рис. 3.6. Плотность распределения хи-квадрат
Математическое ожидание и дисперсия величины c
2 равны соответственно k и 2k.
Распределение хи-квадрат является частным случаем более общего
гамма-распределения, а величина, равная корню квадратному из хи-квадрат с
двумя степенями свободы, подчиняется распределению Рэлея.
С увеличением числа степеней свободы (k >30) распределение хи-квадрат приближается к нормальному распределению с математическим ожиданием k и дисперсией 2k. В таких случаях критическое значение c 2(k; a ) » u1– a (k, 2k), где u1– a (k, 2k) – квантиль нормального распределения. Погрешность аппроксимации не превышает нескольких процентов.
Распределение Стьюдента
Распределение Стьюдента (t-распределение, предложено в 1908 г. английским статистиком В. Госсетом, публиковавшим научные труды под псевдонимом Student) характеризует распределение случайной величины 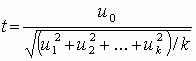 , где u0, u1, …, uk взаимно независимые нормально распределенные случайные величины с нулевым средним и конечной дисперсией. Аргумент t не зависит от дисперсии слагаемых. Функция плотности распределения Стьюдента
, где u0, u1, …, uk взаимно независимые нормально распределенные случайные величины с нулевым средним и конечной дисперсией. Аргумент t не зависит от дисперсии слагаемых. Функция плотности распределения Стьюдента
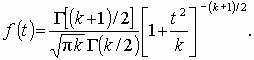
(3.5)
Величина k
характеризует количество степеней свободы. Плотность распределения –
унимодальная и симметричная функция, похожая на нормальное
распределение, рис. 3.7.
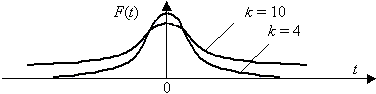
Область изменения аргумента t от –Ґ
до Ґ
. Математическое ожидание и дисперсия равны 0 и k/(k–2) соответственно, при k>2.
По сравнению с нормальным распределение Стьюдента более пологое, оно
имеет меньшую дисперсию. Это отличие заметно при небольших значениях k,
что следует учитывать при проверке статистических гипотез (критические
значения аргумента распределения Стьюдента превышают аналогичные
показатели нормального распределения). Таблицы распределения содержат
значения для односторонней или двусторонней критической области.
Распределение Стьюдента применяется для описания ошибок выборки при k Ј 30. При k >100 данное распределение практически соответствует нормальному, для 30 < k < 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов. Поэтому относительно оценки ошибок малыми считаются выборки объемом не более 30 единиц, большими – объемом более 100 единиц. При аппроксимации распределения Стьюдента нормальным распределением для односторонней критической области вероятность Р{t> t(k; a )} = u1– a (0, k/(k–2)), где u1– a (0, k/(k–2)) – квантиль нормального распределения. Аналогичное соотношение можно составить и для двусторонней критической области.
Распределение Фишера
Распределению Р.А. Фишера (F-распределению Фишера – Снедекора) подчиняется случайная величина х =[(y1/k1)/(y2/k2)],равная отношению двух случайных величин у1и у2, имеющих хи-квадрат распределение с k1 и k2 степенями свободы. Область изменения аргумента х от 0 до ¥
. Плотность распределения
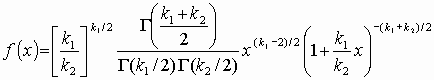
.(3.6)
В этом выражении k1обозначает число степеней свободы величины y1 с большей дисперсией, k2– число степеней свободы величины y2 с меньшей дисперсией. Плотность распределения – унимодальная, несимметричная, рис. 3.8.
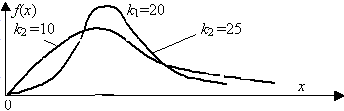
Рис. 3.8. Плотность распределения Фищера
Математическое ожидание случайной величины х равно k2/(k2–2) при k2>2, дисперсия т2 = [2 k22 (k1+k2–2)]/[k1(k2–2)2(k2–4)] при k2 > 4. При k1 > 30 и k2 > 30 величина х распределена приближенно нормально с центром (k1 – k2)/(2 k1 k2) и дисперсией (k1 + k2)/(2 k1 k2).
3.3. Проверка гипотез о законе распределения
Обычно сущность проверки гипотезы о законе распределения ЭД заключается в следующем. Имеется выборка ЭД фиксированного объема, выбран или известен вид закона распределения генеральной совокупности. Необходимо оценить по этой выборке параметры закона, определить степень согласованности ЭД и выбранного закона распределения, в котором параметры заменены их оценками. Пока не будем касаться способов нахождения оценок параметров распределения, а рассмотрим только вопрос проверки согласованности распределений с использованием наиболее употребительных критериев.
Критерий хи-квадрат К. Пирсона
Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределением Fп(x), которая приближенно подчиняется закону распределения c
2. Гипотеза Н0
о согласованности распределений проверяется путем анализа распределения
этой статистики. Применение критерия требует построения статистического
ряда.
Итак, пусть выборка представлена статистическим рядом с количеством разрядов y
. Наблюдаемая частота попаданий в i-й разряд ni. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет Fi. Разность между наблюдаемой и ожидаемой частотой составит величину (n i – Fi). Для нахождения общей степени расхождения между F(x) и Fп(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда
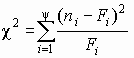
.(3.7)
Величина c
2 при неограниченном увеличении n
имеет распределение хи-квадрат (асимптотически распределена как
хи-квадрат). Это распределение зависит от числа степеней свободы k, т.е. количества независимых значений слагаемых в выражении (3.7). Число степеней свободы равно числу y
минус число линейных связей, наложенных на выборку. Одна связь
существует в силу того, что любая частота может быть вычислена по
совокупности частот в оставшихся y
– 1 разрядах. Кроме того, если параметры распределения неизвестны
заранее, то имеется еще одно ограничение, обусловленное подгонкой
распределения к выборке. Если по выборке определяются f
параметров распределения, то число степеней свободы составит k=y
– f
–1.
Область принятия гипотезы Н0 определяется условием c
2£
c
2(k;a
), где c
2(k;a
) – критическая точка распределения хи-квадрат с уровнем значимости a
. Вероятность ошибки первого рода равна a
, вероятность ошибки второго рода четко определить нельзя, потому что
существует бесконечно большое множество различных способов несовпадения
распределений. Мощность критерия зависит от количества разрядов и объема
выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).
Пример 3.1. Проверить с помощью критерия
хи-квадрат гипотезу о нормальности распределения случайной величины,
представленной статистическим рядом в табл. 2.4 при уровне значимости a
= 0,05.
Решение. В примере 2.3 были вычислены значения оценок моментов: m
1=27,51, m
2 = 0,91, s
= 0,96. На основе табл. 2.4 построим табл. 3.2, иллюстрирующую расчеты.
Таблица 3.2
| Номер интервала, i | 1 | 2 | 3 | 4 | 5 | 6 |
| n i | 5 | 9 | 10 | 9 | 5 | 6 |
| xi | 26,37 | 26,95 | 27,53 | 28,12 | 28,70 | ¥ |
| F(xi) | 0,117 | 0,280 | 0,508 | 0,737 | 0,892 | 1 |
|
D Fi |
0,117 | 0,166 | 0,228 | 0,228 | 0,155 | 0,108 |
| Fi | 5,148 | 7,304 | 10,032 | 10,032 | 6,820 | 4,752 |
| (ni —Fi)2/Fi | 0,004 | 0,394 | 0,0001 | 0,1062 | 0,486 | 0,328 |
В этой таблице:
ni – частота попаданий элементов выборки в i-й интервал;
xi – верхняя граница i-го интервала;
F(xi) – значение функции нормального распределения;
D
Fi – теоретическое значение вероятности попадания случайной величины в i-й интервал
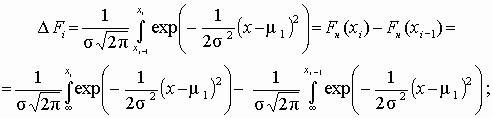
Fi = D
Fi*n – теоретическая частота попадания случайной величины в i-й интервал;
(n i – Fi)2/Fi – взвешенный квадрат отклонения.
Для нормального закона возможные значения случайной величины лежат в диапазоне от – ¥
до ¥
, поэтому при расчетах оценок вероятностей крайний левый и крайний правый интервалы расширяются до – ¥
и ¥
соответственно. Вычислить значения функции нормального распределения
можно, воспользовавшись стандартными функциями табличного процессора или
полиномом наилучшего приближения.
Сумма взвешенных квадратов отклонения c 2=1,32. Число степеней свободы k=6–1–2=3 (уклонения связаны линейным соотношением 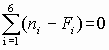 , кроме того, на уклонения наложены еще две связи, так как по выборке были определены два параметра распределения). Критическое значение c 2(3;0,05)= 7,815 определяется по табл. П.3 приложения. Поскольку соблюдается условие c 2 <c 2(3;0,05), то полученный результат нельзя считать значимым и гипотеза о нормальном распределении генеральной совокупности не противоречит ЭД.
, кроме того, на уклонения наложены еще две связи, так как по выборке были определены два параметра распределения). Критическое значение c 2(3;0,05)= 7,815 определяется по табл. П.3 приложения. Поскольку соблюдается условие c 2 <c 2(3;0,05), то полученный результат нельзя считать значимым и гипотеза о нормальном распределении генеральной совокупности не противоречит ЭД.
Критерий А.Н. Колмогорова
Для применения критерия А.Н. Колмогорова ЭД требуется
представить в виде вариационного ряда (ЭД недопустимо объединять в
разряды). В качестве меры расхождения между теоретической F(x) и эмпирической Fn(x) функциями распределения непрерывной случайной величины Х используется модуль максимальной разностиdn = max|F(x) — Fn(x)|.
(3.8)
А.Н. Колмогоров доказал, что какова бы ни была функция распределения F(x) величины Х при неограниченном увеличении количества наблюдений n функция распределения случайной величины dn 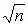 асимптотически приближается к функции распределения
асимптотически приближается к функции распределения 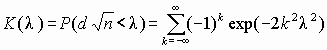 . Иначе говоря, критерий А.Н. Колмогорова характеризует вероятность того, что величина dn не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия
. Иначе говоря, критерий А.Н. Колмогорова характеризует вероятность того, что величина dn не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия 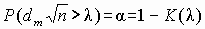 , в силу предположения, что почти невозможно получить это равенство, когда существует соответствие между функциями F(x) и Fn(x). Критерий А.Н. Колмогорова позволяет проверить согласованность распределений по малым выборкам, он проще критерия хи-квадрат, поэтому его часто применяют на практике. Но требуется учитывать два обстоятельства.
, в силу предположения, что почти невозможно получить это равенство, когда существует соответствие между функциями F(x) и Fn(x). Критерий А.Н. Колмогорова позволяет проверить согласованность распределений по малым выборкам, он проще критерия хи-квадрат, поэтому его часто применяют на практике. Но требуется учитывать два обстоятельства.
Во-первых, в точном соответствии с условиями его применения необходимо пользоваться следующим соотношением
![]()
где
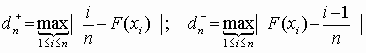
Во-вторых, условия применения критерия
предусматривают, что теоретическая функция распределения известна
полностью (известны вид функции и ее параметры). Но на практике
параметры обычно неизвестны и оцениваются по ЭД. Это приводит к
завышению значения вероятности соблюдения нулевой гипотезы, т.е.
повышается риск принять в качестве правдоподобной гипотезу, которая
плохо согласуется с ЭД (повышается вероятность совершить ошибку второго
рода). В качестве меры противодействия такому выводу следует увеличить
уровень значимости a
, приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.
Пример 3.2. Проверить с помощью критерия А.Н.
Колмогорова гипотезу о том, что ЭД, представленные в табл. 2.3,
подчиняются нормальному распределению при уровне значимости a
=0,1.
Решение. Исходные данные и результаты
вычислений сведены в табл. 3.3. Необходимые вычисления можно провести с
использованием табличного процессора: значение эмпирической функции
распределения Fn(xi)=i/44; значения теоретической функции F(xi) – это значение функции нормального распределения в точке xi.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| xi | 25,79 | 25,98 | 25,98 | 26,12 | 26,13 | 26,49 | 26,52 | 26,60 | 26,66 | 26,69 | 26,74 |
| Fn(xi) | 0,023 | 0,046 | 0,068 | 0,091 | 0,114 | 0,136 | 0,159 | 0,182 | 0,204 | 0,227 | 0,250 |
| F(xi) | 0,036 | 0,055 | 0,055 | 0,073 | 0,075 | 0,144 | 0,151 | 0,170 | 0,188 | 0,196 | 0,211 |
| dn+ | 0,014 | 0,009 | 0,013 | 0,018 | 0,038 | 0,008 | 0,008 | 0,012 | 0,016 | 0,032 | 0,039 |
| dn— | 0,036 | 0,032 | 0,010 | 0,005 | 0,016 | 0,031 | 0,014 | 0,011 | 0,006 | 0,009 | 0,016 |
| i | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| xi | 26,85 | 26,90 | 26,91 | 26,96 | 27,02 | 27,11 | 27,19 | 27,21 | 27,28 | 27,30 | 27,38 |
| Fn(xi) | 0,273 | 0,296 | 0,318 | 0,341 | 0,364 | 0,386 | 0,409 | 0,432 | 0,455 | 0,477 | 0,500 |
| F(xi) | 0,246 | 0,263 | 0,267 | 0,284 | 0,305 | 0,337 | 0,371 | 0,378 | 0,406 | 0,412 | 0,447 |
| dn+ | 0,027 | 0,032 | 0,051 | 0,057 | 0,059 | 0,050 | 0,038 | 0,054 | 0,049 | 0,065 | 0,053 |
| dn— | 0,004 | 0,010 | 0,028 | 0,034 | 0,036 | 0,027 | 0,015 | 0,031 | 0,026 | 0,042 | 0,031 |
| i | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| xi | 27,40 | 27,49 | 27,64 | 27,66 | 27,71 | 27,78 | 27,89 | 27,89 | 28,01 | 28,10 | 28,11 |
| Fn(xi) | 0,523 | 0,546 | 0,568 | 0,591 | 0,614 | 0,636 | 0,659 | 0,682 | 0,705 | 0,727 | 0,750 |
| F(xi) | 0,456 | 0,492 | 0,555 | 0,561 | 0,583 | 0,610 | 0,656 | 0,656 | 0,701 | 0,731 | 0,735 |
| dn+ | 0,067 | 0,053 | 0,013 | 0,030 | 0,031 | 0,026 | 0,003 | 0,026 | 0,003 | 0,004 | 0,015 |
| dn— | 0,044 | 0,031 | 0,010 | 0,007 | 0,008 | 0,003 | 0,019 | 0,003 | 0,020 | 0,027 | 0,008 |
| i | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| xi | 28,37 | 28,38 | 28,50 | 28,63 | 28,67 | 28,90 | 28,99 | 28,99 | 29,03 | 29,12 | 29,28 |
| Fn(xi) | 0,773 | 0,795 | 0,818 | 0,841 | 0,864 | 0,886 | 0,909 | 0,932 | 0,955 | 0,977 | 1,000 |
| F(xi) | 0,817 | 0,819 | 0,851 | 0,879 | 0,888 | 0,928 | 0,939 | 0,940 | 0,944 | 0,954 | 0,968 |
| dn+ | 0,044 | 0,024 | 0,032 | 0,038 | 0,024 | 0,042 | 0,030 | 0,008 | 0,010 | 0,024 | 0,032 |
| dn— | 0,067 | 0,046 | 0,055 | 0,061 | 0,047 | 0,064 | 0,053 | 0,031 | 0,013 | 0,001 | 0,009 |
В данном примере максимальные значения dn+ и dn–одинаковы и равны 0,067. Из табл. П.1 при a =0,1 найдем l =1,22. Для n=44 критическое значение 0,184. Поскольку величина max dn=0,067 меньше критического значения, гипотеза о принадлежности выборки нормальному закону не отвергается.
Критерий Мизеса
В качестве меры различия теоретической функции распределения F(x) и эмпирической Fn(x) по критерию Мизеса (критерию w
2) выступает средний квадрат отклонений по всем значениям аргумента x
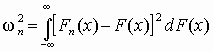
(3.9)
Статистика критерия
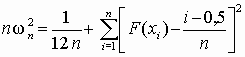
(3.10)
При неограниченном увеличении n существует предельное распределение статистики nw
n2. Задав значение вероятности a
можно определить критические значения nw
n2(a
). Проверка гипотезы о законе распределения осуществляется обычным образом: если фактическое значение nw
n2окажется больше критического или равно ему, то согласно критерию Мизеса с уровнем значимости a
гипотеза Но о том, что закон распределения генеральной совокупности соответствует F(x), должна быть отвергнута.
Пример 3.3. Проверить с помощью критерия
Мизеса гипотезу о том, что ЭД, представленные вариационным рядом, табл.
2.3, подчиняются нормальному распределению при уровне значимости a
= 0,1.
Решение. Исходные данные и результаты вычислений представлены в табл. 3.4.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| xi | 25,79 | 25,98 | 25,98 | 26,12 | 26,13 | 26,49 | 26,52 | 26,60 | 26,66 | 26,69 | 26,74 |
| Fn(xi) | 0,011 | 0,034 | 0,057 | 0,080 | 0,102 | 0,125 | 0,148 | 0,171 | 0,193 | 0,216 | 0,237 |
| F(xi) | 0,036 | 0,055 | 0,055 | 0,073 | 0,075 | 0,144 | 0,151 | 0,170 | 0,188 | 0,196 | 0,211 |
|
D i |
0,618 | 0,429 | 0,003 | 0,047 | 0,726 | 0,378 | 0,009 | 0,000 | 0,025 | 0,409 | 0,742 |
| i | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| xi | 26,85 | 26,90 | 26,91 | 26,96 | 27,02 | 27,11 | 27,19 | 27,21 | 27,28 | 27,30 | 27,38 |
| Fn(xi) | 0,261 | 0,284 | 0,307 | 0,330 | 0,352 | 0,375 | 0,398 | 0,421 | 0,443 | 0,466 | 0,489 |
| F(xi) | 0,246 | 0,263 | 0,267 | 0,284 | 0,305 | 0,337 | 0,371 | 0,378 | 0,406 | 0,412 | 0,447 |
|
D i |
0,231 | 0,439 | 1,572 | 2,071 | 2,243 | 1,467 | 0,717 | 1,790 | 1,391 | 2,866 | 1,755 |
| i | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| xi | 27,40 | 27,49 | 27,64 | 27,66 | 27,71 | 27,78 | 27,89 | 27,89 | 28,01 | 28,10 | 28,11 |
| Fn(xi) | 0,511 | 0,534 | 0,557 | 0,580 | 0,602 | 0,625 | 0,648 | 0,671 | 0,693 | 0,716 | 0,739 |
| F(xi) | 0,456 | 0,492 | 0,555 | 0,561 | 0,583 | 0,610 | 0,656 | 0,656 | 0,701 | 0,731 | 0,735 |
|
D i |
3,103 | 1,765 | 0,003 | 0,332 | 0,374 | 0,216 | 0,063 | 0,213 | 0,067 | 0,238 | 0,013 |
| I | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| xi | 28,37 | 28,38 | 28,50 | 28,63 | 28,67 | 28,90 | 28,99 | 28,99 | 29,03 | 29,12 | 29,28 |
| Fn(xi) | 0,761 | 0,784 | 0,807 | 0,830 | 0,852 | 0,875 | 0,898 | 0,921 | 0,943 | 0,966 | 0,989 |
| F(xi) | 0,817 | 0,819 | 0,851 | 0,879 | 0,888 | 0,928 | 0,939 | 0,940 | 0,944 | 0,954 | 0,968 |
|
D i |
3,090 | 1,230 | 1,908 | 2,461 | 1,271 | 2,791 | 1,737 | 0,381 | 0,001 | 0,149 | 0,432 |
В этой таблице:
Fn(xi)=(i–0,5)/44 – значение эмпирической функции распределения;
F(xi) – значение теоретической функции распределения, соответствует значению функции нормального распределения в точке xi;
D
i =1000[Fn(xi) – F(xi)]2 .Здесь масштабный множитель 1000 введен для удобства отображения данных в таблице, при расчетах он не используется.
Критическое значение статистики критерия Мизеса при заданном уровне значимости равно 0,347, табл. П.2. Фактическое значение статистики , что меньше критического значения. Следовательно, гипотеза Н0 не противоречит имеющимся данным.
Достоинством критерия Мизеса является быстрая
сходимость к предельному закону, для этого достаточно не менее 40
наблюдений в области часто используемых на практике больших значений nw
n (а не несколько сот, как для критерия хи-квадрат).
Сопоставляя возможности различных критериев,
необходимо отметить следующие особенности. Критерий Пирсона устойчив к
отдельным случайным ошибкам в ЭД. Однако его применение требует
группирования данных по интервалам, выбор которых относительно
произволен и подвержен противоречивым рекомендациям. Критерий
Колмогорова слабо чувствителен к виду закона распределения и подвержен
влиянию помех в исходной выборке, но прост в применении. Критерий Мизеса
имеет ряд общих свойств с критерием Колмогорова: оба основаны
непосредственно на результатах наблюдения и не требуют построения
статистического ряда, что повышает объективность выводов; оба не
учитывают уменьшение числа степеней свободы при определении параметров
распределения по выборке, а это ведет к риску принятия ошибочной
гипотезы. Их предпочтительно применять в тех случаях, когда параметры
закона распределения известны априори, например, при проверке датчиков
случайных чисел.
При проверке гипотез о законе распределения следует
помнить, что слишком хорошее совпадение с выбранным законом
распределения может быть обусловлено некачественным экспериментом
(“подчистка” ЭД) или предвзятой предварительной обработкой результатов
(некоторые результаты отбрасываются или округляются).
Выбор критерия проверки гипотезы относительно
произволен. Разные критерии могут давать различные выводы о
справедливости гипотезы, окончательное заключение в таком случае
принимается на основе неформальных соображений. Точно также нет
однозначных рекомендаций по выбору уровня значимости.
Рассмотренный подход к проверке гипотез, основанный
на применении специальных таблиц критических точек распределения,
сложился в эпоху «ручной» обработки ЭД, когда наличие таких таблиц
существенно снижало трудоемкость вычислений. В настоящее время
математические пакеты включают процедуры вычисления стандартных функций
распределений, что позволяет отказаться от использования таблиц, но
может потребовать изменения правил проверки. Например, соблюдению
гипотезы Н0 соответствует такое значение функции распределения критерия, которое не превышает значение доверительной вероятности 1– a
(оценка статистики критерия соответствует доверительному интервалу). В
частности, для примера 3.1 значение статистики критерия хи-квадрат равно
1,318. А значение функции
распределения хи-квадрат для этого значения аргумента при трех степенях
свободы составляет 0,275, что меньше доверительной вероятности 0,95.
Следовательно, нет оснований отвергать нулевую гипотезу.
