Ведение статистики, тестирование различных вариантов данных с отслеживанием эффективности изменений имеет огромное значение в отношении выбора той или иной концепции развития. Однако для анализа важно выбрать только значимые для статистики данные. В этой статье разберемся с понятием статистическая значимость в целом и в A/B тестах, а также рассмотрим, как ее оценивать и рассчитывать.
Что такое статистическая значимость
В процессе любого исследования стоит задача выявить связи между переменными, которые, как правило, характеризуются направлением, силой и надежностью. Чем выше вероятность повторного обнаружения связи, тем она надежнее.
Для проверки гипотез при проведении различных тестов применяется методика статистического анализа. Результатом оценки уровня надежности связи и проверки гипотезы выступает статистическая значимость (statistical significance). Чем меньше вероятность, тем надежнее будет связь.
Статистическая значимость – это параметр, который подтверждает, что результаты исследования были достигнуты не случайно.

Аналитик делает такое заключение, используя метод статистической проверки гипотез. По итогам теста определяется p-значение или значение уровня значимости. Чем оно меньше, тем больше будет статистическая значимость.
Обратите внимание! Слово «значимость» в данном контексте отличается по смыслу от общепринятого. Статистически значимые значения не обязательно являются значимыми или важными. Если же уровень значимости низкий, это не говорит о том, что итоги эксперимента не имеют ценности на практике.
Говоря о статистической значимости, стоит иметь ввиду:
- уровень значимости дает понять, что связь между переменными не случайна;
- уровень значимости в статистике может служить доказательством правдоподобности нулевой гипотезы;
- в ходе проверки получаем информацию о том, что результат эксперимента является или не является статистически значимым.
Значимость статистического критерия применяют при испытаниях вакцин, эффекта новых лекарственных препаратов, изучении болезней, а также при определении, насколько успешна и эффективна работа компании, при A/B тестировании сайтов в маркетинге, а также в различных областях науки, психологии.
История понятия уровня значимости
Статистика помогает решать задачи в различных сферах много веков, однако о статистической значимости заговорили лишь в начале XX столетия. Ввел это понятие в 1925 году британский генетик и статистик сэр Рональд Фишер, который работал над методикой проверки гипотез.

В процессе анализа любого процесса есть вероятность, что произойдут те или иные явления. Итоги эксперимента, которые имели высокую вероятность стать действительными, Фишер описывал словом «значимость» (в переводе с английского significance).
Если данные были недостаточно конкретные для проверки, возникала проблема нулевой гипотезы. Для таких систем в качестве удобной для отклонения нулевой гипотезы выборки исследователем было предложено считать вероятность событий как 5%.
Как оценить статистическую значимость
Для проверки гипотезы используют статистический анализ, при этом уровень значимости определяется с помощью p-значения. Последнее показывает вероятность события, если предположить, что определенная нулевая гипотеза верна.
Весь процесс оценивания уровня значимости можно разделить на 3 стадии, которые, в свою очередь, включают следующие промежуточные этапы.
Постановка эксперимента
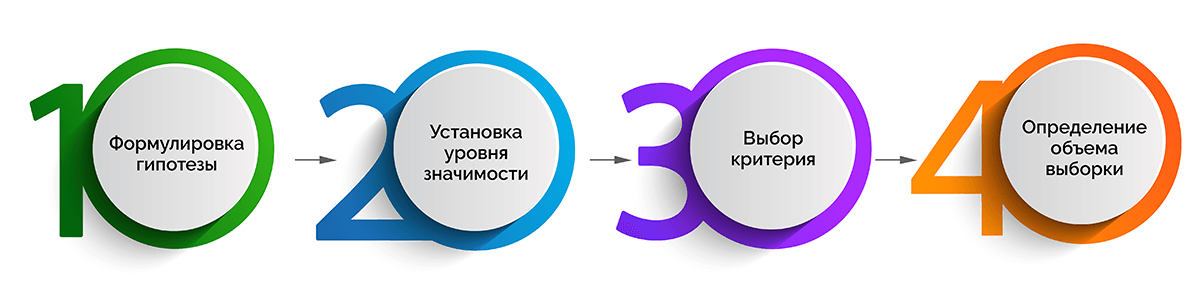
- Формулировка гипотезы.
- Установка уровня значимости, который поможет определить отклонение в распределении данных для идентификации значимого результата.
Если р-значение меньше или равно уровню значимости, данные можно считать статистически значимыми.
- Выбор критерия – одностороннего или двустороннего.
Первый подходит для случаев, когда известно, в какую сторону от нормального значения могут отклониться данные. Второй критерий лучше выбирать, если трудно понять возможное направление отклонения данных от контрольной группы значений. - Определение объема выборки с использованием статистической мощности. Она показывает вероятность того, что при заданной выборке будет получен именно ожидаемый результат. Зачастую пороговая (критическая) цифра мощности – 80%.
Вычисление стандартного отклонения

- Расчет стандартного отклонения, которое показывает величину разброса данных на заданной выборке.
- Поиск среднего значения в каждой исследуемой группе. Для этого осуществляют сложение всех значений, а сумму делят на их количество.
- Определение стандартного отклонения (xi – µ). Разница вычисляется путем вычитания каждого полученного значения из средней величины.
- Возведение полученных величин в квадрат и их суммирование. На данном этапе все числа со знаком «минус» должны исчезнуть.
- Деление суммы на общий объем выборки минус 1. Единица – это генеральная совокупность, которая не учитывается в расчете.
- Извлечение корня квадратного.
Определение значимости
- Определение дисперсии между двумя группами данных по формуле:

sd = √((s1/N1) + (s2/N2)), где:
s1 – стандартной отклонение в первой группе;
s2 – стандартное отклонение во второй группе;
N1 – объем выборки в первой группе;
N2 – объем выборки во 2-й группе. - Поиск t-оценки данных. С ее помощью можно переводить данные в такую форму, которая позволит использовать их в сравнении с другими значениями. T-оценка рассчитывается по формуле:

t = (µ1 – µ2)/sd, где:
µ1 – среднее значение для 1-й группы;
µ2 – среднее значение для 2-й группы;
sd – дисперсия между двумя группами. - Определение степени свободы выборки. Для этого объемы двух выборок складывают и вычитают 2.
- Оценка значимости. Ее осуществляют по таблице значений t-критерия (критерия Стьюдента).
- Повышение уверенности в достоверности выводов путем проведения дальнейшего исследования.
Статистическая значимость и гипотезы
Гипотеза – это теория, предположение. Если требуется проверка гипотез, всегда используется статистическая значимость. Предположение же называется гипотезой до тех пор, пока это утверждение не будет опровергнуто или доказано.

Гипотезы бывают двух типов:
- нулевая гипотеза – теория, не требующая доказательств. Согласно нее, при внесении изменений ничего не произойдет, т. е. стоит задача не доказать это, а опровергнуть;
- альтернативная гипотеза (исследовательская) – теория, в пользу которой нужно отклонить нулевую гипотезу, т. е. предстоит доказать, что одно решение лучше другого.
Рассмотрим, как статистическая значимость влияет на подтверждение или опровержение альтернативной гипотезы на простом примере.
У компании запущена реклама, которая стала давать меньше конверсий и продаж, чем месяц назад. По мнению маркетолога, причина кроется в рекламных креативах, которые приелись аудитории и требуют замены. Специалист предлагает заменить текстовый материал объявления. Гипотеза состоит в том, что после внесенных изменений будет достигнута главная цель эксперимента: клиенты, пришедшие на сайт с рекламы, станут покупать больше. Теперь маркетологу нужно проводить A/B тестирование обоих креативов, чтобы выяснить, какой текст объявления лучше работает. При высоком уровне достоверности данные условия позволят учитывать результаты такого тестирования.
Проверка статистических гипотез
В случаях, когда информация говорит о незначительных изменениях в сравнении с предыдущими значениями, требуется проверка гипотез. Она позволяет определить, действительно ли происходят изменения или это всего лишь результат неточности измерений.
Для этого принимают или отвергают нулевую гипотезу. Задача решается на основании соотношения p-уровня (общей статистической значимости) и α (уровня значимости).
- p-уровень < α – нулевая гипотеза отвергается;
- p-уровень > α – нулевая гипотеза принимается.
Чем меньше значение p-уровня, тем больше шансов, что тестовая статистика актуальна.
Критерии оценки
Уровень значимости для определения степени правдивости полученных результатов обычно устанавливается на отметке 0,05. Таким образом, интервал вероятности между разными вариантами составляет 5%.
После этого необходимо найти подходящий критерий, по которому будут оцениваться выдвинутые гипотезы: односторонний или двусторонний. Для этого применяют разные методы расчета:

- t-критерий Стьюдента;
- u-критерий Манна-Уитни;
- w-критерий Уилкоксона;
- критерий хи-квадрата Пирсона.
T-критерий Стьюдента
предполагает сравнение данных по двум вариантам исследования и позволяет делать выводы о том, по каким параметрам они отличаются. Метод актуален, когда есть сомнения, что данные располагаются ниже или выше относительно нормального распределения.
Установить, все ли данные лежат в заданном пределе, можно с помощью специальной таблицы значений. Но чаще применяют автоматический расчет t-критерия Стьюдента. Существует много калькуляторов, которые работают по схожему принципу:
- Указываем вид расчета (связанные выборки или несвязанные).
- Вносим данные о первой выборке в первую колонку, о второй – во вторую. В одну строку вписываем одно значение, без пропусков и пробелов. Для отделения дробной части от основной используется точка.
- После заполнения обеих колонок, нажимаем кнопку запуска.
Преимущество коэффициента Стьюдента в том, что он применим для любой сферы деятельности, поэтому является самым популярным и используется на практике чаще всего.
Критерий Манна-Уитни
Рассчитывается по иному алгоритму, но предполагает использование аналогичных исходных данных. Его также зачастую рассчитывают онлайн с помощью специальных сервисов.
При расчете критерия Манна-Уитни есть особенности. Показатель применим для малых выборок или выборок с большими выбросами данных. Чем меньше совпадающих значений в выборках, тем корректнее будет работать критерий.
W-критерий Уилкоксона
Непараметрический аналог t-критерия Стьюдента для сравнения показателей до и после эксперимента, основанный на рангах. Его принцип заключается в том, что для каждого участника определяется величина изменения признака. Затем все значения упорядочиваются по абсолютной величине, рангам присваивается знак изменения, после чего «знаковые ранги» суммируются. Данный критерий применяется в медицинской статистике для сравнения показателей пациентов до лечения и после его завершения.
Критерий хи-квадрата Пирсона
Еще один непараметрический метод для оценки уровня значимости двух и более относительных показателей. Применяется для анализа таблиц сопряженности, в которых приведены данные о частотах различных исходов с учетом фактора риска.
Проблема множественного тестирования гипотез
Если сравнивать группы по различным срезам аудитории или метрикам, может возникать проблема множественного тестирования. Дело в том, что учесть абсолютно все проверки достаточно сложно. Это связано со сложностью предварительного прогнозирования их количества. К тому же, зачастую они всё равно не независимы.

Не существует универсального рецепта решения проблемы множественного тестирования гипотез. Аналитики рекомендуют руководствоваться здравым смыслом. Если протестировать много срезов по различным метрикам, любое исследование может показать якобы значимый для статистики результат. Это означает, итоги тестирования следует читать и интерпретировать с осторожностью.
Вычисление объема выборки и стандартного отклонения
После вычисления критерия оценки (критерия Стьюдента или Манна-Уитни) можно определить, какого оптимального объема должна быть выборка. При этом условии должно быть достаточное для признания достоверности результатов исследования количество людей в фокус-группах, на которых будут проверяться разные варианты.
Недостаточное количество участников эксперимента может стать причиной нехватки выборочных данных для того, чтобы сделать статистически значимый вывод и привести к повышению риска получения случайных результатов.
Объем выборки определяют с помощью статистической мощности (распространенный порог находится на уровне 80%). Этот показатель рассчитывают обычно с помощью специального калькулятора.
Затем можно переходить к вычислению уровня стандартного отклонения, по которому можно узнать величину разброса данных. Его рассчитывают по формуле:

s = √∑((xi – µ)2/(N – 1)), где:
xi – i-е значение или полученный результат эксперимента;
µ – среднее значение для конкретной исследуемой группы;
N – общее количество данных.
Для упрощения расчетов также используют онлайн-калькуляторы.
Значение p-уровня
Имея две гипотезы – нулевую и альтернативную, необходимо доказать одну из них (истинную) и опровергнуть другую (ложную).
Для этого основатель теории статистической значимости доктор Рональд Фишер создал определитель, с помощью которого можно было оценить, был эксперимент удачным или нет. Такой определитель получил название индекс достоверности или p-уровень (p-value).
P-уровень или уровень статистической значимости результатов – это показатель, который находится в обратной зависимости от истинного результата и отражает вероятность его ошибочной интерпретации.
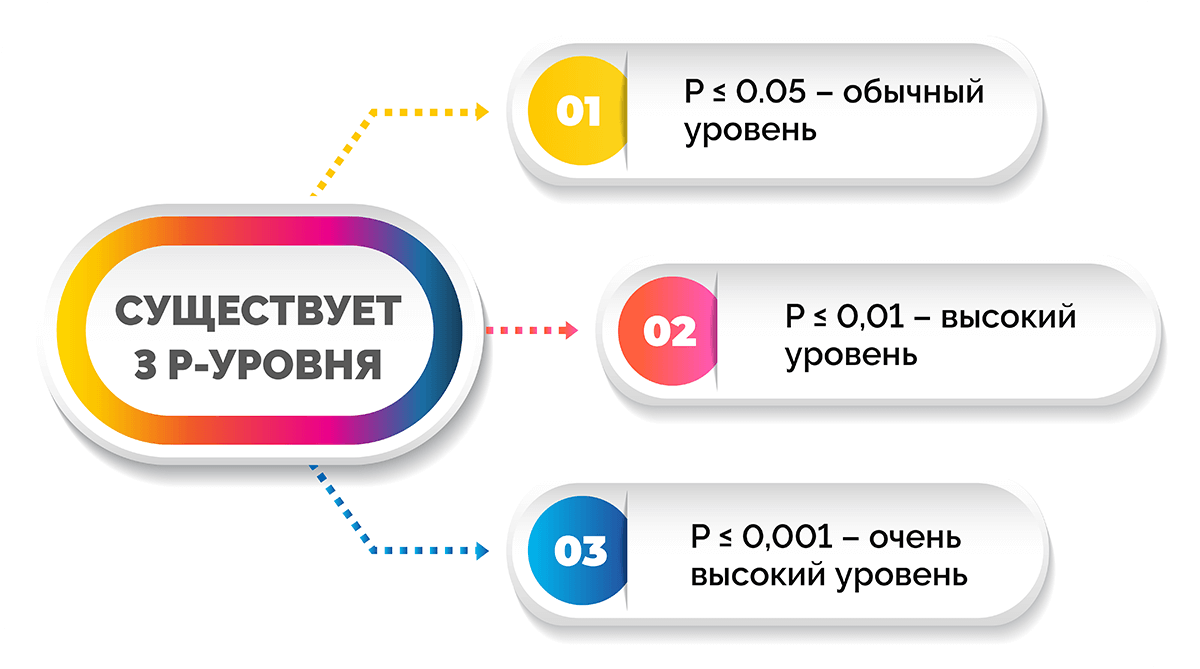
Существует 3 p-уровня.
- P ≤ 0,05 – обычный уровень, т. е. получен статистически значимый результат.
- P ≤ 0,01 – высокий уровень, т. е. выявлена выраженная закономерность.
- P ≤ 0,001 – очень высокий уровень.
Есть и другие значения статистической значимости. Например, уровень p ≥ 0,1 свидетельствует о том, что итог эксперимента не является статистически значимым.
Приближенные к статистически значимым результаты с уровнями p = 0,06 ÷ 0,09 говорят о том, что есть тенденция к существованию искомой закономерности.
Говоря проще, чем ниже значение p-уровня, тем более статистически значимым будет результат эксперимента и тем ниже вероятность ошибки.
Расчет статистической значимости
Выше в статье мы рассматривали порядок оценки уровня статистической значимости. Что касается расчета, то вручную он выполняется редко. Большинство аналитиков определяют уровень значимости с помощью онлайн-калькулятора.
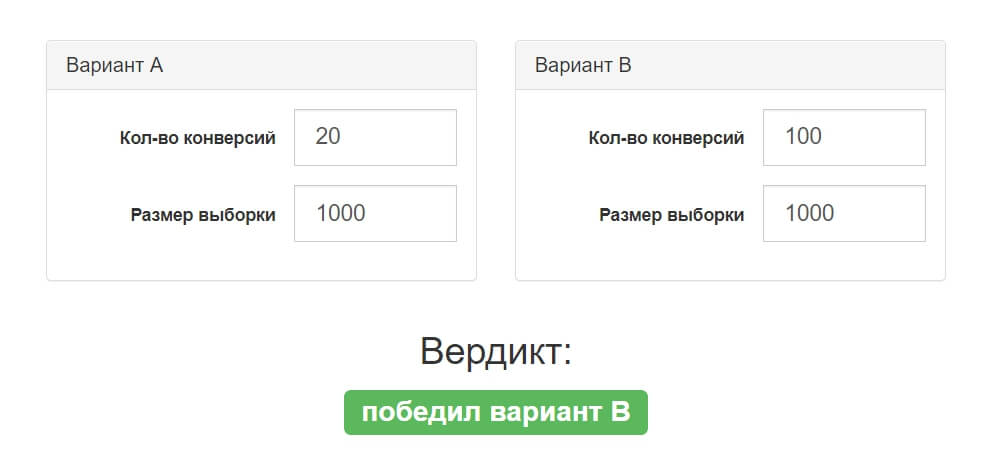
В анализе участвуют две гипотезы, для каждой из которых необходимо задать количество конверсий и размер выборки. Сервис автоматически рассчитывает показатель и определяет уровень значимости результата.
Порог вероятности
Основа статистической значимости – это вероятность получения нужного значения, если принять как факт, что нулевая гипотеза верна. Если предположить, что в процессе эксперимента было получено некое число Х, то при помощи функции плотности вероятности можно узнать, будет ли вероятность получить значение Х или любое другое значение с меньшей вероятностью, чем Х.
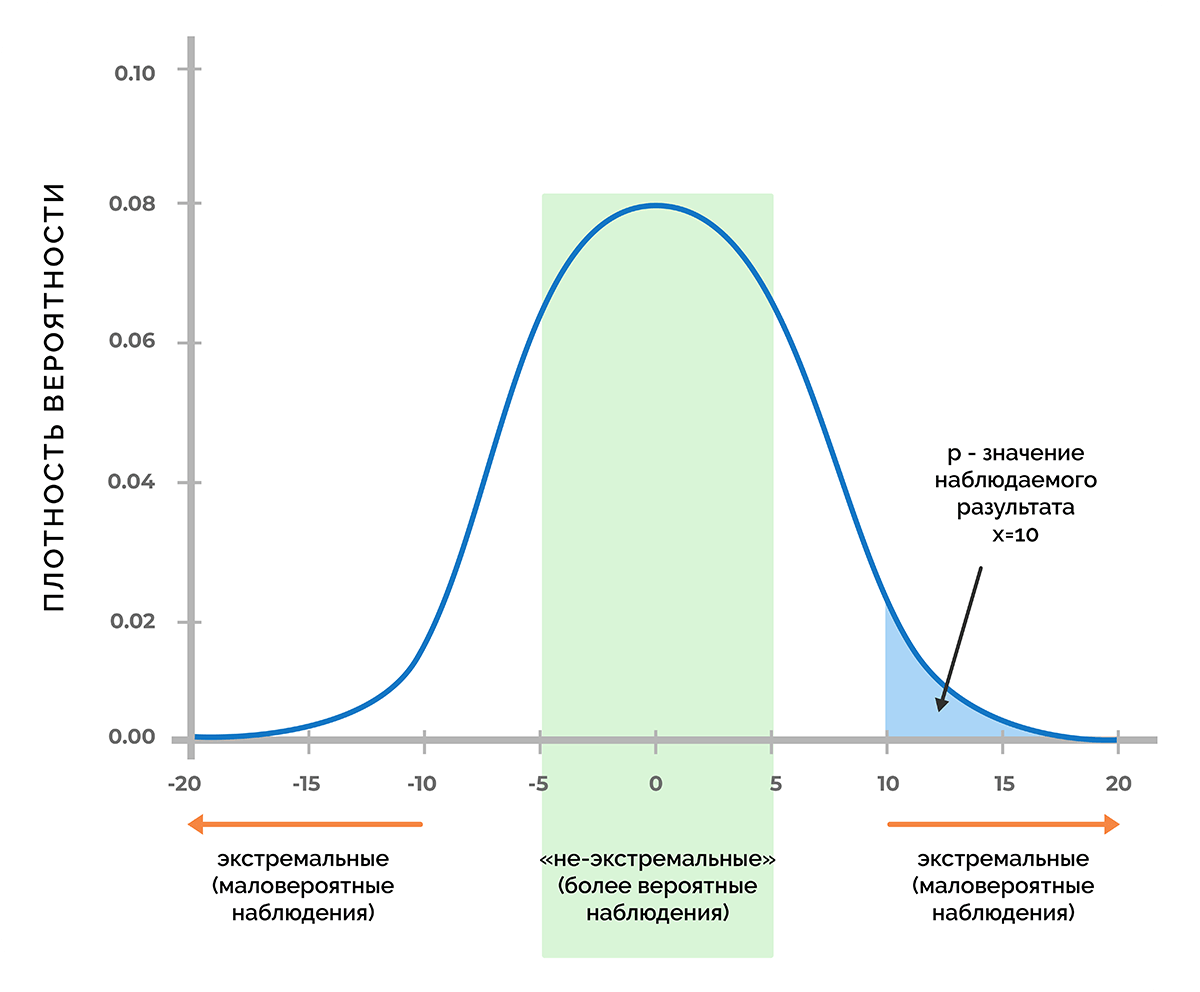
На рисунке изображена кривая Гаусса, соответствующая функции плотности вероятности, которая отвечает распределению значений показателя, при котором верна нулевая гипотеза.
При достаточно низком значении p-уровня не имеет смысла продолжать считать, что переменные не связаны друг с другом. Это позволяет отвергнуть нулевую гипотезу и принять факт того, что связь существует.
Пороги значимости в разных областях могут значительно отличаться. Так, при исследовании вероятности существования бозона Хиггса p-значение равно 1/3,5 млн, в сфере исследования геномов его уровень может достигать 5×10-8.
Статистическая значимость в A/B тестах
Одной из сфер широкого применения статистической значимости является маркетинг. Аналитики используют исследования для поиска оптимальных путей развития бизнеса, интернет-маркетологи оценивают эффективность рекламных кампаний и посещаемость ресурсов.
A/B тестирование – самый распространенный способ оптимизации страниц сайтов. Его результат невозможно предугадать, можно лишь строить алгоритм работы так, чтобы в конце тестирования получить максимальное количество данных, которые позволят сделать вывод о самом удачном варианте.
Важно, чтобы A/B тестирование длилось минимум 7 дней. Это позволит учесть колебания уровней конверсии и других показателей в разные дни.
Процедура A/B тестирования кажется довольно простой:
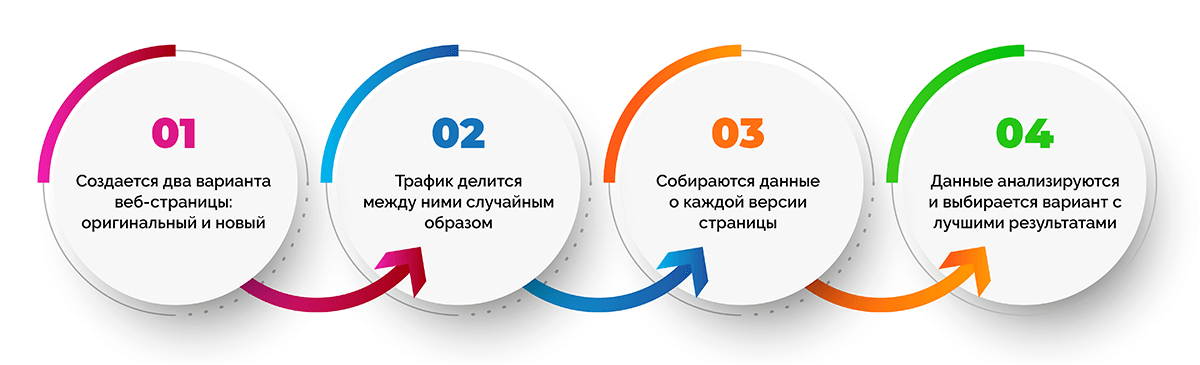
- Создается две веб-страницы (оригинальная и новая).
- Трафик делится между двумя версиями веб-страницы случайным образом.
- Собираются данные о каждой версии страницы.
- Данные анализируются и выбирается вариант с лучшими показателями, а второй отключается.
Важно, чтобы тестирование было достоверным, в противном случае неверное решение может привести к негативным последствиям для сайта.
В данном случае гипотезой считается достижение нужной достоверности. Сама достоверность будет статистической значимостью. Для тестирования гипотезы нужно сформулировать нулевую гипотезу и оценить возможность ее отклонения из-за малой вероятности.
Возможные ошибки
На этапе оценки результатов тестирования можно допустить два типа ошибок:
- ошибка первого рода (type I error) – ложноположительный итог, когда кажется, что различия между показателями двух тестируемых страниц есть, на самом же деле их нет;
- ошибка второго рода (type II error) – ложноотрицательный итог, когда существенная разница между тестируемыми страницами не заметна, но на самом деле она есть, при этом в тестировании видимое ее отсутствие является случайностью.
Как избежать ошибок
Избежать обоих типов ошибок можно, устанавливая при тестировании правильный размер выборки. Чтобы его определить, предстоит в настройках теста задать несколько параметров.
- Чтобы исключить ложноположительные результаты, понадобится указать уровень значимости. Обычно задают значение 0,05, которое будет гарантировать достоверность, превышающую 95%.
- Чтобы избежать ложноотрицательных результатов потребуется минимальная разница в ответах и вероятность обнаружить эту разницу, т. е. статистическая мощность. Последнюю по умолчанию устанавливают на уровне 80%.
Этого достаточно, чтобы вычислить требуемый размер выборки. Обычно расчеты проводятся с помощью спец. калькуляторов.
Можно ли доверять результатам на 100%
К сожалению, даже при правильно проведенной проверке гипотез могут быть допущены ошибки. Это связано с человеческим фактором, а точнее – со скрытыми предположениями, которые зачастую не имеют ничего общего с реальностью.
Вот распространенные предположения, которые приводят к ошибкам:
- посетители сайта, которые просматривают разные варианты веб-страницы, не связаны друг с другом;
- для всех посетителей вероятность конверсии одинакова;
- показатели, которые измеряются в процессе тестирования, имеют нормальное распределение.
На что обратить внимание
Без A/B теста сложно представить развитие современного интернет-продукта. Однако, несмотря на кажущийся простым инструмент, специалисты порой на практике встречаются с подводными камнями. Если знать о них заранее, можно повысить точность тестирования.

Первый узкий момент – проблема подглядывания. Наблюдение за итогами тестирования в реальном времени выступает в качестве соблазна для активных действий, предпринимаемых раньше времени. Обработка «сырых» данных неизменно приводит к статистической погрешности. Чем чаще смотреть на промежуточные результаты A/B теста, тем больше вероятность обнаружить разницу, которой в действительности нет:
- 2 подглядывания с желанием завершить тестирование повышают p-значение в 2 раза;
- 5 подглядывания – в 3,2 раза;
- 10 000 подглядываний – в 12 раз и более.
Решить проблему подглядывания можно тремя способами:
- Заблаговременно фиксировать размер выборки и не смотреть итоги теста до его окончания.
- С помощью математических методов: комбинация Sequential experiment design и байесовского подхода к A/B-тесту.
- С помощью продуктового метода, который предполагает предварительную оценку размера выборки, обеспечивающего эффективность тестирования, и принятие во внимание природы проблемы подглядывания в процессе промежуточных проверок.
Еще один подводный камень заключается в том, что от выигравшей гипотезы ожидают слишком многого. На самом деле в долгосрочной перспективе показатели победителя могут быть менее выдающимися, чем те, которые выдал тест.
Пример статистической значимости
Предположим, разработчики онлайн-игры тестируют два дизайна интерфейса. При A/B тестировании было привлечено 2000 новых игроков: по 1000 пользователей в каждую версию.
В первый день тестирования первая версия дизайна получила 370 возвратов пользователей, вторая – 510.
Как видно, вторая версия дизайна показала лучший результат возвратов. Но разработчики не были уверены, действительно ли это произошло из-за изменения продукта, а не стало следствием случайной погрешности.
Чтобы выяснить это, было принято решение рассчитать уровень значимости для наблюдаемой разницы. Поскольку метрика является простой, можно воспользоваться онлайн-сервисом и вычислить статистическую значимость автоматически.

P-значение < 0,001 в нашем примере свидетельствует о том, что при одинаковых тестовых группах вероятность увидеть наблюдаемую разницу чрезвычайно мала. Это говорит о том, что рост возвратов в первый день с высокой долей вероятности зависит от изменений продукта.
Часто задаваемые вопросы
Маркетинговые исследования статистики чаще всего проводятся путем A/B тестирования. О нем мы рассказали в одном из предыдущих разделов статьи. Однако при тестировании могут возникать некоторые трудности. Например, некорректное определение статистически значимого различия или невозможность определить, чем обусловлено различие. Решить подобные проблемы позволяет увеличение выборки и вариантов.
Оценка необходимости ранжирования данных статистики исключительно на основании статистической значимости может привести к серьезным ошибкам. Предпочтение лишь «значимых» результатов повышает риск искажения фактов.
В процессе тестирования регулярная проверка показателей с готовностью принять решение о завершении теста при обнаружении существенной разницы приводит к кумулятивному накоплению вероятных случайных моментов, при которых разница покидает пределы диапазона. В результате этого каждая новая проверка приводит к росту p-значения.
Заключение
Статистическая значимость является важным методом в ходе проведения экспериментов и исследований несмотря на риск ее неправильной интерпретации. При грамотном подходе погрешность можно свести к минимуму, используя значение в целях повышения достоверности результатов.

Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Уровень
значимости — это вероятность того, что
мы сочли различия существенными, а они
на самом деле случайны.
Когда
мы указываем, что различия достоверны
на 5%-ом уровне значимости, или при р<0,05,
то мы имеем виду, что вероятность того,
что они все-таки недостоверны, составляет
0,05.
Когда
мы указываем, что различия достоверны
на 1%-ом уровне значимости, или при р<0,01,
то мы имеем в виду, что вероятность того,
что они все-таки недостоверны, составляет
0,01.
Если
перевести все это на более формализованный
язык, то уровень значимости — это
вероятность отклонения нулевой гипотезы,
в то время как она верна.
Ошибка,
состоящая в том, что мы отклонили нулевую
гипотезу, в то время как она верна,
называется ошибкой 1 рода.
Вероятность
такой ошибки обычно обозначается как
а. В сущности, мы должны были бы указывать
в скобках не р<0,05 или р<0,01, а а<0,05
или <Х<0,01. В некоторых руководствах
так и делается (Рунион Р., 1982; Захаров
В.П., 1985 и др.).
Если
вероятность ошибки — это а, то вероятность
правильного решения: 1—а. Чем меньше а,
тем больше вероятность правильного
решения.
Исторически
сложилось так, что в психологии принято
считать низшим уровнем статистической
значимости 5%-ый уровень (р<0,05): достаточным
— 1%-ый уровень (р^О.01) и высшим 0,1% -ый
уровень (р<0,001), поэтому в таблицах
критических значений обычно приводятся
значения критериев, соответствующих
уровням статистической значимости
р<0,05 и р<0,01, иногда — р<0,001. Для
некоторых критериев в таблицах указан
точный уровень значимости их разных
эмпирических значений. Например, для
ф*=1,56 р=0,06.
До
тех пор, однако, пока уровень статистической
значимости не достигнет р=0,05, мы еще не
имеем права отклонить нулевую гипотезу.
Правило
отклонения HQ и принятия Hi
Если
эмпирическое значение критерия равняется
критическому значению, соответствующему
р^0,05 или превышает его, то HQ отклоняется,
но мы еще не можем определенно принять
W.
Если
эмпирическое значение критерия равняется
критическому значению, соответствующему
р<0,01 или превышает его, то HQ отклоняется
и принимается Н^.
Исключения:
критерий
знаков G, критерий Т Вилкоксона и критерий
U Манна-Уитни. Для них устанавливаются
обратные соотношения. Для облегчения
процесса принятия решения можно всякий
раз вычерчивать «ось значимости».

Критические
значения критерия обозначены как Qo,O5 и
Qo,O1> эмпирическое значение критерия
как QaMn. Оно заключено в эллипс.
Вправо
от критического значения Qo.oi простирается
«зона значимости» — сюда попадают
эмпирические значения, превышающие
Qooi и, следовательно, безусловно значимые.
Влево
от критического значения Qo,O5 простирается
«зона незначимое™», — сюда попадают
эмпирические значения Q, которые ниже
Qo,O5′ и≫
следовательно, безусловно незначимы.
Мы видим, что Qo,o5=6; Qo.oi=9; Q9Mn=8.
Эмпирическое
значение критерия попадает в область
между Qo,O5 и Qo.oi- Это зона «неопределенности»:
мы уже можем отклонить гипотезу о
недостоверности различий (HQ), НО еще не
можем принять гипотезы об их достоверности
(Hf).
Практически,
однако, исследователь может считать
достоверными уже те различия, которые
не попадают в зону незначимости, заявив,
что они достоверны при р<0,05, или указав
точный уровень значимости полученного
эмпирического значения критерия,
например: р=0,02. С помощью таблиц Приложения
1 это можно сделать по отношению к
критериям Н Крускала-Уоллиса, у}г
Фридмана,
L Пейджа, ф* Фишера, X
Колмогорова.
Уровень
статистической значимости или критические
значения критериев определяются
по-разному при проверке направленных
и ненаправленных статистических гипотез.
При направленной статистической гипотезе
используется односторонний критерий,
при ненаправленной гипотезе — двусторонний
критерий. Двусторонний критерий более
строг, поскольку он проверяет различия
в обе стороны, и поэтому то эмпирическое
значение критерия, которое ранее
соответствовало уровню значимости
р<0,05, теперь соответствует лишь уровню
р<0,10.
Билет 9 Параметрические
и непараметрические методы. Мощность
критериев
-
Параметрические и непараметрические
методы
Методы обучения, т.е. нахождения достаточно
хорошей распознающей функ-
ции f 2 F, традиционно подразделяются на
параметрические и непарамет-
рические в соответствии с тем, просто
или сложно устроено пространство F.
Параметрические — это те методы, в
которых F = fF(w; ¢)jw 2 Wg для неко-
торого достаточно удобного (например,
евклидова) пространства параметров
W и некоторой функции F: W £ X ! Y, а
непараметрические — это мето-
ды, в которых, якобы, пространство F не
зафиксировано заранее, а зависит
от обучающего набора T. На самом деле
разница между параметрическими и
непараметрическими методами — только
в употребляемых словах.
Полезный пример параметрических методов
— методы обучения линейных
распознавателей, которых даже для
простейшей линейной регрессии (X = Rd,
Y
= R,
W
= R
£ Rd,
F(w;
x)
= w0
+Pdj=1
wjxj) довольно много. Подробнее
эти методы рассматриваются в разделе
2.
[А.Б. Мерков]
непараметрические
методы в
математической статистике, методы
непосредственной оценки теоретического
распределения вероятностей и тех или
иных его общих свойств (симметрии и
т.п.) по результатам наблюдений. Название
Н. м. подчёркивает их отличие от
классических (параметрических)
методов, в которых
предполагается, что неизвестное
теоретическое распределение принадлежит
какому-либо семейству, зависящему от
конечного числа параметров (например,
семейству нормальных распределений, и
которые позволяют по результатам
наблюдений оценивать неизвестные
значения этих параметров и проверять
те или иные гипотезы относительно их
значений. Разработка Н. м. является в
значительной степени заслугой советских
учёных.
-
Мощность критериев
Мощность критерия — это его способность
выявлять различия, если они есть. Иными
словами, это его способность отклонить
нулевую гипотезу об отсутствии различий,
если
она неверна.
Ошибка, состоящая в том, что мы приняли
нулевую гипотезу, в то время как
она неверна, называется ошибкой II рода.
Вероятность такой ошибки обозначается
как β. Мощность критерия — это его
способность не допустить ошибку II рода,
поэтому:
Мощность=1—β
Мощность критерия определяется
эмпирическим путем. Одни и те же задачи
могут
быть решены с помощью разных критериев,
при этом обнаруживается, что некоторые
критерии позволяют выявить различия
там, где другие оказываются неспособными
это
сделать, или выявляют более высокий
уровень значимости различий. Возникает
вопрос: а
зачем же тогда использовать менее
мощные критерии? Дело в том, что
основанием для
выбора критерия может быть не только
мощность, но и другие его характеристики,
а
именно:
а) простота;
б) более широкий диапазон использования
(например, по отношению к данным,
определенным по номинативной шкале,
или по отношению к большим n);
в) применимость по отношению к неравным
по объему выборкам;
г) большая информативность результатов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например: 
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид: 
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение: $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение: $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Внимание!Критерий согласия (X^2) чувствителен к низкочастотным (редким) событиям и может ошибаться на таких выборках. Поэтому низкочастотные события нужно либо отбрасывать, либо объединять с другими событиями. Эта процедура называется коррекцией Йетса.
В Учи.ру мы стараемся даже небольшие улучшения выкатывать A/B-тестом, только за этот учебный год их было больше 250. A/B-тест — мощнейший инструмент тестирования изменений, без которого сложно представить нормальное развитие интернет-продукта. В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьёзные ошибки как на этапе дизайна эксперимента, так и при подведении итогов. В этой статье я расскажу о некоторых технических моментах проведения теста: как мы определяем срок тестирования, подводим итоги и как избегаем ошибочных результатов при досрочном завершении тестов и при тестировании сразу нескольких гипотез.

Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:
- Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
- Определяем срок, на который запускается тест.
- Случайно разбиваем пользователей на две группы.
- Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
- В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
- По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
- Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.
Всё выглядит логично и просто, дьявол, как всегда, в деталях.
Статистическая значимость, критерии и ошибки
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:
- Ошибка первого рода происходит, если мы фиксируем разницу между группами, хотя на самом деле её нет. В тексте также будет встречаться эквивалентный термин — ложноположительный результат. Статья посвящена именно таким ошибкам.
- Ошибка второго рода происходит, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.
При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:
- Есть A/B-тест с контрольной группой A и экспериментальной — B. Цель — проверить, что группа B отличается от группы A по какой-то метрике.
- Формулируем нулевую статистическую гипотезу: группы A и B не отличаются, а наблюдаемые различия объясняются шумом. По умолчанию всегда считаем, что разницы нет, пока не доказано обратное.
- Проверяем гипотезу строгим математическим правилом — статистическим критерием, например, критерием Стьюдента.
- В результате получаем величину p-value. Она лежит в диапазоне от 0 до 1 и означает вероятность увидеть текущую или более экстремальную разницу между группами при условии верности нулевой гипотезы, то есть при отсутствии разницы между группами.
- Значение p-value сравнивается с уровнем значимости 0.05. Если оно больше, принимаем нулевую гипотезу о том, что различий нет, иначе считаем, что между группами есть статистически значимая разница.
Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.
Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.
Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.
Проблема множественного тестирования гипотез
Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп и уровне значимости
вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:
Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.
Метод Холма — Бонферрони
Искушенный читатель знает и о методе Холма — Бонферрони, который всегда обладает большей мощностью, чем поправка Бонферрони, то есть реже совершает ошибки второго рода. В этом методе мы сортируем гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага
по формуле:
P-value первой гипотезы сравнивается с уровнем статистический значимости . Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости
, и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.
Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.
Проблема подглядывания
Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.
Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.
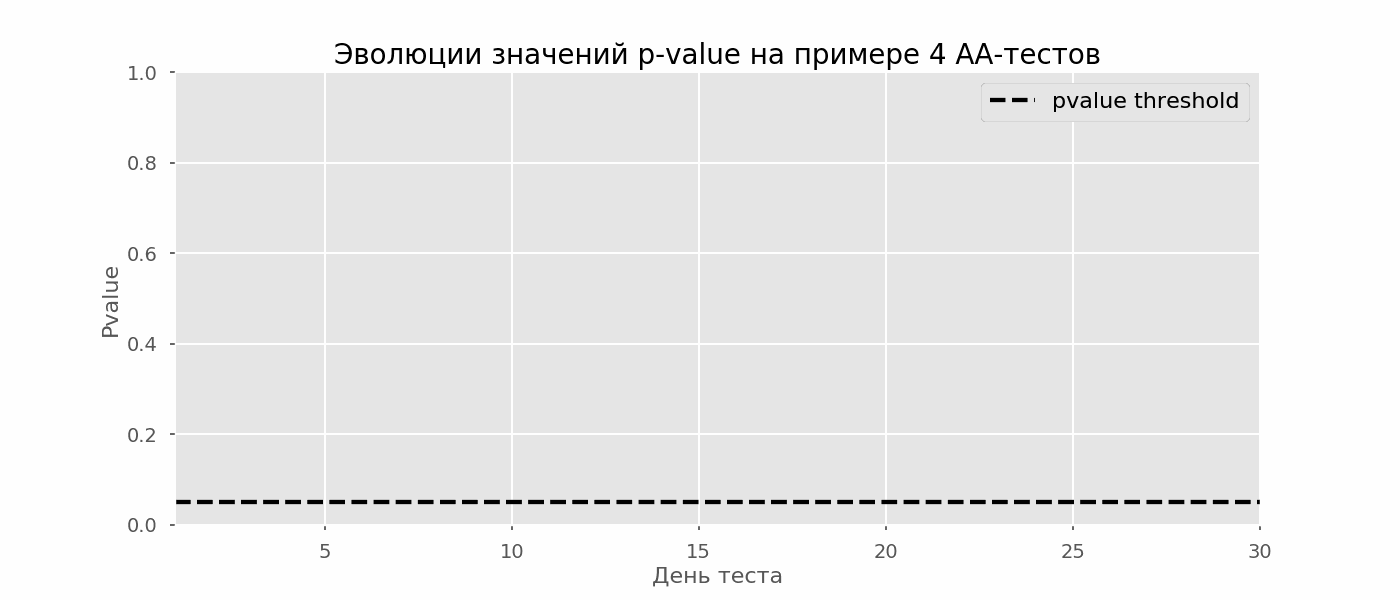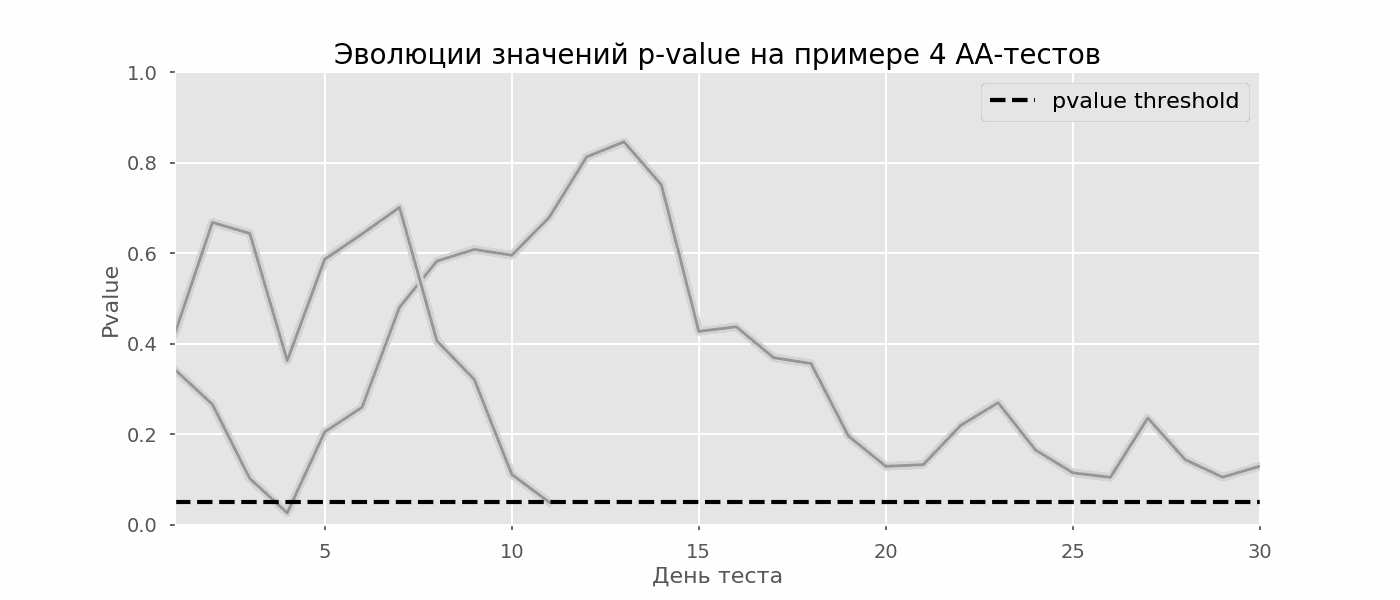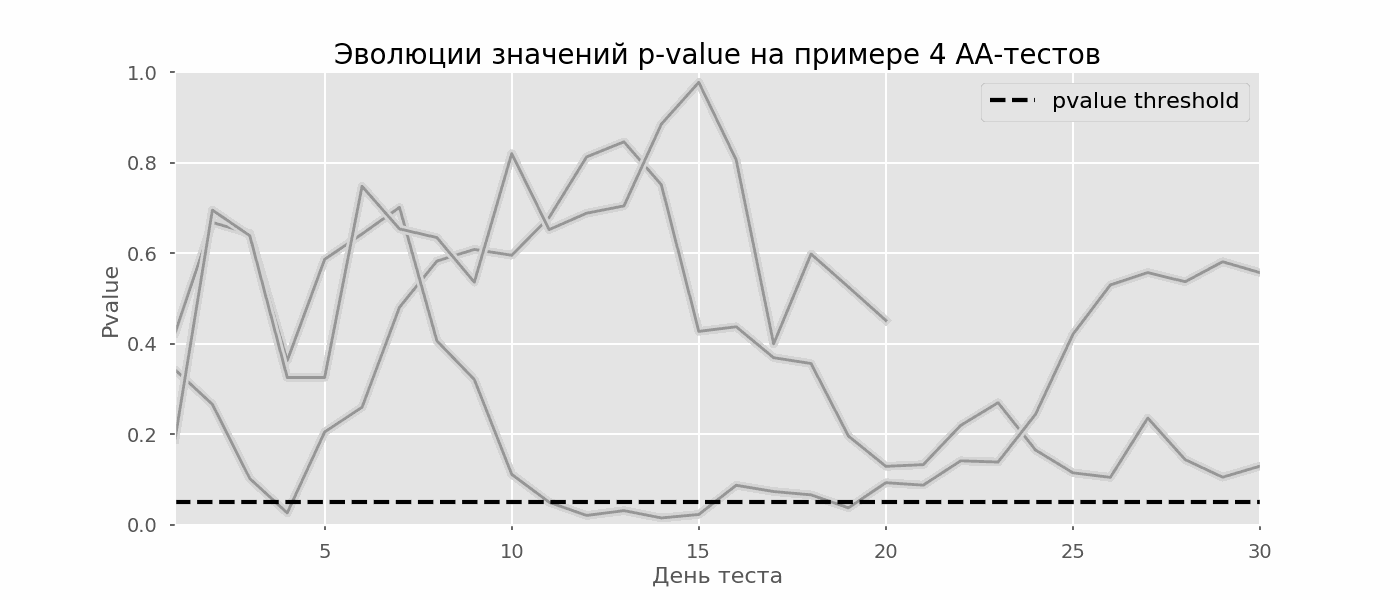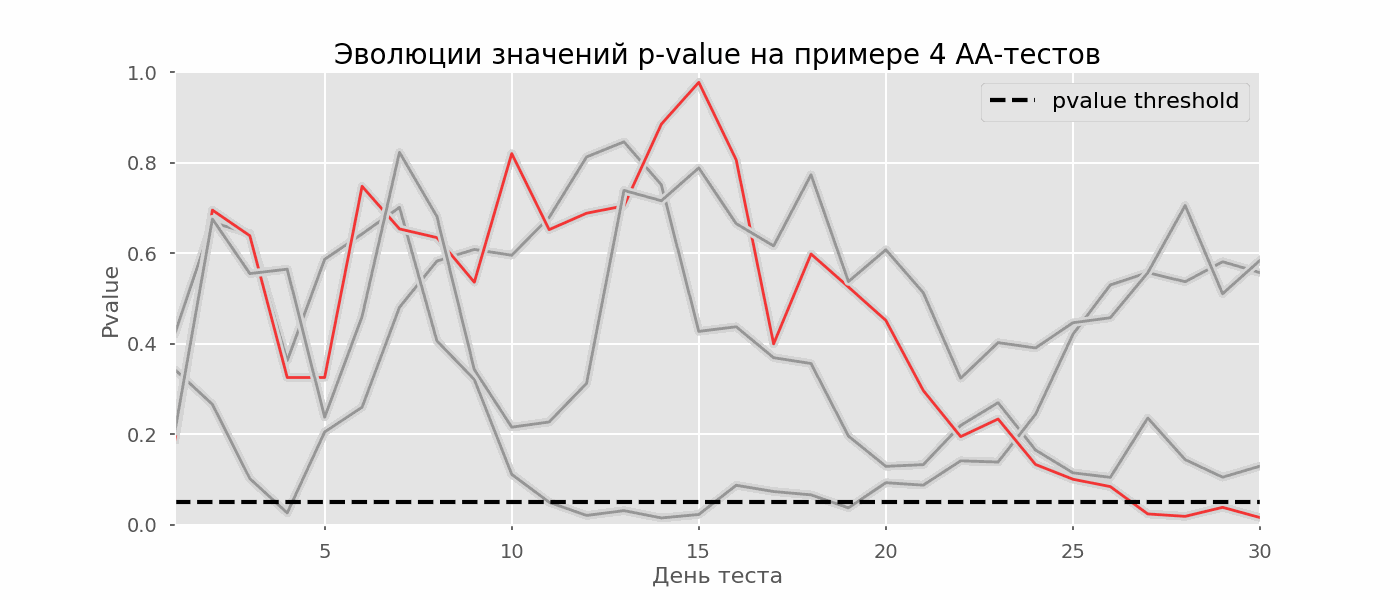
Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.
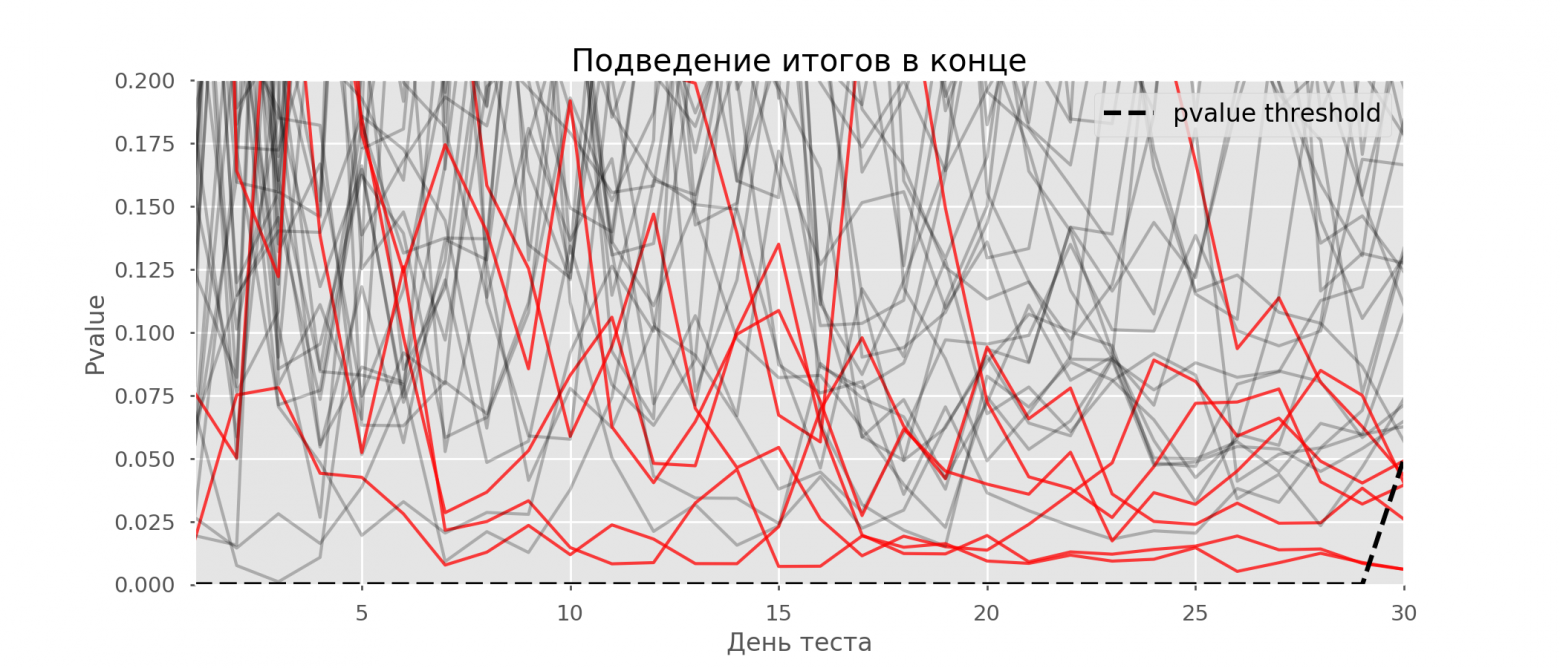
На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:
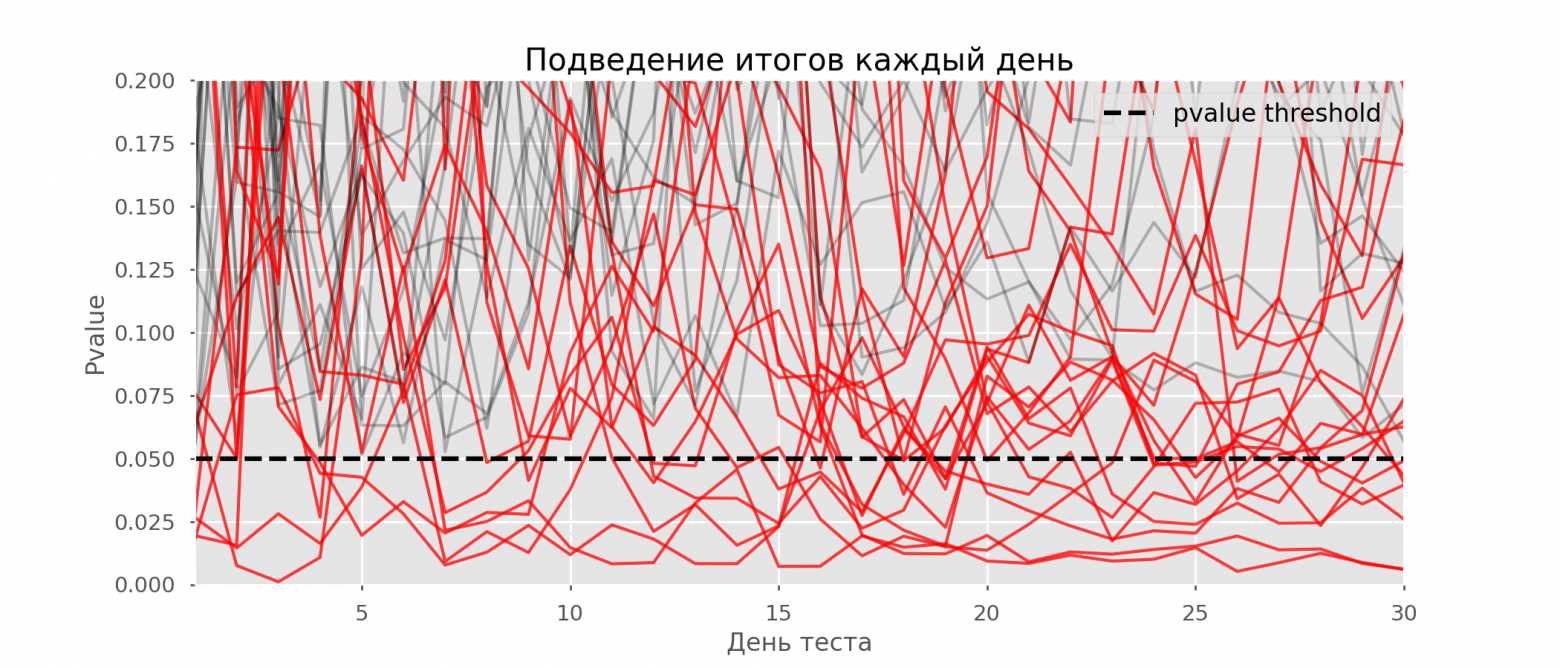
Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:

Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).
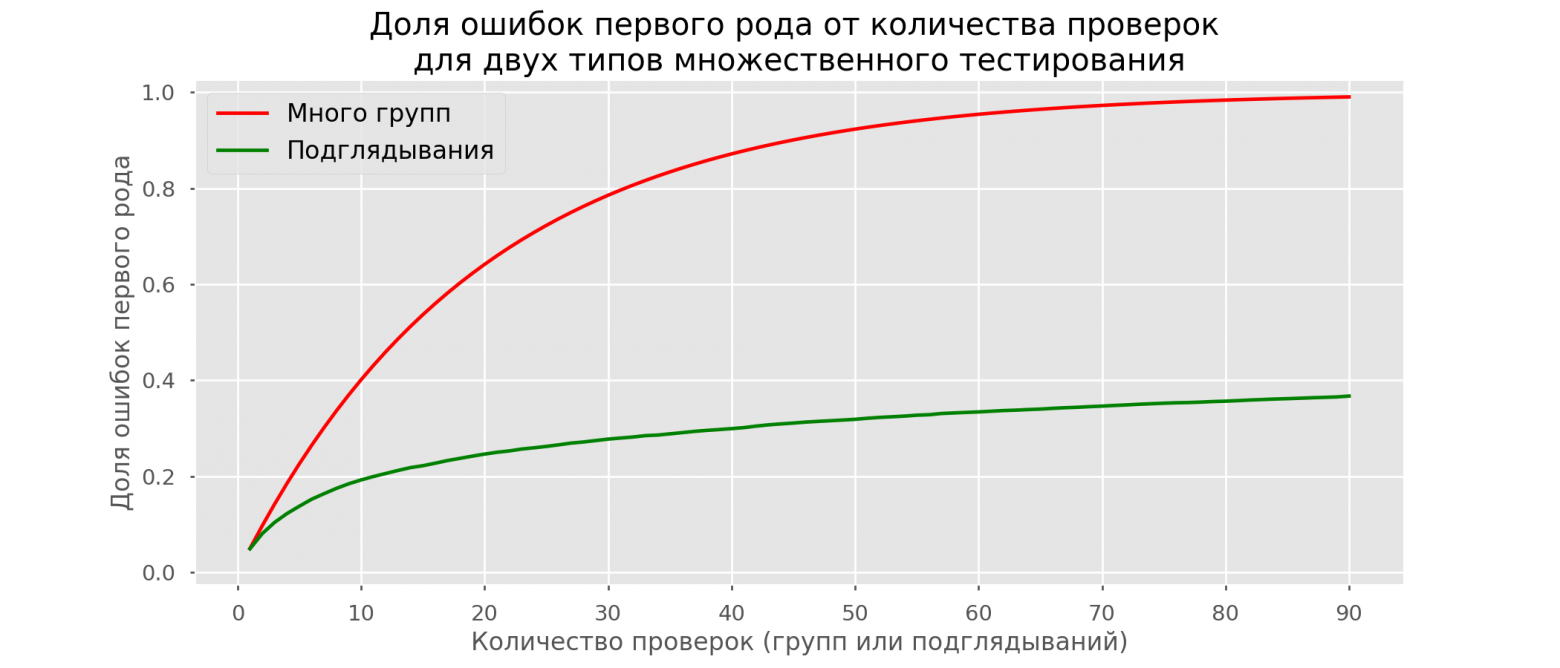
Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.
Байесовский подход и проблема подглядывания
Можно встретить мнение, что Байесовский подход к анализу A/B-тестов избавляет от проблемы подглядывания. Это не так, хотя и его можно настроить соответствующим образом. Отличную статью с дополнительными материалами можно почитать здесь.
Методы досрочного завершения теста
Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O’Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).
Pocock
Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.
O’Brien-Fleming
В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента (в том числе значение на последнем шаге
), соответствующие нужному уровню значимости, зависят от номера проверки
(принимает значения от 1 до общего количества проверок
включительно) и рассчитываются по эмпирически полученной формуле:
Код для воспроизведения коэффициентов
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt
# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081,
2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
[1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_) # [ 0.33729346, -0.63307934]
print(lr.intercept_) # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z)) # 0.999894
total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()
Соответствующие уровни значимости вычисляются через перцентиль стандартного распределения, соответствующий значению статистики Стьюдента
:
perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2
На тех же симуляциях это выглядит так:

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.
Метод Optimizely
Метод Optimizely хорош тем, что позволяет вообще не фиксировать дату окончания теста, а требуемый уровень значимости рассчитывается на каждый момент времени как функция от количества наблюдений в тесте. Интуитивно лично мне их метод нравится меньше, так как в нём жёсткость критерия увеличивается по ходу теста. То есть она минимальна в первые дни, когда случайный шум оказывает наибольшее влияние на метрики. В методе O’Brien-Fleming’a ситуация противоположная.
Калькулятор A/B-тестов
Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:
- какие классы попадают в тест;
- тест раздаётся на учителей или учеников;
- время учебного года;
- тест на всех пользователей или только на новых.
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.

Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте , среднее значение метрики
и её дисперсию
. Зафиксировав доли контрольной группы
, экспериментальной группы
и ожидаемый прирост от теста
в процентах, можно рассчитать ожидаемые значения статистики Стьюдента
и соответствующее p-value на каждый день теста:
Далее легко получить значения p-value на каждый день:
pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2
Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.
Заключение
В качестве заключения хочу напомнить основные посылы статьи:
- Если вы сравниваете средние значения метрики в группах, скорее всего, вам подойдёт критерий Стьюдента. Исключение — экстремально малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я таких не встречал).
- Если в тесте несколько групп, пользуйтесь поправками на множественное тестирование гипотез. Подойдёт простейшая поправка Бонферрони.
- Сравнения по дополнительным метрикам или срезам групп тоже подвержены проблеме множественного тестирования.
- Выбирайте дату завершения теста заранее. Вместо даты также можно зафиксировать количество наблюдений в группе.
- Не подводите итоги теста раньше этой даты. Это можно делать, только если вы заранее решили пользоваться методами, подразумевающими досрочное завершение, например, методом O’Brien-Fleming.
- Когда вносите изменения в схему A/B-тестирования, всегда проверяйте её жизнеспособность A/A-тестами.
Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.
Занырнем глубже в механику классического A/B тестирования, познакомимся с понятием “статистическая значимость” и разберемся, что может угрожать достоверности результатов ваших тестов.
Автор английской версии: Идан Михаэли, директор по Data Science в Hippo Insurance
(Если вы здесь впервые, то лучше начните сначала)
A/B тестирование — это одна из самых популярных техник оптимизации веб-страниц. Техника позволяет маркетологам, владельцам сайтов принимать более взвешенные и обоснованные решения относительно целесообразности внедрения их творческих идей. Другими словами, когда кто-то предлагает что-то на сайте поменять, мы можем оценить эти изменения не интуитивно и не с высоты чьего-то опыта, а объективно, отталкиваясь от конкретных целей: как ближних (например, CTR кнопки), так и долгосрочных (например, конверсия в покупатели). В то же время, тесты страхуют нас от серьезных ошибок, которые могут подорвать вовлеченность.
Давайте же занырнем глубже в механику классического A/B тестирования, познакомимся с понятием статистическая значимость (statistical significance) и разберемся, что может угрожать достоверности результатов ваших тестов. В конце статьи я приведу пару альтернатив классическому A/B тестированию от Dynamic Yield.
На первый взгляд, процедура тестирования предельно проста. Во-первых, мы создаем вариацию некой оригинальной веб-страницы (базы). Далее, мы случайным образом делим трафик между двумя версиями страницы (распределение посетителей проходит случайно, согласно некой вероятности). Наконец, мы собираем данные, как отработала каждая версия страницы (метрики). После этого мы анализируем данные, выбираем версию с наилучшими результатами и отключаем ту, что отработала хуже. Вроде бы все очевидно и просто? Нет.
Важно помнить, что когда мы выбираем одну из версий, то фактически масштабируем показатели, полученные в результате тестирования, на всю аудиторию потенциальных пользователей, а это — серьезный прыжок веры. Поэтому тестирование должно быть достоверным; иначе есть риск принять неверное решение, которое в долгосрочной перспективе негативно скажется на показателях сайта. Процесс достижения нужной достоверности мы называем тестированием гипотезы (hypothesis testing), а саму искомую достоверность — статистической значимостью (statistical significance).
Тестирование гипотезы начинается с того, что мы формулируем нулевую гипотезу (Null hypothesis) — некое утверждение, которое закрепляет статус кво, например “оригинальная страница (база) дает тот же CTR, что и вариация с новым дизайном”. Далее мы смотрим, можно ли отклонить это утверждение как крайне маловероятное.
Как мы это делаем?
Во-первых, нужно понять, где нас подстерегают ошибки. Вариантов тут два: во-первых, мы можем ошибочно опровергнуть нулевую гипотезу. Мельком взглянув на данные, мы можем прийти к выводу, что разница в показателях двух страниц имеется.
Ошибки первого рода. На деле же, этой разницы может не быть, а различия в результатах, на которые мы опираемся — это воля случая. Такой тип ошибок называется ошибки первого рода (type I error) или ложноположительные результаты (false positive).
Ошибки второго рода. Второй тип ошибок наблюдается, когда мы не наблюдаем значительной разницы между вариациями страницы, в то время как разница на самом деле есть, а ее отсутствие в тестировании — это случайность. Такие ошибки называют ошибками второго рода (type II error) или ложноотрицательными результатами (false negative).
Как избежать ошибок первого и второго рода?
Краткий ответ такой: устанавливайте правильный размер выборки. Чтобы определить нужный размер выборки, необходимо задать несколько параметров для нашего теста. Чтобы избежать ложноположительных результатов, нужно установить уровень достоверности (confidence level) или, другими словами, статистическую значимость. Это должно быть небольшое положительное число. Как правило, уровень значимости принимают равным 0,05: это означает, что на действующей модели лишь в 5% случаев есть вероятность выявить ложную разницу между двумя вариациями (то есть пятипроцентная вероятность ошибки). Про эту общепринятую константу обычно говорят “достоверность более 95%”.
Большинство специалистов по проведению тестирований (как и большинство инструментов, доступных на сегодняшний день) довольствуются этим первым параметром. Но, если мы хотим также застраховаться от ложноотрицательных результатов (false negative), нужно определить еще два параметра.
- Первый — это минимальная разница в результатах, которую мы хотим отслеживать (при условии, что разница была выявлена). Второй — это вероятность выявить эту разницу (при условии, что она существует).
- Второй параметр называют статистической мощностью (statistical power) и часто по умолчанию принимают его за 80%. Далее нужный размер выборки рассчитывается на основании этих трёх значений (можно воспользоваться онлайн-калькулятором).
Хотя этот процесс может показаться достаточно сложным, а рассчитанный таким образом размер выборки часто кажется слишком большим, стандартный подход к тестированию диктует именно такую процедуру — иначе о достоверности говорить не приходится. Горькая правда в том, что даже при условии чёткого следования вышеописанному алгоритму, вы всё равно можете получить некорректные результаты. Давайте разберемся почему.
Я провел все вычисления; теперь можно полностью доверять результатам?
Хотя метод проверки гипотез выглядит многообещающе, на практике он совершенно не застрахован от ошибок, потому что при тестировании мы опираемся на определенные скрытые предположения, которые часто не имеют места в реальных жизненных сценариях.
Первое предположение обычно не вызывает сомнений: мы предполагаем, что “образцы” нашей выборки — то есть посетители сайта, которым мы показываем вариации страницы — никак не связаны друг с другом, и их поступки не созависимы. Обычно это предположение достоверно, если конечно мы не показываем наши вариации одному и тому же посетителю по несколько раз, считая каждый раз как отдельный показ.
Второе предположение состоит в том, что элементы каждой выборки распределены одинаково (identically distributed). Проще говоря, это означает, что вероятность конверсии равна для всех посетителей. Конечно, это не так. Вероятность конверсии зависит от времени, местоположения, предпочтений посетителя, источников трафика и многих других факторов. К примеру, если во время проведения эксперимента, на сайте крутится какая-то рекламная кампания, мы можем наблюдать прилив трафика с Facebook. Это может привести к резким изменениям в CTR (click-through rates) — ведь люди, привлеченные рекламой, отличаются от ваших обычных посетителей. Такие колебания влияют не только на A/B тесты, но и на более продвинутые техники оптимизации, которые мы применяем в Dynamic Yield.
Третье предположение заключается в том, что измеряемые нами показатели (например, CTR или конверсия) имеют нормальное распределение. Возможно для вас это звучит как абстрактный математический термин, но правда в том, что все “магические” формулы расчета уровня достоверности основаны на этом предположении, которое, кстати, очень шаткое и соблюдается далеко не всегда. В целом можно выделить такую зависимость: чем больше размер выборки и чем больше мы наблюдаем конверсий, тем сильнее соблюдается это предположение — согласно центральной предельной теореме.
Окей, понятно, что математика не застрахована от ошибок, но на какие подводные камни стоит обратить внимание?
Таких подводных камней два.
Во-первых, платформы для проведения A/B тестов часто предлагают наблюдать за результатами тестирования в реальном времени. С одной стороны, это дает чувство контроля над ситуацией и позволяет специалисту следить за прозрачностью тестирования. Однако, наблюдая за показателями “в прямом эфире”, мы рискуем приступить к активным действиям раньше времени, отталкиваясь от сырых данных. Кто-то останавливает тестирование, получив первые результаты — даже если нужный размер выборки еще не достигнут, кто-то тормозит, как только достигнута статистическая значимость; оба сценария — прямой путь к ошибкам. Это вызывает статистическую погрешность (statistical bias) в сторону выявления разницы, которой на самом деле нет; более того, эту погрешность мы не можем заранее рассчитать и скорректировать (например, установив более высокий уровень значимости). Больше на тему: Как не надо анализировать A/B тесты. Проблема подглядывания →
Второй подводный камень — это завышенные ожидания от вариации-победителя после проведения тестирования. В результате проявления статистического эффекта известного как регрессия к среднему (regression toward the mean), долговременные результаты вариации-победителя могут быть не такими высокими, как в процессе тестирования. Проще говоря, есть вероятность, что вариация-победитель на самом деле была не объективно лучшей, а просто более “везучей”. Это везение со временем заканчивается и сглаживается, в результате чего возникает ощущение, что результаты падают.
Есть ли альтернативы A/B тестированию?
Конечно. Есть множество разных кейсов оптимизации страниц, и A/B тестирование подходит лишь в ряде случаев. Допустим, мы хотим провести тест на странице, которая давно работает и по показателям которой у нас уже собрана определенная история. Изменение, которое мы хотим внести, будет внедрено на страницу надолго и для всей совокупности посетителей сайта. Конечно, в этом случае нужно глубоко и точно измерить все результаты и принять обоснованное решение относительно данного изменения. Однако, на практике часто встречаются другие кейсы.
К примеру, нам нужно узнать, какой из трёх заголовков статей сработает лучше. При этом сайт, на котором будет размещена статья, относительно новый, а сама статья будет висеть на главной странице лишь несколько часов. Это означает, что нам нужно быстро выявить самый эффективный заголовок и применить это знание в рамках нескольких часов. В этом нам поможет метод “многорукого бандита”.
Если кратко, многорукий бандит постоянно делит трафик между вариациями в зависимости от результатов и уровня достоверности, зафиксированных на каждом этапе пути. При таком подходе мы немного теряем в плане уверенности, что вариация-побелитель действительно лучшая вариация, но получаем более быструю конвергенцию. Это первый уровень оптимизации, который мы предлагаем в Dynamic Yield.
Более глубокий уровень оптимизации делает ставку на полную персонализацию. Это можно делать вручную или автоматически. Суть в том, что мы показываем определенным пользователям определенные вариации. Рассмотрим пример персонализации вручную. Допустим мы хотим на День Королевы показывать всем посетителям из Нидерландов оранжевый фон страницы. Очень часто такие ручные изменения приносят свои результаты. Минус в том, что они плохо масштабируются. Допустим, у нас на сайте действует рекламная акция для посетителей с Facebook. Что делать, если с Facebook приходит голландец? По мере появления новых групп посетителей, количество вариаций будет расти, а правила оптимизации — усложняться. Кроме того, здесь в игру вступает метод научного тыка — вроде бы эксперименты должны принести какие-то результаты, но никто не знает какие.
Поэтому в подобных случаях может лучше сработать подход автоматической персонализации. Допустим, у нас кулинарный сайт, на котором есть секция с рекомендованными рецептами. С помощью механизма персонализации мы можем настроить сайт так, чтобы рекомендовать каждому посетителю персональный рецепт, на основании истории его взаимодействия со страницами, разделами и тегами на сайте.
Заключение
A/B тесты — эффективный инструмент, но если проводить их неправильно, можно прийти к ложным выводам. Достижение нужного уровня статистической значимости — это обязательное условие для получения надежных результатов тестирования. Чтобы этого добиться, нужно правильно установить ряд параметров, а также определить необходимый размер выборки и придерживаться его в процессе тестирования.
Классическая ошибка, которая ведет к потере достоверности — это сбор результатов до момента достижения нужного размера выборки. Если вас интересуют быстрые способ оптимизации, присмотритесь к методам из второй части статьи: многорукий бандит и персонализация на базе машинного обучения.
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Стандартная методика проверки статистических гипотез
- 2 Вычисление пи-величины
- 3 Вычисление ROC-кривой
- 4 Литература
- 5 См. также
- 6 Ссылки
Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.
Другая интерпретация:
уровень значимости — это такое (достаточно малое) значение вероятности события, при котором событие уже можно считать неслучайным.
Уровень значимости обычно обозначают греческой буквой (альфа).
Стандартная методика проверки статистических гипотез
В стандартной методике проверки статистических гипотез уровень значимости фиксируется заранее, до того, как становится известной выборка
.
Чрезмерное уменьшение уровня значимости (вероятности ошибки первого рода) может привести к увеличению вероятности ошибки второго рода, то есть вероятности принять нулевую гипотезу, когда на самом деле она не верна (это называется ложноотрицательным решением, false negative).
Вероятность ошибки второго рода связана с мощностью критерия
простым соотношением
.
Выбор уровня значимости требует компромисса между значимостью и мощностью или
(что то же самое, но другими словами)
между вероятностями ошибок первого и второго рода.
Обычно рекомендуется выбирать уровень значимости из априорных соображений.
Однако на практике не вполне ясно, какими именно соображениями надо руководствоваться,
и выбор часто сводится к назначению одного из популярных вариантов
.
В докомпьютерную эпоху эта стандартизация позволяла сократить объём справочных статистических таблиц.
Теперь нет никаких специальных причин для выбора именно этих значений.
Существует две альтернативные методики, не требующие априорного назначения .
Вычисление пи-величины
Достигаемый уровень значимости или пи-величина (p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия .
где
— критическая область критерия.
Другая интерпретация:
достигаемый уровень значимости или пи-величина — это вероятность, с которой (при условии истинности нулевой гипотезы) могла бы реализоваться наблюдаемая выборка, или любая другая выборка с ещё менее вероятным значением статистики
.
Случайная величина имеет равномерное распределение.
Фактически, функция приводит значение статистики критерия
к шкале вероятности.
Маловероятным значениям (хвостам распределения) статистики соотвествуют значения
, близкие к нулю или к единице.
Вычислив значение на заданной выборке
,
статистик имеет возможность решить,
является ли это значение достаточно малым, чтобы отвергнуть нулевую гипотезу.
Данная методика является более гибкой, чем стандартная.
В частности, она допускает «нестандартное решение» — продолжить наблюдения, увеличивая объём выборки, если оценка вероятности ошибки первого рода попадает в зону неуверенности, скажем, в отрезок .
Вычисление ROC-кривой
ROC-кривая (receiver operating characteristic) — это зависимость мощности от уровня значимости
.
Методика предполагает, что статистик укажет подходящую точку на ROC-кривой, которая соответствует компромиссу между вероятностями ошибок I и II рода.
Литература
- Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006.
- Цейтлин Н. А. Из опыта аналитического статистика. — М.: Солар, 2006. — 905 с.
- Алимов Ю. И. Альтернатива методу математической статистики. — М.: Знание, 1980.
См. также
- Проверка статистических гипотез — о стандартной методике проверки статистических гипотез.
- Достигаемый уровень значимости, синонимы: пи-величина, p-Value.
Ссылки
- P-value — статья в англоязычной Википедии.
- ROC curve — статья в англоязычной Википедии.
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например: 
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид: 
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение: $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение: $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
$$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Уровень
значимости — это вероятность того, что
мы сочли различия существенными, а они
на самом деле случайны.
Когда
мы указываем, что различия достоверны
на 5%-ом уровне значимости, или при р<0,05,
то мы имеем виду, что вероятность того,
что они все-таки недостоверны, составляет
0,05.
Когда
мы указываем, что различия достоверны
на 1%-ом уровне значимости, или при р<0,01,
то мы имеем в виду, что вероятность того,
что они все-таки недостоверны, составляет
0,01.
Если
перевести все это на более формализованный
язык, то уровень значимости — это
вероятность отклонения нулевой гипотезы,
в то время как она верна.
Ошибка,
состоящая в том, что мы отклонили нулевую
гипотезу, в то время как она верна,
называется ошибкой 1 рода.
Вероятность
такой ошибки обычно обозначается как
а. В сущности, мы должны были бы указывать
в скобках не р<0,05 или р<0,01, а а<0,05
или <Х<0,01. В некоторых руководствах
так и делается (Рунион Р., 1982; Захаров
В.П., 1985 и др.).
Если
вероятность ошибки — это а, то вероятность
правильного решения: 1—а. Чем меньше а,
тем больше вероятность правильного
решения.
Исторически
сложилось так, что в психологии принято
считать низшим уровнем статистической
значимости 5%-ый уровень (р<0,05): достаточным
— 1%-ый уровень (р^О.01) и высшим 0,1% -ый
уровень (р<0,001), поэтому в таблицах
критических значений обычно приводятся
значения критериев, соответствующих
уровням статистической значимости
р<0,05 и р<0,01, иногда — р<0,001. Для
некоторых критериев в таблицах указан
точный уровень значимости их разных
эмпирических значений. Например, для
ф*=1,56 р=0,06.
До
тех пор, однако, пока уровень статистической
значимости не достигнет р=0,05, мы еще не
имеем права отклонить нулевую гипотезу.
Правило
отклонения HQ и принятия Hi
Если
эмпирическое значение критерия равняется
критическому значению, соответствующему
р^0,05 или превышает его, то HQ отклоняется,
но мы еще не можем определенно принять
W.
Если
эмпирическое значение критерия равняется
критическому значению, соответствующему
р<0,01 или превышает его, то HQ отклоняется
и принимается Н^.
Исключения:
критерий
знаков G, критерий Т Вилкоксона и критерий
U Манна-Уитни. Для них устанавливаются
обратные соотношения. Для облегчения
процесса принятия решения можно всякий
раз вычерчивать «ось значимости».

Критические
значения критерия обозначены как Qo,O5 и
Qo,O1> эмпирическое значение критерия
как QaMn. Оно заключено в эллипс.
Вправо
от критического значения Qo.oi простирается
«зона значимости» — сюда попадают
эмпирические значения, превышающие
Qooi и, следовательно, безусловно значимые.
Влево
от критического значения Qo,O5 простирается
«зона незначимое™», — сюда попадают
эмпирические значения Q, которые ниже
Qo,O5′ и≫
следовательно, безусловно незначимы.
Мы видим, что Qo,o5=6; Qo.oi=9; Q9Mn=8.
Эмпирическое
значение критерия попадает в область
между Qo,O5 и Qo.oi- Это зона «неопределенности»:
мы уже можем отклонить гипотезу о
недостоверности различий (HQ), НО еще не
можем принять гипотезы об их достоверности
(Hf).
Практически,
однако, исследователь может считать
достоверными уже те различия, которые
не попадают в зону незначимости, заявив,
что они достоверны при р<0,05, или указав
точный уровень значимости полученного
эмпирического значения критерия,
например: р=0,02. С помощью таблиц Приложения
1 это можно сделать по отношению к
критериям Н Крускала-Уоллиса, у}г
Фридмана,
L Пейджа, ф* Фишера, X
Колмогорова.
Уровень
статистической значимости или критические
значения критериев определяются
по-разному при проверке направленных
и ненаправленных статистических гипотез.
При направленной статистической гипотезе
используется односторонний критерий,
при ненаправленной гипотезе — двусторонний
критерий. Двусторонний критерий более
строг, поскольку он проверяет различия
в обе стороны, и поэтому то эмпирическое
значение критерия, которое ранее
соответствовало уровню значимости
р<0,05, теперь соответствует лишь уровню
р<0,10.
Билет 9 Параметрические
и непараметрические методы. Мощность
критериев
-
Параметрические и непараметрические
методы
Методы обучения, т.е. нахождения достаточно
хорошей распознающей функ-
ции f 2 F, традиционно подразделяются на
параметрические и непарамет-
рические в соответствии с тем, просто
или сложно устроено пространство F.
Параметрические — это те методы, в
которых F = fF(w; ¢)jw 2 Wg для неко-
торого достаточно удобного (например,
евклидова) пространства параметров
W и некоторой функции F: W £ X ! Y, а
непараметрические — это мето-
ды, в которых, якобы, пространство F не
зафиксировано заранее, а зависит
от обучающего набора T. На самом деле
разница между параметрическими и
непараметрическими методами — только
в употребляемых словах.
Полезный пример параметрических методов
— методы обучения линейных
распознавателей, которых даже для
простейшей линейной регрессии (X = Rd,
Y
= R,
W
= R
£ Rd,
F(w;
x)
= w0
+Pdj=1
wjxj) довольно много. Подробнее
эти методы рассматриваются в разделе
2.
[А.Б. Мерков]
непараметрические
методы в
математической статистике, методы
непосредственной оценки теоретического
распределения вероятностей и тех или
иных его общих свойств (симметрии и
т.п.) по результатам наблюдений. Название
Н. м. подчёркивает их отличие от
классических (параметрических)
методов, в которых
предполагается, что неизвестное
теоретическое распределение принадлежит
какому-либо семейству, зависящему от
конечного числа параметров (например,
семейству нормальных распределений, и
которые позволяют по результатам
наблюдений оценивать неизвестные
значения этих параметров и проверять
те или иные гипотезы относительно их
значений. Разработка Н. м. является в
значительной степени заслугой советских
учёных.
-
Мощность критериев
Мощность критерия — это его способность
выявлять различия, если они есть. Иными
словами, это его способность отклонить
нулевую гипотезу об отсутствии различий,
если
она неверна.
Ошибка, состоящая в том, что мы приняли
нулевую гипотезу, в то время как
она неверна, называется ошибкой II рода.
Вероятность такой ошибки обозначается
как β. Мощность критерия — это его
способность не допустить ошибку II рода,
поэтому:
Мощность=1—β
Мощность критерия определяется
эмпирическим путем. Одни и те же задачи
могут
быть решены с помощью разных критериев,
при этом обнаруживается, что некоторые
критерии позволяют выявить различия
там, где другие оказываются неспособными
это
сделать, или выявляют более высокий
уровень значимости различий. Возникает
вопрос: а
зачем же тогда использовать менее
мощные критерии? Дело в том, что
основанием для
выбора критерия может быть не только
мощность, но и другие его характеристики,
а
именно:
а) простота;
б) более широкий диапазон использования
(например, по отношению к данным,
определенным по номинативной шкале,
или по отношению к большим n);
в) применимость по отношению к неравным
по объему выборкам;
г) большая информативность результатов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Время на прочтение
11 мин
Количество просмотров 20K
В Учи.ру мы стараемся даже небольшие улучшения выкатывать A/B-тестом, только за этот учебный год их было больше 250. A/B-тест — мощнейший инструмент тестирования изменений, без которого сложно представить нормальное развитие интернет-продукта. В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьёзные ошибки как на этапе дизайна эксперимента, так и при подведении итогов. В этой статье я расскажу о некоторых технических моментах проведения теста: как мы определяем срок тестирования, подводим итоги и как избегаем ошибочных результатов при досрочном завершении тестов и при тестировании сразу нескольких гипотез.

Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:
- Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
- Определяем срок, на который запускается тест.
- Случайно разбиваем пользователей на две группы.
- Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
- В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
- По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
- Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.
Всё выглядит логично и просто, дьявол, как всегда, в деталях.
Статистическая значимость, критерии и ошибки
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:
- Ошибка первого рода происходит, если мы фиксируем разницу между группами, хотя на самом деле её нет. В тексте также будет встречаться эквивалентный термин — ложноположительный результат. Статья посвящена именно таким ошибкам.
- Ошибка второго рода происходит, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.
При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:
- Есть A/B-тест с контрольной группой A и экспериментальной — B. Цель — проверить, что группа B отличается от группы A по какой-то метрике.
- Формулируем нулевую статистическую гипотезу: группы A и B не отличаются, а наблюдаемые различия объясняются шумом. По умолчанию всегда считаем, что разницы нет, пока не доказано обратное.
- Проверяем гипотезу строгим математическим правилом — статистическим критерием, например, критерием Стьюдента.
- В результате получаем величину p-value. Она лежит в диапазоне от 0 до 1 и означает вероятность увидеть текущую или более экстремальную разницу между группами при условии верности нулевой гипотезы, то есть при отсутствии разницы между группами.
- Значение p-value сравнивается с уровнем значимости 0.05. Если оно больше, принимаем нулевую гипотезу о том, что различий нет, иначе считаем, что между группами есть статистически значимая разница.
Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.
Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.
Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.
Проблема множественного тестирования гипотез
Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп и уровне значимости
вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:
Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.
Метод Холма — Бонферрони
Искушенный читатель знает и о методе Холма — Бонферрони, который всегда обладает большей мощностью, чем поправка Бонферрони, то есть реже совершает ошибки второго рода. В этом методе мы сортируем гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага
по формуле:
P-value первой гипотезы сравнивается с уровнем статистический значимости . Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости
, и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.
Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.
Проблема подглядывания
Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.
Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.

Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.

На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:

Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:

Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).

Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.
Байесовский подход и проблема подглядывания
Можно встретить мнение, что Байесовский подход к анализу A/B-тестов избавляет от проблемы подглядывания. Это не так, хотя и его можно настроить соответствующим образом. Отличную статью с дополнительными материалами можно почитать здесь.
Методы досрочного завершения теста
Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O’Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).
Pocock
Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.
O’Brien-Fleming
В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента (в том числе значение на последнем шаге
), соответствующие нужному уровню значимости, зависят от номера проверки
(принимает значения от 1 до общего количества проверок
включительно) и рассчитываются по эмпирически полученной формуле:
Код для воспроизведения коэффициентов
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt
# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081,
2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
[1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_) # [ 0.33729346, -0.63307934]
print(lr.intercept_) # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z)) # 0.999894
total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()
Соответствующие уровни значимости вычисляются через перцентиль стандартного распределения, соответствующий значению статистики Стьюдента
:
perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2
На тех же симуляциях это выглядит так:

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.
Метод Optimizely
Метод Optimizely хорош тем, что позволяет вообще не фиксировать дату окончания теста, а требуемый уровень значимости рассчитывается на каждый момент времени как функция от количества наблюдений в тесте. Интуитивно лично мне их метод нравится меньше, так как в нём жёсткость критерия увеличивается по ходу теста. То есть она минимальна в первые дни, когда случайный шум оказывает наибольшее влияние на метрики. В методе O’Brien-Fleming’a ситуация противоположная.
Калькулятор A/B-тестов
Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:
- какие классы попадают в тест;
- тест раздаётся на учителей или учеников;
- время учебного года;
- тест на всех пользователей или только на новых.
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.

Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте , среднее значение метрики
и её дисперсию
. Зафиксировав доли контрольной группы
, экспериментальной группы
и ожидаемый прирост от теста
в процентах, можно рассчитать ожидаемые значения статистики Стьюдента
и соответствующее p-value на каждый день теста:
Далее легко получить значения p-value на каждый день:
pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2
Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.
Заключение
В качестве заключения хочу напомнить основные посылы статьи:
- Если вы сравниваете средние значения метрики в группах, скорее всего, вам подойдёт критерий Стьюдента. Исключение — экстремально малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я таких не встречал).
- Если в тесте несколько групп, пользуйтесь поправками на множественное тестирование гипотез. Подойдёт простейшая поправка Бонферрони.
- Сравнения по дополнительным метрикам или срезам групп тоже подвержены проблеме множественного тестирования.
- Выбирайте дату завершения теста заранее. Вместо даты также можно зафиксировать количество наблюдений в группе.
- Не подводите итоги теста раньше этой даты. Это можно делать, только если вы заранее решили пользоваться методами, подразумевающими досрочное завершение, например, методом O’Brien-Fleming.
- Когда вносите изменения в схему A/B-тестирования, всегда проверяйте её жизнеспособность A/A-тестами.
Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.
