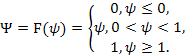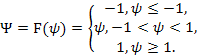Многослойные нейронные сети с сигмовидной функцией — глубокое обучение для новичков (2)
Перевод
Ссылка на автора
Глава 1: Представляем глубокое обучение и нейронные сети
Глава 2. Многослойные нейронные сети с сигмоидальной функцией.
Следуй за мной по щебет узнать больше о жизни в стартапе глубокого обучения.
Привет всем! Добро пожаловать в мой второй пост серииГлубокое обучение для новичков (DLFR)По-настоящему, новичок;) Не стесняйтесь обращаться к мой первый пост здесь или мой блог если вам трудно следовать. Или выделите на этой странице заметки или оставьте комментарий ниже! Ваши отзывы также будут высоко оценены.
На этот раз мы углубимся в нейронные сети, и пост будет несколько более техническим, чем в прошлый раз. Но не беспокойтесь, я сделаю так, чтобы вы могли легко и интуитивно выучить основы без знания CS / Math. Скоро вы сможете похвастаться своим пониманием;)
Обзор от DLFR 1
В прошлый раз мы представили область глубокого обучения и изучили простую нейронную сеть — персептрон … или динозавра … серьезно, однослойный персептрон. Мы также исследовали, как сеть персептрона обрабатывает входные данные, которые мы вводим, и возвращает выходные данные.
Основные понятия: входные данные, веса, суммирование и сложение смещения, функция активации (в частности, функция шага), а затем вывод. Скучно еще? Не беспокойся Я обещаю, что будет … больше глаголов! Но ты скоро к ним привыкнешь. Обещаю.

Еще в 1950-х и 1960-х годах у людей не было эффективного алгоритма обучения однослойного персептрона для изучения и идентификации нелинейных паттернов (помните проблему с воротами XOR?). И публика потеряла интерес к персептрону. В конце концов, большинство проблем в реальном мире нелинейны, и, как отдельные люди, вы и я чертовски хороши в принятии решений по линейным или бинарным задачам, таким какя должен изучать глубокое обучение или нетбез необходимости персептрона. Хорошо, «хорошо» — это сложное слово, так как наш мозг на самом деле не такой рациональный. Но я оставлю это поведенческим экономистам и психологам.
Прорыв: многослойный персептрон
За два десятилетия до 1986 года Джеффри Хинтон, Дэвид Румелхарт и Рональд Уильямс опубликовали статью «Изучение представлений по ошибкам обратного распространения», Который ввел:
- обратное распространениепроцедура длянеоднократно корректировать весачтобы минимизировать разницу между фактическим и желаемым выходом
- Скрытые слои, которыенейронные узлы, расположенные между входами и выходами, позволяя нейронным сетям изучать более сложные функции (такие как логика XOR)
Если вы совершенно новичок в DL, вы должны помнить Джеффри Хинтона, который играет ключевую роль в развитии DL. Итак, это были некоторые важные новости: мы всего 20 лет думали, что у нейронных сетей нет будущего для решения реальных проблем. Теперь мы видим свет от маяка на берегу! Давайте посмотрим на эти 2 новых введения.
Хм, первый,обратное распространениеупоминается в последнем посте. Помните, что мы повторили важность разработки нейронной сети, чтобы сеть могла учиться на разнице междужелаемый вывод(что это за факт) ифактический объем производства(что возвращает сеть), а затем отправить сигнал обратно весам и попросить весы подстроиться? Это сделает выход сети ближе к желаемому результату при следующем запуске.
Как насчет второго, скрытых слоев? Что такое скрытый слой? Скрытый слой превращает однослойный персептрон в многослойный персептрон! Вот план, по техническим причинам,Я сосредоточусь на скрытых слоях в этом посте, а затем расскажу о распространении в следующем посте.,
Просто случайныйзабавный фактздесь: я подозреваю, что Джеффри Хинтон имеет рекорд за то, что был самым старым стажером в Google: D Проверьте эта статья из New York Times и поиск «Хинтон». В любом случае, если вы уже знакомы с машинным обучением, я уверен, что его курс по Coursera подойдет.

Нейронные сети со скрытыми слоями
Скрытые слои нейронной сети буквально просто добавляют больше нейронов между входным и выходным слоями.

Данные во входном слое помечены какИксс подписками1, 2, 3,…, м, Нейроны в скрытом слое помечены какчасс подписками1, 2, 3,…, n, Примечание для скрытого слояегоNи нетм, поскольку количество нейронов скрытого слоя может отличаться от количества во входных данных. И как вы видите на графике ниже, нейроны скрытого слоя также помечены верхним индексом1 Это так, что когда у вас есть несколько скрытых слоев, вы можете определить, какой это скрытый слой:первый скрытый слой имеет верхний индекс 1, второй скрытый слой имеет верхний индекс 2 и т. д., как вГрафик 3, Выход помечен какYсшапка,

Чтобы облегчить жизнь, мы будем использовать некоторые жаргоны, чтобы немного прояснить ситуацию. Я знаю, жаргон может раздражать, но вы привыкнете к нему Во-первых, если у нас естьмвходные данные (х1, х2,…, хм), мы называем этом особенности, Особенность — это только одна переменная, которую мы считаем влияющей на конкретный результат. Как наш пример по итогамесли вы решили изучать DL или нет,у нас есть 3 функции: 1. Будете ли вы зарабатывать больше денег после изучения DL, 2. Трудно с математикой / программированием, 3. Нужен ли вам графический процессор для начала.
Во-вторых, когда мы умножаем каждый из m признаков на вес (w1, w2,…, wm) и суммировать их все вместе, этоскалярное произведение:

Итак, вот вынос на данный момент:
- См особенностина входеИКС,тебе нужномвеса для выполнения точечного произведения
- СNскрытые нейроны в скрытом слое, вам нужноNнаборы весов (W1, W2, … Wn) для выполнения точечных произведений
- С 1 скрытым слоем вы выполняетеNточечные продукты, чтобы получить скрытый выводчас:(h1, h2,…, hn)
- Тогда это как однослойный персептрон, мы используем скрытый выводчас:(h1, h2,…, hn) в качестве входных данных, которые имеютn функций,выполнятьТочечный продукт с 1 наборомNвес (w1, w2,…, wn) чтобы получить окончательный результатy_hat,
Процедура того, как входные значенияраспространяться впередв скрытый слой, а затем из скрытого слоя на выход такой же, как вГрафик 1, Ниже я приведу описание того, как это делается, используя следующую нейронную сеть вГрафик 4,



Теперь вычисляются выходные данные скрытого слоя, мы используем их в качестве входных данных для расчета конечного результата.

Ура! Теперь вы полностью понимаете, как работает персептрон с несколькими слоями Это похоже на однослойный персептрон, за исключением того, что в этом процессе у вас намного больше весов. Когда вы тренируете нейронные сети на больших наборах данных со многими другими функциями (такими как word2vec в Natural Language Processing), этот процесс потребляет много памяти на вашем компьютере. Это была одна из причин, по которой Deep Learning не взлетела до последних нескольких лет, когда мы начали выпускать гораздо более качественное оборудование, которое могло бы обрабатывать потребляющие память глубокие нейронные сети.
Сигмовидные нейроны: введение
Так что теперь у нас есть более сложная нейронная сеть со скрытыми слоями. Но мы не решили проблему активации с помощью функции step.
В последнем посте мы говорили об ограничениях линейности ступенчатой функции. Помните одно:Если функция активации является линейной, то вы можете сложить столько скрытых слоев в нейронной сети, сколько пожелаете, и конечный результат по-прежнему линейная комбинация исходных входных данных, пожалуйста убедитесь, что вы читаете эту ссылку дляобъяснение, если концепции трудно следовать. Эта линейность означает, что она не может действительно понять сложность нелинейных задач, таких как логика XOR или шаблоны, разделенные кривыми или кругами.
Между тем, функция шага также не имеет полезной производной (ее производная равна 0 везде или не определена в точке 0 на оси x). Это не работает дляобратное распространениеОб этом мы обязательно поговорим в следующем посте!

Ну, вот еще одна проблема: Персептрон с пошаговой функцией не очень «стабилен» как «кандидат на отношения» для нейронных сетей. Подумайте об этом: у этой девочки (или мальчика) есть серьезные биполярные проблемы! Один день (дляZ<0), (s) он все «тихий» и «подавленный», что дает вам нулевой ответ. Затем еще один день (дляZ≥ 0), (s) он внезапно становится «разговорчивым» и «живым», разговаривая с вами без остановки. Черт, радикальные перемены! Нет никакого изменения для ее / его настроения, и вы не знаете, когда оно понижается или повышается. Да … это пошаговая функция.
В общем, небольшое изменение любого веса во входном слое нашей сети персептронов может привести к тому, что один нейрон внезапно переключится с 0 на 1, что может снова повлиять на поведение скрытого слоя, а затем повлиять на конечный результат. Как мы уже говорили, нам нужен алгоритм обучения, который мог бы улучшить нашу нейронную сеть за счет постепенного изменения весов, а не путем плоского отсутствия ответа или внезапных скачков. Если мы не можем использовать пошаговую функцию для постепенного изменения веса, то это не должен быть выбор

Попрощайтесь с персептроном с помощью функции шага. Мы находим нового партнера для нашей нейронной сети,сигмовидный нейрон, который идет с сигмовидной функцией (дух). Но не беспокойтесь: единственное, что изменится, — это функция активации, а все остальное, что мы узнали о нейронных сетях, все еще работает для этого нового типа нейронов!


Если функция выглядит очень абстрактно или странно для вас, не стоит слишком беспокоиться о таких деталях, как число Эйлераеили как кто-то придумал эту сумасшедшую функцию. Для тех, кто не разбирается в математике, единственная важная вещь о сигмовидной функции вГрафик 9во-первых, его кривая, а во-вторых, его производная. Вот еще несколько деталей:
- Сигмовидная функция дает результаты, аналогичные шаговой функции, в том случае, если выходной сигнал находится между 0 и 1. Кривая пересекает 0,5г = 0, который мы можем установить правила для функции активации, такие как: Если выходной сигнал сигмоидного нейрона больше или равен 0,5, он выводит 1; если выходное значение меньше 0,5, оно выдает 0.
- Сигмовидная функция не имеет рывка на своей кривой. Он гладкий и имеет очень красивую и простую производную отσ (z) * (1-σ (z)),который дифференцируем повсюду на кривой. Исчисление производной производной можно найти в переполнении стека Вот если хочешь это увидеть. Но вам не нужно знать, как его получить. Здесь нет стресса.
- ЕслиZочень отрицательный, тогда выходной сигнал равен приблизительно 0; еслиZочень положительный результат примерно 1; но вокругг = 0гдеZне является ни слишком большим, ни слишком маленьким (между двумя внешними вертикальными пунктирными линиями сетки вГрафик 9) у нас относительно больше отклонений, чемZменяется.
Теперь это похоже на материал для датировки нашей нейронной сети Функция сигмоида, в отличие от функции шага, вносит нелинейность в нашу модель нейронной сети. Нелинейный просто означает, что выходной сигнал мы получаем от нейрона, который является точечным произведением некоторых входных данных.х (х1, х2,…, хм)и весw (w1, w2,…, wm)плюс смещение, а затем положить в сигмовидную функцию, не может быть представлен линейная комбинация вводах (х1, х2,…, хм),
Эта нелинейная функция активации, когда используется каждым нейроном в многослойной нейронной сети, производит новую « представление Исходных данных, и в конечном итоге учитывает нелинейную границу решения, такую как XOR. Таким образом, в случае XOR, если мы добавим два сигмоидных нейрона в скрытом слое, мы могли бы в другом пространстве преобразовать исходный 2D-график в нечто похожее на 3D-изображение в левой частиГрафик 10ниже. Таким образом, этот гребень позволяет классифицировать затвор XOR и представляет светло-желтоватую область затвора 2D XOR с правой стороныГрафик 10, Таким образом, если наше выходное значение находится в верхней части гребня, то оно должно быть истинным или 1 (например, погода холодная, но не жаркая, или погода жаркая, но не холодная); если наше выходное значение находится в нижней плоской области по двум углам, тогда оно ложно или равно 0, поскольку неправильно говорить, что погода горячая и холодная, а также ни горячая, ни холодная (хорошо, я думаю, что погода может быть не горячей или холодно … вы понимаете, что я имею в виду, хотя … верно?).

Я знаю, что эти разговоры о нелинейности могут сбивать с толку, поэтому, пожалуйста, прочитайте больше о линейности и нелинейности Вот (интуитивно понятный пост с анимацией из отличного блога Кристофера Олаха), Вот (по Вивек Ядав с функцией активации ReLU), и Вот (Себастьян Рашка). Надеюсь, у вас есть понимание того, почему важна функция нелинейной активации, а если нет, то сделайте это легко и дайте некоторое время ее переварить.
Проблема решена … на данный момент;) Мы увидим несколько различных типов функции активации в ближайшем будущем, потому что у сигмоидальной функции тоже есть свои проблемы! Некоторые популярные из них включаютTANHа такжеРЕЛУ, Это, однако, для другого поста.
Многоуровневые нейронные сети: интуитивный подход
Хорошо. Итак, мы внедрили скрытые слои в нейронную сеть и заменили персептрон сигмовидными нейронами. Мы также ввели идею о том, что нелинейная функция активации позволяет классифицировать нелинейные границы решений или шаблоны в наших данных. Вы можете запомнить эти выводы, поскольку они являются фактами, но я призываю вас немного погуглить в Интернете и посмотреть, сможете ли вы лучше понять концепцию (естественно, что мы потратим некоторое время, чтобы понять эти концепции)
Теперь мы никогда не говорили об одном очень важном моменте: с какой стати мы вообще хотим, чтобы скрытые слои в нейронных сетях? Как скрытые слои волшебным образом помогают нам решать сложные проблемы, которые однослойные нейроны не могут решить?
Из приведенного выше примера XOR вы видели, что добавление двух скрытых нейронов в 1 скрытый слой может перевернуть нашу проблему в другое пространство, что волшебным образом позволило нам классифицировать XOR с гребнем. Таким образом, скрытые слои каким-то образом искажают проблему таким образом, чтобы нейронной сети было легко классифицировать проблему или шаблон. Теперь мы будем использовать классический пример из учебника: распознавание рукописных цифр, чтобы помочь вам интуитивно понять, что делают скрытые слои.

Цифры вГрафик 11принадлежат к набору данных под названием MNIST, Он содержит 70000 примеров цифр, написанных руками человека. Каждая из этих цифр представляет собой изображение размером 28×28 пикселей. Таким образом, в целом каждое изображение цифры имеет 28 * 28 = 784 пикселей. Каждый пиксель принимает значение от 0 до 255 (цветовой код RGB). 0 означает цвет белый, а 255 означает цвет черный.

Теперь компьютер не может «видеть» цифру, как мы, люди, но если мы разберем изображение на массив из 784 чисел, таких как [0, 0, 180, 16, 230,…, 4, 77, 0, 0, 0], тогда мы можем передать этот массив в нашу нейронную сеть. Компьютер не может понять изображение, «увидев» его, но он может понимать и анализировать числа пикселей, которые представляют изображение.

Итак, давайте настроим нейронную сеть, как указано выше вГрафик 13, Он имеет 784 входных нейронов для значений 28×28 пикселей. Предположим, у него есть 16 скрытых нейронов и 10 выходных нейронов. Каждый из 10 выходных нейронов, возвращенных нам в массиве, будет отвечать за классификацию цифр от 0 до 9. Поэтому, если нейронная сеть считает, что рукописная цифра равна нулю, то мы должны получить выходной массив [1, 0, 0, 0, 0, 0, 0, 0, 0, 0], первый выход в этом массиве, который воспринимает цифру как ноль, «запускается», чтобы быть нашей 1 нейронной сетью, а остальные 0 Если нейронная сеть считает, что рукописная цифра — 5, то мы должны получить [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]. Шестой элемент, отвечающий за классификацию пяти, срабатывает, а остальные нет. Так далее и тому подобное.
Помните, мы упоминали, что нейронные сети становятся лучше за счет повторного обучения самим данным, чтобы они могли корректировать весовые коэффициенты в каждом слое сети, чтобы приблизить конечные результаты / фактические результаты к желаемым результатам? Поэтому, когда мы на самом деле обучаем эту нейронную сеть всем обучающим примерам в наборе данных MNIST, мы не знаем, какие веса мы должны назначить каждому из слоев. Поэтому мы просто случайным образом просим компьютер назначить веса в каждом слое. (Мы не хотим, чтобы все веса были равны 0, что я объясню в следующем посте, если позволит место).
Эта концепция случайной инициализации весов важна, потому что каждый раз, когда вы тренируете нейронную сеть с глубоким обучением, вы инициализируете разные числа для весов. По сути, вы и я понятия не имеем, что происходит в нейронной сети до тех пор, пока сеть не обучена. Обученная нейронная сеть имеет веса, которые оптимизируются при определенных значениях, которые дают лучший прогноз или классификацию по нашей проблеме. Это черный ящик, буквально. И каждый раз обучаемая сеть будет иметь разные наборы весов.
Ради аргумента, давайте представим следующий случай вГрафик 14, который я позаимствовал у Майкла Нильсена онлайн книга:

После обучения нейронной сети с раундами и раундами помеченных данных в контролируемом обучении, предположим, что первые 4 скрытых нейрона научились распознавать паттерны выше в левой частиГрафик 14, Затем, если мы передадим нейронной сети массив рукописных цифр ноль, сеть должна правильно запустить 4 верхних скрытых нейрона в скрытом слое, в то время как другие скрытые нейроны молчат, а затем снова запустить первый выходной нейрон, в то время как остальные молчит.

Если вы тренируете нейронную сеть с новым набором рандомизированных весов, она может создать следующую сеть (сравнить график 15 с графиком 14), поскольку веса рандомизированы, и мы никогда не знаем, какой из них узнает какой или какой шаблон. Но сеть, если она должным образом обучена, должна по-прежнему вызывать правильные скрытые нейроны и затем правильный вывод

И последнее, что следует упомянуть: в многослойной нейронной сети первый скрытый слой сможет выучить несколько очень простых шаблонов. Каждый дополнительный скрытый слой каким-то образом сможет постепенно выучить более сложные паттерны. Проверять, выписыватьсяГрафик 16от Scientific American с примером распознавания лиц

Некоторые замечательные люди создали следующий сайт для вас, чтобы поиграть с нейронными сетями и посмотреть, как работают скрытые слои. Попробуйте это. Это действительно интересно!
Tensorflow — игровая площадка нейронной сети
Это методика построения компьютерной программы, которая учится на данных. Он очень слабо основан на том, как мы думаем …
playground.tensorflow.org
Офир Самсон писал хороший пост, также объясняющий, что такое нейронная сеть с довольно хорошей визуализацией, и она короткая и лаконичная!
Еженедельник глубокого обучения: что такое нейронная сеть?
Для этой недели я хотел бы сосредоточиться на разъяснении, что такое нейронная сеть, на простом примере, который я собрал…
medium.com
резюмировать
В этом посте мы рассмотрели ограничения персептрона, представили сигмовидные нейроны с новой функцией активации, называемой сигмовидной функцией. Мы также говорили о том, как работают многослойные нейронные сети, и об интуиции скрытых слоев в нейронной сети.
Мы почти заканчиваем полный курс понимания базовых нейронных сетей;) Хе-хе, это еще не конец! В следующем посте я расскажу о так называемой функции потерь, а также об этом загадочном распространении, о котором мы только упоминали, но никогда не посещали! Проверьте следующие ссылки, если вам не терпится ждать:
CS231n сверточные нейронные сети для визуального распознавания
Материалы курса и заметки для Стэнфордского класса CS231n: Сверточные нейронные сети для визуального распознавания.
cs231n.github.io
Шаг за шагом Пример обратного распространения
Фон Backpropagation является распространенным методом обучения нейронной сети. В Интернете нет недостатка в документах, которые …
mattmazur.com
Оставайтесь с нами и, самое главное, получайте удовольствие от обучения: D
Вам понравилось это чтение? Не забудьте подписаться на меня щебет !
Знакомимся с методом обратного распространения ошибки
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!

Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.

Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.

Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:

Для l = 3:

W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.

Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.

b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.

Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:

Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:

Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:

И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:

(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:

Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.

Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:

(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:

(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:

«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
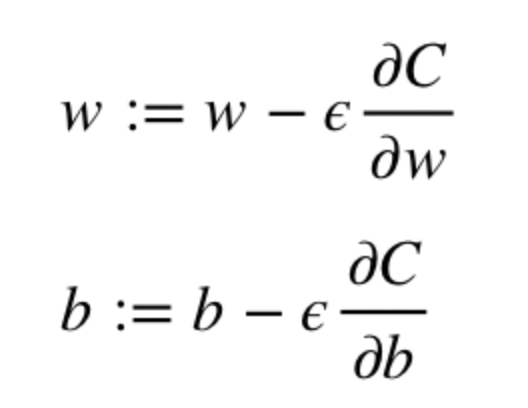
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:

Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z2)3 и (a2)3:

Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
F0:
11196971
F1:
Нейрокомпьютерные системы
F2:
Бозиев О.Л.
F3:
5 курс, 9 семестр, 4 курс,7сем.СП
VI:
1. Введение в искусственные нейронные
сети
I:
ТЗ № 1
S:
Дендрит – это …
-:
тело нейрона
+:
входное волокно нейрона
-:
выходное волокно нейрона
-:
место контакта нервных волокон
I:
ТЗ № 2
S:
Аксон – это …
-:
тело нейрона
-:
входное волокно нейрона
+:
выходное волокно нейрона
-:
место контакта нервных волокон
I:
ТЗ № 3
S:
Синапс – это …
-:
тело нейрона
-:
входное волокно нейрона
-:
выходное волокно нейрона
+:
место контакта нервных волокон
I:
ТЗ № 4
S:
Биологические нейроны …
+:
участвуют в обмене веществ
+:
взаимодействуют с помощью электрохимических
сигналов
-:
взаимодействуют с помощью оптических
сигналов
+:
рассеивают энергию
I:
ТЗ № 5
S:
Биологические нейроны не …
-:
участвуют в обмене веществ
-:
взаимодействуют с помощью электрохимических
сигналов
+:
взаимодействуют с помощью оптических
сигналов
-:
рассеивают энергию
I:
ТЗ № 6
S:
Искусственные нейронные сети обладают
способностью
-:
самоорганизации
+:
обучаемости
+:
обобщения
+:
абстрагирования
I:
ТЗ № 7
S:
Искусственные нейронные сети не обладают
способностью
+:
самоорганизации
-:
обучаемости
-:
обобщения
-:
абстрагирования
I:
ТЗ № 8
S:
Взаимодействуя между собой, нейроны
формируют
+:
нейронные сети
-:
функциональные сети
-:
локальные сети
-:
глобальные сети
I:
ТЗ № 9
S:
Взаимодействующие нейроны не способны
формировать
-:
нейронные сети
+:
функциональные сети
+:
локальные сети
+:
глобальные сети
I:
ТЗ № 10
S:
Искусственная нейронная сеть – это
+:
модель биологической нейронной сети
-:
искусственное объединение биологических
нейронов
-:
естественное объединение биологических
нейронов
-:
математическая формализация нейронной
сети
I:
ТЗ № 11
S:
Искусственная нейронная сеть не является
-:
моделью биологической нейронной сети
+:
искусственным объединением биологических
нейронов
+:
естественным объединением биологических
нейронов
+:
математической формализацией нейронной
сети
I:
ТЗ № 12
S:
Области применения искусственных
нейронных сетей:
+:
распознавание образов
+:
ассоциативный поиск информации
-:
автоматизированное проектирование
-:
управление производством
I:
ТЗ № 13
S:
Искусственные нейронные сети не
применяются для
-:
распознавания образов
-:
ассоциативного поиска информации
+:
автоматизированного проектирования
+:
управления производством
I:
ТЗ № 14
S:
Весовой коэффициент соответствует …
-:
весу нейрона
-:
длине аксона
+:
усилению сигнала синапсом
-:
выходу активационной функции
I:
ТЗ № 15
S:
Весовой коэффициент не соответствует
…
+:
весу нейрона
+:
длине аксона
-:
усилению сигнала синапсом
+:
выходу активационной функции
I:
ТЗ № 16
S:
Назначением активационной функции
является …
-:
преобразование входного вектора
+:
преобразование выходного сигнала
сумматора
-:
получение взвешенной суммы входных
сигналов
-:
преобразование выходного вектора
I:
ТЗ № 17
S:
Назначением активационной функции не
является …
-:
преобразование выходного сигнала
сумматора
+:
получение взвешенной суммы входных
сигналов
+:
преобразование выходного вектора
+:
преобразование входного вектора
I:
ТЗ № 18
S:
Активационная функция «жесткая ступенька»
имеет вид
-:
![]()
+:

-:
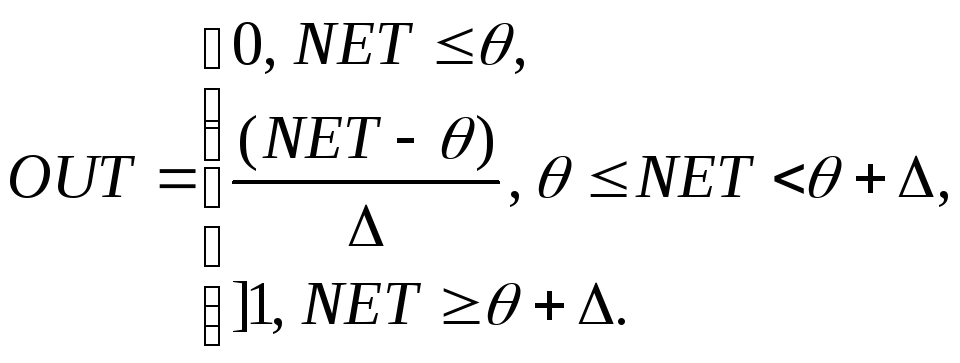
-:

I:
ТЗ № 19
S:
Активационная функция «пологая ступенька»
имеет вид
-:
![]()
-:
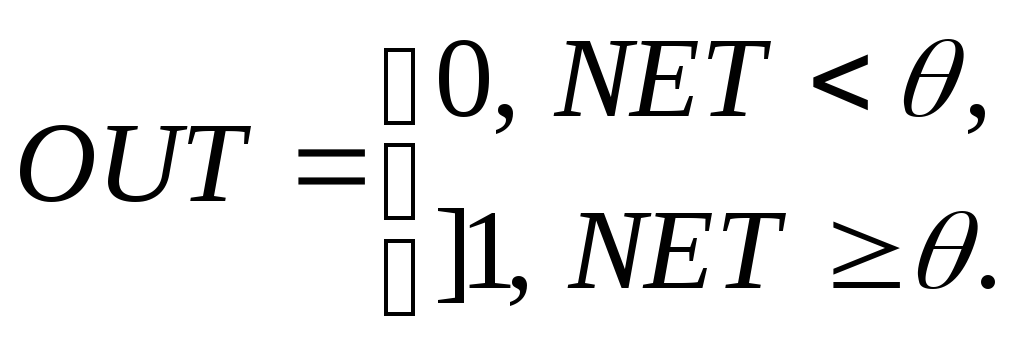
+:
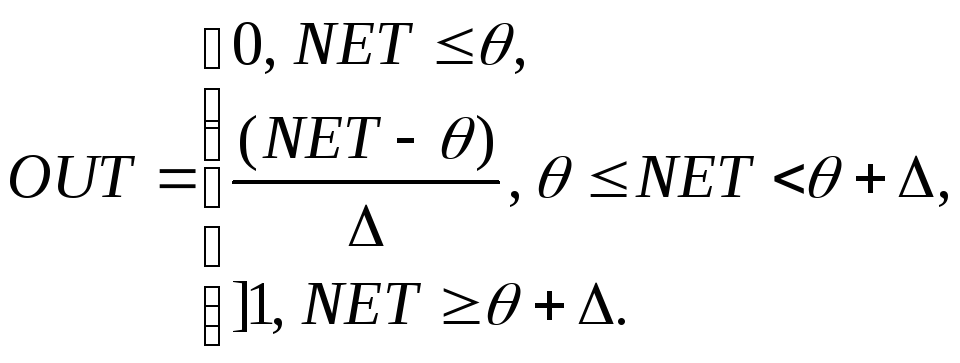
-:

I:
ТЗ № 20
S:
Логистическая активационная функция
имеет вид
+:
![]()
-:

-:

-:

I:
ТЗ № 21
S:
Активационная функция «гиперболический
тангенс» имеет вид
-:
![]()
-:

-:

+:

I:
ТЗ № 22
Q:
Активационным функциям соответствуют
выражения
L1:
жесткая ступенька
L2:
сигмоида
L3:
гиперболический тангенс
L4:
пологая
ступенька
R1:

R2:
![]()
R3:
![]()
R4:

I:
ТЗ № 23
S:
Выбор активационной функции определяется
+:
алгоритмом обучения
+:
спецификой задачи
-:
количеством нейронов
+:
удобством реализации
I:
ТЗ № 24
S:
Выбор активационной функции не
определяется
—
алгоритмом обучения
-:
спецификой задачи
+:
количеством нейронов
-:
удобством реализации
VI: 3. Искусственная нейронная сеть
I:
ТЗ № 25
S:
При создании искусственных нейронных
сетей используется … подход
-:
электрохимический
+:
биологический
-:
компьютерный
+:
информационный
I:
ТЗ № 26
S:
При создании искусственных нейронных
сетей не используется … подход
+:
электрохимический
-:
биологический
+:
компьютерный
-:
информационный
I:
ТЗ № 27
S:
Сети прямого распространения
-:
содержат обратные связи
-:
связывают нейрон с самим собой
-:
соединяют слой сети с предшествующим
+:
не содержат обратных связей
I:
ТЗ № 28
S:
Сети прямого распространения
+:
не содержат обратных связей
+:
не связывают нейрон с самим собой
+:
не соединяют слой сети с предшествующим
-:
содержат обратные связи
I:
ТЗ № 29
S:
Сети с обратными связями
-:
связывают нейроны одного слоя
+:
связывают слой с самим собой
+:
соединяют слой сети с предшествующим
-:
не принимают входных сигналов
I:
ТЗ № 30
S:
Сети с обратными связями
+:
не связывают нейроны одного слоя
-:
не связывают слой с самим собой
-:
не соединяют слой сети с предшествующим
-:
не принимают входных сигналов
I:
ТЗ № 31
S:
Многослойная сеть состоит из
+:
чередующихся множеств нейронов и весов
-:
множества соединений между нейронами
-:
множества входных сигналов и весов
-:
чередующихся множеств весов и активационных
функций
I:
ТЗ № 32
S:
Многослойная сеть содержит
+:
чередующиеся множества нейронов и весов
+:
множества соединений между нейронами
-:
множества входных сигналов и весов
-:
чередующиеся множества весов и
активационных функций
I:
ТЗ № 33
S:
Отличительными признаками многослойных
сетей являются то, что
+:
каждый нейрон сети имеет нелинейную
функцию активации
+:
сеть обладает высокой степенью связанности
-:
каждый нейрон сети имеет линейную
функцию активации
-:
сеть обладает низкой степенью связанности
I:
ТЗ № 34
S:
Искусственные нейронные сети подразделяются
на типы:
+:
полносвязные
+:
многослойные
+:
слабосвязные
-:
циклические сети
I:
ТЗ № 35
S:
В полносвязных сетях
+:
каждый нейрон передает выходной сигнал
остальным нейронам
-:
нейроны имеют соединения от выходов к
входам
-:
каждый слой, кроме последнего, разбит
на возбуждающий и тормозящий блоки
-:
нейроны входного слоя передают сигналы
нейронам 1-го скрытого слоя
I:
ТЗ № 36
S:
В монотонных сетях
-:
каждый нейрон передает выходной сигнал
остальным нейронам
-:
последний слой разбит на возбуждающий
и тормозящий блоки
+:
каждый слой, кроме последнего, разбит
на возбуждающий и тормозящий блоки
-:
нейроны входного слоя передают сигналы
нейронам 1-го скрытого слоя
I:
ТЗ № 37
S:
В слабосвязных сетях
-:
каждый нейрон передает выходной сигнал
остальным нейронам
-:
нейроны имеют соединения от выходов к
входам
-:
каждый слой, кроме последнего, разбит
на возбуждающий и тормозящий блоки
+:
нейроны входного слоя передают сигналы
нейронам 1-го скрытого слоя
I:
ТЗ № 38
S:
Каждый нейрон полносвязной сети передает
выходной сигнал
+:
всем нейронам
-:
двум соседним нейронам
-:
нейрону справа
-:
в последующий слой
I:
ТЗ № 39
S:
Каждый нейрон монотонной сети передает
выходной сигнал
-:
всем нейронам своего слоя
+:
нейронам последующего слоя
-:
одному нейрону последующего слоя
-:
нейронам предыдущего слоя
I:
ТЗ № 40
S:
Каждый нейрон слабосвязной сети передает
выходной сигнал
-:
всем нейронам своего слоя
-:
нейронам последующего слоя
-:
одному нейрону последующего слоя
+:
нейронам первого скрытого слоя
I:
ТЗ № 41
S:
В … сетях каждый нейрон передает выходной
сигнал остальным нейронам
-:
локальных
-:
монотонных
-:
слабосвязных
+:
полносвязных
I:
ТЗ № 42
S:
В … сетях каждый нейрон передает выходной
сигнал нейронам первого скрытого слоя
-:
локальных
+:
монотонных
-:
слабосвязных
-:
полносвязных
I:
ТЗ № 43
S:
В … сетях каждый нейрон передает выходной
сигнал нейронам последующего слоя
-:
локальных
-:
монотонных
+:
слабосвязных
-:
полносвязных
Соседние файлы в папке Нс
- #
- #
- #
- #
- #
- #
- #
- #
1. Что такое функция активации
2. Зачем использовать
3. Какие есть функции активации
4、sigmoid,Relu,softmax
1. Что такое функция активации
Как показано на рисунке ниже, в нейроне входные входы взвешиваются, и после суммирования также применяется функция, которая является функцией активации.

2. Зачем использовать
Если функция возбуждения не используется, выход каждого слоя является линейной функцией от входа верхнего уровня. Независимо от того, сколько слоев в нейронной сети, выход является линейной комбинацией входов.
Если используется, функция активации вводит нелинейные факторы в нейрон, так что нейронная сеть может произвольно приближать любую нелинейную функцию, так что нейронная сеть может применяться ко многим нелинейным моделям.
3. Каковы функции активации
(1) сигмовидная функция
Формула:
Кривая:
Производная:
Сигмовидная функция, также называемая логистической функцией, используется для вывода нейронов скрытого слоя, диапазон значений (0,1), она может отображать действительное число в (0,1) и может использоваться для двоичной классификации.
Эффект лучше, когда различие в функциях более сложное или разница не особенно велика.
Недостатки сигмовидной кишки:
- Функция активации требует больших вычислительных ресурсов, и когда обратное распространение ищет градиент ошибки, дифференциация включает в себя деление
- При обратном распространении градиент легко исчезает, что делает невозможным завершение обучения глубокой сети
- Функция сигмоидов насыщена и убивает градиент.
- Функция сигмоидов сходится медленно.
Ниже объясняется, почему исчезает градиент:
В алгоритме обратного распространения для получения функции активации, производное выражение сигмоиды:

Исходная сигмоидальная функция и производный граф следующие:

Из рисунка видно, что производная скоро приблизится к 0 из 0, что легко вызывает явление «исчезновение градиента»
(2) функция Тан
формула


кривая

Также называется функцией касательной к битам, диапазон значений равен [-1,1].
Эффект Таня будет очень хорошим, когда разница в функциях очевидна, и эффект функции будет продолжать расширяться в течение цикла.
Разница между и сигмоидальным состоянием состоит в том, что tanh имеет значение 0, поэтому в реальном приложении tanh будет лучше сигмовидного.
(3) ReLU
Выпрямленная линейная единица (ReLU) — для выхода нейронов скрытого слоя
формула

кривая

Особенности RELU:
Когда входной сигнал <0, на выходе все 0. Если> 0, выход равен входу
Преимущества ReLU:
Krizhevsky et al.Установлено, что скорость сходимости SGD, полученной с использованием ReLU, будет намного выше, чем сигмоид / танх
Недостатки ReLU:
Обучение очень «хрупкое», его легко «умереть»
Например, через нейрон ReLU протекает очень большой градиент. После обновления параметров этот нейрон больше не будет активировать какие-либо данные, затем градиент этого нейрона Это всегда будет 0.
Если скорость обучения велика, вероятно, что 40% нейронов в сети «мертвы».
(4) функция softmax
Softmax-для мультиклассовых выходов нейронной сети
формула

Возьмите пример, чтобы увидеть значение формулы:

То есть, если определенный zj больше других z, компоненты этого отображения близки к 1, а другие близки к 0. Основное применение — мультиклассификация.
Первая причина, по которой вы хотите получить показатель, состоит в том, чтобы моделировать поведение max, поэтому сделайте его больше.
Вторая причина — это необходимость в производной функции.
4. Сравнение сигмовидной, ReLU, softmax
Сигмоид и ReLU сравнение:
Проблема исчезновения градиента сигмоида, производной ReLU, не имеет такой проблемы, ее производная выражается следующим образом:

Кривая как показано

Основные изменения по сравнению с сигмовидными функциями:
1) Одностороннее подавление
2) Относительно широкая граница возбуждения
3) Разреженная активация.
Разница между сигмоидом и софтмаксом:
softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1.
Сигмоид отображает действительное значение в интервал (0,1), который используется для двоичной классификации.
И softmax отображает k-мерный вектор действительного значения (a1, a2, a3, a4 …) в a (b1, b2, b3, b4 …), где bi — постоянная от 0 до 1, и сумма выходных нейронов Он равен 1,0, поэтому он эквивалентен значению вероятности, и тогда задача мультиклассификации может быть выполнена в соответствии с вероятностью bi.
Для двух задач классификации сигмоид и софтмакс одинаковы, и оба стремятся к потере перекрестной энтропии, а софтмакс можно использовать для задач мультиклассификации
Softmax является расширением сигмовидной кишки, потому что, когда число категорий k = 2, регрессия softmax вырождается в логистическую регрессию. В частности, когда k = 2, предполагаемая функция регрессии softmax равна:

Используя функцию избыточности параметра регрессии softmax, вычтите вектор θ1 из обоих векторов параметров, чтобы получить:

Наконец, θ ′ используется для представления θ2-θ1, и приведенная выше формула может быть выражена как вероятность того, что регрессия softmax предсказывает одну из категорий как

Вероятность другой категории

Это согласуется с логистической регрессией.
Распределение, используемое для моделирования softmax, является полиномиальным распределением, в то время как логистика основана на распределении Бернулли
Множественная логистическая регрессия может также обеспечить эффект мультиклассификации с помощью суперпозиции, но мультиклассификация с помощью регрессии softmax является взаимоисключающей между классами, то есть один вход может быть классифицирован только Это категория, множественные логистические регрессии используются для множественной классификации, и выходные категории не являются взаимоисключающими, то есть слово «яблоко» относится как к категории «фрукты», так и к категории «3C».
5. Как выбрать
При выборе он настраивается в соответствии с преимуществами и недостатками каждой функции, например:
Если вы используете ReLU, будьте осторожны, чтобы установить скорость обучения, и следите за тем, чтобы в сети не появлялось много «мертвых» нейронов. Если это не легко решить, вы можете попробовать Leaky ReLU, PReLU или Maxout.
2.3 ВЫБОР ФУНКЦИИ АКТИВАЦИИ И ОБУЧЕНИЕ НЕЙРОННОЙ СЕТИ
Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи — вес синапса. Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов и внешних входных сигналов. Преобразователь реализует функцию одного аргумента, выхода сумматора, в некоторую выходную величину нейрона. Эта функция называется функцией активации нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента. В общем случае входной сигнал и весовые коэффициенты могут принимать действительные значения. Выход определяется видом функции активации и может быть как действительным, так и целым. Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами — тормозящими.
Таким образом, нейрон полностью описывается своими весами и функцией активации F. Получив набор чисел (вектор) в качестве входов, нейрон выдает некоторое число на выходе.
Активационная функция может быть различного вида [61]. Наиболее широко используемые варианты приведены в таблице (табл.2.1).
Одними из наиболее распространенных функций являются:
- 1. линейная,
- 2. нелинейная с насыщением — логистическая функция или сигмоид,
- 3. гиперболический тангенс.
Линейная функция наилучшим образом соответствует сущности данной задачи. Ее областью определения является диапазон (-∞, ∞). Это позволяет, используя ценовые характеристики товара на входе, получать характеристические значения любой величины на выходе, равные их фактической сумме.
Следует отметить, что сигмоидная функция (2.12) дифференцируема на всей оси абсцисс, что широко используется во многих алгоритмах обучения.
Таблица 2.1
Перечень функций активации нейронов
|
Название |
Формула |
Область значений |
|
Пороговая |
|
0, 1 |
|
Знаковая |
|
-1, 1 |
|
Сигмовидная |
|
(0, 1) |
|
Полулинейная |
|
(0, ∞) |
|
Линейная |
|
(-∞, ∞) |
|
Радиальная базисная |
|
(0, 1) |
|
Полулинейная с насыщением |
|
(0, 1) |
|
Линейная с насыщением |
|
(-1, 1) |
|
Гиперболический тангенс |
|
(-1, 1) |
|
Треугольная |
|
(0, 1) |
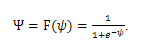 . (2.12)
. (2.12)
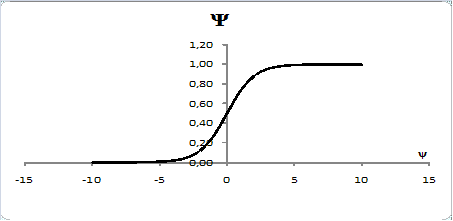
Рис.2.12 Вид сигмоидной функции
Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем сильные, и предотвращает насыщение от сильных сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон (рис.2.12). Эти особенности важны для задачи моделирования совершенной конкуренции. Рынок совершенной конкуренции характеризуется однородностью, которая заключается в том, что все производители выпускают одинаковый по числу, свойствам и неценовым характеристикам товар. Единственное отличие однотипных товаров разных производителей — это его ценовые параметры. В условиях рыночной экономики отличия ценовых параметров достаточно характерны для рынков товаров и услуг. Однако они, чаще всего, носят не значительный характер. Поэтому разница между однотипными ценовыми параметрами разных товаров, подаваемых на вход нейронной сети, будет невелика, что предъявляет к чувствительности функции дополнительные требования. Нейроны должны «распознавать» слабо различающиеся входные сигналы. Это делает (2.12) наиболее применимой.
В условиях конкуренции участники рынка, производящие или потребляющие товар по очень высоким или по слишком низким ценам, соответственно, не определяют положение дел на рынке. Основными участниками конкурентной борьбы являются предприятия, действующие в области наиболее конкурентоспособной цены. Это обстоятельство вполне соответствует виду функции (2.12).
Другой широко используемой активационной функцией является гиперболический тангенс. В отличие от логистической функции гиперболический тангенс принимает значения различных знаков, что для ряда сетей оказывается выгодным.
Важно отметить, что выбор вида активационной функции предлагается осуществлять симметрично в производственном и потребительском сегменте по уровням подсистем. Это обосновывается тем, что производство и потребление товара на рынке являются «зеркальными» процессами и должны протекать по одинаковым принципам. Сам же вид функций определяется исходя из требований точности.
При решении с помощью нейронных сетей задач необходимо собрать достаточный и представительный объем данных для того, чтобы обучить нейронную сеть решению таких задач. Обучающий набор данных — это набор наблюдений, содержащих признаки изучаемого объекта. Нейронные сети работают с числовыми данными, взятыми, как правило, из некоторого ограниченного диапазона. В данной задаче эта выборка может быть построена на основе статистической информации, собранной за время существования рынка. Кроме того, количество производителей и поставщиков на рынке совершенной конкуренции достаточно велико и при отсутствии других данных текущие показатели товара могут быть рассмотрены, как обучающая выборка.
Вопрос о том, сколько нужно иметь наблюдений для обучения сети, часто оказывается непростым. Известен ряд эвристических правил, которые устанавливают связь между количеством необходимых наблюдений и размерами сети. Простейшее из них гласит, что количество наблюдений должно быть в 10 раз больше числа связей в сети. На самом деле это число зависит от сложности того отображения, которое должна воспроизводить нейронная сеть. С ростом числа используемых признаков количество наблюдений возрастает по нелинейному закону, так что уже при довольно небольшом числе признаков, скажем 50, может потребоваться огромное число наблюдений. Эта проблема носит название «проклятие размерности».
Таким образом, в условиях первого слоя нейронной системы примерное число обучающих примеров можно определить:
μ = w x l x m. (2.13)
Процесс обучения нейронной сети заключается в определении значений весовых коэффициентов, обеспечивающих однозначное преобразование входных сигналов в выходные.
Путем анализа имеющихся в распоряжении аналитика входных и выходных данных веса сети автоматически настраиваются так, чтобы минимизировать разность между желаемым сигналом и полученным на выходе в результате моделирования. Эта разность носит название ошибки обучения.
Ошибка обучения для конкретной конфигурации нейронной сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения выходных значений с желаемыми, целевыми значениями. Эти разности позволяют сформировать так называемую функцию ошибок (критерий качества обучения). При моделировании нейронных сетей с линейными функциями активации нейронов можно построить алгоритм, гарантирующий достижение абсолютного минимума ошибки обучения. Для нейронных сетей с нелинейными функциями активации в общем случае нельзя гарантировать достижения глобального минимума функции ошибки.
При таком подходе к процедуре обучения может оказаться полезным геометрический анализ поверхности функции ошибок. Определим веса и смещения как свободные параметры модели и их общее число обозначим через N; каждому набору таких параметров поставим в соответствие одно измерение в виде ошибки сети. Тогда для всевозможных сочетаний весов соответствующую ошибку сети можно изобразить точкой в N-1-мерном пространстве, а все такие точки образуют некоторую поверхность, называемую поверхностью функции ошибок. При таком подходе цель обучения нейронной сети состоит в том, чтобы найти на этой многомерной поверхности глобальный минимум.
В случае линейной модели сети и функции ошибок в виде суммы квадратов такая поверхность будет представлять собой параболоид, который имеет единственный минимум, и это позволяет отыскать такой минимум достаточно просто.
В случае нелинейной модели поверхность ошибок имеет гораздо более сложное строение и обладает рядом неблагоприятных свойств, в частности может иметь локальные минимумы, плоские участки, седловые точки и длинные узкие овраги.
Определить глобальный минимум многомерной функции аналитически невозможно, и поэтому обучение нейронной сети, по сути дела, является процедурой изучения поверхности функции ошибок. Отталкиваясь от случайно выбранной точки на поверхности функции ошибок, алгоритм обучения постепенно отыскивает глобальный минимум. Как правило, для этого вычисляется градиент (наклон) функции ошибок в данной точке, а затем эта информация используется для продвижения вниз по склону. В конце концов алгоритм останавливается в некотором минимуме, который может оказаться лишь локальным минимумом, а если повезет, то и глобальным.
После многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что «сеть обучена». В программных реализациях можно видеть, что в процессе обучения функция ошибки (например, сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда функция ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную сеть считают натренированной и готовой к применению на новых данных.
Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу.
Для решения задачи обучения могут быть использованы следующие (итерационные) алгоритмы:
- 1. алгоритмы локальной оптимизации с вычислением частных производных первого порядка;
- 1. алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка;
- 2. стохастические алгоритмы оптимизации;
- 3. алгоритмы глобальной оптимизации.
К первой группе относятся: градиентный алгоритм (метод скорейшего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряженных градиентов; методы, учитывающие направление антиградиента на нескольких шагах алгоритма [119, 122].
Ко второй группе относятся: метод Ньютона, методы оптимизации с разреженными матрицами Гессе, квазиньютоновские методы, метод Гаусса-Ньютона, метод Левенберга-Марквардта [128, 131] и другие.
Стохастическими методами являются: поиск в случайном направлении, имитация отжига, метод Монте-Карло (численный метод статистических испытаний).
Задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция (функция ошибки).
При использовании алгоритма обратного распространения ошибки сеть рассчитывает возникающую в выходном слое ошибку и вычисляет вектор градиента как функцию весов. Этот вектор указывает направление кратчайшего спуска по поверхности для данной точки, поэтому если продвинуться в этом направлении, то ошибка уменьшится. Последовательность таких шагов в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь вызывает выбор величины шага.
При большой длине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или уйти в неправильном направлении. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. На практике величина шага выбирается пропорциональной крутизне склона (градиенту функции ошибок). Такой коэффициент пропорциональности называется параметром скорости настройки. Правильный выбор параметра скорости настройки зависит от конкретной задачи и обычно осуществляется опытным путем. Этот параметр может также зависеть от времени, уменьшаясь по мере выполнения алгоритма.
Алгоритм действует итеративно, и его шаги принято называть эпохами или циклами. На каждом цикле на вход сети последовательно подаются все обучающие наблюдения, выходные значения сравниваются с целевыми значениями, и вычисляется функция ошибки. Значения функции ошибки, а также ее градиента используются для корректировки весов и смещений, после чего все действия повторяются. Начальные значения весов и смещений сети выбираются случайным образом, и процесс обучения прекращается либо когда реализовано определенное количество циклов, либо когда ошибка достигнет некоторого малого значения или перестанет уменьшаться.
Другой подход к процедуре обучения сети можно сформулировать, если рассматривать ее как процедуру, обратную моделированию. В этом случае требуется подобрать такие значения весов, которые обеспечивали бы нужное соответствие между входами и желаемыми значениями на выходе. Такая процедура обучения носит название процедуры адаптации и достаточно широко применяется для настройки параметров нейронных сетей.
Каждый слой производственного сегмента решает свою функциональную задачу в рамках нейронной системы всего рынка. По этой причине процедуру обучения можно выполнять независимо для каждого слоя.
Процесс обучения требует набора примеров ее желаемого поведения — входов H и целевых выходов Ψоpt. Во время этого процесса веса настраиваются так, чтобы минимизировать некоторый функционал ошибки. По умолчанию, в качестве такого функционала для сетей с прямой передачей сигналов принимается среднеквадратичная ошибка между векторами выхода Ψоpt и Ψ.
При обучении сети рассчитывается некоторый функционал, характеризующий качество обучения:
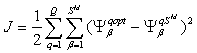 , (2.14)
, (2.14)
где J — функционал; Q — объем выборки; М — число слоев сети; q — номер выборки; Sм — число нейронов выходного слоя; Ψq — вектор сигнала на выходе сети; Ψq opt — вектор желаемых (целевых) значений сигнала на выходе сети для выборки с номером q.
В случае использования линейной активационной функции нейронные сети первого слоя однослойные. В этом случае М = 1 и выражение для функционала принимает вид:
![]() , (2.15)
, (2.15)
где ![]() — функция активации;
— функция активации; ![]() — сигнал на входе функции активации для j-го нейрона;
— сигнал на входе функции активации для j-го нейрона; ![]() — вектор входного сигнала; w — число элементов вектора входа; m — число нейронов в слое;
— вектор входного сигнала; w — число элементов вектора входа; m — число нейронов в слое; ![]() — весовые коэффициенты сети.
— весовые коэффициенты сети.
Включим вектор смещения в состав матрицы весов ![]() , а вектор входа дополним элементом, равным 1.
, а вектор входа дополним элементом, равным 1.
Применяя правило дифференцирования сложной функции, вычислим градиент функционала ошибки, зная при этом, что функция активации дифференцируема:
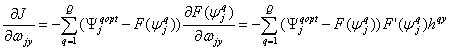 . (2.16)
. (2.16)
Введем обозначение:
![]() . (2.17)
. (2.17)
и преобразуем выражение (2.16) следующим образом:
![]() . (2.18)
. (2.18)
Полученные выражения упрощаются, если сеть линейна. Поскольку для такой сети выполняется соотношение ![]() , то справедливо условие
, то справедливо условие ![]() . В этом случае выражение (2.16) принимает вид:
. В этом случае выражение (2.16) принимает вид:
![]() . (2.19)
. (2.19)
Выражение (2.19) положено в основу алгоритма WH, применяемого для обучения линейных нейронных сетей [132].
Линейные сети могут быть обучены и без использования итерационных методов, а путем решения следующей системы линейных уравнений:
![]() . (2.20)
. (2.20)
Если число неизвестных системы (2.20) равно числу уравнений, то такая система может быть решена, например, методом исключения Гаусса с выбором главного элемента. Если же число уравнений превышает число неизвестных, то решение ищется с использованием метода наименьших квадратов.
В случае нелинейной функции активации для обучения нейронных сетей предлагается применить метод обратного распространения ошибки.
Алгоритм обратного распространения ошибки является одним из эффективных обучающих алгоритмов [130]. По существу он представляет собой минимизационный метод градиентного спуска. Рассмотрим алгоритм обратного распространения ошибки для нейронной сети с одним скрытым слоем. Предположим, что имеется A исходных примеров:
![]() = , (2.21)
= , (2.21)
где ![]() — вектор желаемых выходов сети, соответствующий входному вектору
— вектор желаемых выходов сети, соответствующий входному вектору ![]() .
.
Инициализируем вектор весов Ω случайным образом.
Теперь нужно осуществить настройку весов сети с помощью процесса обучения. Для a-го примера выходы скрытых нейронов будут определяться выражениями:
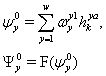 , (2.22)
, (2.22)
а выходы всей нейросети — выражениями:
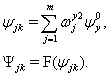 (2.23)
(2.23)
В выражениях (2.22) и (2.23), F() — функция активации, например, сигмоидная функция.
Функционал квадратичной ошибки сети для данного входного образа имеет вид:
![]() (2.24)
(2.24)
Данный функционал подлежит минимизации. Классический градиентный метод оптимизации состоит в итерационном уточнении аргумента согласно формуле:
![]() , (2.25)
, (2.25)
где h — коэффициент скорости обучения 0<η<1.
Параметр η имеет смысл темпа обучения и выбирается достаточно малым для сходимости метода.
Функция ошибки в явном виде не содержит зависимости от веса ![]() , поэтому воспользуемся формулами неявного дифференцирования сложной функции:
, поэтому воспользуемся формулами неявного дифференцирования сложной функции:
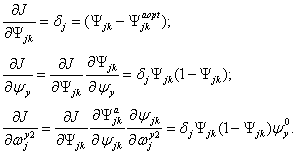 (2.26)
(2.26)
Производная сигмоидной функции выражается только через само значение функции. Таким образом, все необходимые величины для подстройки весов выходного слоя получены.
Выполняется подстройка весов скрытого слоя:
![]() (2.27)
(2.27)
Вычисляются производные функции ошибки:
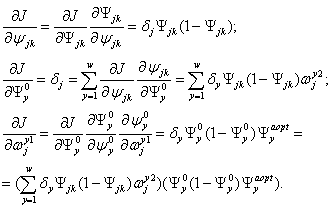 (2.26)
(2.26)
При вычислении d здесь и был применен принцип обратного распространения ошибки: частные производные берутся только по переменным последующего слоя. По полученным формулам модифицируются веса нейронов скрытого слоя.
Вычисления (2.22)-(2.26) повторяются для всех обучающих векторов. Обучение завершается по достижении малой полной ошибки или максимально допустимого числа итераций.
Сходимость метода обратного распространения весьма медленная. Невысокий темп сходимости является особенностью всех градиентных методов, так как локальное направление градиента отнюдь не совпадает с направлением к минимуму. Подстройка весов выполняется независимо для каждой пары образов обучающей выборки. При этом улучшение функционирования на некоторой заданной паре может приводить к ухудшению работы на предыдущих образах.
Несмотря на то, что алгоритм обратного распространения ошибки достаточно прост, он требует обычно тысячи итераций для обучения нейросети. Если требований к точности нет, то следует использовать первый способ (2.14)-(2.20).
Для определения весов входов нейронов второго слоя, а также третьего слоя производственного сегмента нейронной системы обучение не требуется. Значения весов, в силу равнозначности положения всех производителей на рынке, выбираются равными. Никто из них не занимает по условию совершенной конкуренции привилегированного положения. Эти же принципы применимы и к товарам.
По аналогии определяются веса нейронной подсистемы потребительского сегмента рынка.
Главным этапом применения предложенной нейронной системы является процесс ее непосредственной эксплуатации. Цель этого этапа заключается в решении основной задачи — определении характеристик товара, обеспечивающих его производителю конкурентные преимущества и удовлетворяющего запросы потребителей.
Все курсы > Вводный курс > Занятие 21
В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.
Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).
Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.
Смысл, структура и принцип работы
Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).
Отличие нейросети от других алгоритмов заключается в ее структуре.

Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.
Функционирует нейросеть следующим образом.
На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w1, w2, w3, w4). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b1 и b2).
$$ w_{1}cdot x + w_{3}cdot y + b_{1} $$
$$ w_{2}cdot x + w_{4}cdot y + b_{2} $$
Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h1 и h2).
$$ h_{1} = actfun(w_{1}cdot x + w_{3}cdot y + b_{1}) $$
$$ h_{2} = actfun(w_{2}cdot x + w_{4}cdot y + b_{2}) $$
На втором этапе процесс повторяется для нейронов скрытого слоя (h1 и h2), весов (w5 и w6) и смещения (b3) до получения конечного результата (r).
$$ r = actfun(w_{5}cdot h_{1} + w_{6}cdot h_{2} + b_{3}) $$
Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:
- Восприятие информации через сенсоры (входной слой)
- Создание ассоциаций (скрытый слой)
- Реакцию (выходной слой)
Основы нейронных сетей на простом примере
Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.

В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.
$$ f(x) = frac{mathrm{1} }{mathrm{1} + e^{-x}} $$
График сигмоиды выглядит следующим образом.
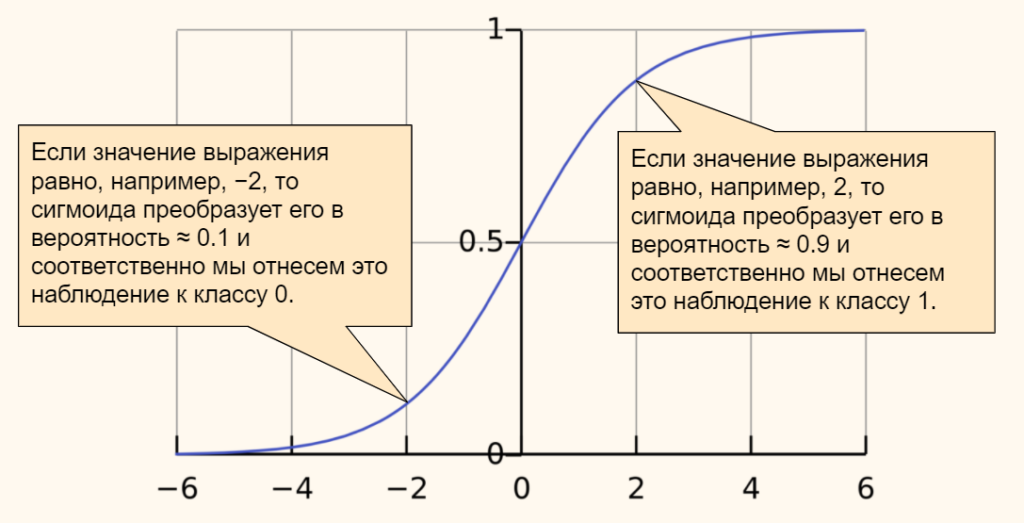
Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.
Общее уравнение нейросети выглядит следующим образом.
$$ r = sigmoid(w_{1}cdot weight + w_{2}cdot height + bias) $$
Теперь предположим, что у нас есть следующие данные и параметры нейросети.
Откроем ноутбук к этому занятию⧉
|
# даны вес и рост трех человек # единицей мы обозначим мужской пол, а нулем — женский. data = { ‘Иван’: [84, 180, 1], ‘Мария’: [57, 165, 0], ‘Анна’: [62, 170, 0] } |
|
# и даны следующие веса и смещение w1, w2, b = 0.3, 0.1, —39 |
Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.
|
r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b |
Теперь к полученному результату (r) применим сигмоиду.
|
np.round(1 / (1 + np.exp(—r)), 3) |
Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.
|
# пройдемся по ключам и значениям нашего словаря с помощью метода .items() for k, v in data.items(): # вначале умножим каждую строчку данных на веса и прибавим смещение r1 = w1 * v[0] + w2 * v[1] + b # затем применим сигмоиду r2 = 1 / (1 + np.exp(—r1)) # если результат больше 0,5, модель предскажет мужской пол if r2 > 0.5: print(k, np.round(r2, 3), ‘male’) # в противном случае, женский else: print(k, np.round(r2, 3), ‘female’) |
|
Иван 0.985 male Мария 0.004 female Анна 0.032 female |
Как мы видим, модель отработала верно.
Обучение нейронной сети
В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).
И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.
В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.
Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).

В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.
Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).
Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.
Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.
Создание нейросети в библиотеке Keras
Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.
|
# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist !pip install tensorflow mnist |
И импортируем их.
|
# импортируем рукописные цифры import mnist # и библиотеку keras from tensorflow import keras |
1. Подготовка данных
Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).
В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).
Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.
|
# сохраним обучающую выборку и соответсвующую целевую переменную X_train = mnist.train_images() y_train = mnist.train_labels() # посмотрим на размерность print(X_train.shape) print(y_train.shape) |
Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.
|
# сделаем то же самое с тестовыми данными X_test = mnist.test_images() y_test = mnist.test_labels() # и также посмотрим на размерность print(X_test.shape) print(y_test.shape) |
Таких изображений и целевых значений 10000.
Посмотрим на сами изображения.
|
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, X_train, y_train): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = ‘gray’) # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f‘Target: {label}’) |

Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.
$$ x’ = 2 frac {x-min(x)}{max(x)-min(x)}-1 $$
Применим эту формулу к нашим данным.
|
# функция np.min() возвращает минимальное значение, # np.ptp() — разницу между максимальным и минимальным значениями (от англ. peak to peak) X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 |
Посмотрим на новый диапазон.
|
# снова воспользуемся функцией np.ptp() np.ptp(X_train) |
Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.
Применим этот метод к нашим данным.
|
# «вытянем» (flatten) наши изображения, с помощью метода reshape # у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1) X_train = X_train.reshape((—1, 784)) X_test = X_test.reshape((—1, 784)) # посмотрим на результат print(X_train.shape) print(X_test.shape) |
Посмотрим на получившиеся значения пикселей.
|
# выведем первое изображение [0], пиксели с 200 по 209 X_train[0][200:210] |
|
array([—1. , —1. , —1. , —0.61568627, 0.86666667, 0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373]) |
Наши данные готовы. Теперь нужно задать конфигурацию модели.
2. Конфигурация нейронной сети
Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.
Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).

В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.
|
# импортируем класс Sequential from tensorflow.keras.models import Sequential # и создадим объект этого класса model = Sequential() |
Далее нам нужно прописать сами слои и связи между нейронами.
Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.
|
# импортируем класс Dense from tensorflow.keras.layers import Dense # и создадим первый скрытый слой (с указанием функции активации и размера входного слоя) model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,))) # затем второй скрытый слой model.add(Dense(64, activation = ‘sigmoid’)) # и наконец выходной слой model.add(Dense(10, activation = ‘softmax’)) |
Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).
Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.
$$ text{softmax}(vec{z})_{i} = frac{e^{z_i}}{sum_{j=1}^K e^{z_i}} $$
Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов zi экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.
На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.

Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.
Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.
|
z = ([1, 2, 0.5]) np.exp(z) / sum(np.exp(z)) |
|
array([0.2312239 , 0.62853172, 0.14024438]) |
Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.
3. Настройки
Настроек будет три:
- тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
- способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
- метрика (metric) покажет, насколько точна наша модель
Функция потерь
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.
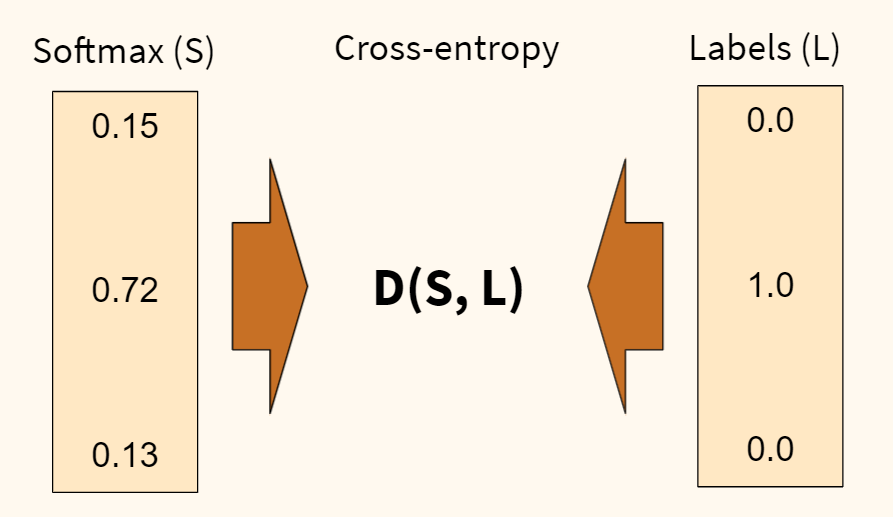
Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.
Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.
Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.

В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).
Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.
Алгоритм оптимизации
Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.

Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w1 и w2, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.
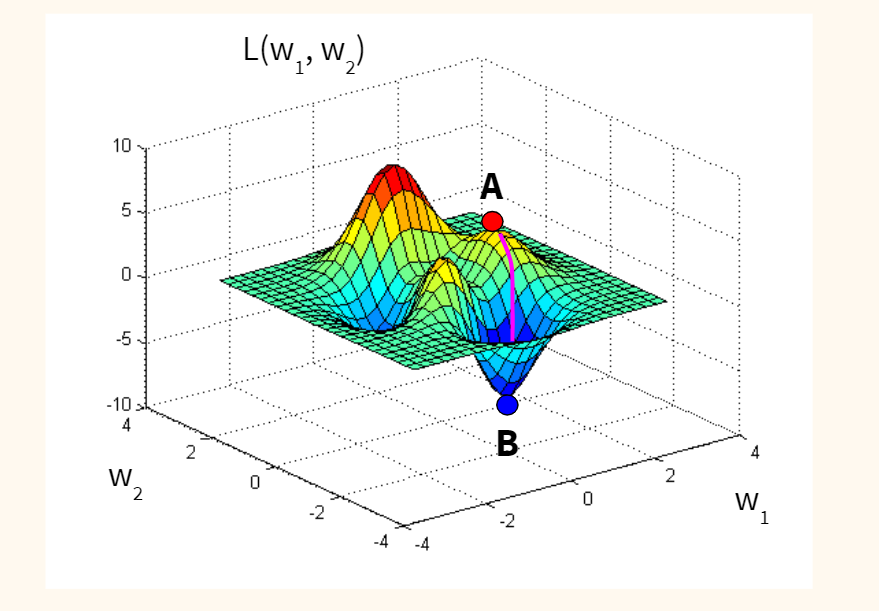
Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.
Метрика
Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.
Посмотрим на используемый код.
|
model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘sgd’, metrics = [‘accuracy’] ) |
4. Обучение модели
Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.
- Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
- Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
- На выходе из функции softmax мы получаем вероятности для каждой из цифр
- После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
- На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
- После этого процесс повторяется, но уже с новыми весами.
Давайте выполним все эти операции в библиотеке Keras.
|
# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding from tensorflow.keras.utils import to_categorical |
|
# обучаем модель model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 2.0324 — accuracy: 0.4785 Epoch 2/10 1875/1875 [==============================] — 3s 2ms/step — loss: 1.2322 — accuracy: 0.7494 Epoch 3/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.7617 — accuracy: 0.8326 Epoch 4/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.5651 — accuracy: 0.8663 Epoch 5/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4681 — accuracy: 0.8827 Epoch 6/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4121 — accuracy: 0.8923 Epoch 7/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3751 — accuracy: 0.8995 Epoch 8/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3487 — accuracy: 0.9045 Epoch 9/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3285 — accuracy: 0.9090 Epoch 10/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3118 — accuracy: 0.9129 <keras.callbacks.History at 0x7f36c3f09490> |
На обучающей выборке мы добились неплохого результата, 91.29%.
5. Оценка качества модели
На этом шаге нам нужно оценить качество модели на тестовых данных.
|
# для оценки модели воспользуемся методом .evaluate() model.evaluate( X_test, # который применим к тестовым данным to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.2972 — accuracy: 0.9173 [0.29716429114341736, 0.9172999858856201] |
Результат «на тесте» оказался даже чуть выше, 91,73%.
6. Прогноз
Теперь давайте в качестве упражнения сделаем прогноз.
|
# передадим модели последние 10 изображений тестовой выборки pred = model.predict(X_test[—10:]) # посмотрим на результат для первого изображения из десяти pred[0] |
|
array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03, 6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01, 5.3100550e-04, 1.9325638e-02], dtype=float32) |
Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.
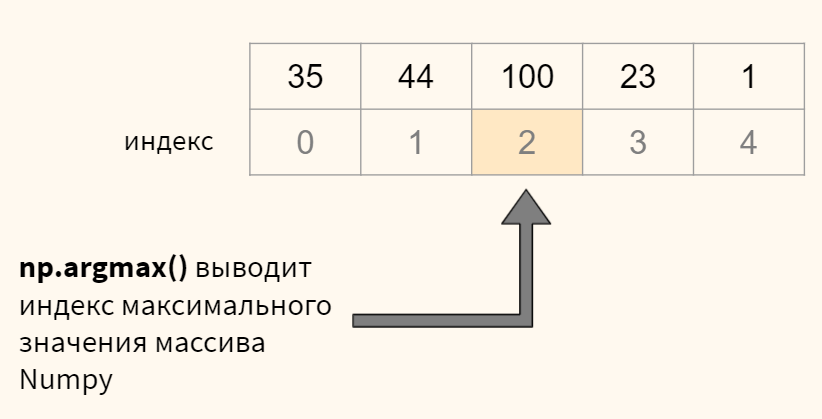
Теперь применим к нашим данным.
|
# для кажого изображения (то есть строки, axis = 1) # выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем print(np.argmax(pred, axis = 1)) # остается сравнить с целевой переменной print(y_test[—10:]) |
|
[7 8 9 0 1 2 3 4 5 6] [7 8 9 0 1 2 3 4 5 6] |
Для первых десяти цифр модель сделала верный прогноз.
7. Пример улучшения алгоритма
Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).
Посмотрим на результат на обучающей и тестовой выборке.
|
# снова укажем настройки модели model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘adam’, # однако заменим алгоритм оптимизации metrics = [‘accuracy’] ) # обучаем модель методом .fit() model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # прописываем количество эпох ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.2572 — accuracy: 0.9252 Epoch 2/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1738 — accuracy: 0.9497 Epoch 3/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1392 — accuracy: 0.9588 Epoch 4/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1196 — accuracy: 0.9647 Epoch 5/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1062 — accuracy: 0.9685 Epoch 6/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0960 — accuracy: 0.9708 Epoch 7/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0883 — accuracy: 0.9732 Epoch 8/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0826 — accuracy: 0.9747 Epoch 9/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0766 — accuracy: 0.9766 Epoch 10/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0699 — accuracy: 0.9780 <keras.callbacks.History at 0x7f36c3d74590> |
|
# и оцениваем результат «на тесте» model.evaluate( X_test, to_categorical(y_test) ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.1160 — accuracy: 0.9647 [0.11602973937988281, 0.9646999835968018] |
Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.
Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.
Подведем итог
На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.
При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.
Вопросы для закрепления
Перечислите типы слоев нейронной сети
Посмотреть правильный ответ
Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.
Из каких двух этапов состоит обучение нейронной сети?
Посмотреть правильный ответ
Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.
Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?
Посмотреть правильный ответ
Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.
Ответы на вопросы
Вопрос. Что означает число 1875 в результате работы модели?
Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).
- в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
- во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
- и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1
В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.
Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.
В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.
Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.
Введение в нейронные сети. Общая постановка задачи. Персептрон. Функции активации нейронов.
Общая постановка задачи
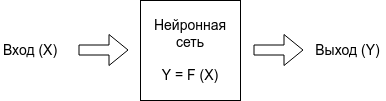
В общем случае задача программирования нейронной сети — это разработать такую нейронную сеть, которая по входу X, будет выдавать правильные ответы Y.
Входом в нейронную сеть могут быть:
- сырые данные, например, звук или фотография.
- либо уже заранее обработанные данные алгоритмом, которые по входу X выдаст признаки (feauture), которые будут передаваться нейронной сети. Данные признаки могут быть определены другой нейронной сетью.
- и т.п.
Выходом могут являться:
- Ответ да или нет.
- Номер категории, к которой принадлежат входные данные.
- Картинка, изображение, звук.
- и т.п.
Задача программиста:
- определить что будет считаться входом в нейронную сеть, а что выходом.
- в каком формате будет принимать нейронная сеть данные.
- структурировать и привести в единую форму входные и выходные данные.
- определить признаки данных, которые могут быть дополнительно поданы на вход в нейронную сеть.
- определить количество слоев нейронной сети.
- определить дополнительные алгоритмы в архитектуре нейронной сети, как отдельные слои.
- создать и разметить DataSet, на котором будет проходить обучение нейронная сеть.
- создать правильную архитектуру нейронной сети.
- обучить нейронную сеть и проверить ее на контрольной выборке.
- внедрить полученную нейронную сеть.
Размеченный DataSet ((D)) — это набор данных и известных ответов к ним. По этому датасету обучаются нейронные сети. При этом датасет делится на две части. Обучающий и контрольный. По обучающему датасету нейронная сеть учится, а по контрольному тестируется. Важно, чтобы данные контрольного датасета не попадали в обучающий, иначе нейронная сеть просто заучит правильные ответы.
Правильным результатом считается, когда нейронная сеть наименьше всего ошибается на обоих дата сетах. Берутся ответы нейронной сети и сравниваются с правильными. Чем меньше ошибка, тем лучше работает нейронная сеть.
Функцией ошибки ((Q)) называется разница между правильными ответами и ответами, которая выдает нейронная сеть на обучающем и контрольном датасете.
Обучение по размеченному датасету называется обучением с учителем. Есть также другие варианты обучения. Например, без учителя. В данном случае правильные ответы отсуствуют и нейронная сеть должна найти их сама. Эта задача хорошо подходит, например, для нахождения общих признаков на большом количестве данных.
Математикой обучения занимаются алгоритмы популярных библиотек TensorFlow, Keros.
Ахитектурой нейронной сети ((F)) — называется цепочка, последовательность слоев этой сети.
Архитектура нейронных сетей может быть разной формы и длины, состоять из нескольких последовательных или паралельных слоев или других цепочек.
Слой — это набор персептронов или определенный алгоритм, который преобразует, по некоторому принципу, входные сигналы p в выходные p’.
Создание архитектуры нейронной сети напоминает конструктор лего, где программист опытным путем подбирает правильный порядок слоев в архитектуре нейронной сети, чтобы она на выходе выдавала правильный результат и значение функии ошибки стремилось к нулю (Q(F, D) to 0)

Каждый слой выполняет определенную функцию. Слои могут отличаться друг от друга.
Примеры слоев:
- простой слой персептронов.
- сверточный слой.
- слой конвертации изображения из двухмерной картинки в одномерный вектор.
- нахождение максимума или минимума.
- фильтрация значения по критерию
- измененя яркости или контрастности.
- удаления или добавление шума.
- Max Pooling и Average Pooling.
- и т.п.
Архитектура нейронной сети может быть иерархической.
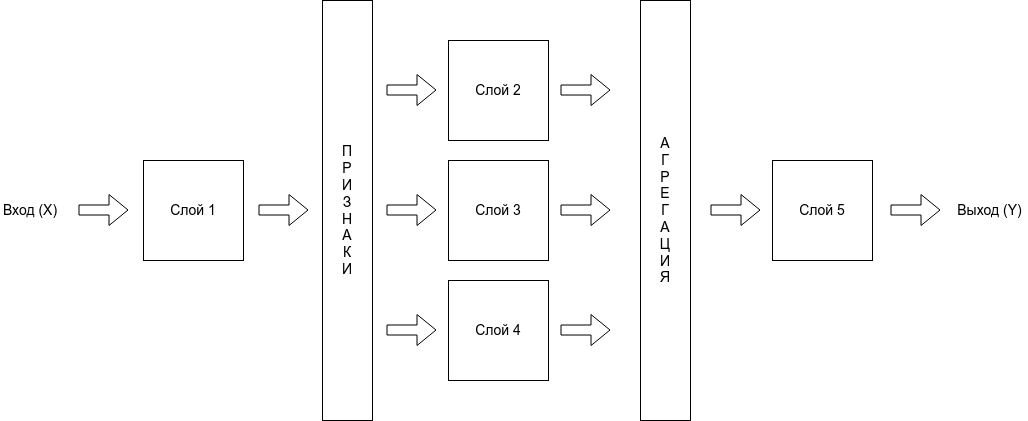
Математическое описание задачи обучения с учителем
Дано:
(X) — это входные тестовые данные. Вектор вида ((x_1, x_2, x_3, … , x_n))
(Y) — выходные тестовые данные. Вектор вида ((y_1, y_2, y_3, … , y_k))
(D) — это обучающая выборка, множество кортежей вида ((X_i,Y_i)), множество входных значений и ответов к ним (выходных значений), где для каждого (X_i) известно (Y_i).
(n) — длинна вектора (X)
(k) — длинна вектора (Y)
(m) — размер выборки, количество кортежей в множестве (D)
Требуется:
Найти функцию (F), которая (Y approx F(X))
Обозначим функцию потерь как:
(L(F,X_i)=|Y_i — F(X_i)|)
Эта функция означает, насколько ошибается функция (F) на конкретном примере ((X_i,Y_i)).
Функция (Q), будет называться функцией ошибки (F) на множестве (D) и определена как сумма всех значений функции (L)
(Q (F) = frac{ sum_{i=1}^{m} L(F,X_i) } {m})
Функция (F) и ее веса будут найдена при условии (Q(F) to 0)
Есть разные варианты формул ошибки:
Абсолютная ошибка:
(Q (F) = frac{ sum_{i=1}^{m} |Y_i — F(X_i)| } {m})
В Tenzorflow loss=’mean_absolute_error’
Среднеквадратическая ошибка:
(Q (F) = frac{ sqrt {sum_{i=1}^{m} (Y_i — F(X_i))^2} } {m})
В Tenzorflow loss=’mean_squared_error’
Математическая модель нейрона
Нейрон — это атом нейронной сети. У каждого нейрона есть несколько входов и один выход.
Ниже представлена математическая модель одного нейрона.
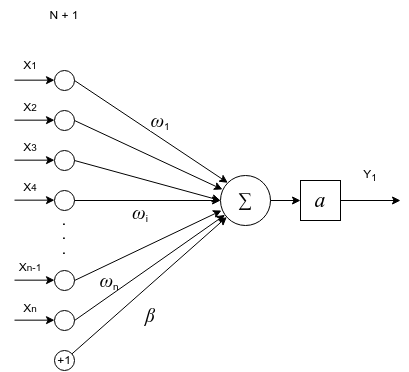
Основная задача нейрона проводить сигнал или гасить его в зависимости от входных значений.
Выходной сигнал нейрона считается как сумма входных значений, умноженная на их веса плюс базис, обработанная функцией активации.
(y = a(sum_{i=1}^{n} omega_i * x_i + beta))
(a(v)) — функция активации нейрона. Функция активации нейрона нужна, чтобы определить при каких входных значениях должен активироваться (включаться) нейрон, т.е. проводить сигнал. А при каких нет. Нейрон включается, если достигается нужный уровень сигнала, после этого нейрон передает сигнал дальше. Поэтому функция и называется функцией активации.
(omega_i) — вес нейронной связи. Задает какой входящий сигнал и с какой силой должен учитываться, а какой нет.
(beta) — смещение bias. Это пороговое значение, которое смещает аргумент активационной функции, потому что активация (включение) нейрона может происходит не в точке 0, а в какой-то другой точке. А т.к. функция активации работает в точке ноль, то аргумент нужно сместить по оси x на смещение bias.
Ниже отображена функция активациции со смещением bias. На графике видно, что нейрон будет включаться после аргумента функции больше 2, а не больше 0. Смещение bias в данном случае равно +2.
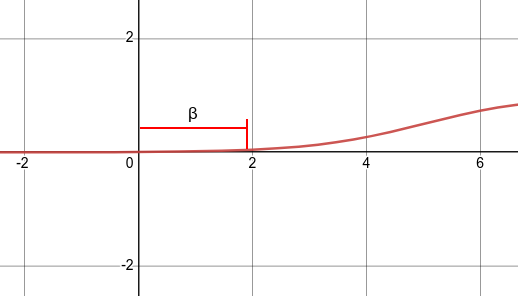
Смещение bias также является входом в нейронную сеть, для которого подбирается свой вес. Этот вес и является смещением. Обычно вес смещения является нулевым весом (omega_0), при входном сигнале равным 1. Получается само смещение вычисляется по формуле (beta = omega_0 *1)
Тогда формула активации нейрона примет вид:
(y = a(omega_0 + sum_{i=1}^{n} omega_i * x_i))
Это удобно, потому что в данном случае формула принимает одинаковый вид, и для обучения нейрона требуется подобрать кортеж весов ((omega_0, omega_1, omega_2, omega_3, … , omega_n))
Функция ошибки и активации являются важными параметрами архитектуры нейронной сети.
Однослойный персептрон
Архитектура нейронной сети состоит из последовательности слоев, которые соединены между собой.
Нейронная сеть состоящая только из входных и выходных слоев называется однослойным персептроном и обозначается упрощенно:
Данная нейронная сеть очень простая. Однослойный персептрон называют более простым термином полносвязный слой. В библиотеке Tensorflow полносвязный слой создается через класс Dense.
Многослойный персептрон
Данный вид нейронной сети имеет следующие названия:
- нейронная сеть с прямой связью
- Feed Forward neural network
- полносвязная сеть
- классификатор
Полносвязная сеть используется очень часто, и хорошо решают задачи на классификацию, например:
- Распознать какая цифра по ее изображению.
- Отличить кошку от собаки.
- Определить какой цветок, по его параметрам (цвет, форма цветка, длинна и т.д.)
- и т.п.
Во сверточных нейронных сетях, полносвязная сеть используется как классификатор на выходе. Сверточная сеть выделяет признаки по картинке и передает ее в полносвязную. А полносвязная уже квалифицирует и выдает ответ.
Многослойный персептрон (полносвязная сеть) — это последовательность полносвязных слоев однослойных персептронов. Основным отличием многослойного персептрона от одногослойного — в наличии одного или более скрытого слоя. Входные и выходные значения соединяются через скрытый слой, а не напрямую, как в однослойном персептроне.
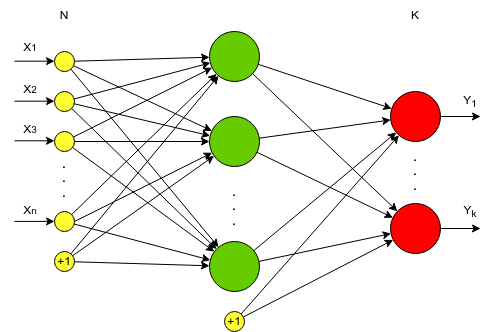
Желтым обозначены входной слой X.
Красным — выходной слой нейронов Y.
Зеленый — это скрытый слой нейронов.
Каждый выход нейрона вычисляется по формуле:
(p’_j = a(omega_0 + sum_{i=1}^{n} omega_i * p_i)), где p — это входные значения, а p’ — это выходные значения нейрона.
В данной нейронной сети 3 слоя. Входной, скрытый и выходной слой. Данную нейронную сеть часто обозначают упрощенно:
Feed Forward neural network
Текстовая нотация Feed Forward:
ff = [
"Input",
"Dense",
"Output"
];Многослойный персептрон с более чем одним скрытым слоем называют Deep Feed Forward.
Текстовая нотация Deep Feed Forward:
dff = [
"Input",
"Dense",
"Dense",
"Output"
]; Функции активации нейрона
Пороговая функция активации
(sign(x) = begin{cases} -1 & ,x < 0 0 & ,x = 0 1 &, x > 0 end{cases})
Сигмоида sigm
(sigm(x) = frac{1}{1+e^{-x}})
relu
(relu(x) = max(0,x) = begin{cases} 0 , x leq 0 x , x > 0 end{cases})
leaky relu
(lerelu(x) = begin{cases} 0.01x & ,x leq 0 x &, x > 0 end{cases})
Материалы
- Обучение многослойного персептрона операции XOR
- Материалы для самостоятельного изучения нейронных сетей
- Базы датасетов для обучения нейронных сетей
- AIML-4-1 Персептроны
- AIML-4-2 Метод обратного распространения ошибки
- Формулы обратного распространения
- Архитектуры нейронных сетей
- Сервис чтобы строить графики
- Ускорение обучения, начальные веса, стандартизация, подготовка выборки
- Переобучение — что это и как этого избежать, критерии останова обучения
- Функции активации, критерии качества работы НС
- Функции активации. Краткий обзор применений CNN и RNN.
- Playground Tensorflow
Все курсы > Оптимизация > Занятие 6
В рамках вводного курса мы начали изучать нейросети. Кроме того, нам знаком важный элемент алгоритма нейронной сети — умножение матриц.
На сегодняшнем занятии мы более подробно поговорим про то, почему нейросеть может оказаться более эффективным алгоритмом, чем рассмотренные ранее линейная и логистическая регрессия.
Кроме того, обладая знаниями о производной и градиенте, мы разберем до сих пор неизученный компонент, а именно процесс оптимизации, который в терминологии нейросетей называется обратным распространением, и построим несколько алгоритмов с нуля.
Зачем нужна нейронная сеть
Нелинейная гипотеза
Мы уже знаем, что некоторые гипотезы нелинейны. В случае задачи классификации и алгоритма логистической регрессии это означает, что, как видно на графике ниже, два класса нельзя разделить прямой линией (еще говорят, что они линейно неразделимы).

Можно обучить полиномиальную логистическую регрессию, однако с ростом количества признаков и степени полинома итоговое количество признаков, а значит и «затратность» алгоритма с точки зрения вычислительных ресурсов будет расти.
Для полинома n-ой степени (с одним признаком!) формула выглядит следующим образом.
$$ y = sum{}^n_{j=0} theta_j x^j $$
Например, полином второй степени будет иметь три коэффициента.
$$ y = theta_0 + theta_{1}x + theta_{2}x^2 $$
Полином второй степени с двумя признаками уже будет иметь шесть коэффициентов.
$$ y = theta_{0} + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
В целом, количество полиномиальных коэффициентов (N) можно рассчитать по формуле.
$$ N(n, d) = C(n+d, d), text{где} $$
- n — количество линейных признаков
- d — степень полинома
- C — количество возможных сочетаний
Используя пример выше, получим
$$ N(2, 2) = C(4, 2) = 6 $$
Полином третьей степени на основе десяти линейных признаков уже потребует создать 286 коэффициентов.
$$ N(10, 3) = C(13, 10) = 286 $$
Если речь идет о картинках 28 х 28 пикселей, то после «вытягивания» каждой картинки у нас появится датасет с 784 признаками. Значит, количество членов полинома второй степени составит
$$ N(784, 2) = C(786, 2) = 308 505 $$
Замечу, что примерное количество признаков полинома второй степени также можно посчитать по формуле $ frac{(n)^2}{2} $, то есть $ frac{(784)^2}{2} = 307 328 $
Такое количество признаков потребует очень больших вычислительных ресурсов. Посмотрим, как нейросеть может помочь справиться с этой сложностью.
Работа нейронной сети
Рассмотрим работу нейронных сетей с трех различных углов зрения.
Нейрон как дополнительный признак
Возьмем упрощенную модель нейронной сети с двумя скрытыми слоями.

Каждый нейрон каждого из скрытых слоев можно рассматривать как новый, дополнительный признак, зачастую нелинейный, способный уловить то, что не могут уловить линейные признаки. При этом умножение матриц, лежащее в основе работы нейронной сети, и векторизация операций позволяют сделать этот алгоритм достаточно быстрым.
Слой как модель логистической регрессии
Одновременно, если считать, что каждый скрытый слой проходит через функцию активации (activation function), зачастую сигмоиду, то каждый слой, кроме выходного, можно представить как, например, модель логистический регрессии.
Для модели представленной выше рассмотрим как из второго скрытого слоя получается значение выходного слоя.
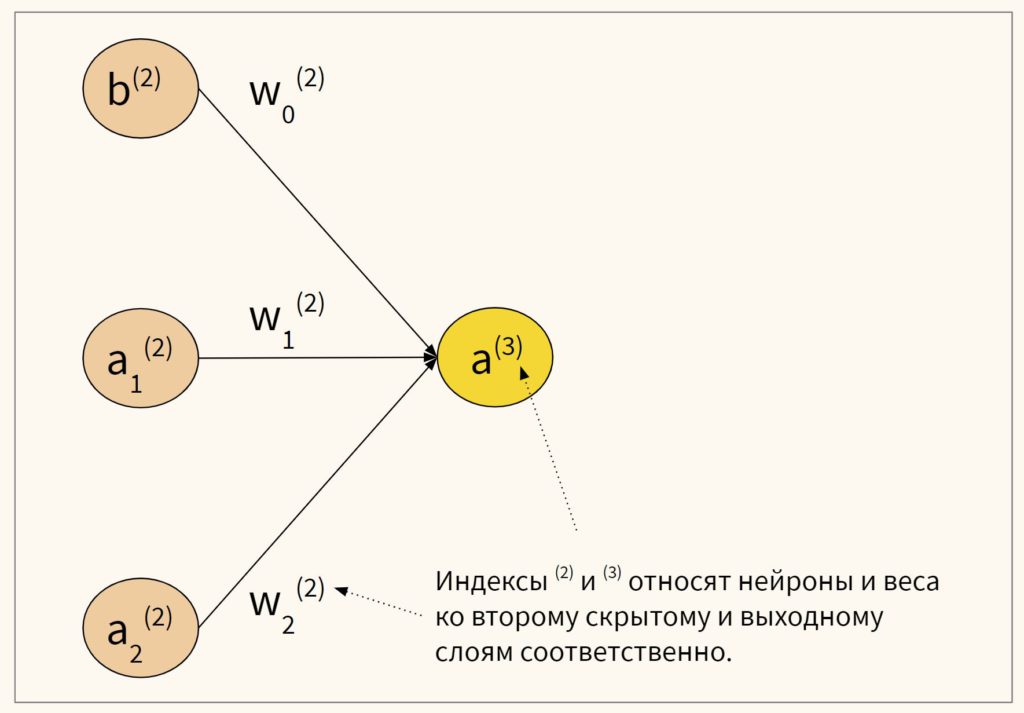
- На основе первого скрытого слоя мы получили некоторые значения нейронов второго скрытого слоя ($a_1^{(2)}$ и $a_2^{(2)}$)
- У нас есть вектор весов ($w_1^{(2)}$ и $w_2^{(2)}$)
- Кроме того, мы добавим смещение (b^{(2))
Замечу, что для удобства матричных операций мы можем добавить еще один нейрон скрытого слоя ($w_0^{(2)}$) со значением 1 так, как мы это делали, например, в модели линейной регрессии.
Результат умножения двух векторов мы пропустим через сигмодиду или функцию активации (отсюда выбор буквы a для обозначения этих нейронов) и таким образом получим значение выходного слоя ($a^{(3)}$). Уверен, вы распознали уравнение логистической регрессии.
$$ a^{(3)} = g(w_0^{(2)} cdot b^{(2)} + w_1^{(2)} cdot a_1^{(2)} + w_2^{(2)} cdot a_2^{(2)}) $$
Соответственно, имея два скрытых слоя, мы строим две связанные между собой логистические регрессии. И вдвоем они могут запомнить более сложные зависимости, чем смогла бы одна такая модель, одновременно преодолевая проблему роста количества признаков полиномиальной модели.
Нейросеть и таблица истинности
Продемонстрируем, как нейросеть обучается на нелинейной гипотезе с помощью таблиц истинности.
Этот пример взят из курса по машинному обучению Эндрю Ына⧉ (Andrew Ng).
Рассмотрим линейно неразделимые данные двух классов (на рисунке слева) и упростим их до четырех наблюдений, которые могут принимать только значения 0 и 1 (на рисунке справа).

Логически такая схема соответствует условию $x_1 XNOR x_2$ или $ NOT x_1 XNOR x_2 $. В таблице истинности это условие выглядит так.

Другими словами, когда наблюдение по обоим признакам $x_1$ и $x_2$ имеет значение 0, то результатом будет класс 1, когда хотя бы один из признаков равен единице, то класс 0.
Построим нейросеть, которая будет предсказывать именно такую зависимость. Начнем с более простого компонента, а именно нейросети, которая делает прогноз в соответствии с логическим И (AND).
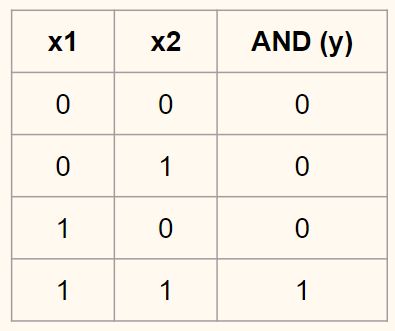
Итак, $x_1. x_2 in {0, 1} $ и $y = x_1 AND x_2 $. В нейросети будет два нейрона для признаков + смещение. Одновременно сразу пропишем веса модели.

Тогда выражение будет иметь вид, $y_{AND} = sigmoid(-30 + 20x_1 + 20x_2)$. Вспомним, как выглядит график сигмоиды.

Рассмотрим четыре варианта значений $x_1, x_2$ применительно к такой гипотезе.
- Если оба признака будут равны нулю, то результат линейного выражения будет равен $-30$. Если «пропустить» это значение через сигмоиду, то результат будет близок к нулю.
- Если один из них будет равен нулю, а второй единице, то результат будет равен $-10$. Сигмоида опять выдаст близкое к нулю значение.
- И только если оба признака равны единице, то результат будет равен 10 и сигмоида выдаст значение близкое к единице.
Это и есть условие логического И. Аналогичным образом можно подобрать веса для логического ИЛИ (OR).

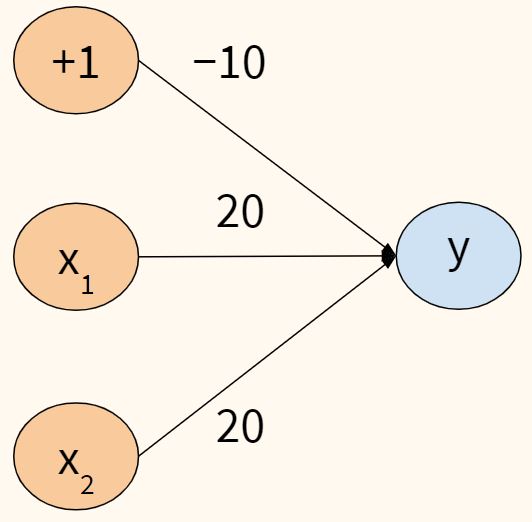
Соответственно $y_{OR} = sigmoid(-10 + 20x_1 + 20x_2)$. Создадим еще более простую сеть для логического НЕ (NOT).


Как следствие, $y_{NOT} = sigmoid(10-20x_1)$. Создадим нейросеть, которая будет предсказывать NOT($x1$) AND NOT($x2$).
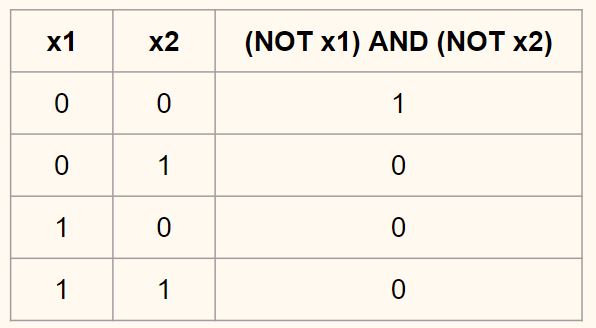

Объединим эти сети в одну.

Рассчитаем таблицу истинности.

Таким образом, мы видим, что на каждом последующем слое нейросеть строит все более сложную зависимость. Первый скрытый слой обучился достаточно простым зависимостям ($x_1$ AND $x_2$ и NOT($x_1$) AND NOT($x_2$)), второй слой дополнил это знание новым ($x1$ OR $x2$), и вместе они обучились выдавать достаточно сложный результат ($x_1$ XNOR $x_2$).
Подготовка данных
Давайте вновь возьмем данные о вине, построим вначале бинарный, а затем мультиклассовый классификатор и посмотрим, сможет ли нейросеть улучшить показатели логистической регрессии.
Откроем ноутбук к этому занятию⧉
Импортируем датасет о вине, удалим класс 2, из признаков оставим спирт и пролин, масштабируем данные.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# импортируем датасет from sklearn import datasets data = datasets.load_wine() # сформируем датафрейм и добавим целевую переменную df = pd.DataFrame(data.data, columns = data.feature_names) df[‘target’] = data.target # удалим класс 2 df = df[df.target != 2] # оставим только спирт и пролин X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # масштабируем признаки X = (X — X.mean()) / X.std() # посмотрим на размерность и оставшиеся классы df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Дополнительно преобразуем датафрейм признаков X в массив Numpy с размерность 2 x 130 и сделаем целевую переменную y двумерным массивом.
|
# каждый столбец — это одно наблюдение X = X.to_numpy().T X.shape |
|
y = y.to_numpy().reshape(1, —1) y.shape |
Нейросеть без смещения
Архитектура сети
Предлагаю идти от простого к сложному и на первом этапе создать алгоритм для бинарной классификации без смещения (bias) с приведенной ниже архитектурой.
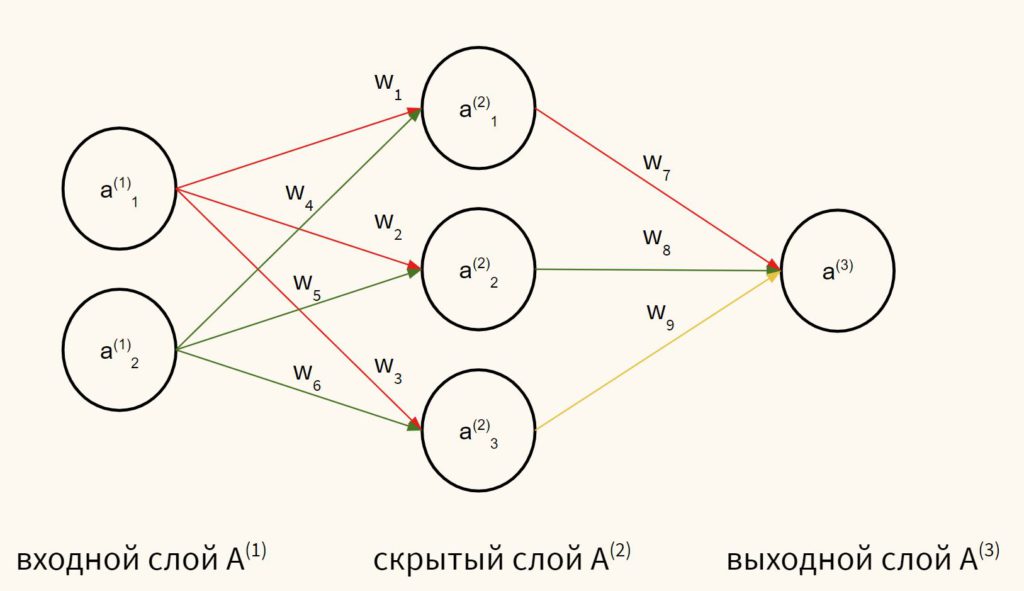
Итак, сеть будет состоять из следующих слоев:
- входной слой $A^{(1)}$ из двух нейронов $a^{(1)}_1$ и $a^{(1)}_2$ т.е. двух признаков, на основе которых мы будем предсказывать класс вина;
- один скрытый слой $A^{(2)}$, состоящий из трех нейронов: $a^{(2)}_1$, $a^{(2)}_2$ и $a^{(2)}_3$; и
- выходной слой из одного нейрона $a^{(3)}$, т.е. вероятности принадлежности к одному из двух классов
Заглавной буквой, например, $A^{(1)}$ обозначаются сразу все нейроны, в данном случае, входного слоя, строчной с соответствющим индексом $a^{(1)}_1$ — отдельный нейрон этого слоя.
Также напомню, что у нас последовательная (sequential) архитектура сети, при которой каждый слой получает один тензор на вход и выдает также только один тензор. Кроме этого, мы используем полносвязные (дословно, «плотно связанные», dense, densely connected) слои, где каждый нейрон одного слоя связан с каждым нейроном последующего (обратите внимание на красные и зеленые стрелки между входным и скрытым слоями).
Размерность матриц
Алгоритм нейронной сети, в конечном счете, не более чем умножение матриц или, в общем случае, тензоров (отсюда, в частности, название библиотеки Tensorflow⧉, которой мы пользовались, изучая основы нейронных сетей) и после выбора архитектуры модели нам важно определиться с размерностью используемых нами матриц.
Первая матрица весов
Начнем со входного слоя, в который мы одновременно (за счет умножения матриц и векторизации кода) подадим матрицу из 130 наблюдений и двух признаков (после транспонирования размерность напомню была 2 x 130).
На нее мы будем умножать матрицу весов ($W^{(1)} cdot X$ или в терминологии слоев $W^{(1)} cdot A^{(1)}$). Как определить размерность матрицы весов? Очень просто, нужно взглянуть на количество нейронов скрытого слоя. Их три. Значит размерность первой матрицы весов составит 3 х 2.

Практический совет. Для того чтобы быстро найти размерность матрицы весов вспомним про две особенности умножения матриц:
- внутренние размеры, т.е. количество столбцов первой и строк второй, должны совпадать, в нашем случае 2 = 2.
- размерность результирующей матрицы будет равна внешним размерам умножаемых матриц, 3 и 130.
Итак, в скрытом слое у нас будет матрица 3 х 130, где каждый столбец — это три (активационных) нейрона для каждого из наблюдений.
Полносвязный слой
Убедимся, что такое умножение матриц обеспечивает умножение каждого нейрона входного слоя на каждый нейрон скрытого слоя (т.е. полносвязность, density, слоев). Для простоты, предположим, что у нас только четыре наблюдения, я не 130.

Рассмотрим первую операцию. Здесь веса $w_1$ и $w_4$ умножаются на нейроны входного слоя $a_1$ и $a_2$ и, таким образом, обеспечивают их «участие» в значении нейрона $a_1$ скрытого слоя. Аналогично, при второй операции за это отвечают $w_2$ и $w_5$. Наконец третий нейрон скрытого слоя рассчитывается благодаря весам $w_3$ и $w_6$ и опять же обоим нейронам входного слоя.
Эти же операции можно посмотреть на стрелках на схеме архитектуры сети.
Вторая матрица весов
Теперь, чтобы получить один единственный нейрон выходного слоя (вернее вектор-строку из 130 таких нейронов, 1 х 130), нам нужно новую матрицу весов умножить на результат скрытого слоя на $W^{(2)} cdot A^{(2)}$.
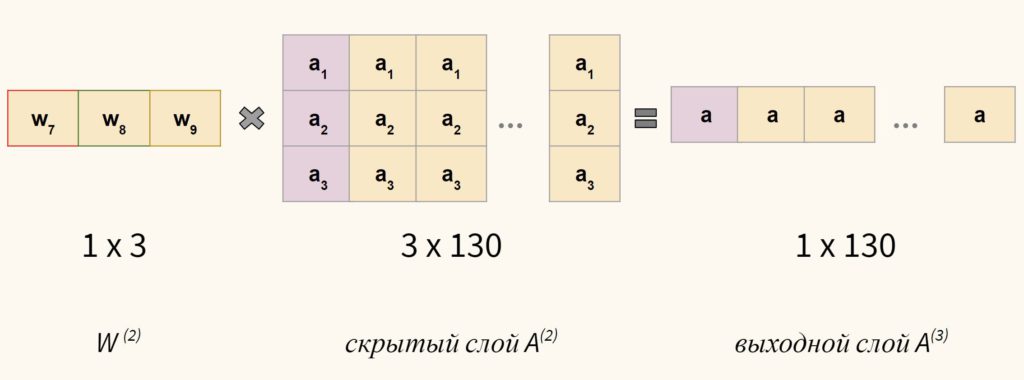
Очевидно, это должна быть матрица 1 х 3, потому что только она даст нам нужную итоговую размерность 1 x 130.
Важная деталь. Как нейроны скрытого слоя, так и нейрон выходного слоя проходят через функцию активации (activation function), в нашем случае сигмоиду (на схемах выше не показана).
В целом мы только что рассмотрели прямое распространение. Давайте напишем соответствующий код.
Код прямого распространения
Вначале объявим знакомые нам функции сигмоиды (функция активации) и логистической ошибки (функция потерь). Их место в архитектуре сети можно увидеть на схеме ниже.
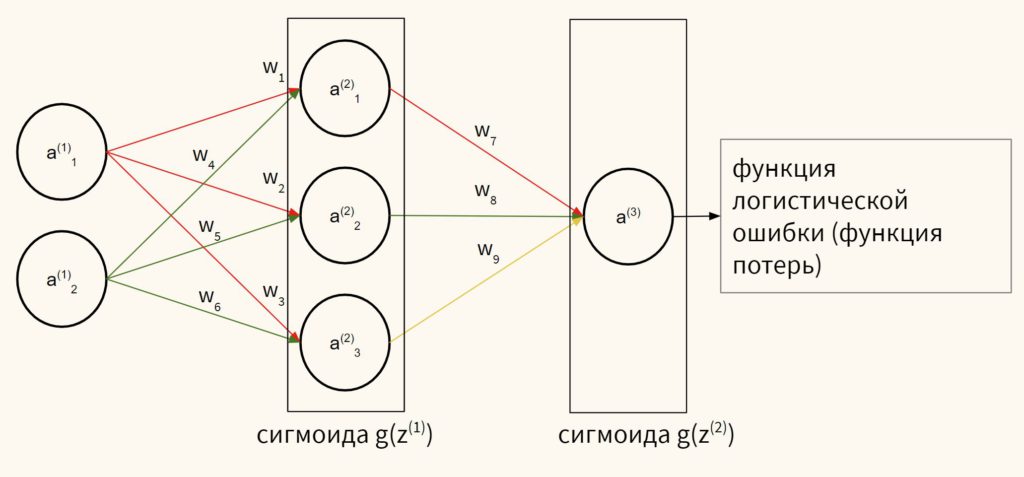
Дополнительно замечу, что в нашей терминологии $z^(1)$ и $z^(2)$ — это результат умножения матрицы весов на матрицу нейронов соответствующего слоя, который мы «пропускаем» через сигмоиду (g). Т.е., например, для скрытого слоя
$$ Z^{(1)} = W^{(1)} cdot A^{(1)} $$
$$ A^{(2)} = g(Z^{(1)}) $$
|
# функция активации def sigmoid(z): s = 1 / (1 + np.exp(—z)) return s # функция потерь def objective(y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) |
Теперь объявим веса и поместим признаки в нейроны скрытого слоя (исключительно ради единнобразия терминологии).
|
# зададим точку отсчета np.random.seed(33) # инициализируем случайные веса, # взятые из стандартного нормального распределения W1 = np.random.randn(3, 2) W2 = np.random.randn(1, 3) # найдем количество наблюдений n = X.shape[1] # поместим признаки в нейроны входного слоя A1 = X |
Последовательно выполним операции умножения весов на нейроны и пропустим результаты через две сигмоиды.
|
# выполним умножение матриц W1 и A1 и «пропустим» результат через сигмоиду # в скобках указана итоговая размерность операции Z1 = np.dot(W1, A1) # (3 x 130) A2 = sigmoid(Z1) # (3 x 130) # поступим аналогично с матрицами W2 и A2 Z2 = np.dot(W2, A2) # (1 x 130) A3 = sigmoid(Z2) # (1 x 130) # посмотрим, какую вероятность модель выдала для первого наблюдения A3[:,0] |
Найдем ошибку при текущих весах.
|
loss = objective(A3, y) loss |
Обратное распространение
Теперь главный вопрос. Как обновить веса так, чтобы уменьшить ошибку?
По большому счету нам нужно рассчитать частную производную функции логистической ошибки ($L$) относительно каждого веса ($w_1, w_2, w_3, …, w_9$), ведь именно их мы и будем обновлять. Начнем с весов второго слоя, а именно, $w_7, w_8, w_9$ (все вместе мы будем обозначать их как $W^{(2)}$).
Частные производные весов $W^{(2)}$
Согласно chain rule градиент (т.е. совокупность частных производных) весов второго слоя будет иметь вид
$$ frac{partial L}{partial w^{(2)}} = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial w^{(2)} } $$
Что нам нужно сделать?
- Вначале найти производную функции логистической ошибки $ frac{partial L}{partial a^{(3)}} $
- После этого производную сигмоиды $frac{partial a^{(3)} }{partial z^{(2)}}$
- И наконец линейной функции $frac{ partial z^{(2)} }{partial w^{(2)} }$
- Перемножить эти производные
Возможно вы заметили, что выше использовались индексы (3) и (2), индекс (3) относит активационную функцию $a^{(3)}$ к третьему выходному слою, а линейную функцию $z^{(2)}$ и веса линейной функции $ w^{(2)} $ ко второму. В такой нотации нам будет удобнее в дальнейшем рассчитывать градиенты и писать код.
На всякий случай также уточню, что это будет поэлементное умножение или произведение Адамара (Hadamard product), которое мы будем обозначать через оператор $circ$.
Далее, уверен, вы обратили внимание на то, что мы выполняем операции в обратном от прямого распространения порядке: сначала производная ошибки, потом сигмоиды третьего слоя, затем линейной функции второго. Именно поэтому процесс называется обратным распространением ошибки (error back propagation).
Производная функции логистической ошибки
$$ frac{partial L}{partial a^{(3)}} = frac{partial}{partial a^{(3)}} left( -y log(a^{(3)})-(1-y) log(1-a^{(3)}) right) $$
Применим правило производной разности и вынесем константы.
$$ -y frac{partial}{partial a^{(3)}} log(a^{(3)})-(1-y) frac{partial}{partial a^{(3)}} log(1-a^{(3)}) $$
Найдем производную натурального логарифма, вынесем минус за скобку и вычтем одну дробь из другой.
$$ -left( frac{y}{a^{(3)}}-frac{(1-y) }{1-a^{(3)}} right) = frac{a^{(3)}-y}{a^{(3)}(1-a^{(3)})} $$
Производная сигмоиды
Производную сигмоиды мы уже находили.
$$ frac{partial a^{(3)} }{partial z^{(2)}} = g(z^{(2)}) (1-g(z^{(2)})) $$
При этом так как результат сигмоиды $ g(z^{(2)}) $ — это нейрон выходного слоя $ a^{(3)} $, то
$$ frac{partial a^{(3)} }{partial z^{(2)}} = a^{(3)} (1-a^{(3)}) $$
Производная линейной функции
Найдем производную линейной функции, расписав умножение для каждого веса и для каждого нейрона.
$$ frac{ partial }{partial w^{(2)} } left( w_7 times a^{(2)}_1 + w_8 times a^{(2)}_2 + w_9 times a^{(2)}_3 right) $$
Для того чтобы найти производную относительно, например, веса $w_7$, мы «замораживаем» (считаем константами, производная которых равна нулю) все веса кроме первого и тогда
$$ w_7^{1-1} times a^{(2)}_1 + 0 times a^{(2)}_2 + 0 times a^{(2)}_3 = $$
$$ 1 times a^{(2)}_1 + 0 times a^{(2)}_2 + 0 times a^{(2)}_3 = a^{(2)}_1 $$
Аналогичный результат мы получим, продифференцировав относительно других весов. Тогда,
$$ frac{ partial z^{(2)} }{partial w^{(2)}} = a^{(2)} $$
Наконец перемножим найденные производные и упростим выражение.
$$ frac{partial L}{partial w^{(2)}} = frac{a^{(3)}-y}{a^{(3)}(1-a^{(3)})} circ a^{(3)} (1-a^{(3)}) circ a^{(2)} = $$
$$ (a^{(3)}-y) circ a^{(2)} $$
В векторной нотации (и матричном умножении) получим
$$ frac{partial L}{partial W^{(2)}} = (A^{(3)}-y) cdot A^{(2)}.T times frac{1}{n} $$
Множитель $ frac{1}{n} $ усредняет градиент на количество наблюдений.
Дельта-правило ($ delta_2 $)
Замечу, что $frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}}$ также обозначают через греческую букву «дельта» (в нашем случае $delta_2$), и тогда градиент для обновления весов $W^{(2)}$, с учетом векторизованного кода, приобретет вид (опять же в векторной нотации)
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
В дальнейшем использование так называемого «дельта-правила» (delta rule) упростит наш код.
Обновление весов $W^{(2)}$
Остается только обновить веса $W^{(2)}$ в направлении антиградиента, умноженного на коэффициент скорости обучения.
$$ W^{(2)} := W^{(2)}-alpha times frac{partial L}{partial W^{(2)}}$$
Частные производные весов $W^{(1)}$
Теперь нужно найти производные относительно весов ($w_1, …, w_6$) или $W^{(1)}$. И мы снова должны «раскручивать» chain rule от функции логистической ошибки. На этот раз цепь будет более длинной.
$$ frac{partial L}{partial w^{(1)}} = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } circ frac{ partial a^{(2)} }{partial z^{(1)} } circ frac{ partial z^{(1)} }{partial w^{(1)} } $$
Нахождение производных
Вспомним, что первые два множителя $frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}}$ мы обозначили через $delta_2$.
Обратим внимание на третий множитель $ frac{ partial z^{(2)} }{partial a^{(2)} } $. В отличие от градиента весов $W^{(2)}$, где мы, напомню, искали производную линейной функции относительно весов $frac{ partial z^{(2)} }{partial w^{(2)} }$, здесь нас интересует частная производная относительно нейронов активационного слоя $a^{(2)}$.
Тогда в данном случае мы «замораживаем» (считаем константами) не веса, а нейроны $ a^{(2)} $ (считая веса просто числами) и, например, частная производная относительно $a^{(2)}_1$ будет равна
$$ frac{ partial }{partial a^{(2)}_1 } left( w_7 times a^{(2)}_1 + w_8 times a^{(2)}_2 + w_9 times a^{(2)}_3 right) $$
$$ w_7 times 1 + w_8 times 0 + w_9 times 0 = w_7 $$
Аналогично находим производные относительно других нейронов. В векторной нотации,
$$ frac{ partial z^{(2)} }{partial a^{(2)} } = W^{(2)}$$
Интересно, что ошибкой скрытого слоя $E_2$ (ошибкой $E_1$ была бы общая ошибка, которую мы рассчитали с помощью функции логистической ошибки) называют произведение
$$ E_2 = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } $$
Это утверждение более понятно, если переписать (в векторной нотации) выражение выше как,
$$ E_2 = W^{(2)}.T cdot delta_2 $$
То есть, мы по сути распространяем «ошибку» $ delta_2 $ (число, скаляр) на каждый из трех весов $W^{(2)}$.
Перейдем к четвертому множителю $ frac{ partial a^{(2)} }{partial z^{(1)} }$. Это снова производная сигмоиды, только уже «на слой раньше»,
$$ frac{ partial a^{(2)} }{partial z^{(1)} } = g(z^{(1)}) (1-g(z^{(1)})) = a^{(2)} (1-a^{(2)}) $$
И наконец пятый компонент,
$$ frac{ partial z^{(1)} }{partial w^{(1)} } = a^{(1)} $$
Дельта-правило ($ delta_1 $)
Аналогично предыдущему слою мы можем обозначить $ frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } circ frac{ partial a^{(2)} }{partial z^{(1)} } $ как $ delta_1 $ (то есть мы опять взяли все множители, кроме последнего).
Градиент относительно $W^{(1)}$
В итоге градиент относительно весов $W^{(1)}$ имел бы вид,
$$ frac{partial L}{partial W^{(1)}} = left( E_2 circ A^{(2)} circ (1-A^{(2)}) right) cdot A^{(1)}.T times frac{1}{n} $$
Или, раскрыв $E_2$,
$$ frac{partial L}{partial W^{(1)}} = left( ( W^{(2)}.T cdot delta_2) circ A^{(2)} circ (1-A^{(2)}) right) cdot A^{(1)}.T times frac{1}{n} $$
Или через $ delta_1 $
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Обратите внимание на паттерн, градиент каждого слоя представляет собой произведение дельты на соответствующие нейроны активационного слоя, усредненное на количество наблюдений.
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Разумеется, это правило справедливо и для большего количества скрытых слоев.
Обновление весов $W^{(1)}$
Обновление весов $W^{(1)}$ аналогично предыдущему слою.
$$ W^{(1)} := W^{(1)}-alpha times frac{partial L}{partial W^{(1)}}$$
Перейдем к коду.
Код обратного распространения
Продолжим писать код, которые мы начали, изучая прямое распространение.
|
# найдем дельту весов между слоями 3 и 2 W2_delta = A3 — y # (1 x 130) |
|
# обратите внимание, это одно число, как и результат # третьего слоя A3 (мы выводим первый столбец из 130) W2_delta[:, 0] |
|
# найдем дельту весов между слоями 1 и 2 W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) |
|
# дельта 1 состоит уже из трех чисел, как и скрытый слой нейросети W1_delta[:, 0] |
|
array([-0.0099838 , 0.06300821, -0.01243332]) |
|
# напомню, что умножение дельты 2 на веса скрытого слоя W2 можно # считать «промежуточной ошибкой» сети или ошибкой скрытого слоя E2 = np.dot(W2.T, W2_delta) # то есть одно число W2_delta мы «распространили» на весь скрытый слой, # поэтому ошибка состоит из трех чисел E2[:, 0] |
|
array([-0.07704936, 1.03666489, -0.04989736]) |
|
# наконец найдем частную производную относительно весов W2 W2_derivative = np.dot(W2_delta, A2.T) / n # (1 x 3) W2_derivative |
|
array([[-0.16738339, -0.23720379, 2.99973404]]) |
|
# и весов W1 # (размерность опять же должна совпадать с размерностью матриц весов) W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 3) W1_derivative |
|
array([[-0.14145948, -0.12624909], [ 1.41742921, 1.87529043], [-0.19429558, -0.21266884]]) |
|
# обновим веса (скорость обучения возьмем равной единице) W2 = W2 — 1 * W2_derivative W1 = W1 — 1 * W1_derivative |
Обучение модели
Теперь соединим прямое и обратное распространение и с помощью цикла произведем обучение нейронной сети.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
np.random.seed(33) W1 = np.random.randn(3, 2) W2 = np.random.randn(1, 3) epochs = 100000 learning_rate = 1 n = X.shape[1] A1 = X for i in range(epochs): # рассчитываем прямое распространение Z1 = np.dot(W1, A1) # (3 x 130) A2 = sigmoid(Z1) # (3 x 130) Z2 = np.dot(W2, A2) # (1 x 130) A3 = sigmoid(Z2) # (1 x 130) # рассчитываем ошибку loss = objective(A3, y) # находим дельту весов между слоями 3 и 2 W2_delta = A3 — y # (1 x 130) # находим дельту весов между слоями 2 и 1 W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # находим частные производные W2_derivative = np.dot(W2_delta, A2.T)/n # (1 x 3) W1_derivative = np.dot(W1_delta, A1.T)/n # (3 x 3) # обновляем веса W2 = W2 — learning_rate * W2_derivative W1 = W1 — learning_rate * W1_derivative # периодически выводим количество итераций и текущую ошибку if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) # можем добавить паузу для более аккуратного вывода time.sleep(0.5) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 7.522291935047792 ———————— Эпоха: 20000 Ошибка: 0.7636370744482613 ———————— Эпоха: 40000 Ошибка: 0.7137144818217118 ———————— Эпоха: 60000 Ошибка: 0.6981278394758277 ———————— Эпоха: 80000 Ошибка: 0.6901729606032463 ———————— Итоговая ошибка 0.6847941294287265 Нейросеть успешно обучена |
Прогноз и оценка качества
Сделаем прогноз и оценим качество.
|
A1 = X Z1 = np.matmul(W1, A1) A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) A3 = sigmoid(Z2) # A3.flatten() делает массив одномерным, # условие выводит True или False (1 или 0) y_pred, y_true = A3.flatten() >= 0.5, y.flatten() |
|
(array([[ 1.59357193e-03, -1.11510787e+00], [-2.70942468e+01, 1.10767378e+01], [-1.78982169e-03, 1.11459111e+00]]), array([[ 14.76831281, 8.70860599, -21.63309402]])) |
|
from sklearn.metrics import accuracy_score accuracy_score(y_true, y_pred) |
Инициализация весов
В моделях линейной и логистической регрессии в качестве начальных значений коэффициентов мы использовали нули, в алгоритме нейронной сети — случайные значения, почему так?

Если веса изначально равны нулю, то произойдет несколько нежелательных событий:
- значения активационных слоев $a_1^(2) = a_2^(2) = a_3^(2) $ будут одинаковыми, то есть запоминать одну и ту же зависимость
- более того, так как веса между вторым и третьим (выходным) слоем будут одинаковыми, то и значения матрицы $ delta_2 $ будут одинаковыми,
- а значит и частные производные, относящиеся к весам одного входного нейрона (например, $w_1, w_2, w_3$) будут одинаковыми
Таким образом, после, например, одного обновления весов, хотя значения весов $w_1, w_2, w_3$ не будут нулевыми, они будут одинаковыми. То же можно сказать про веса $w_4, w_5, w_6$. И снова $a_1^(2) = a_2^(2) = a_3^(2) $.
Как следствие, мы существенно ограничиваем возможности (гибкость) нейронной сети запоминать сложные зависимости.
Масштабирование целевой переменной
Как мы только что убедились, градиент нейронной сети зависит от целевой переменной. Если эта переменная имеет большой диапазон, то это может создать большую ошибку при вычислении градиента, что, в свою очередь, вызовет существенное изменение весов и дестабилизирует процесс обучения.
Очевидно после обучения и прогноза целевую переменную нужно вернуть к прежнему масштабу.
Модель в Tensorflow и Keras
Библиотека Keras представляет собой «надстройку«⧉ (интерфейс, API), через которую удобно создавать нейросети в библиотеке Tensorflow. Реализуем созданную выше несложную нейросеть в библиотеке Keras.
|
# в Google Colab уже установлена вторая версия библиотеки Tensorflow, # которая существенно отличается от первой версии import tensorflow as tf tf.__version__ |
В нейросеть мы будем подавать признаки и целевую переменную таким образом, чтобы объекты были строками.
Перейдем к созданию и обучению нейросети.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# зададим две точки отсчета, одну в библиотеке Numpy np.random.seed(42) # вторую непосредственно в Tensorflow tf.random.set_seed(42) # зададим архитектуру: последовательная модель model = tf.keras.models.Sequential([ # с полносвязными слоями # также укажем нейроны скрытого и выходного слоев # откажемся от смещения tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = False), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = False) ]) # зададим особенности стохастического градиентного спуска (SGD) # в частности, откажемся от импульса # (подробнее об этом на последующих занятиях) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) # соберем все вместе, дополнительно укажем тип функции потерь и метрику качества model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) # зададим количество эпох, # размер batch, после которой мы обновляем веса, равен объему данных (fullbatch) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) |
|
<keras.callbacks.History at 0x7f5f49c0aa90> |
|
Model: «sequential_3» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_6 (Dense) (130, 3) 6 dense_7 (Dense) (130, 1) 3 ================================================================= Total params: 9 Trainable params: 9 Non—trainable params: 0 _________________________________________________________________ |
Оценим качество.
|
model.history.history[‘accuracy’][—1] |
Нейросеть со смещением
Добавим смещение, это должно сделать нашу модель более гибкой.
В отличие от линейных моделей, мы не будем использовать одну и ту же производную и для $b$, и для $W$ (с добавлением столбца из единиц в X). Это связано с тем, что в нейросетях при обратном распространении ошибку на смещение мы не распространяем.
Найдем производные смещения относительно сигмоиды (последний компонент в цепи производных).
$$ frac{ partial z^{(2)} }{partial b^{(2)}} = 1 $$
$$ frac{ partial z^{(2)} }{partial b^{(1)}} = 1 $$
Тогда в целом, используя дельта-правило, частные производные относительно $b^{(2)}$ и $b^{(1)}$ будут равны
$$ frac{partial L}{partial b^{(2)}} = sum delta_2 times frac{1}{n} $$
$$ frac{partial L}{partial b^{(1)}} = sum delta_1 times frac{1}{n} $$
Перейдем к коду.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
np.random.seed(33) # инициализируем веса W1 = np.random.randn(3, 2) # b1 будет иметь размерность 3 х 1, # потому что распространяется на три нейрона скрытого слоя b1 = np.random.randn(3, 1) W2 = np.random.randn(1, 3) b2 = np.random.randn(1, 1) n = X.shape[1] epochs = 100000 learning_rate = 1 A1 = X for i in range(epochs): # 3 х 2 на 2 х 130 Z1 = np.dot(W1, A1) + b1 A2 = sigmoid(Z1) # (3 x 130) # 1 х 3 на 3 х 130 Z2 = np.dot(W2, A2) + b2 A3 = sigmoid(Z2) # (1 x 130) loss = objective(A3, y) W2_delta = A3 — y # (1 x 130) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # keepdims сохраняет исходную размерность # 1 х 130 на 130 х 3 W2_derivative = np.dot(W2_delta, A2.T) / n # (1 x 3) b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) # 3 х 130 на 130 х 2 W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 2) b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) time.sleep(0.5) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 10.080172158274355 ———————————— Эпоха: 20000 Ошибка: 0.5460931772435075 ———————————— Эпоха: 40000 Ошибка: 0.5235933834724054 ———————————— Эпоха: 60000 Ошибка: 0.5153108060799304 ———————————— Эпоха: 80000 Ошибка: 0.5104559107317911 ———————————— Итоговая ошибка 0.5070018571750416 Нейросеть успешно обучена |
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) y_pred, y_true = A3.flatten() > 0.5, y.flatten() accuracy_score(y_true, y_pred) |
TF / Keras. Добавим смещение в нашу модель в библиотеке Keras.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
np.random.seed(42) tf.random.set_seed(42) model = tf.keras.models.Sequential([ tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = True) ]) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) model.summary() |
|
Model: «sequential_6» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_12 (Dense) (130, 3) 9 dense_13 (Dense) (130, 1) 4 ================================================================= Total params: 13 Trainable params: 13 Non-trainable params: 0 _________________________________________________________________ |
|
model.history.history[‘accuracy’][—1] |
|
(array([[ 6.12093182, -12.02342998], [-22.00510547, -9.19535995], [ 14.35718419, 9.69417827]]), array([[ 12.32118926, 15.26008905, -10.91093576]])) |
Два скрытых слоя
Добавим второй скрытый слой.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
np.random.seed(33) W1 = np.random.randn(3, 2) b1 = np.random.randn(3, 1) W2 = np.random.randn(3, 3) b2 = np.random.randn(3, 1) W3 = np.random.randn(1, 3) b3 = np.random.randn(1, 1) n = X.shape[1] epochs = 10000 learning_rate = 1 A1 = X for i in range(epochs): Z1 = np.dot(W1, A1) + b1 # (3 x 130) A2 = sigmoid(Z1) Z2 = np.dot(W2, A2) + b2 # (3 x 130) A3 = sigmoid(Z2) Z3 = np.dot(W3, A3) + b3 # (1 x 130) A4 = sigmoid(Z3) loss = objective(A4, y) W3_delta = A4 — y # (1 x 130) W2_delta = np.dot(W3.T, W3_delta) * A3 * (1 — A3) # (3 x 130) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # 3 х 130 на 130 х 3 W3_derivative = np.dot(W3_delta, A3.T) / n # (3 x 3) b3_derivative = np.sum(W3_delta, keepdims = True) / n # (1 x 1) # 3 х 130 на 130 х 3 W2_derivative = np.dot(W2_delta, A2.T) / n # (3 x 3) b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 2) b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W3 = W3 — learning_rate * W3_derivative b3 = b3 — learning_rate * b3_derivative W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) time.sleep(1) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 11.483275165239569 ———————— Эпоха: 2000 Ошибка: 0.7137240298878413 ———————— Эпоха: 4000 Ошибка: 0.683999037922229 ———————— Эпоха: 6000 Ошибка: 0.6718618481850791 ———————— Эпоха: 8000 Ошибка: 0.6640320570961954 ———————— Итоговая ошибка 0.6583025695728971 Нейросеть успешно обучена |
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = sigmoid(Z3) y_pred, y_true = A4.flatten() > 0.5, y.flatten() accuracy_score(y_true, y_pred) |
Сравним с моделью в Keras.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
np.random.seed(42) tf.random.set_seed(42) model = tf.keras.models.Sequential([ tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = True) ]) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) model.summary() |
|
Model: «sequential_2» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_4 (Dense) (130, 3) 9 dense_5 (Dense) (130, 3) 12 dense_6 (Dense) (130, 1) 4 ================================================================= Total params: 25 Trainable params: 25 Non-trainable params: 0 |
|
model.history.history[‘accuracy’][—1] |
Многоклассовая классификация
Создадим нейросеть, которая будет предсказывать вероятности нескольких классов. Во многом, идея алгоритма совпадает с softmax логистической регрессией.
Постановка задачи и архитектура
Возьмемся за ту же задачу, которую мы решили в рамках вводного курса с помощью библиотеки Keras, а именно создадим нейросеть, которая будет распознавать рукописные цифры из датасета MNIST.
Архитектуру модели сохраним прежней.

Функции активации
Как видно на графике, мы будем использовать сигмоиду для промежуточных слоев и softmax для выходного слоя.
|
def sigmoid(z): s = 1 / (1 + np.exp(—z)) return s |
|
def softmax(z): # на выходном слое тензор будет иметь размерность 10 х 60000, # поэтому складывать мы будем по столбцам z = z — np.max(z, axis = 0, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = 0, keepdims = True) softmax = numerator / denominator return softmax |
Функция потерь
Функцией потерь будет категориальная кросс-энтропия.
|
def cross_entropy(probs, y_enc, epsilon = 1e—9): # опять же, так как softmax выдаст тензор 10 х 60000 # количество наблюдений содержится в атрибуте shape[1] n = probs.shape[1] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Обратное распространение
Очевидно, так как изменилась функция потерь и функция активации выходного слоя (softmax) необходимо заново рассчитать производные. Напомню, для весов $W^{(3)}$ цепное правило будет работать следующим образом.
$$ frac{partial L}{partial w^{(3)}} = frac{partial L}{partial a^{(4)}} circ frac{partial a^{(4)} }{partial z^{(3)}} circ frac{ partial z^{(3)} }{partial w^{(3)} } $$
При этом, оказывается, что производная первых двух компонентов $frac{partial L}{partial a^{(4)}} circ frac{partial a^{(4)} }{partial z^{(3)}}$ (т.е. кросс-энтропии и softmax) сводится к $a^{(4)}-y$ (она аналогична бинарной кросс-энтропии и сигмоиде, но находится⧉, разумеется, иначе).
Одновременно этот компонент производной представляет собой $delta_3$, которую для нахождения градиента необходимо умножить на $A^{(3)}.T$.
$$ frac{partial L}{partial W^{(3)}} = delta_3 cdot A^{(3)}.T times frac{1}{n} $$
Остальные производные находятся аналогично предыдущим моделям.
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Подготовка данных
|
import mnist from tensorflow import keras |
|
def ohe(y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
X_train = mnist.train_images() y_train = mnist.train_labels() X_test = mnist.test_images() y_test = mnist.test_labels() X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 X_train = X_train.reshape((—1, 784)).T X_test = X_test.reshape((—1, 784)).T y_train_enc, y_test_enc = ohe(y_train).T, ohe(y_test).T X_train.shape, y_train_enc.shape |
|
((784, 60000), (10, 60000)) |
Обучение модели
Код ниже исполняется в Google Colab около 10 минут.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
np.random.seed(33) W1 = np.random.randn(64, 784) b1 = np.random.randn(64, 1) W2 = np.random.randn(64, 64) b2 = np.random.randn(64, 1) W3 = np.random.randn(10, 64) b3 = np.random.randn(10, 1) n = X_train.shape[1] epochs = 500 learning_rate = 1 A1 = X_train for i in range(epochs): # 64 x 784 на 784 x 60000 —> 64 x 60000 Z1 = np.dot(W1, A1) + b1 A2 = sigmoid(Z1) # 64 x 64 на 64 x 60000 —> 64 x 60000 Z2 = np.dot(W2, A2) + b2 A3 = sigmoid(Z2) # 10 x 64 на 64 x 60000 —> 10 x 60000 Z3 = np.dot(W3, A3) + b3 A4 = softmax(Z3) loss = cross_entropy(A4, y_train_enc) W3_delta = A4 — y_train_enc # (10 x 60000) W2_delta = np.dot(W3.T, W3_delta) * A3 * (1 — A3) # (64 x 60000) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (64 x 60000) # 10 x 60000 на 60000 x 64 —> 10 x 64 W3_derivative = np.dot(W3_delta, A3.T) / n b3_derivative = np.sum(W3_delta, keepdims = True) / n # (1 x 1) # 64 x 60000 на 60000 x 64 —> 64 x 64 W2_derivative = np.dot(W2_delta, A2.T) / n b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) # 64 x 60000 на 60000 x 784 —> 64 x 784 W1_derivative = np.dot(W1_delta, A1.T) / n b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W3 = W3 — learning_rate * W3_derivative b3 = b3 — learning_rate * b3_derivative W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 6.215969648082527 ———————— Эпоха: 100 Ошибка: 0.9316990279468341 ———————— Эпоха: 200 Ошибка: 0.7055264357349225 ———————— Эпоха: 300 Ошибка: 0.5950572560699322 ———————— Эпоха: 400 Ошибка: 0.5276765625306427 ———————— Итоговая ошибка 0.4813698685793663 Нейросеть успешно обучена |
Прогноз и оценка качества
Сделаем прогноз и оценим качество на обучающей выборке.
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = softmax(Z3) |
|
y_pred = np.argmax(A4, axis = 0) y_pred[:4] |
|
from sklearn.metrics import accuracy_score accuracy_score(y_train, y_pred) |
Теперь на тестовых данных.
|
A1 = X_test Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = softmax(Z3) y_pred = np.argmax(A4, axis = 0) accuracy_score(y_test, y_pred) |
Алгоритм показал достаточно высокую точность и при увеличении количества эпох и настройке скорости обучения мог бы показать более высокий результат.
При этом очевидно, что модель, которую мы создали в рамках вводного курса в библиотеке Keras обучилась гораздо быстрее. На занятии по градиентному спуску мы посмотрим, как можно ускорить работу нашего алгоритма.
Подведем итог
На сегодняшнем занятии мы в деталях посмотрели на математику обратного распространения, а также с нуля построили несколько алгоритмов нейронных сетей.
На следующем занятии мы вернемся к теме качества алгоритмов, а также рассмотрим один из инструментов повышения этого качества, который называется регуляризацией.
Ответы на вопросы
Вопрос. Чем отличается умножение матриц от векторизации?
Ответ. Принцип умножения матриц относится к математике и описывает правила, по которым мы умножаем два двумерных тензора. Векторизация кода — термин из программирования, который позволяет избежать использования циклов в процессе выполнения кода.
Многослойные нейронные сети с сигмовидной функцией — глубокое обучение для новичков (2)
Перевод
Ссылка на автора
Глава 1: Представляем глубокое обучение и нейронные сети
Глава 2. Многослойные нейронные сети с сигмоидальной функцией.
Следуй за мной по щебет узнать больше о жизни в стартапе глубокого обучения.
Привет всем! Добро пожаловать в мой второй пост серииГлубокое обучение для новичков (DLFR)По-настоящему, новичок;) Не стесняйтесь обращаться к мой первый пост здесь или мой блог если вам трудно следовать. Или выделите на этой странице заметки или оставьте комментарий ниже! Ваши отзывы также будут высоко оценены.
На этот раз мы углубимся в нейронные сети, и пост будет несколько более техническим, чем в прошлый раз. Но не беспокойтесь, я сделаю так, чтобы вы могли легко и интуитивно выучить основы без знания CS / Math. Скоро вы сможете похвастаться своим пониманием;)
Обзор от DLFR 1
В прошлый раз мы представили область глубокого обучения и изучили простую нейронную сеть — персептрон … или динозавра … серьезно, однослойный персептрон. Мы также исследовали, как сеть персептрона обрабатывает входные данные, которые мы вводим, и возвращает выходные данные.
Основные понятия: входные данные, веса, суммирование и сложение смещения, функция активации (в частности, функция шага), а затем вывод. Скучно еще? Не беспокойся  Я обещаю, что будет … больше глаголов! Но ты скоро к ним привыкнешь. Обещаю.
Я обещаю, что будет … больше глаголов! Но ты скоро к ним привыкнешь. Обещаю.

Еще в 1950-х и 1960-х годах у людей не было эффективного алгоритма обучения однослойного персептрона для изучения и идентификации нелинейных паттернов (помните проблему с воротами XOR?). И публика потеряла интерес к персептрону. В конце концов, большинство проблем в реальном мире нелинейны, и, как отдельные люди, вы и я чертовски хороши в принятии решений по линейным или бинарным задачам, таким какя должен изучать глубокое обучение или нетбез необходимости персептрона. Хорошо, «хорошо» — это сложное слово, так как наш мозг на самом деле не такой рациональный. Но я оставлю это поведенческим экономистам и психологам.
Прорыв: многослойный персептрон
За два десятилетия до 1986 года Джеффри Хинтон, Дэвид Румелхарт и Рональд Уильямс опубликовали статью «Изучение представлений по ошибкам обратного распространения», Который ввел:
- обратное распространениепроцедура длянеоднократно корректировать весачтобы минимизировать разницу между фактическим и желаемым выходом
- Скрытые слои, которыенейронные узлы, расположенные между входами и выходами, позволяя нейронным сетям изучать более сложные функции (такие как логика XOR)
Если вы совершенно новичок в DL, вы должны помнить Джеффри Хинтона, который играет ключевую роль в развитии DL. Итак, это были некоторые важные новости: мы всего 20 лет думали, что у нейронных сетей нет будущего для решения реальных проблем. Теперь мы видим свет от маяка на берегу! Давайте посмотрим на эти 2 новых введения.
Хм, первый,обратное распространениеупоминается в последнем посте. Помните, что мы повторили важность разработки нейронной сети, чтобы сеть могла учиться на разнице междужелаемый вывод(что это за факт) ифактический объем производства(что возвращает сеть), а затем отправить сигнал обратно весам и попросить весы подстроиться? Это сделает выход сети ближе к желаемому результату при следующем запуске.
Как насчет второго, скрытых слоев? Что такое скрытый слой? Скрытый слой превращает однослойный персептрон в многослойный персептрон! Вот план, по техническим причинам,Я сосредоточусь на скрытых слоях в этом посте, а затем расскажу о распространении в следующем посте.,
Просто случайныйзабавный фактздесь: я подозреваю, что Джеффри Хинтон имеет рекорд за то, что был самым старым стажером в Google: D Проверьте эта статья из New York Times и поиск «Хинтон». В любом случае, если вы уже знакомы с машинным обучением, я уверен, что его курс по Coursera подойдет.

Нейронные сети со скрытыми слоями
Скрытые слои нейронной сети буквально просто добавляют больше нейронов между входным и выходным слоями.

Данные во входном слое помечены какИксс подписками1, 2, 3,…, м, Нейроны в скрытом слое помечены какчасс подписками1, 2, 3,…, n, Примечание для скрытого слояегоNи нетм, поскольку количество нейронов скрытого слоя может отличаться от количества во входных данных. И как вы видите на графике ниже, нейроны скрытого слоя также помечены верхним индексом1 Это так, что когда у вас есть несколько скрытых слоев, вы можете определить, какой это скрытый слой:первый скрытый слой имеет верхний индекс 1, второй скрытый слой имеет верхний индекс 2 и т. д., как вГрафик 3, Выход помечен какYсшапка,

Чтобы облегчить жизнь, мы будем использовать некоторые жаргоны, чтобы немного прояснить ситуацию. Я знаю, жаргон может раздражать, но вы привыкнете к нему  Во-первых, если у нас естьмвходные данные (х1, х2,…, хм), мы называем этом особенности, Особенность — это только одна переменная, которую мы считаем влияющей на конкретный результат. Как наш пример по итогамесли вы решили изучать DL или нет,у нас есть 3 функции: 1. Будете ли вы зарабатывать больше денег после изучения DL, 2. Трудно с математикой / программированием, 3. Нужен ли вам графический процессор для начала.
Во-первых, если у нас естьмвходные данные (х1, х2,…, хм), мы называем этом особенности, Особенность — это только одна переменная, которую мы считаем влияющей на конкретный результат. Как наш пример по итогамесли вы решили изучать DL или нет,у нас есть 3 функции: 1. Будете ли вы зарабатывать больше денег после изучения DL, 2. Трудно с математикой / программированием, 3. Нужен ли вам графический процессор для начала.
Во-вторых, когда мы умножаем каждый из m признаков на вес (w1, w2,…, wm) и суммировать их все вместе, этоскалярное произведение:

Итак, вот вынос на данный момент:
- См особенностина входеИКС,тебе нужномвеса для выполнения точечного произведения
- СNскрытые нейроны в скрытом слое, вам нужноNнаборы весов (W1, W2, … Wn) для выполнения точечных произведений
- С 1 скрытым слоем вы выполняетеNточечные продукты, чтобы получить скрытый выводчас:(h1, h2,…, hn)
- Тогда это как однослойный персептрон, мы используем скрытый выводчас:(h1, h2,…, hn) в качестве входных данных, которые имеютn функций,выполнятьТочечный продукт с 1 наборомNвес (w1, w2,…, wn) чтобы получить окончательный результатy_hat,
Процедура того, как входные значенияраспространяться впередв скрытый слой, а затем из скрытого слоя на выход такой же, как вГрафик 1, Ниже я приведу описание того, как это делается, используя следующую нейронную сеть вГрафик 4,



Теперь вычисляются выходные данные скрытого слоя, мы используем их в качестве входных данных для расчета конечного результата.

Ура! Теперь вы полностью понимаете, как работает персептрон с несколькими слоями  Это похоже на однослойный персептрон, за исключением того, что в этом процессе у вас намного больше весов. Когда вы тренируете нейронные сети на больших наборах данных со многими другими функциями (такими как word2vec в Natural Language Processing), этот процесс потребляет много памяти на вашем компьютере. Это была одна из причин, по которой Deep Learning не взлетела до последних нескольких лет, когда мы начали выпускать гораздо более качественное оборудование, которое могло бы обрабатывать потребляющие память глубокие нейронные сети.
Это похоже на однослойный персептрон, за исключением того, что в этом процессе у вас намного больше весов. Когда вы тренируете нейронные сети на больших наборах данных со многими другими функциями (такими как word2vec в Natural Language Processing), этот процесс потребляет много памяти на вашем компьютере. Это была одна из причин, по которой Deep Learning не взлетела до последних нескольких лет, когда мы начали выпускать гораздо более качественное оборудование, которое могло бы обрабатывать потребляющие память глубокие нейронные сети.
Сигмовидные нейроны: введение
Так что теперь у нас есть более сложная нейронная сеть со скрытыми слоями. Но мы не решили проблему активации с помощью функции step.
В последнем посте мы говорили об ограничениях линейности ступенчатой функции. Помните одно:Если функция активации является линейной, то вы можете сложить столько скрытых слоев в нейронной сети, сколько пожелаете, и конечный результат по-прежнему линейная комбинация исходных входных данных, пожалуйста убедитесь, что вы читаете эту ссылку дляобъяснение, если концепции трудно следовать. Эта линейность означает, что она не может действительно понять сложность нелинейных задач, таких как логика XOR или шаблоны, разделенные кривыми или кругами.
Между тем, функция шага также не имеет полезной производной (ее производная равна 0 везде или не определена в точке 0 на оси x). Это не работает дляобратное распространениеОб этом мы обязательно поговорим в следующем посте!

Ну, вот еще одна проблема: Персептрон с пошаговой функцией не очень «стабилен» как «кандидат на отношения» для нейронных сетей. Подумайте об этом: у этой девочки (или мальчика) есть серьезные биполярные проблемы! Один день (дляZ<0), (s) он все «тихий» и «подавленный», что дает вам нулевой ответ. Затем еще один день (дляZ≥ 0), (s) он внезапно становится «разговорчивым» и «живым», разговаривая с вами без остановки. Черт, радикальные перемены! Нет никакого изменения для ее / его настроения, и вы не знаете, когда оно понижается или повышается. Да … это пошаговая функция.
В общем, небольшое изменение любого веса во входном слое нашей сети персептронов может привести к тому, что один нейрон внезапно переключится с 0 на 1, что может снова повлиять на поведение скрытого слоя, а затем повлиять на конечный результат. Как мы уже говорили, нам нужен алгоритм обучения, который мог бы улучшить нашу нейронную сеть за счет постепенного изменения весов, а не путем плоского отсутствия ответа или внезапных скачков. Если мы не можем использовать пошаговую функцию для постепенного изменения веса, то это не должен быть выбор

Попрощайтесь с персептроном с помощью функции шага. Мы находим нового партнера для нашей нейронной сети,сигмовидный нейрон, который идет с сигмовидной функцией (дух). Но не беспокойтесь: единственное, что изменится, — это функция активации, а все остальное, что мы узнали о нейронных сетях, все еще работает для этого нового типа нейронов!


Если функция выглядит очень абстрактно или странно для вас, не стоит слишком беспокоиться о таких деталях, как число Эйлераеили как кто-то придумал эту сумасшедшую функцию. Для тех, кто не разбирается в математике, единственная важная вещь о сигмовидной функции вГрафик 9во-первых, его кривая, а во-вторых, его производная. Вот еще несколько деталей:
- Сигмовидная функция дает результаты, аналогичные шаговой функции, в том случае, если выходной сигнал находится между 0 и 1. Кривая пересекает 0,5г = 0, который мы можем установить правила для функции активации, такие как: Если выходной сигнал сигмоидного нейрона больше или равен 0,5, он выводит 1; если выходное значение меньше 0,5, оно выдает 0.
- Сигмовидная функция не имеет рывка на своей кривой. Он гладкий и имеет очень красивую и простую производную отσ (z) * (1-σ (z)),который дифференцируем повсюду на кривой. Исчисление производной производной можно найти в переполнении стека Вот если хочешь это увидеть. Но вам не нужно знать, как его получить. Здесь нет стресса.
- ЕслиZочень отрицательный, тогда выходной сигнал равен приблизительно 0; еслиZочень положительный результат примерно 1; но вокругг = 0гдеZне является ни слишком большим, ни слишком маленьким (между двумя внешними вертикальными пунктирными линиями сетки вГрафик 9) у нас относительно больше отклонений, чемZменяется.
Теперь это похоже на материал для датировки нашей нейронной сети  Функция сигмоида, в отличие от функции шага, вносит нелинейность в нашу модель нейронной сети. Нелинейный просто означает, что выходной сигнал мы получаем от нейрона, который является точечным произведением некоторых входных данных.х (х1, х2,…, хм)и весw (w1, w2,…, wm)плюс смещение, а затем положить в сигмовидную функцию, не может быть представлен линейная комбинация вводах (х1, х2,…, хм),
Функция сигмоида, в отличие от функции шага, вносит нелинейность в нашу модель нейронной сети. Нелинейный просто означает, что выходной сигнал мы получаем от нейрона, который является точечным произведением некоторых входных данных.х (х1, х2,…, хм)и весw (w1, w2,…, wm)плюс смещение, а затем положить в сигмовидную функцию, не может быть представлен линейная комбинация вводах (х1, х2,…, хм),
Эта нелинейная функция активации, когда используется каждым нейроном в многослойной нейронной сети, производит новую « представление Исходных данных, и в конечном итоге учитывает нелинейную границу решения, такую как XOR. Таким образом, в случае XOR, если мы добавим два сигмоидных нейрона в скрытом слое, мы могли бы в другом пространстве преобразовать исходный 2D-график в нечто похожее на 3D-изображение в левой частиГрафик 10ниже. Таким образом, этот гребень позволяет классифицировать затвор XOR и представляет светло-желтоватую область затвора 2D XOR с правой стороныГрафик 10, Таким образом, если наше выходное значение находится в верхней части гребня, то оно должно быть истинным или 1 (например, погода холодная, но не жаркая, или погода жаркая, но не холодная); если наше выходное значение находится в нижней плоской области по двум углам, тогда оно ложно или равно 0, поскольку неправильно говорить, что погода горячая и холодная, а также ни горячая, ни холодная (хорошо, я думаю, что погода может быть не горячей или холодно … вы понимаете, что я имею в виду, хотя … верно?).

Я знаю, что эти разговоры о нелинейности могут сбивать с толку, поэтому, пожалуйста, прочитайте больше о линейности и нелинейности Вот (интуитивно понятный пост с анимацией из отличного блога Кристофера Олаха), Вот (по Вивек Ядав с функцией активации ReLU), и Вот (Себастьян Рашка). Надеюсь, у вас есть понимание того, почему важна функция нелинейной активации, а если нет, то сделайте это легко и дайте некоторое время ее переварить.
Проблема решена … на данный момент;) Мы увидим несколько различных типов функции активации в ближайшем будущем, потому что у сигмоидальной функции тоже есть свои проблемы! Некоторые популярные из них включаютTANHа такжеРЕЛУ, Это, однако, для другого поста.
Многоуровневые нейронные сети: интуитивный подход
Хорошо. Итак, мы внедрили скрытые слои в нейронную сеть и заменили персептрон сигмовидными нейронами. Мы также ввели идею о том, что нелинейная функция активации позволяет классифицировать нелинейные границы решений или шаблоны в наших данных. Вы можете запомнить эти выводы, поскольку они являются фактами, но я призываю вас немного погуглить в Интернете и посмотреть, сможете ли вы лучше понять концепцию (естественно, что мы потратим некоторое время, чтобы понять эти концепции)
Теперь мы никогда не говорили об одном очень важном моменте: с какой стати мы вообще хотим, чтобы скрытые слои в нейронных сетях? Как скрытые слои волшебным образом помогают нам решать сложные проблемы, которые однослойные нейроны не могут решить?
Из приведенного выше примера XOR вы видели, что добавление двух скрытых нейронов в 1 скрытый слой может перевернуть нашу проблему в другое пространство, что волшебным образом позволило нам классифицировать XOR с гребнем. Таким образом, скрытые слои каким-то образом искажают проблему таким образом, чтобы нейронной сети было легко классифицировать проблему или шаблон. Теперь мы будем использовать классический пример из учебника: распознавание рукописных цифр, чтобы помочь вам интуитивно понять, что делают скрытые слои.

Цифры вГрафик 11принадлежат к набору данных под названием MNIST, Он содержит 70000 примеров цифр, написанных руками человека. Каждая из этих цифр представляет собой изображение размером 28×28 пикселей. Таким образом, в целом каждое изображение цифры имеет 28 * 28 = 784 пикселей. Каждый пиксель принимает значение от 0 до 255 (цветовой код RGB). 0 означает цвет белый, а 255 означает цвет черный.

Теперь компьютер не может «видеть» цифру, как мы, люди, но если мы разберем изображение на массив из 784 чисел, таких как [0, 0, 180, 16, 230,…, 4, 77, 0, 0, 0], тогда мы можем передать этот массив в нашу нейронную сеть. Компьютер не может понять изображение, «увидев» его, но он может понимать и анализировать числа пикселей, которые представляют изображение.

Итак, давайте настроим нейронную сеть, как указано выше вГрафик 13, Он имеет 784 входных нейронов для значений 28×28 пикселей. Предположим, у него есть 16 скрытых нейронов и 10 выходных нейронов. Каждый из 10 выходных нейронов, возвращенных нам в массиве, будет отвечать за классификацию цифр от 0 до 9. Поэтому, если нейронная сеть считает, что рукописная цифра равна нулю, то мы должны получить выходной массив [1, 0, 0, 0, 0, 0, 0, 0, 0, 0], первый выход в этом массиве, который воспринимает цифру как ноль, «запускается», чтобы быть нашей 1 нейронной сетью, а остальные 0 Если нейронная сеть считает, что рукописная цифра — 5, то мы должны получить [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]. Шестой элемент, отвечающий за классификацию пяти, срабатывает, а остальные нет. Так далее и тому подобное.
Помните, мы упоминали, что нейронные сети становятся лучше за счет повторного обучения самим данным, чтобы они могли корректировать весовые коэффициенты в каждом слое сети, чтобы приблизить конечные результаты / фактические результаты к желаемым результатам? Поэтому, когда мы на самом деле обучаем эту нейронную сеть всем обучающим примерам в наборе данных MNIST, мы не знаем, какие веса мы должны назначить каждому из слоев. Поэтому мы просто случайным образом просим компьютер назначить веса в каждом слое. (Мы не хотим, чтобы все веса были равны 0, что я объясню в следующем посте, если позволит место).
Эта концепция случайной инициализации весов важна, потому что каждый раз, когда вы тренируете нейронную сеть с глубоким обучением, вы инициализируете разные числа для весов. По сути, вы и я понятия не имеем, что происходит в нейронной сети до тех пор, пока сеть не обучена. Обученная нейронная сеть имеет веса, которые оптимизируются при определенных значениях, которые дают лучший прогноз или классификацию по нашей проблеме. Это черный ящик, буквально. И каждый раз обучаемая сеть будет иметь разные наборы весов.
Ради аргумента, давайте представим следующий случай вГрафик 14, который я позаимствовал у Майкла Нильсена онлайн книга:

После обучения нейронной сети с раундами и раундами помеченных данных в контролируемом обучении, предположим, что первые 4 скрытых нейрона научились распознавать паттерны выше в левой частиГрафик 14, Затем, если мы передадим нейронной сети массив рукописных цифр ноль, сеть должна правильно запустить 4 верхних скрытых нейрона в скрытом слое, в то время как другие скрытые нейроны молчат, а затем снова запустить первый выходной нейрон, в то время как остальные молчит.

Если вы тренируете нейронную сеть с новым набором рандомизированных весов, она может создать следующую сеть (сравнить график 15 с графиком 14), поскольку веса рандомизированы, и мы никогда не знаем, какой из них узнает какой или какой шаблон. Но сеть, если она должным образом обучена, должна по-прежнему вызывать правильные скрытые нейроны и затем правильный вывод

И последнее, что следует упомянуть: в многослойной нейронной сети первый скрытый слой сможет выучить несколько очень простых шаблонов. Каждый дополнительный скрытый слой каким-то образом сможет постепенно выучить более сложные паттерны. Проверять, выписыватьсяГрафик 16от Scientific American с примером распознавания лиц 

Некоторые замечательные люди создали следующий сайт для вас, чтобы поиграть с нейронными сетями и посмотреть, как работают скрытые слои. Попробуйте это. Это действительно интересно!
Tensorflow — игровая площадка нейронной сети
Это методика построения компьютерной программы, которая учится на данных. Он очень слабо основан на том, как мы думаем …
playground.tensorflow.org
Офир Самсон писал хороший пост, также объясняющий, что такое нейронная сеть с довольно хорошей визуализацией, и она короткая и лаконичная!
Еженедельник глубокого обучения: что такое нейронная сеть?
Для этой недели я хотел бы сосредоточиться на разъяснении, что такое нейронная сеть, на простом примере, который я собрал…
medium.com
резюмировать
В этом посте мы рассмотрели ограничения персептрона, представили сигмовидные нейроны с новой функцией активации, называемой сигмовидной функцией. Мы также говорили о том, как работают многослойные нейронные сети, и об интуиции скрытых слоев в нейронной сети.
Мы почти заканчиваем полный курс понимания базовых нейронных сетей;) Хе-хе, это еще не конец! В следующем посте я расскажу о так называемой функции потерь, а также об этом загадочном распространении, о котором мы только упоминали, но никогда не посещали! Проверьте следующие ссылки, если вам не терпится ждать:
CS231n сверточные нейронные сети для визуального распознавания
Материалы курса и заметки для Стэнфордского класса CS231n: Сверточные нейронные сети для визуального распознавания.
cs231n.github.io
Шаг за шагом Пример обратного распространения
Фон Backpropagation является распространенным методом обучения нейронной сети. В Интернете нет недостатка в документах, которые …
mattmazur.com
Оставайтесь с нами и, самое главное, получайте удовольствие от обучения: D
Вам понравилось это чтение? Не забудьте подписаться на меня щебет !
Нейрокомпьютерные системы — ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Излагаются основы построения нейрокомпьютеров. Дается детальный обзор и описание важнейших методов обучения нейронных сетей различной структуры, а также задач, решаемых этими сетями. Рассмотрены вопросы реализации нейронных сетей.
Что в наибольшей степени влияет на результат работы нейронной сети?
(1) модель нейрона
(2) топология связей
(3) веса связей
Какие условия являются достаточными для сходимости переходных процессов в сети Хопфилда?
(1) отсутствие автосвязи
(2) неотрицательность весовых коэффициентов
(3) симметричность матрицы весов
Какие сети Хопфилда дают лучшие по качеству решения задачи коммивояжера?
(1) сети со ступенчатой (пороговой) функцией активации
(2) сети с сигмоидальной функцией активации
Как задана обратная связь в сети RMLP?
(1) выходы нейронов второго (выходного) слоя связаны со входами нейронов скрытого слоя
(2) выходы нейронов скрытого слоя связаны со входами нейронов этого же слоя
По какому признаку в методе динамических ядер вектор сигналов относится к заданному классу?
(1) по минимуму квадрата евклидова расстояния до ядра класса
(2) по максимуму квадрата евклидова расстояния до ядра класса
Какой слой сети АРТ осуществляет запоминание векторов данных?
(1) слой сравнения
(2) слой распознавания
Какие из перечисленных ниже свойств присущи традиционным (четким) нейронным сетям?
(1) способность к обучению
(2) высокая степень параллелизма
(3) надежность
(4) простота объяснения полученных результатов
Что понимается под редукцией (сокращением) входных сигналов?
(1) масштабирование наименее значимых сигналов
(2) исключение наименее значимых сигналов
(3) замена наименее значимых сигналов функцией остальных
Какими свойствами обладают нейрокомпьютеры для решения задач распознавания образов?
(1) малая разрядность операндов
(2) полная разрядность операндов
(3) использование операций с фиксированной точкой
(4) использование операций с плавающей точкой
Какой является функция активации персептрона?
(1) ступенчатой
(2) непрерывной
Какой способ построения линейного решающего правила является простейшим?
(1) алгоритм обучения персептрона
(2) разделение центров масс
Как формулируется решающее правило, основанное на формуле Байеса?
(1) объект x принадлежит классу Ci с минимальным значением апостериорной вероятности
P(Ci|x)
(2) объект x принадлежит классу Ci с максимальным значением апостериорной вероятности
P(Ci|x)
Какие из нижеперечисленных сетей после подачи набора входных сигналов функционируют непрерывно?
(1) многослойная сеть
(2) полносвязная сеть
(3) слоисто-циклическая сеть
На каком этапе алгоритма обратного распространения ошибки вычисляются производные функций активации нейронов многослойной сети?
(1) при прямом распространении сигналов
(2) при обратном распространении ошибки
Какие ограничения возникают при попытке осуществить обучение нейронной сети как решение задачи оптимизации?
(1) астрономическое число параметров
(2) необходимость высокого параллелизма при обучении
(3) необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным
(4) необходимость использования алгоритмов целочисленной оптимизации
В каком случае новое решение в алгоритме имитации отжига принимается случайным образом?
(1) при уменьшении значения целевой функции
(2) при увеличении значения целевой функции
Почему радиальные функции называют функциями локальной аппроксимации?
(1) радиальные функции имеют ненулевые значения в ограниченной области пространства
(2) радиальные функции имеют аргументы ограниченной размерности
К чему приводит отказ компонента (нейрона или синаптической связи) сети?
(1) к отказу всей сети
(2) к некоторому ухудшению характеристик сети
Чему равно расстояние Хемминга между двумя векторами?
(1) норме разности двух векторов
(2) числу несовпадающих компонент двух векторов
Какое состояние машины Больцмана считается соседним для данного состояния?
(1) отличающееся состоянием одного нейрона
(2) отличающееся состоянием всех нейронов
(3) отличающееся состоянием половины всех нейронов
Для чего предназначена сеть Эльмана?
(1) для реализации устройств ассоциативной памяти
(2) для моделирования временных рядов
Какое правило обучения реализует алгоритм WTM?
(1) победитель получает все
(2) победитель получает больше
Когда схема сброса считает плохим сходство векторов x и С?
(1) отношение числа единиц в векторах С и x не превышает порог
(2) отношение числа единиц в векторах С и x превышает порог
Какой из модулей системы нечеткого вывода суммирует результаты срабатывания произвольного множества правил вывода?
(1) фазификатор
(2) агрегатор
(3) дефазификатор
Как оценивается значимость входных сигналов сети?
(1) по степени влияния изменения сигнала на функцию оценки качества работы сети
(2) по степени влияния изменения сигнала на выходной сигнал сети
(3) по величине весового коэффициента соответствующей связи
На какие типы подразделяются нейрочипы?
(1) аналоговые
(2) цифровые
(3) символьные
(4) сигнальные
(5) гибридные
Какую задачу решает персептрон?
(1) задачу аппроксимации непрерывных функций
(2) задачу разделения двух классов
В каком случае выходной сигнал персептрона будет положительным?
(1) угол между вектором входных сигналов и вектором весов в расширенном пространстве меньше π/2
(2) угол между вектором входных сигналов и вектором весов больше π/2
Сколько разделяющих гиперплоскостей необходимо для реализации функции ИСКЛЮЧАЮЩЕЕ ИЛИ на нейронной сети?
Какой из видов интерпретации выходных сигналов сети обеспечивает максимальное количество классов при заданном числе нейронов в выходном слое?
(1) правило «победитель забирает все»
(2) знаковая интерпретация
(3) порядковая интерпретация
В чем заключается цель одномерной оптимизации?
(1) выбор направления минимизации целевой функции в пространстве весовых коэффициентов
(2) выбор величины шага в заданном направлении (подбор коэффициента обучения)
В чем преимущество метода случайного выбора направления минимизации оценки?
(1) быстродействие
(2) простота
Чему пропорционален размер популяции?
(1) количеству оптимизируемых параметров
(2) количеству битов хромосомы
Что реализует радиальный нейрон в пространстве входных сигналов?
(1) гиперплоскость
(2) гиперсферу
Каковы типичные приложения нейронных сетей?
(1) классификация образов
(2) обработка символьных строк
(3) ассоциативная память
К какому типу относится двунаправленная ассоциативная память?
(1) автоассоциативная память
(2) гетероассоциативная память
Как интерпретируется отрицательный весовой коэффициент связи в машине Больцмана?
(1) связь нежелательна
(2) связь желательна
Чем сеть RTRN отличается от сети Эльмана?
(1) большим количеством слоев
(2) меньшим количеством слоев
(3) тем, что в сети RTRN не все выходные сигналы нейронов используются в качестве выходных сигналов слоя
Какой вариант компрессии данных реализует сеть Кохонена?
(1) компрессия с потерей части информации
(2) компрессия без потерь информации
В каком случае вектор x проходит на выход слоя сравнения без изменений?
(1) при G1=0
(2) при G1=1
Параметры какой функции рассчитываются при обучении нечетких нейронных сетей?
(1) фазификации
(2) агрегирования
(3) дефазификации
Какие варианты редукции существуют?
(1) редукция «снизу вверх»
(2) редукция «сверху вниз»
(3) редукция «слева направо»
(4) редукция «справа налево»
В чем заключаются преимущества оптической реализации нейронных сетей?
(1) простота реализации большого количества межнейронных соединений
(2) высокая точность вычислений
(3) возможность одновременного срабатывания всех связей
В чем заключается обучение персептрона?
(1) в подборе весовых коэффициентов
(2) в изменении функции активации
Какой вариант алгоритма обучения персептрона обладает наилучшей сходимостью?
(1) обучение по отдельным примерам
(2) обучение по всему задачнику
(3) обучение по страницам
Сколько слоев должна содержать нейронная сеть для выделения выпуклой области?
Что позволяет установить сравнение констант Липшица нейронной сети и аппроксимируемой функции?
(1) принципиальную способность сети аппроксимировать функцию
(2) принципиальную неспособность сети аппроксимировать функцию
Что может вызвать неправильный выбор диапазона случайных значений весов?
(1) слишком раннее насыщение нейронов
(2) слишком позднее насыщение нейронов
(3) колебания выходных сигналов нейронов
В чем заключается сложность использования метода Ньютона для обучения нейронных сетей?
(1) низкая точность вычислений
(2) большие вычислительные затраты
(3) большой объем используемой памяти
Какой способ генерации новых виртуальных частиц является наиболее консервативным?
(1) при падении скорости обучения ниже критической
(2) при рестартах
(3) при каждом вычислении оценок и градиентов
Какую функцию обычно реализует выходной нейрон радиальной сети?
(1) линейную
(2) квадратичную
(3) экспоненту
Какие из нижеперечисленных особенностей присущи традиционным вычислительным системам?
(1) необходимо точное описание алгоритма
(2) искажения данных не влияют существенно на результат
(3) каждый обрабатываемый объект явно указан в памяти
Что является общей чертой рекуррентных сетей?
(1) рекуррентная процедура обучения сети
(2) передача сигналов скрытого или выходного слоя на входной
Какой член функции энергии равен нулю, если каждая строка матрицы нейронов содержит не более одной единицы?
(1) первый
(2) второй
(3) третий
(4) четвертый
Чему равно значение погрешности, управляющей процессом уточнения параметров нейронной сети RMLP?
(1) разности выходного сигнала сети и выходного сигнала динамического объекта
(2) разности выходных сигналов сети на двух, следующих друг за другом итерациях
Каким образом производится отнесение объекта к определенному классу при классификации без учителя?
(1) путем сравнения объекта с типичными элементами разных классов и выбора из них ближайшего
(2) путем сравнения объекта со всеми элементами разных классов и применения процедуры голосования
В чем заключаются положительные качества сети АРТ?
(1) сеть АРТ динамически запоминает новые образы без полного переобучения
(2) сеть АРТ чувствительна к порядку предъявления образов
(3) сеть АРТ не теряет уже запомненные образы при предъявлении новых
Какие параметры сети ТСК изменяются в процессе обучения?
(1) параметры полинома ТСК
(2) параметры матрицы весов второго слоя
(3) параметры функций принадлежности
Какой вариант процедуры отбрасывания наименее значимых параметров является простейшим?
(1) обращение параметра в ноль
(2) замена отбрасываемого параметра на функцию остальных
Что используется в качестве единицы производительности нейросетей?
(1) число сложений в секунду
(2) число умножений в секунду
(3) число соединений в секунду
Что такое персептрон?
(1) нейрон МакКаллока-Питса
(2) сигмоидальный нейрон
(3) адалайн
Как нужно модифицировать вектор весов, если входной вектор ошибочно отнесен персептроном к первому классу (выходной сигнал – 1)?
(1) вычесть часть вектора входных сигналов из вектора весов
(2) сложить с вектором весов часть вектора входных сигналов
Что является формализацией влияния возбуждения в одних областях мозга на возбуждение в других?
(1) введение коэффициента, пропорционального сигналу одного нейрона, в величину веса сигнала другого нейрона
(2) введение обратных связей в структуру нейронной сети
Какие связи между слоями являются возбуждающими?
(1) связи с положительными весами
(2) связи с отрицательными весами
Когда завершается действие алгоритма обратного распространения?
(1) когда фактические выходные сигналы совпадут с заданными
(2) когда норма градиента целевой функции упадет ниже априори заданного значения, характеризующего точность процесса обучения
В каких случаях BFGS-метод превращается в метод сопряженных градиентов?
(1) когда матрица вторых производных функции оценки положительно определена
(2) когда новый градиент практически ортогонален предыдущему направлению спуска
Как ускорить имитацию отжига?
(1) уменьшить коэффициент понижения температуры
(2) заменить случайные начальные значения весов тщательно подобранными значениями с использованием предварительной обработки исходных данных
Каким образом радиальная сеть реализует преобразование всего множества данных?
(1) как сумму локальных преобразований
(2) как произведение локальных преобразований
В каких областях применяются нейрокомпьютеры?
(1) для решения задач искусственного интеллекта
(2) в системах управления и технического контроля
(3) для создания спецвычислителей параллельного действия
(4) как инструмент изучения человеческого мозга
(5) для построения компиляторов программ
Благодаря чему рекуррентные сети можно использовать в качестве ассоциативной памяти?
(1) благодаря наличию аттракторов функции энергии сети
(2) благодаря наличию весовых коэффициентов межнейронных соединений
Что гарантируют связи смещений в машине Больцмана при решении задачи коммивояжера?
(1) хотя бы по одной единице есть в каждом столбце и в каждой строке
(2) ни в одной строке и ни в одном столбце не будет более одной единицы
Какие методы можно применять для прогноза временных рядов?
(1) статистические
(2) рекуррентные нейронные сети на базе персептрона
(3) методы линейной алгебры
Какие данные образуют кодовую таблицу при компрессии?
(1) веса нейронов-победителей
(2) номера нейронов-победителей
Какой тип обучения используется в сетях АРТ?
(1) с учителем
(2) без учителя
Каким методом можно выполнить дефазификацию нечеткого множества?
(1) дефазификация относительно центра
(2) дефазификация относительно среднего центра
(3) дефазификация относительно среднего минимума
(4) дефазификация относительно среднего максимума
Какие этапы включает в себя оценивание показателя значимости?
(1) оценивание показателя значимости для одной компоненты вектора (примера)
(2) оценивание показателя значимости для вектора
(3) оценивание показателя значимости для всей выборки векторов
На какие категории подразделяются оптические НС?
(1) векторно-матричные умножители
(2) дифракционные решетки
(3) голографические корреляторы
В каком интервале изменяются значения униполярной функции сигмоидального нейрона?
(1) (0, 0.5)
(2) (0,1)
(3) (0,2)
Следует ли хранить все входные векторы, на которых нейрон ошибается, при обучении по всему задачнику?
Каким уравнением описывается гиперплоскость, реализующая функцию ИЛИ?
В чем заключается нормировка входных данных нейронной сети?
(1) в отображении входных данных в отрезок [0,1] или [-1,1]
(2) в делении входных данных на заданную константу
Что способствует ускорению процесса обучения сети?
(1) увеличение коэффициента обучения
(2) уменьшение коэффициента обучения
Как обеспечить приобретение нейрокомпьютером новых навыков без существенной утраты старых?
(1) нужно найти общую точку минимума большого числа функций
(2) следует искать такую точку минимума оценки, что в достаточно большой ее окрестности значения оценки незначительно отличаются от минимума
К чему приводит слишком малая популяция хромосом?
(1) к замыканию в неглубоких локальных минимумах
(2) к замедлению поиска глобального минимума
В каких случаях целесообразно использовать радиальную сеть?
(1) в случае нерегулярности данных
(2) в случае круговой симметрии данных
(3) в случае большой размерности пространства данных
Что является главным результатом Розенблатта?
(1) доказательство сходимости процедуры обучения персептрона к решению поставленной задачи
(2) выделение класса задач, которые однослойный персептрон решать не может
(3) разработка алгоритма обратного распространения ошибки для обучения многослойного персептрона
Как связаны между собой нейроны второго слоя сети Хемминга?
(1) образуют кольцевую структуру
(2) образуют тороидальную структуру
(3) по принципу «каждый с каждым»
Какие значения функции энергии соответствуют более коротким маршрутам в задаче коммивояжера?
В каких случаях рекуррентные нейронные сети являются удобным инструментом прогнозирования временных рядов?
(1) когда не существует адекватной математической модели изучаемых временных рядов
(2) когда задача прогнозирования временных рядов может быть решена как задача локальной оптимизации
Когда производится слияние двух классов?
(1) когда расстояние между ядрами классов меньше, чем среднее расстояние от элемента класса до ядра в одном из них
(2) когда расстояние между ядрами классов больше, чем среднее расстояние от элемента класса до ядра в одном из них
Благодаря какому свойству слоя распознавания только один нейрон в слое может быть активирован?
(1) латеральное торможение
(2) латеральное возбуждение
Какие методы включает в себя вычислительный интеллект (мягкие вычисления)?
(1) нейрокомпьютинг
(2) синтаксический анализ
(3) нечеткую логику
(4) метод ветвей и границ
(5) генетические вычисления
Как вычисляется оценка значимости сигнала (параметра) на всей выборке входных сигналов?
(1) как сумма модулей оценок по отдельным примерам
(2) как минимум модуля оценки по отдельным примерам
(3) как максимум модуля оценки по отдельным примерам
Какими свойствами обладают нейрокомпьютеры для решения задач комбинаторной оптимизации?
(1) малая разрядность операндов
(2) полная разрядность операндов
(3) использование операций с фиксированной точкой
(4) использование операций с плавающей точкой
В чем заключается преимущество использования нейрона с непрерывной функцией активации?
(1) возможность определения глобального минимума целевой функции при обучении нейрона
(2) возможность использования градиентных методов оптимизации при обучении нейрона
Если возможно безошибочное разделение классов, то можно ли его получить методом центров масс?
(1) да, безусловно
(2) не всегда
Какой функцией описывается оптимальная разделяющая поверхность при нормальном распределении объектов двух классов?
(1) линейной (первого порядка)
(2) квадратичной (второго порядка)
(3) кубической (третьего порядка)
Какая из многослойных сетей используется наиболее часто?
(1) двухслойная
(2) трехслойная
(3) четырехслойная
В каком направлении осуществляется минимизация целевой функции в алгоритме обратного распространения ошибки?
(1) в направлении градиента целевой функции
(2) в направлении антиградиента целевой функции
Какие методы используются для учета ограничений параметров сети при обучении?
(1) метод штрафных функций
(2) метод проекций
(3) партан-метод
При каких значениях температуры увеличение значения целевой функции становится невозможным?
(1) при повышении температуры до заданного критического значения
(2) при понижении температуры до нуля
Почему аппроксимация, реализуемая сигмоидальной нейронной сетью, называется глобальной?
(1) преобразование значения функции в произвольной точке пространства выполняется объединенными усилиями многих нейронов
(2) преобразование значения функции в произвольной точке пространства выполняется одним нейроном
В чем заключается обучение нейронной сети?
(1) в построении точного алгоритма решения задачи
(2) в минимизации штрафа, как неявной функции связей
На запоминание каких систем векторов рассчитана сеть Хопфилда при обучении по правилу Хебба?
(1) ортогональных
(2) линейно независимых
Какие значения консенсуса соответствуют более коротким маршрутам в задаче коммивояжера?
Что понимается под «памятью» экстраполятора?
(1) его весовые коэффициенты
(2) те входные данные предшествующих тактов работы экстраполятора, которые используются для вычислений в данный момент
Какой тип соседства дает лучшие результаты обучения карты Кохонена?
(1) прямоугольное соседство
(2) гауссовское соседство
Какой сигнал разрешает работу слоя распознавания?
Какие слои сети TSK выполняют фазификацию переменных?
(1) первый
(2) второй
(3) третий
(4) четвертый
(5) пятый
Как оценивается значимость параметра, изменяющегося во времени (например, в результате обучения)?
(1) в качестве оценки значимости изменяющегося параметра берется минимум оценки по значениям параметра
(2) в качестве оценки значимости изменяющегося параметра берется максимум оценки по значениям параметра
(3) в качестве оценки значимости изменяющегося параметра берется среднее арифметическое оценок по значениям параметра
В качестве каких устройств используются электронные нейронные сети в персональных ЭВМ?
(1) аналого-цифровой преобразователь
(2) акселератор
(3) контроллер устройств внешней памяти
Какую функцию реализует Паде-нейрон?
(1) линейную
(2) дробно-линейную
(3) квадратичную
Как нужно модифицировать вектор весов, если входной вектор ошибочно отнесен персептроном ко второму классу (выходной сигнал – 0)?
(1) вычесть часть вектора входных сигналов из вектора весов
(2) сложить с вектором весов часть вектора входных сигналов
Сколько слоев должна содержать нейронная сеть для выделения невыпуклой области?
Для чего выполняется предобработка входных данных нейронной сети?
(1) для того, чтобы отобразить входные данные в заданный числовой отрезок
(2) для фильтрации помех
(3) для повышения точности вычислений
Что подается на входы сети обратного распространения?
(1) фактические выходные сигналы оригинальной нейронной сети
(2) отклонения фактических выходных сигналов оригинальной нейронной сети от ожидаемых
Какой из партан-методов дает лучшие результаты обучения сети?
(1) итерационный партан-метод
(2) модифицированный партан-метод
Что такое мутация?
(1) инверсия случайных битов хромосомы
(2) исключение из популяции случайно выбранных хромосом
Почему для решения задачи классификации (т.е. разбиения пространства входных сигналов на области) в радиальной сети достаточно иметь два слоя нейронов?
(1) в силу локальности преобразования, выполняемого радиальным нейроном
(2) радиальный нейрон реализует в пространстве входных сигналов гипершар, т.е. выпуклую область. Соответственно, двухслойная радиальная сеть может реализовать произвольную невыпуклую область как линейную суперпозицию гипершаров
Какие из перечисленных ниже свойств характерны для нейронных сетей?
(1) массовый параллелизм обработки информации
(2) функционирование по заданному алгоритму
(3) устойчивость к шумам и искажениям сигналов
(4) обобщение результатов обучения
(5) чувствительность к искажениям данных и повреждениям аппаратуры
Какой из нейронов второго слоя сети Хемминга побеждает все остальные нейроны этого слоя?
(1) нейрон с минимальным начальным сигналом на входе
(2) нейрон с максимальным начальным сигналом на входе
Какие связи в машине Больцмана, решающей задачу коммивояжера, обеспечивают хотя бы по одной единице в каждом столбце и в каждой строке матрицы нейронов?
(1) ингибиторные связи
(2) связи смещения
Какая величина минимизируется при идентификации динамического объекта нейронной сетью?
(1) разность между выходными сигналами нейронной сети на двух следующих друг за другом тактах
(2) разность между выходным сигналом сети и выходным сигналом динамического объекта
На каком свойстве сети Кохонена основана компрессия данных?
(1) снижение разрядности компонент векторов сигналов
(2) представление кластера векторов весовым вектором нейрона-победителя
На каком этапе решения задачи классификации сетью АРТ модуль сброса вычисляет второй критерий сходства?
(1) инициализация
(2) распознавание
(3) сравнение
(4) поиск
(5) обучение
В каких слоях сети TSK производится настройка параметров при обучении?
(1) первый
(2) второй
(3) третий
(4) четвертый
(5) пятый
Что собой представляет бинаризация сумматора?
(1) замена действительных значений входных сигналов двоичными значениями
(2) замена действительных значений весовых коэффициентов двоичными значениями
(3) замена сумматора комбинационной схемой на элементах базиса функций И, ИЛИ, НЕ
Что используется для реализации матрицы весовых коэффициентов в оптических умножителях?
(1) фотопленка
(2) интерферометр Майкельсона
(3) жидкокристаллический клапан
Требуется ли обучающая выборка (учитель) для обучения нейронов WTA?
Что является условием остановки выполнения алгоритма обучения персептрона?
(1) совпадение реального выходного сигнала с требуемым для всех векторов обучающей выборки
(2) снижение разности между реальным выходным сигналом и требуемым до заданного ненулевого порога для всех векторов обучающей выборки
Что реализуют нейроны первого слоя многослойной нейронной сети при решении задачи нелинейного разделения двух классов?
(1) гиперплоскости
(2) многогранники
Какое правило интерпретации выходных данных сети является наиболее распространенным?
(1) правило «победитель забирает все»
(2) знаковая интерпретация
(3) порядковая интерпретация
К чему может привести чрезмерное увеличение коэффициента обучения?
(1) к резкому возрастанию значения целевой функции (погрешности обучения)
(2) к насыщению нейронов
Чем обусловлено преимущество квазиньютоновских методов перед методом наискорейшего спуска?
(1) использованием результатов предыдущего шага
(2) использованием матрицы вторых производных оценки
Какие цели преследует метод виртуальных частиц?
(1) вывод сети из возникающих при обучении локальных минимумов оценки
(2) повышение устойчивости обученной сети
(3) снижение сложности вычислений целевой функции
К чему приводит чрезмерное количество весовых коэффициентов сети?
(1) к чрезмерно гладкой разделяющей гиперповерхности в пространстве входных сигналов
(2) к ухудшению обобщающих свойств сети
Что представляет собой задачник при обучении нейронных сетей?
(1) набор примеров с заданными ответами
(2) набор нерешенных задач
В каком режиме функционирует второй слой сети Хемминга?
(1) в режиме знаковой интерпретации
(2) в режиме порядковой интерпретации
(3) в режиме WTA
Какой член функции энергии равен нулю, если каждый столбец матрицы нейронов в задаче коммивояжера содержит не более одной единицы?
(1) первый
(2) второй
(3) третий
(4) четвертый
Какие данные образуют множество входных сигналов скрытого слоя сети Эльмана?
(1) входные сигналы сети вместе с задержанными выходными сигналами сети
(2) входные сигналы сети вместе с задержанными выходными сигналами скрытого слоя
Какие нейроны изменяют свои веса при обучении сети Кохонена алгоритмом WTM?
(1) только нейрон-победитель
(2) нейрон-победитель с заданной его окрестностью
(3) все нейроны сети
Из какого интервала берется значение порога схемы сброса?
(1) (0,1)
(2) (1,2)
(3) (2,3)
Почему модель Мамдани-Заде называют нечеткой нейронной сетью?
(1) в модели используется нечеткий вывод
(2) модель можно представить в виде многослойной структуры, напоминающей структуру классических нейронных сетей
(3) модель использует сигмоидальную функцию активации
Какой вариант процедуры отбрасывания наименее значимых параметров является наилучшим?
(1) обращение параметра в ноль
(2) замена отбрасываемого параметра на функцию остальных
Почему взаимное соединение нейронов с помощью световых лучей не требует изоляции между сигнальными путями?
(1) световые потоки могут пересекаться, не влияя друг на друга
(2) сигнальные пути могут располагаться в трех измерениях
(3) различные световые потоки имеют разные частоты
В каком интервале изменяются значения биполярной функции сигмоидального нейрона?
(1) (-0.5, 0.5)
(2) +(-1,1)
(3) (-2,2)
Как соотносятся вектор весовых коэффициентов и разделяющая гиперплоскость?
(1) вектор весов параллелен гиперплоскости
(2) вектор весов ортогонален гиперплоскости
В каком слое следует увеличить число нейронов, чтобы повысить точность аппроксимации выпуклых областей?
(1) в первом
(2) во втором
(3) в третьем
В какой сети каждый нейрон передает выходной сигнал на вход самому себе?
(1) в слоистой
(2) в полносвязной
(3) в слоисто-циклической
(4) в слоисто-полносвязной
(5) в полносвязно-слоистой
В каком интервале обычно лежат модули допустимых начальных значений весовых коэффициентов сети?
(1) (0,1)
(2) (1,2)
(3) (2,3)
Какие этапы подготовки предшествуют обучению?
(1) создание обучающей выборки
(2) выбор функции оценки
(3) контрастирование нейронной сети
(4) предобработка входных данных
Какая доля хромосом подвергается мутации?
(1) не более 5%
(2) до 50%
(3) все
Какие значения принимает радиальная функция в окрестности центра?
(1) нулевые
(2) отрицательные
(3) ненулевые
Какие состояния имеют нейроны МакКаллока-Питса?
(1) любое значение из интервала (0,1)
(2) 0 и 1
Какой метод обучения обеспечивает большую емкость ассоциативной памяти на основе сети Хопфилда?
(1) метод Хебба
(2) метод проекций
Какой член функции энергии численно равен длине маршрута коммивояжера?
(1) первый
(2) второй
(3) третий
(4) четвертый
Применим ли алгоритм обратного распространения ошибки к обучению рекуррентных персептронных сетей?
(1) неприменим
(2) применим с учетом зависимости сигналов от их значений в предыдущие моменты времени
(3) применим без изменений
Каким образом определяется количество классов в методе динамических ядер?
(1) путем начального задания достаточно большого числа ядер с последующим их слиянием
(2) постепенным наращиванием числа ядер
Какого типа нелинейность используется в нейронах слоя сравнения?
(1) сигмоидальная функция
(2) ступенчатая функция
Какая функция фазификации используется в сети ТСК?
(1) функция Гаусса
(2) треугольная
(3) трапецеидальная
(4) функция вида
μA(x) = 1/(1+((x-C)/σ)2b)
Когда определение значимости через изменение выходного сигнала не имеет альтернатив?
(1) когда рассматриваемая система является лишь подсистемой в некоторой системе
(2) когда рассматриваемая система имеет обратные связи
Какова плотность записи оптических весов в голограммах?
(1) 103 бит на куб. см
(2) 106 бит на куб. см
(3) до 1012 бит на куб. см
Что является важным свойством сигмоидальной функции?
(1) дифференцируемость
(2) скачкообразный характер изменения
Какой способ построения решающего правила всегда достигает безошибочного линейного разделения классов, если оно возможно?
(1) метод центров масс
(2) алгоритм обучения персептрона
В каком слое следует увеличить число нейронов, чтобы увеличить число выпуклых областей, реализуемых сетью?
(1) в первом
(2) во втором
(3) в третьем
Какое правило интерпретации дает минимальное число классов?
(1) правило «победитель забирает все»
(2) знаковая интерпретация
(3) порядковая интерпретация
Какую операцию следует выполнить в алгоритме обратного распространения там, где дуги сходятся к одной вершине?
(1) сложение произведений, полученных на этих дугах
(2) перемножение произведений, полученных на этих дугах
Каковы требования к реализации наиболее трудоемких этапов алгоритма обучения нейрокомпьютера?
(1) распараллеливание вычислений
(2) снижение разрядности обрабатываемых данных
(3) использование нейронной сети
К каким типам возмущений должны быть устойчивы навыки обучения нейрокомпьютера?
(1) к случайным возмущениям входных сигналов
(2) к флуктуациям параметров сети
(3) к изменению типа сети
(4) к разрушению части элементов сети
(5) к обучению новым примерам
Что является аргументом радиальной функции?
(1) скалярное произведение векторов
(2) расстояние от образца до центра функции
(3) вектор входных данных
Какую парадигму искусственного интеллекта реализуют нейронные сети?
(1) символьную
(2) коннекционистскую
Какие нейроны используются в устройствах ассоциативной памяти?
(1) нейроны с сигмоидальной функцией активации
(2) нейроны со ступенчатой функцией активации
Как ведет себя сеть Хопфилда при малых значениях производной сигмовидной функции активации в окрестности нуля?
(1) оказываются в центре гиперкуба решений (некорректное решение)
(2) попадает в вершину гиперкуба, соответствующую локальному минимуму функции энергии
Для чего используется идентифицированная модель объекта?
(1) для управления объектом
(2) для прогнозирования выходных сигналов объекта
Когда в задаче классификации без учителя можно перейти от использования квадрата евклидова расстояния между входным сигналом и ядром к скалярному произведению входного сигнала и ядра?
(1) когда компоненты векторов входных сигналов и ядер имеют действительные значения
(2) когда векторы входных сигналов и ядер нормированы
Способна ли сеть АРТ классифицировать зашумленные векторы?
Какие из следующих особенностей отличают мягкие экспертные системы от нечетких?
(1) представление знаний в форме нечетких продукций
(2) представление знаний в виде обученных нейронных сетей
(3) представление знаний в виде лингвистических переменных
(4) применение генетических алгоритмов
Каковы цели редукции (контрастирования) нейронной сети?
(1) упрощение специализированных устройств
(2) сокращение объема используемой памяти
(3) ускорение обучения
(4) увеличение быстродействия
Что является наиболее сложной проблемой при создании нейрочипов?
(1) создание схем сложения
(2) создание схем умножения
(3) создание межнейронных соединений
Какую функцию реализует адалайн?
(1) линейную
(2) дробно-линейную
(3) квадратичную
Чем полезен метод центров масс?
(1) как средство решения задачи линейного разделения
(2) как средство определения начального значения вектора весов для алгоритма обучения персептрона
Какое устройство реализует оптимальную разделяющую поверхность при нормальном распределении объектов двух классов?
(1) персептрон
(2) паде-нейрон в комбинации с пороговым нелинейным элементом
(3) квадратичный адаптивный сумматор в комбинации с пороговым нелинейным элементом
Сколько нейронов полносвязной сети может быть использовано для выдачи выходных сигналов?
(1) один из нейронов
(2) любое подмножество нейронов
(3) все нейроны
Зависят ли выходные сигналы скрытых слоев оригинальной нейронной сети от весовых коэффициентов нейронов выходного слоя?
Каких значений может достигать число параметров нейронной сети?
(1) не более 103
(2) около 105
(3) более 108
Что происходит с температурой при увеличении числа итераций алгоритма имитации отжига?
(1) температура понижается
(2) температура повышается
(3) температура изменяется случайным образом
Какое утверждение лежит в основе функционирования радиальных сетей?
(1) нелинейные проекции образов в некоторое многомерное пространство могут быть линейно разделены с большей вероятностью, чем их проекции в пространство с меньшей размерностью
(2) нейронная сеть радиального типа функционирует по принципу многомерной интерполяции
На какие классы нейронные сети делятся по структуре?
(1) однослойные
(2) односвязные
(3) многослойные
(4) многосвязные
В каком слое сети Хемминга вычисляется расстояние Хемминга между входным вектором и вектором весов нейрона?
(1) в первом
(2) во втором
(3) в третьем
Как изменяется при понижении температуры вероятность перехода машины Больцмана в состояние с меньшим консенсусом?
(1) уменьшается
(2) увеличивается
(3) остается постоянной
Как задана обратная связь в сети Эльмана?
(1) выходы нейронов второго (выходного) слоя связаны со входами нейронов скрытого слоя
(2) выходы нейронов скрытого слоя связаны со входами нейронов этого же слоя
Какой алгоритм самоорганизации поощряет нейроны с наименьшей активностью?
Чему равен порог нейрона в слое сравнения?
Какая из функций принадлежности обладает наибольшим числом параметров?
(1) функция Гаусса
(2) треугольная
(3) трапецеидальная
Какой показатель должен изменяться минимально при редукции нейронной сети?
(1) значение функции оценки качества работы сети
(2) выходной сигнал сети
(3) скорость обучения сети
Какие подходы сочетают в себе гибридные нейрочипы?
(1) аналоговый
(2) символьный
(3) сигнальный
(4) цифровой
Требуется ли обучающая выборка (учитель) для обучения нейрона Хебба?
Что реализует персептрон в пространстве входных сигналов?
(1) гиперсферу
(2) гиперэллипсоид
(3) гиперплоскость
Каким уравнением описывается гиперплоскость, реализующая функцию И?
Какие из нижеперечисленных сетей относятся к сетям периодического функционирования?
(1) монотонные
(2) слоисто-полносвязные
(3) полносвязно-слоистые
На чем основан поиск минимума целевой функции в заданном направлении?
(1) на случайном переборе значений коэффициента обучения
(2) на полиномиальной аппроксимации целевой функции
Чем обусловлена неэффективность алгоритма наискорейшего спуска?
(1) большой объем вычислений
(2) неиспользование информации о кривизне функции оценки
(3) резкое замедление минимизации в окрестности точки оптимального решения
В чем заключается принцип элитарности?
(1) в мутации наименее приспособленных хромосом
(2) в выборе наиболее приспособленных хромосом
Какая операция лежит в основе функционирования радиального нейрона?
(1) вычисление скалярного произведения вектора сигналов на вектор весовых коэффициентов
(2) определение расстояния от вектора сигналов до центра радиальной функции
Какую функцию реализует ассоциативная память?
(1) классифицирует входной объект
(2) восстанавливает полный образ по частичным данным
(3) задает соответствие между нейронами и входными объектами
Какие пары векторов запоминает двунаправленная ассоциативная память?
(1) пары векторов с действительными значениями компонентов
(2) пары двоичных векторов
(3) пары биполярных векторов
Какая сеть дает лучшие решения задачи коммивояжера?
(1) сеть Хопфилда
(2) машина Больцмана
Для чего используется сеть RTRN?
(1) для идентификации динамических объектов
(2) для обработки сигналов в реальном времени
Что минимизируется при компрессии данных сетью Кохонена?
(1) размер кодовой таблицы
(2) погрешность квантования
Какое устройство тормозит нейроны в слое распознавания?
(1) слой сравнения
(2) прм1
(3) схема сброса
Какая из форм произведения функций принадлежности использует операцию выбора минимального значения?
(1) логическое произведение
(2) алгебраическое произведение
Какой должна быть проекция вектора F на каждом шаге ортогонализации базиса?
(1) отрицательной
(2) минимальной
(3) максимальной
Какой фактор является решающим для обеспечения высокой плотности соединений в оптических реализациях нейронных сетей?
(1) световые лучи имеют малое сечение
(2) световые лучи при взаимном пересечении не взаимодействуют
(3) световые источники и фотоприемники имеют малые размеры
Какое преобразование реализует кубический нейрон ?
(1) вычисляет полином третьей степени от компонент вектора входных сигналов нейрона
(2) использует входной вектор как адрес ячейки памяти, хранящей результат (значение выходного сигнала)
Чем ограничивается размер страницы в методе обучения персептрона по страницам?
(1) емкостью оперативной памяти
(2) скоростью обучения
Может ли персептрон реализовать функцию ИСКЛЮЧАЮЩЕЕ ИЛИ?
Что нужно сделать для повышения константы Липшица многослойной сети?
(1) увеличить число слоев сети
(2) увеличить число нейронов в слоях
(3) увеличить число входов сети
Чем обусловлена возможность попадания целевой функции многослойной сигмоидальной сети в седловую зону?
(1) насыщением сигмоидальной функции активации
(2) наличием скрытых слоев
Когда производится рестарт алгоритма сопряженных градиентов?
(1) когда число выполненных шагов минимизации превышает заданный порог
(2) когда движение вдоль очередного выбранного направления спуска приводит к слишком маленькому шагу либо вообще не дает улучшения
Какой способ генерации новых виртуальных частиц является наиболее перспективным?
(1) при падении скорости обучения ниже критической
(2) при рестартах
(3) при каждом вычислении оценок и градиентов
Какими параметрами описывается радиальная функция Гаусса?
(1) вектор весовых коэффициентов
(2) центр и ширина
Как нейрон МакКаллока-Питса определяет свое состояние?
(1) сравнивает взвешенную сумму входных сигналов с порогом
(2) вычисляет значение непрерывной функции от взвешенной суммы входных сигналов
Что такое автосвязь?
(1) связь выхода сети Хемминга с ее входом
(2) связь между вторым и третьим слоями сети Хемминга
(3) связь выхода нейрона с его собственным входом
Какой член функции энергии равен нулю, если матрица нейронов содержит количество единиц, равное числу городов в маршруте коммивояжера?
(1) первый
(2) второй
(3) третий
(4) четвертый
Какие данные образуют множество входных сигналов скрытого слоя сети RMLP?
(1) входные сигналы сети вместе с задержанными выходными сигналами сети
(2) входные сигналы сети вместе с задержанными выходными сигналами скрытого слоя
Какой тип соседства используется в классическом алгоритме Кохонена?
(1) прямоугольное
(2) гауссовское
Как влияет значение порога схемы сброса на качество работы слоя распознавания?
(1) чем меньше порог, тем менее похожие векторы будут отнесены сетью к одному классу
(2) чем больше порог, тем менее похожие векторы будут отнесены сетью к одному классу
Что утверждает принцип «конструктивной неопределенности»?
(1) точность и смысл противоречат друг другу, начиная с некоторого момента анализа
(2) точность и смысл дополняют друг друга, начиная с некоторого момента анализа
К каким функциям применим метод исключения параметров «сверху вниз» с ортогонализацией?
(1) к любым
(2) только к функциям вида
F(x,w)= ϕ(Σiwifi(x))
Какова разрядность векторного процессора NM6403?
(1) 16
(2) 32
(3) 64
(4) 128
Какой метод позволяет выйти из окрестности локального минимума?
(1) градиентный метод
(2) метод с моментом
Из какого интервала выбирается значение скорости обучения?
(1) (-1,1)
(2) (0,1)
(3) (1,2)
Чему должно быть равно значение t в уравнении
x1 + x2 + x3= t,
чтобы соответствующий нейрон реализовал функцию И?
(1) любому числу из интервала (0,1)
(2) любому числу из интервала (1,2)
(3) любому числу из интервала (2,3)
Какие точки функции наиболее трудно аппроксимировать?
(1) точки, в которых при малом изменении входных сигналов происходит большое изменение значения функции
(2) точки, в которых при большом изменении входных сигналов происходит малое изменение значения функции
Как влияет увеличение числа входов нейронов на выбор начальных значений их весовых коэффициентов (кроме порогов)?
(1) приводит к уменьшению модулей весовых коэффициентов
(2) приводит к увеличению модулей весовых коэффициентов
Как обеспечить ортогональность нового градиента предыдущему направлению спуска в BFGS-методе?
(1) как можно точнее проводить одномерную оптимизацию в поиске шага
(2) учесть изменение градиента на предыдущем шаге
Как происходит отбор хромосом?
(1) по принципу рулетки
(2) случайным образом
(3) по количеству ненулевых битов
Чем могут отличаться друг от друга функции радиальных нейронов?
(1) только параметрами
(2) структурой и параметрами
Как должен изменяться вес входа нейрона по правилу Хебба?
(1) вес входа должен уменьшаться при корреляции между входом и выходом нейрона
(2) вес входа должен увеличиваться при корреляции между входом и выходом нейрона
Что считается достоинством сети Хемминга?
(1) относительно небольшое количество связей между нейронами
(2) сеть Хемминга дает лучшие результаты, чем сеть Хопфилда
(3) отсутствие двунаправленного распространения сигналов
Когда активна связь (Xi,Yj) ∈ Ed машины Больцмана?
(1) когда в маршруте есть прямой путь из города X в город Y
(2) когда длина прямого пути из города X в город Y меньше заданной величины
К какой задаче в общем случае сводится задача прогноза данных на нейронной сети?
(1) к задаче воспроизведения вектор-функции многих переменных по данным обучающей выборки
(2) к задаче интерполяции полиномиальной функции многих переменных
Чем определяется степень адаптации нейронов-соседей при использовании соседства гауссовского типа?
(1) евклидовым расстоянием между нейроном-победителем и нейроном-соседом
(2) уровнем соседства
(3) рангом соседа
Какой нейрон в слое распознавания подавляет все остальные?
(1) нейрон с максимальным выходом
(2) нейрон с минимальным выходом
Какие части должна содержать база знаний мягкой экспертной системы?
(1) функции принадлежности
(2) нечеткие продукции
(3) рекуррентные нейронные сети
(4) нечеткие нейронные сети
(5) сети АРТ
(6) процедуры интерпретации хромосом генетических алгоритмов
(7) функции оптимальности
В чем заключается рекурсивное контрастирование нейронной сети?
(1) в исключении параметров сети – одного за другим
(2) в модификации параметров сети – одного за другим
Каким образом можно объединять нейропроцессоры NM6403 в параллельную систему?
(1) посредством линков
(2) посредством общих модулей памяти
(3) посредством общих векторных регистров
Какая величина минимизируется при аппроксимации функции нейроном?
(1) квадратичная ошибка
(2) четвертая степень ошибки
Какой тип обучения назван обучением с учителем?
(1) обучение, при котором заданы требуемые значения выходных сигналов для всех обучающих входных векторов
(2) обучение, при котором задано допустимое отклонение выходных сигналов от заданных
Чему должно быть равно значение t в уравнении
x1 + x2 + x3= t,
чтобы соответствующий нейрон реализовал функцию ИЛИ?
(1) любому числу из интервала (0,1)
(2) любому числу из интервала (1,2)
(3) любому числу из интервала (2,3)
Что такое контрастер?
(1) система, нормирующая входные сигналы нейронной сети
(2) система, нормирующая выходные сигналы нейронной сети
(3) система, упрощающая нейронную сеть
Почему следует избегать насыщения нейронов?
(1) нейрон, попавший в состояние насыщения, не участвует в преобразовании данных
(2) нейрон, попавший в состояние насыщения, делает сеть неработоспособной
Каким образом в квазиньютоновских и партан-методах выбирается начальное направление спуска?
(1) случайным образом
(2) методом Ньютона
(3) по антиградиенту функции оценки
Когда завершается генетический процесс?
(1) в момент генерации удовлетворительного решения
(2) при выполнении заданного количества мутаций
(3) при выполнении максимально допустимого количества итераций
Как вычисляется вектор весов выходного нейрона радиальной сети?
(1) как результат минимизации функции оценки сети
(2) как результат решения системы линейных алгебраических уравнений
1. Что такое функция активации
2. Зачем использовать
3. Какие есть функции активации
4、sigmoid,Relu,softmax
1. Что такое функция активации
Как показано на рисунке ниже, в нейроне входные входы взвешиваются, и после суммирования также применяется функция, которая является функцией активации.

2. Зачем использовать
Если функция возбуждения не используется, выход каждого слоя является линейной функцией от входа верхнего уровня. Независимо от того, сколько слоев в нейронной сети, выход является линейной комбинацией входов.
Если используется, функция активации вводит нелинейные факторы в нейрон, так что нейронная сеть может произвольно приближать любую нелинейную функцию, так что нейронная сеть может применяться ко многим нелинейным моделям.
3. Каковы функции активации
(1) сигмовидная функция
Формула:
Кривая:
Производная:
Сигмовидная функция, также называемая логистической функцией, используется для вывода нейронов скрытого слоя, диапазон значений (0,1), она может отображать действительное число в (0,1) и может использоваться для двоичной классификации.
Эффект лучше, когда различие в функциях более сложное или разница не особенно велика.
Недостатки сигмовидной кишки:
- Функция активации требует больших вычислительных ресурсов, и когда обратное распространение ищет градиент ошибки, дифференциация включает в себя деление
- При обратном распространении градиент легко исчезает, что делает невозможным завершение обучения глубокой сети
- Функция сигмоидов насыщена и убивает градиент.
- Функция сигмоидов сходится медленно.
Ниже объясняется, почему исчезает градиент:
В алгоритме обратного распространения для получения функции активации, производное выражение сигмоиды:

Исходная сигмоидальная функция и производный граф следующие:

Из рисунка видно, что производная скоро приблизится к 0 из 0, что легко вызывает явление «исчезновение градиента»
(2) функция Тан
формула


кривая

Также называется функцией касательной к битам, диапазон значений равен [-1,1].
Эффект Таня будет очень хорошим, когда разница в функциях очевидна, и эффект функции будет продолжать расширяться в течение цикла.
Разница между и сигмоидальным состоянием состоит в том, что tanh имеет значение 0, поэтому в реальном приложении tanh будет лучше сигмовидного.
(3) ReLU
Выпрямленная линейная единица (ReLU) — для выхода нейронов скрытого слоя
формула

кривая

Особенности RELU:
Когда входной сигнал <0, на выходе все 0. Если> 0, выход равен входу
Преимущества ReLU:
Krizhevsky et al.Установлено, что скорость сходимости SGD, полученной с использованием ReLU, будет намного выше, чем сигмоид / танх
Недостатки ReLU:
Обучение очень «хрупкое», его легко «умереть»
Например, через нейрон ReLU протекает очень большой градиент. После обновления параметров этот нейрон больше не будет активировать какие-либо данные, затем градиент этого нейрона Это всегда будет 0.
Если скорость обучения велика, вероятно, что 40% нейронов в сети «мертвы».
(4) функция softmax
Softmax-для мультиклассовых выходов нейронной сети
формула

Возьмите пример, чтобы увидеть значение формулы:

То есть, если определенный zj больше других z, компоненты этого отображения близки к 1, а другие близки к 0. Основное применение — мультиклассификация.
Первая причина, по которой вы хотите получить показатель, состоит в том, чтобы моделировать поведение max, поэтому сделайте его больше.
Вторая причина — это необходимость в производной функции.
4. Сравнение сигмовидной, ReLU, softmax
Сигмоид и ReLU сравнение:
Проблема исчезновения градиента сигмоида, производной ReLU, не имеет такой проблемы, ее производная выражается следующим образом:

Кривая как показано

Основные изменения по сравнению с сигмовидными функциями:
1) Одностороннее подавление
2) Относительно широкая граница возбуждения
3) Разреженная активация.
Разница между сигмоидом и софтмаксом:
softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1.
Сигмоид отображает действительное значение в интервал (0,1), который используется для двоичной классификации.
И softmax отображает k-мерный вектор действительного значения (a1, a2, a3, a4 …) в a (b1, b2, b3, b4 …), где bi — постоянная от 0 до 1, и сумма выходных нейронов Он равен 1,0, поэтому он эквивалентен значению вероятности, и тогда задача мультиклассификации может быть выполнена в соответствии с вероятностью bi.
Для двух задач классификации сигмоид и софтмакс одинаковы, и оба стремятся к потере перекрестной энтропии, а софтмакс можно использовать для задач мультиклассификации
Softmax является расширением сигмовидной кишки, потому что, когда число категорий k = 2, регрессия softmax вырождается в логистическую регрессию. В частности, когда k = 2, предполагаемая функция регрессии softmax равна:

Используя функцию избыточности параметра регрессии softmax, вычтите вектор θ1 из обоих векторов параметров, чтобы получить:

Наконец, θ ′ используется для представления θ2-θ1, и приведенная выше формула может быть выражена как вероятность того, что регрессия softmax предсказывает одну из категорий как

Вероятность другой категории

Это согласуется с логистической регрессией.
Распределение, используемое для моделирования softmax, является полиномиальным распределением, в то время как логистика основана на распределении Бернулли
Множественная логистическая регрессия может также обеспечить эффект мультиклассификации с помощью суперпозиции, но мультиклассификация с помощью регрессии softmax является взаимоисключающей между классами, то есть один вход может быть классифицирован только Это категория, множественные логистические регрессии используются для множественной классификации, и выходные категории не являются взаимоисключающими, то есть слово «яблоко» относится как к категории «фрукты», так и к категории «3C».
5. Как выбрать
При выборе он настраивается в соответствии с преимуществами и недостатками каждой функции, например:
Если вы используете ReLU, будьте осторожны, чтобы установить скорость обучения, и следите за тем, чтобы в сети не появлялось много «мертвых» нейронов. Если это не легко решить, вы можете попробовать Leaky ReLU, PReLU или Maxout.