Лекция 11 7. Оценки
качества переходного процесса
7.1. Показатели качества переходного
процесса
Если САУ устойчива (см. разд.5), то
переходные процессы в ней затухают с
течением времени, т.е. обеспечивается
принципиальная возможность прихода
системы в некоторое установившееся
состояние при любом внешнем воздействии.
Однако далее требуется, во-первых, чтобы
это установившееся состояние было
достаточно близко к заданному (см.
разд.6), и во-вторых, чтобы затухание
переходного процесса было достаточно
быстрым, а колебания при этом были бы
невелики.
Поэтому после обеспечения устойчивости
системы надо позаботиться о требуемом
качестве процесса управления, в понятие
которого входят, в частности: точность
системы в установившемся состоянии,
качество переходного процесса.
В понятие качества системы входит ряд
показателей, таких как:
-
Установившаяся ошибка (6.5)
![]() .
.
-
Время регулирования

или длительность переходного процесса
(быстродействие).
Теоретически переходной процесс в
устойчивой линейной системе затухает
в бесконечности, т.е. разница между
текущим значение выходной величины
![]()
и установившимся значением
![]()
стремится к нулю
![]()
при
![]() .
.
Практически же длительность переходного
процесса ограничивают тем моментом,
когда отклонения становятся пренебрежительно
малыми, например, величина наперёд
заданного отклонения
![]()
не составит более
![]()
от установившегося значения
![]()
![]() ;
;
где
![]() .
.
-
Время максимального перерегулирования

– момент времени, когда текущее значение

достигает своего максимума.(*) -
Максимальное перерегулирование

![]() .
.
-
Количество колебаний

за время переходного процесса
 .(*)
.(*) -
Период колебаний
 .(*)
.(*)
замечание.
Показатели качества переходного
процесса, отмеченные *, не являются
основными.
Все перечисленные характеристики
переходного процесса приведены на
рис.7.1.

Рис.7.1. Показатели
качества переходного процесса
Как же определить показатели качества
переходного процесса?
-
Прямой путь определения показателей
качества переходного процесса из
аналитического выражения переходной
процесса

или аналитического выражения
переходного процесса для ошибки
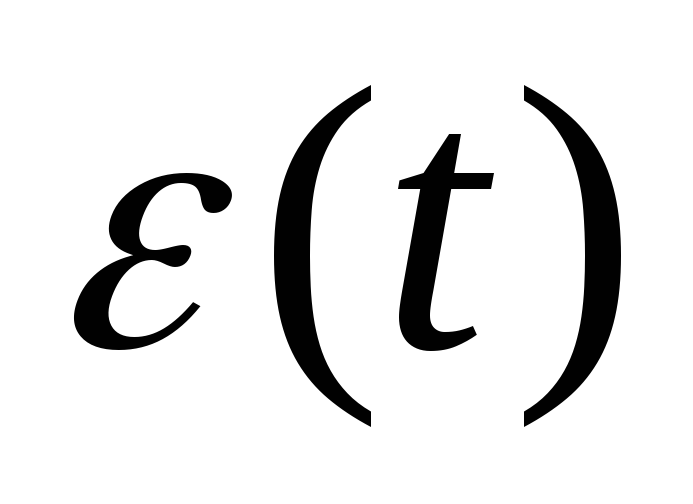 .
.
Установившееся состояние выходной
величины
![]()
определяется при
![]()
из
![]()
![]() .
.
Установившаяся ошибка
![]()
определяется при
![]()
из аналитического выражения переходного
процесса ошибки
![]()
или из выражения (6.7) через коэффициенты
ошибки.
-
Показатели качества переходного
процесса также можно определить
непосредственно из графика переходного
процесса, (см. рис.7.1.) полученного
экспериментальным путем или путем
моделирования численными или
аналоговыми методами.
-
Приближенные или косвенные оценки
качества переходного процесса
определяются корневым методом, если
известен характеристический полином
замкнутой системы управления

(см. подразд.4.4.).
Если известно аналитическое выражение
характеристического полинома
![]() ,
,
то всегда можно определить его корни,
и представить их распределение на
комплексной плоскости, как показано на
рис.7.2.
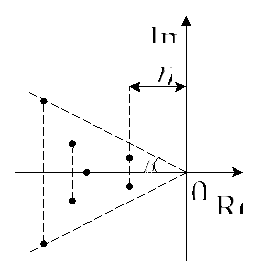
Рис.7.2. Распределение
корней на комплексной плоскости
На рис.7.2. введены следующие обозначения.
-
Степень устойчивости
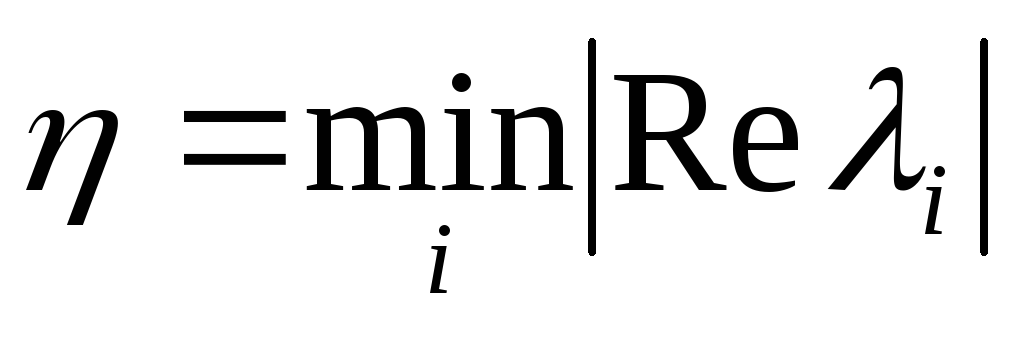 ,
,
действительная часть минимального
корня характеристического полинома
взятая по абсолютной величине. -
длительность
переходного процесса

связана со степенью устойчивости
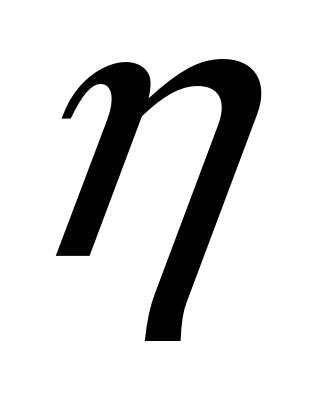
следующей зависимостью
![]() . (7.1)
. (7.1)
-
Колебательность переходного
процесса определяется величиной
 ,
,
где

– максимальное по абсолютному
значению отношение. Т.е
 .
. -
количество
колебаний

за время переходного процесса
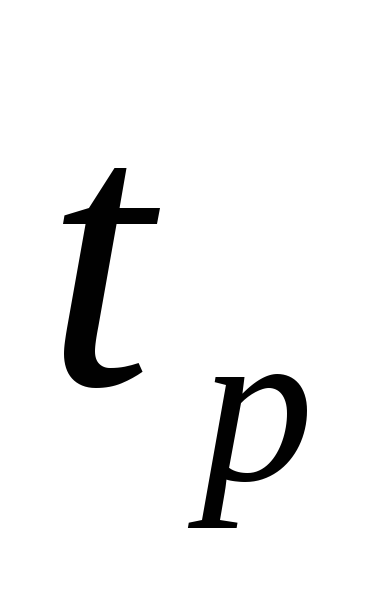
определяется с помощью

по формуле
 .
.
-
Период колебаний переходного процесса
оценивается
 .
. -
Время максимального перерегулирования
равно
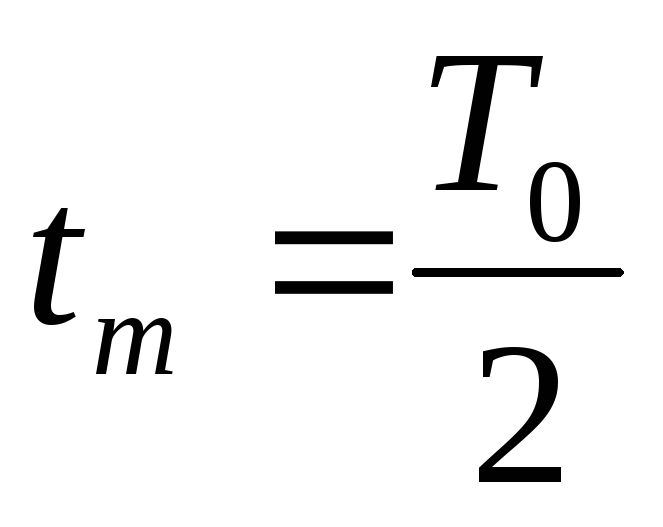 .
. -
Максимальное перерегулирование

связано с колебательностью переходного
процесса

следующей зависимостью .
.
Возникает вопрос, почему в формуле
(7.1) оценки длительности переходного
процесса системы взят интервал
![]() ?
?
Чтобы ответить на него рассмотрим промер
оценки времени регулирования
![]()
апериодического звена первого порядка,
передаточная функция которого
![]() .
.
Соответствующий характеристический
полином имеет вид
![]() .
.
Корень этого характеристического
полинома равен
![]() .
.
Запишем
дифференциальное уравнение относительно
выходной координаты
![]()
и решим его, при следующих начальных
условиях
![]()
и задающем воздействии
![]() .
.
![]() ,
,
![]() .
.
(7.2)
График переходного процесса изображен
на рис.7.3.

Рис.7.3. Пример
переходного процесса апериодического
звена первого порядка
Из решения дифференциального уравнения
(7.2) следует, что установившееся состояние
выходной величины
![]()
при
![]() .
.
тогда 5%-й
допуск от этого установившегося значения
равен
![]() .
.
Подставим положительное значение этого
допуска
![]()
в левую часть решения дифференциального
уравнения (7.2)
![]()
и определим длительность переходного
процесса
![]()
![]() .
.
Если требуется оценить время регулирования
с точностью не хуже, чем 1%, то длительность
переходного процесса
![]()
равна
![]() .
.
Таким образом, если допустимая наперед
заданная точность расчета
![]()
равна 5%, то при оценках длительности
переходного процесса
![]()
по формуле (7.1) выбирается нижняя граница
интервала
![]() .
.
Такая точность расчета характерна для
большинства технических систем. Если
же рассчитывается высокоточная система,
используется 1%-й допуск, и, следовательно,
выбирается верхняя граница интервала
![]() .
.
пример
определения косвенных оценок качества
переходного процесса системы управления,
используя выражение передаточной
функции.
Пусть передаточная функция
разомкнутой части системы имеет вид
![]() .
.
Тогда, согласно (4.8) передаточная функция
замкнутой системы будет равна
![]() , (7.3)
, (7.3)
а передаточная функция для ошибки по
задающему воздействию согласно (4.10)
имеет вид
![]() . (7.4)
. (7.4)
Определим установившуюся ошибку через
коэффициенты ошибки по формуле (6.7)
![]() .
.
Из формулы (6.6) следует, что

,

,
 .
.
Таким образом, установившаяся ошибка
при задающем воздействии
![]()
будет равна
![]() .
.
Исследуемая система обладает астатизмом
нулевого порядка
![]() ,
,
(![]() ).
).
Корни характеристического полинома
![]()
![]()
Равны
![]()
![]() .
.
следовательно,
степень устойчивости
![]() .
.
И можно оценить время регулирования
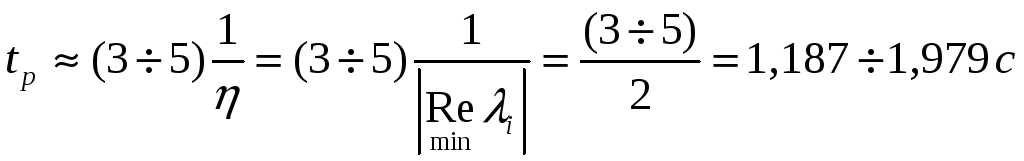 .
.
Также, зная корни характеристического
полинома, можно определить колебательность
переходного процесса
 .
.
количество
колебаний
![]()
за время переходного процесса
![]()
не превышает
![]() .
.
период
колебаний переходного процесса равен
 .
.
Время максимального перерегулирования
определяется по формуле
![]() .
.
Величина максимального перерегулирования
![]()
оценивается по формуле
![]() .
.
На рис.7.4. представлены результаты
моделирования переходной функции по
задающему воздействию
![]()
и для ошибки
![]()
в среде Mat lab.
Из анализа графиков следует, что
предварительные оценки качества
переходных характеристик практически
совпадают с результатами моделирования.


Рис.7.4. Графики
переходной функции
![]()
и
переходной функции
для ошибки
![]()
5
Соседние файлы в папке ТАУ лекции
- #
- #
- #
- #
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: ![]() , рисунок 116.
, рисунок 116.

Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
![]() ,
, ![]() ,
,  и так
и так
далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
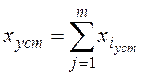 , где
, где
каждое слагаемое, или составляющая сигнала ошибки, ![]() определяется
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
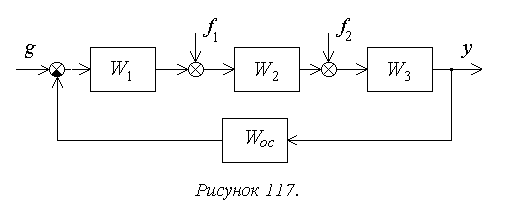
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих ![]() .
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке ![]() при известном изображении задающего
при известном изображении задающего
воздействия G(s):
![]() , где
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
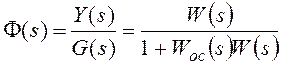 , где
, где ![]() — передаточная функция
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
![]()
В результате:
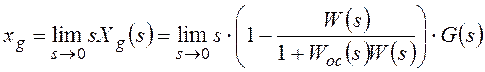 .
.
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения ![]() при известном изображении возмущающего
при известном изображении возмущающего
воздействия F(s):
![]() , где
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
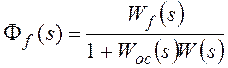 ;
;
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
![]() ,
,
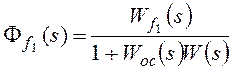 ,
,
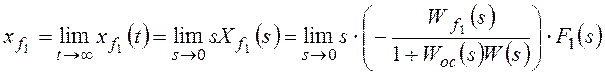 .
.
Для f2:
![]() ,
,
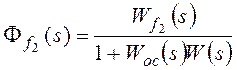 ,
,
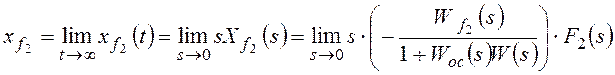 .
.
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
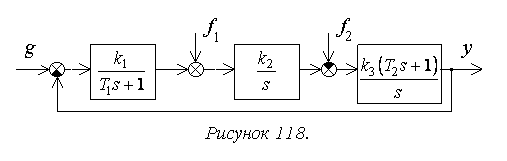
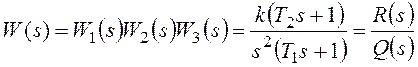 ,
,
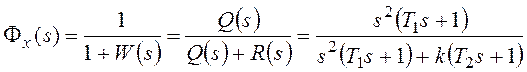 , где k=k1k2k3 – коэффициент передачи
, где k=k1k2k3 – коэффициент передачи
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При ![]() получим:
получим:
![]()
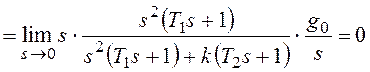 .
.
При ![]() получим:
получим:
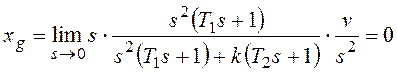 .
.
При  получим:
получим:
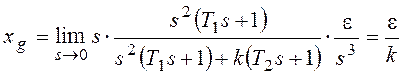 .
.
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
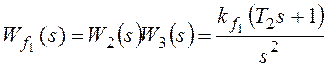 ,
,
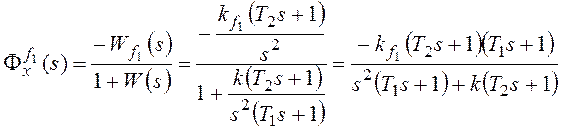 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f1.
При ![]() получим:
получим:
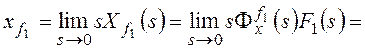
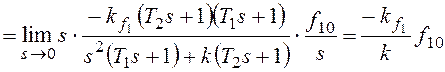 .
.
При ![]() получим:
получим:
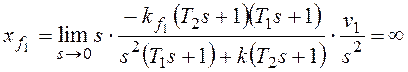 .
.
При 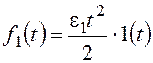 получим
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
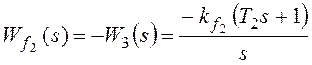 ,
,
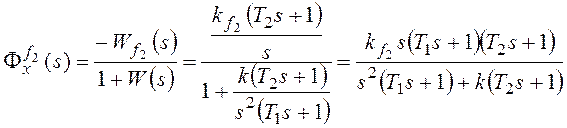 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f2.
При ![]() получим:
получим:
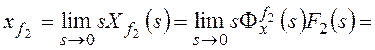
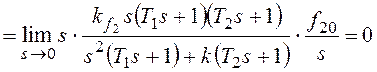 .
.
При ![]() получим:
получим:
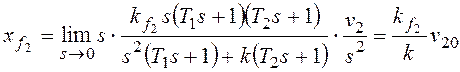 .
.
При 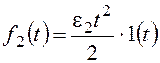 получим:
получим:
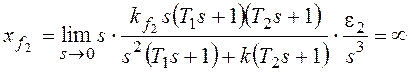 .
.
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.
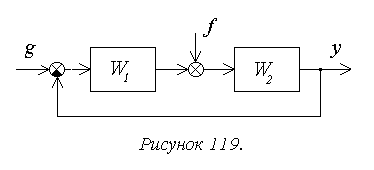
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
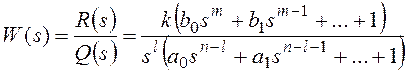 , где l³0.
, где l³0.
Тогда получим:
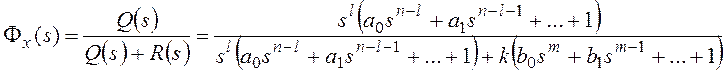
и для общего вида задающего воздействия 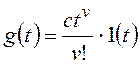 , которому соответствует изображение
, которому соответствует изображение 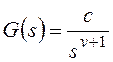 ,
,
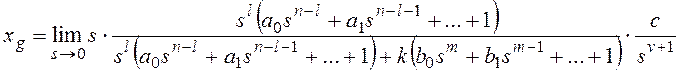 .
.
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
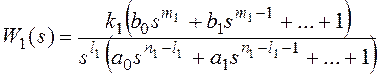 ,
,
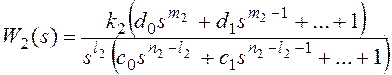 , где l1+l2=l,
, где l1+l2=l,
k1k2=k, m1+m2=m,
n1+n2=n,
причем ![]() и
и ![]() .
.
Тогда получим:
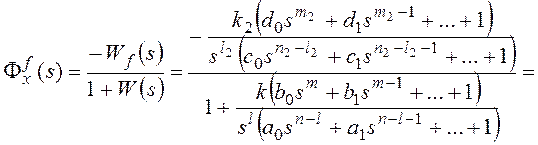
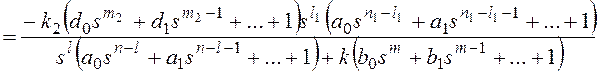
и для общего вида возмущающего воздействия 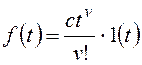 , которому соответствует изображение
, которому соответствует изображение 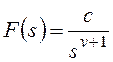 ,
,
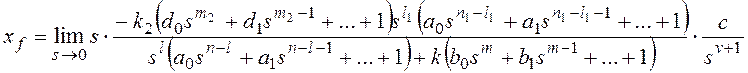 .
.
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Автоматические системы управления
должны быть не только устойчивыми, но и обеспечивать качество процесса
управления. Основные наиболее существенные требования к качеству управления,
которые позволяют оценить работу почти всех систем управления, называют
показателями процесса управления. Они характеризуют поведение системы в
переходном процессе. Показателями качества будет время регулирования,
перерегулирование, колебательность процесса, установившаяся ошибка, характер
затухания переходного процесса, запас устойчивости.
Качество процессов регулирования
обычно оценивают по переходной функции, которая представляет собой реакцию
системы на внешнее воздействие типа единичного скачка. Для следящих систем и
программного регулирования переходную функцию рассматривают по отношению к
задающему воздействию, а для систем стабилизации – по отношению к возмущению.
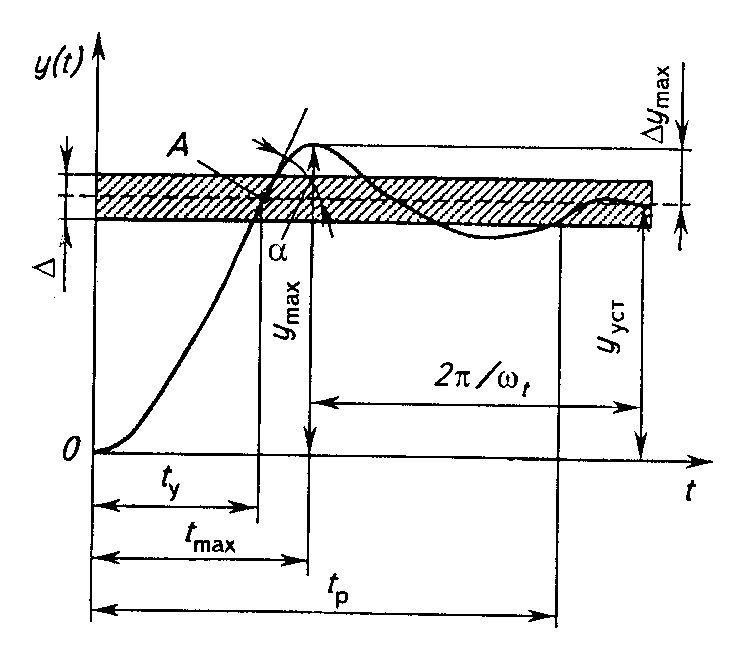
Рисунок 1. Определение показателей
качества регулирования по переходной характеристике.
На рис. 1 изображена переходная
функция по которой можно определить основные показатели качества переходного
процесса: время регулирования, перерегулирование и др.
Время регулирования определяет
длительность переходного процесса. Теоретически переходной процесс длится
бесконечно долго, однако практически его считают законченным, как только
отклонение регулируемой величины от нового ее установившегося значения не будет
превышать допустимых пределов.
Временем регулирования называют
минимальное время, по истечении которого, начиная с момента начала действия
входного сигнала, выходная переменная отклоняется от установившегося значения на величину, не
превышающую некоторую заданную постоянную величину 0,5.
Время регулирования характеризует
быстродействие системы.
Быстродействие может характеризоваться
и временем достижения переходной функцией нового установившегося значения, и
временем достижения максимального значения.
Перерегулированием называется
максимальное отклонение управляемой величины от заданного значения и выраженной
в процентах.
Время регулирования и
перерегулирования взаимосвязаны. Так, перерегулирование зависит от скорости
изменения регулируемой величины, которая графически представляет собой тангенс
угла наклона α (альфа)
касательной в точке А к кривой (рисунок 1).
Чем больше эта скорость, тем больше
перерегулирование. Поэтому для его уменьшения необходимо уменьшить скорость, с
которой система подходит к новому установившемуся состоянию. Но это приведет к
увеличению времени регулирования. Если система подходит к установившемуся
состоянию с нулевой скоростью, то перерегулирования вообще не будет, но время
регулирования значительно увеличится (рисунок 2).
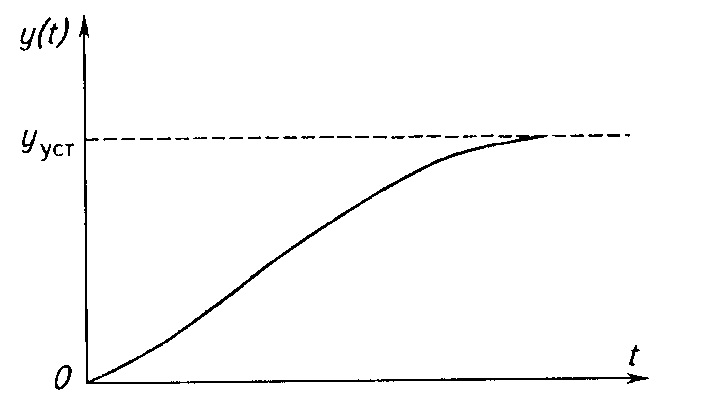
Рисунок 2. Переходная характеристика
системы автоматического регулирования без перерегулирования.
Значения времени регулирования и
перерегулирования часто задают в качестве исходных данных для синтеза
корректирующих устройств, поскольку правильным выбором и настройкой последних
обеспечивается подавление нежелательных колебаний регулируемой величины в
переходном процессе. Для некоторых систем перерегулирование вообще недопустимо,
например для систем автоматического регулирования физических величин в
процессах, связанных с приготовлением продуктов. Необходимо так же иметь в
виду, что стремление уменьшить время регулирования приводит к увеличению
мощности исполнительного устройства.
Колебательность процесса
характеризуется числом колебаний управляемой величины за время регулирования.
Количественно колебательность
оценивается по логарифмическому декременту затухания, который представляет
собой натуральный логарифм отношения двух последующих амплитуд отклонений
управляемой величины одного направления.
Чем больше логарифмический декремент
затухания, тем быстрее происходит затухание переходного процесса.
Установившаяся ошибка показывает
точность управления в установившемся режиме. Она ровняется разности между
заданным значением управляемой величины и ее установившимся значением при
нормальной нагрузке.
Характер затухания переходного
процесса позволяет классифицировать переходные процессы в системах управления и
выделить среди их многообразия четыре основных вида (рисунок 3): колебательный
процесс (кривая 1) – ему присуще несколько значений перерегулирования;
малоколебательный процесс (кривая 2) – процесс с одним перерегулированием;
монотонный процесс (кривая 4), при котором скорость изменения управляемой
величины не изменяет знака в течение всего времени регулирования;
апериодический процесс (кривая 3) – процесс, когда управляемая величина меньше
ее установившегося значения с точностью до зоны нечувствительности регулятора
при всех значениях времени регулирования.
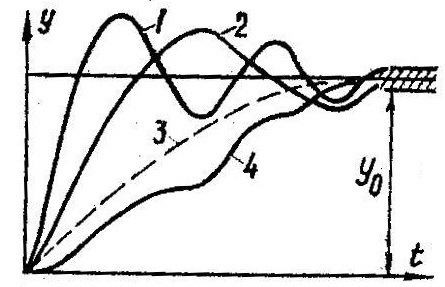
Рисунок 3. Основные виды характеристик
переходных процессов автоматических систем регулирования при типовом единичном
воздействии.
Запас устойчивости – это физическая
сущность и методы определения этого показателя качества управления.
Показатели, которые характеризуют
качество работы системы в переходном режиме, делят на прямые и косвенные.
Прямые показатели – это числовые
оценки качества, получаемые непосредственно по переходной характеристике. Для
получения прямых показателей качества необходимо иметь кривую переходного
процесса, которую можно построить по структурной схеме или дифференциальному
уравнению систем автоматического регулирования, используя аналоговые
вычислительные машины или компьютеры.
Косвенные оценки качества переходного
процесса позволяют определить некоторые особенности переходного процесса и
установить влияние параметров системы на качество переходных процессов. К
косвенным показателям качества относятся корневые, частотные и интегральные
оценки.
Рассмотрим корневые оценки качества.
Геометрически степень устойчивости можно определить как расстояние на плоскости
от мнимой оси до ближайшего к ней корня или ближайшей пары комплексных корней
(рисунок 4).
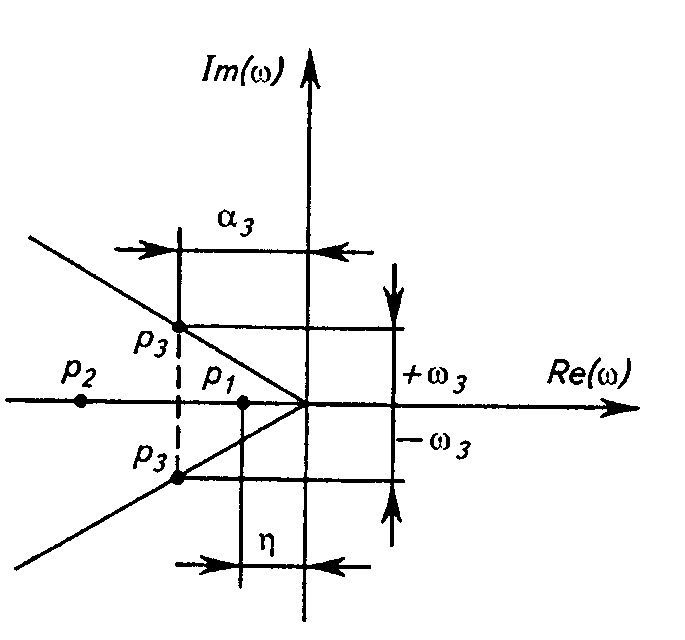
Рисунок 4. Корневые оценки качества
систем автоматического регулирования.
Понятие степени устойчивости
используют для синтеза систем автоматического регулирования.
Рассмотрим
частотные оценки качества. При гармонических воздействиях качество систем
автоматического регулирования принято оценивать по частотным характеристикам.
Для этого используют следующие величины: показатель колебательности и частоту
среза. Показатель колебательности – это отношение максимального значения
амплитудно-частотной характеристики замкнутой системы к ее значению при частоте
равной нулю. Частота среза – это частота при которой амплитудно-частотная
характеристика равна единице. Косвенно она характеризует длительность
переходного процесса.
Рассмотрим интегральные оценки качества.
По кривой переходного процесса можно оценить качество процесса регулирования в
данной системе. Косвенно оценить качество регулирования можно по площади между
кривой переходного процесса и линией установившегося режима. В данном случае
критерием качества будет определенный интеграл по времени от функции,
характеризующей разницу между действительным и заданным значениями регулируемой
величины.
Список
используемой литературы
- В.И. Загинайлов, Л.Н. Шеповалова «Основы
автоматики», Москва «КОЛОС», 2001. - Л.В.Колесов «Основы
автоматики», Москва
«Колос», 1984.
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка
Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.
+ ~ я»
-R(s) —— *~С>——- *
-Y(s)
G(s)
H(s)
Рис. 4.18. Разомкнутая система управления
Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна
ад=ад — ад=[і — стт. (4.48)
В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна
Для вычисления установившейся ошибки используется теорема о конечном значении:
lim e(t)= lims£(s). (4.50)
_ 1 —КО А—>0
Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:
е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).
■v-»0 s -‘->0
В замкнутой системе при H(s) = 1 имеем:
Случай неединичной обратной связи рассматривается в разд. 5.8.
4.5. Установившаяся ошибка
Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.

Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.
Рис. 4.20
Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом
Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию
G(s) = —. (4.53)
TS+ 1
Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна
е0(со) = 1 — 6X0) = 1 — К (4.54)
при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:
Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна
ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).
.v->0 s
Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,
ес(со) = 1 J! Le_L. (4.55)
1+ К 1+ К
В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.
Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит
Ае0(со) 0,1
(4.56)
IKOI 1
т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно
Аес (оо ) = ——(4.57) 91 101
а относительное приращение составит
Аес (оо)
= 0,0011, (4.58)
IKOI
или 0,11%. Как говорится, результат в комментариях не нуждается.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …
Лекция 11 7. Оценки
качества переходного процесса
7.1. Показатели качества переходного
процесса
Если САУ устойчива (см. разд.5), то
переходные процессы в ней затухают с
течением времени, т.е. обеспечивается
принципиальная возможность прихода
системы в некоторое установившееся
состояние при любом внешнем воздействии.
Однако далее требуется, во-первых, чтобы
это установившееся состояние было
достаточно близко к заданному (см.
разд.6), и во-вторых, чтобы затухание
переходного процесса было достаточно
быстрым, а колебания при этом были бы
невелики.
Поэтому после обеспечения устойчивости
системы надо позаботиться о требуемом
качестве процесса управления, в понятие
которого входят, в частности: точность
системы в установившемся состоянии,
качество переходного процесса.
В понятие качества системы входит ряд
показателей, таких как:
-
Установившаяся ошибка (6.5)
![]() .
.
-
Время регулирования

или длительность переходного процесса
(быстродействие).
Теоретически переходной процесс в
устойчивой линейной системе затухает
в бесконечности, т.е. разница между
текущим значение выходной величины
![]()
и установившимся значением
![]()
стремится к нулю
![]()
при
![]() .
.
Практически же длительность переходного
процесса ограничивают тем моментом,
когда отклонения становятся пренебрежительно
малыми, например, величина наперёд
заданного отклонения
![]()
не составит более
![]()
от установившегося значения
![]()
![]() ;
;
где
![]() .
.
-
Время максимального перерегулирования

– момент времени, когда текущее значение

достигает своего максимума.(*) -
Максимальное перерегулирование

![]() .
.
-
Количество колебаний

за время переходного процесса
 .(*)
.(*) -
Период колебаний
 .(*)
.(*)
замечание.
Показатели качества переходного
процесса, отмеченные *, не являются
основными.
Все перечисленные характеристики
переходного процесса приведены на
рис.7.1.

Рис.7.1. Показатели
качества переходного процесса
Как же определить показатели качества
переходного процесса?
-
Прямой путь определения показателей
качества переходного процесса из
аналитического выражения переходной
процесса

или аналитического выражения
переходного процесса для ошибки
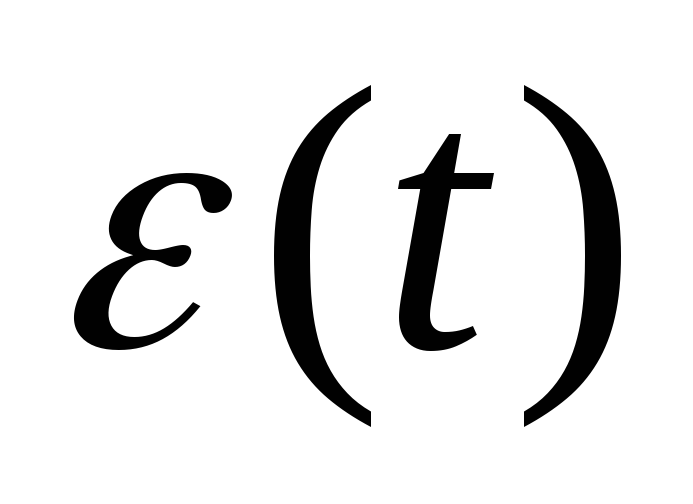 .
.
Установившееся состояние выходной
величины
![]()
определяется при
![]()
из
![]()
![]() .
.
Установившаяся ошибка
![]()
определяется при
![]()
из аналитического выражения переходного
процесса ошибки
![]()
или из выражения (6.7) через коэффициенты
ошибки.
-
Показатели качества переходного
процесса также можно определить
непосредственно из графика переходного
процесса, (см. рис.7.1.) полученного
экспериментальным путем или путем
моделирования численными или
аналоговыми методами.
-
Приближенные или косвенные оценки
качества переходного процесса
определяются корневым методом, если
известен характеристический полином
замкнутой системы управления

(см. подразд.4.4.).
Если известно аналитическое выражение
характеристического полинома
![]() ,
,
то всегда можно определить его корни,
и представить их распределение на
комплексной плоскости, как показано на
рис.7.2.

Рис.7.2. Распределение
корней на комплексной плоскости
На рис.7.2. введены следующие обозначения.
-
Степень устойчивости
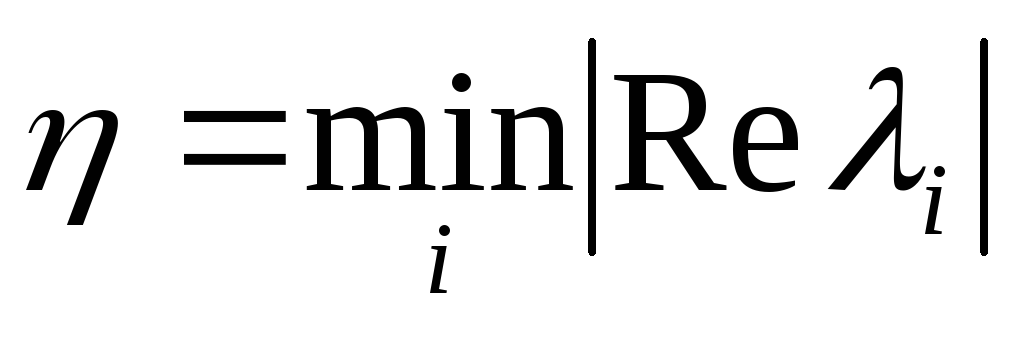 ,
,
действительная часть минимального
корня характеристического полинома
взятая по абсолютной величине. -
длительность
переходного процесса

связана со степенью устойчивости
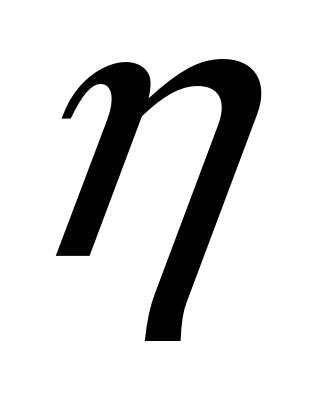
следующей зависимостью
![]() . (7.1)
. (7.1)
-
Колебательность переходного
процесса определяется величиной
 ,
,
где

– максимальное по абсолютному
значению отношение. Т.е
 .
. -
количество
колебаний

за время переходного процесса
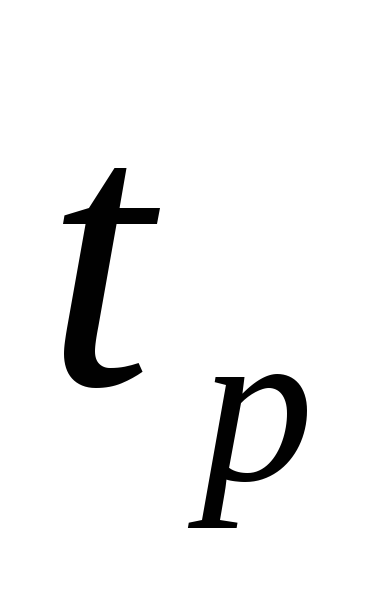
определяется с помощью

по формуле
 .
.
-
Период колебаний переходного процесса
оценивается
 .
. -
Время максимального перерегулирования
равно
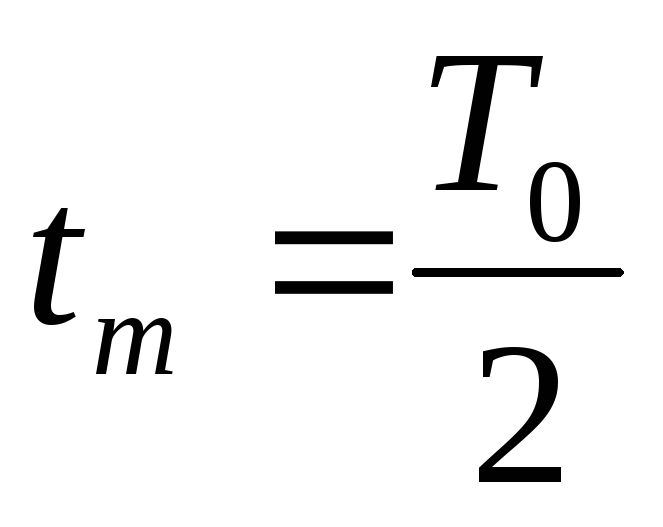 .
. -
Максимальное перерегулирование

связано с колебательностью переходного
процесса

следующей зависимостью .
.
Возникает вопрос, почему в формуле
(7.1) оценки длительности переходного
процесса системы взят интервал
![]() ?
?
Чтобы ответить на него рассмотрим промер
оценки времени регулирования
![]()
апериодического звена первого порядка,
передаточная функция которого
![]() .
.
Соответствующий характеристический
полином имеет вид
![]() .
.
Корень этого характеристического
полинома равен
![]() .
.
Запишем
дифференциальное уравнение относительно
выходной координаты
![]()
и решим его, при следующих начальных
условиях
![]()
и задающем воздействии
![]() .
.
![]() ,
,
![]() .
.
(7.2)
График переходного процесса изображен
на рис.7.3.

Рис.7.3. Пример
переходного процесса апериодического
звена первого порядка
Из решения дифференциального уравнения
(7.2) следует, что установившееся состояние
выходной величины
![]()
при
![]() .
.
тогда 5%-й
допуск от этого установившегося значения
равен
![]() .
.
Подставим положительное значение этого
допуска
![]()
в левую часть решения дифференциального
уравнения (7.2)
![]()
и определим длительность переходного
процесса
![]()
![]() .
.
Если требуется оценить время регулирования
с точностью не хуже, чем 1%, то длительность
переходного процесса
![]()
равна
![]() .
.
Таким образом, если допустимая наперед
заданная точность расчета
![]()
равна 5%, то при оценках длительности
переходного процесса
![]()
по формуле (7.1) выбирается нижняя граница
интервала
![]() .
.
Такая точность расчета характерна для
большинства технических систем. Если
же рассчитывается высокоточная система,
используется 1%-й допуск, и, следовательно,
выбирается верхняя граница интервала
![]() .
.
пример
определения косвенных оценок качества
переходного процесса системы управления,
используя выражение передаточной
функции.
Пусть передаточная функция
разомкнутой части системы имеет вид
![]() .
.
Тогда, согласно (4.8) передаточная функция
замкнутой системы будет равна
![]() , (7.3)
, (7.3)
а передаточная функция для ошибки по
задающему воздействию согласно (4.10)
имеет вид
![]() . (7.4)
. (7.4)
Определим установившуюся ошибку через
коэффициенты ошибки по формуле (6.7)
![]() .
.
Из формулы (6.6) следует, что

,

,
 .
.
Таким образом, установившаяся ошибка
при задающем воздействии
![]()
будет равна
![]() .
.
Исследуемая система обладает астатизмом
нулевого порядка
![]() ,
,
(![]() ).
).
Корни характеристического полинома
![]()
![]()
Равны
![]()
![]() .
.
следовательно,
степень устойчивости
![]() .
.
И можно оценить время регулирования
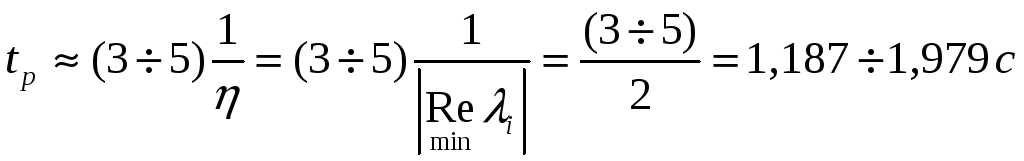 .
.
Также, зная корни характеристического
полинома, можно определить колебательность
переходного процесса
 .
.
количество
колебаний
![]()
за время переходного процесса
![]()
не превышает
![]() .
.
период
колебаний переходного процесса равен
 .
.
Время максимального перерегулирования
определяется по формуле
![]() .
.
Величина максимального перерегулирования
![]()
оценивается по формуле
![]() .
.
На рис.7.4. представлены результаты
моделирования переходной функции по
задающему воздействию
![]()
и для ошибки
![]()
в среде Mat lab.
Из анализа графиков следует, что
предварительные оценки качества
переходных характеристик практически
совпадают с результатами моделирования.


Рис.7.4. Графики
переходной функции
![]()
и
переходной функции
для ошибки
![]()
5
Соседние файлы в папке ТАУ лекции
- #
- #
- #
- #
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: ![]() , рисунок 116.
, рисунок 116.

Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
![]() ,
, ![]() ,
,  и так
и так
далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
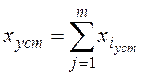 , где
, где
каждое слагаемое, или составляющая сигнала ошибки, ![]() определяется
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).

В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих ![]() .
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке ![]() при известном изображении задающего
при известном изображении задающего
воздействия G(s):
![]() , где
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
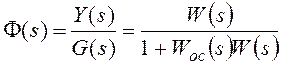 , где
, где ![]() — передаточная функция
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
![]()
В результате:
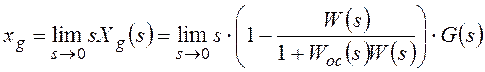 .
.
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения ![]() при известном изображении возмущающего
при известном изображении возмущающего
воздействия F(s):
![]() , где
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
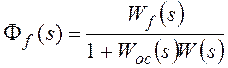 ;
;
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
![]() ,
,
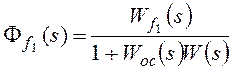 ,
,
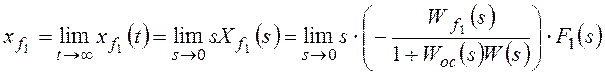 .
.
Для f2:
![]() ,
,
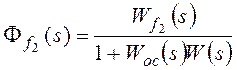 ,
,
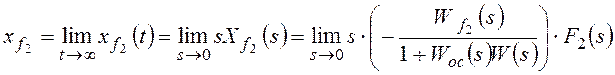 .
.
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):

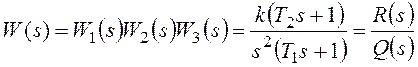 ,
,
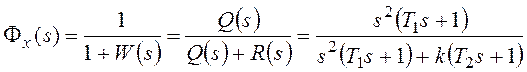 , где k=k1k2k3 – коэффициент передачи
, где k=k1k2k3 – коэффициент передачи
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При ![]() получим:
получим:
![]()
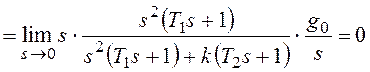 .
.
При ![]() получим:
получим:
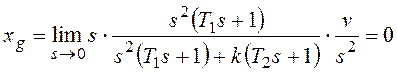 .
.
При  получим:
получим:
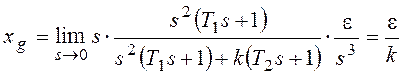 .
.
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
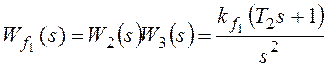 ,
,
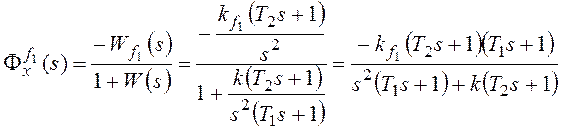 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f1.
При ![]() получим:
получим:
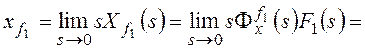
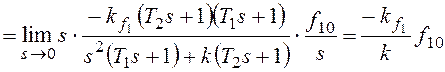 .
.
При ![]() получим:
получим:
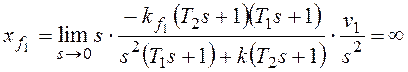 .
.
При 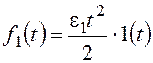 получим
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
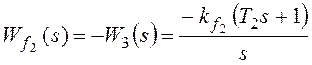 ,
,
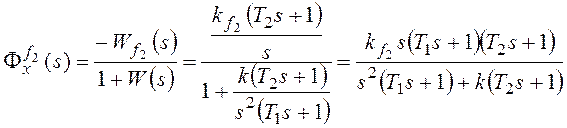 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f2.
При ![]() получим:
получим:
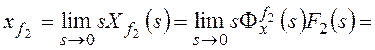
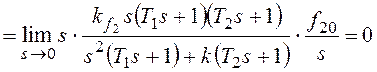 .
.
При ![]() получим:
получим:
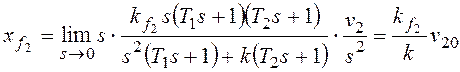 .
.
При 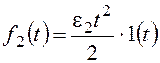 получим:
получим:
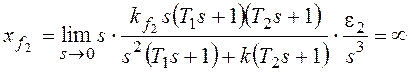 .
.
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.

В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
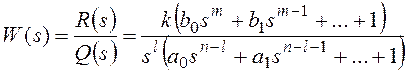 , где l³0.
, где l³0.
Тогда получим:
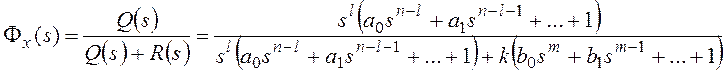
и для общего вида задающего воздействия 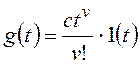 , которому соответствует изображение
, которому соответствует изображение 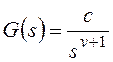 ,
,
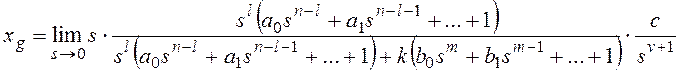 .
.
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
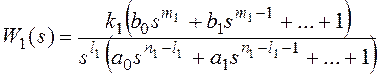 ,
,
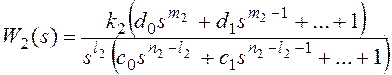 , где l1+l2=l,
, где l1+l2=l,
k1k2=k, m1+m2=m,
n1+n2=n,
причем ![]() и
и ![]() .
.
Тогда получим:
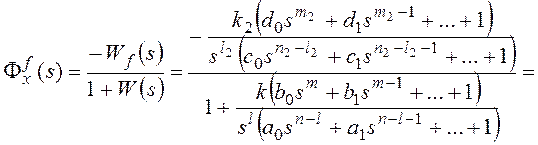
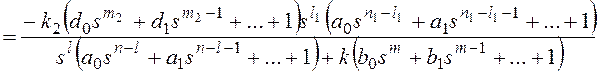
и для общего вида возмущающего воздействия 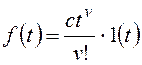 , которому соответствует изображение
, которому соответствует изображение 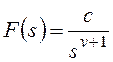 ,
,
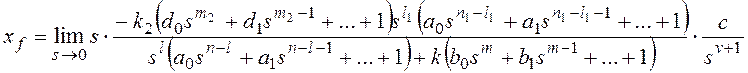 .
.
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка
Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.
+ ~ я»
-R(s) —— *~С>——- *
-Y(s)
G(s)
H(s)
Рис. 4.18. Разомкнутая система управления
Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна
ад=ад — ад=[і — стт. (4.48)
В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна
Для вычисления установившейся ошибки используется теорема о конечном значении:
lim e(t)= lims£(s). (4.50)
_ 1 —КО А—>0
Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:
е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).
■v-»0 s -‘->0
В замкнутой системе при H(s) = 1 имеем:
Случай неединичной обратной связи рассматривается в разд. 5.8.
4.5. Установившаяся ошибка
Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.

Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.
Рис. 4.20
Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом
Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию
G(s) = —. (4.53)
TS+ 1
Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна
е0(со) = 1 — 6X0) = 1 — К (4.54)
при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:
Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна
ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).
.v->0 s
Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,
ес(со) = 1 J! Le_L. (4.55)
1+ К 1+ К
В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.
Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит
Ае0(со) 0,1
(4.56)
IKOI 1
т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно
Аес (оо ) = ——(4.57) 91 101
а относительное приращение составит
Аес (оо)
= 0,0011, (4.58)
IKOI
или 0,11%. Как говорится, результат в комментариях не нуждается.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …

Затухающие колебания — типичный переходной процесс при котором некоторый параметр некоторое время колеблется вокруг установившегося значения
Перехо́дный проце́сс — в теории систем представляет изменения во времени координат динамической системы, до некоторого установившегося состояния; возникает под влиянием возмущающих воздействий, изменяющих её состояние, структуру или параметры, а также вследствие ненулевых начальных условий[B: 1].
Характеристики
Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы. Широкое применение нашло экспериментальное и аналитическое определение и построение переходных процессов для наиболее неблагоприятных условий работы динамической системы при внешних возмущениях типа дельта-функции, ступенчатом или синусоидальных воздействиях[B: 1][B: 2].
Оценка качества САУ по виду кривой переходного процесса производится при помощи так называемых прямых показателей качества — перерегулирования, допустимого числа колебаний и времени переходного процесса. Обычно рассматривают переходный процесс, возникающий в системе при воздействии единичной ступенчатой функции, т. е. переходная функция замкнутой системы[1].
Время переходного процесса
Длительность переходного процесса в системе характеризует её быстродействие, а его характер определяет качество системы. За количественную характеристику длительности переходного процесса принимают время, необходимое выходному сигналу системы для того, чтобы приблизиться к своему установившемуся значению, т. е. время, по истечении которого выполняется равенство:
- [math]displaystyle{ |h(t)-h_{st}| leqslant epsilon, }[/math]
- где [math]displaystyle{ h_{st} }[/math] — установившееся значение;
- [math]displaystyle{ epsilon }[/math] — наперёд заданное положительное число[1].
В линейных непрерывных динамических системах принято рассматривать переходной процесс, вызванный единичным ступенчатым возмущением, но в этом случае установившееся значение достигается за бесконечно большое время. Если же ограничить точность достижения установившегося значения некоторой малой величиной [math]displaystyle{ epsilon }[/math], то тогда длительность переходного процесса [math]displaystyle{ t }[/math] будет конечной величиной[B: 1].
В приложениях теории управления обычно в САУ принимают [math]displaystyle{ epsilon }[/math] равной 0,01—0,05 от [math]displaystyle{ h_{st} }[/math], т. е. переходный процесс считают закончившимся, когда переходная функция отличается не более, чем на 1–5 % от своего установившегося (стационарного) значения[1].
Перерегулирование
Перерегулирование (определяется величиной первого выброса) — отношение разности максимального значения переходной характеристики и её установившегося значения к величине установившегося значения. Измеряется обычно в процентах.
Степень затухания переходного процесса
Степень затухания переходного процесса определяется относительным уменьшением соседних амплитуд переходной характеристики[B: 3].
Числителем является амплитуда первого колебания. Степень затухания показывает во сколько раз уменьшается амплитуда второго колебания по сравнению с первым.
Степень затухания системы зависит от показателя колебательности [math]displaystyle{ M }[/math] (см. ниже).
Логарифмический декремент колебания
Логарифмический декремент колебания — натуральный логарифм отношения амплитуд двух соседних перерегулирований. Обратная ему величина показывает, за какое число колебаний их амплитуда уменьшается в [math]displaystyle{ e }[/math] раз ([math]displaystyle{ e }[/math] — основание натуральных логарифмов). Уместен лишь для характеристики линейных систем[B: 4].
Колебательность
Характеризует склонность системы к колебаниям и определяется как модуль отношения амплитуд второго колебания к амплитудам первого колебания. Колебательность системы характеризуют при помощи показателя колебательности [math]displaystyle{ M }[/math], который представляет собой отношение резонансного пика при резонансной частоте к значению АЧХ при нулевой частоте[2].
Показатель колебательности связан со степенью колебательности формулой:
- [math]displaystyle{ M = frac{1 + m^2}{2m}. }[/math]
При увеличении [math]displaystyle{ M }[/math], уменьшается показатель колебательности [math]displaystyle{ m }[/math] и соответственно происходит уменьшение степени колебательности.
Установившаяся ошибка
Установившаяся ошибка системы — разница между предполагаемым и реальным значением выходного сигнала при времени, стремящемся к бесконечности. В идеальных астатических системах установившаяся ошибка равна нулю.
Примеры
Электрические цепи
В электрической цепи переходный процесс характеризуется плавным инерционным изменением тока и напряжения в цепи в ответ на приложенное внешнее воздействие[B: 5].
Формула, описывающие протекание простейших переходных процессов (разряд конденсатора через резистор):
- [math]displaystyle{ U(t) = U_0 e^{(-t/tau)}, }[/math] [math]displaystyle{ tau=RC, }[/math]
- где [math]displaystyle{ U_0 }[/math] — значение напряжения на конденсаторе в момент перед началом переходного процесса,
- [math]displaystyle{ tau }[/math] — постоянная времени переходного процесса, С — ёмкость, R — сопротивление элементов цепей.
Для цепей, содержащих индуктивность, если можно пренебречь активным сопротивлением, постоянная времени равна:
- [math]displaystyle{ tau=L/R. }[/math]
См. также
- Бифуркационная память
- Время изодрома
- Зона нечувствительности
- Коэффициент демпфирования
- Переходные процессы в электрических цепях
Примечания
- ↑ 1,0 1,1 1,2 Пономарёв, 1974, § 5.7. Оценка запаса устойчивости и быстродействия по кривой процесса регулирования, с. 201—202.
- ↑ МЭИ, 2011, 2.3. Решение линейных дифференциальных уравнений во временной области, с. 44—48.
Литература
- Книги
- ↑ 1,0 1,1 1,2 Энциклопедия кибернетики / Глушков В. М.. — Киев: Глав. ред. УСЭ, 1974. — 624 с.
- ↑ Основы автоматического регулирования и управления / Пономарев В. М. и Литвинов А. П.. — М.: Высшая школа, 1974. — 439 с.
- ↑ Управление и инноватика в теплоэнергетике / Андрюшин А. В., Сабанин В. Р., Смирнов. Н. И.. — М.: МЭИ, 2011. — 392 с. — ISBN 978-5-38300539-2.
- ↑ Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. — 2-е изд., перераб. и испр.. — М.: Наука, 1981. — 918 с.
- ↑ Веников В. А. Переходные электромеханические процессы в электрических системах. — М.: Высшая школа, 1978. — 415 с.
Лекция 11 7. Оценки
качества переходного процесса
7.1. Показатели качества переходного
процесса
Если САУ устойчива (см. разд.5), то
переходные процессы в ней затухают с
течением времени, т.е. обеспечивается
принципиальная возможность прихода
системы в некоторое установившееся
состояние при любом внешнем воздействии.
Однако далее требуется, во-первых, чтобы
это установившееся состояние было
достаточно близко к заданному (см.
разд.6), и во-вторых, чтобы затухание
переходного процесса было достаточно
быстрым, а колебания при этом были бы
невелики.
Поэтому после обеспечения устойчивости
системы надо позаботиться о требуемом
качестве процесса управления, в понятие
которого входят, в частности: точность
системы в установившемся состоянии,
качество переходного процесса.
В понятие качества системы входит ряд
показателей, таких как:
-
Установившаяся ошибка (6.5)
![]() .
.
-
Время регулирования

или длительность переходного процесса
(быстродействие).
Теоретически переходной процесс в
устойчивой линейной системе затухает
в бесконечности, т.е. разница между
текущим значение выходной величины
![]()
и установившимся значением
![]()
стремится к нулю
![]()
при
![]() .
.
Практически же длительность переходного
процесса ограничивают тем моментом,
когда отклонения становятся пренебрежительно
малыми, например, величина наперёд
заданного отклонения
![]()
не составит более
![]()
от установившегося значения
![]()
![]() ;
;
где
![]() .
.
-
Время максимального перерегулирования

– момент времени, когда текущее значение

достигает своего максимума.(*) -
Максимальное перерегулирование

![]() .
.
-
Количество колебаний

за время переходного процесса
 .(*)
.(*) -
Период колебаний
 .(*)
.(*)
замечание.
Показатели качества переходного
процесса, отмеченные *, не являются
основными.
Все перечисленные характеристики
переходного процесса приведены на
рис.7.1.

Рис.7.1. Показатели
качества переходного процесса
Как же определить показатели качества
переходного процесса?
-
Прямой путь определения показателей
качества переходного процесса из
аналитического выражения переходной
процесса

или аналитического выражения
переходного процесса для ошибки
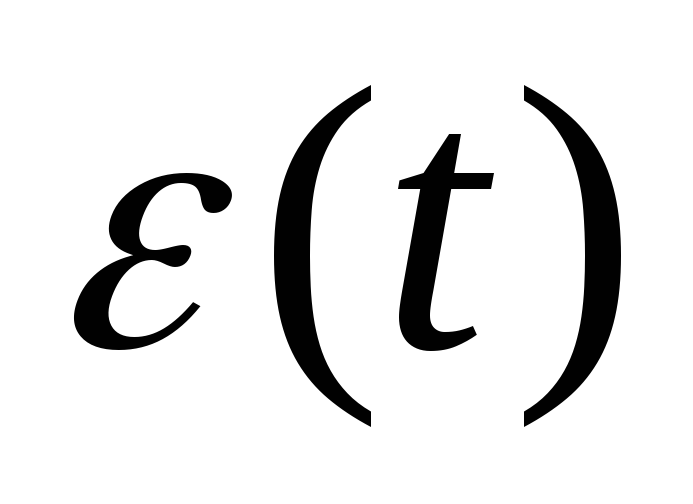 .
.
Установившееся состояние выходной
величины
![]()
определяется при
![]()
из
![]()
![]() .
.
Установившаяся ошибка
![]()
определяется при
![]()
из аналитического выражения переходного
процесса ошибки
![]()
или из выражения (6.7) через коэффициенты
ошибки.
-
Показатели качества переходного
процесса также можно определить
непосредственно из графика переходного
процесса, (см. рис.7.1.) полученного
экспериментальным путем или путем
моделирования численными или
аналоговыми методами.
-
Приближенные или косвенные оценки
качества переходного процесса
определяются корневым методом, если
известен характеристический полином
замкнутой системы управления

(см. подразд.4.4.).
Если известно аналитическое выражение
характеристического полинома
![]() ,
,
то всегда можно определить его корни,
и представить их распределение на
комплексной плоскости, как показано на
рис.7.2.

Рис.7.2. Распределение
корней на комплексной плоскости
На рис.7.2. введены следующие обозначения.
-
Степень устойчивости
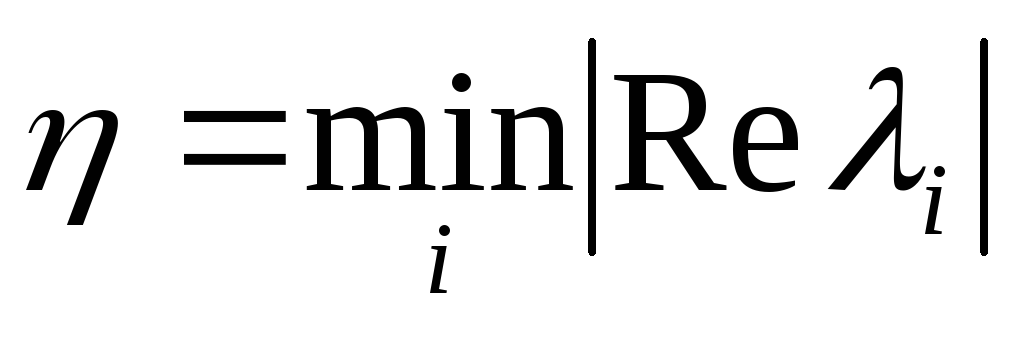 ,
,
действительная часть минимального
корня характеристического полинома
взятая по абсолютной величине. -
длительность
переходного процесса

связана со степенью устойчивости
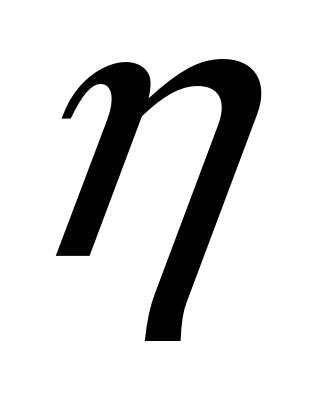
следующей зависимостью
![]() . (7.1)
. (7.1)
-
Колебательность переходного
процесса определяется величиной
 ,
,
где

– максимальное по абсолютному
значению отношение. Т.е
 .
. -
количество
колебаний

за время переходного процесса
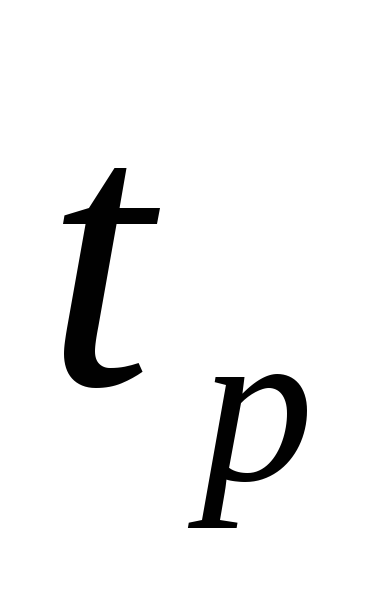
определяется с помощью

по формуле
 .
.
-
Период колебаний переходного процесса
оценивается
 .
. -
Время максимального перерегулирования
равно
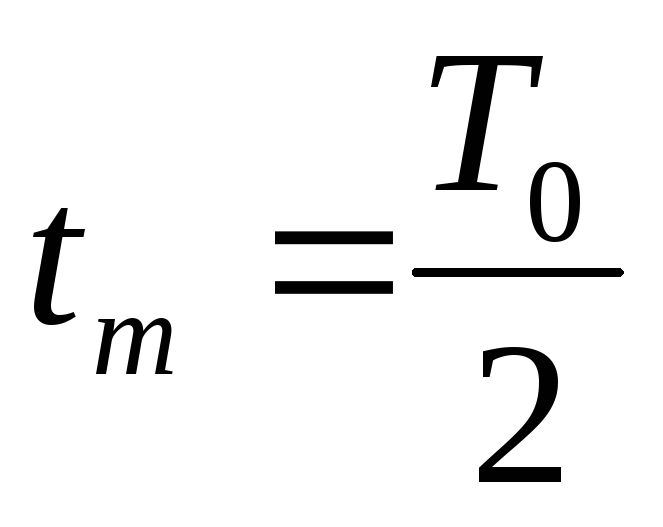 .
. -
Максимальное перерегулирование

связано с колебательностью переходного
процесса

следующей зависимостью .
.
Возникает вопрос, почему в формуле
(7.1) оценки длительности переходного
процесса системы взят интервал
![]() ?
?
Чтобы ответить на него рассмотрим промер
оценки времени регулирования
![]()
апериодического звена первого порядка,
передаточная функция которого
![]() .
.
Соответствующий характеристический
полином имеет вид
![]() .
.
Корень этого характеристического
полинома равен
![]() .
.
Запишем
дифференциальное уравнение относительно
выходной координаты
![]()
и решим его, при следующих начальных
условиях
![]()
и задающем воздействии
![]() .
.
![]() ,
,
![]() .
.
(7.2)
График переходного процесса изображен
на рис.7.3.

Рис.7.3. Пример
переходного процесса апериодического
звена первого порядка
Из решения дифференциального уравнения
(7.2) следует, что установившееся состояние
выходной величины
![]()
при
![]() .
.
тогда 5%-й
допуск от этого установившегося значения
равен
![]() .
.
Подставим положительное значение этого
допуска
![]()
в левую часть решения дифференциального
уравнения (7.2)
![]()
и определим длительность переходного
процесса
![]()
![]() .
.
Если требуется оценить время регулирования
с точностью не хуже, чем 1%, то длительность
переходного процесса
![]()
равна
![]() .
.
Таким образом, если допустимая наперед
заданная точность расчета
![]()
равна 5%, то при оценках длительности
переходного процесса
![]()
по формуле (7.1) выбирается нижняя граница
интервала
![]() .
.
Такая точность расчета характерна для
большинства технических систем. Если
же рассчитывается высокоточная система,
используется 1%-й допуск, и, следовательно,
выбирается верхняя граница интервала
![]() .
.
пример
определения косвенных оценок качества
переходного процесса системы управления,
используя выражение передаточной
функции.
Пусть передаточная функция
разомкнутой части системы имеет вид
![]() .
.
Тогда, согласно (4.8) передаточная функция
замкнутой системы будет равна
![]() , (7.3)
, (7.3)
а передаточная функция для ошибки по
задающему воздействию согласно (4.10)
имеет вид
![]() . (7.4)
. (7.4)
Определим установившуюся ошибку через
коэффициенты ошибки по формуле (6.7)
![]() .
.
Из формулы (6.6) следует, что

,

,
 .
.
Таким образом, установившаяся ошибка
при задающем воздействии
![]()
будет равна
![]() .
.
Исследуемая система обладает астатизмом
нулевого порядка
![]() ,
,
(![]() ).
).
Корни характеристического полинома
![]()
![]()
Равны
![]()
![]() .
.
следовательно,
степень устойчивости
![]() .
.
И можно оценить время регулирования
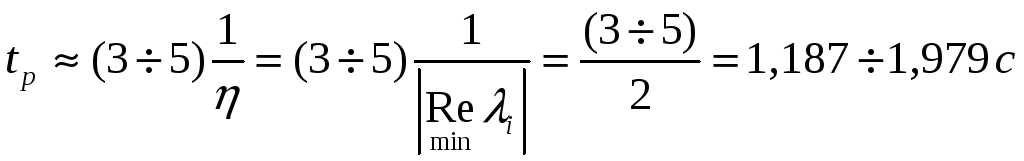 .
.
Также, зная корни характеристического
полинома, можно определить колебательность
переходного процесса
 .
.
количество
колебаний
![]()
за время переходного процесса
![]()
не превышает
![]() .
.
период
колебаний переходного процесса равен
 .
.
Время максимального перерегулирования
определяется по формуле
![]() .
.
Величина максимального перерегулирования
![]()
оценивается по формуле
![]() .
.
На рис.7.4. представлены результаты
моделирования переходной функции по
задающему воздействию
![]()
и для ошибки
![]()
в среде Mat lab.
Из анализа графиков следует, что
предварительные оценки качества
переходных характеристик практически
совпадают с результатами моделирования.


Рис.7.4. Графики
переходной функции
![]()
и
переходной функции
для ошибки
![]()
5
Соседние файлы в папке ТАУ лекции
- #
- #
- #
- #
- #
- #
- #
Лекция 11 7. Оценки
качества переходного процесса
7.1. Показатели качества переходного
процесса
Если САУ устойчива (см. разд.5), то
переходные процессы в ней затухают с
течением времени, т.е. обеспечивается
принципиальная возможность прихода
системы в некоторое установившееся
состояние при любом внешнем воздействии.
Однако далее требуется, во-первых, чтобы
это установившееся состояние было
достаточно близко к заданному (см.
разд.6), и во-вторых, чтобы затухание
переходного процесса было достаточно
быстрым, а колебания при этом были бы
невелики.
Поэтому после обеспечения устойчивости
системы надо позаботиться о требуемом
качестве процесса управления, в понятие
которого входят, в частности: точность
системы в установившемся состоянии,
качество переходного процесса.
В понятие качества системы входит ряд
показателей, таких как:
-
Установившаяся ошибка (6.5)
![]() .
.
-
Время регулирования

или длительность переходного процесса
(быстродействие).
Теоретически переходной процесс в
устойчивой линейной системе затухает
в бесконечности, т.е. разница между
текущим значение выходной величины
![]()
и установившимся значением
![]()
стремится к нулю
![]()
при
![]() .
.
Практически же длительность переходного
процесса ограничивают тем моментом,
когда отклонения становятся пренебрежительно
малыми, например, величина наперёд
заданного отклонения
![]()
не составит более
![]()
от установившегося значения
![]()
![]() ;
;
где
![]() .
.
-
Время максимального перерегулирования

– момент времени, когда текущее значение

достигает своего максимума.(*) -
Максимальное перерегулирование

![]() .
.
-
Количество колебаний

за время переходного процесса
 .(*)
.(*) -
Период колебаний
 .(*)
.(*)
замечание.
Показатели качества переходного
процесса, отмеченные *, не являются
основными.
Все перечисленные характеристики
переходного процесса приведены на
рис.7.1.

Рис.7.1. Показатели
качества переходного процесса
Как же определить показатели качества
переходного процесса?
-
Прямой путь определения показателей
качества переходного процесса из
аналитического выражения переходной
процесса

или аналитического выражения
переходного процесса для ошибки
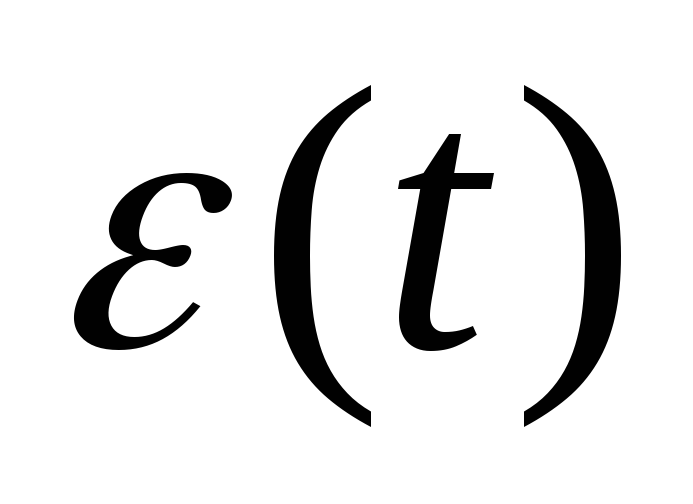 .
.
Установившееся состояние выходной
величины
![]()
определяется при
![]()
из
![]()
![]() .
.
Установившаяся ошибка
![]()
определяется при
![]()
из аналитического выражения переходного
процесса ошибки
![]()
или из выражения (6.7) через коэффициенты
ошибки.
-
Показатели качества переходного
процесса также можно определить
непосредственно из графика переходного
процесса, (см. рис.7.1.) полученного
экспериментальным путем или путем
моделирования численными или
аналоговыми методами.
-
Приближенные или косвенные оценки
качества переходного процесса
определяются корневым методом, если
известен характеристический полином
замкнутой системы управления

(см. подразд.4.4.).
Если известно аналитическое выражение
характеристического полинома
![]() ,
,
то всегда можно определить его корни,
и представить их распределение на
комплексной плоскости, как показано на
рис.7.2.

Рис.7.2. Распределение
корней на комплексной плоскости
На рис.7.2. введены следующие обозначения.
-
Степень устойчивости
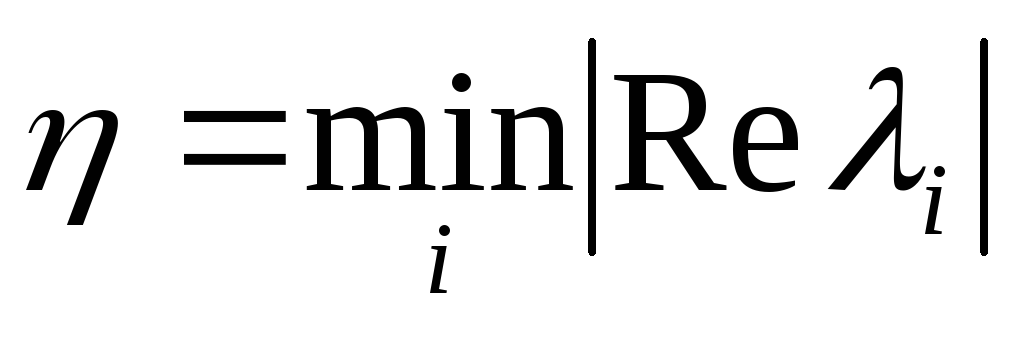 ,
,
действительная часть минимального
корня характеристического полинома
взятая по абсолютной величине. -
длительность
переходного процесса

связана со степенью устойчивости
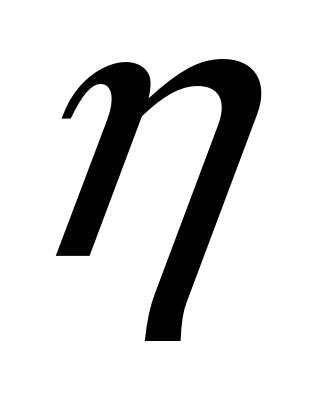
следующей зависимостью
![]() . (7.1)
. (7.1)
-
Колебательность переходного
процесса определяется величиной
 ,
,
где

– максимальное по абсолютному
значению отношение. Т.е
 .
. -
количество
колебаний

за время переходного процесса
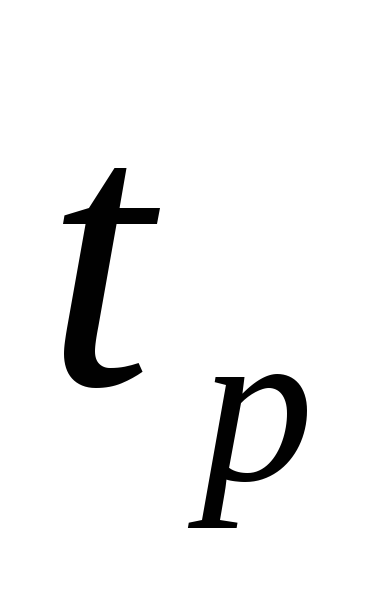
определяется с помощью

по формуле
 .
.
-
Период колебаний переходного процесса
оценивается
 .
. -
Время максимального перерегулирования
равно
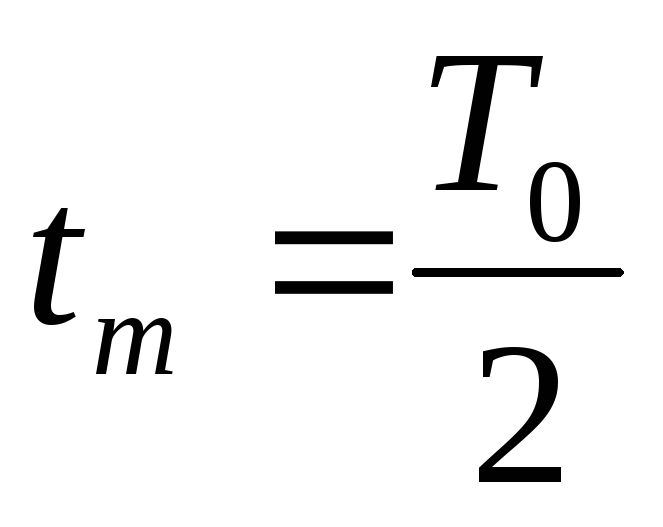 .
. -
Максимальное перерегулирование

связано с колебательностью переходного
процесса

следующей зависимостью .
.
Возникает вопрос, почему в формуле
(7.1) оценки длительности переходного
процесса системы взят интервал
![]() ?
?
Чтобы ответить на него рассмотрим промер
оценки времени регулирования
![]()
апериодического звена первого порядка,
передаточная функция которого
![]() .
.
Соответствующий характеристический
полином имеет вид
![]() .
.
Корень этого характеристического
полинома равен
![]() .
.
Запишем
дифференциальное уравнение относительно
выходной координаты
![]()
и решим его, при следующих начальных
условиях
![]()
и задающем воздействии
![]() .
.
![]() ,
,
![]() .
.
(7.2)
График переходного процесса изображен
на рис.7.3.

Рис.7.3. Пример
переходного процесса апериодического
звена первого порядка
Из решения дифференциального уравнения
(7.2) следует, что установившееся состояние
выходной величины
![]()
при
![]() .
.
тогда 5%-й
допуск от этого установившегося значения
равен
![]() .
.
Подставим положительное значение этого
допуска
![]()
в левую часть решения дифференциального
уравнения (7.2)
![]()
и определим длительность переходного
процесса
![]()
![]() .
.
Если требуется оценить время регулирования
с точностью не хуже, чем 1%, то длительность
переходного процесса
![]()
равна
![]() .
.
Таким образом, если допустимая наперед
заданная точность расчета
![]()
равна 5%, то при оценках длительности
переходного процесса
![]()
по формуле (7.1) выбирается нижняя граница
интервала
![]() .
.
Такая точность расчета характерна для
большинства технических систем. Если
же рассчитывается высокоточная система,
используется 1%-й допуск, и, следовательно,
выбирается верхняя граница интервала
![]() .
.
пример
определения косвенных оценок качества
переходного процесса системы управления,
используя выражение передаточной
функции.
Пусть передаточная функция
разомкнутой части системы имеет вид
![]() .
.
Тогда, согласно (4.8) передаточная функция
замкнутой системы будет равна
![]() , (7.3)
, (7.3)
а передаточная функция для ошибки по
задающему воздействию согласно (4.10)
имеет вид
![]() . (7.4)
. (7.4)
Определим установившуюся ошибку через
коэффициенты ошибки по формуле (6.7)
![]() .
.
Из формулы (6.6) следует, что

,

,
 .
.
Таким образом, установившаяся ошибка
при задающем воздействии
![]()
будет равна
![]() .
.
Исследуемая система обладает астатизмом
нулевого порядка
![]() ,
,
(![]() ).
).
Корни характеристического полинома
![]()
![]()
Равны
![]()
![]() .
.
следовательно,
степень устойчивости
![]() .
.
И можно оценить время регулирования
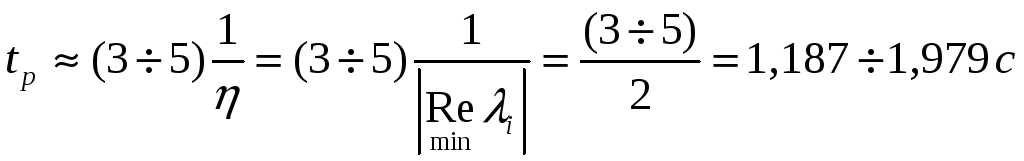 .
.
Также, зная корни характеристического
полинома, можно определить колебательность
переходного процесса
 .
.
количество
колебаний
![]()
за время переходного процесса
![]()
не превышает
![]() .
.
период
колебаний переходного процесса равен
 .
.
Время максимального перерегулирования
определяется по формуле
![]() .
.
Величина максимального перерегулирования
![]()
оценивается по формуле
![]() .
.
На рис.7.4. представлены результаты
моделирования переходной функции по
задающему воздействию
![]()
и для ошибки
![]()
в среде Mat lab.
Из анализа графиков следует, что
предварительные оценки качества
переходных характеристик практически
совпадают с результатами моделирования.


Рис.7.4. Графики
переходной функции
![]()
и
переходной функции
для ошибки
![]()
5
Соседние файлы в папке ТАУ лекции
- #
- #
- #
- #
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: ![]() , рисунок 116.
, рисунок 116.

Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
![]() ,
, ![]() ,
,  и так
и так
далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
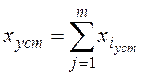 , где
, где
каждое слагаемое, или составляющая сигнала ошибки, ![]() определяется
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).

В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих ![]() .
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке ![]() при известном изображении задающего
при известном изображении задающего
воздействия G(s):
![]() , где
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
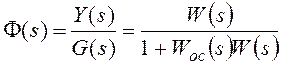 , где
, где ![]() — передаточная функция
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
![]()
В результате:
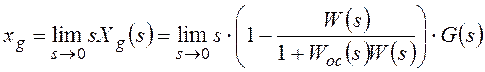 .
.
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения ![]() при известном изображении возмущающего
при известном изображении возмущающего
воздействия F(s):
![]() , где
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
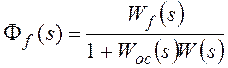 ;
;
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
![]() ,
,
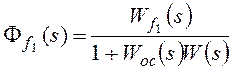 ,
,
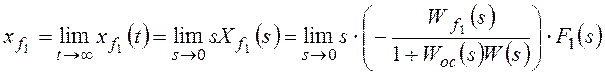 .
.
Для f2:
![]() ,
,
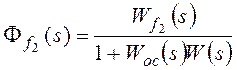 ,
,
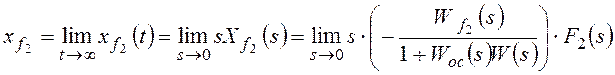 .
.
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):

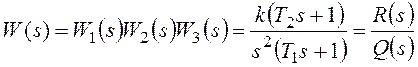 ,
,
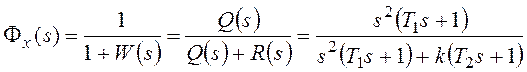 , где k=k1k2k3 – коэффициент передачи
, где k=k1k2k3 – коэффициент передачи
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При ![]() получим:
получим:
![]()
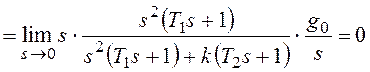 .
.
При ![]() получим:
получим:
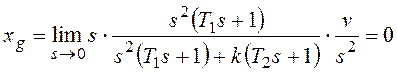 .
.
При  получим:
получим:
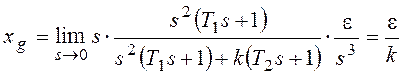 .
.
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
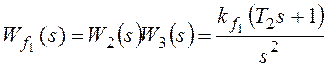 ,
,
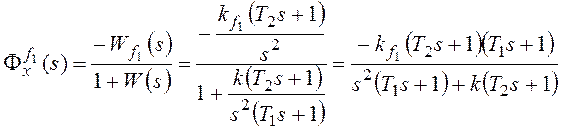 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f1.
При ![]() получим:
получим:
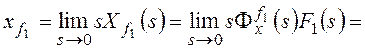
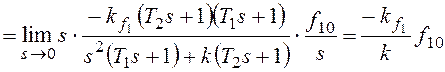 .
.
При ![]() получим:
получим:
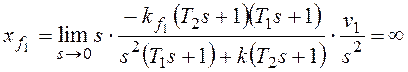 .
.
При 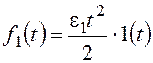 получим
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
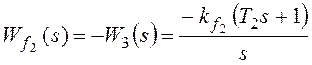 ,
,
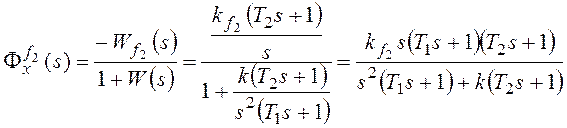 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f2.
При ![]() получим:
получим:
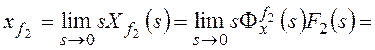
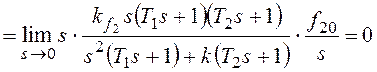 .
.
При ![]() получим:
получим:
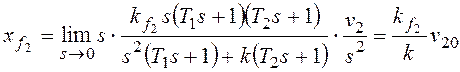 .
.
При 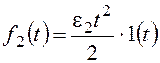 получим:
получим:
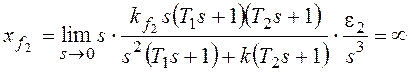 .
.
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.

В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
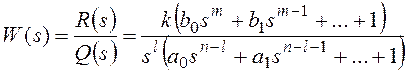 , где l³0.
, где l³0.
Тогда получим:
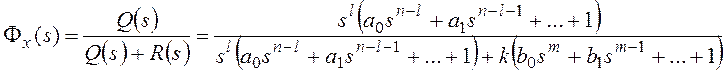
и для общего вида задающего воздействия 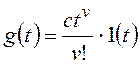 , которому соответствует изображение
, которому соответствует изображение 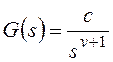 ,
,
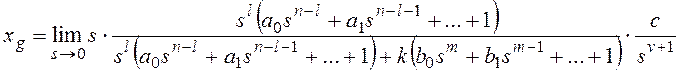 .
.
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
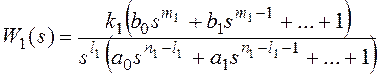 ,
,
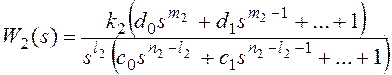 , где l1+l2=l,
, где l1+l2=l,
k1k2=k, m1+m2=m,
n1+n2=n,
причем ![]() и
и ![]() .
.
Тогда получим:
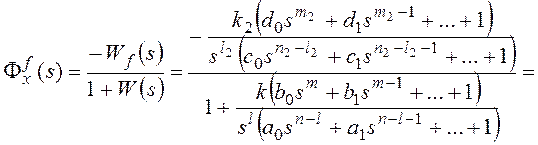
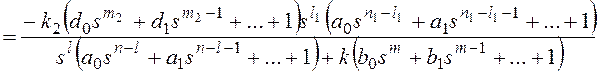
и для общего вида возмущающего воздействия 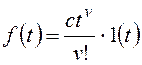 , которому соответствует изображение
, которому соответствует изображение 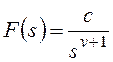 ,
,
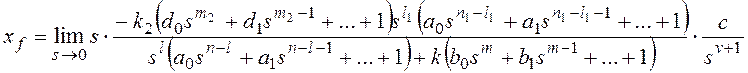 .
.
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Автоматические системы управления
должны быть не только устойчивыми, но и обеспечивать качество процесса
управления. Основные наиболее существенные требования к качеству управления,
которые позволяют оценить работу почти всех систем управления, называют
показателями процесса управления. Они характеризуют поведение системы в
переходном процессе. Показателями качества будет время регулирования,
перерегулирование, колебательность процесса, установившаяся ошибка, характер
затухания переходного процесса, запас устойчивости.
Качество процессов регулирования
обычно оценивают по переходной функции, которая представляет собой реакцию
системы на внешнее воздействие типа единичного скачка. Для следящих систем и
программного регулирования переходную функцию рассматривают по отношению к
задающему воздействию, а для систем стабилизации – по отношению к возмущению.

Рисунок 1. Определение показателей
качества регулирования по переходной характеристике.
На рис. 1 изображена переходная
функция по которой можно определить основные показатели качества переходного
процесса: время регулирования, перерегулирование и др.
Время регулирования определяет
длительность переходного процесса. Теоретически переходной процесс длится
бесконечно долго, однако практически его считают законченным, как только
отклонение регулируемой величины от нового ее установившегося значения не будет
превышать допустимых пределов.
Временем регулирования называют
минимальное время, по истечении которого, начиная с момента начала действия
входного сигнала, выходная переменная отклоняется от установившегося значения на величину, не
превышающую некоторую заданную постоянную величину 0,5.
Время регулирования характеризует
быстродействие системы.
Быстродействие может характеризоваться
и временем достижения переходной функцией нового установившегося значения, и
временем достижения максимального значения.
Перерегулированием называется
максимальное отклонение управляемой величины от заданного значения и выраженной
в процентах.
Время регулирования и
перерегулирования взаимосвязаны. Так, перерегулирование зависит от скорости
изменения регулируемой величины, которая графически представляет собой тангенс
угла наклона α (альфа)
касательной в точке А к кривой (рисунок 1).
Чем больше эта скорость, тем больше
перерегулирование. Поэтому для его уменьшения необходимо уменьшить скорость, с
которой система подходит к новому установившемуся состоянию. Но это приведет к
увеличению времени регулирования. Если система подходит к установившемуся
состоянию с нулевой скоростью, то перерегулирования вообще не будет, но время
регулирования значительно увеличится (рисунок 2).

Рисунок 2. Переходная характеристика
системы автоматического регулирования без перерегулирования.
Значения времени регулирования и
перерегулирования часто задают в качестве исходных данных для синтеза
корректирующих устройств, поскольку правильным выбором и настройкой последних
обеспечивается подавление нежелательных колебаний регулируемой величины в
переходном процессе. Для некоторых систем перерегулирование вообще недопустимо,
например для систем автоматического регулирования физических величин в
процессах, связанных с приготовлением продуктов. Необходимо так же иметь в
виду, что стремление уменьшить время регулирования приводит к увеличению
мощности исполнительного устройства.
Колебательность процесса
характеризуется числом колебаний управляемой величины за время регулирования.
Количественно колебательность
оценивается по логарифмическому декременту затухания, который представляет
собой натуральный логарифм отношения двух последующих амплитуд отклонений
управляемой величины одного направления.
Чем больше логарифмический декремент
затухания, тем быстрее происходит затухание переходного процесса.
Установившаяся ошибка показывает
точность управления в установившемся режиме. Она ровняется разности между
заданным значением управляемой величины и ее установившимся значением при
нормальной нагрузке.
Характер затухания переходного
процесса позволяет классифицировать переходные процессы в системах управления и
выделить среди их многообразия четыре основных вида (рисунок 3): колебательный
процесс (кривая 1) – ему присуще несколько значений перерегулирования;
малоколебательный процесс (кривая 2) – процесс с одним перерегулированием;
монотонный процесс (кривая 4), при котором скорость изменения управляемой
величины не изменяет знака в течение всего времени регулирования;
апериодический процесс (кривая 3) – процесс, когда управляемая величина меньше
ее установившегося значения с точностью до зоны нечувствительности регулятора
при всех значениях времени регулирования.

Рисунок 3. Основные виды характеристик
переходных процессов автоматических систем регулирования при типовом единичном
воздействии.
Запас устойчивости – это физическая
сущность и методы определения этого показателя качества управления.
Показатели, которые характеризуют
качество работы системы в переходном режиме, делят на прямые и косвенные.
Прямые показатели – это числовые
оценки качества, получаемые непосредственно по переходной характеристике. Для
получения прямых показателей качества необходимо иметь кривую переходного
процесса, которую можно построить по структурной схеме или дифференциальному
уравнению систем автоматического регулирования, используя аналоговые
вычислительные машины или компьютеры.
Косвенные оценки качества переходного
процесса позволяют определить некоторые особенности переходного процесса и
установить влияние параметров системы на качество переходных процессов. К
косвенным показателям качества относятся корневые, частотные и интегральные
оценки.
Рассмотрим корневые оценки качества.
Геометрически степень устойчивости можно определить как расстояние на плоскости
от мнимой оси до ближайшего к ней корня или ближайшей пары комплексных корней
(рисунок 4).

Рисунок 4. Корневые оценки качества
систем автоматического регулирования.
Понятие степени устойчивости
используют для синтеза систем автоматического регулирования.
Рассмотрим
частотные оценки качества. При гармонических воздействиях качество систем
автоматического регулирования принято оценивать по частотным характеристикам.
Для этого используют следующие величины: показатель колебательности и частоту
среза. Показатель колебательности – это отношение максимального значения
амплитудно-частотной характеристики замкнутой системы к ее значению при частоте
равной нулю. Частота среза – это частота при которой амплитудно-частотная
характеристика равна единице. Косвенно она характеризует длительность
переходного процесса.
Рассмотрим интегральные оценки качества.
По кривой переходного процесса можно оценить качество процесса регулирования в
данной системе. Косвенно оценить качество регулирования можно по площади между
кривой переходного процесса и линией установившегося режима. В данном случае
критерием качества будет определенный интеграл по времени от функции,
характеризующей разницу между действительным и заданным значениями регулируемой
величины.
Список
используемой литературы
- В.И. Загинайлов, Л.Н. Шеповалова «Основы
автоматики», Москва «КОЛОС», 2001. - Л.В.Колесов «Основы
автоматики», Москва
«Колос», 1984.
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка
Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.
+ ~ я»
-R(s) —— *~С>——- *
-Y(s)
G(s)
H(s)
Рис. 4.18. Разомкнутая система управления
Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна
ад=ад — ад=[і — стт. (4.48)
В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна
Для вычисления установившейся ошибки используется теорема о конечном значении:
lim e(t)= lims£(s). (4.50)
_ 1 —КО А—>0
Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:
е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).
■v-»0 s -‘->0
В замкнутой системе при H(s) = 1 имеем:
Случай неединичной обратной связи рассматривается в разд. 5.8.
4.5. Установившаяся ошибка
Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.

Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.
Рис. 4.20
Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом
Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию
G(s) = —. (4.53)
TS+ 1
Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна
е0(со) = 1 — 6X0) = 1 — К (4.54)
при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:
Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна
ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).
.v->0 s
Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,
ес(со) = 1 J! Le_L. (4.55)
1+ К 1+ К
В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.
Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит
Ае0(со) 0,1
(4.56)
IKOI 1
т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно
Аес (оо ) = ——(4.57) 91 101
а относительное приращение составит
Аес (оо)
= 0,0011, (4.58)
IKOI
или 0,11%. Как говорится, результат в комментариях не нуждается.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: ![]() , рисунок 116.
, рисунок 116.

Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
![]() ,
, ![]() ,
,  и так
и так
далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
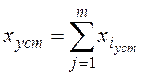 , где
, где
каждое слагаемое, или составляющая сигнала ошибки, ![]() определяется
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).

В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих ![]() .
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке ![]() при известном изображении задающего
при известном изображении задающего
воздействия G(s):
![]() , где
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
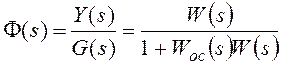 , где
, где ![]() — передаточная функция
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
![]()
В результате:
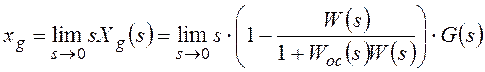 .
.
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения ![]() при известном изображении возмущающего
при известном изображении возмущающего
воздействия F(s):
![]() , где
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
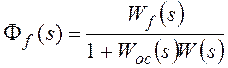 ;
;
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
![]() ,
,
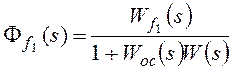 ,
,
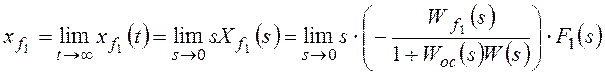 .
.
Для f2:
![]() ,
,
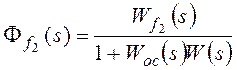 ,
,
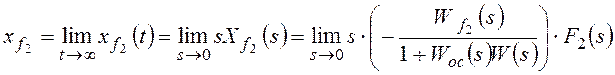 .
.
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):

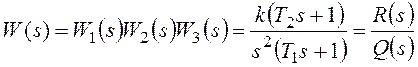 ,
,
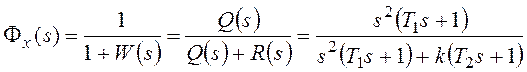 , где k=k1k2k3 – коэффициент передачи
, где k=k1k2k3 – коэффициент передачи
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При ![]() получим:
получим:
![]()
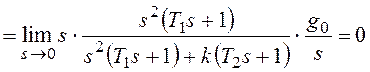 .
.
При ![]() получим:
получим:
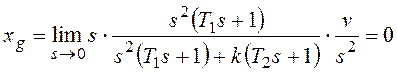 .
.
При  получим:
получим:
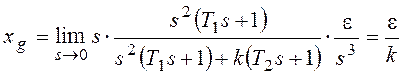 .
.
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
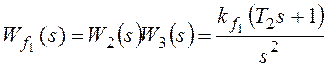 ,
,
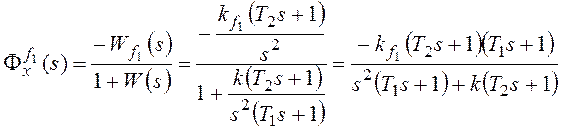 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f1.
При ![]() получим:
получим:
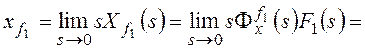
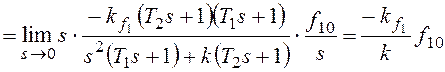 .
.
При ![]() получим:
получим:
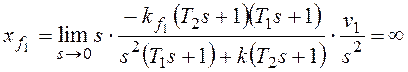 .
.
При 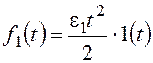 получим
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
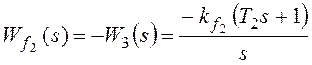 ,
,
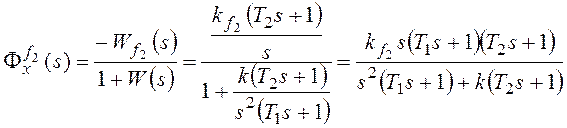 , где
, где ![]() –
–
коэффициент передачи разомкнутой системы по возмущению f2.
При ![]() получим:
получим:
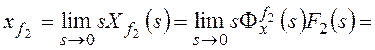
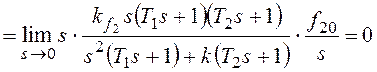 .
.
При ![]() получим:
получим:
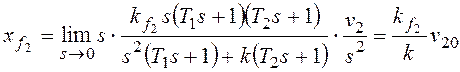 .
.
При 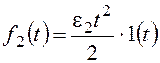 получим:
получим:
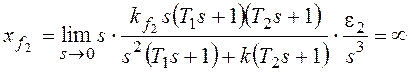 .
.
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.

В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
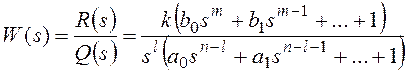 , где l³0.
, где l³0.
Тогда получим:
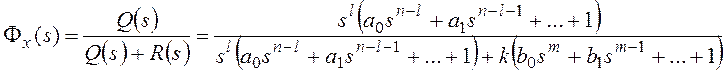
и для общего вида задающего воздействия 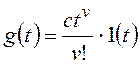 , которому соответствует изображение
, которому соответствует изображение 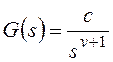 ,
,
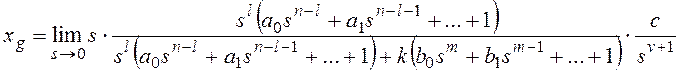 .
.
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
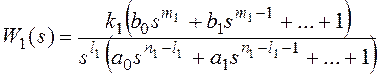 ,
,
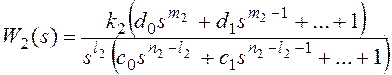 , где l1+l2=l,
, где l1+l2=l,
k1k2=k, m1+m2=m,
n1+n2=n,
причем ![]() и
и ![]() .
.
Тогда получим:
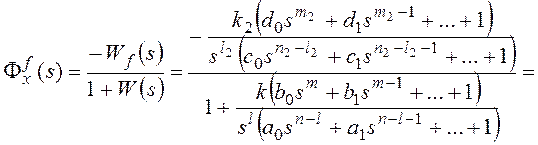
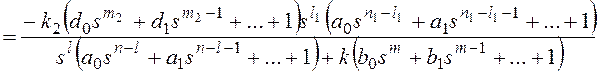
и для общего вида возмущающего воздействия 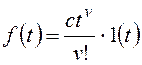 , которому соответствует изображение
, которому соответствует изображение 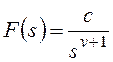 ,
,
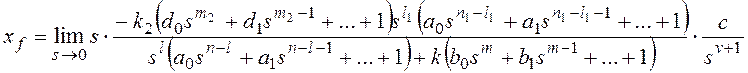 .
.
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.

Если подать на вход системы единичный
скачёк, то переходный процесс, как
правило, имеет следующий вид:
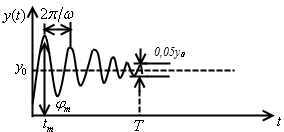
Качество переходного процесса
характеризуется параметрами:
1. максимальное перерегулирование
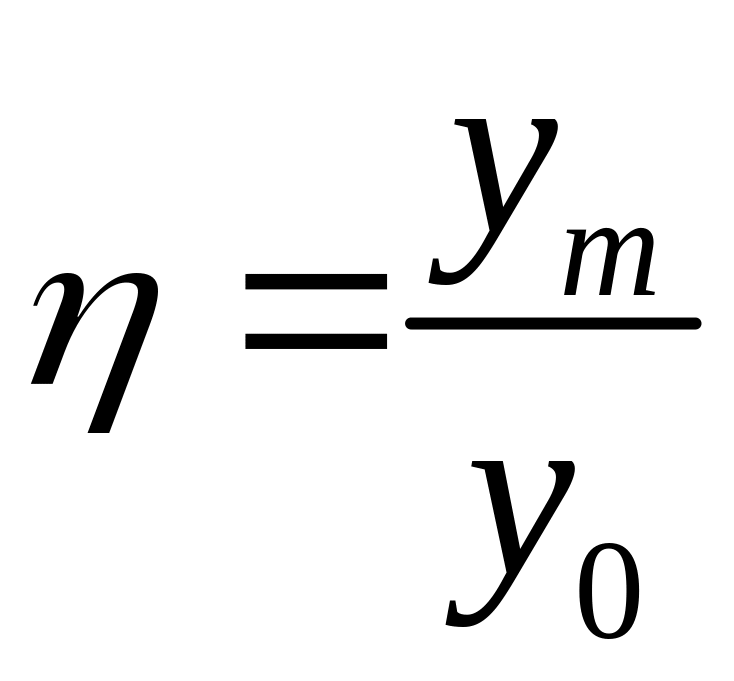
;
2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
![]()
;
3. время достижения первого
максимума
![]()
;
4. частота автоколебаний
;
В литературе приводятся выражения для
этих параметров для типичных передаточных
функций.
Ошибку регулирования в переходном
режиме можно определить, решая
дифференциальное уравнение или используя
преобразования Лапласа.
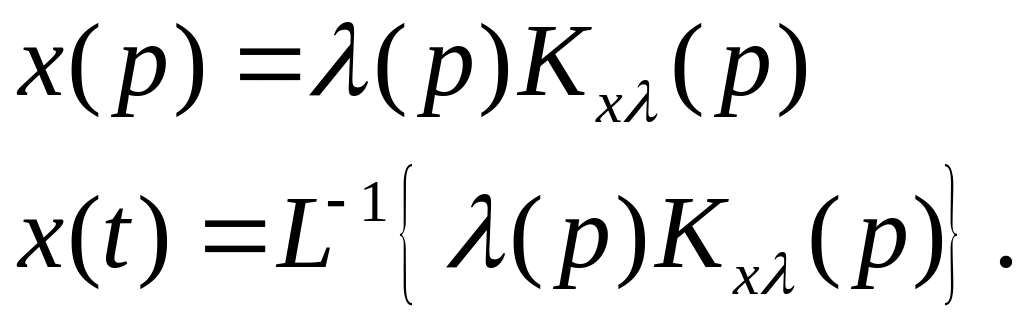
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой
системы:
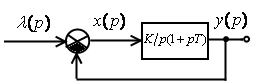

;
![]()
— характеристический полином;
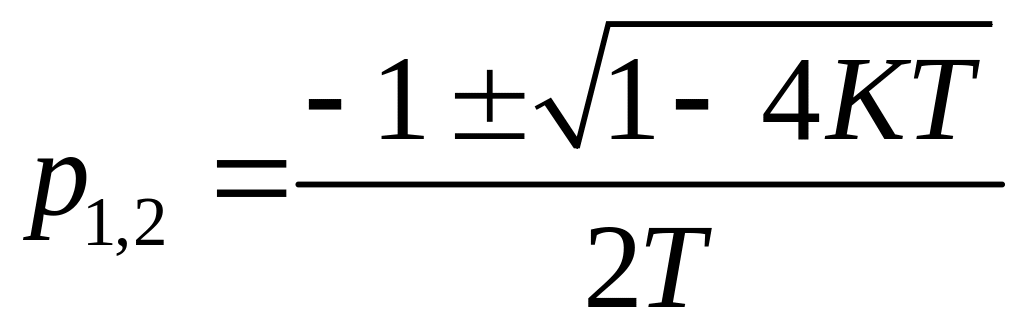
— корни характеристического
полинома.
Если корни действительны
![]()
,
то выходной сигнал определяется
выражением
![]()
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
![]()
![]()
,
то выходной сигнал определяется
выражение
![]()
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
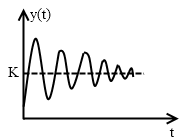
![]()
,
![]()
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
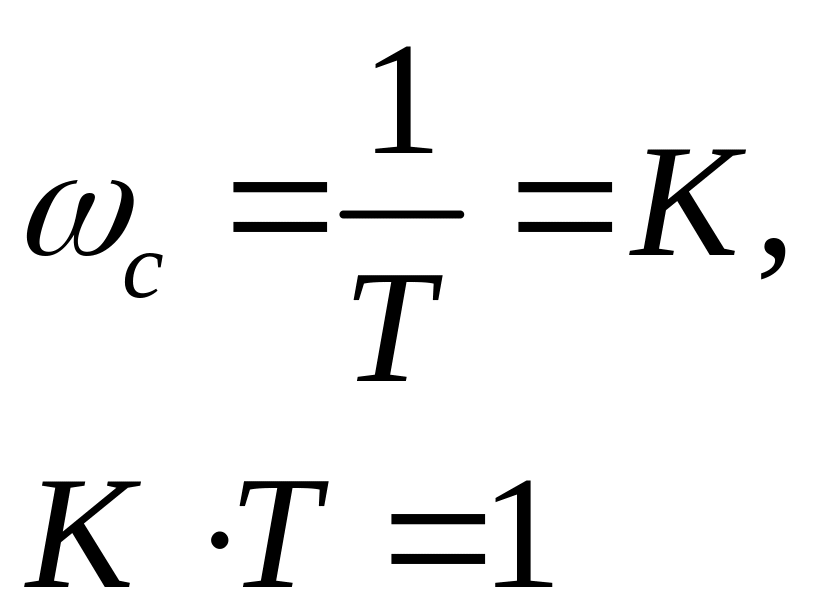
Корни комплексно сопряжённые, на частота
колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:
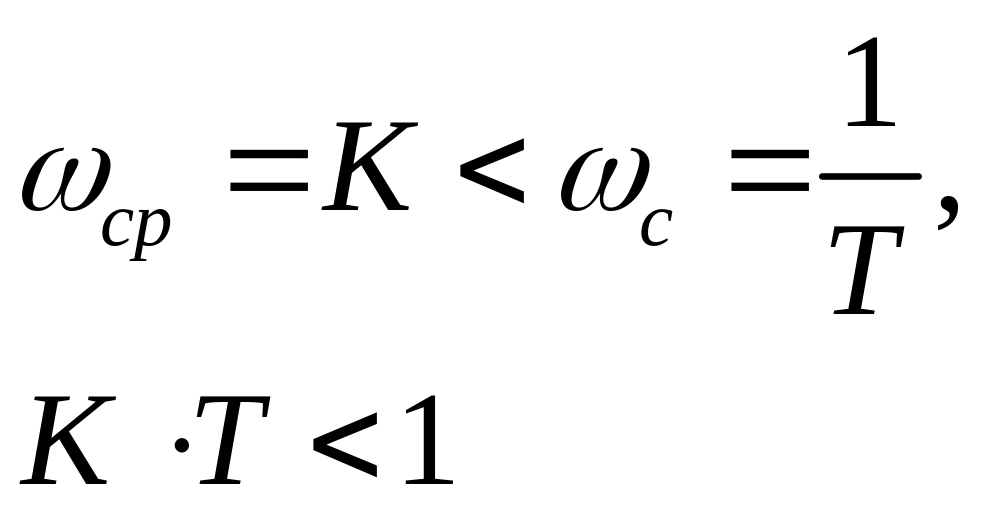
Пусть
![]()
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
![]()
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний
предназначен для решения дифференциальных
уравнений с помощью ЭВМ. Сущность этого
метода состоит в замене скалярного
дифференциального уравнения матричным
дифференциальным уравнением первого
порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
![]()
строк
и
![]()
столбцов,
вида:
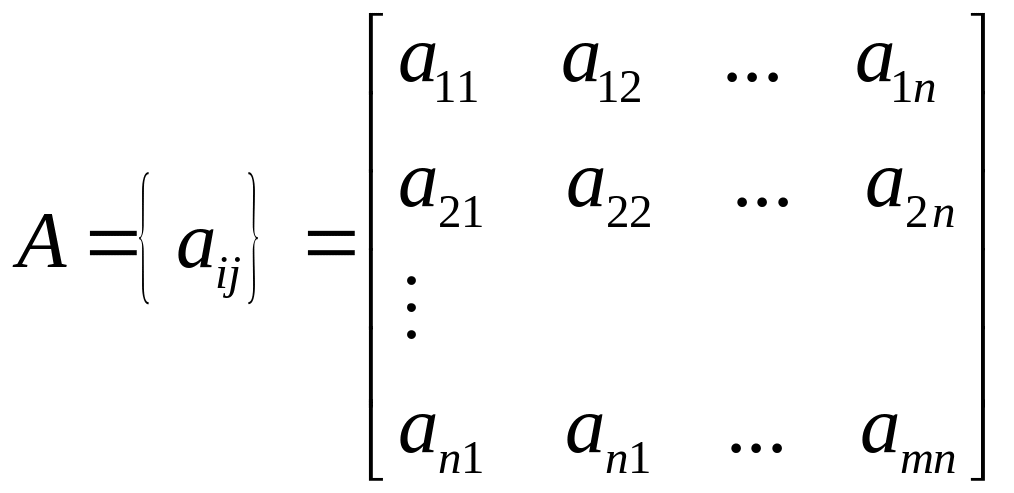
,
где i
– номер строки,
j – номер
столбца.
Матрицу, состоящую из одного столбца,
называют вектор-столбец, а из одной
строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
![]()
и
![]()
одинакового размера
![]()
называют матрицу
![]()
,
элементы которой равны сумме элементов
исходной матрицы
![]()
.
Теорема умножения матриц.
Произведение матрицы
размером
![]()
на матрицу
размера
![]()
называют матрицу, равной
с элементами (произведение взаимно если
![]()
)
:
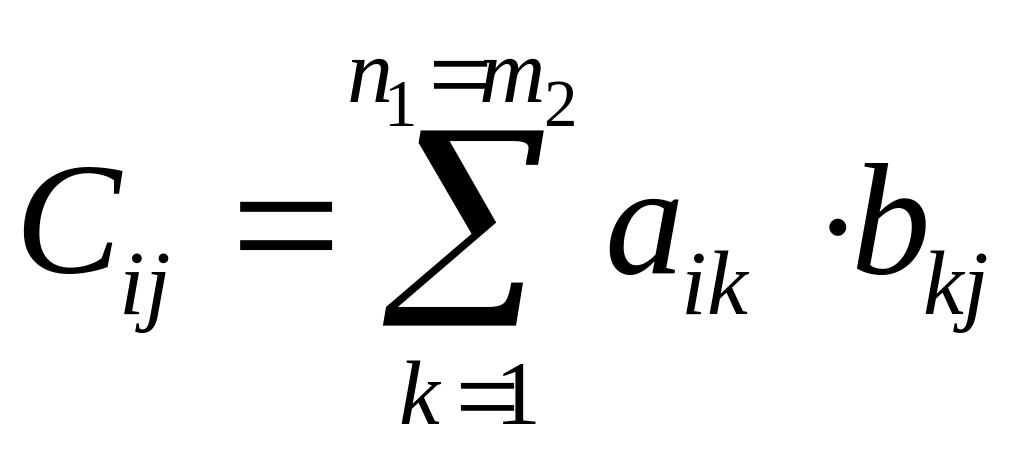
.
Теорема обращения матрицы.
Матрица
![]()
является обратной матрице
,
если выполняется условие
![]()
— единичная матрица размером

.
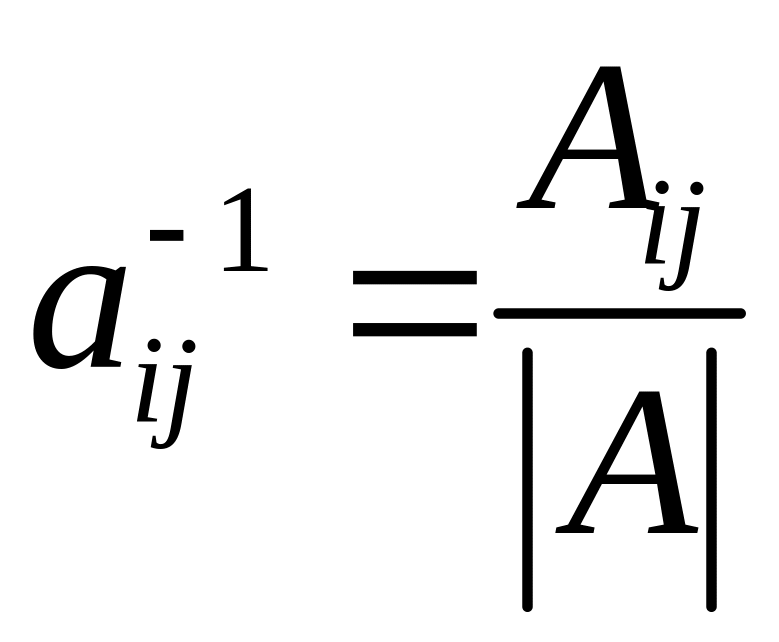
,
где
![]()
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
![]()
— алгебраическое дополнение аргумента,
где
![]()
— минор, равный определителю
![]()
порядка полученному из определителя
вычёркиванием
![]()
строки и
![]()
столбца.
Пример №1.

.
Теорема дифференцирования
и интегрирования матриц.
Для нахождения производной или интеграла
от матрицы по скалярному аргументу
необходимо вычислить их для каждого
элемента матрицы.
Матричной экспонентой называют
матрицу
![]()
,
где
— матрица,
![]()
— скалярный аргумент,
определяющейся бесконечным рядом
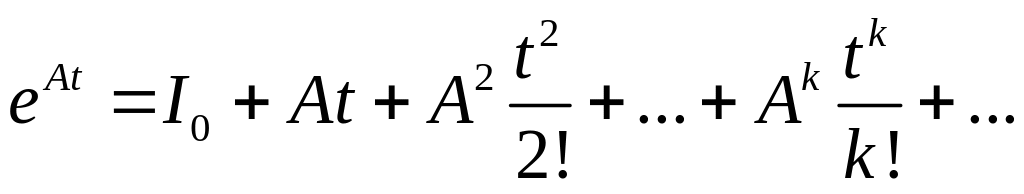
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = 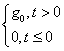 , g(p) =
, g(p) = ![]() ;
;
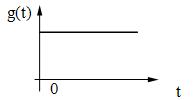
б) линейное воздействие: g(t) = ![]() t , t > 0
t , t > 0
; ![]() ;
;
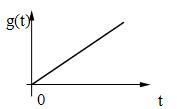
в) квадратичное воздействие:
![]() /2 , t > 0 ;
/2 , t > 0 ;
g(p) = ![]() .
.
В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
![]() , t > 0.
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если ![]() , то
, то ![]() и для g(t) = g0
и для g(t) = g0
получим ![]() .
.
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
![]() ,
,
где Res
x(p)
– вычет функции x(p)
в точке a.
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
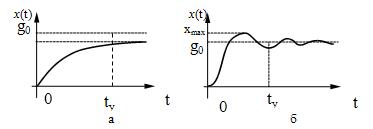
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза ![]() . Для оценки качества системы
. Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением ![]() .
.
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования ![]() .
.
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме ![]() . В зависимости от
. В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: ![]() .
.
При использовании этой теоремы нужно
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).
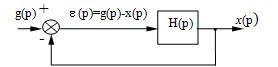
Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда ![]() или e (p) = He(p)g(p)
или e (p) = He(p)g(p)
, где He(p) = ![]() называется передаточной функцией
называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
![]() ,
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
![]() .
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
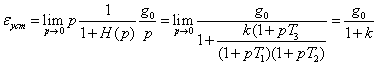 .
.
Предположим теперь, что входное
воздействие изменяется линейно ![]() t или
t или ![]() .
.
Тогда ![]() . Соответствующие входные воздействия и
. Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.
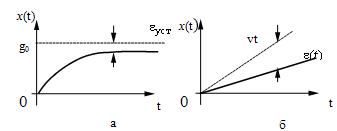
Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с ![]() .
.
Для ступенчатого воздействия g(t) = g0
или g(p) = ![]() получим
получим
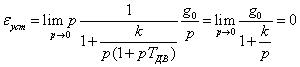 .
.
При линейном входном воздействии
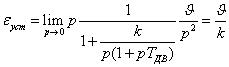 .
.
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.
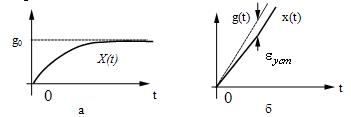
Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, ![]() . При ступенчатом
. При ступенчатом
воздействии 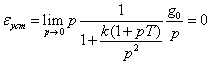 .
.
При линейном 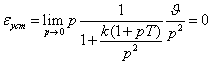 .
.
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
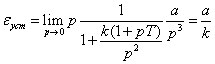 .
.
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии ![]() . Наконец, в системах с астатизмом
. Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)
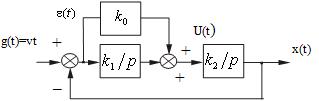
Рис.
25
Пусть входной сигнал системы управления
изменяется линейно: ![]()
![]() t. Как было
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= ![]() t , то на
t , то на
входе второго интегратора должен быть сигнал ![]() . Действительно, при нулевом
. Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора ![]() . Первый интегратор
. Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Динамическая ошибка
Cтраница 3
Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]
Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]
Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]
Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]
Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]
Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]
Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]
Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]
Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]
Страницы:
1
2
3
4
Если подать на вход системы единичный
скачёк, то переходный процесс, как
правило, имеет следующий вид:

Качество переходного процесса
характеризуется параметрами:
1. максимальное перерегулирование
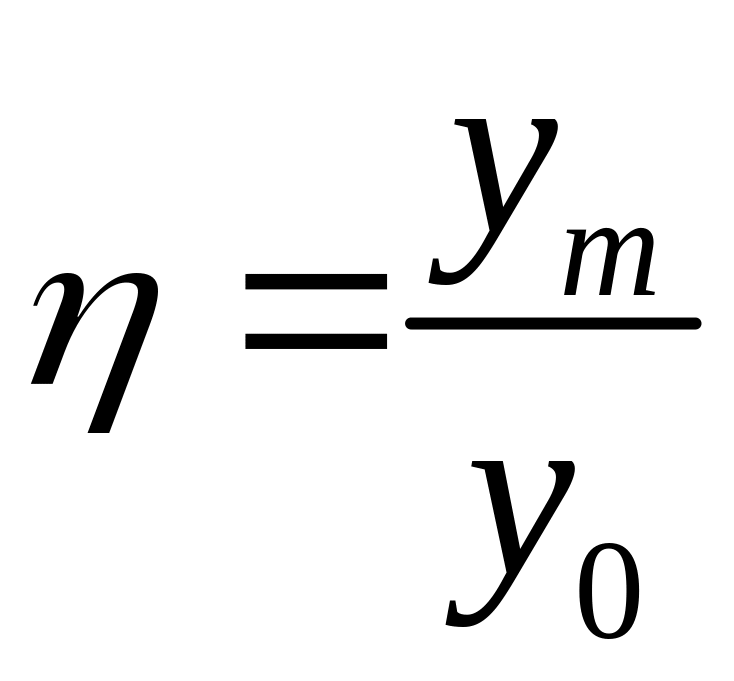
;
2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
![]()
;
3. время достижения первого
максимума
![]()
;
4. частота автоколебаний
;
В литературе приводятся выражения для
этих параметров для типичных передаточных
функций.
Ошибку регулирования в переходном
режиме можно определить, решая
дифференциальное уравнение или используя
преобразования Лапласа.
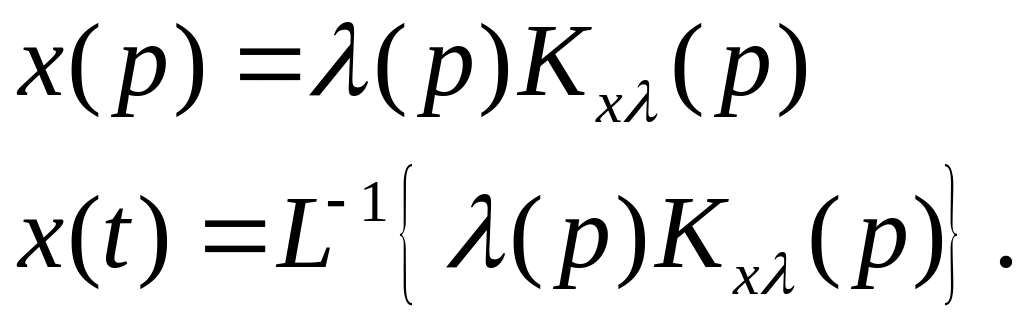
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой
системы:


;
![]()
— характеристический полином;
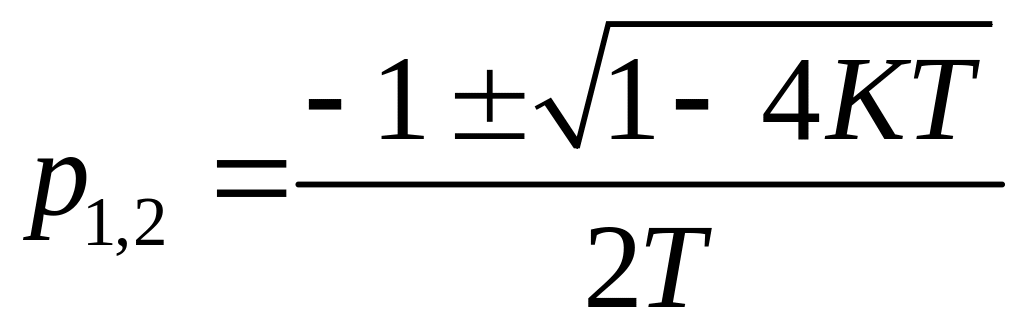
— корни характеристического
полинома.
Если корни действительны
![]()
,
то выходной сигнал определяется
выражением
![]()
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
![]()
![]()
,
то выходной сигнал определяется
выражение
![]()
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
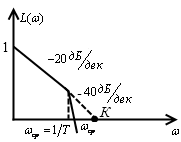

![]()
,
![]()
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
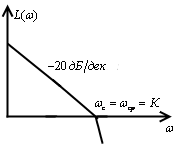

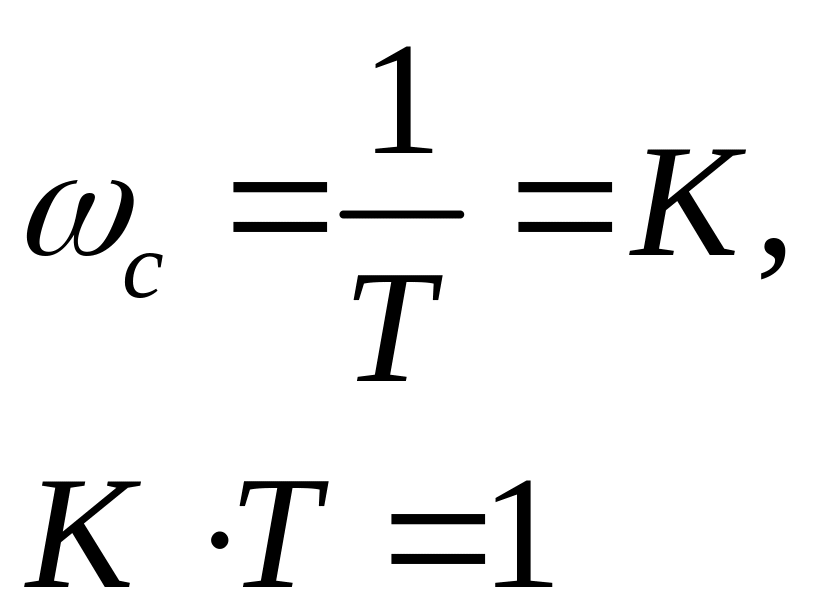
Корни комплексно сопряжённые, на частота
колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:

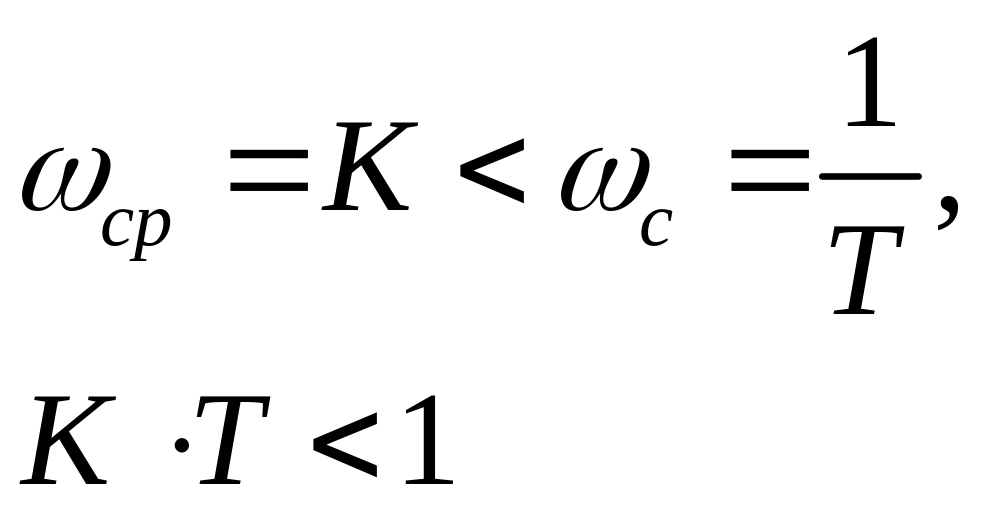
Пусть
![]()
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
![]()
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний
предназначен для решения дифференциальных
уравнений с помощью ЭВМ. Сущность этого
метода состоит в замене скалярного
дифференциального уравнения матричным
дифференциальным уравнением первого
порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
![]()
строк
и
![]()
столбцов,
вида:
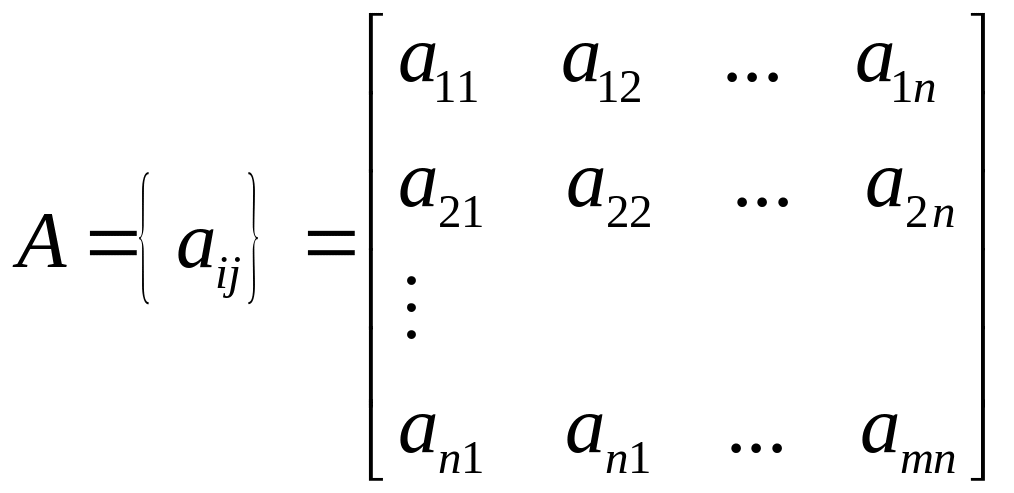
,
где i
– номер строки,
j – номер
столбца.
Матрицу, состоящую из одного столбца,
называют вектор-столбец, а из одной
строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
![]()
и
![]()
одинакового размера
![]()
называют матрицу
![]()
,
элементы которой равны сумме элементов
исходной матрицы
![]()
.
Теорема умножения матриц.
Произведение матрицы
размером
![]()
на матрицу
размера
![]()
называют матрицу, равной
с элементами (произведение взаимно если
![]()
)
:
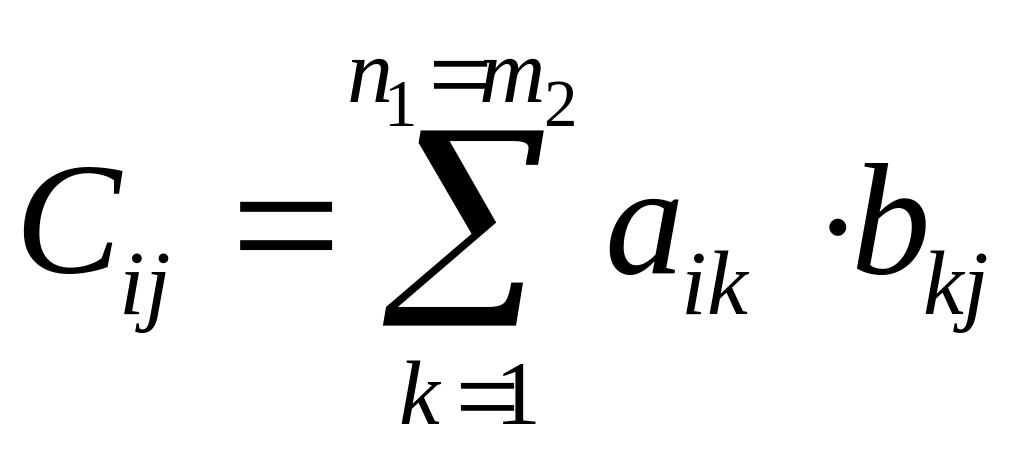
.
Теорема обращения матрицы.
Матрица
![]()
является обратной матрице
,
если выполняется условие
![]()
— единичная матрица размером

.
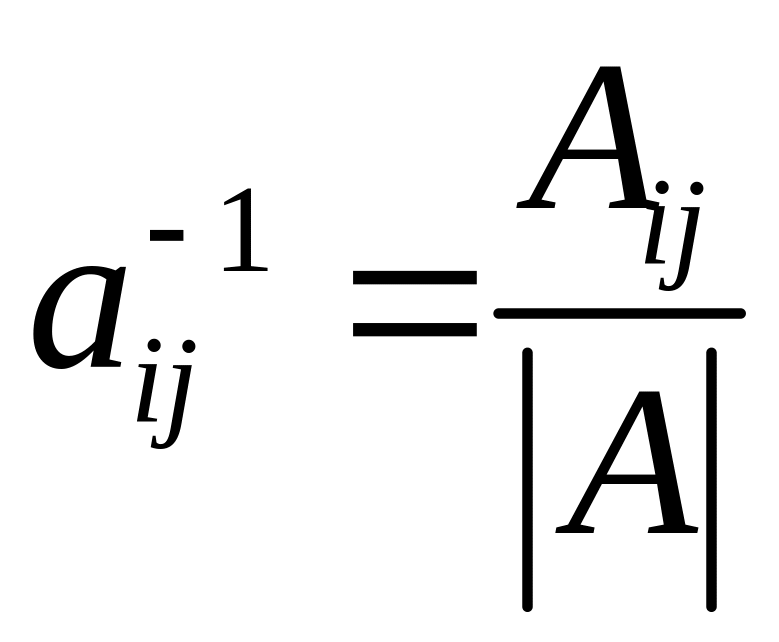
,
где
![]()
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
![]()
— алгебраическое дополнение аргумента,
где
![]()
— минор, равный определителю
![]()
порядка полученному из определителя
вычёркиванием
![]()
строки и
![]()
столбца.
Пример №1.

.
Теорема дифференцирования
и интегрирования матриц.
Для нахождения производной или интеграла
от матрицы по скалярному аргументу
необходимо вычислить их для каждого
элемента матрицы.
Матричной экспонентой называют
матрицу
![]()
,
где
— матрица,
![]()
— скалярный аргумент,
определяющейся бесконечным рядом
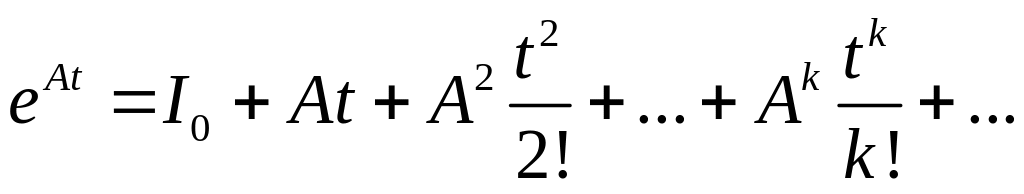
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = 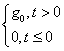 , g(p) =
, g(p) = ![]() ;
;
б) линейное воздействие: g(t) = ![]() t , t > 0
t , t > 0
; ![]() ;
;
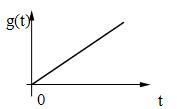
в) квадратичное воздействие:
![]() /2 , t > 0 ;
/2 , t > 0 ;
g(p) = ![]() .
.

В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
![]() , t > 0.
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если ![]() , то
, то ![]() и для g(t) = g0
и для g(t) = g0
получим ![]() .
.
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
![]() ,
,
где Res
x(p)
– вычет функции x(p)
в точке a.
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
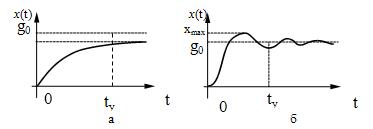
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза ![]() . Для оценки качества системы
. Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением ![]() .
.
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования ![]() .
.
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме ![]() . В зависимости от
. В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: ![]() .
.
При использовании этой теоремы нужно
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).

Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда ![]() или e (p) = He(p)g(p)
или e (p) = He(p)g(p)
, где He(p) = ![]() называется передаточной функцией
называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
![]() ,
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
![]() .
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
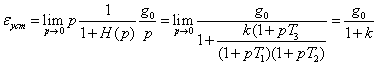 .
.
Предположим теперь, что входное
воздействие изменяется линейно ![]() t или
t или ![]() .
.
Тогда ![]() . Соответствующие входные воздействия и
. Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.

Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с ![]() .
.
Для ступенчатого воздействия g(t) = g0
или g(p) = ![]() получим
получим
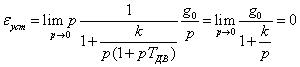 .
.
При линейном входном воздействии
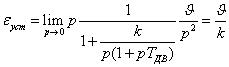 .
.
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.

Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, ![]() . При ступенчатом
. При ступенчатом
воздействии 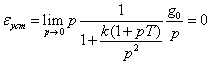 .
.
При линейном 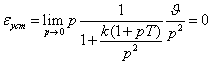 .
.
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
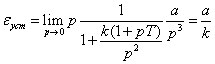 .
.
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии ![]() . Наконец, в системах с астатизмом
. Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)

Рис.
25
Пусть входной сигнал системы управления
изменяется линейно: ![]()
![]() t. Как было
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= ![]() t , то на
t , то на
входе второго интегратора должен быть сигнал ![]() . Действительно, при нулевом
. Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора ![]() . Первый интегратор
. Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Динамическая ошибка
Cтраница 3
Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]
Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]
Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]
Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]
Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]
Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]
Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]
Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]
Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]
Страницы:
1
2
3
4
Если подать на вход системы единичный
скачёк, то переходный процесс, как
правило, имеет следующий вид:

Качество переходного процесса
характеризуется параметрами:
1. максимальное перерегулирование
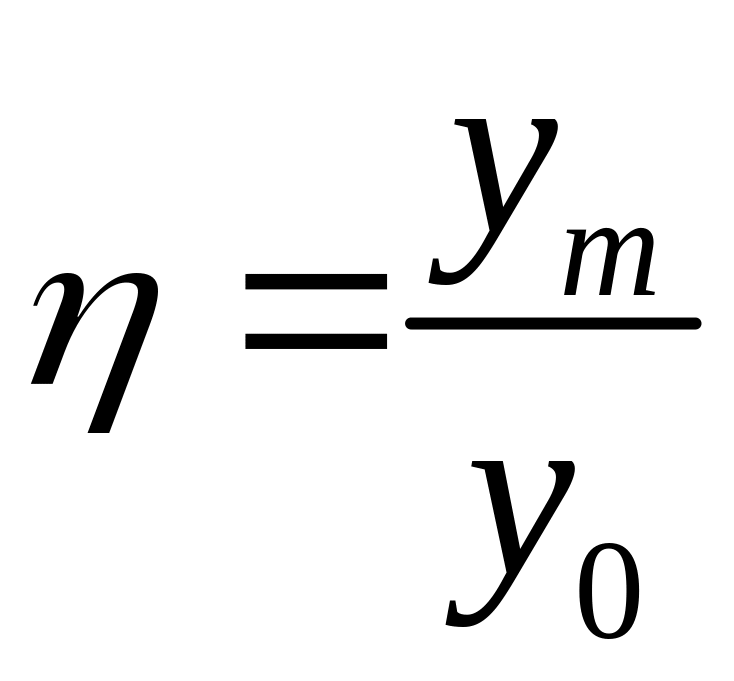
;
2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
![]()
;
3. время достижения первого
максимума
![]()
;
4. частота автоколебаний
;
В литературе приводятся выражения для
этих параметров для типичных передаточных
функций.
Ошибку регулирования в переходном
режиме можно определить, решая
дифференциальное уравнение или используя
преобразования Лапласа.
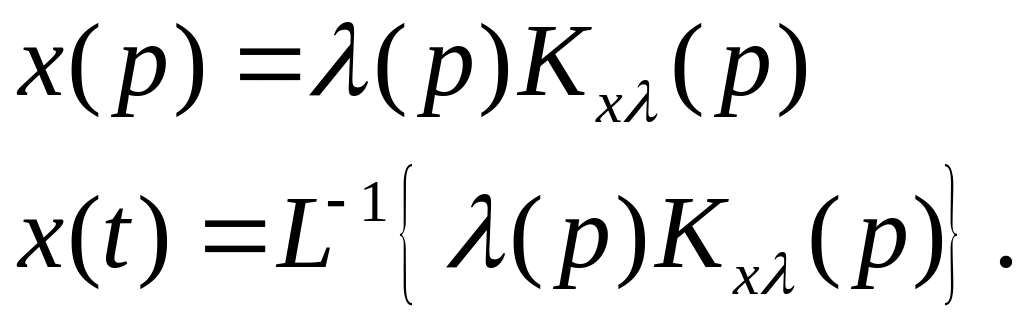
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой
системы:


;
![]()
— характеристический полином;
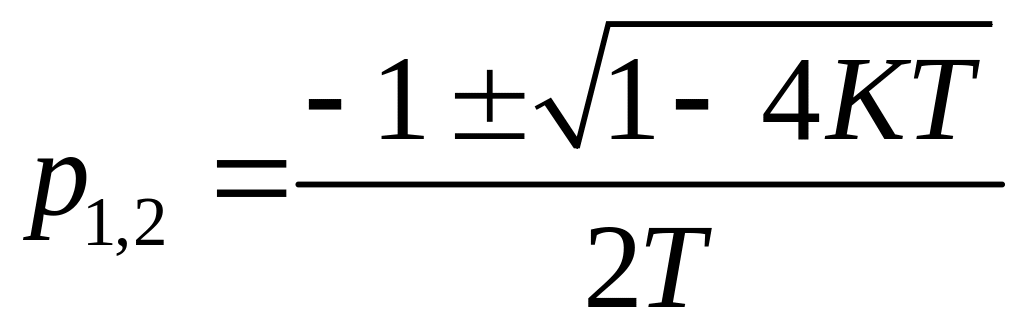
— корни характеристического
полинома.
Если корни действительны
![]()
,
то выходной сигнал определяется
выражением
![]()
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
![]()
![]()
,
то выходной сигнал определяется
выражение
![]()
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
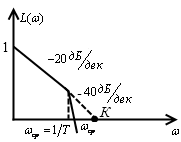

![]()
,
![]()
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
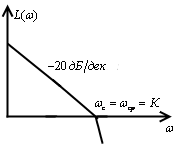

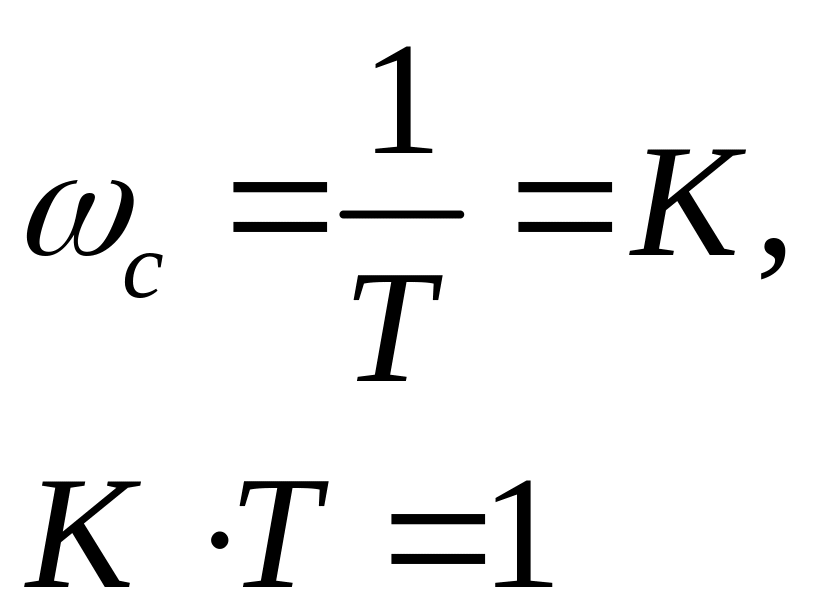
Корни комплексно сопряжённые, на частота
колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:

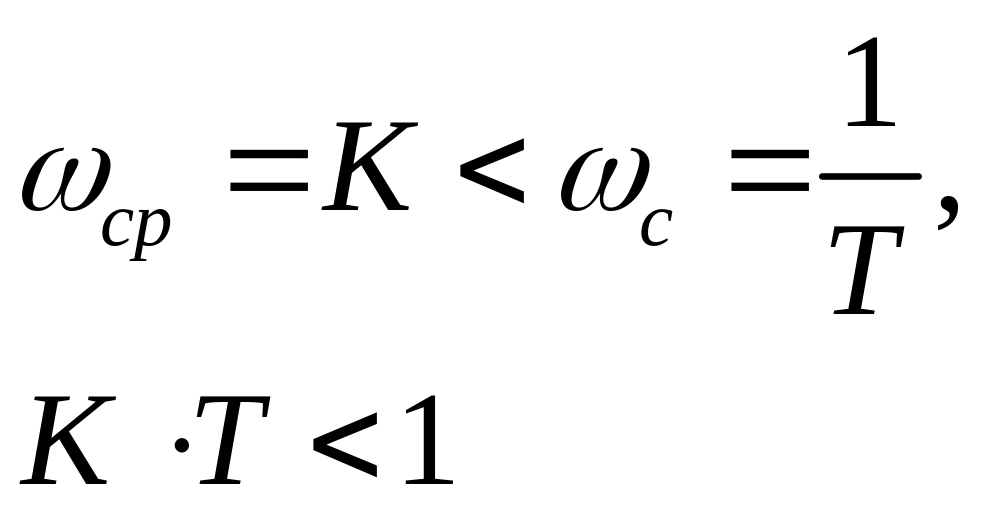
Пусть
![]()
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
![]()
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний
предназначен для решения дифференциальных
уравнений с помощью ЭВМ. Сущность этого
метода состоит в замене скалярного
дифференциального уравнения матричным
дифференциальным уравнением первого
порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
![]()
строк
и
![]()
столбцов,
вида:
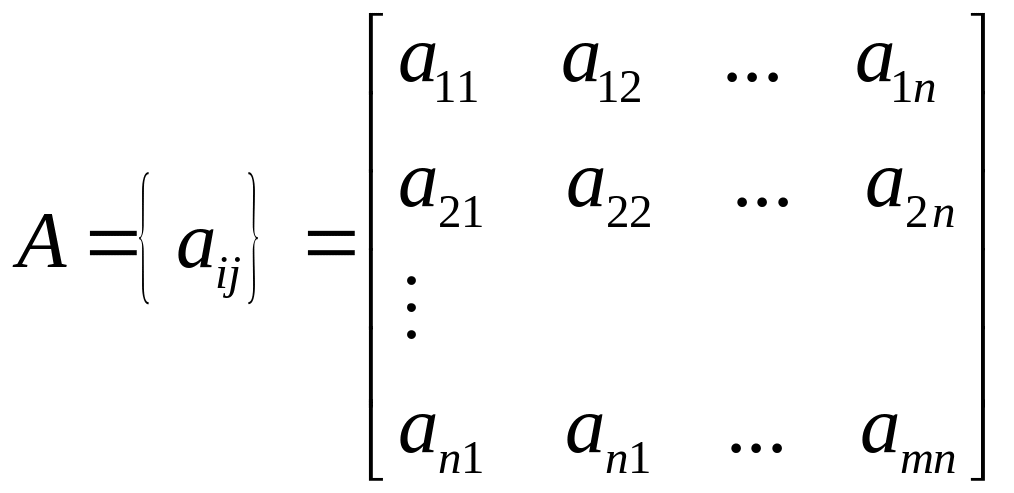
,
где i
– номер строки,
j – номер
столбца.
Матрицу, состоящую из одного столбца,
называют вектор-столбец, а из одной
строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
![]()
и
![]()
одинакового размера
![]()
называют матрицу
![]()
,
элементы которой равны сумме элементов
исходной матрицы
![]()
.
Теорема умножения матриц.
Произведение матрицы
размером
![]()
на матрицу
размера
![]()
называют матрицу, равной
с элементами (произведение взаимно если
![]()
)
:
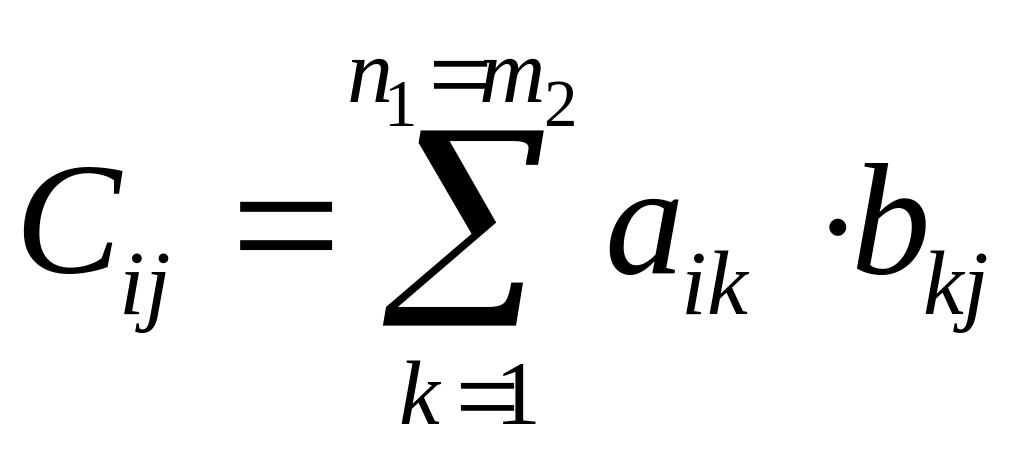
.
Теорема обращения матрицы.
Матрица
![]()
является обратной матрице
,
если выполняется условие
![]()
— единичная матрица размером

.
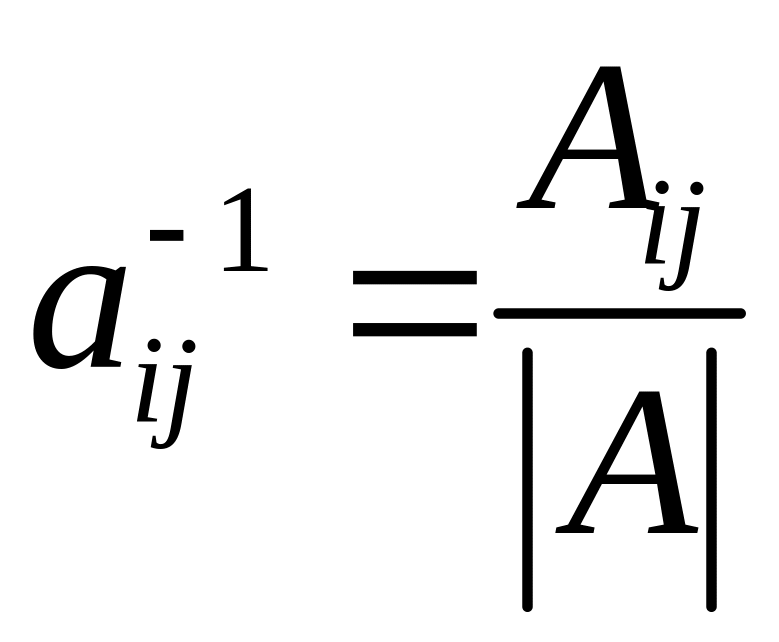
,
где
![]()
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
![]()
— алгебраическое дополнение аргумента,
где
![]()
— минор, равный определителю
![]()
порядка полученному из определителя
вычёркиванием
![]()
строки и
![]()
столбца.
Пример №1.

.
Теорема дифференцирования
и интегрирования матриц.
Для нахождения производной или интеграла
от матрицы по скалярному аргументу
необходимо вычислить их для каждого
элемента матрицы.
Матричной экспонентой называют
матрицу
![]()
,
где
— матрица,
![]()
— скалярный аргумент,
определяющейся бесконечным рядом
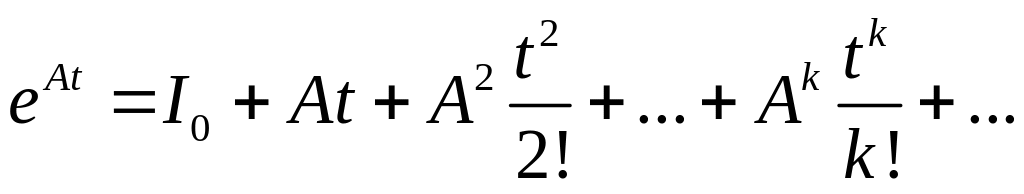
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Динамическая ошибка
Cтраница 3
Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]
Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]
Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]
Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]
Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]
Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]
Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]
Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]
Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]
Страницы:
1
2
3
4
Постановка задачи. Критерии качества переходных процессов
Любая система автоматического регулирования, для того чтобы удовлетворять своему назначению, прежде всего, должна быть устойчивой. Однако устойчивость является необходимым, но недостаточным условием технической пригодности системы регулирования. Помимо устойчивости, к переходному процессу предъявляются требования, обуславливающие его так называемые показатели.
Качество функционирования АСР оценивается прямыми показателями оценки качества переходных процессов в замкнутой АСР. К ним относятся:
Соответственно основными критериями качества системы управления являются:
1) Устойчивость системы;
2) Максимальная динамическая ошибка
3) Статическая ошибка;
4) Время регулирования ;
5) Величина перерегулирования;
6) Степень затухания переходного процесса;
7) Степень колебательности.
Как всякая динамическая система, САУ может находиться в одном из двух режимов — стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью.
Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке САУ необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров САУ. Такие косвенные признаки называются критериями качества переходного процесса.
Существуют три группы критериев качества: корневые, интегральные и частотные.
Группа корневых критериев основана на оценке качества переходного процесса по значениям полюсов и нулей передаточной функции САУ. В частном случае, когда нулей нет, качество переходного процесса определяется только полюсами.
Переходный процесс в устойчивой системе распадается на затухающие и колебательные составляющие. Если найти длительность самой длительной составляющей и величину колебательности самой колебательной составляющей, то по ним можно оценить верхние пределы величин длительности и колебательности всего переходного процесса.
Интегральными критериями качества называются такие, которые одним числом оценивают и величины отклонений, и время затухания переходного процесса. Такие критерии качества используются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки. Применяются интегральные критерии обычно в теории оптимальных систем.
Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик.
Рассмотрим некоторые критерии качества работы САУ:
1) Статическая ошибка (имеет место только в П — регуляторе) — это отклонение регулируемого параметра от заданного в установившемся режиме (точность системы);

.
Если в числителе передаточной функции системы нет свободного члена, то статическая ошибка равна нулю;
2) Динамическая ошибка — это максимальное рассогласование между заданной и текущей траекторией в переходном режиме;
3) Время регулирования — это время, в течение которого переходный процесс войдет в зону допустимой погрешности регулирования , где определяется следующим образом:

.
4)Величина перерегулирования — определяется как отношение амплитуды второй полуволны к первой

.
5)Степень затухания

учитывая, что
.
C данным критерием тесно связан еще один параметр-степень колебательности системы

;
Данные критерии взаимосвязаны следующими соотношениями:

.
Проведя небольшой анализ приведенных соотношений, можно выделить два крайних состояния системы:
а) апериодический процесс , ;
б) незатухающие колебания , .
Часто в расчетах применяют , .
Все системы регулирования рассчитываются с заданным значением либо , либо . Система регулирования считается настроенной оптимально, если она удовлетворяет двум или трем показателям качества. Например, максимальная динамическая ошибка, степень затухания, время регулирования удовлетворяют заданным значениям.
